最新更新时间: ,
doi: 10.6052/1000-0992-25-024
薄壁结构在飞行器领域普遍存在, 随着先进飞行器向宽速域、跨介质、大尺寸等方向发展, 薄壁结构面临的声振环境更加复杂, 对低频宽带和时变减振降噪的需求更加迫切. 超结构/超材料的快速发展为先进飞行器的技术突破提供了新途径, 其中基于局域共振机制的薄壁超结构在解决飞行器振动与噪声控制问题方面具有显著的应用前景. 聚焦薄壁结构的减振和隔声难题, 综述了被动式和压电式薄壁超结构的研究进展, 并对两者的发展脉络和技术特性进行了对比分析, 为先进飞行器薄壁超结构研制提供借鉴. 首先, 介绍了被动式和压电式薄壁超结构的带隙机理和隔声机理, 为后续介绍研究进展提供理论基础. 其次, 从减振和隔声两方面梳理了薄壁超结构设计和性能调控方法, 并针对非线性薄壁超结构减振问题进行了专门讨论. 然后, 探讨了薄壁超结构在飞行器舱室减振降噪、飞行器动力系统减振降噪和高速飞行器壁板颤振等几个方面的应用前景. 最后, 从优化设计、智能调控、多功能融合、极端环境适应性和精密制造等方面展望了飞行器薄壁超结构的发展方向.
最新更新时间: ,
doi: 10.6052/1000-0992-25-015
非晶合金因其独特的原子结构而呈现出复杂的黏弹性行为, 表现为动态弛豫和静态滞后特征, 这不仅是深入理解玻璃转变、塑性变形机制及动态非均匀性等基础物理问题的核心切入点, 也为高性能非晶合金与功能材料的开发及工程应用提供了关键理论支撑. 如何从微观机制出发构建一个能够统一描述并预测其复杂黏弹性行为的理论框架, 仍是非晶固体领域面临的重要挑战. 基于此, 本文聚焦于准点缺陷 (quasi-point defect, QPD) 理论在系统解析非晶合金黏弹性行为中的核心作用及其最新研究进展, 深入探讨了运用 QPD 理论分析非晶合金中的动态弛豫现象, 并揭示了该理论与分数阶模型的内在一致性. 在此基础上, 综述了动态弛豫与宏观准静态黏弹性变形的内在关联, 阐释了两步松弛、蠕变等现象背后由不同尺度缺陷运动主导的物理机制. 针对蠕变行为, 重点讨论了基于QPD理论对非晶合金中缺陷演化和多级幂律蠕变机制的理解. 此外, 本文系统阐述了通过黏弹性变形调控非晶合金能量状态的机制, 以及这种调控如何通过影响准点缺陷的浓度、分布及协同运动, 进而改变材料的动态弛豫特征. 本文旨在展现如何基于准点缺陷理论构建非晶合金微观结构非均匀性、缺陷动力学与宏观黏弹性响应之间的关联, 为理解和预测其复杂力学行为提供重要理论视角.
最新更新时间: ,
doi: 10.6052/1000-0992-25-043
微重力科学是空间科学与应用诸多方向的基础之一. 它不仅是全球科技领域的新兴重点, 也是国家太空科技竞争力的重要标志. 目前, 中国空间站全面建成, 国际空间站将退役. 中国空间站作为国家太空实验室, 将公开征集并实施千余项研究项目, 为我国微重力科学研究提供独一无二的实验条件和前所未有的发展机遇. 基于国家自然科学基金委员会第385期“微重力科学与技术的机遇与挑战”双清论坛, 本文总结了我国微重力科学与技术研究及空间站应用面临的挑战和难点, 梳理了近年来在微重力流体物理、微重力制造与空间技术、微重力生命科学与医工技术等领域取得的主要进展和成就, 凝练了微重力科学与技术领域未来5 ~ 10年所面临的重大关键科学问题, 探讨了前沿研究方向并提出学科发展建议.
最新更新时间: ,
doi: 10.6052/1000-0992-25-026
机器学习正推动金属材料力学性能研究从经验驱动向数据驱动范式转变. 本文系统综述了机器学习在金属材料力学性能智能预测中的研究进展与挑战. 首先, 概述了常用机器学习算法的原理与流程, 重点介绍了可解释人工智能与物理信息机器学习等前沿方法. 进而, 从微介观性能 (如微观结构演化、断裂行为)、宏观性能 (如硬度、应力响应、疲劳寿命) 与跨尺度耦合性能 (如流变应力、屈服强度、本构参数反演) 三个层面, 评述了机器学习模型的典型应用与预测效果, 突出其在高通量计算与多尺度建模中的优势. 最后, 指出该领域面临数据稀缺、异构性及宽温域/宽应变率条件下预测精度不足等挑战, 并提出迁移学习、大型语言模型与多模态融合等解决路径. 展望未来, 本文构建了融合多模态数据与物理机制的机器学习技术路径, 旨在实现对极端环境下金属材料力学行为的精准预测, 推动材料力学研究向数字化、智能化方向发展.
最新更新时间: ,
doi: 10.6052/1000-0992-25-025
从介绍美国和俄罗斯建设特大型低速风洞的背景出发, 重点阐述了国外特大型低速风洞开展的试验研究情况, 包括运用的试验流程、完成的试验型号、使用的试验技术等, 尤其是针对特大型低速风洞而设计的特殊试验技术, 研判了特大型低速风洞试验技术未来的发展趋势. 研究结果表明, 特大型低速风洞的建设主要是为了满足型号试验任务和技术发展的需要, 试验流程突出大模型的安装和试验故障的处理, 试验型号以固定翼飞机、旋翼飞机等各类飞机为主, 也兼顾多种航天飞行器的低速试验研究, 还积极承揽能源、交通及建筑类的试验任务, 并在基础空气动力学问题研究方面发挥了重要的作用. 在试验技术方面, 特大型低速风洞既采用了常规的测力、测压和测速等试验技术, 也发展了全尺寸模型、倾转试验台、特大攻角、模型自由飞行、非接触光学测量、恶劣环境模拟等特殊的试验技术, 试验技术总体呈现向提交高精度数据、组合利用多种测试手段、深度赋能大数据、多学科一体化、虚拟现实与增强现实相结合等方向发展. 最后, 提出了特大型低速风洞分步发展试验技术、打造专业试验平台、突出试验细节尺度优势等几点启示.
最新更新时间: ,
doi: 10.6052/1000-0992-25-020
涡环同轴相互作用是亚音速射流中的典型流动结构和重要的噪声来源. 调控涡环相互作用过程的加减速运动是降低射流噪声的关键. 已有的研究工作发现, 弱涡环径向加速度是低频高振幅噪声的主导因素. 本文基于Dyson薄核涡环模型研究了这一现象的成立条件和规律. 通过将声源分解为涡环轴向和径向动力学参数乘积的形式, 研究了不同初始环量比和初始半径比条件下的涡环相互作用过程, 发现了主导总声源脉冲的临界初始半径比. 只有当初始涡环半径比小于临界初始半径比时, 弱涡环径向加速度声源项对总声源的贡献才大于强涡环. 通过对涡环相互作用过程的定量分析, 发现了声源脉冲峰值与涡环轴向速度、径向加速度峰值的关联关系, 并发现强涡环的反向运动, 会造成强涡环声源项产生反相位脉冲.
最新更新时间: ,
doi: 10.6052/1000-0992-25-018
理解与预测物质微观结构及其演化行为, 并揭示其与宏观性能之间的关联规律, 是固体力学关注的核心科学问题之一. 从 Galileo 的木梁弯曲实验、Cauchy 基于微元的应力定义, 到基于 Arrhenius 关系的加速蠕变实验设计, 力学中的模型假设与理论解析持续推动物质科学的发展和材料、结构工程的进步, 原子模拟、连续介质仿真等方法在学术与工业界得到广泛的应用. 然而, 物质的变形与失效过程常具有多时空尺度、多物理场、多机制耦合与非线性演化特征. 基于“观察−假设−模型”的研究思路在面对上述复杂性时遭遇挑战. 在高性能计算和高通量实验的基础上, 数据科学与人工智能方法的发展使我们可以从互补角度来重新审视复杂性问题, 拓展科学发现与工程设计边界. 相比智能技术在视觉、语言等数字空间中的应用, 工程科学对物质世界的探索在数据质量、模型可解释性与推断能力方面提出更高要求. 在统计学习模型中引入数学约束或物理传递策略有助于克服性能−效率均衡与泛化、可理解性等挑战, 构建具备物理一致性和广度的数据库与数字库有望以“重构现实”的方式理解复杂系统的演化规律. 在认知科学的推动下, 物理智能等技术正逐步具备在复杂、动态场景中协助甚至开展科学探索与推理的能力. 本文聚焦材料力学性能与结构长时服役行为, 探讨固体力学中的典型复杂性, 从学习理论、开放科学的视角展望本领域基础与应用研究的发展方向.
2025, 55(4): 707-746.
doi: 10.6052/1000-0992-25-021
摘要:
非正泊松比力学超材料是一类通过构型设计在宏观尺度上展现零/负泊松比效应的结构型功能材料. 因其在横向变形调控、尺寸稳定性和能量吸收等方面的独特优势, 在航空航天、海洋工程、交通运输、可穿戴防护装备和生物医学等领域展现出广泛的应用前景. 近年来, 随着微结构设计、先进材料制备技术和多材料集成手段的不断演进, 非正泊松比力学超材料在构型多样性、响应调控性与结构功能一体化等方面取得了显著进展. 本文从激活结构横向变形行为的主导机理出发, 系统梳理了非正泊松比力学超材料的典型设计策略. 负泊松比超材料围绕内凹几何、旋转体系 (旋转刚体/桁架、手性/反手性)、剪纸/折纸、弹性不稳定诱导与刚体联动等机制组织. 零泊松比超材料归纳为类矩形/平行四边形、半内凹、正/负泊松比单元组合与刚柔复合等几何范式. 围绕非正泊松比力学超材料在缓冲吸能应用中的关键性能, 重点讨论了多平台响应设计、梯度构型调控、多材料耦合与智能材料介入等性能增强途径. 在结构集成层面, 本文还探讨了模块化组装、夹层结构设计与本征三维结构设计等技术路径. 最后, 结合非正泊松比力学超材料在设计制备、性能调控与系统集成中的研究进展, 梳理了当前面临的核心技术瓶颈, 明确了亟需突破的关键方向, 并提出了面向多尺度制造、多场响应集成与工程化应用的未来发展路径.
非正泊松比力学超材料是一类通过构型设计在宏观尺度上展现零/负泊松比效应的结构型功能材料. 因其在横向变形调控、尺寸稳定性和能量吸收等方面的独特优势, 在航空航天、海洋工程、交通运输、可穿戴防护装备和生物医学等领域展现出广泛的应用前景. 近年来, 随着微结构设计、先进材料制备技术和多材料集成手段的不断演进, 非正泊松比力学超材料在构型多样性、响应调控性与结构功能一体化等方面取得了显著进展. 本文从激活结构横向变形行为的主导机理出发, 系统梳理了非正泊松比力学超材料的典型设计策略. 负泊松比超材料围绕内凹几何、旋转体系 (旋转刚体/桁架、手性/反手性)、剪纸/折纸、弹性不稳定诱导与刚体联动等机制组织. 零泊松比超材料归纳为类矩形/平行四边形、半内凹、正/负泊松比单元组合与刚柔复合等几何范式. 围绕非正泊松比力学超材料在缓冲吸能应用中的关键性能, 重点讨论了多平台响应设计、梯度构型调控、多材料耦合与智能材料介入等性能增强途径. 在结构集成层面, 本文还探讨了模块化组装、夹层结构设计与本征三维结构设计等技术路径. 最后, 结合非正泊松比力学超材料在设计制备、性能调控与系统集成中的研究进展, 梳理了当前面临的核心技术瓶颈, 明确了亟需突破的关键方向, 并提出了面向多尺度制造、多场响应集成与工程化应用的未来发展路径.
2025, 55(4): 747-818.
doi: 10.6052/1000-0992-25-005
摘要:
动力学与控制是研究系统运动规律力学机理及其调控方法的学科, 在现代工程与科学研究中具有重要作用. 来自工程结构、耦合构件间力传递和环境交互中的结构和几何非线性、接触力的非光滑性、环境干扰的不确定性和与环境多场耦合交互等因素的复杂性, 使得传统动力学建模、动力学响应预测和动力学控制的智能化变得异常困难. 数据驱动方法的快速发展为解决这些问题提供了全新思路和新的研究范式. 近年来的研究表明, 数据驱动方法不但可以解决或部分解决传统动力学方法无法解决的问题, 而且可以显著提升动力学行为预测和性能优化的能力, 为动力学与控制研究的智能化奠定必要的基础, 在复杂耦合系统的建模、分析与调控中展现出巨大的潜力与科学价值. 本文简要介绍了近年来数据驱动方法在机器人动力学建模与运动调控、跨声速气动弹性动力学建模、结构动力学设计、随机动力学、基于脑机接口技术和神经动力学模型的运动控制、机械设备故障诊断与剩余寿命预测等方面的应用研究进展, 并探讨了这些领域面临的挑战与发展趋势.
动力学与控制是研究系统运动规律力学机理及其调控方法的学科, 在现代工程与科学研究中具有重要作用. 来自工程结构、耦合构件间力传递和环境交互中的结构和几何非线性、接触力的非光滑性、环境干扰的不确定性和与环境多场耦合交互等因素的复杂性, 使得传统动力学建模、动力学响应预测和动力学控制的智能化变得异常困难. 数据驱动方法的快速发展为解决这些问题提供了全新思路和新的研究范式. 近年来的研究表明, 数据驱动方法不但可以解决或部分解决传统动力学方法无法解决的问题, 而且可以显著提升动力学行为预测和性能优化的能力, 为动力学与控制研究的智能化奠定必要的基础, 在复杂耦合系统的建模、分析与调控中展现出巨大的潜力与科学价值. 本文简要介绍了近年来数据驱动方法在机器人动力学建模与运动调控、跨声速气动弹性动力学建模、结构动力学设计、随机动力学、基于脑机接口技术和神经动力学模型的运动控制、机械设备故障诊断与剩余寿命预测等方面的应用研究进展, 并探讨了这些领域面临的挑战与发展趋势.
2025, 55(4): 819-853.
doi: 10.6052/1000-0992-25-012
摘要:
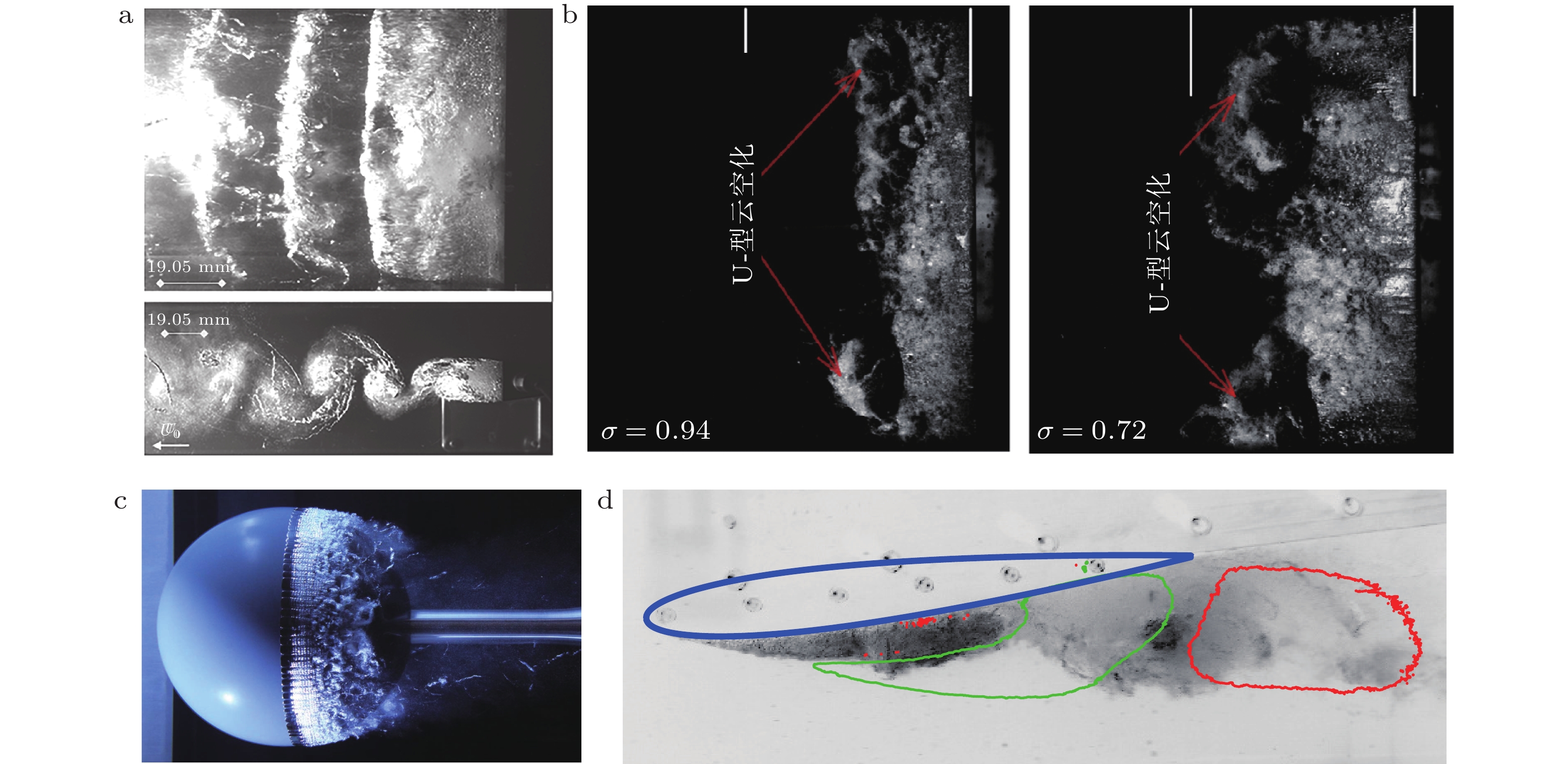
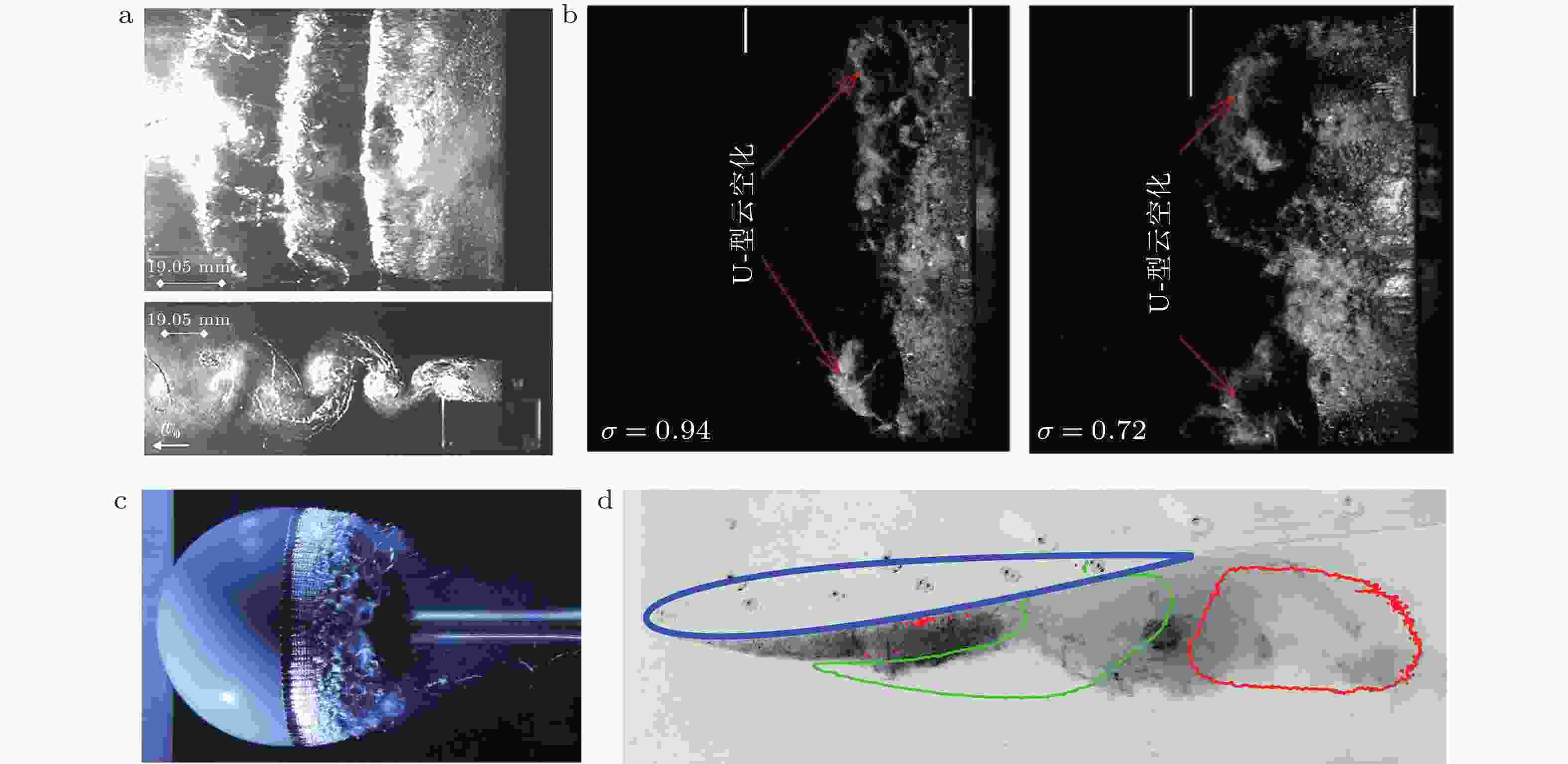
水动力空化是船舶推进、航行体跨介质运动等领域一种常见的物理现象. 针对工程领域空化噪声和空蚀预报对非平衡空化流动研究的迫切需求, 回顾了20余年来空化核与初生、群泡水体介质特性与声传播、空化与湍流相互作用、空泡溃灭瞬态冲击与激波等关键基础科学问题研究的主要进展; 梳理出空化宏观模拟面临的空化相变建模、多相流模拟和多相湍流3个挑战, 指出多尺度空化模拟的重要性并对微介观模拟方法做了简要介绍; 总结了近年来空化流微介观模拟在空化区混合介质基本物理特性、空泡流场时空特性等方面获得的新认识以及高阶数值模拟方法. 面向高精度空化流动多尺度模拟与工程预报, 展望了定量、准确描述空化区域水汽掺混介质特性与空化流时空特性的两个层面迫切需要解决的若干基础性建模问题.
水动力空化是船舶推进、航行体跨介质运动等领域一种常见的物理现象. 针对工程领域空化噪声和空蚀预报对非平衡空化流动研究的迫切需求, 回顾了20余年来空化核与初生、群泡水体介质特性与声传播、空化与湍流相互作用、空泡溃灭瞬态冲击与激波等关键基础科学问题研究的主要进展; 梳理出空化宏观模拟面临的空化相变建模、多相流模拟和多相湍流3个挑战, 指出多尺度空化模拟的重要性并对微介观模拟方法做了简要介绍; 总结了近年来空化流微介观模拟在空化区混合介质基本物理特性、空泡流场时空特性等方面获得的新认识以及高阶数值模拟方法. 面向高精度空化流动多尺度模拟与工程预报, 展望了定量、准确描述空化区域水汽掺混介质特性与空化流时空特性的两个层面迫切需要解决的若干基础性建模问题.
2025, 55(4): 854-907.
doi: 10.6052/1000-0992-25-003
摘要:
工程科学众多问题涉及多物理场耦合效应, 其数值模拟往往面临巨大挑战. 光滑粒子法 (smoothed particle hydrodynamics, SPH) 是一种经典的无网格粒子方法, 在模拟多物理场耦合问题方面具有明显优势, 已在众多科学和工程领域取得广泛应用. 本文重点介绍近期SPH算法研究概况及其在多物理场耦合模拟方面的应用进展. 具体内容包括: (1) 力−热耦合问题, 涉及传热传质、高速撞击、铸造、增材制造等领域; (2) 力−热−化学反应耦合问题, 涵盖聚能射流、爆炸焊接、水下爆炸等应用; (3) 力−热−电磁耦合问题, 包括电磁场流场控制及“X-pinch”等问题. 最后, 对SPH方法模拟多物理场耦合问题的未来发展进行了讨论和展望.
工程科学众多问题涉及多物理场耦合效应, 其数值模拟往往面临巨大挑战. 光滑粒子法 (smoothed particle hydrodynamics, SPH) 是一种经典的无网格粒子方法, 在模拟多物理场耦合问题方面具有明显优势, 已在众多科学和工程领域取得广泛应用. 本文重点介绍近期SPH算法研究概况及其在多物理场耦合模拟方面的应用进展. 具体内容包括: (1) 力−热耦合问题, 涉及传热传质、高速撞击、铸造、增材制造等领域; (2) 力−热−化学反应耦合问题, 涵盖聚能射流、爆炸焊接、水下爆炸等应用; (3) 力−热−电磁耦合问题, 包括电磁场流场控制及“X-pinch”等问题. 最后, 对SPH方法模拟多物理场耦合问题的未来发展进行了讨论和展望.
2025, 55(4): 908-947.
doi: 10.6052/1000-0992-25-007
摘要:
近场动力学作为一种以积分方程为特征的非局部连续介质力学理论, 在模拟裂纹萌生以及裂纹沿任意路径扩展时较传统连续介质理论具有显著优势, 特别在描述脆性以及准脆性材料的瞬态损伤与断裂问题中具有良好的适用性. 本文首先概述了近场动力学的基本理论以及材料断裂与损伤的失效准则. 其次详细介绍了近年来多种脆性以及准脆性材料 (陶瓷、混凝土、玻璃、岩石等) 在近场动力学框架下的损伤预测和断裂建模研究. 最后讨论了该类材料在近场动力学理论中值得深入研究的问题.
近场动力学作为一种以积分方程为特征的非局部连续介质力学理论, 在模拟裂纹萌生以及裂纹沿任意路径扩展时较传统连续介质理论具有显著优势, 特别在描述脆性以及准脆性材料的瞬态损伤与断裂问题中具有良好的适用性. 本文首先概述了近场动力学的基本理论以及材料断裂与损伤的失效准则. 其次详细介绍了近年来多种脆性以及准脆性材料 (陶瓷、混凝土、玻璃、岩石等) 在近场动力学框架下的损伤预测和断裂建模研究. 最后讨论了该类材料在近场动力学理论中值得深入研究的问题.
“最新录用”文章为经过审稿人和编委会评审并已接受录用准备发表的文章. 请您注意:这些文章并未经过排版, 也未经编辑及作者校对. 编辑、排版和校对可能会造成文章的内容变动
当前状态:
, 最新更新时间: ,
doi: 10.6052/1000-0992-25-037
摘要:
凭借其三维波浪状独特外形的胡须, 斑海豹展现出卓越的水下感知能力. 研究证实, 斑海豹可感知流速低至245 μm/s的微弱涡流, 还能追踪180 m外的目标在35 s前遗留下的水中尾迹. 这一能力凸显出斑海豹胡须在水下涡流感知和目标尾迹追踪方面的独特优势. 目前, 以斑海豹胡须为原型的传感器设计已成为仿生科学与工程领域的研究热点, 在水下目标探测与识别等方面展现出广阔应用前景. 本文首先梳理斑海豹胡须形态特征和几何建模方面的研究成果, 总结并对比不同概化模型的优势与不足. 随后, 综述斑海豹胡须仿生模型水动力特性方面的研究进展, 涵盖均匀流场和尾迹流场中仿生模型的尾流特性和振动响应、斑海豹胡须的感知机理、阵列胡须之间的相互作用, 以及人工智能方法在感知信号识别中的应用等方面. 最后, 针对现有研究存在的不足和关键问题, 展望斑海豹胡须仿生科学与工程应用需要关注的若干研究方向.
凭借其三维波浪状独特外形的胡须, 斑海豹展现出卓越的水下感知能力. 研究证实, 斑海豹可感知流速低至245 μm/s的微弱涡流, 还能追踪180 m外的目标在35 s前遗留下的水中尾迹. 这一能力凸显出斑海豹胡须在水下涡流感知和目标尾迹追踪方面的独特优势. 目前, 以斑海豹胡须为原型的传感器设计已成为仿生科学与工程领域的研究热点, 在水下目标探测与识别等方面展现出广阔应用前景. 本文首先梳理斑海豹胡须形态特征和几何建模方面的研究成果, 总结并对比不同概化模型的优势与不足. 随后, 综述斑海豹胡须仿生模型水动力特性方面的研究进展, 涵盖均匀流场和尾迹流场中仿生模型的尾流特性和振动响应、斑海豹胡须的感知机理、阵列胡须之间的相互作用, 以及人工智能方法在感知信号识别中的应用等方面. 最后, 针对现有研究存在的不足和关键问题, 展望斑海豹胡须仿生科学与工程应用需要关注的若干研究方向.
当前状态:
, 最新更新时间: ,
doi: 10.6052/1000-0992-25-032
摘要:
飞行器不确定性设计分析方法作为一种先进的飞行器设计范式, 为解决不确定性精确表征、量化传播与优化设计提供了系统的方法体系. 本文系统梳理了飞行器不确定性设计相关的核心概念与关键技术, 归纳了飞行器关键系统设计与重要环境条件预示涉及的不确定性问题. 在此基础上, 总结提炼了该领域的五个重要发展方向: (1) 高维不确定性量化与高效传播: 通过融合输入空间降维、函数表示稀疏化与低秩张量分解等技术, 构建自适应高维不确定性量化框架, 有效应对“维度灾难”带来的挑战; (2) 混合不确定性量化与高效传播: 构建兼容概率、区间、模糊、证据理论等多种不确定性类型的统一量化分析框架, 并结合代理模型与主动学习策略提升复杂多源不确定性问题的计算效率; (3) 多层级多保真度不确定性量化框架: 融合广义近似控制变量、自适应多指标随机配点等技术, 实现计算资源在不同保真度模型上的动态优化配置; (4) 基于不确定性的设计优化算法与框架: 将概率约束与鲁棒性度量统一到不确定性条件下的多目标优化与决策框架, 通过单层循环与解耦式优化策略, 实现性能、可靠性与鲁棒性的综合权衡优化; (5) 基于人工智能技术的不确定性设计分析: 以物理信息神经网络为核心, 融合物理知识与多源数据, 构建智能不确定性量化与优化框架.
飞行器不确定性设计分析方法作为一种先进的飞行器设计范式, 为解决不确定性精确表征、量化传播与优化设计提供了系统的方法体系. 本文系统梳理了飞行器不确定性设计相关的核心概念与关键技术, 归纳了飞行器关键系统设计与重要环境条件预示涉及的不确定性问题. 在此基础上, 总结提炼了该领域的五个重要发展方向: (1) 高维不确定性量化与高效传播: 通过融合输入空间降维、函数表示稀疏化与低秩张量分解等技术, 构建自适应高维不确定性量化框架, 有效应对“维度灾难”带来的挑战; (2) 混合不确定性量化与高效传播: 构建兼容概率、区间、模糊、证据理论等多种不确定性类型的统一量化分析框架, 并结合代理模型与主动学习策略提升复杂多源不确定性问题的计算效率; (3) 多层级多保真度不确定性量化框架: 融合广义近似控制变量、自适应多指标随机配点等技术, 实现计算资源在不同保真度模型上的动态优化配置; (4) 基于不确定性的设计优化算法与框架: 将概率约束与鲁棒性度量统一到不确定性条件下的多目标优化与决策框架, 通过单层循环与解耦式优化策略, 实现性能、可靠性与鲁棒性的综合权衡优化; (5) 基于人工智能技术的不确定性设计分析: 以物理信息神经网络为核心, 融合物理知识与多源数据, 构建智能不确定性量化与优化框架.
当前状态:
, 最新更新时间: ,
doi: 10.6052/1000-0992-25-029
摘要:
随着全球人口老龄化和慢性病的高发, 心血管疾病、肿瘤、糖尿病等重大难治性疾病已成为全球公共健康和社会经济发展的主要挑战. 其病理进程通常伴随着细胞外基质(ECM)的异常重塑与力学稳态失衡, 导致传统治疗方法难以有效逆转. 近期研究揭示, 结合材料学与工程学原理主动调控ECM的力化属性以精准介导细胞行为, 能够有效激活组织内源性修复从而显著促进组织再生. 该研究策略被称为力材料学, 即通过对材料进行主动设计, 利用力−结构−功能关系对生命系统的力学环境进行主动控制. 基于此概念, 本文提出从基质组学角度系统鉴定ECM的分子组成并解构其力学信息编码; 利用基质力生物学认识细胞-ECM互作机制并解析病理ECM“重编码”过程; 在深入认知和理解ECM力学微环境基础上结合基质力材料学的研究思路, 探索对异常ECM“去编码”与功能恢复的基质工程技术; 最终实现组织内源性修复的基质治疗目的. 具体而言, 本文在介绍ECM的组成与动态编码的基础上, 系统总结了异常ECM力学微环境的生理/病理变化, 着重提出并构建基于分子靶向与材料重建的基质工程与治疗新策略, 旨在为重大难治性疾病的干预和再生医学的发展提供新的理论依据和创新思路.
随着全球人口老龄化和慢性病的高发, 心血管疾病、肿瘤、糖尿病等重大难治性疾病已成为全球公共健康和社会经济发展的主要挑战. 其病理进程通常伴随着细胞外基质(ECM)的异常重塑与力学稳态失衡, 导致传统治疗方法难以有效逆转. 近期研究揭示, 结合材料学与工程学原理主动调控ECM的力化属性以精准介导细胞行为, 能够有效激活组织内源性修复从而显著促进组织再生. 该研究策略被称为力材料学, 即通过对材料进行主动设计, 利用力−结构−功能关系对生命系统的力学环境进行主动控制. 基于此概念, 本文提出从基质组学角度系统鉴定ECM的分子组成并解构其力学信息编码; 利用基质力生物学认识细胞-ECM互作机制并解析病理ECM“重编码”过程; 在深入认知和理解ECM力学微环境基础上结合基质力材料学的研究思路, 探索对异常ECM“去编码”与功能恢复的基质工程技术; 最终实现组织内源性修复的基质治疗目的. 具体而言, 本文在介绍ECM的组成与动态编码的基础上, 系统总结了异常ECM力学微环境的生理/病理变化, 着重提出并构建基于分子靶向与材料重建的基质工程与治疗新策略, 旨在为重大难治性疾病的干预和再生医学的发展提供新的理论依据和创新思路.
当前状态:
, 最新更新时间: ,
doi: 10.6052/1000-0992-25-023
摘要:
当高温引起了流动介质物性变化的时候, 介质微团的物理化学变化显著地改变了介质流动的宏观规律, 超出了气体动力学基本假设和研究范畴, 高温气体动力学诞生了. 当航空航天技术不断拓展人类活动空间的时候, 在探索下一代空天飞行核心技术的过程中, 高温气体动力学发展了. 高温气体动力学是技术科学发展的典范, 在应用驱动学科机制的作用下, 引领着气体动力学的发展与创新. 本文选择了高温气体动力学的四个主要研究领域, 进行了综述和分析, 期望能够助力高温气体流动的学科发展. 第一部分是关于高超声速地面试验装置和测量技术, 重点介绍了三种典型高焓激波风洞, 它们的应用已经能够产生和测量的气流速度达到了1.5 ~ 10 km/s的范围, 可以模拟20 ~ 100 km的飞行高度. 先进科学试验装置对于学科前沿的拓展和流体物理新现象的发现是非常重要的, 该研究领域的进展也凸显了这个道理. 第二部分介绍了高超声速气体流动的理论与实验, 包括物理数学模型的建立、计算方法的发展和实验观测. 到目前为止, 高温气体流动物理模型的发展远低预期, 局限在早期物理模型的应用和改进; 计算方法发展迅速, 能够计算的流动现象越来越多, 准确度也越来越高; 地面实验观测研究进展可期, 表现在一些复现高超声速飞行条件下的大模型实验, 揭示的气动物理现象与飞行试验数据一致良好. 第三部分是关于超声速燃烧和超燃冲压发动机. 这是一个已经持续热了几十年的前沿领域, 虽然理论和技术研究进展巨大、飞行试验硕果累累, 但是超燃冲压发动机依然难以满足工程需求, 超声速燃烧理论依然难以解决超燃冲压发动机研发遇到的问题. 所以, 超声速燃烧和超燃冲压发动机研究都亟需理论创新和技术突破. 第四部分是关于爆轰物理和斜爆轰发动机. 斜爆轰发动机与超燃冲压发动机概念皆生于同一时代, 但它仅在最近20多年才得到重新关注. 爆轰理论和斜爆轰研究都有了创新性突破, 斜爆轰发动机设计方法和风洞实验技术也有了长足的进展. 斜爆轰冲压发动机利用了自然界燃烧速度最快、热效率最高、进气压缩损失最小的增压燃烧现象作为其热力循环, 有着独特的优势. 最后, 论文对于上述研究领域的理论技术及其实践进行了总结和展望, 期望能够给该学科发展提供一些有益的启示.
当高温引起了流动介质物性变化的时候, 介质微团的物理化学变化显著地改变了介质流动的宏观规律, 超出了气体动力学基本假设和研究范畴, 高温气体动力学诞生了. 当航空航天技术不断拓展人类活动空间的时候, 在探索下一代空天飞行核心技术的过程中, 高温气体动力学发展了. 高温气体动力学是技术科学发展的典范, 在应用驱动学科机制的作用下, 引领着气体动力学的发展与创新. 本文选择了高温气体动力学的四个主要研究领域, 进行了综述和分析, 期望能够助力高温气体流动的学科发展. 第一部分是关于高超声速地面试验装置和测量技术, 重点介绍了三种典型高焓激波风洞, 它们的应用已经能够产生和测量的气流速度达到了1.5 ~ 10 km/s的范围, 可以模拟20 ~ 100 km的飞行高度. 先进科学试验装置对于学科前沿的拓展和流体物理新现象的发现是非常重要的, 该研究领域的进展也凸显了这个道理. 第二部分介绍了高超声速气体流动的理论与实验, 包括物理数学模型的建立、计算方法的发展和实验观测. 到目前为止, 高温气体流动物理模型的发展远低预期, 局限在早期物理模型的应用和改进; 计算方法发展迅速, 能够计算的流动现象越来越多, 准确度也越来越高; 地面实验观测研究进展可期, 表现在一些复现高超声速飞行条件下的大模型实验, 揭示的气动物理现象与飞行试验数据一致良好. 第三部分是关于超声速燃烧和超燃冲压发动机. 这是一个已经持续热了几十年的前沿领域, 虽然理论和技术研究进展巨大、飞行试验硕果累累, 但是超燃冲压发动机依然难以满足工程需求, 超声速燃烧理论依然难以解决超燃冲压发动机研发遇到的问题. 所以, 超声速燃烧和超燃冲压发动机研究都亟需理论创新和技术突破. 第四部分是关于爆轰物理和斜爆轰发动机. 斜爆轰发动机与超燃冲压发动机概念皆生于同一时代, 但它仅在最近20多年才得到重新关注. 爆轰理论和斜爆轰研究都有了创新性突破, 斜爆轰发动机设计方法和风洞实验技术也有了长足的进展. 斜爆轰冲压发动机利用了自然界燃烧速度最快、热效率最高、进气压缩损失最小的增压燃烧现象作为其热力循环, 有着独特的优势. 最后, 论文对于上述研究领域的理论技术及其实践进行了总结和展望, 期望能够给该学科发展提供一些有益的启示.
当前状态:
, 最新更新时间: ,
doi: 10.6052/1000-0992-25-044
摘要:
本文综述海洋工程领域中与自由面/界面相关的若干前沿问题的研究现状与最新进展. 主要内容包括热带气旋 (TC) 引发的巨浪、液化天然气 (LNG) 晃荡、空化与气泡动力学、涡激运动 (VIM) 与涡激振动 (VIV). 重点关注上述方向的最新研究进展与所面临的挑战. 过去70年研究成果显示, 人类正在开启新一轮海洋探索活动. 未来将出现从海面向深海拓展、从低中纬度向极地延伸, 从化石能源向可再生能源转型的明显趋势.
本文综述海洋工程领域中与自由面/界面相关的若干前沿问题的研究现状与最新进展. 主要内容包括热带气旋 (TC) 引发的巨浪、液化天然气 (LNG) 晃荡、空化与气泡动力学、涡激运动 (VIM) 与涡激振动 (VIV). 重点关注上述方向的最新研究进展与所面临的挑战. 过去70年研究成果显示, 人类正在开启新一轮海洋探索活动. 未来将出现从海面向深海拓展、从低中纬度向极地延伸, 从化石能源向可再生能源转型的明显趋势.
- 2025 Vol. 3
- 2025 Vol. 2
- 2025 Vol. 1
- 2024 Vol. 4
- 2024 Vol. 3
- 2024 Vol. 2
- 2024 Vol. 1
- 2023 Vol. 4
- 2023 Vol. 3
- 2023 Vol. 2
- 2023 Vol. 1
- 2022 Vol. 4
- 2022 Vol. 3
- 2022 Vol. 2
- 2022 Vol. 1
- 2021 Vol. 4
- 2021 Vol. 3
- 2021 Vol. 2
- 2021 Vol. 1
- 2020 Vol. 1
- 2019 Vol. 1
- 2018 Vol. 1
- 2017 Vol. 1
- 2016 Vol. 1
- 2015 Vol. 1
- 2014 Vol. 1
- 2013 Vol. 6
- 2013 Vol. 5
- 2013 Vol. 4
- 2013 Vol. 3
- 2013 Vol. 2
- 2013 Vol. 1
- 2012 Vol. 6
- 2012 Vol. 5
- 2012 Vol. 4
- 2012 Vol. 3
- 2012 Vol. 2
- 2012 Vol. 1
- 2011 Vol. 6
- 2011 Vol. 5
- 2011 Vol. 4
- 2011 Vol. 3
- 2011 Vol. 2
- 2011 Vol. 1
- 2010 Vol. 6
- 2010 Vol. 5
- 2010 Vol. 4
- 2010 Vol. 3
- 2010 Vol. 2
- 2010 Vol. 1
- 2009 Vol. 6
- 2009 Vol. 5
- 2009 Vol. 4
- 2009 Vol. 3
- 2009 Vol. 2
- 2009 Vol. 1
- 2008 Vol. 6
- 2008 Vol. 5
- 2008 Vol. 4
- 2008 Vol. 3
- 2008 Vol. 2
- 2008 Vol. 1
- 2007 Vol. 4
- 2007 Vol. 3
- 2007 Vol. 2
- 2007 Vol. 1
- 2006 Vol. 4
- 2006 Vol. 3
- 2006 Vol. 2
- 2006 Vol. 1
- 2005 Vol. 4
- 2005 Vol. 3
- 2005 Vol. 2
- 2005 Vol. 1
- 2004 Vol. 4
- 2004 Vol. 3
- 2004 Vol. 2
- 2004 Vol. 1
- 2003 Vol. 4
- 2003 Vol. 3
- 2003 Vol. 2
- 2003 Vol. 1
- 2002 Vol. 4
- 2002 Vol. 3
- 2002 Vol. 2
- 2002 Vol. 1
- 2001 Vol. 4
- 2001 Vol. 3
- 2001 Vol. 2
- 2001 Vol. 1
- 2000 Vol. 4
- 2000 Vol. 3
- 2000 Vol. 2
- 2000 Vol. 1
- 1999 Vol. 4
- 1999 Vol. 3
- 1999 Vol. 2
- 1999 Vol. 1
- 1998 Vol. 4
- 1998 Vol. 3
- 1998 Vol. 2
- 1998 Vol. 1
- 1997 Vol. 4
- 1997 Vol. 3
- 1997 Vol. 2
- 1997 Vol. 1
- 1996 Vol. 4
- 1996 Vol. 3
- 1996 Vol. 2
- 1996 Vol. 1
- 1995 Vol. 4
- 1995 Vol. 3
- 1995 Vol. 2
- 1995 Vol. 1
- 1994 Vol. 4
- 1994 Vol. 3
- 1994 Vol. 2
- 1994 Vol. 1
- 1993 Vol. 4
- 1993 Vol. 3
- 1993 Vol. 2
- 1993 Vol. 1
- 1992 Vol. 4
- 1992 Vol. 3
- 1992 Vol. 2
- 1992 Vol. 1
- 1991 Vol. 4
- 1991 Vol. 3
- 1991 Vol. 2
- 1991 Vol. 1
- 1990 Vol. 4
- 1990 Vol. 3
- 1990 Vol. 2
- 1990 Vol. 1
- 1989 Vol. 4
- 1989 Vol. 3
- 1989 Vol. 2
- 1989 Vol. 1
- 1988 Vol. 4
- 1988 Vol. 3
- 1988 Vol. 2
- 1988 Vol. 1
- 1987 Vol. 4
- 1987 Vol. 3
- 1987 Vol. 2
- 1987 Vol. 1
- 1986 Vol. 4
- 1986 Vol. 3
- 1986 Vol. 2
- 1986 Vol. 1
- 1985 Vol. 4
- 1985 Vol. 3
- 1985 Vol. 2
- 1985 Vol. 1
- 1984 Vol. 4
- 1984 Vol. 3
- 1984 Vol. 2
- 1984 Vol. 1
- 1983 Vol. 4
- 1983 Vol. 3
- 1983 Vol. 2
- 1983 Vol. 1
- 1982 Vol. 4
- 1982 Vol. 3
- 1982 Vol. 2
- 1982 Vol. 1
- 1981 Vol. 4
- 1981 Vol. 3
- 1981 Vol. 2
- 1981 Vol. 1
- 1980 Vol. 4
- 1980 Vol. 2~3
- 1980 Vol. 1
- 1979 Vol. 4
- 1979 Vol. 3
- 1979 Vol. 2
- 1979 Vol. 1
- 1978 Vol. 2
- 1978 Vol. 1
- 1977 Vol. 2
- 1977 Vol. 1
- 1976 Vol. 4
- 1976 Vol. 3
- 1976 Vol. 2
- 1976 Vol. 1
- 1975 Vol. 2
- 1975 Vol. 1
- 1974 Vol. 2
- 1974 Vol. 1
- 1973 Vol. 6
- 1973 Vol. 5
- 1973 Vol. 4
- 1973 Vol. 3
- 1973 Vol. 2
- 1973 Vol. 1
- 1972 Vol. 12
- 1972 Vol. 11
- 1972 Vol. 10
- 1972 Vol. 9
- 1972 Vol. 8
- 1972 Vol. 7
- 1972 Vol. 6
- 1972 Vol. 5
- 1972 Vol. 4
- 1972 Vol. 3
- 1972 Vol. 2
- 1972 Vol. 1
- 1971 Vol. 6
- 1971 Vol. 5
- 1971 Vol. 4
- 1971 Vol. 3
- 1971 Vol. 2
- 1971 Vol. 1











 摘要
摘要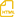 HTML
HTML PDF
PDF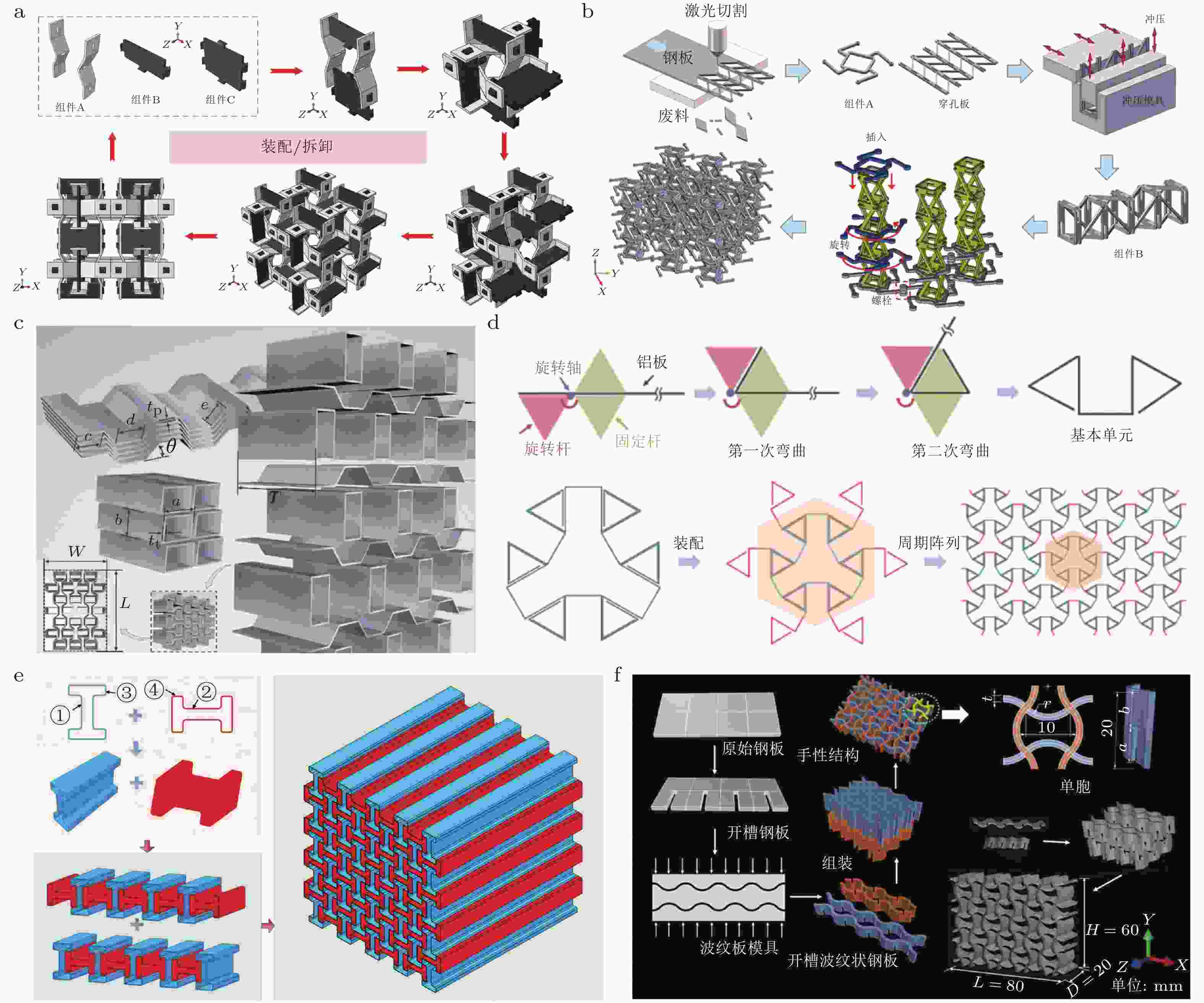



 Email Alert
Email Alert RSS
RSS