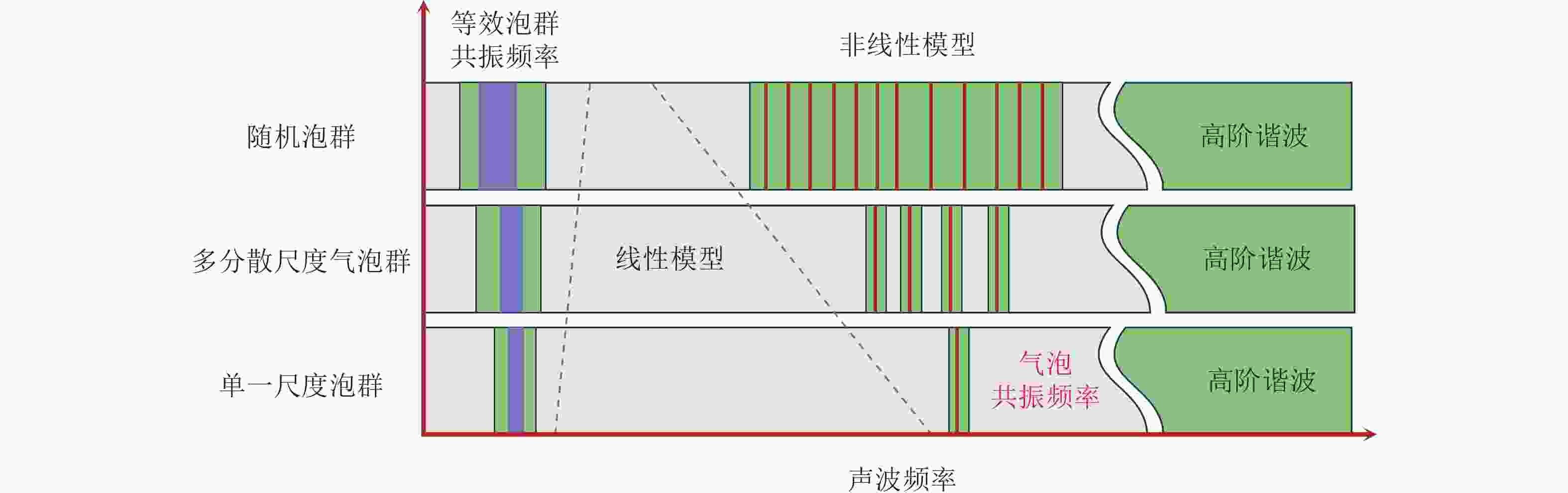
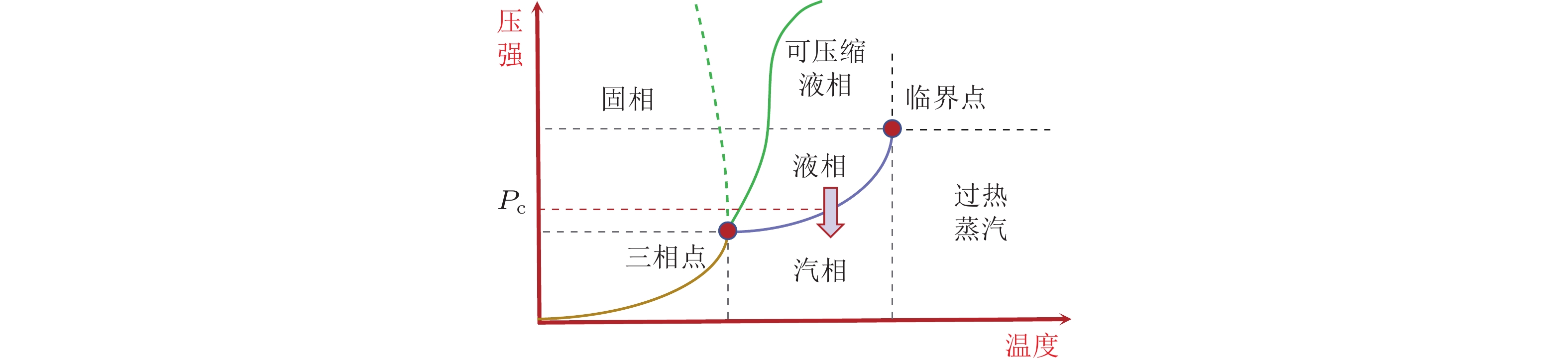
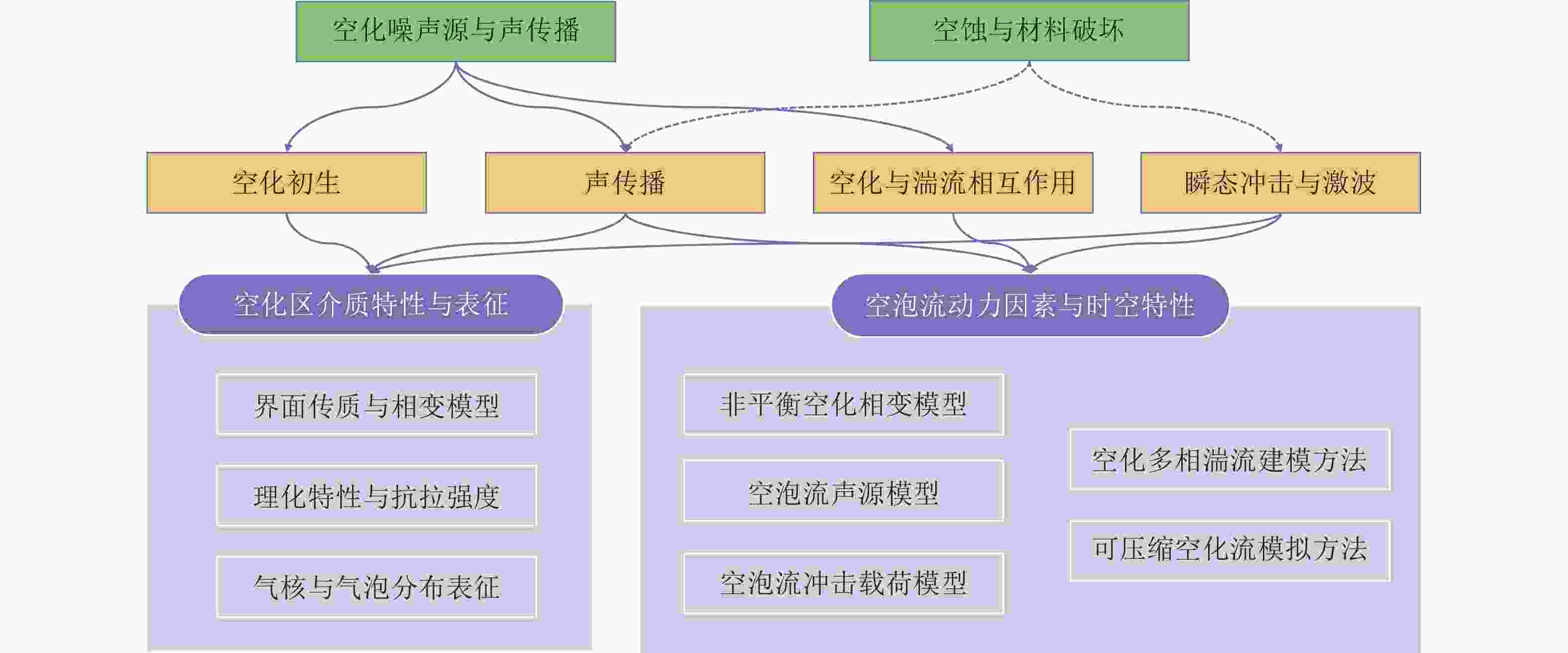
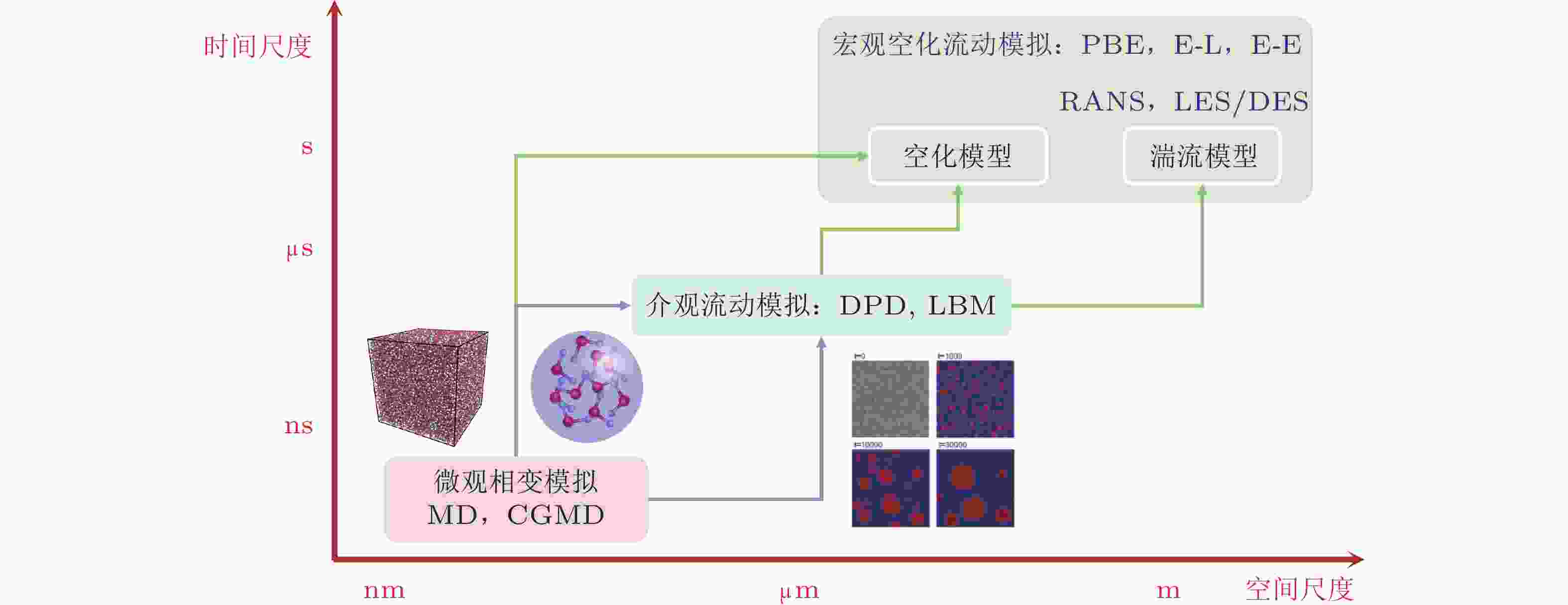
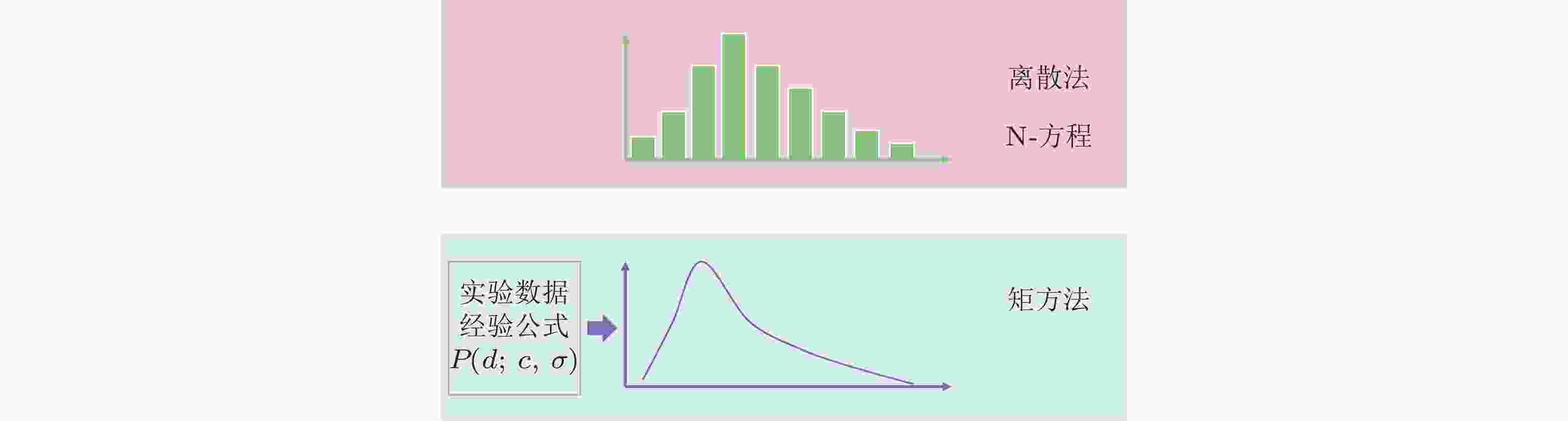
-
摘要: 水动力空化是船舶推进、航行体跨介质运动等领域一种常见的物理现象. 针对工程领域空化噪声和空蚀预报对非平衡空化流动研究的迫切需求, 回顾了二十余年来空化核与初生、群泡水体介质特性与声传播、空化与湍流相互作用、空泡溃灭瞬态冲击与激波等关键基础科学问题研究的主要进展; 梳理出空化宏观模拟面临的空化相变建模、多相流模拟和多相湍流三个挑战, 指出多尺度空化模拟的重要性并对微介观模拟方法做了简要介绍; 总结了近年来空化流微介观模拟在空化区混合介质基本物理特性、空泡流场时空特性等方面获得的新认识以及高阶数值模拟方法. 面向高精度空化流动多尺度模拟与工程预报, 展望了定量、准确描述空化区域水汽掺混介质特性与空化流时空特性的两个层面迫切需要解决的若干基础性建模问题.Abstract: Hydrodynamic cavitation is a prevalent physical phenomenon in ship propulsion and underwater vehicles. To accurate prediction of cavitation noise prediction and cavitation erosion forecasting, this paper reviews key advances over the past two decades: nuclei and inception mechanisms of cavitation, pressure fluctuations and acoustic propagation across cloud cavitating regions, interaction between cavitation and turbulence, transient impact dynamics during cavity collapse and shock wave generation. Current research status and limitations are discussed through perspectives including phase transition model, multiphase flow simulation methodology, and cavitation-turbulence interactions. A concise overview is presented on multi-scale simulation methodologies for cavitating flows, summarizing recent insights into mixed-phase medium characteristics within cavitating zones and spatiotemporal evolution features of cavity fields derived from meso-scale simulations. For future development in multi-scale modeling and engineering forecasting of cavitating flows, the paper identifies two critical theoretical challenges requiring quantitative characterization: (1) fundamental modeling of vapor-water mixture properties in cavitating regions; and (2) precise representation of spatiotemporal dynamics of cavitating flows.
-
Key words:
- phase transition /
- cavitation inception /
- cloud cavitation /
- multiphase flow /
- multiscale simulation
-
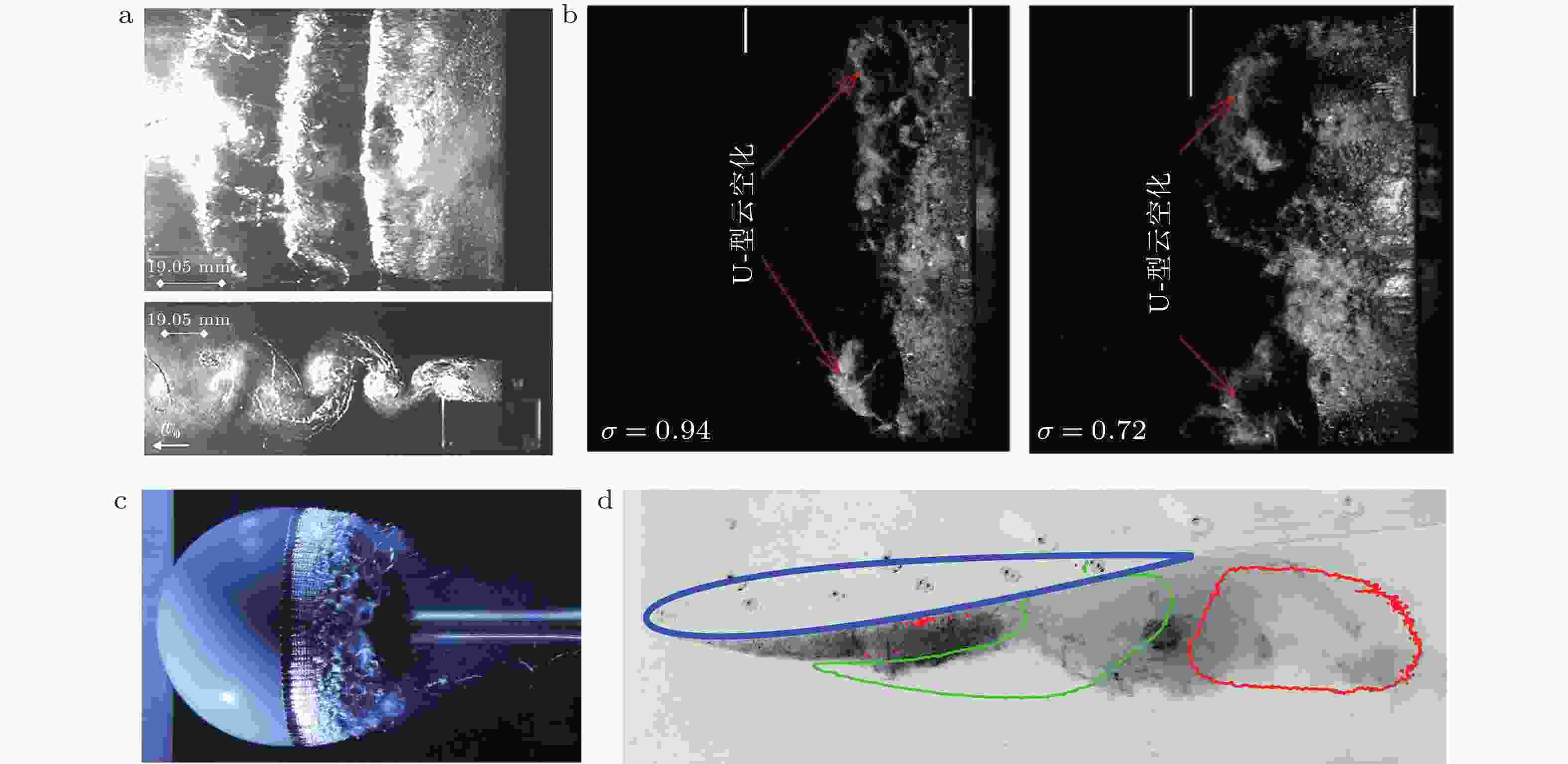
图 3 不同类型空化流场拟序结构实验结果: (a) 楔形体空化区 (Belahadji et al 1995, Wu et al 2021); (b) 水翼U形云空化 (Peng et al 2016), 俯视图; (c)球体云空化 (de Graaf et al 2016); (d)水翼云空化脱落过程 (Zhang et al 2021), 侧视图.
-
[1] 程怀玉, 季斌, 龙新平, 彭晓星. 2024. 旋涡空化水动力学特性研究进展与展望. 力学进展, 54(1): 86-137 (Cheng H Y, Ji B, Long X P, Peng X X. 2024. Research progresses and prospects of vortex cavitation dynamics. Advances in Mechanics, 54(1): 86-137).Cheng H Y, Ji B, Long X P, Peng X X. 2024. Research progresses and prospects of vortex cavitation dynamics. Advances in Mechanics, 54(1): 86-137 [2] 董世汤, 王国强, 唐登海, 等. 2009. 船舶推进器水动力学. 北京: 国防工业出版社 (Dong S T, Wang G Q, Tang D H, et al. 2009. Hydrodynamic of Ship Propulsors. Beijing: National Defense Industry Press).Dong S T, Wang G Q, Tang D H, et al. 2009. Hydrodynamic of Ship Propulsors. Beijing: National Defense Industry Press. [3] 冯先忍. 2024. 喷水推进空化流场特性与尺度效应研究. 上海交通大学博士学位论文 (Feng X R. 2024. Study on the characteristics of cavitation flow field and scale effects in waterjet propulsion. PhD thesis, Shanghai Jiao Tong University).Feng X R. 2024. Study on the characteristics of cavitation flow field and scale effects in waterjet propulsion. PhD thesis, Shanghai Jiao Tong University. [4] 潘森森, 彭晓星. 2013. 空化机理. 北京: 国防工业出版社 (Pan S S, Peng X X. 2013. Physical Mechanism of Cavitation. Beijing: National Defense Industry Press).Pan S S, Peng X X. 2013. Physical Mechanism of Cavitation. Beijing: National Defense Industry Press. [5] 季斌, 程怀玉, 黄彪, 等. 2019. 空化水动力学非定常特性研究进展及展望. 力学进展, 49: 201906 (Ji B, Cheng H Y, Huang B, etc. 2019. Research progresses and prospects of unsteady hydrodynamics characteristics for cavitation. Advances in Mechanics, 49: 201906).Ji B, Cheng H Y, Huang B, etc. 2019. Research progresses and prospects of unsteady hydrodynamics characteristics for cavitation. Advances in Mechanics, 49: 201906. [6] 李游, 李贵, 李桥忠, 代安定, 牛小东. 2024. 正则化相场格子玻尔兹曼两相流模型. 力学学报, 56(8): 2259-2270 (Liu Y, Li G, Li Q Z, Dai A D, Niu X D. 2024. A regularized phase-field lattice Boltzmann model for two-phase flows. Chinese J. Theor. and Appl. Mech., 56(8): 2259-2270).Liu Y, Li G, Li Q Z, Dai A D, Niu X D. 2024. A regularized phase-field lattice Boltzmann model for two-phase flows. Chinese J. Theor. and Appl. Mech., 56(8): 2259-2270. [7] 潘定一, 胡国辉, 陈硕, PHAN-THIEN N. 2024. 复杂多相流体的介观模拟: 耗散粒子动力学方法及应用. 力学进展, 54(1): 173-201 (Pan D Y, Hu G H, Chen S, Phan-Thien N. 2024. Mesoscopic modeling of complex multiphase fluids: Dissipative particle dynamics (DPD) method and its applications. Advances in Mechanics, 2024, 54(1): 173-201).Pan D Y, Hu G H, Chen S, Phan-Thien N. 2024. Mesoscopic modeling of complex multiphase fluids: Dissipative particle dynamics (DPD) method and its applications. Advances in Mechanics, 2024, 54(1): 173-201. [8] 汤渭霖, 俞孟萨, 王斌. 2019. 水动力噪声理论. 科学出版社 (Tang W L, Yu M S, Wang B. 2019. Theory of hydrodynamic noise. Beijing: Science Press).Tang W L, Yu M S, Wang B. 2019. Theory of hydrodynamic noise. Beijing: Science Press. [9] 王本龙, 张浩, 刘筠乔. 2023. 空化区多相混合流体介质特性实验研究进展. 实验流体力学, 37(5): 111-121 (Wang B L, Zhang H, Liu Y Q. 2023. Experimental research on the mixture properties inside cloud cavitation region. J. Exper. Fluid Mech., 37(5): 111-121).Wang B L, Zhang H, Liu Y Q. 2023. Experimental research on the mixture properties inside cloud cavitation region. J. Exper. Fluid Mech., 37(5): 111-121. [10] Abdel-Maksoud M, Hänel D, Lantermann U. 2010. Modeling and computation of cavitation in vortical flow. Int. J. Heat and Fluid Flow, 31: 1065-1074. doi: 10.1016/j.ijheatfluidflow.2010.05.010 [11] Adama Maiga M, Coutier-Delgosha O, Buisine D. 2018. A new cavitation model bashed on bubble-bubble interactions. Phys. Fluids, 30: 123301. doi: 10.1063/1.5052257 [12] Adama Maiga M, Coutier-Delgosha O, Buisine D. 2019. Analysis of sheet cavitation with bubble/bubble interaction models. Phys. Fluids, 31: 073302. doi: 10.1063/1.5095781 [13] Agarwal K, Ram O, Lu Y H, Katz J. 2023. On the pressure field, nuclei dynamics and their relation to cavitation inception in a turbulent shear layer. J. Fluid Mech., 966: A31. doi: 10.1017/jfm.2023.368 [14] Aktas B, Atlar M, Turkmen S, et al. 2016 Propeller cavitation noise investigations of a research vessel using medium size cavitation tunnel tests and full-scale trials. Ocean Eng., 120: 122-135. [15] Alamé K, Mahesh K. 2024. Effect of gas content on cavitation nuclei. J. Fluid Mech., 982: A4. doi: 10.1017/jfm.2024.79 [16] Allan E S C, Barbaca L, Venning J A, Russell P S, Pearce B W, Brandner P A. 2023. Nucleation and cavitation inception in high Reynolds number shear layers. Phys. Fluids, 35: 013317. doi: 10.1063/5.0132054 [17] Amini A, Reclari M, Sano T, Iino M, Dreyer M, Farhat M. 2019. On the physical mechanism of tip vortex cavitation hysteresis. Exp. Fluids, 60: 118. doi: 10.1007/s00348-019-2762-x [18] Amromin E L. 2021. Modeling of the impact of laminar-turbulent transition on cavitation inception. Appl. Ocean Res, 114: 102796. doi: 10.1016/j.apor.2021.102796 [19] Ando K, Colonius T, Brennen C E. 2011. Numerical simulation of shock propagation in a polydisperse bubbly liquid. Int. J. Multiphase Flow., 37: 596-608. doi: 10.1016/j.ijmultiphaseflow.2011.03.007 [20] Angélil R, Diemand J, Tanaka K K, Tanaka H. 2014. Properties of liquid clusters in large-scale molecular dynamics nucleation simulations. J. Chem. Phys., 140: 074303. doi: 10.1063/1.4865256 [21] Apfel R E. 1970. The role of impurities in cavitation-threshold determination. J. Acoust. Soc. Am., 48(5): 1179-1186. [22] Arakeri V H. 1975. Viscous effects on the position of cavitation separation from smooth bodies. J. Fluid Mech., 68(4): 779-799. doi: 10.1017/S0022112075001231 [23] Arndt R E A. 2002. Cavitation in vortical flows. Annu. Rev. Fluid Mech., 34: 143-175. doi: 10.1146/annurev.fluid.34.082301.114957 [24] Asnaghi A, Feymark A, Bensow R R. 2017. Improvement of cavitation mass transfer modeling based on local flow properties. Int. J. Multiphase Flow, 93: 142-157. doi: 10.1016/j.ijmultiphaseflow.2017.04.005 [25] Atchley A A, Prosperetti. 1989. The crevice model of bubble nucleation. Phys. Fluids, 86: 1065-1084. [26] Augier F, Gilli E, Raimundo P M. 2021. One-equation model to assess population balance kernels in turbulent bubbly flows. Chem. Eng. Sci., 229: 116096. doi: 10.1016/j.ces.2020.116096 [27] Azouzi M, Ramboz C, Lenain J, Caupin F. 2013. A coherent picture of water at extreme negative pressure. Nat. Phys., 9: 38-41. doi: 10.1038/nphys2475 [28] Bai X R, Cheng H Y, Ji B. 2022 LES investigation of the noise characteristics of sheet and tip leakage vortex cavitating flows. Int. J. Multiphase Flow, 146: 103880. [29] Balachandar S, Eaton J K. 2010. Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech., 42: 111-133. doi: 10.1146/annurev.fluid.010908.165243 [30] Bauer A A, Patel S. 2009. Properties of water along the liquid-vapor coexistence curve via molecular dynamics simulations using the polarizable TIP4P-QDP-LJ water model. J. Chem. Phys, 131: 084709. doi: 10.1063/1.3200869 [31] Bedeau D, Kjelstrup S. 2004. Irreversible thermodynamics – a tool to describe phase transitions far from global equilibrium. Chem. Eng. Sci., 59: 109-118. [32] Bhatt A, Ganesh H, Ceccio S L. 2021. Cavitating flow behind a backward facing step. Int. J. Multiphase Flow, 139: 103548. [33] Biryukov D A, Gerasimov D N, Yurin E I. 2022. Cavitation and Associated Phenomena. CRC Press. Pp: 68-69; 227. [34] Blake J R, Gibson D C. 1987. Cavitation bubbles near boundaries. Annu. Rev. Fluid Mech., 19: 99-123. doi: 10.1146/annurev.fl.19.010187.000531 [35] Borkent B M, Gekle S, Prosperetti A, Lohse D. 2009. Nucleation threshold and deactivation mechanisms of nanoscopic cavitation nuclei. Phys. Fluids, 21: 102003. doi: 10.1063/1.3249602 [36] Boussonnière A, Liu Q X, Tsai P A. 2020. Cavitation nuclei regeneration in a water-particle suspension. Phys. Rev. Lett., 124: 034501. doi: 10.1103/PhysRevLett.124.034501 [37] Brandao F L, Mahesh K. 2022. Large-eddy simulation of cavitation inception in a shear flow. Int. J. Multiphase Flow, 146: 103865. doi: 10.1016/j.ijmultiphaseflow.2021.103865 [38] Brandner P A, Venning J A, Pearce B W. 2022. Nucleation effects on cavitation about a sphere. J. Fluid Mech, 946: A1. doi: 10.1017/jfm.2022.511 [39] Brennen C E. 2005. Fundamentals of Multiphase Flow. Cambridge University Press. Chapter 10: 199-216. [40] Caflisch R E, Miksis M J, Papanicolaou G C, Ting L. 1985a. Effective equations for wave propagation in bubbly liquids. J. Fluid Mech., 153: 259-273. doi: 10.1017/S0022112085001252 [41] Caflisch R E, Miksis M J, Papanicolaou G C, Ting L. 1985b. Wave propagation in bubbly liquids at finite volume fraction. J. Fluid Mech., 160: 1-14. doi: 10.1017/S0022112085003354 [42] Cai Y, Liu Y Q, Wang B L. 2025. A decoupling approach to analyze sound propagation through inhomogeneous and polydisperse bubbly flows. 12th Int. Conf. Multiphase Flow, Toulouse, France, May. 12-16. [43] Carrica P M, Bonetto F, Drew D, Lahey R T. 1999. A polydisperse model for bubbly two-phase flow around a surface ship. Int. J. Multiphase Flow., 25: 257-305. doi: 10.1016/S0301-9322(98)00047-0 [44] Ceccio S, Gowing S, Shen Y T. 1997. The effects of salt water on bubble cavitation. J. Fluids Eng., 119: 155-163. doi: 10.1115/1.2819102 [45] Chahine G L. 2009. Numerical simulation of bubble flow interactions. J. Hydrodynamics, 21(3): 316-332. doi: 10.1016/S1001-6058(08)60152-3 [46] Chan H, Cherukara M J, Narayanan B, et al 2019. Machine learning coarse grained model for water. Nat. Commn., 10: 379. [47] Chen J L, Xue B, Mahesh K, et al. 2019. Molecular simulations probing the thermophysical properties of homogeneously stretched and bubbly water systems. J. Chem. Eng. Data, 64: 3755-3771. doi: 10.1021/acs.jced.9b00284 [48] Chen J L, Prelesnik J L, Liang B, et al. 2023. Large-scale molecular dynamics simulations of bubble collapse in water: effects of system size, water model, and nitrogen. J. Chem. Phys., 159: 224505. doi: 10.1063/5.0181781 [49] Chen L, Kang Q J, Mu Y T, He Y L, Tao W Q. 2014. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and application. Int. J. Heat Mass Transfer, 76: 210-236. doi: 10.1016/j.ijheatmasstransfer.2014.04.032 [50] Chen L Y, Zhang L X, Peng X X, Shao X M. 2019. Influence of water quality on the tip vortex cavitation inception. Phys. Fluids, 31: 023303. doi: 10.1063/1.5053930 [51] Chen Y, Hu Y, Wang B L, Chu X S, Zhang L W. 2024. Interfacial thermal fluctuations stabilize bulk nanobubbles. Phys. Rev. Lett., 133: 104001. doi: 10.1103/PhysRevLett.133.104001 [52] Chiapolino A, Boivin P, Saurel R. 2017. A simple phase transition relaxation solver for liquid-vapor flows. Int. J. Numer. Meth. Fluids, 83: 583-605. doi: 10.1002/fld.4282 [53] Commander K W, Prosperetti A. 1989. Linear pressure waves in bubbly liquids : Comparison between theory and experiments. J. Acoust. Soc. Am. 85: 732-746. [54] Crialesi-Esposito M, Boffetta G, Brandt L, Chibbaro L, Musacchio S. 2024. How small droplets form in turbulent multiphase flows. Phys. Rev. Fluids, 9: L072301. doi: 10.1103/PhysRevFluids.9.L072301 [55] Crighton D G, Ffowcs Williams J E. 1969. Sound generation by turbulent two-phase flow. J. Fluid Mech., 36(3): 585-603. doi: 10.1017/S0022112069001868 [56] Crum L A. 1979. Tensile strength of water. Nature, 278: 148-149. doi: 10.1038/278148a0 [57] Darmana D, Deen N G, Kuipers J A M. 2006. Parallelization of an Euler-Lagrange model using mixed domain decomposition and a mirror domain technique: application to dispersed gas-liquid two-phase flow. J. Comput. Phys., 220: 216-248. doi: 10.1016/j.jcp.2006.05.011 [58] Diemand J, Angélil R, Tanaka K K, Tanaka H. 2013. Large scale molecular dynamics simulations of homogeneous nucleation. J. Chem. Phys., 139: 074309. doi: 10.1063/1.4818639 [59] d’Agostino L, Brennen C E. 1989. Linearized dynamics of spherical bubble clouds. J. Fluid Mech, 199: 155-176. doi: 10.1017/S0022112089000339 [60] Du T Z, Wang Y W, Liao L J et al. 2016. A numerical model for the evolution of internal structure of cavitation cloud. Phys. Fluids, 28: 077103. doi: 10.1063/1.4958885 [61] Elghobashi S, Truesdell G C. 1993. On the two-way interaction between homogeneous turbulence and dispersed solid particles. I: Turbulence modification. Phys. Fluids, 5: 1790-1801. [62] Epstein P S, Plesset M S. 1950. On the stability of gas bubbles in liquid-gas solutions. J. Chem. Phys., 18: 1505-1509. doi: 10.1063/1.1747520 [63] Farrell K J. 2003. Eulerian/Lagrangian analysis for the prediction of cavitation inception. J. Fluids Eng., 125: 46-52. doi: 10.1115/1.1522411 [64] Ferry J, Balachandar S. 2001. A fast Eulerian method for disperse two-phase flow. Int. J. Multiphase Flow, 27: 1199-1226. doi: 10.1016/S0301-9322(00)00069-0 [65] Franc J P, Michel J M. 2010. Fundamentals of cavitation. Netherlands: Kluwer Academic Publishers. [66] Furness R A, Hutton S P. 1975. Experimental and theoretical studies of two-dimensional fixed-type cavities. J. Fluid Eng., 97(4): 515-521. doi: 10.1115/1.3448098 [67] Fuster D, Colonius T. 2011. Modelling bubble clusters in compressible liquids. J. Fluid Mech., 688: 352-389. doi: 10.1017/jfm.2011.380 [68] Ganesh H, Mäkiharju S A, Ceccio S L. 2016. Bubbly Shock propagation as a mechanism for sheet-to-cloud transition of partial cavities. J. Fluid Mech, 802: 37. doi: 10.1017/jfm.2016.425 [69] Gallo M, Magaletti F, Cocco D, et al. 2020. Nucleation and growth dynamics of vapour bubbles. J. Fluid Mech., 883: A14. doi: 10.1017/jfm.2019.844 [70] Gallo M, Magaletti F, Casciola C M. 2021. Heterogeneous bubble nucleation dynamics. J. Fluid Mech., 906: A20. doi: 10.1017/jfm.2020.761 [71] Gao Z, Wu W X, Wang B. 2021. The effects of nanoscale nuclei on cavitation. J. Fluid Mech., 911: A20. doi: 10.1017/jfm.2020.1049 [72] Garrett C, Li M, Farmer D. 2020. The connection between bubble size spectra and energy dissipation rates in the upper ocean. J. Phys. Oceanogr., 30(9): 2163-2171. [73] Gaylo D B, Hendrickson K, Yue D K P. 2021. Effects of power-law entrainment on bubble fragmentation cascades. J. Fluid Mech., 917: R1. doi: 10.1017/jfm.2021.333 [74] Ge M Y, Svennberg U, Bensow R E. 2021. Improved prediction of sheet cavitation inception using bridged transition sensitive turbulence model and cavitation model. J. Mar. Sci. Eng., 9: 1343. doi: 10.3390/jmse9121343 [75] Ge M Y, Svennberg U, Bensow R E. 2022. Investigation on prediction of ship noise using the FWH acoustic analogy with incompressible flow input. Ocean Eng., 257: 111531. doi: 10.1016/j.oceaneng.2022.111531 [76] Ghahramani E, Mahesh K. 2016. Numerical investigation of near wake characteristics of cavitating flow over a circular cylinder. J. Fluid Mech., 790: 453-491. doi: 10.1017/jfm.2016.19 [77] Ghahramani E, Arabnejad M H, Bensow R E. 2019. A comparative study between numerical methods in simulation of cavitating bubbles. Int. J. Multiphase Flow, 111: 339-359. doi: 10.1016/j.ijmultiphaseflow.2018.10.010 [78] Ghahramani E, Ström H, Bensow R E. 2021. Numerical simulation and analysis of multi-scale cavitating flows. J. Fluid Mech., 922: A22. doi: 10.1017/jfm.2021.424 [79] Giannadakis E, Gavaises M, Arcoumanis C. 2008. Modelling of cavitation in diesel injector nozzles. J. Fluid Mech., 616: 153-193. doi: 10.1017/S0022112008003777 [80] Grandjean H, Jacques N, Zaleski S. 2012. Shock propagation in liquids containing bubbly clusters: a continuum approach. J. Fluid Mech., 701: 304-332. doi: 10.1017/jfm.2012.159 [81] Groβ T F, Bauer J, Ludwig G, Fernandez Rivas D, Pelz P F. 2018. Bubble nucleation from micro-crevices in a shear flow. Exp. Fluids, 59: 12. doi: 10.1007/s00348-017-2459-y [82] Groβ T F, Pelz P F. 2017. Diffusion-driven nucleation from surface nuclei in hydrodynamic cavitation. J. Fluid Mech., 830: 138-164. doi: 10.1017/jfm.2017.587 [83] Gunstensen A K, Rothman D H, Zaleski S, Zanetti G. 1991. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A., 43(8): 4320-4327. doi: 10.1103/PhysRevA.43.4320 [84] Habiyaremye V, Kuerten J G M, Frederix E M A. 2023. Comparison of population balance models for polydisperse bubbly flow. Chem. Eng. Sci., 278: 118932. doi: 10.1016/j.ces.2023.118932 [85] Haller G. 2015. Lagrangian coherent structures. Annu. Rev. Fluid Mech, 47: 137-162. doi: 10.1146/annurev-fluid-010313-141322 [86] Herbert E, Balibar S, Caupin F. 2006. Cavitation pressure in water. 2006. Phys. Rev. E., 74: 041603. [87] Hovem J M. 2012. Marine Acoustics : The Physics of Sound in Underwater Environments. Peninsula Publishing, California. Pp: 60-64. [88] Hsiao C T, Pauley L L. 1999. Study of tip vortex cavitaion inception using Navier-Stokes computation and bubble dynamics model. ASME J. Fluid Mech., 121(1): 198-204. doi: 10.1115/1.2822002 [89] Hsiao C T, Vhahine G L, Liu H L. 2003. Scaling effect on prediction of cavitation inception in a line vortex flow. ASME J. Fluid Eng., 125: 53-60. doi: 10.1115/1.1521956 [90] Hsiao C T, Wu X, Ma J, Chahine G L. 2013. Numerical and experimental study of bubble entrainment due to a horizontal plunging jet. Int. Shipbuilding Progress, 60: 435-469. [91] Hsiao C T, Ma J, Chahine G L. 2017. Multiscale two-phase flow modeling of sheet and cloud cavitation. Int. J. Multiphase Flow, 90: 102-117. doi: 10.1016/j.ijmultiphaseflow.2016.12.007 [92] Hsiao C T, Chahine G L, Ma J. 2020. Dynamics of dispersed bubbly flow over a lifting surface: gas diffusion and bubble breakup effects. Ocean Eng., 213: 107630. doi: 10.1016/j.oceaneng.2020.107630 [93] Hu K, Song M T, Ma C, et al. 2025. Characteristics of radiated noise from the cavitation flow around a NACA16012 twisted hydrofoil, J. Hydrodynamics, XX: XXX. (accepted [94] Hulburt H, Katz S. 1964. Some problems in particle technology. A statistical mechanical formulation. Chem. Eng. Sci., 19: 555-574. doi: 10.1016/0009-2509(64)85047-8 [95] Iben U, Ivanov N G, Isaenko I I, Schmidt A A. 2015. A Eulerian-Lagrangian description of cavitating flow. Tech. Phys. Lett., 41(12): 1159-1162. doi: 10.1134/S1063785015120238 [96] Ilinskii Y A, Hamilton M F, Zabolotskaya E A, Meegan G D. 2006. Influence of compressibility on bubble interaction. AIP Conf. Proc., 838: 303-310. doi: 10.1063/1.2210366 [97] Inanc S, Shy W. 2004. Interfacial dynamics-based modeling of turbulent cavitating flows, Part-Ι: Model development and steady-state computations. Int. J. Numer. Methods Fluids, 44(9): 975-995. doi: 10.1002/fld.692 [98] Ji B, Wang X C, Bai X R, et al. 2023. Cavitation inception noise excited by a tip leakage vortex with various gap sizes: a Eulerian-Lagrangian investigation. Phys. Fluids, 35: 122107. doi: 10.1063/5.0174198 [99] Ji B, Wang Z Y, Cheng H Y, Bensow R E. 2024. Cavitation research with computational fluid dynamics: from Euler-Euler to Euler-Lagrange approach. J. Hydrodynamics, 36(1): 1-23. doi: 10.1007/s42241-024-0001-2 [100] Jiménez J. 2018. Coherent structures in wall-bounded turbulence. J. Fluid Mech., 842: P1. doi: 10.1017/jfm.2018.144 [101] Jones S F, Evans G M, Galvin K P. 1999. Bubble nucleation from gas cavities—a review. Adv. Colloid Interface Sci., 80: 27-50. doi: 10.1016/S0001-8686(98)00074-8 [102] Joshi S Y, Deshmukh S A. 2021. A review of advancements in coarse-grained molecular dynamics simulations. Mole. Simul., 47(10-11): 786-803. doi: 10.1080/08927022.2020.1828583 [103] Joswiak M N, Duff N, Doherty M F, Peters B. 2013. Size-dependent surface free energy and Tolman-corrected droplet nucleation of TIP4P2005 water. Phys. Chem. Lett., 4: 4267-4272. doi: 10.1021/jz402226p [104] Kapila A K, Menikoff R, Bdzil J B, et al. 2001. Two-phase modeling of deflagration-to-detonation transition in granular materials: reduced equations. Phys. Fluids, 13: 3002-3024. doi: 10.1063/1.1398042 [105] Khlifa I, Hocevar M, Vabre A, Fezza K, Fuzier S, Coutier-Delgosha O. 2017. Fast X-ray imaging of cavitating flows. Exp Fluids, 58: 157. doi: 10.1007/s00348-017-2426-7 [106] Kimmerl J, Mertes P, Abdel-Maksoud M. 2021. Application of large eddy simulation to predict underwater noise of marine propulsors. Part 1: cavitation dynamics. J. Mar. Sci. Eng., 9: 792. doi: 10.3390/jmse9080792 [107] Kalová J, Mareš R. 2019. Size dependences of surface tension and measurement accuracy. AIP Conf. Proc., 2189: 020010. [108] Katz J. 1984. Cavitation phenomena within regions of flow separation. J. Fluid Mech., 140: 397-436. doi: 10.1017/S0022112084000665 [109] Kameda M, Matsumoto Y. 1996. Shock waves in a liquid containing small gas bubbles. Phys. Fluids, 8: 322-335. doi: 10.1063/1.868788 [110] Kataoka I, Serizawa A. 1989. Basic equations of turbulence in gas-liquid two-phase flow. Int. J. Multiphase Flow, 15: 843. doi: 10.1016/0301-9322(89)90045-1 [111] Kawanami Y., Kato H, Yamaguchi H, Tanimuri H, Tagaya Y. 1997. Mechanism and control of cloud cavitation. J. Fluid Engng., 119(4): 788-794. doi: 10.1115/1.2819499 [112] Kawakami D T, Qin Q, Arndt R E A. 2005. Water quality and the periodicity of sheet/cloud cavitation. ASME Fluids Engineering Division Summer Meeting and Exhibition, Houston, TX, USA. [113] Kawakami D T, Fuji A, Tsujimoto Y, Arndt R E A. 2008. An assessment of the influence of environmental factors on cavitation instabilities. J. Fluid Engng., 130: 031303. doi: 10.1115/1.2842146 [114] Khoo M T, Venning J A, Pearce B W, et al. 2020. Natural nuclei population dynamics in cavitation tunnels. Exp. Fluids, 61: 34. doi: 10.1007/s00348-019-2843-x [115] Khoo M T, Venning J A, Pearce B W, et al. 2021. Nucleation and cavitation number effects on tip vortex cavitation dynamics and noise. Exp. Fluids, 62: 216. doi: 10.1007/s00348-021-03308-2 [116] Kitagawa A, Murai Y, Yamamoto F. 2001. Two-way coupling of Eulerian-Lagrangian model for dispersed multiphase flows using filtering functions. Int. J. Multiphase Flow, 27: 2129-2153. doi: 10.1016/S0301-9322(01)00040-4 [117] Koumoutsakos P. 2005. Multiscale flow simulations using particles. Annu. Rev. Fluid Mech., 37: 457-487. doi: 10.1146/annurev.fluid.37.061903.175753 [118] Kubota A, Kato H, Yamaguchi H. 1992. A new modelling of cavitating flows: a numerical study of unsteady cavitation on a hydrofoil section. J. Fluid Mech., 240: 59-96. doi: 10.1017/S002211209200003X [119] Kunz R F, Boger D A, Stinebring D R, Chyczewski T S, Lindau J W, Gibeling H J, Venkateswaran S, Govindan T R. 2000. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction. Comput. & Fluids, 29: 849-875. [120] Lavino A D, Smith E, Magnini M, et al. 2021. Surface topography effects on pool boiling via non-equilibrium molecular dynamics simulations. Langmuir, 37: 5731-5744. doi: 10.1021/acs.langmuir.1c00779 [121] Leighton T G. 1996. The Acoustic Bubble. Academic Press, San Diego. [122] Lehr F, Millies M, Mewes D. 2002. Bubble-size distributions and flow fields in bubble columns. AIChE Journal, 48: 2426-2443. doi: 10.1002/aic.690481103 [123] Leroy V, Chastrette N, Thieury M, Lombard O, Tourin A. 2018. Acoustics of bubble arrays: role played by the dipole response of bubbles. Fluids, 3: 95. doi: 10.3390/fluids3040095 [124] Lesnik S, Aghelmaleki A, Mettin R, Brenner G. 2022. Modeling acoustic cavitation with inhomogeneous polydisperse bubble population on a large scale. Ultrason. Sonochem., 89: 106060. doi: 10.1016/j.ultsonch.2022.106060 [125] Li D Q, Hallander J, Johansson T. 2018. Predicting underwater radiated noise of a hull scale ship with model testing and numerical methods. Ocean Eng., 161: 121-135. doi: 10.1016/j.oceaneng.2018.03.027 [126] Li J J, Carrica P M. 2021. A population balance cavitation model. Int. J. Multiphase Flow, 138: 103617. doi: 10.1016/j.ijmultiphaseflow.2021.103617 [127] Li J J, Carrica P M. 2023. Numerical study of the cavitating flow over backward facing step with a polydisperse two-phase flow model. Phys. Fluids, 35: 063313. doi: 10.1063/5.0147595 [128] Li L M, Niu Y B, Wei G L, Manickam S, Sun X, Zhu Z C. 2023. Investigation of cavitation noise using Eulerian-Lagrangian multiscale modeling. Ultrason. Sonochem., 97: 106446. doi: 10.1016/j.ultsonch.2023.106446 [129] Li L M, Wang Z D, Li X J, Zhu Z C. 2021. Multiscale modeling of tip-leakage cavitating flows by a combined volume of fluid and discrete bubble model. Phys. Fluids, 33: 062104. doi: 10.1063/5.0054795 [130] Li Y H, Li M B, Zhang L W, Wang B L. 2024. Bridging the gap: unraveling the role of nano-gas nuclei in the non-equilibrium water-vapor phase transition. Int. J. Heat Mass Transfer, 232: 125958. doi: 10.1016/j.ijheatmasstransfer.2024.125958 [131] Li Y H, Li M B, Zhang L W, Wang B L. 2025. Cavitation inception triggered by transient ambient pressures in electrolyte solutions. Phys. Rev. Fluids, 10: 024202. doi: 10.1103/PhysRevFluids.10.024202 [132] Li Y H, Zhang L W, Wang B L. 2023. Role of mutual diffusion in the dissolution behavior of one primary bulk gas nanobubble in liquid: a molecular dynamics study. Langmuir, 39: 7684-7693. doi: 10.1021/acs.langmuir.3c00484 [133] Li M B, Li Y H, Gao Y W, Sun C, Wang B L. 2024. Effect of nanoscale nuclei on the dynamics of laser-induced cavitation. Phys. Fluids, 36: 093307. doi: 10.1063/5.0226162 [134] Liao Y X, Lucas D. 2009. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci., 64: 3389-3406. doi: 10.1016/j.ces.2009.04.026 [135] Lidtke A K, Turnock S R, Humphrey V F. 2016 Characterisation of sheet cavity noise of a hydrofoil using the Ffowcs Williams-Hawkings acoustic analogy. Comput. Fluids, 130: 8-23. [136] Lin C S, Maxey M, Li Z, Karniadakis G E. 2021. A seamless multiscale operator neural network for inferring bubble dynamics. J. Fluid Mech., 929: A18. doi: 10.1017/jfm.2021.866 [137] Liu Y Q, Wang B L. 2019. Dynamics and surface stability of a cylindrical cavitation bubble in a rectilinear vortex. J. Fluid Mech., 865: 963-992. doi: 10.1017/jfm.2019.103 [138] Liu Y Q, Zhang H, Zhang W etc. 2023. Bubble size distribution at early stage of hydrodynamic cloud cavitation. Phys. Fluids, 35: 063305. doi: 10.1063/5.0154309 [139] Lohse D, Prosperetti A. 2016. Homogeneous nucleation: patching the way form the macroscopic to the nanoscopic description. Proc. Natl. Acd. Sci. USA, 113(48): 13549-13550. doi: 10.1073/pnas.1616271113 [140] Long X P, Cheng H Y, Ji B, Arndt R E A, Peng X X. 2018. Large eddy simulation and Euler-Lagrangian coupling investigation of the transient cavitating turbulent flow around a twisted hydrofoil. Int. J. Multiphase Flow, 100: 41-56. doi: 10.1016/j.ijmultiphaseflow.2017.12.002 [141] Lulli M, Biferale L, Falcucci G, Sbragaglia M, Shan X W. 2022. Mesoscale perspective on the Tolman length. Phys. Rev. E, 105: 015301. doi: 10.1103/PhysRevE.105.015301 [142] Lulli M, Biferale L, Falcucci G, Sbragaglia M, Yang D, Shan X W. 2024. Metastable and unstable hydrodynamics in multiphase lattice Boltzmann. Phys. Rev. E, 109: 045304. [143] Lyu H M, Schlegel F, Rzehak R, Lucas D. 2023. Euler-Euler model of bubbly flow using particle-center-averaging method. Nuclear Sci. Eng., 197(10): 2602-2619. doi: 10.1080/00295639.2022.2131344 [144] Lyu X X, Pan S C, Hu X Y, Adams N A. 2018. Numerical investigation of homogeneous cavitation nucleation in a microchannel. Phys. Rev. Fluids, 3: 064303. doi: 10.1103/PhysRevFluids.3.064303 [145] Lyu X X, Zhu Y J, Zhang C, Hu X Y, Adams N A. 2021. Modeling of cavitation bubble cloud with discrete Lagrangian tracking. Water, 13: 2684. doi: 10.3390/w13192684 [146] Ma J, Oberai A A, Hyman M C, Drew D A, Lahey Jr R T. 2011. Two-fluid modeling of bubbly flows around surface ships using a phenomenological subgrid air entrainment model. Comput. Fluids, 52: 50-57. doi: 10.1016/j.compfluid.2011.08.015 [147] Ma J, Hsiao C T, Chahine G L. 2016. A physical based multiscale modeling of cavitating flows. Comput. Fluids, 145: 68-84. [148] Ma T, Lucas D, Jakirlić S, Fröhlich J. 2020a. Progress in the second-moment closure for bubbly flow based on direct numerical simulation data. J. Fluid Mech., 883: A9. doi: 10.1017/jfm.2019.851 [149] Ma T, Lucas D, Bragg A D. 2020b. Explicit algebraic relation for calculating Reynolds normal stresses in flows dominated by bubble-induced turbulence. Phys. Rev. Fluids, 5: 084305. doi: 10.1103/PhysRevFluids.5.084305 [150] Ma T, Santarelli C, Ziegenhein T, Lucas D, Fröhlich J. 2017. Direct numerical simulation-based Reynolds-average closure for bubble-induced turbulence. Phys. Rev. Fluids, 2: 034301. doi: 10.1103/PhysRevFluids.2.034301 [151] Madabhushi A, Mahesh K. 2023. A compressible multi-scale model to simulate cavitating flows. J. Fluid Mech., 961: A6. doi: 10.1017/jfm.2023.192 [152] Maeda K, Colonius T. 2018. Eulerian-Lagrangian method for simulation of cloud cavitation. J. Comput. Phys., 371: 994-1017. doi: 10.1016/j.jcp.2018.05.029 [153] Maeda K, Colonius T. 2019. Bubble cloud dynamics in an ultrasound field. J. Fluids Mech., 862: 1105-1134. doi: 10.1017/jfm.2018.968 [154] Mao Y J, Hu Z W. 2018. Acoustic analogy for multiphase or multicomponent flow. J. Vib. Acoust., 140: 021006. doi: 10.1115/1.4037702 [155] Marchisio D L, Pikturna J T, Fox R O, Vigil R D, Barresi A A. 2003. Quadrature method of moments for population-balance equations. AIChE J., 49(5): 1266-1276. doi: 10.1002/aic.690490517 [156] Marchisio D L, Fox R O. 2005. Solution of population balance equations using the direct quadrature method of moments. Aerosol Sci., 36: 43-73. doi: 10.1016/j.jaerosci.2004.07.009 [157] Marschall H B, Mørch K A, Keller A P, Kjeldsen M. 2003. Cavitation inception by almost spherical solid particles in water. Phys. Fluids, 15: 545-553. [158] Martínez-Bazán C, Rodríguez-Rodríguez J, Deane G B, Montañés J L, Lasheras J C. 2010. Considerations on bubble fragmentation models. J. Fluid Mech., 661: 159-177. doi: 10.1017/S0022112010003186 [159] Meland R, Frezzotti A, Ytrehus T, Hafskjold B. 2004. Nonequilibrium molecular-dynamics simulation of net evaporation and net condensation, and evaluation of the gas-kinetic boundary condition at the interface. Phys. Fluids, 16(2): 223-243. doi: 10.1063/1.1630797 [160] Menzl G, Gonzalez M A, Geiger P, et al. 2016. Molecular mechanism for cavitation in water under tension. Proc. Natl. Acd. Sci USA, 113(48): 13582-13587. doi: 10.1073/pnas.1608421113 [161] Mishra S K, Deymier P A, Muralidharan K, Frantzskonis G, Pannala S, Simunovic S. 2010. Modeling the coupling of reaction kinetics and hydrodynamics in a collapsing cavity. Ultrason. Sonochem., 17(1): 258-265. doi: 10.1016/j.ultsonch.2009.05.014 [162] Moeendarbary E, Ng T Y, Zangeneh M. 2009. Dissipative particle dynamics : introduction, methodology and complex fluid applications – A review. Int. J. Appl. Mech. 1(4): 737-763. [163] Morciano M, Fasano M, Nold A, et al. 2017. Nonequilibrium molecular dynamics simulations of nanoconfined fluids at solid-liquid interfaces. J. Chem. Phys., 146: 244507. doi: 10.1063/1.4986904 [164] Müller E A, Mejía A. 2014. Resolving discrepancies in the measurements of the interfacial tension for the CO2 + H2O mixture by computer simulation. Phys. Chem. Lett., 5: 1267-1271. doi: 10.1021/jz500417w [165] Pai M G, Subramaniam S. 2009. A comprehensive probability density function formalism for multiphase flows. J. Fluid Mech., 628: 181-228. doi: 10.1017/S002211200900617X [166] Pan D, Zhao G, Lin Y, Shao X. 2018. Mesoscopic modelling of microbubble in liquid with finite density ratio of gas to liquid. EPL Europhys. Lett., 122: 20003. doi: 10.1209/0295-5075/122/20003 [167] Park K, Seol H, Choi W, Lee S. 2009. Numerical prediction of tip vortex cavitation behavior and noise considering nuclei size and distribution. Appl. Acous., 70: 674-680. doi: 10.1016/j.apacoust.2008.08.003 [168] Peng C, Tian S C, Li G S, Sukop M C. 2018. Single-component multiphase lattice Boltzmann simulation of free bubble and crevice heterogeneous cavitation nucleation. Phys Rev. E., 98: 023305. doi: 10.1103/PhysRevE.98.023305 [169] Peng C, Tian S C, Li G S, Sukop M C. 2019. Simulation of multiple cavitation bubbles interaction with single-component multiphase Lattice Boltzmann method. Int. J. Heat Mass Transfer, 137: 301-317. doi: 10.1016/j.ijheatmasstransfer.2019.03.096 [170] Peng C, Tian S C, Li G S, Sukop M C. 2020. Simulation of laser-produced single cavitation bubbles with hybrid thermal Lattice Boltzmann method. Int. J. Heat Mass Transfer, 149: 119136. doi: 10.1016/j.ijheatmasstransfer.2019.119136 [171] Peng H N, He X L, Zhang J M, Wang Y R. 2020. Cavitation bubble collapse between parallel rigid walls with the three-dimensional multi-relaxation time pseudopotential lattice Boltzmann method. AIP Advances, 10: 105104. doi: 10.1063/5.0005048 [172] Peng H N, Zhang J M, He X L, Wang Y R. 2021. Thermal pseudo-potential lattice Boltzmann method for simulating cavitation bubbles collapse near a rigid boundary. Comput. Fluids, 217: 104817. doi: 10.1016/j.compfluid.2020.104817 [173] Peng X X, Wang B L, Li H Y. 2017. Generation of abnormal acoustic noise: singing of a cavitating tip vortex. Phys. Rev. Fluids, 2: 053602. doi: 10.1103/PhysRevFluids.2.053602 [174] Prince M J, Blanch H W. 1990. Bubble coalescence and break-up in air-sparged bubble columns. AIChE J., 46(10): 1485-1499. [175] Prosperetti A, Crum L A, Commander K W. 1988. Nonlinear bubble dynamics. J. Acoust. Soc. Am., 83: 502-514. doi: 10.1121/1.396145 [176] Qi Y, Masuk A U M, Ni R. 2020. Towards a model of bubble breakup in turbulence through experimental constraints. Int. J. Multiphase Flow, 132: 103397. doi: 10.1016/j.ijmultiphaseflow.2020.103397 [177] Rahman A, Stillinger F H. 1971. Molecular dynamics study of liquid water. J. Chem. Phys., 55(7): 3336-3359 doi: 10.1063/1.1676585 [178] Rahmani F, Weathers T, Hosangadi A, Chiew Y C. 2020. A non-equilibrium molecular dynamics study of subcritical, supercritical and transcritical mixing of liquid-gas systems. Chem. Eng. Sci., 214: 115424. doi: 10.1016/j.ces.2019.115424 [179] Ram O, Agarwal K, Katz J. 2020. On the mechanisms that sustain the inception of attached cavitation. J. Fluid Mech., 901: R4. doi: 10.1017/jfm.2020.646 [180] Reis T, Phillips T N. 2007. Lattice Boltzmann model for simulating immiscible two-phase flows. J. Phys. A: Math. Theor., 40: 4033-4053. doi: 10.1088/1751-8113/40/14/018 [181] Reisman G E, Wang Y C, Brennen C E. 1996. Observations of shock waves in cloud cavitation. J. Fluid Mech., 355: 255-283. [182] Risso F, Fabre J. 1998. Oscillations and breakup of a bubble immersed in a turbulent field. J. Fluid Mech., 372: 323-355. doi: 10.1017/S0022112098002705 [183] Rivière A, Mostert W, Perrard S, Deike L. 2021. Sub-Hinze scale bubble production in turbulent bubble break-up. J. Fluid Mech., 917: A40. doi: 10.1017/jfm.2021.243 [184] Rosselló J M, Ohl C. -D. 2023. Clean production and characterization of nanobubbles using laser energy deposition. Ultrason. Sonochem., 94: 106321. [185] Ruth D J, Mostert W, Perrard S, Deike L. 2019. Bubble pinch-off in turbulence. Proc. Natl. Acad. Sci. U. S. A., 116: 25412-25417. doi: 10.1073/pnas.1909842116 [186] Santarelli C, Fröhlich J. 2015. Direct numerical simulations of spherical bubbles in vertical turbulent channel flow. Int. J. Multiphase Flow, 75: 174-193. doi: 10.1016/j.ijmultiphaseflow.2015.05.007 [187] Saurel R, Petitpas F, Abgrall R. 2008. Modelling phase transition in metastable liquids: application to cavitating and flashing flows. J. Fluid Mech., 607: 313-350. doi: 10.1017/S0022112008002061 [188] Schnerr G H, Sauer J. 2001. Physical and numerical modeling of unsteady cavitation dynamics. Proc. 4th Int. Conf. Multiphase Flow. New Orleans, La, USA. [189] Sekine M, Yasuoka K, Kinjo T, Matsumoto M. 2008. Liquid-vapor nucleation simulation of Lennard-Jones fluid by molecular dynamics method. Fluid Dyn. Res., 40: 597-605. doi: 10.1016/j.fluiddyn.2007.12.012 [190] Seo J H, Lele S K, Tryggvason G. 2010. Investigation and modeling of bubble-bubble interaction effect in homogeneous bubbly flows. Phys. Fluids, 22: 063302. doi: 10.1063/1.3432503 [191] Sethi S K, Kadian S, Manik G. 2022. A review of recent progress in molecular dynamics and coarse-grain simulations assisted understanding of wettability. Arch. Compt. Method Eng., 29: 3059-3085. doi: 10.1007/s11831-021-09689-1 [192] Shams E, Finn J, Apte S V. 2011. A numerical scheme for Euler-Lagrange simulation of bubbly flows in complex systems. Int. J. Numer. Meth. Fluids, 67: 1865-1898. doi: 10.1002/fld.2452 [193] Shan X, Chen H. 1993. Lattice Boltzmann model for simulating flows with multiple phase and components. Phys. Rev. E., 47(3): 1815-1819. doi: 10.1103/PhysRevE.47.1815 [194] Shan X, Chen H. 1994. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys. Rev. E., 49(4): 2491-2498. [195] Shiea M, Buffo A, Vanni M, Marchisio D. 2020. Numerical methods for the solution of population balance equations coupled with computational fluid dynamics. Annu. Rev. Chem. Biomol. Eng., 11: 339-366. doi: 10.1146/annurev-chembioeng-092319-075814 [196] Shinoda W, DeVane R, Klein M L. 2007. Multi-property fitting and parameterization a coarse grained model for aqueous surfactants. Mol. Simul., 33(1-2): 27-36. doi: 10.1080/08927020601054050 [197] Simon J M, Bedeaux D, Kjelstrup S, Xu J, Johannessen E. 2006. Interface film resistivities for heat and mass transfer—integral relations verified by non-equilibrium molecular dynamics. J. Phys. Chem., 110: 18528-18536. doi: 10.1021/jp062047y [198] Singhal A K, Athavale M M, Li H Y, et al. 2002. Mathematical basis and validation of the full cavitation model. J. Fluid Eng., 124(3): 617-624. doi: 10.1115/1.1486223 [199] Soligo G, Roccon A, Soldati A. 2021. Turbulent flows with drops and bubbles: what numerical simulations can tell us- Freeman scholar lecture. J. Fluid Eng., 143: 080801. [200] Strasberg M. 1959. Onset of ultrasonic cavitation in tap water. J. Acoust. Soc. Am., 31: 163-176. doi: 10.1121/1.1907688 [201] Subramaniam S. 2001. Statistical modeling of sprarys using the droplet distribution function. Phys. Fluids, 13(3): 624-642. doi: 10.1063/1.1344893 [202] Subramaniam S. 2013. Lagrangian-Eulerian methods for multiphase flows. Prog. Energy Comb. Sci., 39: 215-245. doi: 10.1016/j.pecs.2012.10.003 [203] Sukop M C, Or D. 2005. Lattice Boltzmann method for homogeneous and heterogeneous cavitation. Phys. Rev. E., 71(4): 46703. doi: 10.1103/PhysRevE.71.046703 [204] Swift M R, Orlandini E, Osborn W R, Yeomans J M. 1996. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Phys. Rev. E., 54(5): 5041-5052. doi: 10.1103/PhysRevE.54.5041 [205] Tani G, Viviani M, Felli M, et al. 2020. Noise measurements of a cavitating propeller in different facilities: Results of the round robin test programme. Ocean Eng, 213: 107599. doi: 10.1016/j.oceaneng.2020.107599 [206] Testa C, Ianniello S, Salvatore F. 2018. A Ffowcs Williams and Hawkings formulation for hydroacoustic analysis of propeller sheet cavitation. J. Sound Vib., 413: 421-441. doi: 10.1016/j.jsv.2017.10.004 [207] Tian B C, Huang B, Li L M. 2023. Investigation of transient sheet/cloud cavitating flow dynamics from multiscale perspective. Phys. Fluids, 35: 077115. doi: 10.1063/5.0159763 [208] Thomas R M. 1981. Bubble coalescence in turbulent flows. Int. J. Multiphase Flow, 7(6): 709-717. doi: 10.1016/0301-9322(81)90040-9 [209] Tomar G, Fuster D, Zaleski S, Popinet S. 2010. Multiscale simulations of primary atomization. Computers & Fluids, 39: 1864-1874. [210] Tryggvason G, Dabiri S, Aboulhasanzadeh B, Lu J C. 2013. Multiscale considerations in direct numerical simulations of multiphase flows. Phys. Fluids, 25: 031302. doi: 10.1063/1.4793543 [211] Van Wijngaarden L. 1968. On the equations of motion for mixtures of liquid and gas bubbles. J. Fluid Mech., 33: 465-474. doi: 10.1017/S002211206800145X [212] Venning J A, Pearce B W, Brandner P A. 2022. Nucleation effects on cloud cavitation about a hydrofoil. J. Fluid Mech., 947: A1. doi: 10.1017/jfm.2022.535 [213] Viitanen V M, Hynninen A, Sipilä T, et al. 2018. DDES of wetted and cavitating marine propeller for CHA underwater noise assessment. J. Mar. Sci. Eng., 6: 56. doi: 10.3390/jmse6020056 [214] Wan C R, Wang B L, Wang Q, etc. 2017. Probing and imaging of vapor-water mixture properties inside partial/cloud cavitating flows. J. Fluids Eng., 139: 031303. doi: 10.1115/1.4035013 [215] Wang B L, Liu Z H, Li H Y, etc. 2017. On the numerical simulations of vortical cavitating flows around various hydrofoils. J. Hydrodynamics, 29(6): 926-938. doi: 10.1016/S1001-6058(16)60807-7 [216] Wang Q Y, Wang B L, Wan C R, Zhang H, Liu Y Q. 2023. Modeling the distribution characteristics of vapor bubbles in cavitating flows. Phys. Fluids, 35: 123316. doi: 10.1063/5.0176400 [217] Wang T F, Wang J F, Jin Y. 2003. A novel theoretical breakup kernel function for bubbles/droplets in a turbulent flow. Chem. Eng. Sci., 58: 4629-4637. doi: 10.1016/j.ces.2003.07.009 [218] Wang X C, Bai X R, Cheng H Y, Ji B, Peng X X. 2023. Numerical investigation of how gap size influences tip leakage vortex cavitation inception using a Eulerian-Lagrangian method. Phys. Fluids, 35: 012113. doi: 10.1063/5.0131813 [219] Wang Z J, Valeriani C, Frenkel D. 2009. Homogeneous bubble nucleation driven by local hot spots: a molecular dynamics study. J. Phys. Chem. B, 113: 3776-3784. doi: 10.1021/jp807727p [220] Wang Z Y, Cheng H Y, Ji B. 2021. Euler-Lagrange study of cavitating turbulent flow around a hydrofoil. Phys. Fluids, 33: 112108. doi: 10.1063/5.0070312 [221] Wang Z Y, Cheng H Y, Ji B, Peng X X. 2023. Numerical investigation of inner structure and its formation mechanism of cloud cavitating flow. Int. J. Multiphase Flow, 165: 104484. doi: 10.1016/j.ijmultiphaseflow.2023.104484 [222] Watanabe H, Suzuki M, Ito N. 2010. Cumulative distribution functions associated with bubble-nucleation processes in cavitation. Phys. Rev. E, 82: 051604. doi: 10.1103/PhysRevE.82.051604 [223] Williams F A. 1958. Spray combustion and atomization. Phys. Fluids, 1: 541-545. doi: 10.1063/1.1724379 [224] Wood A B, Weston D E. 1964. The propagation of sound in mud. Acustica, 14: 156-162. [225] Wu J, Deijlen L, Bhatt A, Ganesh H, Ceccio S L. 2021. Cavitation dynamics and vortex shedding in the wake of a bluff body. J. Fluid Mech, 917: A26. doi: 10.1017/jfm.2021.263 [226] Wu J, Ganesh H, Ceccio S. 2019. Multimodal partial cavity shedding on a two-dimensional hydrofoil and its relation to the presence of bubbly shocks. Exp. Fluids, 69: 66. [227] Wu K, Cai H P, Zhang Z Z et al. 2024. Experimental investigation of tip vortex cavitation noise under static and dynamics states. Phys. Fluids, 36: 073329. doi: 10.1063/5.0217994 [228] Wu W B, Liu Y L, Zhang A M, Liu N N, Liu L T. 2020. Numerical investigation on underwater explosion cavitation characteristics near water wave. Ocean Eng., 205: 107321. doi: 10.1016/j.oceaneng.2020.107321 [229] Yamashita K, Daiguji H. 2016. Coarse-grained molecular dynamics simulations of capillary evaporation of water confined in hydrophilic mesopores. Molecular Phys., 114(6): 884-894. doi: 10.1080/00268976.2015.1133858 [230] Yoon S W, Crum L A, Prosperetti A, Lu N Q. 1991. An investigation of the collective oscillations of a bubble cloud. J. Acoust. Soc. Am., 89: 700-706. doi: 10.1121/1.1894629 [231] Young F R. 1999. Cavitaion. Imperial College Press. Pp: 10-11. [232] Yu J, Liu J H, Wang H K, et al. 2021. Numerical simulation of underwater explosion cavitation characteristics based on phase transition model in compressible multicomponent fluids. Ocean Eng., 240: 109934. doi: 10.1016/j.oceaneng.2021.109934 [233] Zhang Y N, Guo Z Y, Du X Z. 2018. Wave propagation in liquids with oscillating vapor-gas bubbles. Appl. Thermal Eng., 133: 483-492. doi: 10.1016/j.applthermaleng.2018.01.056 [234] Zhang H, Liu Y Q, Wang B L. 2021. Spatial-temporal features of the coherent structure of sheet/cloud cavitation flows using a frequency-weighted dynamic mode decomposition approach. Phys. Fluids, 33: 053317. doi: 10.1063/5.0049492 [235] Zhang H, Liu Y Q, Wang B L, etc. 2022. Phase-resolved characteristics of bubbles in cloud cavitation shedding cycles. Ocean Eng., 256: 111529. doi: 10.1016/j.oceaneng.2022.111529 [236] Zhang G, Zhang D, Ge M, Petkovsek M, Coutier-Delgosha O. 2022. Experimental investigation of three distinct mechanisms for the transition from sheet to cloud cavitation. Int. J. Heat Mass Transfer, 197: 123372. doi: 10.1016/j.ijheatmasstransfer.2022.123372 [237] Zhang L X, Zhou Z C, Deng J, Shao X M. 2021. A numerical study on the drag law of a gas bubble using dynamic body force method. Phys. Fluids, 33: 063320. doi: 10.1063/5.0055646 [238] Zheng Q, Durben D J, Wolf G H, Angell C A. 1991. Liquids at large negative pressures: water at the homogeneous nucleation limit. Science, 254: 829-832. doi: 10.1126/science.254.5033.829 [239] Zwart P J, Gerber A G, Belamri. 2004. A two-phase flow model for predicting cavitation dynamics. Fifth Int. Conf. Multiphase Flow. Yokohama, Japan. -
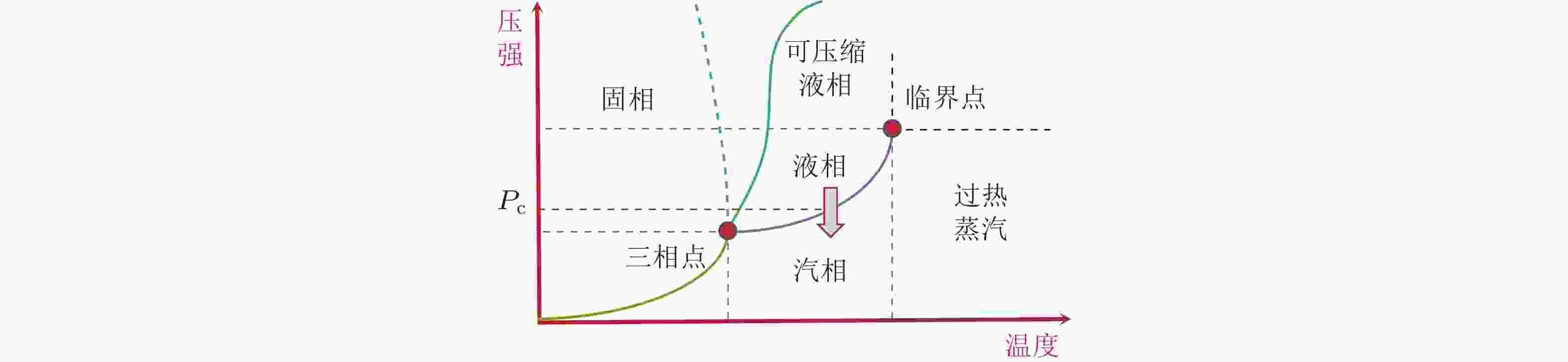
下载:
图(6)
计量
- 文章访问数: 8
- HTML全文浏览量: 6
- PDF下载量: 1
- 被引次数: 0