Intelligent prediction of mechanical properties in metallic materials based on machine learning: A review & perspective
-
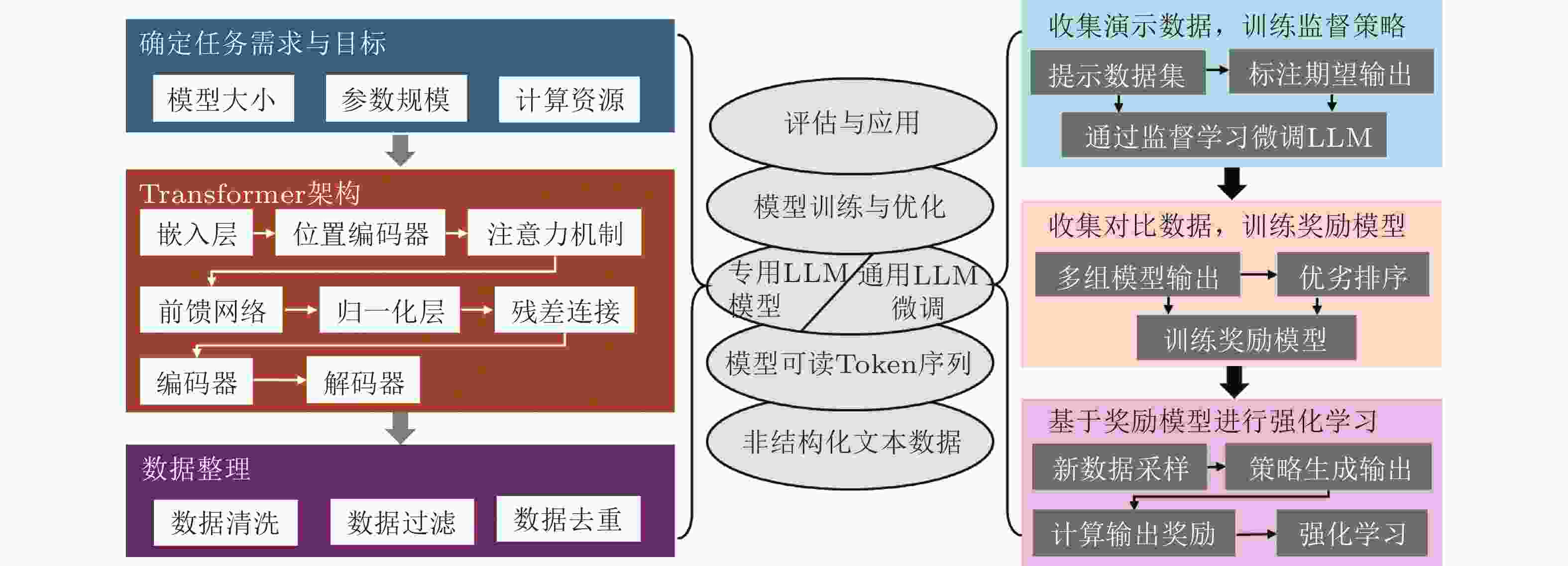
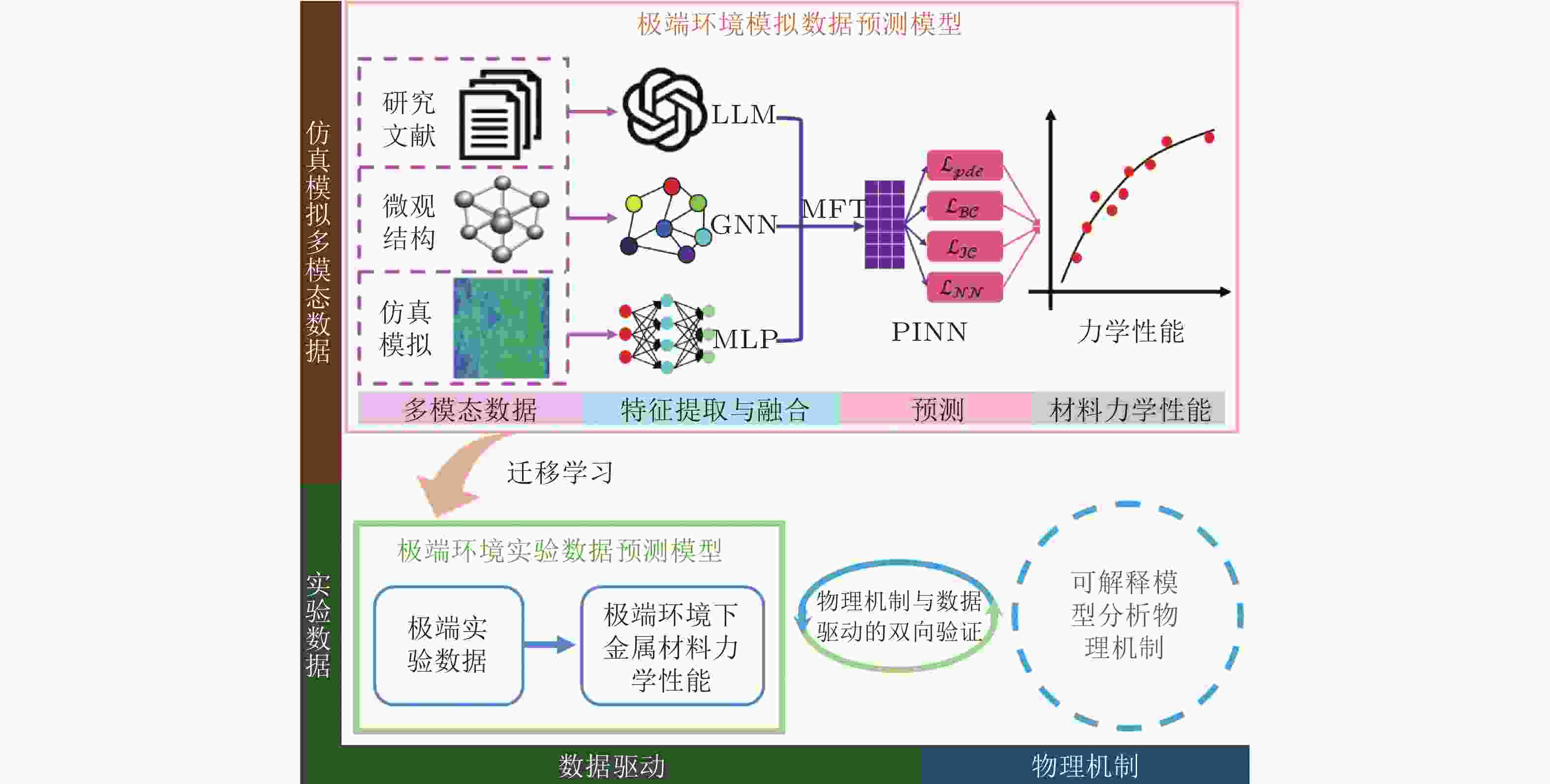
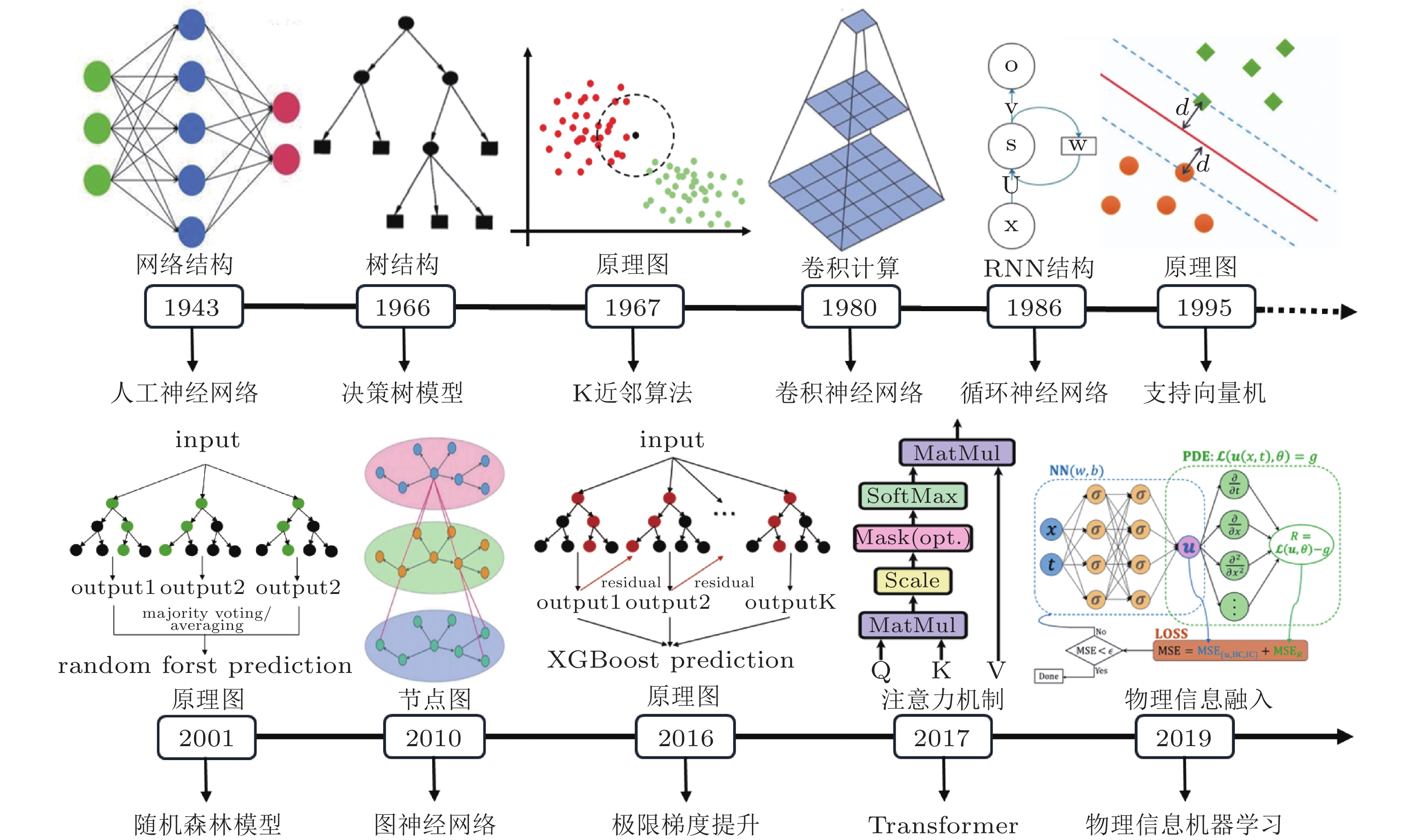
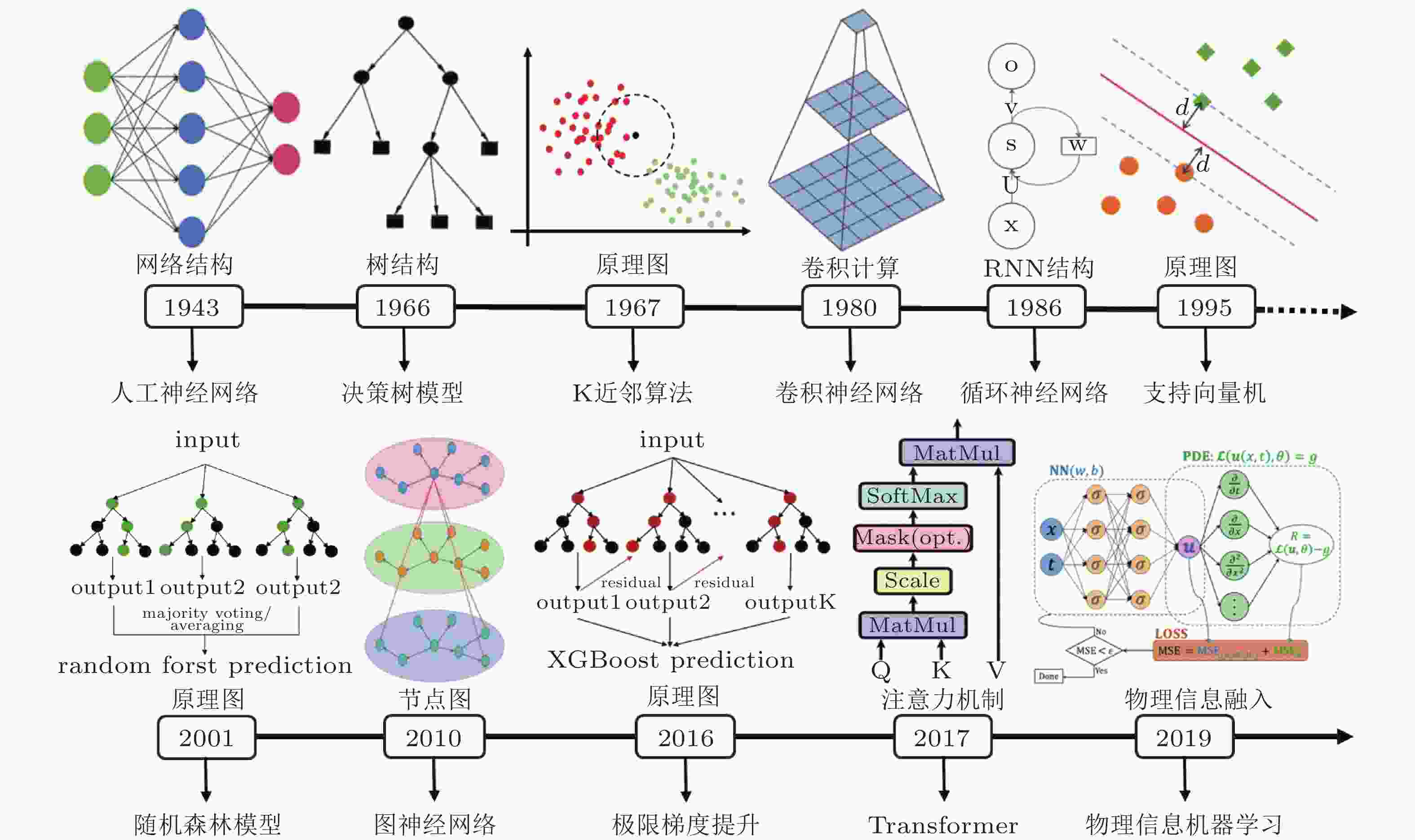
摘要: 机器学习正推动金属材料力学性能研究从经验驱动向数据驱动范式转变. 本文系统综述了机器学习在金属材料力学性能智能预测中的研究进展与挑战. 首先, 概述了常用机器学习算法的原理与流程, 重点介绍了可解释人工智能与物理信息机器学习等前沿方法. 进而, 从微介观性能 (如微观结构演化、断裂行为)、宏观性能 (如硬度、应力响应、疲劳寿命) 与跨尺度耦合性能 (如流变应力、屈服强度、本构参数反演) 三个层面, 评述了机器学习模型的典型应用与预测效果, 突出其在高通量计算与多尺度建模中的优势. 最后, 指出该领域面临数据稀缺、异构性及宽温域/宽应变率条件下预测精度不足等挑战, 并提出迁移学习、大型语言模型与多模态融合等解决路径. 展望未来, 本文构建了融合多模态数据与物理机制的机器学习技术路径, 旨在实现对极端环境下金属材料力学行为的精准预测, 推动材料力学研究向数字化、智能化方向发展.Abstract: The rapid advancement of machine learning is transforming the research paradigm of mechanical properties of metallic materials from experience-driven to data-driven. This review systematically summarizes recent progress and challenges in machine learning based prediction of mechanical properties in metallic materials. We first outline commonly used ML algorithms and workflows, with an emphasis on cutting-edge methods such as explainable AI and physics-informed machine learning. We then review typical applications and predictive performance of ML models across three scales: micro/mesoscopic properties (e.g., microstructural evolution, fracture behavior), macroscopic properties (e.g., hardness, stress response, fatigue life), and cross-scale coupling properties (e.g., flow stress, yield strength, constitutive parameter inversion), highlighting their advantages in high-throughput computation and multi-scale modeling. Finally, we identify persistent challenges such as data scarcity, heterogeneity, and insufficient accuracy under wide temperature/strain-rate ranges, and propose potential solutions including transfer learning, large language models, and multi-modal fusion. Looking forward, we outline a technical pathway integrating multi-modal data and physical mechanisms for accurate prediction of mechanical behavior under extreme conditions, aiming to advance materials mechanics toward digitalization and intelligence.
-
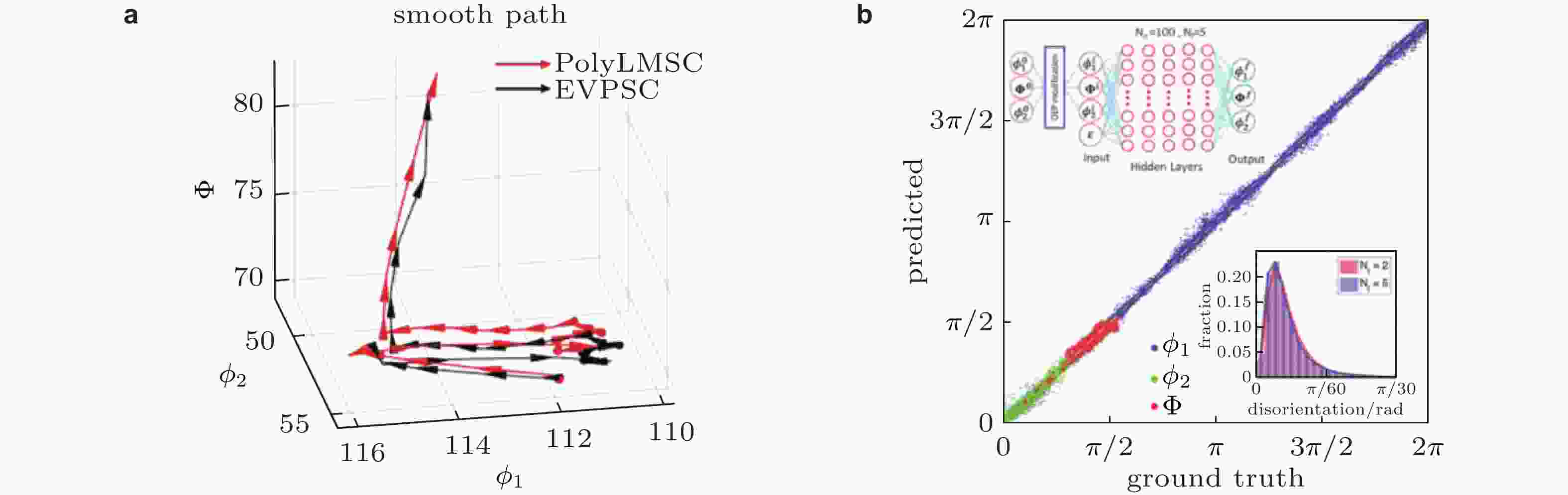
图 5 微观结构演化预测结果对比图. (a) PolyLMSE预测结果(Hu et al. 2025), (b) MOEP-ANN预测结果(Saidi et al. 2022)
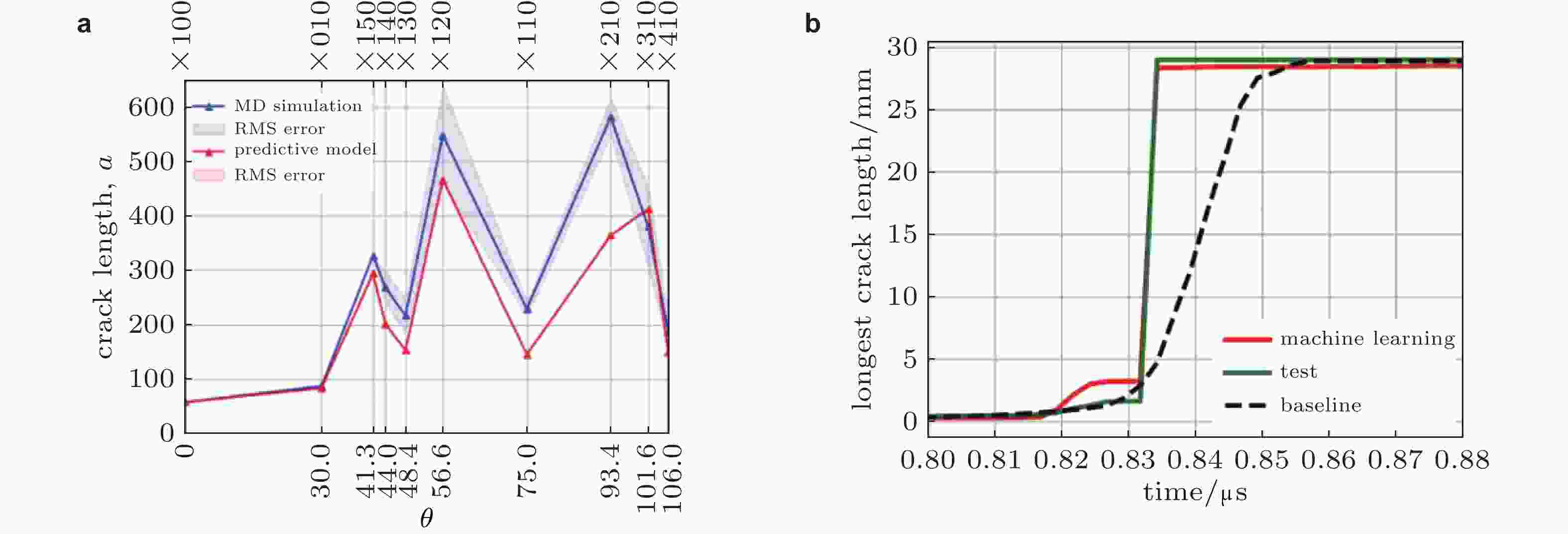
图 6 机器学习预测裂纹长度结果对比图. (a) ConvLSTM裂纹长度预测结果(Hsu et al. 2020), (b) LSTM裂纹长度预测结果(Fernández-Godino et al. 2021)
图 8 材料力学行为预测物理信息神经网络结构与预测结果对比. (a)有限应变弹性塑性的PINN结构; (b)有限应变弹性塑性的PINN预测结果(Niu et al. 2023); (c)数据驱动识别力学行为PINN结构; (d)数据驱动识别力学行为PINN预测结果(Jeong et al. 2024); (e) Finite-PINN模型结构; (f) Finite-PINN模型预测结果(Li et al. 2025b); (g)金属材料数字化框架模型结构; (h)金属材料数字化框架预测结果(Razaei et al. 2025)
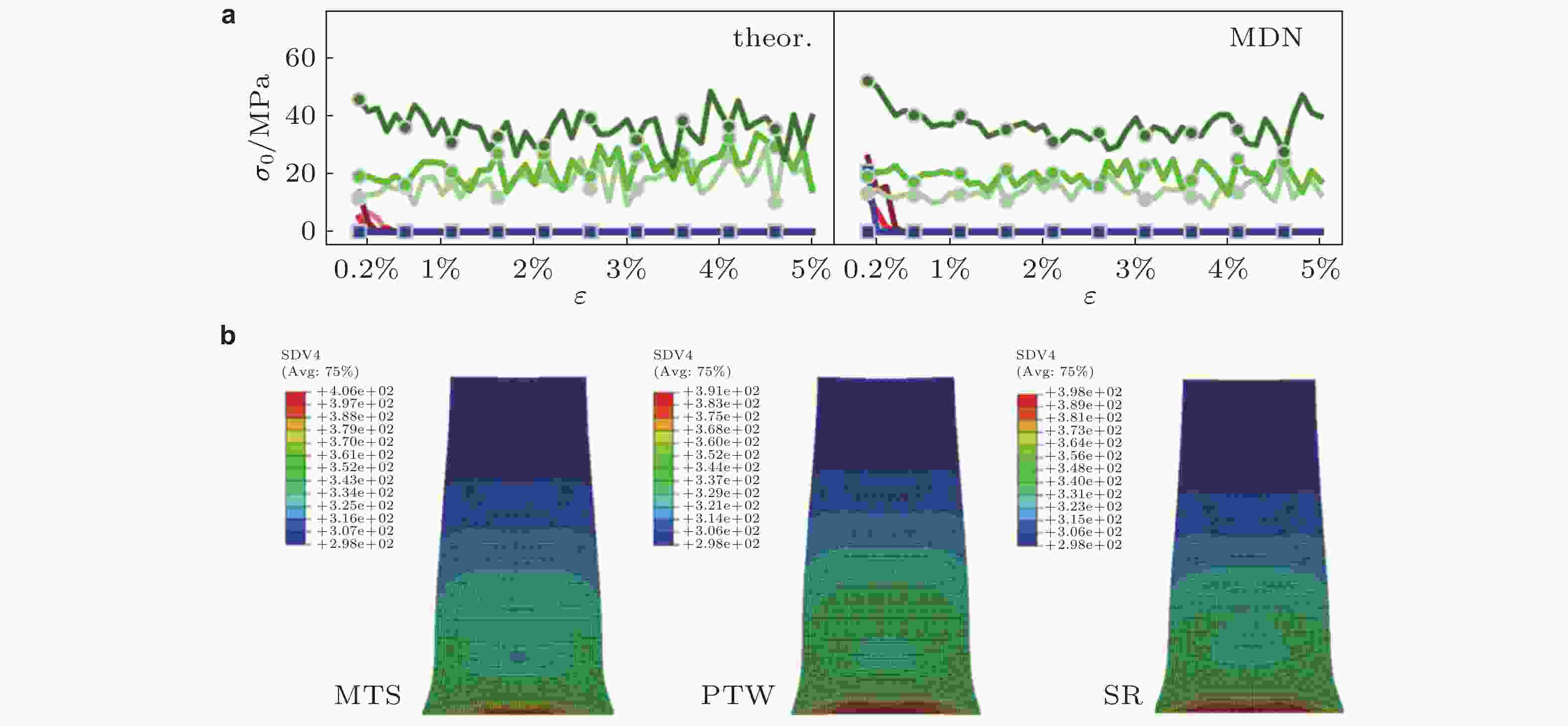
图 10 流变应力预测模型结果对比图. (a) MDN预测结果与理论结果对比(Gu et al. 2024), (b) SR预测结果与经典模型对比(Versino et al. 2017)
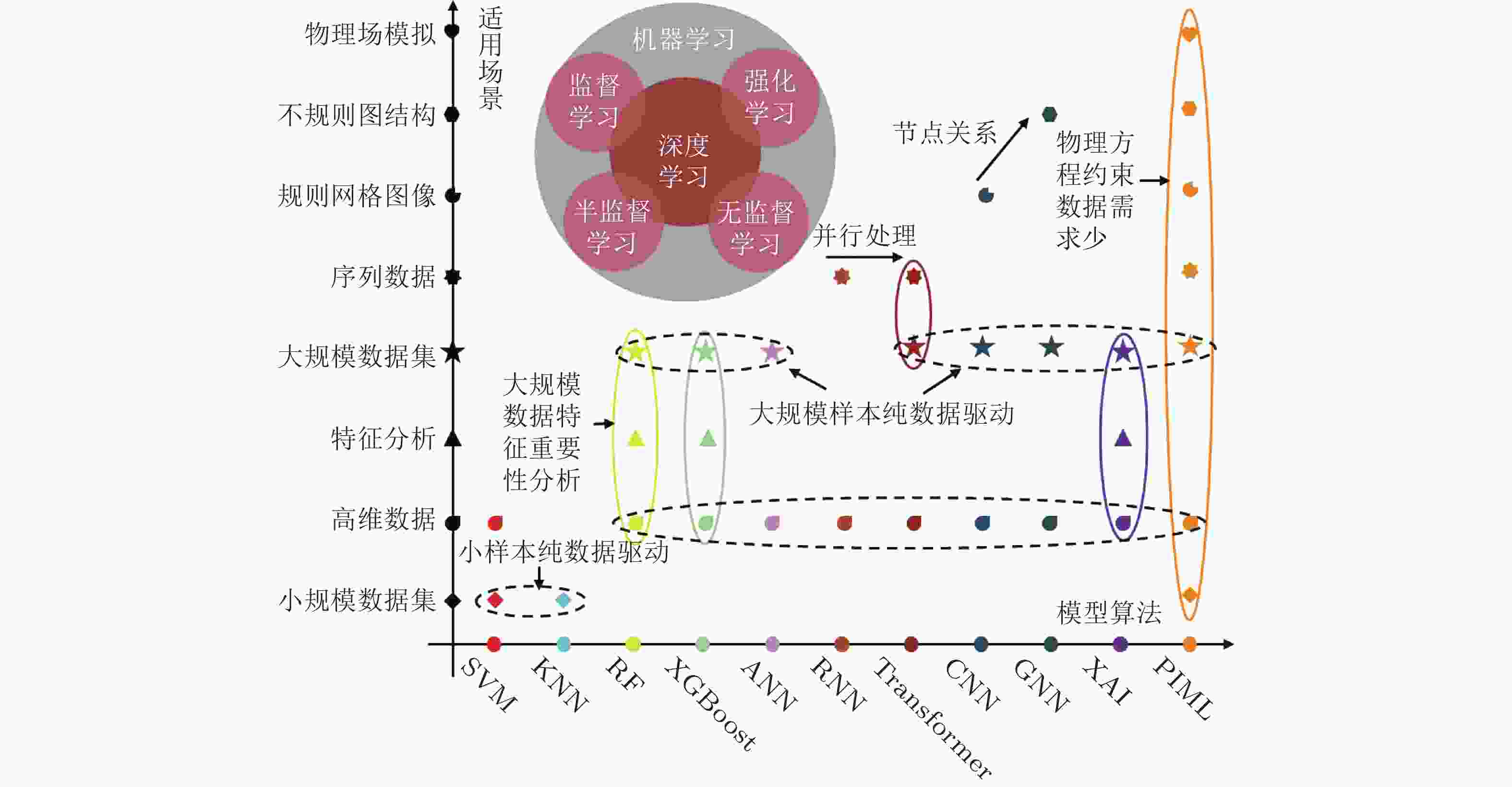
表 1 机器学习算法特征汇总
算法 核心思想 优势 局限性 适用场景 应用案例 支持向
量机在数据集中寻找最优分割超平面, 使得超平面周围正负样本间隔最大化 在高维空间中有效, 内存效率高 对参数和核函数的选择敏感 在材料科学的早期数据挖掘中应用广泛, 适合处理高维度的数据集 预测铝合金硬度和电导率 (Fang et al. 2009) K近邻
算法基于某种距离度量方法找出训练集中与样本最近的k个训练样本进行预测 原理简单易实现, 无需训练过程 对高维数据与不平衡数据敏感 常用于快速原型验证或作为基线模型, 适用于小规模数据集 预测D16T铝合金疲劳断裂图 (Yasnii et al. 2018) 树集成
算法每个节点代表一个逻辑条件用于将输入数据划分为不同类别或分配数值 具有可解释性, 能输出特征重要性排序 模型参数较多, 调参过程复杂 根据材料成分、工艺参数预测其性能特征, 或筛选潜力材料 建立多组分钛合金成分与杨氏模量的关系(Yang et al. 2020) 人工神经网络 利用多层神经元结构实现信息传递与特征映射 能拟合复杂的非线性关系, 对特征要求较低 预测能力严重依赖于数据集质量 用于构建各类结构化材料描述符到目标性能的复杂非线性映射模型 预测铝合金DMD轨迹横截面几何参数(Caiazzo & Caggiano 2018) 循环神经网络 对上一层神经元的输出进行记忆并应用于当前神经元的计算中 有记忆功能, 可以处理长度不一的序列数据 难以实现高效并行化计算 处理序列相关的数据, 如金属材料的力学性能演化等 纤维增强复合材料的疲劳寿命预测 (Al-Assaf & El Kadi 2007) Transformer模型 通过注意力机制建立序列内部各个位置之间的全局依赖关系, 从而捕捉序列中各元素之间的关联 具有强大的全局依赖建模能力, 可以实现高效的并行计算 具有极高的计算复杂度, 需要大规模数据和较高的计算资源 用于处理原子排列、晶格结构等微观结构序列以及文本描述等大规模序列化数据 预测合金耐腐蚀性能(Sasidhar et al. 2023), 预测材料的电导率、带隙等性能(Xu et al. 2023b) 卷积神经网络 通过局部连接、权重共享和多层堆叠, 逐级提取图像中的特征 能自动提取特征, 具有平移不变性, 在图像相关任务上性能卓越 仅能处理规则网格数据, 并且需要大量标注数据 专门用于处理具有空间网格结构的材料数据, 如微观结构图像等 基于微观结构预测增材制造316L不锈钢有效屈服强度 (Herriott & Spear 2020) 图神经
网络通过信息传递机制整合节点及其邻居节点的信息, 迭代地更新节点表示 兼具强大表征能力与可解释性 难以处理长程相互作用, 对图结构定义敏感 用于表征材料的分子或晶体结构等不规则形状图结构 预测材料原子力并支撑分子动力学模拟(Park et al. 2021) 可解释
模型通过约束模型结构或事后解析, 确保其决策逻辑与已知的因果关系或特征贡献度保持一致 透明度高, 能够揭示输入变量与输出目标之间的作用关系 难以兼顾预测精度与机制解释的深度, 且其结论多为统计相关性 常用于分析输入与输出之间的潜在机理, 指导材料设计 基于热轧钢板成分与工艺参数预测屈服强度等力学性能 (Xie et al. 2021) 物理信息机器学习 将已知的物理定律显式地融入到机器学习模型的构建、训练和推理过程中 泛化能力更强, 缓解模型对于数据的依赖 需要将物理知识数学化, 实现更复杂 用于数据获取困难, 成本高昂, 需要对物理过程进行高精度模拟的领域 预测材料均质化位移场, 计算弹性模量 (Li et al. 2024b) 表 2 损失函数及其适用场景
损失函数 公式 适用场景 均方误差 $ L=\dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2} $ 对异常值敏感, 适用于回归任务 平均绝对误差 $ L=\dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}\left\| {{y}_{i}-{\widehat{y}}_{i}} \right\| $ 对异常值不敏感, 适用于回归任务 交叉熵损失 $ L=-\displaystyle\sum\nolimits_{i=1}^{n}{\widehat{y}}_{i}\log\left({\widehat{y}}_{i}\right) $ 适用于分类任务 二元交叉熵 $ L=-\dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}\left[{\widehat{y}}_{i}\log\left({\widehat{y}}_{i}\right) + \left(1-{\widehat{y}}_{i}\right)\log\left({1-\widehat{y}}_{i}\right)\right] $ 二分类任务专用 Hinge loss $ L=\max\left(\mathrm{0,1}-{y}_{i}\cdot {\widehat{y}}_{i}\right) $ 适用于SVM模型, 确保间隔最大化 表 3 评估指标及其特点
评估指标 公式 特点 准确率 $ \mathrm{Accuracy=\dfrac{TP+TN}{TP+TN+FP+FN}} $ 简单直观, 但类别不平衡时失效 精确率 $ \mathrm{Precision=\dfrac{TP}{TP+FP}} $ 关注预测为正类的准确性 召回率 $ \mathrm{Recall=\dfrac{TP}{TP+FN}} $ 关注真实正类的覆盖率 F1分数 $ {\mathrm{F}}1=2\times\mathrm{\dfrac{Precision\times Recall}{Precision+Recall}} $ 平衡精确率与召回率 均方误差 $ \text{MSE}=\dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2} $ 对异常值更加敏感 均方根误差 $ \text{RMSE}=\sqrt{\dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}} $ 可直接与真实值对比 相对均方根误差 $ \text{RRMSE}=\sqrt{\dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}{\left(\dfrac{{y}_{i}-{\widehat{y}}_{i}}{{y}_{i}}\right)}^{2}} $ 以百分比形式表示误差相对大小 平均绝对误差 $ \text{MAE}=\dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}\left\| {{y}_{i}-{\widehat{y}}_{i}} \right\| $ 简单直观, 鲁棒性强 平均绝对百分比误差 $ \text{MAPE}=\dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}\left\| {\dfrac{{y}_{i}-{\widehat{y}}_{i}}{{y}_{i}}} \right\| $ 以百分比形式表示误差相对大小 决定系数 $ {R}^{2}=1-\dfrac{\displaystyle\sum {\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}{\displaystyle\sum {\left({y}_{i}-\stackrel{-}{{y}_{i}}\right)}^{2}} $ 衡量预测结果与真实情况的拟合程度 表 4 高熵合金相选择性能对比(Huang et al. 2019)
机器学习算法 测试准确率 限制因素 SVM 64.3% 不擅长处理多分类非线性问题 KNN (k = 2) 66.8% 数据分布不均衡 加权KNN (k = 3) 68.6% 数据分布不均衡 ANN 74.3% 选取特征并非决定相选择的最关键因素 表 5 不同硬度预测模型的性能比较
模型 输入特征 预测性能 SVR (Whitman & Latypov 2025) ViT提取微观结构特征、成分特征 $ \text{MAPE}=12.6\% $ DNN (Li et al. 2020) 微观结构特征、$ \gamma ' $析出相面积分布、冷却速率 $ {R}^{2}=0.945 $ RFR (Xiong et al. 2021) 平均价电子浓度、混合焓、电负性失配度、平均原子序数、摩尔热容失配度、平均热导率 $\begin{array}{l} {R}^{2}=0.821 \\ \text{RRMSE}=16.7\% \end{array}$ GBDT (Yu et al. 2024) 激光功率、扫描速度、体能量密度、线能量密度 $\begin{array}{l}{R}^{2}=0.963 \\ \text{MAE}=2.059 \\ \text{RMSE}=3.844 \end{array}$ SR (Xiong et al. 2020) 回火温度、碳含量、铬含量、钼含量 $\begin{array}{l} {R}^{2} > 0.888 \\ \text{RRMSE} < 3.25\% \end{array}$ RF (Xiong et al. 2020) $ \begin{array}{l} {R}^{2} > 0.912 \\ \text{RRMSE} < 3.75\% \end{array}$ 表 6 金属材料疲劳寿命预测性能汇总
文献 模型 材料 预测性能 Zhan et al. 2022 CDM-MLP 300M-AerMet100钢 $ {R}^{2}=0.650 $ Wang et al. 2022a SVM AlSi10Mg合金 $ {R}^{2}=0.927 $
$ \mathrm{MAPE}=24.5\% $RF AlSi10Mg合金 $ {R}^{2}=0.874 $
$ \mathrm{MAPE}=32.8\% $Wang et al. 2023b $ \delta \sigma $-ANN (框架A) Al-Mg4.5Mn合金 $ {R}^{2}=0.975 $
$ \mathrm{MAPE}=12.3\% $$ \delta \sigma $-SVR (框架A) Al-Mg4.5Mn合金 $ {R}^{2}=0.942 $
$ \mathrm{MAPE}=15.7\% $$ \delta \sigma $-ANN (框架B) Al-Mg4.5Mn合金 $ {R}^{2}=0.833 $
$ \mathrm{MAPE}=22.6\% $$ \delta \sigma $-SVR (框架B) Al-Mg4.5Mn合金 $ {R}^{2}=0.925 $
$ \mathrm{MAPE}=20.2\% $Paris-ANN (框架A) Al-Mg4.5Mn合金 $ {R}^{2}=0.943 $
$ \mathrm{MAPE}=15.5\% $Paris-SVR (框架A) Al-Mg4.5Mn合金 $ {R}^{2}=0.939 $
$ \mathrm{MAPE}=15.3\% $Paris-ANN (框架B) Al-Mg4.5Mn合金 $ {R}^{2}=0.912 $
$ \mathrm{MAPE}=16.8\% $Paris-SVR (框架B) Al-Mg4.5Mn合金 $ {R}^{2}=0.984 $
$ \mathrm{MAPE}=9.8\% $Feng et al. 2025 MPIBNN 316L不锈钢 $ {R}^{2}=0.895 $
$ \mathrm{MSE}=0.014 $MPIBNN AlMg4.5Mn合金 $ {R}^{2}=0.902 $
$ \mathrm{MSE}=0.032 $MPIBNN Ti6.5Al2ZrMoV合金 $ {R}^{2}=0.867 $
$ \mathrm{MSE}=0.037 $表 7 金属材料屈服强度预测性能汇总
文献 模型 材料 预测性能 Jiang et al. 2022 $ {\sigma _{{y}}} = 79W/\left( {{S^3}\sqrt {{l_{\rm{t}}}} } \right) + 1.2\sqrt {\gamma E/{l_{\rm{t}}}} {d^{ - 0.5}}$ 多晶金属 $ {R}^{2}=0.960 $ Lee et al. 2024 $ \begin{aligned} {{\sigma }}_{{y}}=&{{\sigma }}_{\mathrm{o}}^{\mathrm{*}}\mathrm{exp}\left(-\dfrac{2.526{R}{T}}{\Delta {E}}\mathrm{l}\mathrm{n}\left(\dfrac{0.237{\dot{\mathrm{\varepsilon }}}_{\mathrm{*}}}{\dot{\mathrm{\varepsilon }}}\right)\right) +\\ &\mathrm{\alpha }\dfrac{{G}}{\sqrt{\mathrm{\beta }\cdot \left(\dfrac{{d}}{{{\boldsymbol{b}}}}\right)} + \mathrm{\gamma }\cdot 4\sqrt{\dfrac{{\delta }{{D}}_{\mathrm{g}\mathrm{b}}}{\dot{\mathrm{\varepsilon }}{{d}}^{3}}} + \mathrm{\omega }}\end{aligned} $ 中熵合金
$ \mathrm{\text{Fe}_{60}\text{Co}_{15}\text{Ni}_{15}\text{Cr}_{10}} $$ {R}^{2}=0.957 $
$ {\text{MAE}=35.0\text{MPa}} $集成树回归 $ {R}^{2}=0.925 $
$ {\text{MAE}=53.7\text{MPa}} $Li et al. 2023 $ {{\sigma }}_{{y}}=0.4734 + 2.713\times {10}^{-5}\cdot \dfrac{{T}_{m}^{2}\cdot \text{VED}}{{V}_\text{m}\cdot {\chi }_\text{p}^{2}} $ 非晶合金 $ {R}^{2}=0.930 $ Peng et al. 2020 随机森林 (RF) 9Cr钢 $ {R}^{2}=0.983 $
$ {\text{MAE}=16.4\text{MPa}} $Kateb & Safarian 2025 随机森林 (RF) 钢 $ {R}^{2}=0.845 $ -
[1] 何俊, 张彩庆, 李小珍, 等. 2020. 面向深度学习的多模态融合技术研究综述. 计算机工程, 46(5): 1-11 (He J, Zhang C Q, Li X Z, et al. 2020. A survey on multimodal fusion technology for deep learning. Computer Engineering, 46(5): 1-11). doi: 10.19678/j.issn.1000-3428.0057370He J, Zhang C Q, Li X Z, et al. 2020. A survey on multimodal fusion technology for deep learning. Computer Engineering, 46(5): 1-11 doi: 10.19678/j.issn.1000-3428.0057370 [2] 李航. 2022. 机器学习方法. 北京: 清华大学出版社 (Li H. 2022. Machine learning methods. Beijing: Tsinghua University Press).Li H. 2022. Machine learning methods. Beijing: Tsinghua University Press. [3] 王一铮, 庄晓莹, Timon Rabczcuk, 等. 2025. AI for PDEs在固体力学领域的研究进展. 力学进展, 55(2): 231-287 (Wang Y Z, Zhuang X Y, Timon R, et al. 2025. AI for PDEs in solid mechanics: A review. Advances in Mechanics, 55(2): 231-287). doi: 10.6052/1000-0992-24-016Wang Y Z, Zhuang X Y, Timon R, et al. 2025. AI for PDEs in solid mechanics: A review. Advances in Mechanics, 55(2): 231-287 doi: 10.6052/1000-0992-24-016 [4] 谢建新, 宿彦京, 薛德祯, 等. 2021. 机器学习在材料研发中的应用. 金属学报, 57(11): 1343-1361 (Xie J X, Su Y J, Xue D Z, et al. 2021. Application of machine learning in materials research and development. Acta Metallurgica Sinica, 57(11): 1343-1361).Xie J X, Su Y J, Xue D Z, et al. 2021. Application of machine learning in materials research and development. Acta Metallurgica Sinica, 57(11): 1343-1361. [5] 杨桂通, 熊祝华. 1984. 塑性动力学. 北京: 清华大学出版社 (Yang G T, Xiong Z H. 1984. Plasticity dynamics. Beijing: Tsinghua University Press).Yang G T, Xiong Z H. 1984. Plasticity dynamics. Beijing: Tsinghua University Press. [6] 杨杨, 詹德川, 姜远, 等. 2021. 可靠多模态学习综述. 软件学报, 32(4): 1067-1081 (Yang Y, Zhan D C, Jiang Y, et al. 2021. A survey on trustworthy multimodal learning. Journal of Software, 32(4): 1067-1081). doi: 10.13328/j.cnki.jos.006167Yang Y, Zhan D C, Jiang Y, et al. 2021. A survey on trustworthy multimodal learning. Journal of Software, 32(4): 1067-1081. doi: 10.13328/j.cnki.jos.006167 [7] 周瑞, 熊宇凯, 储节磊, 等. 2023. 基于机器学习和遗传算法的非局部晶体塑性模型参数识别. 力学学报, 56(3): 751-762 (Zhou R, Xiong Y K, Chu J L, et al. 2023. Parameter identification of nonlocal crystal plasticity model based on machine learning and genetic algorithm. Chinese Journal of Theoretical and Applied Mechanics, 56(3): 751-762). doi: 10.6052/0459-1879-23-479Zhou R, Xiong Y K, Chu J L, et al. 2023. Parameter identification of nonlocal crystal plasticity model based on machine learning and genetic algorithm. Chinese Journal of Theoretical and Applied Mechanics, 56(3): 751-762. doi: 10.6052/0459-1879-23-479 [8] 周志华. 2016. 机器学习. 北京: 清华大学出版社 (Zhou Z H. 2016. Machine learning. Beijing: Tsinghua University Press).Zhou Z H. 2016. Machine learning. Beijing: Tsinghua University Press. [9] Agrawal A, Choudhary A. 2016. Perspective: Materials informatics and big data: Realization of the “fourth paradigm” of science in materials science. Apl Materials, 4(5). [10] Ahmad W, Simon E, Chithrananda S, et al. 2022. Chemberta-2: Towards chemical foundation models. arXiv preprint arXiv: 2209.01712. [11] Al-Assaf Y, El Kadi H. 2007. Fatigue life prediction of composite materials using polynomial classifiers and recurrent neural networks. Composite Structures, 77(4): 561-569. doi: 10.1016/j.compstruct.2005.08.012 [12] Alder B J, Wainwright T E. 1957. Phase transition for a hard sphere system. The Journal of Chemical Physics, 27(5): 1208. doi: 10.1063/1.1743957 [13] Amodeo R J, Ghoniem N M. 1990. Dislocation dynamics. I. A proposed methodology for deformation micromechanics. Physical Review B, 41(10): 6958. doi: 10.1103/PhysRevB.41.6958 [14] Ang K, Qiu J, Su B, et al. 2025. Deep learning-based inverse design of programmable disordered metamaterials. International Journal of Mechanical Sciences, 110712. [15] Balamurugan R, Chen J, Meng C, et al. 2024. Data-driven approaches for fatigue prediction of Ti–6Al–4V parts fabricated by laser powder bed fusion. International Journal of Fatigue, 182: 108167. doi: 10.1016/j.ijfatigue.2024.108167 [16] Belianinov A, Vasudevan R, Strelcov E, et al. 2015. Big data and deep data in scanning and electron microscopies: Deriving functionality from multidimensional data sets. Advanced Structural and Chemical Imaging, 1(1): 6. doi: 10.1186/s40679-015-0006-6 [17] Berg J, Nyström K. 2021. Neural networks as smooth priors for inverse problems for PDEs. Journal of Computational Mathematics and Data Science, 1: 100008. doi: 10.1016/j.jcmds.2021.100008 [18] Bishara D, Xie Y, Liu W K, et al. 2023. A state-of-the-art review on machine learning-based multiscale modeling, simulation, homogenization and design of materials. Archives of Computational Methods in Engineering, 30(1). [19] Blaschke D N, Nguyen T, Nitol M, et al. 2023. Machine learning based approach to predict ductile damage model parameters for polycrystalline metals. Computational Materials Science, 229: 112382. doi: 10.1016/j.commatsci.2023.112382 [20] Breiman L. 2001. Random forests. Machine learning, 45(1): 5-32. doi: 10.1023/A:1010933404324 [21] Bruna J, Zaremba W, Szlam A, et al. 2013. Spectral networks and locally connected networks on graphs. arXiv preprint arXiv: 1312.6203. [22] Burov A, Fedorova E. 2021. Modeling of interface failure in a thermal barrier coating system on Ni-based superalloys. Engineering Failure Analysis, 123: 105320. doi: 10.1016/j.engfailanal.2021.105320 [23] Butler K T, Davies D W, Cartwright H, et al. 2018. Machine learning for molecular and materials science. Nature, 559(7715): 547-555. doi: 10.1038/s41586-018-0337-2 [24] Caiazzo F, Caggiano A. 2018. Laser direct metal deposition of 2024 Al alloy: Trace geometry prediction via machine learning. Materials, 11(3): 444. doi: 10.3390/ma11030444 [25] Cecen A, Dai H, Yabansu Y C, et al. 2018. Material structure-property linkages using three-dimensional convolutional neural networks. Acta Materialia, 146: 76-84. doi: 10.1016/j.actamat.2017.11.053 [26] Chen A, Zhang X, Zhou Z. 2020. Machine learning: Accelerating materials development for energy storage and conversion. InfoMat, 2(3): 553-576. doi: 10.1002/inf2.12094 [27] Chen C, Ong S P. 2021. AtomSets as a hierarchical transfer learning framework for small and large materials datasets. npj Computational Materials, 7(1): 173. doi: 10.1038/s41524-021-00639-w [28] Chen C, Ye W, Zuo Y, et al. 2019a. Graph networks as a universal machine learning framework for molecules and crystals. Chemistry of Materials, 31(9): 3564-3572. doi: 10.1021/acs.chemmater.9b01294 [29] Chen K, Dong X, Gao P, et al. 2025. Physics-informed neural networks for topological metamaterial design and mechanical applications. International Journal of Mechanical Sciences, 110489. [30] Chen L, Zhang Z, Lou M, et al. 2023. High-temperature wear mechanisms of TiNbWN films: Role of nanocrystalline oxides formation. Friction, 11(3): 460-472. doi: 10.1007/s40544-022-0621-x [31] Chen T, Guestrin C. 2016. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. [32] Chen X W, Jeong J C. 2007. Enhanced recursive feature elimination. Proceedings of the IEEE conference on machine learning and applications. [33] Chen X, Wang S, Fu B, et al. 2019b. Catastrophic forgetting meets negative transfer: Batch spectral shrinkage for safe transfer learning. Advances in Neural Information Processing Systems, 32. [34] Ciampaglia A, Tridello A, Paolino D S, et al. 2023. Data driven method for predicting the effect of process parameters on the fatigue response of additive manufactured AlSi10Mg parts. International Journal of Fatigue, 170: 107500. doi: 10.1016/j.ijfatigue.2023.107500 [35] Comanici G, Bieber E, Schaekermann M, et al. 2025. Gemini 2.5: Pushing the frontier with advanced reasoning, multimodality, long context, and next generation agentic capabilities. arXiv preprint arXiv: 2507.06261. [36] Cortes C, Vapnik V. 1995. Support-vector networks. Machine Learning, 20(3): 273-297. doi: 10.1023/A:1022627411411 [37] Cover T, Hart P. 1967. Nearest neighbor pattern classification. IEEE Transactions on Information Theory, 13(1): 21-27. doi: 10.1109/TIT.1967.1053964 [38] Das K, Goyal P, Lee S C, et al. 2023. Crysmmnet: Multimodal representation for crystal property prediction. In Uncertainty in Artificial Intelligence. (pp. 507-517). PMLR. [39] De Cao N, Kipf T. 2018. MolGAN: An implicit generative model for small molecular graphs. arXiv preprint arXiv: 1805.11973. [40] Dhuliawala S, Komeili M, Xu J, et al. 2023. Chain-of-verification reduces hallucination in large language models. arXiv preprint arXiv: 2309.11495. [41] Dong S, Wang Y, Li J, et al. 2024. Machine learning aided prediction and design for the mechanical properties of magnesium alloys. Metals and Materials International, 30(3): 593-606. doi: 10.1007/s12540-023-01531-6 [42] Dung C V, Sekiya H, Hirano S, et al. 2019. A vision-based method for crack detection in gusset plate welded joints of steel bridges using deep convolutional neural networks. Automation in Construction, 102: 217-229. doi: 10.1016/j.autcon.2019.02.013 [43] Eswarappa Prameela S, Pollock T M, Raabe D, et al. 2023. Materials for extreme environments. Nature Reviews Materials, 8(2): 81-88. [44] Fang S F, Wang M P, Song M. 2009. An approach for the aging process optimization of Al–Zn–Mg–Cu series alloys. Materials & Design, 30(7): 2460-2467. [45] Feng F, Zhu T, Yang B, et al. 2025. Probabilistic fatigue life prediction in additive manufacturing materials with a physics-informed neural network framework. Expert Systems with Applications, 275: 127098. doi: 10.1016/j.eswa.2025.127098 [46] Fernández-Godino M G, Panda N, O’Malley D, et al. 2021. Accelerating high-strain continuum-scale brittle fracture simulations with machine learning. Computational Materials Science, 186: 109959. doi: 10.1016/j.commatsci.2020.109959 [47] Fida M A F A, Ahmad T, Ntahobari M. 2021. Variance threshold as early screening to Boruta feature selection for intrusion detection system. Proceedings of the IEEE Conference on Information & Communication Technology and System. [48] Frey N C, Akinwande D, Jariwala D, et al. 2020. Machine learning-enabled design of point defects in 2D materials for quantum and neuromorphic information processing. ACS Nano, 14(10): 13406-13417. doi: 10.1021/acsnano.0c05267 [49] Fukushima K. 1980. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics, 36(4): 193-202. doi: 10.1007/BF00344251 [50] Fung V, Zhang J, Juarez E, et al. 2021. Benchmarking graph neural networks for materials chemistry. npj Computational Materials, 7(1): 84. doi: 10.1038/s41524-021-00554-0 [51] Georgiou G P. 2025. Capabilities of GPT-5 across critical domains: Is it the next breakthrough? arXiv preprint arXiv: 2508.19259. [52] Ghiringhelli L M, Vybiral J, Ahmetcik E, et al. 2017. Learning physical descriptors for materials science by compressed sensing. New Journal of Physics, 19(2): 023017. doi: 10.1088/1367-2630/aa57bf [53] Golovneva O, Allen-Zhu Z, Weston J, et al. 2024. Reverse training to nurse the reversal curse. arXiv preprint arXiv: 2403.13799. [54] Goodfellow I, Bengio Y, Courville A, et al. 2016. Deep learning. Cambridge, MA, USA: MIT press. [55] Gu Y, Stiles C D, El-Awady J A. 2024. A statistical perspective for predicting the strength of metals: Revisiting the Hall–Petch relationship using machine learning. Acta Materialia, 266: 119631. doi: 10.1016/j.actamat.2023.119631 [56] Haghighat E, Abouali S, Vaziri R. 2023. Constitutive model characterization and discovery using physics-informed deep learning. Engineering Applications of Artificial Intelligence, 120: 105828. doi: 10.1016/j.engappai.2023.105828 [57] Haghighat E, Raissi M, Moure A, et al. 2021. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Computer Methods in Applied Mechanics and Engineering, 379: 113741. doi: 10.1016/j.cma.2021.113741 [58] Herriott C, Spear A D. 2020. Predicting microstructure-dependent mechanical properties in additively manufactured metals with machine-and deep-learning methods. Computational Materials Science, 175: 109599. doi: 10.1016/j.commatsci.2020.109599 [59] Hochreiter S, Schmidhuber J. 1997. Long short-term memory. Neural Computation, 9(8): 1735-1780. doi: 10.1162/neco.1997.9.8.1735 [60] Holzinger A. 2016. Interactive machine learning for health informatics: When do we need the human-in-the-loop. Brain Informatics, 3(2): 119-131. doi: 10.1007/s40708-016-0042-6 [61] Hsu Y C, Yu C H, Buehler M J. 2020. Using deep learning to predict fracture patterns in crystalline solids. Matter, 3(1): 197-211. doi: 10.1016/j.matt.2020.04.019 [62] Hu Y, Zhou G, Knezevic M, et al. 2025. Multiscale modelling with neural network-based crystal plasticity model from meso-to macroscale. Acta Materialia, 121075. [63] Huang J, Chen X, Mishra S, et al. 2023. Large language models cannot self-correct reasoning yet. arXiv preprint arXiv: 2310.01798. [64] Huang L, Yu W, Ma W, et al. 2025. A survey on hallucination in large language models: Principles, taxonomy, challenges, and open questions. ACM Transactions on Information Systems, 43(2): 1-55. [65] Huang W, Martin P, Zhuang H L. 2019. Machine-learning phase prediction of high-entropy alloys. Acta Materialia, 169: 225-236. doi: 10.1016/j.actamat.2019.03.012 [66] Hutchinson M L, Antono E, Gibbons B M, et al. 2017. Overcoming data scarcity with transfer learning. arXiv preprint arXiv: 1711.05099. [67] Ihuaenyi R C, Li W, Bazant M Z, et al. 2025. Mechanics informatics: A paradigm for efficiently learning constitutive models. Journal of the Mechanics and Physics of Solids, 106239. [68] Indeck J, Cereceda D, Mayeur J R, et al. 2022. Understanding slip activity and void initiation in metals using machine learning-based microscopy analysis. Materials Science and Engineering: A, 838: 142738. doi: 10.1016/j.msea.2022.142738 [69] Jablonka K M, Ai Q, Al-Feghali, et al. 2023. 14 examples of how LLMs can transform materials science and chemistry: A reflection on a large language model hackathon. Digital Discovery, 2(5): 1233-1250. doi: 10.1039/D3DD00113J [70] Jebli I, Belouadha F Z, Kabbaj M I, et al. 2021. Prediction of solar energy guided by pearson correlation using machine learning. Energy, 224: 120109. doi: 10.1016/j.energy.2021.120109 [71] Jeong I, Cho M, Chung H, et al. 2024. Data-driven nonparametric identification of material behavior based on physics-informed neural network with full-field data. Computer Methods in Applied Mechanics and Engineering, 418: 116569. doi: 10.1016/j.cma.2023.116569 [72] Ji Z, Lee N, Frieske R, et al. 2023. Survey of hallucination in natural language generation. ACM Computing Surveys, 55(12): 1-38. [73] Jia X, Li W, Lu Q, et al. 2021. Towards accurate prediction for ultra-low carbon tempered martensite property through the cross-correlated substructures. Materials & Design, 211: 110126. [74] Jiang L, Fu H, Zhang H, et al. 2022. Physical mechanism interpretation of polycrystalline metals’ yield strength via a data-driven method: A novel Hall–Petch relationship. Acta Materialia, 231: 117868. doi: 10.1016/j.actamat.2022.117868 [75] Jolliffe I. 2011. Principal component analysis. In International encyclopedia of statistical science. Springer, Berlin, Heidelberg. [76] Julianto I T, Kurniadi D, Fauziah F A, et al. 2023. Improvement of data mining models using forward selection and backward elimination with cryptocurrency datasets. Journal of Applied Intelligent System, 8(1): 100-109. doi: 10.33633/jais.v8i1.7568 [77] Kabliman E, Kolody A H, Kommenda M, et al. 2019. Prediction of stress-strain curves for aluminium alloys using symbolic regression. AIP Conference Proceedings. AIP Publishing LLC, 2113(1): 180009. [78] Kabliman E, Kolody A H, Kronsteiner J, et al. 2021. Application of symbolic regression for constitutive modeling of plastic deformation. Applications in Engineering Science, 6: 100052. doi: 10.1016/j.apples.2021.100052 [79] Kalidindi S R, De Graef M. 2015. Materials data science: Current status and future outlook. Annual Review of Materials Research, 45(1): 171-193. doi: 10.1146/annurev-matsci-070214-020844 [80] Kateb M, Safarian S. 2025. Machine learning-driven predictive modeling of mechanical properties in diverse steels. Machine Learning with Applications, 20: 100634. doi: 10.1016/j.mlwa.2025.100634 [81] Khoei A R, Seddighian M R, Sameti A R. 2024. Machine learning-based multiscale framework for mechanical behavior of nano-crystalline structures. International Journal of Mechanical Sciences, 265: 108897. doi: 10.1016/j.ijmecsci.2023.108897 [82] Kingma D P, Ba J. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. [83] Kipf T N, Welling M. 2016. Variational graph auto-encoders. arXiv preprint arXiv: 1611.07308. [84] Kirkpatrick J, Pascanu R, Rabinowitz N, et al. 2017. Overcoming catastrophic forgetting in neural networks. Proceedings of the National Academy of Sciences, 114(13): 3521-3526. doi: 10.1073/pnas.1611835114 [85] Kohn W, Sham L J. 1965. Self-consistent equations including exchange and correlation effects. Physical Review, 140(4A): A1133. doi: 10.1103/PhysRev.140.A1133 [86] Kong C S, Luo W, Arapan S, et al. 2012. Information-theoretic approach for the discovery of design rules for crystal chemistry. Journal of Chemical Information and Modeling, 52(7): 1812-1820. doi: 10.1021/ci200628z [87] Kumar A, Dawson P R. 1998. Modeling crystallographic texture evolution with finite elements over neo-Eulerian orientation spaces. Computer Methods in Applied Mechanics and Engineering, 153(3-4): 259-302. doi: 10.1016/S0045-7825(97)00072-8 [88] Lee J A, Figueiredo R B, Park H, et al. 2024. Unveiling yield strength of metallic materials using physics-enhanced machine learning under diverse experimental conditions. Acta Materialia, 275: 120046. doi: 10.1016/j.actamat.2024.120046 [89] Lei G, Docherty R, Cooper S J. 2024. Materials science in the era of large language models: A perspective. Digital Discovery, 3(7): 1257-1272. doi: 10.1039/D4DD00074A [90] Lew A J, Buehler M J. 2022. DeepBuckle: Extracting physical behavior directly from empirical observation for a material agnostic approach to analyze and predict buckling. Journal of the Mechanics and Physics of Solids, 164: 104909. doi: 10.1016/j.jmps.2022.104909 [91] Li C, Xu K, Lou M, et al. 2024a. Machine learning-enabled prediction of high-temperature oxidation resistance for Ni-based alloys. Corrosion Science, 234: 112152. doi: 10.1016/j.corsci.2024.112152 [92] Li C, Yang S, Zheng H, et al. 2025a. Integration of machine learning with finite element analysis in materials science: A review. Journal of Materials Science, 1-23. [93] Li H, Miao Y, Khodaei Z S, et al. 2025b. Finite-PINN: A physics-informed neural network with finite geometric encoding for solid mechanics. Journal of the Mechanics and Physics of Solids, 106222. [94] Li N, Zhao S, Zhang Z. 2021. Property prediction of medical magnesium alloy based on machine learning. Proceedings of the IEEE Conference on Big Data Analytics. [95] Li X, Chen Z, Xie T, et al. 2025. Enhancing sonologist examination performance with large language models: An analytical study of ChatGPT-4 and Claude 3. Medical ultrasonography, 27(3), 294–300. [96] Li X, Yan Z, Du Y, et al. 2024. HomoGenius: A foundation model of homogenization for rapid prediction of effective mechanical properties using neural operators. arXiv: 2404.07943 [97] Li Y, Liu Y, Luo S, et al. 2020. Neural network model for correlating microstructural features and hardness properties of nickel-based superalloys. Journal of Materials Research and Technology, 9(6): 14467-14477. doi: 10.1016/j.jmrt.2020.10.042 [98] Li Y, Tarlow D, Brockschmidt M, et al. 2015. Gated graph sequence neural networks. arXiv preprint arXiv: 1511.05493. [99] Li Z, Long Z, Lei S, et al. 2023. A simple, quantitative expression for understanding and evaluating the yield strength of amorphous alloys based on symbolic regression and dimensional calculation. Journal of Non-Crystalline Solids, 614: 122409. doi: 10.1016/j.jnoncrysol.2023.122409 [100] Liang R, Khan A S. 1999. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures. International Journal of Plasticity, 15(9): 963-980. doi: 10.1016/S0749-6419(99)00021-2 [101] Liu Y C, Wu H, Mayeshiba T, et al. 2022. Machine learning predictions of irradiation embrittlement in reactor pressure vessel steels. npj Computational Materials, 8(1): 85. doi: 10.1038/s41524-022-00760-4 [102] Lu L, Pestourie R, Yao W, et al. 2021. Physics-informed neural networks with hard constraints for inverse design. SIAM Journal on Scientific Computing, 43(6): B1105-B1132. doi: 10.1137/21M1397908 [103] Mao Y, Keshavarz S, Kilic M N T, et al. 2025. A deep learning-based crystal plasticity finite element model. Scripta Materialia, 254: 116315. doi: 10.1016/j.scriptamat.2024.116315 [104] McCulloch W S, Pitts W. 1943. A logical calculus of the ideas immanent in nervous activity. The Bulletin of Mathematical Biophysics, 5(4): 115-133. doi: 10.1007/BF02478259 [105] Morgan D, Jacobs R. 2020. Opportunities and challenges for machine learning in materials science. Annual Review of Materials Research, 50(1): 71-103. doi: 10.1146/annurev-matsci-070218-010015 [106] Murr L E, Meyers M A, Niou C S, et al. 1997. Shock-induced deformation twinning in tantalum. Acta Materialia, 45(1): 157-175. doi: 10.1016/S1359-6454(96)00145-0 [107] Nath D, Neog D R, Gautam S S. 2024. Application of machine learning and deep learning in finite element analysis: A comprehensive review. Archives of Computational Methods in Engineering, 31(5). [108] Niu S, Zhang E, Bazilevs Y, et al. 2023. Modeling finite-strain plasticity using physics-informed neural network and assessment of the network performance. Journal of the Mechanics and Physics of Solids, 172: 105177. doi: 10.1016/j.jmps.2022.105177 [109] Nocedal J. 1980. Updating quasi-Newton matrices with limited storage. Mathematics of Computation, 35(151): 773-782. doi: 10.1090/S0025-5718-1980-0572855-7 [110] Olson G B. 1997. Computational design of hierarchically structured materials. Science, 277(5330): 1237-1242. doi: 10.1126/science.277.5330.1237 [111] Ouyang R, Curtarolo S, Ahmetcik E, et al. 2018. SISSO: A compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates. Physical Review Materials, 2(8): 083802. doi: 10.1103/PhysRevMaterials.2.083802 [112] Park C W, Kornbluth M, Vandermause J, et al. 2021. Accurate and scalable graph neural network force field and molecular dynamics with direct force architecture. npj Computational Materials, 7(1): 73. doi: 10.1038/s41524-021-00543-3 [113] Peng J, Yamamoto Y, Hawk J A, et al. 2020. Coupling physics in machine learning to predict properties of high-temperatures alloys. npj Computational Materials, 6(1): 141. doi: 10.1038/s41524-020-00407-2 [114] Peng X, Wu S, Qian W, et al. 2022. The potency of defects on fatigue of additively manufactured metals. International Journal of Mechanical Sciences, 221: 107185. doi: 10.1016/j.ijmecsci.2022.107185 [115] Penwarden M, Jagtap A D, Zhe S, et al. 2023. A unified scalable framework for causal sweeping strategies for physics-informed neural networks (PINNs) and their temporal decompositions. Journal of Computational Physics, 493: 112464. doi: 10.1016/j.jcp.2023.112464 [116] Penwarden M, Owhadi H, Kirby R M. 2024. Kolmogorov n-widths for multitask physics-informed machine learning (PIML) methods: Towards robust metrics. Neural Networks, 180: 106703. doi: 10.1016/j.neunet.2024.106703 [117] Perry B J, Guo Y, Mahmoud H N. 2022. Automated site-specific assessment of steel structures through integrating machine learning and fracture mechanics. Automation in Construction, 133: 104022. doi: 10.1016/j.autcon.2021.104022 [118] Picard R R, Cook R D. 1984. Cross-validation of regression models. Journal of the American Statistical Association, 79(387): 575-583. doi: 10.1080/01621459.1984.10478083 [119] Polak M P, Morgan D. 2024. Extracting accurate materials data from research papers with conversational language models and prompt engineering. Nature Communications, 15(1): 1569. doi: 10.1038/s41467-024-45914-8 [120] Ponciroli R, Shriwise P, Mei Z G, et al. 2022. Simulation-based methodology to assess the lattice defects creation as energy storing process. Annals of Nuclear Energy, 165: 108691. doi: 10.1016/j.anucene.2021.108691 [121] Qayyum F, Kim D H, Bong S J, et al. 2022. A survey of datasets, preprocessing, modeling mechanisms, and simulation tools based on AI for material analysis and discovery. Materials, 15(4): 1428. doi: 10.3390/ma15041428 [122] Quinlan J R. 1986. Induction of decision trees. Machine Learning, 1(1): 81-106. doi: 10.1023/A:1022643204877 [123] Raccuglia P, Elbert K C, Adler P D, et al. 2016. Machine-learning-assisted materials discovery using failed experiments. Nature, 533(7601): 73-76. doi: 10.1038/nature17439 [124] Rainio O, Teuho J, Klén R. 2024. Evaluation metrics and statistical tests for machine learning. Scientific Reports, 14(1): 6086. doi: 10.1038/s41598-024-56706-x [125] Raissi M, Perdikaris P, Karniadakis G E. 2019. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics, 378: 686-707. doi: 10.1016/j.jcp.2018.10.045 [126] Ramprasad R, Batra R, Pilania G, et al. 2017. Machine learning in materials informatics: Recent applications and prospects. npj Computational Materials, 3(1): 54. doi: 10.1038/s41524-017-0056-5 [127] Ras G, Xie N, Van Gerven M, et al. 2022. Explainable deep learning: A field guide for the uninitiated. Journal of Artificial Intelligence Research, 73: 329-396. doi: 10.1613/jair.1.13200 [128] Rasiwasia N, Costa Pereira J, Coviello E, et al. 2010. A new approach to cross-modal multimedia retrieval. In Proceedings of the 18th ACM international conference on Multimedia. [129] Reiser P, Neubert M, Eberhard A, et al. 2022. Graph neural networks for materials science and chemistry. Communications Materials, 3(1): 93. doi: 10.1038/s43246-022-00315-6 [130] Ren D, Wang C, Wei X, et al. 2023. Building a quantitative composition-microstructure-property relationship of dual-phase steels via multimodal data mining. Acta Materialia, 252: 118954. doi: 10.1016/j.actamat.2023.118954 [131] Rezaei S, Taghikhani K, Viardin A, et al. 2025. Digitalizing metallic materials from image segmentation to multiscale solutions via physics informed operator learning. npj Computational Materials, 11(1): 262. doi: 10.1038/s41524-025-01718-y [132] Rodrigues J F, Lopes Cardoso H, Teixeira Lopes C. 2025. Evaluating llama 3 for text simplification: A study on Wikipedia lead sections. In Companion Proceedings of the ACM on Web Conference 2025. [133] Rosenblatt F. 1958. The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review, 65(6): 386. doi: 10.1037/h0042519 [134] Roy A M, Guha S, Sundararaghavan V, et al. 2024. Physics-infused deep neural network for solution of non-associative Drucker–Prager elastoplastic constitutive model. Journal of the Mechanics and Physics of Solids, 185: 105570. doi: 10.1016/j.jmps.2024.105570 [135] S Schweizer P, Sharma A, Pethö L, et al. 2023. Atomic scale volume and grain boundary diffusion elucidated by in situ STEM. Nature Communications, 14(1): 7601. doi: 10.1038/s41467-023-43103-7 [136] Saidi P, Pirgazi H, Sanjari M, et al. 2022. Deep learning and crystal plasticity: A preconditioning approach for accurate orientation evolution prediction. Computer Methods in Applied Mechanics and Engineering, 389: 114392. doi: 10.1016/j.cma.2021.114392 [137] Salvado F C, Teixeira-Dias F, Walley S M, et al. 2017. A review on the strain rate dependency of the dynamic viscoplastic response of FCC metals. Progress in Materials Science, 88: 186-231. doi: 10.1016/j.pmatsci.2017.04.004 [138] Sasidhar K N, Siboni N H, Mianroodi J R, et al. 2023. Enhancing corrosion-resistant alloy design through natural language processing and deep learning. Science Advances, 9(32): 7992. doi: 10.1126/sciadv.adg7992 [139] Scarselli F, Gori M, Tsoi A C, et al. 2008. The graph neural network model. IEEE Transactions on Neural Networks, 20(1): 61-80. [140] Schmitt J H, Iung T. 2018. New developments of advanced high-strength steels for automotive applications. Comptes Rendus Physique, 19(8): 641-656. doi: 10.1016/j.crhy.2018.11.004 [141] Schütt K T, Sauceda H E, Kindermans P J, et al. 2018. Schnet—A deep learning architecture for molecules and materials. The Journal of Chemical Physics, 148(24). [142] Sen P C, Hajra M, Ghosh M. 2019. Supervised classification algorithms in machine learning: A survey and review. In Emerging technology in modelling and graphics: Proceedings of IEM graph 2018. [143] Song L, Meng S, Zhao J, et al. 2025. Exploration of machine learning approach to predict ultra-high temperature mechanical properties of carbon/carbon composites from multi-scale microstructure parameters. Diamond and Related Materials, 112647. [144] Su T H, Huang S J, Jean J G, et al. 2022. Multiscale computational solid mechanics: Data and machine learning. Journal of Mechanics, 38: 568-585. doi: 10.1093/jom/ufac037 [145] Tan Z, Luo L, Zhong J. 2023. Knowledge transfer in evolutionary multi-task optimization: A survey. Applied Soft Computing, 138: 110182. doi: 10.1016/j.asoc.2023.110182 [146] Tansley S, Tolle K M. 2009. The fourth paradigm: Data-intensive scientific discovery. Redmond, WA: Microsoft research. [147] Tjoa E, Guan C. 2020. A survey on explainable artificial intelligence (xai): Toward medical xai. IEEE Transactions on Neural Networks and Learning Systems, 32(11): 4793-4813. [148] Tripathi M K, Kumar R, Tripathi R. 2020. Big-data driven approaches in materials science: A survey. Materials Today: Proceedings, 26: 1245-1249. doi: 10.1016/j.matpr.2020.02.249 [149] Unke O T, Meuwly M. 2019. PhysNet: A neural network for predicting energies, forces, dipole moments, and partial charges. Journal of Chemical Theory and Computation, 15(6): 3678-3693. doi: 10.1021/acs.jctc.9b00181 [150] Unocic R R, Viswanathan G B, Sarosi P M, et al. 2008. Mechanisms of creep deformation in polycrystalline Ni-base disk superalloys. Materials Science and Engineering: A, 483: 25-32. [151] Vaswani A, Shazeer N, Parmar N, et al. 2017. Attention is all you need. Advances in Neural Information Processing Systems, 30. [152] Versino D, Tonda A, Bronkhorst C A. 2017. Data driven modeling of plastic deformation. Computer Methods in Applied Mechanics and Engineering, 318: 981-1004. doi: 10.1016/j.cma.2017.02.016 [153] Voyiadjis G Z, Almasri A H. 2008. A physically based constitutive model for fcc metals with applications to dynamic hardness. Mechanics of Materials, 40(6): 549-563. doi: 10.1016/j.mechmat.2007.11.008 [154] Wang C, Shen C, Cui Q, et al. 2020a. Tensile property prediction by feature engineering guided machine learning in reduced activation ferritic/martensitic steels. Journal of Nuclear Materials, 529: 151823. doi: 10.1016/j.jnucmat.2019.151823 [155] Wang C, Zhang C, Yang Z, et al. 2016. Microstructure analysis and yield strength simulation in high Co–Ni secondary hardening steel. Materials Science and Engineering: A, 669: 312-317. doi: 10.1016/j.msea.2016.05.069 [156] Wang G, Hu J, Zhou J, et al. 2025a. Knowledge-guided large language model for material science. Review of Materials Research, 100007. [157] Wang H, Li B, Xuan F Z. 2022a. Fatigue-life prediction of additively manufactured metals by continuous damage mechanics (CDM)-informed machine learning with sensitive features. International Journal of Fatigue, 164: 107147. doi: 10.1016/j.ijfatigue.2022.107147 [158] Wang H, Li B, Gong J, et al. 2023a. Machine learning-based fatigue life prediction of metal materials: Perspectives of physics-informed and data-driven hybrid methods. Engineering Fracture Mechanics, 284: 109242. doi: 10.1016/j.engfracmech.2023.109242 [159] Wang J, Guo W G, Gao X, et al. 2015. The third-type of strain aging and the constitutive modeling of a Q235B steel over a wide range of temperatures and strain rates. International Journal of Plasticity, 65: 85-107. doi: 10.1016/j.ijplas.2014.08.017 [160] Wang J, Li Y, Zhao R, et al. 2020b. Physics guided neural network for machining tool wear prediction. Journal of Manufacturing Systems, 57: 298-310. doi: 10.1016/j.jmsy.2020.09.005 [161] Wang L, Zhu S P, Luo C, et al. 2023b. Physics-guided machine learning frameworks for fatigue life prediction of AM materials. International Journal of Fatigue, 172: 107658. doi: 10.1016/j.ijfatigue.2023.107658 [162] Wang P, Jiang Y, Liao W, et al. 2025b. Generalizable descriptors for automatic titanium alloys design by learning from texts via large language model. Acta Materialia, 121275. [163] Wang Q, Ma Y, Zhao K, et al. 2022b. A comprehensive survey of loss functions in machine learning. Annals of Data Science, 9(2): 187-212. doi: 10.1007/s40745-020-00253-5 [164] Wang Z, Cudmani R, Olarte A A P. 2025c. Connecting and distinguishing conventional and data-driven constitutive models: The role of state boundary surfaces. Journal of the Mechanics and Physics of Solids, 200: 106122. doi: 10.1016/j.jmps.2025.106122 [165] Wang Z, Dai Z, Póczos B, et al. 2019. Characterizing and avoiding negative transfer. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. [166] Wang Z, Wang K, Wang Q, et al. 2025d. Ragen: Understanding self-evolution in llm agents via multi-turn reinforcement learning. arXiv preprint arXiv: 2504.20073. [167] Wei Y, Serra Q, Lubineau G, et al. 2023. Coupling physics-informed neural networks and constitutive relation error concept to solve a parameter identification problem. Computers & Structures, 283: 107054. [168] Weiss K, Khoshgoftaar T M, Wang D. 2016. A survey of transfer learning. Journal of Big data, 3(1): 9. doi: 10.1186/s40537-016-0043-6 [169] Whitman S E, Latypov M I. 2025. Machine learning of microstructure–property relationships in materials leveraging microstructure representation from foundational vision transformers. Acta Materialia, 121217. [170] Wolpert D H, Macready W G. 2002. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1): 67-82. [171] Wu J, Yin X, Xiao H. 2018. Seeing permeability from images: Fast prediction with convolutional neural networks. Science Bulletin, 63(18): 1215-1222. doi: 10.1016/j.scib.2018.08.006 [172] Xiao S, Hu R, Li Z, et al. 2020. A machine-learning-enhanced hierarchical multiscale method for bridging from molecular dynamics to continua. Neural Computing and Applications, 32(18): 14359-14373. doi: 10.1007/s00521-019-04480-7 [173] Xie Q, Suvarna M, Li J, et al. 2021. Online prediction of mechanical properties of hot rolled steel plate using machine learning. Materials & Design, 197: 109201. [174] Xiong J, Shi S Q, Zhang T Y. 2021. Machine learning of phases and mechanical properties in complex concentrated alloys. Journal of Materials Science & Technology, 87: 133-142. [175] Xiong J, Zhang T, Shi S. 2020. Machine learning of mechanical properties of steels. Science China Technological Sciences, 63(7): 1247-1255. doi: 10.1007/s11431-020-1599-5 [176] Xu C, Cao B T, Yuan Y, et al. 2023a. Transfer learning based physics-informed neural networks for solving inverse problems in engineering structures under different loading scenarios. Computer Methods in Applied Mechanics and Engineering, 405: 115852. doi: 10.1016/j.cma.2022.115852 [177] Xu C, Wang Y, Barati Farimani A. 2023b. TransPolymer: A transformer-based language model for polymer property predictions. npj Computational Materials, 9(1): 64. doi: 10.1038/s41524-023-01016-5 [178] Xu X, Wang L, Zhu G, et al. 2020. Predicting tensile properties of AZ31 magnesium alloys by machine learning. Jom, 72(11): 3935-3942. doi: 10.1007/s11837-020-04343-w [179] Yang F, Li Z, Wang Q, et al. 2020. Cluster-formula-embedded machine learning for design of multicomponent β-Ti alloys with low Young’s modulus. npj Computational Materials, 6(1): 101. doi: 10.1038/s41524-020-00372-w [180] Yang J, Kang G, Liu Y, et al. 2021a. A novel method of multiaxial fatigue life prediction based on deep learning. International Journal of Fatigue, 151: 106356. doi: 10.1016/j.ijfatigue.2021.106356 [181] Yang L, Meng X, Karniadakis G E. 2021b. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. Journal of Computational Physics, 425: 109913. doi: 10.1016/j.jcp.2020.109913 [182] Yasnii О P, Pastukh O А, Pyndus Y І, et al. 2018. Prediction of the diagrams of fatigue fracture of D16T aluminum alloy by the methods of machine learning. Materials Science, 54(3): 333-338. doi: 10.1007/s11003-018-0189-9 [183] Yu A, Pan Y, Yue L, et al. 2024. Explainable machine learning for hardness prediction of laser powder bed fused Ti-6Al-4V and assisting in understanding effects of process parameters. Journal of Alloys and Compounds, 1008: 176566. doi: 10.1016/j.jallcom.2024.176566 [184] Zeni C, Pinsler R, Zügner D, et al. 2025. A generative model for inorganic materials design. Nature, 639(8055): 624-632. doi: 10.1038/s41586-025-08628-5 [185] Zhan Z, Ao N, Hu Y, et al. 2022. Defect-induced fatigue scattering and assessment of additively manufactured 300M-AerMet100 steel: An investigation based on experiments and machine learning. Engineering Fracture Mechanics, 264: 108352. doi: 10.1016/j.engfracmech.2022.108352 [186] Zhang T, Yang D B. 2025. Multimodal machine learning with large language embedding model for polymer property prediction. Chemistry of Materials, 37(18): 7002-7013. doi: 10.1021/acs.chemmater.5c00940 [187] Zhang Y, Khan S A, Mahmud A, et al. 2025. Exploring the role of large language models in the scientific method: From hypothesis to discovery. npj Artificial Intelligence, 1(1): 14. doi: 10.1038/s44387-025-00019-5 [188] Zhang Z, Sun C. 2021. Structural damage identification via physics-guided machine learning: A methodology integrating pattern recognition with finite element model updating. Structural Health Monitoring, 20(4): 1675-1688. doi: 10.1177/1475921720927488 [189] Zhao P, Wang Y, Jiang B, et al. 2023. Neural network modeling of titanium alloy composition-microstructure−property relationships based on multimodal data. Materials Science and Engineering: A, 879: 145202. doi: 10.1016/j.msea.2023.145202 [190] Zhou T, Jiang S, Han T, et al. 2023. A physically consistent framework for fatigue life prediction using probabilistic physics-informed neural network. International Journal of Fatigue, 166: 107234. doi: 10.1016/j.ijfatigue.2022.107234 [191] Zhou W, Xu Y F. 2024. Damage identification for plate structures using physics-informed neural networks. Mechanical Systems and Signal Processing, 209: 111111. doi: 10.1016/j.ymssp.2024.111111 -




 下载:
下载: