Viscoelastic behaviors of amorphous alloys in the framework of the quasi-point defect theory
-
摘要: 非晶合金因其独特的原子结构而呈现出复杂的粘弹性行为, 表现为动态弛豫和静态滞后特征, 这不仅是深入理解玻璃转变、塑性变形机制及动态非均匀性等基础物理问题的核心切入点, 也为高性能非晶合金与功能材料的开发及工程应用提供了关键理论支撑. 如何从微观机制出发构建一个能够统一描述并预测其复杂粘弹性行为的理论框架, 仍是非晶固体领域面临的重要挑战. 基于此, 本文聚焦于准点缺陷 (Quasi-Point Defect, QPD) 理论在系统解析非晶合金粘弹性行为中的核心作用及其最新研究进展. 深入探讨了运用 QPD 理论分析非晶合金中的动态弛豫现象, 并揭示了该理论与分数阶模型的内在一致性. 在此基础上, 综述了动态弛豫与宏观准静态粘弹性变形的内在关联, 阐释了两步松弛、蠕变等现象背后由不同尺度缺陷运动主导的物理机制. 针对蠕变行为, 重点讨论了基于QPD理论对非晶合金中缺陷演化和多级幂律蠕变机制的理解. 此外, 本文系统阐述了通过粘弹性变形调控非晶合金能量状态的机制, 以及这种调控如何通过影响准点缺陷的浓度、分布及协同运动, 进而改变材料的动态弛豫特征. 本文旨在展现如何基于准点缺陷理论构建非晶合金微观结构非均匀性、缺陷动力学与宏观粘弹性响应之间的关联, 为理解和预测其复杂力学行为提供重要理论视角.Abstract: Amorphous alloys exhibit complex viscoelastic behaviors due to their unique atomic structure, characterized by dynamic relaxation and static hysteresis features. This not only serves as a core entry point for in-depth understanding of fundamental physical issues such as glass transition, plastic deformation mechanisms, and dynamic heterogeneity, but also provides key theoretical support for the development and engineering application of high-performance amorphous alloys. Currently, how to construct a theoretical framework from the microscopic mechanism that can uniformly describe and predict their complex viscoelastic behaviors remains a core challenge in this field. This paper focuses on the core role and latest progress of the Quasi-Point Defect (QPD) theory in systematically analyzing the viscoelastic behaviors. It deeply explores the application of the QPD theory in analyzing dynamic relaxation and reveals the intrinsic consistency between this theory and fractional models. On this basis, it reviews the intrinsic connection between dynamic relaxation and macroscopic quasi-static viscoelastic deformation, and explains the physical mechanisms behind phenomena such as two-step relaxation and creep, which are dominated by defect movements at different scales. Regarding creep behavior, it particularly discusses the understanding of defect evolution and multi-level power-law creep mechanisms. Additionally, this paper systematically expounds the mechanism of regulating the energy state of amorphous alloys through viscoelastic deformation and how this regulation changes the dynamic relaxation of the material by influencing the concentration, distribution, and cooperative movement of quasi-point defects. This paper aims to demonstrate how to establish the correlation between the microstructure heterogeneity, defect dynamics, and viscoelastic response of amorphous alloys based on the QPD theory, providing a theoretical perspective for understanding and predicting their complex mechanical behaviors.
-
Key words:
- Amorphous alloys /
- Viscoelastic behavior /
- Quasi-point defect /
- Dynamic relaxation /
- Creep /
- Stress relaxation /
- rejuvenation.
-
图 2 (a)非晶固体内部原子/分子运动分级关联示意图 (Rinaldi et al., 2011); (b)非晶固体在准点缺陷理论框架下微观变形描述, 包括初始结构QPD位点在热力耦合刺激作用下的激活、扩展和合并过程 (Rinaldi et al., 2011); (c)微剪切畴结构示意图 (Perez, 1984)
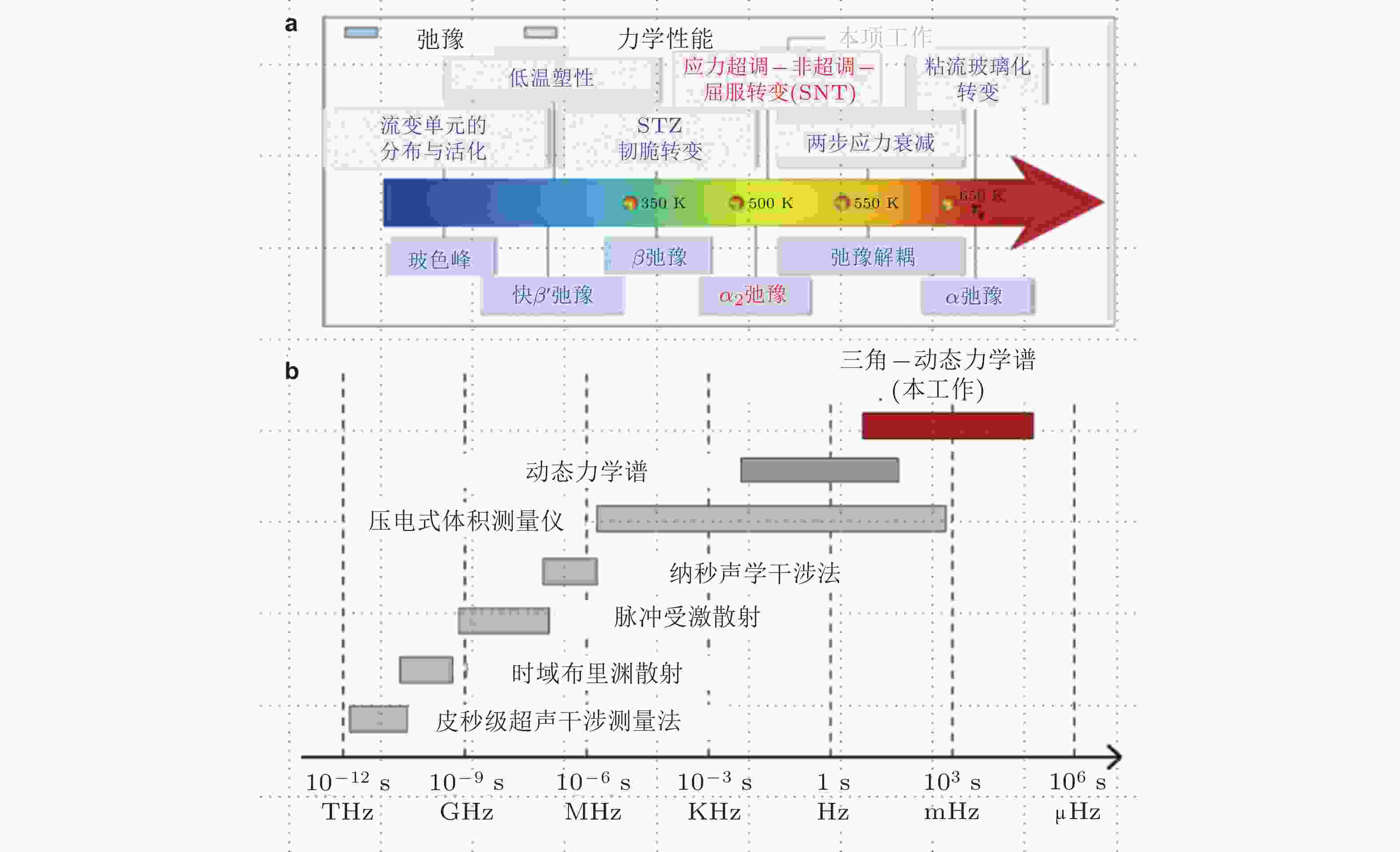
图 3 (a) 弛豫行为与力学性能之间的关联关系图 (Zhou et al., 2021). 特征温度以Al90Sm10非晶合金为例绘制. (b) 各类弛豫谱测试技术的频率范围与时间尺度分布 (Yang et al., 2024c)
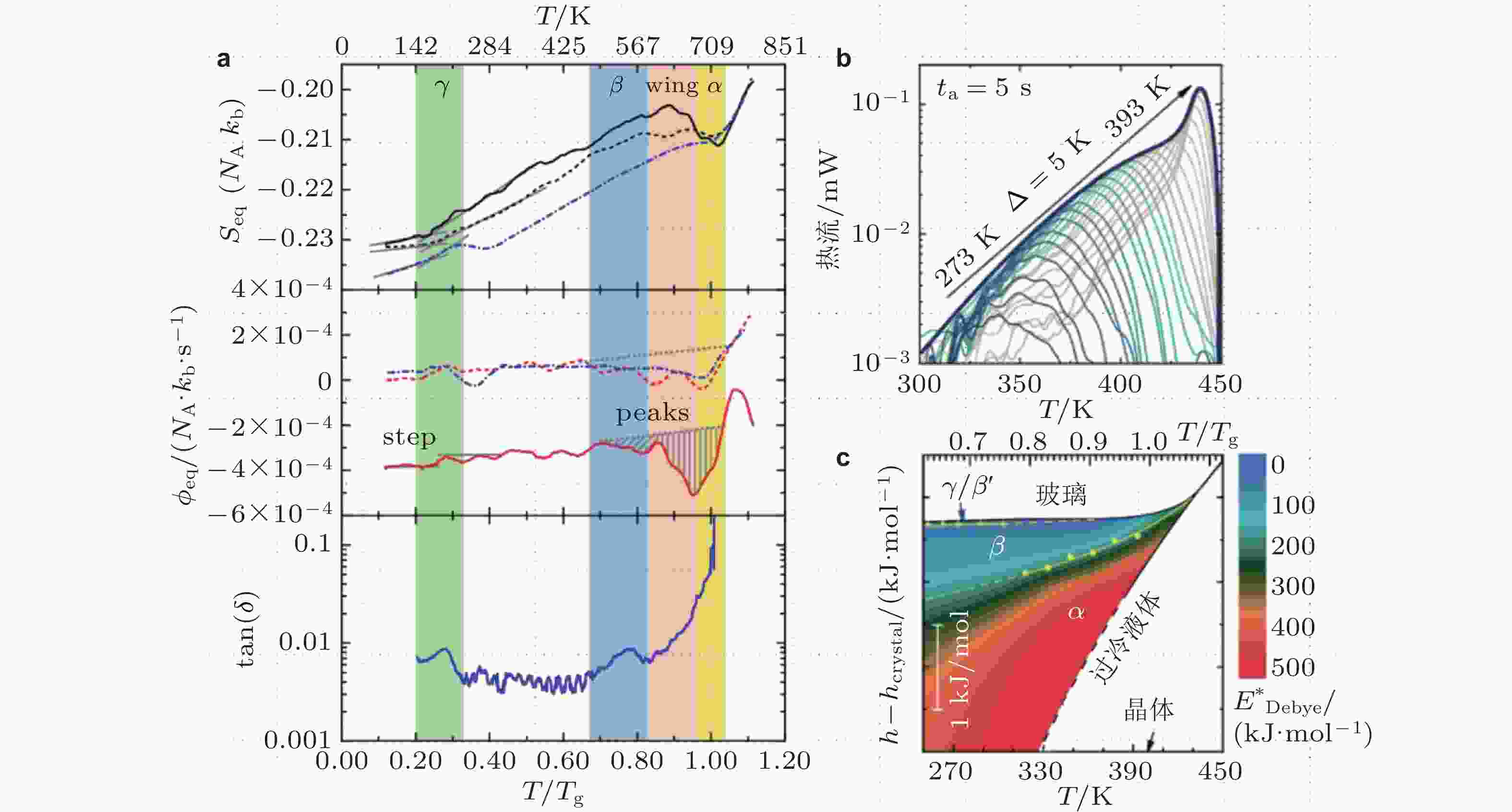
图 4 (a) 从等效构型熵导出等效构型热流过程(Spieckermann et al., 2022). γ 弛豫处的斜率变化由灰色实线标出. 在进入 β 弛豫以及 β 与 α 之间的过剩尾时出现显著的焓弛豫现象. (b)不同退火温度下的热流弛豫峰谱图 (Song et al., 2023). (c) 不同弛豫模式的温度–焓图(Song et al., 2023)
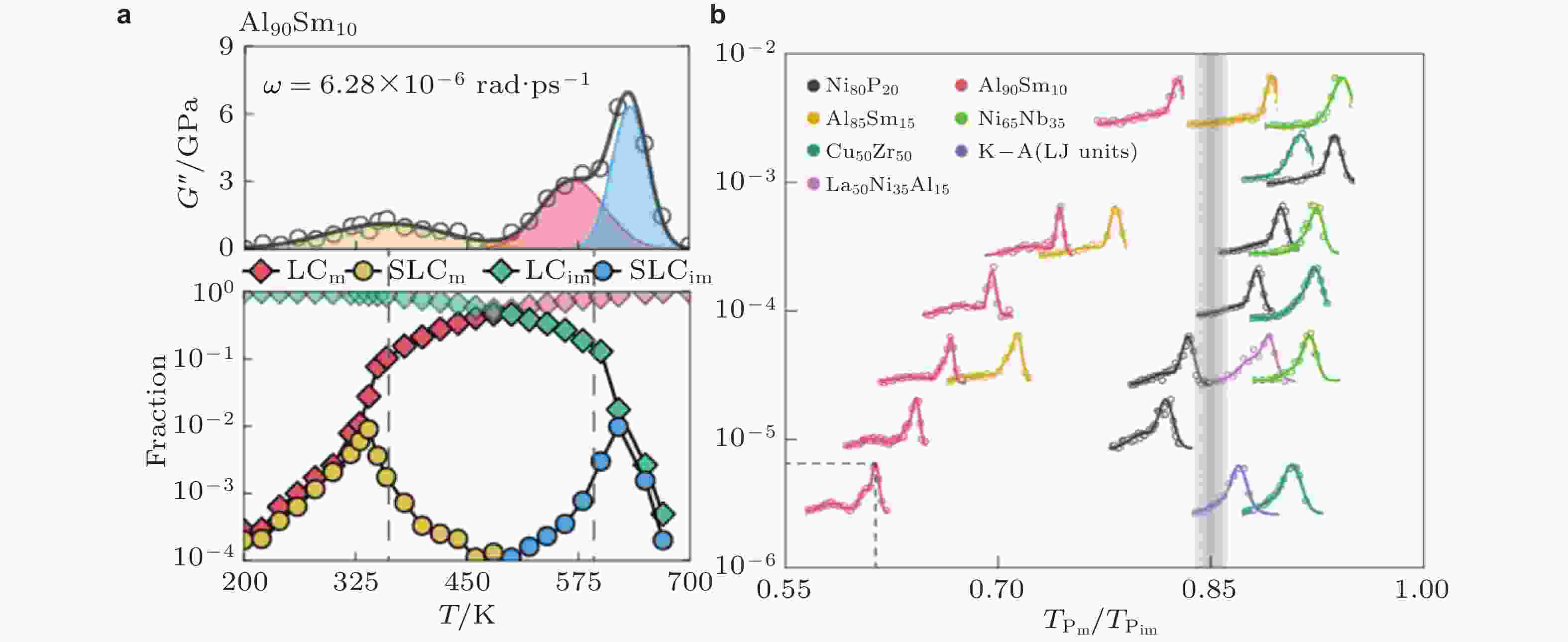
图 5 (a) Al90Sm10体系中, α和 β 弛豫峰分别对应非迁移性粒子逾渗和迁移性粒子逾渗的特征温度 (Gao et al., 2025). (b)三维体系的 β弛豫形态(峰, 肩膀峰或过剩尾)取决于迁移性与非迁移性粒子逾渗温度的比值 (Gao et al., 2025)
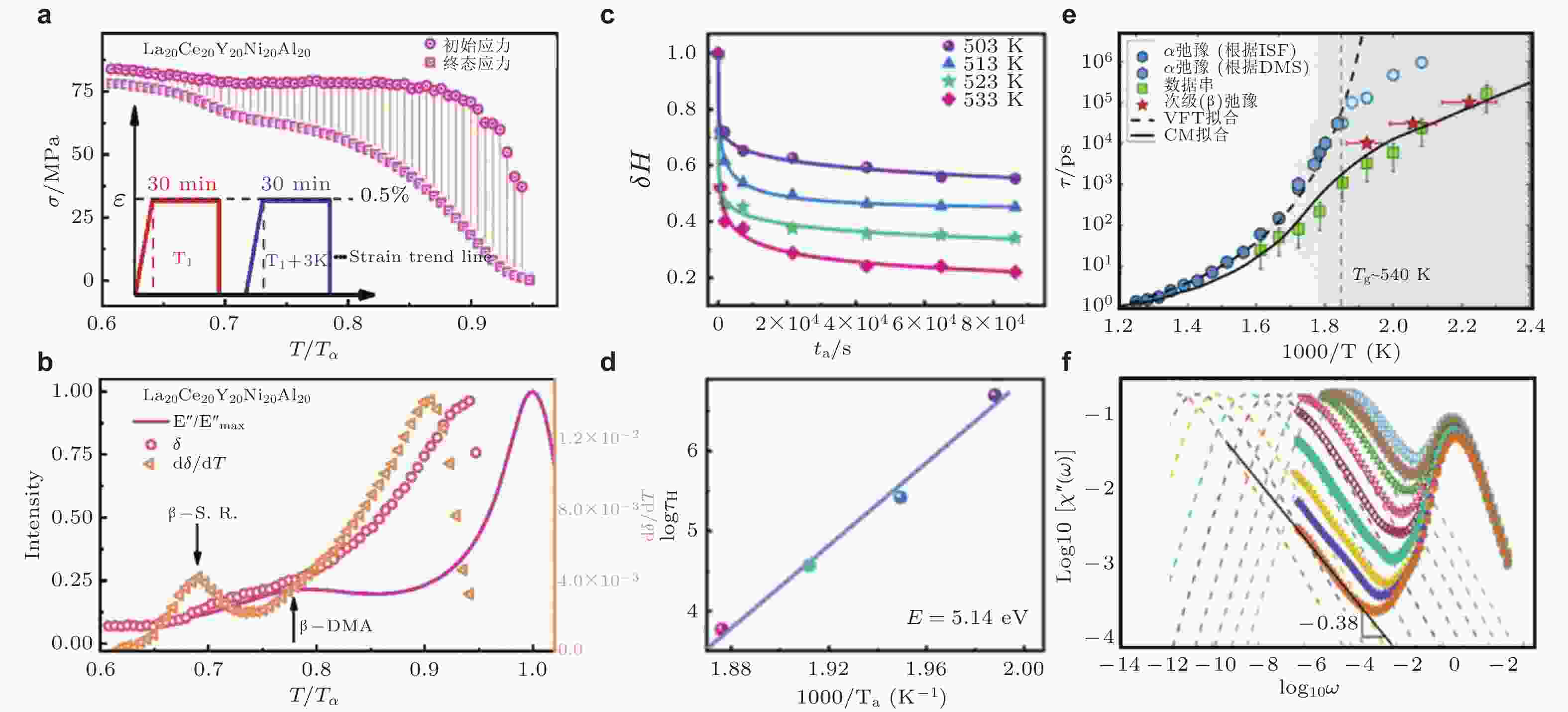
图 6 从室温到
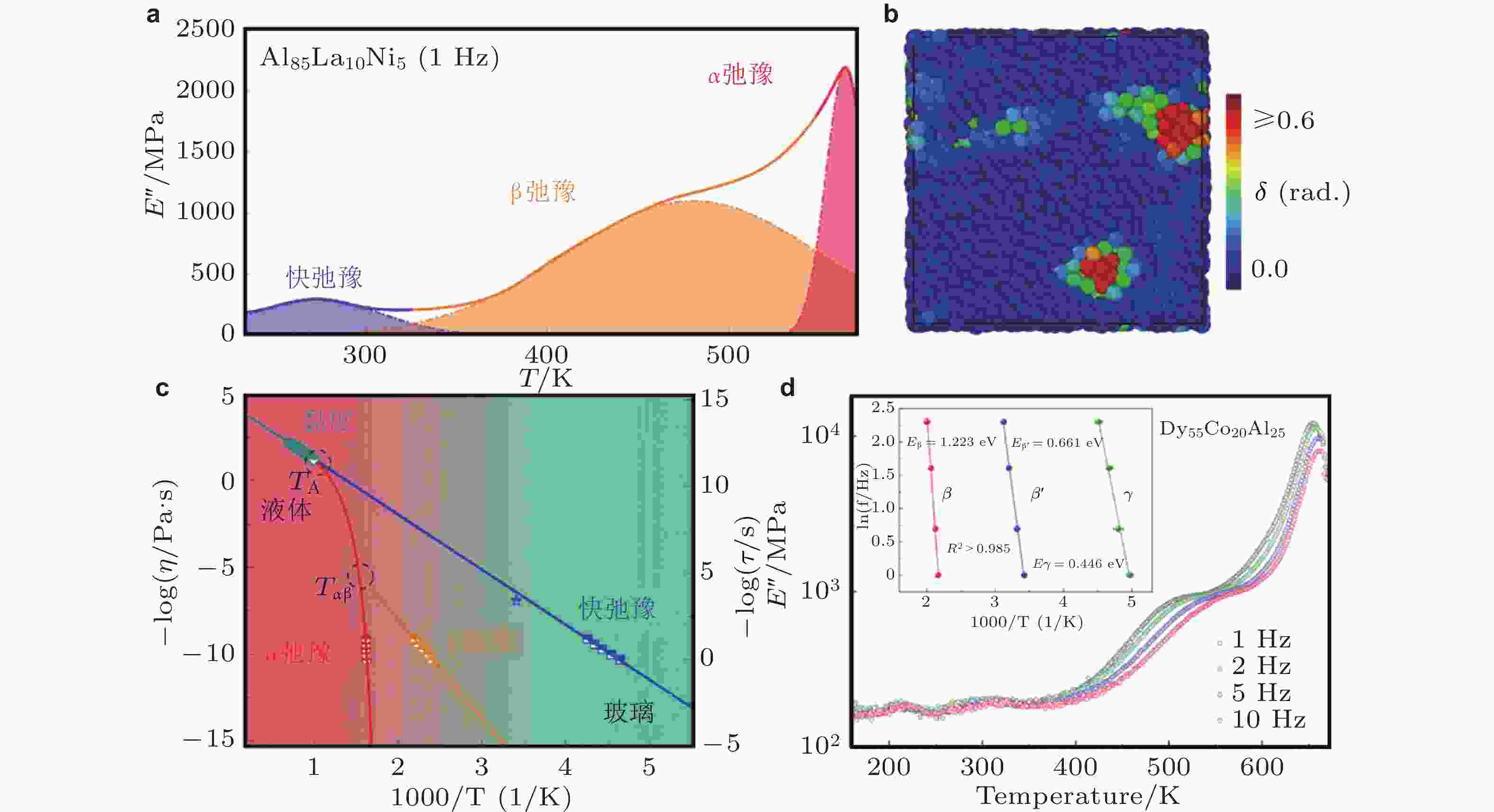
$ {T}_{\alpha } $ 步进温度下, (a) La基高熵非晶合金应力松弛曲线和 (b) 对应的应力变化, 应力变化率以及归一化损耗模量的演化 (Duan et al., 2022). (c) 不同退火温度$ {T}_{a} $ 下归一化过剩焓$ \delta H $ 随退火时间的变化关系 (Duan et al., 2024). (d) 焓弛豫时间$ {\tau }_{H} $ 与退火温度倒数$ 1/{T}_{a} $ 的阿伦尼乌斯关系 (Duan et al., 2024). (e) Ni80P20非晶合金的弛豫图谱 (Zhou et al., 2024b). (f) 三维玻璃中“过剩尾”现象的出现, 虚线表示估算得到的α弛豫峰位置 (Guiselin et al., 2022)
图 7 (a) 非晶合金中快速弛豫过程在动态弛豫谱中的呈现 (Chang et al., 2022); (b) 原子尺度的弹性与耗散(Yu and Wang, 2024); (c) Y68.9Co31.1非晶合金的实验弛豫图谱 (Chang et al., 2022); (d) Dy55Co20A25非晶合金在驱动频率为1-10 Hz时损耗模量随温度的变化情况, 插图展示了根据阿伦尼乌斯关系拟合得到的不同弛豫过程的激活能 (Shao et al., 2023)
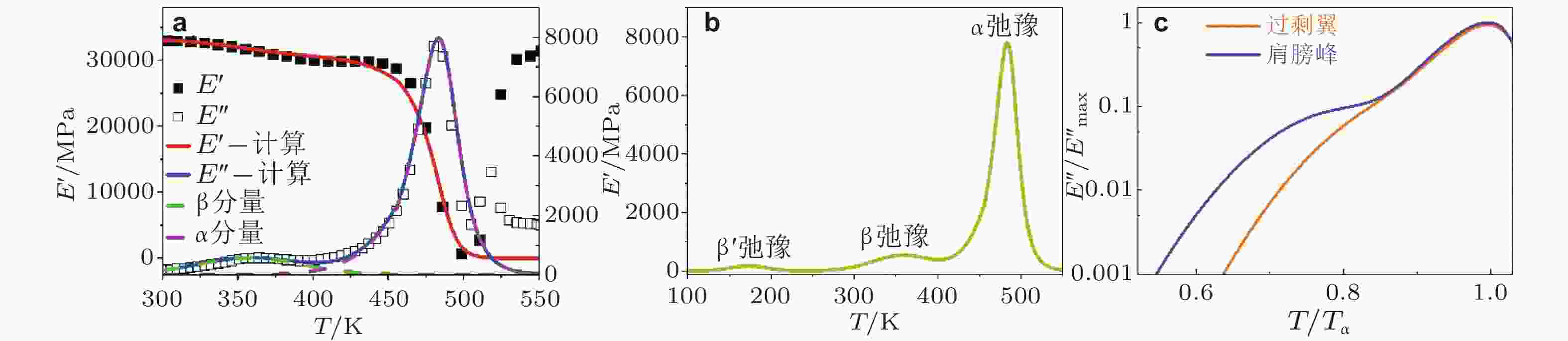
图 8 (a) La60Ni15Al25块体非晶合金动态力学参量随温度的演化. 实线为基于公式 (1.28b) 的拟合曲线, 绿色和紫色虚线分别为α弛豫和β弛豫对损耗模量的贡献. 当前模型对其他形式动态弛豫温度谱图的计算曲线. (b) 当前模型对不同弛豫模式计算, 包括明显分离的快
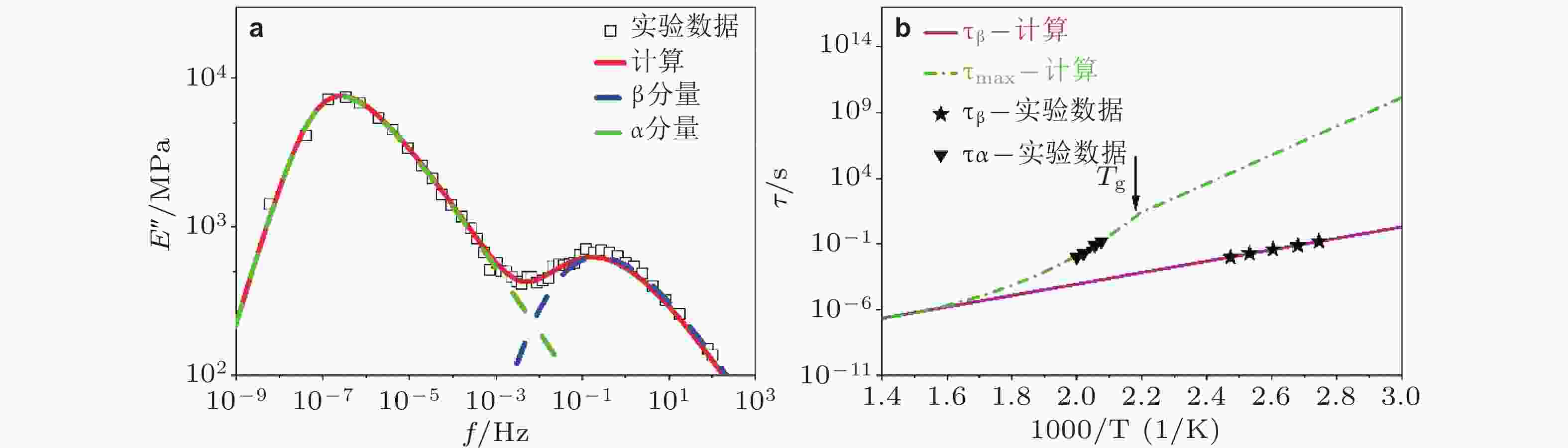
$ \beta ' $ 弛豫过程; (c) 当前模型对$ \beta $ 弛豫的不同表现形式 (肩膀峰和过剩尾)的计算曲线 (Hao et al., 2022)
图 9 (a) La60Ni15Al25非晶合金损耗模量
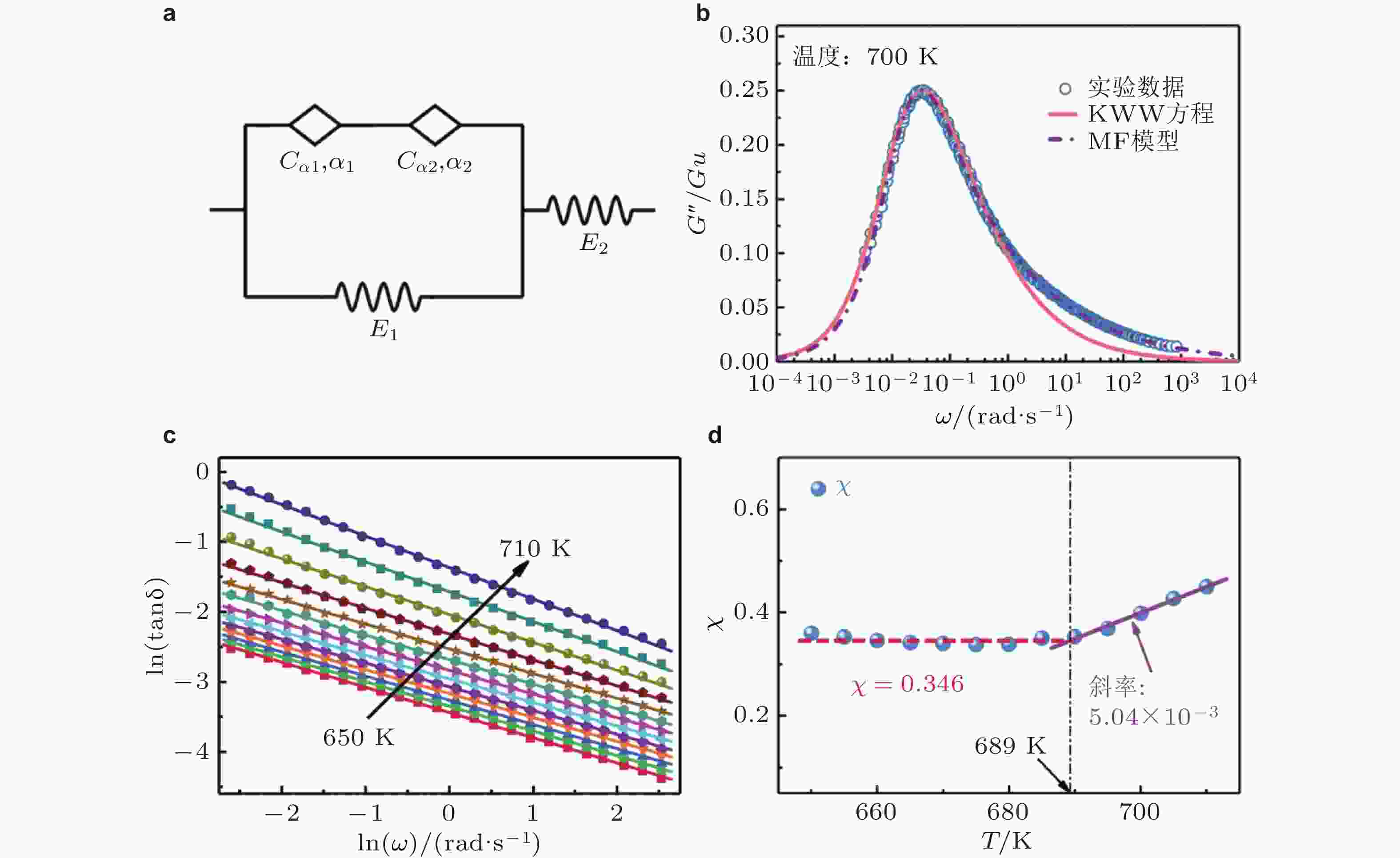
$ {E}'' $ 的频率域主曲线. 红色实线: 基于准点缺陷理论所得计算曲线;绿色和蓝色虚线分别为α和β两个弛豫模式对频率谱图的贡献; (b) α和β两种弛豫模式特征时间随温度的演化. 黑色符号为基于损耗模量曲线峰值位置$ \omega \tau =1 $ 确定的$ {\tau }_{\alpha } $ 和$ {\tau }_{\beta } $ 的实验值; 紫色实线为根据Arrhenius公式计算所得$ {\tau }_{\beta } $ 随温度的演化; 绿色虚线表示为当前模型预测所得$ {\tau }_{\text{max}} $ 随温度演化规律 (Hao et al., 2022)
图 10 (a) 改进分数阶模型 (MF模型); (b) 不同模型描述实验数据的结果. 实线是由KWW方程拟合得到; 虚线是由 MF模型拟合得到的, 其中
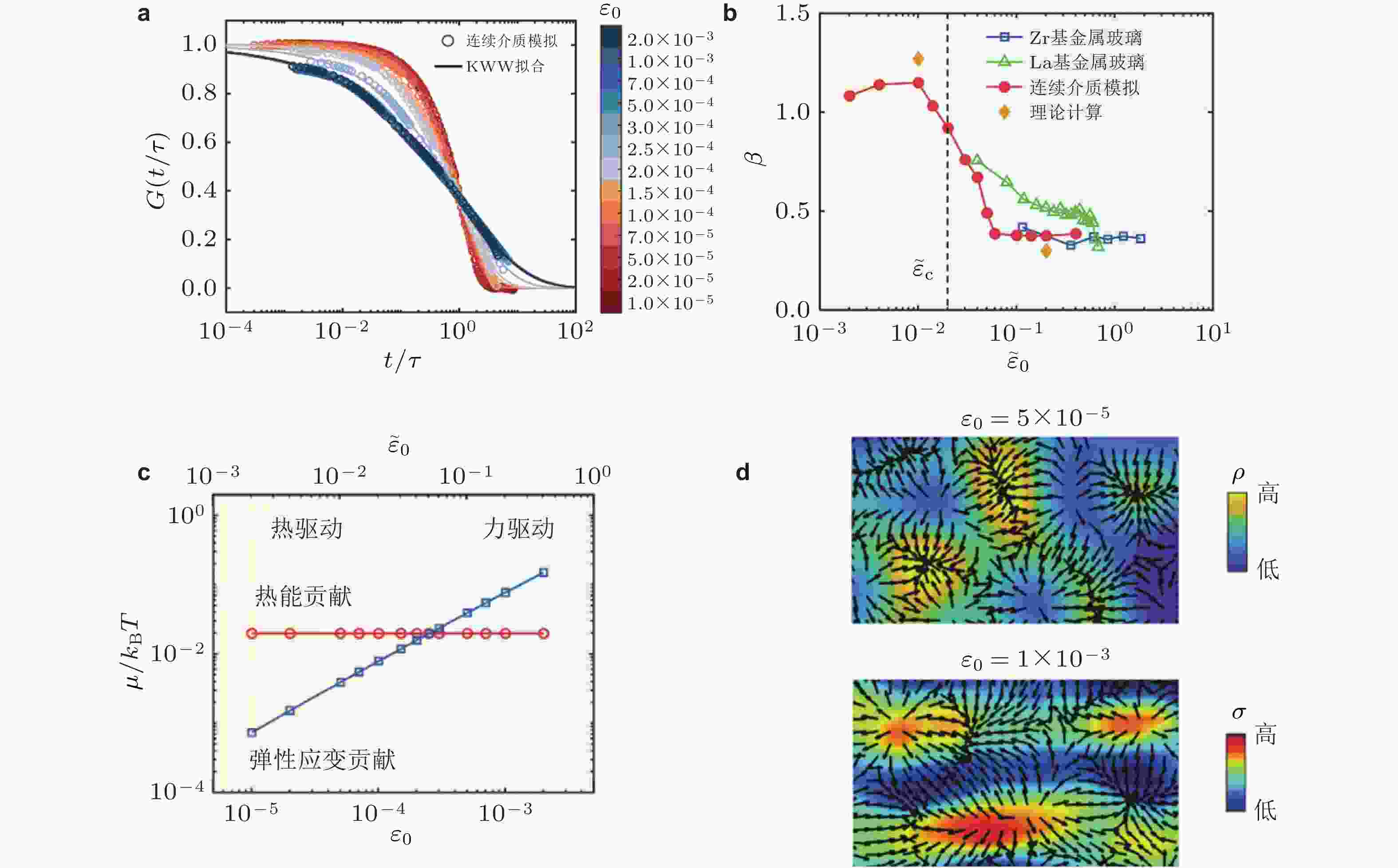
$ \dfrac{\left({G}_{\infty }-{G}_{0}\right)}{{G}_{\infty }}=0.94 $ ,$ {\tau }_{MF}=35.1s $ ,$ \lambda =0.99 $ ,$ {\alpha }_{2}=0.35 $ ; (c) 不同温度下驱动频率与损耗因子$ \mathrm{tan}\delta $ 在对数下的关系; (d) 关联因子$ \mathrm{\chi } $ 随温度的演化趋势 (Zhu et al., 2023)
图 11 (a) 基于连续介质模型, 模拟不同应变下非晶合金的弛豫函数随归一化时间的变化. 实线是使用KWW方程拟合的曲线; (b)形状参数β随应变的演化规律; (c) 热能密度和弹性应变密度部分对化学势的贡献对比; (d) 热驱动和应力驱动弛豫过程中不同的原子动力学 (Zhu et al., 2024b)
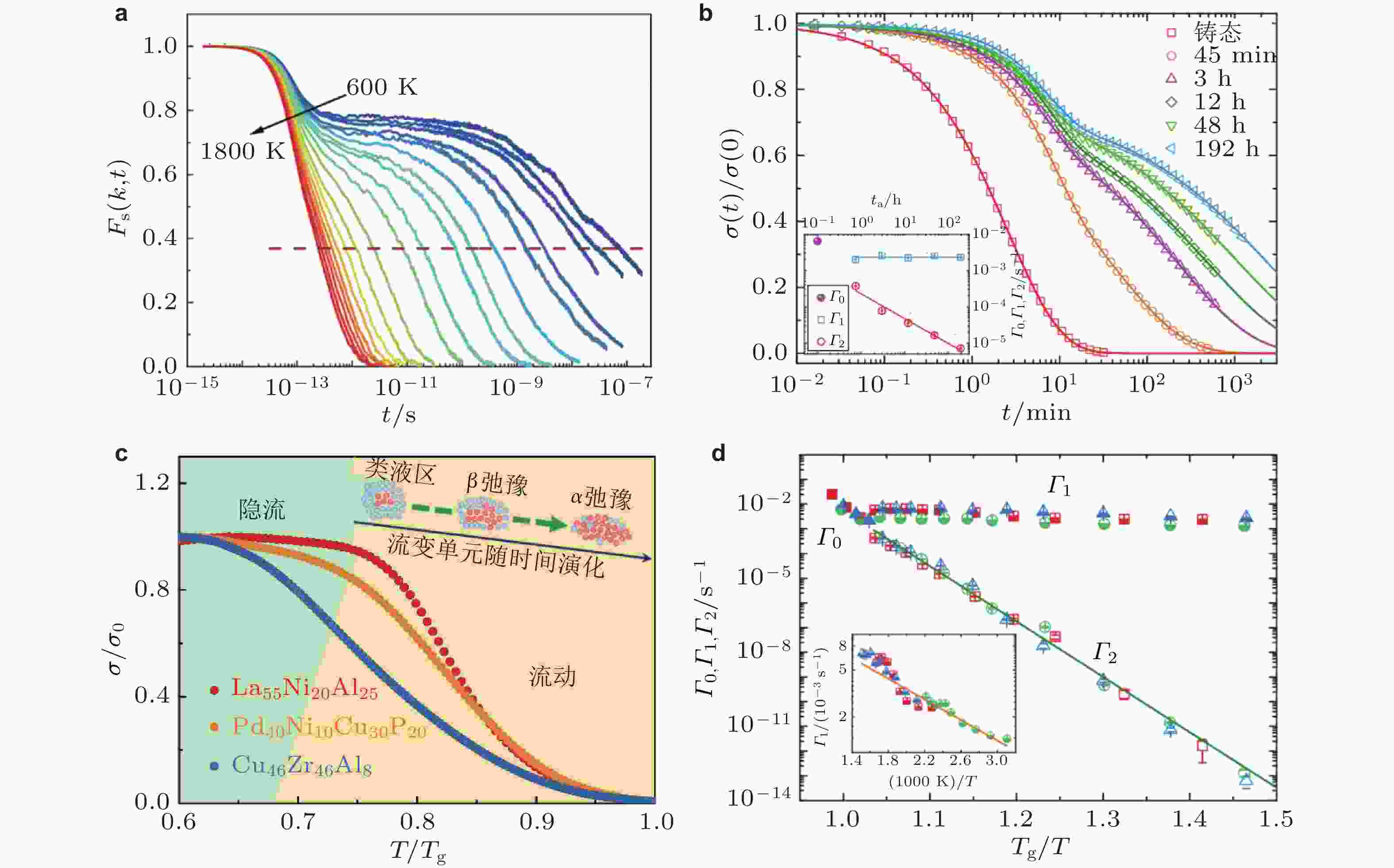
图 12 (a) 分子动力学模拟CuZr非晶合金宽温度范围内的中间散射函数 (Cao and Wang, 2024); (b) Zr44Ti11Cu10Ni10Be25非晶合金的两步应力松弛曲线 (Luo et al., 2017); (c) 三种不同β弛豫形式非晶合金线形升温应力弛豫行为 (Lu et al., 2016); (d) 弛豫速率的劈裂 (Luo et al., 2017)
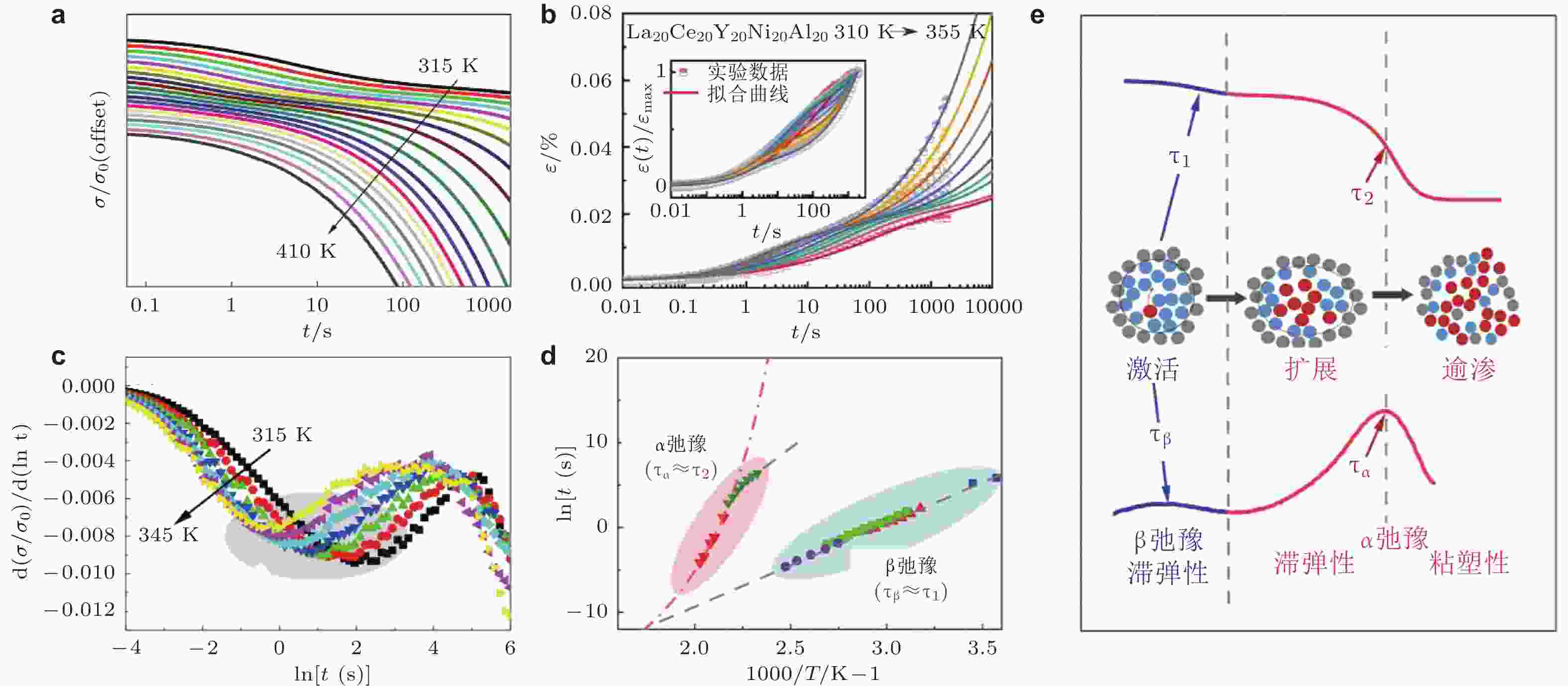
图 13 La基非晶合金(a)应力松弛 (Hao et al., 2023a)和(b)蠕变过程 (Xing et al., 2024)现象; (c)从应力衰减速率与时间的关系中识别快速衰减过程的特征时间 (Hao et al., 2023a). (d) 两步应力松弛特征时间和动态松弛的温度依赖性 (Hao et al., 2023a). (e) STZ的激活, 扩展和湮灭导致的应力衰减和动态弛豫 (Hao et al., 2023a)
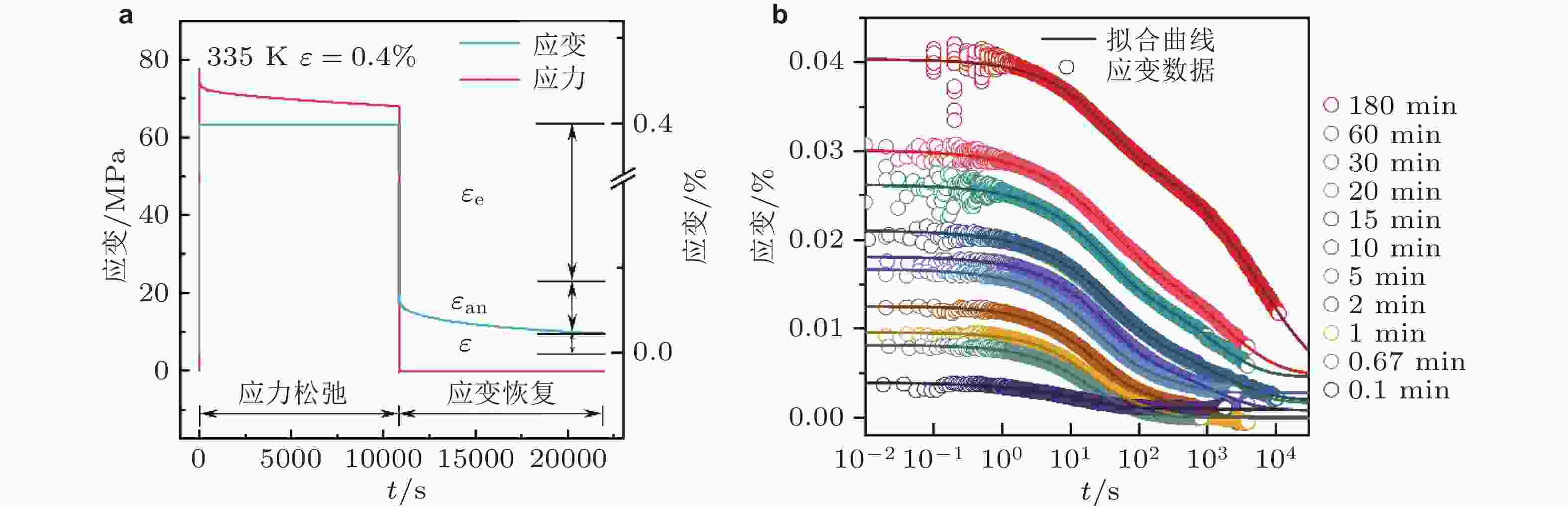
图 14 (a) 335 K下La基非晶合金 应变为0.4%的应力松弛与应变回复过程; (b) 不同松弛时间后的应变回复的非弹性分量结果, 其中的实线为拟合结果 (Xing et al., 2025)
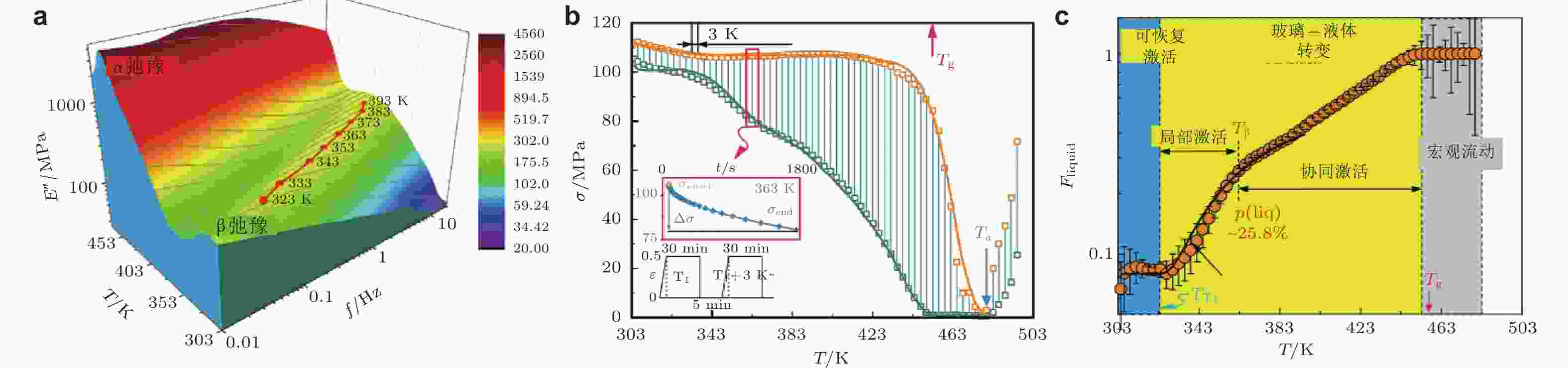
图 15 (a)La基非晶合金在不同温度下的动态力学谱, 以三维形式呈现了损耗模量随温度和频率的变化关系. (b)不同温度下的应力松弛光谱; (c)液态区域比例随温度的演化 (Wang et al., 2014)
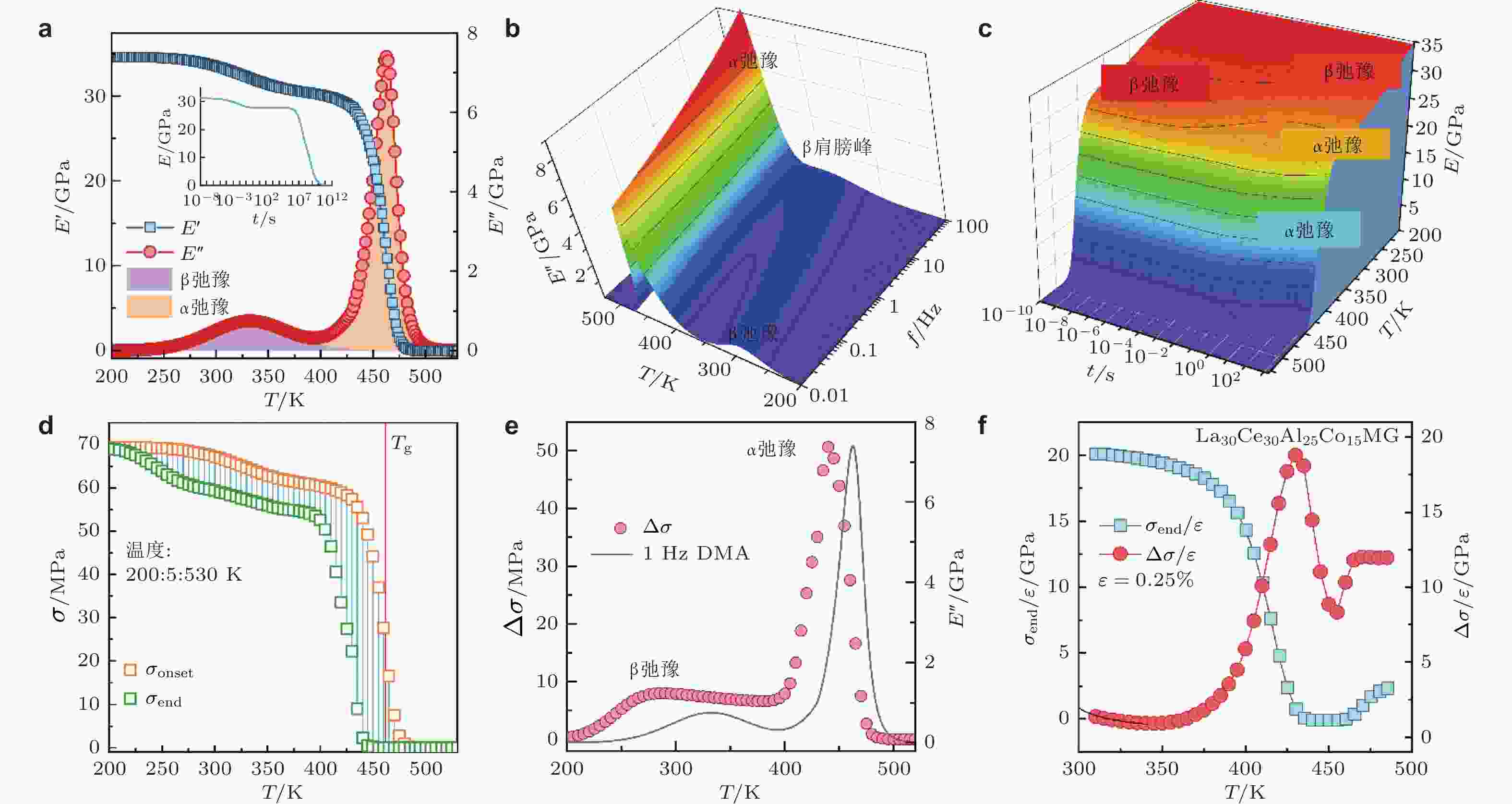
图 16 (a) 等时储能模量和损耗模量的QPD模拟. 插图显示了从300 K开始的大时间尺度的应力衰减模拟. QPD模型计算得到的(b) 三维损耗模量图和(c) 三维应力松弛图. 从冷蓝色到暖红色的颜色过渡表示模值的变化. (d)“竖琴”形应力松弛谱. (e) 应力降Δσ随温度的演化曲线和在1 Hz下获得的等温DMA曲线. (f)La30Ce30Al15Co25非晶合金应力弛豫谱实验结果中σend/ε和Δσ/ε随温度的演化 (Xing et al., 2025)
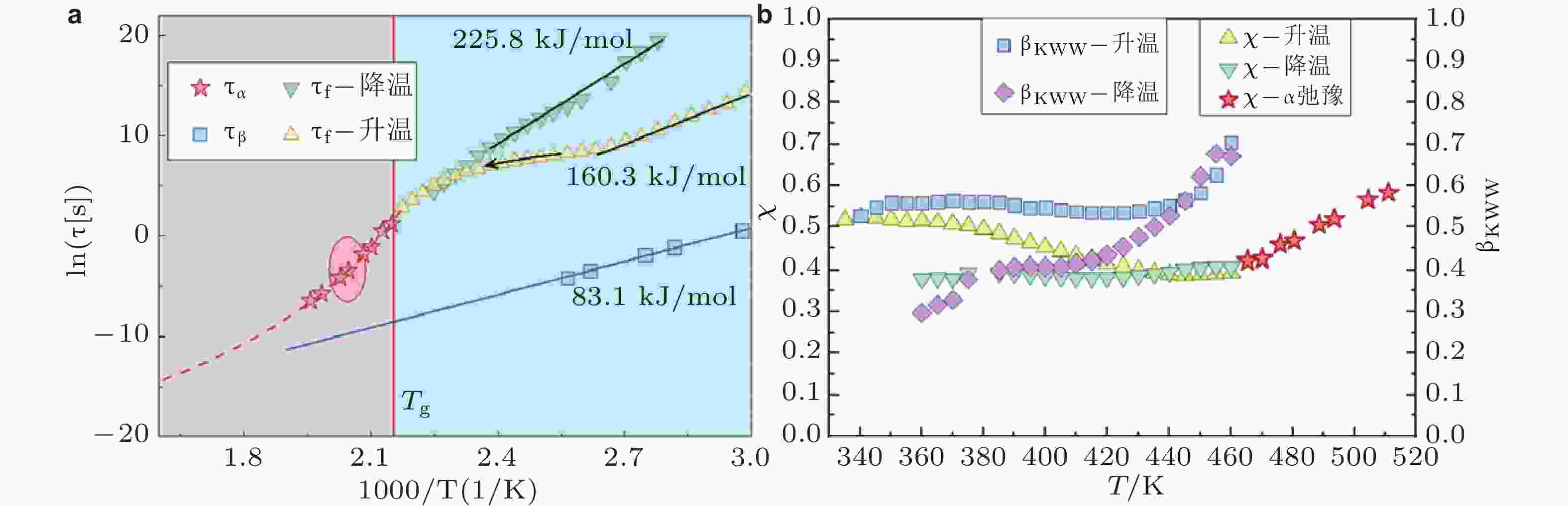
图 17 (a) 加热和冷却过程中所得不同动力学过程特征时间的温度依赖性, 表观激活能利用Arrhenius方程拟合获得; (b) KWW方程中扩展指数参量与准点缺陷理论中关联因子
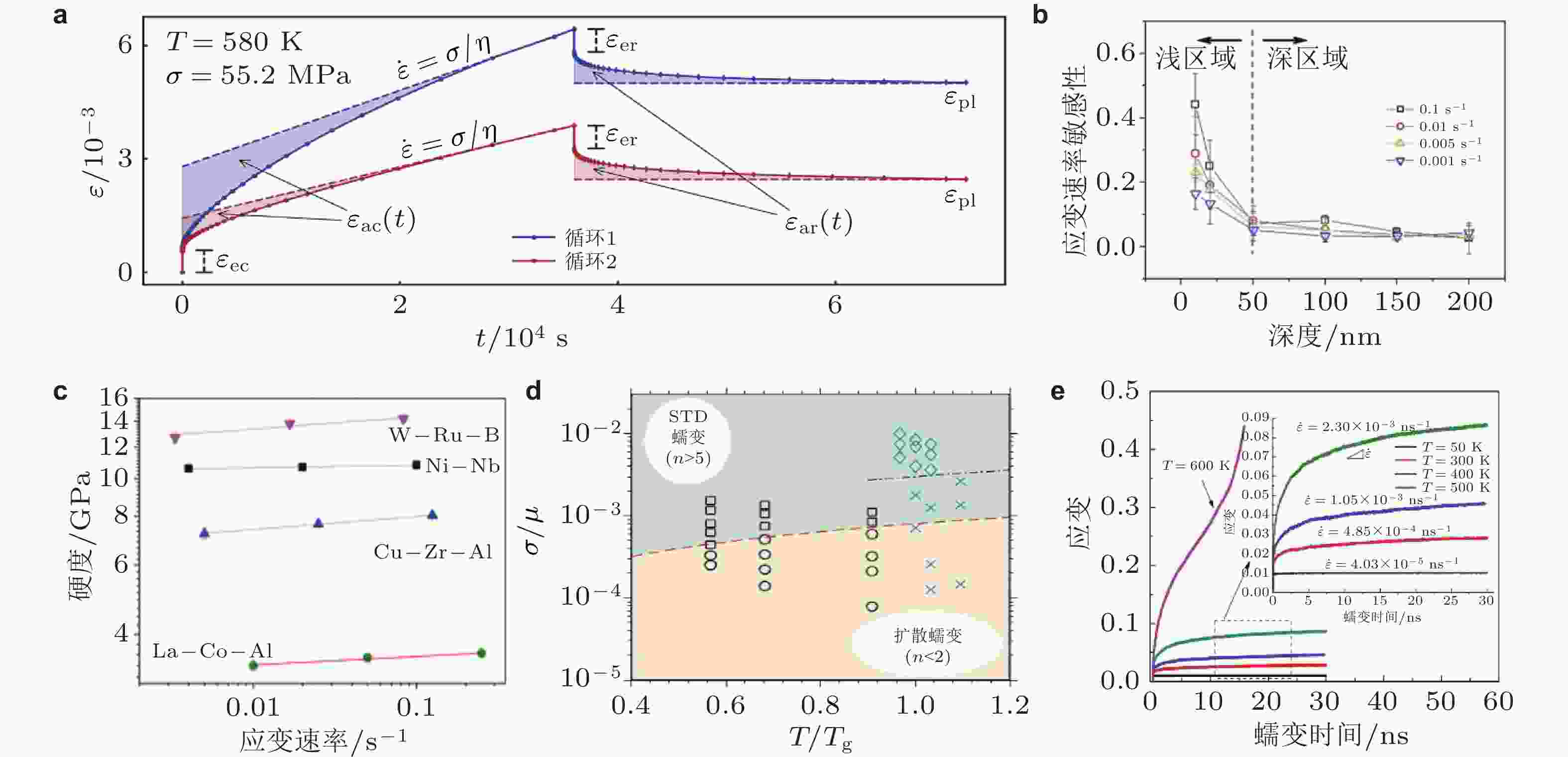
$ \chi $ 的温度依赖性 (Hao et al., 2024)
图 18 (a) Vit105非晶合金的蠕变及回复行为 (Nabahat et al., 2022); (b) 应变速率敏感程度与初始蠕变深度的关系 (Wang et al., 2013); (c) 纳米压痕硬度值与等效应变速率 (Ma et al., 2015); (d) 归一化应力−温度主导区域的蠕变机理图 (Cao et al., 2017); (e) 不同温度下Cu64Zr36非晶合金的蠕变曲线 (Zhu et al., 2024a)
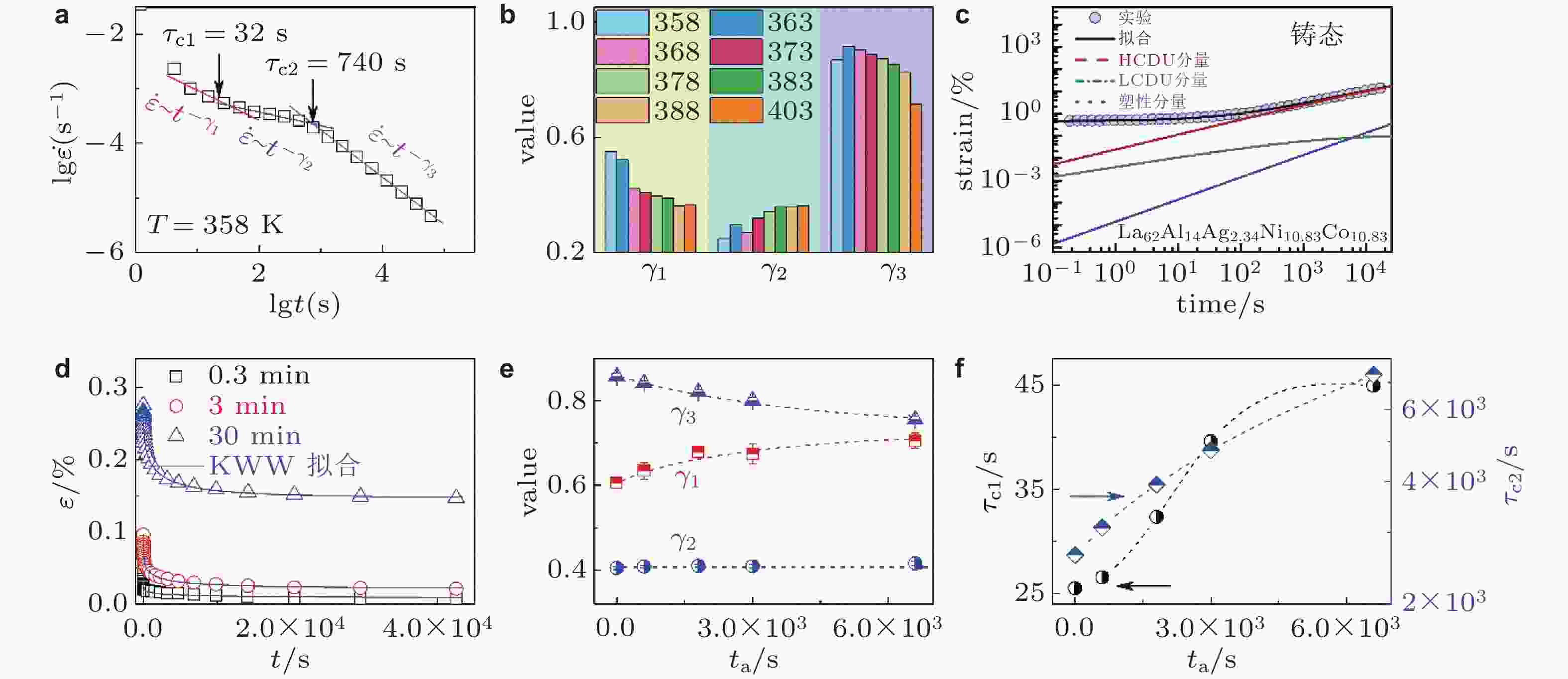
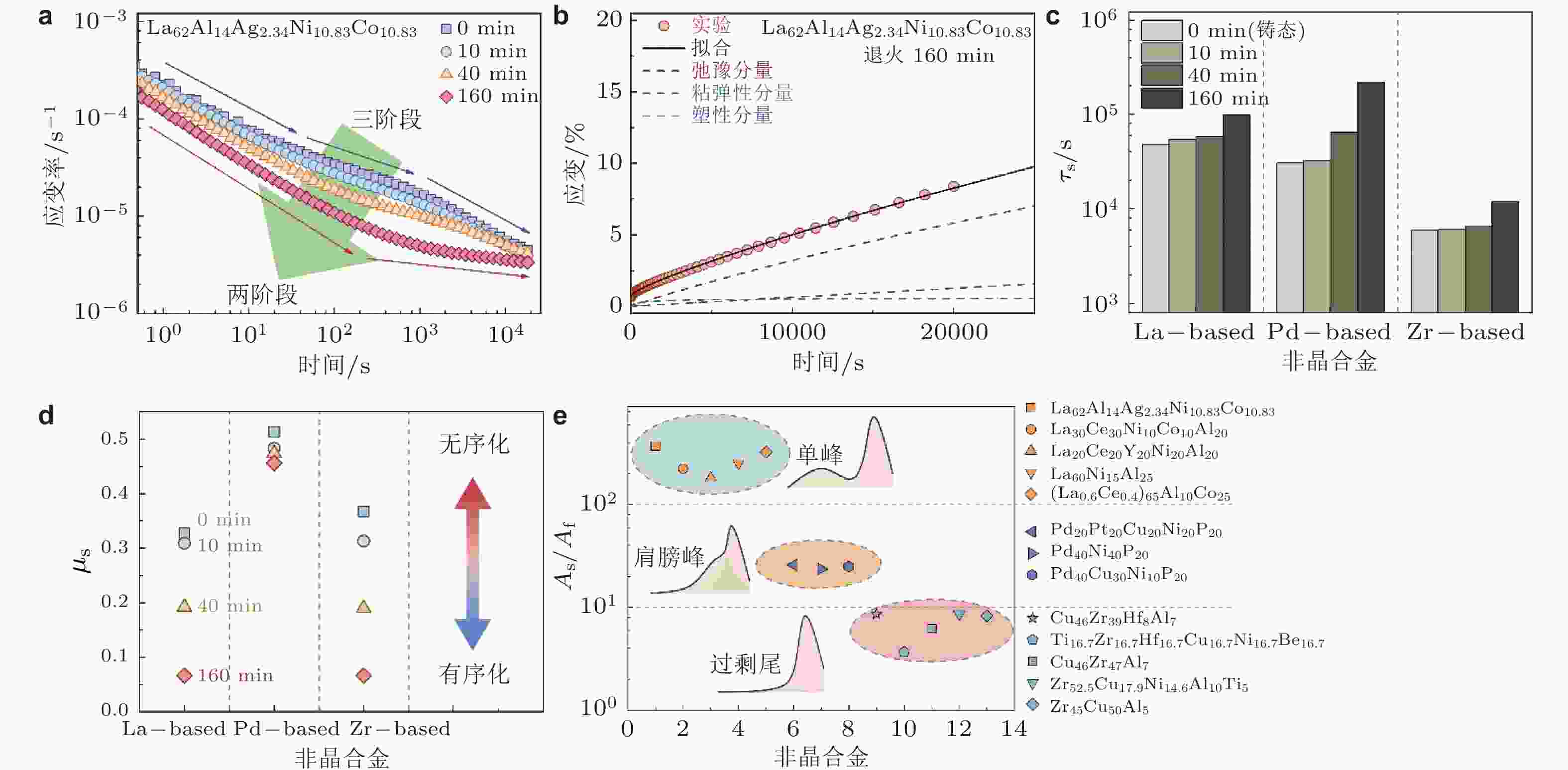
图 19 (a) La30Ce30Ni10Al20Co10非晶合金的三阶段幂律蠕变, 及其(b)幂律指数随温度演化过程 (Zhang et al., 2021); (c) La62Al14Ag2.34Ni10.83Co10.83非晶合金的蠕变实验曲线及基于QPD模型的拟合曲线 (Liang et al., 2024); (d) 358 K时 La30Ce30Ni10Al20Co10非晶合金不同蠕变时间后回复过程中应变随时间的演化, 插图为变形分量的解耦示意图 (Zhang et al., 2021); 三阶段幂律蠕变(e)幂律指数和(f)转折时间随老化时间演化过程 (Zhang et al., 2022a)
图 20 (a) La30Ce30Ni10Al20Co10非晶合金不同老化时间后的三阶段幂律蠕变 (Zhang et al., 2022a); (b) 非晶合金蠕变过程的双机制变形机制示意图 (Zhu et al., 2024a)
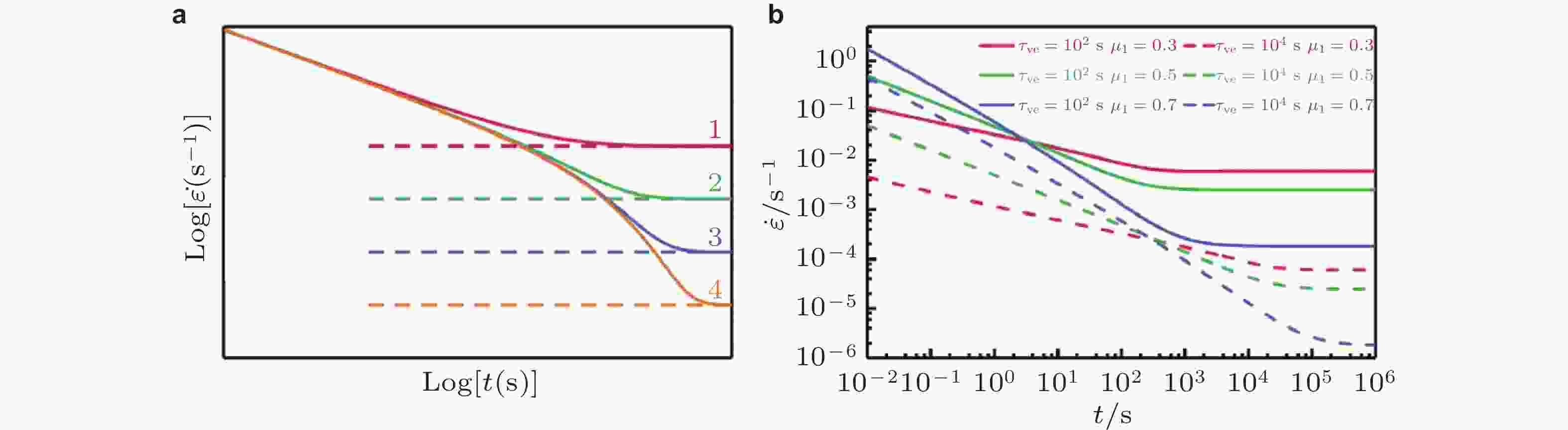
图 21 (a) 通过改变不可逆变形的应变速率, 总应变速率随时间演变示意图; (b) 通过改变
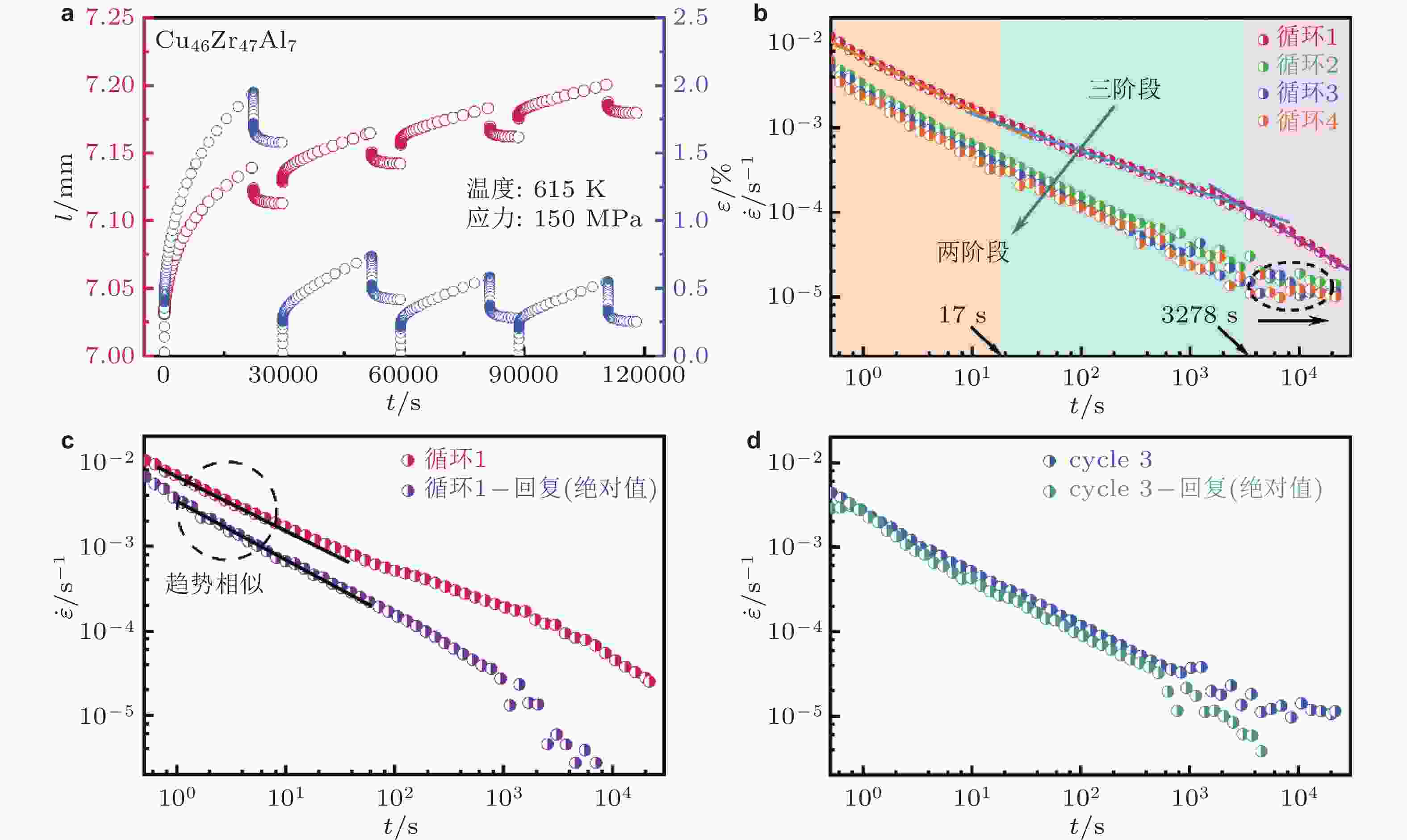
$ {\tau }_{ve} $ 和$ {\mu }_{1} $ 得到的公式(4.1)的应变速率随时间的双对数图, 其中$ {A}_{ve} $ 和$ {A}_{p} $ 被设置为1 (Zhu et al., 2024a)
图 22 (a) 615 K 和 150 MPa 下测得的长度和应变随时间的演变曲线; (b) 四个循环过程中蠕变应变速率随时间的双对数图; (c) 第一次循环期间蠕变和恢复应变速率随时间的双对数演变趋势; (d) 第三次循环期间蠕变和恢复应变速率随时间的双对数演变趋势 (Zhu et al., 2024a)
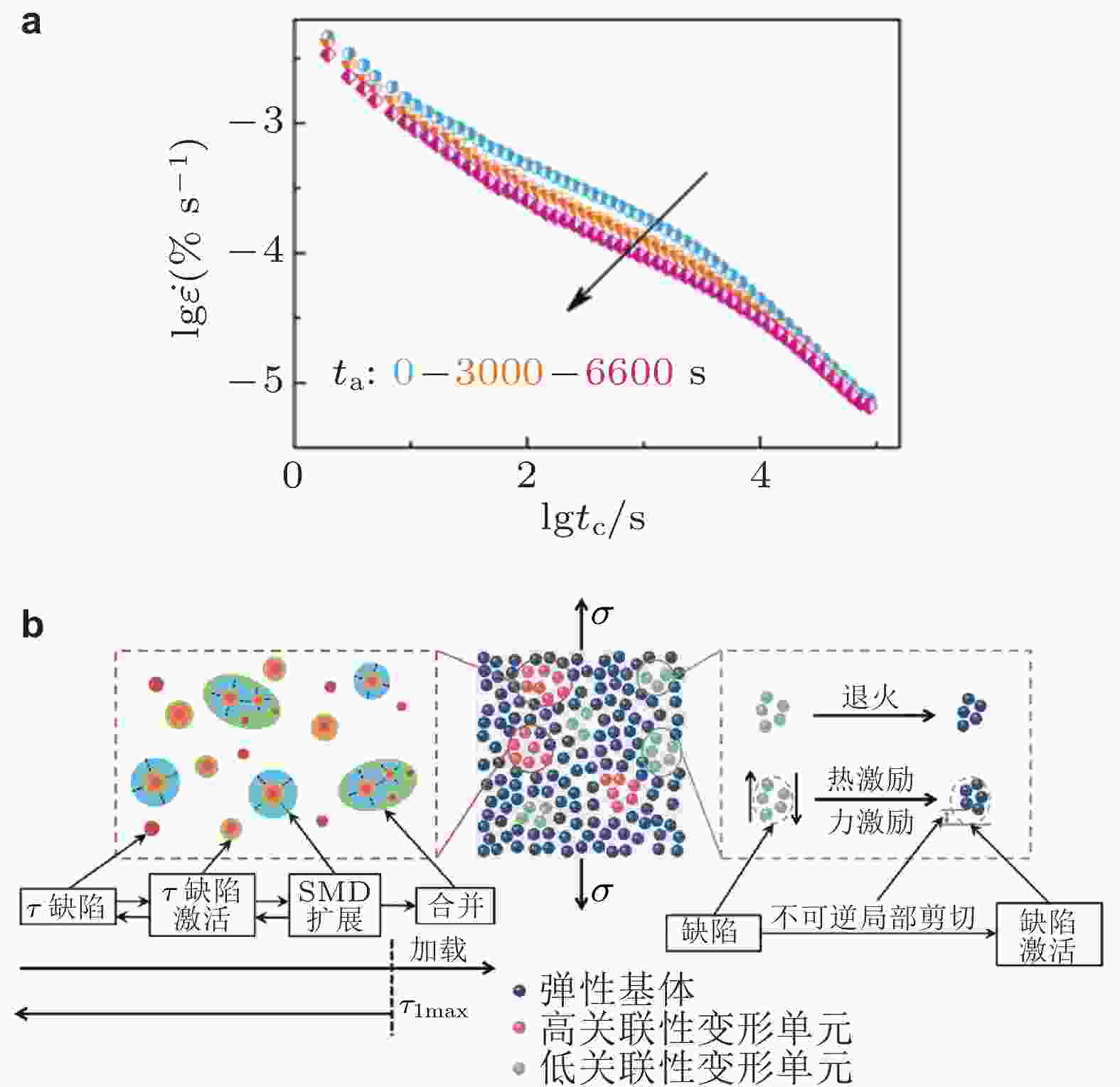
图 23 (a) 不同老化时间的非晶合金蠕变幂律行为 (Liang et al., 2024); (b)非晶合金退火160 min后蠕变变形及其模型拟合 (Liang et al., 2024); (c)不同非晶合金高关联变形单元特征弛豫时间随老化时间的演化 (Liang et al., 2024); (d)非晶合金蠕变过程高关联变形单元关联因子随老化时间的演化 (Liang et al., 2024); (e) 不同非晶合金蠕变过程中高关联变形单元与低关联变形单元的强度比值 (Liang et al., 2024)
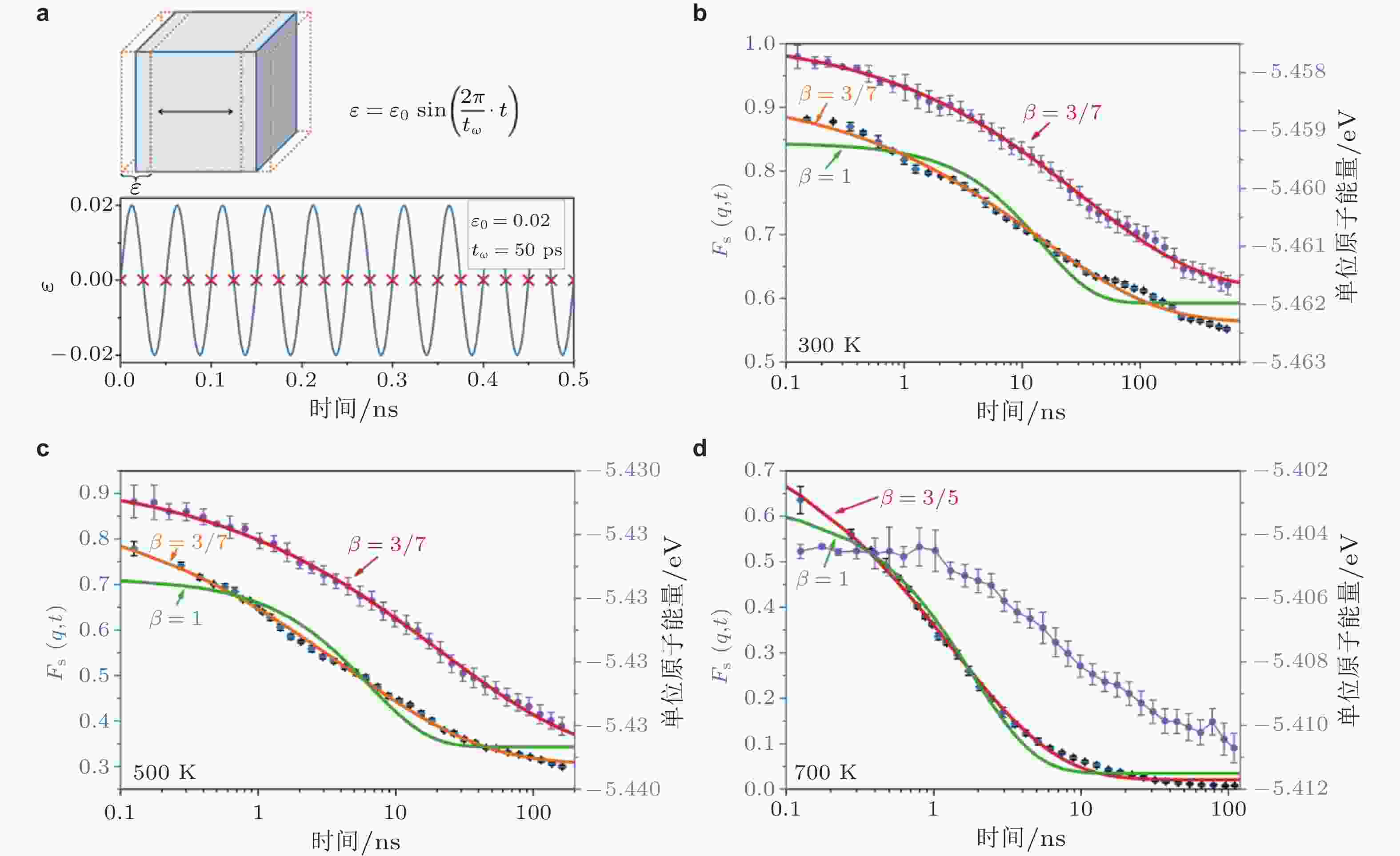
图 24 (a)振动加速Zr70Cu30非晶合金老化仿真过程示意图; 在300 K (b), 500 K (c)和700 K (d)加速时效过程中的自中间散射函数和势能随时间演变 (Sun et al., 2023)
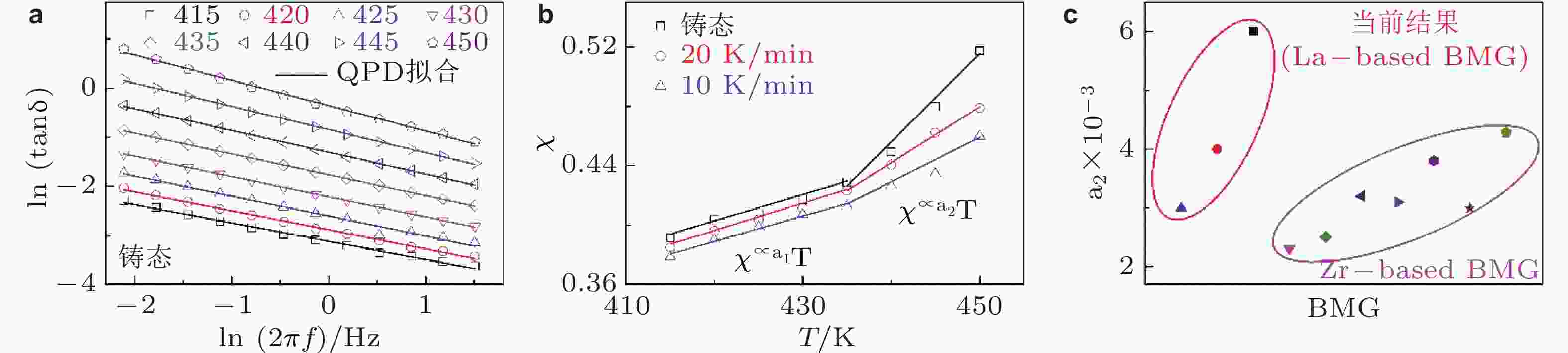
图 25 (a) 多个温度下铸态非晶合金的损耗因子−频率曲线, 实线为QPD理论拟合结果 (Zhang et al., 2023);; (b) 铸态和冷却速率分别为10 K/min和20 K/min时不同状态下关联因子随温度演化过程, 实线为线性拟合结果 (Zhang et al., 2023); (c) 典型玻璃体系a2数值 (Qiao et al., 2018; Wang et al., 2018)
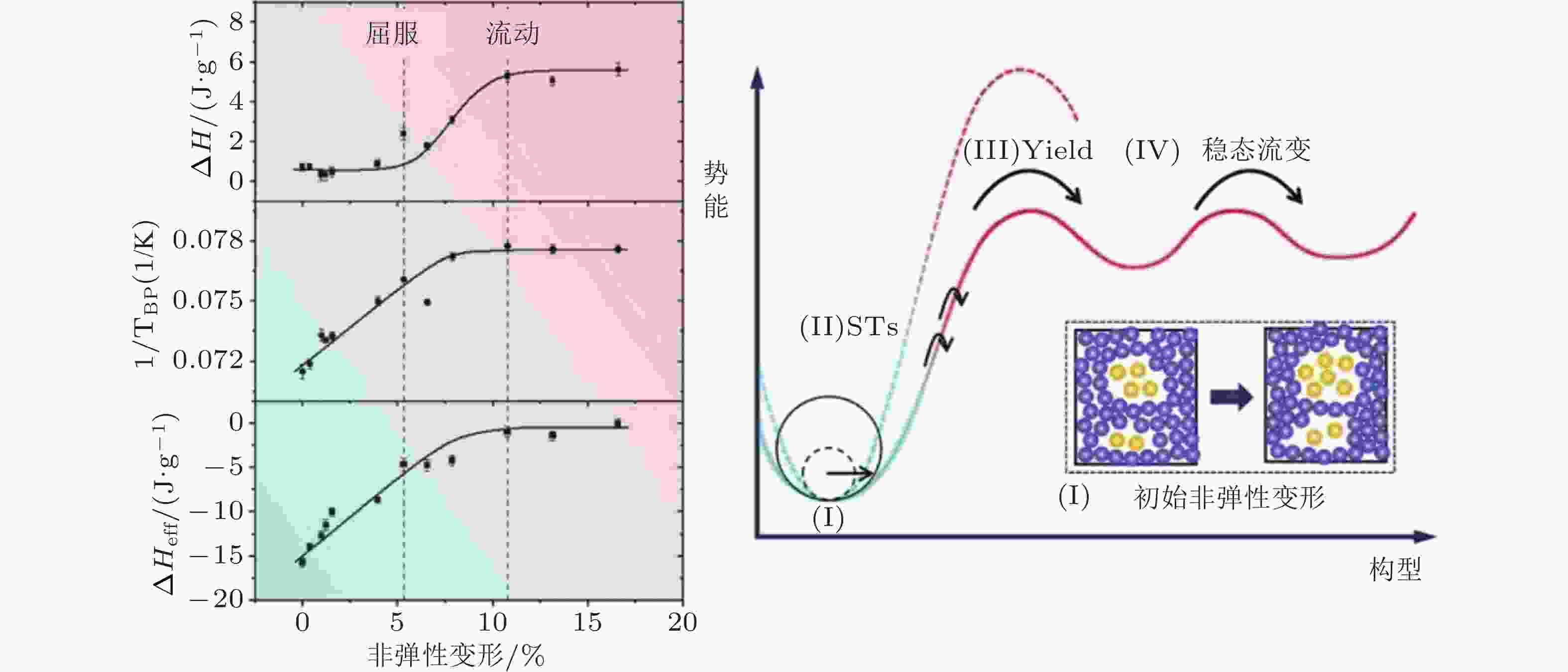
图 26 弛豫焓, 玻色峰温与有效焓随非弹性应变的演化过程 (Gao et al., 2024)
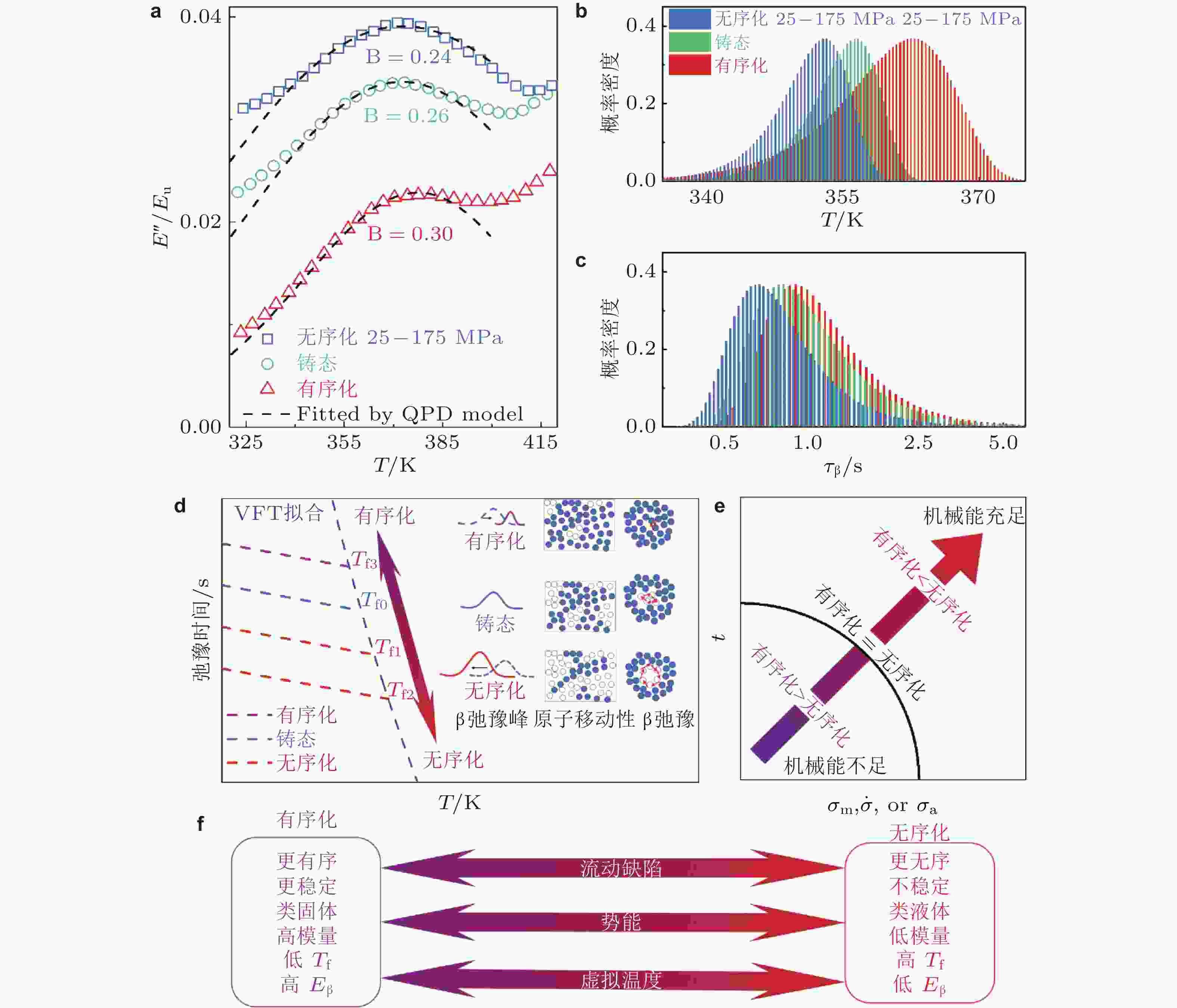
图 27 机械循环实现非晶合金年轻化 (Zhang et al., 2022b). (a) La30Ce30Ni10Al20Co10 非晶合金铸态, 退火态和机械循环处理后样品损耗模量E′′/Eu随温度演化过程, 虚线为QPD模型拟合结果; 弛豫单元分别沿(b) 温度梯度和(c) 特征弛豫时间梯度分布情况; (d) 老化和年轻化对弛豫时间演化影响机制示意图, 构建了缺陷, 老化, 年轻化与β弛豫过程之间关联; (e) 机械循环过程中老化与年轻化动态竞争谱图; (f) 年轻化与老化作用下非晶合金结构指标
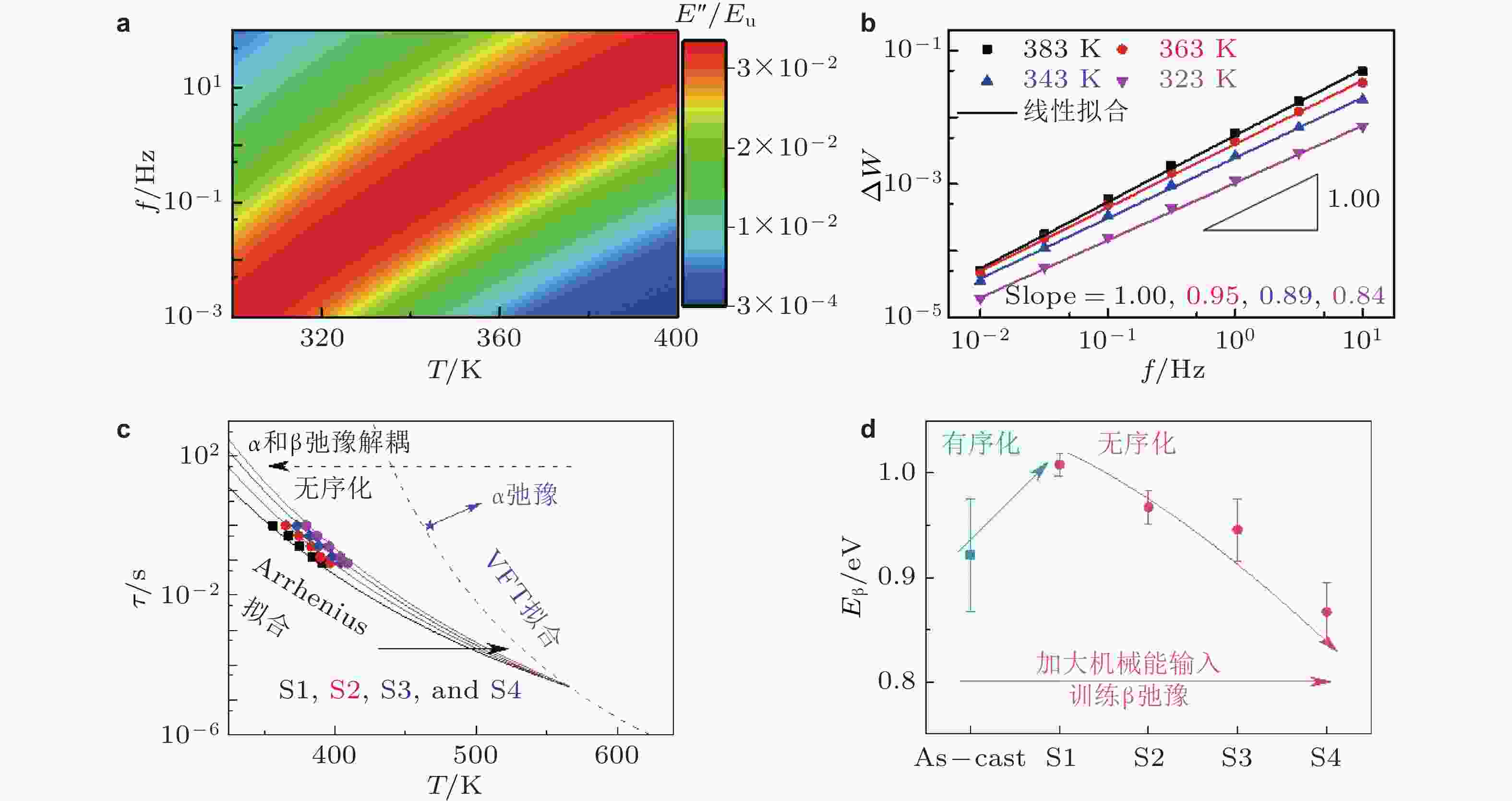
图 28 训练β弛豫实现年轻化 (Zhang et al., 2024a). 理论计算不同训练频率和温度下(a) 归一化损耗模量演化规律; (b) 不同温度下范∆W随训练频率演化过程; (c) 不同训练方案下β弛豫和α弛豫特征时间随温度演化过程; (d) 不同训练方案下β弛豫激活能演化规律
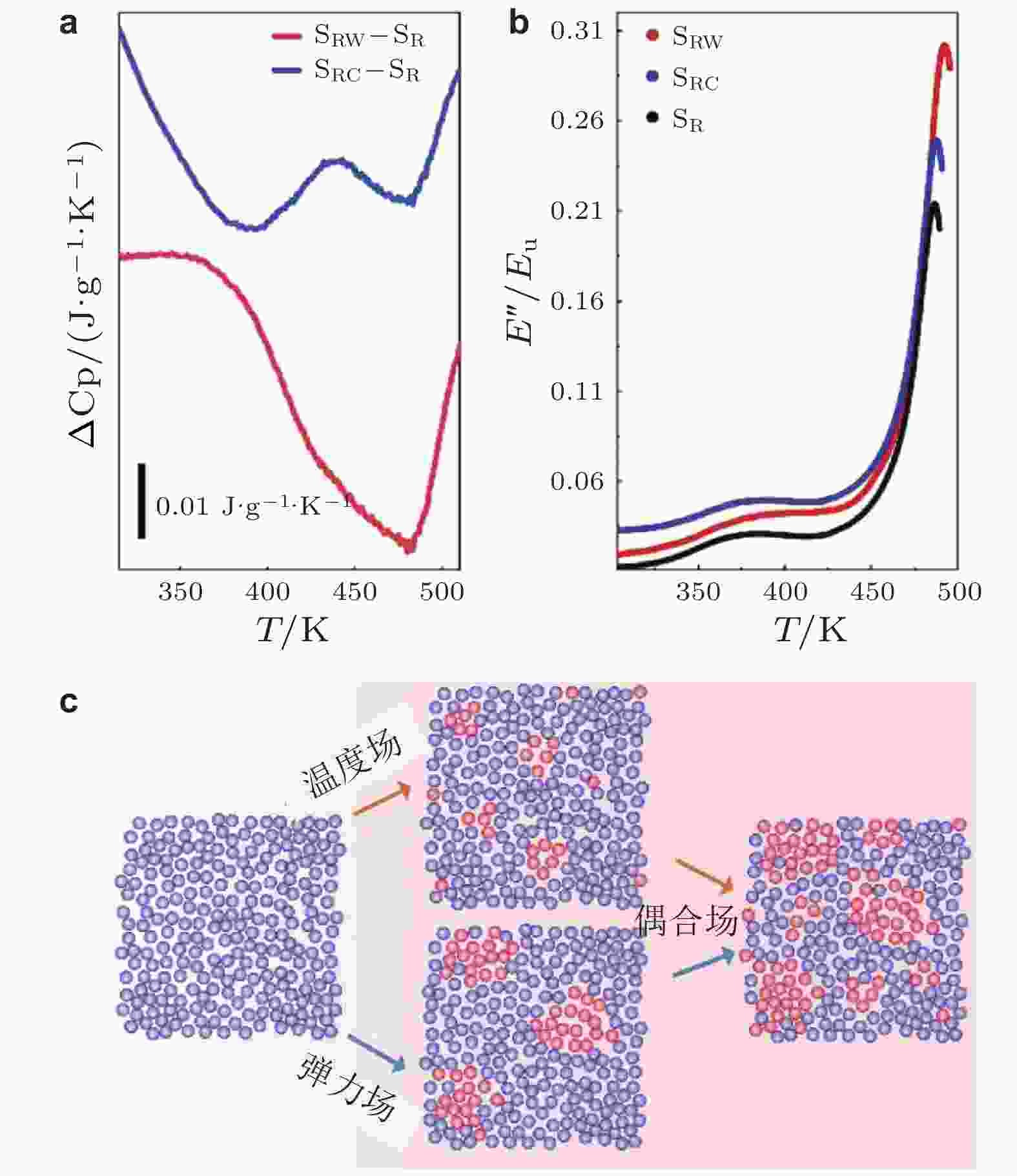
图 29 (a)-(b)室温缠绕、深冷循环与耦合处理样品的热流曲线与损耗模量演化过程 (Yang et al., 2025); (c)处理过程原子演化示意图 (Yang et al., 2025)
-
[1] 汪卫华, 2013. 非晶态物质的本质和特性. 物理学进展, 33: 4-178 (Wang W H 2013. The nature and properties of amorphous matter. Progress in Physics, 33: 4-178).Wang W H 2013. The nature and properties of amorphous matter. Progress in Physics, 33: 4-178. [2] 王云江, 魏丹, 韩懂, 杨杰, 蒋敏强, 戴兰宏, 2020. 非晶态固体的结构可以决定性能吗? 力学学报, 52: 1-15 (Wang Y J, Wei D, Han D, et al. 2020. Does structure determine property in amorphous solids? Chinese Journal of Theoretical and Applied Mechanics, 52: 303-317).Wang Y J, Wei D, Han D, et al. 2020. Does structure determine property in amorphous solids? Chinese Journal of Theoretical and Applied Mechanics, 52: 303-317. [3] Arikoglu A 2014. A new fractional derivative model for linearly viscoelastic materials and parameter identification via genetic algorithms. Rheologica Acta, 53: 219-233. [4] Blair G W S, Veinoglou B C 1944. A Study of the Firmness of Soft Materials Based on Nutting's Equation. Journal of Scientific Instruments, 21: 149. [5] Bruns M, Hassani M, Varnik F, et al. 2021. Decelerated aging in metallic glasses by low temperature thermal cycling. Physical Review Research, 3: 013234. doi: 10.1103/PhysRevResearch.3.013234 [6] Cao L-L, Wang Y-J 2024. Dynamics–Entropy Relationship in Metallic Glasses. Journal of Physical Chemistry Letters, 15: 811-816. [7] Cao P, Short M P, Yip S 2017. Understanding the mechanisms of amorphous creep through molecular simulation. Proceedings of the National Academy of Sciences, 114: 13631-13636. [8] Caputo M, Mainardi F 1971. A new dissipation model based on memory mechanism. Pure and Applied Geophysics, 91: 134-147. [9] Cavaille J Y, Perez J, Johari G P 1989. Molecular theory for the rheology of glasses and polymers. Physical Review B, 39: 2411-2422. [10] Chang C, Zhang H P, Zhao R, et al. 2022. Liquid-like atoms in dense-packed solid glasses. Nature Materials, 21: 1240-1245. doi: 10.1038/s41563-022-01327-w [11] Debenedetti P G, Stillinger F H 2001. Supercooled liquids and the glass transition. Nature, 410: 259-267. [12] Demetriou M D, Harmon J S, Tao M, et al. 2006. Cooperative Shear Model for the Rheology of Glass-Forming Metallic Liquids. Physical Review Letters, 97: 065502. doi: 10.1103/PhysRevLett.97.065502 [13] Ding G, Jiang F, Song X, et al. 2022. Unraveling the threshold stress of structural rejuvenation of metallic glasses via thermo-mechanical creep. Science China Physics, Mechanics & Astronomy, 65: 264613. [14] Duan Y J, Nabahat M, Tong Y, et al. 2024. Connection between mechanical relaxation and equilibration kinetics in a high-entropy metallic glass. Physical Review Letters, 132: 056101. doi: 10.1103/PhysRevLett.132.056101 [15] Duan Y J, Zhang L T, Qiao J C, et al. 2022. Intrinsic correlation between the fraction of liquidlike zones and the β relaxation in high-entropy metallic glasses. Physical Review Letters, 129: 175501. doi: 10.1103/PhysRevLett.129.175501 [16] Ediger M D 2000. Spatially heterogeneous dynamics in supercooled liquids. Annual Review of Physical Chemistry, 51: 99-128. [17] Fujita T, Guan P F, Sheng H W, et al. 2010. Coupling between chemical and dynamic heterogeneities in a multicomponent bulk metallic glass. Physical Review B, 81: 140204. doi: 10.1103/PhysRevB.81.140204 [18] Gao L, Yu H-B, Schrøder T B, et al. 2025. Unified percolation scenario for the α and β processes in simple glass formers. Nature Physics, 21: 1-9. doi: 10.1038/s41567-024-02771-y [19] Gao Y, Yang C, Ding G, et al. 2024. Structural rejuvenation of a well-aged metallic glass. Fundamental Research, 4: 1266-1271. doi: 10.1016/j.fmre.2022.12.004 [20] Gauthier C, David L, Ladouce L, et al. 1997. Nonlinear mechanical response of amorphous polymers below and through glass transition temperature. Journal of Applied Polymer Science, 65: 2517-2528. doi: 10.1002/(SICI)1097-4628(19970919)65:12<2517::AID-APP22>3.0.CO;2-W [21] Gauthier C, Pelletier J M, David L, et al. 2000. Relaxation of non-crystalline solids under mechanical stress. Journal of Non-Crystalline Solids, 274: 181-187. doi: 10.1016/S0022-3093(00)00213-1 [22] Guiselin B, Scalliet C, Berthier L 2022. Microscopic origin of excess wings in relaxation spectra of supercooled liquids. Nature Physics, 18: 468-472. [23] Hao Q, Lyu G J, Pineda E, et al. 2022. A hierarchically correlated flow defect model for metallic glass: Universal understanding of stress relaxation and creep. International Journal of Plasticity, 154: 103288. doi: 10.1016/j.ijplas.2022.103288 [24] Hao Q, Pineda E, Wang Y J, et al. 2023b. Reversible anelastic deformation mediated by β relaxation and resulting two-step deformation in a La60Ni15Al25 metallic glass. Physical Review B, 108: 024101. [25] Hao Q, Xing G, Pineda E, et al. 2024. Deciphering the α relaxation and the anelastic-to-plastic transition in the deep glassy state. Science China Physics, Mechanics & Astronomy, 68: 234611. [26] Harmon J S, Demetriou M D, Johnson W L, et al. 2007. Anelastic to Plastic Transition in Metallic Glass-Forming Liquids. Physical Review Letters, 99: 135502. doi: 10.1103/PhysRevLett.99.135502 [27] Heymans N 1996. Hierarchical models for viscoelasticity: dynamic behaviour in the linear range. Rheologica Acta, 35: 508-519. [28] Hu Y, Guan P, Li M, et al. 2016. Unveiling atomic-scale features of inherent heterogeneity in metallic glass by molecular dynamics simulations. Physical Review B, 93: 214202. doi: 10.1103/PhysRevB.93.214202 [29] Hu Y C, Li Y W, Yang Y, et al. 2018. Configuration correlation governs slow dynamics of supercooled metallic liquids. Proceedings of the National Academy of Sciences, 115: 6375. doi: 10.1073/pnas.1802300115 [30] Ichitsubo T, Matsubara E, Yamamoto T, et al. 2005. Microstructure of fragile metallic glasses inferred from ultrasound-accelerated crystallization in Pd-based metallic glasses. Physical Review Letters, 95: 245501. doi: 10.1103/PhysRevLett.95.245501 [31] Ke H B, Zeng J F, Liu C T, et al. 2014. Structure Heterogeneity in Metallic Glass: Modeling and Experiment. Journal of Materials Science and Technology, 30: 560-565. doi: 10.1016/j.jmst.2013.11.014 [32] Ketov S V, Sun Y H, Nachum S, et al. 2015. Rejuvenation of metallic glasses by non-affine thermal strain. Nature, 524: 200-203. doi: 10.1038/nature14674 [33] Li X, Wei D, Zhang J Y, et al. 2020. Ultrasonic plasticity of metallic glass near room temperature. Applied Materials Today, 21: 100866. doi: 10.1016/j.apmt.2020.100866 [34] Liang S Y, Zhu F, Wang Y-J, et al. 2024. On the kinetics of structural evolution in metallic glasses. International Journal of Engineering Science, 205: 104146. doi: 10.1016/j.ijengsci.2024.104146 [35] Liu Y H, Wang D, Nakajima K, et al. 2011. Characterization of nanoscale mechanical heterogeneity in a metallic glass by dynamic force microscopy. Physical Review Letters, 106: 125504. doi: 10.1103/PhysRevLett.106.125504 [36] Louzguine-Luzgin D V, Zadorozhnyy M Y, Ketov S V, et al. 2019. Influence of cyclic loading on the structure and double-stage structure relaxation behavior of a Zr-Cu-Fe-Al metallic glass. Materials Science and Engineering: A, 742: 526-531. doi: 10.1016/j.msea.2018.11.031 [37] Lu Z, Shang B S, Sun Y T, et al. 2016. Revealing β-relaxation mechanism based on energy distribution of flow units in metallic glass. Journal of Chemical Physics, 144: 144501. doi: 10.1063/1.4945279 [38] Lubchenko V, Wolynes P G 2007. Theory of Structural Glasses and Supercooled Liquids. Annual Review of Physical Chemistry, 58: 235-266. [39] Luckabauer M, Hayashi T, Kato H, et al. 2019. Decreasing activation energy of fast relaxation processes in a metallic glass during aging. Physical Review B, 99: 140202. doi: 10.1103/PhysRevB.99.140202 [40] Lunkenheimer P, Wehn R, Schneider U, et al. 2005. Glassy aging dynamics. Physical Review Letters, 95: 055702. doi: 10.1103/PhysRevLett.95.055702 [41] Luo P, Wen P, Bai H Y, et al. 2017. Relaxation decoupling in metallic glasses at low temperatures. Physical Review Letters, 118: 225901. doi: 10.1103/PhysRevLett.118.225901 [42] Ma Y, Ye J H, Peng G J, et al. 2015. Loading rate effect on the creep behavior of metallic glassy films and its correlation with the shear transformation zone. Materials Science and Engineering: A, 622: 76-81. doi: 10.1016/j.msea.2014.11.022 [43] Magagnosc D J, Kumar G, Schroers J, et al. 2014. Effect of ion irradiation on tensile ductility, strength and fictive temperature in metallic glass nanowires. Acta Materialia, 74: 165-182. doi: 10.1016/j.actamat.2014.04.002 [44] Mainardi F, 1997. Fractals and Fractional Calculus in Continuum Mechanics. [45] Menard K P, Menard N, 2020. Dynamic mechanical analysis. Boca Raton: Taylor and Francis. [46] Nabahat M, Amini N, Pineda E, et al. 2022. Delayed elasticity of metallic glasses: Loading time and temperature dependences of the anelastic relaxation. Physical Review Materials, 6: 125601. doi: 10.1103/PhysRevMaterials.6.125601 [47] Ngai K L 2023. Universal properties of relaxation and diffusion in complex materials: Originating from fundamental physics with rich applications. Progress in Materials Science, 139: 101130. [48] Ngai K L, Wang L M, Yu H B 2017. Relating ultrastable glass formation to enhanced surface diffusion via the Johari-Goldstein beta-relaxation in molecular glasses. Journal of Physical Chemistry Letters, 8: 2739-2744. [49] Nutting P G 1921. A new general law of deformation. Journal of the Franklin Institute, 191: 679-685. [50] Palade L-I, Verney V, Attané P 1996. A modified fractional model to describe the entire viscoelastic behavior of polybutadienes from flow to glassy regime. Rheologica Acta, 35: 265-273. [51] Palmer R G, Stein D L, Abrahams E, et al. 1984. Models of Hierarchically Constrained Dynamics for Glassy Relaxation. Physical Review Letters, 53: 958-961. doi: 10.1103/PhysRevLett.53.958 [52] Perez J 1984. Homogeneous flow and anelastic/plastic deformation of metallic glasses. Acta Metallurgica, 32: 2163-2173. [53] Perez J 1988. Defect diffusion model for volume and enthalpy recovery in amorphous polymers. Polymer, 29: 483-489. [54] Perez J 1990. Quasi-punctual defects in vitreous solids and liquid-glass transition. Solid State Ionics, 39: 69-79. [55] Perez J, 1998. Physics and Mechanics of Amorphous Polymers: Taylor & Francis. [56] Perez J, Cavaille J Y, Etienne S, et al. 1988. Physical interpretation of the rheological behavior of amorphous polymers through the glass-transition. Revue De Physique Appliquee, 23: 125-135. doi: 10.1051/rphysap:01988002302012500 [57] Qiao J, Pelletier J-M 2014. Dynamic mechanical relaxation in bulk metallic glasses: a review. Journal of Materials Science Technology, 30: 523-545. [58] Qiao J C, Cong J, Wang Q, et al. 2018. Effects of iron addition on the dynamic mechanical relaxation of Zr55Cu30Ni5Al10 bulk metallic glasses. Journal of Alloys and Compounds, 749: 262-267. doi: 10.1016/j.jallcom.2018.03.285 [59] Qiao J C, Pelletier J M 2012. Mechanical relaxation in a Zr-based bulk metallic glass: Analysis based on physical models. Journal of Applied Physics, 112: 033518. [60] Qiao J C, Pelletier J M, Esnouf C, et al. 2014. Impact of the structural state on the mechanical properties in a Zr–Co–Al bulk metallic glass. Journal of Alloys and Compounds, 607: 139-149. doi: 10.1016/j.jallcom.2014.04.008 [61] Qiao J C, Wang Q, Pelletier J M, et al. 2019. Structural heterogeneities and mechanical behavior of amorphous alloys. Progress in Materials Science, 104: 250-329. doi: 10.1016/j.pmatsci.2019.04.005 [62] Richert R 2002. Heterogeneous dynamics in liquids: fluctuations in space and time. Journal of Physics: Condensed Matter, 14: R703. [63] Rinaldi R, Gaertner R, Chazeau L, et al. 2011. Modelling of the mechanical behaviour of amorphous glassy polymer based on the Quasi Point Defect theory—Part I: Uniaxial validation on polycarbonate. International Journal of Non-Linear Mechanics, 46: 496-506. doi: 10.1016/j.ijnonlinmec.2010.11.004 [64] Schiessel H, Metzler R, Blumen A, et al. 1995. Generalized viscoelastic models: their fractional equations with solutions. Journal of Physics A: Mathematical and General, 28: 6567. doi: 10.1088/0305-4470/28/23/012 [65] Shao L, Xue L, Qiao J, et al. 2023. Gamma relaxation in Dy-based metallic glasses and its correlation with plasticity. Scripta Materialia, 222: 115017. doi: 10.1016/j.scriptamat.2022.115017 [66] Sharma R, Cherayil B J 2010. Polymer melt dynamics: Microscopic roots of fractional viscoelasticity. Physical Review E, 81: 021804. [67] Song J, Zhu W, Wei X 2021. Correlations between the hierarchical spatial heterogeneity and the mechanical properties of metallic glasses. International Journal of Mechanical Sciences, 204: 106570. [68] Song L, Gao Y, Zou P, et al. 2023. Detecting the exponential relaxation spectrum in glasses by high-precision nanocalorimetry. Proceedings of the National Academy of Sciences, 120: e2302776120. doi: 10.1073/pnas.2302776120 [69] Song S, Zhu F, Chen M 2022. Universal scaling law of glass rheology. Nature Materials, 21: 404-409. [70] Spieckermann F, Şopu D, Soprunyuk V, et al. 2022. Structure-dynamics relationships in cryogenically deformed bulk metallic glass. Nature Communications, 13: 127. doi: 10.1038/s41467-021-27661-2 [71] Srolovitz D, Maeda K, Vitek V, et al. 1981. Structural defects in amorphous solids Statistical analysis of a computer model. Philosophical Magazine A, 44: 847-866. doi: 10.1080/01418618108239553 [72] Sun Y-T, Zhao R, Ding D-W, et al. 2023. Distinct relaxation mechanism at room temperature in metallic glass. Nature Communications, 14: 540. doi: 10.1038/s41467-023-36300-x [73] Sun Y, Concustell A, Greer A L 2016. Thermomechanical processing of metallic glasses: extending the range of the glassy state. Nature Reviews Materials, 1: 16039. [74] Tao K, Khonik V A, Qiao J C 2023. Indentation creep dynamics in metallic glasses under different structural states. International Journal of Mechanical Sciences, 240: 107941. [75] Tong Y, Dmowski W, Bei H, et al. 2018. Mechanical rejuvenation in bulk metallic glass induced by thermo-mechanical creep. Acta Materialia, 148: 384-390. doi: 10.1016/j.actamat.2018.02.019 [76] Wagner H, Bedorf D, Küchemann S, et al. 2011. Local elastic properties of a metallic glass. Nature Materials, 10: 439-442. doi: 10.1038/nmat3024 [77] Wang C H, Hu Y J, Qiao J C, et al. 2018. Mechanical relaxation behavior of Zr64.13Cu15.75Ni10.12Al10 bulk metallic glass. Materials Science & Engineering A, 738: 57-62. [78] Wang F, Li J M, Huang P, et al. 2013. Nanoscale creep deformation in Zr-based metallic glass. Intermetallics, 38: 156-160. doi: 10.1016/j.intermet.2013.03.006 [79] Wang H, Chang C-T, Cui Z-D, et al. 2023. Creep recovery of stress-annealed Zr-based metallic glass: Investigation based on the dynamic viscoelastic model. Materials Today Communications, 37: 107239. doi: 10.1016/j.mtcomm.2023.107239 [80] Wang Q, Liu J J, Ye Y F, et al. 2017. Universal secondary relaxation and unusual brittle-to-ductile transition in metallic glasses. Materials Today, 20: 293-300. doi: 10.1016/j.mattod.2017.05.007 [81] Wang W H 2019. Dynamic relaxations and relaxation-property relationships in metallic glasses. Progress in Materials Science, 106: 100561. [82] Wang X Y, Xu W S, Zhang H, et al. 2019. Universal nature of dynamic heterogeneity in glass-forming liquids: A comparative study of metallic and polymeric glass-forming liquids. Journal of Chemical Physics, 151: 184503. doi: 10.1063/1.5125641 [83] Wang Z, Sun B A, Bai H Y, et al. 2014. Evolution of hidden localized flow during glass-to-liquid transition in metallic glass. Nature Communications, 5. [84] Wei Y, Bower A F, Gao H 2010. Analytical model and molecular dynamics simulations of the size dependence of flow stress in amorphous intermetallic nanowires at temperatures near the glass transition. Physical Review B, 81: 125402. [85] Wu W-P, Şopu D, Yuan X, et al. 2021. Atomistic understanding of creep and relaxation mechanisms of Cu64Zr36 metallic glass at different temperatures and stress levels. Journal of Non-Crystalline Solids, 559: 120676. doi: 10.1016/j.jnoncrysol.2021.120676 [86] Xing G, Hao Q, Zhu F, et al. 2024. Correlating dynamic relaxation and viscoelasticity in metallic glasses. Science China Physics, Mechanics & Astronomy, 67: 256111. [87] Xing G H, Hao Q, Lyu G-J, et al. 2025. Integrating dynamic relaxation with inelastic deformation in metallic glasses: Theoretical insights and experimental validation. Journal of Materials Science & Technology, 218: 135-152. [88] Yang C, Duan J, Ding G, et al. 2024a. Splitting of fast relaxation in a metallic glass by laser shocks. Physical Review B, 109: 024201. [89] Yang X-M, Yang Q, Zhang T, et al. 2024b. Probing slow glass dynamics down to 10−5 Hz. Applied Physics Reviews, 11: 041403. doi: 10.1063/5.0206556 [90] Yang Y, Geng J, Cao Y, et al. 2025. Rejuvenation of La-based metallic glass by controlling different modes of relaxation. Scripta Materialia, 256: 116418. doi: 10.1016/j.scriptamat.2024.116418 [91] Ye J C, Lu J, Liu C T, et al. 2010. Atomistic free-volume zones and inelastic deformation of metallic glasses. Nature Materials, 9: 619-623. doi: 10.1038/nmat2802 [92] Yu H-B, Richert R, Samwer K 2017a. Structural rearrangements governing Johari-Goldstein relaxations in metallic glasses. Science Advances, 3: e1701577. [93] Yu H-B, Yang M-H, Sun Y, et al. 2018. Fundamental Link between β Relaxation, Excess Wings, and Cage-Breaking in Metallic Glasses. Journal of Physical Chemistry Letters, 9: 5877-5883. doi: 10.1021/acs.jpclett.8b02629 [94] Yu H B, Richert R, Samwer K 2017b. Structural rearrangements governing Johari-Goldstein relaxations in metallic glasses. Science Advances, 3: e1701577. [95] Yu H B, Samwer K, Wu Y, et al. 2012. Correlation between β relaxation and self-diffusion of the smallest constituting atoms in metallic glasses. Physical Review Letters, 109: 095508. doi: 10.1103/PhysRevLett.109.095508 [96] Yu H B, Wang Q 2024. Liquid-like clusters in glassy solids as a unique state of matter: Dissipative but non-diffusive. Next Materials, 3: 100168. [97] Yu H B, Wang W H, Bai H Y, et al. 2014. The β-relaxation in metallic glasses. National Science Review, 1: 429-461. doi: 10.1093/nsr/nwu018 [98] Yu H B, Wang W H, Bai H Y, et al. 2010. Relating activation of shear transformation zones to β relaxations in metallic glasses. Physical Review B, 81: 220201. doi: 10.1103/PhysRevB.81.220201 [99] Zhang C, Qiao J C, Pelletier J M, et al. 2016. Thermal activation in the Zr65Cu18Ni7Al10 metallic glass by creep deformation and stress relaxation. Scripta Materialia, 113: 180-184. doi: 10.1016/j.scriptamat.2015.11.001 [100] Zhang L, Duan Y, Crespo D, et al. 2021. Dynamic mechanical relaxation and thermal creep of high-entropy La30Ce30Ni10Al20Co10 bulk metallic glass. Science China Physics, Mechanics & Astronomy, 64: 296111. [101] Zhang L, Duan Y, Pineda E, et al. 2022a. Effect of physical aging and cyclic loading on power-law creep of high-entropy metallic glass. Journal of Materials Science & Technology, 115: 1-9. [102] Zhang L, Duan Y, Wang Y, et al. 2023. Tailoring the mechanical properties of bulk metallic glasses via cooling from the supercooled liquid region. Science China Technological Sciences, 66: 173-180. doi: 10.1007/s11431-022-2237-5 [103] Zhang L, Wang Y, Pineda E, et al. 2022b. Achieving structural rejuvenation in metallic glass by modulating β relaxation intensity via easy-to-operate mechanical cycling. International Journal of Plasticity, 157: 103402. doi: 10.1016/j.ijplas.2022.103402 [104] Zhang L T, Wang Y J, Nabahat M, et al. 2024a. Creep deformation in metallic glasses: A global approach with strain as an indicator within transition state theory. International Journal of Plasticity, 174: 103923. doi: 10.1016/j.ijplas.2024.103923 [105] Zhang L T, Wang Y J, Yang Y, et al. 2024b. Mechanical memory and relaxation decoupling of metallic glasses in homogenous flow. International Journal of Mechanical Sciences, 281: 109661. doi: 10.1016/j.ijmecsci.2024.109661 [106] Zhou Z-Y, Yang Q, Yu H-B 2024a. Toward atomic-scale understanding of structure-dynamics-properties relations for metallic glasses. Progress in Materials Science, 145: 101311. [107] Zhou Z Y, Chen Q, Sun Y, et al. 2021. Unveiling correlation between α relaxation and yielding behavior in metallic glasses. Physical Review B, 103: 094117. doi: 10.1103/PhysRevB.103.094117 [108] Zhou Z Y, Yang Q, Yu H B 2024b. Toward atomic-scale understanding of structure-dynamics-properties relations for metallic glasses. Progress in Materials Science, 145: 101311. [109] Zhu F, Song S X, Reddy K M, et al. 2018. Spatial heterogeneity as the structure feature for structure–property relationship of metallic glasses. Nature Communications, 9: 3965. doi: 10.1038/s41467-018-06476-8 [110] Zhu F, Xing G H, Lyu G J, et al. 2023. Physics-motivated fractional viscoelasticity model for dynamic relaxation in amorphous solids. International Journal of Plasticity, 164: 103588. doi: 10.1016/j.ijplas.2023.103588 [111] Zhu F, Xing G H, Wang Y-J, et al. 2024a. Quantifying contribution of hierarchically correlated shear microdomains underlying creep in metallic glass. International Journal of Plasticity, 174: 103900. doi: 10.1016/j.ijplas.2024.103900 [112] Zhu W, Deng Y, Liu J, et al. 2024b. Strain-dependent transition of the relaxation dynamics in metallic glasses. Modelling and Simulation in Materials Science and Engineering, 32: 035026. doi: 10.1088/1361-651X/ad29b1 -
下载:
计量
- 文章访问数: 13
- HTML全文浏览量: 4
- PDF下载量: 1
- 被引次数: 0