流体力学量子计算研究进展

孟昭远; 卢臻; 熊诗颖; 赵耀民; 杨越

doi:10.6052/1000-0992-24-041

流体力学量子计算研究进展

doi: 10.6052/1000-0992-24-041 cstr: 32046.14.1000-0992-24-041

孟昭远¹,
卢臻¹,
熊诗颖²,
赵耀民^{1, 3},
杨越^{1, 3, ,}

1.
北京大学工学院湍流与复杂系统国家重点实验室, 北京 100871
2.
浙江大学航空航天学院工程力学系, 杭州 310027
3.
北京大学应用物理与技术研究中心, 北京 100871

基金项目: 感谢国家自然科学基金(12432010、11925201)和国家重点研发计划青年科学家项目(2023YF-B4502600)资助

详细信息

作者简介:
杨越, 北京大学工学院教授、副院长. 先后获浙江大学学士、中国科学院力学研究所硕士、加州理工学院博士学位, 于普林斯顿大学与康奈尔大学作博士后. 现任湍流与复杂系统国家重点实验室副主任, 中国力学学会理事, 中国空气动力学会理事, 周培源基金会理事, 空气动力学学报副主编, 力学进展、SCPMA、AMS、ARC期刊编委. 曾获国家杰出青年科学基金、科学探索奖、教育部青年科学奖、求是杰出青年学者奖. 主要研究方向为湍流、涡动力学、燃烧、量子计算

通讯作者:
yyg@pku.edu.cn

计量
- 文章访问数: 366
- HTML全文浏览量: 49
- PDF下载量: 131
- 被引次数: 0
出版历程
- 网络出版日期: 2025-03-11

Advances in quantum computing for fluid dynamics

MENG Zhaoyuan¹,
LU Zhen¹,
XIONG Shiying²,
ZHAO Yaomin^{1, 3},
YANG Yue^{1, 3
, ,}

1.
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing 100871, China
2.
Department of Engineering Mechanics, School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China
3.
HEDPS-CAPT, Peking University, Beijing 100871, China

More Information

Corresponding author: yyg@pku.edu.cn

摘要

摘要: 本文综述流体力学量子计算这一前沿交叉研究领域的进展与挑战. 作为潜在的颠覆性技术, 量子计算预期在未来能够解决部分现实世界中的难题. 流体力学是经典物理与工程应用中极具挑战的问题, 可作为展示量子计算实用性与优越性的范例, 同时量子计算也可为流体力学带来新的研究范式. 本文首先阐述量子计算在量子态叠加与纠缠等方面的特点, 指出流体力学量子计算在初态制备、量子态演化和测量方面的挑战. 随后重点介绍量子−经典混合算法、哈密顿模拟等流体力学量子算法, 以及综述它们在真实量子计算机上的硬件实现进展. 总之, 目前流体力学量子计算仍处于萌芽阶段, 未来在量子计算硬件与算法方面均面临诸多挑战. 与传统方法相比, 尽管量子计算尚未在模拟强非线性的流体力学问题上展示出优越性, 但近期进展显示其有潜力来高效模拟湍流等复杂流动.
- 流体力学 /
- 量子计算 /
- 湍流 /
- 涡动力学 /
- 计算流体力学
Abstract: We review progress and challenges in the emerging field of quantum computing for fluid dynamics (QCFD). Quantum computing, a potentially disruptive technology, is expected to tackle pressing problems in the real world. Fluid dynamics, a complex problem in classical physics and engineering, can serve as an example to demonstrate quantum utility and advantage. Conversely, quantum computing can introduce new paradigms in fluid dynamics research. In this review, we first introduce quantum computing features, such as superposition and entanglement, and highlight the challenges of QCFD in initial state preparation, quantum state evolution, and measurement. We then focus on hybrid quantum-classical algorithms and Hamiltonian simulation for fluid dynamics, reviewing their hardware implementation on current quantum computers. In conclusion, QCFD is in its infancy, facing both challenges in quantum devices and algorithms. Although quantum computing has not yet shown an advantage in simulating strongly nonlinear fluid dynamics over classical methods, recent progress suggests its potential in enhancing simulations of complex flows, including turbulence.
- fluid mechanics /
- quantum computing /
- turbulence /
- vortex dynamics /
- computational fluid dynamics

HTML全文

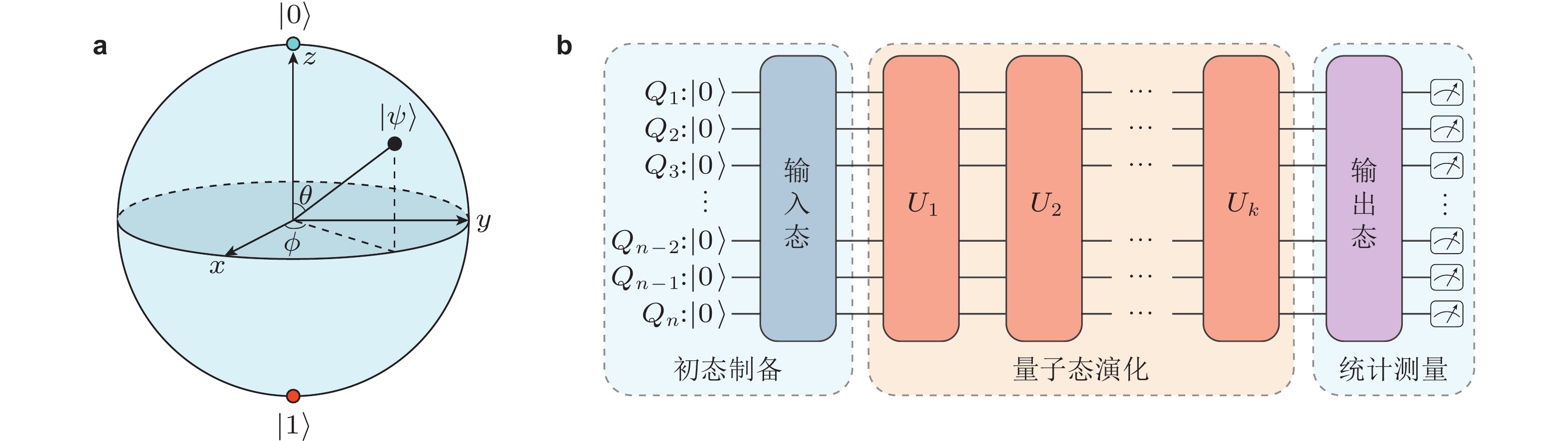
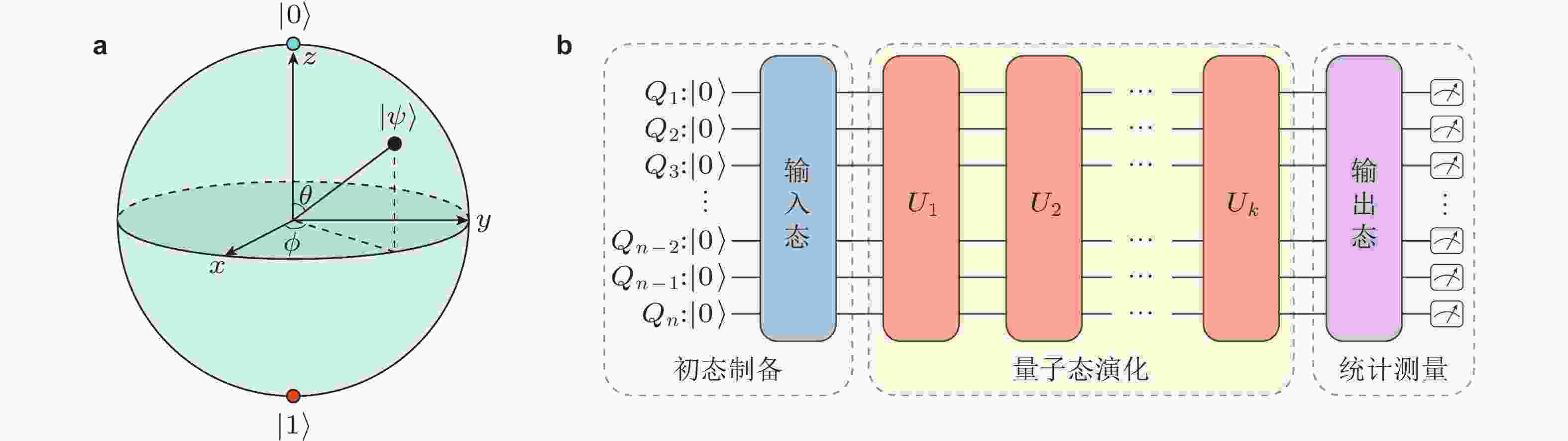
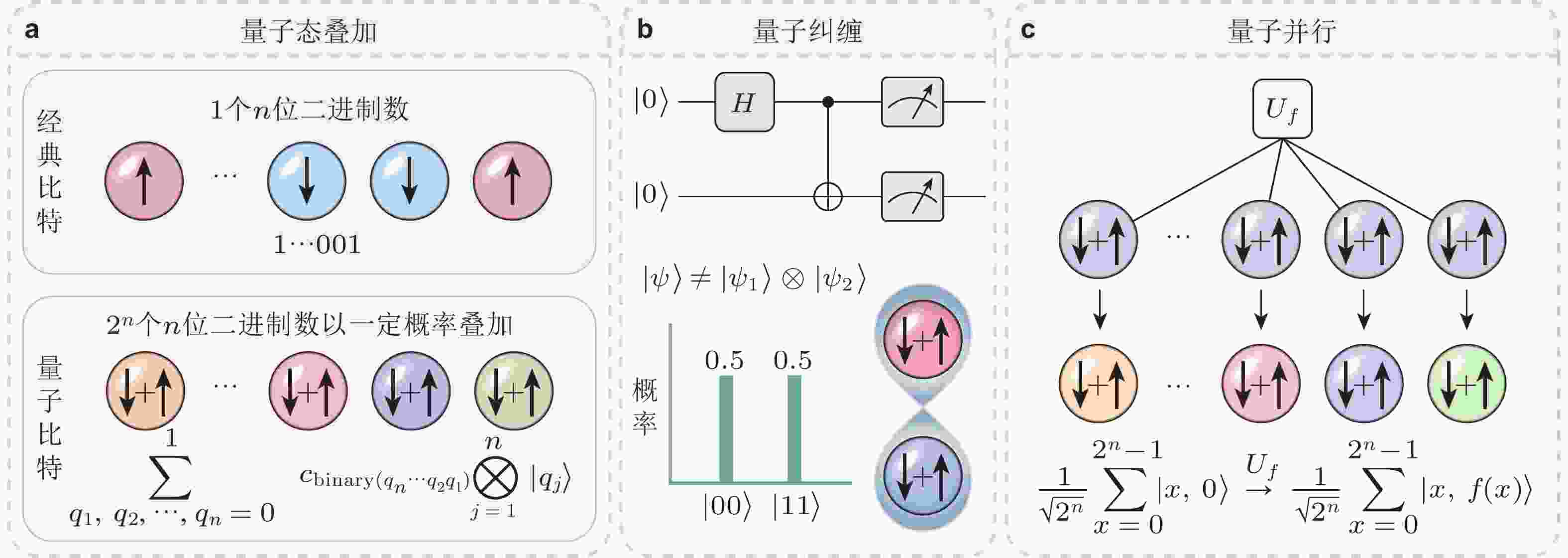
图 1 量子态和量子计算过程示意图. (a)单量子比特状态的Bloch球表示, 可用三维笛卡尔坐标$ x=\sin\theta\cos\varphi $, $ y=\sin\theta\sin\varphi $, $ z=\cos\theta $描述, 为量子态提供几何图像. 任意单量子比特状态$ | {\psi} \rangle=\cos\dfrac{\theta}{2}| {0} \rangle+ {\rm{e}}^{ {\rm{i}}\varphi}\sin\dfrac{\theta}{2}| {1} \rangle $可用球上的一个点来表示, $ | {0} \rangle $态位于北极, $ | {1} \rangle $态位于南极. (b)量子计算机的计算过程分为初态制备、量子态演化和统计测量三步, 图中量子门$ U_1,U_2,\cdots,U_k $均为酉变换

下载: 全尺寸图片幻灯片

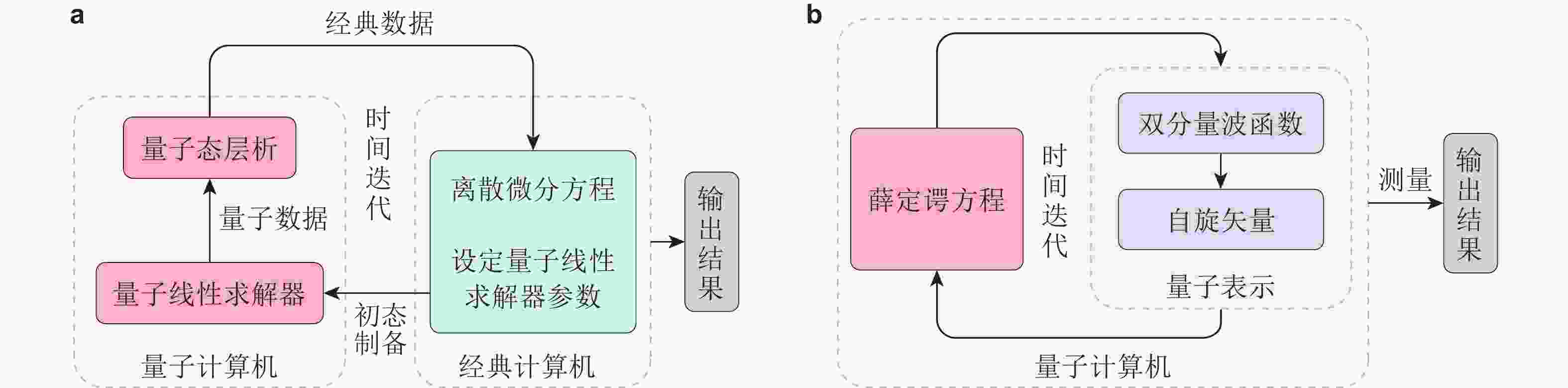
图 2 量子计算基本特性总结. (a)在经典计算机中, n位寄存器中保存 0 到 $ 2^n - 1 $中的一个数; 而在量子计算机中, 处于叠加态的n位量子寄存器中同时保存 0 到 $ 2^n - 1 $ 所有的数, 它们各以一定的概率同时存在. (b)制备两比特纠缠态的最简量子线路: 输出态$ (| {00} \rangle+| {11} \rangle)/\sqrt{2} $不能写成两个量子态的直积, 即两个量子比特处于纠缠态; 测量纠缠中一个量子比特的态, 将使另一个量子比特的态与之相同. (c) 量子计算具有类似于并行的特性, 对叠加的量子态进行一次酉变换, 可产生从0到$ 2^n-1 $所有取值各自所对应的函数值. 其中不同或相同颜色的量子比特分别代表它们之间存在或不存在纠缠

下载: 全尺寸图片幻灯片

图 3 流场的量子初态制备示意图. 将流场信息编码为量子态, 并将该量子初态制备过程分解为多项式复杂度的基本门操作, 是QCFD面临的难题之一

下载: 全尺寸图片幻灯片

图 4 量子−经典混合算法与哈密顿模拟算法计算流程图对比. (a) 利用量子线性求解器的量子−经典混合计算流程图. 在经典计算机上, 首先计算离散微分方程在当前时刻的矩阵和非齐次列向量, 结果用于设定量子线性求解器的参数. 随后进行初态制备, 并利用量子线性求解器求解线性方程组, 获得归一化的解向量. 通过量子态层析将提取出的解向量输入到经典计算机中, 计算下一个时刻的矩阵元素. 推进时间步需重复这一循环过程, 任一时刻的数据处理均在经典计算机上完成. (b) 基于NS方程的自旋量子表示, 将流体动力学模拟转化为求解双分量薛定谔方程 (Meng & Yang 2024b). 在量子计算机上, 对该薛定谔方程进行时间积分, 从而基于该哈密顿模拟流程实现端到端的量子计算

下载: 全尺寸图片幻灯片

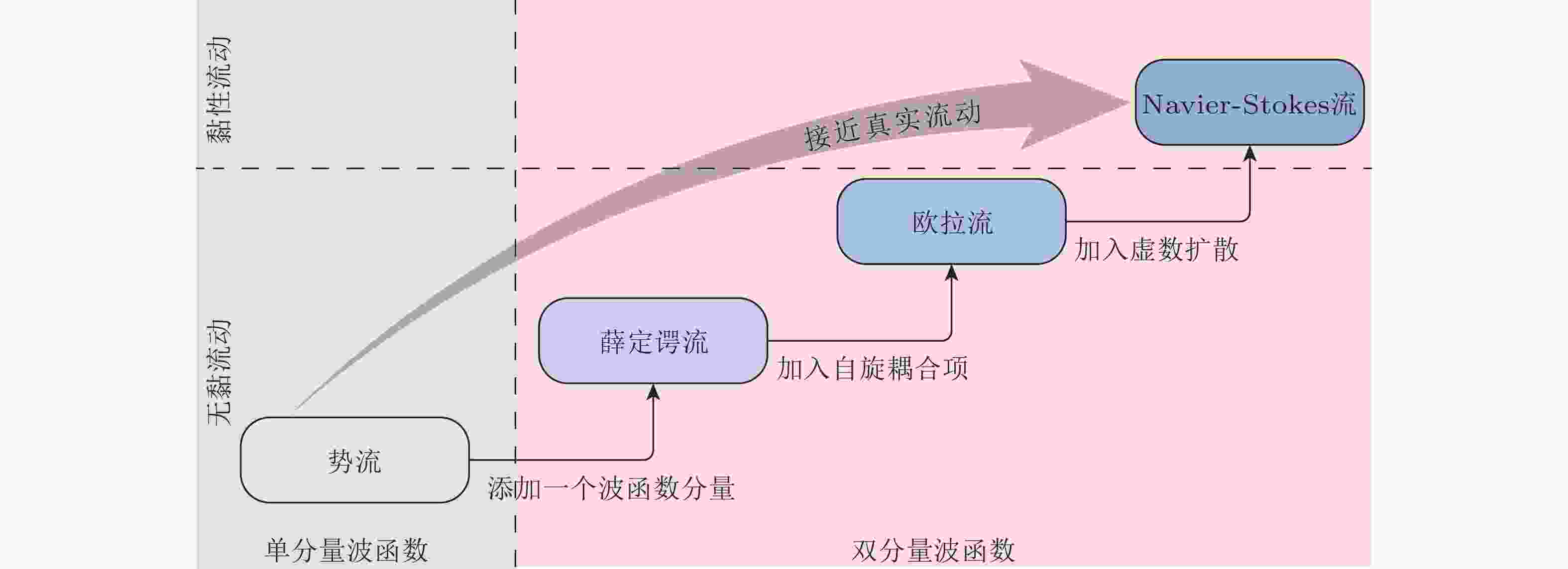
图 5 求解线性方程组Ax = b的HHL算法的量子线路. 首先在量子寄存器$ | {0} \rangle^{\otimes n_b} $中制备列向量b初态, 然后利用量子相位估计得到矩阵A特征值的二进制表示, 对初态为$ | {0} \rangle $的辅助量子比特施加受控旋转, 随后进行量子相位估计的状态反演, 最后对辅助量子比特进行量子测量. 若测量结果为$ | {1} \rangle $, 则量子寄存器中编码的是归一化的解向量$ | {x} \rangle $. 此外, 一些HHL的改进算法可以有效利用辅助量子比特测量结果为$ | {0} \rangle $时量子寄存器中的信息 (Babukhin 2023, Tsemo et al. 2024), 从而避免该预选择过程

下载: 全尺寸图片幻灯片

图 6 从复函数场$ \psi $的零等值面中提取涡丝. 半透明红色曲面为等值面$ \text{Re}(\psi)=0 $, 半透明蓝色曲面为等值面$ \text{Im}(\psi)=0 $, 黄色曲线为$ \text{Re}(\psi)=0 $和$ \text{Im}(\psi)=0 $的交线

下载: 全尺寸图片幻灯片

图 7 “薛定谔化”变换或酉算符线性组合方法的示意图. 对一般线性偏微分方程, 直接对空间方向编码通常无法使状态向量的二范数对应系统的守恒量, 即状态向量不能保持归一化, 对应于系统演化中产生能量集中或耗散现象, 如左图所示对应于非酉的演化算符. 通过引入辅助变量(如右图中的转角), 左图中随时间耗散的量转化为右图中随时间不变的半径, 从而低维空间中的非酉算符映射为高维空间中的酉算符

下载: 全尺寸图片幻灯片

图 8 从简单到复杂流动的流体动力学方程的量子表示层级示意图 (Meng & Yang 2024b)

下载: 全尺寸图片幻灯片

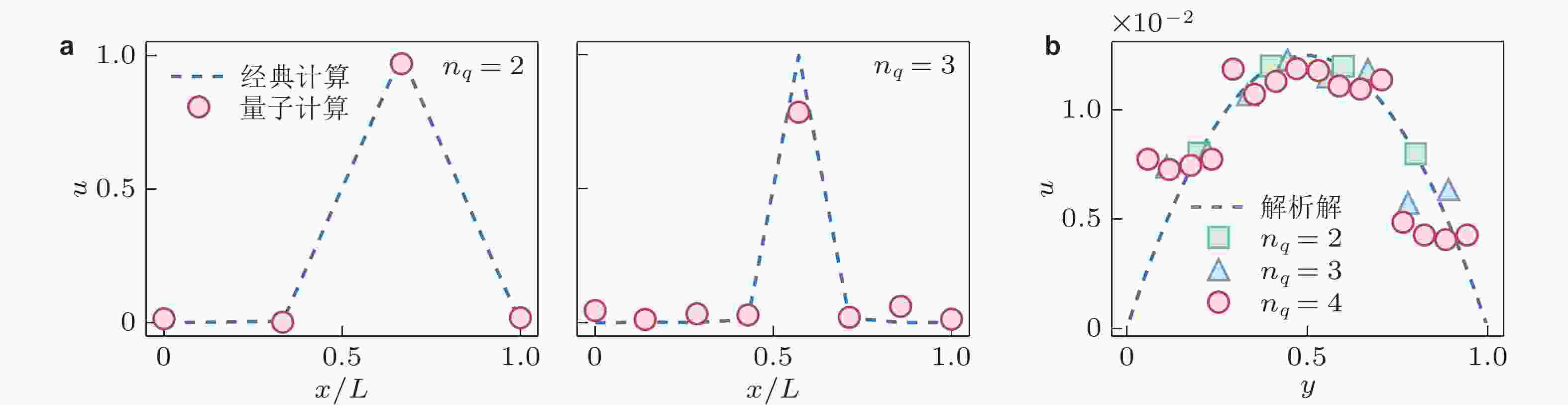
图 9 基于量子线性求解器的量子−经典混合算法的量子计算真机实验结果. (a) 使用2和3个量子比特分别模拟一维对流−扩散问题, 并与经典计算结果进行对比 (Bharadwaj & Sreenivasan 2024a); (b) 使用 2 ~ 4 个量子比特模拟不可压缩 Poiseuille 流 (Chen et al. 2024).

下载: 全尺寸图片幻灯片

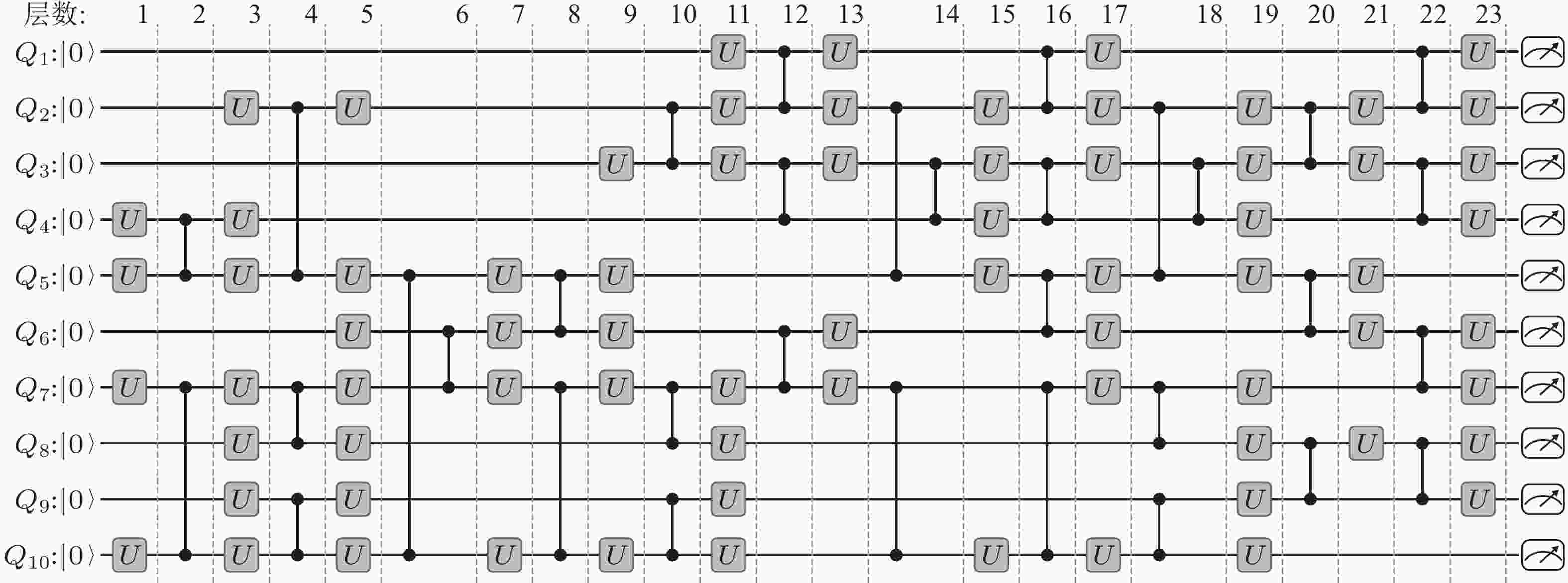
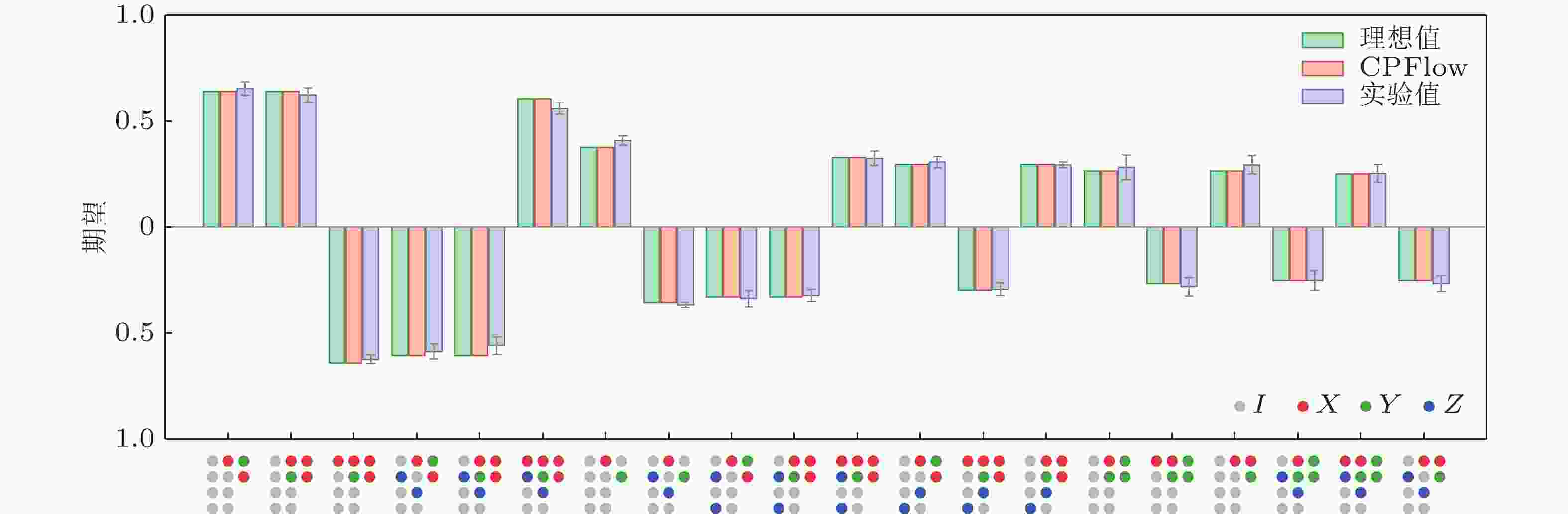
图 10 构建二维旋涡自旋向上波函数分量的10量子比特线路(Meng et al. 2024), 包括任意单量子门U和双量子门CZ. 从基态$ | {0} \rangle^{\otimes 10} $开始, 通过23层同步的单(双)量子门操作, 可以制备目标量子态. 每层操控时间为30(40)纳秒, 总运行时间为810纳秒, 远低于量子比特的寿命. 线路完成后, 需测量所有量子比特以重构流体的密度场和动量场

下载: 全尺寸图片幻灯片

图 11 二维可压缩渐扩势流的初始态下Pauli字符串的期望值(Meng et al. 2024). 按绝对值降序排列, 绘制了精确解(绿色)、CPFlow模拟(橘色)和实验(蓝色)得出的前20个Pauli字符串的期望值. 实验数据的误差棒代表10个标准差, 横轴下的每个点阵序列代表一个Pauli字符串, 每个量子比特根据对应的Pauli算符进行着色

下载: 全尺寸图片幻灯片

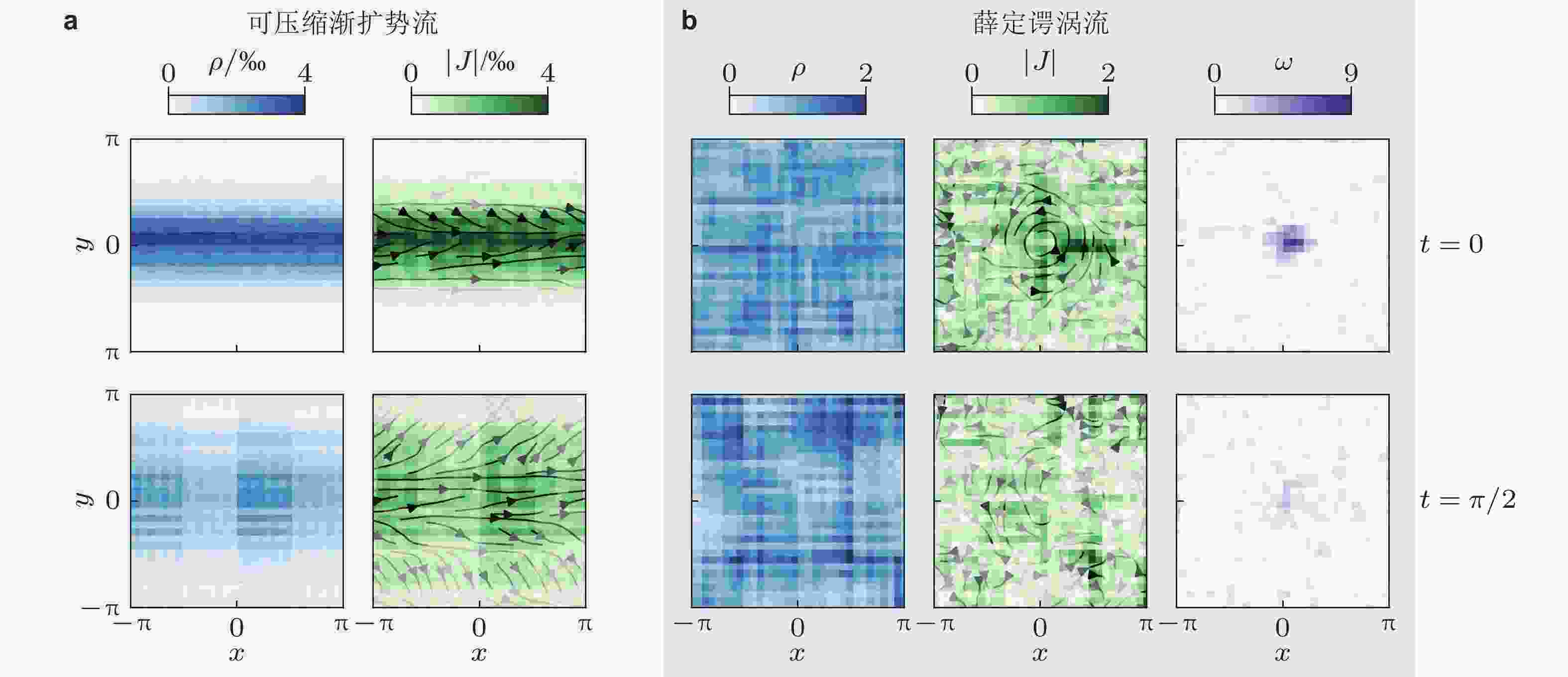
图 12 在超导量子计算机上基于哈密顿模拟的实验结果 (Meng et al. 2024). 其中(a)可压缩渐扩势流, (b)薛定谔涡流. 图中从上至下分别为t = 0和$ \pi/2 $两个时刻的测量结果, 包括密度场(蓝)、动量场(绿)和涡量场(紫), 其中动量场中绘制了若干流线

下载: 全尺寸图片幻灯片

参考文献(165)

[1]	陈坚强, 袁先旭, 涂国华, 郭启龙. 2023. 计算流体力学 2035 愿景. 科学出版社. (Chen J Q, Yuan X X, Tu G H, Guo Q L. 2023. Computational fluid dynamics 2035 vision in China. Science Press). Chen J Q, Yuan X X, Tu G H, Guo Q L. 2023. Computational fluid dynamics 2035 vision in China. Science Press.
[2]	Aaronson S. 2015. Read the fine print. Nat. Phys., 11: 291-293. doi: 10.1038/nphys3272
[3]	Aharonov Y, Davidovich L, Zagury N. 1993. Quantum random walks. Phys. Rev. A, 48: 1687-1690. doi: 10.1103/PhysRevA.48.1687
[4]	Albash T, Lidar D A. 2018. Adiabatic quantum computation. Rev. Mod. Phys., 90: 015002. doi: 10.1103/RevModPhys.90.015002
[5]	An D, Lin L. 2022. Quantum linear system solver based on time-optimal adiabatic quantum computing and quantum approximate optimization algorithm. ACM Transactions on Quantum Computing, 3 .
[6]	An D, Liu J P, Lin L. 2023. Linear combination of Hamiltonian simulation for nonunitary dynamics with optimal state preparation cost. Phys. Rev. Lett., 131: 150603. doi: 10.1103/PhysRevLett.131.150603
[7]	Arute F, Arya K, Babbush R, Bacon D, Bardin J C, Barends R, Biswas R, Boixo S, Brandao F, Buell D A, et al. 2019. Quantum supremacy using a programmable superconducting processor. Nature, 574: 505-510. doi: 10.1038/s41586-019-1666-5
[8]	Ashida Y, Gong Z, Ueda M. 2021. Non-Hermitian physics. Adv. Phys., 69: 249-435.
[9]	Asztalos K, Steijl R, Maulik R. 2024. Reduced-order modeling on a near-term quantum computer. J. Comput. Phys., 510: 113070. doi: 10.1016/j.jcp.2024.113070
[10]	Babbush R, Berry D W, Kothari R, Somma R D, Wiebe N. 2023. Exponential quantum speedup in simulating coupled classical oscillators. Phys. Rev. X, 13: 041041.
[11]	Babukhin D V. 2023. Harrow−Hassidim−Lloyd algorithm without ancilla postselection. Phys. Rev. A, 107: 042408. doi: 10.1103/PhysRevA.107.042408
[12]	Barends R, Shabani A, Lamata L, Kelly J, Mezzacapo A, Las Heras U, Babbush R, Fowler A G, Campbell B, Chen Y, et al. 2016. Digitized adiabatic quantum computing with a superconducting circuit. Nature, 534: 222-226. doi: 10.1038/nature17658
[13]	Basheer A, Afham A, Goyal S K. 2020. Quantum k-nearest neighbors algorithm. arXiv preprint arXiv: 2003.09187,
[14]	Begušić T, Gray J, Chan G K L. 2024. Fast and converged classical simulations of evidence for the utility of quantum computing before fault tolerance. Sci. Adv., 10: eadk4321. doi: 10.1126/sciadv.adk4321
[15]	Benedetti M, Lloyd E, Sack S, Fiorentini M. 2019. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol., 4: 043001. doi: 10.1088/2058-9565/ab4eb5
[16]	Bennett C H, Bernstein E, Brassard G, Vazirani U. 1997. Strengths and weaknesses of quantum computing. SIAM J. Comput., 26: 1510-1523. doi: 10.1137/S0097539796300933
[17]	Bernstein D, Lange T. 2017. Post-quantum cryptography. Nature, 549: 188-194. doi: 10.1038/nature23461
[18]	Bharadwaj S S, Sreenivasan K R. 2020. Quantum computation of fluid dynamics. Indian Acad. Sci. Conf. Ser., 3: 77.
[19]	Bharadwaj S S, Sreenivasan K R. 2023. Hybrid quantum algorithms for flow problems. Proc. Natl. Acad. Sci. U.S.A., 120: e2311014120. doi: 10.1073/pnas.2311014120
[20]	Bharadwaj S S, Sreenivasan K R. 2024a. Compact quantum algorithms that can potentially maintain quantum advantage for solving time-dependent differential equations. arXiv: 2405.09767.
[21]	Bharadwaj S S, Sreenivasan K R. 2024b. Simulating fluid flows with quantum computing. arXiv: 2409.09736.
[22]	Bharti K, Cervera-Lierta A, Kyaw T H, Haug T, Alperin-Lea S, Anand A, Degroote M, Heimonen H, Kottmann J S, Menke T, et al. 2022. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys., 94: 015004. doi: 10.1103/RevModPhys.94.015004
[23]	Biamonte J, Wittek P, Pancotti N, Rebentrost P, Wiebe N, Lloyd S. 2017. Quantum machine learning. Nature, 549: 195-202. doi: 10.1038/nature23474
[24]	Bishwas A K, Mani A, Palade V. 2020. An investigation on support vector clustering for big data in quantum paradigm. Quantum Inf. Process., 19: 108. doi: 10.1007/s11128-020-2606-x
[25]	Borle A, Lomonaco S J. 2022. How viable is quantum annealing for solving linear algebra problems? arXiv: 2206.10576.
[26]	Brearley P, Laizet S. 2024. Quantum algorithm for solving the advection equation using Hamiltonian simulation. Phys. Rev. A, 110: 012430. doi: 10.1103/PhysRevA.110.012430
[27]	Brunton S L, Noack B R, Koumoutsakos P. 2020. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech., 52: 477-508. doi: 10.1146/annurev-fluid-010719-060214
[28]	Brüstle N, Wiebe N. 2024. Quantum and classical algorithms for nonlinear unitary dynamics. arXiv: 2407.07685.
[29]	Budinski L. 2021. Quantum algorithm for the advection-diffusion equation simulated with the lattice Boltzmann method. Quantum Inf. Process., 20: 57. doi: 10.1007/s11128-021-02996-3
[30]	Budinski L. 2022. Quantum algorithm for the Navier−Stokes equations by using the stream function vorticity formulation and the lattice Boltzmann method. Int. J. Quantum Inf., 20: 2150039. doi: 10.1142/S0219749921500398
[31]	Buluta I, Nori F. 2009. Quantum simulators. Science, 326: 108-111. doi: 10.1126/science.1177838
[32]	Cerezo M, Arrasmith A, Babbush R, Benjamin S C, Endo S, Fujii K, McClean J R, Mitarai K, Yuan X, Cincio L, et al. 2021. Variational quantum algorithms. Nat. Rev. Phys., 3: 625-644. doi: 10.1038/s42254-021-00348-9
[33]	Cerezo M, Verdon G, Huang H Y, Cincio L, Coles P J. 2022. Challenges and opportunities in quantum machine learning. Nat. Comput. Sci., 2: 567-576. doi: 10.1038/s43588-022-00311-3
[34]	Chen Z Y, Ma T Y, Ye C C, Xu L, Bai W, Zhou L, Tan M Y, Zhuang X N, Xu X F, Wang Y J, et al. 2024. Enabling large-scale and high-precision fluid simulations on near-term quantum computers. Comput. Methods Appl. Mech. Eng., 432: 117428. doi: 10.1016/j.cma.2024.117428
[35]	Chen Z Y, Xue C, Chen S M, Lu B H, Wu Y C, Ding J C, Huang S H, Guo G P. 2022. Quantum approach to accelerate finite volume method on steady computational fluid dynamics problems. Quantum Inf. Process., 21: 137. doi: 10.1007/s11128-022-03478-w
[36]	Cheng B, Deng X H, Gu X, He Y, Hu G, Huang P, Li J, Lin B C, Lu D, Lu Y, et al. 2023. Noisy intermediate-scale quantum computers. Front. Phys., 18: 21308. doi: 10.1007/s11467-022-1249-z
[37]	Chern A, Knöppel F, Pinkall U, Schröder P. 2017. Inside fluids: Clebsch maps for visualization and processing. ACM Trans. Graphics, 36: 1-11.
[38]	Childs A M, Maslov D, Nam Y, Ross N J, Su Y. 2018. Toward the first quantum simulation with quantum speedup. Proc. Natl. Acad. Sci. U.S.A., 115: 9456-9461. doi: 10.1073/pnas.1801723115
[39]	Chiribella G, D’Ariano G M, Perinotti P. 2008. Quantum circuit architecture. Phys. Rev. Lett., 101: 060401. doi: 10.1103/PhysRevLett.101.060401
[40]	Cirac J I, Zoller P. 2012. Goals and opportunities in quantum simulation. Nat. Phys., 8: 264-266. doi: 10.1038/nphys2275
[41]	Costa P C S, An D, Sanders Y R, Su Y, Babbush R, Berry D W. 2022. Optimal scaling quantum linear-systems solver via discrete adiabatic theorem. PRX Quantum, 3: 040303. doi: 10.1103/PRXQuantum.3.040303
[42]	Cottet G H, Koumoutsakos P. 2000. Vortex methods: Theory and practice. Cambridge University Press.
[43]	Daley A J, Bloch I, Kokail C, Flannigan S, Pearson N, Troyer M, Zoller P. 2022. Practical quantum advantage in quantum simulation. Nature, 607: 667-676. doi: 10.1038/s41586-022-04940-6
[44]	Das A, Chakrabarti B K. 2008. Colloquium: Quantum annealing and analog quantum computation. Rev. Mod. Phys., 80: 1061-1081. doi: 10.1103/RevModPhys.80.1061
[45]	Deutsch D. 1985. Quantum theory, the church-turing principle and the universal quantum computer. Proc. R. Soc. London Ser. A-Math. Phys. Eng. Sci., 400: 97-117.
[46]	Esmaeilifar E, Ahn D, Myong R S. 2024. Quantum algorithm for nonlinear Burgers’ equation for high-speed compressible flows. Phys. Fluids, 36: 106110. doi: 10.1063/5.0231994
[47]	Ferreira G J, Loss D. 2013. Magnetically defined qubits on 3D topological insulators. Phys. Rev. Lett., 111: 106802. doi: 10.1103/PhysRevLett.111.106802
[48]	Feynman R P. 1982. Simulating physics with computers. Int. J. Theor. Phys., 21: 467-488. doi: 10.1007/BF02650179
[49]	Feynman R, Leighton R, Sands M. 2015. The Feynman lectures on physics, Vol. II: The new millennium edition: Mainly electromagnetism and matter. Basic Books.
[50]	Frisch U, Hasslacher B, Pomeau Y. 1986. Lattice-gas automata for the Navier−Stokes equation. Phys. Rev. Lett., 56: 1505-1508. doi: 10.1103/PhysRevLett.56.1505
[51]	Fukagata K. 2022. Towards quantum computing of turbulence. Nat. Comput. Sci., 2: 68-69. doi: 10.1038/s43588-022-00189-1
[52]	Georgescu I M, Ashhab S, Nori F. 2014. Quantum simulation. Rev. Mod. Phys., 86: 153-185. doi: 10.1103/RevModPhys.86.153
[53]	Gilyén A, Su Y, Low G H, Wiebe N. 2019. Quantum singular value transformation and beyond: Exponential improvements for quantum matrix arithmetics. Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing. 193–204.
[54]	Giovannetti V, Lloyd S, Maccone L. 2008. Quantum random access memory. Phys. Rev. Lett., 100: 160501. doi: 10.1103/PhysRevLett.100.160501
[55]	Gourianov N, Lubasch M, Dolgov S, van den Berg Q Y, Babaee H, Givi P, Kiffner M, Jaksch D. 2022. A quantum-inspired approach to exploit turbulence structures. Nat. Comput. Sci., 2: 30-37. doi: 10.1038/s43588-021-00181-1
[56]	Grant E, Wossnig L, Ostaszewski M, Benedetti M. 2019. An initialization strategy for addressing barren plateaus in parametrized quantum circuits. Quantum, 3: 214. doi: 10.22331/q-2019-12-09-214
[57]	Großardt A. 2024. Nonlinear-ancilla aided quantum algorithm for nonlinear Schrödinger equations. arXiv: 2403.10102.
[58]	Grover L K. 1996. A fast quantum mechanical algorithm for database search. Proceedings of the 28th Annual ACM Symposium on Theory of Computing. 212–219.
[59]	Gupta S, Zia R. 2001. Quantum neural networks. J. Comput. System Sci., 63: 355-383. doi: 10.1006/jcss.2001.1769
[60]	Han Z, Yang Y. 2025. Quantum-enriched large-eddy simulation with the incompressible Schrödinger flow. Acta Sin. Mech., 41: 324054. doi: 10.1007/s10409-024-24054-x
[61]	Hangleiter D, Eisert J. 2023. Computational advantage of quantum random sampling. Rev. Mod. Phys., 95: 035001. doi: 10.1103/RevModPhys.95.035001
[62]	Harrow A W, Hassidim A, Lloyd S. 2009. Quantum algorithm for linear systems of equations. Phys. Rev. Lett., 103: 150502. doi: 10.1103/PhysRevLett.103.150502
[63]	Hibat-Allah M, Mauri M, Carrasquilla J, Perdomo-Ortiz A. 2024. A framework for demonstrating practical quantum advantage: Comparing quantum against classical generative models. Commun. Phys., 7: 68. doi: 10.1038/s42005-024-01552-6
[64]	Hu J, Jin S, Liu N, Zhang L. 2024. Quantum circuits for partial differential equations via Schrödingerisation. arXiv: 2403.10032.
[65]	Ishida S, Wojtan C, Chern A. 2022. Hidden degrees of freedom in implicit vortex filaments. ACM Trans. Graph., 41: 241.
[66]	Itani W, Sreenivasan K R, Succi S. 2024. Quantum algorithm for lattice Boltzmann (QALB) simulation of incompressible fluids with a nonlinear collision term. Phys. Fluids, 36: 017112. doi: 10.1063/5.0176569
[67]	Itani W, Succi S. 2022. Analysis of carleman linearization of lattice Boltzmann. Fluids, 7: 24. doi: 10.3390/fluids7010024
[68]	Jain N, Landman J, Mathur N, Kerenidis I. 2024. Quantum fourier networks for solving parametric PDEs. Quantum Sci. Technol., 9: 35026. doi: 10.1088/2058-9565/ad42ce
[69]	Jaksch D, Givi P, Daley A J, Rung T. 2023. Variational quantum algorithms for computational fluid dynamics. AIAA J., 61: 1885-1894. doi: 10.2514/1.J062426
[70]	Jin S, Liu N, Ma C. 2023a. Quantum simulation of Maxwell’s equations via Schrödingerisation. arXiv: 2308.08408.
[71]	Jin S, Liu N, Yu Y. 2023b. Quantum simulation of partial differential equations: Applications and detailed analysis. Phys. Rev. A, 108: 032603. doi: 10.1103/PhysRevA.108.032603
[72]	Jin S, Liu N, Yu Y. 2023c. Time complexity analysis of quantum algorithms via linear representations for nonlinear ordinary and partial differential equations. J. Comput. Phys., 487: 112149. doi: 10.1016/j.jcp.2023.112149
[73]	Jin S, Liu N, Yu Y. 2024a. Quantum simulation of partial differential equations via Schrödingerization. Phys. Rev. Lett., 133: 230602. doi: 10.1103/PhysRevLett.133.230602
[74]	Jin S, Liu N, Yu Y. 2024b. Quantum simulation of the Fokker−Planck equation via Schrödingerization. arXiv: 2404.13585.
[75]	Jin S, Liu N. 2024. Quantum algorithms for nonlinear partial differential equations. Bull. Sci. Math., 194: 103457. doi: 10.1016/j.bulsci.2024.103457
[76]	Joseph I. 2020. Koopman-von Neumann approach to quantum simulation of nonlinear classical dynamics. Phys. Rev. Res., 2: 043102. doi: 10.1103/PhysRevResearch.2.043102
[77]	Kempe J. 2003. Quantum random walks: An introductory overview. Contemp. Phys., 44: 307-327. doi: 10.1080/00107151031000110776
[78]	Kim Y, Eddins A, Anand S, Wei K X, van den Berg E, Rosenblatt S, Nayfeh H, Wu Y, Zaletel M, Temme K, et al. 2023. Evidence for the utility of quantum computing before fault tolerance. Nature, 618: 500-505. doi: 10.1038/s41586-023-06096-3
[79]	Kjaergaard M, Schwartz M E, Braumüller J, Krantz P, Wang J I J, Gustavsson S, Oliver W D. 2020. Superconducting qubits: Current state of play. Annu. Rev. Condens. Matter Phys., 11: 369-395. doi: 10.1146/annurev-conmatphys-031119-050605
[80]	Kocherla S, Song Z, Chrit F E, Gard B, Dumitrescu E F, Alexeev A, Bryngelson S H. 2024. Fully quantum algorithm for mesoscale fluid simulations with application to partial differential equations. AVS Quantum Sci., 6: 033806. doi: 10.1116/5.0217675
[81]	Kuang Z, Xu Y, Huang Q, Yang J, Kihal C E, Hu H. 2025. Quantum computing with error mitigation for data-driven computational homogenization. Compos. Struct., 351: 118625. doi: 10.1016/j.compstruct.2024.118625
[82]	Kumar E D, Frankel S H. 2024. Decomposition of nonlinear collision operator in quantum lattice Boltzmann algorithm. arXiv: 2408.00387.
[83]	Kumar E D, Frankel S H. 2025. Quantum unitary matrix representation of the lattice Boltzmann model for low Reynolds fluid flow simulation. AVS Quantum Sci., 7: 013802. doi: 10.1116/5.0245082
[84]	Kuya Y, Komatsu K, Yonaga K, Kobayashi H. 2024. Quantum annealing-based algorithm for lattice gas automata. Comput. Fluids, 274: 106238. doi: 10.1016/j.compfluid.2024.106238
[85]	Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien J L. 2010. Quantum computers. Nature, 464: 45-53. doi: 10.1038/nature08812
[86]	Lapworth L. 2022. A hybrid quantum-classical CFD methodology with benchmark HHL solutions. arXiv: 2206.00419.
[87]	Leibfried D, Blatt R, Monroe C, Wineland D. 2003. Quantum dynamics of single trapped ions. Rev. Mod. Phys., 75: 281-324. doi: 10.1103/RevModPhys.75.281
[88]	Lewis D, Eidenbenz S, Nadiga B, Subaşı Y. 2024. Limitations for quantum algorithms to solve turbulent and chaotic systems. Quantum, 8: 1509. doi: 10.22331/q-2024-10-24-1509
[89]	Liao S. 2024. A general frame of quantum simulation for nonlinear partial differential equations. arXiv: 2406.15821.
[90]	Lin L, Tong Y. 2020. Optimal polynomial based quantum eigenstate filtering with application to solving quantum linear systems. Quantum, 4: 361. doi: 10.22331/q-2020-11-11-361
[91]	Liu B, Zhu L, Yang Z, He G. 2023. Quantum implementation of numerical methods for convectiondiffusion equations: Toward computational fluid dynamics. Commun. Comput. Phys., 33: 425-451. doi: 10.4208/cicp.OA-2022-0081
[92]	Liu H Y, Lin X, Chen Z Y, Xue C, Sun T P, Li Q S, Zhuang X N, Wang Y J, Wu Y C, Gong M, et al. 2024. Simulation of open quantum systems on universal quantum computers. arXiv: 2405.20712.
[93]	Liu J P, Kolden H O, Krovi H K, Loureiro N F, Trivisa K, Childs A M. 2021. Effcient quantum algorithm for dissipative nonlinear differential equations. Proc. Natl. Acad. Sci. U.S.A., 118: e2026805118. doi: 10.1073/pnas.2026805118
[94]	Liu Y, Ke Y, Zhou J, Liu Y, Luo H, Wen S, Fan D. 2017. Generation of perfect vortex and vector beams based on Pancharatnam−Berry phase elements. Sci. Rep., 7: 44096. doi: 10.1038/srep44096
[95]	Lloyd S, Palma G D, Gokler C, Kiani B, Liu Z W, Marvian M, Tennie F, Palmer T. 2020. Quantum algorithm for nonlinear differential equations. arXiv: 2011.06571.
[96]	Loss D, DiVincenzo D P. 1998. Quantum computation with quantum dots. Phys. Rev. A, 57: 120-126. doi: 10.1103/PhysRevA.57.120
[97]	Louie S G, Chan Y H, da Jornada F H, Li Z, Qiu D Y. 2021. Discovering and understanding materials through computation. Nat. Mater., 20: 728-735. doi: 10.1038/s41563-021-01015-1
[98]	Low G H, Chuang I L. 2017. Optimal hamiltonian simulation by quantum signal processing. Phys. Rev. Lett., 118: 010501. doi: 10.1103/PhysRevLett.118.010501
[99]	Low G H, Chuang I L. 2019. Hamiltonian simulation by qubitization. Quantum, 3: 163. doi: 10.22331/q-2019-07-12-163
[100]	Lu Z, Yang Y. 2024. Quantum computing of reacting flows via Hamiltonian simulation. Proc. Combust. Inst., 40: 105440. doi: 10.1016/j.proci.2024.105440
[101]	Lubasch M, Joo J, Moinier P, Kiffner M, Jaksch D. 2020. Variational quantum algorithms for nonlinear problems. Phys. Rev. A, 101: 010301. doi: 10.1103/PhysRevA.101.010301
[102]	Markidis S. 2022. On physics-informed neural networks for quantum computers. Front. Appl. Math. Stat., 8: 1036711. doi: 10.3389/fams.2022.1036711
[103]	McArdle S, Endo S, Aspuru-Guzik A, Benjamin S C, Yuan X. 2020. Quantum computational chemistry. Rev. Mod. Phys., 92: 015003. doi: 10.1103/RevModPhys.92.015003
[104]	Meng Z, Song C, Yang Y. 2025. Challenges of simulating fluid flows on near-term quantum computer. Sci. China-Phys. Mech. Astron. (in press
[105]	Meng Z, Yang Y. 2023. Quantum computing of fluid dynamics using the hydrodynamic Schrödinger equation. Phys. Rev. Res., 5: 033182. doi: 10.1103/PhysRevResearch.5.033182
[106]	Meng Z, Yang Y. 2024a. Lagrangian dynamics and regularity of the spin Euler equation. J. Fluid Mech., 985: A34. doi: 10.1017/jfm.2024.319
[107]	Meng Z, Yang Y. 2024b. Quantum spin representation for the Navier−Stokes equation. Phys. Rev. Res., 6: 043130. doi: 10.1103/PhysRevResearch.6.043130
[108]	Meng Z, Zhong J, Xu S, Wang K, Chen J, Jin F, Zhu X, Gao Y, Wu Y, Zhang C, et al. 2024. Simulating unsteady flows on a superconducting quantum processor. Commun. Phys., 7: 349. doi: 10.1038/s42005-024-01845-w
[109]	Mujal P, Martínez-Peña R, Nokkala J, García-Beni J, Giorgi G L, Soriano M C, Zambrini R. 2021. Opportunities in quantum reservoir computing and extreme learning machines. Adv. Quantum Technol., 4: 2100027. doi: 10.1002/qute.202100027
[110]	Nayak C, Simon S H, Stern A, Freedman M, Das Sarma S. 2008. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys., 80: 1083-1159. doi: 10.1103/RevModPhys.80.1083
[111]	Nemkov N A, Kiktenko E O, Luchnikov I A, Fedorov A K. 2023. Effcient variational synthesis of quantum circuits with coherent multi-start optimization. Quantum, 7: 993. doi: 10.22331/q-2023-05-04-993
[112]	Novikau I, Joseph I. 2025. Quantum algorithm for the advection-diffusion equation and the Koopmanvon Neumann approach to nonlinear dynamical systems. Comput. Phys. Commun., 309: 109498. doi: 10.1016/j.cpc.2025.109498
[113]	Over P, Bengoechea S, Brearley P, Laizet S, Rung T. 2024. Quantum algorithm for the advectiondiffusion equation with optimal success probability. arXiv: 2410.07909.
[114]	Peddinti R D, Pisoni S, Marini A, Lott P, Argentieri H, Tiunov E, Aolita L. 2024. Quantum-inspired framework for computational fluid dynamics. Commun. Phys., 7: 135. doi: 10.1038/s42005-024-01623-8
[115]	Pfeffer P, Heyder F, Schumacher J. 2022. Hybrid quantum-classical reservoir computing of thermal convection flow. Phys. Rev. Res., 4: 033176. doi: 10.1103/PhysRevResearch.4.033176
[116]	Pfeffer P, Heyder F, Schumacher J. 2023. Reduced-order modeling of two-dimensional turbulent Rayleigh-Bénard flow by hybrid quantum-classical reservoir computing. Phys. Rev. Res., 5: 043242. doi: 10.1103/PhysRevResearch.5.043242
[117]	Pope S B. 2011. Simple models of turbulent flows. Phys. Fluids, 23: 011301. doi: 10.1063/1.3531744
[118]	Prawer S, Greentree A D. 2008. Diamond for quantum computing. Science, 320: 1601-1602. doi: 10.1126/science.1158340
[119]	Rodríguez J D D, Pérez A P, Fernández E I, Valera A J J. 2024. A quantum annealing approach to fluid dynamics problems solving Navier−Stokes equations. 9th International Conference on Smart and Sustainable Technologies (SpliTech).
[120]	Saffman M, Walker T G, Mølmer K. 2010. Quantum information with Rydberg atoms. Rev. Mod. Phys., 82: 2313-2363. doi: 10.1103/RevModPhys.82.2313
[121]	Sajjan M, Li J, Selvarajan R, Sureshbabu S H, Kale S S, Gupta R, Singh V, Kais S. 2022. Quantum machine learning for chemistry and physics. Chem. Soc. Rev., 51: 6475-6573. doi: 10.1039/D2CS00203E
[122]	Salasnich L, Succi S, Tiribocchi A. 2024. Quantum wave representation of dissipative fluids. Int. J. Mod. Phys. C, 35: 2450100. doi: 10.1142/S0129183124501006
[123]	Sanavio C, Mauri E, Succi S. 2024a. Explicit quantum circuit for simulating the advection-diffusionreaction dynamics. arXiv: 2410.05876.
[124]	Sanavio C, Scatamacchia R, de Falco C, Succi S. 2024b. Three Carleman routes to the quantum simulation of classical fluids. Phys. Fluids, 36: 057143. doi: 10.1063/5.0204955
[125]	Santagati R, Aspuru-Guzik A, Babbush R, Degroote M, González L, Kyoseva E, Moll N, Oppel M, Parrish R M, Rubin N C, et al. 2024. Drug design on quantum computers. Nat. Phys., 20: 549-557. doi: 10.1038/s41567-024-02411-5
[126]	Sato Y, Kondo R, Hamamura I, Onodera T, Yamamoto N. 2024. Hamiltonian simulation for hyperbolic partial differential equations by scalable quantum circuits. Phys. Rev. Res., 6: 033246. doi: 10.1103/PhysRevResearch.6.033246
[127]	Schlimgen A W, Head-Marsden K, Sager L M, Narang P, Mazziotti D A. 2021. Quantum simulation of open quantum systems using a unitary decomposition of operators. Phys. Rev. Lett., 127: 270503. doi: 10.1103/PhysRevLett.127.270503
[128]	Schmid P J. 2010. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech., 656: 5-28. doi: 10.1017/S0022112010001217
[129]	Shao C. 2018. Quantum algorithms to matrix multiplication. arXiv: 1803.01601.
[130]	Shao H J, Wang Y X, Zhu D Z, Zhu Y S, Sun H N, Chen S Y, Zhang C, Fan Z J, Deng Y, Yao X C, et al. 2024. Antiferromagnetic phase transition in a 3D fermionic Hubbard model. Nature, 632: 267-272. doi: 10.1038/s41586-024-07689-2
[131]	Shor P W. 1994. Algorithms for quantum computation: Discrete logarithms and factoring. Proceedings 35th Annual Symposium on Foundations of Computer Science. 124–134.
[132]	Shor P W. 1997. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput., 26: 1484. doi: 10.1137/S0097539795293172
[133]	Singh H, McCulloch E, Gopalakrishnan S, Vasseur R. 2024. Emergence of Navier−Stokes hydrodynamics in chaotic quantum circuits. arXiv: 2405.13892.
[134]	Song Z, Deaton R, Gard B, Bryngelson S H. 2025. Incompressible Navier−Stokes solve on noisy quantum hardware via a hybrid quantum-classical scheme. Comput. Fluids, 288: 106507. doi: 10.1016/j.compfluid.2024.106507
[135]	Steijl R, Barakos G N. 2018. Parallel evaluation of quantum algorithms for computational fluid dynamics. Comput. Fluids, 173: 22-28. doi: 10.1016/j.compfluid.2018.03.080
[136]	Su H, Xiong S, Yang Y. 2024. Quantum state preparation for a velocity field based on the spherical Clebsch wave function. arXiv: 2406.04652.
[137]	Subaşı Y, Somma R D, Orsucci D. 2019. Quantum algorithms for systems of linear equations inspired by adiabatic quantum computing. Phys. Rev. Lett., 122: 060504. doi: 10.1103/PhysRevLett.122.060504
[138]	Succi S, Itani W, Sanavio C, Sreenivasan K R, Steijl R. 2024. Ensemble fluid simulations on quantum computers. Comput. Fluids, 270: 106148. doi: 10.1016/j.compfluid.2023.106148
[139]	Succi S, Itani W, Sreenivasan K, Steijl R. 2023. Quantum computing for fluids: Where do we stand? Europhys. Lett., 144: 10001.
[140]	Tennie F, Laizet S, Lloyd S, Magri L. 2025. Quantum computing for nonlinear differential equations and turbulence. Nat. Rev. Phys., arXiv: 2406.04826.
[141]	Tennie F, Magri L. 2024. Solving nonlinear differential equations on quantum computers: A FokkerPlanck approach. arXiv: 2401.13500.
[142]	Terhal B M. 2015. Quantum error correction for quantum memories. Rev. Mod. Phys., 87: 307-346. doi: 10.1103/RevModPhys.87.307
[143]	Thouless D J, Ao P, Niu Q. 1993. Vortex dynamics in superfluids and the Berry phase. Physica A: Stat. Mech. Appl., 200: 42-49. doi: 10.1016/0378-4371(93)90503-V
[144]	Tilly J, Chen H, Cao S, Picozzi D, Setia K, Li Y, Grant E, Wossnig L, Rungger I, Booth G H, et al. 2022. The variational quantum eigensolver: A review of methods and best practices. Phys. Rep., 986: 1-128. doi: 10.1016/j.physrep.2022.08.003
[145]	Tsemo P B, Jayashankar A, Sugisaki K, Baskaran N, Chakraborty S, Prasannaa V S. 2024. Enhancing the Harrow-Hassidim-Lloyd (HHL) algorithm in systems with large condition numbers. arXiv: 2407.21641.
[146]	Vandersypen L M K, Chuang I L. 2005. NMR techniques for quantum control and computation. Rev. Mod. Phys., 76: 1037-1069. doi: 10.1103/RevModPhys.76.1037
[147]	Wang B, Meng Z, Zhao Y, Yang Y. 2025. Quantum lattice Boltzmann method for simulating nonlinear fluid dynamics. arXiv: 2502.16568.
[148]	Wawrzyniak D, Winter J, Schmidt S, Indinger T, Janßen C F, Schramm U, Adams N A. 2025. A quantum algorithm for the lattice-Boltzmann method advection-diffusion equation. Comput. Phys. Commun., 306: 109373. doi: 10.1016/j.cpc.2024.109373
[149]	Weißmann S, Pinkall U, Schröder P. 2014. Smoke rings from smoke. ACM Trans. Graph., 33: 4.
[150]	Williams C A, Gentile A A, Elfving V E, Berger D, Kyriienko O. 2024. Quantum iterative methods for solving differential equations with application to computational fluid dynamics. arXiv: 2404.08605.
[151]	Wootters W K, Zurek W H. 1982. A single quantum cannot be cloned. Nature, 299: 802-803. doi: 10.1038/299802a0
[152]	Wright L, Keever C M, First J T, Johnston R, Tillay J, Chaney S, Rosenkranz M, Lubasch M. 2024. Noisy intermediate-scale quantum simulation of the one-dimensional wave equation. arXiv: 2402.19247.
[153]	Wu Y, Bao W S, Cao S, Chen F, Chen M C, Chen X, Chung T H, Deng H, Du Y, Fan D, et al. 2021. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett., 127: 180501. doi: 10.1103/PhysRevLett.127.180501
[154]	Xiao P, Zheng M, Jiao A, Yang X, Lu L. 2024a. Quantum DeepONet: Neural operators accelerated by quantum computing. arXiv: 2409.15683.
[155]	Xiao Y, Yang L M, Shu C, Chew S C, Khoo B C, Cui Y D, Liu Y Y. 2024b. Physics-informed quantum neural network for solving forward and inverse problems of partial differential equations. Phys. Fluids, 36 .
[156]	Xiong S, Tong Y, He X, Yang S, Yang C, Zhu B. 2021. Nonseparable symplectic neural networks. International Conference on Learning Representations. arXiv: 2010.12636.
[157]	Xu X, Sun J, Endo S, Li Y, Benjamin S C, Yuan X. 2021. Variational algorithms for linear algebra. Sci. Bull., 66: 2181-2188. doi: 10.1016/j.scib.2021.06.023
[158]	Xu Y, Yang J, Kuang Z, Huang Q, Huang W, Hu H. 2024. Quantum computing enhanced distanceminimizing data-driven computational mechanics. Comput. Meth. Appl. Mech. Eng., 419: 116675. doi: 10.1016/j.cma.2023.116675
[159]	Yadav S. 2023. Qpde: Quantum neural network based stabilization parameter prediction for numerical solvers for partial differential equations. AppliedMath, 3: 552-562. doi: 10.3390/appliedmath3030029
[160]	Ye C C, An N B, Ma T Y, Dou M H, Bai W, Sun D J, Chen Z Y, Guo G P. 2024. A hybrid quantum-classical framework for computational fluid dynamics. Phys. Fluids, 36: 127111. doi: 10.1063/5.0238193
[161]	Yuan X, Chen Z, Liu Y, Xie Z, Liu Y, Jin X, Wen X, Tang H. 2023. Quantum support vector machines for aerodynamic classification. Int. Comput., 2: 0057. doi: 10.34133/icomputing.0057
[162]	Zamora A D B, Budinski L, Niemimäki O, Lahtinen V. 2025. Effcient quantum lattice gas automata. Comput. Fluids, 286: 106476. doi: 10.1016/j.compfluid.2024.106476
[163]	Zhong H S, Deng Y H, Qin J, Wang H, Chen M C, Peng L C, Luo Y H, Wu D, Gong S Q, Su H, et al. 2021. Phase-programmable Gaussian Boson sampling using stimulated squeezed light. Phys. Rev. Lett., 127: 180502. doi: 10.1103/PhysRevLett.127.180502
[164]	Zhong H S, Wang H, Deng Y H, Chen M C, Peng L C, Luo Y H, Qin J, Wu D, Ding X, Hu Y, et al. 2020. Quantum computational advantage using photons. Science, 370: 1460-1463. doi: 10.1126/science.abe8770
[165]	Zylberman J, Di Molfetta G, Brachet M, Loureiro N F, Debbasch F. 2022. Quantum simulations of hydrodynamics via the Madelung transformation. Phys. Rev. A, 106: 032408. doi: 10.1103/PhysRevA.106.032408