基于状态空间离散的非线性动力系统全局分析方法进展: 从模型驱动到数据驱动

李自刚; 洪灵; 江俊

doi:10.6052/1000-0992-25-002

基于状态空间离散的非线性动力系统全局分析方法进展: 从模型驱动到数据驱动

doi: 10.6052/1000-0992-25-002 cstr: 32046.14.1000-0992-25-002

李自刚¹,
洪灵²,
江俊^2, ,

1.
西安科技大学理学院, 西安 710054
2.
西安交通大学复杂服役环境重大装备结构强度与寿命全国重点实验室, 西安 710049

基金项目: 国家自然科学基金项目 (12472031, 12172279, 12172267) 资助

详细信息

作者简介:
李自刚, 西安科技大学教授, 项目博导. 全国徐芝纶力学优秀教师. 现任理学院副院长, 动力学与控制学科学术带头人, 信息交叉力学创新团队负责人. 主要从事非线性系统全局振动控制与机器学习方法、转子动力学等研究. 在国内外学术刊物上发表论文40余篇. 主持国家自然科学基金项目3项. 获陕西省自然科学奖一等奖、三等奖, 陕西高等学校科学技术奖特等奖, 西安市科学技术二等奖等. 担任国际动力学与控制学术期刊“International Journal of Dynamics and Control”副主编

洪灵, 西安交通大学教授, 博士生导师. 主要从事非线性复杂系统全局动力学分析方法,模糊非线性系统动力学与最优控制以及机器学习方法等研究. 在国内外学术刊物上发表论文90余篇, 主持国家自然科学基金面上项目4项. 获陕西省自然科学一等奖和教育部自然科学二等奖, 陕西高等学校科学技术奖特等奖等, 2004年全国百篇优秀博士论文提名. 担任国际动力学与控制学术期刊“International Journal of Dynamics and Control”副主编

江俊, 西安交通大学教授, 博士生导师. 主要从事非线性动力学的全局分析方法、非线性模态及其降价模型、智能结构及振动控制; 多体与转子动力学、流固耦合振动等研究. 在国内外学术刊物上发表论文150余篇, 主持完成国家自然科学基金重点项目和面上项目6项. 获陕西省自然科学奖一等奖1项, 教育部科学技术奖二等奖2项, 陕西高等学校科学技术奖特等奖1项. 担任“International Journal of Dynamics and Control” “动力学与控制学报” “应用力学学报”和“西安交通大学学报” 等学术杂志编委

通讯作者:
jun.jiang@xjtu.edu.cn

中图分类号: O322
计量
- 文章访问数: 16
- HTML全文浏览量: 13
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-30
- 录用日期: 2024-11-30
- 网络出版日期: 2024-11-30

State space discretization based methods for global analysis of nonlinear dynamic systems from model-driven to data-driven: A review

LI Zigang¹,
HONG Ling²,
JIANG Jun^{2
, ,}

1.
College of Sciences, Xi’an University of Science and Technology, Xi’an 710054, China
2.
State Key Laboratory for Strength and Vibration, Xi’an Jiaotong University, Xi’an 710049, China

More Information

Corresponding author: jun.jiang@xjtu.edu.cn

摘要

摘要: 非线性动力系统的一切响应行为均受制于其内在的全局结构, 诸如多稳吸引子及其影响域的形貌和空间分布, 不稳定不变集和不变流形等. 因而, 在指定状态空间内开展全局分析, 不仅可以获得认识和预测系统响应的全部信息, 还能深刻揭示诱发系统复杂分岔、激变或边界蜕变等众多动力学现象的内在机制. 目前, 数值方法仍是非线性动力系统全局分析的最有效手段. 相较于点尺度的数值积分方法或点映射法, 基于状态空间离散思想的方法 (如: 胞映射方法等), 其采用子集覆盖来逼近系统的不变集, 一方面可以高效刻画系统的全局结构形貌, 另一方面可以实现对相邻轨道动态特征的集合表征. 胞映射方法经历40余年的发展, 其功能不断增强, 计算效率和精度已显著提升, 应用场景也逐渐拓宽. 本综述第二节将从当前的视角对状态空间离散方式进行简要归类, 以便于读者更好地了解在全局分析实施过程中该框架体系的本质及优势. 文章第三节将着重介绍近些年提出的一系列状态空间离散方法, 展示在非线性系统全局结构的高效刻画和内在特征的数据表征两方面已取得的最新进展, 突出全局分析从模型驱动向数据驱动的思维模式转变. 在文章第四节将总结本综述的意义和价值, 并就如何在状态空间离散框架下进一步泛化全局分析的概念, 以及应对未来发展和应用需求可能面临的问题和可以拓展的方向提出见解.
- 状态空间离散 /
- 全局分析 /
- 胞映射方法 /
- 模型驱动 /
- 数据驱动
Abstract: Response behaviors of nonlinear dynamic systems are subject to their inherent global structures, such as the morphology and distribution of multi-stable attractors and basins of attraction in state space, unstable invariant sets as well as invariant manifolds. Therefore, conducting a global analysis within the specified state space can not only obtain all the information for understanding and predicting the responses, but also profoundly reveal the internal mechanisms that induce numerous dynamic phenomena, like complex bifurcations, catastrophes, or boundary transitions in the system. Currently, numerical methods remain the most effective means for the global analysis of nonlinear dynamic systems. Compared with the pointwise numerical integration or point mapping approaches, the methods based on the state space discretization, such as the cell mapping method, approximate the invariant sets by covering subsets (cells). This pattern, on the one hand, can efficiently depict the morphology of underlying global structure, and on the other hand, it characterizes the dynamics of adjacent orbits. After 40 years of development, the function of cell mapping method is continuously enhanced, the computational efficiency and accuracy are significantly improved, and its scenarios of application are also being broadened. In the second section of this review, the manners of state space discretization will be briefly classified from the perspective of current research, so that readers can understand the essence and advantages of this framework in global analysis clearly. Focusing on a series of state space discretization methods proposed in recent years, in the third section, we follow the shift in the idea of global analysis from model-driven to data-driven, introducing the latest progress achieved in two aspects: the efficient characterization of global structure and the data mining of inherent features. In the fourth section, the significance of this review is summarized, and insights will be put forward on how to further generalize the concept of global analysis within the state space discretization framework, as well as on the possible problems and expandable directions that may be faced in response to future development and application requirements.
- state space discretization /
- global analysis /
- cell mapping /
- model-driven method /
- data-driven method

HTML全文

图 1 非线性动力系统全局结构的基本框架示意图, 如鞍性不变集 (红色“△”)、稳定不变流形 (蓝色线)、不稳定不变流形 (黄色线)、吸引子 (两侧低地势区)、吸引域 (两侧盆地区域), 虚有向线表示吸引域内部遵循于全局不变结构的响应轨迹

下载: 全尺寸图片幻灯片

图 2 面向集合方法的胞尺寸精细化过程

下载: 全尺寸图片幻灯片

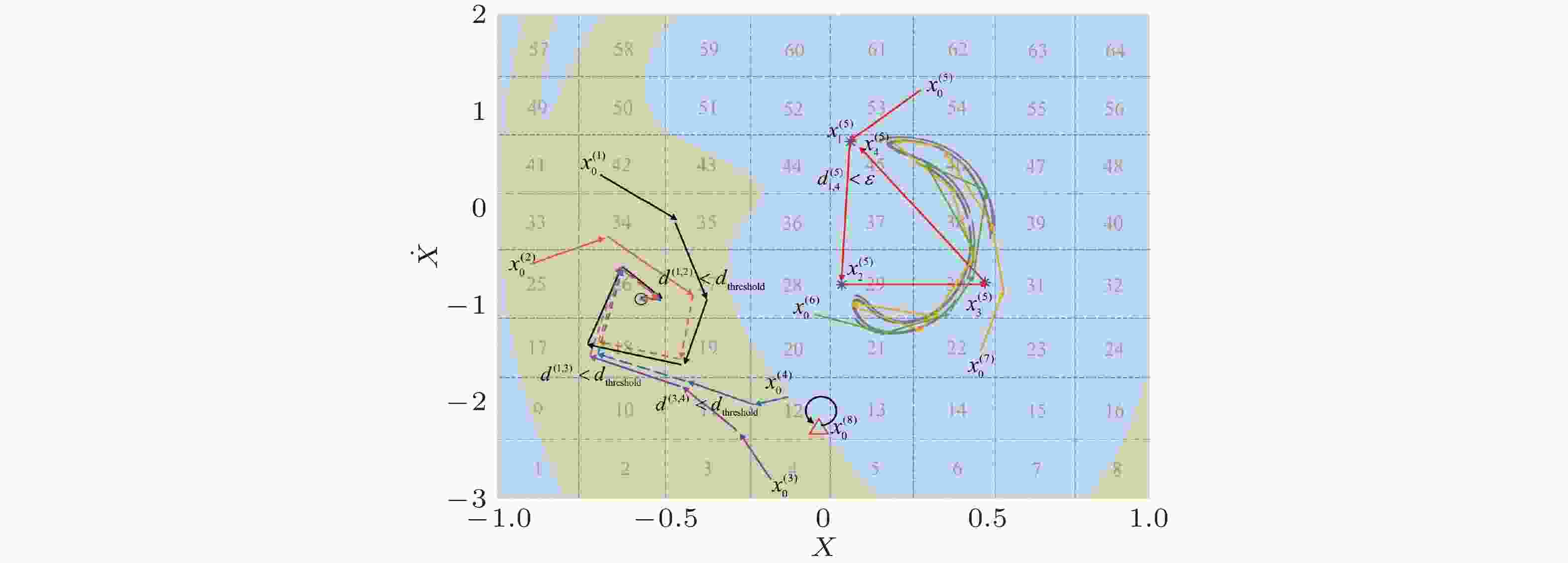
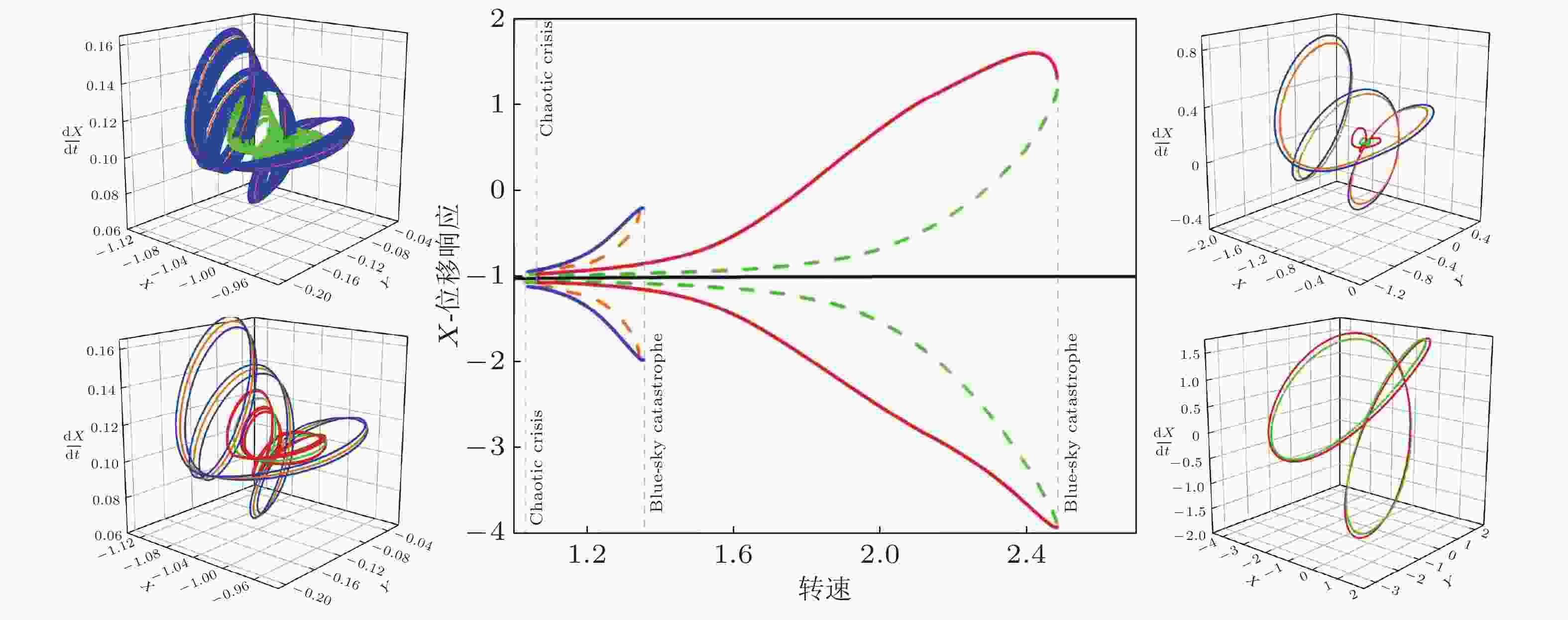
图 3 两尺度胞参考点映射方法的原理示意图. 其中$x_m^{(i)}$表示第i条轨迹的第m个映射状态点, 网格和数字代表胞的区间和编码, 浅黄和浅蓝区域分别对应周期1 (“○”) 和周期3 (“*”) 两个吸引子的全局吸引域, 浅灰色结构为周期3吸引域内部的鞍性混沌, 边界上“△”为不稳定鞍点. 当第j条轨迹进入第i条轨迹的“已访问”胞且触发$ {d^{(i,j)}} \lt {d_{{\text{threshold}}}} $, 则后续轨迹无需计算 (彩色虚线) 并更新相应的$ R(Z) $; 当第i条轨迹的第n个映射状态点再次进入该条轨迹的“访问中”胞且与第m个映射状态点触发$ d_{m,n}^{(i)} \lt \varepsilon $时, 则标记该轨迹的周期性并更新相应的$ R(Z) $

下载: 全尺寸图片幻灯片

图 4 转子/定子碰摩系统的全局结构和动力学分岔(Fan et al. 2022). 其中左图为诱发两种间歇性准周期碰摩行为发生的混沌激变, 左图为导致两种间歇性准周期碰摩行为消亡的突变分岔, 中图为上述现象发生、发展和消亡的动力学分岔图.

下载: 全尺寸图片幻灯片

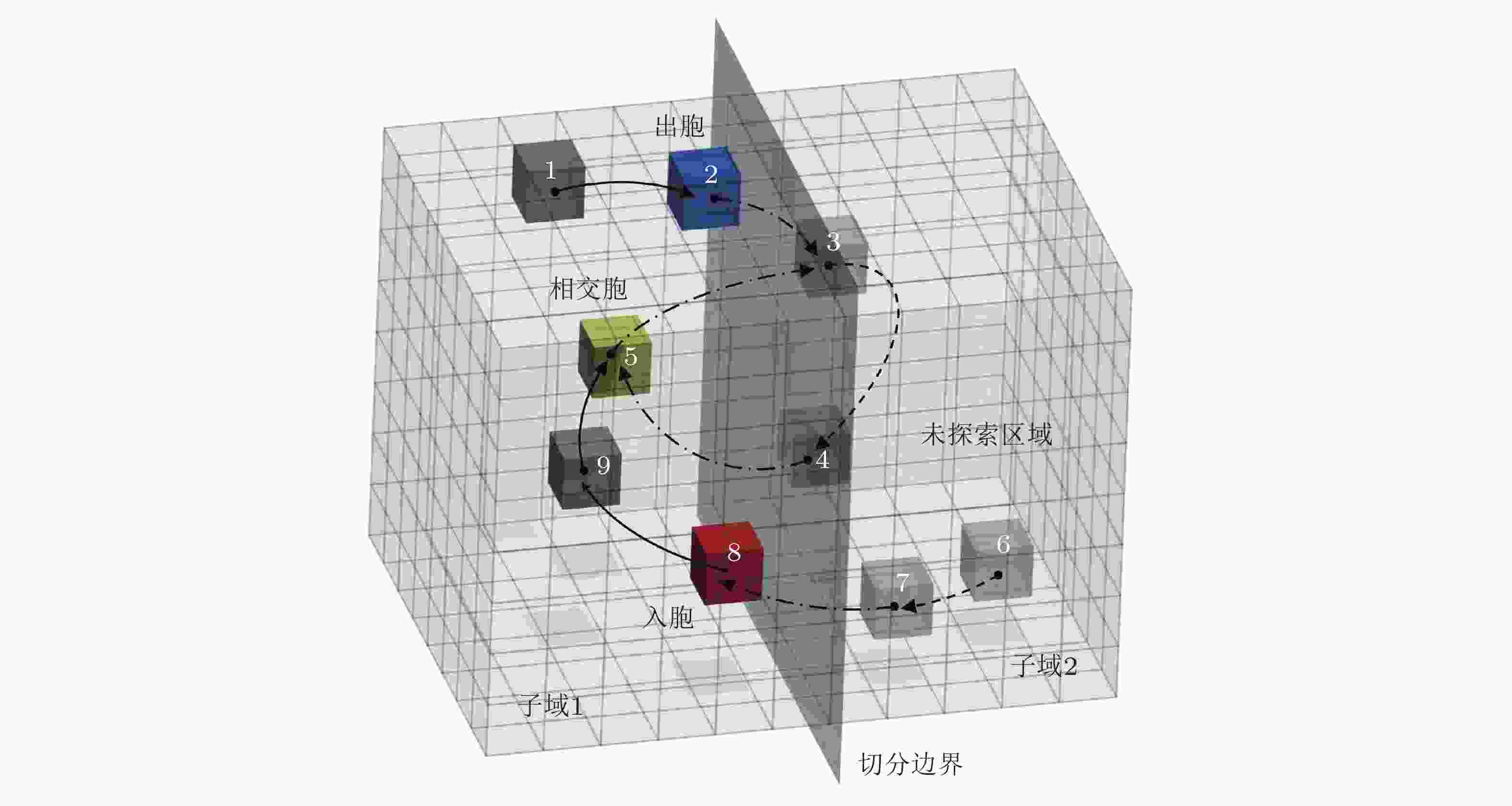
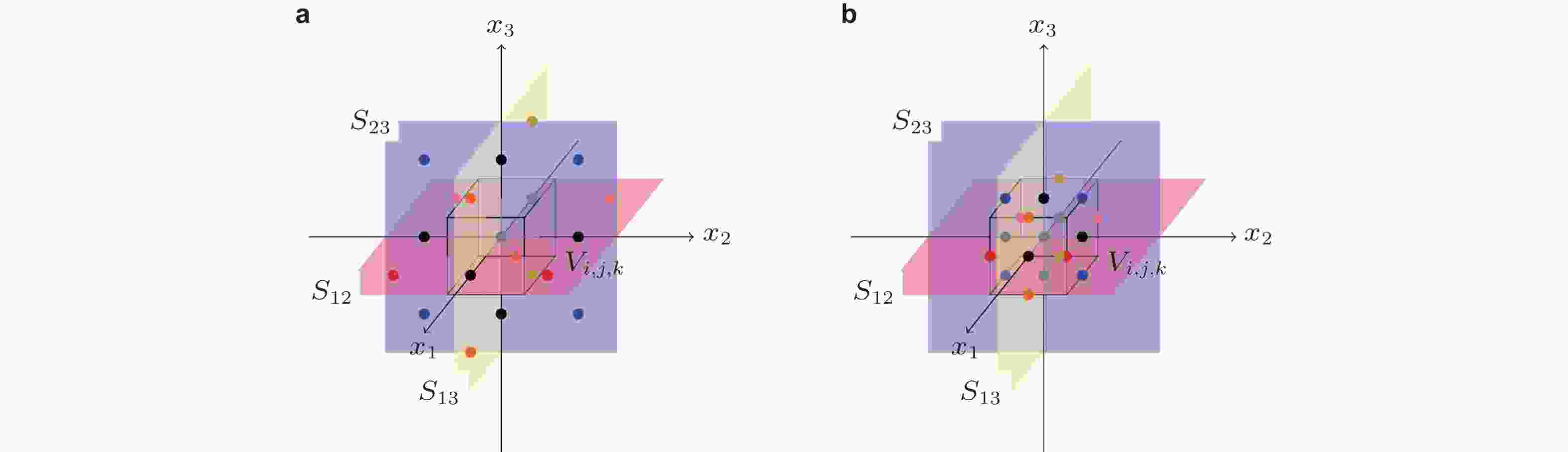
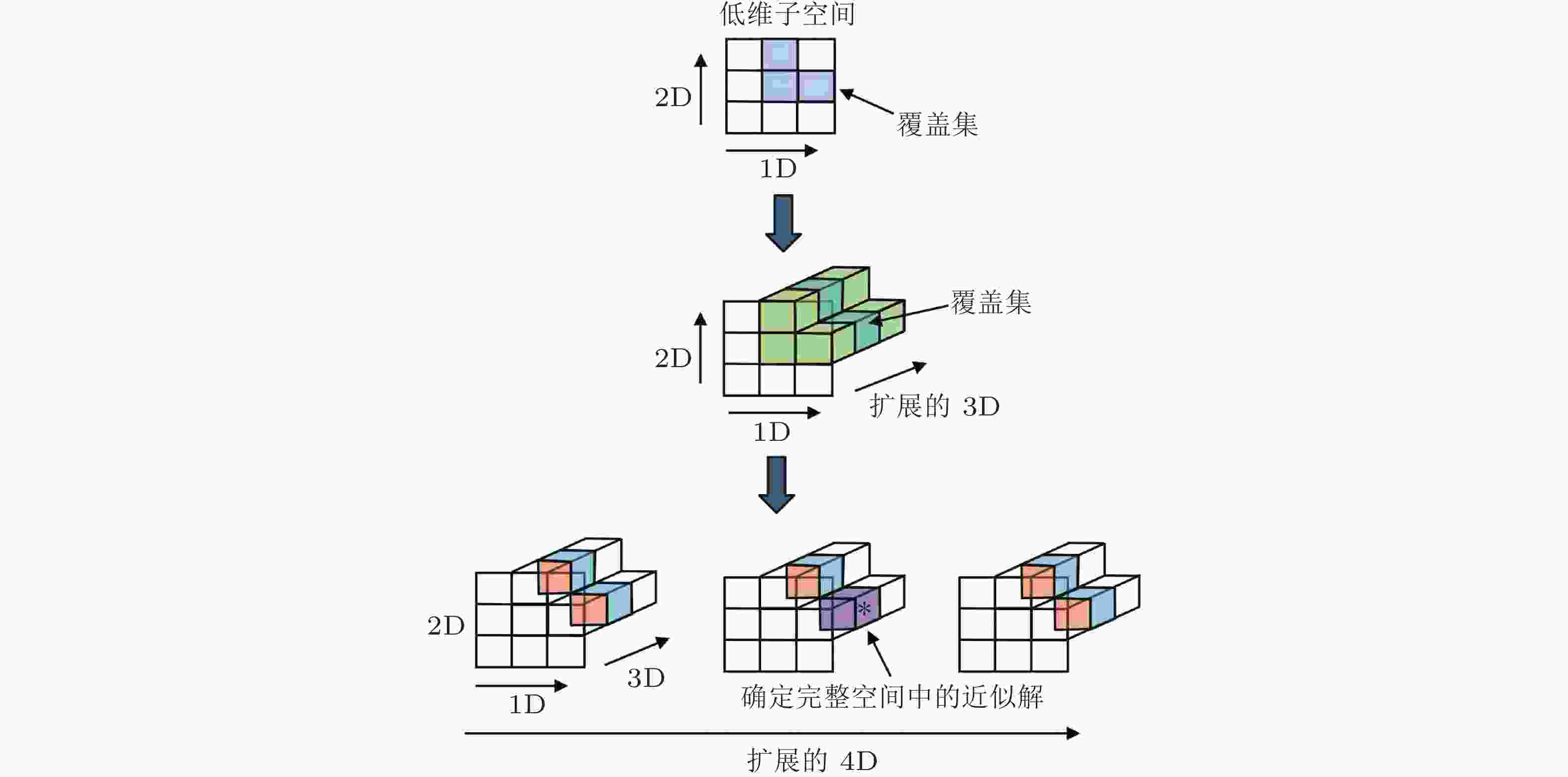
图 5 PSSCM方法的子域划分方式和虚拟不变集(Li et al. 2022). 其中红色胞{8}代表入胞, 蓝色胞{2}代表出胞, 黄色胞{5}代表相交胞, 深灰色胞集合{1,9}是待处理子域1内的瞬态胞, 浅灰色胞集合{6,7}是待处理子域外的潜在 (未知) 转移胞. 集合{5,8,9}即为子域1内的虚拟不变集, 它是跨子域不变集{3,4,5}在子域1中的覆盖集

下载: 全尺寸图片幻灯片

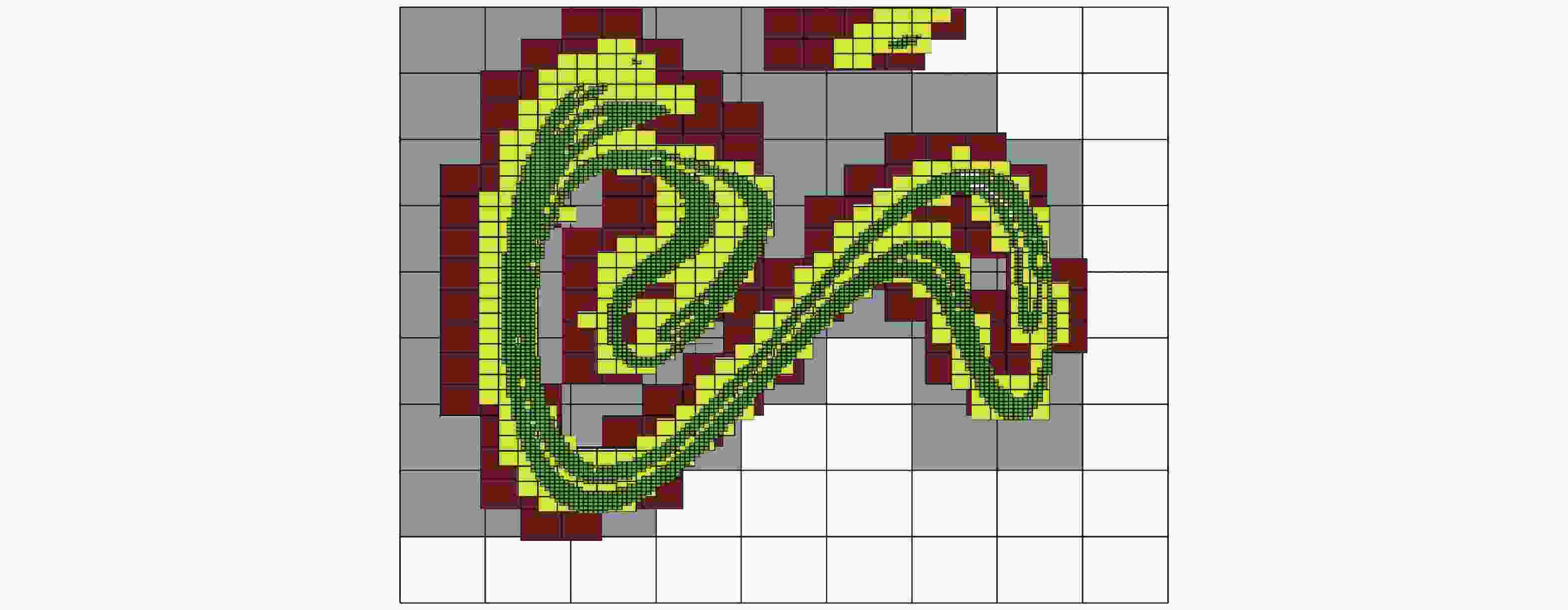
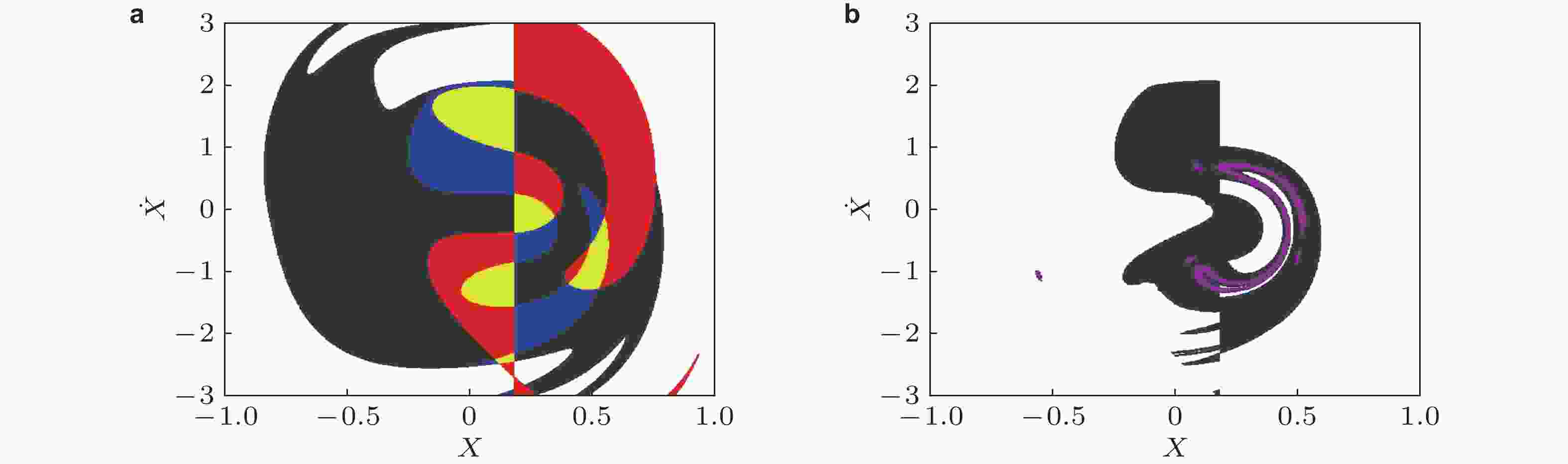
图 6 Mathieu–Duffing系统状态空间子域分割与合成 (空间切分位置为X_d = 0.18)(Li, Jiang, Li, et al. 2019): (a) 子域划分形成的标记胞; (b) 子域综合后恢复的全局不变集. 其中红色胞为入胞, 蓝色胞为出胞, 黄色胞为相交胞, 深灰色胞为子域内的瞬态胞, 紫色为恢复后的全局不变集结构

下载: 全尺寸图片幻灯片

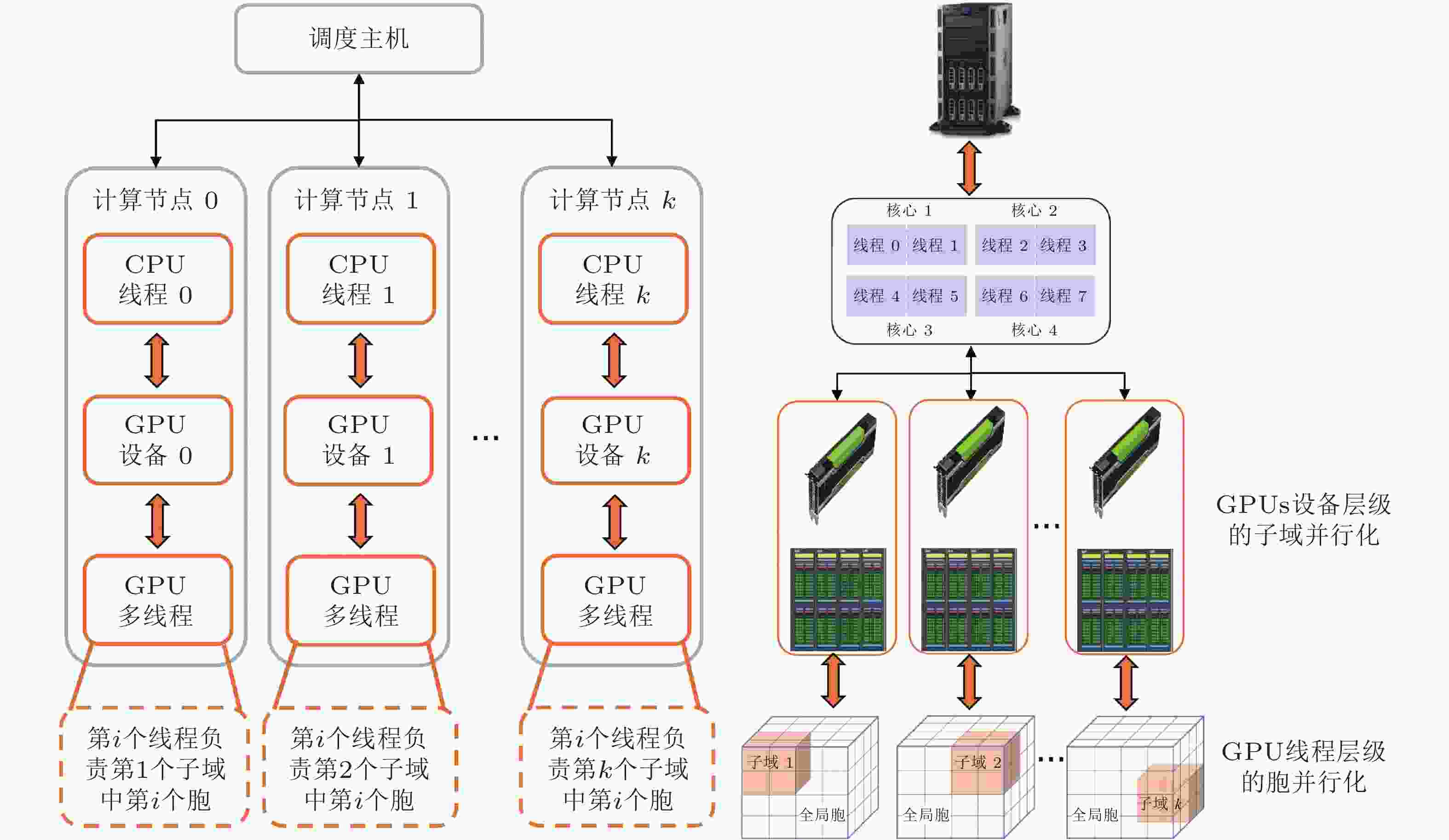
图 7 PSSCM方法采用的GPU集群计算架构(Li et al. 2022). 其中调度主机负责子域分割、合成以及计算资源调配. 每个计算节点由1个CPU线程和1个GPU设备组成, 独立节点中GPU负责处理子域中数据映射并传给对应的CPU执行子域内全局分析, 实现GPUs设备层级的子域并行化. GPU中的每个线程执行一次胞−胞映射, 实现GPU线程层级的胞并行化

下载: 全尺寸图片幻灯片

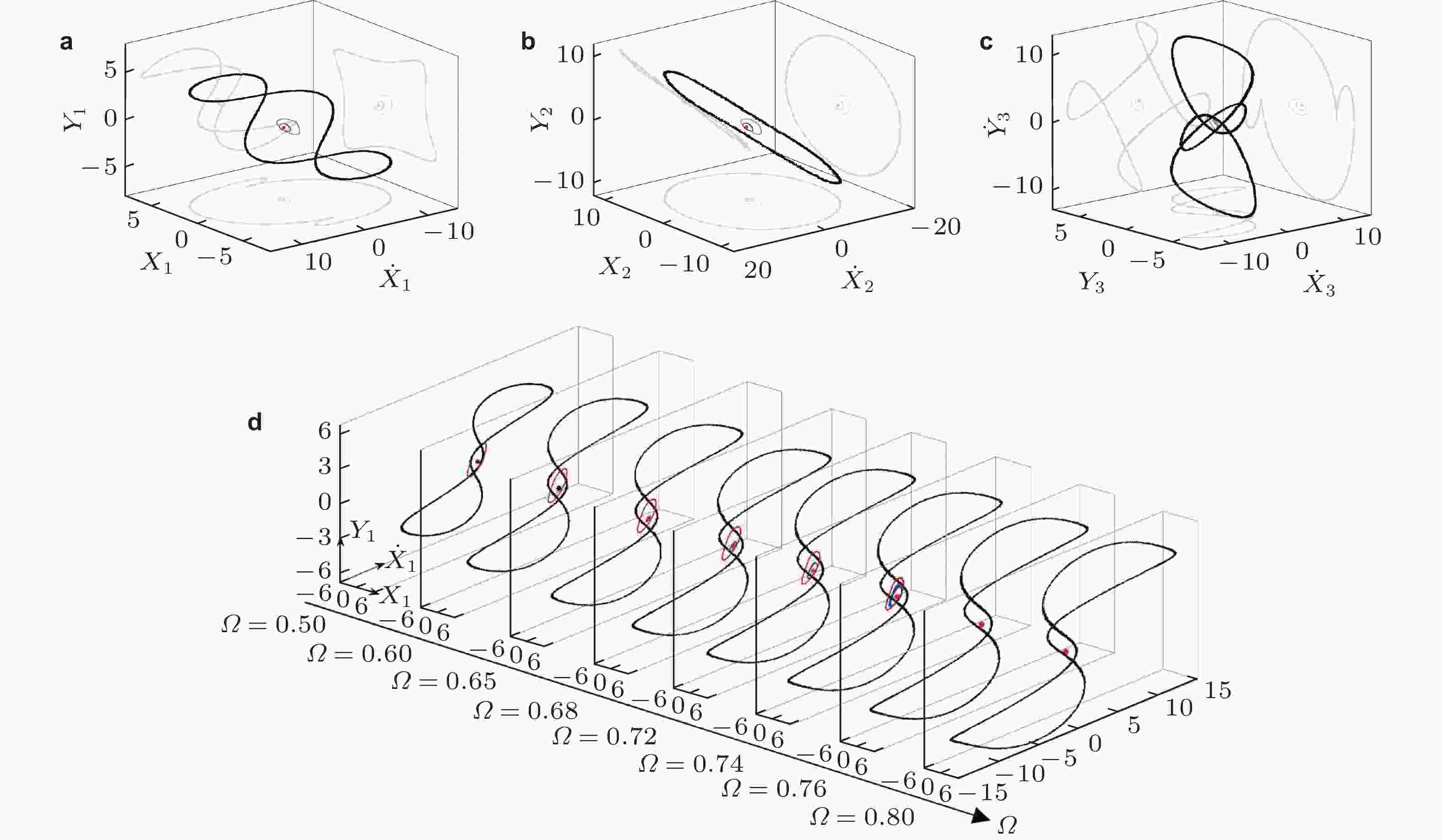
图 8 转子/定子碰摩诱发干摩擦反向涡动的全局响应和12维极限环分岔 (状态空间3维投影展示)(Li et al. 2022): (a)-(c) 多稳态全局响应相图; (d) 无碰摩周期响应Hopf分叉诱发间歇性准周期碰摩响应 (${\varOmega } \approx 0.65$), 间歇性准周期碰摩 (极限环) 由突变分岔而失稳(${\varOmega } \approx 0.74$), 响应最终进入干摩擦反向涡动大幅振荡 (${\varOmega } = 0.76 \to 0.80$)

下载: 全尺寸图片幻灯片

图 9 GCMSAI方法中插值参考点的配置: (a)邻接胞参考点(Liu et al. 2018); (b)插值胞内参考点(Wang et al. 2020)

下载: 全尺寸图片幻灯片

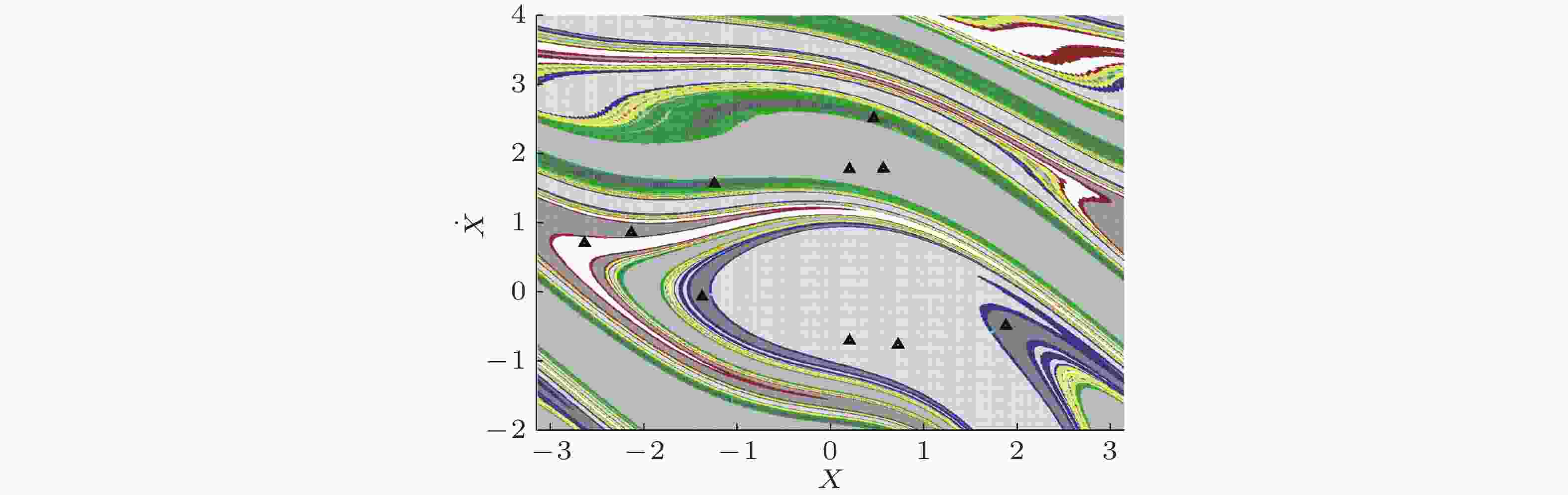
图 10 阻尼摆系统六个共存吸引域间的Wada边界(Liu et al. 2018). 其中黑色“▲”代表共存的多个吸引子, 彩色点为吸引域的影响区域, 不同吸引域间的边界表现出典型分形特征

下载: 全尺寸图片幻灯片

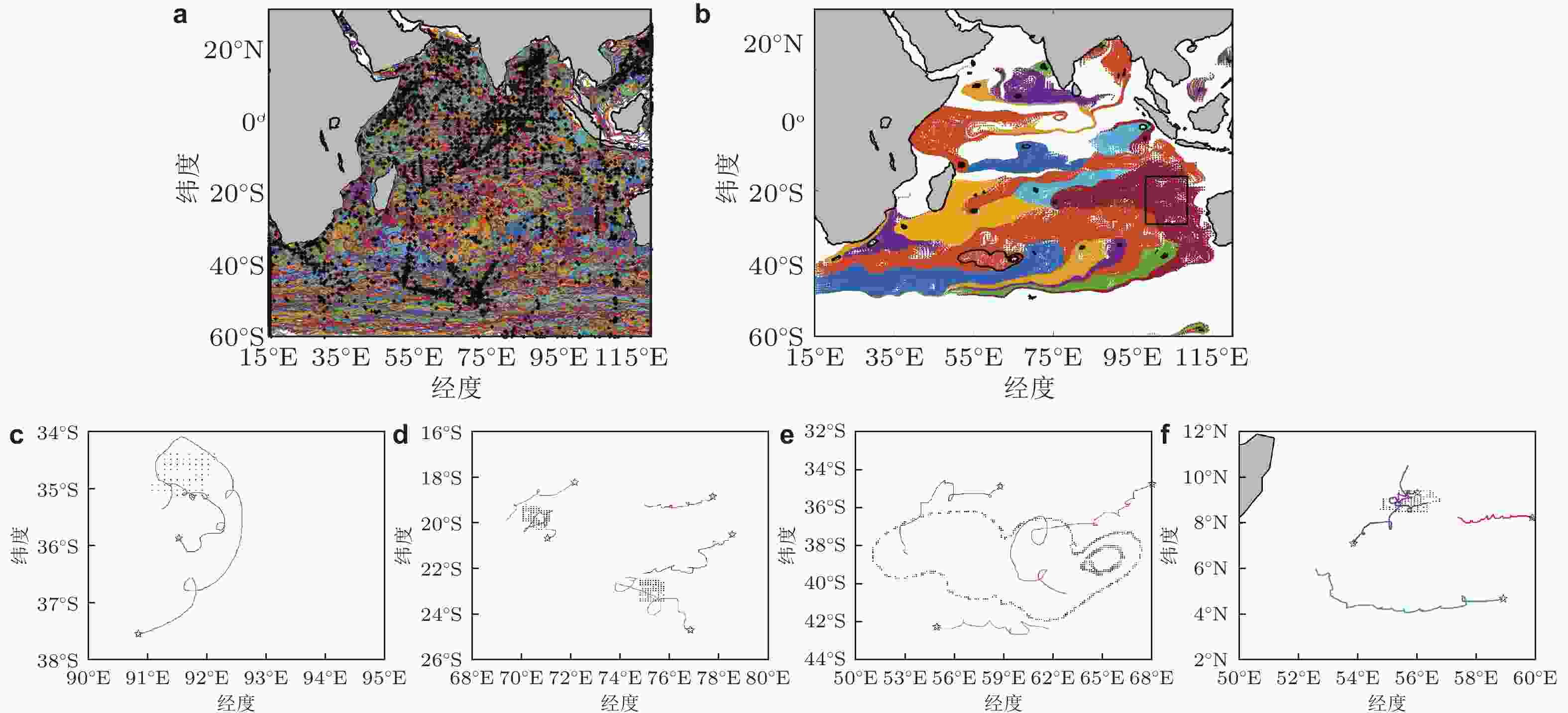
图 11 2014年3月8日—14日印度洋海域洋流短期运动特征及对周围浮漂的吸引性(李自刚等 2021): (a) 印度洋海域布置的浮漂数据及运动轨迹; (b) 短期涡旋中心(黑色点)和涡旋域 (彩色区域); (c)-(f) 不同涡旋中心对周围浮漂运动轨迹 (真实数据) 的吸引性

下载: 全尺寸图片幻灯片

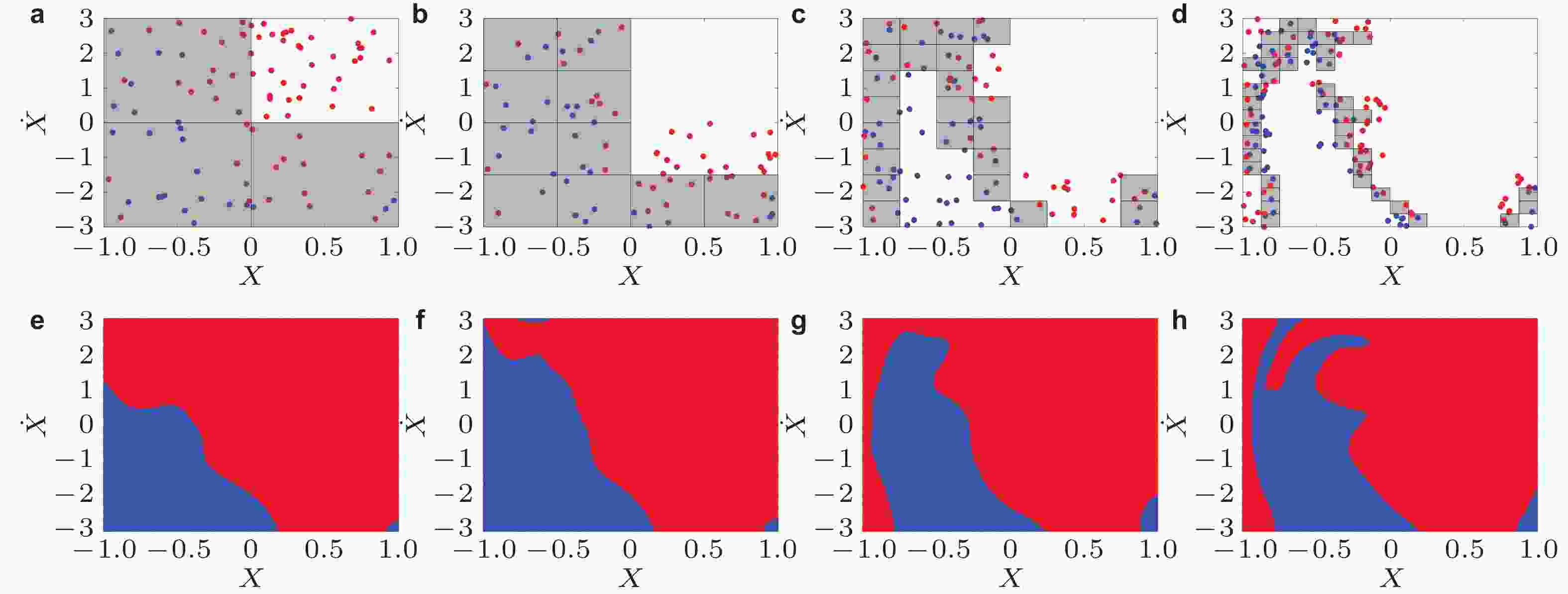
图 12 非线性系统渐进式学习及预测能力的进化过程(Li, Ma, et al. 2024): (a)-(d) 样本提取区域的精细化 (胞分辨率分别为2 × 2, 4 × 4, 8 × 8, 16 × 16); (e)-(h) 数据模型对全局吸引域学习和预测能力的进化过程

下载: 全尺寸图片幻灯片

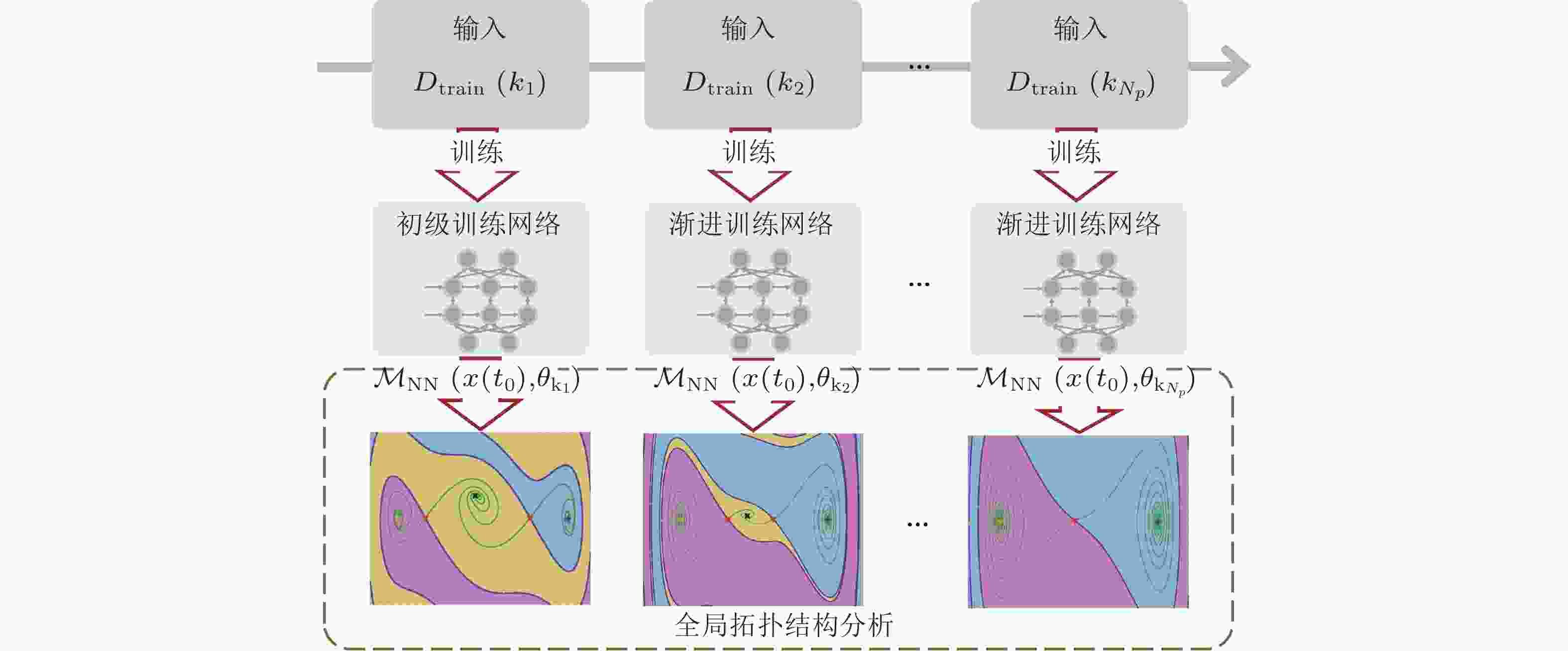
图 13 少数据量下追踪非线性全局拓扑结构的渐进式学习方法(Li, Jiang, et al. 2024)

下载: 全尺寸图片幻灯片

图 14 离散子空间扩展方法示意图

下载: 全尺寸图片幻灯片

表 1 全局动力学结构 (不变特性) 对动力学行为的影响及部分典型应用

全局动力学结构		典型应用	应用场景
吸引子		共存动态特性	机电系统(Kim et al. 2014, Wu et al. 2018, Zhu et al. 2022), 生态共存(Beisner et al. 2003, Schmitt et al. 2019, 杨永均等 2019), 非线性模型(Li, Jiang, et al. 2020, Mitra et al. 2017, Niroomand et al. 2022)
		多目标优化	优化设计(Sun et al. 2015, Sun, Zheng, et al. 2017, Wang et al. 1995)
		复杂行为认知	稀有事件(Hu et al. 2021, Klokov et al. 2011), 混沌特性(Dudkowski et al. 2018, Y. Li et al. 2024, Sahoo et al. 2022), 复杂系统(Heino et al. 2022, Kahana et al. 2023, Rodrigues 2017)
吸引域		稳定性和鲁棒性测度	振动评价(Deng et al. 2019, Yang et al. 2017, Yue et al. 2024), 仿生结构(Andonovski et al. 2022, 柳宁等 2008), 生物种群(Dubey et al. 2019, Pattanayak et al. 2021, Pattanayak et al. 2021), 工程安全域(Lenci et al. 2019, Yan et al. 2021)
		能量势阱刻画	俘能结构(Sun et al. 2024, F. Yang et al. 2023, Zhang et al. 2023), 抑振分析(Mamaghani et al. 2016, Q. Yang et al. 2023)
		几何特征	内在结构特征表征(Brzeski et al. 2018, Danca et al. 2019, Wang et al. 2021, Zhang et al. 2021)
		响应分类与控制	分类指标(Daza et al. 2022, Rega et al. 2005), 疾病诊断(Conforte et al. 2020), 行为预测(Molčan et al. 2023, Orlando et al. 2018), 控制策略(De Rengervé et al. 2015, Qin et al. 2020, Şimşek et al. 2020, Z. Sun et al. 2019)
鞍型不变集		危险分岔	边界分岔(Liu, Jiang, Hong & Tang 2019, Ponce et al. 2018, Szemplinska-Stupnicka et al. 1997)
		早期预警	临界点(Bauch et al. 2016, Grziwotz et al. 2023, Lohmann et al. 2024, Scheffer et al. 2009, Xu et al. 2023)
		特定属性	瞬态混沌(Baroni et al. 2023, Gawroński et al. 2024, Lai et al. 2011), 混沌巡游(郭旭等 2009)
不变流形	不稳定	响应跃迁	三体问题(An et al. 2024, Gómez et al. 2001, Tamakoshi et al. 2019), 路径控制(Yu et al. 2001)
		流形导向	Lagrangian 相干结构(Allshouse et al. 2015, Haller 2015), 特征识别(Bollt 2005, Huang et al. 2015, Nolan et al. 2020)
		特征降维	谱子流形(Alora et al. 2023, Cenedese et al. 2022, Jain et al. 2022)
		瞬态动力学	转迁轨道(Koch et al. 2024, Revuelta et al. 2018, Duguet et al. 2008), 短期演化(Mujica et al. 2018, Nave et al. 2019, Serra et al. 2020)
	稳定	逃逸壁垒	逃逸路径设计(Cilenti et al. 2022, Henkelman et al. 2002, Jin et al. 2017), 噪声驱动响应(Capala et al. 2020), 结构失效(Naik et al. 2017, Zhong et al. 2021)
		形貌刻画	边界属性(Guckenheimer et al. 2015, Huang et al. 2022, Osinga 2018)
		参数优化	运动优化(Horibe et al. 2018, 武朋玮等 2017)

下载: 导出CSV

表 2 数据模型对全局吸引域各区域的预测精度

典型区域	胞分辨率
典型区域	2 × 2	4 × 4	8 × 8	16 × 16
总体	75.14%	85.96%	93.54%	98.87%
吸引域内部	79.21%	90.62%	95.77%	99.06%
吸引域边界	21.47%	30.72%	62.33%	96.40%
状态空间边缘	62.39%	55.67%	91.21%	98.13%

下载: 导出CSV

参考文献(240)

[1]	干思思. 2020. 三十余载初衷不移矢志攻克算法难题−西安交通大学非线性动力学研究所科研侧记. 科学中国人, 60 (Gan S S. 2020. Sticking to the original aspiration for over three decades and determined to solve algorithm problems—A side note on the scientific research of the institute of nonlinear dynamics at Xi’an Jiaotong University. Scientific Chinese, 60). Gan S S. 2020. Sticking to the original aspiration for over three decades and determined to solve algorithm problems—A side note on the scientific research of the institute of nonlinear dynamics at Xi’an Jiaotong University. Scientific Chinese, 60
[2]	郭旭, 孙锋, 江俊. 2009. 耦合神经元模型中的混沌巡游现象及其特性分析. 力学季刊, 30: 511-516 (Guo X, Sun F, Jiang J. 2009. Chaotic Itinerancy Phenomena and Dynamic Characteristics in Coupled Neuron Model. Chinese Quarterly of Mechanics, 30: 511-516). Guo X, Sun F, Jiang J. 2009. Chaotic Itinerancy Phenomena and Dynamic Characteristics in Coupled Neuron Model. Chinese Quarterly of Mechanics, 30: 511-516
[3]	贺群, 徐伟, 李爽, 等. 2008. 图胞映射的一种改进方法. 物理学报, 57: 743-748 (He Q, Li W, Li S, et al. 2008. A modified digraph cell mapping method. Acta Physica Sinica, 57: 743-748). doi: 10.7498/aps.57.743 He Q, Li W, Li S, et al. 2008. A modified digraph cell mapping method. Acta Physica Sinica, 57: 743-748 doi: 10.7498/aps.57.743
[4]	李斌华, 杨汝, 张波, 等. 2016. 基于胞映射方法的异步电机低速信号混沌检测机理及实验研究. 中国电机工程学报, 36: 2270-2279 (Li B H, Yang R, Zhang B, et al. 2016. The chaotic detection mechanism and experimental study of low frequency signal of asynchronous motor based on cell mapping method. Proceedings of the CSEE, 36: 2270-2279). Li B H, Yang R, Zhang B, et al. 2016. The chaotic detection mechanism and experimental study of low frequency signal of asynchronous motor based on cell mapping method. Proceedings of the CSEE, 36: 2270-2279
[5]	柳宁, 李俊峰, 王天舒. 2008. 用胞胞映射计算被动行走模型不动点的吸引盆. 工程力学, 25: 218-223 (Liu N, Li J F, Wang T S. 2008. Study of the Basin of Attraction of Passive Models by the Aid of Cell-to-Cell Mapping Method. Engineering Mechanics, 25: 218-223). Liu N, Li J F, Wang T S. 2008. Study of the Basin of Attraction of Passive Models by the Aid of Cell-to-Cell Mapping Method. Engineering Mechanics, 25: 218-223
[6]	李自刚, 严旺, 康佳琪, 等. 2021. 数据驱动印度洋海域全局动力学研究. 力学学报, 53: 2595-2602 (Li Z G, Yan W, Kang J Q, et al. 2021. Data-driven global dynamics of the Indian ocean. Chinese Journal of Theoretical and Applied Mechanics, 53: 2595-2602). doi: 10.6052/0459-1879-21-218 Li Z G, Yan W, Kang J Q, et al. 2021. Data-driven global dynamics of the Indian ocean. Chinese Journal of Theoretical and Applied Mechanics, 53: 2595-2602 doi: 10.6052/0459-1879-21-218
[7]	武朋玮, 李颖晖, 佘智勇, 等. 2017. 高超声速飞行器纵向动力学系统稳定流形边界与频域设计指标关联规律. 战术导弹技术, 4: 25-31 (Wu P, Li Y H, She Z Y, et al. 2017. Associated orderliness between hypersonic stability manifold boundary and frequency domain performance. Tactical Missile Technology, 4: 25-31). Wu P, Li Y H, She Z Y, et al. 2017. Associated orderliness between hypersonic stability manifold boundary and frequency domain performance. Tactical Missile Technology, 4: 25-31
[8]	徐伟, 孙春艳, 孙建桥, 等. 2013. 胞映射方法的研究和进展. 力学进展, 43: 91-100 (Xu W, Sun C Y, Sun J Q, et al. 2013. Development and study on cell mapping methods. Advances in Mechanics, 43: 91-100). doi: 10.6052/1000-0992-12-022 Xu W, Sun C Y, Sun J Q, et al. 2013. Development and study on cell mapping methods. Advances in Mechanics, 43: 91-100 doi: 10.6052/1000-0992-12-022
[9]	杨永均, 张绍良, 侯湖平. 2019. 基于非线性动力学模型的矿山土地生态系统恢复力机制. 煤炭学报, 40: 3174-3184 (Yang Y J, Zhang S L, Hou H P. 2019. Resilience mechanism of land ecosystem in mining area based on nonlinear dynamic model. Journal of China Coal Society, 40: 3174-3184). Yang Y J, Zhang S L, Hou H P. 2019. Resilience mechanism of land ecosystem in mining area based on nonlinear dynamic model. Journal of China Coal Society, 40: 3174-3184
[10]	Aguirre J, Sanjuán M A F. 2002. Unpredictable behavior in the Duffing oscillator: Wada basins. Physica D: Nonlinear Phenomena, 171: 41-51 doi: 10.1016/S0167-2789(02)00565-1
[11]	Ahamed T, Costa A C, Stephens G J. 2020. Capturing the continuous complexity of behaviour in Caenorhabditis elegans. Nature Physics, 17: 275-283
[12]	Allshouse M R, Peacock T. 2015. Lagrangian based methods for coherent structure detection. Chaos: An Interdisciplinary Journal of Nonlinear Science, 25: 097617 doi: 10.1063/1.4922968
[13]	Alora J I, Cenedese M, Schmerling E, et al. 2023. Data-Driven Spectral Submanifold Reduction for Nonlinear Optimal Control of High-Dimensional Robots. in 2023 IEEE International Conference on Robotics and Automation (ICRA). 2023 IEEE International Conference on Robotics and Automation (ICRA). London, UnitedKingdom: 2627-2633
[14]	Amiri A, Cordero A, Darvishi M T, et al. 2019. A fast algorithm to solve systems of nonlinear equations. Journal of Computational and Applied Mathematics, 354: 242-258 doi: 10.1016/j.cam.2018.03.048
[15]	An S, Liu M, Li H, et al. 2024. Five-impulse low-energy earth-moon transfer using manifolds. Advances in Space Research, 73: 201-224 doi: 10.1016/j.asr.2023.10.013
[16]	Andonovski N, Kovacic I, Lenci S. 2022. On the dynamics of a biomimetic model of a sympodial tree: from bifurcations diagrams and 6D basins of attraction to dynamical integrity and robustness. Journal of Computational and Nonlinear Dynamics, 17: 011002 doi: 10.1115/1.4052570
[17]	Andonovski N, Lenci S. 2020. Six-dimensional basins of attraction computation on small clusters with semi-parallelized SCM method. International Journal of Dynamics and Control, 8: 436-447 doi: 10.1007/s40435-019-00557-2
[18]	Andonovski N, Lenci S, Kovacic I. 2020. Basins of attraction for higher-dimensional nonlinear dynamical systems: preliminary results on the case study of a sympodial tree. in Kovacic I, Lenci S, (Ed. ) IUTAM Symposium on Exploiting Nonlinear Dynamics for Engineering Systems. IUTAM Bookseries. Springer International Publishing, Cham, pp. 27-36
[19]	Andrade M, Gasca E, Lara E R. 2017. Implementation of Incremental Learning in Artificial Neural Networks. in EPiC Series in Computing. 3rd Global Conference on Artificial Intelligence, 50: 221-232
[20]	Baroni R S, Carvalho R D de, Caldas I L, et al. 2023. Chaotic saddles and interior crises in a dissipative nontwist system. Physical Review E, 107: 024216 doi: 10.1103/PhysRevE.107.024216
[21]	Bauch C T, Sigdel R, Pharaon J, et al. 2016. Early warning signals of regime shifts in coupled human-environment systems. Proceedings of the National Academy of Sciences, 113: 14560-14567 doi: 10.1073/pnas.1604978113
[22]	Beisner B, Haydon D, Cuddington K. 2003. Alternative stable states in ecology. Frontiers in Ecology and the Environment, 1: 376-382 doi: 10.1890/1540-9295(2003)001[0376:ASSIE]2.0.CO;2
[23]	Belardinelli P, Lenci S. 2016a. A first parallel programming approach in basins of attraction computation. International Journal of Non-Linear Mechanics, 80: 76-81 doi: 10.1016/j.ijnonlinmec.2015.10.016
[24]	Belardinelli P, Lenci S. 2016b. An efficient parallel implementation of cell mapping methods for MDOF systems. Nonlinear Dynamics, 86: 2279-2290 doi: 10.1007/s11071-016-2849-3
[25]	Belardinelli P, Lenci S. 2017. Improving the global analysis of mechanical systems via parallel computation of basins of attraction. Procedia IUTAM, 22: 192-199 doi: 10.1016/j.piutam.2017.08.028
[26]	Benedetti K C B, Gonçalves P B, Lenci S, et al. 2023. Global analysis of stochastic and parametric uncertainty in nonlinear dynamical systems: adaptative phase-space discretization strategy, with application to Helmholtz oscillator. Nonlinear Dynamics, 111: 15675-15703 doi: 10.1007/s11071-023-08667-5
[27]	Bhalekar S, Gupta D. 2024. Stability and bifurcation analysis of two-term fractional differential equation with delay. arXiv e-prints. arXiv: 2404.01824
[28]	Bollt E. 2005. The path towards a longer life: on invariant sets and the escape time landscape. International Journal of Bifurcation and Chaos, 15: 1615-1624 doi: 10.1142/S0218127405012892
[29]	Broer H W, Osinga H M, Vegter G. 1997. Algorithms for computing normally hyperbolic invariant manifolds. Zeitschrift für angewandte Mathematik und Physik, 48: 480
[30]	Brunton S L, Proctor J L, Kutz J N. 2016. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences, 113: 3932-3937 doi: 10.1073/pnas.1517384113
[31]	Brzeski P, Belardinelli P, Lenci S, et al. 2018. Revealing compactness of basins of attraction of multi-DoF dynamical systems. Mechanical Systems and Signal Processing, 111: 348-361 doi: 10.1016/j.ymssp.2018.04.005
[32]	Cao L. 1997. Practical method for determining the minimum embedding dimension of a scalar time series. Physica D: Nonlinear Phenomena, 110: 43-50 doi: 10.1016/S0167-2789(97)00118-8
[33]	Capala K, Padash A, Chechkin A V, et al. 2020. Lévy noise-driven escape from arctan potential wells. Chaos: An Interdisciplinary Journal of Nonlinear Science, 30: 123103 doi: 10.1063/5.0021795
[34]	Cenedese M, Axås J, Yang H, et al. 2022. Data-driven nonlinear model reduction to spectral submanifolds in mechanical systems. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 380: 20210194 doi: 10.1098/rsta.2021.0194
[35]	Chai F, Zhou B, Xie X, et al. 2023. Incremental learning model for dynamical identification and classification of abnormal vibration in operational underground facilities. Tunnelling and Underground Space Technology, 140: 105251 doi: 10.1016/j.tust.2023.105251
[36]	Chaudhuri R, Gerçek B, Pandey B, et al. 2019. The intrinsic attractor manifold and population dynamics of a canonical cognitive circuit across waking and sleep. Nature Neuroscience, 22: 1512-1520 doi: 10.1038/s41593-019-0460-x
[37]	Chen Z, Bian H, Zhu W. 2025. Incremental data modeling based on neural ordinary differential equations. Complex & Intelligent Systems, 11: 172(1-12
[38]	Cheng Y, Jiang J. 2021. A subdivision strategy for adjoining cell mapping on the global optimal control in multi-input-multi-output systems. Optimal Control Applications and Methods, 42: 1556-1567 doi: 10.1002/oca.2746
[39]	Church K E M, Liu X. 2020. Invariant manifold theory. in Bifurcation Theory of Impulsive Dynamical Systems. Springer International Publishing, Cham: 221-234
[40]	Cilenti L, Cameron M K, Balachandran B. 2022. Most probable escape paths in periodically driven nonlinear oscillators. Chaos: An Interdisciplinary Journal of Nonlinear Science, 32: 083140 doi: 10.1063/5.0093074
[41]	Cobey S, Baskerville E B. 2016. Limits to causal inference with state-space reconstruction for infectious disease. PLOS One, 11: e0169050 doi: 10.1371/journal.pone.0169050
[42]	Conforte A J, Alves L, Coelho F C, et al. 2020. Modeling basins of attraction for breast cancer using Hopfield networks. Frontiers in Genetics, 11: 314 doi: 10.3389/fgene.2020.00314
[43]	Cruz J F, Schütze O, Sun J Q, et al. 2014. Parallel cell mapping for unconstrained multi-objective optimization problems. in Tantar A-A et al., (Ed.) EVOLVE - A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation V. Springer International Publishing, Cham, pp. 133-146
[44]	Dai H, Yue X, Yuan J, et al. 2018. Dealiasing harmonic balance method for obtaining periodic solutions of an aeroelastic system. Aerospace Science and Technology, 77: 244-255 doi: 10.1016/j.ast.2018.03.008
[45]	Danca M F, Bourke P, Kuznetsov N V. 2019. Graphical structure of attraction basins of hidden chaotic attractors: the rabinovich-fabrikant system. Int. J. Bifurc. Chaos, 29: 1930001 doi: 10.1142/S0218127419300015
[46]	Datseris G, Luiz Rossi K, Wagemakers A. 2023. Framework for global stability analysis of dynamical systems. Chaos: An Interdisciplinary Journal of Nonlinear Science, 33: 073151 doi: 10.1063/5.0159675
[47]	Datseris G, Wagemakers A. 2022. Effortless estimation of basins of attraction. Chaos: An Interdisciplinary Journal of Nonlinear Science, 32: 023104 doi: 10.1063/5.0076568
[48]	Daza A, Wagemakers A, Sanjuán M A F. 2022. Classifying basins of attraction using the basin entropy. Chaos, Solitons & Fractals, 159: 112112
[49]	Daza Á, Wagemakers A, Sanjuán M A F. 2024. Multistability and unpredictability. Physics Today, 77: 44-50
[50]	De Rengervé A, Andry P, Gaussier P. 2015. On-line learning and control of attraction basins for the development of sensorimotor control strategiess. Biological Cybernetics, 109: 255-274 doi: 10.1007/s00422-014-0640-4
[51]	Dellnilz M, Junge O. 2006. Set oriented numerical methods in space mission design. in Modern Astrodynamics. Elsevier Astrodynamics Series. Butterworth-Heinemann, 1: 127-153
[52]	Dellnitz M, Froyland G, Junge O. 2001. The algorithms behind GAIO — Set oriented numerical methods for dynamical systems. in Fiedler B, (Ed. ) Ergodic Theory, Analysis, and Efficient Simulation of Dynamical Systems. Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 145-174
[53]	Dellnitz M, Hohmann A. 1997. A subdivision algorithm for the computation of unstable manifolds and global attractors. Numerische Mathematik, 75: 293-317 doi: 10.1007/s002110050240
[54]	Dellnitz M, Schütze O, Sertl S. 2002. Finding zeros by multilevel subdivision techniques. IMA Journal of Numerical Analysis, 22: 167-185 doi: 10.1093/imanum/22.2.167
[55]	Deng Y, Xu B, Chen D, et al. 2019. Stochastic global stability and bifurcation of a hydro-turbine generator. Communications in Nonlinear Science and Numerical Simulation, 72: 64-77 doi: 10.1016/j.cnsns.2018.11.018
[56]	Deyle E R, Sugihara G. 2011. Generalized theorems for nonlinear state space reconstruction. PLOS One, 6: e18295 doi: 10.1371/journal.pone.0018295
[57]	Dhir N, Kosiorek A R, Posner I. 2017. Bayesian Delay Embeddings for Dynamical Systems. in NIPS Timeseries Workshop. 31st Conference on Neural Information Processing Systems, Long Beach, USA
[58]	Dieci L, Lopez L. 2009. Sliding motion in filippov differential systems: Theoretical results and a computational approach. SIAM Journal on Numerical Analysis, 47: 2023-2051 doi: 10.1137/080724599
[59]	Dubey B, Kumar A, Patra A. 2019. Global stability and Hopf-bifurcation of prey-predator system with two discrete delays including habitat complexity and prey refuge. Communications in Nonlinear Science and Numerical Simulation, 67: 528-554. doi: 10.1016/j.cnsns.2018.07.019
[60]	Dudkowski D, Prasad A, Kapitaniak T. 2018. Describing chaotic attractors: Regular and perpetual points. Chaos: An Interdisciplinary Journal of Nonlinear Science, 28: 033604 doi: 10.1063/1.4991801
[61]	Duguet Y, Willis A P, Kerswell R R. 2008. Transition in pipe flow: the saddle structure on the boundary of turbulence. Journal of Fluid Mechanics, 613: 255-274 doi: 10.1017/S0022112008003248
[62]	Durbin J, Koopman S J. 2012. Time Series Analysis by State Space Methods (2nd edn), Oxford University Press
[63]	Eason R P, Dick A J. 2014. A parallelized multi-degrees-of-freedom cell mapping method. Nonlinear Dynamics, 77: 467-479 doi: 10.1007/s11071-014-1310-8
[64]	Erazo C, Homer M E, Piiroinen P T, et al. 2017. Dynamic cell mapping algorithm for computing basins of attraction in planar Filippov systems. International Journal of Bifurcation and Chaos, 27: 1730041 doi: 10.1142/S0218127417300415
[65]	Erem B, Orellana R M, Hyde D E, et al. 2016. Extensions to a manifold learning framework for time-series analysis on dynamic manifolds in bioelectric signals. Physical Review E, 93: 042218 doi: 10.1103/PhysRevE.93.042218
[66]	Fan S, Hong L, Jiang J. 2022. Blue-sky catastrophic bifurcations behind emergence and disappearance of quasiperiodic rubbing oscillations in a piecewise smooth rotor-stator system. International Journal of Bifurcation and Chaos, 32: 2250221 doi: 10.1142/S0218127422502212
[67]	Fan Y, Iwashita T, Egami T. 2017. Energy landscape-driven non-equilibrium evolution of inherent structure in disordered material. Nature Communications, 8: 15417 doi: 10.1038/ncomms15417
[68]	Fang S, Zhou S, Yurchenko D V, et al. 2022. Multistability phenomenon in signal processing, energy harvesting, composite structures, and metamaterials: A review. Mechanical Systems and Signal Processing, 166: 108419 doi: 10.1016/j.ymssp.2021.108419
[69]	Fantino E, Castelli R. 2017. Efficient design of direct low-energy transfers in multi-moon systems. Celestial Mechanics and Dynamical Astronomy, 127: 429-450 doi: 10.1007/s10569-016-9733-9
[70]	Fichthorn K A, Weinberg W H. 1991. Theoretical foundations of dynamical Monte Carlo simulations. The Journal of Chemical Physics, 95: 1090-1096 doi: 10.1063/1.461138
[71]	Freeman R A, Kototovic P V. 1996. Robust nonlinear control design: state-space and Lyapunov techniques, Birkhäuser Boston, MA
[72]	Fuß S, Hawkins S C, Marburg S. 2011. An eigenvalue search algorithm for the modal analysis of a resonator in free space. Journal of Computational Acoustics, 19: 95-109 doi: 10.1142/S0218396X11004304
[73]	Gawroński P, Kwapień J, Kułakowski K. 2024. Transient chaos and memory effect in the Rosenzweig-MacArthur system with dynamics of consumption rates. Physical Review E, 109: 034210 doi: 10.1103/PhysRevE.109.034210
[74]	Gelbrecht M, Kurths J, Hellmann F. 2020. Monte Carlo basin bifurcation analysis. New Journal of Physics, 22: 033032 doi: 10.1088/1367-2630/ab7a05
[75]	Ghahramani Z, Roweis S. 1998. Learning nonlinear dynamical systems using an EM algorithm. in Kearns M, Solla S, Cohn D, (Ed. ) Advances in Neural Information Processing Systems. MIT Press
[76]	Ghil M, Allen M R, Dettinger M, et al. 2002. Advanced spectral methods for climatic time series. Reviews of Geophysics, 40: 3(1-41
[77]	Giannakis D, Majda A. 2012. Nonlinear Laplacian spectral analysis for time series with intermittency and low-frequency variability. Proceedings of the National Academy of Sciences, 109: 2222-2227 doi: 10.1073/pnas.1118984109
[78]	Gilpin W. 2020. Deep reconstruction of strange attractors from time series. in Larochelle H et al. , (Ed. ) Advances in Neural Information Processing Systems. Curran Associates, Inc. , pp. 204-216
[79]	Gómez G, Koon W S, Lo M W, et al. 2004. Connecting orbits and invariant manifolds in the spatial restricted three-body problem. Nonlinearity, 17: 1571-1606 doi: 10.1088/0951-7715/17/5/002
[80]	Gómez G, Koon W S, Lo M W, et al. 2001. Invariant manifolds, the spatial three-body problem and space mission design. in Advances in the Astronautical Sciences. AAS/AIAA Astrodynamics Specialtists Conference. Quebec, Canada
[81]	Grziwotz F, Chang C-W, Dakos V, et al. 2023. Anticipating the occurrence and type of critical transitions. Science Advances, 9: eabq4558 doi: 10.1126/sciadv.abq4558
[82]	Gu X Q, Yang S, Liu Y, et al. 2018. A novel Pareto-based Bayesian approach on extension of the infogram for extracting repetitive transients. Mechanical Systems and Signal Processing, 106: 119-139 doi: 10.1016/j.ymssp.2017.12.034
[83]	Guan L, Qiao F, Zhai X, et al. 2022. Model Evolution Mechanism for Incremental Fault Diagnosis. IEEE Transactions on Instrumentation and Measurement, 71: 1-11
[84]	Guckenheimer J, Krauskopf B, Osinga H M, et al. 2015. Invariant manifolds and global bifurcations. Chaos: An Interdisciplinary Journal of Nonlinear Science, 25: 097604 doi: 10.1063/1.4915528
[85]	Guckenheimer J M, Holmes P. 1983. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer New York, NY
[86]	Gutman Y. 2016. Takens’ embedding theorem with a continuous observable. arXiv e-prints, arXiv: 1510.05843
[87]	Gyebrószki G, Csernák G. 2017. Clustered Simple Cell Mapping: An extension to the Simple Cell Mapping method. Communications in Nonlinear Science and Numerical Simulation, 42: 607-622 doi: 10.1016/j.cnsns.2016.06.020
[88]	Haller G. 2015. Lagrangian Coherent Structures. Annual Review of Fluid Mechanics, 47: 137-162 doi: 10.1146/annurev-fluid-010313-141322
[89]	Han M, Feng S, Chen C L P, et al. 2019. Structured manifold broad learning system: A manifold perspective for large-scale chaotic time series analysis and prediction. IEEE Transactions on Knowledge and Data Engineering, 31: 1809-1821 doi: 10.1109/TKDE.2018.2866149
[90]	Han Q, Xu W, Yue X. 2015. Stochastic response analysis of noisy system with non-negative real-power restoring force by generalized cell mapping method. Applied Mathematics and Mechanics, 36: 329-336 doi: 10.1007/s10483-015-1918-6
[91]	Hao W, Lee S, Xu X, et al. 2025. Stability and robustness of time-discretization schemes for the Allen-Cahn equation via bifurcation and perturbation analysis. Journal of Computational Physics, 521: 113565 doi: 10.1016/j.jcp.2024.113565
[92]	Heino M, Proverbio D, Marchand G, et al. 2022. Attractor landscapes: A unifying conceptual model for understanding behaviour change across scales of observation. Health Psychology Review, 17: 655-672
[93]	Henkelman G, Jóhannesson G, Jónsson H. 2002. Methods for finding saddle points and minimum energy paths. in Schwartz SD, (Ed. ) Theoretical Methods in Condensed Phase Chemistry. Springer Netherlands, Dordrecht, pp. 269-302
[94]	Hitczenko P, Medvedev G S. 2013. The Poincaré map of randomly perturbed periodic motion. Journal of Nonlinear Science, 23: 835-861 doi: 10.1007/s00332-013-9170-9
[95]	Homburg A J, Osinga H M, Vegter G. 1995. On the computation of invariant manifolds of fixed points. Zeitschrift für angewandte Mathematik und Physik ZAMP, 46: 171-187
[96]	Hong L, Jiang J, Sun J-Q. 2015. Fuzzy responses and bifurcations of a forced duffing oscillator with a triple-Well potential. International Journal of Bifurcation and Chaos, 25: 1550005 doi: 10.1142/S0218127415500054
[97]	Hong L, Jiang J, Sun J-Q. 2014. Response analysis of fuzzy nonlinear dynamical systems. Nonlinear Dynamics, 78: 1221-1232 doi: 10.1007/s11071-014-1509-8
[98]	Hong L, Sun J Q. 2006a. A fuzzy blue sky catastrophe. Nonlinear Dynamics, 55: 98-108
[99]	Hong L, Sun J Q. 2006b. Bifurcations of forced oscillators with fuzzy uncertainties by the generalized cell mapping method. Chaos, Solitons & Fractals, 27: 895-904
[100]	Hong L, Sun J Q. 2013. Double crises in fuzzy chaotic systems. International Journal of Dynamics and Control, 1: 32-40 doi: 10.1007/s40435-013-0004-2
[101]	Hong L, Xu J. 1999. Crises and chaotic transients studied by the generalized cell mapping digraph method. Physics Letters A, 262: 361-375 doi: 10.1016/S0375-9601(99)00669-6
[102]	Horibe T, Sakamoto N. 2018. Optimal swing up and stabilization control for inverted pendulum via stable manifold method. IEEE Transactions on Control Systems Technology, 26: 708-715 doi: 10.1109/TCST.2017.2670524
[103]	Hsu C S. 1981. A generalized theory of cell-to-cell mapping for nonlinear dynamical systems. Journal of Applied Mechanics, 48: 634-642 doi: 10.1115/1.3157686
[104]	Hsu C S. 1982. A probabilistic theory of nonlinear dynamical systems based on the cell state space concept. Journal of Applied Mechanics, 49: 895-902 doi: 10.1115/1.3162633
[105]	Hsu C S. 1980. A theory of cell-to-cell mapping dynamical systems. Journal of Applied Mechanics, 47: 931-939 doi: 10.1115/1.3153816
[106]	Hsu C S. 1987. Cell-to-cell mapping: a method of global analysis for nonlinear systems, Springer-Verlag, New York
[107]	Hsu C S. 1992. Global analysis by cell mapping. International Journal of Bifurcation & Chaos, 2: 727-771
[108]	Hsu C S. 1995. Global analysis of dynamical systems using posets and digraphs. International Journal of Bifurcation and Chaos, 5: 1085-1118. doi: 10.1142/S021812749500079X
[109]	Hsu C S, Guttalu R S. 1980. An unravelling algorithm for global analysis of dynamical systems: An application of cell-to-cell mappings. Journal of Applied Mechanics, 47: 940-948 doi: 10.1115/1.3153817
[110]	Hu J, Qi G, Wang Z, et al. 2021. Rare energy-conservative attractors on global invariant hypersurfaces and their multistability. International Journal of Bifurcation and Chaos, 31: 2130007 doi: 10.1142/S021812742130007X
[111]	Huang F L, Chen L Q, Jiang W A. 2024. A Geometric numerical integration with simple cell mapping for global analysis of nonlinear dynamical systems. International Journal of Bifurcation and Chaos, 34: 2450190 doi: 10.1142/S0218127424501906
[112]	Huang W, Zhang Y, Yang X S. 2022. Complicated boundaries of the attraction basin in a class of three-dimensional polynomial systems. International Journal of Bifurcation and Chaos, 32: 2250235 doi: 10.1142/S0218127422502352
[113]	Huang Y, Green M A. 2015. Detection and tracking of vortex phenomena using Lagrangian coherent structures. Experiments in Fluids, 56: 147 doi: 10.1007/s00348-015-2001-z
[114]	Jain S, Haller G. 2022. How to compute invariant manifolds and their reduced dynamics in high-dimensional finite-element models. Nonlinear Dynamics, 107: 1417-1450 doi: 10.1007/s11071-021-06957-4
[115]	Jiang J. 2012. An effective numerical procedure to determine saddle-type unstable invariant limit sets in nonlinear systems. Chinese Physics Letters, 29: 050503 doi: 10.1088/0256-307X/29/5/050503
[116]	Jiang J, Guo X. 2011. Study of evolution of global structure into chaotic itinerancy by point mapping under cell reference method. in 23rd Biennial Conference on Mechanical Vibration and Noise, Parts A and B. ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. ASME, Washington, DC, USA, pp. 625-629
[117]	Jiang J, Xu J X. 1994. A method of point mapping under cell reference for global analysis of nonlinear dynamical systems. Physics Letters A, 188: 137-145 doi: 10.1016/0375-9601(84)90008-2
[118]	Jiang J, Xu J. X 1998. An iterative method of point mapping under cell reference for the global analysis: Theory and a multiscale reference technique. Nonlinear Dynamics, 15: 103-114
[119]	Jiang J, Xu J X. 2012. Point mapping under cell reference - a two scaled numerical method for global analysis. in Sun J-Q, Luo ACJ, (Ed. ) Global Analysis of Nonlinear Dynamics. Springer New York, New York, NY, pp. 107-137
[120]	Jin C, Ge R, Netrapalli P, et al. 2017. How to escape saddle points efficiently. in Precup D, Teh YW, (Ed. ) Proceedings of the 34th International Conference on Machine Learning. Proceedings of Machine Learning Research. PMLR, pp. 1724-1732
[121]	Jung C. 1986. Poincaré map for scattering states. Journal of Physics A: Mathematical and General, 19: 1345-1353 doi: 10.1088/0305-4470/19/8/016
[122]	Kahana A, Segev L, Lancet D. 2023. Attractor dynamics drives self-reproduction in protobiological catalytic networks. Cell Reports Physical Science, 4: 101384 doi: 10.1016/j.xcrp.2023.101384
[123]	Kelley C T. 2003. Solving Nonlinear Equations with Newton’s Method, Society for Industrial and Applied Mathematics.
[124]	Kempf R. 2002. On Ω-limit sets of discrete-time dynamical systems. Journal of Difference Equations and Applications, 8: 1121-1131 doi: 10.1080/10236190290029024
[125]	Kim H S, Eykholt R, Salas J D. 1999. Nonlinear dynamics, delay times, and embedding windows. Physica D: Nonlinear Phenomena, 127: 48-60 doi: 10.1016/S0167-2789(98)00240-1
[126]	Kim P, Seok J. 2014. A multi-stable energy harvester: Dynamic modeling and bifurcation analysis. Journal of Sound and Vibration, 333: 5525-5547 doi: 10.1016/j.jsv.2014.05.054
[127]	Kim W, Perkins N C. 2003. Harmonic balance/Galerkin method for non-smooth dynamic systems. Journal of Sound and Vibration, 261: 213-224 doi: 10.1016/S0022-460X(02)00949-5
[128]	Klokov A V, Zakrzhevsky M V. 2011. Parametrically excited pendulum systems with several equilibrium positions: bifurcation analysis and rare attractors. International Journal of Bifurcation and Chaos, 21: 2825-2836 doi: 10.1142/S0218127411030167
[129]	Koch D, Nandan A, Ramesan G, et al. 2024. Ghost channels and ghost cycles guiding long transients in dynamical systems. Physical Review Letters, 133: 047202 doi: 10.1103/PhysRevLett.133.047202
[130]	Koh D, Anderson R L, Bermejo-Moreno I. 2021. Cell-mapping orbit search for mission design at ocean worlds using parallel computing. The Journal of the Astronautical Sciences, 68: 172-196 doi: 10.1007/s40295-021-00251-6
[131]	Krauskopf B, Osinga H M, Doedel E J, et al. 2005. A survey of methods for computing (un) stable manifolds of vector fields. International Journal of Bifurcation and Chaos, 15: 763-791 doi: 10.1142/S0218127405012533
[132]	Lai Y C, Tél T. 2011. Transient Chaos, Springer New York, New York, NY
[133]	Lenci S, Rega G eds. 2019. Global nonlinear dynamics for engineering design and system safety, Springer International Publishing, Cham
[134]	Li Y, Li C, Zhong Q, et al. 2024. Coexisting hollow chaotic attractors within a steep parameter interval. Chaos, Solitons & Fractals, 179: 114406
[135]	Li Z, Jiang J, Li J, et al. 2019. A subdomain synthesis method for global analysis of nonlinear dynamical systems based on cell mapping. Nonlinear Dynamics, 95: 715-726 doi: 10.1007/s11071-018-4592-4
[136]	Li Z, Jiang J, Hong L, et al. 2020. A subspace expanding technique for global zero finding of multi-degree-of-freedom nonlinear systems. Applied Mathematics and Mechanics - English Edition, 41: 769-784 doi: 10.1007/s10483-020-2604-6
[137]	Li Z, Ma S, Jiang J, et al. 2024. Discretized boundary-oriented progressive learning method for predicting global basins of attraction with few data. Physica D: Nonlinear Phenomena, 470: 134350 doi: 10.1016/j.physd.2024.134350
[138]	Li Z, Qiao L, Jiang J, et al. 2020. Global dynamic analysis of the North Pacific Ocean by data-driven generalized cell mapping method. International Journal of Dynamics and Control, 8: 1141-1146 doi: 10.1007/s40435-020-00678-z
[139]	Li Z, Jiang J, Hong L, et al. 2019. On the data-driven generalized cell mapping method. International Journal of Bifurcation and Chaos, 29: 1950204: 1-1950204: 21
[140]	Li Z, Kang J, Jiang J, et al. 2022. Parallel subdomain synthesis of cell mapping for capturing global invariant sets in higher-dimensional dynamical systems. International Journal of Bifurcation and Chaos, 32: 2250231 doi: 10.1142/S0218127422502315
[141]	Li Z, Jiang J, Hong L. 2017. Noise-induced transition in a piecewise smooth system by generalized cell mapping method with evolving probabilistic vector. Nonlinear Dynamics, 88: 1473-1485 doi: 10.1007/s11071-016-3323-y
[142]	Li Z, Jiang Q, Jiang J. 2024. Tracking global topologies by deep learning-based progressive training with few data. The European Physical Journal Special Topics
[143]	Liu X, Jiang J, Hong L, Li Z, et al. 2019. Fuzzy noise-induced codimension-two bifurcations captured by fuzzy generalized cell mapping with adaptive interpolation. International Journal of Bifurcation and Chaos, 29: 1950151 doi: 10.1142/S0218127419501517
[144]	Liu X, Jiang J, Hong L, et al. 2018. Studying the global bifurcation involving Wada boundary metamorphosis by a method of generalized cell mapping with sampling-adaptive interpolation. International Journal of Bifurcation and Chaos, 28: 1830003 doi: 10.1142/S0218127418300033
[145]	Liu X, Jiang J, Hong L, Tang D. 2019. Wada boundary bifurcations induced by boundary saddle-saddle collision. Physics Letters A, 383: 170-175 doi: 10.1016/j.physleta.2018.10.023
[146]	Lohmann J, Dijkstra H A, Jochum M, et al. 2024. Multistability and intermediate tipping of the Atlantic Ocean circulation. Science Advances, 10: eadi4253 doi: 10.1126/sciadv.adi4253
[147]	López-Ureña S, Torres-Lapasió J R, García-Alvarez-Coque M C. 2019. Enhancement in the computation of gradient retention times in liquid chromatography using root-finding methods. Journal of Chromatography. A, 1600: 137-147 doi: 10.1016/j.chroma.2019.04.030
[148]	Lu Z, Hunt B, Ott E. 2018. Attractor reconstruction by machine learning. Chaos: An Interdisciplinary Journal of Nonlinear Science, 28: 061104 doi: 10.1063/1.5039508
[149]	Ma F, Küpper T. 1994. Numerical calculation of invariant manifolds for maps. Numerical Linear Algebra with Applications, 1: 141-150 doi: 10.1002/nla.1680010205
[150]	Mamaghani A E, Khadem S E, Bab S. 2016. Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink. Nonlinear Dynamics, 86: 1761-1795 doi: 10.1007/s11071-016-2992-x
[151]	Matteo A D, Pirrotta A. 2024. Efficient path integral approach via analytical asymptotic expansion for nonlinear systems under Gaussian white noise. Nonlinear Dynamics, 112: 13995-14018 doi: 10.1007/s11071-024-09822-2
[152]	Menck P J, Heitzig J, Marwan N, et al. 2013. How basin stability complements the linear-stability paradigm. Nature Physics, 9: 89-92 doi: 10.1038/nphys2516
[153]	Mirowski P, LeCun Y. 2009. Dynamic factor graphs for time series modeling. in Buntine W et al., (Ed.) Machine Learning and Knowledge Discovery in Databases. Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 128-143
[154]	Mitra C, Choudhary A, Sinha S, et al. 2017. Multiple-node basin stability in complex dynamical networks. Physical Review E, 95: 032317
[155]	Molčan M, Ferfecki P, Zapoměl J. 2023. The numerical identification of basins of attraction for the vibration response of the rigid rotor with squeeze film dampers. Applied Sciences, 13: 2864 doi: 10.3390/app13052864
[156]	Mujica J, Krauskopf B, Osinga H M. 2018. Tangencies Between Global Invariant Manifolds and Slow Manifolds Near a Singular Hopf Bifurcation. SIAM Journal on Applied Dynamical Systems, 17: 1395-1431 doi: 10.1137/17M1133452
[157]	Naik S, Ross S D. 2017. Geometry of escaping dynamics in nonlinear ship motion. Communications in Nonlinear Science and Numerical Simulation, 47: 48-70 doi: 10.1016/j.cnsns.2016.10.021
[158]	Navarro C A, Hitschfeld-Kahler N, Mateu L. 2014. A survey on parallel computing and its applications in data-parallel problems using GPU architectures. Communications in Computational Physics, 15: 285-329 doi: 10.4208/cicp.110113.010813a
[159]	Nave G K, Nolan P J, Ross S D. 2019. Trajectory-free approximation of phase space structures using the trajectory divergence rate. Nonlinear Dynamics, 96: 685-702 doi: 10.1007/s11071-019-04814-z
[160]	Niroomand M P, Morgan J W R, Cafolla C T, et al. 2022. On the capacity and superposition of minima in neural network loss function landscapes. Machine Learning: Science and Technology, 3: 025004 doi: 10.1088/2632-2153/ac64e6
[161]	Noakes L. 1991. The takens embedding theorem. International Journal of Bifurcation and Chaos, 1: 867-872 doi: 10.1142/S0218127491000634
[162]	Nolan P J, Foroutan H, Ross S. 2020. Pollution transport patterns obtained through generalized Lagrangian coherent structures. Atmosphere, 11: 168 doi: 10.3390/atmos11020168
[163]	Nusse H E, Yorke J A. 1991. A numerical procedure for finding accessible trajectories on basin boundaries. Nonlinearity, 4: 1183-1212 doi: 10.1088/0951-7715/4/4/008
[164]	Nusse H E, Yorke J A. 1989. A procedure for finding numerical trajectories on chaotic saddles. Physica D: Nonlinear Phenomena, 36: 137-156 doi: 10.1016/0167-2789(89)90253-4
[165]	Orlando D, de Castro C H L, Gonçalves P B. 2018. Nonlinear vibrations and instability of a bistable shallow reticulated truss. Nonlinear Dynamics, 94: 1479-1499 doi: 10.1007/s11071-018-4437-1
[166]	Osinga H M. 2014. Computing global invariant manifolds: techniques and applications. in Proceedings of the International Congress of Mathematicians. Seoul, South Korea
[167]	Osinga H M. 2018. Understanding the geometry of dynamics: the stable manifold of the Lorenz system. Journal of the Royal Society of New Zealand, 48: 203-214 doi: 10.1080/03036758.2018.1434802
[168]	Ott E. 2002. Chaos in dynamical systems, Cambridge University Press
[169]	Parker T S, Chua L O. 1989. Practical numerical algorithms for chaotic systems, Springer New York, NY
[170]	Pattanayak D, Mishra A, Dana S K, et al. 2021. Bistability in a tri-trophic food chain model: Basin stability perspective. Chaos: An Interdisciplinary Journal of Nonlinear Science, 31: 073124 doi: 10.1063/5.0054347
[171]	Pérez-Hernández G, Paul F, Giorgino T, et al. 2013. Identification of slow molecular order parameters for Markov model construction. The Journal of Chemical Physics, 139: 015102 doi: 10.1063/1.4811489
[172]	Piiroinen P T, Kuznetsov Y A. 2008. An event-driven method to simulate Filippov systems with accurate computing of sliding motions. ACM Transactions on Mathematical Software, 34: 1-24
[173]	Pisarchik A N, Hramov A E. 2022. Multistability in physical and living systems: Characterization and Applications, Springer Cham
[174]	Ponce E, Ros J, Vela E. 2018. The boundary focus-saddle bifurcation in planar piecewise linear systems. Application to the analysis of memristor oscillators. Nonlinear Analysis: Real World Applications, 43: 495-514 doi: 10.1016/j.nonrwa.2018.03.011
[175]	Qin Z, Xin Y, Sun J. 2020. Multi-objective optimal motion control of a laboratory helicopter based on parallel simple cell mapping method. Asian Journal of Control, 22: 1565-1578 doi: 10.1002/asjc.2040
[176]	Raghav S, Ruggiero M, Marongiu A, et al. 2015. GPU acceleration for simulating massively parallel many-core platforms. IEEE Transactions on Parallel and Distributed Systems, 26: 1336-1349 doi: 10.1109/TPDS.2014.2319092
[177]	Rega G. 2019. Exploiting global dynamics to unveil the nonlinear response and actual safety of systems and structures. in Developments and Novel Approaches in Nonlinear Solid Body Mechanics. International Conference on Nonlinear Solid Mechanics 2019. Springer, Cham, Roma, Italy
[178]	Rega G, Lenci S. 2015. A global dynamics perspective for system safety from macro- to nanomechanics: analysis, control, and design engineering. Applied Mechanics Reviews, 67: 050802 doi: 10.1115/1.4031705
[179]	Rega G, Lenci S. 2005. Identifying, evaluating, and controlling dynamical integrity measures in non-linear mechanical oscillators. Nonlinear Analysis: Theory, Methods & Applications, 63: 902-914
[180]	Revuelta F, Bartsch T, Benito R M, et al. 2018. The geometry of transition states: How invariant manifolds determine reaction rates. Chaotic Modeling and Simulation, 3: 305-318
[181]	Rhodes C, Morari M. 1997. The false nearest neighbors algorithm: An overview. Computers & Chemical Engineering, 21: S1149-S1154
[182]	Rodrigues A A P. 2017. Attractors in complex networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 27: 103105 doi: 10.1063/1.4996883
[183]	Sahoo S, Roy B K. 2022. A new multi-wing chaotic attractor with unusual variation in the number of wings. Chaos, Solitons & Fractals, 164: 112598
[184]	Scheffer M, Bascompte J, Brock W A, et al. 2009. Early-warning signals for critical transitions. Nature, 461: 53-59 doi: 10.1038/nature08227
[185]	Schmitt R J, Holbrook S J, Davis S L, et al. 2019. Experimental support for alternative attractors on coral reefs. Proceedings of the National Academy of Sciences, 116: 4372-4381 doi: 10.1073/pnas.1812412116
[186]	Schöll E, Klapp S H L, Hövel P. 2016. Control of self-organizing nonlinear systems, Springer Cham
[187]	Serra M, Sathe P, Rypina I, et al. 2020. Search and rescue at sea aided by hidden flow structures. Nature Communications, 11: 2525 doi: 10.1038/s41467-020-16281-x
[188]	Sievidova I, Oliynik T, Mandych O, et al. 2019. Optimizing the strategy of activities using numerical methods for determining equilibrium. Eastern-European Journal of Enterprise Technologies, 6: 47-56
[189]	Simó C. 1990. On the analytical and numerical approximation of invariant manifolds. in Modern Methods in Celestial Mechanics. pp. 285-329
[190]	Şimşek M, Bilgen O. 2020. The Duffing-Holmes oscillator under hybrid position feedback controller: response type and basin of attraction analyses. International Journal of Structural Stability and Dynamics, 20: 2050101 doi: 10.1142/S0219455420501011
[191]	Stark J. 1999. Delay embeddings for forced systems. I. deterministic forcing. Journal of Nonlinear Science, 9: 255-332 doi: 10.1007/s003329900072
[192]	Stark J, Broomhead D S, Davies M E, et al. 2003. Delay embeddings for forced systems. II. stochastic forcing. Journal of Nonlinear Science, 13: 519-577 doi: 10.1007/s00332-003-0534-4
[193]	Stark J, Broomhead D S, Davies M E, et al. 1997. Takens embedding theorems for forced and stochastic systems. Nonlinear Analysis: Theory, Methods & Applications, 30: 5303-5314
[194]	Sugihara G, May R, Ye H, et al. 2012. Detecting causality in complex ecosystems. Science, 338: 496-500 doi: 10.1126/science.1227079
[195]	Sun H, Shang H. 2024. Comparisons for global dynamics of a geometrically nonlinear oscillator among single-, double- and quadruple-well configurations. Fractal and Fractional, 8: 202 doi: 10.3390/fractalfract8040202
[196]	Sun J Q, Jia T, Xiong F, et al. 2015. Aircraft landing gear control with multi-objective optimization using generalized cell mapping. Transactions of Tianjin University, 21: 140-146 doi: 10.1007/s12209-015-2584-8
[197]	Sun J Q, Xiong F R, Schütze O, et al. 2019. Cell Mapping Methods, Springer Singapore, Singapore
[198]	Sun J Q, Zheng W, Xiong F, et al. 2017. Multi-objective optimal design of vbration absorber with simple cell mapping algorithm. Transactions of Tianjin University, 23: 488-492 doi: 10.1007/s12209-017-0066-x
[199]	Sun J Q, Hong L. 2012. Fuzzy cell mapping. in Global Analysis of Nonlinear Dynamics. Springer New York, pp. 161-174
[200]	Sun J Q, Hsu C S. 1990a. Global analysis of nonlinear dynamical systems with fuzzy uncertainties by the cell mapping method. Computer Methods in Applied Mechanics and Engineering, 83: 109-120 doi: 10.1016/0045-7825(90)90146-D
[201]	Sun J Q, Hsu C S. 1990b. The generalized cell mapping method in nonlinear random vibration based upon short-time gaussian approximation. Journal of Applied Mechanics-Transactions of the ASME, 57: 1018-1025 doi: 10.1115/1.2897620
[202]	Sun J Q, Luo A C J eds. 2012. Global Analysis of Nonlinear Dynamics, Springer New York, New York, NY
[203]	Sun J Q, Xiong F. 2017. Cell mapping methods-beyond global analysis of nonlinear dynamic systems. Advances in Mechanics, 47: 150-177
[204]	Sun S, Cao Z, Zhu H, et al. 2020. A survey of optimization methods from a machine learning perspective. IEEE Transactions on Cybernetics, 50: 3668-3681 doi: 10.1109/TCYB.2019.2950779
[205]	Sun Z, Zhang X, Fan T, et al. 2019. Nonlinear dynamic characteristics analysis of active magnetic bearing system based on cell mapping method with a case study. Mechanical Systems and Signal Processing, 117: 116-137 doi: 10.1016/j.ymssp.2018.07.030
[206]	Szemplinska-Stupnicka W, Janicki K. 1997. Basin boundary bifurcations and boundary crisis in the twin-well Duffing oscillator: Scenarios related to the saddle of the large resonant orbit. International Journal of Bifurcation and Chaos, 7: 129-146 doi: 10.1142/S0218127497000091
[207]	Tamakoshi D, Kojima H. 2019. Set-oriented design of interplanetary low-thrust trajectories using Earth Gravity Assist. Acta Astronautica, 156: 208-218 doi: 10.1016/j.actaastro.2018.10.012
[208]	Tarjan R. 1971. Depth-first search and linear graph algorithms. in 12th Annual Symposium on Switching and Automata Theory (swat 1971). pp. 114-121
[209]	Tongue B H. 1987. On obtaining global nonlinear system characteristics through interpolated cell mapping. Physica D: Nonlinear Phenomena, 28: 401-408 doi: 10.1016/0167-2789(87)90028-5
[210]	Tongue B H, Gu K. 1988a. A higher order method of interpolated cell mapping. Journal of Sound and Vibration, 125: 169-179 doi: 10.1016/0022-460X(88)90424-5
[211]	Tongue B H, Gu K. 1988b. A theoretical basis for interpolated cell mapping. SIAM Journal on Applied Mathematics, 48: 1206-1214 doi: 10.1137/0148072
[212]	Tongue B H, Gu K. 1988c. Interpolated cell mapping of dynamical systems. Journal of Applied Mechanics, 55: 461-466 doi: 10.1115/1.3173700
[213]	Troger H, Steindl A. 1992. Nonlinear stability and bifurcation theory: An introduction for engineers and applied scientists, Springer Vienna
[214]	Valle D, Wagemakers A, Sanjuán M A F. 2024. Deep learning-based analysis of basins of attraction. Chaos: An Interdisciplinary Journal of Nonlinear Science, 34: 033105 doi: 10.1063/5.0159656
[215]	Wan E A. 1993. Time series prediction by using a connectionist network with internal delay lines. in Time Series Prediction. Forecasting the Future and Understanding the Past. In Santa Fe Institute Studies In The Sciences Of Complexity. Addison-Wesley, pp. 195-195
[216]	Wang F Y, Fan X Y. 1995. Cell-to-cell mapping method for time-optimal trajectory planning of multiple robot arm systems. Journal of Optimization Theory and Applications, 86: 347-368 doi: 10.1007/BF02192084
[217]	Wang N, Zhang G, Kuznetsov N V, et al. 2021. Hidden attractors and multistability in a modified Chua’s circuit. Communications in Nonlinear Science and Numerical Simulation, 92: 105494 doi: 10.1016/j.cnsns.2020.105494
[218]	Wang T, Li J, Lu D, et al. 2024. A point mapping strategy-based sparse grid integration method for statistical moments estimation and structural reliability analysis. Computer Methods in Applied Mechanics and Engineering, 430: 117238 doi: 10.1016/j.cma.2024.117238
[219]	Wang X, Jiang J, Hong L. 2020. Enhancing subdivision technique with an adaptive interpolation sampling method for global attractors of nonlinear dynamical systems. International Journal of Dynamics and Control, 8: 1147-1160 doi: 10.1007/s40435-020-00683-2
[220]	Wu L, Xi X, Li B, et al. 2018. Multi-stable mechanical structural materials. Advanced Engineering Materials, 20: 1700599 doi: 10.1002/adem.201700599
[221]	Xiong F. 2016. Finding zeros of nonlinear functions using the hybrid parallel cell mapping method. Communications in Nonlinear Science and Numerical Simulation, 34: 23-37 doi: 10.1016/j.cnsns.2015.10.008
[222]	Xiong F, Qin Z, Ding Q, et al. 2015. Parallel cell mapping method for global analysis of high-dimensional nonlinear dynamical systems. Journal of Applied Mechanics-Transactions of the ASME, 82: 111010 doi: 10.1115/1.4031149
[223]	Xu C, Xue L, Cui Y, et al. 2023. Critical slowing down phenomenon for predicting the failure of solid rocks and cement mortar materials: Insight from acoustic emission multiparameters. Construction and Building Materials, 399: 132523 doi: 10.1016/j.conbuildmat.2023.132523
[224]	Xu Y, Li Y, Zhang H, et al. 2016. The switch in a genetic toggle system with Lévy noise. Scientific Reports, 6: 31505 doi: 10.1038/srep31505
[225]	Yan Y, Liu G, Wiercigroch M, et al. 2021. Safety estimation for a new model of regenerative and frictional cutting dynamics. International Journal of Mechanical Sciences, 201: 106468 doi: 10.1016/j.ijmecsci.2021.106468
[226]	Yang F, Chen L, Yuan Z, et al. 2023. Transient response of energy harvesting systems with multi-well potential under Poisson white noise excitations. International Journal of Non-Linear Mechanics, 155: 104463 doi: 10.1016/j.ijnonlinmec.2023.104463
[227]	Yang L, Ge Y, Ma X, et al. 2017. Global analysis of stochastic bifurcation in permanent magnet synchronous generator for wind turbine system. Acta Physica Sinica, 66: 190501 doi: 10.7498/aps.66.190501
[228]	Yang Q, Li S, Ma Z. 2023. Global behavior analysis of nonlinear energy sink systems using the parallelized multi-degrees-of-freedom cell mapping method. Journal of Computational and Nonlinear Dynamics, 18: 011002 doi: 10.1115/1.4056198
[229]	Yee H C, Sweby P K, Griffiths D F. 1991. Dynamical approach study of spurious steady-state numerical solutions of nonlinear differential equations. I. The dynamics of time discretization and its implications for algorithm development in computational fluid dynamics. Journal of Computational Physics, 97: 249-310 doi: 10.1016/0021-9991(91)90001-2
[230]	Yi D, Ahn J L, Ji S. 2020. An effective optimization method for machine learning based on ADAM. Applied Sciences, 10: 1073 doi: 10.3390/app10031073
[231]	Yu X, Chen G, Xia Y, et al. 2001. An invariant-manifold-based method for chaos control. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 48: 930-937
[232]	Yue X, Zhang H, Li Y, et al. 2024. Global dynamics and noise-induced transitions for a two-dimensional panel system in subsonic flow. Acta Mechanica Sinica, 40: 523472 doi: 10.1007/s10409-024-23472-x
[233]	Yue X, Xu Y, Xu W, et al. 2019. Global invariant manifolds of dynamical systems with the compatible cell mapping method. International Journal of Bifurcation and Chaos, 29: 1950105 doi: 10.1142/S0218127419501050
[234]	Yue X, Wang Y, Han Q, et al. 2019. Transient responses of nonlinear dynamical systems under colored noise. Europhysics Letters, 127: 24004 doi: 10.1209/0295-5075/127/24004
[235]	Yue X, Xu W, Zhang Y. 2012. Global bifurcation analysis of Rayleigh-Duffing oscillator through the composite cell coordinate system method. Nonlinear Dynamics, 69: 437-457 doi: 10.1007/s11071-011-0276-z
[236]	Zeng S. 2018. On sample-based computations of invariant sets. Nonlinear Dynamics, 94: 2613-2624 doi: 10.1007/s11071-018-4512-7
[237]	Zhang W, Xu W, Niu L, et al. 2023. Bifurcations analysis of a multiple attractors energy harvesting system with fractional derivative damping under random excitation. Communications in Nonlinear Science and Numerical Simulation, 118: 107069 doi: 10.1016/j.cnsns.2022.107069
[238]	Zhang Y, Strogatz S H. 2021. Basins with tentacles. Physical Review Letters, 127: 194101 doi: 10.1103/PhysRevLett.127.194101
[239]	Zhong J, Ross S D. 2021. Global invariant manifolds delineating transition and escape dynamics in dissipative systems: an application to snap-through buckling. Nonlinear Dynamics, 104: 3109-3137 doi: 10.1007/s11071-021-06509-w
[240]	Zhu Y, Shang H. 2022. Global bifurcation behaviors and control in a class of bilateral MEMS resonators. Fractal and Fractional, 6: 538 doi: 10.3390/fractalfract6100538