非线性周期结构动力学与波动调控研究进展

高鹏林; 龚凌云; 王国旭; 罗宇; 朱俊喆; 高昊; 马海斌; 瞿叶高

doi:10.6052/1000-0992-24-047

非线性周期结构动力学与波动调控研究进展

doi: 10.6052/1000-0992-24-047 cstr: 32046.14.1000-0992-24-047

高鹏林^{1, 2},
龚凌云^{1, 2},
王国旭^{1, 2},
罗宇^{1, 2},
朱俊喆^{1, 2},
高昊^{1, 2},
马海斌^{1, 2},
瞿叶高^{1, 2, ,}

1.
上海交通大学机械系统与振动全国重点实验室, 上海 200240
2.
上海交通大学振动、冲击、噪声研究所, 上海 200240

基金项目: 国家自然科学基金(12202267, 12425202, 12393781, U2141244, 12121002, 12202260)、上海市市级科技重大专项资助的课题和上海交通大学机械系统与振动全国重点实验室自主课题(MSVZD202404)的支持

详细信息

作者简介:
高鹏林, 上海交通大学机械与动力工程学院副教授, 博士生导师. 主要研究方向为人工周期结构动力学与振动噪声控制, 在《Physical Reviews Letters》《Nature Communications》《Journal of Sound and Vibration》等学术期刊发表论文30余篇, 入选上海市浦江人才计划、上海市海外高层次青年人才, 获上海市力学学会优秀青年学者一等奖

瞿叶高, 上海交通大学科研院副院长、前沿创新研究院院长, 机械系统与振动全国重点实验室副主任. 主要从事非线性动力学设计及振动与声波操控研究. 主持国家杰出青年科学基金以及基金委重大项目课题、叶企孙基金重点项目等. 获教育部自然科学奖一等奖、上海市科技进步一等奖、中国力学学会青年科技奖、中国振动工程学会青年科技奖等奖励. 担任《Applied Acoustics》副主编以及多个国内外期刊编委. 兼任中国力学学会理性力学和力学中的数学方法专业委员会委员, 中国振动工程学会副秘书长、非线性振动专业委员会副主任等

通讯作者:
quyegao@sjtu.edu.cn

中图分类号: O322
计量
- 文章访问数: 400
- HTML全文浏览量: 124
- PDF下载量: 136
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-26
- 录用日期: 2025-04-14
- 网络出版日期: 2025-05-06

Review on the dynamics and wave control in nonlinear periodic structures

GAO Penglin^{1, 2},
GONG Lingyun^{1, 2},
WANG Guoxu^{1, 2},
LUO Yu^{1, 2},
ZHU Junzhe^{1, 2},
GAO Hao^{1, 2},
MA Haibin^{1, 2},
QU Yegao^{1, 2
, ,}

1.
State Key Laboratory of Mechanical System and Vibration, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 20024, China
2.
Institute of Vibration, Shock and Noise, Shanghai Jiao Tong University, Shanghai 200240, China

More Information

Corresponding author: quyegao@sjtu.edu.cn

摘要

摘要: 周期结构是构建自然界和人类工程结构的一种重要形式, 平移对称性引起的Bloch调制作用赋予其独特的能带结构和丰富的时/频域动力学特性, 为弹性波/声波传播调控、新型声功能器件设计、振动与噪声控制等提供了新思路. 非线性效应可以突破线性理论框架的束缚, 能够增强甚至拓展人工周期结构的功能. 但非线性周期系统在单胞结构设计和建模分析方面存在诸多困难, 也面临时空平移对称性破缺、非线性响应特性及机理复杂等深层次科学难题, 给非线性周期结构动力学设计与实际应用带来挑战. 针对上述问题, 学者们融合力学、声学、材料学和能带物理等多学科研究方法开展了一些卓有成效的研究, 本文旨在及时总结非线性周期结构动力学和波动调控领域的重要研究进展, 梳理研究中存在的不足之处和关键难题, 凝聚力量, 促进该领域的深入发展. 首先, 归纳了力学周期结构非线性效应来源、单胞结构设计方法、非线性周期结构动力学建模与分析方法; 之后, 综述了非线性周期结构在通带、带隙和能量局域束缚等方面的主要特性, 着重介绍了非线性导致的能带频移、模式耦合、低频宽带拓展和带隙内波动模式局域束缚等丰富动力学现象, 梳理了非线性周期结构在波调控装置和减振降噪设计方面的一些应用探索. 最后, 针对现有研究存在的一些不足和关键难题, 展望了未来理论研究和应用探索亟需关注的若干发展方向.
- 非线性周期结构 /
- 动力学设计 /
- 非线性振动 /
- 振动控制 /
- 波动调控
Abstract: Periodic structures are an important form of constructing structures in natural and human engineering. The Bloch modulation caused by translational symmetry gives them unique band structures and rich time/frequency domain dynamic characteristics, providing new avenues for elastic/acoustic wave propagation regulation, novel wave-based functional device design, vibration and noise control, etc. Nonlinear effects can break through the constraints of linear theoretical frameworks and can enhance or even expand the functions of artificial periodic structures. However, nonlinear periodic systems have many difficulties in unit cell design and modeling analysis. They also face key scientific problems such as the broken of space-time invariance, the complexity of nonlinear response characteristics and mechanisms, which brings challenge to the dynamic design and practical application of nonlinear periodic structures. In response to the above problems, scholars have carried out some fruitful research by integrating multidisciplinary research methods in fileds such as mechanics, acoustics, materials science and band physics. This article aims to timely summarize the important research progress concerning about wave dynamics and control in nonlinear periodic structures, sort out the shortcomings and key problems, gather strength and promote the in-depth development of this field. First, the sources of nonlinear effects of periodic structures, unit cell structure design methods, and nonlinear dynamics modeling and analysis methods are summarized. Then, the main characteristics of nonlinear periodic structures in terms of passband, bandgap, and local energy confinement are reviewed, and the rich dynamic phenomena such as amplitude-induced band shift, wave mode coupling, low-frequency broadband bandgap, and spatial confinement of wave modes in the bandgap caused by nonlinearity are introduced. Some application explorations of nonlinear periodic structures in wave control devices, vibration and noise reduction are sorted out. Finally, in view of some shortcomings and key problems in existing research, several development directions that need special attention in future theoretical research and application exploration are prospected.
- nonlinear periodic structure /
- dynamic design /
- nonlinear vibration /
- vibration control /
- wave control

HTML全文

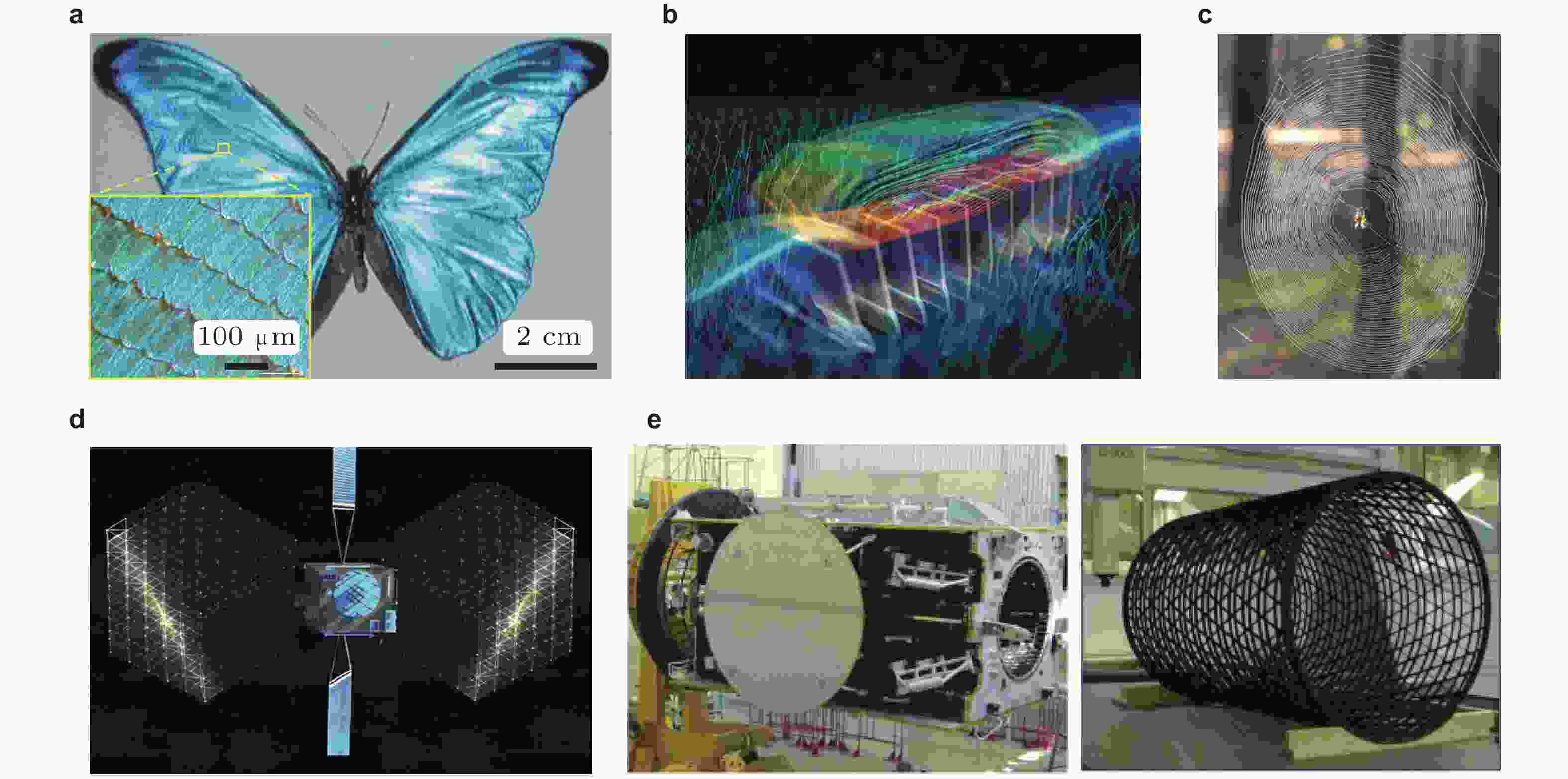
图 1 自然界和人类工程中存在的典型周期结构. (a) 蓝闪蝶翅鳞结构(Plattner 2004), (b) 微纤毛驱动流体运动示意图(Wang et al. 2024b), (c) 蜘蛛网, (d) 由周期桁架结构构成的星载天线(Zheng et al. 2022), (e) 运载火箭中由周期格栅构成的复合材料壳体结构(Vasiliev et al. 2012)

下载: 全尺寸图片幻灯片

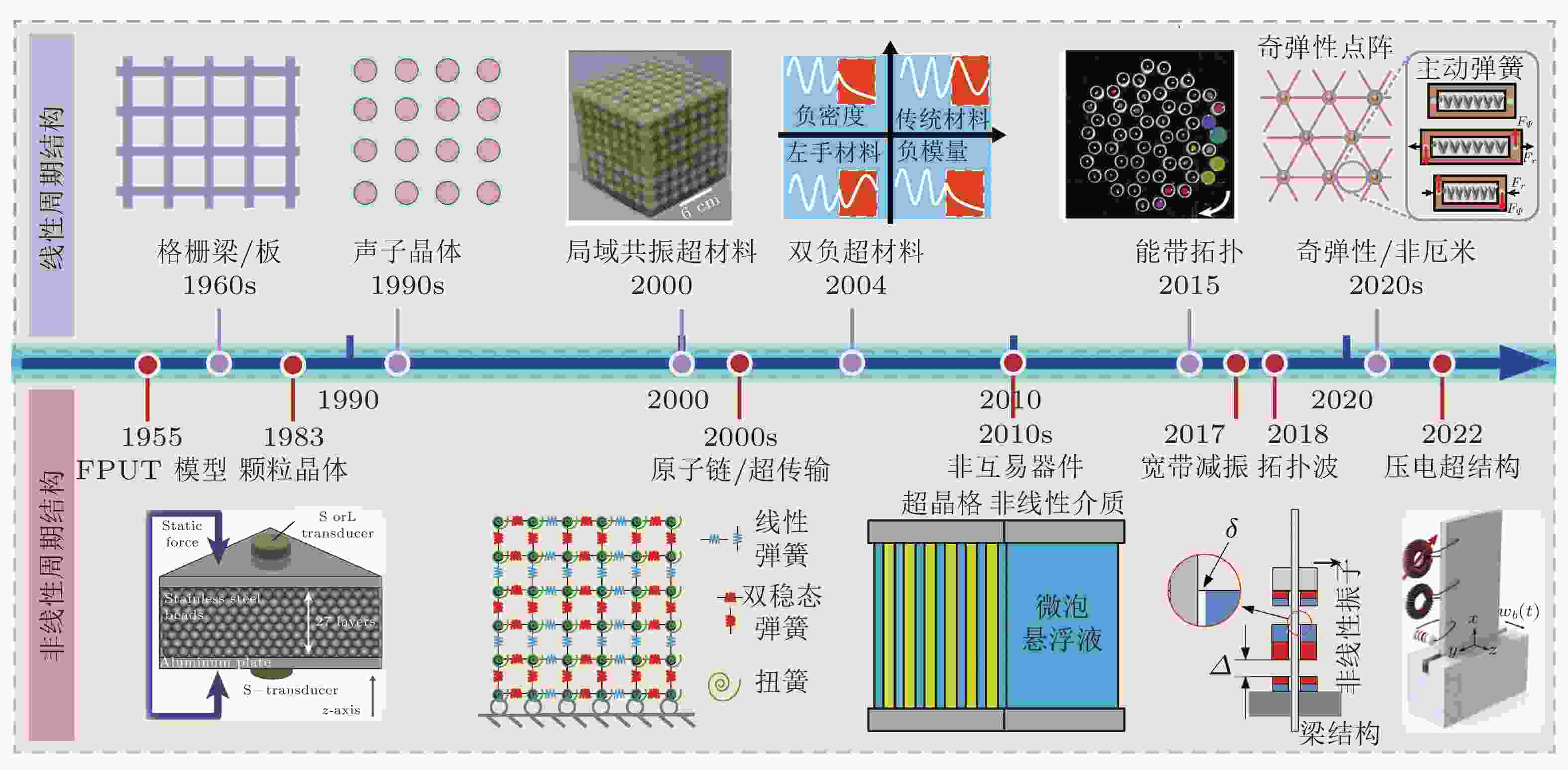
图 2 线性周期结构和非线性周期结构发展历程简图. 来自文献(Liu et al. 2000, 陈毅等 2016, Nash et al. 2015, Gao et al. 2022b, Merkel et al. 2011, Meaud 2020, Liang et al. 2010, Fang et al. 2017a, Alfahmi et al. 2022)

下载: 全尺寸图片幻灯片

图 3 WOS数据库收录的关于周期结构的论文数目变化过程(数据截止于2024年12月)

下载: 全尺寸图片幻灯片

图 4 周期结构非线性效应来源. (a) 几种代表性非线性效应 (b) 非线性作用力示意图

下载: 全尺寸图片幻灯片

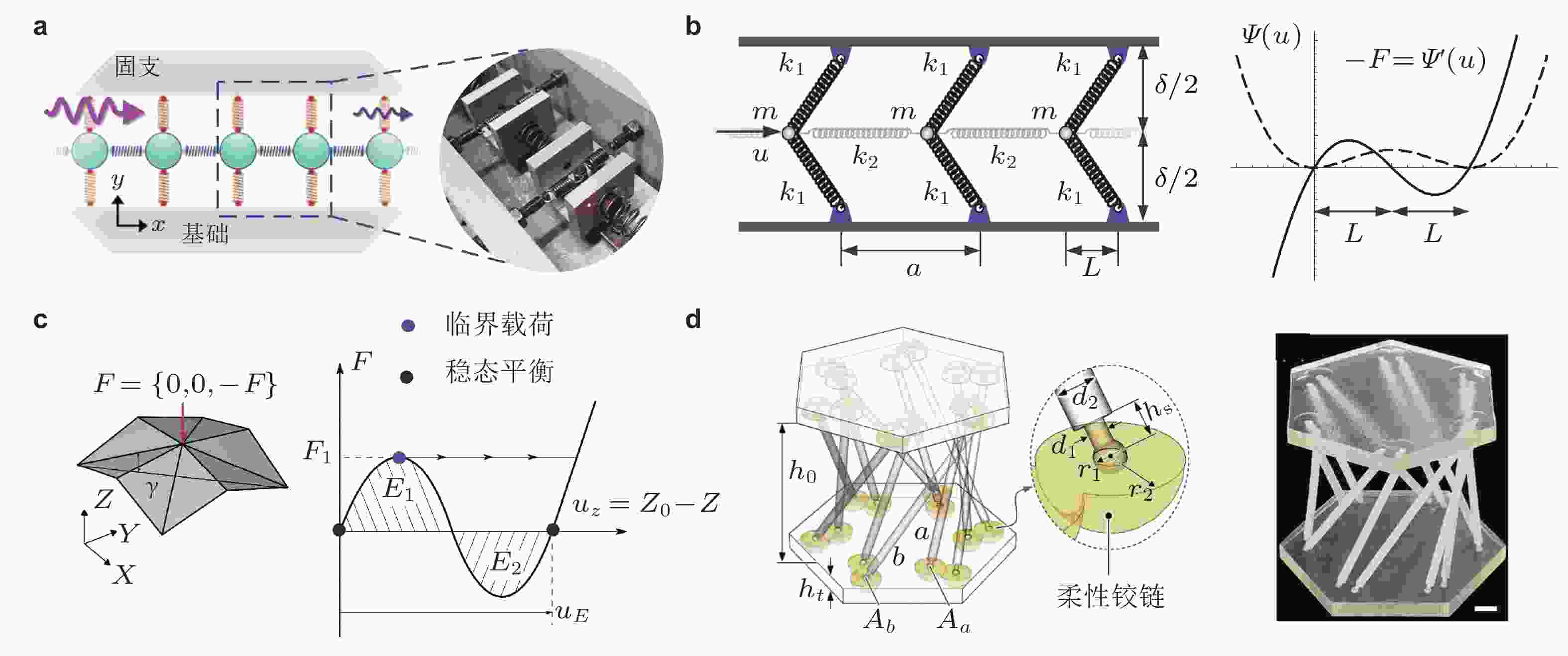
图 5 通过几何构型设计实现非线性回复力. (a) 线性弹簧组合结构, 实现三次非线性回复力(Bae & Oh 2022), (b) 线性弹簧组合结构实现双稳态(Nadkarni et al. 2014), (c) 折纸双稳态结构(Gillman et al. 2018), (d) 连杆−软铰链组合结构(Zhang & Rudykh 2024)

下载: 全尺寸图片幻灯片

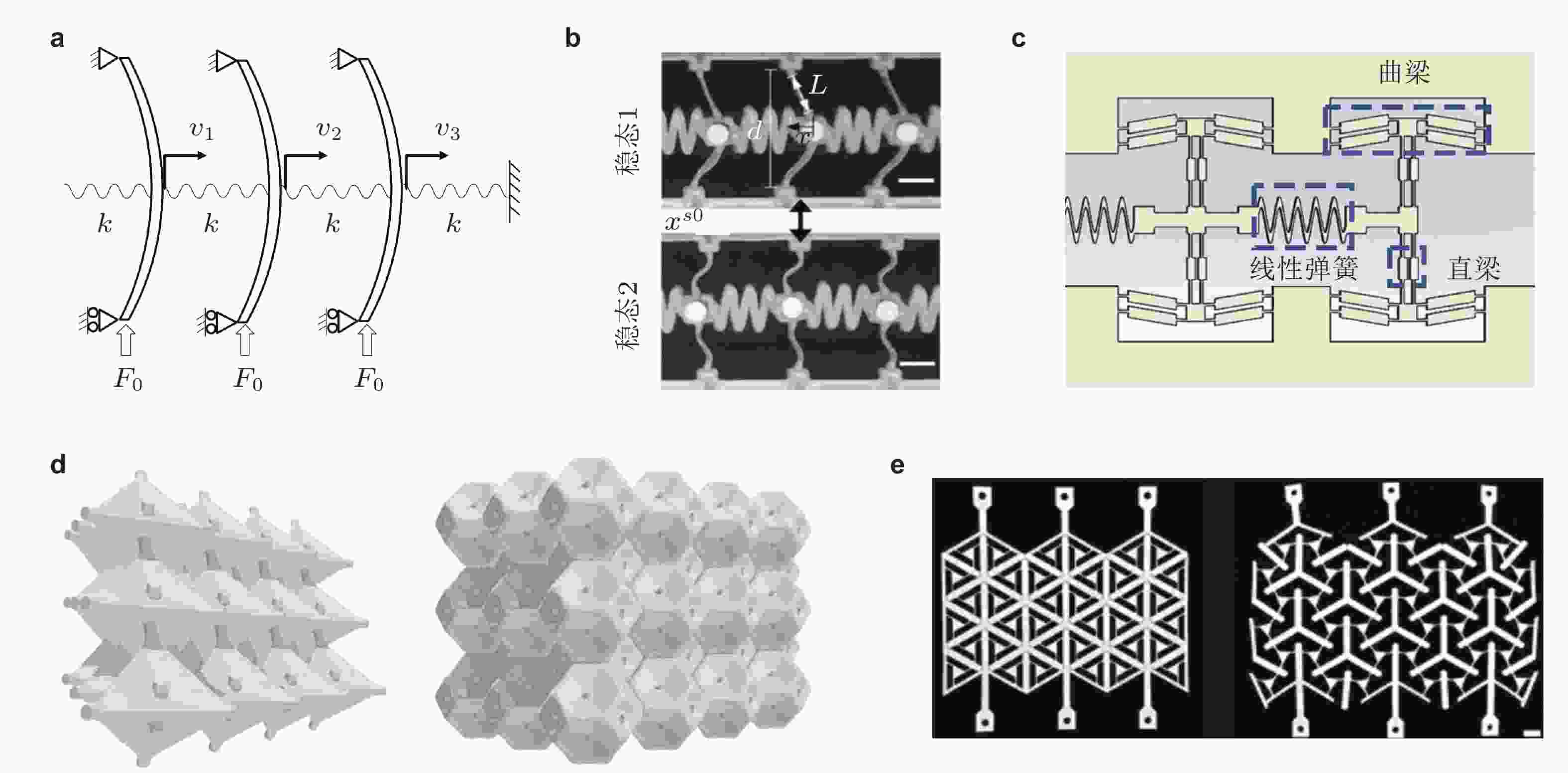
图 6 利用几何大变形和材料非线性实现非线性回复力. (a) 屈曲梁周期结构(Bidhendi 2022), (b) 大变形超弹性梁−弹簧双稳态结构(Raney et al. 2016), (c) 曲梁−直梁−弹簧多稳态结构(Xu & Xiang 2024), (d) 大变形屈曲壳可重构多稳态结构(Khajehtourian & Kochmann 2021), (e) 多稳态网络结构(Jin et al. 2020)

下载: 全尺寸图片幻灯片

图 7 利用接触或碰撞实现非线性回复力. (a) 带间隙的弹簧−质量振子结构(Yu et al. 2024), (b) 颗粒晶体(Allein et al. 2020), (c) 木桩结构(Kim et al. 2015)

下载: 全尺寸图片幻灯片

图 8 通过外界物理场引入非线性效应. (a) 具有非线性力−磁耦合作用的梁结构(Xue et al. 2023), (b) 含永磁体的柔性铰链结构(Jiao et al. 2024), (c) 由介电弹性材料构成一维周期结构(Chen et al. 2020)

下载: 全尺寸图片幻灯片

图 9 非线性惯性力和非线性阻尼力. (a) 惯性放大旋转结构, 实现非线性阻尼力(Zhao et al. 2024), (b) 弹簧−连杆惯性放大机构, 同时实现非线性惯性力和非线性阻尼力(Settimi et al. 2021), (c) 弹簧摆结构, 同时实现非线性惯性力和非线性阻尼力(Zhou et al. 2024a), (d)弹簧−连杆组合结构, 同时实现非线性惯性力、非线性阻尼力和非线性回复力(Zhou et al. 2019)

下载: 全尺寸图片幻灯片

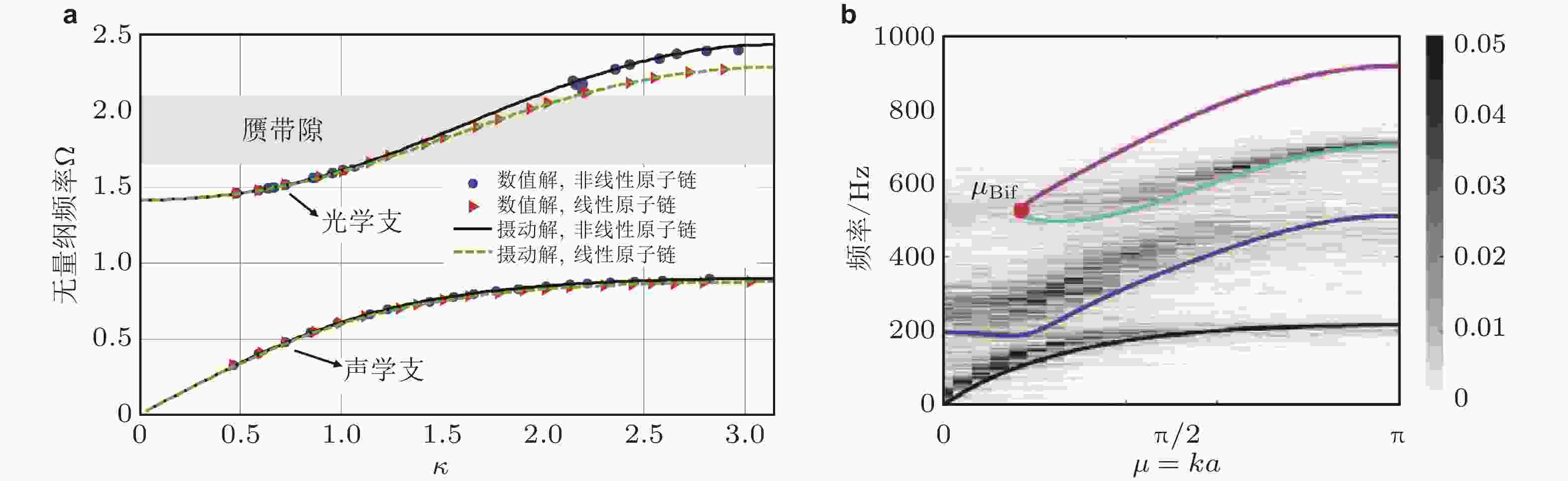
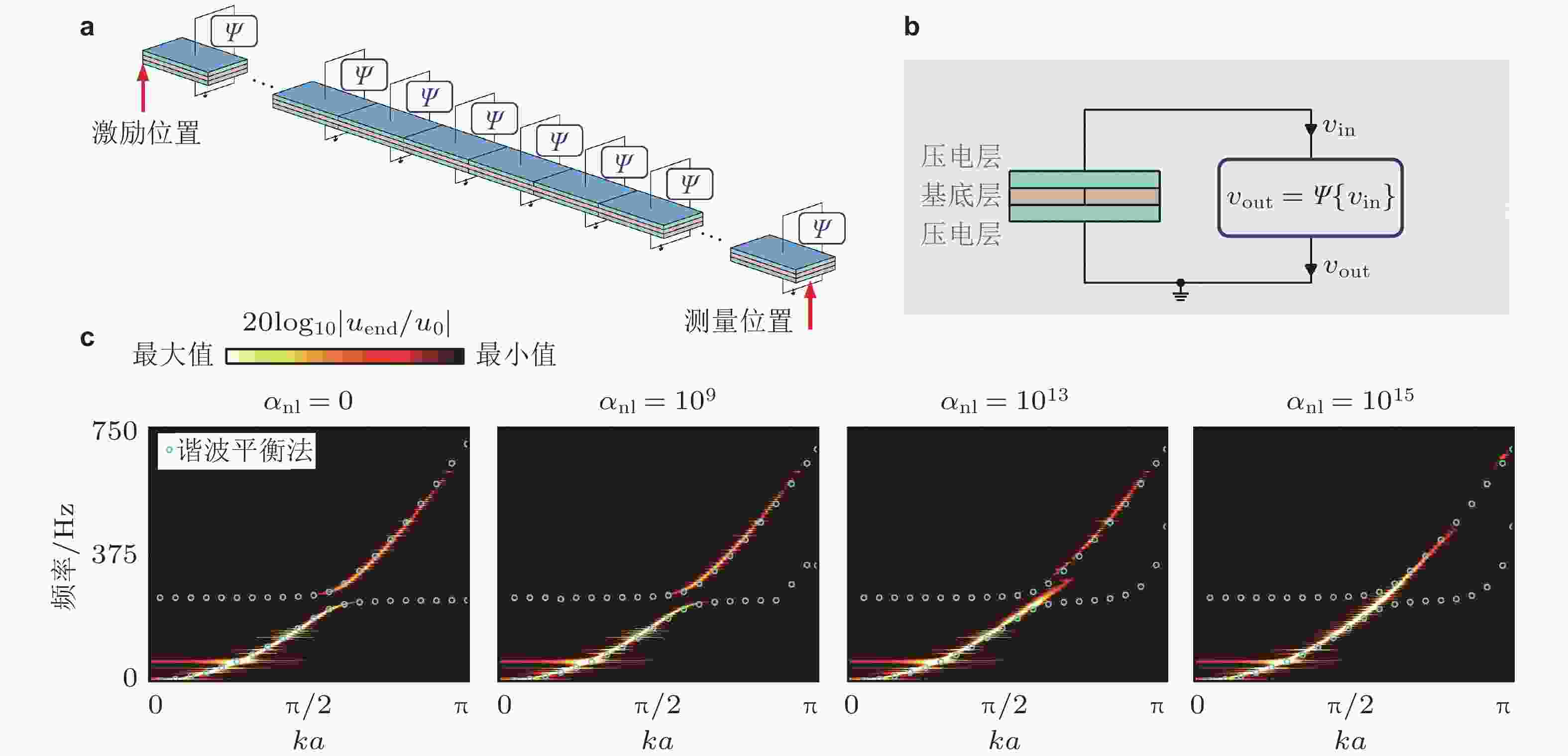
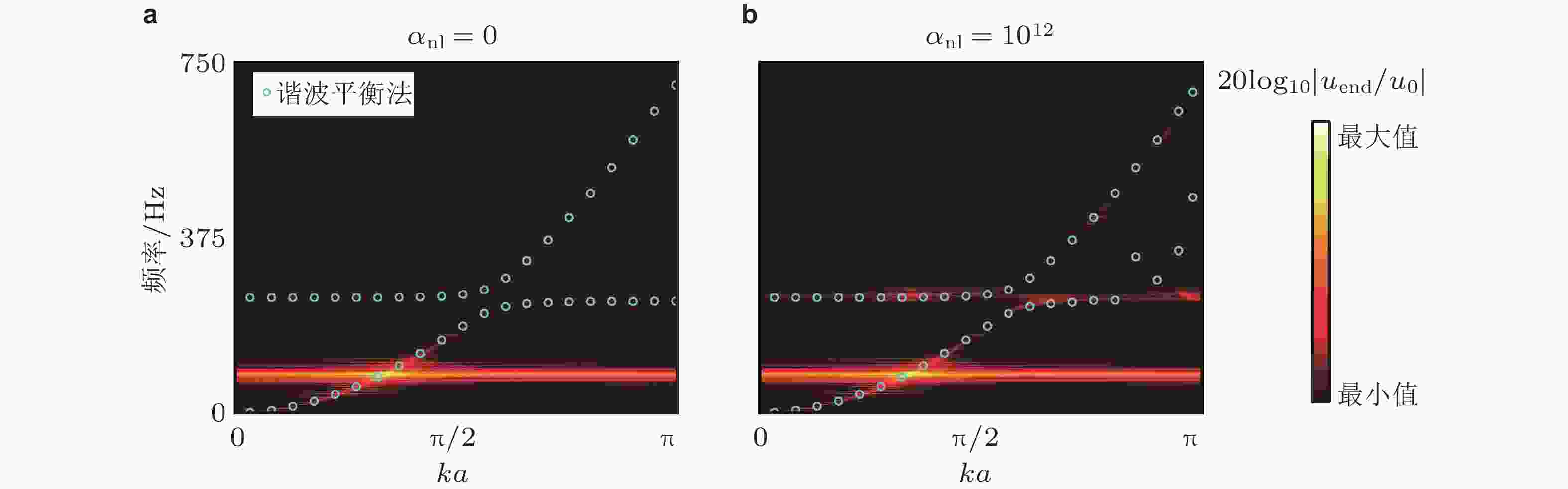
图 10 一维非线性原子链能带结构时/频域分析. (a) 弱非线性原子链(Zhou et al. 2018), (b) 强非线性原子链, 实线为谐波平衡法计算结果, 背景阴影色为时域计算获得的2D FFT结果(Gong et al. 2023)

下载: 全尺寸图片幻灯片

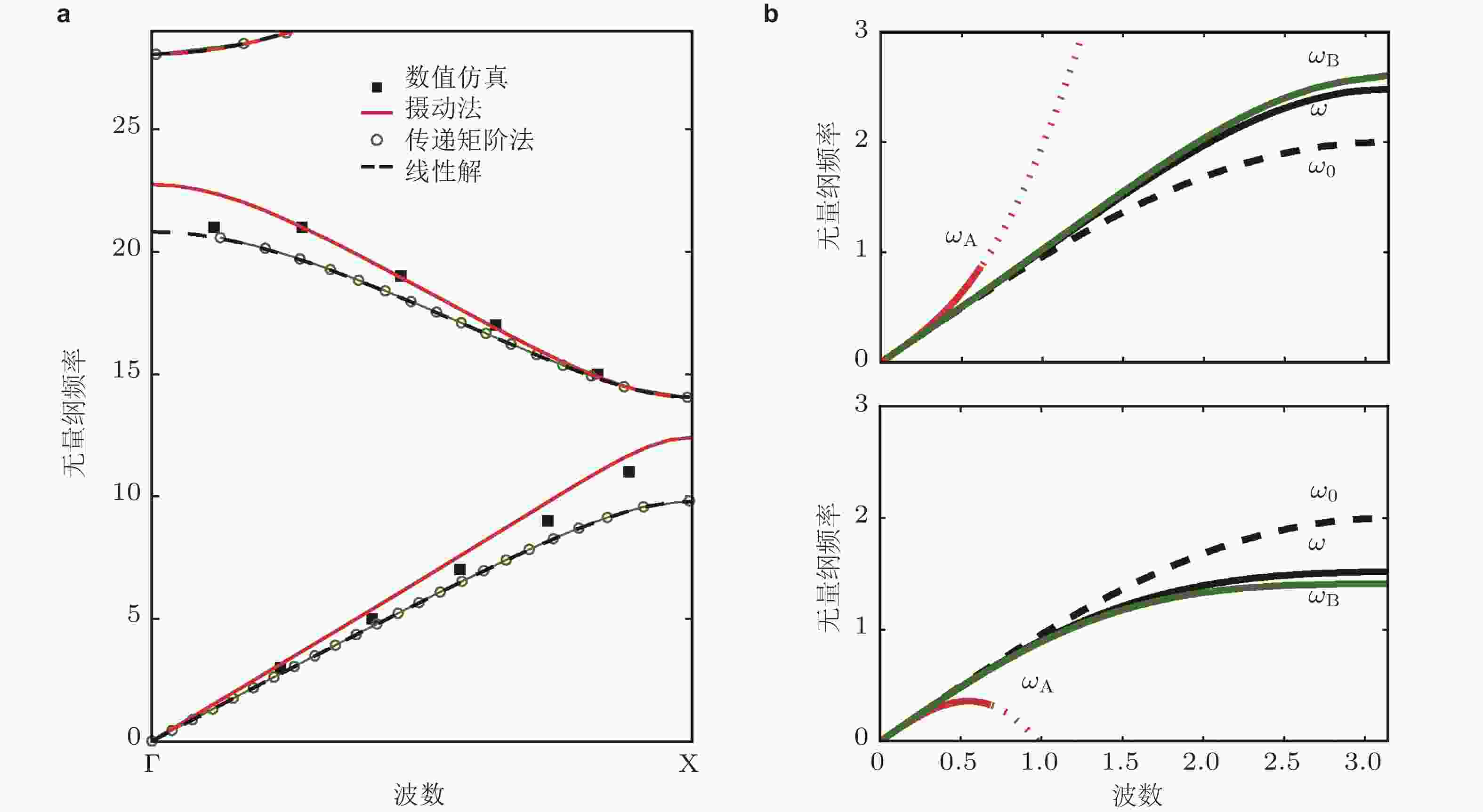
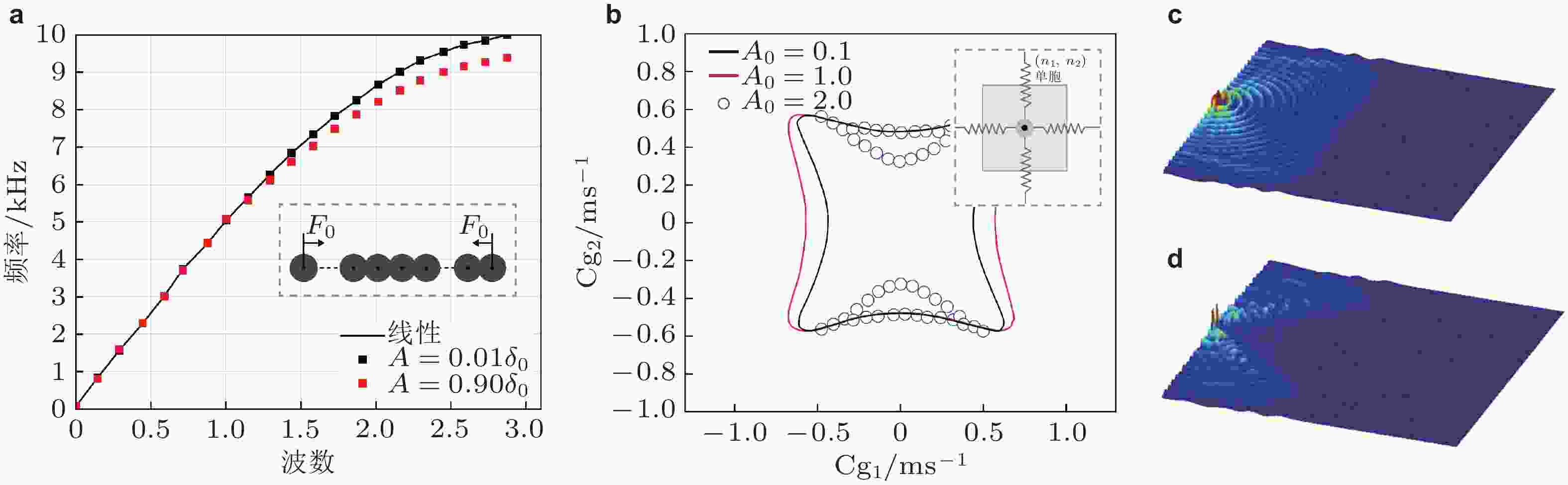
图 11 基于不同频域计算方法获得的非线性周期结构能带曲线. (a) Lindstedt-Poincaré摄动法与传递矩阵法对比(Manktelow et al. 2013a), (b) Lindstedt-Poincaré摄动法与多尺度法对比, $ {\omega _0} $为线性频散曲线, $ \omega $为单谐波近似下两种频域方法的计算结果(Manktelow et al. 2011)

下载: 全尺寸图片幻灯片

图 12 可编程压电周期结构及其带隙性质. (a) 压电梁周期结构, (b) 基于可编程数字电路的力−电耦合单胞, (c) 不同非线性系数$ {\alpha _{{\text{nl}}}} $下能带曲线变化, 青色圆圈和背景颜色分别为采用谐波平衡法和2D FFT方法获得的能带曲线

下载: 全尺寸图片幻灯片

图 13 压电周期结构的频散曲线与2D FFT谱. 青色圆圈和背景颜色分别为采用谐波平衡法和2D FFT计算的能带曲线, 时域仿真中激励脉冲中心频率为82 Hz. (a) 线性电路$ {\alpha _{{\text{nl}}}} = 0 $, (b) 非线性电路$ {\alpha _{{\text{nl}}}} = {10^{12}} $

下载: 全尺寸图片幻灯片

图 14 非线性压电周期结构与缺陷束缚态. (a) 由负电容分流电路构造的压电梁示意图, 通过移除中间区域的2对压电片构造局部缺陷, (b) 不同非线性系数下的传递率频响曲线, 青色背景表示初始线性系统的Bragg带隙范围, (c) 不同非线性系数下压电梁传递率频响, 横坐标为频率, 纵坐标为梁长度方向的归一化坐标

下载: 全尺寸图片幻灯片

图 15 非线性原子链能带频移特性. (a) 不同波幅下单原子颗粒晶体的能带曲线, (b) 不同波幅下二维原子链的群速度方向图, (c) 小振幅激励下弹性波的传播, (d) 大振幅激励下弹性波的传播. 来自文献(Narisetti et al. 2012, 2011)

下载: 全尺寸图片幻灯片

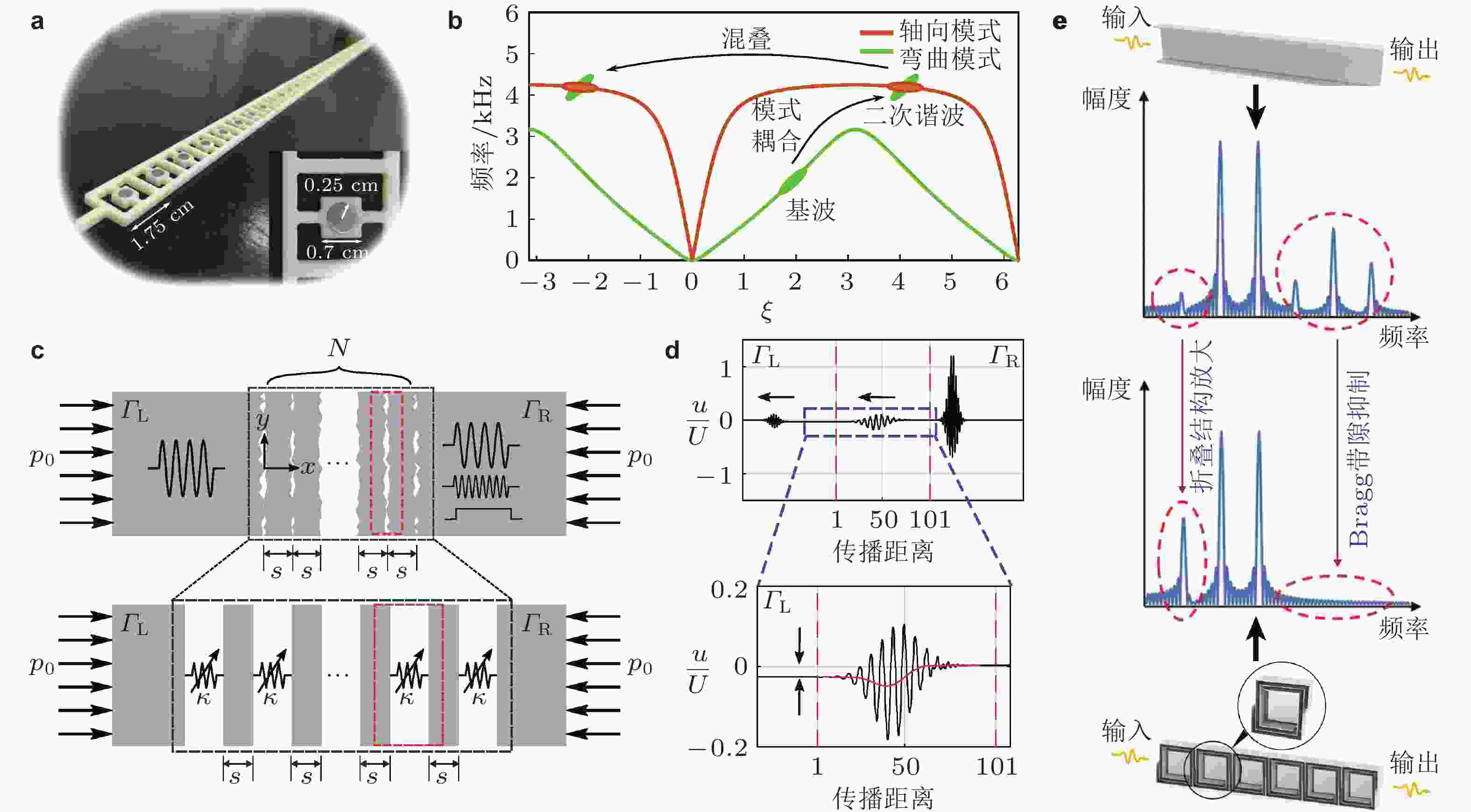
图 16 非线性引起的不同频率间能量转换. (a) 由钢芯谐振结构组成的一维周期结构(Jiao & Gonella 2018a); (b) 基波与超谐波模式耦合效应示意图(Jiao & Gonella 2018a); (c) 由粗糙接触界面构成的非线性周期结构(Patil & Matlack 2021); (d) 某时刻的弹性波位移信号, 红色虚线表示周期结构所在区域(Patil & Matlack 2021); (e) 空间卷绕型声学周期结构与非线性混频现象(Jeon & Oh 2021)

下载: 全尺寸图片幻灯片

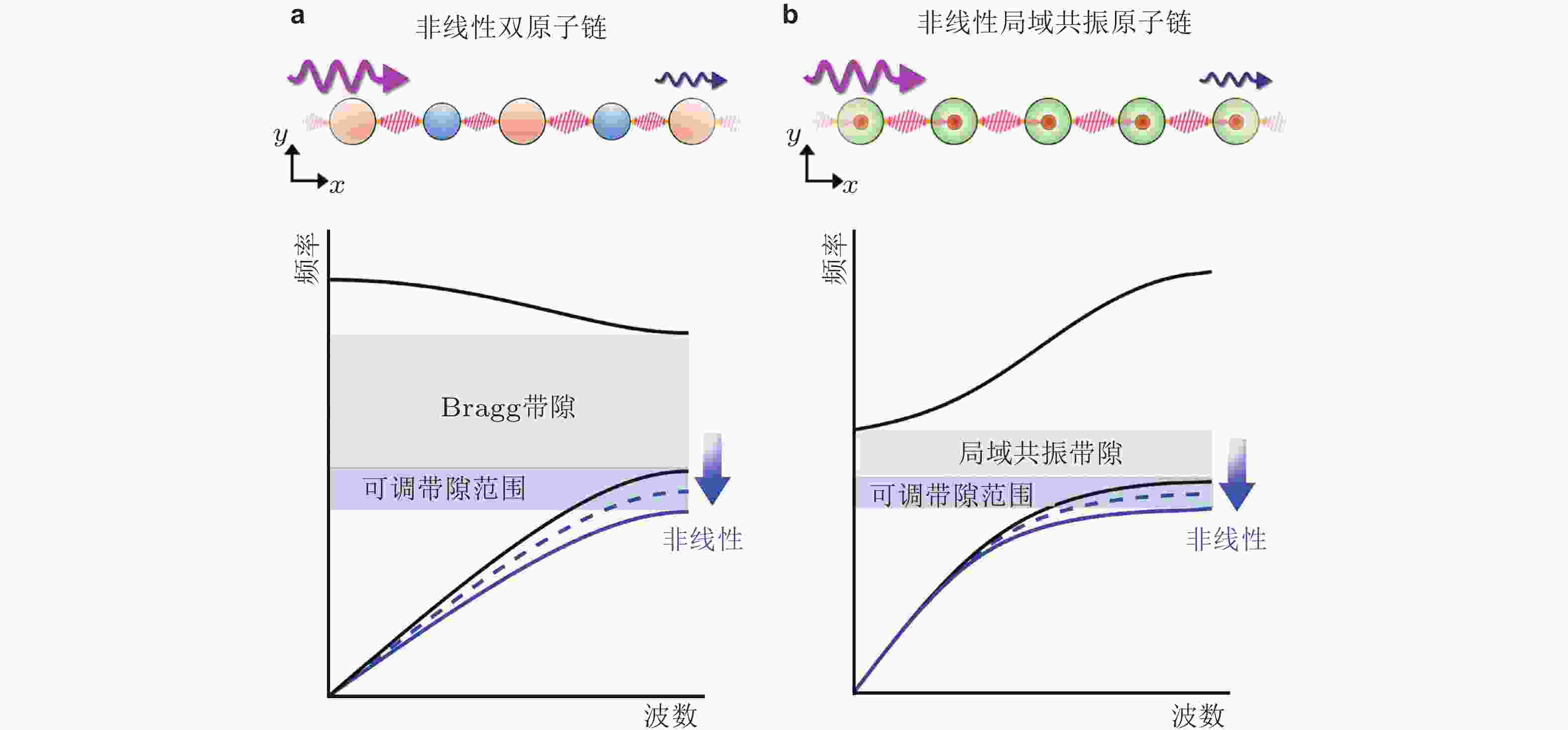
图 17 一维非线性原子链能带曲线与带隙特征. (a) Bragg带隙, (b) 局域共振带隙. 图中黑色实线为线性系统的结果, 蓝色曲线为考虑非线性效应的结果. 来自文献(Bae & Oh 2022)

下载: 全尺寸图片幻灯片

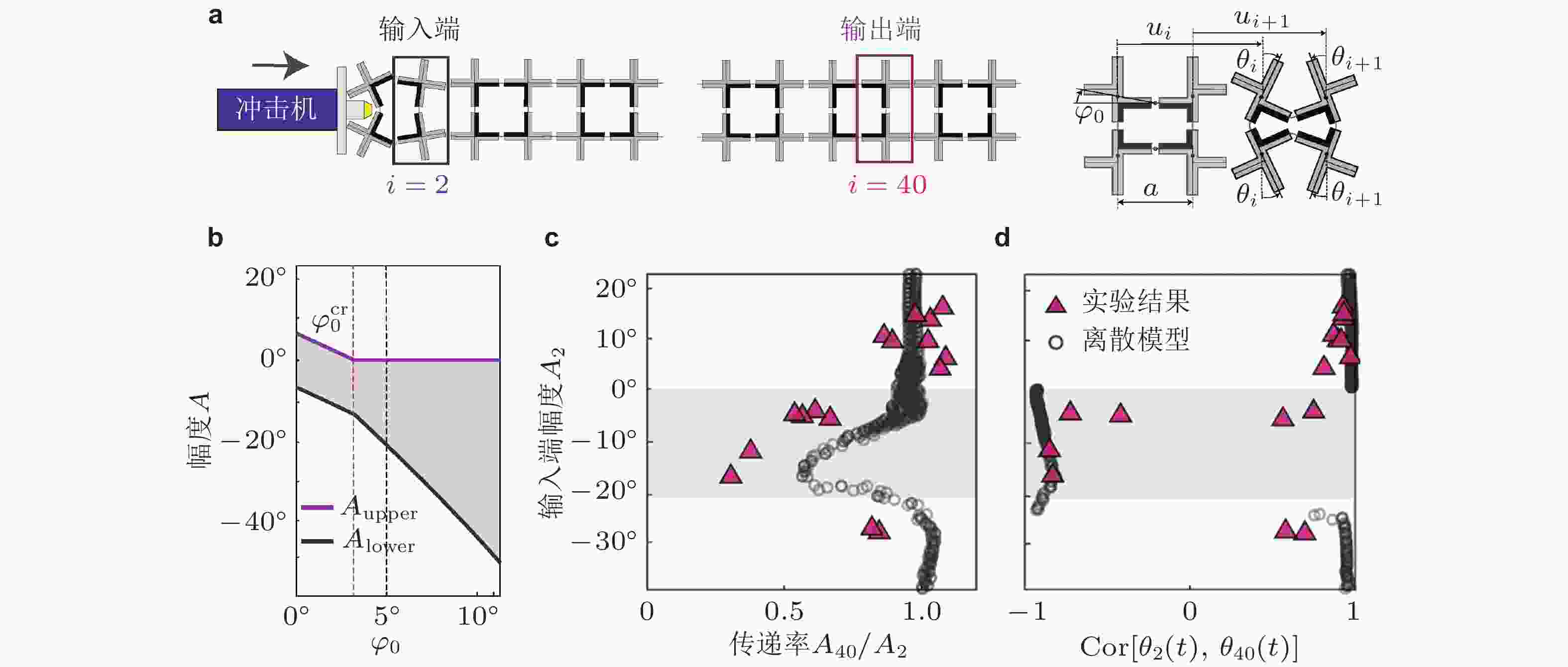
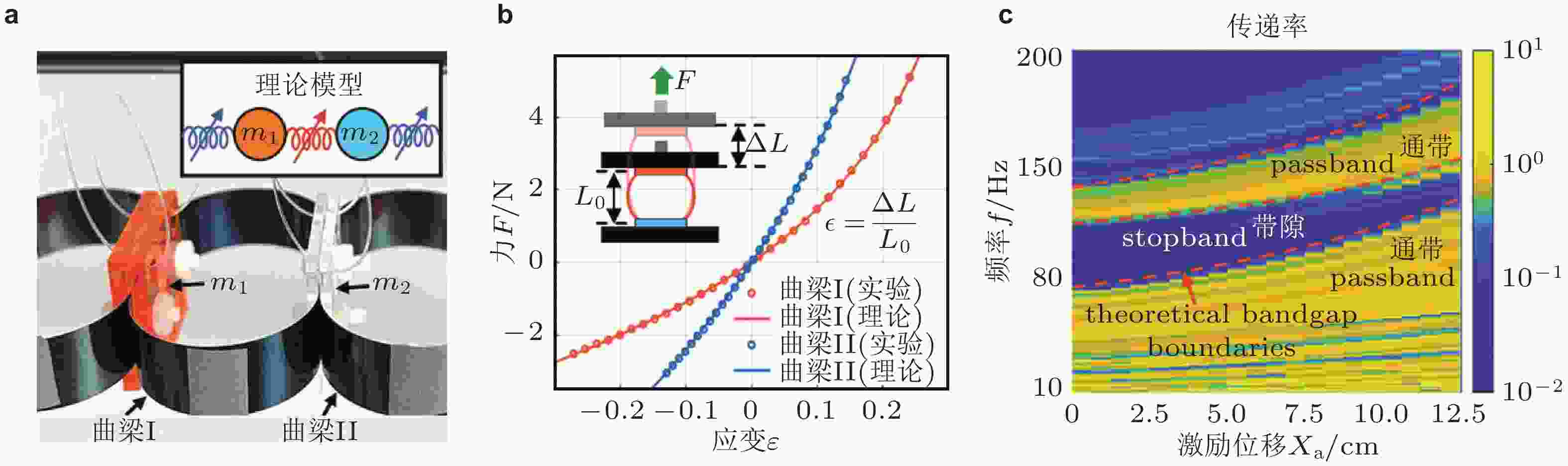
图 18 弹性矢量孤波及幅度带隙. (a) 柔性铰链组成的非线性周期结构, 其可承载弹性矢量孤波, (b) 孤波幅度带隙范围与结构角$ {\varphi _0} $的变化规律, (c) 幅度传递率$ {{{A_{40}}} /{{A_2}}} $, (d) $ {\theta _{40}} $和$ {\theta _2} $相关性关系. (c)和(d)为$ {\varphi _0} = 5^\circ $时的仿真和实验结果. 来自文献(Deng et al. 2018)

下载: 全尺寸图片幻灯片

图 19 非线性周期结构带隙频移特性. (a) 非线性双原子链模型与实物结构, (b) 曲梁结构载荷−变形曲线, (c) 不同激励强度下透射谱实验结果, 橙色虚线表示理论预测的带隙边界, 深蓝区域为带隙范围. 来自文献(Zhang et al. 2023)

下载: 全尺寸图片幻灯片

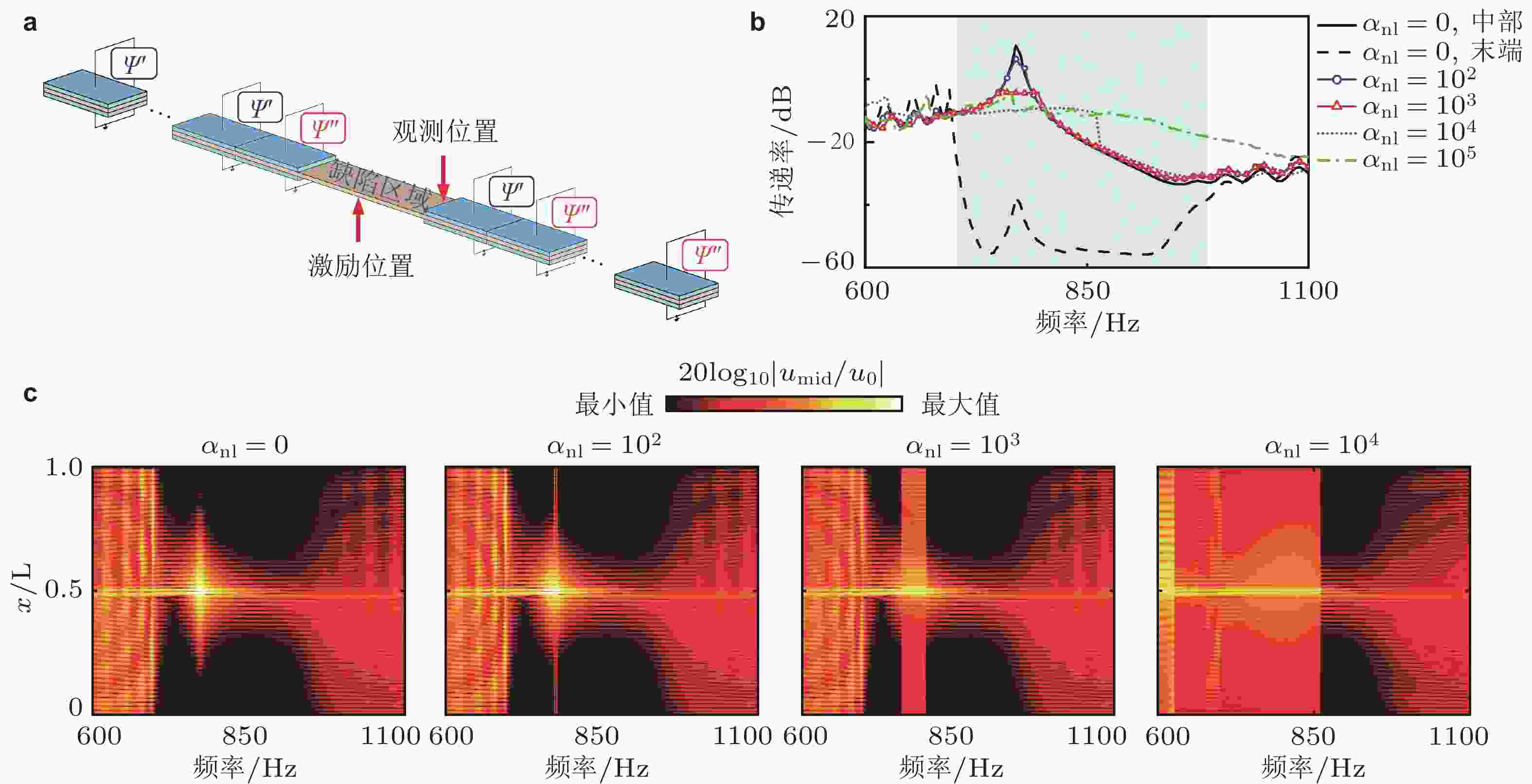
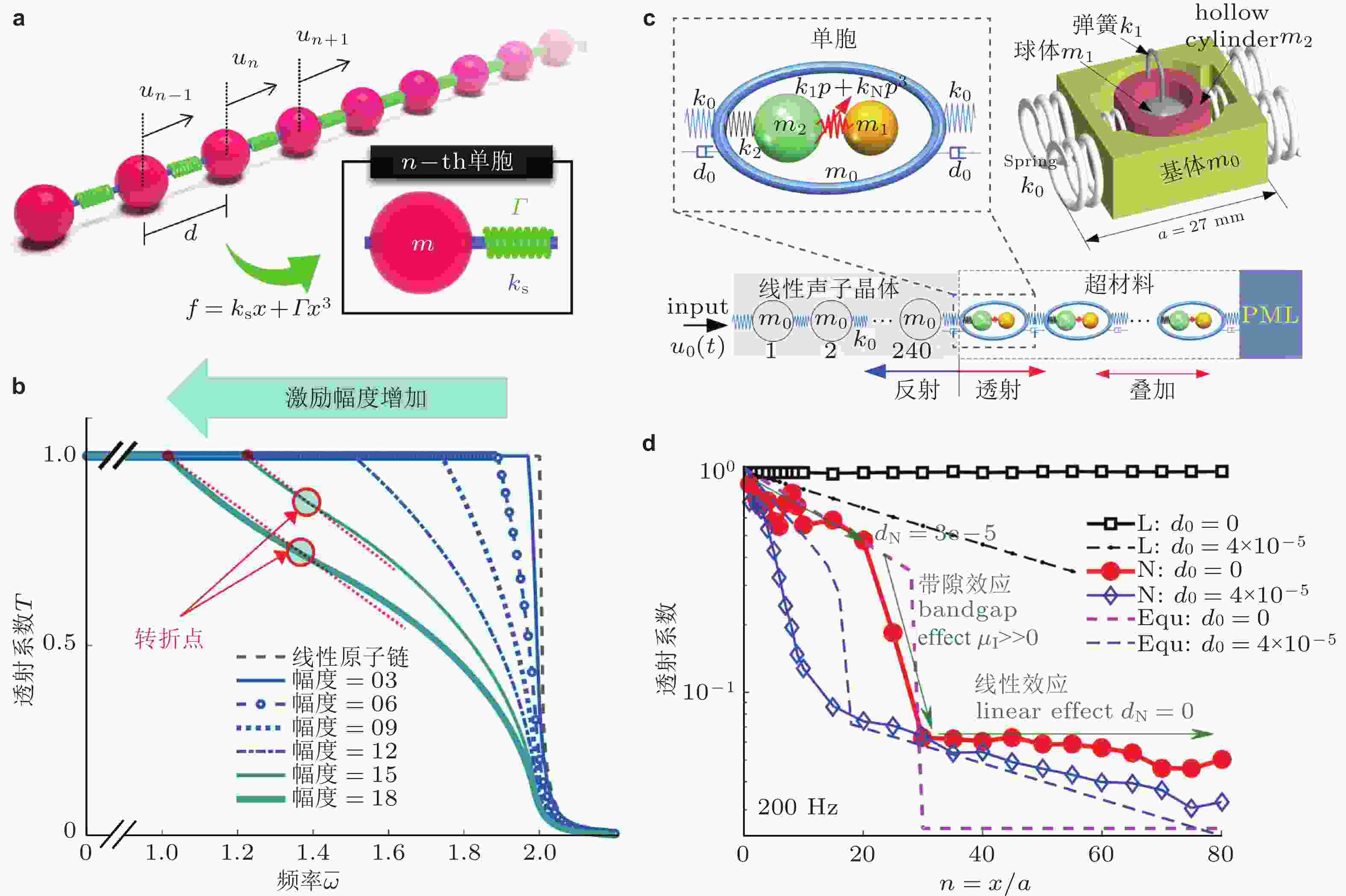
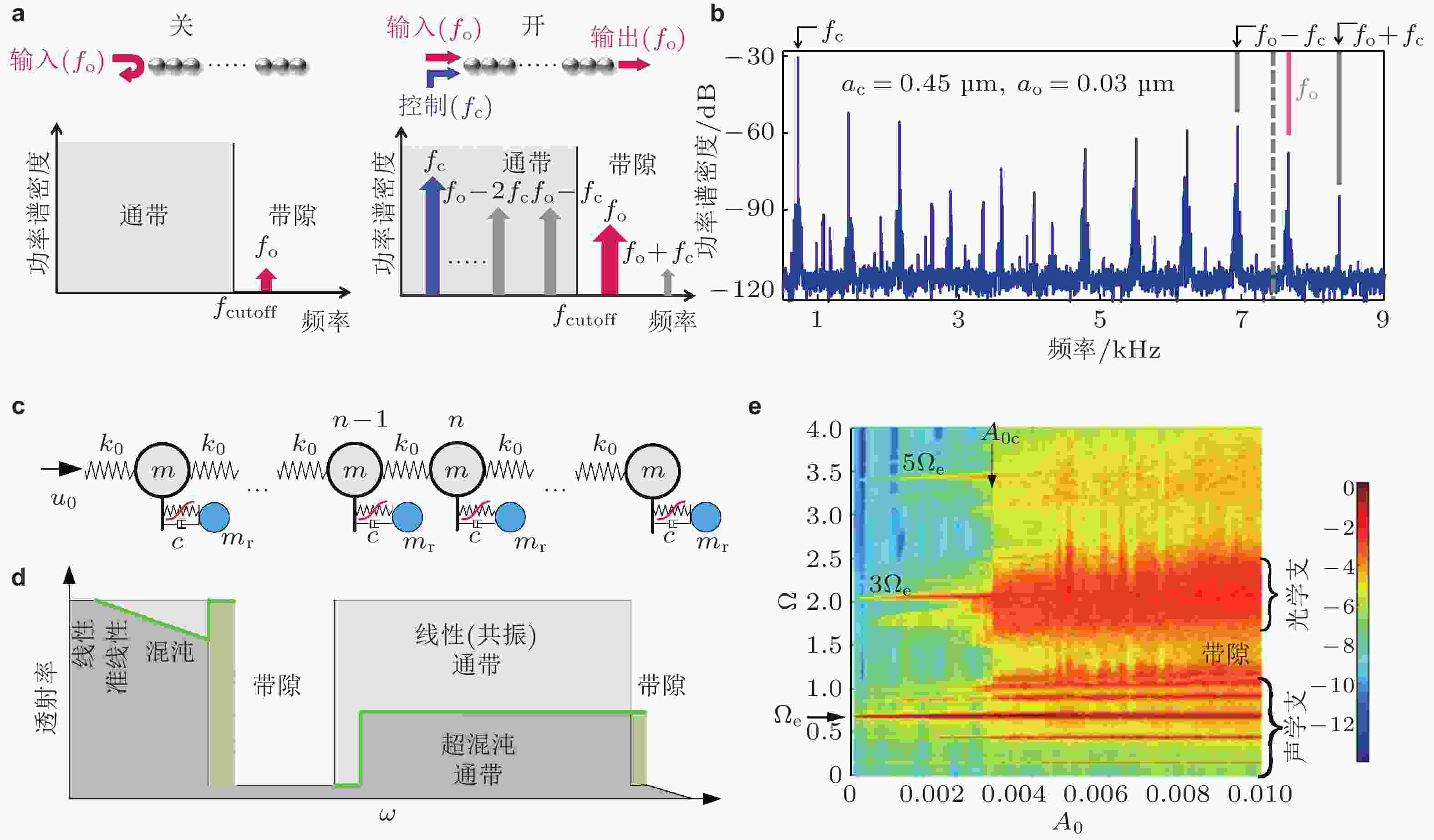
图 20 非线性带隙时空相关特性. (a) 非线性单原子链模型, (b) 不同激励幅度下单原子链透射频谱变化过程, (c) 三原子单胞及原子链模型, 支链采用两自由度非线性振子, (d) 200 Hz激励下, 透射系数随点阵位置$ n = {x / a} $变化过程, 图例中L和N分别表示线性和非线性原子链, $ {d_0} $为阻尼系数. 来自文献(Bae & Oh 2020, Fang et al. 2020)

下载: 全尺寸图片幻灯片

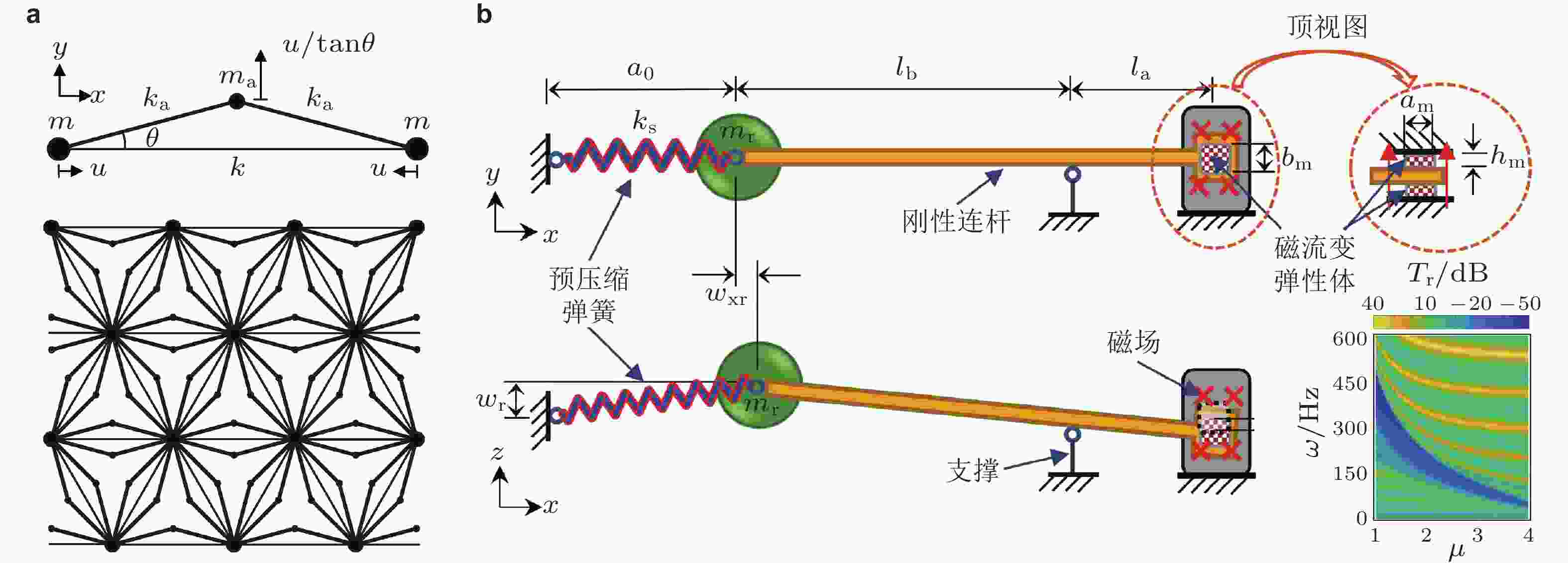
图 21 通带和带隙之间频率成分转换与能量转换. (a) 左图为单频激励$ {f_0} $作用下, 颗粒晶体的透射功率谱密度示意图, 右图施加了频率为$ {f_{\mathrm{c}}} $的高幅控制信号, (b) 施加控制信号$ {f_{\mathrm{c}}} $后, 实验测量的透射功率谱密度, (c) 含非线性振子的一维原子链模型, (d) 混沌对通带和带隙透射率影响示意图, (e) 单频激励下($ {\Omega _{\text{e}}} = 0.678 $), 非线性原子链功率谱密度随激励波幅变化图. 来自文献(Li et al. 2014, Fang et al. 2017b)

下载: 全尺寸图片幻灯片

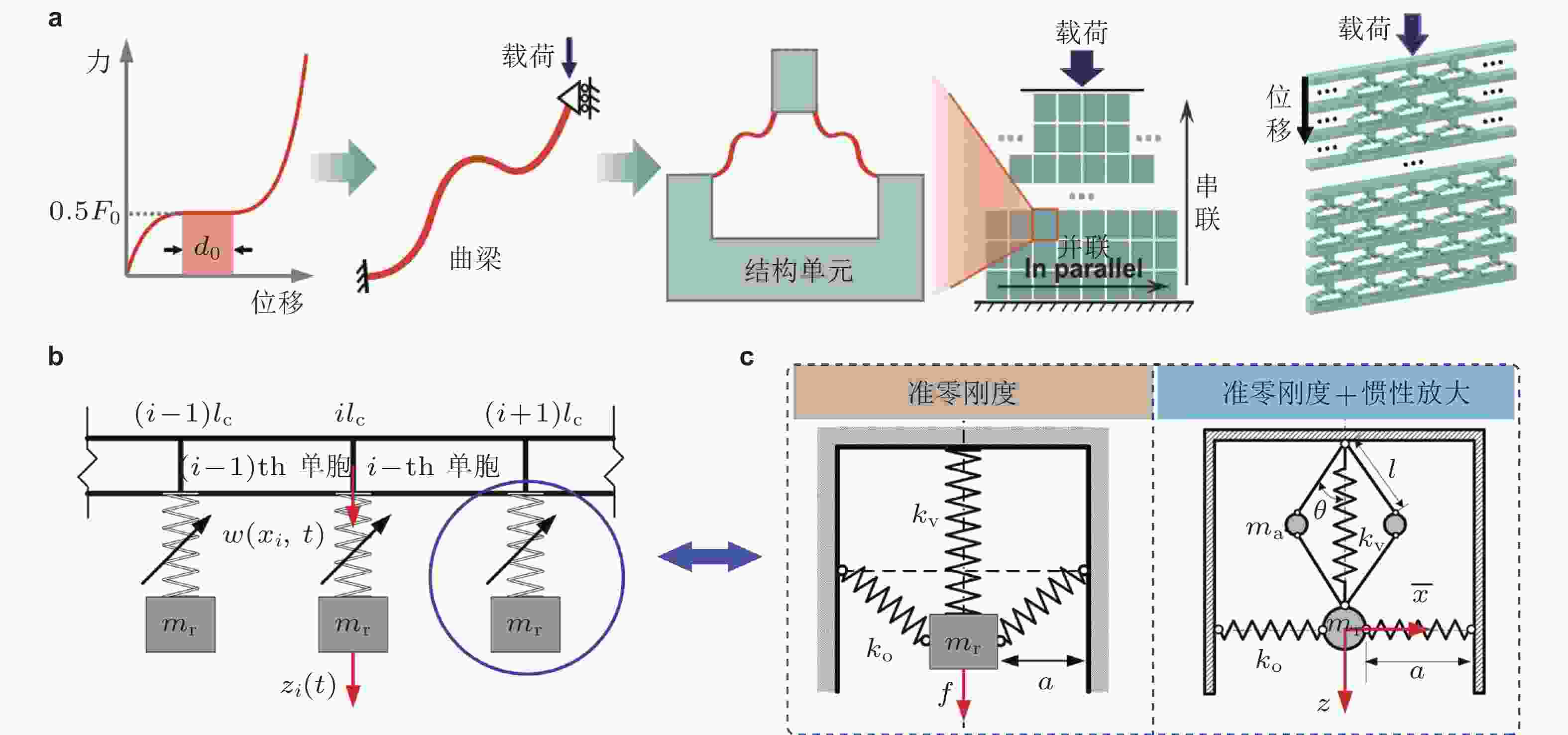
图 22 惯性放大机构. (a) 弹簧−质量位移放大机构及其组成的二维周期结构(Yilmaz et al. 2007), (b) 由磁流变弹性体构成的主动可调惯性放大机构, 右下角插图为传递率, 随着杠杆比$ \mu = {{{l_{\mathrm{b}}}} / {{l_{\mathrm{a}}}}} $增加带隙位置向低频拓展(Xue et al. 2024)

下载: 全尺寸图片幻灯片

图 23 准零刚度周期结构. (a) 曲梁单元及其构成的准零刚度周期结构(Zhang et al. 2021b), (b) 附加准零刚度谐振子的周期梁(Zhou et al. 2019), (c) 基于弹簧正、负刚度抵消效应设计的准零刚度谐振子(Zhou et al. 2019, 2017)

下载: 全尺寸图片幻灯片

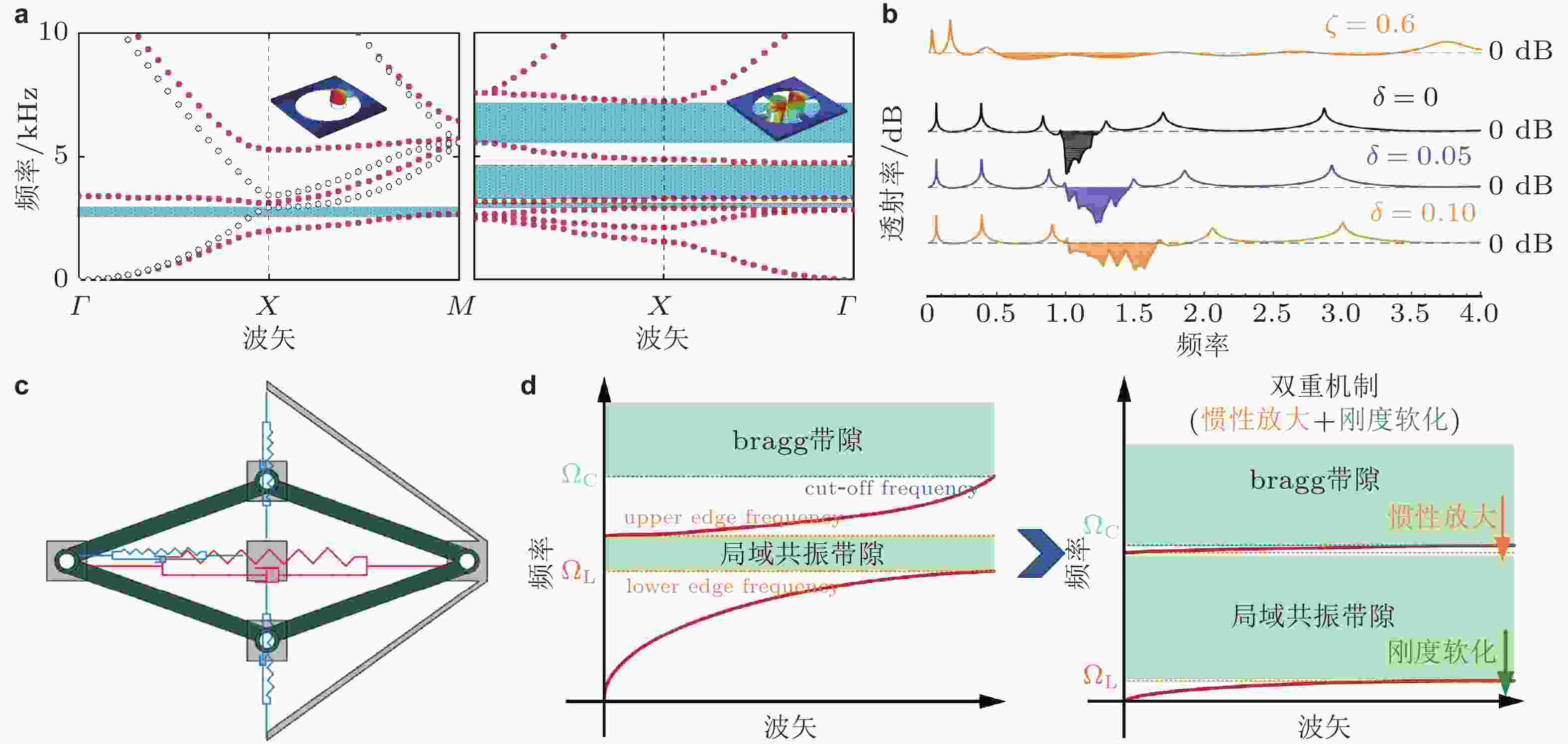
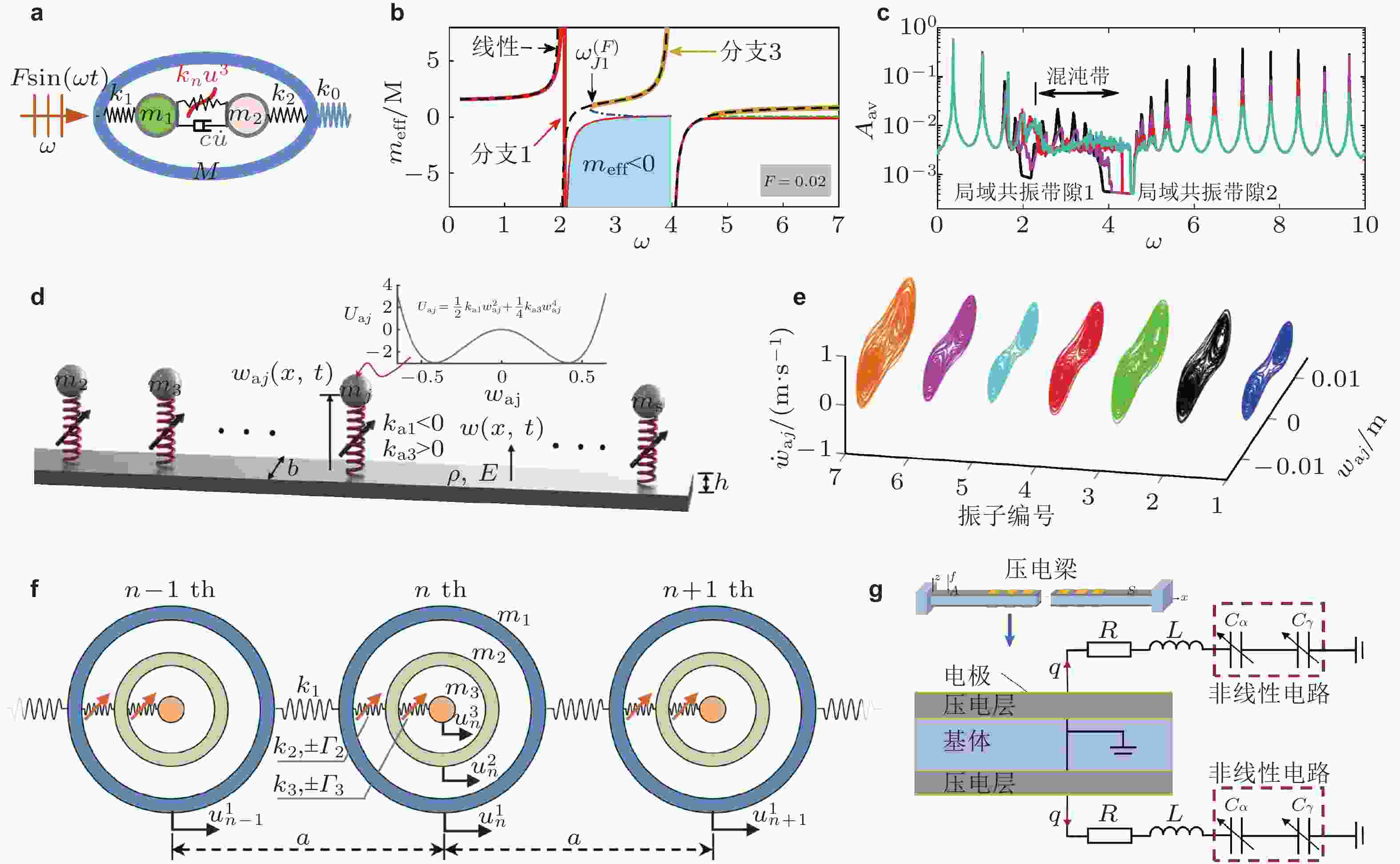
图 24 传统的带隙拓宽方法. (a) 单相多重谐振结构及其能带结构(Gao et al. 2019a), (b) 超材料梁透射率随阻尼$ \zeta $和梯度参数$ \delta $的变化图, 参数$ \left( {\zeta ,\delta } \right) $从上到下分别为(0.6, 0.1)、(0, 0)、(0, 0.05)和(0, 0.1)(Hu et al. 2021), (c) 融合负刚度和惯性放大效应的单胞结构(Zhou et al. 2024b), (d) 带隙低频宽带拓展示意图(Zhou et al. 2024b)

下载: 全尺寸图片幻灯片

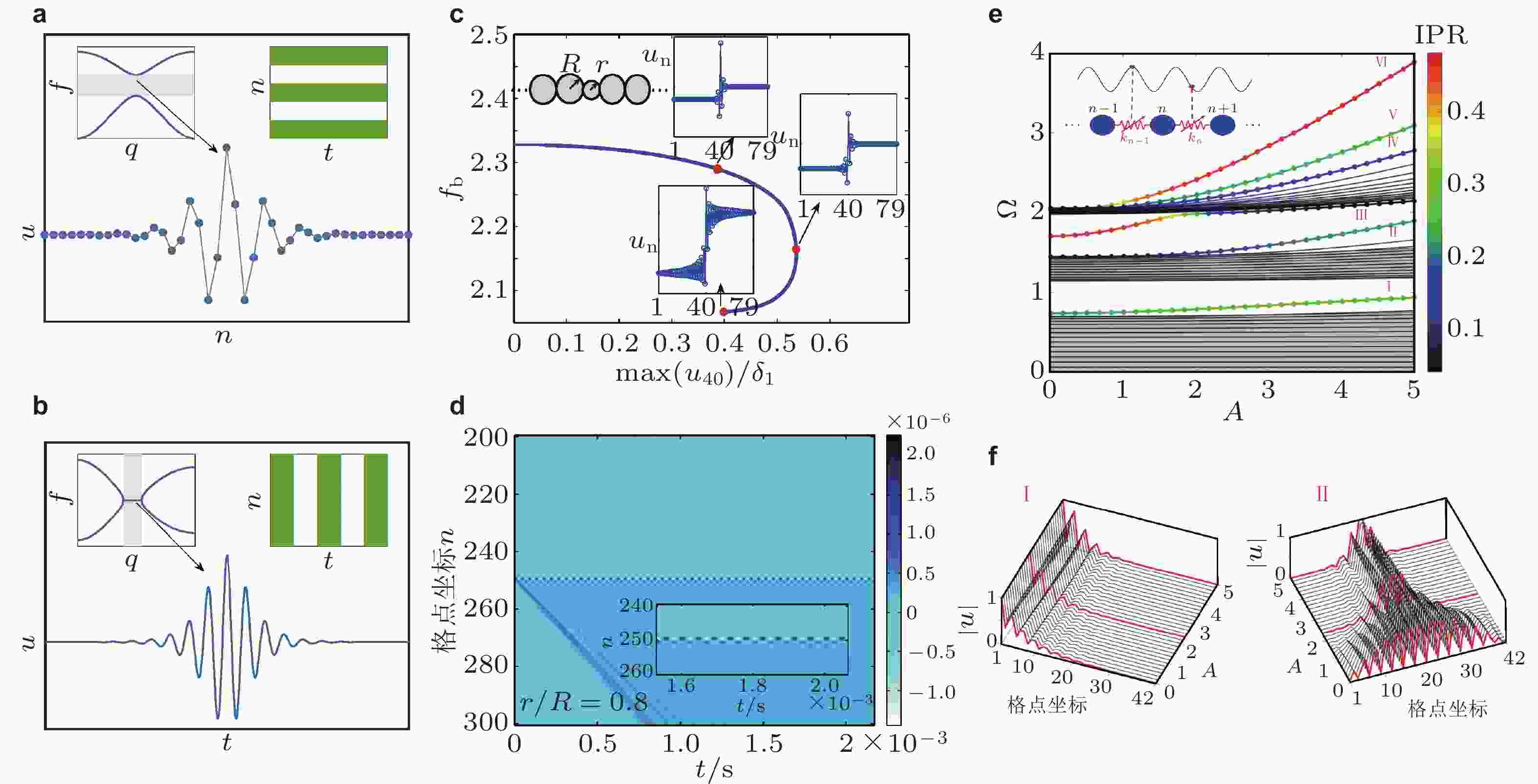
图 25 基于非线性效应的带隙拓宽方法. (a) 非线性弹簧−质量三原子模型, (b) 三原子系统等效质量, (c) 包含20个单胞的非线性原子链频响曲线, 黑色代表线性原子链, 彩色对应不同的非线性系数, $ {{{k_n}} / {{k_1}}} = 100 $(洋红色)、$ {{{k_n}} / {{k_1}}} = 500 $(红色)、$ {{{k_n}} / {{k_1}}} = 1000 $(青色), (d) 附加双稳态振子的周期梁结构, (e) 双稳态振子相图, 周期梁的基底加速度为$ 0.3g $, 激励频率为12.5 Hz, (f) 多重局域共振非线性原子链模型, (g) 压电梁与非线性分流电路. 来自文献(Fang et al. 2018, Xia et al. 2020, Zhao et al. 2023c, Chen et al. 2024a)

下载: 全尺寸图片幻灯片

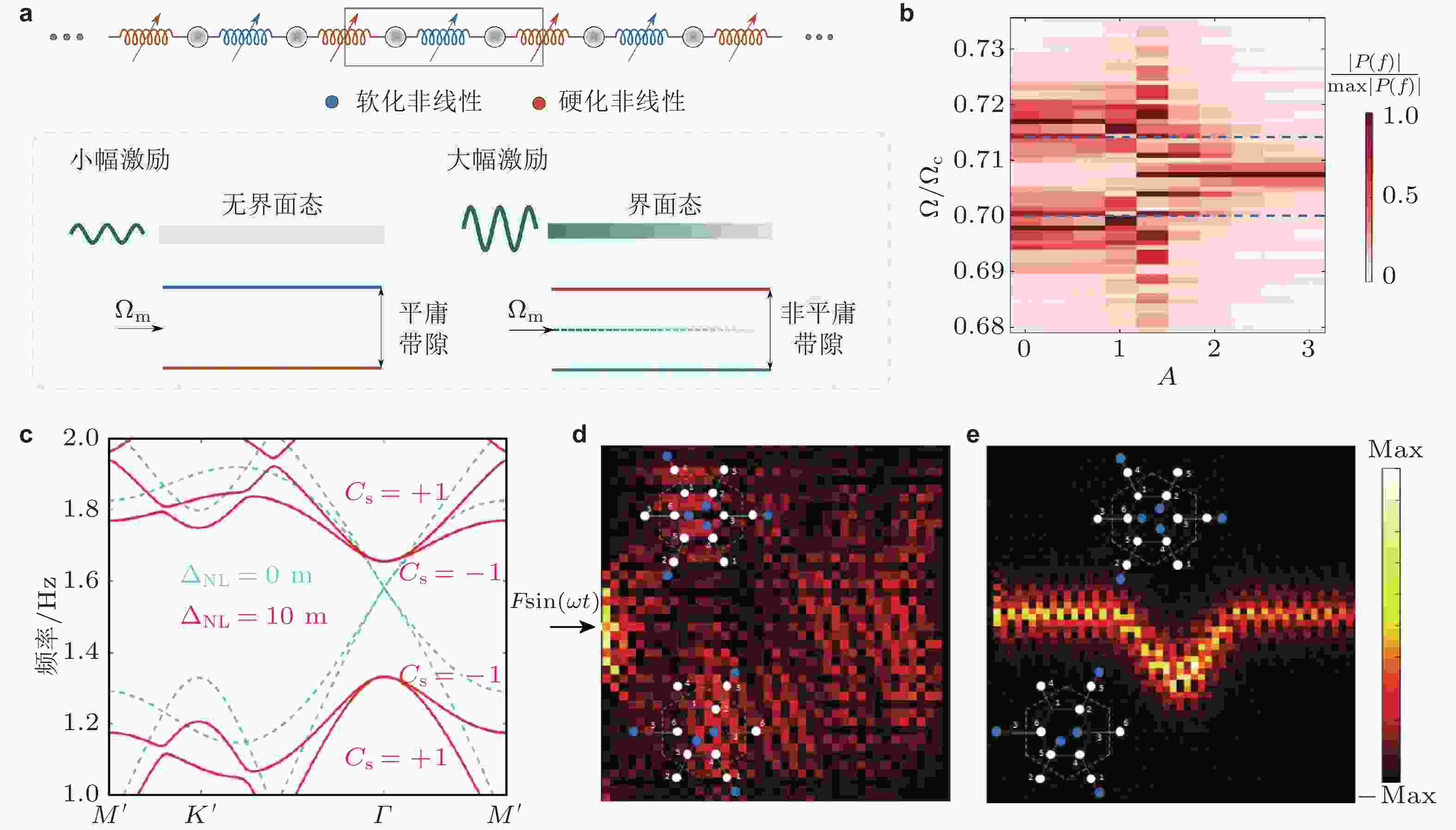
图 26 非线性周期结构能量局域束缚效应. (a) 经典呼吸子波形与频散曲线, (b) 波数带隙呼吸子波形与频散曲线, (c) 颗粒晶体缺陷束缚态频率$ {f_b} $随激励幅度$ {{\max \left( {{u_{40}}} \right)} / {{\delta _1}}} $变化曲线, 插图为颗粒晶体模型和束缚态波形, (d) 大振幅激励下颗粒晶体中弹性波传播和束缚态时空演化过程, 该算例中缺陷束缚态频率为22.47 kHz, (e) 非线性Aubry–André原子链特征频率$ \Omega $随波幅$ A $变化过程, IPR表征波模式的局域状态, 数值越大表示局域束缚程度越高, 插图为非线性Aubry–André模型示意图, (f) 特征模式I和II空间束缚状态随波幅$ A $变化过程. 来自文献(Chong et al. 2024, Theocharis et al. 2009, Rosa et al. 2023)

下载: 全尺寸图片幻灯片

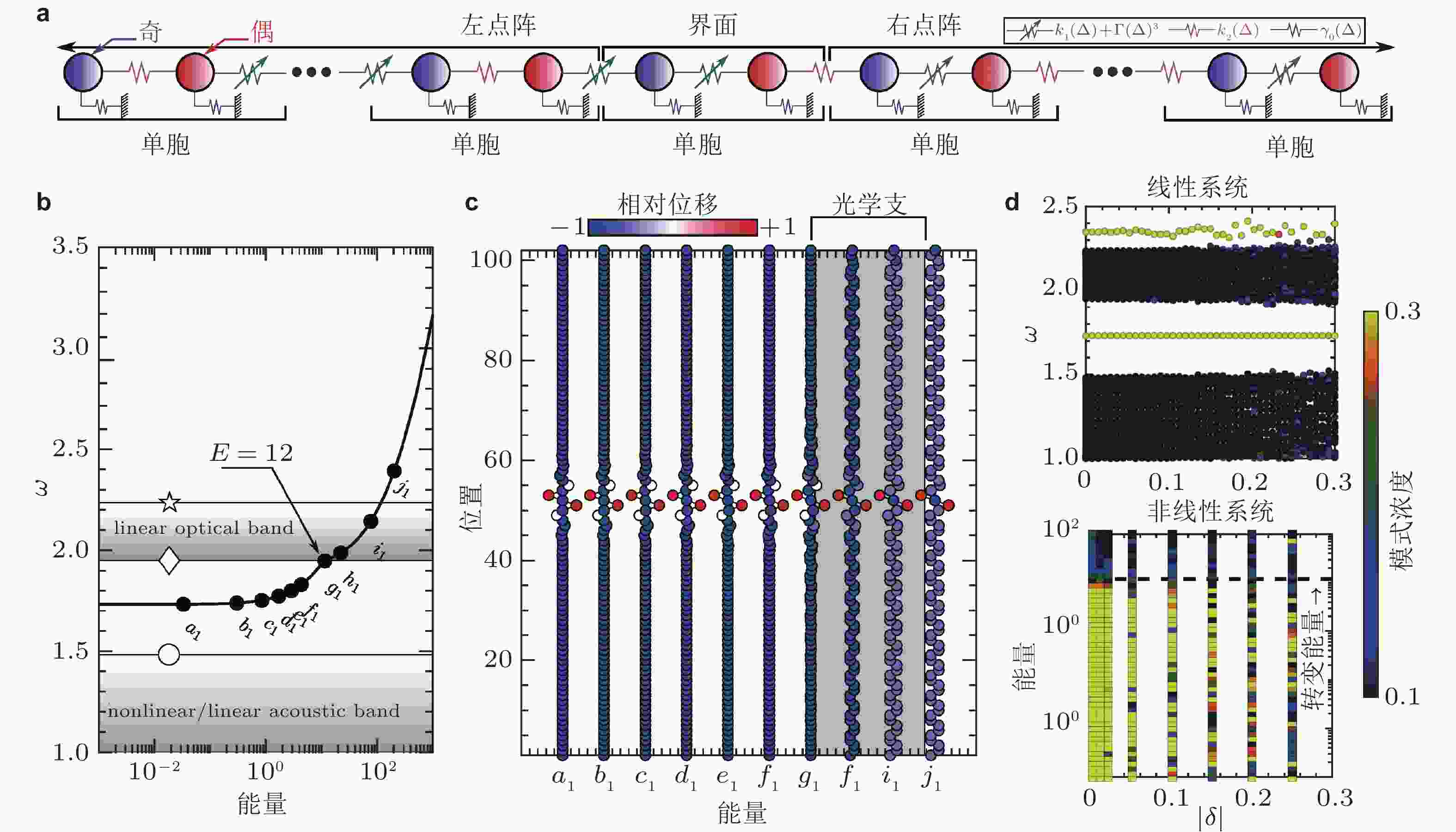
图 27 非线性效应调控拓扑相变. (a) 上图: 基于SSH模型构造的含软化和硬化非线性的原子链模型, 下图: 入射波振幅调控拓扑相变示意图, 大振幅激励可以产生频率为$ {\Omega _{\mathrm{m}}} $的拓扑束缚态, (b) 归一化模态幅度随激励幅度$ A $变化过程, 颜色越深表示能量局域束缚程度越高, (c) 非线性效应破缺四重简并点(青色虚线在$ \Gamma $点构成双Dirac锥结构), 形成拓扑非平庸带隙, (d) F = 1 N激励力作用下六方点阵的位移场分布, 呈现出非局域体波传播现象, (e) F = 100 N 激励力作用下六方点阵的位移场分布, 呈现出界面传播现象. 来自文献(Chaunsali & Theocharis 2019, Darabi & Leamy 2019)

下载: 全尺寸图片幻灯片

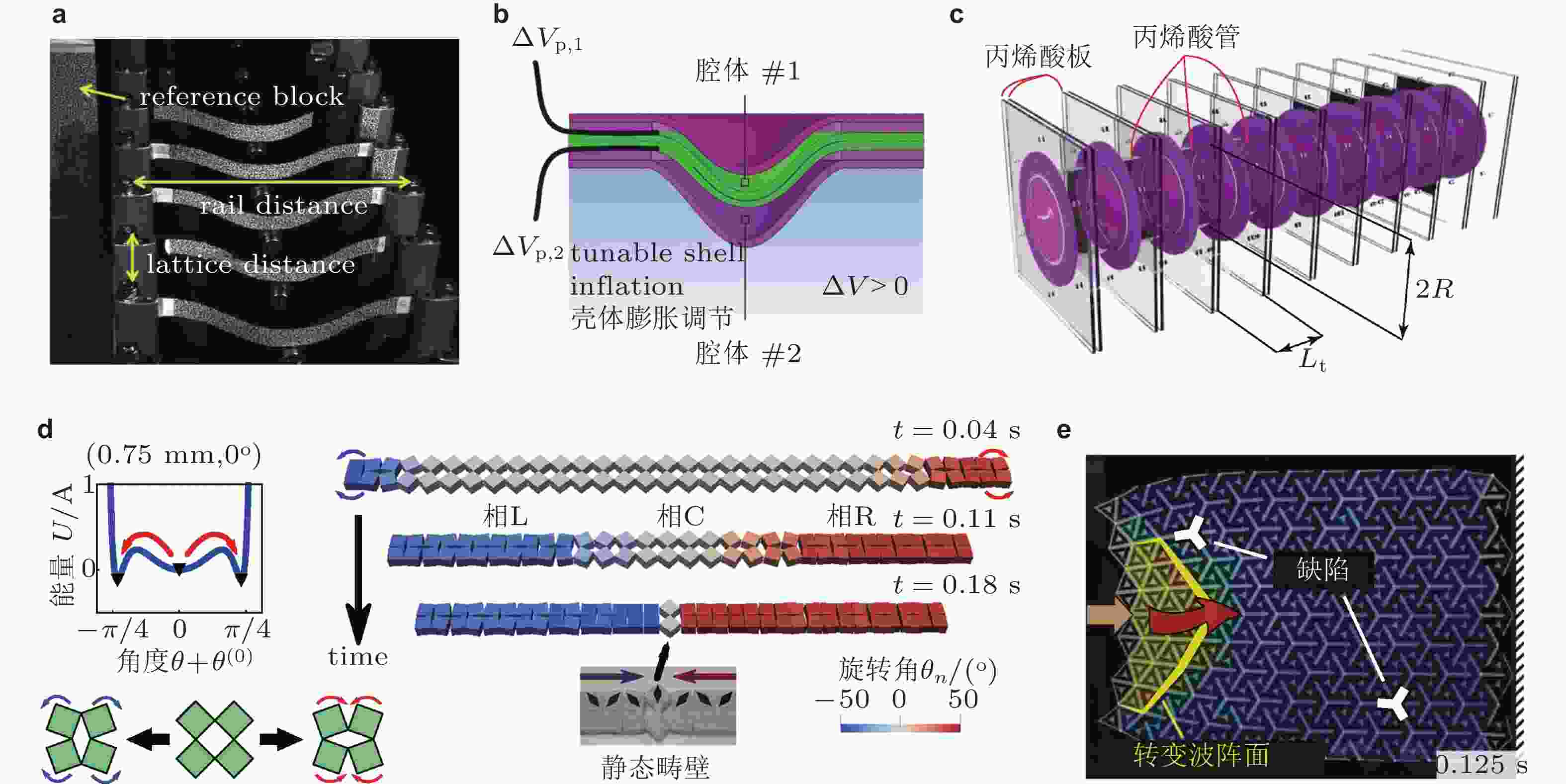
图 28 强非线性效应对拓扑束缚态的影响. (a) 基于SSH模型构造的非线性原子链, (b) 带隙内束缚态特征频率$ \omega $随激励能量的变化趋势, 图中阴影区域对应线性原子链的体能带, (c) 不同激励能量下界面态局域状态变化, $ {a_1} $ ~ $ {j_1} $对应图(b)中标识点, (d) 在线性SSH模型中引入手性对称缺陷后, 束缚态频率随缺陷强度$ \left| \delta \right| $的变化, (e) 手性对称缺陷对非线性界面态鲁棒性的影响, 模式浓度表示波模式的局域束缚程度, 数值越大, 能量局域程度越高. 来自文献(Tempelman et al. 2021)

下载: 全尺寸图片幻灯片

图 29 多稳态周期结构与转变波. (a) 由预压缩复合材料曲梁构成的双稳态周期结构, 利用永磁体在结构单元间产生非线性斥力(Nadkarni et al. 2016), (b) 充气式主动可调双稳态壳体结构(Vasios et al. 2021), (c) 由双稳态壳体构成的一维周期结构(Vasios et al. 2021), (d) 三稳态周期结构与转变波碰撞现象(Yasuda et al. 2020), (e) 利用缺陷和边界引导拉胀周期结构中转变波的传播(Jin et al. 2020)

下载: 全尺寸图片幻灯片

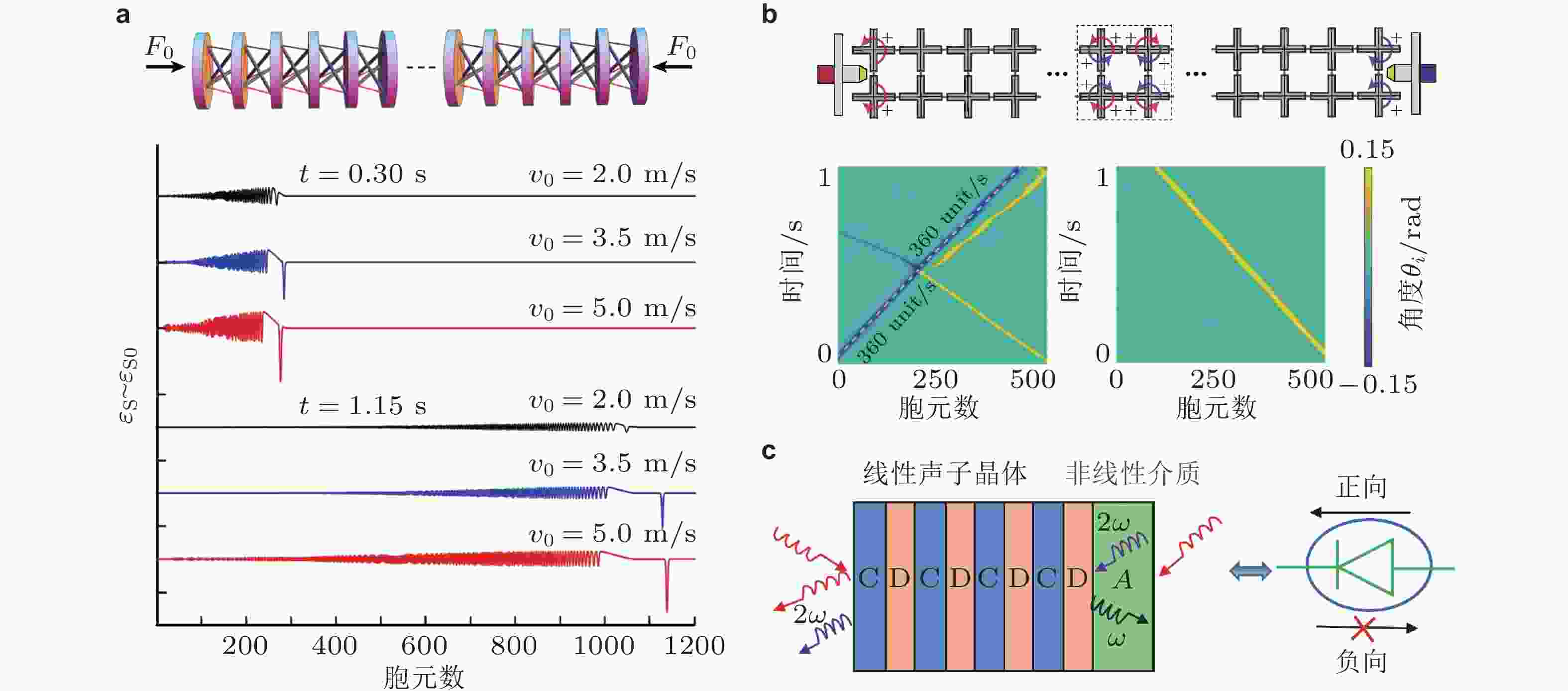
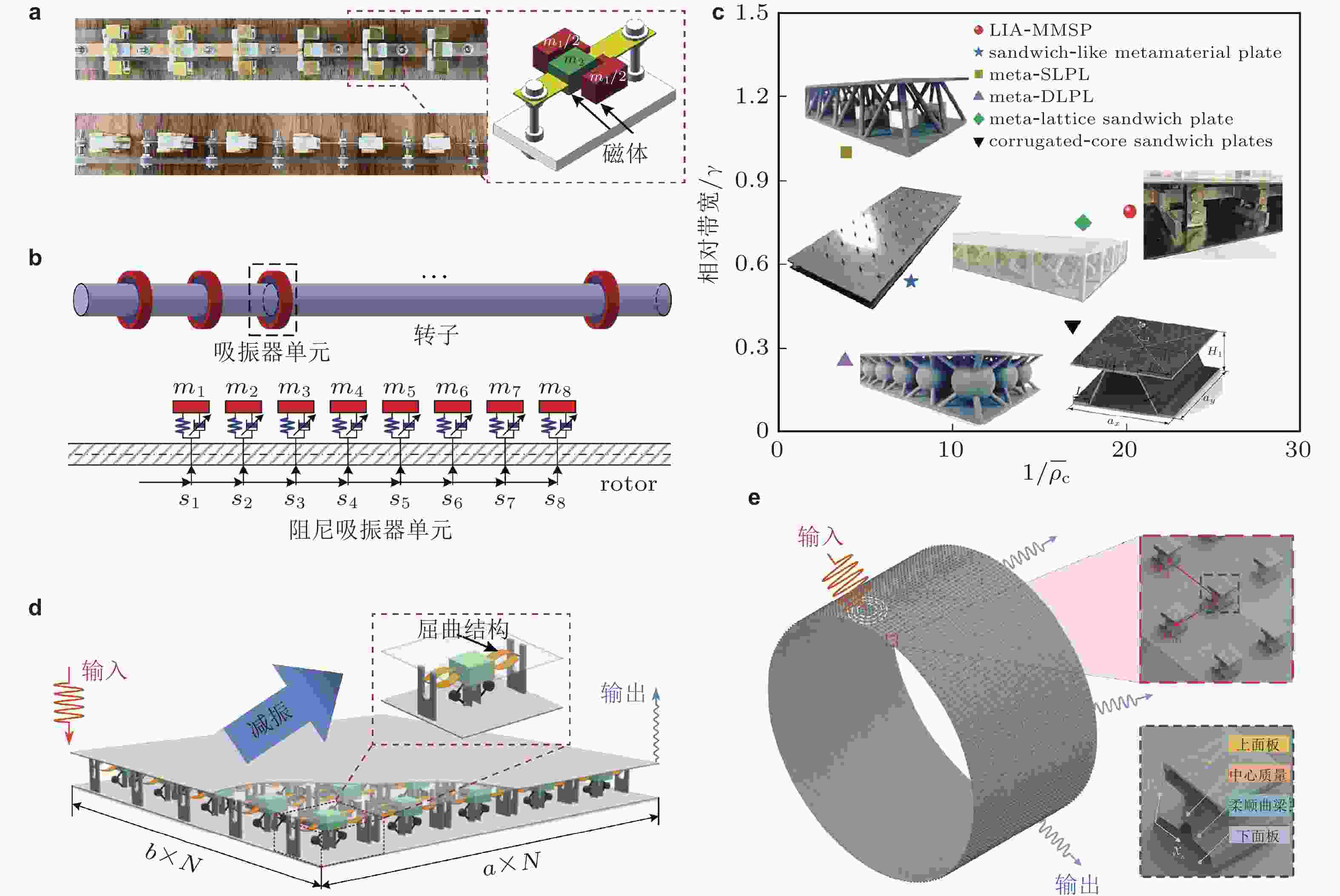
图 30 弹性孤波与非互易波. (a) 上图: 张拉整体结构, 下图: 不同冲击速度$ {v_0} $下压缩脉冲转变为稀疏型孤波的演化过程(Fraternali et al. 2014), (b) 上图: 由柔性铰链构成的一维周期结构, 下图: 矢量孤波传播与碰撞过程(Deng et al. 2019b), (c) 由线性周期结构和非线性介质构成的非互易系统, 实现弹性波/声波二极管功能(Li et al. 2019)

下载: 全尺寸图片幻灯片

图 31 梁/板/壳等代表性结构形式与周期结构设计. (a) 受磁力控制的非线性梁结构(Xue et al. 2023), (b) 周期性排布动力吸振器的转子结构(Xu et al. 2023), (c) 几种轻质夹芯结构的相对密度−带隙宽度对比图(Gao et al. 2024), (d) 含惯性放大共振结构的三明治夹芯板(Yang et al. 2024), (e) 附加准零刚度单元的圆柱壳周期结构(Cai et al. 2024)

下载: 全尺寸图片幻灯片

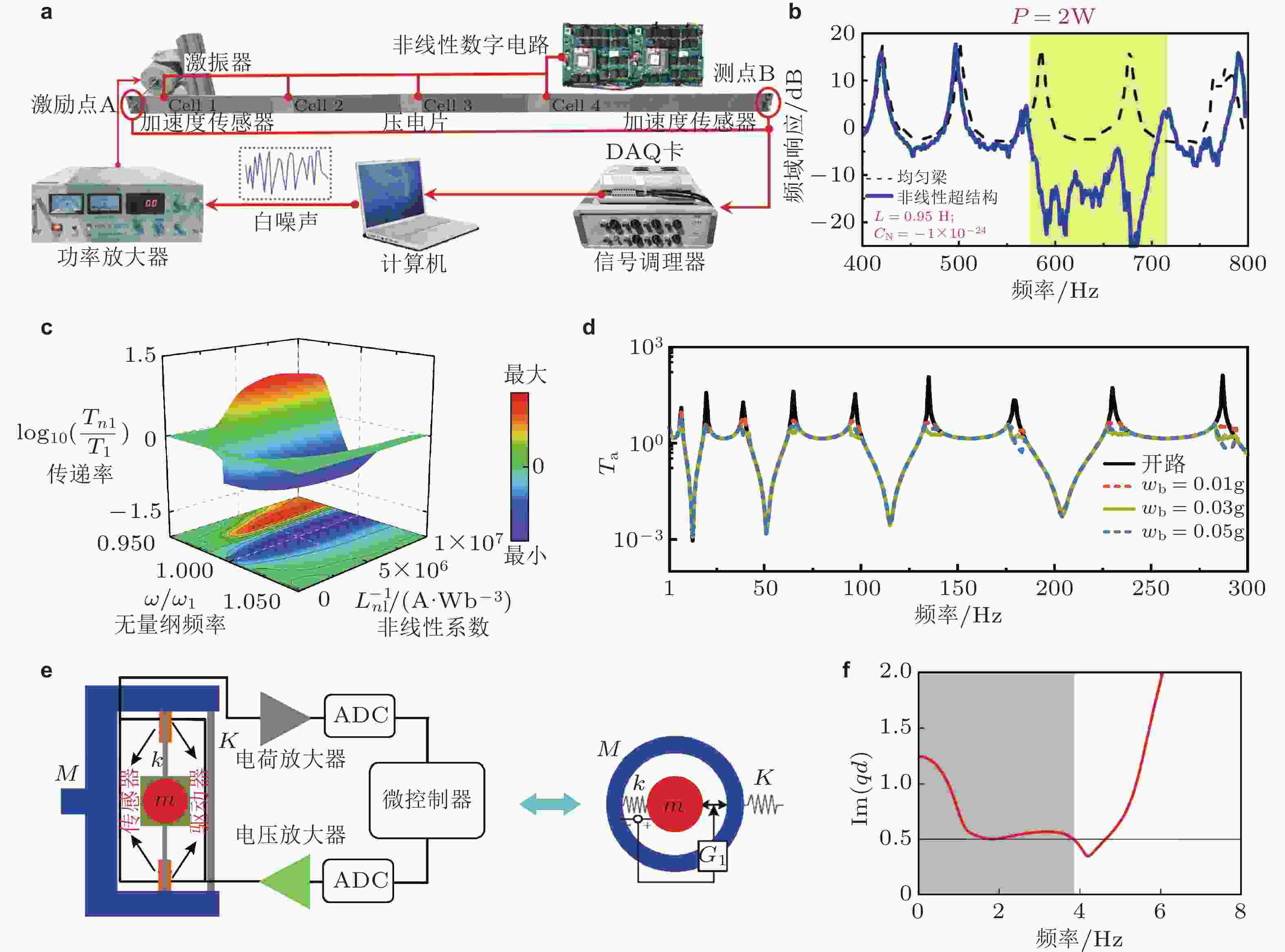
图 32 基于非线性分流电路的压电周期结构与低频振动控制. (a) 压电周期结构实验装置, (b) 压电梁在微幅激励下的振动频响, 黄色阴影区域表示非线性带隙, (c) 压电梁非线性动力学频响特性, (d) 压电梁传递率频响曲线, 调节纯非线性系数实现宽带可调振动控制, (e) 主动胞元结构, 压电片用于实现时滞反馈控制, (f) 优化时滞参数获得的超宽带隙(灰色阴影区域). 来自文献(Zhang et al. 2021c, Gong et al. 2025, Gao & Wang 2023)

下载: 全尺寸图片幻灯片

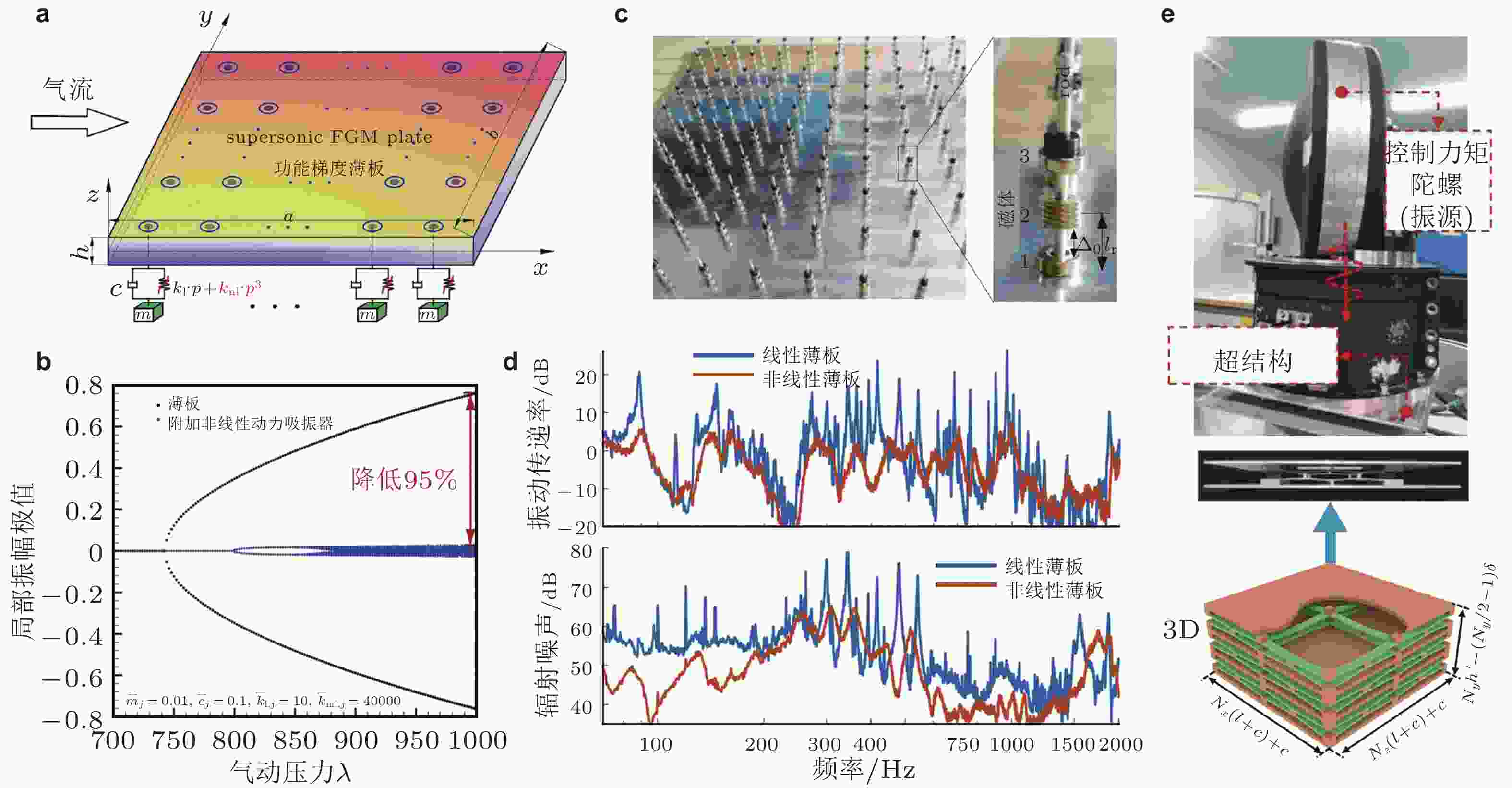
图 33 非线性周期结构在航空航天领域振动控制中的应用. (a) 超音速来流下功能梯度壁板颤振控制示意图, (b)壁板结构局部位移极值分岔图, 壁板上周期排布非线性动力吸振器, (c) 附加非线性振子的薄板周期结构, 局部放大图展示了由永磁体构成的强非线性共振结构, (d) 线性和非线性振子作用下, 薄板结构振动和辐射噪声频谱, (e) 准零刚度周期结构及其在航天器控制力矩陀螺隔振系统中的应用. 来自文献(Tian et al. 2022a, Fang et al. 2022, Zhao et al. 2023b)

下载: 全尺寸图片幻灯片

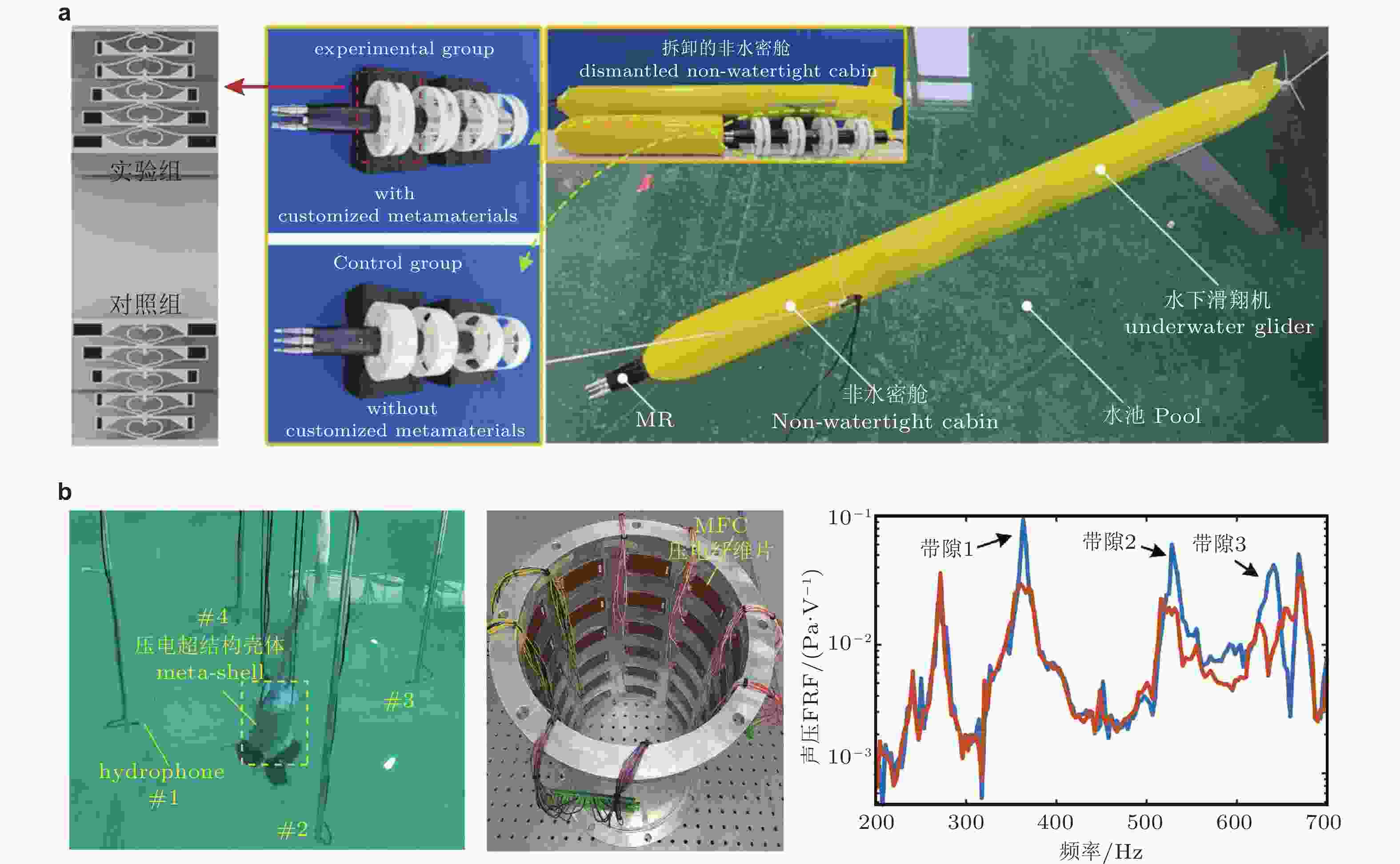
图 34 水下结构声振耦合控制. (a) 左图: 准零刚度周期结构, 右图: 水下滑翔机超低频隔振应用(Liu et al. 2024), (b) 压电周期结构用于水下壳体多模态声振耦合控制(Zheng et al. 2024)

下载: 全尺寸图片幻灯片

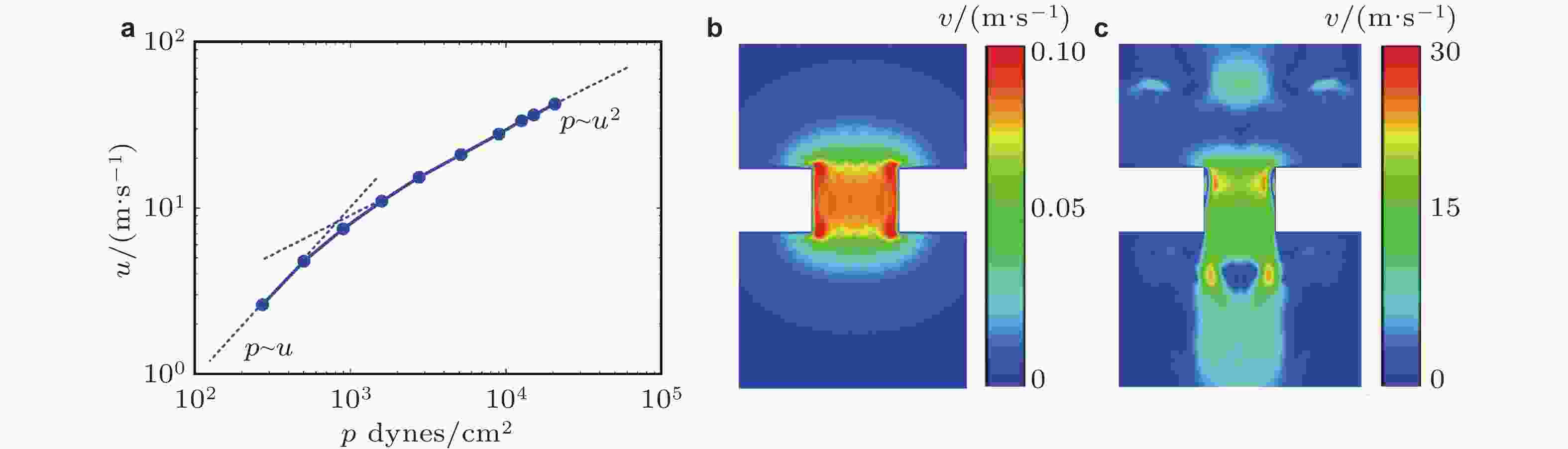
图 35 高声压级下微孔结构非线性声学特性. (a) 孔口粒子振速与激励声压之间呈现非线性关系, (b) 90 dB下Helmholtz共鸣器孔口粒子振速分布, (c) 140 dB下孔口粒子振速分布. 来自文献(Ingard & Ising 1967, Zhu et al. 2022)

下载: 全尺寸图片幻灯片

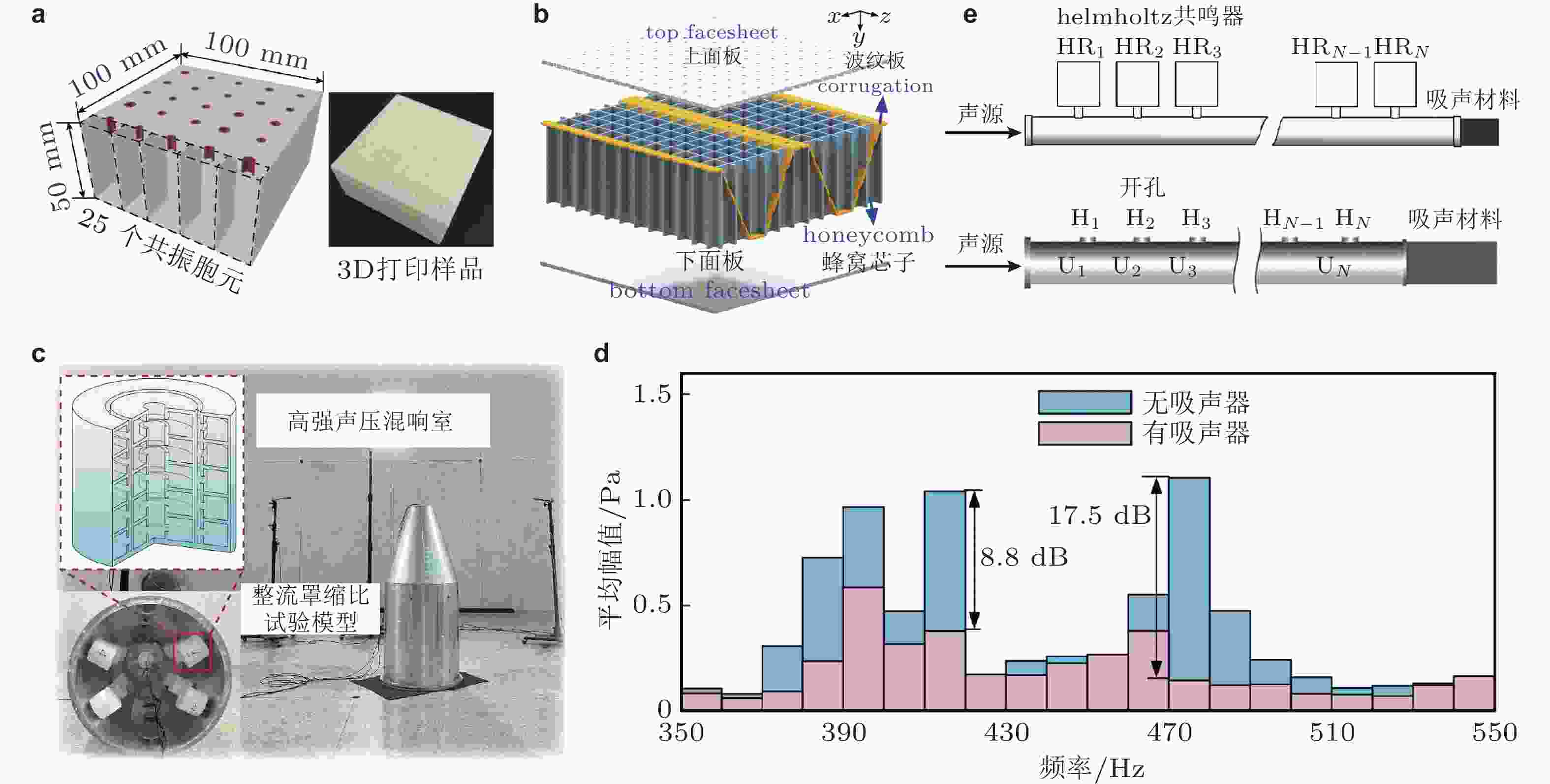
图 36 吸隔声阵列结构. (a) Helmholtz共鸣器平面阵列结构(Huang et al. 2020), (b) 轻质蜂窝夹芯板吸声结构(Tang et al. 2020), (c) 周期性多层嵌套吸声结构(插图)与高声强混响室吸声性能测试装置(Zhu et al. 2023a), (d) 整流罩模型布置吸声器前后, 内声腔噪声频谱(Zhu et al. 2023a), (e) 含Helmholtz共鸣器或微孔阵列的一维声管道(Fan et al. 2013, Lan et al. 2017)

下载: 全尺寸图片幻灯片

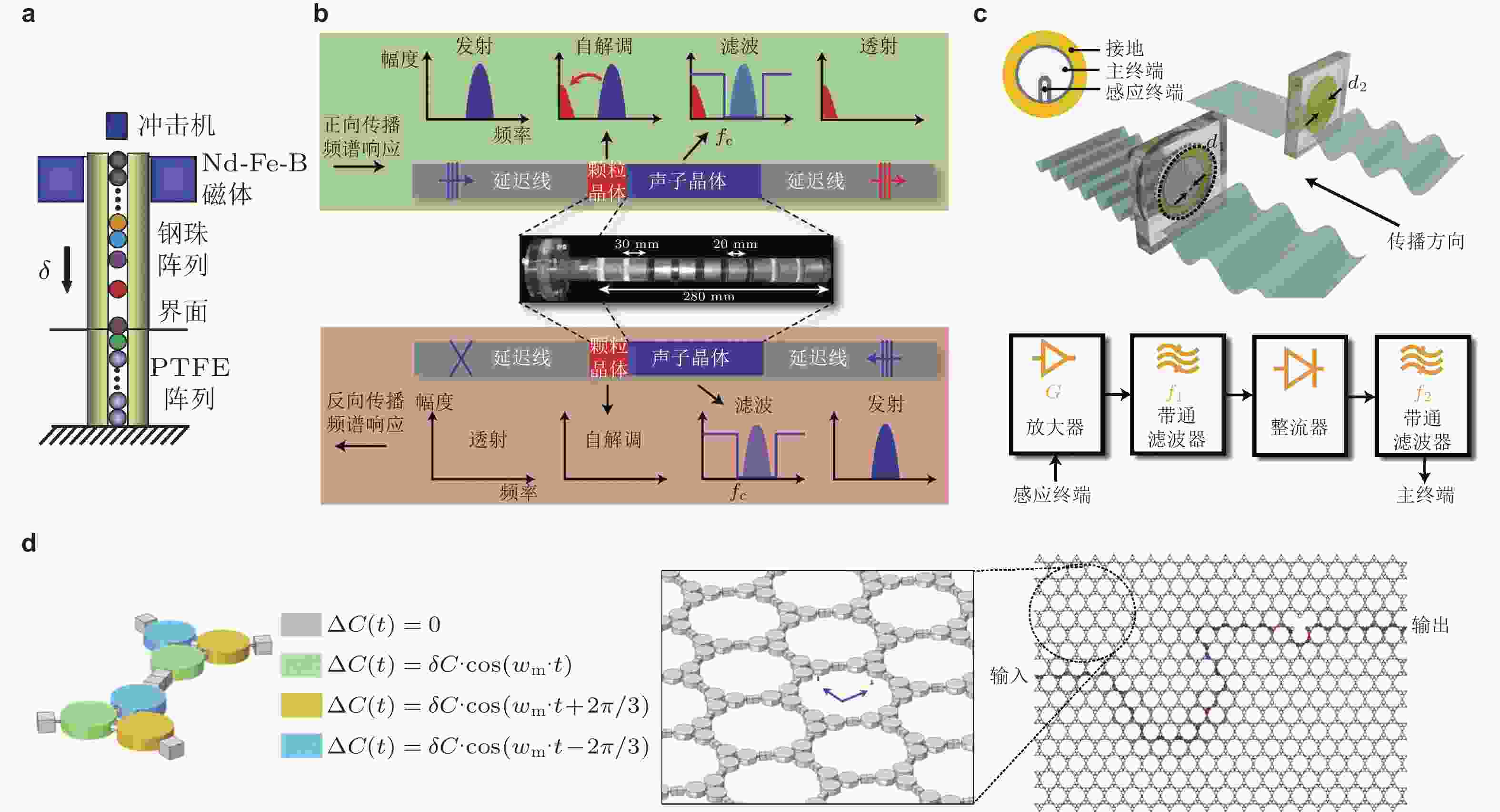
图 37 基于异质界面和有源主动系统构造的非互易整流器件. (a) 钢珠和聚四氟乙烯珠(PTFE)构成的颗粒晶体, 顶端通过磁体施加预紧力(Nesterenko et al. 2005), (b) 弹性波整流器件与工作原理示意图, 整流器件由颗粒晶体和层状周期结构构成(Devaux et al. 2015), (c) 有源声学整流器件(Popa & Cummer 2014), (d) Floquet拓扑绝缘体与单向边界态, 通过对单胞声容进行时变调制引入非互易效应(Fleury et al. 2016)

下载: 全尺寸图片幻灯片

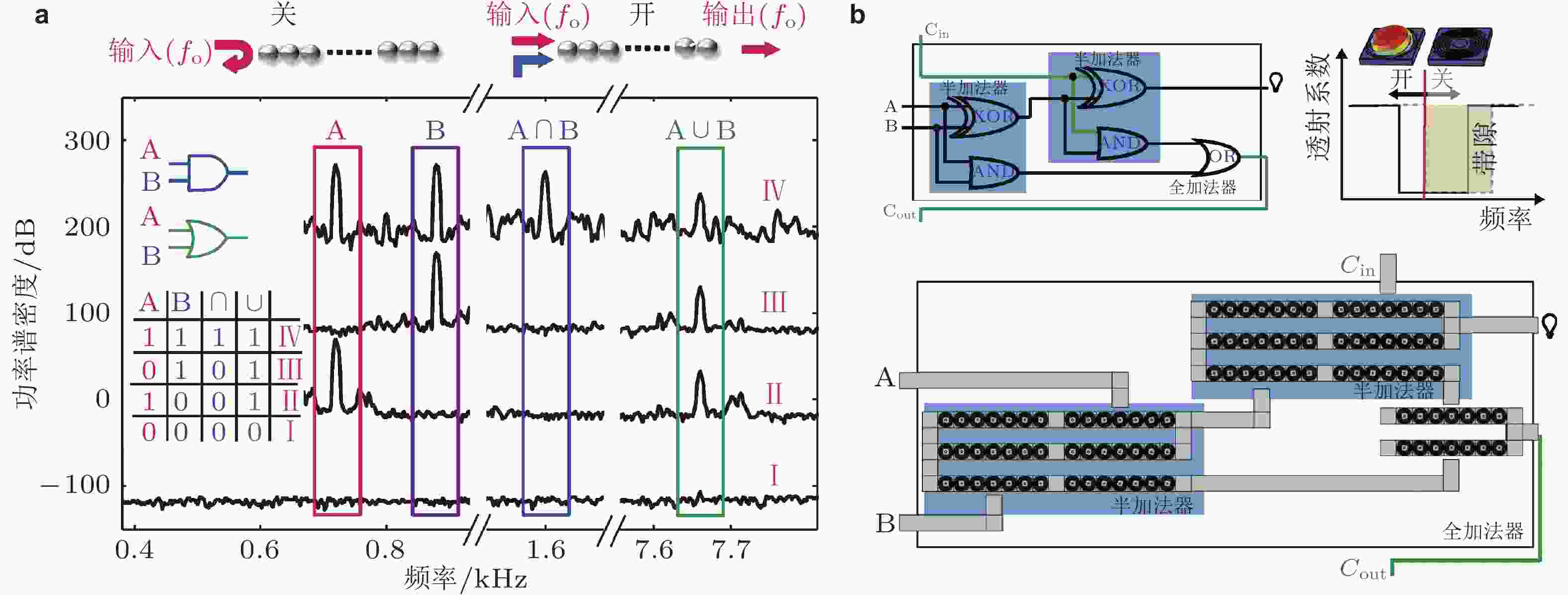
图 38 基于弹性波传播特性设计的逻辑门器件. (a) 颗粒晶体开关功能示意图及OR/AND逻辑运算信号功率谱密度(Li et al. 2014), (b) 全加法器原理图与对应的周期结构实现装置, 右上角插图为弹性波开关原理示意图, 随着单胞构型变化传输信号会在开/关两种状态间切换(Bilal et al. 2017)

下载: 全尺寸图片幻灯片

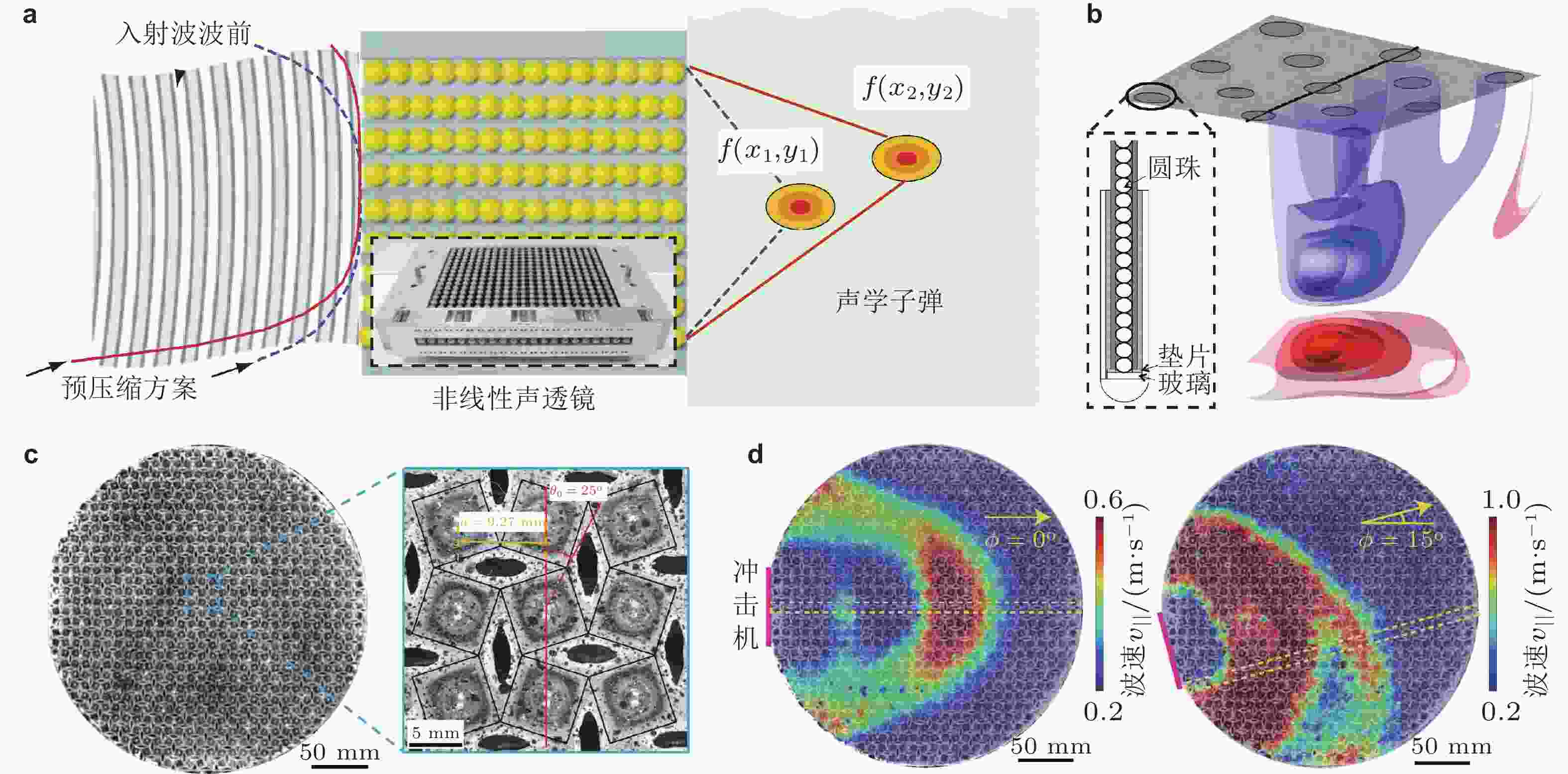
图 39 非线性波束操纵器件. (a) 由颗粒晶体构成的非线性聚焦透镜, 调节静态预紧力空间分布可改变焦点位置(Spadoni & Daraio 2010), (b) 二维非线性声透镜, 彩色表示水中声学子弹恒压面(Donahue et al. 2014), (c) 柔性铰链构成的非线性周期结构(Deng et al. 2019a), (d) 不同冲击角下的孤波脉冲速度场分布(Deng et al. 2019a)

下载: 全尺寸图片幻灯片

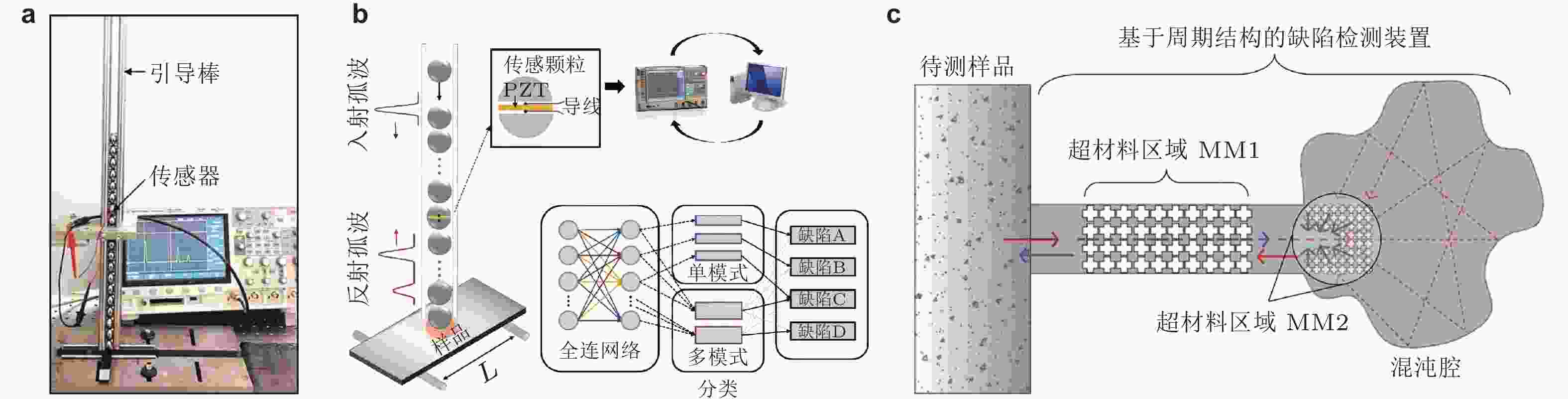
图 40 基于周期结构实现无损检测或健康监测功能. (a) 利用颗粒晶体中孤波反射特性识别复合材料弱粘接区域(Singhal et al. 2017), (b) 颗粒晶体用于复合材料分层损伤实时监测(Yoon et al. 2023), (c) 由周期结构滤波区域(MM1)、周期结构聚焦区域(MM2)和混沌腔构成的缺陷检测装置(Gliozzi et al. 2015)

下载: 全尺寸图片幻灯片

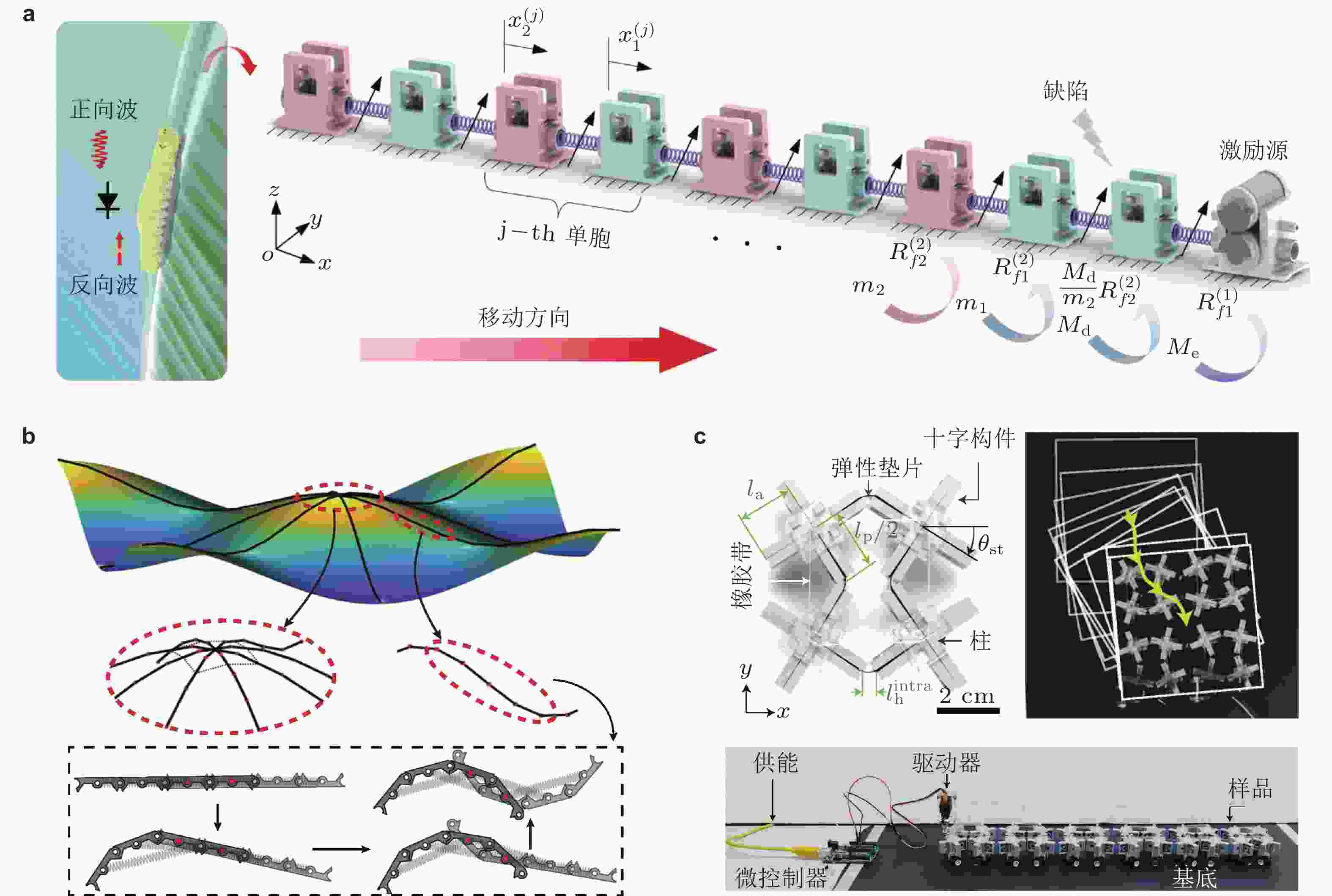
图 41 基于波传播的致动器件. (a) 毛毛虫爬行运动的“二极管”输运特性, 以此可设计能够单向运动的周期结构致动器件(Zhou & Wang 2024), (b) 由刚性杆和双稳态关节组成的机械连杆机构, 利用转变波现象实现空间展开部署(Zareei et al. 2020), (c) 双稳态旋转方块结构单元与其构成的二维周期结构致动器件(Deng et al. 2022a)

下载: 全尺寸图片幻灯片

表 1 常见的非线性周期结构动力学建模方法

示意图	动力学模型	代表性文献
	原子链模型	(Chakraborty & Mallik 2001) (Lazarov & Jensen 2007)
	连续极限模型	(Deng et al. 2019a) (Deng et al. 2020b)
	有限元模型	(Manktelow et al. 2013b) (Mosquera-Sánchez et al. 2024)
	混合模型	(Casalotti et al. 2018) (Fang et al. 2022)

下载: 导出CSV

表 2 压电单胞几何及材料参数

参数	基底层 (铝)	压电层 (PZT-5H)
长度 (mm)	50.00	50.00
宽度 (mm)	25.00	25.00
厚度 (mm)	0.50	0.25
密度 (kg/m³)	2700	7450
杨氏模量 (GPa)	69.0	76.9
压电应力常数$ {\bar e_{31}} $ (C/m²)	—	−14.3
恒应力介电常数$ {\overline{\epsilon }}_{33}^{\text{S}} $ (nF/m)	—	37.2

下载: 导出CSV

参考文献(328)

[1]	陈毅, 刘晓宁, 向平, 等. 2016. 五模材料及其水声调控研究. 力学进展, 46: 201609 (Chen Y, Liu X N, Xiang P, et al. 2016. Pentamode material for underwater acoustic wave control. Advances in Mechanics, 46: 201609). doi: 10.6052/1000-0992-16-010 Chen Y, Liu X N, Xiang P, et al. 2016. Pentamode material for underwater acoustic wave control. Advances in Mechanics, 46: 201609. doi: 10.6052/1000-0992-16-010
[2]	方鑫. 2018. 非线性声学超材料中弹性波传播理论及其减振应用研究. [博士论文]. 国防科技大学 (Fang, X. 2018. Nonlinear acoustic metamaterials: theory of elastic wave propagation and applications on vibration reduction. [Doctor Thesis]. National University of Defense Technology). Fang, X. 2018. Nonlinear acoustic metamaterials: theory of elastic wave propagation and applications on vibration reduction. [Doctor Thesis]. National University of Defense Technology.
[3]	耿琳琳, 袁锦波, 程文, 等. 2024. 非厄米力学系统基本原理与研究进展. 力学进展, 54: 1-60 (Geng L L, Yuan J B, Cheng W, et al. 2024. Fundamental principles and research progress of non-Hermitian mechanical systems. Advances in Mechanics, 54: 1-60). doi: 10.6052/1000-0992-23-049 Geng L L, Yuan J B, Cheng W, et al. 2024. Fundamental principles and research progress of non-Hermitian mechanical systems. Advances in Mechanics, 54: 1-60. doi: 10.6052/1000-0992-23-049
[4]	胡更开, 刘晓宁. 2024. 弹性超材料设计与波动控制//科学出版社: 科学出版社. (Hu G K, Liu X N. 2024. Elastic metamaterials design and wave control. China Science Publishing & Media Ltd). Hu G K, Liu X N. 2024. Elastic metamaterials design and wave control. China Science Publishing & Media Ltd.
[5]	胡海岩, 田强, 张伟, 等. 2013. 大型网架式可展开空间结构的非线性动力学与控制. 力学进展, 43: 390-414 (Hu H Y, Tian Q, Zhang W, et al. 2013. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes. Advances in Mechanics, 43: 390-414). Hu H Y, Tian Q, Zhang W, et al. 2013. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes. Advances in Mechanics, 43: 390-414.
[6]	马大猷. 1996. 高声强下的微穿孔板. 声学学报, 21: 10-14 (Ma D Y. 1996. Microperforated panel at high sound intensity. Acta Acustica, 21: 10-14). Ma D Y. 1996. Microperforated panel at high sound intensity. Acta Acustica, 21: 10-14.
[7]	孟光, 周徐斌, 苗军. 2016. 航天重大工程中的力学问题. 力学进展, 46: 201606 (Meng G, Zhou X B, Miao J. 2016. Mechanical problems in momentous projects of aerospace engineering. Advances in Mechanics, 46: 201606). Meng G, Zhou X B, Miao J. 2016. Mechanical problems in momentous projects of aerospace engineering. Advances in Mechanics, 46: 201606
[8]	苏常伟, 梁冉, 王雪仁, 等. 2023. 水下航行器线谱振动噪声研究进展. 舰船科学技术, 45: 1-8 (Su C W, Liang R, Wang X R, et al. 2023. Research progress of line spectrum vibration and noise of underwater vehicle. Ship Science and Technology, 45: 1-8). doi: 10.3404/j.issn.1672-7649.2023.08.001 Su C W, Liang R, Wang X R, et al. 2023. Research progress of line spectrum vibration and noise of underwater vehicle. Ship Science and Technology, 45: 1-8 doi: 10.3404/j.issn.1672-7649.2023.08.001
[9]	孙秀婷, 钱佳伟, 齐志凤, 等. 2023. 非线性隔振及时滞消振方法研究进展. 力学进展, 53: 308-356 (Sun X T, Qian J W, Qi Z F, et al. 2023. Review on research progress of nonlinear vibration isolation and time-delayed suppression method. Advances in Mechanics, 53: 308-356). doi: 10.6052/1000-0992-22-048 Sun X T, Qian J W, Qi Z F, et al. 2023. Review on research progress of nonlinear vibration isolation and time-delayed suppression method. Advances in Mechanics, 53: 308-356 doi: 10.6052/1000-0992-22-048
[10]	王凯, 周加喜, 蔡昌琦, 等. 2022. 低频弹性波超材料的若干进展. 力学学报, 54: 2678-2694 (Wang K, Zhou J X, Cai C Q, et al. 2022. Review of low-frequency elastic wave metamaterials. Chinese Journal of Theoretical and Applied Mechanics, 54: 2678-2694). doi: 10.6052/0459-1879-22-108 Wang K, Zhou J X, Cai C Q, et al. 2022. Review of low-frequency elastic wave metamaterials. Chinese Journal of Theoretical and Applied Mechanics, 54: 2678-2694. doi: 10.6052/0459-1879-22-108
[11]	王育人, 缪旭弘, 姜恒, 等. 2017. 水下吸声机理与吸声材料. 力学进展, 47: 201703 (Wang Y R, Miao X H, Jiang H, et al. 2017. Review on underwater sound absorption materials and mechanisms. Advances in Mechanics, 47: 201703). Wang Y R, Miao X H, Jiang H, et al. 2017. Review on underwater sound absorption materials and mechanisms. Advances in Mechanics, 47: 201703
[12]	吴林志, 熊健, 马力, 等. 2012. 新型复合材料点阵结构的研究进展. 力学进展, 42: 41-67 (Wu L Z, Xiong J, Ma L, et al. 2012. Processes in the study of novel composite sandwich panels with lattice truss cores. Advances in Mechanics, 42: 41-67). doi: 10.6052/1000-0992-2012-1-lxjzJ2011-095 Wu L Z, Xiong J, Ma L, et al. 2012. Processes in the study of novel composite sandwich panels with lattice truss cores. Advances in Mechanics, 42: 41-67. doi: 10.6052/1000-0992-2012-1-lxjzJ2011-095
[13]	易凯军, 陈洋洋, 朱睿. 2022. 力电耦合主动超材料及其弹性波调控. 科学通报, 67: 1290-1304 (Yi K J, Chen Y Y, Zhu R, et al. 2022. Electromechanical active metamaterials and their applications in controlling elastic wave propagation. Chinese Science Bulletin, 67: 1290-1304). doi: 10.1360/TB-2021-0573 Yi K J, Chen Y Y, Zhu R, et al. 2022. Electromechanical active metamaterials and their applications in controlling elastic wave propagation. Chinese Science Bulletin, 67: 1290-1304 doi: 10.1360/TB-2021-0573
[14]	尹剑飞, 蔡力, 方鑫, 等. 2022. 力学超材料研究进展与减振降噪应用. 力学进展, 52: 508-586 (Yin J F, Cai L, Fang X, et al. 2022. Review on research progress of mechanical metamaterials and their applications in vibration and noise control. Advances in Mechanics, 52: 508-586). doi: 10.6052/1000-0992-22-005 Yin J F, Cai L, Fang X, et al. 2022. Review on research progress of mechanical metamaterials and their applications in vibration and noise control. Advances in Mechanics, 52: 508-586 doi: 10.6052/1000-0992-22-005
[15]	袁毅, 游镇宇, 陈伟球. 2021. 压电超构材料及其波动控制研究: 现状与展望. 力学学报, 53: 2101-2116 (Yuan Y, You Z Y, Chen W Q. 2021. Piezoelectric metamaterials and wave control: Status quo and prospects. Chinese Journal of Theoretical and Applied Mechanics, 53: 2101-2116). doi: 10.6052/0459-1879-21-198 Yuan Y, You Z Y, Chen W Q. 2021. Piezoelectric metamaterials and wave control: Status quo and prospects. Chinese Journal of Theoretical and Applied Mechanics, 53: 2101-2116. doi: 10.6052/0459-1879-21-198
[16]	Akbari-Farahani F, Ebrahimi-Nejad S. 2024. From defect mode to topological metamaterials: A state-of-the-art review of phononic crystals & acoustic metamaterials for energy harvesting. Sensors and Actuators A: Physical, 365: 114871.
[17]	Alfahmi O, Erturk A. 2024. Programmable hardening and softening cubic inductive shunts for piezoelectric structures: Harmonic balance analysis and experiments. Journal of Sound and Vibration, 571: 118029.
[18]	Alfahmi O, Sugino C, Erturk A. 2022. Duffing-type digitally programmable nonlinear synthetic inductance for piezoelectric structures. Smart Materials and Structures, 31: 095044.
[19]	Allein F, Tournat V, Gusev V, et al. 2020. Linear and nonlinear elastic waves in magnetogranular chains. Physical Review Applied, 13: 024023. doi: 10.1103/PhysRevApplied.13.024023
[20]	Allein F, Tournat V, Gusev V E, et al. 2016. Tunable magneto-granular phononic crystals. Applied Physics Letters, 108: 161903. doi: 10.1063/1.4947192
[21]	Alleyne D, Cawley P. 1991. A two-dimensional Fourier transform method for the measurement of propagating multimode signals. The Journal of the Acoustical Society of America, 89: 1159-1168.
[22]	Alshaqaq M, Sugino C, Erturk A. 2023. Digital programming of reciprocity breaking in resonant piezoelectric metamaterials. Physical Review Research, 5: 043003.
[23]	Bae M H, Oh J H. 2020. Amplitude-induced bandgap: New type of bandgap for nonlinear elastic metamaterials. Journal of the Mechanics and Physics of Solids, 139: 103930.
[24]	Bae M H, Oh J H. 2022. Nonlinear elastic metamaterial for tunable bandgap at quasi-static frequency. Mechanical Systems and Signal Processing, 170: 108832.
[25]	Banerjee A, Adhikari S, Hussein M I. 2021. Inertial amplification band-gap generation by coupling a levered mass with a locally resonant mass. International Journal of Mechanical Sciences, 207: 106630.
[26]	Banerjee A, Calius E P, Das R. 2018a. An impact based mass-in-mass unit as a building block of wideband nonlinear resonating metamaterial. International Journal of Non-Linear Mechanics, 101: 8-15.
[27]	Banerjee A, Calius E P, Das R. 2018b. Impact based wideband nonlinear resonating metamaterial chain. International Journal of Non-Linear Mechanics, 103: 138-144.
[28]	Bao B, Guyomar D, Lallart M. 2017. Vibration reduction for smart periodic structures via periodic piezoelectric arrays with nonlinear interleaved-switched electronic networks. Mechanical Systems and Signal Processing, 82: 230-259.
[29]	Bertoldi K, Vitelli V, Christensen J, et al. 2017. Flexible mechanical metamaterials. Nature Reviews Materials, 2: 17066. doi: 10.1038/natrevmats.2017.66
[30]	Bickham S R, Kiselev S A, Sievers A J. 1993. Stationary and moving intrinsic localized modes in one-dimensional monatomic lattices with cubic and quartic anharmonicity. Physical Review B, 47: 14206-14211.
[31]	Bidhendi M R T. 2022. Band gap transmission in a periodic network of coupled buckled beams. International Journal of Solids and Structures, 252: 111766.
[32]	Bilal O R, Foehr A, Daraio C. 2017. Bistable metamaterial for switching and cascading elastic vibrations. Proceedings of the National Academy of Sciences, 114: 4603-4606.
[33]	Boechler N, Theocharis G, Daraio C. 2011. Bifurcation-based acoustic switching and rectification. Nature Materials, 10: 665-668.
[34]	Boechler N, Theocharis G, Job S, et al. 2010. Discrete breathers in one-dimensional diatomic granular crystals. Physical Review Letters, 104: 244302. doi: 10.1103/PhysRevLett.104.244302
[35]	Bordiga G, Medina E, Jafarzadeh S, et al. 2024. Automated discovery of reprogrammable nonlinear dynamic metamaterials. Nature Materials, 23: 1486-1494. doi: 10.1038/s41563-024-02008-6
[36]	Bosia F, Dal Poggetto V F, Gliozzi A S, et al. 2022. Optimized structures for vibration attenuation and sound control in nature: A review. Matter, 5: 3311-3340. doi: 10.1016/j.matt.2022.07.023
[37]	Brooke D C, Umnova O, Leclaire P, et al. 2020. Acoustic metamaterial for low frequency sound absorption in linear and nonlinear regimes. Journal of Sound and Vibration, 485: 115585. doi: 10.1016/j.jsv.2020.115585
[38]	Bukhari M, Barry O. 2020. Spectro-spatial analyses of a nonlinear metamaterial with multiple nonlinear local resonators. Nonlinear Dynamics, 99: 1539-1560.
[39]	Buryak A V, Trapani P D, Skryabin D V, et al. 2002. Optical solitons due to quadratic nonlinearities: From basic physics to futuristic applications. Physics Reports, 370: 63-235. doi: 10.1016/S0370-1573(02)00196-5
[40]	Cabaret J, Tournat V, Béquin P. 2012. Amplitude-dependent phononic processes in a diatomic granular chain in the weakly nonlinear regime. Physical Review E, 86: 041305.
[41]	Cai C, Guo X, Yan B, et al. 2024. Modelling and analysis of the quasi-zero-stiffness metamaterial cylindrical shell for low-frequency band gap. Applied Mathematical Modelling, 135: 90-108. doi: 10.1016/j.apm.2024.06.031
[42]	Cai C, Zhou J, Wang K, et al. 2022. Metamaterial plate with compliant quasi-zero-stiffness resonators for ultra-low-frequency band gap. Journal of Sound and Vibration, 540: 117297. doi: 10.1016/j.jsv.2022.117297
[43]	Casalotti A, El-Borgi S, Lacarbonara W. 2018. Metamaterial beam with embedded nonlinear vibration absorbers. International Journal of Non-Linear Mechanics, 98: 32-42.
[44]	Cha J, Daraio C. 2018. Electrical tuning of elastic wave propagation in nanomechanical lattices at MHz frequencies. Nature Nanotechnology, 13: 1016-1020.
[45]	Chakraborty G, Mallik A K. 2001. Dynamics of a weakly non-linear periodic chain. International Journal of Non-Linear Mechanics, 36: 375-389.
[46]	Chaunsali R, Theocharis G. 2019. Self-induced topological transition in phononic crystals by nonlinearity management. Physical Review B, 100: 014302.
[47]	Chaunsali R, Xu H, Yang J, et al. 2021. Stability of topological edge states under strong nonlinear effects. Physical Review B, 103: 024106. doi: 10.1103/PhysRevB.103.024106
[48]	Chen B, Zheng Y, Dai S, et al. 2024a. Bandgap enhancement of a piezoelectric metamaterial beam shunted with circuits incorporating fractional and cubic nonlinearities. Mechanical Systems and Signal Processing, 212: 111262. doi: 10.1016/j.ymssp.2024.111262
[49]	Chen C, Li X D. 2020. Microscopic fluid dynamics of a wire screen bound to a slit resonator excited by acoustic waves. Physics of Fluids, 32: 116107.
[50]	Chen W, Hao Y X, Zhang W, et al. 2024b. Vibration isolation performance of a novel metamaterials sandwich cylindrical panel by locally resonant band gap. Journal of Vibration Engineering & Technologies, 12: 6121-6136.
[51]	Chen Y, Li X, Nassar H, et al. 2019. Nonreciprocal wave propagation in a continuum-based metamaterial with space-time modulated resonators. Physical Review Applied, 11: 064052. doi: 10.1103/PhysRevApplied.11.064052
[52]	Chen Y, Wu B, Su Y, et al. 2020. Effects of strain stiffening and electrostriction on tunable elastic waves in compressible dielectric elastomer laminates. International Journal of Mechanical Sciences, 176: 105572. doi: 10.1016/j.ijmecsci.2020.105572
[53]	Chong C, Kim B, Wallace E, et al. 2024. Modulation instability and wavenumber bandgap breathers in a time layered phononic lattice. Physical Review Research, 6: 023045. doi: 10.1103/PhysRevResearch.6.023045
[54]	Cui J-G, Yang T, Chen L-Q. 2018. Frequency-preserved non-reciprocal acoustic propagation in a granular chain. Applied Physics Letters, 112: 181904.
[55]	Cummings A. 1984. Acoustic nonlinearities and power losses at orifices. AIAA Journal, 22: 786-792.
[56]	Darabi A, Leamy M J. 2019. Tunable nonlinear topological insulator for acoustic waves. Physical Review Applied, 12: 044030.
[57]	Darabi A, Ni X, Leamy M, et al. 2020. Reconfigurable Floquet elastodynamic topological insulator based on synthetic angular momentum bias. Science Advances, 6: eaba8656. doi: 10.1126/sciadv.aba8656
[58]	De Marqui Junior C, Erturk A, Inman D J. 2009. An electromechanical finite element model for piezoelectric energy harvester plates. Journal of Sound and Vibration, 327: 9-25.
[59]	Deng B, Chen L, Wei D, et al. 2020a. Pulse-driven robot: Motion via solitary waves. Science Advances, 6: eaaz1166. doi: 10.1126/sciadv.aaz1166
[60]	Deng B, Mo C, Tournat V, et al. 2019a. Focusing and mode separation of elastic vector solitons in a 2D soft mechanical metamaterial. Physical Review Letters, 123: 024101. doi: 10.1103/PhysRevLett.123.024101
[61]	Deng B, Raney J R, Bertoldi K, et al. 2021. Nonlinear waves in flexible mechanical metamaterials. Journal of Applied Physics, 130: 040901. doi: 10.1063/5.0050271
[62]	Deng B, Tournat V, Wang P, et al. 2019b. Anomalous collisions of elastic vector solitons in mechanical metamaterials. Physical Review Letters, 122: 044101. doi: 10.1103/PhysRevLett.122.044101
[63]	Deng B, Wang P, He Q, et al. 2018. Metamaterials with amplitude gaps for elastic solitons. Nature Communications, 9: 3410. doi: 10.1038/s41467-018-05908-9
[64]	Deng B, Yu S, Forte A E, et al. 2020b. Characterization, stability, and application of domain walls in flexible mechanical metamaterials. Proceedings of the National Academy of Sciences, 117: 31002-31009. doi: 10.1073/pnas.2015847117
[65]	Deng B, Zanaty M, Forte A E, et al. 2022a. Topological solitons make metamaterials crawl. Physical Review Applied, 17: 014004. doi: 10.1103/PhysRevApplied.17.014004
[66]	Deng B, Zareei A, Ding X, et al. 2022b. Inverse design of mechanical metamaterials with target nonlinear response via a neural accelerated evolution strategy. Advanced Materials, 34: 2206238. doi: 10.1002/adma.202206238
[67]	Devaux T, Tournat V, Richoux O, et al. 2015. Asymmetric acoustic propagation of wave packets via the self-demodulation effect. Physical Review Letters, 115: 234301. doi: 10.1103/PhysRevLett.115.234301
[68]	Deymier P A. 2013. Acoustic metamaterials and phononic crystals//: Springer Science & Business Media.
[69]	Donahue C M, Anzel P W J, Bonanomi L, et al. 2014. Experimental realization of a nonlinear acoustic lens with a tunable focus. Applied Physics Letters, 104: 014103. doi: 10.1063/1.4857635
[70]	Dong E, Cao P, Zhang J, et al. 2022. Underwater acoustic metamaterials. National Science Review, 10: nwac246.
[71]	Dong H-W, Shen C, Liu Z, et al. 2024. Inverse design of phononic meta-structured materials. Materials Today, 80: 824-855. doi: 10.1016/j.mattod.2024.09.012
[72]	Fan L, Ge H, Zhang S-Y, et al. 2013. Nonlinear acoustic fields in acoustic metamaterial based on a cylindrical pipe with periodically arranged side holes. The Journal of the Acoustical Society of America, 133: 3846-3852. doi: 10.1121/1.4803904
[73]	Fang X, Lacarbonara W, Cheng L. 2024. Advances in nonlinear acoustic/elastic metamaterials and metastructures. Nonlinear Dynamics, https://doi.org/10.1007/s11071-024-10219-4.
[74]	Fang X, Sheng P, Wen J, et al. 2022. A nonlinear metamaterial plate for suppressing vibration and sound radiation. International Journal of Mechanical Sciences, 228: 107473. doi: 10.1016/j.ijmecsci.2022.107473
[75]	Fang X, Wen J, Benisty H, et al. 2020. Ultrabroad acoustical limiting in nonlinear metamaterials due to adaptive-broadening band-gap effect. Physical Review B, 101: 104304. doi: 10.1103/PhysRevB.101.104304
[76]	Fang X, Wen J, Bonello B, et al. 2017a. Ultra-low and ultra-broad-band nonlinear acoustic metamaterials. Nature Communications, 8: 1288. doi: 10.1038/s41467-017-00671-9
[77]	Fang X, Wen J, Bonello B, et al. 2017b. Wave propagation in one-dimensional nonlinear acoustic metamaterials. New Journal of Physics, 19: 053007. doi: 10.1088/1367-2630/aa6d49
[78]	Fang X, Wen J, Yin J, et al. 2016. Broadband and tunable one-dimensional strongly nonlinear acoustic metamaterials: Theoretical study. Physical Review E, 94: 052206. doi: 10.1103/PhysRevE.94.052206
[79]	Fang X, Wen J, Yu D, et al. 2018. Bridging-coupling band gaps in nonlinear acoustic metamaterials. Physical Review Applied, 10: 054049. doi: 10.1103/PhysRevApplied.10.054049
[80]	Fermi E, Pasta P, Ulam S, et al. 1955. Studies of the nonlinear problems. Los Alamos National Laboratory (LANL), Los Alamos, NM (United States).
[81]	Flach S, Gorbach A V. 2008. Discrete breathers—Advances in theory and applications. Physics Reports, 467: 1-116.
[82]	Fleury R, Khanikaev A B, Alù A. 2016. Floquet topological insulators for sound. Nature Communications, 7: 11744.
[83]	Florijn B, Coulais C, van Hecke M. 2014. Programmable mechanical metamaterials. Physical Review Letters, 113: 175503.
[84]	Frandsen N M M, Bilal O R, Jensen J S, et al. 2016. Inertial amplification of continuous structures: Large band gaps from small masses. Journal of Applied Physics, 119: 124902.
[85]	Frandsen N M M, Jensen J S. 2017. Modal interaction and higher harmonic generation in a weakly nonlinear, periodic mass–spring chain. Wave Motion, 68: 149-161.
[86]	Fraternali F, Carpentieri G, Amendola A, et al. 2014. Multiscale tunability of solitary wave dynamics in tensegrity metamaterials. Applied Physics Letters, 105: 201903. doi: 10.1063/1.4902071
[87]	Fraternali F, Senatore L, Daraio C. 2012. Solitary waves on tensegrity lattices. Journal of the Mechanics and Physics of Solids, 60: 1137-1144.
[88]	Frazier M J, Kochmann D M. 2017. Band gap transmission in periodic bistable mechanical systems. Journal of Sound and Vibration, 388: 315-326.
[89]	Fronk M D, Fang L, Packo P, et al. 2023. Elastic wave propagation in weakly nonlinear media and metamaterials: A review of recent developments. Nonlinear Dynamics, 111: 10709-10741. doi: 10.1007/s11071-023-08399-6
[90]	Fronk M D, Leamy M J. 2017. Higher-order dispersion, stability, and waveform invariance in nonlinear monoatomic and diatomic systems. Journal of Vibration and Acoustics, 139: 051003.
[91]	Ganesh R, Gonella S. 2015. From modal mixing to tunable functional switches in nonlinear phononic crystals. Physical Review Letters, 114: 054302.
[92]	Ganeshan S, Sun K, Das Sarma S. 2013. Topological zero-energy modes in gapless commensurate Aubry-André-Harper models. Physical Review Letters, 110: 180403.
[93]	Gao L, Mak C M, Ma K W, et al. 2024. Mechanisms of multi-bandgap inertial amplification applied in metamaterial sandwich plates. International Journal of Mechanical Sciences, 277: 109424. doi: 10.1016/j.ijmecsci.2024.109424
[94]	Gao N, Zhang Z, Deng J, et al. 2022a. Acoustic metamaterials for noise reduction: A review. Advanced Materials Technologies, 7: 2100698. doi: 10.1002/admt.202100698
[95]	Gao P, Climente A, Sánchez-Dehesa J, et al. 2017. Theoretical study of platonic crystals with periodically structured N-beam resonators. Journal of Applied Physics, 123: 091707.
[96]	Gao P, Climente A, Sánchez-Dehesa J, et al. 2019a. Single-phase metamaterial plates for broadband vibration suppression at low frequencies. Journal of Sound and Vibration, 444: 108-126. doi: 10.1016/j.jsv.2018.12.022
[97]	Gao P, Qu Y, Christensen J. 2022b. Non-Hermitian elastodynamics in gyro-odd continuum media. Communications Materials, 3: 74.
[98]	Gao P, Torrent D, Cervera F, et al. 2019b. Majorana-like zero modes in Kekulé distorted sonic lattices. Physical Review Letters, 123: 196601. doi: 10.1103/PhysRevLett.123.196601
[99]	Gao P, Willatzen M, Christensen J. 2020. Anomalous topological edge states in non-Hermitian piezophononic media. Physical Review Letters, 125: 206402.
[100]	Gao Y, Wang L. 2022. Nonlocal active metamaterial with feedback control for tunable bandgap and broadband nonreciprocity. International Journal of Mechanical Sciences, 219: 107131.
[101]	Gao Y, Wang L. 2023. Broad bandgap active metamaterials with optimal time-delayed control. International Journal of Mechanical Sciences, 254: 108449.
[102]	Gao Y, Wang L. 2024. An active tunable piezoelectric metamaterial beam for broadband vibration suppression by optimization. Acta Mechanica Sinica, 40: 523235.
[103]	Geniet F, Leon J. 2002. Energy transmission in the forbidden band gap of a nonlinear chain. Physical Review Letters, 89: 134102.
[104]	Gillman A, Fuchi K, Buskohl P R. 2018. Truss-based nonlinear mechanical analysis for origami structures exhibiting bifurcation and limit point instabilities. International Journal of Solids and Structures, 147: 80-93.
[105]	Gilpin W, Bull M S, Prakash M. 2020. The multiscale physics of cilia and flagella. Nature Reviews Physics, 2: 74-88.
[106]	Gliozzi A S, Miniaci M, Bosia F, et al. 2015. Metamaterials-based sensor to detect and locate nonlinear elastic sources. Applied Physics Letters, 107: 161902. doi: 10.1063/1.4934493
[107]	Gong C, Fang X, Cheng L. 2023. Band degeneration and evolution in nonlinear triatomic metamaterials. Nonlinear Dynamics, 111: 97-112.
[108]	Gong L, Zhang G, Gao P, et al. 2025. Tunable nonlinear piezoelectric metabeams for multimode vibration suppression. International Journal of Mechanical Sciences, 295: 110238.
[109]	Guddala S, Ramakrishna S A. 2016. Optical limiting by nonlinear tuning of resonance in metamaterial absorbers. Optics Letters, 41: 5150-5153.
[110]	Guo X, Gusev V E, Tournat V, et al. 2019. Frequency-doubling effect in acoustic reflection by a nonlinear, architected rotating-square metasurface. Physical Review E, 99: 052209. doi: 10.1103/PhysRevE.99.052209
[111]	Guo X, Lissek H, Fleury R. 2020. Improving sound absorption through nonlinear active electroacoustic resonators. Physical Review Applied, 13: 014018.
[112]	Gupta G S. 1970. Natural flexural waves and the normal modes of periodically-supported beams and plates. Journal of Sound and Vibration, 13: 89-101.
[113]	Hatanaka D, Yamaguchi H. 2020. Real-space characterization of cavity-coupled waveguide systems in hypersonic phononic crystals. Physical Review Applied, 13: 024005.
[114]	Heckl M A. 1964. Investigations on the vibrations of grillages and other simple beam structures. The Journal of the Acoustical Society of America, 36: 1335-1343.
[115]	Herbold E B, Nesterenko V F. 2013. Propagation of rarefaction pulses in discrete materials with strain-softening behavior. Physical Review Letters, 110: 144101.
[116]	Hersh A S, Walker B E, Celano J W. 2003. Helmholtz resonator impedance model, part 1: Nonlinear behavior. AIAA Journal, 41: 795-808.
[117]	Hsu C W, Zhen B, Stone A D, et al. 2016. Bound states in the continuum. Nature Reviews Materials, 1: 16048. doi: 10.1038/natrevmats.2016.48
[118]	Hu B, Fang X, Cheng L, et al. 2023. Attenuation of impact waves in a nonlinear acoustic metamaterial beam. Nonlinear Dynamics, 111: 15801-15816. doi: 10.1007/s11071-023-08689-z
[119]	Hu G, Austin A C M, Sorokin V, et al. 2021. Metamaterial beam with graded local resonators for broadband vibration suppression. Mechanical Systems and Signal Processing, 146: 106982. doi: 10.1016/j.ymssp.2020.106982
[120]	Huang S, Li Y, Zhu J, et al. 2023. Sound-absorbing materials. Physical Review Applied, 20: 010501. doi: 10.1103/PhysRevApplied.20.010501
[121]	Huang S, Zhou Z, Li D, et al. 2020. Compact broadband acoustic sink with coherently coupled weak resonances. Science Bulletin, 65: 373-379. doi: 10.1016/j.scib.2019.11.008
[122]	Hussein M I, Leamy M J, Ruzzene M. 2014. Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Applied Mechanics Reviews, 66: 040802.
[123]	Ingard U, Ising H. 1967. Acoustic nonlinearity of an orifice. The Journal of the Acoustical Society of America, 42: 6-17.
[124]	Ingård U, Labate S. 1950. Acoustic circulation effects and the nonlinear impedance of orifices. The Journal of the Acoustical Society of America, 22: 211-218.
[125]	Jeon G J, Oh J H. 2021. Nonlinear acoustic metamaterial for efficient frequency down-conversion. Physical Review E, 103: 012212.
[126]	Jhang K-Y, Kim K-C. 1999. Evaluation of material degradation using nonlinear acoustic effect. Ultrasonics, 37: 39-44.
[127]	Jian Y, Tang L, Hu G, et al. 2022. Design of graded piezoelectric metamaterial beam with spatial variation of electrodes. International Journal of Mechanical Sciences, 218: 107068. doi: 10.1016/j.ijmecsci.2022.107068
[128]	Jiao W, Gonella S. 2018a. Intermodal and subwavelength energy trapping in nonlinear metamaterial waveguides. Physical Review Applied, 10: 024006.
[129]	Jiao W, Gonella S. 2018b. Mechanics of inter-modal tunneling in nonlinear waveguides. Journal of the Mechanics and Physics of Solids, 111: 1-17.
[130]	Jiao W, Gonella S. 2021. Wavenumber-space band clipping in nonlinear periodic structures. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 477: 20210052.
[131]	Jiao W, Shu H, Tournat V, et al. 2024. Phase transitions in 2D multistable mechanical metamaterials via collisions of soliton-like pulses. Nature Communications, 15: 333. doi: 10.1038/s41467-023-44293-w
[132]	Jin L, Khajehtourian R, Mueller J, et al. 2020. Guided transition waves in multistable mechanical metamaterials. Proceedings of the National Academy of Sciences, 117: 2319-2325. doi: 10.1073/pnas.1913228117
[133]	Jin Y, Torrent D, Rouhani B D, et al. 2025. The 2024 phononic crystals roadmap. Journal of Physics D: Applied Physics, 58: 113001. doi: 10.1088/1361-6463/ad9ab2
[134]	Jing X, Sun X. 2002. Sound-excited flow and acoustic nonlinearity at an orifice. Physics of Fluids, 14: 268-276.
[135]	Job S, Santibanez F, Tapia F, et al. 2009. Wave localization in strongly nonlinear Hertzian chains with mass defect. Physical Review E, 80: 025602. doi: 10.1103/PhysRevE.80.025602
[136]	Johnson K L. 1982. One hundred years of Hertz contact. Proceedings of the Institution of Mechanical Engineers, 196: 363-378.
[137]	Kadic M, Bückmann T, Schittny R, et al. 2013. Metamaterials beyond electromagnetism. Reports on Progress in Physics, 76: 126501. doi: 10.1088/0034-4885/76/12/126501
[138]	Khajehtourian R, Kochmann D M. 2021. A continuum description of substrate-free dissipative reconfigurable metamaterials. Journal of the Mechanics and Physics of Solids, 147: 104217.
[139]	Khomeriki R, Lepri S, Ruffo S. 2004. Nonlinear supratransmission and bistability in the Fermi-Pasta-Ulam model. Physical Review E, 70: 066626.
[140]	Khoo I C, Wang Y K. 1976. Multiple time scale analysis of an anharmonic crystal. Journal of Mathematical Physics, 17: 222-227.
[141]	Kim B L, Chong C, Hajarolasvadi S, et al. 2023. Dynamics of time-modulated, nonlinear phononic lattices. Physical Review E, 107: 034211. doi: 10.1103/PhysRevE.107.034211
[142]	Kim E, Li F, Chong C, et al. 2015. Highly nonlinear wave propagation in elastic woodpile periodic structures. Physical Review Letters, 114: 118002. doi: 10.1103/PhysRevLett.114.118002
[143]	Kim E, Yang J. 2019. Review: Wave propagation in granular metamaterials. Functional Composites and Structures, 1: 012002.
[144]	Komkin A, Bykov A, Mironov M. 2020. Experimental study of nonlinear acoustic impedance of circular orifices. The Journal of the Acoustical Society of America, 148: 1391-1403.
[145]	Korpas L M, Yin R, Yasuda H, et al. 2021. Temperature-responsive multistable metamaterials. ACS Applied Materials & Interfaces, 13: 31163-31170.
[146]	Krushynska A O, Miniaci M, Bosia F, et al. 2017. Coupling local resonance with Bragg band gaps in single-phase mechanical metamaterials. Extreme Mechanics Letters, 12: 30-36. doi: 10.1016/j.eml.2016.10.004
[147]	Kumar R, Ezhilarasi D. 2023. A state-of-the-art survey of model order reduction techniques for large-scale coupled dynamical systems. International Journal of Dynamics and Control, 11: 900-916.
[148]	Kushwaha M S, Halevi P, Dobrzynski L, et al. 1993. Acoustic band structure of periodic elastic composites. Physical Review Letters, 71: 2022-2025. doi: 10.1103/PhysRevLett.71.2022
[149]	Laly Z, Atalla N, Meslioui S-A. 2018. Acoustical modeling of micro-perforated panel at high sound pressure levels using equivalent fluid approach. Journal of Sound and Vibration, 427: 134-158.
[150]	Laly Z, Atalla N, Meslioui S-A, et al. 2019. Sensitivity analysis of micro-perforated panel absorber models at high sound pressure levels. Applied Acoustics, 156: 7-20. doi: 10.1016/j.apacoust.2019.06.025
[151]	Lan J, Li Y, Yu H, et al. 2017. Nonlinear effects in acoustic metamaterial based on a cylindrical pipe with ordered Helmholtz resonators. Physics Letters A, 381: 1111-1117. doi: 10.1016/j.physleta.2017.01.036
[152]	Larbi W, Deü J-F. 2019. Reduced order finite element formulations for vibration reduction using piezoelectric shunt damping. Applied Acoustics, 147: 111-120.
[153]	Lazarov B S, Jensen J S. 2007. Low-frequency band gaps in chains with attached non-linear oscillators. International Journal of Non-Linear Mechanics, 42: 1186-1193.
[154]	Leon J. 2003. Nonlinear supratransmission as a fundamental instability. Physics Letters A, 319: 130-136.
[155]	Lepri S, Casati G. 2011. Asymmetric wave propagation in nonlinear systems. Physical Review Letters, 106: 164101.
[156]	Li F, Anzel P, Yang J, et al. 2014. Granular acoustic switches and logic elements. Nature Communications, 5: 5311. doi: 10.1038/ncomms6311
[157]	Li J, Chan C T. 2004. Double-negative acoustic metamaterial. Physical Review E, 70: 055602.
[158]	Li Z-N, Wang Y-Z, Wang Y-S. 2020. Tunable nonreciprocal transmission in nonlinear elastic wave metamaterial by initial stresses. International Journal of Solids and Structures, 182-183: 218-235.
[159]	Li Z-N, Wang Y-Z, Wang Y-S. 2021. Tunable mechanical diode of nonlinear elastic metamaterials induced by imperfect interface. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 477: 20200357.
[160]	Li Z-N, Yuan B, Wang Y-Z, et al. 2019. Diode behavior and nonreciprocal transmission in nonlinear elastic wave metamaterial. Mechanics of Materials, 133: 85-101. doi: 10.1016/j.mechmat.2019.03.010
[161]	Liang B, Guo X S, Tu J, et al. 2010. An acoustic rectifier. Nature Materials, 9: 989-992. doi: 10.1038/nmat2881
[162]	Librandi G, Tubaldi E, Bertoldi K. 2021. Programming nonreciprocity and reversibility in multistable mechanical metamaterials. Nature Communications, 12: 3454.
[163]	Liu E, Fang X, Wen J. 2022a. Harmonic and shock wave propagation in bistable periodic structure: Regularity, randomness, and tunability. Journal of Vibration and Control, 28: 3332-3343.
[164]	Liu J, Wang Y, Yang S, et al. 2024. Customized quasi-zero-stiffness metamaterials for ultra-low frequency broadband vibration isolation. International Journal of Mechanical Sciences, 269: 108958. doi: 10.1016/j.ijmecsci.2024.108958
[165]	Liu Z, Fang H, Xu J, et al. 2023. Discriminative transition sequences of origami metamaterials for mechanologic. Advanced Intelligent Systems, 5: 2200146. doi: 10.1002/aisy.202200146
[166]	Liu Z, Shan S, Cheng L. 2022b. Nonlinear-Lamb-wave-based plastic damage detection assisted by topologically designed metamaterial filters. Structural Health Monitoring, 22: 1828-1843.
[167]	Liu Z, Zhang X, Mao Y, et al. 2000. Locally resonant sonic materials. Science, 289: 1734-1736. doi: 10.1126/science.289.5485.1734
[168]	Macías-Díaz J E. 2008. Numerical study of the transmission of energy in discrete arrays of sine-Gordon equations in two space dimensions. Physical Review E, 77: 016602.
[169]	Man Y, Boechler N, Theocharis G, et al. 2012. Defect modes in one-dimensional granular crystals. Physical Review E, 85: 037601. doi: 10.1103/PhysRevE.85.037601
[170]	Manktelow K, Leamy M J, Ruzzene M. 2011. Multiple scales analysis of wave–wave interactions in a cubically nonlinear monoatomic chain. Nonlinear Dynamics, 63: 193-203.
[171]	Manktelow K, Leamy M J, Ruzzene M. 2013a. Comparison of asymptotic and transfer matrix approaches for evaluating intensity-dependent dispersion in nonlinear photonic and phononic crystals. Wave Motion, 50: 494-508.
[172]	Manktelow K, Narisetti R K, Leamy M J, et al. 2013b. Finite-element based perturbation analysis of wave propagation in nonlinear periodic structures. Mechanical Systems and Signal Processing, 39: 32-46. doi: 10.1016/j.ymssp.2012.04.015
[173]	Manktelow K L, Leamy M J, Ruzzene M. 2013c. Topology design and optimization of nonlinear periodic materials. Journal of the Mechanics and Physics of Solids, 61: 2433-2453.
[174]	Maradudin A A, Mazur P, Montroll E W, et al. 1958. Remarks on the vibrations of diatomic lattices. Reviews of Modern Physics, 30: 175-196. doi: 10.1103/RevModPhys.30.175
[175]	Marathe A, Chatterjee A. 2006. Wave attenuation in nonlinear periodic structures using harmonic balance and multiple scales. Journal of Sound and Vibration, 289: 871-888.
[176]	Mead D J. 1971. Vibration response and wave propagation in periodic structures. Journal of Engineering for Industry, 93: 783-792.
[177]	Meaud J. 2020. Nonlinear wave propagation and dynamic reconfiguration in two-dimensional lattices with bistable elements. Journal of Sound and Vibration, 473: 115239.
[178]	Melling T H. 1973. The acoustic impendance of perforates at medium and high sound pressure levels. Journal of Sound and Vibration, 29: 1-65.
[179]	Merkel A, Tournat V, Gusev V. 2011. Experimental evidence of rotational elastic waves in granular phononic crystals. Physical Review Letters, 107: 225502.
[180]	Miniaci M, Gliozzi A S, Morvan B, et al. 2017. Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals. Physical Review Letters, 118: 214301. doi: 10.1103/PhysRevLett.118.214301
[181]	Mojahed A, Bunyan J, Tawfick S, et al. 2019. Tunable acoustic nonreciprocity in strongly nonlinear waveguides with asymmetry. Physical Review Applied, 12: 034033. doi: 10.1103/PhysRevApplied.12.034033
[182]	Mosquera-Sánchez J A, Alfahmi O, Erturk A, et al. 2024. Broadening the frequency response of a Duffing-type piezoelectric shunt by means of negative capacitance. Journal of Sound and Vibration, 578: 118344. doi: 10.1016/j.jsv.2024.118344
[183]	Mosquera-Sánchez J A, De Marqui C. 2024. Broadband and multimode attenuation in Duffing- and NES-type piezoelectric metastructures. International Journal of Mechanical Sciences, 270: 109084.
[184]	Mosquera-Sánchez J A, De Marqui Jr C. 2021. Dynamics and wave propagation in nonlinear piezoelectric metastructures. Nonlinear Dynamics, 105: 2995-3023.
[185]	Nadkarni N, Arrieta A F, Chong C, et al. 2016. Unidirectional transition waves in bistable lattices. Physical Review Letters, 116: 244501. doi: 10.1103/PhysRevLett.116.244501
[186]	Nadkarni N, Daraio C, Kochmann D M. 2014. Dynamics of periodic mechanical structures containing bistable elastic elements: From elastic to solitary wave propagation. Physical Review E, 90: 023204.
[187]	Narisetti R K, Leamy M J, Ruzzene M. 2010. A perturbation approach for predicting wave propagation in one-dimensional nonlinear periodic structures. Journal of Vibration and Acoustics, 132: 031001.
[188]	Narisetti R K, Ruzzene M, Leamy M J. 2011. A perturbation approach for analyzing dispersion and group velocities in two-dimensional nonlinear periodic lattices. Journal of Vibration and Acoustics, 133: 061020.
[189]	Narisetti R K, Ruzzene M, Leamy M J. 2012. Study of wave propagation in strongly nonlinear periodic lattices using a harmonic balance approach. Wave Motion, 49: 394-410.
[190]	Nash L M, Kleckner D, Read A, et al. 2015. Topological mechanics of gyroscopic metamaterials. Proceedings of the National Academy of Sciences, 112: 14495-14500. doi: 10.1073/pnas.1507413112
[191]	Nassar H, Chen H, Norris A N, et al. 2017. Non-reciprocal wave propagation in modulated elastic metamaterials. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 473: 20170188. doi: 10.1098/rspa.2017.0188
[192]	Nassar H, Yousefzadeh B, Fleury R, et al. 2020. Nonreciprocity in acoustic and elastic materials. Nature Reviews Materials, 5: 667-685. doi: 10.1038/s41578-020-0206-0
[193]	Nesterenko V F. 1983. Propagation of nonlinear compression pulses in granular media. Journal of Applied Mechanics and Technical Physics, 24: 733-743.
[194]	Nesterenko V F. 2018. Waves in strongly nonlinear discrete systems. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 376: 20170130.
[195]	Nesterenko V F, Daraio C, Herbold E B, et al. 2005. Anomalous wave reflection at the interface of two strongly nonlinear granular media. Physical Review Letters, 95: 158702. doi: 10.1103/PhysRevLett.95.158702
[196]	Ni X, Rizzo P, Yang J, et al. 2012. Monitoring the hydration of cement using highly nonlinear solitary waves. NDT & E International, 52: 76-85.
[197]	Norris A N. 2008. Acoustic cloaking theory. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 464: 2411-2434.
[198]	Ou H, Hu L, Wang Y, et al. 2024. High-efficient and reusable impact mitigation metamaterial based on compression-torsion coupling mechanism. Journal of the Mechanics Physics of Solids, 186: 105594. doi: 10.1016/j.jmps.2024.105594
[199]	Pal A, Sitti M. 2023. Programmable mechanical devices through magnetically tunable bistable elements. Proceedings of the National Academy of Sciences, 120: e2212489120.
[200]	Pal R K, Vila J, Leamy M, et al. 2018. Amplitude-dependent topological edge states in nonlinear phononic lattices. Physical Review E, 97: 032209. doi: 10.1103/PhysRevE.97.032209
[201]	Palermo A, Celli P, Yousefzadeh B, et al. 2020. Surface wave non-reciprocity via time-modulated metamaterials. Journal of the Mechanics and Physics of Solids, 145: 104181. doi: 10.1016/j.jmps.2020.104181
[202]	Panigrahi S R, Feeny B F, Diaz A R. 2017. Wave–wave interactions in a periodic chain with quadratic nonlinearity. Wave Motion, 69: 65-80.
[203]	Park S-H. 2013a. Acoustic properties of micro-perforated panel absorbers backed by Helmholtz resonators for the improvement of low-frequency sound absorption. Journal of Sound and Vibration, 332: 4895-4911.
[204]	Park S-H. 2013b. A design method of micro-perforated panel absorber at high sound pressure environment in launcher fairings. Journal of Sound and Vibration, 332: 521-535.
[205]	Patil G U, Matlack K H. 2021. Wave self-interactions in continuum phononic materials with periodic contact nonlinearity. Wave Motion, 105: 102763.
[206]	Patil G U, Matlack K H. 2022. Review of exploiting nonlinearity in phononic materials to enable nonlinear wave responses. Acta Mechanica, 233: 1-46.
[207]	Peng F. 2018. Sound absorption of a porous material with a perforated facing at high sound pressure levels. Journal of Sound and Vibration, 425: 1-20.
[208]	Pernas-Salomón R, Shmuel G. 2020. Fundamental principles for generalized Willis metamaterials. Physical Review Applied, 14: 064005.
[209]	Plattner L. 2004. Optical properties of the scales of morpho rhetenor butterflies: Theoretical and experimental investigation of the back-scattering of light in the visible spectrum. Journal of the Royal Society Interface, 1: 49-59.
[210]	Popa B-I, Cummer S A. 2014. Non-reciprocal and highly nonlinear active acoustic metamaterials. Nature Communications, 5: 3398.
[211]	Porter M A, Kevrekidis P G, Daraio C. 2015. Granular crystals: Nonlinear dynamics meets materials engineering. Physics Today, 68: 44-50.
[212]	Qu R, Guo J, Fang Y, et al. 2023. Broadband quasi-perfect sound absorption by a metasurface with coupled resonators at both low- and high-amplitude excitations. Mechanical Systems and Signal Processing, 204: 110782. doi: 10.1016/j.ymssp.2023.110782
[213]	Qu S, Gao N, Tinel A, et al. 2022. Underwater metamaterial absorber with impedance-matched composite. Science Advances, 8: eabm4206. doi: 10.1126/sciadv.abm4206
[214]	Raney J R, Nadkarni N, Daraio C, et al. 2016. Stable propagation of mechanical signals in soft media using stored elastic energy. Proceedings of the National Academy of Sciences, 113: 9722-9727. doi: 10.1073/pnas.1604838113
[215]	Richoux O, Tournat V, Van Suu T L. 2007. Acoustic wave dispersion in a one-dimensional lattice of nonlinear resonant scatterers. Physical Review E, 75: 026615.
[216]	Rienstra S W, Singh D K. 2018. Nonlinear asymptotic impedance model for a Helmholtz resonator of finite depth. AIAA Journal, 56: 1792-1802.
[217]	Rosa M I N, Leamy M J, Ruzzene M. 2023. Amplitude-dependent edge states and discrete breathers in nonlinear modulated phononic lattices. New Journal of Physics, 25: 103053.
[218]	Rosa M I N, Pal R K, Arruda J R F, et al. 2019. Edge states and topological pumping in spatially modulated elastic lattices. Physical Review Letters, 123: 034301. doi: 10.1103/PhysRevLett.123.034301
[219]	Sadeghi S, Allison S R, Bestill B, et al. 2021. TMP origami jumping mechanism with nonlinear stiffness. Smart Materials and Structures, 30: 065002. doi: 10.1088/1361-665X/abf5b2
[220]	Scheibner C, Irvine W T M, Vitelli V. 2020. Non-Hermitian band topology and skin modes in active elastic media. Physical Review Letters, 125: 118001.
[221]	Sepehri S, Mashhadi M M, Fakhrabadi M M S. 2022. Wave propagation in fractionally damped nonlinear phononic crystals. Nonlinear Dynamics, 110: 1683-1708.
[222]	Serra-Garcia M, Lydon J, Daraio C. 2016. Extreme stiffness tunability through the excitation of nonlinear defect modes. Physical Review E, 93: 010901.
[223]	Settimi V, Lepidi M, Bacigalupo A. 2021. Nonlinear dispersion properties of one-dimensional mechanical metamaterials with inertia amplification. International Journal of Mechanical Sciences, 201: 106461.
[224]	Shan S, Wen F, Cheng L. 2021. Purified nonlinear guided waves through a metamaterial filter for inspection of material microstructural changes. Smart Materials and Structures, 30: 095017.
[225]	Shen H, Wen J, Yu D, et al. 2013. Control of sound and vibration of fluid-filled cylindrical shells via periodic design and active control. Journal of Sound and Vibration, 332: 4193-4209. doi: 10.1016/j.jsv.2013.03.007
[226]	Sheng P, Fang X, Yu D, et al. 2024. Mitigating aeroelastic vibration of strongly nonlinear metamaterial supersonic wings under high temperature. Nonlinear Dynamics, https://doi.org/10.1007/s11071-024-10278-7.
[227]	Sigalas M M, Economou E N. 1992. Elastic and acoustic wave band structure. Journal of Sound and Vibration, 158: 377-382.
[228]	Silva P B, Leamy M J, Geers M G D, et al. 2019a. Emergent subharmonic band gaps in nonlinear locally resonant metamaterials induced by autoparametric resonance. Physical Review E, 99: 063003. doi: 10.1103/PhysRevE.99.063003
[229]	Silva T, Tan D, De Marqui C, et al. 2019b. Vibration attenuation in a nonlinear flexible structure via nonlinear switching circuits and energy harvesting implications. Journal of Intelligent Material Systems and Structures, 30: 965-976. doi: 10.1177/1045389X19828835
[230]	Silva T M, Clementino M A, De Marqui Jr C, et al. 2018. An experimentally validated piezoelectric nonlinear energy sink for wideband vibration attenuation. Journal of Sound and Vibration, 437: 68-78. doi: 10.1016/j.jsv.2018.08.038
[231]	Singh D K, Rienstra S W. 2014. Nonlinear asymptotic impedance model for a Helmholtz resonator liner. Journal of Sound and Vibration, 333: 3536-3549.
[232]	Singhal T, Kim E, Kim T-Y, et al. 2017. Weak bond detection in composites using highly nonlinear solitary waves. Smart Materials and Structures, 26: 055011. doi: 10.1088/1361-665X/aa6823
[233]	Sivian L J. 1935. Acoustic impedance of small orifices. The Journal of the Acoustical Society of America, 7: 94-101.
[234]	Snee D D J M, Ma Y-P. 2019. Edge solitons in a nonlinear mechanical topological insulator. Extreme Mechanics Letters, 30: 100487.
[235]	Spadoni A, Daraio C. 2010. Generation and control of sound bullets with a nonlinear acoustic lens. Proceedings of the National Academy of Sciences, 107: 7230-7234.
[236]	Su J, Rupp J, Garmory A, et al. 2015. Measurements and computational fluid dynamics predictions of the acoustic impedance of orifices. Journal of Sound and Vibration, 352: 174-191. doi: 10.1016/j.jsv.2015.05.009
[237]	Su W P, Schrieffer J R, Heeger A J. 1979. Solitons in polyacetylene. Physical Review Letters, 42: 1698-1701.
[238]	Sugimoto N. 1992. Propagation of nonlinear acoustic waves in a tunnel with an array of Helmholtz resonators. Journal of Fluid Mechanics, 244: 55-78.
[239]	Sugimoto N. 1996. Acoustic solitary waves in a tunnel with an array of Helmholtz resonators. The Journal of the Acoustical Society of America, 99: 1971-1976.
[240]	Sugino C, Ruzzene M, Erturk A. 2020. Digitally programmable resonant elastic metamaterials. Physical Review Applied, 13: 061001.
[241]	Sun Y, Zheng H, Han Q, et al. 2024. Non-contact electromagnetic controlled metamaterial beams for low-frequency vibration suppression. International Journal of Solids and Structures, 290: 112667. doi: 10.1016/j.ijsolstr.2024.112667
[242]	Swinteck N Z, Muralidharan K, Deymier P A. 2013. Phonon scattering in one-dimensional anharmonic crystals and superlattices: Analytical and numerical study. Journal of Vibration and Acoustics, 135: 041016.
[243]	Tam C K W, Auriault L. 1999. Jet mixing noise from fine-scale turbulence. AIAA Journal, 37: 145-153.
[244]	Tam C K W, Ju H, Jones M G, et al. 2010. A computational and experimental study of resonators in three dimensions. Journal of Sound and Vibration, 329: 5164-5193. doi: 10.1016/j.jsv.2010.06.005
[245]	Tam C K W, Ju H, Walker B E. 2008. Numerical simulation of a slit resonator in a grazing flow under acoustic excitation. Journal of Sound and Vibration, 313: 449-471.
[246]	Tam C K W, Kurbatskii K A, Ahuja K K, et al. 2001. A numerical and experimental investigation of the dissipation mechanisms of resonant acoustic liners. Journal of Sound and Vibration, 245: 545-557. doi: 10.1006/jsvi.2001.3571
[247]	Tam C K W, Pastouchenko N N, Jones M G, et al. 2014. Experimental validation of numerical simulations for an acoustic liner in grazing flow: Self-noise and added drag. Journal of Sound and Vibration, 333: 2831-2854. doi: 10.1016/j.jsv.2014.02.019
[248]	Tamura S, Hurley D C, Wolfe J P. 1988. Acoustic-phonon propagation in superlattices. Physical Review B, 38: 1427-1449.
[249]	Tang Y, He W, Xin F, et al. 2020. Nonlinear sound absorption of ultralight hybrid-cored sandwich panels. Mechanical Systems and Signal Processing, 135: 106428. doi: 10.1016/j.ymssp.2019.106428
[250]	Tempelman J R, Matlack K H, Vakakis A F. 2021. Topological protection in a strongly nonlinear interface lattice. Physical Review B, 104: 174306.
[251]	Theocharis G, Boechler N, Daraio C. 2013. Nonlinear periodic phononic structures and granular crystals//P. A. DEYMIER. Acoustic metamaterials and phononic crystals. Berlin, Heidelberg: Springer, 217-251.
[252]	Theocharis G, Kavousanakis M, Kevrekidis P G, et al. 2009. Localized breathing modes in granular crystals with defects. Physical Review E, 80: 066601. doi: 10.1103/PhysRevE.80.066601
[253]	Tian W, Yang Z, Li M, et al. 2025. Theoretical modeling and mechanism analysis of nonlinear metastructure for supersonic aeroelastic suppression. Mechanical Systems and Signal Processing, 224: 111931. doi: 10.1016/j.ymssp.2024.111931
[254]	Tian W, Zhao T, Gu Y, et al. 2022a. Nonlinear flutter suppression and performance evaluation of periodically embedded nonlinear vibration absorbers in a supersonic FGM plate. Aerospace Science and Technology, 121: 107198. doi: 10.1016/j.ast.2021.107198
[255]	Tian W, Zhao T, Yang Z. 2022b. Supersonic meta-plate with tunable-stiffness nonlinear oscillators for nonlinear flutter suppression. International Journal of Mechanical Sciences, 229: 107533.
[256]	Tian Y, Shen Y, Rao D, et al. 2019. Metamaterial improved nonlinear ultrasonics for fatigue damage detection. Smart Materials and Structures, 28: 075038. doi: 10.1088/1361-665X/ab2566
[257]	Tournat V, Gusev V E, Castagnède B. 2004. Self-demodulation of elastic waves in a one-dimensional granular chain. Physical Review E, 70: 056603.
[258]	Trainiti G, Xia Y, Marconi J, et al. 2019. Time-periodic stiffness modulation in elastic metamaterials for selective wave filtering: Theory and experiment. Physical Review Letters, 122: 124301. doi: 10.1103/PhysRevLett.122.124301
[259]	Vakakis A F, King M E. 1998. Resonant oscillations of a weakly coupled, nonlinear layered system. Acta Mechanica, 128: 59-80.
[260]	Vasiliev V V, Barynin V A, Razin A F. 2012. Anisogrid composite lattice structures–development and aerospace applications. Composite Structures, 94: 1117-1127.
[261]	Vasios N, Deng B, Gorissen B, et al. 2021. Universally bistable shells with nonzero Gaussian curvature for two-way transition waves. Nature Communications, 12: 695. doi: 10.1038/s41467-020-20698-9
[262]	Veenstra J, Gamayun O, Guo X, et al. 2024. Non-reciprocal topological solitons in active metamaterials. Nature, 627: 528-533. doi: 10.1038/s41586-024-07097-6
[263]	Vila J, Paulino G H, Ruzzene M. 2019. Role of nonlinearities in topological protection: Testing magnetically coupled fidget spinners. Physical Review B, 99: 125116.
[264]	Wallen S P, Boechler N. 2017. Shear to longitudinal mode conversion via second harmonic generation in a two-dimensional microscale granular crystal. Wave Motion, 68: 22-30.
[265]	Wang K, Zhou J, Cai C, et al. 2019. Mathematical modeling and analysis of a meta-plate for very low-frequency band gap. Applied Mathematical Modelling, 73: 581-597. doi: 10.1016/j.apm.2019.04.033
[266]	Wang T, Touzé C, Li H, et al. 2024a. Nonlinear dispersion relationships and dissipative properties of damped metamaterials embedding bistable attachments. Nonlinear Dynamics, https://doi.org/10.1007/s11071-024-10462-9.
[267]	Wang T, Islam T ul, Steur E, et al. 2024b. Programmable metachronal motion of closely packed magnetic artificial cilia. Lab on a Chip, 24: 1573-1585. doi: 10.1039/D3LC00956D
[268]	Wang Y-F, Wang Y-Z, Wu B, et al. 2020. Tunable and active phononic crystals and metamaterials. Applied Mechanics Reviews, 72: 040801. doi: 10.1115/1.4046222
[269]	Wang Y, Yousefzadeh B, Chen H, et al. 2018. Observation of nonreciprocal wave propagation in a dynamic phononic lattice. Physical Review Letters, 121: 194301. doi: 10.1103/PhysRevLett.121.194301
[270]	Wei L-S, Wang Y-Z, Wang Y-S. 2020. Nonreciprocal transmission of nonlinear elastic wave metamaterials by incremental harmonic balance method. International Journal of Mechanical Sciences, 173: 105433.
[271]	Wen Z, Jin Y, Gao P, et al. 2022. Topological cavities in phononic plates for robust energy harvesting. Mechanical Systems and Signal Processing, 162: 108047. doi: 10.1016/j.ymssp.2021.108047
[272]	Wu B, Destrade M, Chen W. 2020. Nonlinear response and axisymmetric wave propagation in functionally graded soft electro-active tubes. International Journal of Mechanical Sciences, 187: 106006.
[273]	Wu B, Jiang W, Jiang J, et al. 2024. Wave manipulation in intelligent metamaterials: Recent progress and prospects. Advanced Functional Materials, 34: 2316745. doi: 10.1002/adfm.202316745
[274]	Wu G, Lu Z, Xu X, et al. 2019. Numerical investigation of aeroacoustics damping performance of a Helmholtz resonator: Effects of geometry, grazing and bias flow. Aerospace Science and Technology, 86: 191-203. doi: 10.1016/j.ast.2019.01.007
[275]	Wu Z, Wang K W. 2019. On the wave propagation analysis and supratransmission prediction of a metastable modular metastructure for non-reciprocal energy transmission. Journal of Sound and Vibration, 458: 389-406.
[276]	Xia Y, Ruzzene M, Erturk A. 2019. Dramatic bandwidth enhancement in nonlinear metastructures via bistable attachments. Applied Physics Letters, 114: 093501.
[277]	Xia Y, Ruzzene M, Erturk A. 2020. Bistable attachments for wideband nonlinear vibration attenuation in a metamaterial beam. Nonlinear Dynamics, 102: 1285-1296.
[278]	Xiao Y, Wen J, Wen X. 2012. Flexural wave band gaps in locally resonant thin plates with periodically attached spring–mass resonators. Journal of Physics D: Applied Physics, 45: 195401.
[279]	Xiao Z, Gao P, He X, et al. 2023. Multifunctional acoustic metamaterial for air ventilation, broadband sound insulation and switchable transmission. Journal of Physics D: Applied Physics, 56: 044006. doi: 10.1088/1361-6463/acaa44
[280]	Xiao Z, Gao P, He X, et al. 2024. Lightweight cellular multifunctional metamaterials with superior low-frequency sound absorption, broadband energy harvesting and high load-bearing capacity. Materials & Design, 241: 112912.
[281]	Xiao Z, Gao P, Wang D, et al. 2021. Ventilated metamaterials for broadband sound insulation and tunable transmission at low frequency. Extreme Mechanics Letters, 46: 101348. doi: 10.1016/j.eml.2021.101348
[282]	Xu L, Xiang Z. 2024. Chaotic metastructures for frequency self-conversion. Mechanical Systems and Signal Processing, 206: 110927.
[283]	Xu Q, Wang J, Lv Y, et al. 2023. Vibration characteristics of linear and nonlinear dissipative elastic metamaterials rotor with geometrical nonlinearity. International Journal of Non-Linear Mechanics, 157: 104543. doi: 10.1016/j.ijnonlinmec.2023.104543
[284]	Xu X, Barnhart M V, Fang X, et al. 2019. A nonlinear dissipative elastic metamaterial for broadband wave mitigation. International Journal of Mechanical Sciences, 164: 105159. doi: 10.1016/j.ijmecsci.2019.105159
[285]	Xue Y, Li J, Wang Y, et al. 2023. Broadband vibration attenuation in nonlinear meta-structures with magnet coupling mechanism: Theory and experiments. Communications in Nonlinear Science and Numerical Simulation, 127: 107543. doi: 10.1016/j.cnsns.2023.107543
[286]	Xue Y, Li J, Wang Y, et al. 2024. Widely tunable magnetorheological metamaterials with nonlinear amplification mechanism. International Journal of Mechanical Sciences, 264: 108830. doi: 10.1016/j.ijmecsci.2023.108830
[287]	Yablonovitch E 1987. Inhibited spontaneous emission in solid-state physics and electronics. Physical Review Letters, 58: 2059-2062.
[288]	Yang D, Guo X, Zhang W, et al. 2024. Non-linear dynamics and bandgap control in magneto-rheological elastomers metamaterials with inertial amplification. Thin-Walled Structures, 204: 112237. doi: 10.1016/j.tws.2024.112237
[289]	Yao D, Xiong M, Luo J, et al. 2022. Flexural wave mitigation in metamaterial cylindrical curved shells with periodic graded arrays of multi-resonator. Mechanical Systems and Signal Processing, 168: 108721. doi: 10.1016/j.ymssp.2021.108721
[290]	Yao S, Zhou X, Hu G. 2010. Investigation of the negative-mass behaviors occurring below a cut-off frequency. New Journal of Physics, 12: 103025.
[291]	Yasuda H, Korpas L M, Raney J R. 2020. Transition waves and formation of domain walls in multistable mechanical metamaterials. Physical Review Applied, 13: 054067.
[292]	Yi J, Chen C Q. 2024. Delocalization and higher-order topology in a nonlinear elastic lattice. New Journal of Physics, 26: 063004.
[293]	Yi J, Zhang Y, Chen C Q. 2023. Tunable mode conversion in a mechanical metamaterial via second harmonic generation. Journal of Sound and Vibration, 565: 117911.
[294]	Yilmaz C, Hulbert G M, Kikuchi N. 2007. Phononic band gaps induced by inertial amplification in periodic media. Physical Review B, 76: 054309.
[295]	Yin D, Yi K, Liu Z, et al. 2022. Design of cylindrical metashells with piezoelectric materials and digital circuits for multi-modal vibration control. Frontiers in Physics, 10: 958141. doi: 10.3389/fphy.2022.958141
[296]	Yoon S, Kim A, Cantwell W J, et al. 2023. Defect detection in composites by deep learning using solitary waves. International Journal of Mechanical Sciences, 239: 107882. doi: 10.1016/j.ijmecsci.2022.107882
[297]	Yousefzadeh B, Phani A S. 2016. Supratransmission in a disordered nonlinear periodic structure. Journal of Sound and Vibration, 380: 242-266.
[298]	Yu D, Wen J, Shen H, et al. 2012. Propagation of flexural wave in periodic beam on elastic foundations. Physics Letters A, 376: 626-630. doi: 10.1016/j.physleta.2011.11.056
[299]	Yu M, Fang X, Wen J, et al. 2024. Robust nonlinear elastic metamaterial enabled by collision damping. Mechanics of Advanced Materials and Structures, 31: 3630-3637. doi: 10.1080/15376494.2023.2180557
[300]	Yu M, Fang X, Yu D. 2021. Combinational design of linear and nonlinear elastic metamaterials. International Journal of Mechanical Sciences, 199: 106422.
[301]	Zareei A, Deng B, Bertoldi K. 2020. Harnessing transition waves to realize deployable structures. Proceedings of the National Academy of Sciences, 117: 4015-4020.
[302]	Zhang J, Romero-García V, Theocharis G, et al. 2021a. High-amplitude sound propagation in acoustic transmission-line metamaterial. Applied Physics Letters, 118: 104102. doi: 10.1063/5.0040702
[303]	Zhang Q, Fang H, Xu J. 2020. Programmable stopbands and supratransmission effects in a stacked miura-origami metastructure. Physical Review E, 101: 042206.
[304]	Zhang Q, Guo D, Hu G. 2021b. Tailored mechanical metamaterials with programmable quasi-zero-stiffness features for full-band vibration isolation. Advanced Functional Materials, 31: 2101428.
[305]	Zhang Q, Rudykh S. 2024. Propagation of solitary waves in origami-inspired metamaterials. Journal of the Mechanics and Physics of Solids, 187: 105626.
[306]	Zhang X, Yu H, He Z, et al. 2021c. A metamaterial beam with inverse nonlinearity for broadband micro-vibration attenuation. Mechanical Systems and Signal Processing, 159: 107826. doi: 10.1016/j.ymssp.2021.107826
[307]	Zhang Y, Deshmukh A, Wang K-W. 2023. Embodying multifunctional mechano-intelligence in and through phononic metastructures harnessing physical reservoir computing. Advanced Science, 10: 2305074.
[308]	Zhang Z, Gao P, Liu W, et al. 2022. Structured sonic tube with carbon nanotube-like topological edge states. Nature Communications, 13: 5096. doi: 10.1038/s41467-022-32777-0
[309]	Zhao B, Thomsen H R, Pu X, et al. 2024. A nonlinear damped metamaterial: Wideband attenuation with nonlinear bandgap and modal dissipation. Mechanical Systems and Signal Processing, 208: 111079. doi: 10.1016/j.ymssp.2023.111079
[310]	Zhao C, Zhang K, Zhao P, et al. 2023a. Finite-amplitude nonlinear waves in inertial amplification metamaterials: Theoretical and numerical analyses. Journal of Sound and Vibration, 560: 117802. doi: 10.1016/j.jsv.2023.117802
[311]	Zhao J, Zhou G, Zhang D, et al. 2023b. Integrated design of a lightweight metastructure for broadband vibration isolation. International Journal of Mechanical Sciences, 244: 108069. doi: 10.1016/j.ijmecsci.2022.108069
[312]	Zhao J, Zhou H, Yi K, et al. 2023c. Ultra-broad bandgap induced by hybrid hardening and softening nonlinearity in metastructure. Nonlinear Dynamics, 111: 17687-17707. doi: 10.1007/s11071-023-08808-w
[313]	Zhao T, Yang Z, Tian W. 2023d. Tunable nonlinear metastructure with periodic bi-linear oscillators for broadband vibration suppression. Thin-Walled Structures, 191: 110975.
[314]	Zheng S, Li T, Zhao J, et al. 2022. Deployment impact experiment and dynamic analysis of modular truss antenna. International Journal of Aerospace Engineering, 2022: 2038932.
[315]	Zheng Y, Qu Y, Dai S, et al. 2024. Mitigating vibration and sound radiation with a digital piezoelectric meta-shell in heavy fluids. Journal of Sound and Vibration, 573: 118221. doi: 10.1016/j.jsv.2023.118221
[316]	Zhou J, Dou L, Wang K, et al. 2019. A nonlinear resonator with inertial amplification for very low-frequency flexural wave attenuations in beams. Nonlinear Dynamics, 96: 647-665. doi: 10.1007/s11071-019-04812-1
[317]	Zhou J, Wang K, Xu D, et al. 2017. Local resonator with high-static-low-dynamic stiffness for lowering band gaps of flexural wave in beams. Journal of Applied Physics, 121: 044902. doi: 10.1063/1.4974299
[318]	Zhou S, Zhang R, Cheng Y, et al. 2024a. Non-reciprocity and selective wave amplification in nonlinear inertia-induced autoparametric periodic structures. Applied Mathematical Modelling, 130: 457-471. doi: 10.1016/j.apm.2024.03.005
[319]	Zhou W, Li Y, Yan G, et al. 2024b. Quasi-full bandgap generating mechanism by coupling negative stiffness and inertial amplification. European Journal of Mechanics-A/Solids, 103: 105143. doi: 10.1016/j.euromechsol.2023.105143
[320]	Zhou W, Wang Y-Z. 2024. Metamaterial robot driven by nonlinear elastic waves with stop band and nonreciprocal crawling. Nonlinear Dynamics, 112: 5825-5845.
[321]	Zhou W J, Li X P, Wang Y S, et al. 2018. Spectro-spatial analysis of wave packet propagation in nonlinear acoustic metamaterials. Journal of Sound and Vibration, 413: 250-269. doi: 10.1016/j.jsv.2017.10.023
[322]	Zhou X, Liu X, Hu G. 2012. Elastic metamaterials with local resonances: An overview. Theoretical and Applied Mechanics Letters, 2: 041001.
[323]	Zhou X, Zhang W, Geng X, et al. 2025. Broadband sound absorption of micro-perforated sandwich panels with hierarchical honeycomb core at high sound pressure levels. Composite Structures, 354: 118794. doi: 10.1016/j.compstruct.2024.118794
[324]	Zhu J, Gao H, Dai S, et al. 2023a. Multilayer structures for high-intensity sound energy absorption in low-frequency range. International Journal of Mechanical Sciences, 247: 108197. doi: 10.1016/j.ijmecsci.2023.108197
[325]	Zhu J, Qu Y, Gao H, et al. 2022. Nonlinear sound absorption of Helmholtz resonators with serrated necks under high-amplitude sound wave excitation. Journal of Sound and Vibration, 537: 117197. doi: 10.1016/j.jsv.2022.117197
[326]	Zhu J, Qu Y, Gao H, et al. 2024. A tunable sound absorber with perfect sound absorption for suppressing acoustic waves of different intensities. Journal of Sound and Vibration, 577: 118306. doi: 10.1016/j.jsv.2024.118306
[327]	Zhu W, Deng W, Liu Y, et al. 2023b. Topological phononic metamaterials. Reports on Progress in Physics, 86: 106501. doi: 10.1088/1361-6633/aceeee
[328]	Zhuang Y, Li Q, Yang D, et al. 2024. Vibration suppression of power cabin for underwater vehicle based on mechanical metamaterial flanges. Ocean Engineering, 310: 118540. doi: 10.1016/j.oceaneng.2024.118540