-
摘要: 量子计算在算力上有望指数级超越经典计算, 然而亟需拓展实际应用场景. 计算力学应用场景丰富, 但面临多尺度、多物理场、极端环境等问题带来的算力挑战. 因此, 两者在算力和应用场景上的互补融合式发展前景广阔. 本文旨在梳理量子计算在计算力学中的应用现状, 并展望该领域未来的发展趋势.Abstract: Quantum computing has the potential to exponentially surpass classical computing in terms of computational power, but its practical applications need further expansion. At the same time, computational mechanics offers a wide range of applications, but faces challenges of significant computational power requirements arising from multi-scale, multi-physics, and extreme conditions, among others. Therefore, the complementary development of quantum computing and computational mechanics holds great promise. This paper reviews the current state of quantum computing applications in computational mechanics and discusses future trends in this field.
-
Key words:
- quantum computing /
- computational mechanics /
- computing power /
- computational complexity
-
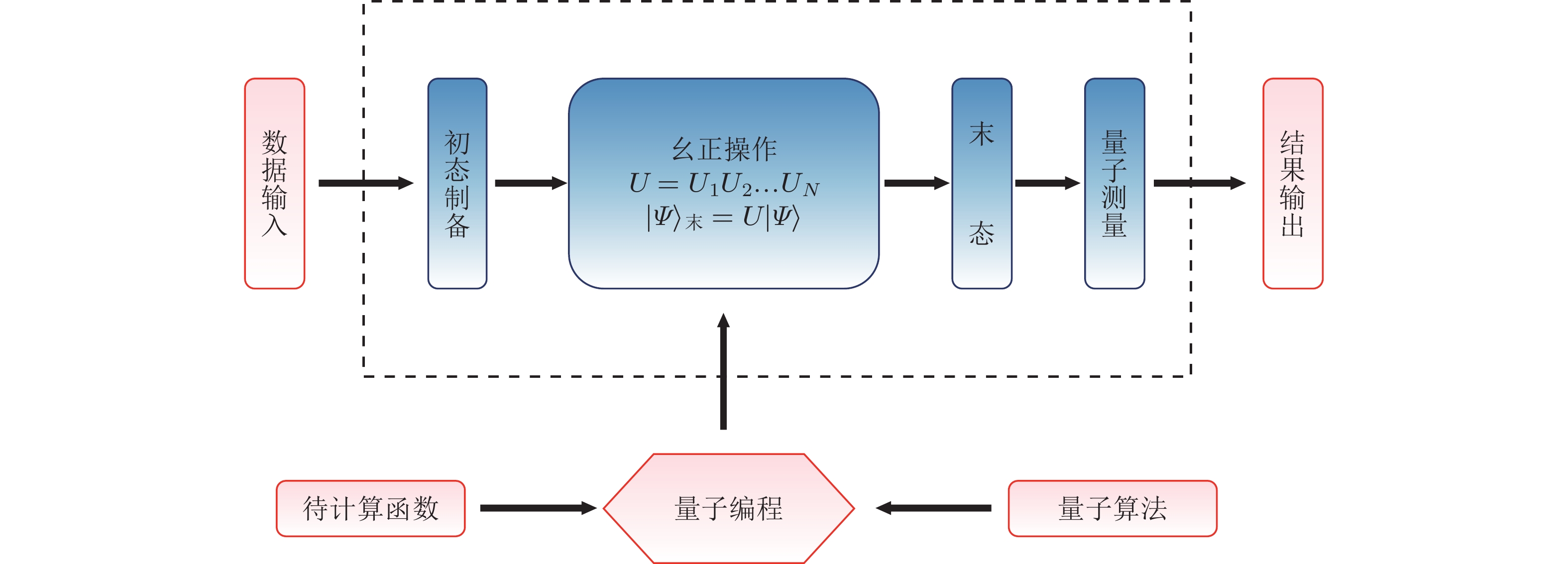
图 1 量子计算流程示意图(郭光灿 2022)
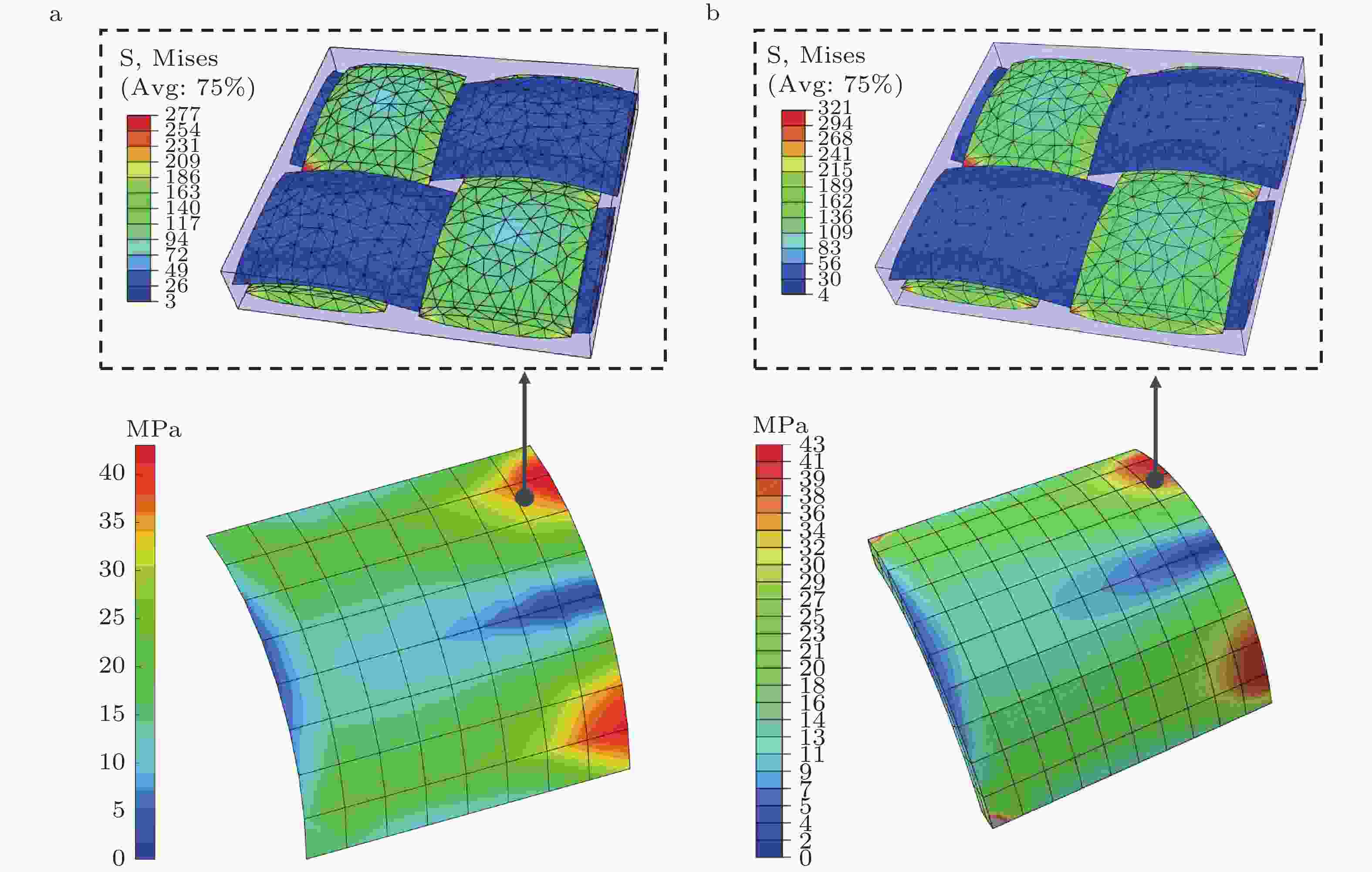
图 2 编织型复合壳体的多尺度仿真对比(Kuang et al. 2025). (a) 量子计算增强的数据驱动计算均匀化方法, (b) 并发多尺度有限元方法
-
[1] 郭光灿. 2022. 颠覆: 迎接第二次量子革命. 北京: 科学出版社 (Guo G C. 2022. Subversion: Embracing the second quantum revolution. Beijing: Science Press).Guo G C. 2022. Subversion: Embracing the second quantum revolution. Beijing: Science Press. [2] Ali M, Kabel M. 2023. Performance study of variational quantum algorithms for solving the poisson equation on a quantum computer. Physical Review Applied, 20: 014054. doi: 10.1103/PhysRevApplied.20.014054 [3] Arute F, Arya K, Babbush R, et al. 2019. Quantum supremacy using a programmable superconducting processor. Nature, 574: 505-510. doi: 10.1038/s41586-019-1666-5 [4] Bharadwaj S S, Sreenivasan K R. 2023. Hybrid quantum algorithms for flow problems. Proceedings of the National Academy of Sciences, 120: e2311014120. doi: 10.1073/pnas.2311014120 [5] Bravo-Prieto C, LaRose R, Cerezo M, et al. 2023. Variational quantum linear solver. Quantum, 7: 1188. doi: 10.22331/q-2023-11-22-1188 [6] Buhrman H, Cleve R, Watrous J, et al. 2001. Quantum fingerprinting. Physical Review Letters, 87: 167902. doi: 10.1103/PhysRevLett.87.167902 [7] Chen Z, Ma T, Ye C, et al. 2024. Enabling large-scale and high-precision fluid simulations on near-term quantum computers. Computer Methods in Applied Mechanics and Engineering, 432: 117428. doi: 10.1016/j.cma.2024.117428 [8] Coppersmith D. 1994. An approximate Fourier transform useful in quantum factoring. IBM Research Report: RC-19642. [9] Feynman R P. 1982. Simulating physics with computers. International Journal of Theoretical Physics, 21: 6-7. [10] Geers M G, Kouznetsova V G, Brekelmans W. 2010. Multi-scale computational homogenization: Trends and challenges. Journal of Computational and Applied Mathematics, 234: 2175-2182. doi: 10.1016/j.cam.2009.08.077 [11] Georgescu I M, Ashhab S, Nori F. 2014. Quantum simulation. Reviews of Modern Physics, 86: 153-185. doi: 10.1103/RevModPhys.86.153 [12] Giovannetti V, Lloyd S, Maccone L. 2008. Quantum random access memory. Physical Review Letters, 100: 160501. doi: 10.1103/PhysRevLett.100.160501 [13] Givois F, Kabel M, Gauger N. 2022. QFT-based homogenization. arXiv preprint arXiv: 2207.12949. [14] Grover L K. 2001. From Schrödinger’s equation to the quantum search algorithm. American Journal of Physics, 69: 769-777. doi: 10.1119/1.1359518 [15] Harrow A W, Hassidim A, Lloyd S. 2009. Quantum algorithm for linear systems of equations. Physical Review Letters, 103: 150502. doi: 10.1103/PhysRevLett.103.150502 [16] Henderson J M, Kath J, Golden J K, et al. 2024. Addressing quantum’s “fine print” with efficient state preparation and information extraction for quantum algorithms and geologic fracture networks. Scientific Reports, 14: 3592. doi: 10.1038/s41598-024-52759-0 [17] Jin S, Liu N, Yu Y. 2023. Quantum simulation of partial differential equations: Applications and detailed analysis. Physical Review A, 108: 032603. doi: 10.1103/PhysRevA.108.032603 [18] Kadowaki T, Nishimori, H. 1998. Quantum annealing in the transverse Ising model. Physical Review E, 58: 5355. doi: 10.1103/PhysRevE.58.5355 [19] Key F, Freinberger L. 2024. A formulation of structural design optimization problems for quantum annealing. Mathematics, 12: 482. doi: 10.3390/math12030482 [20] Kim Y, Eddins A, Anand S, et al. 2023. Evidence for the utility of quantum computing before fault tolerance. Nature, 618: 500-505. doi: 10.1038/s41586-023-06096-3 [21] Kirchdoerfer T, Ortiz M. 2016. Data-driven computational mechanics. Computer Methods in Applied Mechanics and Engineering, 304: 81-101. doi: 10.1016/j.cma.2016.02.001 [22] Kuang Z, Xu Y, Huang Q, et al. 2025. Quantum computing with error mitigation for data-driven computational mechanics. Composite Structures, 351: 118625. doi: 10.1016/j.compstruct.2024.118625 [23] Leyton S K, Osborne T J. 2008. A quantum algorithm to solve nonlinear differential equations. arXiv preprint arXiv: 0812.4423. [24] Li Y, Benjamin S C. 2017. Efficient variational quantum simulator incorporating active error minimization. Physical Review X, 7: 021050. [25] Liu B, Ortiz M, Cirak F. 2024. Towards quantum computational mechanics. Computer Methods in Applied Mechanics and Engineering, 432: 117403. doi: 10.1016/j.cma.2024.117403 [26] Liu B F, Zhu L X, He G W. 2023. Quantum implementation of numerical methods for convection-diffusion equations: Toward computational fluid dynamics. Communications in Computational Physics, 33: 425-451. doi: 10.4208/cicp.OA-2022-0081 [27] Liu J P, Kolden H Ø, Krovi H K, et al. 2021. Efficient quantum algorithm for dissipative nonlinear differential equations. Proceedings of the National Academy of Sciences, 118: 2026805118. doi: 10.1073/pnas.2026805118 [28] Liu Y, Liu J, Raney J R, et al. 2024. Quantum computing for solid mechanics and structural engineering - A demonstration with variational quantum eigensolver. Extreme Mechanics Letters, 67: 102117. doi: 10.1016/j.eml.2023.102117 [29] Lloyd S, Mohseni M, Rebentrost P. 2013. Quantum algorithms for supervised and unsupervised machine learning. arXiv preprint arXiv: 1307.0411. [30] Lloyd S, De Palma G, Gokler C, et al. 2020. Quantum algorithm for nonlinear differential equations. arXiv preprint arXiv: 2011.06571. [31] Lu Z, Yang Y. 2024. Quantum computing of reacting flows via Hamiltonian simulation. Proceedings of the Combustion Institute, 40: 105440. doi: 10.1016/j.proci.2024.105440 [32] Lubasch M, Joo J, Moinier P, et al. 2020. Variational quantum algorithms for nonlinear problems. Physical Review A, 101: 010301. doi: 10.1103/PhysRevA.101.010301 [33] Lundstrom M. 2003. Moore’s law forever. Science, 299: 210-211. doi: 10.1126/science.1079567 [34] Lye K O, Mishra S, Ray D. 2020. Deep learning observables in computational fluid dynamics. Journal of Computational Physics, 410: 109339. doi: 10.1016/j.jcp.2020.109339 [35] Morales M E, Pira L, Schleich P, et al. 2024. Quantum linear system solvers: A survey of algorithms and applications. arXiv preprint arXiv: 2411.02522. [36] Meng Z, Yang Y. 2023. Quantum computing of fluid dynamics using the hydrodynamic Schrödinger equation. Physical Review Research, 5: 033182. doi: 10.1103/PhysRevResearch.5.033182 [37] Meng Z, Zhong J, Xu S, et al. 2024. Simulating unsteady fluid flows on a superconducting quantum processor. Communications Physics, 7: 349. [38] Montanaro A, Pallister S. 2016. Quantum algorithms and the finite element method. Physical Review A, 93: 032324. doi: 10.1103/PhysRevA.93.032324 [39] Moulinec H, Suquet P. 1998. A numerical method for computing the overall response of nonlinear composites with complex microstructure. Computer Methods in Applied Mechanics and Engineering, 157: 69-94. doi: 10.1016/S0045-7825(97)00218-1 [40] Mukherjee S, Lu D, Raghavan B, et al. 2021. Accelerating large-scale topology optimization: State-of-the-art and challenges. Archives of Computational Methods in Engineering, 28: 4549-4571. [41] Nielsen M A, Chuang I L. 2010. Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. [42] Peruzzo A, McClean J, Shadbolt P, et al. 2014. A variational eigenvalue solver on a photonic quantum processor. Nature Communications, 5: 4213. doi: 10.1038/ncomms5213 [43] Preskill J. 2018. Quantum computing in the NISQ era and beyond. Quantum, 2: 79. doi: 10.22331/q-2018-08-06-79 [44] Raisuddin O M, De S. 2022. FEqa: Finite element computations on quantum annealers. Computer Methods in Applied Mechanics and Engineering, 395: 115014. doi: 10.1016/j.cma.2022.115014 [45] Rebentrost P, Mohseni M, Lloyd S. 2014. Quantum support vector machine for big data classification. Physical Review Letters, 113: 130503. doi: 10.1103/PhysRevLett.113.130503 [46] Sato Y, Kondo R, Hamamura I, et al. 2024. Hamiltonian simulation for hyperbolic partial differential equations by scalable quantum circuits. Physical Review Research, 6: 033246. doi: 10.1103/PhysRevResearch.6.033246 [47] Schaller R R. 1997. Moore’s law: Past, present and future. IEEE spectrum 34: 52-59. [48] Shao H J, Wang Y X, Zhu D Z, et al. 2024. Antiferromagnetic phase transition in a 3D fermionic Hubbard model. Nature, 632: 1-6. [49] Song C, Xu K, Li H, et al. 2019. Generation of multicomponent atomic Schrödinger cat states of up to 20 qubits. Science, 365: 574-577. doi: 10.1126/science.aay0600 [50] Temme K, Bravyi S, Gambetta J M. 2017. Error mitigation for short-depth quantum circuits. Physical Review Letters, 119: 180509. doi: 10.1103/PhysRevLett.119.180509 [51] Trahan C J, Loveland M, Davis N, et al. 2023. A variational quantum linear solver application to discrete finite-element methods. Entropy, 25: 580. doi: 10.3390/e25040580 [52] Wiebe N, Kapoor A, Svore K M. 2015. Quantum nearest-neighbor algorithms for machine learning. Quantum Information and Computation, 15: 318-358. [53] Wils K, Chen B Y. 2023. A symbolic approach to discrete structural optimization using quantum annealing. Mathematics, 11: 3451. doi: 10.3390/math11163451 [54] Xiao J, Endo K, Muramatsu M, et al. 2024. Application of factorization machine with quantum annealing to hyperparameter optimization and metamodel-based optimization in granular flow simulations. International Journal for Numerical and Analytical Methods in Geomechanics, 48: 3432-3451. doi: 10.1002/nag.3800 [55] Xu Y, Kuang Z, Huang Q, et al. 2024a, A robust quantum nonlinear solver based on the asymptotic numerical method. arXiv preprint arXiv: 2412.03939. [56] Xu Y, Yang J, Kuang Z, et al. 2024b. Quantum computing enhanced distance-minimizing data-driven computational mechanics. Computer Methods in Applied Mechanics and Engineering, 419: 116675. doi: 10.1016/j.cma.2023.116675 [57] Xue C, Wu Y, Guo G. 2021. Quantum Newton’s method for solving the system of nonlinear equations. World Scientific Publishing Company, 11: 2140004. doi: 10.1142/S201032472140004X [58] Xue C, Xu X, Wu Y, et al. 2022. Quantum algorithm for solving a quadratic nonlinear system of equations. Physical Review A, 106: 032427. doi: 10.1103/PhysRevA.106.032427 [59] Yarkoni S, Raponi E, Bäck T, et al. 2022. Quantum annealing for industry applications: Introduction and review. Reports on Progress in Physics, 85: 104001. doi: 10.1088/1361-6633/ac8c54 [60] Ye Z, Qian X, Pan W. 2023. Quantum topology optimization via quantum annealing. IEEE Transactions on Quantum Engineering, 4: 1-15. doi: 10.1109/TQE.2023.3266410 [61] Zhong H S, Wang H, Deng Y H, et al. 2020. Quantum computational advantage using photons. Science, 370: 1460-1463. doi: 10.1126/science.abe8770 -




 下载:
下载: