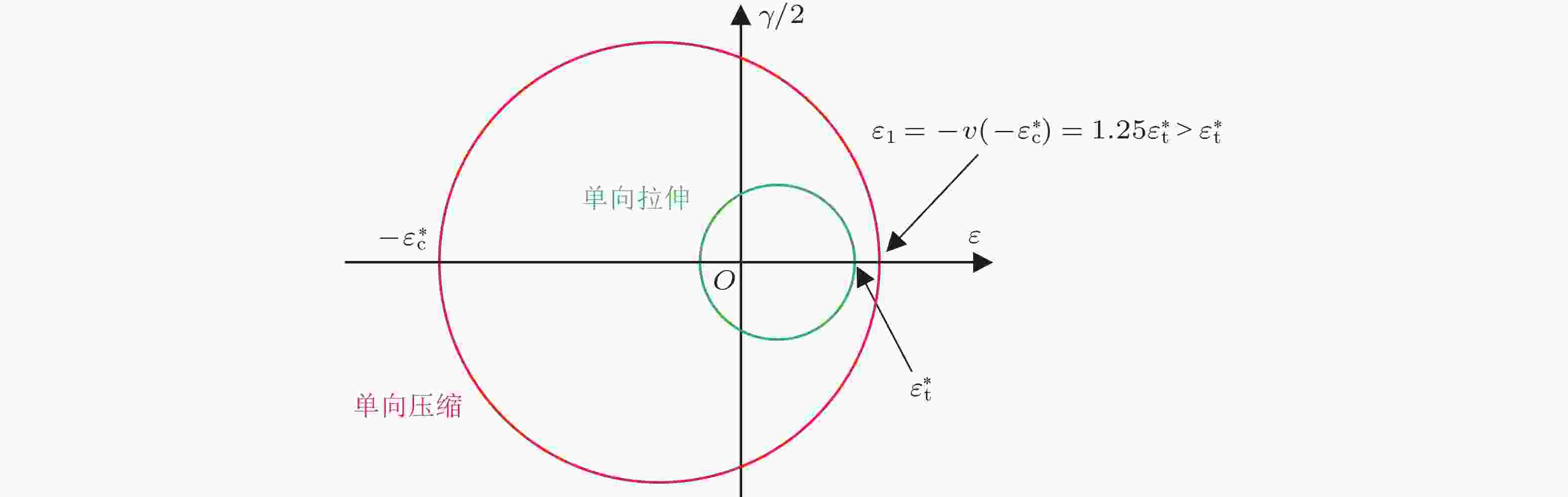
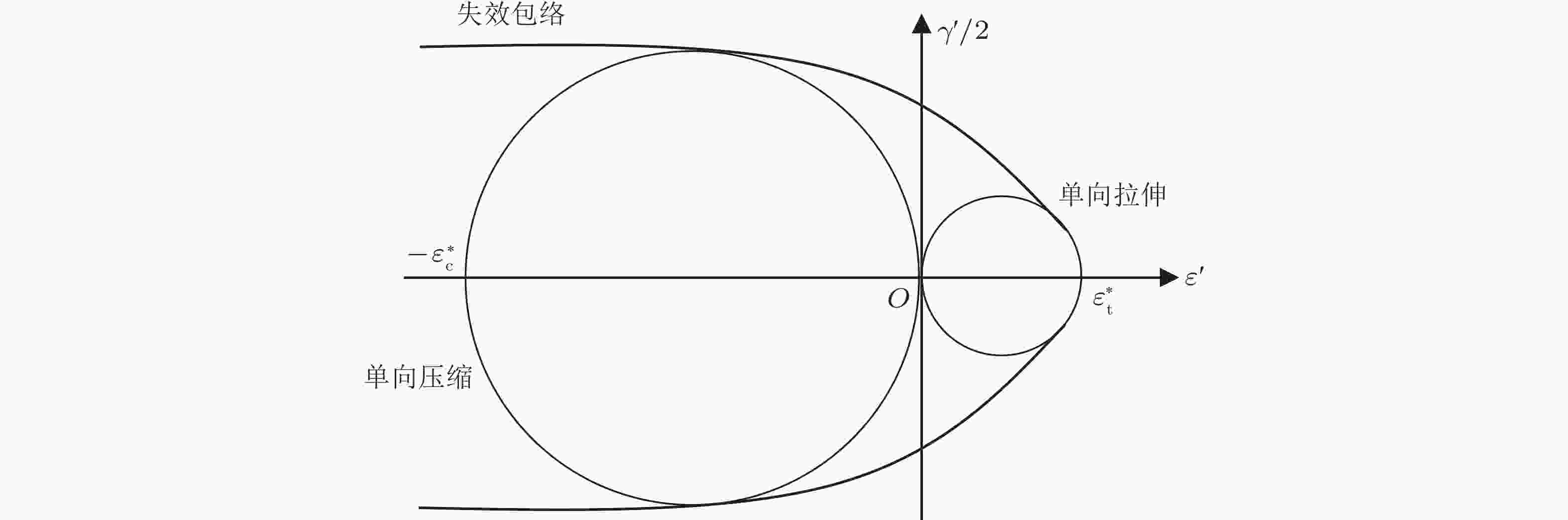
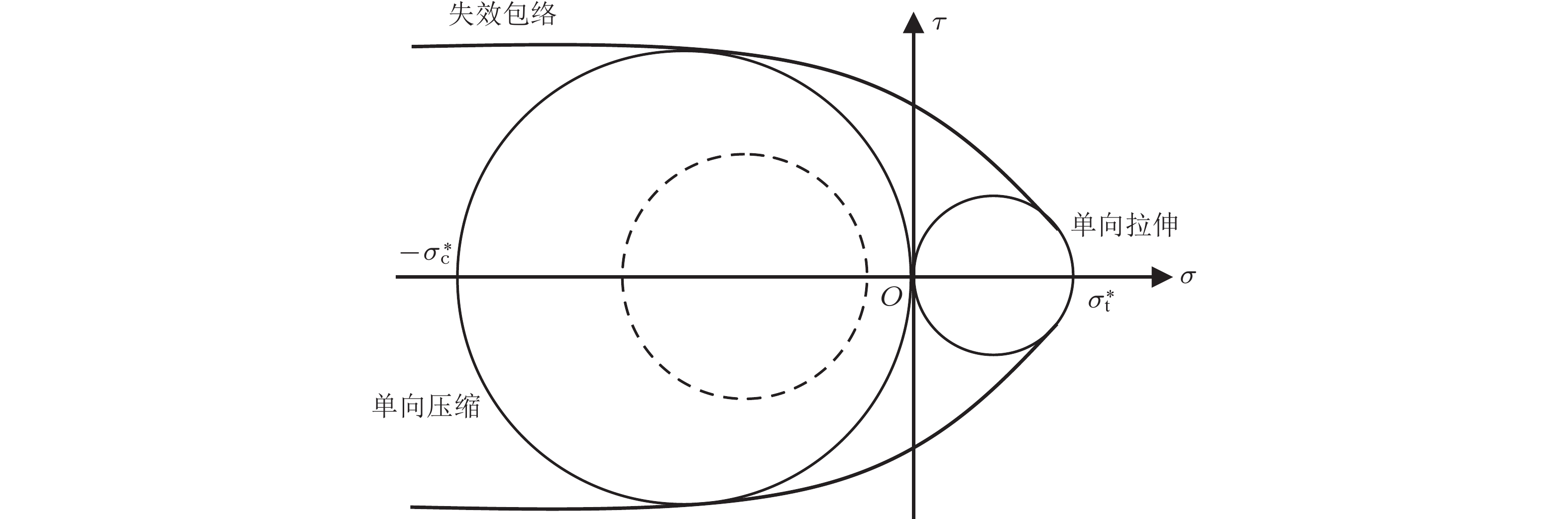
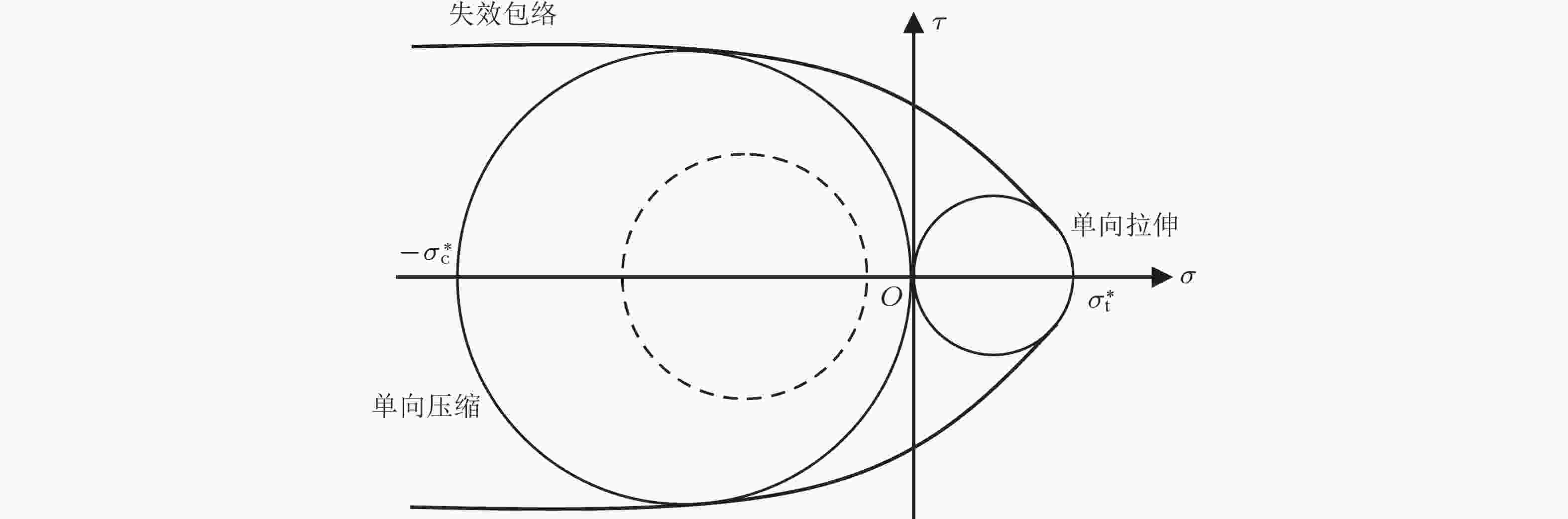
-
摘要: 本文旨在解决建立材料失效准则时该用应力还是用应变作为基本变量之间的纷争, 该纷争源远流长, 两者之间似势不两立. 事实上, 两者之间不会自然而然地相互一致, 它们也不真正地互补. 大多数失效准则开始时都是用应力的形式给出的, 包括最大应力准则、Tresca(最大剪应力)准则、von Mises准则、Raghava-Caddell-Yeh准则和Mohr准则, 它们的形式唯一, 并自洽, 即能够再现输入数据. 而这些准则, 如果以应变形式给出, 譬如, 最大应变准则, 其可视作最大应力准则的应变翻版, 它们的形式就未必唯一、也未必自洽. 本文证明, 自洽的应变准则严格再现其应力准则, 而应用时, 比相应的应力准则, 需多输入一个材料参数, 其他别无优势. 就Mohr准则而言, 其应变形式一般情况并不可行. 所有的应变准则的弊端, 源于一个简单的事实, 即材料的失效应变, 是在单向应力状态(而不是单向应变状态)下测得的. 与单向应力状态相应的应变状态, 一般都是复合应变状态. 如果数学、逻辑与常理比观念与偏见更值得遵从的话, 那么, 本文关于所述纷争的论断就会完全倾向于应力一方.Abstract: This paper is intended to reconcile the stress-based and strain-based formulations for material failure criteria, where a longstanding and deep division is present. The two approaches do not naturally agree with each other, and they not genuinely complement each other, either. Most popular criteria are stress-based when originally proposed, including the maximum stress, Tresca, von Mises, Raghava-Caddell-Yeh and the Mohr criteria. Their formulations are unique and self-consistent, i.e. capable of reproducing the input data. Their strain-based counterparts, with the maximum strain criterion being considered as the strain-based counterpart of the maximum stress criterion, are neither unique nor necessarily self-consistent. It has been proven that the self-consistent ones reproduce their respective stress-based counterparts identically in effect with a disadvantage of requiring an additional material property to apply, without a single benefit. For the Mohr criterion as a special case, a strain-based counterpart is simply infeasible in general. All undesirable features of strain-based criteria are rooted in a single source: the failure strains can only be measured under a uniaxial stress state, which corresponds to a combined strain state in general, not a uniaxial strain state! Given the arguments presented, the reconciliation proves to be biased completely towards the stress-based side if mathematics, logic and common sense prevail over perception and prejudice.
-
Key words:
- Stress /
- Strain /
- Strength /
- Failure /
- Failure strain /
- Failure criterion /
- Tresca /
- von Mises /
- Raghava-Caddell-Yeh /
- Mohr.
-
图 2 单向压缩变形示意, 其中材料在
$ - {\varepsilon _3} < \varepsilon _c^*$ 的情况下, 可能达到${\varepsilon _1} = \varepsilon _t^*$ 
图 3 一个ν=0.25、
${{\varepsilon _c^*} \mathord{\left/ {\vphantom {{\varepsilon _c^*} {\varepsilon _t^*}}} \right. } {\varepsilon _t^*}} = 5$ 的材料在单向拉伸和单向压缩的条件下失效时的Mohr圆 -
[1] Boeing. 2024 (date accessed 23rd Dec. ), https://en.wikipedia.org/wiki/Boeing [2] Christensen R M. 2013. The Theory of Materials Failure, Oxford University Press, Oxford [3] Li S. 2020a. The maximum stress failure criterion and the maximum strain failure criterion: their unification and rationalization. J. Composites Science, 4: 157 doi: 10.3390/jcs4040157 [4] Li S. 2020b. A reflection on the Mohr failure criterion, Mechanics of Materials, 148 : 103442 https://www.sciencedirect.com/science/article/abs/pii/S0167663620302076 [5] Li S. 2024a. Stress invariants and invariants of the failure envelope as a quadric surface: their significances in the formulation of a rational failure criterion, Mechanics of Materials, 196 : 105076 https://authors.elsevier.com/sd/article/S0167-6636(24)00168-6 [6] Li S. 2024b. Rational implementation of the Mohr criterion in its general form. Int. J. Mech. Sci, 278: 109449 doi: 10.1016/j.ijmecsci.2024.109449 [7] Love A E H. 2013 (reprint). A Treatise on the Mathematical Theory of Elasticity, Cambridge University Press, Cambridge [8] von Mises R. 1913. Mechanics of solid bodies in the plastically-deformable state, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse, 1913: 582-592 [9] Mohr O. 1900. Welche Umstände bedingen die Elastizitätsgrenze und den Bruch eines Materials? Civilingenieur, 44 : 1524-1530 & 44 : 1572-1577 [10] Raghava R, Caddell R M, Yeh G S Y. 2024. The macroscopic yield behaviour of polymers. J. Mater. Sci., 8: 225-232,1973 [11] Sokolnikoff I S. 1956. Mathematical theory of elasticity, Chapter 5, McGraw-Hill, London [12] Timoshenko S P. 1963. Strength of Materials, Part II: Advanced Theory and Problems, 3rd edn, D. Van Nostrand Company, Inc. , New York [13] Timoshenko S P, Goodier J N. 1970. Theory of Elasticity, 3rd edn. , McGraw-Hill, London [14] Timoshenko S P. 1983. History of Strength of Materials, Dover Publications, New York [15] Tresca H. 1864. Mémoire sur l’écoulement des corps solides soumis à de fortes pressions. C. R. Acad. Sci. Paris, 59: 754-758 [16] Yu W. 2024. Common misconceptions on rules of mixtures for predicting elastic properties of composites, AIAA J., 62 (5): N/A https://doi.org/10.2514/1.J063863 -
下载:
图(4)
计量
- 文章访问数: 173
- HTML全文浏览量: 24
- PDF下载量: 56
- 被引次数: 0