力学分析中的对称性与守恒律分析方法研究进展

邱志平; 邱宇; 张培宣

doi:10.6052/1000-0992-24-033

力学分析中的对称性与守恒律分析方法研究进展

doi: 10.6052/1000-0992-24-033 cstr: 32046.14.1000-0992-24-033

邱志平^1, ,,
邱宇^{1, 2},
张培宣^{1, 2}

1.
北京航空航天大学, 航空科学与工程学院, 北京 100191
2.
北京航空航天大学, 沈元学院, 北京 100191

基金项目: 国家自然科学基金项目 (12132001, 52192632)、北航沈元学院博士卓越研究基金项目 (230123202) 的支持

详细信息

作者简介:
邱志平, 男, 博士, 1962年出生于吉林省长春市, 教授. 于1994年在吉林大学获博士学位. 1996年12月至今, 在北京航空航天大学固体力学所工作. 洪堡学者, 国家杰出青年基金获得者, 2019—2023年爱思唯尔中国高被引学者, 北航蓝天学者特聘教授. 主要研究方向: 结构动力学、结构强度、结构可靠性、疲劳分析、损伤容限与耐久性设计、结构优化设计、随机振动、复合材料力学、智能材料结构, 气动弹性力学, 热力学, 力学中的非线性问题等

通讯作者:
zpqiu@buaa.edu.cn

计量
- 文章访问数: 105
- HTML全文浏览量: 15
- PDF下载量: 68
- 被引次数: 0
出版历程
- 收稿日期: 2024-10-08
- 录用日期: 2024-12-17
- 网络出版日期: 2024-12-22

A review of research advances in analytical methods for symmetry and conservation laws in mechanical analysis

QIU Zhiping^{1
, ,},
QIU Yu^{1, 2},
ZHANG Peixuan^{1, 2}

1.
Institute of Solid Mechanics, School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China
2.
Shen Yuan Honors College, Beihang University, Beijing 100191, China

More Information

Corresponding author: zpqiu@buaa.edu.cn

摘要

摘要: 本文综述了力学分析中对称性与守恒律的研究进展. 首先, 介绍了连续系统中的Lie群对称性, 包括微分方程和偏微分方程的Lie群对称性、泛函的Lie群对称性及其守恒律, 以及扰动微分方程的近似Lie对称性, 并通过实例分析了这些对称性在实际中的应用. 接着, 探讨了离散系统的对称性与守恒律, 重点介绍了离散系统的动力学方程、Noether对称性、Lie对称性及Mei对称性, 并结合具体应用实例进行了说明. 最后, 综述了随机系统中的对称性与守恒律, 讨论了Ito型和Stratonovich型随机微分方程的对称性, 特别是在统计意义下对随机微分方程对称性的理解. 本文旨在为后续研究提供理论参考, 推动相关领域的进一步发展.
- 对称性 /
- 守恒律 /
- 连续系统 /
- 离散系统 /
- 随机系统
Abstract: This paper reviews the research progress on symmetry and conservation laws in mechanical analysis. It begins by introducing Lie group symmetries in continuous systems, including the symmetries of differential equations, partial differential equations, functionals, and approximate Lie symmetries of perturbed differential equations, with practical applications demonstrated through examples. The paper then explores symmetries and conservation laws in discrete systems, focusing on the dynamics equations, Noether symmetries, Lie symmetries, and Mei symmetries, with explanations supported by specific application examples. Finally, it reviews symmetries and conservation laws in stochastic systems, discussing the symmetries of Ito and Stratonovich stochastic differential equations, particularly in the statistical sense. The aim of this paper is to provide theoretical references for subsequent research and to advance the development of related fields.
- symmetry /
- conservation laws /
- continuous systems /
- discrete systems /
- stochastic systems

HTML全文

图 1 连续对称性和守恒律的关系(夏丽莉和陈立群2015)

下载: 全尺寸图片幻灯片

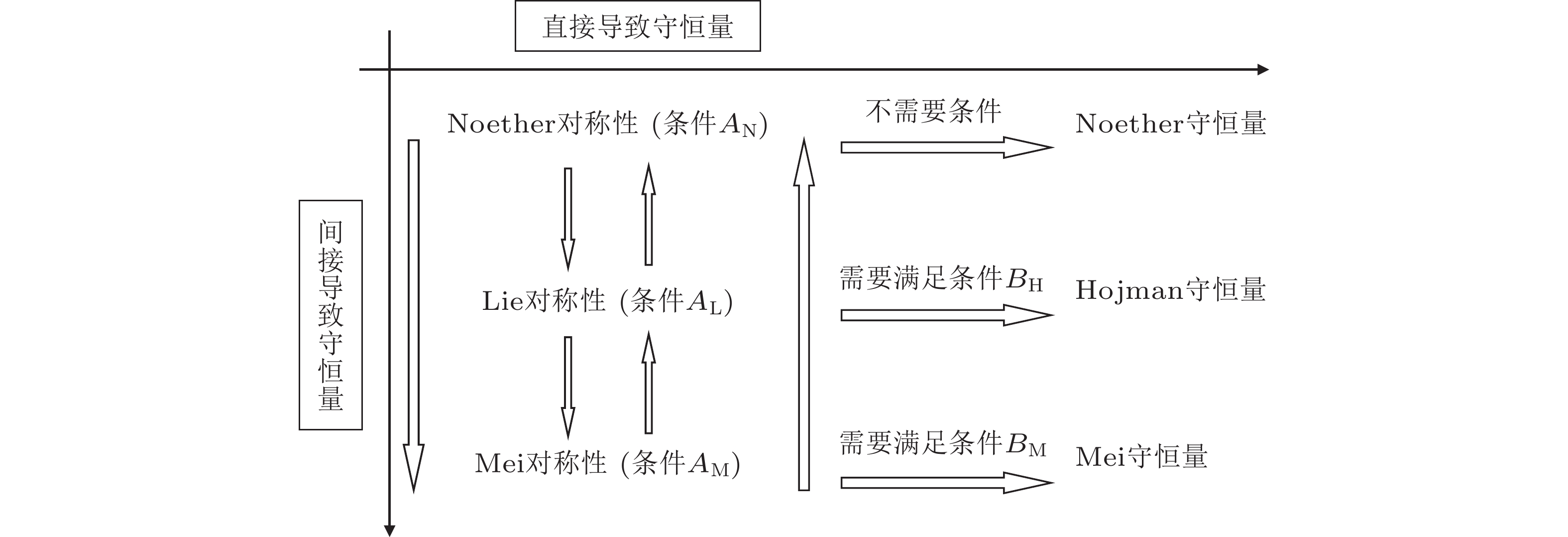
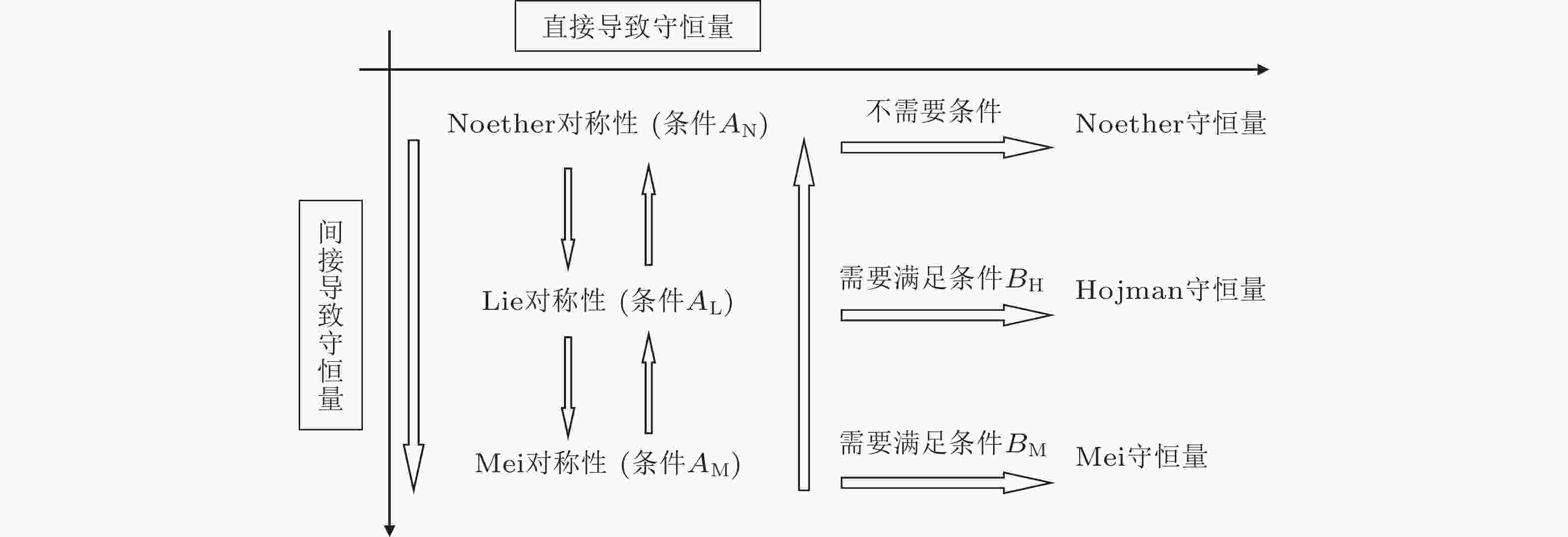
图 2 三种对称性的关系(梅凤翔 2001).

下载: 全尺寸图片幻灯片

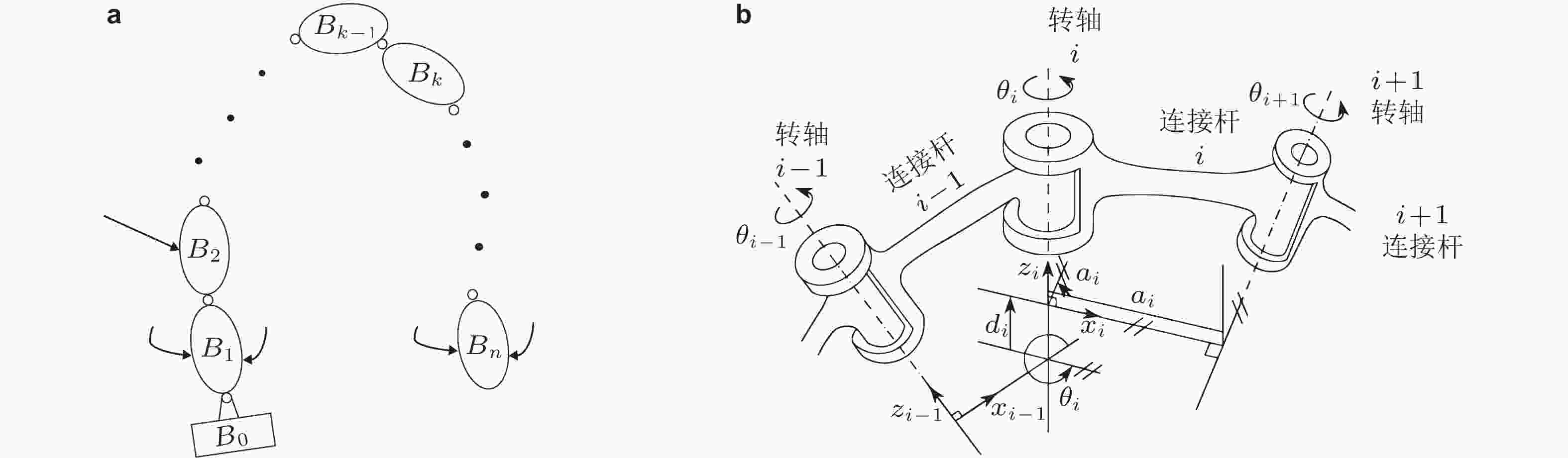
图 3 机械多体系统及其坐标系. (a)受冲击的机械多体系统, (b)多体连杆式D-H坐标系(郑明亮等 2018)

下载: 全尺寸图片幻灯片

参考文献(86)

[1]	冯录祥. 2012. 一类一阶常微分方程的可积性条件及应用. 中央民族大学学报(自然科学版), 021 : 32–36 (Feng L X. 2012. A class of first order differential equation and application of the integrability conditions. Journal of MUC (Natural Sciences Edition), 021: 32–36). Feng L X. 2012. A class of first order differential equation and application of the integrability conditions. Journal of MUC (Natural Sciences Edition), 021: 32–36
[2]	刘胜, 雷锦志. 1998. 判定常微分方程组具有一维李对称群的新方法. 纯粹数学与应用数学, 14 : 6 (Liu S, Lei J Z. 1998. A new method of identifying one-dimensional Lie groups admitted by ordinary differential equation systems. Pure and Applied Mathematics, 14 : 6). Liu S, Lei J Z. 1998. A new method of identifying one-dimensional Lie groups admitted by ordinary differential equation systems. Pure and Applied Mathematics, 14: 6.
[3]	夏丽莉. 2018. 双连杆机械臂的差分离散和Noether对称性. 北京信息科技大学学报(自然科学版), 33 : 1–5 (Xia L L. 2018. Noether symmetry and difference discretization of double-link manipulator. Journal of Beijing Information Science & Technology University, 33 : 1–5). Xia L L. 2018. Noether symmetry and difference discretization of double-link manipulator. Journal of Beijing Information Science & Technology University, 33: 1–5
[4]	夏丽莉, 陈立群. 2015. 基于变分积分子的动力学系统的对称性与守恒量研究. 上海大学博士论文 (Xia L L, Chen L Q. 2015. Study on symmetries and conserved quantities of dynamical systems based on the variational integrators. Shanghai University). Xia L L, Chen L Q. 2015. Study on symmetries and conserved quantities of dynamical systems based on the variational integrators. Shanghai University.
[5]	孙博华. 2016. 量纲分析与Lie群. 北京: 高等教育出版社 (Sun B H. 2016. Dimensional analysis and Lie group. Beijing: Higher Education Press). Sun B H. 2016. Dimensional analysis and Lie group. Beijing: Higher Education Press.
[6]	张学元. 1993. 常微分方程一些新的可积性结果. 岳阳大学学报, 01 : 9–16 (Zhang X Y. 1993. Some new productability results for ordinary differential equations. Journal of Yueyang University, 01 : 9–16). Zhang X Y. 1993. Some new productability results for ordinary differential equations. Journal of Yueyang University, 01: 9–16
[7]	张晓莉, 赵小山. 2011. 基于李群李对称方法求解一类偏微分方程. 天津师范大学学报: 自然科学版, 31 : 4 (Zhang X L, Zhao X S. 2011. Solving a kind of partial differential equations by Lie group Lie symmetry. Journal of Tianjin Normal University (Natural Science Edition), 31 : 4). Zhang X L, Zhao X S. 2011. Solving a kind of partial differential equations by Lie group Lie symmetry. Journal of Tianjin Normal University (Natural Science Edition), 31: 4.
[8]	张锦, 伊贺达赉, 冀书关. 2007. 常微分方程存在广义对称的必要条件. 吉林大学学报(理学版), 045 : 393–395 (Zhang J, Yi H D L, Ji S G. 2007. Necessary condition for existence of generalized symmetry of ordinary differential equations. Journal of Jilin University (Science Edition), 045 : 393–395). Zhang J, Yi H D L, Ji S G. 2007. Necessary condition for existence of generalized symmetry of ordinary differential equations. Journal of Jilin University (Science Edition), 045: 393–395.
[9]	施沈阳. 2008. 离散约束动力学系统的对称性质与守恒量研究. 上海大学博士论文 (Shi S Y. 2008. The investigation on symmetry and conserved quantity of discrete constrained dynamical system. Shanghai University). Shi S Y. 2008. The investigation on symmetry and conserved quantity of discrete constrained dynamical system. Shanghai University.
[10]	梅凤翔. 2001. 关于Noether对称性、Lie对称性和形式不变性. 北京理工大学学报, 535–536 (Mei F X. 2001. On Noether symmetry, Lie symmetry and form invariance. Journal of Beijing Institute of Technology, 535–536). Mei F X. 2001. On Noether symmetry, Lie symmetry and form invariance. Journal of Beijing Institute of Technology, 535–536
[11]	薛崇政, 胡彦霞. 2013. 利用单参数Lie群组的一种可解性求自治系统首次积分的方法. 应用数学学报, 36 : 738–747 (Xue C Z, Hu Y X. 2013. Searching for first integral of autonomous system based on a kind of solvability of one-parameter Lie groups. Acta Mathematicae Applicatae Sinica, 36 : 738–747). Xue C Z, Hu Y X. 2013. Searching for first integral of autonomous system based on a kind of solvability of one-parameter Lie groups. Acta Mathematicae Applicatae Sinica, 36: 738–747
[12]	邱志平, 姜南. 2022. 力学分析中的对称性和守恒律. 北京: 科学出版社 (Qiu Z P, Jiang N. 2022. Symmetry and conservation laws in mechanical analysis. Beijing: China Science Publishing & Media Ltd). Qiu Z P, Jiang N. 2022. Symmetry and conservation laws in mechanical analysis. Beijing: China Science Publishing & Media Ltd.
[13]	郑明亮, 冯鲜, 李文霞, 曹亚玲. 2018. 机械多体系统碰撞动力学的对称性和守恒量研究. 应用数学和力学, 39 : 1292–1299 (Zheng M L, Feng X, Li W X, Cao Y L. 2018. Study on symmetries and conserved quantities of mechanical multibody system collision dynamics. Applied Mathematics and Mechanics, 39 : 1292–1299). Zheng M L, Feng X, Li W X, Cao Y L. 2018. Study on symmetries and conserved quantities of mechanical multibody system collision dynamics. Applied Mathematics and Mechanics, 39: 1292–1299.
[14]	Albeverio S, Fei S-M. 1995. A remark on symmetry of stochastic dynamical systems and their conserved quantities. J. Phys. A: Math. Gen, 28: 6363-6371. doi: 10.1088/0305-4470/28/22/012
[15]	Andriopoulos K, Leach P G L, Flessas G P. 2001. Complete symmetry groups of ordinary differential equations and their integrals: Some basic considerations. Journal of Mathematical Analysis and Applications, 262: 256-273. doi: 10.1006/jmaa.2001.7570
[16]	Arnold L, Jones, C K, Mischaikow K, Raugel G, Arnold L. 1995. Random dynamical systems. Berlin: Springer Berlin Heidelberg,pp. 1-43.
[17]	Bluman G. 1990. Simplifying the form of Lie groups admitted by a given differential equation. Journal of Mathematical Analysis and Applications, 145: 52-62. doi: 10.1016/0022-247X(90)90431-E
[18]	Bordag L A, Yamshchikov I P. 2017. Lie group analysis of nonlinear black-scholes models, in: Ehrhardt M, Günther M, Ter Maten E J W (Eds.), Novel Methods in Computational Finance, Mathematics in Industry. Springer International Publishing, Cham, pp. 109–128.
[19]	Buckwar E, Luchko Y. 1998. Invariance of a partial differential equation of fractional order under the lie group of scaling transformations. Journal of Mathematical Analysis and Applications, 227: 81-97. doi: 10.1006/jmaa.1998.6078
[20]	Cicogna G, Vitali D. 1990. Classification of the extended symmetries of Fokker−Planck equations. Journal of Physics A: Mathematical and General, 23: L85. doi: 10.1088/0305-4470/23/3/001
[21]	Cicogna G, Vitali D. 1989. Generalised symmetries of Fokker−Planck-type equations. Journal of Physics A: Mathematical and General, 22 : L453.
[22]	Donato A, Oliveri F. 1994. Linearization procedure of nonlinear first order system of partial differential equations by means of canonical variables related to lie groups of point transformations. Journal of Mathematical Analysis and Applications, 188: 552-568. doi: 10.1006/jmaa.1994.1445
[23]	Dorodnitsyn V. 2001. Noether-type theorems for difference equations. Applied numerical mathematics, 39: 307-321. doi: 10.1016/S0168-9274(00)00041-6
[24]	Dorodnitsyn V, Kozlov R, Winternitz P. 2000. Lie group classification of second-order ordinary difference equations. Journal of mathematical physics, 41: 480-504. doi: 10.1063/1.533142
[25]	Émery M. 2012. Stochastic calculus in manifolds. Springer Science & Business Media.
[26]	F De Vecchi. 2014. Symmetries of diffusion processes and applications. Milan: Università degli Studi di Milano.
[27]	Finkel F. 1999. Symmetries of the Fokker−Planck equation with a constant diffusion matrix in 2+1 dimensions. Journal of Physics A: Mathematical and General, 32: 2671. doi: 10.1088/0305-4470/32/14/008
[28]	Floreanini R, Vinet L. 1995. Lie symmetries of finite-difference equations. Journal of Mathematical Physics, 36: 7024-7042. doi: 10.1063/1.531205
[29]	Fu J, Dai G, Jiménez S, Tang Y. 2007. Discrete variational principle and first integrals for Lagrange–Maxwell mechanico-electrical systems. Chinese Physics, 16: 570. doi: 10.1088/1009-1963/16/3/002
[30]	Fu J L, Chen L Q, Jiménez S, Tang Y F. 2006. Non-Noether symmetries and Lutzky conserved quantities for mechanico-electrical systems. Physics Letters A, 358: 5-10. doi: 10.1016/j.physleta.2006.04.097
[31]	Gaeta G. 2004. Symmetry of stochastic equations. arXiv preprint math-ph/0401025.
[32]	Gaeta G, Quintero N R. 1999. Lie-point symmetries and stochastic differential equations. Journal of Physics A: Mathematical and General, 32: 8485-8505. doi: 10.1088/0305-4470/32/48/310
[33]	Gomez-Ullate D, Lafortune S, Winternitz P. 1999. Symmetries of discrete dynamical systems involving two species. Journal of Mathematical Physics, 40: 2782-2804. doi: 10.1063/1.532728
[34]	Guerra F. 1981. Structural aspects of stochastic mechanics and stochastic field theory. Physics Reports, 77: 263-312. doi: 10.1016/0370-1573(81)90078-8
[35]	Heredero R H, Levi D, Winternitz P. 1999. Symmetries of the discrete Burgers equation. Journal of Physics A: Mathematical and General, 32: 2685. doi: 10.1088/0305-4470/32/14/009
[36]	Hydon P. 1998. Discrete point symmetries of ordinary differential equations. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 454: 1961-1972.
[37]	Hydon P E. 2000. Symmetry methods for differential equations: A beginner’s guide, 1st ed. Cambridge University Press.
[38]	Khater A, Moussa M, Abdul-Aziz S. 2002. Potential symmetries and invariant solutions for the generalized one-dimensional Fokker–Planck equation. Physica A: Statistical Mechanics and its Applications, 304: 395-408. doi: 10.1016/S0378-4371(01)00496-4
[39]	Kozlov R. 2010a. The group classification of a scalar stochastic differential equation. Journal of Physics A: Mathematical and Theoretical, 43: 055202. doi: 10.1088/1751-8113/43/5/055202
[40]	Kozlov R. 2010b. Symmetries of systems of stochastic differential equations with diffusion matrices of full rank. Journal of Physics A: Mathematical and Theoretical, 43: 245201. doi: 10.1088/1751-8113/43/24/245201
[41]	Levi D, Rodriguez M A. 1999. Lie symmetries for integrable evolution equations on the lattice. Journal of Physics A: Mathematical and General, 32: 8303. doi: 10.1088/0305-4470/32/47/309
[42]	Levi D, Tremblay S, Winternitz P. 2001. Lie symmetries of multidimensional difference equations. Journal of Physics A: Mathematical and General, 34: 9507. doi: 10.1088/0305-4470/34/44/311
[43]	Levi D, Tremblay S, Winternitz P. 2000. Lie point symmetries of difference equations and lattices. Journal of Physics A: Mathematical and General, 33: 8507. doi: 10.1088/0305-4470/33/47/313
[44]	Levi D, Vinet L, Winternitz P. 1997. Lie group formalism for difference equations. Journal of Physics A: Mathematical and General, 30: 633. doi: 10.1088/0305-4470/30/2/024
[45]	Levi D, Winternitz P. 1996. Symmetries of discrete dynamical systems. Journal of Mathematical Physics, 37: 5551-5576. doi: 10.1063/1.531722
[46]	Levi D, Winternitz P. 1993. Symmetries and conditional symmetries of differential-difference equations. Journal of Mathematical Physics, 34: 3713-3730. doi: 10.1063/1.530054
[47]	Levi D, Yamilov R. 1997. Conditions for the existence of higher symmetries of evolutionary equations on the lattice. Journal of Mathematical Physics, 38: 6648-6674. doi: 10.1063/1.532230
[48]	Lie S. 1880. Theorie der transformations gruppen I. Mathematische Annalen, 16: 441-528. doi: 10.1007/BF01446218
[49]	Liu C S, Chang C W. 2016. A real-time Lie-group differential algebraic equations method to solve the inverse nonlinear vibration problems. Inverse Problems in Science and Engineering, 24: 1569-1586. doi: 10.1080/17415977.2015.1130043
[50]	Liu R, Zhang H, Chen L. 2006. Variational principle and dynamical equations of discrete nonconservative holonomic systems. Chinese Physics, 15: 249. doi: 10.1088/1009-1963/15/2/002
[51]	Lutzky M. 1979. Dynamical symmetries and conserved quantities. Journal of Physics A: Mathematical and General, 12: 973. doi: 10.1088/0305-4470/12/7/012
[52]	Lutzky M. 1978a. Noether’s theorem and the time-dependent harmonic oscillator. Physics Letters A, 68: 3-4. doi: 10.1016/0375-9601(78)90738-7
[53]	Lutzky M. 1978b. Symmetry groups and conserved quantities for the harmonic oscillator. Journal of Physics A: Mathematical and General, 11: 249. doi: 10.1088/0305-4470/11/2/005
[54]	Mahomed F M. 2007. Symmetry group classification of ordinary differential equations: Survey of some results. Math Methods in App Sciences, 30: 1995-2012. doi: 10.1002/mma.934
[55]	Márquez A D P, Garrido T M, Recio E, De La Rosa R. 2022. Lie symmetries and exact solutions for a fourth-order nonlinear diffusion equation. Math Methods in App Sciences, 45: 10614-10627. doi: 10.1002/mma.8387
[56]	Marsden J E, West M. 2001. Discrete mechanics and variational integrators. Acta Numerica, 10: 357-514. doi: 10.1017/S096249290100006X
[57]	Mei F. 2000. Form invariance of Lagrange system. Journal of Beijing Institute of Technology, 9 : 120–124.
[58]	Meyer P A. 2006. A differential geometric formalism for the Itô calculus, in: Stochastic Integrals: Proceedings of the LMS Durham Symposium, July 7–17, 1980. Springer, pp. 256–270.
[59]	Meyer P A. 1982. Géométrie différentielle stochastique (bis), in: Séminaire de Probabilités XVI, 1980/81 Supplément: Géométrie Différentielle Stochastique. Springer, pp. 165–207.
[60]	Meyer P A. 1981. Géométrie Stochastique Sans Larmes, in: Séminaire de Probabilités XV 1979/80: Avec Table Générale Des Exposés de 1966/67 à 1978/79. Springer, pp. 44–102.
[61]	Misawa T. 1994a. Conserved quantities and symmetry for stochastic dynamical systems. Physics Letters A, 195: 185-189. doi: 10.1016/0375-9601(94)90150-3
[62]	Misawa T. 1994b. New conserved quantities derived from symmetry for stochastic dynamical systems. Journal of Physics A: Mathematical and General, 27: L777-L782. doi: 10.1088/0305-4470/27/20/004
[63]	Noether E. 1918. Invariante Variations Probleme, Nachr. KoÈnig. Gesell. Wissen. GoÈttingen, Math.-Phys, 186-207.
[64]	Oliveri F. 2010. Lie symmetries of differential equations: Classical results and recent contributions. Symmetry, 2: 658-706. doi: 10.3390/sym2020658
[65]	Olver P J. 1986a. Symmetry groups of differential equations, in: Applications of Lie groups to differential equations, graduate texts in mathematics. New York: Springer New York, 77–185.
[66]	Olver P J. 1986b. Applications of Lie groups to differential equations, graduate texts in mathematics. New York, NY: Springer New York.
[67]	Protter P. 1990. Stochastic differential equations. Stochastic Integration and Differential Equations: A New Approach, 187–284.
[68]	Rudra P. 1990. Symmetry classes of Fokker−Planck-type equations. Journal of Physics A: Mathematical and General, 23: 1663. doi: 10.1088/0305-4470/23/10/009
[69]	Sastri C, Dunn K. 1985. Lie symmetries of some equations of the Fokker–Planck type. Journal of mathematical physics, 26: 3042-3047. doi: 10.1063/1.526681
[70]	Schwartz L. 2006. Géométrie différentielle du 2eme ordre, semi-martingales et équations différentielles stochastiques sur une variété différentielle, in: Séminaire de Probabilités XVI, 1980/81 Supplément: Géométrie Différentielle Stochastique. Springer, pp. 1–148.
[71]	Shapovalov A V, Shirokov I V. 1992. Symmetry algebras of linear differential equations. Theor Math Phy, 92: 697-703. doi: 10.1007/BF01018697
[72]	Shi S, Fu J, Chen L. 2008a. The Lie symmetries and Noether conserved quantities of discrete non-conservative mechanical systems. Chinese Physics B, 17: 385. doi: 10.1088/1674-1056/17/2/005
[73]	Shi S, Fu J, Huang X, Chen L, Zhang X. 2008b. The Lie symmetries and Noether conserved quantities of discrete mechanical systems with variable mass. Chinese Physics B, 17: 754. doi: 10.1088/1674-1056/17/3/003
[74]	Shi S, Huang X. 2008. Noether symmetry and Lie symmetry of discrete holonomic systems with dependent coordinates. Chinese Physics B, 17: 1554. doi: 10.1088/1674-1056/17/5/004
[75]	Shtelen W, Stogny V. 1989. Symmetry properties of one-and two-dimensional Fokker−Planck equations. Journal of Physics A: Mathematical and General, 22: L539. doi: 10.1088/0305-4470/22/13/002
[76]	Spichak S, Stognii V. 1999. Symmetry classification and exact solutions of the one-dimensional Fokker−Planck equation with arbitrary coefficients of drift and diffusion. Journal of Physics A: Mathematical and General, 32: 8341. doi: 10.1088/0305-4470/32/47/312
[77]	Stratonovich R. 1966. A new representation for stochastic integrals and equations. SIAM Journal on Control, 4: 362-371. doi: 10.1137/0304028
[78]	Stroock D W. 2003. Markov processes from K. Itô’s Perspective (AM-155). Princeton University Press.
[79]	Ünal G. 2003. Symmetries of Itô and Stratonovich dynamical systems and their conserved quantities. Nonlinear Dynamics, 32: 417-426. doi: 10.1023/A:1025669920594
[80]	Walcher S. 2023. Symmetries of ordinary differential equations: A short introduction. arXiv preprint arXiv: 1911.01053.
[81]	Winternitz P. 1993. Lie groups and solutions of nonlinear partial differential equations, in: Ibort L A, Rodríguez M A (Eds.), integrable systems, quantum groups, and quantum field theories. Springer Netherlands, Dordrecht, pp. 429–495.
[82]	Zhang H, Chen L, Gu S, Liu C. 2007. The discrete variational principle and the first integrals of Birkhoff systems. Chinese Physics, 16: 582. doi: 10.1088/1009-1963/16/3/004
[83]	Zhang H, Chen L, Liu R. 2005a. First integrals of the discrete nonconservative and nonholonomic systems. Chinese Physics, 14: 238. doi: 10.1088/1009-1963/14/2/003
[84]	Zhang H, Chen L, Liu R. 2005b. Discrete variational principle and the first integrals of the conservative holonomic systems in event space. Chinese Physics, 14: 888. doi: 10.1088/1009-1963/14/5/005
[85]	Zhang H, Chen L, Liu R. 2005c. The discrete variational principle in Hamiltonian formalism and first integrals. Chinese Physics, 14: 1063. doi: 10.1088/1009-1963/14/6/001
[86]	Zhao G L, Chen L Q, Fu J L. 2012. Lie symmetries for discrete electromechanical dynamical systems with irregular lattices. Applied Mechanics and Materials, 138: 267-272. doi: 10.4028/www.scientific.net/AMM.138-139.267