Research progress and performance evaluations for self-starting single-solve explicit time integrators
-
摘要: 直接时间积分法在大型非线性动力系统的数值计算中起着关键作用, 尤其是在工程仿真与设计领域. 自启动单解显式时间积分法因在处理复杂非线性系统时的高效性和可靠性, 成为该领域的重要工具. 然而, 随着此类算法的逐步发展和多样化, 性能表现各异, 因此对其进行系统回顾和深入分析具有急迫性和重要性. 本文首先介绍了评估时间积分法性能的主要指标, 包括精度、稳定性、振幅误差与相位误差等, 为读者提供了理论基础; 接着, 详细回顾了自启动单解显式时间积分法的发展历程, 系统梳理了各种算法的演变过程; 比较了多种自启动单解显式时间积分法在谱特性、精度、稳定性以及误差方面的性能表现并使用典型算例与工程结构进行了数值验证. 重点指出当前性能表现优异的两种显式积分法: 完全显式的GSSE法和速度隐式处理的GSSI法. 这两种方法都具备自启动、单解、显式求解、最大化条件稳定域、可控数值耗散(全历程变化)和一致二阶精度的特点, 而二者之间的区别在于求解阻尼问题的计算量和有阻尼时的条件稳定域大小. 本文还展望了显式时间积分法未来的研究方向, 强调了进一步优化与发展的潜力.Abstract: Direct time integration methods play a critical role in the numerical computation of large-scale nonlinear dynamic systems, particularly in the field of engineering simulation and design. The self-starting single-solve explicit time integration methods have become essential tools in this domain due to their efficiency and reliability in handling complex nonlinear systems. However, as these algorithms continue to evolve and diversify, their performance varies significantly, underscoring the urgent need for a systematic review and in-depth analysis of their capabilities. This paper first introduces the key performance metrics for evaluating time integration methods, including accuracy, stability, amplitude and phase error, providing a theoretical foundation for readers. It then offers a detailed review of the development of self-starting single-solve explicit time integration methods, systematically tracing the evolution of various algorithms. Finally, the performance of several self-starting single-solve explicit methods is compared in terms of spectral properties, accuracy, stability, and error characteristics, with numerical verification performed using typical examples and engineering structures. The paper highlights two explicit methods that currently exhibit superior performance: The fully explicit GSSE method and the velocity-implicit GSSI method. Both methods are characterized by their self-starting capability, single-solution, explicitness, maximized conditional stability, controllable numerical dissipation (over the full range), and identical second-order accuracy. The primary distinction between the two lies in the computational effort required for damping problems and the size of the conditional stability domain in the presence of damping. The paper also explores future research directions for explicit time integration methods, emphasizing the potential for further optimization and development.
-
图 1 EWBZ-
$\alpha $ 法的谱半径变化曲线. (a)在${\rho _{\rm{b}}} = 0.4$ 且$\xi = 0$ 时谱半径随${\rho _{\rm{s}}}$ 变化; (b)在$\xi = 0$ 且${\rho _{\rm{b}}} = {\rho _{\rm{s}}}$ 时谱半径随${\rho _{\rm{b}}}$ 变化
图 2 EWBZ-
$\alpha $ 法的谱半径与条件稳定域. (a)在$\xi = 0.1$ 时谱半径的变化情况; (b)最优EWBZ-$\alpha $ 法的稳定域${\varOmega _{\rm{s}}}$ 的变化情况
图 5 取步长
$\Delta t = 0.02$ s, 最优EWBZ-$\alpha $ 法在求解无阻尼自由振动的单自由度系统$ (\ddot {\boldsymbol{u}}(t) + 4{\boldsymbol{u}}(t) = 0, $ $ {\text{ }}{\boldsymbol{u}}(t) = 1,\;\dot {\boldsymbol{u}}(t) $ $ = 0) $ 时预测的数值解与精确解的比较
图 6 自启动单解显式算法(
${\rho _{\rm{b}}} = {\rho _{\rm{s}}} = 1$ )在求解无阻尼自由振动时的收敛率. (a)全局位移误差; (b)全局速度误差; (c)全局加速度误差
图 7 自启动单解显式算法(
${\rho _{\rm{b}}} = {\rho _{\rm{s}}} = 0.6$ )在求解无阻尼自由振动时的收敛率. (a)全局位移误差; (b)全局速度误差; (c)全局加速度误差
图 8 自启动单解显式算法(
${\rho _{\rm{b}}} = {\rho _{\rm{s}}} = 1$ )在求解无阻尼受迫振动时的收敛率. (a)全局位移误差; (b)全局速度误差; (c)全局加速度误差
图 9 自启动单解显式算法(
${\rho _{\rm{b}}} = {\rho _{\rm{s}}} = 0.6$ )在求解无阻尼受迫振动时的收敛率. (a)全局位移误差; (b)全局速度误差; (c)全局加速度误差
图 10 自启动单解显式算法(
${\rho _{\rm{b}}} = 0.6$ )在求解有阻尼自由振动时的收敛率. (a)全局位移误差; (b)全局速度误差; (c)全局加速度误差
图 11 自启动单解显式算法(
${\rho _{\rm{b}}} = 0.6$ )在求解有阻尼受迫振动时的收敛率. (a) 全局位移误差; (b) 全局速度误差; (c) 全局加速度误差
图 12 GSSE和GSSI法的谱半径. (a)
${\rho _{\rm{b}}} = 1$ 和${\rho _{\rm{s}}} = 0$ ; (b)${\rho _{\rm{b}}} = 0$ 和${\rho _{\rm{s}}} = 0$ 
图 13 GSSE和GSSI法的稳定域曲面. (a) GSSE法(
${\rho _{\rm{s}}} = {\rho _{\rm{b}}}$ ); (b) GSSE法(${\rho _{\rm{s}}} = 0$ ); (c) GSSI法(${\rho _{\rm{s}}} = {\rho _{\rm{b}}}$ ); (d) GSSI法(${\rho _{\rm{s}}} = 0$ )
图 15 GSSE和GSSI法振幅和相位误差的比较. (a) GSSE法(
${\rho _{\rm{s}}} = {\rho _{\rm{b}}}$ )的振幅误差主项; (b) GSSE法(${\rho _{\rm{s}}} = {\rho _{\rm{b}}}$ )的相位误差主项; (c) GSSI法(${\rho _{\rm{s}}} = {\rho _{\rm{b}}}$ )的振幅误差主项; (d) GSSI法(${\rho _{\rm{s}}} = {\rho _{\rm{b}}}$ )的相位误差主项
图 16 GSSE和GSSI法(
${\rho _{\rm{b}}} = {\rho _{\rm{s}}}$ )在取$\Delta t = 0.1$ s解阻尼自由振动问题时预测的数值位移. (a) GSSE法; (b) GSSI法
图 17 受冲击的直杆, 截面积
$A = 1\;{{\text{m}}^2}$ ,$E = 3 \times {10^7}\;{\text{Pa}}$ ,$L = 20\;{\text{m}}$ ,$\rho = 7.4 \times {10^{ - 4}}\;{\text{kg}}/{{\text{m}}^3}$ 表 1 自启动单解显式时间积分法的算法结构特点比较
算法 平衡方程满足的时刻 启动条件 耗散控制 速度处理方式 EN-$\beta $(Hughes & Liu 1978) ${t_{n + 1}}$ ${{\boldsymbol{\ddot u}}_0}$ $0 \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 TW (Mahéo et al. 2009) ${t_{n + 1}}$ ${{\boldsymbol{\ddot u}}_0}$ $0 \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 EDV1 (Zhang & Xing 2019) ${t_{n + \zeta }}$ — $0 \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 TSSE (Li & Yu 2021) ${t_{n + \zeta }}$ — $0 \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 EHHT-$\alpha $(Miranda et al. 1989) ${t_{n + \varsigma }}$ ${{\boldsymbol{\ddot u}}_0}$ $1/2 \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 CL (Chung & Lee 1994) ${t_n}$ — $1/2 \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 NT (Namburu & Tamma 1992) $ {t_{n + 1/2}} $ — $\rho_{\mathrm{b}}=1 $ 隐式 EWBZ-$\alpha $(Hulbert & Chung 1996) ${t_n}$ — $0 \leqslant \left| {{\rho _{\rm{s}}}} \right| \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 YZ (于开平 等 2004) ${t_n}$ — $0 \leqslant \left| {{\rho _{\rm{s}}}} \right| \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 EG-$\alpha $(Li et al. 2021a) ${t_{n + 2/3 - {\alpha _m}}}$ ${{\boldsymbol{\ddot u}}_0}$ $0 \leqslant \left| {{\rho _{\rm{s}}}} \right| \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 E-GSSSS (Shimada 2013) ${t_{n + {W_1}{\Lambda _1}}}$ ${{\boldsymbol{\ddot u}}_0}$ $0 \leqslant \left| {{\rho _{3{\rm{b}}}}} \right| \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 ICL (Kim 2019) ${t_{n + 1}}$ ${{\boldsymbol{\ddot u}}_0}$ $1/2 \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 NE (Newmark 1959) ${t_{n + 1}}$ ${{\boldsymbol{\ddot u}}_0}$ $\rho_{\mathrm{b}}=1 $ 隐式 GSSE (Li et al. 2021a) ${t_{n + p}}$ ${{\boldsymbol{\ddot u}}_0}$ $0 \leqslant \left| {{\rho _{\rm{s}}}} \right| \leqslant {\rho _{\rm{b}}} \leqslant 1$ 显式 GSSI (Zhao et al. 2023) ${t_{n + p}}$ ${{\boldsymbol{\ddot u}}_0}$ $0 \leqslant \left| {{\rho _{\rm{s}}}} \right| \leqslant {\rho _{\rm{b}}} \leqslant 1$ 隐式 注: $\zeta = (3 - {\rho _{\rm{b}}})/(2{\rho _{\rm{b}}} + 2)$和$\varsigma = 2{\rho _{\rm{b}}}/({\rho _{\rm{b}}} + 1)$. 
下载: 导出CSV
表 2 自启动单解显式积分法在求解无阻尼问题
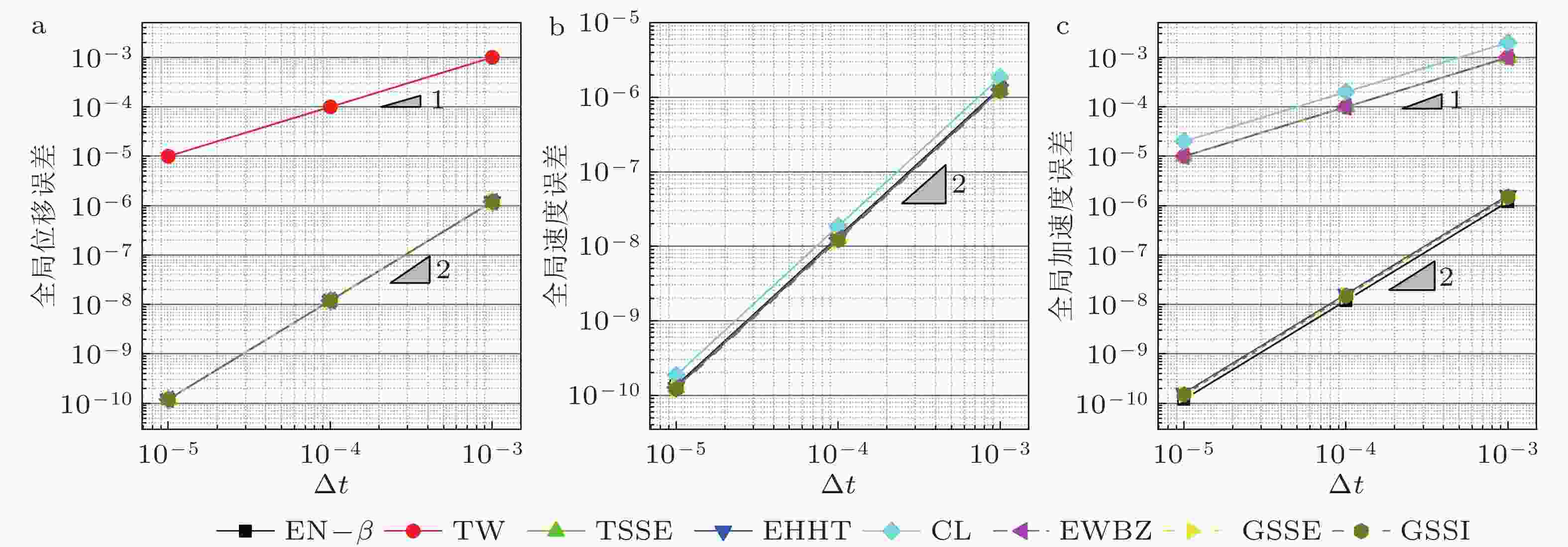
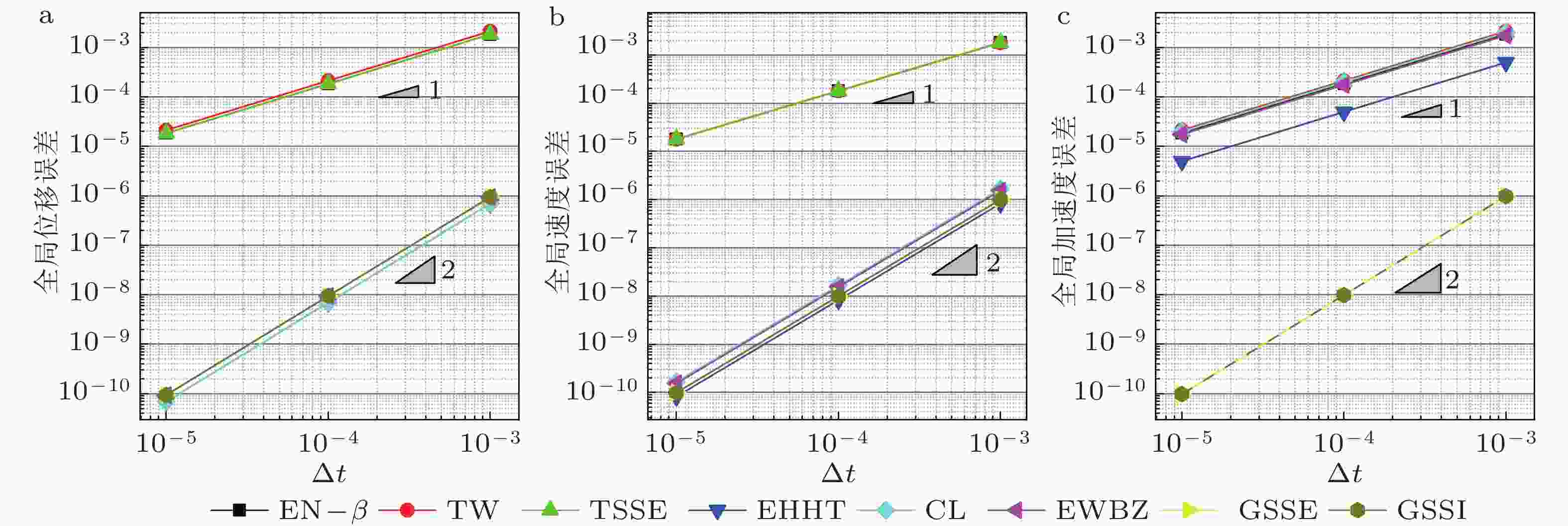
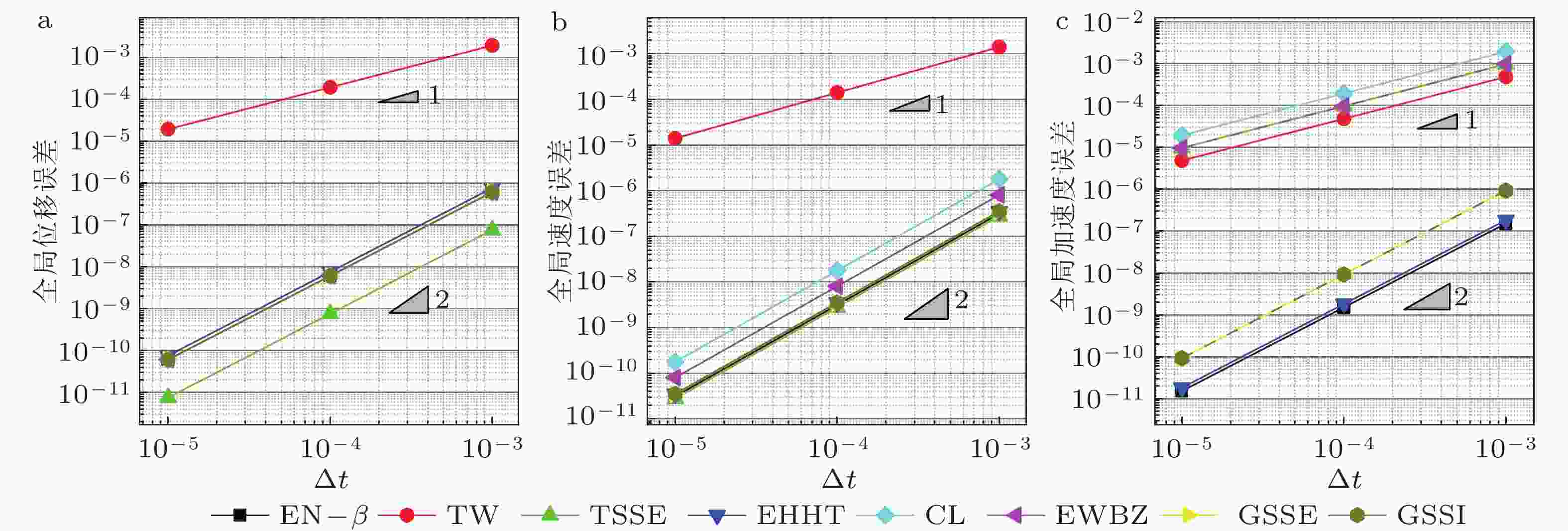
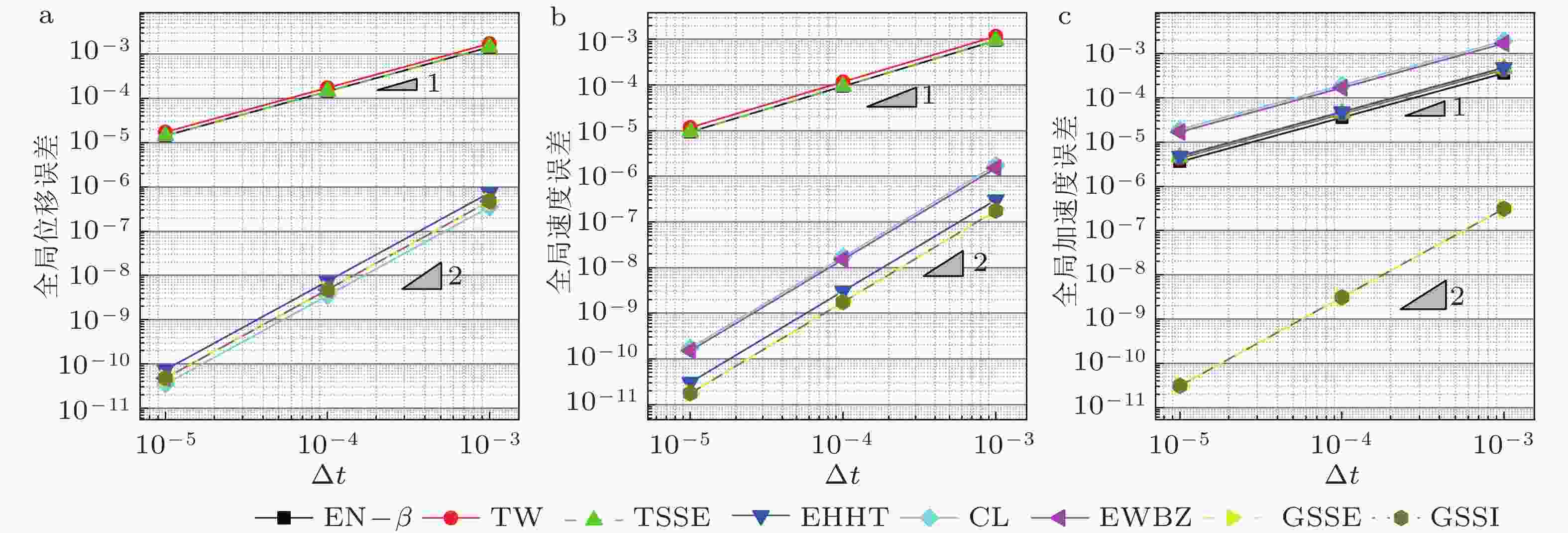
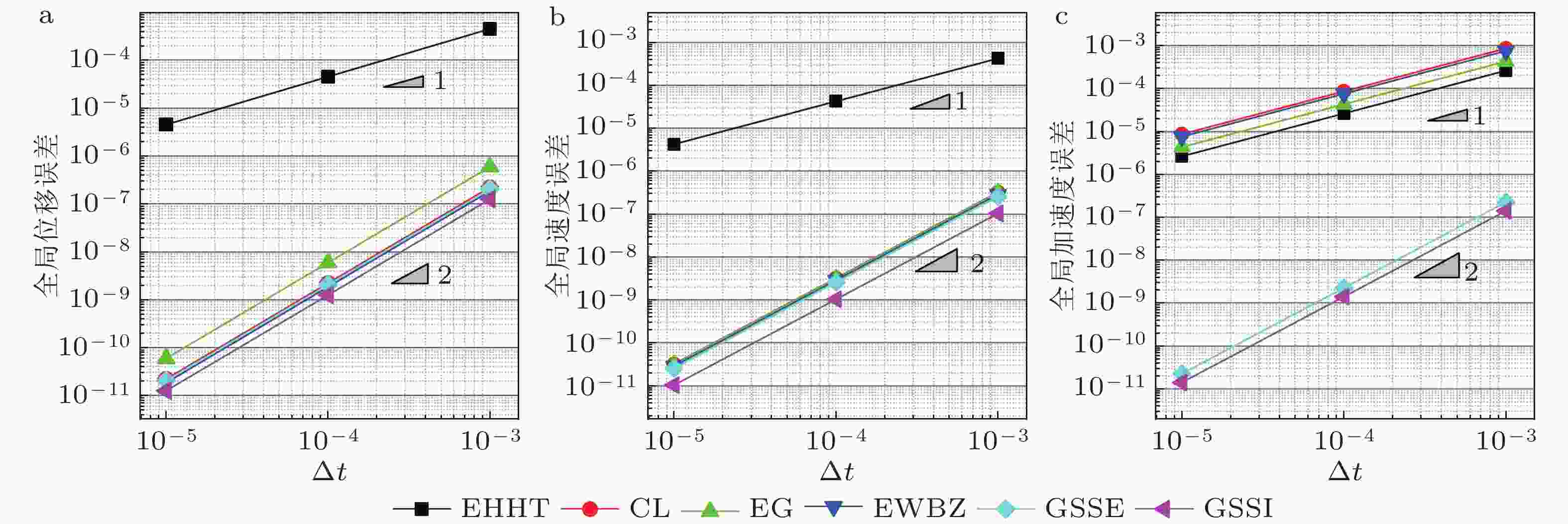
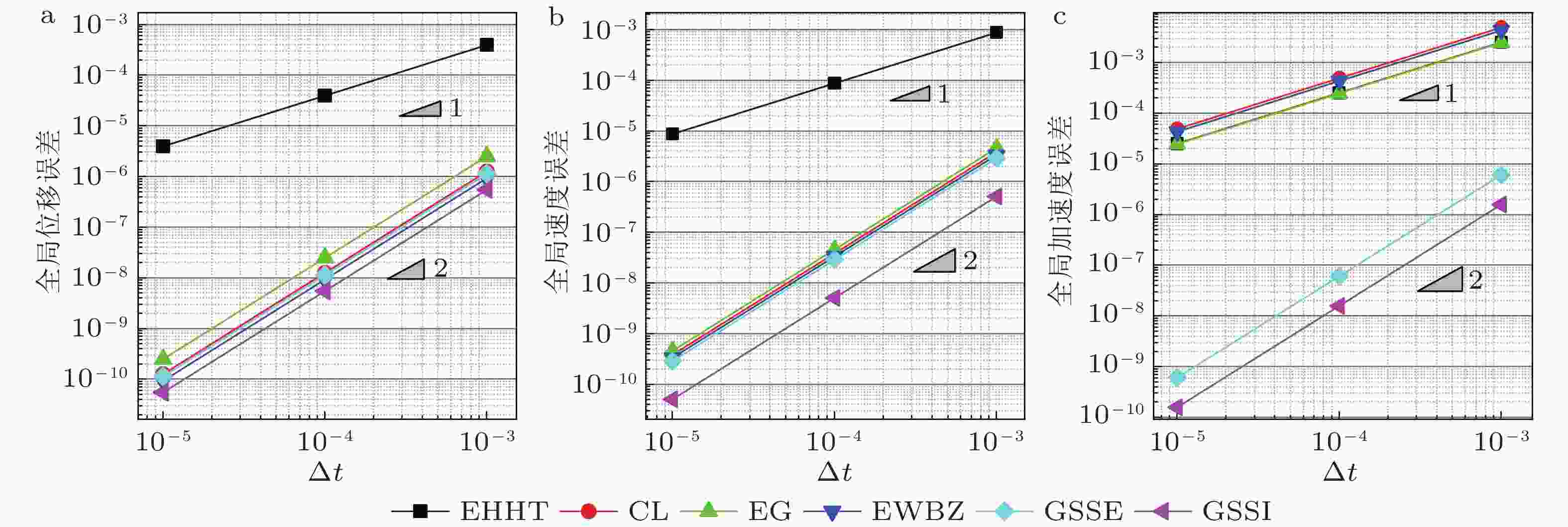
$(\xi = 0)$ 时的精度阶数算法 位移 速度 加速度 $f(t) = 0$ $f(t)\ne 0$ $f(t) = 0$ $f(t)\ne 0$ $f(t) = 0$ $f(t)\ne 0$ ${\rho _{\rm{b}}} = 1$ ${\rho _{\rm{b}}} \ne 1$ ${\rho _{\rm{b}}} = 1$ ${\rho _{\rm{b}}} \ne 1$ ${\rho _{\rm{b}}} = 1$ ${\rho _{\rm{b}}} \ne 1$ ${\rho _{\rm{b}}} = 1$ ${\rho _{\rm{b}}} \ne 1$ ${\rho _{\rm{b}}} = 1$ ${\rho _{\rm{b}}} \ne 1$ ${\rho _{\rm{b}}} = 1$ ${\rho _{\rm{b}}} \ne 1$ TW 1 1 1 1 2 1 1 1 1 1 1 1 EN-$\beta $ 2 1 2 1 2 1 2 1 2 1 2 1 EDV1 2 1 2 1 2 1 2 1 — — — — TSSE 2 1 2 1 2 1 2 1 1 1 1 1 EHHT-$\alpha $ 2 2 2 2 2 1 2 1 2 1 2 1 CL 2 2 2 2 2 2 2 2 1 1 1 1 NT 2 — 2 — 2 — 2 — 1 — 1 — EWBZ-$\alpha $ 2 2 2 2 2 2 2 2 1 1 1 1 YZ 2 2 2 2 2 2 2 2 1 1 1 1 EG-$\alpha $ 2 2 2 2 2 2 2 2 1 1 1 1 ICL 2 2 2 2 2 2 2 2 2 2 2 2 NE 2 — 2 — 2 — 2 — 2 — 2 — GSSE 2 2 2 2 2 2 2 2 2 2 2 2 GSSI 2 2 2 2 2 2 2 2 2 2 2 2
下载: 导出CSV
表 3 自启动单解显式算法在求解有阻尼问题
$(\xi \ne 0)$ 时的精度阶数算法 位移 速度 加速度 $f(t) = 0$ $f(t)\ne 0$ $f(t) = 0$ $f(t)\ne 0$ $f(t) = 0$ $f(t)\ne 0$ EN-$\beta $ 1 1 1 1 1 1 TW 1 1 1 1 1 1 EDV1 1 1 1 1 — — TSSE 1 1 1 1 1 1 EHHT-$\alpha $ 1 1 1 1 1 1 CL 2 2 2 2 1 1 NT 2 2 2 2 1 1 EWBZ-$\alpha $ 2 2 2 2 1 1 YZ 2 2 2 2 1 1 EG-$\alpha $ 2 2 2 2 1 1 ICL 2 2 2 2 2 2 NE 2 2 2 2 2 2 GSSE 2 2 2 2 2 2 GSSI 2 2 2 2 2 2
下载: 导出CSV
表 4 自启动单解显式积分法的条件稳定域
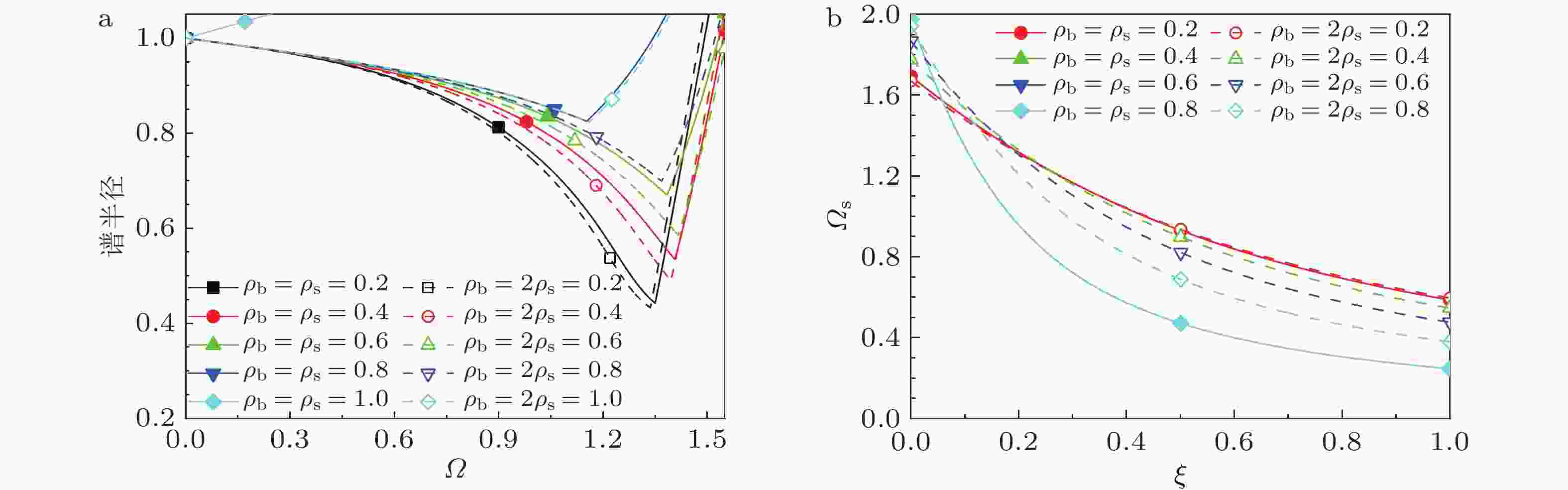
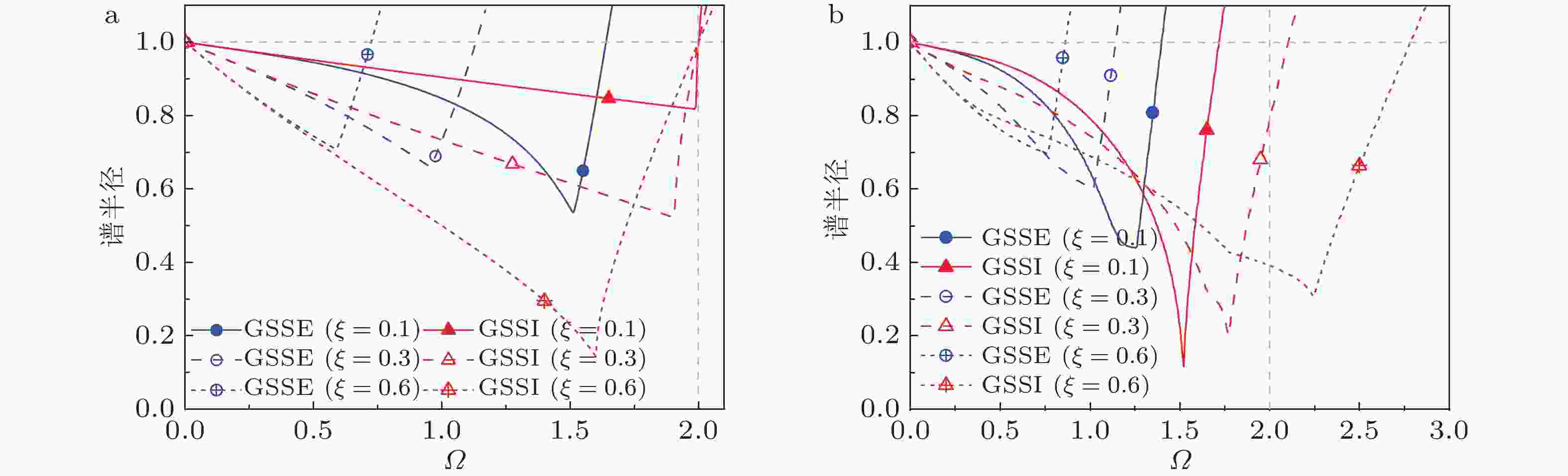
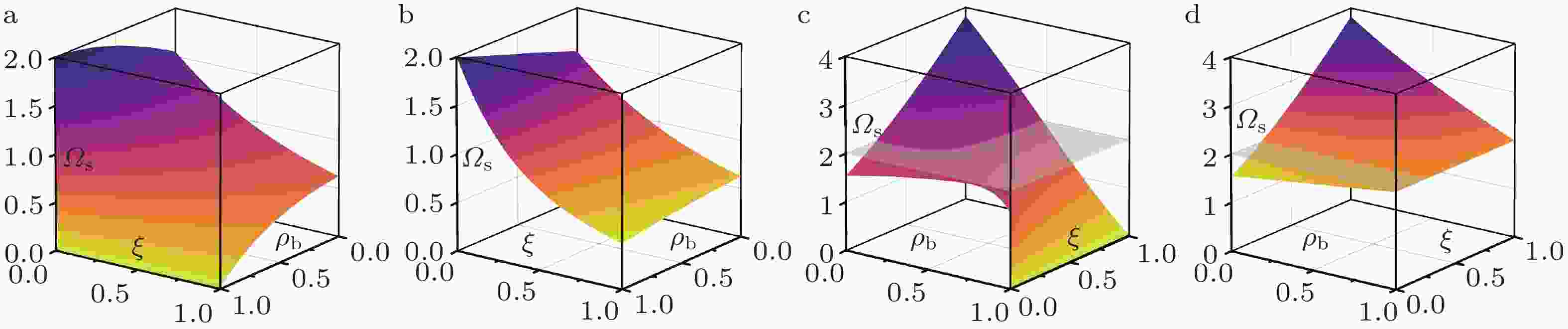
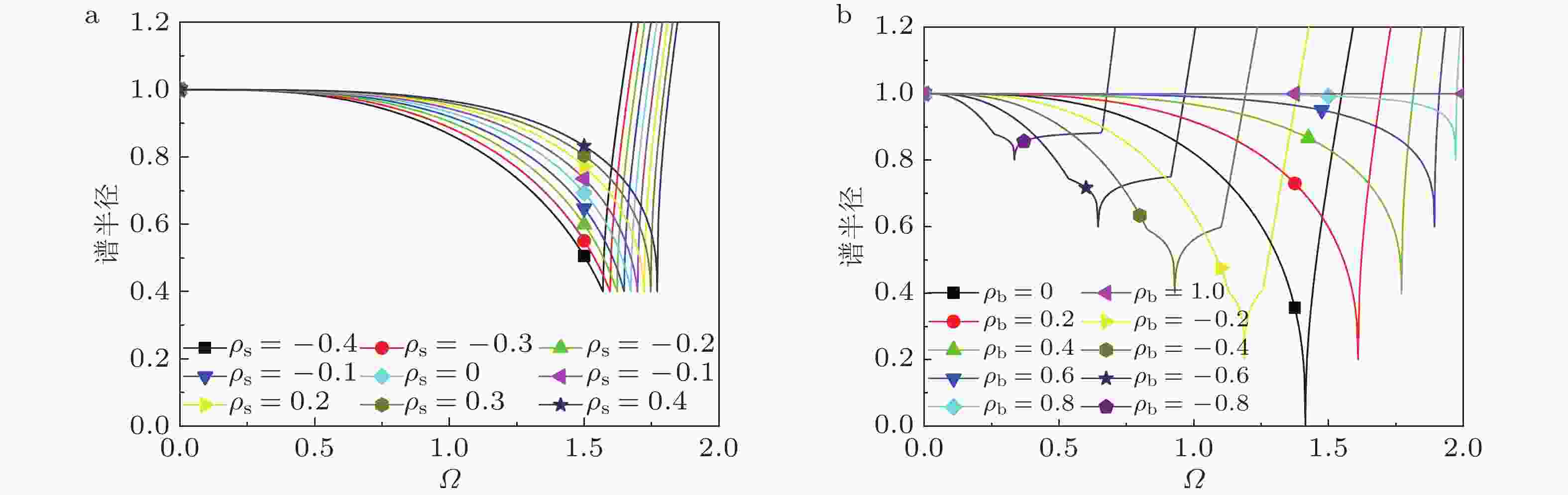
算法 稳定域($\xi \ne 0$) 稳定域($\xi = 0$) 最大值 当$\xi $增大时 最大值 参数取值 EN-$\beta $、TW、EDV1、TSSE <2 减小 2 ${\rho _{\rm{b}}} = 1$ EHHT-$\alpha $ <2 减小 2 ${\rho _{\rm{b}}} = 1$ CL、ICL <2 减小 2 ${\rho _{\rm{b}}} = 1$ NT、NE 2 不变 2 — EWBZ-$\alpha $、YZ、EG-$\alpha $ <2 减小 2 ${\rho _{\rm{b}}} = 1$ GSSE <2 减小 2 ${\rho _{\rm{b}}} = 1$ GSSI <3.8271 增大 2 ${\rho _{\rm{b}}} = 1$
下载: 导出CSV
表 5 自启动单解显式积分算法的振幅与相位误差阶数
算法 有阻尼($\xi \ne 0$) 无阻尼($\xi = 0$) 振幅误差 相位误差 振幅误差 相位误差 EN-$\beta $、TW、EDV1、TSSE 1 1 1 2 EHHT-$\alpha $ 1 1 3 2 CL、ICL 2 2 3 2 NT、NE 2 2 — 2 EWBZ-$\alpha $、EG-$\alpha $、GSSE、YZ 2 2 3 2 GSSI 2 2 3 2
下载: 导出CSV
表 6 不同算法计算间隙非线性舵面的性能比较
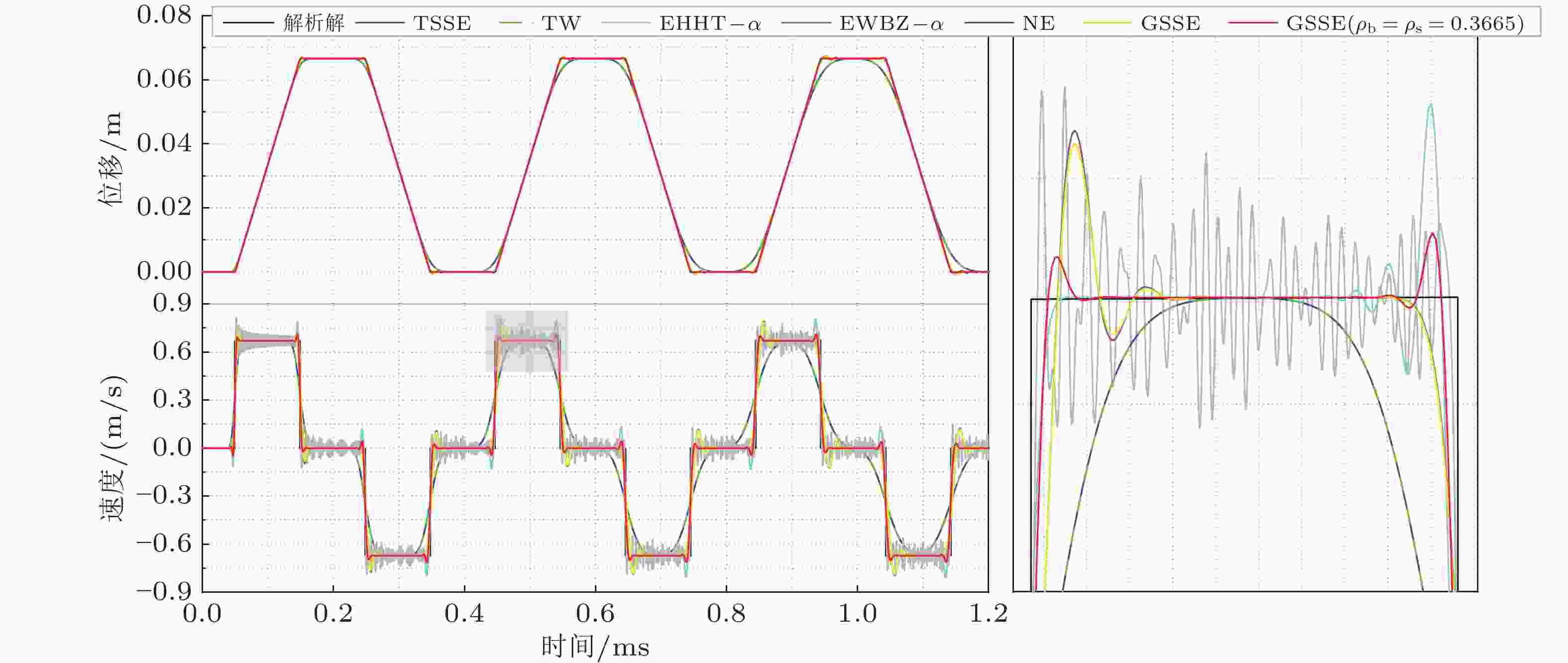
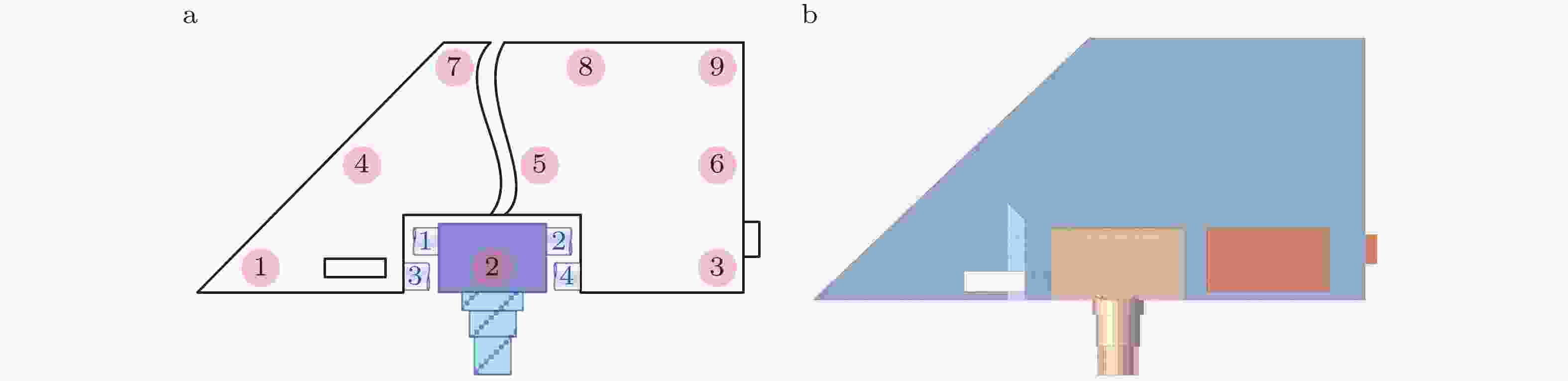
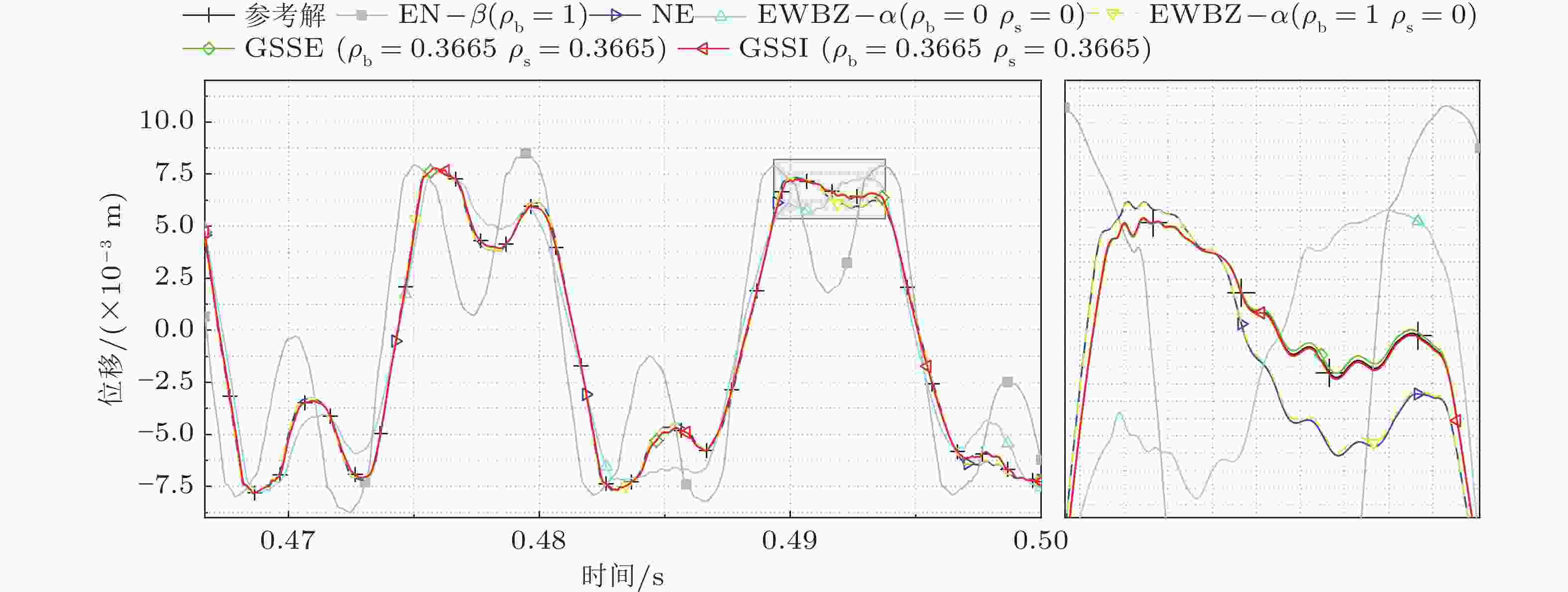
算法 参数取值 全局误差($ \times {10^{ - 4}}$) 运行时间(s) EN-$\beta $(Hughes & Liu 1978) ${\rho _{\rm{b}}} = 1,\beta = 0$ 2 094.65400691130 16.7371675 TW (Mahéo et al. 2009) ${\rho _{\rm{b}}} = 1$ 2 094.65400539673 16.5674646 TSSE (Li & Yu 2021) ${\rho _{\rm{b}}} = 1$ 2 095.11359385971 16.6394112 EHHT-$\alpha $(Miranda et al. 1989) ${\rho _{\rm{b}}} = 1$ 2 094.64833439895 16.7600374 CL (Chung & Lee 1994) ${\rho _{\rm{b}}} = 1$ 122.05490051270 16.5825193 NT (Namburu & Tamma 1992) — 128.74544603336 16.6789087 EWBZ-$\alpha $(Hulbert & Chung 1996) ${\rho _{\rm{b}}} = 1,{\rho _{\rm{s}}} = 0$ 122.05490051270 16.7971924 ${\rho _{\rm{b}}} = 0,{\rho _{\rm{s}}} = 0$ 574.57122300857 16.9433569 ${\rho _{\rm{b}}} = 0.36653,{\rho _{\rm{s}}} = 0.36653$ 8.09663420031 17.0288960 EG-$\alpha $(Li et al. 2021a) ${\rho _{\rm{b}}} = 1,{\rho _{\rm{s}}} = 0$ 120.23431346855 17.0691251 ${\rho _{\rm{b}}} = 0,{\rho _{\rm{s}}} = 0$ 579.63193462968 17.1157046 ${\rho _{\rm{b}}} = 0.36653,{\rho _{\rm{s}}} = 0.36653$ 9.67169868571 16.7288852 ICL (Kim 2019) ${\rho _{\rm{b}}} = 1$ 6.72052405612 16.6451444 NE (Newmark 1959) — 128.86982904751 16.5817191 CD (Fox & Goodwin 1949) — 128.89359314558 16.8137596 GSSE (Li et al. 2021a) ${\rho _{\rm{b}}} = 1,{\rho _{\rm{s}}} = 0$ 122.05489777818 17.0365016 ${\rho _{\rm{b}}} = 0,{\rho _{\rm{s}}} = 0$ 577.66327372322 16.5218805 ${\rho _{\rm{b}}} = 0.36653,{\rho _{\rm{s}}} = 0.36653$ 7.02558590034 16.7662669 GSSI (Zhao et al. 2023) ${\rho _{\rm{b}}} = 1,{\rho _{\rm{s}}} = 0$ 128.86982904751 16.7886440 ${\rho _{\rm{b}}} = 0,{\rho _{\rm{s}}} = 0$ 555.75987795750 16.6073923 ${\rho _{\rm{b}}} = 0.36653,{\rho _{\rm{s}}} = 0.36653$ 2.79079214905 16.6471036 TPO/G-$\alpha $
(Chung & Hulbert 1993, 邵慧萍和蔡承文 1988)${\rho _\infty } = 1$ 233.37572689655 32.7353195 ${\rho _\infty } = 0$ 1091.11262975068 32.8101065 Newmark-$\beta $(Newmark 1959) $\gamma = 0.5,\beta = 0.25$ 233.56743425553 33.1281854 SUCI2 (Li & Yu 2020) ${\rho _\infty } = 1$ 66.39354082933 122.886593 S2E1 (Li & Yu 2021) ${\rho _{\rm{b}}} = 0.99$ 30.98184714029 33.2407046
下载: 导出CSV
-
[1] 陈旻铭, 任旭华, 张继勋. 2024. 显式算法中三维黏弹性人工边界应用及输水隧洞动力响应分析. 水力发电, 50(1): 20-25, 70 (Chen M M, Ren X H, Zhang J X. 2024. Application of 3d viscoelastic artificial boundary and dynamic response analysis of water conveyance tunnel in explicit algorithm. Water Power, 50(1): 20-25, 70). doi: 10.3969/j.issn.0559-9342.2024.01.005Chen M M, Ren X H, Zhang J X. 2024. Application of 3d viscoelastic artificial boundary and dynamic response analysis of water conveyance tunnel in explicit algorithm. Water Power, 50(1): 20-25, 70 doi: 10.3969/j.issn.0559-9342.2024.01.005 [2] 丁峻宏, 金先龙, 郭毅之, 等. 2005. 沉管隧道地震响应的三维非线性数值模拟方法及应用. 振动与冲击, 24(5): 10-14 (Ding J H, Jin X L, Guo Y Z, et al. 2005. 3D numerical simulation method and its application in calculation of seismic response of immersed tunnel. Journal of Vibration and Shock, 24(5): 10-14). doi: 10.3969/j.issn.1000-3835.2005.05.006Ding J H, Jin X L, Guo Y Z, et al. 2005. 3D numerical simulation method and its application in calculation of seismic response of immersed tunnel. Journal of Vibration and Shock, 24(5): 10-14. doi: 10.3969/j.issn.1000-3835.2005.05.006 [3] 杜修力, 王进廷. 2000. 阻尼弹性结构动力计算的显式差分法. 工程力学, 17: 37-43 (Du X L, Wang J T. 2000. An explicit difference formulation of dynamic response calculation of elastic structure with damping. Engineering Mechanics, 17: 37-43). doi: 10.3969/j.issn.1000-4750.2000.05.006Du X L, Wang J T. 2000. An explicit difference formulation of dynamic response calculation of elastic structure with damping. Engineering Mechanics, 17: 37-43. doi: 10.3969/j.issn.1000-4750.2000.05.006 [4] 杜晓琼, 杨迪雄, 赵永亮. 2015. 一种无条件稳定的结构动力学显式算法. 力学学报, 47: 310-319 (Du X Q, Yang D X, Zhao Y L. 2015. An unconditionally stable explicit algorithm for structural dynamics. Chinese Journal of Mechanics, 47: 310-319). doi: 10.6052/0459-1879-14-209Du X Q, Yang D X, Zhao Y L. 2015. An unconditionally stable explicit algorithm for structural dynamics. Chinese Journal of Mechanics, 47: 310-319. doi: 10.6052/0459-1879-14-209 [5] 胡海岩, 田强, 张伟, 等. 2013. 大型网架式可展开空间结构的非线性动力学与控制. 力学进展, 43(4): 390-414 (Hu H Y, Tian Q, Zhang W, et al. 2013. Nonlinear dynamics and control of large mesh deployable space structures. Advances in Mechanics, 43(4): 390-414). doi: 10.6052/1000-0992-13-045Hu H Y, Tian Q, Zhang W, et al. 2013. Nonlinear dynamics and control of large mesh deployable space structures. Advances in Mechanics, 43(4): 390-414. doi: 10.6052/1000-0992-13-045 [6] 胡晓楠, 张建斌, 赵国伟. 2010. 柔性绳索在空气阻力作用下的动力学仿真研究. 机械科学与技术, 29(8): 1334-1337 (Hu X N, Zhang J B, Zhao G W. 2010. Dynamic simulation study of flexible ropes under air resistance. Mechanical Science and Technology, 29(8): 1334-1337).Hu X N, Zhang J B, Zhao G W. 2010. Dynamic simulation study of flexible ropes under air resistance. Mechanical Science and Technology, 29(8): 1334-1337. [7] 姜凯, 陈伟, 韩佳奇, 等. 2023. 鸟撞发动机整机响应显式—隐式仿真. 航空发动机, 49(1): 109-114 (Jiang K, Chen W, Han J Q, et al. 2023. Explicit-implicit simulation of engine response under bird impact. Aeroengine, 49(1): 109-114).Jiang K, Chen W, Han J Q, et al. 2023. Explicit-implicit simulation of engine response under bird impact. Aeroengine, 49(1): 109-114. [8] 兰彬, 叶献辉, 宋顺成, 等. 2015. 304NG不锈钢高应变率材料模型在ABAQUS中的实现技术. 应用数学和力学, 36(2): 167-177 (Lan B, Ye X H, Song S C, et al. 2015. Formulation and programming of a dynamic constitutive model at high strain rates in ABAQUS for the 304NG stainless steel. Applied Mathematics and Mechanics, 36(2): 167-177). doi: 10.3879/j.issn.1000-0887.2015.02.006Lan B, Ye X H, Song S C, et al. 2015. Formulation and programming of a dynamic constitutive model at high strain rates in ABAQUS for the 304NG stainless steel. Applied Mathematics and Mechanics, 36(2): 167-177. doi: 10.3879/j.issn.1000-0887.2015.02.006 [9] 刘学深, 丁培柱. 2004. 量子系统保结构计算新进展. 物理学进展, 24(1): 47-89 (Liu X S, Ding P Z. 2004. New progress of structure-preserving computation for quantum systems. Progress in Physics, 24(1): 47-89). doi: 10.3321/j.issn:1000-0542.2004.01.003Liu X S, Ding P Z. 2004. New progress of structure-preserving computation for quantum systems. Progress in Physics, 24(1): 47-89. doi: 10.3321/j.issn:1000-0542.2004.01.003 [10] 刘祥庆, 刘晶波, 丁桦. 2007. 时域逐步积分算法稳定性与精度的对比分析. 岩石力学与工程学报, 26: 3000-3008 (Liu X Q, Liu J B, Ding H. 2007. Comparative analysis of stability and accuracy of step-by-step time-integration methods. Chinese Journal of Rock Mechanics and Engineering, 26: 3000-3008).Liu X Q, Liu J B, Ding H. 2007. Comparative analysis of stability and accuracy of step-by-step time-integration methods. Chinese Journal of Rock Mechanics and Engineering, 26: 3000-3008. [11] 赖松柏, 陈同祥, 于登云. 2012. 整体壁板填料辅助滚弯成形的动力显式分析方法. 航天器工程, 21(3): 41-47 (Lai S B, Chen T X, Yu D Y. 2012. Dynamic explicit analysis method for roll bending of integral stiffened panel with rubber filler. Spacecraft Engineering, 21(3): 41-47). doi: 10.3969/j.issn.1673-8748.2012.03.021Lai S B, Chen T X, Yu D Y. 2012. Dynamic explicit analysis method for roll bending of integral stiffened panel with rubber filler. Spacecraft Engineering, 21(3): 41-47. doi: 10.3969/j.issn.1673-8748.2012.03.021 [12] 李云飞, 曾祥国, 廖异. 2017. 基于修正Johnson-Cook模型的钛合金热黏塑性动态本构关系及有限元模拟. 中国有色金属学报, 27(7): 1419-1425 (Li Y F, Zeng X G, Liao Y. 2017. Thermal-viscoplastic constitutive relation of Ti-6Al-4V alloy and numerical simulation by modified Johnson-Cook modal. The Chinese Journal of Nonferrous Metals, 27(7): 1419-1425). doi: 10.19476/j.ysxb.1004.0609.2017.07.13Li Y F, Zeng X G, Liao Y. 2017. Thermal-viscoplastic constitutive relation of Ti-6Al-4V alloy and numerical simulation by modified Johnson-Cook modal. The Chinese Journal of Nonferrous Metals, 27(7): 1419-1425 doi: 10.19476/j.ysxb.1004.0609.2017.07.13 [13] 李小军, 刘爱文. 2000. 动力方程求解的显式积分格式及其稳定性与适用性. 世界地震工程, 16: 8-12 (Li X J, Liu A W. 2000. Explicit step-by-step integration formulas for dynamic differential equations and their stability and applicability. World Earthquake Engineering, 16: 8-12).Li X J, Liu A W. 2000. Explicit step-by-step integration formulas for dynamic differential equations and their stability and applicability. World Earthquake Engineering, 16: 8-12. [14] 李小军, 廖振鹏. 1993. 非线性结构动力方程求解的显式差分格式的特性分析. 工程力学, 10: 141-148 (Li X J, Liao Z P. 1993. The analysis of the problems of an explicit difference method for solving the nonlinear structural dynamic equations. Engineering Mechanics, 10: 141-148).Li X J, Liao Z P. 1993. The analysis of the problems of an explicit difference method for solving the nonlinear structural dynamic equations. Engineering Mechanics, 10: 141-148. [15] 李小军, 廖振鹏, 杜修力. 1992. 有阻尼体系动力问题的一种显式差分解法. 地震工程与工程振动, 12: 74-80 (Li X J, Liao Z P, Du X L. 1992. An explicit difference method for dynamic problems of damped systems. Earthquake Engineering and Engineering Vibration, 12: 74-80).Li X J, Liao Z P, Du X L. 1992. An explicit difference method for dynamic problems of damped systems. Earthquake Engineering and Engineering Vibration, 12: 74-80. [16] 李常青, 李正藩, 蒋丽忠. 2024. 单步无条件稳定显式结构动力学算法. 铁道科学与工程学报, 21: 1136-1145 (Li C Q, Li Z F, Jiang L Z. 2024. An explicit finite difference method for viscoelastic dynamic problem. Journal of Railway Science and Engineering, 21: 1136-1145). doi: 10.19713/j.cnki.43-1423/u.T20230761Li C Q, Li Z F, Jiang L Z. 2024. An explicit finite difference method for viscoelastic dynamic problem. Journal of Railway Science and Engineering, 21: 1136-1145. doi: 10.19713/j.cnki.43-1423/u.T20230761 [17] 李常青, 楼梦麟, 余志武, 等. 2011. 近似平衡多项式加速度动力显式算法. 应用力学学报, 28: 475-479, 553 (Li C Q, Lou M L, Yu Z W, et al. 2011. Pseudo-balance polynomial acceleration explicit method. Chinese Journal of Applied Mechanics, 28: 475-479, 553).Li C Q, Lou M L, Yu Z W, et al. 2011. Pseudo-balance polynomial acceleration explicit method. Chinese Journal of Applied Mechanics, 28: 475-479, 553. [18] 李志成, 黄小平, 钱七虎. 1994. 一种提高直接积分精度的方法. 力学与实践, 16: 36-39 (Li Z C, Huang X P, Qian Q H. 1994. A method for improving the accuracy of direct integration. Mechanics and Practice, 16: 36-39). doi: 10.6052/1000-0992-1994-063Li Z C, Huang X P, Qian Q H. 1994. A method for improving the accuracy of direct integration. Mechanics and Practice, 16: 36-39. doi: 10.6052/1000-0992-1994-063 [19] 李艳敏. 2005. 复杂结构的冲击动力学分析与仿真. [硕士论文]. 西北工业大学 (Li Y M. 2005. Impact dynamic analysis and simulation of complex structures. [Master Thesis]. Northwestern Polytechnical University).Li Y M. 2005. Impact dynamic analysis and simulation of complex structures. [Master Thesis]. Northwestern Polytechnical University. [20] 李金泽. 2023. 结构动力学问题自启动逐步时间积分算法的设计与分析. [博士论文]. 哈尔滨工业大学 (Li J Z. 2023. Design and analysis of self-starting step-by-step time integration algorithms for structural dynamics. [PhD Thesis]. Harbin Institute of Technology).Li J Z. 2023. Design and analysis of self-starting step-by-step time integration algorithms for structural dynamics. [PhD Thesis]. Harbin Institute of Technology. [21] 缪建成. 2011. 柔性多体动力学计算方法与大型可展天线动力分析研究. [博士论文]. 上海交通大学 (Miao J C. 2011. Study on computational stretgy for flexible multi-body dynamics and analysis of large deployable antenna. [PhD Thesis].Shanghai Jiao Tong University).Miao J C. 2011. Study on computational stretgy for flexible multi-body dynamics and analysis of large deployable antenna. [PhD Thesis].Shanghai Jiao Tong University. [22] 荣棉水, 李亚琦, 周伯昌. 2007. 求解动力方程的三种显式积分格式的比较. 华南地震, 27: 77-85 (Rong M S, Li Y Q, Zhou B C. 2007. Comparison of dissipation characteristics of 3 kinds of explicit integration formula for dynamic differential equations. South China Seismology, 27: 77-85). doi: 10.3969/j.issn.1001-8662.2007.01.011Rong M S, Li Y Q, Zhou B C. 2007. Comparison of dissipation characteristics of 3 kinds of explicit integration formula for dynamic differential equations. South China Seismology, 27: 77-85. doi: 10.3969/j.issn.1001-8662.2007.01.011 [23] 邵慧萍, 蔡承文. 1988. 结构动力学方程数值积分的三参数算法. 应用力学学报, 5: 76-81 (Shao H P, Cai C W. 1988. A three parameter algorithm for integration of structural dynamic equations. Chinese Journal of Applied Mechanics, 5: 76-81).Shao H P, Cai C W. 1988. A three parameter algorithm for integration of structural dynamic equations. Chinese Journal of Applied Mechanics, 5: 76-81. [24] 王进廷, 杜修力. 2002. 有阻尼体系动力分析的一种显式差分法. 工程力学, 19: 109-112 (Wang J T, Du X L. 2002. An explicit difference method for dynamic analysis of a structure system with damping. Engineering Mechanics, 19: 109-112). doi: 10.3969/j.issn.1000-4750.2002.03.022Wang J T, Du X L. 2002. An explicit difference method for dynamic analysis of a structure system with damping. Engineering Mechanics, 19: 109-112. doi: 10.3969/j.issn.1000-4750.2002.03.022 [25] 王进廷, 张楚汉, 金峰. 2006. 有阻尼动力方程显式积分方法的精度研究. 工程力学, 23: 1-5 (Wang J T, Zhang C H, Jin F. 2006. On the accuracy of several explicit integration schemes for dynamic equation with damping. Engineering Mechanics, 23: 1-5). doi: 10.3969/j.issn.1000-4750.2006.03.001Wang J T, Zhang C H, Jin F. 2006. On the accuracy of several explicit integration schemes for dynamic equation with damping. Engineering Mechanics, 23: 1-5. doi: 10.3969/j.issn.1000-4750.2006.03.001 [26] 谢红飙, 肖宏, 张国民, 等. 2003. 显式动力学有限元法分析板宽对板带轧制压力分布的影响. 塑性工程学报, 10(1): 61-64 (Xie H B, Xiao H, Zhang G M, et al. 2003. Analysis of strip rolling pressure distribution for different width by explicit dynamic FEM. Journal of Plasticity Engineering, 10(1): 61-64). doi: 10.3969/j.issn.1007-2012.2003.01.016Xie H B, Xiao H, Zhang G M, et al. 2003. Analysis of strip rolling pressure distribution for different width by explicit dynamic FEM. Journal of Plasticity Engineering, 10(1): 61-64 doi: 10.3969/j.issn.1007-2012.2003.01.016 [27] 徐圣. 2015. 几何非线性空间梁动力学仿真. [硕士论文]. 上海交通大学 (Xu S. 2015. Dynamic simulation of geometric nonlinear spatial beam. [Master Thesis]. Shanghai Jiao Tong University).Xu S. 2015. Dynamic simulation of geometric nonlinear spatial beam. [Master Thesis]. Shanghai Jiao Tong University. [28] 姚松, 田红旗, 高广军. 2003. 显式有限元法在车辆耐撞性研究中的应用. 交通运输工程学报, 3(1): 13-16, 20 (Yao S, Tian H Q, Gao G J. 2003. Explicit finite element method for vehicle crashworthiness. Journal of Traffic and Transportation Engineering, 3(1): 13-16, 20). doi: 10.3321/j.issn:1671-1637.2003.01.003Yao S, Tian H Q, Gao G J. 2003. Explicit finite element method for vehicle crashworthiness. Journal of Traffic and Transportation Engineering, 3(1): 13-16, 20. doi: 10.3321/j.issn:1671-1637.2003.01.003 [29] 于开平, 李进旺, 杨利芳, 等. 2004. 一个新的显式算法及其在转子动力学中的应用. 中国电机工程学报, 24: 114-118 (Yu K P, Li J W, Yang L F, et al. 2004. A new explicit time integration algorithm for the rotor problem. Proceedings of the CSEE, 24: 114-118). doi: 10.3321/j.issn:0258-8013.2004.05.021Yu K P, Li J W, Yang L F, et al. 2004. A new explicit time integration algorithm for the rotor problem. Proceedings of the CSEE, 24: 114-118. doi: 10.3321/j.issn:0258-8013.2004.05.021 [30] 赵宝友. 2010. 大型岩体洞室地震响应及减震措施研究. [博士论文]. 大连理工大学 (Zhao B Y. 2010. Research on seismic response and seismic resistance measures for large rock cavern under earthquake motion. [PhD Thesis]. Dalian University of Technology).Zhao B Y. 2010. Research on seismic response and seismic resistance measures for large rock cavern under earthquake motion. [PhD Thesis]. Dalian University of Technology. [31] 赵欣, 丁继锋, 韩增尧, 等. 2016. 航天器火工冲击模拟试验及响应预示方法研究综述. 爆炸与冲击, 36(2): 259-268 (Zhao X, Ding J F, Han Z Y, et al. 2016. Review of simulation and response prediction methods in spacecraft. Explosion and Shock Waves, 36(2): 259-268). doi: 10.11883/1001-1455(2016)02-0259-10Zhao X, Ding J F, Han Z Y, et al. 2016. Review of simulation and response prediction methods in spacecraft. Explosion and Shock Waves, 36(2): 259-268. doi: 10.11883/1001-1455(2016)02-0259-10 [32] 郑天骄. 2014. 拖拽下大变形柔性线缆非线性力学特性研究. [硕士论文]. 哈尔滨工业大学 (Zheng T J. 2014. Study on nonlinear mechanical properties of dragging flexible cables with large deformation. [Master Thesis].Harbin Institute of Technology).Zheng T J. 2014. Study on nonlinear mechanical properties of dragging flexible cables with large deformation. [Master Thesis].Harbin Institute of Technology. [33] 翟婉明. 1991. 大型结构动力分析的Newmark显式算法. 重庆交通学院学报, 10: 33-41 (Zhai W M. 1991. The explicit scheme of Newmark’s integration method for large structural dynamic analysis. Journal of Chongqing Jiaotong Institute, 10: 33-41).Zhai W M. 1991. The explicit scheme of Newmark’s integration method for large structural dynamic analysis. Journal of Chongqing Jiaotong Institute, 10: 33-41. [34] 翟婉明. 1990. 非线性结构动力分析的Newmark预测—校正积分模式. 计算结构力学与机器应用, 7: 51-58 (Zhai W M. 1990. The predictor-corrector scheme based on the Newmark’s integration algorithm for nonlinear structural dynamic analysis. Computational Structural Mechanics and Applications, 7: 51-58).Zhai W M. 1990. The predictor-corrector scheme based on the Newmark’s integration algorithm for nonlinear structural dynamic analysis. Computational Structural Mechanics and Applications, 7: 51-58. [35] 张雄, 刘岩, 张帆, 等. 2017. 极端变形问题的物质点法研究进展. 计算力学学报, 34(1): 1-16 (Zhang X, Liu Y, Zhang F, et al. 2017. Recent progress of material point method for extreme deformation problems. Chinese Journal of Computational Mechanics, 34(1): 1-16). doi: 10.7511/jslx201701001Zhang X, Liu Y, Zhang F, et al. 2017. Recent progress of material point method for extreme deformation problems. Chinese Journal of Computational Mechanics, 34(1): 1-16 doi: 10.7511/jslx201701001 [36] 张晓志, 程岩, 谢礼立. 2002. 结构动力反应分析的三阶显式方法. 地震工程与工程振动, 22: 1-8 (Zhang X Z, Cheng Y, Xie L L. 2002. A new explicit solution of dynamic response analysis. Earthquake Engineering and Engineering Vibration, 22: 1-8). doi: 10.3969/j.issn.1000-1301.2002.03.001Zhang X Z, Cheng Y, Xie L L. 2002. A new explicit solution of dynamic response analysis. Earthquake Engineering and Engineering Vibration, 22: 1-8. doi: 10.3969/j.issn.1000-1301.2002.03.001 [37] 周平. 2023. 多体系统动力学中微分代数方程组的数值方法研究. [博士论文]. 哈尔滨工业大学 (Zhou P. 2023. Study on numerical methods fordifferential algebraicequations in multibody systemsdynamics. [PhD Thesis]. Harbin Institute of Technology).Zhou P. 2023. Study on numerical methods fordifferential algebraicequations in multibody systemsdynamics. [PhD Thesis]. Harbin Institute of Technology. [38] 周正华, 李山有, 侯兴民. 1999. 阻尼振动方程的一种显式直接积分方法. 世界地震工程, 15: 41-44 (Zhou Z H, Li S Y, Hou X M. 1999. An explicit method for direct integration of the damped vibration equations. World Earthquake Engineering, 15: 41-44). doi: CNKI:SUN:SJDC.0.1999-01-005Zhou Z H, Li S Y, Hou X M. 1999. An explicit method for direct integration of the damped vibration equations. World Earthquake Engineering, 15: 41-44. doi: CNKI:SUN:SJDC.0.1999-01-005 [39] Amirouche F M L, Xie M. 1993. An explicit matrix formulation of the dynamical equations for flexible multibody systems: A recursive approach. Computers and Structures, 46: 311-321. doi: 10.1016/0045-7949(93)90195-J [40] Bettinotti O, Allix O, Perego U, et al. 2017. Simulation of delamination under impact using a global–local method in explicit dynamics. Finite Elements in Analysis and Design, 125: 1-13. doi: 10.1016/j.finel.2016.11.002 [41] Butcher J C. 2016. Numerical Methods for Ordinary Differential Equations. John Wiley & Sons. [42] Chang S. 2009. An explicit method with improved stability property. International Journal for Numerical Methods in Engineering, 77: 1100-1120. doi: 10.1002/nme.2452 [43] Chang S-Y. 2002. Explicit pseudodynamic algorithm with unconditional stability. Journal of Engineering Mechanics, 128: 935-947. doi: 10.1061/(ASCE)0733-9399(2002)128:9(935) [44] Chen C, Ricles J M. 2008. Development of direct integration algorithms for structural dynamics using discrete control theory. Journal of Engineering Mechanics, 134: 676-683. doi: 10.1061/(ASCE)0733-9399(2008)134:8(676) [45] Chung J. 1992. Numerically dissipative time integration algorithms for structural dynamics. English, University of Michigan. [46] Chung J, Hulbert G M. 1993. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method. Journal of Applied Mechanics, 60: 371-375. doi: 10.1115/1.2900803 [47] Chung J, Lee J M. 1994. A new family of explicit time integration methods for linear and non-linear structural dynamics. International Journal for Numerical Methods in Engineering, 37: 3961-3976. doi: 10.1002/nme.1620372303 [48] Cook R D. 2007. Concepts and applications of finite element analysis. John Wiley & Sons. [49] Dwivedy S K, Eberhard P. 2006. Dynamic analysis of flexible manipulators, a literature review. Mechanism and Machine Theory, 41: 749-777. doi: 10.1016/j.mechmachtheory.2006.01.014 [50] Ettefagh M H, Naraghi M, Towhidkhah F. 2019. Position control of a flexible joint via explicit model predictive control: An experimental implementation. Emerging Science Journal, 3: 146-156. doi: 10.28991/esj-2019-01177 [51] Fox L, Goodwin E T. 1949. Some new methods for the numerical integration of ordinary differential equations. Mathematical Proceedings of the Cambridge Philosophical Society. Cambridge University Press: 373-388. [52] Geradin M, Rixen D J. 2015. Mechanical vibrations: Theory and application to structural dynamics. John Wiley & Sons. [53] Gladwell I, Thomas R M. 1983. Damping and phase analysis for some methods for solving second-order ordinary differential equations. International Journal for Numerical Methods in Engineering, 19: 495-503. doi: 10.1002/nme.1620190404 [54] Großeholz G, Soares D, Von Estorff O. 2015. A stabilized central difference scheme for dynamic analysis. International Journal for Numerical Methods in Engineering, 102: 1750-1760. doi: 10.1002/nme.4869 [55] Gufler V, Wehrle E, Zwölfer A. 2021. A review of flexible multibody dynamics for gradient-based design optimization. Multibody System Dynamics, 53: 379-409. doi: 10.1007/s11044-021-09802-z [56] He H, Tang H, Yu K, et al. 2020. Nonlinear aeroelastic analysis of the folding fin with freeplay under thermal environment. Chinese Journal of Aeronautics, 33: 2357-2371. doi: 10.1016/j.cja.2020.05.005 [57] Heinstein M W, Mello F J, Attaway S W, et al. 2000. Contact-impact modeling in explicit transient dynamics. Computer Methods in Applied Mechanics and Engineering, 187: 621-640. doi: 10.1016/S0045-7825(99)00342-4 [58] Hilber H M, Hughes T J R. 1978. Collocation, dissipation and “overshoot” for time integration schemes in structural dynamics. Earthquake Engineering & Structural Dynamics, 6: 99-117. doi: 10.1002/eqe.4290060111 [59] Hilber H M, Hughes T J R, Taylor R L. 1977. Improved numerical dissipation for time integration algorithms in structural dynamics. Earthquake Engineering & Structural Dynamics, 5: 283-292. doi: 10.1002/eqe.4290050306 [60] Hoff C, Taylor R L. 1990a. Higher derivative explicit one step methods for non-linear dynamic problems. Part I: Design and theory. International Journal for Numerical Methods in Engineering, 29: 275-290. doi: 10.1002/nme.1620290205 [61] Hoff C, Taylor R L. 1990b. Higher derivative explicit one step methods for non-linear dynamic problems. Part II: Practical calculations and comparisons with other higher order methods. International Journal for Numerical Methods in Engineering, 29: 291-301. doi: 10.1002/nme.1620290206 [62] Hughes T J. 1983. Analysis of transient algorithms with particular reference to stability behavior. Computational Methods for Transient Analysis. Computational Methods in Mechanics. North Holland, pp. 67–155. [63] Hughes T J. 2012. The finite element method: linear static and dynamic finite element analysis. Courier Corporation. [64] Hughes T J R, Belytschko T. 1983. A precis of developments in computational methods for transient analysis. Journal of Applied Mechanics, 50: 1033-1041. doi: 10.1115/1.3167186 [65] Hughes T J R, Liu W K. 1978a. Implicit-explicit finite elements in transient analysis: Implementation and numerical examples. Journal of Applied Mechanics, 45: 375-378. doi: 10.1115/1.3424305 [66] Hughes T J R, Liu W K. 1978b. Implicit-explicit finite elements in transient analysis: Stability theory. Journal of Applied Mechanics, 45: 371-374. doi: 10.1115/1.3424304 [67] Hulbert G M, Chung J. 1996. Explicit time integration algorithms for structural dynamics with optimal numerical dissipation. Computer Methods in Applied Mechanics and Engineering, 137: 175-188. doi: 10.1016/S0045-7825(96)01036-5 [68] Hulbert G M, Hughes T J R. 1987. An error analysis of truncated starting conditions in step-by-step time integration: Consequences for structural dynamics. Earthquake Engineering and Structural Dynamics, 15: 901-910. doi: 10.1002/eqe.4290150710 [69] Johnson G R, Beissel S R. 2001. Damping algorithms and effects for explicit dynamics computations. International Journal of Impact Engineering, 25: 911-925. doi: 10.1016/S0734-743X(01)00019-7 [70] Kawamoto A, Krenk S, Suzuki A, et al. 2010. Flexible body dynamics in a local frame with explicitly predicted motion. International Journal for Numerical Methods in Engineering, 81: 246-268. doi: 10.1002/nme.2699 [71] Kim W. 2019. A simple explicit single step time integration algorithm for structural dynamics. International Journal for Numerical Methods in Engineering, 119: 383-403. doi: 10.1002/nme.6054 [72] Kolay C, Ricles J M. 2014. Development of a family of unconditionally stable explicit direct integration algorithms with controllable numerical energy dissipation. Earthquake Engineering and Structural Dynamics, 43: 1361-1380. doi: 10.1002/eqe.2401 [73] Krieg R D. 1973. Unconditional stability in numerical time integration methods. Journal of Applied Mechanics, 40: 417-421. doi: 10.1115/1.3422999 [74] Lambert J D. 1973. Computational methods in ordinary differential equations. Wiley. [75] Leech J W, Hsu P-T, Mack E W. 1965. Stability of a finite-difference method for solving matrix equations. AIAA Journal, 3: 2172-2173. doi: 10.2514/3.3342 [76] Li J, Cui N, Li H, et al. 2024. Directly self-starting second-order explicit integration methods with dissipation control and adjustable bifurcation points for second-order initial value problems. International Journal of Structural Stability and Dynamics, 2450274. [77] Li J, Li H, Lian Y, et al. 2023a. On designing and developing single-step second-order implicit methods with dissipation control and zero-order overshoots via subsidiary variables. International Journal for Numerical Methods in Engineering, 124: 4880-4940. doi: 10.1002/nme.7328 [78] Li J, Li H, Lian Y, et al. 2023b. A suite of second-order composite sub-step explicit algorithms with controllable numerical dissipation and maximal stability bounds. Applied Mathematical Modelling, 114: 601-626. doi: 10.1016/j.apm.2022.10.012 [79] Li J, Li H, Zhao R, et al. 2023c. On second-order s-sub-step explicit algorithms with controllable dissipation and adjustable bifurcation point for second-order hyperbolic problems. European Journal of Mechanics-A/Solids, 97: 104829. doi: 10.1016/j.euromechsol.2022.104829 [80] Li J, Yu K. 2020. A novel family of composite sub-step algorithms with desired numerical dissipations for structural dynamics. Archive of Applied Mechanics, 90: 737-772. doi: 10.1007/s00419-019-01637-7 [81] Li J, Yu K. 2021. Development of composite sub-step explicit dissipative algorithms with truly self-starting property. Nonlinear Dynamics, 103: 1911-1936. [82] Li J, Yu K. 2019. Noniterative integration algorithms with controllable numerical dissipations for structural dynamics. International Journal of Computational Methods, 16: 1850111. doi: 10.1142/S0219876218501116 [83] Li J, Yu K, Li X. 2018. A generalized structure-dependent semi-explicit method for structural dynamics. Journal of Computational and Nonlinear Dynamics, 13: 111008. doi: 10.1115/1.4041239 [84] Li J, Yu K, Li X. 2019. A two-step unconditionally stable explicit method with controllable numerical dissipations. Earthquake Engineering and Engineering Vibration, 18: 285-299. doi: 10.1007/s11803-019-0504-y [85] Li J, Yu K, Li X. 2021a. An identical second-order single step explicit integration algorithm with dissipation control for structural dynamics. International Journal for Numerical Methods in Engineering, 122: 1089-1132. doi: 10.1002/nme.6574 [86] Li J, Yu K, Tang H. 2021b. Further assessment of three bathe algorithms and implementations for wave propagation problems. International Journal of Structural Stability and Dynamics, 21: 2150073. doi: 10.1142/S0219455421500735 [87] Li J, Yu K, Zhao R. 2022a. Two third-order explicit integration algorithms with controllable numerical dissipation for second-order nonlinear dynamics. Computer Methods in Applied Mechanics and Engineering, 395: 114945. doi: 10.1016/j.cma.2022.114945 [88] Li J, Zhao R, Yu K, et al. 2022b. Directly self-starting higher-order implicit integration algorithms with flexible dissipation control for structural dynamics. Computer Methods in Applied Mechanics and Engineering, 389: 114274. doi: 10.1016/j.cma.2021.114274 [89] Lim H, Taylor R L. 2001. An explicit-implicit method for flexible–rigid multibody systems. Finite Elements in Analysis and Design, 37: 881-900. doi: 10.1016/S0168-874X(01)00073-7 [90] Liu W, Ye T, Yuan P, et al. 2023. An explicit integration method with third-order accuracy for linear and nonlinear dynamic systems. Engineering Structures, 274: 115013. doi: 10.1016/j.engstruct.2022.115013 [91] Mahéo L, Grolleau V, Rio G. 2009. Damping efficiency of the Tchamwa−Wielgosz explicit dissipative scheme under instantaneous loading conditions. Comptes Rendus Mécanique, 337: 722-732. doi: 10.1016/j.crme.2009.10.005 [92] Mahéo L, Grolleau V, Rio G. 2013. Numerical damping of spurious oscillations: A comparison between the bulk viscosity method and the explicit dissipative Tchamwa−Wielgosz scheme. Computational Mechanics, 51: 109-128. doi: 10.1007/s00466-012-0708-8 [93] Miranda I, Ferencz R M, Hughes T J R. 1989. An improved implicit-explicit time integration method for structural dynamics. Earthquake Engineering & Structural Dynamics, 18: 643-653. doi: 10.1002/eqe.4290180505 [94] Namburu R, Tamma K. 1992. A generalized $ {\mathrm{\gamma }}_{\mathrm{s}} $-family of self-starting algorithms for computational structural dynamics. 33rd Structures, Structural Dynamics and Materials Conference. American Institute of Aeronautics and Astronautics, Dallas, TX, U.S.A. [95] Newmark N M. 1959. A method of computation for structural dynamics. Journal of the Engineering Mechanics Division, 85: 67-94. doi: 10.1061/JMCEA3.0000098 [96] Nguyen M Q, Elder D J, Bayandor J, et al. 2005. A review of explicit finite element software for composite impact analysis. Journal of Composite Materials, 39: 375-386. doi: 10.1177/0021998305046739 [97] Noh G, Bathe K-J. 2013. An explicit time integration scheme for the analysis of wave propagations. Computers and Structures, 129: 178-193. doi: 10.1016/j.compstruc.2013.06.007 [98] Nsiampa N, Ponthot J-P, Noels L. 2008. Comparative study of numerical explicit schemes for impact problems. International Journal of Impact Engineering, 35: 1688-1694. doi: 10.1016/j.ijimpeng.2008.07.003 [99] Otto P, De Lorenzis L, Unger J F. 2020. Explicit dynamics in impact simulation using a NURBS contact interface. International Journal for Numerical Methods in Engineering, 121: 1248-1267. doi: 10.1002/nme.6264 [100] Park S W, Xia Q, Zhou M. 2001. Dynamic behavior of concrete at high strain rates and pressures: II. Numerical simulation. International Journal of Impact Engineering, 25: 887-910. doi: 10.1016/S0734-743X(01)00021-5 [101] Shimada M. 2013. Integration framework and algorithms by design: Implicit and explicit families of generalized single step single solve algorithms by design in two-and single-field forms. [102] Shimada M, Masuri S, Tamma K K. 2015. A novel design of an isochronous integration framework for first/second order multidisciplinary transient systems. International Journal for Numerical Methods in Engineering, 102: 867-891. doi: 10.1002/nme.4715 [103] Soares D, Großeholz G. 2018. Nonlinear structural dynamic analysis by a stabilized central difference method. Engineering Structures, 173: 383-392. doi: 10.1016/j.engstruct.2018.06.115 [104] Tamma K K, D’Costa J F. 1992. A new explicit variable time-integration self-starting methodology for computational structural dynamics. International Journal for Numerical Methods in Engineering, 33: 1165-1180. doi: 10.1002/nme.1620330605 [105] Tamma K K, Namburu R R. 1988a. A new finite element based Lax-Wendroff/Taylor-Galerkin methodology for computational dynamics. Computer Methods in Applied Mechanics and Engineering, 71: 137-150. doi: 10.1016/0045-7825(88)90082-5 [106] Tamma K K, Namburu R R. 1988b. An explicit velocity based Lax-Wendroff/Taylor-Galerkin methodology of computation for the dynamics of structures. Computers & structures, 30: 1017-1024. doi: 10.1016/0045-7949(88)90146-0 [107] Tamma K K, Wang Y, Maxam D. 2024. A critical review/look at “optimal implicit single-step time integration methods with equivalence to the second-order-type linear multistep methods for structural dynamics: Accuracy analysis based on an analytical framework”. Computer Methods in Applied Mechanics and Engineering, 431: 117272. doi: 10.1016/j.cma.2024.117272 [108] Tarnow N, Simo J C. 1994. How to render second order accurate time-stepping algorithms fourth order accurate while retaining the stability and conservation properties. Computer Methods in Applied Mechanics and Engineering, 115: 233-252. doi: 10.1016/0045-7825(94)90061-2 [109] Tchamwa B. 1997. Contribution a l’etude des methodes d’integration directe explicites en dynamique non lineaire des structures. Doctoral dissertation, Nantes. [110] Trujillo D M. 1975. The direct numerical integration of linear matrix differential equations using Padé approximations. International Journal for Numerical Methods in Engineering, 9: 259-270. doi: 10.1002/nme.1620090202 [111] Wood W L. 1984. A unified set of single step algorithms. Part 2: Theory. International Journal for Numerical Methods in Engineering, 20: 2303-2309. doi: 10.1002/nme.1620201210 [112] Wood W L. 1986. A unified set of single step algorithms. Part 4: Backward error analysis applied to the solution of the dynamic vibration equation. International Journal for Numerical Methods in Engineering, 23: 929-944. doi: 10.1002/nme.1620230513 [113] Wood W L. 1981. Numerical integration of structural dynamics equations including natural damping and periodic forcing terms. International Journal for Numerical Methods in Engineering, 17: 281-289. doi: 10.1002/nme.1620170211 [114] Wood W L, Bossak M, Zienkiewicz O C. 1980. An alpha modification of Newmark’s method. International Journal for Numerical Methods in Engineering, 15: 1562-1566. doi: 10.1002/nme.1620151011 [115] Yang C, Wang X, Li Q, et al. 2020. An improved explicit integration algorithm with controllable numerical dissipation for structural dynamics. Archive of Applied Mechanics, 90: 2413-2431. doi: 10.1007/s00419-020-01729-9 [116] Yang C, Xiao S, Lu L, et al. 2014. Two dynamic explicit methods based on double time steps. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 228: 330-337. doi: 10.1177/1464419314530111 [117] Yankovskii A P. 2017. Applying the explicit time central difference method for numerical simulation of the dynamic behavior of elastoplastic flexible reinforced plates. Journal of Applied Mechanics and Technical Physics, 58: 1223-1241. doi: 10.1134/S0021894417070112 [118] Yu K. 2008. A new family of generalized-α time integration algorithms without overshoot for structural dynamics. Earthquake Engineering and Structural Dynamics, 37: 1389-1409. doi: 10.1002/eqe.818 [119] Yue B, Guddati M N. 2005. Dispersion-reducing finite elements for transient acoustics. Journal of the Acoustical Society of America, 118: 2132-2141. doi: 10.1121/1.2011149 [120] Zhai W. 1996. Two simple fast integration methods for large-scale dynamic problems in engineering. International Journal for Numerical Methods in Engineering, 39: 4199-4214. doi: 10.1002/(SICI)1097-0207(19961230)39:24<4199::AID-NME39>3.0.CO;2-Y [121] Zhang H M, Xing Y F. 2019. Two novel explicit time integration methods based on displacement-velocity relations for structural dynamics. Computers & Structures, 221: 127-141. doi: 10.1016/j.compstruc.2019.05.018 [122] Zhang J, Ankit A, Gravenkamp H, et al. 2021. A massively parallel explicit solver for elasto-dynamic problems exploiting octree meshes. Computer Methods in Applied Mechanics and Engineering, 380: 113811. doi: 10.1016/j.cma.2021.113811 [123] Zhao R, Li J, Yu K. 2023. A self-starting dissipative alternative to the central difference methods. Archive of Applied Mechanics, 93: 571-603. doi: 10.1007/s00419-022-02286-z [124] Zhou X, Tamma K K. 2004. Design, analysis, and synthesis of generalized single step single solve and optimal algorithms for structural dynamics. International Journal for Numerical Methods in Engineering, 59: 597-668. doi: 10.1002/nme.873 -
下载:
图(28) / 表(6)
计量
- 文章访问数: 206
- HTML全文浏览量: 49
- PDF下载量: 51
- 被引次数: 0