-
摘要: 近几年来, 深度学习无所不在, 赋能于各个领域. 尤其是人工智能与传统科学的结合 (AI for science, AI4Science) 引发广泛关注. 在AI4Science领域, 利用人工智能算法求解PDEs (AI4PDEs) 已成为计算力学研究的焦点. AI4PDEs的核心是将数据与方程相融合, 并且几乎可以求解任何偏微分方程问题, 由于其融合数据的优势, 相较于传统算法, 其计算效率通常提升数万倍. 因此, 本文全面综述了AI4PDEs的研究, 总结了现有AI4PDEs算法、理论, 并讨论了其在固体力学中的应用, 包括正问题和反问题, 展望了未来研究方向, 尤其是必然会出现的计算力学大模型. 现有AI4PDEs算法包括基于物理信息神经网络 (physics-informed neural network, PINNs)、深度能量法 (deep energy methods, DEM)、算子学习 (operator learning), 以及基于物理神经网络算子 (physics-informed neural operator, PINO). AI4PDEs在科学计算中有许多应用, 本文聚焦于固体力学, 正问题包括线弹性、弹塑性, 超弹性、以及断裂力学; 反问题包括材料参数, 本构, 缺陷的识别, 以及拓朴优化. AI4PDEs代表了一种全新的科学模拟方法, 通过利用大量数据在特定问题上提供近似解, 然后根据具体的物理方程进行微调, 避免了像传统算法那样从头开始计算, 因此AI4PDEs是未来计算力学大模型的雏形, 能够大大加速传统数值算法. 我们相信, 利用人工智能助力科学计算不仅仅是计算领域的未来重要方向, 同时也是计算力学的未来,即是智能计算力学。
-
关键词:
- PINNs(基于物理信息神经网络) /
- 算子学习 /
- 计算力学 /
- AI for PDEs /
- 固体力学
Abstract: In recent years, deep learning has become ubiquitous and is empowering various fields. In particular, the combination of artificial intelligence and traditional science (AI for science, AI4Science) has attracted widespread attention. In the field of AI4Science, the use of artificial intelligence algorithms to solve partial differential equations (AI4PDEs) has become the focus of computational mechanics research. The core of AI4PDEs is to fuse data with equations and can solve almost any PDEs. Due to the advantages of AI4PDEs in data fusion, computational efficiency using AI4PDEs is usually increased by tens of thousands of times compared to traditional algorithms. Therefore, this article comprehensively reviews the research on AI4PDEs, summarizes the existing AI4PDEs algorithms and theories, discusses its application in solid mechanics, including forward and inverse problems, and outlines future research directions, especially the foundation model of computational mechanics. Existing algorithms of AI4PDEs include physics-informed neural networks (PINNs), deep energy methods (DEM), operator learning, and (physics-informed neural operator, PINO). AI4PDEs has numerous applications in scientific computing, and this paper focuses on application of AI4PDEs in the forward and inverse problems of solid mechanics. The forward problems include linear elasticity, elasto-plasticity, hyperelasticity, and fracture mechanics; while the inverse problems encompass the identification of material parameters, constitutive laws, defect recognition, and topology optimization. AI4PDEs represents a novel method of scientific simulation, which offers approximate solutions for specific problems by leveraging large datasets and then fine-tunes according to the specific physical equations, avoiding the need to start calculations from scratch as traditional algorithms do. Thus, AI4PDEs is a prototype for the foundation model of computational mechanics in the future, capable of significantly accelerating traditional numerical methods. We believe that utilizing artificial intelligence to empower scientific computing is not only a vital direction for the future of computation but also a dawn of humanity in scientific research, laying the foundation for mankind to reach new heights in scientific development.-
Key words:
- PINNs /
- operator learning /
- computational mechanics /
- AI for PDEs /
- solid mechanics
-
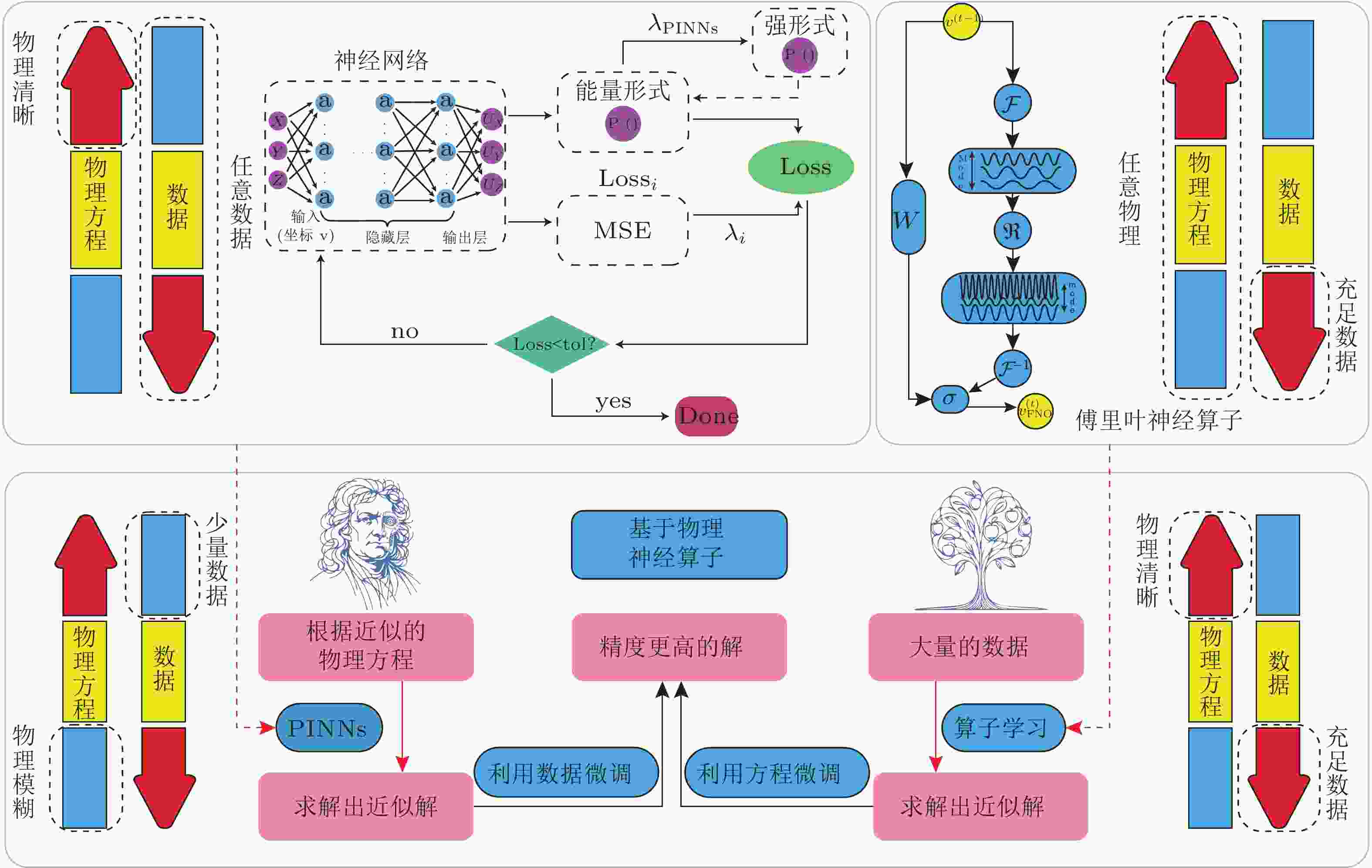
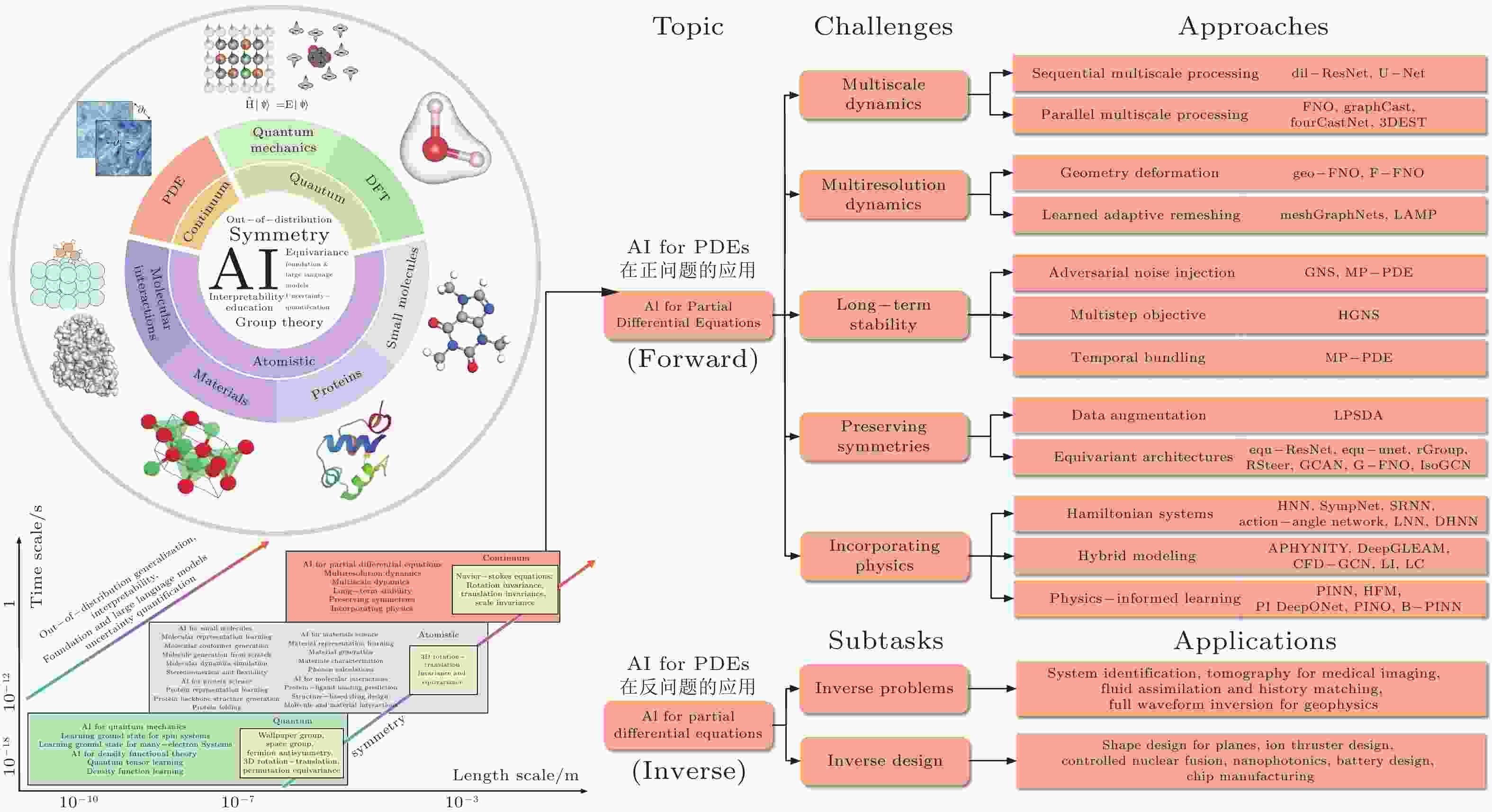
图 1 AI4PDEs在AI4Science中扮演的角色, 以及AI4PDE的介绍, AI4PDEs的核心是利用人工智能算法帮助求解PDEs, AI4PDEs大体分为正问题和反问题 (Zhang et al. 2023)
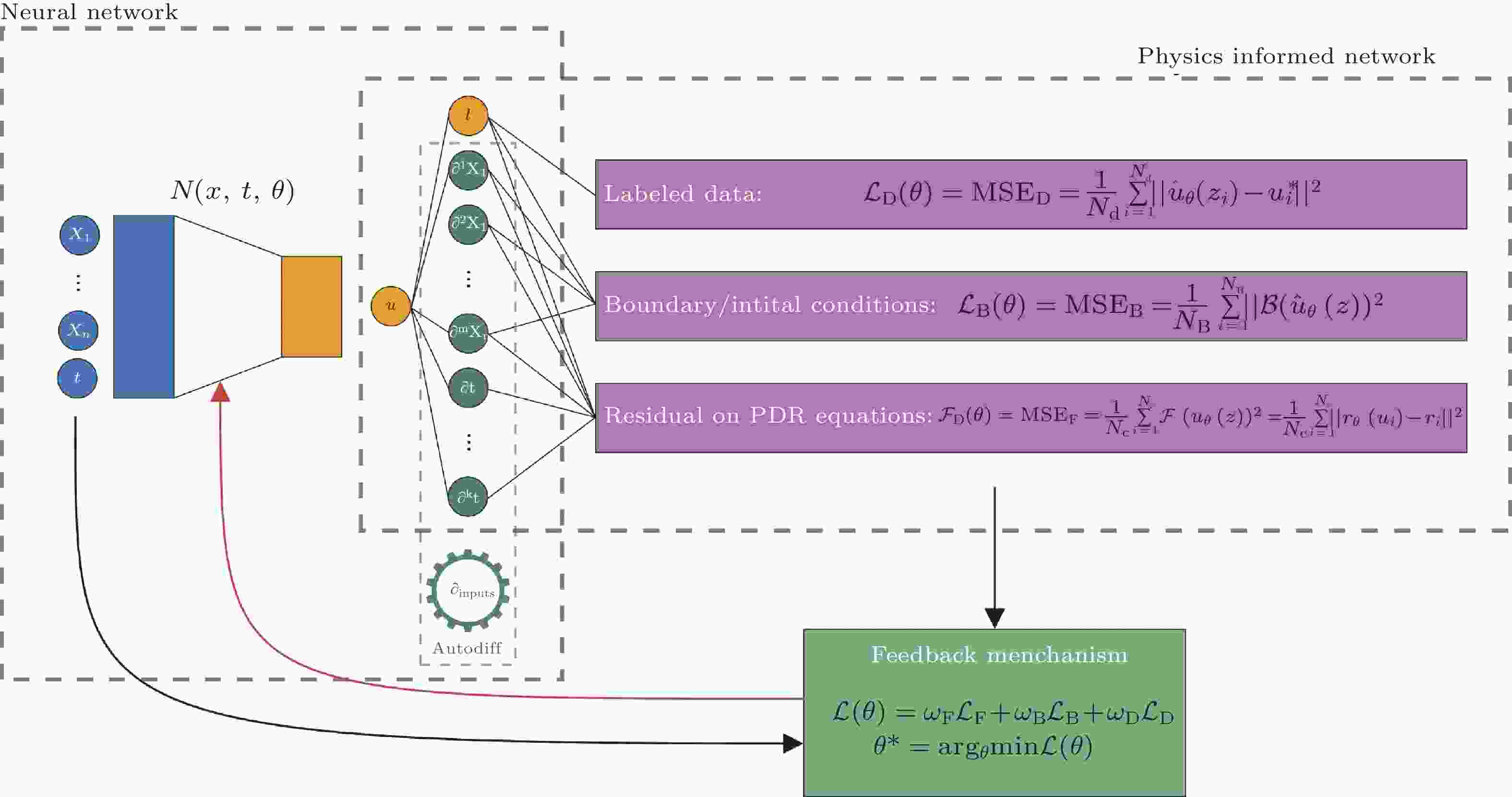
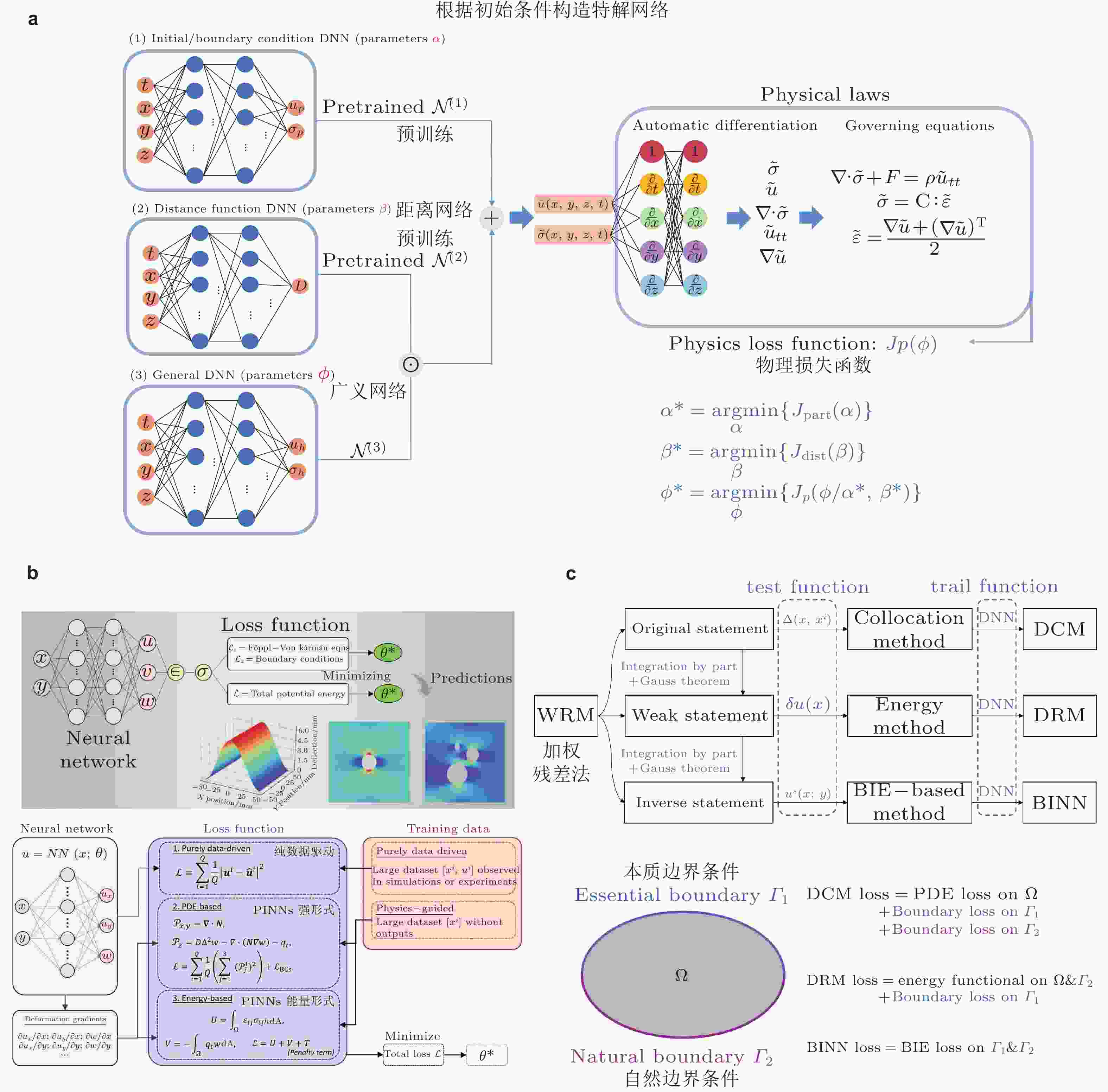
图 3 AI for PDEs方法: PINNs强形式示意图 (Cuomo et al. 2022)
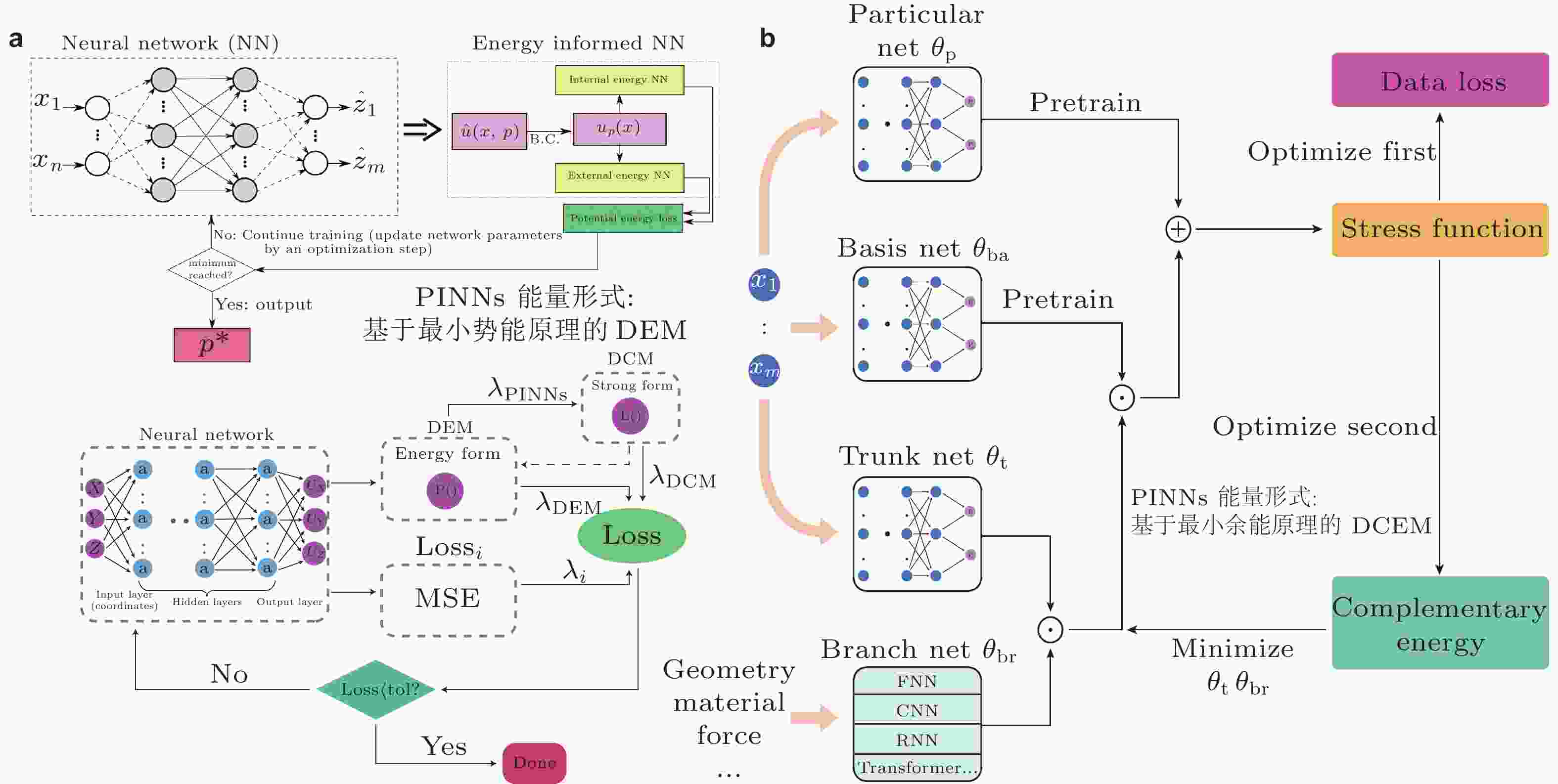
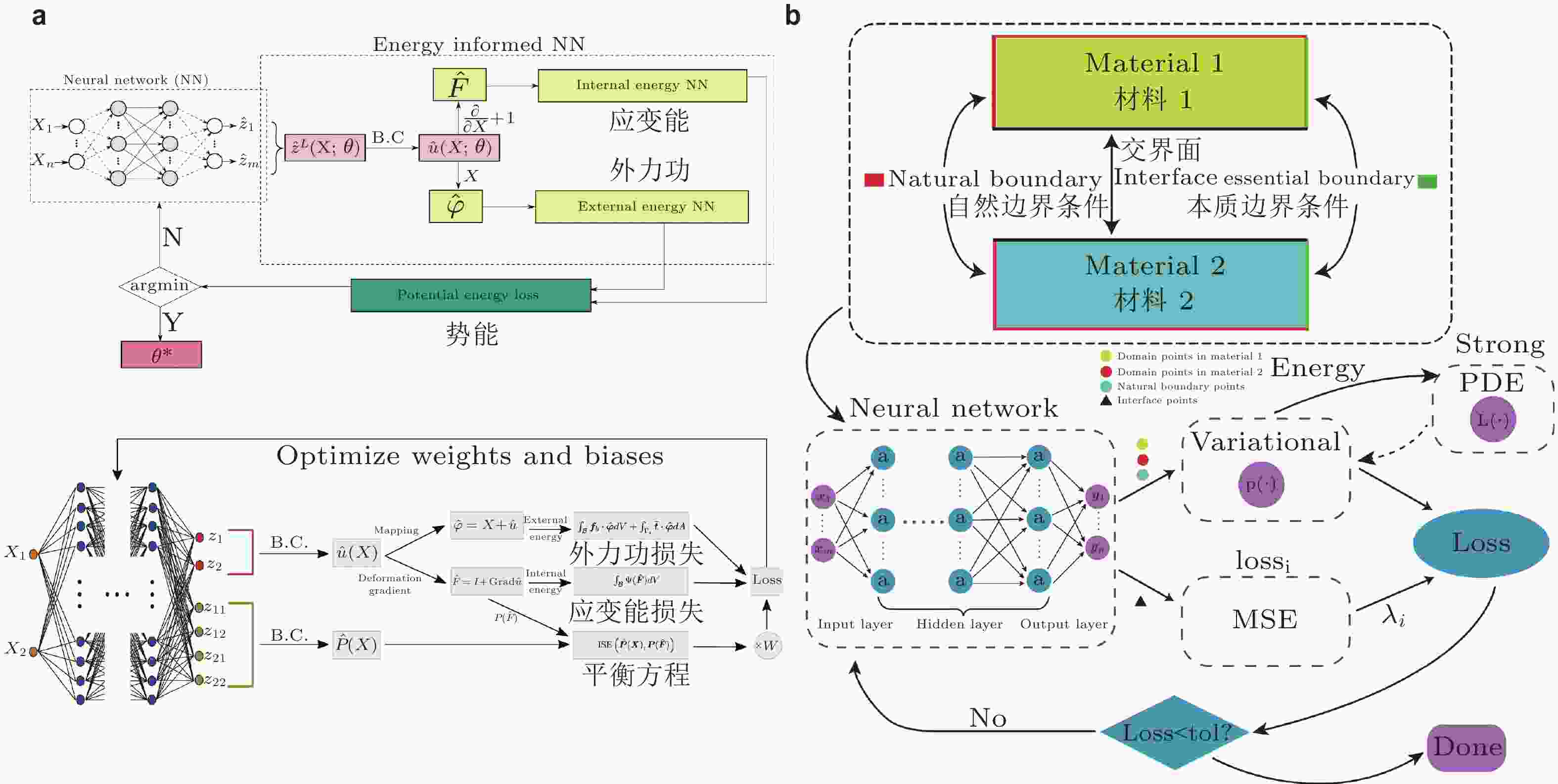
图 4 AI for PDEs方法: PINNs能量原理. (a) 基于最小势能原理的深度能量法DEM (Nguyen-Thanh et al. 2020, Samaniego et al. 2020, Wang Y et al. 2022), (b) 基于最小余能原理的深度余能法(Wang et al. 2023)
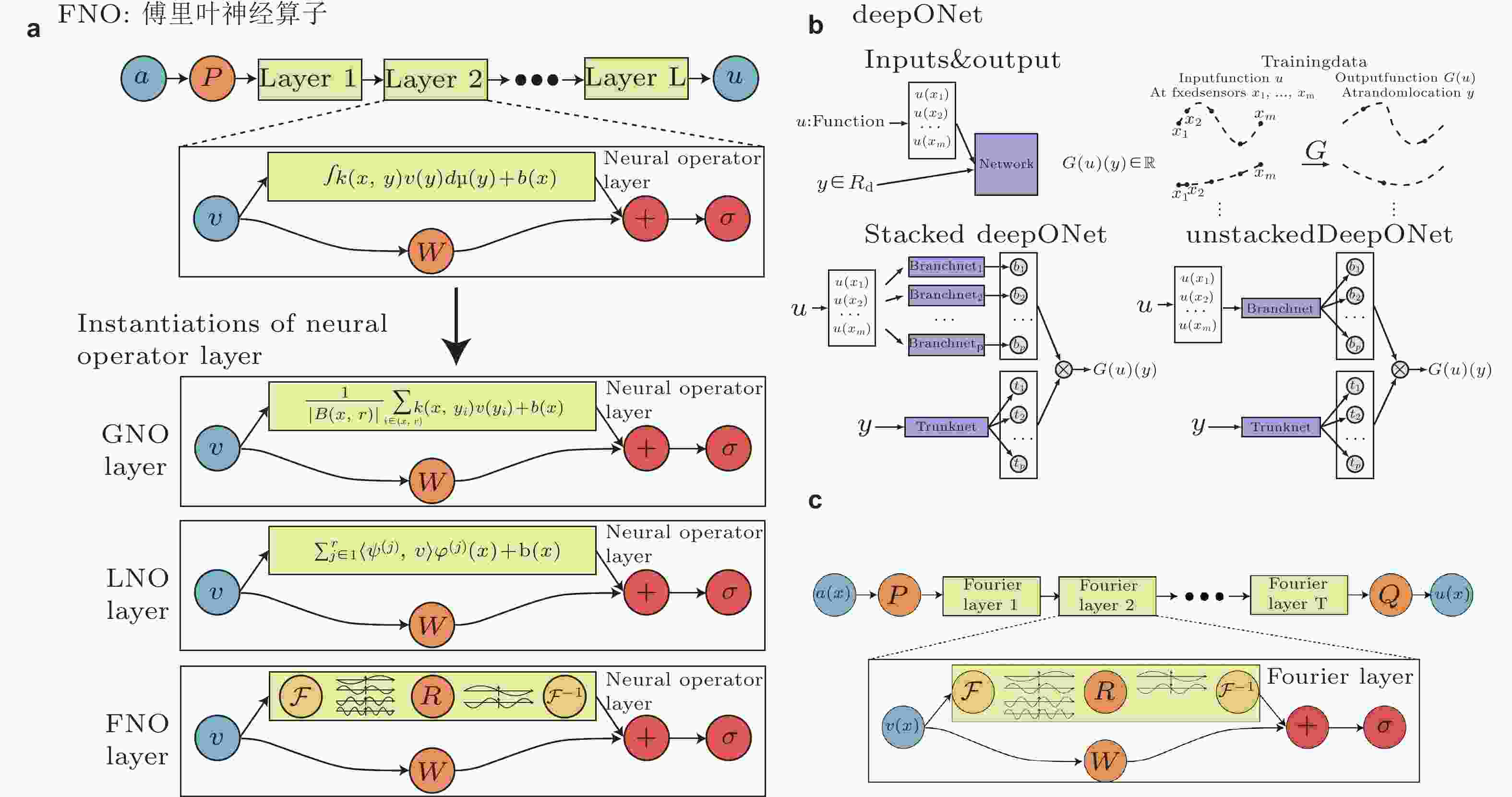
图 5 AI for PDEs方法: 算子学习示意图. (a) 神经算子算法(Kovachki et al. 2023), (b) DeepONet (Lu et al. 2021a), (c) FNO (Li et al. 2020a)
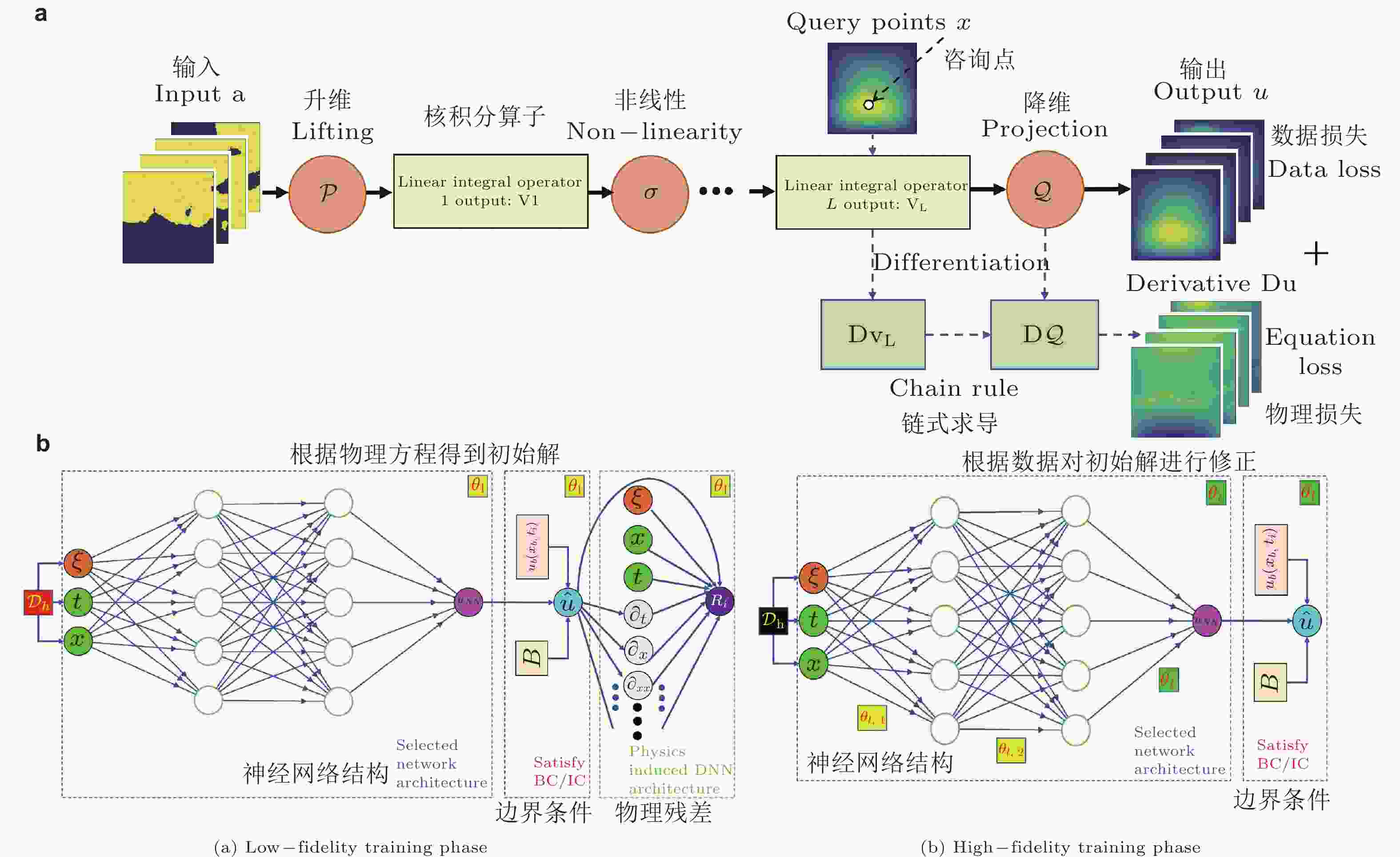
图 6 AI for PDEs方法: 基于物理神经算子示意图. (a) 利用物理方程对算子学习的初解进行微调(Li Z et al. 2021), (b) 利用数据对近似物理方程的低精度解进行微调(Chakraborty 2021)
图 8 PINNs在线弹性力学中的算法上的应用. (a) 强形式: 线弹性动力学(Rao et al. 2021), (b) 强形式和能量形式: Kirchhoff板壳(Li W et al. 2021 ), (c) 反形式: 边界元(Sun et al. 2023a)
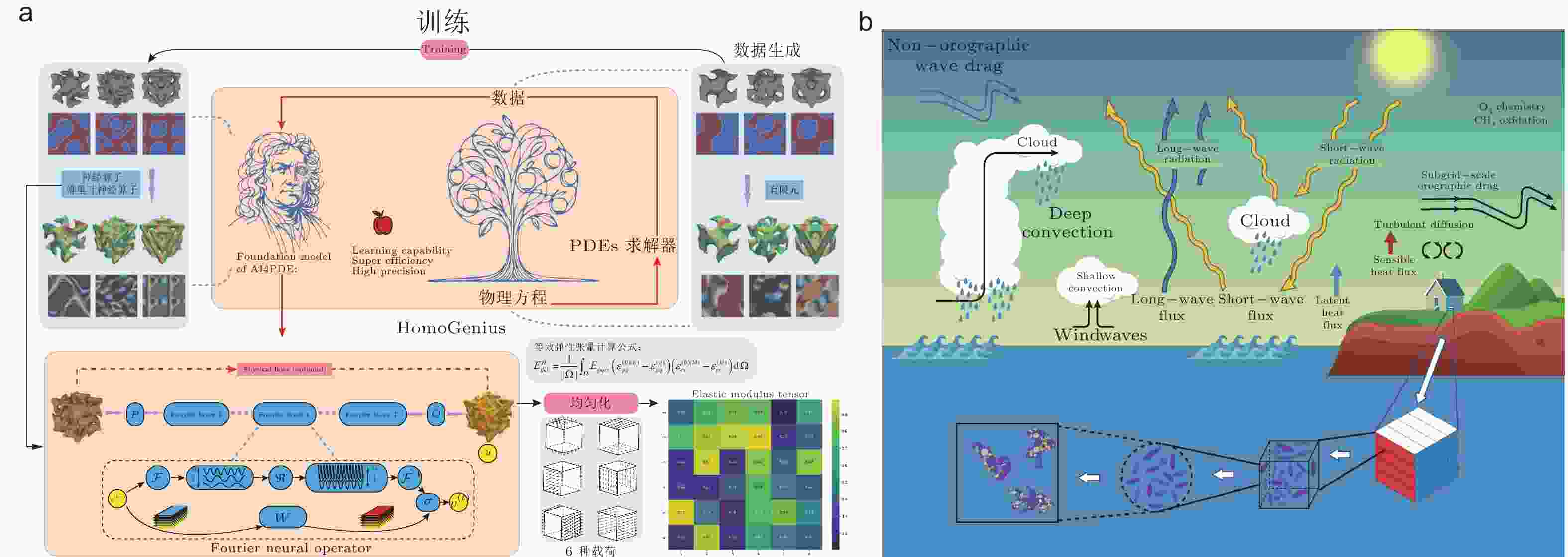
图 9 算子学习在线弹性力学中的均匀化中的应用. (a) 预测等效弹性模量(Wang et al. 2024), (b) 多尺度RVE代表性体积元(Liu et al. 2024a)
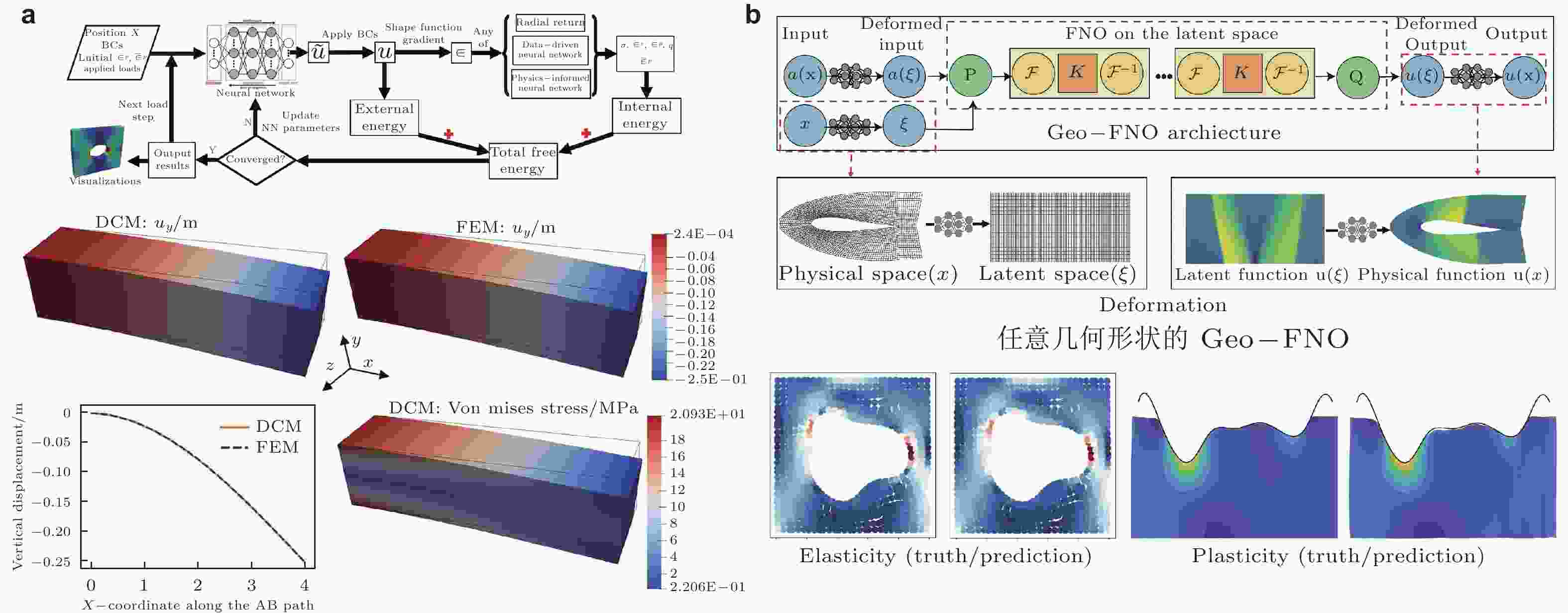
图 10 PINNs和算子学习在弹塑性力学中的应用. (a) PINNs强形式(Abueidda et al. 2021)和能量形式(He et al. 2023a), (b) 算子学习Geo-FNO (Li et al. 2023)
图 11 PINNs能量形式在超弹性力学中的应用. (a) PINNs能量形式(Fuhg & Bouklas 2022, Nguyen-Thanh et al. 2020), (b) PINNs能量子域形式(Wang Y et al. 2022)
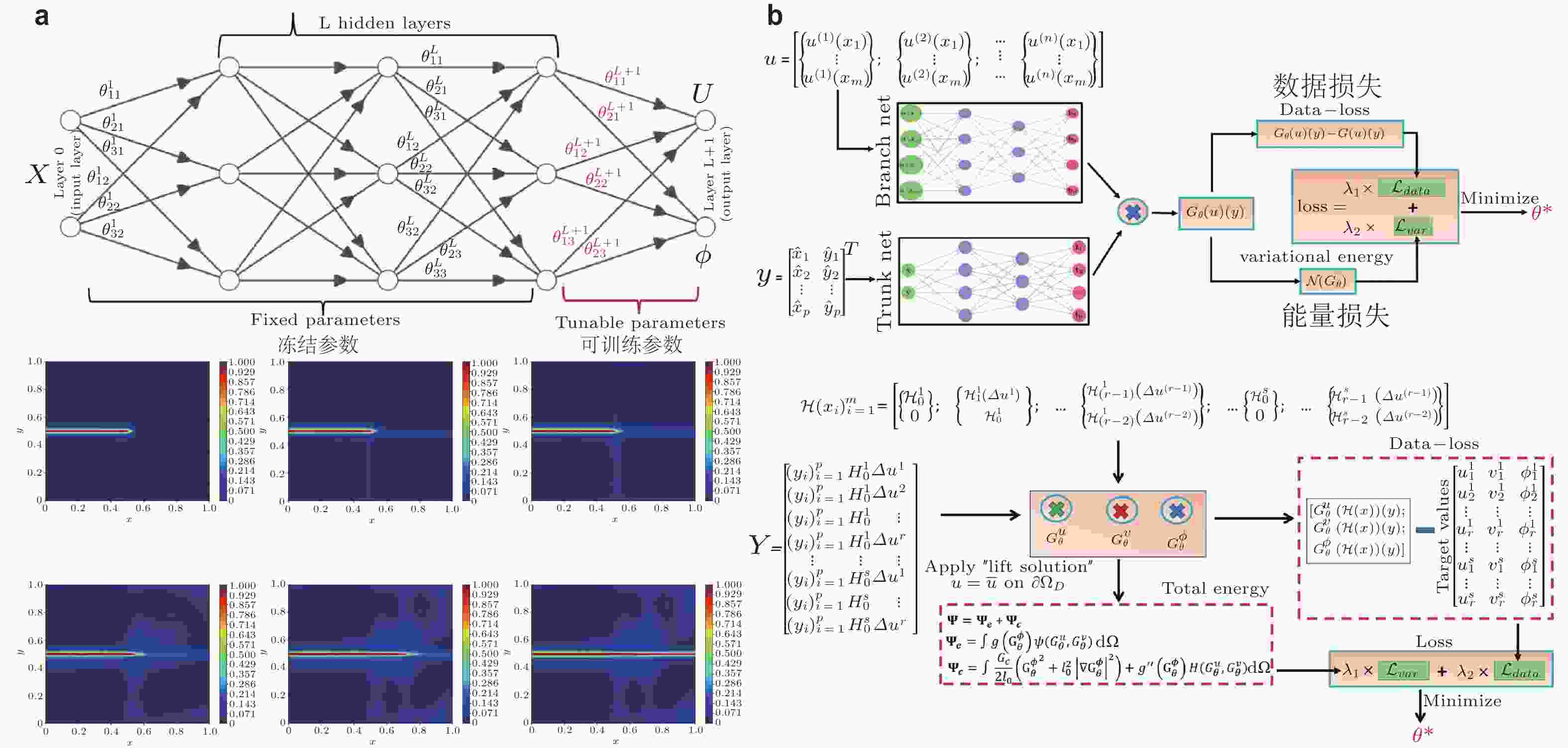
图 12 基于物理信息神经算子在断裂力学相场法中的应用. (a) PINNs能量形式(Goswami et al. 2020), (b) PINNs能量形式和算子结合(Goswami et al. 2022 )
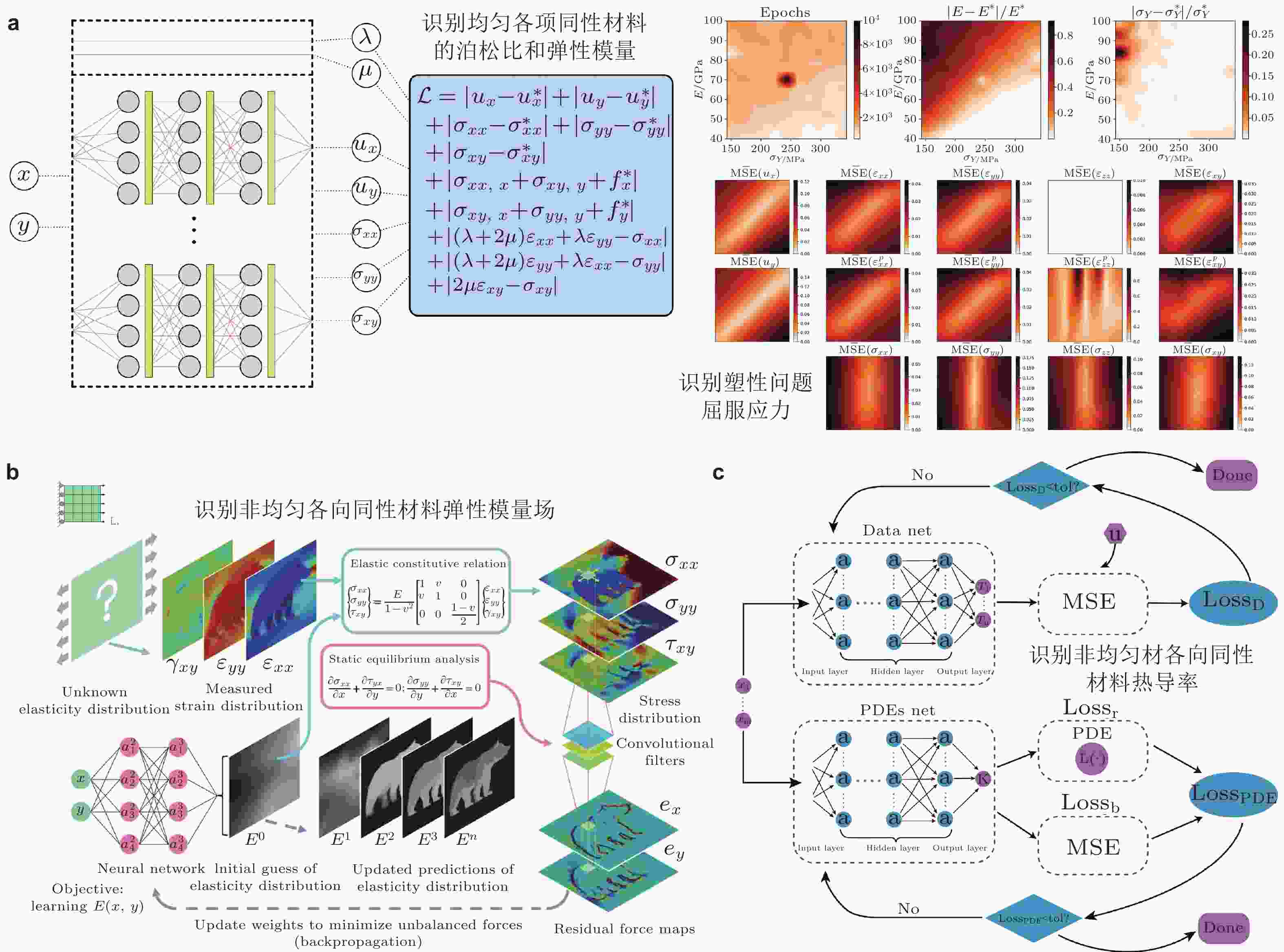
图 13 PINNs在弹性模量和泊松比的识别的应用. (a) 识别均匀各项同性弹塑形材料的弹性模量和泊松比, 以及屈服应力(Haghighat et al. 2021), (b) 识别非均匀各项同性材料的弹性模量场(Chen & Gu 2021), (c) 识别非均匀各项同性材料的热导率(Liu et al. 2024b)
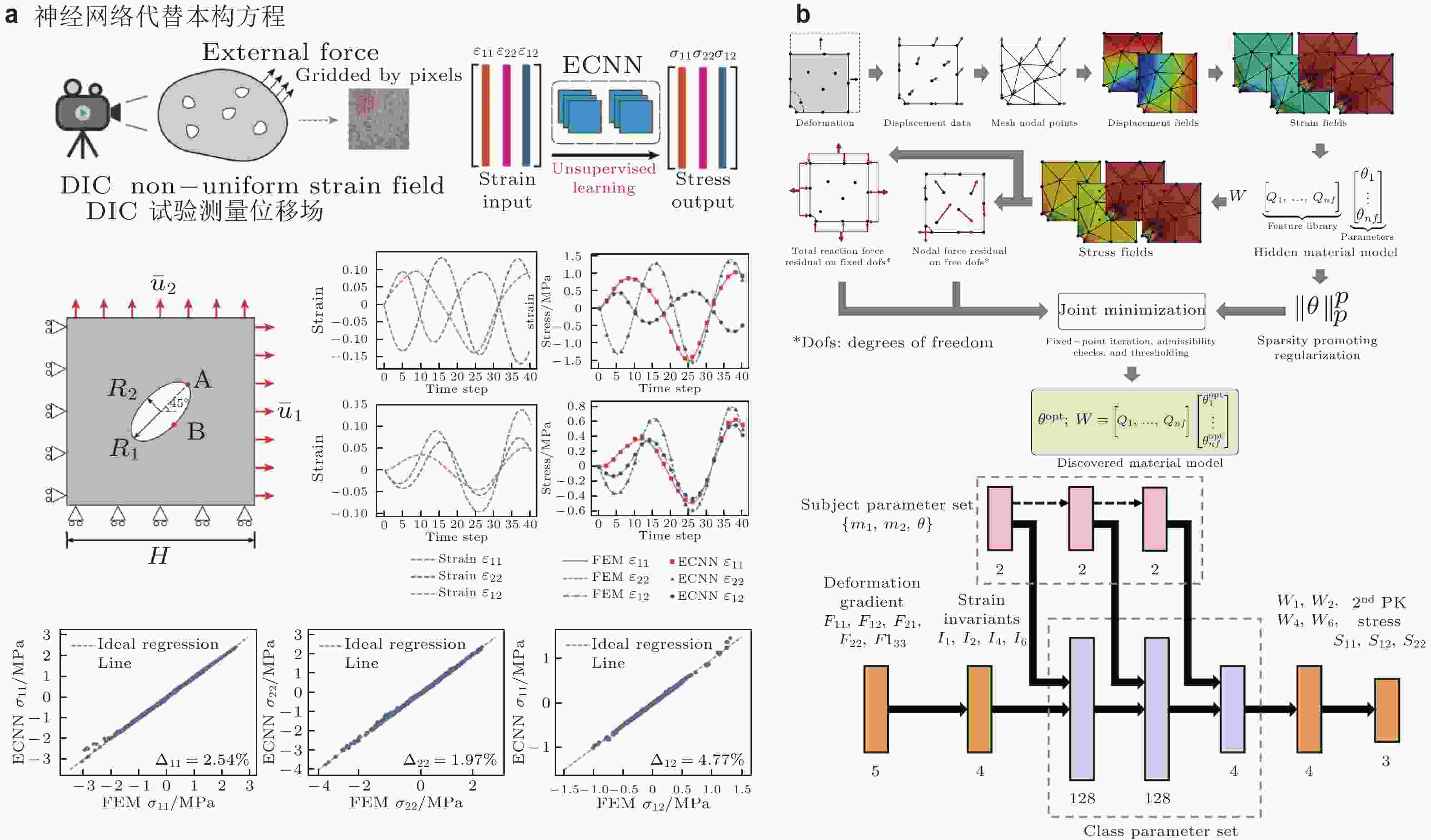
图 14 AI for PDEs在本构方程识别的应用. (a) 神经网络拟合应变和应力的超弹性关系(Li & Chen 2022), (b) 提前给定超弹性本构的形式, 拟合前面的参数(Flaschel et al. 2021)
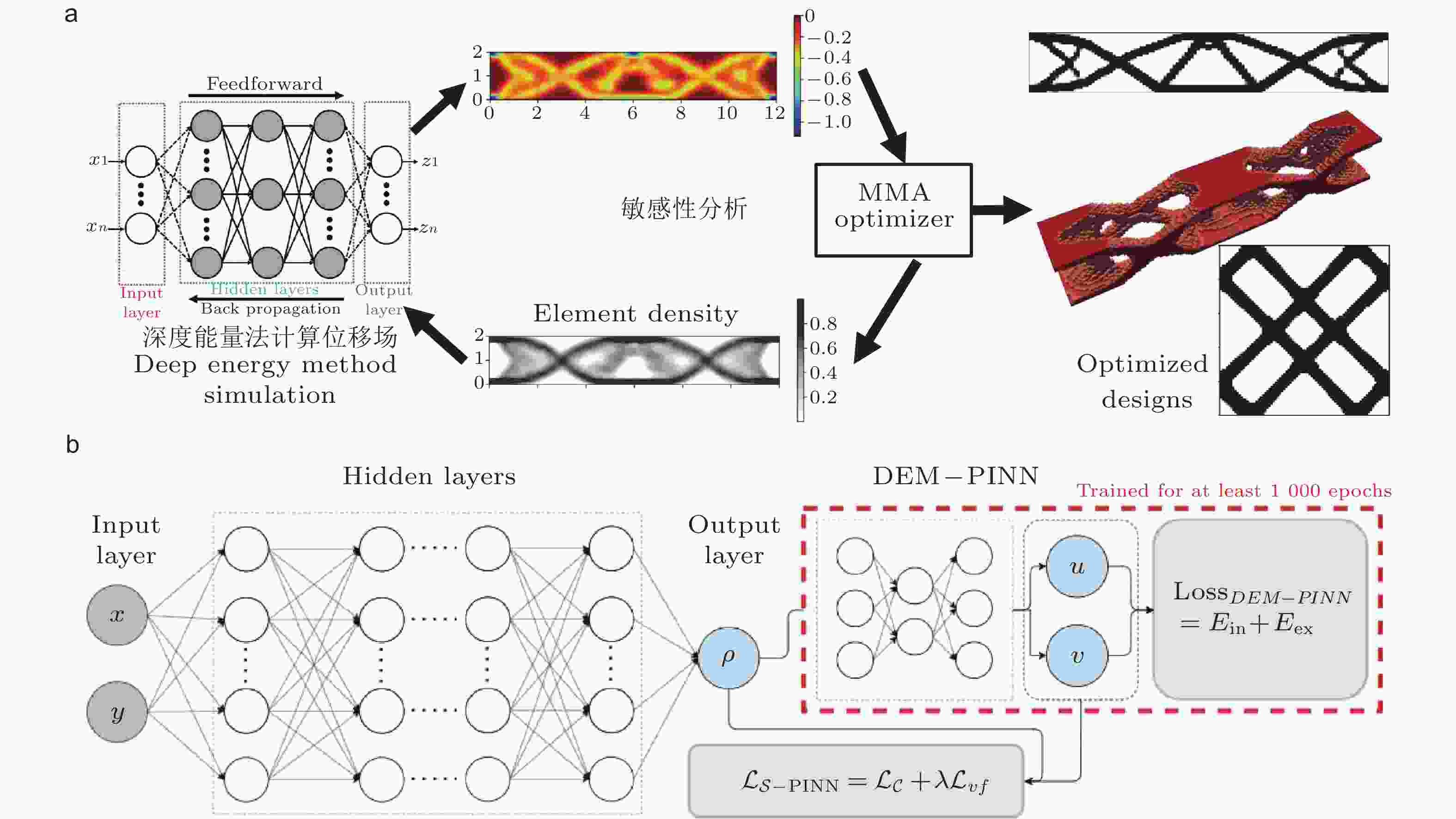
图 15 PINNs能量形式在拓扑优化的应用. (a) 密度场传统方法迭代(He et al. 2023c), (b) 神经网络拟合密度场(Jeong et al. 2023b)
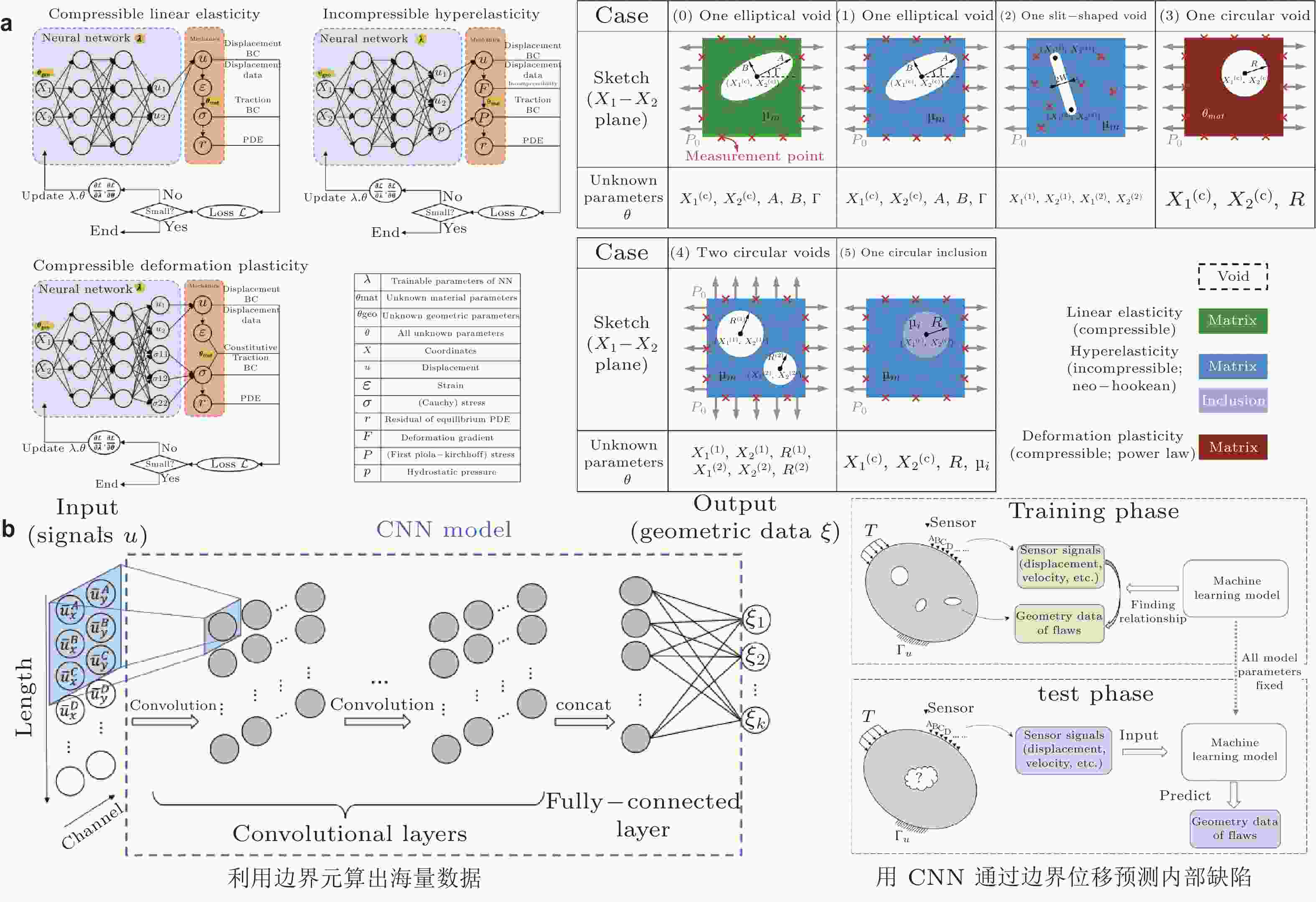
图 16 AI for PDEs在缺陷识别的应用. (a) PINNs识别缺陷(Zhang et al. 2022), (b) 数据驱动识别缺陷(Sun et al. 2023b)
表 1 PINN强形式算法研究现状
文献 方法 试函数分片 权函数分片 试函数类型 权函数类型 本质边界施加方式 Raissi 等 (2019) PINNs 否 (全局) 否 (全局) 全连接 Delta 罚函数 Sirignano和Spiliopoulos (2018) DGM 否 (全局) 否 (全局) 全连接 最小二乘 罚函数 Kharazmi 等 (2019) VPINNs 否 (全局) 否 (全局) 全连接 混合权函数 罚函数 Dwivedi和Srinivasan (2020) PIELM 是 (子域) 否 (全局) ELM
(Huang et al. 2006)Delta 罚函数 Jagtap 等 (2020c) cPINN 是 (子域) 否 (全局) 全连接 Delta 罚函数 Jagtap和Karniadakis (2020) XPINN 是 (子域) 否 (全局) 全连接 Delta 罚函数 Kharazmi 等 (2021) hp-VPINNs 否 (全局) 是 (子域) 全连接 正交多项式 罚函数 Gao 等 (2021) PhyGeoNet 否 (全局) 否 (全局) 卷积网络 Delta 强制施加 Gao 等 (2022) PIGCN 否 (全局) 否 (全局) 图卷积 有限元试函数空间 强制施加 Ramabathiran和Ramachandran (2021) SPINN 否 (全局) 否 (全局) 径向基网络 有限元试函数空间 罚函数 Sun 等 (2023a) BINN 否 (全局) 否 (全局) 全连接 微分方程基本解 边界积分项 表 2 PINN能量形式研究现状
文献 方法 试函数分片 试函数类型 本质边界施加方式 能量原理 (Yu 2018) Deep Ritz 否 (全局) 全连接 罚函数 变分原理 (Samaniego et al. 2020) DEM 否 (全局) 全连接 距离, 边界, 广义网络 最小势能 (Sheng & Yang 2021) PFNN 否 (全局) 全连接 距离, 边界, 广义网络 变分原理 (Fuhg & Bouklas 2022) mDEM 否 (全局) 全连接 距离, 边界, 广义网络 混合形式 (Nguyen-Thanh et al. 2021) P-DEM 否 (全局) 全连接 等参元 最小势能 (Wang Y et al. 2022) CENN 是 (子域) 全连接 距离, 边界, 广义网络 最小势能 (He et al. 2023b) GCN-DEM 否 (全局) 图卷积 距离, 边界, 广义网络 最小势能 (Wang et al. 2023) DCEM 否 (全局) 全连接 距离, 边界, 广义网络 最小余能 表 3 PINNs权重选取研究现状
文献 方法简要描述 (Wang et al. 2021a) 通过比较不同成分的损失函数的梯度来选取权重 (Wang S et al. 2022) 利用NTK理论选取权重 (Wang et al. 2021c) 利用NTK理论识别出神经网络的频率倾向 (Liu & Wang 2021) 将PINNs损失函数修改成鞍点问题 (Xu et al. 2023) 利用最大似然估计修改损失函数 表 4 AI for PDEs收敛性证明
文献 证明简要描述 (Cohen et al. 2016, Cybenko 1989, Hornik et al. 1989, Pinkus 1999) 证明神经网络强大的拟合能力 (Shin et al. 2020) 椭圆的二阶线性微分方程以及抛物线PDE, PINNs收敛性证明 (Mishra & Molinaro 2022) PINNs反问题近似性证明 (Psaros et al. 2023) PINNs不确定性估计 (Kovachki et al. 2023) 神经算子近似任意连续算子的证明 (Kovachki et al. 2021) 神经算子FNO近似任意连续算子的证明 (Chen & Chen 1995) DeepONet理论支撑: 神经网络近似任意连续算子 (Lanthaler et al. 2022) DeepONet近似任意连续算子的证明 (De Ryck & Mishra 2022) PINO可以近似任意的连续函数或者任意的连续算子 -
[1] Abueidda D W, Koric S, Al-Rub R A, et al. 2022. A deep learning energy method for hyperelasticity and viscoelasticity. European Journal of Mechanics-A/Solids, 95: 104639. doi: 10.1016/j.euromechsol.2022.104639 [2] Abueidda D W, Lu Q, Koric S. 2021. Meshless physics-informed deep learning method for three-dimensional solid mechanics. International Journal for Numerical Methods in Engineering, 122(23): 7182-7201. doi: 10.1002/nme.6828 [3] Bathe K J. 2006. Finite Element Procedures. Upper Saddle River: Prentice Hall. [4] Baydin A G, Pearlmutter B A, Radul A A, et al. 2018. Automatic differentiation in machine learning: A survey. Journal of Marchine Learning Research, 18: 1-43. [5] Berg J, Nyström K. 2018. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing, 317: 28-41. doi: 10.1016/j.neucom.2018.06.056 [6] Bi K, Xie L, Zhang H, et al. 2013. Accurate medium-range global weather forecasting with 3D neural networks. Nature, 619: 533-538. [7] Bourdin B, Francfort G A, Marigo J-J. 2000. Numerical experiments in revisited brittle fracture. Journal of the Mechanics and Physics of Solids, 48(4): 797-826. doi: 10.1016/S0022-5096(99)00028-9 [8] Brebbia C A, Telles J C F, Wrobel L C. 2012. Boundary Element Techniques: Theory and Applications in Engineering. Springer Science & Business Media. [9] Brown T, Mann B, Ryder N, et al. 2020. Language models are few-shot learners. Advances in Neural Information Processing Systems, 33: 1877-1901. [10] Cai S, Mao Z, Wang Z, et al. 2021. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mechanica Sinica, 37(12): 1727-1738. doi: 10.1007/s10409-021-01148-1 [11] Chakraborty S. 2021. Transfer learning based multi-fidelity physics informed deep neural network. Journal of Computational Physics, 426: 109942. doi: 10.1016/j.jcp.2020.109942 [12] Chen C-T, Gu G X. 2021. Learning hidden elasticity with deep neural networks. Proceedings of the National Academy of Sciences, 118(31): e2102721118. doi: 10.1073/pnas.2102721118 [13] Chen T, Chen H. 1995. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Transactions on Neural Networks, 6(4): 911-917. doi: 10.1109/72.392253 [14] Cohen N, Sharir O, Shashua A. 2016. On the expressive power of deep learning: A tensor analysis. arXiv:1509.05009v3. [15] Cuomo S, Di Cola V S, Giampaolo F, et al. 2022. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. Journal of Scientific Computing, 92(3): 88. doi: 10.1007/s10915-022-01939-z [16] Cybenko G. 1989. Approximation by superpositions of a sigmoidal function. Mathematics of control, signals and systems, 2(4): 303-314. doi: 10.1007/BF02551274 [17] Darwish M, Moukalled F. 2016. The finite volume method in computational fluid dynamics: An advanced introduction with OpenFOAM® and Matlab®. Springer. [18] De Ryck T, Mishra S. 2022. Generic bounds on the approximation error for physics-informed (and) operator learning. Advances in Neural Information Processing Systems, 35: 10945-10958. [19] Dissanayake M W M G, Phan-Thien N. 1994. Neural-network-based approximations for solving partial differential equations. Communications in Numerical Methods in Engineering, 10(3): 195-201. doi: 10.1002/cnm.1640100303 [20] Dwivedi V, Srinivasan B. 2020. Physics informed extreme learning machine (pielm)–A rapid method for the numerical solution of partial differential equations. Neurocomputing, 391: 96-118. doi: 10.1016/j.neucom.2019.12.099 [21] Fang Z. 2021. A high-efficient hybrid physics-informed neural networks based on convolutional neural network. IEEE Transactions on Neural Networks and Learning Systems, 33(10): 5514-5526. [22] Flaschel M, Kumar S, De Lorenzis L. 2021. Unsupervised discovery of interpretable hyperelastic constitutive laws. Computer Methods in Applied Mechanics and Engineering, 381: 113852. doi: 10.1016/j.cma.2021.113852 [23] Francfort G A, Marigo J J. 1998. Revisiting brittle fracture as an energy minimization problem. Journal of the Mechanics and Physics of Solids, 46(8): 1319-1342. doi: 10.1016/S0022-5096(98)00034-9 [24] Fuhg J N, Bouklas N. 2022. The mixed deep energy method for resolving concentration features in finite strain hyperelasticity. Journal of Computational Physics, 451: 110839. doi: 10.1016/j.jcp.2021.110839 [25] Gao H, Sun L, Wang J X. 2021. PhyGeoNet: Physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain. Journal of Computational Physics, 428: 110079. doi: 10.1016/j.jcp.2020.110079 [26] Gao H, Zahr M J, Wang J X. 2022. Physics-informed graph neural Galerkin networks: A unified framework for solving PDE-governed forward and inverse problems. Computer Methods in Applied Mechanics and Engineering, 390: 114502. doi: 10.1016/j.cma.2021.114502 [27] Goswami S, Anitescu C, Chakraborty S, et al. 2020. Transfer learning enhanced physics informed neural network for phase-field modeling of fracture. Theoretical and Applied Fracture Mechanics, 106: 102447. doi: 10.1016/j.tafmec.2019.102447 [28] Goswami S, Yin M, Yu Y, et al. 2022. A physics-informed variational DeepONet for predicting crack path in quasi-brittle materials. Computer Methods in Applied Mechanics and Engineering, 391: 114587. doi: 10.1016/j.cma.2022.114587 [29] Graves A, Fernández S, Gomez F, et al. 2006. Connectionist temporal classification: Labelling unsegmented sequence data with recurrent neural networks. ICML'06: Proceedings of the 23rd International Conference on Machine learning. 369–376. [30] Guo H, Zhuang X, Chen P, et al. 2022a. Analysis of three-dimensional potential problems in non-homogeneous media with physics-informed deep collocation method using material transfer learning and sensitivity analysis. Engineering with Computers, 38(6): 5423-5444. doi: 10.1007/s00366-022-01633-6 [31] Guo H, Zhuang X, Chen P, et al. 2022b. Stochastic deep collocation method based on neural architecture search and transfer learning for heterogeneous porous media. Engineering with Computers, 38(6): 5173-5198. doi: 10.1007/s00366-021-01586-2 [32] Guo H, Zhuang X, Rabczuk T. 2021. A deep collocation method for the bending analysis of Kirchhoff plate. arXiv preprint arXiv: 2102.02617. [33] Haghighat E, Juanes R. 2021. SciANN: A Keras/TensorFlow wrapper for scientific computations and physics-informed deep learning using artificial neural networks. Computer Methods in Applied Mechanics and Engineering, 373: 113552. doi: 10.1016/j.cma.2020.113552 [34] Haghighat E, Raissi M, Moure A, et al. 2021. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Computer Methods in Applied Mechanics and Engineering, 379: 113741. doi: 10.1016/j.cma.2021.113741 [35] Han J, Jentzen A, Weinan E. 2018. Solving high-dimensional partial differential equations using deep learning. Proceedings of the National Academy of Sciences, 115(34): 8505-8510. doi: 10.1073/pnas.1718942115 [36] Hao K. 2020. AI has cracked a key mathematical puzzle for understanding our world. MIT Technology Review. https://www. technologyreview. com/2020/10/30/1011435/ai-fourier-neural-network-cracks-navier-stokes-and-partial-differential-equations/. Zugegriffen am, 15, 2021. [37] He D, Li S, Shi W, et al. 2023. Learning physics-informed neural networks without stacked back-propagation. International Conference on Artificial Intelligence and Statistics.He D, Li S, Shi W, et al. 2023. Learning physics-informed neural networks without stacked back-propagation. International Conference on Artificial Intelligence and Statistics. [38] He J, Abueidda D, Al-Rub R A, et al. 2023a. A deep learning energy-based method for classical elastoplasticity. International Journal of Plasticity, 103531. [39] He J, Abueidda D, Koric S, et al. 2023b. On the use of graph neural networks and shape-function-based gradient computation in the deep energy method. International Journal for Numerical Methods in Engineering, 124(4): 864-879. doi: 10.1002/nme.7146 [40] He J, Chadha C, Kushwaha S, et al. 2023c. Deep energy method in topology optimization applications. Acta Mechanica, 234(4): 1365-1379. doi: 10.1007/s00707-022-03449-3 [41] He K, Zhang X, Ren S, et al. 2016. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition.He K, Zhang X, Ren S, et al. 2016. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition. [42] Hennigh O, Narasimhan S, Nabian M A, et al. 2021. NVIDIA SimNet: An AI-accelerated multi-physics simulation framework. International conference on computational science.Hennigh O, Narasimhan S, Nabian M A, et al. 2021. NVIDIA SimNet: An AI-accelerated multi-physics simulation framework. International conference on computational science. [43] Hestenes M R. 1969. Multiplier and gradient methods. Journal of optimization theory and applications, 4(5): 303-320. doi: 10.1007/BF00927673 [44] Hornik K, Stinchcombe M, White H. 1989. Multilayer feedforward networks are universal approximators. Neural Networks, 2(5): 359-366. doi: 10.1016/0893-6080(89)90020-8 [45] Huang G-B, Zhu Q-Y, Siew C-K. 2006. Extreme learning machine: Theory and applications. Neurocomputing, 70(1-3): 489-501. doi: 10.1016/j.neucom.2005.12.126 [46] Hughes T J R. 2012. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Courier Corporation. [47] Jacot A, Gabriel F, Hongler C. 2018. Neural tangent kernel: Convergence and generalization in neural networks. Advances in Neural Information Processing Systems, 31. [48] Jagtap A D, Karniadakis G E. 2020. Extended physics-informed neural networks (xpinns): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. Communications in Computational Physics, 28(5): 2002-2041. doi: 10.4208/cicp.OA-2020-0164 [49] Jagtap A D, Kawaguchi K, Em Karniadakis G. 2020a. Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 476(2239): 20200334. doi: 10.1098/rspa.2020.0334 [50] Jagtap A D, Kawaguchi K, Karniadakis G E. 2020b. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. Journal of Computational Physics, 404: 109136. doi: 10.1016/j.jcp.2019.109136 [51] Jagtap A D, Kharazmi E, Karniadakis G E. 2020c. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Computer Methods in Applied Mechanics and Engineering, 365: 113028. doi: 10.1016/j.cma.2020.113028 [52] Jasak H, Jemcov A, Tukovic Z, et al. 2007. OpenFOAM: A C++ library for complex physics simulations. International workshop on coupled methods in numerical dynamics.Jasak H, Jemcov A, Tukovic Z, et al. 2007. OpenFOAM: A C++ library for complex physics simulations. International workshop on coupled methods in numerical dynamics. [53] Jeong H, Bai J, Batuwatta-Gamage C P, et al. 2023a. A physics-informed neural network-based topology optimization (PINNTO) framework for structural optimization. Engineering Structures, 278: 115484. doi: 10.1016/j.engstruct.2022.115484 [54] Jeong H, Batuwatta-Gamage C, Bai J, et al. 2023b. A complete physics-informed neural network-based framework for structural topology optimization. Computer Methods in Applied Mechanics and Engineering, 417: 116401. doi: 10.1016/j.cma.2023.116401 [55] Kendall A, Gal Y, Cipolla R. 2018. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. [56] Kharazmi E, Zhang Z, Karniadakis G E. 2019. Variational physics-informed neural networks for solving partial differential equations. arXiv preprint arXiv: 1912.00873. [57] Kharazmi E, Zhang Z, Karniadakis G E. 2021. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Computer Methods in Applied Mechanics and Engineering, 374: 113547. doi: 10.1016/j.cma.2020.113547 [58] Kirchdoerfer T, Ortiz M. 2016. Data-driven computational mechanics. Computer Methods in Applied Mechanics and Engineering, 304: 81-101. doi: 10.1016/j.cma.2016.02.001 [59] Kirchdoerfer T, Ortiz M. 2018. Data-driven computing in dynamics. International Journal for Numerical Methods in Engineering, 113(11): 1697-1710. doi: 10.1002/nme.5716 [60] Kovachki N, Lanthaler S, Mishra S. 2021. On universal approximation and error bounds for Fourier neural operators. The Journal of Machine Learning Research, 22(1): 13237-13312. [61] Kovachki N B, Li Z, Liu B, et al. 2023. Neural operator: learning maps between function spaces with applications to PDEs. J. Mach. Learn. Res., 24(89): 1-97. [62] Krizhevsky A, Sutskever I, Hinton G E. 2012. Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems, 25: 1097-1105. [63] Lagaris I E, Likas A, Fotiadis D I. 1998. Artificial neural networks for solving ordinary and partial differential equations. IEEE Transactions on Neural Networks, 9(5): 987-1000. doi: 10.1109/72.712178 [64] Lagaris I E, Likas A C, Papageorgiou D G. 2000. Neural-network methods for boundary value problems with irregular boundaries. IEEE Transactions on Neural Networks, 11(5): 1041-1049. doi: 10.1109/72.870037 [65] Lanthaler S, Mishra S, Karniadakis G E. 2022. Error estimates for deeponets: A deep learning framework in infinite dimensions. Transactions of Mathematics and Its Applications, 6(1): 1. [66] Lauer F, Bloch G. 2008. Incorporating prior knowledge in support vector machines for classification: A review. Neurocomputing, 71(7-9): 1578-1594. doi: 10.1016/j.neucom.2007.04.010 [67] Lee H, Kang I S. 1990. Neural algorithm for solving differential equations. Journal of Computational Physics, 91(1): 110-131. doi: 10.1016/0021-9991(90)90007-N [68] LeVeque R J. 2007. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-state and Time-dependent Problems. SIAM. [69] Li L F, Chen C Q. 2022. Equilibrium-based convolution neural networks for constitutive modeling of hyperelastic materials. Journal of the Mechanics and Physics of Solids, 164: 104931. doi: 10.1016/j.jmps.2022.104931 [70] Li W, Bazant M Z, Zhu J. 2021. A physics-guided neural network framework for elastic plates: Comparison of governing equations-based and energy-based approaches. Computer Methods in Applied Mechanics and Engineering, 383: 113933. doi: 10.1016/j.cma.2021.113933 [71] Li X, Liu Z, Cui S, et al. 2019. Predicting the effective mechanical property of heterogeneous materials by image based modeling and deep learning. Computer Methods in Applied Mechanics and Engineering, 347: 735-753. doi: 10.1016/j.cma.2019.01.005 [72] Li Z, Huang D Z, Liu B, et al. 2023. Fourier neural operator with learned deformations for pdes on general geometries. Journal of Machine Learning Research, 24(388): 1-26. [73] Li Z, Kovachki N, Azizzadenesheli K, et al. 2020a. Fourier neural operator for parametric partial differential equations. arXiv preprint arXiv: 2010.08895. [74] Li Z, Kovachki N, Azizzadenesheli K, et al. 2020b. Neural operator: Graph kernel network for partial differential equations. arXiv preprint arXiv: 2003.03485. [75] Li Z, Zheng H, Kovachki N, et al. 2021. Physics-informed neural operator for learning partial differential equations. arXiv preprint arXiv: 2111.03794. [76] Liu B, Wang Y, Liu Y, et al. 2024a. Deep learning-based multi-scale modeling of thermal conductivity in polyurethane with phase change materials via neural operators. Available at SSRN 4702962. [77] Liu B, Wang Y, Rabczuk T, et al. 2024b. Multi-scale modeling in thermal conductivity of polyurethane incorporated with phase change materials using physics-informed neural networks. Renewable Energy, 220: 119565. doi: 10.1016/j.renene.2023.119565 [78] Liu D, Wang Y. 2021. A dual-dimer method for training physics-constrained neural networks with minimax architecture. Neural Networks, 136: 112-125. doi: 10.1016/j.neunet.2020.12.028 [79] Liu G-R, Karamanlidis D. 2003. Mesh free methods: Moving beyond the finite element method. Appl. Mech. Rev., 56(2): 17-18. [80] Liu M, Liang L, Sun W. 2020. A generic physics-informed neural network-based constitutive model for soft biological tissues. Computer Methods in Applied Mechanics and Engineering, 372: 113402. doi: 10.1016/j.cma.2020.113402 [81] Lu L, Jin P, Pang G, et al. 2021a. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature Machine Intelligence, 3(3): 218-229. doi: 10.1038/s42256-021-00302-5 [82] Lu L, Meng X, Cai S, et al. 2022. A comprehensive and fair comparison of two neural operators (with practical extensions) based on fair data. Computer Methods in Applied Mechanics and Engineering, 393: 114778. doi: 10.1016/j.cma.2022.114778 [83] Lu L, Meng X, Mao Z, et al. 2021b. DeepXDE: A deep learning library for solving differential equations. SIAM Review, 63(1): 208-228. doi: 10.1137/19M1274067 [84] Lu L, Pestourie R, Yao W, et al. 2021c. Physics-informed neural networks with hard constraints for inverse design. SIAM Journal on Scientific Computing, 43(6): 1105-1132. doi: 10.1137/21M1397908 [85] Mattey R, Ghosh S. 2022. A novel sequential method to train physics informed neural networks for Allen Cahn and Cahn Hilliard equations. Computer Methods in Applied Mechanics and Engineering, 390: 114474. doi: 10.1016/j.cma.2021.114474 [86] McClenny L D, Braga-Neto U M. 2023. Self-adaptive physics-informed neural networks. Journal of Computational Physics, 474: 111722. doi: 10.1016/j.jcp.2022.111722 [87] McFall K S. 2006. An artificial neural network method for solving boundary value problems with arbitrary irregular boundaries. Georgia Institute of Technology. [88] McFall K S, Mahan J R. 2009. Artificial neural network method for solution of boundary value problems with exact satisfaction of arbitrary boundary conditions. IEEE Transactions on Neural Networks, 20(8): 1221-1233. doi: 10.1109/TNN.2009.2020735 [89] Meng X, Karniadakis G E. 2020. A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems. Journal of Computational Physics, 401: 109020. doi: 10.1016/j.jcp.2019.109020 [90] Meng X, Li Z, Zhang D, et al. 2020. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Computer Methods in Applied Mechanics and Engineering, 370: 113250. doi: 10.1016/j.cma.2020.113250 [91] Miehe C, Hofacker M, Welschinger F. 2010. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Computer Methods in Applied Mechanics and Engineering, 199(45-48): 2765-2778. doi: 10.1016/j.cma.2010.04.011 [92] Mishra S, Molinaro R. 2022. Estimates on the generalization error of physics-informed neural networks for approximating a class of inverse problems for PDEs. IMA Journal of Numerical Analysis, 42(2): 981-1022. doi: 10.1093/imanum/drab032 [93] Nguyen-Thanh V M, Anitescu C, Alajlan N, et al. 2021. Parametric deep energy approach for elasticity accounting for strain gradient effects. Computer Methods in Applied Mechanics and Engineering, 386: 114096. doi: 10.1016/j.cma.2021.114096 [94] Nguyen-Thanh V M, Zhuang X, Rabczuk T. 2020. A deep energy method for finite deformation hyperelasticity. European Journal of Mechanics-A/Solids, 80: 103874. doi: 10.1016/j.euromechsol.2019.103874 [95] Nguyen V P, Rabczuk T, Bordas S, et al. 2008. Meshless methods: A review and computer implementation aspects. Mathematics and computers in simulation, 79(3): 763-813. doi: 10.1016/j.matcom.2008.01.003 [96] Paszke A, Gross S, Chintala S, et al. 2017. Automatic differentiation in pytorch. [97] Pinkus A. 1999. Approximation theory of the MLP model in neural networks. Acta numerica, 8: 143-195. doi: 10.1017/S0962492900002919 [98] Psaros A F, Meng X, Zou Z, et al. 2023. Uncertainty quantification in scientific machine learning: Methods, metrics, and comparisons. Journal of Computational Physics, 477: 111902. doi: 10.1016/j.jcp.2022.111902 [99] Rabczuk T, Belytschko T. 2004. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. International Journal for Numerical Methods in Engineering, 61(13): 2316-2343. doi: 10.1002/nme.1151 [100] Rabczuk T, Belytschko T. 2007. A three-dimensional large deformation meshfree method for arbitrary evolving cracks. Computer Methods in Applied Mechanics and Engineering, 196(29-30): 2777-2799. doi: 10.1016/j.cma.2006.06.020 [101] Rabczuk T, Song J-H, Zhuang X, et al. 2019. Extended finite element and meshfree methods. Academic Press.Rabczuk T, Song J-H, Zhuang X, et al. 2019. Extended finite element and meshfree methods. Academic Press. [102] Rahaman N, Baratin A, Arpit D, et al. 2019. On the spectral bias of neural networks. International conference on machine learning.Rahaman N, Baratin A, Arpit D, et al. 2019. On the spectral bias of neural networks. International conference on machine learning. [103] Raissi M, Karniadakis G E. 2018. Hidden physics models: Machine learning of nonlinear partial differential equations. Journal of Computational Physics, 357: 125-141. doi: 10.1016/j.jcp.2017.11.039 [104] Raissi M, Perdikaris P, Karniadakis G E. 2017a. Inferring solutions of differential equations using noisy multi-fidelity data. Journal of Computational Physics, 335: 736-746. doi: 10.1016/j.jcp.2017.01.060 [105] Raissi M, Perdikaris P, Karniadakis G E. 2017b. Machine learning of linear differential equations using Gaussian processes. Journal of Computational Physics, 348: 683-693. doi: 10.1016/j.jcp.2017.07.050 [106] Raissi M, Perdikaris P, Karniadakis G E. 2017c. Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv preprint arXiv: 1711.10561. [107] Raissi M, Perdikaris P, Karniadakis G E. 2017d. Physics informed deep learning (part II): Data-driven discovery of nonlinear partial differential equations. arXiv preprint arXiv: 1711.10566. [108] Raissi M, Perdikaris P, Karniadakis G E. 2018. Numerical Gaussian processes for time-dependent and nonlinear partial differential equations. SIAM Journal on Scientific Computing, 40(1): 172-198. doi: 10.1137/17M1120762 [109] Raissi M, Perdikaris P, Karniadakis G E. 2019. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378: 686-707. doi: 10.1016/j.jcp.2018.10.045 [110] Ramabathiran A A, Ramachandran P. 2021. SPINN: Sparse, physics-based, and partially interpretable neural networks for PDEs. Journal of Computational Physics, 445: 110600. doi: 10.1016/j.jcp.2021.110600 [111] Rao C, Sun H, Liu Y. 2021. Physics-informed deep learning for computational elastodynamics without labeled data. Journal of Engineering Mechanics, 147(8): 04021043. doi: 10.1061/(ASCE)EM.1943-7889.0001947 [112] Reddy J N. 2019. Introduction to the finite element method. McGraw-Hill Education. [113] Samaniego E, Anitescu C, Goswami S, et al. 2020. An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications. Computer Methods in Applied Mechanics and Engineering, 362: 112790. doi: 10.1016/j.cma.2019.112790 [114] Senior A W, Evans R, Jumper J, et al. 2020. Improved protein structure prediction using potentials from deep learning. Nature, 577(7792): 706-710. doi: 10.1038/s41586-019-1923-7 [115] Sheng H, Yang C. 2021. PFNN: A penalty-free neural network method for solving a class of second-order boundary-value problems on complex geometries. Journal of Computational Physics, 428: 110085. doi: 10.1016/j.jcp.2020.110085 [116] Shin Y, Darbon J, Karniadakis G E. 2020. On the convergence of physics informed neural networks for linear second-order elliptic and parabolic type PDEs. arXiv preprint arXiv: 2004.01806. [117] Shukla K, Jagtap A D, Karniadakis G E. 2021. Parallel physics-informed neural networks via domain decomposition. Journal of Computational Physics, 447: 110683. doi: 10.1016/j.jcp.2021.110683 [118] Silver D, Huang A, Maddison C J, et al. 2016. Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587): 484-489. doi: 10.1038/nature16961 [119] Simo J C, Hughes T J R. 2006. Computational Inelasticity (Vol. 7). Springer Science & Business Media. [120] Sirignano J, Spiliopoulos K. 2018. DGM: A deep learning algorithm for solving partial differential equations. Journal of Computational Physics, 375: 1339-1364. doi: 10.1016/j.jcp.2018.08.029 [121] Sukumar N, Srivastava A. 2022. Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks. Computer Methods in Applied Mechanics and Engineering, 389: 114333. doi: 10.1016/j.cma.2021.114333 [122] Sun J, Liu Y, Wang Y, et al. 2023a. BINN: A deep learning approach for computational mechanics problems based on boundary integral equations. Computer Methods in Applied Mechanics and Engineering, 410: 116012. doi: 10.1016/j.cma.2023.116012 [123] Sun J, Liu Y, Yao Z, et al. 2023b. A data-driven multi-flaw detection strategy based on deep learning and boundary element method. Computational Mechanics, 71(3): 517-542. doi: 10.1007/s00466-022-02231-5 [124] Vinyals O, Babuschkin I, Czarnecki W M, et al. 2019. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature, 575(7782): 350-354. doi: 10.1038/s41586-019-1724-z [125] Wang S, Teng Y, Perdikaris P. 2021a. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM Journal on Scientific Computing, 43(5): 3055-3081. doi: 10.1137/20M1318043 [126] Wang S, Wang H, Perdikaris P. 2021b. Learning the solution operator of parametric partial differential equations with physics-informed DeepONets. Science advances, 7(40): 8605. doi: 10.1126/sciadv.abi8605 [127] Wang S, Wang H, Perdikaris P. 2021c. On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 384: 113938. doi: 10.1016/j.cma.2021.113938 [128] Wang S, Yu X, Perdikaris P. 2022. When and why PINNs fail to train: A neural tangent kernel perspective. Journal of Computational Physics, 449: 110768. doi: 10.1016/j.jcp.2021.110768 [129] Wang Y, Li X, Yan Z, et al. 2024. HomoGenius: A foundation model of homogenization for rapid prediction of effective mechanical properties using neural operators.arXiv preprint arXiv:2404.07943 [130] Wang Y, Sun J, Li W, et al. 2022. CENN: Conservative energy method based on neural networks with subdomains for solving variational problems involving heterogeneous and complex geometries. Computer Methods in Applied Mechanics and Engineering, 400: 115491. doi: 10.1016/j.cma.2022.115491 [131] Wang Y, Sun J, Rabczuk T, et al. 2023. DCEM-PINNs: A deep complementary energy method for solid mechanics. arXiv preprint arXiv: 2302.01538. [132] Wang Z, Zhang Z. 2020. A mesh-free method for interface problems using the deep learning approach. Journal of Computational Physics, 400: 108963. doi: 10.1016/j.jcp.2019.108963 [133] Xu C, Cao B T, Yuan Y, et al. 2023. Transfer learning based physics-informed neural networks for solving inverse problems in engineering structures under different loading scenarios. Computer Methods in Applied Mechanics and Engineering, 405: 115852. doi: 10.1016/j.cma.2022.115852 [134] Xu H, Chen Y, Zhang D. 2024. Worth of prior knowledge for enhancing deep learning. Nexus. [135] Yang L, Zhang D, Karniadakis G E. 2020. Physics-informed generative adversarial networks for stochastic differential equations. SIAM Journal on Scientific Computing, 42(1): 292-317. doi: 10.1137/18M1225409 [136] Yang L, Zhang Z, Song Y, et al. 2022. Diffusion models: A comprehensive survey of methods and applications. ACM Computing Surveys.56(4): 1-39. [137] Yu B. 2018. The deep Ritz method: A deep learning-based numerical algorithm for solving variational problems. Communications in Mathematics and Statistics, 6(1): 1-12. doi: 10.1007/s40304-018-0127-z [138] Yuan L, Ni Y-Q, Deng X-Y, et al. 2022. A-PINN: Auxiliary physics informed neural networks for forward and inverse problems of nonlinear integro-differential equations. Journal of Computational Physics, 462: 111260. doi: 10.1016/j.jcp.2022.111260 [139] Zehnder J, Li Y, Coros S, et al. 2021. Ntopo: Mesh-free topology optimization using implicit neural representations. Advances in Neural Information Processing Systems, 34: 10368-10381. [140] Zhang D, Lu L, Guo L, et al. 2019. Quantifying total uncertainty in physics-informed neural networks for solving forward and inverse stochastic problems. Journal of Computational Physics, 397: 108850. doi: 10.1016/j.jcp.2019.07.048 [141] Zhang E, Dao M, Karniadakis G E, et al. 2022. Analyses of internal structures and defects in materials using physics-informed neural networks. Science advances, 8(7): 0644. [142] Zhang X, Chen Z, Liu Y. 2016. The material point method: A continuum-based particle method for extreme loading cases. Academic Press. [143] Zhang X, Wang L, Helwig J, et al. 2023. Artificial intelligence for science in quantum, atomistic, and continuum systems. arXiv preprint arXiv: 2307.08423. [144] Zhuang X, Guo H, Alajlan N, et al. 2021. Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates with transfer learning. European Journal of Mechanics-A/Solids, 87: 104225. doi: 10.1016/j.euromechsol.2021.104225 [145] Zienkiewicz O C, Emson C, Bettess P. 1983. A novel boundary infinite element. International Journal for Numerical Methods in Engineering, 19(3): 393-404. doi: 10.1002/nme.1620190307 [146] Zienkiewicz O C, Taylor R L, Zhu J Z. 2005. The finite element method: Its basis and fundamentals. Elsevier. [147] Zubov K, McCarthy Z, Ma Y, et al. 2021. Neuralpde: Automating physics-informed neural networks (pinns) with error approximations. arXiv preprint arXiv: 2107.09443. -




 下载:
下载: