Research progress of fatigue crack propagation method based on finite element technology
-
摘要: 疲劳裂纹是引起工程结构断裂失效的重要因素之一. 目前疲劳裂纹扩展的有限元仿真商业软件有ANSYS、ABAQUS、FRANC3D、ZENCRACK等, 这些软件为疲劳裂纹扩展过程的研究提供了有力支撑. 本文对目前疲劳裂纹扩展的有限元仿真方法进行了综述. 阐明了疲劳裂纹的定义以及研究疲劳裂纹扩展行为的必要性; 介绍了三种用于模拟疲劳裂纹扩展的有限元方法: 扩展有限元法 (XFEM)、内聚力模型 (CZM) 和虚拟裂纹闭合技术 (VCCT); 分别总结了三种方法的基本理论和核心思想, 对三种方法的应用与发展进行了分类归纳; 最后对三种有限元方法进行分析, 指出每种方法各自的优势及目前存在的局限性, 并对疲劳裂纹扩展有限元仿真技术的未来改进方向给出了建议.Abstract: Fatigue cracks are one of the important factors causing fracture and failure of engineering structures. At present, the commercial software for fatigue crack propagation finite element simulation includes ANSYS, ABAQUS, FRANC3D, ZENCRACK, etc., which provide strong support for the study of fatigue crack propagation process. The current finite element simulation methods for fatigue crack propagation are reviewed in this paper. The definition of fatigue crack and the necessity of studying fatigue crack propagation behavior are clarified. Three finite element methods for simulating fatigue crack propagation are introduced: Extended Finite Element Method(XFEM), Cohesive Zone Model (CZM) and Virtual Crack Closure Technique (VCCT). The basic theories and core ideas of the three methods were summarized, and the application as well as development of the three methods were classified and summarized. Finally, the three finite element methods are analyzed, the advantages and limitations of each method are pointed out, and suggestions are given for the future improvement of the finite element simulation technology for fatigue crack propagation.
-
图 1 飞机机体上的疲劳裂纹 (Barter & Molent 2013)
图 3 沥青路面上出现的裂纹 (李妍 2016)
图 5 (a)含孔洞和夹杂物的中心裂纹疲劳寿命图, (b)含孔洞、夹杂物和小裂纹的中心裂纹疲劳寿命图 (Singh et al. 2012)
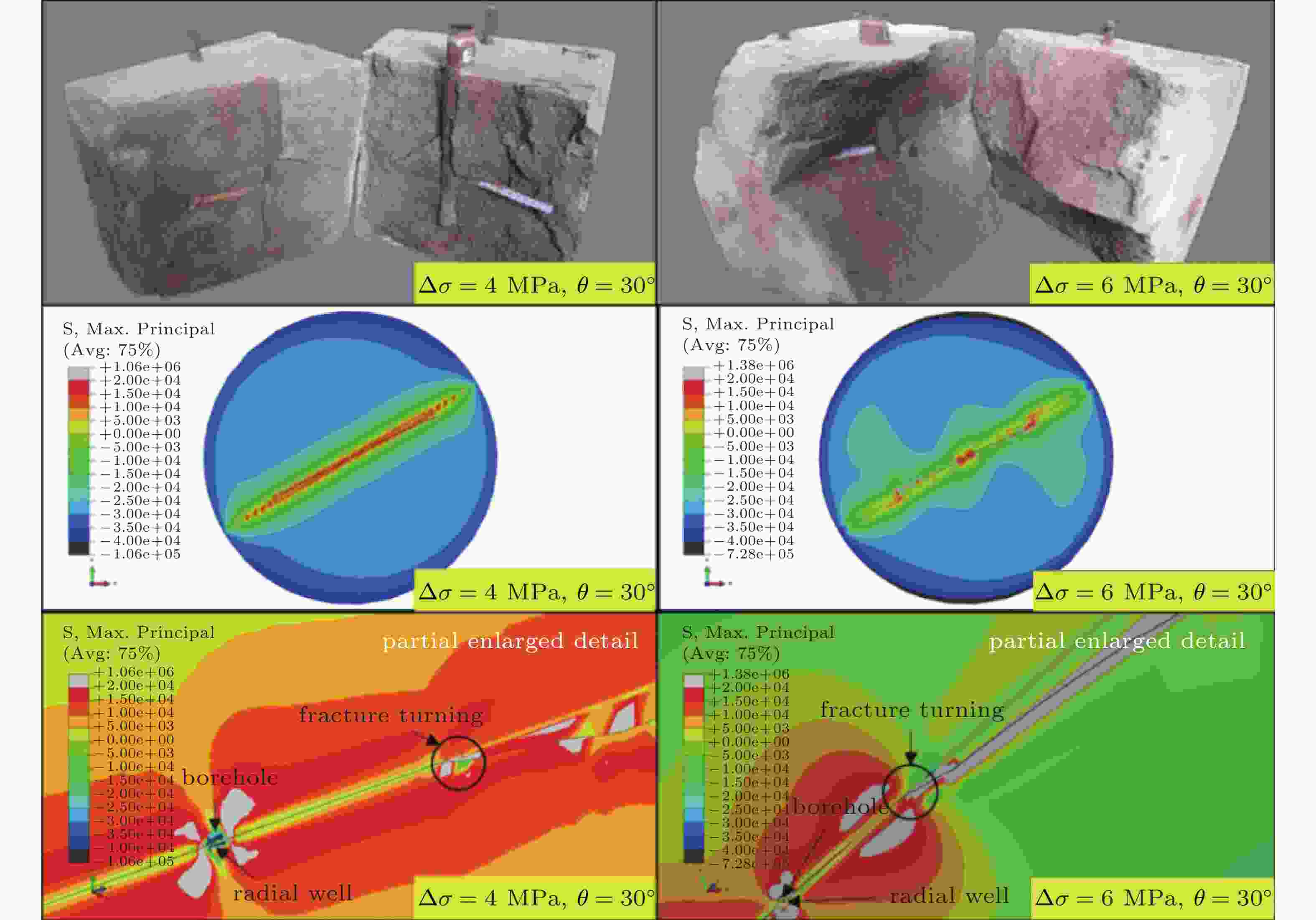
图 6 XFEM对径向井疲劳裂纹扩展仿真结果与实验结果的比较(Li et al. 2018)
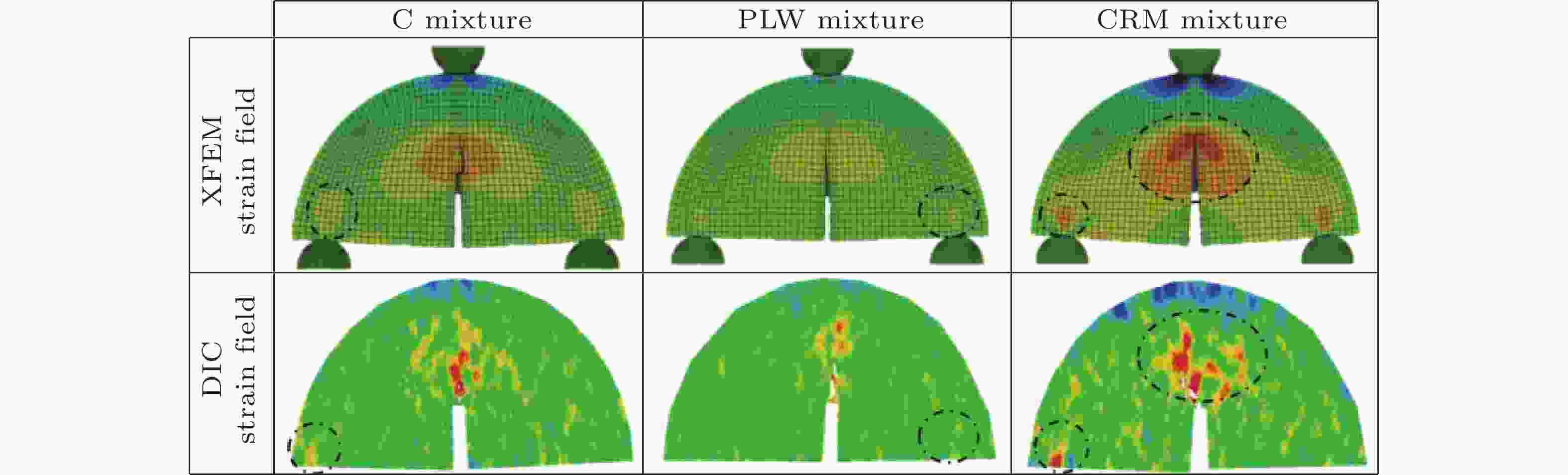
图 7 XFEM模拟应变场与DIC应变场的比较(Radeef et al. 2022)
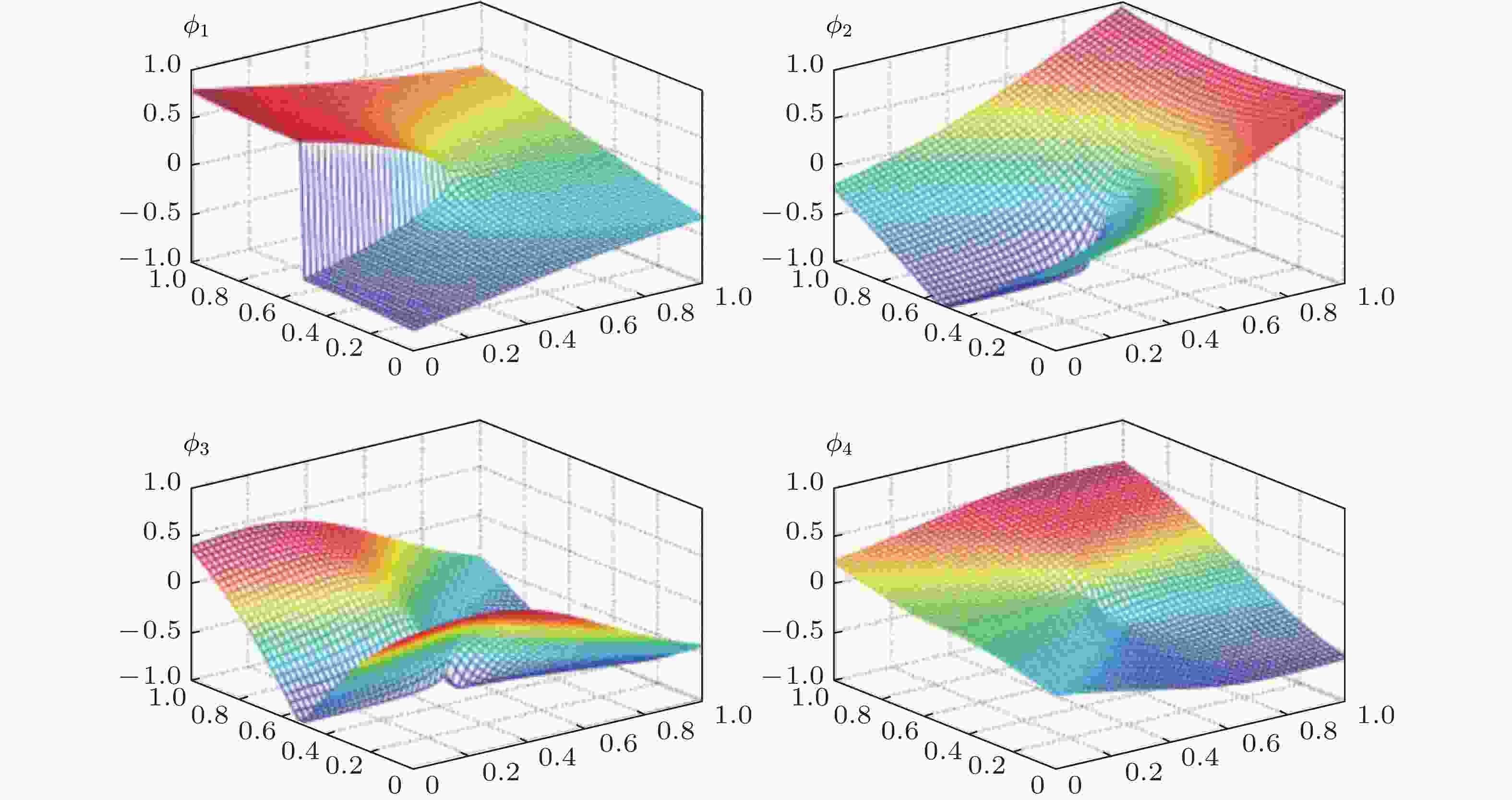
图 8 高阶尖端富集函数节点(Zamani et al. 2012)
图 9 通常用于裂纹前端富集的四种分支函数(Loehnert et al. 2011)
图 10 三维弹塑性离轴单向层合板的边值模型(Higuchi et al. 2017)
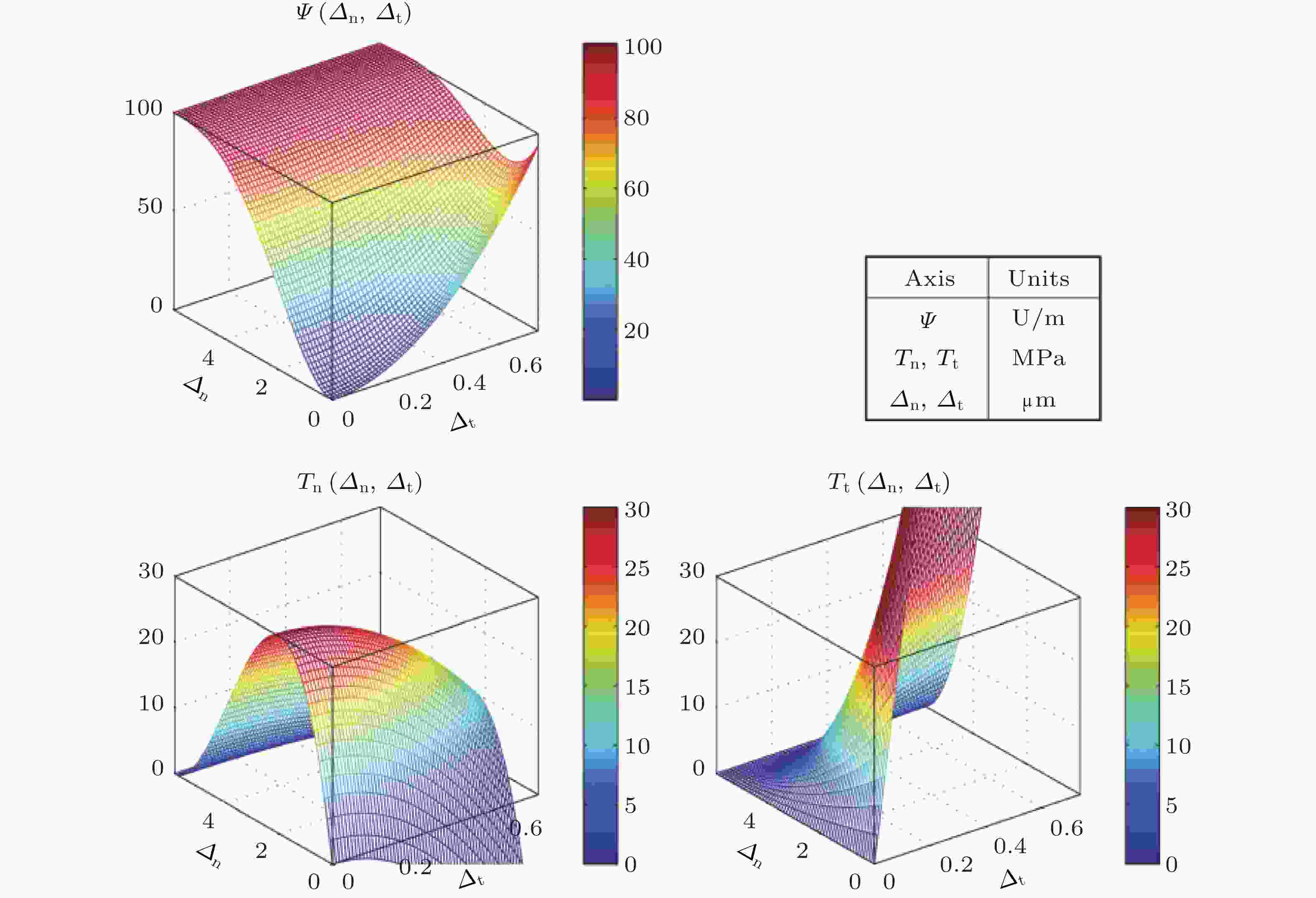
图 13 Needleman提出的三次线性能势模型(Park & Paulino 2011)
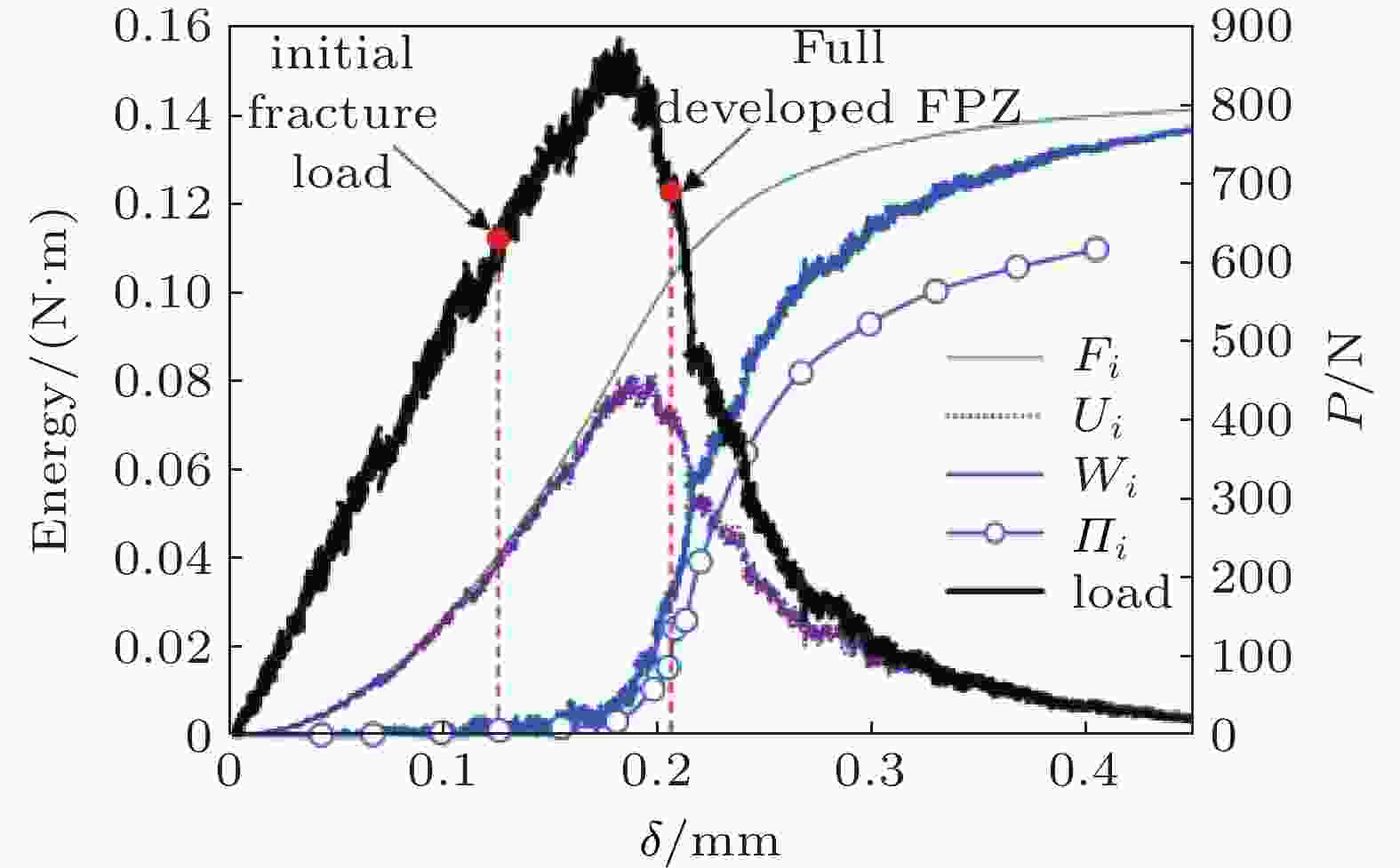
图 14 核石墨压裂过程的能量转换(Tang et al. 2021)
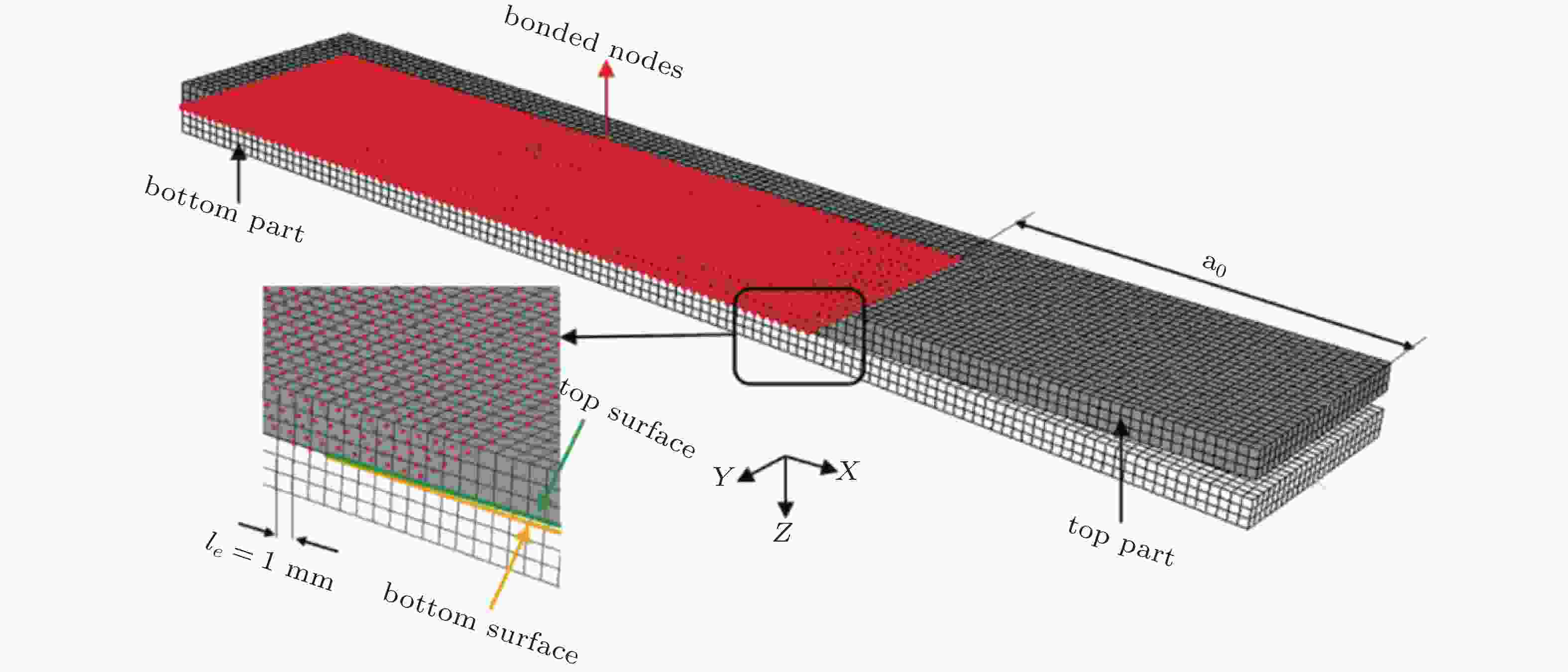
图 17 DCB试件的有限元模型(Teimouri et al. 2021)
表 1 三种有限元方法的特点
有限元方法 优势 局限性 XFEM 1.无需重划网格
2.可以模拟任意方向路径
3.可以解决不连续几何问题
4.具有较好的精度和收敛性1.富集函数收敛耗时较长
2.模拟复杂多个裂纹尚存在局限性
3.计算精度较低CZM 1.使用方便简单
2.计算时间较少
3.计算结果精度较高1.网格敏感性
2.需要提前确定裂纹路径
3.需要预制裂纹VCCT 1. 使用方便简单
2.准确计算应变能释放率1.网格敏感性
2.需要提前确定裂纹路径
3.需要预制裂纹
4.计算时间较长
5.计算精度较低 -
[1] 陈兴. 2014. 基于内聚力模型的不锈钢钎焊接头裂纹扩展研究. 华东理工大学 (Chen X. 2014. The Study on the crack propagation of stainless steel brazed joints by using cohesive zone model. East China University of Science and Technology).Chen X. 2014. The Study on the crack propagation of stainless steel brazed joints by using cohesive zone model. East China University of Science and Technology. [2] 邓殿凯. 2021. 基于内聚力模型的复合材料裂纹扩展研究. 中国民航大学 (Deng D K. 2021. Research on crack propagation of composite materials based on cohesive zone model. Civil Aviation University of China).Deng D K. 2021. Research on crack propagation of composite materials based on cohesive zone model. Civil Aviation University of China. [3] 冯威, 徐绯, 由昊, 李梦琳. 2018. 扩展有限元方法与内聚力模型耦合下斜接修补复合材料的胶层损伤和缺陷. 复合材料学报, 35(5): 1354-1360 (Feng W, Xu F, You H, Li M L. 2018. Adhesive damage and defect analysis of scarf-repaired composite by combining extended finite element method and cohesive zone model. Acta Materiae Compositae Sinica, 35(5): 1354-1360).Feng W, Xu F, You H, Li M L. 2018. Adhesive damage and defect analysis of scarf-repaired composite by combining extended finite element method and cohesive zone model. Acta Materiae Compositae Sinica, 35(5): 1354-1360. [4] 何文涛. 2015. 船体结构疲劳裂纹扩展及其可靠性分析直接计算法研究. 华中科技大学 (He W T. 2015. Research on the direct analysis approach of reliability regarding fatigue crack growth of ship structures. Huazhong University of Science and Technology).He W T. 2015. Research on the direct analysis approach of reliability regarding fatigue crack growth of ship structures. Huazhong University of Science and Technology. [5] 李妍. 2016. 沥青混凝土路面中粘弹性-热力学模型及裂纹扩展. 石家庄铁道大学 (Li Y. 2016. Viscoelasticity -thermal model and crack growth in asphalt concrete pavement. Shijiazhuang Tiedao University).Li Y. 2016. Viscoelasticity -thermal model and crack growth in asphalt concrete pavement. Shijiazhuang Tiedao University. [6] 刘琛. 2021. 复合材料层合板及其夹层结构的界面参数表征方法与裂纹扩展研究. 大连理工大学 (Liu C. 2021. Study on characterization method of interface parameters and crack propagation of composite laminates and their sandwich structures. Dalian University of Technology).Liu C. 2021. Study on characterization method of interface parameters and crack propagation of composite laminates and their sandwich structures. Dalian University of Technology. [7] 苏毅. 2016. 扩展有限元法及其应用中的若干问题研究. 西北工业大学 (Su Y. 2016. Research on extended finite element method and some issues in its application. Northwestern Polytechnical University.).Su Y. 2016. Research on extended finite element method and some issues in its application. Northwestern Polytechnical University. [8] 孙家啟, 纪冬梅, 唐家志. 2016. 内聚力模型在裂纹萌生及扩展中的应用. 上海电力学院学报, 32(2): 129-134 (Sun J Q, Ji D M, Tang J Z. 2016. Application of cohesive zone model on crack initiation and propagation. Journal of Shanghai University of Electric Power, 32(2): 129-134).Sun J Q, Ji D M, Tang J Z. 2016. Application of cohesive zone model on crack initiation and propagation. Journal of Shanghai University of Electric Power, 32(2): 129-134. [9] 王自强, 陈少华. 2009. 高等断裂力学. 北京: 科学出版社 (Wang Z Q, Chen S H. 2009. Advanced fracture mechanics. Beijing: Science Press).Wang Z Q, Chen S H. 2009. Advanced fracture mechanics. Beijing: Science Press. [10] 解德, 钱勤, 李长安. 2009. 断裂力学中的数值计算方法及工程应用. 北京: 科学出版社 (Xie D, Qian Q, Li C A. 2009. Numerical calculation methods and engineering applications in fracture mechanics. Beijing: Science Press).Xie D, Qian Q, Li C A. 2009. Numerical calculation methods and engineering applications in fracture mechanics. Beijing: Science Press. [11] 杨新华, 陈传尧. 2018. 疲劳与断裂. 武汉: 华中科技大学出版社 (Yang X H, Chen C Y. 2018. Fatigue and Fracture. Wuhan: Huazhong University of Science and Technology Press).Yang X H, Chen C Y. 2018. Fatigue and Fracture. Wuhan: Huazhong University of Science and Technology Press [12] 周伟, 张超, 甘淑媛. 2020. 基于 XFEM-CZM 耦合法的胶接接头裂纹扩展分析及强度预测. 北京航空航天大学学报, 46(11) : 2121-2130 (Zhou W, Zhang C, Gan S Y. 2020. Crack propagation analysis and strength prediction of bonded joints based on XFEM-CZM coupling method. Journal of Beijing University of Aeronautics and Astronautics: 46(11) : 2121-2130).Zhou W, Zhang C, Gan S Y. 2020. Crack propagation analysis and strength prediction of bonded joints based on XFEM-CZM coupling method. Journal of Beijing University of Aeronautics and Astronautics: 46(11): 2121-2130. [13] Agathos K, Chatzi E, Bordas S P A. 2018. Multiple crack detection in 3D using a stable XFEM and global optimization. Computational Mechanics, 62: 835-852. doi: 10.1007/s00466-017-1532-y [14] Aure T W, Ioannides A M. Simulation of crack propagation in concrete beams with cohesive elements in ABAQUS. Transportation Research Record, 2010, 2154(1): 12-21. [15] Barenblatt G I. 1962. The mathematical theory of equilibrium cracks in brittle fracture. Advances in applied mechanics, 7: 55-129. [16] Barter S A, Molent L. 2013. Service fatigue cracking in an aircraft bulkhead exposed to a corrosive environment. Engineering Failure Analysis, 34: 181-188. doi: 10.1016/j.engfailanal.2013.07.036 [17] Belytschko T, Black T. 1999. Elastic crack growth in finite elements with minimal remeshing. International Journal for Numerical Methods in Engineering, 45(5): 601-620. doi: 10.1002/(SICI)1097-0207(19990620)45:5<601::AID-NME598>3.0.CO;2-S [18] Belytschko T, Chen H. 2004. Singular enrichment finite element method for elastodynamic crack propagation. International Journal of Computational Methods, 1(01): 1-15. doi: 10.1142/S0219876204000095 [19] Belytschko T, Gracie R, Ventura G. 2009. A review of extended/generalized finite element methods for material modeling. Modelling and Simulation in Materials Science and Engineering, 17(4): 043001. doi: 10.1088/0965-0393/17/4/043001 [20] Bouhala L, Makradi A, Belouettar S, et al. 2015. An XFEM/CZM based inverse method for identification of composite failure parameters. Computers & Structures, 153: 91-97. [21] Bourdin B, Francfort G A, Marigo J J. 2000. Numerical experiments in revisited brittle fracture. Journal of the Mechanics and Physics of Solids, 48(4): 797-826. doi: 10.1016/S0022-5096(99)00028-9 [22] Bourdin B, Francfort G A, Marigo J J. 2008. The variational approach to fracture. Journal of Elasticity, 91: 5-148. doi: 10.1007/s10659-007-9107-3 [23] Busari Y O, Manurung Y H P, Leitner M, et al. 2022. Numerical evaluation of fatigue crack growth of structural steels using energy release rate with VCCT. Applied Sciences, 12(5): 2641. doi: 10.3390/app12052641 [24] Camanho P P, Davila C G, De Moura M F. 2003. Numerical simulation of mixed-mode progressive delamination in composite materials. Journal of Composite Materials, 37(16): 1415-1438. doi: 10.1177/0021998303034505 [25] Chatzi E N, Hiriyur B, Waisman H, et al. 2011. Experimental application and enhancement of the XFEM–GA algorithm for the detection of flaws in structures. Computers & Structures, 89(7-8): 556-570. [26] Chen A, Airey G D, Thom N, et al. 2022. Simulation of micro-crack initiation and propagation under repeated load in asphalt concrete using zero-thickness cohesive elements. Construction and Building Materials, 342: 127934. doi: 10.1016/j.conbuildmat.2022.127934 [27] Conti S, Focardi M, Iurlano F. 2016. Phase field approximation of cohesive fracture models. In Annales de l'Institut Henri Poincaré C, Analyse non linéaire , 33(4) : 1033-1067). [28] Daux C, Moës N, Dolbow J, et al. 2000. Arbitrary branched and intersecting cracks with the extended finite element method. International journal for numerical methods in engineering, 48(12): 1741-1760. doi: 10.1002/1097-0207(20000830)48:12<1741::AID-NME956>3.0.CO;2-L [29] De Carvalho N V, Mabson G E, Krueger R, et al. 2019. A new approach to model delamination growth in fatigue using the Virtual Crack Closure Technique without re-meshing. Engineering Fracture Mechanics, 222: 106614. doi: 10.1016/j.engfracmech.2019.106614 [30] De Maio U, Cendón D, Greco F, et al. 2021. Investigation of concrete cracking phenomena by using cohesive fracture-based techniques: A comparison between an embedded crack model and a refined diffuse interface model. Theoretical and Applied Fracture Mechanics, 115: 103062. doi: 10.1016/j.tafmec.2021.103062 [31] De Maio U, Greco F, Leonetti L, et al. 2022. A cohesive fracture model for predicting crack spacing and crack width in reinforced concrete structures. Engineering Failure Analysis, 139: 106452. doi: 10.1016/j.engfailanal.2022.106452 [32] Deng H, Yan B, Okabe T. 2022. Fatigue crack propagation simulation method using XFEM with variable-node element. Engineering Fracture Mechanics, 269: 108533. doi: 10.1016/j.engfracmech.2022.108533 [33] Deobald L, Mabson G, Dopker B, et al. 2007. Interlaminar fatigue elements for crack growth based on virtual crack closure technique. In 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2091 . [34] Du C, Zhao W, Jiang S, et al. 2020. Dynamic XFEM-based detection of multiple flaws using an improved artificial bee colony algorithm. Computer Methods in Applied Mechanics and Engineering, 365: 112995. doi: 10.1016/j.cma.2020.112995 [35] Dugdale D S. 1960. Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids, 8(2): 100-104. doi: 10.1016/0022-5096(60)90013-2 [36] Esfandiari M, Pak A. 2023. XFEM modeling of the effect of in-situ stresses on hydraulic fracture characteristics and comparison with KGD and PKN models. Journal of Petroleum Exploration and Production Technology, 13(1): 185-201. doi: 10.1007/s13202-022-01545-7 [37] Fageehi Y A. 2021. Fatigue crack growth analysis with extended finite element for 3D linear elastic material. Metals, 11(3): 397. doi: 10.3390/met11030397 [38] Fawaz S A. 1998. Application of the virtual crack closure technique to calculate stress intensity factors for through cracks with an elliptical crack front. Engineering Fracture Mechanics, 59(3): 327-342. doi: 10.1016/S0013-7944(97)00126-4 [39] Francfort G A, Marigo J J. 1998. Revisiting brittle fracture as an energy minimization problem. Journal of the Mechanics and Physics of Solids, 46(8): 1319-1342. doi: 10.1016/S0022-5096(98)00034-9 [40] Freddi F, Iurlano F. 2017. Numerical insight of a variational smeared approach to cohesive fracture. Journal of the Mechanics and Physics of Solids, 98: 156-171. doi: 10.1016/j.jmps.2016.09.003 [41] Freed Y, Zobeiry N, Salviato M. 2022. Development of aviation industry-oriented methodology for failure predictions of brittle bonded joints using probabilistic machine learning. Composite Structures, 297: 115979. doi: 10.1016/j.compstruct.2022.115979 [42] Fries T P. 2008. A corrected XFEM approximation without problems in blending elements. International Journal for Numerical Methods in Engineering, 75(5): 503-532. doi: 10.1002/nme.2259 [43] Gairola S, Rengaswamy J, Verma R. 2023. A study on XFEM simulation of tensile, fracture toughness, and fatigue crack growth behavior of Al 2024 alloy through fatigue crack growth rate models using genetic algorithm. Fatigue & Fracture of Engineering Materials & Structures, 46(6): 2121-2138. [44] Giner E, Sukumar N, Denia F D, et al. 2008. Extended finite element method for fretting fatigue crack propagation. International Journal of Solids and Structures, 45(22-23): 5675-5687. doi: 10.1016/j.ijsolstr.2008.06.009 [45] Gordeliy E, Peirce A. 2015. Enrichment strategies and convergence properties of the XFEM for hydraulic fracture problems. Computer Methods in Applied Mechanics and Engineering, 283: 474-502. doi: 10.1016/j.cma.2014.09.004 [46] Heidari-Rarani M, Sayedain M. 2019. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theoretical and Applied Fracture Mechanics, 103: 102246. doi: 10.1016/j.tafmec.2019.102246 [47] Higuchi R, Okabe T, Nagashima T. 2017. Numerical simulation of progressive damage and failure in composite laminates using XFEM/CZM coupled approach. Composites Part A:Applied Science and Manufacturing, 95: 197-207. doi: 10.1016/j.compositesa.2016.12.026 [48] Hillerborg A, Modéer M, Petersson P E. 1976. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and Concrete Research, 6(6): 773-781. doi: 10.1016/0008-8846(76)90007-7 [49] Iarve E V, Gurvich M R, Mollenhauer D H, et al. 2011. Mesh‐independent matrix cracking and delamination modeling in laminated composites. International Journal for Numerical Methods in Engineering, 88(8): 749-773. doi: 10.1002/nme.3195 [50] Jena J, Singh S K, Gaur V, et al. 2022. A new framework based on XFEM to study the role of electrostatic tractions in semipermeable piezoelectric material. Engineering Fracture Mechanics, 266: 108398. doi: 10.1016/j.engfracmech.2022.108398 [51] Jie Z, Wang W, Chen C, et al. 2021. Local approaches and XFEM used to estimate life of CFRP repaired cracked welded joints under fatigue loading. Composite Structures, 260: 113251. doi: 10.1016/j.compstruct.2020.113251 [52] Jin H, Yu S. 2022. Study on corrosion-induced cracks for the concrete with transverse cracks using an improved CDM-XFEM. Construction and Building Materials, 318: 126173. doi: 10.1016/j.conbuildmat.2021.126173 [53] Jokinen J, Kanerva M, Wallin M, et al. 2019. The simulation of a double cantilever beam test using the virtual crack closure technique with the cohesive zone modelling. International Journal of Adhesion and Adhesives, 88: 50-58. doi: 10.1016/j.ijadhadh.2018.10.015 [54] Jokinen J, Kanerva M. 2019. Simulation of delamination growth at CFRP-tungsten aerospace laminates using VCCT and CZM modelling techniques. Applied Composite Materials, 26: 709-721. doi: 10.1007/s10443-018-9746-5 [55] Jokinen J, Wallin M, Saarela O. 2015. Applicability of VCCT in mode I loading of yielding adhesively bonded joints—a case study. International Journal of Adhesion and Adhesives, 62: 85-91 doi: 10.1016/j.ijadhadh.2015.07.004 [56] Karihaloo B L, Xiao Q Z. 2001a. Accurate determination of the coefficients of elastic crack tip asymptotic field by a hybrid crack element with p-adaptivity. Engineering Fracture Mechanics, 68(15): 1609-1630. doi: 10.1016/S0013-7944(01)00063-7 [57] Karihaloo B L, Xiao Q Z. 2001b. Higher order terms of the crack tip asymptotic field for a notched three-point bend beam. International Journal of Fracture, 112: 111-128. doi: 10.1023/A:1013392324585 [58] Karihaloo B L, Xiao Q Z. 2001c, Higher order terms of the crack tip asymptotic field for a wedge-splitting specimen. International Journal of Fracture, 112 : 129-137. [59] Karimi S, Haji Aboutalebi F, Heidari‐Rarani M. 2022. Developments in remeshing‐free fatigue crack growth simulation including a new adaptive virtual crack closure technique. Fatigue & Fracture of Engineering Materials & Structures, 45(8): 2293-2312. [60] Kaushik V, Ghosh A. 2019. Experimental and numerical characterization of Mode I fracture in unidirectional CFRP laminated composite using XIGA-CZM approach. Engineering Fracture Mechanics, 211: 221-243. doi: 10.1016/j.engfracmech.2019.01.038 [61] Kim J, Bathe K J. 2013. The finite element method enriched by interpolation covers. Computers & Structures, 116: 35-49. [62] Krscanski S, Brnic J. 2020. Prediction of fatigue crack growth in metallic specimens under constant amplitude loading using virtual crack closure and forman model. Metals, 10(7): 977. doi: 10.3390/met10070977 [63] Krueger R. 2004. Virtual crack closure technique: History, approach, and applications. Appl Mech Rev, 57(2): 109-143. doi: 10.1115/1.1595677 [64] Kumar V, Singh I V, Mishra B. 2014. XFEM, Crack growth examination of Cryo-Rolled (CR) 6082 Al alloys. Int. J. Emerg. Technol. Adv. Eng, 4(1): 264-271. [65] Li X, Xiao W, Qu Z, et al. 2018. Rules of fracture propagation of hydraulic fracturing in radial well based on XFEM. Journal of Petroleum Exploration and Production Technology, 8: 1547-1557. doi: 10.1007/s13202-018-0436-5 [66] Liang J, Huang R, Prevost J H, et al. 2003. Evolving crack patterns in thin films with the extended finite element method. International Journal of Solids and Structures, 40(10): 2343-2354. doi: 10.1016/S0020-7683(03)00095-7 [67] Liu G, Chen Z, Zhou J. 2023. Numerical investigation on the residual ultimate strength of central-cracked stiffened plates under tensile and bending loads using XFEM. Journal of Marine Science and Engineering, 11(2): 302. doi: 10.3390/jmse11020302 [68] Liu P F, Yang Y H. 2014. Finite element analysis of the competition between crack deflection and penetration of fiber-reinforced composites using virtual crack closure technique. Applied Composite Materials, 21: 759-771. doi: 10.1007/s10443-013-9375-y [69] Liu X Y, Xiao Q Z, Karihaloo B L. 2004. XFEM for direct evaluation of mixed mode SIFs in homogeneous and bi‐materials. International Journal for Numerical Methods in Engineering, 59(8): 1103-1118. doi: 10.1002/nme.906 [70] Liu Y P, Li T J. 2021. Application of the virtual crack closure technique (VCCT) using tetrahedral finite elements to calculate the stress intensity factor. Engineering Fracture Mechanics, 253: 107853. doi: 10.1016/j.engfracmech.2021.107853 [71] Loehnert S, Mueller‐Hoeppe D S, Wriggers P. 2011. 3D corrected XFEM approach and extension to finite deformation theory. International Journal for Numerical Methods in Engineering, 86(4‐5): 431-452. [72] Mabson G, Deobald L, Dopker B. 2007. Fracture interface elements for the implementation of the virtual crack closure technique. In 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference , 2376 . [73] Máirtín É Ó, Parry G, Beltz G E, et al. 2014. Potential-based and non-potential-based cohesive zone formulations under mixed-mode separation and over-closure–Part II: Finite element applications. Journal of the Mechanics and Physics of Solids, 63: 363-385. doi: 10.1016/j.jmps.2013.08.019 [74] Martulli L M, Bernasconi A. 2023. An efficient and versatile use of the VCCT for composites delamination growth under fatigue loadings in 3D numerical analysis: the Sequential static fatigue algorithm. International Journal of Fatigue, 170: 107493. doi: 10.1016/j.ijfatigue.2022.107493 [75] Marulli M R, Valverde-González A, Quintanas-Corominas A, et al. 2022. A combined phase-field and cohesive zone model approach for crack propagation in layered structures made of nonlinear rubber-like materials. Computer Methods in Applied Mechanics and Engineering, 395: 115007. doi: 10.1016/j.cma.2022.115007 [76] McGarry J P, Máirtín É Ó, Parry G, et al. 2014. Potential-based and non-potential-based cohesive zone formulations under mixed-mode separation and over-closure. Part I: Theoretical analysis. Journal of the Mechanics and Physics of Solids, 63: 336-362. doi: 10.1016/j.jmps.2013.08.020 [77] Melenk J M, Babuška I. 1997. Approximation with harmonic and generalized harmonic polynomials in the partition of unity method. Computer Assisted Mechanics and Engineering Sciences, 4: 607-632. [78] Melenk J M, Babuška I. 1996. The partition of unity finite element method: basic theory and applications. Computer methods in applied mechanics and engineering, 139(1-4): 289-314. doi: 10.1016/S0045-7825(96)01087-0 [79] Menouillard T, Rethore J, Combescure A, et al. 2006. Efficient explicit time stepping for the extended Finite Element Method (XFEM). International Journal for Numerical Methods in Engineering, 68(9): 911-939. doi: 10.1002/nme.1718 [80] Meray F, Chaise T, Gravouil A, et al. 2022. A novel SAM/X-FEM coupling approach for the simulation of 3D fatigue crack growth under rolling contact loading. Finite Elements in Analysis and Design, 206: 103752. doi: 10.1016/j.finel.2022.103752 [81] Meschke G, Dumstorff P. 2007. Energy-based modeling of cohesive and cohesionless cracks via XFEM. Computer Methods in Applied Mechanics and Engineering, 196(21-24): 2338-2357. doi: 10.1016/j.cma.2006.11.016 [82] Miehe C, Hofacker M, Welschinger F. 2010. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Computer Methods in Applied Mechanics and Engineering, 199(45-48): 2765-2778. doi: 10.1016/j.cma.2010.04.011 [83] Moës N, Belytschko T. 2002. Extended finite element method for cohesive crack growth. Engineering Fracture Mechanics, 69(7): 813-833. doi: 10.1016/S0013-7944(01)00128-X [84] Moës N, Dolbow J, Belytschko T. 1999. A finite element method for crack growth without remeshing. International Journal for Numerical Methods in Engineering, 46(1): 131-150. doi: 10.1002/(SICI)1097-0207(19990910)46:1<131::AID-NME726>3.0.CO;2-J [85] Nagashima T, Sawada M. 2016. Development of a damage propagation analysis system based on level set XFEM using the cohesive zone model. Computers & Structures, 174: 42-53. [86] Narayana K B, Dattaguru B, Ramamurthy T S, et al. 1994. A general procedure for modified crack closure integral in 3D problems with cracks. Engineering Fracture Mechanics, 48(2): 167-176. doi: 10.1016/0013-7944(94)90076-0 [87] Needleman A. 1987. A continuum model for void nucleation by inclusion debonding. Journal of Applied Mechanics, 54(3): 525-531. doi: 10.1115/1.3173064 [88] Needleman A. 1990. An analysis of decohesion along an imperfect interface. International Journal of Fracture, 42: 21-40. doi: 10.1007/BF00018611 [89] Nguyen K D, Thanh C L, Vogel F, et al. 2022. Crack propagation in quasi-brittle materials by fourth-order phase-field cohesive zone model. Theoretical and Applied Fracture Mechanics, 118: 103236. doi: 10.1016/j.tafmec.2021.103236 [90] Nguyen O, Repetto E A, Ortiz M, et al. 2001. A cohesive model of fatigue crack growth. International Journal of Fracture, 110: 351-369. doi: 10.1023/A:1010839522926 [91] Osher S, Sethian J A. 1988. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. Journal of computational physics, 79(1): 12-49. doi: 10.1016/0021-9991(88)90002-2 [92] Paggi M, Reinoso J. 2017. Revisiting the problem of a crack impinging on an interface: a modeling framework for the interaction between the phase field approach for brittle fracture and the interface cohesive zone model. Computer Methods in Applied Mechanics and Engineering, 321: 145-172. doi: 10.1016/j.cma.2017.04.004 [93] Park K, Paulino G H, Roesler J R. 2009. A unified potential-based cohesive model of mixed-mode fracture. Journal of the Mechanics and Physics of Solids, 57(6): 891-908. doi: 10.1016/j.jmps.2008.10.003 [94] Park K, Paulino G H, Roesler J. 2010. Cohesive fracture model for functionally graded fiber reinforced concrete. Cement and Concrete Research, 40(6): 956-965. doi: 10.1016/j.cemconres.2010.02.004 [95] Park K, Paulino G H. 2011. Cohesive zone models: A critical review of traction-separation relationships across fracture surfaces. Applied Mechanics Reviews, 64(6): 060802. doi: 10.1115/1.4023110 [96] Pascoe J A, Alderliesten R C, Benedictus R. 2013. Methods for the prediction of fatigue delamination growth in composites and adhesive bonds–a critical review. Engineering Fracture Mechanics, 112: 72-96. [97] Pathak H, Singh A, Singh I V. 2013. Fatigue crack growth simulations of 3-D problems using XFEM. International Journal of Mechanical Sciences, 76 : 112-131. [98] Pirondi A, Giuliese G, Moroni F, et al. 2014. Comparative study of cohesive zone and virtual crack closure techniques for three-dimensional fatigue debonding. The Journal of Adhesion, 90(5-6): 457-481. doi: 10.1080/00218464.2013.859616 [99] Prabel B, Combescure A, Gravouil A, et al. 2007. Level set X‐FEM non‐matching meshes: application to dynamic crack propagation in elastic–plastic media. International Journal for Numerical Methods in Engineering, 69(8): 1553-1569. doi: 10.1002/nme.1819 [100] Pranavi D, Rajagopal A, Reddy J N. 2021. Interaction of anisotropic crack phase field with interface cohesive zone model for fiber reinforced composites. Composite Structures, 270: 114038. doi: 10.1016/j.compstruct.2021.114038 [101] Qi C, Lin S, Yan X. 2023. Damage calculation method for stress corrosion crack of glass fiber reinforced polymer composites. Composite Structures, 306: 116575. doi: 10.1016/j.compstruct.2022.116575 [102] Rabinovich D, Givoli D, Vigdergauz S. 2009. Crack identification by ‘arrival time’using XFEM and a genetic algorithm. International Journal for Numerical Methods in Engineering, 77(3): 337-359. doi: 10.1002/nme.2416 [103] Rabinovich D, Givoli D, Vigdergauz S. 2007. XFEM‐based crack detection scheme using a genetic algorithm. International Journal for Numerical Methods in Engineering, 71(9): 1051-1080. doi: 10.1002/nme.1975 [104] Radeef H R, Hassan N A, Mahmud M Z H, et al. 2022. Linear viscoelastic response of semi-circular asphalt sample based on digital image correlation and XFEM. Measurement, 192: 110866. doi: 10.1016/j.measurement.2022.110866 [105] Raimondo A, Doesburg S A, Bisagni C. 2020. Numerical study of quasi-static and fatigue delamination growth in a post-buckled composite stiffened panel. Composites Part B:Engineering, 182: 107589. doi: 10.1016/j.compositesb.2019.107589 [106] Raju I S. 1987. Calculation of strain-energy release rates with higher order and singular finite elements. Engineering Fracture Mechanics, 28(3): 251-274. doi: 10.1016/0013-7944(87)90220-7 [107] Réthoré J, Gravouil A, Combescure A. 2005. An energy‐conserving scheme for dynamic crack growth using the extended finite element method. International Journal for Numerical Methods in Engineering, 63(5): 631-659. doi: 10.1002/nme.1283 [108] Riahi H, Bressolette P, Chateauneuf A. 2010. Random fatigue crack growth in mixed mode by stochastic collocation method. Engineering Fracture Mechanics, 77(16): 3292-3309. doi: 10.1016/j.engfracmech.2010.07.015 [109] Rose J H, Ferrante J, Smith J R. 1981. Universal binding energy curves for metals and bimetallic interfaces. Physical Review Letters, 47(9): 675. doi: 10.1103/PhysRevLett.47.675 [110] Rybicki E F, Kanninen M F. 1977a. A finite element calculation of stress intensity factors by a modified crack closure integral. Engineering Fracture Mechanics, 9(4): 931-938. doi: 10.1016/0013-7944(77)90013-3 [111] Rybicki E F, Schmueser D W, Fox J. 1977b. An energy release rate approach for stable crack growth in the free-edge delamination problem. Journal of Composite Materials, 11(4): 470-487. doi: 10.1177/002199837701100409 [112] Sethian J A. 1999a. Advancing interfaces: level set and fast marching methods. In Proceedings of the International Conference on Industrial and Applied Mathematics: Plenary Lectures, 222–233. [113] Sethian J A. 1999b. Fast marching methods. SIAM review, 41(2): 199-235. doi: 10.1137/S0036144598347059 [114] Shi J, Chopp D, Lua J, et al. 2010. Abaqus implementation of extended finite element method using a level set representation for three-dimensional fatigue crack growth and life predictions. Engineering Fracture Mechanics, 77(14): 2840-2863. doi: 10.1016/j.engfracmech.2010.06.009 [115] Shivakumar K N, Tan P W, Newman Jr J C. 1988. A virtual crack-closure technique for calculating stress intensity factors for cracked three dimensional bodies. International Journal of Fracture, 36 . [116] Siegmund T. 2004. A numerical study of transient fatigue crack growth by use of an irreversible cohesive zone model. International Journal of Fatigue, 26(9): 929-939. doi: 10.1016/j.ijfatigue.2004.02.002 [117] Singh I V, Mishra B K, Bhattacharya S, et al. 2012. The numerical simulation of fatigue crack growth using extended finite element method. International Journal of Fatigue, 36(1): 109-119. doi: 10.1016/j.ijfatigue.2011.08.010 [118] Solob A, Grbović A, Božić Ž, et al. 2020. XFEM based analysis of fatigue crack growth in damaged wing-fuselage attachment lug. Engineering Failure Analysis, 112: 104516. doi: 10.1016/j.engfailanal.2020.104516 [119] Stolarska M, Chopp D L, Moës N, et al. 2001. Modelling crack growth by level sets in the extended finite element method. International Journal for Numerical Methods in Engineering, 51(8): 943-960. doi: 10.1002/nme.201 [120] Su X, Yang Z, Liu G. 2010. Finite element modelling of complex 3D static and dynamic crack propagation by embedding cohesive elements in Abaqus. Acta Mechanica Solida Sinica, 23(3): 271-282. doi: 10.1016/S0894-9166(10)60030-4 [121] Sukumar N, Moës N, Moran B, et al. 2000. Extended finite element method for three‐dimensional crack modelling. International journal for numerical methods in engineering, 48(11): 1549-1570. doi: 10.1002/1097-0207(20000820)48:11<1549::AID-NME955>3.0.CO;2-A [122] Sukumar N, Srolovitz D J, Baker T J, et al. 2003. Brittle fracture in polycrystalline microstructures with the extended finite element method. International Journal for Numerical Methods in Engineering, 56(14): 2015-2037. doi: 10.1002/nme.653 [123] Sun H, Waisman H, Betti R. 2014a. A multiscale flaw detection algorithm based on XFEM. International Journal for Numerical Methods in Engineering, 100(7): 477-503. doi: 10.1002/nme.4741 [124] Sun H, Waisman H , Betti R. 2014b. A two-scale algorithm for detection of multiple flaws in structures modeled with XFEM. In Nondestructive Characterization for Composite Materials, Aerospace Engineering, Civil Infrastructure, and Homeland Security 2014, 9063 : 503-516. [125] Tang Y X, Su R K L, Chen H N. 2021. Energy dissipation during fracturing process of nuclear graphite based on cohesive crack model. Engineering Fracture Mechanics, 242: 107426. doi: 10.1016/j.engfracmech.2020.107426 [126] Teimouri F, Heidari-Rarani M, Aboutalebi F H. 2021. An XFEM-VCCT coupled approach for modeling mode I fatigue delamination in composite laminates under high cycle loading. Engineering Fracture Mechanics, 249: 107760. doi: 10.1016/j.engfracmech.2021.107760 [127] Tian R, Wen L, Wang L. 2019. Three-dimensional improved XFEM (IXFEM) for static crack problems. Computer Methods in Applied Mechanics and Engineering, 343 : 339-367. [128] Torabi A R, Majidi H R, Ayatollahi M R. 2019. Fracture study in notched graphite specimens subjected to mixed mode I/II loading: Application of XFEM based on the cohesive zone model. Theoretical and Applied Fracture Mechanics, 99: 60-70. doi: 10.1016/j.tafmec.2018.11.008 [129] Verma R, Kumar P, Jayaganthan R, et al. 2022. Extended finite element simulation on tensile, fracture toughness and fatigue crack growth behaviour of additively manufactured Ti6Al4V alloy. Theoretical and Applied Fracture Mechanics, 117: 103163. doi: 10.1016/j.tafmec.2021.103163 [130] Vigueras G, Sket F, Samaniego C, et al. 2015. An XFEM/CZM implementation for massively parallel simulations of composites fracture. Composite Structures, 125: 542-557. doi: 10.1016/j.compstruct.2015.01.053 [131] Waisman H, Chatzi E, Smyth A W. 2010. Detection and quantification of flaws in structures by the extended finite element method and genetic algorithms. International Journal for Numerical Methods in Engineering, 82(3): 303-328. doi: 10.1002/nme.2766 [132] Wang C, Nagashima T. 2023. Damage propagation analysis of CFRP laminate by quasi-3D XFEM using hexahedral elements. Composite Structures, 316: 117024. doi: 10.1016/j.compstruct.2023.117024 [133] Wang Z, Xian G, Yue Q. 2023. Finite element modeling of debonding failure in CFRP-strengthened steel beam using a ductile adhesive. Composite Structures, 311: 116818. doi: 10.1016/j.compstruct.2023.116818 [134] Wen L F, Tian R, Wang L X, et al. 2023. Improved XFEM for multiple crack analysis: Accurate and efficient implementations for stress intensity factors. Computer Methods in Applied Mechanics and Engineering, 411: 116045. doi: 10.1016/j.cma.2023.116045 [135] Wen L F, Tian R. 2014. An extra dof-free and well-conditioned XFEM. Proceedings of the 5th International Conference on Computational Methods, 28th-30th July. [136] Wen L, Tian R. 2015. Evaluation of dynamic stress intensity factors using iXFEM. The 6th International Conference on Computational Methods (ICCM2015). [137] Wittmann F H, Rokugo K, Brühwiler E, et al. 1988. Fracture energy and strain softening of concrete as determined by means of compact tension specimens. Materials and Structures, 21: 21-32. doi: 10.1007/BF02472525 [138] Wu H, Settgast R R, Fu P, et al. 2021. An enhanced virtual crack closure technique for stress intensity factor calculation along arbitrary crack fronts and the application in hydraulic fracturing simulation. Rock Mechanics and Rock Engineering, 54: 2943-2957. doi: 10.1007/s00603-021-02428-9 [139] Xiao G, Wen L, Tian R, et al. 2023. Improved XFEM (IXFEM): 3D dynamic crack propagation under impact loading. Computer Methods in Applied Mechanics and Engineering, 405: 115844. doi: 10.1016/j.cma.2022.115844 [140] Xiao Q Z, Karihaloo B L, Liu X Y. 2004. Direct determination of SIF and higher order terms of mixed mode cracks by a hybrid crack element. International Journal of Fracture, 125: 207-225. doi: 10.1023/B:FRAC.0000022229.54422.13 [141] Xie D, Biggers Jr S B. 2006a. Progressive crack growth analysis using interface element based on the virtual crack closure technique. Finite Elements in Analysis and Design, 42(11): 977-984. doi: 10.1016/j.finel.2006.03.007 [142] Xie D, Biggers Jr S B. 2006b. Strain energy release rate calculation for a moving delamination front of arbitrary shape based on the virtual crack closure technique. Part I: Formulation and validation. Engineering Fracture Mechanics, 73(6): 771-785. doi: 10.1016/j.engfracmech.2005.07.013 [143] Xie D, Biggers Jr S B. 2006c. Strain energy release rate calculation for a moving delamination front of arbitrary shape based on the virtual crack closure technique. Part II: Sensitivity study on modeling details. Engineering Fracture Mechanics, 73(6): 786-801. doi: 10.1016/j.engfracmech.2005.07.014 [144] Xie D, Waas A M, Shahwan K W, et al. 2004. Computation of energy release rates for kinking cracks based on virtual crack closure technique. Computer Modeling in Engineering & Sciences, 6(6): 515-524. [145] Xu X P, Needleman A. 1993. Void nucleation by inclusion debonding in a crystal matrix. Modelling and Simulation in Materials Science and Engineering, 1(2): 111. doi: 10.1088/0965-0393/1/2/001 [146] Yang Q D, Thouless M D. 2001. Mixed-mode fracture analyses of plastically-deforming adhesive joints. International Journal of Fracture, 110: 175-187. doi: 10.1023/A:1010869706996 [147] Yazdani S, Rust W J H, Wriggers P. 2016. An XFEM approach for modelling delamination in composite laminates. Composite Structures, 135: 353-364. doi: 10.1016/j.compstruct.2015.09.035 [148] Zamani A, Gracie R, Reza Eslami M. 2012. Cohesive and non‐cohesive fracture by higher‐order enrichment of XFEM. International Journal for Numerical Methods in Engineering, 90(4): 452-483. doi: 10.1002/nme.3329 [149] Zeng W, Liu G R, Jiang C, et al. 2016. An effective fracture analysis method based on the virtual crack closure-integral technique implemented in CS-FEM. Applied Mathematical Modelling, 40(5-6): 3783-3800. doi: 10.1016/j.apm.2015.11.001 [150] Zhang H, Huang Y, Yang Z, et al. 2022. 3D meso-scale investigation of ultra high performance fibre reinforced concrete (UHPFRC) using cohesive crack model and Weibull random field. Construction and Building Materials, 327: 127013. doi: 10.1016/j.conbuildmat.2022.127013 [151] Zhou L, Wang J, Wang Y, et al. 2023. The enriched finite element method-virtual crack closure technique for cracked structures. Thin-Walled Structures, 187: 110756. doi: 10.1016/j.tws.2023.110756 [152] Zi G, Belytschko T. 2003. New crack‐tip elements for XFEM and applications to cohesive cracks. International Journal for Numerical Methods in Engineering, 57(15): 2221-2240. doi: 10.1002/nme.849 -





 下载:
下载: