海洋工程力学中的若干前沿问题

李家春; 聂冰川

doi:10.6052/1000-0992-25-044

海洋工程力学中的若干前沿问题

doi: 10.6052/1000-0992-25-044 cstr: 32046.14.1000-0992-25-044

李家春^{1, 2, ,},
聂冰川^{3, 4, ,}

1.
中国科学院力学研究所流固耦合系统力学重点实验室, 北京 100190
2.
中国科学院大学工程科学学院, 北京 100049
3.
北京交通大学土木工程学院, 北京 100044
4.
北京市结构风工程与城市风环境重点实验室, 北京 100044

基金项目: 本研究得到国家自然科学基金的资助 (11902024).

详细信息

作者简介:
李家春, 流体力学家, 中国科学院院士. 曾任中国科学院大学工程科学学院院长、中国力学学会理事长、国际理论与应用力学联合会理事、亚洲流体力学委员会主席、《力学快报》主编. 现为中国科学院力学研究所研究员, 研究方向为理论流体力学和海洋、环境工程

聂冰川, 北京交通大学力学系副教授、博士生导师. 从事海洋环境流体力学研究. 现任中国力学学会环境力学专业委员会委员

通讯作者:
jcli05@imech.ac.cn

bcnie@bjtu.edu.cn

中图分类号: O3
计量
- 文章访问数: 165
- HTML全文浏览量: 11
- PDF下载量: 58
- 被引次数: 0
出版历程
- 收稿日期: 2025-12-29
- 录用日期: 2025-01-09
- 网络出版日期: 2025-01-15

A few frontier issues in ocean engineering mechanics

LI Jiachun^{1, 2
, ,},
NIE Bingchuan^{3, 4
, ,}

1.
Key Laboratory for Mechanics in Fluid Solid Coupling System, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
2.
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
3.
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
4.
The Chinese Society of Theoretical and Applied Mechanics, Beijing 100190, China

More Information

Corresponding author: jcli05@imech.ac.cn; bcnie@bjtu.edu.cn

摘要

摘要: 本文综述海洋工程领域中与自由面/界面相关的若干前沿问题的研究现状与最新进展. 主要内容包括热带气旋 (TC) 引发的巨浪、液化天然气 (LNG) 晃荡、空化与气泡动力学、涡激运动 (VIM) 与涡激振动 (VIV). 重点关注上述方向的最新研究进展与所面临的挑战. 过去70年研究成果显示, 人类正在开启新一轮海洋探索活动. 未来将出现从海面向深海拓展、从低中纬度向极地延伸, 从化石能源向可再生能源转型的明显趋势.
- 热带气旋 /
- 风浪 /
- 晃荡 /
- 空化 /
- 气泡 /
- 涡激振动
Abstract: In this review, we primarily address the present state of the arts and latest progresses in a few frontier issues mostly relevant to free surface/interface in ocean engineering. They include TC (tropical cyclone) induced extreme surface wave, sloshing of LNG (liquefied natural gas), cavitation/bubble dynamics and VIM (vortex-induced motion) and VIV (vortex-induced vibration). In addition to general description, we mainly focus on the recent advances and challenging aspects of above-mentioned topics. Inspired by the achievements in the previous 70 years, mankind starts a new round of ocean exploration activities. Then, we can find obvious trends: the realm of ocean engineering is expanding from sea surface to deep sea, from low and middle latitude to polar region and from fossil to renewable energy in near future.
- tropical cyclone /
- wind wave /
- sloshing /
- cavitation /
- bubble /
- vortex-induced vibration

HTML全文

图 1 海洋油气勘探开发作业水深记录

下载: 全尺寸图片幻灯片

图 2 非对称风场与海浪生成示意图

下载: 全尺寸图片幻灯片

图 3 二维矩形储罐在共振附近不同水深下的典型晃荡运动. (a) 浅水, (b) 中等水深, (c) 有限水深, (d) 深水

下载: 全尺寸图片幻灯片

图 4 (a) 近自由面气泡; (b) 自由场中气泡; (c) 近垂直壁面气泡; (d) 近水平底部气泡

下载: 全尺寸图片幻灯片

图 5 锁定状态下的涡脱离模式示意图: 2S模式、2P模式、2C模式以及2T模式

下载: 全尺寸图片幻灯片

参考文献(50)

[1]	刘俊, 高福平. 2019. 近壁面柱体涡激振动的迟滞效应. 力学学报, 51(6): 1630-1640 (Liu J, Gao F P. 2019. Hysteresis in vortex-induced vibrations of a near-wall cylinder. Chinese Journal of Theoretical and Applied Mechanics, 51(6): 1630-1640). doi: 10.6052/0459-1879-19-293 Liu J, Gao F P. 2019. Hysteresis in vortex-induced vibrations of a near-wall cylinder. Chinese Journal of Theoretical and Applied Mechanics, 51(6): 1630-1640 doi: 10.6052/0459-1879-19-293
[2]	Bauer H F. 1984. Oscillations of immiscible liquids in a rectangular container: A new damper for excited structures. Journal of Sound and Vibration, 93(1): 117-133. doi: 10.1016/0022-460X(84)90354-7
[3]	Bearman P W. 1984. Vortex shedding from oscillating bluff bodies. Annual Review of Fluid Mechanics, 16: 195-222. doi: 10.1146/annurev.fl.16.010184.001211
[4]	Benjamin T B, Ellis A T. 1966. The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 260: 221-240. doi: 10.1098/rsta.1966.0046
[5]	Blake J R. 1988. The Kelvin impulse: Application to cavitation bubble dynamics. The Journal of the Australian Mathematical Society. Series B. Applied Mathematics, 30(2): 127-146. doi: 10.1017/S0334270000006111
[6]	Blake J R, Leppinen D M, Wang Q X. 2015. Cavitation and bubble dynamics: The Kelvin impulse and its applications. Interface Focus, 5(5): 20150017. doi: 10.1098/rsfs.2015.0017
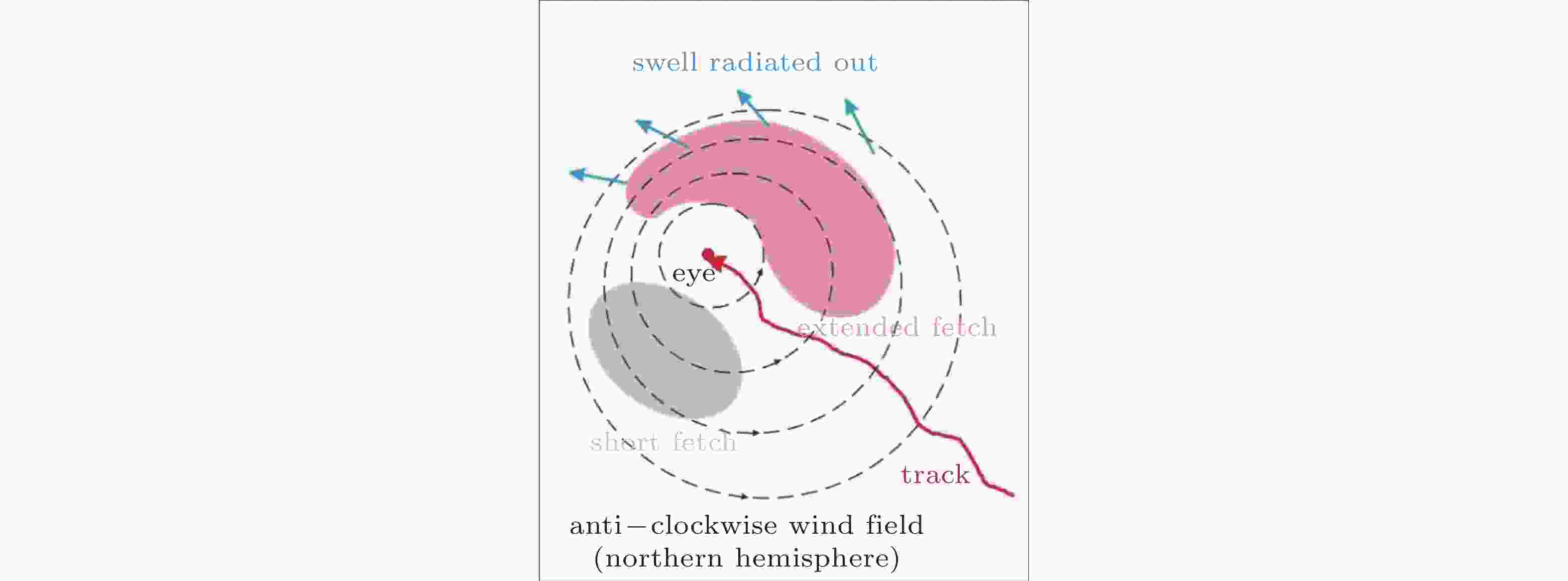
[7]	Bowyer P J, MacAfee A W. 2005. The theory of trapped-fetch waves within tropical cyclones—An operational perspective. Weather Forecast, 20: 229-244. doi: 10.1175/WAF849.1
[8]	Bulian G, Gercos-Pita J L. 2018. Co-simulation of ship motions and sloshing in tanks. Ocean Engineering, 152: 353-376. doi: 10.1016/j.oceaneng.2018.01.028
[9]	Cangialosi J P, Franklin P P. 2016. 2015 hurricane season. National Hurricane Center Forecast Verification Report.
[10]	Cole R H. 1965. Underwater explosions. Dover Publications New York.
[11]	Dias F, Ghidaglia J-M. 2018. Slamming: Recent progress in the evaluation of impact pressure. Annual Review of Fluid Mechanics, 50: 243-273. doi: 10.1146/annurev-fluid-010816-060121
[12]	Eyring V, Bony S, Meehl G A, Senior C A, Stevens B, Stouffer R J, Taylor K E. 2016. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geoscientific Model Development, 9: 1937-1958. doi: 10.5194/gmd-9-1937-2016
[13]	Faltinsen O M, Timokha A N. 2002. Asymptotic modal approximation of nonlinear resonant sloshing in a rectangular tank with small fluid depth. Journal of Fluid Mechanics, 470: 319-357. doi: 10.1017/s0022112002002112
[14]	Faltinsen O M, Rognebakke O, Timokha A. 2005. Resonant three-dimensional nonlinear sloshing in a square-base basin, Part 2, effect of higher modes. Journal of Fluid Mechanics, 523: 199-218. doi: 10.1017/s002211200400196x
[15]	Faltinsen O M. 2017. Sloshing. Advances in Mechanics, 47: 201701. doi: 10.6052/1000-0992-16-017
[16]	Flemming F, Williamson C H K. 2005. Vortex-induced vibrations of a pivoted cylinder. Journal of Fluid Mechanics, 522: 215-252. doi: 10.1017/s0022112004001831
[17]	Fong S W, Ahhikari D, Klaserboer E, Khoo B C. 2009. Interactions of multiple spark-generated bubbles with phase differences. Experiments in Fluids, 46: 705-724. doi: 10.1007/s00348-008-0603-4
[18]	Fujarra A L C, Rosetti G F, Wilde J, Gonçalves R T. 2012. State-of-art on vortex-induced motion: A comprehensive survey after more than one decade of experimental investigation. Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil. July 1–6.
[19]	Ganesh H, Makiharju S A, Ceccio S L. 2016. Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities. Journal of Fluid Mechanics, 802: 37-78. doi: 10.1017/jfm.2016.425
[20]	Gañán-Calvo A M. 2017. Revision of bubble bursting: Universal scaling laws of top jet drop size and speed. Physical Review Letters, 119(20): 204502. doi: 10.1103/PhysRevLett.119.204502
[21]	Gilmore F R. 1952. The growth or collapse of a spherical bubble in a viscous compressible liquid. Hydrodynamics Laboratory, California Institute of Technology, Report No 26-4.
[22]	Govardhan R, Williamson C H K. 2000. Modes of vortex formation and frequency response of a freely vibrating cylinder. Journal of Fluid Mechanics, 420: 85-130. doi: 10.1017/s0022112000001233
[23]	Hsu J-Y, Lien R-C, D’Asaro E A, Sanford T B. 2019. Scaling of drag coefficients under five tropical cyclones. Geophysical Research Letters, 46: 3349-3358. doi: 10.1029/2018GL081574
[24]	Holland G J. 1980. An analytic model of the wind and pressure profiles in hurricanes. Monthly Weather Review, 108: 1212-1218. doi: 10.1175/1520-0493(1980)108<1212:aamotw>2.0.co;2
[25]	Holland G J, Belanger J I, Fritz A. 2010. A revised model for radial profiles of hurricane winds. Monthly Weather Review, 138: 4393-4401. doi: 10.1175/2010MWR3317.1
[26]	Kana D D. 1989. Validated spherical pendulum model for rotary liquid slosh. Journal of Spacecraft and Rockets, 26(3): 188-195. doi: 10.2514/3.26052
[27]	Keller J B, Miksis M. 1980. Bubble oscillations of large amplitude. The Journal of the Acoustical Society of America, 68: 628-633. doi: 10.21236/ada095754
[28]	Khalak A, Williamson C H K. 1999. Motions, forces and mode transitions in vortex-induced vibrations at low mass damping. Journal of Fluids and Structures, 13(7-8): 813-851. doi: 10.1006/jfls.1999.0236
[29]	Kim Y, Nam B W, Kim D W, Kim Y S. 2007. Study on coupling effects of ship motion and sloshing. Ocean Engineering, 34: 2176-2187. doi: 10.1016/j.oceaneng.2007.03.008
[30]	Kossin J P. 2018. A global slowdown of tropical-cyclone translation speed. Nature, 558: 104-107. doi: 10.1038/s41586-018-0158-3
[31]	Lafeber W, Brosset L, Bogaert H. 2012. Elementary Loading Processes (ELP) involved in breaking wave impacts: Findings from the Sloshel project. The Proceedings of the 22nd International Offshore and Polar Engineering Conference.
[32]	Mafi S, Amirinia G. 2017. Forecasting hurricane wave height in Gulf of Mexico using soft computing methods. Ocean Engineering, 146: 352-362. doi: 10.1016/j.oceaneng.2017.10.003
[33]	Nie B C, Li J C, Zhang H Q. 2015. On the regimes of underwater explosion for a submerged slender structure by pulsating bubble. Marine Structure, 44: 85-100. doi: 10.1016/j.marstruc.2015.07.003
[34]	Ogink R H M, Metrikine A V. 2010. A wake oscillator with frequency dependent coupling for the modeling of vortex-induced vibration. Journal of Sound and Vibration, 329: 5452-5473. doi: 10.1016/j.jsv.2010.07.008
[35]	Parlitz U, Englisch V, Scheffczyk C, Lauterborn W. 1990. Bifurcation structure of bubble oscillators. The Journal of the Acoustical Society of America, 88: 1061-1077. doi: 10.1121/1.399855
[36]	Qu Y, Metrikine A V. 2020. A wake oscillator model with nonlinear coupling for the vortex-induced vibration of a rigid cylinder constrained to vibrate in the cross-flow direction. Journal of Sound and Vibration, 469: 115161. doi: 10.1016/j.jsv.2019.115161
[37]	Rayleigh O M F R S. 1917. On the pressure developed in a liquid during the collapse of a spherical cavity. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 34(200): 94-98. doi: 10.1017/CBO9780511704017.076
[38]	Saeki S, Madarame H, Okamoto K. 2001. Self-induced sloshing excited by a horizontally injected plane jet. Journal of Fluid Mechanics, 448: 81-114. doi: 10.1017/s0022112001004153
[39]	Sarpkaya T. 1995. Hydrodynamic damping, flow-induced oscillations, and biharmonic response. Journal of Offshore Mechanics and Arctic Engineering, 117(4): 232-238. doi: 10.1115/1.2827228
[40]	Sarpkaya T. 2004. A critical review of the intrinsic nature of vortex-induced vibrations. Journal of Fluids and Structures, 19: 389-447. doi: 10.1016/j.jfluidstructs.2004.02.005
[41]	Sayar B A, Baumgarten J R. 1981. Pendulum analogy for nonlinear fluid oscillations in spherical containers. Journal of Applied Mechanics, 48: 769-772. doi: 10.1115/1.3157731
[42]	Supponen O, Obreschkow D, Tinguely M, Kobel P, Dorsaz N, Farhat M. 2016. Scaling laws for jets of single cavitation bubbles. Journal of Fluid Mechanics, 802: 263-293. doi: 10.1017/jfm.2016.463
[43]	Tapiador F J, Navarro A, Moreno R, Sánchez J L, García-Ortega E. 2020. Regional climate models: 30 years of dynamical downscaling. Atmospheric Research, 235: 104785. doi: 10.1016/j.atmosres.2019.104785
[44]	Wang L Z, Li J C. 2016. Estimation of extreme wind speed in SCS and NWP by a non-stationary model. Theoretical and Applied Mechanics Letters, 6: 131-138. doi: 10.1016/j.taml.2016.04.001
[45]	Wang Y W, Huang C G, Du T Z, Wu X C, Fang X, Liang N G, Wei Y P. 2012. Shedding phenomenon of ventilated partial cavitation around an underwater projectile. Chinese Physics Letters, 29: 014601. doi: 10.1088/0256-307X/29/1/014601
[46]	Waterhouse D D. 1994. Resonant sloshing near a critical depth. Journal of Fluid Mechanics, 281: 313-318. doi: 10.1017/s0022112094003125
[47]	Wuxi Q Y, Li J C, Nie B C. 2018. Effects of tide-surge interaction and wave set-up/set-down on surge: Case studies of tropical cyclones landing China’s Zhe-Min coast. Theoretical & Applied Mechanics Letters, 8: 153-159. doi: 10.1016/j.taml.2018.03.002
[48]	Young I R. 2017. A review of parametric descriptions of tropical cyclone wind-wave generation. Atmosphere, 8: 194. doi: 10.3390/atmos8100194
[49]	Zeff B W, Kleber B, Fineberg J, Lathrop D P. 2000. Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature, 403: 401-404. doi: 10.1038/35000151
[50]	Zijema M. 2010. Computation of wind-wave spectra in coastal waters with SWAN on unstructured grids. Coastal Engineering, 57: 267-277. doi: 10.1016/j.coastaleng.2009.10.011