Research advances in Uncertainty Quantification and Design Optimization for Flight Vehicles
-
摘要: 飞行器不确定性设计分析方法作为一种先进的飞行器设计范式, 为解决不确定性精确表征、量化传播与优化设计提供了系统的方法体系. 本文系统梳理了飞行器不确定性设计相关的核心概念与关键技术, 归纳了飞行器关键系统设计与重要环境条件预示涉及的不确定性问题. 在此基础上, 总结提炼了该领域的五个重要发展方向: (1) 高维不确定性量化与高效传播: 通过融合输入空间降维、函数表示稀疏化与低秩张量分解等技术, 构建自适应高维不确定性量化框架, 有效应对“维度灾难”带来的挑战; (2) 混合不确定性量化与高效传播: 构建兼容概率、区间、模糊、证据理论等多种不确定性类型的统一量化分析框架, 并结合代理模型与主动学习策略提升复杂多源不确定性问题的计算效率; (3) 多层级多保真度不确定性量化框架: 融合广义近似控制变量、自适应多指标随机配点等技术, 实现计算资源在不同保真度模型上的动态优化配置; (4) 基于不确定性的设计优化算法与框架: 将概率约束与鲁棒性度量统一到不确定性条件下的多目标优化与决策框架, 通过单层循环与解耦式优化策略, 实现性能、可靠性与鲁棒性的综合权衡优化; (5) 基于人工智能技术的不确定性设计分析: 以物理信息神经网络为核心, 融合物理知识与多源数据, 构建智能不确定性量化与优化框架.
-
关键词:
- 不确定性设计分析 /
- 高维不确定性量化 /
- 混合不确定性量化 /
- 基于可靠性的设计分析 /
- 鲁棒性设计优化
Abstract: Uncertainty Quantification (UQ) and Uncertainty-Based Design Optimization (UBDO), as an emerging design paradigm for flight vehicles, provides a systematic methodological framework for addressing the precise characterization, propagation, and design optimization of uncertainties. This paper reviews the core concepts and key technologies in this field. It summarizes the uncertainty challenges associated with critical systems and significant environmental conditions of flight vehicles. Based on the latest research progress, five key research directions are identified: (1) High-dimensional uncertainty quantification and efficient propagation: Constructing an adaptive high-dimensional UQ framework by integrating techniques such as dimensionality reduction, compressed sensing, and low-rank tensor decomposition to effectively address the "curse of dimensionality." (2) Hybrid uncertainty quantification and efficient propagation: A unified framework is established to accommodate various types of uncertainties—including probabilistic, interval, fuzzy, and evidence theory. The computational efficiency for complex, multi-source uncertainty problems is further enhanced by incorporating surrogate modeling and active learning strategies. (3) Multi-level and multi-fidelity UQ framework: Achieving dynamic and optimal allocation of computational resources across models of varying fidelities by integrating techniques like generalized approximate control variates and adaptive multi-index stochastic collocation. (4) Uncertainty-based design optimization algorithms and frameworks: Unifying probabilistic constraints and robustness metrics within a multi-objective optimization and decision-making framework under uncertainty, enabling trade-off optimization among performance, reliability, and robustness through single-loop and decoupled optimization strategies. (5) Uncertainty design and analysis based on artificial intelligence techniques: Centered on physics-informed neural networks, this direction incorporates physical knowledge and multi-source data to establish intelligent frameworks for uncertainty quantification and optimization. -
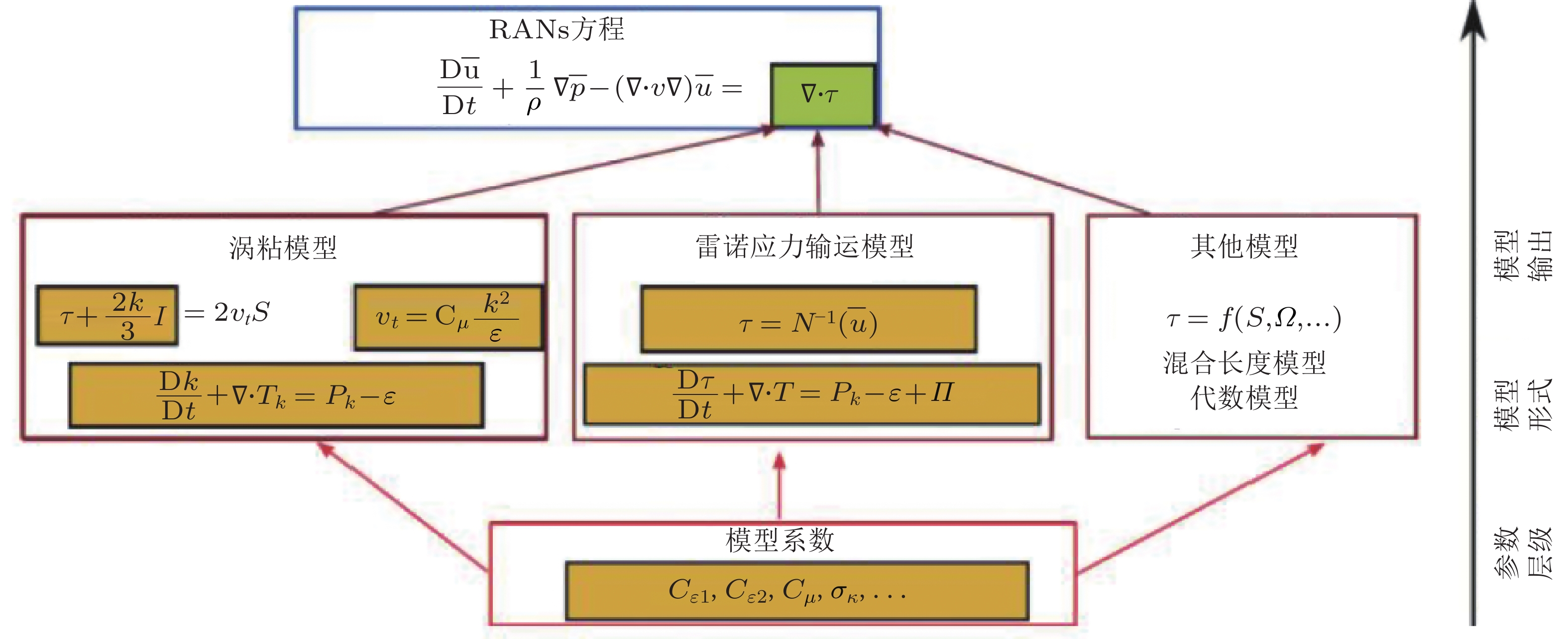
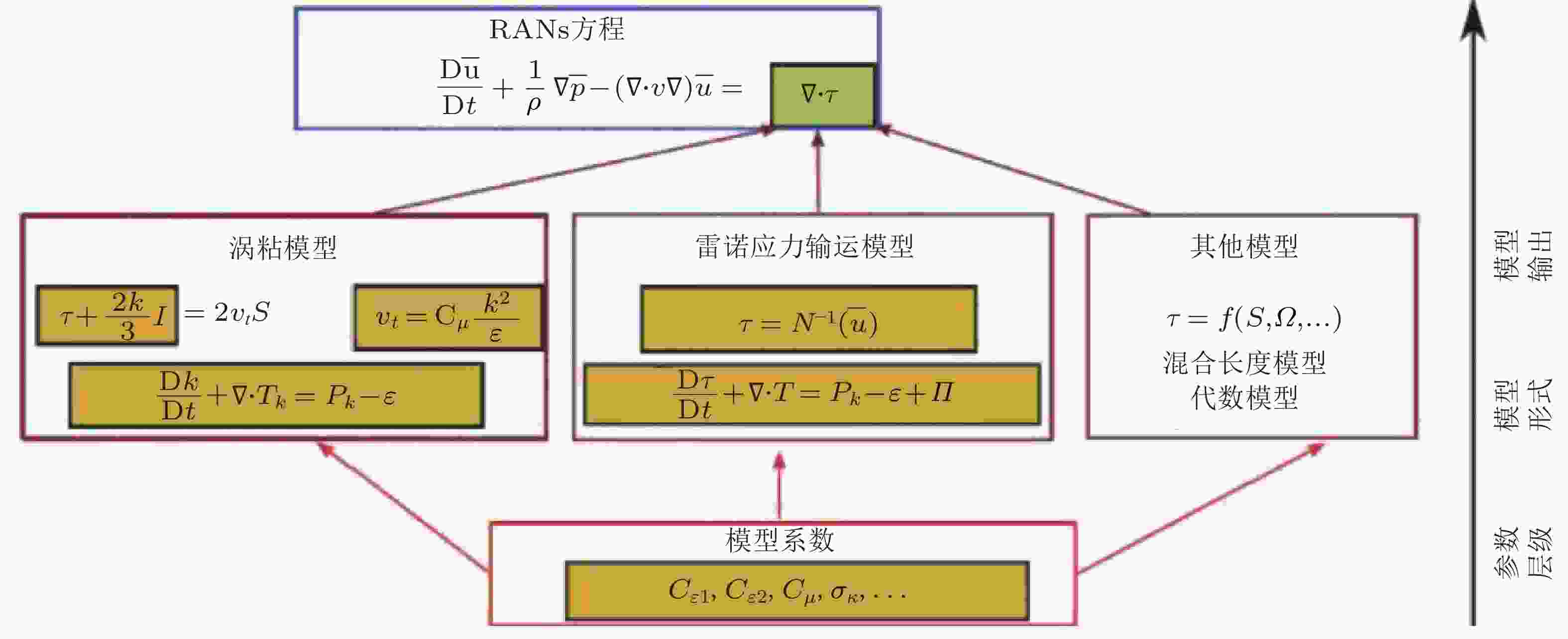
图 1 不同类别湍流模型以及其中的不确定性来源 (Duraisamy et al. 2019, 陈鑫 等 2021)
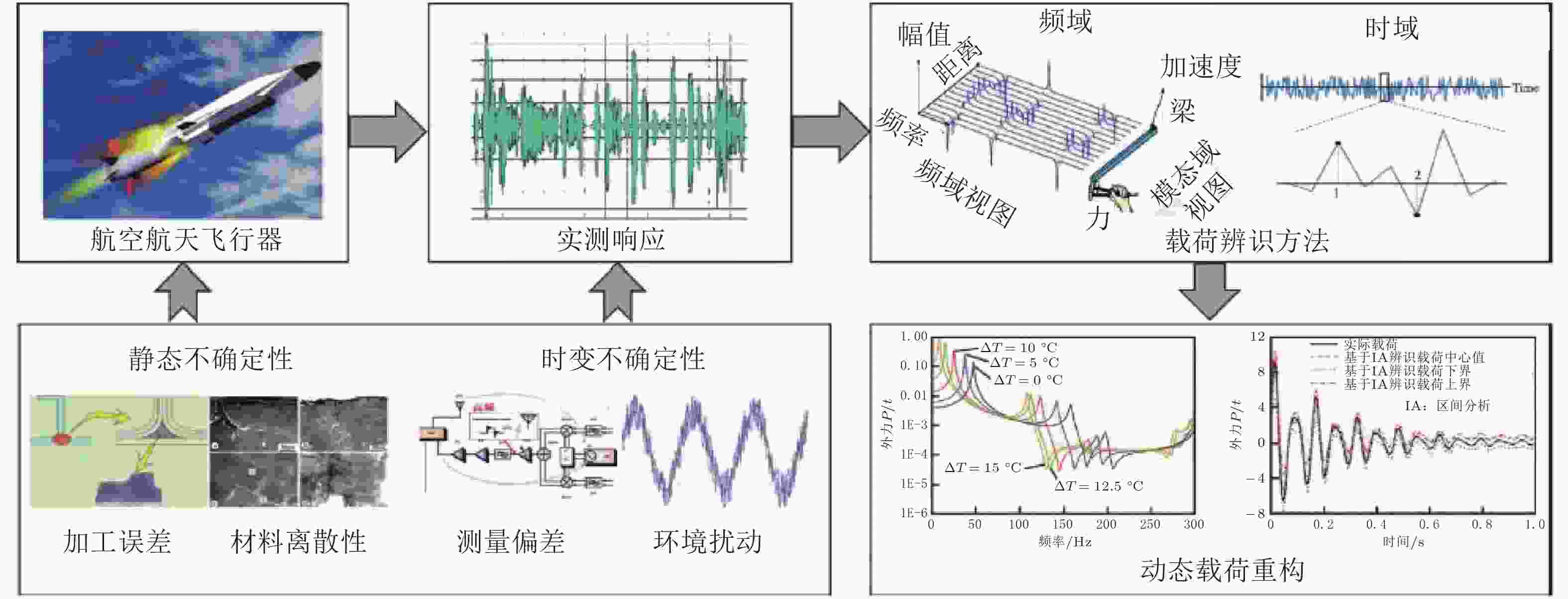
图 2 不确定性影响下的载荷辨识示意图 (Wang et al. 2021)
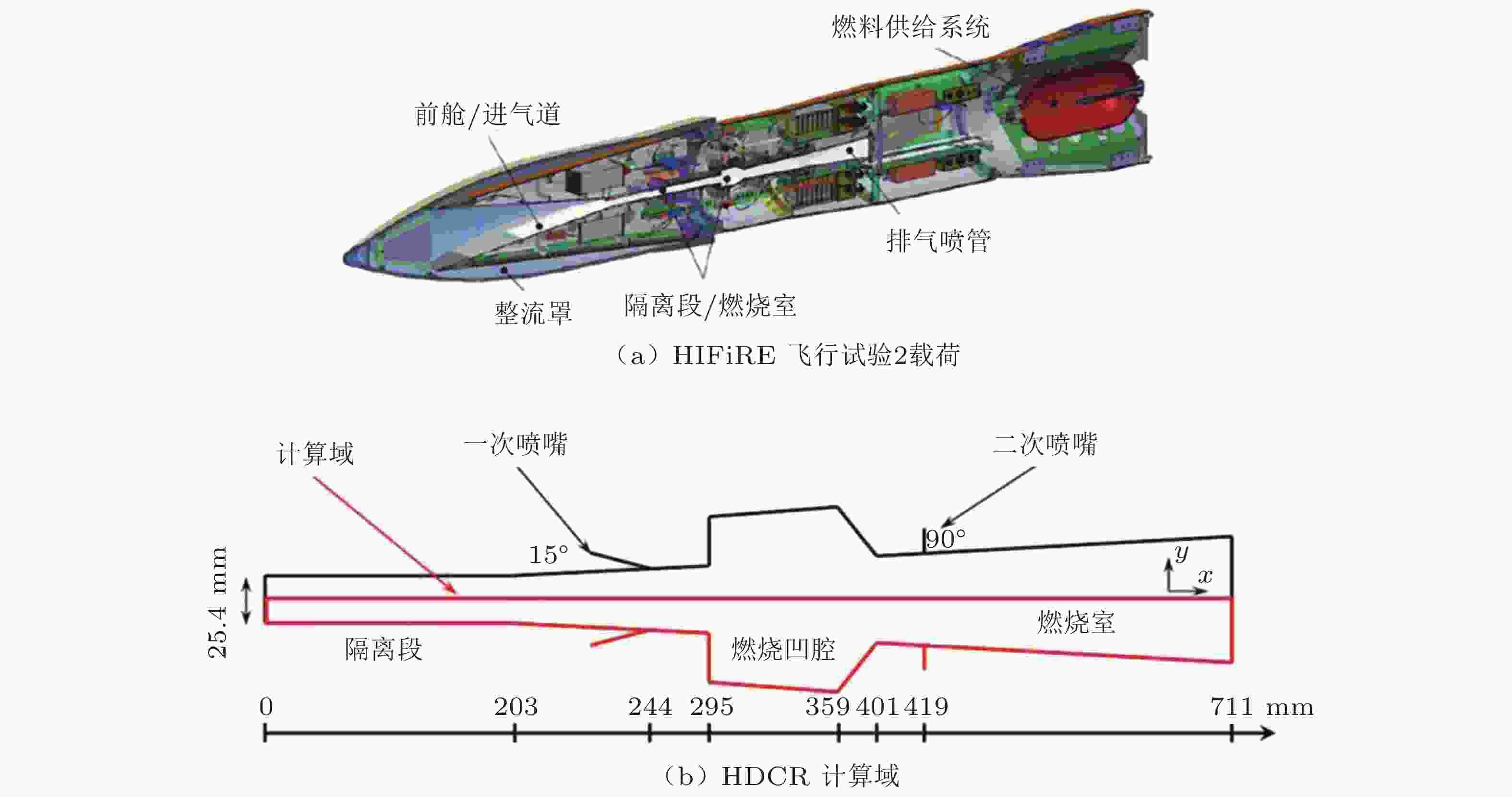
图 3 美国DARPA高超声速国际飞行研究与实验项目 (Hypersonic International Flight Research and Experimentation, HIFiRE) 飞行试验载荷与地面直连试验装置 (HDCR) 示意图 (Geraci et al. 2019)
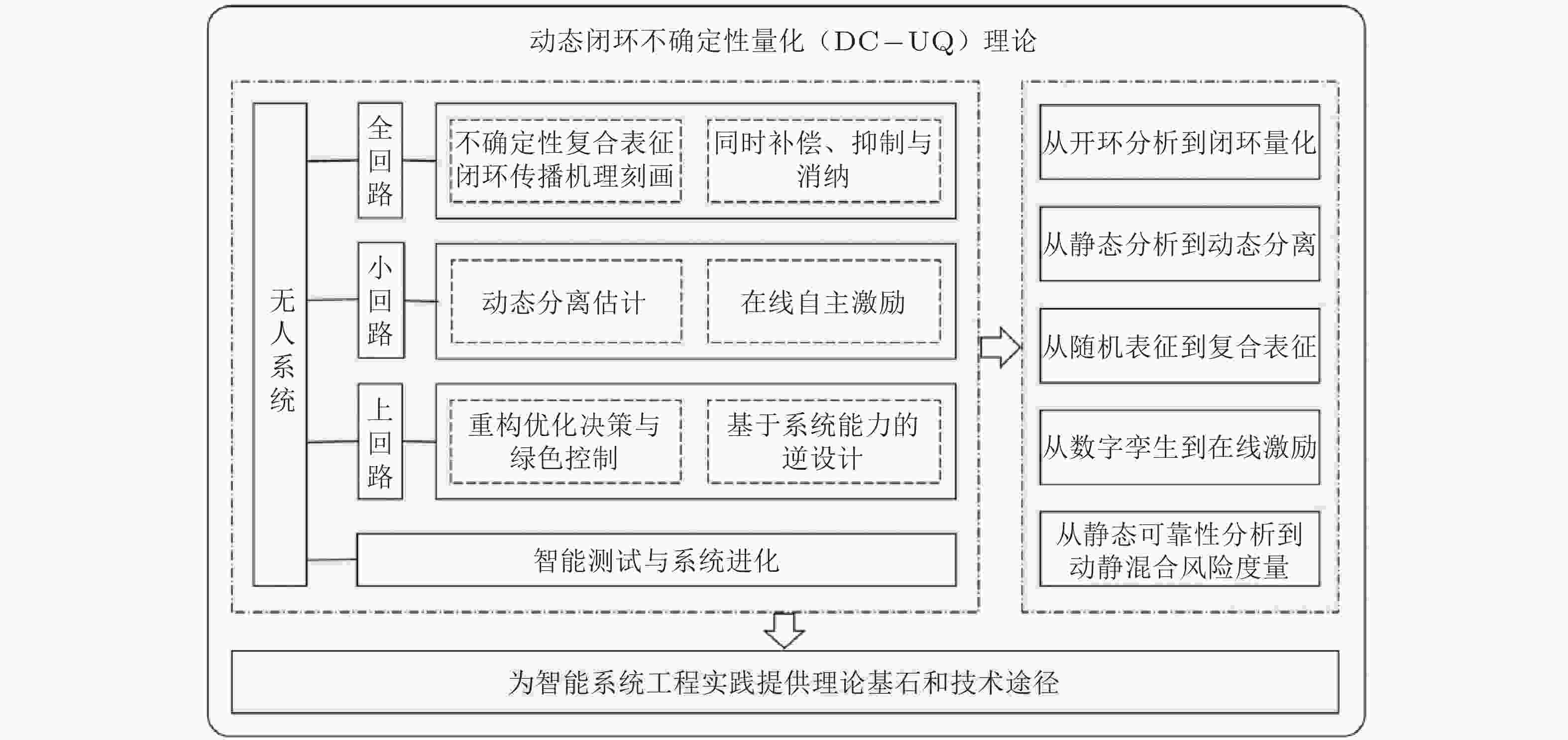
图 4 动态闭环不确定性量化理论与具有“感知−决策−控制−执行”耦合一体化结构特征的无人系统之间的联系 (郭雷 等 2025)
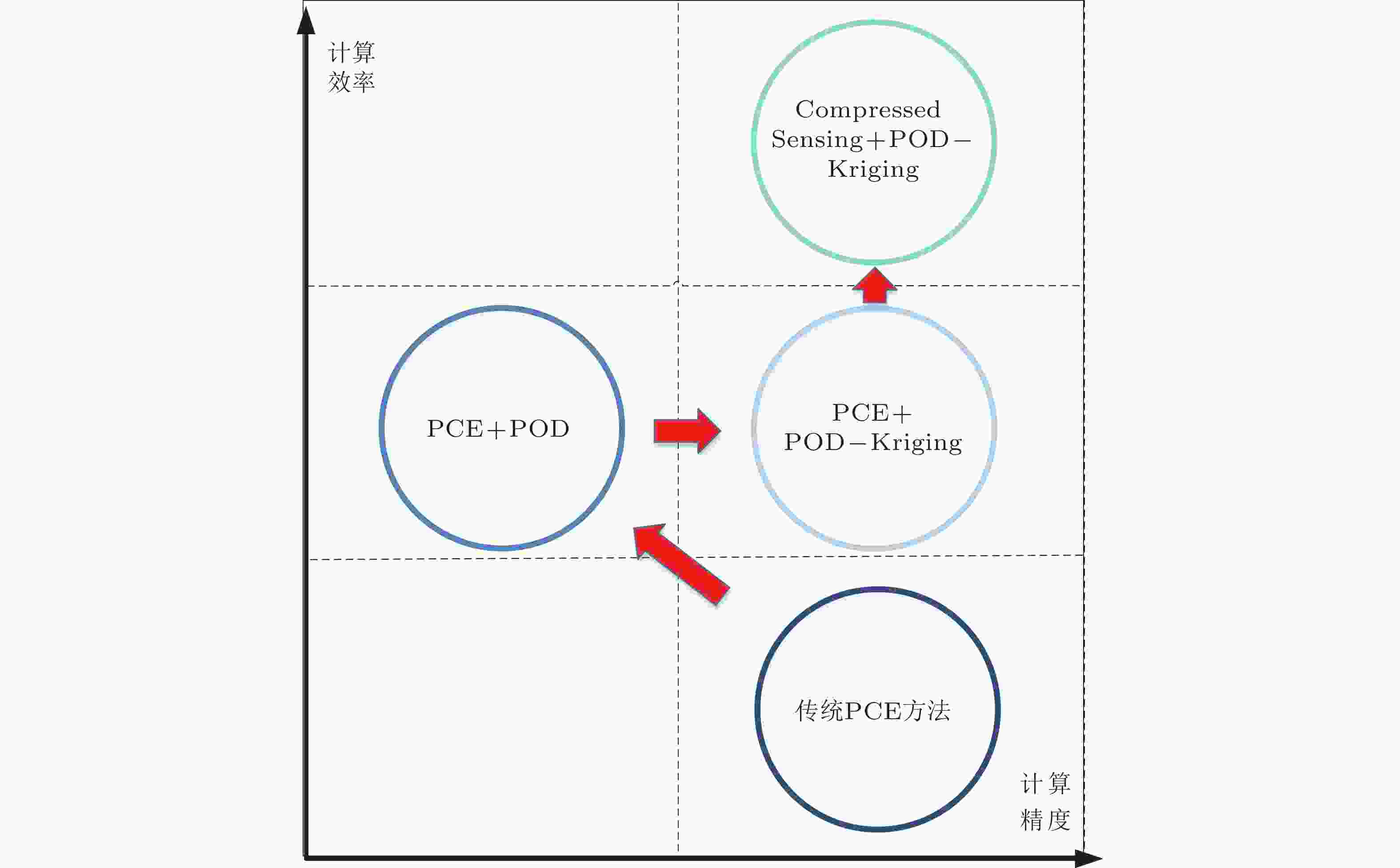
图 5 PCE-POD-Kriging-压缩感知等UQ方法对比 (Lu 等 2022)
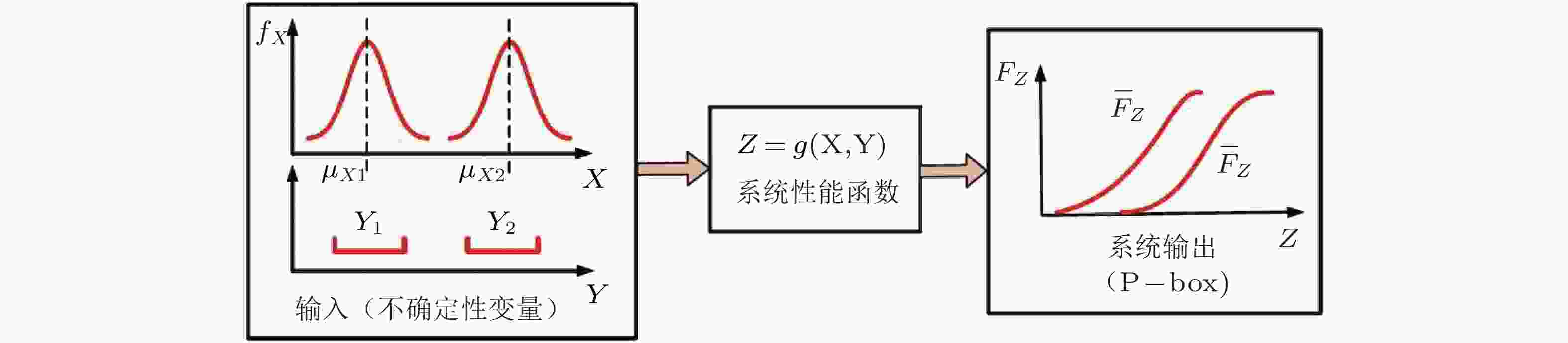
图 6 类型Ⅱ概率−区间混合不确定性传播示意图 (Jiang 等 2017)
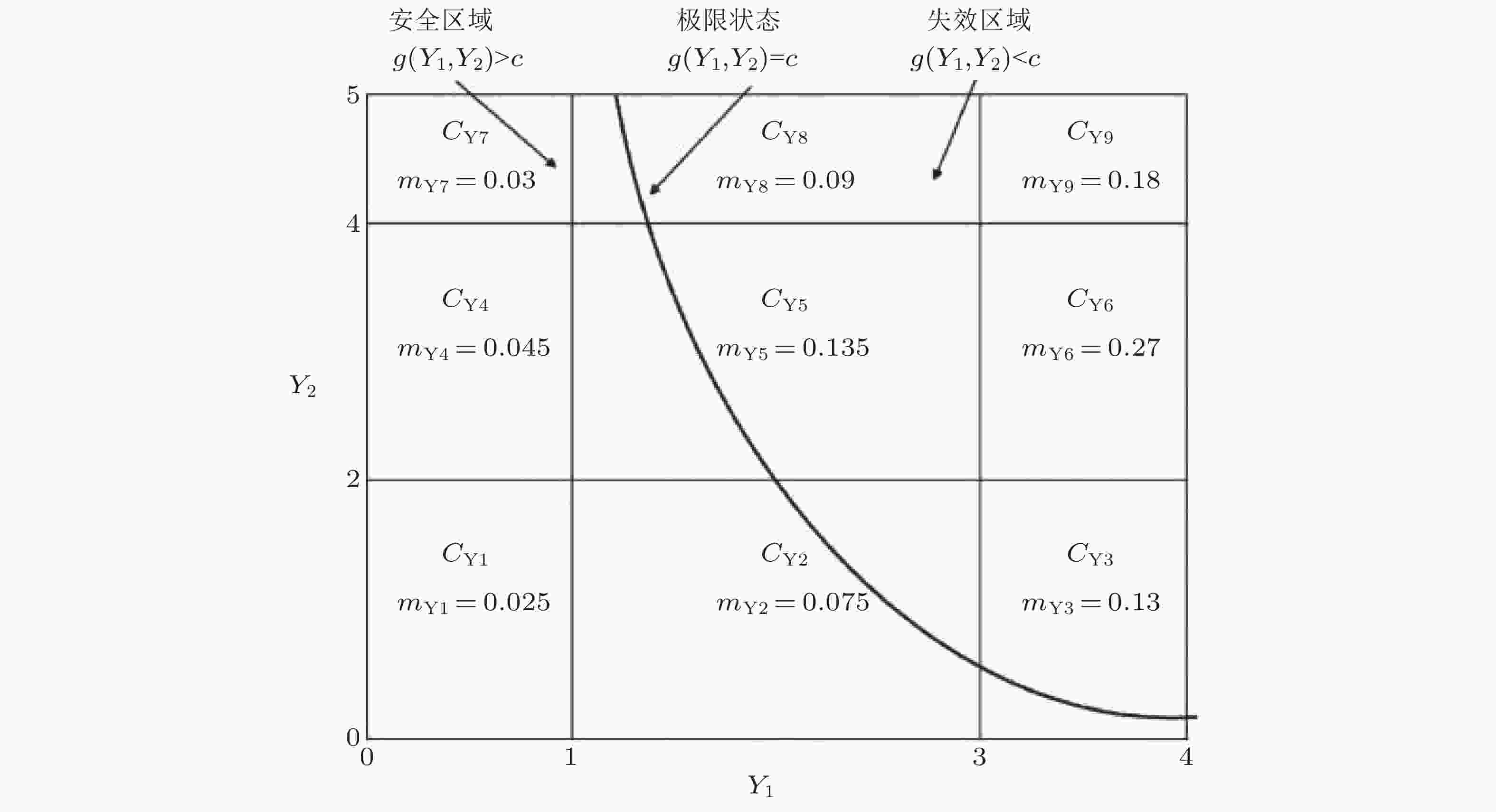
图 7 联合BPA与极限状态曲线的关系示意图 (Du 2008)
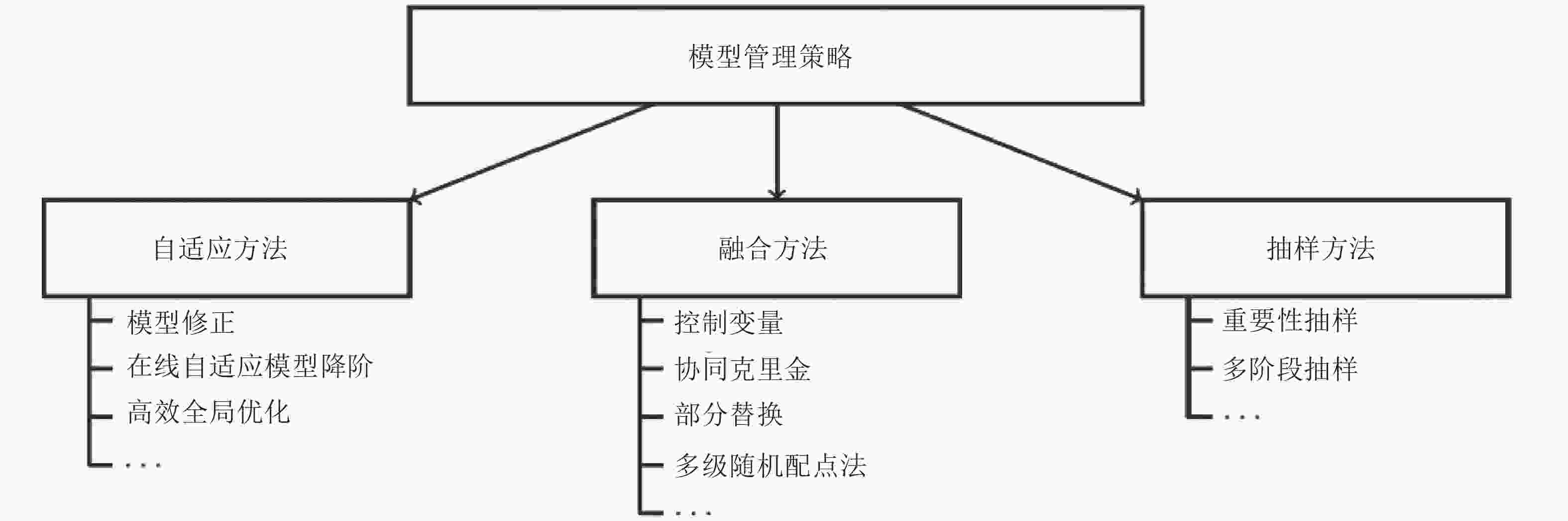
图 8 多保真度方法的三种模型管理策略: 自适应、融合和抽样 (Peherstorfer 等 2018)
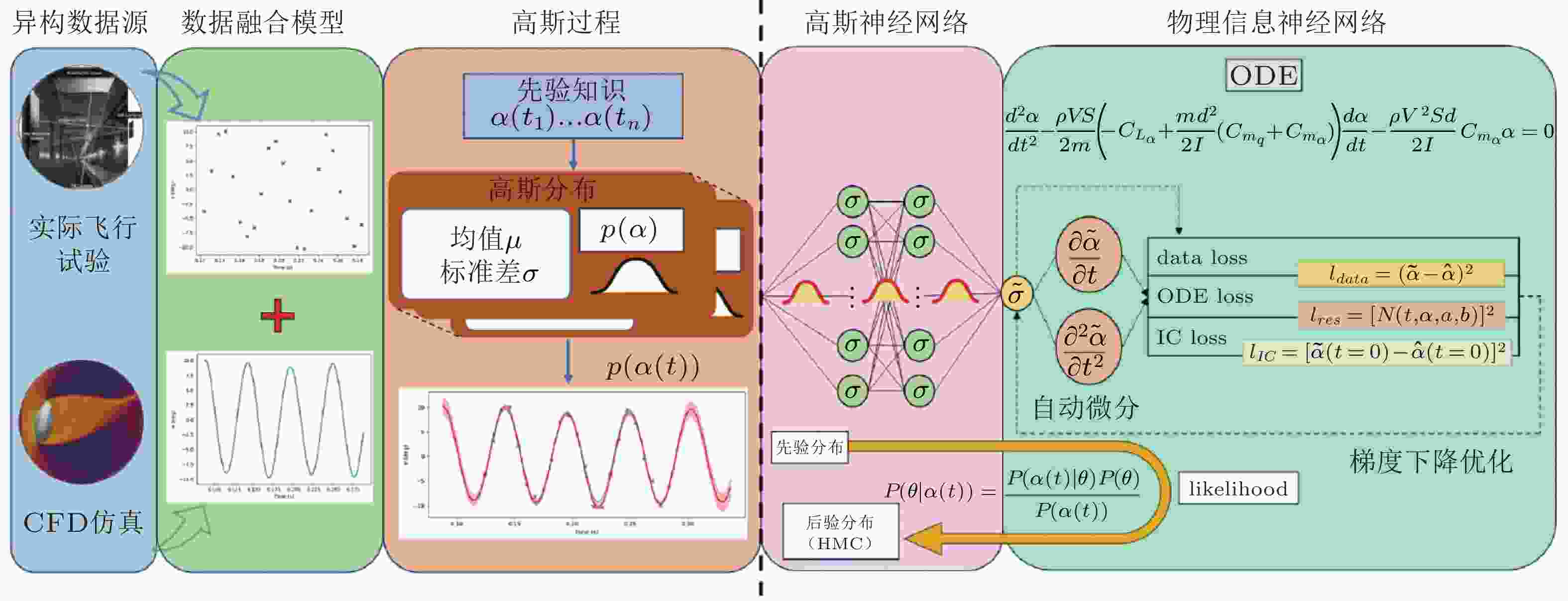
图 10 基于贝叶斯优化的高斯过程模型融合飞试数据和CFD仿真数据的物理信息数据融合框架 (Romeo 等 2024)
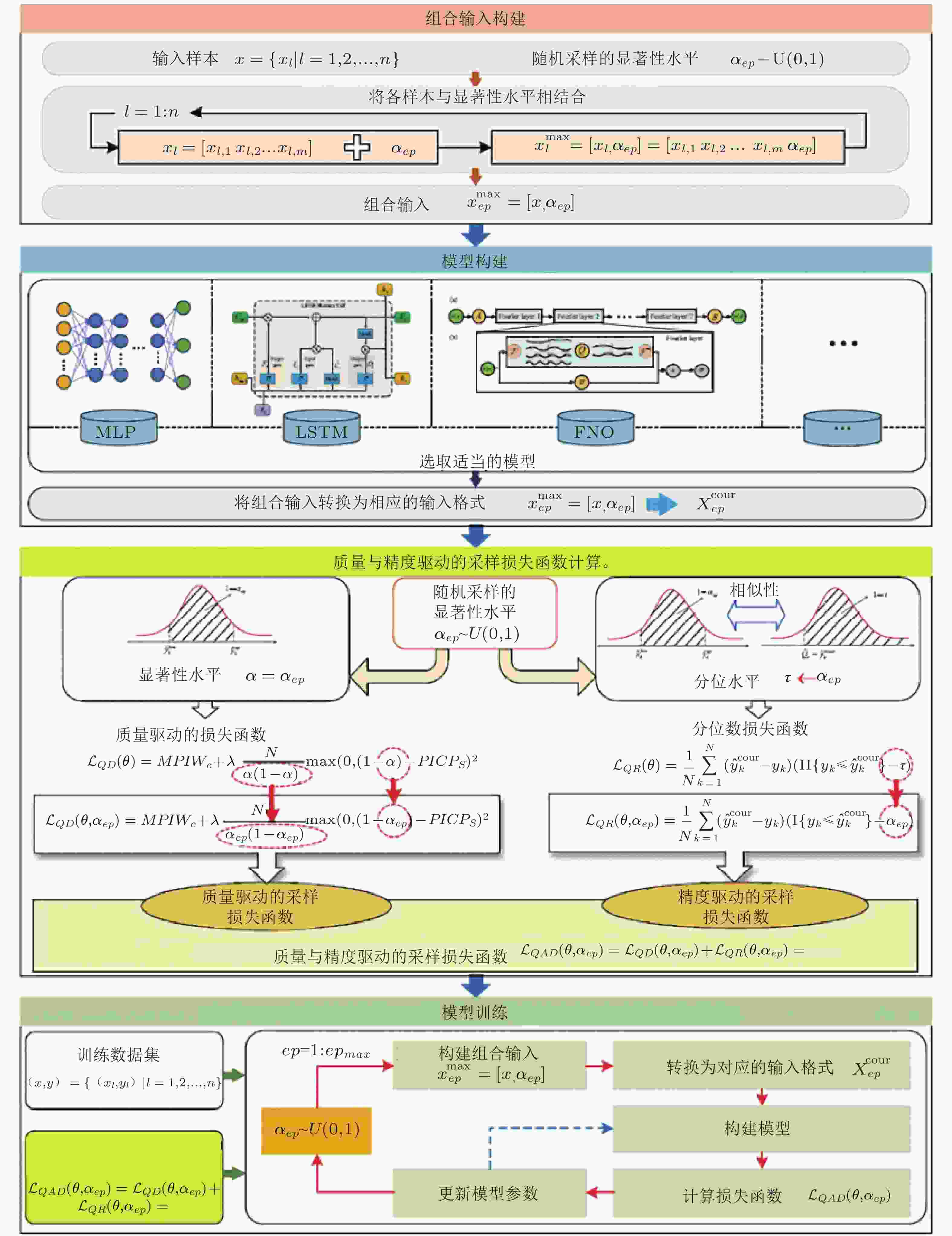
图 11 基于深度学习的质量−精度驱动的通用UQ框架 (Xu等 2025)
表 1 高维不确定性量化技术方法对比分析
方法名称 输入空间降维 函数表示稀疏化 低秩张量分解 计算过程优化 核心思想 高维模型输出的绝大部分变化由少数几个输入变量的线性/非线性组合所主导. 高维模型响应函数可由一个庞大的函数基项中的少数几个关键基函数精确表示. 高维模型内在结构存在变量间的弱耦合性, 可分解为多个低维核心张量的乘积. 复杂模型的计算流程中存在大量因变量依赖稀疏性而产生的冗余计算. 优化对象 输入参数空间: 从高维输入空间识别并投影到一个低维的活跃子空间. 函数表达式 (代理模型) : 在固定的高维输入空间上, 寻找一个系数稀疏、形式简洁的函数表达式. 函数的数据结构: 将表示高维函数的全尺寸张量, 分解为一系列低维 (低秩) 核心张量的组合. 计算执行流程: 重构模型的计算图, 消除在张量网格求值时的重复操作. 关键假设 低维结构假设: 存在一个低维子空间, 模型函数在该空间方向上变化最剧烈, 而在其正交方向上近乎恒定. 稀疏性假设: 在某个合适的正交多项式基下, 模型响应的展开系数向量是稀疏的 (大部分为零或接近零). 低秩/可分离性假设: 高维函数可以近似为一个可分离变量的函数之和/积, 即变量间的耦合程度不高. 计算稀疏性假设: 模型中的许多中间计算步骤仅依赖于小部分输入变量, 计算图存在操作级的稀疏依赖. 技术途径 将高维空间UQ问题转化到降维后的低维空间中进行, 从根本上规避了“维度灾难”. 通过正则化回归等手段, 从组合爆炸的候选基函数中筛选出有效基项, 使所需样本数不依赖于输入维度, 而依赖于解的稀疏度. 通过将高维函数近似为一系列低维核心张量的结构化乘积, 将指数级增长的计算复杂度分解为随维度线性或多项式增长. 通过消除张量化输入下的重复计算, 避免了模型评估成本随维度指数级增长. 优势长处 物理概念直观. 降维效果显著, 识别出子空间之后, 其后续分析成本低. 可与其他代理模型技术 (如Kriging, PCE) 无缝结合. 不改变原始输入空间, 保留了参数的物理意义. 能够处理重要变量非线性组合的情况. 在样本数远少于基函数数量时依然可获得精确解. 对一大类具有可分离结构的函数非常有效. 能够自适应的从少量函数响应样本中构建代理模型. 在求解PDE等问题上效率极高. 不依赖输入空间、函数本身或数据结构的任何特定假设. 不引入模型近似误差, 结果与原始模型完全一致. 局限挑战 识别子空间可能需要梯度信息, 计算成本较高. 降维后的变量通常是原始变量的线性组合, 失去了直接的物理意义. 若模型的低维结构不明显, 则方法失效. 依赖于基函数的选择, 若函数在所选基下不稀疏, 则效果不佳. 正则化超参数的选择对结果影响很大, 需要精细调优. 要求函数具有低秩结构, 对于变量强耦合的函数不适用. 高阶张量分解的理论和算法相对复杂. 主要针对张量网格类输入, 对蒙特卡洛等随机采样输入的加速效果有限. 对于包含高成本隐式操作 (如迭代求解器) 的模型, 加速效果受限. 实现复杂, 需要对模型代码进行深入分析和转换. 代表方法 活跃子空间、主成分
分析压缩感知、正则化回归 张量列车分解 (TT-Cross算法) 计算图转换 (AMTC) 表 2 概率−模糊混合不确定性下的可靠性分析三类问题
序号 分类 解释说明 1 PROFUST问题 失效判据具有模糊性, 而参数只具有随机性, 基于模糊状态假设与概率假设进行混合不确定性下的可靠性分析. 2 POSBIST问题 失效判据不具有模糊性, 而参数具有模糊性, 基于双态假设与可能性假设进行混合不确定性下的可靠性分析. 3 POSFUST问题 失效判据与参数均具有模糊性时, 基于模糊状态假设与可能性假设进行混合不确定性下的可靠性分析. 表 3 混合不确定性量化与高效传播方法对比分析
文献来源 应用场景 核心思路 优势长处 聂兆伟等 (2022) 概率−区间
(Probability-Interval)主动学习Kriging + EGO
将混合不确定性下的可靠性分析转化为无约束优化问题. 利用主动学习Kriging估计多故障模式下的失效概率, 结合EGO搜索区间变量导致的失效概率边界.主动学习Kriging + EGO策略有效解决了区间变量导致的嵌套优化问题, 计算效率得到提升. Meng et al. (2022) 混合指数概率积分法 (HEPIM)
提出混合指数概率积分法. 外层用直接概率积分法 (DPIM) 求解PDF, 内层用指数凸模型处理区间/椭球边界.DPIM避免了蒙特卡洛采样, 从物理方程层面降维求解; 指数凸模型能处理变量间的相关性. You et al. (2020) 概率−模糊
(Probability-Fuzzy)自动更新极值响应面 (AUERS)
基于PSO在模糊变量的α-截集区间内寻找极限状态函数的极值点, 引入均方预测误差指导Kriging模型的局部自适应更新.只在极值点附近精细化模型, 大幅减少了计算代价高昂的功能函数的调用次数. Wang et al. (2023) 非侵入式混合PCE + 稀疏网格
利用Hermite (随机) 和Legendre (区间) 多项式构建混合PCE. 采用稀疏网格积分计算系数, 再用遗传算法在PCE上寻优.非侵入式PCE无需修改原求解器, 便于与商业软件耦合; 稀疏网格策略缓解了中等维度下的“维数灾难”, 兼顾计算精度与效率. Wang & Matthies (2020) 分布参数模糊的随机模型 + RBF + 二分法
建立分布参数模糊的随机模型, 借助λ-截集运算与模糊分解定理, 将模糊随机矩预测转化为一系列区间随机矩; 随后RBF加速从分布参数到随机矩的映射, 并采用二分点嵌套试验设计高效确定截集边界.理论框架严谨, 保留了不精确概率的数学特性; 二分法采样效率高. Elishakoff & Colombi (1993) 概率−凸集
(Probability-Convex)反优化 (Anti-optimization)
采用反优化框架, 将不确定参数约束于椭圆凸集, 并在名义值处对响应函数作一阶泰勒展开, 利用凸集极值定理推导出均方响应上下界的闭式解析解.能够给出解析解, 避免了数值仿真的高计算成本. Zhang et al. (2021) 全局敏感性 + TCR策略 + 主动学习Kriging
针对概率−凸集混合可靠性问题, 提出基于失效概率的矩独立敏感性指标. 利用截断候选域 (TCR) 缩小主动学习Kriging的搜索范围.TCR策略避免了在对结果影响较小的区域浪费采样点; 能识别多失效模式的主导变量. Du (2008) 概率−证据 (Probability-Evidence) 统一FORM框架 (FORM-UUA)
将证据理论的焦元极值分析嵌入到FORM寻找MPP的迭代过程中.解决了证据理论中焦元组合爆炸的问题; 将双层嵌套变为单层优化. Zhang et al. (2019) 针对证据理论焦元的目标失效概率分配策略
通过将目标失效概率合理分解至各焦元, 使得具有较高失效似真度的焦元在迭代过程中承担更大修正权重, 从而更有效的反映不同焦元对系统失效风险的贡献.优化了RBDO中可靠性约束向确定性问题的转换流程, 显著提升了收敛效率, 同时增强了方法的鲁棒性. Liu et al. (2024) 多种不确定性
(Multi-type)Co-Kriging多保真代理模型
面向随机−区间−模糊混合不确定性传播问题, 推导了Co-Kriging预测值的均值和方差的解析表达式. 利用增强期望改进准则平衡高/低保真采样.充分利用低成本 (低保真) 数据, 解析推导避免了后处理误差. Long et al. (2023) T-UUA/ DR/ EGO-UUA
面向概率、证据、模糊和区间四种不确定性的统一框架: 较小不确定度用T-UUA; 较大不确定度用DR/EGO-UUA.更为全面的统一框架, 涵盖4种不确定性; 分策略处理保证了效率与精度的平衡. 表 4 多层级方法与多保真度方法对比分析
方法类别 多层级方法 多保真度方法 模型来源 同质层级: 通常由单一参数 (如网格尺寸) 系统性生成. 模型之间关系明确. 异质集合: 模型来自不同物理原理、降阶技术或数据拟合. 模型之间关系不一定明确. 理论基础 一般基于收敛率, 其分析和资源分配依赖于方差、成本和偏差的渐进收敛率. 一般基于相关性, 其分析和资源分配依赖于模型输出的统计度量. 适用性 最适用于可以系统构建模型层级的问题, 如PDE的有限元/有限体积法. 适用性更加灵活, 可以融合任何类型的低保真度模型, 即使它们的来源和特性非常不同, 甚至是黑箱模型. 模型管理策略 基于伸缩求和 (Telescoping Sum) 的模型管理, 将一个高精度计算任务分解为一个最粗糙模型的计算任务和一系列相邻模型层级之间差异的计算任务. 该策略的核心优势在于能够实现最优资源分配, 即利用已知的成本和误差收敛率, 可以精确计算每个层级需要分配多少次模拟, 从而在满足目标精度的前提下, 将总计算成本降至最低. 多样化的模型管理策略, 主要包括自适应、融合和抽样 (见图8). 例如, 通过高保真度数据在线更新低保真度模型, 或使用低保真度模型作为预筛选器来决定是否调用高保真度模型. 策略选择更加灵活. -
[1] 陈鑫, 王刚, 叶正寅, 等. 2021. CFD不确定度量化方法研究综述. 空气动力学学报, 39(4): 1-13 (Chen X, Wang G, Ye Z Y, et al. 2021. A review of uncertainty quantification methods for Computational Fluid Dynamics. Acta Aerodynamica Sinica, 39(4): 1-13). doi: 10.7638/kqdlxxb-2021.0012Chen X, Wang G, Ye Z Y, et al. 2021. A review of uncertainty quantification methods for Computational Fluid Dynamics. Acta Aerodynamica Sinica, 39(4): 1-13 doi: 10.7638/kqdlxxb-2021.0012 [2] 陈小前, 姚雯, 欧阳琦. 2013. 飞行器不确定性多学科设计优化理论与应用. 科学出版社. [3] 郭雷, 李文硕, 崔洋洋等. 2025. 动态闭环不确定性量化理论与智能无人系统应用. 中国科学: 技术科学, 55(1): 1-13 (Guo L, Li W S, Cui Y Y, et al. 2025. Dynamic closed-loop uncertainty quantification theory with intelligent unmanned systems applications. SCIENTIA SINICA Technologica, 55(1): 1-13). doi: 10.1360/SST-2024-0155Guo L, Li W S, Cui Y Y, et al. 2025. Dynamic closed-loop uncertainty quantification theory with intelligent unmanned systems applications. SCIENTIA SINICA Technologica, 55(1): 1-13. doi: 10.1360/SST-2024-0155 [4] 郭书祥, 吕震宙, 冯元生. 2001. 基于区间分析的结构非概率可靠性模型. 计算力学学报, 18(1): 56-60 (Guo S X, Lu Z Z, Feng Y S. 2001. A non-probabilistic model of structural reliability based on interval analysis. Chinese Journal of Computational Mechanics, 18(1): 56-60).Guo S X, Lu Z Z, Feng Y S. 2001. A non-probabilistic model of structural reliability based on interval analysis. Chinese Journal of Computational Mechanics, 18(1): 56-60. [5] 何佳乐, 王玉惠, 张浩迪. 2023. 高超声速飞行器的非概率可靠性分析. 哈尔滨工业大学学报, 55(12): 1-8 (He J L, Wang Y H, Zhang H D. 2023. Non-probabilistic reliability analysis of hypersonic vehicle. Journal of Harbin Institute of Technology, 55(12): 1-8).He J L, Wang Y H, Zhang H D. 2023. Non-probabilistic reliability analysis of hypersonic vehicle. Journal of Harbin Institute of Technology, 55(12): 1-8. [6] 刘继红, 李连升. 2018. 考虑多源不确定性的多学科可靠性设计优化. 华中科技大学出版社. [7] 李阳天, 李海滨, 韦广梅, 等. 2020. 基于改进型多项式混沌展开的固体火箭发动机药柱低温点火不确定性量化分析. 兵工学报, 41(1): 40-48 (Li Y T, Li H B, Wei G M, et al. 2020. Uncertainty quantification analysis of solid rocket motor grain ignition at low temperature based on improved polynomial chaos expansion. Acta Armamentarii, 41(1): 40-48).Li Y T, Li H B, Wei G M, et al. 2020. Uncertainty quantification analysis of solid rocket motor grain ignition at low temperature based on improved polynomial chaos expansion. Acta Armamentarii, 41(1): 40-48. [8] 聂兆伟, 王浩, 秦梦, 等. 2021. 高维不确定性条件下飞行器级间分离可靠性评估. 宇航学报, 42(12): 1525-1531 (Nie Z W, Wang H, Qin M, et al. 2021. Reliability assessment of flight vehicle stage separation considering high-dimensional uncertainties. Journal of Astronautics, 42(12): 1525-1531).Nie Z W, Wang H, Qin M, et al. 2021. Reliability assessment of flight vehicle stage separation considering high-dimensional uncertainties. Journal of Astronautics, 42(12): 1525-1531. [9] 聂兆伟, 王浩, 秦梦, 等. 2022. 混合不确定条件下的飞行器级间分离可靠性分析. 国防科技大学学报, 44(3): 104-111 (Nie Z W, Wang H, Qin M, et al. 2022. Reliability analysis of flight vehicle stage separation under mixed uncertainties. Journal of National University of Defense Technology, 44(3): 104-111).Nie Z W, Wang H, Qin M, et al. 2022. Reliability analysis of flight vehicle stage separation under mixed uncertainties. Journal of National University of Defense Technology, 44(3): 104-111. [10] 庞煜, 黄洪钟, 刘宇, 等. 2013. 多状态系统的可能可靠性分析. 西安交通大学学报, 47(3): 75-79 (Possibility theory based multi-state system reliability analysis. Journal of Xian Jiaotong University, 47(3): 75-79).Possibility theory based multi-state system reliability analysis. Journal of Xian Jiaotong University, 47(3): 75-79. [11] 邱宇, 邱志平. 2023. 考虑多维相关性的飞行器结构载荷不确定性分析. 空天技术, 4: 66-74 (Qiu Y, Qiu Z P. 2023. Uncertainty analysis of aircraft structures load considering multi-dimensional correlation. Aerospace Technology, 4: 66-74).Qiu Y, Qiu Z P. 2023. Uncertainty analysis of aircraft structures load considering multi-dimensional correlation. Aerospace Technology, 4: 66-74. [12] 邱志平, 胡永明. 2016. 椭球凸模型非概率可靠性度量和区间安全系数的关系. 计算力学学报, 33(4): 522-527 (Qiu Z P, Hu Y M. 2016. The relations of non-probabilistic reliability measures based on ellipsoidal convex model and interval safety factors. Chinese Journal of Computational Mechanics, 33(4): 522-527).Qiu Z P, Hu Y M. 2016. The relations of non-probabilistic reliability measures based on ellipsoidal convex model and interval safety factors. Chinese Journal of Computational Mechanics, 33(4): 522-527. [13] 孙冲, 方群, 袁建平. 2012. 具有模型参数不确定性的高超声速飞行器动态特性分析及控制律设计. 西北工业大学学报, 30(4): 497-502 (Sun C, Fang Q, Yuan J P. 2012. A useful dynamic analysis of hypersonic vehicle and control law design using uncertainty parameter dynamics model. Journal of Northwestern Polytechnical University, 30(4): 497-502). doi: 10.3969/j.issn.1000-2758.2012.04.004Sun C, Fang Q, Yuan J P. 2012. A useful dynamic analysis of hypersonic vehicle and control law design using uncertainty parameter dynamics model. Journal of Northwestern Polytechnical University, 30(4): 497-502. doi: 10.3969/j.issn.1000-2758.2012.04.004 [14] 唐樟春, 吕震宙, 吕媛波. 2011. 随机变量概率信息不充分时的可靠性新模型. 工程力学, 28(4): 18-22 (Tang Z C, Lu Z Z, Lu Y B. 2011. A novel reliability model for random variables lacking sufficient probability information. Engineering Mechanics, 28(4): 18-22).Tang Z C, Lu Z Z, Lu Y B. 2011. A novel reliability model for random variables lacking sufficient probability information. Engineering Mechanics, 28(4): 18-22. [15] 王攀, 吕震宙, 唐樟春. 2012. 模糊分布参数条件下结构系统的近似效应分析. 力学学报, 44(3): 546-556 (Wang P, Lu Z Z, Tang Z C. 2012. An approximate effect analysis of structural system with fuzzy distribution parameters. Chinese Journal of Theoretical and Applied Mechanics, 44(3): 546-556).Wang P, Lu Z Z, Tang Z C. 2012. An approximate effect analysis of structural system with fuzzy distribution parameters. Chinese Journal of Theoretical and Applied Mechanics, 44(3): 546-556. [16] 熊芬芬, 杨树兴, 刘宇, 等. 2015. 工程概率不确定性分析方法. 科学出版社. [17] 张海瑞, 王浩, 王尧, 等. 2019. 基于不确定性的飞行器分离可靠性建模与分析方法. 宇航学报, 40(4): 378-385 (Zhang H R, Wang H, Wang Y. 2019. Uncertainty-based reliability modeling and analysis method of flight vehicle separation. Journal of Astronautics, 40(4): 378-385).Zhang H R, Wang H, Wang Y. 2019. Uncertainty-based reliability modeling and analysis method of flight vehicle separation. Journal of Astronautics, 40(4): 378-385. [18] 张海瑞. 2022. 飞行器总体不确定性分析与优化设计. 中国宇航出版社. [19] 张涵信. 2008. 关于CFD计算结果的不确定度问题. 空气动力学学报, 26(1): 47-49 (Zhang H X. 2008. On the uncertainty about CFD results. Acta Aerodynamica Sinica, 26(1): 47-49).Zhang H X. 2008. On the uncertainty about CFD results. Acta Aerodynamica Sinica, 26(1): 47-49. [20] 张涵信, 查俊. 2010. 关于CFD验证确认中的不确定度和真值估算. 空气动力学学报, 28(1): 39-45 (Zhang H X, Zha J. 2010. The uncertainty and truth-value assessment in the verification and validation of CFD. Acta Aerodynamica Sinica, 28(1): 39-45).Zhang H X, Zha J. 2010. The uncertainty and truth-value assessment in the verification and validation of CFD. Acta Aerodynamica Sinica, 28(1): 39-45 [21] 郑伶华, 陈强, 李彦斌, 等. 2023. 动态大气环境下高速飞行器气动噪声不确定性量化研究. 振动与冲击, 42(14): 306-313 (Zheng L H, Chen Q, Li Y B, et al. 2023. Uncertainty quantification for the aerodynamic noise of high-speed aircrafts in dynamic atmospheric environment. Journal of Vibration and Shock, 42(14): 306-313). doi: 10.13465/j.cnki.jvs.2023.14.036Zheng L H, Chen Q, Li Y B, et al. 2023. Uncertainty quantification for the aerodynamic noise of high-speed aircrafts in dynamic atmospheric environment. Journal of Vibration and Shock, 42(14): 306-313 doi: 10.13465/j.cnki.jvs.2023.14.036 [22] 张伟伟, 邬晓敬, 宋述芳. 2020. 气动外形优化设计中的不确定性及高维问题研究. 西北工业大学出版社. [23] Airbus Group Innovations. 2016. Current engineering practices in UQ&M in aeronautics and associated challenges. [24] Alonso J J, Fenrich R W, Menier V, et al. 2017. Scalable environment for quantification of uncertainty and optimization in industrial applications (SEQUOIA). AIAA SciTech 2017 Forum, 9-13 January 2017, Grapevine, USA. [25] Azarhoosh Z, Ilchi Ghazaan M. 2025. A review of recent advances in surrogate models for uncertainty quantification of high-dimensional engineering applications. Computer Methods in Applied Mechanics and Engineering, 433: 117508. doi: 10.1016/j.cma.2024.117508 [26] Bichon B J, Eldred M S, Swiler L P, et al. 2008. Efficient global reliability analysis for nonlinear implicit performance functions. AIAA Journal, 46(10): 2459-2468. doi: 10.2514/1.34321 [27] Beyer H G, Sendhoff B. 2007. Robust optimization-A comprehensive survey. Computer Methods in Applied Mechanics and Engineering, 196: 3190-3218. doi: 10.1016/j.cma.2007.03.003 [28] Ben-Haim, Y. 1994. A non-probabilistic concept of reliability. Structural Safety, 14(4): 227-245. doi: 10.1016/0167-4730(94)90013-2 [29] Cary A W, Schaefer J A, Duque E P N, et al. 2024. Overview of fluid dynamics uncertainty quantification challenge problem and results. AIAA SciTech 2024 Forum. 8-12 January 2024, Orlando, USA. [30] Chatterjee T, Chakraborty S, Chowdhury R. 2019. A critical review of surrogate assisted robust design optimization. Archives of Computational Methods in Engineering, 26: 245-274. doi: 10.1007/s11831-017-9240-5 [31] Chen X, Zhou W, et al. 2020. The heat source layout optimization using deep learning surrogate modeling. Structural and Multidisciplinary Optimization, 62: 3127-3148. doi: 10.1007/s00158-020-02659-4 [32] Chen X, Zhao X, Gong Z, et al. 2021. A deep neural network surrogate modeling benchmark for temperature field prediction of heat source layout. Science China Physics, Mechanics & Astronomy, 11: 78–107. [33] Dellino G, Meloni C. 2015. Uncertainty management in simulation-optimization of complex systems: algorithms and applications. Springer. [34] Duraisamy K, Iaccarino G, Xiao H. 2019. Turbulence modeling in the age of data. Annual Review of Fluid Mechanics, 51: 1-23. [35] DiGregorio N J, Wright A H. 2024. Efficient global optimization with gradient finish for design under uncertainty. AIAA SciTech 2024 Forum. 8-12 January 2024, Orlando, USA. [36] Dolgov S, Scheichl R. 2017. A hybrid alternating least squares-TT cross algorithm for parametric PDEs. SIAM/ASA Journal on Uncertainty Quantification, 7(1): 1-29. doi: 10.1137/17m1138881 [37] Du X. 2008. Unified uncertainty analysis by the first order reliability method. Journal of Mechanical Design, 130: 091401. doi: 10.1115/1.2943295 [38] Echard B, Gayton N, Lemaire M, et al. 2013. A combined importance sampling and kriging reliability method for small failure probabilities with time-demanding numerical models. Reliability Engineering & System Safety, 111: 232-240. doi: 10.1016/j.ress.2012.10.008 [39] Elishakoff I, Colombi P. 1993. Combination of probabilistic and convex models of uncertainty when scarce knowledge is present on acoustic excitation parameters. Computer Methods in Applied Mechanics and Engineering, 104: 187-209. doi: 10.1016/0045-7825(93)90197-6 [40] Francom D, Nachtsheim A. 2025. A review and comparison of different sensitivity analysis techniques in practice. arXiv preprint arXiv: 2506.11471v1 [stat. ME]. [41] Gorodetsky A A, Geraci G, Eldred M S, et al. 2020. A generalized approximate control variate framework for multifidelity uncertainty quantification. Journal of Computational Physics, 408: 1-29. doi: 10.1016/j.jcp.2020.109257 [42] Geraci G, Eldred M S, Gorodetsky A A, et al. 2018. Leveraging active direction for efficient multifidelity uncertainty quantification. 7th European Conference of Computational Fluid Dynamics, 11-15 June 2018, Glasgow, UK. [43] Geraci G, Eldred M S, Gorodetsky A A, et al. 2019. Recent advancements in Multilevel-Multifidelity techniques for forward UQ in the DARPA SEQUOIA project. AIAA Scitech 2019 Forum, 7-11 January 2019, San Diego, USA. [44] Geraci G, Menhorn F, Huan X, et al. 2019. Progress in scramjet design optimization under uncertainty using simulations of the HIFiRE direct connect rig. AIAA SciTech 2019 Forum, 7-11 January 2019, San Diego, USA. [45] Guo W L, Xu Y, Liu Q, et al. 2024. Reliability of hypersonic airfoil with freeplay and stochasticity via nonlinear energy sink. AIAA Journal, 62(9): 3258-3270. doi: 10.2514/1.J064048 [46] Guo W L, Xu Y, Li Y G, et al. 2023. Dynamic responses of a conceptual two-dimensional airfoil in hypersonic flows with random perturbations. Journal of Fluids and Structures, 121: 103920. doi: 10.1016/j.jfluidstructs.2023.103920 [47] Hirsch C, Wunsch D, Szumbarski J, et al. 2019. Uncertainty management for robust industrial design in aeronautics. Cham: Springer. [48] Hubbard E, Stephens J. 2017. Facility Measurement Uncertainty Analysis at NASA GRC. Supersonic Tunnel Association International (STAI) Meeting. NASA Report Number: GRC-E-DAA-TN31803. [49] Hu H D, Song Y P, Yu J Y, et al. 2024. Investigation on uncertainty quantification of transonic airfoil using compressive sensing greedy reconstruction algorithms. Aerospace Science and Technology, 147: 109000. doi: 10.1016/j.ast.2024.109000 [50] Hu W, Cheng S, Yan J, et al. 2024. Reliability-based design optimization: a state-of-the-art review of its methodologies, applications, and challenges. Structural and Multidisciplinary Optimization, 67: 168. doi: 10.1007/s00158-024-03884-x [51] Huan X, Safta C, Vane Z P, et al. 2019. Uncertainty propagation using conditional random fields in large-eddy simulations of scramjet computations. AIAA SciTech 2019 Forum, 7-11 January 2019, San Diego, USA. [52] Iyengar N, Mavris D. 2023. High-dimensional uncertainty propagation in aerodynamics using polynomial chaos-Kriging. AIAA Aviation 2023 Forum, 12-16 June 2023, San Diego, CA. [53] Jiang C, Zheng J, Han X. 2017. Probability-interval hybrid uncertainty analysis for structures with both aleatory and epistemic uncertainties: a review. Structural and Multidisciplinary Optimization, 57: 2485-2502. doi: 10.1007/s00158-017-1864-4 [54] Jakeman J D, Eldred M S, Geraci G, et al. 2020. Adaptive multi-index collocation for uncertainty quantification and sensitivity analysis. International Journal for Numerical Methods in Engineering, 121: 4471-4472. doi: 10.1002/nme.6450 [55] Liu J X, Shi Y, Ding C, et al. 2024. Hybrid uncertainty propagation based on multi-fidelity surrogate model. Computers & Structures, 293: 107267. doi: 10.1016/j.compstruc.2023.107267 [56] Lu Q H, Wang L, Li L S. 2022. Efficient uncertainty quantification of stochastic problems in CFD by combination of compressed sensing and POD-Kriging. Computer Methods in Applied Mechanics and Engineering, 396: 115118. doi: 10.1016/j.cma.2022.115118 [57] Long X Y, Mao D L, Jiang C, et al. 2023. Unified uncertainty analysis under probability, evidence, fuzzy and interval uncertainties. Computer Methods in Applied Mechanics and Engineering, 355: 1-26. doi: 10.1007/978-981-19-9398-5_23 [58] Liu Y S, Li L Y, Zhao S H, et al. 2021. A global surrogate model technique based on principal component analysis and Kriging for uncertainty propagation of dynamic systems. Reliability Engineering & System Safety, 207: 107365. doi: 10.1016/j.ress.2020.107365 [59] Ma J Z, Li D Y, Wang R F, et al. 2025. Predicting tipping phenomenon in a conceptual airfoil structure under extreme flight environment. Journal of Sound and Vibration, 618: 119306. doi: 10.1016/j.jsv.2025.119306 [60] Michek N E, Mehta P, Huebsch W W. 2024. Flight dynamic uncertainty quantification modeling using physics-informed neural networks. AIAA SciTech 2024 Forum. 8-12 January 2024, Orlando, USA. [61] Ma S J, Xu Y. 2025. Complex dynamics of a conceptual airfoil structure excited by the long-range correlation random load. The European Physical Journal Special Topics, 2025: 1-15. doi: 10.1140/epjs/s11734-025-02038-4 [62] Meng Z, Zhao J Y, Chen G H, et al. 2022. Hybrid uncertainty propagation and reliability analysis using direct probability integral method and exponential convex model. Reliability Engineering and System Safety, 228: 108803. doi: 10.1016/j.ress.2022.108803 [63] Navaneeth N, Chakraborty S. 2022. Surrogate assisted active subspace and active subspace assisted surrogate—A new paradigm for high dimensional structural reliability analysis. Computer Methods in Applied Mechanics and Engineering, 389: 114374. doi: 10.1016/j.cma.2021.114374 [64] Oseledets I, Tyrtyshnikov E. 2010. TT-cross approximation for multidimensional arrays. Linear Algebra and its Applications, 432: 70-88. doi: 10.1016/j.laa.2009.07.024 [65] Paudel A, Thapa M, Gupta S, et al. 2025. Polynomial chaos with modified Tikhonov regularization for uncertainty quantification. AIAA SciTech 2025 Forum. 6-10 January 2025, Orlando, USA. [66] Peherstorfer B, Willcox K, Gunzburger M. 2018. Survey of multifidelity methods in uncertainty propagation, inference, and optimization. SIAM Review, 60(3): 550-591. doi: 10.1137/16M1082469 [67] Phillips B D, Schmidt J, Falck R D, et al. 2024. End-to-end uncertainty quantification with analytical derivatives for design under uncertainty. AIAA SciTech 2024 Forum. 8-12 January 2024, Orlando, USA. [68] Pereira D, Afonso F, Lau F. 2025. End-to-end deep-learning-based surrogate modeling for supersonic airfoil shape optimization. Aerospace, 12: 1-22. doi: 10.3390/aerospace12050389 [69] Peng W, Zhang J, Zhou W, et al. 2021. IDRLnet: A physics-informed neural network library. arXiv preprint arXiv: 2107.04320v1. [70] Romeo S A S, Oz F, Kassem A, et al. 2024. Physics informed data fusion model for uncertainty quantification in atmospheric entry vehicle dynamic stability. AIAA Aviation Forum and Ascend 2024, 29 July-2 August 2024, Las Vegas, USA [71] Stephens J, Hubbard E, Walter J A, et al. 2016. Uncertainty Analysis of NASA Glenn's 8- by 6-Foot Supersonic Wind Tunnel. SciTech Meeting. San Diego, CA. [72] Slotnick J, Khodadoust A, Alonso J, et al. 2014. CFD vision 2030 study: a path to revolutionary computational aerosciences. No. NASA/CR-2014-218178. [73] Schaefer J A, Cary A W, Khurana M S. 2024. Surrogate model and discretization error impacts on the fluid dynamics uncertainty quantification challenge problem. AIAA SciTech 2024 Forum. 8-12 January 2024, Orlando, USA. [74] Sun J L, Zheng X H, Yao W, et al. 2025. Heat source layout optimization using automatic deep learning surrogate and multimodal neighborhood search algorithm. Annals of Operations Research, 348: 345-371. doi: 10.1007/s10479-023-05262-0 [75] Schmidt J N, Phillips B D, Falck R D, et al. 2025. Design under uncertainty with design-dependent uncertain variables. AIAA SciTech 2025 Forum. 6-10 January 2025, Orlando, USA. [76] Shubham S, Kipouros T, Dash S, et al. 2024. Uncertainty propagation and management of mixed uncertainties for multi-fidelity multi-disciplinary analysis of propeller with different blade sweep. AIAA SciTech 2024 Forum. 8-12 January 2024, Orlando, USA. [77] Wong B Y J, Damodaran M, Khoo B C. 2024. Physics-informed machine learning using low-fidelity flowfields for inverse airfoil shape design. AIAA Journal, 62(8): 2846-2861 doi: 10.2514/1.j063570 [78] Wang C, Fan H, Qiang X. 2023. A review of uncertainty-based multidisciplinary design optimization methods based on intelligent strategies. Symmetry, 15: 1875. doi: 10.3390/sym15101875 [79] Wang C, Matthies H G. 2020. Random model with fuzzy distribution parameters for hybrid uncertainty propagation in engineering systems. Computer Methods in Applied Mechanics and Engineering, 1: 112673. doi: 10.1016/j.cma.2019.112673 [80] Wang L, Liu Y R, Xu H Y. 2021. Review: Recent developments in dynamic load identification for aerospace vehicles considering multi-source uncertainties. Transactions of Nanjing University of Aeronautics and Astronautics, 38(2): 271-287. [81] Wang Z F, Wang L Q, Wang X Y, et al. 2023. Propagation algorithm for hybrid uncertainty parameters based on polynomial chaos expansion. International Journal for Numerical Methods in Engineering, 124: 4203-4223. doi: 10.1002/nme.7307 [82] Xu Y, Yao W, Zheng X, et al. 2025. A generic quality and accuracy driven uncertainty quantification framework for reliability analysis. Reliability Engineering & System Safety, 262: 1-21. doi: 10.1016/j.ress.2025.111128 [83] Xiang Z, He X, Zou Y, et al. 2024. An importance sampling method for structural reliability analysis based on interpretable deep generative network. Engineering with Computers, 40(1): 367-380. doi: 10.1007/s00366-023-01790-2 [84] You L F, Zhang J G, Du X S, et al. 2020. A new structural reliability analysis method in presence of mixed uncertainty variables. Chinese Journal of Aeronautics, 33(6): 1673-1682. doi: 10.1016/j.cja.2019.12.008 [85] Yao W, Chen X, Luo W, et al. 2011. Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Progress in Aerospace Sciences, 47(6): 450-479. doi: 10.1016/j.paerosci.2011.05.001 [86] Zhang H R, Wang H, Wang Y, et al. 2019. Incremental shifting vector and mixed uncertainty analysis method for reliability-based design optimization. Structural and Multidisciplinary Optimization, 59: 1597-1616. doi: 10.1007/s00158-018-2178-x [87] Zhang Y D, Liu Y S, Guo Q. 2021. A global sensitivity analysis approach for multiple failure modes based on convex-probability hybrid uncertainty. Engineering Computations, 3: 1263-1286. [88] Zang T A, Hemsch M J, Hilburger M W, et al. 2002. Needs and Opportunities for Uncertainty-Based Multidisciplinary Design Methods for Aerospace Vehicles. No. NASA-TM-2002-211462. -




 下载:
下载: