Recent advances in research on large-deformation dynamics of slender pipes conveying fluid
-
摘要: 细长输流管道是发动机液压装置、航空加油机、核工业热交换器、海洋钻井平台等工程装备系统的一类重要结构. 当流速较高时, 细长管道可能会发生屈曲或颤振等流致失稳现象, 严重时可酿成重大安全事故. 输流管道的流致失稳及其非线性振动是典型的流固耦合力学行为, 已成为结构动力学、流固耦合力学等研究领域的一个普遍性范例. 在建立动力学方程、明确稳定性机理和分析非线性振动规律之后, 近年来人们极其关注输流管道的大变形/大位移动力学问题. 本文系统介绍了细长输流管道非线性振动, 特别是其弯曲大变形动力学的研究进展. 首先, 概述了输流管系统的非线性特征及其分类, 简要分析了一些常用假设的合理性. 其次, 重点介绍了泰勒展开近似模型、几何精确理论模型、绝对节点坐标描述计算模型、数据驱动模型及相关的其他建模与求解方法. 然后, 针对两端支撑管道和悬臂管道两类有本质区别的动力学系统, 回顾了其非线性动力学机理与演化规律, 重点介绍了悬臂管道从小变形假设到大变形响应的一些新近研究进展. 在此基础上, 还介绍了提高输流管稳定性、抑制输流管非线性振动和利用输流管大变形响应的主要方法. 最后, 对细长输流管道大变形动力学的研究现状进行了归纳总结, 并指出值得关注的几个基础性科学问题.Abstract: Slender pipes conveying fluid are an important structure in various engineering equipment systems such as engine hydraulic device, aviation tanker, nuclear heat exchanger and offshore drilling platform. When the flow velocity is sufficiently high, the slender pipe may be subjected to flow-induced instability including buckling and flutter, which may lead to safety accidents in serious cases. Flow-induced instability and nonlinear vibration of pipes conveying fluid are typical fluid-structure interaction behaviors, and have become a generic paradigm and fertile dynamics problem in nonlinear dynamics and fluid-structure interaction mechanics. After establishing governing equation, clarifying the stability mechanism and analyzing the nonlinear vibration mechanism of pipes conveying fluid, much attention has been payed to the large-deformation dynamics of this dynamical system in recent years. In this review, the research progress of nonlinear vibrations, especially the large-deformation bending dynamics of slender pipes are systematically introduced. Firstly, the nonlinear characteristics and classification of the fluid-conveying pipe system are summarized, and the applicability of some common assumptions is briefly analyzed. Secondly, the Taylor expansion approximation model, geometrically exact model, absolute node coordinate formulation model, data-driven model and other related modeling and solving methods are reviewed. Then, the nonlinear dynamics mechanism and evolution law of cantilevered and supported pipes are reviewed, and some recent research progress of cantilevered pipes from small-deformation hypothesis to large-deformation response is emphasized. On this basis, several typical methods of improving the stability of the pipe, suppressing the nonlinear vibrations of the pipe and utilizing the large-deformation response of the pipe are also introduced. Finally, the research status of large-deformation dynamics of slender pipe conveying fluid is summarized, and several basic scientific problems worthy of attention are pointed out.
-
图 1 输流管道在工程技术领域的典型应用. (a)海洋输流管道, (b)航空加油管, (c)发动机燃料管路, (d) 水下仿生水母. (a) ~ (c)来源于网络, (d)源于何毅翔等(2024)
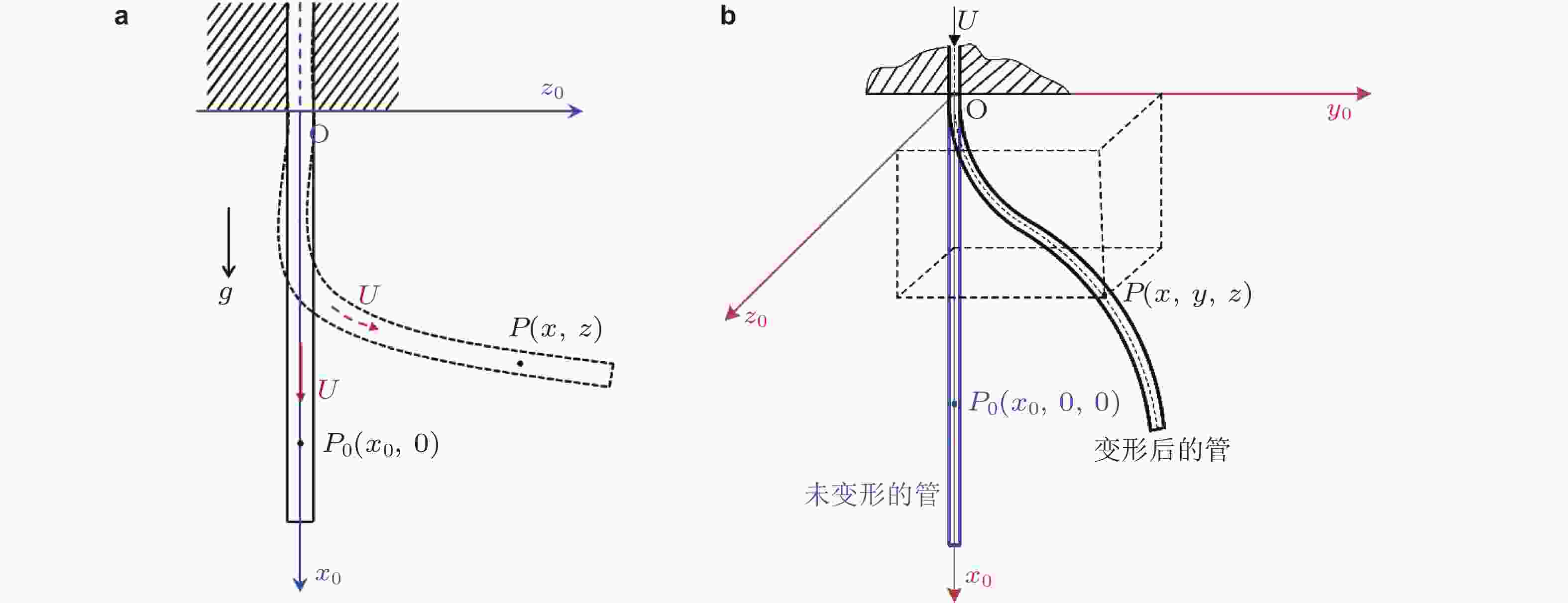
图 2 输流管系统的(a)二维和(b)三维非线性变形示意图(陈伟 2021)
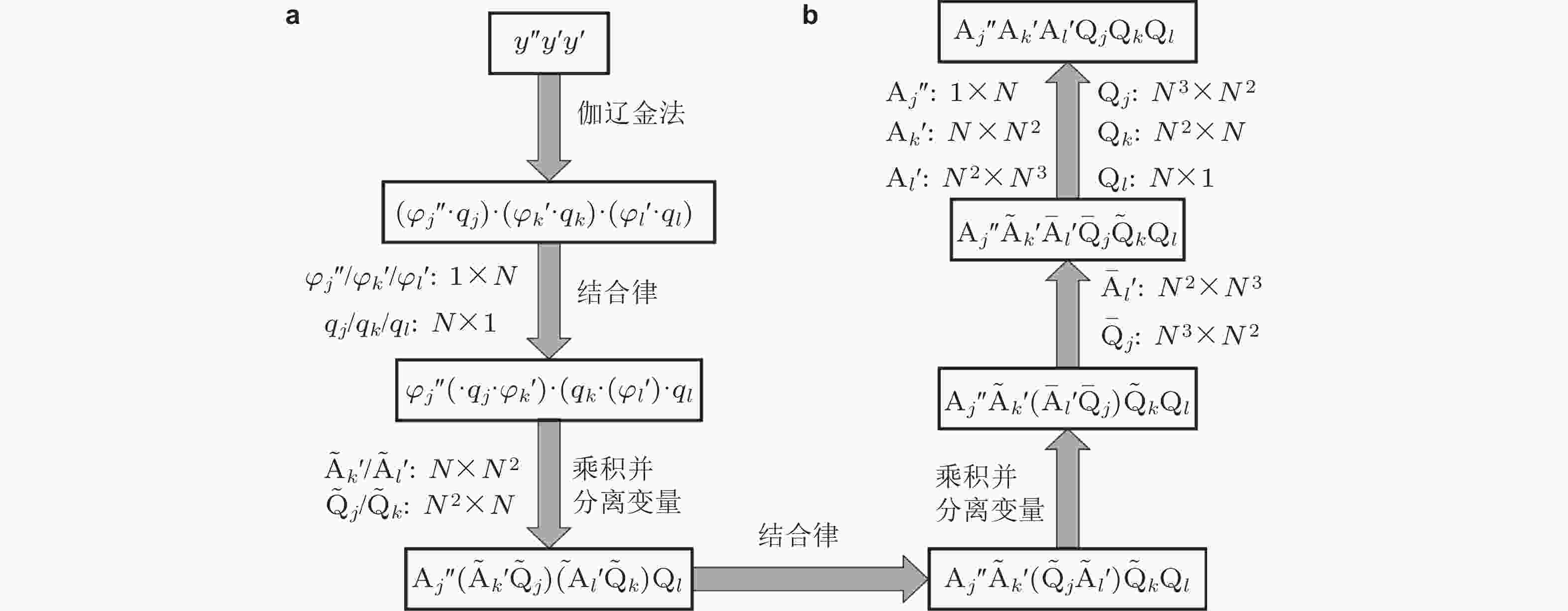
图 3 基于矩阵扩维记法实现时空函数分离的流程图(王乙坤 2017)
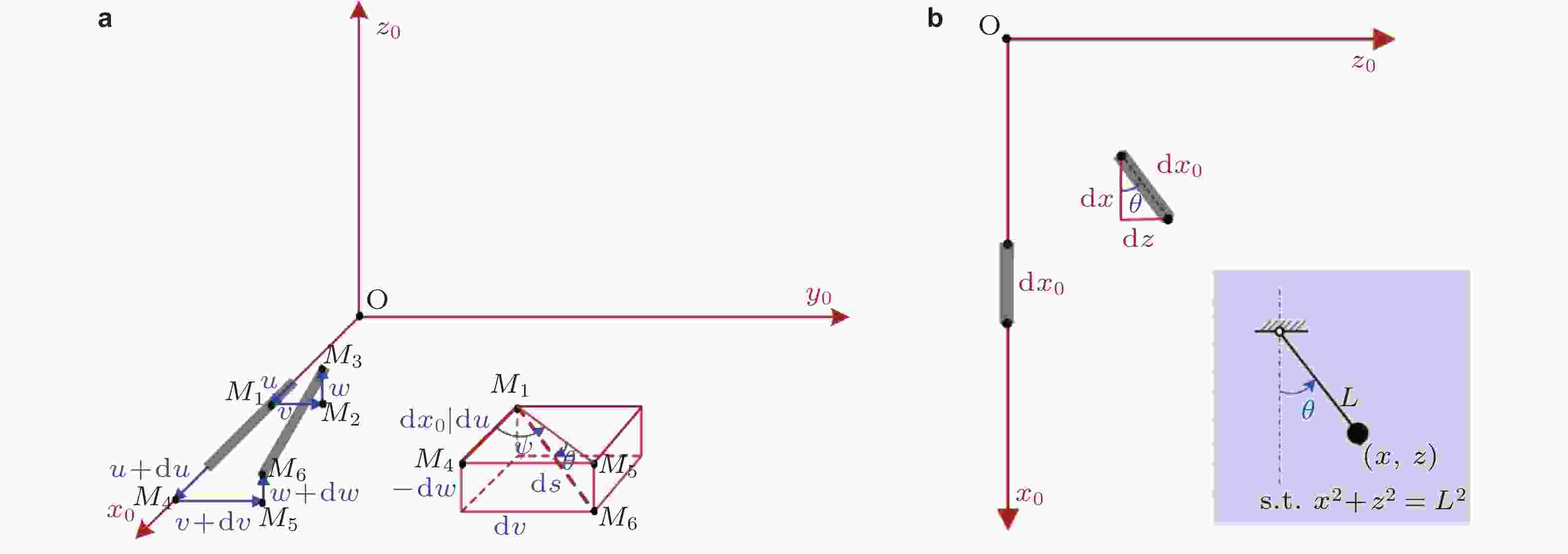
图 4 管道中线的(a)三维和(b)二维精确几何关系示意图(Chen et al. 2021)
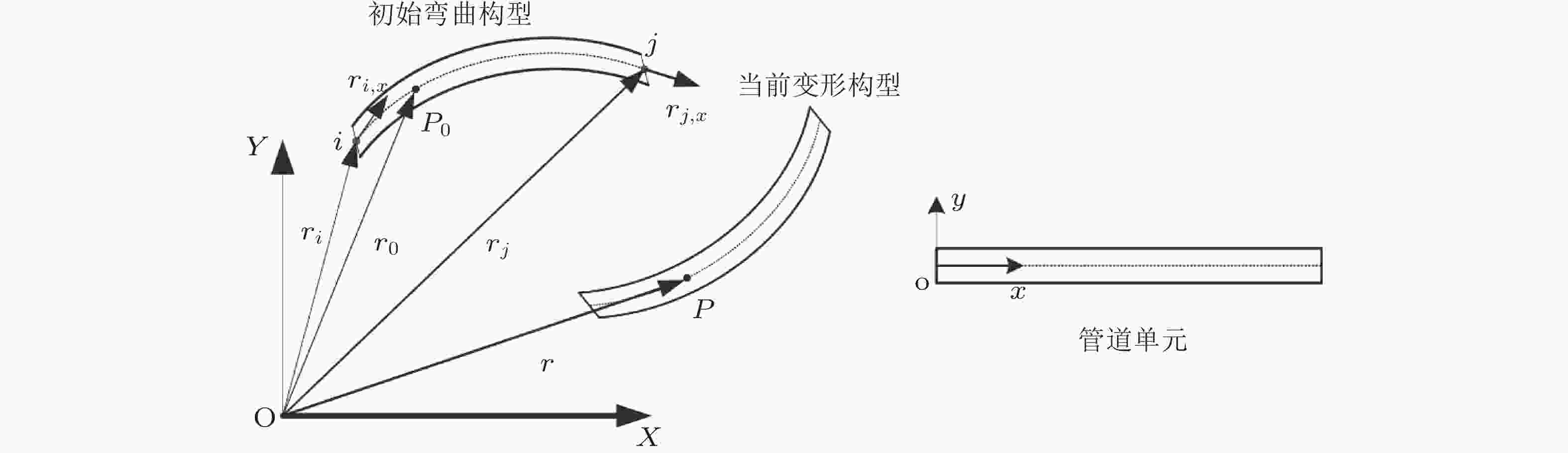
图 5 输流曲管在绝对节点坐标下变形前后的微元几何关系(Zhou et al. 2021a)
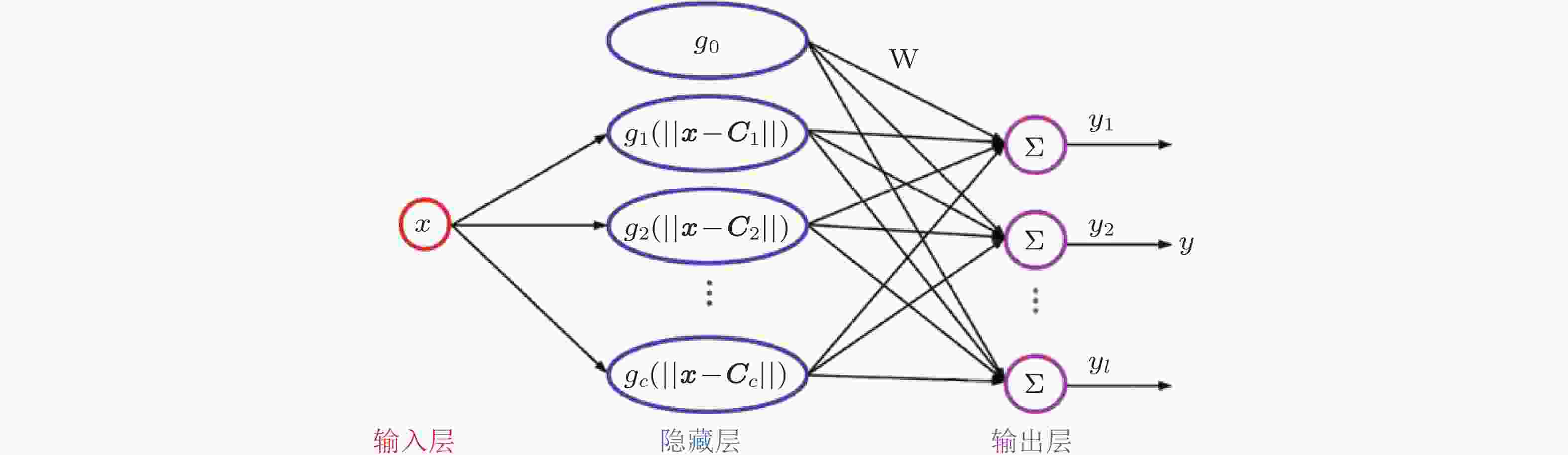
图 6 RBFNN结构示意图(Xu et al. 2023a)
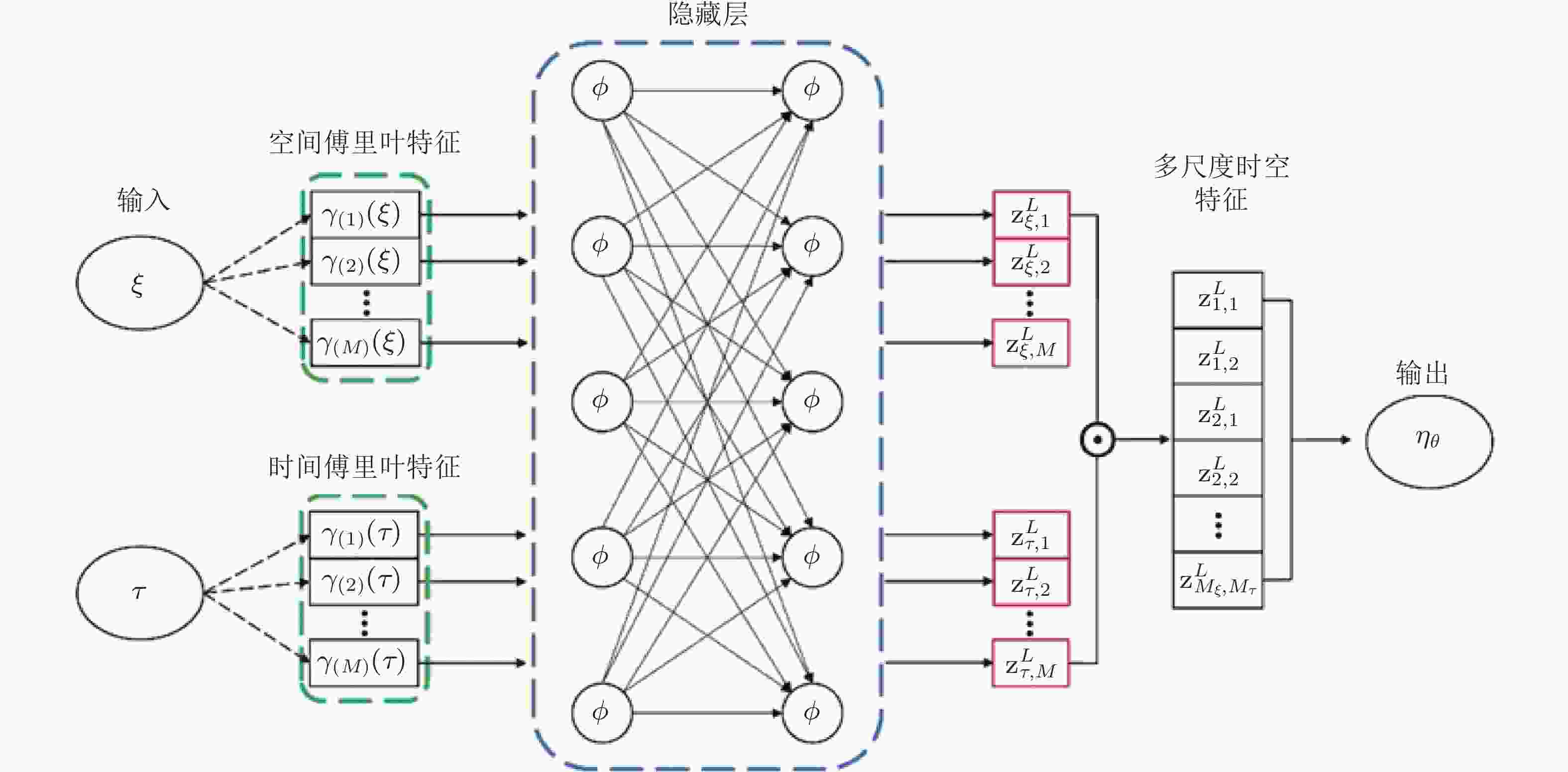
图 7 FF-PINN的网络传递框架示意图(Zhang et al. 2024)
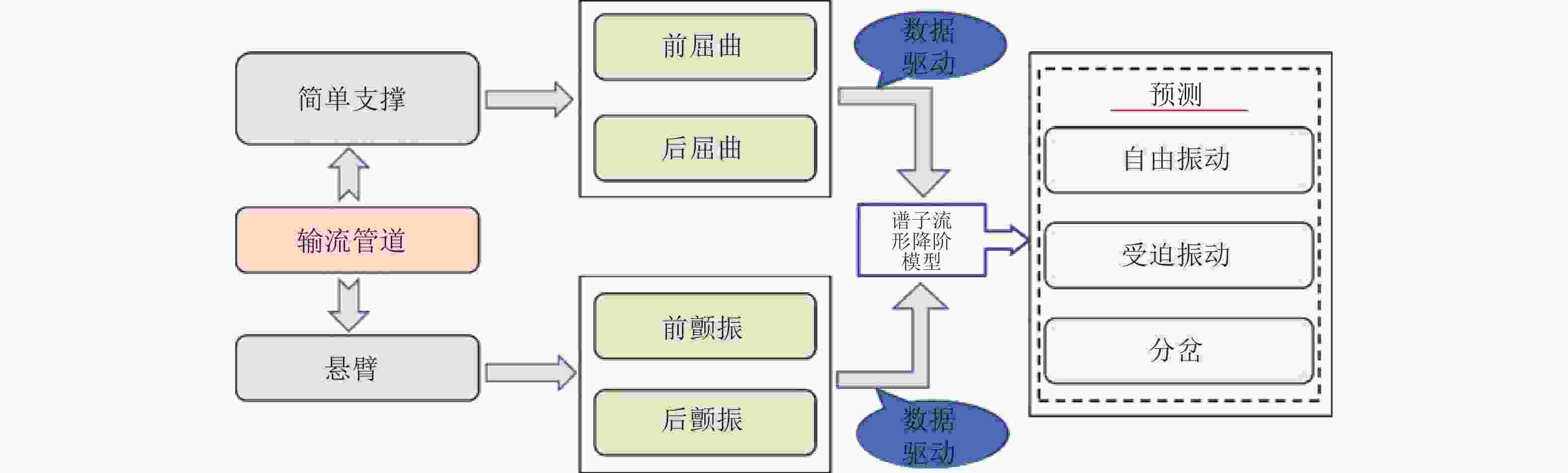
图 8 基于谱子流形(SSM)的输流管道数据驱动模型降阶流程图(Li et al. 2024)
图 10 轴向刚度参数Π0、重力参数γ和张力参数Г对两端支撑输流管道分岔图的影响 (Modarres-Sadeghi & Païdoussis 2009)
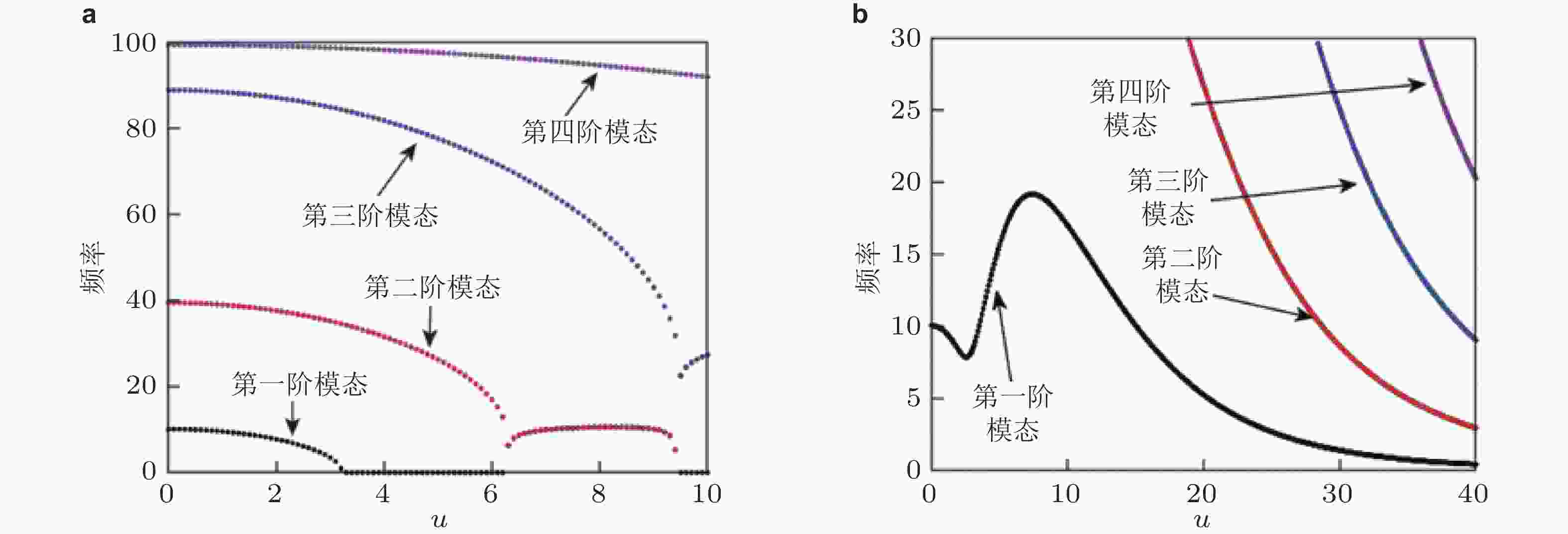
图 11 半个正弦波初始构型输流曲管的前四阶无量纲频率随无量纲流速的演化曲线. (a) 未考虑静变形, (b) 考虑静变形(Zhou et al. 2021b)
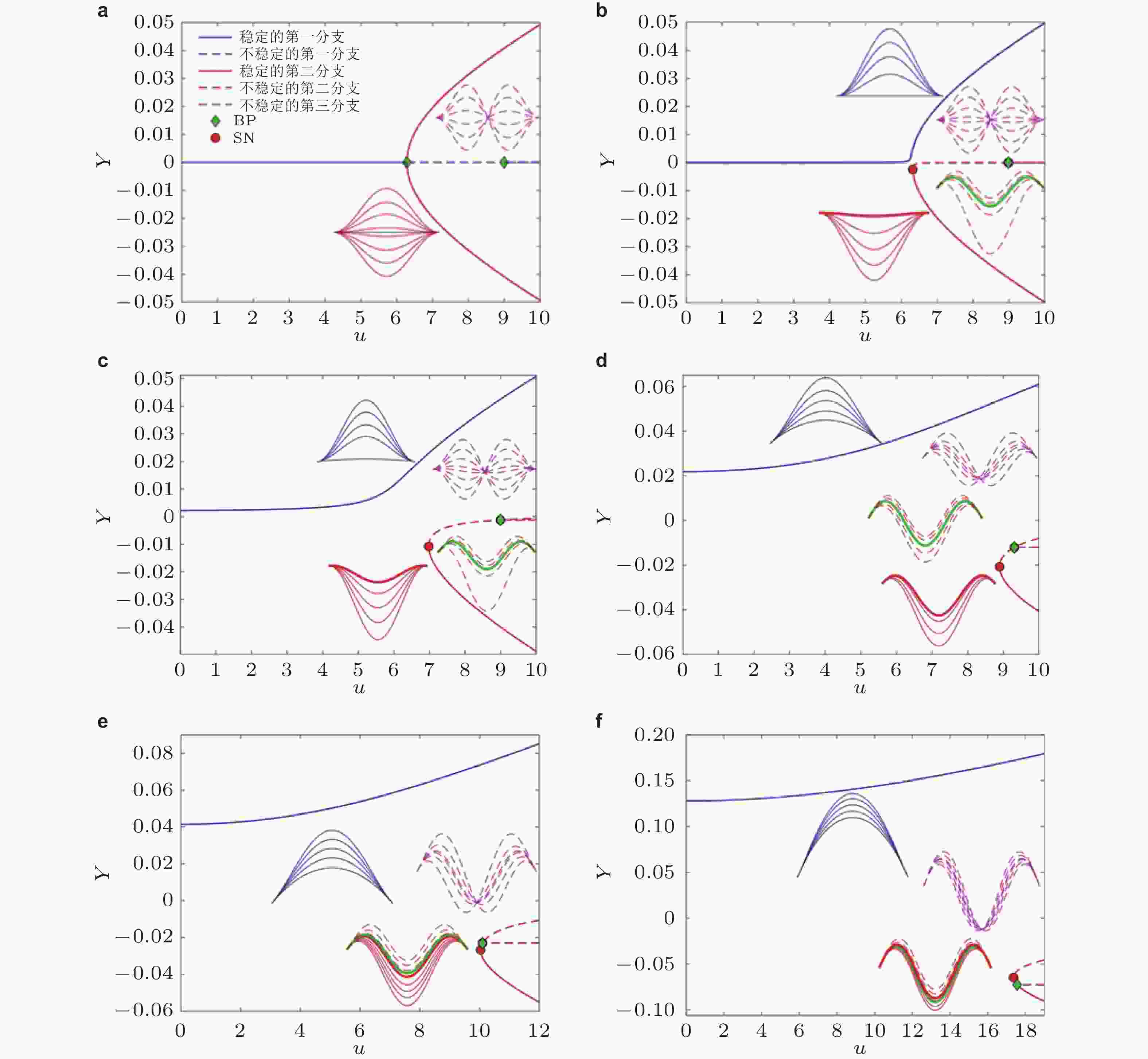
图 12 不同圆弧角曲管的静位移随流速变化的分岔图与静变形构型. (a) 圆弧角为0° (直管), (b)圆弧角为0.01°, (c) 圆弧角为1°, (d) 圆弧角为10°, (e) 圆弧角为19°, (f) 圆弧角为60° (Yan et al. 2023)
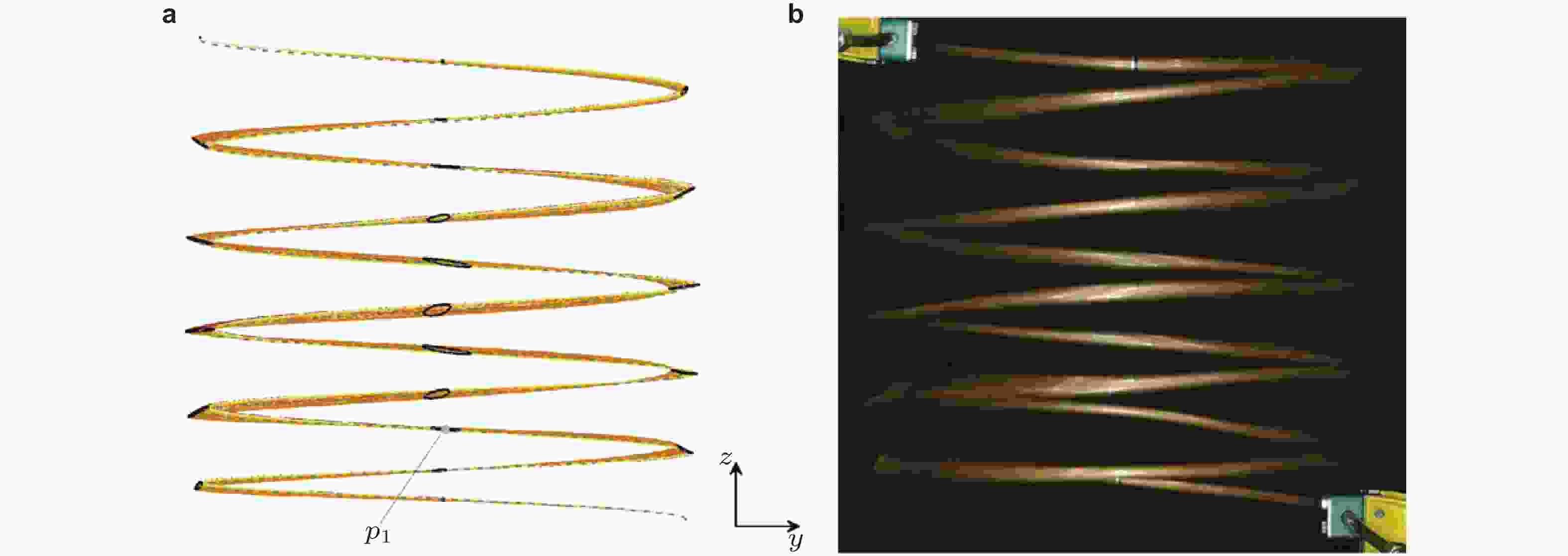
图 13 内流速U0 = 2 m/s时三维螺旋管的振动形状. (a)数值仿真结果, (b)实验测试结果(Czerwinski & Łuczko 2022)
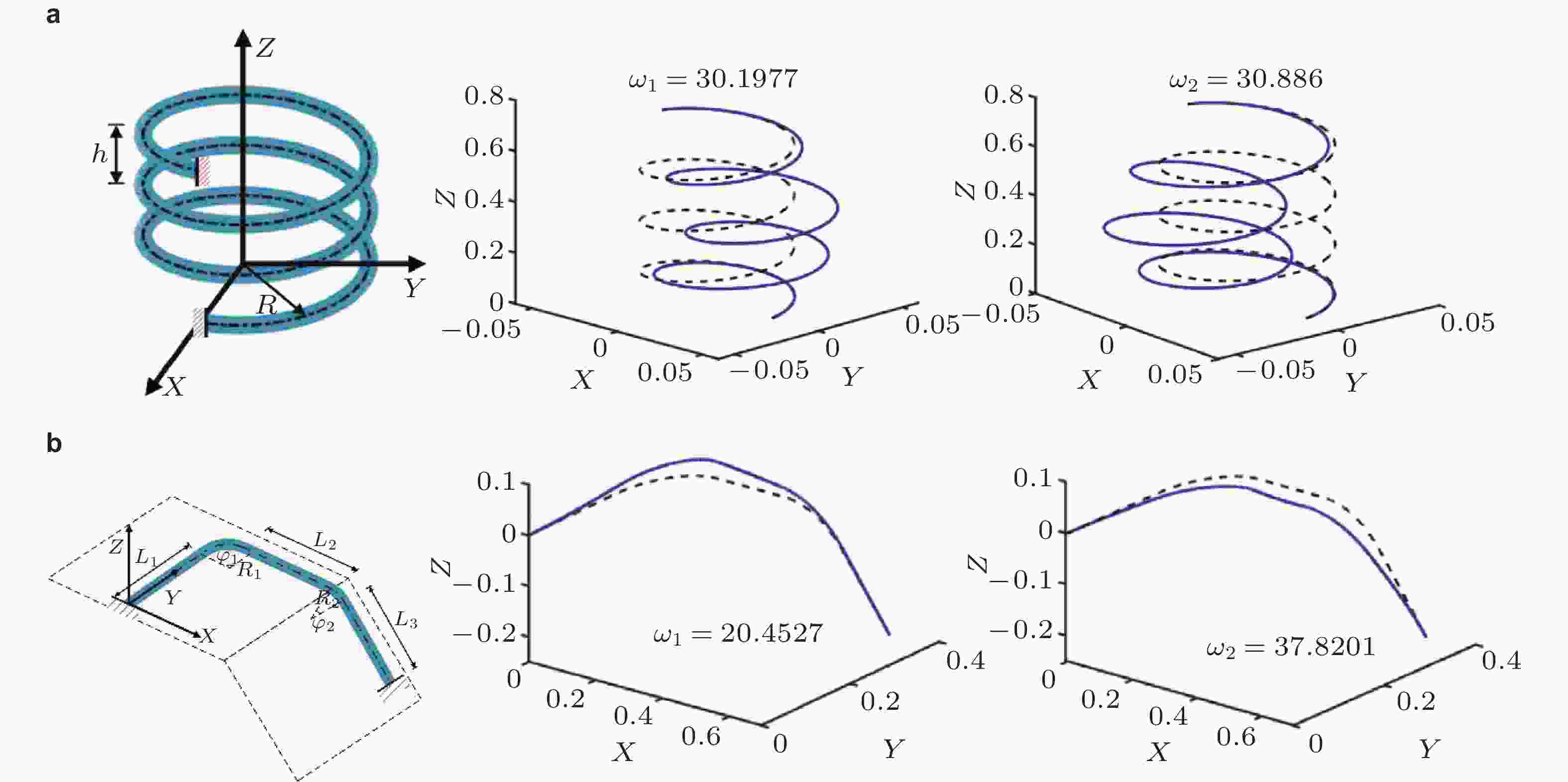
图 14 三维输流曲管示意图和一些典型计算结果. (a) 螺旋输流曲管示意图和u = 0时的前两阶模态形状, (b)直-弯空间管道示意图和u = 0时的前两阶模态形状(Guo et al. 2024a)
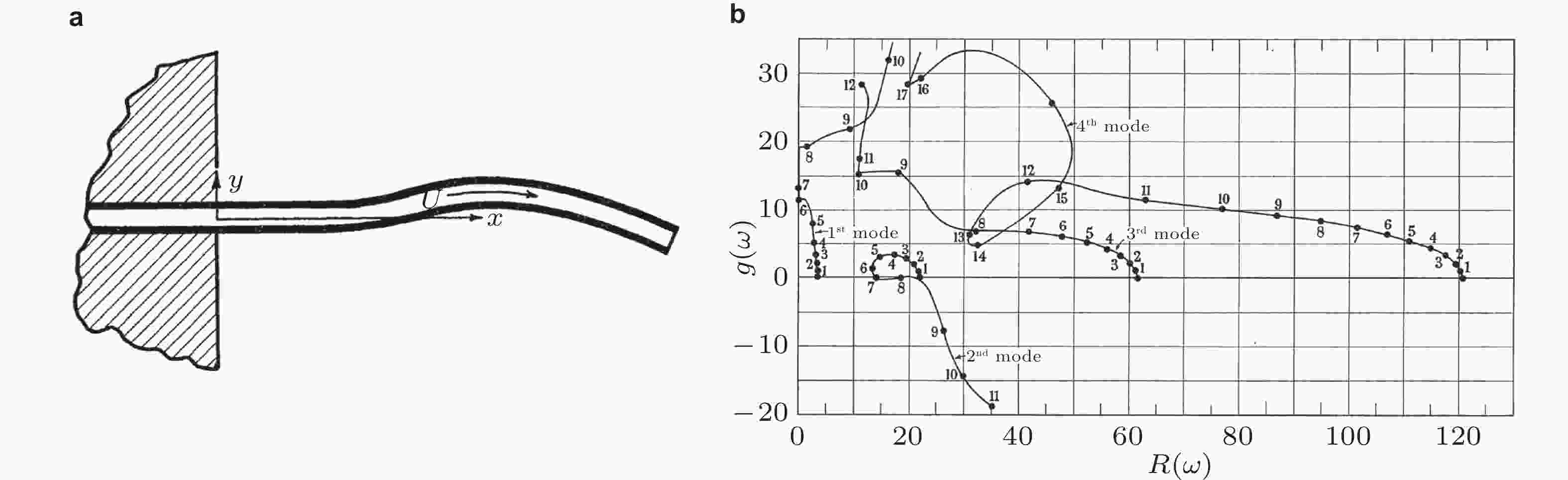
图 15 悬臂输流管道的二阶模态颤振失稳. (a) 悬臂输流管系统模型图, (b) 复特征频率的Argand图(Gregory & Païdoussis 1966)
图 16 侧向弹簧支撑作用下的悬臂输流管道. (a) 模型示意图, (b) 弹簧支撑位于管道末端时的管道屈曲构型, (c) 弹簧支撑位于0.75L (L为管长) 处时管道的静态屈曲构型, (d) 弹簧支撑位于0.5L处时管道的颤振失稳形态(Sugiyama et al. 1985)
图 17 悬臂输流直管模型示意图及其临界流速演化规律. (a) 悬臂输流直管的空间振动模型示意图, (b) 端部含集中质量管道系统的临界流速随质量比参数的演化曲线 (Modarres-Sadeghi et al. 2007)
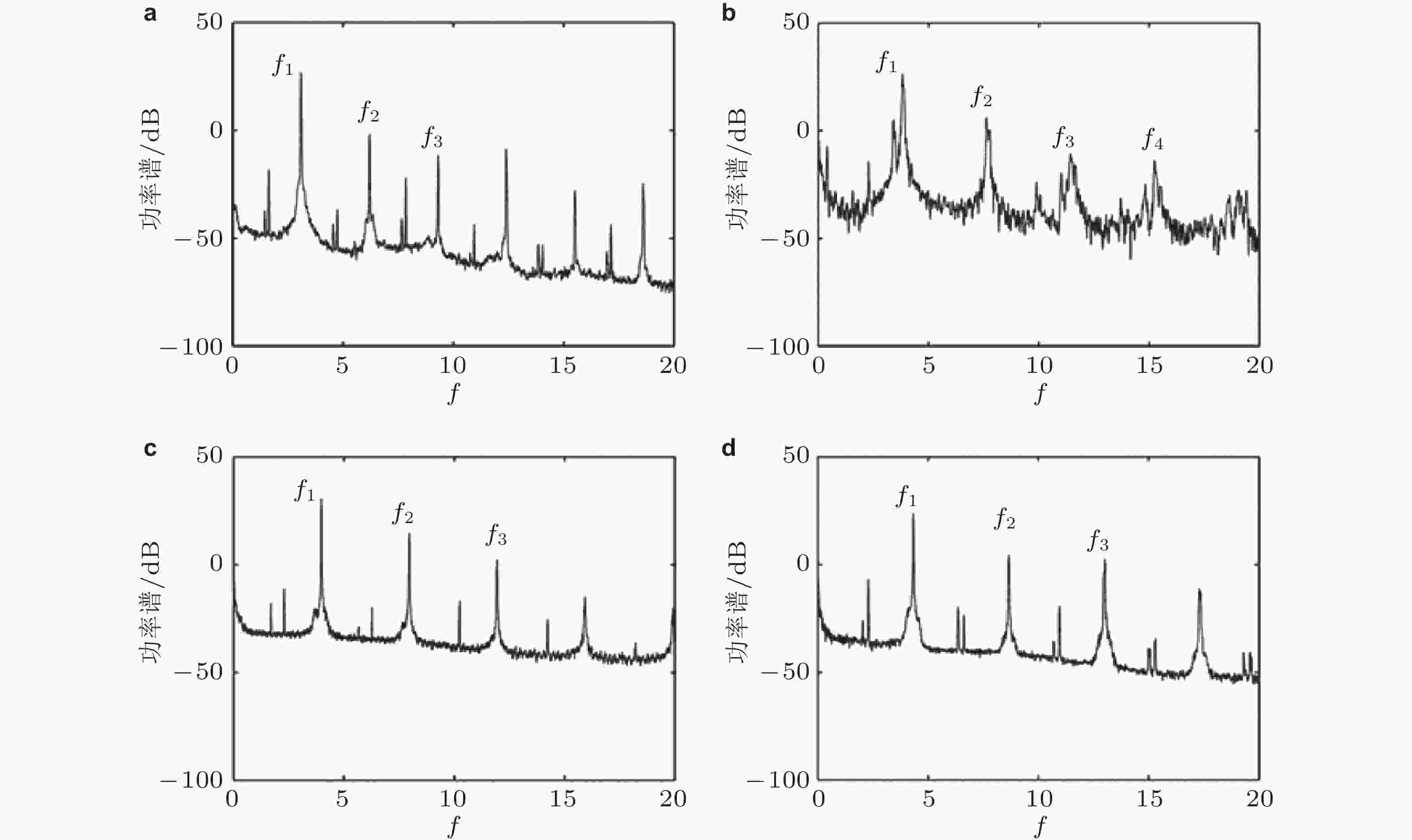
图 18 单点弹簧约束作用下输流直管的动态响应. (a) 流速为6.7, (b) 流速为9.1, (c) 流速为9.3和(d) 流速为10.1时的频谱分析实验结果 (Ghayesh & Païdoussis 2010)
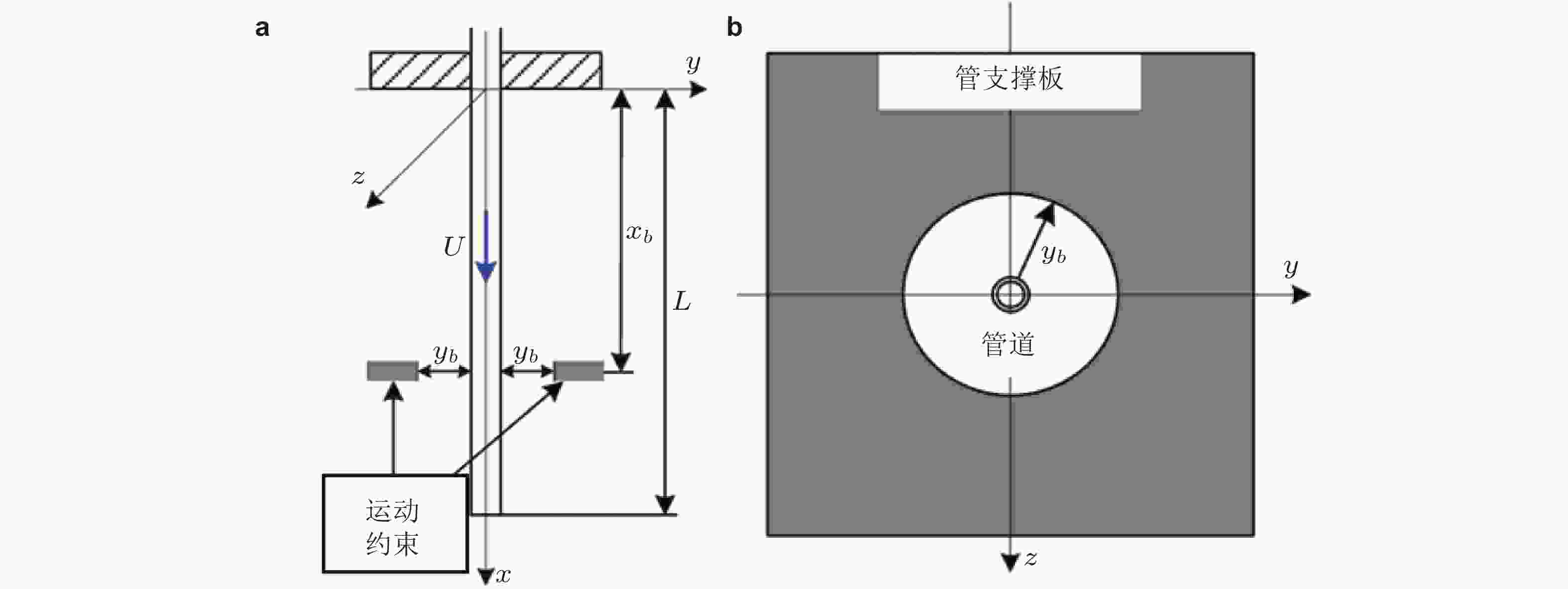
图 19 单点环形碰撞约束下的悬臂输流直管. (a) 管道与碰撞模型示意图, (b) 圆形碰撞约束剖面图 (Wang Y et al. 2018)
图 20 几何精确模型和泰勒展开模型预测的悬臂管道自由端的动态响应结果对比. (a) 悬臂直管模型示意图, (b) 基于几何精确模型预测的管道时域响应和 (c) 相轨迹图, (d) 基于泰勒展开模型预测的管道时域响应和 (e) 相轨迹图 (Chen et al. 2019a)
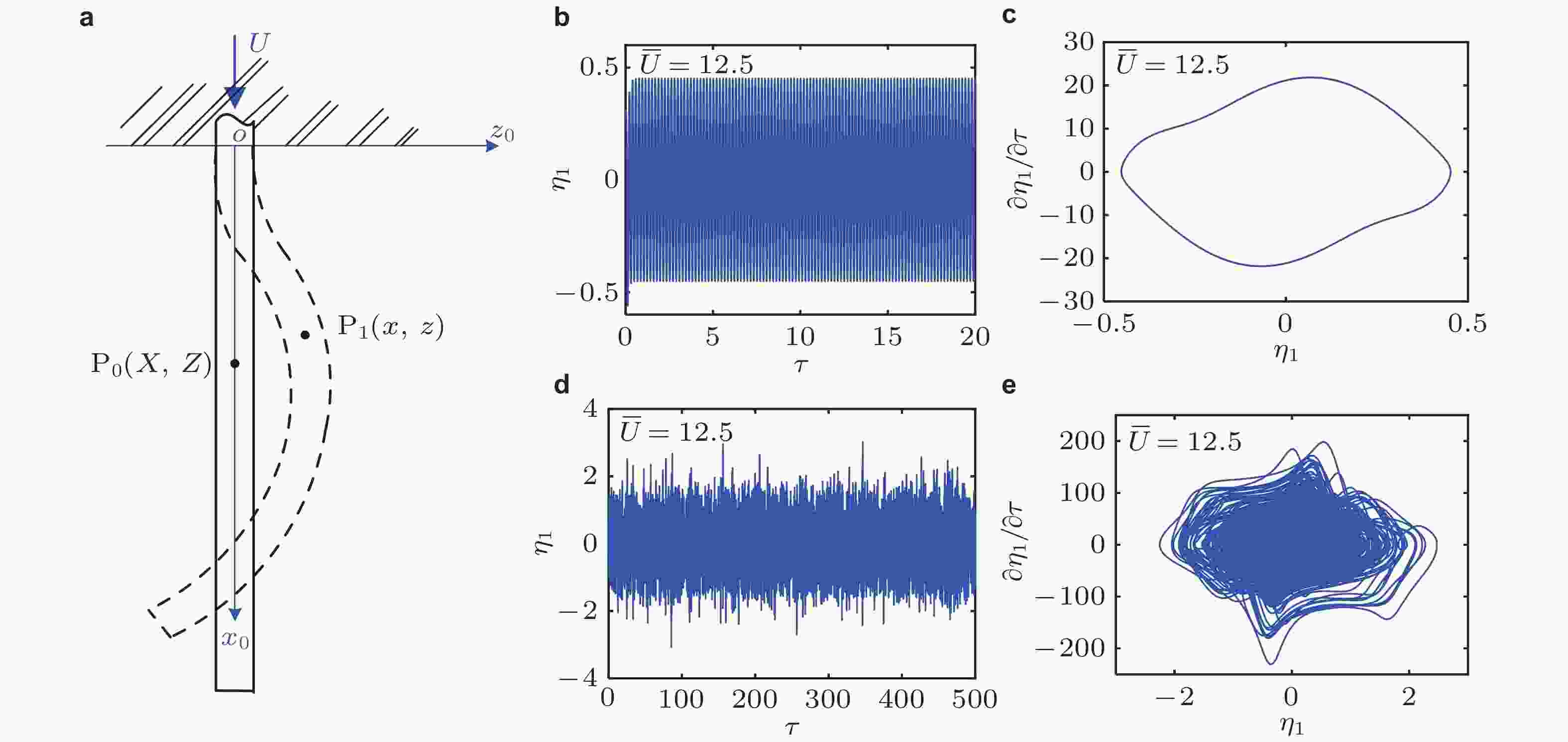
图 21 质量比为0.2时悬臂输流直管动态响应的几何精确理论模型预测结果. (a) 无量纲流速为9时的管道三维振动形态, (b) 无量纲流速为10时的管道三维振动形态, (c)无量纲流速为12时管道二维振动形态及其俯视图 (Chen et al. 2021a)
图 22 含末端质量块的输流直管系统. (a) 管道模型示意图, 无量纲流速 (b) u = 7.42, (c) u = 8.83和(d) u = 10.00时的管道振动形态图 (Farokhi et al. 2021)
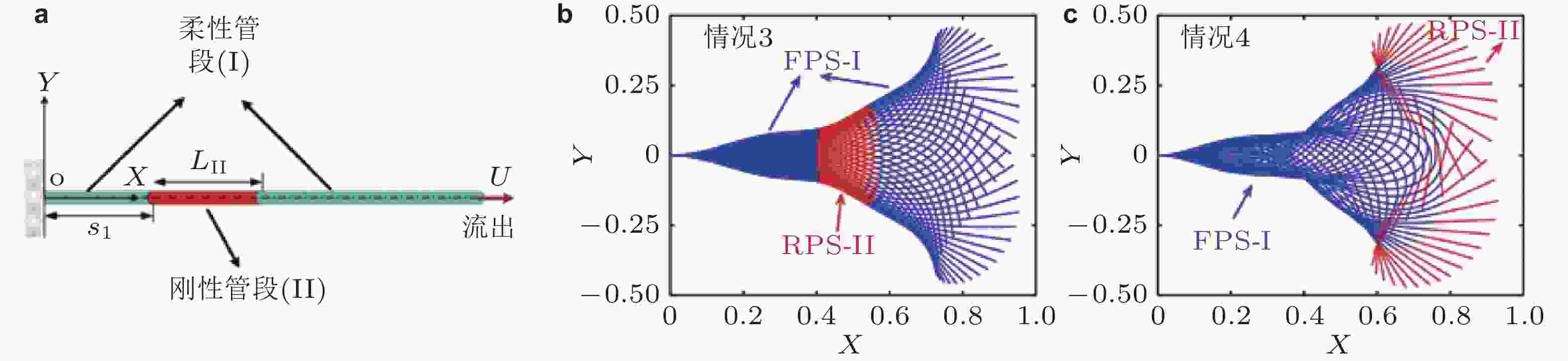
图 23 含有局部刚性段的悬臂输流直管系统 (红色线条为刚性段). (a) 管道模型示意图, (b) ~ (c) 刚性段在不同位置时管道的振动形态图 (Zhou et al. 2020)
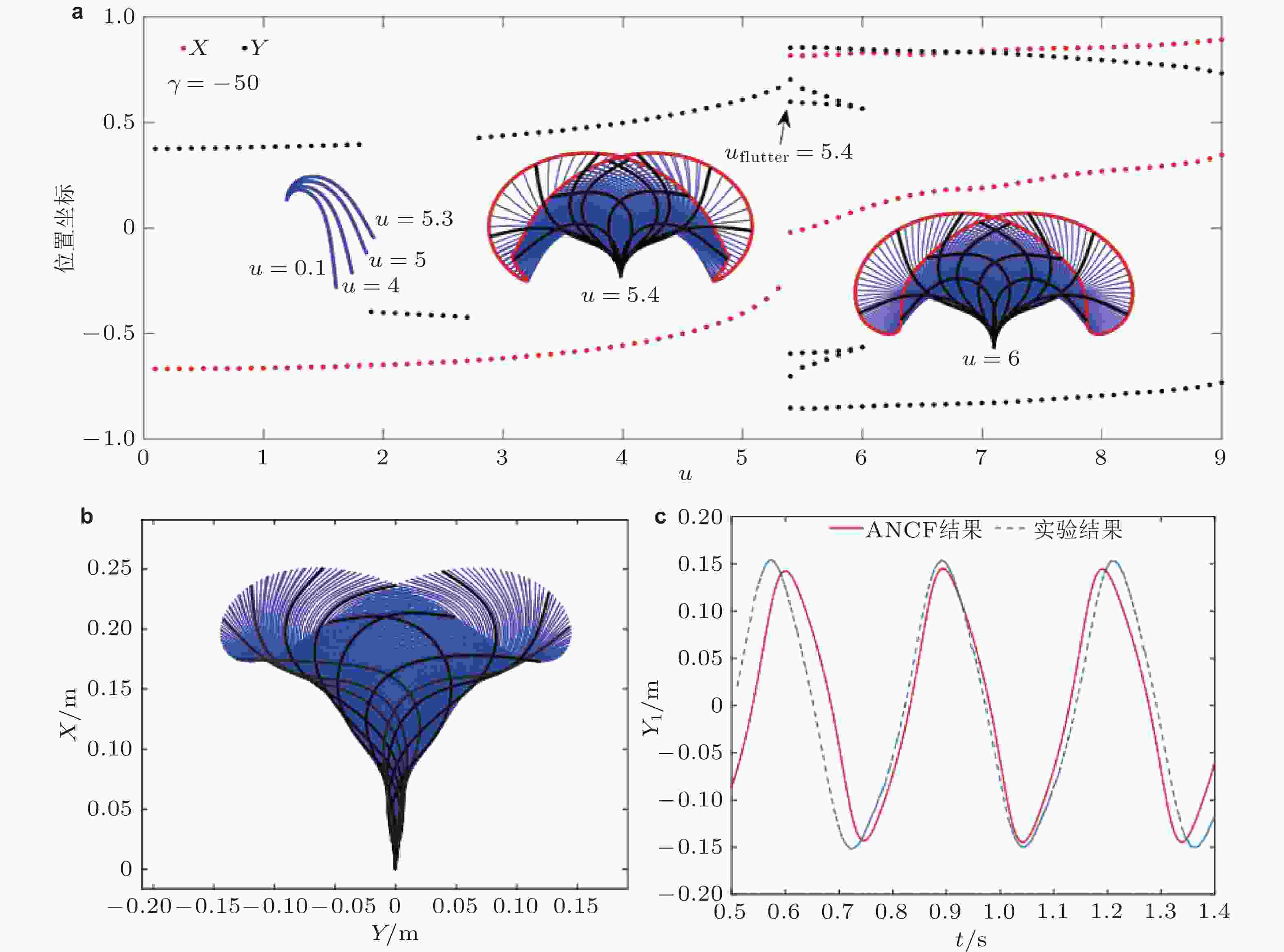
图 24 站立式悬臂输流管道在重力参数γ = −50时的大变形动力学响应. (a) 管道自由端位置随流速变化的分叉图, (b) ~ (c) ANCF模型预测与实验测试结果对比图, (a) ~ (b)中的黑粗线和蓝细线分别为管道构型的实验测试结果与ANCF计算结果 (Chen et al. 2024)
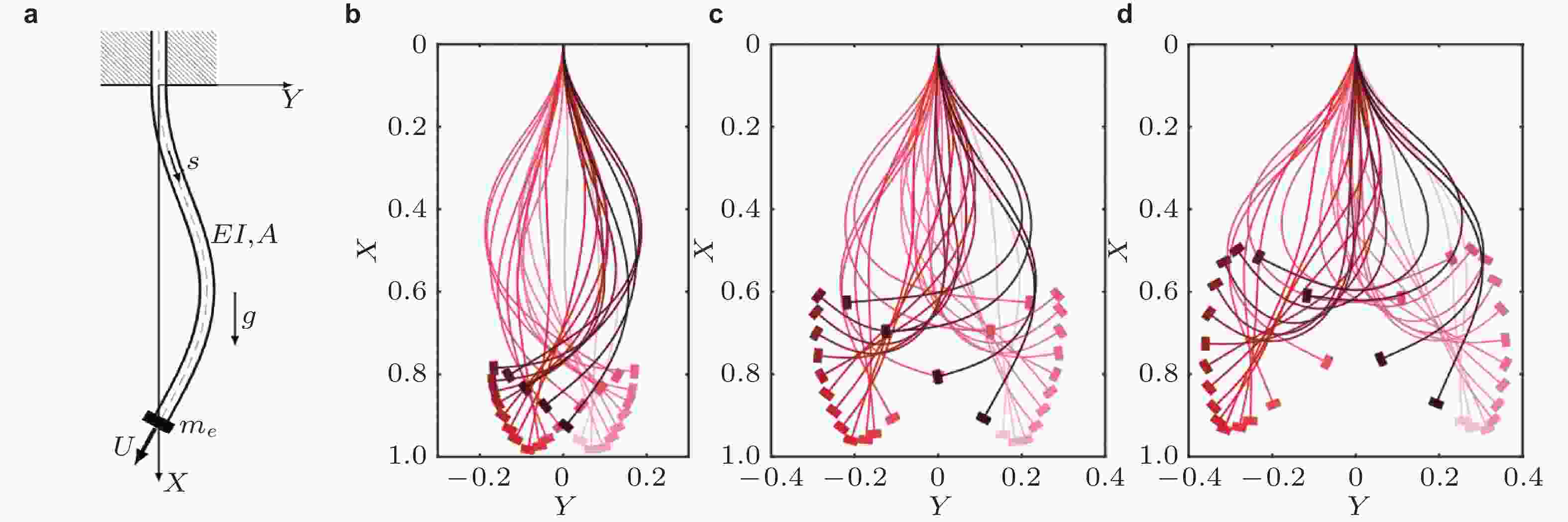
图 25 四种初始构型的微弯悬臂管在高流速下的颤振响应行为. (a) 四种微弯曲管的模型示意图, (b) 四种微弯曲管在高流速下的振动形态图(Zhou et al. 2021a)
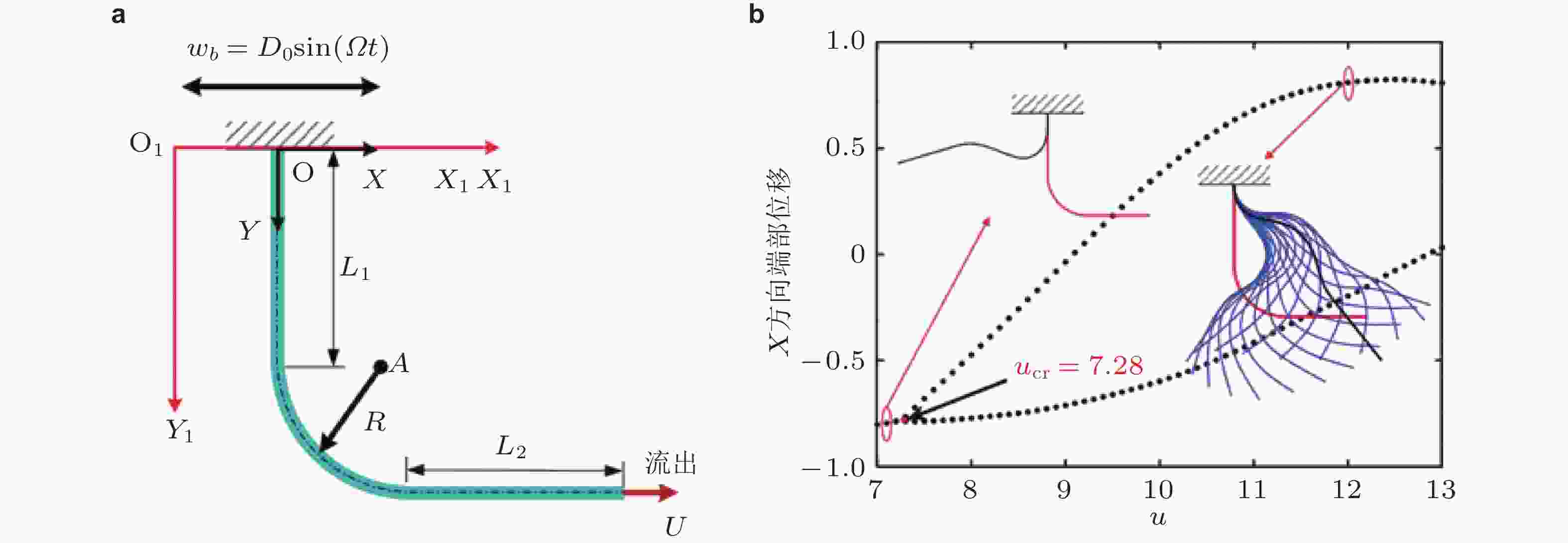
图 26 L形悬臂曲管在定常内流作用下的静态和动态响应. (a) L形输流曲管模型示意图, (b) L形曲管自由端沿X方向位移在不同流速下的分岔图 (Zhou et al. 2022b)
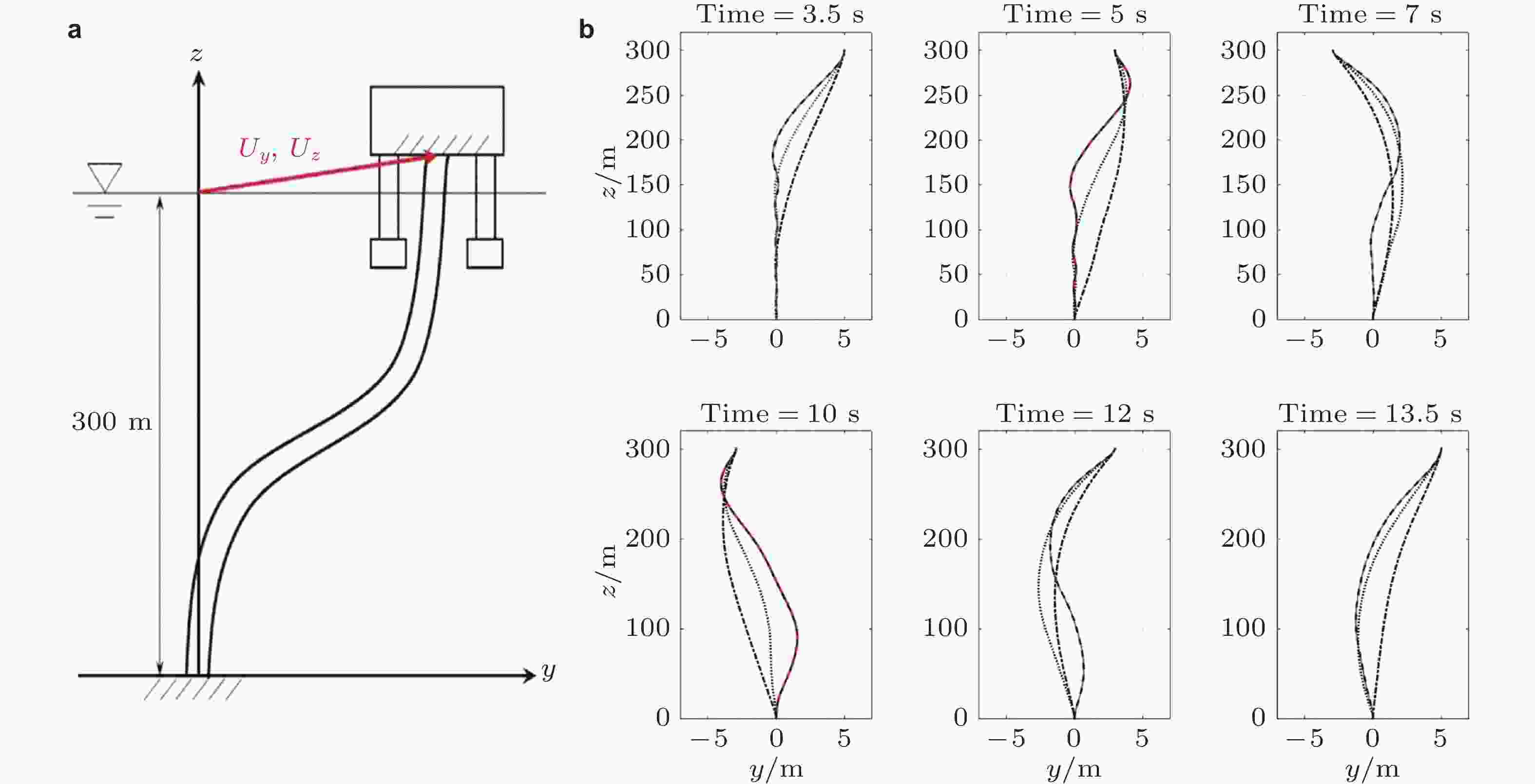
图 27 内流作用下顶端张紧曲管的动力学行为. (a)曲管系统示意图, (b) 不同时刻的管道振动形态图 (Tang & Sweetman 2021)
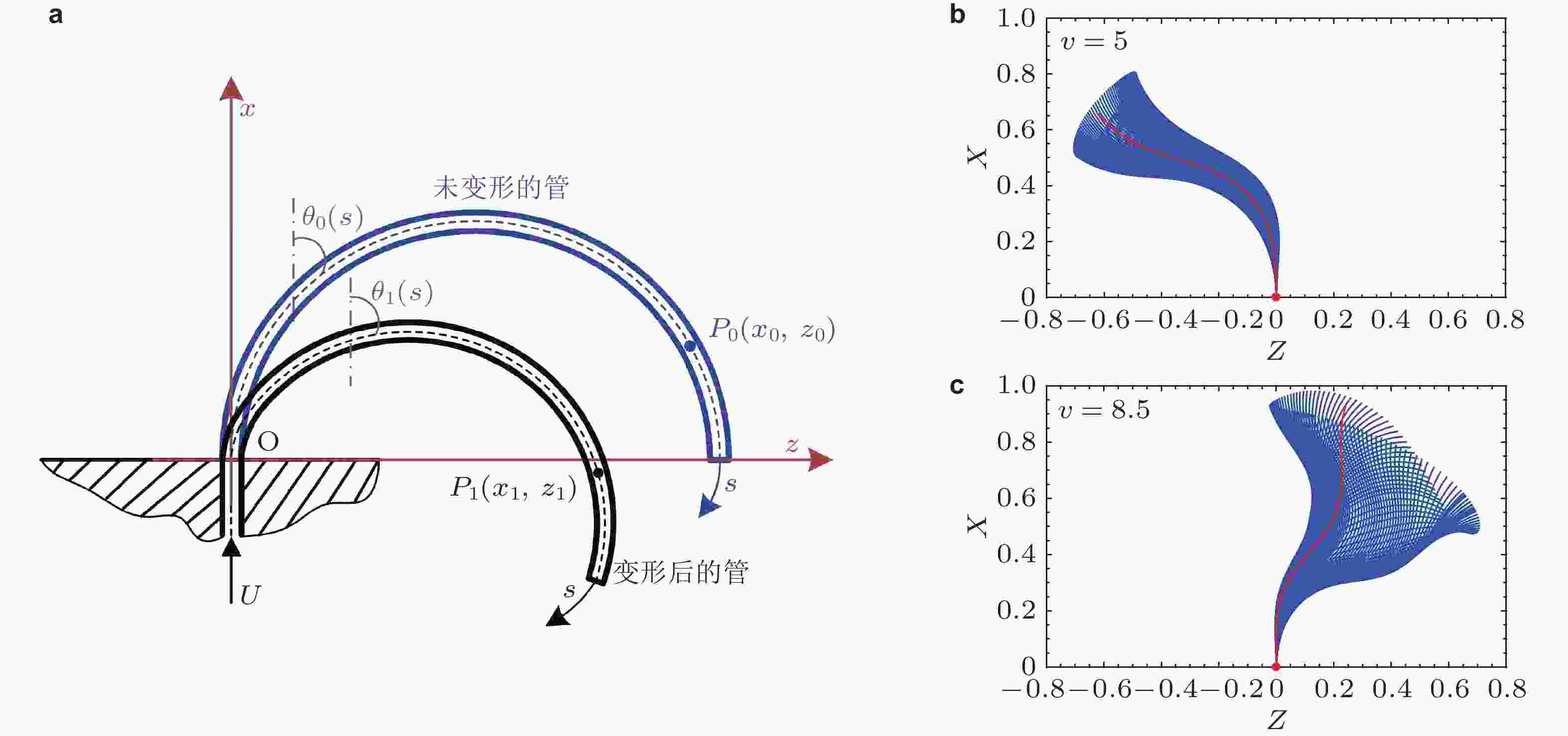
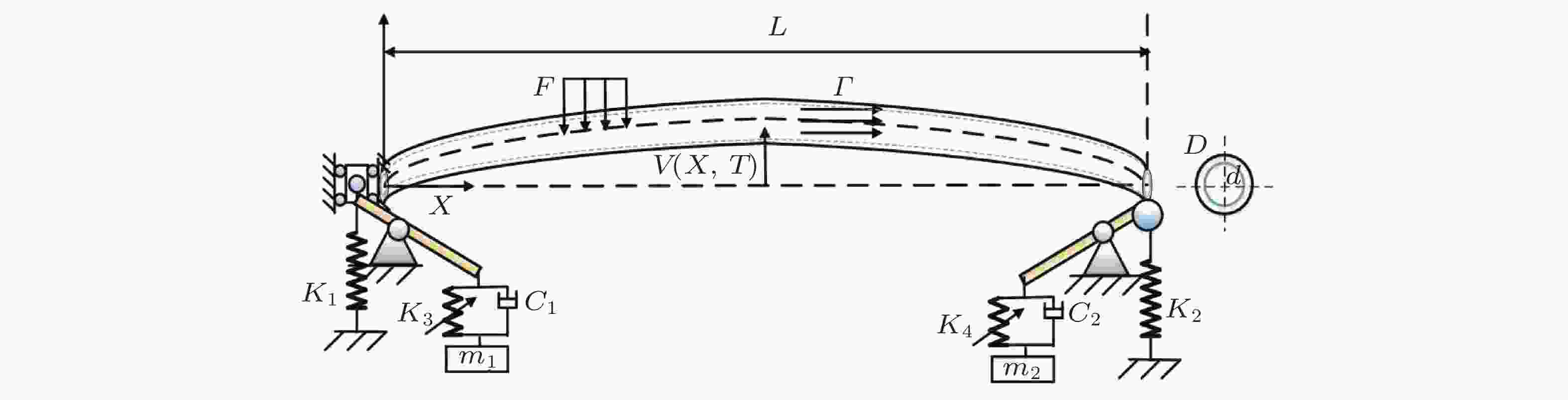
图 28 半圆形悬臂曲管在内流作用下的几何精确动力学模型及其计算结果. (a)半圆形悬臂曲管变形前后的几何描述示意图, (b)流速略高于临界流速值 (v = 5) 时管道的管道静平衡位置 (红色线条) 和振动形态 (蓝色线条) 图, (c)流速远高于临界流速值 (v = 8.5) 时的管道静平衡位置和振动形态图 (Chen et al. 2022)
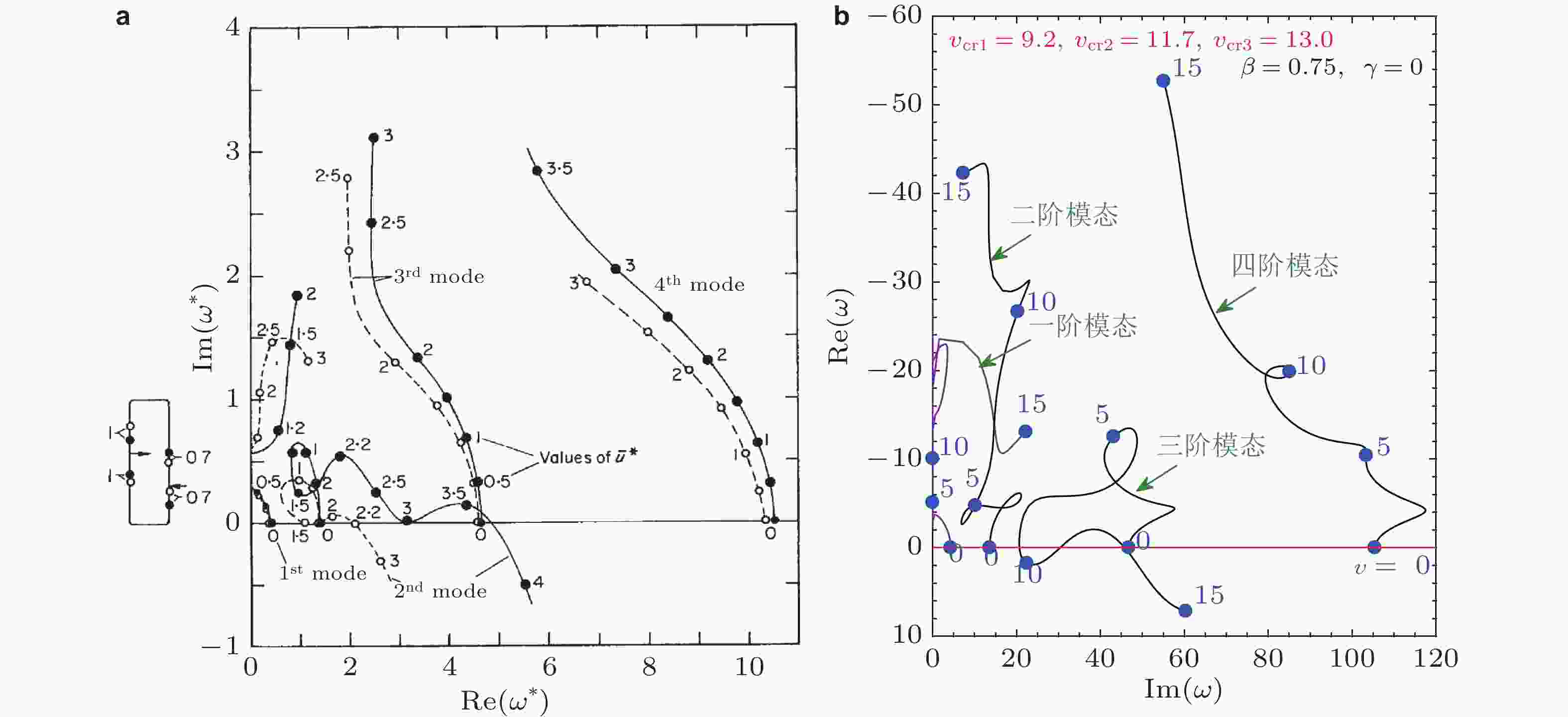
图 29 Misra等人模型和几何精确理论模型预测的半圆形曲管复特征频率. (a) Misra等模型预测的颤振临界流速约为2.2 (Misra et al. 1988), (b) Chen等基于几何精确理论模型预测的颤振临界流速约为9.2 (Chen et al. 2022)
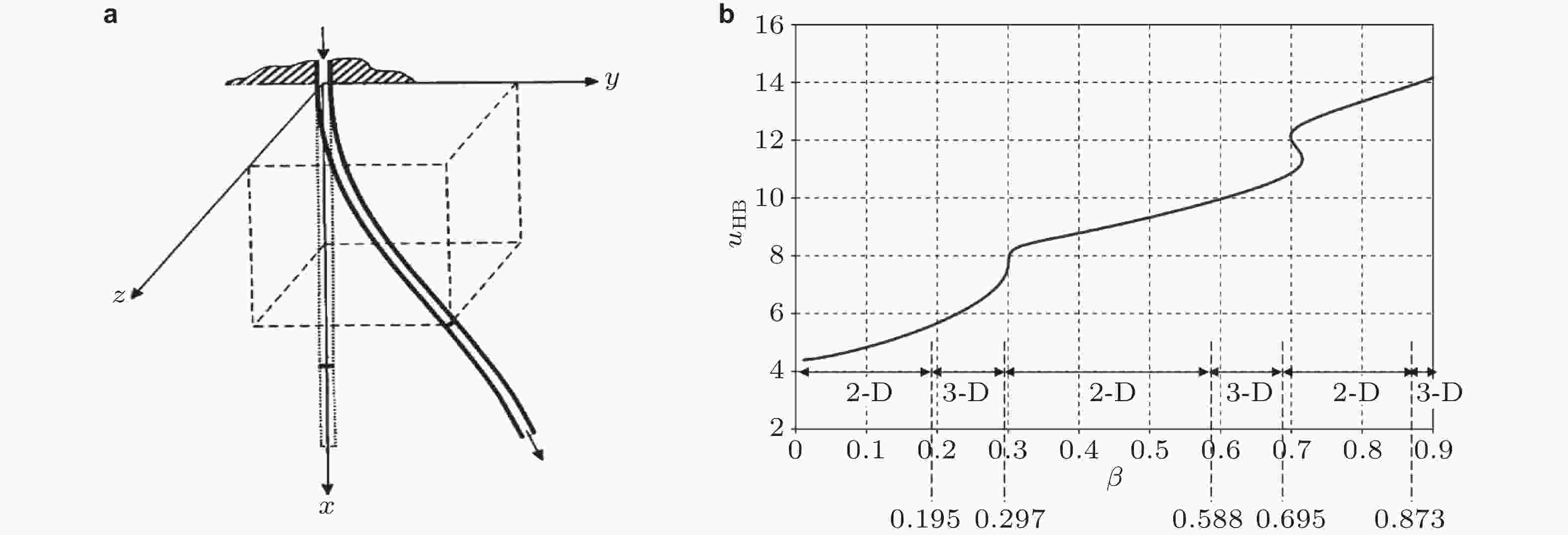
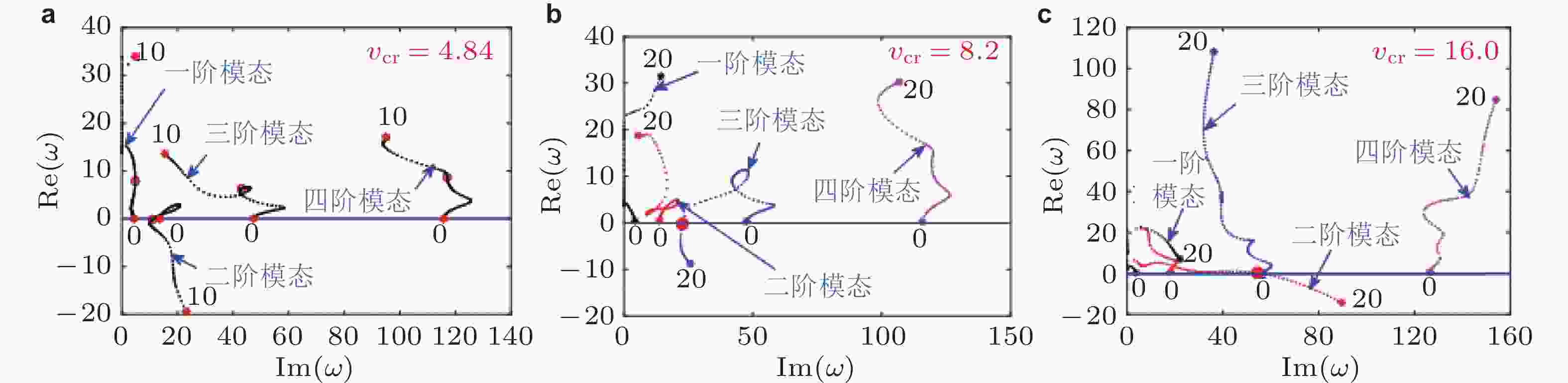
图 30 不同质量比β参数取值下半圆形悬臂曲管的复特征频率. (a) β = 0.2时系统发生二阶模态失稳的Argand图, (b) β = 0.5时系统发生三阶模态失稳的Argand图, (c) β = 0.9时系统发生二阶模态失稳的Argand图 (Cao et al. 2024)
图 31 锥形螺旋线初始构型下悬臂输流曲管的三阶、五阶、六阶模态分析结果. (a) 流速为0的情形, (b) 无量纲流速为6的情形 (Łuczko & Czerwiński 2019)
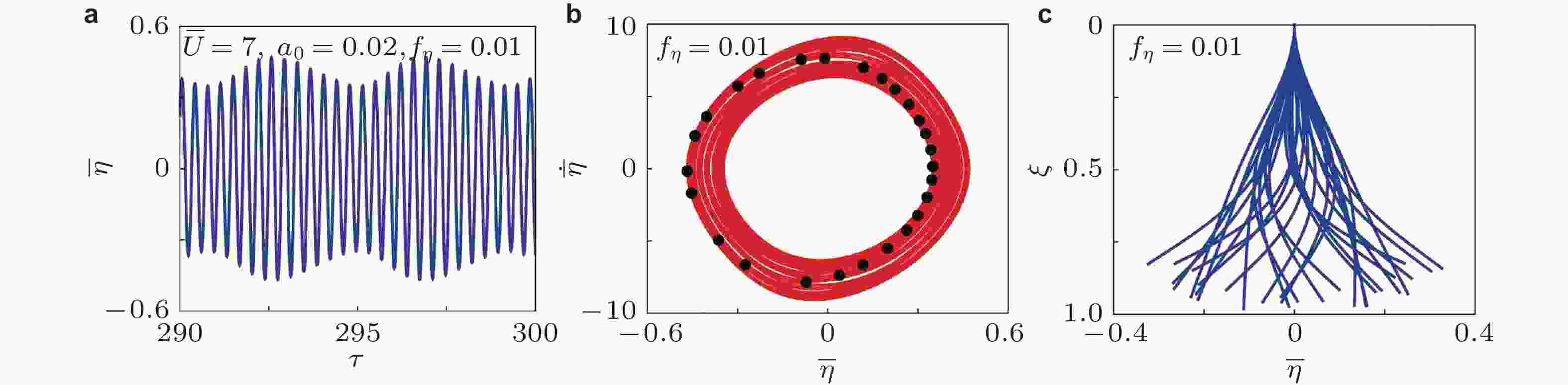
图 32 基础激励下悬臂微弯曲管自由端的准周期运动. (a)位移时间历程曲线, (b)振动相轨迹图, (c) 振动形态图(Zhu et al. 2023)
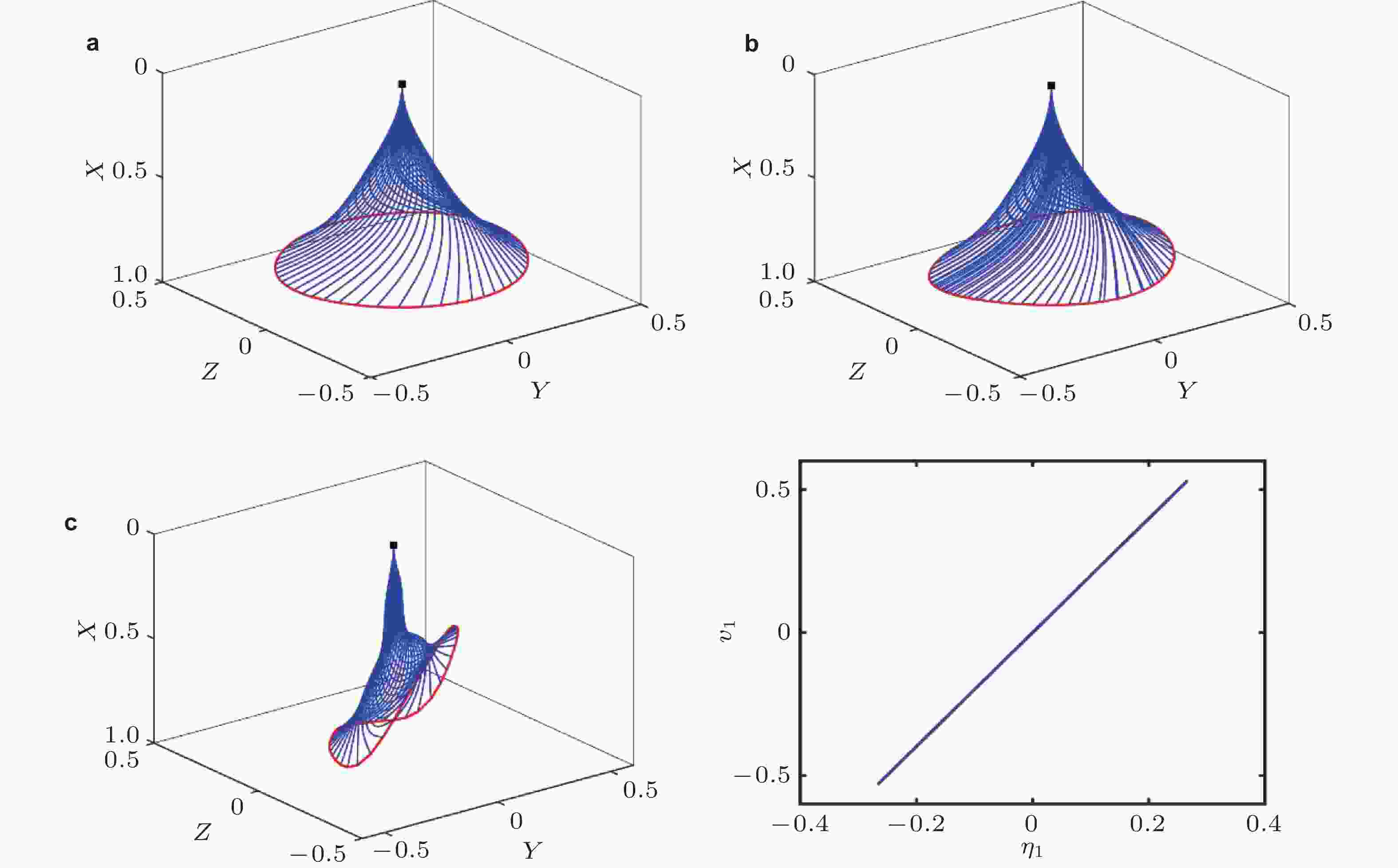
图 33 直-弯组合悬臂平面曲管的稳定性与动态响应. (a)直-弯组合平面曲管模型示意图; (b) 曲管在面内 (蓝线) 和面外 (红线) 的复特征值曲线; (c) 流速略高于临界值时管道的三维振动形态图及其在Y-Z和X-Y平面的投影; (d) 悬臂曲管末端位移在X方向、Y方向和Z方向上的相轨迹曲线 (Guo et al. 2024b)
图 34 杠杆型非线性能量阱在输流管道被动控制中的应用示意图(Cao et al. 2022)
图 35 几种典型的非线性隔振器. (a) NES胞元示意图 (Ding & Shao 2022), (b) NES隔振器 (Ding & Chen 2020), (c)二维逆变器增强型隔振器 (Yang et al. 2024), (d)杠杆型非线性隔振器 (Zang et al. 2021)
图 36 非线性准零刚度隔振器在两端弹性支撑输流管道系统中的应用示意图 (Ding et al. 2019)
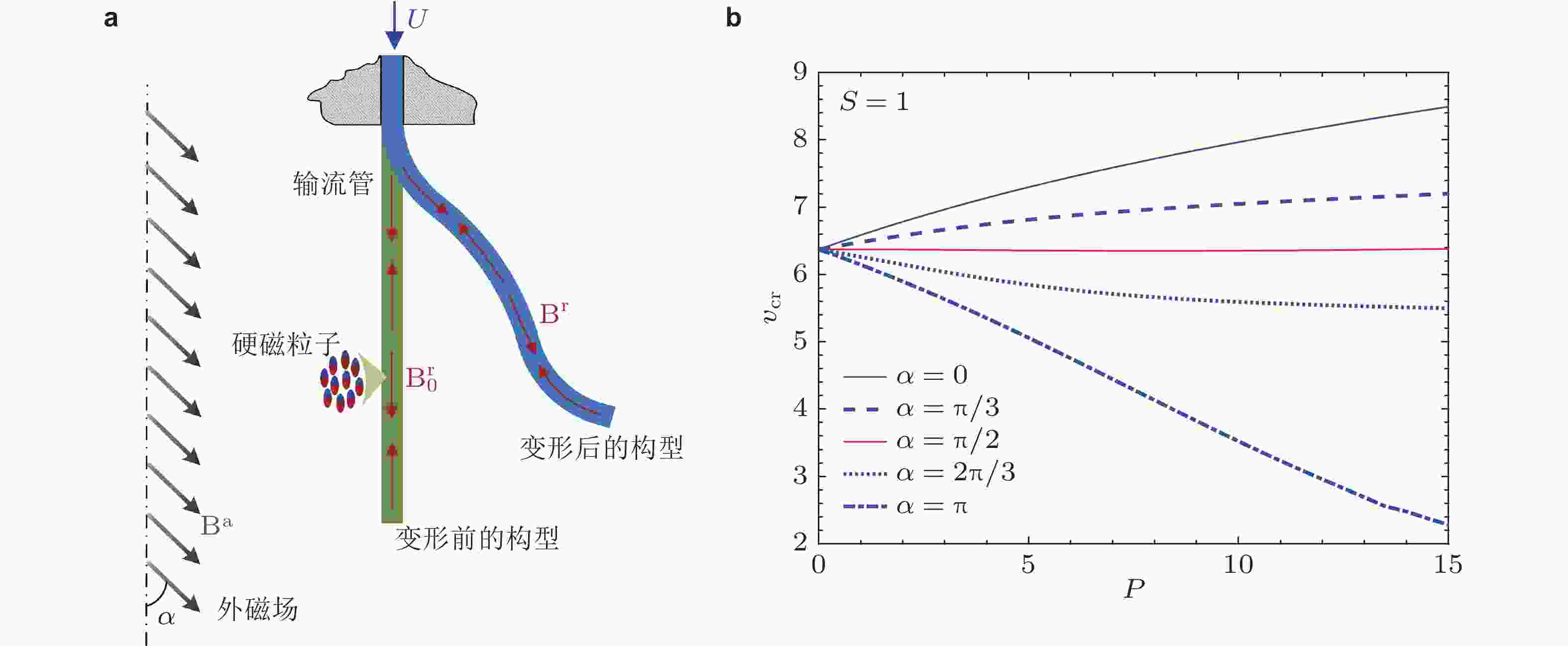
图 37 外磁场作用下的硬磁软材料悬臂输流管道. (a)模型示意图, (b) 不同磁场方向角度下管道失稳临界流速随外部磁场强度的演化曲线 (Chen et al. 2021b)
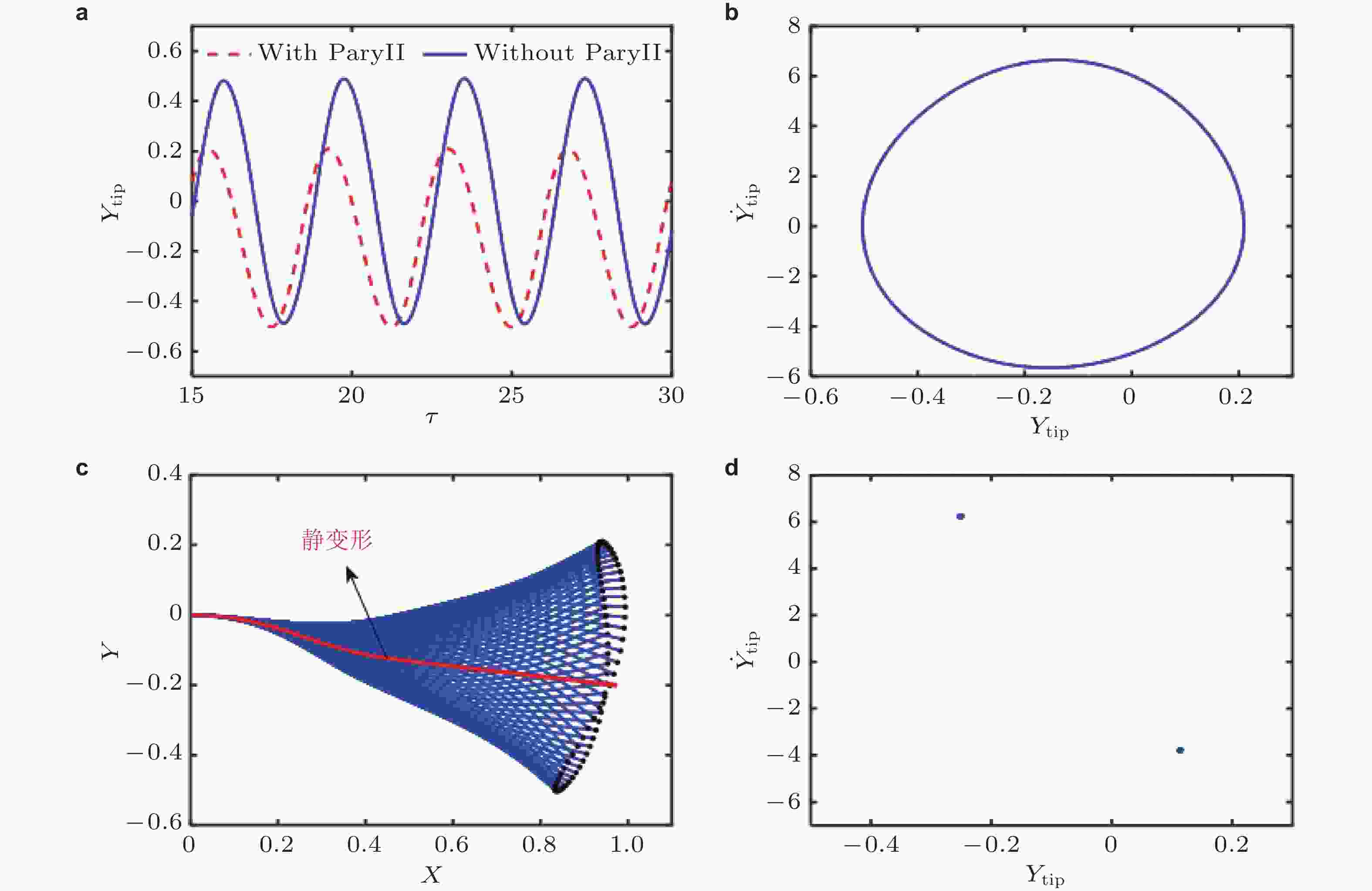
图 38 局部磁化悬臂输流管道的静变形和周期振动响应. (a)磁化和未磁化输流管道端部位移时程曲线对比图, (b) 磁化后输流管道端部相轨迹曲线, (c) 振动形态图和(d) 庞加莱映射图 (Guo et al. 2022a)
图 39 一种协同推进的仿生鱼设计方案 (Strefling et al. 2012)
图 40 一种基于输流管大变形的仿生机器人设计方案. (a) 实验测试照片, (b) CFD仿真计算得到的尾涡脱落云图 (Dai et al. 2022)
图 41 用于微创生物打印的铁磁软导管机器人 (FSCR) 系统. (a) 通过小切口在体内使用功能墨水 (如导电聚合物和生物材料) 进行微创打印的示意图, (b) 使用带有大切口的刚性喷嘴的传统打印系统示意图 (Zhou C et al. 2021)
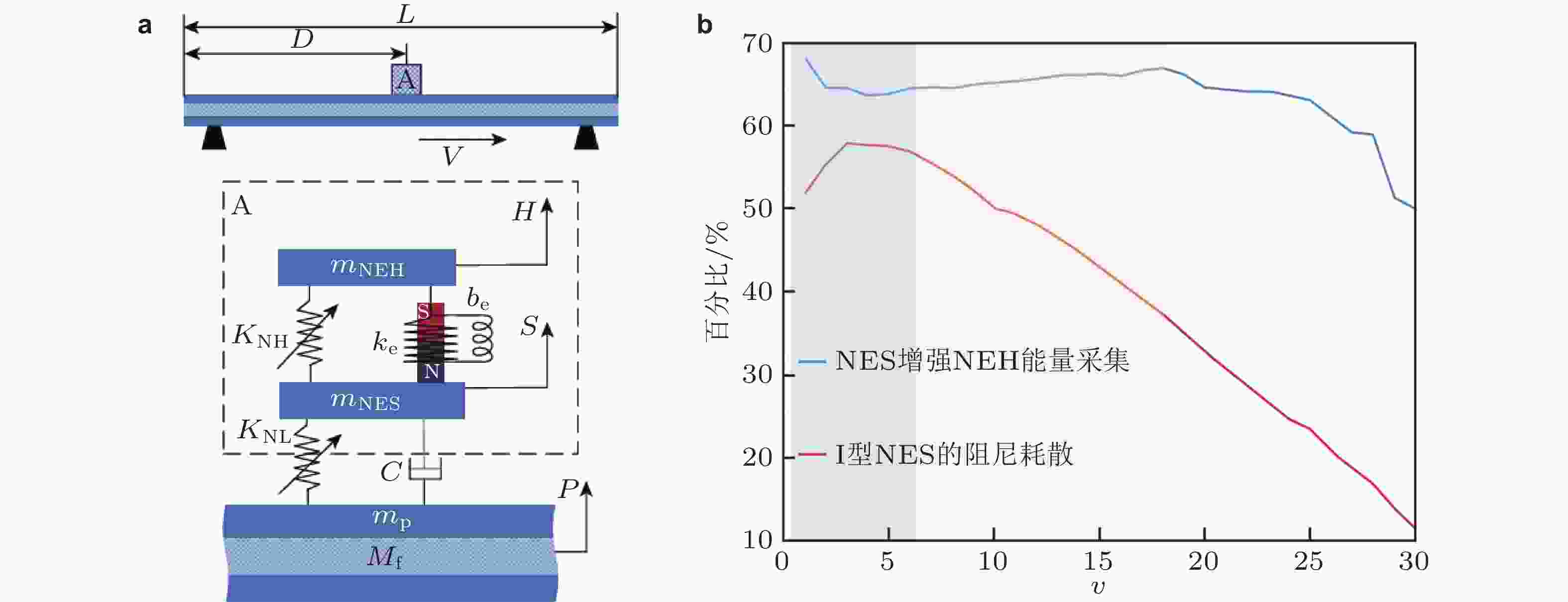
图 42 附有非线性能量阱和能量采集器的两端支撑输流管道. (a) 输流管道系统模型示意图, (b) 能量采集率和阻尼耗散率随流速的变化曲线 (Jin & Yang 2023)
表 1 输流管动力学数据驱动建模的三种方法及其特征对比
作者 方法 主要特征 Xu et al. 2023a, 2023b RBFNN 应用POD降阶处理, 再进行RBFNN建模预测 Zhang et al. 2024 FF-PINN 应用傅里叶特征映射处理数据以改良PINN模型 Li et al. 2024 SSM 应用SSM降阶模型并合理外推预测复杂非线性动力学行为 表 2 环形碰撞约束下悬臂输流直管运动形态所对应的流速区域 (灰色、黑色、绿色分别代表管道的非平面运动、平面运动和粘连现象)(Wang Y et al. 2018)

-
[1] 蔡逢春, 臧峰刚, 叶献辉, 黄茜. 2011. 基于绝对节点坐标法的输流管道非线性动力学分析. 振动与冲击, 30(6): 143-146 (Cai F C, Zang F G, Ye X H, Huang X. 2011. Nonlinear dynamic analysis of flow pipeline based on absolute node coordinate method. Journal of Vibration and Shock, 30(6): 143-146). doi: 10.3969/j.issn.1000-3835.2011.06.030Cai F C, Zang F G, Ye X H, Huang X. 2011. Nonlinear dynamic analysis of flow pipeline based on absolute node coordinate method. Journal of Vibration and Shock, 30(6): 143-146. doi: 10.3969/j.issn.1000-3835.2011.06.030 [2] 陈伟. 2021. 细长软体结构大变形动力学及其磁调控. 华中科技大学: 博士学位论文 (Chen W. 2021. Large deformation dynamics and magnetic control of slender soft structures. Huazhong University of Science and Technology: PhD Thesis).Chen W. 2021. Large deformation dynamics and magnetic control of slender soft structures. Huazhong University of Science and Technology: PhD Thesis. [3] 丁虎. 2022. 输流管道振动的被动控制研究. 中国自然杂志, 44(4): 316-322 (Ding H. 2022. Research on passive control of vibration of flow pipeline. Chinese Journal of Nature, 44(4): 316-322).Ding H. 2022. Research on passive control of vibration of flow pipeline. Chinese Journal of Nature, 44(4): 316-322. [4] 郭梓龙, 王琳, 倪樵, 贾青青, 杨文正. 2021. 接地惯容式减振器对悬臂输流管稳定性和动态响应的影响研究. 力学学报, 53(6): 1769-1780 (Guo Z L, Wang L, Ni Q, Jia Q Q, Yang W Z. 2021. Influence of ground inertial shock absorber on the stability and dynamic response of cantilever flow tube. Acta Mechanica Sinica, 53(6): 1769-1780). doi: 10.6052/0459-1879-21-105Guo Z L, Wang L, Ni Q, Jia Q Q, Yang W Z. 2021. Influence of ground inertial shock absorber on the stability and dynamic response of cantilever flow tube. Acta Mechanica Sinica, 53(6): 1769-1780. doi: 10.6052/0459-1879-21-105 [5] 何毅翔, 邢浩然, 代胡亮, 王琳. 2023. 外流作用下管道流固耦合非线性动力学研究进展. 动力学与控制学报, 21(6): 3-17 (He Y X, Xing H R, Dai H L, Wang L. 2023. Research progress on fluid-structure interaction vibrations of pipes subjected to external flows. Journal of Dynamics and Control, 21(6): 3-17).He Y X, Xing H R, Dai H L, Wang L. 2023. Research progress on fluid-structure interaction vibrations of pipes subjected to external flows. Journal of Dynamics and Control, 21(6): 3-17. [6] 何毅翔, 杨正铖, 邢浩然, 代胡亮, 王琳. 2024. 基于输流软管驱动的仿水母动力学设计、仿真与实验. 中国科学: 物理学 力学 天文学, 54 (6): 116-128 (He Y X, Yang Z C, Xing H R, Dai H L, Wang L. 2024. Dynamic design, simulation and experiment of jellyfish simulation based on flow hose drive. Science in China: Physics, Mechanics and Astronomy, 54 (6): 116-128).He Y X, Yang Z C, Xing H R, Dai H L, Wang L. 2024. Dynamic design, simulation and experiment of jellyfish simulation based on flow hose drive. Science in China: Physics, Mechanics and Astronomy, 54(6): 116-128 [7] 唐冶, 高传康, 丁千, 杨天智. 2023. 输流管道动力学与控制的最新进展. 动力学与控制学报, 21 (6): 18–30 (Tang Y, Gao C K, Ding Q, Yang T Z. 2023. Review on dynamic and control of pipes conveying fluid. Journal of Dynamics and Control, 21 (6): 18-30).Tang Y, Gao C K, Ding Q, Yang T Z. 2023. Review on dynamic and control of pipes conveying fluid. Journal of Dynamics and Control, 21(6): 18-30. [8] 王乙坤. 2017. 碰撞约束下输液管的非线性振动. 华中科技大学: 博士学位论文 (Wang Y K. 2017. Nonlinear vibration of infusion tubes under collision constraints. Huazhong University of Science and Technology: PhD Thesis).Wang Y K. 2017. Nonlinear vibration of infusion tubes under collision constraints. Huazhong University of Science and Technology: PhD Thesis. [9] 王忠民, 邹德志, 姜全友. 2016. 弹性地基上输流管道主参数共振的主动振动控制. 振动与冲击, 35(4): 182-187 (Wang Z M, Zou D Z, Jiang Q Y. 2016. Active vibration control of main parameter resonance of flow pipeline on elastic foundation. Journal of Vibration and Shock, 35(4): 182-187).Wang Z M, Zou D Z, Jiang Q Y. 2016. Active vibration control of main parameter resonance of flow pipeline on elastic foundation. Journal of Vibration and Shock, 35(4): 182-187. [10] 徐鉴. 2015. 振动控制研究进展综述. 力学季刊, 36(4): 547-565 (Xu J. 2015. Review of research progress in vibration control. Chinese Quarterly of Mechanics, 36(4): 547-565).Xu J. 2015. Review of research progress in vibration control. Chinese Quarterly of Mechanics, 36(4): 547-565. [11] 徐鉴, 杨前彪. 2004. 输液管模型及其非线性动力学近期研究进展. 力学进展, 34(2): 182-194 (Xu J, Yang Q B. 2004. Recent development on models and nonlinear dynamics of pipes conveying fluid. Advances in Mechanics, 34(2): 182-194). doi: 10.3321/j.issn:1000-0992.2004.02.003Xu J, Yang Q B. 2004. Recent development on models and nonlinear dynamics of pipes conveying fluid. Advances in Mechanics, 34(2): 182-194. doi: 10.3321/j.issn:1000-0992.2004.02.003 [12] 易浩然, 周坤, 代胡亮, 王琳, 倪樵. 2020. 含集中质量悬臂输流管的稳定性与模态演化特性研究. 力学学报, 52(6): 1800-1810 (Yi H R, Zhou K, Dai H L, Wang L, Ni Q. 2020. Stability and modal evolution characteristics of cantilever flow tube with concentrated mass. Acta Mechanica Sinica, 52(6): 1800-1810). doi: 10.6052/0459-1879-20-280Yi H R, Zhou K, Dai H L, Wang L, Ni Q. 2020. Stability and modal evolution characteristics of cantilever flow tube with concentrated mass. Acta Mechanica Sinica, 52(6): 1800-1810. doi: 10.6052/0459-1879-20-280 [13] 张立翔, 黄文虎, Tijsseling A S. 2000. 输流管道流固耦合振动研究进展. 水动力学研究与进展, 15(3): 366-379 (Zhang L X, Huang W H, Tijsseling A S. 2000. Review of FSI analysis of fluid-conveying pipes. Journal of Hydrodynamics, 15(3): 366-379).Zhang L X, Huang W H, Tijsseling A S. 2000. Review of FSI analysis of fluid-conveying pipes. Journal of Hydrodynamics, 15(3): 366-379. [14] Abdelbaki A R, Païdoussis M P, Misra A K. 2019. A nonlinear model for a hanging tubular cantilever simultaneously subjected to internal and confined external axial flows. Journal of Sound and Vibration, 449: 349-367. doi: 10.1016/j.jsv.2019.02.031 [15] Bajaj A K, Sethna P R. 1982. Bifurcations in three-dimensional motions of articulated tubes, Part 1: Linear systems and symmetry. Journal of Applied Mechanics, 49(3): 606-611. doi: 10.1115/1.3162535 [16] Bajaj A K, Sethna P R. 1984. Flow induced bifurcations to three-dimensional oscillatory motions in continuous tubes. SIAM Journal on Applied Mathematics, 44(2): 270-286. doi: 10.1137/0144020 [17] Bakre S V, Jangid R S, Reddy G R. 2006. Optimum X-plate dampers for seismic response control of piping systems. International Journal of Pressure Vessels and Piping, 83(9): 672-685. doi: 10.1016/j.ijpvp.2006.05.003 [18] Bellman R, Casti J. 1971. Differential quadrature and long-term integration. Journal of mathematical analysis and Applications, 34(2): 235-238. doi: 10.1016/0022-247X(71)90110-7 [19] Bellman R, Kashef B G, Casti J. 1972. Differential quadrature: A technique for the rapid solution of nonlinear partial differential equations. Journal of Computational Physics, 10(1): 40-52. doi: 10.1016/0021-9991(72)90089-7 [20] Benjamin Thomas Brooke. 1961a. Dynamics of a system of articulated pipes conveying fluid-I Theory. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 261(1307): 457-486. [21] Benjamin Thomas Brooke. 1961b. Dynamics of a system of articulated pipes conveying fluid. II. Experiments. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 487–499. [22] Bourrières F J. 1939. Sur un phénomène d’oscillation auto-entretenue en mécanique des fluides réels. Publications Scientifques et Techniques du Ministère de l’ Air, 147 . [23] Cai C, Zhou J, Wang K, Lin Q, Xu D, Wen G. 2023. Quasi-zero-stiffness metamaterial pipe for low-frequency wave attenuation. Engineering Structures, 279: 115580. doi: 10.1016/j.engstruct.2022.115580 [24] Cao R, Guo Z, Chen W, Dai H, Wang L. 2024. Nonlinear dynamics of a circular curved cantilevered pipe conveying pulsating fluid based on the geometrically exact model. Applied Mathematics and Mechanics, 45(2): 261-276. doi: 10.1007/s10483-024-3084-7 [25] Cao R, Wang Z, Zang J, Zhang Y. 2022. Resonance response of fluid-conveying pipe with asymmetric elastic supports coupled to lever-type nonlinear energy sink. Applied Mathematics and Mechanics, 43(12): 1873-1886. doi: 10.1007/s10483-022-2925-8 [26] Chang G H, Modarres-Sadeghi Y. 2014. Flow-induced oscillations of a cantilevered pipe conveying fluid with base excitation. Journal of Sound and Vibration, 333(18): 4265-4280. doi: 10.1016/j.jsv.2014.03.036 [27] Chen W, Dai H, Jia Q, Wang L. 2019a. Geometrically exact equation of motion for large-amplitude oscillation of cantilevered pipe conveying fluid. Nonlinear Dynamics, 98(3): 2097-2114. doi: 10.1007/s11071-019-05310-0 [28] Chen W, Dai H, Wang L. 2021a. Three-dimensional dynamical model for cantilevered pipes conveying fluid under large deformation. Journal of Fluids and Structures, 105: 103329. doi: 10.1016/j.jfluidstructs.2021.103329 [29] Chen W, Hu Z, Dai H, Wang L. 2020. Extremely large-amplitude oscillation of soft pipes conveying fluid under gravity. Applied Mathematics and Mechanics, 41(9): 1381-1400. doi: 10.1007/s10483-020-2646-6 [30] Chen S S. 1970. Forced vibration of a cantilevered tube conveying fluid. The Journal of the Acoustical Society of America, 18(3B): 773-775. [31] Chen W, Wang L. 2021. Large bending deformation of a cantilevered soft beam under external load: The applicability of inextensibility assumption of the centerline. Current Mechanics and Advanced Materials, 1(1): 24-38. doi: 10.2174/2666184501999200909151326 [32] Chen W, Wang G, Li Y, Wang L, Yin Z. 2023. The quaternion beam model for hard-magnetic flexible cantilevers. Applied Mathematics and Mechanics, 44(5): 787-808. doi: 10.1007/s10483-023-2983-8 [33] Chen W, Wang L, Peng Z. 2021b. A magnetic control method for large-deformation vibration of cantilevered pipe conveying fluid. Nonlinear Dynamics, 105(2): 1459-1481. doi: 10.1007/s11071-021-06662-2 [34] Chen W, Zhou K, Wang L, Yin Z. 2022. Geometrically exact model and dynamics of cantilevered curved pipe conveying fluid. Journal of Sound and Vibration, 534: 117074. doi: 10.1016/j.jsv.2022.117074 [35] Chen W, Yan H, Cao R, Dai H, Wang L. 2024. Theoretical and experimental investigations on large-deformation dynamics of the standing cantilevered pipe conveying fluid. Mechanical Systems and Signal Processing, 220: 111688. doi: 10.1016/j.ymssp.2024.111688 [36] Ch’ng E, Dowell E H. 1979. Flow-induced vibration. In: Chen S S and BMD ed. New York: ASME. 65–81 p. [37] Cho S G, Furuya O, Kurabayashi H. 2019. Enhancement of seismic resilience of piping systems in nuclear power plants using steel coil damper. Nuclear Engineering and Design, 350: 147-157. doi: 10.1016/j.nucengdes.2019.05.006 [38] Copeland G S, Moon F C. 1992. Chaotic flow-induced vibration of a flexible tube with end mass. Journal of Fluids and Structures, 6(6): 705-718. doi: 10.1016/0889-9746(92)90004-M [39] Czerwiński A, Łuczko J. 2021. Nonlinear vibrations of planar curved pipes conveying fluid. Journal of Sound and Vibration, 501: 116054. doi: 10.1016/j.jsv.2021.116054 [40] Czerwiński A, Łuczko J. 2022. Experimental and numerical study on vibrations of a helical pipe with fluid flow. Journal of Sound and Vibration, 535: 117116. doi: 10.1016/j.jsv.2022.117116 [41] Dai H, He Y, Zhou K, Peng Z, Wang L, Hagedorn P. 2022. Utilization of nonlinear vibrations of soft pipe conveying fluid for driving underwater bio-inspired robot. Applied Mathematics and Mechanics, 43(7): 1109-1124. doi: 10.1007/s10483-022-2866-7 [42] Dai H L, Wang L. 2016. Dynamics and stability of magnetically actuated pipes conveying fluid. International Journal of Structural Stability and Dynamics, 16(06): 1550026. doi: 10.1142/S0219455415500261 [43] Dai H L, Wang L, Qian Q, Ni Q. 2013. Vortex-induced vibrations of pipes conveying fluid in the subcritical and supercritical regimes. Journal of Fluids and Structures, 39: 322-334. doi: 10.1016/j.jfluidstructs.2013.02.015 [44] Dai H L, Wang L, Qian Q, Gan J. 2012. Vibration analysis of three-dimensional pipes conveying fluid with consideration of steady combined force by transfer matrix method. Applied Mathematics and Computation, 219(5): 2453-2464. doi: 10.1016/j.amc.2012.08.081 [45] Dehrouyeh-Semnani A M. 2023. Nonlinear geometrically exact dynamics of fluid-conveying cantilevered hard magnetic soft pipe with uniform and nonuniform magnetizations. Mechanical Systems and Signal Processing, 188: 110016. doi: 10.1016/j.ymssp.2022.110016 [46] Demir M H, Yesildirek A, Yigit F. 2015. Control of a cantilever pipe conveying fluid using neural network. IEEE. 2015 6th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), 1–6. [47] Ding H, Chen L Q. 2020. Designs, analysis, and applications of nonlinear energy sinks. Nonlinear Dynamics, 100(4): 3061-3107. doi: 10.1007/s11071-020-05724-1 [48] Deng T C, Ding H. 2024. Frequency band preservation: pipe design strategy away from resonance. Acta Mech. Sin, 40: 523201. [49] Ding H, Ji J, Chen L-Q. 2019. Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics. Mechanical Systems and Signal Processing, 121: 675-688. doi: 10.1016/j.ymssp.2018.11.057 [50] Ding H, Shao Y. 2022. NES cell. Applied Mathematics and Mechanics, 43(12): 1793-1804. doi: 10.1007/s10483-022-2934-6 [51] Doki H, Hiramoto K, Skelton R E. 1998. Active control of cantilevered pipes conveying fluid with constraints on input energy. Journal of fluids and structures, 12(5): 615-628. doi: 10.1006/jfls.1997.0154 [52] Duan N, Wu Y, Sun X-M, Zhong C, Wang W. 2020. Lyapunov-based stability analysis for conveying fluid pipe with nonlinear energy sink. IFAC-PapersOnLine, 53(2): 9157-9162. doi: 10.1016/j.ifacol.2020.12.2161 [53] Edelstein W S, Chen S S, Jendrzejczyk J A. 1986. A finite element computation of the flow-induced oscillations in a cantilevered tube. Journal of Sound and Vibration, 107(1): 121-129. doi: 10.1016/0022-460X(86)90287-7 [54] Facchinetti M L, de Langre E, Biolley F. 2004. Coupling of structure and wake oscillators in vortex-induced vibrations. Journal of Fluids and Structures, 19(2): 123-140. doi: 10.1016/j.jfluidstructs.2003.12.004 [55] Farokhi H, Erturk A. 2021. Three-dimensional nonlinear extreme vibrations of cantilevers based on a geometrically exact model. Journal of Sound and Vibration, 510: 116295. doi: 10.1016/j.jsv.2021.116295 [56] Farokhi H, Tavallaeinejad M, Païdoussis M P. 2021. Geometrically exact dynamics of cantilevered pipes conveying fluid. Journal of Fluids and Structures, 106: 103364. doi: 10.1016/j.jfluidstructs.2021.103364 [57] Feodos’Ev V. 1951. Vibrations and stability of a pipe when liquid flows through it. Inzhenernyi Sbornik, 10(1): 69-70. [58] Gendelman O, Manevitch L I, Vakakis A F, et al. 2001. Energy pumping in nonlinear mechanical oscillators: Part I—Dynamics of the underlying Hamiltonian systems. J. Appl Mech, 68(1): 34-41. doi: 10.1115/1.1345524 [59] Ghayesh, M H, Païdoussis M P. 2010. Three-dimensional dynamics of a cantilevered pipe conveying fluid, additionally supported by an intermediate spring array. International Journal of Non-Linear Mechanics, 45(5): 507-524. doi: 10.1016/j.ijnonlinmec.2010.02.001 [60] Ghayesh M H, Païdoussis M P, Amabili M. 2013. Nonlinear dynamics of cantilevered extensible pipes conveying fluid. Journal of Sound and Vibration, 332(24): 6405-6418. doi: 10.1016/j.jsv.2013.06.026 [61] Ghayesh M H, Païdoussis M P, Modarres-Sadeghi Y. 2011. Three-dimensional dynamics of a fluid-conveying cantilevered pipe fitted with an additional spring-support and an end-mass. Journal of Sound and Vibration, 330(12): 2869-2899. doi: 10.1016/j.jsv.2010.12.023 [62] Gregory R W, Païdoussis M P. 1966a. Unstable oscillation of tubular cantilevers conveying fluid II experiments. Proceedings of the Royal Society of London, 293(1435): 528-542. [63] Gregory R W, Païdoussis M P. 1966b. Unstable oscillation of tubular cantilevers conveying fluid I. Theory. Proceedings of the Royal Society of London, 293(1435): 512-527. [64] Gu Z, Bai C, Zhang H. 2019. Stochastic finite-element modeling and dynamic characteristics analysis of pipe-conveying fluid. Journal of Vibration Engineering & Technologies, 7(3): 251-259. [65] Guo Y, Ding H. 2024. Theoretical and experimental study on dynamic characteristics of L-shaped fluid-conveying pipes. Applied Mathematical Modelling, 129: 232-249. doi: 10.1016/j.apm.2024.01.054 [66] Guo Y, Li J, Zhu B, Li Y. 2023. Nonlinear dynamical model of hyperelastic pipes conveying fluid with finite deformation: Roles of hyperelasticity and nonlinearity. Nonlinear Dynamics, 111(15): 13691-13708. doi: 10.1007/s11071-023-08584-7 [67] Guo Q, Liu Y, Chen B, Zhao Y. 2021. An efficient stochastic natural frequency analysis method for axially varying functionally graded material pipe conveying fluid. European Journal of Mechanics-A/Solids, 86: 104155. doi: 10.1016/j.euromechsol.2020.104155 [68] Guo Z, Ni Q, Chen W, Dai H, Wang L. 2022a. Dynamic analysis and regulation of the flexible pipe conveying fluid with a hard-magnetic soft segment. Applied Mathematics and Mechanics, 43(9): 1415-1430. doi: 10.1007/s10483-022-2901-9 [69] Guo Z, Ni Q, Wang L, Zhou K, Meng X. 2022b. Influence of dry friction on the dynamics of cantilevered pipes conveying fluid. Applied Sciences, 12(2): 724. doi: 10.3390/app12020724 [70] Guo Z, Ni Q, Zhou X, Yan H, Chen W, Dai H, Wang L. 2024a. Three-dimensional dynamics of supported pipe conveying fluid with arbitrary initial spatial shape. European Journal of Mechanics-A/Solids, 104: 105196. doi: 10.1016/j.euromechsol.2023.105196 [71] Guo Z, Ni Q, Cao R, et al. 2024b. Large-amplitude vibrations of cantilevered pipe conveying fluid with arbitrary initial configuration in three-dimensional sense. Nonlinear Dynamic, 1-18. [72] Guo C Q, Zhang C H, Païdoussis M P. 2010. Modification of equation of motion of fluid-conveying pipe for laminar and turbulent flow profiles. Journal of Fluids and Structures, 26(5): 793-803. doi: 10.1016/j.jfluidstructs.2010.04.005 [73] Hannoyer M J, Païdoussis M P. 1978. Instabilities of tubular beams simultaneously subjected to internal and external axial flows. Journal of Mechanical Design, 100(2): 328-336. doi: 10.1115/1.3453919 [74] Hellum A M, Mukherjee R, Hull A J. 2010. Dynamics of pipes conveying fluid with non-uniform turbulent and laminar velocity profiles. Journal of Fluids and Structures, 26(5): 804-813. doi: 10.1016/j.jfluidstructs.2010.05.001 [75] Hellum A, Mukherjee R, Hull A J. 2011. Flutter instability of a fluid-conveying fluid-immersed pipe affixed to a rigid body. Journal of Fluids and Structures, 27(7): 1086-1096. doi: 10.1016/j.jfluidstructs.2011.03.002 [76] Holmes P J. 1977. Bifurcations to divergence and flutter in flow-induced oscillations: A finite dimensional analysis. Journal of Sound and Vibration, 53(4): 471-503. doi: 10.1016/0022-460X(77)90521-1 [77] Holmes P J. 1978. Pipes supported at both ends cannot flutter. Journal of Applied Mechanics, 45(3): 619-622. doi: 10.1115/1.3424371 [78] Hong D, Tang J, Ren G. 2011. Dynamic modeling of mass-flowing linear medium with large amplitude displacement and rotation. Journal of Fluids and Structures, 27(8): 1137-1148. doi: 10.1016/j.jfluidstructs.2011.06.006 [79] Housner G W. 1952. Bending vibrations of a pipe line containing flowing fluid. Journal of Applied Mechanics, 19(2): 205-208. doi: 10.1115/1.4010447 [80] Huang Y, Zeng G, Wei F. 2002. A new matrix method for solving vibration and stability of curved pipes conveying fluid. Journal of Sound and Vibration, 251: 215-225. doi: 10.1006/jsvi.2001.3983 [81] Ibrahim R A. 2008. Recent advances in nonlinear passive vibration isolators. Journal of Sound and Vibration, 314(3-5): 371-452. doi: 10.1016/j.jsv.2008.01.014 [82] Ji W, Sun W, Du D, Cao Y. 2023. Dynamics modeling and vibration transmission visualization of fluid-conveying series pipe system based on FEM-TMM. Ocean Engineering, 280: 114693. doi: 10.1016/j.oceaneng.2023.114693 [83] Jin Y, Yang T. 2023. Enhanced vibration suppression and energy harvesting in fluid-conveying pipes. Applied Mathematics and Mechanics, 44(9): 1487-1496. doi: 10.1007/s10483-023-3022-8 [84] Jin J D, Song Z Y. 2005. Parametric resonances of supported pipes conveying pulsating fluid. Journal of Fluids and Structures, 20(6): 763-783. doi: 10.1016/j.jfluidstructs.2005.04.007 [85] Jin J D, Zou G S. 2003. Bifurcations and chaotic motions in the autonomous system of a restrained pipe conveying fluid. Journal of Sound and Vibration, 260(5): 783-805. doi: 10.1016/S0022-460X(02)00982-3 [86] Jung D, Chung J. 2008. In-plane and out-of-plane motions of an extensible semi-circular pipe conveying fluid. Journal of Sound and Vibration, 311(1-2): 408-420. doi: 10.1016/j.jsv.2007.09.011 [87] Khazaee M, Khadem S E, Moslemi A, Abdollahi A. 2020. A comparative study on optimization of multiple essentially nonlinear isolators attached to a pipe conveying fluid. Mechanical Systems and Signal Processing, 141: 106442. doi: 10.1016/j.ymssp.2019.106442 [88] Koo G H, Park Y S. 1996. Vibration analysis of a 3-dimensional piping system conveying fluid by wave approach. International Journal of Pressure and Vessels Piping, 67: 249-256. doi: 10.1016/0308-0161(95)00022-4 [89] Kunieda M, Chiba T, Kobayashi H. 1987. Positive use of damping devices for piping systems—Some experiences and new proposals. Nuclear Engineering and Design, 104(2): 107-120. doi: 10.1016/0029-5493(87)90292-5 [90] Kutin J, Bajsić I. 2014. Fluid-dynamic loading of pipes conveying fluid with a laminar mean-flow velocity profile. Journal of Fluids and Structures, 50: 171-183. doi: 10.1016/j.jfluidstructs.2014.05.014 [91] Ledezma-Ramírez D F, Tapia-González P E, Ferguson N, Brennan M, Tang B. 2019. Recent advances in shock vibration isolation: An overview and future possibilities. Applied Mechanics Reviews, 71 (6): 060802. [92] Lee Y S, Chun I H. 1991. Vibration characteristics of pipe element containing moving medium by a transfer matrix. Transactions of the KSME (A), 15(1): 366-375. [93] Lee S I, Chung J. 2002. New non-linear modelling for vibration analysis of a straight pipe conveying fluid. Journal of Sound and Vibration, 254(2): 313-325. doi: 10.1006/jsvi.2001.4097 [94] Li Y, Sun Z. 2022. Analysis of planar motion for curved pipe conveying fluid with different types of initial configuration. Journal of Vibration Engineering & Technologies, 10(6): 2033-2048. [95] Li M, Wang L. 2024. Parametric model reduction for a cantilevered pipe conveying fluid via parameter-dependent center and unstable manifolds. International Journal of Non-Linear Mechanics, 160: 104629. doi: 10.1016/j.ijnonlinmec.2023.104629 [96] Li M, Yan H, Wang, L. 2023. Nonlinear model reduction for a cantilevered pipe conveying fluid: A system with asymmetric damping and stiffness matrices. Mechanical Systems and Signal Processing, 188: 109993. doi: 10.1016/j.ymssp.2022.109993 [97] Li M, Yan H, Wang L. 2024. Data-driven model reduction for pipes conveying fluid via spectral submanifolds. International Journal of Mechanical Sciences, 109414. [98] Li Y, Yang Y. 2014. Forced vibration of pipe conveying fluid by the Green function method. Archive of Applied Mechanics, 84(12): 1811-1823. doi: 10.1007/s00419-014-0887-1 [99] Liang X, Zha X, Jiang X, Wang L, Leng J, Cao Z. 2018. Semi-analytical solution for dynamic behavior of a fluid-conveying pipe with different boundary conditions. Ocean Engineering, 163: 183-190. doi: 10.1016/j.oceaneng.2018.05.060 [100] Liu Z, Zhou K, Wang L, Jiang T, Dai H. 2019. Dynamical stability of cantilevered pipe conveying fluid in the presence of linear dynamic vibration absorber. Journal of Computational Applied Mechanics, 50(1): 182-190. [101] Lottati I, Kornecki A. 1986. The effect of an elastic foundation and of dissipative forces on the stability of fluid-conveying pipes. Journal of Sound and Vibration, 109(2): 327-338. doi: 10.1016/S0022-460X(86)80012-8 [102] Lu Z-Q, Chen J, Ding H, Chen L-Q. 2022. Energy harvesting of a fluid-conveying piezoelectric pipe. Applied Mathematical Modelling, 107: 165-181. doi: 10.1016/j.apm.2022.02.027 [103] Łuczko J, Czerwiński A. 2019. Three-dimensional dynamics of curved pipes conveying fluid. Journal of Fluids and Structures, 91: 102704. doi: 10.1016/j.jfluidstructs.2019.102704 [104] Lundgren T S, Sethna P R, Bajaj A K. 1979. Stability boundaries for flow induced motions of tubes with an inclined terminal nozzle. Journal of Sound and Vibration, 64(4): 553-571. doi: 10.1016/0022-460X(79)90804-6 [105] Luong K A, Le-Duc T, Lee J. 2023. Deep reduced-order least-square method—A parallel neural network structure for solving beam problems. Thin-Walled Structures, 191: 111044. doi: 10.1016/j.tws.2023.111044 [106] Lyu X, Chen F, Ren Q, Tang Y, Ding Q, Yang T. 2020. Ultra-thin piezoelectric lattice for vibration suppression in pipe conveying fluid. Acta Mechanica Solida Sinica, 33(6): 770-780. doi: 10.1007/s10338-020-00174-z [107] Ma Y, You Y, Chen K, Hu L, Feng A. 2023. Application of harmonic differential quadrature (HDQ) method for vibration analysis of pipes conveying fluid. Applied Mathematics and Computation, 439: 127613. doi: 10.1016/j.amc.2022.127613 [108] Mamaghani A E, Khadem S E, Bab S. 2016. Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink. Nonlinear Dynamics, 86(3): 1761-1795. doi: 10.1007/s11071-016-2992-x [109] Mao X, Ding H, Chen L. 2021. Bending vibration control of pipes conveying fluids by nonlinear torsional absorbers at the boundary. Science China Technological Sciences, 64(8): 1690-1704. doi: 10.1007/s11431-020-1791-2 [110] Mao X-Y, Jing J, Ding H, Chen L-Q. 2023. Dynamics of axially functionally graded pipes conveying fluid. Nonlinear Dynamics, 111(12): 11023-11044. doi: 10.1007/s11071-023-08470-2 [111] Marzani A, Mazzotti M, Viola E, Vittori P, Elishakoff I. 2012. FEM formulation for dynamic instability of fluid-conveying pipe on nonuniform elastic foundation. Mechanics Based Design of Structures and Machines, 40(1): 83-95. doi: 10.1080/15397734.2011.618443 [112] Misra A K, Païdoussis M P, Van K S. 1988a. On the dynamics of curved pipes transporting fluid. Part I: Inextensible theory. Journal of Fluids and Structures, 2(3): 221-244. [113] Misra A K, Païdoussis M P, Van K S. 1988b. On the dynamics of curved pipes transporting fluid Part II: Extensible theory. Journal of Fluids and Structures, 2(3): 245-261. doi: 10.1016/S0889-9746(88)80010-0 [114] Modarres-Sadeghi Y, Païdoussis M P. 2009. Nonlinear dynamics of extensible fluid-conveying pipes, supported at both ends. Journal of Fluids and Structures, 25 (3): 535-543. [115] Modarres-Sadeghi Y, Semler C, Wadham-Gagnon M, Païdoussis M P. 2007. Dynamics of cantilevered pipes conveying fluid. Part 3: Three-dimensional dynamics in the presence of an end-mass. Journal of Fluids and Structures, 23(4): 589-603. [116] Ni Q, Huang Y. 2000. Differential quadrature method to stability analysis of pipes conveying fluid with spring support. Acta Mechanica Solida Sinica, 13(4): 320-327. [117] Ni Q, Tang M, Wang Y, Wang L. 2014. In-plane and out-of-plane dynamics of a curved pipe conveying pulsating fluid. Nonlinear Dynamics, 75(3): 603-619. doi: 10.1007/s11071-013-1089-z [118] Ni Q, Wang L, Qian Q. 2006. Bifurcations and chaotic motions of a curved pipe conveying fluid with nonlinear constraints. Computers & Structures, 84(10-11): 708-717. [119] Ni Q, Wang Y, Tang M, Luo Y, Yan H, Wang L. 2015. Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints. Nonlinear Dynamics, 81(1-2): 893-906. doi: 10.1007/s11071-015-2038-9 [120] Niordson Fin. 1953. Vibrations of a cylindrical tube containing flowing fluid. Lindståhl. [121] Olson L G, Jamison D. 1997. Application of a general purpose finite element method to elastic pipes conveying fluid. Journal of Fluids and Structures, 11(2): 207-222. doi: 10.1006/jfls.1996.0073 [122] Orolu K O, Fashanu T A, Oyediran A A. 2019. Cusp bifurcation of slightly curved tensioned pipe conveying hot pressurized fluid. Journal of Vibration and Control, 25(5): 1109-1121. doi: 10.1177/1077546318813401 [123] Païdoussis M P. 1970. Dynamics of tubular cantilevers conveying fluid. Journal of Mechanical Engineering Science, 12(2): 85-103. doi: 10.1243/JMES_JOUR_1970_012_017_02 [124] Païdoussis M P. 1987. Flow-induced instabilities of cylindrical structures. Applied Mechanics Reviews, 40(2): 163-175. doi: 10.1115/1.3149530 [125] Païdoussis M P. 1976. Hydroelastic ichthyoid propulsion. Journal of Hydronautics, 10(1): 30-32 [126] Païdoussis M P. 1998. Fluid-structure interactions: Slender structures and axial flow (Vol. 1). Academic press. [127] Païdoussis M P. 2021. Dynamics of cylindrical structures in axial flow: A review. Journal of Fluids and Structures, 107: 103374. doi: 10.1016/j.jfluidstructs.2021.103374 [128] Païdoussis M P. 2022. Pipes conveying fluid: A fertile dynamics problem. Journal of Fluids and Structures, 114: 103664. doi: 10.1016/j.jfluidstructs.2022.103664 [129] Païdoussis M P, Denise J-P. 1972. Flutter of thin cylindrical shells conveying fluid. Journal of Sound and Vibration, 20(1): 9-26. doi: 10.1016/0022-460X(72)90758-4 [130] Païdoussis M P, Issid N T. 1974. Dynamic stability of pipes conveying fluid. Journal of Sound and Vibration, 33(3): 267-294. doi: 10.1016/S0022-460X(74)80002-7 [131] Païdoussis M P, Li G X, Rand R H. 1991. Chaotic motions of a constrained pipe conveying fluid: Comparison between simulation, analysis, and experiment. Journal of Applied Mechanics, 58(2): 559-565. doi: 10.1115/1.2897220 [132] Païdoussis M P, Price S J, De Langre E. 2010. Fluid-structure interactions: Cross-flow-induced instabilities. Cambridge,Cambridge University Press. [133] Païdoussis M P, Semler C. 1993a. Nonlinear and chaotic oscillations of a constrained cantilevered pipe conveying fluid: A full nonlinear analysis. Nonlinear Dynamics, 4(6): 655-670. doi: 10.1007/BF00162236 [134] Païdoussis M P, Li G X. 1993b. Pipes conveying fluid: A model dynamical problem. Journal of fluids and Structures, 7(2): 137-204. doi: 10.1006/jfls.1993.1011 [135] Païdoussis M P, Semler C. 1998. Non-linear dynamics of a fluid-conveying cantilevered pipe with a small mass attached at the free end. International Journal of Non-Linear Mechanics, 33(1): 15-32. doi: 10.1016/S0020-7462(97)00002-4 [136] Païdoussis M P, Semler C, Wadham-Gagnon M, Saaid S. 2007. Dynamics of cantilevered pipes conveying fluid. Part 2: Dynamics of the system with intermediate spring support. Journal of Fluids and Structures, 23(4): 569-587. [137] Païdoussis M P, Semler C. 1993b. Nonlinear dynamics of a fluid-conveying cantilevered pipe with an intermediate spring support. Journal of Fluids and Structures, 7(3): 269-298. doi: 10.1006/jfls.1993.1017 [138] Panda L N, Kar R C. 2008. Nonlinear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances. Journal of Sound and Vibration, 309(3-5): 375-406. doi: 10.1016/j.jsv.2007.05.023 [139] Peng G, Xiong Y, Gao Y, Liu L, Wang M, Zhang Z. 2018. Non-linear dynamics of a simply supported fluid-conveying pipe subjected to motion-limiting constraints: Two-dimensional analysis. Journal of Sound and Vibration, 435: 192-204. doi: 10.1016/j.jsv.2018.08.018 [140] Pisarski D, Konowrocki R, Szmidt T. 2018. Dynamics and optimal control of an electromagnetically actuated cantilever pipe conveying fluid. Journal of Sound and Vibration, 432: 420-436. doi: 10.1016/j.jsv.2018.06.045 [141] Qu Y, Metrikine A V. 2021. Modelling of coupled cross-flow and in-line vortex-induced vibrations of flexible cylindrical structures. Part I: Model description and validation. Nonlinear Dynamics, 103(4): 3059-3082. [142] Raissi M, Wang Z, Triantafyllou M S, Karniadakis G E. 2019. Deep learning of vortex induced vibrations. Journal of Fluid Mechanics, 861: 119-137 doi: 10.1017/jfm.2018.872 [143] Rechenberger S, Mair D. 2017. Vibration control of piping systems and structures using tuned mass dampers. American Society of Mechanical Engineers. 57953: V03BT03A035. [144] Rong B, Lu K, Rui X T, Ni X J, Tao L, Wang G P. 2018. Nonlinear dynamics analysis of pipe conveying fluid by Riccati absolute nodal coordinate transfer matrix method. Nonlinear Dynamics, 92(2): 699-708. doi: 10.1007/s11071-018-4084-6 [145] Rousselet J, Herrmann G. 1977. Flutter of articulated pipes at finite amplitude. Journal of Applied Mechanics, 44(1): 154-158. doi: 10.1115/1.3423982 [146] Semler C. 1991. Nonlinear dynamics and chaos of a pipe conveying fluid. McGill University, Montreal, Québec, Canada. [147] Semler C, Li G X, Païdoussis M P. 1994. The non-linear equations of motion of pipes conveying fluid. Journal of Sound and Vibration, 169(5): 577-599. doi: 10.1006/jsvi.1994.1035 [148] Semler C, Païdoussis M P. 1995. Intermittency route to chaos of a cantilevered pipe conveying fluid with a mass effect at the free end. Journal of Applied Mechanics, 62(4): 903-907. doi: 10.1115/1.2896019 [149] Seo Y S, Jeong W B, Jeong S H, Oh J S, Yoo W S. 2005. Finite element analysis of forced vibration for a pipe conveying harmonically pulsating fluid. JSME International Journal Series C, 48(4): 688-694. doi: 10.1299/jsmec.48.688 [150] Shabana A A. 1996. An absolute nodal coordinate formulation for the large rotation and deformation analysis of flexible bodies. Chicago. [151] Shabana A A. 1997. Definition of the slopes and the finite element absolute nodal coordinate formulation. Multibody System Dynamics, 1(3): 339-348. doi: 10.1023/A:1009740800463 [152] Shabana A A, Hussien H A, Escalona J L. 1998. Application of the absolute nodal coordinate formulation to large rotation and large deformation problems. Journal of Mechanical Design, 120(2): 188-195. doi: 10.1115/1.2826958 [153] Srinil N, Rega G, Chucheepsakul S. 2004. Three-dimensional non-linear coupling and dynamic tension in the large-amplitude free vibrations of arbitrarily sagged cables. Journal of Sound and Vibration, 269(3-5): 823-852. doi: 10.1016/S0022-460X(03)00137-8 [154] Stangl M, Gerstmayr J, Irschik H. 2008. An alternative approach for the analysis of nonlinear vibrations of pipes conveying fluid. Journal of Sound and Vibration, 310(3): 493-511. doi: 10.1016/j.jsv.2007.06.020 [155] Strefling P C, Hellum A M, Mukherjee R. 2012. Modeling, simulation, and performance of a synergistically propelled ichthyoid. IEEE/ASME Transactions on Mechatronics, 17(1): 36-45. doi: 10.1109/TMECH.2011.2172950 [156] Sugiyama Y, Tanaka Y, Kishi T, Kawagoe, H. 1985. Effect of a spring support on the stability of pipes conveying fluid. Journal of Sound and Vibration, 100(2): 257-270. doi: 10.1016/0022-460X(85)90419-5 [157] Tang D M, Dowell E H. 1988. Chaotic oscillations of a cantilevered pipe conveying fluid. Journal of Fluids and Structures, 2(3): 263-283. doi: 10.1016/S0889-9746(88)80011-2 [158] Tang S, Sweetman B. 2021. A geometrically-exact momentum-based nonlinear theory for pipes conveying fluid. Journal of Fluids and Structures, 100: 103190. doi: 10.1016/j.jfluidstructs.2020.103190 [159] Tang Y, Zhen Y, Fang B. 2018. Nonlinear vibration analysis of a fractional dynamic model for the viscoelastic pipe conveying fluid. Applied Mathematical Modelling, 56: 123-136. doi: 10.1016/j.apm.2017.11.022 [160] Thurman A L, Mote C D. 1969. Nonlinear oscillation of a cylinder containing a flowing fluid. Journal of Engineering for Industry, 91(4): 1147-1155. doi: 10.1115/1.3591763 [161] Tijsseling A S. 1996. Fluid-structure interaction in liquid-filled pipe systems: A review. Journal of Fluids and Structures, 10(2): 109-146. doi: 10.1006/jfls.1996.0009 [162] Wadham-Gagnon M, Paidoussis M P, Semler C. 2007. Dynamics of cantilevered pipes conveying fluid. Part 1: Nonlinear equations of three-dimensional motion. Journal of Fluids and Structures, 23(4): 545-567. [163] Wang L. 2009. A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid. International Journal of Non-Linear Mechanics, 44(1): 115-121. doi: 10.1016/j.ijnonlinmec.2008.08.010 [164] Wang L, Jiang T L, Dai H L. 2017a. Three-dimensional dynamics of supported pipes conveying fluid. Acta Mechanica Sinica, 33(6): 1065-1074. doi: 10.1007/s10409-017-0718-z [165] Wang L, Jiang T L, Dai H L, Ni Q. 2018a. Three-dimensional vortex-induced vibrations of supported pipes conveying fluid based on wake oscillator models. Journal of Sound and Vibration, 422: 590-612. doi: 10.1016/j.jsv.2018.02.032 [166] Wang L, Liu Z Y, Abdelkefi A, Wang Y K, Dai H L. 2017b. Nonlinear dynamics of cantilevered pipes conveying fluid: Towards a further understanding of the effect of loose constraints. International Journal of Non-Linear Mechanics, 95: 19-29. doi: 10.1016/j.ijnonlinmec.2017.05.012 [167] Wang L, Ni Q. 2008. In-plane vibration analyses of curved pipes conveying fluid using the generalized differential quadrature rule. Computers & Structures, 86(1-2): 133-139. [168] Wang Y, Ni Q, Wang L, et al. 2017c. Nonlinear impacting oscillations of pipe conveying pulsating fluid subjected to distributed motion constraints. Journal of Mechanics of Materials and Structures, 12(5): 563-578. doi: 10.2140/jomms.2017.12.563 [169] Wang Y, Wang L, Ni Q, Dai H, Yan H, Luo Y. 2018b. Non-planar responses of cantilevered pipes conveying fluid with intermediate motion constraints. Nonlinear Dynamics, 93(2): 505-524. doi: 10.1007/s11071-018-4206-1 [170] Wu J-S, Shih P-Y. 2001. The dynamic analysis of a multispan fluid-conveying pipe subjected to external load. Journal of Sound and Vibration, 239(2): 201-215. doi: 10.1006/jsvi.2000.3119 [171] Xu J, Li P, Yang Y. 2023a. An application of data-driven modeling for hydroelasticity of an elastically supported semi-circular pipe conveying fluid. Engineering Computations, 40(5): 1195-1227. doi: 10.1108/EC-05-2022-0343 [172] Xu J, Li P, Yang Y. 2023b. Effects of imperfections on the instability of a pipe conveying fluid: Data-driven modeling and instability transition. International Journal of Structural Stability and Dynamics, 2450175. [173] Yan H, Li M, Wang L. 2023. Bifurcation and stability analysis of static equilibrium configuration of curved pipe conveying fluid. European Journal of Mechanics-A/Solids, 97: 104813. doi: 10.1016/j.euromechsol.2022.104813 [174] Yan B, Ma H, Jian B, Wang K, Wu C. 2019. Nonlinear dynamics analysis of a bi-state nonlinear vibration isolator with symmetric permanent magnets. Nonlinear Dynamics, 97(4): 2499-2519. doi: 10.1007/s11071-019-05144-w [175] Yan B, Wang Z, Ma H, Bao H, Wang K, Wu C. 2021a. A novel lever-type vibration isolator with eddy current damping. Journal of Sound and Vibration, 494: 115862. doi: 10.1016/j.jsv.2020.115862 [176] Yan G, Zou H-X, Wang S, Zhao L-C, Wu Z-Y, Zhang W-M. 2021b. Bio-inspired vibration isolation: Methodology and design. Applied Mechanics Reviews, 73 (2): 020801. [177] Yang T, Dang W, Chen L. 2024. Two-dimensional inerter-enhanced nonlinear energy sink. Nonlinear Dynamics, 112(1): 379-401. doi: 10.1007/s11071-023-09056-8 [178] Yang T-Z, Yang X-D, Li Y, Fang B. 2014. Passive and adaptive vibration suppression of pipes conveying fluid with variable velocity. Journal of Vibration and Control, 20(9): 1293-1300. doi: 10.1177/1077546313480547 [179] Ye S Q, Ding H, Wei S, et al. 2023. Nonlinear forced vibrations of a slightly curved pipe conveying supercritical fluid. Journal of Vibration and Control, 29(15-16): 3634-3645. doi: 10.1177/10775463221102074 [180] Yuan J R, Ding H. 2022. Dynamic model of curved pipe conveying fluid based on the absolute nodal coordinate formulation. International Journal of Mechanical Sciences, 232: 107625. doi: 10.1016/j.ijmecsci.2022.107625 [181] Yuan J R, Ding H. 2023. Three-dimensional dynamic model of the curved pipe based on the absolute nodal coordinate formulation. Mechanical Systems and Signal Processing, 194: 110275. doi: 10.1016/j.ymssp.2023.110275 [182] Yuan J R, Fan X, Shu S, et al. 2022. Free vibration analysis and numerical simulation of slightly curved pipe conveying fluid based on Timoshenko beam theory. International Journal of Applied Mechanics, 14(02): 2250014. doi: 10.1142/S1758825122500144 [183] Zang J, Cao R Q, Zhang Y W. 2021. Steady-state response of a viscoelastic beam with asymmetric elastic supports coupled to a lever-type nonlinear energy sink. Nonlinear Dynamics, 105: 1327-1341. doi: 10.1007/s11071-021-06625-7 [184] Zhang Y L, Chen L Q. 2013. External and internal resonances of the pipe conveying fluid in the supercritical regime. Journal of Sound and Vibration, 332(9): 2318-2337. doi: 10.1016/j.jsv.2012.12.010 [185] Zhang T, Ouyang H, Zhang Y O, Lv B L. 2016. Nonlinear dynamics of straight fluid-conveying pipes with general boundary conditions and additional springs and masses. Applied Mathematical Modelling, 40(17-18): 7880-7900. doi: 10.1016/j.apm.2016.03.050 [186] Zhang T, Yan R, Zhang S, Yang D, Chen A. 2024. Application of Fourier feature physics-information neural network in model of pipeline conveying fluid. Thin-Walled Structures, 198: 111693. doi: 10.1016/j.tws.2024.111693 [187] Zhao X-Y, Zhang Y-W, Ding H, Chen L-Q. 2018. Vibration suppression of a nonlinear fluid-conveying pipe under harmonic foundation displacement excitation via nonlinear energy sink. International Journal of Applied Mechanics, 10(09): 1850096. doi: 10.1142/S1758825118500965 [188] Zhou C, Yang Y, Wang J et al. 2021. Ferromagnetic soft catheter robots for minimally invasive bioprinting. Nat Commun, 12: 5072. [189] Zhou X, Dai H-L, Wang L. 2018. Dynamics of axially functionally graded cantilevered pipes conveying fluid. Composite Structures, 190: 112-118. doi: 10.1016/j.compstruct.2018.01.097 [190] Zhou K, Ni Q, Chen W, Dai H L, Hagedorn P, Wang L. 2021a. Static equilibrium configuration and nonlinear dynamics of slightly curved cantilevered pipe conveying fluid. Journal of Sound and Vibration, 490: 115711. doi: 10.1016/j.jsv.2020.115711 [191] Zhou K, Ni Q, Chen W, Dai H, Peng Z, Wang L. 2021b. New insight into the stability and dynamics of fluid-conveying supported pipes with small geometric imperfections. Applied Mathematics and Mechanics, 42(5): 703-720. doi: 10.1007/s10483-021-2729-6 [192] Zhou K, Ni Q, Guo Z L, Yan H, Dai H L, Wang L. 2022a. Nonlinear dynamic analysis of cantilevered pipe conveying fluid with local rigid segment. Nonlinear Dynamics, 109(3): 1571-1589. doi: 10.1007/s11071-022-07516-1 [193] Zhou K, Ni Q, Wang L, Dai H L. 2020. Planar and non-planar vibrations of a fluid-conveying cantilevered pipe subjected to axial base excitation. Nonlinear Dynamics, 99(4): 2527-2549. doi: 10.1007/s11071-020-05474-0 [194] Zhou J, Xu D, Bishop S. 2015. A torsion quasi-zero stiffness vibration isolator. Journal of Sound and Vibration, 338: 121-133. doi: 10.1016/j.jsv.2014.10.027 [195] Zhou K, Yi H R, Dai H L, Yan H, Guo Z L, Xiong F R, Ni Q, Hagedorn P, Wang L. 2022b. Nonlinear analysis of L-shaped pipe conveying fluid with the aid of absolute nodal coordinate formulation. Nonlinear Dynamics, 107(1): 391-412. doi: 10.1007/s11071-021-07016-8 [196] Zhou S, Yu T J, Yang X D, Zhang W. 2017. Global dynamics of pipes conveying pulsating fluid in the supercritical regime. International Journal of Applied Mechanics, 09(02): 1750029. doi: 10.1142/S1758825117500296 [197] Zhu B, Guo Y, Li Y D, Wang Y Q. 2023. Three-dimensional nonlinear vibrations of slightly curved cantilevered pipes conveying fluid. Journal of Fluids and Structures, 123: 104018. doi: 10.1016/j.jfluidstructs.2023.104018 -





 下载:
下载: