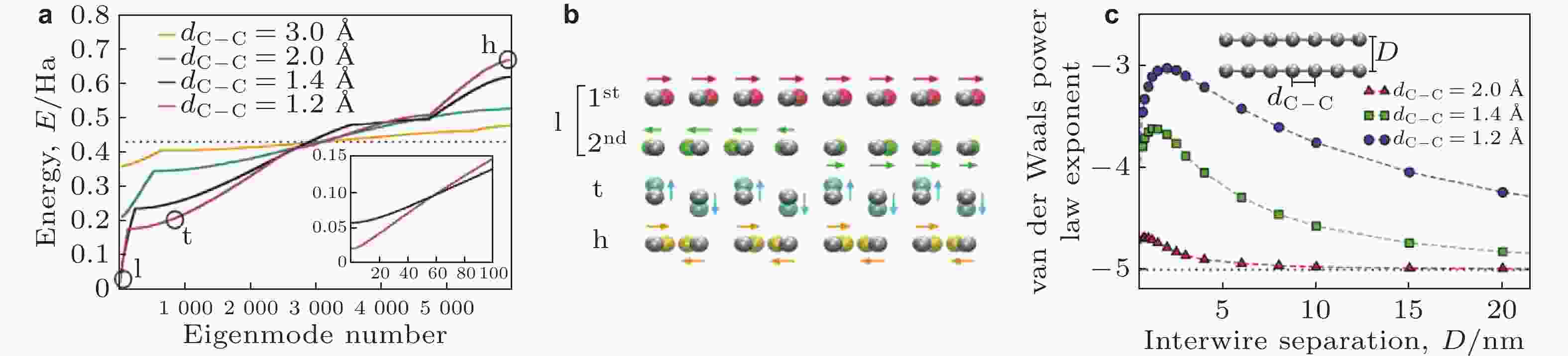Mechanical behaviors of micro-nano systems associated with van der Waals interaction
-
摘要: 起源于量子和热力学涨落的范德华作用在自然界和人造系统中无处不在. 准确描述范德华作用对认识微纳材料及系统的力学行为及其精准设计尤为关键. 本文综述了依赖范德华作用的微纳尺度力学行为方面的最新研究进展. 首先, 简要介绍了适用于原子与分子体系的范德华理论, 如对势近似法、非局域范德华泛函、绝热连接涨落耗散定理和多体色散方法等, 以及适用于连续介质体系的解析、半解析和数值Lifshitz理论等描述方法; 其次, 梳理了范德华作用对二维材料、微纳机电系统等体系典型力学行为的影响; 接着讨论了范德华斥力、非单调范德华势阱、范德华扭转力矩、范德华翻转力矩、范德华屏蔽等新颖效应; 最后总结了范德华理论当前的局限和所面临的挑战, 并展望了未来的发展趋势.Abstract: van der Waals (vdW) interactions originating from quantum and thermal fluctuations are ubiquitous in natural and artificial systems. Accurate descriptions and characterizations of vdW interactions are crucial to understanding the mechanical behavior and realizing the mechanical design of micro-/nano-systems. This review summarized recent research progresses on vdW-dependent mechanical behaviors of micro-/nano-systems. First, we introduced vdW theories for atomic and molecular systems, including pairwise approximation, nonlocal density functional theory, adiabatic-connection fluctuating-dissipation theorem and many-body dispersion theory, as well as theories for continuum systems, including analytic, semi-analytic and numerical Lifshitz theory. Then, we reviewed the effects of vdW interactions on typical mechanical behaviors of two-dimensional materials and nano- and micro-electromechanical systems. We also discussed fascinating effects emerged from vdW interaction, including repulsive vdW force, non-monotonic vdW trap, Casimir rotational torque, Casimir flipping torque and vdW screening. Finally, we analyzed limitations of current vdW theories and presented the outlook for future development.
-
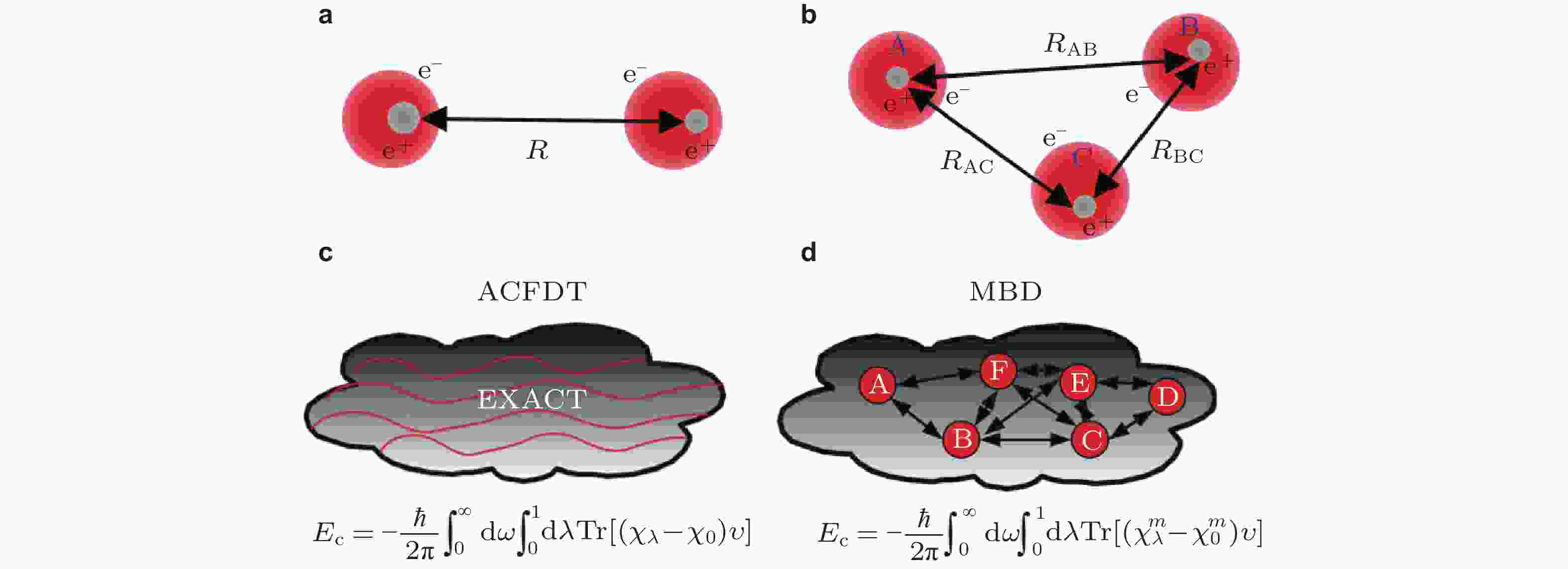
图 1 微观原子分子体系范德华作用示意图. (a) 瞬时涨落偶极矩致双原子范德华作用, (b) 三原子间范德华作用Axilrod–Teller–Muto项, (c) 基于绝热连接涨落耗散定理的精确关联能表述方法示意图 (Woods et al. 2016), (d) 基于耦合量子简谐振子的多体色散表述方法示意图 (Woods et al. 2016)
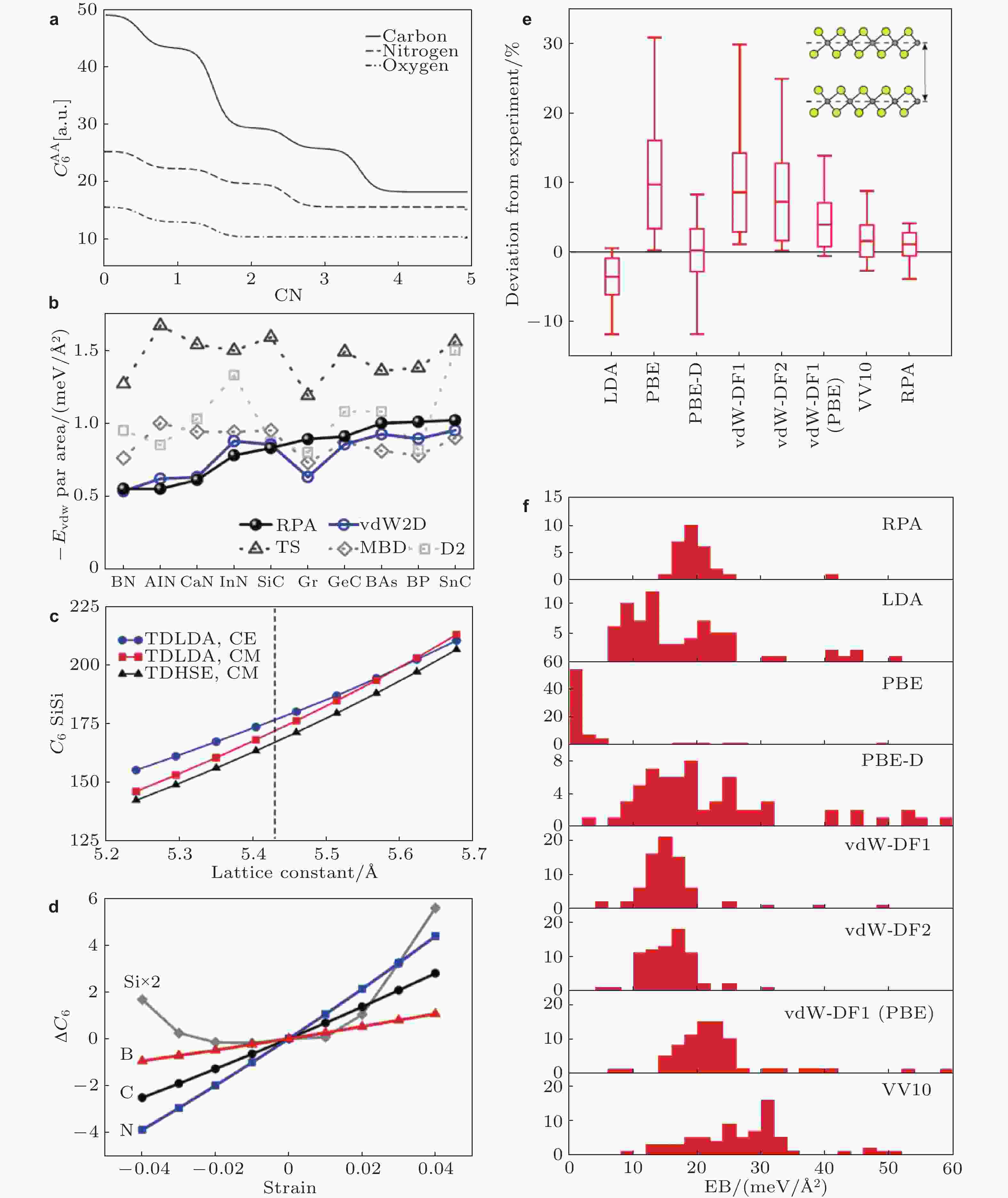
图 2 (a) 不同配位数下C-C、N-N和O-O间C6系数(Grimme et al. 2010), (b) 不同范德华方法预测的双层类石墨烯晶体层间范德华能(Liu et al. 2020), (c) 立方硅中C6系数与晶格常数的依赖关系(Zhang et al. 2011), (d) 石墨烯、h-BN和硅烯面内应变依赖的C6系数(Liu et al. 2020), (e) 常用范德华泛函下对范德华晶体层间距的预测与实验值的差异(Björkman et al. 2012a), (f) 常用范德华泛函所预测范德华晶体结合能的分布(Björkman et al. 2012a)
图 3 (a) 范德华作用理论的发展过程(Casimir & Hendrick 1948, Lifshitz 1956, Canaguier-Durand et al. 2009, Rahi et al. 2009, Reid et al. 2009), (b) 邻近力近似示意图(Jiang et al. 2023)
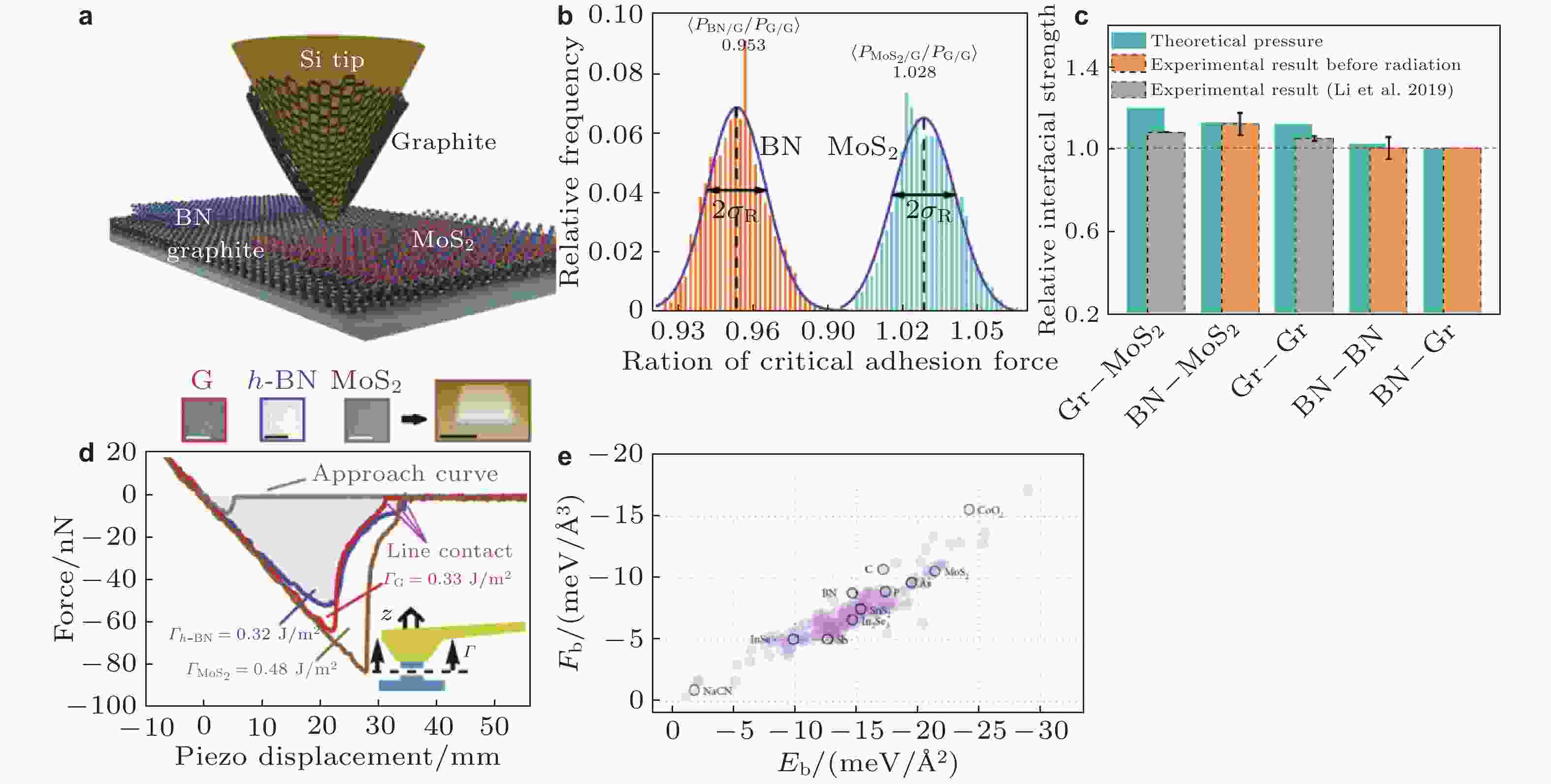
图 4 (a) 石墨层包裹的AFM针尖与h-BN、MoS2、石墨表面接触的示意图(Li et al. 2019); (b) 石墨与石墨、h-BN及MoS2间的界面脱附力相对强度测量值(Li et al. 2019); (c) 5种异质界面相对脱附强度的实验值与vdW2D预测值(Li et al. 2021); (d) 同质范德华晶体界面的黏附力(Rokni & Lu 2020); (e) 230种二维晶体的层间结合能和临界脱附力的理论预测值(Tang et al. 2022)
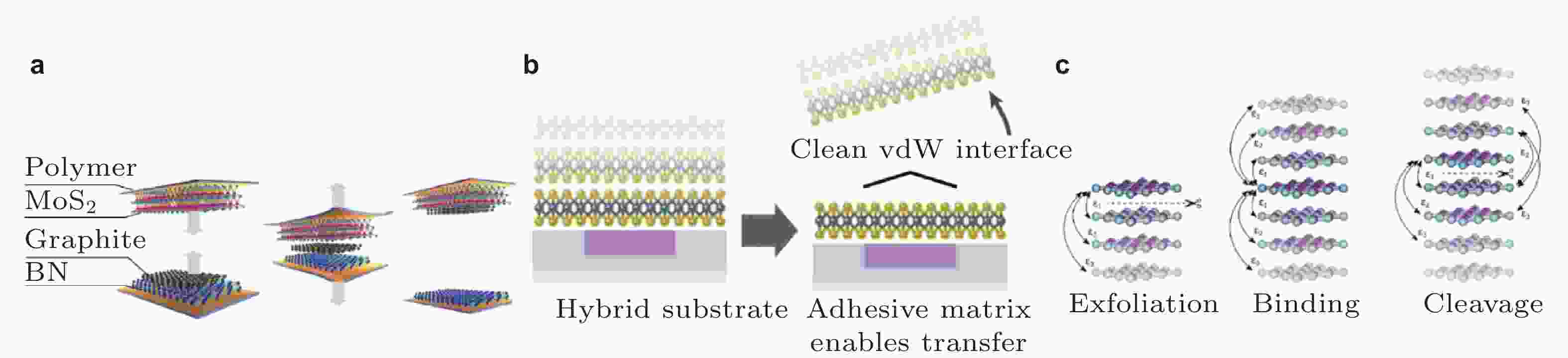
图 5 (a) 利用界面临界脱附力的差异将h-BN表面的石墨片转移至MoS2表面(Li et al. 2019); (b) 利用MoS2-金属的强界面作用, 将单层MoS2晶体从体相转移至弱作用的SiO2表面(Satterthwaite et al. 2024); (c) 范德华晶体剥离能、结合能、解理能的定义(Björkman et al. 2012b)
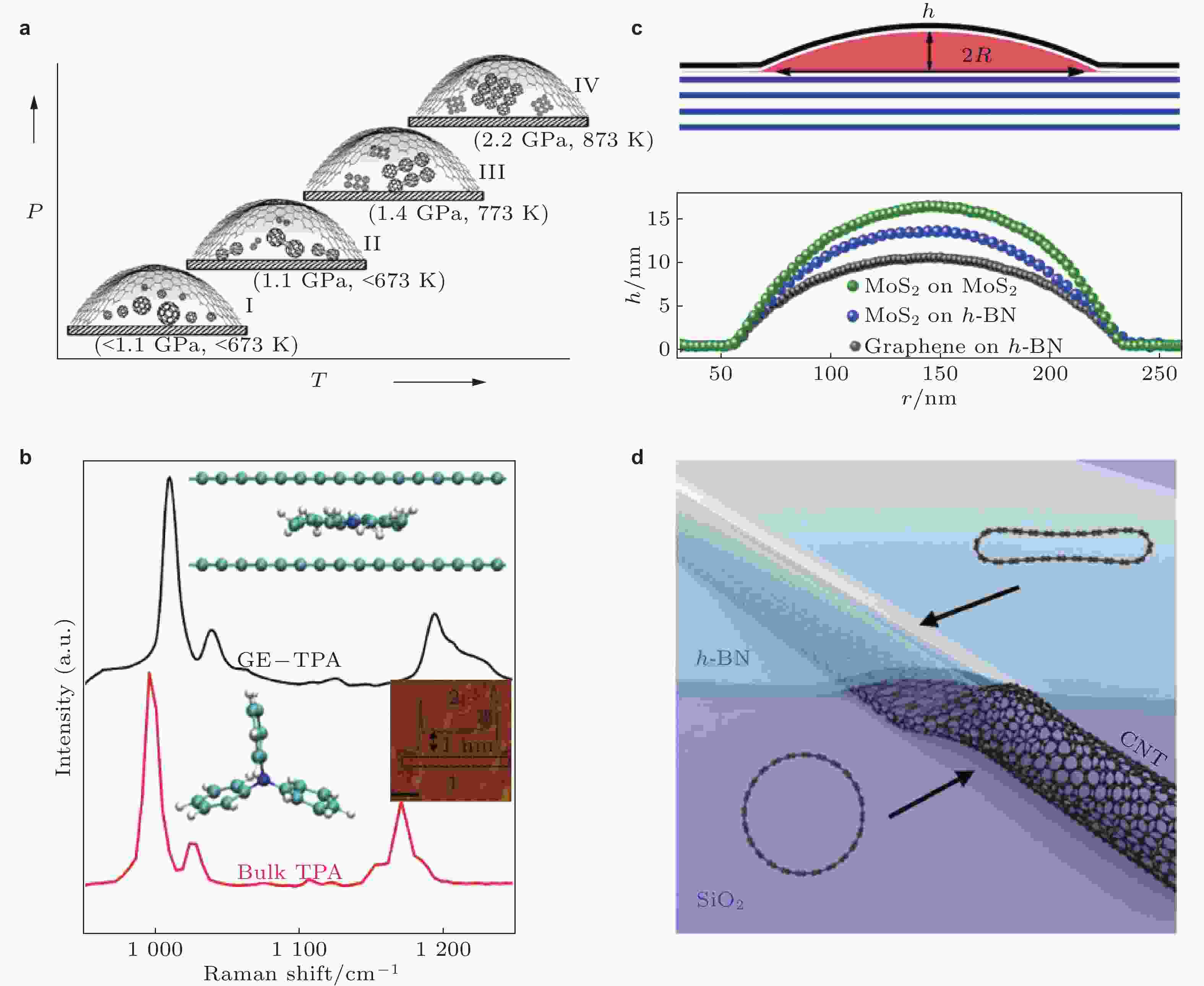
图 6 (a) 富勒烯分子在石墨烯鼓泡施加的高温高压环境下发生聚合反应(Lim et al. 2014); (b) 双层石墨烯包裹的TPA分子结构(上方插图)和拉曼光谱, 体相TPA分子结构(下方插图)和拉曼光谱(Vasu et al. 2016); (c) 二维晶体鼓泡示意图(上侧)和鼓泡的剖面形貌(下侧)(Khestanova et al. 2016); (d) h-BN与基底的范德华压强导致被包裹的碳管坍塌示意图(Hu et al. 2024)
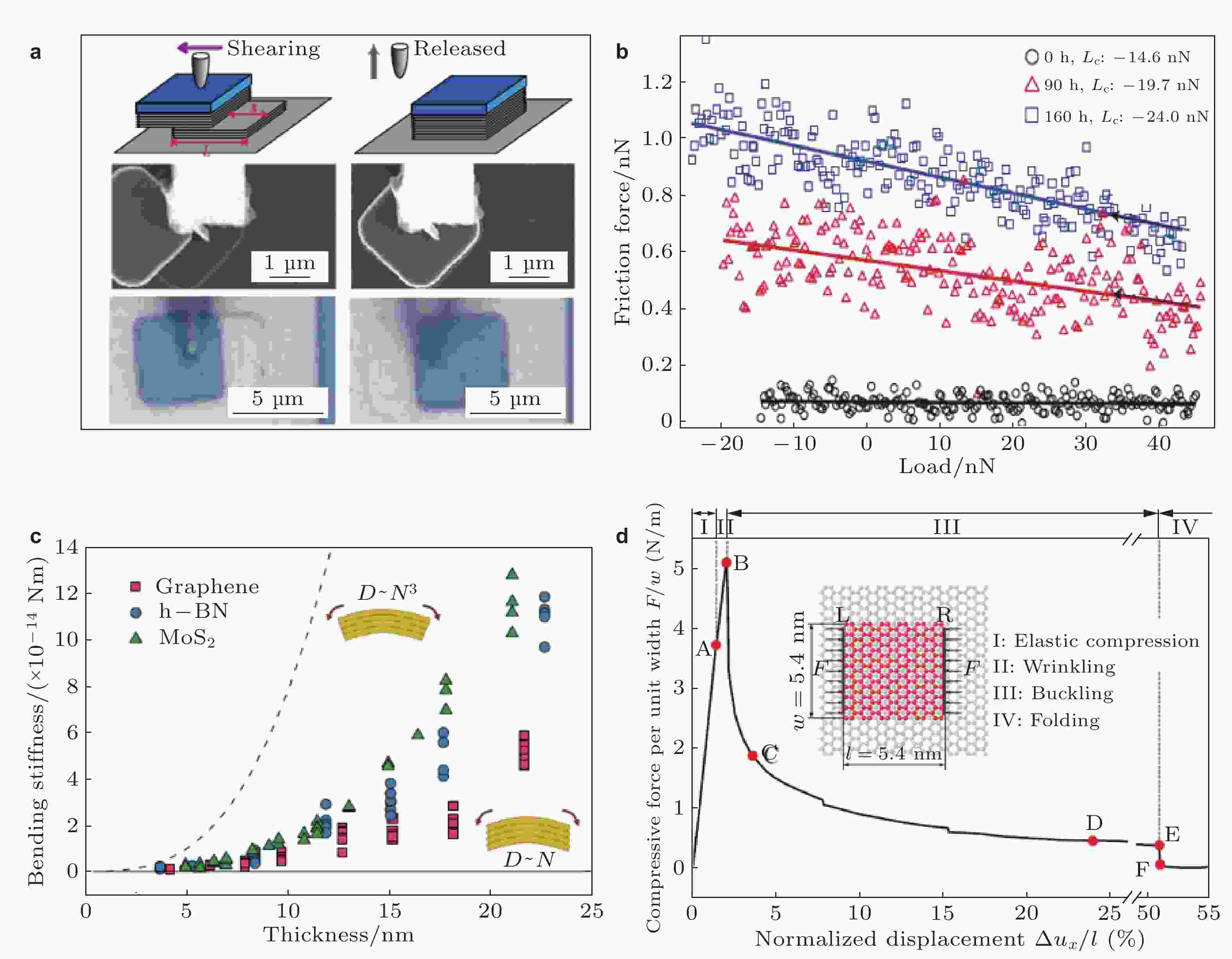
图 7 (a) 通过针尖带动与之接触的几层石墨薄片发生层间剪切, 形成石墨上的自回退装置的示意图(上侧), 此过程的SEM图像(中间), 光学显微镜图像(下侧)(Liu et al. 2012); (b) 不同放置时测得同一针尖与石墨表面的摩擦−载荷曲线(Deng et al. 2012); (c) 石墨烯、h-BN和MoS2弯曲刚度−厚度关系(Wang et al. 2019); (d) 石墨烯衬底上单层石墨烯片的压应力与归一化位移曲线(Yang et al. 2016)
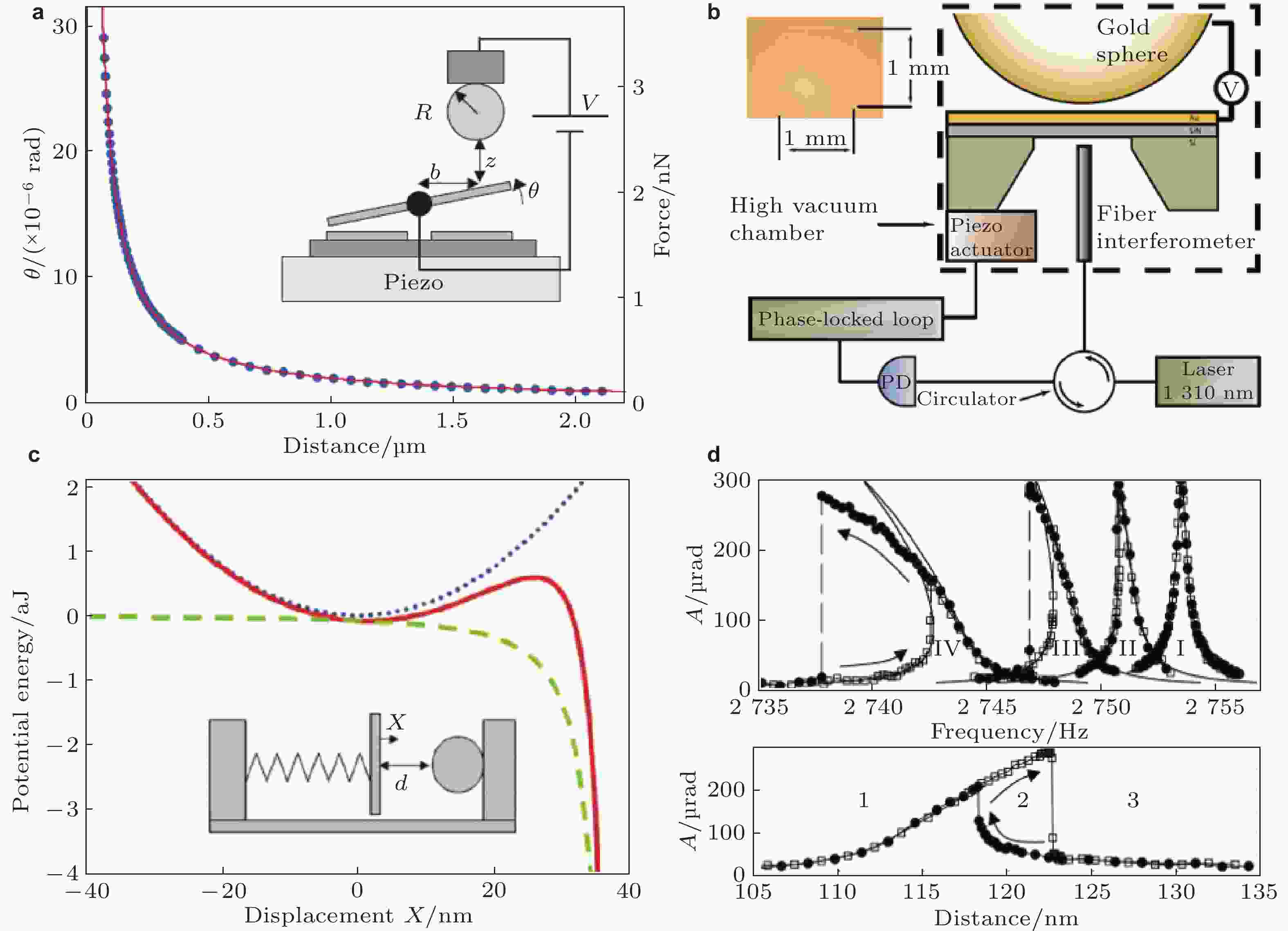
图 8 (a) 电容法测量的卡西米尔力和转角−距离关系, 插图为实验装置示意图(Chan et al. 2001a); (b) 机械共振法测量卡西米尔力示意图(Garcia-Sanchez et al. 2012); (c) 弹性势能(蓝色虚线), 卡西米尔能(绿色虚线)和总势能(红色实线)与平板位移的关系, 插图为非线性卡西米尔振荡器的模型(Chan et al. 2001b); (d) 卡西米尔力对线性振荡器频响的滞后效应(上侧), 激励频率固定时, 振幅随距离的关系(下侧)(Chan et al. 2001b)
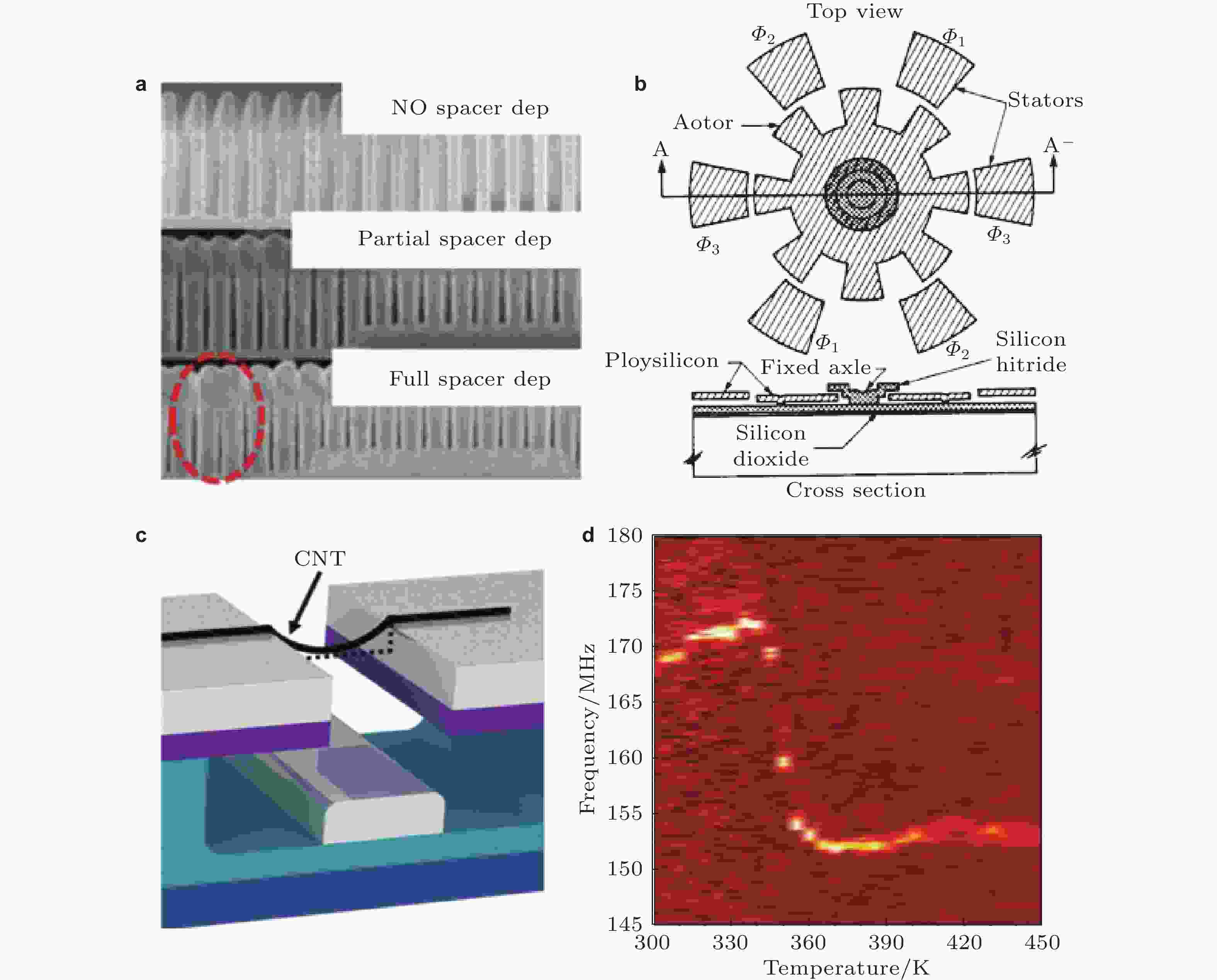
图 9 (a) 鳍式场效应晶体管栅极在沉积隔离层时发生的弯曲, 红圈位置发生屈曲和黏附(Xie et al. 2016); (b) 静电式步进微电机俯视图与剖面图(Fan et al. 1988); (c) 电极沟槽间碳纳米管装置示意图(Aykol et al. 2014); (d)碳纳米管温度-共振频率曲线(Aykol et al. 2014)
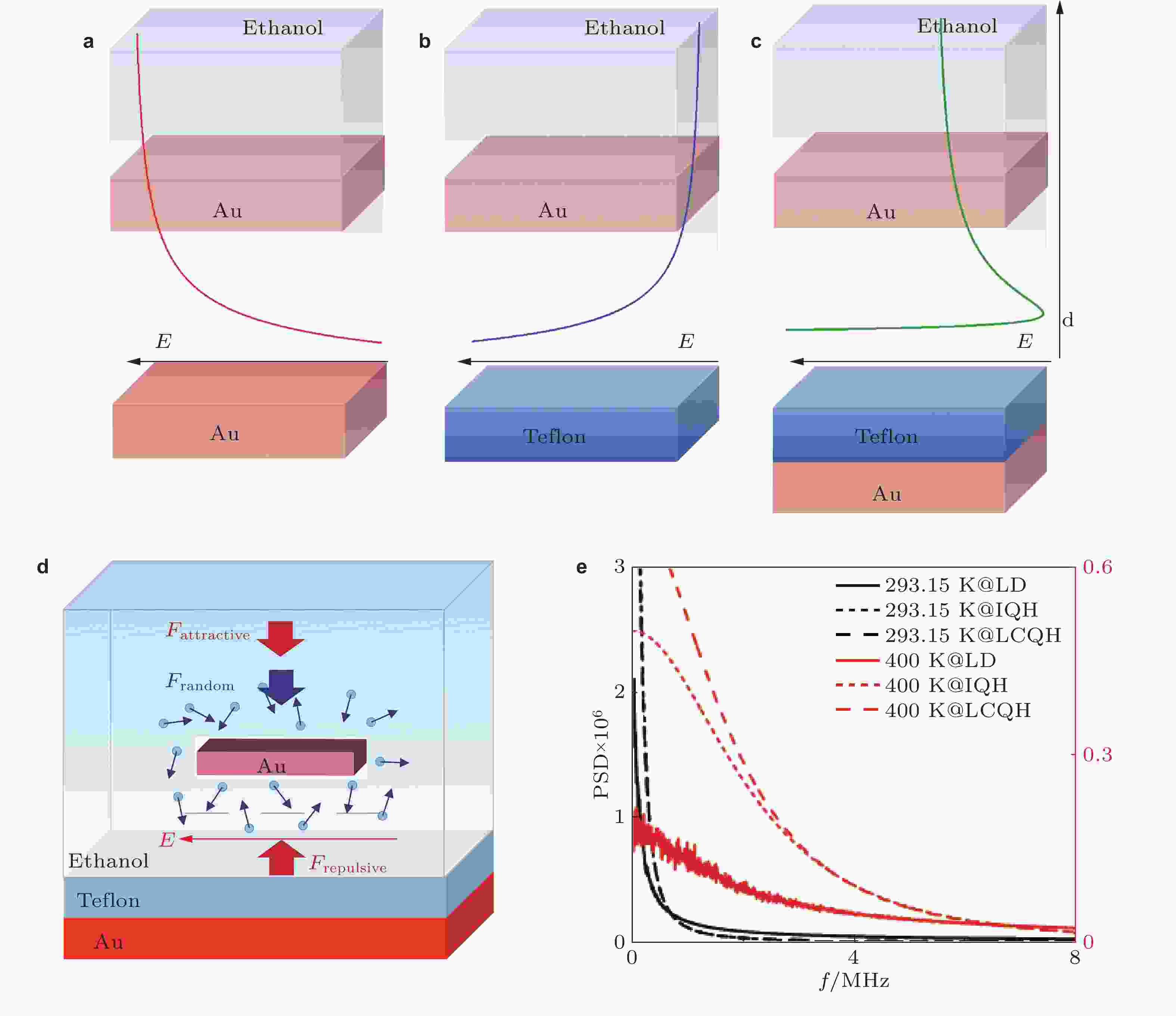
图 10 (a) 乙醇环境下Au板与Au板间的范德华吸引势; (b) 乙醇环境下Au板与Teflon板间的范德华排斥势; (c) 乙醇环境下Au板与Teflon/Au板间的非单调范德华势阱; (d) 沿法向范德华势阱控制下的一维布朗振子(Chen et al. 2024); (e) 具有孔洞阵列的金微板在范德华势阱中的动力学谱密度, 实线为朗之万仿真结果, 虚线为两种准简谐近似结果(Chen et al. 2024)
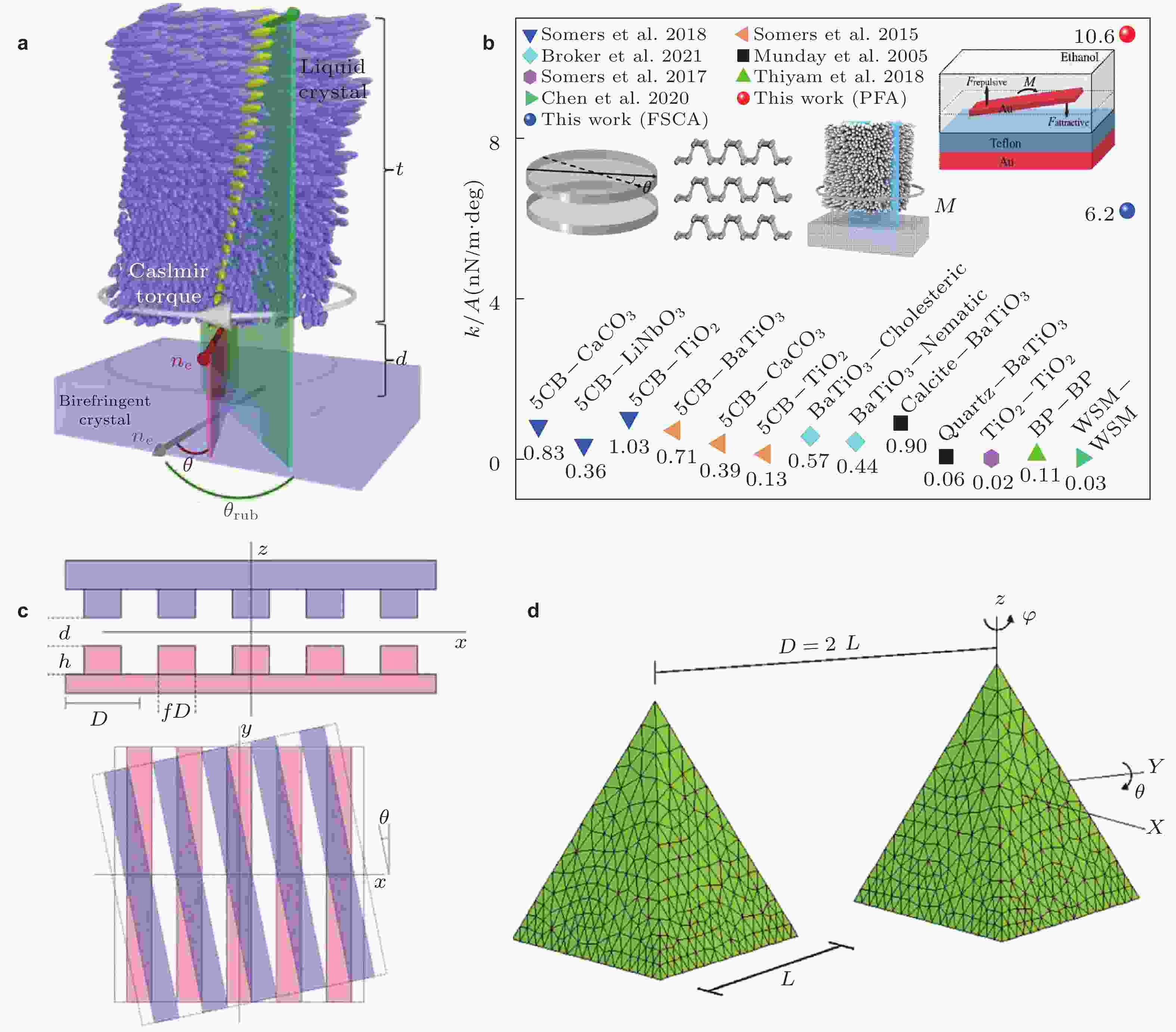
图 11 (a) 卡西米尔扭矩测量装置(Somers et al. 2018); (b) 范德华势阱中悬浮板的卡西米尔翻转力矩与已报导的材料介电各向异性致卡西米尔扭转力矩, 纵坐标为单位面积力矩刚度系数(Somers et al. 2018, 2015, 2017; Broker et al. 2021; Munday et al. 2005; Thiyam et al. 2018; Chen et al. 2020;Jiang et al. 2023); (c) 一维光栅结构相互作用示意图(Antezza et al. 2020); (d) 相互作用的正四面体(Reid 2009)
图 12 (a) 一维碳链在不同晶格常数下的多体色散本征模态频谱(Ambrosetti et al. 2016), (b)不同能量本征模态的极化模式示意图(Ambrosetti et al. 2016), (c) 平行链碳间范德华能与间距幂律关系(Ambrosetti et al. 2016)
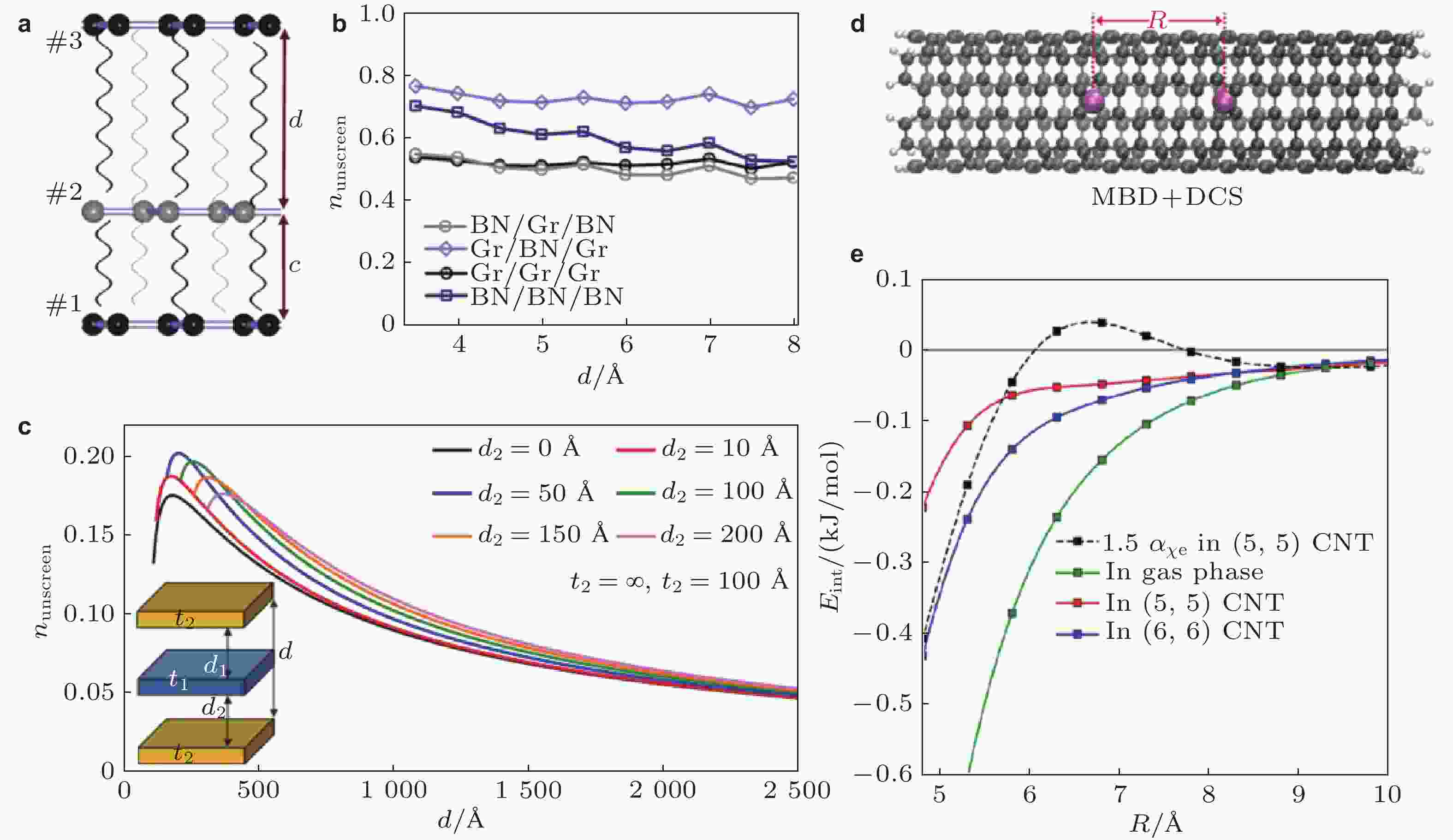
图 13 (a) 三层类石墨烯结构间范德华作用示意图, #1、#2和#3表示AB、CA和AB堆垛的类石墨烯材料, 黑色和灰色波浪线代表不带屏蔽和带屏蔽的范德华作用(Liu et al. 2018); (b) 层#1与层#3间未被屏蔽范德华能的比例与层间距的关系(Liu et al. 2018); (c) 半无限厚h-BN板间范德华能被中间硅板屏蔽比例与间距关系(Yang et al. 2021); (d) 碳纳米管与封装其中的两个氙原子结构示意图(Stöhr et al. 2021); (e) 不同环境下两个氙原子间范德华能与间距关系(Stöhr et al. 2021)
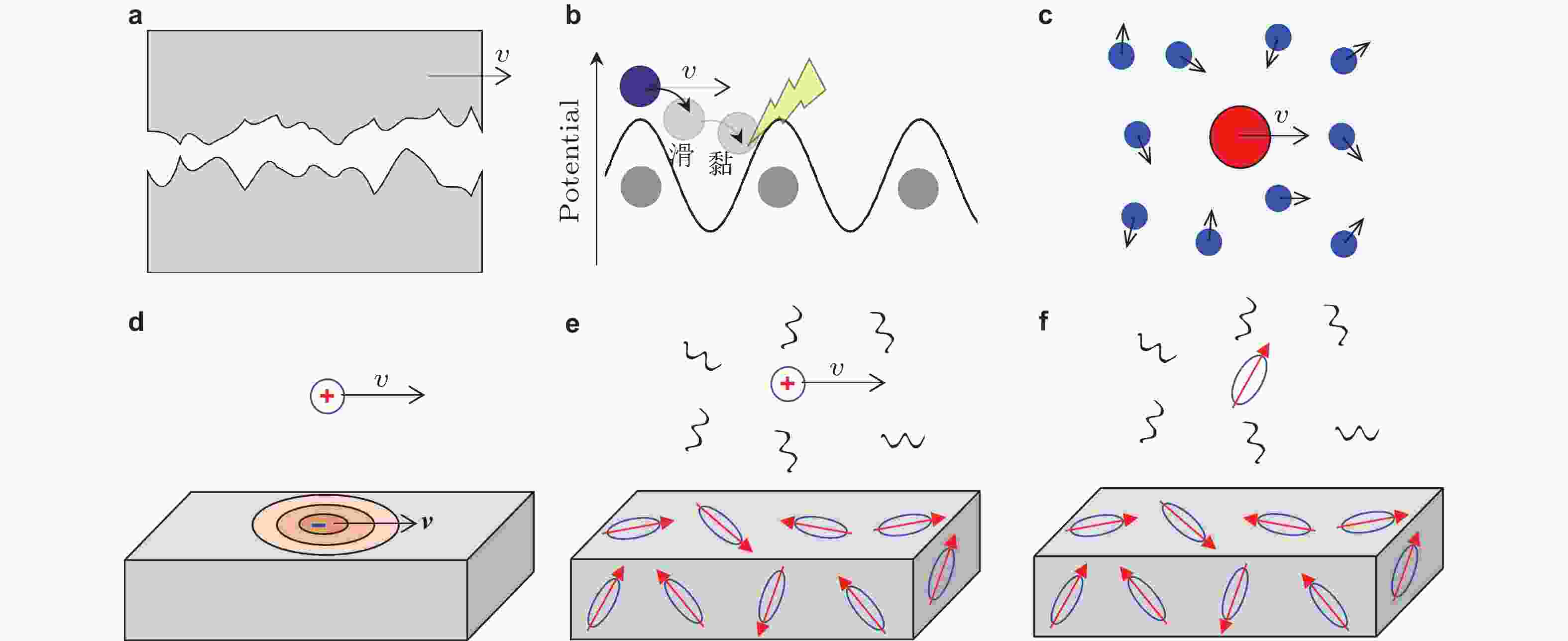
图 14 (a) 宏观摩擦机械啮合模型; (b) 摩擦附在周期性分子势能面上的黏-滑过程(Zhong & Tomanek 1990); (c) 流体内部球体受热力学涨落致随机碰撞, 蓝色表示流体分子; (d) 离子-基底间电子摩擦的焦耳热模型, 基底表层诱导的分布电荷跟随离子移动; (e) 吸收介质电磁涨落致上方离子的电子摩擦示意图, 波浪线表示随机电磁场; (f) 中性原子涨落偶极矩致范德华作用示意图
-
[1] 朗道, 栗弗希兹. 2012. 流体动力学. 李植, 译. 第5版. 北京: 高等教育出版社, 1-608 (Landau, Lifshitz. 2012. Fluid mechanics. Li Z, translate. 5th edition. Beijing: Higher Education Press, 1-608 (in Chinese).Landau, Lifshitz. 2012. Fluid mechanics. Li Z, translate. 5th edition. Beijing: Higher Education Press, 1-608 (in Chinese. [2] 商克栋, 郑韶先, 鞠鹏飞, 等. 2018. 南海海洋大气环境二硫化钼纳米多层薄膜摩擦学行为研究. 摩擦学学报, 38 (4): 417-429 (Shang K D, Zheng S X, Ju P F, et al. 2018. Tribological performance of MoS2/Pb-Ti nano-multilayer coating applied in marine atmospheric environment of South China Sea. Tribology, 38 (4): 417-429 (in Chinese).Shang K D, Zheng S X, Ju P F, et al. 2018. Tribological performance of MoS2/Pb-Ti nano-multilayer coating applied in marine atmospheric environment of South China Sea. Tribology, 38(4): 417-429 (in Chinese. [3] 温诗铸. 2018. 摩擦学原理. 第5版. 北京: 清华大学出版社, 1-484 (Wen S Z. 2018. Principles of tribology. 5th edition. Beijing: Tsinghua University Press, 1-484 (in Chinese)).Wen S Z. 2018. Principles of tribology. 5th edition. Beijing: Tsinghua University Press, 1-484 (in Chinese). [4] Ambrosetti A, Ferri N, DiStasio J R A, et al. 2016. Wavelike charge density fluctuations and van der Waals interactions at the nanoscale. Science, 351(6278): 1171-1176. doi: 10.1126/science.aae0509 [5] Ambrosetti A, Silvestrelli P L. 2019. Faraday-like screening by two-dimensional nanomaterials: A scale-dependent tunable effect. J. Phys. Chem. Lett., 10(9): 2044-2050. doi: 10.1021/acs.jpclett.9b00860 [6] Antezza M, Chan H B, Guizal B, et al. 2020. Giant Casimir torque between rotated gratings and the $\theta $ = 0 anomaly. Phys. Rev. Lett., 124(1): 013903. doi: 10.1103/PhysRevLett.124.013903[7] Aykol M, Hou B, Dhall R, et al. 2014. Clamping instability and van der Waals forces in carbon nanotube mechanical resonators. Nano Lett., 14(5): 2426-2430. doi: 10.1021/nl500096p [8] Barash Y S. 1978. Moment of van der Waals forces between anisotropic bodies. Radiophys. Quantum Electron., 21(11): 1138-1143. doi: 10.1007/BF02121382 [9] Bixon M, Zwanzig R. 1971. Brownian motion of a nonlinear oscillator. J. Stat. Phys., 3(3): 245-260. doi: 10.1007/BF01011383 [10] Björkman T, Gulans A, Krasheninnikov A, et al. 2012a. Are we van der Waals ready. J. Phys.: Condens. Matter, 24(42): 424218. doi: 10.1088/0953-8984/24/42/424218 [11] Björkman T, Gulans A, Krasheninnikov A, et al. 2012b. van der waals bonding in layered compounds from advanced density-functional first-principles calculations. Phys. Rev. Lett., 108(23): 235502. doi: 10.1103/PhysRevLett.108.235502 [12] Boyer T H. 1974. Penetration of the electric and magnetic velocity fields of a nonrelativistic point charge into a conducting plane. Phys. Rev. A, 9(1): 68. doi: 10.1103/PhysRevA.9.68 [13] Broer W, Lu B S, Podgornik R. 2021. Qualitative chirality effects on the Casimir-Lifshitz torque with liquid crystals. Phys. Rev. Res., 3: 033238. [14] Buks E, Roukes M L. 2001. Stiction, adhesion energy, and the Casimir effect in micromechanical systems. Phys. Rev. B, 63(3): 033402. [15] Canaguier-Durand A, Maia N P A, Cavero-Pelaez I, et al. 2009. Casimir interaction between plane and spherical metallic surfaces. Phys. Rev. Lett., 102(23): 230404. doi: 10.1103/PhysRevLett.102.230404 [16] Casimir, Hendrick B G. 1948. On the attraction between two perfectly conducting plates. Proc. K. Ned. Akad. Wet., 51: 793-796. [17] Chan H, Aksyuk V, Kleiman R, et al. 2001a. Nonlinear micromechanical Casimir oscillator. Phys. Rev. Lett., 87(21): 211801. doi: 10.1103/PhysRevLett.87.211801 [18] Chan H, Aksyuk V, Kleiman R, et al. 2001b. Quantum mechanical actuation of microelectromechanical systems by the Casimir force. Science, 291(5510): 1941-1944. doi: 10.1126/science.1057984 [19] Chen F, Kou Z, Jiang Z, et al. 2024. Physical limit of nonlinear brownian oscillators in quantum trap. J. Phys. Chem. Lett., 15: 1719-1725. doi: 10.1021/acs.jpclett.3c03334 [20] Chen L, Chang K. 2020. Chiral-anomaly-driven Casimir-Lifshitz torque between Weyl semimetals. Phys. Rev. Lett., 125: 047402. [21] Chu X, Dalgarno A. 2004. Linear response time-dependent density functional theory for van der Waals coefficients. J. Chem. Phys., 121(9): 4083-4088. doi: 10.1063/1.1779576 [22] Deng Z, Smolyanitsky A, Li Q, et al. 2012. Adhesion-dependent negative friction coefficient on chemically modified graphite at the nanoscale. Nat. Mater., 11(12): 1032-1037. doi: 10.1038/nmat3452 [23] Dienwiebel M, Verhoeven G S, Pradeep N, et al. 2004. Superlubricity of graphite. Phys. Rev. Lett., 92(12): 126101. doi: 10.1103/PhysRevLett.92.126101 [24] Dion M, Rydberg H, Schröder E, et al. 2004. van der Waals density functional for general geometries. Phys. Rev. Lett., 92(24): 246401. doi: 10.1103/PhysRevLett.92.246401 [25] Dobson J F, Wang J, Dinte B P, et al. 2005. Soft cohesive forces. Int. J. Quantum Chem., 101(5): 579-598. doi: 10.1002/qua.20314 [26] Dzyaloshinskii I E, Lifshitz E M, Pitaevskii L P. 1961. The general theory of van der Waals forces. Adv. Phys., 10(38): 165-209. doi: 10.1080/00018736100101281 [27] Fan L S, Tai Y C, Muller R S. 1988. Integrated movable micromechanical structures for sensors and actuators. IEEE Trans. Electron Devices, 35(6): 724-730. doi: 10.1109/16.2523 [28] Franosch T, Grimm M, Belushkin M, et al. 2011. Resonances arising from hydrodynamic memory in brownian motion. Nature, 478(7367): 85-88. doi: 10.1038/nature10498 [29] French R H, Parsegian V A, Podgornik R, et al. 2010. Long range interactions in nanoscale science. Rev. Mod. Phys., 82(2): 1887. doi: 10.1103/RevModPhys.82.1887 [30] Gao H, Yao H. 2004. Shape insensitive optimal adhesion of nanoscale fibrillar structures. Proc. Natl. Acad. Sci., 101(21): 7851-7856. doi: 10.1073/pnas.0400757101 [31] Gao W, Tkatchenko A. 2013. Electronic structure and van der Waals interactions in the stability and mobility of point defects in semiconductors. Phys. Rev. Lett., 111(4): 045501. doi: 10.1103/PhysRevLett.111.045501 [32] Garcia-Sanchez D, Fong K Y, Bhaskaran H, et al. 2012. Casimir force and in situ surface potential measurements on nanomembranes. Phys. Rev. Lett., 109(2): 027202. doi: 10.1103/PhysRevLett.109.027202 [33] Gies H, Klingmüller K. 2006. Casimir effect for curved geometries: Proximity-force-approximation validity limits. Phys. Rev. Lett., 96(22): 220401. doi: 10.1103/PhysRevLett.96.220401 [34] Grimme S. 2004. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem., 25(12): 1463-1473. doi: 10.1002/jcc.20078 [35] Grimme S. 2006. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem., 27(15): 1787-1799. doi: 10.1002/jcc.20495 [36] Grimme S, Antony J, Ehrlich S, et al. 2010. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys, 132(15): 154104. doi: 10.1063/1.3382344 [37] Guo J, Zhao Y. 2004. Influence of van der Waals and Casimir forces on electrostatic torsional actuators. J. Microelectromech. Syst., 13(6): 1027-1035. doi: 10.1109/JMEMS.2004.838390 [38] Harl J, Kresse G. 2008. Cohesive energy curves for noble gas solids calculated by adiabatic connection fluctuation-dissipation theory. Phys. Rev. B, 77(4): 045136. doi: 10.1103/PhysRevB.77.045136 [39] Hartmann M, Ingold G L, Neto P A M. 2018. Advancing numerics for the Casimir effect to experimentally relevant aspect ratios. Phys Scr., 93(11): 114003. doi: 10.1088/1402-4896/aae34e [40] Hiller U. 1971. Form und funktion der hautsinnesorgane bei gekkoniden. Forma Functio, 4: 240-253. [41] Hu C, Chen J, Zhou X, et al. 2024. Collapse of carbon nanotubes due to local high-pressure from van der Waals encapsulation. Nat. Commun., 15(1): 3486. doi: 10.1038/s41467-024-47903-3 [42] Huang J, Rauscher S, Nawrocki G, et al. 2017. Charmm36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods, 14(1): 71-73. doi: 10.1038/nmeth.4067 [43] Jiang Z, Chen F, Kou Z, et al. 2023. Large Casimir flipping torque in quantum trap. J. Phys. Chem. B, 128(1): 350-357. [44] Kardar M, Golestanian R. 1999. The “friction” of vacuum, and other fluctuation-induced forces. Rev. Mod. Phys., 71(4): 1233. doi: 10.1103/RevModPhys.71.1233 [45] Kavokine N, Bocquet M L, Bocquet L. 2022. Fluctuation-induced quantum friction in nanoscale water flows. Nature, 602(7895): 84-90. [46] Khestanova E, Guinea F, Fumagalli L, et al. 2016. Universal shape and pressure inside bubbles appearing in van der Waals heterostructures. Nat. Commun., 7(1): 12587. doi: 10.1038/ncomms12587 [47] Klimchitskaya G, Mohideen U, Mostepanenko V. 2009. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys., 81(4): 1827. doi: 10.1103/RevModPhys.81.1827 [48] Kolmogorov A N, Crespi V H. 2005. Registry-dependent interlayer potential for graphitic systems. Phys. Rev. B, 71(23): 235415. doi: 10.1103/PhysRevB.71.235415 [49] Lebègue S, Harl J, Gould T, et al. 2010. Cohesive properties and asymptotics of the dispersion interaction in graphite by the random phase approximation. Phys. Rev. Lett., 105(19): 196401. doi: 10.1103/PhysRevLett.105.196401 [50] Lee K, Murray É D, Kong L, et al. 2010. Higher-accuracy van der Waals density functional. Phys. Rev. B, 82(8): 081101. doi: 10.1103/PhysRevB.82.081101 [51] Lennard-Jones J E. 1931. Cohesion. Proc. Phys. Soc., 43(5): 461. doi: 10.1088/0959-5309/43/5/301 [52] Leven I, Azuri I, Kronik L, et al. 2014. Inter-layer potential for hexagonal boron nitride. J. Chem. Phys., 140(10): 104106. doi: 10.1063/1.4867272 [53] Levitov L S. 1989. van der Waals’ friction. Europhys. Lett., 8(6): 499-504. doi: 10.1209/0295-5075/8/6/002 [54] Lifshitz E M. 1956. The theory of molecular attractive force between solid bodies. J. Exp. Theor. Phys., 29: 83-94. [55] Lorentz H A. 1907. Abhandlungen über theoretische physik. Teubner, 2: 1907. [56] Li B, Yin J, Liu X, et al. 2019. Probing van der Waals interactions at two-dimensional heterointerfaces. Nat. Nanotechnol., 14(6): 567-572. doi: 10.1038/s41565-019-0405-2 [57] Li B, Liu X, Guo W. 2021. Probing interactions at two-dimensional heterointerfaces by boron nitride-wrapped tip. Nano Res., 14: 692-698. doi: 10.1007/s12274-020-3098-9 [58] Li M, Reimers J R, Dobson J F, et al. 2018. Faraday cage screening reveals intrinsic aspects of the van der Waals attraction. Proc. Natl. Acad. Sci., 115(44): 10295-10302. [59] Liu X, Hermann J, Tkatchenko A. 2016. Communication: Many-body stabilization of non-covalent interactions: Structure, stability, and mechanics of Ag3Co(Cn)6 framework. J. Chem. Phys., 145(24): 241101. doi: 10.1063/1.4972810 [60] Liu X, Zhang Z, Guo W. 2018. van der Waals screening by graphenelike monolayers. Phys. Rev. B, 97(24): 241411. doi: 10.1103/PhysRevB.97.241411 [61] Liu X, Yang J, Guo W. 2020. Semiempirical van der Waals method for two-dimensional materials with incorporated dielectric functions. Phys. Rev. B, 101(4): 045428. doi: 10.1103/PhysRevB.101.045428 [62] Liu Z, Yang J, Grey F, et al. 2012. Observation of microscale superlubricity in graphite. Phys. Rev. Lett., 108(20): 205503. doi: 10.1103/PhysRevLett.108.205503 [63] Lim C H Y X, Nesladek M, Loh K P. 2014. Observing high-pressure chemistry in graphene bubbles. Angew. Chem., Int. Ed., 53(1): 215-219. doi: 10.1002/anie.201308682 [64] Lim C H Y X, Sorkin A, Bao Q, et al. 2013. A hydrothermal anvil made of graphene nanobubbles on diamond. Nat. Commun., 4(1): 1556. [65] London F. 1930. Zur theorie und systematik der molekularkräfte. Z. Angew. Phys., 63(3): 245-279. [66] Mak K F, Lee C, Hone J, et al. 2010. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett., 105(13): 136805. doi: 10.1103/PhysRevLett.105.136805 [67] Marom N, Bernstein J, Garel J, et al. 2010. Stacking and registry effects in layered materials: The case of hexagonal boron nitride. Phys. Rev. Lett., 105(4): 046801. doi: 10.1103/PhysRevLett.105.046801 [68] Mohideen U, Roy A. 1998. Precision measurement of the Casimir force from 0.1 to 0.9 μm. Phys. Rev. Lett., 81(21): 4549. doi: 10.1103/PhysRevLett.81.4549 [69] Munday J N, Capasso F, Parsegian V A. 2009. Measured long-range repulsive Casimir–Lifshitz forces. Nature, 457(7226): 170-173. doi: 10.1038/nature07610 [70] Munday J N, Iannuzzi D, Barash Y, et al. 2005. Torque on birefringent plates induced by quantum fluctuations. Phys. Rev. A, 71: 042102 [71] Neto P M, Lambrecht A, Reynaud S. 2005. Roughness correction to the Casimir force: Beyond the proximity force approximation. Europhys. Lett., 69(6): 924. doi: 10.1209/epl/i2004-10433-9 [72] Neto A C, Guinea F, Peres N M, et al. 2009. The electronic properties of graphene. Rev. Mod. Phys., 81(1): 109. doi: 10.1103/RevModPhys.81.109 [73] Ouyang W, Mandelli D, Urbakh M, et al. 2018. Nanoserpents: Graphene nanoribbon motion on two-dimensional hexagonal materials. Nano Lett., 18(9): 6009-6016. doi: 10.1021/acs.nanolett.8b02848 [74] Parsegian V, Weiss G H. 1972. Dielectric anisotropy and the van der Waals interaction between bulk media. J. Adhes., 3(4): 259-267. doi: 10.1080/00218467208072197 [75] Parsegian V. 2005. Van der Waals forces: A handbook for biologists, chemists, engineers, and physicists. New York: Cambridge University Press, 277-318. [76] Pendry J B. 1997. Shearing the vacuum-quantum friction. J. Phys. Condens. Matter, 9(47): 10301. doi: 10.1088/0953-8984/9/47/001 [77] Persson B, Zhang Z. 1998. Theory of friction: Coulomb drag between two closely spaced solids. Phys. Rev. B, 57(12): 7327. doi: 10.1103/PhysRevB.57.7327 [78] Ponder J W, Case D A. 2003. Force fields for protein simulations. Adv. Protein. Chem., 66: 27-85. [79] Rahi S J, Emig T, Graham N, et al. 2009. Scattering theory approach to electrodynamic Casimir forces. Phys. Rev. D, 80(8): 085021. doi: 10.1103/PhysRevD.80.085021 [80] Rammer J. 2011. Quantum field theory of non-equilibrium states. Cambridge: Cambridge University Press, 79-119. [81] Reid M H, Rodriguez A W, White J, et al. 2009. Efficient computation of Casimir interactions between arbitrary 3D objects. Phys. Rev. Lett., 103(4): 040401. doi: 10.1103/PhysRevLett.103.040401 [82] Reid M H, White J, Johnson S G. 2013. Fluctuating surface currents: An algorithm for efficient prediction of Casimir interactions among arbitrary materials in arbitrary geometries. Phys. Rev. A, 88(2): 022514. doi: 10.1103/PhysRevA.88.022514 [83] Rokni H, Lu W. 2020. Direct measurements of interfacial adhesion in 2d materials and van der Waals heterostructures in ambient air. Nat. Commun., 11(1): 5607. doi: 10.1038/s41467-020-19411-7 [84] Rytov S. 1959. Theory of electrical fluctuations and thermal radiation. Bedford: Air Force Cambridge Research Center, 1-265. [85] Satterthwaite P F, Zhu W, Jastrzebska-Perfect P, et al. 2024. van der Waals device integration beyond the limits of van der Waals forces using adhesive matrix transfer. Nat. Electron., 7(1): 17-28. [86] Schaich W L, Harris J. 1981. Dynamic corrections to van der Waals potentials. J. Phys. F: Met. Phys., 11(1): 65-78. doi: 10.1088/0305-4608/11/1/011 [87] Somers D A, Garrett J L, Palm K J, et al. 2018. Measurement of the Casimir torque. Nature, 564(7736): 386-389. doi: 10.1038/s41586-018-0777-8 [88] Somers D A T, Munday J N. 2015. Rotation of a liquid crystal by the Casimir torque. Phys. Rev. A, 91: 032520. [89] Somers D A, Munday J N. 2017. Casimir-Lifshitz torque enhancement by retardation and intervening dielectrics. Phys. Rev. Lett., 119: 183001. [90] Song Y, Mandelli D, Hod O, et al. 2018. Robust microscale superlubricity in graphite/hexagonal boron nitride layered heterojunctions. Nat. Mater., 17(10): 894-899. doi: 10.1038/s41563-018-0144-z [91] Sparnaay M J. 1958. Measurements of attractive forces between flat plates. Physica, 24(6-10): 751-764. doi: 10.1016/S0031-8914(58)80090-7 [92] Stöhr M, Sadhukhan M, Al-Hamdani Y S, et al. 2021. Coulomb interactions between dipolar quantum fluctuations in van der Waals bound molecules and materials. Nat. Commun., 12(1): 137. doi: 10.1038/s41467-020-20473-w [93] Sun H. 1998. Compass: An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds. J. Phys. Chem. B, 102(38): 7338-7364. doi: 10.1021/jp980939v [94] Tang K, Qi W, Wei Y, et al. 2022. High-throughput calculation of interlayer van der Waals forces validated with experimental measurements. Research, 2022: 9765121. [95] Teodorovich E. 1978. On the contribution of macroscopic van der Waals interactions to frictional force. Proc. R. Soc. London A, 362(1708): 71-77. doi: 10.1098/rspa.1978.0121 [96] Thiyam P, Parashar P, Shajesh K V, et al. 2018. Distance-dependent sign reversal in the Casimir-Lifshitz torque. Phys. Rev. Lett., 120: 131601. [97] Tkatchenko A, Scheffler M. 2009. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett., 102(7): 69-72. [98] Tkatchenko A, Rossi M, Blum V, et al. 2011. Unraveling the stability of polypeptide helices: Critical role of van der Waals interactions. Phys. Rev. Lett., 106(11): 118102. doi: 10.1103/PhysRevLett.106.118102 [99] Tkatchenko A, DiStasio J R A, Car R, et al. 2012. Accurate and efficient method for many-body van der Waals interactions. Phys. Rev. Lett., 108(23): 236402. doi: 10.1103/PhysRevLett.108.236402 [100] Tsoi S, Dev P, Friedman A L, et al. 2014. van der Waals screening by single-layer graphene and molybdenum disulfide. Acs Nano, 8(12): 12410-12417. doi: 10.1021/nn5050905 [101] van der Waals J D. 1873. On the continuity of the gas and liquid state. [Ph. D. thesis]. Netherlands: University of Leiden, 301. [102] Vasu K, Prestat E, Abraham J, et al. 2016. van der Waals pressure and its effect on trapped interlayer molecules. Nat. Commun., 7(1): 12168. doi: 10.1038/ncomms12168 [103] Volokitin A I, Persson B N J. 1999. Theory of friction: The contribution from a fluctuating electromagnetic field. J. Phys. Condens. Matter, 11(2): 345. doi: 10.1088/0953-8984/11/2/003 [104] Volokitin A I, Persson B N J. 2002. Dissipative van der Waals interaction between a small particle and a metal surface. Phys. Rev. B, 65(11): 115419. doi: 10.1103/PhysRevB.65.115419 [105] Volokitin A I, Persson B N J. 2006. Quantum field theory of van der Waals friction. Phys. Rev. B, 74(20): 205413. doi: 10.1103/PhysRevB.74.205413 [106] Volokitin A I, Persson B N J. 2007. Near-field radiative heat transfer and noncontact friction. Rev. Mod. Phys., 79(4): 1291. doi: 10.1103/RevModPhys.79.1291 [107] Vydrov O A, Van V T. 2010. Nonlocal van der Waals density functional: The simpler the better. J. Chem. Phys., 133: 244103. doi: 10.1063/1.3521275 [108] Wang G, Dai Z, Wang Y, et al. 2017. Measuring interlayer shear stress in bilayer graphene. Phys. Rev. Lett., 119(3): 036101. doi: 10.1103/PhysRevLett.119.036101 [109] Wang G, Dai Z, Xiao J, et al. 2019. Bending of multilayer van der Waals materials. Phys. Rev. Lett., 123(11): 116101. doi: 10.1103/PhysRevLett.123.116101 [110] Wang H, Zhang L, Han J, et al. 2018. Deepmd-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun., 228: 178-184. doi: 10.1016/j.cpc.2018.03.016 [111] Wen J, Li W, Chen S, et al. 2016. Simulations of molecular self-assembled monolayers on surfaces: Packing structures, formation processes and functions tuned by intermolecular and interfacial interactions. Phys. Chem. Chem. Phys., 18(33): 22757-22771. doi: 10.1039/C6CP01049K [112] Werder T, Walther J H, Jaffe R, et al. 2003. On the water-carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B, 107(6): 1345-1352. doi: 10.1021/jp0268112 [113] Woods L, Dalvit D A R, Tkatchenko A, et al. 2016. Materials perspective on Casimir and van der Waals interactions. Rev. Mod. Phys., 88(4): 045003. doi: 10.1103/RevModPhys.88.045003 [114] Wu Q, Yang W. 2002. Empirical correction to density functional theory for van der Waals interactions. J. Chem. Phys., 116(2): 515-524. doi: 10.1063/1.1424928 [115] Xie R, Montanini P, Akarvardar K, et al. 2016. A 7 nm finfet technology featuring euv patterning and dual strained high mobility channels. IEEE, 2016 IEEE international electron devices meeting, San Francisco. San Francisco: IEEE, 2016 : 2-7. [116] Yang J, Liu X, Guo W. 2021. Nonmonotonous distance dependence of van der Waals screening by a dielectric layer. J. Phys. Chem. Lett., 12(20): 4993-4999. doi: 10.1021/acs.jpclett.1c00870 [117] Yang K, Chen Y, Pan F, et al. 2016. Buckling behavior of substrate supported graphene sheets. Materials, 9(1): 32. doi: 10.3390/ma9010032 [118] Yu H Y, Eckmann D M, Ayyaswamy P S, et al. 2016. Effect of wall-mediated hydrodynamic fluctuations on the kinetics of a brownian nanoparticle. Proc. R. Soc. A, 472(2196): 20160397. doi: 10.1098/rspa.2016.0397 [119] Yu J, Chary S, Das S, et al. 2011. Gecko-inspired dry adhesive for robotic applications. Adv. Funct. Mater., 21(16): 3010-3018. doi: 10.1002/adfm.201100493 [120] Yuet P K, Blankschtein D. 2010. Molecular dynamics simulation study of water surfaces: Comparison of flexible water models. J. Phys. Chem. B, 114(43): 13786-13795. doi: 10.1021/jp1067022 [121] Zhang G X, Tkatchenko A, Paier J, et al. 2011. van der Waals interactions in ionic and semiconductor solids. Phys. Rev. Lett., 107(24): 245501. doi: 10.1103/PhysRevLett.107.245501 [122] Zhang Y, Wang L. 2020. Effects of the van der Waals force on the vibration of typical multi-layered two-dimensional nanostructures. Sci. Rep., 10(1): 644. doi: 10.1038/s41598-020-57522-9 [123] Zhang Y, Zhang H, Wang X, et al. 2024. Magnetic-field tuning of the Casimir force. Nat. Phys., 20: 1282-1287. doi: 10.1038/s41567-024-02521-0 [124] Zhao W, Qiu H, Guo W. 2022. A deep neural network potential for water confined in graphene nanocapillaries. J. Phys. Chem. C, 126(25): 10546-10553. doi: 10.1021/acs.jpcc.2c02423 [125] Zhao R, Li L, Yang S, et al. 2019. Stable Casimir equilibria and quantum trapping. Science, 364(6444): 984-987. doi: 10.1126/science.aax0916 [126] Zhong W, Tomanek D. 1990. First-principles theory of atomic-scale friction. Phys. Rev. Lett., 64(25): 3054. doi: 10.1103/PhysRevLett.64.3054 -




 下载:
下载: