-
摘要: 固体界面的不稳定性增长是武器内爆物理、惯性约束聚变点火和材料动力学行为研究等工程和科学领域中的关键物理过程, 它可能导致固体表面出现轻重介质相互侵入、物质微喷射乃至湍流混合等复杂的物理现象, 对其发展规律的研究具有重要的意义. 本文在第二、三章分别介绍了对固体界面Richtmyer−Meshkov (RM) 和Rayleigh−Taylor (RT) 不稳定性发展规律的研究现状, 总结了现有的不稳定性增长理论模型并探讨了其局限性. 与纯流体界面不稳定性增长所不同的是, 由于固体材料存在强度, 其界面不稳定性发展过程中扰动增长的部分能量会被强度这一耗散因素转化为晶格的热能, 从而降低扰动增长速率乃至抑制扰动增长, 因此如何衡量动态加载过程中固体的强度效应成为认识其不稳定增长规律的关键. 另一方面, 由于固体界面不稳定性的发展结果蕴含着材料的本构、状态方程等信息, 人们提出可以应用不稳定性的增长规律来获取材料的动态屈服强度、校验材料的高压本构模型和抑制不稳定性的增长, 本文在第四章中对这部分内容进行了介绍, 并指出建立能精确描述不稳定性增长现象与材料性质间“关联性机制”的理论模型是成功进行应用的关键. 在这些基础上, 本文于第五章展望了该领域存在的机遇和挑战.Abstract: The growth of interface instability in solids is a critical phenomenon affecting various fields of engineering and science, including implosion physics, inertial confinement fusion ignition, and the dynamic behavior of materials. This instability can lead to complex phenomena such as the interpenetration of light and heavy media at solid surfaces, material micro-jetting, and turbulent mixing, highlighting the significance of understanding its underlying mechanisms. This paper reviews the current research status of Richtmyer−Meshkov (RM) and Rayleigh−Taylor (RT) instabilities at solid interfaces in Chapters 2 and 3. We summarize existing theoretical models of instability growth and discuss their limitations. Unlike the instability growth observed in pure fluid interfaces, solid materials possess inherent strength, which enables some of the energy from perturbation growth to be transformed into lattice thermal energy through dissipative mechanisms. This energy conversion reduces the rate of perturbation growth and may even suppress the development of instabilities. Consequently, understanding the effects of material strength under dynamic loading conditions is crucial for comprehending instability growth behavior. Moreover, the outcomes of solid interface instability are indicative of various material properties, including constitutive relationships and equations of state. Researchers have proposed that instability growth can be leveraged to determine the dynamic yield strength of materials, validate high-pressure constitutive models, and mitigate instability growth. Chapter 4 focuses on this aspect, emphasizing the need to establish a theoretical model that accurately describes the “correlation mechanism” between instability phenomena and material properties for effective applications. Building on these foundations, Chapter 5 explores future opportunities and challenges in this field.
-
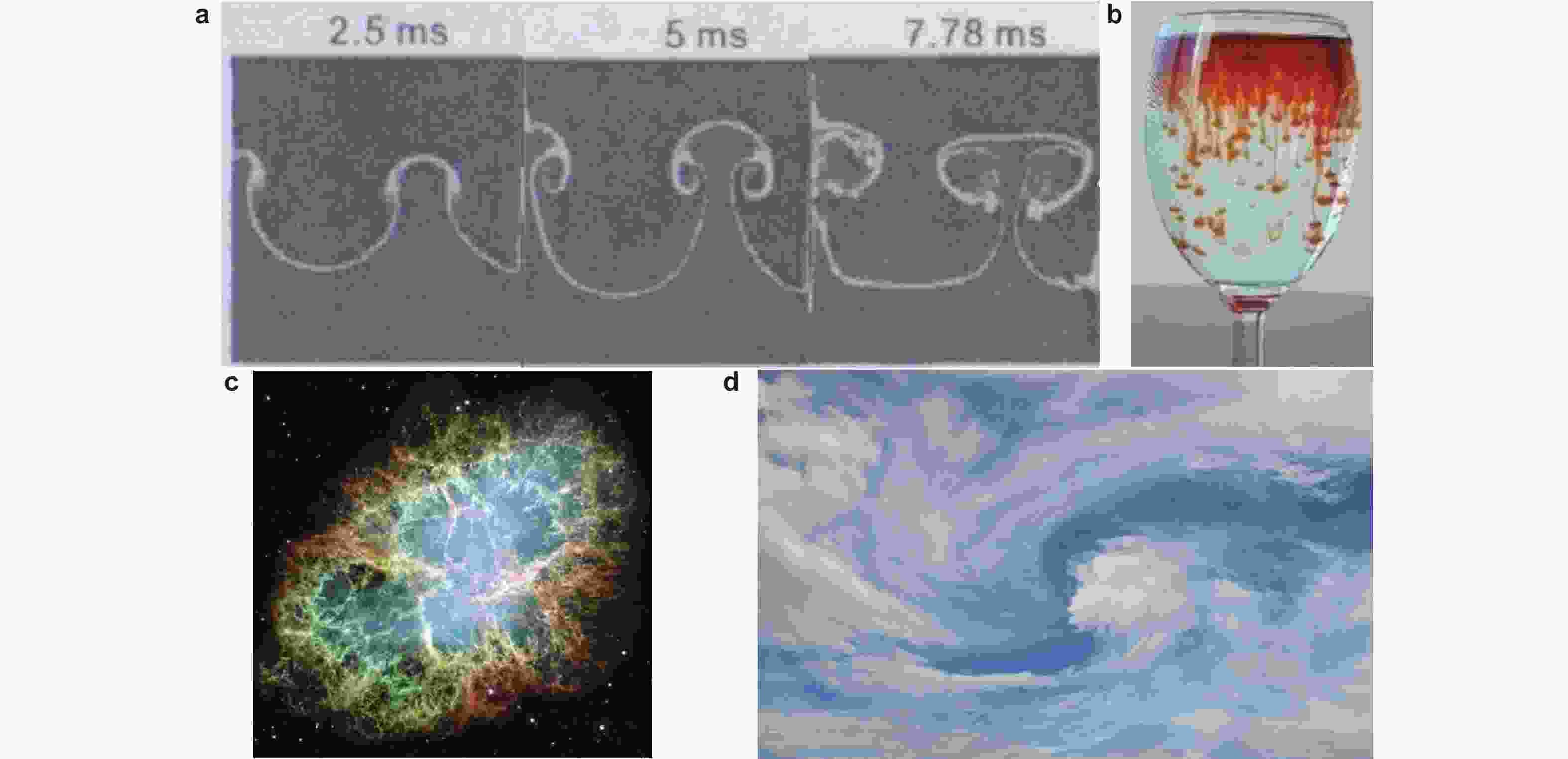
图 1 典型的流动不稳定性现象. (a) 平面激波作用下空气/SF6界面的演化(Collins & Jacobs 2002), (b) 水杯中轻重流体间的混合, (c) 火箭发动机推进剂喷注与燃烧, (d) 大气中环流的云涡
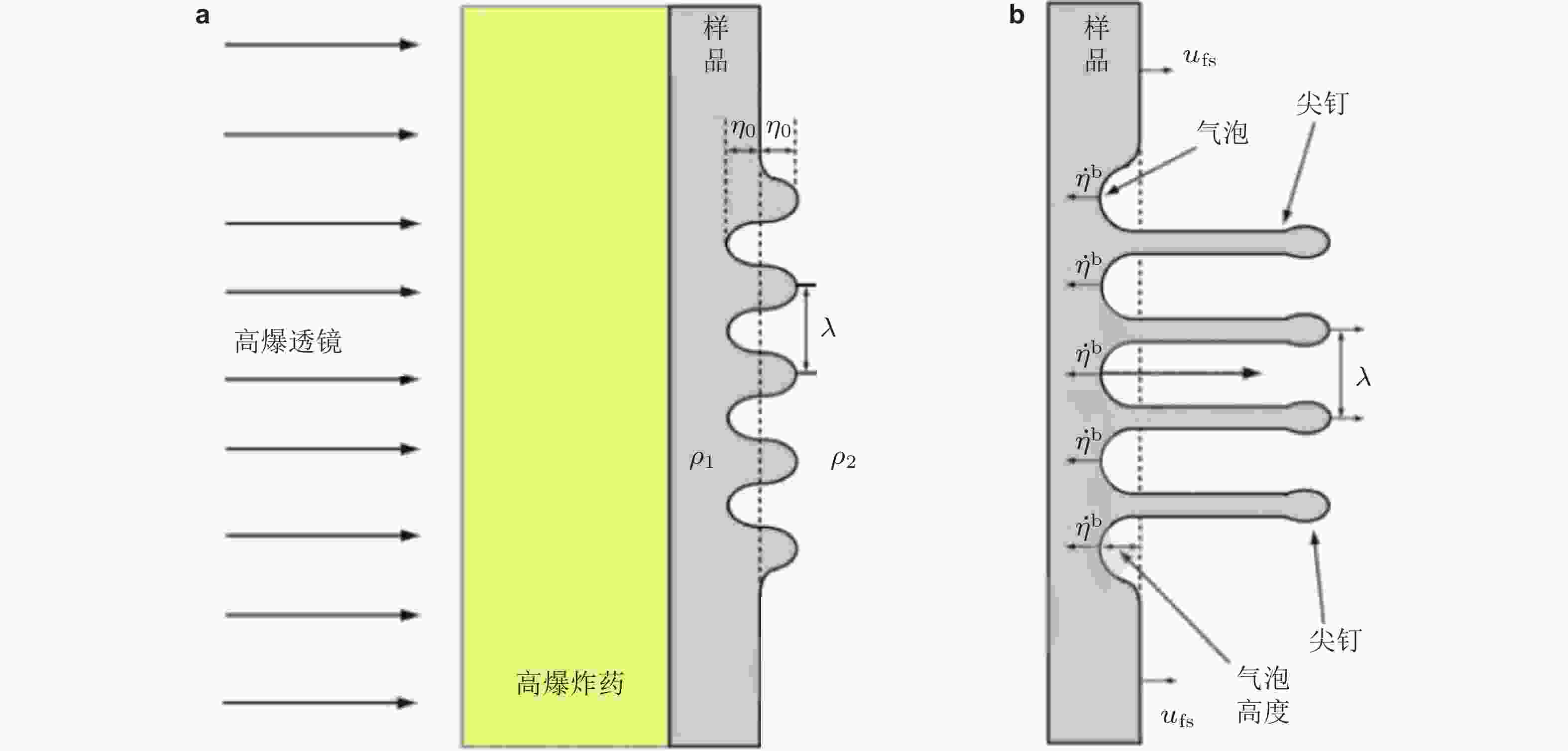
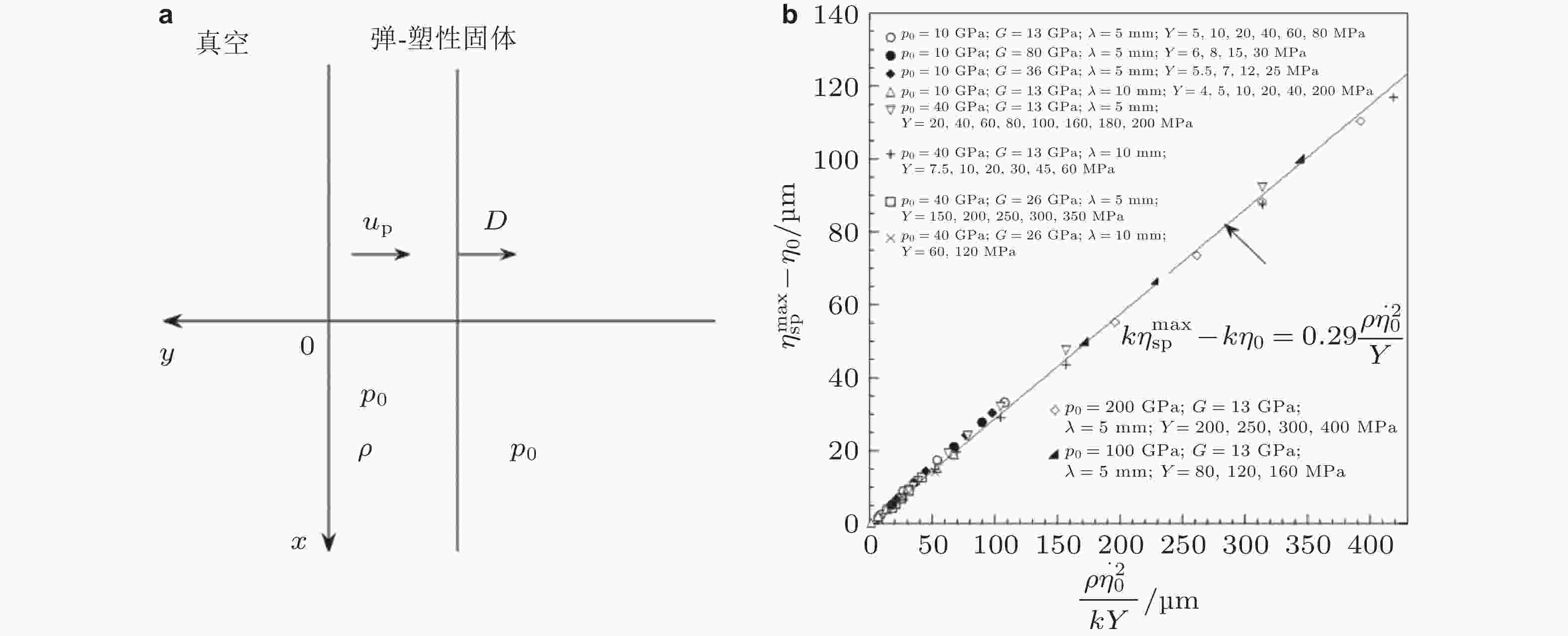
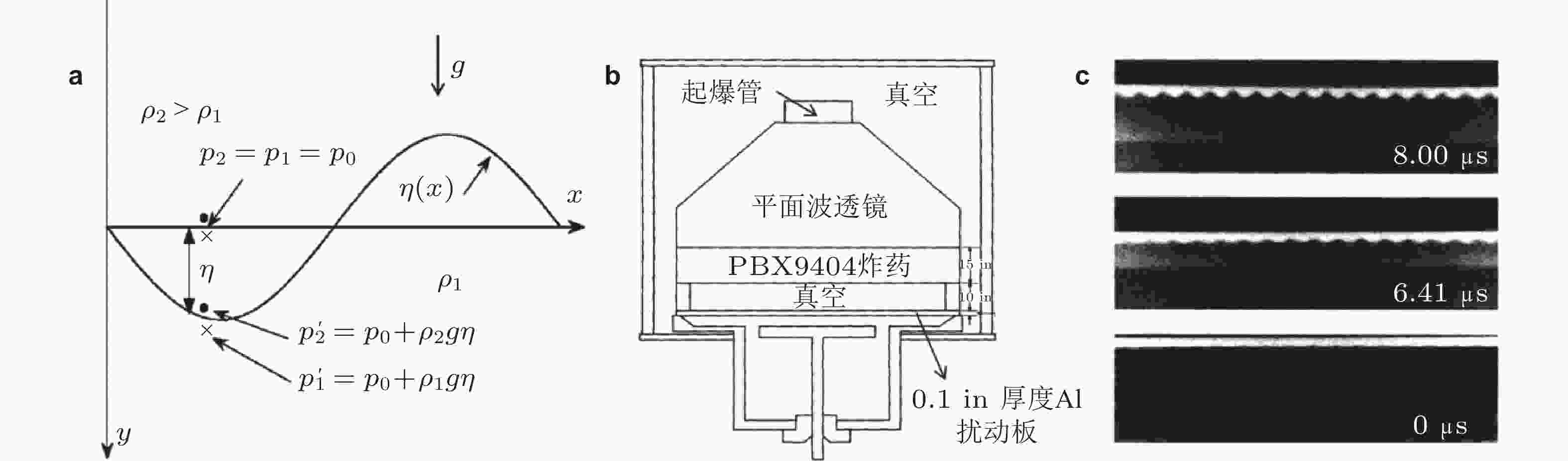
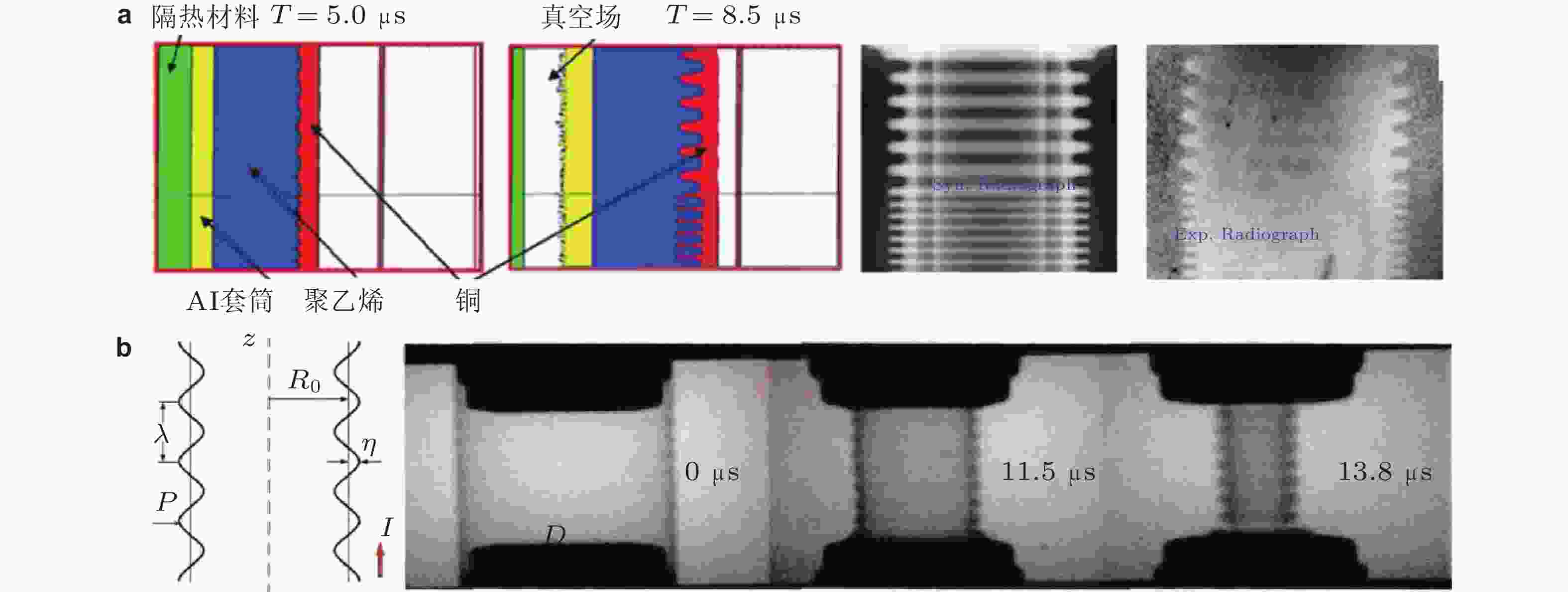
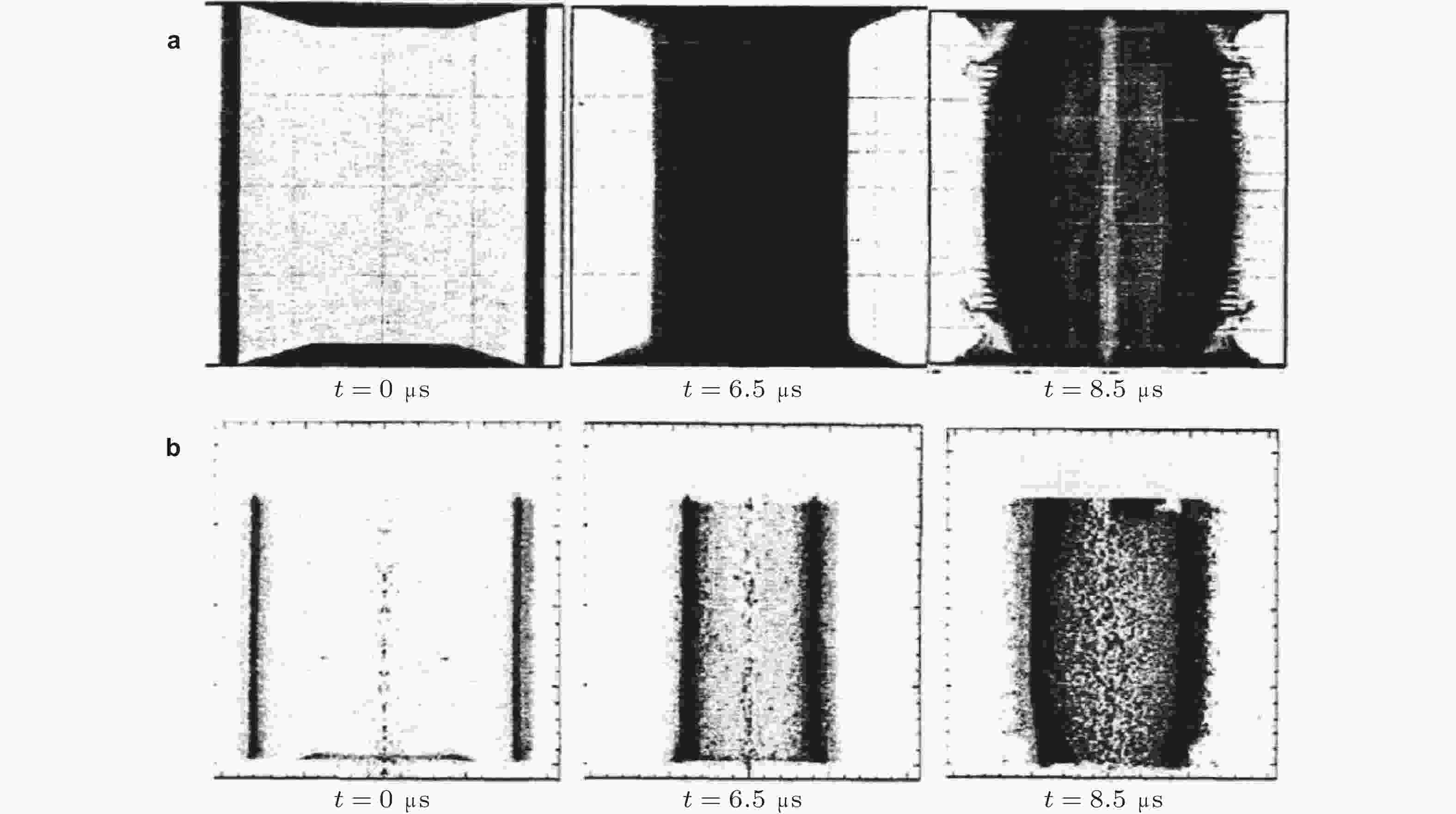
图 3 高爆炸药 (HE) 产生的平面冲击波加载到初始有正弦型扰动的样品前 (a) 和加载后 (b) 界面的几何构型示意图 (Buttler et al. 2012)
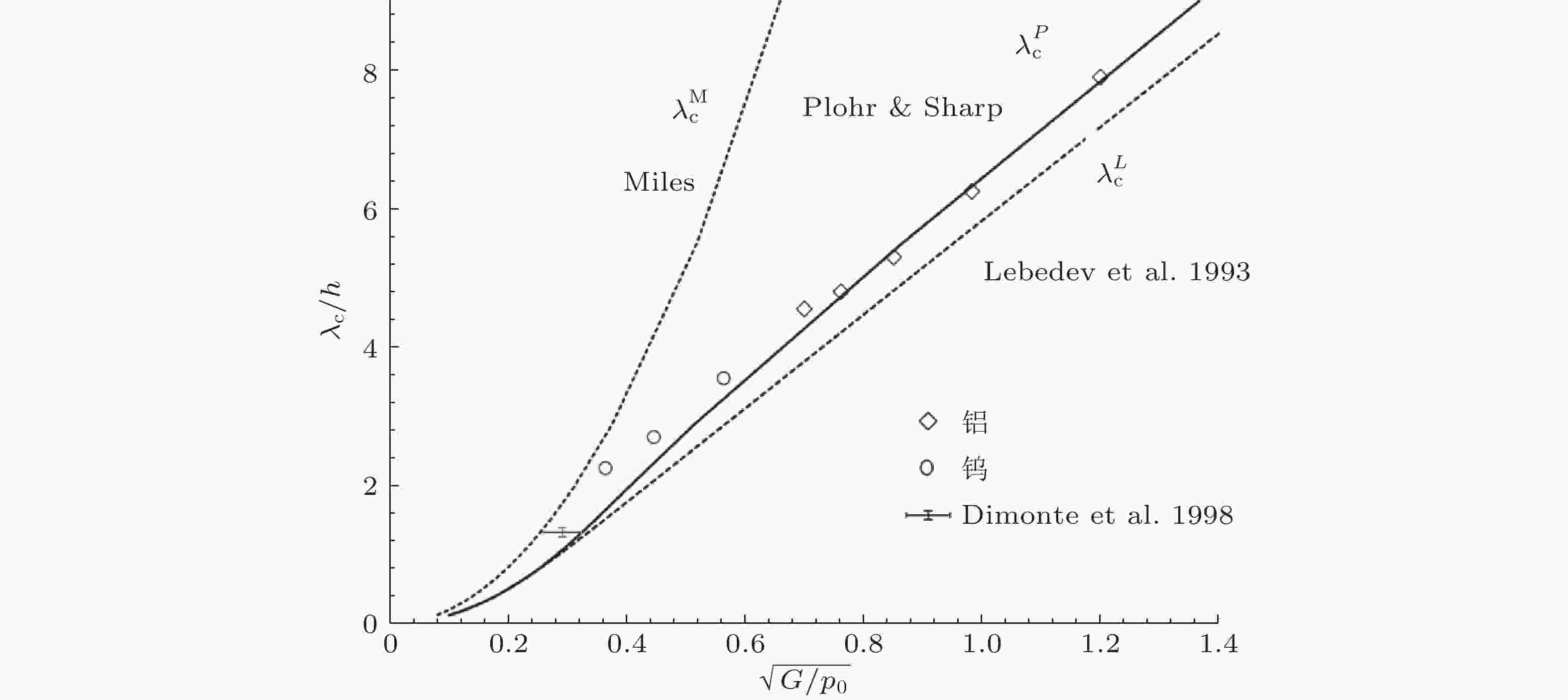
图 19 弹性平板RTI增长临界波长与平板厚度比值λc/h随
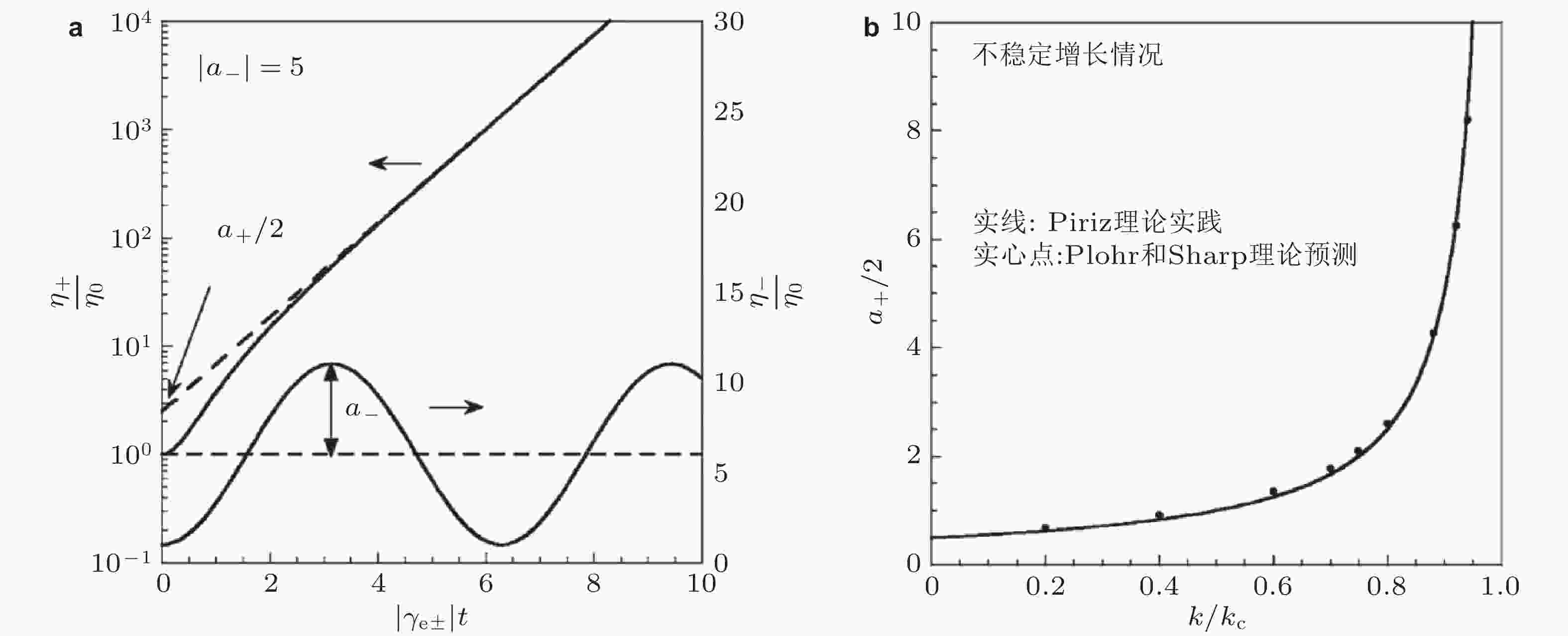
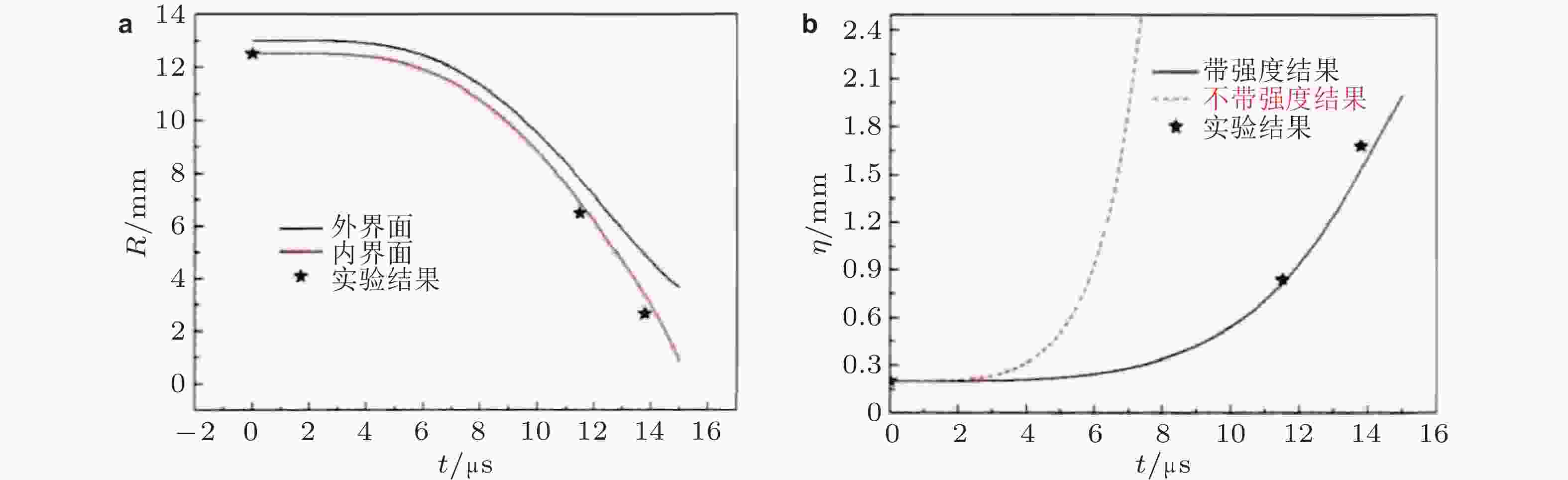
$ \sqrt{{G}/{{p}}_{0}} $ 变化. 其中实线代表Plohr和Sharp (1998) 理论结果, 两条虚线分别代表Miles (1966) 和Lebedev (Lebedev et al. 1993) 理论预测, 图中数据点为Swegle和Robinson (1989) 对铝 (棱形) 和钨 (圆圈) 材料的数值模拟结果, 误差符号代表Dimonte等(1998)的实验结果图 20 弹性固体/固体界面RT扰动增长过程中 (a) 无量纲扰动振幅
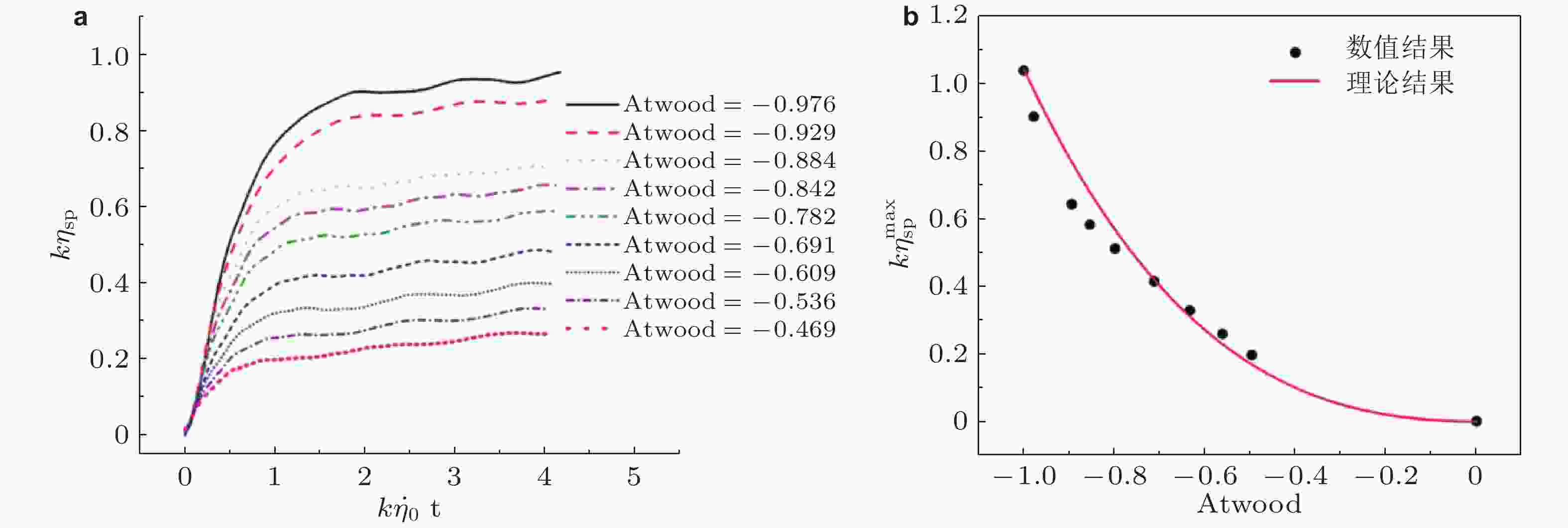
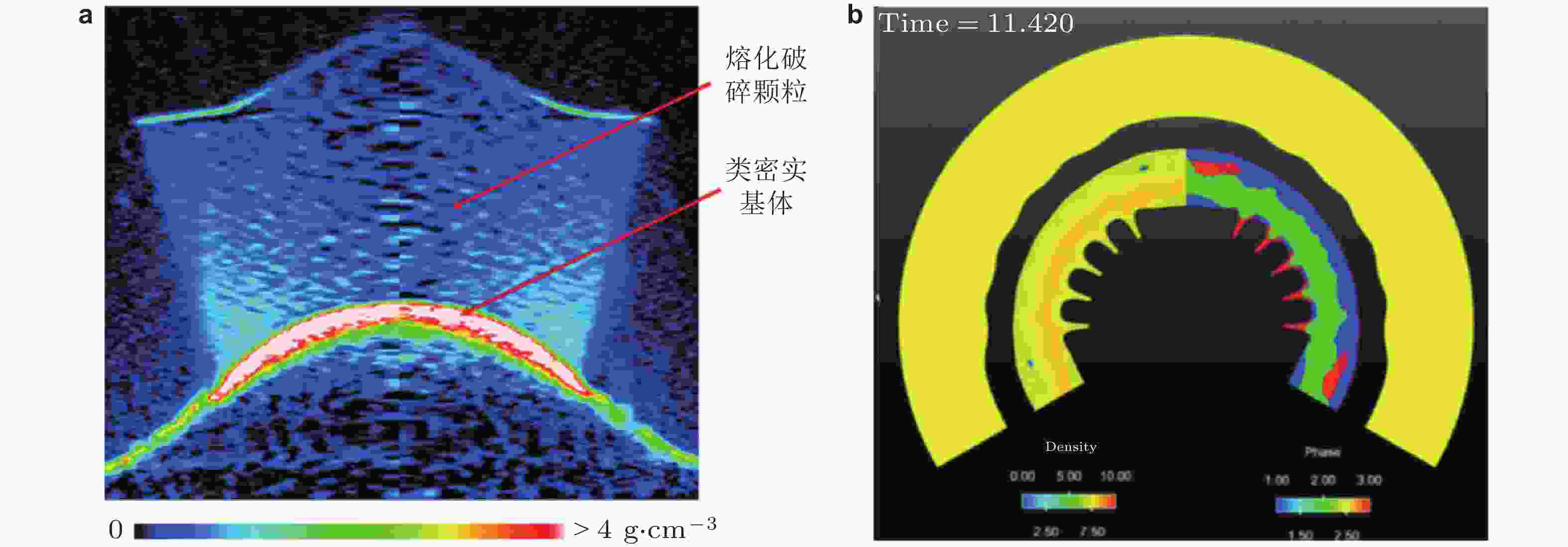
$ {\mathrm{\eta }}_{\pm }/{\mathrm{\eta }}_{0} $ 随无量纲时间$ \left|{\gamma }_{{\mathrm{e}}\pm }\right| $ t的演化, 实线代表式 (49) 理论预测; (b) 对于不稳定扰动增长情况, 渐进无量纲振幅随无量纲扰动波数的变化, 实线和实心点分别代表Piriz (Piriz et al. 2005)、Plohr和Sharp (1998) 理论预测,图 32 (a) 爆轰加载后金属Sn样品的熔化破碎密度图像 (陈永涛等 2013); (b) 磁驱动柱面Sn样品汇聚过程中的组分分布 (t = 11.42 μs), 红色为液相, 绿色为伽马相, 蓝色为β相 (Rousculp et al. 2016)
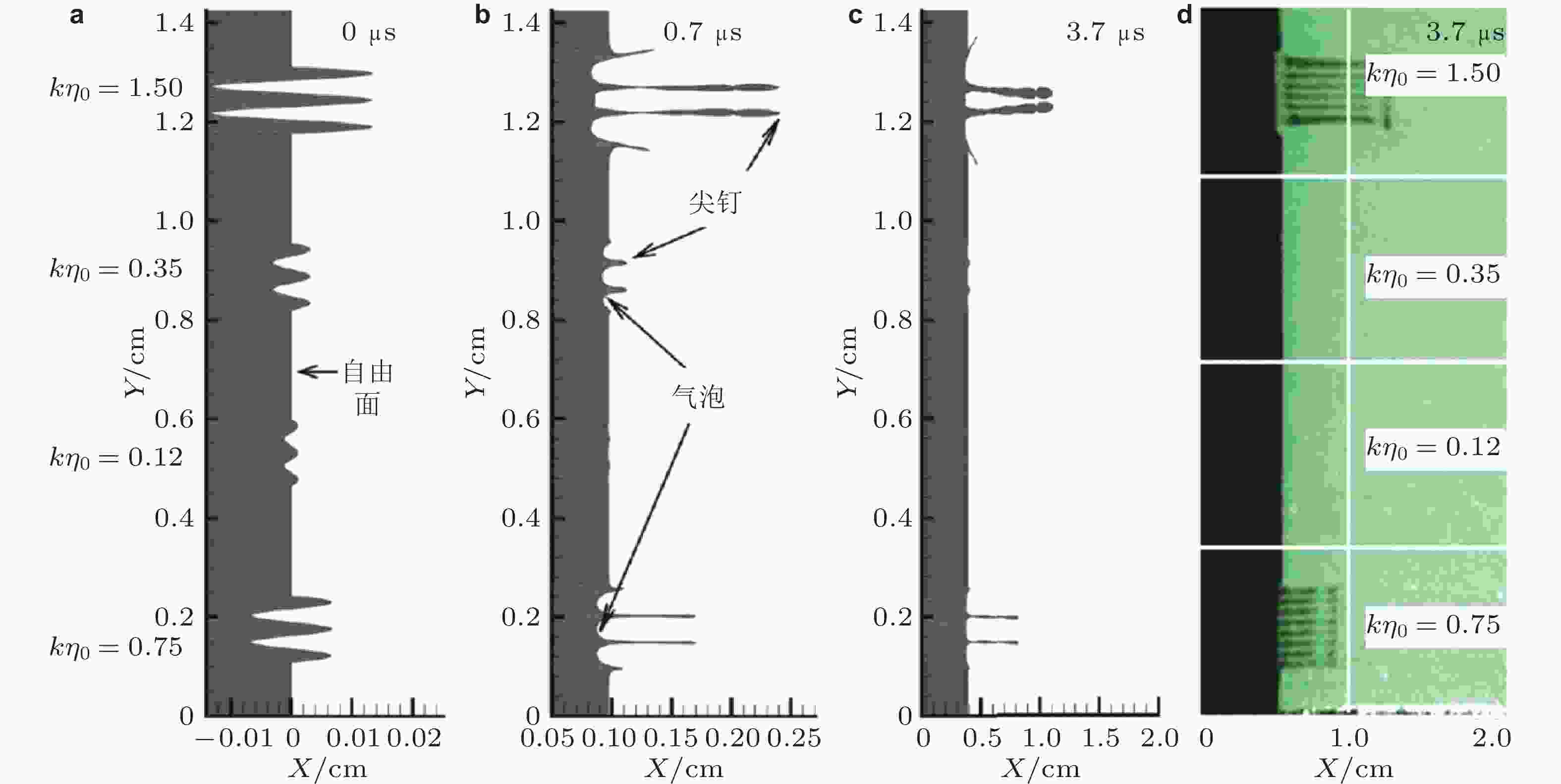
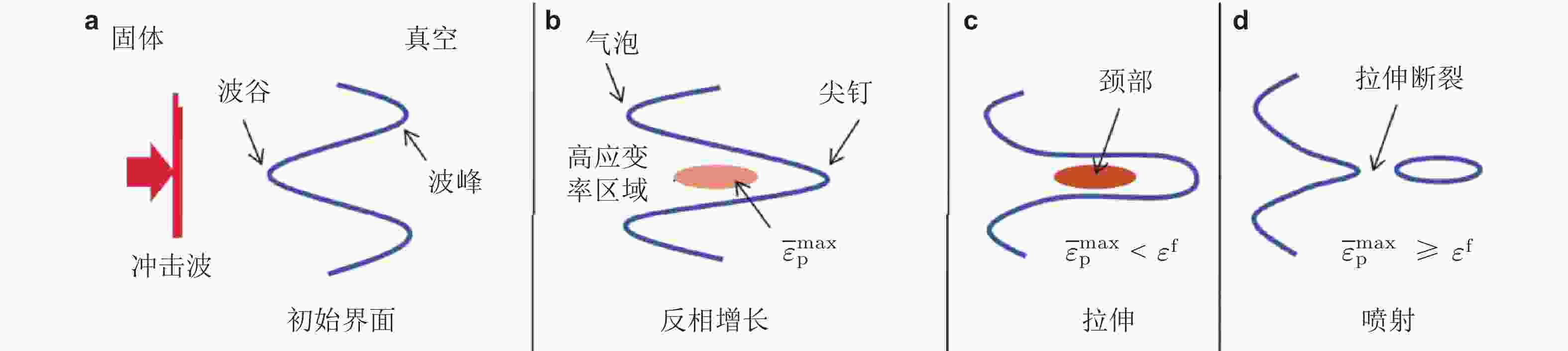
图 33 扰动发展过程中拉升断裂导致尖钉破碎形成射流和微喷示意图 (殷建伟 2018)
表 1 固体界面RM扰动增长理论模型总结
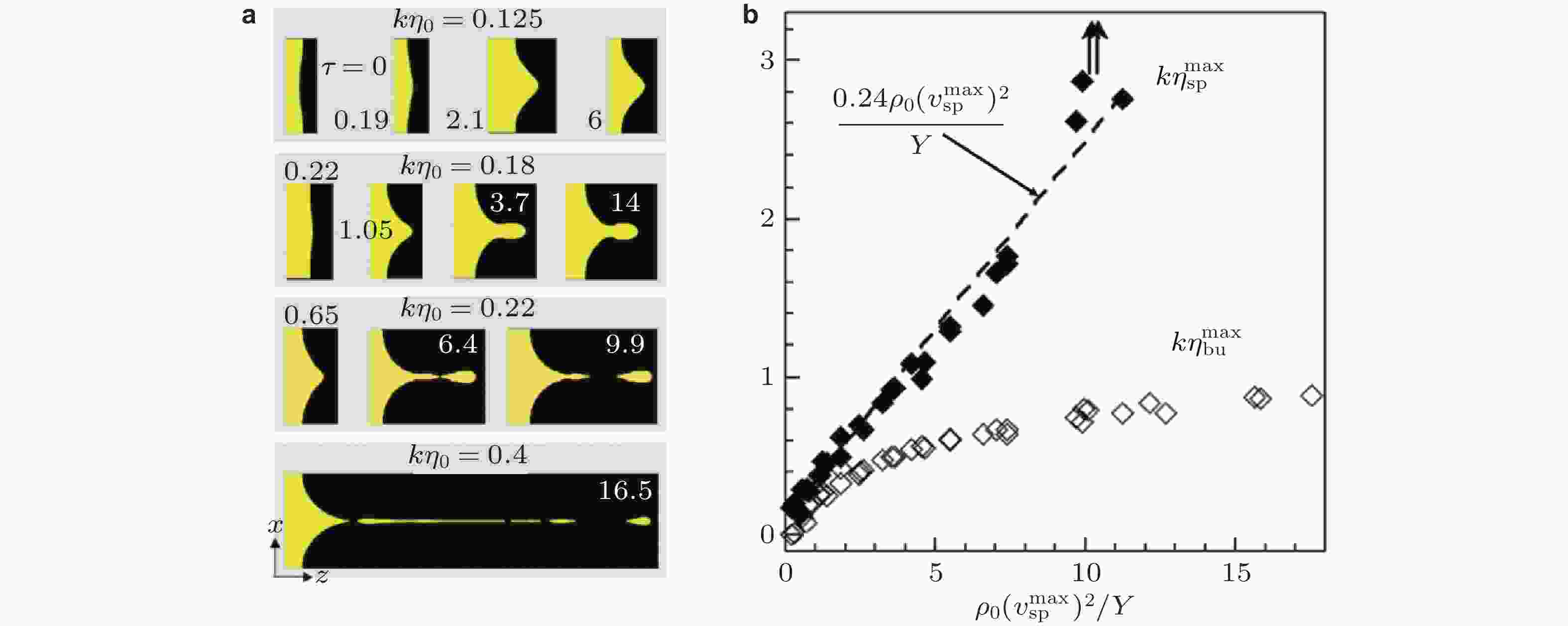
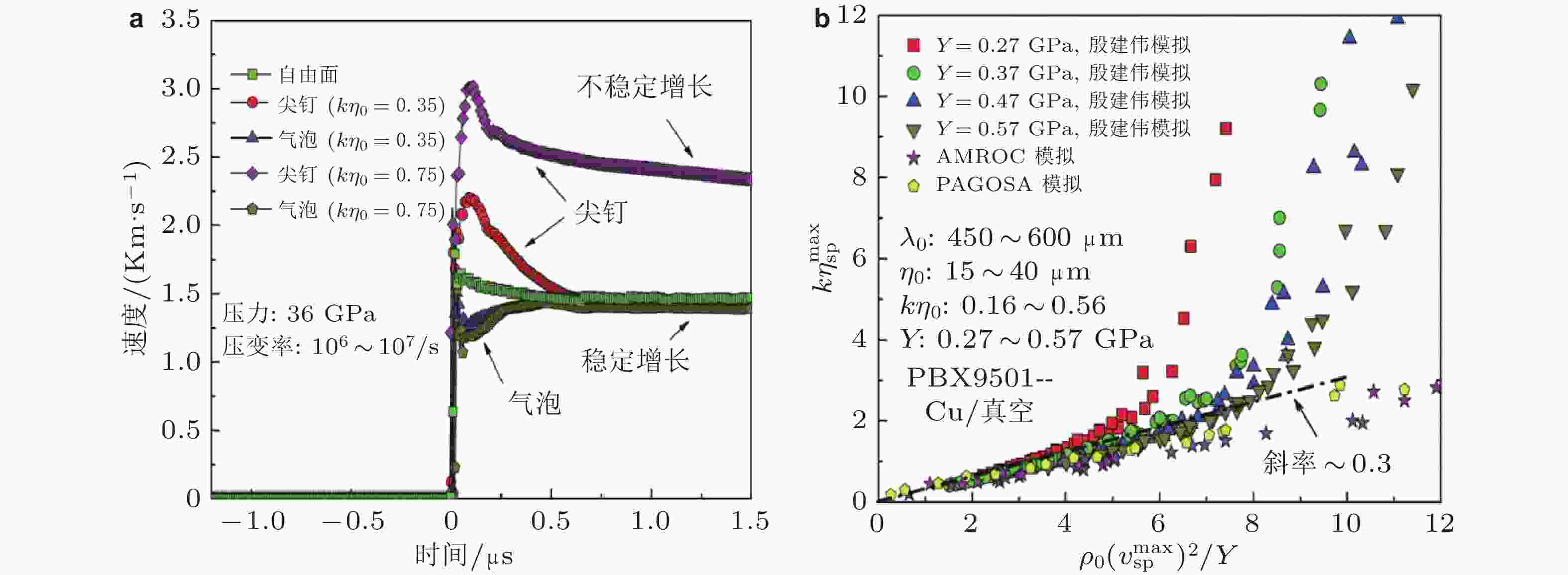
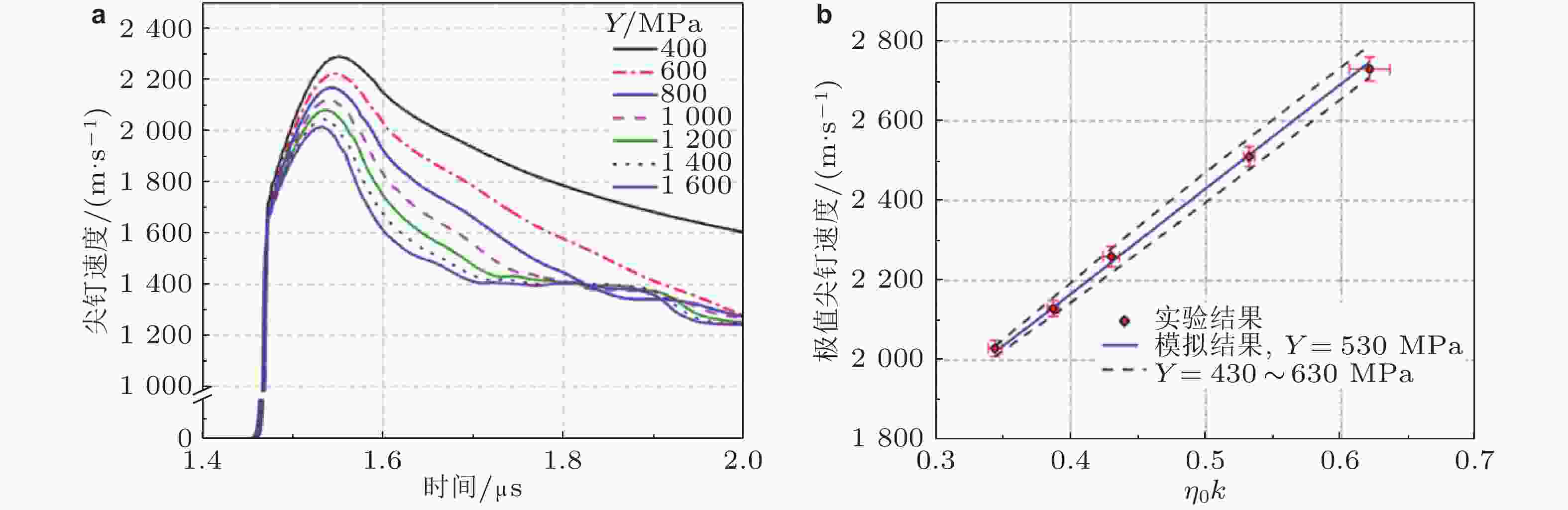
理论模型 无量纲尖钉极值振幅与无量纲尖钉极值增长速度关系 斜率(拟合系数) 截距 Piriz 2008 $ {{k}}\eta _{{\text{sp}}}^{\max } = {{k}}{\eta _0} + {C_{\mathrm{p}}}\dfrac{{{\rho _0}\mathop {\eta _0^2}\limits^ \cdot }}{Y} $ $ {C_{\mathrm{p}}} = 0.29 $ $ {{k}}{\eta _0} $ Dimonte 2011 $ {{k}}\eta _{{\text{sp}}}^{\max } = 0.08 + {C_{\mathrm{D}}}\dfrac{{{\rho _0}{{{{(v}}_{{\mathrm{sp}}}^{\max })}^2}}}{Y} $ $ {C_{\mathrm{D}}} = 0.24 $ 0.08 Buttler 2012 $ {k}{\eta }_{\text{sp}}^{\mathrm{max}}={k}{\eta }_{0} + {C}_{{\mathrm{B}}} \left(\dfrac{1{-}\Delta{V/(2D)}}{1-\Delta {V/D}}\right)^{2}\dfrac{{\rho }_{\text{0}}{{\eta }_{0}^{2}}}{Y} $ $ {C_{\mathrm{B}}} = 0.29 $ $ {{k}}{\eta _0} $ Mikaelian 2013 $ {{k}}\eta _{{\text{sp}}}^{\max } = {{k}}{\eta _0} + {C_{\mathrm{M}}}\dfrac{{({\rho ^{\text{h}}} + {\rho ^{\text{l}}})\mathop {\eta _0^2}\limits^ \cdot }}{{{Y^{\text{h}}} + {Y^{\text{l}}}}} $ $ {C_{\mathrm{M}}} = 0.33 $ $ {{k}}{\eta _0} $ 殷建伟 2018 $ {{k}}\eta _{{\text{sp}}}^{\max } = {C_{\mathrm{Y}}}\dfrac{{{\rho _0}{{({{v}}_{{\mathrm{sp}}}^{\max })}^2}}}{Y} $ $ {C_{\mathrm{Y}}} = 0.3 $ 0 Chen et al. 2019 $ {{k}}\eta _{{\mathrm{sp}}}^{{\text{max}}} = \dfrac{Y}{{4\sqrt 3 kG}} + {C_{\mathrm{C}}}\dfrac{{{\rho _S} {\eta _0^2} }}{Y} $ $ {C_{\mathrm{C}}} = {{f}}(A) $ $ \dfrac{Y}{{4\sqrt 3 kG}} $ 表 2 固体界面 RT 扰动增长理论模型总结
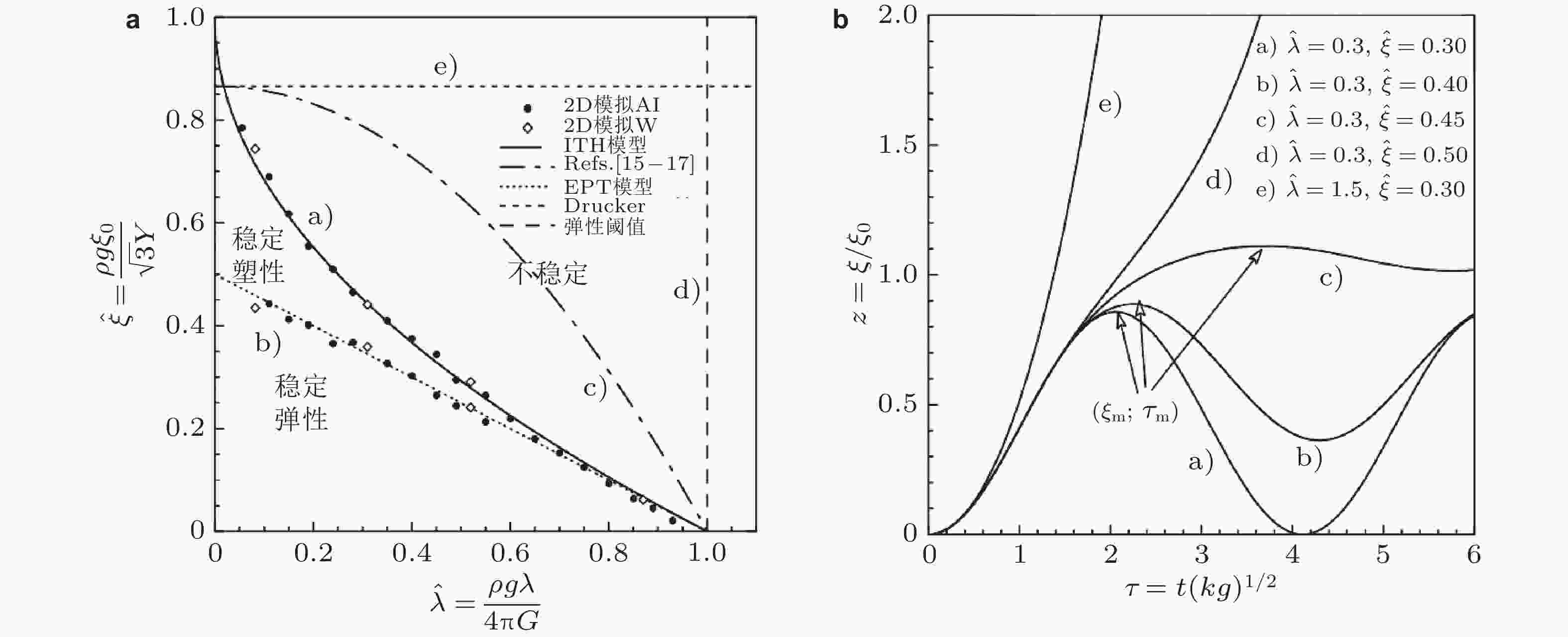
模型 界面运动方程/色散关系 渐进界面扰动增长率 (t$ \to \mathrm{\infty } $) Remington2004: 任意A, 任意kh, 显含应变率 $ \begin{gathered} {\gamma ^2} + 2{k^2}{\nu _{{\mathrm{eff}}}}\gamma + k \times \tanh kh\times \left(\dfrac{{kG}}{\rho } - Ag\right) = 0 \\ {{{v}}_{{\mathrm{eff}}}} = Y/(\sqrt 6 \rho \mathop \varepsilon \limits^ \cdot ) \\ \end{gathered} $ $ \gamma = {\nu _{{\mathrm{eff}}}}{{{k}}^2}\left[{\left(1 - \dfrac{{\tanh kh\times (kG/\rho - Ag)}}{{\nu _{_{{\mathrm{eff}}}}^2{k^3}}}\right)^{1/2}} - 1\right] $ Piriz 2009: 固体/理想流体界面, A = 1, kh >> 1 $ \mathop \eta \limits^{ \cdot \cdot } = \left\{ \begin{gathered} {{k}}g(\eta + {\eta _0})- 2{k^2}G\eta /\rho \begin{array}{*{20}{c}} &{\eta \leqslant {\eta _p}} \end{array} \\ {{k}}g(\eta + {\eta _0})- \alpha Yk/\rho \sqrt 3 \begin{array}{*{20}{c}} &{\eta \geqslant {\eta _p}} \end{array} \\ \end{gathered} \right. $
$ \gamma = \sqrt {{{k}}g} $Piriz 2014: 固体/黏性流体界面, 任意A, kh >> 1 $ \begin{gathered} \mathop \eta \limits^{ \cdot \cdot } + \dfrac{{2\mu {k^2}}}{{{\rho _2} + {\rho _1}}}\mathop \eta \limits^ \cdot = \\ \left\{ \begin{gathered} {{Ak}}g(\eta + {\eta _0})- 2{k^2}G\eta /({\rho _2} + {\rho _1})\begin{array}{*{20}{c}} &{\eta \leqslant {\eta _p}} \end{array} \\ {{Ak}}g(\eta + {\eta _0})- \sqrt 3 Yk/({\rho _2} + {\rho _1})\begin{array}{*{20}{c}} &{\eta \geqslant {\eta _p}} \end{array} \\ \end{gathered} \right. \\ \end{gathered} $ $ \gamma = \sqrt {\dfrac{{{\mu ^2}{k^4}}}{{{{({\rho _2} + {\rho _1})}^2}}} + A{{k}}g} - \dfrac{{\mu {k^2}}}{{({\rho _2} + {\rho _1})}} $ Piriz 2019: 固体/理想流体界面, 任意A, 任意kh $ {\left(\dfrac{{kg}}{{{\gamma ^2}}}\right)^2} - 1 = \left(\dfrac{{kg}}{{{\gamma ^2}}} + 1\right)\dfrac{{1 - A}}{{1 + A}}[\dfrac{{kg}}{{{\gamma ^2}}} + \coth kh] $ $ \begin{gathered} {\gamma _{1,2}} = \pm \sqrt {\dfrac{{2A{{kg}}}}{{1 + A + (1 - A)\coth kh}}} \\ {\gamma _{3,4}} = \pm \sqrt { - kg} \\ \end{gathered} $ -
[1] 陈永涛, 洪仁楷, 汤铁钢, 等. 2016. 熔化状态下锡样品微喷射现象的诊断. 高压物理学报, 30(4): 323-327. (Chen Y T, Hong R K, Tang T G et al. 2016. Diagnosis of micro spray phenomenon of tin samples in melting state. Chin J High Press Phy., 30(4): 323-327).Chen Y T, Hong R K, Tang T G et al. 2016. Diagnosis of micro spray phenomenon of tin samples in melting state. Chin J High Press Phy., 30(4): 323-327. [2] 陈永涛, 任国武, 汤铁钢, 等. 2013. 爆轰加载下金属样品的熔化破碎现象诊断. 物理学报, 62(11): 116202. (Chen Y T, Ren G W, Tang T G, et al. 2013. Experimental diagnostic of melting fragments underexplosive loading. Acta Phys. Sin., 62(11): 116202). doi: 10.7498/aps.62.116202Chen Y T, Ren G W, Tang T G, et al. 2013. Experimental diagnostic of melting fragments underexplosive loading. Acta Phys. Sin., 62(11): 116202. doi: 10.7498/aps.62.116202 [3] 郝鹏程, 冯其京, 胡晓棉. 2016. 内爆加载金属界面不稳定性的数值分析. 爆炸与冲击, 36 (6): 739–744. (Hao P C, Feng Q J, Hu X M. 2016, A numerical study of the instability of the metal shell in the implosion. Expl Shock Wave., 36 (6): 739–744).Hao P C, Feng Q J, Hu X M. 2016, A numerical study of the instability of the metal shell in the implosion. Expl Shock Wave., 36(6): 739–744. [4] 李碧勇, 彭建祥, 谷岩, 等. 2020. 爆轰加载下高纯铜界面 Rayleigh—Taylor 不稳定性实验研究. 物理学报. (Li B Y, Peng J X, Gu Y, et al. 2020. Experimental research on the Rayleigh-Taylor instability of OFHC copper under explosive loading. Acta Phys. Sin. ).Li B Y, Peng J X, Gu Y, et al. 2020. Experimental research on the Rayleigh-Taylor instability of OFHC copper under explosive loading. Acta Phys. Sin. . [5] 罗喜胜, 翟志刚, 司廷, 等. 2014. 激波诱导下的气体界面不稳定性实验研究. 力学进展, 44(1): 260-290. (Luo X S, Zhai Z G, Si T, et al. 2014. Experimental study on the interfacial instabilityinduced by shock waves. Advances in Mechanics, 44(1): 260-290).Luo X S, Zhai Z G, Si T, et al. 2014. Experimental study on the interfacial instabilityinduced by shock waves. Advances in Mechanics, 44(1): 260-290. [6] 刘军, 冯其京, 周海兵. 2014. 柱面内爆驱动金属界面不稳定性的数值模拟研究. 物理学报, 63(15): 155201. (Liu J, Feng Q J, Zhou H B. 2014. Simulation study of interface instability in metals drivenby cylindrical implosion. Acta Phys. Sin., 63(15): 155201). doi: 10.7498/aps.63.155201Liu J, Feng Q J, Zhou H B. 2014. Simulation study of interface instability in metals drivenby cylindrical implosion. Acta Phys. Sin., 63(15): 155201. doi: 10.7498/aps.63.155201 [7] 陆逸然, 王晋军. 2024. 高效合成射流激励器研究进展及展望. 力学进展, 54(1): 61-85. (Lu Y R, Wang J J. 2024. Review and prospect on the efficient synthetic jet. Advances in Mechanics, 54(1): 61-85).Lu Y R, Wang J J. 2024. Review and prospect on the efficient synthetic jet. Advances in Mechanics, 54(1): 61-85. [8] 潘昊, 胡晓棉, 吴子辉, 等. 2012. 铈低压冲击相变数值模拟研究. 物理学报, 61(20): 351-357. (Pan H, Hu X M, Wu Z H, et al. 2012. Numerical simulation study on cerium low-pressure impact phase transition. Acta Phys. Sin., 61(20): 351-357).Pan H, Hu X M, Wu Z H, et al. 2012. Numerical simulation study on cerium low-pressure impact phase transition. Acta Phys. Sin., 61(20): 351-357. [9] 任九生, 程昌钧. 2009. 超弹性材料的不稳定性问题. 力学进展, 39(5): 566-575. (Ren J S, Cheng C J. 2009. Instability problems for hyper-elastic materials. Advances in Mechanics, 39(5): 566-575).Ren J S, Cheng C J. 2009. Instability problems for hyper-elastic materials. Advances in Mechanics, 39(5): 566-575. [10] 汤文辉, 张若棋. 2008. 物态方程理论及计算概论(第二版). 北京: 高等教育出版社. (Tang W H, Zhang R Q. 2008. Introduction to the Theory and Computation of Equation of State. Beijing: Higher Education Press).Tang W H, Zhang R Q. 2008. Introduction to the Theory and Computation of Equation of State. Beijing: Higher Education Press. [11] 谭华. 2007. 实验冲击波物理导引. 北京: 国防工业出版社 (Tan H. 2007. Experimental shock wave physics guidance. Beijing: National Defence Industry Press).Tan H. 2007. Experimental shock wave physics guidance. Beijing: National Defence Industry Press. [12] 王洪建, 冯永祯, 罗笔瀚, 等. 2023. 强激光加载下金属材料微喷诊断实验研究进展. 强激光与粒子束, 35(10): 1-12. (Wang H J, Feng Y Z, Luo B H, et al. 2023. Research progress on diagnostic experiments of metal material micro spraying under strong laser loading. High Power Laser and Particle Beams, 35(10): 1-12). doi: 10.11884/HPLPB202335.230225Wang H J, Feng Y Z, Luo B H, et al. 2023. Research progress on diagnostic experiments of metal material micro spraying under strong laser loading. High Power Laser and Particle Beams, 35(10): 1-12. doi: 10.11884/HPLPB202335.230225 [13] 王立锋, 叶文华, 陈竹, 等. 2021. 激光聚变内爆流体不稳定性基础问题研究进展. 强激光与粒子束, 33(1): 012001-012001. (Wang L F, Ye W H, Chen Z, et al. 2021. Review of hydrodynamic instabilities in inertial confinement fusion implosions. High Power Laser and Particle Beams, 33(1): 012001-012001).Wang L F, Ye W H, Chen Z, et al. 2021. Review of hydrodynamic instabilities in inertial confinement fusion implosions. High Power Laser and Particle Beams, 33(1): 012001-012001. [14] 王涛, 汪兵, 林健宇, 等. 2020. 柱形汇聚几何中内爆驱动金属界面不稳定性. 爆炸与冲击, 40(5): 1-12 (Wang T, Wang B, Lin J Y, et al. 2020. Numerical investigations of the interface instabilities of metallic material under implosion in cylindrical convergent geometry. Expl Shock Wave., 40(5): 1-12).Wang T, Wang B, Lin J Y, et al. 2020. Numerical investigations of the interface instabilities of metallic material under implosion in cylindrical convergent geometry. Expl Shock Wave., 40(5): 1-12. [15] 殷建伟. 2018. 强度介质界面的 Richtmyer—Meshkov 扰动增长规律研究. [博士论文]. 北京理工大学. (Yin J W. 2018. Study on the growth regularity of Richtmyer-Meshkov flow in solid medias with strength. [PhD Thesis]. Beijing Institute of Technology).Yin J W. 2018. Study on the growth regularity of Richtmyer-Meshkov flow in solid medias with strength. [PhD Thesis]. Beijing Institute of Technology. [16] 朱建士, 胡晓棉, 王裴, 等. 2010. 爆炸与冲击动力学若干问题研究进展. 力学进展, 40(4): 400-423. (Zhu J S, Hu X M, Wang P, et al. 2010. A review on research progress in explosion mechaanics and impact dynamics. Advances in Mechanics, 40(4): 400-423).Zhu J S, Hu X M, Wang P, et al. 2010. A review on research progress in explosion mechaanics and impact dynamics. Advances in Mechanics, 40(4): 400-423. [17] 郑宇轩, 周风华, 胡时胜, 等. 2016. 固体的冲击拉伸碎裂. 力学进展, 46(1): 506-540. (Zheng Y X, Zhou F H, Hu S S, et al. 2016. Fragmentations of solids under impact tension. Advances in Mechanics, 46(1): 506-540).Zheng Y X, Zhou F H, Hu S S, et al. 2016. Fragmentations of solids under impact tension. Advances in Mechanics, 46(1): 506-540. [18] 张维岩, 叶文华, 吴俊峰, 等. 2014. 激光间接驱动聚变内爆流体不稳定性研究. 中国科学: 物理学力学天文学, 1-23. (Zhang W Y, Ye W H, Wu J F, et al. 2014. Study on the instability of laser driven fusion implosion fluid. Chinese Science: Physics, Mechanics, Astronomy, 1-23).Zhang W Y, Ye W H, Wu J F, et al. 2014. Study on the instability of laser driven fusion implosion fluid. Chinese Science: Physics, Mechanics, Astronomy, 1-23. [19] 章征伟. 2020. 磁驱动固体套筒内爆理论与实验研究. [博士论文]. 中国工程物理研究院. (Zhang Z W. 2020. Theoretic and experimental study on magnetically driven solid liner implosion. [PhD Thesis]. China Academy of Engineering Physics).Zhang Z W. 2020. Theoretic and experimental study on magnetically driven solid liner implosion. [PhD Thesis]. China Academy of Engineering Physics. [20] 章征伟, 魏懿, 孙奇志, 等. 2016. 材料强度对电磁驱动固体套筒内爆过程的影响. 强激光与粒子束, 28(4): 156-160. (Zhang Z W, Wei Y, Sun Q Z, et al. 2016. The influence of material strength on the implosion process of electromagnetic driven solid sleeves. High Power Laser and Particle Beams, 28(4): 156-160).Zhang Z W, Wei Y, Sun Q Z, et al. 2016. The influence of material strength on the implosion process of electromagnetic driven solid sleeves. High Power Laser and Particle Beams, 28(4): 156-160. [21] Aglitskiy Y, Velikovich A L, Karasik M, et al. 2010. Basic hydrodynamics of Richtmyer−Meshkov-type growth and oscillations in the inertial confinement fusionrelevant conditions. Phil TransR Soc A, 368: 1739-1768 doi: 10.1098/rsta.2009.0131 [22] Al’tshuler L V, Il’kaev R I, Fortov V E. 2021. Use of powerful shock and detonation waves to study extreme states of matter. Physics-Uspekhi, 64(11): 1167 doi: 10.3367/UFNe.2021.09.039092 [23] Arinin V A, Baltakov F N, Burenkov O M. 2004. A series of joint VNIIEF/LANL experiments on radiographic studies of perturbation growth at the interface of a polyethylene liner with polyethylene or water. Proc. MG-X, 348-353. [24] Atchison W L, Zocher M A, Kaul A M. 2008. Studies of material constitutive behavior using perturbation growth in explosive and magnetically driven liner systems. Russian Journal of Physical Chemistry B, 2(3): 387-401 doi: 10.1134/S199079310803010X [25] Avdeev P A, Artamonov M V, Bakhrakh S M. 2001. LEGAK program complex aimed to compute nonsteady-state flows of multi-component continuum media and the principles for realization of this complex on the distributed-memory multiprocessor computer. Ser.: Math. modeling physical processes, 3: 14 [26] Bakhrakh S M, Drennov O B, Kovalev N P, et al. 1997. Hydrodynamic instability in strong media. UCRL-CR-126710. [27] Bakhrakh S M, Velichko S V, Spiridonov V F, et al. 2004. LEGAK-3D technique aimed to compute 3D nonsteady-state flows of multi-component continuum media and the principles for its realization on the distributed-memory multiprocessor computer. Ser. : Math. modeling physical processes, 4: 41 [28] Barnes J F, Blewett P J, Mc Queen R G, el al. 1974. Taylor instability in solids. Journal of Applied Physics, 45(2): 727-732 doi: 10.1063/1.1663310 [29] Bell G I. 1951. Taylor instability on cylinders and spheres in the small amplitude approximation. Report No. LA-1321, LANL,1321: 91873-9 [30] Bellman R, Pennington R H. 1954. Effects of surface tension and viscosity on Taylor instability. Quarterly of Applied Mathematics, 12(2): 151-162 doi: 10.1090/qam/63198 [31] Betti R, Hurricane O A. 2016. Inertial-confinement fusion with lasers. Nature Physics, 12(5): 435-448 doi: 10.1038/nphys3736 [32] Buttler W T, Oró D M, Preston D L, et al. 2012. Unstable Richtmyer–Meshkov growth of solid and liquid metals in vacuum. Journal of Fluid Mechanics, 703: 60-84 doi: 10.1017/jfm.2012.190 [33] Buyko A M, Zmushko V V, Mokhov V N, et al. 2005. Dynamic copper and polyethylene strengths in shockless loading to 15 GPa according to the data of explosive magnetic experiments with cylindrical three-layer liner systems//2005 IEEE Pulsed Power Conference. IEEE: 1242-1245. [34] Buyko A M, Gorbachev Y N, Zmushko V V, et al. 2002. Study of dynamic strength of copper in joint VNIIEF/LANL liner experiments on capacitor bank ATLAS (RUS-6 7). Proc. Int. Conf. Megagauss-9. 718-724. [35] Buyko A M, Zmushko V V, Atchison W L, et al. 2008. Results and prospects of material strength studies on electrophysical facilities based on perturbation growth in liner systems. IEEE transactions on plasma science, 36(1): 104-111 doi: 10.1109/TPS.2007.914072 [36] Casner A, Masse L, Delorme B, et al. 2014. Progress in indirect and direct-drive planar experiments on hydrodynamic instabilities at the ablation front. Phys Plasmas, 21: 122702 doi: 10.1063/1.4903331 [37] Casner A, Galmiche D, Huser G, et al. 2009. Indirect drive ablative Rayleight−Taylor experiments with rugby hohlraums on OMEGA. Phys Plasmas, 16: 092701 doi: 10.1063/1.3224027 [38] Casey D T, Woods D T, Smalyuk V A, et al. 2015. Performance and mix measurements of indirect drive Cu-doped Be implosions. Physical Review Letters, 114(20): 205002 doi: 10.1103/PhysRevLett.114.205002 [39] Chandrasekhar S. 2013. Hydrodynamic and hydromagnetic stability. North Chemsford, Massachusetts, Courier Corporation. [40] Chen Q, Li L, Zhang Y, et al. 2019. Effects of the Atwood number on the Richtmyer−Meshkov instability in elastic-plastic media. Physical Review E, 99(5): 053102 doi: 10.1103/PhysRevE.99.053102 [41] Collins B D, Jacobs J W. 2002. PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/SF6 interface. Journal of Fluid Mechanics, 464: 113-136 doi: 10.1017/S0022112002008844 [42] Colvin J D, Legrand M, Remington B A, et al. 2003. A model for instability growth in accelerated solid metals. Journal of applied physics, 93(9): 5287-5301 doi: 10.1063/1.1565188 [43] Dimonte G, Gore R, Schneider M. 1998. Rayleigh−Taylor instability in elastic-plastic materials. Physical review letters, 80(6): 1212 doi: 10.1103/PhysRevLett.80.1212 [44] Dimonte G, Terrones G, Cherne F J, et al. 2011. Use of the Richtmyer−Meshkov instability to infer yield stress at high-energy densities. Physical review letters, 107(26): 264502 doi: 10.1103/PhysRevLett.107.264502 [45] Dimonte G, Remington B. 1993. Richtmyer−Meshkov experiments on the Nova laser at high compression. Physical review letters, 70(12): 1806 doi: 10.1103/PhysRevLett.70.1806 [46] Drucker D C. 1980. Taylor instability of the surface of an elastic plastic-plate. Pergamon, Mechanics Today. [47] Fermi E. 1962. The Collected Papers of Enrico Fermi, edited by E. Amaldi et al. 813-815. [48] Frachet V, Geleznikoff F, Guix R, et al. 1989. Rayleigh Taylor instability in cylindrical configuration. Proceedings of 2nd International Workshop on the Physics of Compressible Turbulent Mixing, 862−849, Pleasanton, CA. [49] Gao C Y, Zhang L C. 2012. Constitutive modelling of plasticity of fcc metals under extremely high strain rates. International Journal of Plasticity, 32: 121-133 [50] Goldstein W, Rosner R. 2012. Workshop on the science of fusion ignition on NIF. LLNL-TR-570412. [51] Goncharov V N, McKenty P, Skupsky S, et al. 2000. Modeling hydrodynamic instabilities in inertial confinement fusion targets. Physics of Plasmas, 7(12): 5118-5139 doi: 10.1063/1.1321016 [52] Grady D. 2007. Fragmentation of rings and shells: The legacy of NF Mott. Berlin, Springer Science & Business Media. [53] Grigoryev S Y, Dyachkov S A, Parshikov A N, et al. 2022. Limited and unlimited spike growth from grooved free surface of shocked solid. Journal of Applied Physics, 131 (6). [54] Guo H Y, Wang L F, Ye W H, et al. 2018. Weakly nonlinear Rayleigh–Taylor instability in cylindrically convergent geometry. Chinese Physics Letters, 35(5): 055201 doi: 10.1088/0256-307X/35/5/055201 [55] Haan S W, Huang H, Johnson M A, et al. 2015. Instability growth seeded by oxygen in CH shells on the national ignition facility. Physics of Plasmas, 22 (3). [56] Hide R. 1955. The character of the equilibrium of an incompressible heavy viscous fluid of variable density: An approximate theory. Mathematical Proceedings of the Cambridge Philosophical Society. Cambridge University Press, 51(1): 179-201 doi: 10.1017/S030500410003005X [57] Huntington C M, Belof J L, Blobaum K J M, et al. 2017. Investigating iron material strength up to 1 Mbar using Rayleigh−Taylor growth measurements. AIP Conference Proceedings. AIP Publishing, 1793 (1). [58] Jensen B J, Cherne F J, Prime M B, et al. 2015. Jet formation in cerium metal to examine material strength. Journal of Applied Physics, 118 (19). [59] Karkhanis V, Ramaprabhu P, Cherne F J, et al. 2018. A numerical study of bubble and spike velocities in shock-driven liquid metals. Journal of Applied Physics, 123 (2). [60] Kozlov E A, Petrovtsev A V. 2014. Cumulation of a spherically converging shock wave in metals and its dependence on elastic-plastic properties, phase transitions, spall and shear fractures. Journal of Physics: Conference Series. IOP Publishing, 490 (1): 012191. [61] Kozlov E A. 2012. 2D-and 3D-explosive experiments for verification of spall and shear strength models for some steels. AIP Conference Proceedings. American Institute of Physics, 1426(1): 945-948 [62] Landau L D, Lifshitz E M. 1987. Fluid Mechanics: Volume 6. Vol 6. Elsevier. [63] Lebedev A I, Nisovtsev P N, Rayevsky V A. 1993. Rayleigh−Taylor Instability in solids. Proceedings of the 4th International Workshop on the Physics of Compressible Turbulent Mixing, 81-93, Cambridge University Press, Cambridge, UK. [64] Lebedev A I, Nizovtsev P N, Raevskii V A, et al. 1996. Rayleigh−Taylor instability in firm substances. Physics-Doklady, 41(7): 328-330 [65] Lim H, Battaile C C, Brown J L, et al. 2016. Physically-based strength model of tantalum incorporating effects of temperature, strain rate and pressure. Modelling and Simulation in Materials Science and Engineering, 24(5): 055018 doi: 10.1088/0965-0393/24/5/055018 [66] Linhart J G. 1961. Dynamic stability of a conducting, cylindrical shell in a magnetic field. Journal of Applied Physics, 32(3): 500-505 doi: 10.1063/1.1736032 [67] Lorenz K T, Edwards M J, Glendinning S G, et al. 2005. Accessing ultrahigh-pressure, quasi-isentropic states of matter. Physics of plasmas, 12 (5). [68] Marsh S P. 1980. LASL shock Hugoniot data. California, Univ of California Press. [69] McGlaun J M, Thompson S L, Elrick M G. 1990. CTH: A three-dimensional shock wave physics code. International Journal of Impact Engineering, 10(1-4): 351-360 doi: 10.1016/0734-743X(90)90071-3 [70] Mikaelian K O. 1996. Rayleigh−Taylor instability in finite-thickness fluids with viscosity and surface tension. Physical Review E, 54(4): 3676 doi: 10.1103/PhysRevE.54.3676 [71] Meshkov E E. 1969. Instability of the interface of two gases accelerated by a shock wave. Fluid Dynamics, 4(5): 101-104 [72] Mikaelian K O. 2005. Rayleigh—Taylor and Richtmyer—Meshkov instabilities and mixing in stratified cylindrical shells. Physics of Fluids, 17 (9). [73] Mikaelian K O. 2013. Shock-induced interface instability in viscous fluids and metals. Physical Review E, 87(3): 031003 doi: 10.1103/PhysRevE.87.031003 [74] Mikaelian K O. 1993. Effect of viscosity on Rayleigh−Taylor and Richtmyer−Meshkov instabilities. Physical Review E, 47(1): 375 doi: 10.1103/PhysRevE.47.375 [75] Miles J W. 1966. Taylor instability of a flat plate. General Dynamics Report No. GAMD-7335, AD643161. General Dynamics, San Diego, CA. [76] Monfared S K, Oró D M, Grover M, et al. 2014. Experimental observations on the links between surface perturbation parameters and shock-induced mass ejection. Journal of Applied Physics, 116 (6). [77] Olles J D, Hudspeth M C, Tilger C F, et al. 2021. The effect of liquid tamping media on the growth of Richtmyer−Meshkov instability in copper. Journal of Dynamic Behavior of Materials, 7(2): 338-351 doi: 10.1007/s40870-021-00305-8 [78] Olles J D, Hudspeth M, Tilger C F, et al. 2020. Hydrodynamic Richtmyer−Meshkov instability of metallic solids used to assess material deformation at high strain-rates. Dynamic Behavior of Materials, Volume 1: Proceedings of the 2019 Annual Conference on Experimental and Applied Mechanics, 149-155, Springer International Publishing, Berlin, Germang. [79] Opie S, Loomis E, Peralta P, et al. 2017. Strength and viscosity effects on perturbed shock front stability in metals. Physical Review Letters, 118(19): 195501 doi: 10.1103/PhysRevLett.118.195501 [80] Ortega A L, Hill D J, Pullin D I, et al. 2010. Linearized Richtmyer−Meshkov flow analysis for impulsively accelerated incompressible solids. Physical Review E, 81(6): 066305 doi: 10.1103/PhysRevE.81.066305 [81] Ortega A L, Lombardini M, Pullin D I, et al. 2014. Numerical simulations of the Richtmyer−Meshkov instability in solid-vacuum interfaces using calibrated plasticity laws. Physical Review E, 89(3): 033018 doi: 10.1103/PhysRevE.89.033018 [82] Park H S, Lorenz K T, Cavallo R M. 2010a. Viscous Rayleigh−Taylor instability experiments at high pressure and strain rate. Physical Review Letter, 104(13): 5504-5507 [83] Park H S, Remington B A, Becker R C, et al. 2010b. Strong stabilization of the Rayleigh−Taylor instability by material strength at megabar pressures. Physics of Plasmas, 17 (5). [84] Plesset M S. 1954. On the stability of fluid flows with spherical symmetry. Journal of Applied Physics, 25(1): 96-98 doi: 10.1063/1.1721529 [85] Plohr J N, Plohr B J. 2005. Linearized analysis of Richtmyer–Meshkov flow for elastic materials. Journal of Fluid Mechanics, 537: 55-89 doi: 10.1017/S0022112005004647 [86] Plohr B J, Sharp D H. 1998. Instability of accelerated elastic metal plates. Zeitschrift für angewandte Mathematik und Physik ZAMP, 49: 786-804 [87] Piriz A R, Cela J J L, Cortazar O D, et al. 2005. Rayleigh−Taylor instability in elastic solids. Physical Review E, 72(5): 056313 doi: 10.1103/PhysRevE.72.056313 [88] Piriz A R, Cela J J L, Tahir N A, et al. 2006a. Richtmyer−Meshkov flow in elastic solids. Physical Review E, 74(3): 037301 doi: 10.1103/PhysRevE.74.037301 [89] Piriz A R, Cela J J L, Tahir N A. 2009. Linear analysis of incompressible Rayleigh−Taylor instability in solids. Physical Review E, 80(4): 046305 doi: 10.1103/PhysRevE.80.046305 [90] Piriz A R, Cela J J L, Tahir N A, et al. 2008. Richtmyer−Meshkov instability in elastic-plastic media. Physical Review E, 78(5): 056401 doi: 10.1103/PhysRevE.78.056401 [91] Piriz A R, Cela J J L, Tahir N A. 2010. Comment on “viscous Rayleigh−Taylor instability experiments at high pressure and strain rate”. Physical review letters, 105(17): 179601 doi: 10.1103/PhysRevLett.105.179601 [92] Piriz A R, Cortazar O D, Lopez Cela J J, et al. 2006b. The Rayleigh−Taylor instability. American Journal of Physics, 74(12): 1095-1098 doi: 10.1119/1.2358158 [93] Piriz A R, Piriz S A, Tahir N A. 2021. Elastic-plastic Rayleigh−Taylor instability at a cylindrical interface. Physical Review E, 104(3): 035102 doi: 10.1103/PhysRevE.104.035102 [94] Piriz A R, Sun Y B, Tahir N A. 2013. Rayleigh−Taylor stability boundary at solid−liquid interfaces. Physical Review E, 88(2): 023026 doi: 10.1103/PhysRevE.88.023026 [95] Piriz A R, Sun Y B, Tahir N A. 2014. Rayleigh−Taylor linear growth at an interface between an elastoplastic solid and a viscous liquid. Physical Review E, 89(6): 063022 doi: 10.1103/PhysRevE.89.063022 [96] Piriz S A, Piriz A R, Tahir N A. 2019. Magneto-Rayleigh–Taylor instability in an elastic finite-width medium overlying an ideal fluid. Journal of Fluid Mechanics, 867: 1012-1042 doi: 10.1017/jfm.2019.193 [97] Preston D L, Tonks D L, Wallace D C. 2003. Model of plastic deformation for extreme loading conditions. Journal of Applied Physics, 93(1): 211-220 doi: 10.1063/1.1524706 [98] Prime M B, Buttler W T, Buechler M A, et al. 2017. Estimation of metal strength at very high rates using free-surface Richtmyer–Meshkov instabilities. Journal of Dynamic Behavior of Materials, 3: 189-202 doi: 10.1007/s40870-017-0103-9 [99] Prime M B, Buttler W T, Fensin S J, et al. 2019. Tantalum strength at extreme strain rates from impact-driven Richtmyer−Meshkov instabilities. Physical Review E, 100(5): 053002 doi: 10.1103/PhysRevE.100.053002 [100] Prudhomme G, De Rességuier T, Roland C, et al. 2020. Velocity and mass density of the ejecta produced from sinusoidal grooves in laser shock-loaded tin. Journal of Applied Physics, 128 (15). [101] Remington B A, Bazan G, Belak J, et al. 2004. Materials science under extreme conditions of pressure and strain rate. Metal Lurgical and Materials Transactions A, 35 : 2587-2607. [102] Reinovsky R E, Atchison W L, Dimonte G, et al. 2008. Pulsed-power hydrodynamics: An application of pulsed-power and high magnetic fields to the exploration of material properties and problems in experimental hydrodynamics. IEEE transactions on plasma science, 36(1): 112-124 doi: 10.1109/TPS.2007.914708 [103] Richtmyer R D. 1954. Taylor instability in shock acceleration of compressible fluids. Los Alamos Scientific Lab., N. Mex. [104] Roberts M S. 2012. Experiments and simulations on the incompressible, Rayleigh−Taylor instability with small wavelength initial perturbations. PhD of the University of Arizona. [105] Robinson A C, Swegle J W. 1989. Acceleration instability in elastic-plastic solids. II. Analytical techniques. Journal of applied physics, 66(7): 2859-2872 doi: 10.1063/1.344191 [106] Rousculp C L, Oro D M, Griego J R, et al. 2016. Investigation of surface phenomena in shocked tin in converging geometry. Los Alamos National Lab. (LANL), Los Alamos, NM (United States). [107] Ruden E L, Bell D E. 1997. Rayleigh–Taylor stability criteria for elastic-plastic solid plates and shells. Journal of applied physics, 82(1): 163-170 doi: 10.1063/1.365795 [108] Sheppard M G, Atchison W L, Anderson W E, et al. 1997. Rayleigh−Taylor mix experiment on Pegasus. Digest of Technical Papers. 11th IEEE International Pulsed Power Conference (Cat. No. 97CH36127). IEEE, 2: 1399-1404 [109] Smalyuk V A, Weber C R, Landen O L, et al. 2020. Review of hydrodynamic instability experiments in inertially confined fusion implosions on national ignition facility. Plasma Phys Control Fusion, 62: 014007 doi: 10.1088/1361-6587/ab49f4 [110] Stebner A P, Wehrenberg C E, Li B, et al. 2018. Strength of tantalum shocked at ultrahigh pressures. Materials Science and Engineering: A, 732 : 220-227. [111] Steinberg D J, Cochran S G, Guinan M W. 1980. A constitutive model for metals applicable at high-strain rate. Journal of applied physics, 51(3): 1498-1504 doi: 10.1063/1.327799 [112] Sun Q, Jia Y, Zhang Z, et al. 2022. Cylindrical metal liner implosion at extremes of pressure and material velocity on an intense pulsed power facility-FP-2. Review of Scientific Instruments, 93 (1). [113] Swegle J W, Robinson A C. 1989. Acceleration instability in elastic-plastic solids. I. Numerical simulations of plate acceleration. Journal of Applied Physics, 66(7): 2838-2858 doi: 10.1063/1.344190 [114] Sun Y B, Zeng R H, Tao J J. 2021. Effects of viscosity and elasticity on Rayleigh—Taylor instability in a cylindrical geometry. Physics of Plasmas, 28 (6). [115] Taylor G I. 1950. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 201(1065): 192-196 [116] Terrones G. 2005. Fastest growing linear Rayleigh−Taylor modes at solid/fluid and solid/solid interfaces. Physical Review E, 71(3): 036306 doi: 10.1103/PhysRevE.71.036306 [117] Terrones G, Carrara M D. 2015. Rayleigh−Taylor instability at spherical interfaces between viscous fluids: Fluid/vacuum interface. Physics of Fluids, 27 (5). [118] Terrones G, Heberling T. 2020. Rayleigh–Taylor instability at spherical interfaces between viscous fluids: The fluid/fluid interface. Physics of Fluids, 32 (9). [119] Velikovich A L. 1996. Analytic theory of Richtmyer–Meshkov instability for the case of reflected rarefaction wave. Physics of Fluids, 8(6): 1666-1679 doi: 10.1063/1.868938 [120] Vogler T J, Hudspeth M C. 2021. Tamped Richtmyer–Meshkov instability experiments to probe high-pressure material strength. Journal of Dynamic Behavior of Materials, 7: 262-278 doi: 10.1007/s40870-020-00288-y [121] Wang L F, Ye W H, He X T, et al. 2017. Theoretical and simulation research of hydrodynamic instabilities in inertial-confinement fusion implosions. Sci China Phys Mech Astron, 60: 055201 doi: 10.1007/s11433-017-9016-x [122] Wang P, He A M, Shao J L, et al. 2018. Numerical and theoretical investigations of shock-induced material ejection and ejecta-gas mixing. Scientia Sinica, 48(9): 106-116 [123] Weinwurm M, Bland S N, Chittenden J P. 2014. Metal liner-driven cylindrically convergent isentropic compression of cryogenic deuterium. Journal of Physics: Conference Series. IOP Publishing, 500(8): 082002 doi: 10.1088/1742-6596/500/8/082002 [124] White G N. 1973. Los Alamos National Laboratory Report No. LA-5225-MS (unpublished [125] Wouchuk J G. 2001. Growth rate of the linear Richtmyer−Meshkov instability when a shock is reflected. Physical Review E, 63(5): 056303 doi: 10.1103/PhysRevE.63.056303 [126] Zhao Z, Wang P, Liu N, et al. 2020. Analytical model of nonlinear evolution of single-mode Rayleigh–Taylor instability in cylindrical geometry. Journal of Fluid Mechanics, 900: A24 doi: 10.1017/jfm.2020.526 [127] Zhang Y, Dai Z H, et al. 2017. One-dimensional magneto-hydrodynamics simulation of magnetically driven solid liner implosions on FP-1 facility. Acta Phys. Sin., 67 (7): 070703. [128] Zhang S, Liu W, Wang G, et al. 2019. Investigation of convergent Richtmyer—Meshkov instability at tin/xenon interface with pulsed magnetic driven imploding. Chinese Physics B, 28 (4): 044702. -




 下载:
下载: