-
摘要: 力学超材料是一种有别于传统力学行为的工程材料, 它源于人工可编程的微结构以及材料的固有属性. 在过去的十年中, 随着计算性能和复杂微观结构制造能力的巨大进步, 力学超材料已经吸引了研究人员的广泛关注, 因为它能够实现自然界中不可能出现的多重物理属性. 该领域迅速崛起的趋势之一是将材料行为和单元结构与其他不同的多种物理因素(如电场或磁场)以及温度、光或化学反应等刺激相结合, 从而扩大按需主动调制力学响应的范围. 在本文中, 我们旨在概述有关超材料的力学和多物理性质调制的相关文献, 重点介绍双能级设计的新兴趋势, 着重讨论力学超材料在关键工程领域应用中的巨大潜力. 本文对该领域的发展趋势、挑战和未来路线进行了系统深入分析, 涵盖实时可重构性和功能编程、4D打印、纳米超材料、人工智能和机器学习、多物理折纸/剪纸、活性物质、软物质和保形超材料、复杂微结构制造、服役寿命效应和可扩展性等概念.Abstract: Mechanical metamaterials are engineered materials with unconventional mechanical behavior that originates from artificially programmed microstructures along with intrinsic material properties. With tremendous advancement in computational and manufacturing capabilities to realize complex microstructures over the last decade, the field of mechanical metamaterials has been attracting wide attention due to immense possibilities of achieving unprecedented multi-physical properties which are not attainable in naturally-occurring materials. One of the rapidly emerging trends in this field is to couple the mechanics of material behavior and the unit cell architecture with different other multi-physical aspects such as electrical or magnetic fields, and stimuli like temperature, light or chemical reactions to expand the scope of actively programming on-demand mechanical responses. In this article, we aim to abridge outcomes of the relevant literature concerning mechanical and multi-physical property modulation of metamaterials focusing on the emerging trend of bi-level design, and subsequently highlight the broad-spectrum potential of mechanical metamaterials in their critical engineering applications. The evolving trends, challenges and future roadmaps have been critically analyzed here involving the notions of real-time reconfigurability and functionality programming, 4D printing, nano-scale metamaterials, artificial intelligence and machine learning, multi-physical origami/kirigami, living matter, soft and conformal metamaterials, manufacturing complex microstructures, service-life effects and scalability.
-
图 1 材料和结构在超材料中相互作用. (a)在材料尺度上利用力学设计和人工微结构来提高性能(Schaedler & Carter 2016). 随着技术的进步, 功能结构的定义变得更加复杂, 并从宏观走向更精细的微观和纳米尺度. (b)跨尺度点阵结构的适用性和工程应用(Mukhopadhyay & Adhikari 2017a). (c)泊松比可编程的六边形晶格微结构: (i)正泊松比; (ii)负泊松比; (iii) ~ (v)零泊松比(Mukhopadhyay & Adhikari 2017b). (d)超平面弯曲的高斯曲率编程结构: (i)负; (ii)正(Mirzaali et al. 2021). (e) Sarrus模块化折纸设计: (i)描述Sarrus机制的立方单位; (ii) Sarrus连杆的装配; (iii) ~ (v)模块变换顺序; (vi) ~ (viii) Sarrus超材料(Yang & You 2020)的变形构型. (f)基于折纸/剪纸的模块材料: (i)一个典型的截断八面体; (ii) ~ (iii)由截断的八面体衍生的对称和非对称单胞; (iv)由对称单元格堆叠得到二维元表面; (v)承受压缩载荷时的超板材结构; (vi)受拉伸载荷(Sinha & Mukhopadhyay 2022c)时的板材超结构. (g)基于水弹折纸的管状超材料: (i)基于水弹折纸的折痕图; (ii)水弹管的3D视图; (iii)管状元结构的宏观图示; (iv)微观结构和远场驱动相关的形状变形; (v)基于微观结构的本构关系编程(Mukhopadhyay et al. 2020a)
图 3 多功能超材料总览 (a)电磁超材料: (i)由铜制分裂环谐振器和导线构成的2维周期阵列组成一种“左手材料”(LHM), 呈现出负折射(Shelby et al. 2001); (ii)圆形、方形、单环和多环结构的分裂环谐振器, 分裂环谐振器(SRR)是一种高导电性结构, 其电感由两个环之间的电容平衡; (iii)瑞士卷结构的透视图和俯视图, 瑞士卷结构内的电流是由结构的自身电容引起的, 能够形成完整交流电路; (iv)圆锥形瑞士卷的侧视图和俯视图, 圆锥形瑞士卷结构有助于电磁波在相对较大的距离上传输, 同时减少了阻尼; (v)用于制作手性瑞士卷结构的导电片展开结构和手性瑞士卷结构的俯视图, 导电片的每一层都填充有介质材料(Grimberg 2013). (b)光学超材料: (i)常规透镜聚焦光线; (ii)负折射率超材料; (iii)给出负电响应的等离子体纳米棒; (iv)提供负磁共振的分裂纳米环; (v)与双分裂纳米环配对的纳米棒, 产生负的磁和电响应; (vi)耦合纳米棒在特定情况下也能呈现负的磁和电响应; (vii)由双开口环组成的3D光学超材料单胞(Gardner et al. 2011). (c)声学超材料: (i)带有侧孔图案的管状结构, 显示出负有效模量, 单胞结构如侧图显示; (ii)测量相位和传输速度的实验装置(Lee et al. 2009b). (d)力学超材料: 显示出拉胀性和可逆变形的微观点阵(Schaedler & Carter 2016)
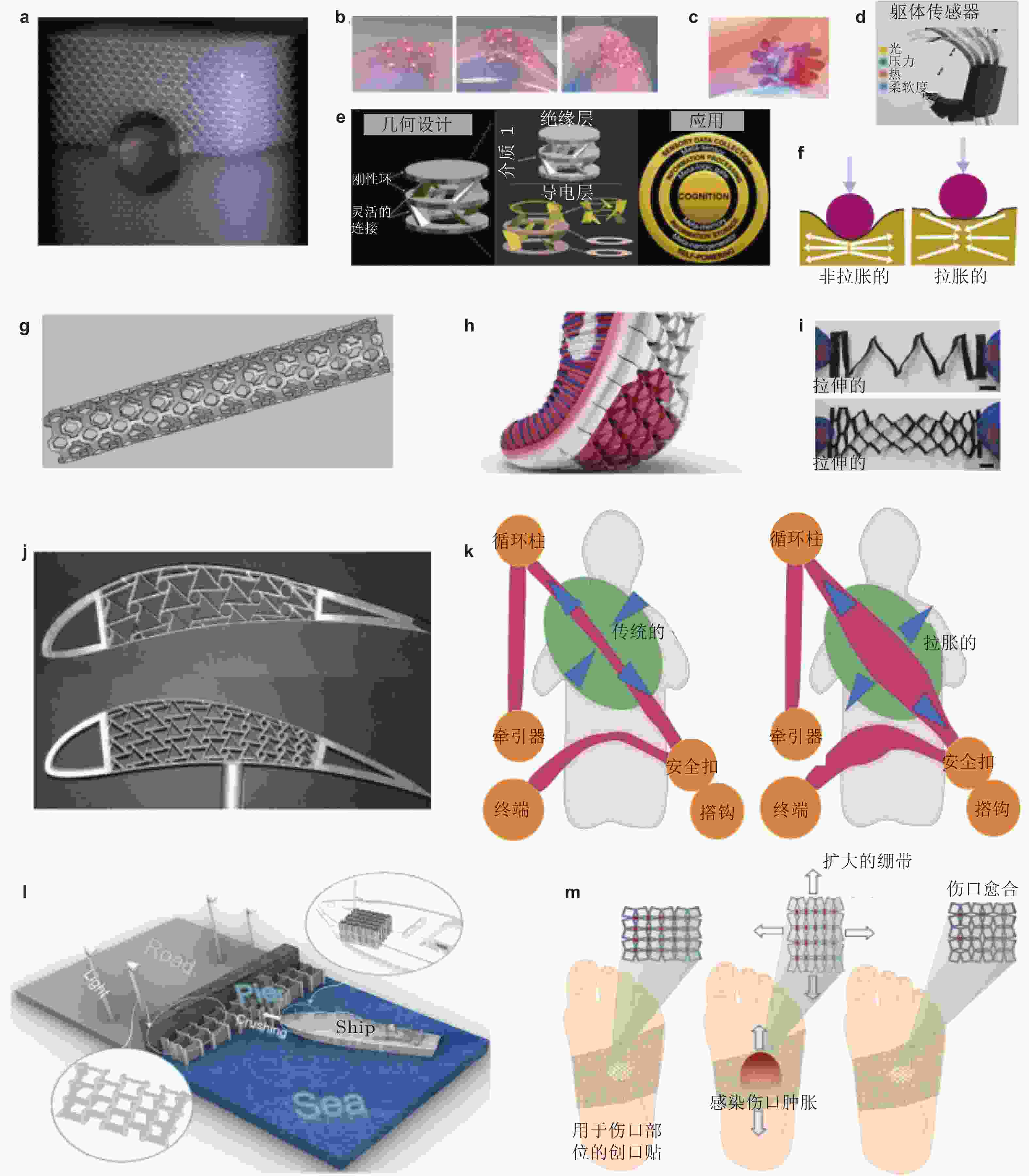
图 4 力学超材料的实际应用 (a)隐身斗篷(Bückmann et al. 2014). (b)电子皮肤(Li K et al. 2019). (c)软体机器人(Cheng et al. 2020). (d)仿生夹具(Wang X Q et al. 2020). (e)通过超材料进行力学计算(Zhang et al. 2023). (f)抗冲击结构(Evans & Alderson 2000). (g)血管支架(Jia et al. 2018). (h)跑鞋(Gleeson 2020). (i)柔性电池(Bao et al. 2020). (j)桁架芯翼型(Spadoni & Ruzzene 2007). (k)拉胀安全带(Balan P et al. 2023). (l)海洋防护结构应用中的组装蜂窝结构(Lang et al. 2023). (m)拉胀绷带(Balan P et al. 2023). 值得注意的是, 我们在这里只提到了几个有代表性的应用, 实际上这个列表是无穷无尽的
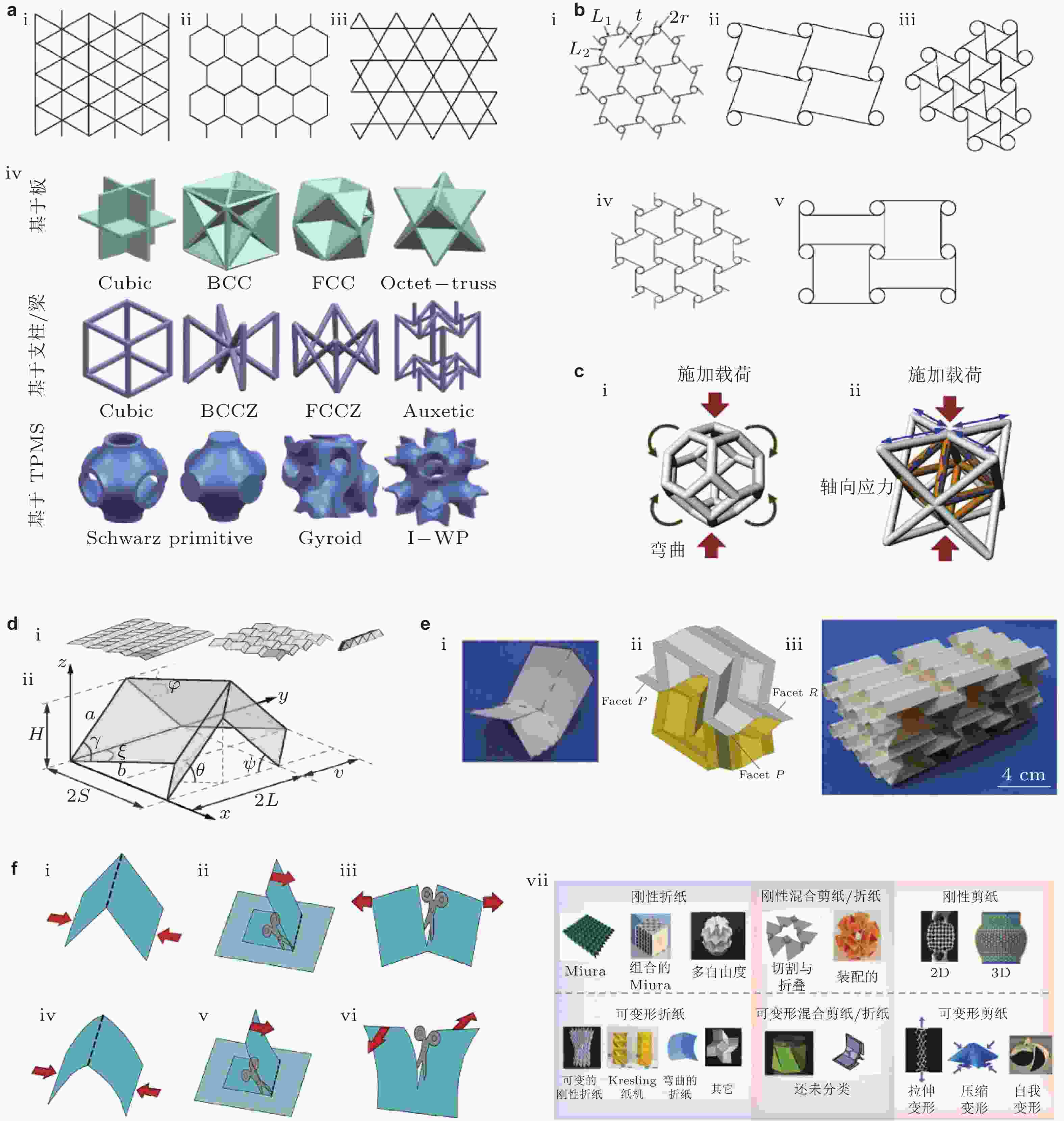
图 5 超材料的微结构构型 (a)不同形状的晶格: (i)规则的三角形网格; (ii)正六边形晶格; (iii)被称为Kagome的半正三角形-六边形晶格(Ongaro 2018); (iv)具有不同类型组成元素的晶格超材料, 例如基于板、基于支柱/梁和基于TPMS的构件(Zhong et al. 2023). (b)手性和反手性蜂窝(Ongaro 2018): (i)三手性蜂窝(Alderson et al. 2010); (ii)四手性蜂窝; (iii)六手性蜂窝; (iv)反三手性蜂窝(Alderson et al. 2010); (v)反四手性蜂巢. (c)基本变形模式: (i)弯曲占优势的晶格晶胞; (ii)受拉伸支配的晶格单胞(Zheng et al. 2014). (d)基于折纸的力学超材料: (i) Miura-ori层的运动行为; (ii) Miura-ori折纸结构的单胞几何形状(Schenk & Guest 2013). (e)混合折纸超材料: (i)标准Miura-ori图案化的晶胞, 可表现出面内拉胀性; (ii)混合折纸单元的3D视图, 由常规凹六边形蜂窝单元和常规Miura-ori图案组合而成; (iii)通过周期性重复单胞获得的超材料微结构(Wang H et al. 2020). (f)基于折纸和剪纸不同类别的超材料: (i)刚性折纸; (ii)刚性混合折纸/剪纸; (iii)刚性剪纸; (iv)可变形折纸; (v)可变形的混合折纸/剪纸; (vi)可变形的剪纸; (vii)基于折纸和剪纸的超材料的子类(Zhai et al. 2021)
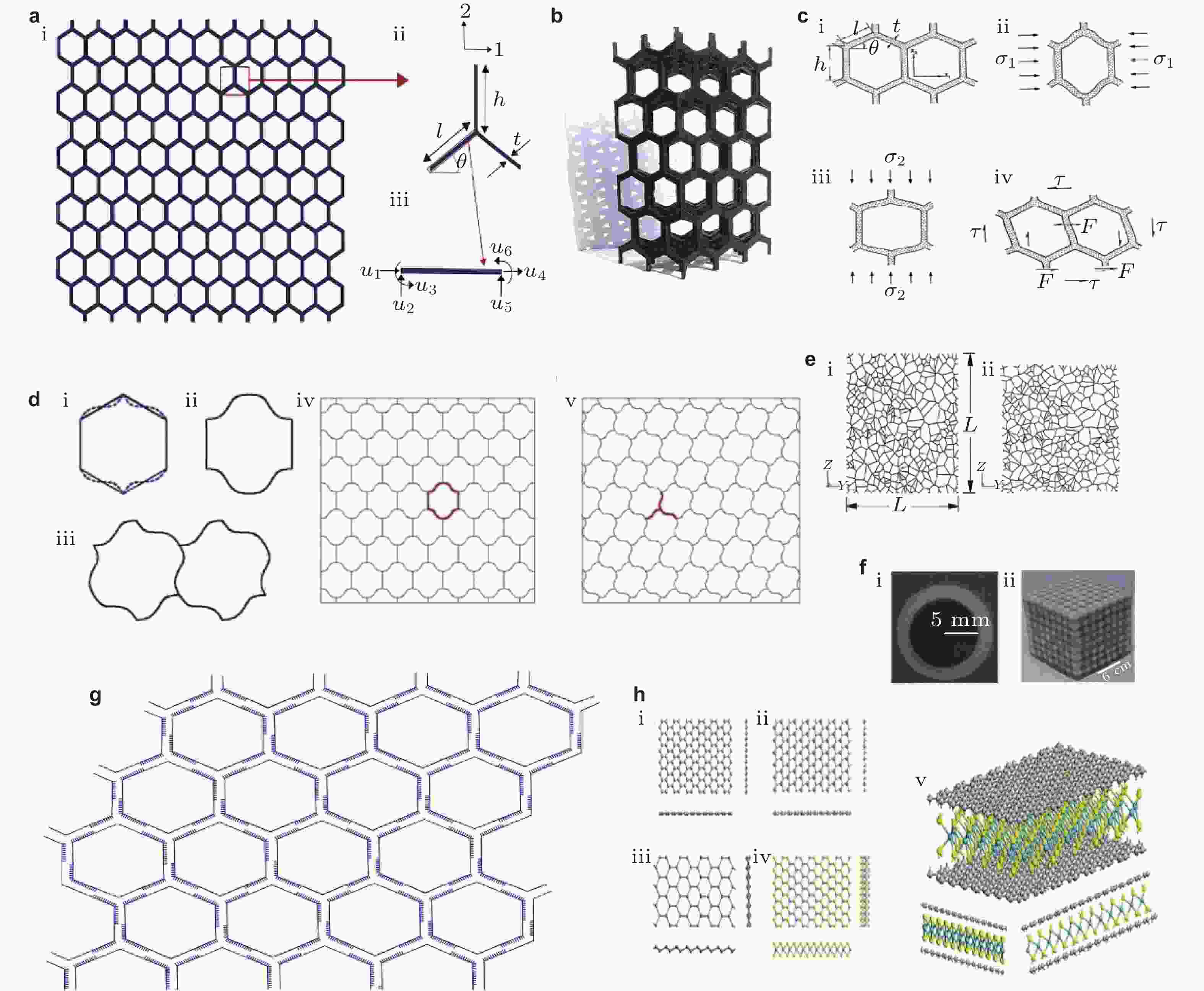
图 6 力学超材料的被动特性调制 (a)基于单胞自下而上的方法对蜂窝结构分析: (i)规则的2D蜂窝状晶格; (ii)堆叠时形成整个晶格的蜂窝的单胞; (iii)蜂窝的单元壁, 将其视为具有自由度的梁单元(P Sinha & Mukhopadhyay 2022). (b)规则的3D蜂窝晶格(Sinha et al. 2023a). (c) 2D六边形蜂窝结构的力学特性: (i)未变形的蜂窝; (ii)沿X1方向承受面内载荷的单胞; (iii)沿X2方向承受面内载荷的单胞; (iv)承受面内剪切载荷的单胞(Andrews et al. 1999). 对于其他2D和3D晶格, 需要适当分析单胞的力学特性. (d)不同应力条件下晶格中的抗弯曲效应: (i)正六边形晶格的单胞; (ii)在经受沿X1方向的拉伸载荷的压应力时, 具有弯曲胞壁的单胞; (iii)当受到剪切应力时获得的具有弯曲细胞壁的单胞; (iv)针对X1方向上的拉伸正应力, 蜂窝网格单元壁中具有的反曲率; (v)蜂窝晶格单元壁在抗逆时针剪应力具有的反曲率(Ghuku & Mukhopadhyay 2023). (e) 2D Voronoi蜂窝的单元不规则性: (i)未变形构型中的随机Voronoi蜂窝; (ii)具有周期性边界条件的变形Voronoi蜂窝结构(Zhu et al. 2001). (f)波在力学超材料中的传播: (i)共振球形原子的横截面; (ii)声波晶体中具有单胞的声学超材料(Lu et al. 2009). (g)具有区域不连续性的典型非不变蜂窝晶格(Sinha et al. 2023b). (h)基于纳米异质结构的纳米级超材料概念: (i)典型纳米结构的侧视图和俯视图, 其中单一类型的原子在单一平面中形成整个结构; (ii)典型纳米结构的侧视图和俯视图, 其中不同类型的原子在单个平面中形成整个结构; (iii)典型纳米结构的侧视图和俯视图, 其中原子在多个平面中形成整个结构; (iv)典型纳米结构的侧视图和俯视图, 其中不同类型的原子在多个平面中形成整个结构; (v)由不同2D材料组成的多层异质结构(Mukhopadhyay et al. 2020b)
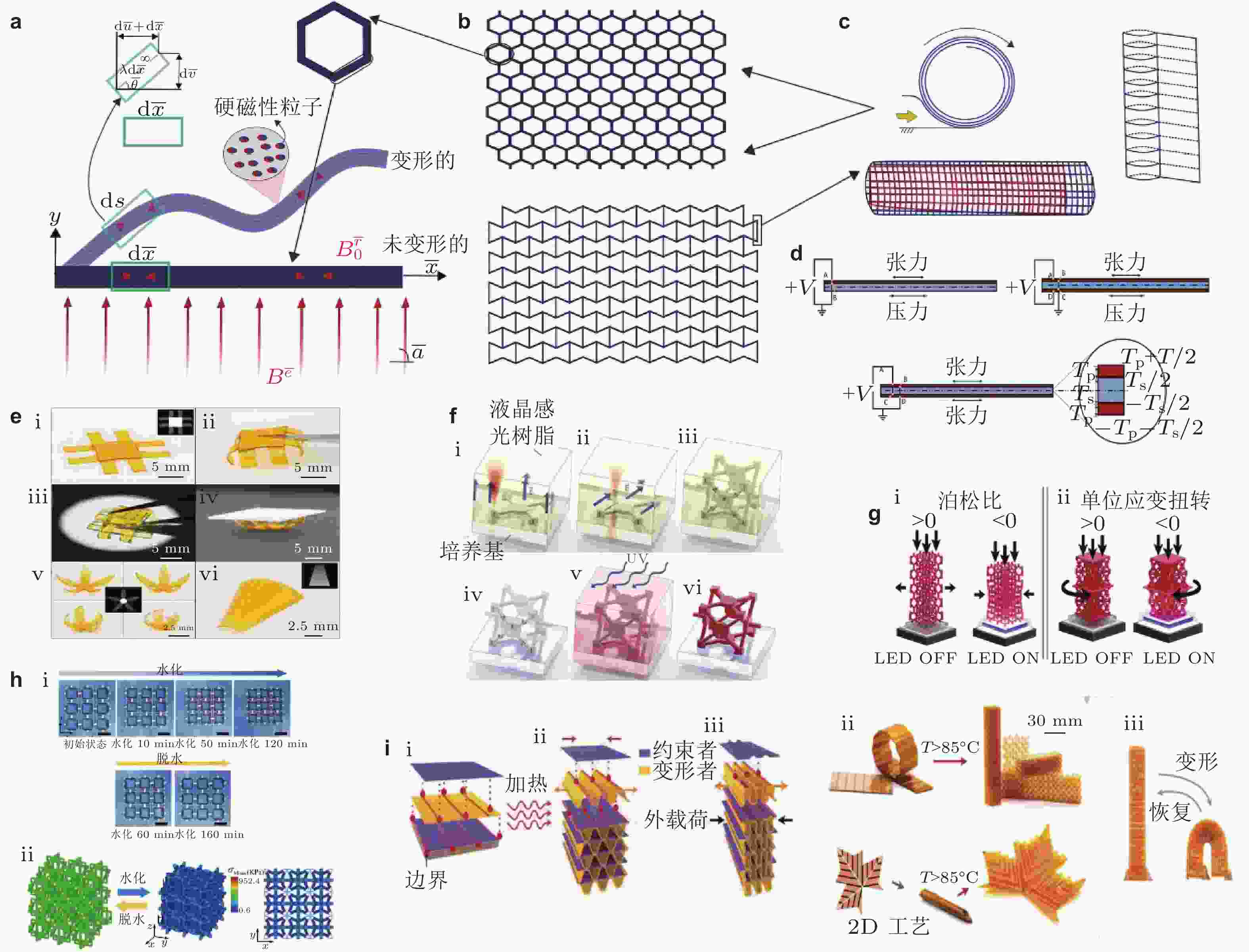
图 7 力学超材料的主动特性调制 (a) ~ (d)双能级主动晶格超材料: (b)中所示的晶格(拉胀型和非拉胀型)由(a)、(c)和(d)中所示的不同主动梁组件制成; 基于(a)中所示的硬磁软(HMS)梁形成磁驱动主动力学超材料, 图中显示了外磁驱动下未变形和变形配置的HMS梁(Sinha & Mukhopadhyay 2023); 压力驱动的主动力学超材料是基于(c)所示的可充气梁形成的, 在这种可膨胀的晶格中可以进行卷绕和密实堆叠(P Sinha et al. 2023); 电驱动主动力学超材料基于压电复合梁形成, 如(d)所示, 其中通过单晶形和双晶形构型可以实现纯弯曲、纯拉伸和弯曲/拉伸组合模式(Singh et al. 2022b). (e)光驱动主动力学超材料: (i)光聚合后的聚合物片; (ii)空间的、 不同固化板的自由弯曲; (iii)用后固化法在均匀光线下对弯曲结构进行定形; (iv)后固化后的硬样品; (v)花结构的不同开放程度; (vi)聚合物板材曲率的连续变化(Zhao et al. 2017). (f) 3D光学力学超材料: (i)使用外部准静态电场
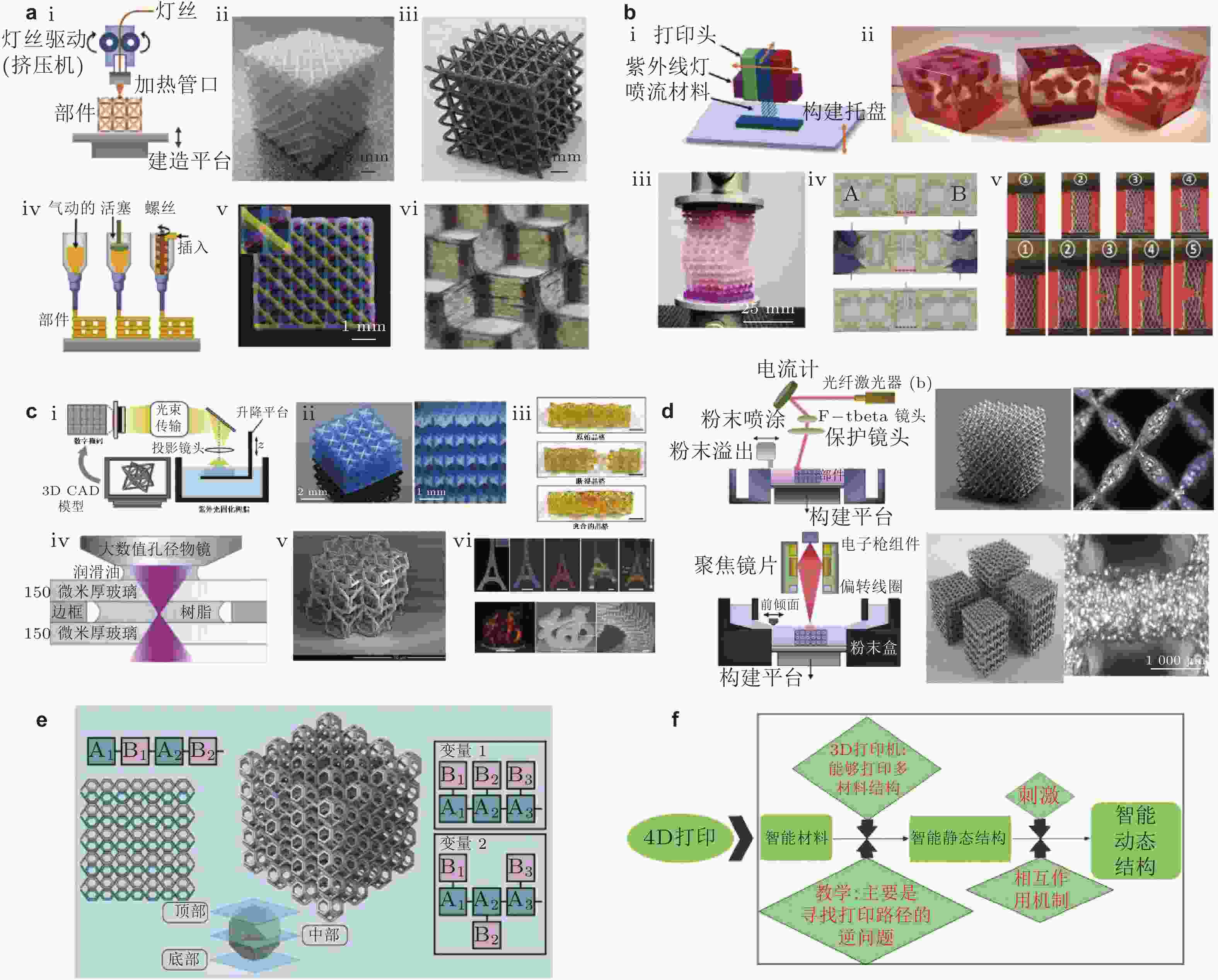
$ \overrightarrow{E} $ 来定向光敏树脂的液晶方向, 然后通过双光子聚合(TPP)打印的体素进行局部固定; (ii)结构的另一部分具有不同的方向排列, 导致电场的排列发生变化; (iii)结构的聚合和未聚合区域; (iv)包含定向3D液晶导向场的光学透明聚合结构; (v)样品浸泡在染料溶液中, 染料溶液扩散到样品中, 并作为吸收剂与刺激光耦合; (vi)最终超材料(Münchinger et al. 2022). (g)受光刺激的力学超材料: 基于晶格的结构, 当外部LED关闭和打开时, 分别显示正的和负的(i)泊松比和(ii)扭转应变(Münchinger et al. 2022). (h)化学驱动的主动力学超材料: (i) 2D超材料在水合和脱水时的变形模式; (ii) 3D超材料的负水化膨胀变形(Wei et al. 2020). (i)热驱动主动力学超材料: (i)热致动超弹性超材料的变形; (ii)弹性薄层压板向体积材料的转变; (iii)超材料的大变形, 卸载后可恢复其形状(Wu et al. 2021)图 8 力学超材料的物理实现 (a)材料挤压工艺: (i)熔融沉积建模 (FDM) 的设置和工作方法演示 (Surjadi et al. 2019); (ii)基于FDM的聚合物八重桁架晶格(Kaur et al. 2017); (iii)通过化学镀和FDM制造的具有Ni外壳和聚合物芯的复合晶格(Song et al. 2018); (iv)直接墨水书写(DIW)的基本工作方法说明 (Surjadi et al. 2019); (v)一种基于3D微点阵的DIW (Rozvany 2009); (vi)使用DIW (Compton & Lewis 2014)制造的纤维填充环氧蜂窝复合材料. (b)喷墨打印: (i)喷墨打印设置示意图(IJP) (Ding et al. 2017); (ii)使用Polyjet打印尺寸和形状可调的颗粒复合材料(Tee et al. 2020); (iii)由于使用Polyjet在周期性晶格中插入刚性缺陷, 导致周期性晶格屈曲(Janbaz et al. 2019); (iv)使用PolyJet印刷制造的物理与门, 允许逻辑可调属性(Waheed et al. 2020); (v)通过改变数字材料的比例来控制2D复合材料 (PolyJet打印) 的断裂特性(Lei et al. 2018). (c)光固化技术: (i)数字光处理(DLP)技术图示(Chen & Zheng 2018); (ii)使用多材料μDLP方法(Chen & Zheng 2018)创建具有可定制泊松比的超材料; (iii)由于光固化技术的灵活性, 晶格的愈合得以实现(Yu et al. 2020); (iv)双光子聚合 (TPP) 技术说明(Serbin et al. 2004); (v) TPP可以产生具有可调屈曲特性的微晶格(Vangelatos et al. 2019); (vi) TPP工艺可以导致更大的晶格间距, 因为它允许结构收缩, 从而使结构显示出光子性质(Liu Y et al. 2019). (d)粉末床熔融: (i)选择性激光熔化(SLM)装置演示(Surjadi et al. 2019); (ii)使用SLM印刷的五模超材料(Hedayati et al. 2017); (iii)电子束熔化(EBM)装置演示(Surjadi et al. 2019); (iv)使用EBM制造的晶格(Yang et al. 2015). (e)六边形晶格结构的运动动力学, 用于将其从平面配置折叠. 晶格结构的设计基于重复晶胞(Janbaz et al. 2017). (f)利用4D打印制造主动超材料, 并实现主动的时间依赖性和可编程响应(Boley et al. 2019, Kim et al. 2022, Zeng et al. 2022). 这本质上是通过耦合3D打印和主动材料来制造时间依赖性和外部刺激敏感的超材料来实现的
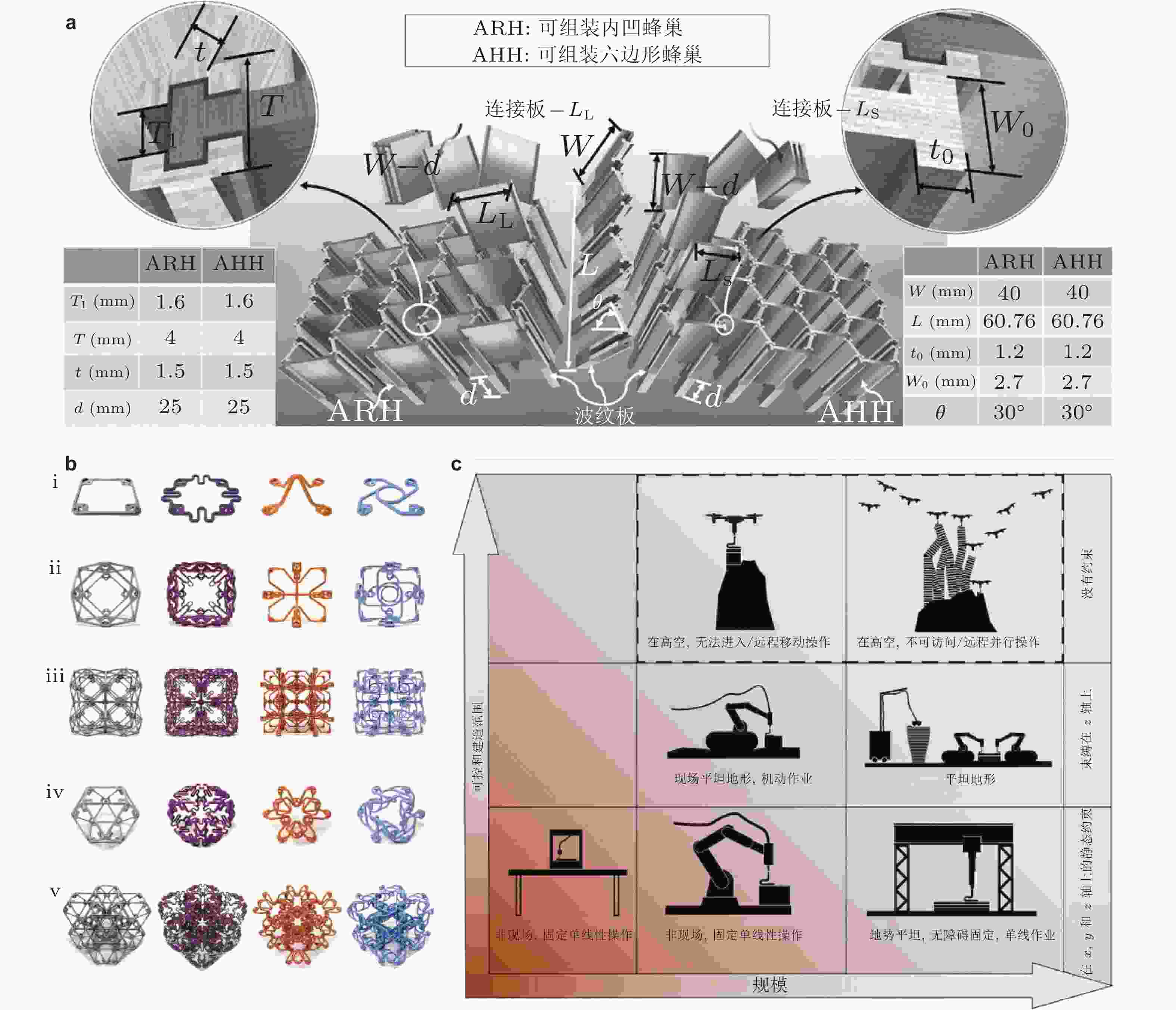
图 9 力学超材料的可扩展性和大型建造体积增材制造的途径. (a)通过组装过程制造超材料(Lang et al. 2023). 这里, 每个超材料晶胞(或一组几个晶胞)可以额外制造并随后组装以实现大的构建体积. (b)离散组装的力学超材料. 从左到右显示了四种不同类型的超材料, 即刚性、柔性、拉胀性和手性. (i)端面轮廓; (ii)单个体素的前视图; (iii) 2 × 2 × 2立方体的前视图; (iv)单个体素的斜视图; (v) 2 × 2 × 2斜视图(Jenett et al. 2020). (c)用于实现大构建体积和规模的常规、机器人和无人机辅助(空中)增材制造(Zhang et al. 2022)
-
[1] Abd El-Sayed F K, Jones R, Burgess I W. 1979. A theoretical approach to the deformation of honeycomb based composite materials. Composites, 10: 209-214. doi: 10.1016/0010-4361(79)90021-1 [2] Adhikari S, Mukhopadhyay T, Liu X. 2021. Broadband dynamic elastic moduli of honeycomb lattice materials: A generalized analytical approach. Mechanics of Materials, 157: 103796. doi: 10.1016/j.mechmat.2021.103796 [3] Adhikari S, Mukhopadhyay T, Shaw A, Lavery N P. 2020. Apparent negative values of Young’s moduli of lattice materials under dynamic conditions. International Journal of Engineering Science, 150: 103231. doi: 10.1016/j.ijengsci.2020.103231 [4] Aghighi F, Morris J, Amirkhizi A V. 2019. Low-frequency micro-structured mechanical metamaterials. Mechanics of Materials, 130: 65-75. doi: 10.1016/j.mechmat.2018.12.008 [5] Alderson A, Alderson K L, Chirima G, Ravirala N, Zied K M. 2010. The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs. Composites Science and Technology, Special issue on Chiral Smart Honeycombs, 70: 1034-1041. [6] Al-Mulla T, Buehler M J. 2015. Folding creases through bending. Nature Mater., 14: 366-368. doi: 10.1038/nmat4258 [7] Alturki M, Burgueño R. 2019. Multistable cosine-curved dome system for elastic energy dissipation. Journal of Applied Mechanics, 86 : 091002 [8] Alù A, Engheta N. 2008. Dielectric sensing in $ \mathrm{\epsilon } $ -near-zero narrow waveguide channels. Phys. Rev. B, 78: 1098-1121.[9] Ambati M, Fang N, Sun C, Zhang X. 2007. Surface resonant states and superlensing in acoustic metamaterials. Phys. Rev. B, 75: 195447. doi: 10.1103/PhysRevB.75.195447 [10] Andrews E W, Gibson L J, Ashby M F. 1999. The creep of cellular solids. Acta Materialia, 47: 2853-2863. doi: 10.1016/S1359-6454(99)00150-0 [11] Ashby M F. 2005. The properties of foams and lattices. Philosophical Transactions of the Royal Society A: Mathematical. Physical and Engineering Sciences, 364: 15-30. [12] Bacquet C L, Al Ba’ba’a H, Frazier M J, Nouh M, Hussein M I. 2018. Metadamping: Dissipation emergence in elastic metamaterials. Advances in Applied Mechanics, 51: 115-164. [13] Bakhvalov N, Panasenko G. 1989. Homogenisation: Averaging processes in periodic media: Mathematical problems in the mechanics of composite materials. Netherlands, 36 . [14] Balan P M, Mertens A J, Bahubalendruni M V A R. 2023. Auxetic mechanical metamaterials and their futuristic developments: A state-of-art review. Materials Today Communications, 34: 105285. doi: 10.1016/j.mtcomm.2022.105285 [15] Banerjee A, Das R, Calius E P. 2017. Frequency graded 1d metamaterials: A study on the attenuation bands. Journal of Applied Physics, 122: 075101. doi: 10.1063/1.4998446 [16] Bao Y, Hong G, Chen Y, Chen J, Chen H, Song W-L, Fang D. 2020. Customized kirigami electrodes for flexible and deformable lithium-ion batteries. ACS Appl. Mater. Interfaces, 12: 780-788. doi: 10.1021/acsami.9b18232 [17] Bassik N, Abebe B T, Laflin K E, Gracias D H. 2010. Photolithographically patterned smart hydrogel based bilayer actuators. Polymer, 51: 6093-6098. doi: 10.1016/j.polymer.2010.10.035 [18] Bauer J, Schroer A, Schwaiger R, Kraft O. 2016. Approaching theoretical strength in glassy carbon nanolattices. Nature Mater., 15: 438-443. doi: 10.1038/nmat4561 [19] Benedetti M, du Plessis A, Ritchie R O, Dallago M, Razavi N, Berto F. 2021. Architected cellular materials: A review on their mechanical properties towards fatigue-tolerant design and fabrication. Materials Science and Engineering: R: Reports, 144: 100606. doi: 10.1016/j.mser.2021.100606 [20] Bertoldi K, Vitelli V, Christensen J, van Hecke M. 2017. Flexible mechanical metamaterials. Nat. Rev. Mater., 2: 1-11. [21] Bessa M A, Glowacki P, Houlder M. 2019. Bayesian machine learning in metamaterial design: Fragile becomes supercompressible. Advanced Materials, 31: 1904845. doi: 10.1002/adma.201904845 [22] Bigoni D, Guenneau S, Movchan A B, Brun M. 2013. Elastic metamaterials with inertial locally resonant structures: Application to lensing and localization. Phys. Rev. B, 87: 174303. doi: 10.1103/PhysRevB.87.174303 [23] Blees M K, Barnard A W, Rose P A, Roberts S P, McGill K L, Huang P Y, Ruyack A R, Kevek J W, Kobrin B, Muller D A, McEuen P L. 2015. Graphene kirigami. Nature, 524: 204-207. doi: 10.1038/nature14588 [24] Boatti E, Vasios N, Bertoldi K. 2017. Origami metamaterials for tunable thermal expansion. Advanced Materials, 29: 1700360. doi: 10.1002/adma.201700360 [25] Boley J W, van Rees W M, Lissandrello C, Horenstein M N, Truby R L, Kotikian A, Lewis J A, Mahadevan L. 2019. Shape-shifting structured lattices via multimaterial 4D printing. Proceedings of the National Academy of Sciences, 116: 20856-20862. doi: 10.1073/pnas.1908806116 [26] Brillouin L N. 1953. Wave propagation in periodic structures: Electric filters and crystal lattices. New York: Dover Publications. [27] Brunet T, Merlin A, Mascaro B, Zimny K, Leng J, Poncelet O, Aristégui C, Mondain-Monval O. 2015. Soft 3D acoustic metamaterial with negative index. Nature Mater., 14: 384-388. doi: 10.1038/nmat4164 [28] Bückmann T, Thiel M, Kadic M, Schittny R, Wegener M. 2014. An elasto-mechanical unfeelability cloak made of pentamode metamaterials. Nat. Commun., 5: 4130. doi: 10.1038/ncomms5130 [29] Buckner T L, Bilodeau R A, Kim S Y, Kramer-Bottiglio R. 2020. Roboticizing fabric by integrating functional fibers. Proceedings of the National Academy of Sciences, 117: 25360-25369. doi: 10.1073/pnas.2006211117 [30] Cai R, Jin Y, Rabczuk T, Zhuang X, Djafari-Rouhani B. 2021. Propagation and attenuation of rayleigh and pseudo surface waves in viscoelastic metamaterials. Journal of Applied Physics, 129: 124903. doi: 10.1063/5.0042577 [31] Cai W, Chettiar V, Kildishev A, V Shalaev. 2007. Optical cloaking with metamaterials. Nature Photon, 1: 224-227. doi: 10.1038/nphoton.2007.28 [32] Carrara M, Cacan M R, Leamy M J, Ruzzene M, Erturk A. 2012. Dramatic enhancement of structure-borne wave energy harvesting using an elliptical acoustic mirror. Applied Physics Letters, 100: 204105. doi: 10.1063/1.4719098 [33] Carrara M, Cacan M R, Toussaint J, Leamy M J, Ruzzene M, Erturk A. 2013. Metamaterial-inspired structures and concepts for elastoacoustic wave energy harvesting. Smart Mater. Struct., 22: 065004. doi: 10.1088/0964-1726/22/6/065004 [34] Chandra Y, Adhikari S, Mukherjee S, Mukhopadhyay T. 2022. Unfolding the mechanical properties of buckypaper composites: Nano-to-macro-scale coupled atomistic-continuum simulations. Engineering with Computers, 38: 5199-5229. doi: 10.1007/s00366-021-01538-w [35] Chandra Y, Mukhopadhyay T, Adhikari S, Figiel Ł. 2020. Size-dependent dynamic characteristics of graphene based multi-layer nano hetero-structures. Nanotechnology, 31: 145705. doi: 10.1088/1361-6528/ab6231 [36] Chaurha A, Malaji P V, Mukhopadhyay T. 2022. Dual functionality of vibration attenuation and energy harvesting: Effect of gradation on non-linear multi-resonator metastructures. Eur. Phys. J. Spec. Top., 231: 1403-1413. doi: 10.1140/epjs/s11734-022-00506-9 [37] Che K, Yuan C, Wu J, Jerry Qi H, Meaud J. 2016. Three-dimensional-printed multistable mechanical metamaterials with a deterministic deformation sequence. Journal of Applied Mechanics, 84 : 011004. [38] Chen B G, Upadhyaya N, Vitelli V. 2014. Nonlinear conduction via solitons in a topological mechanical insulator. Proceedings of the National Academy of Sciences, 111: 13004-13009. doi: 10.1073/pnas.1405969111 [39] Chen C, Lu T J, Fleck N A. 1999. Effect of imperfections on the yielding of two-dimensional foams. Journal of the Mechanics and Physics of Solids, 47: 2235-2272. doi: 10.1016/S0022-5096(99)00030-7 [40] Chen D, Zheng X. 2018. Multi-material additive manufacturing of metamaterials with giant, tailorable negative poisson’s ratios. Sci. Rep., 8: 9139. doi: 10.1038/s41598-018-26980-7 [41] Chen J S, Su W J, Cheng Y, Li W C, Lin C Y. 2019. A metamaterial structure capable of wave attenuation and concurrent energy harvesting. Journal of Intelligent Material Systems and Structures, 30: 2973-2981. doi: 10.1177/1045389X19880023 [42] Chen S, Cao Y, Sarparast M, Yuan H, Dong L, Tan X, Cao C. 2020. Soft crawling robots: Design, actuation, and locomotion. Advanced Materials Technologies, 5: 1900837. doi: 10.1002/admt.201900837 [43] Chen Y, Ai B, Wong Z J. 2020. Soft optical metamaterials. Nano Convergence, 7: 1-17. doi: 10.1186/s40580-019-0212-3 [44] Chen Y, Jin L. 2018. Geometric role in designing pneumatically actuated pattern-transforming metamaterials. Extreme Mechanics Letters, 23: 55-66. doi: 10.1016/j.eml.2018.08.001 [45] Chen Y, Ma Y, Yin Q, Pan F, Cui C, Zhang Z, Liu B. 2021. Advances in mechanics of hierarchical composite materials. Composites Science and Technology, 214: 108970. doi: 10.1016/j.compscitech.2021.108970 [46] Chen Y, Mai Y W, Ye L. 2023. Perspectives for multiphase mechanical metamaterials. Materials Science and Engineering: R: Reports, 153: 100725. doi: 10.1016/j.mser.2023.100725 [47] Cheng Y C, Lu H C, Lee X, Zeng H, Priimagi A. 2020. Kirigami-based light-induced shape-morphing and locomotion. Advanced Materials, 32: 1906233. doi: 10.1002/adma.201906233 [48] Cho Y, Shin J H, Costa A, Kim T A, Kunin V, Li J, Lee S Y, Yang S, Han H N, Choi I S, Srolovitz D J. 2014. Engineering the shape and structure of materials by fractal cut. Proceedings of the National Academy of Sciences, 111: 17390-17395. doi: 10.1073/pnas.1417276111 [49] Choi G P T, Dudte L H, Mahadevan L. 2019. Programming shape using kirigami tessellations. Nat. Mater., 18: 999-1004. doi: 10.1038/s41563-019-0452-y [50] Claeys C, Pluymers B, Sas P, Desmet W. 2014. Design of a resonant metamaterial based acoustic enclosure. Proceedings of the 26th International Conference on Noise and Vibration Engineering, 325 . [51] Compton B G, Lewis J A. 2014. 3d-printing of lightweight cellular composites. Advanced materials, 26: 5930-5935. doi: 10.1002/adma.201401804 [52] Cummer S A, Christensen J, Alù A. 2016. Controlling sound with acoustic metamaterials. Nat Rev Mater., 1: 1-13. [53] Cummer S A, Schurig D. 2007. One path to acoustic cloaking. New J. Phys., 9: 45. doi: 10.1088/1367-2630/9/3/045 [54] Cundy H M, Rollett A P. 1961. Mathematical Models. Oxford: Oxford University Press. [55] de Bruijn N G. 1981. Algebraic theory of penrose’s non-periodic tilings of the plane, kon. Nederl. Akad. Wetensch. Proc, Ser, 84: 1-7. doi: 10.1016/1385-7258(81)90013-5 [56] de Loos M, Feringa B L, van Esch J H. 2005. Design and application of self-assembled low molecular weight hydrogels. European Journal of Organic Chemistry, 17: 3615-3631. [57] de Moura B, Machado M R, Mukhopadhyay T, Dey S. 2022. Dynamic and wave propagation analysis of periodic smart beams coupled with resonant shunt circuits: Passive property modulation. Eur. Phys. J. Spec. Top., 231: 1415-1431. doi: 10.1140/epjs/s11734-022-00504-x [58] Del Vescovo D, Giorgio I. 2014. Dynamic problems for metamaterials: Review of existing models and ideas for further research. International Journal of Engineering Science, 80: 153-172. doi: 10.1016/j.ijengsci.2014.02.022 [59] dell’Isola F, Steigmann D, Corte A D. 2016. Synthesis of fibrous complex structures: Designing microstructure to deliver targeted macroscale response. Applied Mechanics Reviews, 67: 060804. [60] Demaine E, O’Rourke J. 2007. Geometric folding algorithms: linkages, origami, polyhedra, Cambridge university press. [61] Deshpande V S, Ashby M F, Fleck N A. 2001. Foam topology: Bending versus stretching dominated architectures. Acta Materialia, 49: 1035-1040. doi: 10.1016/S1359-6454(00)00379-7 [62] Dey S, Mukhopadhyay T, Adhikari S. 2018. Uncertainty quantification in laminated composites: A meta-model based approach. CRC Press. [63] Deymier P A. 2013. Acoustic metamaterials and phononic crystals. Springer science & Business media, 173 . [64] Dima A, Bhaskarla S, Becker C, Brady M, Campbell C, Dessauw P, Hanisch R, Kattner U, Kroenlein K, Newrock M, Peskin A, Plante R, Li S Y, Rigodiat P F, Amaral G S, Trautt Z, Schmitt X, Warren J, Youssef S. 2016. Informatics infrastructure for the materials genome initiative. JOM, 68: 2053-2064. doi: 10.1007/s11837-016-2000-4 [65] Ding Z, Yuan C, Peng X, Wang T, Qi H J, Dunn M L. 2017. Direct 4d printing via active composite materials. Science Advances, 3: e1602890. doi: 10.1126/sciadv.1602890 [66] Dudek K K, Gatt R, Dudek M R, Grima J N. 2018. Negative and positive stiffness in auxetic magneto-mechanical metamaterials. Proceedings of the Royal Society A: Mathematical. Physical and Engineering Sciences, 474: 20180003. doi: 10.1098/rspa.2018.0003 [67] Dudek K K, Gatt R, Grima J N. 2020. 3D composite metamaterial with magnetic inclusions exhibiting negative stiffness and auxetic behaviour. Materials & Design, 187: 108403. [68] Dudek K K, Martínez J A I, Ulliac G, Kadic M. 2022. Micro-scale auxetic hierarchical mechanical metamaterials for shape morphing. Advanced Materials, 34: 2110115. doi: 10.1002/adma.202110115 [69] Dudek K K, Wolak W, Gatt R, Grima J N. 2019. Impact resistance of composite magnetic metamaterials. Sci. Rep., 9: 3963. doi: 10.1038/s41598-019-40610-w [70] Dudek M R, Dudek K K, Wolak W, Wojciechowski K W, Grima J N. 2019. Magnetocaloric materials with ultra-small magnetic nanoparticles working at room temperature. Sci. Rep., 9:17607. doi: 10.1038/s41598-018-37186-2 [71] Dudte L H, Vouga E, Tachi T, Mahadevan L. 2016. Programming curvature using origami tessellations. Nature Mater., 15: 583-588. doi: 10.1038/nmat4540 [72] Eidini M, Paulino G H. 2015. Unraveling metamaterial properties in zigzag-base folded sheets. Science Advances, 1: e1500224. doi: 10.1126/sciadv.1500224 [73] El Helou C, Buskohl P R, Tabor C E, Harne R L. 2021. Digital logic gates in soft, conductive mechanical metamaterials. Nat. Commun., 12: 1-8. doi: 10.1038/s41467-020-20314-w [74] Evans A A, Silverberg J L, Santangelo C D. 2015. Lattice mechanics of origami tessellations. Phys. Rev. E, 92: 013205. doi: 10.1103/PhysRevE.92.013205 [75] Evans K E, Alderson A. 2000. Auxetic materials: Functional materials and structures from lateral thinking! Advanced Materials, 12 : 617–628. [76] Fahy F, Walker J. 2018. Advanced Applications in Acoustics, Noise and Vibration. Boca Raton: CRC Press. [77] Fan H, Yang L, Tian Y, Wang Z. 2020. Design of metastructures with quasi-zero dynamic stiffness for vibration isolation. Composite Structures, 243: 112244. doi: 10.1016/j.compstruct.2020.112244 [78] Fan Y, Collet M, Ichchou M, Li L, Bareille O, Dimitrijevic Z. 2017. Enhanced wave and finite element method for wave propagation and forced response prediction in periodic piezoelectric structures. Chinese Journal of Aeronautics, 30: 75-87. doi: 10.1016/j.cja.2016.12.011 [79] Fang H, Chu S C A, Xia Y, Wang K W. 2018. Programmable self-locking origami mechanical metamaterials. Advanced Materials, 30: 1706311. doi: 10.1002/adma.201706311 [80] Fang H, Li S, Ji H, Wang K W. 2016. Uncovering the deformation mechanisms of origami metamaterials by introducing generic degree-four vertices. Phys. Rev. E, 94: 043002. doi: 10.1103/PhysRevE.94.043002 [81] Fang N, Lee H, Sun C, Zhang X. 2005. Sub-diffraction-limited optical imaging with a silver superlens. Science, 308: 534-537. doi: 10.1126/science.1108759 [82] Fang Z, Song H, Zhang Y, Jin B, Wu J, Zhao Q, Xie T. 2020. Modular 4d printing via interfacial welding of digital light-controllable dynamic covalent polymer networks. Matter., 2: 1187-1197. doi: 10.1016/j.matt.2020.01.014 [83] Fathers R K, Gattas J M, You Z. 2015. Quasi-static crushing of eggbox, cube, and modified cube foldcore sandwich structures. International Journal of Mechanical Sciences, 101: 421-428. [84] Filipov E T, Tachi T, Paulino G H. 2015. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proceedings of the National Academy of Sciences, 112: 12321-12326. doi: 10.1073/pnas.1509465112 [85] Fleck N A, Deshpande V S, Ashby M F. 2010. Micro-architectured materials: Past, present and future. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 466: 2495-2516. doi: 10.1098/rspa.2010.0215 [86] Florijn B, Coulais C, van Hecke M. 2014. Programmable mechanical metamaterials. Phys. Rev. Lett., 113: 175503. doi: 10.1103/PhysRevLett.113.175503 [87] Frenzel T, Kadic M, Wegener M. 2017. Three-dimensional mechanical metamaterials with a twist. Science, 358: 1072-1074. doi: 10.1126/science.aao4640 [88] Galea R, Dudek K K, Farrugia P S, Zammit Mangion L, Grima J N, Gatt R. 2022. Reconfigurable magneto-mechanical metamaterials guided by magnetic fields. Composite Structures, 280: 114921. doi: 10.1016/j.compstruct.2021.114921 [89] Gao H, Ji B, Jäger I L, Arzt E, Fratzl P. 2003. Materials become insensitive to flaws at nanoscale: Lessons from nature. Proceedings of the National Academy of Sciences, 100: 5597-5600. doi: 10.1073/pnas.0631609100 [90] Gardner D F, Evans J S, Smalyukh I I. 2011. Towards reconfigurable optical metamaterials: Colloidal nanoparticle self-assembly and self-alignment in liquid crystals. Molecular Crystals and Liquid Crystals, 545: 3-1227. [91] Gatt R, Grima J N. 2008. Negative compressibility. Physica Status Solidi, 2: 236-238. [92] Gatt R, Mizzi L, Azzopardi J I, Azzopardi K M, Attard D, Casha A, Briffa J, Grima J N. 2015. Hierarchical auxetic mechanical metamaterials. Sci. Rep., 5: 8395. doi: 10.1038/srep08395 [93] Ge Q, Dunn C K, Qi H J, Dunn M L. 2014. Active origami by 4D printing. Smart Mater. Struct., 23: 094007. doi: 10.1088/0964-1726/23/9/094007 [94] Ge Q, Qi H J, Dunn M L. 2013. Active materials by four-dimension printing. Applied Physics Letters, 103: 131901. doi: 10.1063/1.4819837 [95] Ghuku S, Mukhopadhyay T. 2023. On enhancing mode-dependent failure strength under large deformation: The concept of anti-curvature in honeycomb lattices. Composite Structures, 305: 116318. doi: 10.1016/j.compstruct.2022.116318 [96] Ghuku S, Mukhopadhyay T. 2022. Anti-curvature honeycomb lattices for mode-dependent enhancement of nonlinear elastic properties under large deformation. International Journal of Non-Linear Mechanics, 140: 103887. doi: 10.1016/j.ijnonlinmec.2021.103887 [97] Gibson I J, Ashby M F. 1997. The mechanics of three-dimensional cellular materials. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 382: 43-59. [98] Gibson L J. 2012. The hierarchical structure and mechanics of plant materials. Journal of The Royal Society Interface, 9: 2749-2766. doi: 10.1098/rsif.2012.0341 [99] Gibson L J, Ashby M F, Schajer G S, Robertson, C I. 1997. The mechanics of two-dimensional cellular materials. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 382: 25-42. [100] Giri T R, Mailen R. 2021. Controlled snapping sequence and energy absorption in multistable mechanical metamaterial cylinders. International Journal of Mechanical Sciences, 204: 106541. doi: 10.1016/j.ijmecsci.2021.106541 [101] Gleeson H. 2020. Stretching the limits. Phys. World, 33: 36. [102] Goldsmith B R, Esterhuizen J, Liu J X, Bartel C J, Sutton C. 2018. Machine learning for heterogeneous catalyst design and discovery. AIChE Journal, 64: 2311-2323. doi: 10.1002/aic.16198 [103] Gómez L R, Turner A M, van Hecke M, Vitelli V. 2012. Shocks near Jamming. Phys. Rev. Lett., 108: 058001. doi: 10.1103/PhysRevLett.108.058001 [104] Greer J R, Deshpande V S. 2019. Three-dimensional architected materials and structures: Design, fabrication, and mechanical behavior. MRS Bulletin, 44: 750-757. doi: 10.1557/mrs.2019.232 [105] Grima J N, Caruana-Gauci R, Dudek M R, Wojciechowski K W, Gatt, R. 2013. Smart metamaterials with tunable auxetic and other properties. Smart Mater. Struct., 22: 084016. doi: 10.1088/0964-1726/22/8/084016 [106] Grimberg R. 2013. Electromagnetic metamaterials. Materials Science and Engineering, 178: 1285-1295. doi: 10.1016/j.mseb.2013.03.022 [107] Grosskopf A K, Truby R L, Kim H, Perazzo A, Lewis J A, Stone H A. 2018. Viscoplastic matrix materials for embedded 3d printing. ACS Appl. Mater. Interfaces, 10: 23353-23361. doi: 10.1021/acsami.7b19818 [108] Gu G X, Chen C T, Buehler M J. 2018a. De novo composite design based on machine learning algorithm. Extreme Mechanics Letters, 18: 19-28. doi: 10.1016/j.eml.2017.10.001 [109] Gu G X, Chen C T, Richmond D J, Buehler M J. 2018b. Bioinspired hierarchical composite design using machine learning: Simulation, additive manufacturing, and experiment. Mater. Horiz., 5: 939-945. doi: 10.1039/C8MH00653A [110] Gu G X, Wettermark, S, Buehler, M J. 2017. Algorithm-driven design of fracture resistant composite materials realized through additive manufacturing. Additive Manufacturing, 17: 47-54. doi: 10.1016/j.addma.2017.07.002 [111] Gu H, Boehler Q, Cui H, Secchi E, Savorana G, De Marco C, Gervasoni S, Peyron Q, Huang T Y, Pane S, Hirt A M, Ahmed D, Nelson B J. 2020. Magnetic cilia carpets with programmable metachronal waves. Nat. Commun., 11: 2637. doi: 10.1038/s41467-020-16458-4 [112] Guenneau S, Movchan A, Pétursson G, Ramakrishna S A. 2007. Acoustic metamaterials for sound focusing and confinement. New J. Phys., 9: 399. doi: 10.1088/1367-2630/9/11/399 [113] Guo K, Yang Z, Yu C H, Buehler M J. 2021. Artificial intelligence and machine learning in design of mechanical materials. Mater. Horiz., 8: 1153-1172. doi: 10.1039/D0MH01451F [114] Gupta K, Mukhopadhyay T, Roy L, Dey S. 2022. High-velocity ballistics of twisted bilayer graphene under stochastic disorder. Adv. Nano Res, 12: 529-547. [115] Gupta K K, Roy A, Mukhopadhyay T, Roy L, Dey S. 2022. Probing the stochastic fracture behavior of twisted bilayer graphene: Efficient ann based molecular dynamics simulations for complete probabilistic characterization. Materials Today Communications, 32: 103932. doi: 10.1016/j.mtcomm.2022.103932 [116] Gupta S, Mukhopadhyay T, Kushvaha V. 2023. Microstructural image based convolutional neural networks for efficient prediction of full-field stress maps in short fiber polymer composites. Defence Technology, 24: 58-82. doi: 10.1016/j.dt.2022.09.008 [117] Ha C S, Lakes R S, Plesha M E. 2018. Design, fabrication, and analysis of lattice exhibiting energy absorption via snap-through behavior. Materials & Design, 141: 426-437. [118] Hahn V, Kiefer P, Frenzel T, Qu J, Blasco E, Barner-Kowollik C, Wegener M. 2020. Rapid assembly of small materials building blocks (voxels) into large functional 3d metamaterials. Advanced Functional Materials, 30: 1907795. doi: 10.1002/adfm.201907795 [119] Hao X P, Xu Z, Li C Y, Hong W, Zheng Q, Wu Z L. 2020. Kirigami-design-enabled hydrogel multimorphs with application as a multistate switch. Advanced Materials, 32: 2000781. doi: 10.1002/adma.202000781 [120] He L, Wen Z, Jin Y, Torrent D, Zhuang X, Rabczuk T. 2021. Inverse design of topological metaplates for flexural waves with machine learning. Materials & Design, 199: 109390. [121] Hedayati R, Leeflang A M, Zadpoor A A. 2017. Additively manufactured metallic pentamode meta-materials. Applied Physics Letters, 110: 091905. doi: 10.1063/1.4977561 [122] Helma C, Cramer T, Kramer S, De Raedt L. 2004. Data mining and machine learning techniques for the identification of mutagenicity inducing substructures and structure activity relationships of noncongeneric compounds. J. Chem. Inf. Comput. Sci, 44: 1402-1411. doi: 10.1021/ci034254q [123] Hewage T A M, Alderson K L, Alderson A, Scarpa F. 2016. Double-negative mechanical metamaterials displaying simultaneous negative stiffness and negative poisson’s ratio properties. Advanced Materials, 28: 10323-10332. doi: 10.1002/adma.201603959 [124] Hu N, Burgueño R. 2015. Buckling-induced smart applications: Recent advances and trends. Smart Mater. Struct, 24: 063001. doi: 10.1088/0964-1726/24/6/063001 [125] Hua J, Lei H, Gao C F, Guo X, Fang D. 2020. Parameters analysis and optimization of a typical multistable mechanical metamaterial. Extreme Mechanics Letters, 35: 100640. doi: 10.1016/j.eml.2020.100640 [126] Huang C, Chen L. 2016. Negative poisson’s ratio in modern functional materials. Advanced Materials, 28: 8079-8096. doi: 10.1002/adma.201601363 [127] Huang J, Zhang J, Xu D, Zhang S, Tong H, Xu N. 2023. From jammed solids to mechanical metamaterials : A brief review. Current Opinion in Solid State and Materials Science, 27: 101053. doi: 10.1016/j.cossms.2022.101053 [128] Hussein M I. 2009. Reduced bloch mode expansion for periodic media band structure calculations. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 465: 2825-2848. doi: 10.1098/rspa.2008.0471 [129] Hussein M I, Frazier M J. 2013. Metadamping: An emergent phenomenon in dissipative metamaterials. Journal of Sound and Vibration, 332: 4767-4774. doi: 10.1016/j.jsv.2013.04.041 [130] Hussein M I, Leamy M J, Ruzzene M. 2014. Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Applied Mechanics Reviews, 66 : 040802. [131] Imre A R. 2014. Metamaterials with negative compressibility—A novel concept with a long history. Mater. Sci. -Pol., 32: 126-129. doi: 10.2478/s13536-013-0179-4 [132] Inman D J. 2017. Vibration with control. John Wiley & Sons. [133] Isanaka B R, Mukhopadhyay T, Varma R K, Kushvaha V. 2022. On exploiting machine learning for failure pattern driven strength enhancement of honeycomb lattices. Acta Materialia, 239: 118226. doi: 10.1016/j.actamat.2022.118226 [134] Isobe M, Okumura K. 2016. Initial rigid response and softening transition of highly stretchable kirigami sheet materials. Sci. Rep., 6: 24758. doi: 10.1038/srep24758 [135] Jackson J A, Messner M C, Dudukovic N A, Smith W L, Bekker L, Moran B, Golobic A M, Pascall A J, Duoss E B, Loh K J, Spadaccini C M. 2018. Field responsive mechanical metamaterials. Science Advances, 4: eaau6419. doi: 10.1126/sciadv.aau6419 [136] Jacob Z, Alekseyev L V, Narimanov E. 2006. Optical hyperlens: Far-field imaging beyond the diffraction limit. Opt. Express, 14: 8247. doi: 10.1364/OE.14.008247 [137] Jain A, Ong S P, Hautier G, Chen W, Richards W D, Dacek S, Cholia S, Gunter D, Skinner D, Ceder G, Persson K A. 2013. Commentary: The materials project: A materials genome approach to accelerating materials innovation. APL Materials, 1: 011002. doi: 10.1063/1.4812323 [138] Jakšić Z, Jakšić O, Djurić Z, Kment C. 2007. A consideration of the use of metamaterials for sensing applications: Field fluctuations and ultimate performance. J. Opt. A: Pure Appl. Opt., 9: S377. doi: 10.1088/1464-4258/9/9/S16 [139] Janbaz S, Bobbert F S L, Mirzaali M J, Zadpoor A A. 2019. Ultra-programmable buckling-driven soft cellular mechanisms. Mater. Horiz., 6: 1138-1147. doi: 10.1039/C9MH00125E [140] Janbaz S, Noordzij N, Widyaratih D S, Hagen C W, Fratila-Apachitei L E, Zadpoor A A. 2017. Origami lattices with free-form surface ornaments. Science Advances, 3: eaao1595. doi: 10.1126/sciadv.aao1595 [141] Jang D, Greer J R. 2010. Transition from a strong-yet-brittle to a stronger-and-ductile state by size reduction of metallic glasses. Nature Mater., 9: 215-219. doi: 10.1038/nmat2622 [142] Jena D P, Panigrahi S N, Kumar R. 2013. Gear fault identification and localization using analytic wavelet transform of vibration signal. Measurement, 46: 1115-1124. doi: 10.1016/j.measurement.2012.11.010 [143] Jenett B, Cameron C, Tourlomousis F, Rubio A P, Ochalek M, Gershenfeld N. 2020. Discretely assembled mechanical metamaterials. Science Advances, 6: eabc9943. doi: 10.1126/sciadv.abc9943 [144] Ji X, Deng L, Zhang J, Luan Y, Duan Y. 2022. Energy absorption characteristics of 3d lattice structure filled with periodic inner core based on 3d printing. J. of Materi Eng and Perform, 31: 6784-6794. doi: 10.1007/s11665-022-06692-w [145] Jia H, Gu S Y, Chang K. 2018. 3D printed self-expandable vascular stents from biodegradable shape memory polymer. Advances in Polymer Technology, 37: 3222-3228. doi: 10.1002/adv.22091 [146] Jiang C, Rist F, Wang H, Wallner J, Pottmann H. 2022. Shape-morphing mechanical metamaterials. Computer-Aided Design, 143: 103146. doi: 10.1016/j.cad.2021.103146 [147] Jikov V V, Kozlov S M, Oleinik O A. 1994. Homogenization of differential operators and integral functionals. Springer Science & Business Media. [148] Jin L, Forte A E, Deng B, Rafsanjani A, Bertoldi K. 2020. Kirigami-inspired inflatables with programmable shapes. Advanced Materials, 32: 2001863. doi: 10.1002/adma.202001863 [149] Jin Y, He L, Wen Z, Mortazavi B, Hongwei G, Torrent D, Djafari-Rouhani B, Rabczuk T, Zhuang X, Li Y. 2022. Intelligent on-demand design of phononic metamaterials. Nanophotonics, 11: 439-460. doi: 10.1515/nanoph-2021-0639 [150] Jones D R H, Ashby M F. 2011. Engineering Materials 1: An Introduction to Properties, Application and Design. Oxford: Elsevier. [151] Kadic M, Bückmann T, Stenger N, Thiel M, Wegener M. 2012. On the practicability of pentamode mechanical metamaterials. Applied Physics Letters, 100: 191901. doi: 10.1063/1.4709436 [152] Kadic M, Milton G W, van Hecke M, Wegener M. 2019. 3d metamaterials. Nat Rev Phys, 1: 198-210. doi: 10.1038/s42254-018-0018-y [153] Kaur M, Yun T G, Han S M, Thomas E L, Kim W S. 2017. 3D printed stretching-dominated micro-trusses. Materials & Design, 134: 272-280. [154] Kim D, Ferretto I, Leinenbach C, Lee W. 2022. 3d and 4d printing of complex structures of Fe-mn-Si-based shape memory alloy using laser powder bed fusion. Advanced Materials Interfaces, 9: 2200171. doi: 10.1002/admi.202200171 [155] Kim W, Byun J, Kim J K, Choi W Y, Jakobsen K, Jakobsen J, Lee D Y, Cho K J. 2019. Bioinspired dual-morphing stretchable origami. Science Robotics, 4: eaay3493. doi: 10.1126/scirobotics.aay3493 [156] Kim Y, Parada G A, Liu S, Zhao X. 2019. Ferromagnetic soft continuum robots. Science Robotics, 4: eaax7329. doi: 10.1126/scirobotics.aax7329 [157] Kim Y, Yuk H, Zhao R, Chester S A, Zhao X. 2018. Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature, 558: 274-279. doi: 10.1038/s41586-018-0185-0 [158] Kirklin S, Saal J E, Meredig B, Thompson A, Doak J W, Aykol M, Rühl S, Wolverton C. 2015. The open quantum materials database (oqmd): Assessing the accuracy of dft formation energies. npj Comput Mater., 1: 1-15. [159] Kokkinis D, Bouville F, Studart A R. 2018. 3d printing of materials with tunable failure via bioinspired mechanical gradients. Advanced Materials, 30: 1705808. doi: 10.1002/adma.201705808 [160] Kokkinis D, Schaffner M, Studart A R. 2015. Multimaterial magnetically assisted 3d printing of composite materials. Nat. Commun., 6: 8643. doi: 10.1038/ncomms9643 [161] Kozin V K, Shelykh I A, Nalitov A V, Iorsh I V. 2018. Topological metamaterials based on polariton rings. Phys. Rev. B, 98: 125115. doi: 10.1103/PhysRevB.98.125115 [162] Krishnamoorthy H N S, Jacob Z, Narimanov E, Kretzschmar I, Menon V M. 2012. Topological transitions in metamaterials. Science, 336: 205-209. doi: 10.1126/science.1219171 [163] Krödel S, Thomé N, Daraio C. 2015. Wide band-gap seismic metastructures. Extreme Mechanics Letters, 4: 111-117. doi: 10.1016/j.eml.2015.05.004 [164] Kruk S S, Wong Z J, Pshenay-Severin E, O’Brien K, Neshev D N, Kivshar Y S, Zhang X. 2016. Magnetic hyperbolic optical metamaterials. Nat. Commun., 7: 11329. doi: 10.1038/ncomms11329 [165] Kruth J P, Froyen L, Van Vaerenbergh J, Mercelis P, Rombouts M, Lauwers B. 2004. Selective laser melting of iron-based powder. Journal of Materials Processing Technology, 149: 616-622. doi: 10.1016/j.jmatprotec.2003.11.051 [166] Kuang X, Roach D J, Wu J, Hamel C M, Ding Z, Wang T, Dunn M L, Qi H J. 2019a. Advances in 4d printing: Materials and applications. Advanced Functional Materials, 29: 1805290. doi: 10.1002/adfm.201805290 [167] Kuang X, Wu J, Chen K, Zhao Z, Ding Z, Hu F, Fang D, Qi H J. 2019. Grayscale digital light processing 3D printing for highly functionally graded materials. Science Advances, 5: eaav5790. doi: 10.1126/sciadv.aav5790 [168] Kundu D, Ghuku S, Naskar S, Mukhopadhyay T. 2023. Extreme specific stiffness through interactive cellular networks in bi-level micro-topology architected metamaterials. Advanced Engineering Materials, 25: 2201407. doi: 10.1002/adem.202201407 [169] Kuribayashi K, Tsuchiya K, You Z, Tomus D, Umemoto M, Ito T, Sasaki M. 2006. Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil. Materials Science and Engineering: A, 419: 131-137. doi: 10.1016/j.msea.2005.12.016 [170] Lakes R. 1993. Advances in negative Poisson’s ratio materials. Advanced Materials, 5: 293-296. doi: 10.1002/adma.19930050416 [171] Lakes R. 1987. Foam structures with a negative Poisson’s ratio. Science, 235: 1038-1040. doi: 10.1126/science.235.4792.1038 [172] Lakes R, Wojciechowski K W. 2008. Negative compressibility, negative Poisson’s ratio, and stability. Physica Status Solidi, 245: 545-551. doi: 10.1002/pssb.200777708 [173] Lakes R S, Lee T, Bersie A, Wang Y C. 2001. Extreme damping in composite materials with negative-stiffness inclusions. Nature, 410: 565-567. doi: 10.1038/35069035 [174] Lamoureux A, Lee K, Shlian M, Forrest S R, Shtein M. 2015. Dynamic kirigami structures for integrated solar tracking. Nat. Commun., 6: 8092. doi: 10.1038/ncomms9092 [175] Lang J P, Jiang W, Teng X C, Zhang X G, Han D, Hao J, Xu H H, Ni X H, Xie Y M, Qin Q H, Yang J, Ren X. 2023. Assembled mechanical metamaterials with transformable shape and auxeticity. Construction and Building Materials, 378: 131181. doi: 10.1016/j.conbuildmat.2023.131181 [176] Lang R J. 2012. Origami design secrets: Mathematical methods for an ancient art. CRC Press. [177] Lee D Y, Kim J S, Kim S R, Koh J S, Cho K J. 2014. The deformable wheel robot using magic-ball origami structure. International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 55942. [178] Lee H J, Yook J G. 2008. Biosensing using split-ring resonators at microwave regime. Applied Physics Letters, 92: 254103. doi: 10.1063/1.2946656 [179] Lee J H, Singer J P, Thomas E L. 2012. Micro-/nanostructured mechanical metamaterials. Advanced Materials, 24: 4782-4810. doi: 10.1002/adma.201201644 [180] Lee N, Yoon B, Kim T, Bae J Y, Lim J S, Chang I, Cho H H. 2020. Multiple resonance metamaterial emitter for deception of infrared emission with enhanced energy dissipation. ACS Appl. Mater. Interfaces, 12: 8862-8869. doi: 10.1021/acsami.9b21030 [181] Lee S H, Park C M, Seo Y M, Wang Z G, Kim C K. 2009a. Acoustic metamaterial with negative density. Physics Letters A, 373: 4464-4469. doi: 10.1016/j.physleta.2009.10.013 [182] Lee S H, Park C M, Seo Y M, Wang Z G, Kim C K. 2009b. Acoustic metamaterial with negative modulus. J. Phys: Condens. Matter, 21: 175704. doi: 10.1088/0953-8984/21/17/175704 [183] Lei M, Hamel C M, Yuan C, Lu H, Qi H J. 2018. 3d printed two-dimensional periodic structures with tailored in-plane dynamic responses and fracture behaviors. Composites Science and Technology, 159: 189-198. doi: 10.1016/j.compscitech.2018.02.024 [184] Lei M, Hong W, Zhao Z, Hamel C, Chen M, Lu H, Qi H J. 2019. 3d printing of auxetic metamaterials with digitally reprogrammable shape. ACS Appl. Mater. Interfaces, 11: 22768-22776. doi: 10.1021/acsami.9b06081 [185] Levine D J, Turner K T, Pikul J H. 2021. Materials with electroprogrammable stiffness. Advanced Materials, 33: 2007952. doi: 10.1002/adma.202007952 [186] Li J, Chan C T. 2004. Double-negative acoustic metamaterial. Phys. Rev. E, 70: 055602. doi: 10.1103/PhysRevE.70.055602 [187] Li K, Cheng X, Zhu F, Li L Z, Xie Z, Luan H, Wang Z, Ji Z, Wang H, Liu F, Xue Y, Jiang C, Feng X, Li L M, Rogers J A, Huang Y, Zhang Y. 2019. A generic soft encapsulation strategy for stretchable electronics. Advanced Functional Materials, 29: 1806630. doi: 10.1002/adfm.201806630 [188] Li S, Stampfli J J, Xu H J, Malkin E, Diaz E V, Rus D, Wood R J. 2019. A vacuum-driven origami “magic-ball” soft gripper. 2019 International Conference on Robotics and Automation (ICRA), 7401–7408. [189] Li S, Wang K W. 2015. Fluidic origami: A plant-inspired adaptive structure with shape morphing and stiffness tuning. Smart Mater. Struct., 24: 105031. doi: 10.1088/0964-1726/24/10/105031 [190] Li T, Wang J, Zhang L, Yang J, Yang M, Zhu D, Zhou X H, Handschuh-Wang S, Liu Y, Zhou X C. 2017. “Freezing”, morphing, and folding of stretchy tough hydrogels. J. Mater. Chem. B, 5: 5726-5732. doi: 10.1039/C7TB01265A [191] Li W, Matsuhisa N, Liu Z Y, Wang M, Luo Y, Cai P, Chen G, Zhang F, Li C, Liu Z H, Lv Z, Zhang W, Chen X. 2021. An on-demand plant-based actuator created using conformable electrodes. Nat. Electron., 4: 134-142. doi: 10.1038/s41928-020-00530-4 [192] Libonati F, Buehler M J. 2017. Advanced structural materials by bioinspiration. Advanced Engineering Materials, 19: 1600787. doi: 10.1002/adem.201600787 [193] Lier E, Shaw R K. 2008. Design and simulation of metamaterial-based hybrid-mode horn antennas. Electronics Letters, 44: 1444-1445. doi: 10.1049/el:20082639 [194] Lier E, Werner D H, Scarborough C P, Wu Q, Bossard J A. 2011. An octave-bandwidth negligible-loss radiofrequency metamaterial. Nat. Mater., 10: 216-222. doi: 10.1038/nmat2950 [195] Ligon S C, Liska R, Stampfl J, Gurr M, Mülhaupt R. 2017. Polymers for 3d printing and customized additive manufacturing. Chem. Rev., 117: 10212-10290. doi: 10.1021/acs.chemrev.7b00074 [196] Lim T C. 2015. Auxetic materials and structures. Engineering Materials. [197] Liu J, Gu T, Shan S, Kang S H, Weaver J C, Bertoldi K. 2016. Harnessing buckling to design architected materials that exhibit effective negative swelling. Advanced Materials, 28: 6619-6624. doi: 10.1002/adma.201600812 [198] Liu Q, Wang W, Reynolds M F, Cao M C, Miskin M Z, Arias T A, Muller D A, McEuen P L, Cohen I. 2021. Micrometer-sized electrically programmable shape-memory actuators for low-power microrobotics. Science Robotics, 6: eabe6663. doi: 10.1126/scirobotics.abe6663 [199] Liu R, Yabansu Y C, Yang Z, Choudhary A N, Kalidindi S R, Agrawal A. 2017. Context aware machine learning approaches for modeling elastic localization in three-dimensional composite microstructures. Integr Mater Manuf Innov, 6: 160-171. doi: 10.1007/s40192-017-0094-3 [200] Liu S, Azad A I, Burgueño R. 2019. Architected materials for tailorable shear behavior with energy dissipation. Extreme Mechanics Letters, 28: 1-7 doi: 10.1016/j.eml.2019.01.010 [201] Liu X N, Hu G K, Huang G L, Sun C T. 2011. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Applied Physics Letters, 98: 251907. doi: 10.1063/1.3597651 [202] Liu Y, Shaw B, Dickey M D, Genzer J. 2017. Sequential self-folding of polymer sheets. Science Advances, 3: e1602417. doi: 10.1126/sciadv.1602417 [203] Liu Y, Wang H, Ho J, Ng R C, Ng R J H, Hall-Chen V H, Koay E H H, Dong Z, Liu H, Qiu C W, Greer J R, Yang J K W. 2019. Structural color three-dimensional printing by shrinking photonic crystals. Nat. Commun., 10: 4340. doi: 10.1038/s41467-019-12360-w [204] Liu Z, Du H, Li J, Lu L, Li Z Y, Fang N X. 2018. Nano-kirigami with giant optical chirality. Science Advances, 4: eaat4436. doi: 10.1126/sciadv.aat4436 [205] Liu Z, Zhang X, Mao Y, Zhu Y Y, Yang Z, Chan C T, Sheng P. 2000. Locally resonant sonic materials. Science, 289: 1734-1736. doi: 10.1126/science.289.5485.1734 [206] Lockwood E H, MacMillan R H, Geometric Symmetry. cambridge university press, 1978. [207] Lorna J Gibson, Michael F Ashby. 1999. Cellular solids structure and properties. Cambridge University Press. [208] Lu M H, Feng L, Chen Y F. 2009. Phononic crystals and acoustic metamaterials. Materials Today, 12: 34-42. [209] Lum G Z, Ye Z, Dong X, Marvi H, Erin O, Hu W, Sitti M. 2016. Shape-programmable magnetic soft matter. Proceedings of the National Academy of Sciences, 113(41): E6007-E6015. [210] Luo C, Ning S, Liu Z, Zhuang Z. 2020. Interactive inverse design of layered phononic crystals based on reinforcement learning. Extreme Mechanics Letters, 36: 100651. doi: 10.1016/j.eml.2020.100651 [211] Lv H, Tian X, Wang M Y, Li, D. 2013. Vibration energy harvesting using a phononic crystal with point defect states. Applied Physics Letters, 102: 034103. doi: 10.1063/1.4788810 [212] Ma G, Yang M, Xiao S, Yang Z, Sheng P. 2014. Acoustic metasurface with hybrid resonances. Nat. Mater., 13: 873-878. doi: 10.1038/nmat3994 [213] Ma H, Wang K, Zhao H, Shi W, Xue J, Zhou Y, Li Q, Wang G, Yan B. 2022. Energy dissipation and shock isolation using novel metamaterials. International Journal of Mechanical Sciences, 228: 107464. doi: 10.1016/j.ijmecsci.2022.107464 [214] Ma H S, Prévost J H, Jullien R, Scherer G W. 2001. Computer simulation of mechanical structure–property relationship of aerogels. Journal of Non-Crystalline Solids, 285: 216-221. doi: 10.1016/S0022-3093(01)00456-2 [215] Ma W, Cheng F, Liu Y. 2018. Deep-learning-enabled on-demand design of chiral metamaterials. ACS Nano, 12: 6326-6334. doi: 10.1021/acsnano.8b03569 [216] Machado M R, Moura B B, Dey S, Mukhopadhyay T. 2022. Bandgap manipulation of single and multi-frequency smart metastructures with random impedance disorder. Smart Mater. Struct., 31: 105020. doi: 10.1088/1361-665X/ac8ef9 [217] Mahata A, Mukhopadhyay T. 2018. Probing the chirality-dependent elastic properties and crack propagation behavior of single and bilayer stanene. Phys. Chem. Chem. Phys., 20: 22768-22782. doi: 10.1039/C8CP03892A [218] Malek S, Gibson L. 2015. Effective elastic properties of periodic hexagonal honeycombs. Mechanics of Materials, 91: 226-240. doi: 10.1016/j.mechmat.2015.07.008 [219] Mao M, He J, Li X, Zhang B, Lei Q, Liu Y, Li D. 2017. The emerging frontiers and applications of high-resolution 3d printing. Micromachines, 8: 113. doi: 10.3390/mi8040113 [220] Mao Y, He Q, Zhao X. 2020. Designing complex architectured materials with generative adversarial networks. Science Advances, 6: eaaz4169. doi: 10.1126/sciadv.aaz4169 [221] Mead D M. 1996. Wave propagation in continuous periodic structures: Research contributions from southampton, 1964–1995. Journal of Sound and Vibration, 190: 495-524. doi: 10.1006/jsvi.1996.0076 [222] Meeussen A S, Paulose J, Vitelli V. 2016. Geared topological metamaterials with tunable mechanical stability. Phys. Rev. X, 6: 041029. [223] Meza L R, Das S, Greer J R. 2014. Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science, 345: 1322-1326. doi: 10.1126/science.1255908 [224] Milton G W. 2015. New examples of three-dimensional dilational materials. Physica Status Solidi, 252: 1426-1430. doi: 10.1002/pssb.201552297 [225] Milton G W, Cherkaev A V. 1995. Which elasticity tensors are realizable. Journal of Engineering Materials and Technology, 117: 483-493. doi: 10.1115/1.2804743 [226] Mirzaali M J, Caracciolo A, Pahlavani H, Janbaz S, Vergani L, Zadpoor A A. 2018. Multi-material 3d printed mechanical metamaterials: rational design of elastic properties through spatial distribution of hard and soft phases. Applied Physics Letters, 113: 241903. doi: 10.1063/1.5064864 [227] Mirzaali M J, Ghorbani A, Nakatani K, Nouri-Goushki M, Tümer N, Callens S J P, Janbaz S, Accardo A, Bico J, Habibi M, Zadpoor A A. 2021. Curvature induced by deflection in thick meta-plates. Advanced Materials, 33: 2008082. doi: 10.1002/adma.202008082 [228] Mishin Y. 2021. Machine-learning interatomic potentials for materials science. Acta Materialia, 214: 116980. doi: 10.1016/j.actamat.2021.116980 [229] Mishra A K, Wallin T J, Pan W, Xu A, Wang K, Giannelis E P, Mazzolai B, Shepherd R F. 2020. Autonomic perspiration in 3d-printed hydrogel actuators. Science Robotics, 5: eaaz3918. doi: 10.1126/scirobotics.aaz3918 [230] Montgomery S M, Wu S, Kuang X, Armstrong C D, Zemelka C, Ze Q, Zhang R, Zhao R, Qi H J. 2021. Magneto-mechanical metamaterials with widely tunable mechanical properties and acoustic bandgaps. Advanced Functional Materials, 31: 2005319. doi: 10.1002/adfm.202005319 [231] Mortazavi B, Zhuang X, Rabczuk T, Shapeev A V. 2023. Atomistic modeling of the mechanical properties: The rise of machine learning interatomic potentials. Mater. Horiz., 10: 1956-1968. doi: 10.1039/D3MH00125C [232] Moruzzi M C, Cinefra M, Bagassi S. 2021. Vibroacoustic analysis of an innovative windowless cabin with metamaterial trim panels in regional turboprops. Mechanics of Advanced Materials and Structures, 28: 1509-1521. doi: 10.1080/15376494.2019.1682729 [233] Mousanezhad D, Haghpanah B, Ghosh R, Hamouda A M, Nayeb-Hashemi H, Vaziri A. 2016. Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: A simple energy-based approach. Theoretical and Applied Mechanics Letters, 6: 81-96. doi: 10.1016/j.taml.2016.02.004 [234] Mueller T, Hernandez A, Wang C. 2020. Machine learning for interatomic potential models. The Journal of Chemical Physics, 152: 050902. doi: 10.1063/1.5126336 [235] Mukhopadhyay T, Adhikari S. 2017a. Effective in-plane elastic moduli of quasi-random spatially irregular hexagonal lattices. International Journal of Engineering Science, 119: 142-179. doi: 10.1016/j.ijengsci.2017.06.004 [236] Mukhopadhyay T, Adhikari S. 2017b. Stochastic mechanics of metamaterials. Composite Structures, 162: 85-97. doi: 10.1016/j.compstruct.2016.11.080 [237] Mukhopadhyay T, Adhikari S. 2016a. Effective in-plane elastic properties of auxetic honeycombs with spatial irregularity. Mechanics of Materials, 95: 204-222. doi: 10.1016/j.mechmat.2016.01.009 [238] Mukhopadhyay T, Adhikari S. 2016b. Free-vibration analysis of sandwich panels with randomly irregular honeycomb core. Journal of Engineering Mechanics, 142: 06016008. [239] Mukhopadhyay T, Adhikari S. 2016c. Equivalent in-plane elastic properties of irregular honeycombs: An analytical approach. International Journal of Solids and Structures, 91: 169-184. doi: 10.1016/j.ijsolstr.2015.12.006 [240] Mukhopadhyay T, Adhikari S, Alu A. 2019a. Probing the frequency-dependent elastic moduli of lattice materials. Acta Materialia, 165: 654-665. doi: 10.1016/j.actamat.2018.11.012 [241] Mukhopadhyay T, Adhikari S, Alu A. 2019b. Theoretical limits for negative elastic moduli in subacoustic lattice materials. Phys. Rev. B, 99: 094108. doi: 10.1103/PhysRevB.99.094108 [242] Mukhopadhyay T, Adhikari S, Batou A. 2019c. Frequency domain homogenization for the viscoelastic properties of spatially correlated quasi-periodic lattices. International Journal of Mechanical Sciences, 150: 784-806. doi: 10.1016/j.ijmecsci.2017.09.004 [243] Mukhopadhyay T, Kundu D. 2022. Mixed-mode multidirectional Poisson’s ratio modulation in auxetic 3D lattice metamaterials. Advanced Engineering Materials, 24: 2101183. doi: 10.1002/adem.202101183 [244] Mukhopadhyay T, Ma J, Feng H, Hou D, Gattas J M, Chen Y, You Z. 2020a. Programmable stiffness and shape modulation in origami materials: Emergence of a distant actuation feature. Applied Materials Today, 19: 100537. doi: 10.1016/j.apmt.2019.100537 [245] Mukhopadhyay T, Mahata A, Adhikari S, Zaeem M A. 2018. Probing the shear modulus of two-dimensional multiplanar nanostructures and heterostructures. Nanoscale, 10: 5280-5294. doi: 10.1039/C7NR07261A [246] Mukhopadhyay T, Mahata A, Adhikari S, Zaeem M A. 2017a. Effective elastic properties of two dimensional multiplanar hexagonal nanostructures. 2D Mater., 4: 025006. doi: 10.1088/2053-1583/aa551c [247] Mukhopadhyay T, Mahata A, Adhikari S, Zaeem M A. 2017b. Effective mechanical properties of multilayer nano-heterostructures. Sci. Rep., 7: 15818. doi: 10.1038/s41598-017-15664-3 [248] Mukhopadhyay T, Mahata A, Naskar S, Adhikari S. 2020b. Probing the effective Young’s modulus of ‘magic angle’ inspired multi-functional twisted nano-heterostructures. Advanced Theory and Simulations, 3: 2000129. doi: 10.1002/adts.202000129 [249] Mukhopadhyay T, Naskar S, Adhikari S. 2020c. Anisotropy tailoring in geometrically isotropic multi-material lattices. Extreme Mechanics Letters, 40: 100934. doi: 10.1016/j.eml.2020.100934 [250] Mukhopadhyay T, Naskar S, Chakraborty S, Karsh P K, Choudhury R, Dey S. 2021. Stochastic oblique impact on composite laminates: A concise review and characterization of the essence of hybrid machine learning algorithms. Arch Computat Methods Eng, 28: 1731-1760. doi: 10.1007/s11831-020-09438-w [251] Münchinger A, Hsu L Y, Fürniß F, Blasco E, Wegener M. 2022. 3D optomechanical metamaterials. Materials Today, 59: 9-17. doi: 10.1016/j.mattod.2022.08.020 [252] Nabian M A, Meidani H. 2018. Deep learning for accelerated seismic reliability analysis of transportation networks. Computer-Aided Civil and Infrastructure Engineering, 33: 443-458. doi: 10.1111/mice.12359 [253] Narang Y S, Vlassak J J, Howe R D. 2018. Mechanically versatile soft machines through Laminar Jamming. Advanced Functional Materials, 28: 1707136. doi: 10.1002/adfm.201707136 [254] Nash L M, Kleckner D, Read A, Vitelli V, Turner A M, Irvine W T M. 2015. Topological mechanics of gyroscopic metamaterials. Proceedings of the National Academy of Sciences, 112: 14495-14500. doi: 10.1073/pnas.1507413112 [255] Neelakantan S, Bosbach W, Woodhouse J, Markaki A E. 2014. Characterization and deformation response of orthotropic fibre networks with auxetic out-of-plane behaviour. Acta Materialia, 66: 326-339. doi: 10.1016/j.actamat.2013.11.020 [256] Ngo T D, Kashani A, Imbalzano G, Nguyen K T Q, Hui D. 2018. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Composites Part B: Engineering, 143: 172-196. doi: 10.1016/j.compositesb.2018.02.012 [257] Nguyen C, Zhuang X, Chamoin L, Zhao X, Nguyen-Xuan H, Rabczuk T. 2020. Three-dimensional topology optimization of auxetic metamaterial using isogeometric analysis and model order reduction. Computer Methods in Applied Mechanics and Engineering, 371: 113306. doi: 10.1016/j.cma.2020.113306 [258] Nick Z H, Tabor C E, Harne R L. 2020. Liquid metal microchannels as digital sensors in mechanical metamaterials. Extreme Mechanics Letters, 40: 100871. doi: 10.1016/j.eml.2020.100871 [259] Nicolaou Z G, Motter A E. 2012. Mechanical metamaterials with negative compressibility transitions. Nature Mater., 11: 608-613. doi: 10.1038/nmat3331 [260] Ning X, Wang X, Zhang Y, Yu X, Choi D, Zheng N, Kim D S, Huang Y, Zhang Y H, Rogers, J A. 2018. Assembly of advanced materials into 3d functional structures by methods inspired by origami and kirigami: A review. Advanced Materials Interfaces, 5: 1800284. doi: 10.1002/admi.201800284 [261] Nouh M, Aldraihem O, Baz A. 2014. Vibration characteristics of metamaterial beams with periodic local resonances. Journal of Vibration and Acoustics, 136 : 061012. [262] Novelino L S, Ze Q, Wu S, Paulino G H, Zhao R. 2020. Untethered control of functional origami microrobots with distributed actuation. Proceedings of the National Academy of Sciences, 117: 24096-24101. doi: 10.1073/pnas.2013292117 [263] O’Brien K, Suchowski H, Rho J, Salandrino A, Kante B, Yin X, Zhang X. 2015. Predicting nonlinear properties of metamaterials from the linear response. Nat. Mater., 14: 379-383. doi: 10.1038/nmat4214 [264] O’Connor H J, Dickson A N, Dowling D P. 2018. Evaluation of the mechanical performance of polymer parts fabricated using a production scale multi jet fusion printing process. Additive Manufacturing, 22: 381-387. doi: 10.1016/j.addma.2018.05.035 [265] Oh J H, Seung H M, Kim Y Y. 2016. Adjoining of negative stiffness and negative density bands in an elastic metamaterial. Applied Physics Letters, 108: 093501. doi: 10.1063/1.4943095 [266] Ongaro F. 2018. Estimation of the effective properties of two-dimensional cellular materials: A review. Theoretical and Applied Mechanics Letters, 8: 209-230. doi: 10.1016/j.taml.2018.04.010 [267] Overvelde J T B, de Jong T A, Shevchenko Y, Becerra S A, Whitesides G M, Weaver J C, Hoberman C, Bertoldi K. 2016. A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom. Nat. Commun., 7: 1-8. [268] Pahlavani H, Amani M, Saldívar M C, Zhou J, Mirzaali M J, Zadpoor A A. 2022. Deep learning for the rare-event rational design of 3D printed multi-material mechanical metamaterials. Commun Mater., 3: 1-11. doi: 10.1038/s43246-021-00223-1 [269] Palermo A, Marzani A. 2016. Extended bloch mode synthesis: Ultrafast method for the computation of complex band structures in phononic media. International Journal of Solids and Structures, 100: 29-40. [270] Palleau E, Morales D, Dickey M D, Velev O D. 2013. Reversible patterning and actuation of hydrogels by electrically assisted ionoprinting. Nat. Commun., 4: 2257. doi: 10.1038/ncomms3257 [271] Pan Q, Chen S, Chen F, Zhu X. 2020. Programmable soft bending actuators with auxetic metamaterials. Sci. China Technol. Sci., 63: 2518-2526. doi: 10.1007/s11431-020-1741-2 [272] Parthasarathy J, Starly B, Raman S, Christensen A. 2010. Mechanical evaluation of porous titanium (Ti6Al4V) structures with electron beam melting (EBM). Journal of the Mechanical Behavior of Biomedical Materials, 3: 249-259. doi: 10.1016/j.jmbbm.2009.10.006 [273] Paulose J, Chen B G, Vitelli V. 2015. Topological modes bound to dislocations in mechanical metamaterials. Nature Phys, 11: 153-156. doi: 10.1038/nphys3185 [274] Pendry J B. 2000. Negative refraction makes a perfect lens. Phys. Rev. Lett., 85: 3966-3969. doi: 10.1103/PhysRevLett.85.3966 [275] Peng X, Li Y, Zhang Q, Shang C, Bai Q W, Wang H. 2016. Tough hydrogels with programmable and complex shape deformations by ion dip-dyeing and transfer printing. Advanced Functional Materials, 26: 4491-4500. doi: 10.1002/adfm.201601389 [276] Poddubny A, Iorsh I, Belov P, Kivshar Y. 2013. Hyperbolic metamaterials. Nature Photon, 7: 948-957. doi: 10.1038/nphoton.2013.243 [277] Podolskiy V A, Kuhta N A, Milton G W. 2005. Optimizing the superlens: Manipulating geometry to enhance the resolution. Applied Physics Letters, 87: 231113. doi: 10.1063/1.2139620 [278] Prajwal P, Ghuku S, Mukhopadhyay T. 2022. Large-deformation mechanics of anti-curvature lattice materials for mode-dependent enhancement of non-linear shear modulus. Mechanics of Materials, 171: 104337. doi: 10.1016/j.mechmat.2022.104337 [279] Prall D, Lakes R S. 1997. Properties of a chiral honeycomb with a Poisson’s ratio of −1. International Journal of Mechanical Sciences, 39: 305-314. doi: 10.1016/S0020-7403(96)00025-2 [280] Pratapa P P, Suryanarayana P, Paulino G H. 2018. Bloch wave framework for structures with nonlocal interactions: Application to the design of origami acoustic metamaterials. Journal of the Mechanics and Physics of Solids, 118: 115-132. doi: 10.1016/j.jmps.2018.05.012 [281] Qi S, Oudich M, Li Y, Assouar, B. 2016. Acoustic energy harvesting based on a planar acoustic metamaterial. Applied Physics Letters, 108: 263501. doi: 10.1063/1.4954987 [282] Rafi H K, Karthik N V, Gong H, Starr T L, Stucker B E. 2013. Microstructures and mechanical properties of Ti6Al4V parts fabricated by selective laser melting and electron beam melting. J. of Materi Eng and Perform, 22: 3872-3883. doi: 10.1007/s11665-013-0658-0 [283] Rafsanjani A, Bertoldi K. 2017. Buckling-induced kirigami. Phys. Rev. Lett., 118: 084301. doi: 10.1103/PhysRevLett.118.084301 [284] Rafsanjani A, Jin L, Deng B, Bertoldi K. 2019. Propagation of pop ups in kirigami shells. Proceedings of the National Academy of Sciences, 116: 8200-8205. doi: 10.1073/pnas.1817763116 [285] Raghunath G, Flatau A B. 2015. Study of magnetic domain evolution in an auxetic plane of Galfenol using kerr microscopy. Journal of Applied Physics, 117: 17E704. doi: 10.1063/1.4913727 [286] Reid D R, Pashine N, Bowen A S, Nagel S R, Pablo J J de. 2019. Ideal isotropic auxetic networks from random networks. Soft Matter, 15: 8084-8091. doi: 10.1039/C9SM01241A [287] Ren Z, Hu W, Dong X, Sitti M. 2019. Multi-functional soft-bodied jellyfish-like swimming. Nat. Commun., 10: 2703. doi: 10.1038/s41467-019-10549-7 [288] Roach D, Hamel C, Dunn C, Johnson M, Kuang X, Qi H. 2019. The m4 3d printer: A multi-material multi-method additive manufacturing platform for future 3d printed structures. Additive Manufacturing, 29: 100819. doi: 10.1016/j.addma.2019.100819 [289] Robertson I D, Yourdkhani M, Centellas P J, Aw J E, Ivanoff D G, Goli E, Lloyd E M, Dean L M, Sottos N R, Geubelle P H, Moore J S, White S R. 2018. Rapid energy-efficient manufacturing of polymers and composites via frontal polymerization. Nature, 557: 223-227. doi: 10.1038/s41586-018-0054-x [290] Rogers J, Huang Y, Schmidt O G, Gracias D H. 2016. Origami mems and nems. MRS Bulletin, 41: 123-129. doi: 10.1557/mrs.2016.2 [291] Rothemund P W K. 2006. Folding DNA to create nanoscale shapes and patterns. Nature, 440: 297-302. doi: 10.1038/nature04586 [292] Rozvany G I N. 2009. A critical review of established methods of structural topology optimization. Struct Multidisc Optim, 37: 217-237. doi: 10.1007/s00158-007-0217-0 [293] Scarpa F, Bullough W A, Lumley P. 2004. Trends in acoustic properties of iron particle seeded auxetic polyurethane foam. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 218: 241-244. doi: 10.1243/095440604322887099 [294] Scarpa F, Panayiotou P, Tomlinson G. 2000. Numerical and experimental uniaxial loading on in-plane auxetic honeycombs. The Journal of Strain Analysis for Engineering Design, 35: 383-388. doi: 10.1243/0309324001514152 [295] Scarpa F, Smith F C. 2004. Passive and mr fluid-coated auxetic pu foam–mechanical, acoustic, and electromagnetic properties. Journal of Intelligent Material Systems and Structures, 15: 973-979. doi: 10.1177/1045389X04046610 [296] Schaedler T A, Carter W B. 2016. Architected cellular materials. Annual Review of Materials Research, 46: 187-210. doi: 10.1146/annurev-matsci-070115-031624 [297] Schaedler T A, Jacobsen A J, Torrents A, Sorensen A E, Lian J, Greer J R, Valdevit L, Carter W B. 2011. Ultralight metallic microlattices. Science, 334: 962-965. doi: 10.1126/science.1211649 [298] Schaeffer Marshall, Ruzzene M. 2015. Homogenization of 1d and 2d magnetoelastic lattices. EPJ Applied Metamaterials, 2: 13. doi: 10.1051/epjam/2015013 [299] Schaeffer M, Ruzzene M. 2015. Wave propagation in multistable magneto-elastic lattices. International Journal of Solids and Structures, 56: 78-95. [300] Schenk M, Guest S D. 2013. Geometry of miura-folded metamaterials. Proceedings of the National Academy of Sciences, 110: 3276-3281. doi: 10.1073/pnas.1217998110 [301] Schurig D, Mock J J, Justice B J, Cummer S A, Pendry J B, Starr A F, Smith D R. 2006. Metamaterial electromagnetic cloak at microwave frequencies. Science, 314: 977-980. doi: 10.1126/science.1133628 [302] Serbin J, Ovsianikov A, Chichkov B. 2004. Fabrication of woodpile structures by two-photon polymerization and investigation of their optical properties. Opt. Express, 12: 5221-5228. doi: 10.1364/OPEX.12.005221 [303] Shadrivov I V. 2010. Nonlinear metamaterials. Nonlinearities in Periodic Structures and Metamaterials, Springer, pp: 241-257. [304] Shalaev V M. 2007. Optical negative-index metamaterials. Nat. Photoics, 1: 41-48. doi: 10.1038/nphoton.2006.49 [305] Shalaev V M, Cai W, Chettiar U K, Yuan H K, Sarychev A K, Drachev V P, Kildishev A V. 2005. Negative index of refraction in optical metamaterials. Opt. Lett, 30: 3356-3358. doi: 10.1364/OL.30.003356 [306] Shan S, Kang S H, Raney J R, Wang P, Fang L, Candido F, Lewis J A, Bertoldi K. 2015. Multistable architected materials for trapping elastic strain energy. Advanced Materials, 27: 4296-4301. doi: 10.1002/adma.201501708 [307] Sharma A, Mukhopadhyay T, Rangappa S M, Siengchin S, Kushvaha V. 2022. Advances in computational intelligence of polymer composite materials: Machine learning assisted modeling, analysis and design. Arch Computat Methods Eng, 29: 3341-3385. doi: 10.1007/s11831-021-09700-9 [308] Shelby R A, Smith D R, Schultz S. 2001. Experimental verification of a negative index of refraction. Science, 292: 77-79. doi: 10.1126/science.1058847 [309] Silva M J, Hayes W C, Gibson L J. 1995. The effects of non-periodic microstructure on the elastic properties of two-dimensional cellular solids. International Journal of Mechanical Sciences, 37: 1161-1177. doi: 10.1016/0020-7403(94)00018-F [310] Silverberg J L, Evans A A, McLeod L, Hayward R C, Hull T, Santangelo C D, Cohen I. 2014. Using origami design principles to fold reprogrammable mechanical metamaterials. Science, 345: 647-650. doi: 10.1126/science.1252876 [311] Silverberg J L, Na J H, Evans A A, Liu B, Hull T C, Santangelo C D, Lang R J, Hayward R C, Cohen I. 2015. Origami structures with a critical transition to bistability arising from hidden degrees of freedom. Nat. Mater., 14: 389-393. doi: 10.1038/nmat4232 [312] Singh A, Mukhopadhyay T, Adhikari S, Bhattacharya B. 2022a. Extreme on-demand contactless modulation of elastic properties in magnetostrictive lattices. Smart Mater. Struct., 31: 125005. doi: 10.1088/1361-665X/ac9cac [313] Singh A, Mukhopadhyay T, Adhikari S, Bhattacharya B. 2022b. Active multi-physical modulation of Poisson’s ratios in composite piezoelectric lattices: On-demand sign reversal. Composite Structures, 280: 114857. doi: 10.1016/j.compstruct.2021.114857 [314] Singh A, Mukhopadhyay T, Adhikari S, Bhattacharya B. 2021. Voltage-dependent modulation of elastic moduli in lattice metamaterials: Emergence of a programmable state-transition capability. International Journal of Solids and Structures, 208: 31-48. [315] Singh K, Tipton C R, Han E, Mullin T. 2013. Magneto-elastic buckling of an Euler beam. Proc. R. Soc. A., 469: 20130111. doi: 10.1098/rspa.2013.0111 [316] Sinha A, Mukhopadhyay T. 2022c. Kirigami-inspired metamaterials for programming constitutive laws: Mixed-mode multidirectional auxeticity and contact-induced stiffness modulation. iScience, 25: 105656. doi: 10.1016/j.isci.2022.105656 [317] Sinha P, Mukhopadhyay T. 2023. On-demand contactless programming of nonlinear elastic moduli in hard magnetic soft beam based broadband active lattice materials. Smart Mater. Struct., 32: 055021. doi: 10.1088/1361-665X/acc43b [318] Sinha P, Mukhopadhyay T. 2022. Effective elastic properties of lattice materials with intrinsic stresses. Thin-Walled Structures, 173: 108950. doi: 10.1016/j.tws.2022.108950 [319] Sinha P, Mukhopadhyay T. 2023b. Elastostatics of inflatable lattices: realization of extreme specific stiffness along with multi-functionality in active modulation and deployability. In press. [320] Sinha P, Kundu D, Mukhopadhyay T. 2023a. Effective in-plane and out-of-plane elastic properties of 3d lattice materials with intrinsic stresses: an analytical approach. In press. [321] Sinha P, Walker M G, Mukhopadhyay T. 2023b. Non-invariant elastic moduli of bi-level architected lattice materials through programmed domain discontinuity. Mechanics of Materials, 184: 104691. doi: 10.1016/j.mechmat.2023.104691 [322] Slesarenko V. 2020. Planar mechanical metamaterials with embedded permanent magnets. Materials, 13: 1313. doi: 10.3390/ma13061313 [323] Smith D R, Pendry J B, Wiltshire M C K. 2004. Metamaterials and negative refractive index. Science, 305: 788-792. doi: 10.1126/science.1096796 [324] Song J, Gao L, Cao K, Zhang H, Xu S, Jiang C, Surjadi J U, Xu Y, Lu Y. 2018. Metal-coated hybrid meso-lattice composites and their mechanical characterizations. Composite Structures, 203: 750-763. doi: 10.1016/j.compstruct.2018.07.074 [325] Song Z, Ma T, Tang R, Cheng Q, Wang X, Krishnaraju D, Panat R, Chan C K, Yu H, Jiang H. 2014. Origami lithium-ion batteries. Nat. Commun., 5: 3140. doi: 10.1038/ncomms4140 [326] Soukoulis C M, Wegener M. 2010. Optical metamaterials—More bulky and less lossy. Science, 330: 1633-1634. doi: 10.1126/science.1198858 [327] Spadoni A, Ruzzene M. 2007. Numerical and experimental analysis of the static compliance of chiral truss-core airfoils. Journal Of Mechanics Of Materials And Structures, 2: 965-981. doi: 10.2140/jomms.2007.2.965 [328] Sugino C, Leadenham S, Ruzzene M, Erturk A. 2016. On the mechanism of bandgap formation in locally resonant finite elastic metamaterials. Journal of Applied Physics, 120: 134501. doi: 10.1063/1.4963648 [329] Sundararaghavan V, Zabaras N. 2005. Classification and reconstruction of three-dimensional microstructures using support vector machines. Computational Materials Science, 32: 223-239. doi: 10.1016/j.commatsci.2004.07.004 [330] Surjadi J U, Gao L, Du H, Li X, Xiong X, Fang N X, Lu Y. 2019. Mechanical metamaterials and their engineering applications. Advanced Engineering Materials, 21: 1800864. doi: 10.1002/adem.201800864 [331] Sussman D M, Cho Y, Castle T, Gong X, Jung E, Yang S, Kamien R D. 2015. Algorithmic lattice kirigami: A route to pluripotent materials. Proceedings of the National Academy of Sciences, 112: 7449-7453. doi: 10.1073/pnas.1506048112 [332] Tan X, Chen S, Wang B, Tang J, Wang L, Zhu S, Yao K, Xu P. 2020. Real-time tunable negative stiffness mechanical metamaterial. Extreme Mechanics Letters, 41: 100990. doi: 10.1016/j.eml.2020.100990 [333] Tan X, Wang B, Zhu S, Chen S, Yao K, Xu P, Wu L, Sun Y. 2019. Novel multidirectional negative stiffness mechanical metamaterials. Smart Materials and Structures, 29 : 015037. [334] Tang Y, Li Y, Hong Y, Yang S, Yin J. 2019. Programmable active kirigami metasheets with more freedom of actuation. Proceedings of the National Academy of Sciences, 116: 26407-26413. doi: 10.1073/pnas.1906435116 [335] Tao R, Ji L, Li Y, Wan Z, Hu W, Wu W, Liao B, Ma L, Fang D. 2020. 4D printed origami metamaterials with tunable compression twist behavior and stress-strain curves. Composites Part B: Engineering, 201: 108344. doi: 10.1016/j.compositesb.2020.108344 [336] Tee Y L, Peng C, Pille P, Leary M, Tran P. 2020. Polyjet 3d printing of composite materials: Experimental and modelling approach. JOM, 72: 1105-1117. doi: 10.1007/s11837-020-04014-w [337] Thijs L, Verhaeghe F, Craeghs T, Humbeeck J V, Kruth J P. 2010. A study of the microstructural evolution during selective laser melting of Ti–6Al–4V. Acta Materialia, 58: 3303-3312. doi: 10.1016/j.actamat.2010.02.004 [338] Thomson B K, William. 2010. Baltimore lectures on molecular dynamics and the wave theory of light, cambridge library collection-physical sciences. Cambridge University Press, Cambridge. [339] Tian Y, Shen Y. 2020. Selective guided wave mode transmission enabled by elastic metamaterials. Journal of Sound and Vibration, 485: 115566. doi: 10.1016/j.jsv.2020.115566 [340] Tipton C R, Han E, Mullin T. 2012. Magneto-elastic buckling of a soft cellular solid. Soft Matter, 8: 6880-6883. doi: 10.1039/c2sm25965f [341] Tiwari P, Naskar S, Mukhopadhyay T. 2023. Programmed out-of-plane curvature to enhance multimodal stiffness of bending-dominated composite lattices. AIAA Journal, 61: 1820-1838. doi: 10.2514/1.J062573 [342] Vaishali Mukhopadhyay T, Naskar S, Dey S. 2023. On machine learning assisted data-driven bridging of fsdt and hozt for high-fidelity uncertainty quantification of laminated composite and sandwich plates. Composite Structures, 304: 116276. doi: 10.1016/j.compstruct.2022.116276 [343] Valentine J, Zhang S, Zentgraf T, Ulin-Avila E, Genov D A, Bartal G, Zhang X. 2008. Three-dimensional optical metamaterial with a negative refractive index. Nature, 455: 376-379. doi: 10.1038/nature07247 [344] Valipour A, Kargozarfard M H, Rakhshi M, Yaghootian A, Sedighi H M. 2022. Metamaterials and their applications: An overview. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 236: 2171-2210. doi: 10.1177/1464420721995858 [345] van Manen T, Janbaz S, Ganjian M, Zadpoor A A. 2020. Kirigami-enabled self-folding origami. Materials Today, 32: 59-67. doi: 10.1016/j.mattod.2019.08.001 [346] Vangelatos Z, Gu G X, Grigoropoulos C P. 2019. Architected metamaterials with tailored 3d buckling mechanisms at the microscale. Extreme Mechanics Letters, 33: 100580. doi: 10.1016/j.eml.2019.100580 [347] Vyatskikh A, Delalande S, Kudo A, Zhang X, Portela C M, Greer J R. 2018. Additive manufacturing of 3D nano-architected metals. Nat. Commun., 9: 593. doi: 10.1038/s41467-018-03071-9 [348] Waheed U, Myant C W, Dobson S N. 2020. Boolean and/or mechanical logic using multi-plane mechanical metamaterials. Extreme Mechanics Letters, 40: 100865. doi: 10.1016/j.eml.2020.100865 [349] Waitukaitis S, Menaut R, Chen B G, van Hecke M. 2015. Origami multistability: From single vertices to metasheets. Phys. Rev. Lett., 114: 055503. doi: 10.1103/PhysRevLett.114.055503 [350] Wang A J, McDowell D L. 2003. Effects of defects on in-plane properties of periodic metal honeycombs. International Journal of Mechanical Sciences, 45: 1799-1813. doi: 10.1016/j.ijmecsci.2003.12.007 [351] Wang C, Tan X P, Tor S B, Lim C S. 2020. Machine learning in additive manufacturing: State-of-the-art and perspectives. Additive Manufacturing, 36: 101538. doi: 10.1016/j.addma.2020.101538 [352] Wang H, Zhao D, Jin Y, Wang M, Mukhopadhyay T, You Z. 2020. Modulation of multi-directional auxeticity in hybrid origami metamaterials. Applied Materials Today, 20: 100715. doi: 10.1016/j.apmt.2020.100715 [353] Wang L C, Song W L, Zhang Y J, Qu M J, Zhao Z, Chen M, Yang Y, Chen H, Fang D. 2020. Active reconfigurable tristable square-twist origami. Advanced Functional Materials, 30: 1909087. doi: 10.1002/adfm.201909087 [354] Wang P, Shim J, Bertoldi K. 2013. Effects of geometric and material nonlinearities on tunable band gaps and low-frequency directionality of phononic crystals. Phys. Rev. B, 88: 014304. doi: 10.1103/PhysRevB.88.014304 [355] Wang S, Shen Z A, Shen Z Y, Dong Y, Li Y, Cao Y, Zhang Y, Guo S, Shuai J, Yang Y, Lin C, Chen X, Zhang X, Huang Q. 2021. Machine-learning micropattern manufacturing. Nano Today, 38: 101152. doi: 10.1016/j.nantod.2021.101152 [356] Wang W, Lu H, Liu Y, Leng J. 2014. Sodium dodecyl sulfate/epoxy composite: Water-induced shape memory effect and its mechanism. J. Mater. Chem. A, 2: 5441-5449. doi: 10.1039/c3ta15204a [357] Wang X Q, Chan K H, Cheng Y, Ding T, Li T, Achavananthadith S, Ahmet S, Ho J S, Ho G W. 2020. Somatosensory, light-driven, thin-film robots capable of integrated perception and motility. Advanced Materials, 32: 2000351. doi: 10.1002/adma.202000351 [358] Wang Z, Li K, He Q, Cai S. 2019. A light-powered ultralight tensegrity robot with high deformability and load capacity. Advanced Materials, 31: 1806849. doi: 10.1002/adma.201806849 [359] Wang Z J, Zhu C N, Hong W, Wu Z L, Zheng Q. 2017. Cooperative deformations of periodically patterned hydrogels. Science Advances, 3: e1700348. doi: 10.1126/sciadv.1700348 [360] Ward L, Agrawal A, Choudhary A, Wolverton C. 2016. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput Mater., 2: 1-7. doi: 10.1038/s41524-016-0001-z [361] Wei Y L, Yang Q S, Ma L H, Tao R, Shang J J. 2020. Design and analysis of 2d/3d negative hydration expansion metamaterial driven by hydrogel. Materials & Design, 196: 109084. [362] Wilt J K, Yang C, Gu G X. 2020. Accelerating auxetic metamaterial design with deep learning. Advanced Engineering Materials, 22: 2070018. doi: 10.1002/adem.202070018 [363] Wu L, Liu L, Wang Y, Zhai Z, Zhuang H, Krishnaraju D, Wang Q, Jiang H. 2020. A machine learning-based method to design modular metamaterials. Extreme Mechanics Letters, 36: 100657. doi: 10.1016/j.eml.2020.100657 [364] Wu R, Roberts P C E, Lyu S, Zheng F, Soutis C, Diver C, Zhou D, Li L, Deng Z. 2021. Lightweight self-forming super-elastic mechanical metamaterials with adaptive stiffness. Advanced Functional Materials, 31: 2008252. doi: 10.1002/adfm.202008252 [365] Wu W, Tao Y, Xia Y, Chen J, Lei H, Sun L, Fang D. 2017. Mechanical properties of hierarchical anti-tetrachiral metastructures. Extreme Mechanics Letters, 16: 18-32. doi: 10.1016/j.eml.2017.08.004 [366] Wu X, Jin Y, Khelif A, Zhuang X, Rabczuk T, Djafari-Rouhani B. 2022. Topological surface wave metamaterials for robust vibration attenuation and energy harvesting. Mechanics of Advanced Materials and Structures, 29: 4759-4767. doi: 10.1080/15376494.2021.1937758 [367] Wyart M, Liang H, Kabla A, Mahadevan L. 2008. Elasticity of floppy and stiff random networks. Phys. Rev. Lett., 101: 215501. doi: 10.1103/PhysRevLett.101.215501 [368] Xia X, Afshar A, Yang H, Portela C M, Kochmann D M, Di Leo C V, Greer J R. 2019. Electrochemically reconfigurable architected materials. Nature, 573: 205-213. doi: 10.1038/s41586-019-1538-z [369] Xia X, Spadaccini C M, Greer J R. 2022. Responsive materials architected in space and time. Nat. Rev. Mater., 7: 683-701. doi: 10.1038/s41578-022-00450-z [370] Xiang X M, Lu G, You Z. 2020. Energy absorption of origami inspired structures and materials. Thin-Walled Structures, 157: 107130. doi: 10.1016/j.tws.2020.107130 [371] Xin X, Liu L, Liu Y, Leng J. 2020. Origami-inspired self-deployment 4d printed honeycomb sandwich structure with large shape transformation. Smart Mater. Struct., 29: 065015. doi: 10.1088/1361-665X/ab85a4 [372] Xu C, Quinn B, L’Espérance G, Lebel L, Daniel T. 2019. Multi-material direct ink writing (DIW) for complex 3d metallic structures with removable supports. ACS Applied Materials & Interfaces, 11: 8499-8506. [373] Xu L, Wang X, Kim Y, Shyu T C, Lyu J, Kotov N A. 2016. Kirigami nanocomposites as wide-angle diffraction gratings. Acs Nano, 10: 6156-6162. doi: 10.1021/acsnano.6b02096 [374] Yang C, Boorugu M, Dopp A, Ren J, Martin R, Han D, Choi W, Lee H. 2019. 4d printing reconfigurable, deployable and mechanically tunable metamaterials. Mater. Horiz., 6: 1244-1250. doi: 10.1039/C9MH00302A [375] Yang H, D’Ambrosio N, Liu P, Pasini D, Ma L. 2023. Shape memory mechanical metamaterials. Materials Today, 66: 36-49. doi: 10.1016/j.mattod.2023.04.003 [376] Yang H, Ma L. 2020. 1d to 3d multi-stable architected materials with zero Poisson’s ratio and controllable thermal expansion. Materials & Design, 188: 108430. [377] Yang H, Ma L. 2019. Multi-stable mechanical metamaterials by elastic buckling instability. J Mater Sci, 54: 3509-3526. doi: 10.1007/s10853-018-3065-y [378] Yang L, Harrysson O, Cormier D, West H, Gong H, Stucker B. 2015. Additive manufacturing of metal cellular structures: Design and fabrication. JOM, 67: 608-615. doi: 10.1007/s11837-015-1322-y [379] Yang Y, You Z. 2020. A Modular Origami-inspired Mechanical Metamaterial. arXiv:2012.09567 [380] Yao J, Sun R, Scarpa F, Remillat C, Gao Y, Su Y. 2021. Two-dimensional graded metamaterials with auxetic rectangular perforations. Composite Structures, 261: 113313. doi: 10.1016/j.compstruct.2020.113313 [381] Yu K, Du H, Xin A, Lee K H, Feng Z, Masri S F, Chen Y, Huang G, Wang Q. 2020. Healable, memorizable, and transformable lattice structures made of stiff polymers. NPG Asia Mater., 12: 1-16. doi: 10.1038/s41427-019-0187-x [382] Yu X, Zhou J, Liang H, Jiang Z, Wu L. 2018. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Progress in Materials Science, 94: 114-173. doi: 10.1016/j.pmatsci.2017.12.003 [383] Zadpoor A A. 2016. Mechanical meta-materials. Mater. Horiz., 3: 371-381. doi: 10.1039/C6MH00065G [384] Zeng C, Liu L, Bian W, Leng J, Liu Y. 2022. Temperature-dependent mechanical response of 4d printed composite lattice structures reinforced by continuous fiber. Composite Structures, 280: 114952. doi: 10.1016/j.compstruct.2021.114952 [385] Zeng H, Wani O M, Wasylczyk P, Priimagi A. 2018. Light-driven, caterpillar-inspired miniature inching robot. Macromolecular Rapid Communications, 39: 1700224. doi: 10.1002/marc.201700224 [386] Zhai Z, Wang Y, Jiang H. 2018. Origami-inspired, on-demand deployable and collapsible mechanical metamaterials with tunable stiffness. Proceedings of the National Academy of Sciences, 115: 2032-2037. doi: 10.1073/pnas.1720171115 [387] Zhai Z, Wang Y, Lin K, Wu L, Jiang H. 2020. In situ stiffness manipulation using elegant curved origami. Science Advances, 6: eabe2000. doi: 10.1126/sciadv.abe2000 [388] Zhai Z, Wu L, Jiang H. 2021. Mechanical metamaterials based on origami and kirigami. Applied Physics Reviews, 8: 041319. doi: 10.1063/5.0051088 [389] Zhang J, Ashby M F. 1992. The out-of-plane properties of honeycombs. International Journal of Mechanical Sciences, 34: 475-489. doi: 10.1016/0020-7403(92)90013-7 [390] Zhang J, Lu G, You Z. 2020. Large deformation and energy absorption of additively manufactured auxetic materials and structures: A review. Composites Part B: Engineering, 201: 108340. doi: 10.1016/j.compositesb.2020.108340 [391] Zhang K, Chermprayong P, Xiao F, Tzoumanikas D, Dams B, Kay S, Kocer B B, Burns A, Orr L, Choi C, Darekar D D, Li W, Hirschmann S, Soana V, Ngah S A, Sareh S, Choubey A, Margheri L, Pawar V M, Ball R J, Williams C, Shepherd P, Leutenegger S, Stuart-Smith R, Kovac M. 2022. Aerial additive manufacturing with multiple autonomous robots. Nature, 609: 709-717. doi: 10.1038/s41586-022-04988-4 [392] Zhang Q, Barri K, Jiao P, Lu W, Luo J, Meng W, Wang J, Hong L, Mueller J, Lin Wang Z, Alavi A H. 2023. Meta-mechanotronics for self-powered computation. Materials Today, 65: 78-89. doi: 10.1016/j.mattod.2023.03.026 [393] Zhang Q, Kuang X, Weng S, Zhao Z, Chen H, Fang D, Qi H J. 2020. Rapid volatilization induced mechanically robust shape-morphing structures toward 4d printing. ACS Appl. Mater. Interfaces, 12: 17979-17987. doi: 10.1021/acsami.0c02038 [394] Zhang Q, Wommer J, O’Rourke C, Teitelman J, Tang Y, Robison J, Lin G, Yin J. 2017. Origami and kirigami inspired self-folding for programming three-dimensional shape shifting of polymer sheets with light. Extreme Mechanics Letters, 11: 111-120. doi: 10.1016/j.eml.2016.08.004 [395] Zhang S, Yin L, Fang N. 2009. Focusing ultrasound with an acoustic metamaterial network. Phys. Rev. Lett., 102: 194301. doi: 10.1103/PhysRevLett.102.194301 [396] Zhang X, Liu Z. 2008. Superlenses to overcome the diffraction limit. Nature Mater., 7: 435-441. doi: 10.1038/nmat2141 [397] Zhang Y, Wang Q, Tichem M, van Keulen F. 2020. Design and characterization of multi-stable mechanical metastructures with level and tilted stable configurations. Extreme Mechanics Letters, 34: 100593. doi: 10.1016/j.eml.2019.100593 [398] Zhang Y, Yan Z, Nan K, Xiao D, Liu Y, Luan H, Fu H, Wang X, Yang Q, Wang J C, Ren W, Si H, Liu F, Yang L, Li H, Wang J T, Guo X, Luo H, Wang L, Huang Y, Rogers J A. 2015. A mechanically driven form of kirigami as a route to 3d mesostructures in micro/nanomembranes. Proceedings of the National Academy of Sciences, 112: 11757-11764. doi: 10.1073/pnas.1515602112 [399] Zhang Z, Dou J, He J, Xiao C, Shen L, Yang J, Wang Y, Zhou Z. 2017. Electrically/infrared actuated shape memory composites based on a bio-based polyester blend and graphene nanoplatelets and their excellent self-driven ability. J. Mater. Chem. C, 5: 4145-4158. doi: 10.1039/C7TC00828G [400] Zhang Z, Krushynska A O. 2022. Programmable shape morphing of rose mechanical metamaterials. APL Mater., 10: 080701. doi: 10.1063/5.0099323 [401] Zhang Z, Scarpa F, Bednarcyk B A, Chen Y. 2021. Harnessing fractal cuts to design robust lattice metamaterials for energy dissipation. Additive Manufacturing, 46: 102126. doi: 10.1016/j.addma.2021.102126 [402] Zhao Z, Wu J, Mu X, Chen H, Qi H J, Fang D. 2017. Origami by frontal photopolymerization. Science Advances, 3: e1602326. doi: 10.1126/sciadv.1602326 [403] Zheng X, Lee H, Weisgraber T H, Shusteff M, DeOtte J, Duoss E B, Kuntz J D, Biener M M, Ge Q, Jackson J A, Kucheyev S O, Fang N X, Spadaccini C M. 2014. Ultralight, ultrastiff mechanical metamaterials. Science, 344: 1373-1377. doi: 10.1126/science.1252291 [404] Zhong H, Song T, Li C, Das R, Gu J, Qian M. 2023. The gibson-ashby model for additively manufactured metal lattice materials: Its theoretical basis, limitations and new insights from remedies. Current Opinion in Solid State and Materials Science, 27: 101081. doi: 10.1016/j.cossms.2023.101081 [405] Zhou X H, Li T, Wang J, Chen F, Zhou D, Liu Q, Li B, Cheng J, Zhou X C, Zheng B. 2018. Mechanochemical regulated origami with tough hydrogels by ion transfer printing. ACS Appl. Mater. Interfaces, 10: 9077-9084. doi: 10.1021/acsami.8b01610 [406] Zhu H X, Hobdell J R, Windle A H. 2001. Effects of cell irregularity on the elastic properties of 2d voronoi honeycombs. Journal of the Mechanics and Physics of Solids, 49: 857-870. doi: 10.1016/S0022-5096(00)00046-6 [407] Zhu R, Huang G L, Huang H H, Sun C T. 2011. Experimental and numerical study of guided wave propagation in a thin metamaterial plate. Physics Letters A, 375: 2863-2867. doi: 10.1016/j.physleta.2011.06.006 [408] Zhu S, Wang B, Tan X, Hu J, Wang L, Zhou Z, Chen S. 2021. A novel bi-material negative stiffness metamaterial in sleeve-type via combining rigidity with softness. Composite Structures, 262: 113381. doi: 10.1016/j.compstruct.2020.113381 [409] Zhu Y, Birla M, Oldham K R, Filipov E T. 2020. Elastically and plastically foldable electrothermal micro-origami for controllable and rapid shape morphing. Advanced Functional Materials, 30: 2003741. doi: 10.1002/adfm.202003741 -





 下载:
下载: