Advances in vibration testing and model updating for nonlinear aerospace structures
-
摘要: 面向质量更轻、承载能力更强, 柔性变形更大的先进飞行器, 首先对其地面振动试验及使役过程中观察到的非线性振动现象进行梳理, 归纳出两类典型的非线性结构模型−局部非线性结构和分布式非线性结构, 对其基本概念进行了阐述. 随后, 从频响函数试验、纯模态试验、自由衰减试验等技术路径总结了非线性振动试验方法的研究进展. 最后, 根据两类非线性结构动力学方程的特点分别归纳了与之相适应的有限元模型修正流程及关键辨识方法, 展望了发展趋势并给出研究建议. 有望为未来飞行器非线性振动试验与精准建模提供有益参考.Abstract: For lighter, stronger and more flexible aerospace structures, the nonlinear phenomena observed during ground vibration tests and in-service operations are first sorted out. Two types of typical nonlinear structures-localised and distributed nonlinear structures—are then highlighted, the basic concepts of which are explained. Secondly, the vibration testing techniques developed for these nonlinear structures are compared, and the research progress is summarised from the perspective of frequency response test, pure modal test, free decay test and others. Finally, model updating procedures of the two types of nonlinear structures are analysed, with identification methods discussed. Future perspectives are pointed out and research suggestions are also highlighted. It is expected to provide a useful reference for the future development of vibration testing techniques and accurate modelling methods of nonlinear aerospace structures.
-
Key words:
- aerospace structure /
- nonlinear vibration /
- vibration testing /
- model updating
-
图 1 欧洲机械臂地面振动试验(Göge et al. 2005a). (a)试验场景, (b)辨识得到模态刚度的非线性曲线
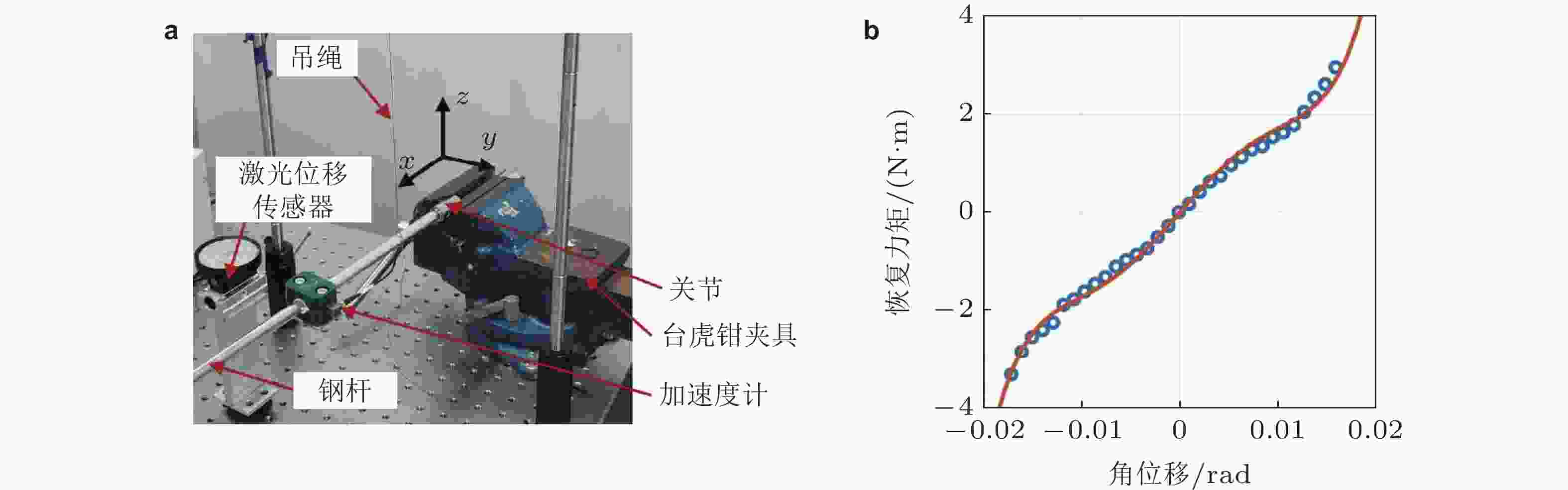
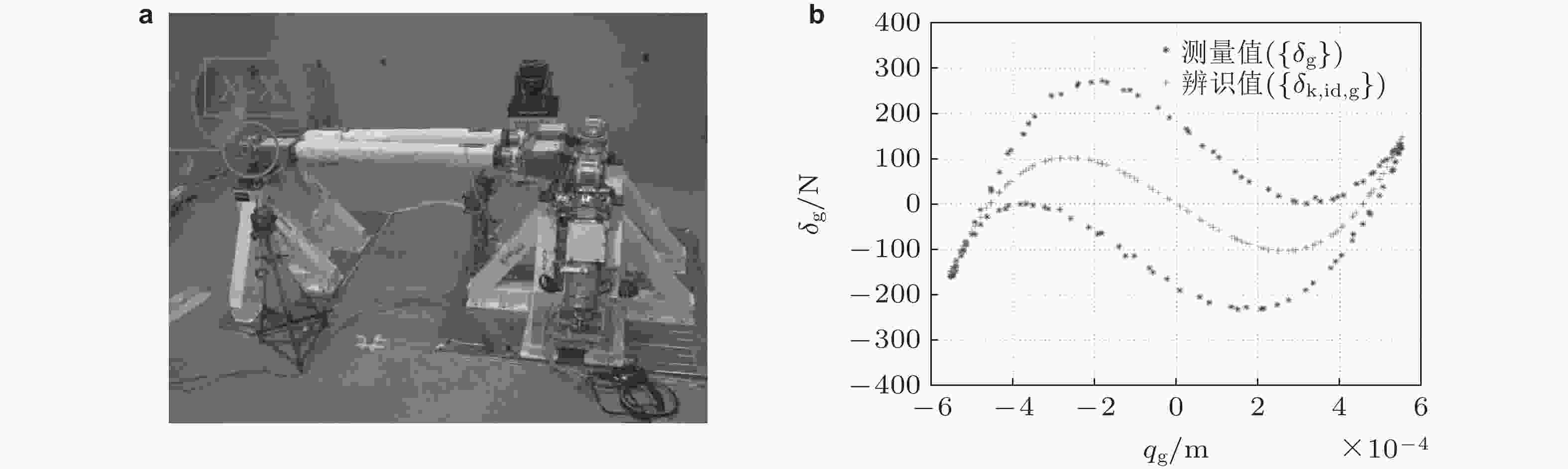
图 2 航天器桁架关节的非线性振动试验(Li et al. 2022a, 2023). (a)试验场景, (b)辨识得到的力矩-转角曲线
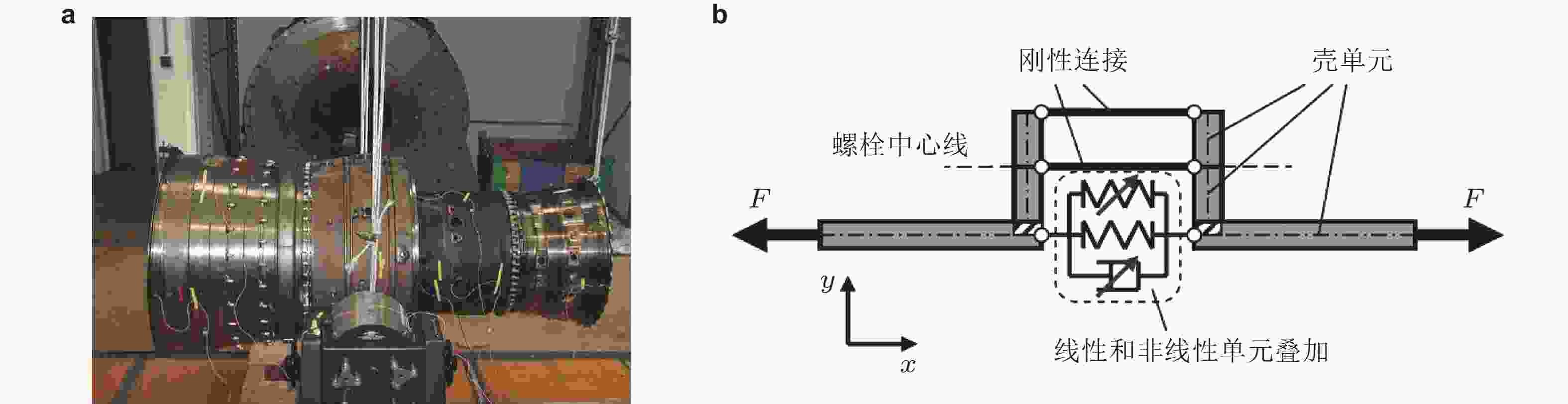
图 3 航空发动机部段连接结构的振动试验(Boswald & Link 2004). (a)试验场景, (b)单个螺栓结构的非线性模型
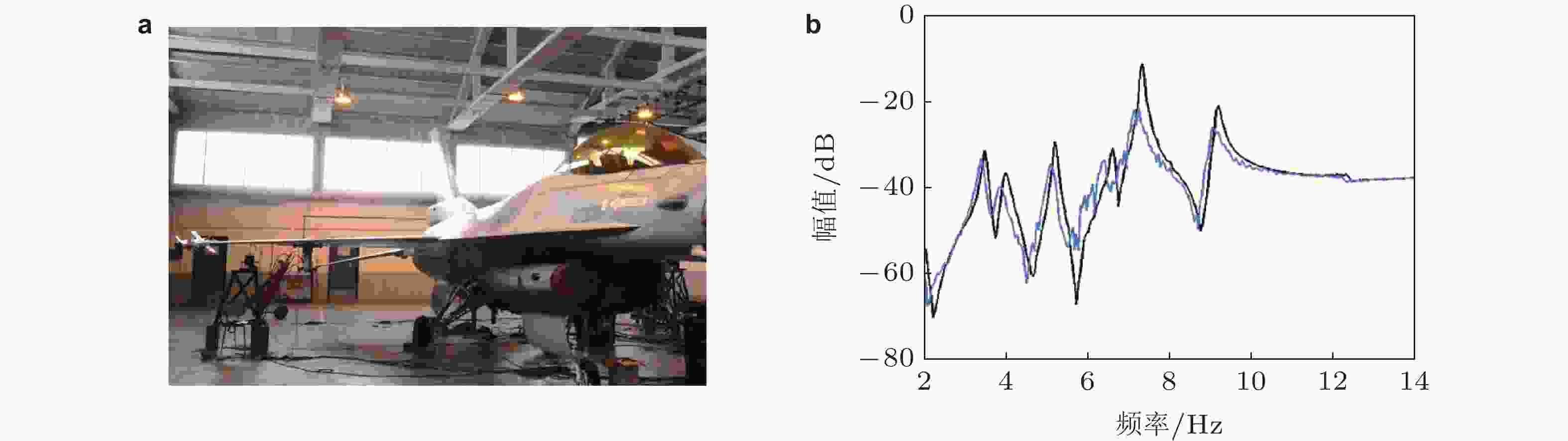
图 4 美国F-16翼尖挂架的地面振动试验 (Noël et al. 2013). (a)试验场景, (b) 频响函数测量结果
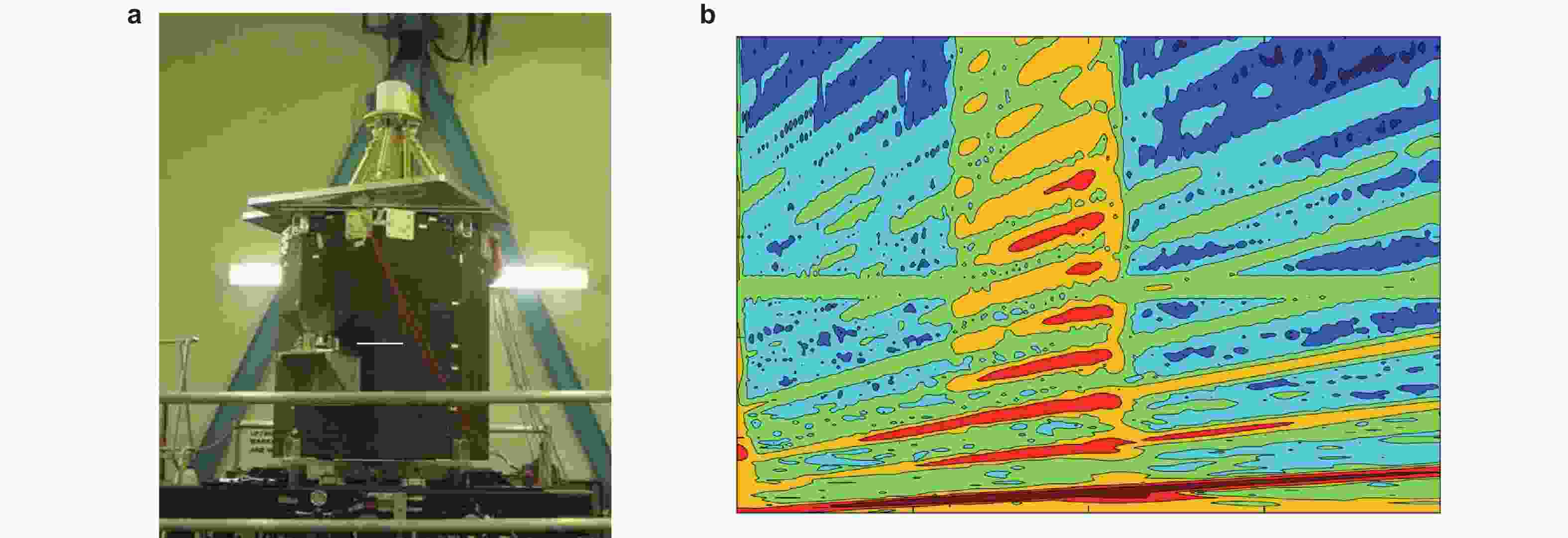
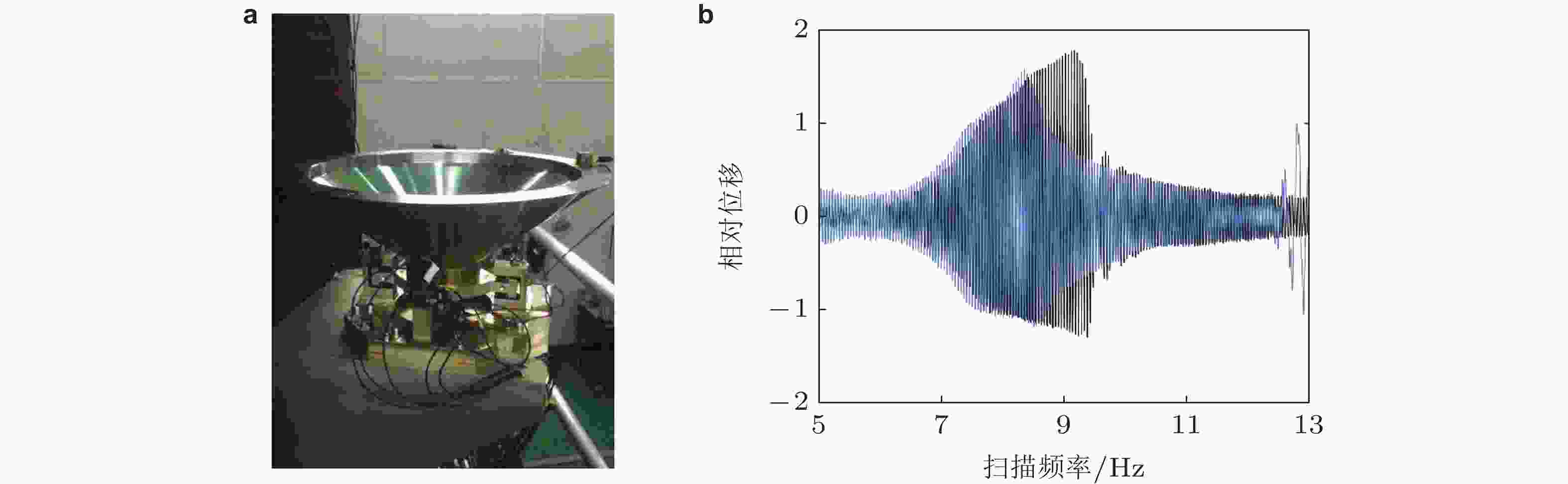
图 5 欧洲SmallSat地面振动试验(Noël & Kerschen 2017). (a)扫频试验场景, (b) 试验测得的复杂非线性振动响应
图 7 欧洲SmallSat卫星飞轮支架振动试验(Noël & Kerschen 2017). (a)飞轮支架局部图, (b)正扫和反扫试验中测得的支架处相对位移响应
图 8 航空发动机风扇叶片的纯模态试验(Wang et al. 2022). (a)振动试验场景, (b)全场加速度与激振力的相位差图
图 9 基于数字图像相关的连接结构非线性振动试验(Chen et al. 2022). (a)相机与被测结构, (b)多点响应测量结果
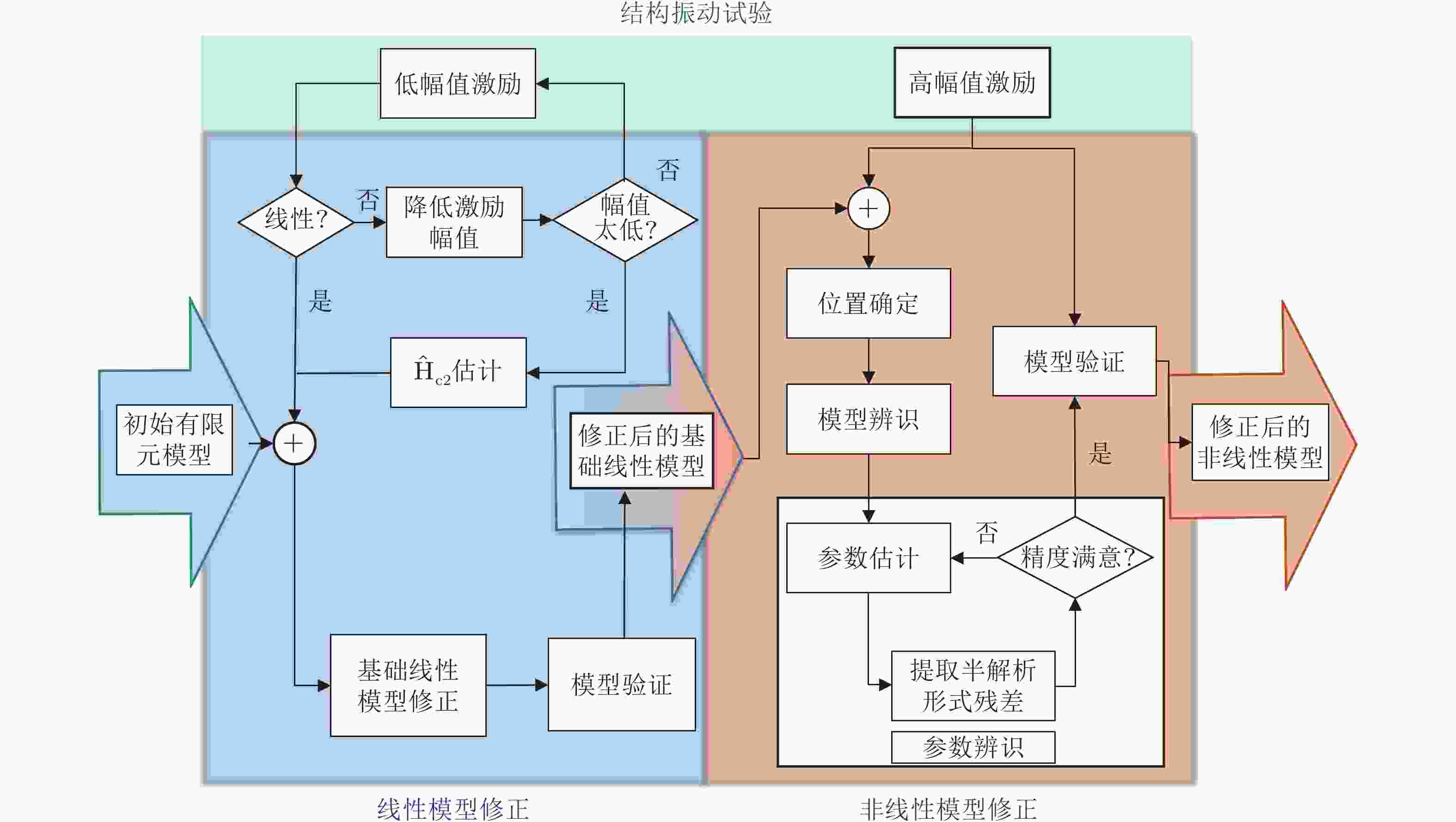
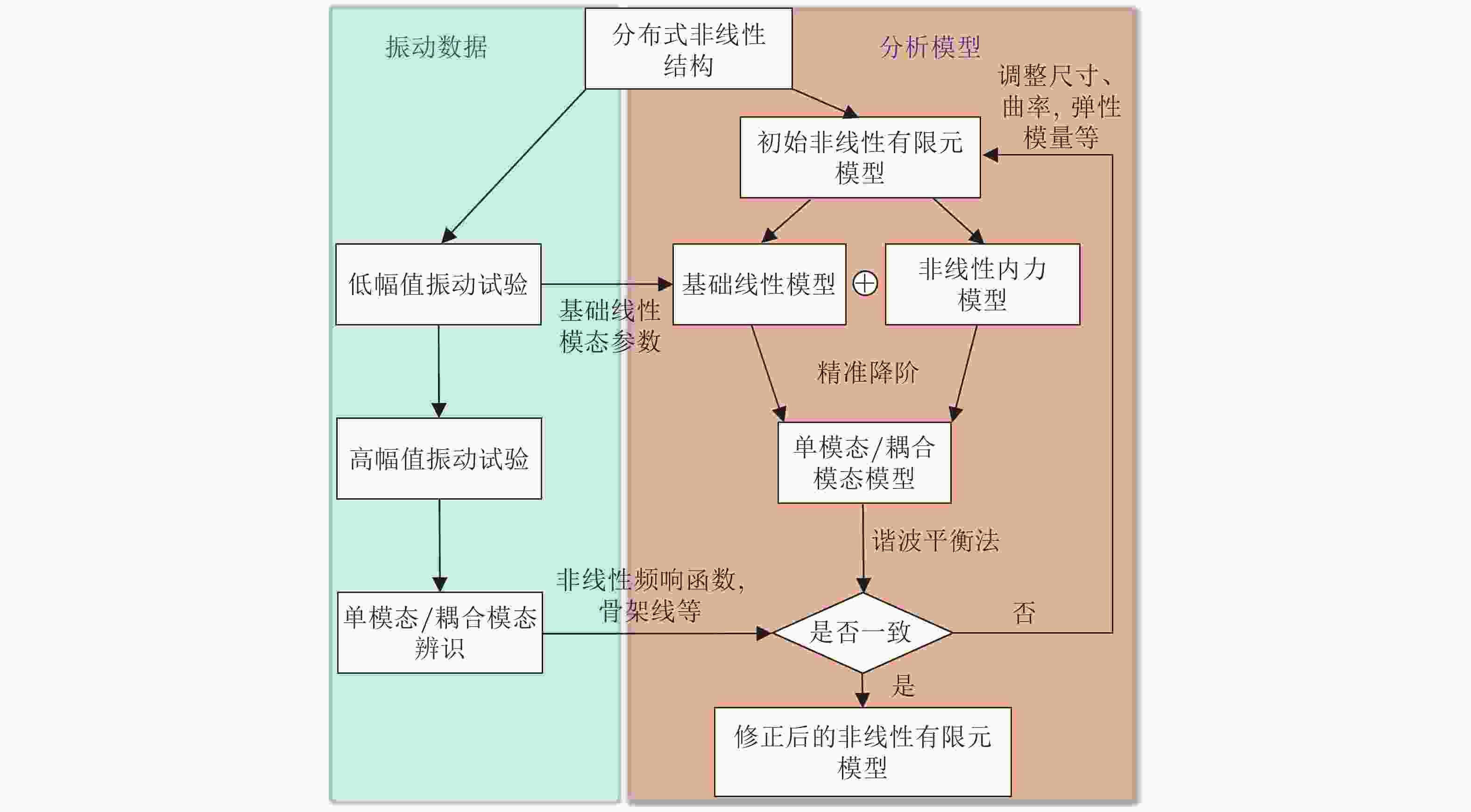
图 10 基于频响函数数据的局部非线性结构有限元模型修正的一般流程(Wang et al. 2018b)
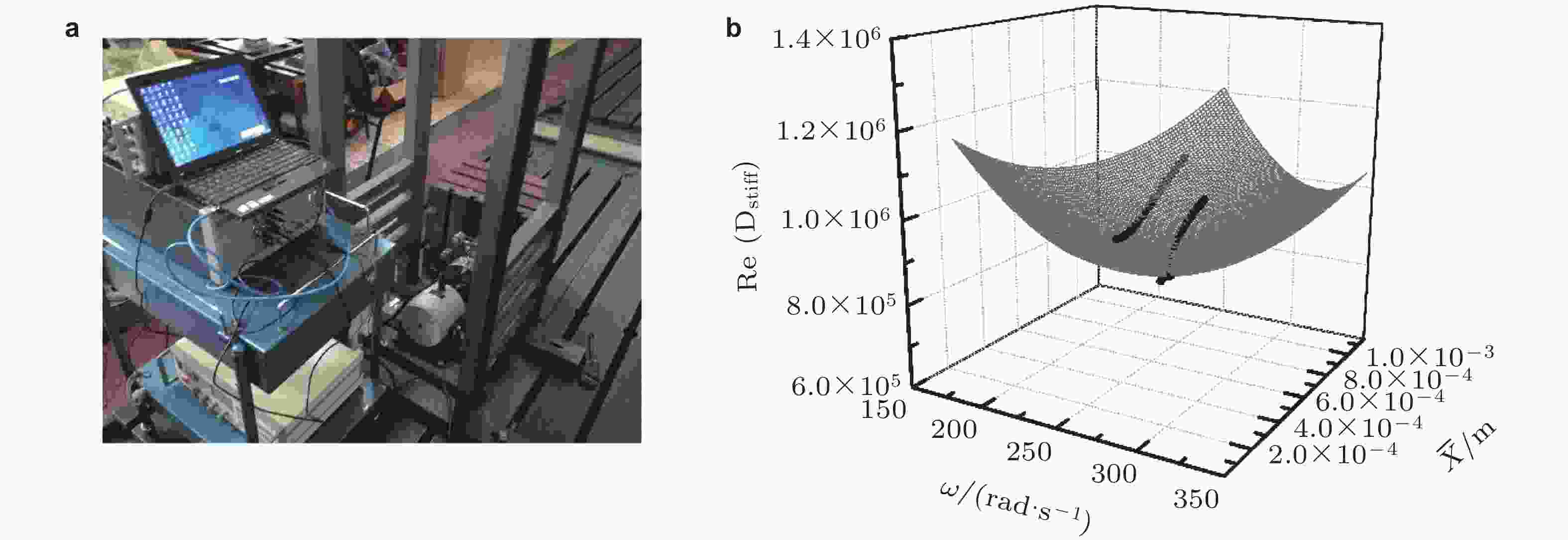
图 11 利用等效动刚度图法辨识卫星金属橡胶阻尼器参数(Wang & Zheng 2016). (a)试验场景, (b)等效动刚度实部图
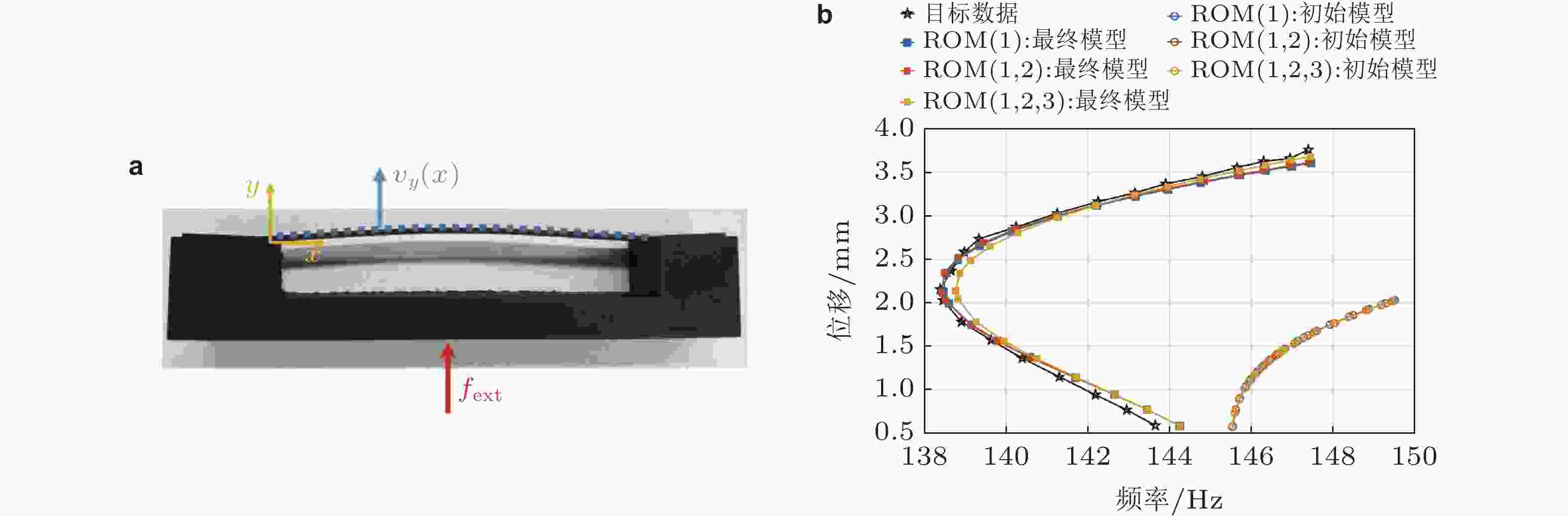
图 13 基于骨架线匹配的曲梁结构单模态辨识 (Van Damme et al. 2020). (a)曲梁结构, (b)骨架线迭代过程
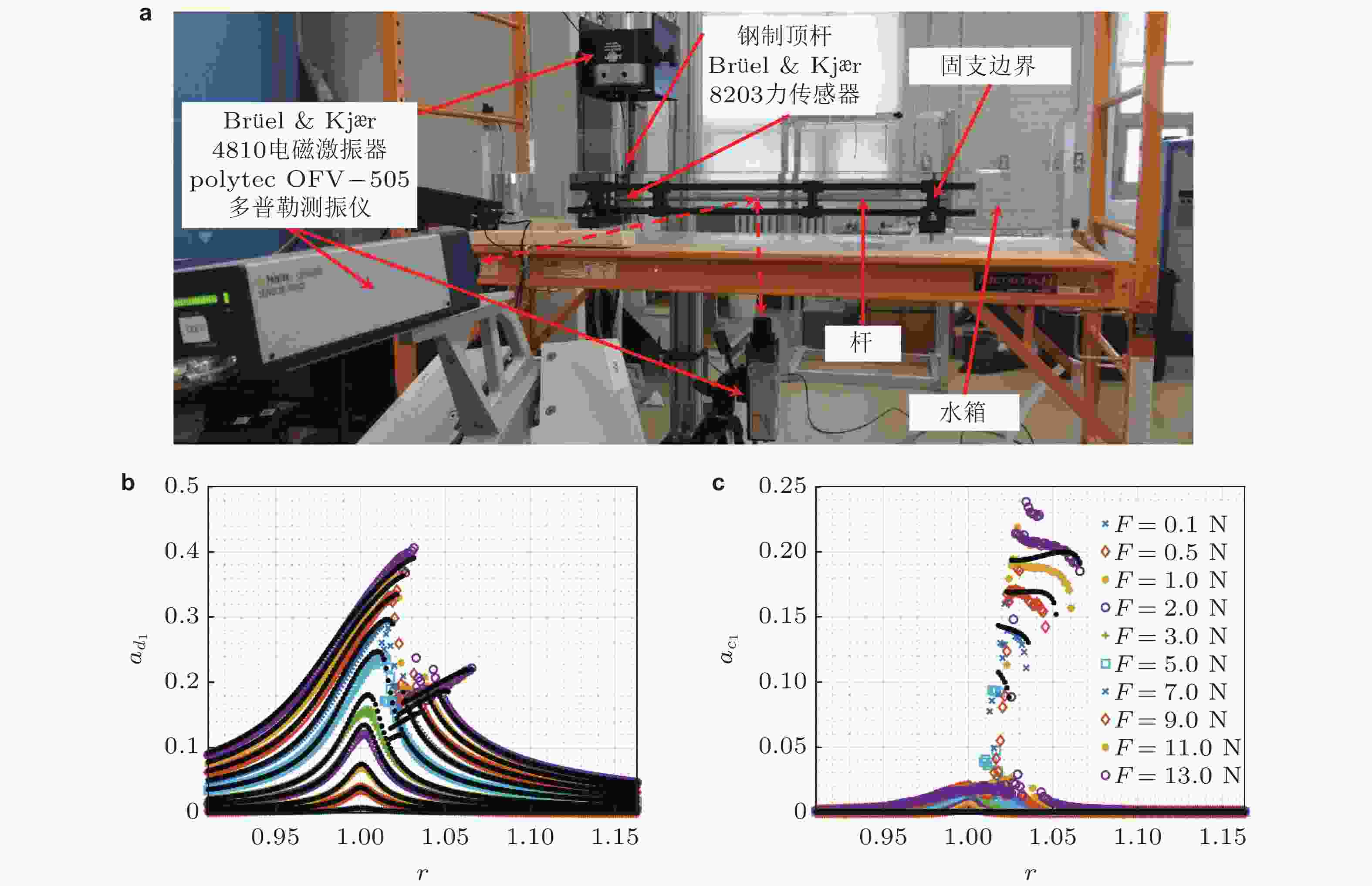
图 14 浸入水中圆杆的非线性振动试验与耦合模态辨识 (Le Guisquet & Amabili 2021b). (a)试验场景, (b)驱动模态(driven mode)频响函数对比, (c)伴随模态(companion mode)频响函数对比
-
[1] 陈昌亚, 宋汉文, 王德禹, 等. 2003. 卫星振动试验中固有频率 “漂移” 现象初步研究. 振动与冲击, 22: 23-25 (Chen C Y, Song H W, Wang D Y, et al. 2003. Preliminary research on natural frequency drift in satellite vibration test. Journal of vibration and shock, 22: 23-25). doi: 10.3969/j.issn.1000-3835.2003.01.006Chen C Y, Song H W, Wang D Y, et al. 2003. Preliminary research on natural frequency drift in satellite vibration test. Journal of vibration and shock, 22: 23-25. doi: 10.3969/j.issn.1000-3835.2003.01.006 [2] 丁继锋, 韩增尧, 马兴瑞. 2010. 大型复杂航天器结构有限元模型的验证策略研究. 宇航学报, 31: 547-555 (Ding J F, Han Z Y, Ma X R. 2010. Finite element model verification strategy of large complex spacecraft. Journal of Astronautics, 31: 547-555). doi: 10.3873/j.issn.1000-1328.2010.02.039Ding J F, Han Z Y, Ma X R. 2010. Finite element model verification strategy of large complex spacecraft. Journal of Astronautics, 31: 547-555. doi: 10.3873/j.issn.1000-1328.2010.02.039 [3] 东巳宙, 白照广, 白云鹤, 等. 2023. 卫星对接环减振装置设计与验证. 宇航学报, 01 : 143-154 (Dong S Z, Bai Z G, Bai Y H, et al. 2023. Design and verification of satellite docking ring damping device. Journal of Astronautics, 01 : 143-154).Dong S Z, Bai Z G, Bai Y H, et al. 2023. Design and verification of satellite docking ring damping device. Journal of Astronautics, 01: 143-154. [4] 郝淑英, 陈予恕, 张琪昌, 等. 2001. 连结子结构在非线性动力学分析中的应用. 天津大学学报, 34: 295-299 (Hao S Y, Chen Y S, Zhang Q C, et al. 2001. Application of link substructure to nonlinear dynamic system analysis. Journal of Tianjin University, 34: 295-299). doi: 10.3969/j.issn.0493-2137.2001.03.003Hao S Y, Chen Y S, Zhang Q C, et al. 2001. Application of link substructure to nonlinear dynamic system analysis. Journal of Tianjin University, 34: 295-299. doi: 10.3969/j.issn.0493-2137.2001.03.003 [5] 黄文虎, 武新华, 焦映厚, 等. 2000. 非线性转子动力学研究综述. 振动工程学报, 13: 497-509 (Huang W H, Wu X H, Jiao Y H, et al. 2000. Review of nonlinear rotor dynamics. Journal of vibration engineering, 13: 497-509). doi: 10.3969/j.issn.1004-4523.2000.04.001Huang W H, Wu X H, Jiao Y H, et al. 2000. Review of nonlinear rotor dynamics. Journal of vibration engineering, 13: 497-509. doi: 10.3969/j.issn.1004-4523.2000.04.001 [6] 何昊南, 于开平, 唐宏, 等. 2019. 有间隙折叠舵面的振动实验与非线性建模研究. 力学学报, 51: 1476-1488 (He H N, Yu K P, Tang H, et al. 2019. Vibration experiment and nonlinear modelling research on the folding fin with freeplay. Chinese Journal of Theoretical and Applied Mechanics, 51: 1476-1488). doi: 10.6052/0459-1879-19-119He H N, Yu K P, Tang H, et al. 2019. Vibration experiment and nonlinear modelling research on the folding fin with freeplay. Chinese Journal of Theoretical and Applied Mechanics, 51: 1476-1488 doi: 10.6052/0459-1879-19-119 [7] 何贵勤, 曹登庆, 陈帅, 等. 2021. 挠性航天器太阳翼全局模态动力学建模与实验研究. 力学学报, 53 : 2312-2322 (He G Q, Cao D Q, Chen S, et al. Study on global mode dynamic modeling and experiment for a solar array of the flexible spacecraft. 2021. Chinese Journal of Theoretical and Applied Mechanics, 53 2312-2322).He G Q, Cao D Q, Chen S, et al. Study on global mode dynamic modeling and experiment for a solar array of the flexible spacecraft. 2021. Chinese Journal of Theoretical and Applied Mechanics, 53 2312-2322. [8] 凯歌, 刘涛, 斯日古楞, 等. 2019. 美国SMAP卫星失效的一个可能性分析. 科学通报, 64: 3196-3203 (Kai G, Liu T, Siriguleng, et al. 2019. A possible analysis for failure of U. S. SMAP satellite. Chinese science bulletin, 64: 3196-3203).Kai G, Liu T, Siriguleng, et al. 2019. A possible analysis for failure of U. S. SMAP satellite. Chinese science bulletin, 64: 3196-3203. [9] 陆秋海, 李德葆. 2015 工程振动试验分析(第2版). 北京: 清华大学出版社 (Lu Q H, Li D B. 2015. Experimental vibration analysis in engineering (second Edition).Beijing: Tsinghua University Press).Lu Q H, Li D B. 2015. Experimental vibration analysis in engineering (second Edition).Beijing: Tsinghua University Press. [10] 马兴瑞, 韩增尧, 等. 2014. 卫星与运载火箭力学环境分析方法及试验技术. 北京: 科学出版社 (Ma X R, Han Z Y, et al. 2014. Mechanical environment analysis and test for satellites and launch vehicles. Beijing: China Science Publishing & Media Ltd).Ma X R, Han Z Y, et al. 2014. Mechanical environment analysis and test for satellites and launch vehicles. Beijing: China Science Publishing & Media Ltd. [11] 孟光, 周徐斌, 苗军. 2016. 航天重大工程中的力学问题. 力学进展, 46: 201606 (Meng G, Zhou X B, Miao J. 2016. Mechanical problems in momentous projects of aerospace engineering. Advances in Mechanics, 46: 201606). doi: 10.6052/1000-0992-15-018Meng G, Zhou X B, Miao J. 2016. Mechanical problems in momentous projects of aerospace engineering. Advances in Mechanics, 46: 201606 doi: 10.6052/1000-0992-15-018 [12] 钱志英, 韩世泽, 马为佳, 等. 2018. 航天器振动试验中的频率漂移现象研究. 航天器环境工程, 35: 342-347 (Qian Z Y, Han S Z, Ma W J, et al. 2018. Natural frequency drift in the vibration test of spacecraft. Spacecraft Environment Engineering, 35: 342-347). doi: 10.12126/j.issn.1673-1379.2018.04.006Qian Z Y, Han S Z, Ma W J, et al. 2018. Natural frequency drift in the vibration test of spacecraft. Spacecraft Environment Engineering, 35: 342-347. doi: 10.12126/j.issn.1673-1379.2018.04.006 [13] 邱吉宝, 张正平, 向树红, 等. 2015. 结构动力学及其在航天工程中的应用. 合肥: 中国科学技术大学出版社. [14] 孙业凯, 吴亚光, 王兴, 等. 2022. 叶片/叶盘摩擦阻尼结构的非线性模态分析综述. 航空动力学报, 37: 2167-2187 (Sun Y K, Wu Y G, Wang X, et al. 2022. Review of nonlinear modal analysis in friction damping structures of blades/blade disks. Journal of Aerospace Power, 37: 2167-2187).Sun Y K, Wu Y G, Wang X, et al. 2022. Review of nonlinear modal analysis in friction damping structures of blades/blade disks. Journal of Aerospace Power, 37: 2167-2187. [15] 沈民民, 杨晓东. 连接结构界面摩擦力学建模研究进展. 力学进展, 2024, 54 (3): 477-521. (Shen M M, Yang X D. Modeling of joint structure interface friction mechanics: A review. Advances in Mechanics, 2024, 54 (3): 477-521).Shen M M, Yang X D. Modeling of joint structure interface friction mechanics: A review. Advances in Mechanics, 2024, 54(3): 477-521 [16] 王强, 马志赛, 张欣, 等. 2020. 基于模态综合法的含间隙折叠舵面动态特性分析. 航空学报, 05 , 223507 (Wang Q, Ma Z S, Zhang X, et al. 2020. Dynamic characteristic analysis for a folding fin with freeplay nonlinearities based on mode synthesis method. Acta Aeronautica ET Astronautica Sinica, 05 : 223507).Wang Q, Ma Z S, Zhang X, et al. 2020. Dynamic characteristic analysis for a folding fin with freeplay nonlinearities based on mode synthesis method. Acta Aeronautica ET Astronautica Sinica, 05: 223507. [17] 王兴. 2023. 飞行器结构的非线性动力学试验与模型修正研究. 第五届全国连接结构动力学学术研讨会, 中国苏州 (Wang X. 2023. Nonlinear dynamic testing and model updating for aerospace structures. The fifth national symposium on jointed structures, Suzhou, China).Wang X. 2023. Nonlinear dynamic testing and model updating for aerospace structures. The fifth national symposium on jointed structures, Suzhou, China. [18] 王东, 万强, 张周锁. 2024. 连接结构动力学预测与辨识. 国防工业出版社 (Wang D, Wan Q, Zhang Z S. 2024. Dynamic prediction and identification of jointed structures. National Defense Industry Press).Wang D, Wan Q, Zhang Z S. 2024. Dynamic prediction and identification of jointed structures. National Defense Industry Press. [19] 张皓, 李东升, 李宏男. 2019. 有限元模型修正研究进展: 从线性到非线性. 力学进展, 49: 201909 (Zhang H, Li D S, Li H N. 2019. Recent progress on finite element model updating: From linearity to nonlinearity. Advances in Mechanics, 49: 201909). doi: 10.6052/1000-0992-18-004Zhang H, Li D S, Li H N. 2019. Recent progress on finite element model updating: From linearity to nonlinearity. Advances in Mechanics, 49: 201909 doi: 10.6052/1000-0992-18-004 [20] Adams D E, Allemang R J. 2000. A frequency domain method for estimating the parameters of a non-linear structural dynamic model through feedback. Mechanical Systems and Signal Processing, 14: 637-656. doi: 10.1006/mssp.2000.1292 [21] Ajjan Al-Hadid M, Wright J R. 1989. Developments in the force-state mapping technique for non-linear systems and the extension to the location of non-linear elements in a lumped-parameter system. Mechanical Systems and Signal Processing, 3: 269-290. doi: 10.1016/0888-3270(89)90053-8 [22] Arslan O, Aykan M, Nevzat O H. 2011. Parametric identification of structural nonlinearities from measured frequency response data. Mechanical Systems and Signal Processing, 25: 1112-1125. doi: 10.1016/j.ymssp.2010.10.010 [23] Avitabile P, Singhal R, Peeters B, et al. 2006. Modal parameter estimation for large, complicated MIMO tests. Sound and Vibration, 40: 14-20. [24] Aykan M, Ozguven H N. 2013. Identification of restoring force surfaces in nonlinear MDOF systems from FRF data using nonlinearity matrix. Proceedings of the 31st IMAC, A Conference on Structural Dynamics, Springer New York. [25] Avin O, Raveh D E, Drachinsky A, et al. 2022. Experimental aeroelastic benchmark of a very flexible wing. AIAA Journal, 60: 1745-1768. doi: 10.2514/1.J060621 [26] Allemang R, Avitabile P (Eds.). 2022. Handbook of experimental structural dynamics. Springer Nature. [27] Anastasio D, Marchesiello S. 2023. Nonlinear frequency response curves estimation and stability analysis of randomly excited systems in the subspace framework. Nonlinear Dynamics, 111: 8115-8133. doi: 10.1007/s11071-023-08280-6 [28] Barton D A W, Mann B P, Burrow S G. 2012. Control-based continuation for investigating nonlinear experiments. Journal of Vibration and Control, 18: 509-520. doi: 10.1177/1077546310384004 [29] Belytschko T, Liu W K, Moran B, et al. 2014. Nonlinear finite elements for continua and structures. John Wiley & Sons. [30] Boswald M, Link M. 2004. Identification of non-linear joint parameters by using frequency response residuals. Proceedings of the 2004 International Conference on Noise and Vibration Engineering, Leuven: Belgium. [31] Brake M R W (ed.). 2017. The mechanics of jointed structures: Recent research and open challenges for developing predictive models for structural dynamics. Springer International Publishing. [32] Brunton S L, Proctor J L, Kutz J N. 2016. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences, 113: 3932-3937. doi: 10.1073/pnas.1517384113 [33] Bi S, Beer M, Mottershead J. 2022. Recent advances in stochastic model updating. Mechanical Systems and Signal Processing, 172: 108971. doi: 10.1016/j.ymssp.2022.108971 [34] Carney K, Yunis I, Smith K, et al. 1997. Nonlinear dynamic behavior in the Cassini spacecraft modal survey. Proceedings of SPIE, the International Society for Optical Engineering. [35] Carrella A, Ewins D J. 2011. Identifying and quantifying structural nonlinearities in engineering applications from measured frequency response functions. Mechanical Systems and Signal Processing, 25: 1011-1027. doi: 10.1016/j.ymssp.2010.09.011 [36] Crawley E F, Aubert A C. 1986. Identification of nonlinear structural elements by force-state mapping. AIAA Journal, 24: 155-162. doi: 10.2514/3.9236 [37] Crawley E F, O'DONNELL K J. 1987. Force-state mapping identification of nonlinear joints. AIAA Journal, 25: 1003-1010. doi: 10.2514/3.9733 [38] Cesnik C E, Senatore P J, Su W, et al. 2012. X-HALE: A very flexible unmanned aerial vehicle for nonlinear aeroelastic tests. AIAA Journal, 50: 2820-2833. doi: 10.2514/1.J051392 [39] Csurcsia P Z, Peeters B, Schoukens J, et al. 2020. Simplified analysis for multiple input systems: A toolbox study illustrated on F-16 measurements. Vibration, 3: 70-84. doi: 10.3390/vibration3020007 [40] Chen W, Zang X, Wu S, et al. 2020. Gradient-based point tracking method and its application in the modal test of a solar array model. Measurement, 154: 107503. doi: 10.1016/j.measurement.2020.107503 [41] Chen W, Jana D, Singh A, et al. 2022. Measurement and identification of the nonlinear dynamics of a jointed structure using full-field data, part I: Measurement of nonlinear dynamics. Mechanical Systems and Signal Processing, 166: 108401. doi: 10.1016/j.ymssp.2021.108401 [42] Denis V, Jossic M, Giraud-Audine C, et al. 2018. Identification of nonlinear modes using phase-locked-loop experimental continuation and normal form. Mechanical Systems and Signal Processing, 106: 430-452. doi: 10.1016/j.ymssp.2018.01.014 [43] Ehrhardt D A, Allen M S, Beberniss T J, et al. 2017. Finite element model calibration of a nonlinear perforated plate. Journal of Sound and Vibration, 392: 280-294. doi: 10.1016/j.jsv.2016.12.037 [44] Ewins D J, Weekes B, Delli Carri A. 2015. Modal testing for model validation of structures with discrete nonlinearities. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 373: 20140410. doi: 10.1098/rsta.2014.0410 [45] Feldman M. 1994. Non-linear system vibration analysis using Hilbert transform-I. Free vibration analysis method ‘Freevib’. Mechanical systems and signal processing, 8 : 119-127. [46] Friswell M I, Mottershead J E. 1995. Finite element model updating in structural dynamics. Springer Science & Business Media. [47] Fuellekrug U, Göge D. 2012. Identification of weak non-linearities within complex aerospace structures. Aerospace Science and Technology, 23: 53-62. doi: 10.1016/j.ast.2011.04.012 [48] Farokhi H, Xia Y, Erturk A. 2022. Experimentally validated geometrically exact model for extreme nonlinear motions of cantilevers. Nonlinear dynamics, 107: 457-475. doi: 10.1007/s11071-021-07023-9 [49] Gibert C. 2003. Fitting measured frequency response using non-linear modes. Mechanical systems and signal processing, 17: 211-218. doi: 10.1006/mssp.2002.1562 [50] Göge D. 2003. Automatic updating of large aircraft models using experimental data from ground vibration testing. Aerospace science and technology, 7: 33-45. doi: 10.1016/S1270-9638(02)01184-7 [51] Göge D, Fuellekrug U, Sinapius M, et al. 2005a. Advanced test strategy for identification and characterization of nonlinearities of aerospace structures. AIAA Journal, 43: 974-986. doi: 10.2514/1.5651 [52] Göge D, Sinapius M, Füllekrug U, et al. 2005b. Detection and description of non-linear phenomena in experimental modal analysis via linearity plots. International Journal of Non-Linear Mechanics, 40: 27-48. doi: 10.1016/j.ijnonlinmec.2004.05.011 [53] Goege D. 2007. Fast identification and characterization of nonlinearities in experimental modal analysis of large aircraft. Journal of aircraft, 44: 399-409. doi: 10.2514/1.20847 [54] Geng X F, Ding H, Ji J C, et al. 2024. A state-of-the-art review on the dynamic design of nonlinear energy sinks. Engineering Structures, 313: 118228. doi: 10.1016/j.engstruct.2024.118228 [55] Haddow A G, Barr A D S, Mook D T. 1984. Theoretical and experimental study of modal interaction in a two-degree-of-freedom structure. Journal of Sound and Vibration, 97: 451-473. doi: 10.1016/0022-460X(84)90272-4 [56] Haller G, Ponsioen S. 2016. Nonlinear normal modes and spectral submanifolds: Existence, uniqueness and use in model reduction. Nonlinear dynamics, 86: 1493-1534. doi: 10.1007/s11071-016-2974-z [57] Haroon M, Adams D E, Luk Y W, et al. 2005. A time and frequency domain approach for identifying nonlinear mechanical system models in the absence of an input measurement. Journal of Sound and Vibration, 283: 1137-1155. doi: 10.1016/j.jsv.2004.06.008 [58] Hollkamp J J, Gordon R W. 2008. Reduced-order models for nonlinear response prediction: Implicit condensation and expansion. Journal of Sound and Vibration, 318: 1139-1153. doi: 10.1016/j.jsv.2008.04.035 [59] Hubbard S A, McFarland D M, Bergman L A, et al. 2014. Targeted energy transfer between a swept wing and winglet-housed nonlinear energy sink. AIAA Journal, 52: 2633-2651. doi: 10.2514/1.J052538 [60] Jain S, Tiso P, Haller G. 2018. Exact nonlinear model reduction for a von Kármán beam: Slow-fast decomposition and spectral submanifolds. Journal of Sound and Vibration, 423: 195-211. doi: 10.1016/j.jsv.2018.01.049 [61] Jalali H, Ahmadian H. 2012. Characterization of dominant mechanisms in contact interface restoring forces. International Journal of Mechanical Sciences, 65: 75-82. doi: 10.1016/j.ijmecsci.2012.09.005 [62] Jezequel L, Lamarque C H. 1991. Analysis of non-linear dynamical systems by the normal form theory. Journal of sound and vibration, 149: 429-459. doi: 10.1016/0022-460X(91)90446-Q [63] Jin M, Brake M R, Song H. 2019. Comparison of nonlinear system identification methods for free decay measurements with application to jointed structures. Journal of Sound and Vibration, 453: 268-293. doi: 10.1016/j.jsv.2019.04.021 [64] Kerschen G, Golinval J C, Worden K. 2001. Theoretical and experimental identification of a non-linear beam. Journal of Sound and vibration, 244: 597-613. doi: 10.1006/jsvi.2000.3490 [65] Kerschen G, Worden K, Vakakis A F, et al. 2006. Past, present and future of nonlinear system identification in structural dynamics. Mechanical systems and signal processing, 20: 505-592. doi: 10.1016/j.ymssp.2005.04.008 [66] Kerschen G, Peeters M, Golinval J C, et al. 2009. Nonlinear normal modes, part I: A useful framework for the structural dynamicist. Mechanical systems and signal processing, 23: 170-194. doi: 10.1016/j.ymssp.2008.04.002 [67] Kerschen G, Soula L, Vergniaud J B, et al. 2011. Assessment of nonlinear system identification methods using the SmallSat spacecraft structure. Proceedings of the 29th IMAC, A Conference on Structural Dynamics, New York. [68] Kwarta M, Allen M S. 2022. Nonlinear normal mode backbone estimation with near-resonant steady state inputs. Mechanical Systems and Signal Processing, 162: 108046. doi: 10.1016/j.ymssp.2021.108046 [69] Lacayo R M, Allen M S. 2019. Updating structural models containing nonlinear Iwan joints using quasi-static modal analysis. Mechanical systems and signal processing, 118: 133-157. doi: 10.1016/j.ymssp.2018.08.034 [70] Laible M, Fitzpatrick K, Grygier M. 2013. International Space Station 2A array modal analysis. Proceedings of the 31st IMAC, A Conference on Structural Dynamics, 2013. Springer New York. [71] Karaağaçlı T, Özgüven H N. 2021. Experimental modal analysis of nonlinear systems by using response-controlled stepped-sine testing. Mechanical Systems and Signal Processing, 146: 107023. doi: 10.1016/j.ymssp.2020.107023 [72] Le Guisquet S, Amabili M. 2021a. Identification by means of a genetic algorithm of nonlinear damping and stiffness of continuous structures subjected to large-amplitude vibrations. Part I: Single-degree-of-freedom responses. Mechanical Systems and Signal Processing, 153: 107470. doi: 10.1016/j.ymssp.2020.107470 [73] Le Guisquet S, Amabili M. 2021b. Identification by means of a genetic algorithm of nonlinear damping and stiffness of continuous structures subjected to large-amplitude vibrations. Part II: One-to-one internal resonance. Mechanical Systems and Signal Processing, 161: 107972. doi: 10.1016/j.ymssp.2021.107972 [74] Li X Y, Wei G, Liu F S, et al. 2022a. Multi-harmonic equivalent modeling for a planar repetitive structure with polynomial-nonlinear joints. Acta Mechanica Sinica, 38: 122020. doi: 10.1007/s10409-022-22020-x [75] Li X Y, Wei G, Guo J, et al. 2023. Multi-harmonic equivalent dynamic model of the gyroelastic repetitive truss with nonlinear joints. Acta Mechanica Sinica, 234: 3361-3375. doi: 10.1007/s00707-023-03560-z [76] Li X L, Wei S, Ding H, et al. 2024. A subspace parameter identification method for nonlinear structures under oversampling conditions. Journal of Sound and Vibration, 118590. [77] Li M, Jain S, Haller G. 2022b. Nonlinear analysis of forced mechanical systems with internal resonance using spectral submanifolds, part I: Periodic response and forced response curve. Nonlinear Dynamics, 110: 1005-1043. doi: 10.1007/s11071-022-07714-x [78] Lin C, Zhao Z, Wang Z, et al. 2022. Quantifying uncertainties in nonlinear dynamics of a modular assembly using the resonance decay method. Actuators, 11: 350. doi: 10.3390/act11120350 [79] Link M, Boeswald M, Laborde S, et al. 2011. Non-linear experimental modal analysis and application to satellite vibration test data. Proceedings of the 3rd International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering. [80] Londoño J M, Neild S A, Cooper J E. 2015. Identification of backbone curves of nonlinear systems from resonance decay responses. Journal of Sound and Vibration, 348: 224-238. doi: 10.1016/j.jsv.2015.03.015 [81] Lubrina P, Giclais S, Stephan C. et al. 2014. AIRBUS A350 XWB GVT: State-of-the-art techniques to perform a faster and better GVT campaign. Topics in Modal Analysis II, Springer: Cham. [82] Ma Z S, Pang Z Y, Liang J X, et al. 2021. A novel output-only time-domain nonlinear subspace approach for identifying vibrating structures with clearance nonlinearity. Journal of Sound and Vibration, 511: 116332. doi: 10.1016/j.jsv.2021.116332 [83] Masri S F, Caughey T K. 1979. A nonparametric identification technique for nonlinear dynamic problems. Journal of Applied Mechanics, 46: 433-447. doi: 10.1115/1.3424568 [84] Masters B P, Crawley E F. 1994. Multiple degree-of-freedom force-state component identification. AIAA Journal, 32: 2276-2285. doi: 10.2514/3.12287 [85] Muravyov A A, Rizzi S A. 2003. Determination of nonlinear stiffness with application to random vibration of geometrically nonlinear structures. Computers & Structures, 81: 1513-1523. [86] Marchesiello S, Garibaldi L. 2008. A time domain approach for identifying nonlinear vibrating structures by subspace methods. Mechanical Systems and Signal Processing, 22: 81-101. doi: 10.1016/j.ymssp.2007.04.002 [87] Neild S A, Wagg D J. 2011. Applying the method of normal forms to second-order nonlinear vibration problems. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 467: 1141-1163. doi: 10.1098/rspa.2010.0270 [88] Noël J P, Renson L, Kerschen G, et al. 2013. Nonlinear dynamic analysis of an F-16 aircraft using GVT data. International Forum on Aeroelasticity and Structural Dynamics, IFASD 2013. [89] Noël J P, Marchesiello S, Kerschen G. 2014a. Subspace-based identification of a nonlinear spacecraft in the time and frequency domains. Mechanical Systems and Signal Processing, 43: 217-236. doi: 10.1016/j.ymssp.2013.10.016 [90] Noël J P, Kerschen G, Foltete E, et al. 2014b. Grey-box identification of a non-linear solar array structure using cubic splines. International Journal of Non-Linear Mechanics, 67: 106-119. doi: 10.1016/j.ijnonlinmec.2014.08.012 [91] Noël J P, Renson L, Kerschen G. 2014c. Complex dynamics of a nonlinear aerospace structure: Experimental identification and modal interactions. Journal of Sound and Vibration, 333: 2588-2607. [92] Noël J P, Kerschen G. 2017. Nonlinear system identification in structural dynamics: 10 more years of progress. Mechanical Systems and Signal Processing, 83: 2-35. doi: 10.1016/j.ymssp.2016.07.020 [93] Ondra V, Sever I A, Schwingshackl C W. 2019. A method for non-parametric identification of non-linear vibration systems with asymmetric restoring forces from a resonant decay response. Mechanical Systems and Signal Processing, 114: 239-258. doi: 10.1016/j.ymssp.2018.05.010 [94] Opreni A, Vizzaccaro A, Touzé C, et al. 2023. High-order direct parametrisation of invariant manifolds for model order reduction of finite element structures: Application to generic forcing terms and parametrically excited systems. Nonlinear Dynamics, 111: 5401-5447. doi: 10.1007/s11071-022-07978-3 [95] Peeters B, Hendricx W, Debille J, et al. 2009. Modern solutions for ground vibration testing of large aircraft. Sound and vibration, 43: 8-15. [96] Peeters M, Kerschen G, Golinval J C. 2011a. Dynamic testing of nonlinear vibrating structures using nonlinear normal modes. Journal of Sound and Vibration, 330: 486-509. doi: 10.1016/j.jsv.2010.08.028 [97] Peeters M, Kerschen G, Golinval J C. 2011b. Modal testing of nonlinear vibrating structures based on nonlinear normal modes: Experimental demonstration. Mechanical Systems and Signal Processing, 25: 1227-1247. doi: 10.1016/j.ymssp.2010.11.006 [98] Pesaresi L, Salles L, Jones A, et al. 2017. Modelling the nonlinear behaviour of an underplatform damper test rig for turbine applications. Mechanical Systems and Signal Processing, 85: 662-679. doi: 10.1016/j.ymssp.2016.09.007 [99] Peter S, Leine R I. 2017. Excitation power quantities in phase resonance testing of nonlinear systems with phase-locked-loop excitation. Mechanical Systems and Signal Processing, 96: 139-158. doi: 10.1016/j.ymssp.2017.04.011 [100] Platten M F, Wright J R, Dimitriadis G, et al. 2009. Identification of multi-degree of freedom non-linear systems using an extended modal space model. Mechanical Systems and Signal Processing, 23: 8-29. doi: 10.1016/j.ymssp.2007.11.016 [101] Rasband S N. 2015. Chaotic dynamics of nonlinear systems. Courier Dover Publications. [102] Renson L, Gonzalez-Buelga A, Barton D A W, et al. 2016. Robust identification of backbone curves using control-based continuation. Journal of Sound and Vibration, 367: 145-158. doi: 10.1016/j.jsv.2015.12.035 [103] Rice H J, Fitzpatrick J A. 1991. A procedure for the identification of linear and non-linear multi-degree-of-freedom systems. Journal of Sound and Vibration, 149: 397-411. doi: 10.1016/0022-460X(91)90444-O [104] Richards C M, Singh R. 1998. Identification of multi-degree-of-freedom non-linear systems under random excitations by the “reverse path” spectral method. Journal of Sound and Vibration, 213: 673-708. doi: 10.1006/jsvi.1998.1522 [105] Rosenberg R M. 1966. On nonlinear vibrations of systems with many degrees of freedom. Advances in applied mechanics, 9: 155-242. [106] Roncen T, Sinou J J, Lambelin J P. 2019. Experiments and nonlinear simulations of a rubber isolator subjected to harmonic and random vibrations. Journal of Sound and Vibration, 451: 71-83. doi: 10.1016/j.jsv.2019.03.017 [107] Rostamijavanani A, Li S, Yang Y. 2023. A study on data-driven identification and representation of nonlinear dynamical systems with a physics-integrated deep learning approach: Koopman operators and nonlinear normal modes. Communications in Nonlinear Science and Numerical Simulation, 123: 107278. doi: 10.1016/j.cnsns.2023.107278 [108] Schoukens J, Dobrowiecki T, Pintelon R. 1998. Parametric and nonparametric identification of linear systems in the presence of nonlinear distortions—A frequency domain approach. IEEE Transactions on Automatic Control, 43: 176-190. doi: 10.1109/9.661066 [109] Schwarz S, Kohlmann L, Hartung A, et al. 2020. Validation of a turbine blade component test with frictional contacts by phase-locked-loop and force-controlled measurements. Journal of Engineering for Gas Turbines and Power, 142: 051006. doi: 10.1115/1.4044772 [110] Setio S, Setio H D, Jezequel L. 1992. A method of non-linear modal identification from frequency response tests. Journal of Sound and Vibration, 158: 497-515. doi: 10.1016/0022-460X(92)90421-S [111] Shaw S, Pierre C. 1991. Non-linear normal modes and invariant manifolds. Journal of sound and Vibration, 150: 170-173. doi: 10.1016/0022-460X(91)90412-D [112] Liu S, Zhao R, Yu K, et al. 2022. Nonlinear system identification framework of folding fins with freeplay using backbone curves. Chinese Journal of Aeronautics, 35: 183-194. doi: 10.1016/j.cja.2022.05.011 [113] Singh A, Allen M S, Kuether R J. 2023. Multi-mode quasi-static excitation for systems with nonlinear joints. Mechanical Systems and Signal Processing, 185: 109601. doi: 10.1016/j.ymssp.2022.109601 [114] Szalai R, Ehrhardt D, Haller G. 2017. Nonlinear model identification and spectral submanifolds for multi-degree-of-freedom mechanical vibrations. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 473: 20160759. doi: 10.1098/rspa.2016.0759 [115] Thomas O, Touzé C, Chaigne A. 2003. Asymmetric non-linear forced vibrations of free-edge circular plates. Part II: Experiments. Journal of Sound and Vibration, 265: 1075-1101. doi: 10.1016/S0022-460X(02)01564-X [116] Touzé C, Thomas O, Chaigne A. 2002. Asymmetric non-linear forced vibrations of free-edge circular plates. Part 1: Theory. Journal of Sound and Vibration, 258: 649-676. doi: 10.1006/jsvi.2002.5143 [117] Touzé C, Amabili M. 2006. Nonlinear normal modes for damped geometrically nonlinear systems: Application to reduced-order modelling of harmonically forced structures. Journal of sound and vibration, 298: 958-981. doi: 10.1016/j.jsv.2006.06.032 [118] Touzé C, Vidrascu M, Chapelle D. 2014. Direct finite element computation of non-linear modal coupling coefficients for reduced-order shell models. Computational Mechanics, 54: 567-580. doi: 10.1007/s00466-014-1006-4 [119] Tsialiamanis G, Champneys M D, Dervilis N, et al. 2022. On the application of generative adversarial networks for nonlinear modal analysis. Mechanical Systems and Signal Processing, 166: 108473. doi: 10.1016/j.ymssp.2021.108473 [120] Van Damme C I, Allen M S, Hollkamp J J. 2020. Updating geometrically nonlinear reduced-order models using nonlinear modes and harmonic balance. AIAA Journal, 58: 3553-3568. doi: 10.2514/1.J058698 [121] Vizzaccaro A, Shen Y, Salles L, et al. 2021. Direct computation of nonlinear mapping via normal form for reduced-order models of finite element nonlinear structures. Computer Methods in Applied Mechanics and Engineering, 384: 113957. doi: 10.1016/j.cma.2021.113957 [122] Wang X, Zheng G T. 2016. Equivalent dynamic stiffness mapping technique for identifying nonlinear structural elements from frequency response functions. Mechanical Systems and Signal Processing, 68: 394-415. [123] Wang X, Khodaparast H H, Shaw A D, et al. 2018a. Localisation of local nonlinearities in structural dynamics using spatially incomplete measured data. Mechanical Systems and Signal Processing, 99: 364-383. doi: 10.1016/j.ymssp.2017.06.021 [124] Wang X, Hill T L, Neild S A, et al. 2018b. Model updating strategy for structures with localised nonlinearities using frequency response measurements. Mechanical Systems and Signal Processing, 100: 940-961. doi: 10.1016/j.ymssp.2017.08.004 [125] Wang X, Hill T L, Neild S A. 2019. Frequency response expansion strategy for nonlinear structures. Mechanical Systems and Signal Processing, 116: 505-529. doi: 10.1016/j.ymssp.2018.06.027 [126] Wang X, Szydlowski M, Yuan J, et al. 2022. A multi-step interpolated-FFT procedure for full-field nonlinear modal testing of turbomachinery components. Mechanical Systems and Signal Processing, 169: 108771. doi: 10.1016/j.ymssp.2021.108771 [127] Wei S, Peng Z K, Dong X J, et al. 2018. A nonlinear subspace-prediction error method for identification of nonlinear vibrating structures. Nonlinear Dynamics, 91: 1605-1617. doi: 10.1007/s11071-017-3967-2 [128] Wei S, Li X L, Ding H, et al. 2023. A two-step method to locate multiple local nonlinearities. Mechanical Systems and Signal Processing, 202: 110712. doi: 10.1016/j.ymssp.2023.110712 [129] Worden K, Tomlinson G R. 2001. Nonlinearity in structural dynamics: Detection, identification and modelling. Institute of Physics Publishing, Bristol and Philadelphia. [130] Yang K, Zhang Y W, Ding H, et al. 2017. Nonlinear energy sink for whole-spacecraft vibration reduction. Journal of Vibration and Acoustics, 139: 021011. doi: 10.1115/1.4035377 [131] Zhang M W, Wei S, Peng Z K, et al. 2017. A two-stage time domain subspace method for identification of nonlinear vibrating structures. International Journal of Mechanical Sciences, 120: 81-90. doi: 10.1016/j.ijmecsci.2016.11.008 [132] Zhang G, Zang C, Friswell M I. 2020. Measurement of the multivalued phase curves of a strongly nonlinear system by fixed frequency tests. Archive of Applied Mechanics, 90: 2543-2560. doi: 10.1007/s00419-020-01736-w [133] Zhu T, Zhang G, Zang C. 2022a. Frequency-domain nonlinear model updating based on analytical sensitivity and the multi-harmonic balance method. Mechanical Systems and Signal Processing, 163: 108169. doi: 10.1016/j.ymssp.2021.108169 [134] Zhu R, Fei Q, Jiang D, et al. 2022b. Bayesian model selection in nonlinear subspace identification. AIAA Journal, 60: 92-101. [135] Zhou T, Kerschen G. 2024. Identification of secondary resonances of nonlinear systems using phase-locked loop testing. arXiv preprint arXiv: 2401.01151. -




 下载:
下载: