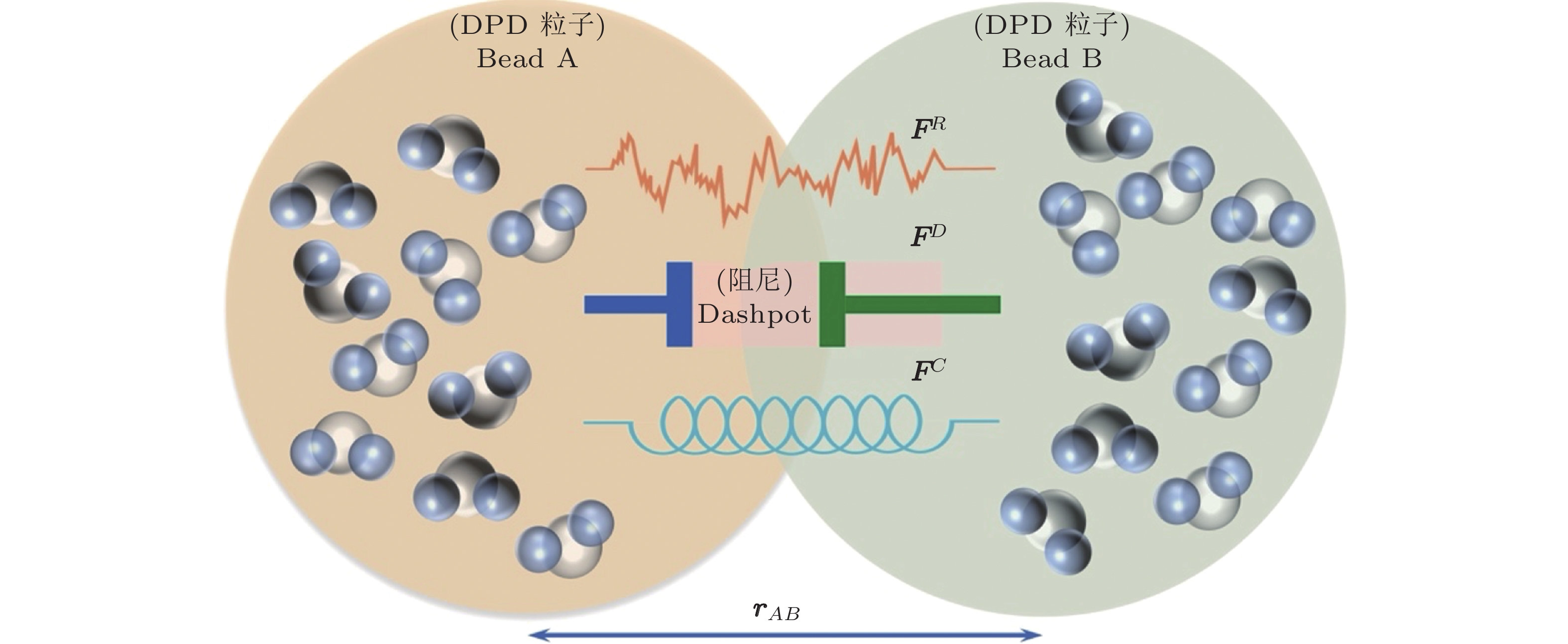
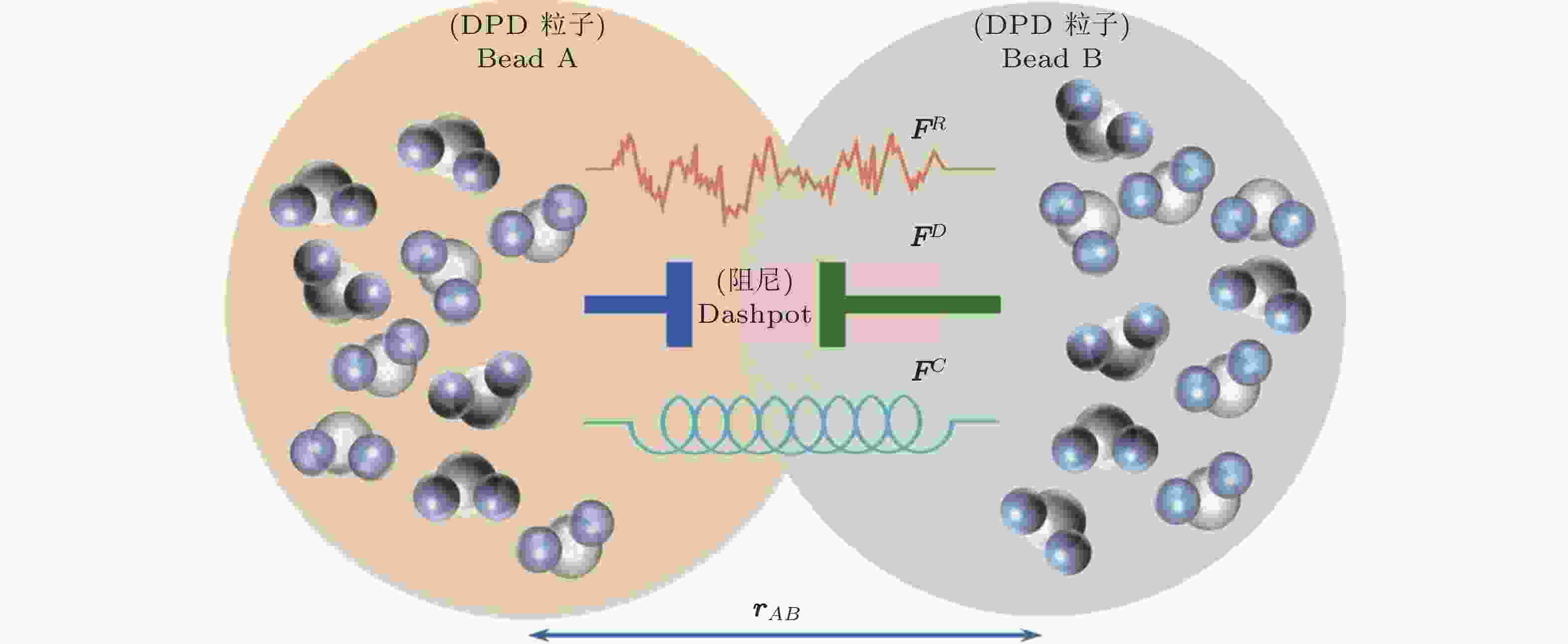
Mesoscopic modeling of complex multiphase fluids: Dissipative particle dynamics (DPD) method and its applications
-
摘要: 在悬浮液、乳液和泡沫等复杂多相流体中, 离散分布着大量的纳米至微米尺度的颗粒、液滴和气泡等, 在流动作用下这些离散相物质呈现出复杂的个体或群体运动行为, 进而显著影响这些复杂多相流体的宏观流变和流动行为. 针对这类流体, 开展介观尺度数值模拟成为一种有效且相对经济的研究手段. 其中, 耗散粒子动力学 (dissipative particle dynamics, DPD) 方法是一种具有代表性的介观尺度数值模拟方法, 由于其粒子方法的特质, DPD方法适合用于上述复杂多相流体内部结构的数值建模和数值模拟研究. 本文对近年来DPD方法在颗粒悬浮液、乳液和气泡等复杂多相流体模拟方面研究进展进行了系统的介绍, 深入探讨了DPD方法在复杂多相流体介观模拟方面的针对性改进以及当前存在的不足, 并对DPD方法的研究和应用进行了总结和展望.Abstract: Complex multiphase fluids, such as suspension, emulsion and foam, which contain large number of particles, droplets and bubbles, respectively, with characteristic scale ranges from nanometer to micron. For these kinds of dispersed materials, either individually or in clusters, complex kinematic behavior is exhibited under the imposed flow, affecting the bulk rheological properties of these multiphase fluids. Investigations of these complex fluids by using mesoscopic numerical methods are among the most effective and economic approaches. In particular, dissipative particle dynamics (DPD) is a typical mesoscopic numerical method. Due to its particle-based nature, it is especially suitable for the modeling and investigating of these types of complex fluids. In this review, we thoroughly introduce the applications of DPD methods in the modeling of suspension, emulsion and bubbles as well as the corresponding developments in DPD methods. Meanwhile, we also discuss relevant shortcomings and certain aspects that require further improvement. Finally, we provide a conclusion and outlook for DPD methods.
-
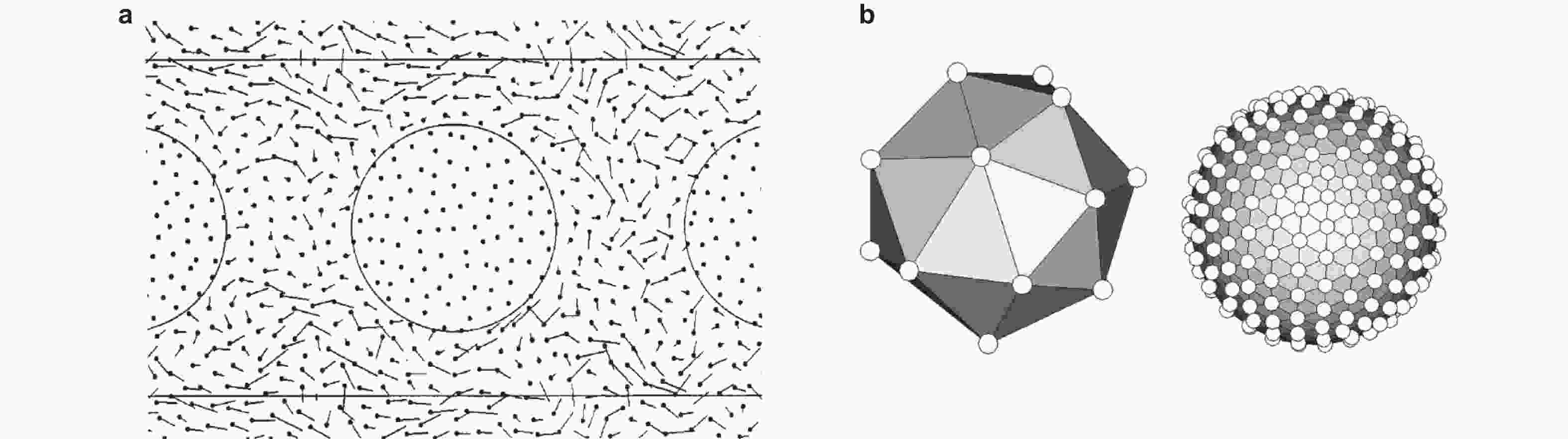
图 2 冻结粒子模型示意图. (a)二维颗粒模型(Hoogerbrugge & Koelman 1992), (b)三维球形颗粒模型(Chen S et al. 2006)
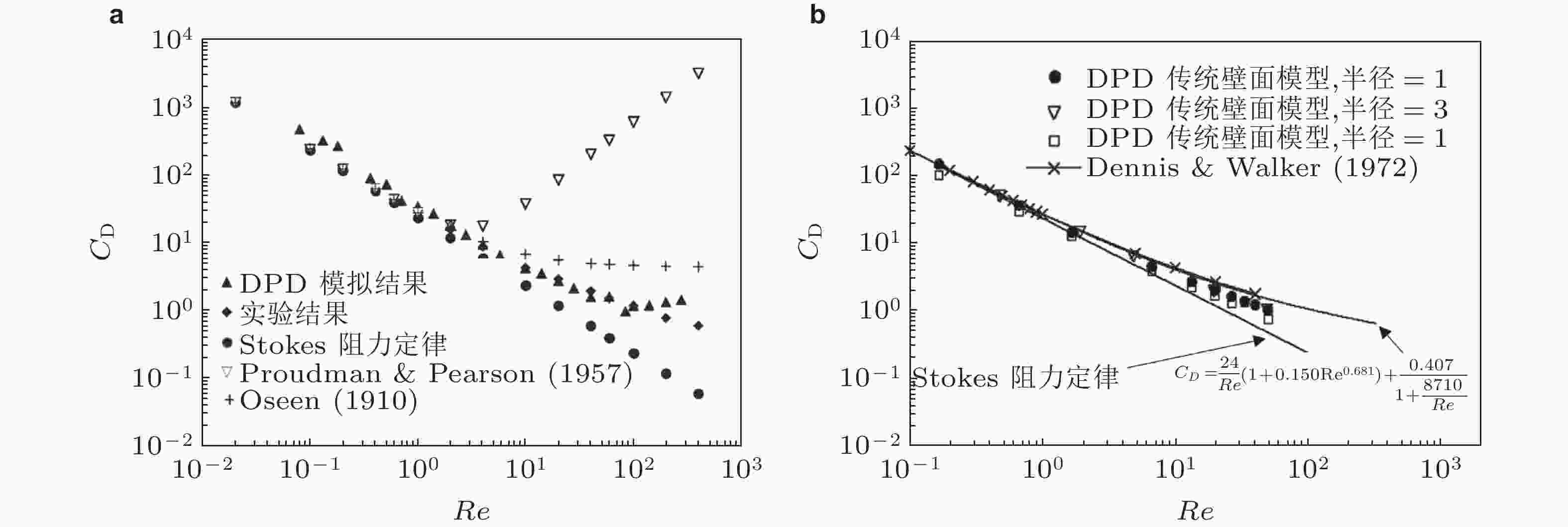
图 3 DPD模拟得到的单颗粒阻力系数与流动Re关系图及其与实验和理论结果的对比验证. (a) Kim和Phillips(2004)的模拟结果与实验结果(Perry & Green 1999)以及渐进分析结果(Oseen 1910, Proudman & Pearson 1957)的对比, (b) Chen等(2006)的模拟结果与理论结果(Dennis & Walker 1971)的对比
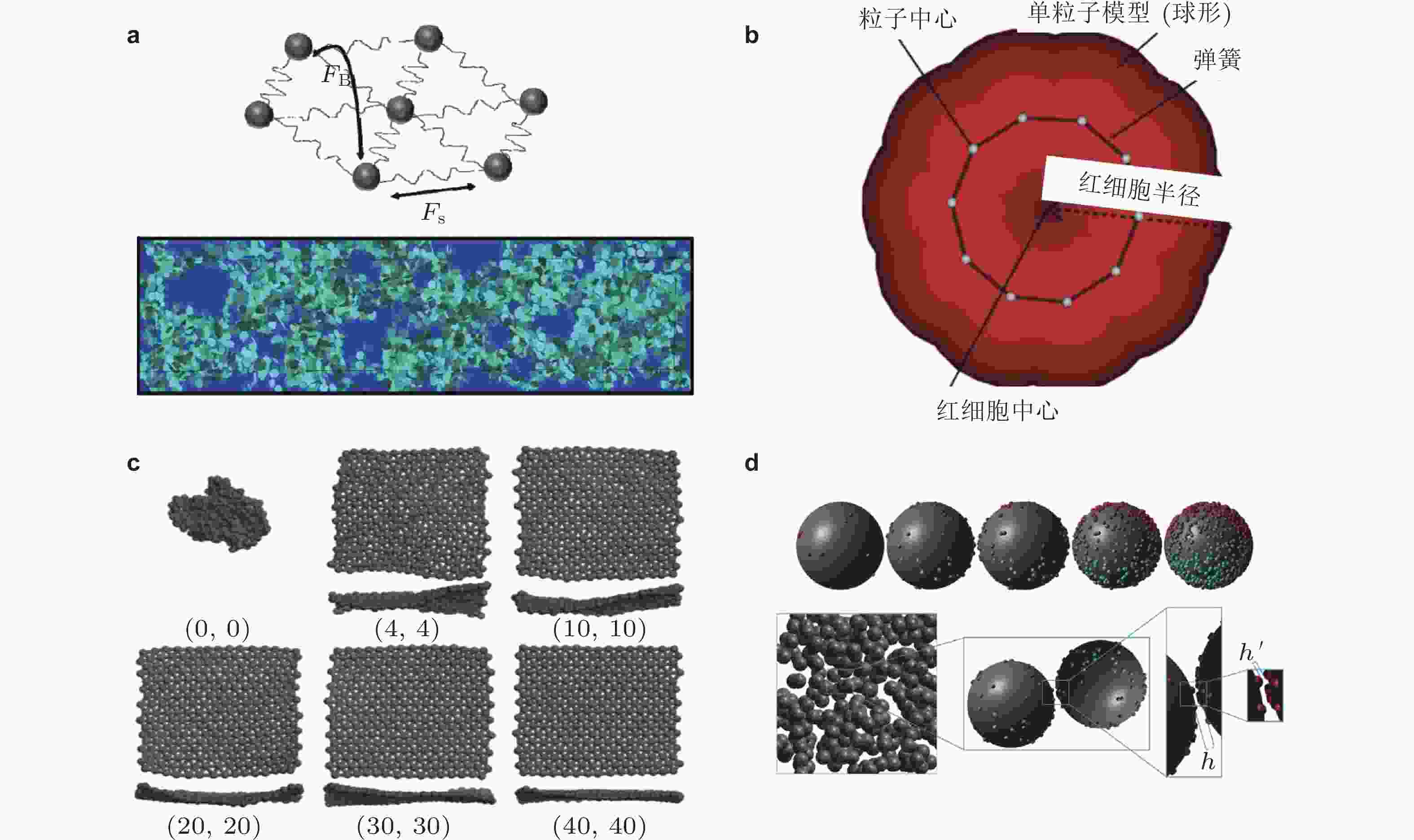
图 4 基于DPD-DEM模拟得到的颗粒悬浮液内部颗粒团结构的演变过程, 上行为半浓相悬浮液, 下行为浓相悬浮液, 不同颜色颗粒表示不同数量悬浮颗粒组成的颗粒团结构(Boromand et al. 2018)
图 5 复杂颗粒的DPD方法建模. (a) 碟形颗粒模型(Jamali et al. 2017), (b) 低维红细胞模型(Pan W et al. 2010b), (c) 石墨烯片状颗粒模型(Min et al. 2012), (d) 颗粒表面粗糙度模型(Jamali & Brady 2019)
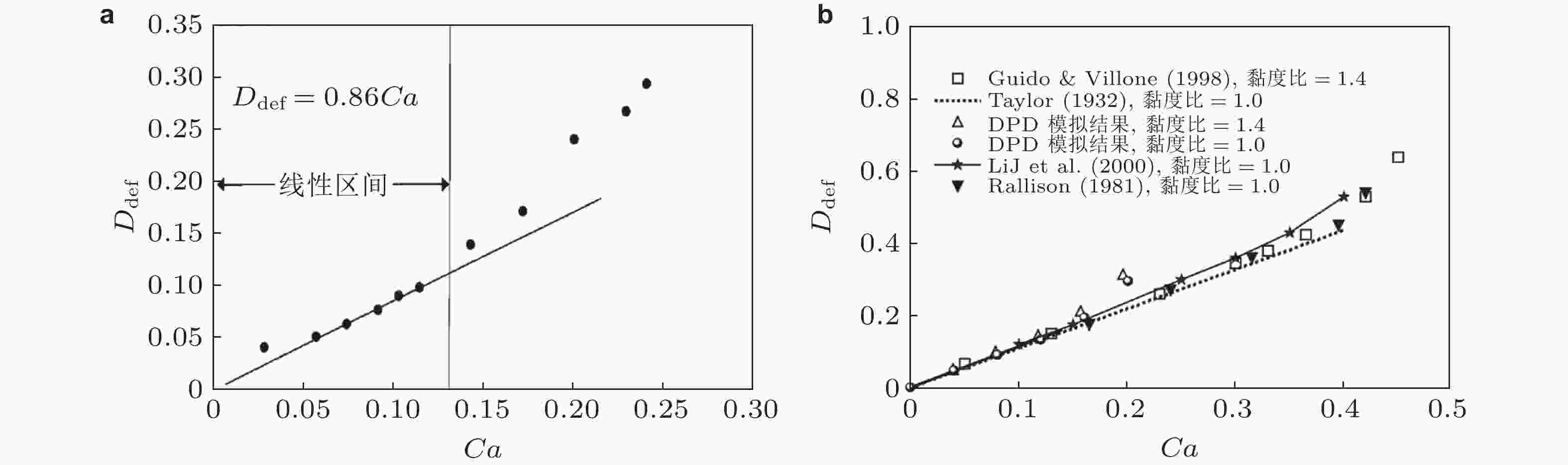
图 7 (a) 改进的DPD模拟液滴在剪切流作用下变形结果与实验和前人模拟的对比(Pan D et al. 2014), (b) 液滴在剪切作用下的瞬态变形结果与实验和前人模拟的对比(Zhao G et al. 2021)
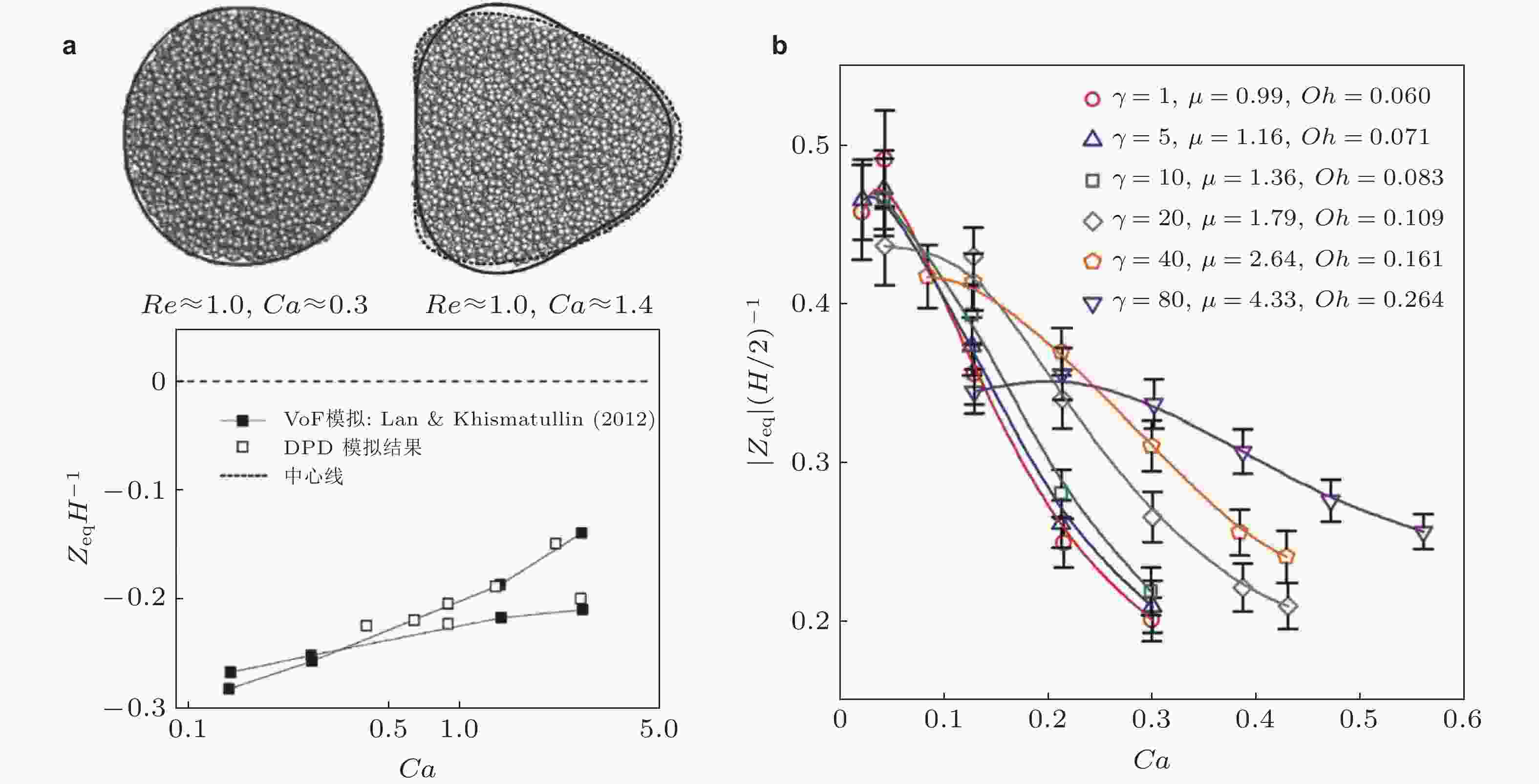
图 8 (a) 平板泊肃叶流动中液滴变形以及横向平衡位置的DPD模拟与理论 (实线) 和VoF模拟 (虚线) 结果的验证(Pan D et al. 2016), (b) 液滴在泊肃叶流动中横向平衡位置随Oh数的变化规律(Marson et al. 2018)
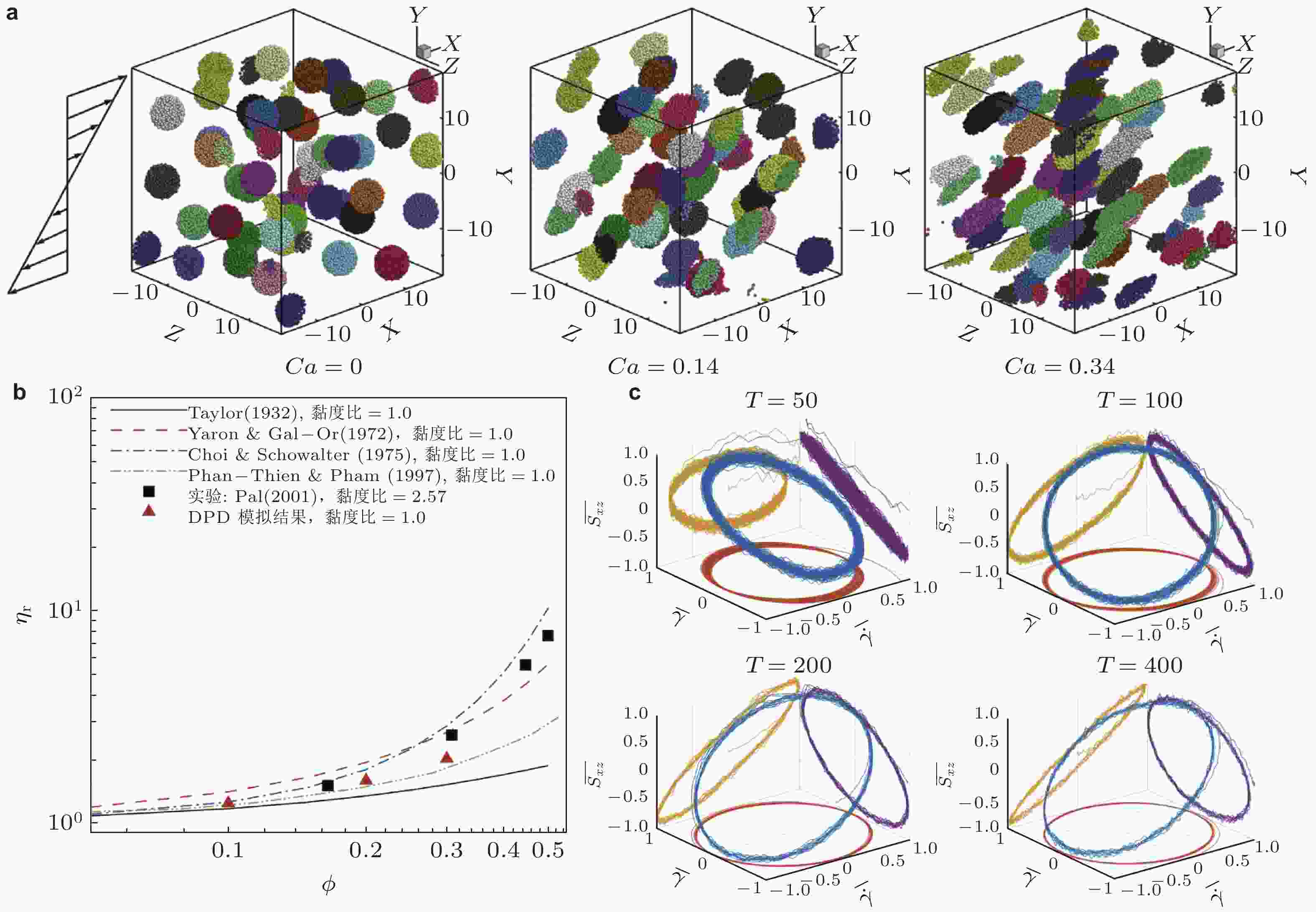
图 9 (a) 剪切流作用下乳液液滴变形的DPD模拟(Pan D et al. 2014), (b) 乳液相对黏度随体积分数的变化情况(Pan D et al. 2014)及其与相关理论模型(Choi & Schowalter 1975, Phan-Thien & Pham 1997, Taylor 1932, Yaron & Gal-Or 1972)和实验结果(Pal 2001)的对比, (c) 振荡剪切作用下乳液的Lissajous曲线(赵庚尧 2023)
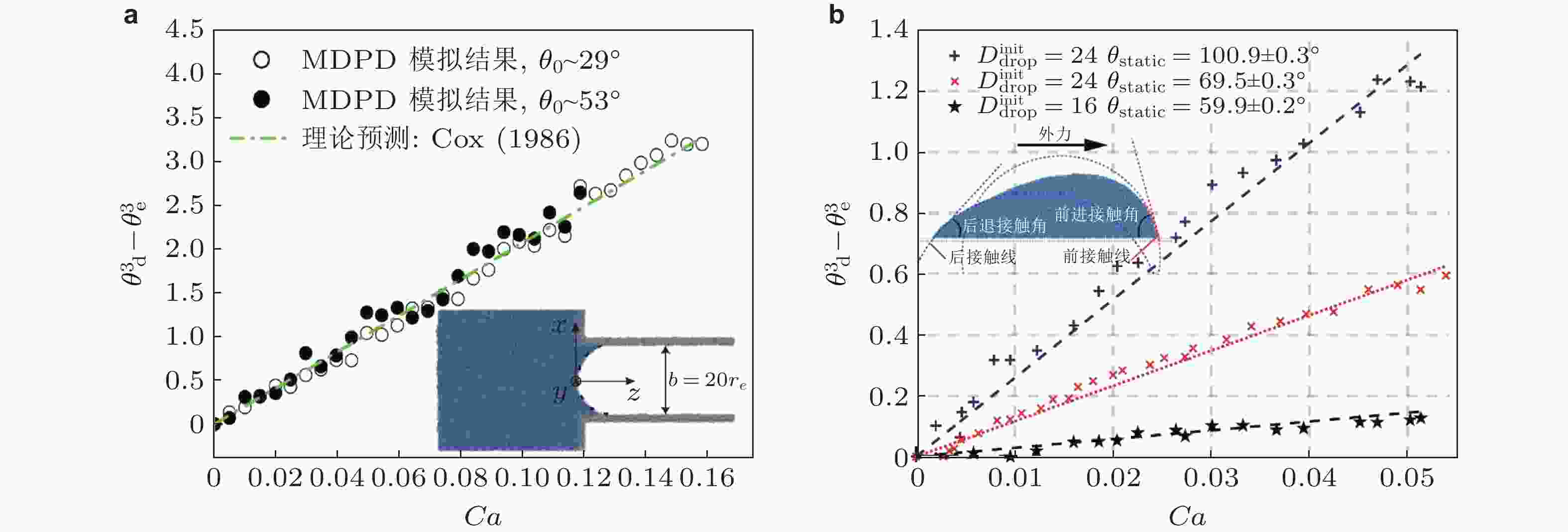
图 10 (a) 微尺度流道内气液两相流动模拟(Chen C et al. 2010), (b) 微纳尺度液柱模拟(Tiwari et al. 2008), (c) 壁面上液滴运动模拟(Li Z et al. 2013), (d) 平行壁面间的液桥模拟(Zhao J et al. 2020a)
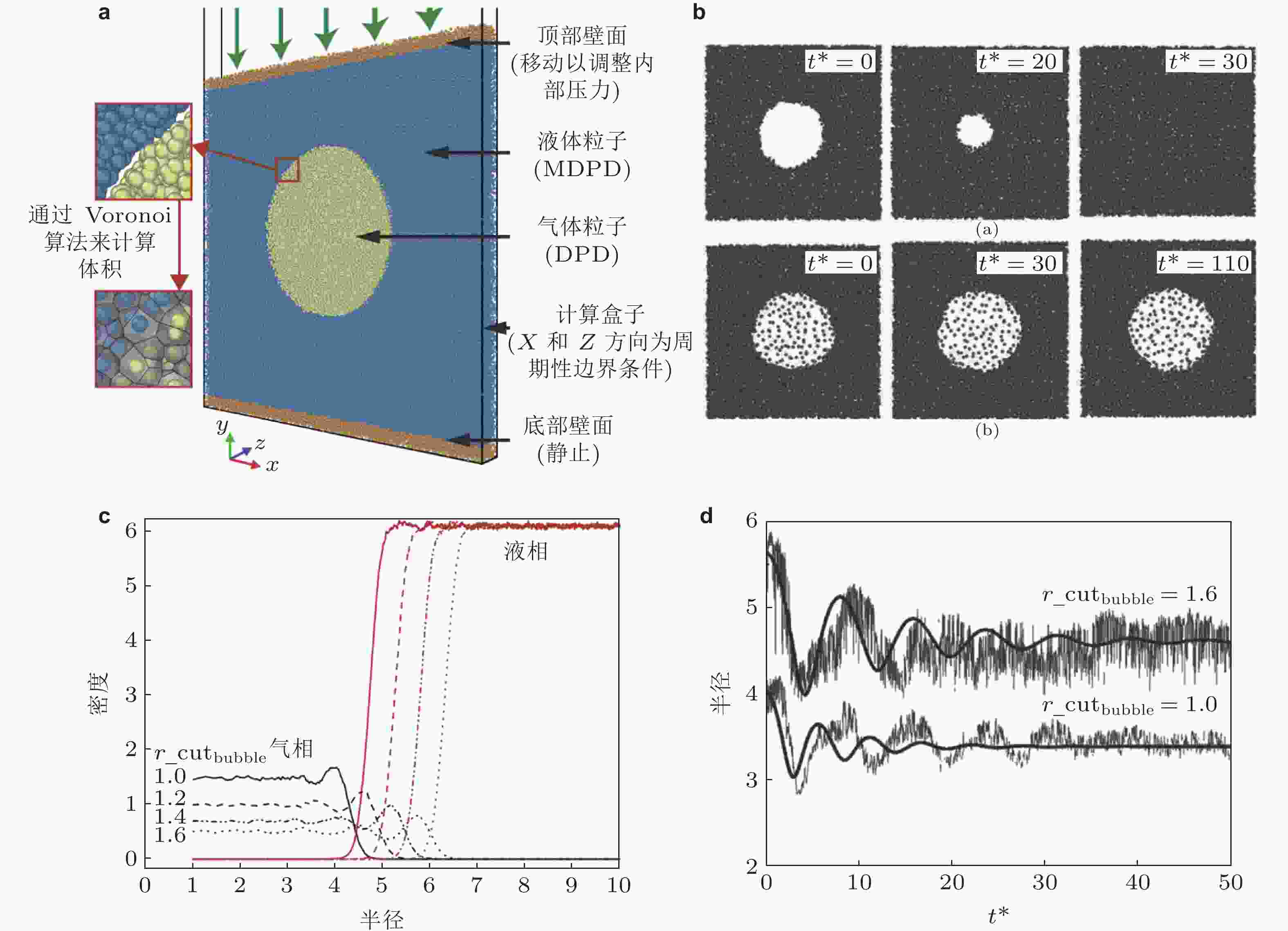
图 12 传统DPD和many-body DPD相结合的气泡DPD模型. (a) 模型示意图(Lin C et al. 2021a), (b) 稳态气泡的DPD模拟结果(Pan D et al. 2018), (c) 气泡内外密度分布(Pan D et al. 2018), (d) 外场压力作用下的气泡振荡模拟结果与Rayleigh-Plesset方程对比(Pan D et al. 2018)
-
[1] 陈硕, 赵钧, 范西俊, 王丹. 2006. 复杂流体流动的耗散粒子动力学研究进展. 科技通报, 22, 596–602. [2] 李振. 2011. 微流控芯片中液滴操控的耗散粒子动力学模拟 (博士论文). 上海大学, 上海. [3] 李红霞, 强洪夫. 2009. 耗散粒子动力学模拟方法的发展和应用. 力学进展, 39: 165-175. doi: 10.6052/1000-0992-2009-2-J2008-002 [4] 林雨青. 2017. 基于耗散粒子动力学方法的微泡动力学介观模拟研究 (硕士论文). 浙江大学, 杭州. [5] 唐梓涵, 李学进, 李德昌. 2023. 耗散粒子动力学方法在生物学领域的应用与研究进展:从蛋白质结构到细胞力学. 科学通报, 68(7): 741-761 [6] 赵庚尧. 2023. 单液滴变形特性及乳浊液流变特性的介观模拟研究 (博士论文). 浙江大学, 杭州. [7] Ahmadi M, Aliabadian E, Liu B, Lei X, Khalilpoorkordi P, Hou Q, Wang Y, Chen Z. 2022. Comprehensive review of the interfacial behavior of water/oil/surfactant systems using dissipative particle dynamics simulation. Adv. Colloid Interface Sci., 309: 102774. doi: 10.1016/j.cis.2022.102774 [8] Allen M P, Tildesley D J. 2017. Computer simulation of liquids, 2nd ed. Oxford University Press, Oxford. [9] Arienti M, Pan W, Li X, Karniadakis G. 2011. Many-body dissipative particle dynamics simulation of liquid/vapor and liquid/solid interactions. J. Chem. Phys., 134: 204114. doi: 10.1063/1.3590376 [10] Atashafrooz M, Mehdipour N. 2016. Many-body dissipative particle dynamics simulation of liquid–vapor coexisting curve in sodium. J. Chem. Eng. Data, 61: 3659-3664. doi: 10.1021/acs.jced.6b00586 [11] Avalos J B, Mackie A D. 1997. Dissipative particle dynamics with energy conservation. Europhys. Lett. EPL, 40: 141-146. doi: 10.1209/epl/i1997-00436-6 [12] Balmforth N J, Frigaard I A, Ovarlez G. 2014. Yielding to stress: recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech., 46: 121-146. doi: 10.1146/annurev-fluid-010313-141424 [13] Bentley B J, Leal L G. 1986. An experimental investigation of drop deformation and breakup in steady, two-dimensional linear flows. J. Fluid Mech., 167: 241. doi: 10.1017/S0022112086002811 [14] Bian X, Litvinov S, Qian R, Ellero M, Adams N A. 2012. Multiscale modeling of particle in suspension with smoothed dissipative particle dynamics. Phys. Fluids, 24: 012002. doi: 10.1063/1.3676244 [15] Boek E S, Coveney P V, Lekkerkerker H N W. 1996. Computer simulation of rheological phenomena in dense colloidal suspensions with dissipative particle dynamics. J. Phys. Condens. Matter, 8: 9509-9512. doi: 10.1088/0953-8984/8/47/053 [16] Boek E S, Coveney P V, Lekkerkerker H N W, Van Der Schoot P. 1997. Simulating the rheology of dense colloidal suspensions using dissipative particle dynamics. Phys. Rev. E, 55: 3124-3133. [17] Boromand A, Jamali S, Grove B, Maia J M. 2018. A generalized frictional and hydrodynamic model of the dynamics and structure of dense colloidal suspensions. J. Rheol., 62: 905-918. doi: 10.1122/1.5006937 [18] Boromand A, Jamali S, Maia J M. 2017. Structural fingerprints of yielding mechanisms in attractive colloidal gels. Soft Matter, 13: 458-473. doi: 10.1039/C6SM00750C [19] Chan K C, Li Z, Wenzel W. 2023. A mori–zwanzig dissipative particle dynamics approach for anisotropic coarse grained molecular dynamics. J. Chem. Theory Comput., 19: 910-923. doi: 10.1021/acs.jctc.2c00960 [20] Chen C, Gao C, Zhuang L, Li X, Wu P, Dong J, Lu J. 2010. A many-body dissipative particle dynamics study of spontaneous capillary imbibition and drainage. Langmuir, 26: 9533-9538. doi: 10.1021/la100105f [21] Chen C, Zhuang L, Li X, Dong J, Lu J. 2012. A many-body dissipative particle dynamics study of forced water–oil displacement in capillary. Langmuir, 28: 1330-1336. doi: 10.1021/la204207s [22] Chen S, Phan-Thien N, Fan X-J, Khoo B C. 2004. Dissipative particle dynamics simulation of polymer drops in a periodic shear flow. J. Non-Newton. Fluid Mech., 118: 65-81. doi: 10.1016/j.jnnfm.2004.02.005 [23] Chen S, Phan-Thien N, Khoo B C, Fan X J. 2006. Flow around spheres by dissipative particle dynamics. Phys. Fluids, 18: 103605. doi: 10.1063/1.2360421 [24] Chen Z, Cheng X, Cui H, Cheng P, Wang H. 2007. Dissipative particle dynamics simulation of the phase behavior and microstructure of CTAB/octane/1-butanol/water microemulsion. Colloids Surf. Physicochem. Eng. Asp., 301: 437-443. doi: 10.1016/j.colsurfa.2007.01.022 [25] Choi S J, Schowalter W R. 1975. Rheological properties of nondilute suspensions of deformable particles. Phys. Fluids, 18: 420-427. doi: 10.1063/1.861167 [26] Clark A T, Lal M, Ruddock J N, Warren P B. 2000. Mesoscopic simulation of drops in gravitational and shear fields. Langmuir, 16: 6342-6350. doi: 10.1021/la991565f [27] Clift R, Grace J, Weber M. 2005. Bubbles, drops, and particles, 2nd ed, Dover Civil and Mechanical Engineering Series, Courier Corporation. [28] Conti A, Kamimura H A S, Novell A, Duggento A, Toschi N. 2020. Magnetic resonance methods for focused ultrasound-induced blood-brain barrier opening. Front. Phys., 8: 547674. doi: 10.3389/fphy.2020.547674 [29] Coussios C C, Roy R A. 2008. Applications of acoustics and cavitation to noninvasive therapy and drug delivery. Annu. Rev. Fluid Mech., 40: 395-420. doi: 10.1146/annurev.fluid.40.111406.102116 [30] Coveney P V, Novik K E. 1996. Computer simulations of domain growth and phase separation in two-dimensional binary immiscible fluids using dissipative particle dynamics. Phys. Rev. E, 54: 5134-5141. doi: 10.1103/PhysRevE.54.5134 [31] Cox R G. 1986. The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech., 168: 169. doi: 10.1017/S0022112086000332 [32] Crowe C T, Schwarzkopf J D, Sommerfeld M, Tsuji Y. 2011. Multiphase flows with droplets and particles, 0 ed. CRC Press. [33] Cupelli C, Henrich B, Glatzel T, Zengerle R, Moseler M, Santer M. 2008. Dynamic capillary wetting studied with dissipative particle dynamics. New J. Phys., 10: 043009. doi: 10.1088/1367-2630/10/4/043009 [34] Deguillard E, Pannacci N, Creton B, Rousseau B. 2013. Interfacial tension in oil–water–surfactant systems: On the role of intra-molecular forces on interfacial tension values using DPD simulations. J. Chem. Phys., 138: 144102. doi: 10.1063/1.4799888 [35] Deng M, Li Z, Borodin O, Karniadakis G E. 2016. cDPD: A new dissipative particle dynamics method for modeling electrokinetic phenomena at the mesoscale. J. Chem. Phys., 145: 144109. doi: 10.1063/1.4964628 [36] Deng M, Pan W, Karniadakis G E. 2017. Anisotropic single-particle dissipative particle dynamics model. J. Comput. Phys., 336: 481-491. doi: 10.1016/j.jcp.2017.01.033 [37] Denn M M, Morris J F. 2014. Rheology of non-brownian suspensions. Annu. Rev. Chem. Biomol. Eng., 5: 203-228. doi: 10.1146/annurev-chembioeng-060713-040221 [38] Dennis S C R, Walker J D A. 1971. Calculation of the steady flow past a sphere at low and moderate Reynolds numbers. J. Fluid Mech., 48: 771-789. doi: 10.1017/S0022112071001848 [39] Derkach S R. 2009. Rheology of emulsions. Adv. Colloid Interface Sci., 151: 1-23. doi: 10.1016/j.cis.2009.07.001 [40] Duong-Hong D, Phan-Thien N, Fan X. 2004. An implementation of no-slip boundary conditions in DPD. Comput. Mech., 35: 24-29. doi: 10.1007/s00466-004-0595-8 [41] Duong-Hong D, Phan-Thien N, Yeo K S, Ausias G. 2010. Dissipative particle dynamics simulations for fibre suspensions in newtonian and viscoelastic fluids. Comput. Methods Appl. Mech. Eng., 199: 1593-1602. doi: 10.1016/j.cma.2010.01.010 [42] Dzwinel W, Yuen D A. 2000. Matching macroscopic properties of binary fluids to the interactions of dissipative particle dynamics. Int. J. Mod. Phys. C, 11: 1-25. doi: 10.1142/S012918310000002X [43] Ellero M, Español P. 2018. Everything you always wanted to know about SDPD* (*but were afraid to ask). Appl. Math. Mech., 39: 103-124. doi: 10.1007/s10483-018-2255-6 [44] Epstein P S, Plesset M S. 1950. On the stability of gas bubbles in liquid-gas solutions. J. Chem. Phys., 18: 1505-1509. doi: 10.1063/1.1747520 [45] Español P. 1998. Fluid particle model. Phys. Rev. E, 57: 2930-2948. doi: 10.1103/PhysRevE.57.2930 [46] Español P. 1997a. Dissipative particle dynamics with energy conservation. Europhys. Lett. EPL, 40: 631-636. doi: 10.1209/epl/i1997-00515-8 [47] Español P. 1997b. Fluid particle dynamics: A synthesis of dissipative particle dynamics and smoothed particle dynamics. Europhys. Lett. EPL, 39: 605-610. doi: 10.1209/epl/i1997-00401-5 [48] Español P, Warren P. 1995. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. EPL, 30: 191-196. doi: 10.1209/0295-5075/30/4/001 [49] Español P, Warren P B. 2017. Perspective: Dissipative particle dynamics. J. Chem. Phys., 146: 150901. doi: 10.1063/1.4979514 [50] Fan X, Phan-Thien N, Yong N T, Wu X, Xu D. 2003. Microchannel flow of a macromolecular suspension. Phys. Fluids, 15: 11-21. doi: 10.1063/1.1522750 [51] Ferziger J H, Perić M, Street R L. 2020. Computational methods for fluid dynamics. Springer International Publishing, Cham. [52] Filipovic N, Kojic M, Ferrari M. 2011. Dissipative particle dynamics simulation of circular and elliptical particles motion in 2D laminar shear flow. Microfluid. Nanofluidics, 10: 1127-1134. doi: 10.1007/s10404-010-0742-9 [53] Fu H, Comer J, Cai W, Chipot C. 2015. Sonoporation at small and large length scales: effect of cavitation bubble collapse on membranes. J. Phys. Chem. Lett., 6: 413-418. doi: 10.1021/jz502513w [54] Groot R D, Warren P B. 1997. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys., 107: 4423-4435. doi: 10.1063/1.474784 [55] Guazzelli É, Morris J F, Pic S. 2011. A physical introduction to suspension dynamics, 1st ed. Cambridge University Press. [56] Guido S, Simeone M. 1998. Binary collision of drops in simple shear flow by computer-assisted video optical microscopy. J. Fluid Mech., 357: 1-20. doi: 10.1017/S0022112097007921 [57] Guido S, Villone M. 1999. Measurement of interfacial tension by drop retraction analysis. J. Colloid Interface Sci., 209: 247-250. doi: 10.1006/jcis.1998.5818 [58] Guido S, Villone M. 1998. Three-dimensional shape of a drop under simple shear flow. J. Rheol., 42: 395-415. doi: 10.1122/1.550942 [59] Henrich B, Cupelli C, Moseler M, Santer M. 2007. An adhesive DPD wall model for dynamic wetting. Europhys. Lett. EPL, 80: 60004. doi: 10.1209/0295-5075/80/60004 [60] Hoang Viet M, Derreumaux P, Nguyen P H. 2016. Nonequilibrium all-atom molecular dynamics simulation of the bubble cavitation and application to dissociate amyloid fibrils. J. Chem. Phys., 145: 174113. doi: 10.1063/1.4966263 [61] Hoogerbrugge P J, Koelman J M V A. 1992. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. EPL, 19: 155-160. doi: 10.1209/0295-5075/19/3/001 [62] Howard M P, Truskett T M, Nikoubashman A. 2019. Cross-stream migration of a Brownian droplet in a polymer solution under Poiseuille flow. Soft Matter, 15: 3168-3178. doi: 10.1039/C8SM02552E [63] Huang Y, Marson R L, Larson R G. 2018. Inertial migration of a rigid sphere in plane poiseuille flow as a test of dissipative particle dynamics simulations. J. Chem. Phys., 149: 164912. doi: 10.1063/1.5047923 [64] Jamali S, Armstrong R C, McKinley G H. 2019. Multiscale nature of thixotropy and rheological hysteresis in attractive colloidal suspensions under shear. Phys. Rev. Lett., 123: 248003. doi: 10.1103/PhysRevLett.123.248003 [65] Jamali S, Boromand A, Wagner N, Maia J. 2015. Microstructure and rheology of soft to rigid shear-thickening colloidal suspensions. J. Rheol., 59: 1377-1395. doi: 10.1122/1.4931655 [66] Jamali S, Brady J F. 2019. Alternative frictional model for discontinuous shear thickening of dense suspensions: Hydrodynamics. Phys. Rev. Lett., 123: 138002. doi: 10.1103/PhysRevLett.123.138002 [67] Jamali S, McKinley G H, Armstrong R C. 2017. Microstructural rearrangements and their rheological implications in a model thixotropic elastoviscoplastic fluid. Phys. Rev. Lett., 118: 048003. doi: 10.1103/PhysRevLett.118.048003 [68] Jamali S, Yamanoi M, Maia J. 2013. Bridging the gap between microstructure and macroscopic behavior of monodisperse and bimodal colloidal suspensions. Soft Matter, 9: 1506-1515. doi: 10.1039/C2SM27104D [69] Jeffery G B. 1922. The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character, 102: 161-179. [70] Kim J, Phillips R. 2004. Dissipative particle dynamics simulation of flow around spheres and cylinders at finite Reynolds numbers. Chem. Eng. Sci., 59: 4155-4168. doi: 10.1016/S0009-2509(04)00209-X [71] Koelman J M V A, Hoogerbrugge P J. 1993. Dynamic simulations of hard-sphere suspensions under steady shear. Europhys. Lett. EPL, 21: 363-368. doi: 10.1209/0295-5075/21/3/018 [72] Koos E, Willenbacher N. 2011. Capillary forces in suspension rheology. Science, 331: 897-900. doi: 10.1126/science.1199243 [73] Lan C, Pal S, Li Z, Ma Y. 2015. Numerical simulations of the digital microfluidic manipulation of single microparticles. Langmuir, 31: 9636-9645. doi: 10.1021/acs.langmuir.5b02011 [74] Lan H, Khismatullin D B. 2012. A numerical study of the lateral migration and deformation of drops and leukocytes in a rectangular microchannel. Int. J. Multiph. Flow, 47: 73-84. doi: 10.1016/j.ijmultiphaseflow.2012.07.004 [75] Larson R G, Desai P S. 2015. Modeling the rheology of polymer melts and solutions. Annu. Rev. Fluid Mech., 47: 47-65. doi: 10.1146/annurev-fluid-010814-014612 [76] Li J, Renardy Y Y, Renardy M. 2000. Numerical simulation of breakup of a viscous drop in simple shear flow through a volume-of-fluid method. Phys. Fluids, 12: 269-282. doi: 10.1063/1.870305 [77] Li W, Ouyang J, Zhuang X. 2016. Dissipative particle dynamics simulation for the microstructures of ferromagnetic fluids. Soft Mater., 14: 87-95. doi: 10.1080/1539445X.2016.1150293 [78] Li Y, Guo Y, Bao M, Gao X. 2011. Investigation of interfacial and structural properties of CTAB at the oil/water interface using dissipative particle dynamics simulations. J. Colloid Interface Sci., 361: 573-580. doi: 10.1016/j.jcis.2011.05.078 [79] Li Y, Guo Y, Xu G, Wang Z, Bao M, Sun N. 2013. Dissipative particle dynamics simulation on the properties of the oil/water/surfactant system in the absence and presence of polymer. Mol. Simul., 39: 299-308. doi: 10.1080/08927022.2012.724173 [80] Li Y, Zhang H, Bao M, Wang Z. 2012. Dissipative particle dynamics simulation on the association between polymer and surfactant: Effects of surfactant and polymer feature. Comput. Mater. Sci., 63: 154-162. doi: 10.1016/j.commatsci.2012.06.007 [81] Li Z, Bian X, Caswell B, Karniadakis G E. 2014a. Construction of dissipative particle dynamics models for complex fluids via the Mori–Zwanzig formulation. Soft Matter, 10: 8659-8672. doi: 10.1039/C4SM01387E [82] Li Z, Bian X, Li X, Deng M, Tang Y-H, Caswell B, Karniadakis G E. 2017. Dissipative particle dynamics: foundation, evolution, implementation, and applications, in: Bodnár, T., Galdi, G. P., Nečasová, Š. (Eds.), Particles in Flows, Advances in Mathematical Fluid Mechanics, Springer International Publishing, Cham, pp. 255–326. [83] Li Z, Bian X, Li X, Karniadakis G E. 2015a. Incorporation of memory effects in coarse-grained modeling via the Mori-Zwanzig formalism. J. Chem. Phys., 143: 243128. doi: 10.1063/1.4935490 [84] Li Z, Hu G-H, Wang Z-L, Ma Y-B, Zhou Z-W. 2013. Three dimensional flow structures in a moving droplet on substrate: A dissipative particle dynamics study. Phys. Fluids, 25: 072103. doi: 10.1063/1.4812366 [85] Li Z, Tang Y-H, Lei H, Caswell B, Karniadakis G E. 2014b. Energy-conserving dissipative particle dynamics with temperature-dependent properties. J. Comput. Phys., 265: 113-127. doi: 10.1016/j.jcp.2014.02.003 [86] Li Z, Yazdani A, Tartakovsky A, Karniadakis G E. 2015b. Transport dissipative particle dynamics model for mesoscopic advection-diffusion-reaction problems. J. Chem. Phys., 143: 014101. doi: 10.1063/1.4923254 [87] Lin C, Chen S, Xiao L, Liu Y. 2018. Tuning drop motion by chemical chessboard-patterned surfaces: A many-body dissipative particle dynamics study. Langmuir, 34: 2708-2715. doi: 10.1021/acs.langmuir.7b04162 [88] Lin C, Li Z, Lu L, Cai S, Maxey M, Karniadakis G E. 2021a. Operator learning for predicting multiscale bubble growth dynamics. J. Chem. Phys., 154: 104118. doi: 10.1063/5.0041203 [89] Lin C, Maxey M, Li Z, Karniadakis G E. 2021b. A seamless multiscale operator neural network for inferring bubble dynamics. J. Fluid Mech., 929: A18. doi: 10.1017/jfm.2021.866 [90] Lin Y, Pan D, Li J, Zhang L, Shao X. 2017. Application of Berendsen barostat in dissipative particle dynamics for nonequilibrium dynamic simulation. J. Chem. Phys., 146: 124108. doi: 10.1063/1.4978807 [91] Liu M B, Liu G R, Zhou L W, Chang J Z. 2015. Dissipative particle dynamics (DPD): An overview and recent developments. Arch. Comput. Methods Eng., 22: 529-556. doi: 10.1007/s11831-014-9124-x [92] Liu M, Meakin P, Huang H. 2006. Dissipative particle dynamics with attractive and repulsive particle-particle interactions. Phys. Fluids, 18: 017101. doi: 10.1063/1.2163366 [93] Loewenberg M, Hinch E J. 1997. Collision of two deformable drops in shear flow. J. Fluid Mech., 338: 299-315. doi: 10.1017/S0022112097005016 [94] Loewenberg M, Hinch E J. 1996. Numerical simulation of a concentrated emulsion in shear flow. J. Fluid Mech., 321: 395-419. doi: 10.1017/S002211209600777X [95] Lohse D, Zhang X. 2015. Surface nanobubbles and nanodroplets. Rev. Mod. Phys., 87: 981-1035. doi: 10.1103/RevModPhys.87.981 [96] Luciani A, Champagne M F, Utracki L A. 1997. Interfacial tension coefficient from the retraction of ellipsoidal drops. J. Polym. Sci. Part B Polym. Phys., 35: 1393-1403. doi: 10.1002/(SICI)1099-0488(19970715)35:9<1393::AID-POLB9>3.0.CO;2-N [97] Lukianova-Hleb E Y, Kim Y-S, Belatsarkouski I, Gillenwater A M, O’Neill B E, Lapotko D O. 2016. Intraoperative diagnostics and elimination of residual microtumours with plasmonic nanobubbles. Nat. Nanotechnol., 11: 525-532. doi: 10.1038/nnano.2015.343 [98] Mackie A D, Bonet Avalos J, Navas V. 1999. Dissipative particle dynamics with energy conservation: Modelling of heat flow. Phys. Chem. Chem. Phys., 1: 2039-2049. doi: 10.1039/a809502g [99] Mai-Duy N, Pan D, Phan-Thien N, Khoo B C. 2013. Dissipative particle dynamics modeling of low Reynolds number incompressible flows. J. Rheol., 57: 585-604. doi: 10.1122/1.4789444 [100] Mai-Duy N, Phan-Thien N, Khoo B C. 2015. Investigation of particles size effects in Dissipative Particle Dynamics (DPD) modelling of colloidal suspensions. Comput. Phys. Commun., 189: 37-46. doi: 10.1016/j.cpc.2014.12.003 [101] Marson R L, Huang Y, Huang M, Fu T, Larson R G. 2018. Inertio-capillary cross-streamline drift of droplets in Poiseuille flow using dissipative particle dynamics simulations. Soft Matter, 14: 2267-2280. doi: 10.1039/C7SM02294H [102] Martys N S. 2005. Study of a dissipative particle dynamics based approach for modeling suspensions. J. Rheol., 49: 401-424. doi: 10.1122/1.1849187 [103] Menzl G, Gonzalez M A, Geiger P, Caupin F, Abascal J L F, Valeriani C, Dellago C. 2016. Molecular mechanism for cavitation in water under tension. Proc. Natl. Acad. Sci., 113: 13582-13587. doi: 10.1073/pnas.1608421113 [104] Merabia S, Bonet-Avalos J, Pagonabarraga I. 2008. Modelling capillary phenomena at a mesoscale: From simple to complex fluids. J. Non-Newton. Fluid Mech., 154: 13-21. doi: 10.1016/j.jnnfm.2008.01.009 [105] Mewis J, Wagner N J. 2012. Colloidal suspension rheology, Cambridge Series in Chemical Engineering, Cambridge University Press, Cambridge; New York. [106] Mills Z G, Mao W, Alexeev A. 2013. Mesoscale modeling: solving complex flows in biology and biotechnology. Trends Biotechnol., 31: 426-434. doi: 10.1016/j.tibtech.2013.05.001 [107] Min S H, Lee C, Jang J. 2012. Dissipative particle dynamics modeling of a graphene nanosheet and its self-assembly with surfactant molecules. Soft Matter, 8: 8735. doi: 10.1039/c2sm26029h [108] Mo C, Qin L, Zhao F, Yang L. 2016. Application of the dissipative particle dynamics method to the instability problem of a liquid thread. Phys. Rev. E, 94: 063113. doi: 10.1103/PhysRevE.94.063113 [109] Moeendarbary E, Ng T Y, Zangeneh M. 2009. Dissipative particle dynamics: introduction, methodology and complex fluid applications — A review. Int. J. Appl. Mech., 1: 737-763. doi: 10.1142/S1758825109000381 [110] Morris J F. 2020. Shear thickening of concentrated suspensions: Recent developments and relation to other phenomena. Annu. Rev. Fluid Mech., 52: 121-144. doi: 10.1146/annurev-fluid-010816-060128 [111] Ness C, Seto R, Mari R. 2022. The physics of dense suspensions. Annu. Rev. Condens. Matter Phys., 13: 97-117. doi: 10.1146/annurev-conmatphys-031620-105938 [112] Novik K E, Coveney P V. 2000. Spinodal decomposition of off-critical quenches with a viscous phase using dissipative particle dynamics in two and three spatial dimensions. Phys. Rev. E, 61: 435-448. doi: 10.1103/PhysRevE.61.435 [113] Novik K E, Coveney P V. 1997. Using dissipative particle dynamics to model binary immiscible fluids. Int. J. Mod. Phys. C, 8: 909-918. doi: 10.1142/S0129183197000783 [114] Olapade P O, Singh R K, Sarkar K. 2009. Pairwise interactions between deformable drops in free shear at finite inertia. Phys. Fluids, 21: 063302. doi: 10.1063/1.3153905 [115] Oseen C W. 1910. Uber die stokes’ sche formel und uber eine verwandte aufgabe in der hydrodynamik. Ark. Mat. Astron. Phisik, 6: 29. [116] Pagonabarraga I, Frenkel D. 2001. Dissipative particle dynamics for interacting systems. J. Chem. Phys., 115: 5015-5026. doi: 10.1063/1.1396848 [117] Pagonabarraga I, Frenkel D. 2000. non-Ideal DPD fluids. Mol. Simul., 25: 167-175. doi: 10.1080/08927020008044122 [118] Pal R. 2011. Rheology of simple and multiple emulsions. Curr. Opin. Colloid Interface Sci., 16: 41-60. doi: 10.1016/j.cocis.2010.10.001 [119] Pal R. 2001. Novel viscosity equations for emulsions of two immiscible liquids. J. Rheol., 45: 509-520. doi: 10.1122/1.1339249 [120] Pan D, Lin Y, Zhang L, Shao X. 2016. Motion and deformation of immiscible droplet in plane Poiseuille flow at low Reynolds number. J. Hydrodyn., 28: 702-708. doi: 10.1016/S1001-6058(16)60673-X [121] Pan D, Phan-Thien N, Khoo B C. 2015. Studies on liquid–liquid interfacial tension with standard dissipative particle dynamics method. Mol. Simul., 41: 1166-1176. doi: 10.1080/08927022.2014.952636 [122] Pan D, Phan-Thien N, Khoo B C. 2014. Dissipative particle dynamics simulation of droplet suspension in shear flow at low Capillary number. J. Non-Newton. Fluid Mech., 212: 63-72. doi: 10.1016/j.jnnfm.2014.08.011 [123] Pan D, Phan-Thien N, Mai-Duy N, Khoo B C. 2013. Numerical investigations on the compressibility of a DPD fluid. J. Comput. Phys., 242: 196-210. doi: 10.1016/j.jcp.2013.02.013 [124] Pan D, Zhao G, Lin Y, Shao X. 2018. Mesoscopic modelling of microbubble in liquid with finite density ratio of gas to liquid. EPL Europhys. Lett., 122: 20003. doi: 10.1209/0295-5075/122/20003 [125] Pan W, Caswell B, Karniadakis G E. 2010a. Rheology, microstructure and migration in brownian colloidal suspensions. Langmuir, 26: 133-142. doi: 10.1021/la902205x [126] Pan W, Caswell B, Karniadakis G E. 2010b. A low-dimensional model for the red blood cell. Soft Matter, 6: 4366. doi: 10.1039/c0sm00183j [127] Pan W, Fedosov D A, Karniadakis G E, Caswell B. 2008. Hydrodynamic interactions for single dissipative-particle-dynamics particles and their clusters and filaments. Phys. Rev. E, 78: 046706. doi: 10.1103/PhysRevE.78.046706 [128] Pan W, Tartakovsky A M. 2013. Dissipative particle dynamics model for colloid transport in porous media. Adv. Water Resour., 58: 41-48. doi: 10.1016/j.advwatres.2013.04.004 [129] Perry R H, Green D W. 1999. Perry’s Chemical Engineers’ handbook, 7th ed., McGraw-Hill, New York. [130] Phan-Thien N, Mai-Duy N, Khoo B C. 2014a. A spring model for suspended particles in dissipative particle dynamics. J. Rheol., 58: 839-867. doi: 10.1122/1.4874679 [131] Phan-Thien N, Mai-Duy N, Pan D, Khoo B C. 2014b. Exponential-time differencing schemes for low-mass DPD systems. Comput. Phys. Commun., 185: 229-235. doi: 10.1016/j.cpc.2013.09.022 [132] Phan-Thien N, Pham D C. 1997. Differential multiphase models for polydispersed suspensions and particulate solids. J. Non-Newton. Fluid Mech., 72: 305-318. doi: 10.1016/S0377-0257(97)90002-1 [133] Proudman I, Pearson J R A. 1957. Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech., 2: 237-262. doi: 10.1017/S0022112057000105 [134] Pryamitsyn V, Ganesan V. 2005. A coarse-grained explicit solvent simulation of rheology of colloidal suspensions. J. Chem. Phys., 122: 104906. doi: 10.1063/1.1860557 [135] Rallison J M. 1981. A numerical study of the deformation and burst of a viscous drop in general shear flows. J. Fluid Mech., 109: 465-482. doi: 10.1017/S002211208100116X [136] Rekvig L, Kranenburg M, Hafskjold B, Smit B. 2003a. Effect of surfactant structure on interfacial properties. Europhys. Lett. EPL, 63: 902-907. doi: 10.1209/epl/i2003-00607-5 [137] Rekvig Live, Kranenburg M, Vreede J, Hafskjold B, Smit B. 2003b. Investigation of surfactant efficiency using dissipative particle dynamics. Langmuir, 19: 8195-8205. doi: 10.1021/la0346346 [138] Revenga M, Zúñiga I, Español P. 1999. Boundary conditions in dissipative particle dynamics. Comput. Phys. Commun., 121–122 : 309–311. [139] Revenga M, Zúñiga I, Español P, Pagonabarraga I. 1998. Boundary models in DPD. Int. J. Mod. Phys. C, 9: 1319-1328. doi: 10.1142/S0129183198001199 [140] Santo K P, Neimark A V. 2021. Dissipative particle dynamics simulations in colloid and Interface science: a review. Adv. Colloid Interface Sci., 298: 102545. doi: 10.1016/j.cis.2021.102545 [141] Segré G, Silberberg A. 1962. Behaviour of macroscopic rigid spheres in poiseuille flow Part 2. Experimental results and interpretation. J. Fluid Mech., 14: 136-157. doi: 10.1017/S0022112062001111 [142] Serrano M, Español P. 2001. Thermodynamically consistent mesoscopic fluid particle model. Phys. Rev. E, 64: 046115. doi: 10.1103/PhysRevE.64.046115 [143] Stickel J J, Powell R L. 2005. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech., 37: 129-149. doi: 10.1146/annurev.fluid.36.050802.122132 [144] Taylor G I. 1934. The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character, 146: 501-523. [145] Taylor G I. 1932. The viscosity of a fluid containing small drops of another fluid. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character, 138: 41-48. [146] Tiwari A, Abraham J. 2009. A two-component two-phase dissipative particle dynamics model. Int. J. Numer. Methods Fluids, 59: 519-533. doi: 10.1002/fld.1830 [147] Tiwari A, Abraham J. 2006. Dissipative-particle-dynamics model for two-phase flows. Phys. Rev. E, 74: 056701. doi: 10.1103/PhysRevE.74.056701 [148] Tiwari A, Reddy H, Mukhopadhyay S, Abraham J. 2008. Simulations of liquid nanocylinder breakup with dissipative particle dynamics. Phys. Rev. E, 78: 016305. doi: 10.1103/PhysRevE.78.016305 [149] Tran-Duc T, Phan-Thien N, Cheong Khoo B. 2013. Rheology of bubble suspensions using dissipative particle dynamics. Part I: A hard-core DPD particle model for gas bubbles. J. Rheol., 57: 1715-1737. doi: 10.1122/1.4824387 [150] Trofimov S Y, Nies E L F, Michels M A J. 2005. Constant-pressure simulations with dissipative particle dynamics. J. Chem. Phys., 123: 144102. doi: 10.1063/1.2052667 [151] Trofimov S Y, Nies E L F, Michels M A J. 2002. Thermodynamic consistency in dissipative particle dynamics simulations of strongly nonideal liquids and liquid mixtures. J. Chem. Phys., 117: 9383-9394. doi: 10.1063/1.1515774 [152] Tsouka S, Dimakopoulos Y, Tsamopoulos J. 2016. Stress-gradient induced migration of polymers in thin films flowing over smoothly corrugated surfaces. J. Non-Newton. Fluid Mech., 228: 79-95. doi: 10.1016/j.jnnfm.2015.12.011 [153] Visser D C, Hoefsloot H C J, Iedema P D. 2006. Modelling multi-viscosity systems with dissipative particle dynamics. J. Comput. Phys., 214: 491-504. doi: 10.1016/j.jcp.2005.09.022 [154] Wang J, Han Y, Xu Z, Yang X, Ramakrishna S, Liu Y. 2021. Dissipative particle dynamics simulation: A review on investigating mesoscale properties of polymer systems. Macromol. Mater. Eng., 306: 2000724. doi: 10.1002/mame.202000724 [155] Wang J, Li J, Pan D. 2022. Mesoscopic simulation of liquid bridge spreading under squeezing of parallel plates. Phys. Fluids, 34: 123101. doi: 10.1063/5.0127420 [156] Wang X, Santo K P, Neimark A V. 2020. Modeling gas–liquid interfaces by dissipative particle dynamics: Adsorption and surface tension of cetyl trimethyl ammonium bromide at the air–water interface. Langmuir, 36: 14686-14698. doi: 10.1021/acs.langmuir.0c02572 [157] Wang Y, Ouyang J, Wang X. 2021. Machine learning of lubrication correction based on GPR for the coupled DPD–DEM simulation of colloidal suspensions. Soft Matter, 17: 5682-5699. doi: 10.1039/D1SM00250C [158] Warren P B. 2003. Vapor-liquid coexistence in many-body dissipative particle dynamics. Phys. Rev. E, 68: 066702. doi: 10.1103/PhysRevE.68.066702 [159] Weijs J H, Snoeijer J H, Lohse D. 2012. Formation of surface nanobubbles and the universality of their contact angles: A molecular dynamics approach. Phys. Rev. Lett., 108: 104501. doi: 10.1103/PhysRevLett.108.104501 [160] Whittle M, Travis K P. 2010. Dynamic simulations of colloids by core-modified dissipative particle dynamics. J. Chem. Phys., 132: 124906. doi: 10.1063/1.3364011 [161] Wu C J, Chu K C, Sheng Y J, Tsao H K. 2017. Sliding dynamic behavior of a nanobubble on a surface. J. Phys. Chem. C, 121: 17932-17940. doi: 10.1021/acs.jpcc.7b04924 [162] Xia Y, Blumers A, Li Z, Luo L, Tang Y-H, Kane J, Goral J, Huang H, Deo M, Andrew M. 2020. A GPU-accelerated package for simulation of flow in nanoporous source rocks with many-body dissipative particle dynamics. Comput. Phys. Commun., 247: 106874. doi: 10.1016/j.cpc.2019.106874 [163] Xiao L, Zhang K, Zhao J, Chen S, Liu Y. 2021. Viscosity measurement and simulation of microbubble wetting on flat surfaces with many-body dissipative particle dynamics model. Colloids Surf. Physicochem. Eng. Asp., 608: 125559. doi: 10.1016/j.colsurfa.2020.125559 [164] Yaron I, Gal-Or B. 1972. On viscous flow and effective viscosity of concentrated suspensions and emulsions: Effect of particle concentration and surfactant impurities. Rheol. Acta, 11: 241-252. doi: 10.1007/BF01974767 [165] Ye T, Jing B, Pan D. 2023. Intelligent dissipative particle dynamics: Bridging mesoscopic models from microscopic simulations via deep neural networks. J. Comput. Phys., 475: 111857. doi: 10.1016/j.jcp.2022.111857 [166] Ye T, Pan D, Huang C, Liu M. 2019. Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids, 31: 011301. doi: 10.1063/1.5068697 [167] Zhang Y, Xu J, He X. 2018. Effect of surfactants on the deformation of single droplet in shear flow studied by dissipative particle dynamics. Mol. Phys., 116: 1851-1861. doi: 10.1080/00268976.2018.1459916 [168] Zhao G, Pan D, Zeng L, Shao X. 2021. Numerical study on droplet deformation in periodic pulsatile shear flow and effects of inertia. J. Non-Newton. Fluid Mech., 289: 104494. doi: 10.1016/j.jnnfm.2021.104494 [169] Zhao J, Chen S, Zhang K, Liu Y. 2021. A review of many-body dissipative particle dynamics (MDPD): Theoretical models and its applications. Phys. Fluids, 33: 112002. doi: 10.1063/5.0065538 [170] Zhao J, Zhou N, Zhang K, Chen S, Liu Y. 2020a. Study on stretching liquid bridges with symmetric and asymmetric surface wettability. Phys. Rev. Fluids, 5: 064003. doi: 10.1103/PhysRevFluids.5.064003 [171] Zhao J, Zhou N, Zhang K, Chen S, Liu Y, Wang Y. 2020b. Rupture process of liquid bridges: The effects of thermal fluctuations. Phys. Rev. E, 102: 023116. [172] Zhao L, Li Z, Wang Z, Caswell B, Ouyang J, Karniadakis G E. 2021. Active- and transfer-learning applied to microscale-macroscale coupling to simulate viscoelastic flows. J. Comput. Phys., 427: 110069. doi: 10.1016/j.jcp.2020.110069 -




 下载:
下载: