面向流体力学的多范式融合研究展望

张伟伟; 王旭; 寇家庆

doi:10.6052/1000-0992-22-050

面向流体力学的多范式融合研究展望

doi: 10.6052/1000-0992-22-050

张伟伟^{1, 2, ,},
王旭¹,
寇家庆³

1.
西北工业大学航空学院, 西安 710072
2.
西北工业大学流体力学智能化国际联合研究所, 西安 710072
3.
亚琛工业大学空气动力学所, 德国亚琛 52062

基金项目: 国家自然科学基金重大计划集成项目 (92152301) 、国家自然科学基金面上项目 (12072282) 、国家数值风洞项目 (NNW2018-ZT1B01, NNW2019ZT2-A05) 资助

详细信息

作者简介:
张伟伟，西北工业大学航空学院博士生导师，长江学者特聘教授，中国空气动力学会副理事长、流体力学智能化国际联合研究所中方负责人。主要从事智能空气动力学、气动弹性力学和飞行器设计研究，是国内智能流体力学研究的倡导者和主要推动者之一。发展了高效高精度的空气动力模型和气动弹性分析方法，揭示了复杂流固耦合问题的诱发机理，主持国家自然科学基金等国家级项目10余项，有力支撑了我国航空、航天、兵器等十多个单位20多个型号的研制，获得省部级科研成果奖5项。在PAS、JFM等国内外知名刊物发表论文100余篇，撰写著作3部。曾获得国家优秀青年基金、中国航空学会青年科技奖、中国空气动力学会青年科技奖等荣誉。担任中国空气动力学会智能流体力学专业组主任、空气弹性力学专业委员会副主任，中国力学学会流固耦合力学专业委员会副主任，智能流体力学产业联合体副理事长兼秘书长，《空气动力学学报》副主编，AST、TAML、AAMM、AIA等国际期刊编委

通讯作者:
aeroelastic@nwpu.edu.cn

中图分类号: V211
计量
- 文章访问数: 1981
- HTML全文浏览量: 775
- PDF下载量: 603
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-19
- 录用日期: 2023-03-16
- 网络出版日期: 2023-04-17
- 刊出日期: 2023-06-25

Prospects of multi-paradigm fusion methods for fluid mechanics research

ZHANG Weiwei^{1, 2
, ,},
WANG Xu¹,
KOU Jiaqing³

1.
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China
2.
International Joint Institute of Artificial Intelligence on Fluid Mechanics, Northwestern Polytechnical University, Xi'an 710072, China
3.
Institute of Aerodynamics, RWTH Aachen University, Wüllnerstraße 5a, 52062, Aachen, Germany

Funds: The project was supported by the (12345678) and (9876543)

More Information

Corresponding author: aeroelastic@nwpu.edu.cn

摘要

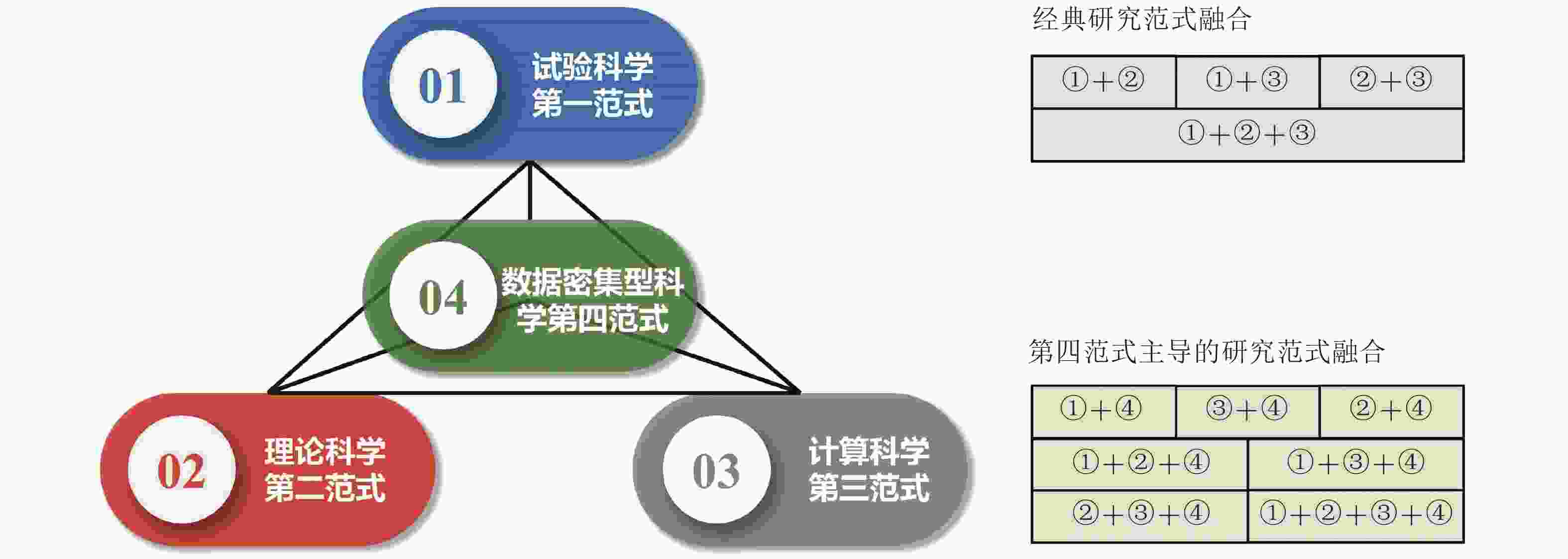
摘要: 实验观测、理论研究以及数值模拟是包括流体力学在内很多学科的基本研究范式. 21世纪以来, 大数据驱动下的人工智能成为引领新一轮科技革命和产业变革的重要驱动力, 也被称为数据密集型科学研究范式, 即第四范式. 同样, 数据驱动的机器学习方法也成为流体力学的新兴方向, 并助推智能流体力学方向的发展. 然而, 与面向社会依赖“互联网 + 大数据”的数据密集型范式相比, 流体力学智能化研究有其特有的背景. 例如有限工程样本中产生的海量流动数据, 与流动状态、几何边界条件的高维度以及复杂流动固有的高维、跨尺度、随机、非线性特征相比, 数据驱动的流体力学研究面临着大数据小样本问题. 经典流体力学虽然有三大研究范式, 但融合度很低, 工程设计师通常只能对不同来源的数据进行拼凑使用或简单修正. 多源数据融合一定程度上可缓解单一样本量来源少、建模难, 以及低精度样本利用不充分等困境, 但仍未能实现基本范式中的理论模型或者专家知识和经验的充分利用. 因此, 在人工智能技术支撑的第四范式架构下, 有机融合实验、理论模型以及数值模拟三大手段, 发展“数据 + 知识”双驱动的流体力学多范式融合方法, 成为解决重大实际工程研制问题的迫切需求, 也是新时代流体力学学科内涵、特色发展的迫切需求.
- 数据驱动 /
- 人工智能 /
- 流体力学 /
- 智能流体力学 /
- 多范式融合
Abstract: Experimental observation, theoretical research and numerical simulation are the basic research paradigms in many disciplines, including fluid mechanics. Since the 21st century, artificial intelligence based on big data has become an important driving force, leading to new scientific and technological revolution and industrial transformation. This is known as the data-intensive scientific research paradigm, which forms the fourth research paradigm. Similarly, data-driven machine learning has also become an emerging research direction in fluid mechanics and promoted the progress in intelligent fluid mechanics. However, compared to traditional data-intensive research paradigm that relies on "Internet and big data", research on intelligent fluid mechanics has its own unique background. For example, compared to high-dimensional flow state, geometric boundary conditions, and the inherent high-dimensional, cross-scale, random, and nonlinear characteristics of complex flow, research in data-driven fluid mechanics essentially handles large data but small samples. Although there are three major research paradigms in fluid mechanics, the integration among research paradigms is very low, where engineering optimization simply corrects data from multiple sources. Multi-source data fusion can alleviate several dilemmas, like small data sample from a single source, difficulties in modelling, and the insufficient utilization of low-fidelity data, it still fails to fully integrate theoretical models, expert knowledge and experience from the basic paradigms.Therefore, based on the fourth paradigm driven by artificial intelligence, the organic combination of three major research topics including experiment, theoretical model and numerical simulation, developing date and knowledge jointly driven multi-paradigm fusion methods for fluid mechanics, have become urgent to solve major practical engineering problems, as well as to satisfy the need for the development of the connotation and the characteristics of fluid mechanics in the new era.
- data-driven /
- artificial intelligence /
- fluid mechanics /
- intelligent fluid mechanics /
- multi-paradigm fusion

HTML全文

图 1 达芬奇对水流现象的描摹

下载: 全尺寸图片幻灯片

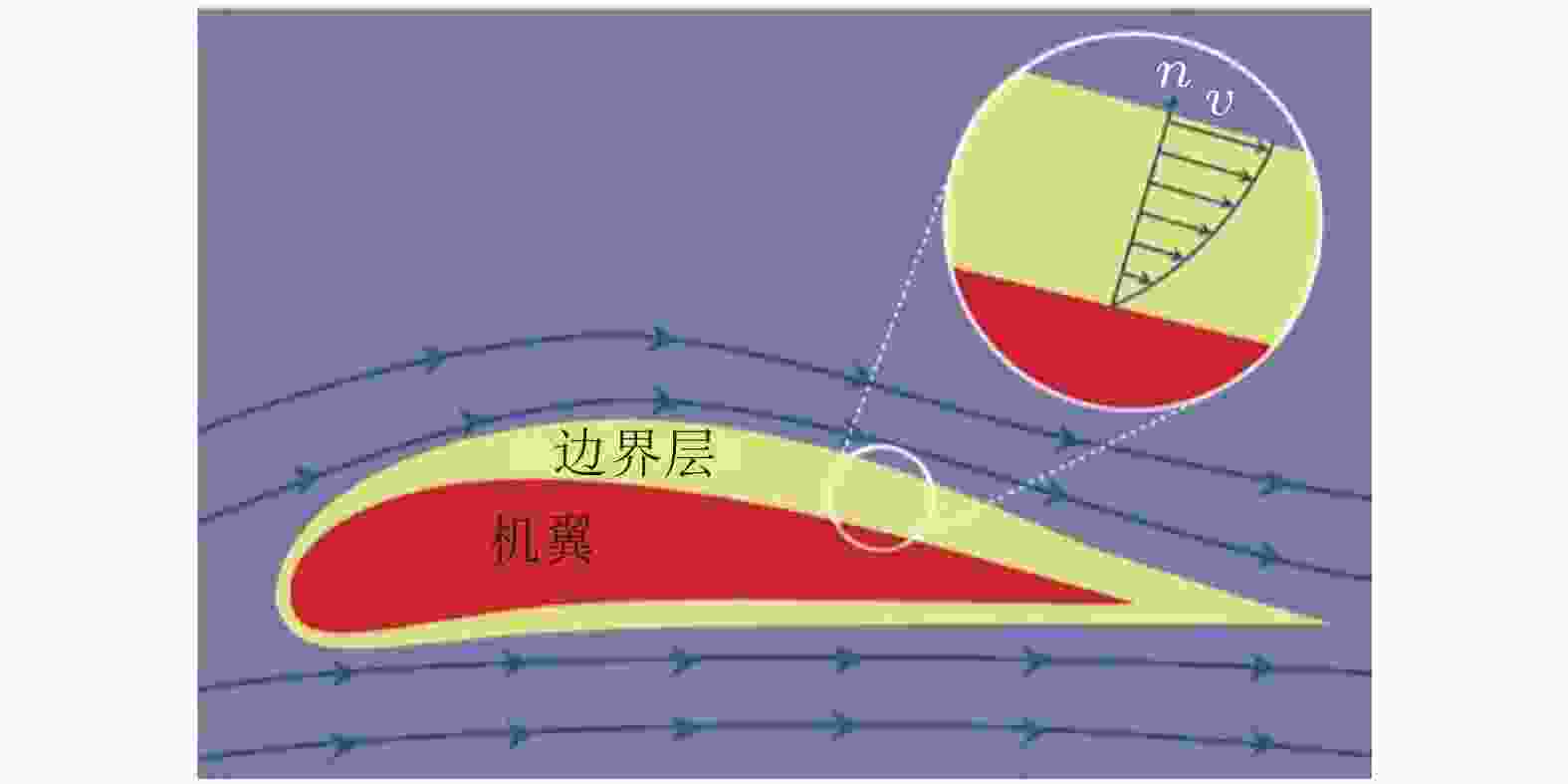
图 2 边界层内外流动(Anderson 2005)

下载: 全尺寸图片幻灯片

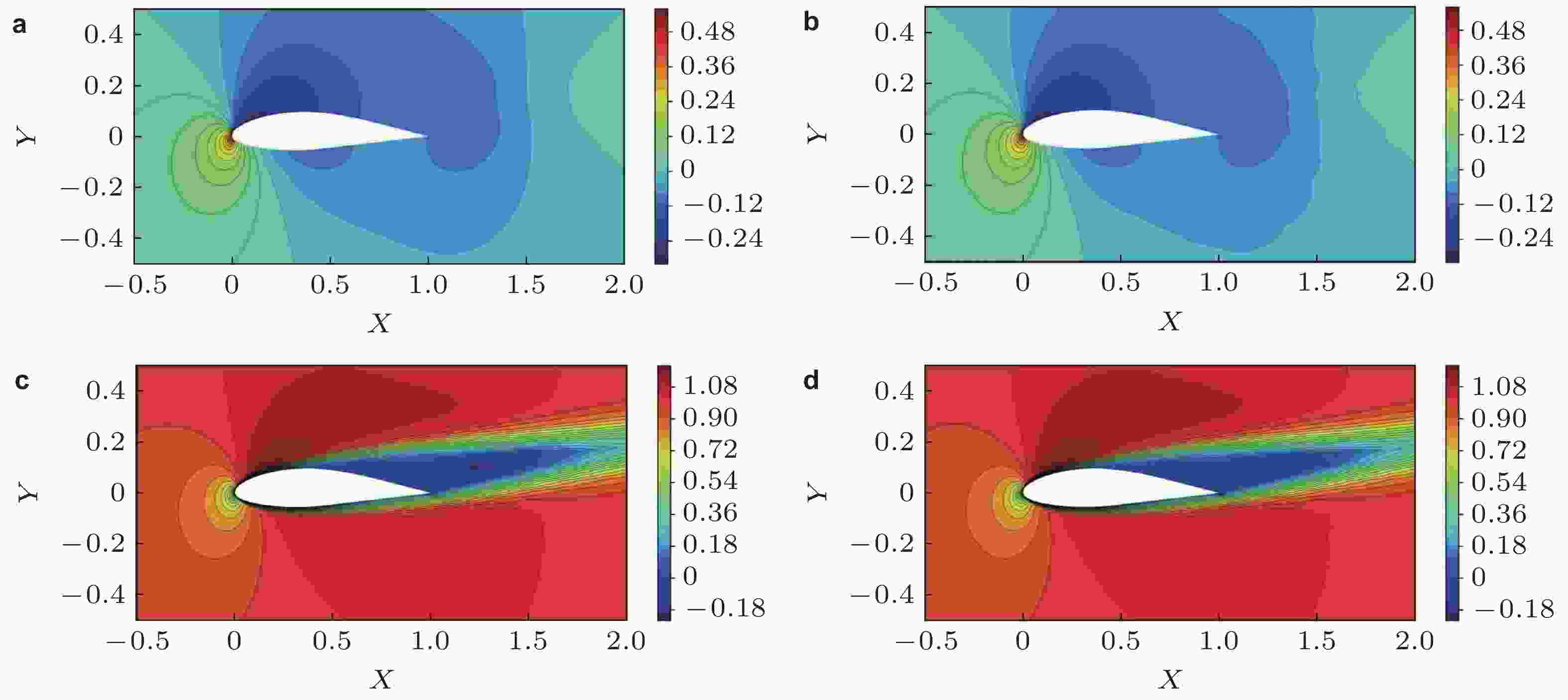
图 3 NACA63415翼型流场压力分布和速度分布结果与CFD样本数据结果对比 (Re=1900, α=7°) ( a、b: 压力场; c、d: 速度场; 左: CFD样本数据; 右: 神经网络模型预测结果) (Sekar et al. 2019)

下载: 全尺寸图片幻灯片

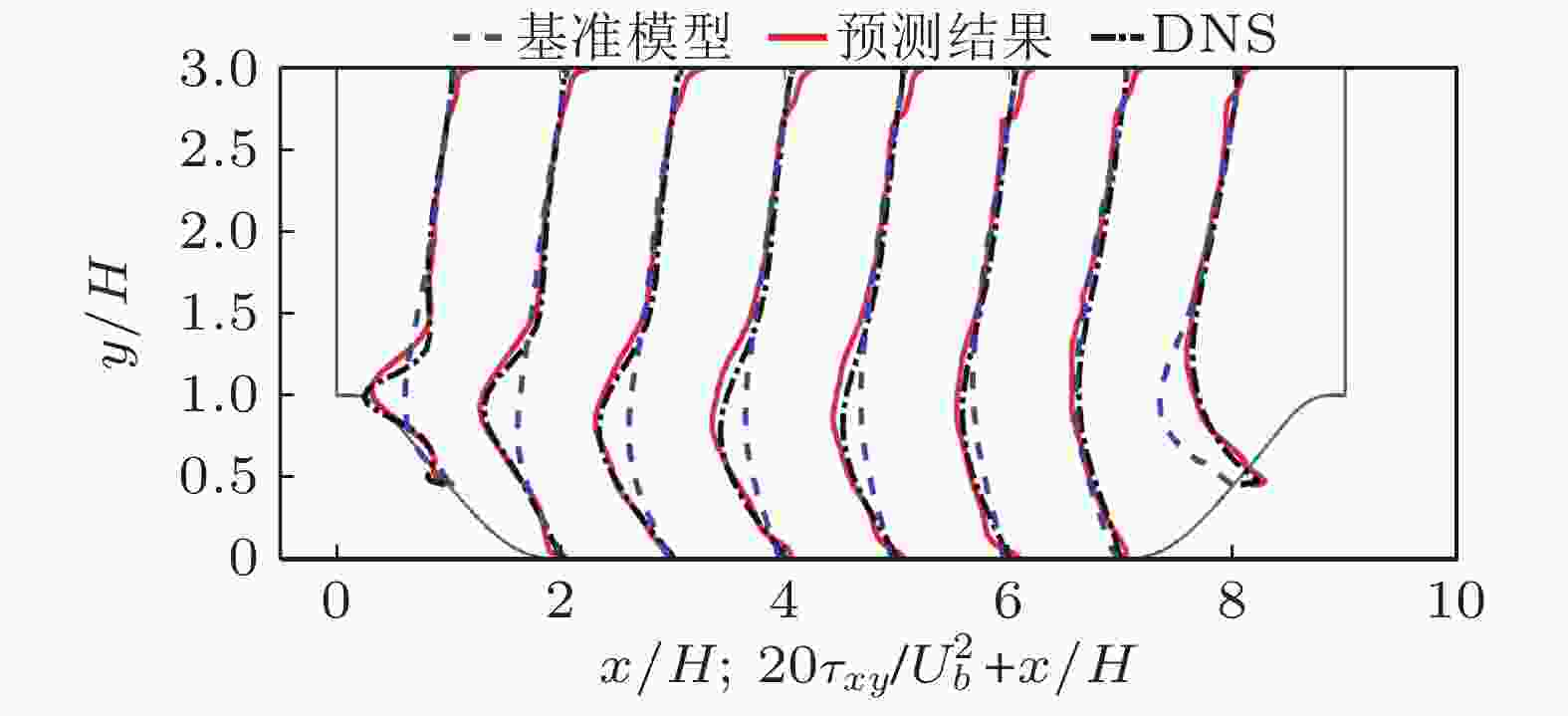
图 4 机器学习湍流模型预测周期山算例壁面湍流剪切应力分布(Wang et al. 2017)

下载: 全尺寸图片幻灯片

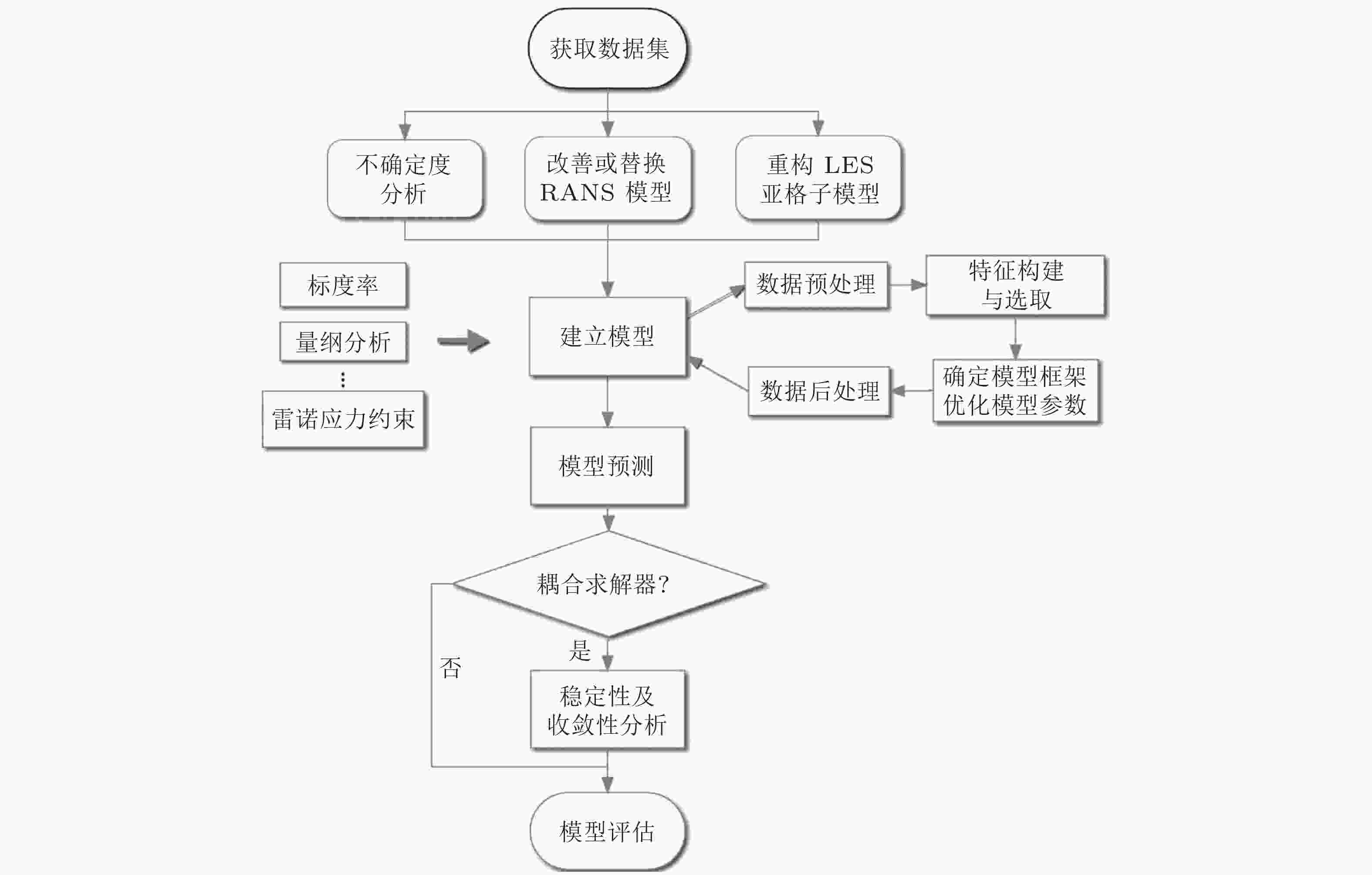
图 5 机器学习应用于湍流建模的主要研究方向及流程(张伟伟等 2021)

下载: 全尺寸图片幻灯片

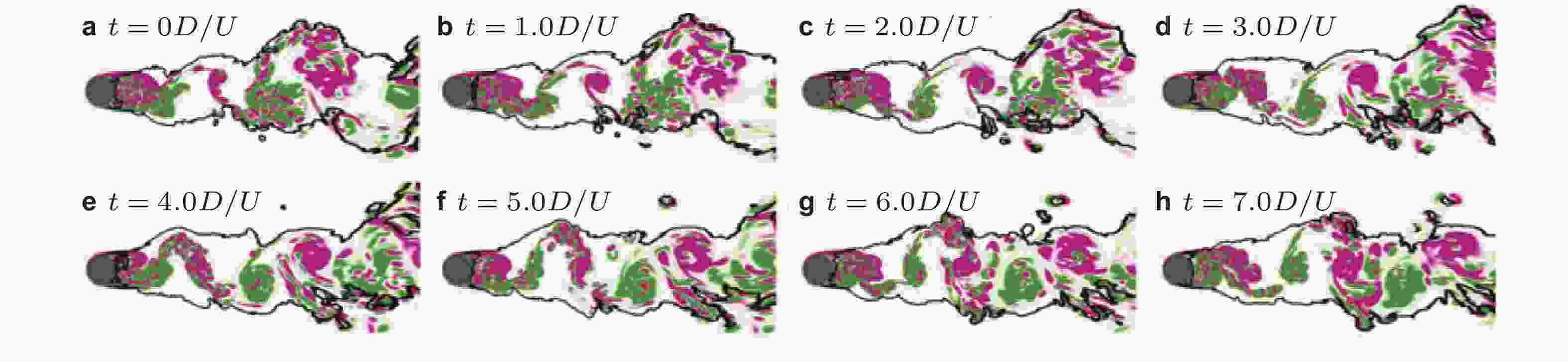
图 6 不同流场快照下机器学习方法的湍流区域识别结果对比(Li B et al. 2020)

下载: 全尺寸图片幻灯片

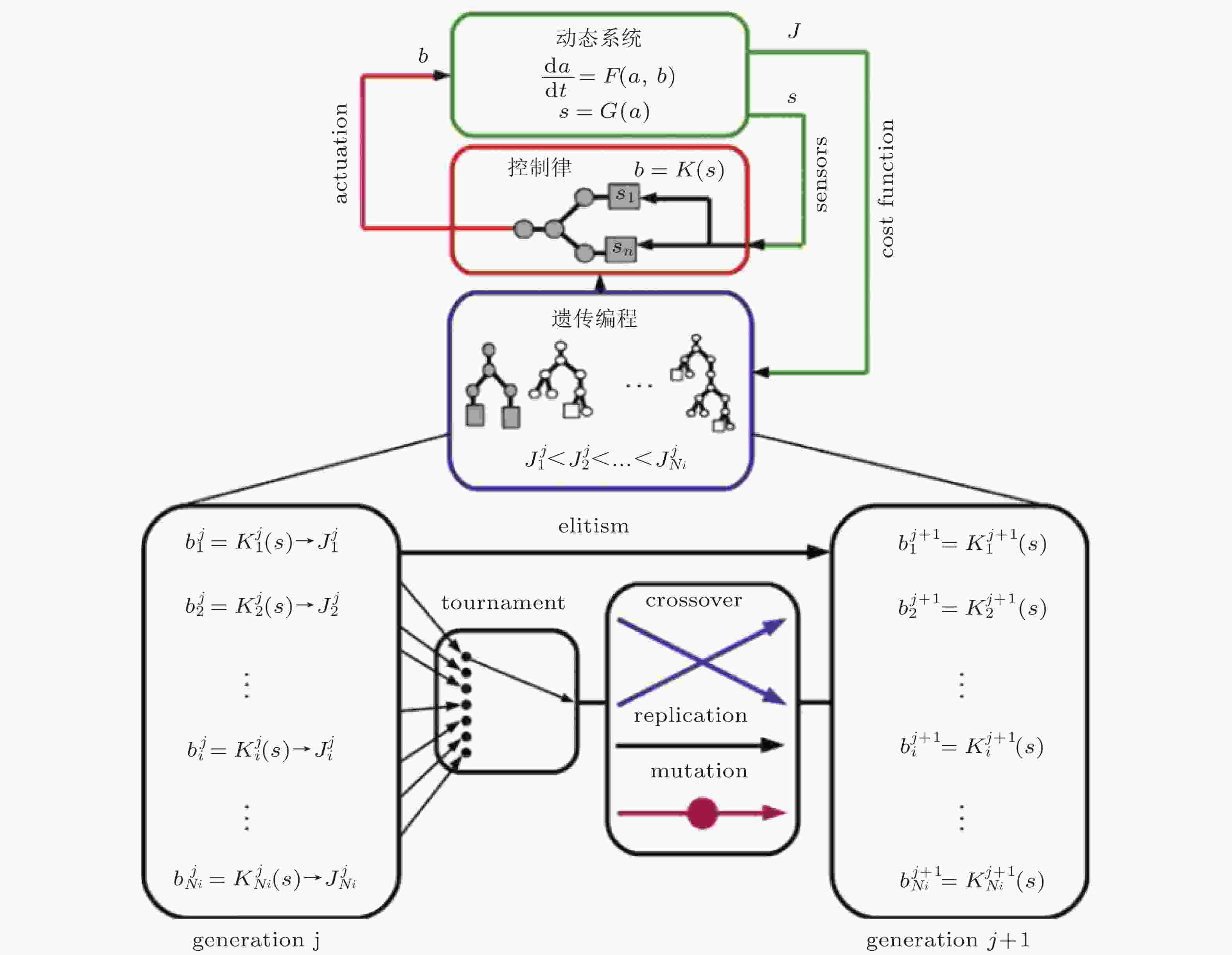
图 7 基于遗传编程的无模型智能化控制设计思路(Duriez et al. 2017)

下载: 全尺寸图片幻灯片

图 8 层流状态下圆柱流动控制结果(Ren et al. 2021)

下载: 全尺寸图片幻灯片

图 9 多范式融合的研究脉络

下载: 全尺寸图片幻灯片

图 10 分布载荷稀疏重构流程(赵旋等 2022)

下载: 全尺寸图片幻灯片

图 11 不同试验数据驱动模型的预测能力对比(Holierhoek et al. 2013)

下载: 全尺寸图片幻灯片

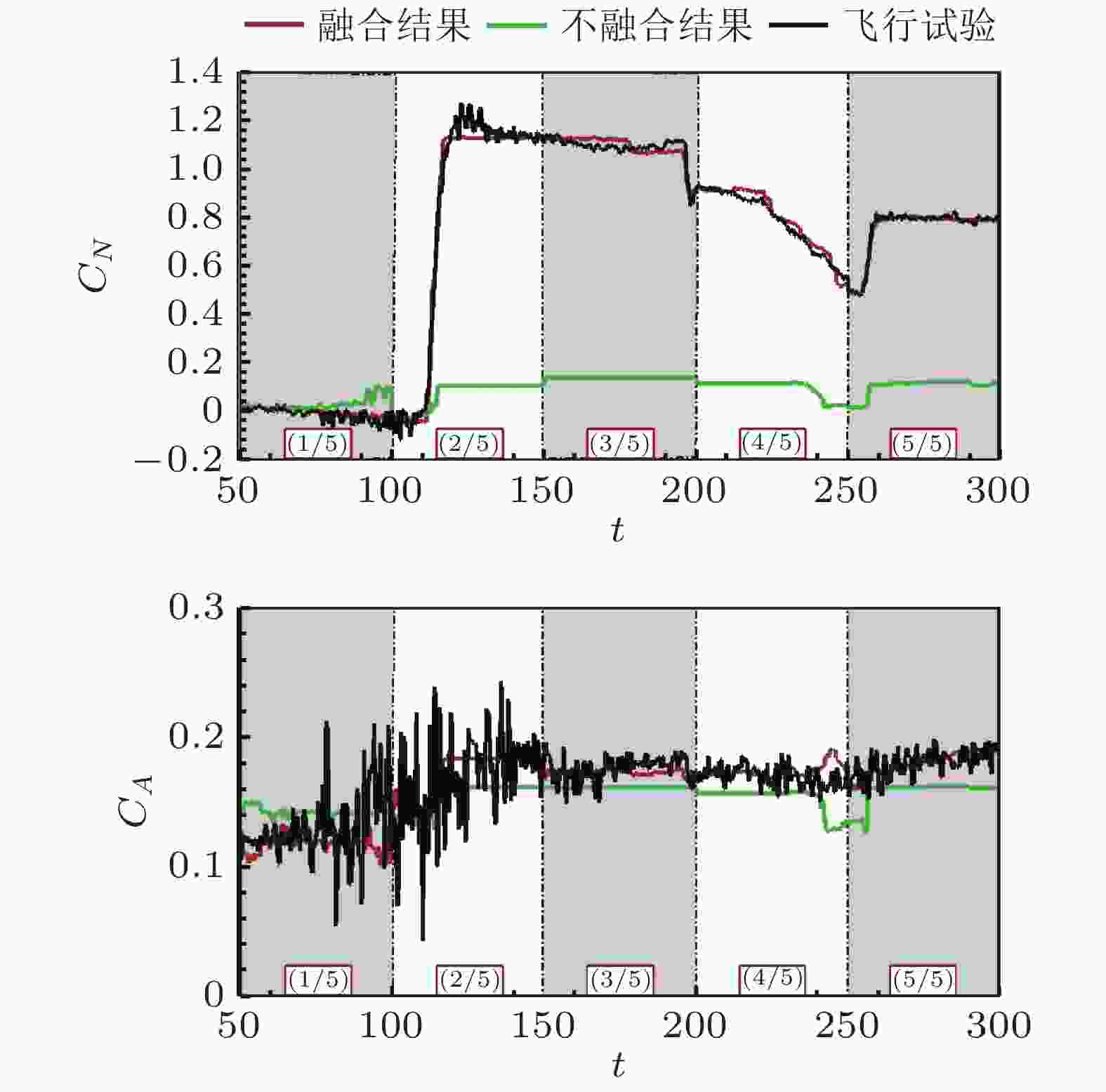
图 12 基于随机森林的天地气动数据融合(王旭等 2023)

下载: 全尺寸图片幻灯片

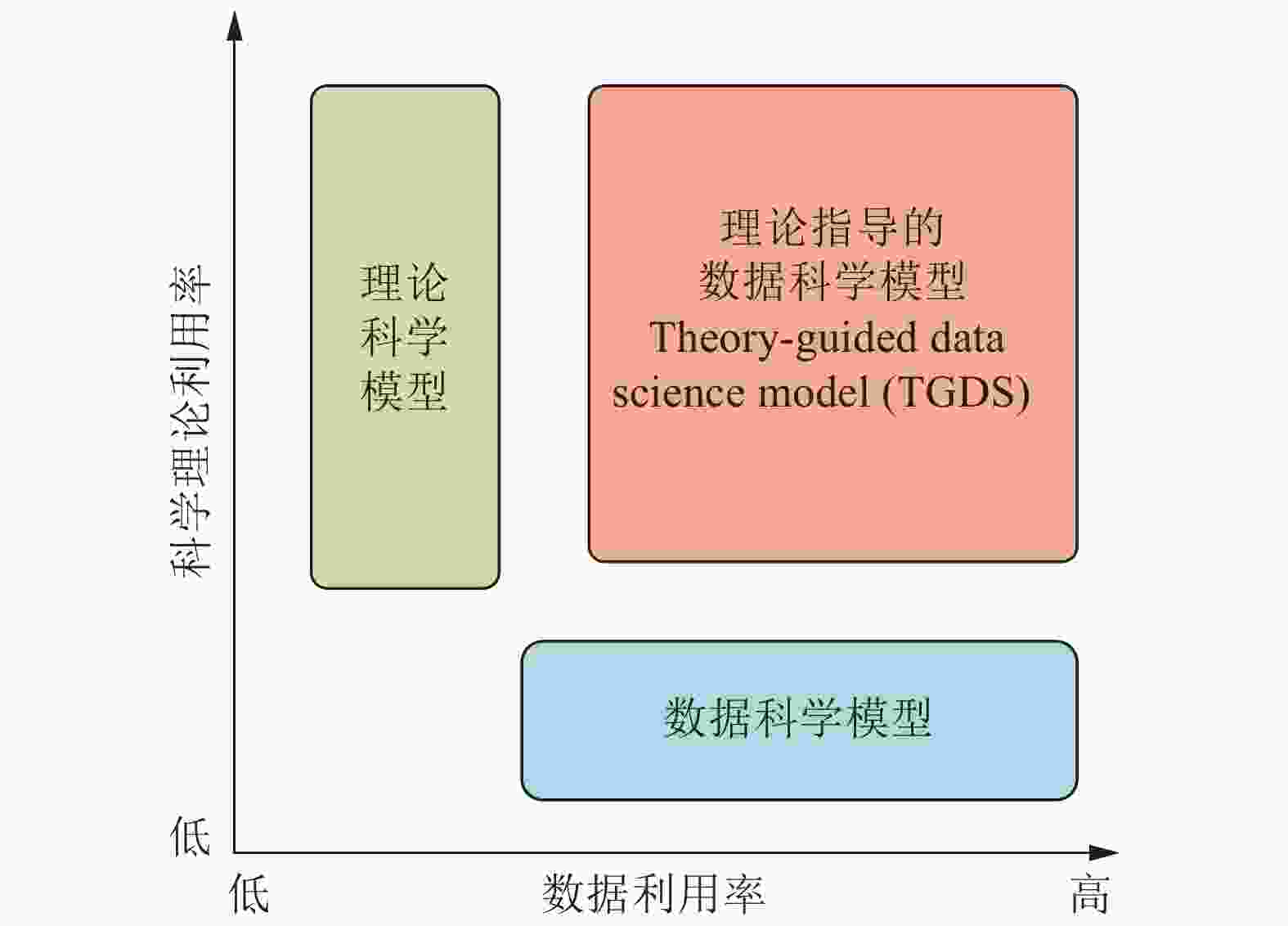
图 13 第二与第四范式的关系(Karpatne et al. 2017)

下载: 全尺寸图片幻灯片

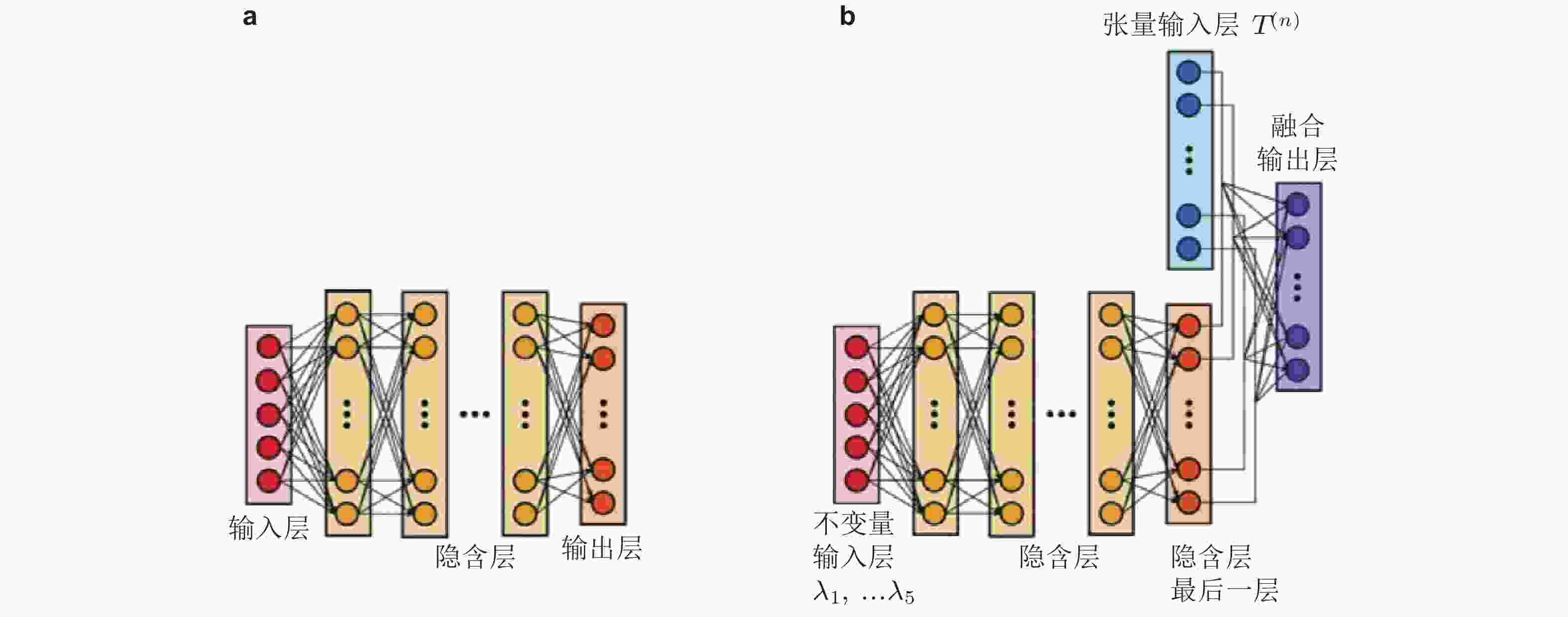
图 14 Ling等人的TBNN网络架构 (Ling et al. 2016)

下载: 全尺寸图片幻灯片

图 15 Zhu等人引入标度分析的网络架构(Zhu L Y et al. 2021)

下载: 全尺寸图片幻灯片

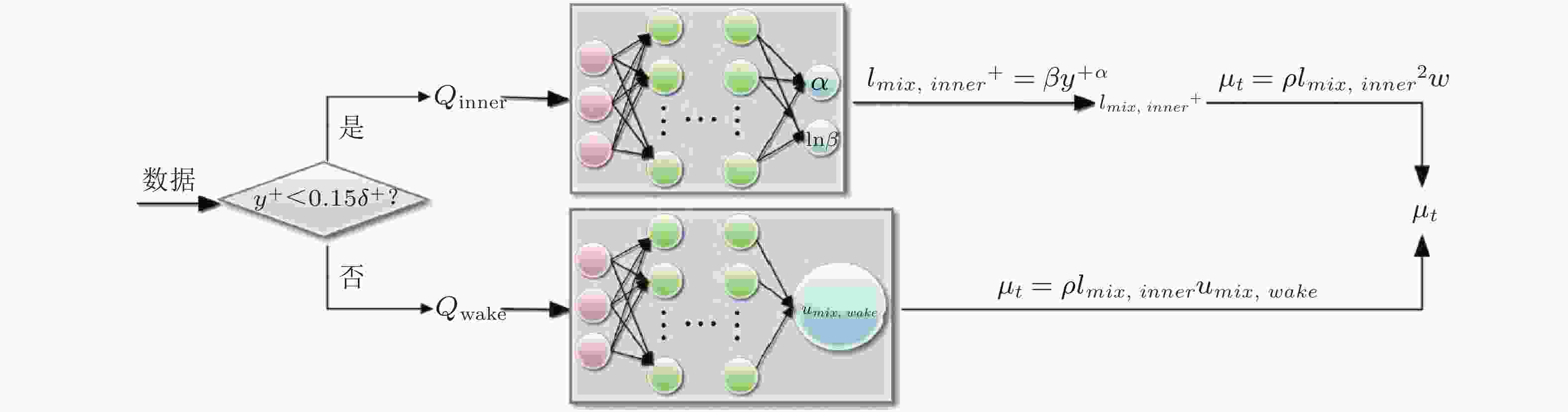
图 16 基于机器学习的湍流模型修正(Singh et al. 2017b)

下载: 全尺寸图片幻灯片

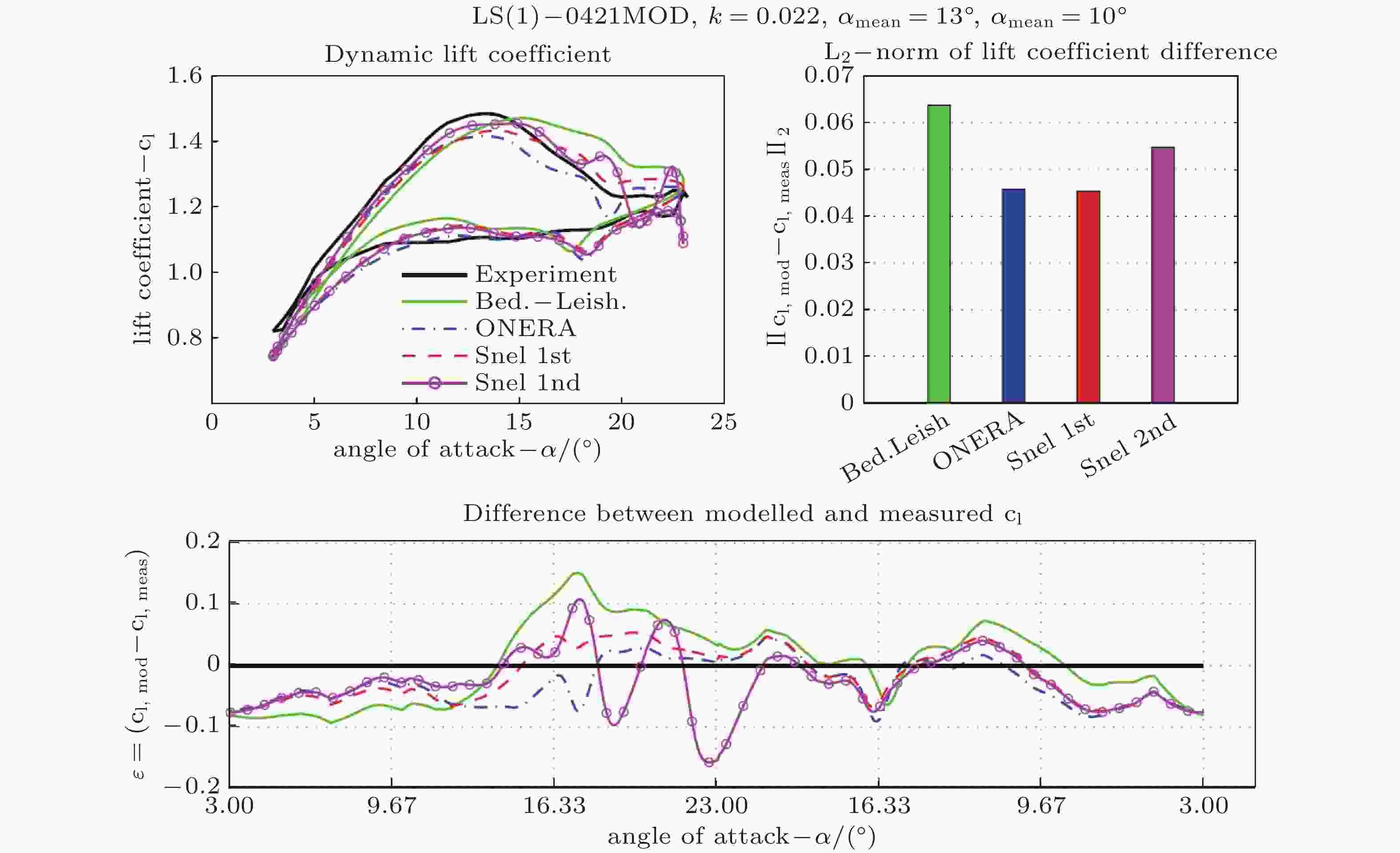
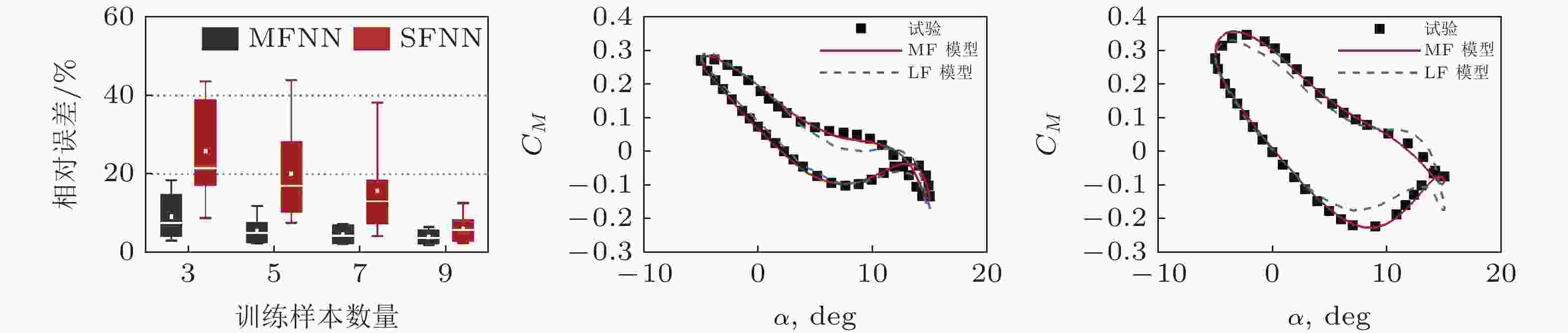
图 17 集成神经网络融合模型实现小样本动态失速预测(Wang X et al. 2022)

下载: 全尺寸图片幻灯片

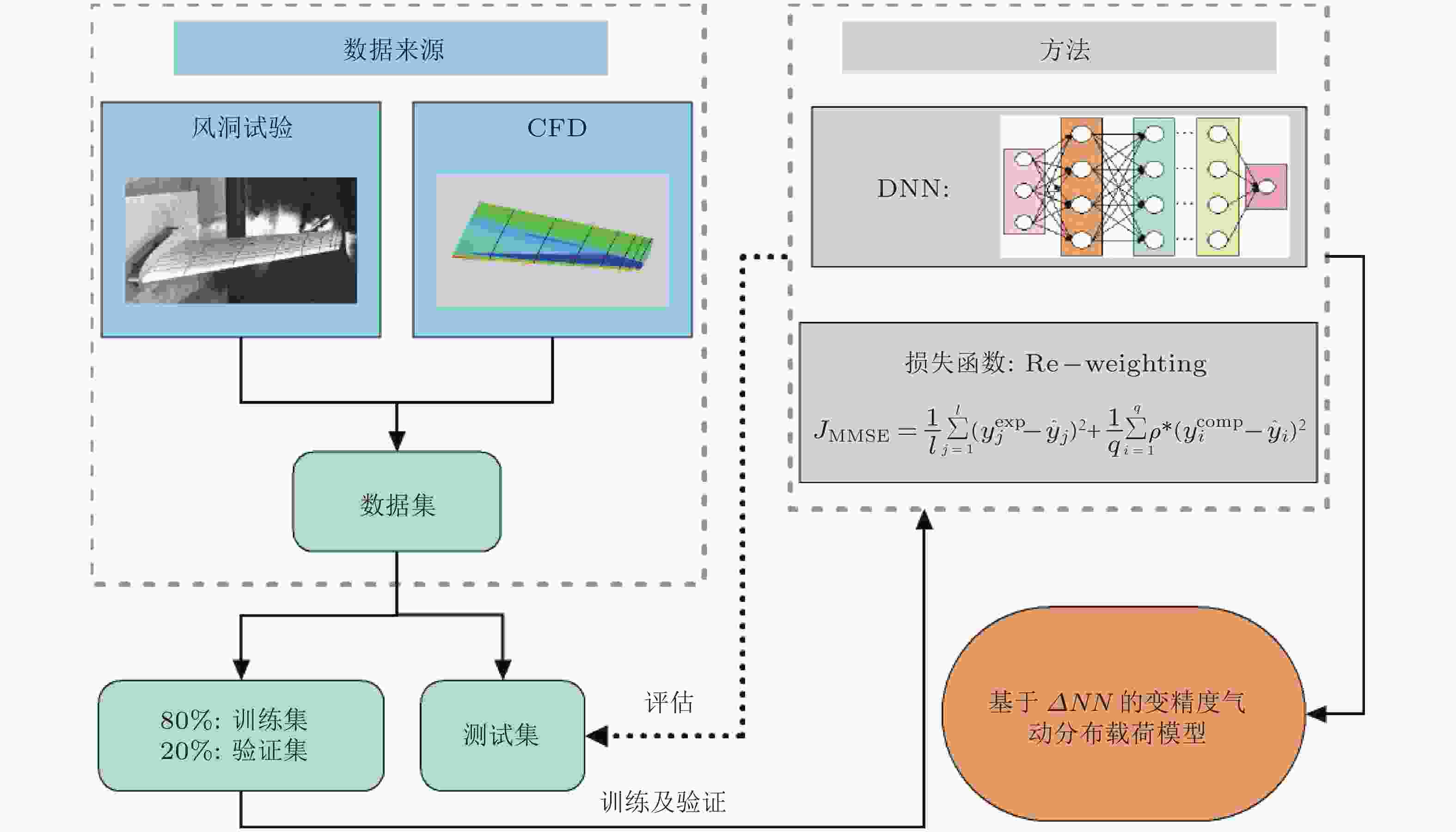
图 18 基于深度学习的计算-试验范式融合(Li K et al. 2022)

下载: 全尺寸图片幻灯片

表 1 Zhu L Y等(2019)对涡粘建模的输入特征

Feature	Description	Sign
1	Horizontal	u
2	Density	ρ
3	Normal wall distance	d
4	Normal wall distance squared times the vorticity	${{\rm{d}}^2}\varOmega$
5	Exponential function	${F_s}$
6	Projection of free stream to normal direction of streamline	${{\rm{sgn}}} (y)[ - v + u\tan (\alpha )]$
7	Velocity direction	$\arctan [\left\| {v/u} \right\|]$
8	Entropy	${{{\boldsymbol{S}}'}}$
9	Normalized strain rate	$\left\\| {{{\boldsymbol{S}}}} \right\\|/(\left\\| {{{\boldsymbol{S}}}} \right\\| + \left\\| {\boldsymbol{\varOmega }} \right\\|)$

下载: 导出CSV

表 2 Xiao等(2017)对雷诺应力建模的输入特征

Feature (${q_\beta }$)	Description	Raw feature(${\hat q_\beta }$)	Normalization factor ($ q{_\beta *_{}} $)
${q_1}$	Ratio of excess Rotation rate to strain rate (Q criterion)	$\dfrac{1}{2}({\left\\| {\boldsymbol{\varOmega }} \right\\|^2} - {\left\\| {{\boldsymbol{S}}} \right\\|^2})$	${\left\\| {{\boldsymbol{S}}} \right\\|^2}$
${q_2}$	Turbulence intensity	k	$\dfrac{1}{2}{U_i}{U_i}$
${q_3}$	Wall-distance based Reynolds number	$\min \left(\dfrac{ {\sqrt k {\rm{d}}} }{ {50v} },2\right)$	Not applicable ^a
${q_4}$	Pressure gradient along streamline	${U_k}\dfrac{{\partial P}}{{\partial {x_k}}}$	$ \sqrt {\dfrac{{\partial P}}{{\partial {x_j}}}\dfrac{{\partial P}}{{\partial {x_j}}}{U_i}{U_i}} $
$ {q_5} $	Ratio of turbulence time scale to mean strain time scale	$\dfrac{k}{\varepsilon }$	$\dfrac{1}{{\left\\| {S} \right\\|}}$
${q_6}$	Cratio of pressure normal stresses to shear stresses	$ \sqrt {\dfrac{{\partial P}}{{\partial {x_j}}}\dfrac{{\partial P}}{{\partial {x_j}}}} $	$\dfrac{1}{2}\rho \dfrac{{\partial U_k^2}}{{\partial {x_k}}}$
${q_7}$	Nonorthogonality between velocity and its gradient	$\left\| {{U_i}{U_j}\dfrac{{\partial {U_i}}}{{\partial {x_j}}}} \right\|$	$\sqrt {{U_l}{U_l}{U_i}\dfrac{{\partial {U_i}}}{{\partial {x_j}}}{U_k}\dfrac{{\partial {U_k}}}{{\partial {x_j}}}} $
${q_8}$	Ratio of convection to production of TKE	${U_i}\dfrac{{{\rm{d}}k}}{{{\rm{d}}{x_i}}}$	$ \left\| {\overline {{{u'}_j}{{u'}_k}} {S_{jk}}} \right\| $
${q_9}$	Ratio of total to normal Reynolds stresses	$ \left\\| {\overline {{{u'}_i}{{u'}_j}} } \right\\| $	k
${q_{10}}$	Streamline curvature	$ \begin{gathered} \left\| {\dfrac{{{\rm D}\varGamma }}{{{\rm D}s}}} \right\|where \to \varGamma \equiv {U} /\left\| {U} \right\|, \\ {\rm D}s = \left\| {U} \right\|{\rm D}t \\ \end{gathered} $	$\dfrac{1}{{{L_c}}}$
^a Normalization is not necessary as the Reynolds number is nondimensional.

下载: 导出CSV

参考文献(180)

[1]	蔡声泽, 许超, 高琪, 等. 2019. 基于深度神经网络的粒子图像测速算法. 空气动力学学报, 37: 455-461 (Cai S Z, Xu C, Gao Q, et al. 2019. Particle image velocimetry algorithm based on depth neural network. Acta Aerodynamica Sinica, 37: 455-461). Cai S Z, Xu C, Gao Q, et al. Particle image velocimetry algorithm based on depth neural network [J] Acta Aerodynamica Sinica, 2019, 37 (3): 455-461.
[2]	高高. 1998. 从流体力学的发展史看科学发展模式. 武汉交通科技大学学报(哲学社会科学版), 67-70 (Gao G. 1998. Viewing scientific development mode from the development history of fluid mechanics. Journal of Wuhan Jiaotong University of Science and Technology (Philosophy and Social Sciences Edition), 67-70). Gao G. Viewing scientific development mode from the development history of fluid mechanics [J]. Journal of Wuhan Jiaotong University of Science and Technology (Philosophy and Social Sciences Edition), 1998 (01): 67-70.
[3]	韩忠华. 2016. Kriging模型及代理优化算法研究进展. 航空学报, 37: 3197-3255 (Han Z H. 2016. Research progress of Kriging model and agent optimization algorithm. Acta Aeronautica et Astronautica Sinica, 37: 3197-3255). Han Z H. Research progress of Kriging model and agent optimization algorithm [J] Acta Aeronautica et Astronautica Sinica, 2016, 37 (11): 3197 – 3255.
[4]	何磊, 钱炜祺, 汪清, 等. 2019. 机器学习方法在气动特性建模中的应用. 空气动力学学报, 37: 470-479 (He L, Qian W Q, Wang Q, et al. 2019. Applications of machine learning for aerodynamic characteristics modeling. Acta Aerodynamica Sinica, 37: 470-479). He L, Qian W Q, Wang Q, et al. Applications of machine learning for aerodynamic characteristics modeling[J]. Acta Aerodynamica Sinica, 2019, 37(3): 470-479.
[5]	何志昆, 刘光斌, 赵曦晶, 等. 2013. 高斯过程回归方法综述. 控制与决策, 28: 1121-1129 (He Z K, Liu G B, Zhao X J, et al. 2013. Overview of Gaussian process regression methods. Control and Decision Making, 28: 1121-1129). He Z K, Liu G B, Zhao X J, et al. Overview of Gaussian process regression methods [J] Control and Decision Making, 2013, 28 (8): 1121 – 1129.
[6]	李家春. 1995. 现代流体力学发展的回顾与展望. 力学进展, 25: 442-450 (Li J C. 1995. Review and prospect of the development of modern fluid mechanics. Advances in Mechanics, 25: 442-450). doi: 10.6052/1000-0992-1995-4-J1995-002 LI J C. Review and prospect of the development of modern fluid mechanics [J]. Advances in Mechanics, 1995 (04): 442-450. doi: 10.6052/1000-0992-1995-4-J1995-002
[7]	任峰, 高传强, 唐辉. 2021. 机器学习在流动控制领域的应用及发展趋势. 航空学报, 42: 152-166 (Ren Feng, Gao Chuanqiang, Tang Hui. 2021. Application and development trend of machine learning in the field of flow control. Acta Aeronautica et Astronautica Sinica, 42: 152-166). Ren Feng, Gao Chuanqiang, Tang Hui. Application and development trend of machine learning in the field of flow control [J]. Acta Aeronautica et Astronautica Sinica, 2021, 42 (04): 152-166.
[8]	任海杰, 袁先旭, 陈坚强, 等. 2022. 宽速域下神经网络对雷诺应力各向异性张量的预测. 力学学报, 54: 347-358 (Haijie R, Xianxu Y, Jianqiang C, et al. 2022. Prediction of Reynolds stress anisotropic tensor by neural network within wide speed range. Chinese Journal of Theoretical and Applied Mechanics, 54: 347-358). doi: 10.6052/0459-1879-21-518 Haijie R, Xianxu Y, Jianqiang C, et al. Prediction of Reynolds stress anisotropic tensor by neural network within wide speed range[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(2): 347-358). doi: 10.6052/0459-1879-21-518
[9]	托马斯·库恩. 1962. 科学革命的结构. 芝加哥: 芝加哥大学出版社 Thomas Kuhn. 1962. The Structure of Scientific Revolutions. Chicago: University of Chicago Press.
[10]	王超, 王贵东, 白鹏. 2019. 飞行仿真气动力数据机器学习建模方法. 空气动力学学报, 37: 488-497 (Wang C, Wang G D, Bai P. 2019. Machine learning method for aerodynamic modeling based on flight simulation data. Acta Aerodynamica Sinica, 37: 488-497). Wang C, Wang G D, Bai P. Machine learning method for aerodynamic modeling based on flight simulation data[J]. Acta Aerodynamica Sinica, 2019, 37(3): 488-497.
[11]	王旭, 宁晨伽, 王文正, 等. 2023. 面向飞行试验的多源气动数据智能融合方法. 空气动力学学报, 41: 12-20 (Xu W, Chenjia N, Wenzheng W, et al. 2023. Intelligent fusion method of multi-source aerodynamic data for flight tests. Acta Aerodynamica Sinica, 41: 12-20). doi: 10.7638/kqdlxxb-2021.0428 Xu W, Chenjia N, Wenzheng W, et al. Intelligent fusion method of multi-source aerodynamic data for flight tests[J]. Acta Aerodynamica Sinica, 2023, 41(02): 12-20. ). doi: 10.7638/kqdlxxb-2021.0428
[12]	熊俊涛, 乔志德, 韩忠华. 2006. 基于响应面法的跨声速机翼气动优化设计. 航空学报, 27: 399-402
[13]	张伟伟, 寇家庆, 刘溢浪. 2021. 智能赋能流体力学展望. 航空学报, 42: 26-71 (Zhang W W, Kou J Q, Liu Y L. 2021. Prospect of intelligent energized hydrodynamics. Acta Aeronautica et Astronautica Sinica, 42: 26-71). ZHANG W W, KOU J Q, LIU Y L. Prospect of Intelligent Energized Hydrodynamics [J]. Acta Aeronautica et Astronautica Sinica, 2021, 42 (04): 26-71.
[14]	张亦知, 程诚, 范钇彤, 等. 2020. 基于物理知识约束的数据驱动式湍流模型修正及槽道湍流计算验证. 航空学报, 41: 123282 (Zhang Y Z, Cheng C, Fan Y T, et al. 2020. Data-driven correction of turbulence model with physics knowledge constrains in channel flow. Acta Aeronautica et Astronautica Sinica, 41: 123282). doi: 10.7527/S1000-6893.2019.23282 Zhang Y Z, Cheng C, Fan Y T, et al. Data-driven correction of turbulence model with physics knowledge constrains in channel flow [J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(3): 123282. doi: 10.7527/S1000-6893.2019.23282
[15]	赵凯琳, 靳小龙, 王元卓. 2021. 小样本学习研究综述. 软件学报, 32: 349-369 (Zhao Kailin, Jin Xiaolong, Wang Yuanzhuo. 2021. Summary of small sample learning research. Journal of Software, 32: 349-369). doi: 10.13328/j.cnki.jos.006138 Zhao Kailin, Jin Xiaolong, Wang Yuanzhuo. Summary of small sample learning research [J]. Journal of Software, 2021, 32 (02): 349-369). doi: 10.13328/j.cnki.jos.006138
[16]	赵旋, 彭绪浩, 邓子辰, 等. 2022. 基于多源数据融合的翼型表面压强精细化重构方法. 实验流体力学, 36: 93-101 (Xuan Z, Xuhao P, Zichen D, et al. 2022. Fine reconstruction method of airfoil surface pressure based on multi-source data fusion. Journal of Experiments in Fluid Mechanics, 36: 93-101). doi: 10.11729/syltlx20210166 Xuan Z, Xuhao P, Zichen D, et al. Fine reconstruction method of airfoil surface pressure based on multi-source data fusion[J]. Journal of Experiments in Fluid Mechanics, 2022, 36(3): 93-101). doi: 10.11729/syltlx20210166
[17]	Alfonsi G. 2009. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Applied Mechanics Reviews, 62: 040802. doi: 10.1115/1.3124648
[18]	Anderson J D, Wendt J. 1995. Computational Fluid Dynamics. New York: McGraw-Hill.
[19]	Anderson J D. 2005. Ludwig Prandtl’s boundary layer. Physics Today, 58: 42-48. doi: 10.1063/1.2169443
[20]	Andrés E, Salcedo-Sanz S, Monge F, et al. 2012. Efficient aerodynamic design through evolutionary programming and support vector regression algorithms. Expert Systems with Applications, 39: 10700-10708. doi: 10.1016/j.eswa.2012.02.197
[21]	Baldwin B, Lomax H. 1978. Thin-layer approximation and algebraic model for separated turbulentflows//16th Aerospace Sciences Meeting.
[22]	Batten P, Craft T J, Leschziner M A, et al. 1999. Reynolds-stress-transport modeling for compressible aerodynamics applications. AIAA Journal, 37: 785-797. doi: 10.2514/2.801
[23]	Beck A D, Zeifang J, Schwarz A, et al. 2020. A neural network based shock detection and localization approach for discontinuous Galerkin methods. Journal of Computational Physics, 423: 109824. doi: 10.1016/j.jcp.2020.109824
[24]	Bhattacharya K, Hosseini B, Kovachki N B, et al. 2021. Model reduction and neural networks for parametric PDEs. Journal of Computational Mathematics, 7: 121-157. doi: 10.5802/smai-jcm.74
[25]	Buhendwa A B, Bezgin D A, Adams N A. 2022. Consistent and symmetry preserving data-driven interface reconstruction for the level-set method. Journal of Computational Physics, 457: 111049. doi: 10.1016/j.jcp.2022.111049
[26]	Cai S, Wang Z, Fuest F, et al. 2021. Flow over an espresso cup: inferring 3-D velocity and pressure fields from tomographic background oriented Schlieren via physics-informed neural networks. Journal of Fluid Mechanics, 915: A102. doi: 10.1017/jfm.2021.135
[27]	Cai S, Wang Z, Lu L, et al. 2021. DeepM&Mnet: Inferring the electroconvection multiphysics fields based on operator approximation by neural networks. Journal of Computational Physics, 436: 110296. doi: 10.1016/j.jcp.2021.110296
[28]	Cai S, Zhou S, Xu C, et al. 2019. Dense motion estimation of particle images via a convolutional neural network. Experiments in Fluids, 60: 1-16. doi: 10.1007/s00348-018-2646-5
[29]	Chaouat B. 2006. Reynolds stress transport modeling for high-lift airfoil flows. AIAA Journal, 44: 2390-2403. doi: 10.2514/1.21228
[30]	Chen S, Doolen G D. 1998. Lattice Boltzmann method for fluid flows. Annual review of fluid mechanics, 30: 329-364. doi: 10.1146/annurev.fluid.30.1.329
[31]	Chen T, Chen H. 1995. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Transactions on Neural Networks, 6: 911-917. doi: 10.1109/72.392253
[32]	Chen X, Yang G, Yao Q, et al. 2021. A compressed lattice Boltzmann method based on ConvLSTM and ResNet. Computers & Mathematics with Applications, 97: 162-174.
[33]	Cheung S H, Oliver T A, Prudencio E E, et al. 2011. Bayesian uncertainty analysis with applications to turbulence modeling. Reliability Engineering & System Safety, 96: 1137-1149.
[34]	Constantin P, Foias C. 2020. Navier-stokes Equations. Chicago: University of Chicago Press.
[35]	Cowan T J, Arena Jr A S, Gupta K K. 2001. Accelerating computational fluid dynamics based aeroelastic predictions using system identification. Journal of Aircraft, 38: 81-87. doi: 10.2514/2.2737
[36]	De S, Doostan A. 2022. Neural network training using ℓ1-regularization and bi-fidelity data. Journal of Computational Physics, 458: 111010. doi: 10.1016/j.jcp.2022.111010
[37]	Deng Z, He C, Wen X, et al. 2018. Recovering turbulent flow field from local quantity measurement: turbulence modeling using ensemble-Kalman-filter-based data assimilation. Journal of Visualization, 21: 1043-1063. doi: 10.1007/s12650-018-0508-0
[38]	Discacciati N, Hesthaven J S, Ray D. 2020. Controlling oscillations in high-order discontinuous Galerkin schemes using artificial viscosity tuned by neural networks. Journal of Computational Physics, 409: 109304. doi: 10.1016/j.jcp.2020.109304
[39]	Duan Y, Cai J, Li Y. 2012. Gappy proper orthogonal decomposition-based two-step optimization for airfoil design. AIAA Journal, 50: 968-971. doi: 10.2514/1.J050997
[40]	Duraisamy K, Zhang Z J, Singh A P. 2015. New approaches in turbulence and transition modeling using data-driven techniques//53rd AIAA Aerospace sciences meeting.
[41]	Duriez T, Brunton S L, Noack B R. 2017. Machine Learning Control-Taming Nonlinear Dynamics and Turbulence. Switzerland: Springer International Publishing.
[42]	Duriez T, Parezanovic V, Laurentie J C, et al. Closed-loop control of experimental shear flows using machine learning//7th AIAA Flow Control Conference. 2014: 2219.
[43]	Edeling W N, Cinnella P, Dwight R P, et al. 2014. Bayesian estimates of parameter variability in the k–ε turbulence model. Journal of Computational Physics, 258: 73-94. doi: 10.1016/j.jcp.2013.10.027
[44]	Ekaterinaris J A, Platzer M F. 1998. Computational prediction of airfoil dynamic stall. Progress in aerospace sciences, 33: 759-846. doi: 10.1016/S0376-0421(97)00012-2
[45]	Fang R, Sondak D, Protopapas P, et al. 2020. Neural network models for the anisotropic Reynolds stress tensor in turbulent channel flow. Journal of Turbulence, 21: 525-543. doi: 10.1080/14685248.2019.1706742
[46]	Fukami K, Fukagata K, Taira K. 2019. Super-resolution reconstruction of turbulent flows with machine learning. Journal of Fluid Mechanics, 870: 106-120. doi: 10.1017/jfm.2019.238
[47]	Fukami K, Nakamura T, Fukagata K. 2020. Convolutional neural network based hierarchical autoencoder for nonlinear mode decomposition of fluid field data. Physics of Fluids, 32: 095110. doi: 10.1063/5.0020721
[48]	Galilei G. 1914. Two new sciences. Dover.
[49]	Gao C, Zhang W, Kou J, et al. 2017b. Active control of transonic buffet flow. Journal of Fluid Mechanics, 824: 312-351. doi: 10.1017/jfm.2017.344
[50]	Gao C, Zhang W, Li X, et al. 2017a. Mechanism of frequency lock-in in transonic buffeting flow. Journal of Fluid Mechanics, 818: 528-561. doi: 10.1017/jfm.2017.120
[51]	Gautier N, Aider J L, Duriez T, et al. 2015. Closed-loop separation control using machine learning. Journal of Fluid Mechanics, 770: 442-457. doi: 10.1017/jfm.2015.95
[52]	Geneva N, Zabaras N. 2020. Modeling the dynamics of PDE systems with physics-constrained deep auto-regressive networks. Journal of Computational Physics, 403: 109056. doi: 10.1016/j.jcp.2019.109056
[53]	Geneva N, Zabaras N. 2019. Quantifying model form uncertainty in Reynolds-averaged turbulence models with Bayesian deep neural networks. Journal of Computational Physics, 383: 125-147. doi: 10.1016/j.jcp.2019.01.021
[54]	Guastoni L, Encinar M P, Schlatter P, et al. 2020. Prediction of wall-bounded turbulence from wall quantities using convolutional neural networks//Journal of Physics: Conference Series. IOP Publishing 1522(1): 012022.
[55]	Gupta G, Xiao X, Bogdan P. 2021. Multiwavelet-based operator learning for differential equations. Advances in Neural Information Processing Systems, 34: 24048-24062.
[56]	Han J, Zhou X H, Xiao H. 2022. An equivariant neural operator for developing nonlocal tensorial constitutive models. arXiv, . doi: 10.48550/arXiv.2201.01287
[57]	Han Z H, Goertz S. 2012. Hierarchical Kriging Model for Variable-Fidelity Surrogate Modeling. AIAA Journal, 50: 1885-1896. doi: 10.2514/1.J051354
[58]	Han Z H, Zimmermann, Görtz S. 2012. Alternative cokriging method for variable-fidelity surrogate modeling. AIAA Journal, 50: 1205-1210. doi: 10.2514/1.J051243
[59]	Hartmann F, Katz C. 2004. Structural analysis with finite elements. Springer Science & Business Media.
[60]	Hey T, Tansley S, Tolle K M. 2009. Jim Gray on eScience: a transformed scientific method. The Fourth Paradigm, 17-31.
[61]	Hirt C W, Nichols B D. 1981. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 39: 201-225. doi: 10.1016/0021-9991(81)90145-5
[62]	Holierhoek J G, De Vaal J B, Van Zuijlen A H, et al. 2013. Comparing different dynamic stall models. Wind Energy, 16: 139-158. doi: 10.1002/we.548
[63]	Hu J W, Zhang W W. 2022. Mesh-Conv: Convolution operator with mesh resolution independence for flow field modeling. Journal of Computational Physics, 452: 110896. doi: 10.1016/j.jcp.2021.110896
[64]	Huang J, Liu H, Cai W. 2019. Online in situ prediction of 3-D flame evolution from its history 2-D projections via deep learning. Journal of Fluid Mechanics, 875: R2. doi: 10.1017/jfm.2019.545
[65]	Iuliano E, Quagliarella D. 2013. Proper orthogonal decomposition, surrogate modelling and evolutionary optimization in aerodynamic design. Computers & Fluids, 84: 327-350.
[66]	Jahangirian A, Shahrokhi A. 2011. Aerodynamic shape optimization using efficient evolutionary algorithms and unstructured CFD solver. Computers & Fluids, 46: 270-276.
[67]	Jiang Z, Tahmasebi P, Mao Z. 2021. Deep residual U-net convolution neural networks with autoregressive strategy for fluid flow predictions in large-scale geosystems. Advances in Water Resources, 150: 103878. doi: 10.1016/j.advwatres.2021.103878
[68]	Jin X, Cai S, Li H, et al. 2021. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. Journal of Computational Physics, 426: 109951. doi: 10.1016/j.jcp.2020.109951
[69]	Jones W P, Launder B E. 1973. The calculation of low-Reynolds-number phenomena with a two-equation model of turbulence. International Journal of Heat and Mass Transfer, 16: 1119-1130. doi: 10.1016/0017-9310(73)90125-7
[70]	Jones W P, Launder B E. 1972. The prediction of laminarization with a two-equation model of turbulence. International Journal of Heat and Mass Transfer, 15: 301-314. doi: 10.1016/0017-9310(72)90076-2
[71]	Jouhaud J C, Sagaut P, Montagnac M, et al. 2007. A surrogate-model based multidisciplinary shape optimization method with application to a 2D subsonic airfoil. Computers & Fluids, 36: 520-529.
[72]	Karpatne A, Watkins W, Read J, et al. 2017. Physics-guided neural networks (PGNN): An application in lake temperature modeling. arXiv Preprint arXiv: 1710.11431.
[73]	Karumuri S, Tripathy R, Bilionis I, et al. 2020. Simulator-free solution of high-dimensional stochastic elliptic partial differential equations using deep neural networks. Journal of Computational Physics, 404: 109120. doi: 10.1016/j.jcp.2019.109120
[74]	Kato H, Yoshizawa A, Ueno G, et al. 2015. A data assimilation methodology for reconstructing turbulent flows around aircraft. Journal of Computational Physics, 283: 559-581. doi: 10.1016/j.jcp.2014.12.013
[75]	Kawthar-Ali M, Acharya M. 1996. Artificial neural networks for suppression of the dynamic-stall vortex over pitching airfoils//34th Aerospace Sciences Meeting and Exhibit.
[76]	Kendall A, Gal Y, Cipolla R, et al. 2018. Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics. 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).
[77]	Kennedy M C, O'hagan A. 2001. Bayesian calibration of computer models. Journal of the Royal Statistical Society Series B-Statistical Methodology, 63: 425-450. doi: 10.1111/1467-9868.00294
[78]	Kloss C, Goniva C, Hager A, et al. 2012. Models, algorithms and validation for opensource DEM and CFD–DEM. Progress in Computational Fluid Dynamics, an International Journal, 12: 140-152.
[79]	Kou J, Ning C, Zhang W. 2022. Transfer Learning for Flow Reconstruction Based on Multifidelity Data. AIAA Journal, 60: 5821-5842. doi: 10.2514/1.J061647
[80]	Kou J, Zhang W. 2019. A hybrid reduced-order framework for complex aeroelastic simulations. Aerospace Science and Technology, 84: 880-894. doi: 10.1016/j.ast.2018.11.014
[81]	Kou J, Zhang W. 2017a. Layered reduced-order models for nonlinear aerodynamics and aeroelasticity. Journal of Fluids and Structures, 68: 174-193. doi: 10.1016/j.jfluidstructs.2016.10.011
[82]	Kou J, Zhang W. 2017b. Multi-kernel neural networks for nonlinear unsteady aerodynamic reduced-order modeling. Aerospace Science and Technology, 67: 309-326. doi: 10.1016/j.ast.2017.04.017
[83]	Kou J, Zhang W. 2018. Reduced-order modeling for nonlinear aeroelasticity with varying Mach numbers. Journal of Aerospace Engineering, 31: 04018105. doi: 10.1061/(ASCE)AS.1943-5525.0000932
[84]	Kovachki N, Lanthaler S, Mishra S. 2021. On Universal Approximation and Error Bounds for Fourier Neural Operators. Journal of Machine Learning Research, 22: 1-76.
[85]	Kurtulus D F. 2009. Ability to forecast unsteady aerodynamic forces of flapping airfoils by artificial neural network. Neural Computing and Applications, 18: 359-368. doi: 10.1007/s00521-008-0186-2
[86]	Kutz J N. 2013. Data-driven Modeling & Scientific Computation: Methods for Complex Systems & Big Data. London: Oxford University Press.
[87]	Kutz J N. 2017. Deep learning in fluid dynamics. Journal of Fluid Mechanics, 814: 1-4. doi: 10.1017/jfm.2016.803
[88]	Lagemann C, Lagemann K, Mukherjee S, et al. 2021. Deep recurrent optical flow learning for particle image velocimetry data. Nature Machine Intelligence, 3: 641-651. doi: 10.1038/s42256-021-00369-0
[89]	Lee C, Kim J, Babcock D, et al. 1997. Application of neural networks to turbulence control for drag reduction. Physics of Fluids, 9: 1740-1747. doi: 10.1063/1.869290
[90]	Leishman J G, Beddoes T S. 1989. A Semi‐Empirical model for dynamic stall. Journal of the American Helicopter Society, 34: 3-17.
[91]	Li B, Yang Z, Zhang X, et al. 2020. Using machine learning to detect the turbulent region in flow past a circular cylinder. Journal of Fluid Mechanics, 905: A10. doi: 10.1017/jfm.2020.725
[92]	Li K, Kou J, Zhang W. 2022. Deep learning for multifidelity aerodynamic distribution modeling from experimental and simulation data. AIAA Journal, 60: 4413-4427. doi: 10.2514/1.J061330
[93]	Li K, Kou J, Zhang W. 2019. Deep neural network for unsteady aerodynamic and aeroelastic modeling across multiple Mach numbers. Nonlinear Dynamics, 96: 2157-2177. doi: 10.1007/s11071-019-04915-9
[94]	Li W, Laima S, Jin X, et al. 2020. A novel long short-term memory neural-network-based self-excited force model of limit cycle oscillations of nonlinear flutter for various aerodynamic configurations. Nonlinear Dynamics, 100: 2071-2087. doi: 10.1007/s11071-020-05631-5
[95]	Li Y, Chang J, Wang Z, et al. 2019. Inversion and reconstruction of supersonic cascade passage flow field based on a model comprising transposed network and residual network. Physics of Fluids, 31: 126102. doi: 10.1063/1.5124133
[96]	Li Z, Kovachki N, Azizzadenesheli K, et al. Fourier neural operator for parametric partial differential equations. arXiv Preprint arXiv: 2010.08895, 2020.
[97]	Lin C, Maxey M, Li Z, et al. 2021. A seamless multiscale operator neural network for inferring bubble dynamics. Journal of Fluid Mechanics, 929: A18. doi: 10.1017/jfm.2021.866
[98]	Ling J, Kurzawski A, Templeton J. 2016. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. Journal of Fluid Mechanics, 807: 155-166. doi: 10.1017/jfm.2016.615
[99]	Liu Y, Cao W, Zhang W, et al. 2022. Analysis on numerical stability and convergence of Reynolds averaged Navier–Stokes simulations from the perspective of coupling modes. Physics of Fluids, 34: 015120. doi: 10.1063/5.0076273
[100]	Liu Y, Zhang W, Kou J. 2019. Mode multigrid-a novel convergence acceleration method. Aerospace Science and Technology, 92: 605-619. doi: 10.1016/j.ast.2019.06.001
[101]	Lu L, Jin P, Pang G, et al. 2021. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature Machine Intelligence, 3: 218-229. doi: 10.1038/s42256-021-00302-5
[102]	Luo C, Hu Z, Zhang S L, et al. 2015. Adaptive space transformation: An invariant based method for predicting aerodynamic coefficients of hypersonic vehicles. Engineering Applications of Artificial Intelligence, 46: 93-103. doi: 10.1016/j.engappai.2015.09.001
[103]	Luo S, Vellakal M, Koric S, et al. Parameter identification of RANS turbulence model using physics-embedded neural network. High Performance Computing: ISC High Performance 2020 International Workshops, Frankfurt, Germany, June 21–25, 2020, Revised Selected Papers, 2020: 137-149.
[104]	Markidis S. 2021. The old and the new: Can physics-informed deep-learning replace traditional linear solvers? Frontiers in big Data, 92.
[105]	McAlister K W, Carr L W, McCroskey W J. Dynamic stall experiments on the NACA 0012 airfoil. 1978.
[106]	Meng X, Babaee H, Karniadakis G E. 2021. Multi-fidelity Bayesian neural networks: Algorithms and applications. Journal of Computational Physics, 438: 110361. doi: 10.1016/j.jcp.2021.110361
[107]	Menter F R. 1994. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal, 32: 1598-1605. doi: 10.2514/3.12149
[108]	Menter F, Rumsey C. Assessment of two-equation turbulence models for transonic flows//Fluid Dynamics Conference. 1994: 2343.
[109]	Mifsud M, Vendl A, Hansen L U, et al. 2019. Fusing wind-tunnel measurements and CFD data using constrained gappy proper orthogonal decomposition. Aerospace Science and Technology, 86: 312-326. doi: 10.1016/j.ast.2018.12.036
[110]	Milano M, Koumoutsakos P. 2002. Neural network modeling for near wall turbulent flow. Journal of Computational Physics, 182: 1-26. doi: 10.1006/jcph.2002.7146
[111]	Mohammadi-Amin M, Entezari M M, Alikhani A. 2018. An efficient surrogate-based framework for aerodynamic database development of manned reentry vehicles. Advances in Space Research, 62: 997-1014. doi: 10.1016/j.asr.2018.06.022
[112]	Moin P, Mahesh K. 1998. Direct numerical simulation: a tool in turbulence research. Annual Review of Fluid Mechanics, 30: 539-578. doi: 10.1146/annurev.fluid.30.1.539
[113]	Monaghan J J. 2012. Smoothed particle hydrodynamics and its diverse applications. Annual Review of Fluid Mechanics, 44: 323-346. doi: 10.1146/annurev-fluid-120710-101220
[114]	Mons V, Chassaing J C, Sagaut P. 2017. Optimal sensor placement for variational data assimilation of unsteady flows past a rotationally oscillating cylinder. Journal of Fluid Mechanics, 823: 230-277. doi: 10.1017/jfm.2017.313
[115]	Murata T, Fukami K, Fukagata K. 2020. Nonlinear mode decomposition with convolutional neural networks for fluid dynamics. Journal of Fluid Mechanics, 882: A13. doi: 10.1017/jfm.2019.822
[116]	Newton I. The Principia: mathematical principles of natural philosophy[M]. Univ of California Press, 1999.
[117]	Omata N, Shirayama S. 2019. A novel method of low-dimensional representation for temporal behavior of flow fields using deep autoencoder. Aip Advances, 9: 015006. doi: 10.1063/1.5067313
[118]	Pan S J, Yang Q. 2010. A Survey on Transfer Learning. Ieee Transactions on Knowledge and Data Engineering, 22: 1345-1359. doi: 10.1109/TKDE.2009.191
[119]	Parussini L, Venturi D, Perdikaris P, et al. 2017. Multi-fidelity Gaussian process regression for prediction of random fields. Journal of Computational Physics, 336: 36-50. doi: 10.1016/j.jcp.2017.01.047
[120]	Perdikaris P, Venturi D, Royset J O, et al. 2015. Multi-fidelity modelling via recursive co-kriging and Gaussian–Markov random fields. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 471: 20150018. doi: 10.1098/rspa.2015.0018
[121]	Piomelli U. 1999. Large-eddy simulation: achievements and challenges. Progress in Aerospace Sciences, 35: 335-362. doi: 10.1016/S0376-0421(98)00014-1
[122]	Rabault J, Kuchta M, Jensen A, et al. 2019. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. Journal of Fluid Mechanics, 865: 281-302. doi: 10.1017/jfm.2019.62
[123]	Raissi M, Perdikaris P, Karniadakis G E. 2019a. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378: 686-707. doi: 10.1016/j.jcp.2018.10.045
[124]	Raissi M, Wang Z, Triantafyllou M S, et al. 2019b. Deep learning of vortex-induced vibrations. Journal of Fluid Mechanics, 861: 119-137. doi: 10.1017/jfm.2018.872
[125]	Raissi M, Yazdani A, Karniadakis G E. 2020. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science, 367: 1026-1030. doi: 10.1126/science.aaw4741
[126]	Rapaport D C, Rapaport D C R. The Art of Molecular Dynamics Simulation. Cambridge University Press, 2004.
[127]	Ray D, Hesthaven J S. 2019. Detecting troubled-cells on two-dimensional unstructured grids using a neural network. Journal of Computational Physics, 397: 108845. doi: 10.1016/j.jcp.2019.07.043
[128]	Ren F, Wang C, Tang H. 2021. Bluff body uses deep-reinforcement-learning trained active flow control to achieve hydrodynamic stealth. Physics of Fluids, 33: 093602. doi: 10.1063/5.0060690
[129]	Ren K, Chen Y, Gao C, et al. 2020. Adaptive control of transonic buffet flows over an airfoil. Physics of Fluids, 32: 096106. doi: 10.1063/5.0020496
[130]	Renganathan S A, Harada K, Mavris D N. 2020. Aerodynamic data fusion toward the digital twin paradigm. AIAA Journal, 58: 3902-3918. doi: 10.2514/1.J059203
[131]	Robinson D F, Harris J E, Hassan H A. 1995. Unified turbulence closure model for axisymmetric and planar free shear flows. AIAA Journal, 33: 2325-2331. doi: 10.2514/3.12987
[132]	Schlichting H, Gersten K. Boundary-layer Theory. Springer, 2016.
[133]	Sekar V, Jiang Q, Shu C, et al. 2019. Fast flow field prediction over airfoils using deep learning approach. Physics of Fluids, 31: 057103. doi: 10.1063/1.5094943
[134]	Shih T H, Liou W W, Shabbir A, et al. 1995. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Computers & fluids, 24: 227-238.
[135]	Silva W A. 1993. Application of nonlinear systems theory to transonic unsteady aerodynamic responses. Journal of Aircraft, 30: 660-668. doi: 10.2514/3.46395
[136]	Singh A P, Duraisamy K, Zhang Z J. Augmentation of turbulence models using field inversion and machine learning//55th AIAA Aerospace Sciences Meeting. 2017a: 0993.
[137]	Singh A P, Medida S, Duraisamy K. 2017b. Machine-learning-augmented predictive modeling of turbulent separated flows over airfoils. AIAA Journal, 55: 2215-2227. doi: 10.2514/1.J055595
[138]	Spalart P, Allmaras S. A one-equation turbulence model for aerodynamic flows//30th Aerospace Sciences Meeting and Exhibit. 1992: 439.
[139]	Sun L, Gao H, Pan S, et al. 2020. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Computer Methods in Applied Mechanics and Engineering, 361: 112732. doi: 10.1016/j.cma.2019.112732
[140]	Sun S, Liu S, Liu J, et al. 2018. Wind field reconstruction using inverse process with optimal sensor placement. IEEE Transactions on Sustainable Energy, 10: 1290-1299.
[141]	Sun X, Cao W, Liu Y, et al. 2022. High Reynolds number airfoil turbulence modeling method based on machine learning technique. Computers & Fluids, 236: 105298.
[142]	Tan S, Liu Y, Kou J, et al. 2021. Improved mode multigrid method for accelerating turbulence flows. AIAA Journal, 59: 3012-3024.
[143]	Tang M, Liu Y, Durlofsky L J. 2020. A deep-learning-based surrogate model for data assimilation in dynamic subsurface flow problems. Journal of Computational Physics, 413: 109456. doi: 10.1016/j.jcp.2020.109456
[144]	Tipping M E. Bayesian inference: An introduction to principles and practice in machine learning. Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2-14, 2003, Tübingen, Germany, August 4-16, 2003, Revised Lectures, 2004: 41-62.
[145]	Tracey B D, Duraisamy K, Alonso J J. A machine learning strategy to assist turbulence model development//53rd AIAA Aerospace Sciences Meeting. 2015: 1287.
[146]	Tran C T, Petot D. Semi-empirical model for the dynamic stall of airfoils in view of the application to the calculation of responses of a helicopter blade in forward flight[J]. ONERA TP, 103-1980.
[147]	Udrescu S M, Tegmark M. 2020. AI Feynman: A physics-inspired method for symbolic regression. Science Advances, 6: eaay2631. doi: 10.1126/sciadv.aay2631
[148]	Venturi D, Karniadakis G E. 2004. Gappy data and reconstruction procedures for flow past a cylinder. Journal of Fluid Mechanics, 519: 315-336. doi: 10.1017/S0022112004001338
[149]	Voet L J A, Ahlfeld R, Gaymann A, et al. 2021. A hybrid approach combining DNS and RANS simulations to quantify uncertainties in turbulence modelling. Applied Mathematical Modelling, 89: 885-906. doi: 10.1016/j.apm.2020.07.056
[150]	Von Karman T. 1948. Progress in the statistical theory of turbulence. Proceedings of the National Academy of Sciences, 34: 530-539. doi: 10.1073/pnas.34.11.530
[151]	von Kármán T. 1940. The engineer grapples with nonlinear problems. Bulletin of the American Mathematical Society, 46: 615-683. doi: 10.1090/S0002-9904-1940-07266-0
[152]	Wang H, Liu Y, Wang S. 2022. Dense velocity reconstruction from particle image velocimetry/particle tracking velocimetry using a physics-informed neural network. Physics of Fluids, 34: 017116. doi: 10.1063/5.0078143
[153]	Wang H, Zhu X, Du Z. 2010. Aerodynamic optimization for low pressure turbine exhaust hood using Kriging surrogate model. International Communications in Heat and Mass Transfer, 37: 998-1003. doi: 10.1016/j.icheatmasstransfer.2010.06.022
[154]	Wang J X, Wu J L, Xiao H. 2017. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Physical Review Fluids, 2: 034603. doi: 10.1103/PhysRevFluids.2.034603
[155]	Wang S, Teng Y, Perdikaris P. 2021. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. Siam Journal on Scientific Computing, 43: A3055-A3081. doi: 10.1137/20M1318043
[156]	Wang S, Yu X, Perdikaris P. 2022. When and why PINNs fail to train: A neural tangent kernel perspective. Journal of Computational Physics, 449: 110768. doi: 10.1016/j.jcp.2021.110768
[157]	Wang X, Kou J, Zhang W, et al. 2022. Incorporating physical models for dynamic stall prediction based on machine learning. AIAA Journal, 60: 4428-4439. doi: 10.2514/1.J061210
[158]	Wang X, Kou J, Zhang W. 2021. A new dynamic stall prediction framework based on symbiosis of experimental and simulation data. Physics of Fluids, 33: 127119. doi: 10.1063/5.0075083
[159]	Wang Z, Luo K, Li D, et al. 2018b. Investigations of data-driven closure for subgrid-scale stress in large-eddy simulation. Physics of Fluids, 30: 125101. doi: 10.1063/1.5054835
[160]	Wang Z, Zhang W, Wu X, et al. 2018a. A novel unsteady aerodynamic Reduced-Order Modeling method for transonic aeroelastic optimization. Journal of Fluids and Structures, 82: 308-328. doi: 10.1016/j.jfluidstructs.2018.07.001
[161]	Wei S, Jin X, Li H. 2019. General solutions for nonlinear differential equations: a rule-based self-learning approach using deep reinforcement learning. Computational Mechanics, 64: 1361-1374. doi: 10.1007/s00466-019-01715-1
[162]	Weiss K, Khoshgoftaar T M, Wang D. 2016. A survey of transfer learning. Journal of Big Data, 3: 1-40. doi: 10.1186/s40537-015-0036-x
[163]	Wilcox D, Traci R. A complete model of turbulence//9th Fluid and Plasma Dynamics Conference. 1976: 351.
[164]	Winter M, Breitsamter C. 2016. Neurofuzzy-model-based unsteady aerodynamic computations across varying freestream conditions. AIAA Journal, 54: 2705-2720. doi: 10.2514/1.J054892
[165]	Wu J L, Xiao H, Paterson E. 2018. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Physical Review Fluids, 3: 074602. doi: 10.1103/PhysRevFluids.3.074602
[166]	Xiao H, Wang J X, Ghanem R G. 2017. A random matrix approach for quantifying model-form uncertainties in turbulence modeling. Computer Methods in Applied Mechanics and Engineering, 313: 941-965. doi: 10.1016/j.cma.2016.10.025
[167]	Xie C, Wang J, Li H, et al. 2019. Artificial neural network mixed model for large eddy simulation of compressible isotropic turbulence. Physics of Fluids, 31: 085112. doi: 10.1063/1.5110788
[168]	Yan X, Zhu J, Kuang M, et al. 2019. Aerodynamic shape optimization using a novel optimizer based on machine learning techniques. Aerospace Science and Technology, 86: 826-835. doi: 10.1016/j.ast.2019.02.003
[169]	Yin Y, Yang P, Zhang Y, et al. 2020. Feature selection and processing of turbulence modeling based on an artificial neural network. Physics of Fluids, 32: 105117. doi: 10.1063/5.0022561
[170]	Zhang K, Zuo Y, Zhao H, et al. 2022. Fourier neural operator for solving subsurface oil/water two-phase flow partial differential equation. Spe Journal, 27: 1815-1830. doi: 10.2118/209223-PA
[171]	Zhang W, Wang B, Ye Z, et al. 2012. Efficient method for limit cycle flutter analysis based on nonlinear aerodynamic reduced-order models. AIAA Journal, 50: 1019-1028. doi: 10.2514/1.J050581
[172]	Zhang Y, Han Z-H, Zhang K-S. 2018. Variable-fidelity expected improvement method for efficient global optimization of expensive functions. Structural and Multidisciplinary Optimization, 58: 1431-1451. doi: 10.1007/s00158-018-1971-x
[173]	Zhang Z J, Duraisamy K. Machine learning methods for data-driven turbulence modeling//22nd AIAA Computational Fluid Dynamics Conference. 2015: 2460.
[174]	Zhao L, Li Z, Wang Z, et al. 2021. Active-and transfer-learning applied to microscale-macroscale coupling to simulate viscoelastic flows. Journal of Computational Physics, 427: 110069. doi: 10.1016/j.jcp.2020.110069
[175]	Zhao Y, Akolekar H D, Weatheritt J, et al. 2020. RANS turbulence model development using CFD-driven machine learning. Journal of Computational Physics, 411: 109413. doi: 10.1016/j.jcp.2020.109413
[176]	Zhou Q, Wu Y, Guo Z, et al. 2020. A generalized hierarchical co-Kriging model for multi-fidelity data fusion. Structural and Multidisciplinary Optimization, 62: 1885-1904. doi: 10.1007/s00158-020-02583-7
[177]	Zhou Z, He G, Wang S, et al. 2019. Subgrid-scale model for large-eddy simulation of isotropic turbulent flows using an artificial neural network. Computers & Fluids, 195: 104319.
[178]	Zhu L, Zhang W, Kou J, et al. 2019. Machine learning methods for turbulence modeling in subsonic flows around airfoils. Physics of Fluids, 31: 015105. doi: 10.1063/1.5061693
[179]	Zhu L, Zhang W, Sun X, et al. 2021. Turbulence closure for high Reynolds number airfoil flows by deep neural networks. Aerospace Science and Technology, 110: 106452. doi: 10.1016/j.ast.2020.106452
[180]	Zhu Y, Zabaras N, Koutsourelakis P S, et al. 2019. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. Journal of Computational Physics, 394: 56-81. doi: 10.1016/j.jcp.2019.05.024