Review on research progress of nonlinear vibration isolation and time-delayed suppression method
-
摘要: 振动问题与人类日常生活和科技发展紧密相关. 振动不但会干扰人类的生活、影响人类健康, 也会造成建筑物、机械设备和精密仪器无法正常使用甚至损坏. 于是, 在航空航天、汽车工程、船舶工程、大型结构及精密仪器加工等领域, 人们利用弹性元件或控制装置形成有效的振动隔离或消除装备, 有效的隔振能够提高人员和装备的安全性、稳定性、可控性和舒适性. 现代结构的大型化和复杂化发展, 对隔振和消振器的宽频抑振效果提出了新挑战. 然而, 基于线性理论的设计优化方法在分析和应用中出现了无法调和的矛盾, 即, 如果要拓宽隔振频带, 就必须降低隔振结构的刚度, 这导致结构承载能力下降. 本文对典型的非线性隔振器高静低动设计方法、动力学建模、动力学分析进行了详细的综述, 阐明不同机理下呈现的恢复力本构和准零刚度设计准则, 在面向航空航天、精密加工、汽车船舶等领域的不同需求时, 能够从动力学特征上进行选型; 另外, 关注到基于仿生和超结构的隔振和消振设计方法, 在非线性恢复力本构的力学机理解释和调控上产生了新的问题和挑战, 引发出变刚度、大变形动力学分析及其控制新方法、新策略和实验新技术的研究; 最后, 随着结构零部件向着轻质化和柔性化的方向发展, 运动部件末端的隔振效果受限于部件的柔性, 即使通过耦合多层准零刚度结构也难以实现被隔结构在空间上的快速定位, 关注到时滞控制的调幅调频机理, 本文对时滞抑振原理及设计方法进行讨论, 提供时滞抑制柔性低频振动成功案例, 为极端工况下的有效、简单、快速的主动隔振消振提供了可能性. 未来, 基于大数据时代的数据密集型研究范式, 非线性隔振和消振技术将面向复杂工况实现更精确、更智能的控制效果, 在精密仪器、航空航天等国家重大需求领域实现泛化应用.Abstract: Vibration problem is closely related to human daily life and the development of science and technology. Undersigned vibration would affect human health, also cause the failure of buildings, mechanical equipment and precision instruments. In the fields of aerospace, automotive engineering, marine engineering, large structure and precision instrument processing, elastic components or control devices are utilized to form effective vibration isolation environment. Effective vibration isolation can improve the safety, stability, controllability and comfort of human and equipment. However, the design method based on linear theory appears irreconcilable contradiction for applications. The stiffness of the vibration isolation structure reduces for wider band for vibration isolation, which results the decrease of loading capacity. In this paper, the high-static-low-dynamic design methods of nonlinear vibration isolators are reviewed in detail. Based on the dynamic modeling and analysis of nonlinearity induced by different mechanisms, the quasi-zero stiffness design criteria are presented, which provides the selection principle of the kind of isolator in aerospace, precision machining, automobile and ship. Then, attentions are paid on the design methods of bionics and metastructure for vibration suppression, which causes new problems and challenges in the explanation on mechanical bionic mechanism and regulation on the nonlinear restoring force constitutive. The studies on new methods, strategies and experimental techniques are introduced. Finally, faced to the development of light-weight and flexibility of structures, the vibration isolation effect is limited by the flexibility of parts. Even through coupling multi-layer quasi-zero-stiffness structures are assembled, it is difficult to realize the rapid positioning of the isolated structure in space. Considering the amplitude and frequency modulation by time delay, different design methods of vibration suppression with time delay are proposed. Successful cases of time-delayed suppression of flexible low-frequency vibration are given, which provides a possibility for effective, simple and rapid active vibration isolation and vibration elimination under extreme working conditions. In the future, based on the new analysis method according to data-driven, the nonlinear vibration isolation and suppression technology would realize more accurate and intelligent control effect in complex working conditions.
-
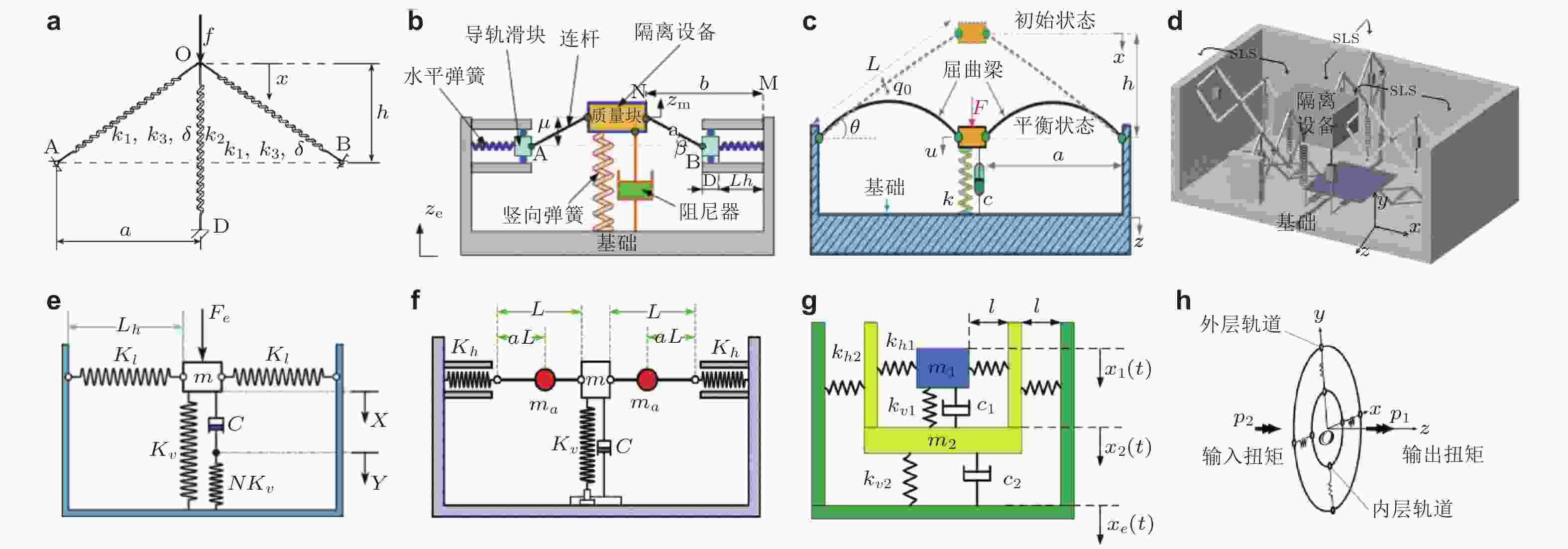
图 2 几类三弹簧设计准零刚度隔振器原理图(Lee & Goverdovski 2012)
图 3 几类三弹簧设计准零刚度非线性隔振器的结构简图及拓展设计. (a)通过水平方向弹簧预压实现负刚度 (Kovacic et al. 2008), (b)水平方向弹簧串联连杆增大负刚度效果(Le & Ahn 2013), (c)屈曲梁实现负刚度 (Liu X T et al. 2013), (d)利用菱形机构实现负刚度(Sun & Jing 2015), (e)考虑串并联阻尼的三弹簧隔振器(Liu C R et al. 2020a), (f) 增加附加小球的三弹簧准零刚度隔振器(Liu C R et al. 2021a), (g)具有三弹簧设计二级隔振模型 (Lu et al. 2017), (h)三弹簧设计的径向扭转准零刚度隔振器(Miyasato et al. 2021)
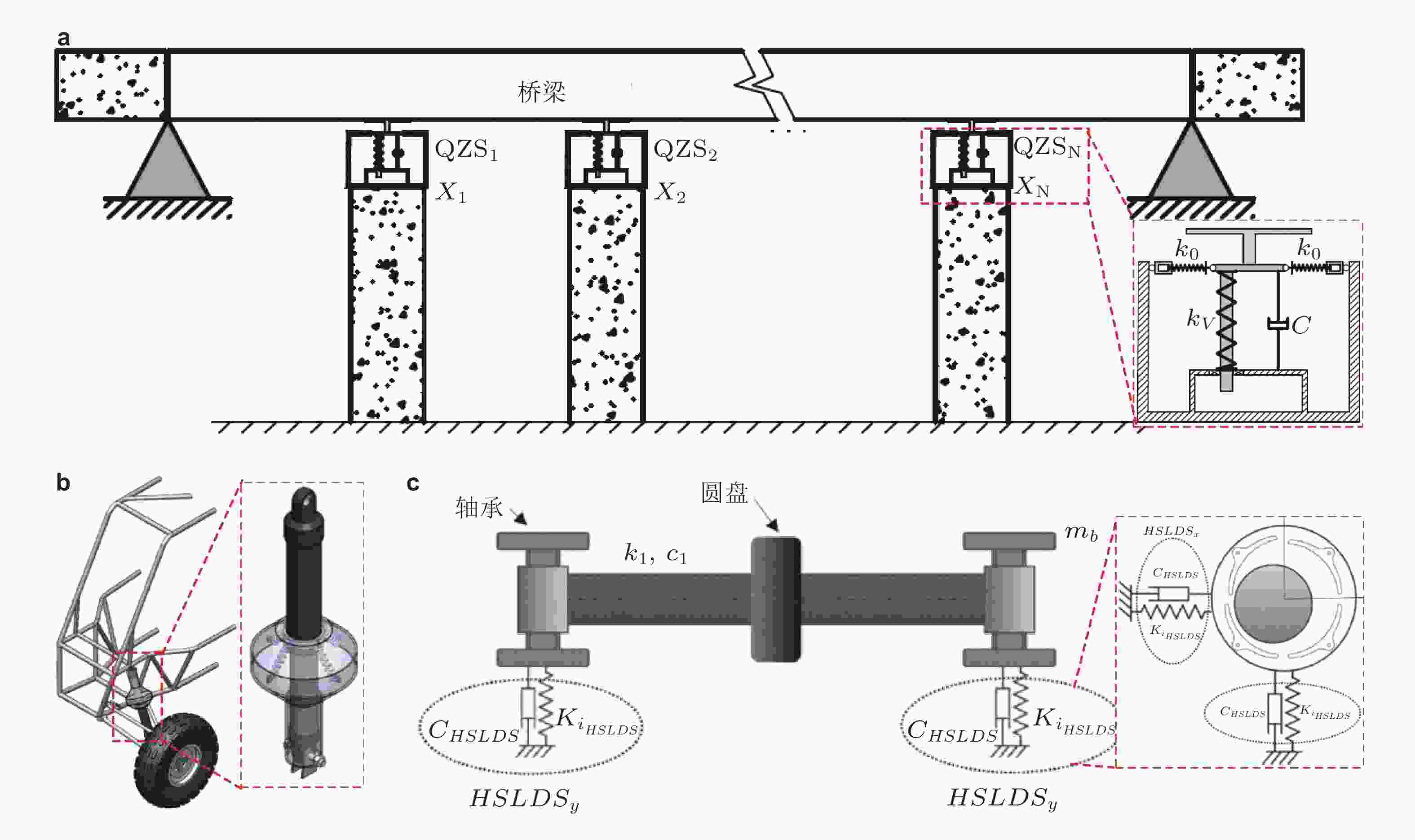
图 4 三弹簧隔振器的高静低动特性应用. (a)三弹簧准零刚度隔振器作为桥梁支座(Bouna et al. 2020), (b)三弹簧隔振器作为汽车悬挂系统(Suman et al. 2021), (c)三弹簧隔振器作为转子系统弹性支座(Abbasi et al. 2021)
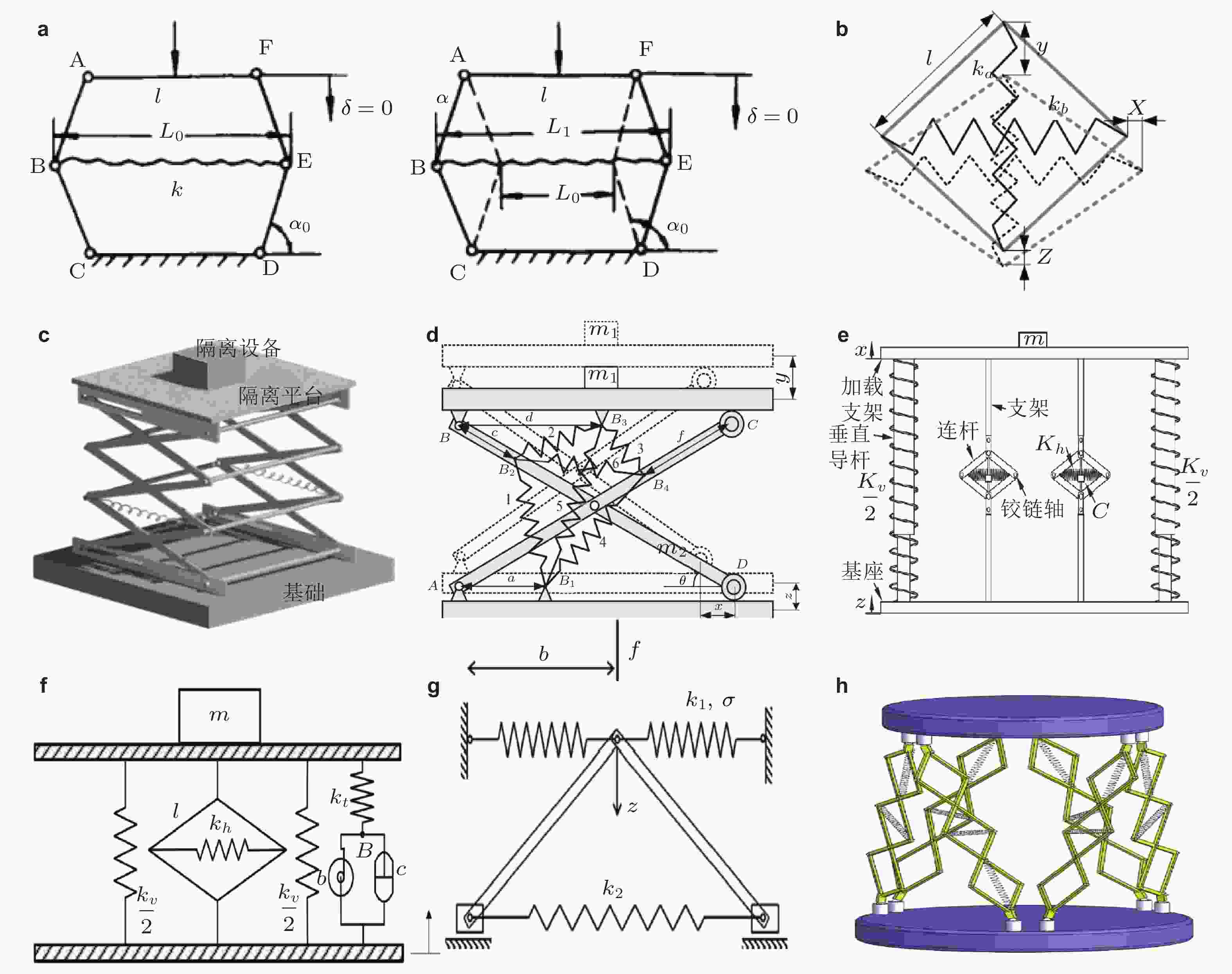
图 5 典型的复合型三弹簧准零刚度隔振器. (a) 嵌套型三弹簧准零刚度隔振器及其宽幅零刚度特性(Wang K et al. 2020), (b) 连杆嵌套三弹簧准零刚度隔振器及其宽幅零刚度特性(Yang et al. 2021a), (c) 空间多组斜弹簧布置的准零刚度隔振器(徐道临 等 2014), (d)四弹簧准零刚度隔振器(Gatti 2020), (e)多组斜弹簧准零刚度隔振器(Zhao et al. 2020, 2021), (f)斜向连杆框架型负刚度隔振设备(张也 等 2018)
图 6 多连杆多弹簧单方向/多方向准零刚度隔振器.(a)负刚度的产生(彭献 等 1997), (b)装配水平和竖直两方向弹簧的菱形机构(陈然 2019), (c)剪刀型隔振平台(Sun XT et al. 2014a), (d)装配多组弹性元件的剪刀型隔振平台(Zhang W & Zhao JB 2016), (e)菱形机构与竖向正刚度并联形成的准零刚度隔振平台(姚国 等 2020), (f)菱形机构并联竖向弹簧、阻尼器和控制器形成隔振平台(Wang Y et al. 2021), (g)连杆和弹簧串并联形成非线性隔振器(Gatti 2021), (h)利用菱形机构形成六自由度稳定平台(Wang X et al. 2020)
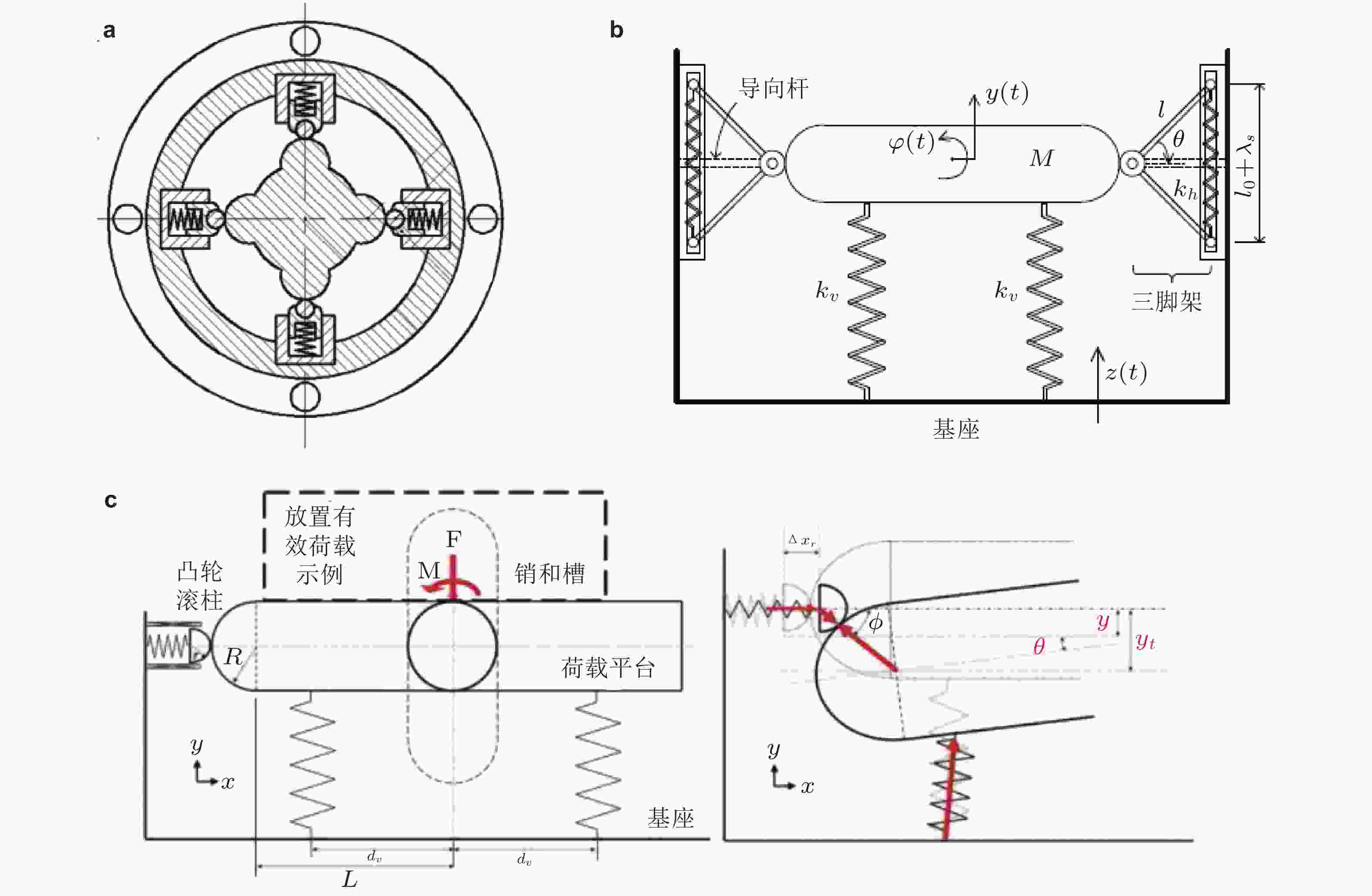
图 7 几类凸轮−滚子型的分段准零刚度隔振器. (a)凸轮滚子形成准零刚度隔振器(王毅 等 2015, 周加喜 等 2015, Zhou et al. 2015a), (b)融合连杆机构和凸轮滚子的准零刚度隔振器(Sun et al. 2018b), (c)串联气动弹簧的凸轮滚子分段准零刚度隔振器(Vo et al. 2021, Vo & Le 2022), (d)具有可设计接触曲面的凸轮滚子隔振器(Li M et al. 2020), (e)三弹簧链杆融合凸轮滚子的准零刚度隔振器(Zhang Y L et al. 2021), (f)凸轮约束曲面的高阶准零刚度隔振设计方法(Wang & Wang, 2022), (g)不倒翁原理的滚轮隔振结构(Yan B et al. 2022b), (h)多个凸轮构成的变刚度隔振器及其阶梯式高静低动特性(Ye et al. 2020), (i)水平方向布置耗散元件的准零刚度隔振器(Donmez et al. 2020)
图 8 凸轮滚子扭转方向准零刚度隔振装置. (a)凸轮滚子设计的扭转隔振器(Zhou et al. 2015b), (b) 融合叉形结构和凸轮滚子两方向隔振平台(孙秀婷和富展展 2018), (c)凸轮滚子摆振−颠振两方向隔振平台(Ye et al. 2021)
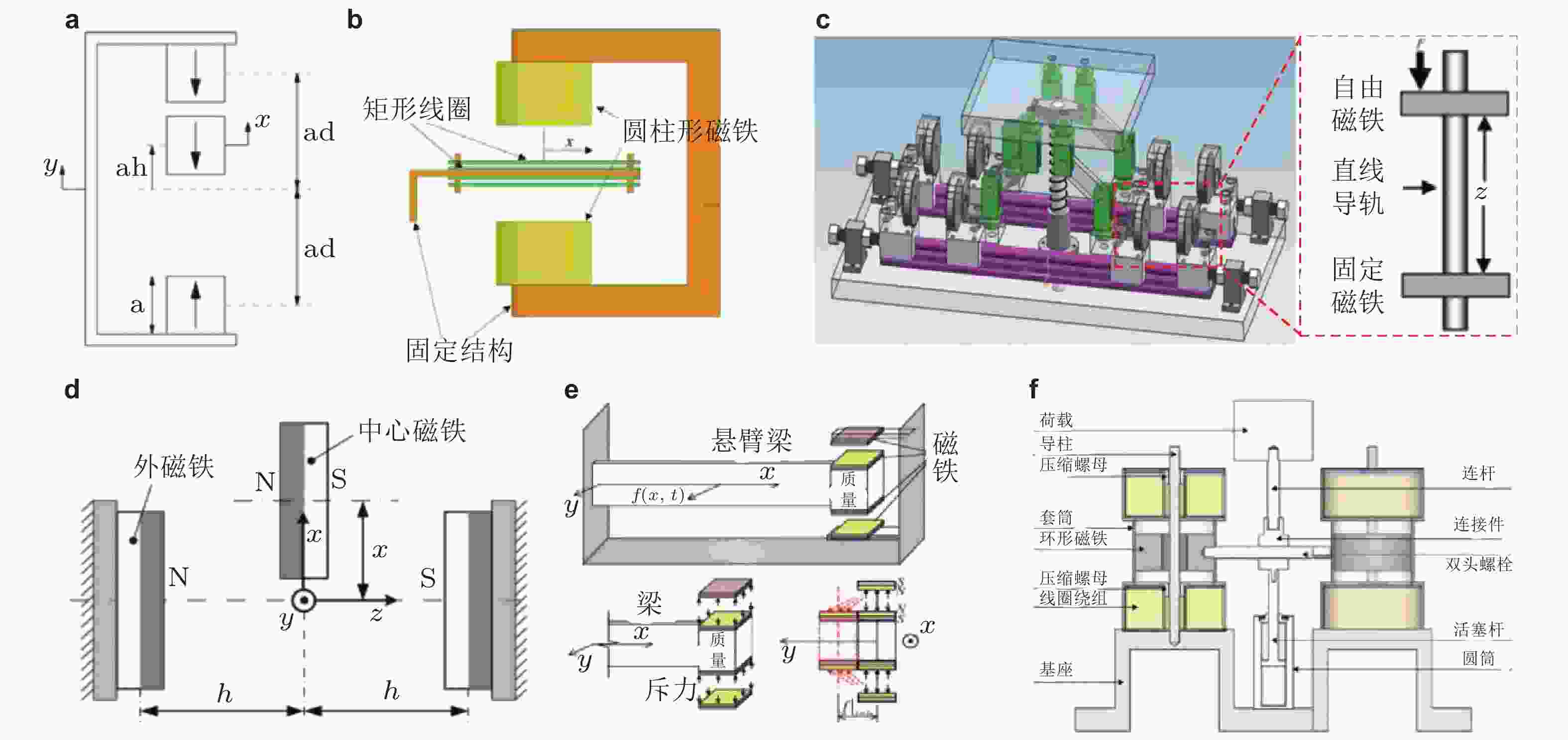
图 9 利用磁效应实现非线性隔振器. (a) 通过磁场实现低频隔振器(Carrella et al. 2008), (b)电磁场设计准零刚度隔振器(Chen et al. 2021), (c)磁铁连杆串联设计的准零刚度隔振平台(Xu et al. 2013), (d)两对磁铁形成负刚度特性原理图(Wu W et al. 2014), (e)磁铁并联连续梁形成准零刚度隔振器(Sun X T et al. 2019a), (f)环形磁铁套筒装配形成准零刚度隔振器(Xie et al. 2022)
图 10 磁体负刚度多方向高静低动隔振平台. (a)应用于婴儿转运车的磁力准零刚度隔振平台(Wang Q et al. 2020), (b)利用磁力负刚度构建的Stewart隔振平台(Zheng et al. 2018), (c)应用于空间天线的电磁双稳态隔振器(Yan B et al. 2022a), (d)电磁弹簧与三弹簧准零刚度构型混合的隔振平台(Jiang et al. 2020)
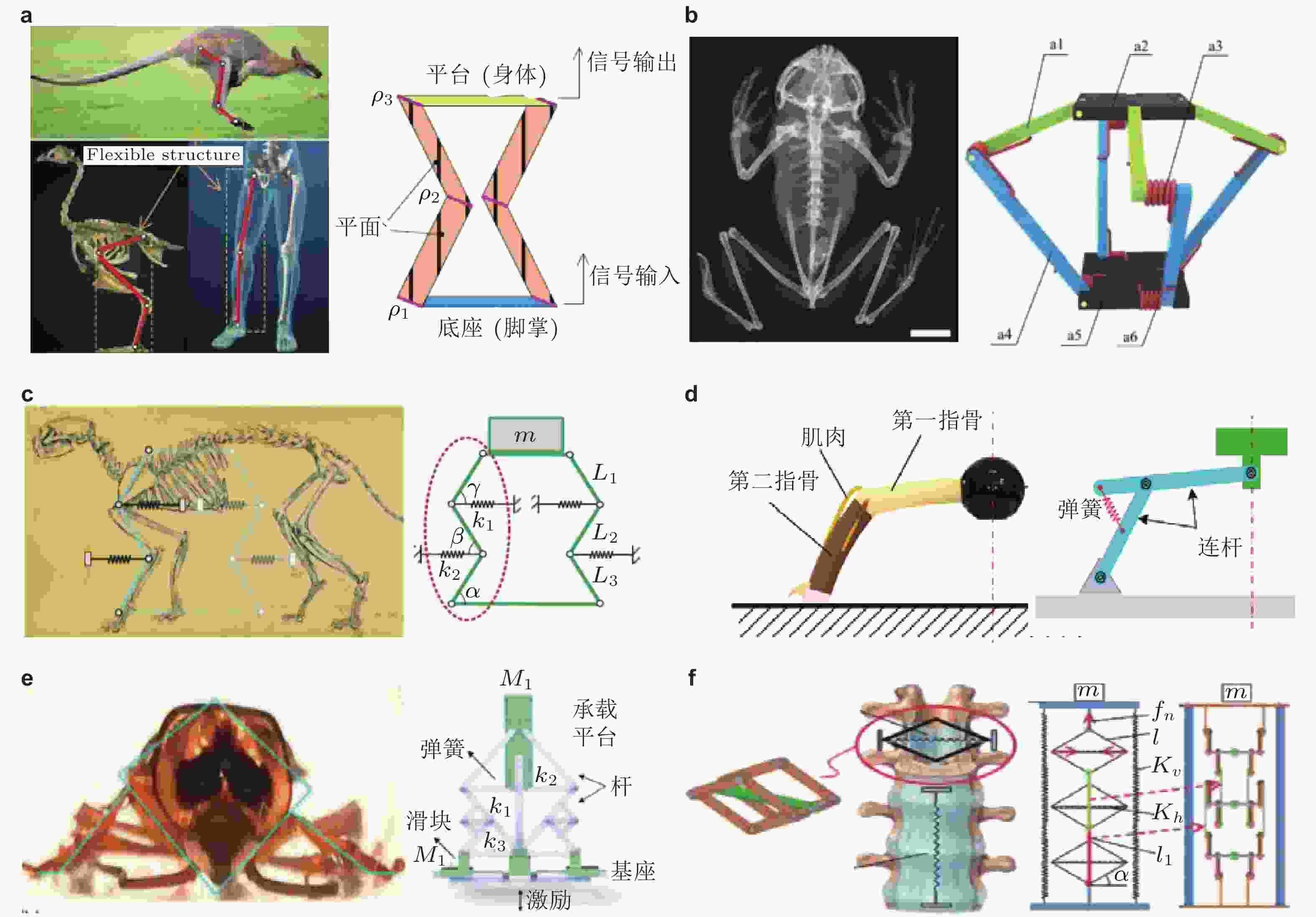
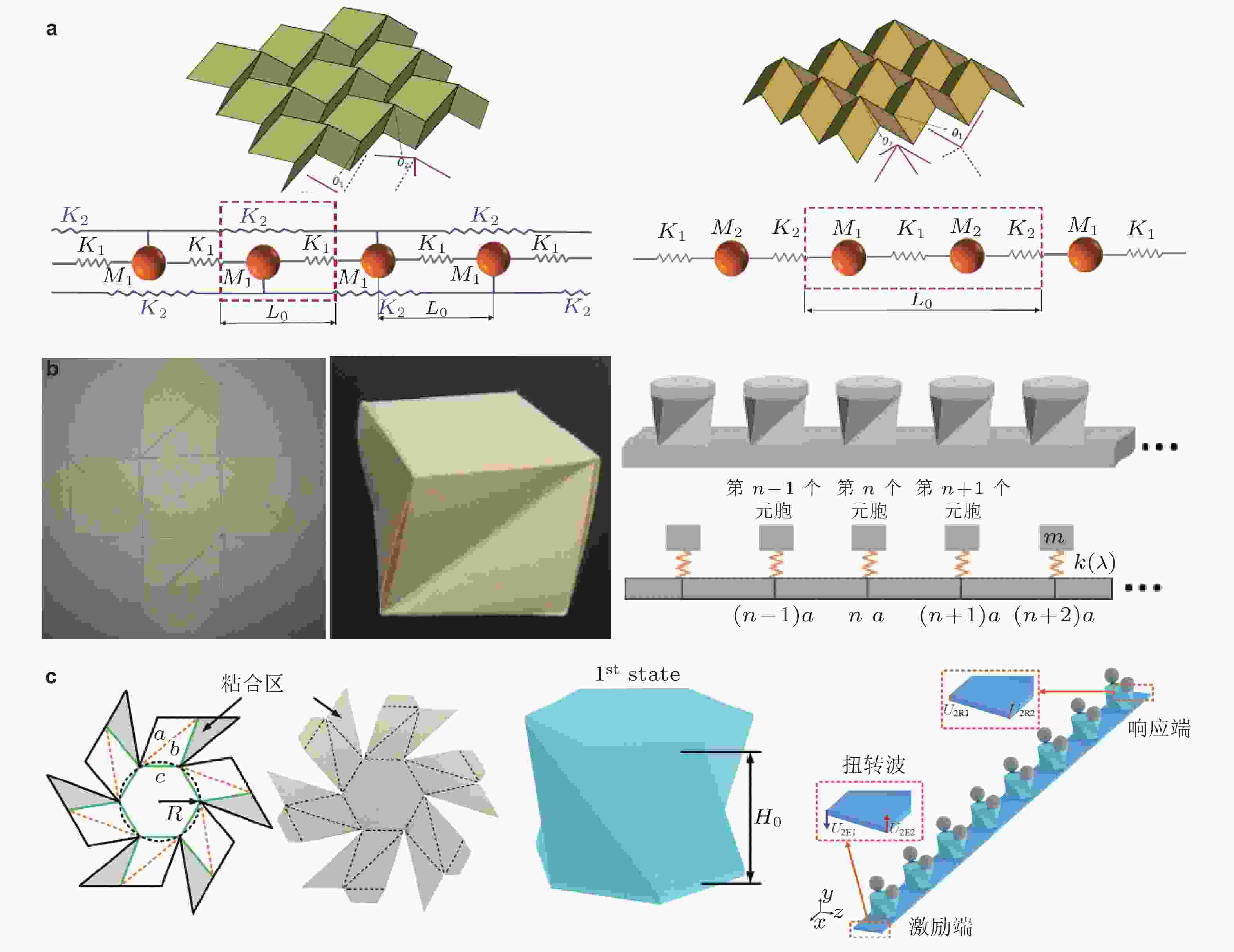
图 11 仿动物单自由度非线性隔振器. (a)仿腿部构型的隔振元胞(Sun et al. 2018a), (b)仿青蛙腿部的隔振单元(Zeng et al. 2021), (c)仿猫腿构型的隔振器连杆仿生机理(Yan G et al. 2020a), (d)仿猫爪构型隔振器力学模型(Yan G et al. 2022a), (e)仿蟑螂身体和腿部的多连杆隔振器(Ling et al. 2022), (f)仿脊椎的多层串联菱形连杆非线性隔振器(Jin et al. 2022)
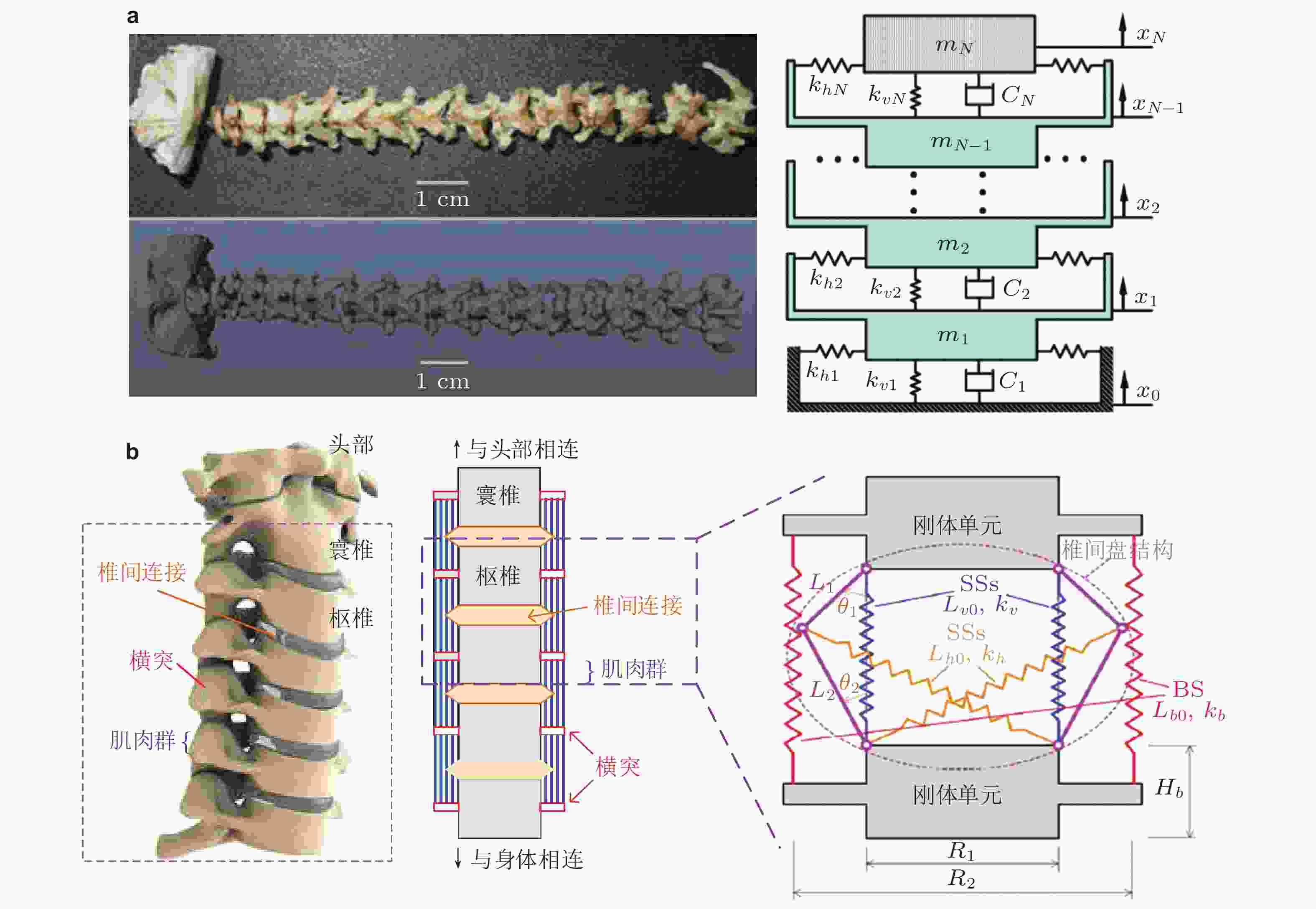
图 12 仿禽类颈部的多层隔振器仿生机理及力学原理图. (a)仿一类鸟脖子的多层准零刚度隔振器(Deng et al. 2020), (b)仿脖子的多层隔振结构及标准单元结构图(Sun X T et al. 2021, Sun X T et al. 2022)
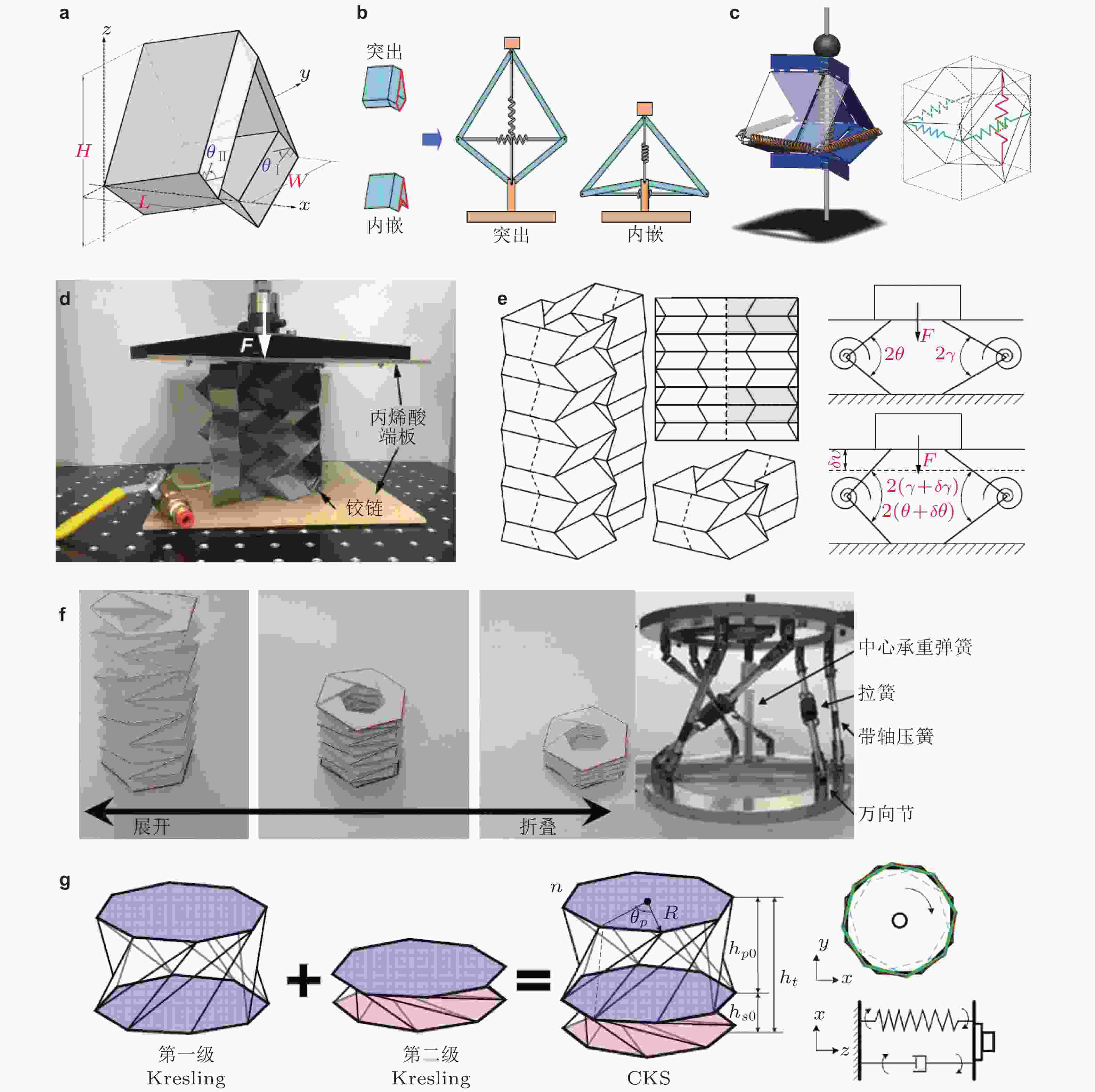
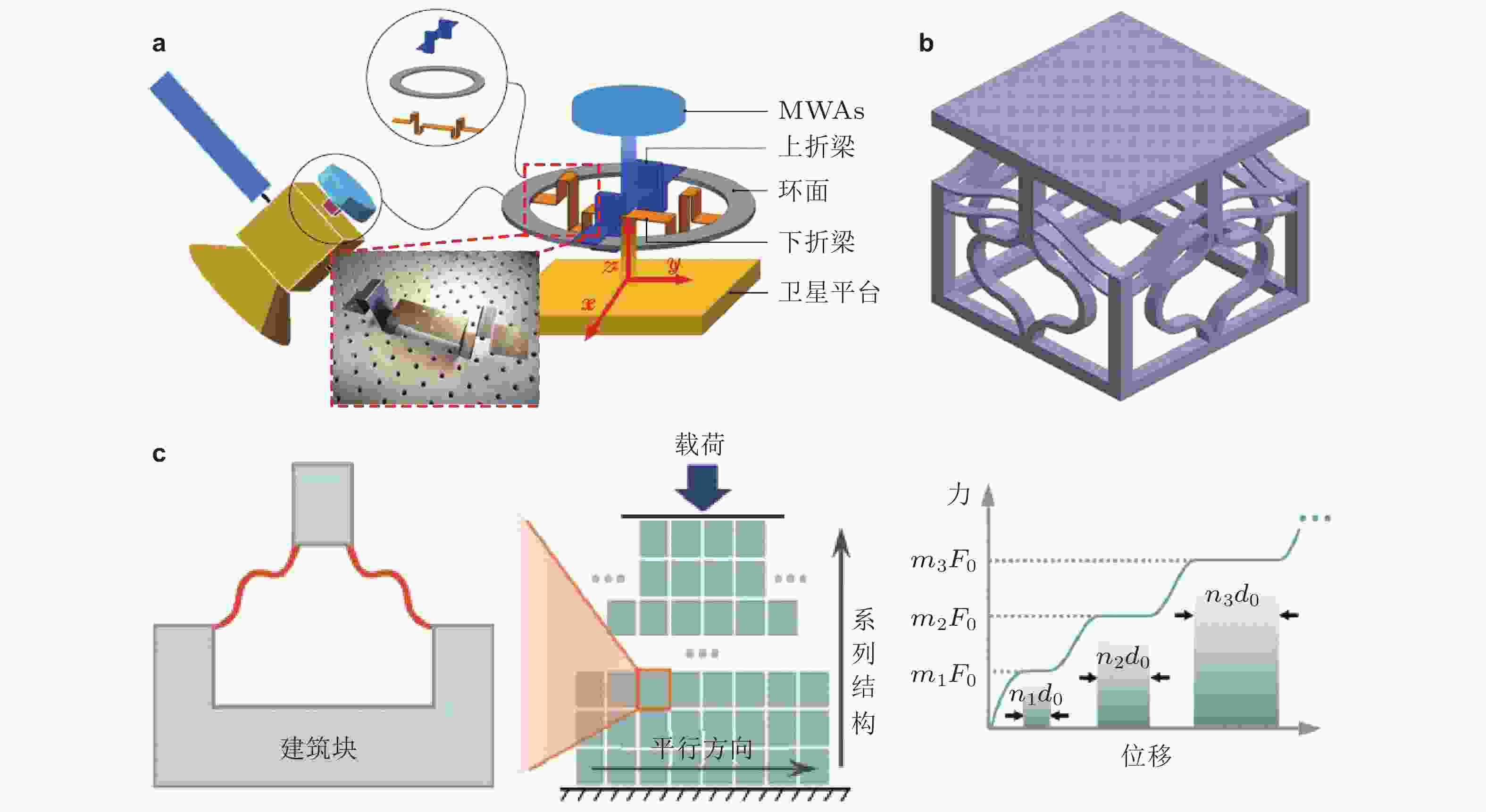
图 13 Miura折纸和Kresling折纸结构作为隔振器的结构设计和准零刚度机理. (a)Miura-Ori单胞结构及其恢复力本构(Sadeghi & Li 2017), (b) Miura-Ori等效多连杆结构机理及变刚度特性(Han et al. 2021), (c)Miura-Ori等效空间桁架结构及准零刚度特性(Ye et al. 2022), (d) Miura-Ori串联形成管状射流折纸结构作为隔振器的原理和实验图(Sadeghi & Li 2019), (e) Tachi-Miura折纸串并联形成的隔振器(Liu S W et al. 2021), (f) Kresling折纸结构及其等效变形框架(Ishida et al. 2017a), (g)两级Kresling隔振结构(Li Z et al. 2020)
图 14 折纸超材料吸振隔振结构. (a)可调谐、可编程的Miura折纸结构的材料及其等效动力学系统(Phanisri et al. 2018), (b)用Kresling折纸结构实现变刚度的局部振子(Zhang M K et al. 2021), (c) Kresling折纸结构实现变刚度扭转振动的局部振子(Xu et al. 2021)
图 15 基于折纸概念的柔性隔振器. (a) Z型折型柔性梁形成卫星动量轮多方向隔振结构(Yan G et al. 2020b), (b) 双稳屈曲梁隔振微结构(Dalela et al. 2022), (c)可编程隔振超材料单胞构造及堆叠(Zhang Q et al. 2021)
图 16 利用时滞的隔振器和隔振平台. (a)考虑时滞的主动LGQ控制的隔振结构 (Weng et al. 2011), (b)时滞反馈控制非线性隔振结构(Zhou et al. 2012, Li et al. 2011, 2013), (c)具有两层独立时滞隔振系统(Nia & Sipahi 2013), (d)两方向时滞控制隔振器均匀布置形成六自由度主动隔振平台(Sun & Kim 2012, 2013)
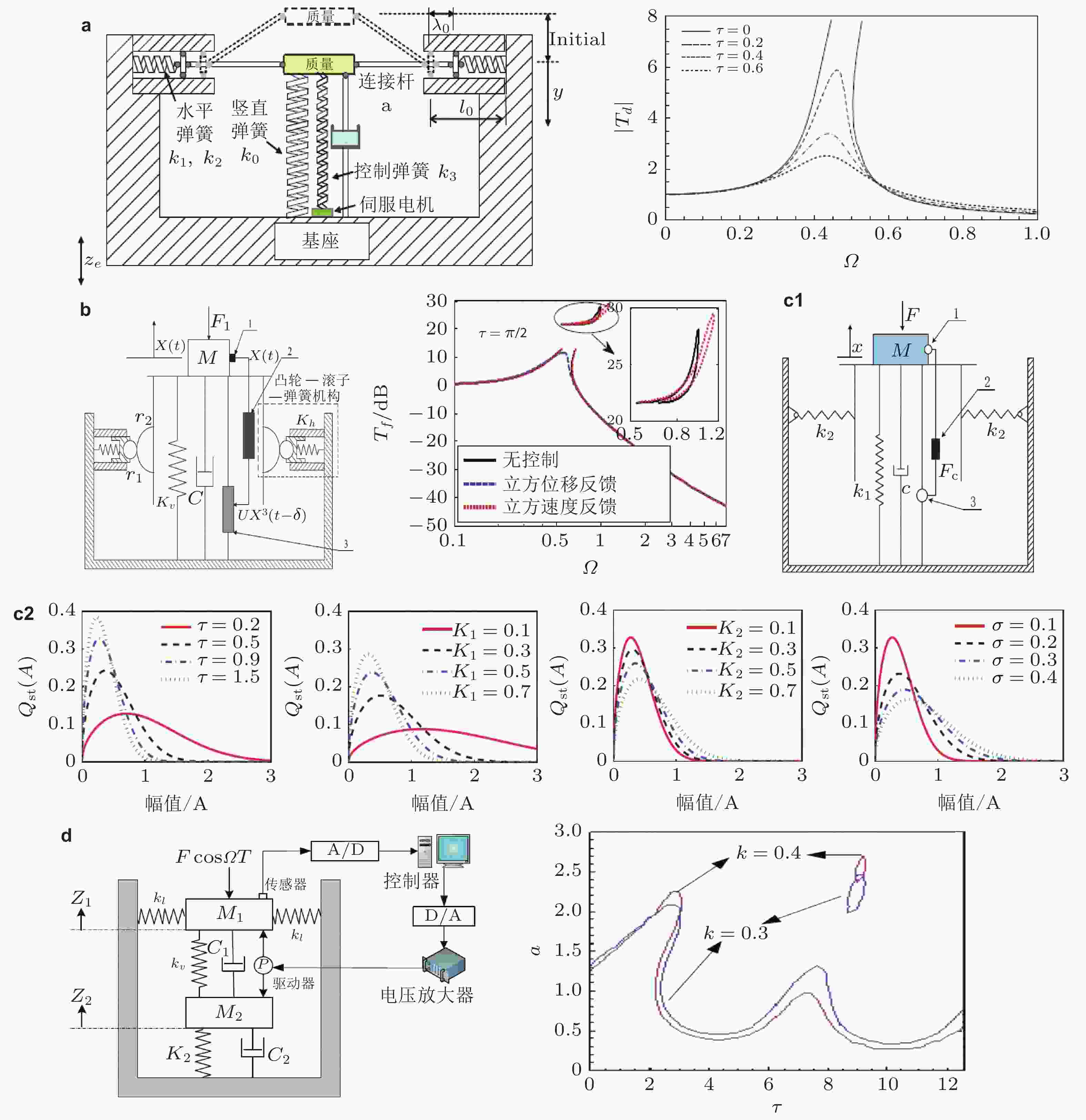
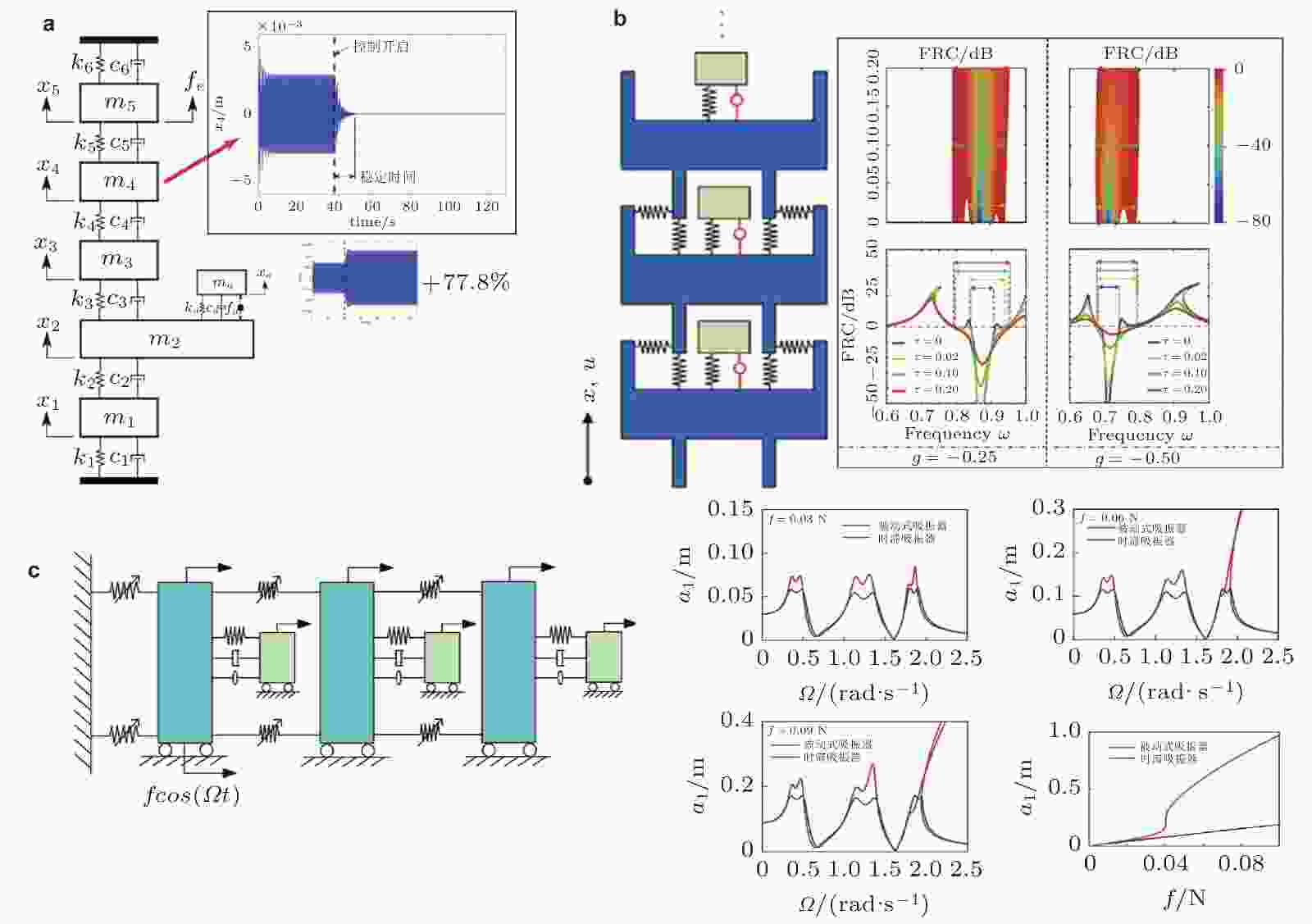
图 17 时滞反馈控制下的准零刚度隔振器的力学简图和幅频变化. (a)时滞线性反馈控制下的连杆弹簧准零刚度隔振器及时滞的抑振效果(Sun et al. 2014b), (b)时滞非线性反馈控制下的凸轮滚子准零刚度隔振器及不同控制策略和时滞下的幅频曲线的变化(Cheng et al. 2016), (c)时滞控制准零刚度隔振器在谐波和随机激励下的稳定性和共振幅值(Yang & Cao, 2017, 2018), (d)时滞线性反馈下的双层隔振器及幅值随时滞的变化(Zhang H P et al. 2020)
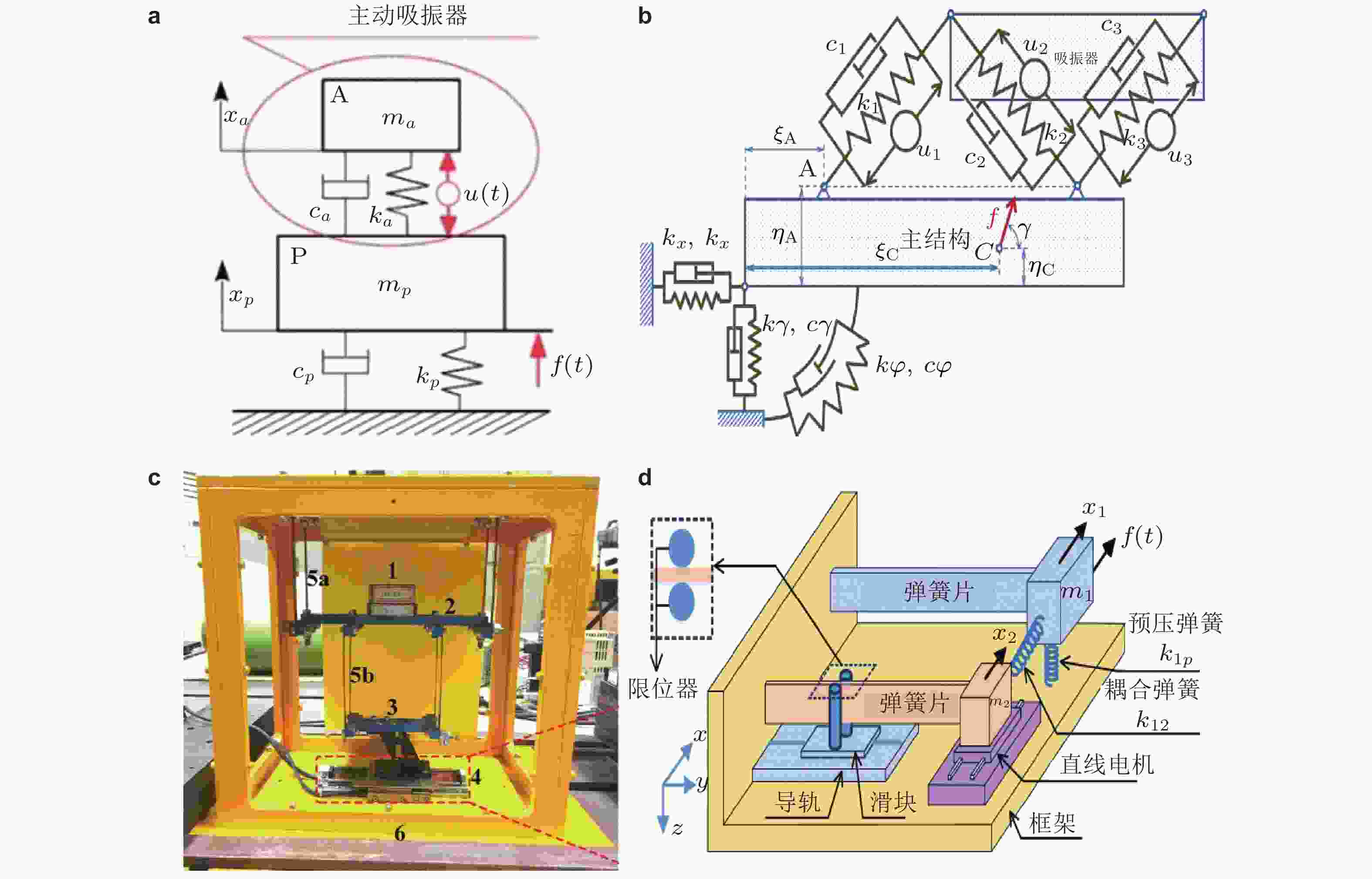
图 18 时滞反馈吸振器. (a)单自由度主系统的时滞吸振设计(Vyhlídal et al. 2019), (b)平面运动的主系统时滞吸振设计(Sika et al. 2021), (c)时滞反馈控制吸振器(Wang & Xu 2019), (d)时滞反馈控制非线性隔振系统(Wang F et al. 2021)
图 19 时滞反馈吸振器对多自由度线性/非线性主系统的吸振效果. (a)单个时滞吸振器的吸振机理和效果(Jenkins & Olgac 2019), (b)时滞吸振器形成吸−隔复合周期结构(Wang F et al. 2022), (c)多自由度非线性系统时滞吸振器结构图(Meng et al. 2021a)
-
[1] 蔡国平, 陈龙祥. 2013. 时滞反馈控制的若干问题. 力学进展, 43: 21-28 (Cai G P, Chen L X. 2013. Some problems of delayed feedback control. Advances in Mechanics, 43: 21-28). doi: 10.6052/1000-0992-12-014Cai G P, Chen L X. 2013. Some problems of delayed feedback control. Advances in Mechanics, 43: 21-28). doi: 10.6052/1000-0992-12-014 [2] 柴凯, 朱石坚, 杨庆超, 等. 2018. 三磁体型隔振器的性能分析和实验研究. 振动与冲击, 37: 6 (Chai K, Zhu S J, Yang Q C, et al. 2018. Analysis and test for the performances of a tri-magnet vibration isolator. Journal of Vibration and Shock, 37: 6). doi: 10.13465/j.cnki.jvs.2018.06.006Chai K, Zhu S J, Yang Q C, et al. 2018. Analysis and test for the performances of a tri-magnet vibration isolator. Journal of Vibration and Shock, 37: 6). doi: 10.13465/j.cnki.jvs.2018.06.006 [3] 陈关荣, 汪小帆. 2006. 动力系统的混沌化: 理论方法与应用. 上海: 上海交通大学出版社(Chen G R, Wang X F. 2006. Chaos of dynamical systems: Theoretical methods and applications. Shanghai: Shanghai Jiao Tong University Press). [4] 陈然. 2019. 一种正交菱形准零刚度隔振器的设计与分析. 山东农业大学学报(自然科学版), 50: 837-841 (Chen R. 2019. The design and analysis of a vibration isolator with orthogonal diamond quasi zero stiffness. Journal of Shandong Agricultural University (Natural Science Edition) , 50: 837-841).Chen R. 2019. The design and analysis of a vibration isolator with orthogonal diamond quasi zero stiffness. Journal of Shandong Agricultural University (Natural Science Edition), 50: 837-841). [5] 城市区域环境振动标准. 1989. GB10070-1988. 中国标准出版社(Environmental vibration standards for urban areas. 1989. GB10070-1988. Standards Press of China). [6] 韩俊淑, 孙景工, 孟令帅. 2019. 一种曲面−弹簧−滚子机构的非线性隔振器特性分析. 振动与冲击, 38: 9 (Han J S, Sun J G, Meng L S. 2019. Design and characteristics analysis of a nonlinear vibration isolator using a curved surface-spring-roller mechanism as negative stiffness element. Journal of Vibration and Shock, 38: 9).Han J S, Sun J G, Meng L S. 2019. Design and characteristics analysis of a nonlinear vibration isolator using a curved surface-spring-roller mechanism as negative stiffness element. Journal of Vibration and Shock, 38: 9). [7] 胡海岩, 王在华. 2010. 论迟滞与时滞. 力学学报, 42: 740-746 (Hu H Y, Wang Z H. 2010. On hysteresis and retardation. Chinese Journal of Theoretical and Applied Mechanics, 42: 740-746). doi: 10.6052/0459-1879-2010-4-lxxb2009-414Hu H Y, Wang Z H. 2010. On hysteresis and retardation. Chinese Journal of Theoretical and Applied Mechanics, 42: 740-746). doi: 10.6052/0459-1879-2010-4-lxxb2009-414 [8] 刘永强. 2011. 基于磁流变阻尼器的高速动车组半主动控制与时滞分析. 北京交通大学(Liu Y Q. 2011. Semi-active control of high-speed EMUs and time delay analysis based on magnetorheological damper. Beijing Jiaotong University). [9] 陆泽琦, 陈立群. 2017. 非线性被动隔振的若干进展. 力学学报, 49: 550-564 (Lu Z Q, Chen L Q. 2017. Some recent progresses in nonlinear passive isolations of vibrations. Chinese Journal of Theoretical and Applied Mechanics, 49: 550-564). doi: 10.6052/0459-1879-17-064(Lu Z Q, Chen L Q. 2017. Some recent progresses in nonlinear passive isolations of vibrations. Chinese Journal of Theoretical and Applied Mechanics, 49: 550-564). doi: 10.6052/0459-1879-17-064 [10] 孟光, 董瑶海, 周徐斌, 等. 2019. 风云四号卫星微振动抑制和试验技术研究. 中国科学: 物理学力学天文学, 49: 024508 (Meng G, Dong Y H, Zhou X B, et al. 2019. Research on micro-vibration control and testing of FY-4 meteorological satellite. Scientia Sinica(Physica, Mechanica and Astronomica) , 49: 024508). doi: 10.1360/SSPMA2018-00108Meng G, Dong Y H, Zhou X B, et al. 2019. Research on micro-vibration control and testing of FY-4 meteorological satellite. Scientia Sinica(Physica, Mechanica and Astronomica), 49: 024508). doi: 10.1360/SSPMA2018-00108 [11] 彭献, 黎大志, 陈树年. 1997. 准零刚度隔振器及其弹性特性设计. 振动, 17: 3 (Peng X, Li D Z, Chen S N. 1997. Quasi-zero stiffness vibration isolators and design for their elastic characteristics. Journal of Vibration, Measurement & Diagnosis, 17: 3).Peng X, Li D Z, Chen S N. 1997. Quasi-zero stiffness vibration isolators and design for their elastic characteristics. Journal of Vibration, Measurement & Diagnosis, 17: 3). [12] 任晨辉, 杨德庆. 2018. 船用新型多层负刚度冲击隔振器性能分析. 振动与冲击, 37: 81-87 (Ren C H, Yang D Q. 2018. Characteristics of a novel multilayer negative stiffness shock isolation system for a marine structure. Journal of Vibration and Shock, 37: 81-87).Ren C H, Yang D Q. 2018. Characteristics of a novel multilayer negative stiffness shock isolation system for a marine structure. Journal of Vibration and Shock, 37: 81-87). [13] 邵栋, 陆泽琦, 陈立群. 2017. 非线性刚度非线性阻尼隔振系统功率流研究. 振动工程学报, 30: 764-773(Shao D, Lu Z Q, Chen L Q. 2017. Power flow characteristics of a two-stage nonlinear vibration isolation system. Journal of Vibration Engineering, 30: 764-772). [14] 束立红, 胡宗成, 吕志强. 2006. 国外舰船隔振器研究进展. 舰船科学技术, 28: 109-112 (Shu L H, Hu Z C, Lv Z Q. 2006. Overseas research progress on vibration isolator. Ship Science and Technology, 28: 109-112).Shu L H, Hu Z C, Lv Z Q. 2006. Overseas research progress on vibration isolator. Ship Science and Technology, 28: 109-112). [15] 孙秀婷, 富展展. 2018. 一类新型多方向准零刚度隔振平台. 力学季刊, 39: 9 (Sun X T, Fu Z Z. 2018. A novel multi-direction quasi-zero-stiffness vibration isolation platform. Chinese Quarterly of Mechanics, 39: 9). doi: 10.15959/j.cnki.0254-0053.2018.02.003Sun X T, Fu Z Z. 2018. A novel multi-direction quasi-zero-stiffness vibration isolation platform. Chinese Quarterly of Mechanics, 39: 9). doi: 10.15959/j.cnki.0254-0053.2018.02.003 [16] 王毅, 徐道临, 周加喜. 2015. 滚球型准零刚度隔振器的特性分析. 振动与冲击, 34: 6 (Wang Y, Xu D L, Zhou J X. 2015. Characteristic analysis of a ball-type vibration isolator with quasi-zero-stiffness. Journal of Vibration and Shock, 34: 6). doi: 10.13465/j.cnki.jvs.2015.04.024Wang Y, Xu D L, Zhou J X. 2015. Characteristic analysis of a ball-type vibration isolator with quasi-zero-stiffness, Journal of Vibration and Shock, 34: 6). doi: 10.13465/j.cnki.jvs.2015.04.024 [17] 王哲, 杜嘉峰, 张传伟, 等. 2016. 车辆电动静液压作动器的半主动悬架时滞补偿控制. 中国机械工程, 27: 2111-2117 (Wang Z, Du J F, Zhang C W, et al. 2016. Time delay compensation control of semi-active suspension with vehicle electro-hydrostatic actuator. China Mechanical Engineering, 27: 2111-2117). doi: 10.3969/j.issn.1004-132X.2016.15.022Wang Z, Du J F, Zhang C W, et al. 2016. Time delay compensation control of semi-active suspension with vehicle electro-hydrostatic actuator. China Mechanical Engineering, 27: 2111-2117). doi: 10.3969/j.issn.1004-132X.2016.15.022 [18] 徐道临, 张月英, 周加喜, 等. 2014. 一种准零刚度隔振器的特性分析与实验研究. 振动与冲击, 33: 208-213 (Xu D L, Zhang Y Y, Zhou J X, et al. 2014. Characteristic analysis and experimental investigation for a vibration isolator with quasi-zero stiffness. Journal of Vibration and Shock, 33: 208-213). doi: 10.13465/j.cnki.jvs.2014.11.036Xu D L, Zhang Y Y, Zhou J X, et al. 2014. Characteristic analysis and experimental investigation for a vibration isolator with quasi-zero stiffness. Journal of Vibration and Shock, 33: 208-213). doi: 10.13465/j.cnki.jvs.2014.11.036 [19] 徐鉴, 裴利军. 2006. 时滞系统动力学近期研究进展与展望. 力学进展, 36: 17-30 (Xu J. Pei L J. 2006. Advances in dynamics for delayed systems. Advances in Mechanics, 36: 17-30). doi: 10.6052/1000-0992-2006-1-J2005-095Xu J. Pei L J. 2006. Advances in dynamics for delayed systems. Advances in Mechanics, 36: 17-30). doi: 10.6052/1000-0992-2006-1-J2005-095 [20] 徐鉴. 2015. 振动控制研究进展综述. 力学季刊, 36: 547-565 (Xu J. 2015. Advances of research on vibration control. Chinese Quarterly of Mechanics, 36: 547-565). doi: 10.15959/j.cnki.0254-0053.2015.04.001Xu J. 2015. Advances of research on vibration control. Chinese Quarterly of Mechanics, 36: 547-565). doi: 10.15959/j.cnki.0254-0053.2015.04.001 [21] 徐龙河, 周云, 等. 2001. MRFD半主动控制系统的时滞与补偿. 地震工程与工程振动, 3: 127-131 (Xu L H, Zhou Y, et al. 2001. Time-delay and compensation for MRFD semi-active control system. Earthquake Engineering and Engineering Dynamics, 3: 127-131). doi: 10.3969/j.issn.1000-1301.2001.03.023Xu L H, Zhou Y, et al. 2001. Time-delay and compensation for MRFD semi-active control system. Earthquake Engineering and Engineering Dynamics, 3: 127-131). doi: 10.3969/j.issn.1000-1301.2001.03.023 [22] 徐平. 2014. 蜂窝状空腔屏障隔振效果分析. 振动与冲击, 33: 5 (Xu P. 2014. Analysis of vibration isolation effects of honeycomb-cell barriers. Journal of Vibration and Shock, 33: 5). doi: 10.3969/j.issn.1000-3835.2014.03.003Xu P. 2014. Analysis of vibration isolation effects of honeycomb-cell barriers. Journal of Vibration and Shock, 33: 5). doi: 10.3969/j.issn.1000-3835.2014.03.003 [23] 姚国, 于永恒, 张义民, 等. 2020. X型准零刚度隔振器的隔振特性分析. 东北大学学报: 自然科学版, 41: 5 (Yao G, Yu Y H, Zhang Y M, et al. 2020. Vibration isolation characteristics analysis of x-shaped quasi-zero stiffness vibration isolator. Journal of Northeastern University(Natural Science) , 41: 5).Yao G, Yu Y H, Zhang Y M, et al. 2020. Vibration isolation characteristics analysis of x-shaped quasi-zero stiffness vibration isolator. Journal of Northeastern University(Natural Science), 41: 5). [24] 张也, 薛松领, 常军. 2018. 基于负刚度的减振设备参数优化及其应用. 地震工程与工程振动, 38: 201-209 (Zhang Y, Xue S L, Chang J. 2018. Parameter optimization and application of vibration damping device based on negative stiffness. Earthquake Engineering and Engineering Dynamics, 38: 201-209). doi: 10.13197/j.eeev.2018.02.201.zhangy.023Zhang Y, Xue S L, Chang J. 2018. Parameter optimization and application of vibration damping device based on negative stiffness. Earthquake Engineering and Engineering Dynamics, 38: 201-209). doi: 10.13197/j.eeev.2018.02.201.zhangy.023 [25] 中国工程院全球工程前沿项目组. 2021. 全球工程前沿2021. 高等教育出版社(Chinese Academy of Engineering Global Engineering Frontier Project Team. 2021. Global Engineering Frontiers 2021. Higher Education Press). [26] 周加喜, 王心龙, 徐道临, 等. 2015. 含凸轮−滚轮机构的准零刚度系统隔振特性实验研究. 振动工程学报, 28: 7 (Zhou J X, Wang X L, Xu D L, et al. 2015. Experimental study on vibration isolation characteristics of the quasi-zero stiffness isolator with cam-roller mechanism. Journal of Vibration Engineering, 28: 7).Zhou J X, Wang X L, Xu D L, et al. 2015. Experimental study on vibration isolation characteristics of the quasi-zero stiffness isolator with cam-roller mechanism. Journal of Vibration Engineering, 28: 7). [27] Abbasi A, Khadem S E, Bab S. 2021. Applications of adaptive stiffness suspensions to vibration control of a high-speed stiff rotor with tilting pad bearings. Archive of Applied Mechanics, 91: 1819-1835. doi: 10.1007/s00419-020-01856-3 [28] Abbasi A, Khadem S E, Bab S. 2018. Vibration control of a continuous rotating shaft employing high-static low-dynamic stiffness isolators. Journal of vibration and control, 24: 760-783. doi: 10.1177/1077546316651559 [29] Alhazza K A, Majeed M A. 2012. Free vibrations control of a cantilever beam using combined time delay feedback. Journal of Vibration and Control, 18: 609-621. doi: 10.1177/1077546311405700 [30] Bouna H S, Nbendjo B R N, Woafo P. 2020. Isolation performance of a quasi-zero stiffness isolator in vibration isolation of a multi-span continuous beam bridge under pier base vibrating excitation. Nonlinear Dynamics, 100: 1125-1141. doi: 10.1007/s11071-020-05580-z [31] Cai G P, Chen L X. 2010. Delayed feedback control experiments on some flexible structures. Acta Mechanica Sinica, 6: 951-965. [32] Carrella A, Brennan M J, Waters T P, et al. 2008. On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets. Journal of Sound and Vibration, 315: 712-720. doi: 10.1016/j.jsv.2008.01.046 [33] Carrella A, Brennan M J, Waters T P. 2007. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. Journal of Sound and Vibration, 301: 678-689. doi: 10.1016/j.jsv.2006.10.011 [34] Chang P H, Han D K, Shin Y H, et al. 2010. Effective suppression of pneumatic vibration isolators by using input-output linearization and time delay control. Journal of Sound and Vibration, 329: 1636-1652. doi: 10.1016/j.jsv.2009.12.003 [35] Chatterjee S. 2008. Vibration control by recursive time-delayed acceleration feedback. Journal of Sound and Vibration, 317: 67-90. doi: 10.1016/j.jsv.2008.03.020 [36] Chen T F, Zheng Y X, Song L H, et al. 2022. Design of a new quasi-zero-stiffness isolator system with nonlinear positive stiffness configuration and its novel features. Nonlinear Dynamics, Online. [37] Chen Y, Wen H, Jin D. 2021. Design of a Quasi-Zero Stiffness System Based on Electromagnetic Vibration Isolation. In: Oberst, S. , Halkon, B. , Ji, J. , Brown, T. (eds) Vibration Engineering for a Sustainable Future. Springer. [38] Cheng C, Li S M, Wang Y, et al. 2016. On the analysis of a high-static-low-dynamic stiffness vibration isolator with time-delayed cubic displacement feedback. Journal of Sound and Vibration, 378: 76-91. doi: 10.1016/j.jsv.2016.05.029 [39] Cheng C, Li S M, Wang Y, et al. 2017. Performance analysis of high-static-low-dynamic stiffness vibration isolator with time-delayed displacement feedback. Journal of Central South University, 24: 2294-2305. doi: 10.1007/s11771-017-3641-3 [40] Chong X Q, Wu Z J, Li F M. 2022. Vibration isolation properties of the nonlinear X-combined structure with a high-static and low-dynamic stiffness: Theory and experiment. Mechanical Systems & Signal Processing, 179: 109352. [41] Coppola G, Liu K F. 2012. Time‐delayed position feedback control for a unique active vibration isolator. Structural Control and Health Monitoring, 19: 646-666. doi: 10.1002/stc.460 [42] Dai H H, Cao X Y, Jing X J, et al. 2020. Bio-inspired anti-impact manipulator for capturing non-cooperative spacecraft: theory and experiment. Mechanical Systems and Signal Processing, 142: 106785. doi: 10.1016/j.ymssp.2020.106785 [43] Dai H H, Jing X J, Wang Y, et al. 2018. Post-capture vibration suppression of spacecraft via a bio-inspired isolation system. Mechanical Systems and Signal Processing, 105: 214-240. doi: 10.1016/j.ymssp.2017.12.015 [44] Dalela S, Balaji P S, Jena D P. 2022. Design of a metastructure for vibration isolation with quasi-zero-stiffness characteristics using bistable curved beam. Nonlinear Dynamics, 108: 1931-1971. doi: 10.1007/s11071-022-07301-0 [45] Dan P, Vyhlídal T, Michiels W. 2018. Optimized design of robust resonator with distributed time-delay. Journal of Sound and Vibration, 443: 576-590. [46] Dan P, Vyhlídal T, Olgac N. 2015. Delayed resonator with distributed delay in acceleration feedback-design and experimental verification. IEEE/ASME Transactions on Mechatronics, 21: 2120-2131. [47] Demir M U, Yilmaz C. 2022. Analysis and design of an adjustable stiffness three-axis horizontal vibration isolator using elastic columns and a string in tension. Journal of Sound and Vibration, 523: 22. [48] Deng T C, Wen G L, Ding H, et al. 2020. A bio-inspired isolator based on characteristics of quasi-zero stiffness and bird multi-layer neck. Mechanical Systems and Signal Processing, 145: 106967. doi: 10.1016/j.ymssp.2020.106967 [49] Dong X M, Yu M, Li Z S, et al. 2009. Neural network compensation of semi-active control for magneto-rheological suspension with time delay uncertainty. Smart Materials and Structures, 18: 015014. doi: 10.1088/0964-1726/18/1/015014 [50] Donmez A, Cigeroglu E, Ozgen G O. 2020. Correction to: an improved quasi-zero stiffness vibration isolation system utilizing dry friction damping. Nonlinear Dynamics, 101: 107-121. doi: 10.1007/s11071-020-05685-5 [51] Eskandary-Malayery F, Ilanko S, Mace B, et al. 2022. Experimental and numerical investigation of a vertical vibration isolator for seismic applications. Nonlinear Dynamics, 109: 303-322. doi: 10.1007/s11071-022-07613-1 [52] Fulcher B A, Shahan D W, Haberman M R, et al. 2014. Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems. Journal of Vibration and Acoustics, 136: 031009. doi: 10.1115/1.4026888 [53] Gao X, Chen Q. 2014. Nonlinear analysis, design and vibration isolation for a bilinear system with time-delayed cubic velocity feedback. Journal of Sound and Vibration, 333: 1562-1576. doi: 10.1016/j.jsv.2013.11.009 [54] Gatti G, Brennan M J, Tang B. 2019. Some diverse examples of exploiting the beneficial effects of geometric stiffness nonlinearity. Mechanical Systems and Signal Processing, 125: 4-20. doi: 10.1016/j.ymssp.2018.08.024 [55] Gatti G, Kovacic I, Brennan M J. 2010. On the response of a harmonically excited two degree-of-freedom system consisting of a linear and a nonlinear quasi-zero stiffness oscillator. Journal of Sound and Vibration, 329: 1823-1835. doi: 10.1016/j.jsv.2009.11.019 [56] Gatti G, Shaw A D, Gonçalves P J P, et al. 2022. On the detailed design of a quasi-zero stiffness device to assist in the realisation of a translational Lanchester damper. Mechanical Systems and Signal Processing, 164: 108258. doi: 10.1016/j.ymssp.2021.108258 [57] Gatti G. 2020. Statics and dynamics of a nonlinear oscillator with quasi-zero stiffness behaviour for large deflections. Communications in Nonlinear Science and Numerical Simulation, 83: 105143. doi: 10.1016/j.cnsns.2019.105143 [58] Gatti G. 2021. Optimizing elastic potential energy via geometric nonlinear stiffness. Communications in Nonlinear Science and Numerical Simulation, 103: 1-18. [59] Gatti G. 2022b. An adjustable device to adaptively realise diverse nonlinear force-displacement characteristics. Mechanical Systems and Signal Processing, 180: 1-21. [60] Ghasabi S A, Arbabtafti M, Shahgholi M. 2022. Time-delayed control of a nonlinear asymmetrical rotor near the major critical speed with flexible supports. Mechanics Based Design of Structures and Machines, 50: 242-267. doi: 10.1080/15397734.2020.1715230 [61] Gu K, Niculescu S L. 2003. Survey on recent results in the stability and control of time-delay systems. Journal of Dynamic Systems, 125: 158-165. [62] Hamdi M, Belhaq M. 2009. Self-excited vibration control for axially fast excited beam by a time delay state feedback. Chaos Solitons and Fractals, 41: 521-532. doi: 10.1016/j.chaos.2008.02.023 [63] Han H S, Sorokin V, Tang L H, et al. 2021. A nonlinear vibration isolator with quasi-zero-stiffness inspired by Miura-origami tube. Nonlinear Dynamics, 105: 1313-1325. doi: 10.1007/s11071-021-06650-6 [64] Han Y W, Cao Q J, Chen Y S, et al. 2012. A novel smooth and discontinuous oscillator with strong irrational nonlinearities. Science China Physics. Mechanics and Astronomy, 55: 1832-1843. doi: 10.1007/s11433-012-4880-9 [65] Hao Z F, Cao Q J. 2015. The isolation characteristics of an archetypal dynamical model with stable-quasi-zero-stiffness. Journal of Sound and Vibration, 340: 61-79. doi: 10.1016/j.jsv.2014.11.038 [66] Heiden U A D, Walther H O. 1983. Existence of chaos in control system with delayed feedback. Journal of Differential Equations, 47: 273-295. doi: 10.1016/0022-0396(83)90037-2 [67] Huang D M, Xu W, Xie W X, et al. 2015. Dynamical properties of a forced vibration isolation system with real-power nonlinearities in restoring and damping forces. Nonlinear Dynamics, 81: 641-658. doi: 10.1007/s11071-015-2016-2 [68] Huang D M, Xu W. 2017. Performance characteristics of a real-power viscoelastic isolation system under delayed PPF control and base excitation. Nonlinear Dynamics, 88: 2035-2050. doi: 10.1007/s11071-017-3360-1 [69] Huang D M, Zhou S X, Li R H, et al. 2022. On the analysis of the tristable vibration isolation system with delayed feedback control under parametric excitation. Mechanical Systems and Signal Processing, 164: 108207. doi: 10.1016/j.ymssp.2021.108207 [70] Huang X C, Liu X T, Hua H X. 2014. Effects of stiffness and load imperfection on the isolation performance of a high-static-low-dynamic-stiffness non-linear isolator under base displacement excitation. International Journal of Non-Linear Mechanics, 65: 32-43. doi: 10.1016/j.ijnonlinmec.2014.04.011 [71] Ibrahim R A. 2008. Recent advances in nonlinear passive vibration isolators. Journal of Sound and Vibration, 314: 371-452. doi: 10.1016/j.jsv.2008.01.014 [72] Ishida S, Suzuki K, Shimosaka H. 2016. Design and experimental analysis of Origami-Inspired vibration isolators with quasi-zero-stiffness characteristic//Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 5B: V05BT07A015. [73] Ishida S, Suzuki K, Shimosaka H. 2017b. Design and experimental analysis of Origami-Inspired vibration isolator with quasi-zero-stiffness characteristic. Journal of Vibration and Acoustics-Transactions of the ASME, 139: 051004. doi: 10.1115/1.4036465 [74] Ishida S, Uchida H, Shimosaka H, et al. 2017a. Design and numerical analysis of vibration isolators with quasi-zero-stiffness characteristics using bistable foldable structures. Journal of Vibration and Acoustics-Transactions of the ASME, 139: 031015. doi: 10.1115/1.4036096 [75] Jazar G N, Golnaraghi M F. 2002. Nonlinear modeling, experimental verification, and theoretical analysis of a hydraulic engine mount. Journal of Vibration and Control, 8: 87-116. doi: 10.1177/1077546302008001519 [76] Jenkins R, Olgac N. 2019. Real-time tuning of delayed resonator-based absorbers for spectral and spatial variations. Journal of Vibration and Acoustics, 141: 021011. doi: 10.1115/1.4041592 [77] Jiang Y, Song C, Ding C, et al. 2020. Design of magnetic-air hybrid quasi-zero stiffness vibration isolation system. Journal of Sound and Vibration, 477: 115346. doi: 10.1016/j.jsv.2020.115346 [78] Jin G X, Wang Z H, Yang T Z. 2022. Cascaded quasi-zero stiffness nonlinear low-frequency vibration isolator inspired by human spine. Applied Mathematics and Mechanics (English Edition) , 43: 813-824. doi: 10.1007/s10483-022-2852-5 [79] Johnson M, Chen Y, Hovet S, et al. 2017. Fabricating biomedical origami: a state-of-the-art review. International Journal of Computer Assisted Radiology and Surgery, 12: 2023-2032. doi: 10.1007/s11548-017-1545-1 [80] Kamaruzaman N A , Robertson W , Ghayesh MH , et al. 2018. Improving passive stability of a planar quasi-zero stiffness magnetic levitation system via lever arm// 2018 IEEE International Magnetics Conference (INTERMAG). [81] Kamaruzaman N A, Robertson W S P, Ghayesh M H, et al. 2021. Six degree of freedom quasi-zero stiffness magnetic spring with active control: Theoretical analysis of passive versus active stability for vibration isolation. Journal of Sound and Vibration, 502: 116086. doi: 10.1016/j.jsv.2021.116086 [82] Kim J H, Jeon Y J, Um S W, et al. 2019. A Novel Passive Quasi-Zero Stiffness Isolator for Ultra-Precision Measurement Systems. International Journal of Precision Engineering and Manufacturing, 20: 1573-1580. doi: 10.1007/s12541-019-00149-2 [83] Korytov M S, Shcherbakov V S, Titenko V V, et al. 2021. Study of the antivibration suspended seat oscillations with quasi-zero stiffness effect under sinusoidal excitation. Journal of Physics:Conference Series, 1901: 012120. doi: 10.1088/1742-6596/1901/1/012120 [84] Kovacic I, Brennan M J, Waters T P. 2008. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic. Journal of Sound and Vibration, 315: 700-711. doi: 10.1016/j.jsv.2007.12.019 [85] Kucera V, Pilbauer D, Vyhlídal T. 2017. Extended delayed resonators-Design and experimental verification. Mechatronics, 41: 29-44. [86] Lan C C, Yang S A, Wu Y S. 2014. Design and experiment of a compact quasi-zero-stiffness isolator capable of a wide range of loads. Journal of Sound and Vibration, 333: 4843-4858. doi: 10.1016/j.jsv.2014.05.009 [87] Le T D, Ahn K K. 2013. Experimental investigation of a vibration isolation system using negative stiffness structure. International Journal of Mechanical Sciences, 70: 99-112. doi: 10.1016/j.ijmecsci.2013.02.009 [88] Ledezma-Ramirez D F, Tapia-Gonzalez P E, Ferguson N, et al. 2019. Recent Advances in Shock Vibration Isolation: An Overview and Future Possibilities. Applied Mechanics Reviews, 71: 060802. doi: 10.1115/1.4044190 [89] Lee C M, Goverdovskiy V N. 2012. A multi-stage high-speed railroad vibration isolation system with “negative” stiffness. Journal of Sound and Vibration, 331: 914-921. doi: 10.1016/j.jsv.2011.09.014 [90] Li H, Li H Y, Chen Z B, et al. 2016. Experiments on active precision isolation with a smart conical adapter. Journal of Sound and Vibration, 374: 17-28. doi: 10.1016/j.jsv.2016.03.039 [91] Li M, Cheng W, Xie R L. 2020. A quasi-zero-stiffness vibration isolator using a cam mechanism with user-defined profile. International Journal of Mechanical Sciences, 189: 105938. [92] Li S Y, Fang H B, Sadeghi S, et al. 2019. Architected origami materials: how folding creates sophisticated mechanical properties. Advanced materials, 31: e1805282. doi: 10.1002/adma.201805282 [93] Li Y L, Xu D L, Fu Y M, et al. 2011. Stability and chaotification of vibration isolation floating raft systems with time-delayed feedback control. Chaos, 21: 033115. doi: 10.1063/1.3615710 [94] Li Y L, Xu D L, Fu Y M, et al. 2013. Chaotification of a nonlinear vibration isolation system by dual time delayed feedback control. International Journal of Bifurcation and Chaos, 23: 1350096. doi: 10.1142/S021812741350096X [95] Li Y L, Xu D L, Fu Y M, et al. 2014. Dynamic effects of delayed feedback control on nonlinear vibration isolation floating raft systems. Journal of Sound and Vibration, 333: 2665-2676. doi: 10.1016/j.jsv.2014.02.012 [96] Li Y L, Xu D L. 2016. Chaotification of quasi-zero-stiffness system with time delay control. Nonlinear Dynamics, 86: 353-368. doi: 10.1007/s11071-016-2893-z [97] Li Y L, Xu D L. 2017. Vibration attenuation of high dimensional quasi-zero stiffness floating raft system. International Journal of Mechanical Sciences, 126: 186-195. doi: 10.1016/j.ijmecsci.2017.03.029 [98] Li Z, Kidambi N, Wang L M, et al. 2020. Uncovering rotational multifunctionalities of coupled Kresling modular structures. Extreme Mechanics Letters, 39: 100795. doi: 10.1016/j.eml.2020.100795 [99] Ling P, Miao L L, Zhang W M, et al. 2022. Cockroach-inspired structure for low-frequency vibration isolation. Mechanical Systems and Signal Processing, 171: 108955. doi: 10.1016/j.ymssp.2022.108955 [100] Liu B Y, Gu L, Dong M M. 2022. Design and characteristic analysis of an X-shaped negative stiffness structure. Acta Mechanica, 233: 4549-4587. doi: 10.1007/s00707-022-03343-y [101] Liu C C, Jing X J, Daley S, et al. 2015. Recent advances in micro-vibration isolation. Mechanical Systems and Signal Processing, 56: 55-80. [102] Liu C R, Tang J, Yu K P, et al. 2020a. On the characteristics of a quasi-zero-stiffness vibration isolator with viscoelastic damper. Applied Mathematical Modelling, 88: 367-381. doi: 10.1016/j.apm.2020.06.068 [103] Liu C R, Yu K P, Liao B P, et al. 2021a. Enhanced vibration isolation performance of quasi-zero-stiffness isolator by introducing tunable nonlinear inerter. Communications in Nonlinear Science and Numerical Simulation, 95: 105654. doi: 10.1016/j.cnsns.2020.105654 [104] Liu C R, Yu K P, Tang J. 2020b. New insights into the damping characteristics of a typical quasi-zero-stiffness vibration isolator. International Journal of Non-Linear Mechanics, 124: 103511. doi: 10.1016/j.ijnonlinmec.2020.103511 [105] Liu C R, Zhao R, Yu K P, et al. 2021b. In-plane quasi-zero-stiffness vibration isolator using magnetic interaction and cables: Theoretical and experimental study. Applied Mathematical Modelling, 96: 497-522. doi: 10.1016/j.apm.2021.03.035 [106] Liu S W, Peng G L, Jin K. 2021. Design and characteristics of a novel QZS vibration isolation system with origami-inspired corrector. Nonlinear Dynamics, 106: 255-277. doi: 10.1007/s11071-021-06821-5 [107] Liu S W, Peng G L, Jin K. 2022. Towards accurate modeling of the Tachi-Miura origami in vibration isolation platform with geometric nonlinear stiffness and damping. Applied Mathematical Modelling, 103: 674-695. doi: 10.1016/j.apm.2021.11.012 [108] Liu X T, Huang X C, Hua H X. 2013. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. Journal of Sound and Vibration, 332: 3359-3376. doi: 10.1016/j.jsv.2012.10.037 [109] Liu Y Q, Xu L L, Song C F, et al. 2019. Dynamic characteristics of a quasi-zero stiffness vibration isolator with nonlinear stiffness and damping. Archive of Applied Mechanics, 89: 1743-1759. doi: 10.1007/s00419-019-01541-0 [110] Liu Z L, Xu J, Fang H B. 2022. Extracting inherent model structures and identifying parameters of time-varying systems using local linear neuro-fuzzy networks. IEEE Transactions on Fuzzy Systems:A Publication of the IEEE Neural Networks Council, 30: 233-247. [111] Lu J J, Yan G, Qi W H, et al. 2022. Sliding-boundary-constrained cantilever structure for vibration isolation via nonlinear stiffness modulation. International Journal of Mechanical Sciences, 235: 107733. doi: 10.1016/j.ijmecsci.2022.107733 [112] Lu Z Q, Yang T J, Brennan M J, et al. 2017. Experimental investigation of a two-stage nonlinear vibration isolation system with high-static-low-dynamic stiffness. Journal of Applied Mechanics, 84: 021001. doi: 10.1115/1.4034989 [113] Ma Z Z, Zhou R P, Yang Q C. 2022. Recent advances in quasi-zero stiffness vibration isolation systems: an overview and future possibilities. Machines, 10: 813. doi: 10.3390/machines10090813 [114] Maccari A. 2008. Vibration amplitude control for a van der Pol-Duffing oscillator with time delay. Journal of Sound and Vibration, 317: 20-29. doi: 10.1016/j.jsv.2008.03.029 [115] Mao X Y, Yin M M, Ding H, et al. 2022. Modeling, analysis, and simulation of X-shape quasi-zero-stiffness-roller vibration isolators. Applied Mathematics and Mechanics (English Edition) , 43: 1027-1044. doi: 10.1007/s10483-022-2871-6 [116] Meng H, Sun X T, Xu J, et al. 2020. The generalization of equal-peak method for delay-coupled nonlinear system. Physica D Nonlinear Phenomena, 403: 132340. doi: 10.1016/j.physd.2020.132340 [117] Meng H, Sun X T, Xu J, et al. 2021a. Establishment of the equal-peak principle for a multiple-DOF nonlinear system with multiple time-delayed vibration absorbers. Nonlinear Dynamics, 104: 241-266. doi: 10.1007/s11071-021-06301-w [118] Meng H, Sun X T, Xu J, et al. 2021b. Multimodal vibration suppression of nonlinear Euler-Bernoulli beam by multiple time-delayed vibration absorbers. Meccanica, 56: 2429-2449. doi: 10.1007/s11012-021-01384-6 [119] Meng L S, Sun J G, Wu W J. 2015. Theoretical design and characteristics analysis of a quasi-zero stiffness isolator using a disk spring as negative stiffness element. Shock and Vibration, 2015: 1-19. [120] Miyasato H H, Simionatto V G S, Dias M. 2021. Study of a torsional link with radial springs: Periodic responses under base excitation. European Journal of Mechanics-A/Solids, 89: 104267. doi: 10.1016/j.euromechsol.2021.104267 [121] Mokni L, Belhaq M. 2012. Using delayed damping to minimize transmitted vibrations. Communications in Nonlinear Science and Numerical Simulation, 17: 1980-1985. doi: 10.1016/j.cnsns.2011.08.034 [122] Nakamura Y, Goto S, Horie T, et al. 2013. Implementation of a smith predictor for pneumatic vibration isolators with dead time//39th Annual Conference of the IEEE Industrial Electronics Society, IEEE Industrial Electronics Society: 3574-3579. [123] Nakamura Y, Kawakami H, Wakui S. 2015. Suppression of anti-resonance and resonance in pneumatic system of vibration isolator considering time delay//IECON 2015 - 41st Annual Conference of the IEEE Industrial Electronics Society, IEEE Industrial Electronics Society: 2509-2514. [124] Nia P M, Sipahi R. 2013. Controller design for delay-independent stability of linear time-invariant vibration systems with multiple delays. Journal of Sound and Vibration, 332: 3589-3604. doi: 10.1016/j.jsv.2013.01.016 [125] Olgac N, Holm-Hansen B T. 1994. A novel active vibration absorption technique: delayed resonator. Journal of Sound and Vibration, 176: 93-104. doi: 10.1006/jsvi.1994.1360 [126] Phanisri P P, Phanish S, Glaucio H P, 2018, Bloch wave framework for structures with nonlocal interactions: Application to the design of origami acoustic metamaterials, Journal of the Mechanics and Physics of Solids, 118: 115–132 [127] Pratapa P P, Suryanarayana P, Paulino G H. 2018. Bloch wave framework for structures with nonlocal interactions: Application to the design of origami acoustic metamaterials. Journal of the Mechanics and Physics and Solids, 118: 115-132. doi: 10.1016/j.jmps.2018.05.012 [128] Qi W H, Yan G, Lu J J, et al. 2022. Magnetically modulated sliding structure for low frequency vibration isolation. Journal of Sound and Vibration, 526: 116819. doi: 10.1016/j.jsv.2022.116819 [129] Qiao P, Wang J. 2005. Transverse shear stiffness of composite honeycomb cores and efficiency of material. Mechanics of Advanced Materials and Structures, 12: 159-172. doi: 10.1080/15376490590913576 [130] Ravindra B, Mallik A K. 1994. Performance of non-linear vibration isolators under harmonic excitation. Journal of Sound and Vibration, 170: 325-337. doi: 10.1006/jsvi.1994.1066 [131] Robertson WS, Kidner MRF, Cazzolato BS, et al. 2009. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation. Journal of Sound and Vibration, 326: 88-103. doi: 10.1016/j.jsv.2009.04.015 [132] Sadeghi S, Li S Y. 2017. Harnessing the quasi-zero stiffness from fluidic Origami for low frequency vibration isolation// Proceedings of the ASME Conference on Smart Materials, Adaptive Structures and Intelligent Systems, 2: UNSP V002T03A008. [133] Sadeghi S, Li S Y. 2019. Fluidic origami cellular structure with asymmetric quasi-zero stiffness for low-frequency vibration isolation. Smart Materials and Structures, 28: 065006. doi: 10.1088/1361-665X/ab143c [134] Salvatore A, Carboni B, Lacarbonara W. 2022. Nonlinear dynamic response of an isolation system with superelastic hysteresis and negative stiffness. Nonlinear dynamics, 107: 1765-1790. doi: 10.1007/s11071-021-06666-y [135] Shahraeeni M, Sorokin V, Mace B, et al. 2022. Effect of damping nonlinearity on the dynamics and performance of a quasi-zero-stiffness vibration isolator. Journal of Sound and Vibration, 526: 116822. doi: 10.1016/j.jsv.2022.116822 [136] Shaw A D, Gatti G, Goncalves P, et al. 2021. Design and test of an adjustable quasi-zero stiffness device and its use to suspend masses on a multi-modal structure. Mechanical Systems and Signal Processing, 152: 107354. doi: 10.1016/j.ymssp.2020.107354 [137] Shaw A D, Neild S A, Wagg D J, et al. 2013. Experimental investigation into a passive vibration isolator incorporating a bistable composite plate// 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. [138] Shin Y H, Kim K J, Chang P H, et al. 2010. Control of pneumatic vibration isolation table by pneumatic and time delay control technique. Journal of Vibration and Acoustics, 132: 051013-1. doi: 10.1115/1.4001509 [139] Shin Y H, Kim K J. 2009. Performance enhancement of pneumatic vibration isolation tables in low frequency range by time delay control. Journal of Sound and Vibration, 321: 537-553. doi: 10.1016/j.jsv.2008.10.030 [140] Sika Z, Vyhlidal T, Neusser Z. 2021. Two-dimensional delayed resonator for entire vibration absorption. Journal of Sound and Vibration, 500: 116010. doi: 10.1016/j.jsv.2021.116010 [141] Singh K V, Ouyang H J. 2013. Pole assignment using state feedback with time delay in friction-induced vibration problems. Acta Mechanica, 224: 645-656. doi: 10.1007/s00707-012-0778-x [142] Suman S, Balaji P S, Selvakumar K, et al. 2021. Nonlinear vibration control device for a vehicle suspension using negative stiffness mechanism. Journal of Vibration Engineering and Technologies, 9: 957-966. doi: 10.1007/s42417-020-00275-6 [143] Sun J O, Kim K J. 2012. Six-degree of freedom active pneumatic table based on time delay control technique. Proceedings of the Institution of Mechanical Engineers, Part I. Journal of Systems and Control Engineering, 226: 622-637. [144] Sun J O, Kim KJ. 2013. Control of transient vibrations due to stage movements in 6-dof active pneumatic table by inertial force compensation. Journal of Sound and Vibration, 332: 5241-5254. doi: 10.1016/j.jsv.2013.05.013 [145] Sun X T, Jing X J, Xu J, et al. 2014a. Vibration isolation via a scissor-like structured platform. Journal of Sound and Vibration, 333: 2404-2420. [146] Sun X T, Jing X J. 2015. Multi-direction vibration isolation with quasi-zero stiffness by employing geometrical nonlinearity. Mechanical Systems and Signal Processing, 62: 149-163. [147] Sun X T, Qi Z F, Xu J. 2022. A novel multi-layer isolation structure for transverse stabilization inspired by neck structure. Acta Mechanica Sinica, 38: 521543. doi: 10.1007/s10409-022-09039-x [148] Sun X T, Wang F, Xu J. 2019a. Analysis, design and experiment of continuous isolation structure with Local Quasi-Zero-Stiffness property by magnetic interaction. International Journal of Non-Linear Mechanics, 116: 289-301. doi: 10.1016/j.ijnonlinmec.2019.07.008 [149] Sun X T, Wang F, Xu J. 2019b. Dynamics and realization of a feedback-controlled nonlinear isolator with variable time delay. Journal of Vibration and Acoustics, 141: 021005. doi: 10.1115/1.4041369 [150] Sun X T, Wang F, Xu J. 2021. A novel dynamic stabilization and vibration isolation structure inspired by the role of avian neck. International Journal of Mechanical Sciences, 193: 106166. doi: 10.1016/j.ijmecsci.2020.106166 [151] Sun X T, Xu J, Fu J S. 2017. The effect and design of time delay in feedback control for a nonlinear isolation system. Mechanical Systems and Signal Processing, 87: 206-217. doi: 10.1016/j.ymssp.2016.10.022 [152] Sun X T, Xu J, Jing X J, et al. 2014b. Beneficial performance of a quasi-zero- stiffness vibration isolator with time-delayed active control. International Journal of Mechanical Sciences, 82: 32-40. doi: 10.1016/j.ijmecsci.2014.03.002 [153] Sun X T, Xu J, Wang F. 2018a. A Novel isolation structure with flexible joints for impact and ultralow-frequency excitations. International Journal of Mechanical Sciences, 146-147: 366-376. doi: 10.1016/j.ijmecsci.2018.08.009 [154] Sun X T, Zhang S, Xu J, et al. 2018b. Dynamical analysis and realization of an adaptive Isolator. ASME Trans Journal of Applied Mechanics, 85: 011002. doi: 10.1115/1.4038285 [155] Sun X T, Zhang S, Xu J. 2018c. Parameter design of a multi-delayed isolator with asymmetrical nonlinearity. International Journal of Mechanical Sciences, 138-139: 398-408. doi: 10.1016/j.ijmecsci.2018.02.026 [156] Sun Y X, Xu J. 2015. Experiments and analysis for a controlled mechanical absorber considering delay effect. Journal of Sound and Vibration, 339: 25-37. doi: 10.1016/j.jsv.2014.11.005 [157] Valeev A R, Zotov A N, Kharisov S A. 2015. Application of disk springs for manufacturing vibration isolators with quasi-zero stiffness. Chemical and Petroleum Engineering, 51: 194-200. doi: 10.1007/s10556-015-0023-2 [158] Vo N Y P, Le T D. 2022. Dynamic Analysis of Quasi-Zero Stiffness Pneumatic Vibration Isolator. Applied sciences, 12: 2378. doi: 10.3390/app12052378 [159] Vo N Y P, Nguyen M K, Le T D. 2021. Analytical study of a pneumatic vibration isolation platform featuring adjustable stiffness. Communications in Nonlinear Science and Numerical Simulation, 98: 105775. doi: 10.1016/j.cnsns.2021.105775 [160] Vyhlídal T, Dan P, Alikoc B, et al. 2019. Analysis and design aspects of delayed resonator absorber with position, velocity or acceleration feedback. Journal of Sound and Vibration, 459: 114831. doi: 10.1016/j.jsv.2019.06.038 [161] Wang F, Sun X T, Meng H, et al. 2021. Time-delayed feedback control design and its application for vibration absorption. IEEE Transactions on Industrial Electronics, 68: 8593-8602. doi: 10.1109/TIE.2020.3009612 [162] Wang F, Sun X T, Meng H, et al. 2022. Tunable broadband low-frequency band gap of multiple-layer metastructure induced by time-delayed vibration absorbers. Nonlinear Dynamics, 107: 1903-1918. doi: 10.1007/s11071-021-07065-z [163] Wang F, Xu J. 2019. Parameter design for a vibration absorber with time-delayed feedback control. Acta Mechanica Sinica, 35: 624-640. doi: 10.1007/s10409-018-0822-8 [164] Wang K, Zhou J X, Chang Y P, et al. 2020. A nonlinear ultra-low-frequency vibration isolator with dual quasi-zero-stiffness mechanism. Nonlinear Dynamics, 101: 755-773. doi: 10.1007/s11071-020-05806-0 [165] Wang Q, Zhou J X, Xu D L, et al. 2020. Design and experimental investigation of ultra-low frequency vibration isolation during neonatal transport. Mechanical Systems and Signal Processing, 139: 19. [166] Wang Q B, Wu H, Yang Y J. 2022. The effect of fractional damping and time-delayed feedback on the stochastic resonance of asymmetric SD oscillator. Nonlinear Dynamics, 107: 2099-2114. doi: 10.1007/s11071-021-07105-8 [167] Wang S L, Wang Z C. 2022. Curved surface-based vibration isolation mechanism with designable stiffness: Modeling, simulation, and applications. Mechanical Systems and Signal Processing, 181: 109489. doi: 10.1016/j.ymssp.2022.109489 [168] Wang X, Yue X K, Dai H H, et al. 2020. Vibration suppression for post-capture spacecraft via a novel bio-inspired Stewart isolation system. Acta Astronautica, 168: 1-22. doi: 10.1016/j.actaastro.2019.11.033 [169] Wang Y, Li H X, Jiang W A, et al. 2021. A base excited mixed-connected inerter-based quasi-zero stiffness vibration isolator with mistuned load. Mechanics of Advanced Materials and Structures, 29: 4224-4242. [170] Weng X T, Yan Z T, Zeng Q H. 2011. Research on time delay of control in hybrid vibration isolation system. Procedia Engineering, 15: 1224-1228. doi: 10.1016/j.proeng.2011.08.226 [171] Wu J L, Che J X, Chen X D, et al. 2022a. Design of a combined magnetic negative stiffness mechanism with high linearity in a wide working region. Science China Technological Sciences, 65: 2127-2142. doi: 10.1007/s11431-022-2121-7 [172] Wu J L, Zeng L Z, Han B, et al. 2022b. Analysis and design of a novel arrayed magnetic spring with high negative stiffness for low-frequency vibration isolation. International Journal of Mechanical Sciences, 216: 106980. doi: 10.1016/j.ijmecsci.2021.106980 [173] Wu W, Chen X, Shan Y. 2014. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness. Journal of Sound and Vibration, 333: 2958-2970. doi: 10.1016/j.jsv.2014.02.009 [174] Wu Y, Yu K P, Jiao J, et al. 2015. Dynamic modeling and robust nonlinear control of a six-DOF active micro-vibration isolation manipulator with parameter uncertainties. Mechanism and Machine Theory, 92: 407-435. doi: 10.1016/j.mechmachtheory.2015.06.008 [175] Xie Y, Niu F, Sun J, et al. 2022. Design and analysis of a novel quasi-zero stiffness isolator under variable loads. Mathematical Problems in Engineering, 602: 657-663. [176] Xu D L, Yu Q P, Zhou J X, et al. 2013. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic. Journal of Sound and Vibration, 332: 3377-3389. doi: 10.1016/j.jsv.2013.01.034 [177] Xu J, Sun X T. 2015a. A multi-directional vibration isolator based on Quasi-Zero-Stiffness structure and time-delayed active control. International Journal of Mechanical Sciences, 100: 126-135. doi: 10.1016/j.ijmecsci.2015.06.015 [178] Xu J, Sun Y X. 2015b. Experimental studies on active control of a dynamic system via a time-delayed absorber. Acta Mechanica Sinica, 31: 229-247. doi: 10.1007/s10409-015-0411-z [179] Xu Z L, Wang Y Q, Zhu R, et al. 2021. Torsional bandgap switching in metamaterials with compression-torsion interacted origami resonators. Journal of Applied Physics, 130: 045105. doi: 10.1063/5.0056179 [180] Yan B, Ling P, Zhou Y, et al. 2022a. Shock isolation characteristics of a bistable vibration isolator with tunable magnetic controlled stiffness. Journal of Vibration and Acoustics, 144: 021008. doi: 10.1115/1.4051850 [181] Yan B, Ma H, Zhang L, et al. 2020. Electromagnetic shunt damping for shock isolation of nonlinear vibration isolators. Journal of Sound and Vibration, 479: 115370. doi: 10.1016/j.jsv.2020.115370 [182] Yan B, Pan X G, Su R, et al. 2022b. Nonlinear dynamics characteristics of a tumbler on an arc. Journal of Sound and Vibration, 525: 116810. doi: 10.1016/j.jsv.2022.116810 [183] Yan B, Yu N, Wu C Y. 2022c. A state-of-the-art review on low-frequency nonlinear vibration isolation with electromagnetic mechanisms. Applied Mathematics and Mechanics (English Edition) , 43: 1045-1062. doi: 10.1007/s10483-022-2868-5 [184] Yan G, Qi W H, Shi J W, et al. 2022a. Bionic paw-inspired structure for vibration isolation with novel nonlinear compensation mechanism. Journal of Sound and Vibration, 525: 116799. doi: 10.1016/j.jsv.2022.116799 [185] Yan G, Wang S, Zou H X, et al. 2020a. Bio-inspired polygonal skeleton structure for vibration isolation: Design, modelling, and experiment. Science China Technological Sciences, 63: 14. doi: 10.1007/s11431-019-9542-5 [186] Yan G, Wu Z Y, Wei X S, et al. 2022b. Nonlinear compensation method for quasi-zero stiffness vibration isolation. Journal of Sound and Vibration, 523: 116743. doi: 10.1016/j.jsv.2021.116743 [187] Yan G, Zou H X, Wang S, et al. 2021. Bio-inspired vibration isolation: Methodology and design. Applied Mechanics Reviews, 73: 020801. doi: 10.1115/1.4049946 [188] Yan G, Zou H X, Wang S, et al. 2022a. Bio-inspired toe-like structure for low-frequency vibration isolation. Mechanical Systems and Signal Processing, 162: 108010. doi: 10.1016/j.ymssp.2021.108010 [189] Yan G, Zou H X, Yan H, et al. 2020b. Multi-direction vibration isolator for momentum wheel assemblies. Journal of Vibration and Acoustics- Transactions of the ASME, 142: 041007. doi: 10.1115/1.4046680 [190] Yang T, Cao Q J, Hao Z F. 2021a. A novel nonlinear mechanical oscillator and its application in vibration isolation and energy harvesting. Mechanical systems and signal processing, 155: 107636. doi: 10.1016/j.ymssp.2021.107636 [191] Yang T, Cao Q J. 2017. Nonlinear transition dynamics in a time-delayed vibration isolator under combined harmonic and stochastic excitations. Journal of Statistical Mechanics:Theory and Experiment, 4: 043202. [192] Yang T, Cao Q J. 2018. Delay-controlled primary and stochastic resonances of the SD oscillator with stiffness nonlinearities. Mechanical Systems and Signal Processing, 103: 216-235. doi: 10.1016/j.ymssp.2017.10.002 [193] Yang T, Cao Q J. 2019. Noise- and delay-enhanced stability in a nonlinear isolation system. International Journal of Non-Linear Mechanics, 110: 81-93. doi: 10.1016/j.ijnonlinmec.2019.01.010 [194] Yang T, Cao Q J. 2021. Modeling and analysis of a novel multi-directional micro-vibration isolator with spring suspension struts. Archive of Applied Mechanics, 92: 801-819. [195] Yang T, Zhou S X, Fang S T, et al. 2021. Nonlinear vibration energy harvesting and vibration suppression technologies: Designs, analysis, and applications. Applied Physics Reviews, 8: 031317. doi: 10.1063/5.0051432 [196] Yang X L, Wu H T, Chen B, et al. 2019. Dynamic modeling and decoupled control of a flexible Stewart platform for vibration isolation. Journal of Sound and Vibration, 439: 398-412. doi: 10.1016/j.jsv.2018.10.007 [197] Yang X L, Wu H T, Li Y, et al. 2017. Dynamic isotropic design and decentralized active control of a six-axis vibration isolator via Stewart platform. Mechanism and Machine Theory, 117: 244-252. doi: 10.1016/j.mechmachtheory.2017.07.017 [198] Ye K, Ji J C, Brown T. 2020. Design of a quasi-zero stiffness isolation system for supporting different loads. Journal of Sound and Vibration, 471: 115198. doi: 10.1016/j.jsv.2020.115198 [199] Ye K, Ji J C, Brown T. 2021. A novel integrated quasi-zero stiffness vibration isolator for coupled translational and rotational vibrations. Mechanical Systems and Signal Processing, 149: 107340. doi: 10.1016/j.ymssp.2020.107340 [200] Ye K, Ji J C. 2022. An origami inspired quasi-zero stiffness vibration isolator using a novel truss-spring based stack Miura-ori structure. Mechanical Systems and Signal Processing, 165: 108383. doi: 10.1016/j.ymssp.2021.108383 [201] Zeng R, Wen G L, Zhou J X, et al. 2021. A limb-inspired bionic quasi-zero stiffness vibration isolator. Acta Mechanica Sinica, 37: 1152-1167. doi: 10.1007/s10409-021-01070-6 [202] Zeng R, Yin S, Wen G, et al. 2022. A non-smooth quasi-zero-stiffness isolator with displacement constraints. International Journal of Mechanical Sciences, 225: 107351. doi: 10.1016/j.ijmecsci.2022.107351 [203] Zhang H P, Yang L H, Su P, et al. 2020. The influence of the controlling delay time on two-degree-of-freedom system with a high-static-low-dynamic-stiffness isolator. Journal of Vibroengineering, 22: 751-761. doi: 10.21595/jve.2020.20720 [204] Zhang J, Xu D, Zhou J, et al. 2012. Chaotification of vibration isolation floating raft system via nonlinear time-delay feedback control. Chaos Solitons and Fractals, 45: 1255-1265. doi: 10.1016/j.chaos.2012.05.012 [205] Zhang M K, Yang J Y, Zhu R. 2021. Origami-based bistable metastructures for low-frequency vibration control. Journal of Applied Mechanics- Transactions of the ASME, 88: 051009. doi: 10.1115/1.4049953 [206] Zhang Q, Guo D K, Hu G K. 2021. Tailored mechanical metamaterials with programmable quasi-zero-stiffness features for full-band vibration Isolation. Advanced Functional Materials, 31: 2101428. doi: 10.1002/adfm.202101428 [207] Zhang W, Zhao J B. 2016. Analysis on nonlinear stiffness and vibration isolation performance of scissor-like structure with full types. Nonlinear Dynamics, 86: 17-36. doi: 10.1007/s11071-016-2869-z [208] Zhang X X, Ji J, Xu J. 2019. Parameter identification of time-delayed nonlinear systems: An integrated method with adaptive noise correction. Journal of the Franklin Institute, 356: 5858-5880. doi: 10.1016/j.jfranklin.2019.03.023 [209] Zhang X X, Xu J, Feng Z C. 2017. Nonlinear equivalent model and its identification for a delayed absorber with magnetic action using distorted measurement. Nonlinear Dynamics, 88: 937-954. doi: 10.1007/s11071-016-3286-z [210] Zhang X X, Xu J, Ji J. 2018. Modelling and tuning for a time-delayed vibration absorber with friction. Journal of Sound and Vibration, 424: 137-157. doi: 10.1016/j.jsv.2018.03.019 [211] Zhang X X, Xu J. 2014. Identification of time delay in nonlinear systems with delayed feedback control. Journal of the Franklin Institute, 352: 2987-2998. [212] Zhang X X, Xu J. 2016. Time delay identifiability and estimation for the delayed linear system with incomplete measurement. Journal of Sound and Vibration, 361: 330-340. doi: 10.1016/j.jsv.2015.09.034 [213] Zhang Y, Liu Q H, Lei Y G, et al. 2023. Halbach high negative stiffness isolator: Modeling and experiments. Mechanical Systems and Signal Processing, 188: 110014. doi: 10.1016/j.ymssp.2022.110014 [214] Zhang Y L, Wei G, Wen H, et al. 2021. Design and analysis of a vibration isolation system with cam-roller-spring-rod mechanism. Journal of Vibration and Control, 28: 1781-1791. [215] Zhang Y T, Cao Q J, Huang W H. 2021. Bursting oscillations in an isolation system with quasi-zero stiffness. Mechanical Systems and Signal Processing, 161: 107916. doi: 10.1016/j.ymssp.2021.107916 [216] Zhao F, Ji J C, Luo Q T, et al. 2021. An improved quasi-zero stiffness isolator with two pairs of oblique springs to increase isolation frequency band. Nonlinear Dynamics, 104: 1-17. doi: 10.1007/s11071-021-06413-3 [217] Zhao F, Ji J C, Ye K, et al. 2020. Increase of quasi-zero stiffness region using two pairs of oblique springs. Mechanical Systems and Signal Processing, 144: 106975. doi: 10.1016/j.ymssp.2020.106975 [218] Zhao F, Cao S Q, Ji J C, et al. 2022a. Enhanced design of the quasi-zero stiffness vibration isolator with three pairs of oblique springs: theory and experiment. Journal of Vibration and Control, 0: 1-15. [219] Zhao F, Cao S Q, Luo Q T, et al. 2022b. Practical design of the QZS isolator with one pair of oblique bars by considering pre-compression and low-dynamic stiffness. Nonlinear Dynamics, 108: 3313-3330. doi: 10.1007/s11071-022-07368-9 [220] Zheng Y S, Li Q P, Yan B, et al. 2018. A Stewart isolator with high-static-low-dynamic stiffness struts based on negative stiffness magnetic springs. Journal of Sound and Vibration, 422: 390-408. doi: 10.1016/j.jsv.2018.02.046 [221] Zhou J X, Wang K, Xu D L, et al. 2018. Vibration isolation in neonatal transport by using a quasi-zero-stiffness isolator. Journal of Vibration and Control, 24: 3278-3291. doi: 10.1177/1077546317703866 [222] Zhou J X, Wang X L, Xu D L, et al. 2015a. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms. Journal of Sound and Vibration, 346: 53-69. doi: 10.1016/j.jsv.2015.02.005 [223] Zhou J X, Xu D L, Bishop S. 2015b. A torsion quasi-zero stiffness vibration isolator. Journal of Sound and Vibration, 338: 121-133. doi: 10.1016/j.jsv.2014.10.027 [224] Zhou J X, Xu D L, Zhang J, et al. 2012. Spectrum optimization-based chaotification using time-delay feedback control. Chaos Solitons and Fractals, 45: 815-824. doi: 10.1016/j.chaos.2012.02.015 [225] Zhou N, Liu K. 2010. A tunable high-static-low-dynamic stiffness vibration isolator. Journal of Sound and Vibration, 329: 1254-1273. doi: 10.1016/j.jsv.2009.11.001 [226] Zhu G N, Cao Q J, Chen Y S. 2022. An archetypal zero- or quasi-zero-stiffness model with three degrees of freedom based upon an inverse method. Nonlinear Dynamics, Online. [227] Zhu T, Cazzolato B, Robertson W, et al. 2015. Vibration isolation using six degree-of-freedom quasi-zero stiffness magnetic levitation. Journal of Sound and Vibration, 358: 48-73. doi: 10.1016/j.jsv.2015.07.013 [228] Zhu T, Cazzolato B S, Robertson W S, et al. 2011. The development of a 6 degree of freedom quasi-zero stiffness Maglev vibration isolator with adaptive-passive load support// Icmt Secretariat, 2011. -




 下载:
下载: