-
摘要: 非线性随机动力学是力学、数学、工程等多个领域关注的热点, 在航空航天、机械工程、生物生态等领域有广泛的应用. 多稳态动力系统作为其最重要的研究对象, 在随机扰动下具有丰富的动力学行为, 如随机分岔、随机共振等, 尤其是随机共振, 已经被应用于机械故障诊断、微弱信号检测和振动能量俘获等工程实际问题中. 本文主要综述了多稳态动力系统中的随机共振理论、方法及工程应用. 首先, 通过几类典型的非线性随机动力学系统, 介绍了随机共振的经典理论和度量指标; 其次, 重点阐述了多稳态动力学系统, 尤其是三稳态和周期势系统, 在各类噪声激励下的随机共振现象, 分析了其诱发机理、演化规律和研究方法; 最后, 介绍了多稳态动力系统中随机共振的几类应用实例, 并进一步给出了随机共振当前面临的难题和未来的发展趋势等开放性问题.Abstract: The nonlinear stochastic dynamical system has been an important subject in areas of mechanics, mathematics, engineering and so on, and finds various applications in different fields like mechanical engineering, aerospace engineering, ocean engineering, and biology. The multi-stable dynamical systems are conceptual nonlinear systems, coupling with stochastic excitations, which can exhibit complex dynamical behaviors, such as stochastic resonance and stochastic bifurcation. The stochastic resonance theory has been utilized effectively in many areas related to stochastic dynamics such as mechanical fault diagnosis, weak signal detection and vibration energy harvesting. This paper overviews the fundamental theories, methods and engineering applications of stochastic resonance in multi-stable dynamical systems. We introduce recent advances in theories and measure index of stochastic resonance via several classic examples of nonlinear dynamical systems. Then, we summarize the results of multi-stable dynamical systems under the excitation of different types of noise. The tri-stable and periodic systems are illustrated to show the occurrence principle, evolution mechanism and investigated techniques. Finally, three engineering applications of multi-stable dynamical systems are surveyed. Some open problems are presented to close this paper.
-
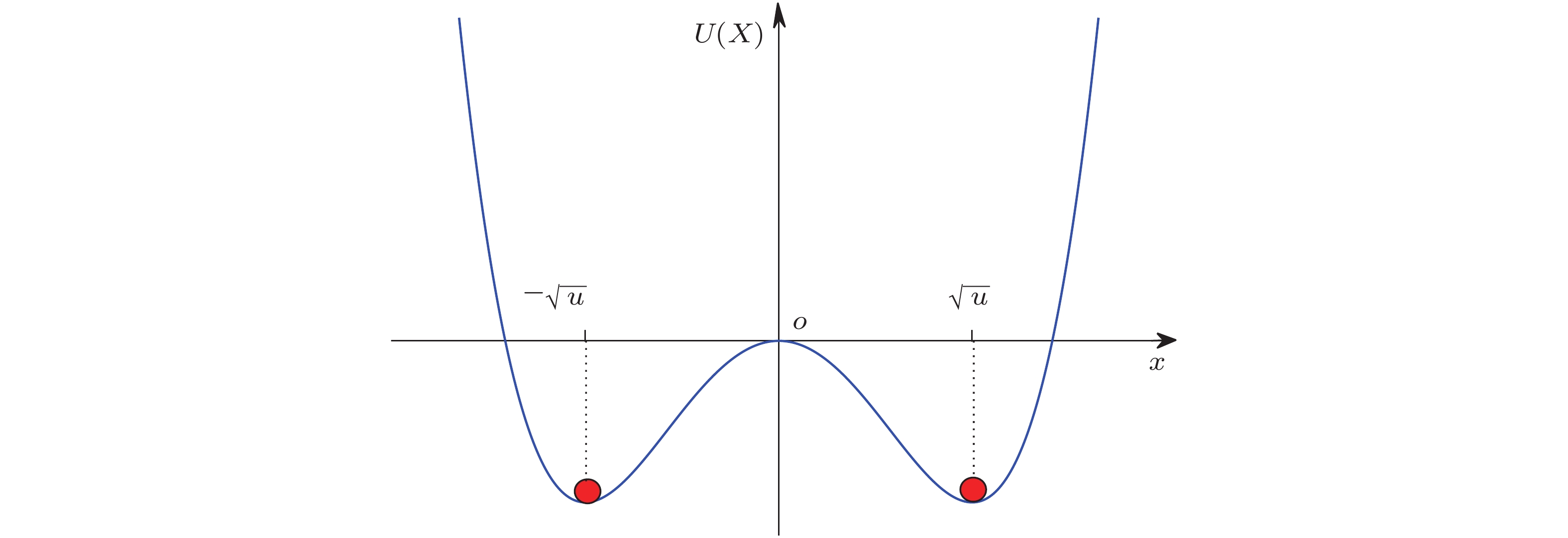
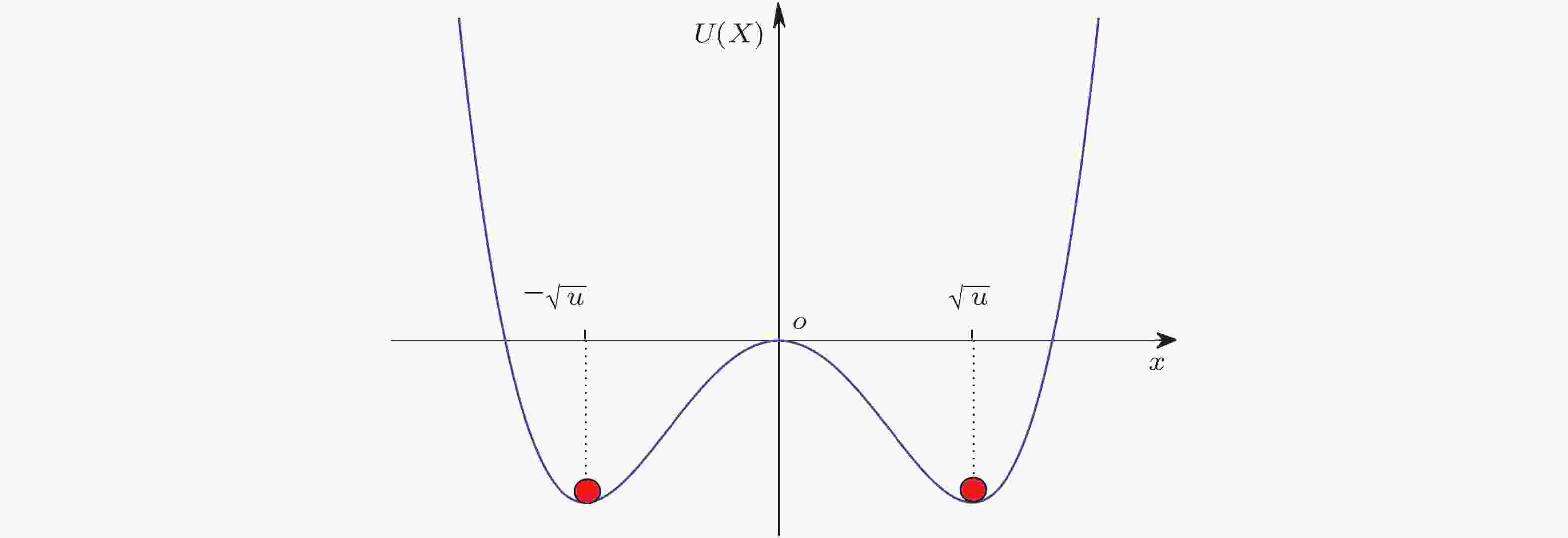
图 2 对称双稳态系统(1)的随机共振示意图(Gammaitoni et al. 1998)
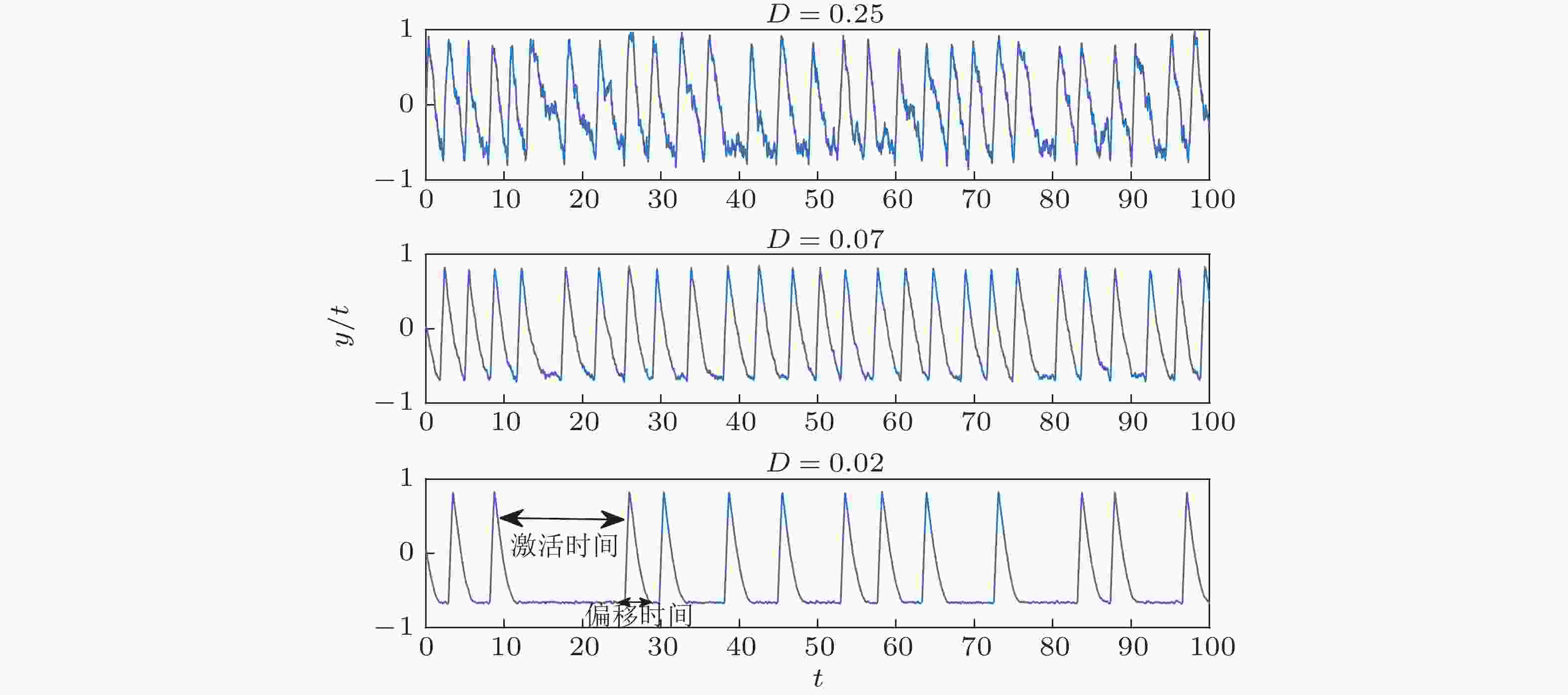
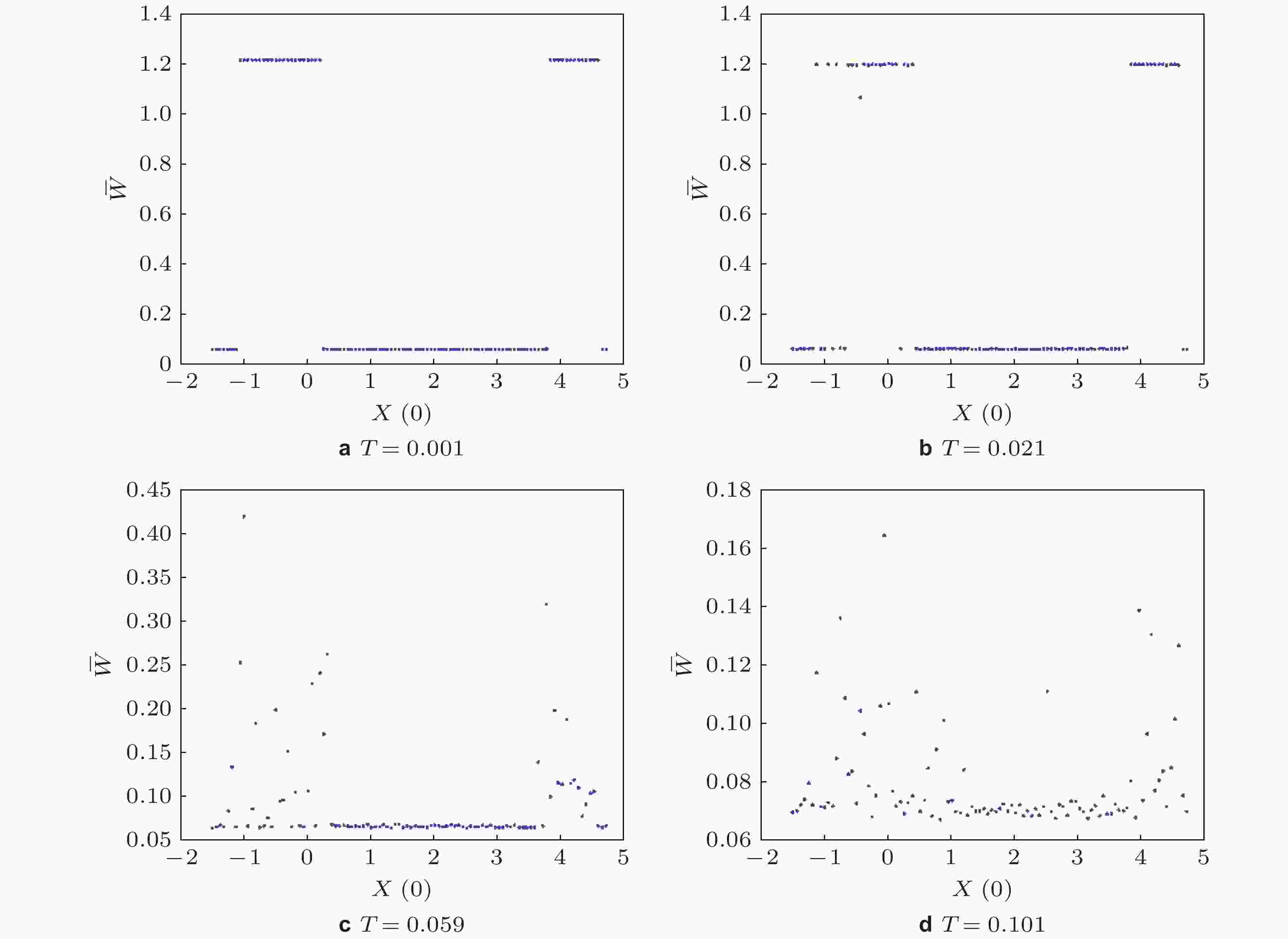
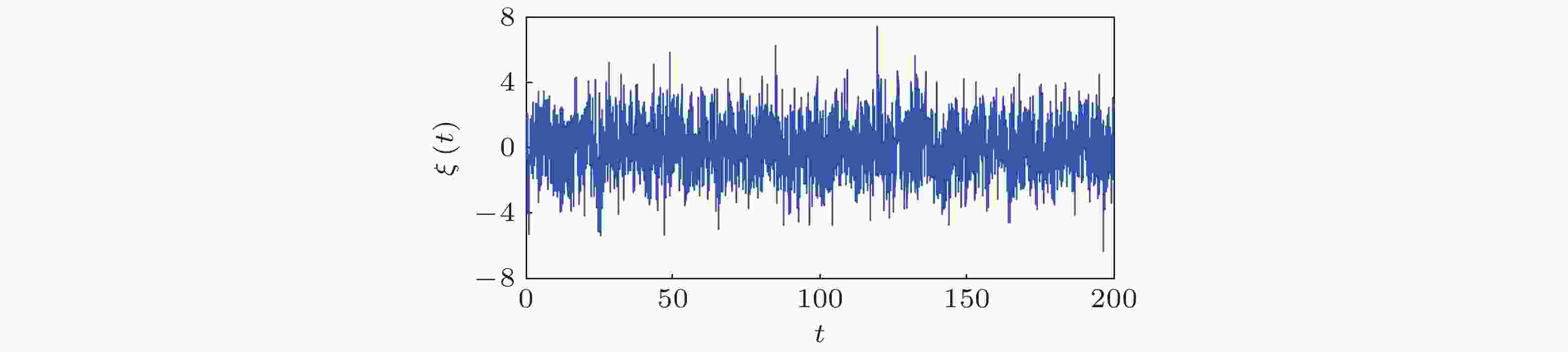
图 3 不同噪声强度下模型(7)的动力学响应, 其中
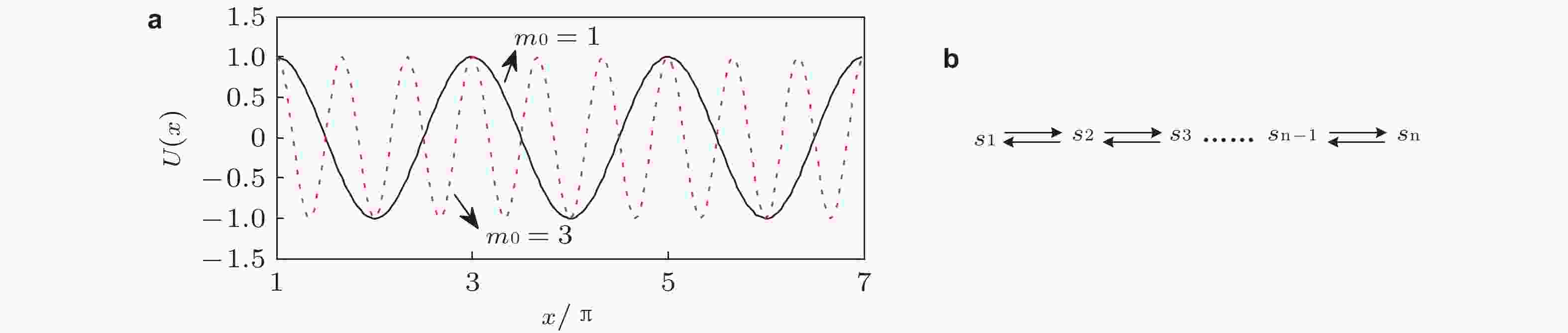
$a = 1.05$ ,$\varepsilon = 0.01$ ,$(x(0),y(0)) = (0,0)$ (Pikovsky & Kurths 1997)图 5 (a)周期势函数(
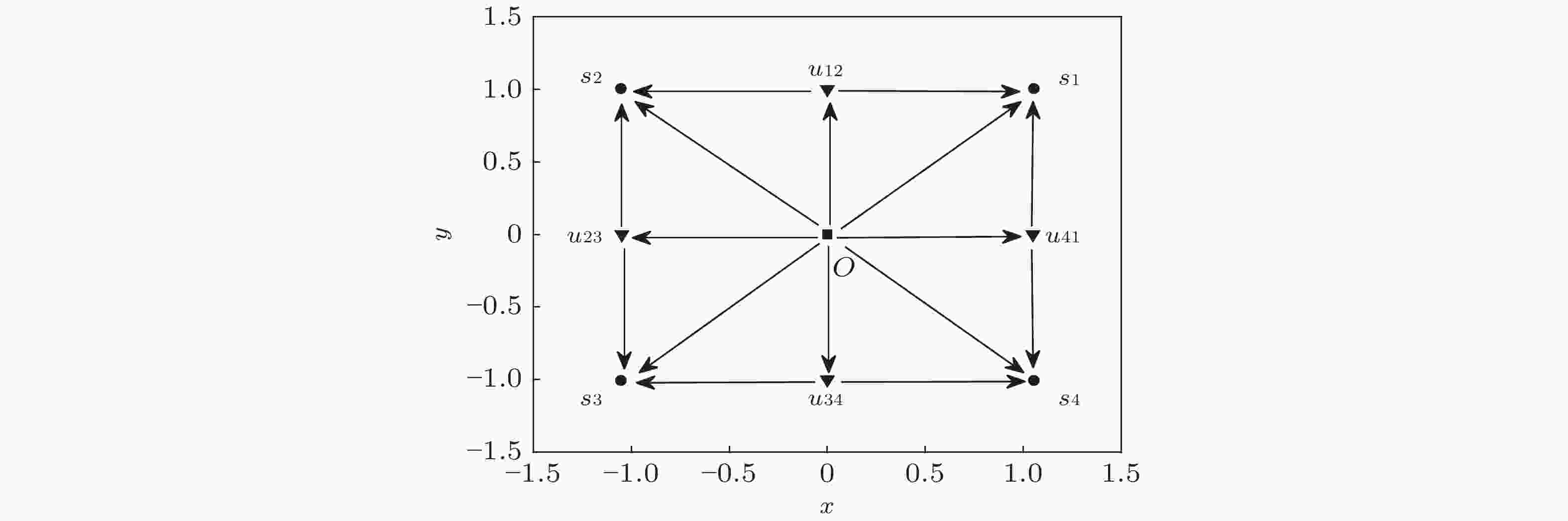
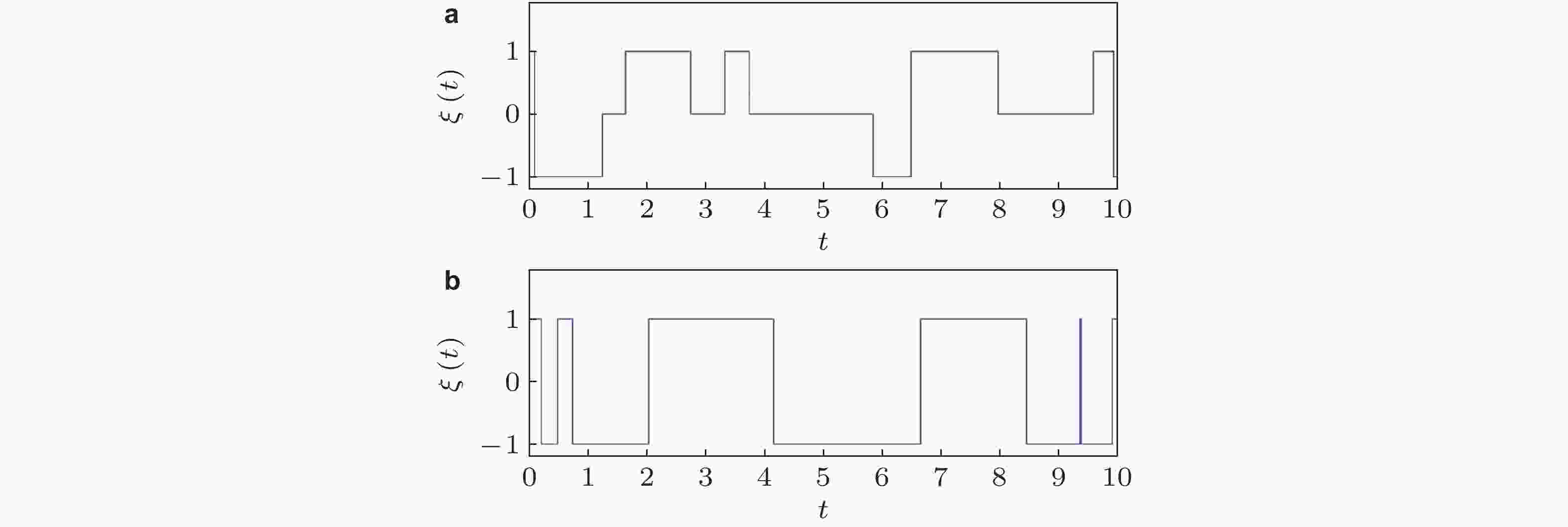
$ a = 1 $ ), (b)离散的多稳态过程(靳艳飞和许鹏飞 2021)图 6 耦合势函数(15)的平衡点在
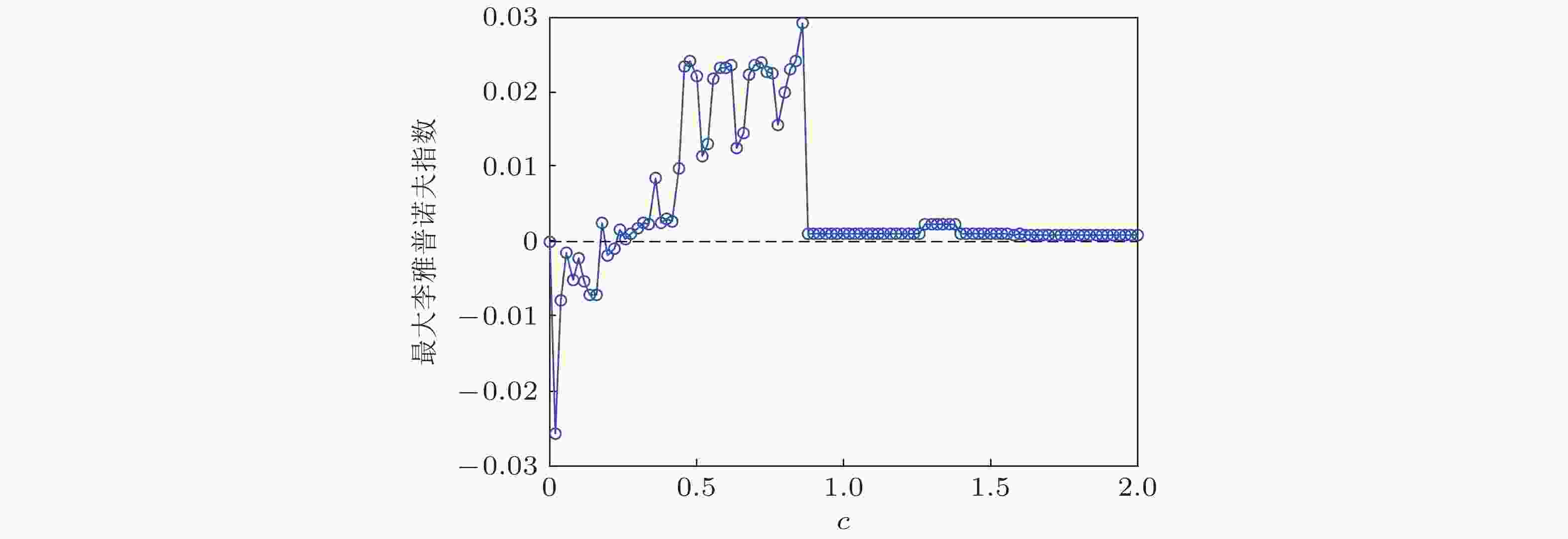
$ x - y $ 相平面上的分布, 其中$ s $ ,$ u $ 和$ o $ 分别表示稳定结点、鞍点和不稳定结点(Xu & Jin 2018)图 7 最大李雅普诺夫指数作为耦合强度
$ c $ 的函数曲线, 其中$ {{{\varepsilon _y}} \mathord{\left/ {\vphantom {{{\varepsilon _y}} {{\varepsilon _x}}}} \right. } {{\varepsilon _x}}} = 1 $ ,$ {{{\omega _y}} \mathord{\left/ {\vphantom {{{\omega _y}} {{\omega _x}}}} \right. } {{\omega _x}}} = {1 \mathord{\left/ {\vphantom {1 {12}}} \right. } {12}} $ (Xu & Jin 2018)图 8 不同热噪声强度下系统平均输入能量相对初始位置出现的相外状态和相内状态(Liu & Jin 2013)
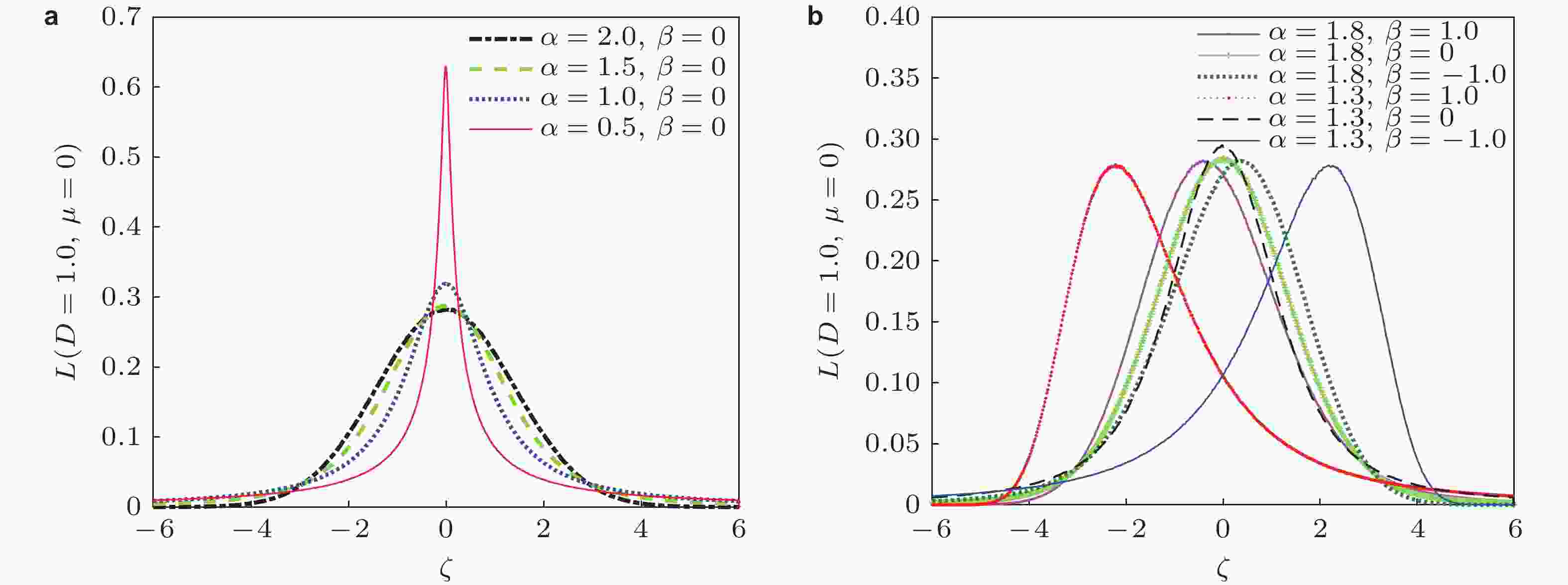
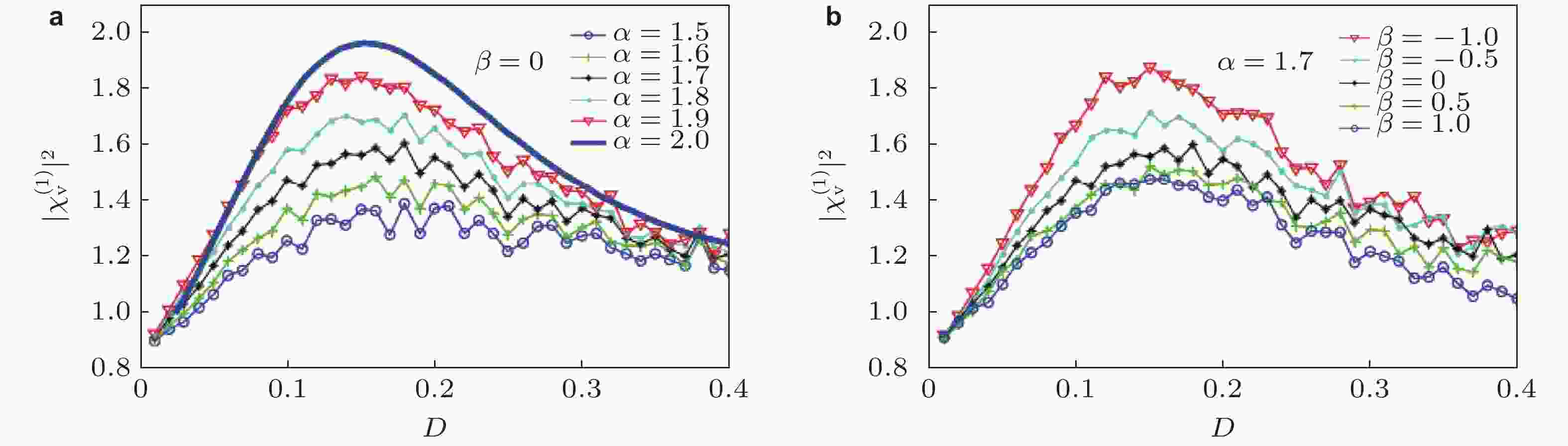
图 10 功率谱放大因子作为噪声强度的函数随不同Lévy噪声参数
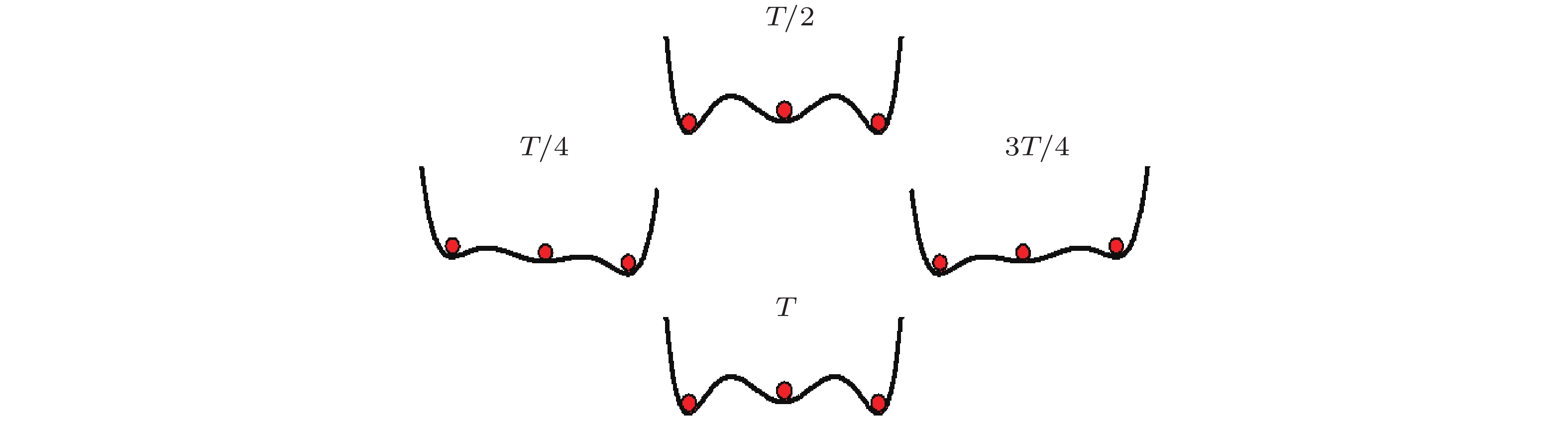
$ \alpha $ 和$ \beta $ 的变换情况(Liu & Kang 2018)图 14 三稳态系统跃迁示意图(Nicolis 2012)
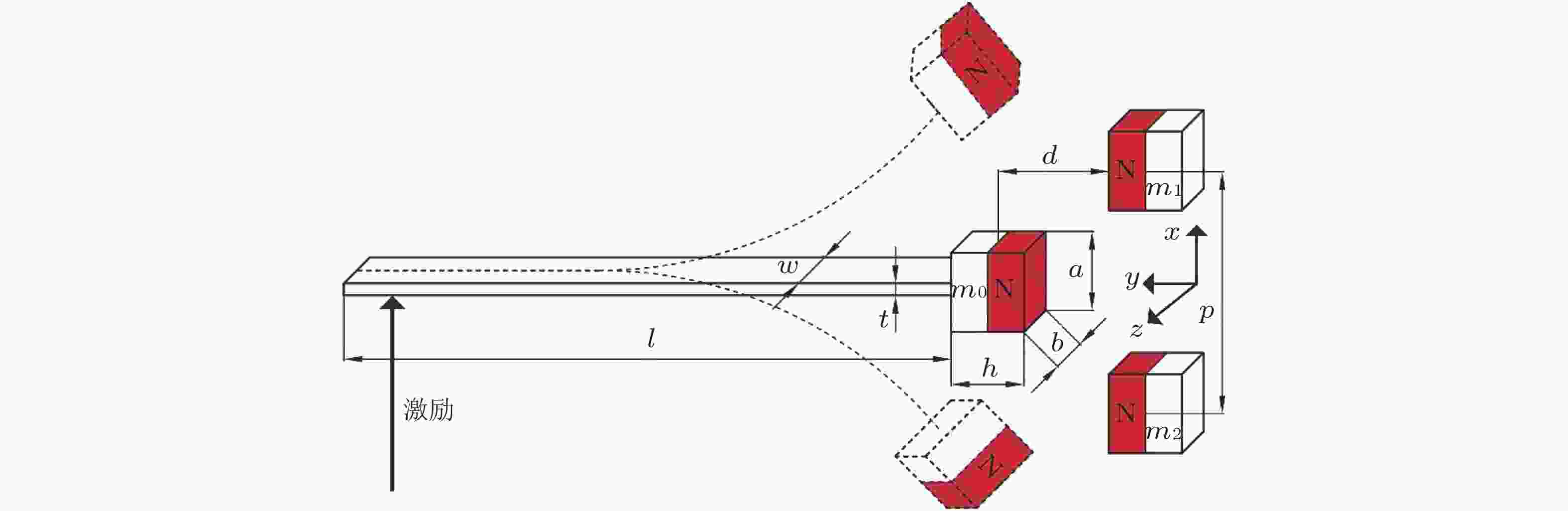
图 15 三稳态随机共振悬臂梁结构示意图(Lu et al. 2013)
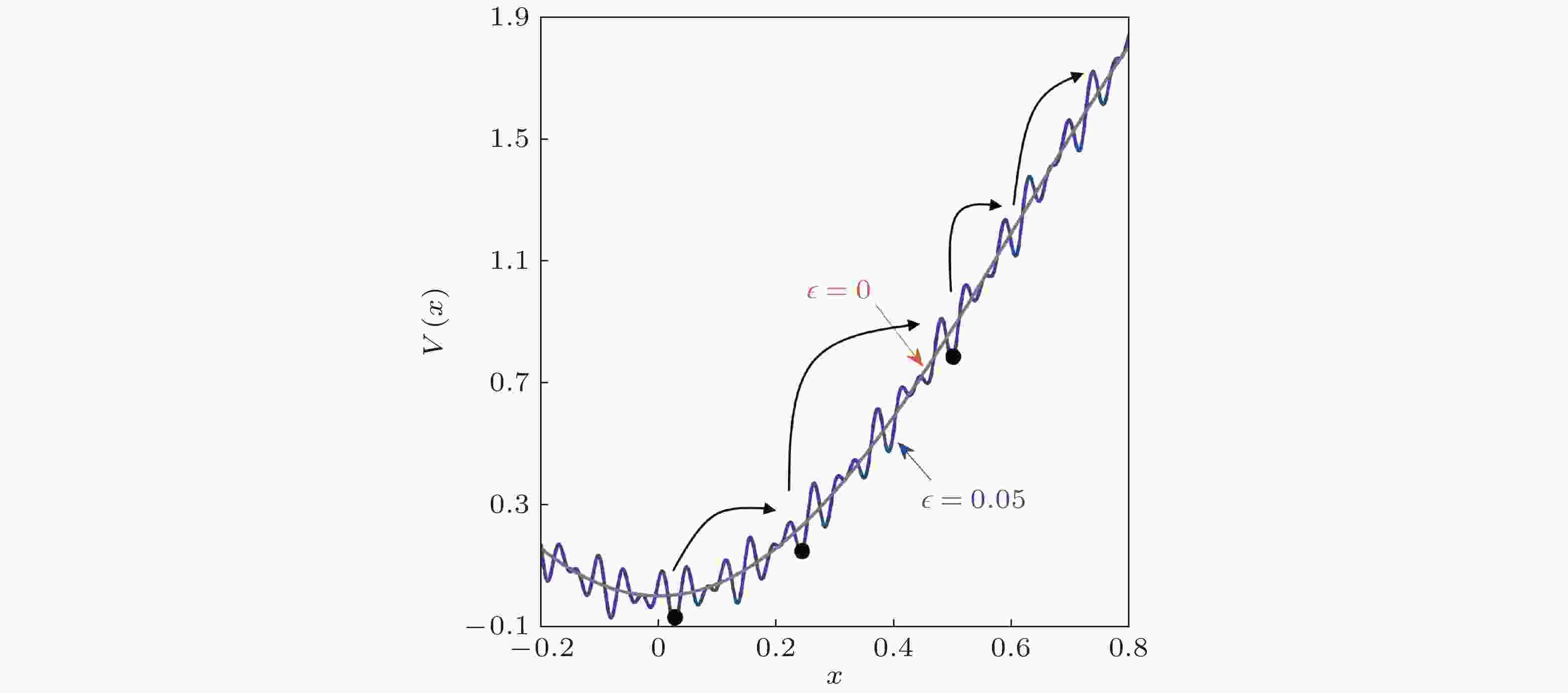
图 16 系统在粗糙三势阱中的跃迁示意图(Li et al. 2016)
图 17 信噪比(
$ {\rm{SNR}} $ )作为阻尼系数$ {\gamma _0} $ 的函数随五次非线性刚度系数$ {\kappa _5} $ 的变化曲线(Xu et al. 2019)图 18 记忆时间
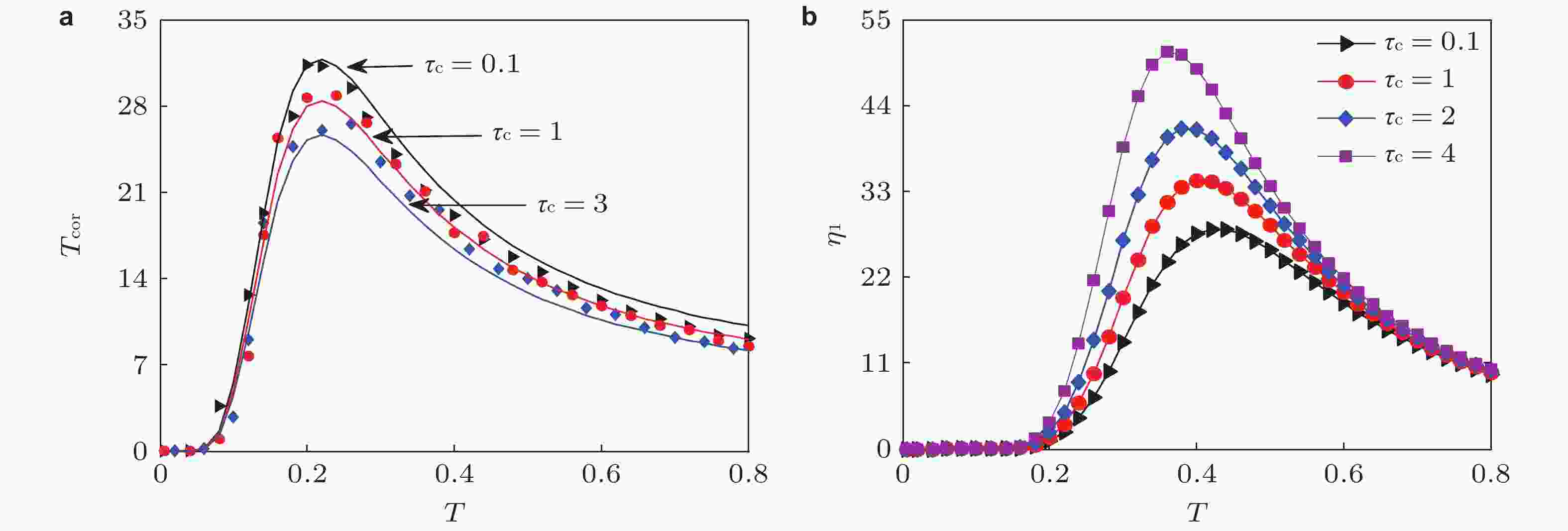
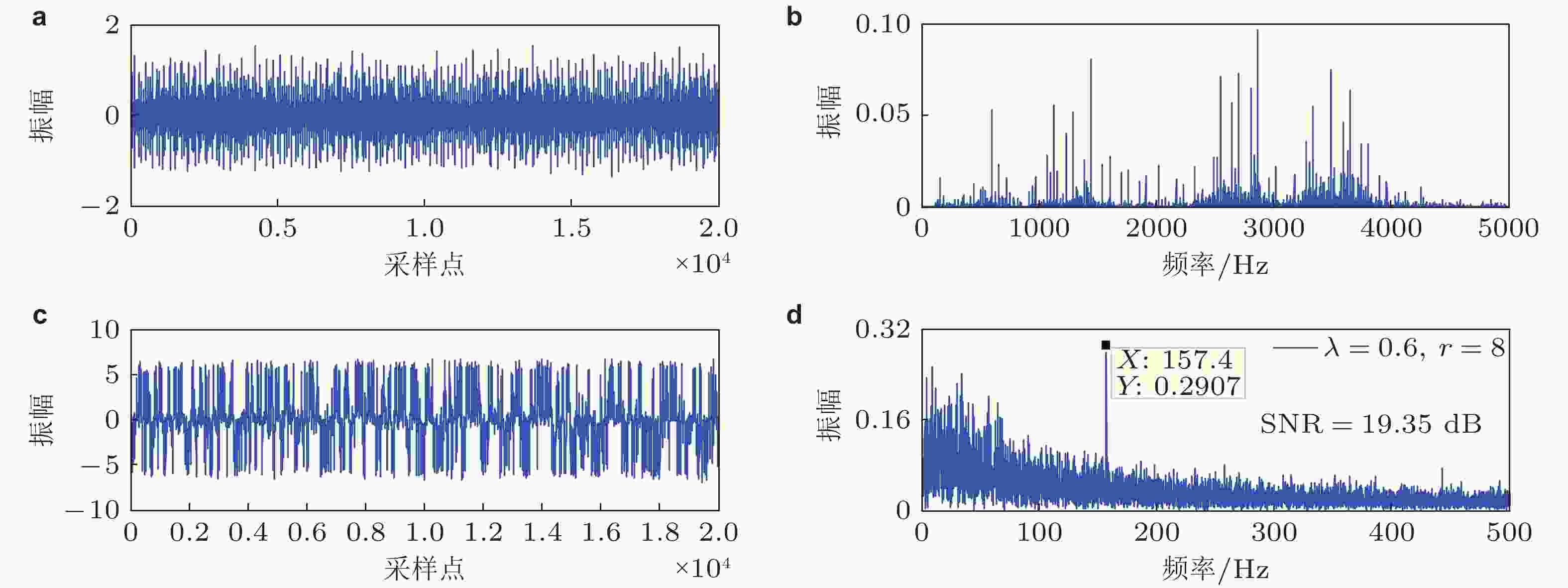
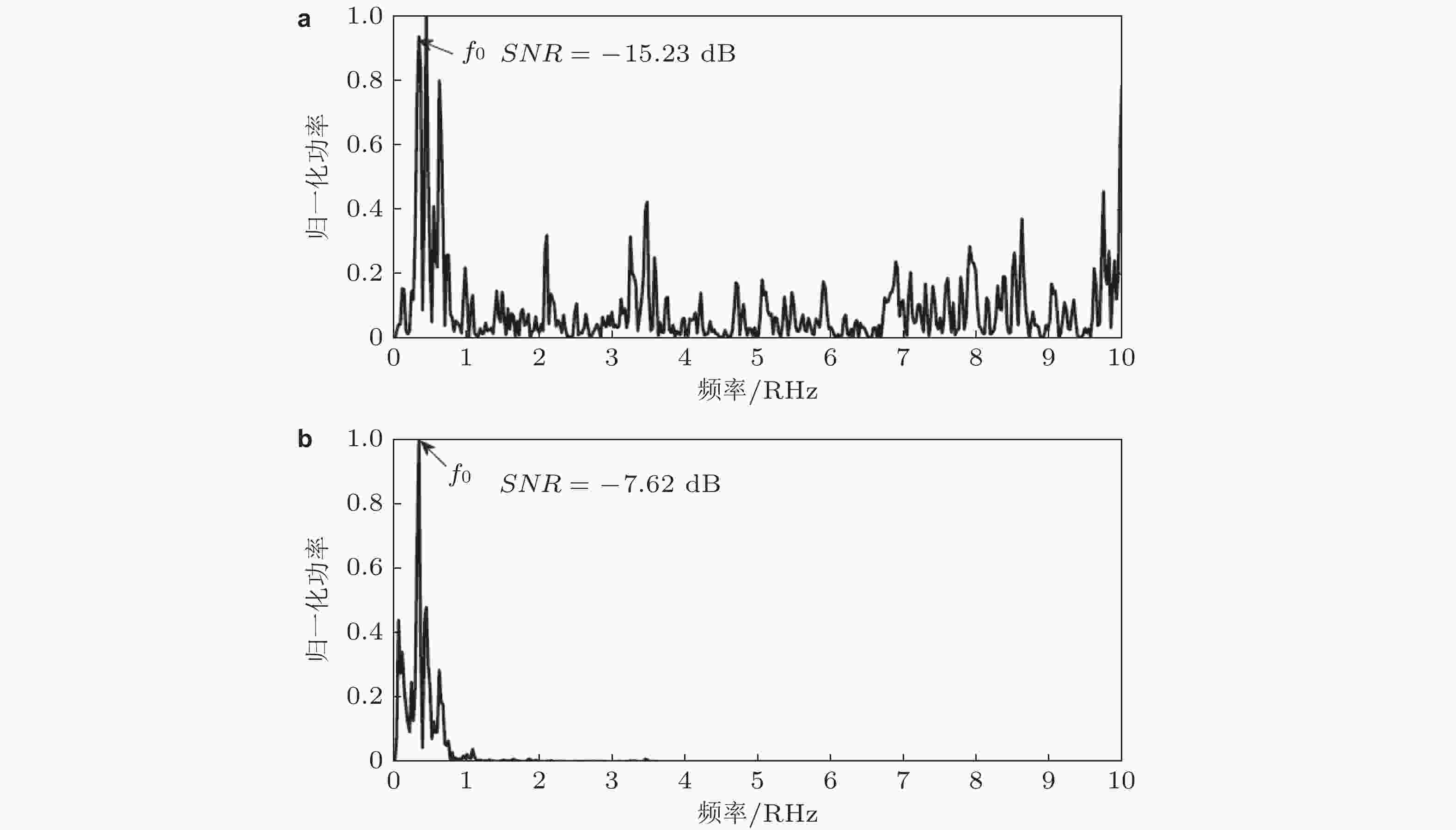
$ {\tau _c} $ 对噪声诱导共振的影响. (a)特征相关时间和(b)功率谱放大因子(Xu & Jin 2020)图 20 轴承内圈故障信号检测. (a)和(b)原始信号和频谱, (c)和(d)随机共振条件下输出信号和频谱(Xu & Jin 2020)
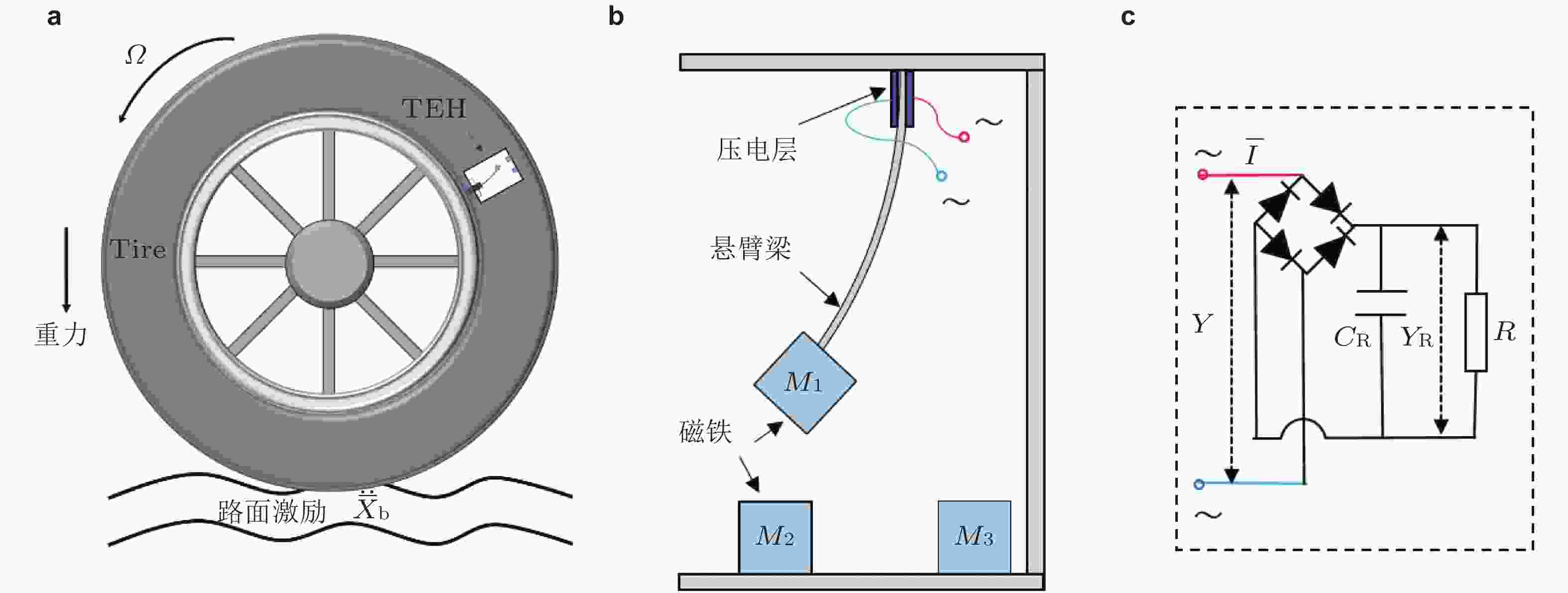
图 22 旋转环境下三稳态能量采集装置示意图. (a)安装在车轮上的三稳态能量收集装置, (b)三稳态压电能量采集器(THE)原理图, (c)与THE相连的标准整流电路(Zhang et al. 2022)
-
[1] 方同. 1995. 工程随机振动. 北京: 国防工业出版社(Fang T. 1995. Engineering Stochastic Vibration. Beijing: National Defense Industry Press). [2] 顾仁财, 许勇, 郝孟丽, 杨志强. 2011. Lévy 稳定噪声激励下的Duffing-van der Pol 振子的随机分岔. 物理学报, 60: 060513 (Gu R C, Xu Y, Hao M L, Yang Z Q. 2011. Stochastic bifurcations in Duffing-van der Pol oscillator with Lévy stable noise. Acta Physica Sinica, 60: 060513). doi: 10.7498/aps.60.060513(Gu R C, Xu Y, Hao M L, Yang Z Q. 2011. Stochastic bifurcations in Duffing-van der Pol oscillator with Lévy stable noise. Acta Physica Sinica, 60: 060513). doi: 10.7498/aps.60.060513 [3] 顾仁财, 许勇, 张慧清, 孙中奎. 2011. 非高斯Lévy噪声驱动下的非对称双稳系统的相转移和平均首次穿越时间. 物理学报, 60: 110514 (Gu R C, Xu Y, Zhang H Q, Sun Z K. 2011. Phase transitions and the mean first passage time of an asymmetric bistable system with non-Gaussian Lévy noise. Acta Physica Sinica, 60: 110514). doi: 10.7498/aps.60.110514(Gu R C, Xu Y, Zhang H Q, Sun Z K. 2011. Phase transitions and the mean first passage time of an asymmetric bistable system with non-Gaussian Lévy noise. Acta Physica Sinica, 60: 110514) doi: 10.7498/aps.60.110514 [4] 郭书祥, 冯元生, 吕震宙. 2000. 随机有限元方法与结构可靠性. 力学进展, 30: 343-350 (Guo S X, Feng Y S, Lü Z Z. 2000. Stochastic finite element method and structural reliability. Advances in Mechanics, 30: 343-350). doi: 10.6052/1000-0992-2000-3-J1998-026(Guo S X, Feng Y S, Lv Z Y. 2000. Stochastic finite element method and structural reliability. Advances in Mechanics, 30: 343-350). doi: 10.6052/1000-0992-2000-3-J1998-026 [5] 郝颖, 吴志强. 2013. 三稳态Van der Pol-Duffing振子的随机P分岔. 力学学报, 45: 257-264 (Hao Y, Wu Z Q. 2013. Stochastic P-bifurcation of tri-stable Van Der Pol-Duffing oscillator. Chinese Journal of Theoretical and Applied Mechanics, 45: 257-264). doi: 10.6052/0459-1879-12-169(Hao Y, Wu Z Q. 2013. Stochastic P-bifurcation of tri-stable Van Der Pol-Duffing oscillator. Chinese Journal of Theoretical and Applied Mechanics, 45: 257-264). doi: 10.6052/0459-1879-12-169 [6] 胡岗. 1994. 随机力与非线性系统. 上海: 上海科技教育出版社(Hu G. 1994. Stochastic Forces and Nonlinear Systems. Shanghai: Shanghai Scientific and Technological Education Press). [7] 江俊, 陈艳华. 2013. 转子与定子碰摩的非线性动力学研究. 力学进展, 43: 132-148 (Jiang J, Chen Y H. 2013. Advances in the research on nonlinear phenomena in rotor/stator rubbing systems. Advances in Mechanics, 43: 132-148). doi: 10.6052/1000-0992-12-033(Jiang J, Chen Y H. 2013. Advances in the research on nonlinear phenomena in rotor/stator rubbing systems. Advances in Mechanics, 43: 132-148). doi: 10.6052/1000-0992-12-033 [8] 金肖玲, 王永, 黄志龙. 2013. 多自由度非线性随机系统的响应与稳定性. 力学进展, 43: 56-62 (Jin X L, Wang Y, Huang Z L. 2013. Response and stability of multi-degree-of-freedom nonlinear stochastic systems. Advances in Mechanics, 43: 56-62). doi: 10.6052/1000-0992-12-026(Jin X L, Wang Y, Huang Z L. 2013. Response and stability of multi-degree-of-freedom nonlinear stochastic systems. Advances in Mechanics, 43: 56-62). doi: 10.6052/1000-0992-12-026 [9] 冷永刚, 王太勇. 2003. 二次采样用于随机共振从强噪声中提取弱信号的数值研究. 物理学报, 52: 2432-2437 (Leng Y G, Wang T Y. 2003. Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise. Acta Physica Sinica, 52: 2432-2437). doi: 10.7498/aps.52.2432(Leng Y G, Wang T Y. 2003. Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise. Acta Physica Sinica, 52: 2432-2437). doi: 10.7498/aps.52.2432 [10] 李杰, 陈建兵. 2010. 随机动力系统中的概率密度演化方程及其研究进展. 力学进展, 40: 170-188 (Li J, Chen J B. 2010. Advance in the research on probability density evolution equations of stochastic dynamical systems. Advances in Mechanics, 40: 170-188). doi: 10.6052/1000-0992-2010-2-J2009-105(Li J, Chen J B. 2010. Advance in the research on probability density evolution equations of stochastic dynamical systems. Advances in Mechanics, 40: 170-188. ). doi: 10.6052/1000-0992-2010-2-J2009-105 [11] 李扬, 赵锋, 刘先斌. 2022. 基于大偏差理论非高斯随机动力系统离出行为研究. 力学进展, 52: 79-116 (Li Y, Zhao F, Liu X B. 2022. On the exit behaviors of non-Gaussian stochastic dynamical systems based on large deviation theory. Advances in Mechanics, 52: 79-116).(Li Y, Zhao F, Liu X B. 2022. On the exit behaviors of non-Gaussian stochastic dynamical systems based on large deviation theory. Advances in Mechanics, 52: 79-116). [12] 林敏, 张美丽, 黄咏梅. 2011. 双稳系统的随机能量共振和作功效率. 物理学报, 60: 080509 (Lin M, Zhang M L, Huang Y M. 2011. The stochastic energetics resonance of bistable systems and efficiency of doing work. Acta Physica Sinica, 60: 080509). doi: 10.7498/aps.60.080509(Lin M, Zhang M L, Huang Y M. 2011. The stochastic energetics resonance of bistable systems and efficiency of doing work. Acta Physica Sinica, 60: 080509). doi: 10.7498/aps.60.080509 [13] 刘开贺, 靳艳飞, 马正木. 2016. 相关乘性和加性高斯白噪声激励下周期势系统的随机共振. 动力学与控制学报, 14: 59-63 (Liu K H, Jin Y F, Ma Z M. 2016. Stochastic resonance in a periodic potential system driven by correlated additive and multiplicative white noises. Journal of Dynamics and Control, 14: 59-63). doi: 10.6052/1672-6553-2015-031(Liu K H, Jin Y F, Ma Z M. 2016. Stochastic resonance in a periodic potential system driven by correlated additive and multiplicative white noises. Journal of Dynamics and Control, 14: 59-63). doi: 10.6052/1672-6553-2015-031 [14] 靳晓琴, 许勇, 张慧清. 2013. 非高斯噪声驱动下一维双稳系统的逻辑操作. 物理学报, 62: 190510 (Jin X Q, Xu Y, Zhang H Q. 2013. The reliability of logical operation in a one-dimensional bistable system induced by non-Gaussian noise. Acta Physica Sinica, 62: 190510).(Jin X Q, Xu Y, Zhang H Q. 2013. The reliability of logical operation in a one-dimensional bistable system induced by non-Gaussian noise. Acta Physica Sinica 62: 190510). [15] 靳艳飞, 许鹏飞. 2021. 典型非线性多稳态系统的随机动力学. 北京: 科学出版社(Jin Y F, Xu P F. Stochastic dynamics of the classical nonlinear multi-stable systems. Beijing: Science Press). [16] 王喜英, 许勇, 徐伟, 张慧清. 2011. 非高斯列维噪声激励下非线性系统的Lyapunov 指数. 动力学与控制学报, 9: 135-138 (Wang X Y, Xu Y, Xu W, Zhang H Q. 2011. Lyapunov exponents for nonlinear systems driven by Lévy noise. Journal of Dynamics and Control, 9: 135-138).(Wang X Y, Xu Y, Xu W, Zhang H Q. 2011. Lyapunov exponents for nonlinear systems driven by Lévy noise. Journal of Dynamics and Control, 9: 135-138). [17] 徐伟. 2016. 非线性随机动力学的若干数值方法及应用. 北京: 科学出版社Xu W. 2016. Numerical Analysis Methods for Stochastic Dynamical System. Beijing: Science Press. [18] 许勇, 裴斌, 徐伟. 2017. 随机平均原理研究若干进展. 动力学与控制学报, 15: 193-199 (Xu Y, Pei B, Xu W. 2017. Some recent developments of stochastic averaging principle. Journal of Dynamics and Control, 15: 193-199). doi: 10.6052/1672-6553-2017-022(Xu Y, Pei B, Xu W. 2017. Some recent developments of stochastic averaging principle. Journal of Dynamics and Control, 15: 193-199). doi: 10.6052/1672-6553-2017-022 [19] 杨强, 孟松鹤, 仲政, 解维华, 郭早阳, 金华, 张幸红. 2020. 力学研究中"大数据"的启示、应用与挑战. 力学进展, 50: 202011 (Yang Q, Meng S H, Zhong Z, Xie W H, Guo Z Y, Jin H, Zhang X H. 2020. Big Data in mechanical research: Potentials, applications and challenges. Advances in Mechanics, 50: 202011). doi: 10.6052/1000-0992-19-002Yang Q, Meng S H, Zhong Z, Xie W H, Guo Z Y, Jin H, Zhang X H. 2020. Big Data in mechanical research: Potentials, applications and challenges. Advances in Mechanics, 50: 202011). doi: 10.6052/1000-0992-19-002 [20] 赵雷, 陈虬. 1999. 随机有限元动力分析方法的研究进展. 力学进展, 29: 9-18 (Zhao L, Chen Q. 1999. Advances of dynamic response analysis based on stochastic finite element method. Advances in Mechanics, 29: 9-18). doi: 10.6052/1000-0992-1999-1-J1998-052(Zhao L, Chen Q. 1999. Advances of dynamic response analysis based on stochastic finite element method. Advances in Mechanics, 29: 9-18). doi: 10.6052/1000-0992-1999-1-J1998-052 [21] 朱金杰, 陈朕, 孔琛, 刘先斌. 2020. 基于大偏差理论的随机动力学. 力学进展, 50: 202000 (Zhu J J, Chen Z, Kong C, Liu X B. 2020. The researches on the stochastic dynamics based on the large deviation theory. Advances in Mechanics, 50: 202000).(Zhu J J, Chen Z, Kong C, Liu X B. 2020. The researches on the stochastic dynamics based on the large deviation theory. Advances in Mechanics, 50: 202000). [22] 朱位秋. 2003. 非线性随机动力学与控制: Hamilton理论体系框架. 北京: 科学出版社(Zhu W Q. 2003. Nonlinear Stochastic Dynamics and Control-the Framework of Hamilton Theory. Beijing: Science Press). [23] 朱位秋, 蔡国强. 2017. 随机动力学引论. 北京: 科学出版社(Zhu W Q, Cai G Q. 2017. Introduction to Stochastic Dynamics. Beijing: Science Press). [24] 朱位秋. 1994. 非线性随机振动理论的近期进展. 力学进展, 24: 163-173 (Zhu W Q. 1994. Recent developments in theory of nonlinear random vibration. Advances in Mechanics, 24: 163-173).Zhu W Q. 1994. Recent developments in theory of nonlinear random vibration. Advances in Mechanics, 24: 163-173). [25] 朱位秋, 黄志龙. 2000. 随机激励的耗散的Hamilton系统理论的研究进展. 力学进展, 30: 481-494 (Zhu W Q, Huang Z L. 2000. Advances in theory of stochastically excited and dissipated Hamiltonian systems. Advances in Mechanics, 30: 481-494).Zhu W Q, Huang Z L. 2000. Advances in theory of Stochastically excited and dissipated Hamiltonian systems. Advances in Mechanics, 30: 481-494. [26] 张峻铭, 杨伟东, 李岩. 2021. 人工智能在复合材料研究中的应用. 力学进展, 51: 865-900 (Zhang J M, Yang W D, Li Y. 2021. Application of artificial intelligence in composite materials. Advances in Mechanics, 51: 865-900). doi: 10.6052/1000-0992-21-019Zhang J M, Yang W D, Li Y. 2021. Application of artificial intelligence in composite materials. Advances in Mechanics, 51: 865-900). doi: 10.6052/1000-0992-21-019 [27] 张刚, 李红威. 2018. 小波-EMD和随机共振级联微弱信号检测. 电子测量与仪器学报, 32: 57-65 (Zhang G, Li H W. 2018. Wavelet-EMD and stochastic resonance cascade weak signal detection. Journal of Electronic Measurement and Instrumentation, 32: 57-65).(Zhang G, Li H W. 2018. Wavelet-EMD and stochastic resonance cascade weak signal detection. Journal of Electronic Measurement and Instrumentation, 32: 57-65). [28] Arathi S, Rajasekar S. 2011. Impact of the depth of the wells and multifractal analysis on stochastic resonance in a triple-well system. Physica Scripta, 84: 065011. doi: 10.1088/0031-8949/84/06/065011 [29] Bai S Y, Duan F B, Chapeau-Blondeau F, Abbott D. 2022. Generalization of stochastic-resonance-based threshold networks with Tikhonov regularization. Physics Review E, 106: L012101. doi: 10.1103/PhysRevE.106.L012101 [30] Bao J D, Zhou Y Z, Wu X Z. 1996. Diffusion current for a system in a periodic potential driven by multiplicative colored noise. Physics Letters A, 215: 154-159. doi: 10.1016/0375-9601(96)00150-8 [31] Benzi R, Sutera A, Vulpiani A. 1981. The mechanism of stochastic resonance. Journal of Physics A, 14: L453-L457. doi: 10.1088/0305-4470/14/11/006 [32] Berdichevsky V, Gitterman M. 1997. Josephson junction with noise. Physical Review E, 56: 6340-6354. doi: 10.1103/PhysRevE.56.6340 [33] Berdichevsky V, Gitterman M. 1999. Stochastic resonance in linear systems subject to multiplicative and additive noise. Physical Review E, 60: 1494-1499. doi: 10.1103/PhysRevE.60.1494 [34] Borland L. 1998. Ito-Langevin equations within generalized thermostatistics. Physics Letters A, 245: 67-72. doi: 10.1016/S0375-9601(98)00467-8 [35] Boukobza E, Moore M G, Cohen D, Vardi A. 2010. Nonlinear phase dynamics in a driven bosonic Josephson junction. Physical Review Letters, 104: 240402. doi: 10.1103/PhysRevLett.104.240402 [36] Caroli B, Caroli C, Roulet B, Saint-James D. 1981. On fluctuations and relaxation in systems described by a one-dimensional Fokker-Planck equation with a time-dependent potential. Physica A, 108: 233-256. doi: 10.1016/0378-4371(81)90177-1 [37] Castro F J, Kuperman M N, Fuentes M, Wio H S. 2001. Experimental evidence of stochastic resonance without tuning due to non-Gaussian noises. Physical Review E, 64: 051105. doi: 10.1103/PhysRevE.64.051105 [38] Chapeau-Blondeau F, Godivier X. 1997. Theory of stochastic resonance in signal transmission by static nonlinear systems. Physical Review E, 55: 1478-1495. doi: 10.1103/PhysRevE.55.1478 [39] Chechkin A, Gonchar V, Klafter J, Metzler R, Tanatarov L. 2002. Stationary states of non-linear oscillators driven by Lévy noise. Chemical Physics, 284: 233-251. doi: 10.1016/S0301-0104(02)00551-7 [40] Chen B, Dong J. 1991. Thermally assisted vortex diffusion in layered high-tc superconductors. Physical Review B, 44: 10206-10209. doi: 10.1103/PhysRevB.44.10206 [41] Christiansen L E, Lehn-Schioler T, Mosekilde E, Granasy P, Matsushita H. 2002. Nonlinear characteristics of randomly excited transonic flutter. Mathematics and Computers in Simulation, 58: 385-405. doi: 10.1016/S0378-4754(01)00379-2 [42] Covaci C, Gontean A. 2020. Piezoelectric energy harvesting solutions: A review. Sensors, 20: 3512. [43] Cui H J, Guan Y, Deng W. 2021. Fault diagnosis using cascaded adaptive second-order tristable stochastic resonance and empirical mode decomposition. Applied Sciences, 11: 11480. doi: 10.3390/app112311480 [44] Daqaq M F. 2011. Transduction of a bistable inductive generator driven by white and exponentially correlated Gaussian noise. Journal of Sound and Vibration, 330: 2554-2564. doi: 10.1016/j.jsv.2010.12.005 [45] Dean A R, Hänggi P. 2002. Brownian motors. Physics Today, 55: 11-33. doi: 10.1063/1.4796664 [46] Debnath G, Zhou T, Moss F. 1989. Remarks on stochastic resonance. Physical Review A, 39: 4323-4326. doi: 10.1103/PhysRevA.39.4323 [47] Dhara A K, Mukhopadhyay T. 1999. Coherent stochastic resonance in the case of two absorbing boundaries. Physical Review E, 60: 2727-2736. doi: 10.1103/PhysRevE.60.2727 [48] Dong H T, Shen X H, He K, Wang H Y. 2020. Nonlinear filtering effects of intrawell matched stochastic resonance with barrier constrainted duffing system for ship radiated line signature extraction. Chaos, Solitons & Fractals, 141: 110428. [49] Dong H T, He K, Shen X H, Ma S L, Wang H Y, Qiao C. C. 2020. Adaptive intrawell matched stochastic resonance with a potential constraint aided line enhancer for passive sonars. Sensors, 20: 3269. doi: 10.3390/s20113269 [50] Dong H T, Wang H Y, Shen X H, He K. 2019. Parameter matched stochastic resonance with damping for passive sonar detection. Journal of Sound and Vibration, 458: 479-496. doi: 10.1016/j.jsv.2019.06.021 [51] Douglass J K, Wilkens L, Pantazelou E, Moss F. 1993. Noise enhancement of the information transfer in crayfish mechanoreceptors by stochastic resonance. Nature, 365: 337-340. doi: 10.1038/365337a0 [52] Duan F B, Pan Y, Chapeau-Blondeau F, Abbott D. 2019. Noise benefits in combined nonlinear Bayesian estimators. IEEE Transactions on Signal Processing, 67: 4611-4623. doi: 10.1109/TSP.2019.2931203 [53] Duan L, Ren Y H, Duan F B. 2022. Adaptive stochastic resonance based convolutional neural network for image classification. Chaos Solitons and Fractrals, 162: 112429. doi: 10.1016/j.chaos.2022.112429 [54] Dykman M I, Luchinsky D G, Mannella R, McClintock P V E, Stein N D, Stocks N G. 1993. Stochastic resonance: Linear response and giant nonlinearity. Journal of Statistical Physics, 70: 463-478. doi: 10.1007/BF01053982 [55] Dykman M I, Mannella R, McClintock P V E, Moss F, Soskin S M. 1988. Spectral density fluctuations of a double-well Duffing oscillator driven by white noise. Physical Review A, 37: 1303-1312. [56] Fauve S, Heslot F. 1983. Stochastic resonance in a bistable system. Physics Letters A, 97: 5-7. doi: 10.1016/0375-9601(83)90086-5 [57] Fox R F. 1989. Stochastic resonance in a double well. Physical Review A, 39: 4148-4153. doi: 10.1103/PhysRevA.39.4148 [58] Fronzoni L, Mannella R. 1993. Stochastic resonance in periodic potentials. Journal of Statistical Physics, 70: 501-512. doi: 10.1007/BF01053984 [59] Fuentes M A, Wio H S, Toral R. 2002. Effective Markovian approximation for non-Gaussian noises: A path integral approach. Physica A, 303: 91-104. doi: 10.1016/S0378-4371(01)00435-6 [60] Galin M A, Rudau F, Borodianskyi E A, Kurin V V, Koelle D, Kleiner R, Krasnov V M, Klushin A M. 2020. Direct visualization of phase-locking of large Josephson junction arrays by surface electromagnetic waves. Physical Review Applied, 14: 024051. doi: 10.1103/PhysRevApplied.14.024051 [61] Gammaitoni L, Hänggi P, Jung P, Marchesoni F. 1998. Stochastic resonance. Reviews of Modern Physics, 70: 223-287. doi: 10.1103/RevModPhys.70.223 [62] Gammaitoni L, Marchesoni F, Santucci S. 1995. Stochastic resonance as a bona fide resonance. Physical Review Letters, 74: 1052-1055. doi: 10.1103/PhysRevLett.74.1052 [63] Gammaitoni L, Neri I, Vocca H. 2009. Nonlinear oscillators for vibration energy harvesting. Applied Physics Letters, 94: 164102. doi: 10.1063/1.3120279 [64] Gandhimathi V M, Rajasekar S, Kurths J. 2006. Vibrational and stochastic resonances in two coupled overdamped anharmonic oscillators. Physics Letters A, 360: 279-286. doi: 10.1016/j.physleta.2006.08.051 [65] Ghosh A W, Khare S V. 2000. Rotation in an asymmetric multidimensional periodic potential due to colored noise. Physical Review Letters, 84: 5243-5246. doi: 10.1103/PhysRevLett.84.5243 [66] Ghosh P K, Bag B C, Ray D S. 2007. Noise correlation-induced splitting of Kramers’ escape rate from a metastable state. Journal of Chemical Physics, 127: 044510. doi: 10.1063/1.2756042 [67] Gong D C, Qing G R, Hu G, Wen X D. 1991. Experimental study of stochastic resonance. Physics Letters A, 159: 147-152. doi: 10.1016/0375-9601(91)90262-7 [68] Guarcello C, Valenti D, Carollo A, Spagnolo B. 2015. Stabilization effects of dichotomous noise on the lifetime of the superconducting state in a long Josephson junction. Entropy, 17: 2862-2875. doi: 10.3390/e17052862 [69] Guarcello C, Valenti D, Carollo A, Spagnolo B. 2016. Effects of Lévy noise on the dynamics of sine-Gordon solitons in long Josephson junctions. Journal of Statistical Mechanics:Theory & Experiment, 2016: 054012. [70] Han J, Liu H J, Huang N, Wang Z L, Zhang Y. B. Chi J. 2019. Reconstructing a scattered image via spatial cross-phase modulation instability in partially incoherent beams. Applied Physics Express, 12: 012007. doi: 10.7567/1882-0786/aaf713 [71] Hänggi P, Marchesoni F. 2009. Artificial Brownian motors: Controlling transport on the nanoscale. Review of Modern Physics, 81: 387-442. doi: 10.1103/RevModPhys.81.387 [72] Hänggi P, McClintock P V E. 1985. Bistablity driven by colored noise: theory and experiment. Physical Review A, 32: 695-698. doi: 10.1103/PhysRevA.32.695 [73] Hänggi P, Talkner P, Borkovec M. 1990. Reaction-rate theory: fifty years after Kramers. Reviews of Modern Physics, 62: 251-341. doi: 10.1103/RevModPhys.62.251 [74] Hu B B, Guo C, Wu J M, Tang J H, Zhang J L, Wang Y. 2019. An adaptive periodical stochastic resonance method based on grey wolf optimizer algorithm and its application in rolling bearing fault diagnosis. Journal of Vibration and Acoustics-Transactions of the ASME, 141: 041016. doi: 10.1115/1.4043063 [75] Hu G, Ditzinger T, Ning C Z, Haken H. 1993. Stochastic resonance without external periodic force. Physics Review Letter, 71: 807-810. doi: 10.1103/PhysRevLett.71.807 [76] Huang D W, Yang J H, Zhang J L, Liu H G. 2018. An improved adaptive stochastic resonance with general scale transformation to extract high-frequency characteristics in strong noise. International Journal of Modern Physics B, 32: 1850185. doi: 10.1142/S0217979218501850 [77] Huisman J, Weissing F. 2001. Fundamental unpredictability in multispecies competition. American Naturalist, 157: 171-187. [78] Jiang W A, Chen L Q. 2014. An equivalent linearization technique for nonlinear piezoelectric energy harvesters under Gaussian white noise. Communications in Nonlinear Science and Numerical Simulation, 19: 2897-2904. doi: 10.1016/j.cnsns.2013.12.037 [79] Jin Y F, Ma Z M, Xiao S M. 2017. Coherence and stochastic resonance in a periodic potential driven by multiplicative dichotomous and additive white noise. Chaos, Solitons & Fractals, 103: 470-475. [80] Jin Y F, Wang H Q. 2020. Noise-induced dynamics in a Josephson junction driven by trichotomous noises. Chaos, Solitons & Fractals, 133: 109633. [81] Jin Y F, Xiao S M, Zhang Y X. 2018. Enhancement of tristable energy harvesting using stochastic resonance. Journal of Statistical Mechanics, 123211. [82] Jin Y F, Xie W X, Liu K H. 2017. Noise-induced resonances in a periodic potential driven by correlated noises. Procedia IUTAM, 22: 267-274. doi: 10.1016/j.piutam.2017.08.035 [83] Jin Y F, Xu P F. 2018. Noise-induced dynamics in a delayed triple-well potential system driven by correlated noises. IFAC PapersOnLine, 51: 189-194. [84] Jin Y F, Xu W, Xu M, Fang T. 2005. Stochastic resonance in linear system due to dichotomous noise modulated by bias signal. Journal of Physics A, 38: 3733-3742. doi: 10.1088/0305-4470/38/17/002 [85] Jung P. 1995. Stochastic resonance and optimal design of threshold detectors. Physical Review A, 220: 219-223. [86] Kay S. 2000. Can detectability be improved by adding noise. IEEE Signal Processing Letters, 7: 8-10. doi: 10.1109/97.809511 [87] Kim P, Seok J. 2014. A multi-stable energy harvester: dynamic modeling and bifurcation analysis. Journal of Sound and Vibration, 333: 5525-5547. doi: 10.1016/j.jsv.2014.05.054 [88] Kim Y W, Sung W. 1998. Does stochastic resonance occur in periodic potentials. Physical Review E, 57: R6237-R6240. doi: 10.1103/PhysRevE.57.R6237 [89] Kramers H A. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica, 7: 284-304. doi: 10.1016/S0031-8914(40)90098-2 [90] Kraut S, Feudel U, Grebogi C. 1999. Preference of attractors in noisy multistable systems. Physical Review E, 59: 5253-5260. doi: 10.1103/PhysRevE.59.5253 [91] Kumar P, Narayanan S, Adhikari S, Friswell M I. 2014. Fokker-Planck equation analysis of randomly excited nonlinear energy harvester. Journal of Sound and Vibration, 333: 2040-2053. doi: 10.1016/j.jsv.2013.11.011 [92] Lan C B, Qin W Y. 2014. Energy harvesting from coherent resonance of horizontal vibration of beam excited by vertical base motion. Applied Physics Letters, 105: 113901. doi: 10.1063/1.4895921 [93] Lee DeVille R E, Vanden-Eijnden E, Muratov C B. 2005. Two distinct mechanisms of coherence in randomly perturbed dynamical systems. Physical Review E, 72: 31105. doi: 10.1103/PhysRevE.72.031105 [94] Leiber T, Marchesoni F, Risken H. 1987. Colored noise and bistable Fokker-Planck equations. Physical Review Letters, 59: 1381-1384. doi: 10.1103/PhysRevLett.59.1381 [95] Leiber T, Marchesoni F, Risken H. 1989. Bistability and colored noise: Application to one-dimensional periodic model potentials. Physical Review A, 40: 6107-6110. doi: 10.1103/PhysRevA.40.6107 [96] Li F H, Zhu F L, Zhang Y J, Zhang B, Li W, Luo W Y. 2021. Synthetic adaptive matched field processing for moving source with a horizontal line array. Journal of the Acoustical Society of America, 149: 1138-1146. doi: 10.1121/10.0003531 [97] Li J L, Xu B H. 2006. Effects of signal spectrum varying on signal processing by parameter-induced stochastic resonance. Physica A, 361: 11-23. doi: 10.1016/j.physa.2005.07.015 [98] Li J M, Chen X F, He Z J. 2013. Multi-stable stochastic resonance and its application research on mechanical fault diagnosis. Journal of Sound and Vibration, 332: 5999-6015. doi: 10.1016/j.jsv.2013.06.017 [99] Li Y G, Xu Y, Kurths J, Yue X L. 2016. Lévy-noise-induced transport in a rough triple-well potential. Physical Review E, 94: 042222. doi: 10.1103/PhysRevE.94.042222 [100] Li Z J, Zuo L, Luhrs G, Lin L J, Qin Y X. 2013. Electromagnetic energy-harvesting shock absorbers: Design, modeling, and road tests. IEEE Transactions on Vehicular Technology, 62: 1065-1074. doi: 10.1109/TVT.2012.2229308 [101] Liang G L, Wan G M, Wang J J, Wang X. 2020. A novel underwater location beacon signal detection method based on mixing and normalizing stochastic resonance. Sensors, 20: 1292. doi: 10.3390/s20051292 [102] Lin Y K, Cai G Q. 1995. Probabilistic Structural Dynamics, Advanced Theory and Applications. New York: McGraw-Hil. [103] Lindner B, García-Ojalvo J, Neiman A, Schimansky-Geier L. 2004. Effects of noise in excitable systems. Physics Reports, 392: 321-424. doi: 10.1016/j.physrep.2003.10.015 [104] Liu B, Xu T, Tharmarasa R, Kirubarajan T, Jassemi R, Halle S. 2020. Underwater target tracking in uncertain multipath ocean environments. IEEE Transactions on Aerospace and Electronic Systems, 56: 4899-4915. doi: 10.1109/TAES.2020.3003703 [105] Liu D, Xu Y, Li J. 2017. Probabilistic response analysis of nonlinear vibration energy harvesting system driven by Gaussian colored noise. Chaos Solitons and Fractals, 104: 806-812. doi: 10.1016/j.chaos.2017.09.027 [106] Liu K H, Jin Y F. 2013. Stochastic resonance in periodic potentials driven by colored noise. Physica A, 392: 5283-5288. doi: 10.1016/j.physa.2013.06.050 [107] Liu Q, Xu Y, Li Y G, Kurths J, Liu X C. 2021. Fixed-interval smoothing of an aeroelastic airfoil model with cubic or free-play nonlinearity in incompressible flow. Acta Mechanica Sinica, 37: 1168-1182. doi: 10.1007/s10409-021-01091-1 [108] Liu R N, Kang Y M. 2018. Stochastic resonance in underdamped periodic potential systems with alpha stable Lévy noise. Physics Letters A, 382: 1656-1664. doi: 10.1016/j.physleta.2018.03.054 [109] Liu Y J, Wang F Z, Liu L, Zhu Y M. 2019. Symmetry tristable stochastic resonance induced by parameter under lévy noise background. European Physical Journal B, 92: 168. doi: 10.1140/epjb/e2019-90759-8 [110] Liu Y L, Liang J, Jiao S B, Xiao N, Zhang Z H. 2017. The phenomenon of tristable stochastic resonance driven by α-noise. Pramana-Journal of Physics, 89: 73. doi: 10.1007/s12043-017-1471-3 [111] Longtin A. 1997. Autonomous stochastic resonance in bursting neurons. Physics Review E, 55: 868-876. doi: 10.1103/PhysRevE.55.868 [112] Lu S L, He Q B, Zhang H B, Zhang S B, Kong F R. 2013. Note: Signal amplification and filtering with a tristable stochastic resonance cantilever. Review of Scientific Instruments, 84: 026110. doi: 10.1063/1.4792603 [113] Ma J Z, Xu Y, Li Y G, Tian R L, Ma S J, Kurths J. 2021. Quantifying the parameter dependent basin of the unsafe regime of asymmetric Lévy-noise-induced critical transitions. Applied Mathematics and Mechanics (English Edition) , 42: 65-84. doi: 10.1007/s10483-021-2672-8 [114] Ma J Z, Xu Y, Liu D, Tian R L, Ma S J, Feudel U, Kurths J. 2021. Suppression of noise-induced critical transitions: a linear augmentation method. European Physical Journal Special Topics, 230: 3281-3290. doi: 10.1140/epjs/s11734-021-00112-1 [115] Ma J Z, Xu Y, Li Y G, Kurths J. 2019. Slowing down critical transitions via Gaussian white noise and periodic force. Science China-Technological Sciences, 62: 2144-2152. doi: 10.1007/s11431-019-9557-2 [116] Makris N C. 2021. The effect of attenuation from fish on passive detection of sound sources in ocean waveguide environments. Remote Sensing, 13: 4369. doi: 10.3390/rs13214369 [117] Martinez-Zerega B E, Pisarchik A N. 2012. Stochastic control of attractor preference in a multistable system. Communications in Nonlinear Science and Numerical Simulation, 17: 4023-4028. doi: 10.1016/j.cnsns.2012.03.010 [118] Masoliver J, Robinson A. 1995. Coherent stochastic resonance. Physical Review E, 51: 4021-4026. doi: 10.1103/PhysRevE.51.4021 [119] McDonnell M D, Abbott D. 2009. What is stochastic resonance? Definitions, misconceptions, debates, and its relevance to biology. PLOS Computational Biology, 5: e1000348. doi: 10.1371/journal.pcbi.1000348 [120] McDonnell M D, Stocks N G, Pearce C E M, Abbott D. 2008. Stochastic Resonance from Suprathreshold Stochastic Resonance to Stochastic Signal Quantization. New York: Cambridge University Press. [121] McInnes C R, Gorman D G, Cartmell M P. 2008. Enhanced vibrational energy harvesting using nonlinear stochastic resonance. Journal of Sound and Vibration, 318: 655-662. doi: 10.1016/j.jsv.2008.07.017 [122] McNamara B, Wiesenfeld K. 1989. Theory of stochastic resonance. Physical Review A, 39: 4854-4869. doi: 10.1103/PhysRevA.39.4854 [123] McNamara B, Wiesenfeld K, Roy R. 1988. Observation of stochastic resonance in a ring laser. Physical Review Letters, 1: 3-4. [124] Mei R X, Xu Y, Li Y G, Kurths J. 2021. Characterizing stochastic resonance in a triple cavity. Philosophical Transactions of the Royal Society A, 379: 20200230. doi: 10.1098/rsta.2020.0230 [125] Mitaim S, Kosko B. 1998. Adaptive stochastic resonance with fuzzy systems. Fuzzy Information Processing Society-Nafips, 355-359. [126] Moss F, Ward L M, Sannita W G. 2004. Stochastic resonance and sensory information processing: a tutorial and review of application. Clinical Neurophysiology, 115: 267-281. doi: 10.1016/j.clinph.2003.09.014 [127] Muratov C B, Vanden-Eijnden E, Weinan E. 2005. Self-induced stochastic resonance in excitable systems. Physica D, 210: 227-240. doi: 10.1016/j.physd.2005.07.014 [128] Mutothya N M, Xu Y, Li Y G, Metzler R. 2021. Characterising stochastic motion in heterogeneous media driven by coloured non-Gaussian noise. Journal of Physics A, 54: 295002. doi: 10.1088/1751-8121/abfba6 [129] Mutothya N M, Xu Y, Li Y G, Metzler R, Mutua N M. 2021. First passage dynamics of stochastic motion in heterogeneous media driven by correlated white Gaussian and coloured non-Gaussian noises. Journal of Physics:Complexity, 2: 045012. doi: 10.1088/2632-072X/ac35b5 [130] Nicolis C. 2010. Stochastic resonance in multistable systems: the role of intermediate states. Physical Review E, 82: 011139. doi: 10.1103/PhysRevE.82.011139 [131] Nicolis C. 2012. Stochastic resonance in multistable systems: The role of dimensionality. Physical Review E, 86: 011133. doi: 10.1103/PhysRevE.86.011133 [132] Nicolis C, Nicolis G. 2017. Stochastic resonance across bifurcation cascades. Physical Review E, 95: 032219. doi: 10.1103/PhysRevE.95.032219 [133] Oliver N, Larger L, Fischer I. 2016. Consistency in experiments on multistable driven delay systems. Chaos, 26: 103115. doi: 10.1063/1.4966021 [134] Panyam M, Daqaq M F. 2017. Characterizing the effective bandwidth of tri-stable energy harvesters. Journal of Sound and Vibration, 386: 336-358. doi: 10.1016/j.jsv.2016.09.022 [135] Paolo A, Giovanni F, Vincenzo P. 2012. Characterization of escape times of Josephson junctions for signal detection. Physical Review E, 85: 016708. doi: 10.1103/PhysRevE.85.016708 [136] Papoulis A. 1965. Probability Random Variables, and Stochastic Processes. New York: McGraw-Hill. [137] Patel A, Kosko B. 2009. Optimal noise benefits in Neyman–Pearson and inequality-constrained statistical signal detection. IEEE Transactions on Signal Process, 57: 1655-1669. doi: 10.1109/TSP.2009.2012893 [138] Pereira T L, Paula A S D, Fabro A T, Savi M A. 2019. Random effects in a nonlinear vibration-based piezoelectric energy harvesting system. International Journal of Bifurcation and Chaos, 29: 1950046. doi: 10.1142/S0218127419500469 [139] Peng C, Sun H X, Cheng E. 2015. Radiated noise measurement of ships based on stochastic resonance. The Open Mechanical Engineering Journal, 9: 927-932. doi: 10.2174/1874155X01509010927 [140] Pikovsky A S, Kurths J. 1997. Coherence resonance in a noise-driven excitable system. Physics Review Letter, 78: 775-778. doi: 10.1103/PhysRevLett.78.775 [141] Pisarchik A N, Barmenkov Y O, Kir’yanov A V. 2003. Experimental characterization of bifurcation structure in an erbium-doped fiber laser with pump modulation. IEEE Journal of Quantum Electronics, 39: 1567-1571. doi: 10.1109/JQE.2003.819559 [142] Pisarchik A N, Feudel U. 2014. Control of multistability. Physics Reports, 540: 167-218. doi: 10.1016/j.physrep.2014.02.007 [143] Porra J M. 1997. When coherent stochastic resonance appears. Physical Review E, 55: 6533-6539. doi: 10.1103/PhysRevE.55.6533 [144] Postnov D E, Sosnovtseva O V, Han S K, Yim T G. 2000. Stochastic synchronization of coupled coherence resonance oscillators. International Journal of Bifurcation and Chaos, 10: 2541-2550. doi: 10.1142/S0218127400001705 [145] Pradines J R, Osipov G V, Collins J J. 1999. Coherence resonance in excitable and oscillatory systems: The essential role of slow and fast dynamics. Physics Review E, 60: 6407-6410. doi: 10.1103/PhysRevE.60.6407 [146] Qiao Z J, Lei Y G, Li N P. 2019. Applications of stochastic resonance to machinery fault detection: A review and tutorial. Mechanical Systems and Signal Processing, 122: 502-536. doi: 10.1016/j.ymssp.2018.12.032 [147] Reenbohn W L, Pohlong S S, Mahato M C. 2012. Periodically driven underdamped periodic and washboard potential systems: Dynamical states and stochastic resonance. Physical Review E, 85: 031144. doi: 10.1103/PhysRevE.85.031144 [148] Reimann P, Hänggi P. 2002. Introduction to the physics of Brownian motors. Applied Physics A, 75: 169. doi: 10.1007/s003390201331 [149] Risken H. 1984. The Fokker-Planck Equation-methods of Solution and Applications. Springer-Verlag. [150] Roberts J B, Spanos P D. 1990. Random Vibration and Statistical Linearization. Chichester etc. : John Wiley & Sons. [151] Ryu H, Yoon H J, Kim S W. 2019. Hybrid energy harvesters: toward sustainable energy harvesting. Advanced Materials, 31: 1802898. doi: 10.1002/adma.201802898 [152] Saikia S. 2014. The role of damping on Stochastic Resonance in a periodic potential. Physica A, 416: 411-420. doi: 10.1016/j.physa.2014.08.060 [153] Saikia S, Jayannavar A M, Mahato M C. 2011. Stochastic resonance in periodic potentials. Physical Review E, 83: 061121. doi: 10.1103/PhysRevE.83.061121 [154] Sbitney V I, Pustovoit M A. 2000. Stochastic resonance in 2D coupled map lattice model of field-like neural tissue. International Journal of Bifurcation and Chaos, 10: 1961-1971. doi: 10.1142/S0218127400001195 [155] Sekimoto K. 1998. Langevin equation and thermodynamics. Progress of Theoretical Physics Supplement, 130: 17-27. doi: 10.1143/PTPS.130.17 [156] Sekimoto K. 2010. Stochastic Energetics. Heidelberg: Springer. [157] Serdukova L, Zheng Y Y, Duan J Q, Kurths J. 2016. Stochastic basins of attraction for metastable states. Chaos, 26: 073117. doi: 10.1063/1.4959146 [158] Shi P M, Yuan D Z, Han D Y, Zhang Y, Fu R R. 2018. Stochastic resonance in a time-delayed feedback tristable system and its application in fault diagnosis. Journal of Sound and Vibration, 424: 1-14. doi: 10.1016/j.jsv.2018.03.007 [159] Siewert U, Schimansky-Geier L. 1998. Analytical study of coupled two-state stochastic resonance. Physical Review E, 58: 2843-2852. doi: 10.1103/PhysRevE.58.2843 [160] Storni R, Ando H, Aihara K, Murali K, Sinha S. 2012. Manipulating potential wells in logical stochastic resonance to obtain XOR logic. Physics Letters A, 376: 930-937. doi: 10.1016/j.physleta.2011.12.036 [161] Sun J Q, Xiong F R. 2017. Cell mapping methods-beyond global analysis of nonlinear dynamic systems. Advances in Mechanics, 47: 201705. [162] Tan J Y, Chen X F, Wang J Y, Chen H X, Cao H R, Zi Y Y, He Z J. 2009. Study of frequency-shifted and re-scaling stochastic resonance and its application to fault diagnosis. Mechanical Systems and Signal Processing, 23: 811-822. doi: 10.1016/j.ymssp.2008.07.011 [163] Tessone C J, Plastino A, Wio H S. 2003. Stochastic resonance and generalized information measures. Physica A, 326: 37-54. doi: 10.1016/S0378-4371(03)00273-5 [164] Toprak A, Tigli O. 2014. Piezoelectric energy harvesting: State-of-the-art and challenges. Applied Physics Reviews, 1: 031104. doi: 10.1063/1.4896166 [165] Tvedt L G W, Nguyen D S, Halvorsen E. 2010. Nonlinear behavior of an electrostatic energy harvester under wide-and narrowband excitation. Journal of Microelectromechanical Systems, 19: 305-316. doi: 10.1109/JMEMS.2009.2039017 [166] Van der Sande G, Verschaffelt G, Danckaert J, Mirasso C R. 2005. Ghost stochastic resonance in vertical-cavity surface-emitting lasers: Experiment and theory. Physical Review E, 72: 016113. doi: 10.1103/PhysRevE.72.016113 [167] Wang J, He Q B, Kong F R. 2014. An improved multiscale noise tuning of stochastic resonance for identifying multiple transient faults in rolling element bearings. Journal of Sound and Vibration, 333: 7401-7421. doi: 10.1016/j.jsv.2014.08.041 [168] Wang Z L, Liu H J, Huang N, Zhang Y B, Chi J. 2019. Nonlinear reconstruction of weak optical diffused images under turbid water. Optics Letters, 44: 3502-3505. doi: 10.1364/OL.44.003502 [169] Wang Z L, Yang J H, Guo Y. 2022. Unknown fault feature extraction of rolling bearings under variable speed conditions based on statistical complexity measures. Mechanical Systems and Signal Processing, 172: 108964. doi: 10.1016/j.ymssp.2022.108964 [170] Wang Z Q, Li Y G, Xu Y, Kapitaniak T, Kurths J. 2022. Coherence-resonance chimeras in coupled HR neurons with alpha-stable Lévy noise. Journal of Statistical Mechanics, 2022: 053501. doi: 10.1088/1742-5468/ac6254 [171] Wang Z Q, Xu Y, Yang H. 2016. Lévy noise induced stochastic resonance in an FHN model. Science China Technological Sciences, 59: 371-375. doi: 10.1007/s11431-015-6001-2 [172] Wellens T, Buchleitner A. 2000. Stochastic resonance in the coherence of a quantum system. Physical Review Letters, 84: 5118-5121. doi: 10.1103/PhysRevLett.84.5118 [173] Wu C J, Yang J H, Huang D W, Liu H G, Hu E Y. 2019. Weak signal enhancement by fractional-order system resonance and its application in bearing fault diagnosis. Measurement Science and Technology, 30: 035004. doi: 10.1088/1361-6501/aaf904 [174] Wu J, Xu Y. 2014. Damping coefficient induces stochastic multiresonance in bistable system with asymmetric dichotomous noise. Discrete Dynamics in Nature and Society, 2014: 850361. [175] Wu J, Xu Y, Wang H Y, Kurths J. 2017. Information-based measures for logical stochastic resonance in a synthetic gene network under Lévy flight superdiffusion. Chaos, 27: 063105. doi: 10.1063/1.4984806 [176] Xu B H, Duan F B, Bao R G, Li J L. 2002. Stochastic resonance with tuning system parameters: the application of bistable systems in signal processing. Chaos, Solitons and Fractals, 13: 633-644. doi: 10.1016/S0960-0779(00)00266-6 [177] Xu P F, Jin Y F. 2018. Stochastic resonance in multi-stable coupled systems driven by two driving signals. Physica A, 492: 1281-1289. doi: 10.1016/j.physa.2017.11.056 [178] Xu P F, Jin Y F. 2019. Mean first-passage time in a delayed tristable system driven by correlated multiplicative and additive white noises. Chaos, Solitons and Fractals, 112: 75-82. [179] Xu P F, Jin Y F. 2020. Coherence and stochastic resonance in a second-order asymmetric tri-stable system with memory effects. Chaos, Solitons and Fractals, 138: 109857. doi: 10.1016/j.chaos.2020.109857 [180] Xu P F, Jin Y F. 2020. Stochastic resonance in an asymmetric tristable system driven by correlated noises. Applied Mathematical Modelling, 77: 408-425. doi: 10.1016/j.apm.2019.07.053 [181] Xu P F, Jin Y F, Xiao S M. 2017. Stochastic resonance in a delayed triple-well potential driven by correlated noises. Chaos, 27: 113109. doi: 10.1063/1.4994638 [182] Xu P F, Jin Y F, Zhang Y X. 2019. Stochastic resonance in an underdamped triple-well potential system. Applied Mathematics and Computation, 346: 352-362. doi: 10.1016/j.amc.2018.10.060 [183] Xu Y, Guo R, Xu W. 2014. A limit theorem for the solutions of slow-fast systems with fractional Brownian motion. Theoretical and Applied Mechanics Letters, 4: 013003. doi: 10.1063/2.1401303 [184] Xu Y, Li J J, Feng J, Zhang H Q, Xu W, Duan J Q. 2013. Lévy noise-induced stochastic resonance in a bistable system. European Physical Journal B, 86: 198. doi: 10.1140/epjb/e2013-31115-4 [185] Xu Y, Wu J, Du L, Yang H. 2016. Stochastic resonance in a genetic toggle model with harmonic excitation and Lévy noise. Chaos, Solitons and Fractals, 92: 91-100. doi: 10.1016/j.chaos.2016.09.015 [186] Xu Y, Zan W, Jia W, Kurths J. 2019. Path integral solutions of the governing equation of SDEs excited by Lévy white noise. Journal of Computational Physics, 394: 41-55. doi: 10.1016/j.jcp.2019.05.023 [187] Yamakou M E, Jost J. 2019. Control of coherence resonance by self-induced stochastic resonance in a multiplex neural network. Physical Review E, 100: 022313. [188] Yang C, Yang J H, Zhu Z C, Shen G, Zheng Y Q. 2020. Distinguish coherence resonance and stochastic resonance in bearing fault evaluation. Measurement Science and Technology, 31: 045001. doi: 10.1088/1361-6501/ab50aa [189] Yang J H, Yang C, Zhuang X Z, Liu H G, Wang Z L. 2022. Unknown bearing fault diagnosis under time-varying speed conditions and strong noise background. Nonlinear Dynamics, 107: 2177-2193. doi: 10.1007/s11071-021-07078-8 [190] Yang T, Cao Q J. 2019. Time delay improves beneficial performance of a novel hybrid energy harvester. Nonlinear Dynamics, 96: 1511-1530. doi: 10.1007/s11071-019-04868-z [191] Yao H Y, Wang H Y, Xu Y, Juergen K. 2020. A recurrent plot based stochastic nonlinear ray propagation model for underwater signal propagation. New Journal of Physics, 22: 063025. doi: 10.1088/1367-2630/ab8caf [192] Yao H Y, Wang H Y, Zhang Z C, Xu Y, Juergen K. 2021. A stochastic nonlinear differential propagation model for underwater acoustic propagation: theory and solution. Chaos, Solitons and Fractals, 150: 111105. doi: 10.1016/j.chaos.2021.111105 [193] Yao H Y, Zhang Z C, Wang H Y, Wang Y. 2021. Narrow band time-frequency space matched passive detector for underwater signal. Applied Acoustics, 183: 108287. doi: 10.1016/j.apacoust.2021.108287 [194] Zan W R, Jia W T, Xu Y. 2022. Reliability of dynamical systems with combined Gaussian and Poisson white noise via path integral method. Probabilistic Engineering Mechanics, 68: 103252. doi: 10.1016/j.probengmech.2022.103252 [195] Zan W R, Jia W T, Xu Y. 2022. Response statistics of single-degree-of-freedom systems with Lévy noise by improved path integral method. International Journal of Applied Mechanics, 14: 2250029. doi: 10.1142/S1758825122500296 [196] Zan W R, Xu Y, Kurths J, Chechkin A V, Metzler R. 2020. Stochastic dynamics driven by combined Lévy-Gaussian noise: fractional Fokker–Planck–Kolmogorov equation and solution. Journal of Physics A, 53: 385001. doi: 10.1088/1751-8121/aba654 [197] Zan W R, Xu Y, Metzler R, Kurths J. 2021. First-passage problem for stochastic differential equations with combined parametric Gaussian and Lévy white noises via path integral method. Journal of Computational Physics, 435: 110264. doi: 10.1016/j.jcp.2021.110264 [198] Zhang G, Yang Y L, Zhang T Q. 2019. The characteristic analysis of stochastic resonance and bearing fault diagnosis based on NWSG model driven by trichotomous noise. Chinese Journal of Physics, 60: 107-121. doi: 10.1016/j.cjph.2019.05.005 [199] Zhang H, Xu Y, Li Y G, Kurths J. 2020. Statistical solution to SDEs with α-stable Lévy noise via deep neural network. International Journal of Dynamics and Control, 8: 1129-1140. doi: 10.1007/s40435-020-00677-0 [200] Zhang H Q, Xu Y, Xu W, Li X C. 2012. Logical stochastic resonance in triple-well potential systems driven by colored noise. Chaos, 22: 043130. doi: 10.1063/1.4768729 [201] Zhang H Q, Yang T T, Xu W, Xu Y. 2014. Effects of non-Gaussian noise on logical stochastic resonance in a triple-well potential system. Nonlinear Dynamics, 76: 649-656. doi: 10.1007/s11071-013-1158-3 [202] Zhang H W, Wang H Y, Yao H Y, Dong H T, Shen X H. 2021. Phase trajectory entropy: A promising tool for passive diver detection. Journal of the Acoustical Society of America Express Letters, 1: 076003. [203] Zhang T T, Jin Y F, Zhang Y X. 2022. Performance improvement of the stochastic-resonance-based tri-stable energy harvester under random rotational vibration. Theoretical and Applied Mechanics Letters, 12: 100365. doi: 10.1016/j.taml.2022.100365 [204] Zhang T T, Jin Y F, Zhang Y X. 2023. Stochastic dynamics of a tri-stable piezoelectric vibration energy harvester interfaced with standard rectifier circuit. Journal of Sound and Vibration, 543: 117379. doi: 10.1016/j.jsv.2022.117379 [205] Zhang X J. 2001. Stochastic resonance in second-order autonomous systems subjected only to white noise. Journal of Physics A, 34: 10859-10868. doi: 10.1088/0305-4470/34/49/308 [206] Zhang X Y, Xu Y, Liu Q, Kurths J. 2020. Rate-dependent tipping-delay phenomenon in a thermoacoustic system with colored noise. Science China-Technological Sciences, 63: 2315-2327. doi: 10.1007/s11431-020-1589-x [207] Zhang Y, Hu G, Gammaitoni L. 1998. Signal transmission in one-way coupled bistable system: noise effect. Physical Review E, 58: 2952-2956. doi: 10.1103/PhysRevE.58.2952 [208] Zhang Y L, Wang T Y, Luo A X, Hu Y S, Li X X, Wang F. 2018. Micro electrostatic energy harvester with both broad bandwidth and high normalized power density. Applied Energy, 212: 362-371. doi: 10.1016/j.apenergy.2017.12.053 [209] Zhang Y S, Zheng R C, Kaizuka T, Su D, Nakano K, Cartmell M P. 2015. Broadband vibration energy harvesting by application of stochastic resonance from rotational environments. European Physical Journal Special Topics, 224: 2687-2701. doi: 10.1140/epjst/e2015-02583-7 [210] Zhang Y S, Zheng R C, Shimono K, Kaizuka T, Nakano K. 2016. Effectiveness testing of a piezoelectric energy harvester for an automobile wheel using SR. Sensors, 16: 1727-1742. doi: 10.3390/s16101727 [211] Zhang Y X, Jin Y F, Xu P F. 2019. Stochastic resonance and bifurcations in a harmonically driven tri-stable potential with colored noise. Chaos, 29: 023127. doi: 10.1063/1.5053479 [212] Zhang Y X, Jin Y F, Xu P F. 2020. Dynamics of a coupled nonlinear energy harvester under colored noise and periodic excitations. International Journal of Mechanical Sciences, 172: 105418. doi: 10.1016/j.ijmecsci.2020.105418 [213] Zhang Y X, Jin Y F, Xu P F, Xiao S M. 2020. Stochastic bifurcations in a nonlinear tri-stable energy harvester under colored noise. Nonlinear Dynamics, 99: 879-897. doi: 10.1007/s11071-018-4702-3 [214] Zhang Y X, Jin Y F. 2021. Colored Lévy noise-induced stochastic dynamics in a tristable hybrid energy harvester. Journal of Computational and Nonlinear Dynamics, 16: 041005. doi: 10.1115/1.4050038 [215] Zheng R C, Nakano K, Hu H G, Su D X, Cartmell M P. 2014. An application of stochastic resonance for energy harvesting in a bistable vibrating system. Journal of Sound and Vibration, 333: 2568-2587. doi: 10.1016/j.jsv.2014.01.020 [216] Zhou S X, Cao J Y, Inman D J, Lin J, Liu S S, Wang Z Z. 2014. Broadband tristable energy harvester: Modeling and experiment verification. Applied Energy, 133: 33-39. doi: 10.1016/j.apenergy.2014.07.077 [217] Zhou S X, Cao J Y, Lin J, Wang Z Z. 2014. Exploitation of a tristable nonlinear oscillator for improving broadband vibration energy harvesting. European Physical Journal Applied Physics, 67: 30902. doi: 10.1051/epjap/2014140190 [218] Zhou T, Moss F. 1990. Analog simulations of stochastic resonance. Physical Review A, 41: 4255-4264. doi: 10.1103/PhysRevA.41.4255 [219] Zhou T, Moss F, Jung P. 1990. Escape-time distributions of a periodically modulated bistable system with noise. Physical Review A, 42: 3161-3169. doi: 10.1103/PhysRevA.42.3161 [220] Zhou Z Y, Qin W Y, Yang Y F, Zhu P. 2017. Improving efficiency of energy harvesting by a novel penta-stable configuration. Sensor Actuators A:Physical, 265: 297-305. doi: 10.1016/j.sna.2017.08.039 [221] Zhou Z Y, Qin W Y, Zhu P. 2018. Harvesting performance of quad-stable piezoelectric energy harvester: modeling and experiment. Mechanical Systems and Signal Processing, 110: 260-272. doi: 10.1016/j.ymssp.2018.03.023 [222] Zhu J J, Liu X B. 2016. Locking induced by distance-dependent delay in neuronal networks. Physical Review E, 94: 052405. doi: 10.1103/PhysRevE.94.052405 -




 下载:
下载: