Advances in control of turbulence by artificial intelligence: Systems, algorithms, achievements and data analysis methods
-
摘要: 湍流控制涉及流体力学和控制理论, 对航空航天、运载工具、风力发电等众多领域具有重要的科学意义和应用价值. 由于湍流的复杂性, 传统控制方法在湍流控制领域面临很多瓶颈, 人工智能技术的发展为突破这些瓶颈提供了工具. 本文简要综述了文献报道的有模型和无模型的人工智能控制湍流的进展, 总结了研究中采用的典型的人工智能控制系统、算法、在不同湍流控制应用中取得的突出成果. 作者所在团队在国际上首次尝试对人工智能控制系统产生的海量数据进行分析, 从而挖掘出重要的信息乃至发现控制相似律. 对面临的挑战和未来的展望进行了分析.Abstract: Turbulence control involves fluid dynamics and control theory, and is of great importance to many fields such as aeronautics and astronautics, vehicle, wind power generation, etc. Due to the complexity of turbulence, traditional control methods face many bottlenecks in the field of turbulence control. The development of artificial intelligence (AI) technology provides a tool to break through these bottlenecks. This paper briefly summarizes the applications of AI in turbulence control reported in the literature, focusing on AI control systems, algorithms, and the outstanding achievements achieved in different turbulence control applications, as well as the first attempt by the author's team to analyze the big data generated by the AI control system to discover important information and even the control scaling law. The challenges and future prospects are also analyzed.
-
Key words:
- artificial intelligence /
- big data /
- flow control /
- turbulence /
- neural network /
- genetic programming /
- deep reinforcement learning
-
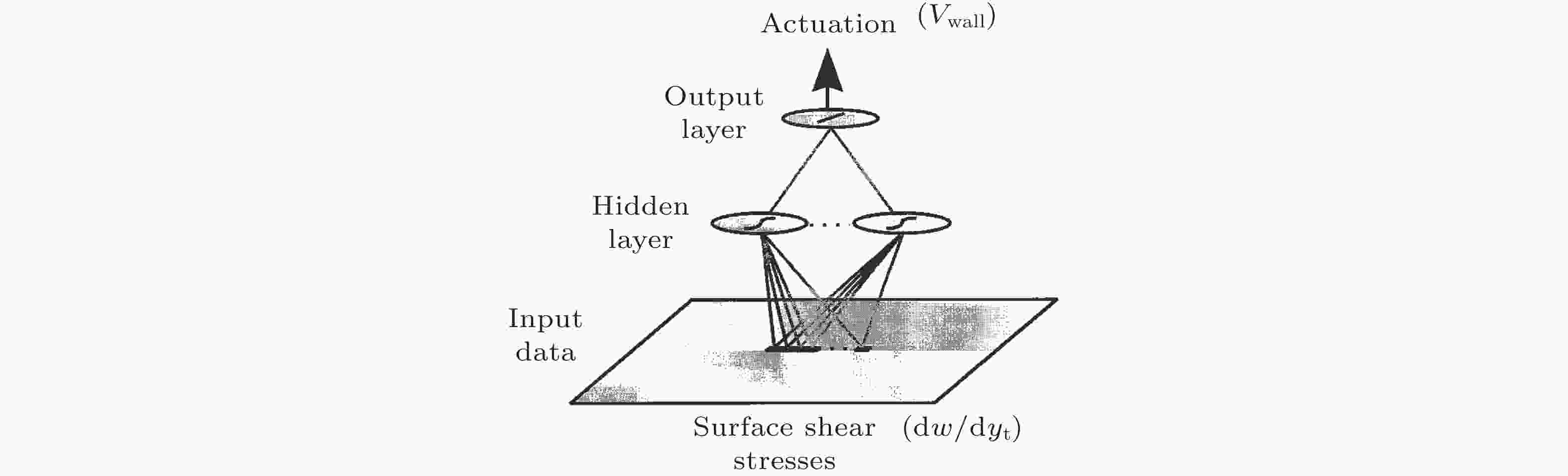
图 4 槽道湍流减阻控制中的神经网络结构图(Lee et al. 1997)
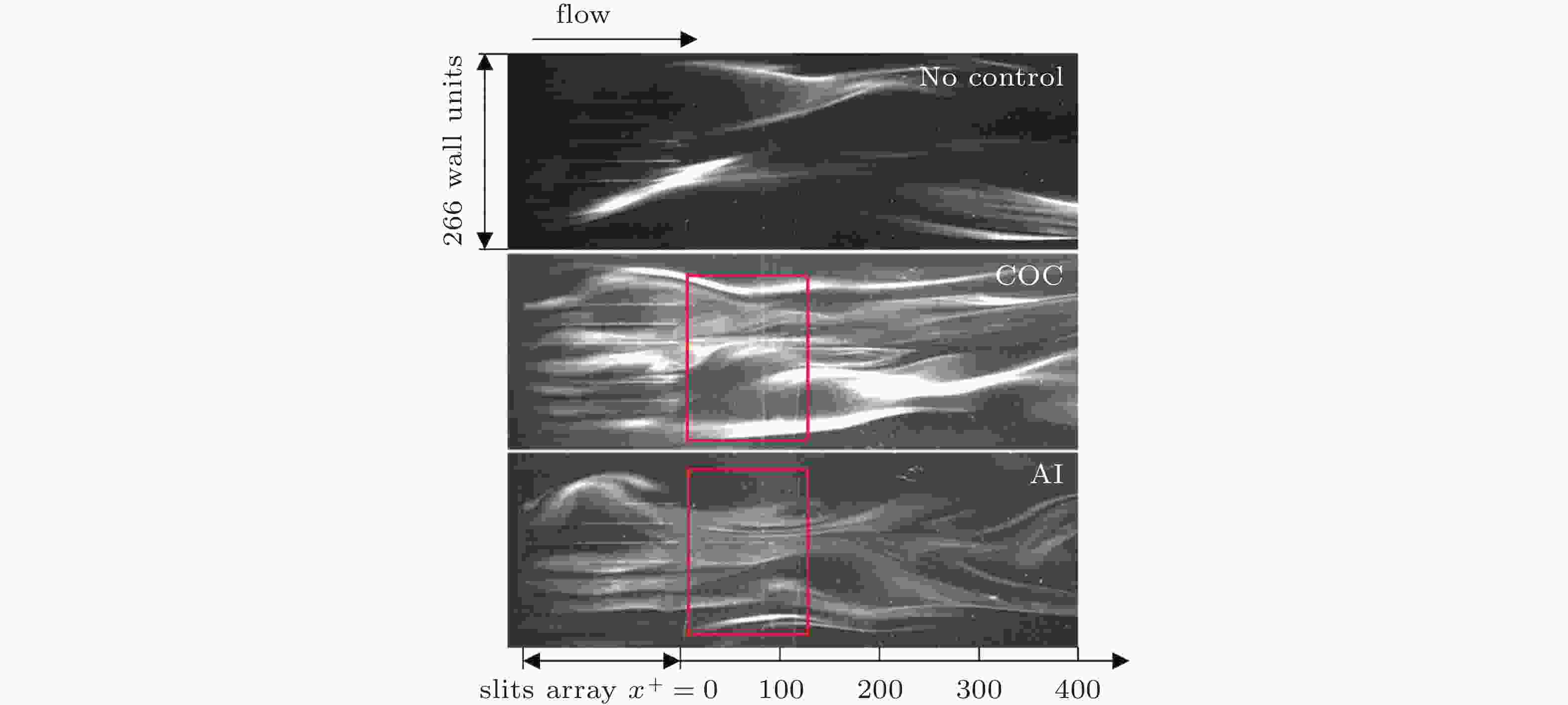
图 6 x-z平面上在y+ = 7时在无控制、传统开环控制 (COC) 和人工智能 (AI) 控制下典型的烟线流动显示图像, 红框区域所示为稳定条带结构(Yu et al. 2021)
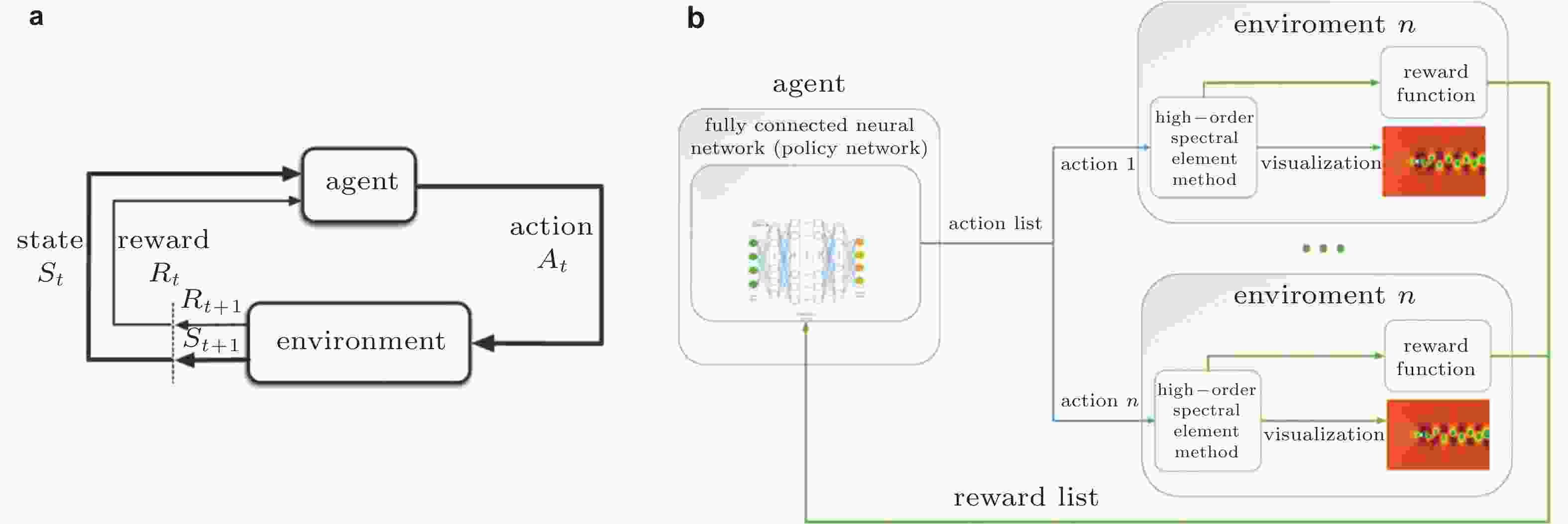
图 7 强化学习(a)和简化的强化学习算法(b)的控制框图(Lai et al. 2021)
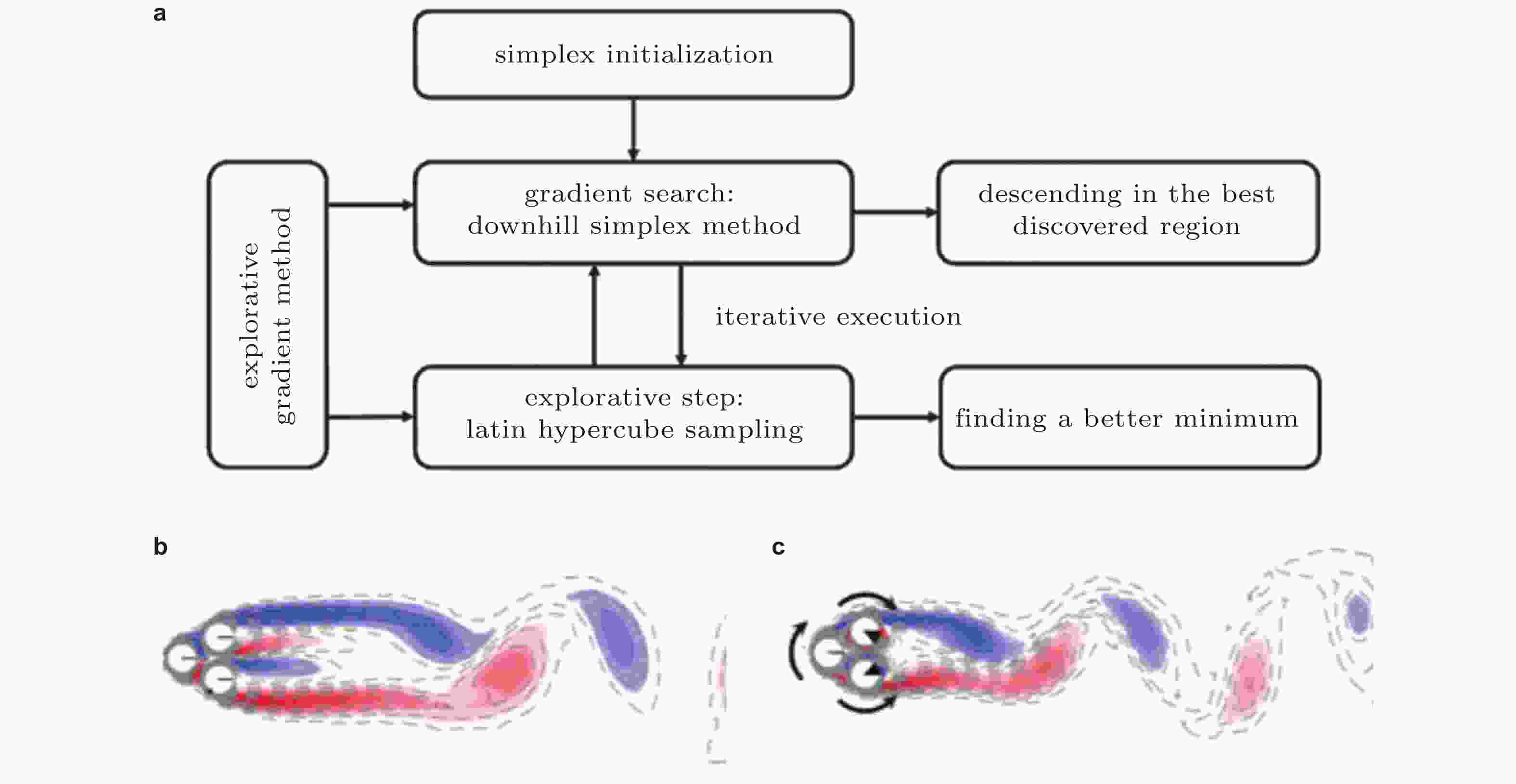
图 8 (a)探索梯度法运行框图, (b)无控制下三圆柱涡量图和(c) EGM搜索到的最优控制参数下的涡量图, 箭头表示旋转方向, 黑色扇区大小与转速成正比(Li et al. 2021)
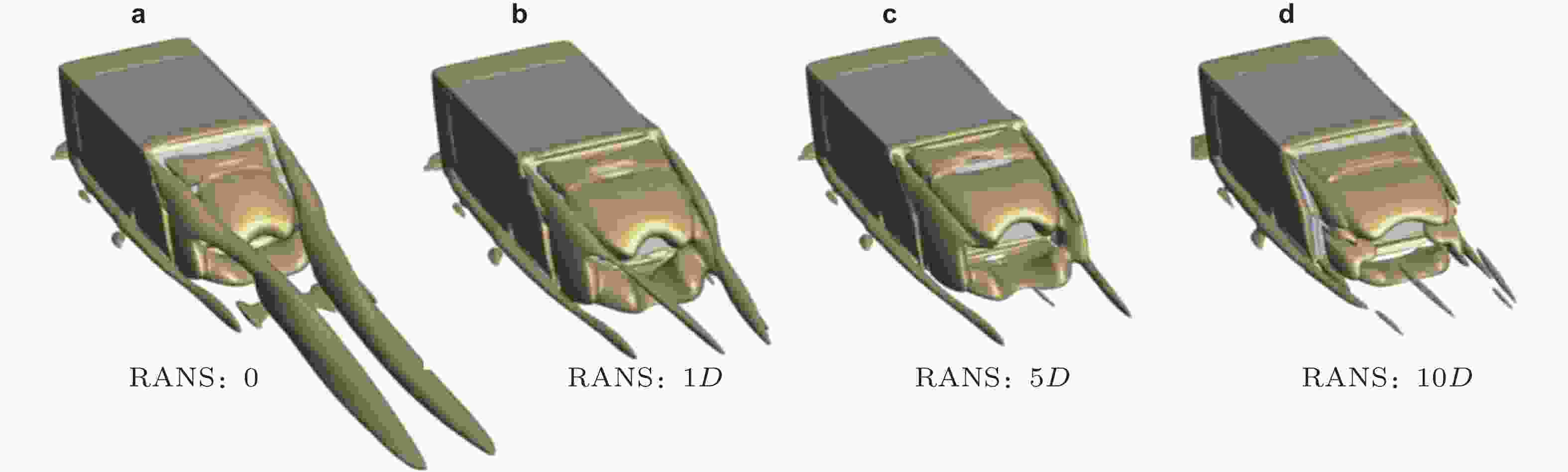
图 9 利用Okubo-Weiss参数法得到的Ahmed车模绕流的在Q = 20000时的等值面(Li et al. 2021)
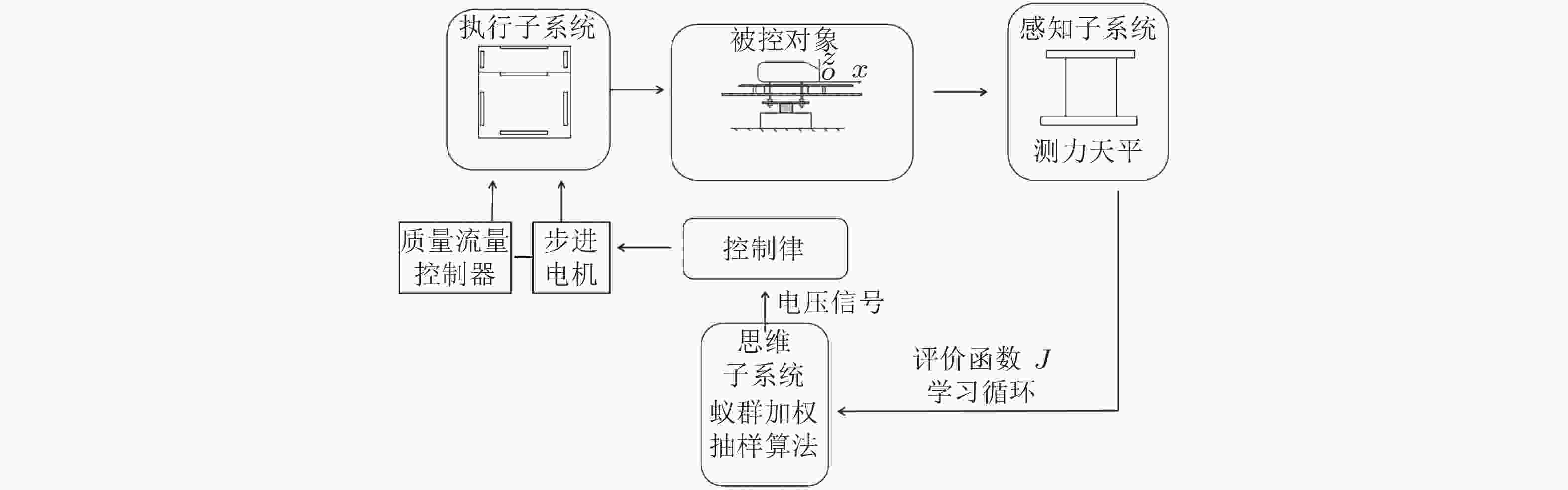
图 10 基于改进蚁群加权抽样算法的汽车模型减阻控制系统逻辑框图 (沈子凡2021)
图 11 基于蚁群算法下的学习曲线. 正方形符号表示第n代中最佳个体An (Zhang et al. 2022)
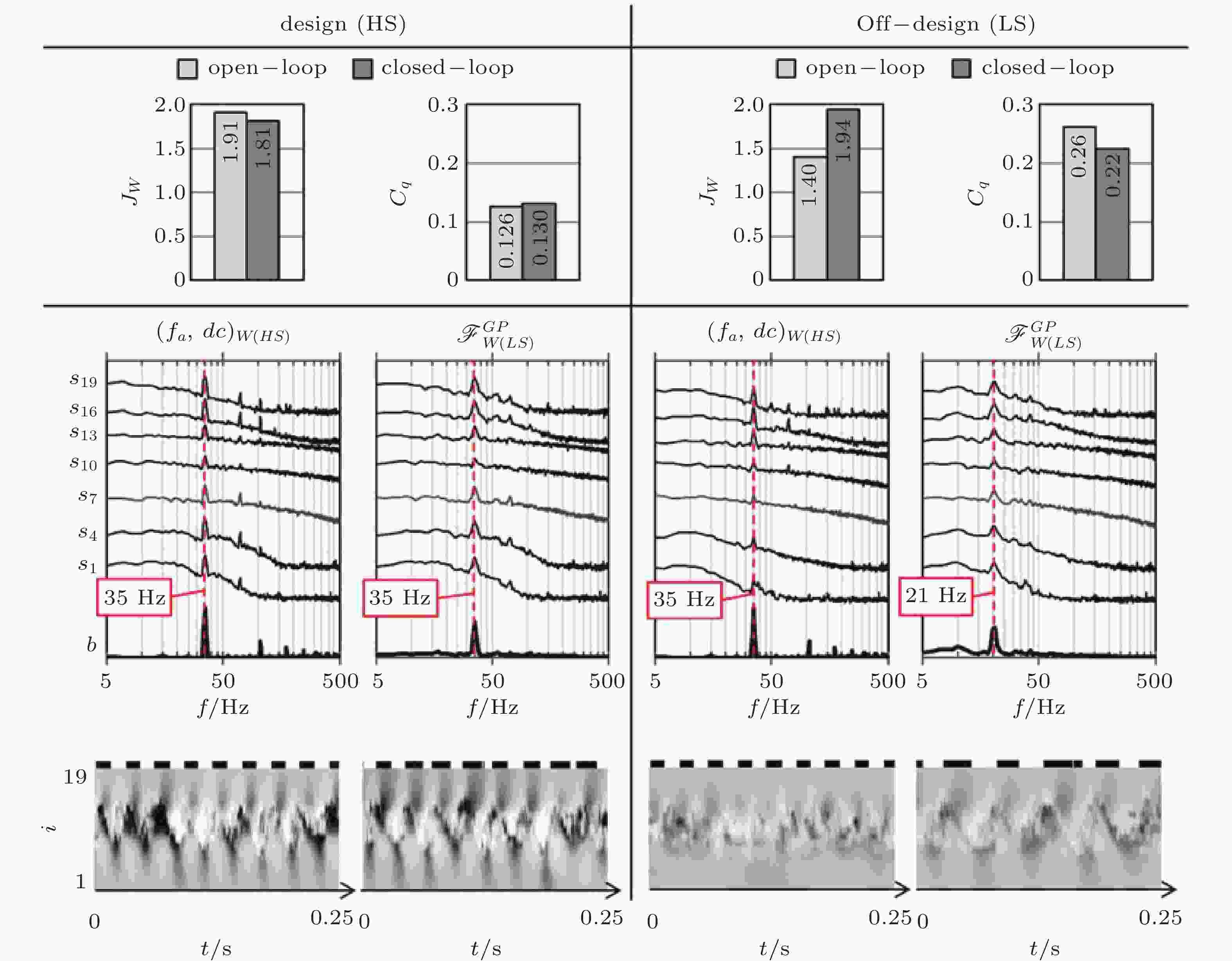
图 13 最优开环控制(fa,dc)w(HS)和最优闭环控制律
$ {\mathcal{F}}_{W\left(HS\right)}^{GP} $ 分别在设计工况 (高速环境HS) 和非设计工况 (低速环境LS) 下对比测试. 第一行是不同控制条件下的JW和对应的质量流率系数Cq, 第二行是每三个热线探针信号的频率谱密度函数 (PSD) , 第三行是t = 0.25 s范围内流场的伪可视化结果, 灰度表示−1.5 ~ 1.5 m/s范围内的脉动速度u' (Parezanović et al. 2015)图 14 GP得到的最佳控制律对平均流场的影响. (a)无控制下和(b)最佳控制下的平均流线图. 颜色表示速度的模
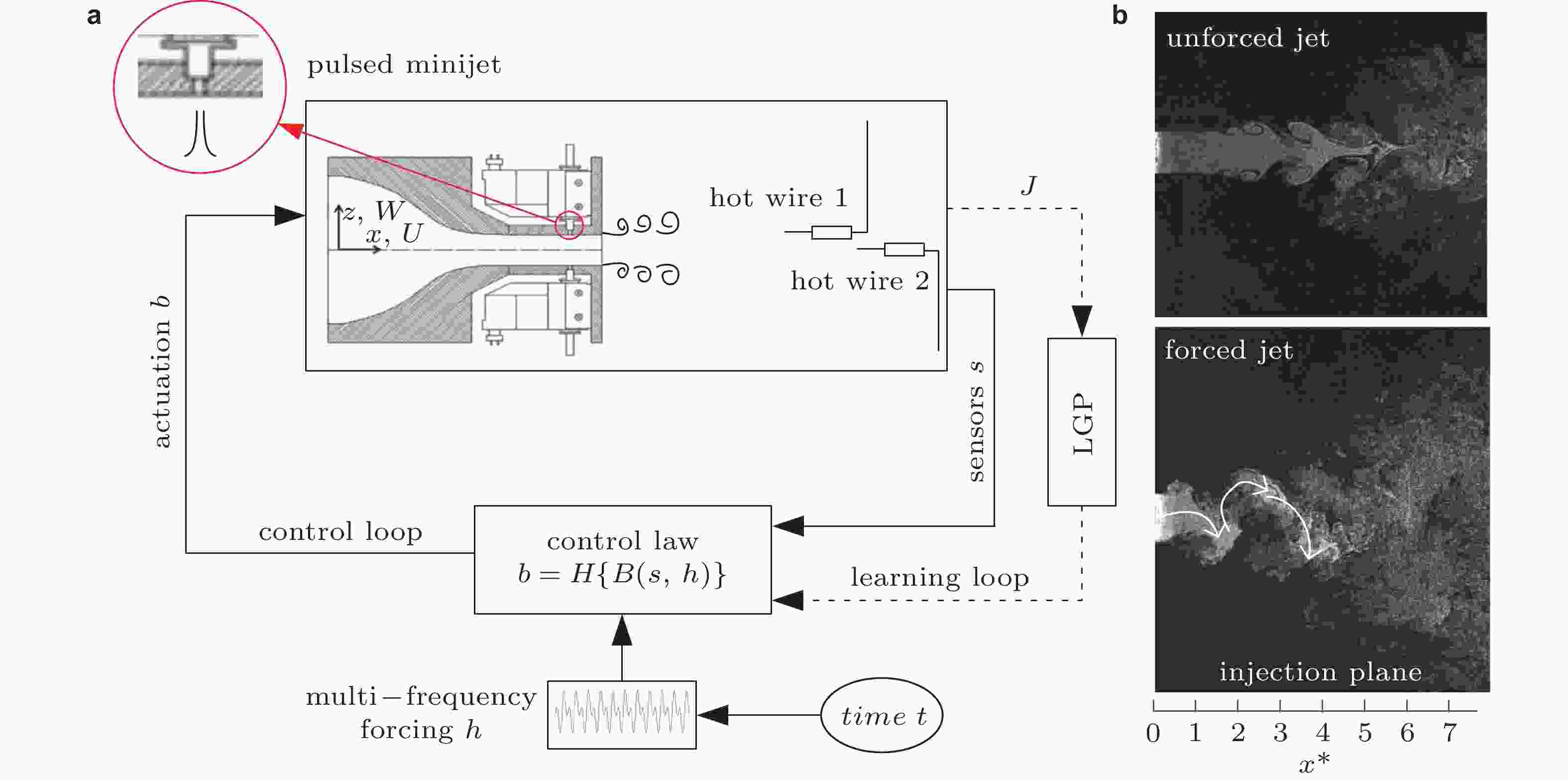
$ \left\| {\boldsymbol{u}} \right\| = \sqrt {({{\overline u }^2} + {{\overline w }^2})} $ (Li et al. 2017)图 15 (a)基于LGP的系统控制框图, (b)无控制与LGP最优控制律下的流动显示图 (Wu et al. 2018a)
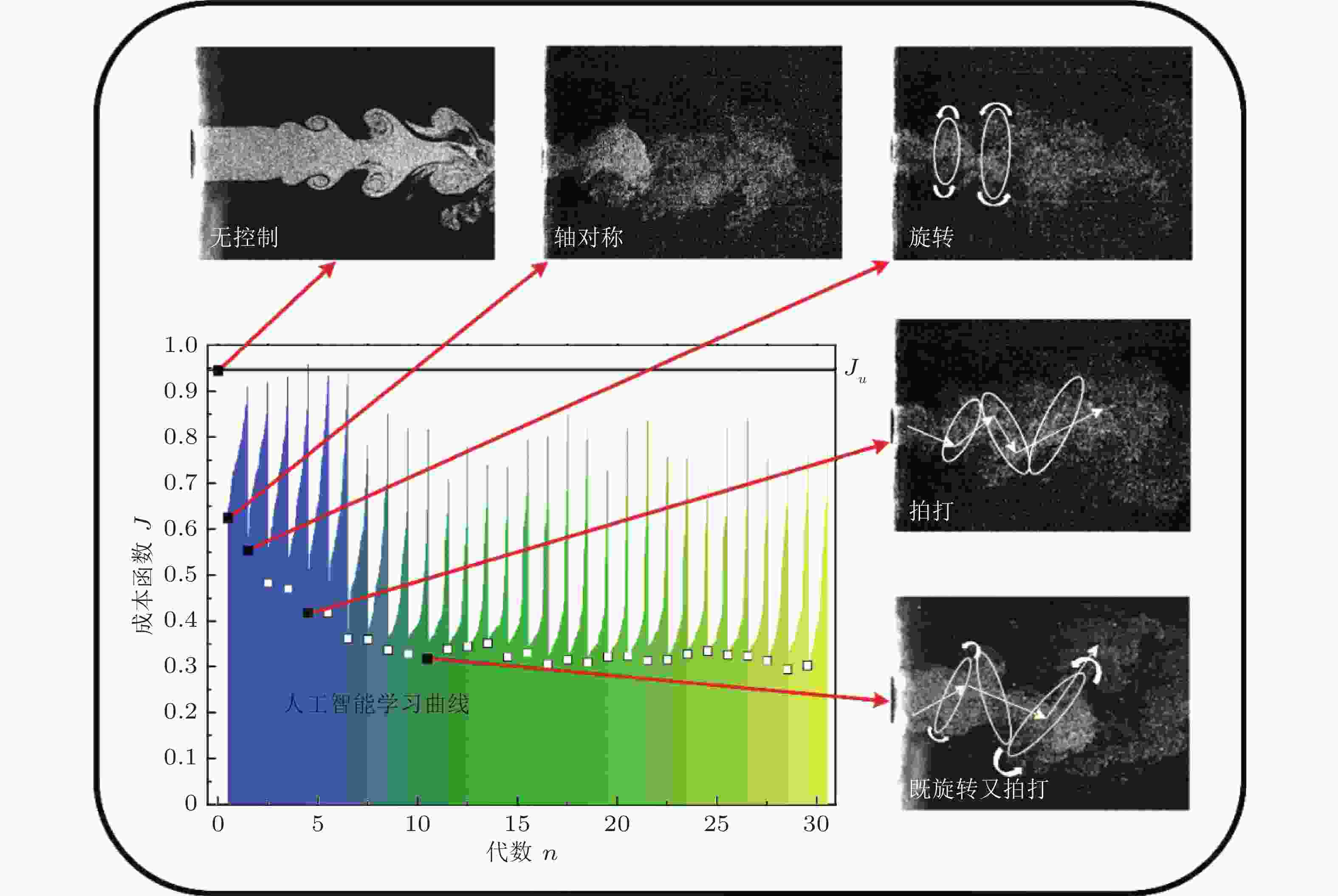
图 16 遗传编程算法在射流混合控制中的学习曲线及特定控制律下的流动显示图 (Zhou et al. 2020)
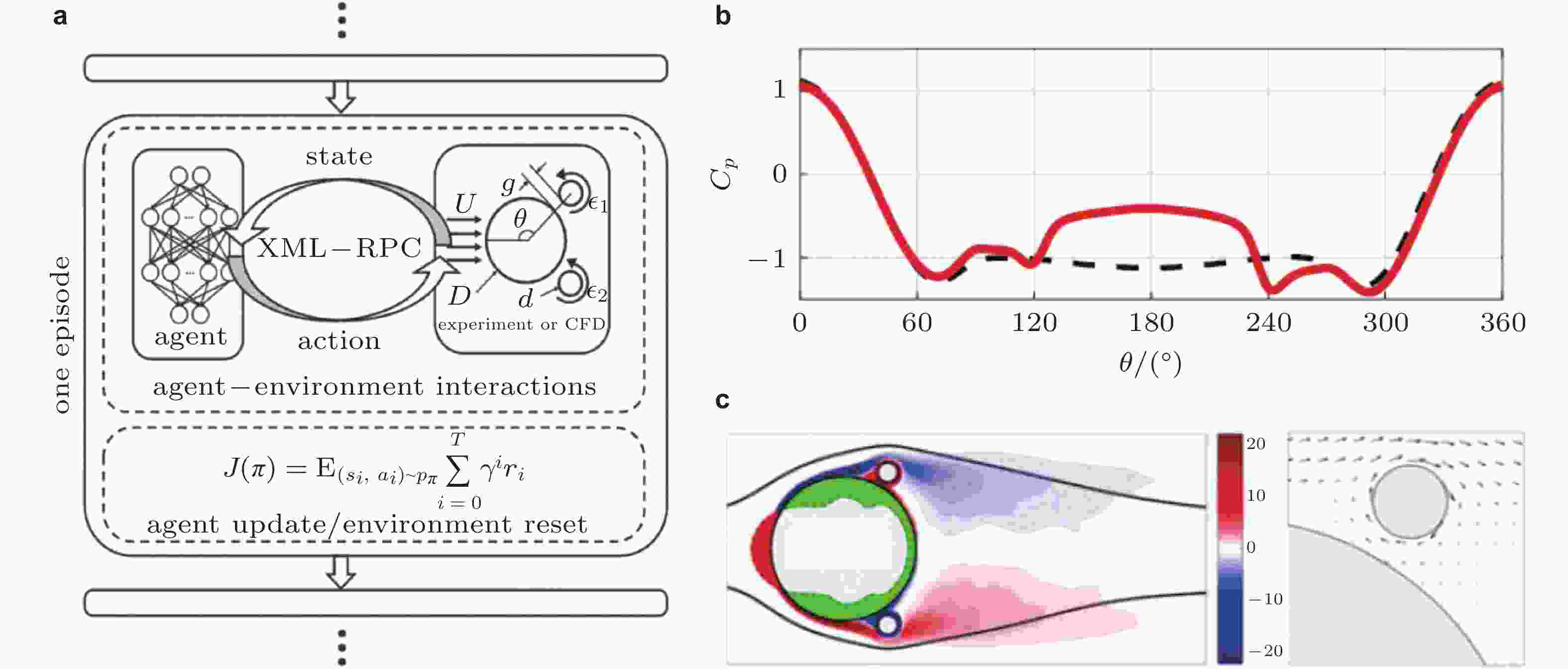
图 17 (a)DRL在一次训练过程中的运行过程示意图, (b)训练500次后圆柱表面压力分布, (c)展向平均涡量的时间平均以及上方小圆柱附近速度分布(Fan et al. 2020a)
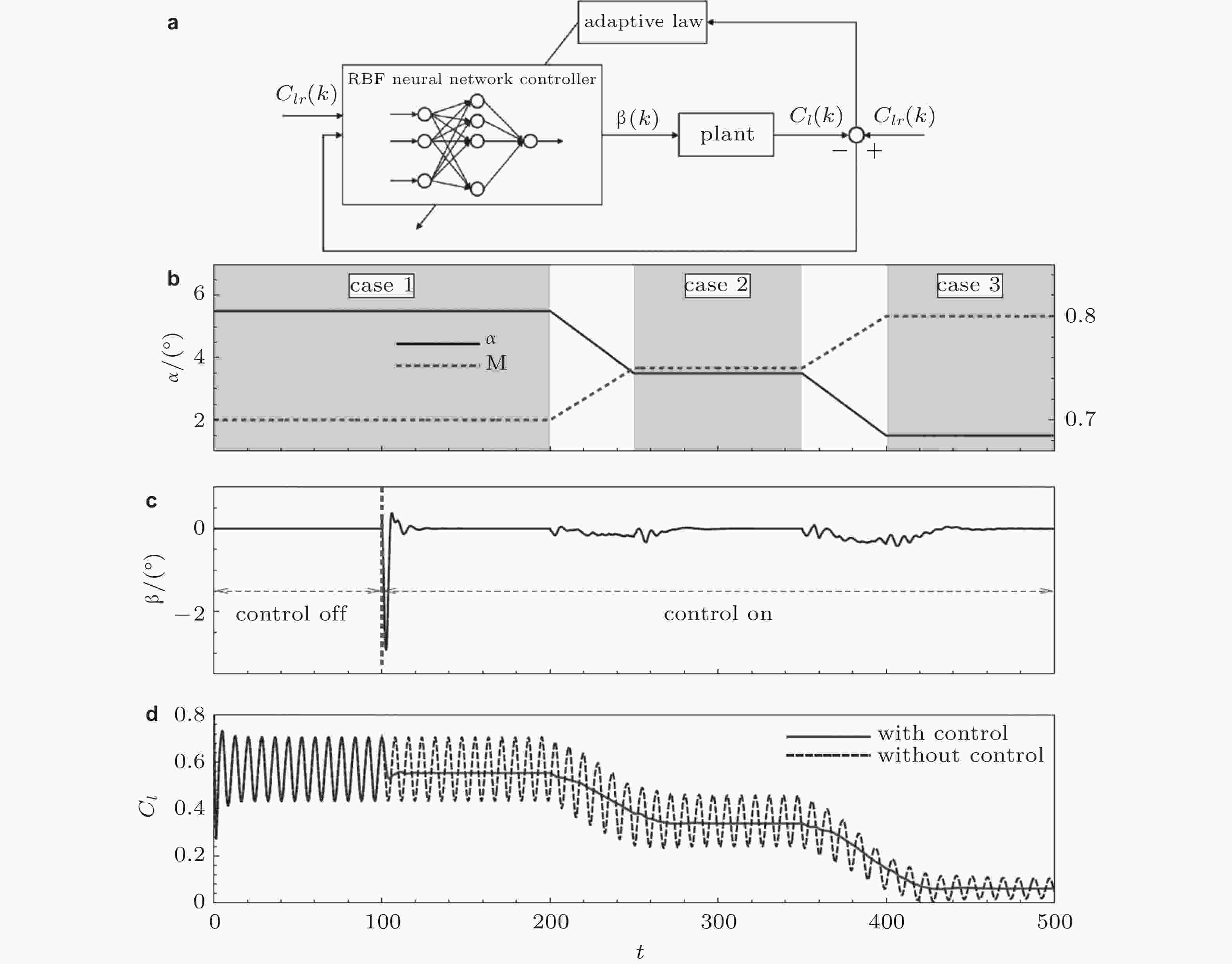
图 18 (a) 径向基函数神经网络自适应控制系统程序框图及(b)其在来流马赫数M和攻角α连续改变时控制系统后缘襟翼角度β和升力系数Cl的响应(Ren et al. 2020b)
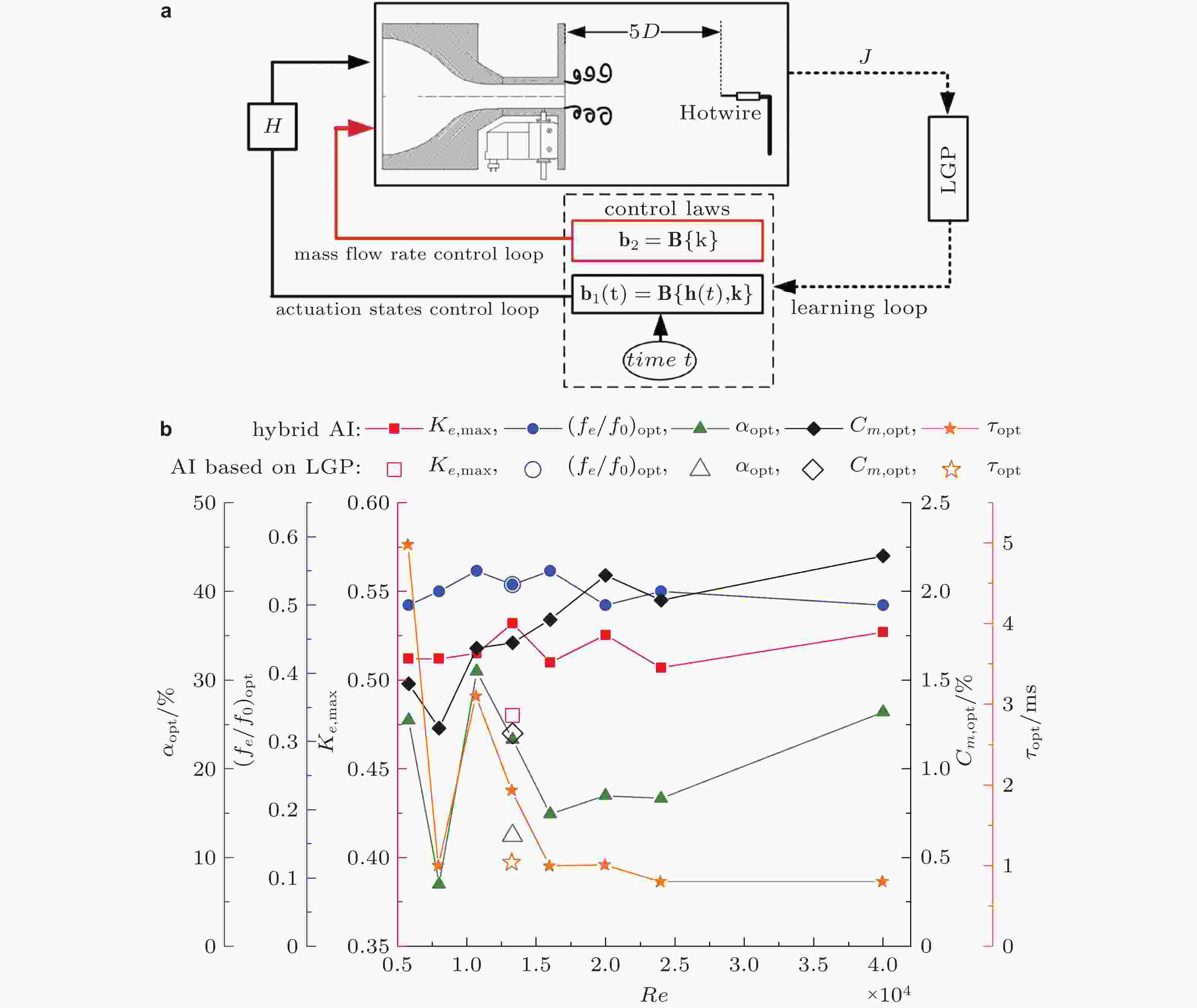
图 19 (a)混合人工智能控制系统的结构示意图, (b)不同雷诺数下混合人工智能控制系统优化得到的最佳控制参数(Perumal et al. 2022)
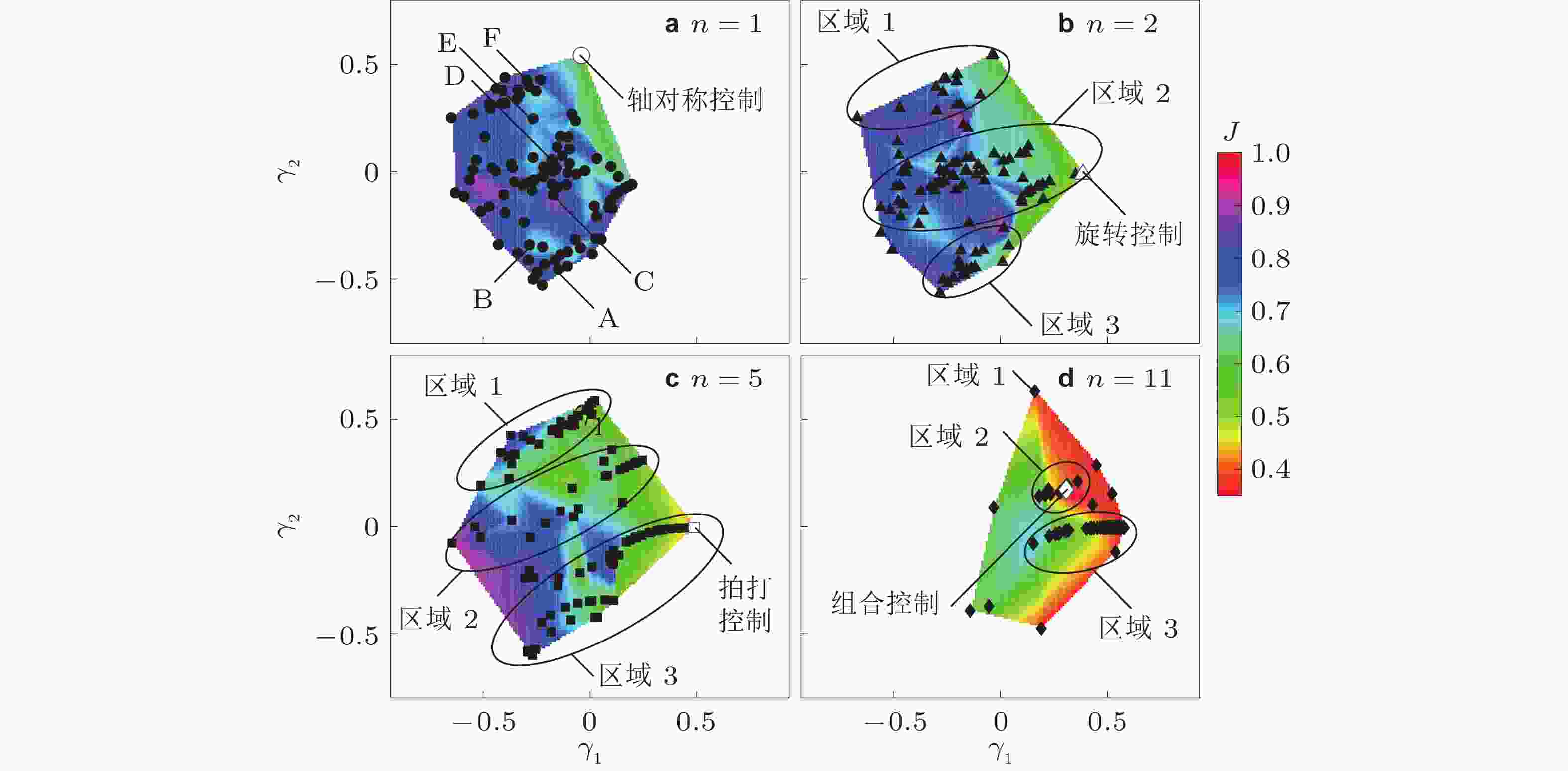
图 20 第 1, 2, 5 和 11 代 (共 400 个控制律) 的近邻图. 每个符号代表一个单独的控制律. 背景颜色对应于控制律的目标函数值J (Zhou et al. 2020). (a) ~ (d) 中的空心圆、三角、方和钻石形符号分别代表第 1, 2, 5 和 11 代的最优控制律
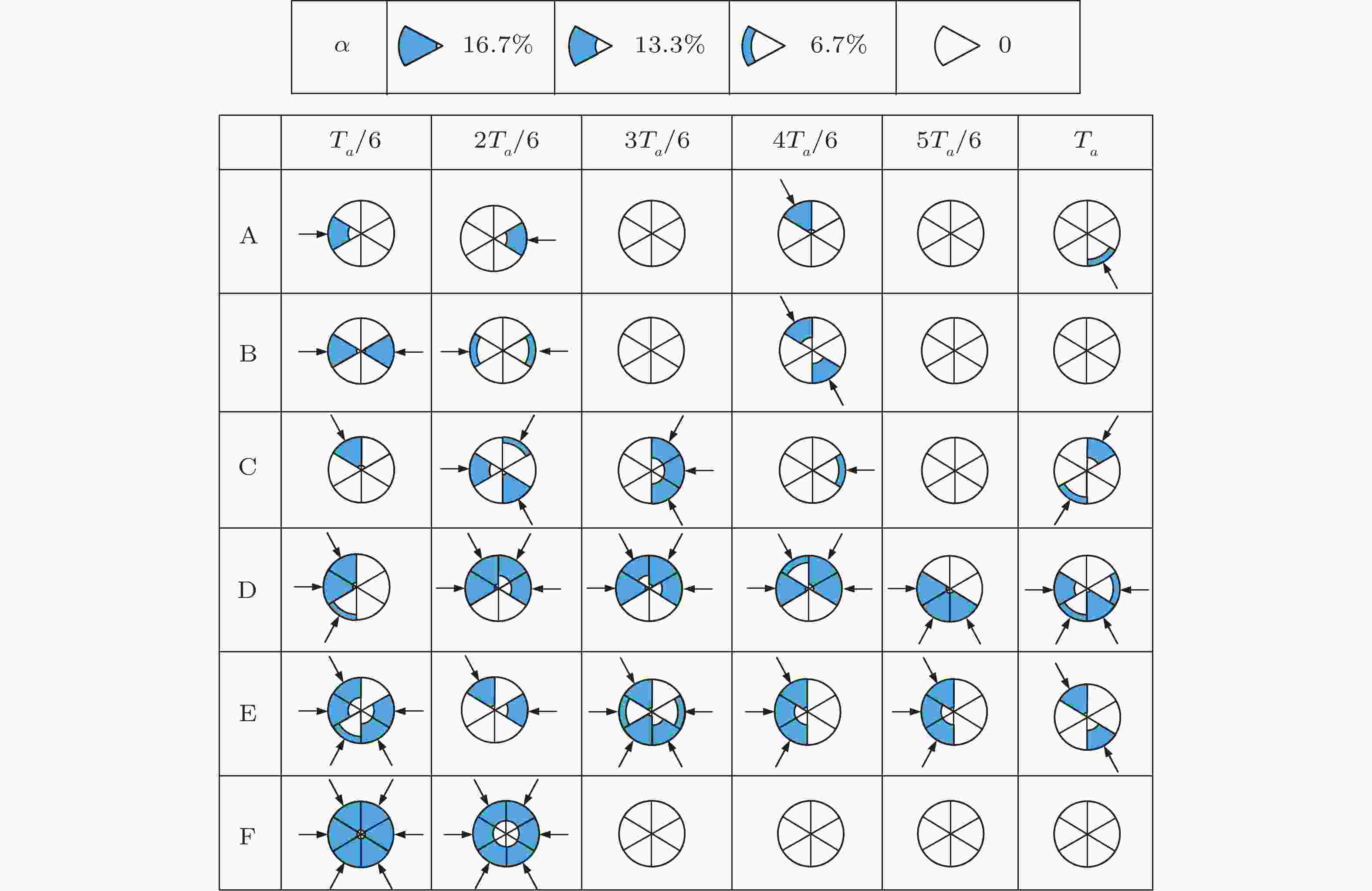
图 21 从图20(a)中提取的与控制律 A ~ F 相关联的控制模式(Zhou et al. 2020). 每个扇形部分对应激励周期的六分之一, 而六个扇区的位置则代表六个微射流. 箭头表示微射流处于开启状态, 蓝色阴影的径向深度与微射流喷射持续时间成正比
图 22 雷诺数5800 ~ 40000范围内变量ζ = (Cm/α)(D/d)1−n(1/Re)(fe/fe,opt)m对Ke/K0的影响. 人工智能实验数据选取了占空比α = 0.07 ~ 0.9, fe/f0 = 0.1 ~ 1.5范围内的测试点. 红线是实验数据根据最小二乘法得到的多项式拟合曲线. 蓝色点对应给定雷诺数的最大混合速率Ke,max/K0 (Perumal et al. 2022)
表 1 基于模型的人工智能湍流控制应用统计
文献 控制方法 控制对象 激励方式 传感器 研究手段 Lee et al. (1997) NN & 反向控制 槽道湍流减阻 动态吹吸气 壁面剪切应力传感器 CFD Lorang et al. (2008) NN & 反向控制 槽道湍流减阻 动态吹吸气 壁面剪切应力传感器 CFD Kaiser et al. (2017) 基于聚类的控制 斜坡流动分离 脉冲吹吸气 速度传感器 CFD Han和Huang (2020) CNN & 反向控制 槽道湍流减阻 动态吹吸气 壁面剪切应力传感器 CFD Park和Choi (2020) CNN & 反向控制 槽道湍流减阻 动态吹吸气 壁面剪切应力传感器、
压力传感器CFD Bieker et al. (2020) RNN & MPC 流体弹球
尾流控制三个独立
旋转的圆柱测力传感器 CFD RNN: recurrent neural network; MPC: model predictive control; NN: neural network; CNN: convolutional neural networks; CFD: computational fluid dynamics. 表 2 控制参数优化在无模型人工智能流动控制中的应用
文献 控制方法 控制对象 激励方式 传感器 研究手段 Koumoutsakos et al. (2001) ES 射流混合 正弦狭缝射流 速度传感器 CFD Hilgers和Boersma (2001) ES 射流混合 螺旋激励和轴向激励 速度传感器 CFD Benard et al. (2016) GA 后向台阶流动分离 等离子体激励 压力传感器 Exp. Minelli et al. (2020) GA 方柱体减阻 前缘吹吸气多频率扰动 测力传感器 CFD Qiao et al. (2021) GA 俯仰方柱体减阻 前缘吹吸气多频率扰动 测力传感器 Exp. Zigunov et al. (2021) GA 倾斜圆柱体减阻 定常微射流阵列组合 粒子图像测速仪 Exp. Yu et al. (2021) GA 湍流边界层减阻 独立控制合成射流阵列 热线传感器 Exp. Fan et al. (2020b) EGM Ahmed 模型减阻 脉冲狭缝射流 测力传感器 Exp. Maceda et al. (2021) EGM 三圆柱组合体尾流控制 三个独立旋转的圆柱 速度传感器 CFD Li et al. (2021) EGM 三圆柱组合体尾流控制 三个独立旋转的圆柱 测力传感器 CFD Ahmed模型减阻 五个独立定常狭缝射流 测力传感器 Lai et al. (2021) SDRL 圆柱减阻 旋转圆柱 测力传感器 CFD 沈子凡 (2021) ACO Ahmed模型减阻 五个角度可调节定常
狭缝射流测力传感器 Exp. Zhang et al. (2022) ACO Ahmed模型减阻 五组定常或非定常狭
缝射流激励测力传感器 Exp. ES: evolution strategies; GA: genetic algorithm; EGM: explorative gradient method; SDRL: simplified deep reinforcement learning; ACO: ant colony optimization; CFD: computational fluid dynamics; Exp: experiments. 表 3 无模型控制律优化在流动控制中的应用
文献 控制方法 控制对象 激励方式 传感器 研究手段 Gautier et al. (2015) GP 后台阶流动分离 动态狭缝射流 粒子图像测速仪 Exp. Parezanović et al. (2015, 2016) GP 混合层 脉冲微射流阵列 热线传感器 Exp. Debien et al. (2016) GP 斜坡流动分离 脉冲主动涡流发生器阵列 热膜传感器 Exp. Chovet et al. (2017) GP 后台阶流动分离 脉冲微射流阵列 压力传感器 Exp. Li et al. (2017) GP Ahmed模型减阻 模型尾部脉冲微射流阵列 测力传感器 Exp. Wu et al. (2018a) GP 射流掺混 单个径向脉冲微射流 热线传感器 Exp. Ren et al. (2019) GP 圆柱涡激振动 动态吹吸气 位移传感器 CFD Li et al. (2020) GP 混合层 动态体积力扰动 速度传感器 CFD Raibaudo和Martinuzzi (2021), Raibaudo et al. (2020) GP 三圆柱组合体尾流 三个旋转的圆柱 速度传感器 Exp. Zhou et al. (2020) GP 射流掺混 六支径向脉冲微射流 热线传感器 Exp. Maceda et al. (2021) GP 三圆柱组合体尾流 三个旋转的圆柱 速度传感器 CFD Nair et al. (2019) CBC 翼型绕流 动态吹吸气 测力传感器 CFD Rabault et al. (2019a),
Rabault和Kuhnle (2019b)DRL 圆柱绕流 动态吹吸气 速度、测力
传感器CFD Fan et al. (2020a) DRL 圆柱绕流 两个旋转圆柱体 测力传感器 Exp Rabault et al. (2020) DRL 圆柱绕流 动态吹吸气 速度、测力
传感器CFD Ren et al. (2020b) DRL 翼型跨音速抖振 后缘襟翼角度 测力传感器 CFD Shimomura et al. (2020) DRL 翼型绕流 等离子激励器 压力传感器 Exp. Tang et al. (2020) DRL 圆柱绕流 四个合成射流激励器 速度、测力
传感器CFD Tokarev et al. (2020) DRL 圆柱绕流 旋转圆柱 速度、测力
传感器CFD Ghraieb et al. (2021) DRL 翼型绕流; 翼型攻角; 角度、测力
传感器CFD Ghraieb et al. (2021) DRL 两串联分布圆柱
绕流;两圆柱间距 测力传感器 CFD Ghraieb et al. (2021) DRL 三圆柱组合体尾流 三个圆柱转速 测力传感器 CFD Mei et al. (2021) DRL 圆柱涡激振动 三个合成射流的质量流率 速度、测力
传感器CFD Mei et al. (2022) DRL 钝体减阻 多个合成射流 速度、测力
传感器CFD Paris et al. (2021) DRL 圆柱绕流 两个合成射流 速度、测力
传感器CFD Zeng和Graham (2021) DRL KSE流动控制
问题均匀分布的激励器 速度传感器 CFD Zheng et al. (2021) DRL 圆柱涡激振动 两支动态射流 速度、测力
传感器CFD Ren et al. (2021a) DRL 圆柱绕流 一对反相射流 速度、测力
传感器CFD Ren et al. (2021b) DRL 圆柱尾迹 前缘吸气后缘吹气 速度传感器 CFD Perumal et al. (2022) DRL 射流增混 一支径向微射流 热线传感器 Exp. Wang et al. (2022) DRL 翼型绕流 合成射流 速度、测力
传感器CFD GP: genetic programming; CBC: cluster-based control; DRL: deep reinforcement learning. 表 4 典型湍流控制方法的优缺点及适用范围
控制方法 优点 缺点 适用范围 基于神经网络的反向控制 对槽道湍流控制效果好 要求传感器数量多、适用
范围小仅适用于反向控制的应用 基于聚类降阶模型的控制 可以处理高维、非线性系统 模型具有不准确性、要求传感器数量多 系统状态易测量的控制应用 RNN和MPC 对传感器数量要求低 需要提供系统期望状态轨迹 使系统输出达到预设目标的应用 参数优化方法: ES, GA, EGM, ACO, SDRL 不依赖模型、对传感器数量要求低、鲁棒性强、简单
通用参数维数高时不易收敛, 仅可以用于 参数优化 形式固定的控制律中参数的优化 GP 对传感器数量要求低、不依赖模型、鲁棒性强、简单
通用优化反馈控制律时抗噪声干扰能力差 优化开环、闭环控制律的
应用DRL 不依赖模型、适用范围广 对传感器数量要求高、
对计算资源要求高、优化闭环控制律的应用 基于聚类的无模型反馈控制 对传感器数量要求低、不依赖模型、收敛时间短 实验研究还需要验证 实时反馈控制应用 基于LGP的混合模式人工智能控制 不依赖模型、可同时实现对控制律和控制参数的优化 优化反馈控制律时抗
噪声干扰能力差优化开环、闭环控制律或
控制参数的应用 -
[1] 刘加利, 李明高, 张继业, 张卫华, 李明. 2013. 高速列车流线型头部多目标气动优化设计. 中国科学:技术科学, 43: 689-698 (Liu J, Li MG, Zhang J, Zhang W, Li M. 2013. Multi-objective aerodynamic optimization design for streamlined head shape of high-speed trains. SCIENTIA SINICA Technologica, 43: 689-698). doi: 10.1360/092012-1475Liu J, Li MG, Zhang J, Zhang W, Li M. 2013. Multi-objective aerodynamic optimization design for streamlined head shape of high-speed trains. SCIENTIA SINICA Technologica, 43(06): 689-698 doi: 10.1360/092012-1475 [2] 刘晓冬, 张沛良, 何光洪, 王永恩, 杨旭东. 2021. 基于伴随方法的飞翼布局多目标气动优化设计. 西北工业大学学报, 39: 753-760 (Liu X, Zhang P, He G, Wang Y, Yang X. 2021. Multi-objective aerodynamic optimization of flying-wing configuration based on adjoint method. Journal of Northwestern Polytechnical University, 39: 753-760). doi: 10.1051/jnwpu/20213940753Liu X, Zhang P, He G, Wang Y, Yang X. 2021. Multi-objective aerodynamic optimization of flying-wing configuration based on adjoint method. Journal of Northwestern Polytechnical University, 39: 753-760 doi: 10.1051/jnwpu/20213940753 [3] 亓昌, 韩元吉, 杨姝, 吕振华. 2020. 考虑气动阻力和横风稳定的汽车车身多目标优化设计. 汽车安全与节能学报, 11: 53-60 (Qi C, Han Y, Yang S, Lu Z. 2020. Multi-objective optimization design of auto body considering aerodynamic resistance and crosswind stability. Journal of Automotive Safety and Energy, 11: 53-60).Qi C, Han Y, Yang S, Lu Z. 2020. Multi-objective optimization design of auto body considering aerodynamic resistance and crosswind stability. Journal of Automotive Safety and Energy, 11(01): 53-60 [4] 任峰, 高传强, 唐辉. 2021. 机器学习在流动控制领域的应用及发展趋势. 航空学报, 42: 152-166 (Ren F, Gao C, Tang H. 2021. Machine learning for flow control: Applications and development trends. Acta Aeronautica et Astronautica Sinica, 42: 152-166).Ren F, Gao C, Tang H. 2021. Machine learning for flow control: Applications and development trends. Acta Aeronautica et Astronautica Sinica, 42: 152-166 [5] 沈子凡 2021 基于人工智能与组合激励的变角度Ahmed模型气动减阻研究 [硕士论文], 哈尔滨: 哈尔滨工业大学Shen Z. 2021. Aerodynamic drag reduciton of Ahmed model using variable angle combined actuators and artificial inteligence [Master Thesis], Harbin: Harbin Institute of Technology [6] 张伟伟, 朱林阳, 刘溢浪, 寇家庆. 2019. 机器学习在湍流模型构建中的应用进展. 空气动力学学报, 37: 444-454 (Zhang W, Zhu L, Liu Y, Kou J. 2019. Progresses in the application of machine learning in turbulence modeling. Acta Aerodynamica Sinica, 37: 444-454).Zhang W, Zhu L, Liu Y, Kou J. 2019. Progresses in the application of machine learning in turbulence modeling. Acta Aerodynamica Sinica, 37: 444-454 [7] Asadi E, Silva M G D, Antunes C H, Dias L, Glicksman L. 2014. Multi-objective optimization for building retrofit: A model using genetic algorithm and artificial neural network and an application. Energy and Buildings, 81: 444-456. doi: 10.1016/j.enbuild.2014.06.009 [8] Benard N, Pons-Prats J, Periaux J, Bugeda G, Braud P, Bonnet J P, Moreau E. 2016. Turbulent separated shear flow control by surface plasma actuator: experimental optimization by genetic algorithm approach. Experiments in Fluids, 57: 22. doi: 10.1007/s00348-015-2107-3 [9] Bieker K, Peitz S, Brunton S L, Kutz J N, Dellnitz M. 2020. Deep model predictive flow control with limited sensor data and online learning. Theoretical and Computational Fluid Dynamics, 34: 577-591. doi: 10.1007/s00162-020-00520-4 [10] Blanchard A B, Cornejo Maceda G Y, Fan D, Li Y, Zhou Y, Noack B R, Sapsis T P. 2022. Bayesian optimization for active flow control. Acta Mechanica Sinica, 37: 1786-1798. [11] Cai S, Mao Z, Wang Z, Yin M, Karniadakis G E. Physics-informed neural networks (PINNs) for fluid mechanics: a review. Acta Mechanica Sinica. 2022. 37(12). 1727-1738 [12] Cai S, Zhou S, Xu C, Gao Q. 2019. Dense motion estimation of particle images via a convolutional neural network. Experiments in Fluids, 60: 73. doi: 10.1007/s00348-019-2717-2 [13] Chen X, Agarwal R K. 2013. Optimization of Wind Turbine Blade Airfoils Using a Multi-Objective Genetic Algorithm. Journal of Aircraft, 50: 519-527. doi: 10.2514/1.C031910 [14] Choi H, Moin P, Kim J. 1994. Active Turbulence Control for Drag Reduction in Wall-Bounded Flows. Journal of Fluid Mechanics, 262: 75-110. doi: 10.1017/S0022112094000431 [15] Chovet C, Keirsbulck L, Noack B R, Lippert M, Foucaut J-M. 2017. Machine learning control for experimental shear flows targeting the reduction of a recirculation bubble. IFAC-PapersOnLine, 50: 12307-12311. doi: 10.1016/j.ifacol.2017.08.2157 [16] Coello C C A, Lechuga M S. 2002. MOPSO: a proposal for multiple objective particle swarm optimization//Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No. 02TH8600). 2: 1051-1056 [17] Corre C, Renaud T, Lerat A. 2003. Transonic flow control using a Navier-Stokes solver and a multi-objective genetic algorithm//In IUTAM Symposium Transsonicum IV: Proceedings of the IUTAM Symposium held in Göttingen, Germany, 2–6 September 2002 (pp. 297-302). Springer Netherlands. [18] Debien A, von Krbek K A F F, Mazellier N, Duriez T, Cordier L, Noack B R, Abel M W, Kourta A. 2016. Closed-loop separation control over a sharp edge ramp using genetic programming. Experiments in Fluids, 57: 40. doi: 10.1007/s00348-016-2126-8 [19] Deng G, Fan D, Zhang B, Liu K, Zhou Y. 2022. Sensitivity analysis of large body of control parameters in machine learning control of a square-back Ahmed body. Proceedings of the Royal Society A. Submitted [20] Dorigo M, Maniezzo V, Colorni A. 1999. Positive feedback as a search strategy. Technical Report. 91-016. [21] Duraisamy K, Iaccarino G, Xiao H. 2019. Turbulence Modeling in the Age of Data. Annual Review of Fluid Mechanics, 51: 357-377. doi: 10.1146/annurev-fluid-010518-040547 [22] Fan D, Yang L, Wang Z, Triantafyllou M S, Karniadakis G E. 2020a. Reinforcement learning for bluff body active flow control in experiments and simulations. Proceedings of the National Academy of Sciences of The United States of America, 117: 26091-26098. doi: 10.1073/pnas.2004939117 [23] Fan D, Zhang B, Zhou Y, Noack B R. 2020b. Optimization and sensitivity analysis of active drag reduction of a square-back Ahmed body using machine learning control. Physics of Fluids, 32: 125117. doi: 10.1063/5.0033156 [24] Fan D W, Zhou Y, Noack B R. 2020c. Fast triple-parameter extremum seeking exemplified for jet control. Experiments in Fluids, 61: 152. doi: 10.1007/s00348-020-02953-3 [25] Gautier N, Aider J L, Duriez T, Noack B R, Segond M, Abel M. 2015. Closed-loop separation control using machine learning. Journal of Fluid Mechanics, 770: 442-457. doi: 10.1017/jfm.2015.95 [26] Ghraieb H, Viquerat J, Larcher A, Meliga P, Hachem E. 2021. Single-step deep reinforcement learning for open-loop control of laminar and turbulent flows. Physical Review Fluids, 6: 053902. doi: 10.1103/PhysRevFluids.6.053902 [27] Han B-Z, Huang W-X. 2020. Active control for drag reduction of turbulent channel flow based on convolutional neural networks. Physics of Fluids, 32: 095108. [28] Hilgers A, Boersma B J. 2001. Optimization of turbulent jet mixing. Fluid Dynamics Research, 29: 345-368. doi: 10.1016/S0169-5983(01)00035-1 [29] Huang L, Huang G, LeBeau R, Hauser T. 2007. Optimization of aifoil flow control using a genetic algorithm with diversity control. Journal of Aircraft, 44: 1337-1349. doi: 10.2514/1.27020 [30] Jahanmiri M, Abbaspour M. 2011. Experimental investigation of drag reduction on Ahmed car model using a combination of active flow control methods. International Journal of Engineering, 24: .403-410. doi: 10.5829/idosi.ije.2011.24.04a.09 [31] Jovanović M R. 2021. From bypass transition to flow control and data-driven turbulence modeling: An input–output viewpoint. Annual Review of Fluid Mechanics, 53: 311-345. doi: 10.1146/annurev-fluid-010719-060244 [32] Kaiser E, Noack B R, Spohn A, Cattafesta L N, Morzynski M. 2017. Cluster-based control of a separating flow over a smoothly contoured ramp. Theoretical and Computational Fluid Dynamics, 31: 579-593. doi: 10.1007/s00162-016-0419-4 [33] Karniadakis G E, Kevrekidis I G, Lu L, Perdikaris P, Wang S, Yang L. 2021. Physics-informed machine learning. Nature Reviews Physics, 3: 422-440. doi: 10.1038/s42254-021-00314-5 [34] Kim J, Bewley T R. 2007. A linear systems approach to flow control. Annual Review of Fluid Mechanics, 39: 383-417. doi: 10.1146/annurev.fluid.39.050905.110153 [35] Koumoutsakos P, Freund J, Parekh D. 2001. Evolution strategies for automatic optimization of jet mixing. AIAA Journal, 39: 967-969. doi: 10.2514/2.1404 [36] Lai P, Wang R, Zhang W, Xu H. 2021. Parameter optimization of open-loop control of a circular cylinder by simplified reinforcement learning. Physics of Fluids, 33: 107110. doi: 10.1063/5.0068454 [37] Laumanns M, Thiele L, Deb K, Zitzler E. 2002. Combining convergence and diversity in evolutionary multiobjective optimization. Evolutionary Computation, 10: 263-282. doi: 10.1162/106365602760234108 [38] Lee C, Kim J, Babcock D, Goodman R. 1997. Application of neural networks to turbulence control for drag reduction. Physics of Fluids, 9: 1740-1747. doi: 10.1063/1.869290 [39] Li H, Tan J G, Gao Z W, Noack B R. 2020. Machine learning open-loop control of a mixing layer. Physics of Fluids, 32: 111701. doi: 10.1063/5.0030071 [40] Li J, Du X, Martins J R R A. 2022. Machine learning in aerodynamic shape optimization. Progress in Aerospace Sciences, 134: 100849. doi: 10.1016/j.paerosci.2022.100849 [41] Li R, Noack B R, Cordier L, Borée J, Harambat F. 2017. Drag reduction of a car model by linear genetic programming control. Experiments in Fluids, 58: 103. doi: 10.1007/s00348-017-2382-2 [42] Li R, Xu P, Peng Y, Ji P. 2016. Multi-objective optimization of a high-speed train head based on the FFD method. Journal of Wind Engineering and Industrial Aerodynamics, 152: 41-49. doi: 10.1016/j.jweia.2016.03.003 [43] Li Y, Cui W, Jia Q, Li Q, Yang Z, Morzyński M, Noack B R. 2021. Explorative gradient method for active drag reduction of the fluidic pinball and slanted Ahmed body. Journal of Fluid Mechanics, 932: A7. [44] Lorang L V, Podvin B, Le Quéré P. 2008. Application of compact neural network for drag reduction in a turbulent channel flow at low Reynolds numbers. Physics of Fluids, 20: 045104. doi: 10.1063/1.2904993 [45] Maceda G Y C, Li Y, Lusseyran F, Morzyński M, Noack B R. 2021. Stabilization of the fluidic pinball with gradient-enriched machine learning control. Journal of Fluid Mechanics, 917. [46] Mei Y-F, Zheng C, Aubry N, Li M-G, Wu W-T, Liu X. 2021. Active control for enhancing vortex induced vibration of a circular cylinder based on deep reinforcement learning. Physics of Fluids, 33: 103604. doi: 10.1063/5.0063988 [47] Mei Y-F, Zheng C, Hua Y, Zhao Q, Wu P, Wu W-T. 2022. Active control for the flow around various geometries through deep reinforcement learning. Fluid Dynamics Research, 54: 015510. doi: 10.1088/1873-7005/ac4f2d [48] Milano M, Koumoutsakos P. 2002. A clustering genetic algorithm for cylinder drag optimization. Journal of Computational Physics, 175: 79-107. doi: 10.1006/jcph.2001.6882 [49] Minelli G, Dong T, Noack B R, Krajnović S. 2020. Upstream actuation for bluff-body wake control driven by a genetically inspired optimization. Journal of Fluid Mechanics, 893: A1. doi: 10.1017/jfm.2020.220 [50] Nair A G, Yeh C A, Kaiser E, Noack B R, Brunton S L, Taira K. 2019. Cluster-based feedback control of turbulent post-stall separated flows. Journal of Fluid Mechanics, 875: 345-375. doi: 10.1017/jfm.2019.469 [51] Niknam T, Kavousifard A, Tabatabaei S, Aghaei J. 2011. Optimal operation management of fuel cell/wind/photovoltaic power sources connected to distribution networks. Journal of Power Sources, 196: 8881-8896. doi: 10.1016/j.jpowsour.2011.05.081 [52] Noack B R, Morzynski M, Tadmor G. Reduced-order Modelling for Flow Control. Springer Science & Business Media. 2011. [53] Parezanović V, Cordier L, Spohn A, Duriez T, Noack B R, Bonnet J P, Segond M, Abel M, Brunton S L. 2016. Frequency selection by feedback control in a turbulent shear flow. Journal of Fluid Mechanics, 797: 247-283. doi: 10.1017/jfm.2016.261 [54] Parezanović V, Laurentie J C, Fourment C, Delville J, Bonnet J P, Spohn A, Duriez T, Cordier L, Noack B R, Abel M, et al. 2015. Mixing layer manipulation experiment: From open-loop forcing to closed-loop machine learning control. Flow, Turbulence and Combustion, 94: 155-173. doi: 10.1007/s10494-014-9581-1 [55] Paris R, Beneddine S, Dandois J. 2021. Robust flow control and optimal sensor placement using deep reinforcement learning. Journal of Fluid Mechanics, 913: A25. doi: 10.1017/jfm.2020.1170 [56] Park J, Choi H. 2020. Machine-learning-based feedback control for drag reduction in a turbulent channel flow. Journal of Fluid Mechanics, 904: A24. doi: 10.1017/jfm.2020.690 [57] Perumal A K, Wu Z, Fan D W, Zhou Y. 2022. A hybrid artificial intelligence control of a turbulent jet: Reynolds number effect and scaling. Journal of Fluid Mechanics, 942: A47. doi: 10.1017/jfm.2022.341 [58] Qiao Z X, Minelli G, Noack B R, Krajnović S, Chernoray V. 2021. Multi-frequency aerodynamic control of a yawed bluff body optimized with a genetic algorithm. Journal of Wind Engineering and Industrial Aerodynamics, 212: 104600. doi: 10.1016/j.jweia.2021.104600 [59] Rabault J, Kuchta M, Jensen A, Réglade U, Cerardi N. 2019. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. Journal of Fluid Mechanics, 865: 281-302. doi: 10.1017/jfm.2019.62 [60] Rabault J, Kuhnle A. 2019. Accelerating deep reinforcement learning strategies of flow control through a multi-environment approach. Physics of Fluids, 31: 094105. doi: 10.1063/1.5116415 [61] Rabault J, Ren F, Zhang W, Tang H, Xu H. 2020. Deep reinforcement learning in fluid mechanics: A promising method for both active flow control and shape optimization. Journal of Hydrodynamics, 32: 234-246. doi: 10.1007/s42241-020-0028-y [62] Raibaudo C, Martinuzzi R J. 2021. Unsteady actuation and feedback control of the experimental fluidic pinball using genetic programming. Experiments in Fluids, 62: 219. doi: 10.1007/s00348-021-03309-1 [63] Raibaudo C, Zhong P, Noack B R, Martinuzzi R J. 2020. Machine learning strategies applied to the control of a fluidic pinball. Physics of Fluids, 32: 015108. doi: 10.1063/1.5127202 [64] Ren F, Hu H-B, Tang H. 2020. Active flow control using machine learning: A brief review. Journal of Hydrodynamics, 32: 247-253. doi: 10.1007/s42241-020-0026-0 [65] Ren F, Rabault J, Tang H. 2021a. Applying deep reinforcement learning to active flow control in weakly turbulent conditions. Physics of Fluids, 33: 037121. doi: 10.1063/5.0037371 [66] Ren F, Wang C, Tang H. 2019. Active control of vortex-induced vibration of a circular cylinder using machine learning. Physics of Fluids, 31: 093601. doi: 10.1063/1.5115258 [67] Ren F, Wang C, Tang H. 2021b. Bluff body uses deep-reinforcement-learning trained active flow control to achieve hydrodynamic stealth. Physics of Fluids, 33: 093602. doi: 10.1063/5.0060690 [68] Ren K, Chen Y, Gao C, Zhang W. 2020. Adaptive control of transonic buffet flows over an airfoil. Physics of Fluids, 32: 096106. doi: 10.1063/5.0020496 [69] Rosenberg R S. 1970. Stimulation of genetic populations with biochemical properties: I. The model. Mathematical Biosciences, 7: 223-257. doi: 10.1016/0025-5564(70)90126-4 [70] Samad A, Kim K Y. 2008. Shape optimization of an axial compressor blade by multi-objective genetic algorithm. Journal of Power and Energy, 222: 599-611. doi: 10.1243/09576509JPE596 [71] Sengupta T K, Deb K, Talla S B. 2007. Control of flow using genetic algorithm for a circular cylinder executing rotary oscillation. Computers & Fluids, 36: 578-600. [72] Shimomura S, Sekimoto S, Oyama A, Fujii K, Nishida H. 2020. Closed-loop flow separation control using the deep Q network over airfoil. AIAA Journal, 58: 4260-4270. doi: 10.2514/1.J059447 [73] Silver D, Schrittwieser J, Simonyan K, Antonoglou I, Huang A, Guez A, Hubert T, Baker L, Lai M, Bolton A, et al. 2017. Mastering the game of Go without human knowledge. Nature, 550: 354-359. doi: 10.1038/nature24270 [74] Tang H, Rabault J, Kuhnle A, Wang Y, Wang T. 2020. Robust active flow control over a range of Reynolds numbers using an artificial neural network trained through deep reinforcement learning. Physics of Fluids, 32: 053605. doi: 10.1063/5.0006492 [75] Tokarev M, Palkin E, Mullyadzhanov R. 2020. Deep reinforcement learning control of cylinder flow using rotary oscillations at low Reynolds number. Energies, 13: 5920. doi: 10.3390/en13225920 [76] Wang J-X, Wu J-L, Xiao H. 2017. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Physical Review Fluids, 2: 034603. doi: 10.1103/PhysRevFluids.2.034603 [77] Wang Y-Z, Mei Y-F, Aubry N, Chen Z, Wu P, Wu W-T. 2022. Deep reinforcement learning based synthetic jet control on disturbed flow over airfoil. Physics of Fluids, 34: 033606. doi: 10.1063/5.0080922 [78] Wen X, Li Z, Liu J, Zhou W, Liu Y. 2019. Machine learning approach to construct global phase-averaged flow field based on local flow features. Flow Measurement and Instrumentation, 67: 41-54. doi: 10.1016/j.flowmeasinst.2019.04.006 [79] Wu J-L, Xiao H, Paterson E. 2018. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Physical Review Fluids, 3: 074602. doi: 10.1103/PhysRevFluids.3.074602 [80] Wu Z, Fan D, Zhou Y, Li R, Noack B R. 2018. Jet mixing optimization using machine learning control. Experiments in Fluids, 59: 131. doi: 10.1007/s00348-018-2582-4 [81] Wu Z, Wong C W, Zhou Y. 2018. Dual-input/single-output extremum-seeking system for jet control. AIAA Journal, 56: 1463-1471. doi: 10.2514/1.J056675 [82] Yu J N, Fan D W, Noack B R, Zhou Y. 2021. Genetic-algorithm-based artificial intelligence control of a turbulent boundary layer. Acta Mechanica Sinica, 37: 1739-1747. doi: 10.1007/s10409-021-01145-4 [83] Yu J N, Fan D W, Zhou Y. Artificial intelligence control of turbulent boundary layer//23rd Australasian Fluid Mechanics Conference – 23AFMC, 4-8th, December, 2022. Sydney, Australia [84] Zeng K, Graham M D. 2021. Symmetry reduction for deep reinforcement learning active control of chaotic spatiotemporal dynamics. Phys Rev E, 104: 014210. doi: 10.1103/PhysRevE.104.014210 [85] Zhang B F, Fan D W, Zhou Y. 2022. Artificial intelligence control of a low-drag Ahmed body using distributed jet arrays. Journal of Fluid Mechanics. (in press) [86] Zhang W W, Noack B R. 2021. Artificial intelligence in fluid mechanics. Acta Mechanica Sinica, 37: 1715-1717. doi: 10.1007/s10409-021-01154-3 [87] Zheng C, Ji T, Xie F, Zhang X, Zheng H, Zheng Y. 2021. From active learning to deep reinforcement learning: Intelligent active flow control in suppressing vortex-induced vibration. Physics of Fluids, 33: 063607. doi: 10.1063/5.0052524 [88] Zhou Y, Fan D, Zhang B, Li R, Noack B R. 2020. Artificial intelligence control of a turbulent jet. Journal of Fluid Mechanics, 897: A27. doi: 10.1017/jfm.2020.392 [89] Zhu L, Zhang W, Kou J, Liu Y. 2019. Machine learning methods for turbulence modeling in subsonic flows around airfoils. Physics of Fluids, 31: 015105. doi: 10.1063/1.5061693 [90] Zigunov F, Sellappan P, Alvi F. 2021. Beyond actuator line arrays in active flow control studies: Lessons from a genetic algorithm approach. Physical Review Fluids, 6: 083903. doi: 10.1103/PhysRevFluids.6.083903 -





 下载:
下载: