-
摘要: 随着21世纪折纸工程学的发展, 折纸不再仅仅是一项民间艺术, 一方面数学家前期的大量工作随之浮出水面, 另一方面工程应用对折纸结构折叠过程的描述与分析都提出了新的挑战. 同时, 折纸的对象也不再局限于简单的纸张, 工程中存在大量的厚度不可忽略的平板结构, 他们的折叠展开问题一直困扰着相关的工程应用. 近几年超材料的发展给模块化折纸带来了一次从玩具到高科技的飞跃, 然而如何协调地安排这些折纸模块使得整体结构展现出超常且可变化调控的性能是折纸领域的新热点. 由此可见, 折纸运动学在诸多应用与探索方面都起到了决定性的基础作用. 本文重点介绍了已有的机构学理论与方法及其在各种折纸结构分析设计中的应用, 旨在为折纸工程学的发展提供坚实的理论技术基础.Abstract: Origami is no longer a folk art with the development of origami engineering in this century, in which a lot of previous work of mathematicians has surfaced and the engineering applications present new challenges to describe the folding process of rigid origami. Meanwhile, origami is not limited to the thin sheet, the folding and unfolding of thick panels have always hindered their related engineering applications. Recently, the development of metamaterials has brought a leap from toys to high technology for modular origami. How to coordinately set up the origami modules to enable the entire structure with excellent and tunable performance is a new hotspot in modular origami. Hence, origami kinematics has played a decisive role in many applications and explorations. This review focuses on the developed mechanism theories and their applications in the analysis and design of origami structures, which hopefully could be able to provide the theoretical foundation for origami engineering.
-
Key words:
- origami /
- origami kinematics /
- rigid origami /
- thick-panel origami /
- modular origami
-
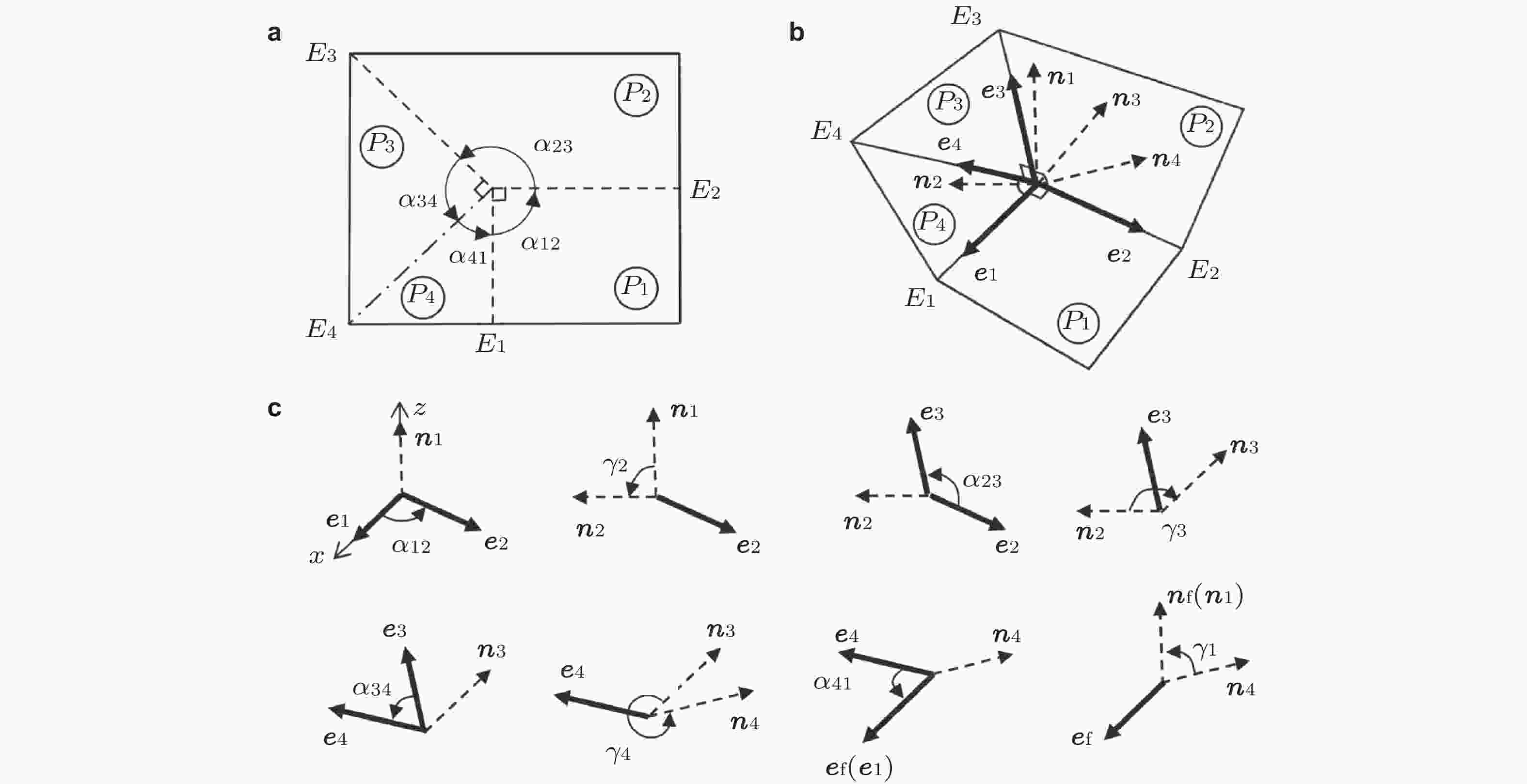
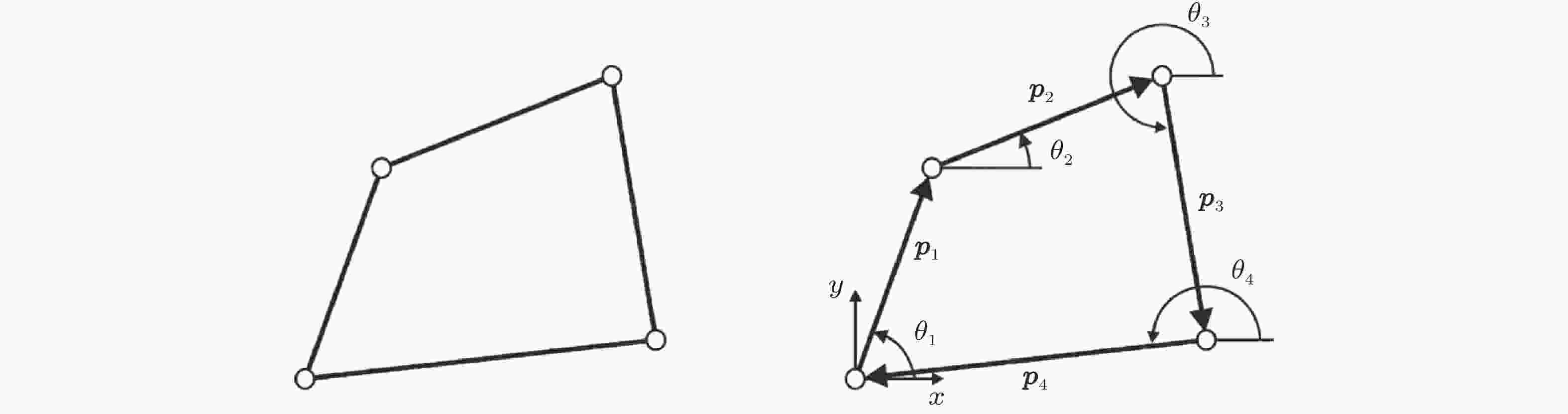
图 1 平面机构及其矢量法表达(You & Chen 2011)
图 2 (a)四折痕顶点折纸图案的平面构型, (b)三维构型中的特征向量, (c)旋转序列(Wu & You 2010)
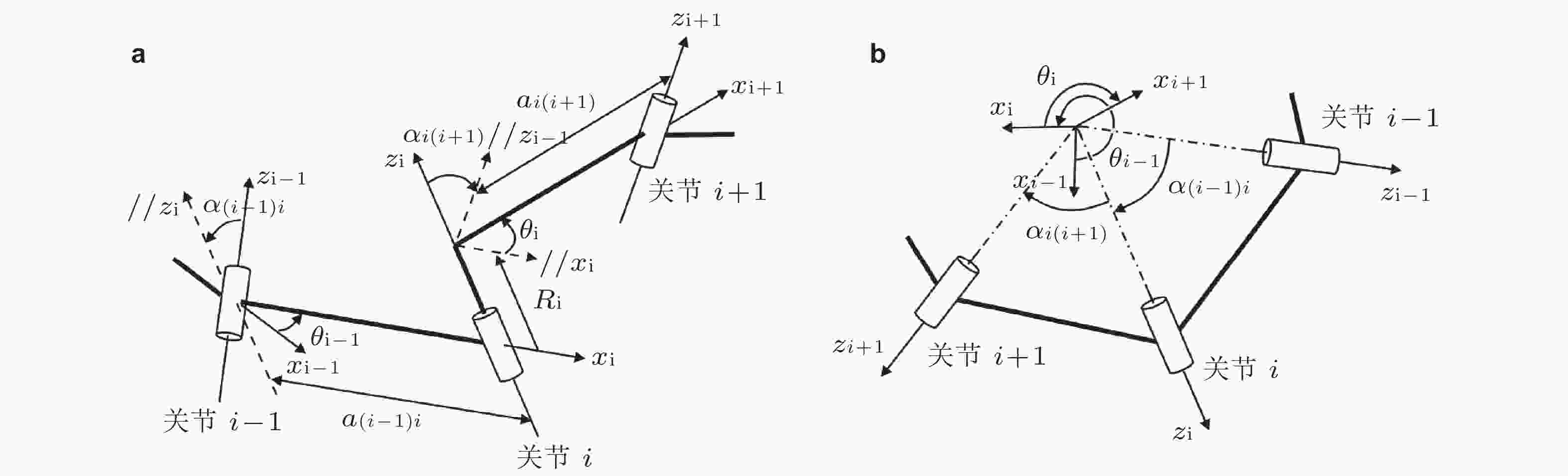
图 3 D-H标注法. (a)空间机构与, (b)球面机构(Denavit & Hartenberg 1955)
图 4 旋量轴线及其位置向量(Hunt 1978)
图 5 连杆桁架理论. (a) 常见情况, (b) 两个相交的转动轴,(c)两个具有瞬时可动性的平行转动轴,(d)两个平行的转动轴(Yang et al. 2016a)
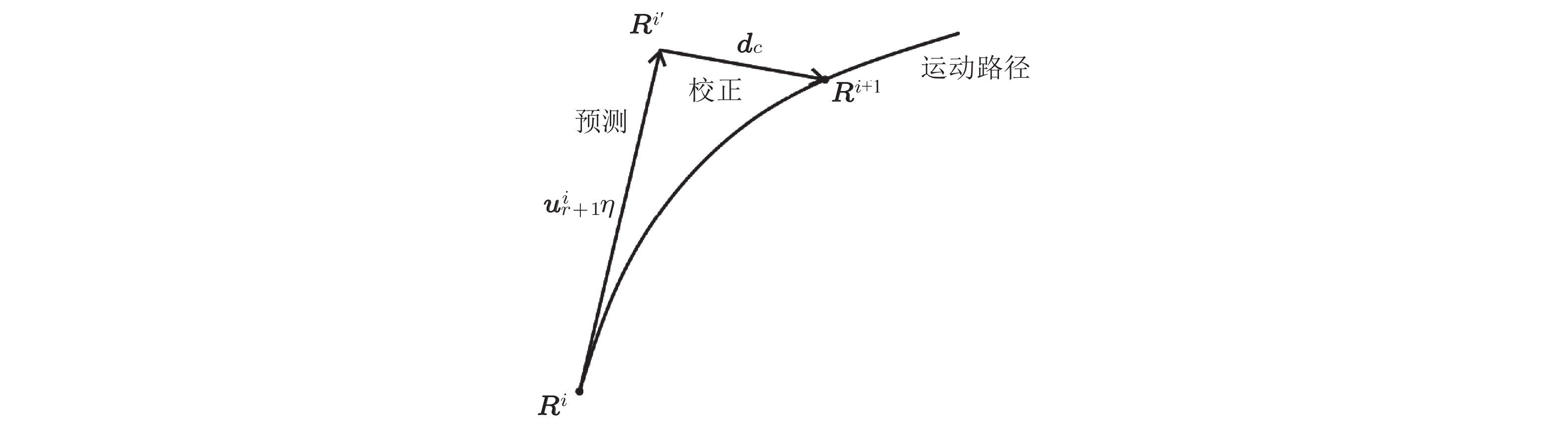
图 6 迭代步骤中的预测-校正算法(Kumar & Pellegrino 2000)
图 7 (a)折纸顶点, (b)四边形网格折纸(Tachi 2009)
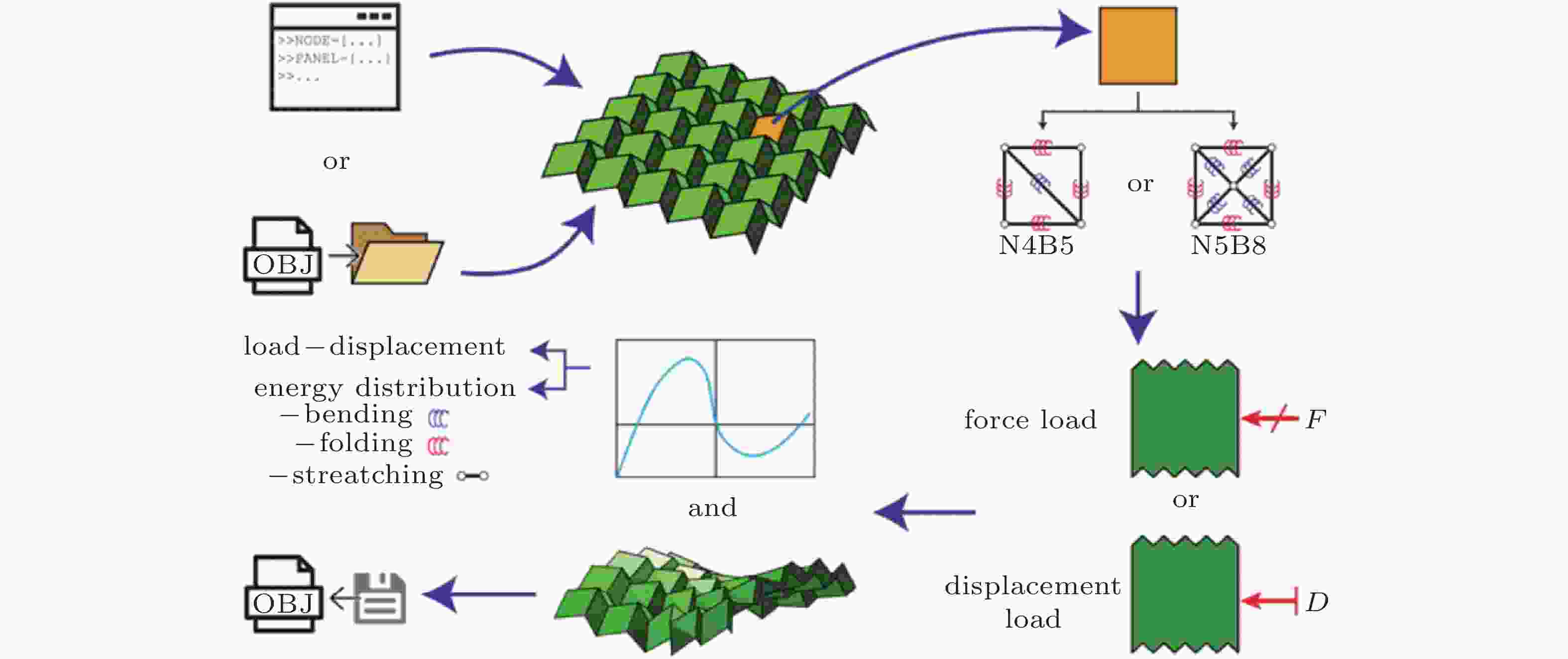
图 8 “MERLIN 2”典型的工作流程(Liu & Paulino 2018)
图 9 四折痕顶点及其等效的球面四杆机构(Chen et al. 2019b)
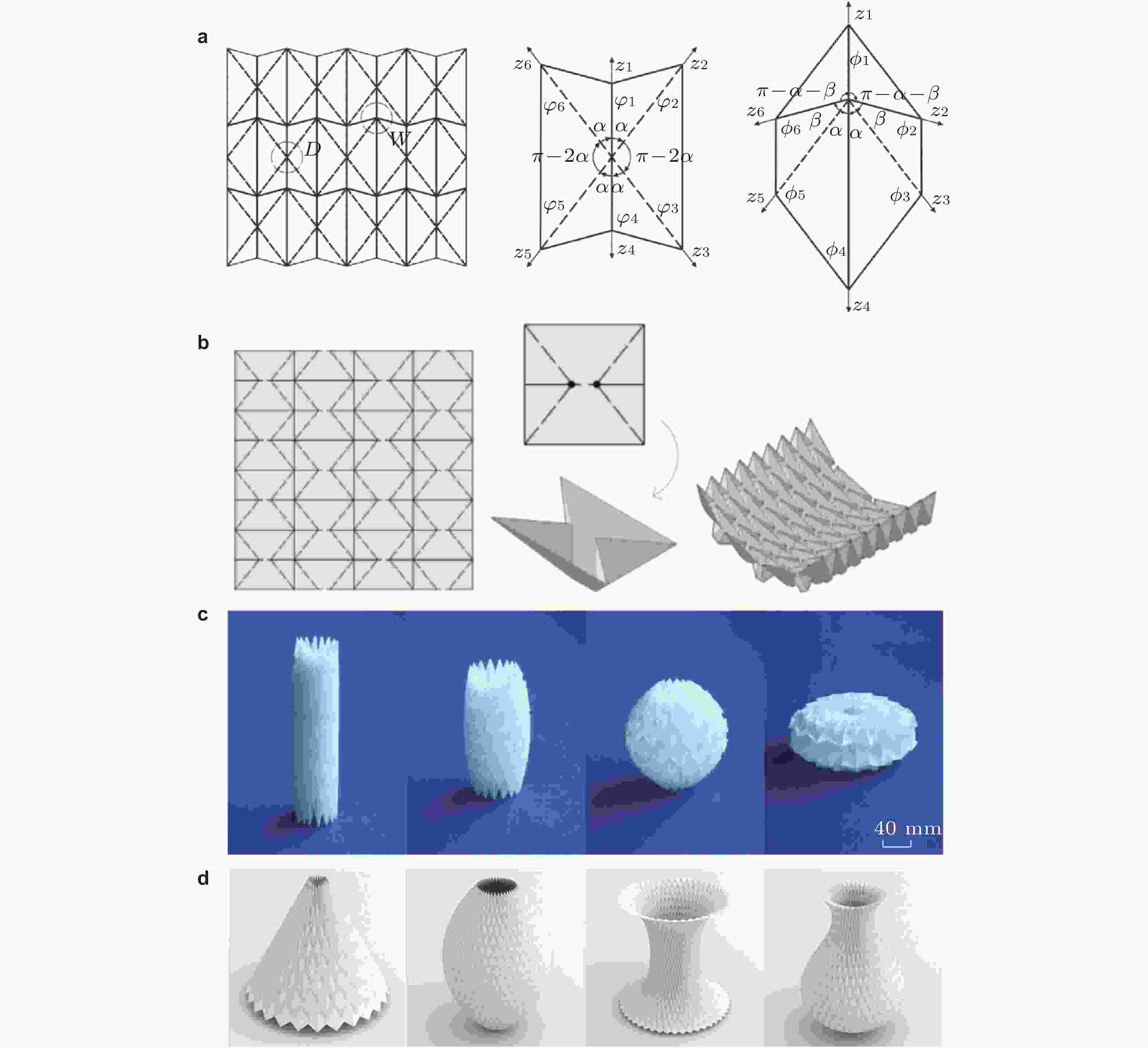
图 10 三浦折纸(Miura 1985)
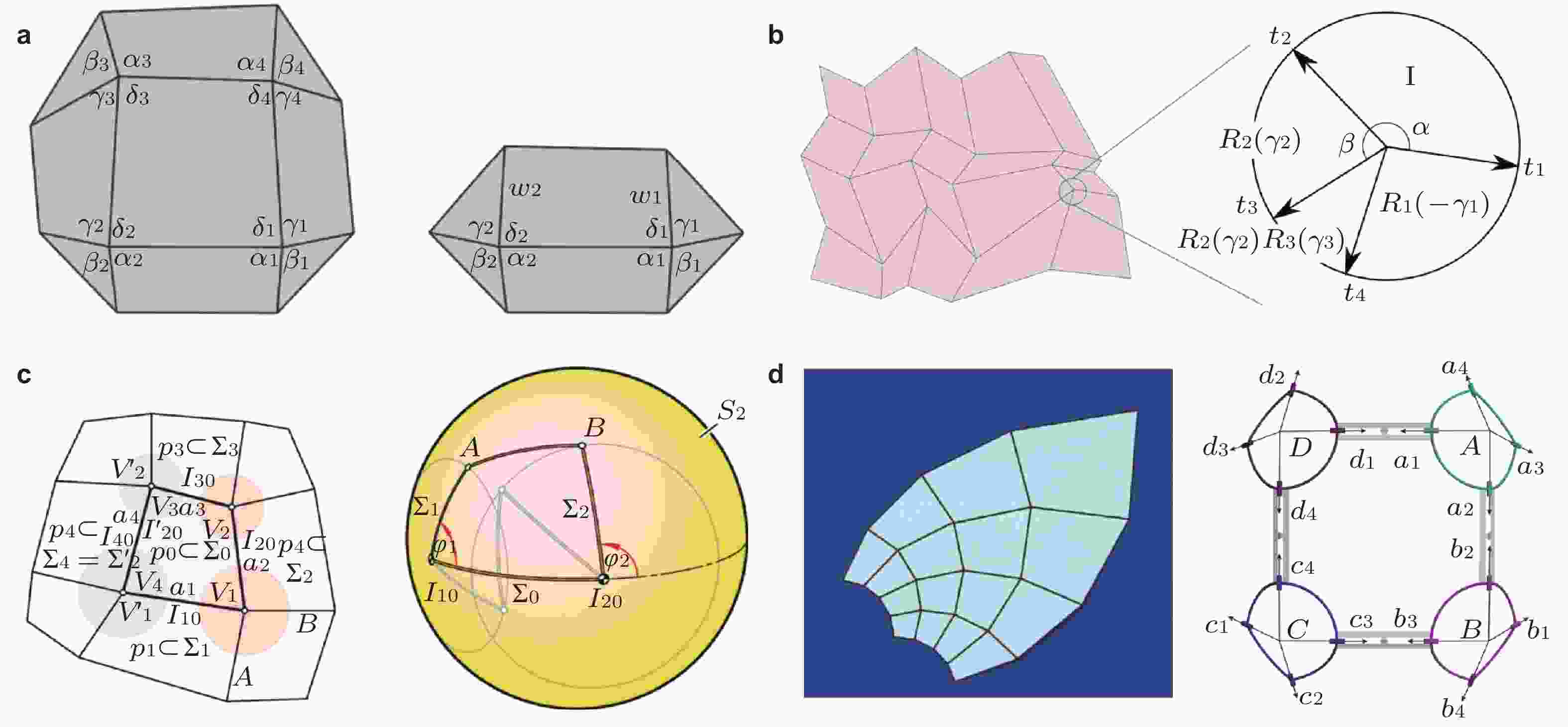
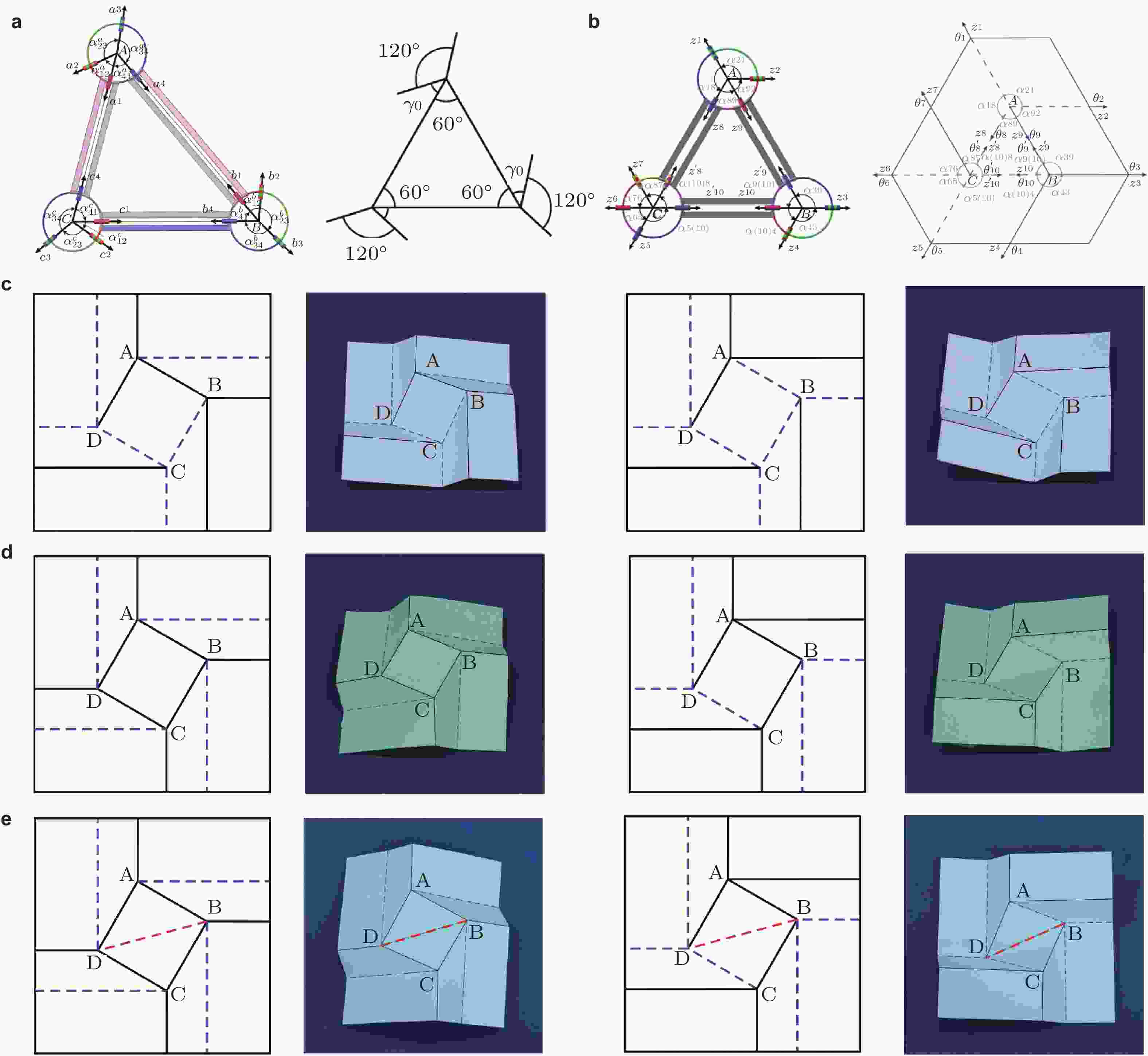
图 11 四边形网格刚性折纸的设计与分析方法. (a) Kokotsakis折纸整合法(He & Guest 2020), (b) 变形梯度法(Feng et al. 2020a), (c) 离散微分几何法(Stachel 2010), (d) 球面机构网格的运动协调法(Chen et al. 2019b)
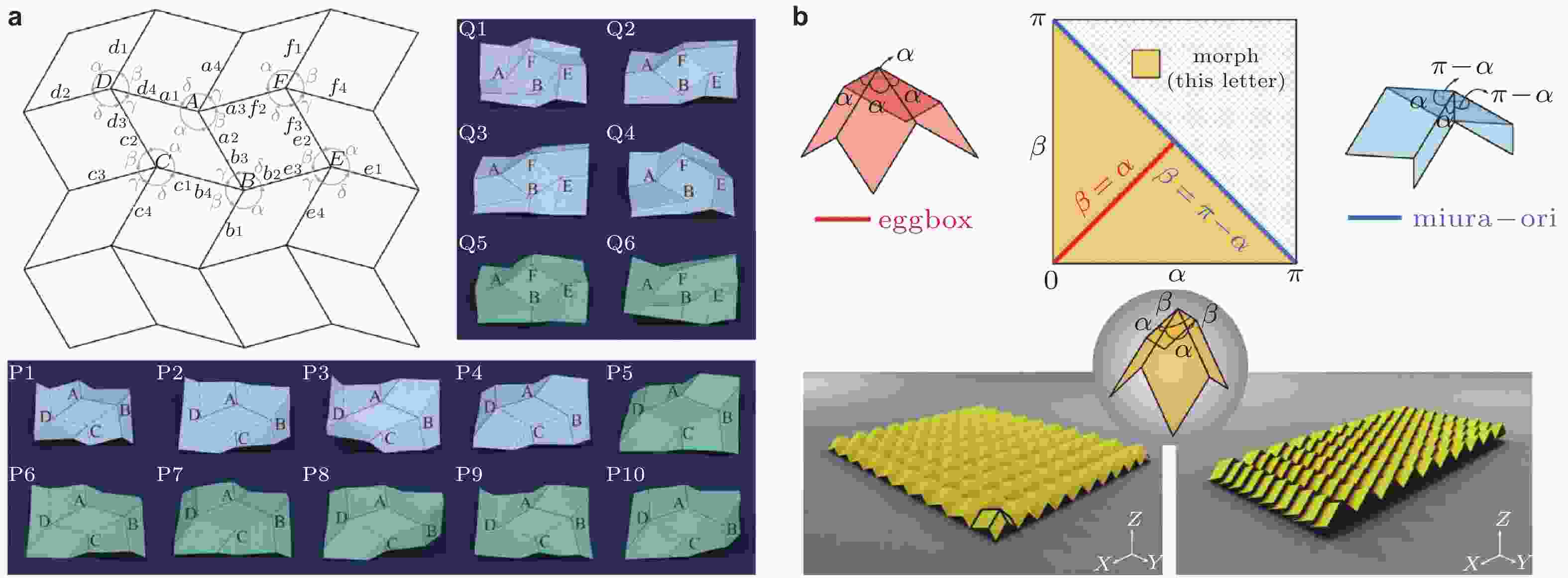
图 12 山谷折痕(M-V)分配. (a)双波纹折纸单元折痕分布(Peng et al. 2018), (b) Eggbox和Miura-ori模式的切换(Pratapa et al. 2019)
图 13 扭转图案. (a)广义三角形扭转图案(Feng et al. 2018b), (b)Plane linkage折纸单元(Chen et al. 2019a). 方形扭转图案. (c)刚性图案, (d)非刚性图案, (e)修正的刚性图案(Feng et al. 2020c, Ma et al. 2021)
图 14 缠绕折纸图案. (a) 机构运动阶段的方形缠绕折纸(Xu et al. 2018), (b)引入切割线的单自由度缠绕折纸(Lang et al. 2016)
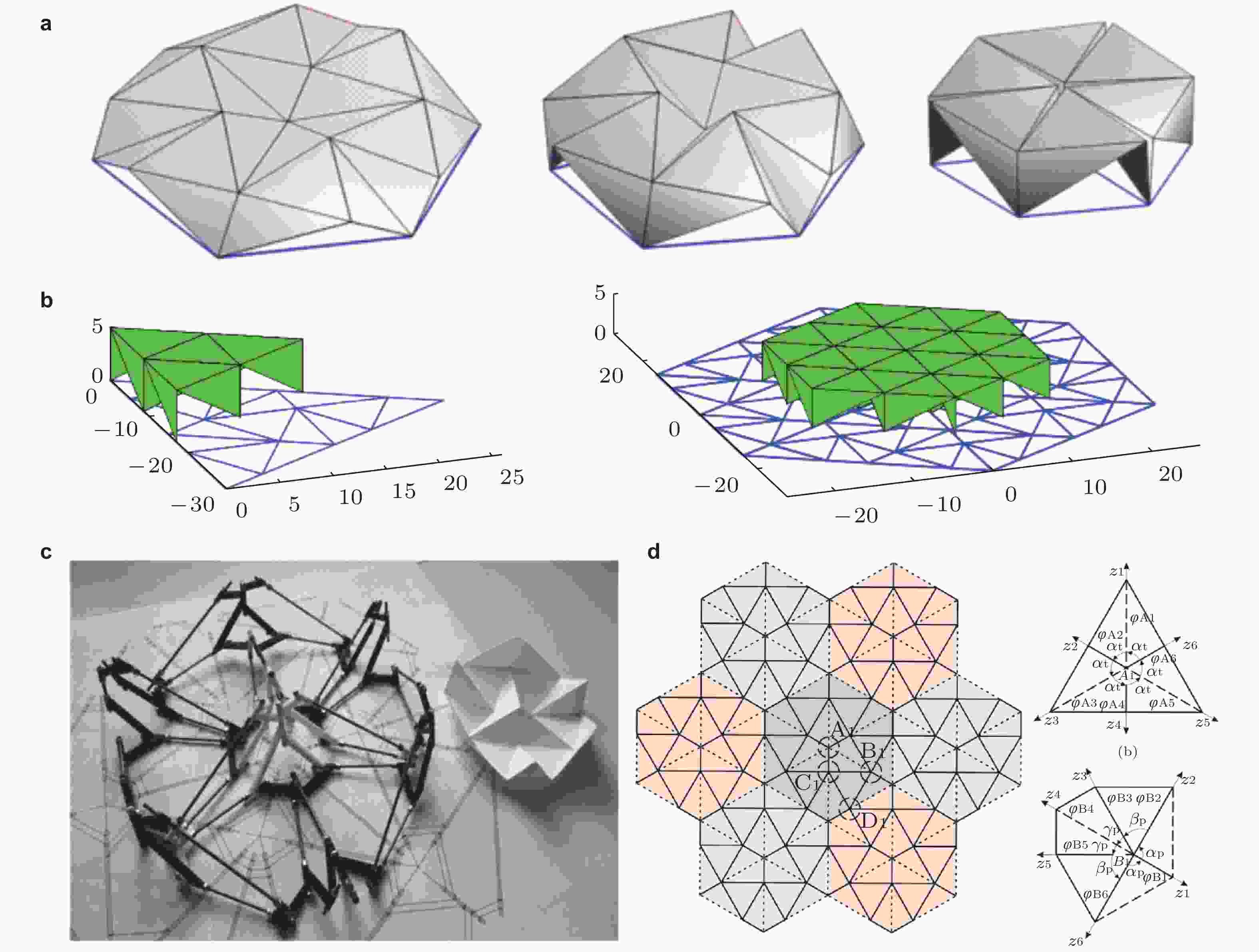
图 15 Resch折纸图案. (a) 施加节点轨迹后的运动路径(Magliozzi et al. 2017), (b) 在目标函数下运动方向(Li 2020), (c) 等效杆件模型(Mazzucchi 2018), (d) 两种典型顶点的运动学解析(Yang et al. 2022a)
图 16 Waterbomb折纸图案. (a)对称折叠模式(Chen et al. 2016), (b)曲面构型(Deng et al. 2022),(c)刚性运动阶段的管状结构(Ma et al. 2020), (d)复杂轴对称构型(Zhao et al. 2021)
图 17 Yoshimura折纸图案. (a)原始图案, (b)节点拆分后的四、六折痕混合图案(Zhang & Chen 2019), (c)其管状结构对称与非对称的拼接方式(Lang 2017)
图 18 Kresling折纸图案. (a)倾斜对称形式(Zhai et al. 2018); (b)水平对称形式(Georgakopoulos et al. 2021)
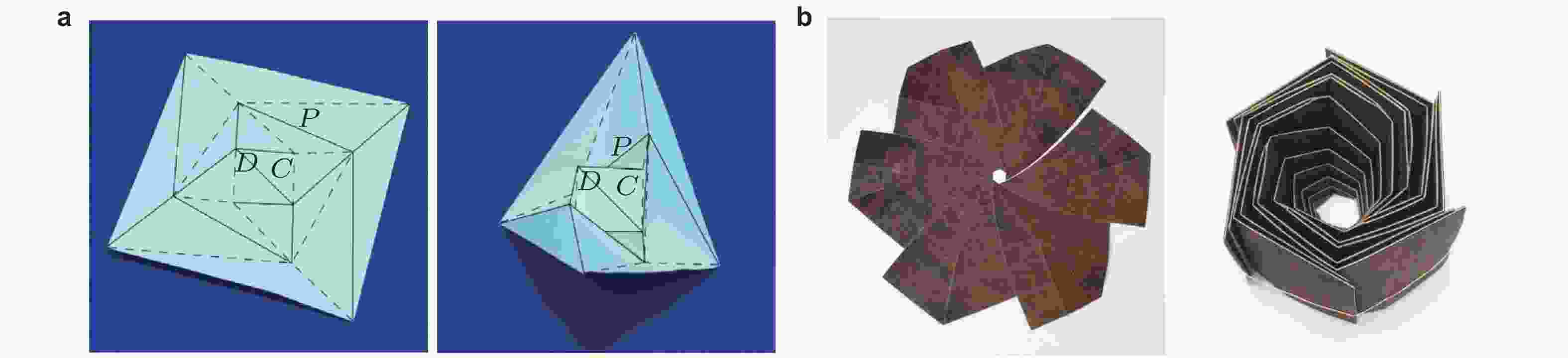
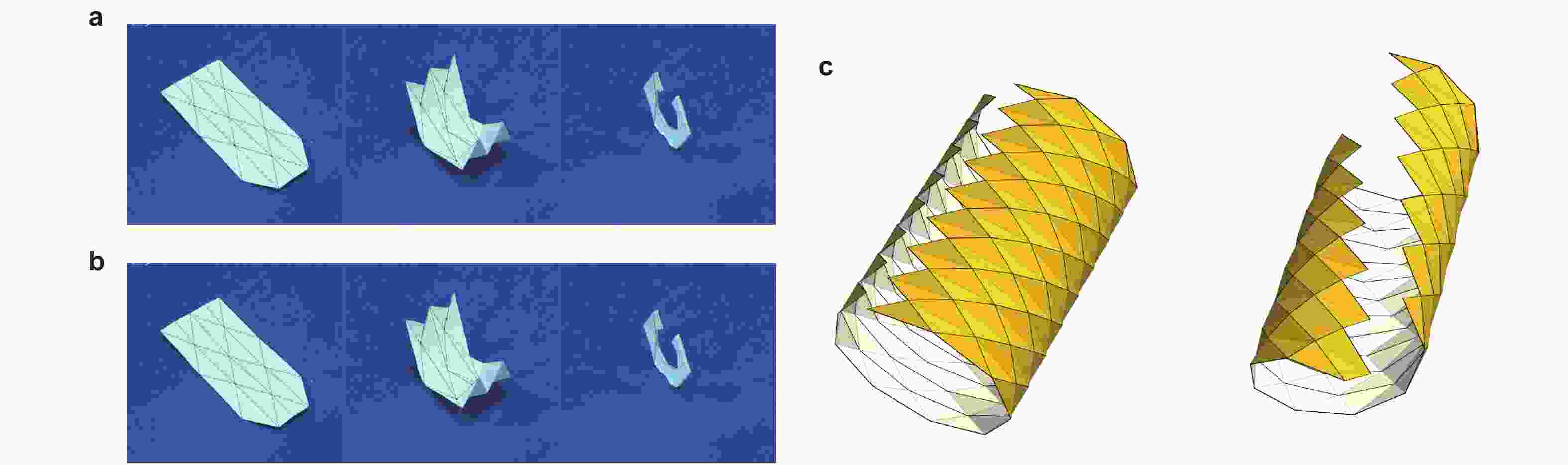
图 19 可刚性平折的管状结构及其组合结构. (a)平行四边形截面的管状结构(Tachi 2010d), (b) 筝形截面的管状结构(Liu et al. 2016), (c)不规则截面的管状结构(Chen et al. 2017), (d)刚性折纸管耦合组装以增加结构刚度(Filipov et al. 2015), (e)模块化管状折纸结构(Mousanezhad et al. 2017)
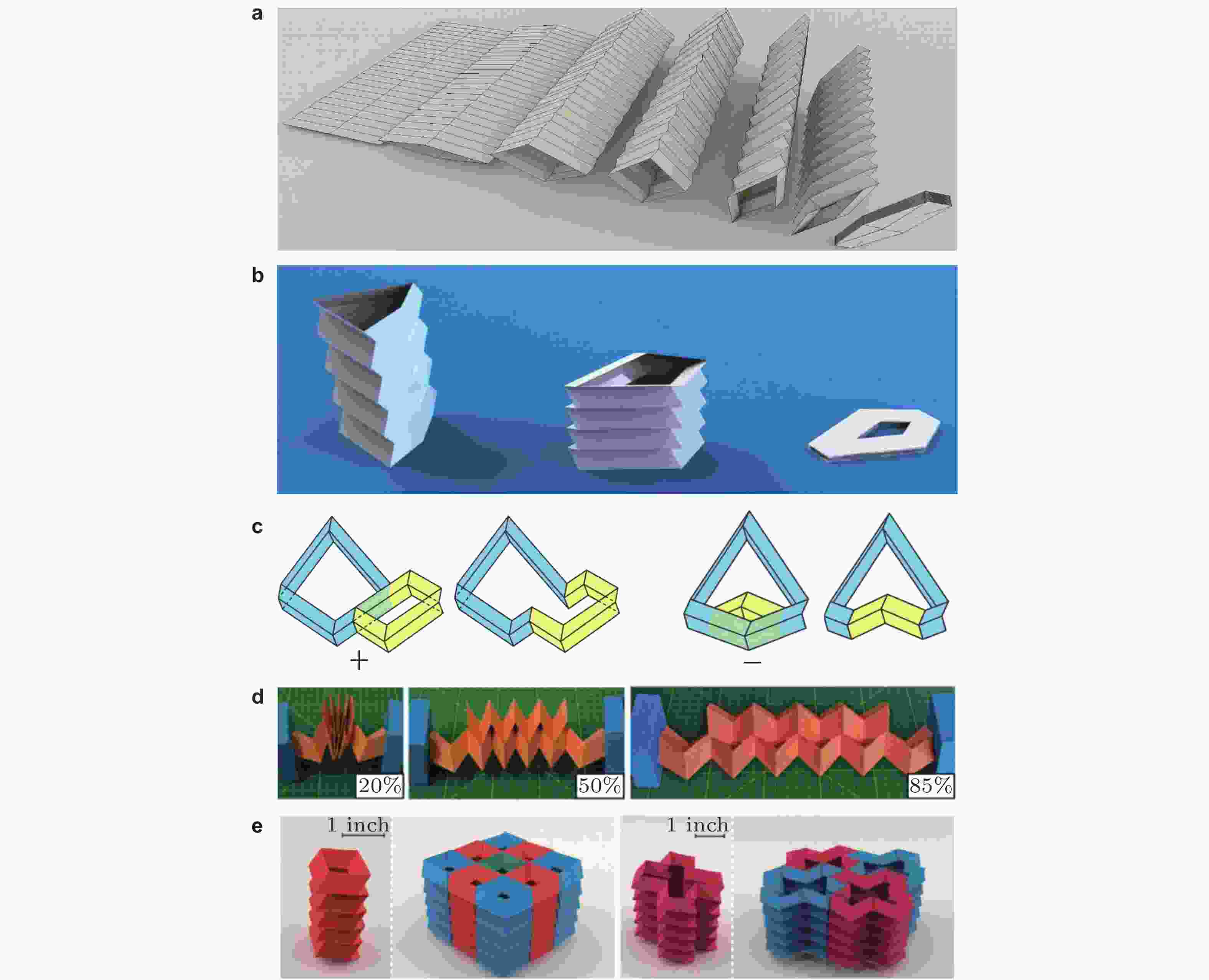
图 20 立体折纸结构. (a) 刚性平折的高购物袋(Wu & You 2011), (b)折纸盒子机构(Wei 2014), (c) 单自由度刚性可平折立方体(Gu & Chen 2020), (d)可折展长方体剪纸结构(Zhang et al. 2022)
图 21 基于球面机构的板厚容纳方法. (a)楔形面板技术(Tachi 2011), (b)偏置面板技术(Edmondson et al. 2014), (c)节点拆分技术(Tolman et al. 2017)
图 22 基于空间机构的板厚容纳方法. (a)偏置铰链技术(Chen et al. 2015), (b)辅助面板技术(Gu et al. 2021), (c)双铰链技术(Ku & Demaine 2016), (d)剪纸技术(Yang et al. 2022b)
图 23 基于铰链变化的板厚容纳方法. (a)滚动接触技术(Lang et al. 2017), (b)柔性铰链技术(Pehrson et al. 2016); (c)薄膜技术(Zirbel et al. 2013)
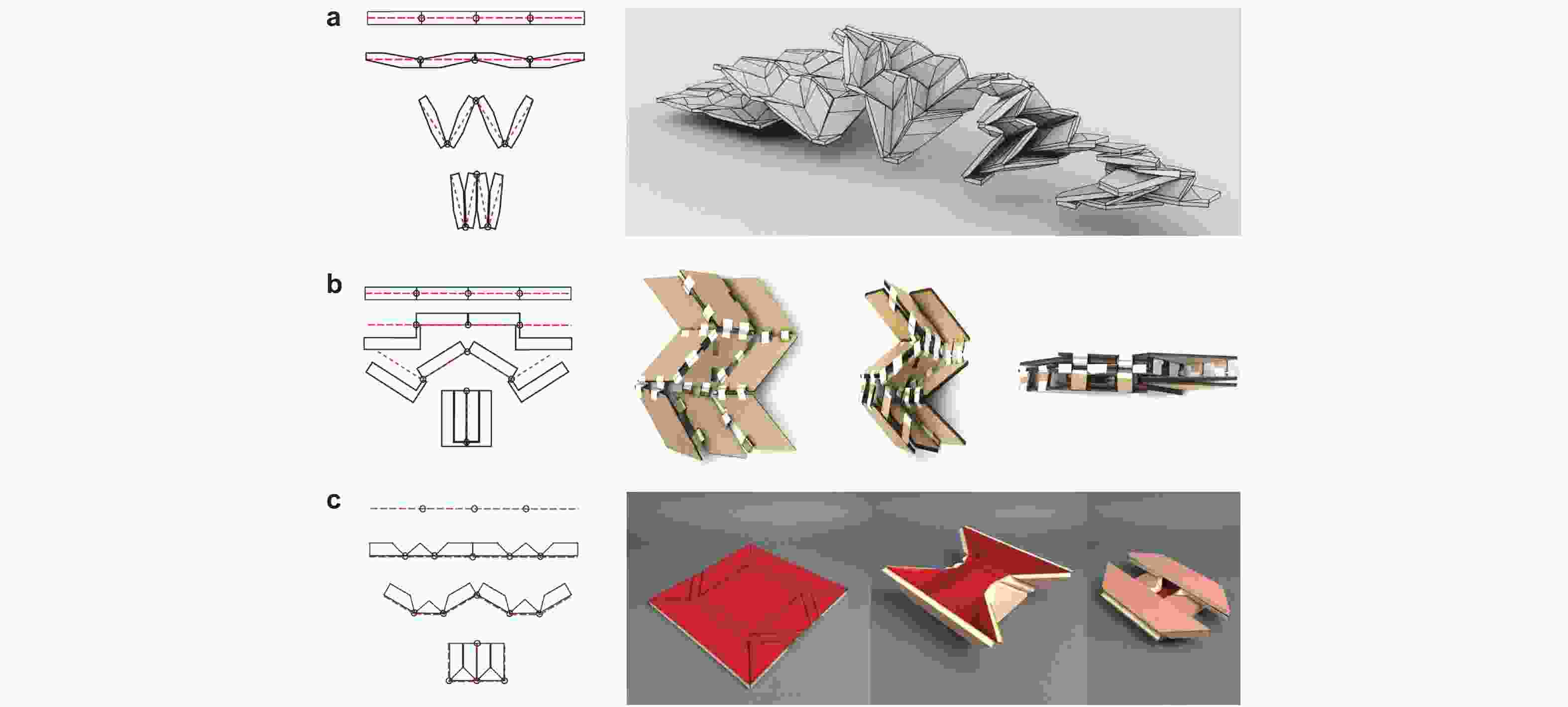
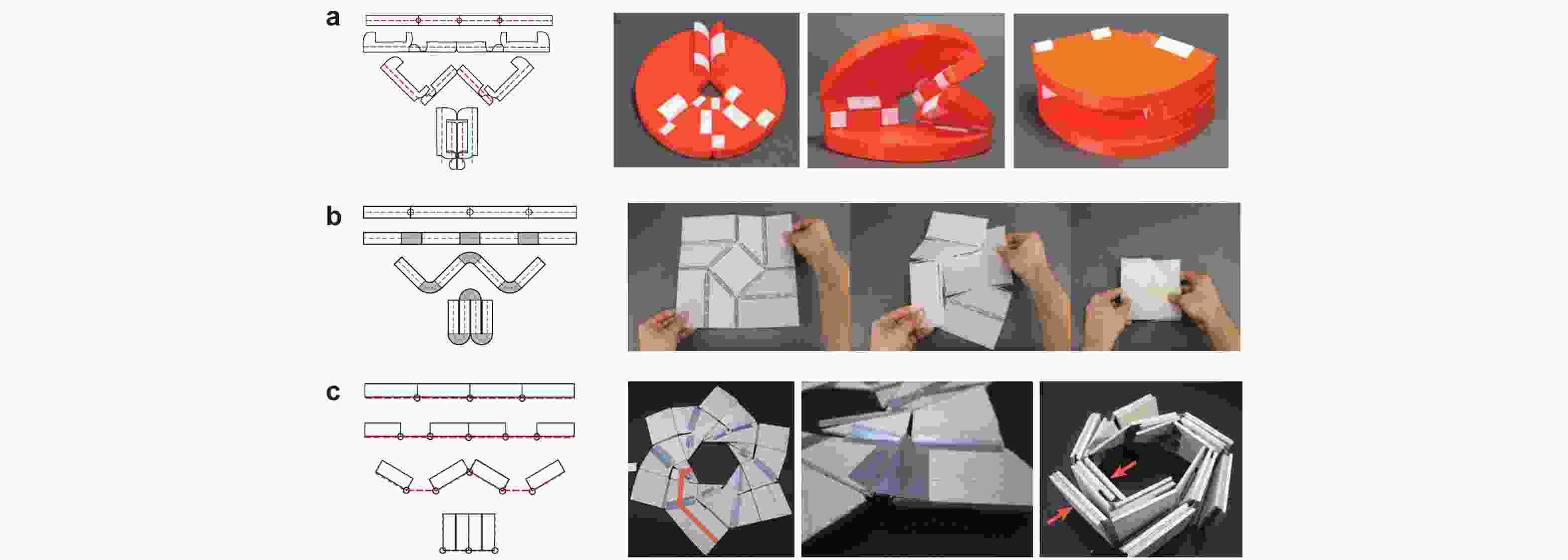
图 24 2D 模块化折纸. (a)正方形镶嵌图案(Resch 1965), (b)非规则菱形平铺(Warisaya et al. 2021), (c)广义剪纸图案(Choi et al. 2019), (d)具有多步自引导折叠路径的可变形材料(Coulais et al. 2018)
图 25 3D 模块化折纸. (a) 三维运动学超材料(Yang et al. 2021), (b) 三维模块化超结构(Ma et al. 2022b), (c)三维可编程超材料(Liu et al. 2022), (d)可转换架构(Li & Yin 2021), (e) 可重构棱柱材料(Overvelde et al. 2017)
表 1 折纸运动学理论方法在各类折纸结构中的应用
折纸结构 矢量法 四元数法 矩阵法 旋量法 桁架法 SVD法 程序法 刚性折纸 折纸顶点 




四边形网格折纸 



扭转图案 

缠绕图案 


Resch图案 


Waterbomb图案 


Yoshimura图案 

Kresling图案 

管状折纸结构 

立体折纸结构 



厚板折纸 




模块化折纸 2D模块化折纸 


3D模块化折纸 




-
陈焱. 2020. 基于机构运动的大变形超材料. 机械工程学报, 56: 2-13 (Chen Y. 2020. Review on kinematic metamaterials. Journal of Mechanical Engineering, 56(19): 2-13 (in Chinese)). 杨富富. 2017. 基于桁架方法的空间过约束机构分析与可变多面体设计.[博士论文]. 天津: 天津大学 (Yang F F. 2017. Truss method for kinematic analysis of 3D overconstrained linkages and design of transformable polyhedrons. [PhD Thesis]. Tianjin: Tianjin University). 张霄. 2018. 空间机构网格与刚性折纸的关联研究.[博士论文]. 天津: 天津大学 (Zhang X. 2018. Study on the relationship between mobile assemblies of spatial linkages and rigid origami. [PhD Thesis]. Tianjin: Tianjin University). Altmann S. 1986. Rotations, Quaternions, and Double Groups. Oxford University Press. Ball R S. 1876. The Theory of Screws: A Study in the Dynamics of a Rigid Body. Dublin, Hodges, Forster and Co. Beech R. 2009. The Practical Illustrated Encyclopedia of Origami: the Complete Guide to the Art of Paperfolding. Anness. Beggs J S. 1966. Advanced Mechanism. Macmillan. Belcastro S, Hull T C. 2002. Modelling the folding of paper into three dimensions using affine transformations. Linear Algebra its Applications, 348: 273-282. doi: 10.1016/S0024-3795(01)00608-5 Bennett G T. 1903. A new mechanism. Engineering, 76: 777. Bricard R. 1927. Leçons de cinématique Tome II Cinématique Appliquée. Paris: Gauthier-Villars. Cai J. 2016. Kinematic analysis of foldable plate structures with rolling joints. Journal of Mechanisms and Robotics, 8: 034502. doi: 10.1115/1.4032269 Cai J, Deng X, Xu Y, Feng J. 2016. Motion analysis of a foldable barrel vault based on regular and irregular Yoshimura origami. Journal of Mechanisms and Robotics, 8: 021017. doi: 10.1115/1.4031658 Cai J, Deng X, Zhou Y, Feng J, Tu Y. 2015. Bistable behavior of the cylindrical origami structure with Kresling pattern. Journal of Mechanical Design, 137: 061406. doi: 10.1115/1.4030158 Cai J, Liu Y, Ma R, Feng J, Zhou Y. 2017. Nonrigidly foldability analysis of Kresling cylindrical origami. Journal of Mechanisms and Robotics, 9: 041018. doi: 10.1115/1.4036738 Cai J, Zhang Q, Feng J, Xu Y. 2019. Modeling and kinematic path selection of retractable kirigami roof structures. Computer-Aided Civil Infrastructure Engineering, 34: 352-363. doi: 10.1111/mice.12418 Chen X, Feng H, Ma J, Chen Y. 2019a. A plane linkage and its tessellation for deployable structure. Mechanism and Machine Theory, 142: 103605. doi: 10.1016/j.mechmachtheory.2019.103605 Chen Y, Chai W H. 2011. Bifurcation of a special line and plane symmetric Bricard linkage. Mechanism and Machine Theory, 46: 515-533. doi: 10.1016/j.mechmachtheory.2010.11.015 Chen Y, Fan L, Bai Y, Feng J, Sareh P. 2020. Assigning mountain-valley fold lines of flat-foldable origami patterns based on graph theory and mixed-integer linear programming. Computers and Structures, 239: 106328. doi: 10.1016/j.compstruc.2020.106328 Chen Y, Feng H, Ma J, Peng R, You Z. 2016. Symmetric waterbomb origami. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 472: 20150846. doi: 10.1098/rspa.2015.0846 Chen Y, Lv W, Li J, You Z. 2017. An extended family of rigidly foldable origami tubes. Journal of Mechanisms and Robotics, 9: 021002. doi: 10.1115/1.4035559 Chen Y, Lv W, Peng R, Wei G. 2019b. Mobile assemblies of four-spherical-4R-integrated linkages and the associated four-crease-integrated rigid origami patterns. Mechanism and Machine Theory, 142: 103613. doi: 10.1016/j.mechmachtheory.2019.103613 Chen Y, Peng R, You Z. 2015. Origami of thick panels. Science, 349: 396-400. doi: 10.1126/science.aab2870 Chen Y, You Z. 2009. Two-fold symmetrical 6R foldable frame and its bifurcations. International Journal of Solids Structures, 46: 4504-4514. doi: 10.1016/j.ijsolstr.2009.09.012 Chen Z, Wu T, Nian G, Shan Y, Liang X, Jiang H, Qu S. 2019c. Ron Resch origami pattern inspired energy absorption structures. Journal of Applied Mechanics, 86: 011005. doi: 10.1115/1.4041415 Chiang C-H. 1988. Kinematics of Spherical Mechanisms. Cambridge University Press. Choi G P, Dudte L H, Mahadevan L. 2019. Programming shape using kirigami tessellations. Nature materials, 18: 999-1004. doi: 10.1038/s41563-019-0452-y Choi G P, Dudte L H, Mahadevan L. 2021. Compact reconfigurable kirigami. Physical Review Research, 3: 043030. doi: 10.1103/PhysRevResearch.3.043030 Chu C C, Keong C K. 2017. The review on tessellation origami inspired folded structure//AIP Conference Proceedings, 020025. AIP Publishing LLC. Connelly R, Sabitov I, Walz A. 1997. The bellows conjecture. Beitr. Algebra Geom, 38: 1-10. Coulais C, Sabbadini A, Vink F, van Hecke M. 2018. Multi-step self-guided pathways for shape-changing metamaterials. Nature Materials, 561: 512-515. Dai J S. 2012. Finite displacement screw operators with embedded Chasles’ motion. Journal of Mechanisms and Robotics, 4: 041002. doi: 10.1115/1.4006951 Dai J S, Rees Jones J. 1999. Mobility in metamorphic mechanisms of foldable/erectable kinds. Journal of Mechanical Design, 121: 375-382. doi: 10.1115/1.2829470 Davies T. 1981. Kirchhoff's circulation law applied to multi-loop kinematic chains. Mechanism and Machine Theory, 16: 171-183. doi: 10.1016/0094-114X(81)90033-1 De Temmerman I a N, Mollaert M, Van Mele I a T, De Laet I a L. 2007. Design and analysis of a foldable mobile shelter system. International Journal of Space Structures, 22: 161-168. doi: 10.1260/026635107782218868 Demaine E D, O'Rourke J. 2007. Geometric Folding Algorithms: Linkages, Origami, Polyhedra. Cambridge University Press. Denavit J, Hartenberg R S. 1955. A kinematic notation for lower-pair mechanisms based on matrices. ASME Journal of Applied Mechanics, 22: 215-221. doi: 10.1115/1.4011045 Deng A, Ji B, Zhou X, You Z. 2020. Geometric design and mechanical properties of foldcores based on the generalized Resch patterns. Thin-Walled Structures, 148: 106516. doi: 10.1016/j.tws.2019.106516 Deng X, Zhao J, Cai J, Liu X. 2022. Tunable origami metamaterial with arbitrary single-curvature configuration. Mechanism and Machine Theory, 171: 104745. doi: 10.1016/j.mechmachtheory.2022.104745 Edmondson B J, Lang R J, Magleby S P, Howell L L. 2014. An offset panel technique for thick rigidily foldable origami//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V05BT08A054. American Society of Mechanical Engineers. Edmondson B J, Lang R J, Morgan M R, Magleby S P, Howell L L. 2015. Thick rigidly foldable structures realized by an offset panel. Origami, 6: 149-161. Evans T A, Lang R J, Magleby S P, Howell L L. 2015a. Rigidly foldable origami gadgets and tessellations. Royal Society Open Science, 2: 150067. doi: 10.1098/rsos.150067 Evans T A, Lang R J, Magleby S P, Howell L L. 2015b. Rigidly foldable origami twists. Origami, 6: 119-130. Fang H, Zhang Y, Wang K. 2017. Origami-based earthworm-like locomotion robots. Bioinspiration and Biomimetics, 12: 065003. doi: 10.1088/1748-3190/aa8448 Farnham J, Hull T C, Rumbolt A. 2022. Rigid folding equations of degree-6 origami vertices. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Science, 478: 20220051. doi: 10.1098/rspa.2022.0051 Fei L J, Sujan D. 2013. Origami theory and its applications: a literature review. International Journal of Humanities and Social Sciences, 7: 229-233. Felton S, Tolley M, Demaine E, Rus D, Wood R. 2014. A method for building self-folding machines. Science, 345: 644-646. doi: 10.1126/science.1252610 Feng F, Dang X, James R D, Plucinsky P. 2020a. The designs and deformations of rigidly and flat-foldable quadrilateral mesh origami. Journal of the Mechanics Physics of Solids, 142: 104018. doi: 10.1016/j.jmps.2020.104018 Feng H, Ma J, Chen Y. 2020b. Rigid folding of generalized waterbomb origami tubes. Chinese Journal of Mechanical engineering, 56: 143-159. Feng H, Ma J, Chen Y, You Z. 2018a. Twist of tubular mechanical metamaterials based on waterbomb origami. Scientific reports, 8: 1-13. Feng H, Peng R, Ma J, Chen Y. 2018b. Rigid foldability of generalized triangle twist origami pattern and its derived 6R linkages. Journal of Mechanisms and Robotics, 10: 051003. doi: 10.1115/1.4040439 Feng H, Peng R, Zang S, Ma J, Chen Y. 2020c. Rigid foldability and mountain-valley crease assignments of square-twist origami pattern. Mechanism and Machine Theory, 152: 103947. doi: 10.1016/j.mechmachtheory.2020.103947 Filipov E, Liu K, Tachi T, Schenk M, Paulino G H. 2017. Bar and hinge models for scalable analysis of origami. International Journal of Solids Structures, 124: 26-45. doi: 10.1016/j.ijsolstr.2017.05.028 Filipov E T, Tachi T, Paulino G H. 2015. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proceedings of the National Academy of Sciences, 112: 12321-12326. doi: 10.1073/pnas.1509465112 Fonseca L M, Savi M A. 2021. On the symmetries of the origami waterbomb pattern: kinematics and mechanical investigations. Meccanica, 56: 2575-2598. doi: 10.1007/s11012-021-01388-2 Gan W, Pellegrino S. 2003. Closed-loop deployable structures//44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 1450. Gan W W, Pellegrino S. 2006. Numerical approach to the kinematic analysis of deployable structures forming a closed loop. Journal of Mechanical Engineering Science, 220: 1045-1056. doi: 10.1243/09544062JMES245 Georgakopoulos S V, Zekios C L, Sattar-Kaddour A, Hamza M, Biswas A, et al. 2021. Origami antennas. IEEE Open Journal of Antennas Propagation, 2: 1020-1043. doi: 10.1109/OJAP.2021.3121102 Ghassaei A, Demaine E D, Gershenfeld N. 2018. Fast, interactive origami simulation using GPU computation, Origami, 7: 1151-1166. Gillman A, Fuchi K, Buskohl P. 2018. Truss-based nonlinear mechanical analysis for origami structures exhibiting bifurcation and limit point instabilities. International Journal of Solids and Structures, 147: 80-93. doi: 10.1016/j.ijsolstr.2018.05.011 Gogu G. 2005. Mobility of mechanisms: a critical review. Mechanism and Machine Theory, 40: 1068-1097. doi: 10.1016/j.mechmachtheory.2004.12.014 Goldman F. 2011. Using the snapology technique to teach convex polyhedra//Fifth International Meeting of Origami Science, Mathematics, and Education, 99-110. Grünbaum B, Shephard G C. 1987. Tilings and Patterns. Courier Dover Publications. Gu Y, Chen Y. 2020. Origami cubes with one-DOF rigid and flat foldability. International Journal of Solids and Structures, 207: 250-261. doi: 10.1016/j.ijsolstr.2020.09.008 Gu Y, Chen Y. 2021. One-DOF origami boxes with rigid and flat foldability//IFToMM Asian Conference on Mechanism and Machine Science, 80-88. Springer. Gu Y, Wei G, Chen Y. 2021. Thick-panel origami cube. Mechanism and Machine Theory, 164: 104411. doi: 10.1016/j.mechmachtheory.2021.104411 Guest S, Pellegrino S. 1992. Inextensional wrapping of flat membranes//Proceedings of the First International Seminar on Structural Morphology, Citeseer. Guest S, Pellegrino S. 1996a. A new concept for solid surface deployable antennas. Acta Astronautica, 38: 103-113. doi: 10.1016/0094-5765(96)00009-4 Guest S D, Pellegrino S. 1994a. The folding of triangulated cylinders, part I: geometric considerations, Journal of Applied Mechanics, 61: 773-777. Guest S D, Pellegrino S. 1994b. The folding of triangulated cylinders, part II: the folding process, Journal of Applied Mechanics, 61: 778-783. Guest S D, Pellegrino S. 1996b. The folding of triangulated cylinders, part III: experiments, Journal of Applied Mechanics, 63: 77-83. Hagiwara I. 2008. From origami to “Origamics”. The Japan Journal, 5: 22-25. Hamilton W R. 1866. Elements of Quaternions. London: Longmans, Green, & Company. Hartenberg R S, Danavit J. 1964. Kinematic Synthesis of Linkages. New York: McGraw-Hill. He Z, Guest S D. 2020. On rigid origami II: quadrilateral creased papers. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Science, 476: 20200020. doi: 10.1098/rspa.2020.0020 Howell L L. 2013. Compliant Mechanisms. McCathy J, eds. 21st Century Kinematics. Springer. Howell L L, Olsen B M, Magleby S P. 2013. Handbook of Compliant Mechanisms. John Wiley & Sons Ltd. Huang C, Chen C. 1994. The linear representation of the screw triangle: a unification of finite and infinitesimal kinematics//In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 449-458. Huang Z, Li Q. 2002. General methodology for type synthesis of symmetrical lower-mobility parallel manipulators and several novel manipulators. The International Journal of Robotics Research, 21: 131-145. doi: 10.1177/027836402760475342 Huang Z, Li Q. 2003. Type synthesis of symmetrical lower-mobility parallel mechanisms using the constraint-synthesis method. The International Journal of Robotics Research, 22: 59-79. Hull T. 2012. Project Origami: Activities for Exploring Mathematics. CRC Press. Hull T C. 2014. Counting mountain-valley assignments for flat folds. arXiv: 1410.5022. Hull T C, Tachi T. 2017. Double-line rigid origami//Proceedings of the 11th Asian Forum on Graphic Science, Tokyo. Hunt K H. 1978. Kinematic Geometry of Mechanisms. Oxford University Press, USA. Iniguez-Rabago A, Li Y, Overvelde J T. 2019. Exploring multistability in prismatic metamaterials through local actuation. Nature Communications, 10: 1-10. doi: 10.1038/s41467-018-07882-8 Ionescu T G, Antonescu P, Biro I, Bögelsack G, Breteler A K. 2003. Terminology for the mechanism and machine science. Mechanism and Machine Theory, 38: 767-901. doi: 10.1016/S0094-114X(03)00015-6 Izmestiev I. 2017. Classification of flexible Kokotsakis polyhedra with quadrangular base. International Mathematics Research Notices, 2017: 715-808. Jeong D, Lee K. 2018. Design and analysis of an origami-based three-finger manipulator. Robotica, 36: 261-274. doi: 10.1017/S0263574717000340 Jiao Z, Ji C, Zou J, Yang H, Pan M. 2019a. Vacuum‐powered soft pneumatic twisting actuators to empower new capabilities for soft robots. Advanced Materials Technologies, 4: 1800429. doi: 10.1002/admt.201800429 Jiao Z, Zhang C, Wang W, Pan M, Yang H, Zou J. 2019b. Advanced artificial muscle for flexible material‐based reconfigurable soft robots. Advanced Science, 6: 1901371. doi: 10.1002/advs.201901371 Justin J. 1986. Mathematics of origami, part 9. British Origami, 118: 28-30. Justin J. 1994. Mathematical remarks about origami bases. Symmetry:Culture Science, 5: 153-165. Kawasaki T, Yoshida M. 1988. Crystallographic flat origamis. Memoirs of the Faculty of Science, Kyushu University. Series A, Mathematics, 42: 153-157. doi: 10.2206/kyushumfs.42.153 Kokotsakis A. 1933. Über bewegliche polyeder. Mathematische Annalen, 107: 627-647. doi: 10.1007/BF01448912 Kresling B. 2002. Folded tubes as compared to kikko (‘tortoise-shell55’) bamboo. Origami, 3: 197-207. Kshad M A E, Popinigis C, Naguib H E. 2018. 3D printing of Ron-Resch-like origami cores for compression and impact load damping. Smart Materials Structures, 28: 015027. Ku J S, Demaine E D. 2016. Folding flat crease patterns with thick materials. Journal of Mechanisms and Robotics, 8: 031003. doi: 10.1115/1.4031954 Kuipers J B. 1999. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality. Princeton University Press. Kumar P, Pellegrino S. 2000. Computation of kinematic paths and bifurcation points. International Journal of Solids and Structures, 37: 7003-7027. doi: 10.1016/S0020-7683(99)00327-3 Kuribayashi K, Tsuchiya K, You Z, Tomus D, Umemoto M, Ito T, Sasaki M. 2006. Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil. Materials Science Engineering:A, 419: 131-137. doi: 10.1016/j.msea.2005.12.016 Lam T. 2003. Hamilton's Quaternions. Elsevier. Lang R J. 2015. Treemaker. https://www.langorigami.com/article/treemaker/. Lang R J. 2017. Twists, Tilings, and Tessellations: Mathematical Methods for Geometric Origami. AK Peters/CRC Press. Lang R J, Brown N, Ignaut B, Magleby S, Howell L. 2020. Rigidly foldable thick origami using designed-offset linkages. Journal of Mechanisms and Robotics, 12: 021106. Lang R J, Howell L. 2018. Rigidly foldable quadrilateral meshes from angle arrays. Journal of Mechanisms and Robotics, 10: 021004. Lang R J, Howell L L. 2022. Laminar emergent flexural fold joints: Planar compliant mechanisms with large-angle near-revolute motion. Extreme Mechanics Letters, 52: 101657. doi: 10.1016/j.eml.2022.101657 Lang R J, Magleby S, Howell L. 2016. Single degree-of-freedom rigidly foldable cut origami flashers. Journal of Mechanisms and Robotics, 8: 031005. doi: 10.1115/1.4032102 Lang R J, Nelson T, Magleby S, Howell L. 2017. Thick rigidly foldable origami mechanisms based on synchronized offset rolling contact elements. Journal of Mechanisms and Robotics, 9: 021013. doi: 10.1115/1.4035686 Lang R J, Tolman K A, Crampton E B, Magleby S P, Howell L L. 2018. A review of thickness-accommodation techniques in origami-inspired engineering. Applied Mechanics Reviews, 70: 010805. Lee D-Y, Kim S-R, Kim J-S, Park J-J, Cho K-J. 2017. Origami wheel transformer: a variable-diameter wheel drive robot using an origami structure. Soft robotics, 4: 163-180. doi: 10.1089/soro.2016.0038 Lee T-U, Yang X, Ma J, Chen Y, Gattas J M. 2019. Elastic buckling shape control of thin-walled cylinder using pre-embedded curved-crease origami patterns. International Journal of Mechanical Sciences, 151: 322-330. doi: 10.1016/j.ijmecsci.2018.11.005 Li Y. 2020. Motion paths finding for multi-degree-of-freedom mechanisms. International Journal of Mechanical Sciences, 185: 105709. doi: 10.1016/j.ijmecsci.2020.105709 Li Y, Yin J. 2021. Metamorphosis of three-dimensional kirigami-inspired reconfigurable and reprogrammable architected matter. Materials Today Physics, 21: 100511. doi: 10.1016/j.mtphys.2021.100511 Li Y, Zhang Q, Hong Y, Yin J. 2021. 3D transformable modular Kirigami based programmable metamaterials. Advanced Functional Materials, 31: 2105641. doi: 10.1002/adfm.202105641 Lin Y, Yang G, Liang Y, Zhang C, Wang W, Qian D, Yang H, Zou J. 2020. Controllable stiffness origami “skeletons” for lightweight and multifunctional artificial muscles. Advanced Functional Materials, 30: 2000349. doi: 10.1002/adfm.202000349 Liu K, Paulino G H. 2016. MERLIN: A MATLAB implementation to capture highly nonlinear behavior of non-rigid origami//Proceedings of IASS Annual Symposia, 1-10. Liu K, Paulino G H. 2018. Highly efficient nonlinear structural analysis of origami assemblages using the MERLIN2 software, Origami, 7: 1167-1182. Liu L, Choi G P, Mahadevan L. 2021a. Wallpaper group kirigami. Proceedings of the Royal Society A:Mathematical, Physical, 477: 20210161. Liu P, Ma J, Chen Y, Yuan L, Zhao H, Wang K. 2021b. The kinematic analysis and bistable characteristics of the winding origami structure//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V08BT08A032. American Society of Mechanical Engineers. Liu S. 2014. Deployable structure associated with rigid origami and its mechanics. [PhD thesis]. Singapore: School of Mechanical and Aerospace Engineering, Nanyang Technological University. Liu S, Lv W, Chen Y, Lu G. 2016. Deployable prismatic structures with rigid origami patterns. Journal of Mechanisms and Robotics, 8: 031002. doi: 10.1115/1.4031953 Liu W, Jiang H, Chen Y. 2022. 3D programmable metamaterials based on reconfigurable mechanism modules. Advanced Functional Materials, 32: 2109865. doi: 10.1002/adfm.202109865 Liu Z, Fang H, Xu J, Wang K. 2021c. A novel origami mechanical metamaterial based on Miura-variant designs: exceptional multistability and shape reconfigurability. Smart Materials Structures, 30: 085029. doi: 10.1088/1361-665X/ac0d0f Lv C, Krishnaraju D, Konjevod G, Yu H, Jiang H. 2014. Origami based mechanical metamaterials. Scientific Reports, 4: 1-6. Ma J, Chai S, Chen Y. 2022a. Geometric design, deformation mode, and energy absorption of patterned thin-walled structures. Mechanics of Materials, 168: 104269. doi: 10.1016/j.mechmat.2022.104269 Ma J, Feng H, Chen Y, Hou D, You Z. 2020. Folding of tubular waterbomb. Research, 2020: 1735081. Ma J, Jiang X, Chen Y. 2022b. A 3D modular meta-structure with continuous mechanism motion and bistability. Extreme Mechanics Letters, 51: 101584. doi: 10.1016/j.eml.2021.101584 Ma J, Song J, Chen Y. 2018. An origami-inspired structure with graded stiffness. International Journal of Mechanical Sciences, 136: 134-142. doi: 10.1016/j.ijmecsci.2017.12.026 Ma J, You Z. 2013. Energy absorption of thin-walled beams with a pre-folded origami pattern. Thin-Walled Structures, 73: 198-206. doi: 10.1016/j.tws.2013.08.001 Ma J, Zang S, Feng H, Chen Y, You Z. 2021. Theoretical characterization of a non-rigid-foldable square-twist origami for property programmability. International Journal of Mechanical Sciences, 189: 105981. doi: 10.1016/j.ijmecsci.2020.105981 Magliozzi L, Micheletti A, Pizzigoni A, Ruscica G. 2017. On the design of origami structures with a continuum of equilibrium shapes. Composites Part B:Engineering, 115: 144-150. doi: 10.1016/j.compositesb.2016.10.023 Maxwell J C. 1864. On the calculation of the equilibrium and stiffness of frames. The London, Edinburgh, Dublin Philosophical Magazine, 27: 294-299. doi: 10.1080/14786446408643668 Mazzucchi A. 2018. A kinetic module for modular structures based on rigid origami. Nexus Network Journal, 20: 41-57. doi: 10.1007/s00004-017-0351-y McCarthy J M. 1990. Introduction to theoretical kinematics. MIT Press. Meloni M, Cai J, Zhang Q, Sang‐Hoon Lee D, Li M, Ma R, Parashkevov T E, Feng J. 2021. Engineering origami: a comprehensive review of recent applications, design methods, and tools. Advanced Science, 8: 2000636. doi: 10.1002/advs.202000636 Micheletti A, Giannetti I, Mattei G, Tiero A. 2022. Kinematic and static design of rigid origami structures: Application to modular yoshimura patterns. Journal of Architectural Engineering, 28: 04022009. doi: 10.1061/(ASCE)AE.1943-5568.0000531 Mitani J. 2017. 3D Origami Art. CRC Press. Miura K. 1985. Method of packaging and deployment of large membranes in space. The Institute of Space Astronautical Science report: 1-9. Miura K, Tachi T. 2010. Synthesis of rigid-foldable cylindrical polyhedra. Symmetry: Art Science, 1: 204-213. Miyashita S, Guitron S, Yoshida K, Li S, Damian D D, Rus D. 2016. Ingestible, controllable, and degradable origami robot for patching stomach wounds//2016 IEEE International Conference on Robotics and Automation (ICRA), 909-916.IEEE. Morgan M R, Lang R J, Magleby S P, Howell L L. 2016. Towards developing product applications of thick origami using the offset panel technique. Mechanical Sciences, 7: 69-77. doi: 10.5194/ms-7-69-2016 Mousanezhad D, Kamrava S, Vaziri A. 2017. Origami-based building blocks for modular construction of foldable structures. Scientific Reports, 7: 1-8. doi: 10.1038/s41598-016-0028-x Mukhopadhyay T, Ma J, Feng H, Hou D, Gattas J M, Chen Y, You Z. 2020. Programmable stiffness and shape modulation in origami materials: Emergence of a distant actuation feature. Applied Materials Today, 19: 100537. doi: 10.1016/j.apmt.2019.100537 Myard F E. 1931. Contribution à la géométrie des systèmes articulés. Bulletin de la Société Mathématique de France, 59: 183-210. Novelino L S, Ze Q, Wu S, Paulino G H, Zhao R. 2020. Untethered control of functional origami microrobots with distributed actuation. Proceedings of the National Academy of Sciences, 117: 24096-24101. doi: 10.1073/pnas.2013292117 Onal C D, Wood R J, Rus D. 2012. An origami-inspired approach to worm robots. IEEE/ASME Transactions on Mechatronics, 18: 430-438. Ou J, Ma Z, Peters J, Dai S, Vlavianos N, Ishii H. 2018. KinetiX-designing auxetic-inspired deformable material structures. Computers Graphics, 75: 72-81. doi: 10.1016/j.cag.2018.06.003 Overvelde J T, De Jong T A, Shevchenko Y, Becerra S A, Whitesides G M, Weaver J C, Hoberman C, Bertoldi K. 2016. A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom. Nature Communications, 7: 1-8. Overvelde J T, Weaver J C, Hoberman C, Bertoldi K. 2017. Rational design of reconfigurable prismatic architected materials. Nature Communications, 541: 347-352. doi: 10.1038/nature20824 Pehrson N A, Magleby S P, Lang R J, Howell L L. 2016. Introduction of monolithic origami with thick-sheet materials//Proceedings of IASS Annual Symposia, 1-10. Pellegrino S. 1990. Analysis of prestressed mechanisms. International Journal of Solids and Structures, 26: 1329-1350. doi: 10.1016/0020-7683(90)90082-7 Pellegrino S. 1993. Structural computations with the singular value decomposition of the equilibrium matrix. International Journal of Solids and Structures, 30: 3025-3035. doi: 10.1016/0020-7683(93)90210-X Pellegrino S, Calladine C R. 1986. Matrix analysis of statically and kinematically indeterminate frameworks. International Journal of Solids and Structures, 22: 409-428. doi: 10.1016/0020-7683(86)90014-4 Peng R, Chen Y. 2014. The metamaterial generated from rigid-origami pattern//The 6th International Meeting on Origami in Science, Mathematics and Education, Tokyo, Japan, August. Peng R, Ma J, Chen Y. 2018. The effect of mountain-valley folds on the rigid foldability of double corrugated pattern. Mechanism and Machine Theory, 128: 461-474. doi: 10.1016/j.mechmachtheory.2018.06.012 Pratapa P P, Liu K, Paulino G H. 2019. Geometric mechanics of origami patterns exhibiting Poisson’s ratio switch by breaking mountain and valley assignment. Physical Review Letters, 122: 155501. doi: 10.1103/PhysRevLett.122.155501 Pratapa P P, Liu K, Paulino G H. 2020. Kinematics of the morph origami pattern and its hybrid states//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V010T010A076. American Society of Mechanical Engineers. Pratapa P P, Liu K, Vasudevan S P, Paulino G H. 2021. Reprogrammable kinematic branches in tessellated origami structures. Journal of Mechanisms and Robotics, 13: 031004. doi: 10.1115/1.4049949 Qiu C, Zhang K, Dai J S. 2016. Repelling-screw based force analysis of origami mechanisms. Journal of Mechanisms and Robotics, 8: 031001. doi: 10.1115/1.4031458 Rafsanjani A, Pasini D. 2016. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extreme Mechanics Letters, 9: 291-296. doi: 10.1016/j.eml.2016.09.001 Randlett S. 1963. The Art of Origami: Paper Folding, Traditional and Modern. Faber & Faber. Resch R D. 1965. Geometrical device having articulated relatively movable sections. U.S. Patent 3201894. Resch R D. 1968. Self-supporting structural unit having a series of repetitious geometrical modules. U.S. Patent 3407558. Resch R D. 1973. The topological design of sculptural and architectural systems//Proceedings of the June 4-8, 1973, National Computer Conference and Exposition, 643-650. Reuleaux F. 1875. The Kinematics of Machinery. London. Macmillan and Co. Salazar R, Murthy S, Pellazar C, Stoica A. 2017. Transformers for lunar extreme environments: large origami deployable solar reflectors//2017 IEEE Aerospace Conference, 1-7.IEEE. Sarrus P. 1853. Note Sur la transformation des mouvements rectilignes alternatifs, en mouvements circulaires, et reciproquement, comptes. rendus. Acad. Sci. , Paris, 36: 1036. Schenk M, Guest S D. 2011. Origami folding: a structural engineering approach. Origami, 5: 291-304. Schenk M, Guest S D. 2013. Geometry of Miura-folded metamaterials. Proceedings of the National Academy of Sciences, 110: 3276-3281. doi: 10.1073/pnas.1217998110 Song C, Chen Y. 2012. Multiple linkage forms and bifurcation behaviours of the double-subtractive-Goldberg 6R linkage. Mechanism and Machine Theory, 57: 95-110. doi: 10.1016/j.mechmachtheory.2012.07.002 Stachel H. 2010. A kinematic approach to Kokotsakis meshes. Computer Aided Geometric Design, 27: 428-437. doi: 10.1016/j.cagd.2010.05.002 Stavric M, Wiltsche A. 2014. Quadrilateral patterns for rigid folding structures. International Journal of Architectural Computing, 12: 61-79. doi: 10.1260/1478-0771.12.1.61 Sun T, Yang S, Huang T, Dai J S. 2017. A way of relating instantaneous and finite screws based on the screw triangle product. Mechanism and Machine Theory, 108: 75-82. Tachi T. 2009. Generalization of rigid-foldable quadrilateral-mesh origami. Journal of the International Association for Shell Spatial Structures, 50: 173-179. Tachi T. 2010a. “Freeform Origami”. www.tsg.ne.jp/TT/software/. Tachi T. 2010b. Freeform rigid-foldable structure using bidirectionally flat-foldable planar quadrilateral mesh. Advances in Architectural Geometry, 14: 203-215. Tachi T. 2010c. Geometric considerations for the design of rigid origami structures//Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium, 458-460. Elsevier Ltd. Tachi T. 2010d. One-DOF cylindrical deployable structures with rigid quadrilateral panels//Symposium of the International Association for Shell and Spatial Structures (50th. 2009. Valencia). Evolution and Trends in Design, Analysis and Construction of Shell and Spatial Structures: Proceedings. Editorial Universitat Politècnica de València. Tachi T. 2011. Rigid-foldable thick origami. Origami, 5: 253-264. Tachi T. 2013. Designing freeform origami tessellations by generalizing Resch's patterns. Journal of Mechanical Design, 135: 111006. doi: 10.1115/1.4025389 Tachi T, Masubuchi M, Iwamoto M. 2012. Rigid origami structures with vacuumatics: geometric considerations//Proc. the IASS-APCS Seoul, Korea, 21–24 May. Tang J, Tian M, Wang C, Wang X, Mao H. 2021. A novel scheme of folding discretized surfaces of revolution inspired by waterbomb origami. Mechanism and Machine Theory, 165: 104431. doi: 10.1016/j.mechmachtheory.2021.104431 Tang Y, Li Y, Hong Y, Yang S, Yin J. 2019. Programmable active kirigami metasheets with more freedom of actuation. Proceedings of the National Academy of Sciences, 116: 26407-26413. doi: 10.1073/pnas.1906435116 Tarnai T. 2001. Infinitesimal and finite mechanisms. //Pellegrinos eds. Deployable Structures. New York: Springer, 2001. Tolman K A, Lang R J, Magleby S P, Howell L L. 2017. Split-vertex technique for thickness-accommodation in origami-based mechanisms//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V05BT08A054. American Society of Mechanical Engineers. Turner N, Goodwine B, Sen M. 2016. A review of origami applications in mechanical engineering. Journal of Mechanical Engineering Science, 230: 2345-2362. doi: 10.1177/0954406215597713 Varadarajan V. 1974. Lie GRoups, Lie Algebras, and Their Representations. Prentice-Hall. Vasudevan S P, Pratapa P P. 2021. Origami metamaterials with near-constant poisson functions over finite strains. Journal of Engineering Mechanics, 147: 04021093. Wang C, Guo H, Liu R, Deng Z. 2022a. A programmable origami-inspired space deployable structure with curved surfaces. Engineering Structures, 256: 113934. doi: 10.1016/j.engstruct.2022.113934 Wang C, Li J, Zhang D. 2021. Optimization design method for kirigami-inspired space deployable structures with cylindrical surfaces. Applied Mathematical Modelling, 89: 1575-1598. doi: 10.1016/j.apm.2020.07.005 Wang K, Chen Y. 2011. Folding a patterned cylinder by rigid origami, Origami, 5: 265-276. Wang L-C, Song W-L, Fang D. 2018. Twistable origami and kirigami: from structure-guided smartness to mechanical energy storage. ACS Applied Materials and Interfaces, 11: 3450-3458. Wang L C, Song W L, Zhang Y J, Qu M J, Zhao Z, Chen M, Yang Y, Chen H, Fang D. 2020. Active reconfigurable tristable square‐twist origami. Advanced Functional Materials, 30: 1909087. doi: 10.1002/adfm.201909087 Wang S, Gao Y, Huang H, Li B, Guo H, Liu R. 2022b. Design of deployable curved-surface rigid origami flashers. Mechanism and Machine Theory, 167: 104512. doi: 10.1016/j.mechmachtheory.2021.104512 Warisaya K, Hamanaka H, Tokolo A, Tachi T. 2021. Auxetic structures based on rhombic tiling//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V08BT08A031. American Society of Mechanical Engineers. Watanabe N, Kawaguchi K. 2009. The method for judging rigid foldability. Origami, 4: 165-174. Webb D, Hirsch B, Bach V, Sauder J F, Bradford S, Thomson M. 2016. Starshade mechanical architecture & technology effort//3rd AIAA Spacecraft Structures Conference, 2165. Wei G, Dai J S. 2014. Origami-inspired integrated planar-spherical overconstrained mechanisms. Journal of Mechanical Design, 136: 051003. doi: 10.1115/1.4025821 Wei G, Ding X, Dai J S. 2010. Mobility and geometric analysis of the Hoberman switch-pitch ball and its variant. Journal of Mechanisms and Robotics, 2: 031010. doi: 10.1115/1.4001730 Wohlhart K. 2001. Regular polyhedral linkages//Proceedings of the 2nd Workshop on Computational Kinematics, Seoul: 239-248. Wu W, You Z. 2010. Modelling rigid origami with quaternions and dual quaternions. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Science, 466: 2155-2174. doi: 10.1098/rspa.2009.0625 Wu W, You Z. 2011. A solution for folding rigid tall shopping bags. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 467: 2561-2574. doi: 10.1098/rspa.2011.0120 Xu R, Zhang X, Ma J, Chen Y, Cao Y, You Z. 2018. Folding a rigid flat surface around a square hub//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V05BT07A060. American Society of Mechanical Engineers. Yamaguchi K, Yasuda H, Tsujikawa K, Kunimine T, Yang J. 2022. Graph-theoretic estimation of reconfigurability in origami-based metamaterials. Materials and Design, 213: 110343. doi: 10.1016/j.matdes.2021.110343 Yang F, Chen Y, Kang R, Ma J. 2016a. Truss transformation method to obtain the non-overconstrained forms of 3D overconstrained linkages. Mechanism and Machine Theory, 102: 149-166. doi: 10.1016/j.mechmachtheory.2016.04.005 Yang F, Zhang M, Ma J, You Z, Yu Y, Chen Y, Paulino G H. 2022a. Design of single degree-of-freedom triangular resch patterns with thick-panel origami. Mechanism and Machine Theory, 169: 104650. doi: 10.1016/j.mechmachtheory.2021.104650 Yang J, Zhang X, Chen Y, You Z. 2022b. Folding arrays of uniform-thickness panels to compact bundles with a single degree of freedom. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Science, 478: 20220043. doi: 10.1098/rspa.2022.0043 Yang S, Sun T, Huang T, Li Q, Gu D. 2016b. A finite screw approach to type synthesis of three-DOF translational parallel mechanisms. Mechanism and Machine Theory, 104: 405-419. Yang Y, Maiolino P, Chen Y, You Z. 2021. Three-dimensional kinematic metamaterial with tuneable directional permeability, arXiv preprint arXiv: 2102.08821. Yang Y, You Z. 2018a. 3D construction of a tilted cuboid mechanical metamaterial//ASME International Mechanical Engineering Congress and Exposition, V009T012A021. American Society of Mechanical Engineers. Yang Y, You Z. 2018b. Geometry of transformable metamaterials inspired by modular origami. Journal of Mechanisms and Robotics, 10: 021001. doi: 10.1115/1.4038969 Yang Y, You Z. 2018c. A modular origami-inspired mechanical metamaterial. Origami, 7: 715-730. Yasuda H, Miyazawa Y, Charalampidis E G, Chong C, Kevrekidis P G, Yang J. 2019. Origami-based impact mitigation via rarefaction solitary wave creation. Science advances, 5: eaau2835. doi: 10.1126/sciadv.aau2835 Yasuda H, Tachi T, Lee M, Yang J. 2017. Origami-based tunable truss structures for non-volatile mechanical memory operation. Nature Communications, 8. Yasuda H, Yein T, Tachi T, Miura K, Taya M. 2013. Folding behaviour of Tachi–Miura polyhedron bellows. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 469: 20130351. doi: 10.1098/rspa.2013.0351 Ye H, Ma J, Zhou X, Wang H, You Z. 2019. Energy absorption behaviors of pre-folded composite tubes with the full-diamond origami patterns. Composite Structures, 221: 110904. doi: 10.1016/j.compstruct.2019.110904 Ye H, Zhou X, Ma J, Wang H, You Z. 2020. Axial crushing behaviors of composite pre-folded tubes made of KFRP/CFRP hybrid laminates. Thin-Walled Structures, 149: 106649. doi: 10.1016/j.tws.2020.106649 Yellowhorse A, Lang R J, Tolman K, Howell L L. 2018. Creating linkage permutations to prevent self-intersection and enable deployable networks of thick-origami. Scientific Reports, 8: 1-9. Yellowhorse A D, Brown N, Howell L L. 2020. Design of regular one-dimensional, two-dimensional, and three-dimensional linkage-based tessellations. Journal of Mechanisms and Robotics, 12: 021104. doi: 10.1115/1.4045936 Yoshimura Y. 1955. On the mechanism of buckling of a circular cylindrical shell under axial compression//National Advisory Committee for Aeronautics Technical Memorandum. You Z, Chen Y. 2011. Motion Structures: Deployable Structural Assemblies of Mechanisms. Crc Press. Yu Y, Chen Y, Paulino G H. 2019. On the unfolding process of triangular Resch patterns: a finite particle method investigation//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V05BT07A048. American Society of Mechanical Engineers. Zang S, Ma J, You Z, Chen Y. 2022. Deformation characteristics and mechanical properties tuning of a non-rigid square-twist origami structure with rotational symmetry. Thin-Walled Structures, 179: 109570. doi: 10.1016/j.tws.2022.109570 Zhai Z, Wang Y, Jiang H. 2018. Origami-inspired, on-demand deployable and collapsible mechanical metamaterials with tunable stiffness. Proceedings of the National Academy of Sciences, 115: 2032-2037. doi: 10.1073/pnas.1720171115 Zhakypov Z, Paik J. 2018. Design methodology for constructing multimaterial origami robots and machines. IEEE Transactions on Robotics, 34: 151-165. doi: 10.1109/TRO.2017.2775655 Zhang K, Dai J S. 2013. Classification of origami-enabled foldable linkages and emerging applications//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V06BT07A024. American Society of Mechanical Engineers. Zhang K, Fang Y, Fang H, Dai J S. 2010. Geometry and constraint analysis of the three-spherical kinematic chain based parallel mechanism. Journal of Mechanisms and Robotics, 2: 191-200. Zhang T, Kawaguchi K i, Wu M. 2018. A folding analysis method for origami based on the frame with kinematic indeterminacy. International Journal of Mechanical Sciences, 146: 234-248. Zhang X, Chen Y. 2018a. The diamond thick-panel origami and the corresponding mobile assemblies of plane-symmetric Bricard linkages. Mechanism and Machine Theory, 130: 585-604. doi: 10.1016/j.mechmachtheory.2018.09.005 Zhang X, Chen Y. 2018b. Mobile assemblies of Bennett linkages from four-crease origami patterns. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 474: 20170621. doi: 10.1098/rspa.2017.0621 Zhang X, Chen Y. 2019. Vertex-splitting on a diamond origami pattern. Journal of Mechanisms and Robotics, 11: 031014. doi: 10.1115/1.4043214 Zhang X, Ma J, Li M, You Z, Wang X, Luo Y, Ma K, Chen Y. 2022. Kirigami-based metastructures with programmable multistability. Proceedings of the National Academy of Sciences, 119: e2117649119. doi: 10.1073/pnas.2117649119 Zhao Y, Endo Y, Kanamori Y, Mitani J. 2018a. Approximating 3D surfaces using generalized waterbomb tessellations. Journal of Computational Design Engineering, 5: 442-448. doi: 10.1016/j.jcde.2018.01.002 Zhao Y, Kanamori Y, Mitani J. 2018b. Design and motion analysis of axisymmetric 3D origami with generic six-crease bases. Computer Aided Geometric Design, 59: 86-97. doi: 10.1016/j.cagd.2017.10.002 Zhao Y, Li S, Zhang M, Zeng L, Yang Y, Kanamori Y, Mitani J. 2021. Computational design methods for cylindrical and axisymmetric waterbomb tessellations. Computer Aided Geometric Design, 91: 102037. doi: 10.1016/j.cagd.2021.102037 Zhou C, Wang B, Ma J, You Z. 2016. Dynamic axial crushing of origami crash boxes. International Journal of Mechanical Sciences, 118: 1-12. doi: 10.1016/j.ijmecsci.2016.09.001 Zimmermann L, Shea K, Stanković T. 2020. Conditions for rigid and flat foldability of degree-n vertices in origami. Journal of Mechanisms and Robotics, 12: 011020. doi: 10.1115/1.4045249 Zimmermann L, Stanković T. 2020. Rigid and flat foldability of a degree-four vertex in origami. Journal of Mechanisms and Robotics, 12: 011004. doi: 10.1115/1.4044737 Zirbel S A, Lang R J, Thomson M W, Sigel D A, Walkemeyer P E, Trease B P, Magleby S P, Howell L L. 2013. Accommodating thickness in origami-based deployable arrays. Journal of Mechanical Design, 135: 111005. doi: 10.1115/1.4025372 -




 下载:
下载: