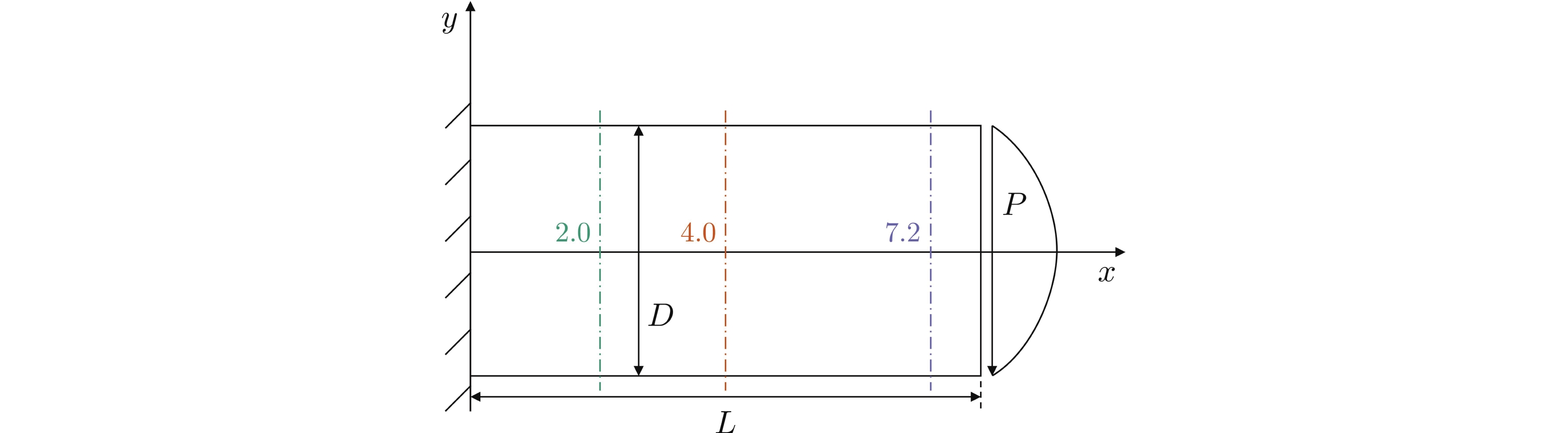
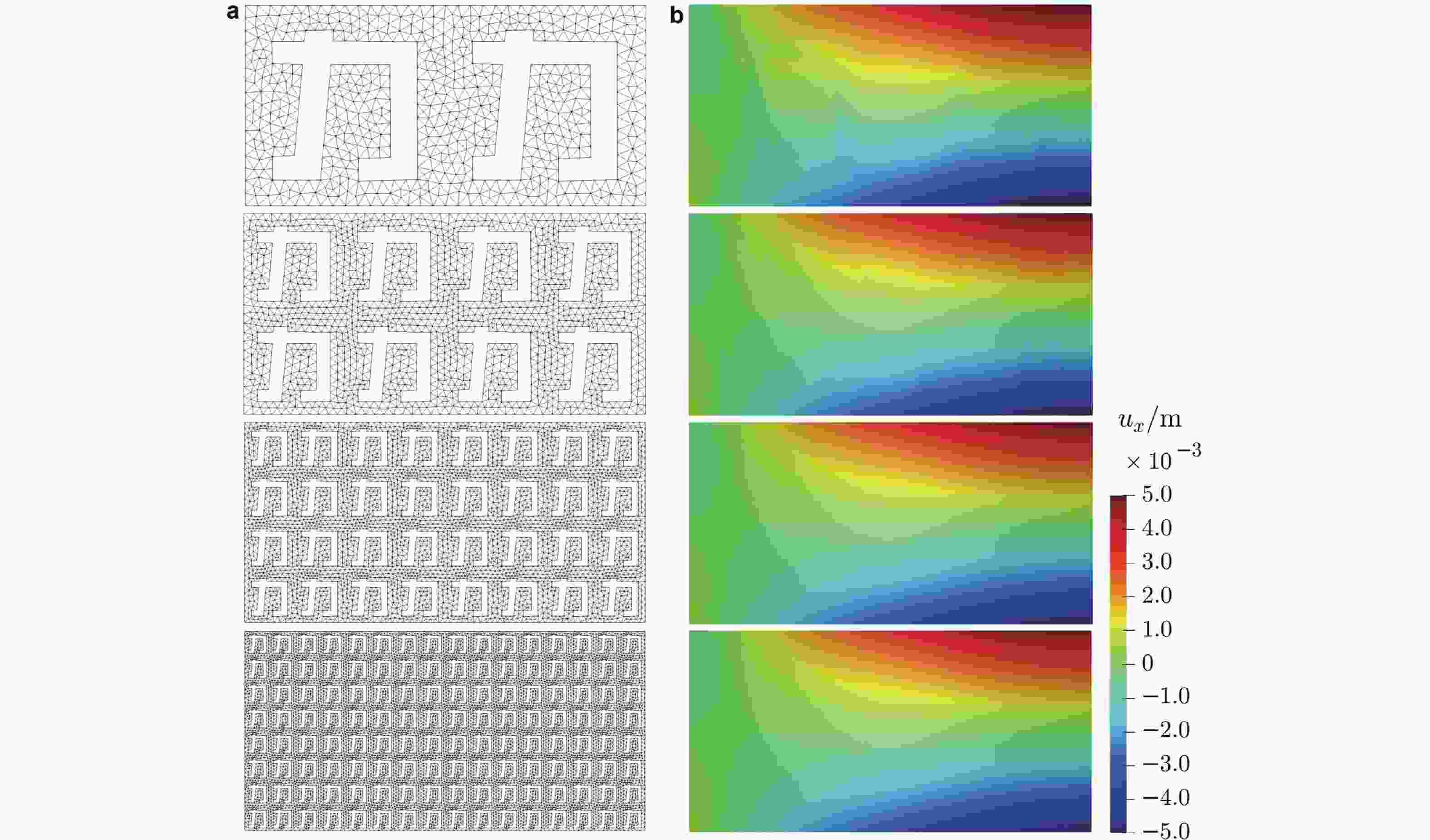
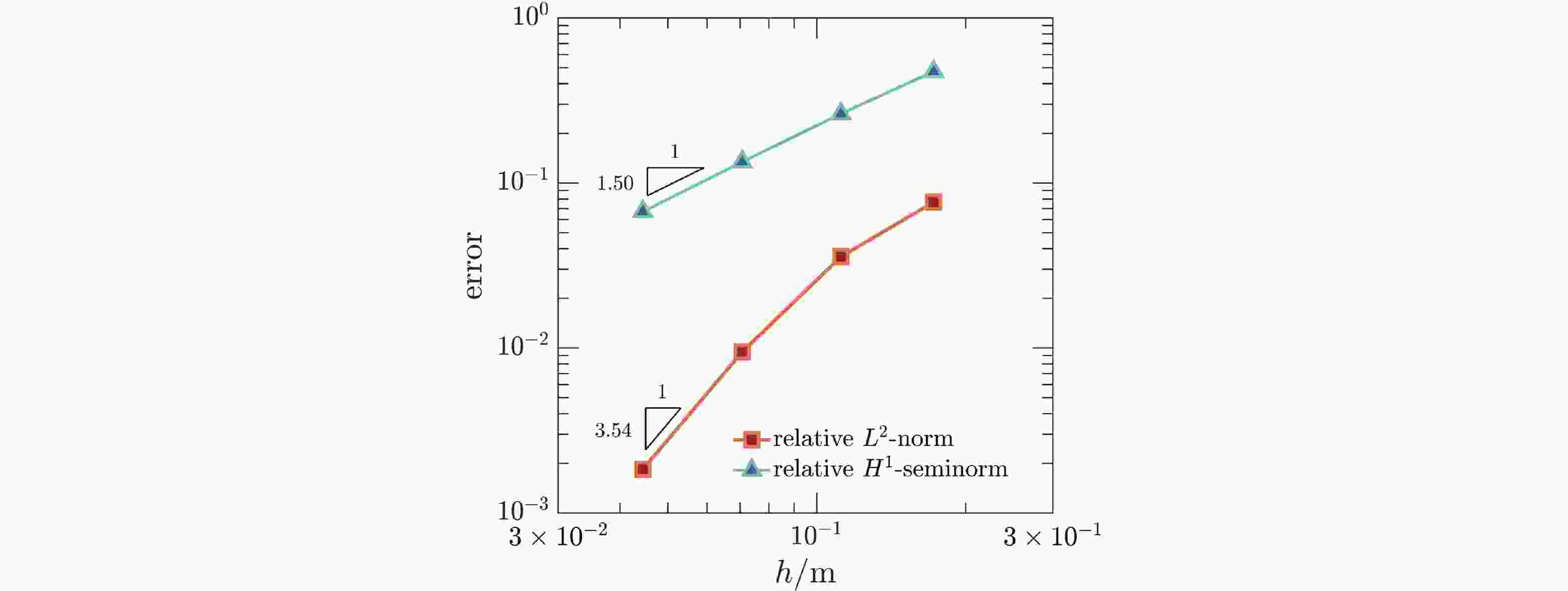
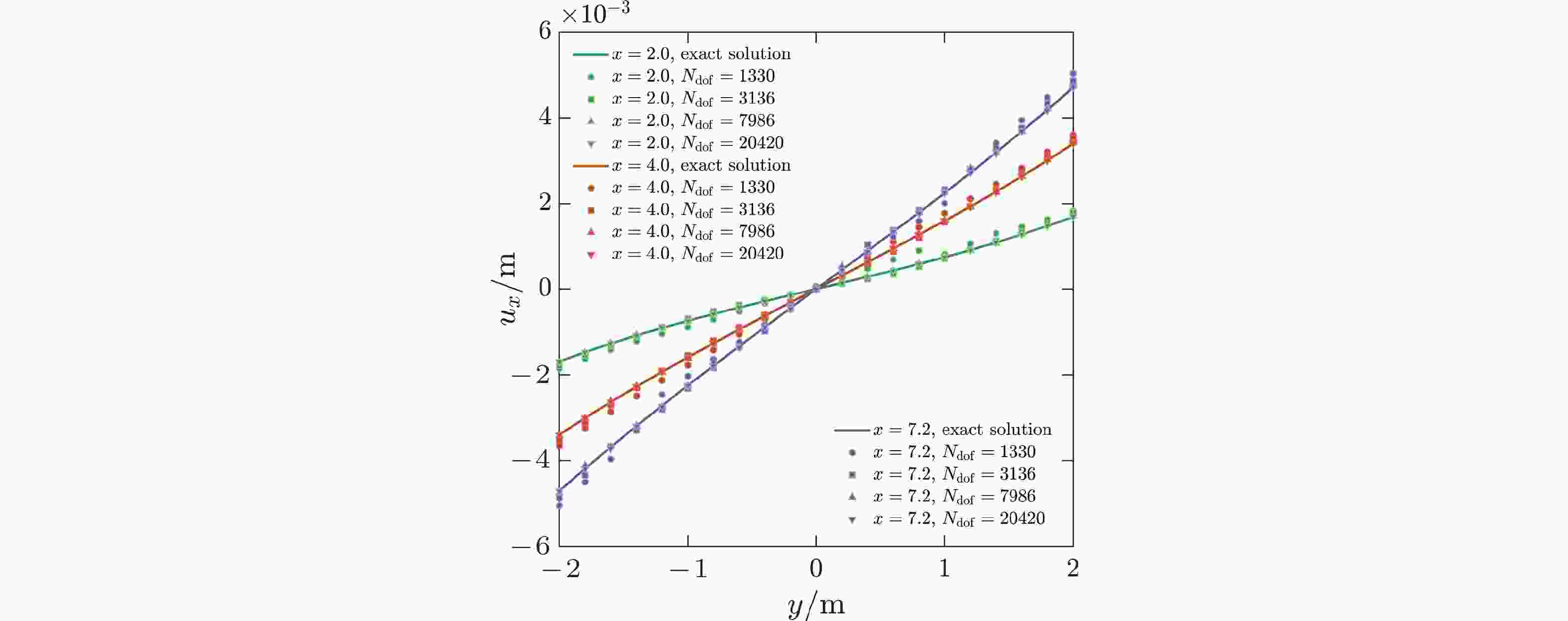
-
摘要: 虚单元方法是近几年在计算领域迅速发展的一种先进数值方法, 相比于有限元方法, 该方法放松了对单元凸凹性的限制, 可适用于任意形状的多边形单元, 因而在处理悬挂节点、接触、多晶体变形等特定问题方面具有优势, 是当前计算力学领域的国际前沿与热点方向. 本文全面综述了虚单元方法的理论发展, 通过介绍该方法在泊松方程、线弹性、非线性等问题中的应用, 向读者展示了虚单元法的理论核心以及它和有限元方法的异同. 尽管虚单元法的发展目前还处在起步阶段, 但该方法在诸多的非线性问题、接触问题、裂纹扩展以及多场耦合等方面展现出了巨大潜力. 通过对虚单元方法最新理论与应用进展的综述, 为面临单元凸凹性等问题苦恼的计算领域科研工作者提供一种新的解决方案; 同时为对工程科学计算感兴趣的青年科研人员提供关于虚单元方法的快速而系统的全面认知, 以期青年学者能融会贯通, 发展出适应我国计算力学需求的新型算法与高性能软件.Abstract: Virtual Element Method (VEM) is a recently-developed numerical method suitable for arbitrarily convex or concave cells. This benefits the VEM to handle hanging nodes, contacts and polycrystalline deformations. We here illustrate the theory of the VEM via the Poisson equation and the elastic problem, and summarize its applications to non-linear problems. Compared to the Finite Element Method (FEM), the characteristics of the VEM are explained in details. The VEM has demonstrated potentials to model contacts, cracks, coupling of multiple physics, and etc. We hope that this review can provides an alternative means for software developers in computational mechanics.
-
1. 发展历程
虚单元方法(virtual element method, VEM)的基本驱动来源于对任意形状多边形的处理. 传统意义的有限元或有限差分需要将具备显著几何特征的物理实体离散化而求解, 这在一定程度上丧失了对实体几何信息的“宏观”描述. 而实际的工程需求中, 越来越多的计算涉及到处理特定几何体结构, 如非凸性多边形的变形以及复杂结构的接触等问题. 2013 年, 由意大利 Milano-Bicocca 大学的 L. Beirão da Veiga 教授组首先提出可适用于任意形状多边形的虚单元数值方法 (Beirão Da Veiga et al. 2013a, 2013b; Beirão da Veiga et al. 2014). 由于该方法和有限元方法的高度兼容性, 同时在处理悬挂节点(适用于含任意数目节点的单元)、接触(均可转化为点−点接触)、晶体变形(对形状、晶格匹配等无特殊要求)等问题方面具有特定优势, 近年来得到计算力学领域的广泛关注与发展. 国际上不同的团队将该方法从理论上进行了拓展, 并应用到不同的力学问题, 如弹性问题 (Gain et al. 2014, Artioli et al. 2017a)、接触问题 (Wriggers et al. 2016, Wriggers and Rust 2019)、高阶单元 (Beirão da Veiga et al. 2017a)、大变形 (Beirão da Veiga et al. 2015, Wriggers and Rust 2019)、断裂问题 (Hussein et al. 2018, Aldakheel et al. 2019a), 等工程科学/力学问题的计算.
对比有限元方法, 虚单元法也需要对几何空间进行离散, 通过形成并求解线性方程组对实际问题进行近似. 不同之处在于: (1)有限元中所采用的近似函数为显式多项式函数; 虚单元法中, 近似函数除了多项式函数外, 还有在单元边界为连续多项式且单元内部满足某些条件(如进行拉普拉斯运算后为多项式)的函数. 这些函数在单元域内无显式表达, 这也是虚单元方法中“虚”字的由来. (2)有限元方法中自由度均是近似函数的取值, 虚单元方法通过定义合理的自由度, 在形成刚度矩阵时避免计算单元内部近似函数的取值; (3)有限元的刚度矩阵中仅含有一项, 虚单元法的刚度矩阵包含了协调矩阵和稳定矩阵, 以此来保证计算的收敛.
为了实现摘要中所提出的目标, 本文将采取有别于传统综述论文的行文方式, 大幅度地增加了关于虚单元法基本原理和最新理论的详细介绍. 这样处理的目的是双重性的: 一方面, 读者能够了解该方法在一些典型问题中所体现的有别于有限元方法的能力; 与此同时, 对该方法感兴趣的读者将可以通过对本文的通读和理解, 全面掌握虚单元法的理论基础和实现途径, 为利用该方法来发展适用于自身面临的科学与工程计算问题提供一份全面的参考资料. 基于这一设想, 文章的基本框架为: 第 2 章简略介绍有限元法与虚单元法的区别与联系, 以便具有力学背景的同行对虚单元法有个直观了解; 第 3 章详细介绍虚单元法基本原理方面的发展, 以熟知的泊松方程为对象, 介绍了虚单元法的核心理论; 第 4 章针对线弹性问题的求解, 全面综述了求解过程中涉及自由度、单元刚度矩阵构建、相应计算流程的具体方法和步骤, 并给出了典型的计算实例来考察这一计算方法; 第 5 章详细介绍了当前虚单元在非线性问题、断裂问题、接触问题、多场耦合等涉及复杂几何边界处理的典型应用; 第 6 章总结该方法的利弊并展望虚单元法的发展前景.
为便于介绍, 需要在此做一些符号及其运算的基本设定. 以二维问题为例, 下文中黑斜体表示张量（张量函数）或矩阵, 比如位移场u, 刚度矩阵K; 斜体表示标量函数, 比如泊松方程的解u; 若带有下标则表示矢量的分量形式, 比如u = ui ei(i=1, 2), 下文为描述简单省去单位基矢量ei.
$ \nabla() $ 表示空间梯度运算, 比如$ \nabla u = {\rm{d}}u/{\rm{d}}x_i $ 为矢量;$ \nabla \cdot() $ 表示散度运算, 比如$ \nabla \cdot {\boldsymbol{{u}}} = {\rm{d}}u_i/{\rm{d}}x_i $ 为标量, 这里重复下标采用了爱因斯坦求和约定;$ \Delta() = \nabla \cdot \nabla() $ 表示拉普拉斯运算, 比如$ \Delta u = \sum_{i=1}^2 {\rm{d}}^2 u/{\rm{d}}x^2_i $ 为标量.2. 虚单元法与有限元法的异同概述
在详细阐述虚单元法的基本理论前, 需要对比有限元法并指出两种方法的异同, 以便工程力学背景的同行对该方法有个直观了解. 需要指出, 该章意为对比基本概念, 相关定义并不严格, 更严格推导与解释详见下两章.
考虑
$ \varOmega $ 域内定义的标量场$ u({\boldsymbol{{x}}}), \; {\boldsymbol{{x}}} \in \varOmega $ , 为得到该场的近似解$ u^h({\boldsymbol{{x}}}) $ , 两种方法均需进行空间离散$ \varOmega \approx \cup_i E_i $ , 其中$ E_i $ 为单元网格.网格要求的不同: 有限元需要网格为特定节点数目的凸单元, 如三角形单元、四边形单元等; 虚单元法中单元可为任意节点数目, 且对单元凸/凹性没有限制. 其原因为: 有限元中需要进行单元映射, 单元为凸才能保证映射矩阵的雅可比行列式为正, 即单元体积恒正; 而虚单元法无需进行单元映射, 可直接采用空间离散单元的几何信息进行近似.
在单元
$ E $ 上, 近似函数$ u^{h}({\boldsymbol{{x}}}) $ 均表示成形函数与待解自由度的乘积, 即$$ \begin{array}{*{20}{l}} u^{h}({\boldsymbol{{x}}}) = \displaystyle\sum\limits_{i=1}^{n_d} \phi_i({\boldsymbol{{x}}}) {{\rm{dof}}}_i(u^h) \end{array} $$ (1) 其中,
$ n_d $ 为待解自由度的数目,$ \phi_i({\boldsymbol{{x}}}) $ 为节点$ i $ 的形函数,$ {{\rm{dof}}}_i(u^h) $ 为节点$ i $ 处的自由度. 根据变分原理, 刚度矩阵分量的一般形式为$$ \begin{array}{*{20}{l}} k_{ij} = \int_E f(\nabla \phi_i, \nabla \phi_j) {{\rm{d}}}\varOmega = \int_{\partial E} g(\phi_i, \phi_j, \nabla \phi_i, \nabla \phi_j) {{\rm{d}}}\partial \varOmega - \displaystyle\int_E l(\phi_i, \phi_j, \Delta \phi_i, \Delta \phi_j) {{\rm{d}}}\varOmega \end{array} $$ (2) 式中推导采用了高斯公式,
$ f, g, l $ 为根据具体问题确定的函数. 有限元确定刚度矩阵主要依赖式(2)中第二个等号左边直接进行体积积分, 而虚单元主要依赖式(2)中第二个等号右边, 需要在单元边界上进行线积分以及单元内部进行体积积分(通过自由度设定可避免). 因而, 形函数与自由度的设定均有不同.形函数
$ \phi_i({\boldsymbol{{x}}}) $ 形式的不同: 有限元中单元形函数为显式的多项式函数; 虚单元法形函数除了多项式函数也可以为在单元边界上$ \partial E $ 为多项式、单元内部满足拉普拉斯运算后$ \Delta \phi_i $ 为多项式的函数, 该函数可没有显式表达. 如此, 虚单元方法将形函数的形式进行了扩充.自由度
$ {{\rm{dof}}}_i(u^h) $ 设定的不同: 有限元中待解量为函数在节点处的取值, 即:$ {{\rm{dof}}}_i(u^h) = u^h({\boldsymbol{{x}}}_i) $ ; 虚单元法中, 在单元边界上的节点处的待解量为函数取值, 但在单元内部的待解量为形函数的拉普拉斯运算与多项式的乘积. 如此, 可避免对没有显式表达的形函数进行体积分.具体实施起来, 有限元法由于形函数形式确定, 可直接对式(2)中第二个等号左边进行体积积分, 刚度矩阵因而仅有一项. 需要指出, 在特定单元与积分格式会造成“沙漏”, 需要进行积分格式的调整或者增加稳定项. 而对于虚单元方法需进行线积分以及体积分, 由于形函数在边界上为多项式, 因而线积分容易求得; 通过自由度设定可避免进行单个形函数的体积分, 但对于牵扯两个形函数
$ \phi_i, \phi_j $ 的积分便需要引入映射操作符$ \Pi $ 来使得$ \Pi \phi_i $ 为多项式, 如此$$ \begin{array}{*{20}{l}} k_{ij}(\phi_i, \phi_j) = k^c_{ij}(\Pi \phi_i, \Pi \phi_j) + k^s_{ij}(\phi_i - \Pi \phi_i, \phi_j - \Pi \phi_j) \end{array} $$ (3) 式中,
$ k^c_{ij} $ 为协调刚度矩阵分量,$ k^s_{ij} $ 为稳定刚度矩阵分量, 其具体形式可根据收敛准则给出.刚度矩阵的不同: 有限元的刚度矩阵可直接通过体积积分获得, 仅含有一项; 虚单元法的刚度矩阵包含协调刚度矩阵和稳定刚度矩阵, 其中稳定刚度矩阵通过收敛准则确定.
至此, 通过对比有限元中的概念, 简述了虚单元法的基本理论, 第三章从数学角度探讨虚单元法的完备性; 第四章从应用角度介绍虚单元方法在弹性问题中的应用流程, 若对数学完备不感兴趣的读者, 可直接跳至第四章.
3. 虚单元法的基本原理与其在泊松方程中的应用
为解释虚单元法的基本理论, 特别是数学上的完备性, 需要补充部分基本理论, 涉及到函数空间、离散方程推导的基本流程、解的存在唯一性与收敛条件、以及多项式函数空间与虚单元法特定的近似函数形式等的讨论. 为便于理解且从信息的全面性考虑, 这里作一些基本介绍.
3.1 函数空间
实数的集合称为实数集, 类似的, 函数的集合称为函数空间. 比如函数
$ u(x) $ 和$ v(x) $ 隶属于同一个函数空间(为表述更简洁, 下文中省去自变量$ x $ ), 若在作用域$ \varOmega $ 内定义了两者的内积$$ \begin{array}{*{20}{l}} (u, v) := \displaystyle\int_\varOmega u(x) v(x) {{\rm{d}}}x \end{array} $$ (4) 则称这样的函数空间为内积空间. 对于内积空间的任意函数
$ u $ , 进一步定义一个实数$ \|u\|_{L^{p}(\Omega)} $ 表示其大小, 称为函数的模$$ \begin{array}{*{20}{l}} \|u\|_{L^{p}(\varOmega)}:=\left(\displaystyle\int_{\varOmega}|u(x)|^{p} {{\rm{d}}}x \right)^{1 / p} \end{array} $$ (5) 其中,
$ p $ 为整数. 若$ \|u\|_{L^{p}(\varOmega)} < \infty $ , 则称 Lebesgue 空间(下标$ L $ 的来源). 在本文讨论中仅涉及$ L^2 $ 空间(即$ p=2 $ , 并略去了作用域$ \varOmega $ 的符号). 进一步, 若函数及其导数满足$$ \begin{array}{*{20}{l}} H^k = \left\{\left.u\; \right|\; u\in L^2, \; \dfrac{{{\rm{d}}}^\alpha u}{{{\rm{d}}}x^\alpha} \in L^2, \; \alpha= 1,2, \cdots, k\right\} \end{array} $$ (6) 其中,
$ k $ 为整数, 则称为 Hilbert 空间(符号$ H $ 的来源). 在本文讨论中仅涉及$ H^1 $ 空间(即$ k=1 $ ). 因为考虑了函数的导数, 需要将函数的模进一步细化为半模(单竖线表示)与模(双竖线表示), 分别定义为$$ \begin{array}{*{20}{l}} |u|_0 = \left(\displaystyle\int_{\varOmega}u^2{{\rm{d}}} x\right)^{\textstyle\frac{1}{2}} = \|u\|_{L^{2}}, \quad |u|_1 = \left(\displaystyle\int_{\varOmega}u^{\prime}u^{\prime}{{\rm{d}}} x\right)^{\textstyle\frac{1}{2}} = \|u^{\prime}\|_{L^{2}}, \quad \|u\|_1 = |u|_0+ |u|_1 \end{array} $$ (7) 其中, 下标表示最高求导阶次.
3.2 离散化方程组(泊松方程及其离散化)
无论何种数值方法最终都将变为求解线性方程组, 因而本小节将以简单的泊松方程为例, 简述推导离散方程组的基本流程, 以便后续的讨论.
记空间域
$ \varOmega $ 的边界为$ \partial \varOmega $ , 考虑$$ \begin{array}{*{20}{l}} -\Delta u = f\quad {{\rm{in}}}\; \varOmega, \quad u = 0 \quad{{\rm{on}}}\; \partial \varOmega \end{array} $$ (8) 将包含真实物理解的函数空间记为
$ V $ , 则方程(8)对应的弱形式可通过分部积分并考虑边界条件推得, 即寻找$ u \in V $ , 使得$$ \begin{array}{*{20}{l}} a(u, v) = (f, v), \quad \; \forall v \in V \end{array} $$ (9) 其中,
$ a(u, v) $ ,$ (f, v) $ 分别称为双线性格式与线性格式, 与式(4)相对应, 分别定义为$$ \begin{array}{*{20}{l}} a(u, v) = \int_\varOmega \nabla u \cdot \nabla v {{\rm{d}}}x, \quad (f, v) = \int_\varOmega f v {{\rm{d}}}x \end{array} $$ (10) 将包含有限个元素的近似函数空间记为
$ V^h \subset V $ , 待解问题变为: 寻找$ u^h \in V^h $ , 使得$$ \begin{array}{*{20}{l}} a_h (u^h, v^h) = (f, v^h), \quad \; \forall v^h \in V^h \end{array} $$ (11) 需要指出, 由于
$ V^h \subset V $ , 对于$ \forall u^h, v^h \in V^h $ , 除了在$ V^h $ 空间内定义双线性格式$ a_h (u^h, v^h) $ , 还可以在$ V $ 空间内定义相应的$ a(u^h, v^h) $ . 为避免引入过多的数学定义, 而不能专注于问题本身, 在下文不引起混淆的情况下, 把$ a_h $ 中的下标$ h $ 略去①, 但在考虑解的收敛性时需要加以区分.进一步, 将
$ V^h $ 中线性无关的基函数记为$ \phi_i \; (i=1,2, \cdots, n) $ (考虑到$ V^h $ 的定义,$ n $ 为有限值), 则对于函数$ u^h, v^h\in V^h $ , 将有如下线性组合形式$$ \begin{array}{*{20}{l}} u^h = U_j \phi_j, \quad v^h = V_i \phi_i \end{array} $$ (12) 其中,
$ U_j $ ,$ V_i $ 为实数. 将式(12)代入到式(11)中, 并考虑到$ v^h $ 的任意性, 则有$$ \begin{array}{*{20}{l}} \displaystyle\sum\limits^n_{j=1} a(\phi_j, \phi_i) U_j = (f, \phi_i) \end{array} $$ (13) 由于双线性格式的对称性, 记
$ K_{ij} = a(\phi_i, \phi_j) $ ,$ F_i = (f, \phi_i) $ , 若采用矩阵写法$ {\boldsymbol{{K}}} = (K_{ij}) $ ,$ {\boldsymbol{{U}}} = (U_j) $ ,$ {\boldsymbol{{F}}} = (F_i) $ , 则式(13)可写为$$ \begin{array}{*{20}{l}} {\boldsymbol{{K}}}{\boldsymbol{{U}}}={\boldsymbol{{F}}} \end{array} $$ (14) 再进一步, 将空间域
$ \varOmega $ 离散为有限个空间单元,$ \varOmega \approx \varOmega^h \equiv \cup_i E_i $ , 此时, 作用于整个空间域$ \varOmega $ 上的函数空间$ V^h $ 将由作用在单元$ E $ 上的函数空间$ V^{h|E} $ 集合构成, 对应着整体刚度矩阵与右端项将由单元内积分(亦可以理解为全域积分, 但在单元外部的函数取值为零)组装得到, 即$$ \begin{array}{*{20}{l}} {\boldsymbol{{K}}} = \displaystyle\sum\limits_E {\boldsymbol{{K}}}_E, \quad {\boldsymbol{{F}}} = \displaystyle\sum\limits_E {\boldsymbol{{F}}}_E \end{array} $$ (15) 其中,
$ \sum $ 为组装操作, 由于不易产生歧义, 直接采用了相加符号.至此, 上述理论是有限元法与虚单元法共同的理论基础.
3.3 存在性、唯一性和收敛条件
对于数值求解, 自然地需要考虑式(9)、式(11)是否存在解且解是否唯一; 当将计算域进行空间离散后(记空间离散特征尺寸为
$ h $ ), 还需要考虑收敛性, 即$ h\rightarrow 0 $ 时,$ \|u-u^h\|\rightarrow 0 $ 是否成立. 分别讨论如下:(1)解的存在性与唯一性
对于式(9), 真实解所在的空间为在边界取值为零的一阶 Hilbert 空间, 即
$ V=H^1_0 $ , 下标$ 0 $ 表示函数在边界处取值为零. 如果存在$ C>0 $ , 使得$$ \begin{array}{*{20}{l}} |a(u, v)| \leqslant C\|u\|_m\|v\|_m, \quad \forall u, v \in H^m \end{array} $$ (16) 称双线性格式
$ a(\cdot, \cdot) $ 为连续的, 类似地, 连续性需要$ |(f, v)| \leqslant ||f|| \cdot ||v||_m $ . 进一步如果存在$ \alpha >0 $ , 使得$$ \begin{array}{*{20}{l}} a(v, v) \geqslant \alpha\|v\|^{2}_m, \quad \forall v \in H^m \end{array} $$ (17) 称
$ a(\cdot, \cdot) $ 为强制的(coercive) 或者$ H^m $ −椭圆的(elliptic). 可以证明强制的双线性格式对应的方程存在且具有唯一解, 即著名的 Lax-Milgram 定理. 需要指出, 式(16)、式(17)中不等式右端项采用模度量或半模度量是等价的. 对于式(9), 可以证明$$ \begin{array}{*{20}{l}} a(u, v) \leqslant |u|_{1}|v|_{1}, \quad a(v, v) \geqslant |v|_{1}^{2}, \quad \forall u, v \in V \end{array} $$ (18) 因而, 式(9)存在唯一解. 上述理论与相关证明, 可参阅 (Braess 2007, Brenner and Scott 2008). 对于式(11), 其解的存在性亦需要验证
$ a_h(u^h, v^h) $ 是否是强制的, 即: 是否满足式(16)和式(17), 相关讨论将在下一节展开.(2)解的收敛性
判断解是否收敛, 需要验证协调性(consistency)和稳定性(stability)(Ralston and Rabinowitz 2001). 协调性指当
$ h\rightarrow 0 $ 时, 式(14)的解满足微分方程与边界条件, 即趋向真实解; 稳定性指式(14)有解, 即:$ {\boldsymbol{{K}}} $ 非奇异. 因而可以通过给定一些简单的真实解, 来判断方程的解是否满足协调性与稳定性, 即进行分片测试(patch test) (Taylor et al. 1986).3.4 多项式函数空间与虚单元法特定的近似函数形式
3.4.1 多项式函数空间
函数空间中, 最直观的为多项式函数构成的空间. 记
$ {\cal{P}}_k $ 为最高阶次不超过$ k $ 的多项式函数构成的空间,$ {\boldsymbol{{{\cal{P}}}}}_k $ 为对应的矢量函数空间.(1) 在一维问题中, 记
$ \xi $ 为无量纲坐标, 则有$$ {\cal{P}}_0 = \{1\}, \quad {\cal{P}}_1 = \{{\cal{P}}_0, \xi\}, \; \cdots\;,\quad {\cal{P}}_k = \{{\cal{P}}_{k-1}, \xi^k\} $$ $ {\cal{P}}_k $ 共有$ k+1 $ 个线性无关函数, 此外, 记$ {\cal{P}}_{-1} = 0 $ ;(2) 在二维几何空间的标量问题中, 记
$ \xi $ ,$ \eta $ 为无量纲坐标, 则有$$ {\cal{P}}_0 = \{1\}, \quad {\cal{P}}_1 = \{{\cal{P}}_0, \xi, \eta\}, \; \cdots, \; {\cal{P}}_k = \{{\cal{P}}_{k-1}, \xi^k, \xi^{k-1}\eta, \cdots, \eta^{k} \} $$ $ {\cal{P}}_k $ 共有$ (k+2)(k+1)/2 $ 个线性无关的函数;(3) 在二维几何空间的矢量问题中, 则有
$$ {\boldsymbol{{{\cal{P}}}}}_0 = \left\{ \left(\begin{array}{l} 1 \\ 0 \end{array}\right), \left(\begin{array}{l} 0 \\ 1 \end{array}\right)\right\}, \quad {\boldsymbol{{{\cal{P}}}}}_1 = \left\{{\boldsymbol{{{\cal{P}}}}}_0, \left(\begin{array}{l} \xi \\ 0 \end{array}\right), \left(\begin{array}{l} 0 \\ \xi \end{array}\right), \left(\begin{array}{l} \eta \\ 0 \end{array}\right), \left(\begin{array}{l} 0 \\ \eta \end{array}\right)\right\}, \cdots $$ $$ {\boldsymbol{{{\cal{P}}}}}_k = \left\{ {\boldsymbol{{{\cal{P}}}}}_{k-1}, \left(\begin{array}{l} \xi^k \\ 0 \end{array}\right), \left(\begin{array}{l} 0 \\ \xi^k \end{array}\right), \left(\begin{array}{l} \xi^{k-1}\eta \\ 0 \end{array}\right), \left(\begin{array}{l} 0 \\ \xi^{k-1}\eta \end{array}\right), \cdots, \left(\begin{array}{l} \eta^k \\ 0 \end{array}\right), \left(\begin{array}{l} 0 \\ \eta^k \end{array}\right)\right\} $$ 共有
$ (k+2)(k+1) $ 个线性无关的矢量函数. 对于小变形下的弹性问题, 将$ {\boldsymbol{{{\cal{P}}}}}_1 $ 变为$$ {\boldsymbol{{{\cal{P}}}}}_1 = \left\{ \left(\begin{array}{l} 1 \\ 0 \end{array}\right), \left(\begin{array}{l} 0 \\ 1 \end{array}\right), \left(\begin{array}{l} -\eta \\ \xi \end{array}\right), \left(\begin{array}{l} \eta \\ \xi \end{array}\right), \left(\begin{array}{l} \xi \\ 0 \end{array}\right), \left(\begin{array}{l} 0 \\ \eta \end{array}\right)\right\} $$ 如此, 并不改变函数空间内线性无关多项式矢量函数的数目, 但利用前三项对位移矢量
$ {\boldsymbol{{u}}} $ 进行近似时, 可对应着应变为零的情况, 即发生刚体位移. 比如, 若$ {\boldsymbol{{u}}} = C(-\eta, \xi)^{{\rm{T}}} $ , 其中,$ C $ 为常数, 对应的应变为$ {\boldsymbol{{\epsilon}}} = \left[\nabla {\boldsymbol{{u}}} + (\nabla {\boldsymbol{{u}}})^{{\rm{T}}} \right] /2 = {\boldsymbol{{0}}} $ . 如此调整, 在生成刚度矩阵时, 仅需少量操作, 便可避免刚性位移, 具体讨论将在下一章给出.3.4.2 虚单元法特定的近似函数形式
首先考虑如下问题, 在二维多边形
$ E $ 域内, 标量函数$ u\in H^{1} $ 满足$$ \begin{array}{*{20}{l}} u = g \in {\cal{P}}_k\cap C^{0} \quad {{\rm{on}}}\; \partial E, \qquad \Delta u= f\in {\cal{P}}_{k-2} \quad {{\rm{in}}}\; E \end{array} $$ (19) 即函数
$ u $ 进行拉普拉斯运算后得到最高阶次不超过$ k-2 $ 的多项式, 并且在多边形边界上$ u $ 为连续的且不超过$ k $ 次的多项式, 那么函数$ u $ 一定是多项式么？通过反证法, 显然答案是否定的. 下文将介绍虚单元法的函数空间由满足上述条件的函数构成(多项式函数以及非多项式函数), 因为所对应的非多项式没有显式形式(或者不易求出), 而被称为虚单元法. 与之对应, 有限元法的函数空间仅为多项式空间, 因而, 不同方法的核心区别是近似函数空间
$ V^h $ 的差异.3.5 虚单元法在泊松方程中的应用
由于泊松方程待解量为标量函数, 相对简单, 本节将以泊松方程为例, 介绍虚单元法的基本思路与流程. 相比于下一节介绍的弹性方程, 本节略侧重于数学理论, 以保证方法的数学完备. 本节按照逆序的思路, 首先给出式(11)存在唯一解以及收敛的条件, 其次引出虚单元方法来实现上述条件, 最后给出具体的实施细节.
3.5.1 目标
空间离散后, 对于任意的
$ V^h \subset V $ , 假定$$ \begin{array}{*{20}{l}} a_h(u^h, v^h) = \displaystyle\sum_E a^E_h(u^h, v^h), \quad \forall u^h, v^h \in V^h \end{array} $$ (20) 即整体的双线性格式可由单元内的双线性格式组装得到, 如此仅需对单元内的双线性格式进行讨论. 对于任意的多边形单元
$ E $ , 相应的空间离散特征尺度$ h $ , 以及定义在单元上的近似空间$ V^{h|E} $ , 如果存在一个正整数$ k\geqslant 1 $ , 使得$ {\cal{P}}_k(E) \subset V^{h|E} $ , 且有(1) 对于
$ \forall p\in{\cal{P}}_k(E) $ 以及$ \forall v^h \in V^{h|E} $ , 满足$$ \begin{array}{*{20}{l}} a^E_h(p, v^h) = a^E(p, v^h) \end{array} $$ (21) (2) 存在两个不依赖于
$ E $ 以及$ h $ 的正数$ \alpha_* $ 和$ \alpha^* $ , 对于$ \forall v^h \in V^{h|E} $ , 满足$$ \begin{array}{*{20}{l}} \alpha_{*} a^{E}\left(v^{h}, v^{h}\right) \leqslant a_{h}^{E}\left(v^{h}, v^{h}\right) \leqslant \alpha^{*} a^{E}\left(v^{h}, v^{h}\right) \end{array} $$ (22) 此时, 可以证明式(11)存在唯一解, 且有足够的精度, 保证
$$ \begin{array}{*{20}{l}} \left|u-u^{h}\right|_{1} \leqslant C h^{k}|u|_{k+1, \Omega} \end{array} $$ (23) 条件(1)保证真实解为最高阶次不超过
$ k $ 的多项式时, 近似解可逼近真实解, 即协调性条件; 条件(2)保证$ a_h $ 的度量与$ a $ 相同, 此时能保证生成的刚度矩阵是满秩的, 称为稳定性条件. 上述证明可参考 (Beirão Da Veiga et al. 2013a).为满足条件(1), 首先定义函数空间
$ V^{E, k} $ 为式(19)的解所构成的空间. 其次, 定义映射操作符$ \Pi^E_k: V^{E, k} \rightarrow {\cal{P}}_k(E)\subset V^{E, k} $ , 满足: 对于$ \forall v \in V^{E, k} $ 有$$ \left. \begin{gathered} a^{E}\left(\Pi_{k}^{E} v, p\right)=a^{E}(v, p), \quad \forall p \in {\cal{P}}_{k}(E) \\ \overline{\Pi_{k}^{E} v}=\bar{v} \end{gathered}\right\} $$ (24) 其中,
$ \bar{(\cdot)} $ 为平均操作符, 对于任意函数$ \varphi $ , 有:$ \overline{\varphi} := \dfrac{1}{n} \sum_{v=1}^n \varphi({\boldsymbol{{x}}}_v) $ , 其中$ {\boldsymbol{{x}}}_v $ 为单元$ E $ 的顶点位置 (共有$ n $ 个顶点). 可以证明(函数以及函数梯度均相等)$$ \begin{array}{*{20}{l}} \Pi_{k}^{E} p = p, \quad \forall p \in {\cal{P}}_{k}(E) \end{array} $$ (25) 至此, 对于
$ \forall u, v \in V^{h|E} $ , 令$ a^E_h(u, v) = a^E(\Pi_{k}^{E}u, \Pi_{k}^{E}v) $ , 则能满足条件(1), 即式(21).为满足条件(2), 假定一个对称正定的双线性格式
$ S^E(u, v) $ , 对于$ \forall v \in V^{E, k} $ 满足$ \Pi_{k}^{E} v= 0 $ 的前提下, 满足$$ \begin{array}{*{20}{l}} c_0 a^E(v, v) \leqslant S^E(v, v) \leqslant c_1 a^E(v, v) \end{array} $$ (26) 其中, 正数
$ c_0, \; c_1 $ 与单元和单元尺度无关. 根据式(25), 对于$ \forall u \in V^{E, k} $ , 则有:$ \Pi_{k}^{E} \left(u-\Pi_{k}^{E}u \right) = 0 $ . 令$ v = u-\Pi_{k}^{E}u $ , 代入式(26), 则对于$ \forall u \in V^{E, k} $ , 有$$ \begin{array}{*{20}{l}} c_0 a^E(u-\Pi_{k}^{E}u, u-\Pi_{k}^{E}u) \leqslant S^E(u-\Pi_{k}^{E}u, u-\Pi_{k}^{E}u) \leqslant c_1 a^E(u-\Pi_{k}^{E}u, u-\Pi_{k}^{E}u) \end{array} $$ (27) 至此, 令
$$ \begin{array}{*{20}{l}} a^E_h(u, v) = a^E(\Pi_{k}^{E}u, \Pi_{k}^{E}v) + S^E(u-\Pi_{k}^{E}u, v-\Pi_{k}^{E}v), \quad \forall u, v \in V^{h|E} \end{array} $$ (28) 此时, 考虑式(25), 易证明式(28)的定义满足条件(1), 即式(21); 考虑到式(26)以及
$ a^E(\Pi_{k}^{E}v, \Pi_{k}^{E}v) + a^E(v-\Pi_{k}^{E}v, v-\Pi_{k}^{E}v) = a^E(v, v) $ , 亦可证明式(28)满足条件(2), 即式(22), 其中$ \alpha^*= \max\{1, c_1\} $ ,$ \alpha_* = \min\{1, c_0\} $ .基于上述讨论, 虚单元法的总体思路可以简述为: 在满足式(19)的
$ V^{E, k} $ 空间中, 定义满足式(24)的映射操作符$ \Pi^E_k: V^{E, k} \rightarrow {\cal{P}}_k (E) \subset V^{E, k} $ , 并选用满足式(27)的$ S^E $ 来定义双线性格式(28).3.5.2 实施方案
虚单元法的具体实施中, 包括三个核心细节: 根据
$ V^{E, k} $ 设定自由度; 构造$ S^E $ ; 以及计算线性格式(离散方程组的右端项). 现分别予以讨论.(1)根据
$ V^{E, k} $ 设定自由度考虑多边形单元
$ E $ , 记其形心为$ {\boldsymbol{{x}}}_E $ , 边数为$ n $ , 特征尺寸为$ h_E $ .对于式(19)的第一个条件, 对于多边形的任意边, 需该边上
$ k+1 $ 个点的函数取值则可确定最高阶次为$ k $ 的多项式函数, 这些点可由该边的 2 个顶点, 以及边内$ k-1 $ 个平均分布的点(或位于边内线积分点的 位置)构成(当$ k=1 $ 时, 每个多项式函数均为线性函数, 则无需边内节点). 由于多边形的顶点被 2 条边共用, 因而, 共需要$ n + (k-1)n = nk $ 个自由度即可确定$ \partial E $ 上连续的多项式函数.对于式(19)的第二个条件, 对于任意给定的
$ f $ , 则式(19)的解是唯一的. 因而若满足$ f\in {\cal{P}}_{k-2}(E) $ , 由于$ {\cal{P}}_{k-2} $ 共有$ k(k-1)/2 $ 个线性无关的多项式函数(预备知识 3.4.1 中已予以讨论), 需要增加$ k(k-1)/2 $ 个自由度来保证式(19)的解的函数空间的维度, 这些自由度设定在单元内部点上.因而, 共需
$ N_{{\rm{dof}}} = {\rm{dim}} \; V^{E, k} = nk + k(k-1)/2 $ 个自由度. 图 1 表示了五边形($ n=5 $ )单元在$ k=2 $ 时, 自由度的设定位置.在确定完自由度位置后, 现在确定自由度的取值. 将节点与单元边界上的设定自由度的点的集合记为
$ n_f $ , 单元内部设定自由度的点的集合记为$ n_b $ , 并记$ {\boldsymbol{{x}}}_i $ 处自由度取值为$ {\rm{dof}}_i(v^h) $ .若
$ {\boldsymbol{{x}}}_i \in n_f $ , 则该点处自由度取值为近似函数的取值, 即:$ {\rm{dof}}_i(v^h) = v^h({\boldsymbol{{x}}}_i) $ ;若
$ {\boldsymbol{{x}}}_i \in n_b $ , 则该点处自由度取值需要考虑双线性格式的定义, 即, 对于$ \forall u^h, v^h \in V^{E, k} $ $$ \begin{array}{*{20}{l}} a^E_h(u^h, v^h)=\displaystyle\int_E \nabla u^h \cdot \nabla v^h {{\rm{d}}}x = \displaystyle\int_{\partial E} {\boldsymbol{{n}}} \cdot \nabla u^h v^h {{\rm{d}}}x - \displaystyle\int_E \Delta u^h v^h {{\rm{d}}}x \end{array} $$ (29) 上式推导中采用了分部积分以及高斯定理,
$ {\boldsymbol{{n}}} $ 为单元的外法向, 且有:$ {\boldsymbol{{n}}}\cdot\nabla v^h = \partial v^h / \partial n $ . 由于$ V^{E, k} $ 为满足式(19)的解构成的空间, 因而, 在$ \partial E $ 上$ v^h $ ,$ \partial u^h / \partial n $ 为多项式, 可由$ {\boldsymbol{{x}}}_i \in n_f $ 上设定的自由度确定(可设定边内自由度的点位于线积分点的位置, 从而可以精确计算上式右端第一项的单元边界积分); 单元内部积分仅包含右端第二项, 而考虑到式(19)中$ \Delta u^h \in {\cal{P}}_{k-2}(E) $ , 因而把$ {\boldsymbol{{x}}}_i \in n_b $ 处的自由度取值设定为$$ \begin{array}{*{20}{l}} {\rm{dof}}_i(v^h) = \dfrac{1}{A_E} \displaystyle\int_E p v^h {{\rm{d}}}x, \quad \forall p \in {\cal{P}}_{k-2}(E) \end{array} $$ (30) 其中,
$ A_E $ 为单元面积. 需要指出, 一个$ {\boldsymbol{{x}}}_i \in n_b $ 对应一个$ p $ ,$ {\cal{P}}_{k-2} $ 共有$ k(k-1)/2 $ 项, 则共有$ k(k-1)/2 $ 个单元内部点设定了自由度. 如此, 可以避免体积分来确定刚度矩阵, 且避免了确定$ u^h $ 在单元内的取值. 因而, 虚单元的一个优势为: 通过设定合理的自由度取值, 在规避求解形函数在单元内部的取值的同时, 避免进行体积分来确定刚度矩阵.对自由度的取值进一步讨论如下.
① 式(30)中
$ p $ 为无量纲的多项式, 因而式(30)的量纲与$ v^h $ 的量纲相同. 特别的, 当$ p=1 $ 时, 该自由度对应着$ v^h $ 在单元内部的平均值. 在单元$ E $ 内的无量纲度量可以为$$ \begin{array}{*{20}{l}} \xi =\dfrac{x- x_E}{h_E}, \quad \eta = \dfrac{y-y_E}{h_E} \end{array} $$ (31) ② 与有限元类似, 每个自由度对应着一个基函数
$ \phi_i(x) $ , 使得$$ \begin{array}{*{20}{l}} v^h(x) = \displaystyle\sum\limits_{i=1}^{N_{{\rm{dof}}}} { {\rm{dof}}}_i (v^h) \phi_i(x) \end{array} $$ (32) 此时, 亦有:
$ { {\rm{dof}}}_i(\phi_j) = \delta_{ij} $ . 由于$ v^h(x) $ 无显式表达式, 则$ \phi_i(x) $ 亦无显式表达式.③ 考虑到式(28), 与上述自由度对应的局部刚度矩阵为
$$ \begin{array}{*{20}{l}} a^E_h(\phi_i, \phi_j) = a^E(\Pi_{k}^{E}\phi_i, \Pi_{k}^{E}\phi_j) + S^E(\phi_i-\Pi_{k}^{E}\phi_i, \phi_j-\Pi_{k}^{E}\phi_j) \end{array} $$ (33) (2)稳定项
$ S^E $ 的构造式(33)右端第一项生成的刚度矩阵并不满秩, 因而需要增加稳定项. 考虑到稳定性需要满足式(27), 最直观的设定为
$$ \begin{array}{*{20}{l}} \begin{aligned} & S^E(\phi_i-\Pi_{k}^{E}\phi_i, \phi_j-\Pi_{k}^{E}\phi_j) = a^E(\phi_i-\Pi_{k}^{E}\phi_i, \phi_j-\Pi_{k}^{E}\phi_j) =\\ & a^E\left(\sum_{r=1}^{N_{{\rm{dof}}}} { {\rm{dof}}}_{r} (\phi_i-\Pi_{k }^{E}\phi_i) \phi_{r}, \sum_{r=1}^{N_{{\rm{dof}}}} { {\rm{dof}}}_r (\phi_j-\Pi_{k}^{E}\phi_j) \phi_r\right) =\\ & \sum_{r=1}^{N_{{\rm{dof}}}} { {\rm{dof}}}_r (\phi_i-\Pi_{k}^{E}\phi_i) { {\rm{dof}}}_r (\phi_j-\Pi_{k}^{E}\phi_j) a^E(\phi_r, \phi_r) \end{aligned} \end{array} $$ (34) 需要指出, 在上述推导中,
$ \phi_i $ 和$ \Pi_{k}^{E}\phi_i $ 被表示成基函数$ \phi_r $ 的线性组合, 即:$ \phi_i = \displaystyle\sum_{r=1}^{N_{{\rm{dof}}}} { {\rm{dof}}}_r (\phi_i) \phi_r $ , 对于$ \Pi_{k}^{E}\phi_i $ 同理. 在合理的$ h_E $ 的设定下, 可以保证$ a^E(\phi_r, \phi_r) = O(1) $ , 因而可以设定$$ \begin{array}{*{20}{l}} S^E(\phi_i-\Pi_{k}^{E}\phi_i, \phi_j-\Pi_{k}^{E}\phi_j) = \displaystyle\sum\limits_{r=1}^{N_{{\rm{dof}}}} {\rm{dof}}_r(\phi_i-\Pi_{k}^{E}\phi_i) {\rm{dof}}_r(\phi_j-\Pi_{k}^{E}\phi_j) \end{array} $$ (35) 来满足式(27). 需要指出稳定项的设定有多种形式, 更多的讨论可参考 (Beirão da Veiga et al. 2017b).
(3)离散方程组右端项的构造
考虑到单元离散, 有
$$ \begin{array}{*{20}{l}} (f, \phi_i) \approx (f_h, \phi_i) = \displaystyle\sum\limits_E (f_h, \phi_i)_E \end{array} $$ (36) 根据
$ k $ 的取值不同,$ f_h $ 的定义与$ (f_h, \phi_i)_E $ 的构造可分为三种情况① 对于
$ k=1 $ ,$ f_h $ 为$ f $ 在单元$ E $ 内的平均值, 即$$ \begin{array}{*{20}{l}} f_h = \frac{1}{A_E} \displaystyle\int_E f {{\rm{d}}}x \approx f({\boldsymbol{x_E}}) \end{array} $$ (37) 此时
$$ \begin{array}{*{20}{l}} (f_h, \phi_i)_E = \displaystyle\int_E f({\boldsymbol{x_E}}) \phi_{i} {{\rm{d}}}x = A_E f({\boldsymbol{x_E}}) \dfrac{1}{n}\displaystyle\sum\limits_{v =1}^{n} \phi_i ({\boldsymbol{{x}}}_v) = \dfrac{A_E}{n} f({\boldsymbol{x_E}}) \end{array} $$ (38) 上述推导中, 考虑了
$ \phi_i ({\boldsymbol{{x}}}_v) = \delta_{iv} $ .② 对于
$ k=2 $ , 类似式(24), 需要定义线性格式的映射操作符$ \Pi_{k}^0: L^2(E) \rightarrow {\cal{P}}_{k}(E) $ , 对于$ \forall w \in L^2(E) $ , 满足$$ \begin{array}{*{20}{l}} (p, \Pi_k^0 w - w) = 0 , \quad \forall p \in {\cal{P}}_{k}(E) \end{array} $$ (39) 此时,
$ f_h = \Pi_{k}^0 f $ , 类似可定义$ \Pi_{k}^0 \phi_i $ . 如此, 反复利用式(39), 可构造单元右端项为$$ \begin{array}{*{20}{l}} (f_h, \phi_i)_E = \displaystyle\int_E \Pi_{k}^0 f \cdot \phi_i {{\rm{d}}}x = \displaystyle\int_E \Pi_{k}^0 f \cdot \Pi_{k}^0 \phi_i {{\rm{d}}}x = \displaystyle\int_E f \cdot \Pi_{k}^0 \phi_i {{\rm{d}}}x \end{array} $$ (40) 其中,
$ \Pi_{k}^0 $ 可以通过单元内部自由度式(30)求出, 更多实施细节可参考 4.2.4 节.③ 对于
$ k>2 $ , 类似的, 定义映射操作符$ \Pi_{k-2}^0: L^2(E) \rightarrow {\cal{P}}_{k-2}(E) $ ,$ f_h = \Pi_{k-2}^0 f $ 以及$ \Pi_{k-2}^0 \phi_i $ . 构造单元右端项为$$ \begin{array}{*{20}{l}} (f_h, \phi_i)_E = \displaystyle\int_E \Pi_{k-2}^0 f \cdot \phi_i {{\rm{d}}}x = \displaystyle\int_E f \cdot \Pi_{k-2}^0 \phi_i {{\rm{d}}}x \end{array} $$ (41) 其中,
$ \Pi_{k-2}^0 $ 的计算可参考 4.2.4 节.如此, 可证明(Beirão Da Veiga et al. 2013a)
$$ \begin{array}{*{20}{l}} (f_h, \phi_i) - (f, \phi_i) \leqslant Ch^k \left(\displaystyle\sum\limits_E \left|f\right|^2_{k-1, E}\right)^{1/2} \left|\phi_i\right|_1 \end{array} $$ (42) 至此, 虚单元求解泊松问题时单元内部的刚度矩阵为式(33), 右端项根据
$ k $ 的取值在式 (38)、式(40)、式(41)三者中选择合适的公式计算, 进行组装后, 便可进行近似求解.4. 虚单元法处理线弹性问题
上一章以泊松方程为例, 介绍了虚单元法的核心理论, 侧重解释为什么引入一些处理, 比如自由度的设定、多项式映射等, 并强调数学完备. 本章以弹性问题为例, 通过对比有限元, 具体介绍虚单元法的应用过程. 为独立于上一章节, 本章直接从应用角度理解虚单元, 部分概念略有重复, 但更侧重物理意义.
4.1 弹性问题描述
以二维连续弹性体为例, 如图 2 所示, 物体
$ \varOmega $ 在准静态、小变形条件下的平衡条件为$$ \begin{array}{*{20}{l}} \nabla \cdot {{\boldsymbol{{\sigma}}}} + {\boldsymbol{{f}}} = {\boldsymbol{{0}}} \end{array} $$ (43) 其中,
$ {\boldsymbol{{\sigma}}} $ 为柯西应力张量,$ {\boldsymbol{{f}}} $ 是为单位体积的体力. 物体边界记为$ \partial \varOmega $ , 边界条件为$$ \begin{array}{*{20}{l}} \left. \begin{aligned} {\boldsymbol{{\sigma}}} \cdot {\boldsymbol{{n}}} & = \bar{{\boldsymbol{{t}}}}, \quad{{\rm{on}}} \;\; \partial \varOmega_t \\ {\boldsymbol{{u}}} & = {\boldsymbol{{0}}} , \quad{{\rm{on}}} \;\; \partial \varOmega_u \end{aligned} \right\} \end{array} $$ (44) 其中,
$ {\boldsymbol{{n}}} $ 为边界法向,$ \bar{{\boldsymbol{{t}}}} $ 为指定应力, 且有$ \partial \varOmega = \partial \varOmega_{t} \cup \partial \varOmega_{u} $ 以及$ \partial \varOmega_{t} \cap \partial \varOmega_{u} = \emptyset $ . 本构方程为$ {\boldsymbol{{\sigma}}} = {\boldsymbol{{{{C}}}}} {\boldsymbol{{\epsilon}}} $ , 其中$ {\boldsymbol{{{{C}}}}} $ 为四阶材料弹性常数,$ {\boldsymbol{{\epsilon}}} $ 为应变张量, 定义为位移梯度的对称部分, 即$ {\boldsymbol{{\epsilon}}} = \left[\nabla {\boldsymbol{{u}}} + (\nabla {\boldsymbol{{u}}})^{{\rm{T}}} \right] / 2 $ .控制方程的弱形式为: 寻找
$ {\boldsymbol{{u}}} \in {\boldsymbol{{{\cal{V}}}}} $ 使得②$$ \begin{array}{*{20}{l}} \displaystyle\int_\varOmega(\nabla \cdot {{\boldsymbol{{\sigma}}}} + {\boldsymbol{{f}}}) \cdot {\boldsymbol{{v}}} \; {\rm{d}}\varOmega = 0,\quad \forall {\boldsymbol{{v}}} \in {\boldsymbol{{{\cal{V}}}}} \end{array} $$ (45) 其中,
$ {\boldsymbol{{v}}} $ 为试矢量,$ {\boldsymbol{{{\cal{V}}}}} $ 为包含真实解的矢量函数空间, 其中每个分量隶属于$ H^1(\varOmega) $ . 通过分部积分, 考虑应力的对称性以及代入边界条件, 式(45)可写成如下形式$$ \begin{array}{*{20}{l}} a({\boldsymbol{{u}}}, {\boldsymbol{{v}}}) = L({\boldsymbol{{v}}}),\quad \forall {\boldsymbol{{v}}} \in {\boldsymbol{{{\cal{V}}}}} \end{array} $$ (46) 其中,
$ a({\boldsymbol{{u}}}, {\boldsymbol{{v}}}) $ 与$ L({\boldsymbol{{v}}}) $ 分别为弹性问题的双线性与线性形式, 定义为$$ \begin{array}{*{20}{l}} a({\boldsymbol{{u}}}, {\boldsymbol{{v}}}) = \displaystyle\int_\varOmega {\boldsymbol{{\sigma}}}({\boldsymbol{{u}}}) : {\boldsymbol{{\epsilon}}}({\boldsymbol{{v}}}) \; {{\rm{d}}} \varOmega \end{array} $$ (47) $$ \begin{array}{*{20}{l}} L({\boldsymbol{{v}}}) = \displaystyle\int_\varOmega {\boldsymbol{{v}}} \cdot {\boldsymbol{{f}}} \; {{\rm{d}}} \varOmega + \displaystyle\int_{\partial \varOmega_t} {\boldsymbol{{v}}} \cdot \bar{{\boldsymbol{{t}}}} \; {{\rm{d}}} \partial \varOmega \end{array} $$ (48) 同样, 记含有限个基函数的近似空间为
$ {\boldsymbol{{{\cal{V}}}}}^h $ , 相应地, 近似的双线性格式$ a_h({\boldsymbol{{u}}}^h, {\boldsymbol{{v}}}^h) $ 和线性格式$ L_h({\boldsymbol{{v}}}^h) $ 形式与式(47)、式(48)类似, 这里不再重复.4.2 离散方程
如前所述, 虚单元法与有限元法类似, 也需要将计算域近似为有限个单元构成的区域, 即:
$ \varOmega \approx \varOmega^h \equiv \cup_i E_i $ . 不同于有限元中单元需要为凸多边形来保证雅可比矩阵的行列式为正, 在虚单元中单元$ E_i $ 可以为任意形状多边形(凸、凹). 本节将重复虚单元法的映射操作符与自由度设定, 并给出刚度矩阵与右端项的具体矩阵表达.4.2.1 映射操作符
对于矢量函数空间, 同样定义映射操作符
$ \Pi^{E}_k $ , 将定义在单元$ E $ 上的近似函数空间$ {\boldsymbol{{{\cal{V}}}}}^h(E) $ 映射到最高阶次不超过$ k $ 的多项式空间$ {\boldsymbol{{{\cal{P}}}}}_k(E) $ ,$ \Pi^{E}_k: {\boldsymbol{{{\cal{V}}}}}^h(E) \rightarrow {\boldsymbol{{{\cal{P}}}}}_k(E) $ , 下文中在不产生歧义的情况下,$ \Pi \equiv \Pi^{E}_k $ . 式(24)亦称为正交条件, 即:$$ \begin{array}{*{20}{l}} a^E ({\boldsymbol{{u}}}^h - \Pi {\boldsymbol{{u}}}^h, \; {\boldsymbol{{p}}}) = 0,\quad \forall {\boldsymbol{{p}}} \in {\boldsymbol{{{\cal{P}}}}}_k(E) \end{array} $$ (49) 由于双线性形式在某种程度上表示了单元内部的能量, 因而正交条件表示了以能量为度量时,
$ {\boldsymbol{{u}}}^h $ 与$ \Pi {\boldsymbol{{u}}}^h $ 的误差并不能通过不超过$ k $ 次的多项式空间进行度量.如此, 利用式(49), 定义在单元上的双线性格式为:
$ {\boldsymbol{{u}}}^h, {\boldsymbol{{v}}}^h \in {\boldsymbol{{{\cal{V}}}}}^h $ $$ \begin{split} a^E({\boldsymbol{{u}}}^h, {\boldsymbol{{v}}}^h) =& a^E({\boldsymbol{{u}}}^h - \Pi{\boldsymbol{{u}}}^h + \Pi {\boldsymbol{{u}}}^h, {\boldsymbol{{v}}}^h - \Pi{\boldsymbol{{v}}}^h + \Pi {\boldsymbol{{v}}}^h) =\\ & a^E(\Pi{\boldsymbol{{u}}}^h, \Pi{\boldsymbol{{v}}}^h) + a^E({\boldsymbol{{u}}}^h - \Pi{\boldsymbol{{u}}}^h, {\boldsymbol{{v}}}^h - \Pi{\boldsymbol{{v}}}^h) \end{split} $$ (50) 右端第一项为映射操作符对
$ {\boldsymbol{{u}}}^h, {\boldsymbol{{v}}}^h $ 操作后在单元$ E $ 内的积分, 第二项为进行映射操作后没能考虑的能量, 又被称为稳定项, 需要能够确保$ a^E({\boldsymbol{{u}}}^h, {\boldsymbol{{v}}}^h) $ 为强制的, 保证存在唯一解.4.2.2 自由度设定
在弹性问题中, 近似函数空间中的分量亦需满足式(19). 对于
$ n_v $ 边形单元, 且边界上近似函数为最高阶次不超过$ k $ 的多项式时, 需在●
$ n_v $ 个节点布置函数取值的自由度;● 每条边界上存在
$ k-1 $ 个边界内部节点, 在其上布置函数取值的自由度;● 在单元内部布置
$ {\boldsymbol{{v}}}^h $ 与最高阶次不超过$ k-2 $ 的多项式内积的自由度(矩形式)$$ \begin{array}{*{20}{l}} \dfrac{1}{A_E}\displaystyle\int_E {\boldsymbol{{v}}}^h \cdot {\boldsymbol{{p}}} \; {{\rm{d}}} E, \quad \forall {\boldsymbol{{p}}} \in {\boldsymbol{{{\cal{P}}}}}_{k-2}(E) \end{array} $$ (51) 如第三章关于自由度的讨论所述, 对于标量问题共需
$ n_d = n_v k + k(k-1) / 2 $ 个自由度, 因而对于二维矢量问题, 共需$ 2n_d $ 个自由度.在一个维度的函数空间内定义操作符
$ {\rm{dof}}_i(v^h), \; i = 1, 2,\cdots, \; n_d $ , 表示$ v^h $ 在第$ i $ 个自由度的取值,$ \phi_i({\boldsymbol{x}}) $ 为第$ i $ 个自由度对应的基函数, 如前所述, 此时有$$ \begin{array}{*{20}{l}} v^h({\boldsymbol{{x}}}) = \displaystyle\sum\limits_{i=1}^{n_d} \phi_i({\boldsymbol{{x}}}) {{\rm{dof}}}_i(v^h) \end{array} $$ (52) 当设定自由度的点处均有两个自由度(二维矢量)时,
$ {\boldsymbol{{\phi}}} $ 表示基函数的向量表达, 有$ {\boldsymbol{{\phi}}}_1=[\phi_1, 0]^{{\rm{T}}}, \; {\boldsymbol{{\phi}}}_2=[0, \phi_1]^{{\rm{T}}}\;, \cdots, \; {\boldsymbol{{\phi}}}_{2n_d-1}=[\phi_{n_d}, 0]^{{\rm{T}}}, \; {\boldsymbol{{\phi}}}_{2n_d}=[0, \phi_{n_d}]^{{\rm{T}}} $ , 且有$$ \begin{array}{*{20}{l}} {\boldsymbol{{v}}}^h({\boldsymbol{{x}}}) = \displaystyle\sum\limits_{i=1}^{2n_d} {\boldsymbol{{\phi}}}_i({\boldsymbol{{x}}}) {{\rm{dof}}}_i({\boldsymbol{{v}}}^h) \end{array} $$ (53) 需要指出, 尽管虚单元法的空间离散格式(53)与有限元法相同, 但由于节点形函数并无显示表达, 单元内部任意位置处的位移并不能直接获取. 但网格节点的位移是待解量, 可通过节点位移后处理插值获取位移场、应力场等信息.
4.2.3 单元刚度矩阵
首先回顾传统有限元中单元刚度矩阵的构造. 二维弹性问题的自由度为节点位移
$$ \begin{array}{*{20}{l}} {\boldsymbol{{u}}}^E=\left[ \begin{array}{lllll} u^1_1 & u_2^1 & \ldots & u_1^{n_d} & u_2^{n_d} \end{array}\right]^{{\rm{T}}} \end{array} $$ (54) 其中, 下标
$ 1, 2 $ 分别表示两个维度, 上标$ 1, 2,\cdots, n_d $ 为单元节点编号. 形函数矩阵为$$ \begin{array}{*{20}{l}} \boldsymbol{N}=\left[ \begin{array}{lllll} {\boldsymbol{{\phi}}}_{1} & {\boldsymbol{{\phi}}}_{2} & \ldots & {\boldsymbol{{\phi}}}_{2n_{d}-1} & {\boldsymbol{{\phi}}}_{2n_{d}} \end{array} \right] \end{array} $$ (55) 应变为:
$ \boldsymbol{\epsilon} = {\boldsymbol{{B}}}{\boldsymbol{{u}}}^E = \boldsymbol{\partial}\boldsymbol{N} {\boldsymbol{{u}}}^E $ , 其中$ \boldsymbol{\partial} $ 在二维 Voigt 表示下, 为$$ \begin{array}{*{20}{l}} \boldsymbol{\partial} = \left[ \begin{array}{cc} \partial_{x_1} & 0\\ 0 & \partial_{x_2} \\ \partial_{x_2} & \partial_{x_1} \\ \end{array} \right] \end{array} $$ (56) 从式(47)出发, 并考虑
$ {\boldsymbol{{v}}}^h $ 的任意性, 可以推得有限单元法中单元刚度矩阵为$$ \begin{array}{*{20}{l}} {\boldsymbol{{K}}}_E = \displaystyle\int_E {\boldsymbol{{B}}}^{\rm{T}} {\boldsymbol{{C}}} {\boldsymbol{{B}}} \; {{\rm{d}}}E \end{array} $$ (57) 其中,
$ {\boldsymbol{{C}}} $ 是材料弹性常数矩阵.虚单元法中的刚度矩阵构造过程与有限元法类似, 但如式(50)所示, 需包含两部分
$$ \begin{array}{*{20}{l}} {\boldsymbol{{K}}}_E = {\boldsymbol{{K}}}^c_E + {\boldsymbol{{K}}}^s_E \end{array} $$ (58) 其中,
$ {\boldsymbol{{K}}}^c_E $ 为协调刚度矩阵(与映射操作符的协调性相关),$ {\boldsymbol{{K}}}^s_E $ 为稳定刚度矩阵(与稳定项相关).(1)协调刚度矩阵
最高阶次不超过
$ k $ 的多项式基矢量集为:$ \{{\boldsymbol{{p}}}_\alpha\}_{\alpha = 1,2, \cdots, n_k} $ , 且$ {\boldsymbol{{p}}}_\alpha \in {\boldsymbol{{{\cal{P}}}}}_k(E) $ , 如 3.4.1 中所述,$ n_k = (k+2)(k+1) $ . 映射操作符$ \Pi $ 对式(53)中的矢量基函数$ \boldsymbol{\phi}_i $ 的操作定义为多项式基的线性组合, 即$$ \begin{array}{*{20}{l}} \Pi(\boldsymbol{\phi}_i) = \displaystyle\sum\limits_{\beta=1}^{n_k}s_{i, \beta} {\boldsymbol{{p}}}_{\beta} \in {\boldsymbol{{{\cal{P}}}}}_k(E) \end{array} $$ (59) 式中,
$ s_{i, \beta} $ 为常数. 按照正交条件式(49), 需要满足$$ \begin{array}{*{20}{l}} a^E (\boldsymbol{\phi}_i, \; {\boldsymbol{{p}}}_\alpha) = \displaystyle\sum\limits_{\beta=1}^{n_k}s_{i, \beta} a^E ({\boldsymbol{{p}}}_{\beta}, \; {\boldsymbol{{p}}}_\alpha), \quad \forall {\boldsymbol{{p}}}_\alpha \in {\boldsymbol{{{\cal{P}}}}}_k(E) \end{array} $$ (60) 令
$ \alpha=1, 2,\cdots, n_k $ , 则可以得到如下矩阵形式$$ \begin{array}{*{20}{l}} {\boldsymbol{{b}}}_i = {\boldsymbol{{G}}} {\boldsymbol{{s}}}_i \end{array} $$ (61) 其中
$$ \begin{array}{*{20}{l}} {\boldsymbol{{b}}}_{i}=\left[\begin{array}{c}a^{E}\left(\boldsymbol{p}_{1}, \boldsymbol{\phi}_{i}\right) \\ a^{E}\left(\boldsymbol{p}_{2}, \boldsymbol{\phi}_{i}\right) \\ \vdots \\ a^{E}\left(\boldsymbol{p}_{n_{k}}, \boldsymbol{\phi}_{i}\right)\end{array}\right], \quad {\boldsymbol{{s}}}_{i}=\left[\begin{array}{c}s_{i, 1} \\ s_{i, 2} \\ \vdots \\ s_{i, n_{k}}\end{array}\right] \end{array} $$ (62) 以及
$$ \begin{array}{*{20}{l}} {\boldsymbol{{G}}}=\left[\begin{array}{cccc}a^{E}\left(\boldsymbol{p}_{1}, \boldsymbol{p}_{1}\right) & a^{E}\left(\boldsymbol{p}_{1}, \boldsymbol{p}_{2}\right) & \cdots & a^{E}\left(\boldsymbol{p}_{1}, \boldsymbol{p}_{n_{k}}\right) \\ a^{E}\left(\boldsymbol{p}_{2}, \boldsymbol{p}_{1}\right) & a^{E}\left(\boldsymbol{p}_{2}, \boldsymbol{p}_{2}\right) & \cdots & a^{E}\left(\boldsymbol{p}_{2}, \boldsymbol{p}_{n_{k}}\right) \\ \vdots & \vdots & \ddots & \vdots \\ a^{E}\left(\boldsymbol{p}_{n_{k}}, \boldsymbol{p}_{1}\right) & a^{E}\left(\boldsymbol{p}_{n_{k}}, \boldsymbol{p}_{2}\right) & \cdots & a^{E}\left(\boldsymbol{p}_{n_{k}}, \boldsymbol{p}_{n_{k}}\right)\end{array}\right] \end{array} $$ (63) 代入所有的矢量基函数
$ {\boldsymbol{{\phi}}}_i, \; i=1, 2,\cdots, 2 n_{d} $ ,$ {\boldsymbol{{b}}}_{i} $ 组装成矩阵$ \tilde{{\boldsymbol{{B}}}} $ , 映射系数$ {\boldsymbol{{s}}}_{i} $ 组装成矩阵$ \tilde{{\boldsymbol{{\varPi}}}} $ , 即$$ \begin{array}{*{20}{l}} \tilde{{\boldsymbol{{B}}}}=\left[ \begin{array}{*{20}{l}}{\boldsymbol{{b}}}_{1} & {\boldsymbol{{b}}}_{2} & \ldots & {\boldsymbol{{b}}}_{2 n_{d}}\end{array}\right] \end{array} $$ (64) $$ \begin{array}{*{20}{l}} \tilde{{\boldsymbol{{\varPi}}}}=\left[\begin{array}{*{20}{l}}{\boldsymbol{{s}}}_{1} & {\boldsymbol{{s}}}_{2} & \ldots & {\boldsymbol{{s}}}_{2 n_{d}}\end{array}\right] \end{array} $$ (65) 此时, 由式(61), 得
$$ \begin{array}{*{20}{l}} \tilde{{\boldsymbol{{B}}}} = {\boldsymbol{{G}}} \tilde{{\boldsymbol{{\varPi}}}}\rightarrow \tilde{{\boldsymbol{{\varPi}}}} = {\boldsymbol{{G}}}^{-1}\tilde{{\boldsymbol{{B}}}} \end{array} $$ (66) 需要指出, 由于矩阵
$ \tilde{{\boldsymbol{{B}}}} $ 和矩阵$ {\boldsymbol{G}} $ 中前三行的每一项均需求解$ \nabla {\boldsymbol{{p}}}_\alpha $ ,$ \alpha=1, 2, 3 $ , 如 3.4.1 所述, 此时对应刚性位移模式, 即应变为零的情况. 因而, 需要扩充映射操作符$ \Pi $ 的定义, 使得$$ \begin{array}{*{20}{l}} \dfrac{1}{n_{v}} \displaystyle\sum\limits_{i=1}^{2 n_{v}} {{\rm{dof}}}_{i}\left({\boldsymbol{{v}}}^h \right) {{{\rm{dof}}}}_{i}\left({\boldsymbol{{p}}}_{\alpha}\right) = \dfrac{1}{n_{v}} \displaystyle\sum\limits_{i=1}^{2 n_{v}} {{\rm{dof}}}_{i}\left(\Pi {\boldsymbol{{v}}}^h \right) {{{\rm{dof}}}}_{i}\left({\boldsymbol{{p}}}_{\alpha}\right),\quad \alpha=1, 2, 3 \end{array} $$ (67) 该条件可视为
$ {\boldsymbol{{v}}}^h $ 和$ \Pi {\boldsymbol{{v}}}^h $ 在$ {\boldsymbol{p}} _{\alpha} (\alpha = 1, 2, 3) $ 度量下的平均值相等. 如此, 矩阵$ \tilde{{\boldsymbol{{B}}}} $ 和矩阵$ {\boldsymbol{G}} $ 需要做如下修正 (Mengolini et al. 2019)$$ \begin{array}{*{20}{l}} \tilde{{\boldsymbol{{B}}}}_{\alpha I}=\dfrac{1}{n_{v}} \displaystyle\sum\limits_{i=1}^{2 n_{v}} {\rm dof}_{i}\left(\boldsymbol{\phi}_{I}\right) {\rm{dof}}_{i}\left(\boldsymbol{p}_{\alpha}\right) ,\quad \alpha=1, 2, 3 \end{array} $$ (68) $$ \begin{array}{*{20}{l}} {\boldsymbol{{G}}}_{\alpha \beta}=\dfrac{1}{n_{v}} \displaystyle\sum\limits_{i=1}^{2 n_{v}} {\rm{dof}}_{i}\left({\boldsymbol{{p }}}_{\alpha }\right) {\rm{dof}}_{i}\left({\boldsymbol{{p}}}_{\beta }\right) ,\quad \alpha=1, 2, 3 \end{array} $$ (69) 对于矩阵
$ {\boldsymbol{G}} $ , 前三行外的其他元素均可通过数值积分直接求得, 从而可完全确定矩阵$ {\boldsymbol{G}} $ 的各个元素.对于矩阵
$ \tilde{{\boldsymbol{{B}}}} $ , 前三行外的其他元素均可通过分部积分将原来的双线性格式分解成两个可以直接计算的积分项, 从而避免对形函数(在单元内部一般没有显式表达)求体积分$$ \begin{array}{*{20}{l}} a^{E}\left({\boldsymbol{{\phi}}}_{i}, {\boldsymbol{{p}}}_{\alpha} \right) = \displaystyle\int_{E} {\boldsymbol{{\epsilon}}}({\boldsymbol{{\phi}}}_i)^{{\rm{T}}} {\boldsymbol{{\sigma}}}({\boldsymbol{{p}}}_{\alpha}) \; {\rm{d}}E = -\displaystyle\int_{E} {\boldsymbol{{\phi}}}_i \cdot \left[ \nabla \cdot ({\boldsymbol{{C}}}\; {\boldsymbol{{\epsilon}}}({\boldsymbol{{p}}}_{\alpha})) \right] {\rm{d}}E +\displaystyle\int_{\partial E} {\boldsymbol{{\phi}}}_i \cdot {\boldsymbol{{\sigma}}}({\boldsymbol{{p}}}_{\alpha}) \hat{{\boldsymbol{{n}}}}_e \; {\rm{d}} \partial E \end{array} $$ (70) 其中,
$ \hat{{\boldsymbol{{n}}}}_e $ 为单元边界$ \partial E $ 的外法向量.对于式(70)右端第一项, 如前所述,
$ {\boldsymbol{{p}}}_\alpha \in {\boldsymbol{{{\cal{P}}}}}_k(E) $ , 则:$ \nabla \cdot ({\boldsymbol{{C}}}\; {\boldsymbol{{\epsilon}}}({\boldsymbol{{p}}}_{\alpha})) \in {\boldsymbol{{\cal {P}}}}_{k-2}(E) $ , 进一步考虑线性组合$$ \begin{array}{*{20}{l}} -\displaystyle\int_{E} {\boldsymbol{{\phi}}}_i \cdot \left[ \nabla \cdot ({\boldsymbol{{C}}}\; {\boldsymbol{{\epsilon}}}({\boldsymbol{{p}}}_{\alpha})) \right] {\rm{d}}E = -\displaystyle\sum\limits_{\beta =1}^{n_{k-2}} d_{\alpha, \beta} \; \displaystyle\int_{E}{\boldsymbol{{\phi}}}_i \cdot {\boldsymbol{{p}}}_{\beta} \; {\rm{d}}E = -A_E\displaystyle\sum\limits_{\beta =1}^{n_{k-2}} d_{\alpha, \beta} \; {\rm{dof}}_{2n_v k+\beta}({\boldsymbol{{\phi}}}_i) \end{array} $$ (71) 其中,
$ d_{\alpha, \beta} $ 为有量纲的系数. 考虑到内部自由度的定义式(51), 可以看出, 式(70)右端第一项与单元内部自由度相关, 且有$ {\rm{dof}}_{2n_v k+\beta}({\boldsymbol{{\phi}}}_i) = \delta_{2n_v k+\beta, i} $ .对于式(70)右端第二项, 单元边界积分为各条边上线积分的贡献之和, 每条边上的线积分按如下数值积分计算
$$ \begin{array}{*{20}{l}} \displaystyle\int_{\partial E} {\boldsymbol{{\phi}}}_i \cdot {\boldsymbol{{\sigma}}}({\boldsymbol{{p}}}_{\alpha}) \hat{{\boldsymbol{{n}}}}_e \; {\rm{d}} \partial E = \displaystyle\sum\limits_{j =1}^{n_v} \int_{e_j} {\boldsymbol{{\phi}}}_i \cdot {\boldsymbol{{\sigma}}}({\boldsymbol{{p}}}_{\alpha}) \hat{{\boldsymbol{{n}}}}_{e_j} \; {\rm{d}}e = \displaystyle\sum\limits_{j =1}^{n_v} \frac{|{\boldsymbol{e}}_j|}{2} \displaystyle\sum\limits_{r =1}^{k+1} w_r \; {\boldsymbol{{\phi}}}_i\bigg|_{\xi_r} \cdot \left({\boldsymbol{{\sigma}}}({\boldsymbol{{p}}}_{\alpha})\bigg|_{\xi_r} \cdot \hat{{\boldsymbol{{n}}}}_{e_j} \right) \end{array} $$ (72) 其中,
${\boldsymbol{ e}}_j $ 为单元边界$ \partial E $ 的第$ j $ 条边,$ \hat{{\boldsymbol{{n}}}}_{e_j} $ 是该边外法线矢量. 可将边界与顶点设定的自由度置于每条边界上的数值积分点$ \xi_r $ (其相对应的权重为$ w_r $ ), 如此, 可提高计算精度.作为总结, 矩阵
$ {\boldsymbol{{G}}} $ 的前三行按照式(69)求得, 剩余行可直接数值积分得到; 矩阵$ \tilde{{\boldsymbol{{B}}}} $ 的前三行按照式(68)求得, 剩余行通过式(70)~式(72)求得; 矩阵$ \tilde{{\boldsymbol{{\varPi}}}} $ 按照式(66)求得. 进一步, 将矩阵$ {\boldsymbol{G}} $ 作一变换, 令其前三行所有元素设为 0, 其他行所有元素不变, 记此矩阵为$ \tilde {{\boldsymbol{G}}} $ .如此, 协调刚度矩阵的分量形式可表示为
$$ \begin{split} \left({\boldsymbol{{k}}}^c_E\right)_{ij} &= \int_E {\boldsymbol{{\epsilon}}}\left(\Pi({\boldsymbol{{\phi}}}_i)\right)^{{\rm{T}}} {\boldsymbol{{C}}} {\boldsymbol{{\epsilon}}}\left(\Pi({\boldsymbol{{\phi}}}_j)\right) {{\rm{d}}}E = \int_E {\boldsymbol{{\epsilon}}}\left(\sum_{\alpha=1}^{n_k}s_{i, \alpha} {\boldsymbol{{p}}}_{\alpha}\right)^{{\rm{T}}} {\boldsymbol{{C}}} {\boldsymbol{{\epsilon}}}\left(\sum_{\beta=1}^{n_k}s_{j, \beta} {\boldsymbol{{p}}}_{\beta}\right) {{\rm{d}}}E =\\ & \sum_{\alpha=1}^{n_k} \sum_{\beta=1}^{n_k} s_{i, \alpha} s_{j, \beta} \int_E {\boldsymbol{{\epsilon}}}\left({\boldsymbol{{p}}}_{\alpha}\right)^{{\rm{T}}} {\boldsymbol{{C}}} {\boldsymbol{{\epsilon}}}\left({\boldsymbol{{p}}}_{\beta}\right) {{\rm{d}}}E = \sum_{\alpha=1}^{n_k} \sum_{\beta=1}^{n_k} s_{i, \alpha} s_{j, \beta} a^E({\boldsymbol{{p}}}_\alpha, {\boldsymbol{{p}}}_\beta)= \\ & \sum_{\alpha=1}^{n_k} \sum_{\beta=1}^{n_k} \tilde{{\boldsymbol{{\varPi}}}}_{i\alpha} \tilde{{\boldsymbol{{\varPi}}}}_{j\beta} {\tilde{{\boldsymbol{{G}}}}_{\alpha\beta} } = \left[ \tilde{{\boldsymbol{{\varPi}}}}^{{\rm{T}}} \tilde{{\boldsymbol{{G}}}} \tilde{{\boldsymbol{{\varPi}}}} \right]_{ij} \end{split} $$ (73) 相应地, 协调刚度矩阵为
$$ \begin{array}{*{20}{l}} {\boldsymbol{{k}}}^c_E = \tilde{{\boldsymbol{{\varPi}}}}^{{\rm{T}}}{\tilde{{\boldsymbol{{G}}}}} \tilde{{\boldsymbol{{\varPi}}}} \end{array} $$ (74) (2)稳定刚度矩阵
与有限元法不同, 虚单元法中需要增加稳定刚度矩阵.
首先, 定义矩阵
$ {\boldsymbol{{D}}}_{2n_d \times n_k} $ 为多项式基$ {\boldsymbol{{p}}}_\alpha $ 在自由度设定位置上的自由度取值, 即$$ \begin{array}{*{20}{l}} {\boldsymbol{{D}}}_{i\alpha} = {{\rm{dof}}}_i ({\boldsymbol{{p}}}_\alpha) ,i = 1,2, \cdots, 2n_d, \; \alpha = 1,2, \cdots, n_k \end{array} $$ (75) 对应的矩阵形式为
$$ \boldsymbol{D}=\left[\begin{array}{cccc} \operatorname{dof}_{1}\left(\boldsymbol{p}_{1}\right) & \operatorname{dof}_{1}\left(\boldsymbol{p}_{2}\right) & \cdots & \operatorname{dof}_{1}\left(\boldsymbol{p}_{n_{k}}\right) \\ \operatorname{dof}_{2}\left(\boldsymbol{p}_{1}\right) & \operatorname{dof}_{2}\left(\boldsymbol{p}_{2}\right) & \cdots & \operatorname{dof}_{2}\left(\boldsymbol{p}_{n_{k}}\right) \\ \vdots & \vdots & \ddots & \vdots \\ \operatorname{dof}_{2 n_{d}}\left(\boldsymbol{p}_{1}\right) & \operatorname{dof}_{2 n_{d}}\left(\boldsymbol{p}_{2}\right) & \cdots & \operatorname{dof}_{2 n_{d}}\left(\boldsymbol{p}_{n_{k}}\right) \end{array}\right] $$ (76) 考虑到自由度取值可为函数本身取值, 亦可为函数与多项式乘积的积分(矩形式). 由此, 可以确定矩阵
$ {\boldsymbol{D}} $ 的各个元素:① 对于边界自由度:
$ 1\leqslant i \leqslant 2n_{v}k $ ,$ {\rm{dof}}_i ({\boldsymbol{p}}_{\alpha}) $ 定义为基矢量$ {\boldsymbol{p}}_{\alpha} $ 在第$ i $ 个自由度所属节点的矢量分量值.②对于单元内部自由度:
$ 2n_{v}k + 1\leqslant i \leqslant 2n_d $ , 考虑到单元内部自由度的定义式(51)$$ \begin{array}{*{20}{l}} {\rm{dof}}_{2n_{v}k+\beta} ({\boldsymbol{p}}_{\alpha}) = \dfrac{1}{A_E} \displaystyle\int_{E} {\boldsymbol{p}}_{\alpha} \cdot {\boldsymbol{p}}_\beta \; {\rm{d}}E , \quad\forall \; {\boldsymbol{p}}_\beta \in {\boldsymbol{{{\cal{P}}}}}_{k-2}(E) \end{array} $$ (77) 按照数值积分即可求得矩阵
$ {\boldsymbol{{D}}} $ 的剩余元素.进一步, 定义
$$ \begin{array}{*{20}{l}} {\boldsymbol{{\varPi}}}_{ij} = {{\rm{dof}}}_i\left(\Pi({\boldsymbol{{\phi}}}_j)\right) = {{\rm{dof}}}_i\left(\displaystyle\sum\limits_{\alpha=1}^{n_k} s_{j, \alpha} {\boldsymbol{{p}}}_\alpha\right) = \displaystyle\sum\limits_{\alpha=1}^{n_k} {\boldsymbol{{D}}}_{i\alpha}\tilde{{\boldsymbol{{\varPi}}}}_{\alpha j} = \left({\boldsymbol{{D}}} \tilde{{\boldsymbol{{\varPi}}}} \right)_{ij} \rightarrow {\boldsymbol{{\varPi}}} = {\boldsymbol{{D}}} \tilde{{\boldsymbol{{\varPi}}}} \end{array} $$ (78) 与式(35)相对应, 二维弹性问题的稳定项可以取
$$ \begin{array}{*{20}{l}} S^E({\boldsymbol{{\phi}}}_i-\Pi ({\boldsymbol{{\phi}}}_i), {\boldsymbol{{\phi}}}_j-\Pi ({\boldsymbol{{\phi}}}_j)) = \displaystyle\sum\limits_{r=1}^{2n_{d}} {\rm{dof}}_r({\boldsymbol{{\phi}}}_i-\Pi ({\boldsymbol{{\phi}}}_i)) {\rm{dof}}_r({\boldsymbol{{\phi}}}_j-\Pi ({\boldsymbol{{\phi}}}_j)) \end{array} $$ (79) 将式(78)中
$ {\boldsymbol{{\varPi}}}_{ij} $ 的定义, 以及单位矩阵$ {\boldsymbol{{I}}}_{ij} = {{\rm{dof}}}_i\left(\phi_j\right) $ 的定义代入式(79), 则稳定项的矩阵形式为$$ \begin{array}{*{20}{l}} {\boldsymbol{{S}}}^E = ({\boldsymbol{{I}}} - {\boldsymbol{{\varPi}}})^{{\rm{T}}}({\boldsymbol{{I}}} - {\boldsymbol{{\varPi}}}) \end{array} $$ (80) 可以证明(Beirão da Veiga et al. 2014, 2013b), 若存在一个因子
$ \sigma_E > 0 $ , 满足$$ \begin{array}{*{20}{l}} 0 < \sigma_* \leqslant \sigma_E \leqslant \sigma^* \end{array} $$ (81) 其中, 常数
$ \sigma_*, \; \sigma^* $ 均不依赖于单元特征尺寸$ h $ , 则稳定项式(80)乘以该因子$ \sigma_E $ 依然能够保证计算结果收敛. 通常取$ \sigma_E=\tau^h \cdot {\rm{tr}}({\boldsymbol{{k}}}^c_E)>0 $ , 从而得到稳定刚度矩阵$$ \begin{array}{*{20}{l}} {\boldsymbol{{k}}}^s_E = \tau^h {\rm{tr}}({\boldsymbol{{k}}}^c_E)({\boldsymbol{{I}}} - {\boldsymbol{{\varPi}}})^{{\rm{T}}}({\boldsymbol{{I}}} - {\boldsymbol{{\varPi}}}) \end{array} $$ (82) 式中,
$ \tau^h $ 为稳定系数, 对于弹性问题,$ \tau^h=0.5 $ , 更多选择可参考 (Gain et al. 2014);$ {\rm{tr}}(\cdot) $ 为矩阵的迹, 引入此项可保证单元内部的能量相对于单元尺寸和材料弹性常数为相对正确的比例 (Artioli et al. 2017a).最后, 需要指出矩阵
$ {\boldsymbol{G}} $ 恰好可以表示成矩阵$ \tilde{{\boldsymbol{{B}}}} $ 和矩阵$ {\boldsymbol{D}} $ 的乘积:$ {\boldsymbol{G}} = \tilde{{\boldsymbol{{B}}}} {\boldsymbol{D}} $ . 因此, 如果在计算过程中首先求出了矩阵$ \tilde{{\boldsymbol{{B}}}} $ 和矩阵$ {\boldsymbol{D}} $ , 就无需再通过式(63)进行求解. 当然, 按式(63)求出矩阵$ {\boldsymbol{G}} $ , 可帮助检查两种方式的求解结果是否相同.4.2.4 右端项
如式(48), 单元内部的线性格式为
$$ \begin{array}{*{20}{l}} L_h^E({\boldsymbol{{v}}}^h) = \displaystyle\int_E {\boldsymbol{{v}}}^h \cdot {\boldsymbol{{f}}} \; {{\rm{d}}} E + \displaystyle\int_{\partial E \cap \partial \varOmega_t} {\boldsymbol{{v}}}^h \cdot \bar {{\boldsymbol{{t}}}} \; {{\rm{d}}} \partial E \end{array} $$ (83) 由于近似函数在单元边界上为多项式, 式中第二项无需特别处理, 但对于第一项, 近似函数在单元内部无显式表达, 因此需要进行近似处理. 在不产生歧义的情况下, 本节下述右端项均指与体积力
$ {\boldsymbol{{f}}} $ 对应的右端项.与泊松方程类似, 对于弹性问题, 右端项也需要进行合理近似
$$ \begin{array}{*{20}{l}} ({\boldsymbol{f}}, {\boldsymbol{\phi}}_i) \approx ({{{\boldsymbol{f}}_h}}, {\boldsymbol{\phi}}_i) = \displaystyle\sum\limits_E ({{{\boldsymbol{f}}_h}}, {\boldsymbol{\phi}}_i)_E \end{array} $$ (84) 根据
$ k $ 的取值不同,$ {{{\boldsymbol{f}}_h}} $ 的定义与$ ({{{\boldsymbol{f}}_h}}, {\boldsymbol{\phi}}_i)_E $ 的构造可分为三种情况(1) 对于
$ k=1 $ ,$ {{{\boldsymbol{f}}_h}} $ 为$ {\boldsymbol{f}} $ 在单元$ E $ 内的平均值, 即$$ \begin{array}{*{20}{l}} {{{\boldsymbol{f}}_h}} \approx \dfrac{1}{n_v} \displaystyle\sum_{v=1}^{n_v} {\boldsymbol{{f}}}({\boldsymbol{{x}}}_v)=\bar {{\boldsymbol{f}} } \end{array} $$ (85) 考虑到
$ \bar{{\boldsymbol{\phi}}_i} = \dfrac{1}{n_v} \displaystyle\sum\nolimits_{v=1}^{n_v} {\boldsymbol{{\phi}}}_i({\boldsymbol{x_v}}) $ ,$ {\boldsymbol{{\phi}}}_i ({\boldsymbol{{x}}}_v) = {\boldsymbol{\delta}}_{iv} $ , 有$$ \begin{array}{*{20}{l}} ({{{\boldsymbol{f}}_h}}, {\boldsymbol{{\phi}}}_i)_E = \displaystyle\int_E \bar{{\boldsymbol{f}}} \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E = A_E \bar{{\boldsymbol{f}}} \dfrac{1}{n_v} \displaystyle\sum\limits_{v=1}^{n_v} {\boldsymbol{{\phi}}}_i({\boldsymbol{x_v}}) = \dfrac{A_E}{n_v}\bar {{\boldsymbol{f}}} \end{array} $$ (86) (2) 对于
$ k=2 $ , 类似式(49)定义的双线性格式的正交条件, 首先定义线性格式的映射操作符$ \Pi^0_k: {\boldsymbol{{{\cal{V}}}}}^{E, k} \rightarrow {\boldsymbol{{{\cal{P}}}}}_{k}(E) $ , 对于$ \forall {\boldsymbol{{\phi}}}_i \in {\boldsymbol{{{\cal{V}}}}}^{E, k} $ , 满足$$ \begin{array}{*{20}{l}} \displaystyle\int_{E} {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E = \displaystyle\int_{E} {\boldsymbol{{p}}}_\alpha \cdot \Pi_k^0({\boldsymbol{{\phi}}}_i) \; {\rm{d}}E ,\quad\forall \; {\boldsymbol{{p}}}_\alpha \in {\boldsymbol{{{\cal{P}}}}}_{k}(E) \end{array} $$ (87) 其中
$$ \begin{array}{*{20}{l}} \Pi_k^0({\boldsymbol{{\phi}}}_i) = \displaystyle\sum\limits_{\beta=1}^{n_k}s_{i, \beta} {\boldsymbol{{p}}}_{\beta} \end{array} $$ (88) 式中,
$ s_{i, \beta} $ 为常数. 下面将讨论如何计算$ s_{i, \beta} $ .将式(88)代入式(87), 可得方程组
$$ \begin{array}{*{20}{l}} \displaystyle\int_{E} {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E = \displaystyle\sum\limits_{\beta=1}^{n_k}s_{i, \beta} \displaystyle\int_{E} {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{p}}}_{\beta} \; {\rm{d}}E ,\quad\forall \; {\boldsymbol{{p}}}_\alpha \in {\boldsymbol{{{\cal{P}}}}}_{k}(E) \end{array} $$ (89) 将其写成矩阵形式
$$ {\boldsymbol{q_i}}^0 = {\boldsymbol{H}}^0 {\boldsymbol{s_i}}^0 $$ (90) 其中
$$ \begin{array}{*{20}{l}} {\boldsymbol{{q}}}_{i}^0=\left[ \begin{array}{*{20}{l}} \displaystyle\int_{E} {\boldsymbol{{p}}}_1 \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E \\ \displaystyle\int_{E} {\boldsymbol{{p}}}_2 \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E \\ \quad \quad \quad \vdots \\ \displaystyle\int_{E} {\boldsymbol{{p}}}_{n_k } \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E \end{array}\right], \quad {\boldsymbol{{s}}}_{i}^0=\left[\begin{array}{c}s_{i, 1} \\ s_{i, 2} \\ \vdots \\ s_{i, n_{k}}\end{array}\right] \end{array} $$ (91) 以及
$$ \begin{array}{*{20}{l}} {\boldsymbol{{H}}}^0 =\left[\begin{array}{*{20}{l}} \displaystyle\int_{E} {\boldsymbol{{p}}}_1 \cdot {\boldsymbol{{p}}}_1 \; {\rm{d}}E & \displaystyle\int_{E} {\boldsymbol{{p}}}_1 \cdot {\boldsymbol{{p}}}_2 \; {\rm{d}}E & \cdots & \displaystyle\int_{E} {\boldsymbol{{p}}}_1 \cdot {\boldsymbol{{p}}}_{n_k} \; {\rm{d}}E \\ \displaystyle\int_{E} {\boldsymbol{{p}}}_2 \cdot {\boldsymbol{{p}}}_1 \; {\rm{d}}E & \displaystyle\int_{E} {\boldsymbol{{p}}}_2 \cdot {\boldsymbol{{p}}}_2 \; {\rm{d}}E & \cdots & \displaystyle\int_{E} {\boldsymbol{{p}}}_2 \cdot {\boldsymbol{{p}}}_{n_k} \; {\rm{d}}E \\ \quad \quad \quad \vdots & \quad \quad \quad\vdots & \ddots &\quad \quad \quad \vdots \\ \displaystyle\int_{E} {\boldsymbol{{p}}}_{n_k} \cdot {\boldsymbol{{p}}}_1 \; {\rm{d}}E & \displaystyle\int_{E} {\boldsymbol{{p}}}_{n_k} \cdot {\boldsymbol{{p}}}_2 \; {\rm{d}}E & \cdots & \displaystyle\int_{E} {\boldsymbol{{p}}}_{n_k} \cdot {\boldsymbol{{p}}}_{n_k} \; {\rm{d}}E \end{array}\right] \end{array} $$ (92) 代入所有矢量基函数
$ {\boldsymbol{{\phi}}}_i, \; i=1,2, \; \cdots, 2n_{d} $ , 将$ {\boldsymbol{q_i}}^0 $ 组装成矩阵$ {\boldsymbol{Q}}^0 $ , 将映射系数$ {\boldsymbol{s_i}}^0 $ 组装成矩阵$ \boldsymbol\varPi^0_k $ , 即$$ \begin{array}{*{20}{l}} {\boldsymbol{{Q}}}^0=\left[ \begin{array}{*{20}{l}} {\boldsymbol{{q}}}_{1}^0 & {\boldsymbol{{q}}}_{2}^0 & \ldots & {\boldsymbol{{q}}}_{2 n_{d}}^0 \end{array}\right] \end{array} $$ (93) $$ \begin{array}{*{20}{l}} {\boldsymbol{{\varPi}}}^0_k=\left[\begin{array}{*{20}{l}} {\boldsymbol{{s}}}_{1}^0 & {\boldsymbol{{s}}}_{2}^0 & \ldots & {\boldsymbol{{s}}}_{2 n_{d}}^0 \end{array}\right] \end{array} $$ (94) 方程组(90)可整理为
$$ \begin{array}{*{20}{l}} {\boldsymbol{Q}}^0 = {\boldsymbol{H}}^0 {{\boldsymbol{{\varPi}}}}^0_k \rightarrow {{\boldsymbol{{\varPi}}}}^0_k = ({\boldsymbol{H}}^0)^{-1} {\boldsymbol{Q}}^0 \end{array} $$ (95) 至此, 系数矩阵
$ {{\boldsymbol{{\varPi}}}}^0_k $ 可由式(95)求得. 下面讨论$ {\boldsymbol{H}}^0 $ ,$ {\boldsymbol{Q}}^0 $ 的求解. 对于矩阵$ {\boldsymbol{H}}^0_{{n_k}\times{n_k}} $ 可通过已知的基矢量$ {\boldsymbol{{p}}}_\alpha\; (\alpha = 1,2,\cdots, n_k) $ 完全确定. 对于$ {\boldsymbol{Q}}^0 $ 的前$ n_{k-2} $ 行$$ \begin{array}{*{20}{l}} {\boldsymbol{{Q}}}_{\alpha i}^{0}= {\boldsymbol{{Q}}}_{\alpha i} ,\alpha = 1,2, \cdots, n_{k-2}, \quad i = 1,2, \cdots, 2n_d \end{array} $$ (96) 其中
$$ \begin{array}{*{20}{l}} {\boldsymbol{{Q}}} =\left[\begin{array}{*{20}{l}} \displaystyle\int_{E} {\boldsymbol{{p}}}_1 \cdot {\boldsymbol{{\phi}}}_1 \; {\rm{d}}E & \displaystyle\int_{E} {\boldsymbol{{p}}}_1 \cdot {\boldsymbol{{\phi}}}_2 \; {\rm{d}}E & \cdots & \displaystyle\int_{E} {\boldsymbol{{p}}}_1 \cdot {\boldsymbol{{\phi}}}_{2n_d} \; {\rm{d}}E \\ \displaystyle\int_{E} {\boldsymbol{{p}}}_2 \cdot {\boldsymbol{{\phi}}}_1 \; {\rm{d}}E & \displaystyle\int_{E} {\boldsymbol{{p}}}_2 \cdot {\boldsymbol{{\phi}}}_2 \; {\rm{d}}E & \cdots & \displaystyle\int_{E} {\boldsymbol{{p}}}_2 \cdot {\boldsymbol{{\phi}}}_{2n_d} \; {\rm{d}}E \\ \quad \quad \quad \vdots &\quad \quad \quad \vdots & \ddots &\quad \quad \quad \vdots \\ \displaystyle\int_{E} {\boldsymbol{{p}}}_{n_{k-2}} \cdot {\boldsymbol{{\phi}}}_1 \; {\rm{d}}E & \displaystyle\int_{E} {\boldsymbol{{p}}}_{n_{k-2}} \cdot {\boldsymbol{{\phi}}}_2 \; {\rm{d}}E & \cdots & \displaystyle\int_{E} {\boldsymbol{{p}}}_{n_{k-2}} \cdot {\boldsymbol{{\phi}}}_{2n_d} \; {\rm{d}}E \end{array}\right] \end{array} $$ (97) 考虑到单元内部自由度的定义式(51), 可将基函数在单元内部的自由度写成
$$ \begin{array}{*{20}{l}} {\rm{dof}}_{2n_{v}k+\alpha} ({\boldsymbol{{\phi}}}_i) = \dfrac{1}{A_E} \displaystyle\int_{E} {\boldsymbol{{\phi}}}_i \cdot {\boldsymbol{{p}}}_{\alpha} \; {\rm{d}}E ,\quad \forall \; {\boldsymbol{{p}}}_\alpha \in {\boldsymbol{{{\cal{P}}}}}_{k-2}(E) \end{array} $$ (98) 因此, 矩阵
$ {\boldsymbol{Q}} $ 中的元素均可以确定$$ \begin{array}{*{20}{l}} \displaystyle\int_{E} {\boldsymbol{{p}}}_{\alpha} \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E = A_E {\rm{dof}}_{2n_{v}k+\alpha} ({\boldsymbol{{\phi}}}_i) = \left\{\begin{array}{l} A_E ,\quad 2n_{v}k+\alpha = i \\ 0, \quad\quad 2n_{v}k+\alpha \neq i \end{array} \right . \end{array} $$ (99) 对于
$ {\boldsymbol{Q}}^0 $ 的第$ n_{k-2}+1 $ 行至第$ n_{k} $ 行(需要特别注意$ n_{k-2} $ 和$ n_{k} $ 分别是$ {\boldsymbol{{{\cal{P}}}}}_{k-2} $ 和$ {\boldsymbol{{{\cal{P}}}}}_{k} $ 空间的线性无关基函数的个数, 两者并非相差 2), 需要计算基函数$ {\boldsymbol{{\phi}}}_i $ 和基矢量$ {\boldsymbol{{p}}}_\alpha $ 在单元内部的积分, 然而$ {\boldsymbol{{\phi}}}_i $ 没有显式表达, 考虑到式(60)与式(89), 由于$ \tilde{{\boldsymbol{{\varPi}}}} $ 已按照式(66)求得, 可直接采用$ \tilde{{\boldsymbol{{\varPi}}}} $ 的第$ n_{k-2}+1 $ 行至第$ n_{k} $ 行进行替换, 即$$ \begin{array}{*{20}{l}} {\boldsymbol{Q}}_{\alpha i}^0 = \left[{\boldsymbol{H}}^0 {\boldsymbol{G}}^{-1} \tilde{{\boldsymbol{B}}} \right]_{\alpha i} ,\quad \alpha = n_{k-2}, \; n_{k-1}, n_k; \quad i = 1,2, \cdots, 2n_d \end{array} $$ (100) 如此, 矩阵
$ {\boldsymbol{Q}}^0_{{n_k}\times{2n_d}} $ 的计算公式如下$$ \begin{array}{*{20}{l}} {\boldsymbol{{Q}}}_{\alpha i}^{0}= \left\{\begin{array}{l} {\boldsymbol{{Q}}}_{\alpha i} ,\qquad \qquad \quad\; \alpha =1,2, \cdots, n_{k-2}, \quad i = 1,2, \cdots, 2n_d \\ \left[{\boldsymbol{{H}}}^{0} {\boldsymbol{{G}}}^{-1} \tilde{{\boldsymbol{{B}}}}\right]_{\alpha i} ,\quad \alpha =n_{k-2}+1,2, \cdots, n_k, i = 1, 2,\cdots, 2n_d \end{array} \right. \end{array} $$ (101) 通过式(95)求出
$ {{\boldsymbol{{\varPi}}}}_k^0 $ , 反复利用式(87), 可构造右端项为$$ \begin{split} ({{{\boldsymbol{f}}_h}}, {\boldsymbol{{\phi}}}_i)_E &= \int_E {\boldsymbol{\varPi}}_{k}^0 {\boldsymbol{f}} \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E = \int_E {\boldsymbol{\varPi}}_{k}^0 {\boldsymbol{f}} \cdot {\boldsymbol{\varPi}}_{k}^0 {\boldsymbol{{\phi}}}_i \; {\rm{d}}E = \int_E {\boldsymbol{f}} \cdot {\boldsymbol{\varPi}}_{k}^0 {\boldsymbol{{\phi}}}_i \; {\rm{d}}E =\\ & \int_E {\boldsymbol{f}} \cdot \left(\sum_{\beta=1}^{n_k} s_{i, \beta} {\boldsymbol{{p}}}_{\beta}\right) \; {\rm{d}}E = \int_E {\boldsymbol{f}} \cdot \left(\sum_{\beta=1}^{n_k} \left({\boldsymbol{{\varPi}}}^0_{k} \right)_{\beta i} {\boldsymbol{{p}}}_{\beta} \right) \; {\rm{d}}E \end{split} $$ (102) (3) 对于
$ k>2 $ , 类似的, 定义映射操作符$ \Pi^0_{k-2}: {\boldsymbol{{{\cal{V}}}}}^{E, k} \rightarrow {\boldsymbol{{{\cal{P}}}}}_{k-2}(E) $ , 对于$ \forall {\boldsymbol{{\phi}}}_i \in {\boldsymbol{{{\cal{V}}}}}^{E, k} $ , 满足$$ \begin{array}{*{20}{l}} \displaystyle\int_{E} {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E = \displaystyle\int_{E} {\boldsymbol{{p}}}_\alpha \cdot \Pi^0_{k-2}({\boldsymbol{{\phi}}}_i) \; {\rm{d}}E ,\quad \forall \; {\boldsymbol{{p}}}_\alpha \in {\boldsymbol{{{\cal{P}}}}}_{k-2}(E) \end{array} $$ (103) 其中
$$ \begin{array}{*{20}{l}} \Pi^0_{k-2} ({\boldsymbol{{\phi}}}_i) = \displaystyle\sum\limits_{\beta=1}^{n_{k-2}} r_{i, \beta} {\boldsymbol{{p}}}_{\beta} \end{array} $$ (104) 式中,
$ r_{i, \beta} $ 为常数. 将式(104)代入式(103), 则有方程组$$ \begin{array}{*{20}{l}} \displaystyle\int_{E} {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E = \displaystyle\sum\limits_{\beta=1}^{n_{k-2}} r_{i, \beta} \displaystyle\int_{E} {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{p}}}_{\beta} \; {\rm{d}}E ,\quad\forall \; {\boldsymbol{{p}}}_\alpha \in {\boldsymbol{{{\cal{P}}}}}_{k-2}(E) \end{array} $$ (105) 其矩阵形式为
$$ \begin{array}{*{20}{l}} {\boldsymbol{q_i}} = {\boldsymbol{H}} {\boldsymbol{r_i}} \end{array} $$ (106) 代入所有矢量基函数
$ {\boldsymbol{{\phi}}}_i, \; i=1, 2,\; \cdots, 2n_{d} $ , 将$ {\boldsymbol{q_i}} $ 组装成矩阵$ {\boldsymbol{Q}} $ , 恰好为式(97), 将映射系数$ {\boldsymbol{r_i}} $ 组装成矩阵$ {\boldsymbol{{\varPi}}}^0_{k-2} $ , 即$$ \begin{array}{*{20}{l}} {\boldsymbol{{Q}}} =\left[ \begin{array}{*{20}{l}} {\boldsymbol{{q}}}_{1} & {\boldsymbol{{q}}}_{2} & \ldots & {\boldsymbol{{q}}}_{2 n_{d}} \end{array}\right] \end{array} $$ (107) $$ \begin{array}{*{20}{l}} {\boldsymbol{{\varPi}}}^0_{k-2} =\left[\begin{array}{*{20}{l}} {\boldsymbol{{r}}}_{1} & {\boldsymbol{{r}}}_{2} & \ldots & {\boldsymbol{{r}}}_{2 n_{d}} \end{array}\right] \end{array} $$ (108) 方程组(106)可以整理为
$$ \begin{array}{*{20}{l}} {\boldsymbol{Q}} = {\boldsymbol{H}} {\boldsymbol{{\varPi}}}^0_{k-2} \rightarrow {\boldsymbol{{\varPi}}}^0_{k-2} = {\boldsymbol{H}}^{-1} {\boldsymbol{Q}} \end{array} $$ (109) 其中, 矩阵
$ {\boldsymbol{H}}_{n_{k-2}\times n_{k-2}} $ 可通过已知的基矢量$ {\boldsymbol{{p}}}_\alpha\; (\alpha = 1,2, \; \cdots, n_{k-2}) $ 完全确定; 矩阵$ {\boldsymbol{Q}}_{n_{k-2}\times {2n_d}} $ 可通过式(97)、式(99)确定.此时, 通过式(109)求出操作符
$ \Pi^0_{k-2} $ 的矩阵表达式$ {{\boldsymbol{{\varPi}}}}^0_{k-2} $ , 可构造右端项$$ \begin{array}{*{20}{l}} ({{{\boldsymbol{f}}_h}}, {\boldsymbol{{\phi}}}_i)_E = \displaystyle\int_E {\boldsymbol{f}} \cdot \Pi^0_{k-2} \left({\boldsymbol{{\phi}}}_i\right) \; {\rm{d}}E = \displaystyle\int_E {\boldsymbol{f}} \cdot \left(\displaystyle\sum\limits_{\beta=1}^{n_{k-2}} r_{i, \beta} {\boldsymbol{{p}}}_{\beta}\right) \; {\rm{d}}E = \displaystyle\int_E {\boldsymbol{f}} \cdot \left(\displaystyle\sum\limits_{\beta=1}^{n_{k-2}} \left({\boldsymbol{{\varPi}}}^0_{k-2} \right)_{\beta i} {\boldsymbol{{p}}}_{\beta} \right) \; {\rm{d}}E \end{array} $$ (110) 如上所述, 可以在三种不同情况下求得基函数
$ {\boldsymbol{{\phi}}}_i $ 所对应的离散方程右端项. 如此, 单元内与体积力$ {\boldsymbol{{f}}} $ 对应的右端项为$$ \begin{array}{*{20}{l}} {\boldsymbol{{r}}}_{E}^{{\boldsymbol{{f}}}}=\left[\begin{array}{c} \left({\boldsymbol{{f}}}_h, \boldsymbol{\phi}_{1}\right)_{E} \\ \left({\boldsymbol{{f}}}_h, \boldsymbol{\phi}_{2}\right)_{E} \\ \vdots \\ \left({\boldsymbol{{f}}}_h, \boldsymbol{\phi}_{2n_d}\right)_{E} \end{array}\right] \end{array} $$ (111) 4.3 计算流程
本小节给出单元矩阵与右端项的计算流程, 如统一输入量为: 内插阶数
$ k $ , 多边形单元$ E $ , 单元节点坐标$ {\boldsymbol{{X}}} = \left[{\boldsymbol{{x}}}_1, {\boldsymbol{{x}}}_2,\cdots, {\boldsymbol{{x}}}_{n_v}\right] $ , 积分点坐标为$ {\boldsymbol{{\xi}}} $ , 权重为$ {\boldsymbol{{\gamma}}} $ , 材料弹性常数矩阵$ {\boldsymbol{{C}}} $ , 体积力$ {\boldsymbol{{f}}} $ ; 输出量为: 单元矩阵$ {\boldsymbol{{k}}}_E $ , 单元右端项$ {\boldsymbol{{r}}}_E $ (包含与体积力$ {\boldsymbol{{f}}} $ 对应的右端项$ {\boldsymbol{{r}}}^{{\boldsymbol{f}}}_E $ ).算法 1: 虚单元计算弹性问题的基本流程
(1)
$\tau^h \leftarrow 0.5$ //稳定系数(2)
$ {\boldsymbol{{x}}}_E, A_E, h_E, n_v \leftarrow {\boldsymbol{{X}}} $ //单元的形心、面积、几何尺寸、节点数目(3)
$ n_d \leftarrow 2n_vk + k(k-1) $ //自由度数目(4)
$ n_k \leftarrow (k+1)(k+2) $ //多项式空间维度(5)
$ \tilde{{\boldsymbol{B}}}_{\beta i} \leftarrow a^E_h({\boldsymbol{{p}}}_\beta, \boldsymbol{\phi}_i) $ //$ \tilde{{\boldsymbol{B}}}_{n_k \times 2n_d } $ 矩阵式 (64)、式(68)(6)
$ {{\boldsymbol{D}}}_{i\alpha} \leftarrow {\rm{dof}}_i({\boldsymbol{{p}}}_\alpha)$ //$ {\boldsymbol{{D}}}_{2n_d \times n_k } $ 矩阵式(75)(7)
${\boldsymbol{{G}}} \leftarrow \tilde{{\boldsymbol{{B}}}} {\boldsymbol{{D}}}$ //$ {\boldsymbol{{G}}}_{n_k \times n_k } $ 矩阵, 也可用式(63)、式(69)进行验证(8)
$\tilde{\boldsymbol{G}} \leftarrow\left[\begin{array}{cc}\mathbf{0}_{3 \times n_{k}} & \\\boldsymbol{G}\left[4: n_{k}, \quad:\right]\end{array}\right] $ //$ \tilde{{\boldsymbol{G}}}_{n_k \times n_k } $ 矩阵, 由$ {\boldsymbol{{G}}}_{n_k \times n_k } $ 矩阵给出(9)
$\tilde{{\boldsymbol{{\varPi}}}} \leftarrow {\boldsymbol{{G}}}^{-1}\tilde{{\boldsymbol{{B}}}}$ //映射到$ {\boldsymbol{{\cal {P}}}}_k(E) $ 空间的操作符式(66)(10)
${\boldsymbol{{\varPi}}} \leftarrow {\boldsymbol{{D}}} \tilde{{\boldsymbol{{\varPi}}}} $ //映射到$ {\boldsymbol{{\cal {V}}}}^h(E) $ 空间的操作符式(78)(11) //计算刚度矩阵
(12)
${\boldsymbol{{k}}}^c_E \leftarrow \tilde{{\boldsymbol{{\varPi}}}}^{{\rm{T}}} \tilde{{\boldsymbol{{G}}}} \tilde{{\boldsymbol{{\varPi}}}}$ //协调刚度矩阵式(74)(13)
${\boldsymbol{{k}}}^s_E \leftarrow \tau^h {\rm{tr}}({\boldsymbol{{k}}}^c_E)({\boldsymbol{{I}}} - {\boldsymbol{{\varPi}}})^{{\rm{T}}} ({\boldsymbol{{I}}} - {\boldsymbol{{\varPi}}}) $ //稳定刚度矩阵式(82)(14)
${\boldsymbol{{k}}}_E \leftarrow {\boldsymbol{{k}}}^c_E + {\boldsymbol{{k}}}^s_E $ (15) // 计算右端项
(16)
${\boldsymbol{{r}}}^{{\boldsymbol{f}}}_E ,$ $ {\boldsymbol{{r}}}_E \leftarrow {\boldsymbol{{0}}}_{2n_d\times1} $ //初始化(17) if:
$ k=1 $ then(18) 根据
$ {\boldsymbol{{X}}} $ 和$ {\boldsymbol{{f}}} $ 计算$ {\boldsymbol{{r}}}^{{\boldsymbol{f}}}_E $ ,$ {\boldsymbol{{r}}}_E $ //右端项式(86)、式(83)(19) end
(20) else if
$ k=2 $ then(21)
$ {\boldsymbol{{H}}}^0_{\alpha\beta} \leftarrow \int_E {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{p}}}_\beta \; {\rm{d}}E $ //$ {\boldsymbol{{H}}}^0_{n_k \times n_k } $ 矩阵式(92)(22)
$ {\boldsymbol{{Q}}}_{\alpha i} \leftarrow \int_E {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E$ //$ {\boldsymbol{{Q}}}_{n_{k-2} \times 2n_d } $ 矩阵式(97)(23)
$ {\boldsymbol{{Q}}}^0 \leftarrow {\boldsymbol{{Q}}}, {\boldsymbol{{H}}}^0, {\boldsymbol{{G}}}, \tilde{{\boldsymbol{{B}}}} $ //$ {\boldsymbol{{Q}}}^0_{n_k \times 2n_d } $ 矩阵式(101)(24)
$ {{{{\boldsymbol{\varPi}}}}}_{k}^{0} \leftarrow \left({\boldsymbol{{H}}}^{0}\right)^{-1} {\boldsymbol{{Q}}}^{0} $ //$ {n_k \times 2n_d } $ 的$ {{{\Pi}}}_{k}^{0} $ 矩阵式(95)(25) 根据
$ {\boldsymbol{{X}}} $ ,$ {\boldsymbol{{f}}} $ ,$ {\boldsymbol{{\varPi}}}_{k}^{0} $ 计算$ {\boldsymbol{{r}}}^{{\boldsymbol{f}}}_E $ ,$ {\boldsymbol{{r}}}_E $ //右端项式(102)、式(83)(26) end
(27) else
(28)
$ {\boldsymbol{{H}}}_{\alpha\beta} \leftarrow \int_E {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{p}}}_\beta \; {\rm{d}}E $ //$ {\boldsymbol{{H}}}_{n_{k-2} \times n_{k-2} } $ 矩阵式(105)(29)
$ {\boldsymbol{{Q}}}_{\alpha i} \leftarrow \int_E {\boldsymbol{{p}}}_\alpha \cdot {\boldsymbol{{\phi}}}_i \; {\rm{d}}E $ //$ {\boldsymbol{{Q}}}_{n_{k-2} \times 2n_d } $ 矩阵式(97)(30)
$ {\boldsymbol{{\varPi}}}^0_{k-2} \leftarrow {\boldsymbol{{H}}}^{-1} {\boldsymbol{{Q}}} $ //$ {n_{k-2} \times 2n_d } $ 的$ {{{{\boldsymbol{\varPi}}}}}^0_{k-2} $ 矩阵式(109)(31) 根据
$ {\boldsymbol{{X}}} $ ,$ {\boldsymbol{{f}}} $ ,$ {\boldsymbol{{\varPi}}}^0_{k-2} $ 计算$ {\boldsymbol{{r}}}^{{\boldsymbol{f}}}_E $ ,$ {\boldsymbol{{r}}}_E $ //右端项式(110)、式(83)(32) end
4.4 应用实例
如前所述, 虚单元法可处理任意节点数目的多边形且对单元凸凹性没有限制. 为做出直观展示, 本小节以含有“力”字单元的悬臂梁模型为例, 讨论收敛性. 本小节结果为阶次为
$ k=1 $ 的情况.考虑到悬臂梁的位移场存在理论解(Timoshenko and Goodier 1951). 如图 3 所示, 在平面应变状态下单位厚度的悬臂梁左端, 根据理论解施加位移边界条件, 右端施加沿 y 轴分布的剪应力:
$$ \begin{array}{*{20}{l}} \tau_{xy} = \dfrac{P}{2I}\left(\dfrac{D^2}{4} - y^2\right) \end{array} $$ (112) 此时, 水平向与垂向的位移为
$$ \begin{align} &u_{x}=-\frac{P y}{6 \bar{E}_{Y} I}\left[(6 L-3 x) x+(2+\bar{\nu}) y^{2}-\frac{3 D^{2}}{2}(1+\bar{\nu})\right] \end{align} $$ (113) $$ \begin{align} &u_{y}=\frac{P}{6 \bar{E}_{Y} I}\left[3 \bar{\nu} y^{2}(L-x)+(3 L-x) x^{2}\right] \end{align} $$ (114) 其中,
$ \bar{E}_{Y} = E_Y/(1-\nu^2) $ ,$ \bar{\nu} = \nu / (1-\nu) $ ,$ I = D^3/12 $ . 模型参数为$ E_Y = 200 $ GPa,$ \nu = 0.3 $ ,$ L=8 $ m,$ D=4 $ m, 右端载荷$ P = -1\times 10^5 $ kN.为展示虚单元的优势, 采用含“力”字单元的网格, 分别计算四种网格密度, 如图 4(a) 所示. 图 4(b) 为计算得到的水平向位移场, 可以看出位移场连续且光滑.
图 5 展示了收敛曲线, 横轴为单元平均特征尺寸
$ h=\displaystyle\sum_{E\subset \Omega^h } h^E / n_v $ , 纵轴为不同的误差估计, 可以看出含有“力”字单元的网格是满足收敛的.图 6 展示了不同纵向剖面(如图 3 所示
$ x=2.0 $ m,$ x=4.0 $ m,$ x=7.2 $ m)的水平向位移与理论解的比较, 可以看出虚单元方法在不均匀的多边形网格下, 随着网格的加密能够趋于收敛.5. 虚单元方法的深入应用
上一章系统梳理了理解虚单元基本理论的预备知识; 侧重数学推导, 阐述了虚单元在泊松方程的应用; 侧重物理解释, 介绍了虚单元在二维弹性问题的应用过程. 如前言所述, 虚单元方法的相关研究已从计算数学领域逐渐拓展到工程科学/力学领域. 本章对虚单元方法在计算力学领域的研究进展进行归纳与总结, 包括材料与几何非线性、接触与界面问题、断裂问题等. 为避免内容过度重合, 每部分仅引用近 5 年的代表性工作.
5.1 材料与几何非线性
本节首先梳理小变形的相关工作, 侧重于单元曲直、阶数的研究进展, 其次按照准静态问题与动力学问题进行区分, 讨论材料与几何非线性问题的研究进展. 需要指出, 晶体塑性的相关工作在下一节接触与界面问题中予以讨论.
5.1.1 小变形问题
对于低阶直线单元, Artioli et al. (2017a) 提出虚单元方法求解线弹性问题的标准化代码实现流程, 详细介绍了协调项、稳定项和载荷右端项的构造过程, 结果表明, 同阶的虚单元方法与有限元方法具有相近的准确性和相同的收敛阶数, 且对网格畸变几乎不敏感. 此后, Artioli et al. (2017b) 将其工作扩展到非线性材料中, 研究了黏弹性模型、含各向同性与运动硬化的 Mises 塑性模型、以及记忆合金本构模型. Beirão da Veiga et al. (2015) 对小变形条件下, 虚单元的非线性弹性本构与 Mises 屈服准则的弹塑性本构的应用过程进行了总结. Gain et al. (2014) 将虚单元法应用到三维的小变形弹性问题中, 并对比了不同类型网格的收敛性.
针对单元阶数, Beirão da Veiga et al. (2017a) 提出了高阶单元方法求解对流反应方程, Beirão da Veiga et al.(2016)类比高阶 Serendipity 有限元方法, 提出了高阶 Serendipity 虚单元方法求解弹性问题. 与高阶有限元方法类似, 高阶虚单元法对网格畸变问题具有更高的鲁棒性, 并且由于增加了自由度, 计算精度更高. 为避免离散曲线边界时需要“以直代曲”, 针对单元曲直, Beirão da Veiga et al. (2019) 将单元边界的描述转化为自然坐标, 提出了曲边单元, 并对椭圆方程进行了求解. Artioli et al. (2020) 将其方法应用到二维线弹性问题中, 但曲线形状不能任意. Wriggers et al. (2020) 提出可将参考构型的单元(直线边)映射到初始构型(曲线边)中, 实现任意形状的单元离散, 对于映射操作可采用等参映射或者 NURBS 映射. 而后, Wriggers et al. (2021b) 将该方法扩展到高阶单元中.
5.1.2 准静态问题的几何与材料非线性
对于弹性条件下的几何非线性问题, Wriggers et al. (2017) 通过对应变能的讨论, 提出了有限变形的稳定项构建方法, 通过可压缩和不可压缩材料的模拟, 验证了其方法的收敛性和鲁棒性, 如图 7 所示. 同一时期, Chi et al.(2017) 通过构造局部位移空间准确求得体积变化, 根据切线模量的迹构建稳定项, 讨论了混合单元(位移、压力)格式与纯位移格式的有限变形模型. 图 8 是其模型对弹性多孔材料的模拟结果. 针对不可压缩材料, Taylor-Hood 是混合单元格式, 采用不同的阶数插值位移与压力, 以保证 LBB 稳定条件, Wriggers et al. (2021a) 将 Taylor-Hood 单元引入到虚单元法中, 构造了不可压缩材料的有限变形格式.
图 7 有限变形下的冲压问题. (a)模型, (b)可压缩材料的冲压变形, (c)不可压缩材料冲压变形(修改自 (Wriggers et al. 2017))
图 8 弹性多孔材料的有限变形. (a)模型, (b)剪应变为 1.345 下的最大应变分布(修改自(Chi et al. 2017))若进一步考虑材料非线性, Wriggers and Hudobivnik (2017) 采用低阶单元从最小能量增量出发, 构造了二维弹塑性本构下有限变形的虚单元格式, 并对精度和收敛性进行了讨论. Hudobivnik et al. (2019) 将该方法扩展到三维问题中, 并对比了不同收敛算法对结果的影响. 图 9 是对冲压以及扭转过程的模拟结果.
图 9 准静态大变形弹塑性问题的等效塑性应变分布. (a)冲压, (b)扭转 (修改自(Hudobivnik et al. 2019))需要指出, 大部分虚单元方法在处理非线性问题时, 均采用低阶单元, De Bellis et al. (2019) 成功将高阶单元应用到非线性弹性问题中.
5.1.3 动力学问题的几何与材料非线性
对于动力学问题, Cihan et al. (2021b) 指出不同于刚度矩阵需要稳定项, 虚单元方法的质量矩阵只需要进行映射操作即可, 其中时间积分可按照隐式 Newmark 格式进行. 图 10 是不考虑阻尼条件下, 悬臂梁的振动模拟结果.
图 10 悬臂梁振动问题. (a)模型, (b)垂向位移时间演化(修改自 (Cihan et al. 2021b))对于弹塑性的动力学问题, Cihan et al. (2021a) 按照 Hu-Washizu 泛函求极值的基本思路, 提出了混合单元格式, 以避免弹塑性不可压条件引入的体积自锁问题, 其中的时间积分亦采用隐式 Newmark 格式. 图 11 为泰勒杆与冲压过程中的塑性应变. 若采用显式时间积分, Park et al. (2020) 对弹性不可压缩材料、Park et al. (2019) 对弹塑性材料分别进行了讨论, 其中临界时间步长都是通过矩阵最大的特征值确定.
图 11 弹塑性动力学问题的塑性应变. (a)泰勒杆, (b)冲压 (修改自 (Cihan et al. 2021a))上述讨论的都是各向同性材料, 对于横观各向同性材料（比如纤维增强）, 虚单元法也被逐步应用到小变形 (Wriggers et al. 2018b, Reddy and van Huyssteen 2019) 与有限变形模拟中 (Wriggers et al. 2018a, van Huyssteen and Reddy 2021).
5.2 接触与界面问题
由于虚单元法对网格形状没有要求, 因而在网格配对处理上可得到极大简化, 在处理接触与界面问题上具有先天优势. 本节分别从接触问题、非均匀材料的界面问题以及衍生的晶体塑性三个方面总结虚单元的研究进展.
5.2.1 接触问题
采用虚单元法处理接触问题, 是该方法一个非常重要的应用. 处理接触问题需要判断两个物体间的相对位置, 对于有限元网格(含节点、网格边界线), 如图 12(a)~图 12(c)所示, 常用的方法有点-点、点-线、Mortar 型, 其中点-点型最容易实现, 但需要网格匹配. 由于虚单元对单元节点数目没有要求, 可任意增加节点, 如图 12(d)所示, 可以将潜在接触面的节点向目标面做映射生成新的节点, 采用点-点格式进行接触判断, 如此可避免复杂的网格匹配、助于各体间独立建模. 需要指出, 虚单元法中增加了单元节点后, 增加节点的单元形式会发生改变, 待解自由度增加, 而其他单元没有变化, 这是与有限元节点插值最大的区别.
对于两体接触, Wriggers et al. (2016) 对虚单元法在接触问题中的应用进行了梳理, 分别采用拉格朗日乘子法和罚函数法施加约束, 其结果表明虚单元法利用插点格式处理接触问题, 精度高、操作简单. 图 13 是采用不同方法对接触问题进行的分片测试, 可以看出相对于有限元中的点-线格式, 虚单元法求得的应力均匀, 精度更高. Wriggers and Rust (2019) 将该方法扩展到大变形的摩擦接触问题中, 图 14 为其模拟的赫兹接触过程. 对于接触体具有曲线边界的情况, Aldakheel et al. (2020) 引入了曲边单元处理接触, 其中插入的节点需要按照曲边单元进行处理.
图 13 接触问题的分片测试. (a)虚单元法, (b)有限元点−线格式(修改自(Wriggers et al. 2016))
图 14 大变形条件下的赫兹接触问题(修改自 (Wriggers and Rust, 2019))颗粒材料中颗粒间的相互作用涉及多体接触问题, 常采用离散元进行描述, 其核心假定为颗粒为刚体. 虚单元法在网格上的任意性以及接触处理的优势, 使得快捷准确地捕捉变形颗粒间的相互作用变为可能. Gay Neto et al. (2021) 首次做出了尝试, 采用完全的隐式时间积分、并且研究了刚度与质量矩阵参数的敏感性. 图 15 模拟多面体颗粒集合的沙漏过程. 该方法为颗粒材料研究提供一个新的思路与方向.
图 15 颗粒材料沙漏过程(修改自 (Gay Neto et al. 2021))5.2.2 不考虑断裂的非均匀材料界面问题
对于非均匀材料, 考虑两方面的研究: 材料界面与均质化.
关于材料界面问题, Lo Cascio et al. (2021) 采用虚单元法描述基材、边界元法描述内嵌材料, 边界元获取的应力−位移方程转化为力−位移方程, 组装到虚单元法的方程组中, 实现两者的耦合. 该方法有效地描述了非均匀材料的变形及损伤演化, 图 16 为典型算例的模拟结果.
图 16 虚单元法与边界元法模拟非均匀材料. (a)网格, (b)单轴拉伸条件下的应力分布(修改自 (Lo Cascio et al. 2021))多晶材料的均质化是进行多尺度建模的核心. 对于有限元, 增加晶粒的各向异性需增加大量的自由度, 而虚单元法将任意形状的晶粒视为一个网格, 自由度数目自然大大降低. Marino et al. (2019)对线性和非线性的均质化格式开展研究. 若考虑电−磁−力耦合的多晶材料, Böhm et al. (2021b) 计算了不同晶格结构和不同程度的各向异性材料, 发现虚单元方法在低自由度条件下计算的均质化性能都表现出很好的精度, 如图 17 所示.
图 17 多晶结构均质化. (a)虚单元法网格, (b)粗糙的四面体网格, (c)精细的四面体网格, (d)$ \mathrm{BaNiO_3} $ ，中度各向异性，六方晶系晶胞(修改自 (Böhm et al. 2021b))5.2.3 晶体塑性
晶体塑性采用虚单元方法进行模拟具有巨大潜力. 虚单元法中单元的任意性可以完美地契合晶粒结构, 无需进行精细的网格剖分, 但该部分工作尚属起步阶段. Böhm et al. (2021a) 采用虚单元模拟了 FCC 晶格结构受单向拉伸的滑移过程, 其中映射操作在晶粒的表面进行以产生协调矩阵, 稳定项需要将晶格内部划分为多个四面体. 图 18 为单元分解过程与单滑的模拟结果. 工业应用方面, Behrens et al. (2020)将基于虚单元的晶体塑性模型应用到轴承衬套的生产设计中, 以描述多种材料连接处多晶材料的损伤与疲劳性质, 图 19 为模拟结果.
图 18 虚单元法模拟晶体塑性. (a)单个晶格网格分解为界面网格与内部四面体网格, (b)单轴拉伸条件下 FCC 晶格结构的剪应变(修改自 (Böhm et al. 2021a))
图 19 虚单元方法分析轴承衬套中不同材料连接区域的多晶塑性模型. (a)轴承衬套示意, (b)三种材料连接区域的代表性体积单元, (c) FCC 晶格在$ (1 1 1) $ 滑移面上剪切应变率$ \dot{\gamma}_1 $ 的分布, (d)等效 von Mises 应力分布(修改自 (Behrens et al. 2020))5.3 断裂问题
虚单元法中网格的任意性简化了空间离散的难度、并能随意增加/减少节点. 虚单元法处理断裂问题可以从直接单元切割(强间断)以及与其他方法(相场、内聚力、扩展有限元等)的结合两个角度进行总结.
5.3.1 直接单元切割
针对直接单元切割, Hussein et al. (2019)提出了沿裂纹扩展方向增加新的单元节点并进行单元分割的裂纹扩展技术, 对比不同形状的网格, 验证其方法的有效性. 图 20 为单元切割算法与单轴拉伸下的裂纹扩展. 直接切割算法的优势是可直接确定裂纹面的位移间隔, 在采用位移差求解应力强度因子时大大简化了程序设计, 并且由于可任意增加节点, 虚单元法在裂纹交叉、分叉、三维曲面裂纹的扩展模拟中具有潜力.
图 20 虚单元法在断裂问题中的应用. (a)单元切割, (b)裂纹扩展(修改自 (Hussein et al. 2019))5.3.2 与其他方法结合模拟断裂
断裂问题一直是计算力学的热点, 在虚单元法提出以前, 适用于不同场景的描述断裂的方法已被广泛发展.
与相场法耦合. 考虑到裂纹扩展方向可以容易从相场方法获得, Hussein et al. (2020) 将相场法与单元切割融合, 采用虚单元法中单元切割表征裂纹扩展, 未开裂部分的网格采用自适应方案, 来求解相场. 该方法为裂纹扩展模拟提供了高效、鲁棒性强的模拟方案. 图 21 展示了该方法模拟的裂纹扩展过程.
图 21 单元切割与自适性相场耦合模拟裂纹扩展. (a)自适应网格求解相场, (b)单元切割模拟裂纹扩展(修改自 (Hussein et al. 2020))与内聚力模型结合. Marfia et al. (2022)将虚单元法与内聚力模型相结合, 按照单元域内平均的最大主应力确定裂纹方向, 通过内聚力模型以及单元切割, 模拟裂纹的起裂与扩展过程, 如图 22 所示. 进一步考虑非均匀材料的界面引起的断裂问题, Benedetto et al. (2018) 应用零厚度的界面单元模拟应力−裂纹张开过程, 结果如图 23 所示.
图 22 虚单元法与内聚力模型模拟 L 形状板的裂纹扩展(修改自 (Marfia et al. 2022))
图 23 虚单元法与内聚力模型模拟耦合. (a)接触脱离模拟, (b)非均匀材料三点弯曲梁模拟(修改自 (Benedetto et al. 2018))与扩展有限元法结合. 扩展有限元法是将近似函数空间进行扩充, 采用间断函数以及奇异函数描述物理场的间断. Benvenuti et al. (2019) 将扩展有限元法与虚单元进行结合, 对拉普拉斯方程的裂纹尖端进行了描述, 其中满足拉普拉斯方程的间断函数以及奇异函数被扩充到基函数空间中, 并推导了扩充映射操作符, 以便将扩充的基函数空间映射到线性多项式与扩充函数上. 图 24 所示为含裂纹的薄膜受 III 型载荷作用的模拟结果. Benvenuti 等 (2022)将扩展有限元法与虚单元结合的方法进一步应用到线弹性断裂问题中, 着重讨论了应力强度因子的求解.
图 24 虚单元法与扩展有限元结合模拟含裂纹的薄膜在 III 型载荷作用下变形. (a)100 个网格, (b)1600个网格(修改自 (Benvenuti et al. 2019))5.4 多场耦合、拓扑优化与地下裂隙网络流体流动
本节总结了虚单元法在其他领域的应用, 包括热−力耦合作用、拓扑优化、以及地下裂隙网络流体流动模拟等.
5.4.1 热−力耦合作用
对于热−力耦合问题, Dhanush and Natarajan (2019) 采用 Matlab 生成多边形网格以及 Abaqus 的输入文件, 将虚单元法成功应用到 Abaqus 中来处理小变形下的热−力耦合问题, 并给出了详细的数据格式. 进一步, Aldakheel et al. (2019b) 将虚单元法中有限变形下的弹塑性模型引入到热−力耦合问题中, 如此, 自由能包含弹性能、弹−热耦合部分、纯热部分、以及塑性势能. 图 25 为三维钢螺栓成型过程模拟.
5.4.2 拓扑优化
拓扑优化问题需要求解各种几何形状的边值问题, 由于虚单元法放松了对网格形状的要求, 简化了复杂形状的网格剖分难度, 特别适用于优化问题. Gain et al. (2015) 对比了虚单元法与有限元法的优化结果, 指出虚单元法只需要少量的单元, 便可得到足够精度. 图 26 展示了对悬臂梁的优化结果, 六面体网格需要 50000 多个网格, 而非规则多面体仅需 10000 个网格. 对于复合材料的大变形优化问题, Zhang et al. (2020) 引入虚单元法提高计算效率, 其中材料性能的确定是通过插值能量函数确定, 而非插值材料参数, 且该函数可以解决粗糙网格面临的单元畸变问题. 进一步, 对于纤维增强的软物质的拓扑优化问题, Zhang 等 (2021) 将基材与纤维参数作为两组设计参数, 其中纤维的方向是预先设定的一组离散方向, 并采用虚单元法求解有限变形的边值问题. 图 27 为三点弯曲梁的优化结果.
图 26 拓扑优化问题. (a)悬臂梁模型, (b)六面体网格, (c)非规则多面体网格(修改自 (Gain et al. 2015))
图 27 拓扑优化问题. (a)目标承载体, (b)优化结果(修改自 (Zhang et al. 2021))5.4.3 地下裂隙网络流体流动模拟
地下裂隙网络中流体的流动是地质力学中的重要问题. 相对于裂隙流动, 孔隙渗流过程一般忽略不计, 但三维空间中二维裂隙平面相互交叉、独立, 若采用传统有限元协调网格, 无法对每个裂隙单独建模, 必需整体考虑, 如此网格生成变得十分困难. 考虑到虚单元法对网格节点数目没有要求, 因而处理连接处的悬挂节点等十分自然, 可以大大简化网格生成的难度. Benedetto et al. (2016) 采用虚单元法对多种裂隙网络下的流动进行了尝试, 如图 28 所示. 此后, Benedetto et al. (2017) 将该方法扩展到混合单元与高阶单元.
图 28 地下裂隙流体流动问题. (a)网格生成, (b)裂隙网络中水头分布(修改自 (Benedetto et al. 2016))6. 结论与展望
正如在该综述的开头所强调的, 通过有别于传统综述论文的行文方式, 详述了虚单元方法的基本原理和最新理论进展, 同时也展示了目前该方法在一些典型问题中所体现的有别于有限元方法的潜力: 包括它对单元凸凹性的处理, 以及因此延伸到如悬挂节点、接触、裂纹扩展、多晶体变形等问题方面的应用. 基于处理非凸性单元任意多边形单元的考虑, 虚单元方法引入了和有限元方法迥异的处理方法, 最为显著的是(1)虚单元法中的近似函数既包含了多项式函数, 同时也引入了在单元域内无法显式表达的函数, 这也是虚单元方法中“虚”字的由来; (2) 自由度取值在节点以及单元边界上为近似函数的取值, 在单元内部为矩形式(近似函数与多项函数的乘积在单元内的积分), 避免计算非多项式在单元内部的取值; (3)为保证计算的收敛性, 虚单元法的刚度矩阵包含了协调矩阵和稳定矩阵两部分, 对应于多项式的精确解和多项式未被考虑的部分, 比有限元方法更为复杂.
虚单元法尚属于发展阶段, 在几何与材料非线性问题、接触与界面问题、断裂问题等诸多方面具有发展潜力, 尤其需要关注它在以下几个方面的应用.
(1) 裂纹扩展: 断裂问题一直是计算力学的热点, 在虚单元法提出以前, 适用于不同场景的描述断裂的方法已被广泛发展. 当前虚单元法在这一类问题方面展现了非常好的兼容性. 将相场法与单元切割融合, 采用虚单元法中单元切割表征裂纹扩展 (Hussein et al. 2020), 可以为裂纹扩展模拟提供了高效、鲁棒性强的模拟方案. 将虚单元法与内聚力模型相结合, 通过内聚力模型以及虚单元法中的单元切割 (Marfia et al. 2022), 可高效模拟裂纹的起裂与扩展过程. 将扩展有限元法与虚单元进行结合 (Benvenuti et al. 2019, 2022), 可模拟诸多的线弹性断裂问题.
(2) 接触问题: 虚单元法对单元形状没有要求, 可任意增加接触面节点, 因而在处理接触与界面问题时, 可避免网格配对带来的挑战, 简化计算与单元划分问题. (Wriggers et al. 2016) 对虚单元法在接触问题中的应用进行了梳理, 分别采用拉格朗日乘子法和罚函数法施加约束, 其结果表明虚单元法利用插点格式处理接触问题, 精度高、操作简单. 对涉及大变形的摩擦接触问题 Wriggers and Rust (2019)和具有曲线接触边界的情况 (Aldakheel et al. 2020), 虚单元法也具有高效的处理方案. 同样对于涉及多体接触的问题, 虚单元法在网格上的任意性以及接触处理方面, 也具超越离散元的优势, 可快捷准确捕捉变形颗粒间的相互作用 (Gay Neto et al. 2021). 工程中涉及到类似的接触问题不胜枚举.
(3) 多晶体变形: 利用虚单元法来模拟晶体塑性具有巨大潜力. 这是因为虚单元法中对多边形单元的包容将可以和晶粒结构完美地契合, 一方面无需进行精细地网格剖分, 可以确保具有晶体取向的晶粒的整体性, 同时又可以保持晶粒内部不同区域之间的非局域作用, 使得变形梯度、位错塞积等晶体变形特征能够得到妥善处理. 尽管目前一些研究组已经采用虚单元方法开展了晶格塑性模拟方面的应用 (Böhm et al. 2021a, Behrens et al. 2020), 该方面的工作还亟待开发, 以充分利用虚单元法对非规则单元处理方面的优势.
以上是笔者从自身的科研背景和需求出发所展望的虚单元计算方法的发展潜力, 因此它不可能是全面的. 同时需要强调的是, 虚单元方法在这些特定问题方面, 具有超越传统有限元方法的某些优势, 因此为饱受这些问题困扰的科研工作者提供了一种新的解决方案, 但这并不意味着它能全面地替代有限元方法的成熟性、便利性以及历经长时间发展带来的高可靠性. 它作为一个特定模块, 结合相应的有限元方法, 将丰富和提升计算力学的处理能力和便利性. 通过对两者的融会贯通, 促进发展出适应我国力学计算需求的新型算法与高性能软件.
1)$ h $ 一般代表空间离散尺寸, 考虑到单元离散后必对应近似函数空间, 为避免引入过多符号, 直接采用$ h $ 符号表示近似空间, 且在定义变量时是上标、在定义运算时是下标.2) 计算数学的微元符号常采用 dx(如上章所述), 本章更侧重于力学解释, 因而体积微元为${\rm{d}} \varOmega $ , 界面微元为${\rm{d}}\partial \varOmega $ -
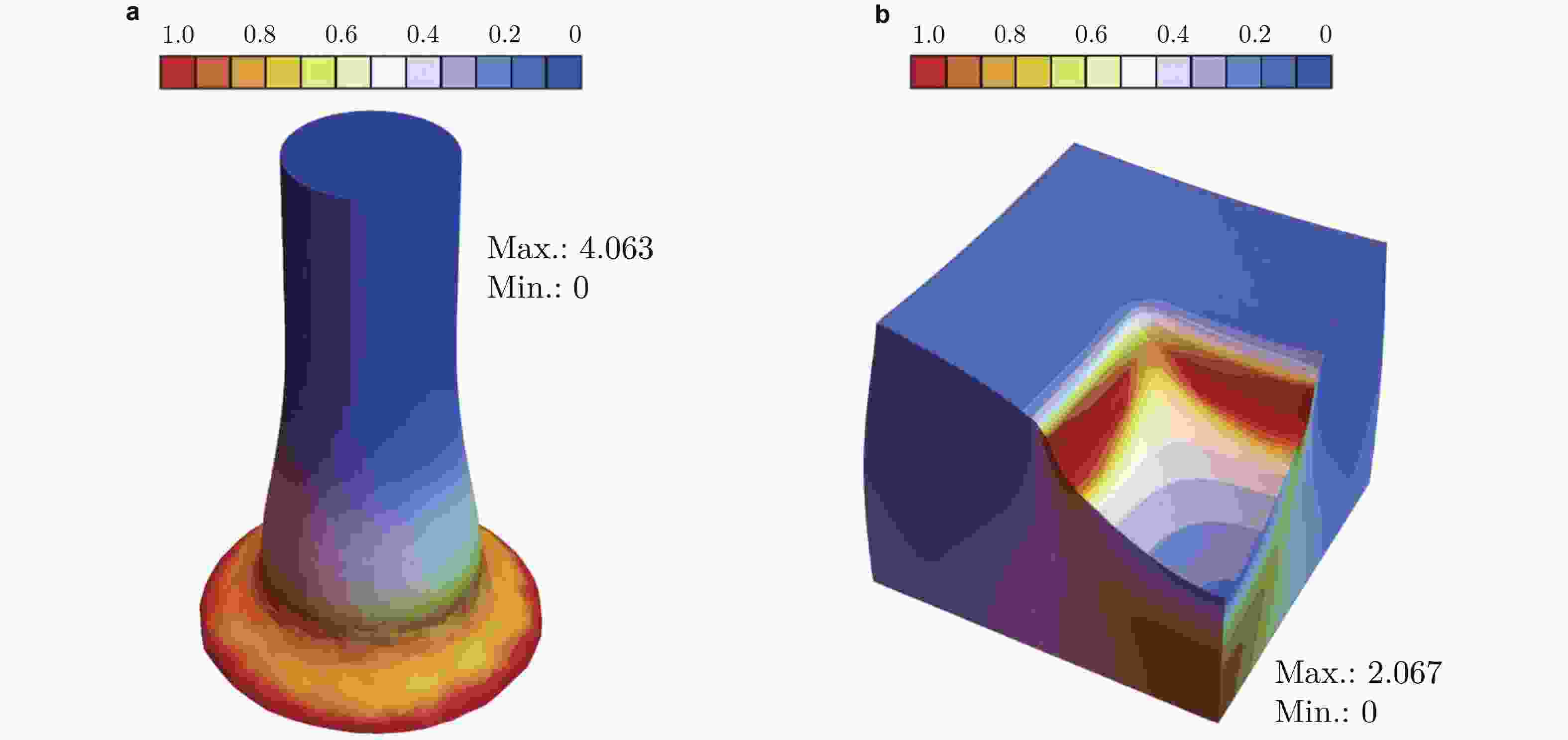
图 7 有限变形下的冲压问题. (a)模型, (b)可压缩材料的冲压变形, (c)不可压缩材料冲压变形(修改自 (Wriggers et al. 2017))
图 8 弹性多孔材料的有限变形. (a)模型, (b)剪应变为 1.345 下的最大应变分布(修改自(Chi et al. 2017))
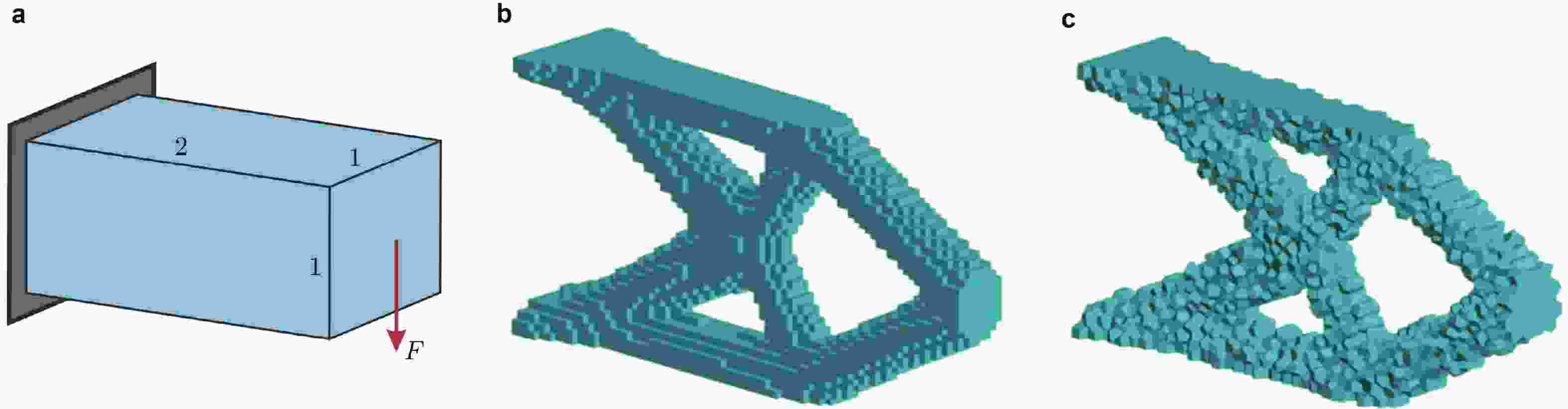
图 9 准静态大变形弹塑性问题的等效塑性应变分布. (a)冲压, (b)扭转 (修改自(Hudobivnik et al. 2019))
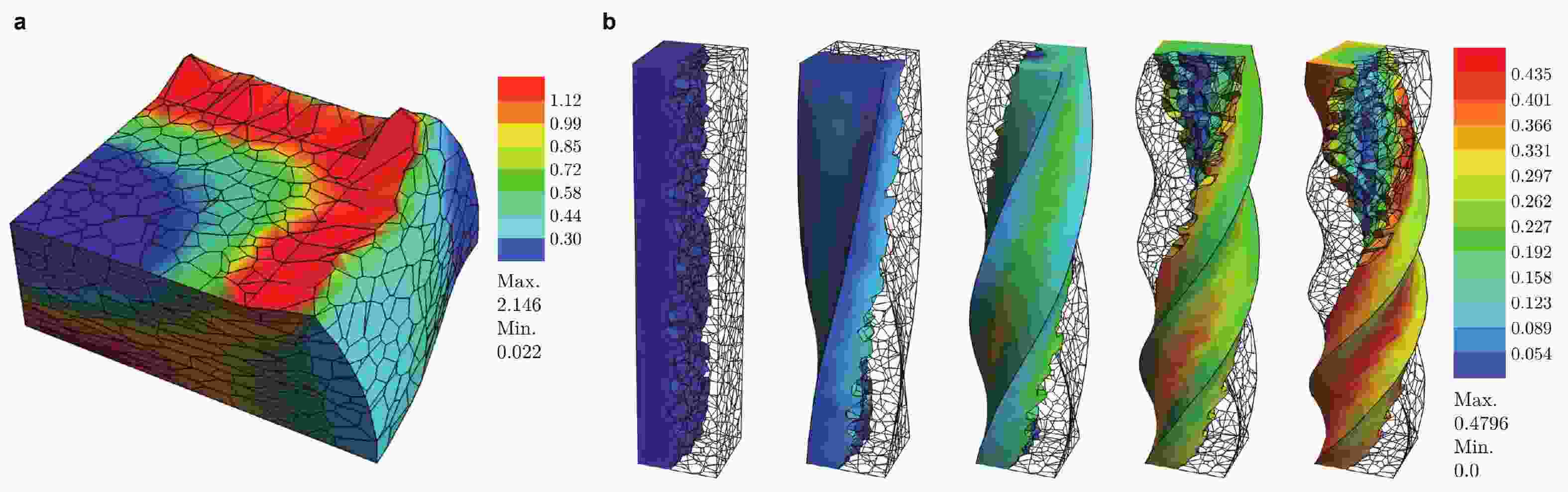
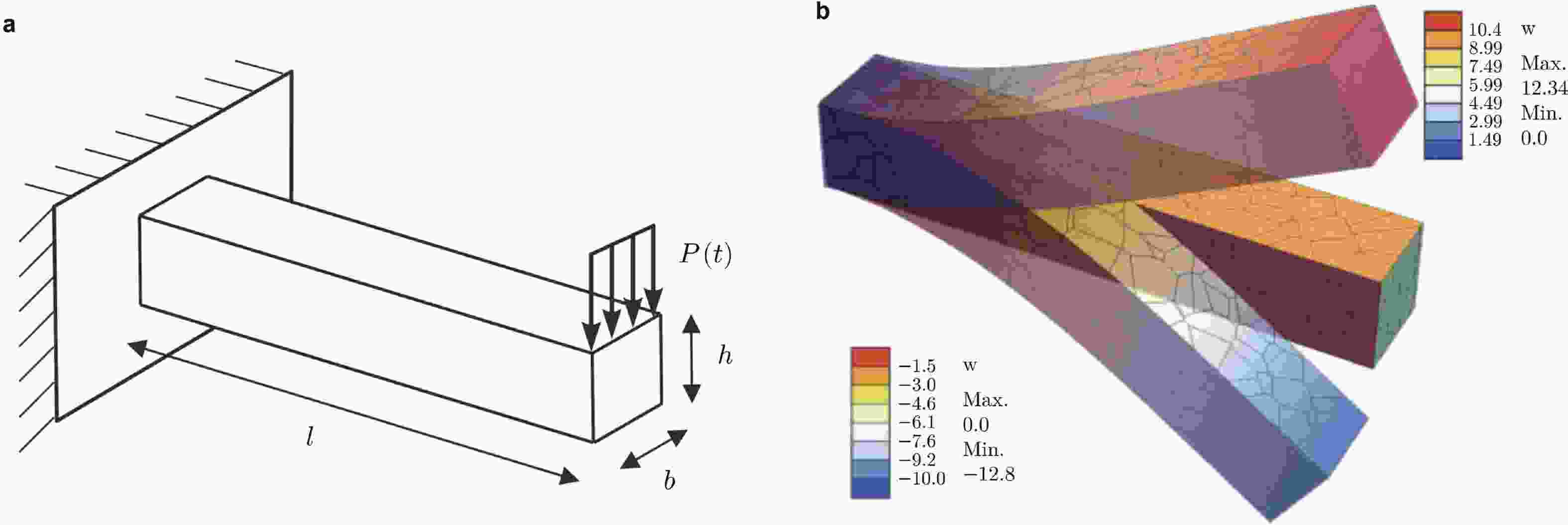
图 10 悬臂梁振动问题. (a)模型, (b)垂向位移时间演化(修改自 (Cihan et al. 2021b))
图 11 弹塑性动力学问题的塑性应变. (a)泰勒杆, (b)冲压 (修改自 (Cihan et al. 2021a))
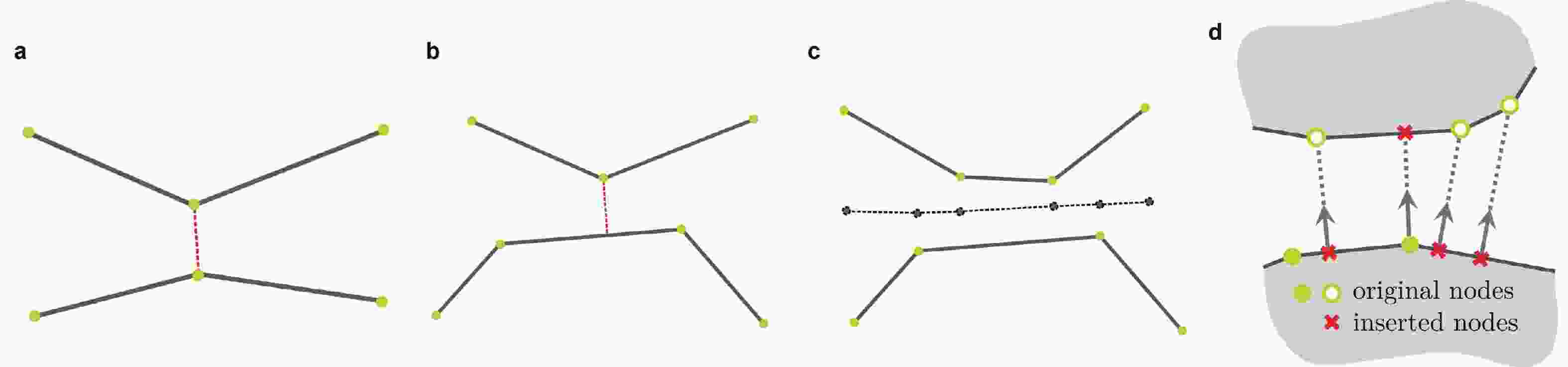
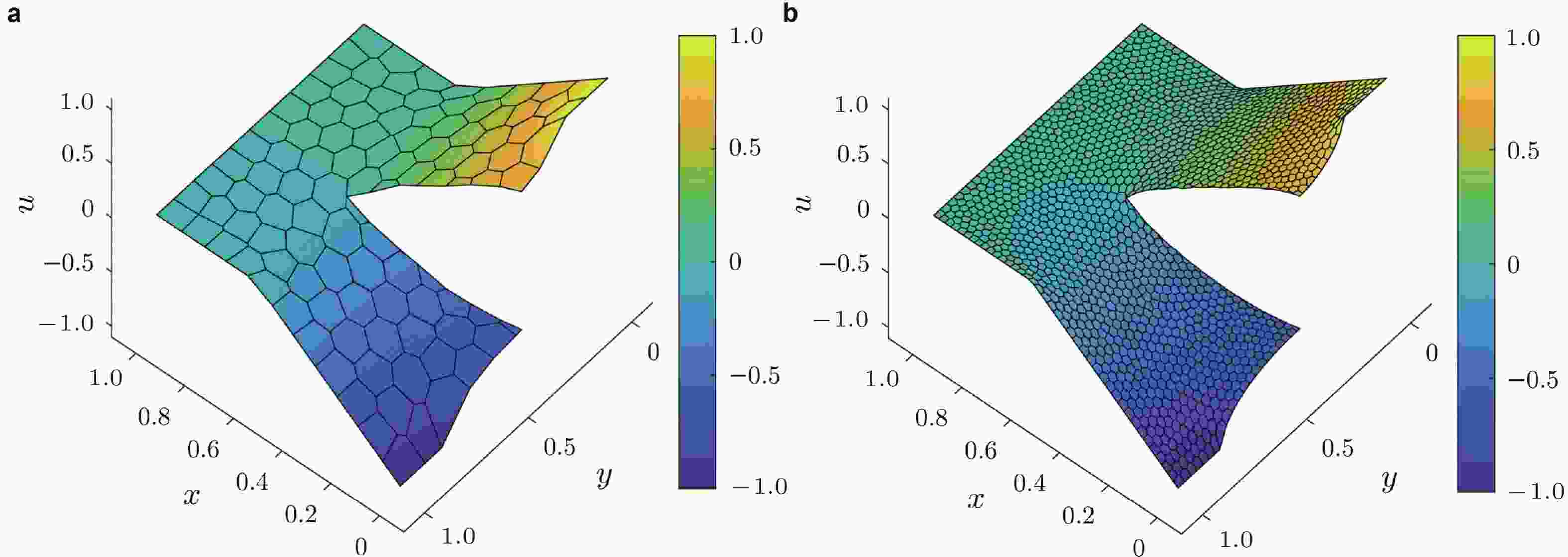
图 13 接触问题的分片测试. (a)虚单元法, (b)有限元点−线格式(修改自(Wriggers et al. 2016))
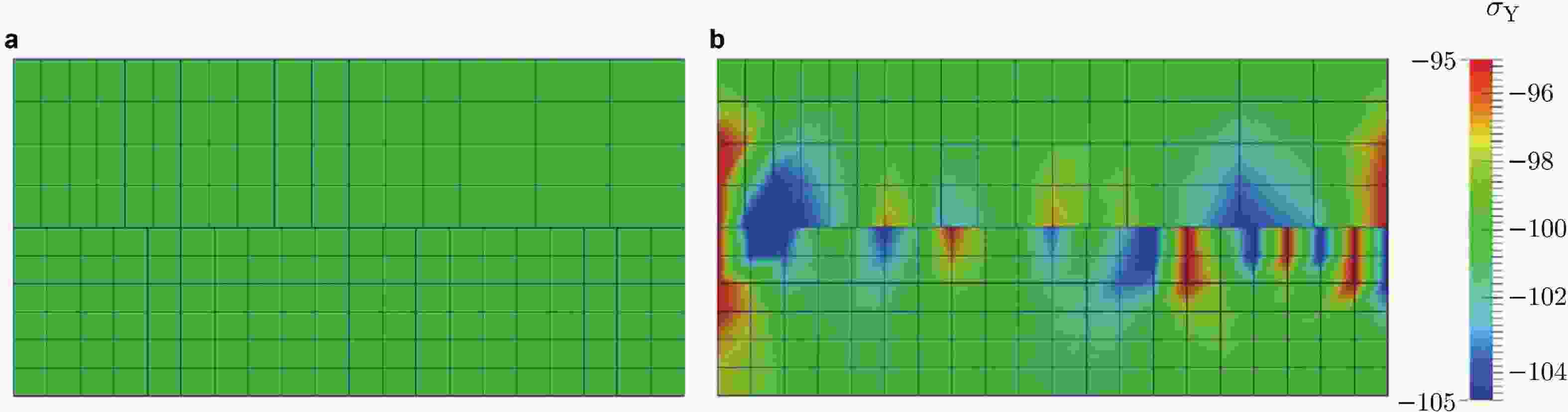
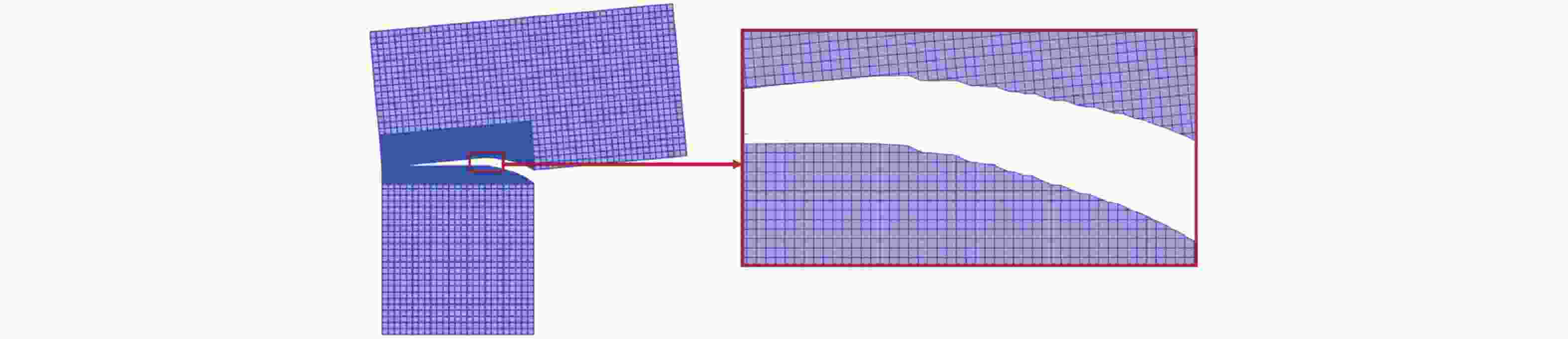
图 14 大变形条件下的赫兹接触问题(修改自 (Wriggers and Rust, 2019))
图 15 颗粒材料沙漏过程(修改自 (Gay Neto et al. 2021))
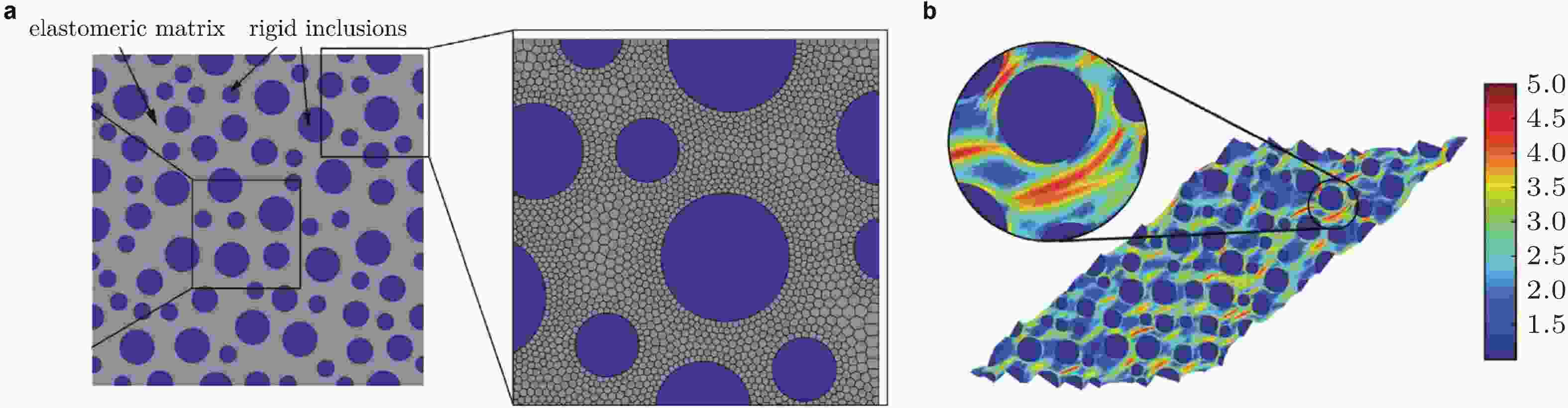
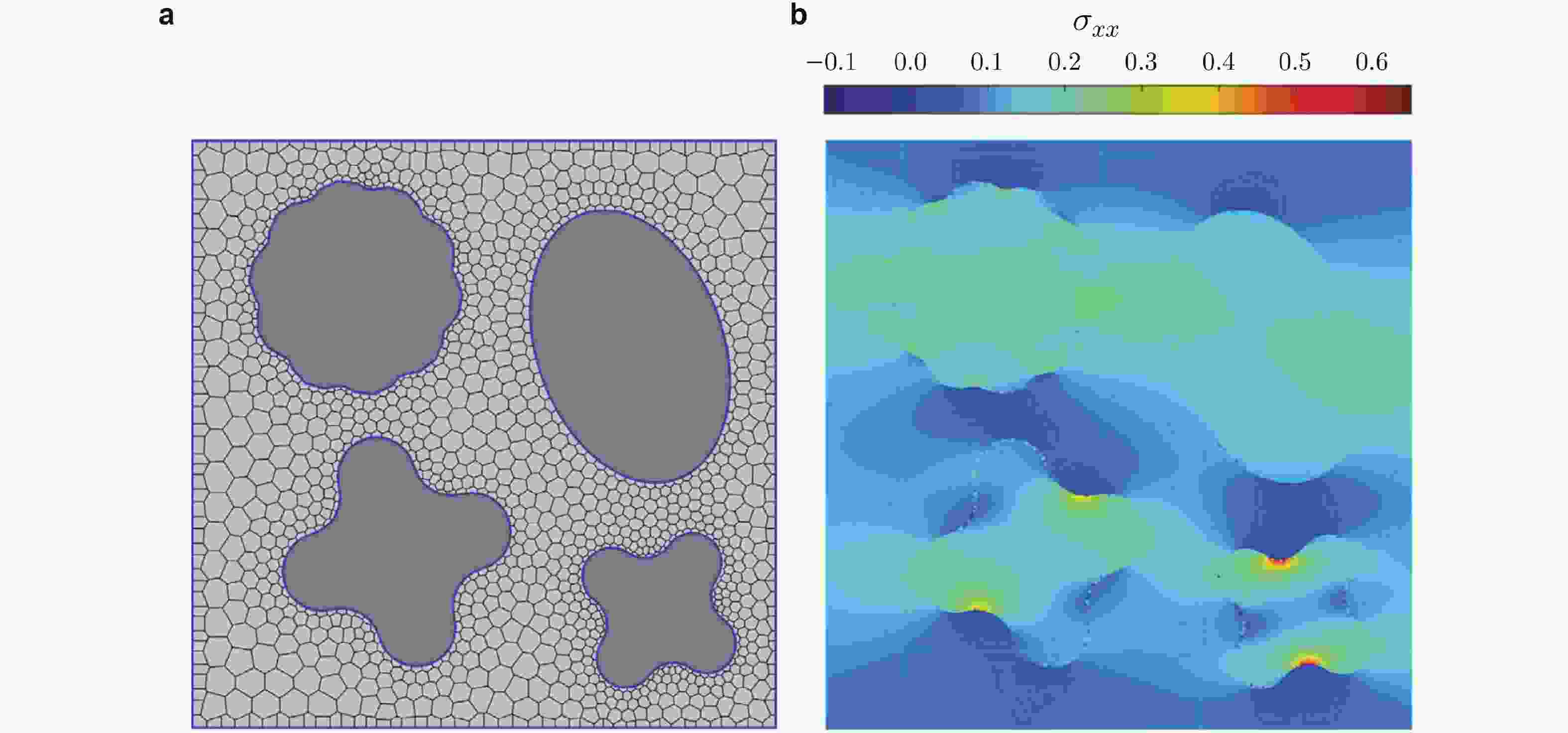
图 16 虚单元法与边界元法模拟非均匀材料. (a)网格, (b)单轴拉伸条件下的应力分布(修改自 (Lo Cascio et al. 2021))
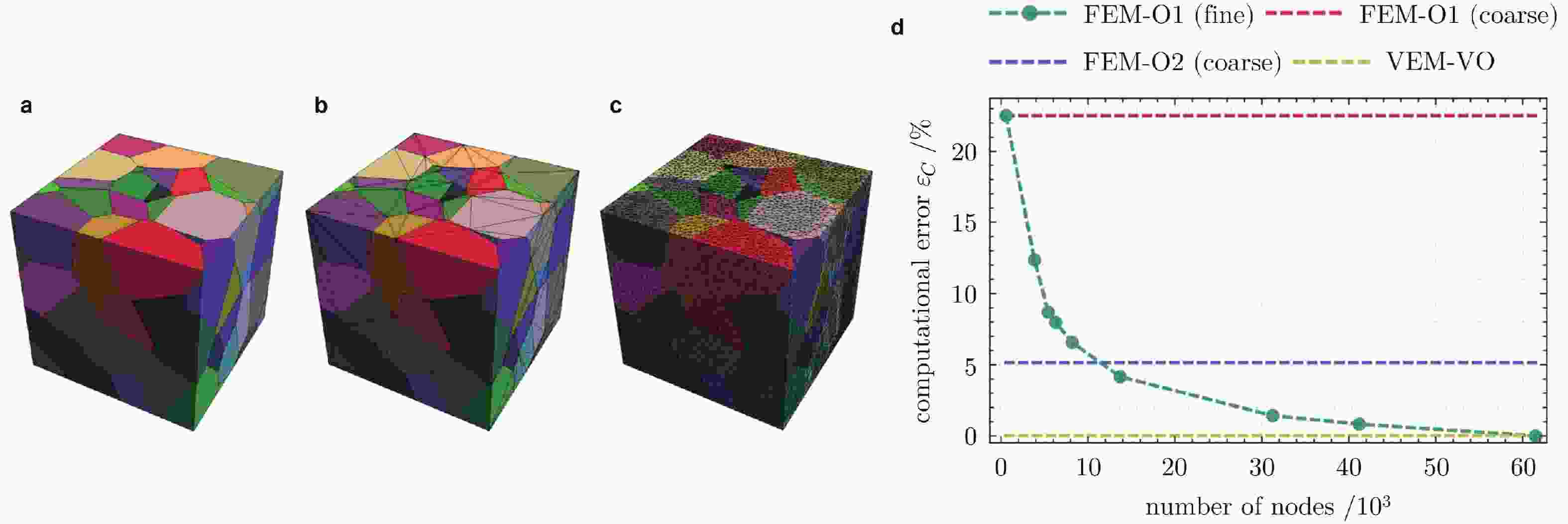
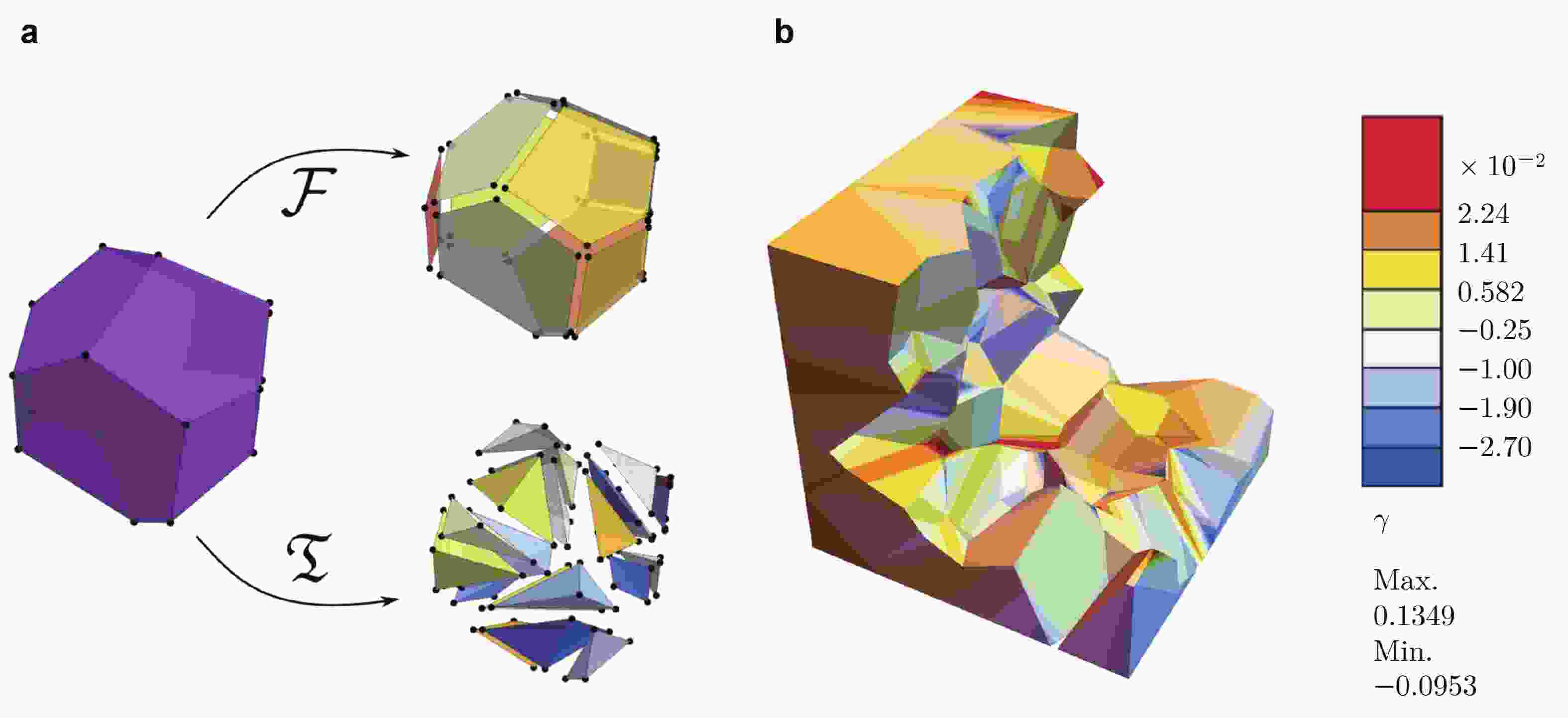
图 17 多晶结构均质化. (a)虚单元法网格, (b)粗糙的四面体网格, (c)精细的四面体网格, (d)
$ \mathrm{BaNiO_3} $ ，中度各向异性，六方晶系晶胞(修改自 (Böhm et al. 2021b))
图 18 虚单元法模拟晶体塑性. (a)单个晶格网格分解为界面网格与内部四面体网格, (b)单轴拉伸条件下 FCC 晶格结构的剪应变(修改自 (Böhm et al. 2021a))
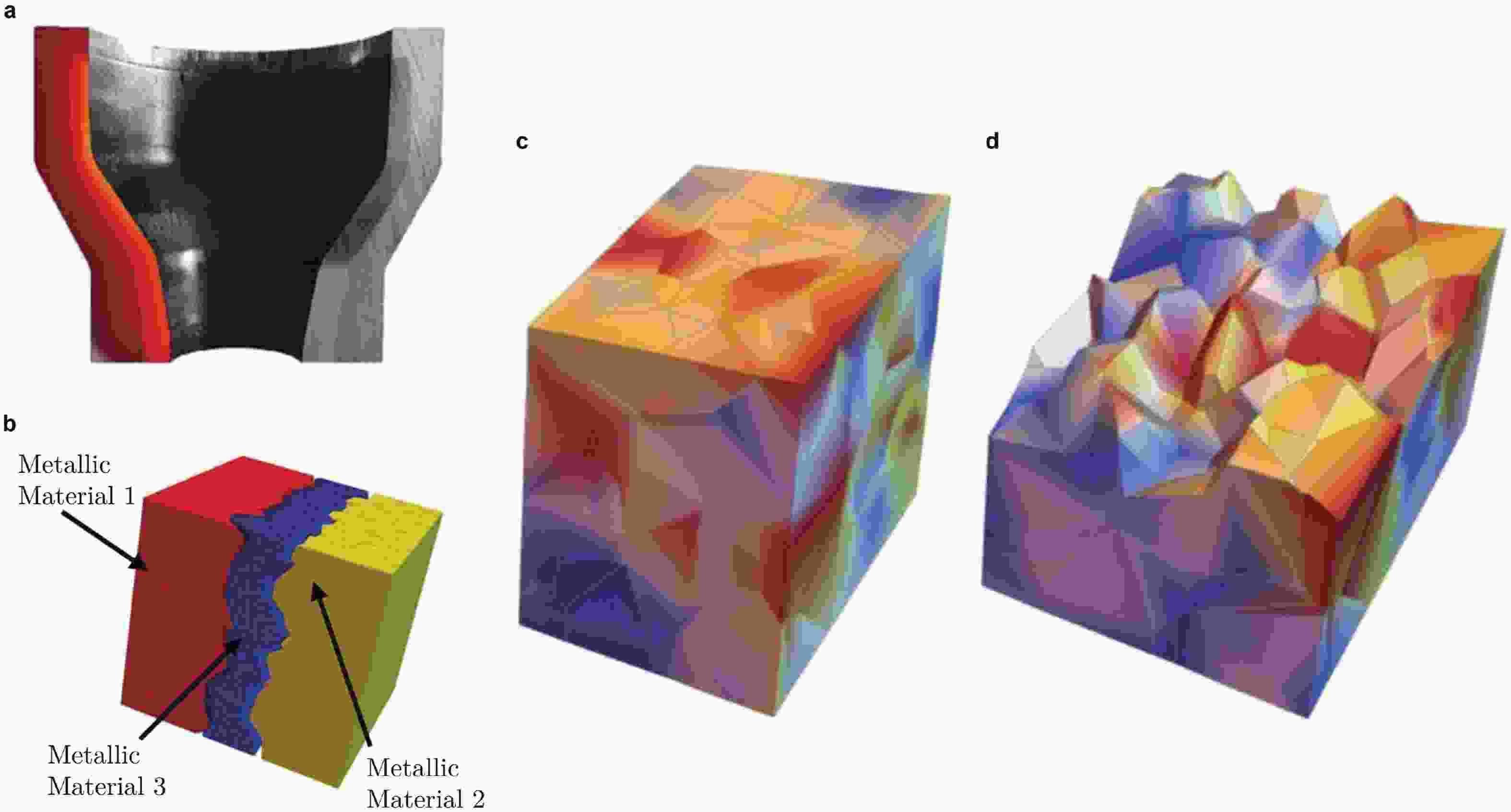
图 19 虚单元方法分析轴承衬套中不同材料连接区域的多晶塑性模型. (a)轴承衬套示意, (b)三种材料连接区域的代表性体积单元, (c) FCC 晶格在
$ (1 1 1) $ 滑移面上剪切应变率$ \dot{\gamma}_1 $ 的分布, (d)等效 von Mises 应力分布(修改自 (Behrens et al. 2020))
图 20 虚单元法在断裂问题中的应用. (a)单元切割, (b)裂纹扩展(修改自 (Hussein et al. 2019))
图 21 单元切割与自适性相场耦合模拟裂纹扩展. (a)自适应网格求解相场, (b)单元切割模拟裂纹扩展(修改自 (Hussein et al. 2020))
图 22 虚单元法与内聚力模型模拟 L 形状板的裂纹扩展(修改自 (Marfia et al. 2022))
图 23 虚单元法与内聚力模型模拟耦合. (a)接触脱离模拟, (b)非均匀材料三点弯曲梁模拟(修改自 (Benedetto et al. 2018))
图 24 虚单元法与扩展有限元结合模拟含裂纹的薄膜在 III 型载荷作用下变形. (a)100 个网格, (b)1600个网格(修改自 (Benvenuti et al. 2019))
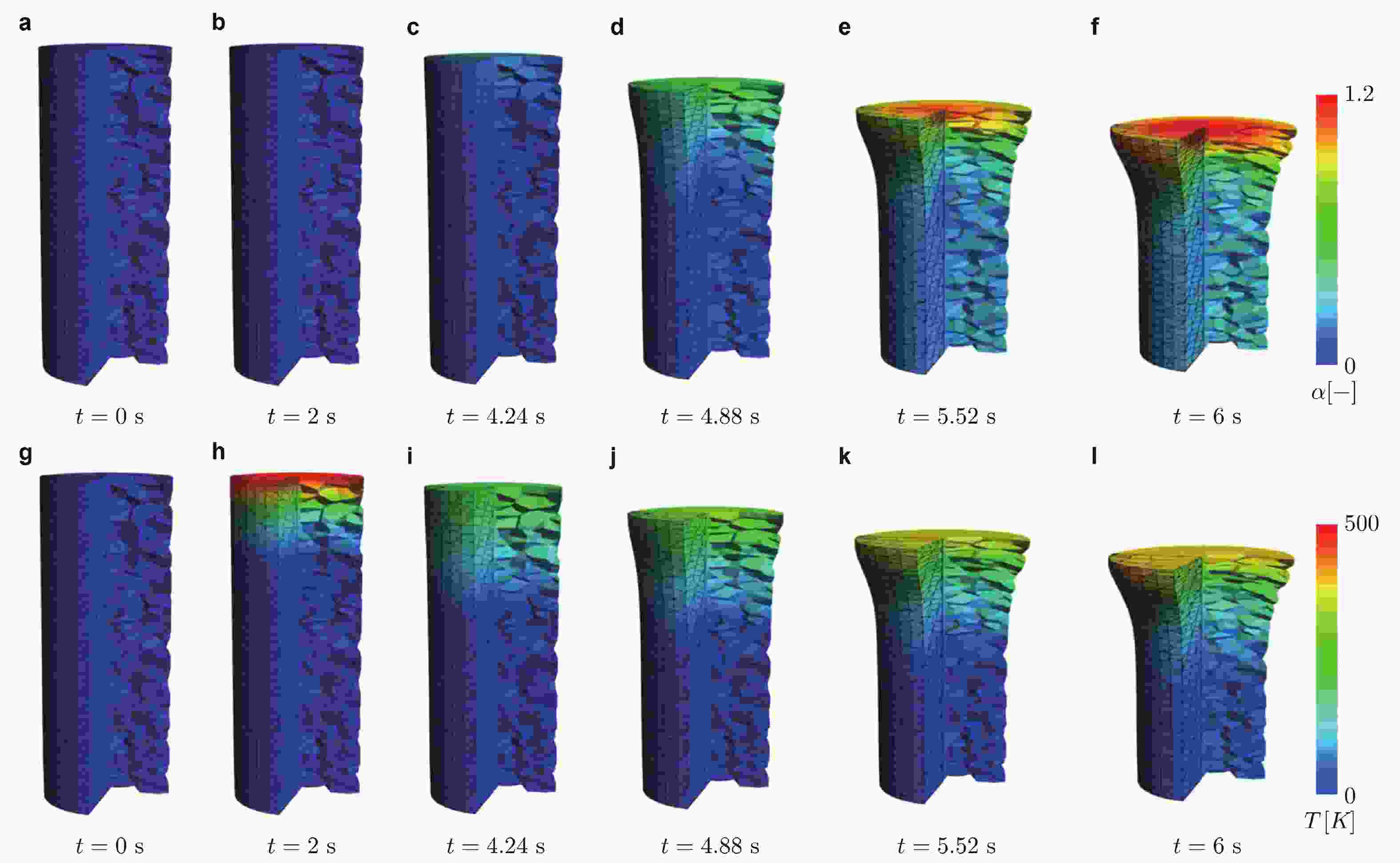
图 25 三维钢螺栓成型的热力耦合过程. (a)~(f)等效塑性应变, (g)~(l)绝对温度场
$ T $ (Aldakheel et al. 2019b)
图 26 拓扑优化问题. (a)悬臂梁模型, (b)六面体网格, (c)非规则多面体网格(修改自 (Gain et al. 2015))
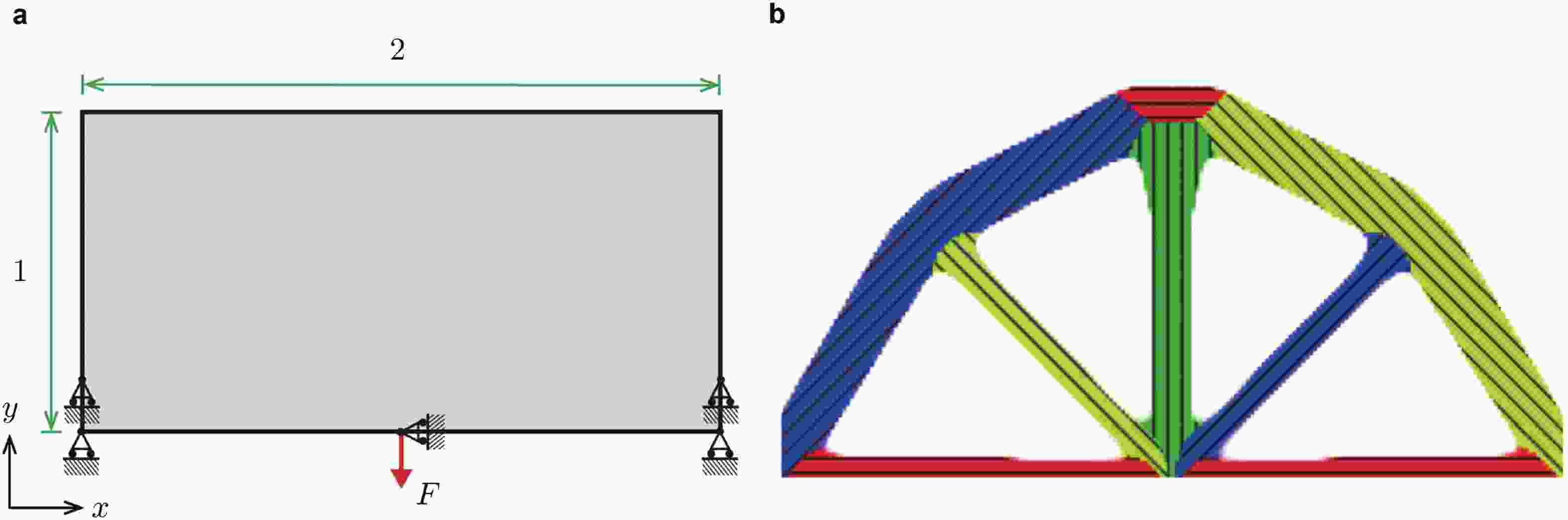
图 27 拓扑优化问题. (a)目标承载体, (b)优化结果(修改自 (Zhang et al. 2021))
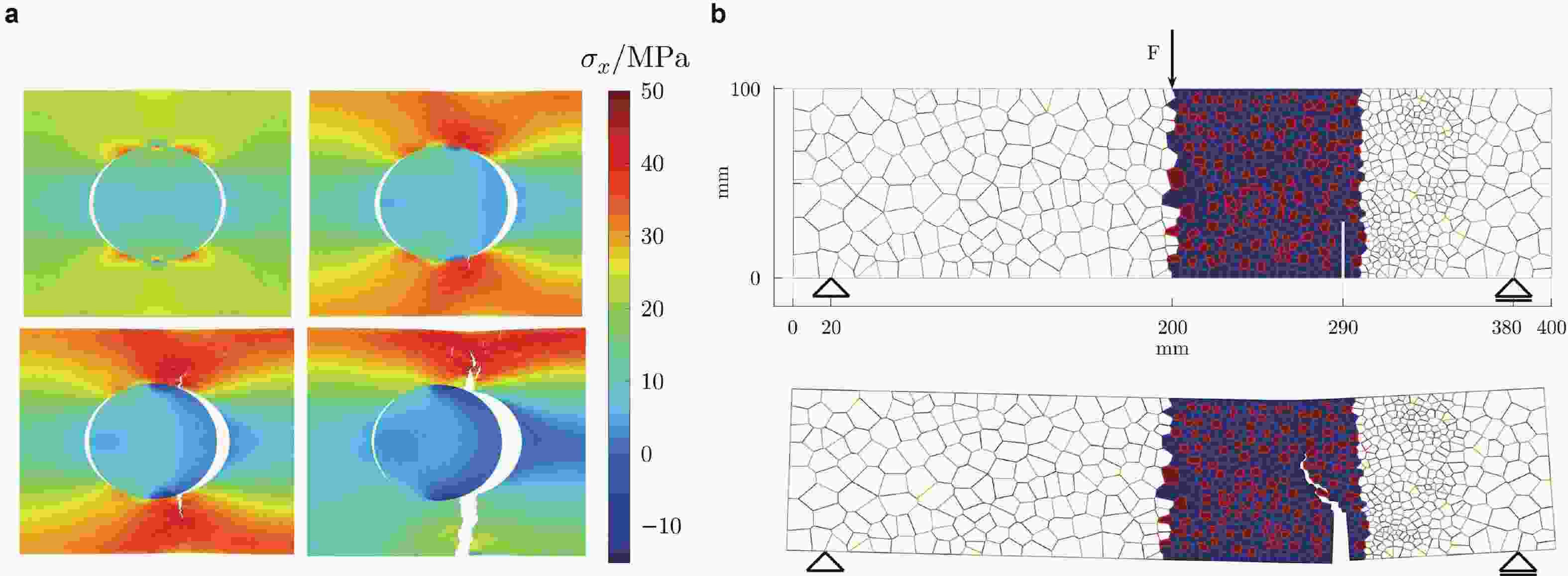
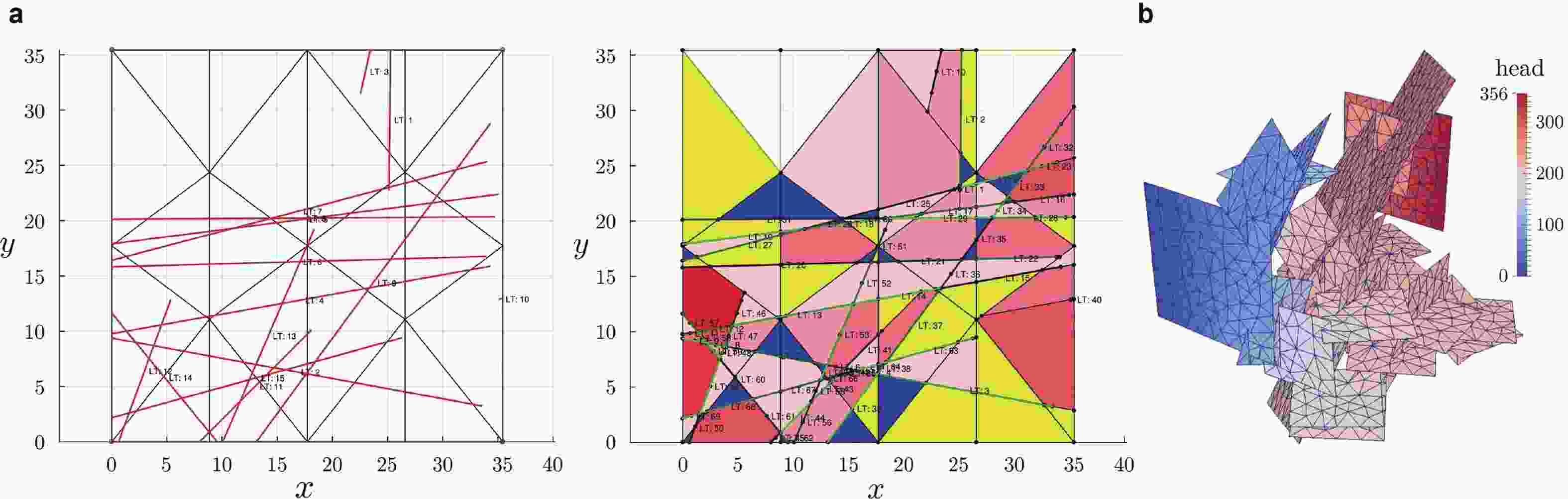
图 28 地下裂隙流体流动问题. (a)网格生成, (b)裂隙网络中水头分布(修改自 (Benedetto et al. 2016))
-
Aldakheel F, Hudobivnik B, Artioli E, Beirão da Veiga L, Wriggers P. 2020. Curvilinear virtual elements for contact mechanics. Computer Methods in Applied Mechanics and Engineering, 372: 113394. doi: 10.1016/j.cma.2020.113394 Aldakheel F, Hudobivnik B, Wriggers P. 2019a. Virtual element formulation for phase-field modeling of ductile fracture. International Journal for Multiscale Computational Engineering, 17: 181-200. doi: 10.1615/IntJMultCompEng.2018026804 Aldakheel F, Hudobivnik B, Wriggers P, 2019b. Virtual elements for finite thermo-plasticity problems. Computational Mechanics, 64: 1347–1360. Artioli E, Beirão da Veiga L, Dassi F. 2020. Curvilinear virtual elements for 2d solid mechanics applications. Computer Methods in Applied Mechanics and Engineering, 359: 112667. doi: 10.1016/j.cma.2019.112667 Artioli E, Beirão da Veiga L, Lovadina C, Sacco E. 2017a. Arbitrary order 2d virtual elements for polygonal meshes: Part i, elastic problem. Computational Mechanics, 60: 355-377. doi: 10.1007/s00466-017-1404-5 Artioli E, Beirão da Veiga L, Lovadina C, Sacco E. 2017b. Arbitrary order 2d virtual elements for polygonal meshes: Part ii, inelastic problem. Computational Mechanics, 60: 643-657. doi: 10.1007/s00466-017-1429-9 Behrens B A, Maier H J, Poll G, Wriggers P, Aldakheel F, Klose C, Nürnberger F, Pape F, Böhm C, Chugreeva A, et al. 2020. Numerical investigations regarding a novel process chain for the production of a hybrid bearing bushing. Production Engineering, 14: 569-581. doi: 10.1007/s11740-020-00992-7 Beirão da Veiga L, Brezzi F, Cangiani A, Manzini G, Marini L D, Russo A. 2013a. Basic principles of virtual element methods. Mathematical Models and Methods in Applied Sciences, 23: 199-214. doi: 10.1142/S0218202512500492 Beirão da Veiga L, Brezzi F, Marini L D. 2013b. Virtual elements for linear elasticity problems. SIAM Journal on Numerical Analysis, 51: 794-812. doi: 10.1137/120874746 Beirão da Veiga L, Brezzi F, Marini L D, Russo A. 2014. The hitchhiker's guide to the virtual element method. Mathematical Models and Methods in Applied Sciences, 24: 1541-1573. doi: 10.1142/S021820251440003X Beirão da Veiga L, Brezzi F, Marini L D, Russo A. 2016. Serendipity nodal vem spaces. Computers & Fluids, 141: 2-12. Beirão da Veiga L, Dassi F, Russo A. 2017a. High-order virtual element method on polyhedral meshes. Computers & Mathematics with Applications, 74: 1110-1122. Beirão da Veiga L, Lovadina C, Mora D. 2015. A virtual element method for elastic and inelastic problems on polytope meshes. Computer Methods in Applied Mechanics and Engineering, 295: 327-346. doi: 10.1016/j.cma.2015.07.013 Beirão da Veiga L, Lovadina C, Russo A. 2017b. Stability analysis for the virtual element method. Mathematical Models and Methods in Applied Sciences, 27: 2557-2594. doi: 10.1142/S021820251750052X Beirão da Veiga L, Russo A, Vacca G. 2019. The virtual element method with curved edges. ESAIM: Mathematical Modelling and Numerical Analysis, 53: 375-404. doi: 10.1051/m2an/2018052 Benedetto M F, Berrone S, Borio A, Pieraccini S, Scialò S. 2016. A hybrid mortar virtual element method for discrete fracture network simulations. Journal of Computational Physics, 306: 148-166. doi: 10.1016/j.jcp.2015.11.034 Benedetto M F, Borio A, Scialò S. 2017. Mixed virtual elements for discrete fracture network simulations. Finite Elements in Analysis and Design, 134: 55-67. doi: 10.1016/j.finel.2017.05.011 Benedetto M F, Caggiano A, Etse G. 2018. Virtual elements and zero thickness interface-based approach for fracture analysis of heterogeneous materials. Computer Methods in Applied Mechanics and Engineering, 338: 41-67. doi: 10.1016/j.cma.2018.04.001 Benvenuti E, Chiozzi A, Manzini G, Sukumar N. 2019. Extended virtual element method for the laplace problem with singularities and discontinuities. Computer Methods in Applied Mechanics and Engineering, 356: 571-597. doi: 10.1016/j.cma.2019.07.028 Benvenuti E, Chiozzi A, Manzini G, Sukumar N. 2022. Extended virtual element method for two-dimensional linear elastic fracture. Computer Methods in Applied Mechanics and Engineering, 390: 114352. doi: 10.1016/j.cma.2021.114352 Böhm C, Hudobivnik B, Aldakheel F, Wriggers P. 2021a. Modeling of single-slip finite strain crystal plasticity via the virtual element method. Proc. Appl. Math. Mech., 20: e202000205. Böhm C, Hudobivnik B, Marino M, Wriggers P. 2021b. Electro-magneto-mechanically response of polycrystalline materials: Computational homogenization via the virtual element method. Computer Methods in Applied Mechanics and Engineering, 380: 113775. doi: 10.1016/j.cma.2021.113775 Braess D. 2007. Finite elements: Theory, fast solvers, and applications in solid mechanics. Cambridge University Press Brenner S C, Scott L R. 2008. The mathematical theory of finite element methods. volume 15 of Texts in Applied Mathematics. Springer New York Chi H, Beirão da Veiga L, Paulino G. 2017. Some basic formulations of the virtual element method (vem) for finite deformations. Computer Methods in Applied Mechanics and Engineering, 318: 148-192. doi: 10.1016/j.cma.2016.12.020 Cihan M, Hudobivnik B, Aldakheel F, Wriggers P. 2021a. 3d mixed virtual element formulation for dynamic elasto-plastic analysis. Computational Mechanics, 68: 1-18. Cihan M, Hudobivnik B, Aldakheel F, Wriggers P. 2021b. Virtual element formulation for finite strain elastodynamics. Computer Modeling in Engineering & Sciences, 129: 1151-1180. De Bellis M L, Wriggers P, Hudobivnik B. 2019. Serendipity virtual element formulation for nonlinear elasticity. Computers & Structures, 223: 106094. Dhanush V, Natarajan S. 2019. Implementation of the virtual element method for coupled thermo-elasticity in abaqus. Numerical Algorithms, 80: 1037-1058. doi: 10.1007/s11075-018-0516-0 Gain A L, Paulino G H, Duarte L S, Menezes I F M. 2015. Topology optimization using polytopes. Computer Methods in Applied Mechanics and Engineering, 293: 411-430. doi: 10.1016/j.cma.2015.05.007 Gain A L, Talischi C, Paulino G H. 2014. On the virtual element method for three-dimensional linear elasticity problems on arbitrary polyhedral meshes. Computer Methods in Applied Mechanics and Engineering, 282: 132-160. doi: 10.1016/j.cma.2014.05.005 Gay Neto A, Hudobivnik B, Moherdaui T F, Wriggers P. 2021. Flexible polyhedra modeled by the virtual element method in a discrete element context. Computer Methods in Applied Mechanics and Engineering, 387: 114163. doi: 10.1016/j.cma.2021.114163 Hudobivnik B, Aldakheel F, Wriggers P. 2019. A low order 3d virtual element formulation for finite elasto–plastic deformations. Computational Mechanics, 63: 253-269. doi: 10.1007/s00466-018-1593-6 Hussein A, Aldakheel F, Hudobivnik B, Wriggers P, Guidault P A, Allix O. 2019. A computational framework for brittle crack-propagation based on efficient virtual element method. Finite Elements in Analysis and Design, 159: 15-32. doi: 10.1016/j.finel.2019.03.001 Hussein A, Hudobivnik B, Aldakheel F, Wriggers P, Guidault P A, Allix O. 2018. A virtual element method for crack propagation. Proc. Appl. Math. Mech., 18: e201800104. Hussein A, Hudobivnik B, Wriggers P. 2020. A combined adaptive phase field and discrete cutting method for the prediction of crack paths. Computer Methods in Applied Mechanics and Engineering, 372: 113329. doi: 10.1016/j.cma.2020.113329 Lo Cascio M, Milazzo A, Benedetti I. 2021. A hybrid virtual–boundary element formulation for heterogeneous materials. International Journal of Mechanical Sciences, 199: 106404. doi: 10.1016/j.ijmecsci.2021.106404 Marfia S, Monaldo E, Sacco E. 2022. Cohesive fracture evolution within virtual element method. Engineering Fracture Mechanics, 269: 108464. doi: 10.1016/j.engfracmech.2022.108464 Marino M, Hudobivnik B, Wriggers P. 2019. Computational homogenization of polycrystalline materials with the virtual element method. Computer Methods in Applied Mechanics and Engineering, 355: 349-372. doi: 10.1016/j.cma.2019.06.004 Mengolini M, Benedetto M F, Aragón A M. 2019. An engineering perspective to the virtual element method and its interplay with the standard finite element method. Computer Methods in Applied Mechanics and Engineering, 350: 995-1023. doi: 10.1016/j.cma.2019.02.043 Park K, Chi H, Paulino G H. 2019. On nonconvex meshes for elastodynamics using virtual element methods with explicit time integration. Computer Methods in Applied Mechanics and Engineering, 356: 669-684. doi: 10.1016/j.cma.2019.06.031 Park K, Chi H, Paulino G H. 2020. Numerical recipes for elastodynamic virtual element methods with explicit time integration. International Journal for Numerical Methods in Engineering, 121: 1-31. doi: 10.1002/nme.6173 Ralston A, Rabinowitz P. 2001. A first course in numerical analysis. Courier Corporation Reddy B D, van Huyssteen D. 2019. A virtual element method for transversely isotropic elasticity. Computational Mechanics, 64: 971-988. doi: 10.1007/s00466-019-01690-7 Taylor R L, Simo J C, Zienkiewicz O C, Chan A C H. 1986. The patch test—a condition for assessing fem convergence. International Journal for Numerical Methods in Engineering, 22: 39-62. doi: 10.1002/nme.1620220105 Timoshenko S P, Goodier J N. 1951. Theory of Elasticity. McGraw-Hill Book Company van Huyssteen D, Reddy B. 2021. A virtual element method for transversely isotropic hyperelasticity. Computer Methods in Applied Mechanics and Engineering, 386: 114108. doi: 10.1016/j.cma.2021.114108 Wriggers P, De Bellis M, Hudobivnik B. 2021a. A taylor–hood type virtual element formulations for large incompressible strains. Computer Methods in Applied Mechanics and Engineering, 385: 114021. doi: 10.1016/j.cma.2021.114021 Wriggers P, Hudobivnik B. 2017. A low order virtual element formulation for finite elasto-plastic deformations. Computer Methods in Applied Mechanics and Engineering, 327: 459-477. doi: 10.1016/j.cma.2017.08.053 Wriggers P, Hudobivnik B, Aldakheel F. 2020. A virtual element formulation for general element shapes. Computational Mechanics, 66: 963-977. doi: 10.1007/s00466-020-01891-5 Wriggers P, Hudobivnik B, Aldakheel F. 2021b. Nurbs-based geometries: A mapping approach for virtual serendipity elements. Computer Methods in Applied Mechanics and Engineering, 378: 113732. doi: 10.1016/j.cma.2021.113732 Wriggers P, Hudobivnik B, Korelc J. 2018a. Efficient low order virtual elements for anisotropic materials at finite strains, in: Advances in Computational Plasticity: A Book in Honour of D. Roger J. Owen. Springer International Publishing. Computational Methods in Applied Sciences, pp. 417–434 Wriggers P, Hudobivnik B, Schröder J. 2018b. Finite and virtual element formulations for large strain anisotropic material with inextensive fibers, in: Multiscale Modeling of Heterogeneous Structures. Springer International Publishing. Lecture Notes in Applied and Computational Mechanics, pp. 205–231 Wriggers P, Reddy B D, Rust W, Hudobivnik B. 2017. Efficient virtual element formulations for compressible and incompressible finite deformations. Computational Mechanics, 60: 253-268. doi: 10.1007/s00466-017-1405-4 Wriggers P, Rust W T. 2019. A virtual element method for frictional contact including large deformations. Engineering Computations, 36: 2133-2161. doi: 10.1108/EC-02-2019-0043 Wriggers P, Rust W T, Reddy B D. 2016. A virtual element method for contact. Computational Mechanics, 58: 1039-1050. doi: 10.1007/s00466-016-1331-x Zhang X S, Chi H, Paulino G H. 2020. Adaptive multi-material topology optimization with hyperelastic materials under large deformations: A virtual element approach. Computer Methods in Applied Mechanics and Engineering, 370: 112976. doi: 10.1016/j.cma.2020.112976 Zhang X S, Chi H, Zhao Z. 2021. Topology optimization of hyperelastic structures with anisotropic fiber reinforcement under large deformations. Computer Methods in Applied Mechanics and Engineering, 378: 113496. doi: 10.1016/j.cma.2020.113496 期刊类型引用(3)
1. 丁聪，刘杨，阳莺，沈瑞刚. 一种三维Poisson-Nernst-Planck方程的虚单元计算. 吉林大学学报(理学版). 2024(02): 293-301 . 
百度学术2. 徐兵兵，彭帆. 基于新型虚单元法的超弹性材料变形研究. 力学学报. 2024(09): 2635-2645 . 百度学术3. 崔辉如. 基于虚单元法(VEM)的固体推进剂药柱结构完整性分析. 固体火箭技术. 2023(04): 528-534 . 百度学术其他类型引用(3)
-
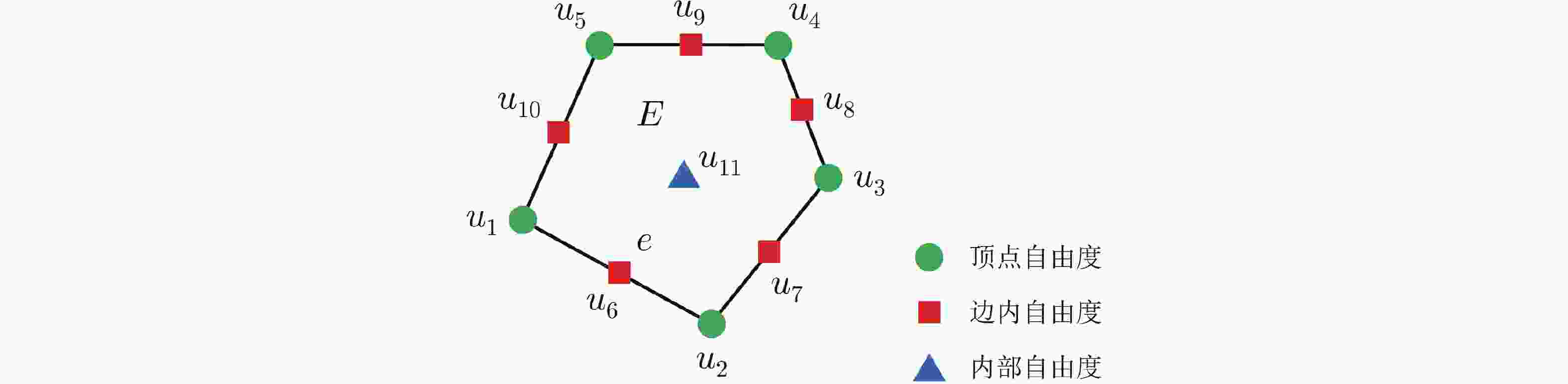
下载:
下载:
百度学术
计量
- 文章访问数: 3974
- HTML全文浏览量: 2171
- PDF下载量: 1321
- 被引次数: 6