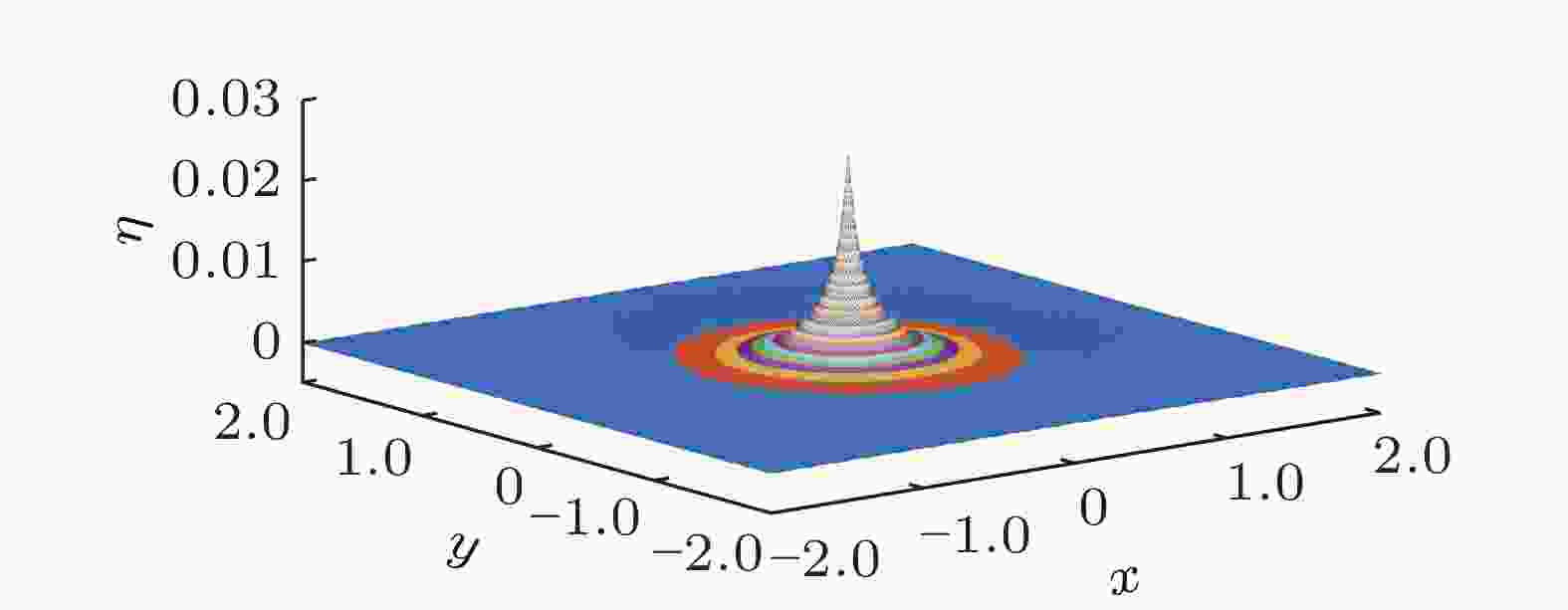
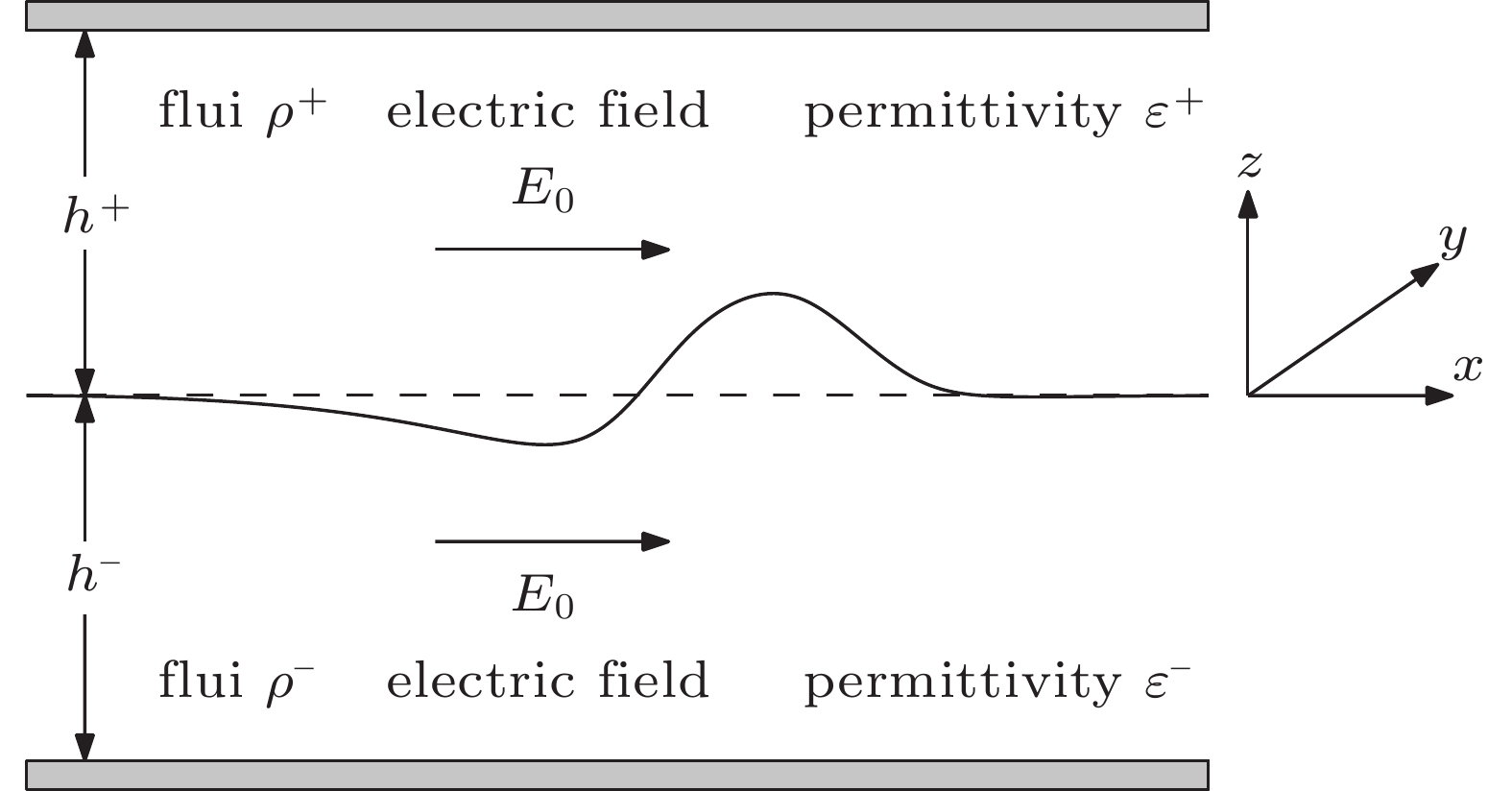
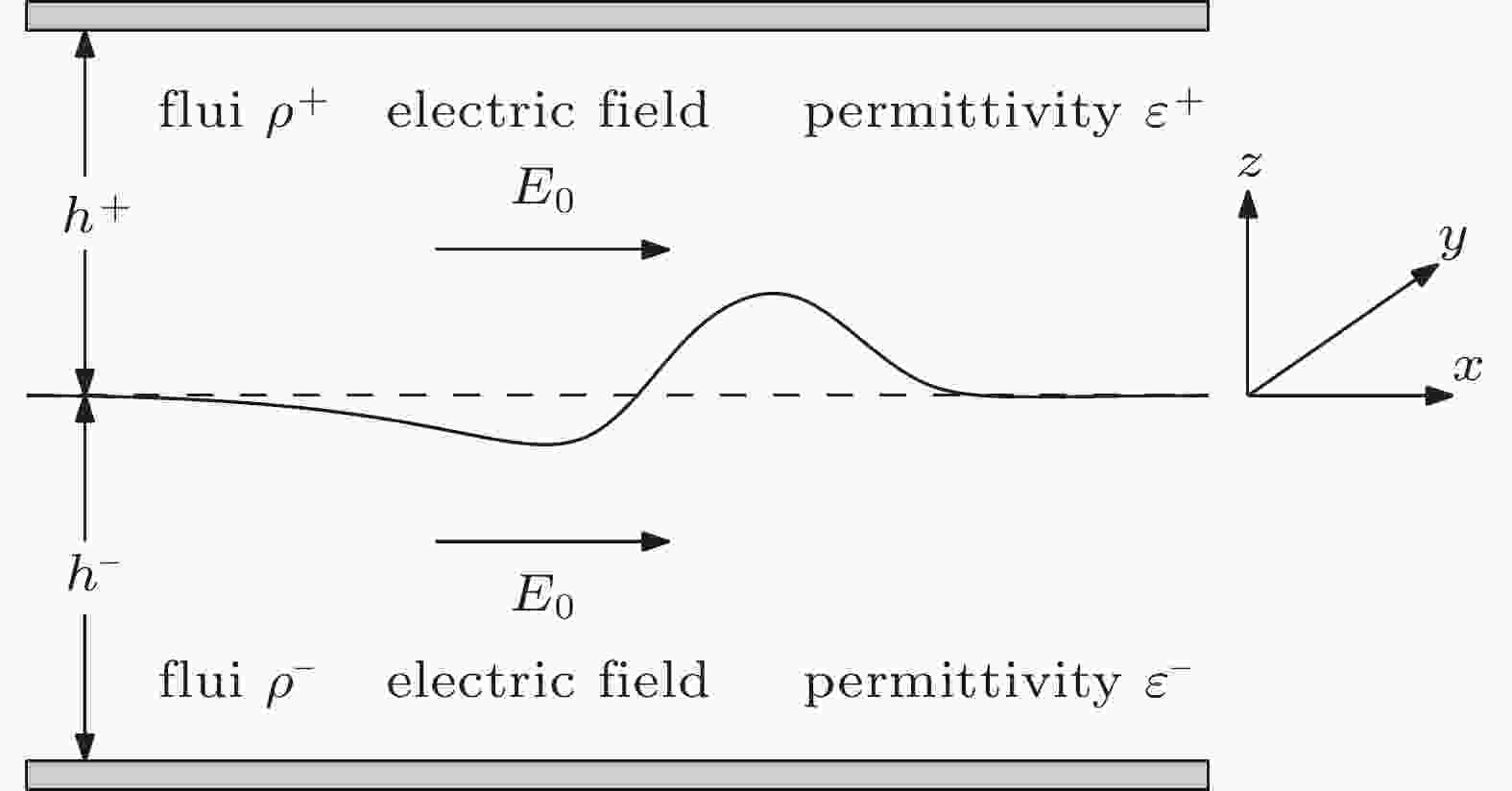
Interfacial electrohydrodynamic waves under horizontal electric fields: Hamilton’s principle and multi-scale modeling
-
摘要: 本文研究水平电场下两层电介质流体间界面波动的多尺度建模. 首先对此系统的Hamilton原理给出详细证明; 然后基于Hamilton结构和Dirichlet–Neumann算子的解析性质, 将Hamilton量中的动能与电势能展开成收敛级数形式并确定截断阶数, 最后通过计算截断后近似总能量的变分导数得到约化模型. 上述过程对该问题给出了一套建立多尺度非线性模型的系统方法. 文章再以“上层深水、下层浅水”为例详细阐述了多尺度建模的全过程, 并利用修正的Petviashvili迭代方法计算了新模型中的非线性相干结构. 本文所发展的渐近分析技巧不同于之前的工作, 其优点在于所导出的约化模型自然保留能量守恒的性质; 同时, 本文亦将原有结果推广至三维情形.Abstract: This paper is concerned with the multi-scale modeling of interfacial waves between two dielectric fluids under a horizontal electric field. First, we give a detailed proof of the Hamilton principle for this system. Next, based on the Hamiltonian structure and the analytical property of the Dirichlet-Neumann operator, the kinetic energy and electric potential energy in the Hamiltonian are expanded into the form of convergent series, and the order of truncation is determined. Finally, the reduced model is obtained by calculating the variational derivatives of the approximate total energy after truncation. The above process provides a systematic method for establishing nonlinear multi-scale models. Taking the case of “deep upper layer and shallow lower layer” as an example, we describe the whole modeling process in detail. Furthermore, the nonlinear coherent structure in the newly proposed model is computed using the modified Petviashvili iterative method. The asymptotic technique developed in this paper differs from previous work. Its advantage is that the derived reduced models naturally retain the energy conservation property; at the same time, this paper also extends the previous results to the three-dimensional situation.
-
Key words:
- Hamiltonian /
- interfacial waves /
- electrohydrodynamics /
- multi-scale modeling
-
张宝善, 卢东强, 戴世强, 程友良. 1998. 非线性水波Hamilton系统理论与应用研究进展. 力学进展, 28: 521-531 doi: 10.3321/j.issn:1000-0992.1998.04.010 Zakharov V E. 2021. 深水表面有限振幅周期波的稳定性. 王展译, 卢东强校. 力学进展, 51(4): 920–930.Zakharov V E. 2021. Stability of periodic waves of finite amplitude on the surface of a deep fluid. Wang Z trans, Lu D Q proof. Advances in Mechanics, 51(4): 920–930. Barannyk L L, Papageorgiou D T, Petropoulos P G, Vanden-Broeck J-M. 2015. Nonlinear dynamics and wall touch-up in unstably stratified multilayer flows in horizontal channels under the action of electric fields. SIAM Journal of Applied Mathematics, 75: 92-113. doi: 10.1137/140968070 Benjamin T B. 1992. A new kind of solitary wave. Journal of Fluid Mechanics, 245: 401-411. doi: 10.1017/S002211209200051X Benjamin T B, Bridges T J. 1997. Reappraisal of the Kelvin-Helmholtz problem. Part 1. Hamiltonian structure. Journal of Fluid Mechanics, 333: 301-325. doi: 10.1017/S0022112096004272 Craig W, Sulem C. 1993. Numerical simulation of gravity waves. Journal of Computational Physics, 108: 73-83. doi: 10.1006/jcph.1993.1164 Guan X, Wang Z. 2022. Interfacial electrohydrodynamic solitary waves under horizontal electric fields. Journal of Fluid Mechanics, 940: A15. doi: 10.1017/jfm.2022.244 Kuznetsov E A, Spector M D, Zakharov V E. 1993. Surface singularities of ideal fluid. Physics Letters A, 182: 387-393. doi: 10.1016/0375-9601(93)90413-T Melcher J R. 1963. Field-coupled Surface Waves. MIT Press. Melcher J R, Schwarz W J. 1968. Interfacial relaxation overstability in a tangential electric field. Physics of Fluids, 11: 2604. doi: 10.1063/1.1691866 Mohamed A A, El Shehawey E F. 1983. Nonlinear electrohydrodynamic Rayleigh-Taylor instability. part 1. A perpendicular field in the absence of surface charges. Journal of Fluid Mechanics, 129: 473-494. doi: 10.1017/S0022112083000877 Papageorgiou D T. 2019. Film flows in the presence of electric fields. Annual Review of Fluid Mechanics, 51: 155-187. doi: 10.1146/annurev-fluid-122316-044531 Taylor G I. 1964. Disintegration of water droplets in an electric field. Proceedings of the Royal Society A, 280: 383-397. Wang Z, Wang Z, Yuan C X. 2022. Oceanic internal solitary waves in three-layer fluids of great depth. Acta Mechanica Sinica, 38: 321473. doi: 10.1007/s10409-021-09012-x Zubarev N M, Kochurin E A. 2013. Three-dimensional nonlinear waves at the interface between dielectric fluid in an external horizontal electric field. Journal of Applied Mechanics and Technical Physics, 54: 212-217. doi: 10.1134/S0021894413020053 -




 下载:
下载: