-
摘要: 热湍流 (浮力驱动湍流) 作为一种典型的湍流现象, 广泛存在于自然界和工程应用中. Rayleigh-Bénard (RB) 湍流是从众多自然现象中抽象出来研究热湍流的经典模型, RB湍流的典型特征是系统中存在大尺度环流和羽流等不同尺度的湍流结构, 这些结构通过作用于边界层, 影响RB湍流的输运效率. 因此, 明确不同尺度湍流结构的生成、演化和作用机理, 对理解RB湍流的输运特性至关重要, 也是通过控制湍流结构调控输运效率的科学基础. 本文重点从湍流结构的时空演化规律、输运特性、湍流调控和热湍流在其他领域的拓展四个方面评述近十年来RB湍流研究所取得的新进展, 并对今后的研究方向做出展望.Abstract: Turbulent convection is ubiquitous in nature and industry. Turbulent Rayleigh-Bénard convection (RBC) is a model system for studying various turbulent convection phenomena. One of the characteristics of turbulent RBC is the formation of coherent structures of different scales, i.e., large-scale circulation and thermal plumes. These structures interact with the thermal and viscous boundary layers. As a result, they inevitably affect the transport properties of the system. Thus, understanding the formation, evolution, and interaction of coherent structures plays a vital role in understanding the transport properties in turbulent convection. This review summarizes progress in the spatial and temporal evolution of coherent structures and their effects on heat transport in the past decade. Special attention was paid to the progress in controlling turbulent convection and its extension to nontraditional cases, such as turbulent convection with rotation, viscoelastic turbulent convection, multiphase turbulent convection, inclined convection, and horizontal convection. A short outlook into future research directions will be given.
-
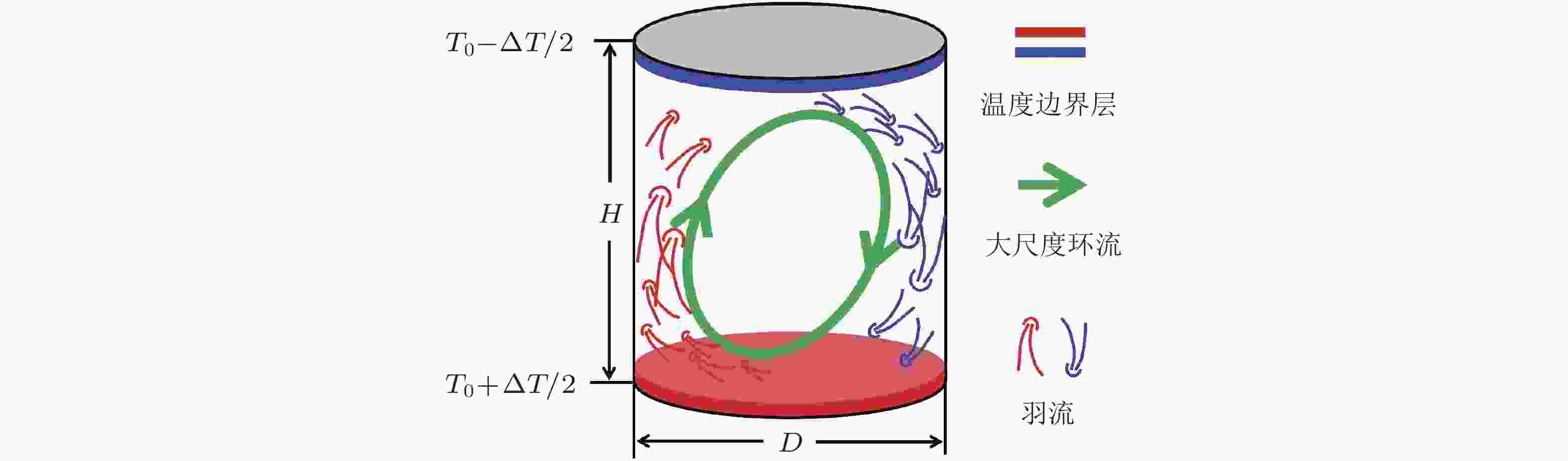
图 1 Rayleigh-Bénard (RB) 湍流系统示意图 (周全和夏克青 2012)
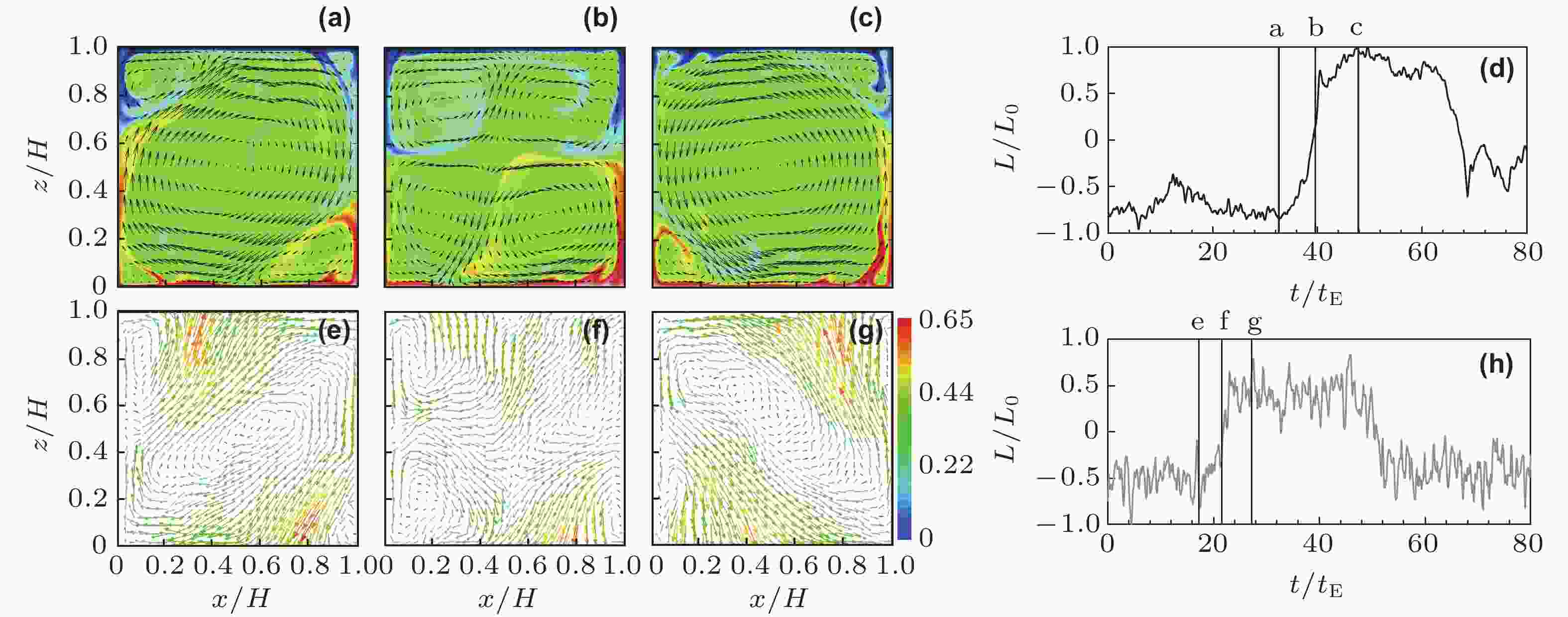
图 2 大尺环流反转过程. (a)~(c) 和 (e)~(g) 分别为直接数值模拟 (Ra = 108, Pr = 4.3) 和通过PIV实验测量 (Ra = 3.8 × 108, Pr = 4.3) 得到的大尺度环流反转过程, (d) 和 (h)分别为直接数值模拟和通过PIV实验测量得到的大尺度环流角动量随时间的变化曲线 (Sugiyama et al. 2010)
图 3 阴影法拍摄的圆盘对流腔体流场图像 (Ra = 6.2 × 109, Pr = 4.4). (a)大尺度环流长时间处于的稳定状态, (b)大尺度环流短暂出现的爆发状态 (Wang, Lai et al. 2018)
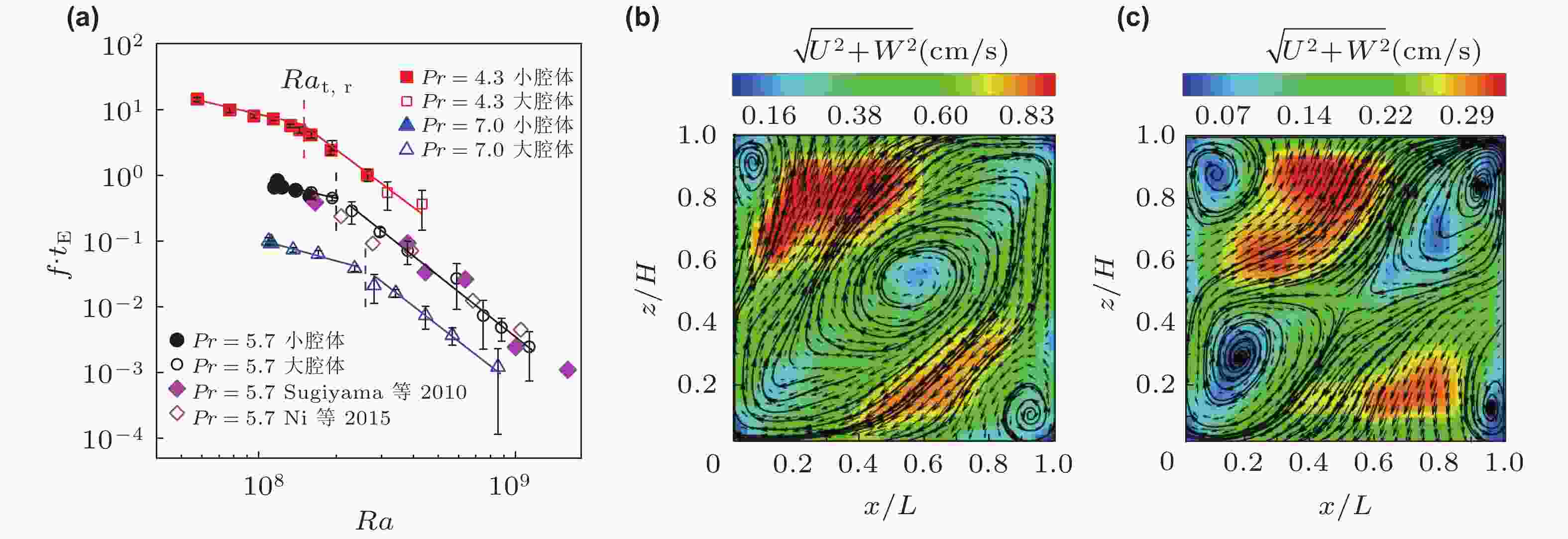
图 4 (a)实验测得的准二维矩形对流腔体中大尺度环流反转频率f随Ra数的变化关系 (为了清晰显示, Pr = 5.7和Pr = 4.3的数据分别上移了10倍和100倍), (b)正常单环结构 (Ra = 7.94 × 108, Pr = 7.0), (c)反常单环结构(Ra = 1.16 × 108, Pr = 7.0) (Chen et al., 2019)
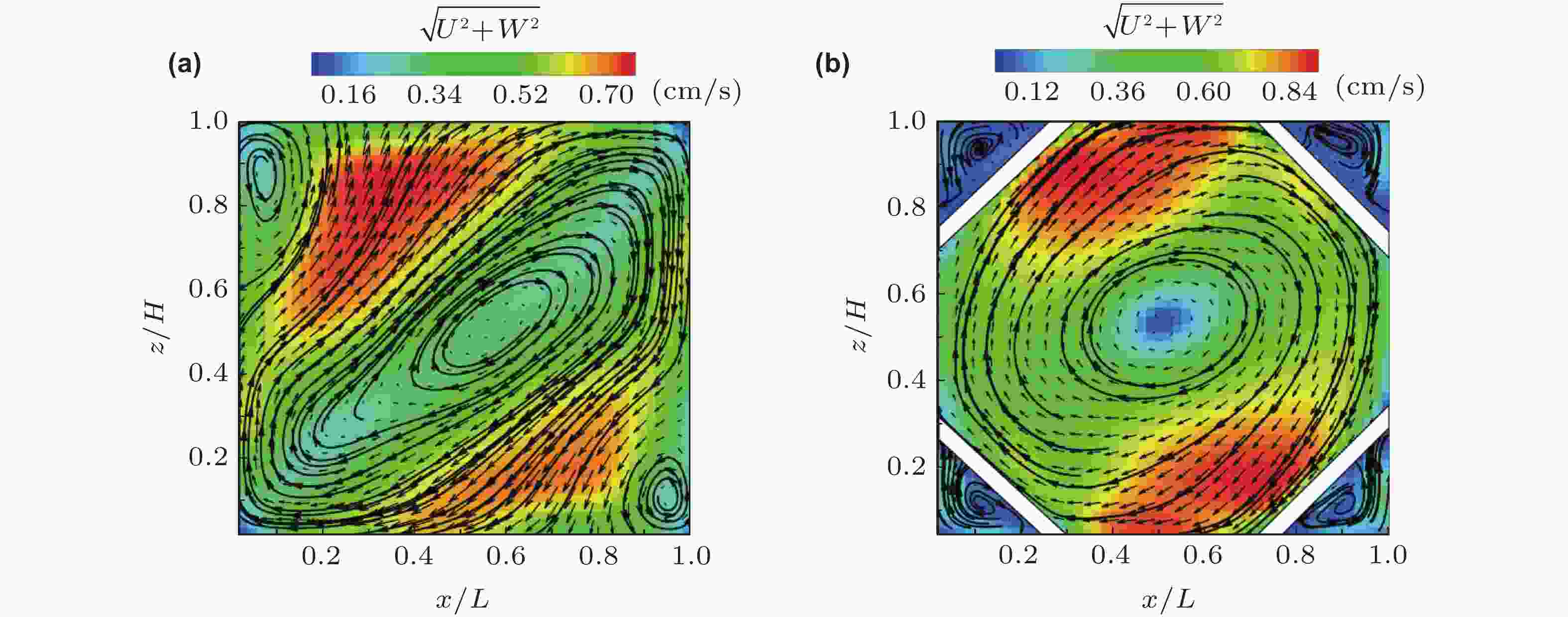
图 5 PIV测量得到的准二维矩形对流腔体中有角涡和无角涡的流场.(a)有角涡的流场 (Ra = 7.94 × 108, Pr = 7.0), (b)无角涡的流场 (Ra = 7.56 ×108, Pr = 7.0) (Chen et al. 2020)
图 6 (a)直接数值模拟所得的平均温度剖面 (空心圆) 与理论值 (实线) 的比较图, 虚线为PB边界层理论的预测值, (b)大尺度环流方向的平均速度剖面比较图, 图例与(a)一致 (Ching et al. 2019)
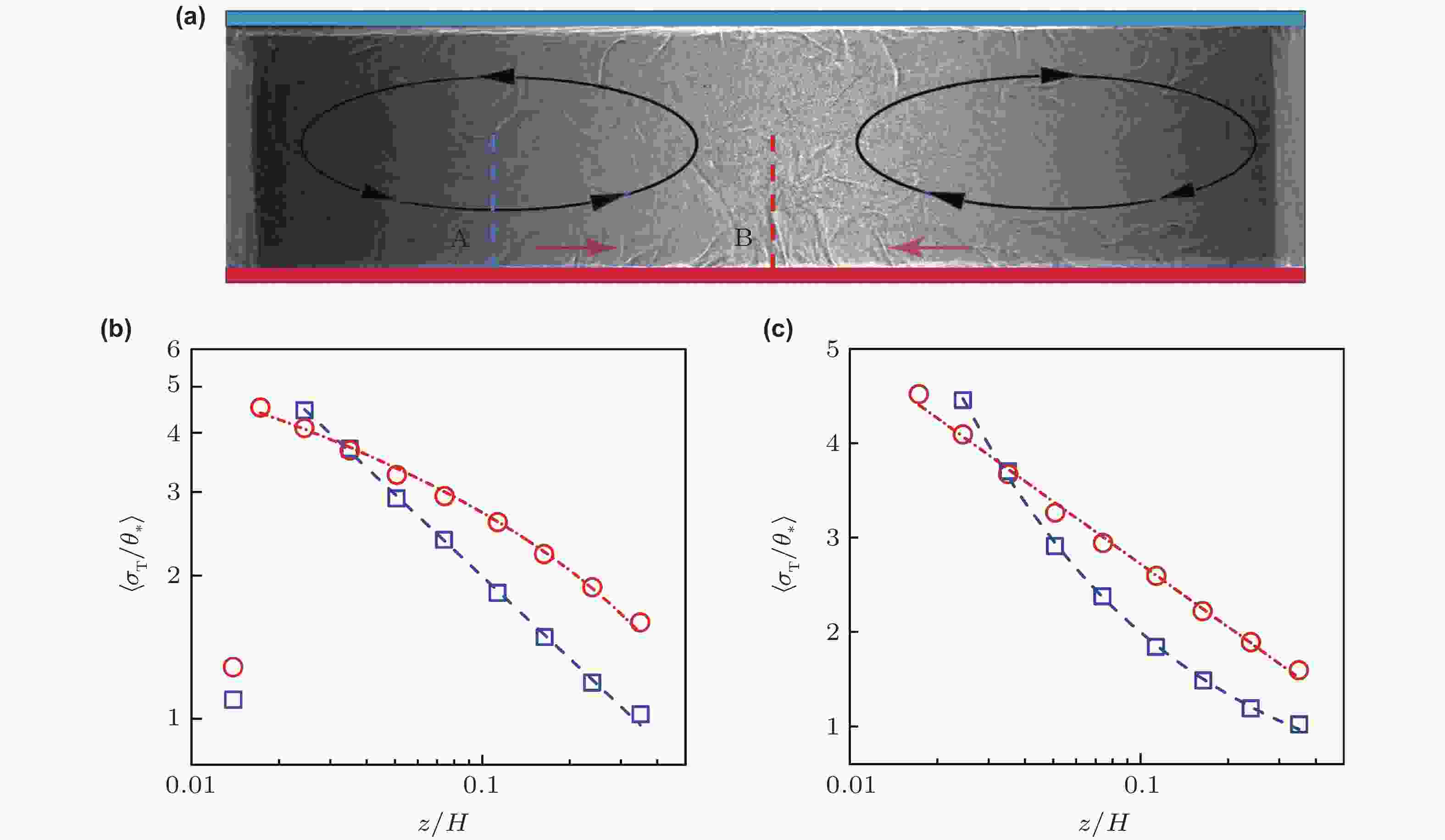
图 7 剪切区和羽流发射区的温度涨落剖面. (a)阴影法观测得到的大尺度流动结构示意图, 其中A为大尺度环流主导的强剪切区, B 为羽流主导的发射区, (b)双对数坐标下的羽流区与剪切区温度涨落剖面, (c)半对数坐标下的羽流区与剪切区温度涨落剖面 (He & Xia 2019)
图 8 单环与双环大尺度环流结构及输运效率与大尺度环流结构的关系. PIV测得的 (a)单环大尺度环流, (b)双环大尺度环流, (c) 双环大尺度环流消失后的单环大尺度环流, (d) Nu随着大尺度湍流结构流态的变化规律, 其中|δφ|top,bot的绝对值代表不同高度大尺度环流的角向方位, 当|δφ|top,bot=0时对应于单环大尺度环流, 当|δφ|top,bot=180时对应于双环大尺度环流 (Xi & Xia 2008)
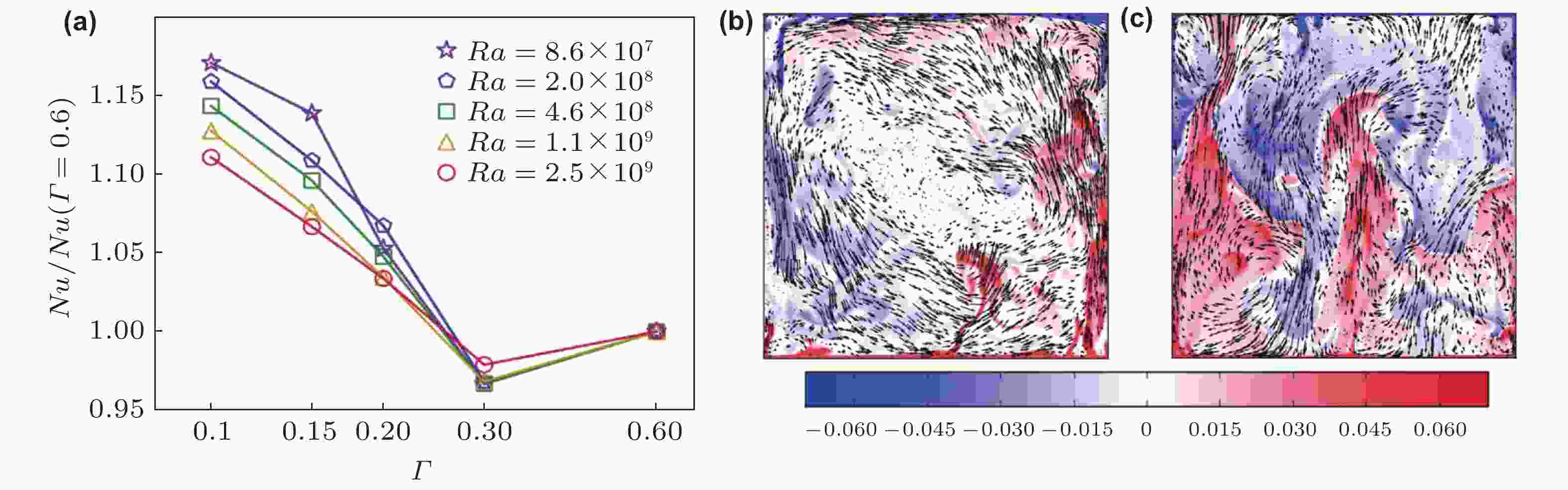
图 9 空间约束对热湍流输运特性和湍流结构的影响. (a)不同Ra时归一化的Nu随着方腔对流腔体厚度方向宽高比Γ的变化规律, 这里Nu (Γ = 0.6)对应宽高比为Γ = 0.6时RB系统的Nu, (b) Γ = 1/2对流腔体中的瞬时温度场(颜色)和速度场(箭头), (c)Γ = 1/8对流腔体中的瞬时温度场(颜色)和速度场(箭头) (Huang et al. 2013)
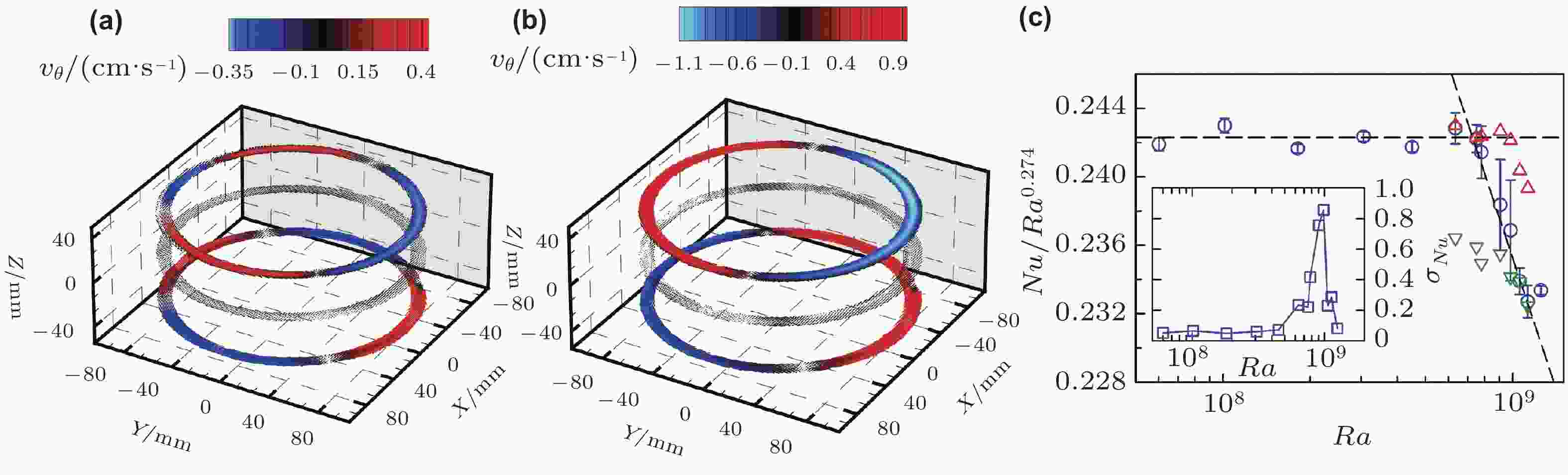
图 10 实验测量得到的圆环对流腔体中大尺度湍流结构. (a)时间平均后的四极矩湍流态空间结构, 红色代表顺时针流动, 蓝色代表逆时针流动 (b) 时间平均后的偶极矩湍流态空间结构, (c) Nu随着Ra数的变化关系, 插入图为Nu的涨落σNu随着Ra数的变化关系 (Xie et al. 2018)
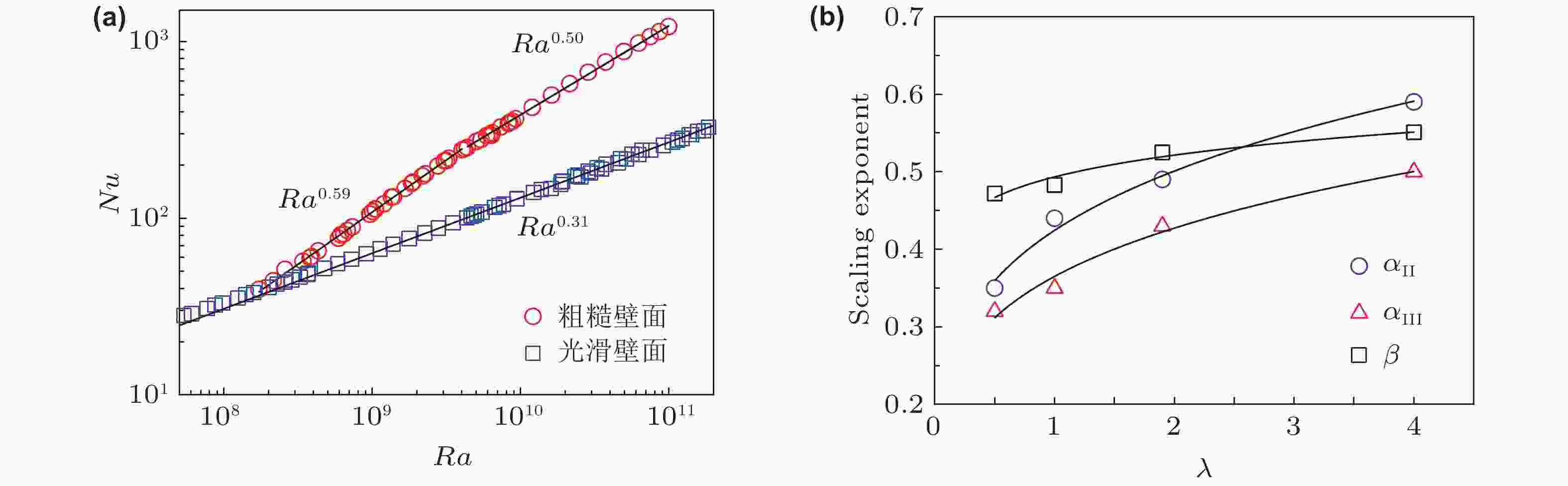
图 11 实验获得的粗糙壁面热湍流不同区间热输运特性, 此处粗糙元宽高比λ = 4.0. (a) Nu和Ra的标度律关系, 图中实线为拟合获得的标度律. (b) Nu Ra标度律指数α (Nu ~ Raα) 和Re与Ra标度律指数β (Re ~ Raβ) 随着粗糙元宽高比λ的变化关系 (Xie & Xia 2017)
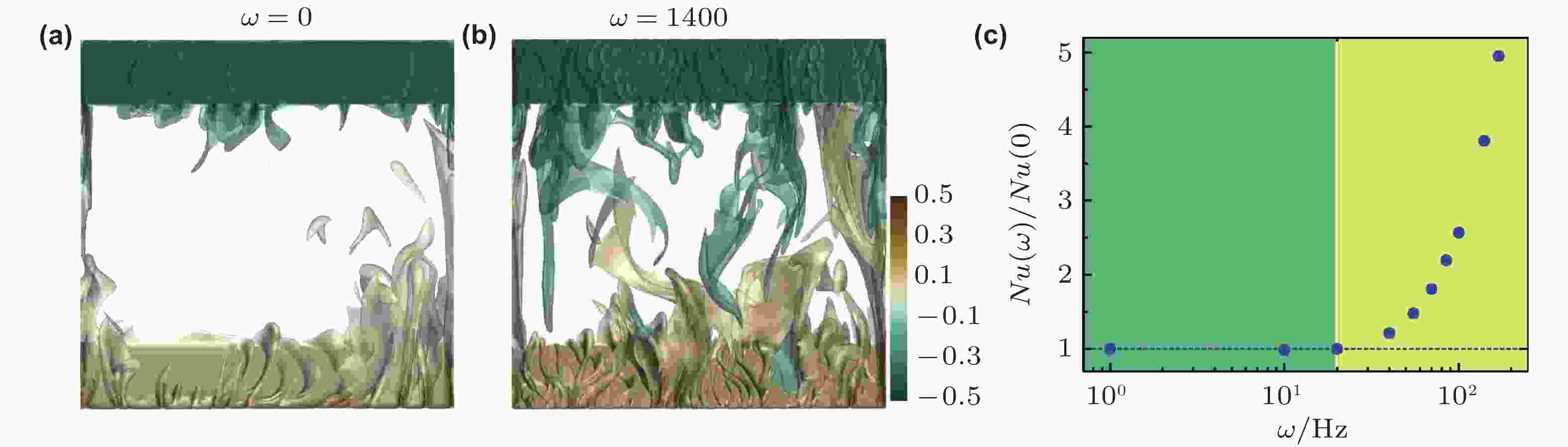
图 12 引入振动调制的热湍流不同振动频率ω时的瞬时流动结构. (a) ω = 0, (b) ω = 1400, (c)归一化的Nu随着振动频率ω的变化关系, 这里Nu(0)对应于ω = 0时RB系统的Nu (Wang, Zhou et al. 2020)
图 13 地转区间不同
$ Ra/R{a}_{c} $ 条件下的温度脉动等值面. (a) 涡胞区间($ Ra/R{a}_{c}=1.2,Pr=7 $ ), (b)泰勒涡区间($ Ra/R{a}_{c}=3.5,Pr=7 $ ), (c)羽流区间 ($ Ra/R{a}_{c}=8.0,Pr=7 $ ), (d) 地转湍流区间 ($ Ra/R{a}_{c}= $ $ 10.3,Pr=1 $ ), 图中的直接数值模拟上下边界均为无滑移条件, 旋转控制参数为$ Ek={10}^{-7} $ (Plumley et al. 2016)图 14 归一化的泰勒涡均方位移随着归一化的时间的变化曲线 (Chong et al. 2020)
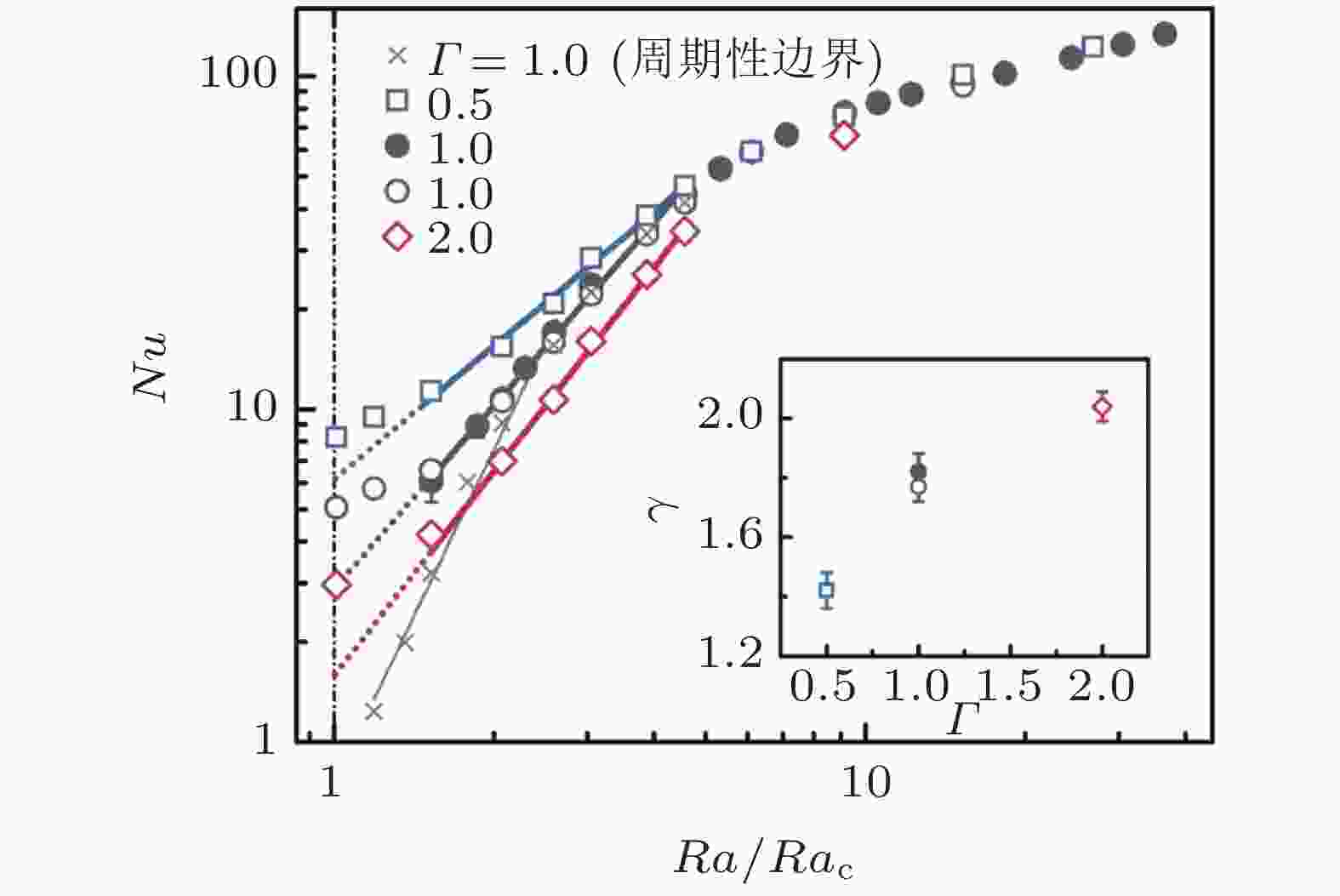
图 15 旋转热湍流不同宽高比Γ 的圆柱对流腔体的Nu随Ra/Rac的变化关系, 插图为标度律指数γ 随着Γ 的变化关系. 图中Ek = 1.85 × 10−6, Pr = 4.38 (Lu et. al 2021)
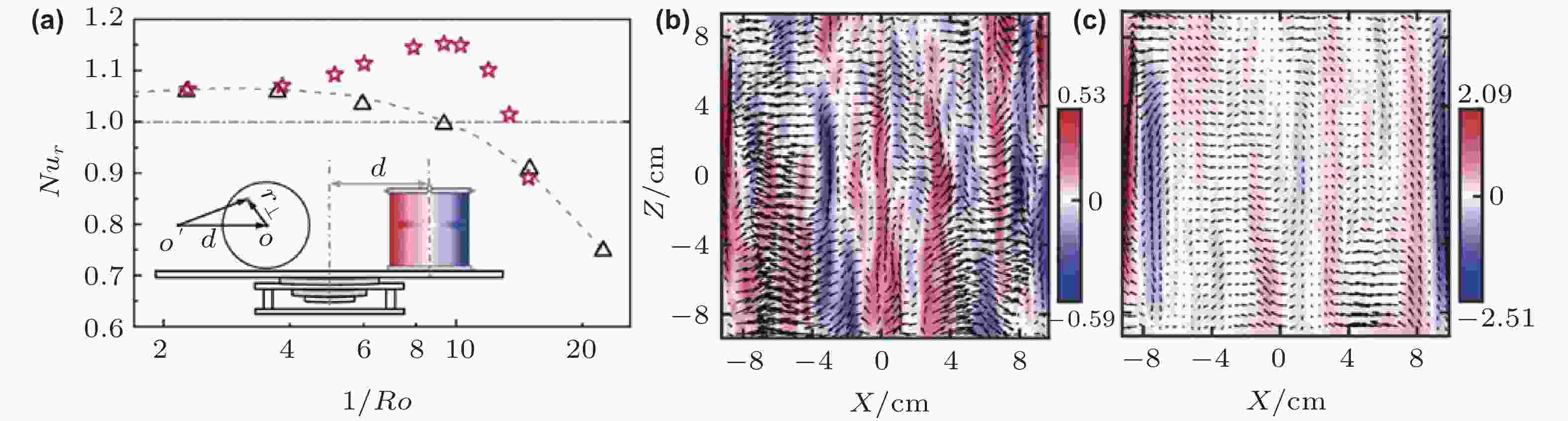
图 16 离心力效应对热湍流输运特性和湍流结构的影响. (a) 归一化的努赛尔数Nur = Nu/Nu(1/Ro = 1) 随着1/Ro的变化曲线, 三角形和五角星分别为为无偏心和偏心率d/R = 5.15时的Nur, 插图为实验装置示意图, (b)和(c)分别为PIV测量得到的无偏心及偏心率为
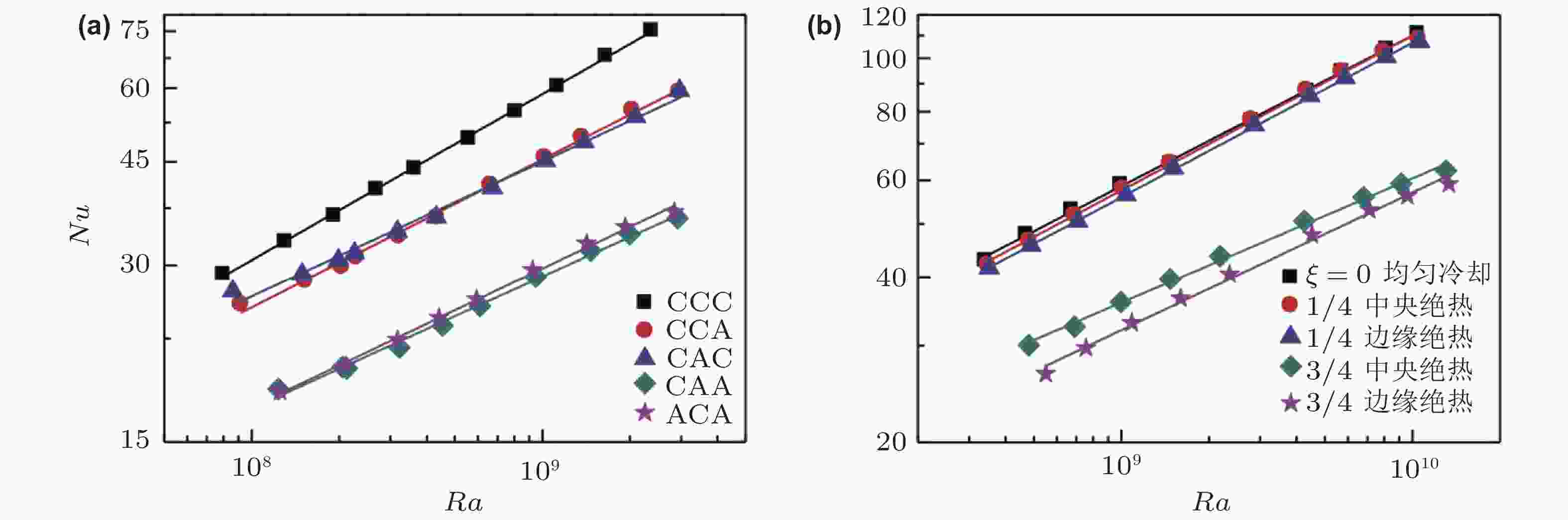
$ d/R=3.5 $ 时,$ 1/Ro\approx 7.6 $ 对应的时均速度场垂直剖面图, 其颜色代表以cm/s为单位的垂直速度大小 (Hu et al. 2021)图 17 混合边界RB湍流的Nu. (a)长方体对流腔体, 图例表示导热板和绝热板的分布形式, 其中C表示导热板, A表示绝热板, (b)圆柱对流腔体, 图例的
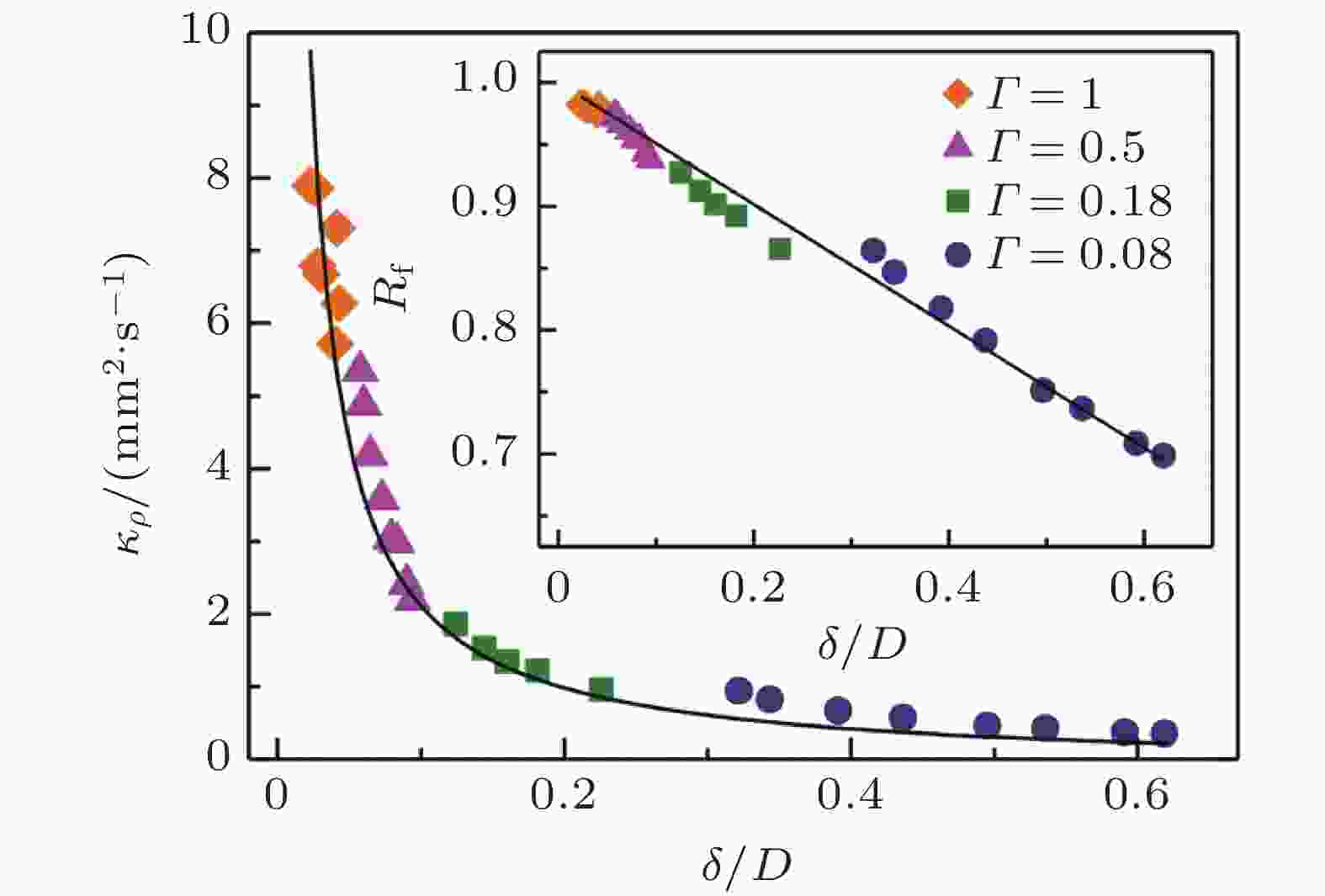
$ \xi $ 及分数表示绝热板占据的面积比, 中央绝热和边缘绝热分别表示绝热板置于冷板中心和边缘 (Wang et al 2017)图 18 混合率 (mixing rate) κρ随无量纲边界层厚度δ/D的变化规律; 插图为混合效率Rf随无量纲边界层厚度的变化规律 (Wang, Huang & Xia 2018)
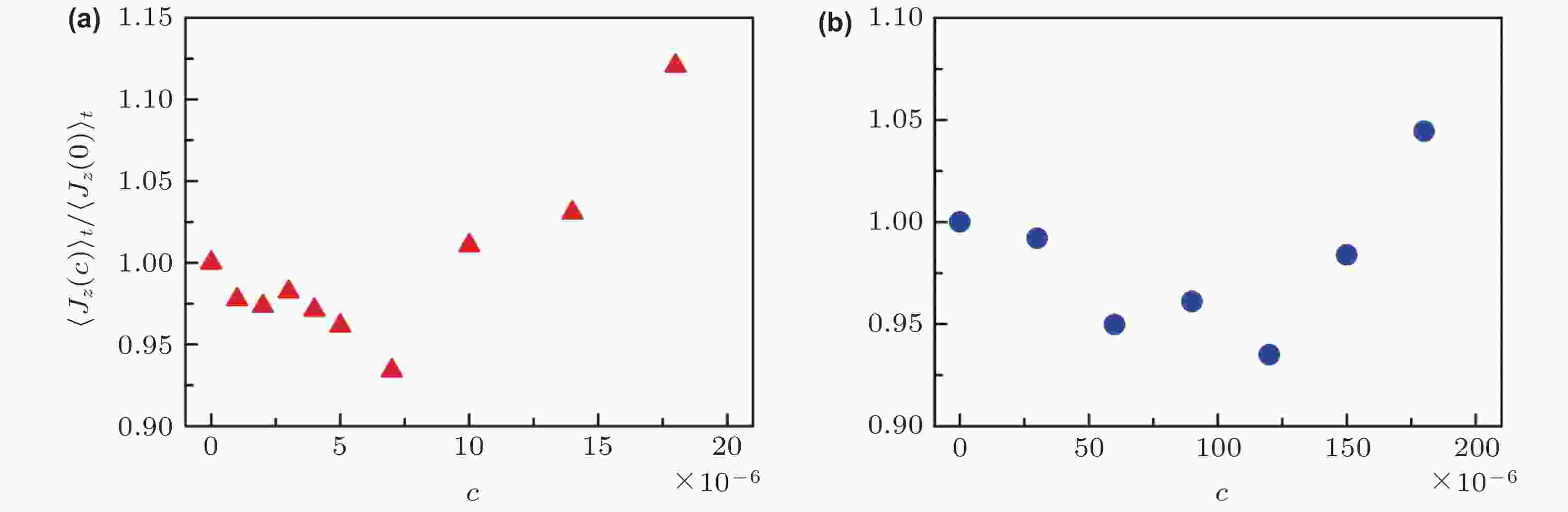
图 19 对流腔体中心区域时间平均的局域热流密度Jz随高聚物浓度c的变化曲线. (a)聚丙烯酰胺 (PAM) , (b) 聚氧化乙烯 (PEO) (Xie et al. 2015)
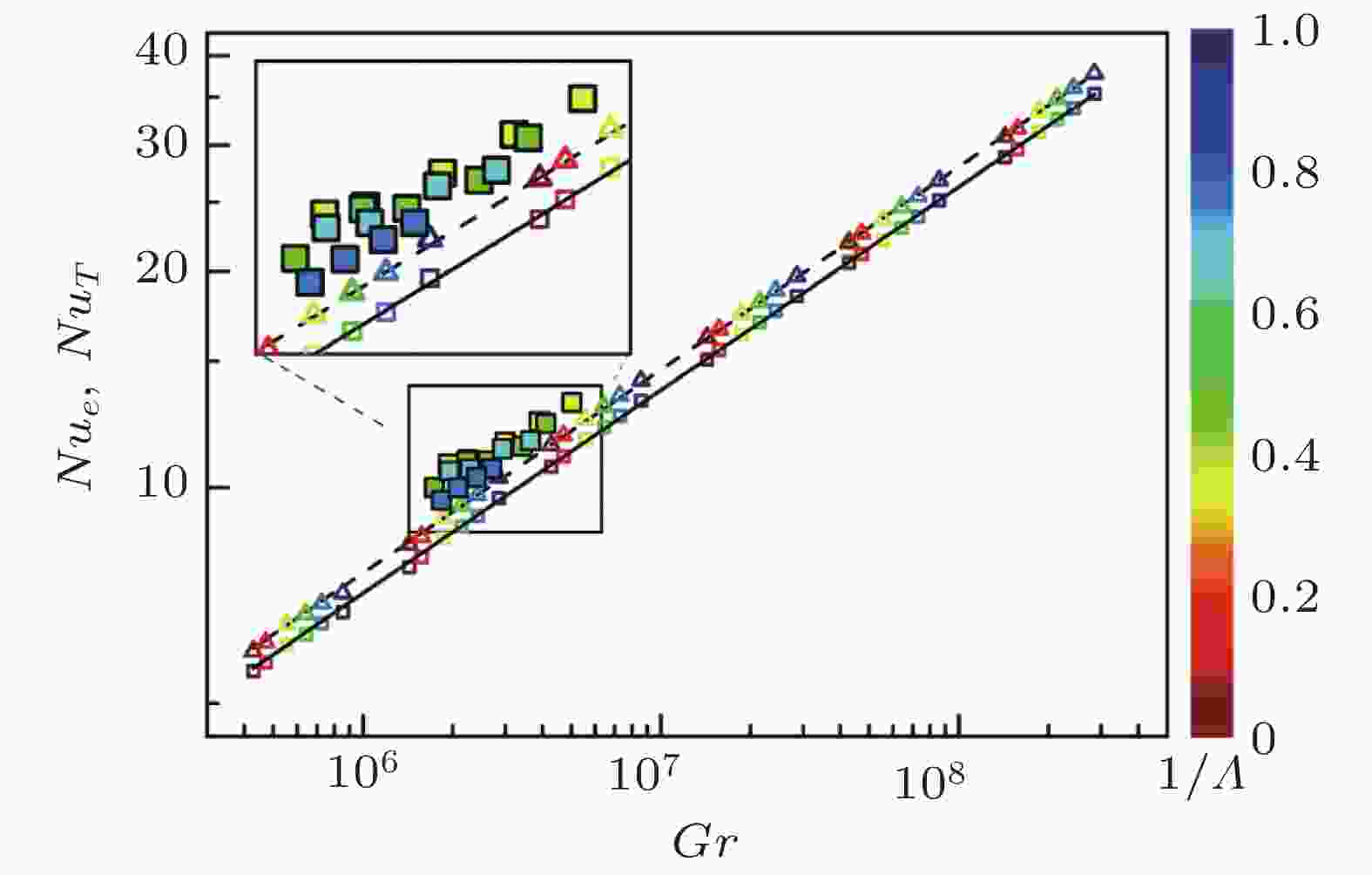
图 20 水汽输运努塞尔数Nue和热输运努塞尔数NuT随格拉晓夫数Gr变化曲线 (Zhang et al. 2019)
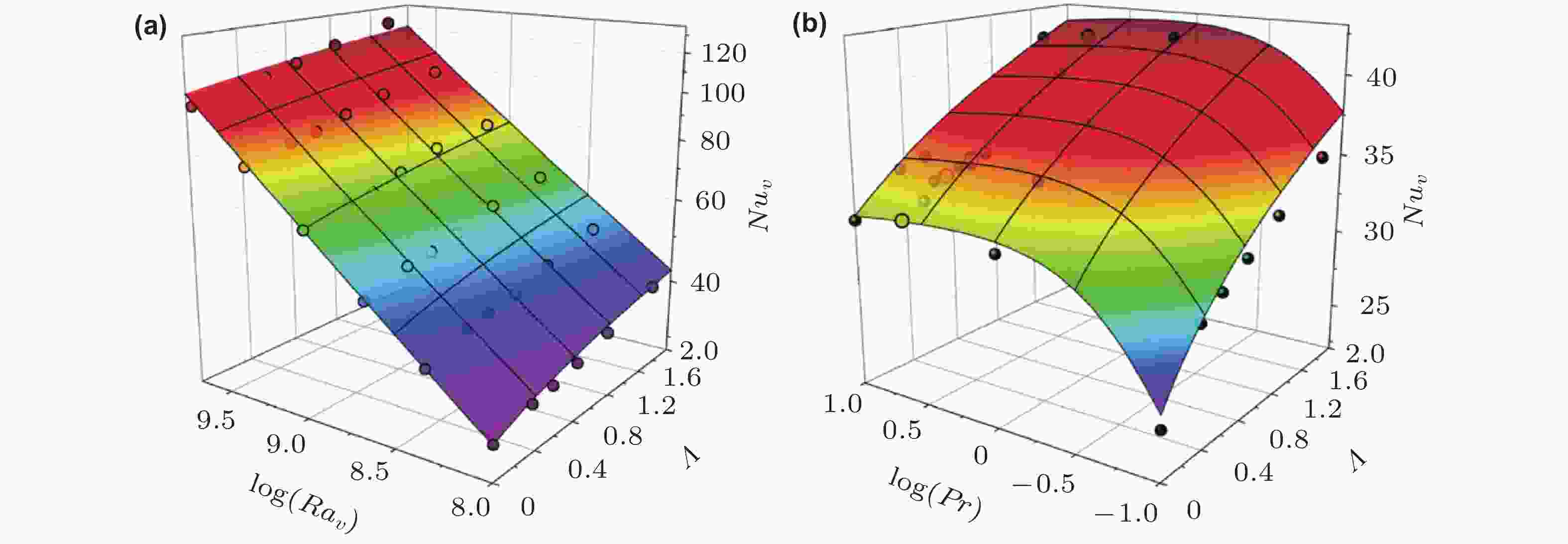
图 21 (a)含水平浮力热对流系统中垂直方向努塞尔数Nuv随Ra以及浮力比例Λ的变化规律, (b)该系统中垂向努塞尔数Nuv随Pr以及浮力比例Λ的变化规律, 图中的曲面表示新理论模型的预测值 (Zhang et al. 2021)
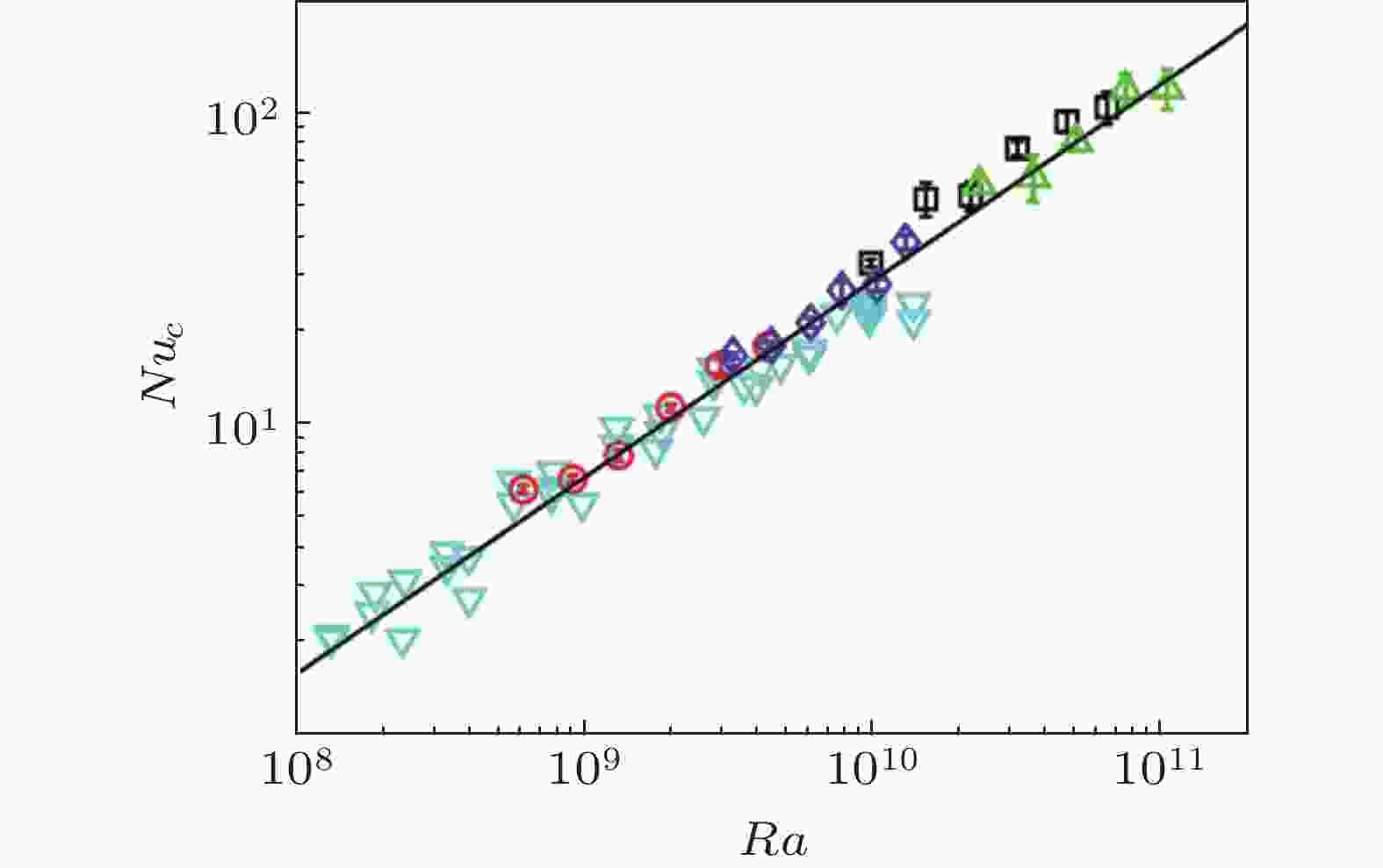
图 22 热湍流中央区域局部能量耗散率εu,c与局部努塞尔数Nuc的平衡关系实验验证.倒三角为直接测量得到的中央区域的局部努塞尔数Nuc, 其他图标为通过式9计算得到的Nuc. 两种方法得到的Nuc互相重叠在一起, 验证了εu,c与Nuc的平衡关系 (Ni et al. 2011)
-
陈鑫, 郗恒东. 2022. 瑞利-伯纳德热湍流中的多湍流态现象. 空气动力学学报, 40: 147−155Chen X, Xi H D. Multiple flow states in turbulent Rayleigh-Bénard convection. Acta Aerodynamica Sinica, 2022, 40: 147-155 (in Chinese) 倪明玖. 2010. 磁约束核聚变关键能量转换部件的磁流体力学研究. 力学与实践, 32: 1-9 (Ni M J. 2010. Magnetohydrodynamics relevant to liquid blanket of fusion. Mechanics in Engineering, 32: 1-9 (in Chinese)). 夏振华. 2019. 湍流中的多态现象. 科学通报, 64(4): 373−383.Xia Z. 2019. Multiple states in turbulence. Chinese Science Bulletin, 64: 373 – 383. (in Chinese) 谢毅超, 陶鑫, 任磊, 夏克青. 2022. 热湍流多重态与热输运效率实验研究. 空气动力学学报, 40(2): 1-11.Xie Y C, Tao X, Ren L, Xia K Q. 2022. Experimental study of multiple states and heat transport in turbulent thermal convection. Acta Aerodynamica Sinica, 40: 188−198 (in Chinese) 周全, 夏克青. 2012. Rayleigh-Bénard 湍流热对流研究的进展、现状及展望. 力学进展, 42: 231-251.Zhou Q, Xia K Q. 2012. Advances and outlook in turbulent Rayleigh- Bénard convection. Advances in Mechanics, 42: 231-251(in Chinese) Ahlers G, Bodenschatz E, Hartmann R, He X, Lohse D, Reiter P, et al. 2022. Aspect ratio dependence of heat transfer in a cylindrical Rayleigh-Bénard cell. Phys. Rev. Lett., 128: 084501. doi: 10.1103/PhysRevLett.128.084501 Ahlers G, Brown E, Nikolaenko A. 2006. The search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh-Bénard convection. J. Fluid Mech., 557: 347-367. doi: 10.1017/S0022112006009888 Ahlers G, Grossmann S, Lohse D. 2009. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection. Rev. Mod. Phys., 81: 503-537. doi: 10.1103/RevModPhys.81.503 Ahlers G, Nikolaenko A. 2010. Effect of a polymer additive on heat transport in turbulent Rayleigh-Bénard convection. Phys. Rev. Lett., 104: 034503. doi: 10.1103/PhysRevLett.104.034503 Alards K M J, Rajaei H, Kunnen R P J, Toschi F, Clercx H J H. 2018. Directional change of tracer trajectories in rotating Rayleigh-Bénard convection. Phys. Rev. E, 97: 063105. doi: 10.1103/PhysRevE.97.063105 Araujo F F, Grossmann S, Lohse D. 2005. Wind reversals in turbulent Rayleigh-Bénard convection. Phys. Rev. Lett., 95: 084502. doi: 10.1103/PhysRevLett.95.084502 Aurnou J M, Bertin V, Grannan A M, Horn S, Vogt T. 2018. Rotating thermal convection in liquid gallium: multi-modal flow, absent steady columns. J. Fluid Mech., 846: 846-876. doi: 10.1017/jfm.2018.292 Bakhuis D, Ostilla-Mónico R, Van Der Poel E P, Verzicco R, Lohse D. 2018. Mixed insulating and conducting thermal boundary conditions in Rayleigh-Bénard convection. J. Fluid Mech., 835: 491-511. doi: 10.1017/jfm.2017.737 Barkan R, Winters K B, Smith S G L. 2013. Rotating horizontal convection. J. Fluid Mech., 723: 556-586. doi: 10.1017/jfm.2013.136 Behringer R P. 1985. Rayleigh-Bénard convection and turbulence in liquid helium. Rev. Mod. Phys., 57: 657-687. doi: 10.1103/RevModPhys.57.657 Benzi R. 2005. Flow reversal in a simple dynamical model of turbulence. Phys. Rev. Lett., 95: 024502. doi: 10.1103/PhysRevLett.95.024502 Benzi R, Ching E S C, De Angelis E. 2010. Effect of polymer additives on heat transport in turbulent thermal convection. Phys. Rev. Lett., 104: 024502. doi: 10.1103/PhysRevLett.104.024502 Benzi R, Ching E S C, De Angelis E. 2016. Turbulent Rayleigh-Benard convection with polymers: Understanding how heat flux is modified. Phys. Rev. E, 94: 063110. doi: 10.1103/PhysRevE.94.063110 Benzi R, Ching E S C. 2018. Polymers in fluid flows. Annu. Rev. Conden. Matt. Phys, 9: 163-181. doi: 10.1146/annurev-conmatphys-033117-053913 Blass A, Zhu X, Verzicco R, Lohse D, Stevens R J A M. 2020. Flow organization and heat transfer in turbulent wall sheared thermal convection. J. Fluid Mech. , 897: A22. Boffetta G, Mazzino A, Musacchio S, Vozella, L. 2010. Polymer heat transport enhancement in thermal convection: the case of Rayleigh-Taylor turbulence. Phys. Rev. Lett., 104: 184501. doi: 10.1103/PhysRevLett.104.184501 Boussinesq J. 1903. Theorie Analytique de la Chaleur (Gauthier-Villars, Paris). 2 Brown E, Ahlers G. 2007. Large-scale circulation model for turbulent Rayleigh-Bénard convection. Phys. Rev. Lett., 98: 134501. doi: 10.1103/PhysRevLett.98.134501 Brown E, Nikolaenko A, Ahlers G. 2005. Reorientation of the large-scale circulation in turbulent Rayleigh-Bénard convection. Phys. Rev. Lett., 95: 084503. doi: 10.1103/PhysRevLett.95.084503 Brown R A. 1988. Theory of transport processes in single crystal growth from the melt. AIChE Journal, 34: 881-911. doi: 10.1002/aic.690340602 Cai W, Wei T, Tang X, Liu Y, Li B, Li F. 2019. The polymer effect on turbulent Rayleigh-Bénard convection based on PIV experiments. Exp. Therm. Fluid Sci., 103: 214-221. doi: 10.1016/j.expthermflusci.2019.01.011 Castaing B, Gunaratne G, Heslot F, Kadanoff L, Libchaber A, Thomae S, Wu X Z, Zaleski S, Zanetti G. 1989. Scaling of hard thermal turbulence in Rayleigh-Bénard convection. J. Fluid Mech., 204: 1-30. doi: 10.1017/S0022112089001643 Castillo-Castellanos A, Sergent A, Rossi M. 2016. Reversal cycle in square Rayleigh-Bénard cells in turbulent regime. J. Fluid Mech., 808: 614-640. doi: 10.1017/jfm.2016.647 Chandra M, Verma M K. 2011. Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E, 83: 067303. doi: 10.1103/PhysRevE.83.067303 Chandra M, Verma M K. 2013. Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett., 110: 114503. doi: 10.1103/PhysRevLett.110.114503 Chandrakar K K, Cantrell W, Chang K, Ciochetto D, Niedermeier D, Ovchinnikov M, Shaw R A, Yang F. 2016. Aerosol indirect effect from turbulence-induced broadening of cloud-droplet size distributions. Proc. Natl. Acad. Sci., 113: 14243-14248. doi: 10.1073/pnas.1612686113 Chandrakar K K, Cantrell W, Krueger S, Shaw R A, Wunsch S. 2019. Supersaturation fluctuations in moist turbulent Rayleigh-Bénard convection: A two-scalar transport problem. J. Fluid Mech., 884: A19. Chandrasekhar S. 1961. Hydrodynamic and Hydromagnetic Stability. Oxford University Press. Chen X, Huang S D, Xia K Q, Xi H D. 2019. Emergence of substructures inside the large-scale circulation induces transition in flow reversals in turbulent thermal convection. J. Fluid Mech., 877: R1. doi: 10.1017/jfm.2019.624 Chen X, Wang D P, Xi H D. 2020. Reduced flow reversals in turbulent convection in the absence of corner vortices. J. Fluid Mech., 891: R5. doi: 10.1017/jfm.2020.202 Cheng J S, Aurnou J M, Julien K, Kunnen R P J. 2018. A heuristic framework for next-generation models of geostrophic convective turbulence. Geophys. Astrophys. Fluid Dyn., 112: 277-300. doi: 10.1080/03091929.2018.1506024 Cheng J S, Madonia M, Aguirre Guzmán A J, Kunnen R P J. 2020. Laboratory exploration of heat transfer regimes in rapidly rotating turbulent convection. Phys. Rev. Fluids, 5: 113501. doi: 10.1103/PhysRevFluids.5.113501 Cheng J S, Stellmach S, Ribeiro A, Grannan A, King E M, Aurnou J M. 2015. Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Int., 201: 1-17. doi: 10.1093/gji/ggu480 Cheng J P, Zhang H N, Cai W H, Li S N, Li F C. 2017. Effect of polymer additives on heat transport and large-scale circulation in turbulent Rayleigh-Bénard convection. Phys. Rev. E, 96: 013111. doi: 10.1103/PhysRevE.96.013111 Chilla F, Schumacher J. 2012. New perspectives in turbulent Rayleigh-Bénard convection. Eur. Phys. J. E, 35: 58. doi: 10.1140/epje/i2012-12058-1 Ching E S C, Leung H S, Zwirner L, Shishkina O. 2019. Velocity and thermal boundary layer equations for turbulent Rayleigh-Bénard convection. Phys. Rev. Research, 1: 033037. doi: 10.1103/PhysRevResearch.1.033037 Chong K L, Shi J Q, Ding G Y, Ding S S, Lu H Y, Zhong J Q, Xia K Q. 2020. Vortices as Brownian particles in turbulent flows. Sci. Adv., 6: eaaz1110. doi: 10.1126/sciadv.aaz1110 Chong K L, Yang Y, Huang S D, Zhong J Q, Stevens R J A M, Verzicco R, Lohse D, Xia K Q. 2017. Confined Rayleigh-Bénard, rotating Rayleigh-Bénard, and double diffusive convection: a unifying view on turbulent transport enhancement through coherent structure manipulation. Phys. Rev. Lett., 119: 064501. doi: 10.1103/PhysRevLett.119.064501 Ciliberto S, Cioni S, Laroche C. 1996. Large-scale flow properties of turbulent thermal convection. Phys. Rev. E, 54: R5901-R5904. doi: 10.1103/PhysRevE.54.R5901 Ciliberto S, Laroche C. 1999. Random roughness of boundary increases the turbulent convection scaling exponent. Phys. Rev. Lett., 82: 3998-4001. doi: 10.1103/PhysRevLett.82.3998 Cioni S, Ciliberto S, Sommeria J. 1997. Strongly turbulent RBC in mercury: Comparison with results at moderate Prandtl numbers. J. Fluid Mech., 335, s 111-140. Cooper C M, Moresi L N, Lenardic A. 2013. Effects of continental configuration on mantle heat loss. Geophys. Res. Lett., 40: 2647-2651. doi: 10.1002/grl.50547 Cross M C, Hohenberg P C. 1993. Pattern formation outside of equilibrium. Rev. Mod. Phys., 65: 851-1112. doi: 10.1103/RevModPhys.65.851 Daniels K E, Bodenschatz E. 2002. Defect turbulence in inclined layer convection. Phys. Rev. Lett., 88: 034501. doi: 10.1103/PhysRevLett.88.034501 Daniels K E, Plapp B B, Bodenschatz E. 2000. Pattern formation in inclined layer convection. Phys. Rev. Lett. , 84: 5320-5323. Daniels K E, Wiener R J, Bodenschatz E. 2003. Localized transverse bursts in inclined layer convection. Phys. Rev. Lett., 91: 114501. doi: 10.1103/PhysRevLett.91.114501 de Wit X M, Guzmán A J, Madonia M, Cheng J S, Clercx H J H, Kunnen R P J. 2020. Turbulent rotating convection confined in a slender cylinder: the sidewall circulation. Phys. Rev. Fluids, 5: 023502. doi: 10.1103/PhysRevFluids.5.023502 Deardorff J W. 1970. Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J. Atmos. Sci., 27: 1211-1213. doi: 10.1175/1520-0469(1970)027<1211:CVATSF>2.0.CO;2 Deusebio E, Boffetta G, Lindborg E, Musacchio S. 2014. Dimensional transition in rotating turbulence. Phys. Rev. E, 90: 023005. doi: 10.1103/PhysRevE.90.023005 Ding G Y, Chong K L, Xia K Q. 2021. A comparative study of linear and step forcing temperature profiles in horizontal convection. Europhys. Lett., 135: 24006. doi: 10.1209/0295-5075/ac29ef Ding G Y, He Y H, Xia K Q. 2022. The effect of tidal force and topography on horizontal convection. J. Fluid Mech., 932: A32. doi: 10.1017/jfm.2021.1021 Ding S S, Chong K L, Shi J Q, Ding G Y, Lu H Y, Xia K Q, Zhong J Q. 2021. Inverse centrifugal effect induced by collective motion of vortices in rotating thermal convection. Nat. Commun., 12: 5585. doi: 10.1038/s41467-021-25838-3 du Puits R, Resagk C, Tilgner A. 2007. Structure of thermal boundary layer for turbulent Rayleigh-Bénard convection. J. Fluid Mech., 572: 231-254. doi: 10.1017/S0022112006003569 du Puits R, Resagk C, Thess A. 2009. Structure of viscous boundary layers in turbulent Rayleigh-Bénard convection. Phys. Rev. E, 80: 036318. doi: 10.1103/PhysRevE.80.036318 Du Y B, Tong P. 2000. Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech., 407: 57-84. doi: 10.1017/S0022112099007624 Ecke R E, Zhong F, Knobloch E. 1992. Hopf bifurcation with broken reflection symmetry in rotating Rayleigh-Bénard convection. Europhys. Lett., 19: 177-182. doi: 10.1209/0295-5075/19/3/005 Favier B, Knobloch E. 2020. Robust wall states in rapidly rotating Rayleigh-Bénard convection. J. Fluid Mech., 895: R1. doi: 10.1017/jfm.2020.310 Frick P, Khalilov R, Kolesnichenko I, Mamykin A, Pakholkov V, Pavlinov A, Rogozhkin S. 2015. Turbulent convective heat transfer in a long cylinder with liquid sodium. EuroPhys. Lett, 109: 14002. doi: 10.1209/0295-5075/109/14002 Funfschilling D, Ahlers G. 2004. Plume motion and large-scale circulation in a cylindrical Rayleigh-Bénard cell. Phys. Rev. Lett., 92: 194502. doi: 10.1103/PhysRevLett.92.194502 Gasteuil Y, Shew W L, Gibert M, Chillà F, Castaing B, Pinton J F. 2007. Lagrangian temperature, velocity, and local heat flux measurement in Rayleigh-Bénard convection. Phys. Rev. Lett., 99: 234302. doi: 10.1103/PhysRevLett.99.234302 Gayen B, Griffiths R W, Hughes G O, Saenz J A. 2013. Energetics of horizontal convection. J. Fluid Mech., 716: R10. doi: 10.1017/jfm.2012.592 Gayen B, Griffiths R W, Hughes G O. 2014. Stability transitions and turbulence in horizontal convection. J. Fluid Mech., 751: 698-724. doi: 10.1017/jfm.2014.302 Gayen B, Griffiths R W. 2022. Rotating horizontal convection. Annu. Rev. Fluid Mech., 54: 105-132. doi: 10.1146/annurev-fluid-030121-115729 Glatzmaiers G A, Roberts P H. 1995. A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature, 377: 203-209. doi: 10.1038/377203a0 Grossmann S, Lohse D, Sun C. 2016. High-Reynolds number Taylor-Couette turbulence. Annu. Rev. Fluid Mech., 48: 53-80. doi: 10.1146/annurev-fluid-122414-034353 Grossmann S, Lohse D. 2000. Scaling in thermal convection: A unifying view. J. Fluid Mech., 407: 27-56. doi: 10.1017/S0022112099007545 Grossmann S, Lohse D. 2001. Thermal convection for large Prandtl number. Phys. Rev. Lett., 86: 3316-3319. doi: 10.1103/PhysRevLett.86.3316 Grossmann S, Lohse D. 2002. Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E, 66: 016305. doi: 10.1103/PhysRevE.66.016305 Grossmann S, Lohse D. 2004. Fluctuations in turbulent Rayleigh-Bénard convection: The role of plumes. Phys. Fluids, 16: 4462-4472. doi: 10.1063/1.1807751 Guo, S X, Zhou S Q, Cen X R, Qu L, Lu Y Z, Sun L, Shang X D. 2014. The effect of cell tilting on turbulent thermal convection in a rectangular cell. J. Fluid Mech., 762: 273-287. Guzman D N, Xie Y, Chen S, Rivas D F, Sun C, Lohse D, Ahlers G. 2015. Heat-flux enhancement by vapour-bubble nucleation in Rayleigh–Bénard turbulence. J. Fluid Mech., 787: 331-366. Guzman D N, Frączek T, Reetz C, Sun C, Lohse D, Ahlers G. 2016. Vapour-bubble nucleation and dynamics in turbulent Rayleigh–Bénard convection. J. Fluid Mech., 795: 60-95. doi: 10.1017/jfm.2016.178 Hartmann D L, Moy L A, Fu Q. 2001. Tropical convection and the energy balance at the top of the atmosphere. J. Climate, 14: 4495-4511. doi: 10.1175/1520-0442(2001)014<4495:TCATEB>2.0.CO;2 Hazewinkel J, Paparella F, Young W R. 2012. Stressed horizontal convection. J. Fluid Mech., 692: 317-331. doi: 10.1017/jfm.2011.514 He X, Funfschilling D, Nobach H, Bodenschatz E, Ahlers G. 2012. Transition to the ultimate state of turbulent Rayleigh-Benard convection. Phys. Rev. Lett., 108: 024502. doi: 10.1103/PhysRevLett.108.024502 He Y H, Xia K Q. 2019. Temperature fluctuation profiles in turbulent thermal convection: a logarithmic dependence versus a power-law dependence. Phys. Rev. Lett., 122: 014503. doi: 10.1103/PhysRevLett.122.014503 Hogg A M, Gayen B. 2020. Ocean gyres driven by surface buoyancy forcing. Geophys. Res. Lett., 47: 1-10. Horn S, Aurnou J M. 2018. Regimes of Coriolis-Centrifugal convection. Phys. Rev. Lett., 120: 204502. doi: 10.1103/PhysRevLett.120.204502 Horn S, Aurnou J M. 2019. Rotating convection with centrifugal buoyancy: Numerical predictions for laboratory experiments. Phys. Rev. Fluids, 4: 073501. doi: 10.1103/PhysRevFluids.4.073501 Horn S, Schmid P J. 2017. Prograde, retrograde, and oscillatory modes in rotating Rayleigh-Bénard convection. J. Fluid Mech., 831: 182-211. Hu Y B, Huang S D, Xie Y C, Xia K Q. 2021. Centrifugal-force-induced flow bifurcations in turbulent thermal convection. Phys. Rev. Lett., 127: 244501. doi: 10.1103/PhysRevLett.127.244501 Hu Y B, Xie Y C, Xia K Q. 2022. On the centrifugal effect in turbulent rotating thermal convection: onset and heat transport. J. Fluid Mech., 938: R1. doi: 10.1017/jfm.2022.190 Huang R X. 1999. Mixing and energetics of the oceanic thermohaline circulation. J. Phys. Oceanogr., 29: 727-746. doi: 10.1175/1520-0485(1999)029<0727:MAEOTO>2.0.CO;2 Huang S D, Kaczorowski M, Ni R, Xia K Q. 2013. Confinement-induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett., 111: 104501. doi: 10.1103/PhysRevLett.111.104501 Huang S D, Wang F, Xi H D, Xia K Q. 2015. Comparative experimental study of fixed temperature and fixed heat flux boundary conditions in turbulent thermal convection. Phys. Rev. Lett., 115: 154502. Huang S D, Xia K Q. 2016. Effects of geometric confinement in quasi-2-D turbulent Rayleigh–Bénard convection. J. Fluid Mech., 794: 639-654. doi: 10.1017/jfm.2016.181 Hughes G O, Griffiths R W, Mullarney J C, Peterson W H. 2007. A theoretical model for horizontal convection at high Rayleigh number. J. Fluid Mech., 581: 251-276. doi: 10.1017/S0022112007005630 Hughes G O, Griffiths R W. 2008. Horizontal convection. Annu. Rev. Fluid Mech, 40: 185-208. doi: 10.1146/annurev.fluid.40.111406.102148 Hughes G O, Hogg A M C, Griffiths R W. 2009. Available potential energy and irreversible mixing in the meridional overturning circulation. J. Phys. Oceanogr., 39: 3130-3146. doi: 10.1175/2009JPO4162.1 Jiang H, Zhu X, Mathai V, Verzicco R, Lohse D, Sun C. 2018. Controlling heat transport and flow structures in thermal turbulence using ratchet surfaces. Phys. Rev. Lett., 120: 044501. doi: 10.1103/PhysRevLett.120.044501 Jiang H, Zhu X, Wang D, Huisman S G, Sun C. 2020. Supergravitational turbulent thermal convection. Sci. Adv., 6: eabb8676. doi: 10.1126/sciadv.abb8676 Jiang L, Sun C, Calzavarini E. 2019. Robustness of heat transfer in confined inclined convection at high Prandtl number. Phys. Rev. E, 99: 013108. doi: 10.1103/PhysRevE.99.013108 Jin T C, Wu J Z, Zhang Y Z, Liu Y L, Zhou Q. 2022. Shear-induced modulation on thermal convection over rough plates. J. Fluid Mech., 936: A28. doi: 10.1017/jfm.2021.1111 Julien K, Aurnou J M, Calkins M A, Knobloch E, Marti P, Stellmach S, Vasil G M. 2016. A nonlinear model for rotationally constrained convection with Ekman pumping. J. Fluid Mech., 798: 50-87. doi: 10.1017/jfm.2016.225 Julien K, Knobloch E, Plumley M. 2018. Impact of domain anisotropy on the inverse cascade in geostrophic turbulent convection. J. Fluid Mech., 837: R4. doi: 10.1017/jfm.2017.894 Julien K, Knobloch E, Rubio A M, Vasil G M. 2012. Heat transport in low-Rossby-number Rayleigh-Bénard convection. Phys. Rev. Lett., 109: 254503. doi: 10.1103/PhysRevLett.109.254503 Julien K, Knobloch E, Werne J. 1998. A new class of equations for rotationally constrained flows. Theor. Comput. Fluid Dyn., 11: 251-261. doi: 10.1007/s001620050092 Kar P K, Kumar Y N, Das P K, Lakkaraju R. 2020. Thermal convection in octagonal-shaped enclosures. Phys. Rev. Fluids, 5: 103501. doi: 10.1103/PhysRevFluids.5.103501 Kerswell R R. 2002. Elliptical instability. Annu. Rev. Fluid Mech., 34: 83-113. doi: 10.1146/annurev.fluid.34.081701.171829 King E M, Aurnou J M. 2013. Turbulent convection in liquid metal with and without rotation. Proc. Natl. Acad. Sci., 110: 6688-6693. doi: 10.1073/pnas.1217553110 King E M, Stellmach S, Aurnou J M. 2012. Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech., 691: 568-582. doi: 10.1017/jfm.2011.493 King E M, Stellmach S, Noir J, Hansen U, Aurnou J M. 2009. Boundary layer control of rotating convection systems. Nature, 457: 301-304. doi: 10.1038/nature07647 Kraichnan R H. 1962. Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids, 5: 1374-1389. doi: 10.1063/1.1706533 Krishnamurti R, Howard L N. 1981. Large-scale flow generation in turbulent convection. Proc. Natl. Acad. Sci., 78: 1981-1985. doi: 10.1073/pnas.78.4.1981 Lakkaraju R, Stevens R J, Oresta P, Verzicco R, Lohse D, Prosperetti A. 2013. Heat transport in bubbling turbulent convection. Proc. Natl. Acad. Sci., 110: 9237-9242. doi: 10.1073/pnas.1217546110 Landau L D, Lifshitz E M. 1987. Fluid Mechanics. Oxford: Pergamon. Li X M, Huang S D, Ni R, Xia K Q. 2021. Lagrangian velocity and acceleration measurements in plume-rich regions of turbulent Rayleigh-Bénard convection. Phys. Rev. Fluids, 6: 053503. doi: 10.1103/PhysRevFluids.6.053503 Li Y Z, Chen X, Xu A, Xi H D. 2022. Counter-flow orbiting of the vortex centre in turbulent thermal convection. J. Fluid Mech., 935: A19. doi: 10.1017/jfm.2022.11 Lim Z L, Chong K L, Ding G Y, Xia K Q. 2019. Quasistatic magnetoconvection: heat transport enhancement and boundary layer crossing. J. Fluid Mech., 870: 519-542. doi: 10.1017/jfm.2019.232 Liot O, Seychelles F, Zonta F, Chibbaro S, Coudarchet T, Gasteuil Y, Pinton J F, Salort J, Chillà F. 2016. Simultaneous temperature and velocity Lagrangian measurements in turbulent thermal convection. J. Fluid Mech., 794: 655-675. doi: 10.1017/jfm.2016.190 Lohse D, Xia K Q. 2010. Small-scale properties of turbulent Rayleigh-Bénard Convection. Annu. Rev. Fluid Mech., 42: 335-364. doi: 10.1146/annurev.fluid.010908.165152 Lu H Y, Ding G Y, Shi J Q, Xia K Q, Zhong J Q. 2021. Heat transport scaling and transition in geostrophic rotating convection with varying aspect ratio. Phys. Rev. Fluids, 6: L071501. doi: 10.1103/PhysRevFluids.6.L071501 Malkus M V R. 1954. The heat transport and spectrum of thermal turbulence. Proc. R. Soc. London, Ser. A, 225: 196-212. doi: 10.1098/rspa.1954.0197 Marshall J, Schott F. 1999. Open-ocean convection: observations, theory, and models. Rev. Geophys., 37: 1-64. doi: 10.1029/98RG02739 Mathai V, Calzavarini E, Brons J, Sun C, Lohse D. 2016. Microbubbles and microparticles are not faithful tracers of turbulent acceleration. Phys. Rev. Lett., 117: 024501. doi: 10.1103/PhysRevLett.117.024501 Mullarney J C, Griffiths R W, Hughes G O. 2004. Convection driven by differential heating at a horizontal boundary. J. Fluid Mech., 516: 181-209. doi: 10.1017/S0022112004000485 Ni R, Huang S D, Xia K Q. 2011. Local energy dissipation rate balances local heat flux in the center of turbulent thermal convection. Phys. Rev. Lett., 107: 174503. doi: 10.1103/PhysRevLett.107.174503 Ni R, Huang S D, Xia K Q. 2012. Lagrangian acceleration measurements in convective thermal turbulence. J. Fluid Mech., 692: 395-419. doi: 10.1017/jfm.2011.520 Ni R, Huang S D, Xia K Q. 2015. Reversals of the large-scale circulation in quasi-2D Rayleigh–Bénard convection. J. Fluid Mech., 778: R5. doi: 10.1017/jfm.2015.433 Nieves D, Rubio A M, Julien K. 2014. Statistical classification of flow morphology in rapidly rotating Rayleigh-Bénard convection. Phys. Fluids, 26: 086602. Noto D, Tasaka Y, Yanagisawa T, Murai Y. 2019. Horizontal diffusive motion of columnar vortices in rotating Rayleigh-Bénard convection. J. Fluid Mech., 871: 401-426. doi: 10.1017/jfm.2019.313 Oberbeck A. 1879. Über die wärmeleitung der flüssigkeiten bei berücksichtigung der strömungen infolge von temperaturdifferenzen. Ann. Phys. Chem., 243: 271-292. doi: 10.1002/andp.18792430606 Ostilla-Mónico R, Amritkar A. 2020. Regime crossover in Rayleigh-Bénard convection with mixed boundary conditions. J. Fluid Mech., 903: A39. doi: 10.1017/jfm.2020.623 Ovsyannikov M, Krasnov D, Emran M S, Schumacher J. 2016. Combined effects of prescribed pressure gradient and buoyancy in boundary layer of turbulent Rayleigh–Bénard convection. European Journal of Mechanics - B/Fluids, 57: 64-74. doi: 10.1016/j.euromechflu.2016.02.001 Paparella F, Young W R. 2002. Horizontal convection is non-turbulent. J. Fluid Mech., 466: 205-214. doi: 10.1017/S0022112002001313 Pauluis O, Schumacher J. 2011. Self-aggregation of clouds in conditionally unstable moist convection. Proc. Natl. Acad. Sci., 108: 12623-12628. doi: 10.1073/pnas.1102339108 Plumley M, Julien K, Marti P, Stellmach S. 2016. The effects of Ekman pumping on quasi-geostrophic Rayleigh-Bénard convection. J. Fluid Mech., 803: 51-71. doi: 10.1017/jfm.2016.452 Plumley M, Julien K, Marti P, Stellmach S. 2017. Sensitivity of rapidly rotating Rayleigh-Bénard convection to Ekman pumping. Phys. Rev. Fluids., 2: 094801. doi: 10.1103/PhysRevFluids.2.094801 Qiu X L, Xia K Q, Tong P. 2005. Experimental study of the velocity boundary layer near a rough conducting surface in turbulent thermal convection. J. Turb., 6: N30. doi: 10.1080/14685240500460733 Rajaei H, Joshi P, Alards K M J, Kunnen R P J, Toschi F, Clercx H J H. 2016. Transitions in turbulent rotating convection: A Lagrangian perspective. Phys. Rev. E, 93: 043129. doi: 10.1103/PhysRevE.93.043129 Reiter P, Shishkina O. 2020. Classical and symmetrical horizontal convection: detaching plumes and oscillations. J. Fluid Mech., 892: R1. doi: 10.1017/jfm.2020.211 Roche P E, Castaing B, Chabaud B, Hebral B. 2001. Observation of the 1/2 power law in Rayleigh-Bénard convection. Phys. Rev. E, 63: 045303. doi: 10.1103/PhysRevE.63.045303 Rossby H T. 1965. On thermal convection driven by non-uniform heating from below: an experimental study. Deep Sea Res. Oceanogr. Abstr., 12: 9-16. doi: 10.1016/0011-7471(65)91336-7 Rubio A M, Julien K, Knobloch E, Weiss J B. 2014. Upscale energy transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett., 112: 144501. doi: 10.1103/PhysRevLett.112.144501 Rusaouën E, Liot O, Castaing B, Salort J, Chillà F. 2018. Thermal transfer in Rayleigh–Bénard cell with smooth or rough boundaries. J. Fluid Mech., 837: 443-460. doi: 10.1017/jfm.2017.852 Sakai S. 1997. The horizontal scale of rotating convection in the geostrophic regime. J. Fluid Mech., 333: 85-95. doi: 10.1017/S0022112096004168 Schaeffer N, Jault D, Nataf H C, Fournier A. 2017. Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Intl, 211: 1-29. doi: 10.1093/gji/ggx265 Schindler F, Eckert S, Zürner T, Schumacher J, Vogt T. 2022. Collapse of coherent large scale flow in strongly turbulent liquid metal convection. Phys. Rev. Lett., 128: 164501. doi: 10.1103/PhysRevLett.128.164501 Schneide C., Pandey A., Padberg-Gehle K. Schumacher J. 2018. Probing turbulent superstructures in Rayleigh-Bénard convection by Lagrangian trajectory clusters. Phys. Rev. Fluids, 3: 113501. doi: 10.1103/PhysRevFluids.3.113501 Schumacher J, Sreenivasan K R. 2020. Colloquium: Unusual dynamics of convection in the Sun. Rev. Mod. Phys., 92: 041001. doi: 10.1103/RevModPhys.92.041001 Shang X D, Qiu X L, Tong P, Xia K Q. 2003. Measured local heat transport in turbulent Rayleigh-Bénard convection. Phys. Rev. Lett., 90: 074501. doi: 10.1103/PhysRevLett.90.074501 Sheard G J, Hussam W K, Tsai T. 2016. Linear stability and energetics of rotating radial horizontal convection. J. Fluid Mech., 795: 1-35. doi: 10.1017/jfm.2016.193 Shen Y, Tong P, Xia K Q. 1996. Turbulent convection over rough surfaces. Phys. Rev. Lett., 76: 908-911. doi: 10.1103/PhysRevLett.76.908 Shew W L, Gasteuil Y, Gibert M, Metz P, Pinton J F. 2007. Instrumented tracer for Lagrangian measurements in Rayleigh-Bénard convection. Rev. Sci. Instrum., 78: 065105. doi: 10.1063/1.2745717 Shi N, Emran M S, Schumacher J. 2012. Boundary layer structure in turbulent Rayleigh-Bénard convection. J. Fluid Mech., 706: 5-33. doi: 10.1017/jfm.2012.207 Shishkina O, Grossmann S, Lohse D. 2016. Heat and momentum transport scalings in horizontal convection. Geophys. Res. Lett., 43: 1219-1225. doi: 10.1002/2015GL067003 Shishkina O, Horn S, Emran M S, Ching E S C. 2017. Mean temperature profiles in turbulent thermal convection. Phys. Rev. Fluids, 2: 113502. doi: 10.1103/PhysRevFluids.2.113502 Shishkina O, Horn S, Wagner S, Ching E S C. 2015. Thermal boundary layer equation for turbulent Rayleigh-Bénard convection. Phys. Rev. Lett., 114: 114302. doi: 10.1103/PhysRevLett.114.114302 Shishkina O, Horn S. 2016. Thermal convection in inclined cylindrical containers. J. Fluid Mech., 790: R3. doi: 10.1017/jfm.2016.55 Shishkina O, Thess A. 2009. Mean temperature profiles in turbulent Rayleigh-Bénard convection of water. J. Fluid Mech., 633: 449-460. doi: 10.1017/S0022112009990528 Shishkina O, Wagner S. 2016. Prandtl-number dependence of heat transport in laminar horizontal convection. Phys. Rev. Lett., 116: 024302. doi: 10.1103/PhysRevLett.116.024302 Shishkina O. 2017. Mean flow structure in horizontal convection. J. Fluid Mech., 812: 525-540. doi: 10.1017/jfm.2016.866 Shishkina, O, Horn S, Wagner S. 2013. Falkner-skan boundary layer approximation in Rayleigh-Bénard convection. J. Fluid Mech., 730: 442-463. doi: 10.1017/jfm.2013.347 Shraiman B I, Siggia E D. 1990. Heat transport in high-Rayleigh-number convection. Phys. Rev. A, 42: 3650-3653. doi: 10.1103/PhysRevA.42.3650 Siggers J H, Kerswell R R, Balmoforth N J. 2004. Bounds on horizontal convection. J. Fluid Mech., 517: 55-70. doi: 10.1017/S0022112004000497 Siggia E D. 1994. High Rayleigh Number convection. Annu. Rev. Fluid Mech., 26: 137-168. doi: 10.1146/annurev.fl.26.010194.001033 Sohail T, Gayen B, Hogg A M C. 2018. Convection enhances mixing in the southern ocean. Geophys. Res. Lett., 45: 4198-4207. doi: 10.1029/2018GL077711 Sprague M, Julien K, Knobloch E, Werne J. 2006. Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech., 551: 141-174. doi: 10.1017/S0022112005008499 Sreenivasan K R, Bershadskii A, Niemela J J. 2002. Mean wind and its reversal in thermal convection. Phys. Rev. E, 65: 056306. doi: 10.1103/PhysRevE.65.056306 Stellmach S, Lischper M, Julien K, Vasil G, Cheng J S, Ribeiro A, King E M, Aurnou J M. 2014. Approaching the asymptotic regime of rapidly rotating convection: boundary layers versus interior dynamics. Phys. Rev. Lett., 113: 254501. doi: 10.1103/PhysRevLett.113.254501 Sterl S, Li H M, Zhong J Q. 2016. Dynamical and statistical phenomena of circulation and heat transfer in periodically forced rotating turbulent Rayleigh-Bénard convection. Phys. Rev. Fluids, 1: 084401. doi: 10.1103/PhysRevFluids.1.084401 Stevens R J A M, Zhong J Q, Clercx H J H, Ahlers G, Lohse D. 2009. Transitions between turbulent states in rotating Rayleigh-Bénard convection. Phys. Rev. Lett., 103: 024503. doi: 10.1103/PhysRevLett.103.024503 Stevens R J A M, Zhou Q, Grossmann S, Verzicco R, Xia K Q, Lohse D. 2012. Thermal boundary layer profiles in turbulent Rayleigh-Bénard convection in a cylindrical sample,. Phys. Rev. E, 85: 027301. doi: 10.1103/PhysRevE.85.027301 Stevens, R J A M, Erwin P van der Poel, Grossmann S, Lohse D. 2013. The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech., 730: 295-308. doi: 10.1017/jfm.2013.298 Stringano G, Pascazio G, Verzicco R. 2006. Turbulent thermal convection over grooved plates,. J. Fluid Mech., 557: 307-336. doi: 10.1017/S0022112006009785 Stringano G, Verzicco R. 2006. Mean flow structure in thermal convection in a cylindrical cell of aspect ratio one half. J. Fluid Mech., 548: 1-16. doi: 10.1017/S0022112005007378 Sugiyama K, Ni R, Stevens R J, Cheng T S, Zhou S Q, Xi H D, Sun C, Grossmann S, Xia K Q, Lohse D. 2010. Flow reversals in thermally driven turbulence. Phys. Rev. Lett., 105: 034503. doi: 10.1103/PhysRevLett.105.034503 Sun C, Xi H D, Xia K Q. 2005. Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett., 95: 074502. doi: 10.1103/PhysRevLett.95.074502 Tisserand J C, Creyssels M, Gasteuil Y, Pabiou H, Gibert M, Csataing B, Chilla F. 2011. Comparison between rough and smooth plates within the same Rayleigh–Bénard cell. Phys. Fluids, 23: 015105. doi: 10.1063/1.3540665 Toppaladoddi S, Succi S, Wettlaufer J S. 2017. Roughness as a route to the ultimate regime of thermal convection. Phys. Rev. Lett., 118: 074503. doi: 10.1103/PhysRevLett.118.074503 Valet J P, Fournier A, Courtillot V, Herrero-Bervera E. 2012. Dynamical similarity of geomagnetic field reversals. Nature, 490: 89-93. doi: 10.1038/nature11491 Vogt T, Horn S, Aurnou J M. 2021. Thermal-inertial oscillatory flows in liquid metal rotating convection,. J. Fluid Mech., 911: A5. doi: 10.1017/jfm.2020.976 Vogt T, Horn S, Grannan A M, Aurnou, J. M. 2018. Jump rope vortex in liquid metal convection. Proc. Natl. Acad. Sci., 115: 12674-12679. doi: 10.1073/pnas.1812260115 Vogt T, Yang J C, Schindler F, Eckert S. 2021. Free-fall velocities and heat transport enhancement in liquid metal magneto-convection. J. Fluid Mech., 915: A68. doi: 10.1017/jfm.2021.108 Vreugdenhil C A, Gayen B, Griffiths R W. 2016. Mixing and dissipation in a geostrophic buoyancy-driven circulation,. J. Geophys. Res. Ocean, 121: 6076-6091. doi: 10.1002/2016JC011691 Vreugdenhil C A, Griffiths R W, Gayen B. 2017. Geostrophic and chimney regimes in rotating horizontal convection with imposed heat flux. J. Fluid Mech., 823: 57-99. doi: 10.1017/jfm.2017.249 Wagner S, Shishkina O. 2015. Heat flux enhancement by regular surface roughness in turbulent thermal convection. J. Fluid Mech., 763: 109-135. doi: 10.1017/jfm.2014.665 Wang B F, Zhou Q, Sun C. 2020. Vibration-induced boundary-layer destabilization achieves massive heat-transport enhancement. Sci. Adv., 6: eaaz8239. doi: 10.1126/sciadv.aaz8239 Wang F, Huang S D, Xia K Q. 2018. Contribution of surface thermal forcing to mixing in the ocean. J. Geophys. Res. Ocean., 123: 855-863. doi: 10.1002/2017JC013578 Wang F, Huang S D, Zhou S Q, Xia K Q. 2016. Laboratory simulation of the geothermal heating effects on ocean overturning circulation. J. Geophys. Res. Ocean, 121: 7589-7598. doi: 10.1002/2016JC012068 Wang F, Huang S, Xia K. 2017. Thermal convection with mixed thermal boundary conditions : effects of insulating lid at the top, J. Fluid Mech., 817: R1. Wang Q, Verzicco R, Lohse D, Shishkina O. 2020. Multiple states in turbulent large-aspect-ratio thermal convection: what determines the number of convection rolls. Phys. Rev. Lett., 125: 074501. doi: 10.1103/PhysRevLett.125.074501 Wang Q, Wan Z H, Yan R, Sun D J. 2018. Multiple states and heat transfer in two-dimensional tilted convection with large aspect ratios. Phys. Rev. Fluids, 3: 113503. doi: 10.1103/PhysRevFluids.3.113503 Wang Q, Xia S N, Wang B F, Sun D J, Zhou Q, Wan Z H. 2018. Flow reversals in two-dimensional thermal convection in tilted cells. J. Fluid Mech., 849: 355-372. doi: 10.1017/jfm.2018.451 Wang W, Huang R X. 2005. An experimental study on thermal circulation driven by horizontal differential heating. J. Fluid Mech., 540: 49-73. doi: 10.1017/S002211200500577X Wang Y, He X, Tong P. 2016. Boundary layer fluctuations and their effects on mean and variance temperature profiles in turbulent Rayleigh-Bénard convection. Phys. Rev. Fluids, 1: 082301. doi: 10.1103/PhysRevFluids.1.082301 Wang Y, Lai P Y, Song H, Tong P. 2018. Mechanism of large-scale flow reversals in turbulent thermal convection. Sci. Adv., 4: eaat7480. doi: 10.1126/sciadv.aat7480 Wang Y, Xu W, He X, Yik H, Wang X, Schumacher J, Tong P. 2018. Boundary layer fluctuations in turbulent Rayleigh-Bénard convection. J. Fluid Mech., 840: 408-431. doi: 10.1017/jfm.2018.68 Wang Z, Mathai V, Sun C. 2019. Self-sustained biphasic catalytic particle turbulence. Nat. Commun., 10: 3333. doi: 10.1038/s41467-019-11221-w Wei P, Chan T S, Ni R, Zhao X Z, Xia K Q. 2014. Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection. J. Fluid Mech., 740: 28-46. doi: 10.1017/jfm.2013.638 Wei P, Ni R, Xia K Q. 2012. Enhanced and reduced heat transport in turbulent thermal convection with polymer additives. Phys Rev E, 86: 016325. doi: 10.1103/PhysRevE.86.016325 Wei P, Xia K Q. 2013. Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting. J. Fluid Mech., 720: 140-168. doi: 10.1017/jfm.2013.17 Weiss S, Ahlers G. 2011. Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ratio Γ = 0.50 and Prandtl number Pr = 4.38. J. Fluid Mech., 676: 5-40. doi: 10.1017/S0022112010005963 Weiss S, Ahlers G. 2013. Effect of tilting on turbulent convection: cylindrical samples with aspect ratio 0.5. J. Fluid Mech., 715: 314-334. doi: 10.1017/jfm.2012.520 Winters K B, Lombard P N, Riley J J, D’Asaro E A. 1995. Available potential energy and mixing in density-stratified fluids. J. Fluid Mech., 289: 115-128. doi: 10.1017/S002211209500125X Winters K B, Young W R. 2009. Available potential energy and buoyancy variance in horizontal convection. J. Fluid Mech., 629: 221-230. doi: 10.1017/S0022112009006685 Wunsch C, Ferrari R. 2004. Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech., 36: 281-314. doi: 10.1146/annurev.fluid.36.050802.122121 Wunsch C. 2000. Moon, tides and climate. Nature, 405: 743-744. doi: 10.1038/35015639 Xi H D, Bodenschatz E, Xu H. 2013. Elastic energy flux by flexible polymers in fluid turbulence. Phys. Rev. Lett., 111: 024501. doi: 10.1103/PhysRevLett.111.024501 Xi H D, Lam S, Xia K Q. 2004. From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech., 503: 47-56. doi: 10.1017/S0022112004008079 Xi H D, Zhou S Q, Zhou Q, Chan T S, Xia K Q. 2009. Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett., 102: 044503. doi: 10.1103/PhysRevLett.102.044503 Xi H D, Xia K Q. 2007. Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E, 75: 066307. doi: 10.1103/PhysRevE.75.066307 Xi H D, Xia K Q. 2008. Flow mode transitions in turbulent thermal convection. Phys. Fluids, 20: 055104. doi: 10.1063/1.2920444 Xi H D, Zhang Y B, Hao J T, Xia K Q. 2016. Higher-order flow modes in turbulent Rayleigh–Bénard convection. J. Fluid Mech., 805: 31-51. doi: 10.1017/jfm.2016.572 Xia K Q. 2013. Current trends and future directions in turbulent thermal convection. Theoretical and Applied Mechanics Letters, 3: 052001. doi: 10.1063/2.1305201 Xia K Q, Sun C, Zhou S Q. 2003. Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys Rev E., 68: 066303. doi: 10.1103/PhysRevE.68.066303 Xia K Q. 2019. Tuning heat transport via boundary layer topographies. J. Fluid Mech., 876: 1-4. doi: 10.1017/jfm.2019.526 Xia S, Wan Z, Liu S, Wang Q, Sun D. 2016. Flow reversals in Rayleigh–Bénard convection with non-Oberbeck–Boussinesq effects. J. Fluid Mech., 798: 628-642. doi: 10.1017/jfm.2016.338 Xie Y C, Cheng B Y C, Hu Y B, Xia K Q. 2019. Universal fluctuations in the bulk of Rayleigh–Bénard turbulence. J. Fluid Mech., 878: R1. doi: 10.1017/jfm.2019.667 Xie Y C, Ding, G Y, Xia K Q. 2018. Flow topology transition via global bifurcation in thermally driven turbulence. Phys. Rev. Lett., 120: 214501. doi: 10.1103/PhysRevLett.120.214501 Xie Y C, Huang S D, Funfschilling D, Li X M, Ni R, Xia K Q. 2015. Effects of polymer additives in the bulk of turbulent thermal convection. J. Fluid Mech., 784: R3. doi: 10.1017/jfm.2015.618 Xie Y C, Wei P, Xia K Q. 2013. Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection. J. Fluid Mech., 717: 322-346. doi: 10.1017/jfm.2012.574 Xie Y C, Xia K Q. 2013. Dynamics and flow coupling in two-layer turbulent thermal convection. J. Fluid Mech., 728: R1. doi: 10.1017/jfm.2013.313 Xie Y C, Xia K Q. 2017. Turbulent thermal convection over rough plates with varying roughness geometries. J. Fluid Mech., 825: 573-599. doi: 10.1017/jfm.2017.397 Xu A, Chen X, Wang F, Xi H D. 2020. Correlation of internal flow structure with heat transfer efficiency in turbulent Rayleigh–Bénard convection. Phys. Fluids, 32: 105112. doi: 10.1063/5.0024408 Xu A, Chen X, Xi H D. 2021. Tristable flow states and reversal of the large-scale circulation in two-dimensional circular convection cells. J. Fluid Mech., 910: A33. doi: 10.1017/jfm.2020.964 Xu B L, Wang Q, Wan Z H, Yan R, Sun D J. 2018. Heat transport enhancement and scaling law transition in two-dimensional Rayleigh-Bénard convection with rectangular-type roughness. International Journal of Heat and Mass Transfer, 121: 872-883. doi: 10.1016/j.ijheatmasstransfer.2018.01.051 Xu W, Wang Y, He X, Wang X, Schumacher J, Huang S D, Tong P. 2021. Mean velocity and temperature profiles in turbulent Rayleigh–Bénard convection at low Prandtl numbers. J. Fluid Mech., 918: A1. doi: 10.1017/jfm.2021.255 Yan B, Shishkina O, He X. 2021. Thermal boundary-layer structure in laminar horizontal convection. J. Fluid Mech., 915: R5. doi: 10.1017/jfm.2021.226 Yang R, Chong K L, Wang Q, Verzicco R, Shishkina O, Lohse D. 2020. Periodically modulated thermal convection. Phys. Rev. Lett., 125: 154502. doi: 10.1103/PhysRevLett.125.154502 Yang Y, Chen W, Verzicco R, Lohse D. 2020. Multiple states and transport properties of double-diffusive convection turbulence. Proc. Nat. Acad. Sci., 117: 14676-14681. doi: 10.1073/pnas.2005669117 Zhang K, Liao X. 2009. The onset of convection in rotating circular cylinders with experimental boundary conditions. J. Fluid Mech., 622: 63-73. doi: 10.1017/S002211200800517X Zhang L, Chong K L, Xia K Q. 2019. Moisture transfer by turbulent natural convection. J. Fluid Mech., 874: 1041-1056. doi: 10.1017/jfm.2019.463 Zhang L, Ding G Y, Xia K Q. 2021. On the effective horizontal buoyancy in turbulent thermal convection generated by cell tilting. J. Fluid Mech., 914: A15. doi: 10.1017/jfm.2020.825 Zhang L, Dong J, Xia K Q. 2022. Exploring the plume and shear effects in turbulent Rayleigh-Bénard convection with effective horizontal buoyancy under stream-wise and span-wise geometrical confinements. J. Fluid Mech., 940: A37. doi: 10.1017/jfm.2022.187 Zhang S, Xia Z, Zhou Q, Chen S. 2020. Controlling flow reversal in two-dimensional Rayleigh–Bénard convection. J. Fluid Mech., 891: R4. doi: 10.1017/jfm.2020.210 Zhang X, van Gils D P M, Horn S, Wedi M, Zwirner L, Ahlers G, Ecke R, Weiss S, Bodenschatz E, Shishkina O. 2019. Boundary Zonal Flow in Rotating Turbulent Rayleigh-Bénard Convection. Phys. Rev. Lett., 124: 084505. Zhang Y B, Bodenschatz E, Xu H, Xi H D. 2021. Experimental observation of the elastic range scaling in turbulent flow with polymer additives. Sci. Adv., 7: eabd3525. doi: 10.1126/sciadv.abd3525 Zhang Y Z, Sun C, Bao Y, Zhou Q. 2018. How surface roughness reduces heat transport for small roughness heights in turbulent Rayleigh–Bénard convection. J. Fluid Mech., 836: R2. doi: 10.1017/jfm.2017.786 Zhong F, Ecke R, Steinberg V. 1991. Asymmetric modes and the transition to vortex structures in rotating Rayleigh-Bénard convection. Phys. Rev. Lett., 67: 2473-2476. doi: 10.1103/PhysRevLett.67.2473 Zhong F, Ecke R, Steinberg V. 1993. Rotating Rayleigh–Bénard convection: asymmetric modes and vortex states. J. Fluid Mech., 249: 135-159. doi: 10.1017/S0022112093001119 Zhong J Q, Funfschilling D, Ahlers G. 2009. Enhanced heat transport by turbulent two-phase Rayleigh-Benard convection. Phys. Rev. Lett., 102: 124501. doi: 10.1103/PhysRevLett.102.124501 Zhong J Q, Sterl S, Li H M. 2015. Dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection with modulated rotation. J. Fluid Mech., 778: R4. doi: 10.1017/jfm.2015.400 Zhong J Q, Stevens R J A M, Clercx H J H, Verzicco R, Lohse D, Ahlers G. 2009. Prandtl-, Rayleigh-, and Rossby-Number dependence of heat transport in turbulent rotating Rayleigh-Bénard convection. Phys. Rev. Lett., 102: 044502. doi: 10.1103/PhysRevLett.102.044502 Zhou Q, Stevens R J A M, Sugiyama K, Grossmann S. Lohse D, Xia K Q. 2010. Prandtl-Blasius temperature and velocity boundary layer profiles in turbulent Rayleigh- Bénard convection. J. Fluid Mech., 664: 297-312. doi: 10.1017/S0022112010003824 Zhou Q, Sugiyama K, Stevens R J A M, Grossmann S, Lohse D, Xia K Q. 2011 Horizontal structures of velocity and temperature boundary layers in two-dimensional numerical turbulent Rayleigh- Bénard convection. Phys. Fluids, 23: 125104. Zhou Q, Xia K Q. 2010. Measured instantaneous viscous boundary layer in turbulent Rayleigh-Benard convection. Phys. Rev. Lett., 104: 104301. doi: 10.1103/PhysRevLett.104.104301 Zhou Q, Xia K Q. 2013. Thermal boundary layer structure in turbulent Rayleigh-Bénard convection in a rectangular cell. J. Fluid Mech., 721: 199-224. doi: 10.1017/jfm.2013.73 Zhu X, Stevens R J A M, Shishkina O, Verzicco R, Lohse D. 2019. Nu~Ra 1/2 scaling enabled by multiscale wall roughness in Rayleigh-Bénard turbulence. J. Fluid Mech., 869: R4. doi: 10.1017/jfm.2019.228 Zhu X, Stevens R J A M, Verzicco R, Lohse D. 2017. Roughness-facilitated local 1/2 scaling does not imply the onset of the ultimate regime of thermal convection. Phys. Rev. Lett., 119: 154501. doi: 10.1103/PhysRevLett.119.154501 Zwirner L, Shishkina O. 2018. Confined inclined thermal convection in low-Prandtl-number fluids. J. Fluid Mech., 850: 984-1008. doi: 10.1017/jfm.2018.477 Zwirner L, Tilgner A, Shishkina O. 2020. Elliptical instability and multiple-roll flow modes of the large-scale circulation in confined turbulent Rayleigh-Bénard convection. Phys. Rev. Lett., 125: 054502. doi: 10.1103/PhysRevLett.125.054502 -




 下载:
下载: