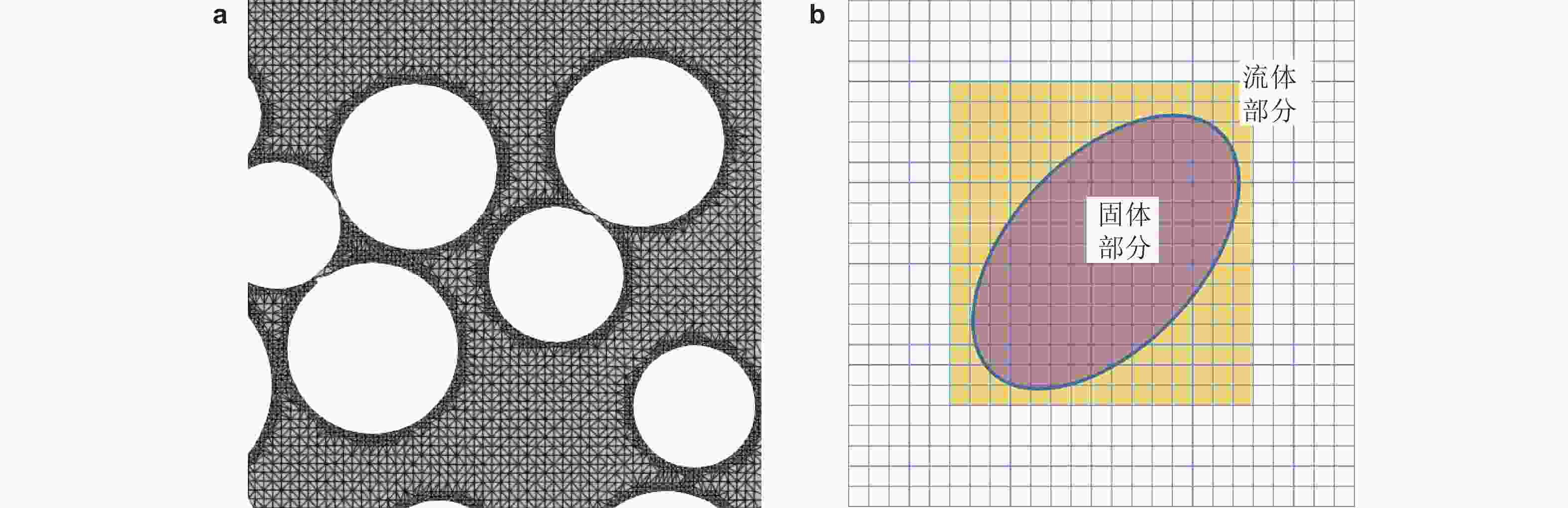
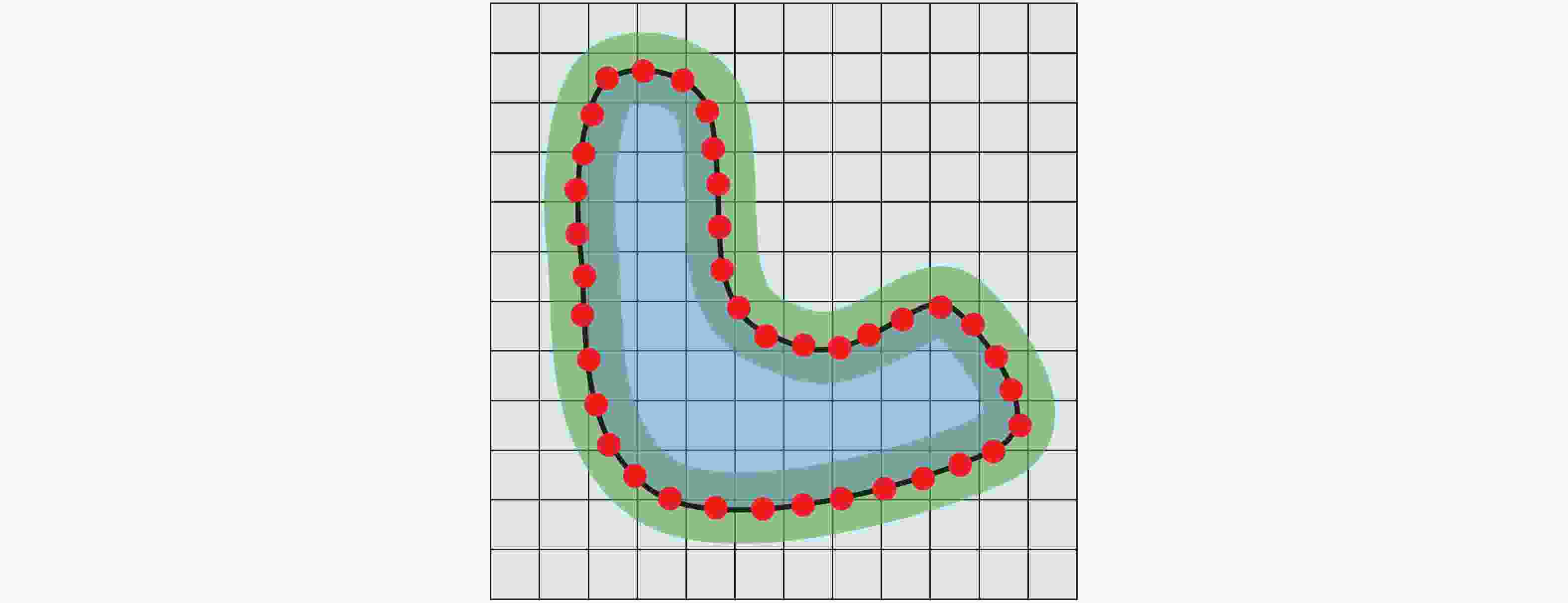
-
摘要: 非球形颗粒两相流是多相流的重要研究方向之一, 常见于自然界及工业生产过程中. 不同于球形颗粒, 由于非球形颗粒形状的各向异性, 除了颗粒平动行为, 还需要考虑颗粒的转动与取向行为, 颗粒的取向与转动行为会影响颗粒所受的力和力矩. 为了准确模拟非球形颗粒的运动行为, 目前非球形颗粒两相流的数值模拟研究主要基于欧拉−拉格朗日的求解框架展开, 常见的非球形颗粒两相流数值模拟方法主要包括点颗粒法与全分辨颗粒法. 本文将对这两类方法进行介绍, 同时会全面介绍非球形颗粒两相流研究的基础理论模型, 并系统总结非球形颗粒在简单基本流和复杂湍流中的研究进展, 包括对于非球形颗粒在湍流中的取向与转动行为机理, 以及颗粒对湍流减阻调制作用的研究. 最后, 本文提出了非球形颗粒两相流研究存在的问题及未来研究方向.Abstract: Non-spherical particle-laden flows are commonly seen and important in nature and industrial processes. The particle's rotational and orientational behaviors could affect the forces and torques acting on the particle from ambient fluid flow. To accurately capture the motion of non-spherical particles, especially for angular particle dynamics, most numerical studies of non-spherical particle-laden flows are carried out in the Euler-Lagrange frame. There are two most popular numerical approaches: the point-particle method and the particle-resolved method. This paper comprehensively and systematically summarizes these methods and significant recent findings about non-spherical particles in simple and turbulent flows. The mechanism of particle orientation and rotation by suspended non-spherical particles, as well as the modulation effect of particles on turbulent drag reduction, are discussed. Furthermore, the key and unsolved problems of non-spherical particle-laden flows for future study are proposed at the end of the paper.
-
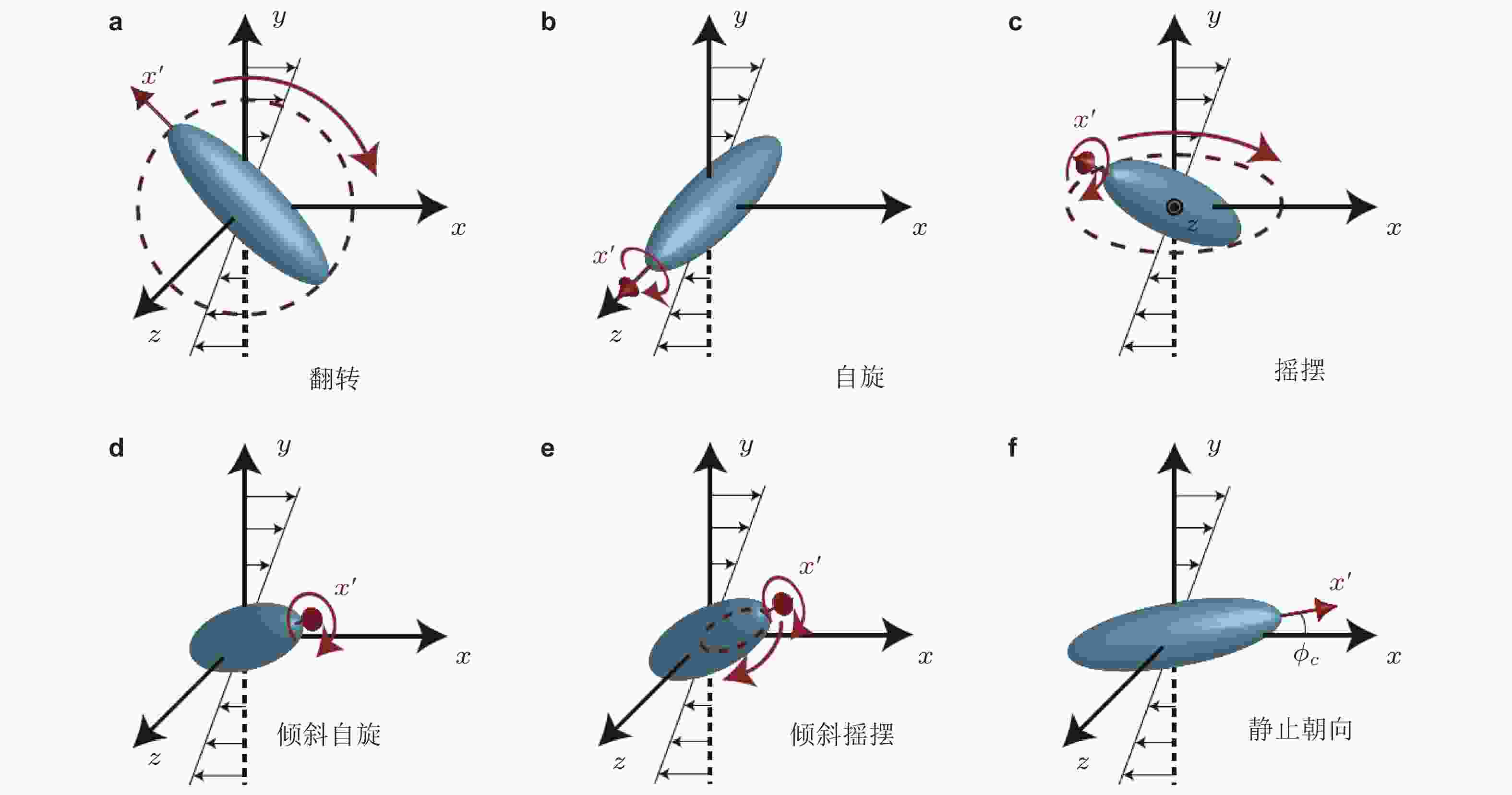
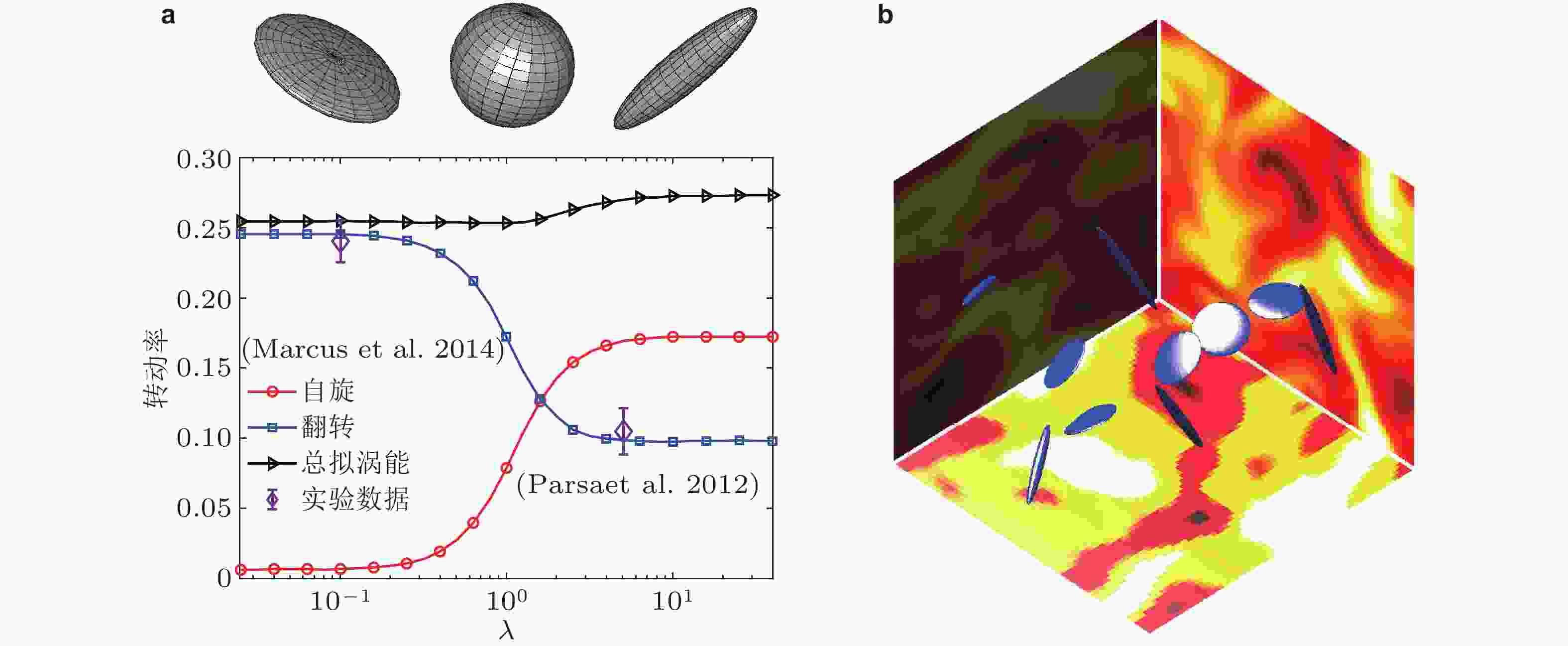
图 9 颗粒在剪切流中转动的不同模态(Rosén et al. 2014)
图 12 有限尺寸杆状颗粒在湍流中分布示意图(a)与(b)自适应网格加密(Schneiders et al. 2019)
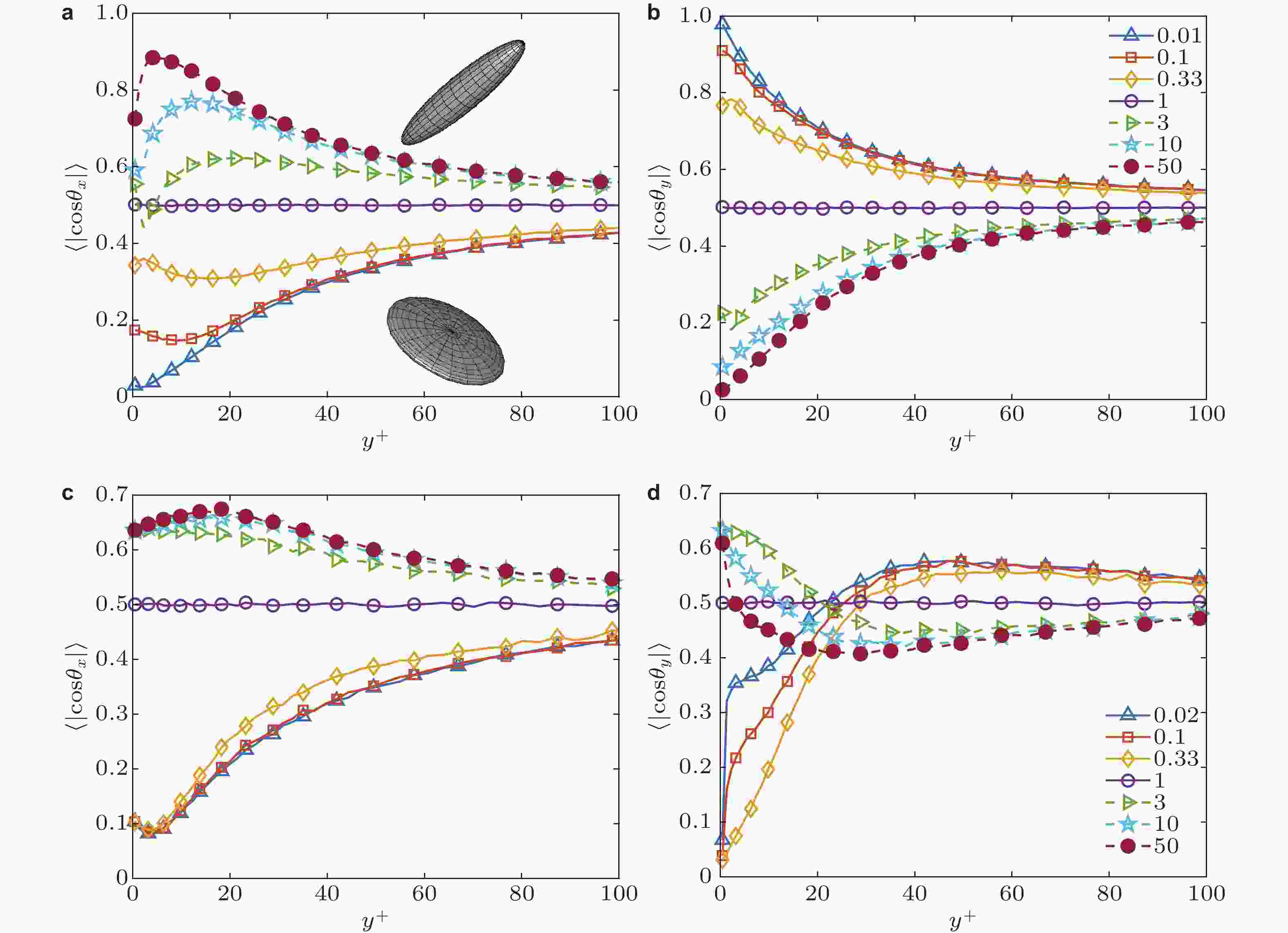
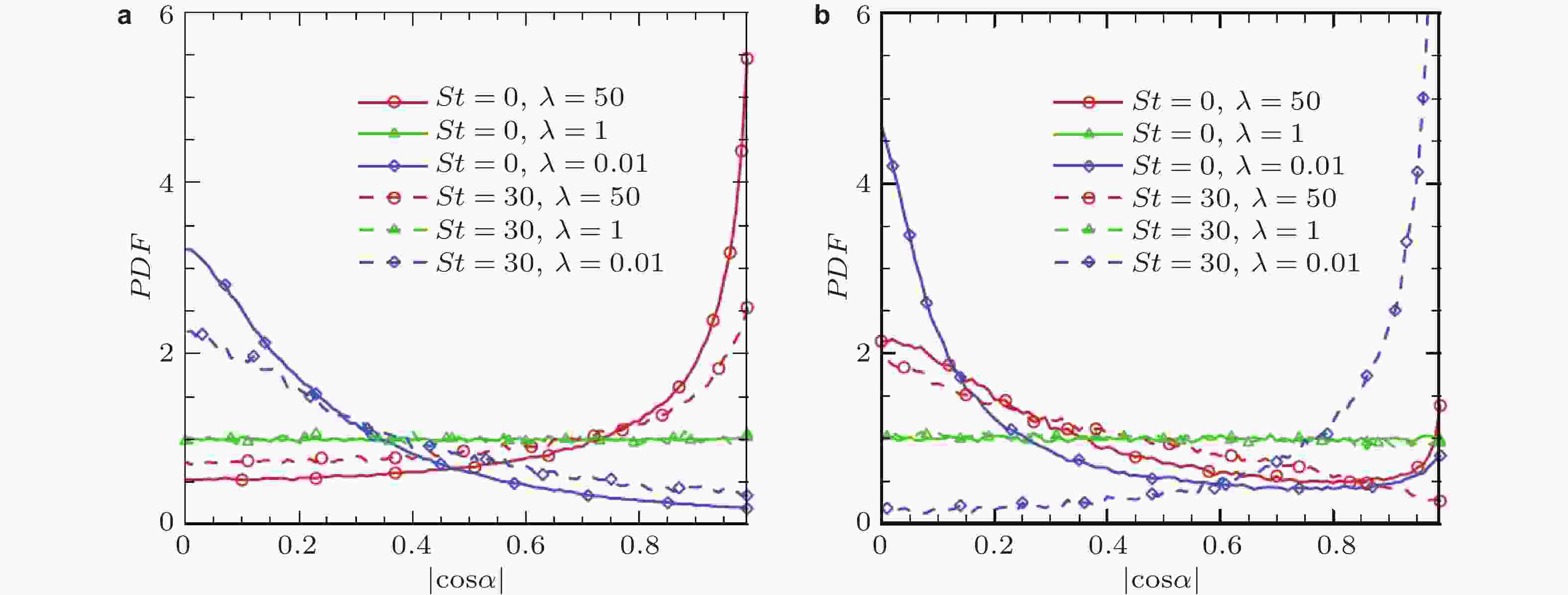
图 13 椭球颗粒在槽道湍流中的取向分布. (a)(b)无惯性椭球颗粒(Challabotla et al. 2015b); (c)(d)St = 30椭球颗粒
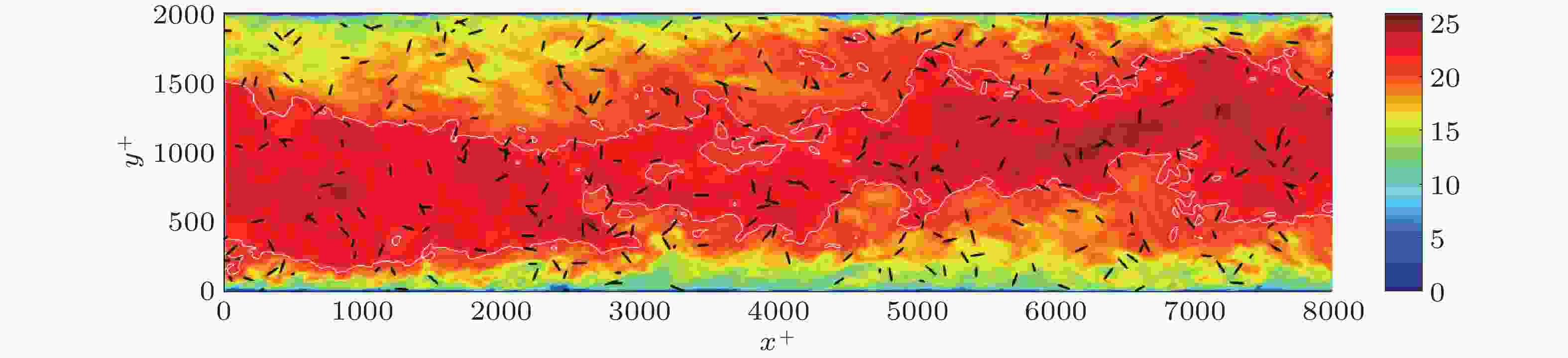
图 14 颗粒在近壁流向涡结构影响下的取向行为及区域划分(Cui Z et al. 2021). (a)(b)分别为细长杆状与扁平颗粒在瞬时流向涡附近的取向分布; (c)(d)条件系综平均后的颗粒取向分布, 其中(c)细长杆状颗粒与流向夹角余弦值
$ \left|\mathrm{cos}{\theta }_{x}\right| $ ; (d) 扁平颗粒与展向夹角余弦值$ \left|\mathrm{cos}{\theta }_{z}\right| $ ; (e)依据颗粒取向行为特点进行的区域划分示意图图 16 无惯性杆状颗粒在壁面取向行为与流体拉格朗日拉伸方向的差异(Cui Z et al. 2020)
图 18 不同形状和颗粒惯性的非球形颗粒回转轴方向与涡量的夹角分布(Zhao et al. 2015). (a)槽道中部, (b)近壁区
图 19 纤维与拉格朗日拉伸结构的关系. (a)周期流动(Parsa et al. 2011), (b)非周期流动(Parsa et al. 2011), (c)拉格朗日拉伸(黑色箭头)与压缩(红色箭头)与拉格朗日结构的关系(Cui Z & Zhao 2021)
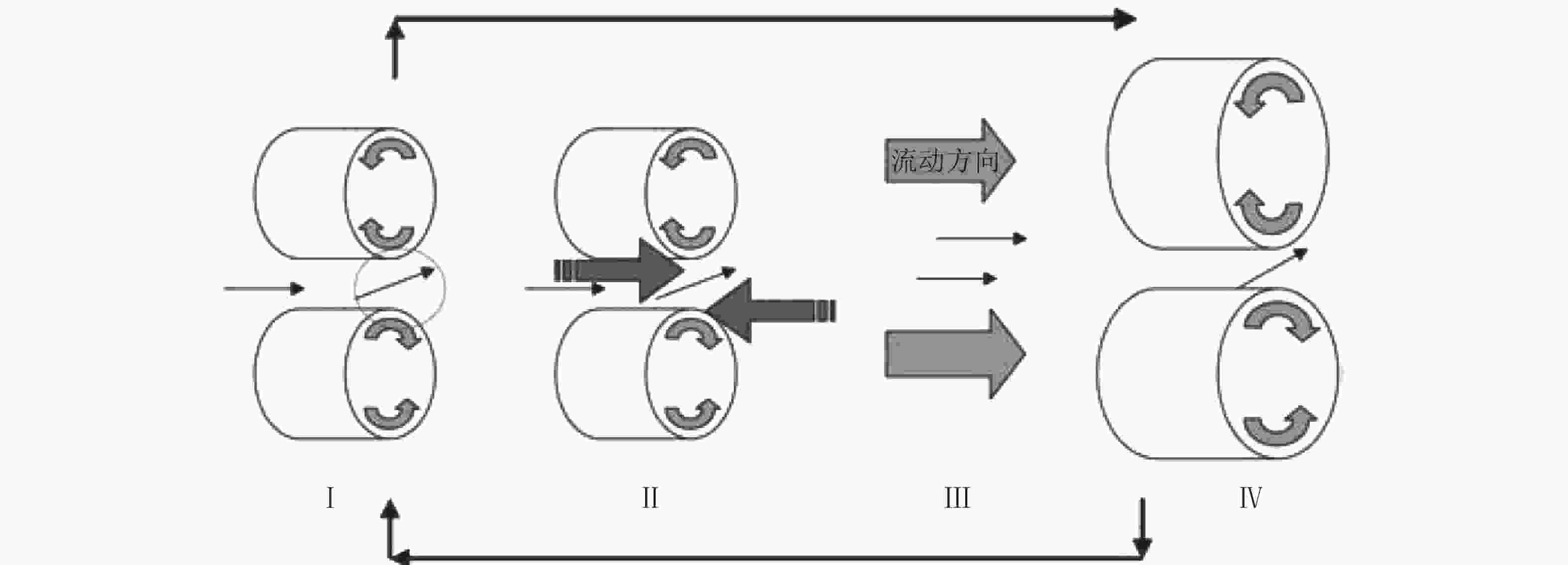
图 20 纤维减阻机制示意图(Paschkewitz et al. 2004)
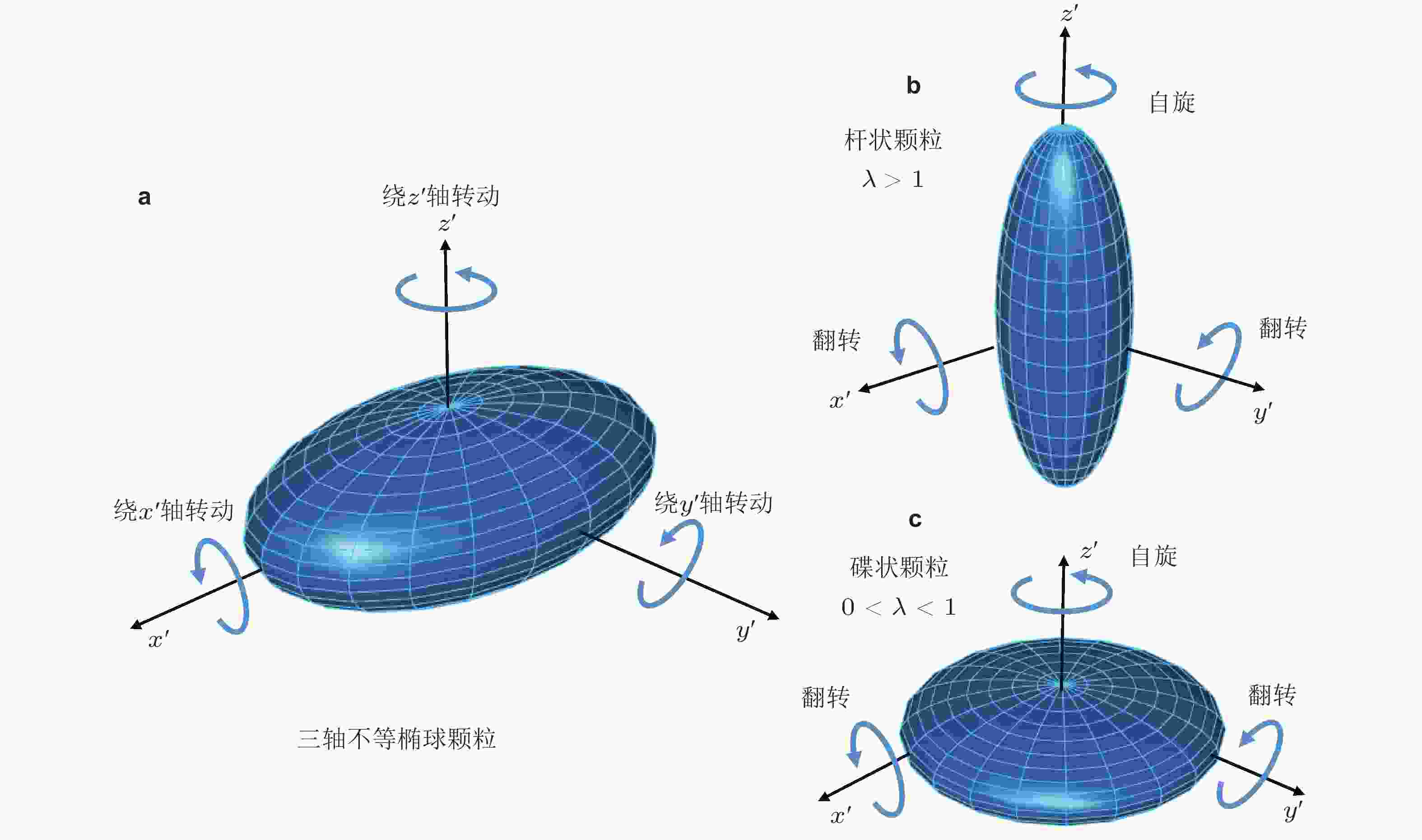
表 1 轴对称椭球颗粒相关的形状参数
碟状椭球颗粒
(${\bf{0} } < \boldsymbol{\lambda } < {\bf{1} }$)球形颗粒
(${\lambda }={\bf{1} }$)杆状椭球颗粒
(${\lambda } > {\bf{1} }$)α = β $-\dfrac{ {{B} }-\pi}{2\left(1-\lambda^{2}\right)^{{3}/{2} } }-\dfrac{\lambda}{1-\lambda^{2} }$ $ \dfrac{2}{3} $ $-\dfrac{{A} }{2{\left({{\lambda } }^{2}-1\right)}^{{3}/{2} } }+\dfrac{\lambda }{ {\lambda }^{2}-1}$ γ $-\dfrac{{B}-{\pi } }{ {\left(1-{\boldsymbol{\lambda } }^{2}\right)}^{{3}/{2} } }+\frac{2}{\left(1-{\lambda }^{2}\right)\lambda }$ $ \dfrac{2}{3} $ $\dfrac{{A} }{ {\left({{\lambda } }^{2}-1\right)}^{{3}/{2} } }-\dfrac{2}{\left({\lambda }^{2}-1\right)\lambda }$ χ $-\dfrac{ { {B} }-\pi}{\left(1-\lambda^{2}\right)^{ {1}/{2} } }$ $ 2 $ $\dfrac{{A} }{ {\left({{\lambda } }^{2}-1\right)}^{{1}/{2} } }$ 其中 ${A}=2{\ln}\left({\lambda }+\sqrt{ {\lambda }^{2}-1}\right),\;{ {{B} } }=2{\rm{arctan} }\dfrac{\lambda}{\sqrt{1-\lambda^{2}} }$ 表 2 有限尺寸杆状颗粒在剪切流中不同
$ {{Re}}_{\mathrm{s}} $ 对应的转动模态$ \mathrm{\lambda }=2 $(Huang et al. 2012) $\mathrm{\lambda }=4$(Rosén et al. 2014) ${{Re} }_{\mathrm{s} }$ 状态 ${Re}_{\mathrm{s} }$ 状态 0 Jeffery 轨迹 0 Jeffery 轨迹 0 ~ 120 翻转 0 ~ 14 翻转 120 ~ 235 翻转或自旋 15 ~ 62 翻转或自旋 235 ~ 305 翻转或倾斜自旋 63 ~ 71 翻转或倾斜自旋 305 ~ 345 翻转或倾斜摇摆 72 ~ 74 翻转或倾斜摇摆 345 ~ 385 翻转或摇摆 75 翻转或摇摆 385 ~ 445 翻转 76 ~ 89 翻转 445 ~ 700 翻转或静止朝向 90 ~ 150 翻转或静止朝向 表 3 有限尺寸碟状颗粒在剪切流中不同
$ {{R}{e}}_{\mathrm{s}} $ 对应的转动模态$ \mathrm{\lambda }=1/2 $(Huang et al. 2012) ${{R}{e} }_{\mathrm{s} }$ 状态 0 Jeffery 轨迹 0 ~ 112 自旋 112 ~ 168 翻转/倾斜自旋 168 ~ 520 静止朝向 -
崔智文, 赵立豪. 2021. 近壁湍流中微小非球形颗粒取向行为研究综述. 空气动力学学报, 39: 99-108 (Cui Z W, Zhao L H. 2021. Reviews on alignment of non-spherical particles in wall-bounded turbulence. Acta Aerodynamica Sinica, 39: 99-108). doi: 10.7638/kqdlxxb-2021.0045 何雅玲, 王勇, 李庆. 2009. 格子Boltzmann方法的理论及应用. 北京: 科学出版社He Y L, Wang Y, Li Q. 2009. Lattice Boltzmann Method Theory and Applications. Beijing: Science Press 邱敬然, 赵立豪. 2021. 复杂流动中的智能颗粒游动策略研究进展. 力学学报, 53: 2630-2639 (Qiu J R, Zhao L H. 2021. Progresses in swimming strategy of smart particles in complex flows. Chinese Journal of Theoretical and Applied Mechanics, 53: 2630-2639). doi: 10.6052/0459-1879-21-402 许春晓. 2015. 壁湍流相干结构和减阻控制机理. 力学进展, 45: 201504 (Xu C X. 2015. Coherent structures and drag-reduction mechanism in wall turbulence. Advances in Mechanics, 45: 201504). doi: 10.6052/1000-0992-15-006 张兆顺, 崔桂香, 许春晓, 黄伟希. 2017. 湍流理论与模拟. 北京: 清华大学出版社Zhang Z S, Cui G X, Xu C X, Huang W X. 2017. Theory and Modeling of Turbulence. Beijing: Tsinghua University Press Abbasi Hoseini A, Lundell F, Andersson H I. 2015. Finite-length effects on dynamical behavior of rod-like particles in wall-bounded turbulent flow. International Journal of Multiphase Flow, 76: 13-21. doi: 10.1016/j.ijmultiphaseflow.2015.05.015 Aidun C K, Clausen J R. 2010. Lattice-Boltzmann method for complex flows. Annual Review of Fluid Mechanics, 42: 439-472. doi: 10.1146/annurev-fluid-121108-145519 Anand P, Ray S S, Subramanian G. 2020. Orientation dynamics of sedimenting anisotropic particles in turbulence. Physical Review Letters, 125: 034501. doi: 10.1103/PhysRevLett.125.034501 Andersson H I, Zhao L, Barri M. 2012. Torque-coupling and particle–turbulence interactions. Journal of Fluid Mechanics, 696: 319-329. doi: 10.1017/jfm.2012.44 Andersson H I, Zhao L, Variano E A. 2015. On the anisotropic vorticity in turbulent channel flows. Journal of Fluids Engineering, 137: 084503-084503–3. Andersson H I, Jiang F. 2018. Forces and torques on a prolate spheroid: Low-Reynolds-number and attack angle effects. Acta Mechanica, 230: 431-447. Angot P, Bruneau C H, Fabrie P. 1999. A penalization method to take into account obstacles in incompressible viscous flows. Numerische Mathematik, 81: 497-520. doi: 10.1007/s002110050401 Ardekani M N, Costa P, Breugem W P, Brandt L. 2016. Numerical study of the sedimentation of spheroidal particles. International Journal of Multiphase Flow, 87: 16-34. doi: 10.1016/j.ijmultiphaseflow.2016.08.005 Ardekani M N, Costa P, Breugem W-P, Picano F, Brandt L. 2017b. Drag reduction in turbulent channel flow laden with finite-size oblate spheroids. Journal of Fluid Mechanics, 816: 43-70. doi: 10.1017/jfm.2017.68 Ardekani M N, Sardina G, Brandt L, Karp-Boss L, Bearon R N, Variano E A. 2017a. Sedimentation of inertia-less prolate spheroids in homogenous isotropic turbulence with application to non-motile phytoplankton. Journal of Fluid Mechanics, 831: 655-674. doi: 10.1017/jfm.2017.670 Bagchi P, Balachandar S. 2002. Effect of free rotation on the motion of a solid sphere in linear shear flow at moderate Re. Physics of Fluids, 14: 2719-2737. doi: 10.1063/1.1487378 Balachandar S, Eaton J K. 2010. Turbulent dispersed multiphase flow. Annual Review of Fluid Mechanics, 42: 111-133. doi: 10.1146/annurev.fluid.010908.165243 Balkovsky E, Fouxon A. 1999. Universal long-time properties of Lagrangian statistics in the Batchelor regime and their application to the passive scalar problem. Physical Review E, 60: 4164-4174. Batchelor G K. 1952. The effect of homogeneous turbulence on material lines and surfaces. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 213: 349-366. Batchelor G K. 1970. The stress system in a suspension of force-free particles. Journal of Fluid Mechanics, 41: 545-570. doi: 10.1017/S0022112070000745 Bec J, Homann H, Ray S S. 2014. Gravity-driven enhancement of heavy particle clustering in turbulent flow. Physical Review Letters, 112: 184501. doi: 10.1103/PhysRevLett.112.184501 Boivin M, Simonin O, Squires K D. 1998. Direct numerical simulation of turbulence modulation by particles in isotropic turbulence. Journal of Fluid Mechanics, 375: 235-263. doi: 10.1017/S0022112098002821 Bounoua S, Bouchet G, Verhille G. 2018. Tumbling of inertial fibers in turbulence. Physical Review Letters, 121: 124502. Brenner H, Cox R G. 1963a. The resistance to a particle of arbitrary shape in translational motion at small Reynolds numbers. Journal of Fluid Mechanics, 17: 561-595. doi: 10.1017/S002211206300152X Brenner H. 1961. The Oseen resistance of a particle of arbitrary shape. Journal of Fluid Mechanics, 11: 604-610. doi: 10.1017/S0022112061000755 Brenner H. 1963b. The Stokes resistance of an arbitrary particle. Chemical Engineering Science, 18: 1-25. doi: 10.1016/0009-2509(63)80001-9 Brenner H. 1974. Rheology of a dilute suspension of axisymmetric Brownian particles. International Journal of Multiphase Flow, 1: 195-341. doi: 10.1016/0301-9322(74)90018-4 Breugem W-P. 2012. A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. Journal of Computational Physics, 231: 4469-4498. doi: 10.1016/j.jcp.2012.02.026 Byron M, Einarsson J, Gustavsson K, Voth G, Mehlig B, Variano E. 2015. Shape-dependence of particle rotation in isotropic turbulence. Physics of Fluids, 27: 035101. doi: 10.1063/1.4913501 Candelier F, Mehlig B. 2016. Settling of an asymmetric dumbbell in a quiescent fluid. Journal of Fluid Mechanics, 802: 174-185. doi: 10.1017/jfm.2016.350 Challabotla N R, Nilsen C, Andersson H I. 2015a. On rotational dynamics of inertial disks in creeping shear flow. Physics Letters A, 379: 157-162. doi: 10.1016/j.physleta.2014.10.045 Challabotla N R, Zhao L, Andersson H I. 2015b. Shape effects on dynamics of inertia-free spheroids in wall turbulence. Physics of Fluids, 27: 061703. doi: 10.1063/1.4922864 Challabotla N R, Zhao L, Andersson H I. 2015c. Orientation and rotation of inertial disk particles in wall turbulence. Journal of Fluid Mechanics, 766. Challabotla N R, Zhao L, Andersson H I. 2016a. Orientation and rotation dynamics of triaxial ellipsoidal tracers in wall turbulence. Physics of Fluids, 28: 123304. doi: 10.1063/1.4971318 Challabotla N R, Zhao L, Andersson H I. 2016b. Gravity effects on fiber dynamics in wall turbulence. Flow, Turbulence and Combustion, 97: 1095-1110. doi: 10.1007/s10494-016-9742-5 Challabotla N R, Zhao L, Andersson H I. 2016c. On fiber behavior in turbulent vertical channel flow. Chemical Engineering Science, 153: 75-86. doi: 10.1016/j.ces.2016.07.002 Chen J, Jin G, Zhang J. 2016. Large eddy simulation of orientation and rotation of ellipsoidal particles in isotropic turbulent flows. Journal of Turbulence, 17: 308-326. doi: 10.1080/14685248.2015.1093638 Chen S, Doolen G D. 1998. Lattice Boltzmann method for fluid flows. Annual Review of Fluid Mechanics, 30: 329-364. doi: 10.1146/annurev.fluid.30.1.329 Cheung H, Ho M, Lau K, Cardona F, Hui D. 2009. Natural fibre-reinforced composites for bioengineering and environmental engineering applications. Composites Part B:Engineering, 40: 655-663. doi: 10.1016/j.compositesb.2009.04.014 Chevillard L, Meneveau C. 2013. Orientation dynamics of small, triaxial–ellipsoidal particles in isotropic turbulence. Journal of Fluid Mechanics, 737: 571-596. doi: 10.1017/jfm.2013.580 Chrust M, Bouchet G, Dusek J. 2013. Numerical simulation of the dynamics of freely falling discs. Physics of Fluids, 25: 044102. doi: 10.1063/1.4799179 Costa P, Boersma B J, Westerweel J, Breugem W-P. 2015. Collision model for fully resolved simulations of flows laden with finite-size particles. Physical Review E, 92: 053012. doi: 10.1103/PhysRevE.92.053012 Crowe C T, Sharma M P, Stock D E. 1977. The particle-source-in cell (PSI-CELL) model for gas-droplet flows. Journal of Fluids Engineering, 99: 325-332. doi: 10.1115/1.3448756 Cui Y, Ravnik J, Hriberšek M, Steinmann P. 2018. A novel model for the lift force acting on a prolate spheroidal particle in an arbitrary non-uniform flow. Part I. Lift force due to the streamwise flow shear. International Journal of Multiphase Flow, 104: 103-112. doi: 10.1016/j.ijmultiphaseflow.2018.03.007 Cui Y, Ravnik J, Hriberšek M, Steinmann P. 2020. Towards a unified shear-induced lift model for prolate spheroidal particles moving in arbitrary non-uniform flow. Computers & Fluids, 196: 104323. Cui Y, Ravnik J, Verhnjak O, Hriberšek M, Steinmann P. 2019. A novel model for the lift force acting on a prolate spheroidal particle in arbitrary non-uniform flow. Part II. Lift force taking into account the non-streamwise flow shear. International Journal of Multiphase Flow, 111: 232-240. doi: 10.1016/j.ijmultiphaseflow.2018.12.003 Cui Z, Dubey A, Zhao L, Mehlig B. 2020. Alignment statistics of rods with the Lagrangian stretching direction in a channel flow. Journal of Fluid Mechanics, 901: A16. doi: 10.1017/jfm.2020.547 Cui Z, Huang W-X, Xu C-X, Andersson H I, Zhao L. 2021. Alignment of slender fibers and thin disks induced by coherent structures of wall turbulence. International Journal of Multiphase Flow, 145: 103837. doi: 10.1016/j.ijmultiphaseflow.2021.103837 Cui Z, Zhao L, Huang W-X, Xu C-X. 2019. Stability analysis of rotational dynamics of ellipsoids in simple shear flow. Physics of Fluids, 31: 023301. doi: 10.1063/1.5080316 Cui Z, Zhao L. 2021. A method for long-time integration of Lyapunov exponent and vectors along fluid particle trajectories. Physics of Fluids, 33: 125107. doi: 10.1063/5.0071064 Dabade V, Marath N K, Subramanian G. 2015. Effects of inertia and viscoelasticity on sedimenting anisotropic particles. Journal of Fluid Mechanics, 778: 133-188. doi: 10.1017/jfm.2015.360 Dabade V, Marath N K, Subramanian G. 2016. The effect of inertia on the orientation dynamics of anisotropic particles in simple shear flow. Journal of Fluid Mechanics, 791: 631-703. doi: 10.1017/jfm.2016.14 Daitche A. 2015. On the role of the history force for inertial particles in turbulence. Journal of Fluid Mechanics, 782: 567-593. doi: 10.1017/jfm.2015.551 Den Toonder J M J, Hulsen M A, Kuiken G D C, Nieuwstadt F T M. 1997. Drag reduction by polymer additives in a turbulent pipe flow: numerical and laboratory experiments. Journal of Fluid Mechanics, 337: 193-231. doi: 10.1017/S0022112097004850 Derksen J J. 2011. Simulations of granular bed erosion due to laminar shear flow near the critical Shields number. Physics of Fluids, 23: 113303. doi: 10.1063/1.3660258 Do-Quang M, Amberg G, Brethouwer G, Johansson A V. 2014. Simulation of finite-size fibers in turbulent channel flows. Physical Review E, 89: 013006. doi: 10.1103/PhysRevE.89.013006 Einarsson J, Angilella J R, Mehlig B. 2014. Orientational dynamics of weakly inertial axisymmetric particles in steady viscous flows. Physica D: Nonlinear Phenomena, 278–279: 79–85. Einarsson J, Candelier F, Lundell F, Angilella J-R, Mehlig B. 2015. Rotation of a spheroid in a simple shear at small Reynolds number. Physics of Fluids, 27. Einarsson J, Mihiretie B M, Laas A, Ankardal S, Angilella J R, Hanstorp D, Mehlig B. 2016. Tumbling of asymmetric microrods in a microchannel flow. Physics of Fluids, 28: 013302. doi: 10.1063/1.4938239 Ern P, Risso F, Fabre D, Magnaudet J. 2012. Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annual Review of Fluid Mechanics, 44: 97-121. doi: 10.1146/annurev-fluid-120710-101250 Eshghinejadfard A, Abdelsamie A, Janiga G, Thevenin D. 2016. Direct-forcing immersed boundary lattice Boltzmann simulation of particle/fluid interactions for spherical and non-spherical particles. Particuology, 25: 93-103. doi: 10.1016/j.partic.2015.05.004 Eshghinejadfard A, Hosseini S A, Thévenin D. 2017. Fully-resolved prolate spheroids in turbulent channel flows: A lattice Boltzmann study. AIP Advances, 7: 095007. doi: 10.1063/1.5002528 Eshghinejadfard A, Hosseini S A, Thévenin D. 2019. Effect of particle density in turbulent channel flows with resolved oblate spheroids. Computers & Fluids, 184: 29-39. Eshghinejadfard A, Zhao L, Thévenin D. 2018. Lattice Boltzmann simulation of resolved oblate spheroids in wall turbulence. Journal of Fluid Mechanics, 849: 510-540. doi: 10.1017/jfm.2018.441 Fadlun E A, Verzicco R, Orlandi P, Mohd-Yusof J. 2000. Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. Journal of Computational Physics, 161: 35-60. doi: 10.1006/jcph.2000.6484 Fan F-G, Ahmadi G. 1995. A sublayer model for wall deposition of ellipsoidal particles in turbulent streams. Journal of Aerosol Science, 26: 813-840. doi: 10.1016/0021-8502(95)00021-4 Feng Y, Kleinstreuer C. American Institute of Physics, 2013. 2013. Analysis of non-spherical particle transport in complex internal shear flows. Physics of Fluids, 25: 091904. doi: 10.1063/1.4821812 Fries J, Einarsson J, Mehlig B. 2017. Angular dynamics of small crystals in viscous flow. Physical Review Fluids, 2: 014302. doi: 10.1103/PhysRevFluids.2.014302 Frohlich K, Meinke M, Schroeder W. 2020. Correlations for inclined prolates based on highly resolved simulations. Journal of Fluid Mechanics, 901: A5. doi: 10.1017/jfm.2020.482 Gillissen J J J, Boersma B J, Mortensen P H, Andersson H I. 2008. Fibre-induced drag reduction. Journal of Fluid Mechanics, 602: 209-218. doi: 10.1017/S0022112008000967 Girimaji S S, Pope S B. 1990. Material-element deformation in isotropic turbulence. Journal of Fluid Mechanics, 220: 427-458. doi: 10.1017/S0022112090003330 Glowinski R, Pan T W, Hesla T I, Joseph D D. 1999. A distributed Lagrange multiplier fictitious domain method for particulate flows. International Journal of Multiphase Flow, 25: 755-794. doi: 10.1016/S0301-9322(98)00048-2 Goldstein D, Handler R, Sirovich L. 1993. Modeling a no-slip flow boundary with an external force-field. Journal of Computational Physics, 105: 354-366. doi: 10.1006/jcph.1993.1081 Griffith B E, Patankar N A. 2020. Immersed methods for fluid-structure interaction. Annual Review of Fluid Mechanics, Vol 52, 52: 421-448. doi: 10.1146/annurev-fluid-010719-060228 Guala M, Lüthi B, Liberzon A, Tsinober A, Kinzelbach W. 2005. On the evolution of material lines and vorticity in homogeneous turbulence. Journal of Fluid Mechanics, 533: 339-359. Guazzelli E, Morris J F. 2011. A physical introduction to suspension dynamics. Cambridge University Press. Gustavsson K, Einarsson J, Mehlig B. 2014. Tumbling of small axisymmetric particles in random and turbulent flows. Physical Review Letters, 112. Gustavsson K, Jucha J, Naso A, Lévêque E, Pumir A, Mehlig B. 2017. Statistical model for the orientation of non-spherical particles settling in turbulence. Physical Review Letters, 119. Gustavsson K, Sheikh M Z, Lopez D, Naso A, Pumir A, Mehlig B. 2019. Effect of fluid inertia on the orientation of a small prolate spheroid settling in turbulence. New Journal of Physics, 21: 083008. doi: 10.1088/1367-2630/ab3062 Gyr A, Bewersdorff H-W. 1995. Drag reduction of turbulent flows by additives. Springer Netherlands. Haeri S, Shrimpton J S. 2012. On the application of immersed boundary, fictitious domain and body-conformal mesh methods to many particle multiphase flows. International Journal of Multiphase Flow, 40: 38-55. doi: 10.1016/j.ijmultiphaseflow.2011.12.002 Håkansson K M O, Fall A B, Lundell F, Yu S, Krywka C, Roth S V, Santoro G, Kvick M, Prahl Wittberg L, Wågberg L, Söderberg L D. 2014. Hydrodynamic alignment and assembly of nanofibrils resulting in strong cellulose filaments. Nature Communications, 5: 4018. doi: 10.1038/ncomms5018 Harper E Y, Chang I-D. 1968. Maximum dissipation resulting from lift in a slow viscous shear flow. Journal of Fluid Mechanics, 33: 209-225. doi: 10.1017/S0022112068001254 Heymsfield A J. 1977. Precipitation development in stratiform ice clouds: A microphysical and dynamical study. Journal of the Atmospheric Sciences, 34: 367-381. doi: 10.1175/1520-0469(1977)034<0367:PDISIC>2.0.CO;2 Hinch E J, Leal L G. 1979. Rotation of small non-axisymmetric particles in a simple shear flow. Journal of Fluid Mechanics, 92: 591. doi: 10.1017/S002211207900077X Hölzer A, Sommerfeld M. 2008. New simple correlation formula for the drag coefficient of non-spherical particles. Powder Technology, 184: 361-365. doi: 10.1016/j.powtec.2007.08.021 Huang H, Yang X, Krafczyk M, Lu X-Y. 2012. Rotation of spheroidal particles in Couette flows. Journal of Fluid Mechanics, 692: 369-394. doi: 10.1017/jfm.2011.519 Huang W-X, Chang C B, Sung H J. 2011. An improved penalty immersed boundary method for fluid-flexible body interaction. Journal of Computational Physics, 230: 5061-5079. doi: 10.1016/j.jcp.2011.03.027 Jain R, Tschisgale S, Froehlich J. 2019. A collision model for DNS with ellipsoidal particles in viscous fluid. International Journal of Multiphase Flow, 120: 103087. doi: 10.1016/j.ijmultiphaseflow.2019.103087 Jeffery G B. 1922. The motion of ellipsoidal particles in a viscous fluid. Proceedings of the Royal Society of London Series a-Containing Papers of a Mathematical and Physical Character, 102: 161-179. Jeffrey D J. 1982. Low-Reynolds-number flow between converging spheres. Mathematika, 29: 58-66. doi: 10.1112/S002557930001216X Jiang F, Zhao L, Andersson H I, Gustavsson K, Pumir A, Mehlig B. 2021. Inertial torque on a small spheroid in a stationary uniform flow. Physical Review Fluids, 6: 024302. doi: 10.1103/PhysRevFluids.6.024302 Jie Y, Xu C, Dawson J R, Andersson H I, Zhao L. 2019. Influence of the quiescent core on tracer spheroidal particle dynamics in turbulent channel flow. Journal of Turbulence: 1–15. Johnson P L, Hamilton S S, Burns R, Meneveau C. 2017. Analysis of geometrical and statistical features of Lagrangian stretching in turbulent channel flow using a database task-parallel particle tracking algorithm. Physical Review Fluids, 2: 014605. doi: 10.1103/PhysRevFluids.2.014605 Jucha J, Naso A, Lévêque E, Pumir A. 2018. Settling and collision between small ice crystals in turbulent flows. Physical Review Fluids, 3: 014604. doi: 10.1103/PhysRevFluids.3.014604 Kempe T, Froehlich J. 2012. Collision modelling for the interface-resolved simulation of spherical particles in viscous fluids. Journal of Fluid Mechanics, 709: 445-489. doi: 10.1017/jfm.2012.343 Khayat R E, Cox R G. 1989. Inertia effects on the motion of long slender bodies. Journal of Fluid Mechanics, 209: 435-462. doi: 10.1017/S0022112089003174 Kim W, Choi H. 2019. Immersed boundary methods for fluid-structure interaction: A review. International Journal of Heat and Fluid Flow, 75: 301-309. doi: 10.1016/j.ijheatfluidflow.2019.01.010 Ladd A J C. 1994a. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. Journal of Fluid Mechanics, 271: 285-309. doi: 10.1017/S0022112094001771 Ladd A J C. 1994b. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. Journal of Fluid Mechanics, 271: 311-339. doi: 10.1017/S0022112094001783 Lai M C, Peskin C S. 2000. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity. Journal of Computational Physics, 160: 705-719. doi: 10.1006/jcph.2000.6483 Lawrence C J, Weinbaum S. 1986. The force on an axisymmetric body in linearized, time-dependent motion: a new memory term. Journal of Fluid Mechanics, 171: 209. doi: 10.1017/S0022112086001428 Lawrence C J, Weinbaum S. 1988. The unsteady force on a body at low Reynolds number; the axisymmetric motion of a spheroid. Journal of Fluid Mechanics, 189: 463-489. doi: 10.1017/S0022112088001107 Lees A W, Edwards S F. 1972. The computer study of transport processes under extreme conditions. Journal of Physics Part C Solid State Physics, 5: 1921-1929. doi: 10.1088/0022-3719/5/15/006 Legendre D, Magnaudet J. 1998. The lift force on a spherical bubble in a viscous linear shear flow. Journal of Fluid Mechanics, 368: 81-126. doi: 10.1017/S0022112098001621 Li R-Y, Cui Z-W, Huang W-X, Zhao L-H, Xu C-X. 2019. On rotational dynamics of a finite-sized ellipsoidal particle in shear flows. Acta Mechanica, 239: 449-467. Lundell F, Carlsson A. 2010. Heavy ellipsoids in creeping shear flow: Transitions of the particle rotation rate and orbit shape. Physical Review E, 81: 016323. doi: 10.1103/PhysRevE.81.016323 Lundell F, Söderberg L D, Alfredsson P H. 2011a. Fluid mechanics of papermaking. Annual Review of Fluid Mechanics, 43: 195-217. doi: 10.1146/annurev-fluid-122109-160700 Lundell F. 2011b. The effect of particle inertia on triaxial ellipsoids in creeping shear: From drift toward chaos to a single periodic solution. Physics of Fluids, 23: 011704. doi: 10.1063/1.3548864 Magnaudet J, Takagi S, Legendre D. 2003. Drag, deformation and lateral migration of a buoyant drop moving near a wall. Journal of Fluid Mechanics, 476: 115-157. doi: 10.1017/S0022112002002902 Magnaudet J. 2003. Small inertial effects on a spherical bubble, drop or particle moving near a wall in a time-dependent linear flow. Journal of Fluid Mechanics, 485: 115-142. doi: 10.1017/S0022112003004464 Majumdar S, Iaccarino G, Durbin P. 2001. RANS solvers with adaptive structured boundary non-conforming grids. Annual Research Briefs, NASA Ames Research Center/Stanford University Center for Turbulence Research, Stanford, CA. 353-366 Mandø M, Roséndahl L. 2010. On the motion of non-spherical particles at high Reynolds number. Powder Technology, 202: 1-13. doi: 10.1016/j.powtec.2010.05.001 Mao W, Alexeev A. 2014. Motion of spheroid particles in shear flow with inertia. Journal of Fluid Mechanics, 749: 145-166. doi: 10.1017/jfm.2014.224 Marchioli C, Fantoni M, Soldati A. 2010. Orientation, distribution, and deposition of elongated, inertial fibers in turbulent channel flow. Physics of fluids, 22: 033301. doi: 10.1063/1.3328874 Marchioli C, Soldati A. 2013. Rotation statistics of fibers in wall shear turbulence. Acta Mechanica, 224: 2311-2329. doi: 10.1007/s00707-013-0933-z Marchioli C, Zhao L, Andersson H. 2016. On the relative rotational motion between rigid fibers and fluid in turbulent channel flow. Physics of Fluids, 28: 013301. doi: 10.1063/1.4937757 Marcus G G, Parsa S, Kramel S, Ni R, Voth G A. 2014. Measurements of the solid-body rotation of anisotropic particles in 3D turbulence. New Journal of Physics, 16: 102001. doi: 10.1088/1367-2630/16/10/102001 Maxey M R, Patel B K, Chang E J, Wang L-P. 1997. Simulations of dispersed turbulent multiphase flow. Fluid Dynamics Research, 20: 143-156. doi: 10.1016/S0169-5983(96)00042-1 Maxey M R, Riley J J. 1983. Equation of motion for a small rigid sphere in a nonuniform flow. The Physics of Fluids, 26: 883-889. doi: 10.1063/1.864230 Maxey M R. 1987. The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. Journal of Fluid Mechanics, 174: 441-465. doi: 10.1017/S0022112087000193 Maxey M. 2017. Simulation methods for particulate flows and concentrated suspensions. Annual Review of Fluid Mechanics, 49: 171-193. doi: 10.1146/annurev-fluid-122414-034408 McLaughlin J B. 1991. Inertial migration of a small sphere in linear shear flows. Journal of Fluid Mechanics, 224: 261-274. doi: 10.1017/S0022112091001751 Meibohm J, Candelier F, Rosén T, Einarsson J, Lundell F, Mehlig B. 2016. Angular velocity of a spheroid log rolling in a simple shear at small Reynolds number. Physical Review Fluids, 1: 084203. doi: 10.1103/PhysRevFluids.1.084203 Michel A, Arcen B. 2021a. Long time statistics of prolate spheroids dynamics in a turbulent channel flow. International Journal of Multiphase Flow, 135: 103525. doi: 10.1016/j.ijmultiphaseflow.2020.103525 Michel A, Arcen B. 2021b. Reynolds number effect on the concentration and preferential orientation of inertial ellipsoids. Physical Review Fluids, 6: 114305. doi: 10.1103/PhysRevFluids.6.114305 Milici B, De Marchis M, Sardina G, Napoli E. 2014. Effects of roughness on particle dynamics in turbulent channel flows: a DNS analysis. Journal of Fluid Mechanics, 739: 465-478. doi: 10.1017/jfm.2013.633 Mittal R, Iaccarino G. 2005. Immersed boundary methods. Annual Review of Fluid Mechanics, 37: 239-261. doi: 10.1146/annurev.fluid.37.061903.175743 Moosaie A, Manhart M. 2013. Direct Monte Carlo simulation of turbulent drag reduction by rigid fibers in a channel flow. Acta Mechanica, 224: 2385-2413. doi: 10.1007/s00707-013-0919-x Moriche M, Uhlmann M, Dusek J. 2021. A single oblate spheroid settling in unbounded ambient fluid: A benchmark for simulations in steady and unsteady wake regimes. International Journal of Multiphase Flow, 136: 103519. doi: 10.1016/j.ijmultiphaseflow.2020.103519 Mortensen P H, Andersson H I, Gillissen J J J, Boersma B J. 2008a. Dynamics of prolate ellipsoidal particles in a turbulent channel flow. Physics of Fluids, 20: 093302. doi: 10.1063/1.2975209 Mortensen P H, Andersson H I, Gillissen J J J, Boersma B J. 2008b. On the orientation of ellipsoidal particles in a turbulent shear flow. International Journal of Multiphase Flow, 34: 678-683. doi: 10.1016/j.ijmultiphaseflow.2007.12.007 Ni R, Ouellette N T, Voth G A. 2014. Alignment of vorticity and rods with Lagrangian fluid stretching in turbulence. Journal of Fluid Mechanics, 743. Nilsen C, Andersson H I. 2013. Chaotic rotation of inertial spheroids in oscillating shear flow. Physics of Fluids, 25: 013303. doi: 10.1063/1.4789376 Olivieri S, Picano F, Sardina G, Iudicone D, Brandt L. 2014. The effect of the Basset history force on particle clustering in homogeneous and isotropic turbulence. Physics of Fluids, 26: 041704. doi: 10.1063/1.4871480 Ouchene R, Khalij M, Arcen B, Taniere A. 2016. A new set of correlations of drag, lift and torque coefficients for non-spherical particles and large Reynolds numbers. Powder Technology, 303: 33-43. doi: 10.1016/j.powtec.2016.07.067 Ouchene R, Khalij M, Tanière A, Arcen B. 2015. Drag, lift and torque coefficients for ellipsoidal particles: From low to moderate particle Reynolds numbers. Computers & Fluids, 113: 53-64. Parsa S, Calzavarini E, Toschi F, Voth G A. 2012. Rotation rate of rods in turbulent fluid flow. Physical Review Letters, 109. Parsa S, Guasto J S, Kishore M, Ouellette N T, Gollub J P, Voth G A. 2011. Rotation and alignment of rods in two-dimensional chaotic flow. Physics of Fluids, 23: 043302. doi: 10.1063/1.3570526 Paschkewitz J S, Dimitropoulos C D, Hou Y X, Somandepalli V S R, Mungal M G, Shaqfeh E S G, Moin P. 2005. An experimental and numerical investigation of drag reduction in a turbulent boundary layer using a rigid rodlike polymer. Physics of Fluids, 17: 085101. doi: 10.1063/1.1993307 Paschkewitz J S, Dubief Y, Dimitropoulos C D, Shaqfeh E S G, Moin P. 2004. Numerical simulation of turbulent drag reduction using rigid fibres. Journal of Fluid Mechanics, 518: 281-317. doi: 10.1017/S0022112004001144 Paschkewitz J S, Dubief Y, Shaqfeh E S G. 2005. The dynamic mechanism for turbulent drag reduction using rigid fibers based on Lagrangian conditional statistics. Physics of Fluids, 17: 063102. doi: 10.1063/1.1925447 Pedley T J, Kessler J O. 1992. Hydrodynamic phenomena in suspensions of swimming microorganisms. Annual Review of Fluid Mechanics, 24: 313-358. doi: 10.1146/annurev.fl.24.010192.001525 Peng C, Teng Y, Hwang B, Guo Z, Wang L-P. 2016. Implementation issues and benchmarking of lattice Boltzmann method for moving rigid particle simulations in a viscous flow. Computers & Mathematics with Applications, 72: 349-374. Peskin C S. 1972. Flow patterns around heart valves: A numerical method. Journal of Computational Physics, 10: 252-271. Peskin C S. 1977. Numerical analysis of blood flow in heart. Journal of Computational Physics, 25: 220-252. doi: 10.1016/0021-9991(77)90100-0 Peskin C S. 2002. The immersed boundary method. Acta Numerica, 11: 479-517. doi: 10.1017/S0962492902000077 Prasath S G, Vasan V, Govindarajan R. 2019. Accurate solution method for the Maxey–Riley equation, and the effects of Basset history. Journal of Fluid Mechanics, 868: 428-460. doi: 10.1017/jfm.2019.194 Pujara N, Arguedas-Leiva J-A, Lalescu C C, Bramas B, Wilczek M. 2021. Shape- and scale-dependent coupling between spheroids and velocity gradients in turbulence. Journal of Fluid Mechanics, 922: R6. Pujara N, Variano E A. 2017. Rotations of small, inertialess triaxial ellipsoids in isotropic turbulence. Journal of Fluid Mechanics, 821: 517-538. doi: 10.1017/jfm.2017.256 Pujara N, Voth G A, Variano E A. 2019. Scale-dependent alignment, tumbling and stretching of slender rods in isotropic turbulence. Journal of Fluid Mechanics, 860: 465-486. doi: 10.1017/jfm.2018.866 Pumir A, Wilkinson M. 2011. Orientation statistics of small particles in turbulence. New Journal of Physics, 13: 093030. doi: 10.1088/1367-2630/13/9/093030 Qi D, Luo L. 2002. Transitions in rotations of a nonspherical particle in a three-dimensional moderate Reynolds number Couette flow. Physics of Fluids, 14: 4440-4443. doi: 10.1063/1.1517053 Qi D, Luo L S. 2003. Rotational and orientational behaviour of three-dimensional spheroidal particles in Couette flows. Journal of Fluid Mechanics, 477: 201-213. Qiu J, Marchioli C, Andersson H I, Zhao L. 2019. Settling tracer spheroids in vertical turbulent channel flows. International Journal of Multiphase Flow, 118: 173-182. doi: 10.1016/j.ijmultiphaseflow.2019.06.012 Radin I, Zakin J L, Patterson G K. 1975. Drag reduction in solid-fluid systems. AIChE Journal, 21: 358-371. doi: 10.1002/aic.690210218 Reddy G V, Singh R P. 1985. Drag reduction effectiveness and shear stability of polymer-polymer and polymer-fibre mixtures in recirculatory turbulent flow of water. Rheologica Acta, 24: 296-311. doi: 10.1007/BF01332609 Rosén T, Do-Quang M, Aidun C K, Lundell F. 2015a. The dynamical states of a prolate spheroidal particle suspended in shear flow as a consequence of particle and fluid inertia. Journal of Fluid Mechanics, 771: 115-158. doi: 10.1017/jfm.2015.127 Rosén T, Einarsson J, Nordmark A, Aidun C K, Lundell F, Mehlig B. 2015b. Numerical analysis of the angular motion of a neutrally buoyant spheroid in shear flow at small Reynolds numbers. Physical Review E, 92: 063022. Rosén T, Kotsubo Y, Aidun C K, Do-Quang M, Lundell F. 2017b. Orientational dynamics of a triaxial ellipsoid in simple shear flow: Influence of inertia. Physical Review E, 96: 013109. Rosén T, Lundell F, Aidun C K. 2014. Effect of fluid inertia on the dynamics and scaling of neutrally buoyant particles in shear flow. Journal of Fluid Mechanics, 738: 563-590. doi: 10.1017/jfm.2013.599 Rosén T, Nordmark A, Aidun C K, Do-Quang M, Lundell F. 2016. Quantitative analysis of the angular dynamics of a single spheroid in simple shear flow at moderate Reynolds numbers. Physical Review Fluids, 1: 044201. doi: 10.1103/PhysRevFluids.1.044201 Rosén T. 2017a. Chaotic rotation of a spheroidal particle in simple shear flow. Chaos:An Interdisciplinary Journal of Nonlinear Science, 27: 063112. doi: 10.1063/1.4985640 Roy A, Gupta A, Ray S S. 2018. Inertial spheroids in homogeneous, isotropic turbulence. Physical Review E, 98: 021101. doi: 10.1103/PhysRevE.98.021101 Saffman P G. 1965. The lift on a small sphere in a slow shear flow. Journal of Fluid Mechanics, 22: 385-400. doi: 10.1017/S0022112065000824 Saffman P G. 1968. The lift on a small sphere in a slow shear flow Corrigendum. Journal of Fluid Mechanics, 31: 624-624. doi: 10.1017/S0022112068999990 Saintillan D. 2018. Rheology of active fluids. Annual Review of Fluid Mechanics, 50: 563-592. doi: 10.1146/annurev-fluid-010816-060049 Sanjeevi S K P, Kuipers J A M, Padding J T. 2018. Drag, lift and torque correlations for non-spherical particles from Stokes limit to high Reynolds numbers. International Journal of Multiphase Flow, 106: 325-337. doi: 10.1016/j.ijmultiphaseflow.2018.05.011 Sardina G, Schlatter P, Brandt L, Picano F, Casciola C M. 2012. Wall accumulation and spatial localization in particle-laden wall flows. Journal of Fluid Mechanics, 699: 50-78. doi: 10.1017/jfm.2012.65 Schneiders L, Fröhlich K, Meinke M, Schröder W. 2019. The decay of isotropic turbulence carrying non-spherical finite-size particles. Journal of Fluid Mechanics, 875: 520-542. doi: 10.1017/jfm.2019.516 Schneiders L, Meinke M, Schröder W. 2017. On the accuracy of Lagrangian point-mass models for heavy non-spherical particles in isotropic turbulence. Fuel, 201: 2-14. doi: 10.1016/j.fuel.2016.11.096 Shapiro M, Goldenberg M. 1993. Deposition of glass fiber particles from turbulent air flow in a pipe. Journal of Aerosol Science, 24: 65-87. doi: 10.1016/0021-8502(93)90085-N Sheikh M Z, Gustavsson K, Lopez D, Lévêque E, Mehlig B, Pumir A, Naso A. 2020. Importance of fluid inertia for the orientation of spheroids settling in turbulent flow. Journal of Fluid Mechanics, 886: A9. Shin M, Koch D L. 2005. Rotational and translational dispersion of fibres in isotropic turbulent flows. Journal of Fluid Mechanics, 540: 143-173. doi: 10.1017/S0022112005005690 Siewert C, Kunnen R P J, Meinke M, Schröder W. 2014. Orientation statistics and settling velocity of ellipsoids in decaying turbulence. Atmospheric Research, 142: 45-56. doi: 10.1016/j.atmosres.2013.08.011 Siewert C, Kunnen R P J, Schröder W. 2014. Collision rates of small ellipsoids settling in turbulence. Journal of Fluid Mechanics, 758: 686-701. doi: 10.1017/jfm.2014.554 Soutis C. 2005. Fibre reinforced composites in aircraft construction. Progress in Aerospace Sciences, 41: 143-151. doi: 10.1016/j.paerosci.2005.02.004 Taira K, Colonius T. 2007. The immersed boundary method: A projection approach. Journal of Computational Physics, 225: 2118-2137. doi: 10.1016/j.jcp.2007.03.005 Taylor G I. 1923. The motion of ellipsoidal particles in a viscous fluid. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 103: 58-61. Tenneti S, Subramaniam S. 2014. Particle-resolved direct numerical simulation for gas-solid flow model development. Annual Review of Fluid Mechanics, 46: 199-230. doi: 10.1146/annurev-fluid-010313-141344 Udaykumar H S, Shyy W, Rao M M. 1996. ELAFINT: A mixed Eulerian-Lagrangian method for fluid flows with complex and moving boundaries. International Journal for Numerical Methods in Fluids, 22: 691-712. doi: 10.1002/(SICI)1097-0363(19960430)22:8<691::AID-FLD371>3.0.CO;2-U Uhlmann M. 2005. An immersed boundary method with direct forcing for the simulation of particulate flows. Journal of Computational Physics, 209: 448-476. doi: 10.1016/j.jcp.2005.03.017 Voth G A, Soldati A. 2017. Anisotropic particles in turbulence. Annual Review of Fluid Mechanics, 49: 249-76. doi: 10.1146/annurev-fluid-010816-060135 Vreman A W. 2015. Turbulence attenuation in particle-laden flow in smooth and rough channels. Journal of Fluid Mechanics, 773: 103-136. doi: 10.1017/jfm.2015.208 Wang L-P, Maxey M R. 1993. Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. Journal of Fluid Mechanics, 256: 27-68. doi: 10.1017/S0022112093002708 Wang Z, Xu C-X, Zhao L. 2021. Turbulence modulations and drag reduction by inertialess spheroids in turbulent channel flow. Physics of Fluids, 33: 123313. doi: 10.1063/5.0074857 Wang Z, Zhao L. 2020. The particle stress in dilute suspensions of inertialess spheroids in turbulent channel flow. Physics of Fluids, 32: 013302. doi: 10.1063/1.5139028 Xia Y, Xiong H, Yu Z, Zhu C. 2020. Effects of the collision model in interface-resolved simulations of particle-laden turbulent channel flows. Physics of Fluids, 32: 103303. doi: 10.1063/5.0020995 Xu H, Pumir A, Bodenschatz E. 2011. The pirouette effect in turbulent flows. Nature Physics, 7: 709-712. doi: 10.1038/nphys2010 Yang K, Zhao L, Andersson H I. 2018. Particle segregation in turbulent Couette–Poiseuille flow with vanishing wall shear. International Journal of Multiphase Flow, 98: 45-55. doi: 10.1016/j.ijmultiphaseflow.2017.09.001 Yarin A L, Gottlieb O, Roisman I V. 1997. Chaotic rotation of triaxial ellipsoids in simple shear flow. Journal of Fluid Mechanics, 340: 83-100. doi: 10.1017/S0022112097005260 Yin C, Roséndahl L, Knudsen Kær S, Sørensen H. 2003. Modelling the motion of cylindrical particles in a nonuniform flow. Chemical Engineering Science, 58: 3489-3498. doi: 10.1016/S0009-2509(03)00214-8 Yu Z, Phan-Thien N, Tanner R I. 2007a. Rotation of a spheroid in a Couette flow at moderate Reynolds numbers. Physical Review E, 76: 026310. Yu Z, Shao X. 2007b. A direct-forcing fictitious domain method for particulate flows. Journal of Computational Physics, 227: 292-314. doi: 10.1016/j.jcp.2007.07.027 Yu Z, Shao X. 2010. Direct numerical simulation of particulate flows with a fictitious domain method. International Journal of Multiphase Flow, 36: 127-134. doi: 10.1016/j.ijmultiphaseflow.2009.10.001 Yuan W, Andersson H I, Zhao L, Challabotla N R, Deng J. 2017. Dynamics of disk-like particles in turbulent vertical channel flow. International Journal of Multiphase Flow, 96: 86-100. doi: 10.1016/j.ijmultiphaseflow.2017.06.008 Yuan W, Zhao L, Andersson H I, Deng J. 2018. Three-dimensional Voronoï analysis of preferential concentration of spheroidal particles in wall turbulence. Physics of Fluids, 30: 063304. doi: 10.1063/1.5031117 Zastawny M, Mallouppas G, Zhao F, van Wachem B. 2012. Derivation of drag and lift force and torque coefficients for non-spherical particles in flows. International Journal of Multiphase Flow, 39: 227-239. doi: 10.1016/j.ijmultiphaseflow.2011.09.004 Zhang H, Ahmadi G, Fan F-G, McLaughlin J B. 2001. Ellipsoidal particles transport and deposition in turbulent channel flows. International Journal of Multiphase Flow, 27: 971-1009. doi: 10.1016/S0301-9322(00)00064-1 Zhao L, Challabotla N R, Andersson H I, Variano E A. 2015. Rotation of nonspherical particles in turbulent channel flow. Physical review letters, 115: 244501. doi: 10.1103/PhysRevLett.115.244501 Zhao L, Challabotla N R, Andersson H I, Variano E A. 2019a. Mapping spheroid rotation modes in turbulent channel flow: effects of shear, turbulence and particle inertia. Journal of Fluid Mechanics, 876: 19-54. doi: 10.1017/jfm.2019.521 Zhao L, Gustavsson K, Ni R, Kramel S, Voth G A, Andersson H I, Mehlig B. 2019b. Passive directors in turbulence. Physical Review Fluids, 4: 054602. doi: 10.1103/PhysRevFluids.4.054602 Zhong W Q, Yu A B, Liu X J, Tong Z B, Zhang H. 2016. DEM/CFD-DEM modelling of non-spherical particulate systems: Theoretical developments and applications. Powder Technology, 302: 108-152. doi: 10.1016/j.powtec.2016.07.010 Zhu C, Yu Z, Pan D, Shao X. 2020. Interface-resolved direct numerical simulations of the interactions between spheroidal particles and upward vertical turbulent channel flows. Journal of Fluid Mechanics, 891: A6. Zhu C, Yu Z, Shao X. 2018. Interface-resolved direct numerical simulations of the interactions between neutrally buoyant spheroidal particles and turbulent channel flows. Physics of Fluids, 30: 115103. doi: 10.1063/1.5051592 -







 下载:
下载: