Neurological disease and cognitive dynamics (I): Dynamics and control of epileptic seizures
-
摘要: 研究表明癫痫发作过程与神经系统本身的非线性动力学行为密切相关. 因此, 开展癫痫发作的非线性网络动力学建模与调控问题的研究, 有助于理解癫痫临床表征的动力学机理和定位致痫灶网络, 进而设计有效的网络调控策略. 本文回顾了癫痫脑神经疾病网络动力学与控制方面的研究进展, 系统总结了本文作者近年来在癫痫发作动力学建模分析及其调控等方面取得的研究成果. 首先, 基于海马齿状回CA3区环路神经元网络模型, 分析了影响颞叶癫痫发作的分子和网络结构因素, 阐释了癫痫发作转迁的动力学机制. 其次, 由于脑神经系统的集群编码特性, 基于神经场模型和平均场模型建模方法完善了皮质−基底节−丘脑环路网络动力学理论框架, 并基于此框架分析了失神癫痫发作转迁的动力学分岔机制, 探讨了不同类型癫痫发作的转迁路径, 发现了失神癫痫发作转迁的多稳态共存现象, 揭示了时滞对失神癫痫同步发作的控制效果, 设计了丰富有效的癫痫深脑刺激调控策略, 给出了电刺激调控失神癫痫发作的动力学解释. 最后, 通过数据驱动的统计建模和神经元群模型动力学建模分析, 提出了局灶癫痫致痫灶定位及寻找有效控制癫痫发作网络关键节点的理论新方法. 这些研究成果为理解难治性癫痫发作动力学本质及在临床诊疗的应用方面提供重要理论支撑. 最后对进一步研究给出若干建议.Abstract: Studies have shown that the process of epileptic seizures is closely related to the nonlinear dynamics of the nervous system itself. Therefore, the study of nonlinear network dynamics modeling and regulation of epileptic seizures is helpful in understanding the dynamic mechanism of clinical manifestations of epilepsy, locating the epileptic foci network, and then designing effective network regulation strategies. This article reviews the research progress in network dynamics and control of epileptic neurological diseases and systematically summarizes our research results in recent years in the modeling and analysis of epileptic seizure dynamics and their regulation. Firstly, based on the neuron network model of the hippocampal dentate gyrus-CA3 loop, the molecular and network structural factors that affect temporal lobe seizures were analyzed, and the dynamic mechanism of seizure transition was explained. Secondly, due to the cluster coding characteristics of the brain nervous system, based on the methods of both the neural field model and mean field model, the network dynamics framework of the basal ganglia-thalamocortical (BGCT) circuit was improved. Based on this framework, the dynamic bifurcation mechanism of absence epileptic seizure transition was analyzed, the transition path of different types of seizures was explored, and the multi-stable coexistence phenomenon of absence seizure transition was discovered. The effect of time delay on the synchronization seizures was also revealed. We also designed rich and effective deep brain stimulation (DBS) control strategies for epilepsy and gave a dynamic explanation of electrical stimulation to control absence epileptic seizures. Finally, based on the data-driven statistical modeling and the dynamics analysis of the neuronal population model, new theoretical methods for the foci localization of focal epileptics and finding the key network nodes for effectively controlling seizures were proposed. These results provide important theoretical support for understanding the dynamic nature of refractory seizures and their application in clinical diagnosis and treatment. Lastly, some suggestions are given for further research.
-
Key words:
- epileptic seizure dynamics /
- mean field model /
- delay /
- synchronization /
- neurofeedback and modulation
-
图 1 DG-CA3网络模型连接示意图. (a)反向投射位置从CA3区锥体神经元到DG区苔藓纤维细胞的胞体, (b)反向投射位置从CA3区锥体神经元到DG区中间神经元 (Zhang et al. 2017)
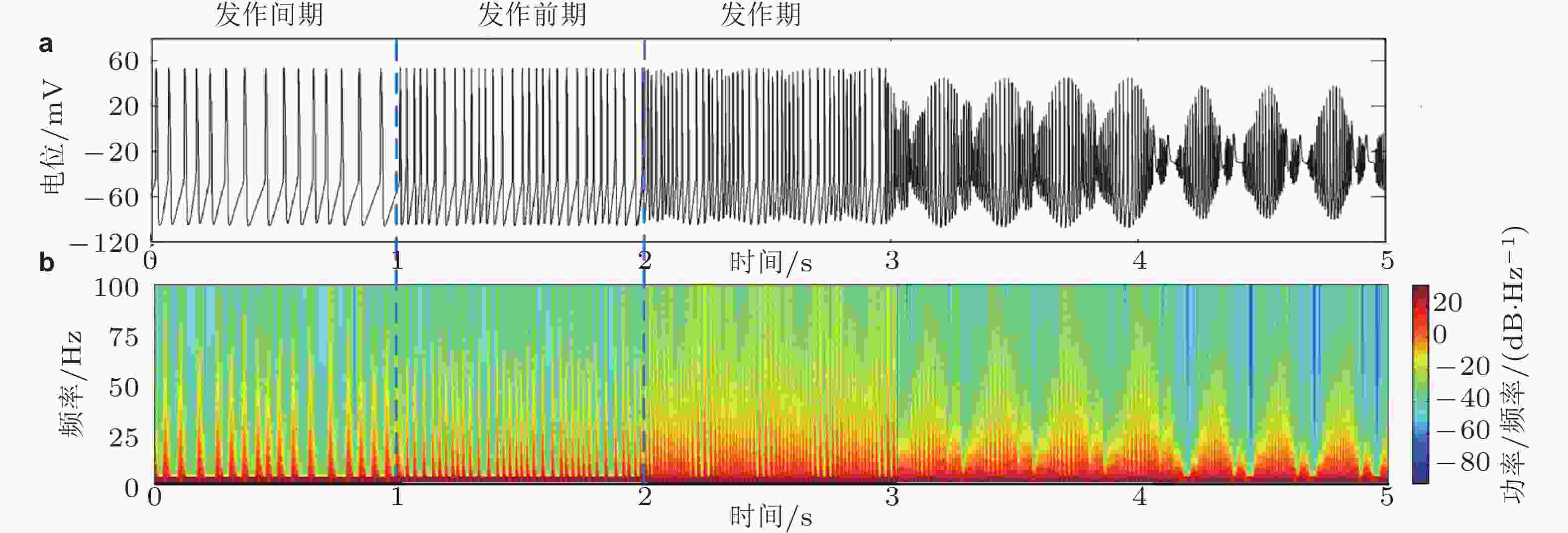
图 2 (a)锥体神经元的放电时序图, (b)随时间变化的能量谱图 (Zhang et al. 2017)
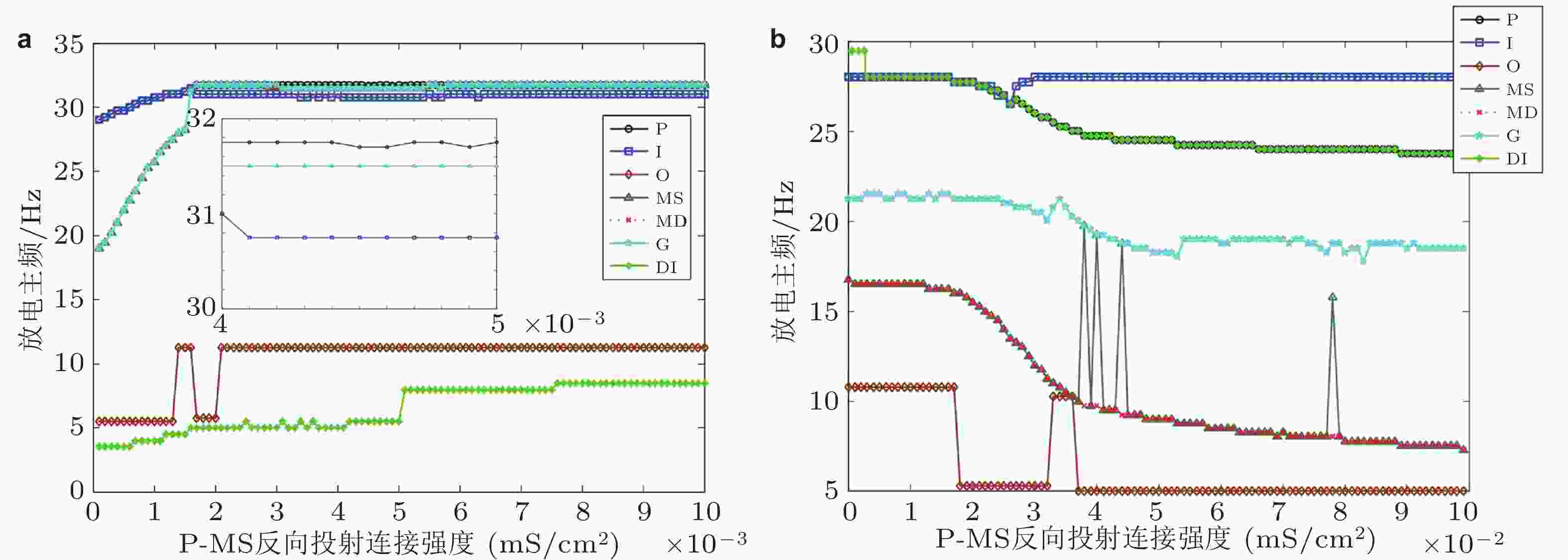
图 3 DG-CA3区神经元放电主频随反向投射强度变化示意图. (a)反向投射位置从P到MS, (b)反向投射位置从P到DI (Zhang et al. 2017)
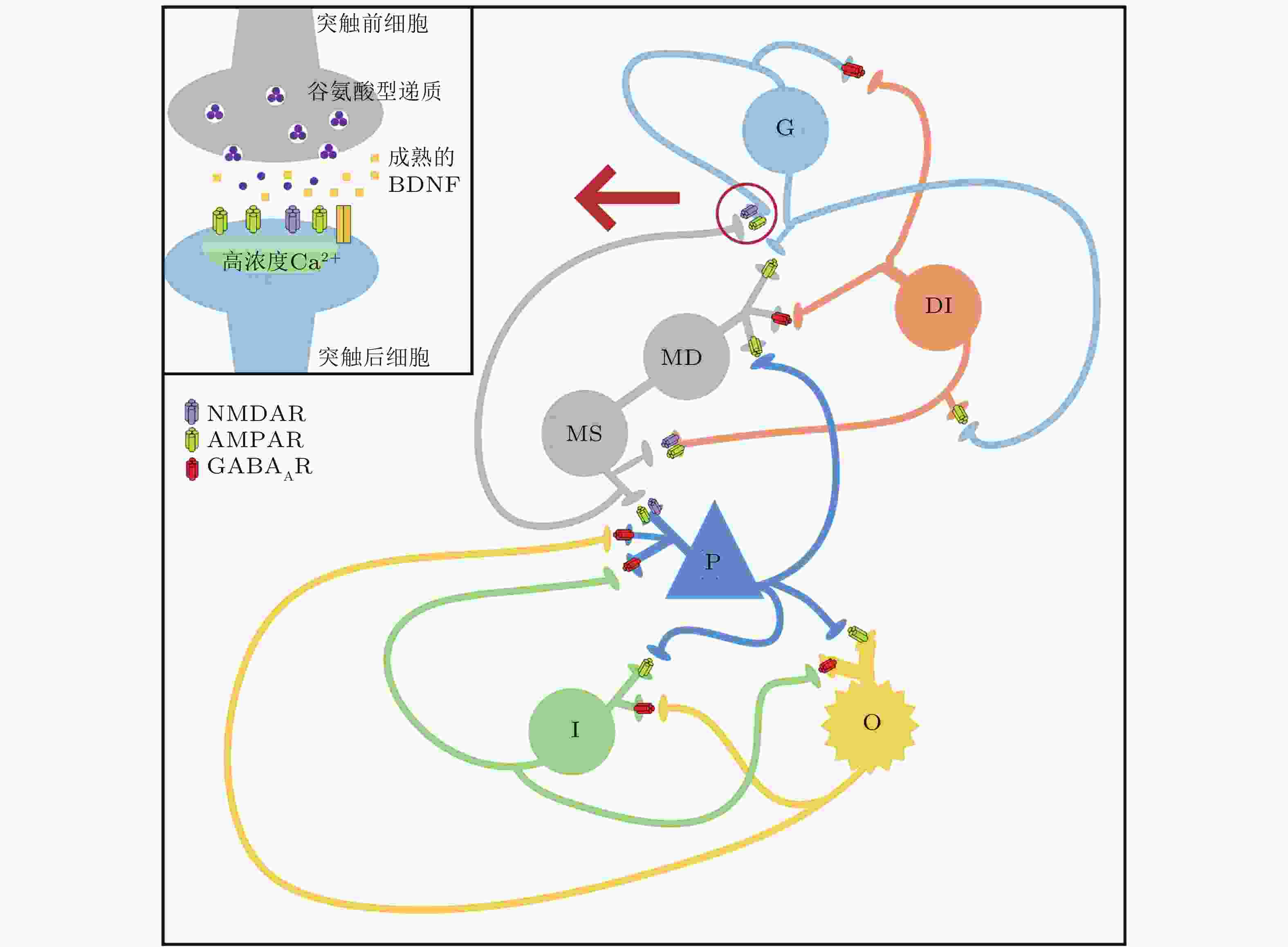
图 4 改进型DG-CA3网络模型结构图 (Zhang et al. 2018a)
图 5 网络平均膜电位在BDNF和神经噪声联合作用下的转迁情况. (a)噪声强度为2 μA/cm2, (b)噪声强度为8 μA/cm2 (Zhang et al. 2018a)
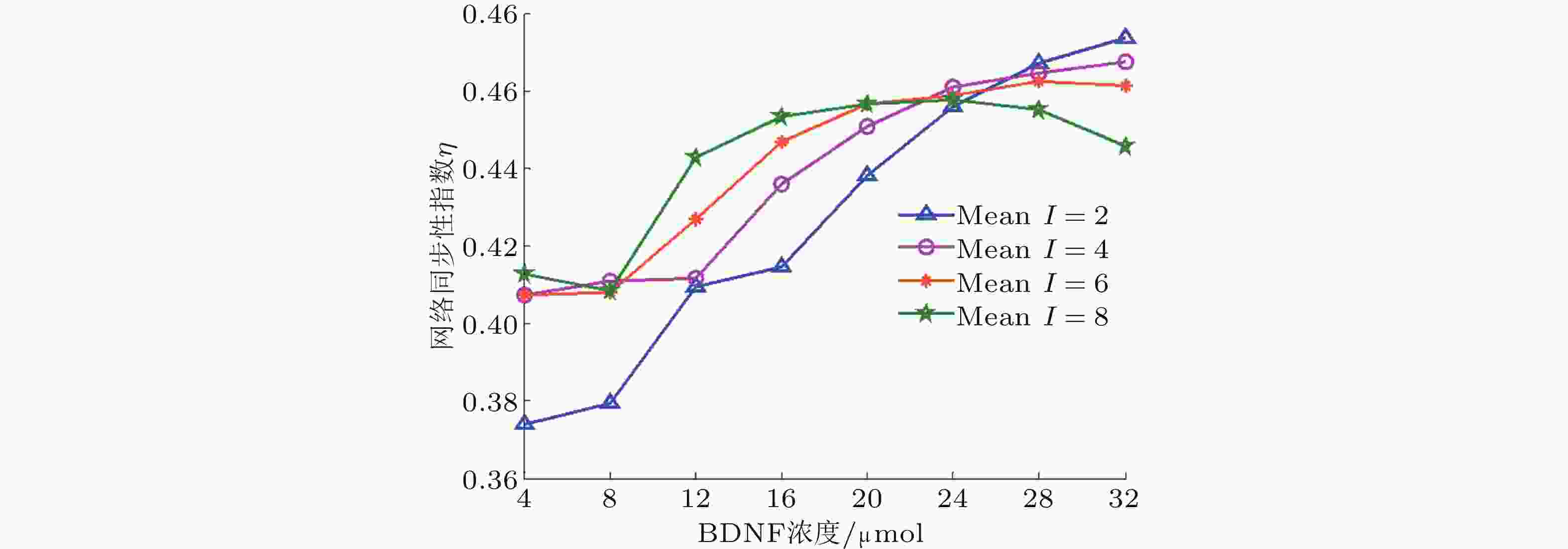
图 6 在固定噪声强度下, 网络同步性指数随BDNF浓度变化的演化图 (Zhang et al. 2018a)
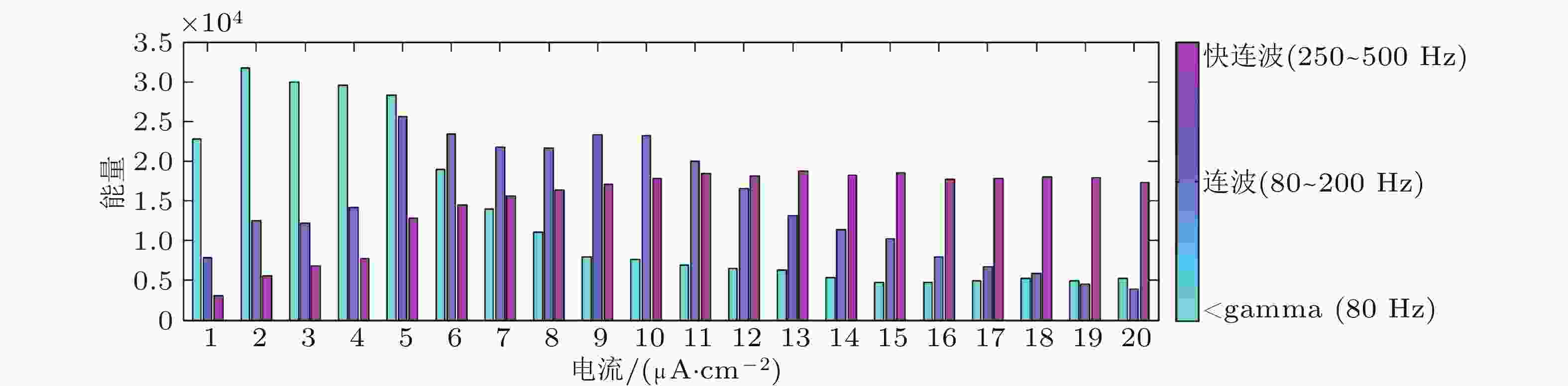
图 7 节点随外部刺激变化的频带能量直方图 (Zhang et al. 2018b)
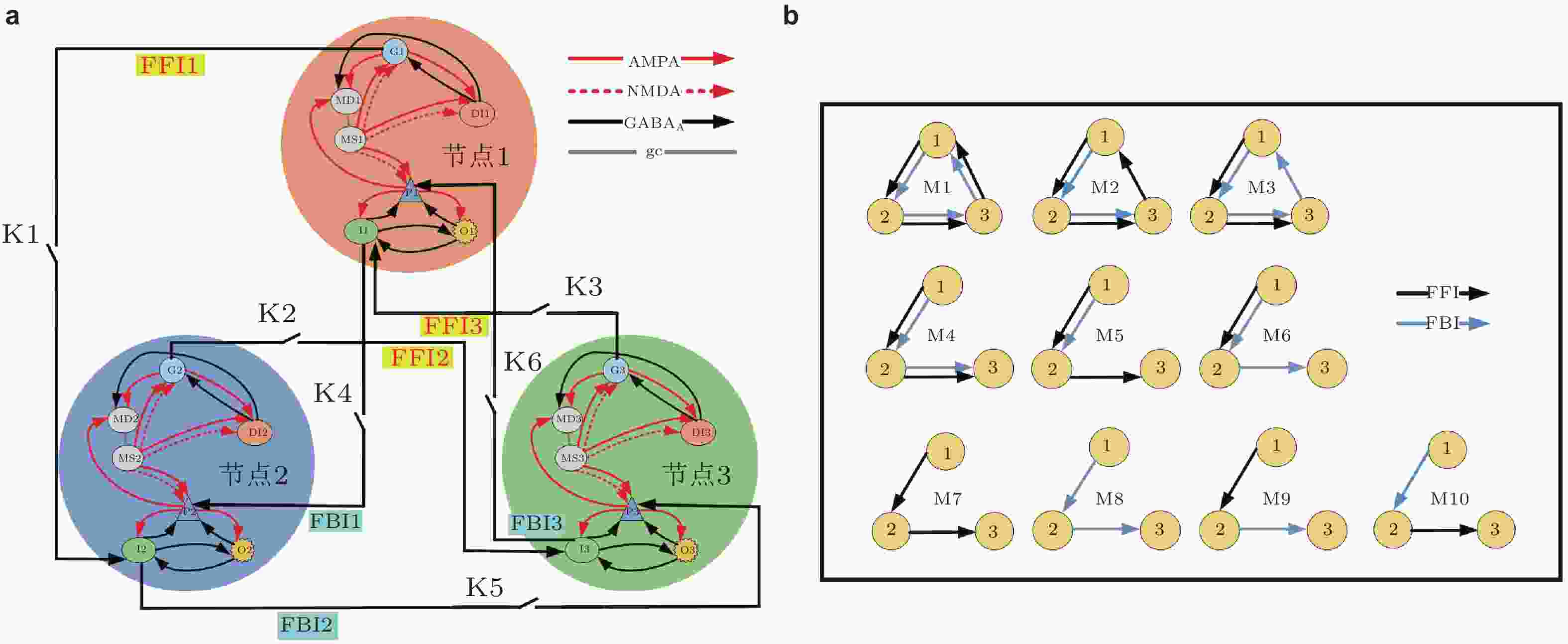
图 8 (a)基于DG-CA3系统模体结构的详细原理图, (b)是基于(a)得出10种可能的连接结构示意图 (Zhang et al. 2018b)
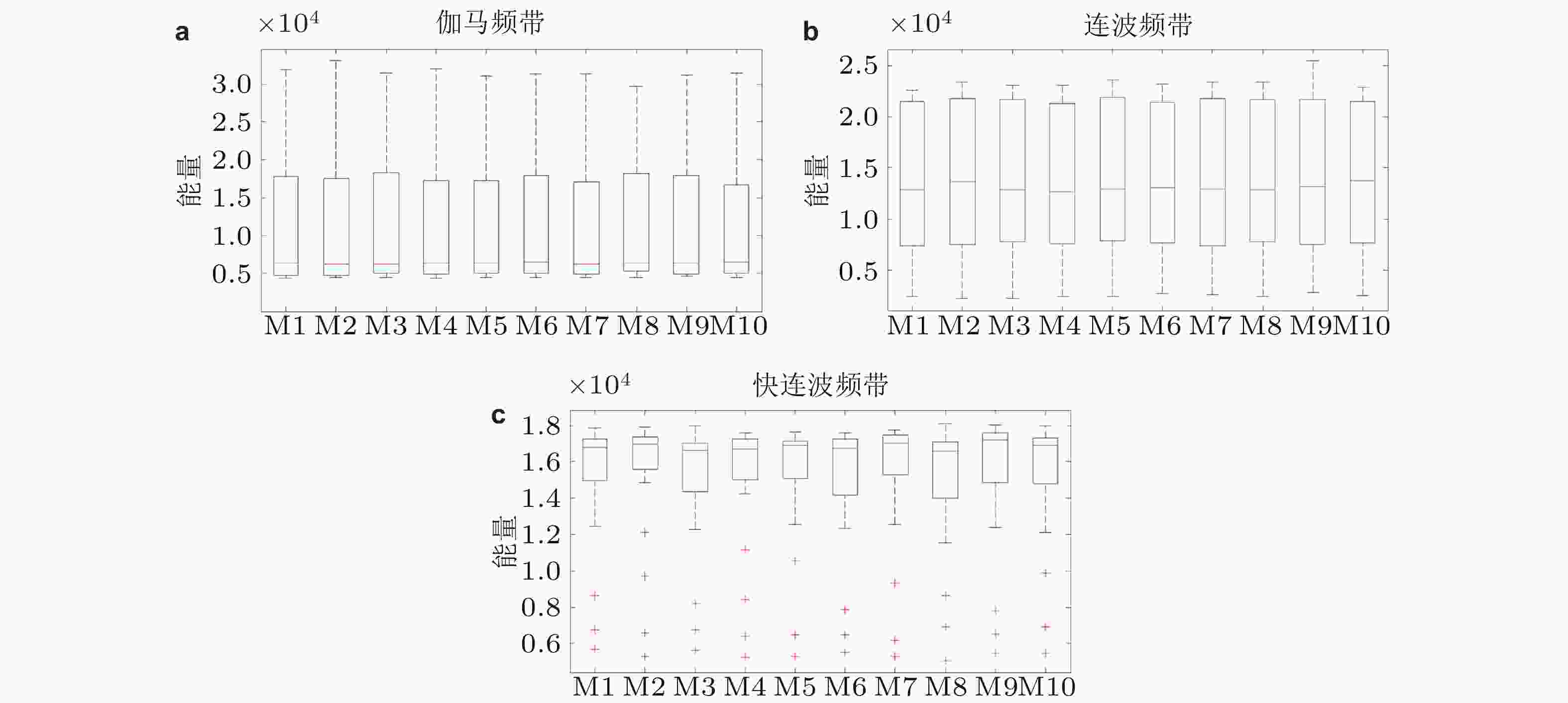
图 9 HFOs对于模体连接结构和外部刺激响应的箱状图. (a)为γ频带, (b)为连波频带, (c)为快连波频带 (Zhang et al. 2018b)
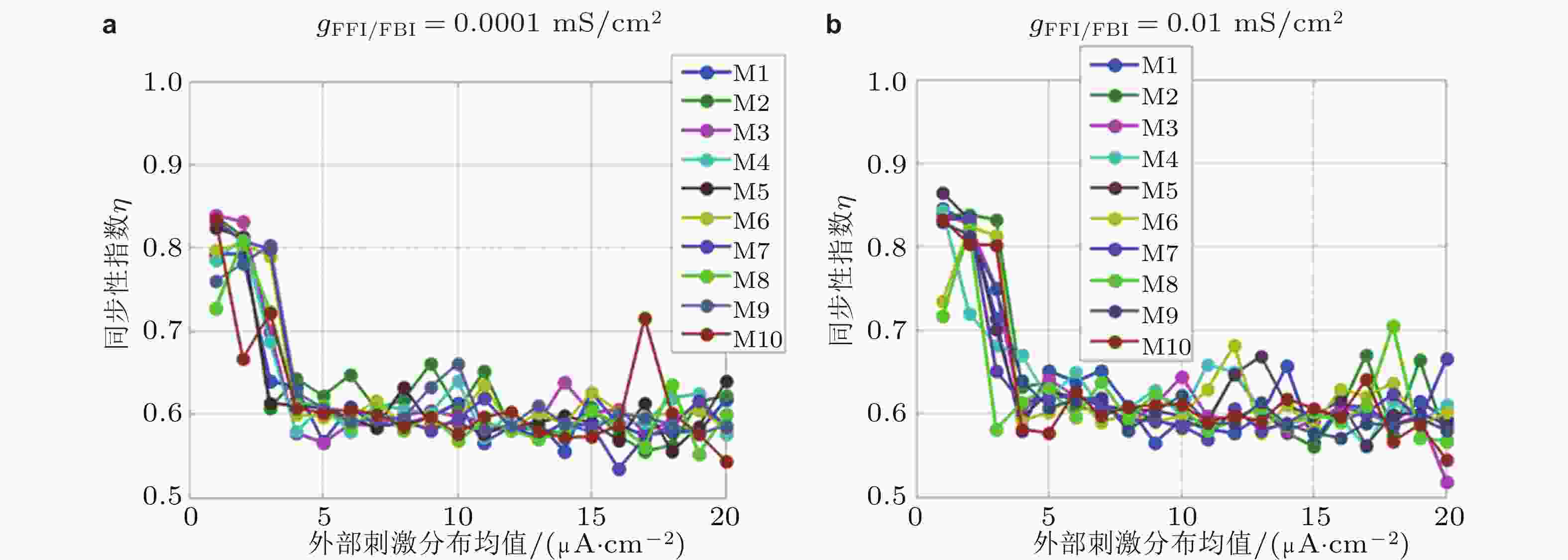
图 10 同步性指数对不同模体结构、外部刺激和抑制性连接强度变化的响应曲线. FFI和FBI抑制性连接电导强度分别为 (a) 0.0001 mS/cm2, (b) 0.01 mS/cm2 (Zhang et al. 2018b)
图 12 (a)慢变量调控的双耦合振子结构示意图 (Zhang L Y et al. 2020b) , (b)由全局慢变量调控的无标度局灶性致痫网络结构示意图, (c)为网络连接矩阵, (d)为耦合强度矩阵图 (Zhang et al. 2020a)
图 13 具有相同时间尺度的耦合振子模型模拟癫痫发作状态 (红色局部极大值, 蓝色局部极小值) 关于耦合参数演化的转迁动力学 (Zhang et al. 2020b)
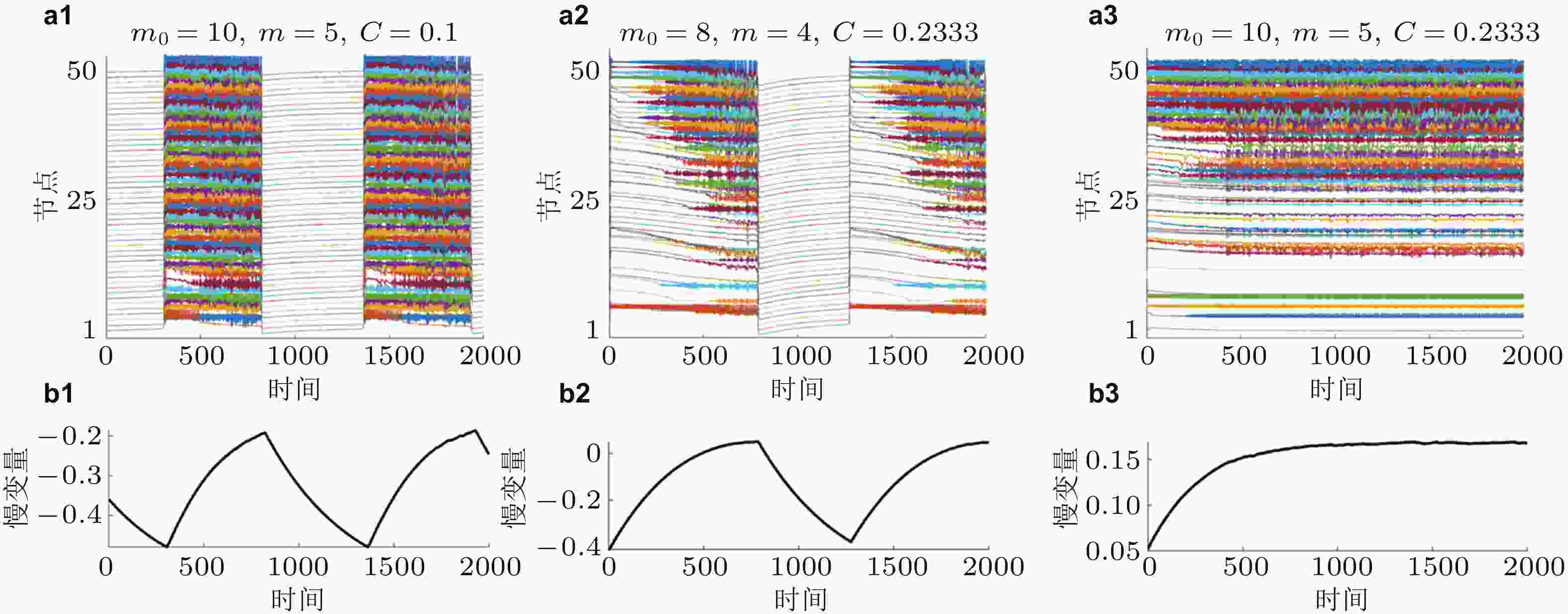
图 14 网络振子 (上) 和慢变量 (下) 的时间序列图. (a1)和(b1)为间歇性癫痫的慢速高幅值发作状态, (a2)和(b2)为间歇性癫痫的快速低幅值发作状态, (a3)和(b3)为持续性癫痫发作状态 (Zhang et al. 2020a)
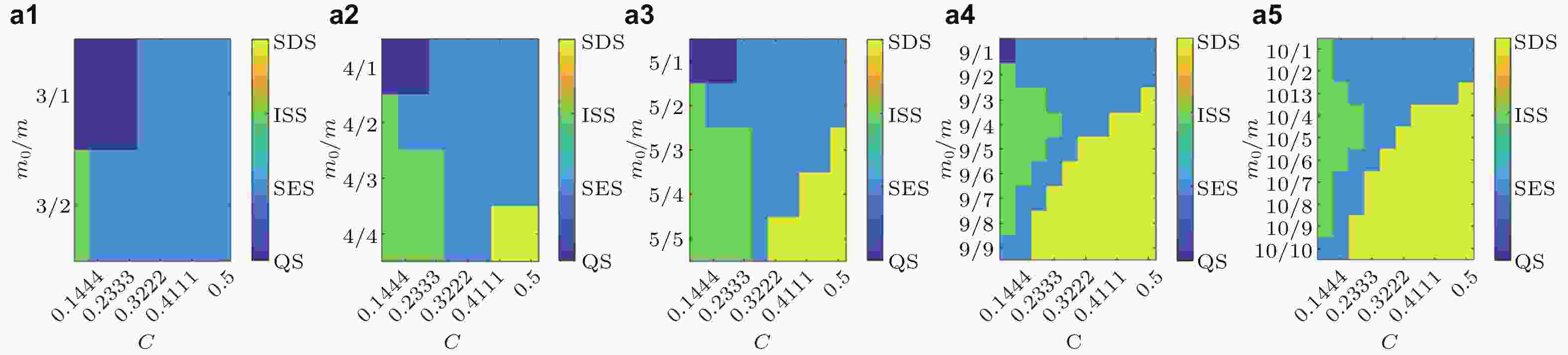
图 15 局灶性癫痫致痫网络的状态转迁空间. 横坐标为平均耦合强度, 纵坐标为网络结构参数的比例, 不同的颜色代表不同的状态. 从(a1)到(a5), 初始节点的个数分别为3,4,5,9和10. 横坐标为耦合强度C, 纵坐标为网络结构系数的比例m0/m (Zhang et al. 2020a)
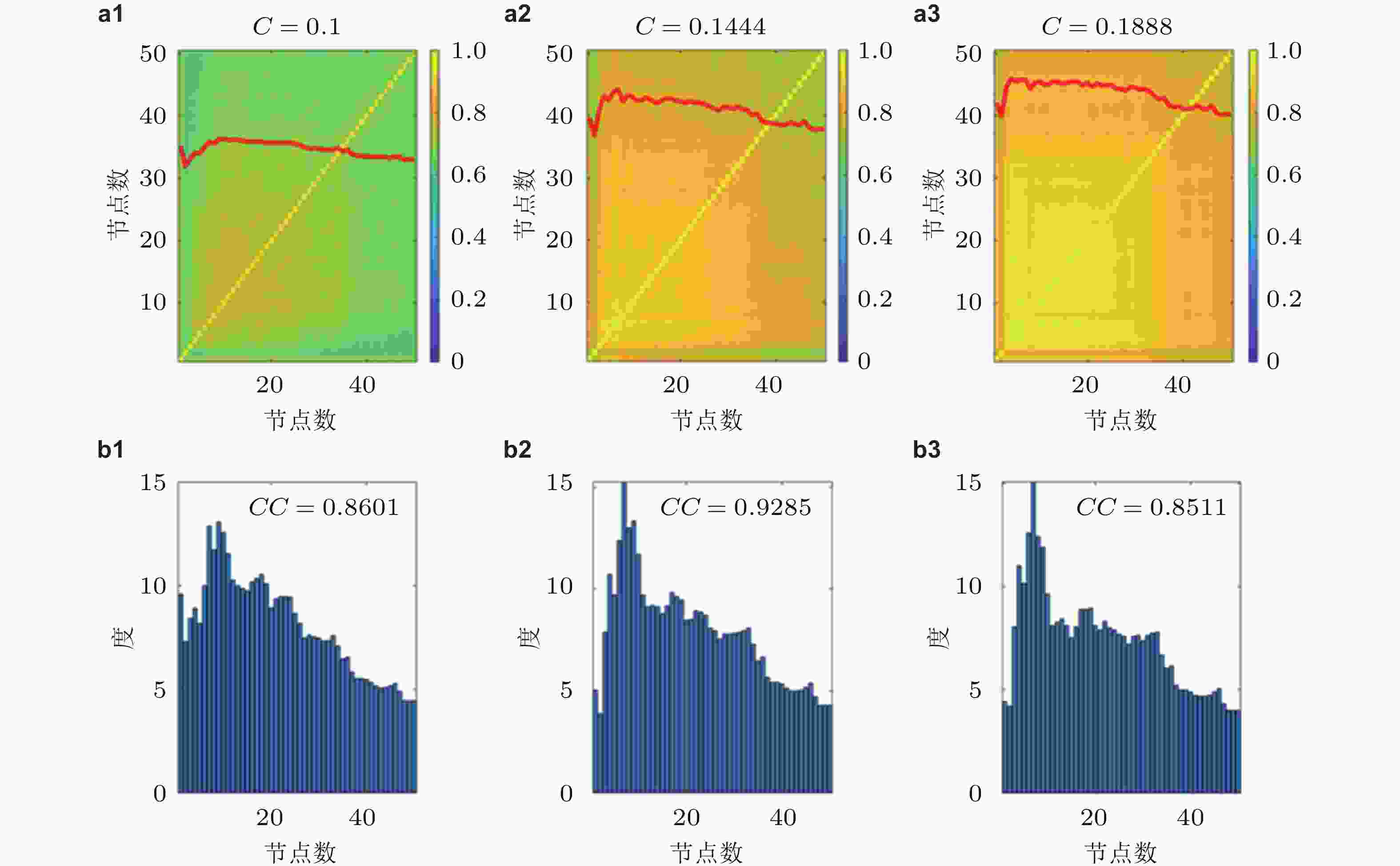
图 16 平均PLV值的矩阵热图(a), 耦合强度分别为0.1, 0.1444和0.1888, 与对应的平均网络度分布直方图(b), CC为节点PLV与度的相关系数 (Zhang et al. 2020a)
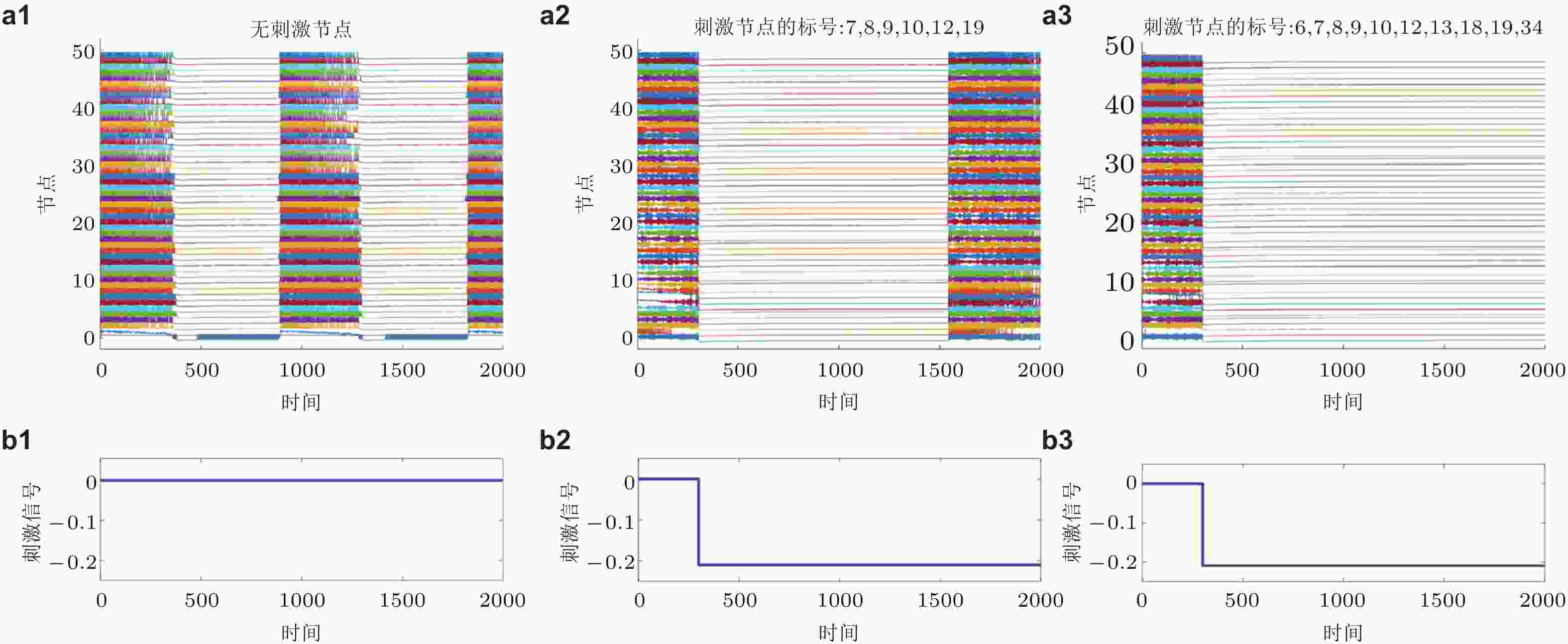
图 17 牵制控制策略的示例. (a)为时间序列, (b)为刺激信号. (a1)(b1)为无刺激节点, (a2)(b2)为刺激PLV值排名前六的节点, (a3)(b3)为刺激PLV值排名前十的节点 (Zhang et al. 2020a)
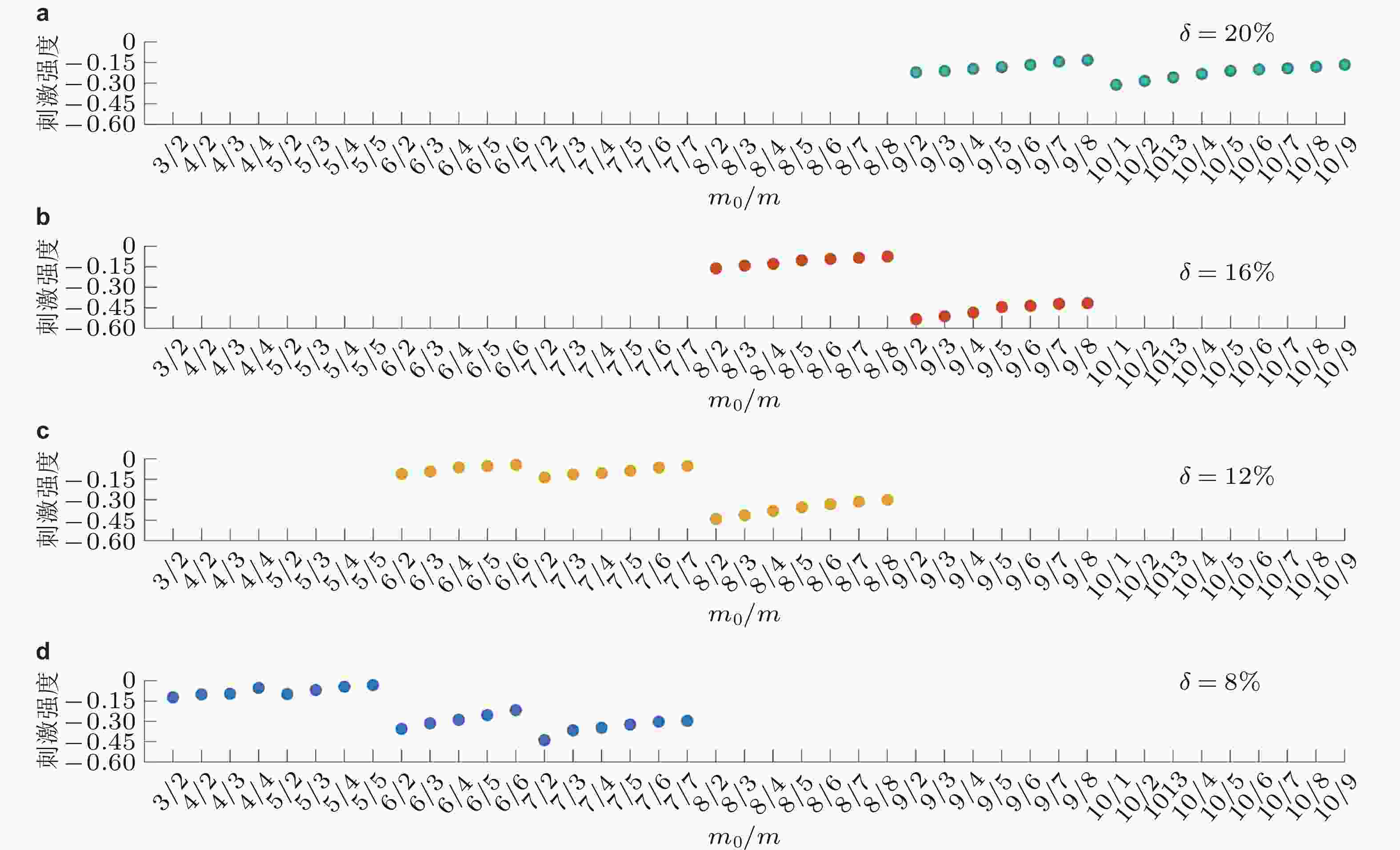
图 18 基于多样网络结构的牵制刺激策略效果图. (a) ~ (d)分别为刺激20%, 16%, 12%和8%的节点 (Zhang et al. 2020a)
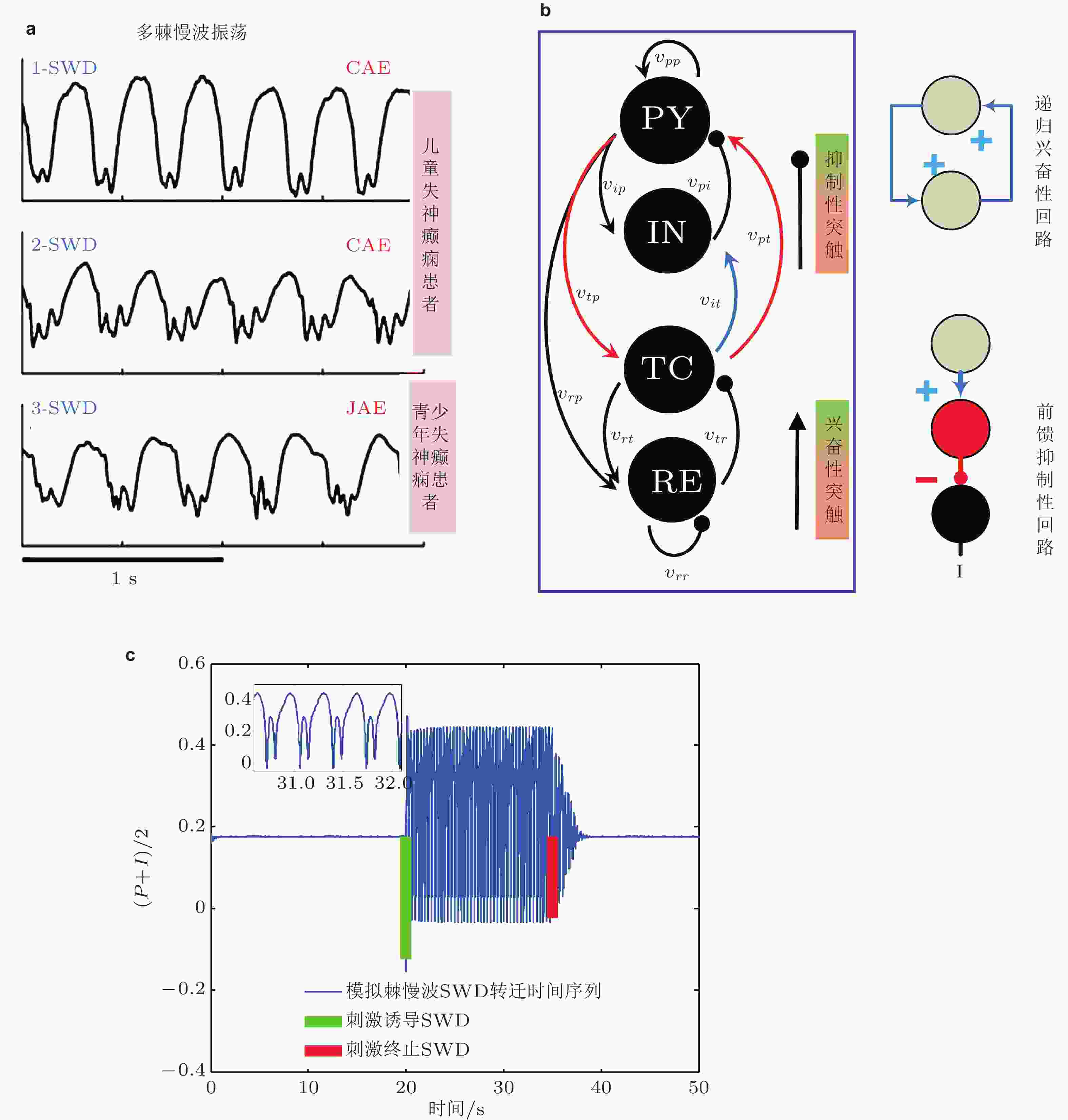
图 19 (a)来自三名不同癫痫患者发作的脑电图记录 (Marten et al. 2009) , 上图和中图为儿童失神癫痫患者 (CAE) 脑电图, 下图为青少年失神癫痫患者 (JAE) 脑电图. (b)皮质−丘脑网络框架: 皮质子系统由兴奋性 (PY) 锥体神经元集群和抑制性 (IN) 中间神经元集群组成; 丘脑子系统由丘脑网状核 (RE) 和中继核 (TC) 组成 (Fan & Duan 2017) . 皮层-丘脑环路 (PY-TC) 形成的递归兴奋性微回路和 (TC-IN-PY) 形成的前馈抑制性微回路 (Paz et al. 2015). (c)皮质−丘脑环路中皮质子网络神经元集群PY (P) 和IN (I) 平均动力学 ( (P+I) /2) 时间序列图: 单脉冲刺激 (绿竖直线) 诱导的SWD振荡和单脉冲刺激 (红竖直线) 诱导的SWD振荡终止 (Fan & Liu 2016)
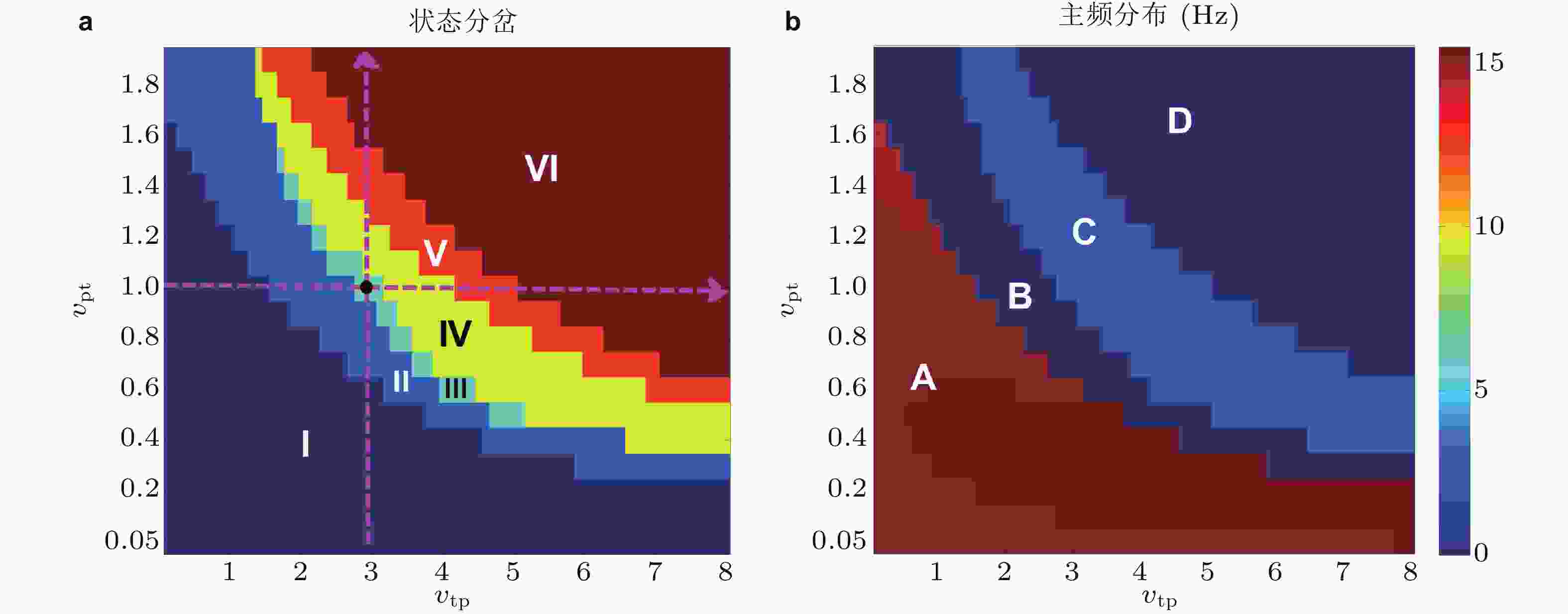
图 20 丘脑中继核与皮质组成的递归兴奋性回路作用下皮质网络中集群平均动力学关于参数状态变化分岔分析. (a) 状态分岔图, 包括失神癫痫SWD振荡 (III,IV) , 强直 (tonic) (I) 和阵挛性 (clonic) 振荡 (V) , 以及低/高 (II/VI) 饱和放电 (saturated firing) 等; (b) 对应状态的主频演化, A/C对应高/低频振荡, B和D对应背景正常状态 (Fan & Liu 2016)
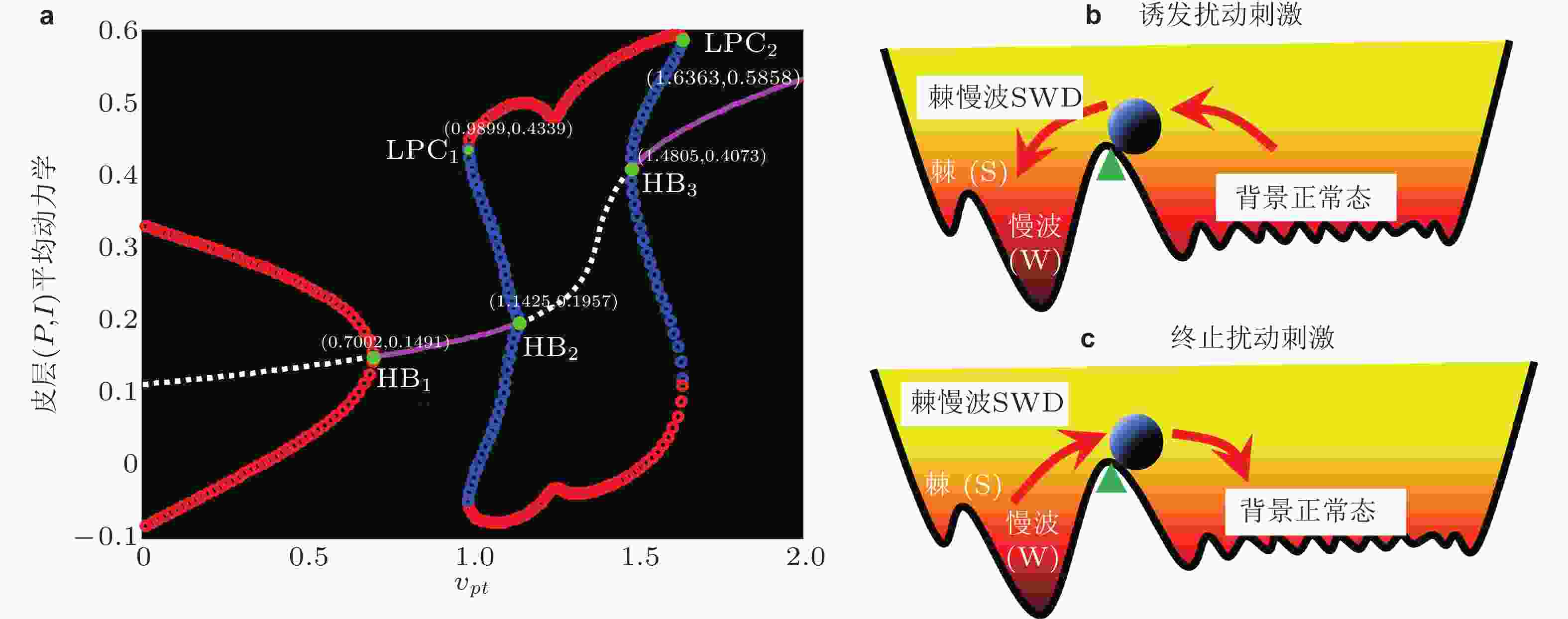
图 21 (a)皮质平均动力学分岔分析 (对应图20竖直线虚线箭头) , 其中粉色/白线代表稳定/不稳定的平衡点, 红/蓝线代表稳定/不稳定的极限环. 系统依次经历超临界和亚临界霍普夫分岔 (HB) 以及极限环分岔 (LPC) . 双稳定吸引子及其吸引域示意图: (b) SWD诱导刺激扰动, (c) SWD终止刺激扰动. 扰动使得系统 (小球) 从一个稳定状态越过临界状态 (三角形) 转迁到另外一个稳定状态 (Fan & Liu 2016)
图 22 由前馈抑制和前馈兴奋组成的2D参数平面上可以确定癫痫失神发作与强直阵挛性发作之间的相互转迁路径. (a)状态演化, 包括高饱和 (HS) 和低饱和 (LS) 放电, (多) 棘慢波SWD, 2-SWD和3-SWD振荡, 反向棘慢波 (r-SWD) , 强直 (TO) 和低/高频阵挛性 (l/h-CO) 以及反向阵挛性 (r-CO) 振荡等; (b)对应的主频演化 (Fan & Duan 2017)
图 23 (a)实验观察到的睡眠纺锤波(spindle)向癫痫棘慢波 (SWD) 转迁 (Kostopoulos 1981, Kostopoulos et al. 2000), (b)癫痫患者睡眠期间颞叶电极的脑电图记录显示10 s的睡眠纺锤波和棘慢波振荡 (Fan et al. 2017c)
图 24 (a) (b) (c)环式连接的3室耦合模型网络, 周期单脉冲刺激 (红色竖直线) 从
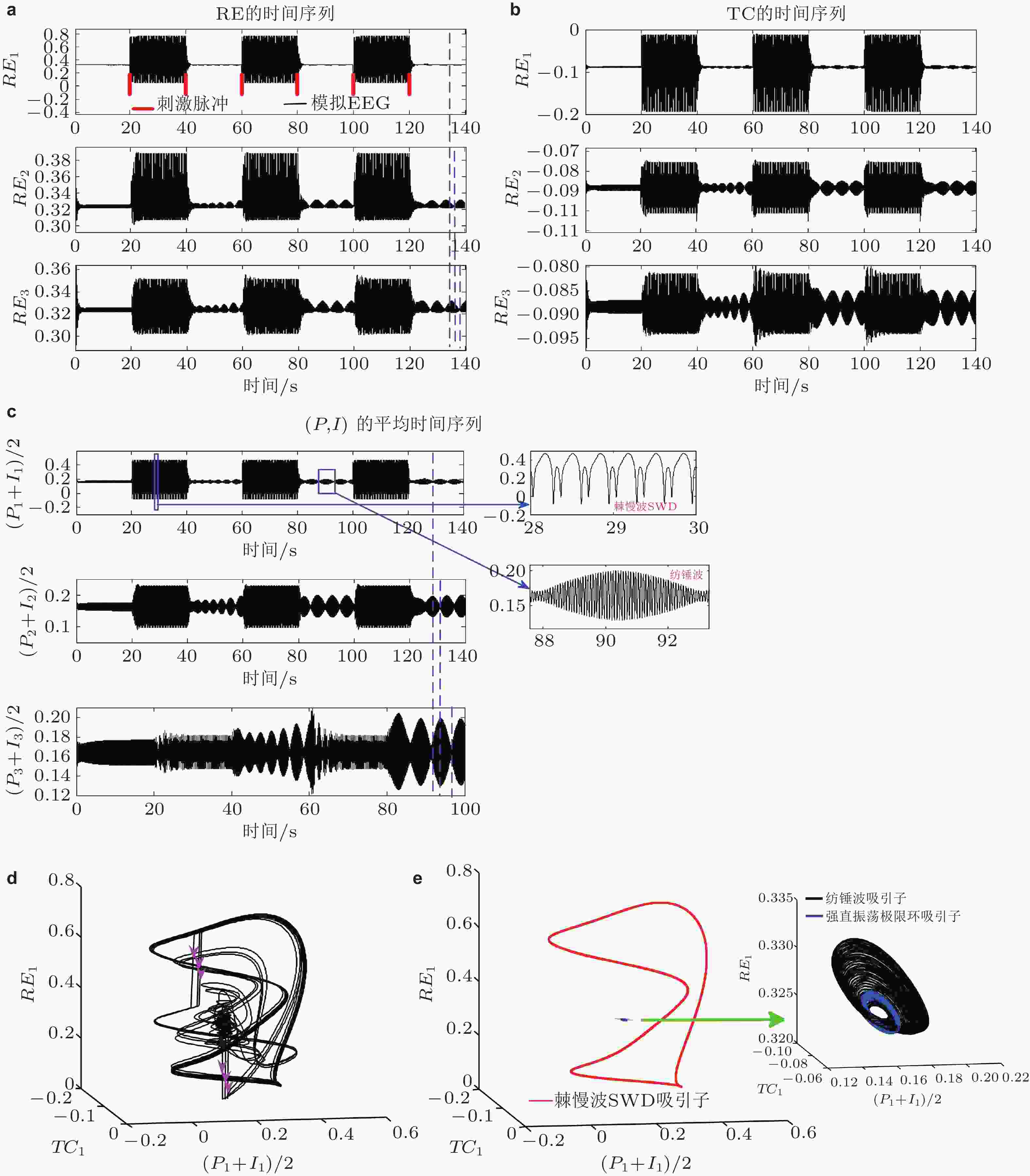
$t = 20\;{\text{s}}$ 开始间隔20 s依次施加刺激在第一室的RE, 三室的不同核团都呈现SWD与纺锤波振荡的周期性转迁(c)右侧为局部放大图. (d) (e)纺锤波吸引子 (spindle, 黑色) , 极限环吸引子 (低幅度强直振荡, 背景正常状态, 蓝色) 和SWD吸引子 (红色) 共存状态. 粉色箭头代表对RE施加的刺激. (e)右侧的局部放大图 (Fan et al. 2017b)图 25 皮质−丘脑环路时滞网络动力学模型示意图,
$ {D_{\text{1}}} $ 为丘脑中继核到皮质时滞,${D_2}$ 为皮质到丘脑中继核时滞,${D_{\text{3}}}$ 为丘脑网状核到中继核时滞,${D_4}$ 是耦合时滞 (Fan et al. 2018)图 26 (a)皮质平均动力学关于D3的分岔图, 系统状态连续地从纺锤波振荡 (spindle) 转迁到SWD, 2-SWD和3-SWD; (b) D1诱导的SWD精确发作, D1与其诱导SWD的发作时刻呈线性增长关系 (白色虚线); (c)随着D2增加 (向下箭头) 和D3增加 (向右箭头) , 在三维空间 (D1X, D1Y, R)及其投影平面(D1X,D1Y) (等高线图) 上D3诱导的SWD (左列) , 2SWD (中列) 和3SWD (右列) 的同步 (R1, R2, R3) 演变, 其中发现D2能有效规范同步发作模式. (d)驱动系统驱动响应系统的癫痫多棘慢波放电终止, 绿线表示控制输入 (Fan et al. 2018)
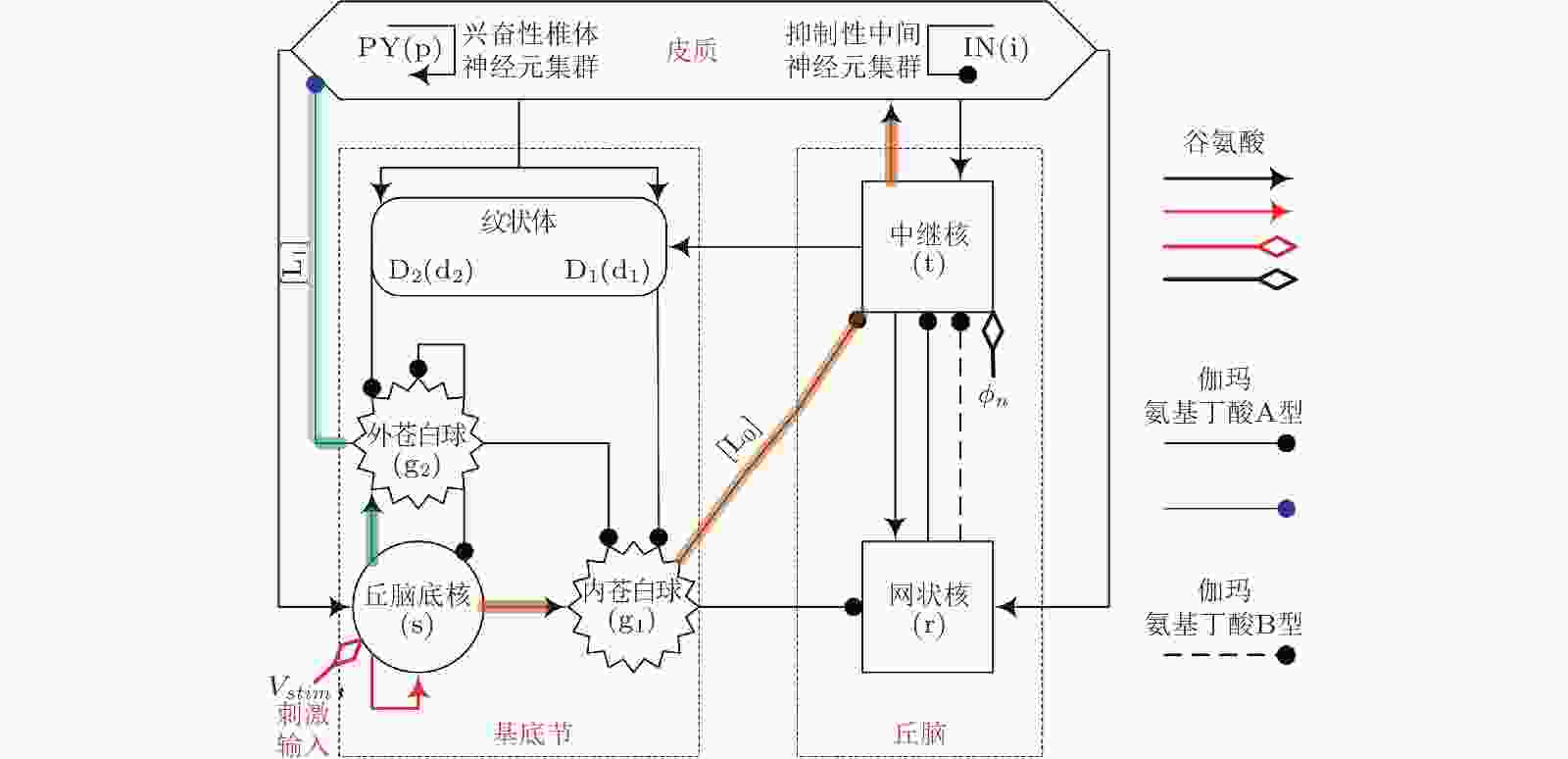
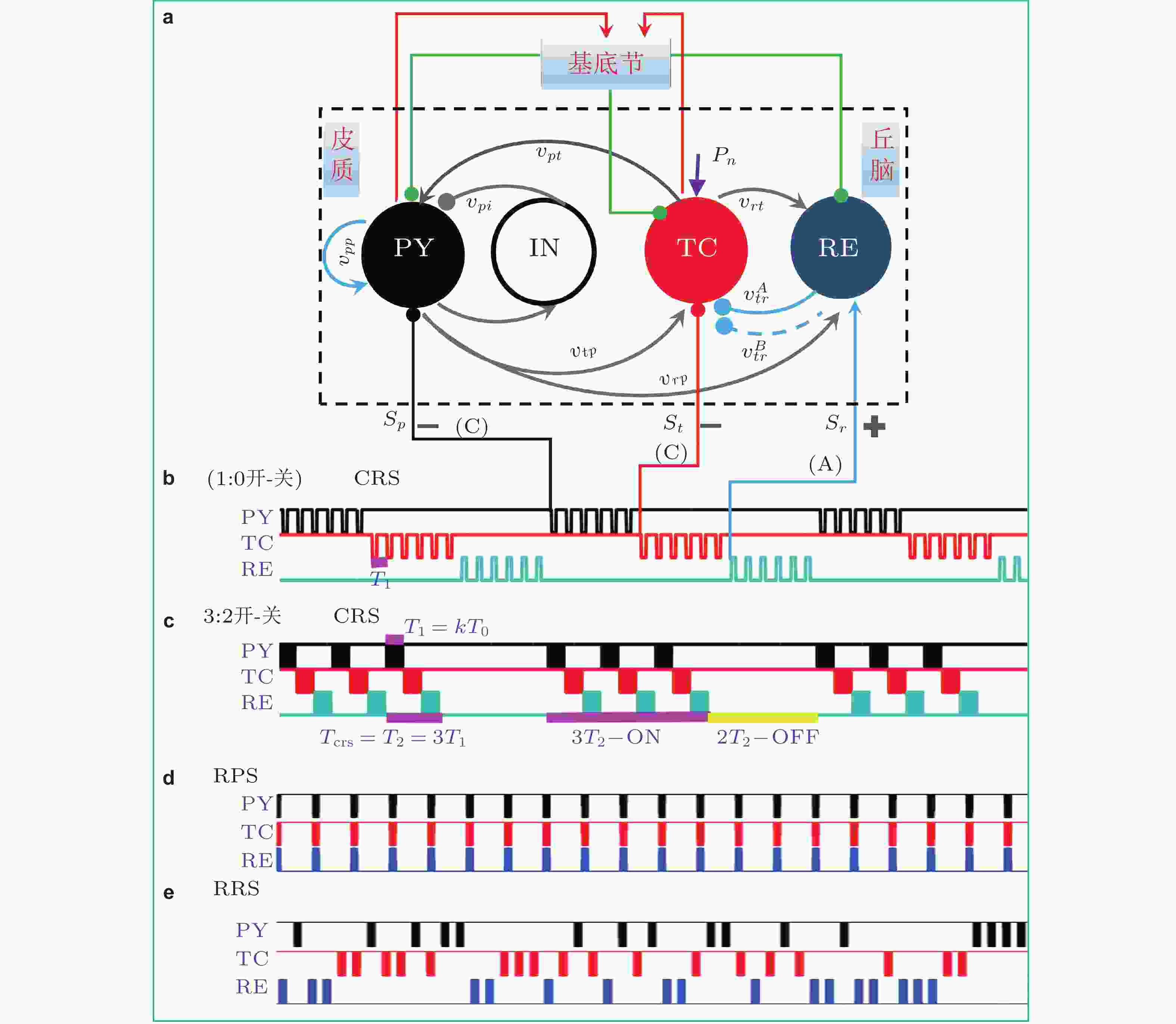
图 27 皮质−基底节−丘脑环路网络框架图: 皮质由兴奋性椎体神经元(PY)和抑制性中间神经元 (IN) 组成; 丘脑由中继核 (TC) 和网状核 (RE) 组成; 基底节由纹状体 (D1/D2) , 丘脑底核 (STN) , 内苍白球 (GPi) 和外苍白球 (GPe) 组成. 箭头代表神经元集群之间的兴奋性投射作用, 带有实心圆端点的射线代表由GABAA (实线) 和GABAB (虚线) 调节的抑制性投射作用.
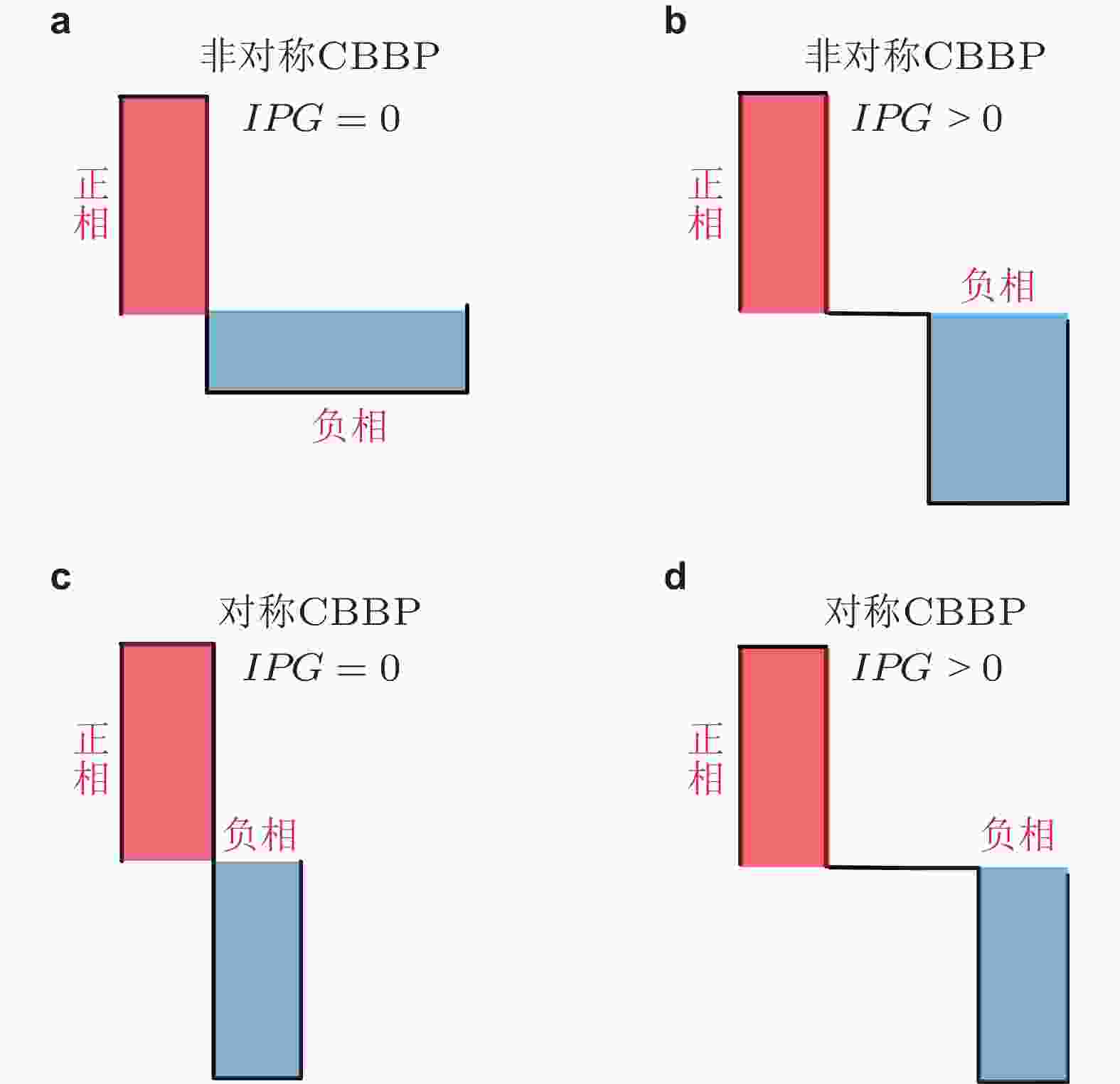
${\phi _n}$ 代表到TC的非特定外部输入. 红色箭头代表新引入的STN自突触作用,${V_{stim}}$ 为注入的外部刺激干扰. 阴影线分别代表从STN到皮质的前驱 (L0) 和后驱 (L1) 投射路径 (Fan & Wang 2018)图 28 具有 (b) (d) 和不具有 (a) (b) 脉冲间期 (IPG) 的电荷平衡的双相脉冲刺激模式, 其中 (a) (b) 为非对称形式, (c) (d) 为对称形式 (Fan & Wang 2018)
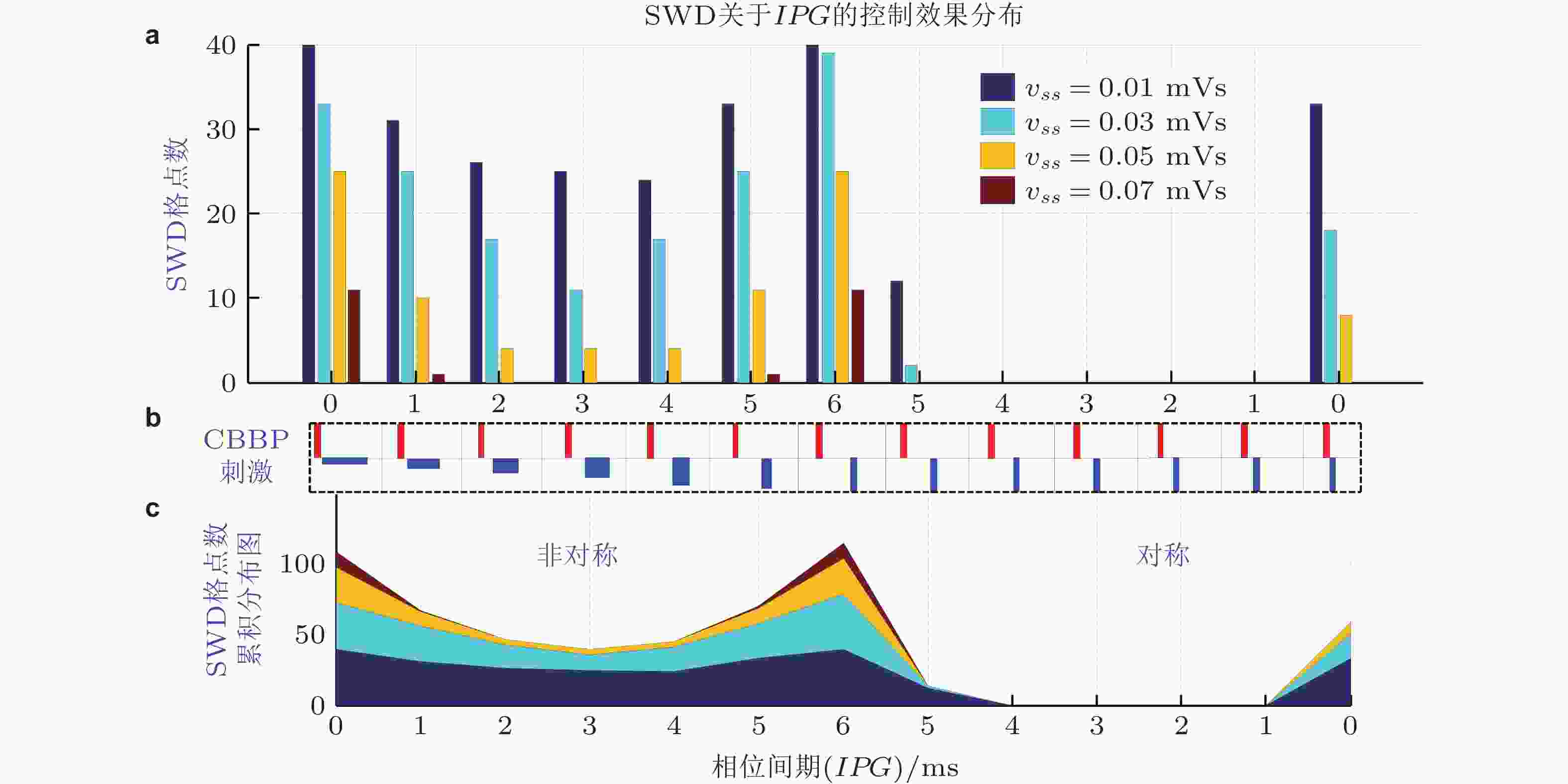
图 29 具有不同相位间期的双相脉冲刺激以及丘脑底核自突触vss对SWD的控制效果. 为了定量观察SWD的控制效果, 将2D参数区域进行均匀网格划分, 得到n × n个网格点, 统计系统显示SWD的参数网格点数 (Fan & Wang 2018)
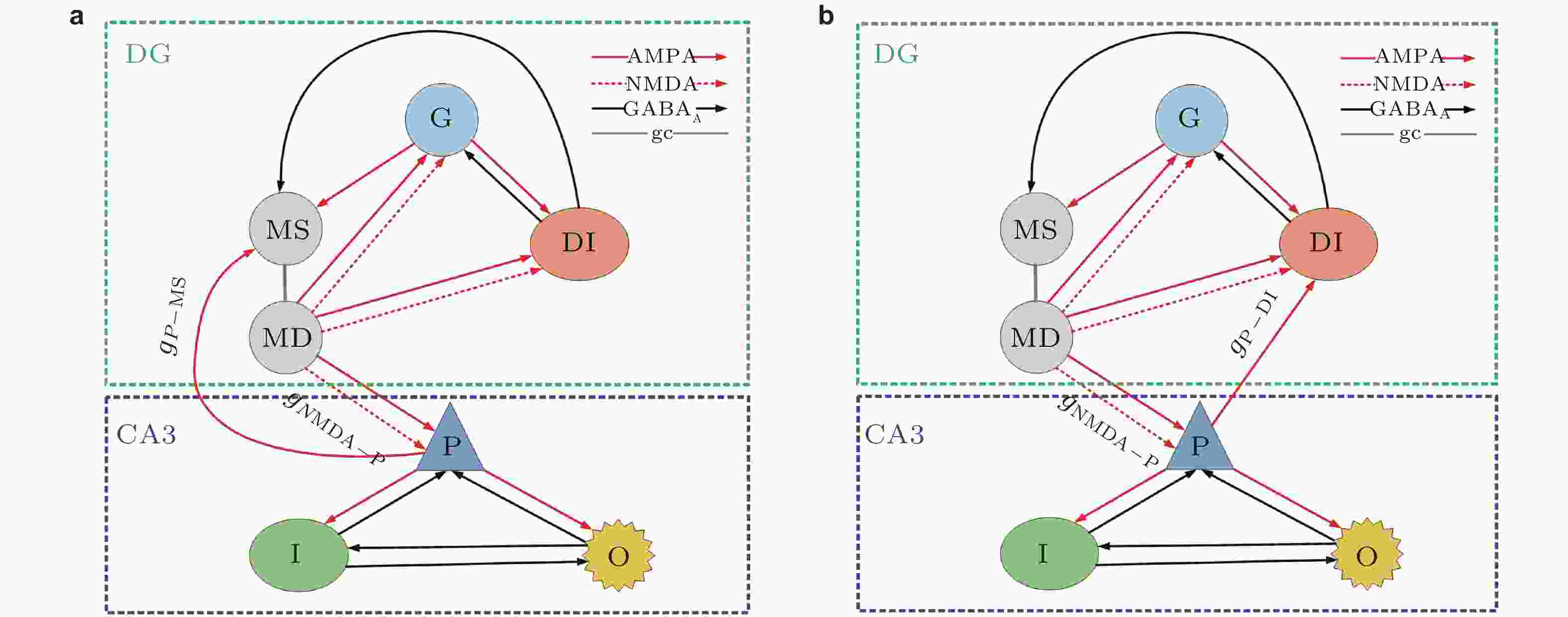
图 30 (a) BGCT环路示意图, 由皮层兴奋性锥体神经元 (PY, p) 和抑制性中间神经元 (IN, i) ; 丘脑中继核 (TC, t) 和网状核 (RE, r) ; 基底节中纹状体D1和D2型神经元群、苍白球内侧部 (GPi, g1) 和外侧部 (GPe, g2) 、丘脑底核 (STN, s) 组成. 箭头代表由谷氨酸介导的兴奋性突触, 圆圈代表GABAA (实线) / GABAB (虚线) 介导的抑制性投射. 红色和蓝色线条分别表示BG接收来自皮质−丘脑环路的兴奋性输入和反馈回皮质−丘脑环路的抑制性输出. (b)简化的BGCT模型(SBGCT), 其中BG被看作一个2I:3O调制器, 即接收来自皮质−丘脑环路2个核团的兴奋性输入和反馈回皮质−丘脑环路3个核团的抑制性输出. (c)简化的CT模型 (RCT) , 这里将来自BG的3个反馈抑制信号作为皮质−丘脑环路的特定输入常数,
$ {P}_{\text{p}}, {P}_{\text{t}}, {P}_{\text{r}} $ .$ {S}_{\text{p}}, {S}_{\text{t}}, {S}_{\text{r}} $ 是用于神经调节的外部刺激输入 (Fan & Wang 2020)图 31 (a)在SBGCT模型上对PY(p),TC(t)和RE(r)施加的协调重置刺激 (CRS) , 其中PY和TC接收负相脉冲 (Cathodic, C) 刺激, RE接收正相脉冲 (Anodic, A) 刺激; (b) (1:0开-关) CCA-CRS刺激模式, T0是在一个CRS刺激周期Tcrs内施加单个核团上的刺激脉冲的周期; (c)m:n = 3:2开−关CCA-CRS: 每进行3个周期的CRS刺激 (3开) 之后附带2个周期的刺激间歇期 (2关) , 其中每个周期的CRS (Tcrs = T2 = 3T1) 刺激过程中每个核团平均接收T1 = kT0时长的脉冲刺激. (d) CCA规则并行刺激 (regular parallel stimulation-RPS) . (e)CCA随机重置刺激 (random resetting stimulation-RRS) (Fan et al. 2020)
图 32 皮质−丘脑方向可控的刺激原理 (a) (b) 及其对SWD的最优控制效果(c). (a)由(RE, TC, PY)生成的三维空间中, 给出了SWD振荡的吸引子, 并建立了一个原点(0, 0, 0)的笛卡尔坐标系
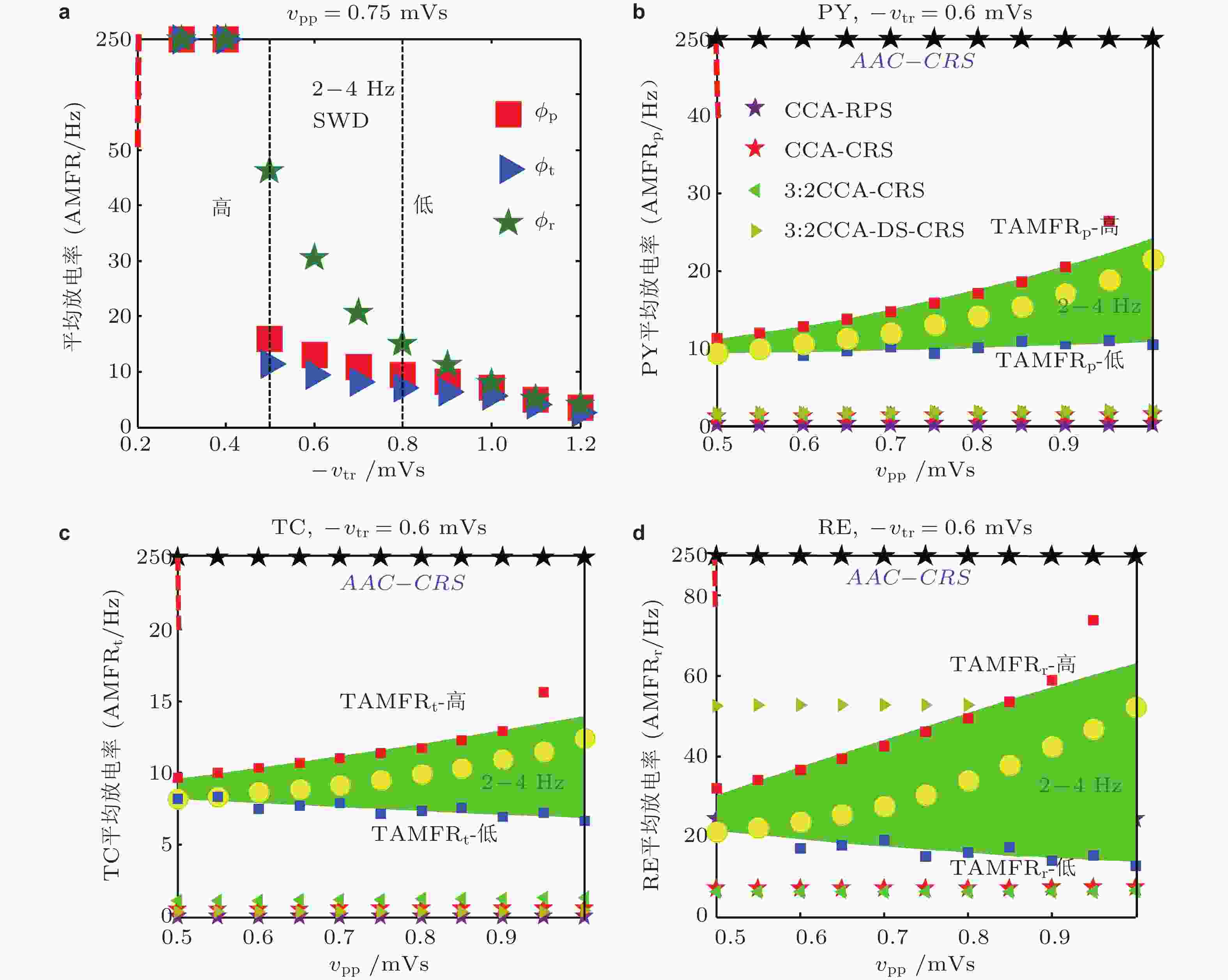
${O_{XYZ}}$ ,${{ {\boldsymbol{V}}}}$ 表示有向刺激 (directional stimulation-DS) 的方向,${\theta _p}$ ,$ {\theta }_{t} $ ,$ {\theta }_{r} $ 分别是有向刺激与三个坐标轴正向的夹角. (b) 笛卡尔3D空间直角坐标系中的单位球面, 球面上的散点是随机选取的并满足${\theta _p} \in \left( {{{90}^\circ },{{180}^\circ }} \right)$ ,${\theta }_{t}\in \left({90}^\circ,{180}^\circ\right), {\theta }_{r}\in \left({0}^\circ,{90}^\circ\right)$ , 代表对TC和PY的负相 (C,$\cos {\theta _{\text{p}}} \lt 0,\cos {\theta _{\text{t}}} \lt 0$ ) 脉冲刺激及对RE的正相 (A,$\cos {\theta _{\text{r}}} \gt 0$ ) 脉冲刺激. (c) 3:2开−关CCA有向刺激 (CCA-DS) 对SWD的控制效果, 其中标记①②③表示取得最好控制效果的刺激方向角、SWD参数格点数和相应的电流消耗 (Fan & Zheng 2020)图 33 电刺激调控SWD的动力学解释. (a) PY(“■”), TC(“►”), RE(“★”)的AMFR随着-vtr的增大而降低. 两条虚线之间的区域表示的是典型的2 ~ 4 Hz的SWD振荡区域, 两条虚线分别对应着-vtr高和低2-4Hz的SWD触发平均放电率(TAMFR); (b)(c)(d)在AAC-CRS(黑色★), CCA-CRS(红色★),CCA-RPS(紫色★), 3:2开−关CCA-CRS(◄), 3:2开−关CCA-DS-CRS(►)以及控制组(○)下, PY, TC, RE的AMFR与对应-vtr 的高 (红色■) 和低 (蓝色■) TAMFR随着vpp的增大的演化图. 图(b)到图(d)中绿色区域表示由-vtr 确定的典型2 ~ 4 Hz的SWD振荡区域 (Fan et al. 2020)
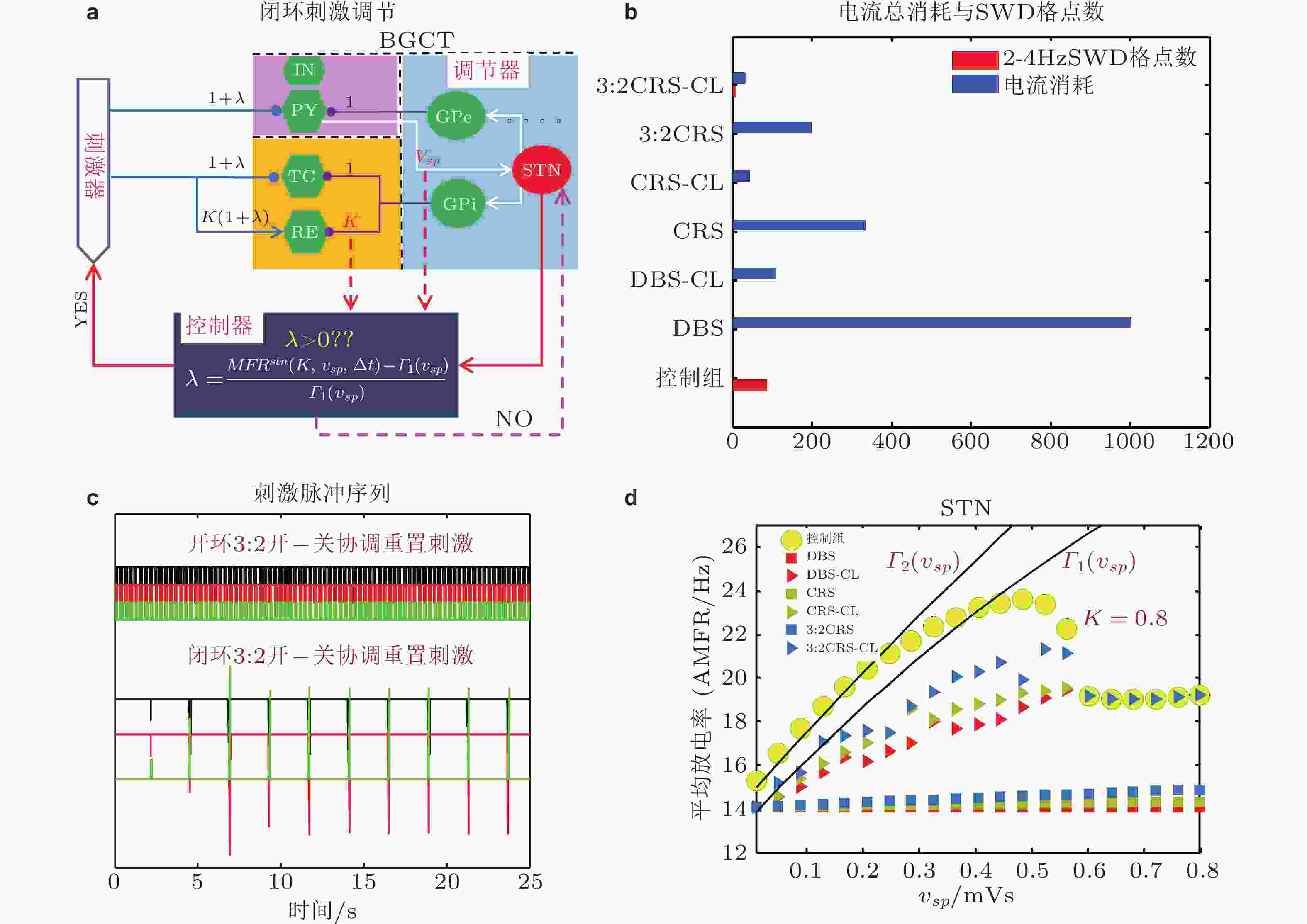
图 34 (a) 基于STN的TAMFR设计的闭环刺激策略, 其中包括了调节器 (基底节) , 控制器和刺激器; (b)不同刺激模式对SWD的控制效果和电流消耗柱状图. (c) 开环和闭环3:2开−关CRS刺激脉冲序列图; (d)常规深脑刺激 (DBS) , 闭环DBS (DBS-CL) , 协调重置刺激 (CRS), 闭环CRS (CRS-CL) , 3:2开−关CRS和闭环3:2开−关CRS (3:2CRS-CL) 等六种不同刺激模式以及无刺激时 (控制组) STN的AMFR随着
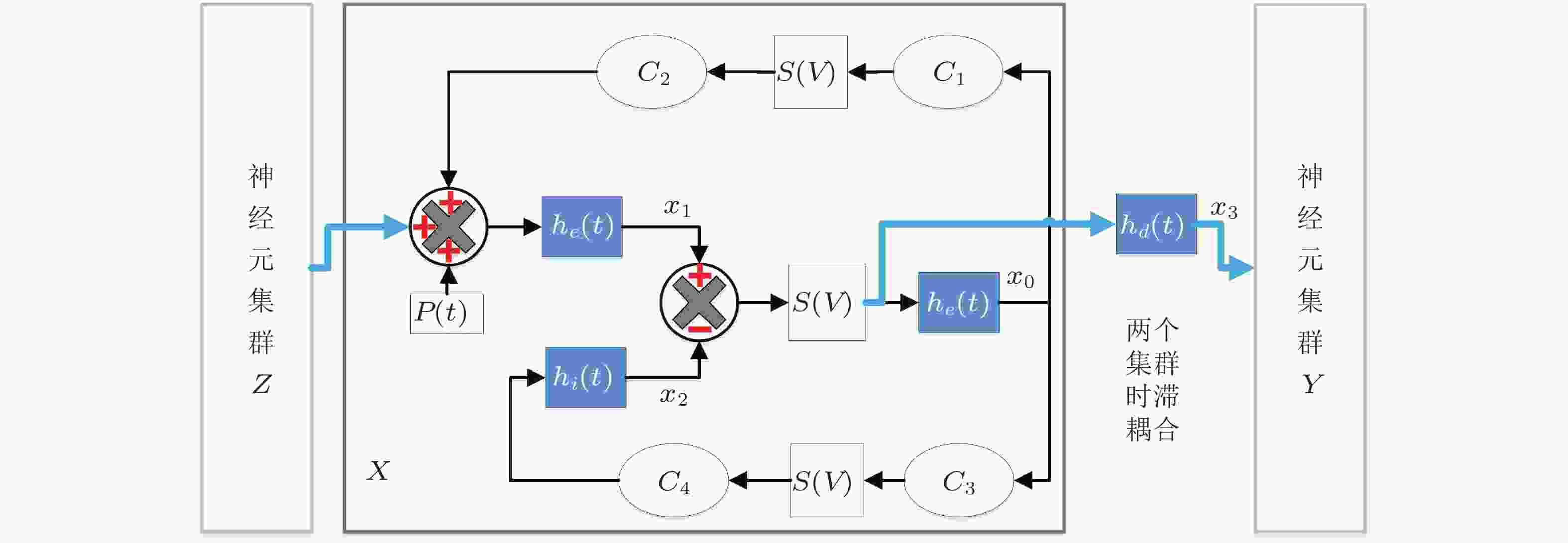
${v_{sp}}$ 的变化趋势,${\varGamma _1}$ 和${\varGamma _2}$ 为GPi作用下确定的低触发TAMFR随着${v_{sp}}$ 增大的演化图 (Fan & Wang 2020)图 35 时滞耦合神经元群模型结构. 虚线矩形框展示了单个神经元群模型X的内在动力学机理, Y和Z与之类似.
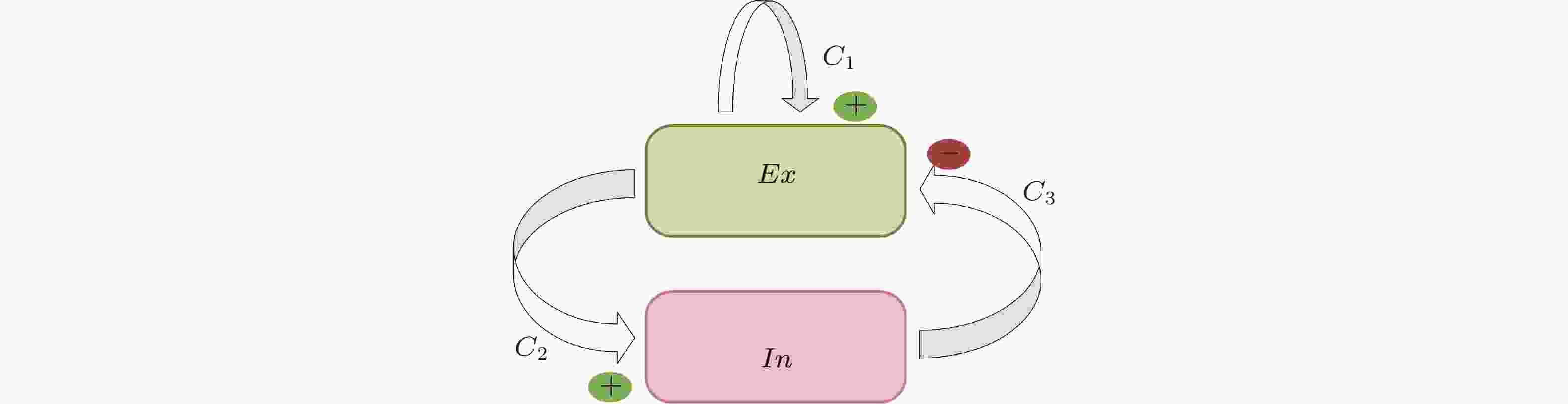
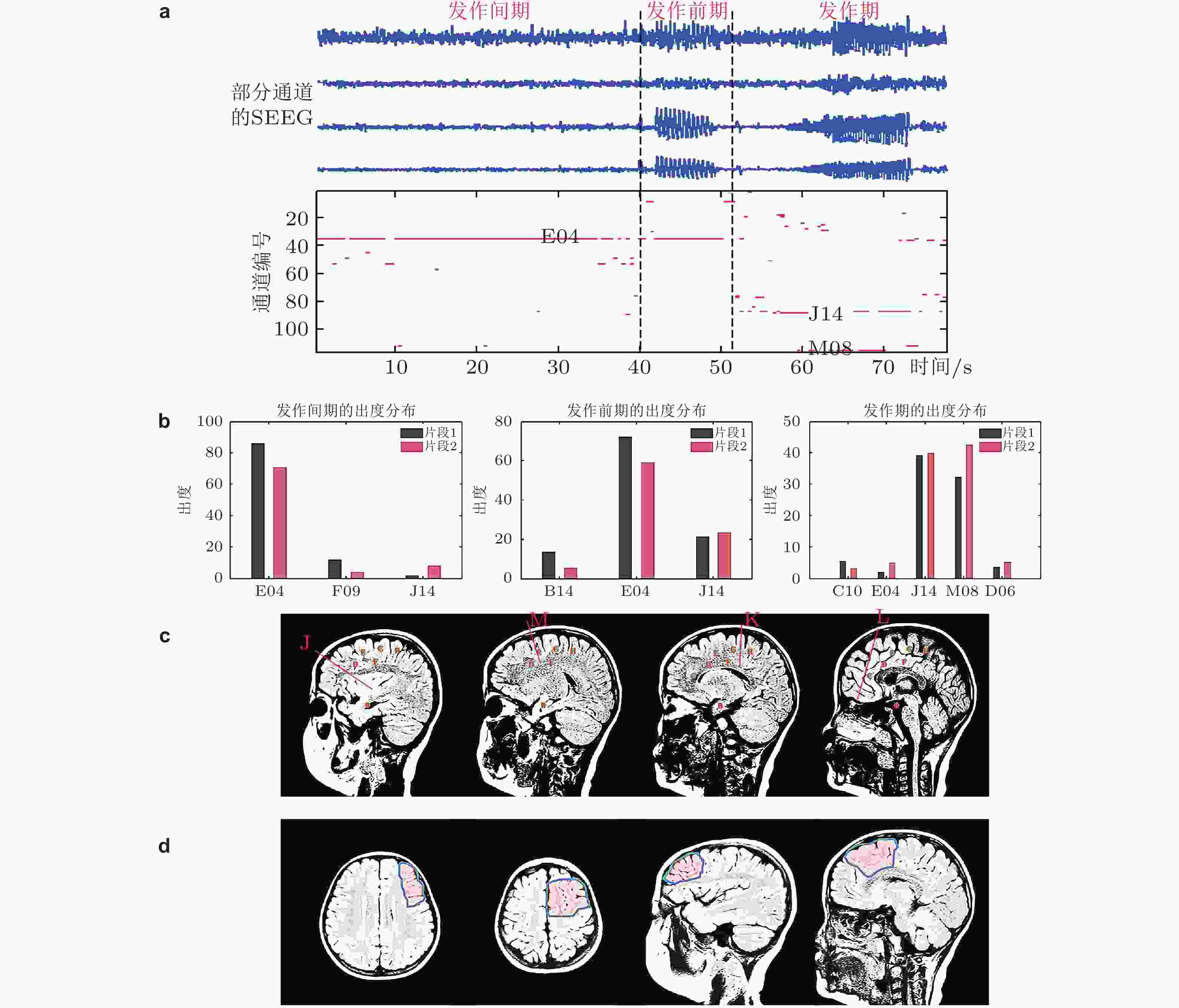
$ {h}_{e},{h}_{i},{h}_{d} $ 分别是兴奋性突触后电位EPSP和抑制性突触后电位IPSP的线性转迁函数,$S\left( v \right)$ 是非线性转迁函数,${{{C}}_{\text{1}}}{\text{,}}{{{C}}_{\text{2}}}{\text{,}}{{{C}}_{\text{3}}}{\text{,}}{{{C}}_{\text{4}}}$ 表示关联突触的平均数量.$p\left( t \right)$ 是高斯白噪声, 是对环境影响的建模.${x_0}$ 表示中间神经元EPSP转迁函数${h_e}$ 的输出,${x_1}$ 表示锥体神经元EPSP转迁函数${h_e}$ 的输出,${x_2}$ 表示锥体神经元IPSP转迁函数${h_i}$ 的输出,${x_{\text{3}}}$ 表示EPSP转迁函数${h_d}$ 的输出.图 36 选取的癫痫患者病灶定位的计算结果. (a)上半部分是部分通道的SEEG数据, 下半部分是对应时刻每个通道的出度变化 (为了突出出度较大的通道, 仅将出度大于30的用红色点显示); (b)发作间期、发作前期和发作期的出度分布 (仅列举出度较大的通道) , 不同的片段计算的结果类似, 表明结果的可重复性; (c)电极位置的示意图; (d)手术切除区域的示意图 (Yang et al. 2018)
图 37 神经元集群时空扩展网络模型的仿真结果. (a)选定患者某个通道的真实脑电数据, 发作间期和发作期各30 s; (b)切除前的仿真结果; (c)随机切除理论病灶之外的一个通道后的仿真结果; (d)切除一个理论致痫通道后的仿真结果; (e)统计三种条件下各重复30次仿真后发作间期和发作期的棘波数量; (f)另一个病人的真实数据 (上) 、切除前的仿真 (中) 和准确切除病灶后的仿真 (下) (Yang et al. 2018)
图 38 选取的癫痫患者 (见表1中编号为1的病人) 大脑通道G05对其他9个通道信号 (F08, M09, C09, D03, D04, H10, J07, K01, K02) 的因果性随时间的演化. 垂直虚线标出了癫痫发作位置, 水平虚线分别标出了因果阈值
${q^\tau }\left( n \right) = $ 0和${q^\tau }\left( n \right) = $ 10的位置. 选取${q^\tau }\left( n \right) = $ 10作为阈值来表示显著的因果关系. 其他每个通道与其余通道的信息流因果关系分析类似 (Fan et al. 2021)图 39 基于多通道信息流因果关系分析 (见图38) 进行癫痫发作的效应网络构建: 基于表1中编号为1的患者数据的因果关系与同步度分析构建的有向加权网络, 这里将每个通道视作一个网络节点 (10个通道对应10个节点, 1-F08, 2-M09, 3-C09, 4-D03, 5-D04, 6-G05, 7-H10, 8-J07, 9-K01, 10-K02) . (a)10个通道EEG信号假设为癫痫脑动力系统中的10个变量
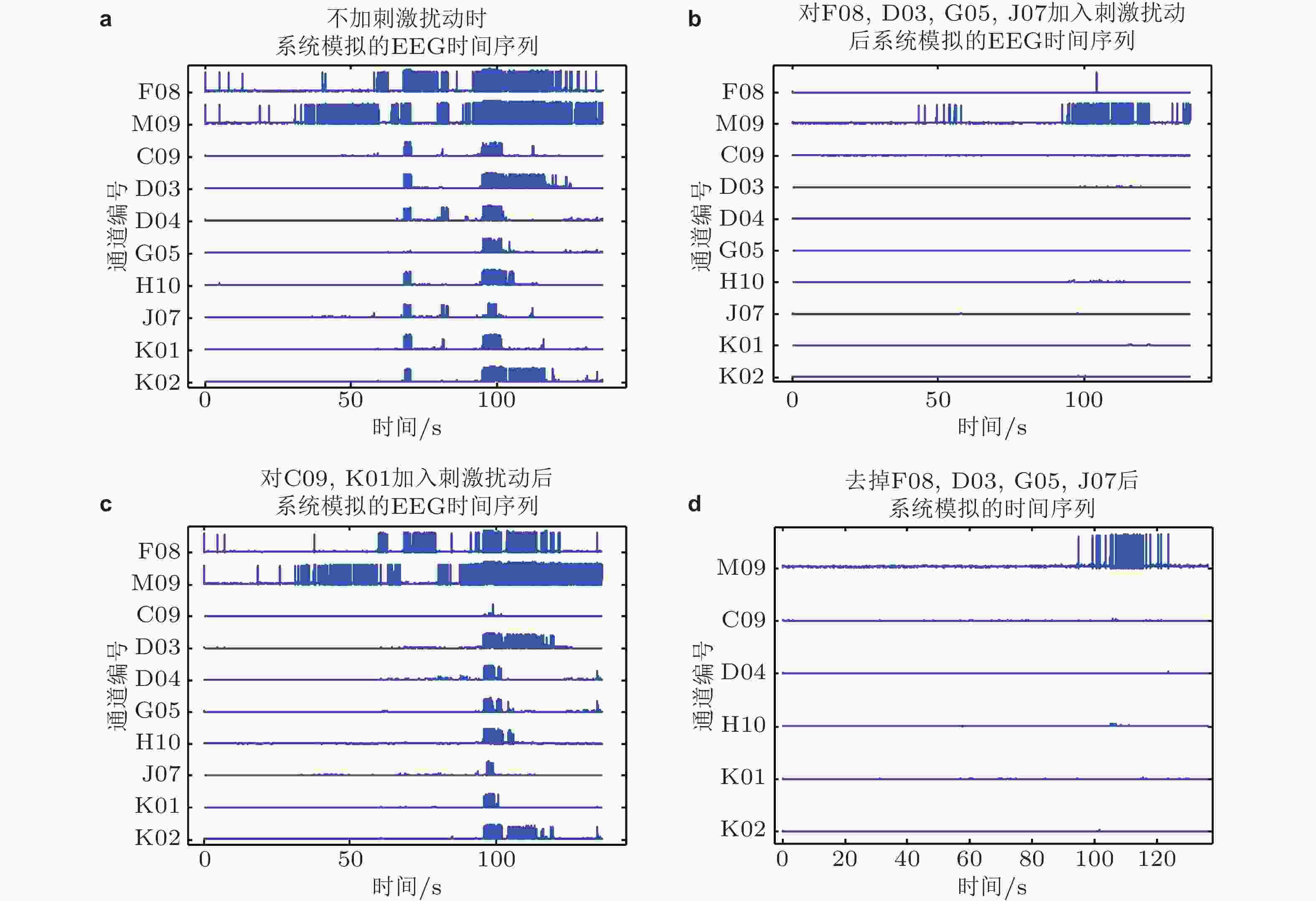
${x_1},{x_2}, \ldots ,{x_{10}}$ , 从初始状态出发, 网络在癫痫发作间期的状态(b)和癫痫发作期的状态(c)可以通过控制到达任意预期的最终状态 ((a)中向右的黄色箭头) , 这个控制为对无匹配节点 (如: 节点1, 4, 6和8, 是针对(c)癫痫发作期计算所得) 的输入刺激扰动$u\left( t \right) = \left( {{u_1}\left( t \right),{u_2}\left( t \right),{u_3}\left( t \right),{u_4}\left( t \right)} \right)$ . (b)和(c)左侧的网络呈现了多种形态的度分布, 节点大小表示网络的出度, 黄色的节点只有入度, 箭头的粗细表示因果性的大小 (只有$q\left( n \right) \gt 10$ 才会被绘制出来) . (c)右侧图展示了所有匹配路径 (由绿色箭头标出) , 通过粉色的箭头被依序连接, 其他连接用浅灰色表示 (Fan et al. 2021)图 40 数值模拟效果. (a)表1中编号为1的癫痫患者原始EEG时间序列; (b)对计算所得的关键控制节点F08, D03, G05, J07进行刺激扰动后模拟的时间序列; (c)对任意两条非病灶通道 (C09, K01为例) 进行刺激扰动后模拟的时间序列; (d)移除时间序列中的病灶通道F08, D03, G05, J07信号后模拟的时间序列 (Fan et al. 2021)
表 1 基于10位局灶性癫痫患者计算的网络关键控制节点与临床定位的病灶节点对比
患者编号 年龄 选择
通道数临床定位的
病灶节点计算的网络关
键控制节点1 ≤6 10 F08,D03 F08,D03,G05,J07 2 15 ~ 20 12 D11,D12 D12,M09,W03,C03,E02 3 5 ~ 10 10 L11,H13,L09 L11,L09 4 5 ~ 10 9 G10,H10 G10,H10,G06 5 ≤6 9 P08,E07,G06 F11,E07,E09 6 25 ~ 30 9 A01,B01 A01 7 15 ~ 20 10 L04,H04 L04,H04,J02 8 10 ~ 15 10 K09,G11 G10,K09,D06,H01 9 30 ~ 35 12 C02,D01,E10 D01,E03 10 5 ~ 10 11 E04,J14,M05 M05,M04,J14,C08 -
[1] Ahn S, Jun S B, Lee H W, et al. 2016. Computational modeling of epileptiform activities in medial temporal lobe epilepsy combined with in vitro experiments. Journal of Computational Neuroscience, 41: 207-223. doi: 10.1007/s10827-016-0614-8 [2] Albert R, Barabási A L. 2002. Statistical mechanics of complex networks. Reviews of Modern Physics, 74: 47-97. doi: 10.1103/RevModPhys.74.47 [3] Amaral D G, Scharfman H E, Lavenex P. 2007. The dentate gyrus: fundamental neuroanatomical organization (dentate gyrus for dummies). Progress in Brain Research, 163: 3-22. [4] Arrais M, Modolo J, Mogul D, et al. 2021. Design of optimal multi-site brain stimulation protocols via neuro-inspired epilepsy models for abatement of interictal discharges. Journal of Neural Engineering, 18: 016024. [5] Astolfi L, Cincotti F, Mattia D, et al. 2008. Tracking the time-varying cortical connectivity patterns by adaptive multivariate estimators. IEEE Transactions on Biomedical Engineering, 55: 902-913. doi: 10.1109/TBME.2007.905419 [6] Badawy R A B, Lai A, Vogrin S J, et al. 2013. Subcortical epilepsy? Neurology, 80: 1901-1907. doi: 10.1212/WNL.0b013e3182929f4f [7] Baier G, Goodfellow M, Taylor P N, et al. 2012. The importance of modeling epileptic seizure dynamics as spatio-temporal patterns. Frontiers in Physiology, 3: 281. [8] Baier G, Rosch R, Taylor P N, et al. 2018. Design Principle for A Population-based Model of Epileptic Dynamics//In Complexity and Synergetics. Cham: Springer, 333-347 [9] Barabási A L, Albert R. 1999. Emergence of scaling in random networks. Science, 286: 509-512. doi: 10.1126/science.286.5439.509 [10] Bartolomei F, Wendling F, Chauvel P. 2008. The concept of an epileptogenic network in human partial epilepsies. Neuro-chirurgie, 54: 174-184. doi: 10.1016/j.neuchi.2008.02.013 [11] Battaglia D, Witt A, Wolf F, et al. 2012. Dynamic effective connectivity of inter-areal brain circuits. PLoS Computational Biology, 8: e1002438. doi: 10.1371/journal.pcbi.1002438 [12] Berényi A, Belluscio M, Mao D, et al. 2012. Closed-loop control of epilepsy by transcranial electrical stimulation. Science, 337: 735-737. doi: 10.1126/science.1223154 [13] Berman R, Negishi M, Vestal M, et al. 2010. Simultaneous EEG, fMRI, and behavior in typical childhood absence seizures. Epilepsia, 51: 2011-2022. doi: 10.1111/j.1528-1167.2010.02652.x [14] Beverlin B, Kakalios J, Nykamp D, et al. 2012. Dynamical changes in neurons during seizures determine tonic to clonic shift. Journal of Computational Neuroscience, 33: 41-51. doi: 10.1007/s10827-011-0373-5 [15] Beverlin B, Netoff T I. 2013. Dynamic control of modeled tonic-clonic seizure states with closed-loop stimulation. Frontiers in Neural Circuits, 6: 126. [16] Bjerknes S, Toft M, Konglund A E, et al. 2018. Multiple microelectrode recordings in STN‐DBS surgery for parkinson's disease: A randomized study. Movement Disorders Clinical Practice, 5: 296-305. doi: 10.1002/mdc3.12621 [17] Blümcke I, Thom M, Aronica E, et al. 2013. International consensus classification of hippocampal sclerosis in temporal lobe epilepsy: A task force report from the ILAE commission on diagnostic methods. Epilepsia, 54: 1315-1329. doi: 10.1111/epi.12220 [18] Boon P, Vonck K, De Herdt V, et al. 2007. Deep brain stimulation in patients with refractory temporal lobe epilepsy. Epilepsia, 48: 1551-1560. doi: 10.1111/j.1528-1167.2007.01005.x [19] Breakspear M, Roberts J A, Terry J R, et al. 2006. A unifying explanation of primary generalized seizures through nonlinear brain modeling and bifurcation analysis. Cerebral Cortex, 16: 1296-1313. doi: 10.1093/cercor/bhj072 [20] Brogin J A F, Faber J, Bueno D D. 2020. An efficient approach to define the input stimuli to suppress epileptic seizures described by the epileptor model. International Journal of Neural Systems, 30: 2050062. doi: 10.1142/S0129065720500628 [21] Burdette D E, Haykal M A, Jarosiewicz B, et al. 2020. Brain-responsive corticothalamic stimulation in the centromedian nucleus for the treatment of regional neocortical epilepsy. Epilepsy & Behavior, 112: 107354. [22] Buskila Y, Bellot-Saez A, Morley J W. 2019. Generating brain waves, the power of astrocytes. Frontiers in Neuroscience, 13: 1125. doi: 10.3389/fnins.2019.01125 [23] Cappaert N L M, Ramekers D, Martens H C F, et al. 2013. Efficacy of a new charge-balanced biphasic electrical stimulus in the isolated sciatic nerve and the hippocampal slice. International Journal of Neural Systems, 23: 1250031. doi: 10.1142/S0129065712500311 [24] Centeno M, Carmichael D W. 2014. Network connectivity in epilepsy: Resting state fMRI and EEG–fMRI contributions. Frontiers in Neurology, 5: 93. [25] Chen M, Guo D, Li M, et al. 2015. Critical roles of the direct GABAergic pallido-cortical pathway in controlling absence seizures. PLoS Computational Biology, 11: e1004539. doi: 10.1371/journal.pcbi.1004539 [26] Chen M, Guo D, Wang T, et al. 2014. Bidirectional control of absence seizures by the basal ganglia: A computational evidence. PLoS Computational Biology, 10: e1003495. doi: 10.1371/journal.pcbi.1003495 [27] Cossart R. 2014. Operational hub cells: A morpho-physiologically diverse class of GABAergic neurons united by a common function. Current Opinion in Neurobiology, 26: 51-56. doi: 10.1016/j.conb.2013.12.002 [28] Cossu M, Cardinale F, Colombo N, et al. 2005. Stereoelectroencephalography in the presurgical evaluation of children with drug-resistant focal epilepsy. Journal of Neurosurgery:Pediatrics, 103: 333-343. doi: 10.3171/ped.2005.103.4.0333 [29] Cukiert A, Lehtimaki K. 2017. Deep brain stimulation targeting in refractory epilepsy. Epilepsia, 58: 80-84. [30] Dobesberger J, Ristic A J, Walser G, et al. 2015. Duration of focal complex, secondarily generalized tonic-clonic, and primarily generalized tonic-clonic seizures—A video-EEG analysis. Epilepsy & Behavior, 49: 111-117. [31] Drover J D, Schiff N D, Victor J D. 2010. Dynamics of coupled thalamocortical modules. Journal of Computational Neuroscience, 28: 605-616. doi: 10.1007/s10827-010-0244-5 [32] Du M, Li J, Chen L, et al. 2018. Astrocytic Kir4.1 channels and gap junctions account for spontaneous epileptic seizure. PloS Computational Biology, 14: e1005877. doi: 10.1371/journal.pcbi.1005877 [33] Dumpelmann M. 2019. Early seizure detection for closed loop direct neurostimulation devices in epilepsy. Journal of Neural Engineering, 16: 041001. doi: 10.1088/1741-2552/ab094a [34] Engel J, Pedley T A, Aicardi J. 2008. Epilepsy: A Comprehensive Textbook (Vol. 3). Lippincott Williams & Wilkins. [35] Ermentrout G B, Kopell N. 1998. Fine structure of neural spiking and synchronization in the presence of conduction delay. Proceedings of the National Academy of Sciences of the United States of America, 95: 1259-1264. doi: 10.1073/pnas.95.3.1259 [36] Fan D, Duan L, Wang Q, et al. 2017a. Combined effects of feedforward inhibition and excitation in thalamocortical circuit on the transitions of epileptic seizures. Frontiers in Computational Neuroscience, 11: 59. doi: 10.3389/fncom.2017.00059 [37] Fan D, Liao F, Wang Q. 2017b. The pacemaker role of thalamic reticular nucleus in controlling spike-wave discharges and spindles. Chaos:An Interdisciplinary Journal of Nonlinear Science, 27: 073103. doi: 10.1063/1.4991869 [38] Fan D, Liu S, Wang Q. 2016a. Stimulus-induced epileptic spike-wave discharges in thalamocortical model with disinhibition. Scientific Reports, 6: 37703. doi: 10.1038/srep37703 [39] Fan D, Wang Q, Su J, et al. 2017c. Stimulus-induced transitions between spike-wave discharges and spindles with the modulation of thalamic reticular nucleus. Journal of Computational Neuroscience, 43: 203-225. doi: 10.1007/s10827-017-0658-4 [40] Fan D, Wang Q. 2018. Improved control effect of absence seizures by autaptic connections to the subthalamic nucleus. Physical Review E, 98: 052414. doi: 10.1103/PhysRevE.98.052414 [41] Fan D, Wang Q. 2020. Closed-loop control of absence seizures inspired by feedback modulation of basal ganglia to the corticothalamic circuit. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 28: 581-590. doi: 10.1109/TNSRE.2020.2969426 [42] Fan D, Wang Z, Wang Q. 2016b. Optimal control of directional deep brain stimulation in the parkinsonian neuronal network. Communications in Nonlinear Science and Numerical Simulation, 36: 219-237. doi: 10.1016/j.cnsns.2015.12.005 [43] Fan D, Yang Z, Yang C, et al. 2021. Clinically localized seizure focus maybe not exactly the position of abating seizures: A computational evidence. Nonlinear Dynamics, 105: 1773-1789. doi: 10.1007/s11071-021-06676-w [44] Fan D, Zhang L, Wang Q. 2018. Transition dynamics and adaptive synchronization of time-delay interconnected corticothalamic systems via nonlinear control. Nonlinear Dynamics, 94: 2807-2825. doi: 10.1007/s11071-018-4526-1 [45] Fan D, Zheng Y, Yang Z, et al. 2020. Improving control effects of absence seizures using single-pulse alternately resetting stimulation (SARS) of corticothalamic circuit. Applied Mathematics and Mechanics, 41: 1287-1302. doi: 10.1007/s10483-020-2644-8 [46] Fan Z, Chen G. 2005. Pinning control of scale-free complex networks//IEEE International Symposium on Circuits and Systems, 2005: 284-287. [47] Frank T D, Richardson M J. 2010. On a test statistic for the Kuramoto order parameter of synchronization: An illustration for group synchronization during rocking chairs. Physica D:Nonlinear Phenomena, 239: 2084-2092. doi: 10.1016/j.physd.2010.07.015 [48] Freyer F, Roberts J A, Becker R, et al. 2011. Biophysical mechanisms of multistability in resting-state cortical rhythms. The Journal of Neuroscience, 31: 6353-6361. doi: 10.1523/JNEUROSCI.6693-10.2011 [49] Fröhlich F. 2016. Network Neuroscience. London: Academic Press. [50] Gao J, Feng S T, Wu B, et al. 2015. Microstructural brain abnormalities of children of idiopathic generalized epilepsy with generalized tonic-clonic seizure: A voxel-based diffusional kurtosis imaging study. Journal of Magnetic Resonance Imaging, 41(4): 1088-1095. [51] Gong J, Jiang S, Li Z, et al. 2021. Distinct effects of the basal ganglia and cerebellum on the thalamocortical pathway in idiopathic generalized epilepsy. Human Brain Mapping, 42: 3440-3449. doi: 10.1002/hbm.25444 [52] Goodfellow M, Schindler K, Baier G. 2011. Intermittent spike-wave dynamics in a heterogeneous, spatially extended neural mass model. NeuroImage, 55: 920-932. doi: 10.1016/j.neuroimage.2010.12.074 [53] Guekht A, Brodie M, Secco M. 2021. The road to a world health organization global action plan on epilepsy and other neurological disorder. Epilepsia, 62: 1057-1063. doi: 10.1111/epi.16856 [54] Guo Y, Rubin J E. 2011. Multi-site stimulation of subthalamic nucleus diminishes thalamocortical relay errors in a biophysical network model. Neural Network, 24: 602-616. doi: 10.1016/j.neunet.2011.03.010 [55] Guye M, Régis J, Tamura M, et al. 2006. The role of corticothalamic coupling in human temporal lobe epilepsy. Brain, 129: 1917-1928. doi: 10.1093/brain/awl151 [56] Hardesty D E, Sackeim H A. 2007. Deep brain stimulation in movement and psychiatric disorders. Biological Psychiatry, 61: 831-835. doi: 10.1016/j.biopsych.2006.08.028 [57] Harvey A S, Cross J H, Shinnar S, et al. 2008. Defining the spectrum of international practice in pediatric epilepsy surgery patients. Epilepsia, 49: 146-155. doi: 10.1111/j.1528-1167.2007.01421.x [58] Hauptmann C, Popovych O, Tass P A. 2005. Effectively desynchronizing deep brain stimulation based on a coordinated delayed feedback stimulation via several sites: A computational study. Biological Cybernetics, 93: 463-470. doi: 10.1007/s00422-005-0020-1 [59] He B J, Zempel J M, Snyder A Z, et al. 2010. The temporal structures and functional significance of scale-free brain activity. Neuron, 66: 353-369. doi: 10.1016/j.neuron.2010.04.020 [60] He X, Chaitanya G, Asma B, et al. 2020. Disrupted basal ganglia–thalamocortical loops in focal to bilateral tonic-clonic seizures. Brain, 143: 175-190. doi: 10.1093/brain/awz361 [61] Hodgkin A L, Huxley A F. 1952. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. Journal of Physiology, 116: 449. doi: 10.1113/jphysiol.1952.sp004717 [62] Hu B, Chen S, Chi H, et al. 2017. Controlling absence seizures by tuning activation level of the thalamus and striatum. Chaos, Solitons & Fractals, 95: 65-76. [63] Hu B, Guo Y, Zou X, et al. 2018. Controlling mechanism of absence seizures by deep brain stimulus applied on subthalamic nucleus. Cognitive Neurodynamics, 12: 103-119. doi: 10.1007/s11571-017-9457-x [64] Iasemidis L D, Sabesan S, Good L, et al. 2009. A new look into epilepsy as a dynamical disorder: Seizure prediction, resetting and control. Encyclopedia of Basic Epilepsy Research, 3: 1295-1302. [65] Inoue J, Doi S, Tsuneki R. 2003. Synchronization. Cambridge University Press. [66] Izhikevich E M. 2007. Dynamical systems in neuroscience: The geometry of excitability and bursting. Cambridge: The MIT Press. [67] Jayakar P. 1993. Physiological principles of electrical stimulation. Advances in Neurology, 63: 17-27. [68] Jedynak M, Pons A J, Ojalvo J G, et al. 2017. Temporally correlated fluctuations drive epileptiform dynamics. Neuroimage, 146: 188-196. doi: 10.1016/j.neuroimage.2016.11.034 [69] Jin X Z, Wang S F, Yang G H, et al. 2017a. Robust adaptive hierarchical insensitive tracking control of a class of leader-follower agents. Information Sciences, 406: 234-247. [70] Jin X, Wang S, Qin J, et al. 2017b. Adaptive fault-tolerant consensus for a class of uncertain nonlinear second-order multi-agent systems with circuit implementation. IEEE Transactions on Circuits and Systems I:Regular Papers, 65: 2243-2255. [71] Jirsa V K, Haken H. 1996. Field theory of electromagnetic brain activity. Physical Review Letters, 77: 960-963. doi: 10.1103/PhysRevLett.77.960 [72] Jirsa V K, Stacey W C, Quilichini P P, et al. 2014. On the nature of seizure dynamics. Brain, 137: 2210-2230. doi: 10.1093/brain/awu133 [73] Jirsch J D, Urrestarazu E, Levan P, et al. 2006. High-frequency oscillations during human focal seizures. Brain, 129: 1593-1608. doi: 10.1093/brain/awl085 [74] Kalman R E. 1963. Mathematical description of linear dynamical systems. Journal of the Society for Industrial and Applied Mathematics, Series A: Control, 1(2): 152-192. [75] Kaminski M, Ding M, Truccolo W A, et al. 2001. Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biological Cybernetics, 85: 145-157. doi: 10.1007/s004220000235 [76] Kim Y. 2017. Autaptic effects on synchrony of neurons coupled by electrical synapses. Journal of the Korean Physical Society, 71: 63-69. doi: 10.3938/jkps.71.63 [77] Kobayashi K, Akiyama T, Ohmori I, et al. 2015. Action potentials contribute to epileptic high-frequency oscillations recorded with electrodes remote from neurons. Clinical Neurophysiology, 126: 873-881. doi: 10.1016/j.clinph.2014.08.010 [78] Kostopoulos G K. 2000. Spike-and-wave discharges of absence seizures as a transformation of sleep spindles: The continuing development of a hypothesis. Clinical Neurophysiology, 111: S27-S38. doi: 10.1016/S1388-2457(00)00399-0 [79] Kostopoulos G, Gloor P, Pellegrini A, et al. 1981. A study of the transition from spindles to spike and wave discharge in feline generalized penicillin epilepsy: Microphysiological features. Experimental Neurology, 73: 55-77. doi: 10.1016/0014-4886(81)90045-5 [80] Kramer M A, Cash S S. 2012. Epilepsy as a disorder of cortical network organization. The Neuroscientist, 18: 360-372. doi: 10.1177/1073858411422754 [81] Lalo U, Palygin O, Rasooli-Nejad S, et al. 2014. Exocytosis of atp from astrocytes modulates phasic and tonic inhibition in the neocortex. PLoS Biology, 12: e1001747. doi: 10.1371/journal.pbio.1001747 [82] Lee J, Song K, Lee K, et al. 2013. Sleep spindles are generated in the absence of T-type calcium channel-mediated low-threshold burst firing of thalamocortical neurons. Proceedings of the National Academy of Sciences, 110: 20266-20271. doi: 10.1073/pnas.1320572110 [83] Leyden K M, Kucukboyaci N E, Puckett O K, et al. 2015. What does diffusion tensor imaging (DTI) tell us about cognitive networks in temporal lobe epilepsy? Quantitative Imaging in Medicine and Surgery, 5: 247. [84] Li J, Wang R, Du M, et al. 2016. Dynamic transition on the seizure-like neuronal activity by astrocytic calcium channel block. Chaos, Solitons & Fractals, 91: 702-708. [85] Li J, Tang J, Ma J, et al. 2016. Dynamic transition of neuronal firing induced by abnormal astrocytic glutamate oscillation. Scientific Reports, 6: 32343. doi: 10.1038/srep32343 [86] Liao W, Zhang Z, Pan Z, et al. 2011. Default mode network abnormalities in mesial temporal lobe epilepsy: A study combining fMRI and DTI. Human Brain Mapping, 32: 883-895. doi: 10.1002/hbm.21076 [87] Liley D T, Matthew W. 2013. The mesoscopic modeling of burst suppression during anesthesia. Frontiers in Computational Neuroscience, 7: 46. [88] Liu Y Y, Slotine J J, Barabasi A L. 2011. Controllability of complex networks. Nature, 473: 167-173. doi: 10.1038/nature10011 [89] Lopes da Silva F H, Pijn J P, Wadman W J. 1994. Dynamics of local neuronal networks: Control parameters and state bifurcations in epileptogenesis. Progress in Brain Research, 102: 359-370. doi: 10.1016/s0079-6123(08)60552-x [90] Lopes da Silva F L, Blanes W, Kalitzin S N, et al. 2003a. Epilepsies as dynamical diseases of brain systems: basic models of the transition between normal and epileptic activity. Epilepsia, 44: 72-83. doi: 10.1111/j.0013-9580.2003.12005.x [91] Lopes da Silva F, Blanes W, Kalitzin S, et al. 2003b. Dynamical diseases of brain systems: Different routes to epileptic seizures. IEEE Transactions on Biomedical Engineering, 50: 540-548. doi: 10.1109/TBME.2003.810703 [92] Luenberger D G. 1979. Introduction to dynamic systems: Theory, models, and applications (No. 04; QA402, L8. ). [93] Mackey M C and Milton J G. 1987. Dynamical disease. Annals of the New York Academy of Sciences, 504: 16-32. [94] Markoula S, Chaudhary U J, Perani S, et al. 2018. The impact of mapping interictal discharges using EEG-fMRI on the epilepsy presurgical clinical decision making process: A prospective study. Seizure, 61: 30-37. doi: 10.1016/j.seizure.2018.07.016 [95] Marten F, Rodrigues S, Benjamin O, et al. 2009. Onset of polyspike complexes in a mean-field model of human electroencephalography and its application to absence epilepsy. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 367: 1145-1161. doi: 10.1098/rsta.2008.0255 [96] Matsumoto H, Marsan C A. 1964. Cortical cellular phenomena in experimental epilepsy: Ictal manifestations. Experimental Neurology, 9: 305-326. doi: 10.1016/0014-4886(64)90026-3 [97] Mayville C, Fakhoury T, Abou-Khalil B. 2000. Absence seizures with evolution into generalized tonic-clonic activity: Clinical and EEG features. Epilepsia, 41: 391-394. doi: 10.1111/j.1528-1157.2000.tb00178.x [98] Meeren H K M, Pijn J P M, Van Luijtelaar E L J M, et al. 2002. Cortical focus drives widespread corticothalamic networks during spontaneous absence seizures in rats. Journal of Neuroscience, 22: 1480-1495. doi: 10.1523/JNEUROSCI.22-04-01480.2002 [99] Meeren H, van Luijtelaar G, da Silva F L, et al. 2005. Evolving concepts on the pathophysiology of absence seizures: The cortical focus theory. Archives of Neurology, 62: 371-376. doi: 10.1001/archneur.62.3.371 [100] Merrill D R, Bikson M, Jefferys J G R. 2005. Electrical stimulation of excitable tissue: Design of efficacious and safe protocols. Journal of Neuroscience Methods, 141: 171-198. doi: 10.1016/j.jneumeth.2004.10.020 [101] Milo R, Shen-Orr S, Itzkovitz S, et al. 2002. Network motifs: Simple building blocks of complex networks. Science, 298: 824-827. doi: 10.1126/science.298.5594.824 [102] Milton J G, Black D. 1995. Dynamic diseases in psychiatry and neurology. Chaos, 5: 8-13. doi: 10.1063/1.166103 [103] Miocinovic S, Lempka S F, Russo G S, et al. 2009. Experimental and theoretical characterization of the voltage distribution generated by deep brain stimulation. Experimental Neurology, 216: 166-176. doi: 10.1016/j.expneurol.2008.11.024 [104] Morgan R J, Soltesz I. 2008. Nonrandom connectivity of the epileptic dentate gyrus predicts a major role for neuronal hubs in seizures. Proceedings of the National Academy of Sciences, 105: 6179-6184. doi: 10.1073/pnas.0801372105 [105] Neishabouri A, Faisal A A. 2014. Axonal noise as a source of synaptic variability. PLoS Computational Biology, 10: e1003615. doi: 10.1371/journal.pcbi.1003615 [106] Nelson T S, Suhr C L, Freestone D R, et al. 2011. Closed-loop seizure control with very high frequency electrical stimulation at seizure onset in the GAERS model of absence epilepsy. International Journal of Neural Systems, 21: 163-173. doi: 10.1142/S0129065711002717 [107] Neubrandt M, Oláh V J, Brunner J, et al. 2017. Feedforward inhibition is randomly wired from individual granule cells onto CA3 pyramidal cells. Hippocampus, 27: 1034-1039. doi: 10.1002/hipo.22763 [108] Olufsen M, Whittington M, Camperi M, et al. 2003. New functions for the gamma rhythm: population tuning and preprocessing for the beta rhythm. Journal of Computational Neuroscience, 14: 33-54. doi: 10.1023/A:1021124317706 [109] Palmigiano A, Geisel T, Wolf F, et al. 2017. Flexible information routing by transient synchrony. Nature Neuroscience, 20: 1014-1022. doi: 10.1038/nn.4569 [110] Panzica F, Varotto G, Rotondi F, et al. 2013. Identification of the epileptogenic zone from stereo-EEG signals: A connectivity-graph theory approach. Frontiers in Neurology, 4: 175. [111] Paz J T, Davidson T J, Frechette E S, et al. 2013. Closed-loop optogenetic control of thalamus as a tool for interrupting seizures after cortical injury. Nature Neuroscience, 16: 64. doi: 10.1038/nn.3269 [112] Paz J T, Huguenard J R. 2015. Microcircuits and their interactions in epilepsy: Is the focus out of focus? Nature Neuroscience, 18: 351-359. doi: 10.1038/nn.3950 [113] Picardo M A, Guigue P, Bonifazi P, et al. 2011. Pioneer GABA cells comprise a subpopulation of hub neurons in the developing hippocampus. Neuron, 71: 695-709. doi: 10.1016/j.neuron.2011.06.018 [114] Pinsky P F, Rinzel J. 1994. Intrinsic and network rhythmogenesis in a reduced Traub model for CA3 neurons. Journal of Computational Neuroscience, 1: 39-60. doi: 10.1007/BF00962717 [115] Pizzo F, Roehri N, Giusiano B, et al. 2021. The ictal signature of thalamus and basal ganglia in focal epilepsy: A seeg study. Neurology, 96: e280-e293. doi: 10.1212/WNL.0000000000011003 [116] Popovych O V, Tass P A. 2018. Multisite delayed feedback for electrical brain stimulation. Frontiers in Physiology, 9: 46. doi: 10.3389/fphys.2018.00046 [117] Quiroga R Q, Kreuz T, Grassberger P. 2002. Event synchronization: A simple and fast method to measure synchronicity and time delay patterns. Physical Review E, 66: 041904. doi: 10.1103/PhysRevE.66.041904 [118] Ratnadurai-Giridharan S, Stefanescu R A, Khargonekar P P, et al. 2014. Genesis of interictal spikes in the CA1: A computational investigation. Front Neural Circuits, 8: 2. doi: 10.3389/fncir.2014.00002 [119] Ratnadurai-Giridharan S, Stefanescu R A, Khargonekar P P, et al. 2012. Genesis of interictal spikes in the CA1: A computational investigation. BMC Neuroscience, 13: P30. doi: 10.1186/1471-2202-13-S1-P30 [120] Rektor I, Kuba R, Brázdil M, et al. 2012. Do the basal ganglia inhibit seizure activity in temporal lobe epilepsy? Epilepsy & Behavior, 25: 56-59. [121] Robinson P A, Rennie C J, Wright J J, et al. 1998. Steady states and global dynamics of electrical activity in the cerebral cortex. Physical Review E, 58: 3557. doi: 10.1103/PhysRevE.58.3557 [122] Rodrigues S, Barton D, Szalai R, et al. 2009. Transitions to spike-wave oscillations and epileptic dynamics in a human cortico-thalamic mean-field model. Journal of Computational Neuroscience, 27: 507-526. doi: 10.1007/s10827-009-0166-2 [123] Rodrigues S, Gonçalves J, Terry J R. 2007. Existence and stability of limit cycles in a macroscopic neuronal population model. Physica D:Nonlinear Phenomena, 233: 39-65. doi: 10.1016/j.physd.2007.06.010 [124] Rosch R, Baldeweg T, Moeller F, et al. 2017. Network dynamics in the healthy and epileptic developing brain. Network Neuroscience, 2: 41-59. [125] Salem K M I, Goodger L, Bowyer K, et al. 2016. Does transcranial stimulation for motor evoked potentials (TcMEP) worsen seizures in epileptic patients following spinal deformity surgery? European Spine Journal, 25: 3044-3048. doi: 10.1007/s00586-015-3993-z [126] Scharfman H E, Goodman J H, Sollas A L. 1999. Actions of Brain-derived neurotrophic factor in slices from rats with spontaneous seizures and mossy fiber sprouting in the dentate gyrus. The Journal of Neuroscience, 19: 5619-5631. doi: 10.1523/JNEUROSCI.19-13-05619.1999 [127] Scharfman H E. 2007. The CA3 “backprojection” to the dentate gyrus. Progress in Brain Research, 163: 627-637. [128] Scharfman H E. 2016. The enigmatic mossy cell of the dentate gyrus. Nature Reviews Neuroscience, 17: 562-575. doi: 10.1038/nrn.2016.87 [129] Schiff S J, Colella D, Jacyna G M, et al. 2000. Brain chirps: Spectrographic signatures of epileptic seizures. Clinical Neurophysiology, 111: 953-958. doi: 10.1016/S1388-2457(00)00259-5 [130] Schiller Y, Bankirer Y. 2007. Cellular mechanisms underlying antiepileptic effects of low-and high-frequency electrical stimulation in acute epilepsy in neocortical brain slices in vitro. Journal of Neurophysiology, 97: 1887-1902. doi: 10.1152/jn.00514.2006 [131] Shaari H M, Haerian B S, Baum L, et. Al. 2016. Association of BDNF polymorphisms with the risk of epilepsy: A multicenter study. Molecular Neurobiology, 53: 2869-2877. doi: 10.1007/s12035-015-9150-1 [132] Sharma N K, Pedreira C, Chaudhary U J, et al. 2019. BOLD mapping of human epileptic spikes recorded during simultaneous intracranial EEG-fMRI: The impact of automated spike classification. Neuroimage, 184: 981-992. doi: 10.1016/j.neuroimage.2018.09.065 [133] Shih T T, Hirsch L J. 2003. Tonic-Absence seizures: An underrecognized seizure type. Epilepsia, 44: 461-465. doi: 10.1046/j.1528-1157.2003.39602.x [134] Shouse M N, Farber P R, Staba R J. 2000. Physiological basis: How NREM sleep components can promote and REM sleep components can suppress seizure discharge propagation. Clinical Neurophysiology, 111: S9-S18. doi: 10.1016/S1388-2457(00)00397-7 [135] Siapas A G, Wilson M A. 1998. Coordinated interactions between hippocampal ripples and cortical spindles during slow-wave sleep. Neuron, 21: 1123-1128. doi: 10.1016/S0896-6273(00)80629-7 [136] Sitnikova E, Hramov A E, Grubov V, et al. 2014. Time-frequency characteristics and dynamics of sleep spindles in WAG/Rij rats with absence epilepsy. Brain Research, 1543: 290-299. doi: 10.1016/j.brainres.2013.11.001 [137] Sitnikova E, Hramov A E, Grubov V, et al. 2016. Rhythmic activity in EEG and sleep in rats with absence epilepsy. Brain Research Bulletin, 120: 106-116. doi: 10.1016/j.brainresbull.2015.11.012 [138] Sitnikova E. 2010. Thalamo-cortical mechanisms of sleep spindles and spike-wave discharges in rat model of absence epilepsy (a review). Epilepsy Research, 89(1): 17-26. [139] Slaght S J, Paz T, Mahon S, et al. 2002. Functional organization of the circuits connecting the cerebral cortex and the basal ganglia: Implications for the role of the basal ganglia in epilepsy. Epileptic Disorders, 4: 9-22. [140] Slotine J J E, Li W. 1991. Applied Nonlinear Control (Vol. 199, No. 1). Englewood Cliffs, NJ: Prentice hall. [141] Sporns O, Kotter R, Friston K J. 2004. Motifs in brain networks. PLoS Biology, 2: e369. doi: 10.1371/journal.pbio.0020369 [142] Steriade M, Deschenes M, Domich L, et al. 1985. Abolition of spindle oscillations in thalamic neurons disconnected from nucleus reticularis thalami. Journal of Neurophysiology, 54: 1473-1497. doi: 10.1152/jn.1985.54.6.1473 [143] Steriade M, Domich L, Oakson G, et al. 1987. The deafferented reticular thalamic nucleus generates spindle rhythmicity. Journal of Neurophysiology, 57: 260-273. doi: 10.1152/jn.1987.57.1.260 [144] Su Y, Radman T, Vaynshteyn J, et al. 2008. Effects of high-frequency stimulation on epileptiform activity in vitro: ON/OFF control paradigm. Epilepsia, 49: 1586-1593. doi: 10.1111/j.1528-1167.2008.01592.x [145] Suffczynski P, Kalitzin S, Da Silva F L. 2004. Dynamics of non-convulsive epileptic phenomena modeled by a bistable neuronal network. Neuroscience, 126: 467-484. doi: 10.1016/j.neuroscience.2004.03.014 [146] Suffczynski P, Kalitzin S, Lopes Da Silva F, et al. 2008. Active paradigms of seizure anticipation: Computer model evidence for necessity of stimulation. Physical Review E, 78: 051917. doi: 10.1103/PhysRevE.78.051917 [147] Sun X, Lei J, Perc M, et al. 2011. Effects of channel noise on firing coherence of small-world Hodgkin-Huxley neuronal networks. The European Physical Journal B, 79: 61-66. doi: 10.1140/epjb/e2010-10031-3 [148] Sun X, Perc M, Lu Q, et al. 2010. Effects of correlated Gaussian noise on the mean firing rate and correlations of an electrically coupled neuronal network. Chaos, 20: 033116. doi: 10.1063/1.3483876 [149] Tang E, Ju H, Baum G L, et al. 2020. Control of brain network dynamics across diverse scales of space and time. Physical Review E, 101: 062301. [150] Tass P A, Qin L, Hauptmann C, et al. 2013. Coordinated reset has sustained aftereffects in Parkinsonian monkeys. Annals of Neurology, 72: 816-820. [151] Tass P A, Silchenko A N, Hauptmann C, et al. 2009. Long-lasting desynchronization in rat hippocampal slice induced by coordinated reset stimulation. Physical Review E, 80: 011902. doi: 10.1103/PhysRevE.80.011902 [152] Taxidis J, Coombes S, Mason R, et al. 2012. Modeling sharp wave-ripple complexes through a CA3-CA1 network model with chemical synapses. Hippocampus, 22: 995-1017. doi: 10.1002/hipo.20930 [153] Taylor P N, Baier G. 2011. A spatially extended model for macroscopic spike-wave discharges. Journal of Computational Neuroscience, 31: 679-684. doi: 10.1007/s10827-011-0332-1 [154] Taylor P N, Thomas J, Sinha N, et al. 2015. Optimal control based seizure abatement using patient derived connectivity. Frontiers in Neuroscience, 9: 202. [155] Taylor P N, Wang Y, Goodfellow M, et al. 2014. A computational study of stimulus driven epileptic seizure abatement. PLoS One, 9: 114316. doi: 10.1371/journal.pone.0114316 [156] Temprana S G, Mongiat L A, Yang S M, et al. 2014. Delayed coupling to feedback inhibition during a critical period for the integration of adult-born granule cells. Neuron, 85: 116-130. [157] Toprani S, Durand D M. 2013. Long-lasting hyperpolarization underlies seizure reduction by low frequency deep brain electrical stimulation. The Journal of Physiology, 591: 5765-5790. doi: 10.1113/jphysiol.2013.253757 [158] Tort A B, Kramer M A, Thorn C, et al. 2008. Dynamic cross-frequency couplings of local field potential oscillations in rat striatum and hippocampus during performance of a T-maze task. Proceedings of the National Academy of Sciences of the United States of America, 105: 20517-20522. doi: 10.1073/pnas.0810524105 [159] Touboul J, Hermann G, Faugeras O. 2011. Noise-induced behaviors in neural mean field dynamics. SIAM Journal on Applied Dynamical Systems, 11: 49-81. [160] Traub R D, Bibbig A. 2000. A model of high-frequency ripples in the hippocampus based on synaptic coupling plus axon-axon gap junctions between pyramidal neurons. Journal of Neuroscience, 20: 2086-2093. doi: 10.1523/JNEUROSCI.20-06-02086.2000 [161] Van D W, Lee H C, Hereld M, et al. 2005. Emergent epileptiform activity in neural networks with weak excitatory synapses. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 13: 236-241. doi: 10.1109/TNSRE.2005.847387 [162] Van Mierlo P, Carrette E, Hallez H, et al. 2011. Accurate epileptogenic focus localization through time-variant functional connectivity analysis of intracranial electroencephalographic signals. Neuroimage, 56: 1122-1133. doi: 10.1016/j.neuroimage.2011.02.009 [163] Vercueil L, Benazzouz A, Deransart C, et al. 1998. High-frequency stimulation of the sub-thalamic nucleus suppresses absence seizures in the rat: comparison with neurotoxic lesions. Epilepsy Research, 31: 39-46. doi: 10.1016/S0920-1211(98)00011-4 [164] Verghese J, Rapin I. 2014. Subcortical epilepsy? Neurology, 82: 373-373. doi: 10.1212/01.wnl.0000443818.22087.0d [165] Von Krosigk M, Bal T, McCormick D A. 1993. Cellular mechanisms of a synchronized oscillation in the thalamus. Science, 261: 361-364. doi: 10.1126/science.8392750 [166] Wang W X, Ni X, Lai Y C, et al. 2012. Optimizing controllability of complex networks by minimum structural perturbations. Physical Review E, 85: 026115. doi: 10.1103/PhysRevE.85.026115 [167] Wang X J, Buzs´aki G. 1996. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. Journal of Neuroscience, 16: 6042-6413. [168] Wang Z, Wang Q. 2017. Eliminating absence seizures through the deep brain stimulation to thalamus reticular nucleus. Frontiers in Computational Neuroscience, 11: 22. [169] Wang Z, Wang Q. 2019. Stimulation strategies for absence seizures: Targeted therapy of the focus in coupled thalamocortical model. Nonlinear Dynamics, 96: 1649-1663. doi: 10.1007/s11071-019-04876-z [170] Wendling F, Bartolomei F, Bellanger J J, et al. 2002. Epileptic fast activity can be explained by a model of impaired GABAergic dendritic inhibition. European Journal of Neuroscience, 15: 1499-1508. doi: 10.1046/j.1460-9568.2002.01985.x [171] Wendling F, Bellanger J J, Bartolomei F, et al. 2000. Relevance of nonlinear lumped-parameter models in the analysis of depth-EEG epileptic signals. Biological Cybernetics, 83: 367-378. doi: 10.1007/s004220000160 [172] Wendling F, Benquet P, Bartolomei F, et al. 2016. Computational models of epileptiform activity. Journal of Neuroscience Methods, 260: 233-251. doi: 10.1016/j.jneumeth.2015.03.027 [173] Wiles L, Gu S, Pasqualetti F, et al. 2017. Autaptic connections shift network excitability and bursting. Scientific Reports, 7: 44006. doi: 10.1038/srep44006 [174] Wilke C, Van Drongelen W, Kohrman M, et al. 2009. Identification of epileptogenic foci from causal analysis of ECoG interictal spike activity. Clinical Neurophysiology, 120: 1449-1456. doi: 10.1016/j.clinph.2009.04.024 [175] Wilke C, Worrell G, He B. 2011. Graph analysis of epileptogenic networks in human partial epilepsy. Epilepsia, 52: 84-93. doi: 10.1111/j.1528-1167.2010.02785.x [176] Womelsdorf T, Valiante T A, Sahin N T, et al. 2014. Dynamic circuit motifs underlying rhythmic gain control, gating and integration. Nature Neuroscience, 17: 1031-1039. doi: 10.1038/nn.3764 [177] Worrell G A, Jerbi K, Kobayashi K, et al. 2012. Recording and analysis techniques for high-frequency oscillations. Progress in Neurobiology, 98: 265-278. doi: 10.1016/j.pneurobio.2012.02.006 [178] Xu Y, Ying H, Jia Y, et al. 2017. Autaptic regulation of electrical activities in neuron under electromagnetic induction. Scientific Reports, 7: 43452. doi: 10.1038/srep43452 [179] Yang C, Luan G, Wang Q, et al. 2018. Localization of epileptogenic zone with the correction of pathological networks. Frontiers in Neurology, 9: 143. doi: 10.3389/fneur.2018.00143 [180] Yuen G L, Durand D. 1991. Reconstruction of hippocampal granule cell electrophysiology by computer simulation. Neuroscience, 41: 411-423. doi: 10.1016/0306-4522(91)90337-N [181] Zhang L Y, Fan D G, Wang Q Y, Baier, G. 2018a. Effects of brain-derived neurotrophic factor and noise on transitions of temporal lobe epilepsy in a hippocampal network. Chaos, 28: 106322. doi: 10.1063/1.5036690 [182] Zhang L Y, Fan D G, Wang Q Y. 2017. Transitions dynamics of a dentate gyrus-CA3 neuronal network during temporal lobe epilepsy. Frontiers in Computational Neuroscience, 11: 61. doi: 10.3389/fncom.2017.00061 [183] Zhang L Y, Fan D G, Wang Q Y. 2018b. Synchronous high-frequency oscillations in inhibitory-dominant network motifs consisting of three dentate gyrus-CA3 systems. Chaos, 28: 063101. doi: 10.1063/1.5017012 [184] Zhang L Y, Wang Q Y, Baier G. 2020a. Dynamical features of a focal epileptogenic network model for stimulation-based control. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 28: 1856-1865. doi: 10.1109/TNSRE.2020.3002350 [185] Zhang L Y, Wang Q Y, Baier G. 2020b. Spontaneous transitions to focal-onset epileptic seizures: A dynamical study. Chaos, 30: 103114. doi: 10.1063/5.0021693 [186] Zhang T, Zhang Y, Ren J, et al. 2021. Aberrant basal ganglia-thalamo-cortical network topology in juvenile absence epilepsy: A resting-state EEG-fMRI study. Seizure, 84: 78-83. doi: 10.1016/j.seizure.2020.11.015 [187] Zou Y, Chen G. 2009. Choosing effective controlled nodes for scale-free network synchronization. Physica A, 388: 2931-2940. doi: 10.1016/j.physa.2009.03.040 -




 下载:
下载: