-
摘要: 断裂力学是工程材料和结构的疲劳与断裂分析、损伤容限设计和结构完整性评定的理论基础. 应力强度因子作为线弹性裂纹尖端奇异场的单一表征参量和裂纹扩展驱动力, 在裂纹体的断裂力学分析中发挥着关键作用. 权函数法为复杂受载裂纹体的应力强度因子求解计算提供了强有力的解析工具, 不但具有远高于各类数值解法的计算效率, 而且精度可靠, 使用方便. 本文结合笔者团队在权函数法方面的长期研究工作, 对该方法自20世纪70年代初提出至今半个世纪以来, 国际断裂界在二维和三维权函数理论与应用方面的主要研究进展作了回顾和评述, 并对其未来发展提出了展望. 主要内容涵盖: 当前国际断裂界广泛应用的3种二维裂纹解析权函数法简介和以格林函数为基准的验证评价; 三维裂纹问题的片条合成权函数法和点载荷权函数法; 权函数法在复杂受载裂纹体的应力强度因子和裂纹张开位移等关键力学参量计算、内聚力/桥连等裂纹模型分析、共线多裂纹权函数理论及其在剩余强度预测等方面的应用, 以及复杂裂纹几何的工程化权函数分析和权函数法的反向应用问题.Abstract: Fracture mechanics is the theoretical foundation for fatigue and fracture analyses of engineering materials and structures, damage tolerance design, and structural integrity assessment. Being the single characterizing parameter of the linear elastic crack tip singular stress/strain field and the crack deriving force, the stress intensity factor (SIF) plays a vital role in fracture mechanics analysis. The weight function method (WFM) is a powerful method for the determination of SIFs for cracks under complex load conditions, with remarkable computational efficiency and reliable solution accuracy, and is easy to use. Combined with the authors’ teamwork on WFM research in the past several decades, this article presents a comprehensive review of the historical developments of various WFMs over the past 50 years and also a brief outlook. The main topics include: a brief introduction of three types of analytical weight function approaches for 2D crack problems and accuracy verification based on Green’s functions; the slice synthesis weight function method and the point weight function method for 3D crack problems; various practical applications of WFMs, including determination of the key fracture mechanics parameters of SIFs and crack opening displacements under complex loadings, cohesive/bridging model analyses, WFM for multiple collinear cracks and residual strength prediction of panels containing multiple site damage, engineering weight function approaches to complex crack configurations, and inverse application of WFM for the determination of stress distributions in un-cracked bodies.
-
图 1 推动断裂力学和损伤容限设计准则发展的“里程碑”事故. (a)斯克内克塔迪自由轮在平静的港湾中整体断裂为两段(Tetelman & McEvily 1967), 该事故引起人们对裂纹尖端场的关注与研究; (b) 锻造缺陷引起的裂纹导致美国空军F-111战斗轰炸机机翼断裂坠毁, 该事故推动了损伤容限设计准则和规范的建立(Wanhill 2003); (c) 多位置损伤MSD导致阿罗哈航空公司波音737-200机身压力舱上部蒙皮被撕脱,该事故改变了大型运输机的适航规范 (Wanhill 2003, FAA 2010); (d) 疲劳裂纹导致CF6-6D航空发动机钛合金一级风扇盘破裂, DC-10客机坠毁(McEvily 2002), 它推动了发动机损伤容限设计准则和规范的建立.
图 14 无限板孔边径向单裂纹, 用Jin 等 (2017)权函数计算得到的两种载荷下的K值与其他方法的比较.
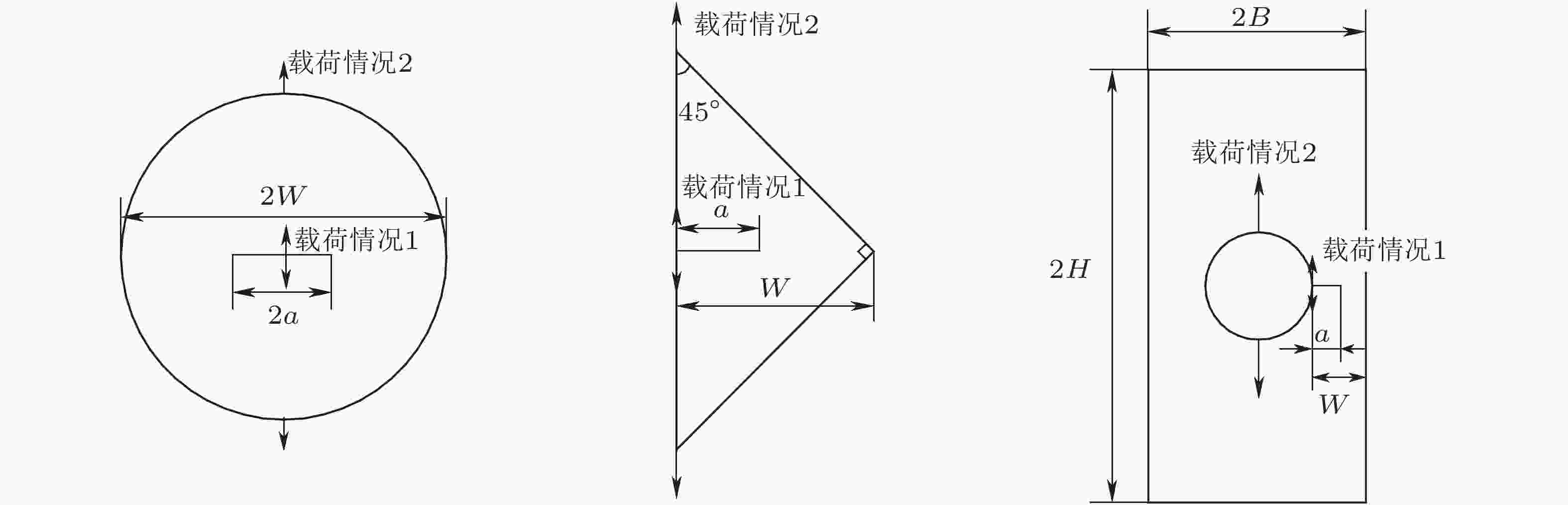
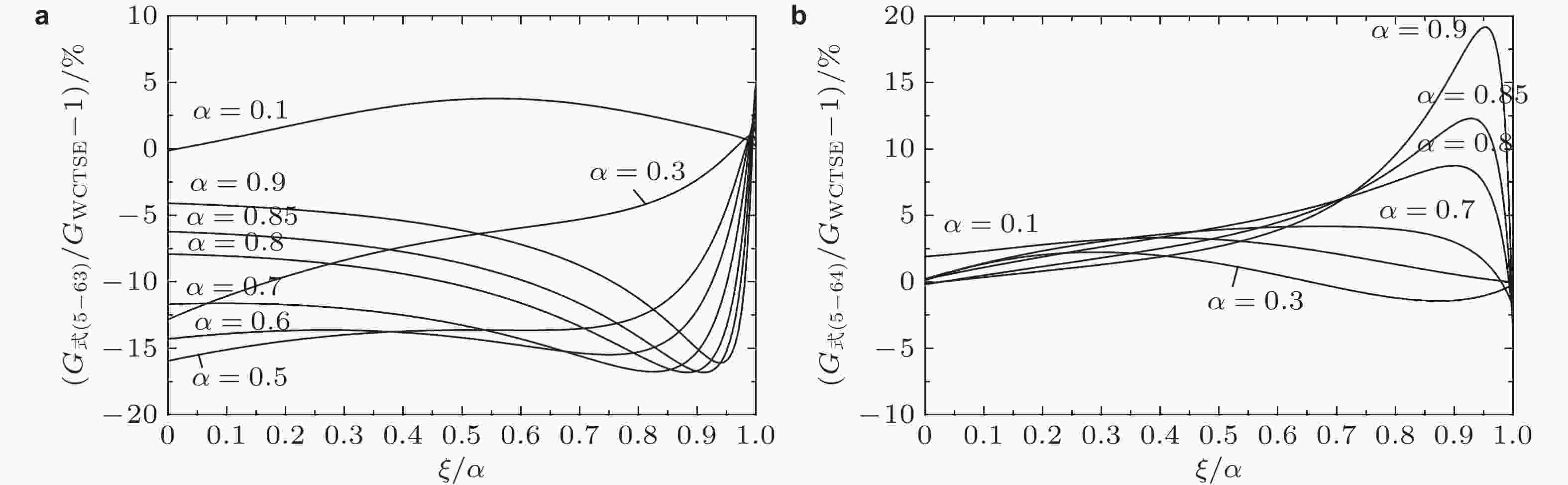
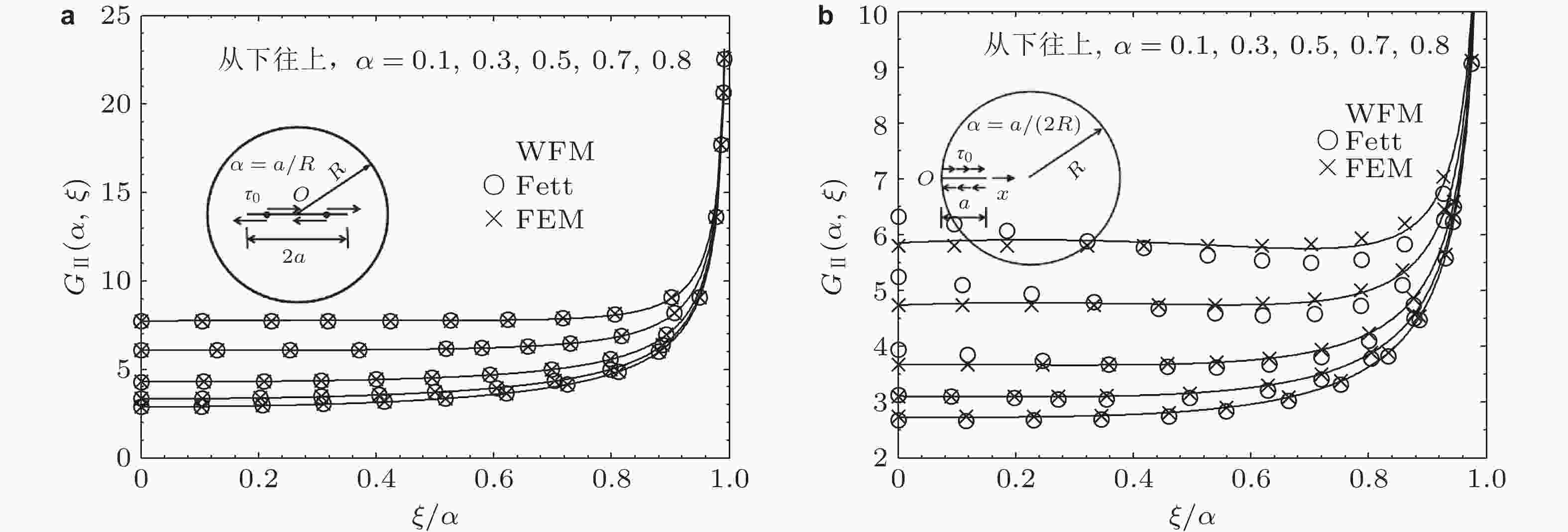
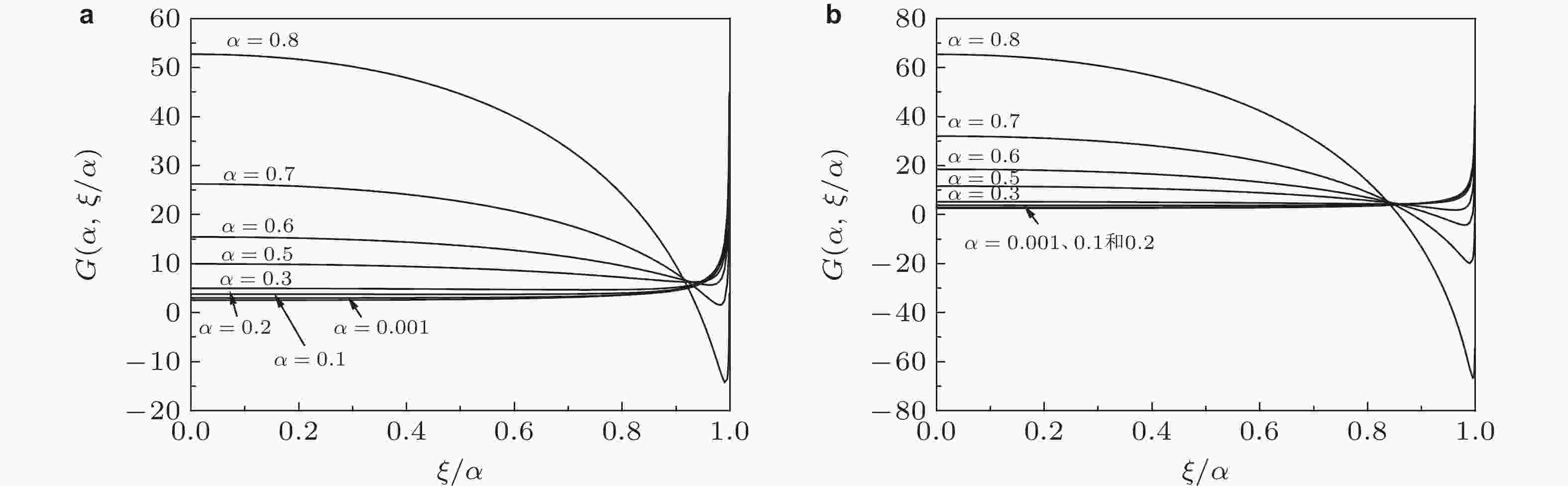
图 22 圆盘中心和边缘裂纹的三种II型格林函数结果比较. (a) 中心裂纹, (b) 边缘裂纹 (Xu et al. 2020a)
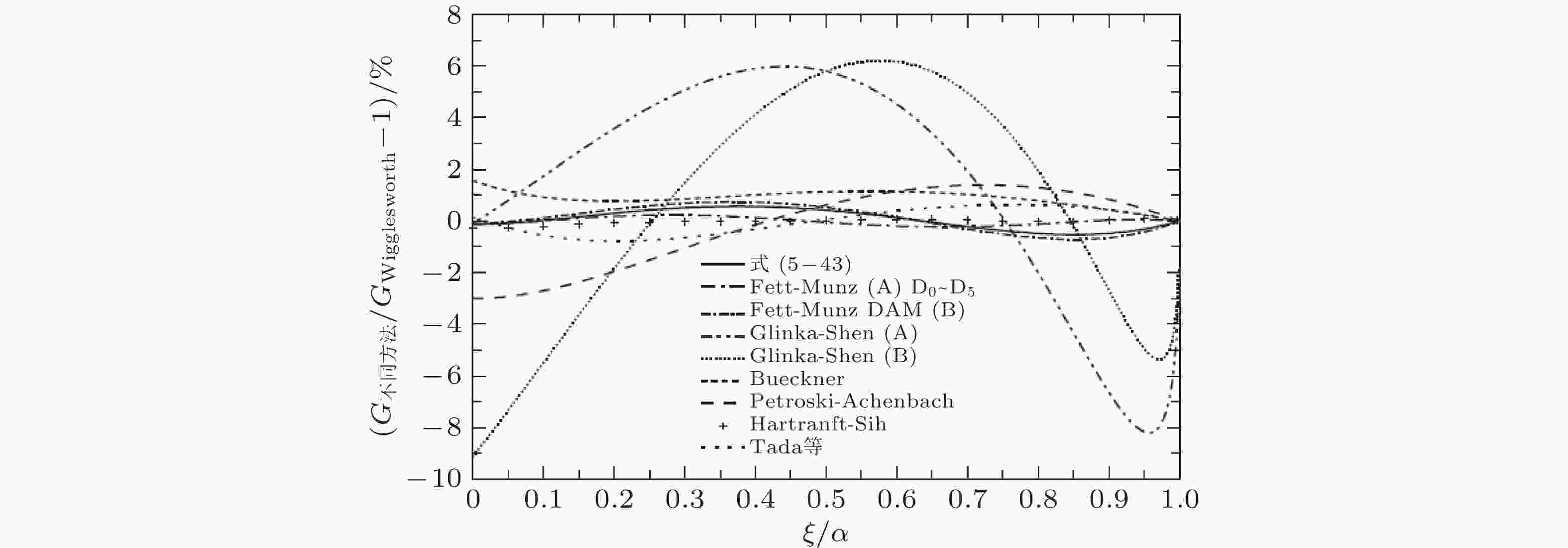
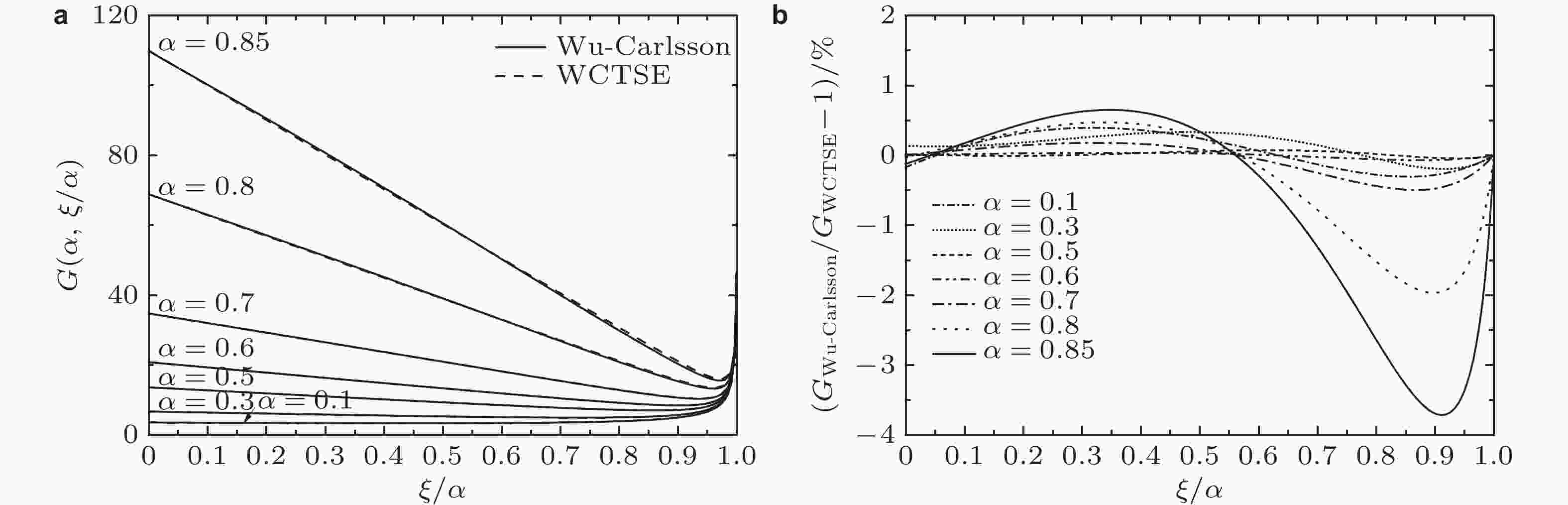
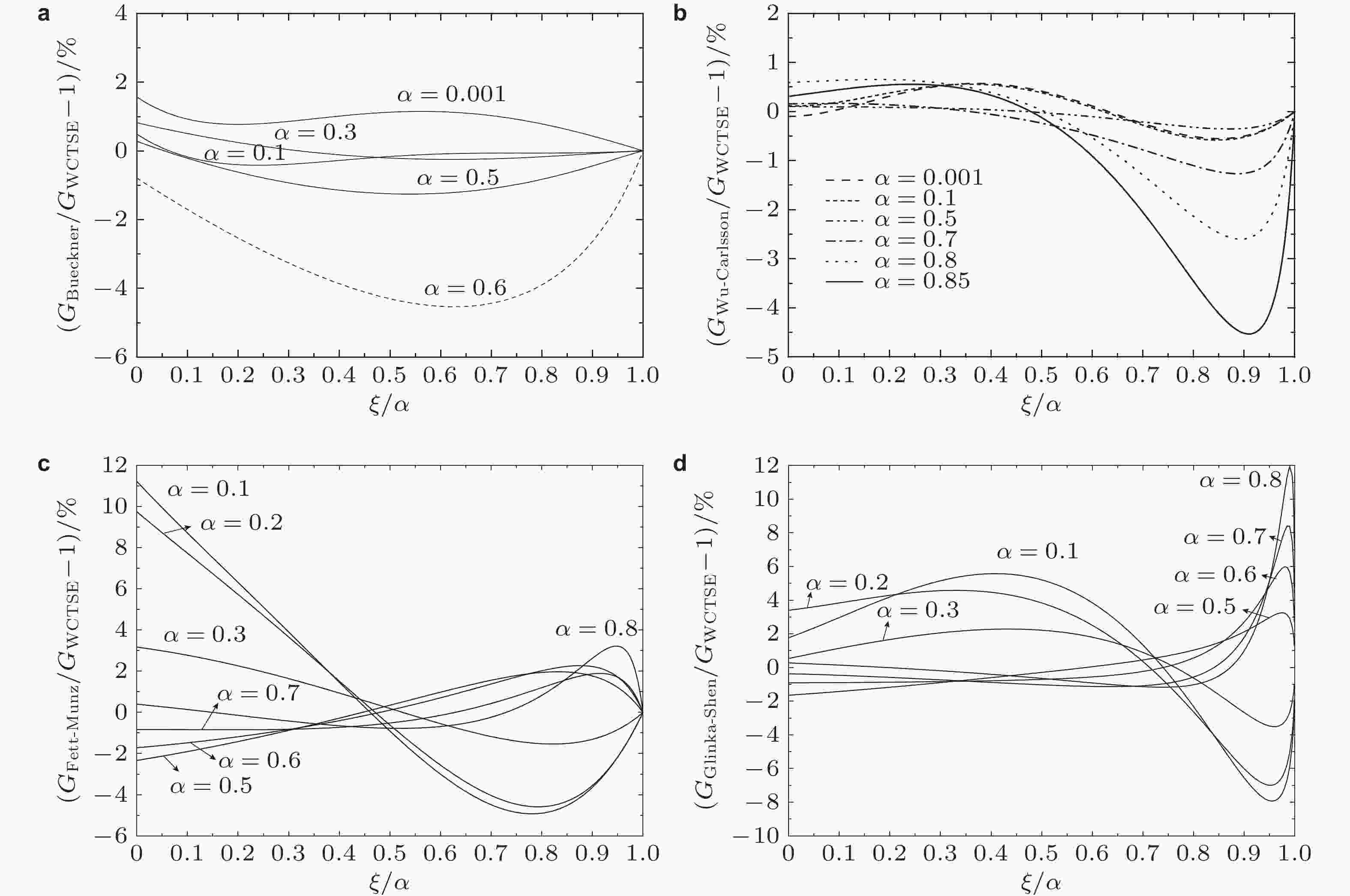
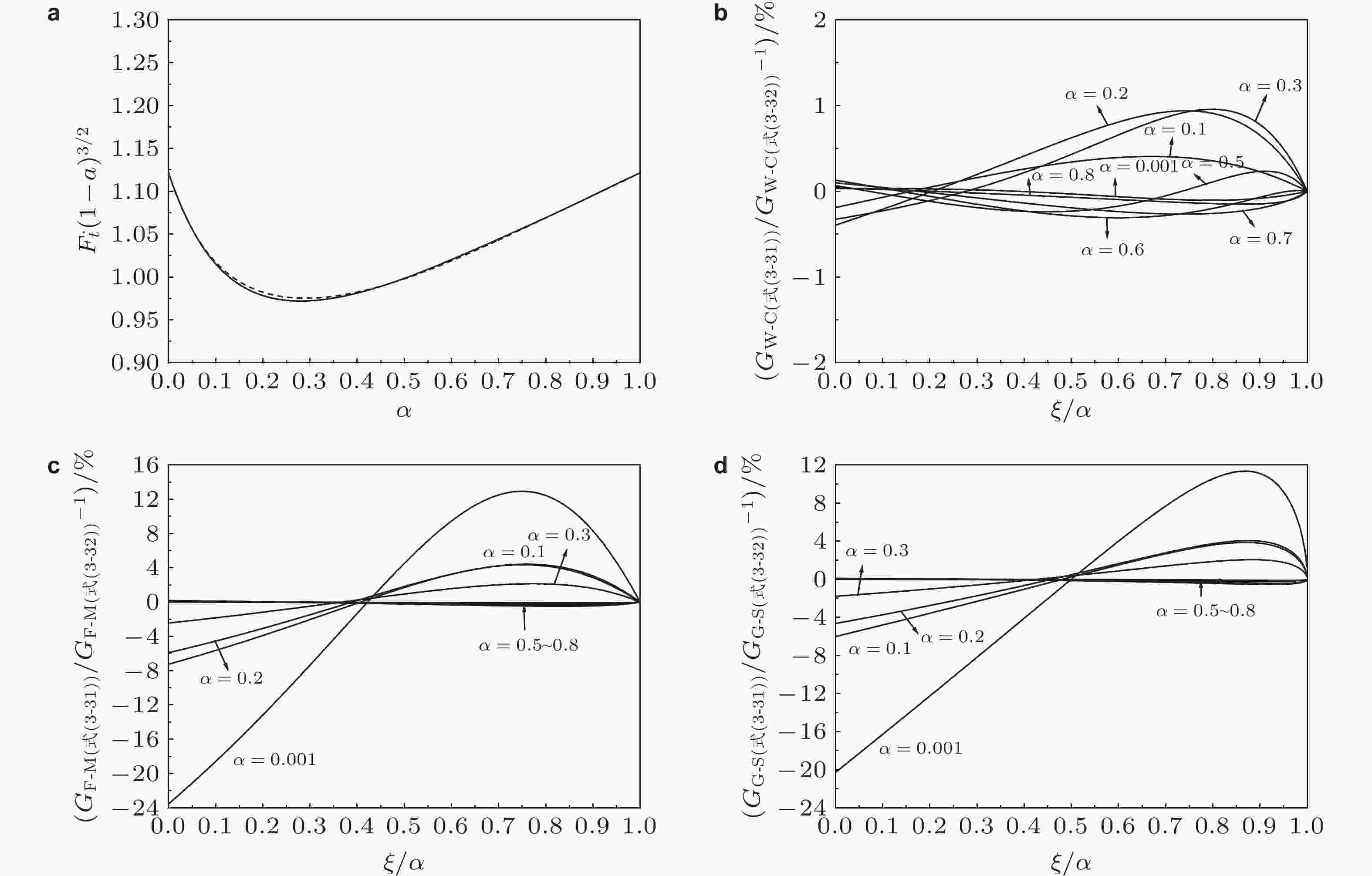
图 27 三种权函数法对有限宽板单边缘裂纹参考解精度的敏感性比较(吴学仁等2019). (a) 远方拉伸的两个无量纲应力强度因子曲线, (b) Wu-Carlsson, (c) Fett-Munz, (d) Glinka-Shen
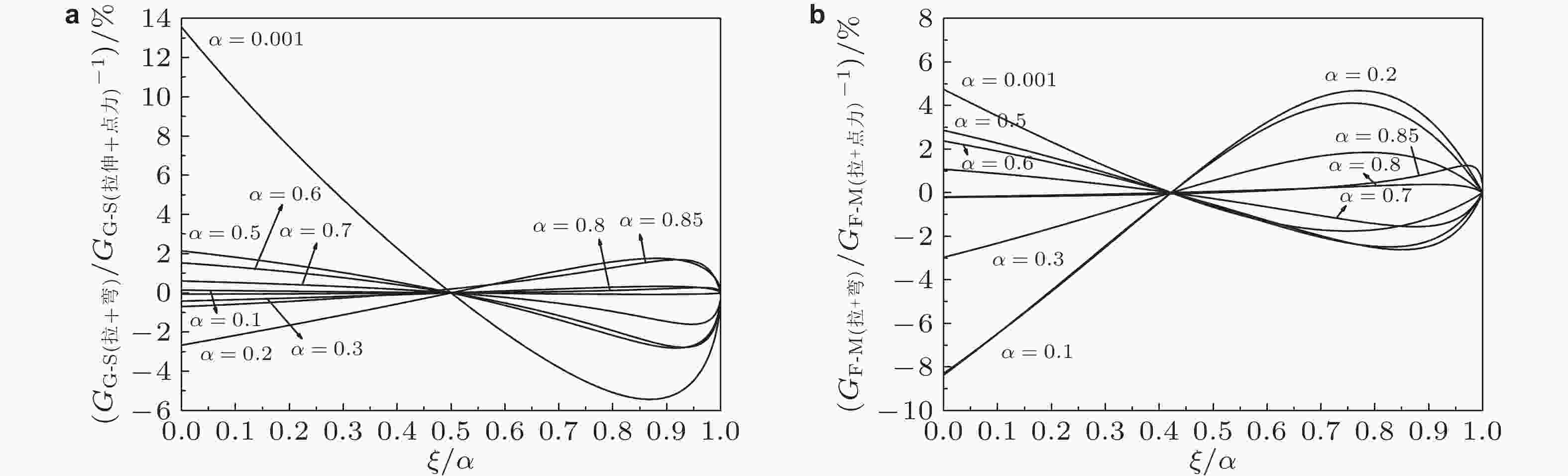
图 28 由Glinka-Shen通用权函数法得到的有限板单边缘裂纹格林函数(采用几何条件m´ = 0). 参考载荷: (a) 拉伸+弯曲, (b) 拉伸+集中力 (吴学仁等2019)
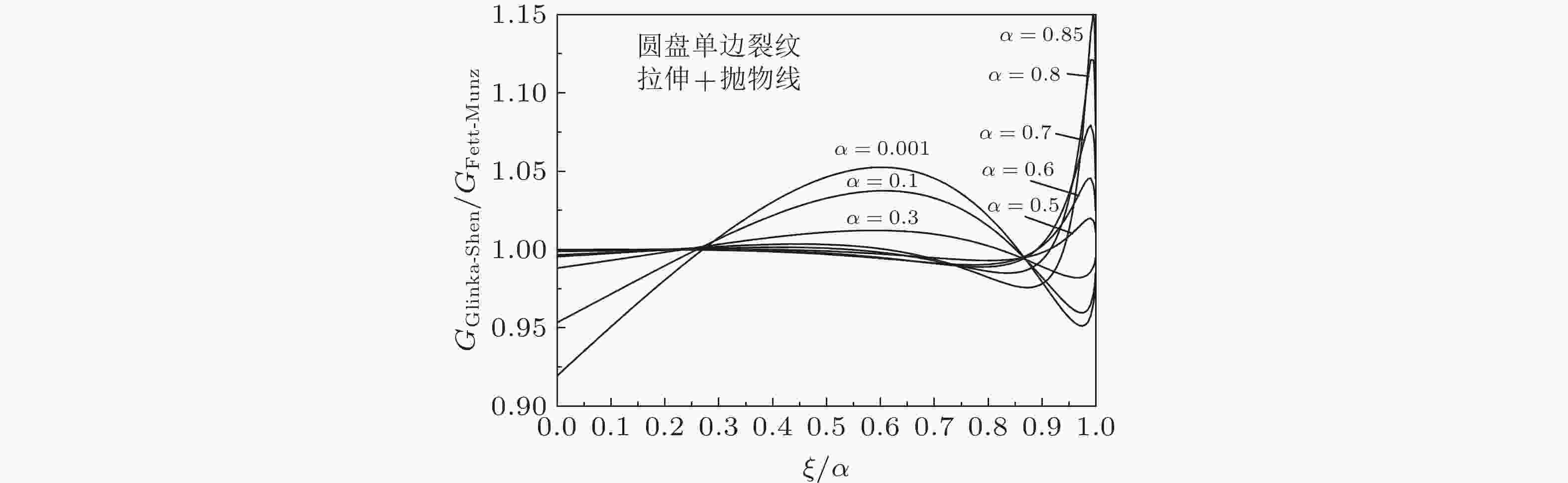
图 29 采用相同的两个精确参考解和几何条件, 反向解得的圆盘单边缘裂纹两种MRS权函数的比值(吴学仁等2019)
图 30 三种解析权函数方法综合比较的雷达图 (吴学仁等 2019)
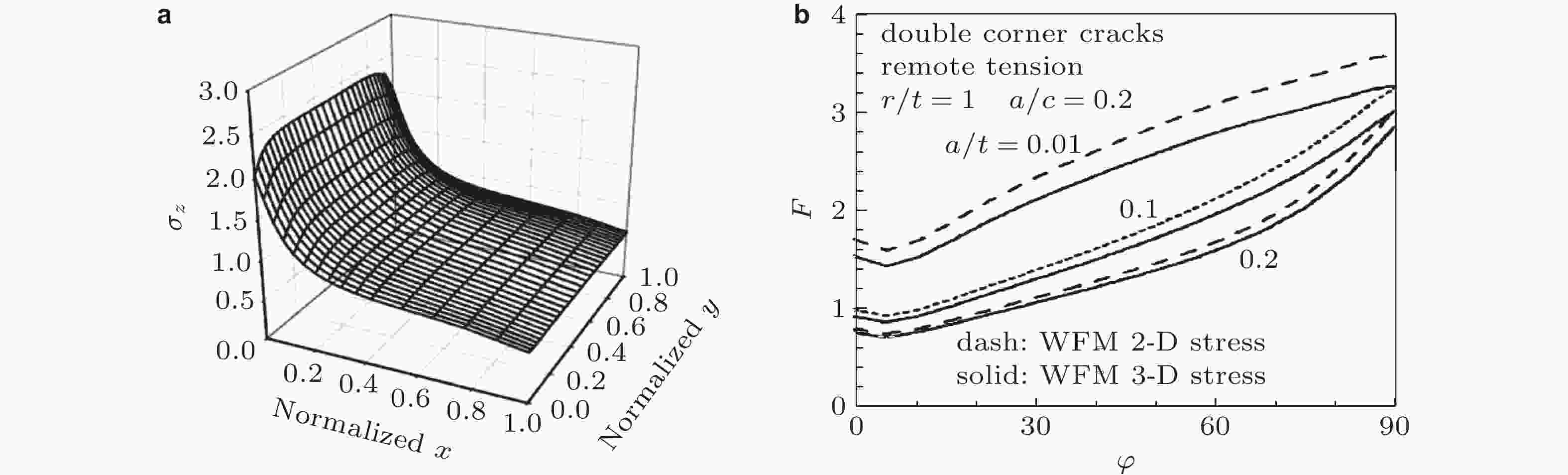
图 32 (a) 无限板圆孔边沿x和y两个方向变化的三维应力场, (b) 用SSWFM结合二维和三维有限元分析的应力场得到的孔边角裂纹无量纲应力强度因子. 实线: 用2D应力解, 虚线: 用3D应力解 (Zhao et al. 1997b)
图 33 (a) 孔边表面裂纹远方拉伸下的应力强度因子: SSWFM结果与有限元解的比较(Newman et al. 1994, Wu et al. 1998), (b) 孔边对称双角裂纹远方拉伸下的应力强度因子: SSWFM与各种数值解法的比较(Bakuckas 2001)
图 34 远方拉伸SENT半圆缺口试样三维应力强度因子: SSWFM与有限元结果以及拟合方程比较. (a) 表面裂纹, (b) 角裂纹 (Newman et al. 1994; Wu et al. 1998)
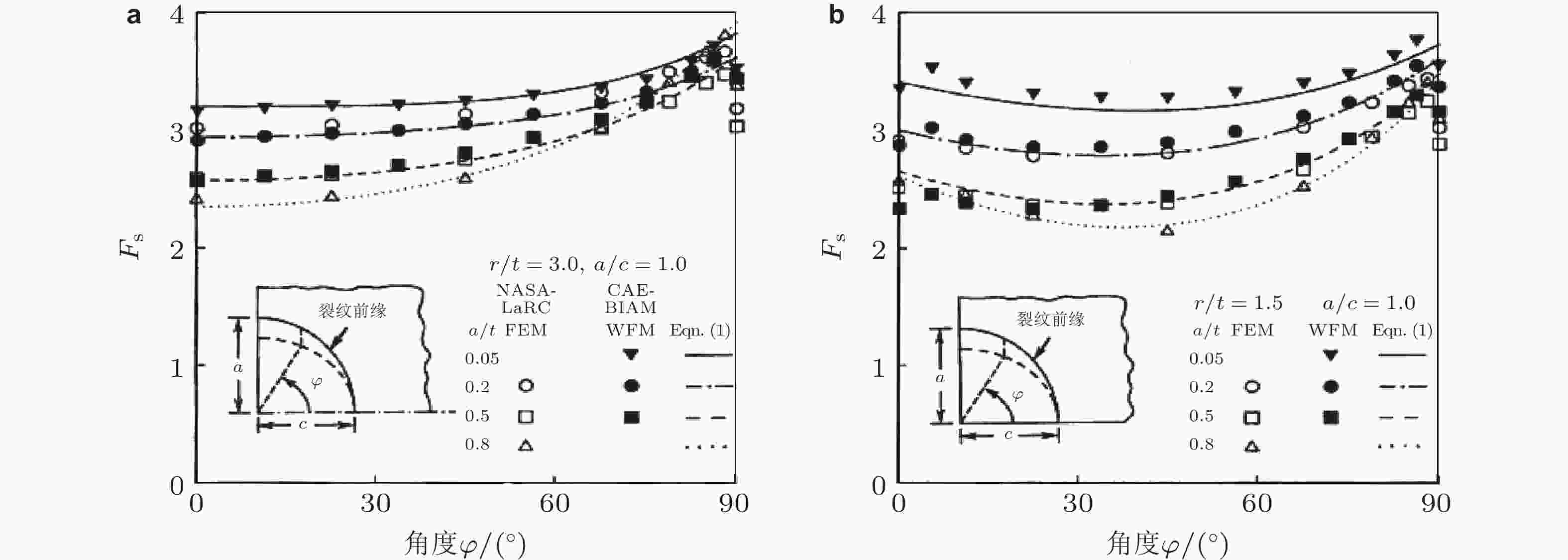
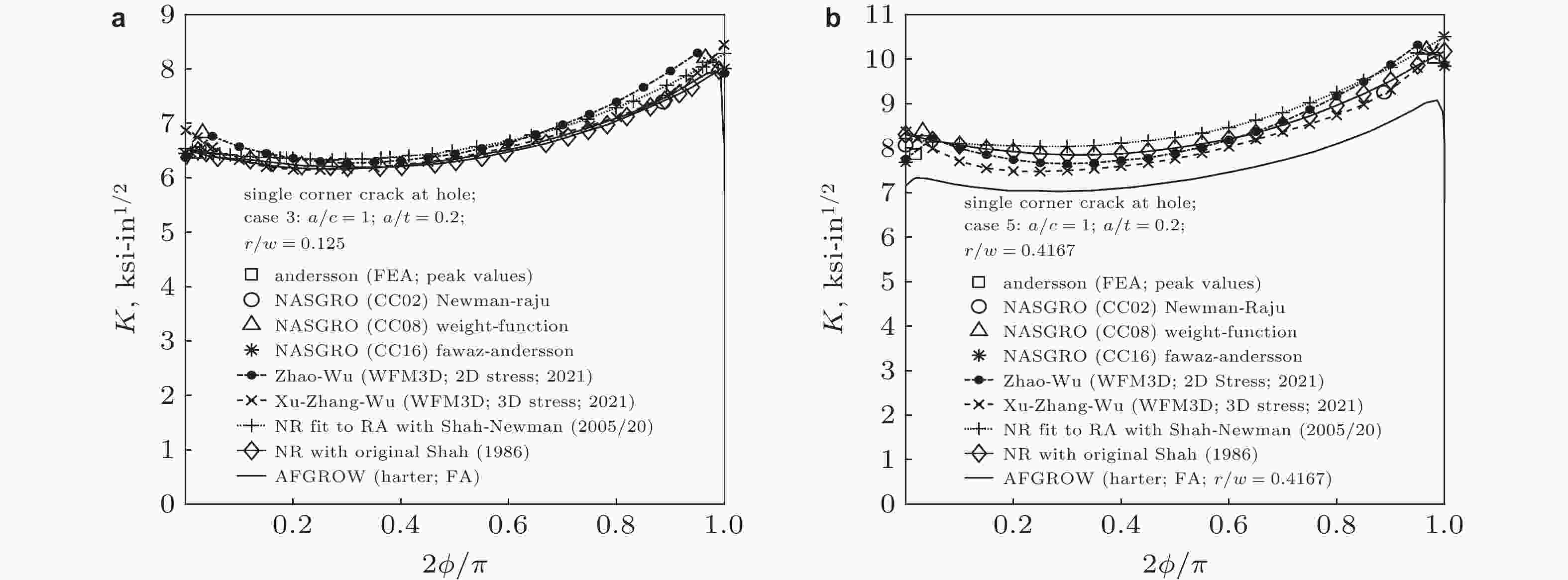
图 35 9种方法求得的远方拉伸无限板孔边角裂纹(r/t = 1.0, a/c = 1.0, a/t = 0.2)三维应力强度因子比较(ERSI-USA). (a) r/W = 0.125, (b) r/W = 0.4167 (Newman & Wu 2021)
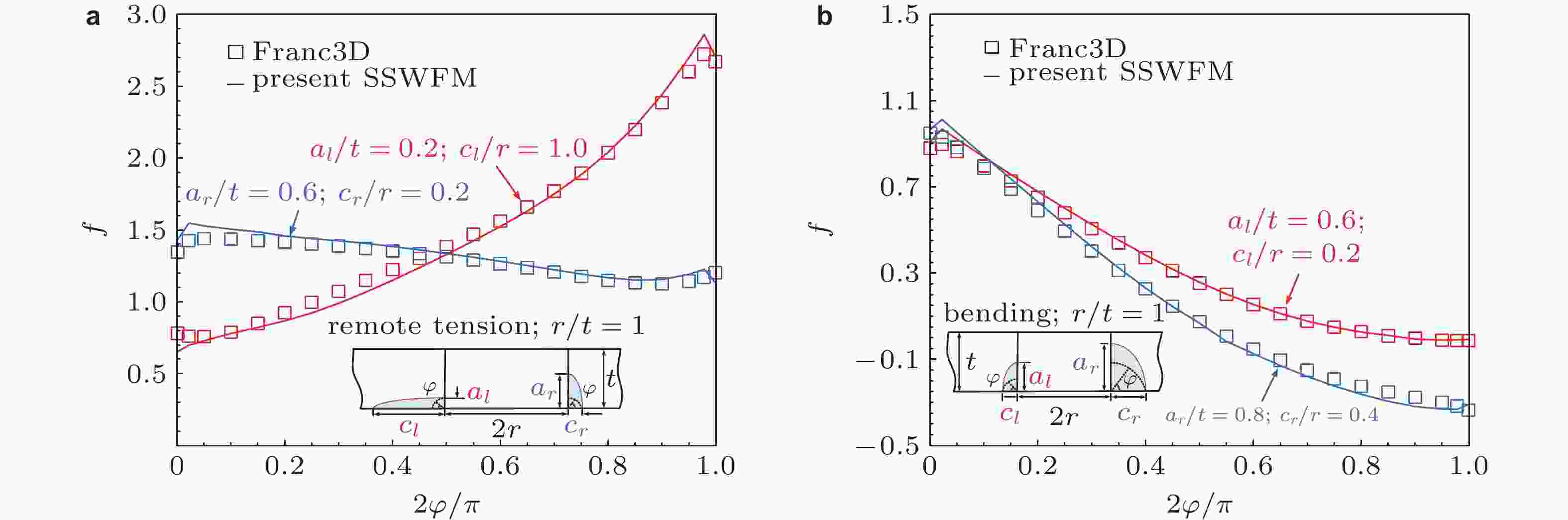
图 36 无限板孔边两条非对称角裂纹(r/t = 1.0)在远方拉伸和面外弯曲载荷下的三维应力强度因子: SSWFM与有限元软件Franc3D结果的比较. 裂纹面应力分布σ(x, y)采用了3D有限元分析结果(Zhang et al. 2022)
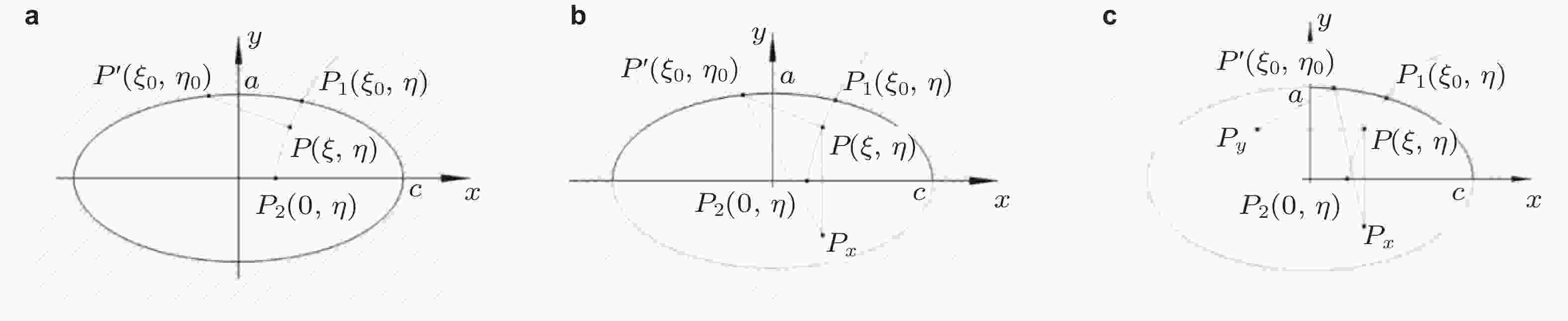
图 38 Rice (1989)点载荷权函数分析模型. (a) 内埋椭圆裂纹, (b) 半椭圆表面裂纹
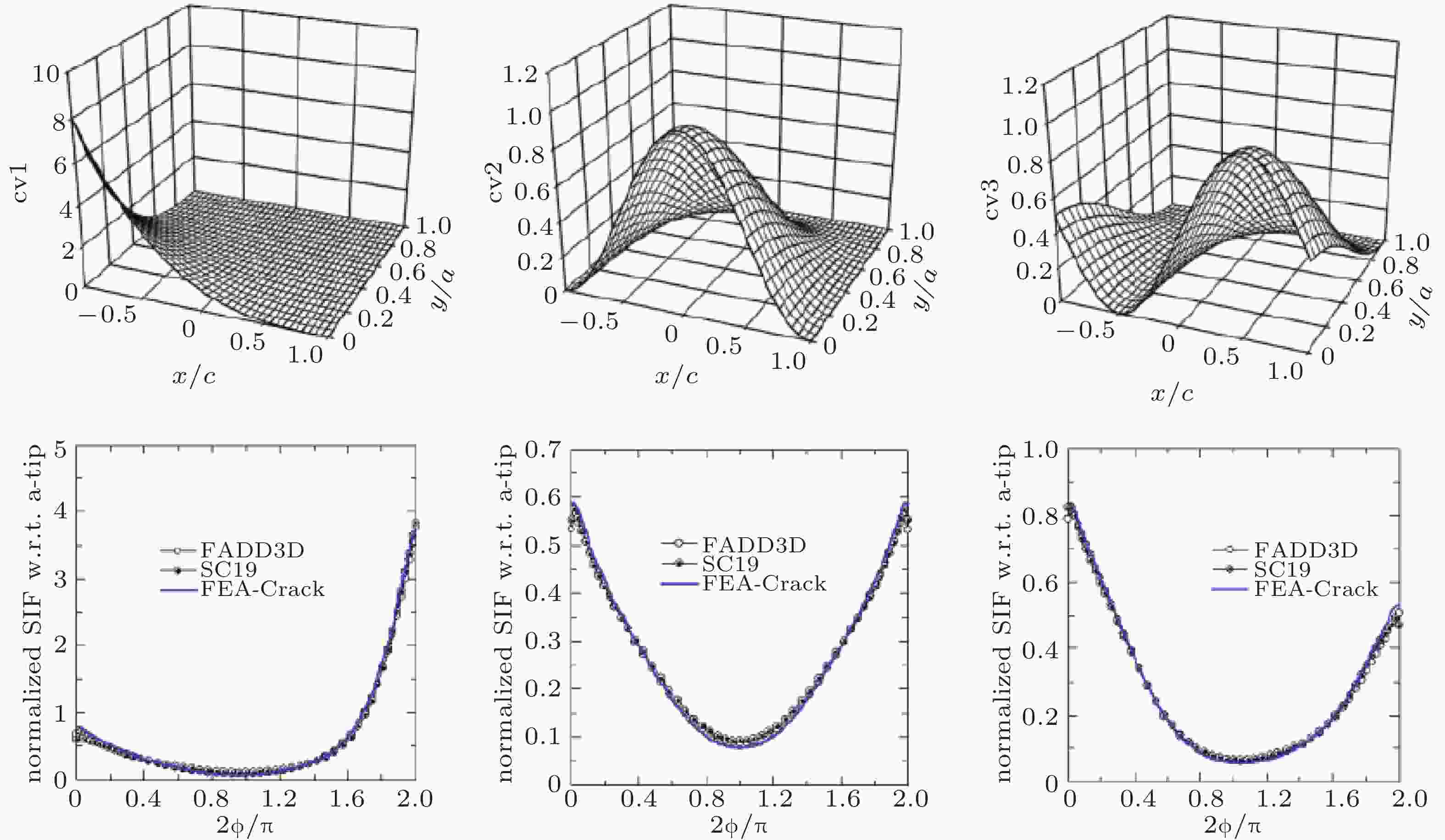
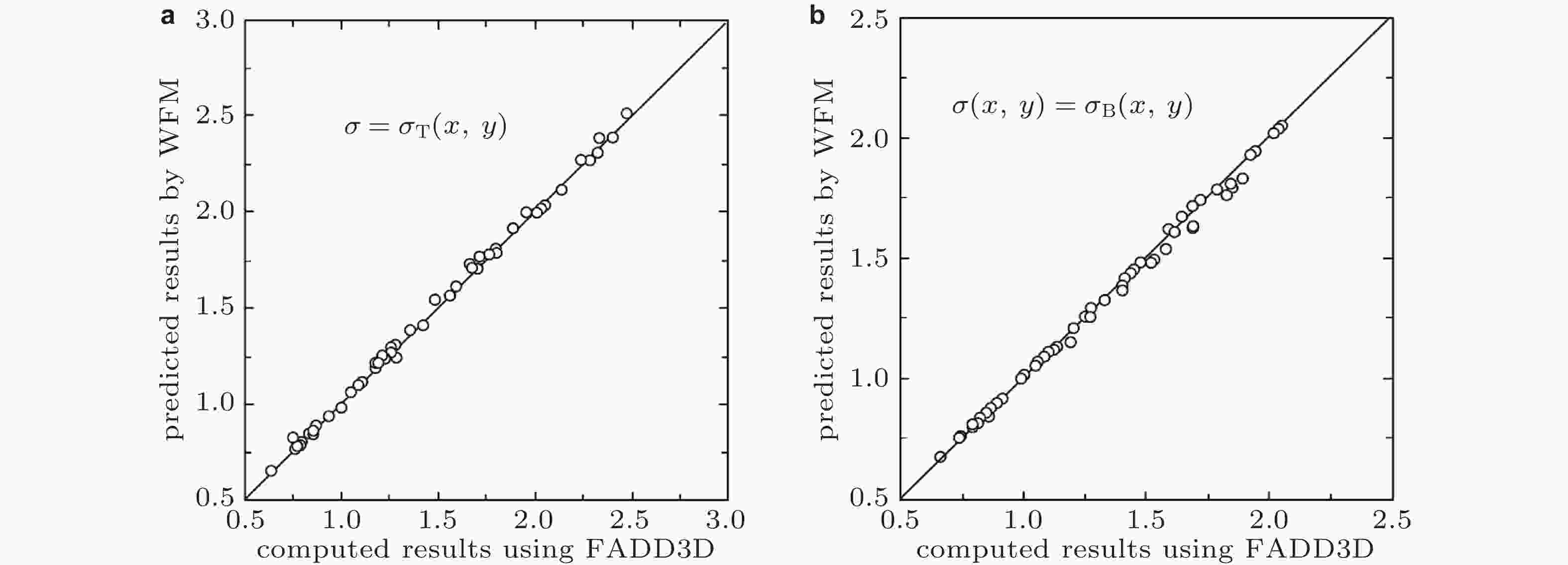
图 39 有限板半椭圆表面裂纹在3种双变应力作用下的无量纲应力强度因子3种解法的结果比较. 点载荷权函数法, 边界元数值法- FADD3D, 有限元法- FEACrack (McClung et al. 2013)
图 40 点载荷权函数法(PWFM)与边界元法(FADD3D)计算的孔边角裂纹无量纲应力强度因子比较. (a) 拉伸, (b) 弯曲 (McClung et al. 2013)
图 41 平板三维裂纹权函数的参数定义. (a) 半椭圆表面裂纹, (b) 四分之一椭圆角裂纹 (Zheng et al. 1996)
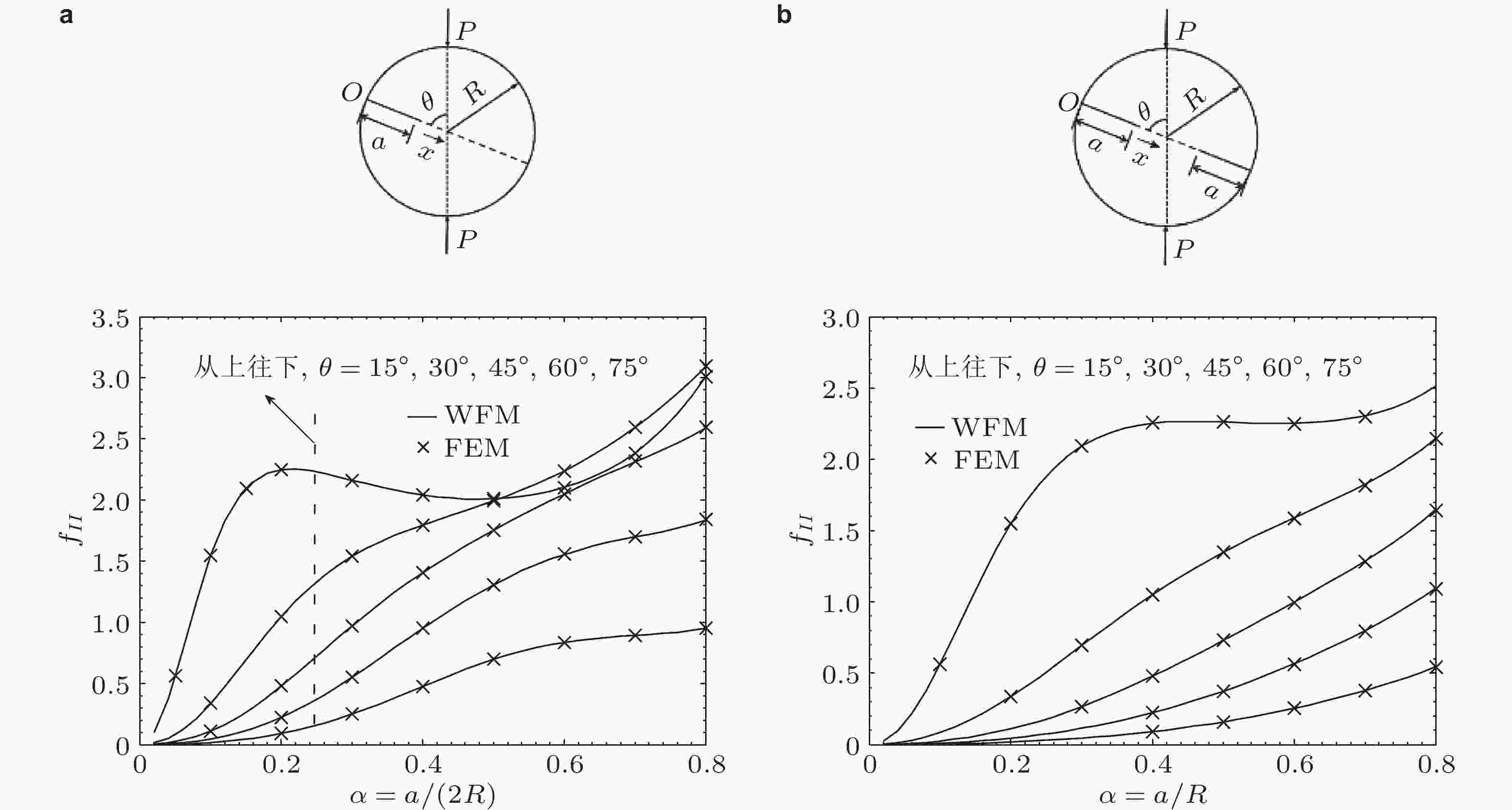
图 43 含单/双边缘裂纹圆盘在一对径向集中力P作用下的II型无量纲应力强度因子: 规范化解析权函数解与有限元解的比较. (a) 单裂纹, (b) 双裂纹 (Xu et al. 2020a; Wu & Xu 2022)
图 44 典型热应力和残余应力分布. (a) 圆柱体热冲击应力, (b) 冷挤压孔边残余应力, (c) 飞机机翼铝合金锻件的简化残余应力, (d) 圆管焊缝轴向残余应力 (吴学仁等 2019)
图 46 两种残余应力场作用下的无量纲应力强度因子. (a) 有限宽板激光冲击残余应力和三种方法计算的边缘裂纹K结果的比较 (Ribeiro & Hill 2016), (b) 无限板冷挤压孔的残余应力(虚线)和不同挤压量孔边裂纹的K
图 47 权函数/格林函数法在洛−马公司联合攻击机含残余应力的机翼梁锻件损伤容限设计中的应用成效. (a) 最终设计许用应力与基线设计许用应力的比值, (b) 因许用应力提高导致的翼梁970个控制部位的局部厚度相对变化(Ball 2008)
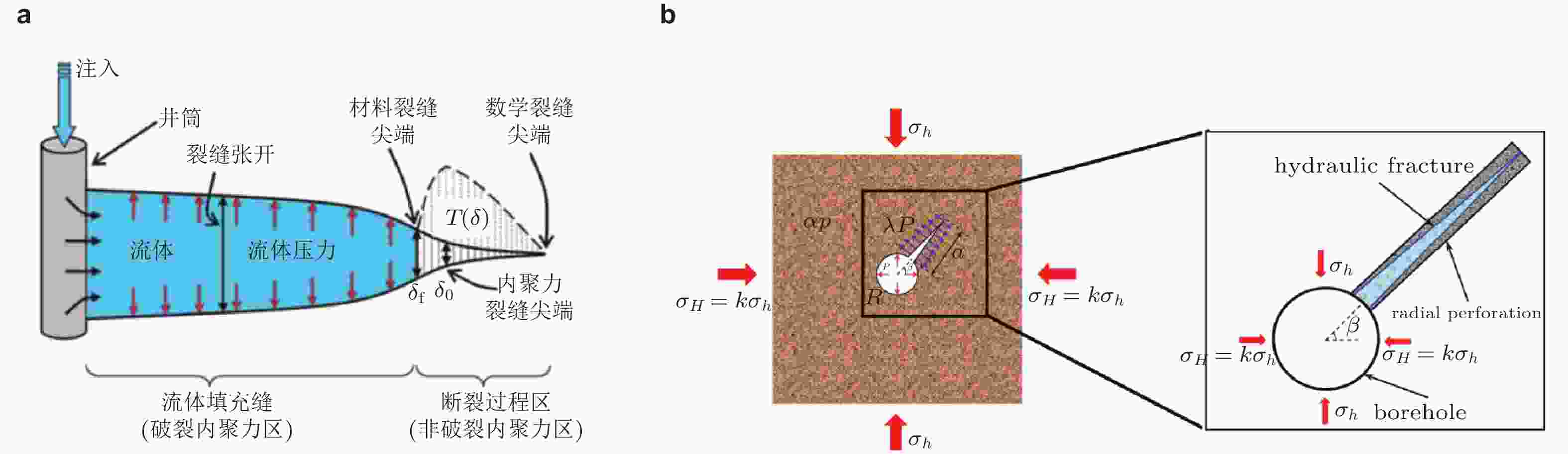
图 48 (a) 内聚力水力压裂模型(刘曰武等 2019, Chen 2012), (b) 孔边裂纹水力压裂分析模型(Dong et al. 2018)
图 49 混凝土重力大坝高压水劈裂分析模型. (a) 扩展有限元模型(XFEM), (b) 裂纹面水压分布 (Wang et al. 2015)
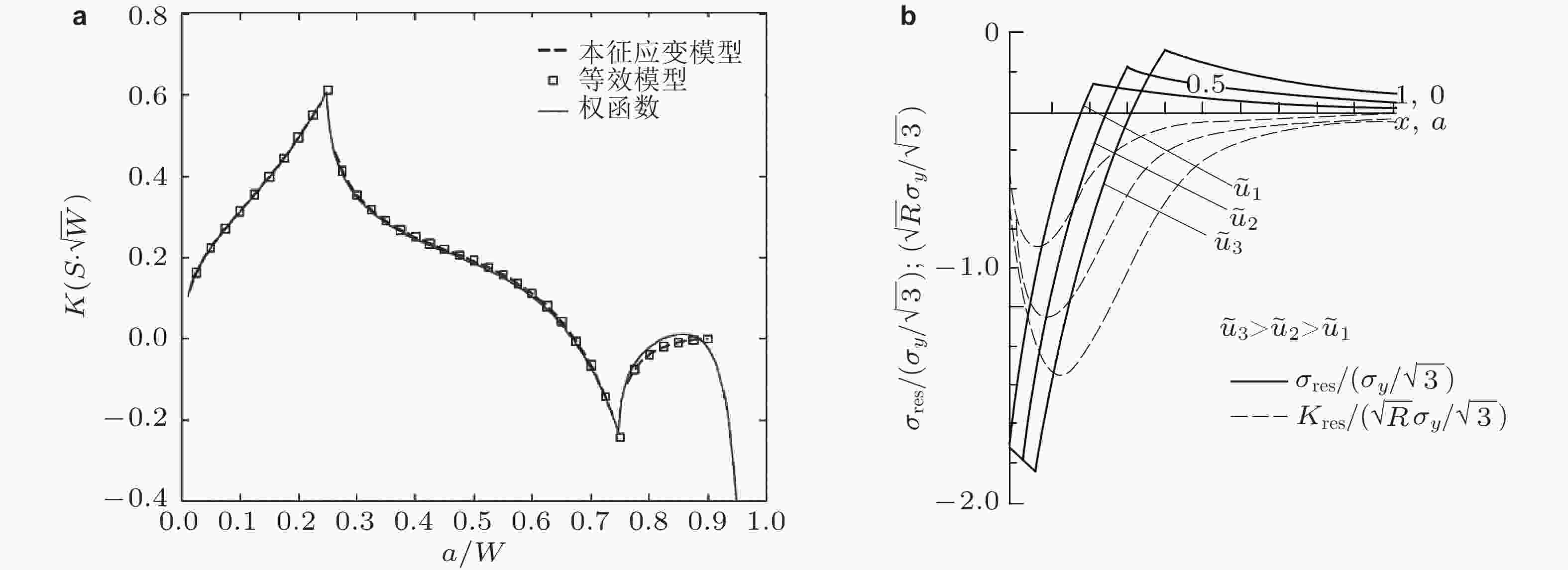
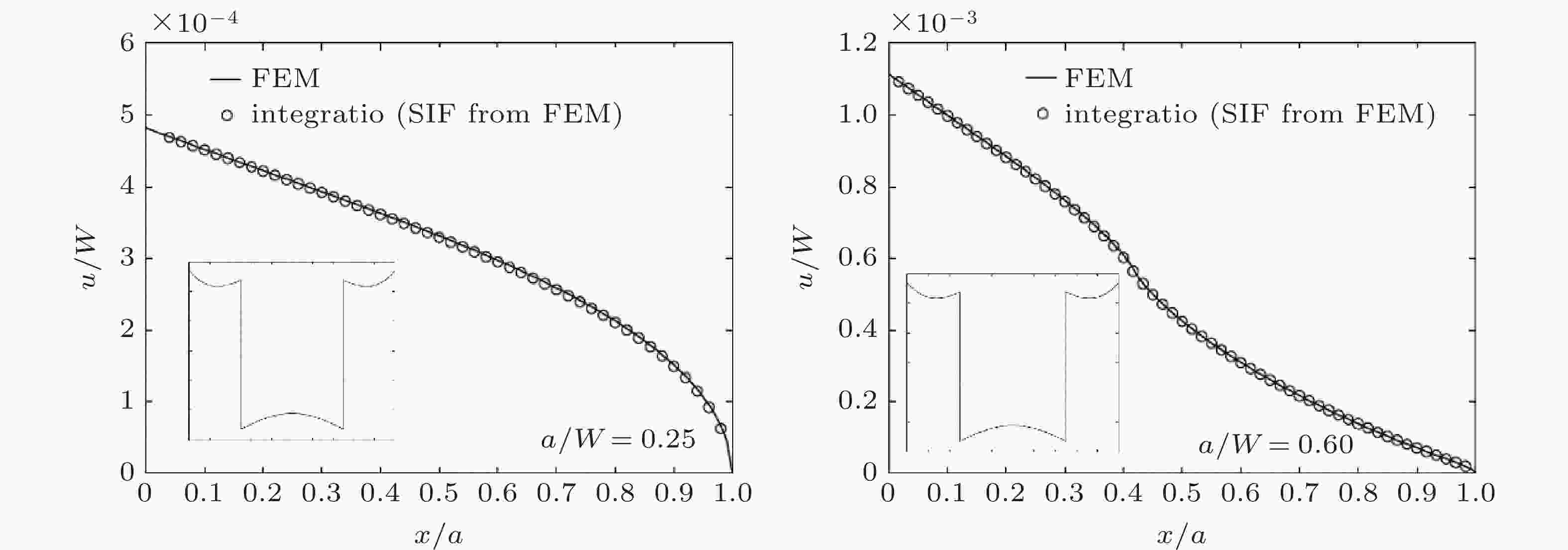
图 53 在激光冲击导致的剧烈变化残余应力作用下, 有限宽板边缘裂纹张开位移的解析权函数解与有限元结果比较(a/W = 0.25, 0.6). 图中左下方的插图是残余应力分布 (Ribeiro & Hill 2016)
图 57 用权函数法得到的桥连应力结果验证 (Buchanan et al. 1997). (a) 预设的3种桥连应力分布, (b) 采用权函数法结合最小二乘法获得的桥连应力与有限元结果的对比
图 58 用权函数法结合桥连应力离散化方法求得的无限板中心裂纹的内聚力模型解(Xu & Waas 2017). (a) 裂纹尖端过程区的大小及应力分布, (b) 裂纹尖端过程区内的张开位移
图 59 用权函数法求得的几种裂纹几何的裂纹张开应力以及与有限元等数值解的比较. (a) 半无限大板边缘裂纹的裂纹张开应力(R = 0), (b) 缺口和孔边裂纹的张开应力与裂纹长度与缺口/孔半径的关系(平面应力) (吴学仁等 2019)
图 60 三条等长裂纹受集中载荷及其无量纲应力强度因子解. (a) 各裂纹中心线受一对对称集中力, (b) 裂纹尖端A的无量纲应力强度因子, (c) 裂纹尖端B的无量纲应力强度因子, (d) 裂纹尖端C的无量纲应力强度因子 (Xu & Wu 2012)
图 61 (a) 加筋板三条对称共线裂纹受远端均匀应力, (b) 中心裂纹应力强度因子与文献结果比较(Zhang et al. 2020)
图 62 (a) 两条等长裂纹, (b) 三条对称裂纹, (c) 两条等长裂纹, 内侧裂尖A的无量纲应力强度因子, (d) 三条对称裂纹, 内侧裂尖A的无量纲应力强度因子 (Xu et al. 2011, Xu & Wu 2012,徐武 2012)
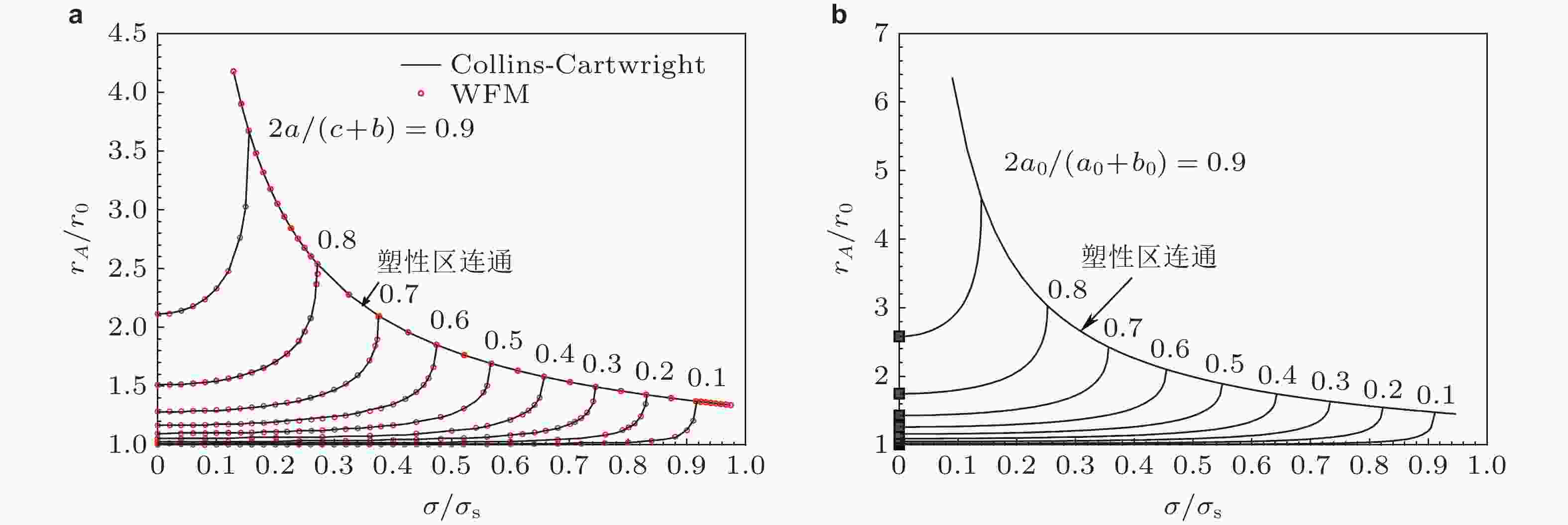
图 63 裂纹尖端A的塑性区尺寸与外载荷σ/σs关系, r0 = a0[sec(0.5πσ/σs). (a) 两条等长裂纹, (b) 三条等长裂纹(Xu et al. 2011; Xu & Wu 2012)
图 66 裂纹尖端正则化塑性区尺寸和张开位移与外载荷关系r0 = a[sec(0.5πσ/σs) − 1], δ0 = 8aσs/(πE)ln[sec(0.5πσ/σs)], (2a + b)/w = 0.5. (a) 裂纹尖端A的塑性区尺寸, (b) 裂纹张开位移, a = b = 1/6 (徐武2012, Xu et al. 2014)
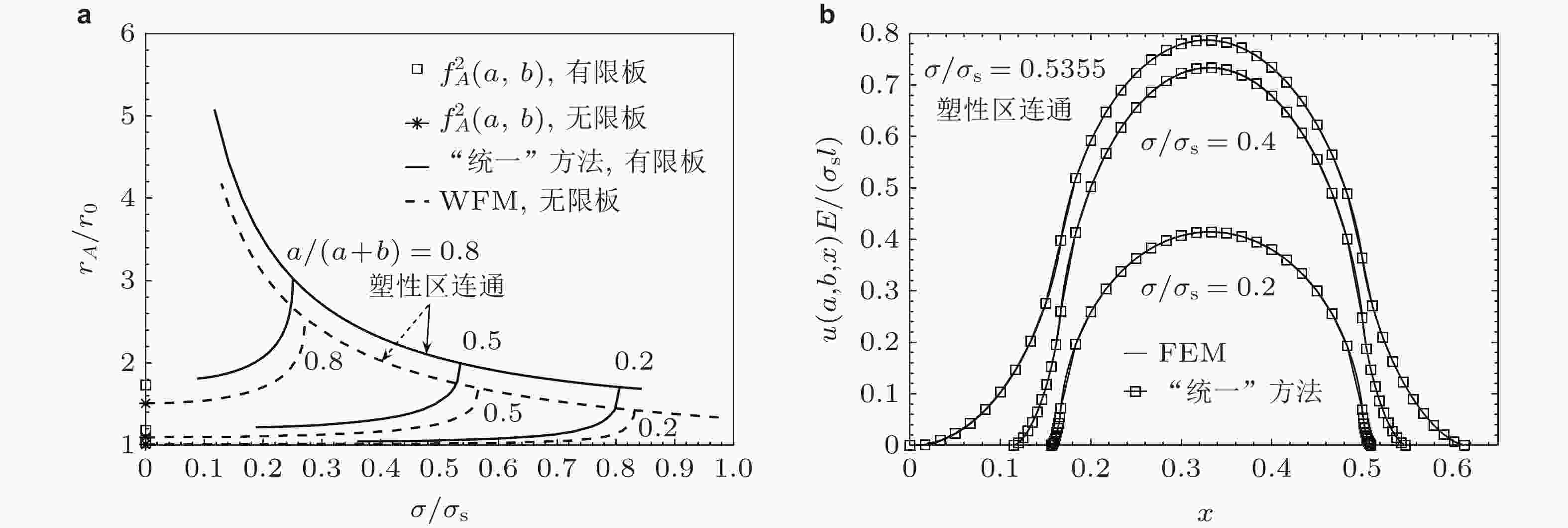
图 67 基于单裂纹权函数的“统一”分析方法和有限元法预测的共线多裂纹板剩余强度比较 (Xu et al. 2014, 吴学仁2019)
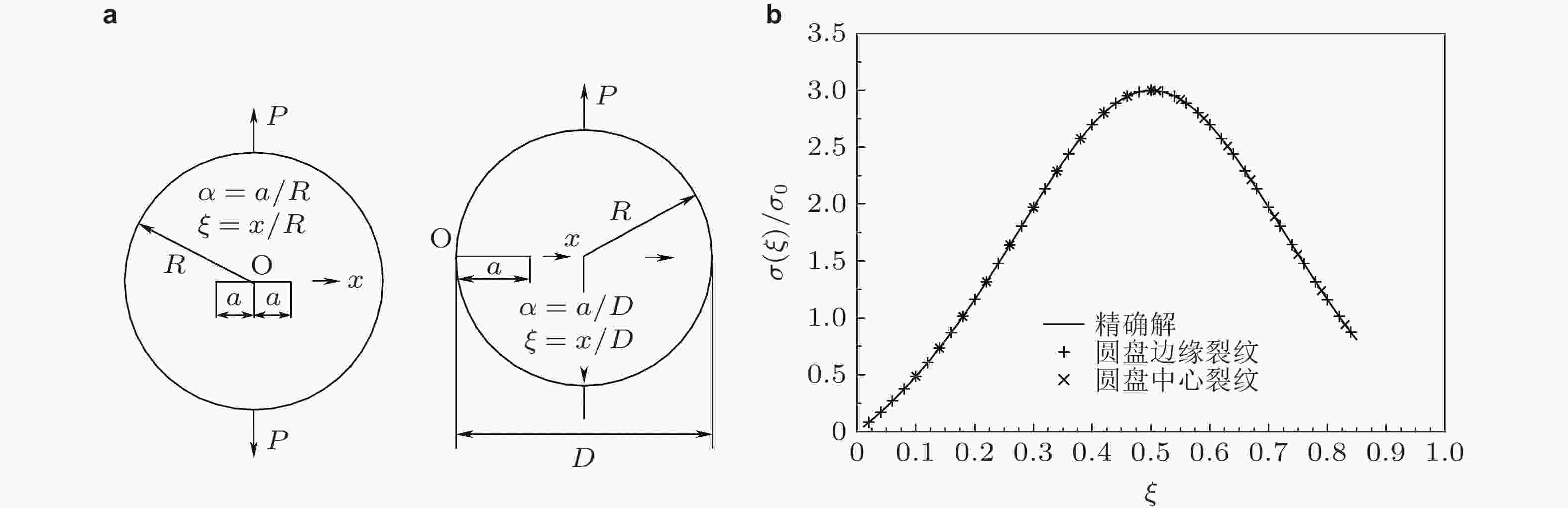
图 68 用逆向权函数法解得的两种圆盘裂纹几何受一对集中力P的无裂纹应力及与精确解比较 (吴学仁等 2019)
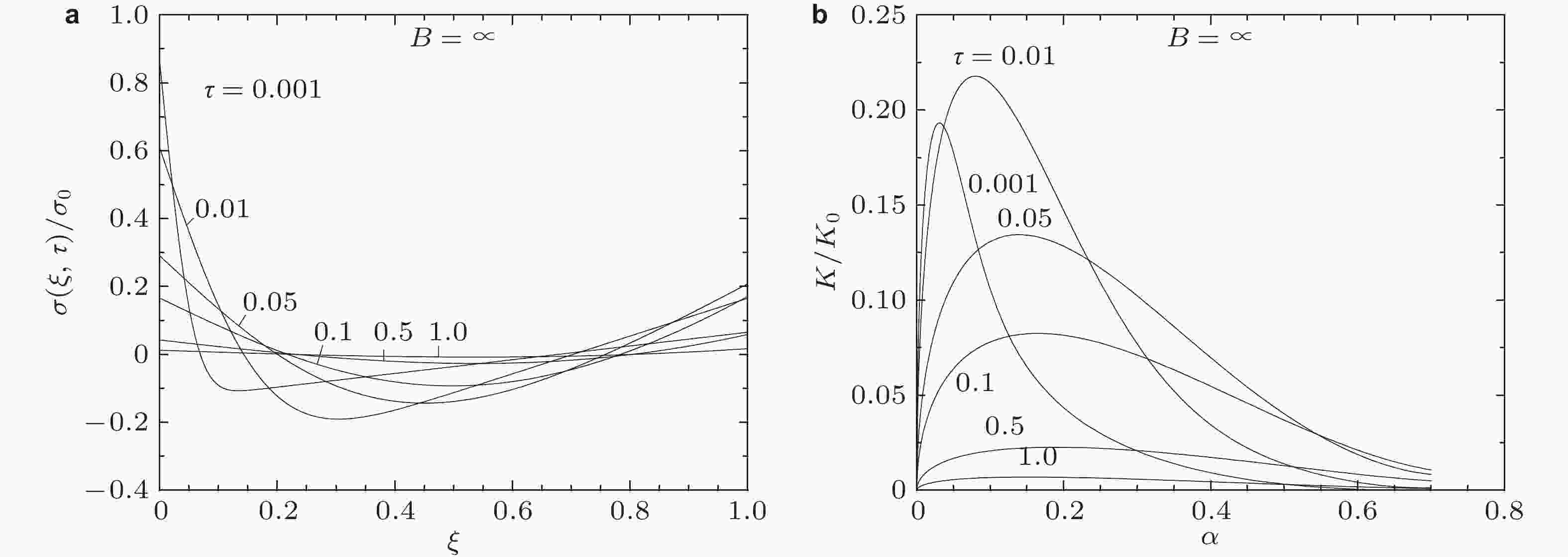
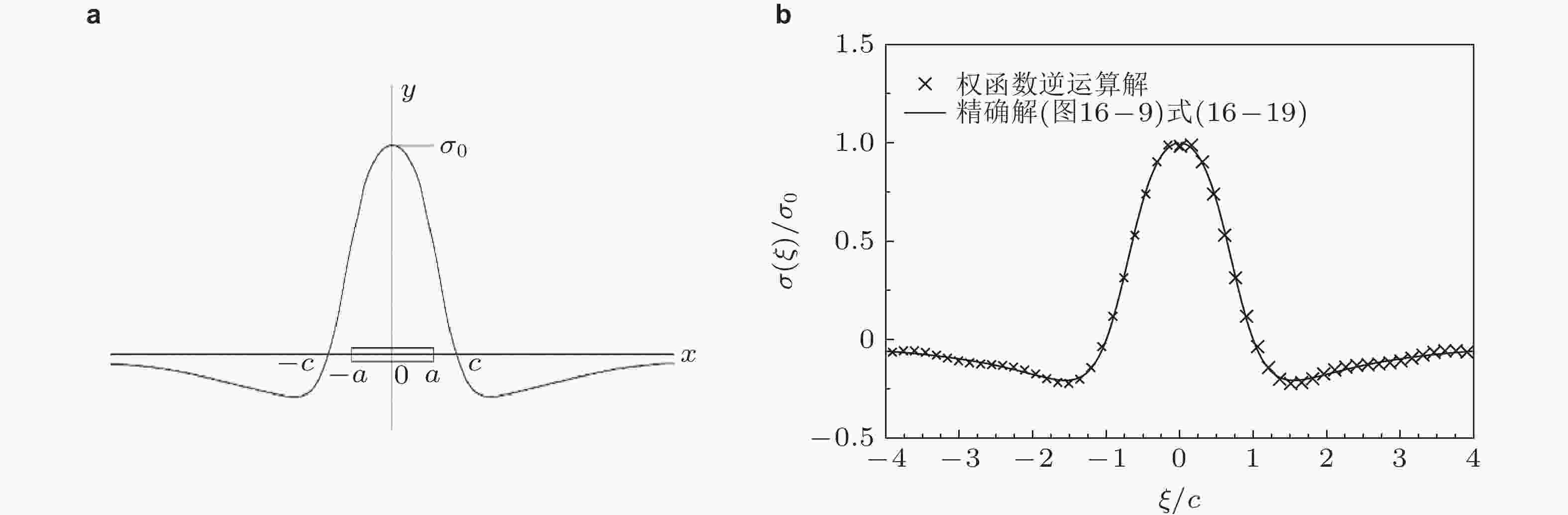
图 69 (a) 无限大板中心裂纹受焊接残余应力作用; (b) 用逆向权函数法求得的无限大板中心裂纹所受残余应力σ(ξ)/σ0, 以及与已知精确解的比较 (吴学仁等 2019)
图 70 利用替代几何计算复杂裂纹体的应力强度因子(Zerbst et al. 2007)
图 71 替代几何示例. (a) T形焊接板和平直板, (b) 远方拉伸T形板焊趾根部的无裂纹应力分布, (c) T形板和平直板的格林函数比较, (d) 4种方法计算的应力强度因子及与有限元结果比较 (吴学仁等 2019)
图 72 (a) 权函数合成原理(weight function composition principle), (b) 用合成权函数法得到的有限板半圆缺口边缘裂纹受纯弯曲的应力强度因子以及与Wu-Carlsson (1991)权函数结果比较(Brennan & Teh 2004)
-
黄克智, 余寿文. 1985. 弹塑性断裂力学. 北京: 清华大学出版社Huang K Z, Yu S W. 1985. Elastoplastic Fracture Mechanics. Beijing: Tsinghua University Press [2] 匡震邦, 马法尚. 2002. 裂纹端部场. 西安: 西安交通大学出版社Kuang Z B, Ma F S. 2002. Crack Tip Fields. Xi'an: Xi'an Jiaotong University Press 郦正能(主编). 2012. 应用断裂力学. 北京: 北京航空航天大学出版社 李宗利, 任青文, 王亚红. 2005. 岩石与混凝土水力劈裂缝内水压力分布的计算. 水利学报, 36: 656-661 (Li Z L, Ren Q W, Wang Y H. 2005. Formula for water pressure distribution in rock or concrete fractures formed by hydraulic fracturing. Shuili Xuebao, 36: 656-661). doi: 10.3321/j.issn:0559-9350.2005.06.004 刘曰武, 高大鹏, 李奇等. 2019. 页岩气开采中的若干力学前沿问题. 力学进展, 49: 201901 (Liu Y W, Gao D P, Li Q, et al. 2019. Mechanical frontiers in shale-gas development. Advancesin Mechanics, 49: 201901). doi: 10.6052/1000-0992-17-020 刘正和, 杨录胜, 廉浩杰等. 2019. 砂岩钻孔轴向预制裂缝定向压裂试验研究. 煤炭学报, 44: 2057-2065 (Liu Z H, Yang L S, Lian H J, et al. 2019. Experimental study of directional fracturing in sandstones with prefabricated cracks in the axial direction of borehole. Journal of China Coal Society, 44: 2057-2065). 彭中伏, 陈学军. 2018. 热对流作用下筒壁涂层的边裂行为. 力学学报, 50: 307-314 (Peng Z F, Chen X J. 2018. Edge cracking behavior of a coated hollow cylinder due to thermal convection. Chinese Journal of Theoretical and Applied Mechanics, 50: 307-314). doi: 10.6052/0459-1879-17-412 唐世斌, 刘向君, 罗江, 董卓. 2017. 水压诱发裂缝拉伸与剪切破坏的理论模型研究. 岩石力学与工程学报, 36: 2124-2135 (Tang S B, Liu X J, Luo J, Dong Z. 2017. Theoretical model for tensile and shear crack initiation at the crack tip in rock subjected to hydraulic pressure. Chinese Journal of Rock Mechanics and Engineering, 36: 2124-2135). 汤英, 张晓晶, 吴学仁. 2012. 单边缺口拉伸试样喷丸强化残余应力及其三维应力强度因子分析. 航空学报, 33: 1265-1274 (Tang Y, Zhang X J, Wu X R. 2012. Analysis of residual stresses and three-dimensional stress intensity factors for shot peened single edge notch tension specimens. Acta Aeronutica et Astronautica Sinica, 33: 1265-1274). 童第华, 吴学仁. 2013. 无限大板圆孔边双裂纹的裂纹面位移权函数解. 航空学报, 34: 2341-2348 (Tong D H, Wu X R. 2013. Weight function solutions of crack surface displacements for double cracks emanating from a circular hole in an infinite plate. Acta Aeronautica et Astronautica Sinica, 34: 2341-2348). 童第华, 吴学仁, 胡本润, 陈勃. 2017. 半无限板边缘裂纹的权函数解法与评价. 力学学报, 49: 848-857 (Tong D H, Wu X R, Hu B R, Chen B. 2017. Weight function methods and assessment for an edge crack in a semi-infinite plate. Chinese Journal of Theoretical and Applied Mechanics, 49: 848-857). 童第华, 吴学仁, 赵晓辰, 徐武, 胡本润. 2000. 任意跨宽比三点弯曲梁断裂力学参数的权函数法求解. 航空材料学报, 40: 127-136 (Tong D H, Wu X R, Zhao X C, Xu W, Hu B R. 2000. SIF and CMOD for three-point bending beams with arbitrary span-to-width ratios by using analytical weight function method. Journal of Aeronautical Materials, 40: 127-136). 王自强, 陈少华. 2009. 高等断裂力学. 北京: 科学出版社Wang Z Q, Chen S H. 2009. Advanced Fracture Mechanics. Beijing: Science Press 吴学仁, 黄新跃. 1988. 受任意钉载圆孔边径向裂纹分析. 航空学报, 10: A442-447 (Wu X R, Huang X Y. 1988. On the problem of radial cracks emanaing from an arbitrarily loaded circular hole. Acta Aeronautica et Astronautica Sinica, 10: A442-447). 吴学仁. 1989. 冷挤压孔边残余应力场中裂纹的应力强度因子. 航空学报, 9: A434-439 (Wu X R. 1989. Residual stress intensity factors for radial cracks at the edge of a cold worked hole. Acta Aeronautica et Astronautica Sinica, 9: A434-439). 吴学仁, 郭亚军. 1999a. 纤维金属层板疲劳寿命预测的研究进展. 力学进展, 29: 304-316 (Wu X R, Guo Y J. 1999a. Development of methodology for predicting fatigue life of fiber reinforced metal laminates. Advances in Mechanics, 29: 304-316). doi: 10.3321/j.issn:1000-0992.1999.03.002 吴学仁, 郭亚军. 1999b. 变幅载荷下纤维金属层板的疲劳与寿命预测. 中国工程科学, 1: 35-40 (Wu X R, Guo Y J. 1999b. Fatigue life prediction of fiber reinforced metal laminates under variable amplitude loading. Engineering Science, 1: 35-40). doi: 10.3969/j.issn.1009-1742.1999.03.007 吴学仁, 赵伟, Newman Jr J C. 2000. 裂纹体分析的三维权函数法一模型、评价与应用. 固体力学学报, 21(增刊): 14-22Wu X R, Zhao W, Newman J C, Jr. 2000. A three-dimensional weight function method for crack analysis: modeling, evaluation and application, Acta Mechanica Solida Sinica. 21 (Special Issue): 14-22 吴学仁, 童第华, 徐武, 赵晓辰. 2019. 断裂力学的权函数理论与应用. 北京: 航空工业出版社 徐世烺. 2011. 混凝土断裂力学. 北京: 科学出版社Xu S L. 2011. Fracture Mechanics of Concrete. Beijing: Science Press 徐世烺, 王建敏. 2009. 水压作用下大坝混凝土裂缝控制与双K断裂参数. 土木工程学报, 42: 119-125 (Xu S, Wang J. 2009. Crack propogation in a concrete dam under water pressure and determination of the double-K fracture parameters. China Civil Engineering Journal, 42: 119-125). doi: 10.3321/j.issn:1000-131X.2009.07.018 徐武. 2012. 飞机结构多位置损伤分析的权函数法与剩余强度预测. [博士论文]. 上海: 上海交通大学Xu W. 2012. Weight function method and residual strength prediction for multi-position damage analysis of aircraft structure. [PhD Thesis]. Shanghai: Shanghai Jiao Tong University 杨卫. 1995. 宏微观断裂力学. 北京: 国防工业出版社Yang W. 1995. Macro and Micro Fracture Mechanics. Beijing: National Defense Industry Press 袁奎霖, 周忠华, 赵峰, 洪明. 2019. 双向应力场中表面裂纹应力强度因子的权函数法. 船舶力学, 23: 976-987 (Yuan K L, Zhou Z H, Zhao F, Hong M. 2019. Improved point load weight function for stress intensity factor of surface cracks under two-dimensional stress field. Journal of Ship Mechanics, 23: 976-987). doi: 10.3969/j.issn.1007-7294.2019.08.010 张秀芳, 徐世烺. 2011. 权函数法计算的混凝土断裂韧度. 工程力学, 28: 58-62 (Zhang X F, Xu S L. 2011. Fracture toughness determined using weight function approach. Engineering Mechanics, 28: 58-62). 张正国, 孟庆臣, 杨国义, 邹广平. 1998. Dugdale模型解法研究. 哈尔滨工程大学学报, 19: 85-93 (Zhang Z G, Meng Q C, Yang G Y, Zou G P. 1998. Study of solutions of Dugdale model. Journal of Harbin Engineering University, 19: 85-93). doi: 10.3969/j.issn.1006-7043.1998.01.014 赵伟. 1988. 三维裂纹分析的权函数理论及应用[博士论文]. 北京: 北京航空材料研究院Zhao W. 1988. Theory and applications of three-dimensional crack analysis[PhD thesis]. Beijing: Beijing Institute of Aeronautical Materials 赵伟, 吴学仁, 颜鸣皋. 1990. 一种高效准确的三维权函数法及其应用. 航空材料学报, 10增刊: 9-22Zhao W, Wu Xueren, Yan Minggao. 1990. An efficient and accurate three-dimensional weight function method and its application. Journal of Aeronautical Materials, 10 S: 9-22 赵伟, 吴学仁, 颜鸣皋. 1991a. 受远方拉伸的孔边角裂纹的应力强度因子. 力学学报, 23: 315-322 (Zhao W, Wu Xueren, Yan Minggao. 1991a. Stress intensity factors for corner cracks at a hole under uniform tension. Acta Mechanica Sinica, 23: 315-322). 赵伟, 吴学仁, 颜鸣皋. 1991b. 小表面裂纹应力强度因子的权函数解. 航空学报, 12: B44-49 (Zhao W, Wu X R, Yan M G. 1991b. Solution of stress intensity factors by weight function for small corner cracks in plates. Acta Aeronautica et Astronautica Sinica, 12: B44-49). 赵伟, 吴学仁, 颜鸣皋. 1991c. 小角裂纹应力强度因子的权函数解. 力学学报, 24: 376-380 (Zhao W, Wu X R, Yan M G. 1991c. Solution of stress intensity factors by weight function for small corner cracks in plates. Acta Mechanica Sinica, 24: 376-380). 赵晓辰. 2016. 复杂应力场三维裂纹宽范围点载荷权函数法[博士论文]. 北京: 北京航空材料研究院Zhao X C. 2016. A wide-range point weight function method for analysis of three-dimensional crack problems[PhD thesis]. Beijing: Beijing Institute of Aeronautical Materials 赵晓辰, 吴学仁, 童第华, 徐武. 2018. 无限板孔边裂纹问题的高精度解析权函数解. 航空学报, 39: 221976 (Zhao X C, Wu X R, Tong D H, Xu W. 2018. Accurate analytical weight function solitions for crack at edge of circular hole in infinite plate. Acta Aeronautica et Astronautica Sinica, 39: 221976). 中国航空研究院. 1993. 应力强度因子手册. 北京: 科学出版社Chinese Aeronautical Establishment. 1993. Stress Intensity Factor Handbook. Beijing: Science Press 王世伟, 李先达, 吴学仁, 贾国荣 主编. 1994. 军用飞机疲劳-损伤容限-耐久性设计手册. 北京: 中国航空研究院.Wang S W, Li X D, Wu X R, Jia G R. 1994. Military Aircracft Fatigue - Damage Tolerance - Durability Design Handbook. Beijing: Chinese Aeronautical Establishment. 庄茁, 蒋持平. 2004. 工程断裂与损伤. 北京: 机械工业出版社Zhuang Z, Jiang C P. 2004. Engineering Fracture and Damage. Beijing: China Machine Press Adamson R M, Dempsey J P, Mulmule S V. 1996. Fracture analysis of semi-circular and semi-circular-bend geometries. International Journal of Fracture, 77: 213-222. doi: 10.1007/BF00018778 Alderliesten R C. 2007. On the available relevant approach for fatigue crack propagation prediction in Glare. International Journal of Fatigue, 29: 289-304. doi: 10.1016/j.ijfatigue.2006.03.003 Aliabadi M, Rooke D, Cartwright D. 1987. An improved boundary element formulation for calculating stress intensity factors: application to aerospace structures. The Journal of Strain Analysis for Engineering Design, 22: 203-207. doi: 10.1243/03093247V224203 Andersson P, Bergman M, Brickstad B, Dahlberg L, Nilsson F, Sattari-Far I. 1999. A procedure for safety assessment of components with cracks – handbook, 3rd revised edition. Stockholm, Sweden: SKI Report 99: 49. Anderson T L. 2005. Fracture Mechanics, Fundamentals and Applications, 3rd Edition. Boca Raton: CRC Press, Taylor & Francis Group, LLC Andrasic C, Parker A. 1980. Weight functions for cracked, curved beams// Numerical Methods in Fracture Mechanics. Proceedings of the 2nd Int. Conf. , Swansea, UK: 67-82. Andrasic C, Parker A. 1984. Dimensionless stress intensity factors for cracked thick cylinders under polynomial crack face loadings. Engineering Fracture Mechanics, 19: 187-193. doi: 10.1016/0013-7944(84)90078-X Anisworth A, Schwalbe H, Zerbst U. 2003. Comprehensive Structural Integrity: Crack Driving Forces Estimation Methods. Pergamon Elsevier: 133-176. API 579. 2000. Recommended practice for fitness-for-service. Washington, DC. American Petroleum Institute. ASTM E08.04. 01. 2018. Standard Guide for the Verification and Validation of Fatigue Crack Growth Life Prediction Models and Software Implementations of Models Pre-release Draft. Babolian E, Masouri Z. 2008. Direct method to solve Volterra integral equation of the first kind using operational matrix with block-pulse functions. Journal of Computational and Applied Mathematics, 220: 51-57. doi: 10.1016/j.cam.2007.07.029 Bahr H A, Balke H, Kuna M, Liesk H. 1987 Fracture analysis of a single edge cracked strip under thermal shock. Theoretical and Applied Fracture Mechanics, 8: 33-39. Bakuckas Jr J G. 2001. Comparison of boundary correction factor solutions for two symmetric cracks in a straight-shank hole. Engineering Fracture Mechanics, 68: 1095-1106. doi: 10.1016/S0013-7944(01)00013-3 Ball D L. 2008. The influence of residual stress on the design of aircraft primary structure. Journal of ASTM International, 5: 1-18. Ball D L, Watton J D. 2011. Fatigue life variability in large aluminum forgings with residual stress// 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 19th AIAA/ASME /AHS Adaptive Structures Conference, Denver, Colorado, 4-7 April 2011. AIAA 2011-1867. Ball D L, James M A, Bucci R J, Watton J D. 2014. A detailed evaluation of the effects of bulk residual stress on fatigue in aluminum. Advanced Materials Research, 891: 1205-1211. Bao R, Zhang X, Yahaya N A. 2010. Evaluating stress intensity factors due to weld residual stresses by the weight function and finite element methods. Engineering Fracture Mechanics, 77: 2550-2566. doi: 10.1016/j.engfracmech.2010.06.002 Barenblatt G I. 1962. The mathematical theory of equilibrium cracks in brittle fracture. Advances in Applied Mechanics, 7: 55-129. Bazant Z P, Planas J. 1997. Fracture and Size Effect in Concrete and Other Quasibrittle Materials. Boca Raton, Boston, London, New York, Washington D C: CRC Press Beghini M, Bertini L, Vitale E. 1991. A numerical approach for determining weight functions in fracture mechanics. International Journal for Numerical Methods in Engineering, 32: 595-607. doi: 10.1002/nme.1620320309 Brennan F. 1994. Evaluation of stress intensity factors by multiple reference state weight function approach. Theoretical and Applied Fracture Mechanics, 20: 249-256. doi: 10.1016/0167-8442(94)90017-5 Brennan F, Teh L. 2004. Determination of crack‐tip stress intensity factors in complex geometries by the composition of constituent weight function solutions. Fatigue & Fracture of Engineering Materials & Structures, 27: 1-7. BS 7910: 2013+A1: 2015. Guide to methods for assessing the acceptability of flaws in metallic structures. BSI Standards Publication. The British Standards Institution. Buchanan D J, John R, Johnson D A. 1997. Determination of crack bridging stresses from crack opening displacement profiles. International Journal of Fracture, 87: 101-117. doi: 10.1023/A:1007495331890 Budiansky B, Amazigo. 1989. Toughning by aligned, frictionally constrained fibers. Journal of the Mechanics and Physics of Solids, 37: 93-109. doi: 10.1016/0022-5096(87)90006-8 Bueckner H F. 1958. The propagation of cracks and the energy of elastic deformation. Transaction of the ASME, Series E, 80: 1225-1230. Bueckner H. 1970. A novel principle for the computation of stress intensity factors. Journal of Applied Mathematics and Mechanics, 50: 529-546. Bueckner H F. 1971. Weight functions for the notched bar. Journal of Applied Mathematics and Mechanics, 51: 97-109. Cardona D, Barney C, Bowen P. 1993. Micromodelling of effective stress intensities for bridged cracks in fibre-reinforced titanium metal-matrix composites. Composites, 24: 122-128. doi: 10.1016/0010-4361(93)90008-V Carpinteri A, Massabó R. 1996. Bridged versus cohesive crack in the flexural behavior of brittle-matrix composites. International Journal of Fracture, 81: 125-145. doi: 10.1007/BF00033178 Chang P Y, Yeh P C, Yang J M. 2011. Fatigue crack growth in fibre metal laminates with multiple open holes. Fatigue & Fracture of Engineering Materials & Structures, 35: 93-107. Chen F, Sun Z, Xu J. 2001. Mode I fracture analysis of the double edge cracked Brazilian disk using a weight function method. International Journal of Rock Mechanics and Mining Sciences (1997) , 38: 475-479. doi: 10.1016/S1365-1609(01)00008-9 Chen X, Albrecht P. 1994. Weight functions for eccentric cracks// Fracture Mechanics, 24th volume. ASTM International. Chen X G, Wu X R, Yan M G. 1992. Dugdale model for strain hardening materials. Engineering Fracture Mechanics, 41: 843-871. doi: 10.1016/0013-7944(92)90236-8 Chen X J, You Y. 2014. Weight functions for multiple edge cracks in a coating. Engineering Fracture Mechanics, 116: 31-40. doi: 10.1016/j.engfracmech.2013.12.012 Chen X, Du C, You M, Jiang S. 2017. Experimental study on water fracture interactions in concrete. Engineering Fracture Mechanics, 179: 314-327. doi: 10.1016/j.engfracmech.2017.04.050 Chen Z. 2012. Finite element modelling of viscosity-dominated hydraulic fractures. Journal of Petroleum Science and Engineering, 88: 136-144. Collins R, Cartwright D, Gregson P. 1999. A direct complex stress function approach for modelling stiffened panels containing multiple site damage. Theoretical and Applied Fracture Mechanics, 31: 105-117. doi: 10.1016/S0167-8442(99)00005-1 Collins R, Cartwright D. 2001. An analytical solution for two equal-length collinear strip yield cracks. Engineering Fracture Mechanics, 68: 915-924. doi: 10.1016/S0013-7944(00)00086-2 Cox B N, Marshall D B. 1991a. Stable and unstable solutions for bridged cracks in various specimens. Acta Metallurgica et Materialia, 39: 579-589. doi: 10.1016/0956-7151(91)90126-L Cox B N, Marshall D B. 1991b. The determination of crack bridging forces. International Journal of Fracture, 49: 159-176. doi: 10.1007/BF00035040 Cruse T A, Besuner P M. 1975. Residual life prediction for surface cracks in complex structural details. Journal of Aircraft, 12: 369-375. doi: 10.2514/3.44458 Daniewicz S R. 1994. A closed-form small-scale yielding collinear strip yield model for strain hardening materials. Engineering Fracture Mechanics, 49: 95-103. doi: 10.1016/0013-7944(94)90114-7 Daniewicz S, Bloom J. 1996. An assessment of geometry effects on plane stress fatigue crack closure using a modified strip-yield model. International Journal of Fatigue, 18: 483-490. doi: 10.1016/0142-1123(96)00084-9 Daniewicz S. 1998. A modified strip-yield model for prediction of plasticity-induced closure in surface flaws. Fatigue & Fracture of Engineering Materials & Structures, 21: 885-901. Daniewicz S, Aveline C. 2000. Strip-yield and finite element analysis of part-through surface flaws. Engineering Fracture Mechanics, 67: 21-39. doi: 10.1016/S0013-7944(00)00032-1 Daniewicz S, Ismonov S. 2010. Simulation and comparison of several crack closure assessment methodologies. International Journal of Fatigue, 32: 428-433. doi: 10.1016/j.ijfatigue.2009.08.008 DARWIN®. 2008. Design Assessment of Reliability With Inspection. DARWIN Theory, Version 6.1. Developed by Southwest Research Institute. de Matos P, Nowell D. 2007. On the accurate assessment of crack opening and closing stresses in plasticity-induced fatigue crack closure problems. Engineering Fracture Mechanics, 74: 1579-1601. doi: 10.1016/j.engfracmech.2006.09.007 Dempsey J, Adamson R, Defranco S. 1995. Fracture analysis of base-edge-cracked reverse-tapered plates. International Journal of Fracture, 69: 281-294. doi: 10.1007/BF00037379 Dempsey J, Mu Z. 2014. Weight function for an edge-cracked rectangular plate. Engineering Fracture Mechanics, 132: 93-103. doi: 10.1016/j.engfracmech.2014.10.023 Deng P, Matsumoto T. 2017. Weight function determinations for shear cracks in reinforced concrete beams based on finite element method. Engineering Fracture Mechanics, 177: 61-78. doi: 10.1016/j.engfracmech.2017.03.046 Dill H D, Saff C R. 1978. Environmental-load interaction effects on crack growth. McDonnell Aircraft Co. , Saint Louis, MO, United States Dillstrom P, Gunnars J, Unge P, Mangard D. 2018. Procedure for Safety Assessment of Components with Defects. Handbook Edition 5. Report number: 18 ISSN: 2000-0456. Swedish Radiation Safety Authority. Dong Z, Tang S, Ranjith P G, Lang Y. 2018. A theoretical model for hydraulic fracturing through a single radial perforation emanating from a borehole. Engineering Fracture Mechanics, 196: 28-42. doi: 10.1016/j.engfracmech.2018.04.029 Dong S, Wang Y, Xia Y. 2004. Stress intensity factors for central cracked circular disk subjected to compression. Engineering Fracture Mechanics, 71: 1135-1148. doi: 10.1016/S0013-7944(03)00120-6 Dugdale D S. 1960. Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids, 8: 100-104. doi: 10.1016/0022-5096(60)90013-2 Elber W. 1970. Fatigue crack closure under cyclic tension. Engineering Fracture Mechanics, 2: 37-45. doi: 10.1016/0013-7944(70)90028-7 FAA. 2010. Aging airplane program: widespread fatigue damage. Federal Register Rules and Regulations, 75: 69746-69789. Fett T, Mattheck C, Munz D. 1987. On the calculation of crack opening displacement from the stress intensity factor. Engineering Fracture Mechanics, 7: 697-715. Fett T. 1988. Limitations of the Petroski-Achenbach procedure demonstrated for a simple load case. Engineering Fracture Mechanics, 29: 713-716. doi: 10.1016/0013-7944(88)90173-7 Fett T. 1992. Direct determination of weight functions from reference loading cases and geometrical conditions. Engineering Fracture Mechanics, 42: 435-444. doi: 10.1016/0013-7944(92)90165-B Fett T, Diegele E, Munz D, Rizzi G. 1996. Weight functions for edge cracks in thin surface layers. International Journal of Fracture, 81: 205-215. doi: 10.1007/BF00039571 Fett T. 1997. A semi-analytical study of the edge-cracked circular disc by use of the boundary collocation method. Engineering Fracture Mechanics, 56: 331-346. doi: 10.1016/S0013-7944(96)00069-0 Fett T, Munz D. 1997. Stress Intensity Factors and Weight Functions. Southampton, UK. Computational Mechanics Publications Fett T, Bahr H. 1999. Mode I stress intensity factors and weight functions for short plates under different boundary conditions. Engineering Fracture Mechanics, 62: 593-606. doi: 10.1016/S0013-7944(99)00014-4 Fett T, Munz D, Yang Y Y. 2000a. Direct adjustment procedure for weight functions of graded materials. Fatigue & Fracture of Engineering Materials & Structures, 23: 191-198. Fett T. 2001. Stress intensity factors and T-stress for internally cracked circular disks under various boundary conditions. Engineering Fracture Mechanics, 68: 1119-1136. doi: 10.1016/S0013-7944(01)00025-X Fett T. 2002. Stress intensity factors and T-stress for single and double edge cracked circular disks under mixed boundary conditions. Engineering Fracture Mechanics, 69: 69-83. doi: 10.1016/S0013-7944(01)00078-9 Fett T, Pham V-B, Bahr H-A. 2004. Weight functions for kinked semi-infinite cracks. Engineering Fracture Mechanics, 71: 1987-1995. doi: 10.1016/j.engfracmech.2003.10.003 Fett T. 2008. Stress intensity factors, T-stresses, weight functions. IKM 50. Institute of Ceramics in Mechanical Engineering, University of Karlsruhe, Germany. Fitzpatrick M E, Edwards L. 1998. Fatigue crack/residual stress field interactions and their implications for damage tolerant design. Journal of Materials Engineering and Performance, 7: 190-198. doi: 10.1361/105994998770347918 Fleck N, Sutcliffe M, Sivashanker S, Xin X. 1996. Compressive R-curve of a carbon fibre-epoxy matrix composite. Composites Part B:Engineering, 27: 531-541. Fujimoto W. 1976. Determination of crack growth and fracture toughness parameters for surface flaws emanating from fastener holes// 17th Structures, Structural Dynamics and Materials Conference: 1552. Gao H, Rice J R. 1987. Somewhat circular tensile cracks. International Journal of Fracture, 33: 155-174. doi: 10.1007/BF00013168 Gao Y, Li B, Wang J, Feng X Q. 2021. Fracture toughness analysis of helical fiber-reinforced biocomposites. Journal of the Mechanics and Physics of Solids, 146: 104206. doi: 10.1016/j.jmps.2020.104206 Garagash D, Detournay E. 1997. An analysis of the influence of the pressurization rate on the borehole breakdown pressure. International Journal of Solids and Structures, 34: 3099-3118. doi: 10.1016/S0020-7683(96)00174-6 Glinka G, Shen G. 1991. Universal features of weight functions for cracks in mode I. Engineering Fracture Mechanics, 40: 1135-1146. doi: 10.1016/0013-7944(91)90177-3 Glinka G. 1996. Development of weight functions and computer integration procedures for calculating stress intensity factors around cracks subjected to complex stress fields. Stress and Fatigue-Fracture Design, Petersburg Ontario, Canada, Progress Report Glinka G. 2020. Department of Mechanical and Mechatronics Engineering, University of Waterloo, Waterloo, Ontario, Canada. Private communications. Görner F, Mattheck C, Morawietz P, Munz D. 1985. Limitations of the Petroski-Achenbach crack opening displacement approximation for the calculation of weight functions. Engineering Fracture Mechanics, 22: 269-277. doi: 10.1016/S0013-7944(85)80029-1 Grandt A F. 1975. Stress intensity factors for some through-cracked fastener holes. International Journal of Fracture, 11: 283-294. doi: 10.1007/BF00038895 Gregory R. 1977. A circular disc containing a radial edge crack opened by a constant internal pressure. Mathematical Proceedings of the Cambridge Philosophical Society, 81: 497-521. doi: 10.1017/S030500410005355X Gregory R D. 1979. The edge-cracked circular disc under symmetric pin-loading. Mathematical Proceedings of the Cambridge Philosophical Society, 85: 523-538. doi: 10.1017/S030500410005595X Gregory R D. 1989. The spinning circular disc with a radial edge crack: An exact solution. International Journal of Fracture, 41: 39-50. doi: 10.1007/BF00014836 Guagliano M, Vergani L. 2001. Mode I stress intensity factors for curved cracks in gears by a weight functions method. Fatigue & Fracture of Engineering Materials & Structures, 24: 41-52. Guidera J, Lardner R. 1975. Penny-shaped cracks. Journal of Elasticity, 5: 59-73. doi: 10.1007/BF01389258 Guo W, Zhang J, Guo W. 2021. Two-dimensional weight function of stress intensity factors for corner cracks emanating from a circular hole. Engineering Fracture Mechanics, 252: 107821. doi: 10.1016/j.engfracmech.2021.107821 Guo Y J, Wu X R. 1998. A theoretical model for predicting fatigue crack growth rates in fibre‐reinforced metal laminates. Fatigue & Fracture of Engineering Materials & Structures, 21: 1133-1145. Guo Y J, Wu X R. 1999. Bridging stress distribution in center-cracked fiber reinforced metal laminates: modeling and experiment. Engineering Fracture Mechanics, 63: 147-163. doi: 10.1016/S0013-7944(99)00018-1 Harter J A. 2008. AFGROW user guider and technical manual. Wright-Patterson Air Force Base OH 45433-7542. HB 7705—2001. 2001. 中华人民共和国航空行业标准: 金属材料疲劳小裂纹扩展速率试验方法. He X, Dong Y, Yang B, Li Y. 2018. A wide range stress intensity factor solution for an eccentrically cracked middle tension specimen with clamped ends. Engineering Fracture Mechanics, 191: 461-475. doi: 10.1016/j.engfracmech.2018.01.007 Heaton M. 1976. On the calculation of stress intensity factors due to thermal and residual stress fields. CEGB Research Report NW/SSD/RR/158. Hill M R, Kim J. 2016. Weight functions for a finite width plate with a radial crack at a circular hole. AFGROW Workshop. Hutchinson J W. 1979. A course on nonlinear fracture mechanics: Department of Solid Mechanics, Technical University of Denmark. Ince R. 2012a. Determination of concrete fracture parameters based on peak-load method with diagonal split-tension cubes. Engineering Fracture Mechanics, 82: 100-114. doi: 10.1016/j.engfracmech.2011.11.026 Ince R. 2012b. Determination of the fracture parameters of the Double-K model using weight functions of split-tension specimens. Engineering Fracture Mechanics, 96: 416-432. doi: 10.1016/j.engfracmech.2012.08.024 Irwin G R. 1957. Analysis of stresses and strains near the end of a crack traversing a plate. Journal of Applied Mechanics, 24: 361-364. doi: 10.1115/1.4011547 Ismonov S, Daniewicz S. 2010. Simulation and comparison of several crack closure assessment methodologies using three-dimensional finite element analysis. International Journal of Fatigue, 32: 1322-1329. doi: 10.1016/j.ijfatigue.2010.01.016 Jin X, Zeng Y, Ding S, et al. 2017. Weight function of stress intensity factor for single radial crack emanating from hollow cylinder. Engineering Fracture Mechanics, 170: 77-86. doi: 10.1016/j.engfracmech.2016.11.031 Jin Z, Wang X. 2011. Point load weight functions for semi-elliptical cracks in finite thickness plate. Journal of ASTM International, 9: JAI103962. Jin Z, Wang X. 2013. Weight functions for the determination of stress intensity factor and T-stress for semi-elliptical cracks in finite thickness plate. Fatigue & Fracture of Engineering Materials & Structures, 36: 1051-1066. Jing Z, Wu X R. 2015. Wide-range weight functions and stress intensity factors for arbitrarily shaped crack geometries using complex Taylor series expansion method. Engineering Fracture Mechanics, 138: 215-232. doi: 10.1016/j.engfracmech.2015.03.006 John R, Kaldon S G, Johnson D A, Coker D. 1995. Weight function for a single edge cracked geometry with clamped ends. International Journal of Fracture, 72: 145-158. doi: 10.1007/BF00042825 Jones I. 1998. A wide range weight function for a single edge cracked geometry with clamped ends. International Journal of Fracture, 89: 1-18. doi: 10.1023/A:1007463205924 Karihaloo B, Xiao Q Z. 2003. Comprehensive Structural Integrity: Linear and Non-linear Fracture Mechanics. Pergamon: Elsevier, 81-212. Kaya A, Erdogan F. 1980. Stress intensity factors and COD in an orthotropic strip. International Journal of Fracture, 16: 171-190. doi: 10.1007/BF00012620 Kiciak A, Glinka G, Eman M, Shiratori M. 1998. Weight functions and stress intensity factors for corner quarter-elliptical crack in finite thickness plate subjected to in-plane loading. Engineering Fracture Mechanics, 60: 221-238. doi: 10.1016/S0013-7944(98)00006-X Kim J, Lee S-B. 2000. Prediction of crack opening stress for part-through cracks and its verification using a modified strip-yield model. Engineering Fracture Mechanics, 66: 1-14. doi: 10.1016/S0013-7944(00)00006-0 Kumar S, Barai S V. 2010a. Determining the double-K fracture parameters for three-point bending notched concrete beams using weight function. Fatigue & Fracture of Engineering Materials & Structures, 33: 645-660. Kumar S, Barai S. 2010b. Determining double-K fracture parameters of concrete for compact tension and wedge splitting tests using weight function. Engineering Fracture Mechanics, 76: 935-948. Kumar S, Barai S V. 2011. Concrete Fracture Models and Applications. Springer Science & Business Media. Kuna M. 2013. Finite Elements in Fracture Mechanics. Springer Science & Business Media. . Kuutti J, Virkkunen I. 2019. The effect of subsurface crack opening on the stress intensity factor under cyclic thermal loads. Engineering Fracture Mechanics, 218: 106600. doi: 10.1016/j.engfracmech.2019.106600 Lee H Y, Biglari F R, Wimpory R, Nikbin K M. 2006. Treatment of residual stress in failure assessment procedure. Engineering Fracture Mechanics, 73: 1755-1771. doi: 10.1016/j.engfracmech.2006.03.005 Lee H Y, Hong C S. 1995. A new weight function approach using indirect boundary integral method. Engineering Fracture Mechanics, 52: 1087-1105. doi: 10.1016/0013-7944(95)00055-Z Lee Y D, Mcclung R, Chell G. 2008. An efficient stress intensity factor solution scheme for corner cracks at holes under bivariant stressing. Fatigue & Fracture of Engineering Materials & Structures, 31: 1004-1016. Li V C, Lin Z, Matsumoto T. 1998. Influence of fiber bridging on structural size-effect. International Journal of Solids and Structures, 35: 4223-4238. doi: 10.1016/S0020-7683(97)00311-9 Lim W-K, Song J-H, Sankar B V. 2003. Effect of ring indentation on fatigue crack growth in an aluminum plate. International Journal of Fatigue, 25: 1271-1277. doi: 10.1016/j.ijfatigue.2003.08.011 Lindhagen J E, Gamstedt E K, Berglund L A. 2000. Application of bridging-law concepts to short-fibre composites Part 3: Bridging law derivation from experimental crack profiles. Composites Science and Technology, 60: 2883-2894. doi: 10.1016/S0266-3538(99)00177-3 Liu J Z, Wu X R. 1997. Study on fatigue crack closure behavior for various cracked geometries. Engineering Fracture Mechanics, 57: 475-491. doi: 10.1016/S0013-7944(97)00052-0 Liu T, Tomsett A, Zhang H. 2000. Thermal shock behaviour of industrial carbon anodes. Carbon, 38: 1401-1409. doi: 10.1016/S0008-6223(99)00275-4 Liu Z, Xu W, Yu Y, Wu X. 2019. Weight functions and stress intensity factors for two unequal-length collinear cracks in an infinite sheet. Engineering Fracture Mechanics, 209: 173-186. doi: 10.1016/j.engfracmech.2019.01.025 Lorenzo J, Cartwright D, Aliabadi M. 1994. Boundary-element weight-function analysis for crack surface displacements and strip-yield cracks. Engineering Analysis with Boundary Elements, 13: 283-289. doi: 10.1016/0955-7997(94)90054-X Love A E H. 1944. A Treatise on the Mathematical Theory of Elasticity. Courier Corporation. Lu Y-L, Liu H, Jia H, Yu Z-Q. 2001. Finite element implementation of thermal weight function method for calculating transient SIFs of a body subjected to thermal shock. International Journal of Fracture, 108: 95-117. doi: 10.1023/A:1007665116534 Lyness J N, Moler C B. 1967. Numerical differentiation of analytic functions. SIAM Journal on Numerical Analysis, 4: 202-210. doi: 10.1137/0704019 Mattheck C, Morawietz P, Munz D. 1983. Stress intensity factor at the surface and at the deepest point of a semi-elliptical surface crack in plates under stress gradients. International Journal of Fracture, 23: 201-212. doi: 10.1007/BF00028823 Mawatari T, Nelson D. 2011. Method for efficient computation of stress intensity factors from weight functions by singular point elimination. Engineering Fracture Mechanics, 78: 2713-2730. doi: 10.1016/j.engfracmech.2011.07.006 McClung R C. 1994. Finite element analysis of specimen geometry effects on fatigue crack closure. Fatigue & Fracture of Engineering Materials & Structures, 17: 861-872. McClung R C, Enright M P, Lee Y-D, Huyse L J. 2004. Efficient fracture design for complex turbine engine components. Turbo Expo: Power for Land, Sea, and Air, 41715: 291-300. McClung R C, Leverant G, Enright M. 2008. Turbine rotor material design—Phase II. Washington, DC: FAA Grant. McClung R C, Lee Y-D, Cardinal J W, Guo Y. 2013. The pursuit of K: Reflections on the current state-of-the-art in stress intensity factor solutions for practical aerospace applications// 27th ICAF Symposium, Jerusalem, 2013. McEvily A J. 2002. Metal Failures: Mechanisms, Analysis, Prevention. John Wiley & Sons, Inc. New Meng Q, Li B, Li T, Feng X Q. 2018. Effects of nanofiber orientations on the fracture toughness of cellulose nanopaper. Engineering Fracture Mechanics, 194: 35-361. Millwater H R, Enright M P, Fitch S H. 2007. Convergent zone-refinement method for risk assessment of gas turbine disks subject to low-frequency metallurgical defects. Journal of Engineerng for Gas Turbines and Power, 129: 827-835. doi: 10.1115/1.2431393 NASCRACTM. 1994. Fracture Mechanics Life Analytical Methods Verification Testing (Verification and Validation of NASCRACTM), NAS8-38103. NASA-CR-196555. 1994. (Nichols Research Corp. ) NASGRO®. 2012. Fracture mechanics and fatigue crack growth analysis software, Version 7.0. NASA Johnson Space Center and Southwest Research Institute. Nabavi SM, Rekavandi S S H. 2020. A weight function for multiple longitudinal cracks in functionally graded hollow cylinders. Theoretical and Applied Fracture Mechanics, 110: 102789. Nazmul I M, Matsumoto. 2004. Inverse analysis to determine re-bars’ force from external crack widths measurement. Journal of Applied Mechanics, 7: 1179-1186. doi: 10.2208/journalam.7.1179 Nazmul I M, Matsumoto. 2008a. High resolution COD image analysis for health mornitoring of reinforced concrete structures through inverse analsis. International Journal of Solids and Structures, 45: 159-174. doi: 10.1016/j.ijsolstr.2007.07.014 Nazmul I M, Matsumoto. 2008b. Regularization of inverse problems in reinforced concrete fracture. Journal of Engineering Mechanics, 134: 811-819. doi: 10.1061/(ASCE)0733-9399(2008)134:10(811) Newman Jr J C. 1983. A nonlinear fracture mechanics approach to the growth of small cracks. NASA Langley Research Center, Hamptong, VA, USA. Newman Jr J C. 1986. Evaluation of the crack-tip-opening-displacement (VR) resistance curve method// The Crack Tip Opening Displacement in Elastic-Plastic Fracture Mechanics. Springer, 157-176. Newman Jr J C. Fastran-II. 1992. Fatigue Crack Growth Structural Analysis Program, NASA TM-104159. National Aeronautics and Space Administration, Langley, VA. Newman Jr J C, Wu X R, Venneri S L, Li C G. 1994. Small-crack effects in high-strength aluminum alloys, NASA RP-1309. Newman Jr J C, Wu X R. 2021. Private communications of stress intensity factors on corner crack at a circular hole in infinite/finite plate. March 2021. Ng S W, Lau K J. 1999. A new weight function expression for through cracks. Engineering Fracture Mechanics, 64: 515-537. doi: 10.1016/S0013-7944(99)00095-8 Nishimura T. 1991. Stress intensity factors of multiple cracked sheet with riveted stiffeners. Journal of Engineering Materials and Technology, 113: 280-284. doi: 10.1115/1.2903406 Nilsson K F, Hutchinson J. 1994. Interaction between a major crack and small crack damage in aircraft sheet material. International Journal of Solids and Structures, 31: 2331-2346. doi: 10.1016/0020-7683(94)90155-4 Niu X, Glinka G. 1987. On the “Limitations of the Petroski-Achenbach crack opening displacement approximation for the calculation of weight function”-Do they really exist? Engineering Fracture Mechanics, 26: 701-706. doi: 10.1016/0013-7944(87)90135-4 Ojdrovic R P, Petroski H J. 1991. Weight functions from multiple reference states and crack profile derivatives. Engineering Fracture Mechanics, 39: 105-111. doi: 10.1016/0013-7944(91)90026-W Oliveira R, Wu X R. 1987. Stress intensity factors for axial cracks in hollow cylinders subjected to thermal shock. Engineering Fracture Mechanics, 27: 185-197. doi: 10.1016/0013-7944(87)90167-6 Orange T W. 1972. Crack shapes and stress intensity factors for edge-cracked specimens// Proceedings of the 1971 National Symposium on Fracture Mechanics: Part I. ASTM STP 513, 71-78. Orange T W. 1985. Wide-range weight functions for the strip with a single edge crack// Fracture Mechanics: Sixteenth Symposium. Orynyak I, Borodii M. 1995. Point weight function method application for semi-elliptical mode I cracks. International Journal of Fracture, 70: 117-124. doi: 10.1007/BF00034135 Orynyak I, Borodii M, Torop V. 1994. Approximate construction of a weight function for quarter-elliptical, semi-elliptical and elliptical cracks subjected to normal stresses. Engineering Fracture Mechanics, 49: 143-151. doi: 10.1016/0013-7944(94)90118-X Östlund S, Nilsson F. 1993. Cohesive modelling of process regions for cracks in linear elastic structures—fundamental aspects. Fatigue & Fracture of Engineering Materials & Structures, 16: 215-235. Östlund S. 1995. Fracture modelling of brittle matrix composites with spatially dependent crack bridging. Fatigue & Fracture of Engineering Materials & Structures, 18: 1213-1230. Östlund S, Kärenlampi P. 2001. Structural geometry effect on the size-scaling of strength. International Journal of Fracture, 109: 141-151. doi: 10.1023/A:1011045510152 Parker A P. 1982. Stress intensity factors, crack profiles, and fatigue crack growth rates in residual stress fields//Residual Stress Effects in Fatigue. ASTM International. Petroski H, Achenbach J. 1978. Computation of the weight function from a stress intensity factor. Engineering Fracture Mechanics, 10: 257-266. doi: 10.1016/0013-7944(78)90009-7 R6. 2009. Assessment of the integrity of structures containing defects. Revision 4. British Energy Generation Ltd (BEGL), Barnwood, Gloucester. Ribeiro R L, Hill M R. 2016. A benchmark fracture mechanics solution for a two-dimensional eigenstrain problem considering residual stress, the stress intensity factor, and superposition. Engineering Fracture Mechanics, 163: 313-326. doi: 10.1016/j.engfracmech.2016.06.007 Rice J R. 1972. Some remarks on elastic crack-tip stress fields. International Journal of Solids and Structures, 8: 751-758. doi: 10.1016/0020-7683(72)90040-6 Rice J R. 1989. Weight function theory for three-dimensional elastic crack analysis// Fracture Mechanics: Perspectives and Directions (ASTM Twentieth Symposium). Saff C R, Sanger K B. 1984. Part-through flaw stress intensity factors developed by a slice synthesis technique. Fracture Mechanics: Fifteenth Symposium, ASTM STP 833. Schajer G S, Prime M B. 2006. Use of inverse solutions for residual stress measurements. Journal of Engineering Materials and Technology, 128: 375-382. doi: 10.1115/1.2204952 Schijve J. 1992. Multiple-site-damage fatigue of riveted joints: International workshop on structural integrity of aging airplanes, Atlanta, 31 March-2 April, 1992. Delft University of Technology, Faculty of Aerospace Engineering, Report LR-679. Schneider G, Danzer R. 1989. Calculation of the stress intensity factor of an edge crack in a finite elastic disc using the weight function method. Engineering Fracture Mechanics, 34: 547-552. doi: 10.1016/0013-7944(89)90117-3 Schneider G A, Petzow G. 1991. Thermal shock testing of ceramics—A new testing method. Journal of the American Ceramic Society, 74: 98-102. doi: 10.1111/j.1151-2916.1991.tb07303.x Sha G T, Yang C. 1986. Weight functions of radial cracks emanating from a circular hole in a plate// Fracture Mechanics: Seventeenth Volume. ASTM International. Sham T L. 1987. A unified finite element method for determining weight functions in two and three dimensions. International Journal of Solids and Structures, 23: 1357-1372. doi: 10.1016/0020-7683(87)90002-3 Shao Y, Zhao H P, Feng X Q, Gao H. 2012. Discontinuous crack-bridging model for fracture toughness analysis of nacre. Journal of the Mechanics and Physics of Solids, 60: 1400-1419. doi: 10.1016/j.jmps.2012.04.011 Shen G, Glinka G. 1991. Weight functions for a surface semi-elliptical crack in a finite thickness plate. Theoretical and Applied Fracture Mechanics, 15: 247-255. doi: 10.1016/0167-8442(91)90023-D Shivakumar V, Forman R G. 1980. Green's function for a crack emanating from a circular hole in an infinite sheet. International Journal of Fracture, 16: 305-316. doi: 10.1007/BF00018234 Sih G C. 1964. Boundary problems for longitudinal shear cracks// Proceedings of Second Conference of Theoretical and Appllied Mechanics, 2: 117-130. Sivashanker S. 1998. Damage growth in carbon fibre–PEEK unidirectional composites under compression. Materials Science and Engineering:A, 249: 259-276. doi: 10.1016/S0921-5093(98)00484-5 Sobotka J C, Mcclung R C. 2019. Verification of stress-intensity factor solutions by uncertainty quantification. Journal of Verification, Validation and Uncertainty Quantification, 4: 021003. doi: 10.1115/1.4044868 Stefanescu D. 2004. Measurement and prediction of fatigue crack growth from cold expanded holes Part 2: Prediction of fatigue crack growth from cold expanded holes. The Journal of Strain Analysis for Engineering Design, 39: 41-52. doi: 10.1177/030932470403900104 Swift T. 1994. Damage tolerance capability. International Journal of Fatigue, 16: 75-94. doi: 10.1016/0142-1123(94)90446-4 Tada H, Paris P C, Irwin G R. 1973. The Stress Analysis of Cracks Handbook, Del Research Corp. Hellertown, PA. Tada H, Paris P C, Irwin G R. 1985. The Stress Analysis of Cracks Handbook, 2nd Edition. Paris Productions Inc, St.Louis. Tada H, Paris P C, Irwin G R. 2000. The Stress Analysis of Cracks Handbook, 3rd Edition. New York: ASME Press. Tan P W, Raju I S, Shivakumar K N, Newman Jr J C. 1988. A re-evaluation of finite element models and stress intensity factors for surface cracks emanating from stress concentrations. NASA TM-101527. Tan P W, Raju I S, Shivakumar K N, Newman Jr J C. 1990. Evaluation of finite-element models and stress intensity factors for surface cracks emanating from stress concentrations// Surface-Crack Growth: Models, Experiments, and Structures: ASTM STP 1060. 1990: 34-48. Teh L S. 2002. Library of geometric influences for stress intensity factor weight functions. University of London, University College London (United Kingdom). Teh L S, Brennan F P. 2005. Stress intensity factors for 2-D semicircular notches using the superposition of SIF weight functions. Fatigue and Fracture of Engineering Materials and Structures, 28: 423-435. doi: 10.1111/j.1460-2695.2005.00872.x Teh L, Love A, Brennan F. 2006. Mode I stress intensity factors for edge cracks emanating from 2-D U-notches using composition of SIF weight functions. International Journal of Fatigue, 28: 355-365. doi: 10.1016/j.ijfatigue.2005.07.021 Teh L, Brennan F. 2007. Evaluation of mode I stress intensity factors for edge cracks from 2-D V-notches using composition of constituent SIF weight functions. International Journal of Fatigue, 29: 1253-1268. doi: 10.1016/j.ijfatigue.2006.10.012 Terada H. 1976. An analysis of the stress intensity factor of a crack perpendicular to the welding bead. Engineering Fracture Mechanics, 8: 441-444. doi: 10.1016/0013-7944(76)90024-2 Tetelman A S, McEvily Jr A J. 1967. Fracture of Structural Materials. New York: John Wiley & Sons, INC. Tong D H, Wu X R. 2013. Determination of crack surface displacements for cracks emanating from a circular hole using weight function method. Fatigue & Fracture of Engineering Materials & Structures, 36: 340-348. Tong D-H, Wu X R. 2014. Analysis of crack opening stresses for center-and edge-crack tension specimens. Chinese Journal of Aeronautics, 27: 291-298. doi: 10.1016/j.cja.2013.07.007 Tong D H, Wu X R. 2015. Determination of crack surface displacements for a radial crack emanating from a semi-circular notch using weight function method. Acta Mechanica Solida Sinica, 28: 305-312. doi: 10.1016/S0894-9166(15)30017-3 Tsai C H, Ma C C. 1989. Weight functions for cracks in finite rectangular plates. International Journal of Fracture, 40: 43-63. doi: 10.1007/BF01150865 Tsai C H, Ma C C. 1992. Thermal weight function of cracked bodies subjected to thermal loading. Engineering Fracture Mechanics, 41: 27-40. doi: 10.1016/0013-7944(92)90092-S Wang K, Zhang Q, Xia X, Wang L. 2015. Analysis of hydraulic fracturing in concrete dam considering fluid–structure interaction using XFEM-FVM model. Engineering Failure Analysis, 57: 399-412. doi: 10.1016/j.engfailanal.2015.07.012 Wang R, Kemeny J M. 1993. Micromechanical modeling of tuffaceous rock for application in nuclear waste storage. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 30: 1351-1357. Wang X, Lambert S. 1995. Stress intensity factors for low aspect ratio semi-elliptical surface cracks in finite thickness plates subjected to nonuniform stresses. Engineering Fracture Mechanics, 51: 517-532. doi: 10.1016/0013-7944(94)00311-5 Wang X, Lambert S. 1997. Stress intensity factors and weight functions for high aspect ratio semi-elliptical surface cracks in finite-thickness plates. Engineering Fracture Mechanics, 57: 13-24. doi: 10.1016/S0013-7944(97)00018-0 Wang X, Glinka G. 2009. Determination of approximate point load weight functions for embedded elliptical cracks. International Journal of Fatigue, 31: 1816-1827. doi: 10.1016/j.ijfatigue.2008.12.002 Wang Y C, Zhu Y B, He Z Z, Wu H A. 2020. Multiscale investigations into the fracture toughness of SiC/graphene composites: Atomistic simulations and crack-bridging model. Ceramics International 46: 29101-29110. Wagner D, Millwater H. 2012. 2D weight function development using a complex Taylor series expansion method. Engineering Fracture Mechanics, 86: 23-37. doi: 10.1016/j.engfracmech.2012.02.006 Wanhill R. 2003. Milestone case histories in aircraft structural integrity. Comprehensive Structural Integrity, 1: 61-72. Wigglesworth L. 1957. Stress distribution in a notched plate. Mathematika, 4: 76-96. doi: 10.1112/S002557930000111X Wu S J, Knott J F. 2001. Comments on spread of plasticity from edge crack close to interface of dissimilar metal joint. Science and Technology of Welding and Joining, 6: 1-8. doi: 10.1179/136217101101538479 Wu X, Bowen P. 2000. Fatigue crack growth resistance of unidirectional fiber reinforced titanium metal matrix composites under transverse loading. Metallurgical and Materials Transactions A, 31A: 2083-2092. Wu X R, Carlsson J. 1983. The generalised weight function method for crack problems with mixed boundary conditions. Journal of the Mechanics and Physics of Solids, 31: 485-497. doi: 10.1016/0022-5096(83)90012-1 Wu X R. 1984. Approximate weight functions for center and edge cracks in finite bodies. Engineering Fracture Mechanics, 20: 35-49. doi: 10.1016/0013-7944(84)90113-9 Wu X R, Carlsson A J. 1991. Weight Functions and Stress Intensity Factor Solutions. Oxford, England: Pergamon Press Wu X R. 1991a. The arbitrarily loaded single-edge cracked circular disc; accurate weight function solutions. International Journal of Fracture, 49: 239-256. doi: 10.1007/BF00042194 Wu X R. 1991b. On the influence of reference load case on the crack face weight functions. International Journal of Fracture, 48: 179-192. doi: 10.1007/BF00036630 Wu X R. 1992. Analytical wide-range weight functions for various finite cracked bodies. Engineering Analysis with Boundary Elements, 9: 307-322. doi: 10.1016/0955-7997(92)90016-Z Wu X R. 1993. Application of weight function method for crack analysis in thermal stress fields.//in Thermal Shock and Thermal Fatigue Behavior of Advanced Ceramics. Springer: 119-141 Wu X R, Newman Jr J C, Zhao W, et al. 1998. Small-crack growth and fatigue life predictions for high-strength aluminium alloys. Part I: Experimental and fracture mechanics analysis. Fatigue & Fracture of Engineering Materials & Structures, 21: 1289-1306. Wu X R, Tong D H. 2014. Determination of stress intensity factors and crack-line stresses from crack mouth opening displacements: an inverse weight function approach// 20th European Conference on Fracture: Fracture at All Scales, Trondheim, Norway. Wu X R, Tong D H. 2018. Evaluation of various analytical weight function methods base on exact K-solutions of an edge-cracked circular disc. Engineering Fracture Mechanics, 189: 64-80. doi: 10.1016/j.engfracmech.2017.09.024 Wu X R, Tong D H, Zhao X C, Xu W. 2018a. Review and evaluation of weight functions and stress intensity factors for edge-cracked finite-width plate. Engineering Fracture Mechanics, 195: 200-221. doi: 10.1016/j.engfracmech.2018.04.001 Wu X R, Zhao X C, Xu W, Tong D H. 2018b. Discussions on weight functions and stress intensity factors for radial crack(s) emanating from a circular hole in an infinite plate. Engineering Fracture Mechanics, 192: 192-204. doi: 10.1016/j.engfracmech.2018.02.001 Wu X R. 2019. A review and verification of analytical weight function methods in fracture mechanics. Fatigue & Fracture of Engineering Materials & Structures, 42: 2017-2042. Wu X R, Xu W. 2022. Weight Function Methods in Fracture Mechanics: Theory and Applications. Springer Nature and China Aviation Publishing & Media Co. LTD. ISBN: 978-981-16-8960-4 Xiao Q, Karihaloo B L. 2002. Approximate Green's functions for singular and higher order terms of an edge crack in a finite plate. Engineering Fracture Mechanics, 69: 959-981. doi: 10.1016/S0013-7944(01)00114-X Xu R X, Wu X R. 1989. A weight function approach to stress-intensity factors for half-elliptical surface cracks in cylindrical pressure vessels subjected to thermal shock. International Journal of Pressure Vessels and Piping, 39: 375-391. doi: 10.1016/0308-0161(89)90108-7 Xu W, Wu X R, Wang H. 2011. Weight functions and strip yield solution for two equal-length collinear cracks in an infinite sheet. Engineering Fracture Mechanics, 78: 2356-2368. doi: 10.1016/j.engfracmech.2011.05.007 Xu W, Wu X R. 2012. Weight functions and strip-yield model analysis for three collinear cracks. Engineering Fracture Mechanics, 85: 73-87. doi: 10.1016/j.engfracmech.2012.02.009 Xu W, Wang H, Wu X R, Zhang X J. 2014. A novel method for residual strength prediction for sheets with multiple site damage: Methodology and experimental validation. International Journal of Solids and Structures, 51: 551-565. doi: 10.1016/j.ijsolstr.2013.10.012 Xu W, Waas A M. 2017. Multiple solutions in cohesive zone models of fracture. Engineering Fracture Mechanics, 177: 104-122. doi: 10.1016/j.engfracmech.2017.03.026 Xu W, Rao D, Wu X, Tong D H. 2020a. Wide‐range and accurate mixed‐mode weight functions and stress intensity factors for cracked discs. Fatigue & Fracture of Engineering Materials & Structures, 43: 1022-1037. Xu W, Zhang C, Wu X R, Yu Y. 2020b. Weight function method and its application for orthotropic single edge notched specimens. Composite Structures, 252: 112695. doi: 10.1016/j.compstruct.2020.112695 Zerbst U, Schwalbe K-H, Anisworth R A. 2003. Comprehensive Structural Integrity: An Overview of Failure Assessment Methods in Codes and Standards, Vol. 7 (7.01): 1-48. Eds. Milne I, Ritchie R O, Karihaloo B, Elsevier Pergamon. Zerbst U, Vormwald M, Andersch C, Mädler K. 2005. The development of a damage tolerance concept for railway components and its demonstration for a railway axle. Engineering Fracture Mechanics, 72: 209-239. doi: 10.1016/j.engfracmech.2003.11.011 Zerbst U, Schodel M, Webster S, Ainsworth R. 2007. Fitness-for-service Fracture Assessment of Structures Containing Cracks - A Workbook Based on European SINTAP/FITNET Procedure. 1st edition. Elsevier Ltd. Zhang B, Xu W, Wu X R, Yu Y. 2020. Stress intensity factors and plastic zones of stiffened panels with multiple collinear cracks. Theoretical and Applied Fracture Mechanics, 110: 102816. doi: 10.1016/j.tafmec.2020.102816 Zhang B, Xu W, Wu X R. 2022. Weight function methods and stress intensity factors for two unsymmetric through and corner cracks at a circular hole. Engineering Fracture Mechanics, 264: 108361. doi: 10.1016/j.engfracmech.2022.108361 Zhang J, Leung C K, Gao Y. 2011. Simulation of crack propagation of fiber reinforced cementitious composite under direct tension. Engineering Fracture Mechanics, 78: 2439-2454. doi: 10.1016/j.engfracmech.2011.06.003 Zhang J, Li V C. 2004. Simulation of crack propagation in fiber-reinforced concrete by fracture mechanics. Cement and Concrete Research, 34: 333-339. doi: 10.1016/j.cemconres.2003.08.015 Zhang Y, Ren X, Zhou J Z, et al. 2009. Investigation of the stress intensity factor changing on the hole crack subject to laser shock processing. Materials & Design, 30: 2769-2773. Zhao W, Wu X R, Yan M G. 1989a. Weight function method for three dimensional crack problems—I. Basic formulation and application to an embedded elliptical crack in finite plates. Engineering Fracture Mechanics, 34: 593-607. doi: 10.1016/0013-7944(89)90122-7 Zhao W, Wu X R. 1990a. Stress intensity factor evaluation by weight function for surface crack in edge notch. Theoretical and Applied Fracture Mechanics, 13: 225-238. doi: 10.1016/0167-8442(90)90090-M Zhao W, Wu X R. 1990b. Stress intensity factors for corner cracks at a semi-circular notch under stress gradients. Fatigue & Fracture of Engineering Materials & Structures, 13: 347-360. doi: 10.1111/j.1460-2695.1990.tb00606.x Zhao W, Wu X R, Yan M G. 1991. Stress intensity factors for corner cracks at a hole under remote tension. Acta Mechanica Sinica, 7: 76-81. doi: 10.1007/BF02486599 Zhao W, Wu X R, Yan M G. 1989b. Weight function method for three dimensional crack problems—II. Application to surface cracks at a hole in finite thickness plates under stress gradients. Engineering Fracture Mechanics, 34: 609-624. doi: 10.1016/0013-7944(89)90123-9 Zhao W, Sutton M A, Shivakumar K N, Newman Jr J C. 1994. Stress intensity factors for surface and corner cracks emanating from a wedge-loaded hole// FAA/NASA International Symposium on Advanced Structural Integrity Methods for Airframe Durability and Damage Tolerance. Hampton, VA, USA, May 1994. NASA Conference Publication 3274. Zhao W, Newman Jr J C, Sutton M A. 1997a. A three-dimensional weight function method—evaluation and applications// Fatigue and Fracture Mechanics: 27th Volume: ASTM STP 1296. Zhao W, Newman Jr J C, Sutton M A, Wu X R, Shivakumar K N. 1997b. Stress intensity factors for corner cracks at a hole by a 3-D weight function method with stresses from the finite element method. Fatigue & Fracture of Engineering Materials & Structures, 20: 1255-1267. Zhao W, Newman Jr J C, Sutton M A, Shivakumar K N, Wu X R. 1998. Stress intensity factors for surface cracks at a hole by a three-dimensional weight function method with stresses from the finite element method. Fatigue & Fracture of Engineering Materials & Structures, 21: 229-239. Zhao X C, Wu X R, Newman J C, Tong D H. 2016. Stress intensity factors for surface cracks in single‐edge notch bend specimen by a three-dimensional weight function method. Fatigue & Fracture of Engineering Materials & Structures, 39: 1407-1418. Zhao X C, Wu X R, Newman Jr J C, Tong D H. 2017. Stress intensity factors for corner cracks in single-edge notch bend specimen by a three-dimensional weight function method. Fatigue & Fracture of Engineering Materials & Structures, 40: 277-287. Zheng X J, Glinka G, Dubey R N. 1996. Stress intensity factors and weight functions for a corner crack in a finite thickness plate. Engineering Fracture Mechanics, 54: 49-61. doi: 10.1016/0013-7944(95)00171-9 Zhou Y C, Long S G, Liu Y W. 2003. Thermal failure mechanism and failure threshold of SiC particle reinforced metal matrix composites induced by laser beam. Mechanics of Materials, 35: 1003-1020. doi: 10.1016/S0167-6636(02)00322-8 Zhuang W. 2000. Prediction of crack growth from bolt holes in a disc. International Journal of Fatigue, 22: 241-250. doi: 10.1016/S0142-1123(99)00122-X -





 下载:
下载: