Mechancial properties of amorphous alloys: In the framework of the microstructure heterogeneity
-
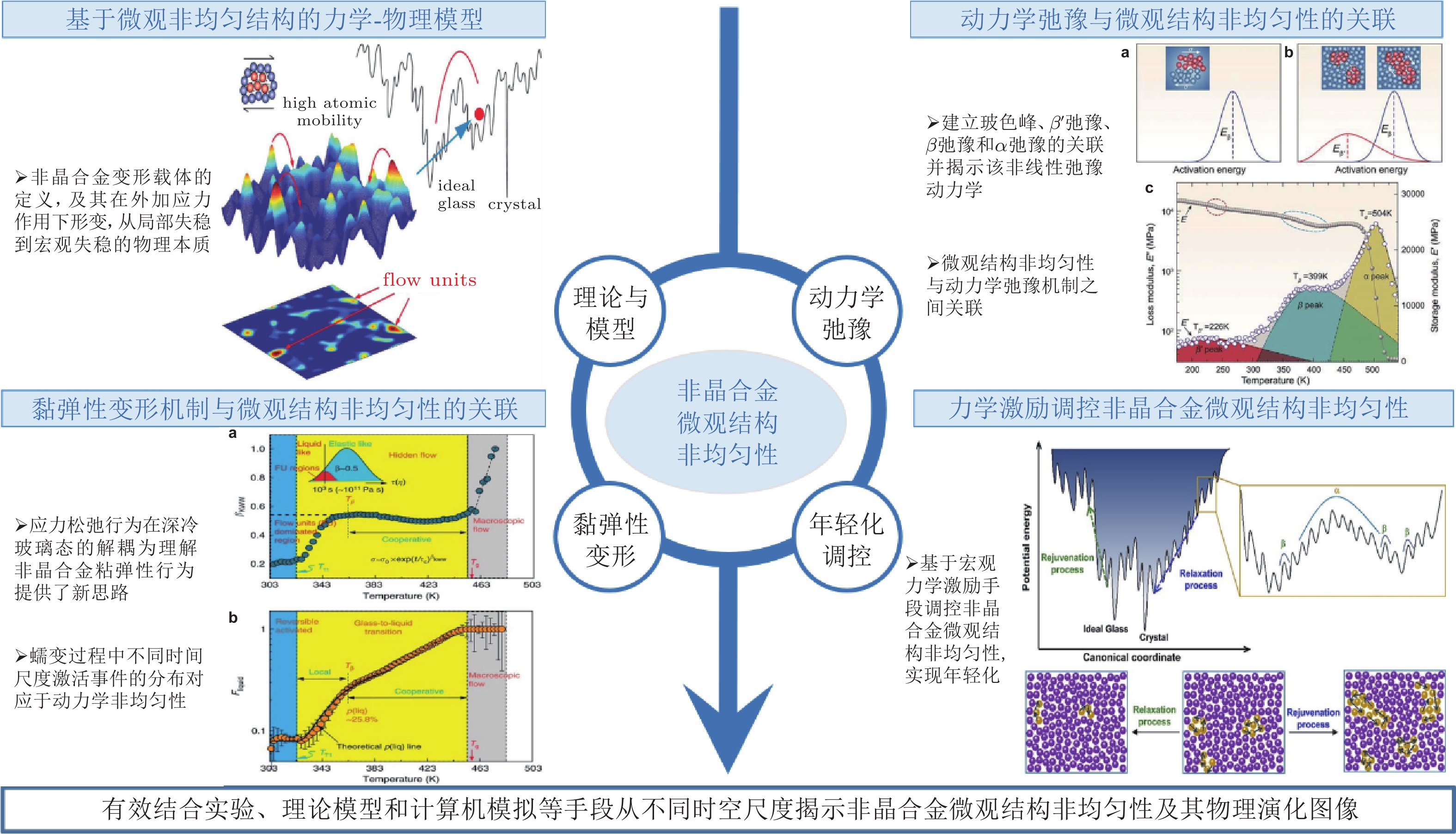
摘要: 非晶合金弛豫/晶化、玻璃转变、塑性变形等热力学和动力学行为都与其固有的结构非均匀性密切相关. 但是, 由于淹没在亚稳的长程无序结构中, 探究非晶合金的结构非均匀性十分困难. 尤其, 非晶合金微观结构非均匀性与其力学性能之间的本征关联是一个亟待解决的重要科学问题. 本文基于多尺度时空下的力学激励阐述非晶合金微观结构非均匀性特征与演化规律. 从实验、理论和数值模拟方面出发, 梳理了非晶合金微观结构非均匀性与弛豫机制和力学行为之间的关联. 最后, 针对非晶合金微观结构非均匀性与其物理/力学性能研究的方向提出了建议和展望.Abstract: The intrinsic structural heterogeneities of amorphous alloys are closely related to the thermodynamics and dynamical behavior, such as relaxation/crystallization, glass transition phenomenon and plastic deformation. However, the structural information is submerged into the meta-stable disordered long-range structure, which made it very difficult to explore the structural heterogeneities of amorphous alloys. Specificlly, the correlation between the microstructural heterogeneity and mechanical properties of amorphous alloys is one of important scientific issues. The current paper reviews the structural heterogeneity of dynamics into the amorphous alloys from the time-scale point of view and inspected the relaxation of structure with various spatial scales. From the perspective of experimental results, theoretical analysis and numerical simulations, the correlation between heterogeneous structure and the dynamic relaxations, deformation mechanisms, mechanical properties and dynamic characteristics were discussed. Finally, we discuss the further development of structural heterogeneity of amorphous alloys.
-
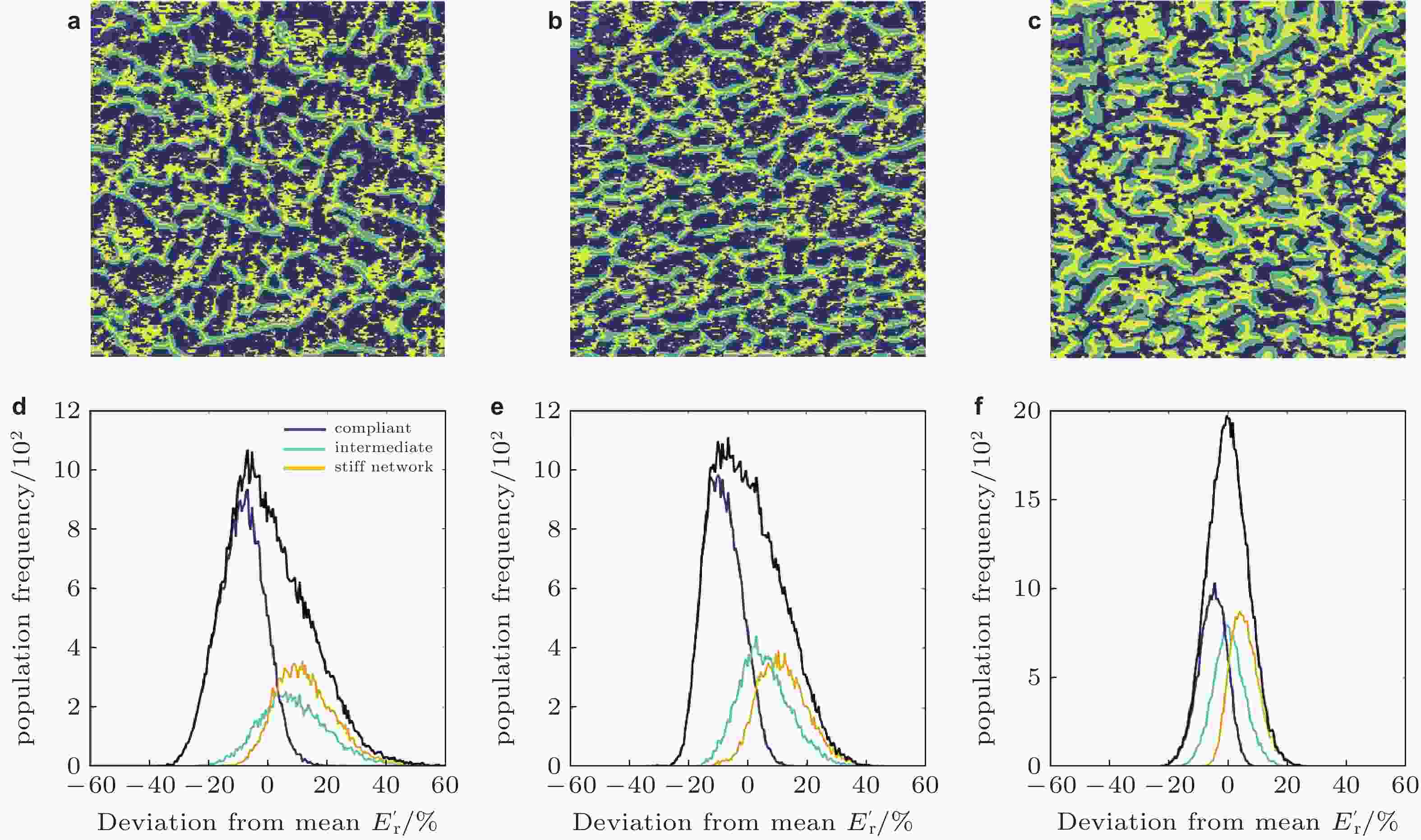
图 2 均值聚类分析表征弹性微观结构非均匀性: (a) ~ (c)模量图的示例三色表示, 其中像素根据模量 (蓝色为软区, 绿色为中间区, 黄色为硬区) 分组, 图像(a)表示铸态样品的中心位置, (b)为样品退火后的中心位置, (c)180 W激光脉冲处理的样品; (d) ~ (f)反卷积直方图, 显示了三种结构
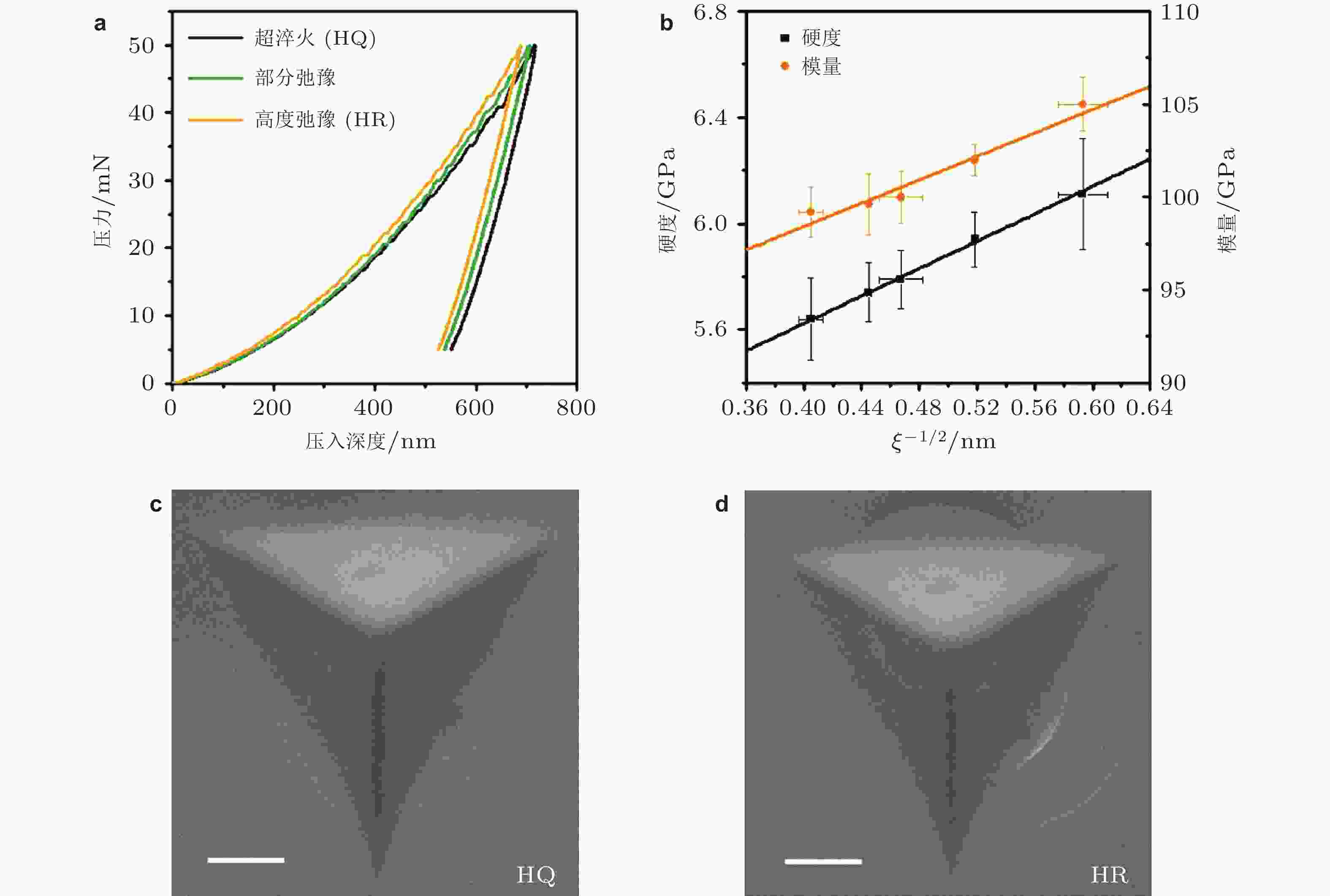
${{E}}_{\mathrm{r}}^{\mathrm{{'}}}$ 分布 (Tsai et al. 2017)图 3 (a)超淬火, 部分弛豫和高度弛豫样品的纳米压痕力−深度曲线; (b)纳米压痕硬度和模量与结构非均匀性的特征长度关系; (c)超淬火样品和高度弛豫样品的压痕形貌 (Zhu et al. 2018)
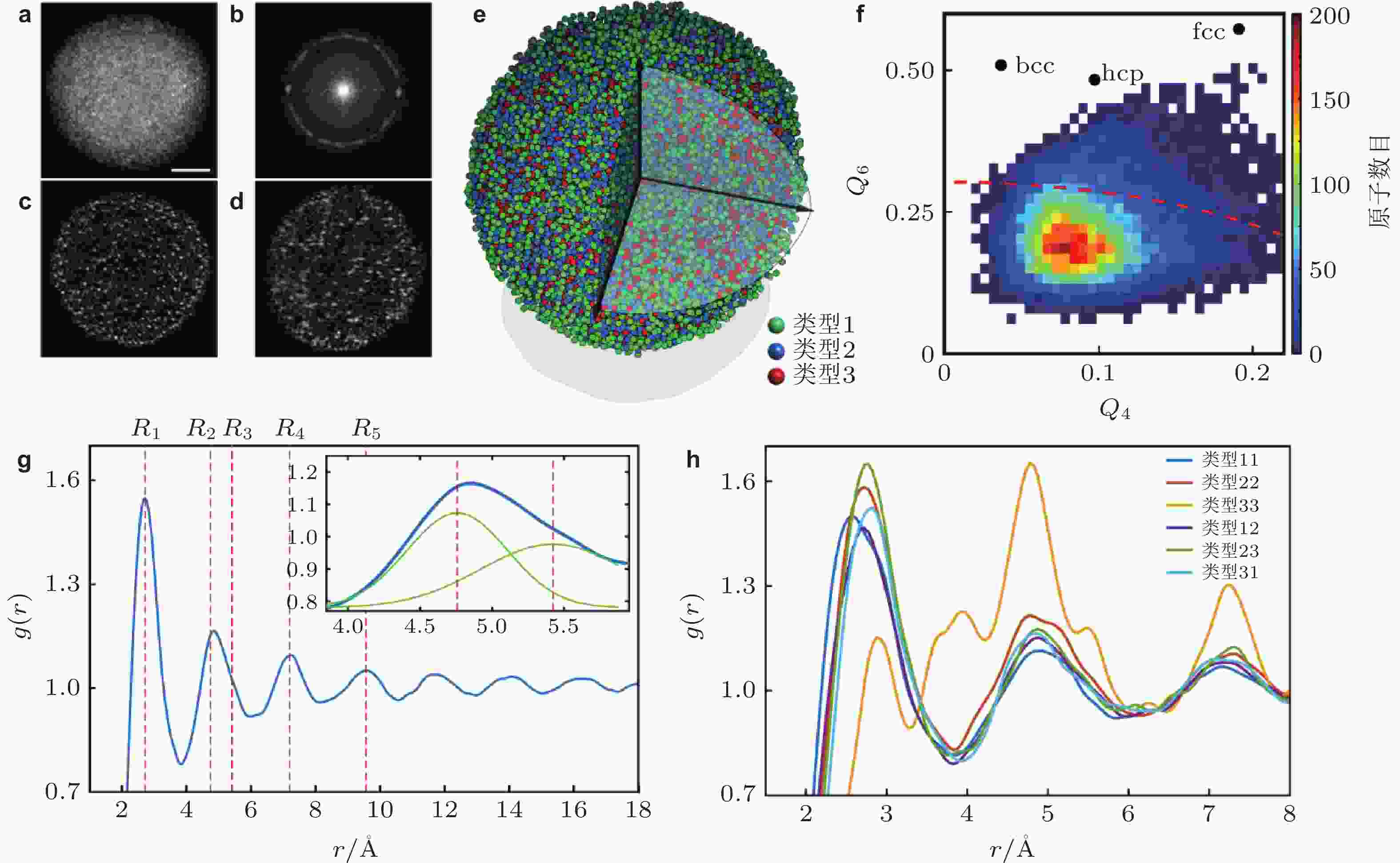
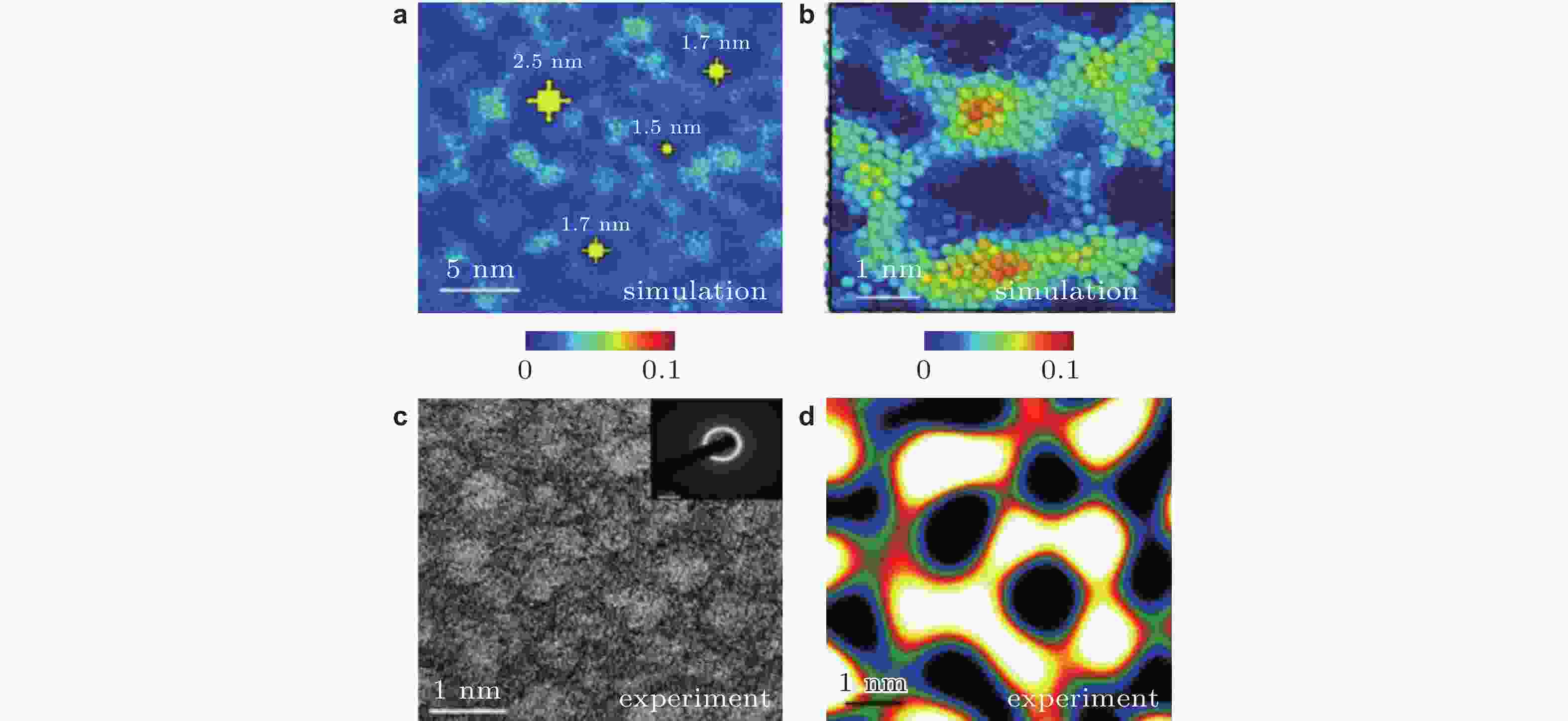
图 4 利用原子电子断层扫描技术观测到非晶固体中的三维原子结构, 1 Å = 0.1 nm (Yang et al. 2021)
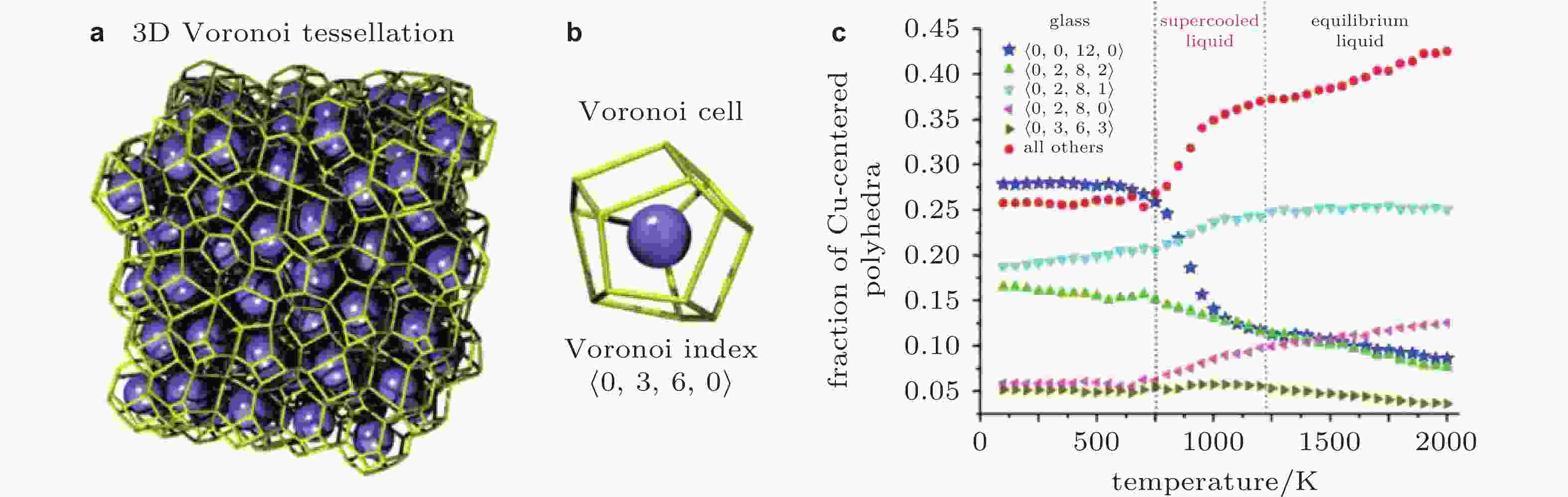
图 5 (a)Voronoi多面体结构, (b)中心原子的Voronoi指数 (Cheng & Ma 2011), (c) Cu64Zr36非晶合金中以Cu原子为中心的多面体含量随温度的演变 (Cheng et al. 2009)
图 6 CuZr非晶合金在分子动力学模拟和实验中的结构特征: (a)压应变为1%时的原子应变分布; (b)图(a)中的局域结构放大图; (c)高分辨透射电镜下的显微结构; (d)密度分布图 (Feng et al. 2016)
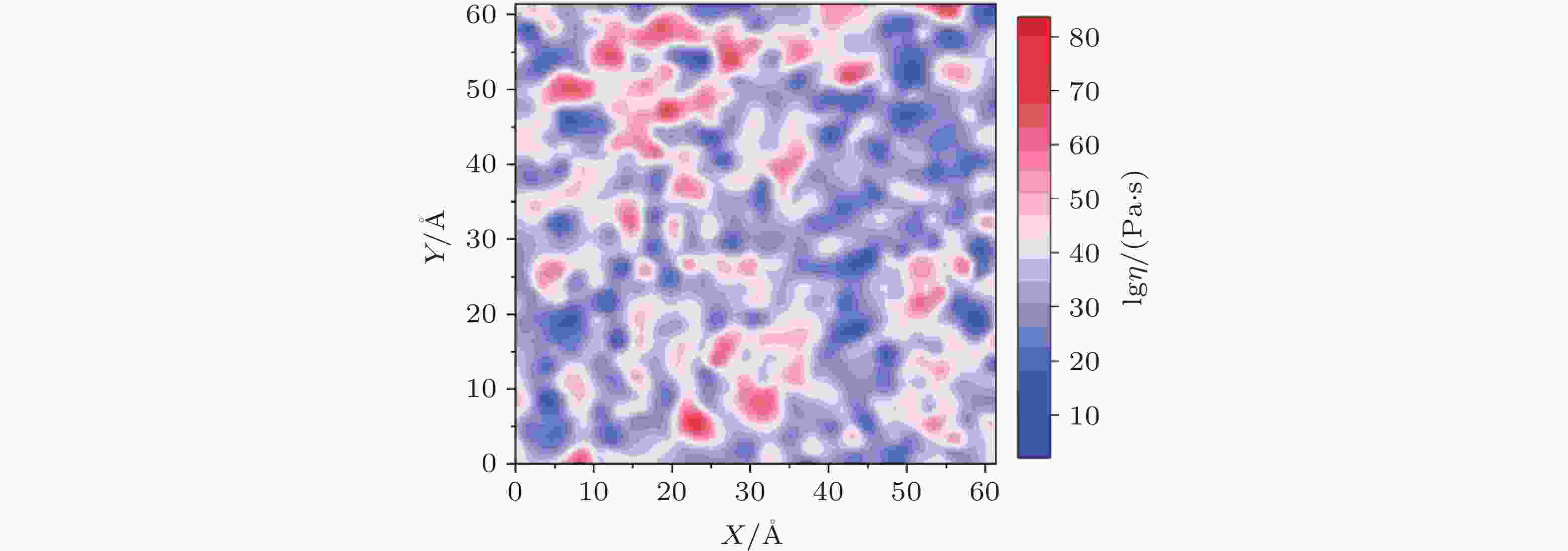
图 7 典型CuZr非晶合金黏度空间分布 (王云江等2020)
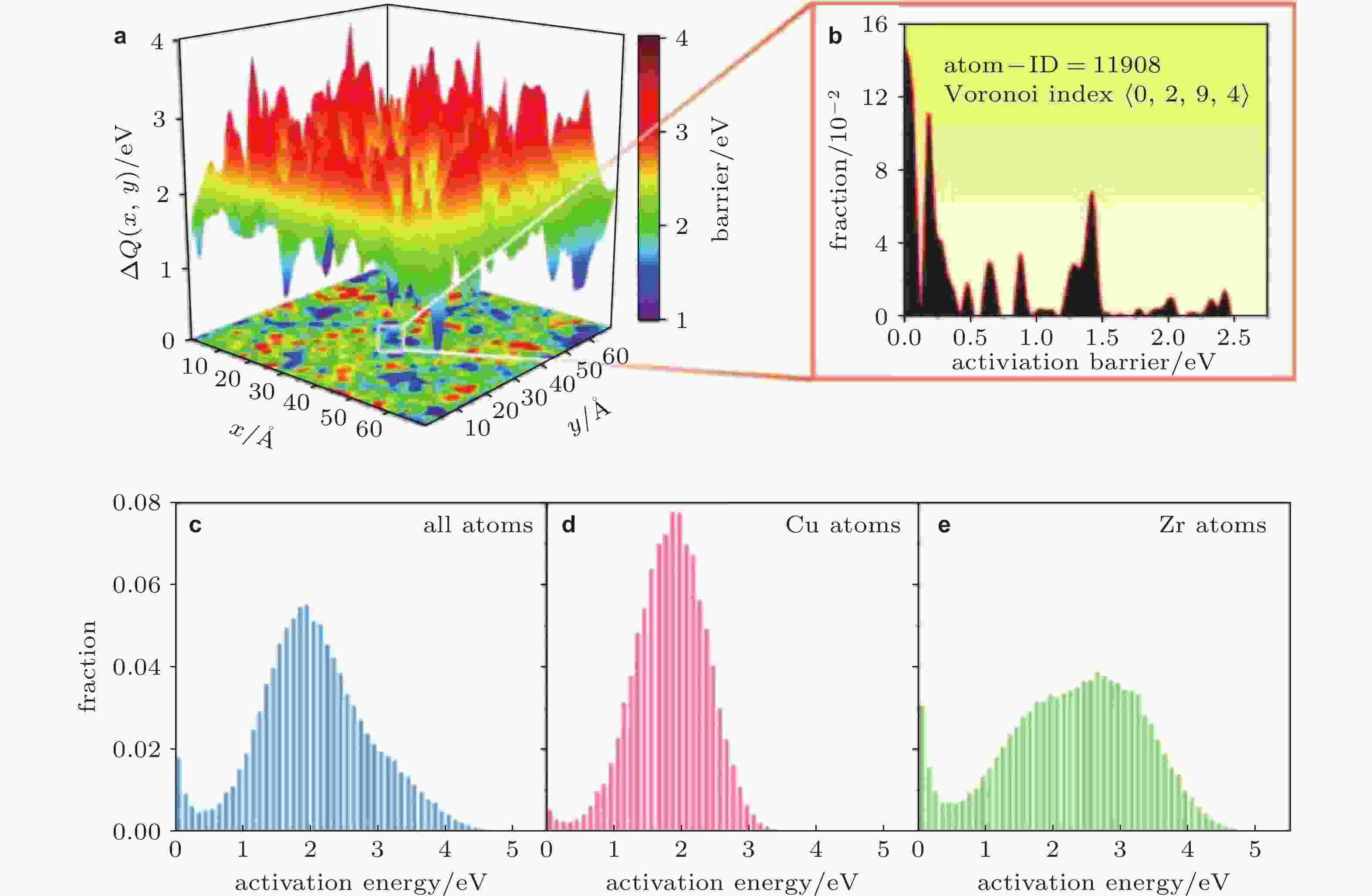
图 8 (a) Cu50Zr50非晶合金的局域事件激活能的空间分布特点; (b)体系中某个Zr原子沿不同方向激活1000次的激活能分布; (c) ~ (e)体系中原子的激活能分布谱 (Wei et al. 2019)
图 9 非晶合金中单原子扩散跃迁过程示意图 (卢博斯基 1989)
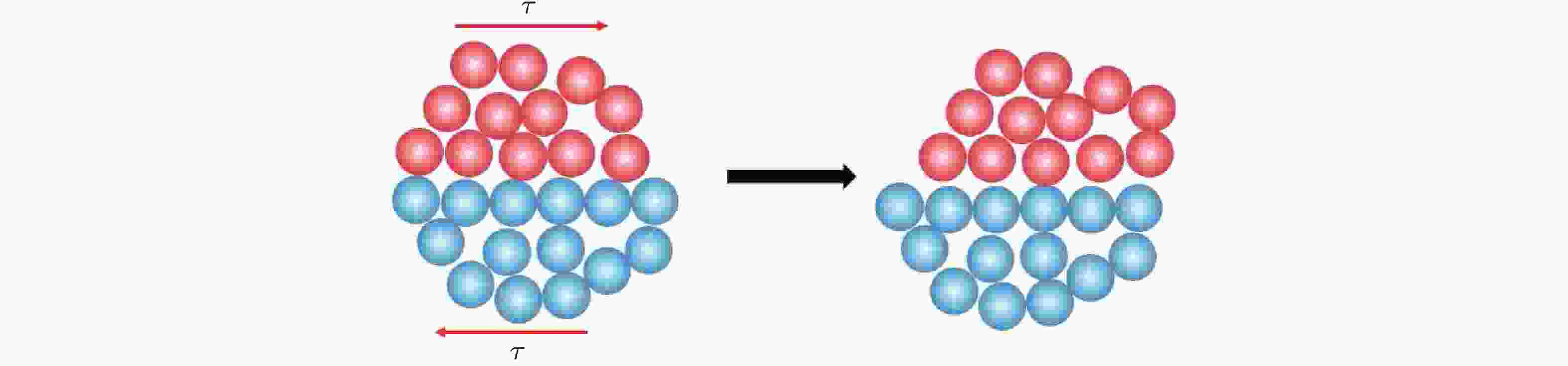
图 10 非晶合金中二维剪切转变区示意图 (Argon 1979)
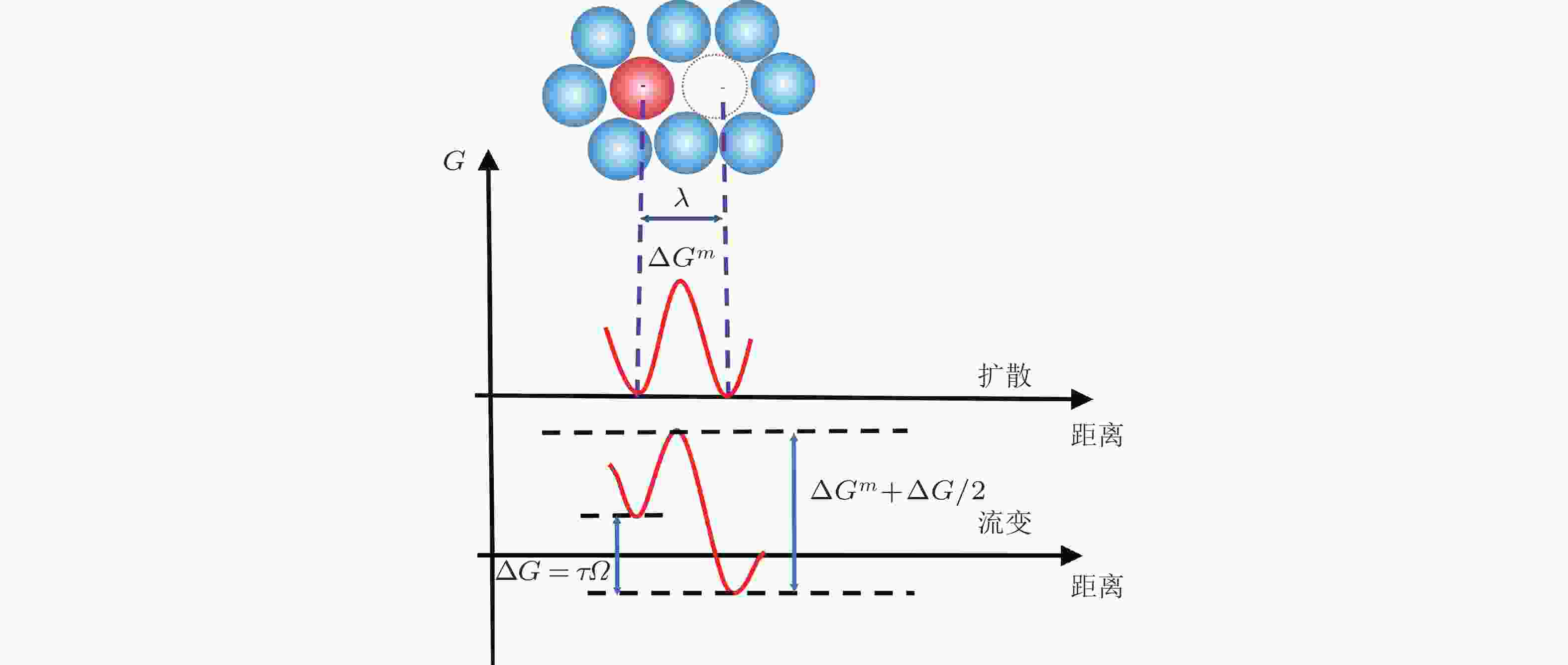
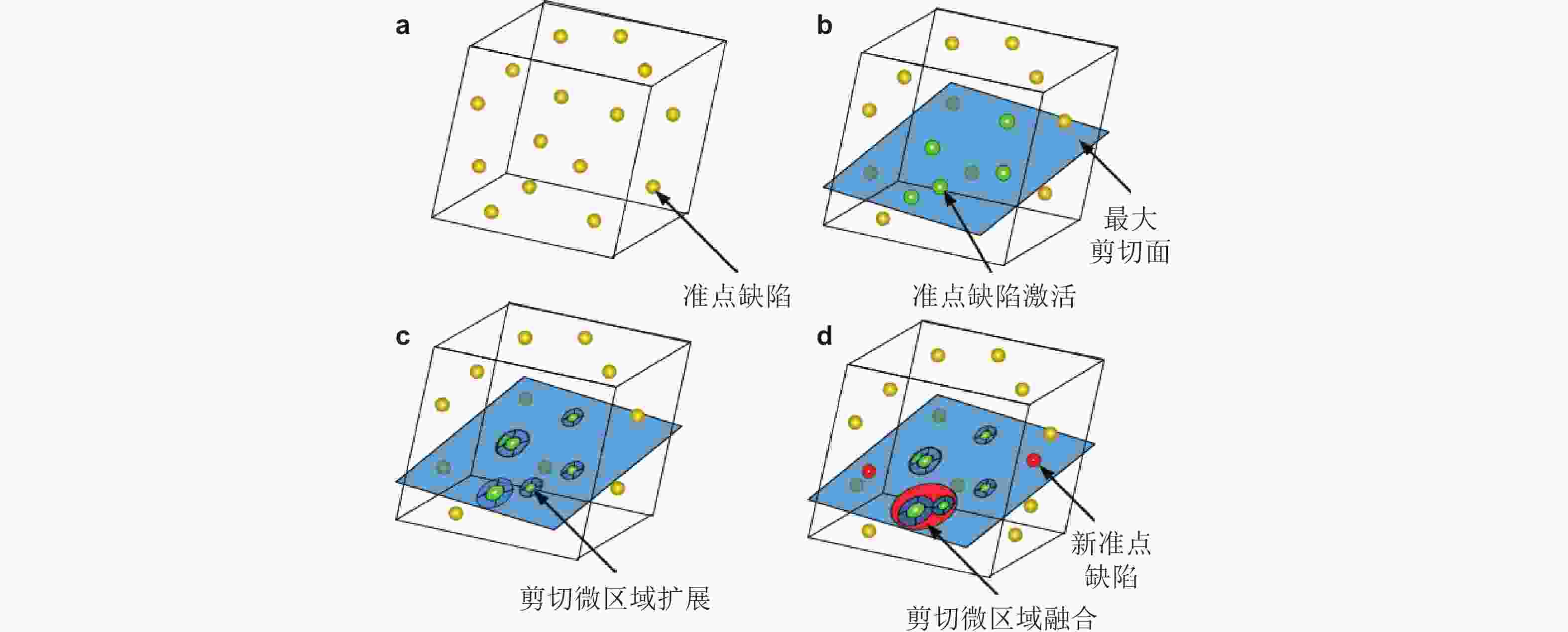
图 11 非晶态物质在准点缺陷理论框架下的微观变形描述. (a) 初始结构, (b) ~ (d) 为热力耦合激励作用下的激活、扩展和融合行为 (Rinaldi et al. 2011)
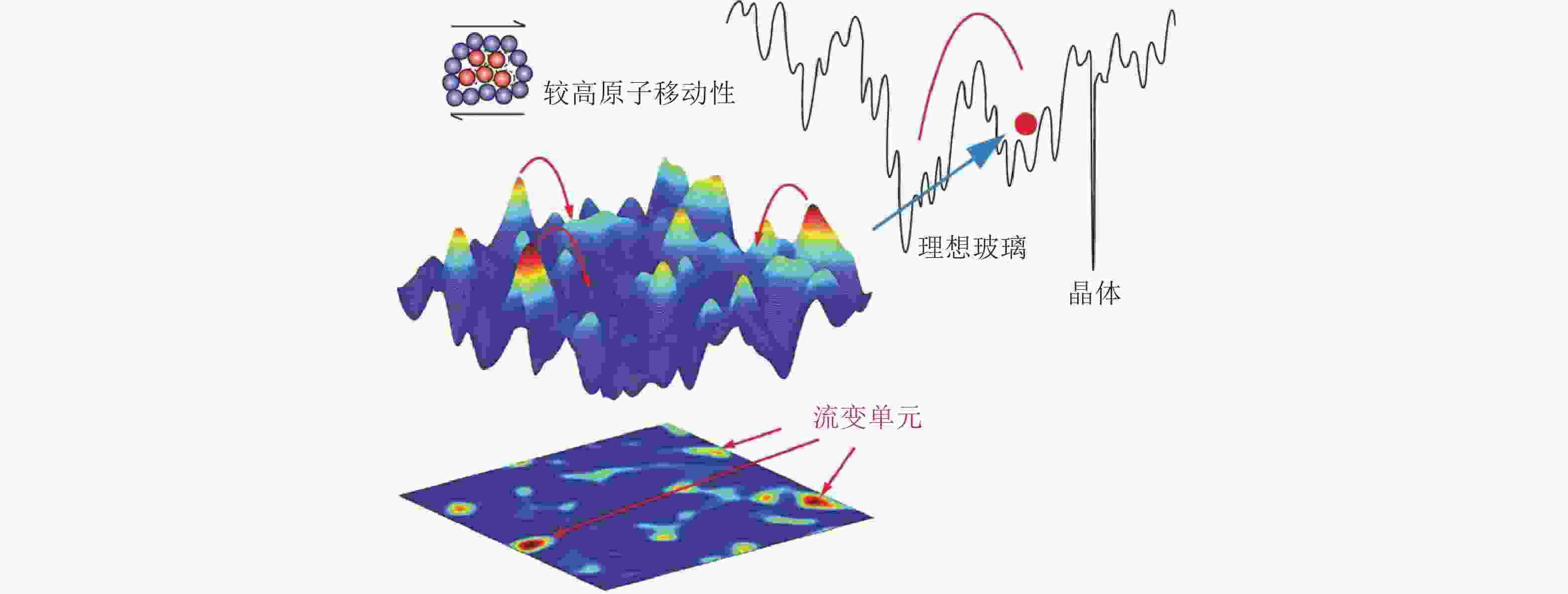
图 12 高能量状态流变单元示意图(Wang & Wang 2019)
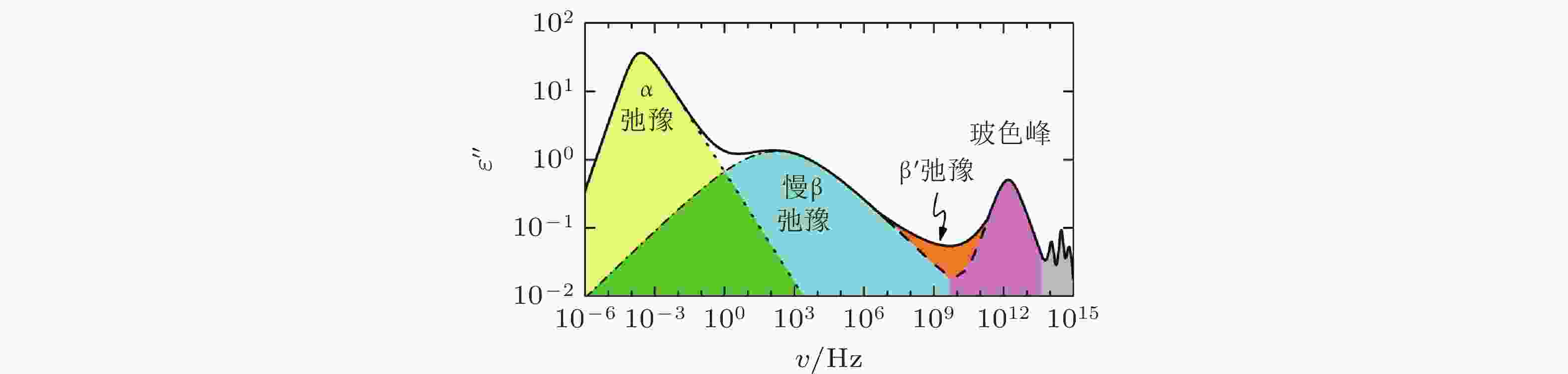
图 13 在极宽频率域内测得高分子玻璃中的介电损耗谱(弛豫现象) (Lunkenheimer et al. 2000)
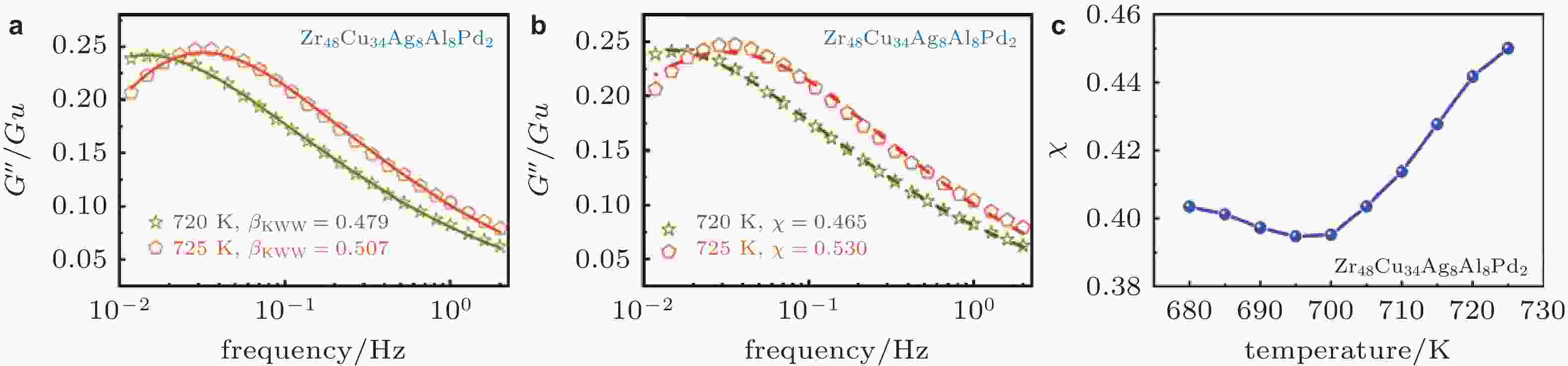
图 14 不同温度下Zr基非晶合金损耗模量G''/Gu随频率演化. (a)实线根据KWW模型拟合, (b)实线根据QPD模型拟合, (c)关联因子随温度的演化 (Cheng et al. 2021)
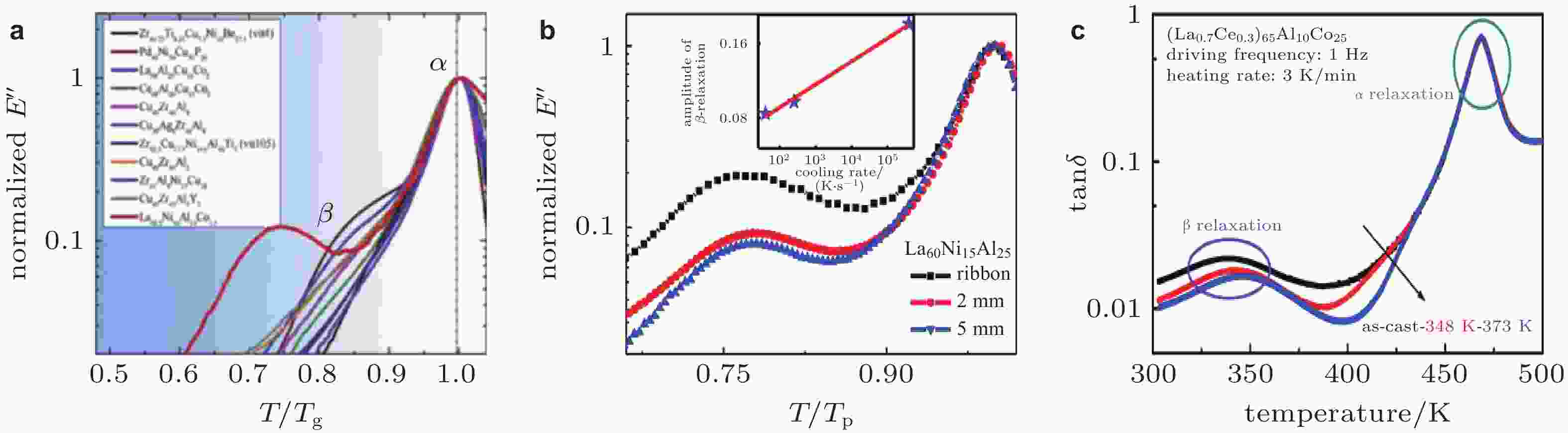
图 15 (a)典型非晶合金体系归一化损耗模量随温度的演化 (Yu et al. 2013), (b)不同初始状态La基非晶合金损耗模量随温度的演化 (Zhao et al. 2014), (c) La基铸态和弛豫态非晶合金内耗随温度的演化 (Zhang et al. 2021b)
图 16 结构非均匀性与β弛豫关联示意图. (a)非晶合金(铸态)的接触共振频率云图, (b) 接触共振频率在(a)的分布, (c) 铸态玻璃能量势垒图, (d) 小能谷跃迁积累为β弛豫, (e)非晶合金(物理老化后)的接触共振频率云图, (f) 接触共振频率在(e)中的分布, (g) 退火后玻璃能量势垒图, (h) β弛豫强度减少 (Wang et al. 2019)
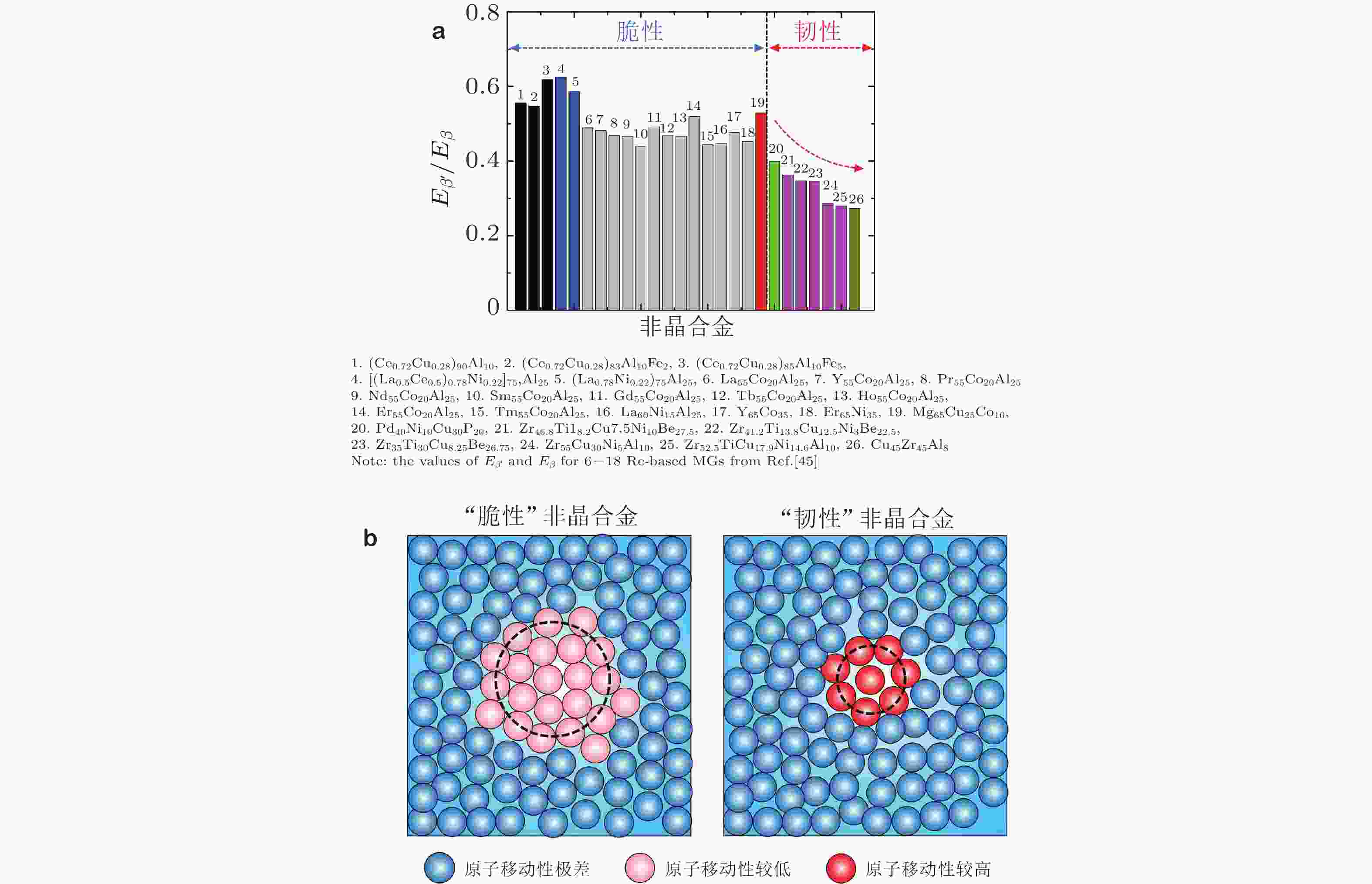
图 17 (a) 典型非晶合金体系快β′弛豫与慢β弛豫激活能之间的关系, (b)“脆性”非晶合金和“韧性”非晶合金微观原子排布示意图 (Wang et al. 2017)
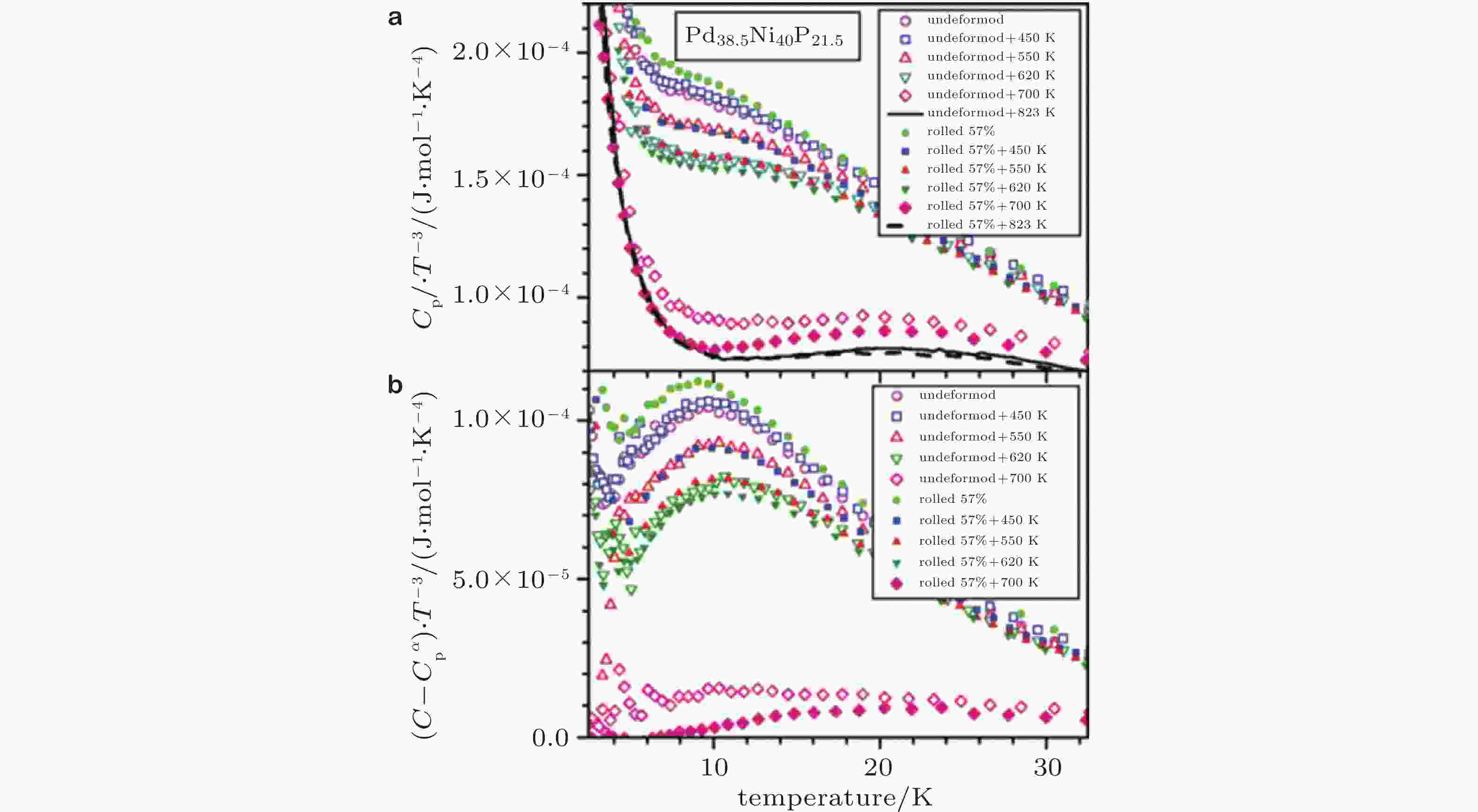
图 18 (a) 不同状态下非晶合金热流随温度的演化, (b) 剔除晶化影响后的热流随温度的演化 (Mitrofanov et al. 2014)
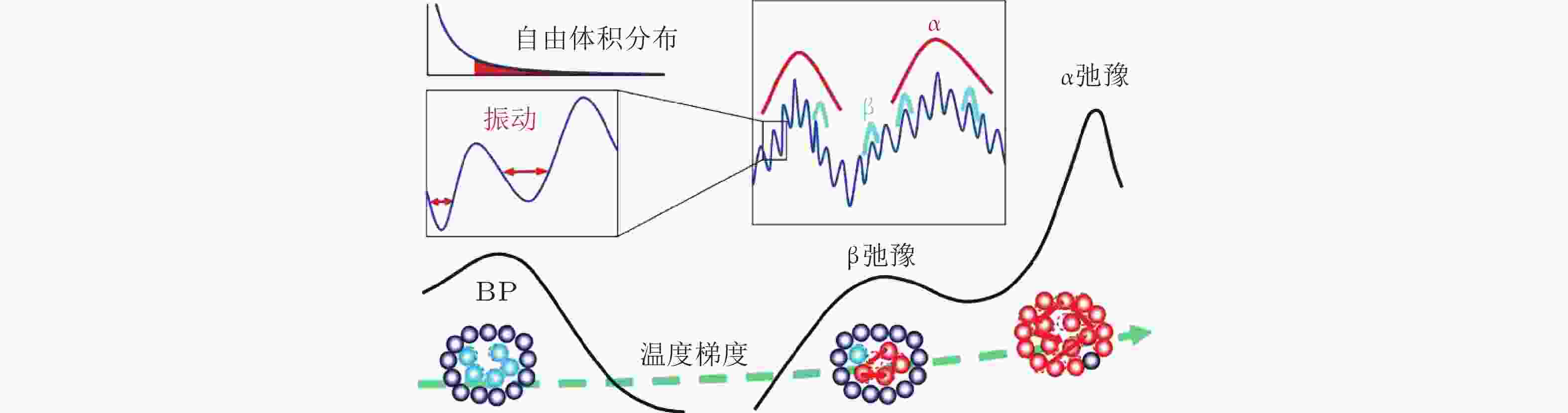
图 19 具有温度依赖性的动力学相关的自由体积分布(左上角). 沿温度升高梯度, 分别为玻色峰、β弛豫峰和α弛豫峰 (Huang et al. 2016)
图 20 (a)部分区域晶化的Pd42.5Ni7.5Cu30P20非晶合金的高分辨电镜图 (Ichitsubo et al. 2005); (b)不同温度下La60Ni15Al25非晶合金的应力松弛曲线, 其中实线为KWW拟合曲线 (Wang et al. 2014); (c)弛豫分布宽度相关指数
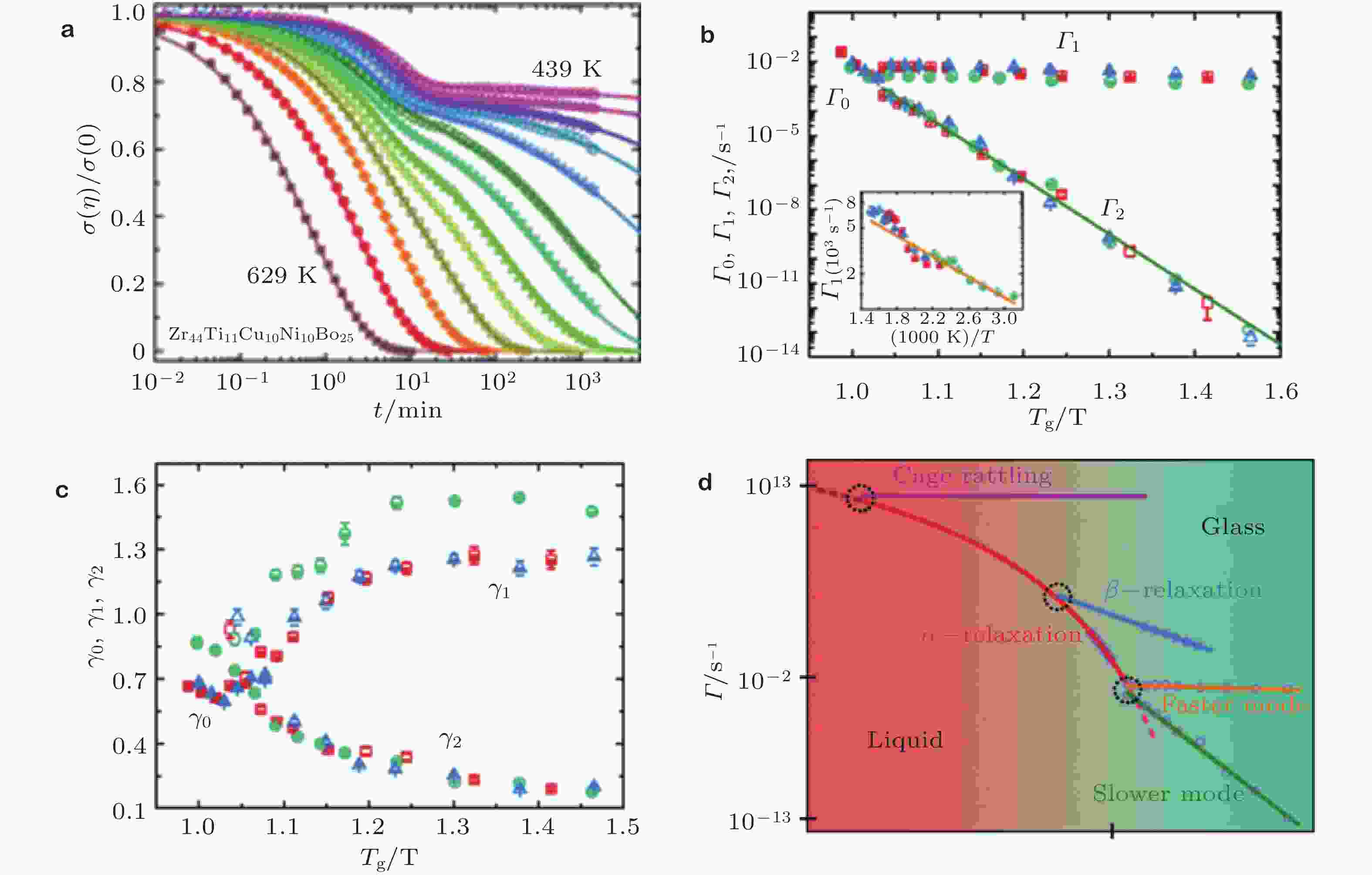
$ {\mathrm{\beta }}_{\mathrm{K}\mathrm{W}\mathrm{W}} $ 随温度的演化 (Wang et al. 2014); (d)通过X射线光子关联谱实验测量的Mg65Cu25Y10非晶合金在不同温度下的关联函数和弛豫指数 (Ruta et al. 2012)图 21 (a) Zr44Ti11Cu10Ni10Be25非晶的应力弛豫曲线, (b)弛豫速率及(c)指数随温度的演化, (d)非晶合金及其高温前驱液体的动力学行为的Arrhenius图 (Luo et al. 2017)
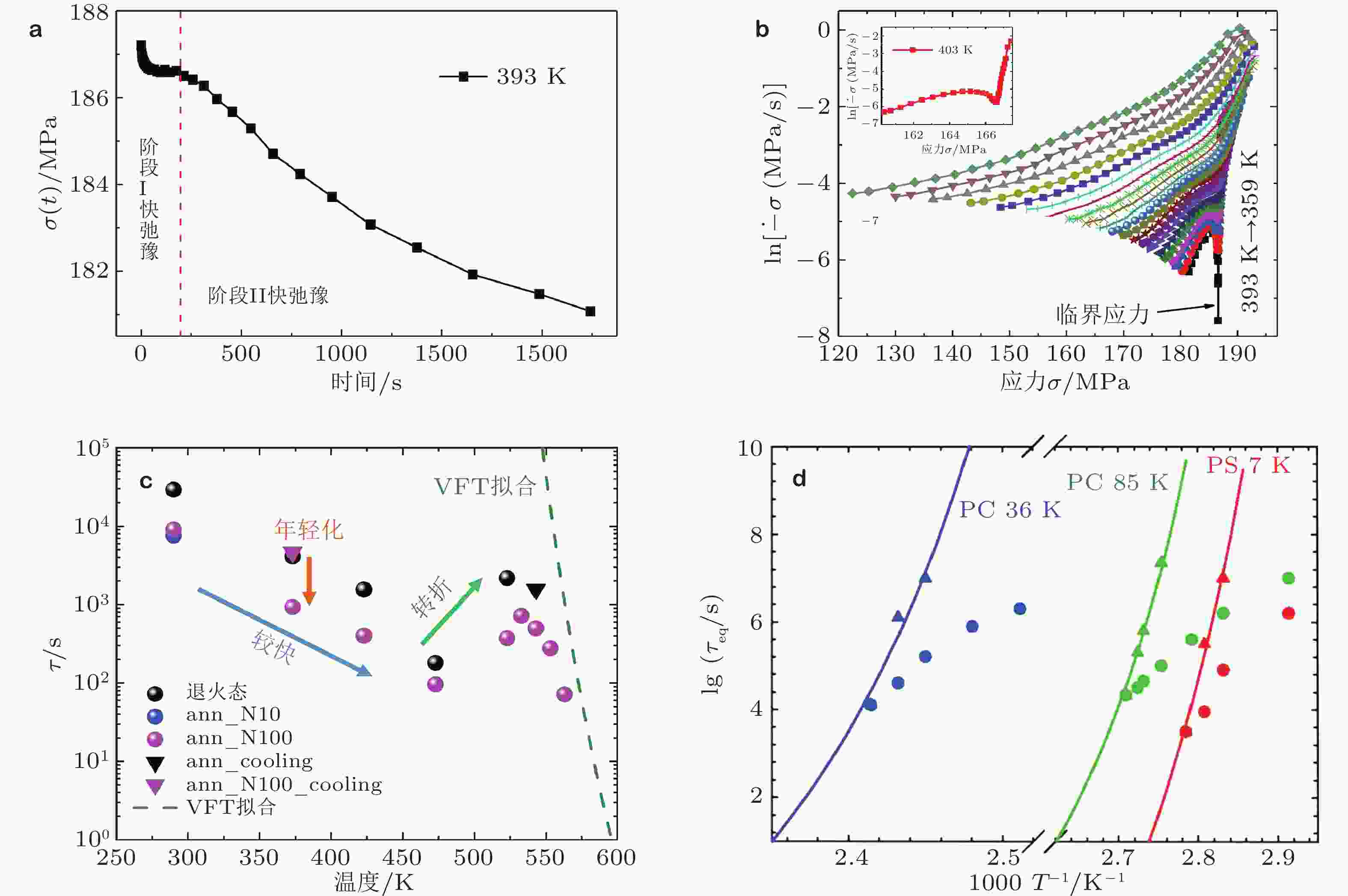
图 22 (a)Cu46Zr46Al8 非晶合金在低温弛豫时的双阶段现象 (Qiao et al. 2016b); (b)应力驱动到热激活应力松弛的转变. 插图显示例如在403 K, 表明松弛机制随应力变化的明显转变 (Qiao et al. 2016b) ; (c) Pd40Ni40P20非晶合金在X射线光子关联谱下的弛豫时间随温度的演化(Zhou et al. 2020); (d)聚合物的焓弛豫时间随温度变化 (Cangialosi et al. 2013)
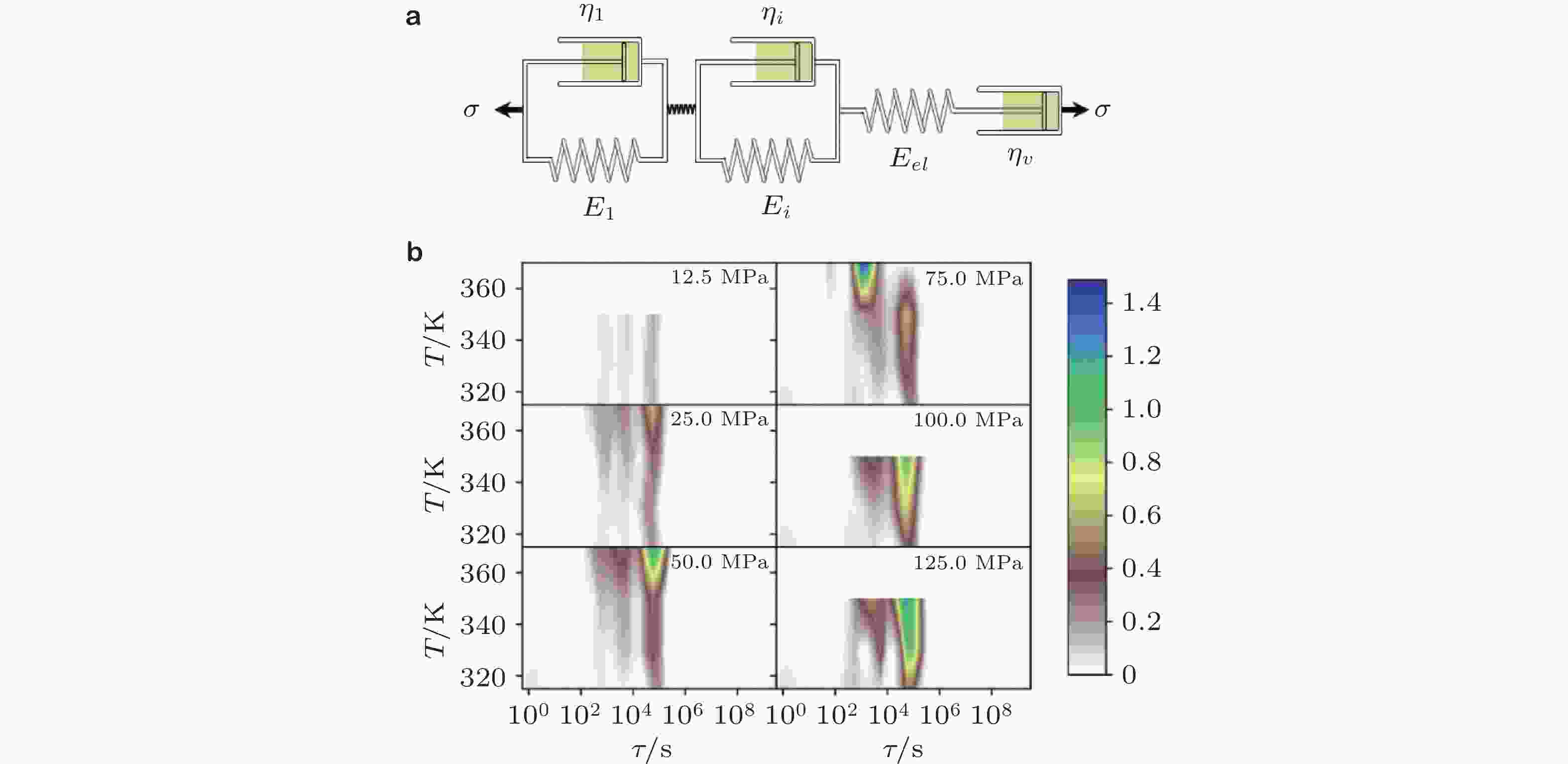
图 23 (a)由n个Kelvin单元和1个Maxwell单元组成的广义Kelvin模型; (b)不同应力及温度下La56.16Ce14.04Ni19.8Al10非晶合金蠕变过程的弛豫时间分布图谱 (Xu et al. 2020)
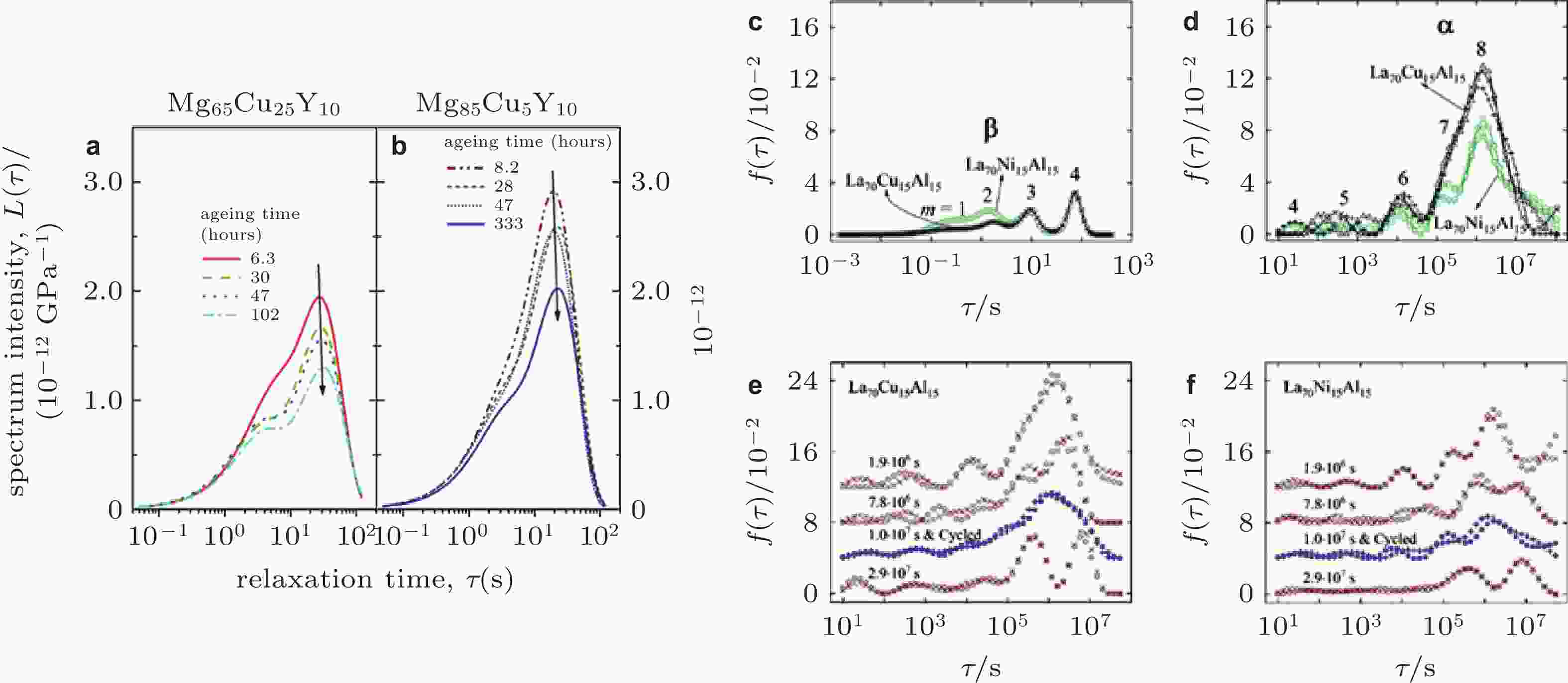
图 24 (a) Mg65Cu25Y10和(b) Mg85Cu5Y10非晶合金的弛豫时间谱 (Castellero et al. 2008), (c) La70Cu15Al15 和(d) La70Ni15Al15 非晶合金物理时效后的弛豫时间谱 (Lei et al. 2020), (e) La70Cu15Al15 和(f) La70Ni15Al15在物理时效和低温循环下非晶合金的弛豫时间谱 (Lei et al. 2019a)
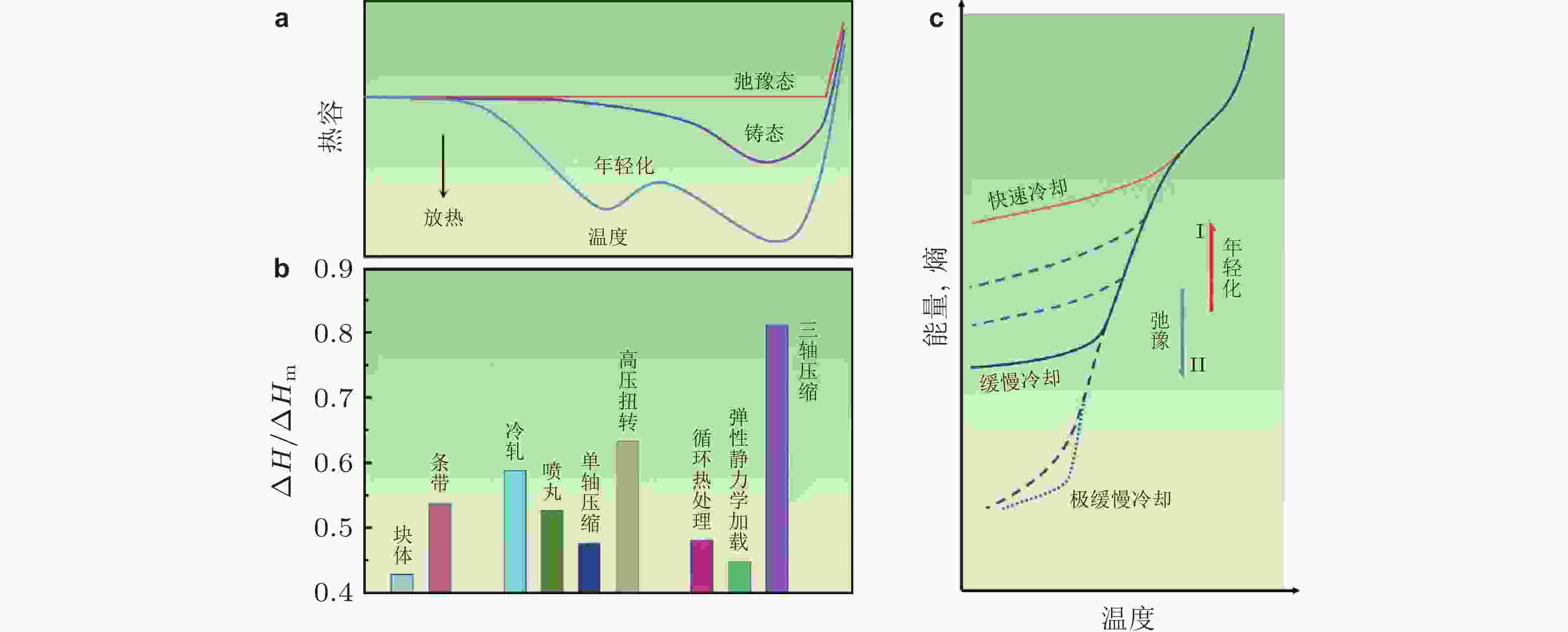
图 25 (a)铸态、弛豫态、年轻化样品热流曲线; (b)不同处理方式样品的相对焓变变化; (c)不同冷却速率条件下冷却过程中能量演化 (Sun et al. 2016)
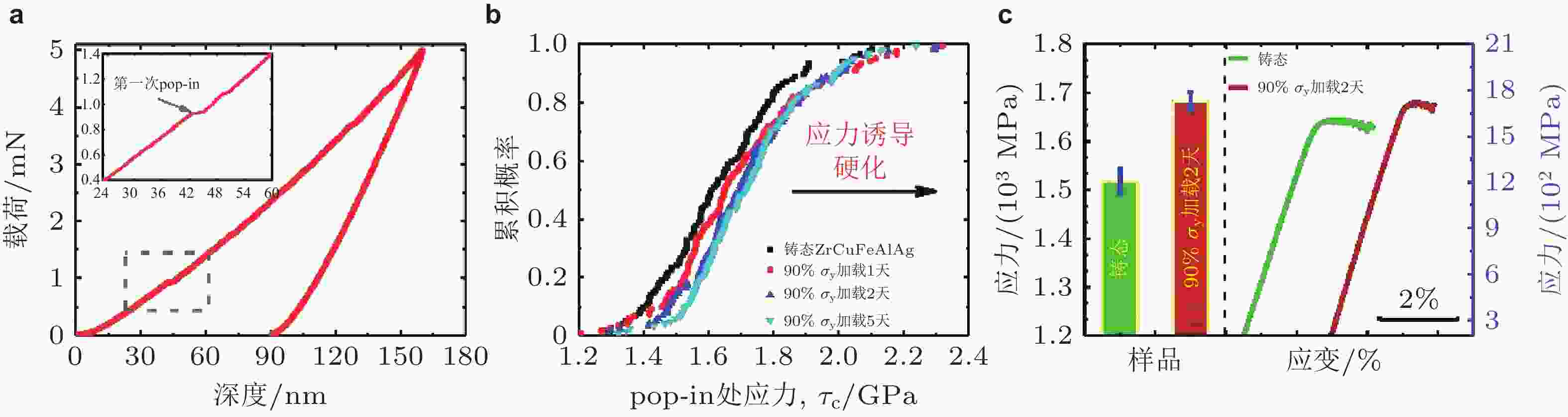
图 26 (a)铸态Zr基非晶合金荷载−深度曲线, (b)铸态及预加载不同时长的非晶合金试样临界剪切应力的累积概率分布, (c)弹性静力压缩2天前后的屈服应力和应力−应变曲线 (Wang et al. 2015c)
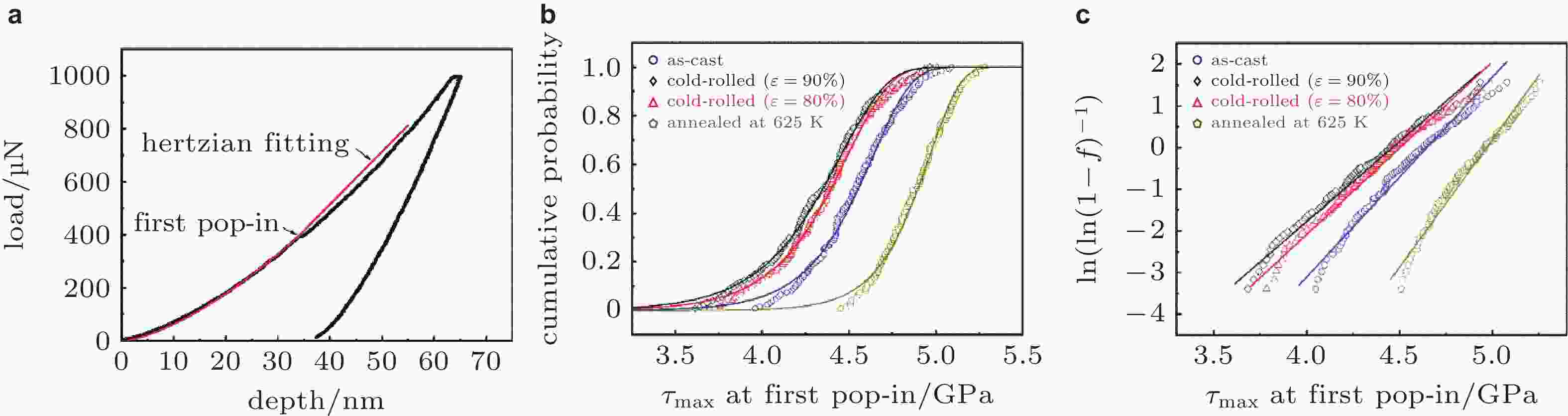
图 27 (a)代表性荷载位移曲线, (b)不同结构状态下pop-in事件累计分布函数, (c)
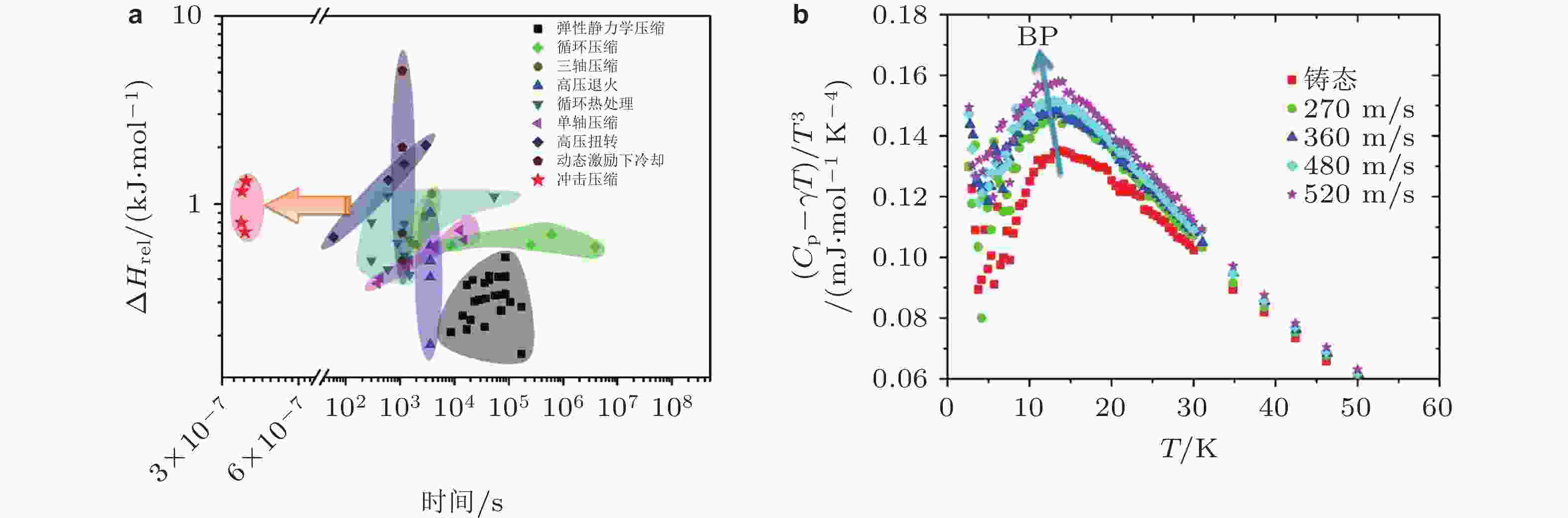
$ \mathrm{l}\mathrm{n}\left[\mathrm{ln}{\left(1-\mathrm{f}\right)}^{-1}\right] $ 与不同结构状态(铸态, 冷轧程度为 80% 和 90%, 退火态)$ {\mathrm{\tau }}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 分布的线性拟合 (Tao et al. 2021)图 28 不同年轻化方式的时间尺度(a)与不同年轻化程度的玻色峰演化(b) (Ding et al. 2019)
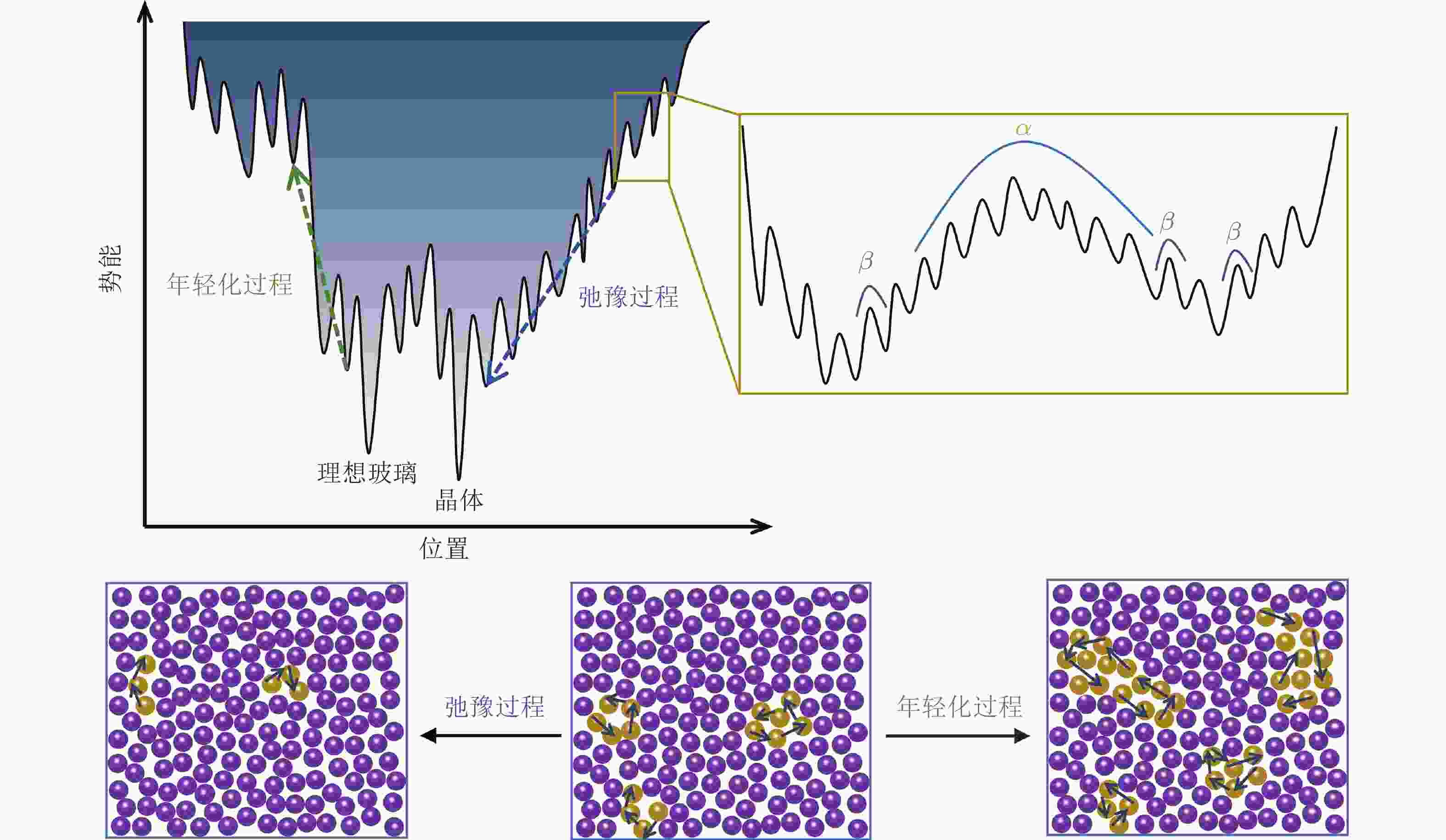
图 29 结构年轻化和弛豫的能量地形关系图 (Tao et al. 2021)
-
[1] 陈迎红, 王云江, 乔吉超. 2020. La30Ce30Al15Co25 金属玻璃应力松弛行为. 力学学报, 52: 740-748 (Chen Y H, Wang Y J, Qiao J C. 2020. Stress relaxation of La30Ce30Al15Co25 metallic glass. Chinese Journal of Theoretical and Applied Mechanics, 52: 740-748 (in Chinese)). doi: 10.6052/0459-1879-20-013 [2] 管鹏飞, 王兵, 吴义成, 张珊, 尚宝双, 胡远超, 苏锐, 刘琪. 2017. 不均匀性: 非晶合金的灵魂. 物理学报, 66: 176112 (Guan P F, Wang B, Wu Y C, Zhang S, Shang B S, Hu Y C, Su R, Liu Q. 2017. Heterogeneity: The soul of metallic glasses. Acta Physica Sinica, 66: 176112 (in Chinese)). doi: 10.7498/aps.66.176112 [3] 蒋敏强, 高洋. 2021. 金属玻璃的结构年轻化及其对力学行为的影响. 金属学报, 57: 425-438 (Jiang M Q, Gao Y. 2021. Structural rejuvenation of metallic glasses and its effect on mechanical behaviors. Acta Metallurgica Sinica, 57: 425-438 (in Chinese)). doi: 10.11900/0412.1961.2020.00431 [4] 蒋敏强, 戴兰宏. 2017. 非晶合金“拉伸转变区”模型. 科学通报, 21: 2346-2357 (Jiang M Q, Dai L H. 2017. The “tension transformation zone” model of amorphous alloys. Chin Sci Bull, 21: 2346-2357 (in Chinese)). [5] 卢博斯基.1989. 非晶态金属合金. 北京: 冶金工业出版社. [6] 汪卫华. 2013. 非晶态物质的本质和特性. 物理学进展, 33: 177-351 (Wang W H. 2013. The nature and properties of amorphous matter. Progress in Physics, 33: 177-351 (in Chinese)). [7] 王云江, 魏丹, 韩懂, 杨杰, 蒋敏强, 戴兰宏. 2020. 非晶态固体的结构可以决定性能吗? 力学学报, 52: 303-317 (Wang Y J, Wei D , Han D , Yang J , Jiang M Q, Dai L H. 2020. Does structure determine property in amorphous solids? Chinese Journal of Theoretical and Applied Mechanics, 52: 303-317 (in Chinese)). doi: 10.6052/0459-1879-19-368 [8] 王峥, 2013. 金属玻璃中流动单元的探测和表征 [博士论文], 北京: 中国科学院物理研究所.Wang Z, 2013. Verification and characterization of flow units in metallic glasses [PhD Thesis ]. Beijing: Institute of Physics, Chinese Academy of Sciences (in Chinese). [9] Afonin G V, Mitrofanov Y P, Kobelev N P, da Silva Pinto M W, Wilde G, Khonik V A. 2019. Relationship between the enthalpies of structural relaxation, crystallization and melting in metallic glass-forming systems. Scr. Mater, 166: 6-9. doi: 10.1016/j.scriptamat.2019.02.030 [10] Argon A. 1979. Plastic deformation in metallic glasses. Acta Metall., 27: 47-58. doi: 10.1016/0001-6160(79)90055-5 [11] Barkema G T, Mousseau N. 1996. Event-Based Relaxation of Continuous Disordered Systems. Phys. Rev. Lett., 77: 4358-4361. doi: 10.1103/PhysRevLett.77.4358 [12] Bei H B, Xie S J, George E P. 2006. Softening caused by profuse shear banding in a bulk metallic glass. Phys. Rev. Lett., 96: 105503. doi: 10.1103/PhysRevLett.96.105503 [13] Bergman R. 2000. General susceptibility functions for relaxations in disordered systems. J. Appl. Phys., 88: 1356-1365. doi: 10.1063/1.373824 [14] Bouchaud J P, Dupuis V, Hammann J, Vincent E. 2001. Separation of time and length scales in spin glasses: Temperature as a microscope. Phys. Rev. B., 65: 024439. doi: 10.1103/PhysRevB.65.024439 [15] Bünz J, Brink T, Tsuchiya K, Meng F, Wilde G, Albe K. 2014. Low temperature heat capacity of a severely deformed metallic glass. Phys. Rev. Lett., 112: 135501. doi: 10.1103/PhysRevLett.112.135501 [16] Cangialosi D, Boucher V. M, Alegría A, Colmenero. 2013. Direct evidence of two equilibration mechanisms in glassy polymers. Phys. Rev. Lett., 111: 095701. doi: 10.1103/PhysRevLett.111.095701 [17] Cao P, Short M P, Yip S. 2017. Understanding the mechanisms of amorphous creep through molecular simulation. Proc. Natl. Acad. Sci., 114: 13631-13636. doi: 10.1073/pnas.1708618114 [18] Carini G, Carin G, D’Angelo G, Tripodo G, Di Marco G, Vasi C, Gilioli E. 2013. Influence of Packing on Low Energy Vibrations of Densified Glasses. Phys. Rev. Lett., 111: 245502. doi: 10.1103/PhysRevLett.111.245502 [19] Casalini R, Roland C M. 2009. Aging of the Secondary Relaxation to Probe Structural Relaxation in the Glassy State. Phys. Rev. Lett., 102: 035701. doi: 10.1103/PhysRevLett.102.035701 [20] Castellero A, Moser B, Uhlenhaut D I, Torre F H. D, Löffler J F. 2008. Room-temperature creep and structural relaxation of Mg–Cu–Y metallic glasses. Acta Mater, 56: 3777-3785. doi: 10.1016/j.actamat.2008.04.021 [21] Cheng Y Q, Cao A J, Ma E. 2009. Correlation between the elastic modulus and the intrinsic plastic behavior of metallic glasses: The roles of atomic configuration and alloy composition. Acta Mater., 57: 3253-3267. doi: 10.1016/j.actamat.2009.03.027 [22] Cheng Y Q, Ma E. 2011. Atomic-level structure and structure-property relationship in metallic glasses. Prog. Mater. Sci., 56: 379-473. doi: 10.1016/j.pmatsci.2010.12.002 [23] Cheng Y T, Hao Q, Qiao J C, Crespo D, Pineda E, Pelletier J M. 2021. Effect of minor addition on dynamic mechanical relaxation in ZrCu-based metallic glasses. J. Non·Cryst. Solids, 553: 120496. doi: 10.1016/j.jnoncrysol.2020.120496 [24] Cohen M H, Turnbull D. 1959. Molecular transport in liquids and glasses. J. Chem. Phys., 31: 1164-1169. doi: 10.1063/1.1730566 [25] Cost J R. 1983. Nonlinear regression least-squares method for determining relaxation time spectra for processes with first-order kinetics. J. Appl. Phys., 54: 2137-2146. doi: 10.1063/1.332390 [26] Debenedetti P G, Stillinger F H. 2001. Supercooled liquids and the glass transition. Nature, 410: 259-267. doi: 10.1038/35065704 [27] Ding G, Li C, Zaccone A, Wang W, Lei H, Jiang F, Ling Z, Jiang M Q. 2019. Ultrafast extreme rejuvenation of metallic glasses by shock compression. Sci. Adv., 5: eaaw6249. doi: 10.1126/sciadv.aaw6249 [28] Ding J, Cheng Y Q, Ma E. 2014a. Full icosahedra dominate local order in Cu64Zr34 metallic glass and supercooled liquid. Acta Mater., 69: 343-354. doi: 10.1016/j.actamat.2014.02.005 [29] Ding J, Patinet S, Falk M L, Cheng Y, Ma E. 2014b. Soft spots and their structural signature in a metallic glass. Proc. Natl. Acad. Sci., 111: 14052-14056. doi: 10.1073/pnas.1412095111 [30] Dixon P K, Wu L, Nagel S R, Williams B D, Carini J P. 1990. Scaling in the relaxation of supercooled liquids. Phys. Rev. Lett., 65: 1108-1111. doi: 10.1103/PhysRevLett.65.1108 [31] Dmowski W, Yokoyama Y, Chuang A, Ren Y, Umemoto M, Tsuchiya K, Inoue A, Egami T. 2010. Structural rejuvenation in a bulk metallic glass induced by severe plastic deformation. Acta Mater., 58: 429-438. doi: 10.1016/j.actamat.2009.09.021 [32] Ebner C, Escher B, Gammer C, Eckert J, Pauly S, Rentenberger C. 2018. Structural and mechanical characterization of heterogeneities in a CuZr-based bulk metallic glass processed by high pressure torsion. Acta Mater., 160: 147-157. doi: 10.1016/j.actamat.2018.08.032 [33] Egami T, Iwashita T, Dmowski W. 2013. Mechanical properties of metallic glasses. Metals, 3: 77-113. doi: 10.3390/met3010077 [34] Elliott S R. 1991. Medium-range structural order in covalent amorphous solids. Nature, 354: 445-452. doi: 10.1038/354445a0 [35] Elliott S R. 1992. A Unified Model for the Low-Energy Vibrational Behaviour of Amorphous Solids. Europhysics Letters (EPL) , 19: 201-206. doi: 10.1209/0295-5075/19/3/009 [36] Falk M L, Langer J S. 1998. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E, 57: 7192-7205. doi: 10.1103/PhysRevE.57.7192 [37] Fan Y, Iwashita T, Egami T. 2014. How thermally activated deformation starts in metallic glass. Nat. Commun., 5: 5083. doi: 10.1038/ncomms6083 [38] Fan Y, Iwashita T, Egami T. 2017. Energy landscape-driven non-equilibrium evolution of inherent structure in disordered material. Nat. Commun., 8: 15417. doi: 10.1038/ncomms15417 [39] Feng S D, Qi L, Wang L M, Yu P F, Zhang S L, Ma M Z, Zhang X Y, Jing Q, Ngai K L, Greer A L, Li G, Liu R P. 2016. Structural feature of Cu64Zr36 metallic glass on nanoscale: Densely-packed clusters with loosely-packed surroundings. Scr. Mater., 115: 57-61. doi: 10.1016/j.scriptamat.2015.12.038 [40] Gauthier C, David L, Ladouce L, Quinson R, Perez J. 1997. Nonlinear mechanical response of amorphous polymers below and through glass transition temperature. J. Appl. Polym. Sci., 65: 2517-2528. doi: 10.1002/(SICI)1097-4628(19970919)65:12<2517::AID-APP22>3.0.CO;2-W [41] Greer A, Sun Y. 2016. Stored energy in metallic glasses due to strains within the elastic limit. Philos. Mag., 96: 1643-1663. doi: 10.1080/14786435.2016.1177231 [42] Grigera T S, Martín-Mayor V, Parisi G, Verrocchio P. 2003. Phonon interpretation of the ‘boson peak’ in supercooled liquids. Nature, 422: 289-292. doi: 10.1038/nature01475 [43] Gurevich V, Parshin D, Pelous J, Schober H. 1993. Theory of low-energy Raman scattering in glasses. Phys. Rev. B, 48: 16318. doi: 10.1103/PhysRevB.48.16318 [44] Herrero-Gomez C, Samwer K. 2016. Stress and temperature dependence of the avalanche dynamics during creep deformation of metallic glasses. Sci. Rep., 6: 33503. doi: 10.1038/srep33503 [45] Huang B, Bai H Y, Wang W H. 2014. Relationship between boson heat capacity peaks and evolution of heterogeneous structure in metallic glasses. J. Appl. Phys., 115: 153505. doi: 10.1063/1.4871676 [46] Huang B, Zhu Z G, Ge T P, Bai H Y, Sun B A., Yang Y, Liu C T, Wang W H. 2016. Hand in hand evolution of boson heat capacity anomaly and slow β-relaxation in La-based metallic glasses. Acta Mater., 110: 73-83. doi: 10.1016/j.actamat.2016.03.016 [47] Hufnagel T C, Schuh C A, Falk M L. 2016. Deformation of metallic glasses: Recent developments in theory, simulations, and experiments. Acta Mater., 109: 375-393. doi: 10.1016/j.actamat.2016.01.049 [48] Hutnik M, Argon A S, Suter U W. 1993. Simulation of elastic and plastic response in the glassy polycarbonate of 4, 4'-isopropylidenediphenol. Macromolecules, 26: 1097-1108. doi: 10.1021/ma00057a034 [49] Ichitsubo T., Matsubara E, Yamamoto T, Chen H, Nishiyama N, Saida J, Anazawa K. 2005. Microstructure of fragile metallic glasses inferred from ultrasound-accelerated crystallization in Pd-based metallic glasses. Phys. Rev. Lett., 95: 245501. doi: 10.1103/PhysRevLett.95.245501 [50] Inoue A, Takeuchi A. 2011. Recent development and application products of bulk glassy alloys. Acta Materialia, 59: 2243-2267. doi: 10.1016/j.actamat.2010.11.027 [51] Jiang M Q, Ling Z, Meng J X, Dai L H. 2008. Energy dissipation in fracture of bulk metallic glasses via inherent competition between local softening and quasi-cleavage. Philos. Mag., 88: 407-426. doi: 10.1080/14786430701864753 [52] Jiang M Q, Ling Z, Meng J X, Gao J B, Dai L H. 2010. Nanoscale periodic corrugation to dimple transition due to “beat” in a bulk metallic glass. Scr. Mater, 62: 572-575. doi: 10.1016/j.scriptamat.2009.12.046 [53] Johari G P, Goldstein M. 1970. Viscous liquids and the glass transition. II. Secondary relaxations in glasses of rigid molecules. J. Chem. Phys., 53: 2372-2388. doi: 10.1063/1.1674335 [54] Johnson W L. 1986. Thermodynamic and kinetic aspects of the crystal to glass transformation in metallic materials. Prog. Mater. Sci., 30: 81-134. doi: 10.1016/0079-6425(86)90005-8 [55] Johnson W L. 1999. Bulk Glass-Forming Metallic Alloys: Science and Technology. MRS Bulletin, 24: 42-56. doi: 10.1557/S0883769400069980 [56] Ju J D, Jang D, Nwankpa A, Atzmon M. 2011. An atomically quantized hierarchy of shear transformation zones in a metallic glass. J. Appl. Phys., 109: 053522. doi: 10.1063/1.3552300 [57] Kelton K F, Lee G W, Gangopadhyay A K, Hyers R W, Rathz T J, Rogers J R, Robinson M B, Robinson D S. 2003. First X-Ray Scattering Studies on Electrostatically Levitated Metallic Liquids: Demonstrated Influence of Local Icosahedral Order on the Nucleation Barrier. Phys. Rev. Lett., 90: 195504. doi: 10.1103/PhysRevLett.90.195504 [58] Krisponeit J O, Pitikaris S, Avila K E, Kuchemann S, Kruger A, Samwer K. 2014. Crossover from random three-dimensional avalanches to correlated nano shear bands in metallic glasses. Nat. Commun., 5: 3616. doi: 10.1038/ncomms4616 [59] Lei T J, DaCosta L R, Liu M, Shen J, Sun Y H, Wang W H, Atzmon M. 2020. Composition dependence of metallic glass plasticity and its prediction from anelastic relaxation – A shear transformation zone analysis. Acta Mater., 195: 81-86. doi: 10.1016/j.actamat.2020.04.053 [60] Lei T J, DaCosta L R, Liu M, Wang W H, Sun Y H, Greer A L, Atzmon M. 2019a. Microscopic characterization of structural relaxation and cryogenic rejuvenation in metallic glasses. Acta Mater, 164: 165-170. doi: 10.1016/j.actamat.2018.10.036 [61] Lei T J, Rangel DaCosta L, Liu M, Wang W H, Sun Y H, Greer A L, Atzmon M. 2019b. Shear transformation zone analysis of anelastic relaxation of a metallic glass reveals distinct properties of alpha and beta relaxations. Phys Rev E, 100: 033001. doi: 10.1103/PhysRevE.100.033001 [62] Lewandowski J J, Greer A L. 2006. Temperature rise at shear bands in metallic glasses. Nat. Mater., 5: 15-18. doi: 10.1038/nmat1536 [63] Li B S, Xie S H, Kruzic J J. 2019. Toughness enhancement and heterogeneous softening of a cryogenically cycled Zr–Cu–Ni–Al–Nb bulk metallic glass. Acta Mater., 176: 278-288. doi: 10.1016/j.actamat.2019.07.012 [64] Li Y, Yu P, Bai H Y. 2008. Study on the boson peak in bulk metallic glasses. J. Appl. Phys., 104: 013520. doi: 10.1063/1.2948926 [65] Liu Y H, Wang D, Nakajima K, Zhang W, Hirata A, Nishi T, Inoue A, Chen M W. 2011. Characterization of nanoscale mechanical heterogeneity in a metallic glass by dynamic force microscopy. Phys. Rev. Lett., 106: 125504. doi: 10.1103/PhysRevLett.106.125504 [66] Lunkenheimer P, Schneider U, Brand R, Loid A. 2000. Glassy dynamics. Contemp. Phys., 41: 15-36. doi: 10.1080/001075100181259 [67] Lunkenheimer P, Wehn R, Schneider U, Loidl A. 2005. Glassy Aging Dynamics. Phys. Rev. Lett., 95: 055702. doi: 10.1103/PhysRevLett.95.055702 [68] Luo P, Wen P, Bai H, Ruta B, Wang W H. 2017. Relaxation decoupling in metallic glasses at low temperatures. Phys. Rev. Lett., 118: 225901. doi: 10.1103/PhysRevLett.118.225901 [69] Ma E. 2015. Tuning order in disorder. Nat. Mater., 14: 547-552. doi: 10.1038/nmat4300 [70] Mitrofanov Y P, Peterlechner M, Divinski S V, Wilde G. 2014. Impact of Plastic Deformation and Shear Band Formation on the Boson Heat Capacity Peak of a Bulk Metallic Glass. Phys. Rev. Lett., 112: 135901. doi: 10.1103/PhysRevLett.112.135901 [71] Monnier X, Cangialosi D, Ruta B, Busch R, Gallino I. 2020. Vitrification decoupling from α-relaxation in a metallic glass. Sci. Adv., 6: eaay1454. doi: 10.1126/sciadv.aay1454 [72] Ngai K L, Wang Z, Gao X Q, Yu H B, Wang W H. 2013. A connection between the structural α-relaxation and the β-relaxation found in bulk metallic glass-formers. J. Chem. Phys., 139: 014502. doi: 10.1063/1.4812281 [73] Nomoto K, Ceguerra A V, Gammer C, Li B, Bilal H, Hohenwarter A, Gludovatz B, Eckert J, Ringer S P, Kruzic J J. 2021. Medium-range order dictates local hardness in bulk metallic glasses. Mater. Today, 44: 48-57. doi: 10.1016/j.mattod.2020.10.032 [74] Pan J, Wang Y X, Guo Q, Zhang D, Greer A L, Li Y. 2018. Extreme rejuvenation and softening in a bulk metallic glass. Nat. Commun., 9: 560. doi: 10.1038/s41467-018-02943-4 [75] Pelletier J M , Louzguine-Luzgin D V , Li S , Inoue A. 2011. Elastic and viscoelastic properties of glassy, quasicrystalline and crystalline phases in Zr65Cu5Ni10Al7.5Pd12.5 alloys. Acta Mater, 59: 2797-2806. doi: 10.1016/j.actamat.2011.01.018 [76] Peng H L, Li M Z, Wang W H. 2011. Structural Signature of Plastic Deformation in Metallic Glasses. Phys. Rev. Lett., 106: 135503. doi: 10.1103/PhysRevLett.106.135503 [77] Perez J. 1990. Quasi-punctual defects in vitreous solids and liquid-glass transition. Solid State Ionics, 39: 69-79. doi: 10.1016/0167-2738(90)90028-P [78] Peter G W. 2009. Spatiotemporal structures in aging and rejuvenating glasses. Proc. Natl. Acad. Sci., 106: 1353-1358. doi: 10.1073/pnas.0812418106 [79] Priezjev N V. 2019. Aging and rejuvenation during elastostatic loading of amorphous alloys: A molecular dynamics simulation study. Comput. Mater. Sci., 168: 125-130. doi: 10.1016/j.commatsci.2019.05.054 [80] Qiao J C, Liu X D, Wang Q, Liu C T, Lu J, Yang Y. 2018. Fast secondary relaxation and plasticity initiation in metallic glasses. Natl. Sci. Rev., 5: 616-618. doi: 10.1093/nsr/nwx113 [81] Qiao J C, Pelletier J M. 2012. Mechanical relaxation in a Zr-based bulk metallic glass: Analysis based on physical models. J. Appl. Phys., 112: 033518. doi: 10.1063/1.4745019 [82] Qiao J C, Pelletier J M, Yao Y. 2019a. Creep in bulk metallic glasses. Transition from linear to non linear regime. Mater. Sci. Eng. A, 743: 185-189. doi: 10.1016/j.msea.2018.11.066 [83] Qiao J C, Wang Q, Pelletier J M, Kato H, Casalini R, Crespo D, Pineda E, Yao Y, Yang Y. 2019b. Structural heterogeneities and mechanical behavior of amorphous alloys. Prog. Mater. Sci., 104: 250-329. doi: 10.1016/j.pmatsci.2019.04.005 [84] Qiao J C, Wang Y J, Zhao L Z, Dai L H, Crespo D, Pelletier J M, Keer L M, Yao Y. 2016a. Transition from stress-driven to thermally activated stress relaxation in metallic glasses. Phys. Rev. B, 94: 104203. doi: 10.1103/PhysRevB.94.104203 [85] Qiao J C, Yao Y, Pelletier J M, Keer L M. 2016b. Understanding of micro-alloying on plasticity in Cu46Zr47− xAl7Dy x (0≤ x ≤ 8) bulk metallic glasses under compression: Based on mechanical relaxations and theoretical analysis. Int. J. Plast., 82: 62-75. doi: 10.1016/j.ijplas.2016.02.002 [86] Rinaldi R, Gaertner R, Chazeau L, Gauthier C. 2011. Modelling of the mechanical behaviour of amorphous glassy polymer based on the Quasi Point Defect theory—Part I: Uniaxial validation on polycarbonate. International Journal of Non-Linear Mechanics, 46: 496-506. doi: 10.1016/j.ijnonlinmec.2010.11.004 [87] Ross P, Küchemann S, Derlet P M, Yu H, Arnold W, Liaw P, Samwer K, Maaß R. 2017. Linking macroscopic rejuvenation to nano-elastic fluctuations in a metallic glass. Acta Mater., 138: 111-118. doi: 10.1016/j.actamat.2017.07.043 [88] Ruta B, Chushkin Y, Monaco G, Cipelletti L, Pineda E, Bruna P, Giordano V, Gonzalez-Silveira M. 2012. Atomic-scale relaxation dynamics and aging in a metallic glass probed by x-ray photon correlation spectroscopy. Phys. Rev. Lett., 109: 165701. doi: 10.1103/PhysRevLett.109.165701 [89] Schall P, Weitz D A, Spaepen F. 2007. Structural rearrangements that govern flow in colloidal glasses. Science, 318: 1895-1899. doi: 10.1126/science.1149308 [90] Schirmacher W, Diezemann G, Ganter C. 1998. Harmonic vibrational excitations in disordered solids and the “boson peak”. Phys. Rev. Lett., 81: 136. doi: 10.1103/PhysRevLett.81.136 [91] Sokolov A P, Kisliuk A, Soltwisch M, Quitmann D. 1992. Medium-range order in glasses: Comparison of Raman and diffraction measurements. Phys. Rev. Lett., 69: 1540-1543. doi: 10.1103/PhysRevLett.69.1540 [92] Song K K , Pauly S, Zhang Y, Scudino S, Gargarella P, Surreddi K B, Kühn U, Eckert J. 2011. Significant tensile ductility induced by cold rolling in Cu47.5Zr47.5Al5 bulk metallic glass. Intermetallics, 19: 1394-1398. doi: 10.1016/j.intermet.2011.05.001 [93] Spaepen F. 1977. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall., 25: 407-415. doi: 10.1016/0001-6160(77)90232-2 [94] Spaepen F, Turnbull D. 1974. A mechanism for the flow and fracture of metallic glasses. Scripta Metallurgica, 8: 563-568. doi: 10.1016/0036-9748(74)90070-2 [95] Sun Y, Concustell A, Greer A L. 2016. Thermomechanical processing of metallic glasses: extending the range of the glassy state. Nat. Rev. Mater., 1: 16036. [96] Tan P, Xu N, Schofield A B, Xu L. 2012. Understanding the Low-Frequency Quasilocalized Modes in Disordered Colloidal Systems. Phys. Rev. Lett., 108: 095501. doi: 10.1103/PhysRevLett.108.095501 [97] Tang C, Harrowell P. 2013. Anomalously slow crystal growth of the glass-forming alloy CuZr. Nat. Mater, 12: 507-511. doi: 10.1038/nmat3631 [98] Tang M B, Bai H Y, Pan M X, Zhao D Q, Wang W H. 2005. Einstein oscillator in highly-random-packed bulk metallic glass. Appl. Phys. Lett., 86: 021910. doi: 10.1063/1.1849420 [99] Tao K, Qiao J C, He Q F, Song K K, Yang Y. 2021. Revealing the structural heterogeneity of metallic glass: Mechanical spectroscopy and nanoindentation experiments. Int. J. Mech. Sci. ,, 201: 106469. doi: 10.1016/j.ijmecsci.2021.106469 [100] Taraskin S, Loh Y, Natarajan G, Elliott S. 2001. Origin of the boson peak in systems with lattice disorder. Phys. Rev. Lett., 86: 1255. doi: 10.1103/PhysRevLett.86.1255 [101] Tong Y, Iwashita T, Dmowski W, Bei H, Yokoyama Y, Egami T. 2015. Structural rejuvenation in bulk metallic glasses. Acta Mater., 86: 240-246. doi: 10.1016/j.actamat.2014.12.020 [102] Tsai P, Kranjc K, Flores K M. 2017. Hierarchical heterogeneity and an elastic microstructure observed in a metallic glass alloy. Acta Mater., 139: 11-20. doi: 10.1016/j.actamat.2017.07.061 [103] Turnbull D, Cohen M H. 1970. On the free‐volume model of the iquid‐glass transition. J. Chem. Phys., 52: 3038-3041. doi: 10.1063/1.1673434 [104] Wagner H, Bedorf D, Küchemann S, Schwabe M, Zhang B, Arnold W, Samwer K. 2011. Local elastic properties of a metallic glass. Nat. Mater., 10: 439-442. doi: 10.1038/nmat3024 [105] Wang D P, Qiao J C, Liu C T. 2019. Relating structural heterogeneity to β relaxation processes in metallic glasses. Mater. Res. Lett., 7: 305-311. doi: 10.1080/21663831.2019.1604441 [106] Wang L M, Liu R, Wang W H. 2008. Relaxation time dispersions in glass forming metallic liquids and glasses. J. Chem. Phys., 128: 164503. doi: 10.1063/1.2904559 [107] Wang Q, Liu J, Ye Y, Liu T, Wang S., Liu C, Lu J, Yang Y. 2017. Universal secondary relaxation and unusual brittle-to-ductile transition in metallic glasses. Mater. Today, 20: 293-300. doi: 10.1016/j.mattod.2017.05.007 [108] Wang Q, Zhang S T, Yang Y, Dong Y D, Liu C T, Lu J. 2015a. Unusual fast secondary relaxation in metallic glass. Nat. Commun., 6: 7876. doi: 10.1038/ncomms8876 [109] Wang W H. 2012. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci., 57: 487-656. doi: 10.1016/j.pmatsci.2011.07.001 [110] Wang W H. 2019. Dynamic relaxations and relaxation-property relationships in metallic glasses. Prog. Mater. Sci., 106: 100561. doi: 10.1016/j.pmatsci.2019.03.006 [111] Wang Y J, Ishii A, Ogata S. 2013. Entropic effect on creep in nanocrystalline metals. Acta Mater., 61: 3866-3871. doi: 10.1016/j.actamat.2013.03.026 [112] Wang Y J, Zhang M, Liu L, Ogata S, Dai L H. 2015b. Universal enthalpy-entropy compensation rule for the deformation of metallic glasses. Phys. Rev. B, 92: 174118. doi: 10.1103/PhysRevB.92.174118 [113] Wang Y M, Zhang M, Liu L. 2015c. Mechanical annealing in the homogeneous deformation of bulk metallic glass under elastostatic compression. Scr. Mater., 102: 67-70. doi: 10.1016/j.scriptamat.2015.02.015 [114] Wang Y W, Li M, Xu J W. 2016. Toughen and harden metallic glass through designing statistical heterogeneity. Scr. Mater., 113: 10-13. doi: 10.1016/j.scriptamat.2015.09.038 [115] Wang Z, Sun B A, Bai H Y, Wang W H. 2014. Evolution of hidden localized flow during glass-to-liquid transition in metallic glass. Nat. Commun., 5: 5823. doi: 10.1038/ncomms6823 [116] Wang Z, Wang W H. 2019. Flow units as dynamic defects in metallic glassy materials. Natl. Sci. Rev., 6: 304-323. doi: 10.1093/nsr/nwy084 [117] Wei D, Yang J, Jiang M Q, Wei B C, Wang Y J, Dai L H. 2019. Revisiting the structure-property relationship of metallic glasses: Common spatial correlation revealed as a hidden rule. Phys. Rev. B, 99: 014115. doi: 10.1103/PhysRevB.99.014115 [118] Xu Z R, Yang D S, Qiao J C, Pelletier J M, Crespo D, Pineda E, Wang Y J. 2020. Unified perspective on structural heterogeneity of a LaCe-based metallic glass from versatile dynamic stimuli. Intermetallics, 125: 106922. doi: 10.1016/j.intermet.2020.106922 [119] Yang J, Wang Y J, Ma E, Zaccone A, Dai L H, Jiang M Q. 2019. Structural Parameter of Orientational Order to Predict the Boson Vibrational Anomaly in Glasses. Phys. Rev. Lett., 122: 015501. doi: 10.1103/PhysRevLett.122.015501 [120] Yang Q, Peng S X, Wang Z, Yu H B. 2020. Shadow glass transition as a thermodynamic signature of β relaxation in hyper-quenched metallic glasses. Natl. Sci. Rev., 7: 1896-1905. doi: 10.1093/nsr/nwaa100 [121] Yang Y, Zeng J F, Volland A, Blandin J J, Gravier S, Liu C T. 2012. Fractal growth of the dense-packing phase in annealed metallic glass imaged by high-resolution atomic force microscopy. Acta Mater., 60: 5260-5272. doi: 10.1016/j.actamat.2012.06.025 [122] Yang Y, Zhou J, Zhu F, Yuan Y, Chang D J, Kim D S, Pham M, Rana A, Tian X, Yao Y, Osher S J, Schmid A K, Hu L, Ercius P, Miao J. 2021. Determining the three-dimensional atomic structure of an amorphous solid. Nature, 592: 60-64. doi: 10.1038/s41586-021-03354-0 [123] Ye J C, Lu J, Liu C T, Wang Q, Yang Y. 2010. Atomistic free-volume zones and inelastic deformation of metallic glasses. Nat. Mater., 9: 619-623. doi: 10.1038/nmat2802 [124] Yu H B, Wang W H, Samwer K. 2013. The β relaxation in metallic glasses: an overview. Materials Today, 16: 183-191. doi: 10.1016/j.mattod.2013.05.002 [125] Yu H, Wang W, Bai H, Wu Y, Chen M. 2010. Relating activation of shear transformation zones to β relaxations in metallic glasses. Phys. Rev. B, 81: 220201. doi: 10.1103/PhysRevB.81.220201 [126] Yu H B, Richert R, Samwer K. 2017. Structural rearrangements governing Johari-Goldstein relaxations in metallic glasses. Sci. Adv., 3: e1701577. doi: 10.1126/sciadv.1701577 [127] Yu H B, Samwer K, Wu Y, Wang W H. 2012. Correlation between beta relaxation and self-diffusion of the smallest constituting atoms in metallic glasses. Phys. Rev. Lett., 109: 095508. doi: 10.1103/PhysRevLett.109.095508 [128] Zhang L T, Duan Y J, Crespo D, Pineda E, Wang Y, Pelletier J M, Qiao J C. 2021a. Dynamic mechanical relaxation and thermal creep of high-entropy La30Ce30Ni10Al20Co10 bulk metallic glass. Sci. China:Phys. , Mech. Astron., 64: 296111. doi: 10.1007/s11433-021-1722-y [129] Zhang L T, Pelletier J M, Qiao J C. 2021b. Dynamic mechanical behavior of (La0.7Ce0.3)65Al10Co25 bulk metallic glass: Influence of the physical aging and heat treatment. J. Alloys Compd, 869: 159271. doi: 10.1016/j.jallcom.2021.159271 [130] Zhang M, Chen Y, Li W. 2019. On the origin of softening in the plastic deformation of metallic glasses. Int. J. Plast., 116: 24-38. doi: 10.1016/j.ijplas.2018.12.004 [131] Zhang P, Maldonis J J, Liu Z, Schroers J, Voyles P M. 2018. Spatially heterogeneous dynamics in a metallic glass forming liquid imaged by electron correlation microscopy. Nat. Commun., 9: 1129. doi: 10.1038/s41467-018-03604-2 [132] Zhao L Z, Wang W H, Bai H Y. 2014. Modulation of β-relaxation by modifying structural configurations in metallic glasses. J. Non·Cryst. Solids, 405: 207-210. doi: 10.1016/j.jnoncrysol.2014.08.034 [133] Zhao L Z, Xue R J, Zhu Z G, Ngai K L, Wang W H, Bai H Y. 2016. A fast dynamic mode in rare earth based glasses. J. Chem. Phys., 144: 204507. doi: 10.1063/1.4952421 [134] Zhong L, Wang J, Sheng H, Zhang Z, Mao S X. 2014. Formation of monatomic metallic glasses through ultrafast liquid quenching. Nature, 512: 177-180. doi: 10.1038/nature13617 [135] Zhou H, Hilke S, Pineda E, Peterlechner M, Chushkin Y, Shanmugam S, Wilde G. 2020. X-ray photon correlation spectroscopy revealing the change of relaxation dynamics of a severely deformed Pd-based bulk metallic glass. Acta Mater., 195: 446-453. doi: 10.1016/j.actamat.2020.05.064 [136] Zhu F, Song S X, Reddy K M, Hirata A, Chen M W. 2018. Spatial heterogeneity as the structure feature for structure–property relationship of metallic glasses. Nat. Commun., 9: 3965. doi: 10.1038/s41467-018-06476-8 [137] Zhu W Q, Liu J J, Mao S, Wei X D. 2021. A new continuum model for viscoplasticity in metallic glasses based on thermodynamics and its application to creep tests. J. Mech. Phys. Solids, 146: 104216. doi: 10.1016/j.jmps.2020.104216 -




 下载:
下载: