-
摘要: 自20世纪70年代以来, 类固体非晶态材料变形与失效的理论模型相继出现, 这些模型基于应力驱动分子重排从而在局部流动缺陷处发生剪切转变这一物理图像. 该图像是现代剪切转变区理论的基础, 也是本综述的焦点. 我们将首先概述该理论框架并给出一些应用案例, 特别是块体金属玻璃应力−应变测量结果的阐释, 剪切带数值模拟分析和剪切转变区运动方程在自由边界计算中的应用. 在本综述的第二部分, 为简单起见, 将关注非晶塑性的非热模型, 并基于该模型说明剪切转变区理论是如何从非平衡热力学的系统描述中发展起来的.Abstract: Since the 1970s, theories of deformation and failure of amorphous, solidlike materials have started with models in which stress-driven, molecular rearrangements occur at localized flow defects via shear transformations. This picture is the basis for the modern theory of shear transformation zones (STZs), which is the focus of this review. We begin by describing the structure of the theory in general terms and by showing several applications, specifically, interpretation of stress-strain measurements for a bulk metallic glass, analysis of numerical simulations of shear banding, and the use of the STZ equations of motion in free-boundary calculations. In the second half of this review, we focus for simplicity on what we call an athermal model of amorphous plasticity, and use that model to illustrate how the STZ theory emerges within a systematic formulation of nonequilibrium thermodynamics.
-
Key words:
- plasticity /
- nonequilibrium thermodynamics /
- shear transformation zones
-
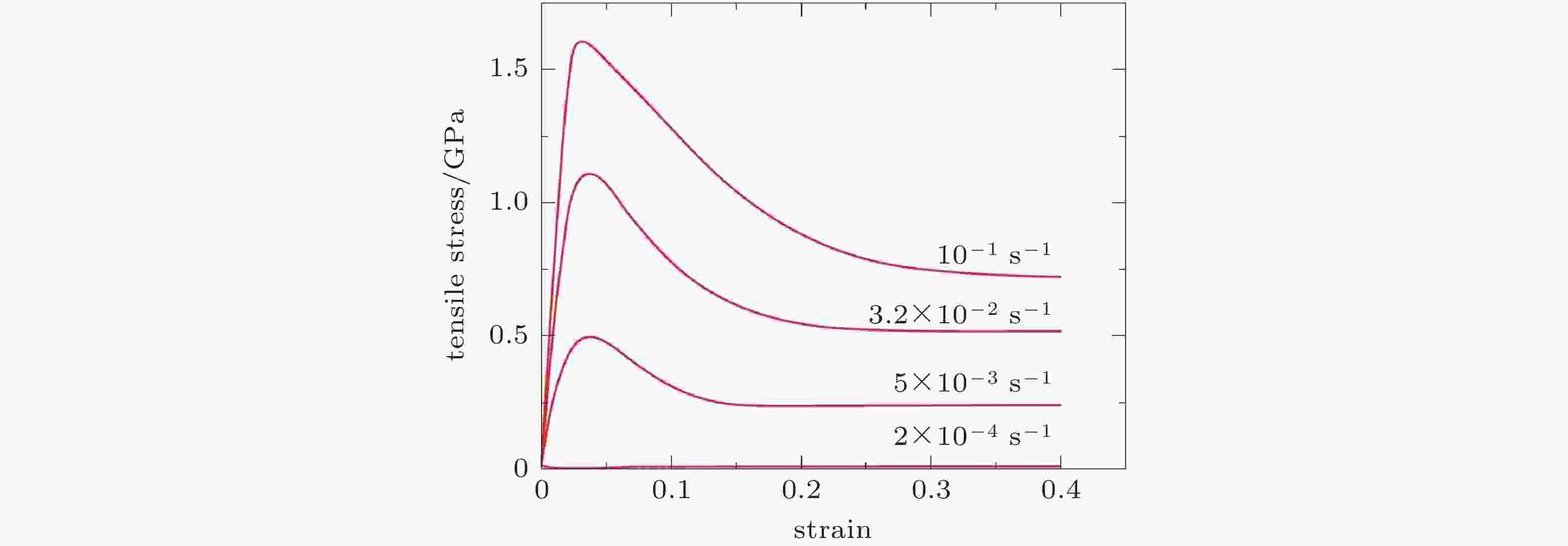
图 1 Vitreloy 1金属玻璃在643 K下, 不同应变率对应的应力−应变理论预测曲线. 这些曲线可以与Lu等(2003)的实验结果很好吻合. 最上面的曲线是个例外, 此曲线在峰值应力处没有对应的实验数据点, 这大概是因为样品在此时已发生破坏
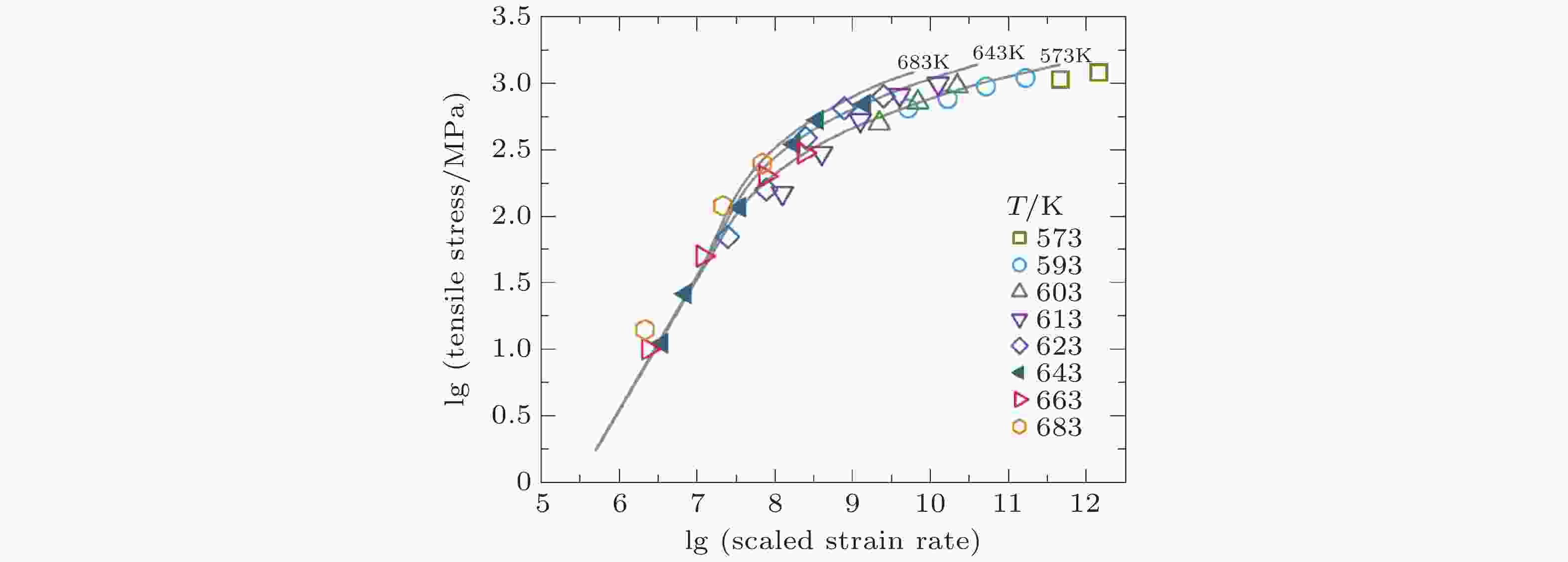
图 2 Vitreloy 1拉伸应力关于约化应变率
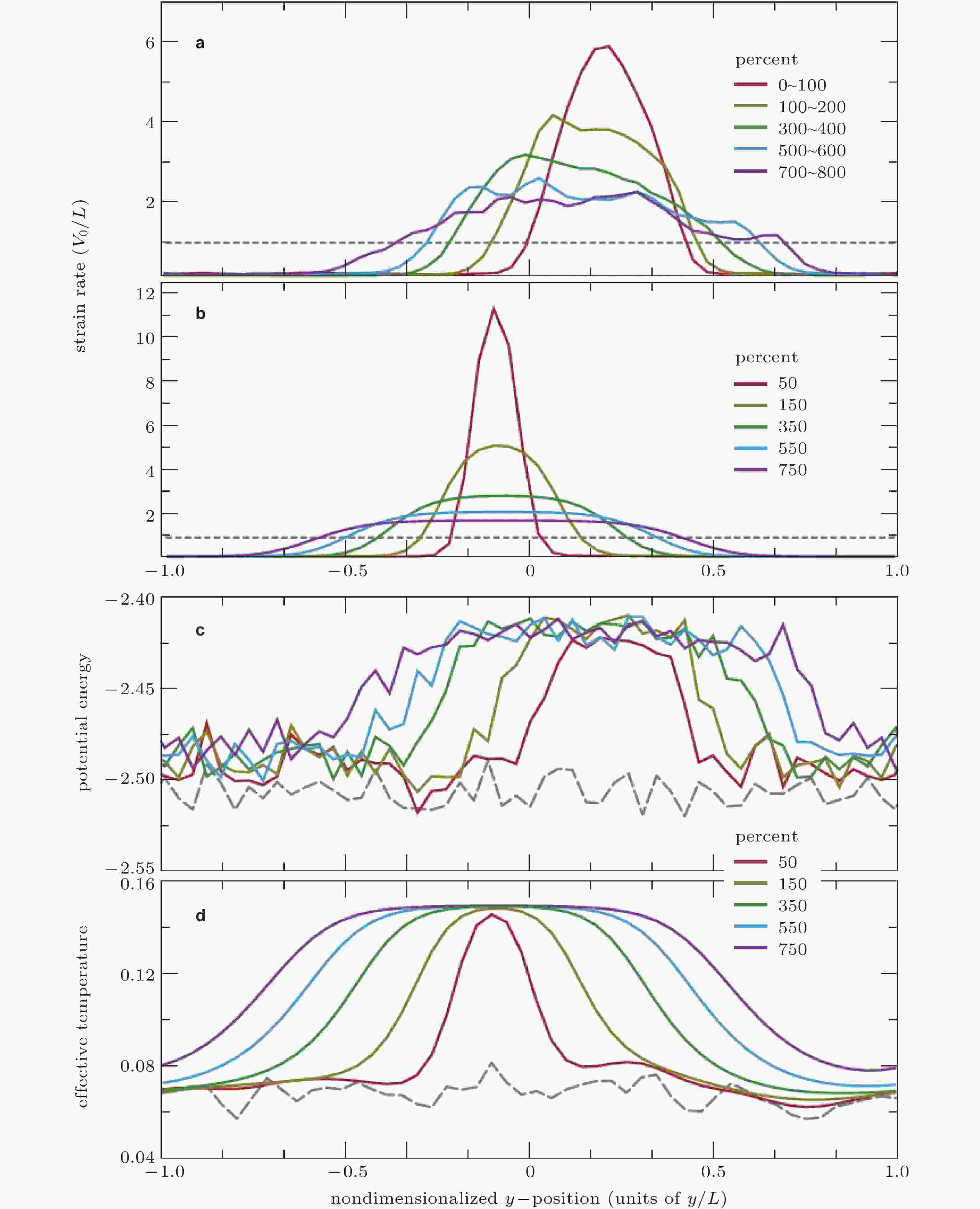
$2{\eta _N}\dot \gamma $ 的函数曲线, 其中${\eta _N}$ 是牛顿粘度. 标注温度的数据点来自Lu等(2003). 三条灰色的曲线, 从下到上, 分别对应于T = 573 K, 643 K和683 K的理论预测结果图 4 Rycroft & Gibou (2012)通过求解有关剪切转变区塑性的弹塑性运动方程得到的颈缩失稳的演化形貌. 相比蓝色区域, 红色区域有效温度更高, 即它们具有更高的有效无序温度, 因此经历了更多的不可逆塑性变形
-
[1] Angell C A, Ngai K L, McKenna G B, McMillan PF, Martin S W. 2000. Relaxation in glassforming liquids and amorphous solids. Appl. Phys. Rev., 88: 3113-57. doi: 10.1063/1.1286035 [2] Argon A S. 1979. Plastic-deformation in metallic glasses. Acta Metall., 27: 47-58. doi: 10.1016/0001-6160(79)90055-5 [3] Argon A S, Shi L T. 1983. Development of visco-plastic deformation in metallic glasses. Acta Metall., 31: 499-507. doi: 10.1016/0001-6160(83)90038-X [4] Bailey N P, Schiotz J, Jacobsen K W. 2006. Atomistic simulation study of the shear-band deformation mechanism in Mg-Cu metallic glasses. Phys. Rev. B, 73: 064108. doi: 10.1103/PhysRevB.73.064108 [5] Bouchbinder E, Langer J S, Procaccia I. 2007a. Athermal shear-transformation-zone theory of amorphous plastic deformation. I. Basic principles. Phys. Rev. E, 75: 036107. doi: 10.1103/PhysRevE.75.036107 [6] Bouchbinder E, Langer J S, Procaccia I. 2007b. Athermal shear-transformation-zone theory of amorphous plastic deformation. II. Analysis of simulated amorphous silicon. Phys. Rev. E, 75: 036108. doi: 10.1103/PhysRevE.75.036108 [7] Bouchbinder E, Langer J S, Lo T S, Procaccia I. 2007c. Free-boundary dynamics in elastoplastic amorphous solids: the circular hole problem. Phys. Rev. E, 76: 026115. doi: 10.1103/PhysRevE.76.026115 [8] Bouchbinder E, Lo T S, Procaccia I. 2008a. Dynamic failure in amorphous solids via a cavitation instability. Phys. Rev. E, 77: 025101. doi: 10.1103/PhysRevE.77.025101 [9] Bouchbinder E, Lo T S, Procaccia I, Shtilerman E. 2008b. Stability of an expanding circular cavity and the failure of amorphous solids. Phys. Rev. E, 78: 026124. doi: 10.1103/PhysRevE.78.026124 [10] Bouchbinder E, Langer J S. 2009a. Nonequilibrium thermodynamics of driven amorphous materials. I. Internal degrees of freedom and volume deformation. Phys. Rev. E, 80: 031131. doi: 10.1103/PhysRevE.80.031131 [11] Bouchbinder E, Langer J S. 2009b. Nonequilibrium thermodynamics of driven amorphous materials. II. Effective-temperature theory. Phys. Rev. E, 80: 031132. doi: 10.1103/PhysRevE.80.031132 [12] Bouchbinder E, Langer J S. 2009c. Nonequilibrium thermodynamics of driven amorphous materials. III. Shear-transformation-zone plasticity. Phys. Rev. E, 80: 031133. doi: 10.1103/PhysRevE.80.031133 [13] Bouchbinder E, Langer J S. 2010. Nonequilibrium thermodynamics of the Kovacs effect. Soft Matter, 6: 3065-73. doi: 10.1039/c001388a [14] Brader J M, Voigtmann T, Fuchs M, Larson RG, Cates M. 2009. Glass rheology: From mode-coupling theory to a dynamical yield criterion. Proc. Natl. Acad. ci. USA, 106: 15186-91. doi: 10.1073/pnas.0905330106 [15] Cao A J, Cheng Y, Ma E. 2009. Structural processes that initiate shear localization in metallic glass. Acta Mater., 57: 5146. doi: 10.1016/j.actamat.2009.07.016 [16] Cohen M, Turnbull D. 1959. Molecular transport in liquids and glasses. J. Chem. Phys., 31: 1164-69. doi: 10.1063/1.1730566 [17] Coleman B D, Gurtin M E. 1967. Thermodynamics with internal state variables. J. Chem. Phys., 47: 597-613. doi: 10.1063/1.1711937 [18] Coleman B D, Noll W. 1963. The thermodynamics of elastic materials with heat conduction and viscosity. Arch. Ration. Mech. Anal., 13: 167-78. doi: 10.1007/BF01262690 [19] Daub E G, Carlson J M. 2010. Friction, Fracture and Earthquakes. Annu. Rev. Condens. Matter Phys., 1: 397-418. doi: 10.1146/annurev-conmatphys-070909-104025 [20] Daub E G, Manning M L, Carlson J M. 2008. Shear strain localization in elastodynamic rupture simulations. Geophys. Res. Lett., 35: L12310. [21] Dieter G E. 1986. Mechanical Metallurgy. London: McGraw-Hill [22] Eastgate L, Langer J S, Pechenik L. 2003. Dynamics of large-scale plastic deformation and the necking instability in amorphous solids. Phys. Rev. Lett., 90: 045506. doi: 10.1103/PhysRevLett.90.045506 [23] Edwards S F, Oakeshott R B S. 1989. Theory of powers. Physica A, 157: 1080-90. doi: 10.1016/0378-4371(89)90034-4 [24] Falk M L, Langer J S. 1998. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E, 57: 7192-205. doi: 10.1103/PhysRevE.57.7192 [25] Falk M L, Maloney C E. 2010. Simulating the mechanical response of amorphous solids using atomistic methods. Eur. Phys. J. B, 75: 405-13. doi: 10.1140/epjb/e2010-00157-7 [26] Falk M L, Langer J S, Pechenik L. 2004. Thermal effects in the shear-transformation-zone theory of amorphous plasticity: comparisons to metallic glass data. Phys. Rev. E, 70: 011507. doi: 10.1103/PhysRevE.70.011507 [27] Goldstein M. 1969. Viscous liquids and glass transition – a potential energy barrier picture. J. Chem. Phys., 51: 3728-39. doi: 10.1063/1.1672587 [28] Götze W. 1991. In Liquids, Freezing and Glass Transition, ed. J-P Hansen, D Levesque, J Zinn-Justin pp. 289–504. Amsterdam: North-Holland [29] Götze W, Sjögren L. 1992. Relaxation processes in supercooled liquids. Rep. Prog. Phys., 55: 241-376. doi: 10.1088/0034-4885/55/3/001 [30] Gurtin M E, Fried E, Anand L. 2010. The Mechanics and Thermodynamics of Continua. New York: Cambridge Univ. Press [31] Haxton T K, Liu A J. 2007. Activated dynamics and effective temperature in a steady state sheared glass. Phys. Rev. Lett., 99: 195701. doi: 10.1103/PhysRevLett.99.195701 [32] Heggen M, Spaepen F, Feuerbacher M. 2005. Creation and annihilation of free volume during homogeneous flow of a metallic glass. J. Appl. Phys., 97: 033506. doi: 10.1063/1.1827344 [33] Hentschel H G E, Karmakar S, Lerner E, Procaccia I. 2010. Size of plastic events in strained amorphous solids at finite temperatures. Phys. Rev. Lett., 104: 025501. doi: 10.1103/PhysRevLett.104.025501 [34] Langer J S, Pechenik L. 2003. Dynamics of shear-transformation zones in amorphous plasticity: Energetic constraints in a minimal theory. Phys. Rev. E, 68: 061507. doi: 10.1103/PhysRevE.68.061507 [35] Langer J S. 2004. Dynamics of shear-transformation zones in amorphous plasticity: Formulation in terms of an effective disorder temperature. Phys. Rev. E, 70: 041502. doi: 10.1103/PhysRevE.70.041502 [36] Langer J S. 2008. Shear-transformation-zone theory of plastic deformation near the glass transition. Phys. Rev. E, 77: 021502. doi: 10.1103/PhysRevE.77.021502 [37] Langer J S, Manning M L. 2007. Steady-state, effective-temperature dynamics in a glassy material. Phys. Rev. E, 76: 056107. doi: 10.1103/PhysRevE.76.056107 [38] Langer J S, Bouchbinder E, Lookman T. 2010. Thermodynamic theory of dislocation-mediated plasticity. Acta Mater., 58: 3718. doi: 10.1016/j.actamat.2010.03.009 [39] Lemaitre A. 2002. Rearrangements and dilatancy for sheared dense materials. Phys. Rev. Lett., 89: 195503. doi: 10.1103/PhysRevLett.89.195503 [40] Lemaitre A. 2006. In Lecture Notes in Physics: Jamming, Yielding, and Irreversible Deformation in Condensed Matter, ed. C Miguel, M Rubi, 688: 129–36. Berlin: Springer-Verlag [41] Lemaitre A, Caroli C. 2007. Plastic response of a two-dimensional amorphous solid to quasistatic shear: Transverse particle diffusion and phenomenology of dissipative events. Phys. Rev. E, 76: 036104. doi: 10.1103/PhysRevE.76.036104 [42] Lemaitre A, Caroli C. 2009. Rate-dependent avalanche size in athermally sheared amorphous solids. Phys. Rev. Lett., 103: 065501. doi: 10.1103/PhysRevLett.103.065501 [43] Lerner E, Procaccia I. 2009. Locality and nonlocality in elastoplastic responses of amorphous solids. Phys. Rev. E, 79: 066109. doi: 10.1103/PhysRevE.79.066109 [44] Lewandowski J J, Greer A L. 2006. Temperature rise at shear bands in metallic glasses. Nat. Mater., 5: 15-18. doi: 10.1038/nmat1536 [45] Li Q K, Li M. 2005. Effects of surface imperfections on deformation and failure of amorphous metals. Appl. Phys. Lett., 87: 031910. doi: 10.1063/1.1999013 [46] Lu J, Ravichandran G, Johnson W L. 2003. Deformation behavior of the Zr41.2Ti13.8CU12.5Ni10Be22.5 bulk metallic glass over a wide range of strain-rates and temperatures. Acta Mater., 51: 3429-43. doi: 10.1016/S1359-6454(03)00164-2 [47] Lubliner J. 1990. Plasticity Theory. New York: Macmillan [48] Lundberg M, Krishnan K, Xu N, O’Hern CS, Dennin M. 2008. Reversible plastic events in amorphous materials. Phys. Rev. E., 77: 041505. doi: 10.1103/PhysRevE.77.041505 [49] Maloney C, Lemaitre A. 2004a. Subextensive scaling in the athermal, quasistatic limit of amorphous matter in plastic shear flow. Phys. Rev. Lett., 93: 016001. doi: 10.1103/PhysRevLett.93.016001 [50] Maloney C, Lemaitre A. 2004. Universal breakdown of elasticity at the onset of material failure. Phys. Rev. Lett., 93: 195501. doi: 10.1103/PhysRevLett.93.195501 [51] Maloney C, Robbins M. 2009. Anisotropic power law strain correlations in sheared amorphous 2D solids. Phys. Rev. Lett., 102: 225502. doi: 10.1103/PhysRevLett.102.225502 [52] Manning M L, Daub E G, Langer J S, Carlson J M. 2009. Rate-dependent shear bands in a shear-transformation-zone model of amorphous solids. Phys. Rev. E, 79: 016110. doi: 10.1103/PhysRevE.79.016110 [53] Manning M L, Langer J S, Carlson J M. 2007. Strain localization in a shear transformation zone model for amorphous solids. Phys. Rev. E, 76: 056106. doi: 10.1103/PhysRevE.76.056106 [54] Maugin G A. 1999. The Thermomechanics of Nonlinear Irreversible Behaviors. Singapore: World Sci. [55] Mehta A, Edwards S F. 1989. Statistical-mechanics of power mixtures. Physica A, 157: 1091-97. doi: 10.1016/0378-4371(89)90035-6 [56] Nemat-Nasser S. 2004. Plasticity. Cambridge, UK: Cambridge Univ. Press [57] Pechenik L. 2005. Dynamics of shear-transformation zones in amorphous plasticity: nonlinear theory at low temperatures. Phys. Rev. E, 72: 021507. doi: 10.1103/PhysRevE.72.021507 [58] Rycroft C H, Gibou F. 2012. Simulations of a stretching bar using a plasticity model from the shear transformation zone theory. J. Chem. Phys., 231: 2155-79. [59] Shi Y, Falk M L. 2006. Atomic-scale simulations of strain localization in three-dimensional model amorphous solids. Phys. Rev. B, 73: 214201. doi: 10.1103/PhysRevB.73.214201 [60] Shi Y, Katz M B, Li H, Falk M L. 2007. Evaluation of the disorder temperature and free-volume formalisms via simulations of shear banding in amorphous solids. Phys. Rev. Lett., 98: 185505. doi: 10.1103/PhysRevLett.98.185505 [61] Shi Y, Falk M. 2005. Strain localization and percolation of stable structure in amorphous solids. Phys. Rev. Lett., 95: 095502. doi: 10.1103/PhysRevLett.95.095502 [62] Sollich P. 1998. Rheological constitutive equation for a model of soft glassy materials. Phys. Rev. E, 58: 738-59. doi: 10.1103/PhysRevE.58.738 [63] Sollich P, Lequeux F, Hebraud P, Cates M E. 1997. Rheology of soft glassy materials. Phys. Rev. Lett., 78: 2020-23. doi: 10.1103/PhysRevLett.78.2020 [64] Spaepen F. 1977. Mircroscopic mechanism for steady-state inhomogeneous flow in metallic glasses. Acta Metall., 25: 407-15. doi: 10.1016/0001-6160(77)90232-2 [65] Spaepen F, Taub A. 1981. In Physics of Defects, ed. R Balian, M Kleman, p. 133. Les Houches Lect. XXV. Amsterdam: North-Holland [66] Stillinger F H. 1988. Supercooled liquids, glass transitions, and the Kauzmann paradox. J. Chem. Phys., 88: 7818-25. doi: 10.1063/1.454295 [67] Stillinger F H, Weber T A. 1982. Hidden structure in liquids. Phys. Rev. A, 25: 978-89. doi: 10.1103/PhysRevA.25.978 [68] Tool A Q. 1946. Relation between inelastic deformability and thermal expansion of glass in its anneling range. J. Am. Ceram. Soc., 29: 240-53. doi: 10.1111/j.1151-2916.1946.tb11592.x [69] Turnbull D, Cohen M H. 1970. On free-volume model of liquid-glass transition. J. Chem. Phys., 52: 3038. doi: 10.1063/1.1673434 -




 下载:
下载: