On the exit behaviors of non-Gaussian stochastic dynamical systems based on large deviation theory
-
摘要: 本文介绍了大偏差理论的基本思想及其在非高斯随机动力系统的离出问题研究中的应用. 依据不同的非高斯噪声类型, 本文分别评述了随机混合系统、指数轻跳跃过程和
$\alpha $ 稳定Lévy噪声驱动的随机动力系统的离出问题的主要研究方法和近期研究进展. 针对随机混合系统, 本文介绍了利用随机微分方程对其进行近似的拟稳态扩散近似方法, 计算拟势和最优离出路径的WKB近似方法与细致平衡条件的研究, 以及求解随机混合系统的简化版本 (即生灭过程) 的离出问题的研究进展. 对于指数轻跳跃过程驱动的随机动力系统, 本文介绍了其大偏差原理和中度偏差原理的泛函极值问题的建立, 拟势概念的定义和平均离出时间的估计. 针对具有$\alpha $ 稳定Lévy噪声的随机动力系统, 本文介绍了计算平均首次离出时间和离出概率的理论和数值方法, 计算最优离出路径的Onsager-Machlup理论、机器学习方法、最大似然法和数据驱动方法. 最后, 给出了非高斯随机动力系统的离出现象相关的一些开放性问题.Abstract: This paper introduces the basic ideas of large deviation theory and its applications in the study of exit problems of non-Gaussian stochastic dynamical systems. According to different types of non-Gaussian noise, the main research methods and recent progresses of exit problems are reviewed for stochastic hybrid systems, stochastic dynamical systems with exponentially light jump fluctuations, and stochastic systems with$\alpha $ -stable Lévy noises. For the stochastic hybrid systems, the quasi-steady-state diffusion approximation which is approximated by stochastic differential equations, the WKB approximation for computing quasi-potential and optimal exit paths, the research on detailed balance conditions, and progresses in exit problems of the simplified version of stochastic hybrid systems (i.e. birth-and-death processes) are introduced. For the stochastic dynamical systems driven by the exponential light jump processes, the establishment of the functional extremum problems of large deviation principle and moderate deviation principle, the definition of the quasi-potential concept and the estimation of the mean exit time are discussed. For stochastic systems with stable Lévy noises, the theoretical and numerical methods for calculating the mean exit time and exit probability, and Onsager-Machlup theory, machine learning method, maximum likelihood method and data-driven method for computing the optimal exit paths are illustrated. Finally, some open problems related to the exit phenomena of non-Gaussian stochastic dynamical systems are given. -
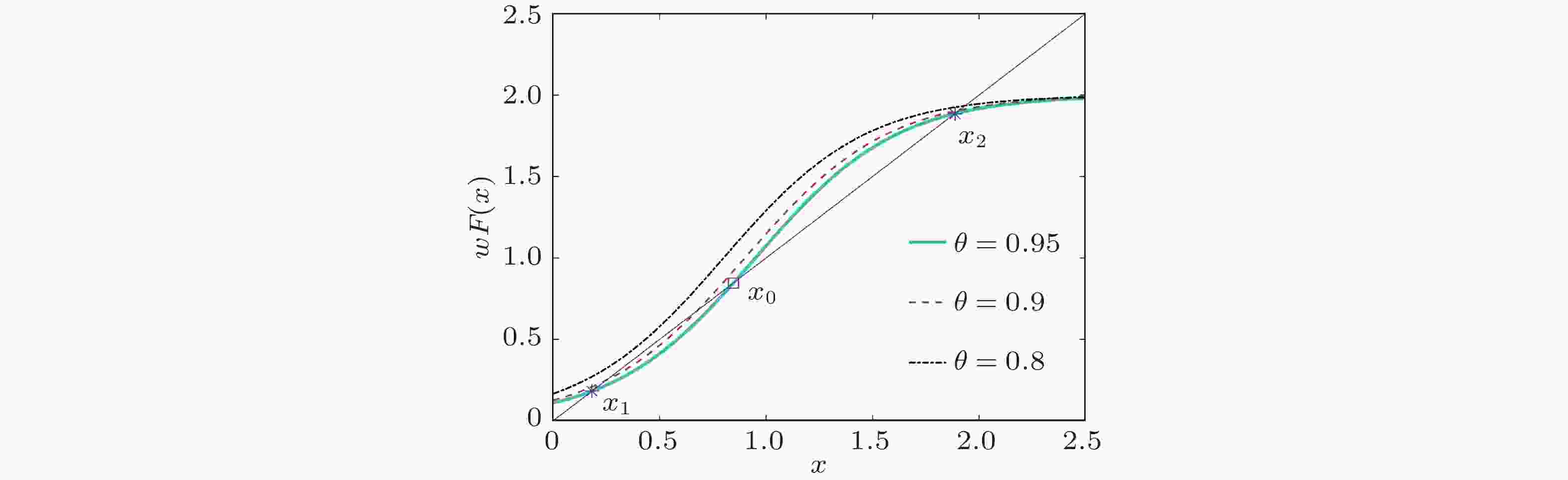
表 1 几种典型随机过程的细致平衡条件
随机过程 细致平衡条件 文献 扩散过程 加性高斯、
有势系统满足细致平衡 朱位秋 (1992) 一般情况 $\begin{array}{c} {b_i}\left( {\boldsymbol{x} } \right){p_s}\left( {\boldsymbol{x} } \right) + {\varepsilon _i}{b_i}\left( {\varepsilon {\boldsymbol{x} } } \right){p_s}\left( {\boldsymbol{x} } \right) - \displaystyle\sum\limits_j {\frac{\partial }{ {\partial {x_j} } }\left[ { {a_{ij} }\left( {\boldsymbol{x} } \right){p_s}\left( {\boldsymbol{x} } \right)} \right]} = 0 \\ {\varepsilon _i}{\varepsilon _j}{a_{ij} }\left( {\varepsilon{\boldsymbol{ x} } } \right) - {a_{ij} }\left( {\boldsymbol{x} } \right) = 0 \end{array}$
($b$为漂移系数, $a$为扩散矩阵, ${p_s}$为平稳概率分布,
${\varepsilon _i} = \pm 1$依赖于变量奇偶性)跳跃Markov过程 ${W_{ji}}{P_i} = {W_{ij}}{P_j}$
(${W_{ij}}$为转移率, ${P_i}$为平稳概率)Dykman 等 (1994) 随机混合系统 不满足细致平衡 Li 和 Liu (2019) -
[1] 陈朕. 2018. 基于大偏差理论的几类非线性随机系统动力学行为研究. [博士论文]. 南京: 南京航空航天大学Chen Z. 2018. Dynamical behaviors of several nonlinear stochastic systems based on the large deviation theory. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics [2] 孔琛. 2018. 噪声扰动下非线性动力系统离出行为研究. [博士论文]. 南京: 南京航空航天大学Kong C. 2018. On the exit problems in nonlinear dynamical systems driven by random perturbations. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics [3] 孔琛, 刘先斌. 2014. 受周期和白噪声激励的分段线性系统的吸引域与离出问题研究. 力学学报, 46: 447-456 (Kong C, Liu X B. 2014. Research for attracting region and exit problem of a piecewise linear system under periodic and white noise excitations. Chinese Journal of Theoretical and Applied Mechanics, 46: 447-456). doi: 10.6052/0459-1879-13-300 [4] 李扬. 2021. 基于大偏差理论和机器学习的随机动力学研究. [博士论文]. 南京: 南京航空航天大学Li Y. 2021. On the stochastic dynamical behaviors based on large deviation theory and machine learning. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics [5] 刘先斌, 陈虬, 陈大鹏. 1996. 非线性随机动力系统的稳定性和分岔研究. 力学进展, 26: 437-452 (Liu X B, Chen Q, Chen D P. 1996. The researches on the stability and bifurcation of nonlinear stochastic dynamical systems. Advances in Mechanics, 26: 437-452). doi: 10.6052/1000-0992-1996-4-J1996-041 [6] 王炜. 2020. 分数Brownian运动及其在反常扩散过程中的应用研究. [博士论文]. 南京: 南京航空航天大学Wang W. 2020. Fractional Brownian motion and its application in modeling the anomalous diffusion processes. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics [7] 徐伟, 孙春艳, 孙建桥, 贺群. 2013. 胞映射方法的研究和进展. 力学进展, 43: 91-100 (Xu W, Sun C Y, Sun J Q, He Q. 2013. Development and study on cell mapping methods. Advances in Mechanics, 43: 91-100). doi: 10.6052/1000-0992-12-022 [8] 颜志. 2021. 几类分数阶系统的随机共振、振动共振和非线性振动研究. [博士论文]. 南京: 南京航空航天大学Yan Z. 2021. Stochastic resonance, vibrational resonance and nonlinear vibration of several fractional order systems. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics [9] 朱金杰, 陈朕, 孔琛, 刘先斌. 2020. 基于大偏差理论的随机动力学研究. 力学进展, 50: 202010 (Zhu J J, Chen Z, Kong C, Liu X B. 2020. The researches on the stochastic dynamics based on the large deviation theory. Advances in Mechanics, 50: 202010). doi: 10.6052/1000-0992-18-021 [10] 朱金杰. 2018. 神经元同步、共振及离出问题研究. [博士论文]. 南京: 南京航空航天大学Zhu J J. 2018. Synchronization, resonance and exit problem for neuronal dynamical systems. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics [11] 朱位秋. 1992. 随机振动. 北京: 科学出版社Zhu W Q. 1992. Stochastic Vibration. Beijing: Science Press [12] 朱位秋, 蔡国强. 2017. 随机动力学引论. 北京: 科学出版社Zhu W Q, Cai G Q. 2017. Introduction to Stochastic Dynamics. Beijing: Science Press [13] Allen R J, Warren P B, Ten Wolde P R. 2005. Sampling rare switching events in biochemical networks. Physical Review Letters, 94: 018104. doi: 10.1103/PhysRevLett.94.018104 [14] Applebaum D. 2009. Lévy Processes and Stochastic Calculus. New York: Cambridge University Press. [15] Assaf M, Roberts E, Luthey-Schulten Z. 2011. Determining the stability of genetic switches: Explicitly accounting for mRNA noise. Physical Review Letters, 106: 248102. doi: 10.1103/PhysRevLett.106.248102 [16] Beri S, Mannella R, Luchinsky D G, Silchenko A N, McClintock P V E. 2005. Solution of the boundary value problem for optimal escape in continuous stochastic systems and maps. Physical Review E, 72: 036131. doi: 10.1103/PhysRevE.72.036131 [17] Bernt Øksendal. 2010. Stochastic Differential Equations. Berlin, Heidelberg: Springer-Verlag. [18] Böttcher B. 2010. Feller processes: The next generation in modeling. Brownian motion, Lévy processes and beyond. PLoS ONE, 5: e15102. [19] Bressloff P C. 2010. Metastable states and quasicycles in a stochastic Wilson-Cowan model of neuronal population dynamics. Physical Review E, 82: 051903. doi: 10.1103/PhysRevE.82.051903 [20] Bressloff P C. 2017. Stochastic switching in biology: from genotype to phenotype. Journal of Physics A: Mathematical and Theoretical, 50: 133001. doi: 10.1088/1751-8121/aa5db4 [21] Bressloff P C, Lawley S D. 2017. Mean first passage times for piecewise deterministic Markov processes and the effects of critical points. Journal of Statistical Mechanics: Theory and Experiment, 2017: 063202. doi: 10.1088/1742-5468/aa71df [22] Bressloff P C, Newby J M. 2011. Quasi-steady-state analysis of two-dimensional random intermittent search processes. Physical Review E, 83: 061139. doi: 10.1103/PhysRevE.83.061139 [23] Bressloff P C, Newby J M. 2013. Metastability in a stochastic neural network modeled as a velocity jump Markov process. SIAM Journal on Applied Dynamical Systems, 12: 1394-1435. doi: 10.1137/120898978 [24] Bressloff P C, Newby J M. 2014. Path integrals and large deviations in stochastic hybrid systems. Physical Review E, 89: 042701. [25] Brooks H A, Bressloff P C. 2015. Quasicycles in the stochastic hybrid Morris-Lecar neural model. Physical Review E, 92: 012704. [26] Budhiraja A, Chen J, Dupuis P. 2013. Large deviations for stochastic partial differential equations driven by a Poisson random measure. Stochastic Processes and Their Applications, 123: 523-560. doi: 10.1016/j.spa.2012.09.010 [27] Budhiraja A, Dupui P, Maroulas V. 2011. Variational representations for continuous time processes. Annales de l′Institut Henri Poincaré Probabilités et Statistiques, 47: 725-747. [28] Budhiraja A, Fischer D M. 2012. Large deviation properties of weakly interacting processes via weak convergence methods. Annals of Probability, 40: 74-102. [29] Cai R, Chen X, Duan J, Kurths J, Li X. 2017. Lévy noise-induced escape in an excitable system. Journal of Statistical Mechanics: Theory and Experiment, 2017: 063503. doi: 10.1088/1742-5468/aa727c [30] Cameron M K. 2012. Finding the quasipotential for nongradient SDEs. Physica D: Nonlinear Phenomena, 241: 1532-1550. doi: 10.1016/j.physd.2012.06.005 [31] Chao Y, Duan J. 2019. The Onsager–Machlup function as Lagrangian for the most probable path of a jump-diffusion process. Nonlinearity, 32: 3715. doi: 10.1088/1361-6544/ab248b [32] Chen L C, Zhu W Q. 2009. The first passage failure of SDOF strongly nonlinear stochastic system with fractional derivative damping. Journal of Vibration and Control, 15: 1247-1266. doi: 10.1177/1077546308091456 [33] Chen L C, Zhu W Q. 2010. First passage failure of quasi non-integrable generalized Hamiltonian systems. Archive of Applied Mechanics, 80: 883-893. doi: 10.1007/s00419-009-0346-6 [34] Chen X, Wu F, Duan J, Kurths J, Li X. 2019. Most probable dynamics of a genetic regulatory network under stable Lévy noise. Applied Mathematics and Computation, 348: 425-436. doi: 10.1016/j.amc.2018.12.005 [35] Chen X, Yang L, Duan J, Karniadakis G E. 2020. Solving inverse stochastic problems from discrete particle observations using the Fokker-Planck equation and physics-informed neural networks. arXiv preprint, arXiv: 2008.10653. [36] Chen Z, Li Y, Liu X. 2016. Noise induced escape from a nonhyperbolic chaotic attractor of a periodically driven nonlinear oscillator. Chaos, 26: 935-992. [37] Chen Z, Liu X. 2016. Patterns and singular features of extreme fluctuational paths of a periodically driven system. Physics Letters A, 380: 1953-1958. doi: 10.1016/j.physleta.2016.04.004 [38] Chen Z, Liu X. 2017. Noise induced transitions and topological study of a periodically driven system. Communications in Nonlinear Science and Numerical Simulation, 48: 454-461. doi: 10.1016/j.cnsns.2017.01.016 [39] Chen Z, Zhu J, Liu X. 2017. Crossing the quasi-threshold manifold of a noise-driven excitable system. Proceedings of the Royal Society A, 473: 20170058. doi: 10.1098/rspa.2017.0058 [40] Chen Z, Zhu J, Liu X. 2019. Non-differentiability of quasi-potential and non-smooth dynamics of optimal paths in the stochastic Morris–Lecar model: Type I and II excitability. Nonlinear Dynamics, 96: 2293-2305. doi: 10.1007/s11071-019-04922-w [41] Cheng X, Wang H, Wang X, Duan J, Li X. 2019. Most probable transition pathways and maximal likely trajectories in a genetic regulatory system. Physica A: Statistical Mechanics and its Applications, 531: 121779. doi: 10.1016/j.physa.2019.121779 [42] Cognata A, Valenti D, Dubkov A, Spagnolo B. 2010. Dynamics of two competing species in the presence of Lévy noise sources. Physical Review E, 82: 011121. doi: 10.1103/PhysRevE.82.011121 [43] Cramér, H. 1944. On a new limit theorem in probability theory. Usp. Mat. Nauk, 10: 166-178. [44] Dai M, Gao T, Lu Y, Zheng Y, Duan J. 2020. Detecting the maximum likelihood transition path from data of stochastic dynamical systems. Chaos, 30: 113124. doi: 10.1063/5.0012858 [45] de Oliveira Gomes A. 2018. Large deviations studies for small noise limits of dynamical systems perturbed by Lévy processes. [PhD. Thesis] Humboldt-Universität zu Berlin. [46] Dembo A, Zeitouni O. 1998. Large Deviations Techniques and Applications. New York: Springer. [47] Deuschel J D, Stroock D W. 2001. Large deviations. American Mathematical Society. [48] Ditlevsen P D. 1999. Observation of -stable noise induced millennial climate changes from an ice-core record. Geophysical Research Letters, 26: 1441-1444. doi: 10.1029/1999GL900252 [49] Donsker M D, Varadhan S S. 1975a. Asymptotic evaluation of certain Markov process expectations for large time, I. Communications on Pure and Applied Mathematics, 28: 1-47. [50] Donsker M D, Varadhan S S. 1975b. Asymptotic evaluation of certain Markov process expectations for large time, II. Communications on Pure and Applied Mathematics, 28: 279-301. doi: 10.1002/cpa.3160280206 [51] Donsker M D, Varadhan S S. 1976. Asymptotic evaluation of certain Markov process expectations for large time—III. Communications on Pure and Applied Mathematics, 29: 389-461. doi: 10.1002/cpa.3160290405 [52] Donsker M D, Varadhan S S. 1983. Asymptotic evaluation of certain Markov process expectations for large time. IV. Communications on Pure and Applied Mathematics, 36: 183-212. [53] Duan J. 2015 An Introduction to Stochastic Dynamics. New York: Cambridge University Press. [54] Dürr D, Bach A. 1978. The Onsager-Machlup function as Lagrangian for the most probable path of a diffusion process. Communications in Mathematical Physics, 60: 153-170. doi: 10.1007/BF01609446 [55] Dykman M I, McClintock P V E, Smelyanski V N, Stein N D, Stocks N G. 1992. Optimal paths and the prehistory problem for large fluctuations in noise-driven systems. Physical Review Letters, 68: 2718-2721. doi: 10.1103/PhysRevLett.68.2718 [56] Dykman M I, Mori E, Ross J, Hunt P M. 1994. Large fluctuations and optimal paths in chemical kinetics. The Journal of Chemical Physics, 100: 5735-5750. doi: 10.1063/1.467139 [57] Feng J, Kurtz T G. 2006. Large Deviations for Stochastic Processes. American Mathematical Society. [58] Freidlin M I, Wentzell A D. 2012. Random Perturbations of Dynamical Systems. Berlin Heidelberg: Springer. [59] Gao T, Duan J, Li X. 2016. Fokker–Planck equations for stochastic dynamical systems with symmetric Lévy motions. Applied Mathematics and Computation, 278: 1-20. doi: 10.1016/j.amc.2016.01.010 [60] Gao T, Duan J, Li X, Song R. 2014. Mean exit time and escape probability for dynamical systems driven by Lévy noises. SIAM Journal on Scientific Computing, 36: A887-A906. doi: 10.1137/120897262 [61] Gardiner C W. 1985. Handbook of Stochastic Methods. Berlin: Springer. [62] Gärtner J. 1977. On large deviations from the invariant measure. Theory of Probability & Its Applications, 22: 24-39. [63] Ge H, Qian H. 2011. Non-equilibrium phase transition in mesoscopic biochemical systems: from stochastic to nonlinear dynamics and beyond. Journal of The Royal Society Interface, 8: 107-116. doi: 10.1098/rsif.2010.0202 [64] Graham R, Haken H. 1971. Generalized thermodynamic potential for Markoff systems in detailed balance and far from thermal equilibrium. Zeitschrift für Physik A: Hadrons and Nuclei, 243: 289-302. [65] Guarcello C, Valenti D, Carollo A, Spagnolo B. 2016. Effects of Lévy noise on the dynamics of sine-Gordon solitons in long Josephson junctions. Journal of Statistical Mechanics: Theory and Experiment, 2016: 054012. doi: 10.1088/1742-5468/2016/05/054012 [66] Han Q, Xu W, Yue X. 2016. Exit location distribution in the stochastic exit problem by the generalized cell mapping method. Chaos, Solitons and Fractals, 87: 302-306. doi: 10.1016/j.chaos.2016.04.017 [67] Heymann M, Vanden-Eijnden E. 2008. The geometric minimum action method: A least action principle on the space of curves. Communications on Pure and Applied Mathematics, 61: 1052-1117. doi: 10.1002/cpa.20238 [68] Hu Y, Shi Z. 2004. Moderate deviations for diffusions with Brownian potentials. Annals of Probability, 32: 3191-3220. [69] Imkeller P, Pavlyukevich I, Wetzel T. 2009. First exit times for Lévy-driven diffusions with exponentially light jumps. Annals of Probability, 37: 530-64. [70] Kang Y M, Chen X, Lin X D, Tan N. 2017. Mean first passage time and stochastic resonance in a transcriptional regulatory system with non-Gaussian noise. Fluctuation and Noise Letters, 16: 1750007. doi: 10.1142/S0219477517500079 [71] Keener J P, Newby J M. 2011. A perturbation analysis of spontaneous action potential initiation by stochastic ion channels. Physical Review E, 84: 011918. doi: 10.1103/PhysRevE.84.011918 [72] Khovanov I A, Polovinkin A V, Luchinsky D G, McClintock P V E. 2013. Noise-induced escape in an excitable system. Physical Review E, 87: 032116. [73] Kłosek-Dygas M M, Matkowsky B J, Schuss Z. 1988. Stochastic stability of nonlinear oscillators. SIAM Journal on Applied Mathematics, 48: 1115-1127. doi: 10.1137/0148066 [74] Kong C, Liu X. 2017. Noise-induced chaos in a piecewise linear system. International Journal of Bifurcation and Chaos, 27: 1750137. doi: 10.1142/S0218127417501371 [75] Kramers H A. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica, 7: 284-304. doi: 10.1016/S0031-8914(40)90098-2 [76] Kraut S, Feudel U. 2003. Enhancement of noise-induced escape through the existence of a chaotic saddle. Physical Review E, 67: 015204. doi: 10.1103/PhysRevE.67.015204 [77] Li Y, Duan J. 2021. A data-driven approach for discovering stochastic dynamical systems with non-Gaussian Lévy noise. Physica D: Nonlinear Phenomena, 417: 132830. doi: 10.1016/j.physd.2020.132830 [78] Li Y, Duan J, Liu X. 2021a. Machine learning framework for computing the most probable paths of stochastic dynamical systems. Physical Review E, 103: 012124. doi: 10.1103/PhysRevE.103.012124 [79] Li Y, Duan J, Liu X, Zhang Y. 2020a. Most probable dynamics of stochastic dynamical systems with exponentially light jump fluctuations. Chaos, 30: 063142. doi: 10.1063/5.0006292 [80] Li Y, Liu X. 2019. Noise induced escape in one-population and two-population stochastic neural networks with internal states. Chaos, 29: 023137. doi: 10.1063/1.5055051 [81] Li Y, Wang J, Liu X. 2020b. Quasi-threshold phenomenon in noise-driven Higgins model. Communications in Nonlinear Science and Numerical Simulation, 91: 105441. doi: 10.1016/j.cnsns.2020.105441 [82] Liptser R, Pukhalskii A. 1992. Limit theorems on large deviations for semimartingales. Stochastics and Stochastic Reports, 38: 201-49. doi: 10.1080/17442509208833757 [83] Liu Q, Jiang D, Hayat T, Ahmad B. 2018. Analysis of a delayed vaccinated SIR epidemic model with temporary immunity and Lévy jumps. Nonlinear Analysis: Hybrid Systems, 27: 29-43. doi: 10.1016/j.nahs.2017.08.002 [84] Maier R S, Stein D L. 1992. Transition-rate theory for nongradient drift fields. Physical Review Letters, 69: 3691-3695. doi: 10.1103/PhysRevLett.69.3691 [85] Matkowsky B J, Schuss Z. 1982. Diffusion across characteristic boundaries. SIAM Journal on Applied Mathematics, 42: 822-834. doi: 10.1137/0142057 [86] Matkowsky B J, Schuss Z, Tier C. 1983. Diffusion across characteristic boundaries with critical points. SIAM Journal on Applied Mathematics, 43: 673-695. doi: 10.1137/0143046 [87] Naeh T, Kłosek M M, Matkowsky B J, Schuss Z. 1990. A direct approach to the exit problem. SIAM Journal on Applied Mathematics, 50: 595-627. doi: 10.1137/0150036 [88] Newby J M. 2014a. Bistable switching asymptotics for the self regulating gene. Journal of Physics A Mathematical and Theoretical, 48: 185001. [89] Newby J M. 2014b. Spontaneous excitability in the Morris-Lecar model with ion channel noise. SIAM Journal on Applied Dynamical Systems, 13: 1756-1791. doi: 10.1137/140971385 [90] Onsager L, Machlup S. 1953. Fluctuations and irreversible processes. Physical Review, 91: 1505. doi: 10.1103/PhysRev.91.1505 [91] Patel A, Kosko B. 2008. Stochastic resonance in continuous and spiking neuron models with Lévy noise. IEEE Transactions on Neural Networks, 19: 1993-2008. doi: 10.1109/TNN.2008.2005610 [92] Poirot J, Tankov P. 2006. Monte Carlo option pricing for tempered stable (CGMY) processes. Asia-Pacific Financial Markets, 13: 327-344. [93] Qiao H, Duan J. 2015. Asymptotic methods for stochastic dynamical systems with small non-Gaussian Lévy noise. Stochastics and Dynamics, 15: 1550004. doi: 10.1142/S0219493715500045 [94] Ryashko L. 2018. Sensitivity analysis of the noise-induced oscillatory multistability in Higgins model of glycolysis. Chaos, 28: 033602. doi: 10.1063/1.4989982 [95] Sanov I N. 1957. On the probability of large deviations of random magnitude. Matematicheskii Sbornik Novaya Seriya, 42: 11-44. [96] Schuss Z. 2009. Theory and Applications of Stochastic Processes: An Analytical Approach. New York: Springer Science & Business Media. [97] Serdukova L, Zheng Y, Duan J, Kurths J. 2017. Metastability for discontinuous dynamical systems under Lévy noise: Case study on Amazonian Vegetation. Scientific Reports, 7: 9336. doi: 10.1038/s41598-017-07686-8 [98] Silchenko A N, Beri S, Luchinsky D G, McClintock P V E. 2005. Fluctuational transitions across different kinds of fractal basin boundaries. Physical Review E, 71: 046203. doi: 10.1103/PhysRevE.71.046203 [99] Shi J, Chen T, Yuan R, Yuan B, Ao P. 2012. Relation of a new interpretation of stochastic differential equations to Ito process. Journal of Statistical Physics, 148: 579-590. doi: 10.1007/s10955-012-0532-8 [100] Tamás T, Lai Y. 2010. Quasipotential approach to critical scaling in noise-induced chaos. Physical Review E, 81: 056208. doi: 10.1103/PhysRevE.81.056208 [101] Tang Y, Yuan R, Ao P. 2014. Summing over trajectories of stochastic dynamics with multiplicative noise. The Journal of Chemical Physics, 141: 044125. doi: 10.1063/1.4890968 [102] Tang Y, Yuan R, Wang G, Zhu X. 2017. Potential landscape of high dimensional nonlinear stochastic dynamics with large noise. Scientific Reports, 7: 1-11. doi: 10.1038/s41598-016-0028-x [103] Tisza L, Manning I. 1957. Fluctuations and irreversible thermodynamics. Physical Review, 105: 1695. doi: 10.1103/PhysRev.105.1695 [104] Van Kampen N G. 1957. Derivation of the phenomenological equations from the master equation: I. Even variables only. Physica, 23: 707-719. [105] Varadhan S S. 1967. Diffusion processes in a small time interval. Communications on Pure and Applied Mathematics, 20: 659-685. doi: 10.1002/cpa.3160200404 [106] Varadhan S S. 1984. Large Deviations and Applications. Society for Industrial and Applied Mathematics. [107] Varadhan S S. 2016. Large Deviations. American Mathematical Society. [108] Ventsel' A D, Freidlin M I. 1970. On small random perturbations of dynamical systems. Russian Mathematical Surveys, 25: 1-55. doi: 10.1070/RM1970v025n01ABEH001254 [109] Wang H, Tsiairis A, Duan J. 2020. Bifurcation in mean phase portraits for stochastic dynamical systems with multiplicative Gaussian noise. International Journal of Bifurcation and Chaos, 30: 2050216. doi: 10.1142/S0218127420502168 [110] Wentzell A D. 2012. Limit Theorems on Large Deviations for Markov Stochastic Processes. New York: Springer Science & Business Media. [111] Wu F, Chen X, Zheng Y, Duan J, Kurths J, Li X. 2018. Lévy noise induced transition and enhanced stability in a gene regulatory network. Chaos, 28: 075510. doi: 10.1063/1.5025235 [112] Xu Y, Li Y, Zhang H, Li X, Kurths J. 2016. The switch in a genetic Toggle system with Lévy noise. Scientific Reports, 6: 31505. doi: 10.1038/srep31505 [113] Xu Y, Zhang H, Li Y, Zhou K, Liu Q, Kurths J. 2020. Solving Fokker-Planck equation using deep learning. Chaos, 30: 013133. doi: 10.1063/1.5132840 [114] Yuan S, Duan J. 2019. Action functionals for stochastic differential equations with Lévy noise. Communications on Stochastic Analysis, 13: 10. [115] Zhang Y, Cheng Z, Zhang X, Chen X, Duan J, Li X. 2017. Data assimilation and parameter estimation for a multiscale stochastic system with alpha-stable Levy noise. Journal of Statistical Mechanics: Theory and Experiment, 2017: 113401. doi: 10.1088/1742-5468/aa9343 [116] Zhang Y, Duan J, Jin Y, Li Y. 2020. Extracting non-Gaussian governing laws from data on mean exit time. Chaos, 30: 113112. doi: 10.1063/5.0018812 [117] Zhang Y, Jin Y, Li Y. 2021. Enhanced energy harvesting using time-delayed feedback control from random rotational environment. Physica D: Nonlinear Phenomena, 422: 132908. doi: 10.1016/j.physd.2021.132908 [118] Zheng Y, Yang F, Duan J, Sun X, Fu L, Kurths J. 2020. The maximum likelihood climate change for global warming under the influence of greenhouse effect and Lévy noise. Chaos, 30: 013132. doi: 10.1063/1.5129003 [119] Zhu J, Chen Z, Liu X. 2018. Probability evolution method for exit location distribution. Physics Letters A, 382: 771-775. doi: 10.1016/j.physleta.2018.01.027 -











 下载:
下载: