基于模板的子结构多分辨率拓扑优化

黄孟成; 霍文栋; 刘畅; 杨东生; 黄佳; 杜宗亮; 郭旭

doi:10.6052/1000-0992-21-030

基于模板的子结构多分辨率拓扑优化

doi: 10.6052/1000-0992-21-030

黄孟成^{1, 2, 3},
霍文栋^{1, 2, 3},
刘畅^{1, 2, 3},
杨东生⁴,
黄佳⁵,
杜宗亮^{1, 2, 3, ,},
郭旭^{1, 2, 3,}

1.
大连理工大学, 工业装备结构分析国家重点实验室, 工程力学系, 辽宁大连 116023
2.
大连理工大学, 国际计算力学研究中心, 辽宁大连 116023
3.
大连理工大学宁波研究院, 浙江宁波 315016
4.
中国运载火箭技术研究院, 北京 100076
5.
北京强度环境研究所，北京 100076

基金项目: 本工作得到了国家自然科学基金(11821202, 11732004, 12002073, 12002077), 国家重点研发计划(2020YFB1709401, 2016YFB0201601), 大连理工大学科研启动项目(DUT20RC(3)020)和博士后科学基金(2020T130078, 2020M680944)的支持.

详细信息

作者简介:
杜宗亮, 大连理工大学工程力学系副教授. 2016年获得大连理工大学博士学位, 2017—2019先后在美国加州大学圣地亚哥校区和密苏里大学从事博士后研究, 2020年1月回到大连理工大学工作. 当前研究兴趣包括: 结构优化、拓扑力学、基于机器学习的建模与力学分析、非光滑力学等. 在JMPS, CMAME, PRL等杂志发表论文30余篇. 曾获亚洲结构与多学科优化学会青年科学家奖, 入选大连市高层次人才、大连市青年科技之星, 担任《力学进展》青年编委

通讯作者:
zldu@dlut.edu.cn

中图分类号: O302
计量
- 文章访问数: 1671
- HTML全文浏览量: 646
- PDF下载量: 257
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-27
- 录用日期: 2021-07-29
- 网络出版日期: 2021-08-10
- 刊出日期: 2021-11-26

Substructuring multi-resolution topology optimization with template

HUANG Mengcheng^{1, 2, 3},
HUO Wendong^{1, 2, 3},
LIU Chang^{1, 2, 3},
YANG Dongsheng⁴,
HUANG Jia⁵,
DU Zongliang^{1, 2, 3
, ,},
GUO Xu^{1, 2, 3
,}

1.
State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian 116023, Liaoning, China
2.
International Research Center for Computational Mechanics, Dalian University of Technology, Dalian 116023, Liaoning, China
3.
Ningbo Institute of Dalian University of Technology, Ningbo 315016, Zhejiang, China
4.
China Academy of Launch Vehicle Technology, Beijing 100076, China
5.
Beijing Institute of Structure and Environment Engineering, Beijing 100076, China.

More Information

Corresponding author: zldu@dlut.edu.cn

摘要

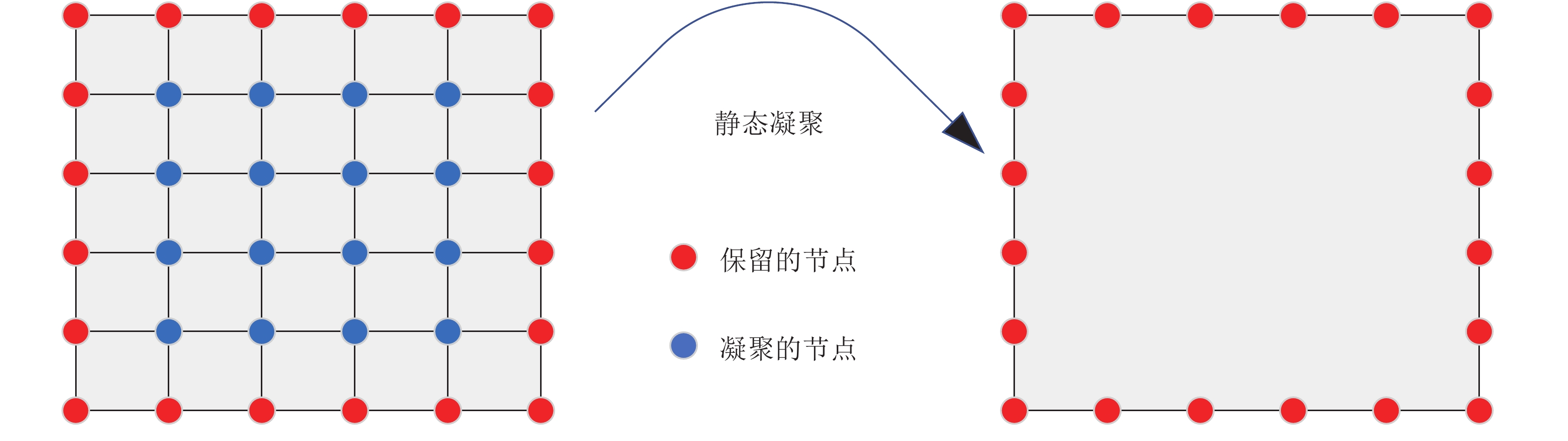
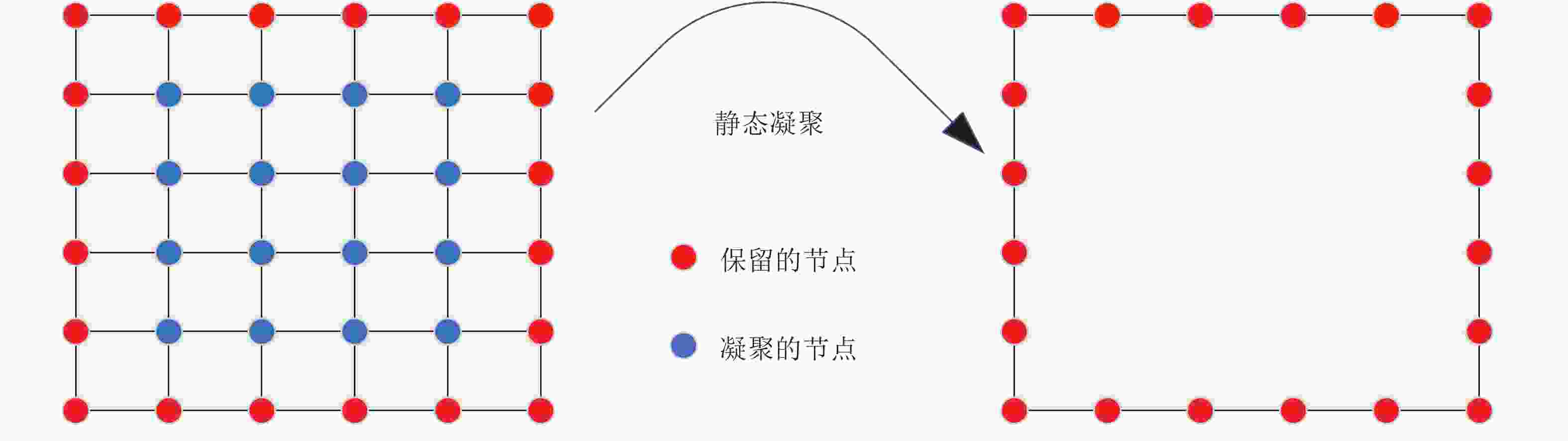
摘要: 多分辨率拓扑优化(multi-resolution topology optimization, MTOP)方法将有限元网格和密度网格解耦, 采用较粗的网格(超单元)进行有限元分析, 从而大大降低了拓扑优化过程中的结构分析成本. 但MTOP方法每次迭代都需要根据超单元内的平均密度计算有限元单刚, 不仅精度不够且在过滤半径较小的情况容易出现棋盘格现象和QR模式. 为解决相应问题, 本文将超单元视为子结构, 通过静态凝聚得到超单元刚度阵, 并进一步根据拓扑优化过程中子结构的密度分布特征组建了其模板库, 从而省去了超单元单刚的重复计算, 显著提高了MTOP方法的分析精度, 有效抑制了数值不稳定现象.
- 多分辨率拓扑优化 /
- 子结构 /
- 模板
Abstract: In the multi-resolution topology optimization (MTOP) method, by decoupling the finite element mesh and discretization of density field, the finite element analysis is carried out with a coarser mesh (i.e., super-elements), and the computational cost is thus greatly reduced in the process of topology optimization. However, the elemental stiffness matrix is calculated each iteration using the average density of super-elements, and this treatment is actually not only inaccurate but also leads to the checkerboard phenomenon and QR patterns when the filter radius is relatively small. In order to alleviate such issues, the super-element is treated as a substructure and the corresponding elemental stiffness matrix is obtained using static condensation. Furthermore, a template library is developed for the substructure based on its density distribution during the topology optimization process. By this means, the elemental stiffness matrix is not required to be calculated repeatedly, the accuracy of the MTOP method is improved significantly and the checkerboard patterns are effectively inhibited as well.
- multi-resolution topology optimization /
- substructure /
- template

HTML全文

图 1 子结构的静态凝聚示意图

下载: 全尺寸图片幻灯片

图 2 (a) 含有5 × 5密度网格的超单元, (b) 超单元内部的9个独立密度值及其分布

下载: 全尺寸图片幻灯片

图 3 受均布力的悬臂梁示意图

下载: 全尺寸图片幻灯片

图 4 (a) MTOP方法的优化设计, (b) 局部细节出现了棋盘格现象和QR模式

下载: 全尺寸图片幻灯片

表 1 结果对比

优化结果目标函数单次循环时间/s

模板法 10.71(10.69) 98.95
SIMP法 10.54 115.67

下载: 导出CSV

表 2 密度阈值对比

密度阈值优化结果目标函数

0.1 11.8551
(10.7433)
0.45 10.71
(10.69)
0.8 11.0542
(11.5824)

下载: 导出CSV

参考文献(21)

[1]	Borrvall T, Petersson J. 2001. Large-scale topology optimization in 3D using parallel computing. Computer Methods in Applied Mechanics and Engineering, 190: 6201-6229. doi: 10.1016/S0045-7825(01)00216-X
[2]	Bruns T E, Tortorelli D A. 2003. An element removal and reintroduction strategy for the topology optimization of structures and compliant mechanisms. International Journal for Numerical Methods in Engineering, 57: 1413-1430. doi: 10.1002/nme.783
[3]	de Sturler E, Paulino G H, Wang S. 2008. Topology optimization with adaptive mesh refinement// Proceedings of the 6th International Conference on Computation of Shell and Spatial Structures IASS-IACM (pp. 28-31).
[4]	Groen J P, Langelaar M, Sigmund O, Ruess M. 2017. Higher‐order multi‐resolution topology optimization using the finite cell method. International Journal for Numerical Methods in Engineering, 110: 903-920. doi: 10.1002/nme.5432
[5]	Guo X, Zhang W, Zhong W. 2014. Doing topology optimization explicitly and geometrically—a new moving morphable components based framework. Journal of Applied Mechanics, 81: 081009. doi: 10.1115/1.4027609
[6]	Gupta D K, Langelaar M, van Keulen F. 2018. QR-patterns: artefacts in multiresolution topology optimization. Structural and Multidisciplinary Optimization, 58: 1335-1350. doi: 10.1007/s00158-018-2048-6
[7]	Guyan R J. 1965. Reduction of stiffness and mass matrices. AIAA Journal, 3: 380-380. doi: 10.2514/3.2874
[8]	Liang Y, Cheng G. 2019. Topology optimization via sequential integer programming and canonical relaxation algorithm. Computer Methods in Applied Mechanics and Engineering, 348: 64-96. doi: 10.1016/j.cma.2018.10.050
[9]	Liu C, Zhu Y, Sun Z, Li D, Du Z, Zhang W, Guo X. 2018. An efficient moving morphable component (MMC)-based approach for multi-resolution topology optimization. Structural and Multidisciplinary Optimization, 58: 2455-2479. doi: 10.1007/s00158-018-2114-0
[10]	Nguyen T H, Le C H, Hajjar J F. 2017. Topology optimization using the p-version of the finite element method. Structural and Multidisciplinary Optimization, 56: 571-586. doi: 10.1007/s00158-017-1675-7
[11]	Nguyen T H, Paulino G H, Song J, Le C H. 2010. A computational paradigm for multiresolution topology optimization (MTOP). Structural and Multidisciplinary Optimization, 41: 525-539. doi: 10.1007/s00158-009-0443-8
[12]	Ortigosa R, Martínez-Frutos J. 2021. Multi-resolution methods for the topology optimization of nonlinear electro-active polymers at large strains. Computational Mechanics, 1-23.
[13]	Park J, Zobaer T, Sutradhar A. 2021. A two-scale multi-resolution topologically optimized multi-material design of 3D printed craniofacial bone implants. Micromachines, 12: 101. doi: 10.3390/mi12020101
[14]	Querin O M, Steven G P, Xie Y M. 1998. Evolutionary structural optimisation (ESO) using a bidirectional algorithm. Engineering Computations, 15: 1031-1048. doi: 10.1108/02644409810244129
[15]	Sigmund O. 2001. A 99 line topology optimization code written in Matlab. Structural and Multidisciplinary Optimization, 21: 120-127. doi: 10.1007/s001580050176
[16]	Svanberg K. 1987. The method of moving asymptotes—A new method for structural optimization. International Journal for Numerical Methods in Engineering, 24: 359-373. doi: 10.1002/nme.1620240207
[17]	Wang H, Liu J, Wen G. 2020. An efficient multi-resolution topology optimization scheme for stiffness maximization and stress minimization. Engineering Optimization, 1-21.
[18]	Wang M Y, Wang X, Guo D. 2003. A level set method for structural topology optimization. Computer Methods in Applied Mechanics and Engineering, 192: 227-246. doi: 10.1016/S0045-7825(02)00559-5
[19]	Xie Y M, Steven G P. 1993. A simple evolutionary procedure for structural optimization. Computers & Structures, 49: 885-896.
[20]	Yoo J, Jang I G, Lee I. 2021. Multi-resolution topology optimization using adaptive isosurface variable grouping (MTOP-aIVG) for enhanced computational efficiency. Structural and Multidisciplinary Optimization, 63: 1743-1766. doi: 10.1007/s00158-020-02774-2
[21]	Zhang W, Yang W, Zhou J, Li D, Guo X. 2017. Structural topology optimization through explicit boundary evolution. Journal of Applied Mechanics, 84: 011011. doi: 10.1115/1.4034972