固体的弹性模量和内耗测量方法研究进展

谢明宇; 李法新

doi:10.6052/1000-0992-21-013

固体的弹性模量和内耗测量方法研究进展

doi: 10.6052/1000-0992-21-013

谢明宇,
李法新^,

北京大学工学院力学与工程科学系, 北京 100871

基金项目: 本文工作得到国家自然科学基金重大项目课题 (11890684) 的资助

详细信息

作者简介:
李法新, 男, 北京大学工学院力学与工程科学系, 研究员. 2004年获清华大学固体力学博士学位, 2005—2007在加拿大不列颠哥伦比亚大学(UBC)做博士后, 2007年10月进入北京大学工作. 目前担任SCI期刊《Smart Materials & Structures》副主编、《固体力学学报》编委等职务. 主要从事智能材料与结构力学、无损检测及结构健康监测方法、高温合金与陶瓷表征的研究. 已发表SCI论文100余篇, 总引用1500余次, 授权发明专利18项, 出版学术专著1部. 曾获基金委优秀青年基金(2014)、中国力学青年科技奖(2015)、三次荣获北京大学优秀博士论文指导教师称号(2014, 2016, 2020)

通讯作者:
lifaxin@pku.edu.cn

中图分类号: O329
计量
- 文章访问数: 2444
- HTML全文浏览量: 868
- PDF下载量: 434
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-15
- 录用日期: 2021-05-26
- 网络出版日期: 2021-07-06
- 刊出日期: 2022-03-25

Review of the measurement methods for elastic moduli and internal friction of solids

XIE Mingyu,
LI Faxin^,

LTCS and Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, China

More Information

Corresponding author: lifaxin@pku.edu.cn

摘要

摘要: 弹性模量和内耗是固体材料的基本力学性质, 其测量的准确性和便捷性对工业生产和科学研究都很重要. 本文回顾了近一百年来固体材料弹性模量和内耗的测量方法, 主要分为四类: 准静态方法、低频法、共振法和波传播法. 首先对每类方法的测量原理进行了简单介绍及总体评价. 接着对几种共振方法, 包括自由梁共振法、脉冲激励法、超声共振谱方法和压电超声复合振动技术(PUCOT)进行了详细介绍和评价. 然后, 重点介绍了本课题组最新提出的基于机电阻抗的模量内耗测量方法(称之为M-PUCOT或Q-EMI), 它可以同时、准确、快速地测量杨氏/剪切模量及相应内耗. 最后, 对这种新型弹性模量/内耗测量方法的意义和应用前景进行了讨论和展望.
- 弹性模量 /
- 内耗 /
- 测量方法 /
- 机电阻抗 /
- 压电
Abstract: Elastic moduli and internal frictions are fundamental properties of solid materials. The accuracy and convenience of the measurements these properties are of great significance to industrial production and scientific research. This paper reviews the measurement methods of elastic moduli and internal frictions of solid materials in the past 100 years. These methods can be divided into four categories: quasi-static method, low frequency method, resonance method, and wave propagation method. Firstly, the measurement principle of each type method is introduced and evaluated. Then the resonance methods, including free-free beam method, impulse excitation technique, resonant ultrasound spectrum and piezoelectric ultrasonic composite oscillator technique (PUCOT) are presented and discussed in detail. After that, a new method called modified piezoelectric ultrasonic composite oscillator technique (M-PUCOT), proposed by the authors, are introduced. This new method is based on the principle of electro-mechanical impedance, and can measure the Young’s modulus/shear modulus and the related internal frictions simultaneously, accurately, and quickly. Finally, the significance and prospective of this new method are discussed.
- elastic moduli /
- internal frictions /
- measurement methods /
- electromechanical impedance /
- piezoelectric

HTML全文

图 1 弹性体的蠕变过程

下载: 全尺寸图片幻灯片

图 2 低频法测量弹性模量与内耗的装置. (a) 扭摆仪, (b) 动态热机械分析仪DMA

下载: 全尺寸图片幻灯片

图 3 波传播法测量材料的模量与内耗. (a) 波传播法测量示意图, (b) 超声波通过滞弹性的衰减过程

下载: 全尺寸图片幻灯片

图 4 (a) 自由梁共振法; (b) 脉冲激励法

下载: 全尺寸图片幻灯片

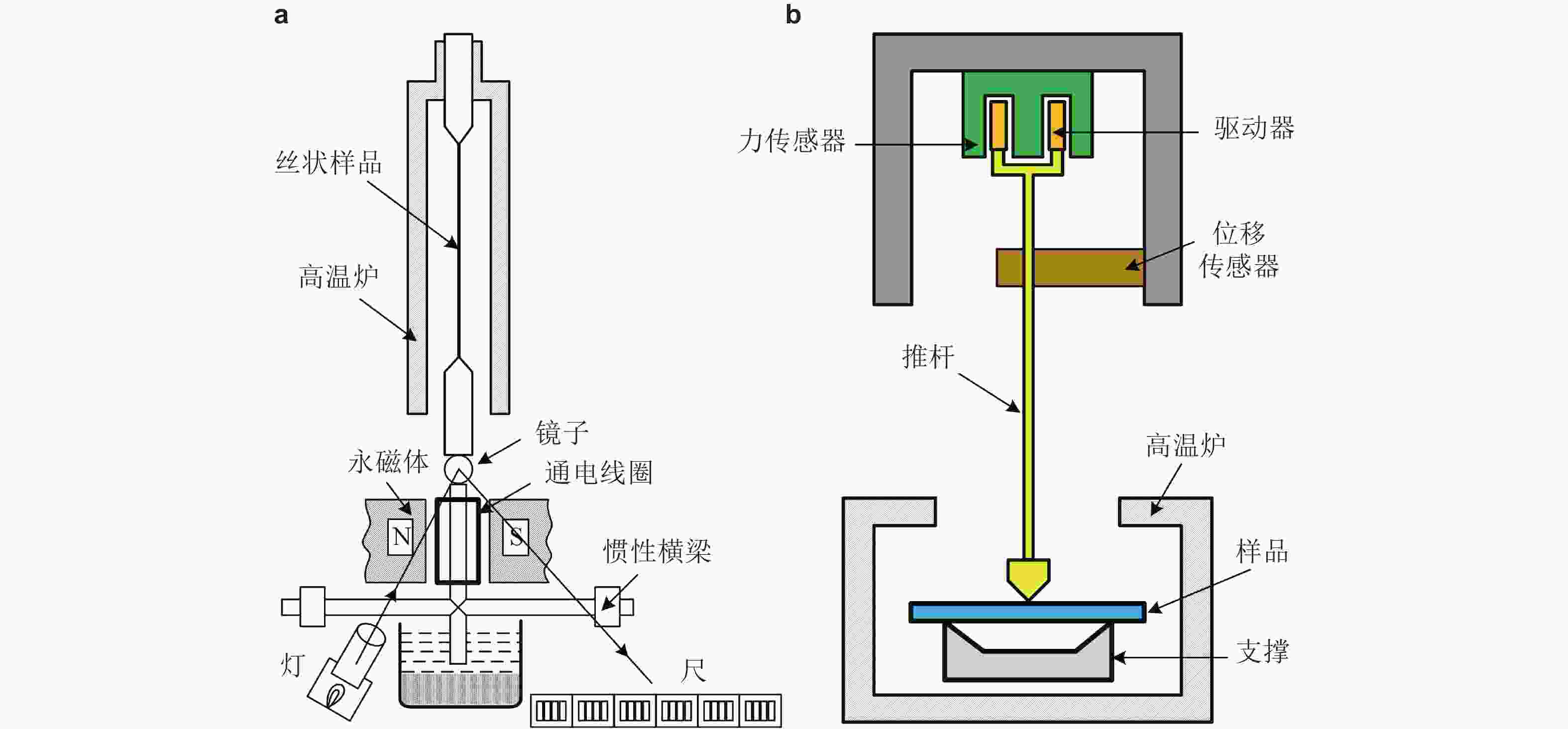
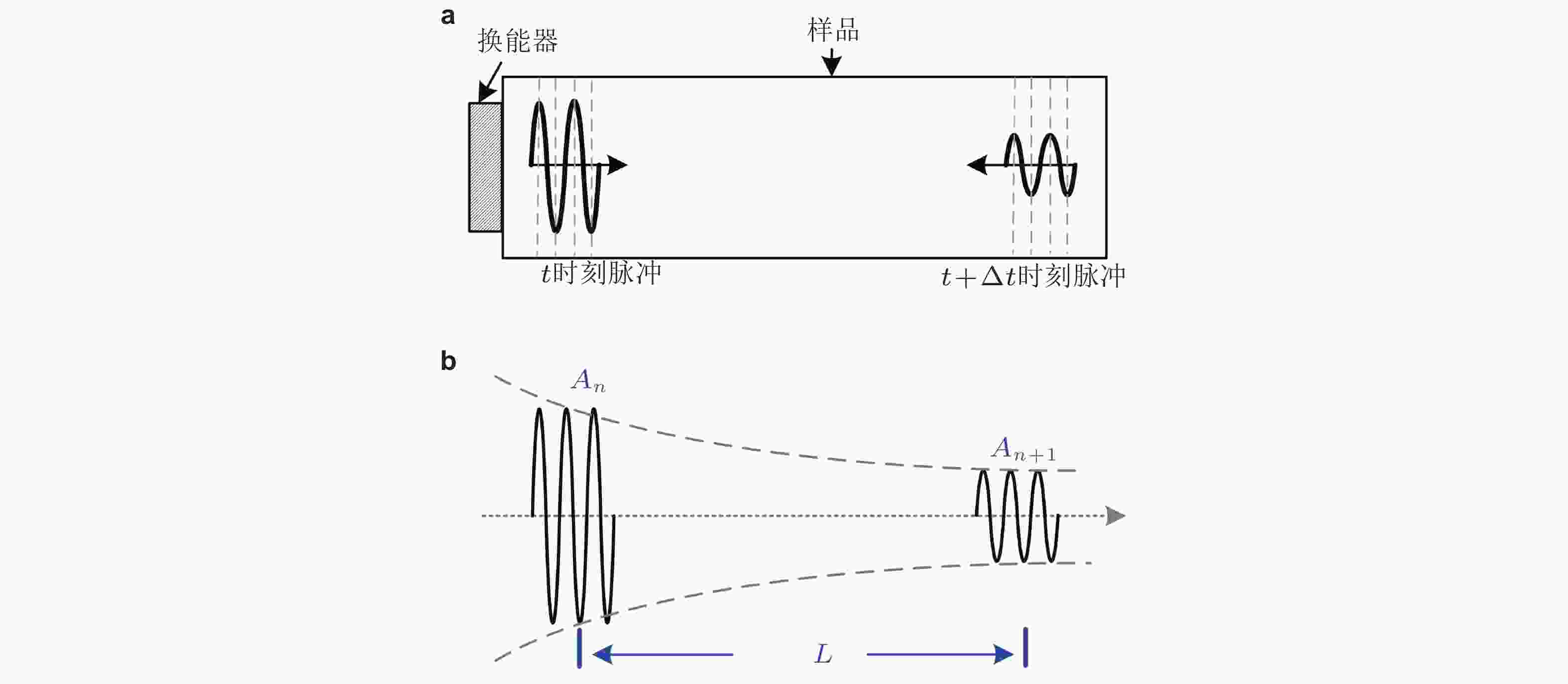
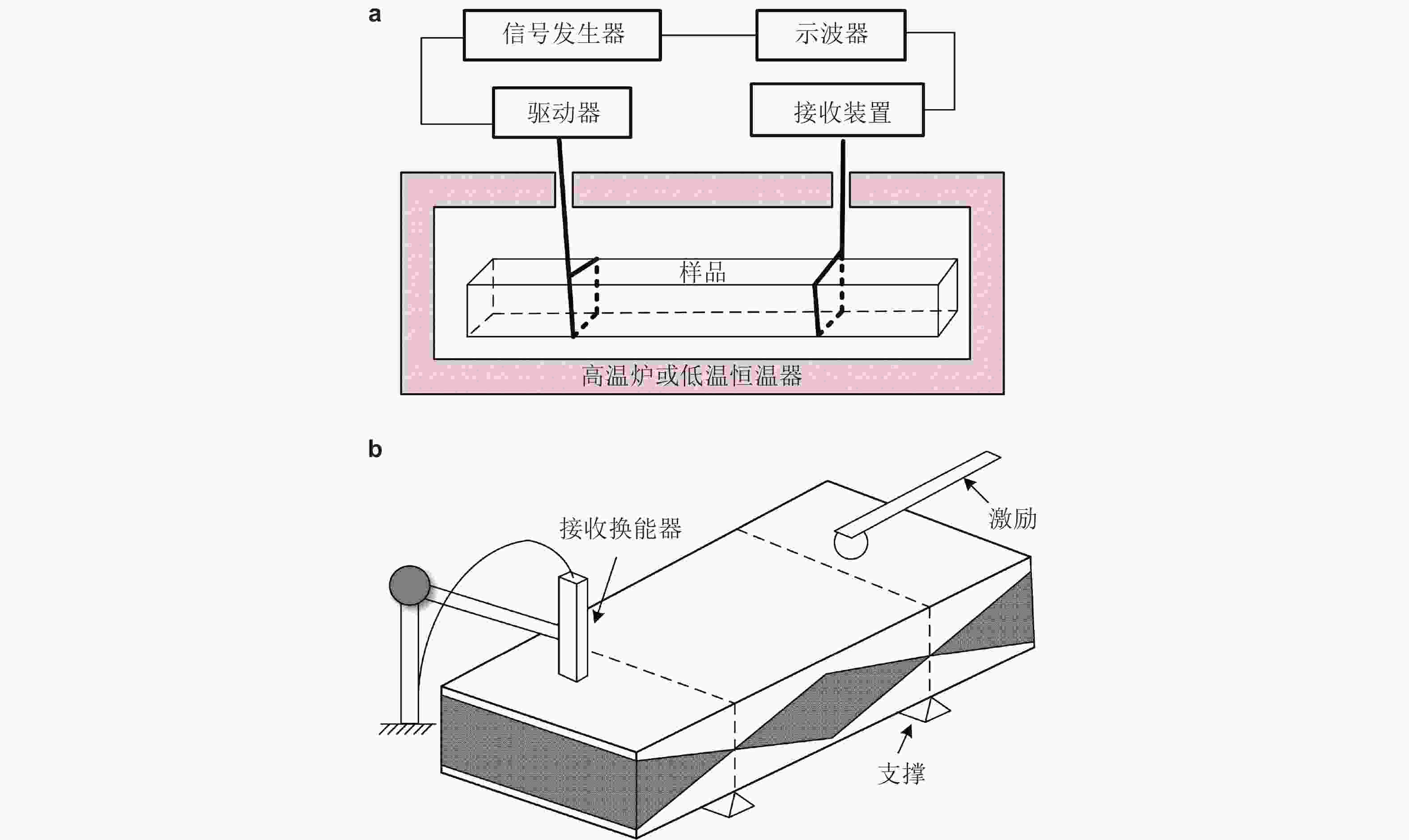
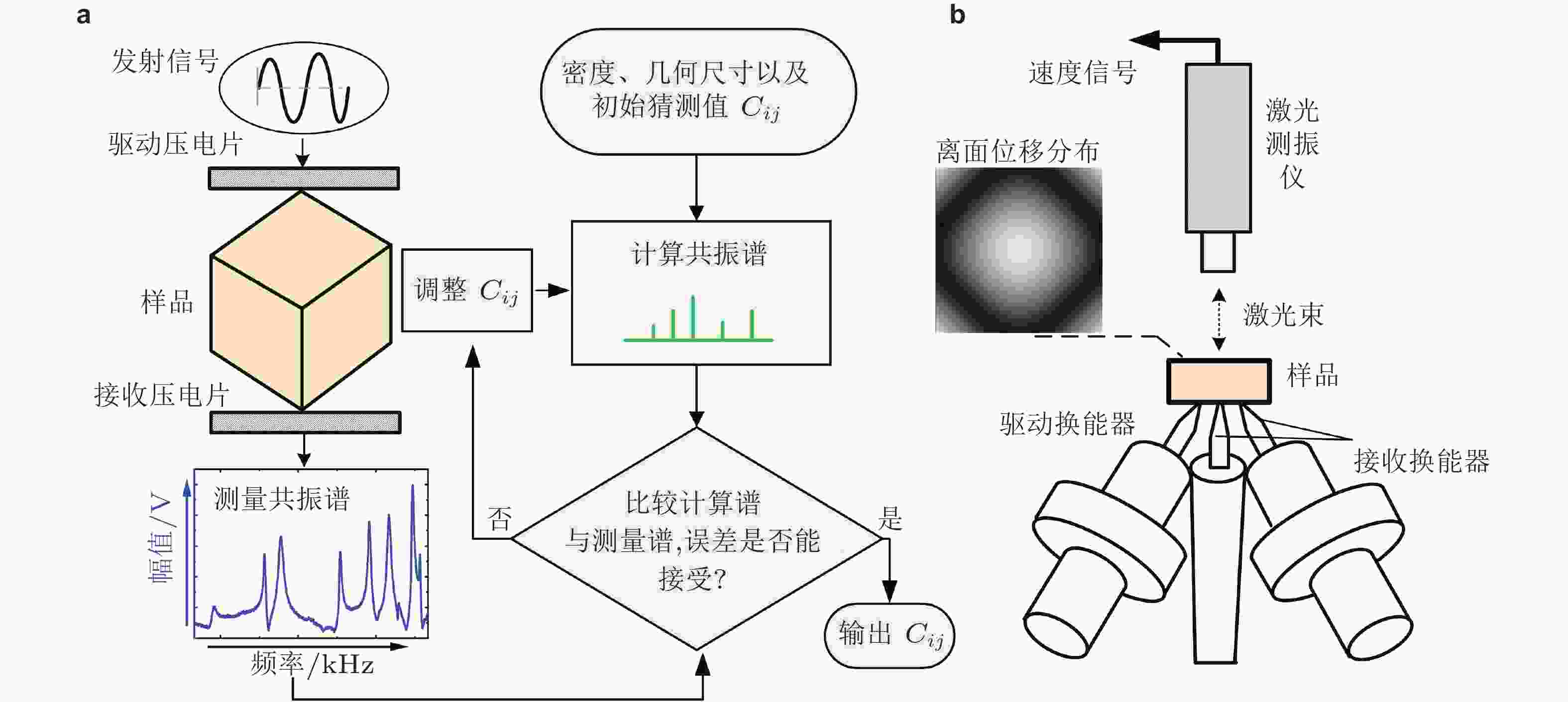
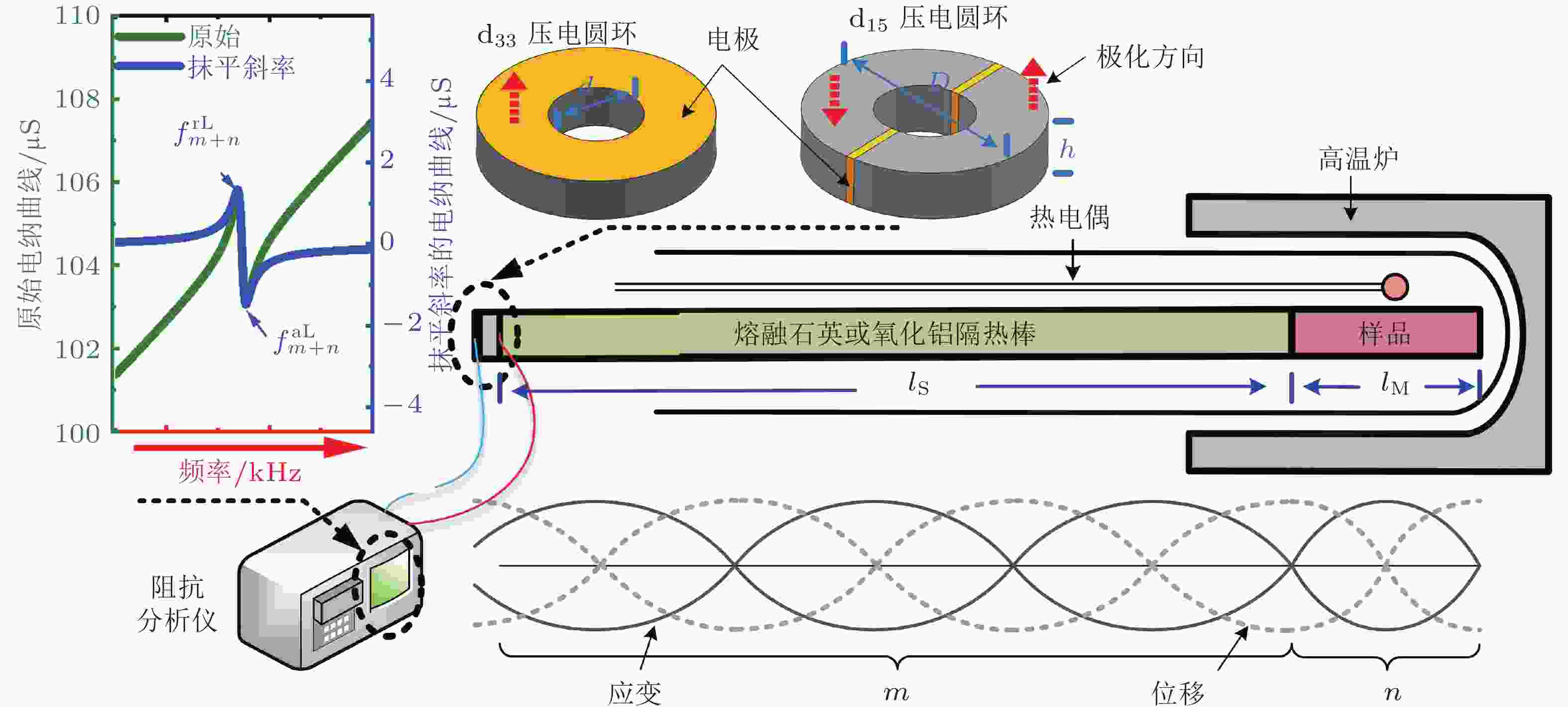
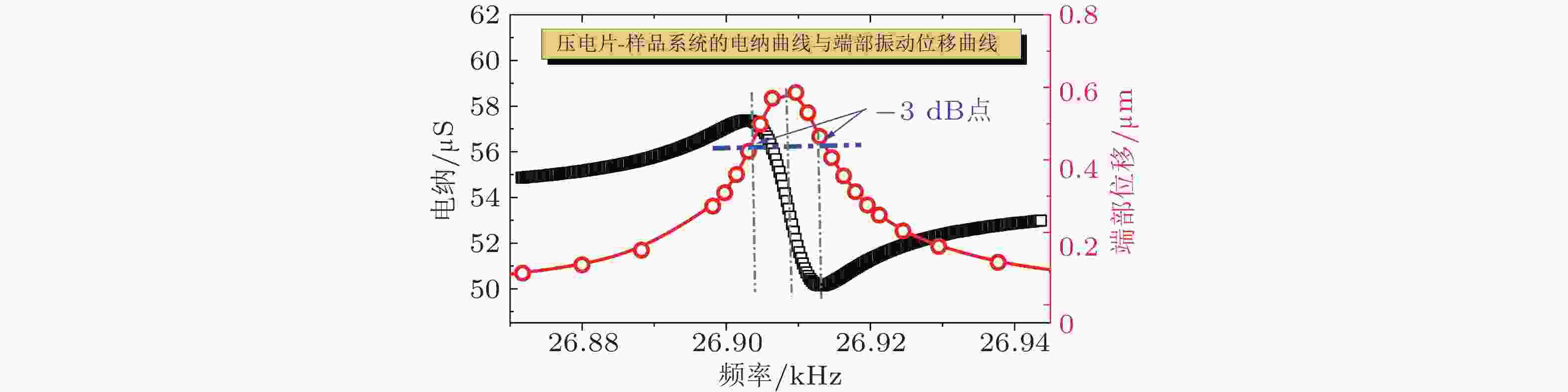
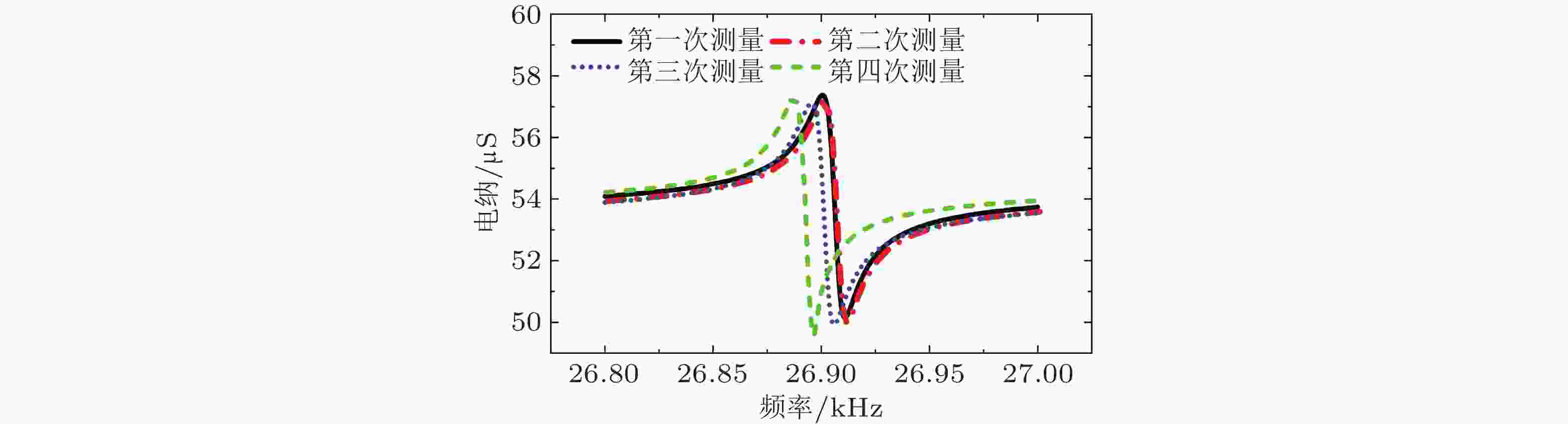
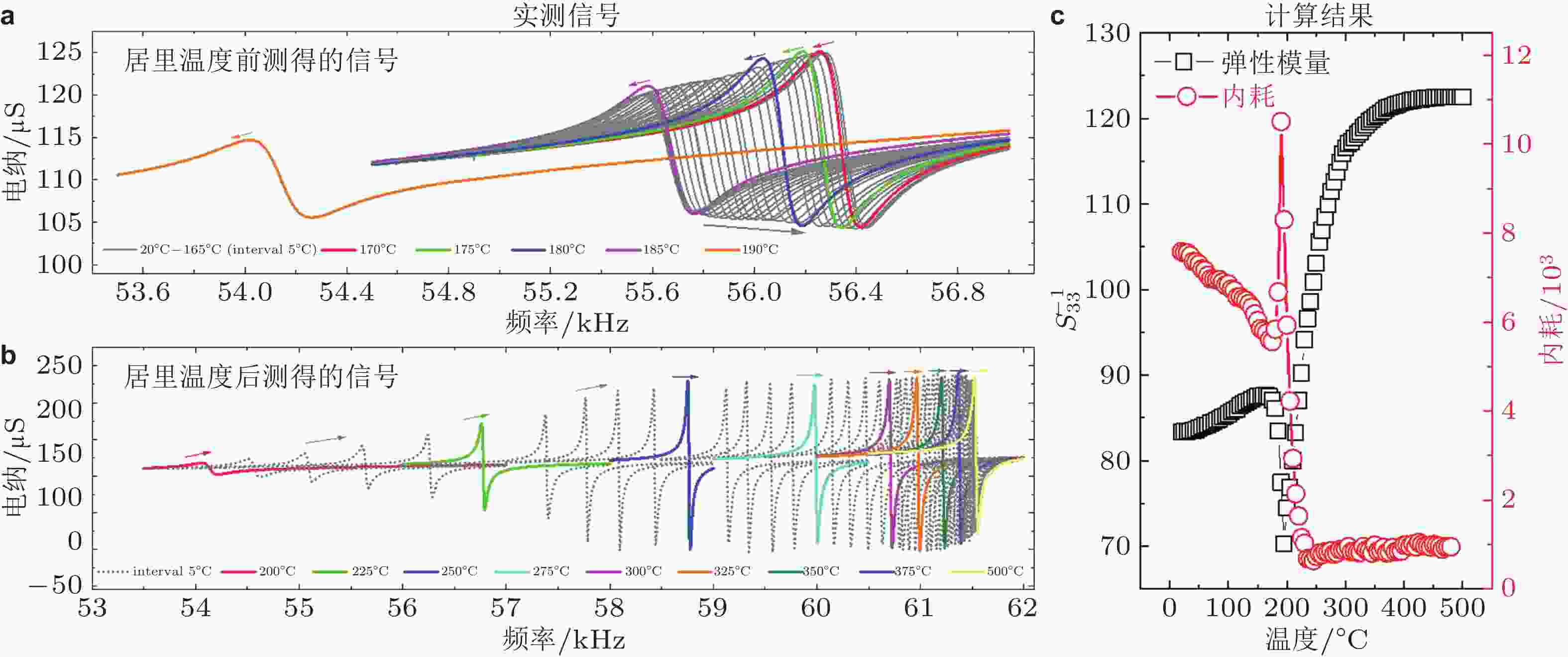
图 5 超声共振谱法RUS. (a) RUS测量各向异性样品弹性常数矩阵示意图; (b) 在RUS中利用激光测振仪扫描离面位移进行模态识别(Ogi et al. 2002)

下载: 全尺寸图片幻灯片

图 6 三组分压电超声复合振动技术

下载: 全尺寸图片幻灯片

图 7 基于机电阻抗法的M-PUCOT测量系统

下载: 全尺寸图片幻灯片

图 8 换能器−被测试件双组分系统的电纳曲线与端部位移幅频特性曲线

下载: 全尺寸图片幻灯片

图 9 采用M-PUCOT方法测量金属棒杨氏模量和内耗(纵向振动模式)时得到的电纳曲线. (1)采用压电换能器A的第一次测量; (2)采用压电换能器A的第二次测量; (3)将换能器A取下, 再次粘结后的测量结果; (4)采用另外一个换能器B的测量结果

下载: 全尺寸图片幻灯片

图 10 利用M-PUCOT的纵振动模式测量轴向极化PZT-5H的弹性模量和纵向振动内耗. (a) 居里温度前电纳曲线随温度的变化; (b) 居里温度后电纳曲线随温度的变化; (c) 根据电纳曲线计算得到的弹性模量与内耗

下载: 全尺寸图片幻灯片

图 11 利用M-PUCOT测量大块金属玻璃Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5玻璃化转变与晶化过程中的弹性模量与内耗. (a) 循环升温与冷却过程中的弹性模量与内耗随温度的变化; (b) 不同温度热处理后金属玻璃的XRD图案

下载: 全尺寸图片幻灯片

图 12 房山汉白玉岩石在压缩过程中的典型应力应变曲线

下载: 全尺寸图片幻灯片

图 13 房山汉白玉岩石在压缩破坏前的模量和内耗变化. (a) 1号样品; (b) 2号样品; (c) 3号样品

下载: 全尺寸图片幻灯片

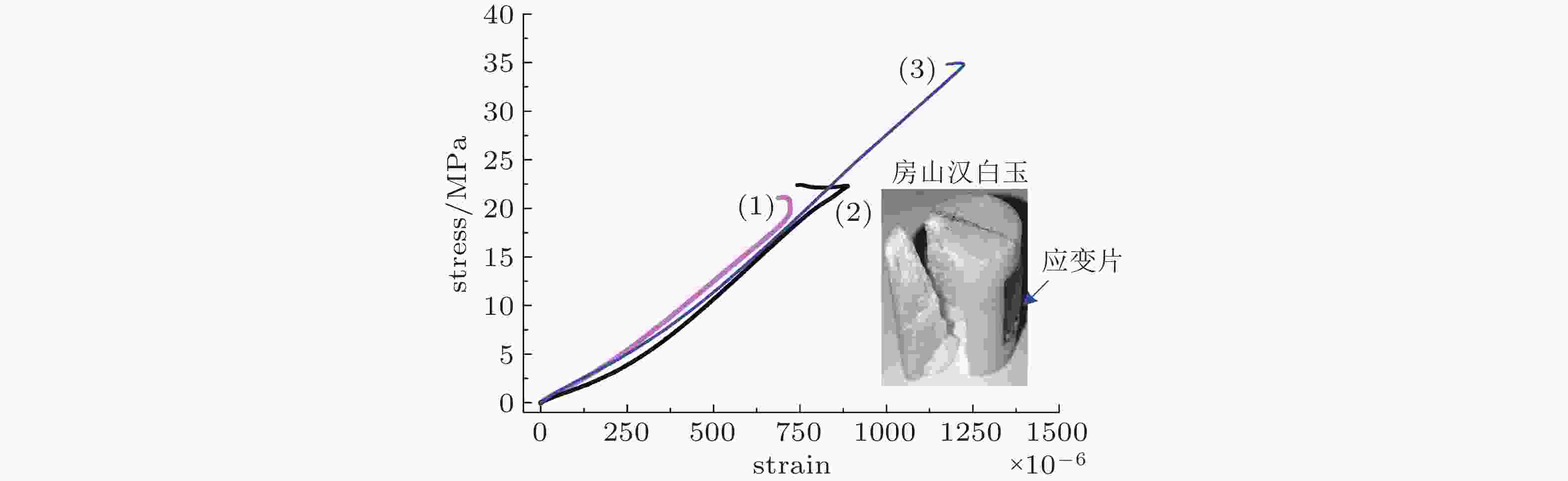
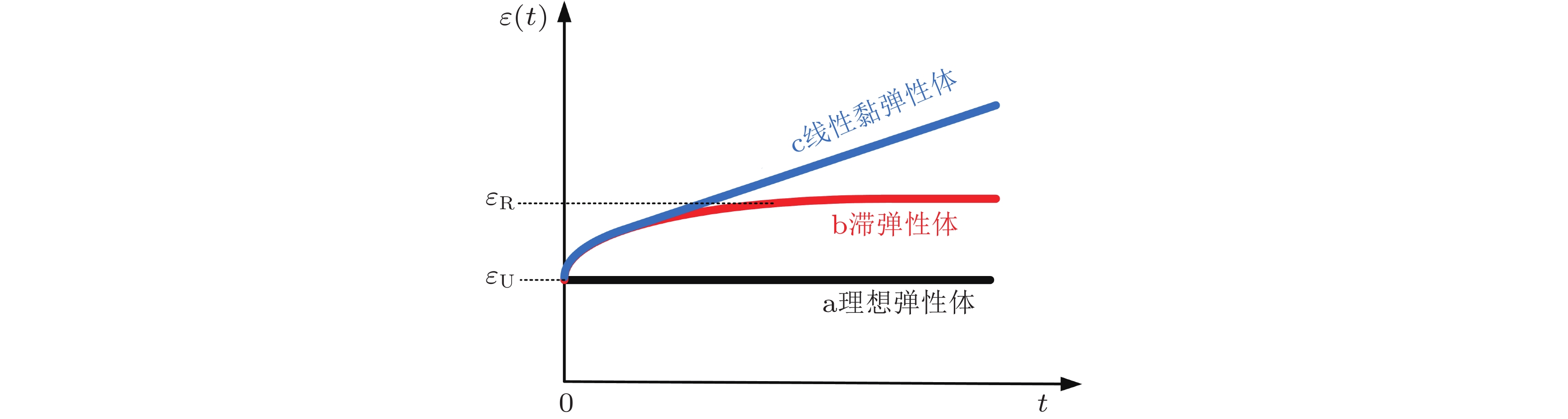
表 1 按应变($ \mathrm{\varepsilon } $)−应力($ \mathrm{\sigma } $)关系对固体材料不同力学行为进行分类


	$ \varepsilon $与$ \sigma $成单值关系	$ \varepsilon $对$ \sigma $瞬时响应	$ \varepsilon $与$ \sigma $成线性关系
理想弹性	是	是	是
非线性弹性	是	是	否
塑性	否	是	否
滞弹性	是	否	是
线性黏弹性	否	否	是

下载: 导出CSV

参考文献(60)

[1]	冯端. 1999. 金属物理学(第三卷): 金属力学性质. 北京: 科学出版社.
[2]	葛庭燧. 1994. 扭摆内耗仪的发明和内耗研究的开拓与发展. 力学进展, 24: 336-352
[3]	徐芝纶. 1979. 弹性力学(上册). 北京: 人民教育出版社.
[4]	Alers G A, Thompson D O. 1961. Dislocation contributions to the modulus and damping in copper at megacycle frequencies. Journal of Applied Physics, 32: 283-293. doi: 10.1063/1.1735992
[5]	Asano S. 1970. Theory of nonlinear damping due to dislocation hysteresis. Journal of the Physical Society of Japan, 29: 952-963. doi: 10.1143/JPSJ.29.952
[6]	ASTME494-10. 2002. Standard practice for measuring ultrasonic velocity in materials. Annual book of ASTM standards.
[7]	ASTME1875-13. 2013. Standard test method for dynamic Young’s modulus, shear modulus, and Poisson’s ratio by sonic resonance. Annual Book of ASTM Standards.
[8]	ASTME1876-15. 2015. Standard test method for dynamic young’s modulus, shear modulus, and poisson’s ratio by impulse excitation of vibration. Annual Book of ASTM Standards.
[9]	Ayres J W, Lalande F, Chaudhry Z, Rogers C A. 1998. Qualitative impedance-based health monitoring of civil infrastructures. Smart Materials and Structures, 7: 599. doi: 10.1088/0964-1726/7/5/004
[10]	Balakirev F F, Ennaceur S M, Migliori R J, Maiorov B, Migliori A. 2019. Resonant ultrasound spectroscopy: The essential toolbox. Review of Scientific Instruments, 90: 121401. doi: 10.1063/1.5123165
[11]	Bauer C L, Gordon R B. 1960. Dislocation damping effects in rock salt. Journal of Applied Physics, 31: 945-949. doi: 10.1063/1.1735780
[12]	Blanter M S, Golovin I S, Neuhauser H, Sinning H. 2010. Internal friction in metallic materials : a handbook. New York: Springer.
[13]	Brook G B, Sully A H. 1955. Some observations on the internal friction of polycrystalline aluminium during the early stages of creep. Acta Metallurgica, 3: 460-469. doi: 10.1016/0001-6160(55)90136-X
[14]	Devine S, Robinson W. 1998. Flexural composite oscillators for the measurement of anelastic and elastic properties of solids at frequencies of 1 to 10 kHz. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 45: 11-22. doi: 10.1109/58.646898
[15]	Fu J, Tan C, Li F. 2015. Quantitative electromechanical impedance method for nondestructive testing based on a piezoelectric bimorph cantilever. Smart Materials and Structures, 24: 065038. doi: 10.1088/0964-1726/24/6/065038
[16]	Golovin I, Sinning H-R, Göken J, Riehemann W. 2004. Fatigue-related damping in some cellular metallic materials. Materials Science and Engineering: A, 370: 537-541. doi: 10.1016/j.msea.2003.08.090
[17]	Granato A V, Lücke K. 1956. Theory of mechanical damping due to dislocations. Journal of Applied Physics, 27: 583-593. doi: 10.1063/1.1722436
[18]	Kê T S. 1947. Stress relaxation across grain boundaries in metals. Physical Review, 72: 41-46. doi: 10.1103/PhysRev.72.41
[19]	Kê T S. 1950. Internal friction of metals at very high temperatures. Journal of Applied Physics, 21: 414-419. doi: 10.1063/1.1699675
[20]	Kê T S, Mehl R F. 1999. Fifty-year study of grain-boundary relaxation. Metallurgical and Materials Transactions A, 30: 2267-2295. doi: 10.1007/s11661-999-0238-y
[21]	Kustov S, Golyandin S, Sapozhnikov K, Van Humbeeck J, De Batist R. 1998. Low-temperature anomalies in Young's modulus and internal friction of Cu–Al–Ni single crystals. Acta Materialia, 46: 5117-5126. doi: 10.1016/S1359-6454(98)00168-2
[22]	Kustov S, Gremaud G, Benoit W, Golyandin S, Sapozhnikov K, Nishino Y, Asano S. 1999. Strain amplitude-dependent anelasticity in Cu–Ni solid solution due to thermally activated and athermal dislocation–point obstacle interactions. Journal of Applied Physics, 85: 1444-1459. doi: 10.1063/1.369276
[23]	Lakes R S. 2004. Viscoelastic measurement techniques. Review of Scientific Instruments, 75: 797-810. doi: 10.1063/1.1651639
[24]	Lee T, Lakes R S, Lal A. 2000. Resonant ultrasound spectroscopy for measurement of mechanical damping: Comparison with broadband viscoelastic spectroscopy. Review of Scientific Instruments, 71: 2855-2861. doi: 10.1063/1.1150703
[25]	Leisure R G, Willis F A. 1997. Resonant ultrasound spectroscopy. Journal of Physics: Condensed Matter, 9: 6001-6029. doi: 10.1088/0953-8984/9/28/002
[26]	Marx J. 1951. Use of the piezoelectric gauge for internal friction measurements. Review of Scientific Instruments, 22: 503-509. doi: 10.1063/1.1745981
[27]	Marx J W, Sivertsen J M. 1953. Temperature dependence of the elastic moduli and internal friction of silica and glass. Journal of Applied Physics, 24: 81-87. doi: 10.1063/1.1721138
[28]	Mason W. 1956. Internal friction and fatigue in metals at large strain amplitudes. The Journal of the Acoustical Society of America, 28: 1207-1218. doi: 10.1121/1.1908595
[29]	Migliori A, Sarrao J L, Visscher W M, Bell T M, Lei M, Fisk Z, Leisure R G. 1993. Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids. Physica B: Condensed Matter, 183: 1-24. doi: 10.1016/0921-4526(93)90048-B
[30]	Ninomiya K, Ferry J D, Ōyanagi Y. 1963. Viscoelastic properties of polyvinyl acetates. II. Creep studies of blends1. The Journal of Physical Chemistry, 67: 2297-2308. doi: 10.1021/j100805a012
[31]	Nowick A S. 2012. Anelastic Relaxation in Crystalline Solids. Amsterdam: Elsevier.
[32]	Nowick A S, Heller W R. 1963. Anelasticity and stress-induced ordering of point defects in crystals. Advances in Physics , 12: 251-298. doi: 10.1080/00018736300101293
[33]	Ogi H, Sato K, Asada T, Hirao M. 2002. Complete mode identification for resonance ultrasound spectroscopy. The Journal of the Acoustical Society of America , 112: 2553-2557. doi: 10.1121/1.1512700
[34]	Ohno I. 1976. Free vibration of a rectangular parallelepiped crystal and its application to determination of elastic constants of orthorhombic crystals. Journal of Physics of the Earth , 24: 355-379. doi: 10.4294/jpe1952.24.355
[35]	Periyannan S, Balasubramaniam K. 2015. Simultaneous moduli measurement of elastic materials at elevated temperatures using an ultrasonic waveguide method. Review of Scientific Instruments , 86: 114903. doi: 10.1063/1.4935556
[36]	Press W H, Flannery B P, Teukolsky S A, Vetterling W T. 1986. Numerical Recipes: The Art of Scientific Computing. Cambridge and New York: Cambridge University Press.
[37]	Quimby S L. 1925. On the experimental determination of viscosity of vibrating solids. Physical Review, 25: 558-573.
[38]	Robinson W H, Carpenter S H, Tallon J L. 1974. Piezoelectric method of determining torsional mechanical damping between 40 and 120 kHz. Journal of Applied Physics , 45: 1975-1981. doi: 10.1063/1.1663533
[39]	Robinson W H, Edgar A. 1974. The piezoelectric method of determining mechanical damping at frequencies of 30 to 200 kHz. IEEE Transactions on Sonics and Ultrasonics , 21: 98-105. doi: 10.1109/T-SU.1974.29798
[40]	Roebben G, Bollen B, Brebels A, Van Humbeeck J, Van der Biest O. 1997. Impulse excitation apparatus to measure resonant frequencies, elastic moduli, and internal friction at room and high temperature. Review of Scientific Instruments , 68: 4511-4515. doi: 10.1063/1.1148422
[41]	Rose J L. 1999. Ultrasonic waves in solid media. Cambridge: Cambridge University Press.
[42]	Salje E K, Schranz W. 2011. Low amplitude, low frequency elastic measurements using dynamic mechanical analyzer (DMA) spectroscopy. Zeitschrift für Kristallographie Crystalline Materials, 226: 1-17.
[43]	Sapozhnikov K, Golyandin S, Kustov S, Van Humbeeck J, De Batist R. 2000. Motion of dislocations and interfaces during deformation of martensitic Cu–Al–Ni crystals. Acta Materialia , 48: 1141-1151. doi: 10.1016/S1359-6454(99)00374-2
[44]	Schaller R, Fantozzi G, Gremaud G. 2001. Mechanical spectroscopy Q−1 2001, with applications to materials science. Trans Tech Publications Inc.
[45]	Sternstein S S, Ho T C. 1972. Biaxial stress relaxation in glassy polymers: polymethylmethacrylate. Journal of Applied Physics , 43: 4370-4383. doi: 10.1063/1.1660930
[46]	Sumino Y, Ohno I, Goto T, Kumazawa M. 1976. Measurement of elastic constants and internal frictions on single-crystal MgO by rectangular parallelepiped resonance. Journal of Physics of the Earth , 24: 263-273. doi: 10.4294/jpe1952.24.263
[47]	Sutton P M. 1953. The variation of the elastic constants of crystalline aluminum with temperature between 63k and 773k. Physical Review , 91: 816-821. doi: 10.1103/PhysRev.91.816
[48]	Thompson D O, Holmes D K. 1956. Effects of neutron irradiation upon the Young's modulus and internal friction of copper single crystals. Journal of Applied Physics , 27: 713-723. doi: 10.1063/1.1722471
[49]	Weertman J, Salkovitz E I. 1955. The internal friction of dilute alloys of lead. Acta Metallurgica , 3: 1-9. doi: 10.1016/0001-6160(55)90002-X
[50]	Woirgard J, Sarrazin Y, Chaumet H. 1977. Apparatus for the measurement of internal friction as a function of frequency between 10− 5 and 10 Hz. Review of Scientific Instruments , 48: 1322-1325. doi: 10.1063/1.1134874
[51]	Wolfenden A, Harmouche M R, Blessing G V, Chen Y T, Terranova P, Dayal V, Kinra V K, Lemmens J W, Phillips R R and Smith J S. 1989. Dynamic Young's modulus measurements in metallic materials: results of an interlaboratory testing program. Journal of Testing and Evaluation , 17: 2-13. doi: 10.1520/JTE11527J
[52]	Xie M, Ding G, Jiang M, Li F. 2021. High-frequency elastic moduli and internal frictions of Zr_41.2Ti_{13. 8}Cu1_2. ₅Ni₁₀Be_{22. 5} bulk metallic glass during glass transition and crystallization. Journal of Non-Crystalline Solids , 560: 120754. doi: 10.1016/j.jnoncrysol.2021.120754
[53]	Xie M, Huan Q, Li F. 2020. Quick and repeatable shear modulus measurement based on torsional resonance using a piezoelectric torsional transducer. Ultrasonics , 103: 106101. doi: 10.1016/j.ultras.2020.106101
[54]	Xie M, Li F. 2020a. A modified piezoelectric ultrasonic composite oscillator technique for simultaneous measurement of elastic moduli and internal frictions at varied temperature. Review of Scientific Instruments , 91: 015110. doi: 10.1063/1.5135360
[55]	Xie M, Li F. 2020b. Anomalous elastic moduli and internal frictions in unpoled and poled lead titanate zirconate ceramics near the Curie temperature. AIP Advances , 10: 045007. doi: 10.1063/5.0003808
[56]	Xie M and Li F. 2020c. New method enables multifunctional measurement of elastic moduli and internal frictions. Journal of Applied Physics , 128: 230902. doi: 10.1063/5.0034801
[57]	Zacharias J. 1933. The temperature dependence of Young’s modulus for nickel. Physical Review , 44: 116-122. doi: 10.1103/PhysRev.44.116
[58]	Zener C. 1943. Internal friction in an alpha-brass crystal. Trans. AIME, 152: 122-126.
[59]	Zener C. 1947. Stress induced preferential orientation of pairs of solute atoms in metallic solid solution. Physical Review , 71: 34. doi: 10.1103/PhysRev.71.34
[60]	Zener C. 1948. Elasticity and Anelasticity of Metals. Chicage: University of Chicago Press.