A review of the study on coherent structures in turbulence by the clustering method
-
摘要: 湍流的无序性要求对拟序结构的研究必须从统计的角度出发, 而聚类连通法 (clustering method) 则是实现拟序结构与统计方法深度融合的有力工具. 该方法是一种基于数据的流动特征提取方法, 它将每个连通域, 即单个拟序结构作为一个统计样本. 此外, 其衍生的基于连通域空间重叠的时空追踪方法可以进一步研究这些结构的时空演化, 该方法将每个拟序结构从生成到消亡的演化过程也视为统计样本, 从而实现了对拟序结构运动学特征和动力学过程的统计刻画. 本文回顾了聚类连通法的发展历程并着重介绍了人们采用该方法在雷诺切应力结构、速度条带和能量级串方面取得的重大进展, 这些结果表明该方法极大拓展了人们基于传统的逐点统计方法对湍流的认识, 因而具有很大的潜力. 最后, 对该方法在湍流中的应用给出了建议和展望.Abstract: The intrinsic randomness of turbulence requires that the study of coherent structures has to be from the statistical point of view. The data-based clustering method is a powerful tool to realize the deep integration of coherent structures and statistics. It makes each continuous region, i.e., an individual structure, as a statistical sample. In addition, the spatial-temporal tracking method based on the spatial overlap of individual structure between consecutive snapshots makes the evolution of individual structure during its lifetime also as a statistical sample. Thus, both the kinematics and dynamics of coherent structures can be statistically described. We reviewed the history of this method and introduced the progress on Reynolds stress structures, velocity streaks, and cascades with emphasis. These results suggest that the clustering method extraordinarily extended our understanding of turbulence compared with the traditional point-wise statistics. Further prospects are also provided for future research.
-
图 2 槽道湍流中提取的涡簇(上)和雷诺应力结构(下). 结构以离壁面距离着色, 坐标以黏性长度δν为单位 (Lozano-Durán 2015)
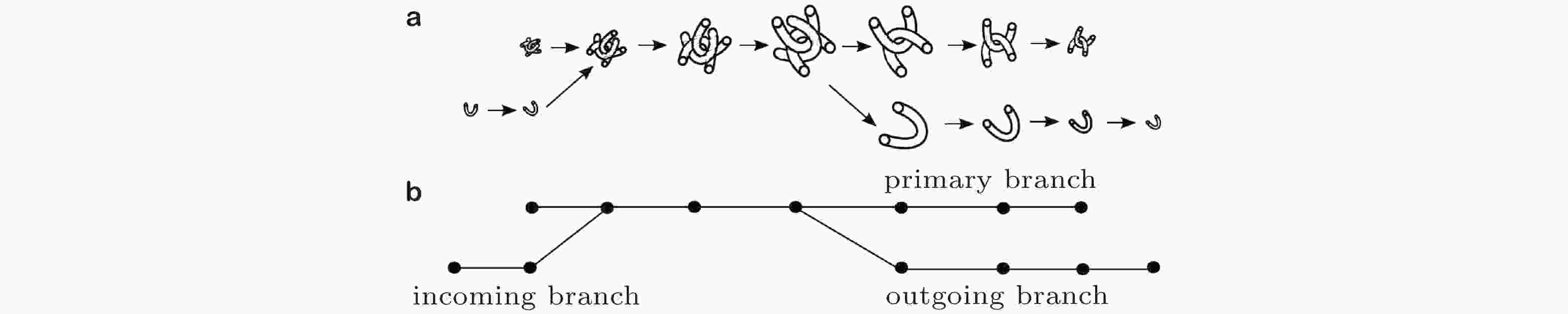
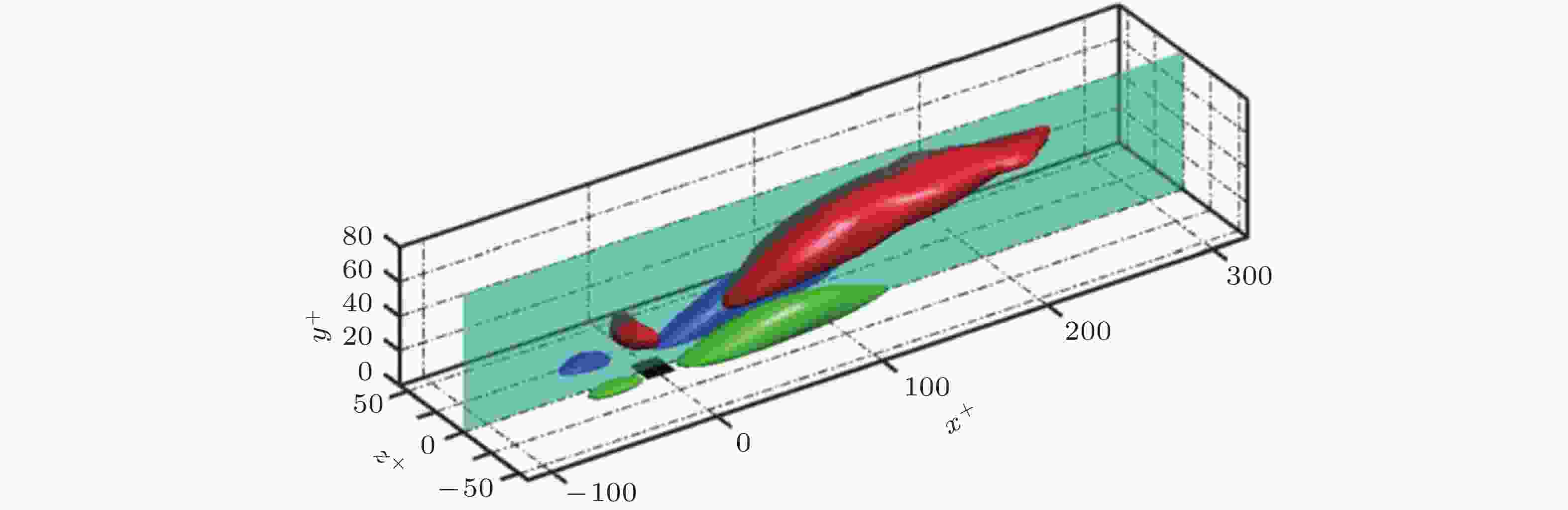
图 3 拟序结构从生成到消亡的示意图, (b)为用节点、边和图表示的(a)中拟序结构的演化 (Lozano-Durán & Jiménez 2014a)
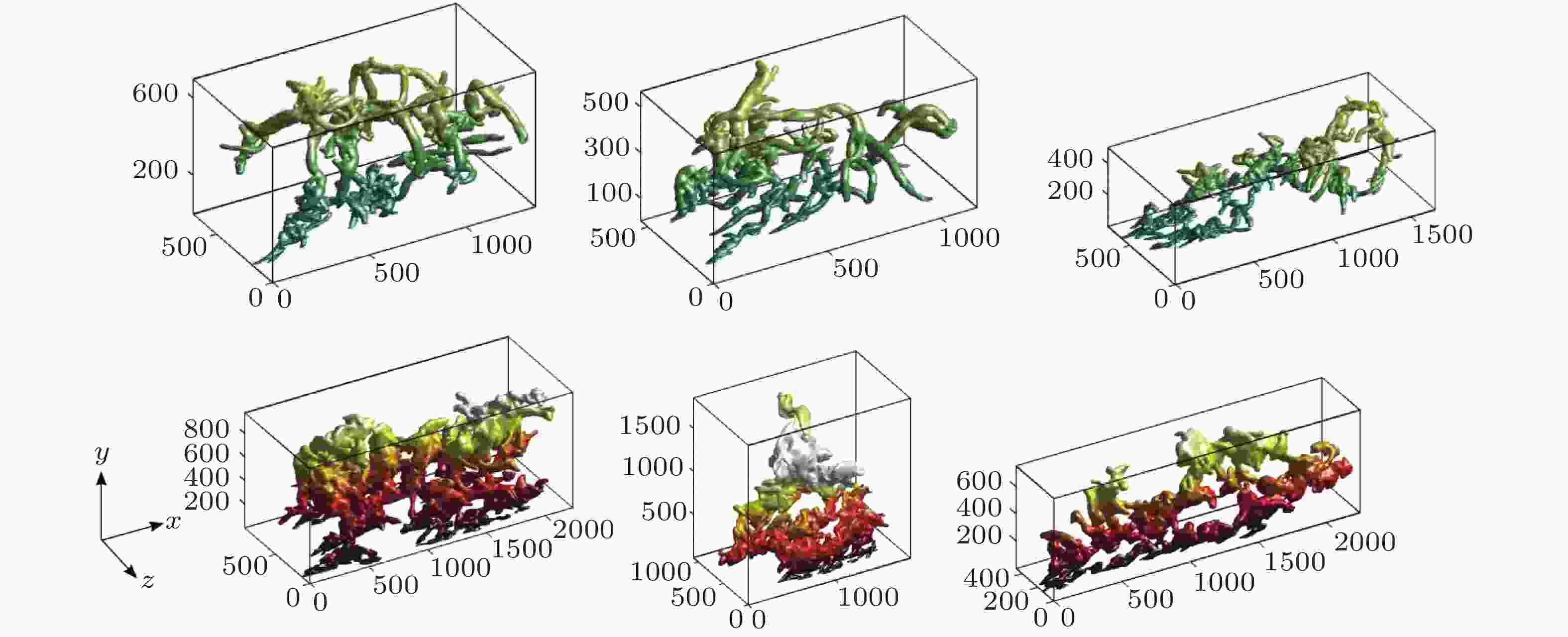
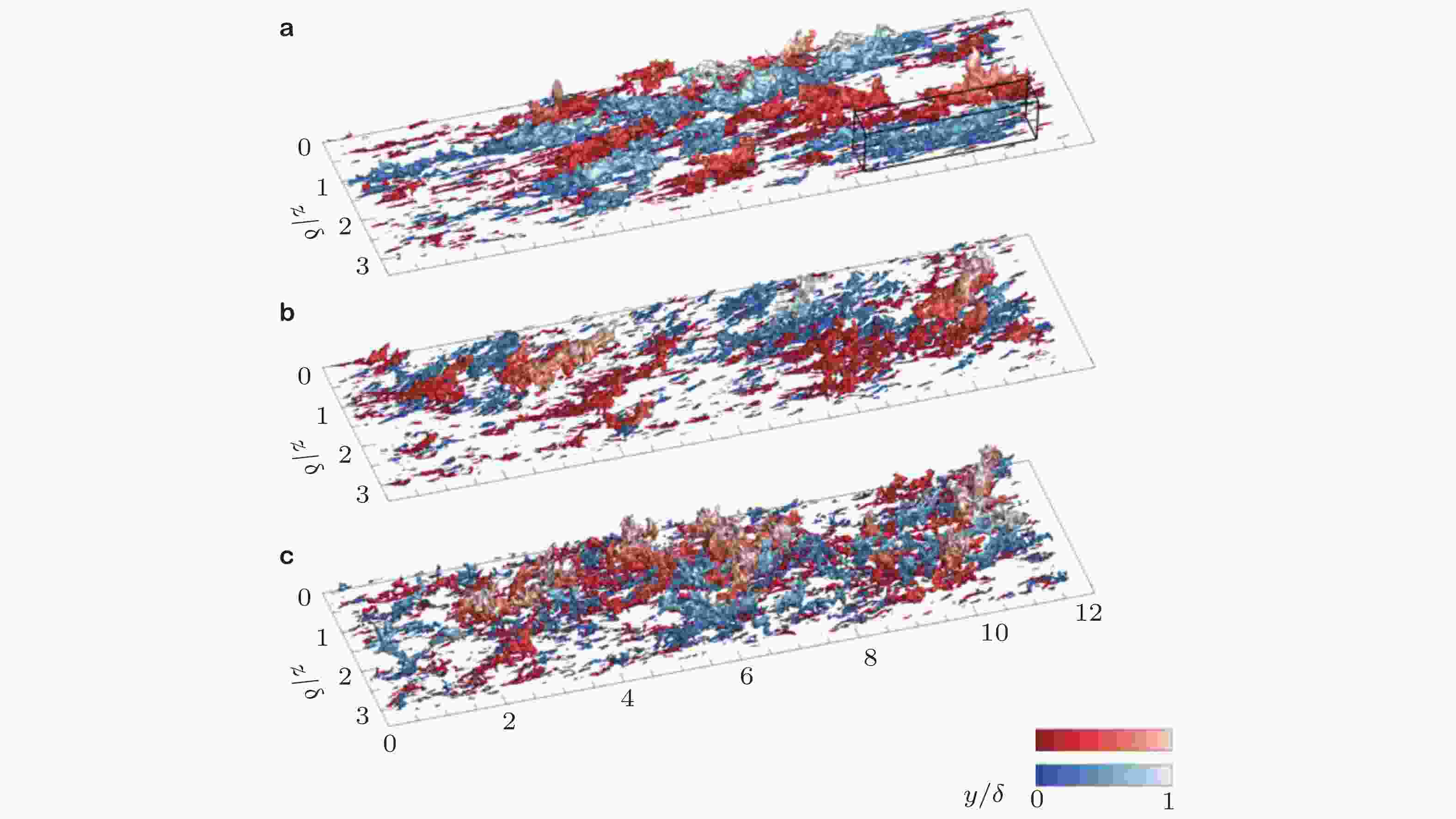
图 4 (a) Reτ ≈ 4200的槽道湍流中瞬时的涡簇和(b)雷诺应力结构. (b)中暖色为上抛, 冷色为下扫. 结构以离壁面距离着色 (Lozano-Durán & Jiménez 2014a)
图 5 (a) Reτ ≈ 4200的槽道湍流中构成一个图的涡簇随时间的演化. (b)涡簇演化构成的1个graph, 实线代表分支, 红色和蓝色虚线分别代表结构的合并和分裂. (c)一个主分支中上抛结构从生成到消亡的演化过程 (Lozano-Durán & Jiménez 2014a)
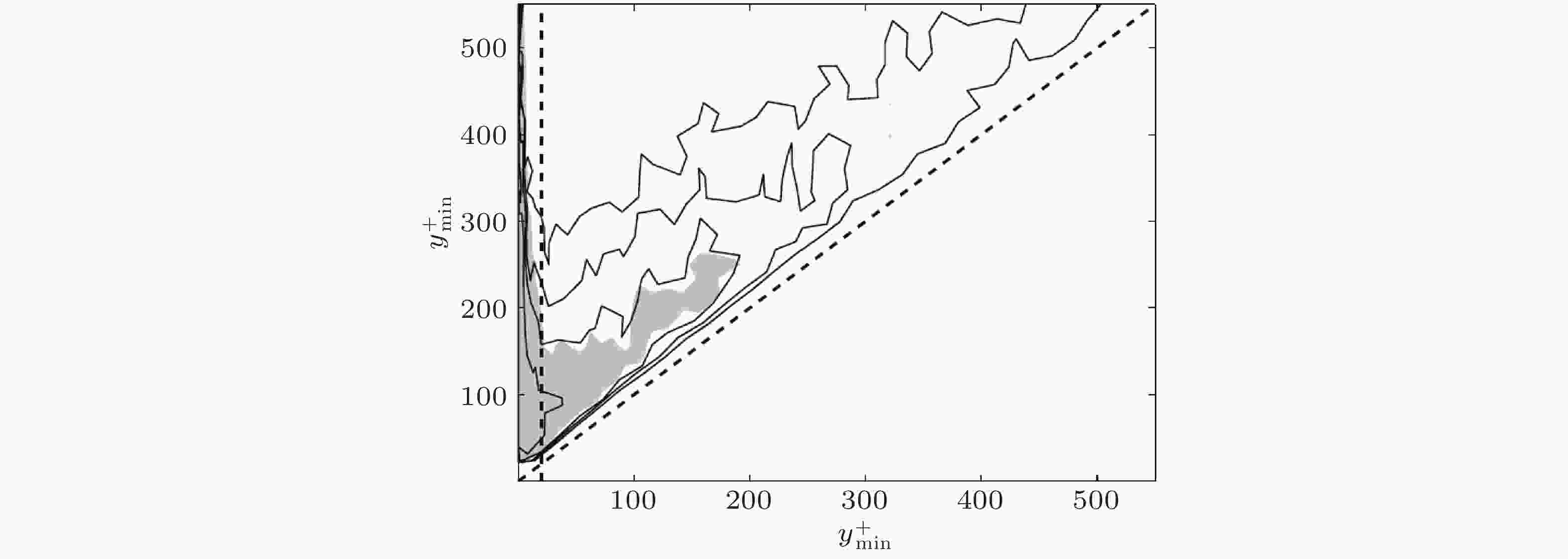
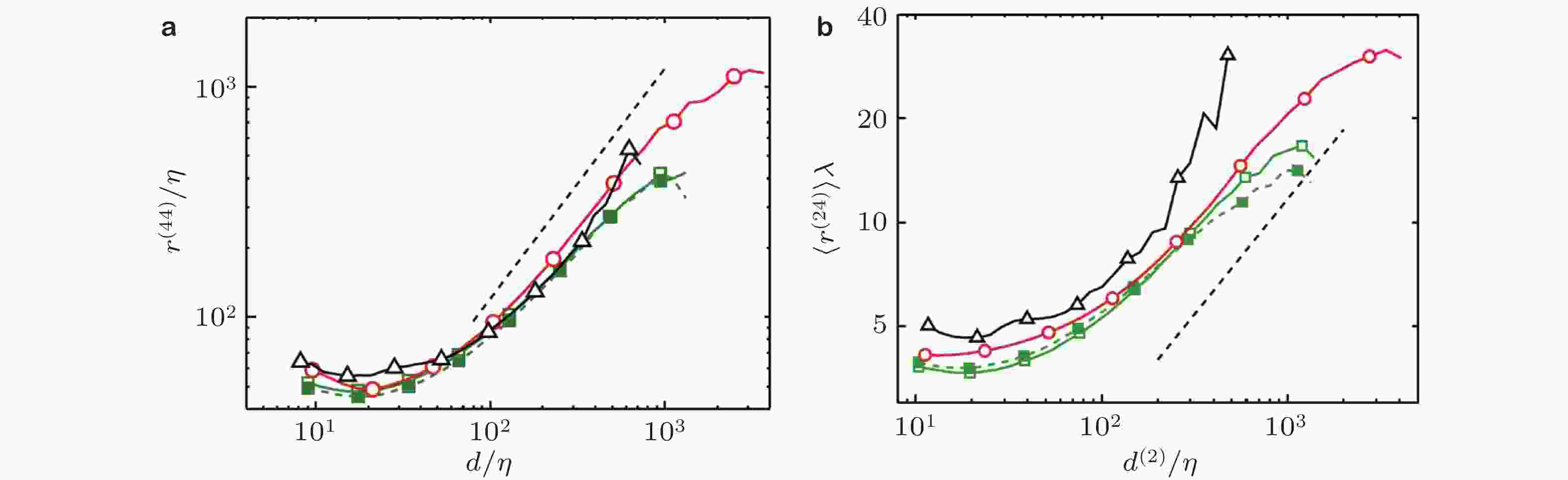
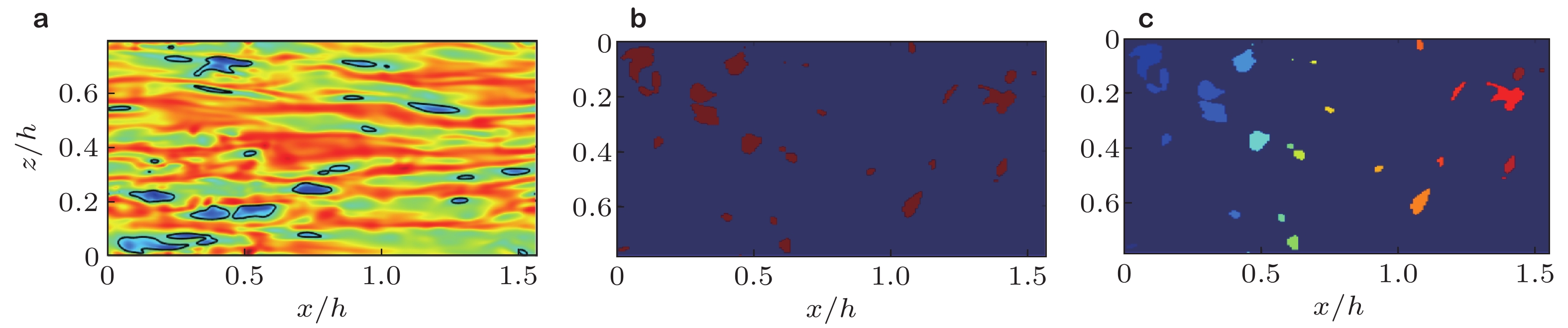
图 6 涡簇体积的概率密度函数, 其中虚线表示ymin+ = 20及ymax = ymin. 等值线分别包含20%, 40%, 60%和80%的数据. 有阴影的等值线为另一阈值的结果, 包含40%的数据 (del Álamo et al. 2006)
图 7 对ymax+ > 100的壁面附着涡簇作条件平均之后涡簇中心xy截面上(
$\{u'\},\{v'\}$ )的矢量图. 阴影为网格点属于涡簇的概率密度函数, 分别包含50%和75%的数据. 实线表示$\{u'\}$ = 0 (del Álamo et al. 2006)图 8 对壁面附着且ymax+>100的涡簇做条件平均之后的平均流场. 其中红色和蓝色等值面分别为
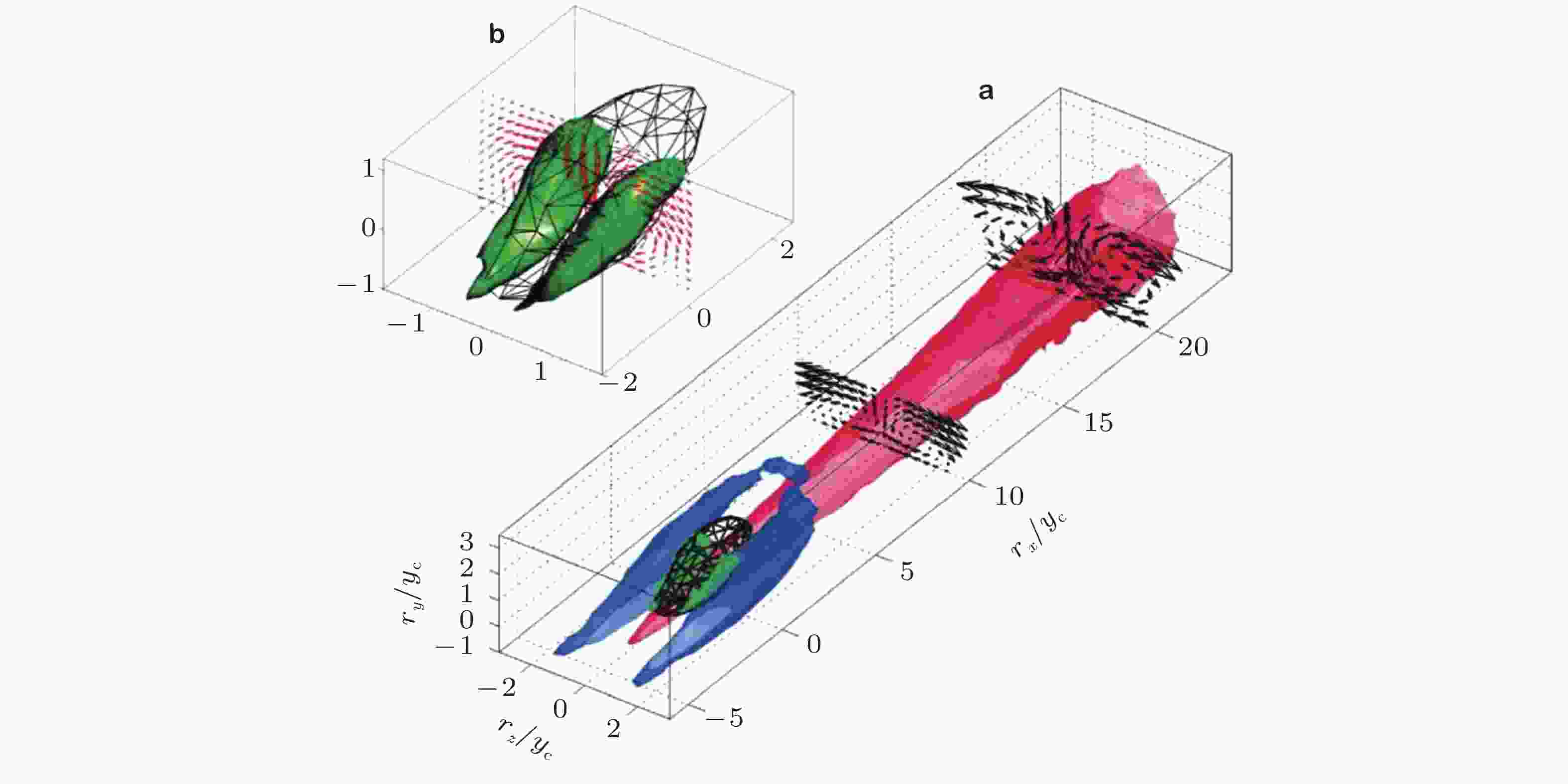
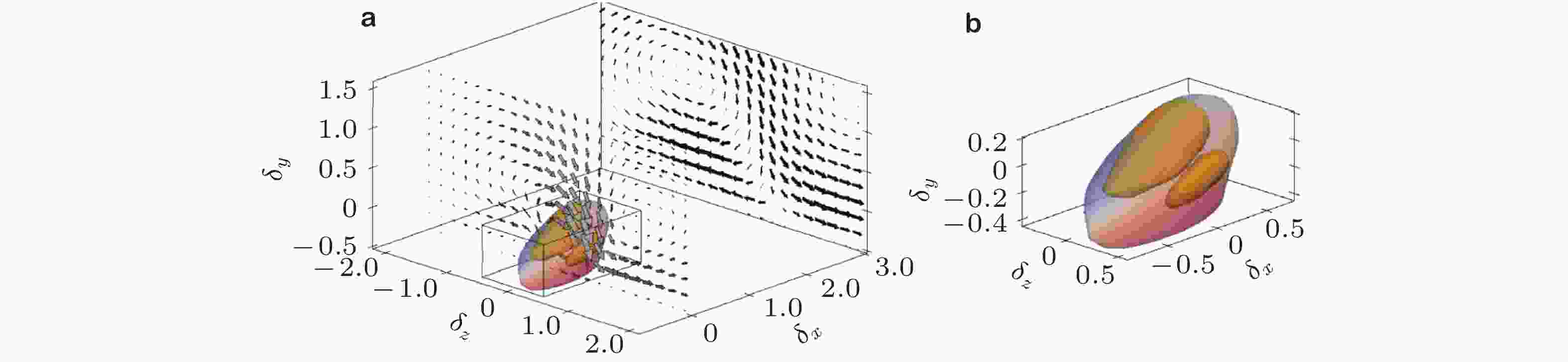
$\{u'\}^+$ = 0.3和−0.1. 箭头代表($ \{v'\},\{w'\}$ ), 黑色代表网格点属于涡簇的概率密度函数等值面, 绿色等值面为平均流场速度梯度的判别式 (del Álamo et al. 2006)图 9 Reτ = 2000的槽道湍流中一个超大尺度上抛. 坐标轴以槽道半高h为单位 (Lozano-Durán et al. 2012)
图 10 壁面附着结构流向和展向相对位置的概率密度函数. (a)上抛之间, (b)下扫之间, (c)涡簇之间, (d)上抛相对于下扫, (e)涡簇相对上抛, (f)涡簇相对下扫 (Lozano-Durán et al. 2012)
图 11 (a)网格点属于上抛、下扫和涡簇的概率密度函数等值面; (b) 瞬时的上抛、下扫和涡簇; (c) 平均流向脉动速度, 红色和蓝色分别表示
$\{u'\}^+$ = 0.5和−0.5; (d) rx = 0截面上的平均流场, 云图为$\{u'\}^+$ , 箭头代表($\{v'\},\{w'\} $ ), 虚线为(a)中概率密度函数的截面 (Lozano-Durán et al. 2012)图 12 下扫分别与(a)下扫和(b)上抛之间的最短距离与特征长度的关系. Δ为槽道湍流中壁面分离的雷诺应力结构(ymin+ > 100), 其他符号为统计平稳均匀剪切湍流中结果. (a)和(b)中虚线的斜率分别为1和2/3 (Dong et al. 2017)
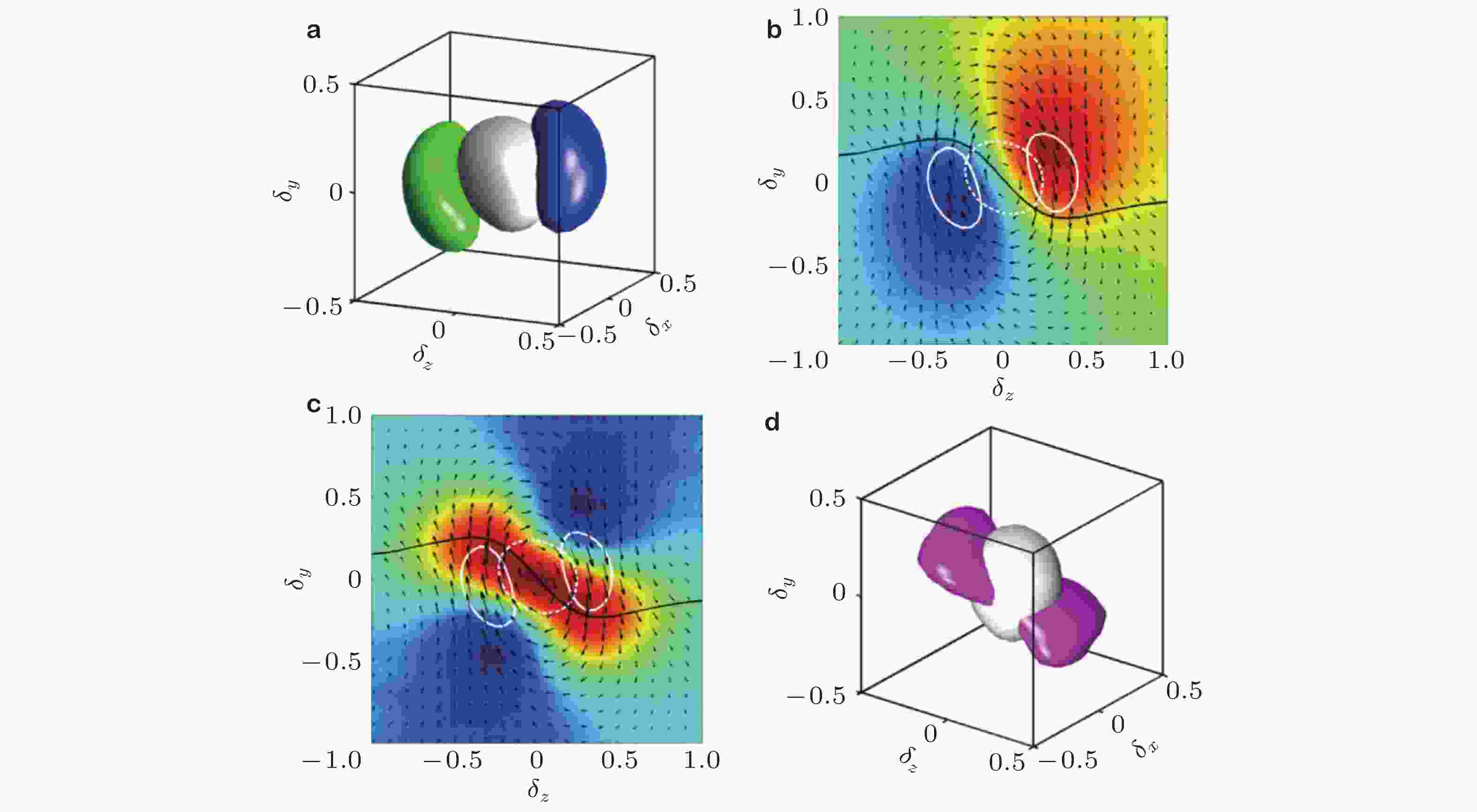
图 13 统计平稳均匀剪切湍流中, 下扫分别与(a)下扫和(b)上抛之间相对位置的三维概率密度函数等值面 (Dong et al. 2017)
图 14 对统计平稳均匀剪切湍流中上抛−下扫对做条件平均之后的流场. (a)属于上抛(绿色)、下扫(蓝色)和涡簇(银灰色)的概率密度函数等值面; (b)和(c)中云图分别为δx = 0截面上的
$\{u'\} $ 和${\partial_y u'}$ , 箭头代表($\{v'\},\{w'\} $ ), 黑线为总的平均速度$\{u'\} $ + Sδy = 0, 白色线条为(a)中的截面; (d)涡簇和平均剪切(粉红) (Dong et al. 2017)图 15 统计平稳均匀剪切湍流中的Q2−Q4对(a) (d)以及槽道湍流中的壁面分离(b) (e)和壁面附着(c) (f)的Q2−Q4对周围的统计平均流场. 其中云图和线条与图13(a)中含义相同 (Dong et al. 2017)
图 16 Reτ = 934的槽道湍流中壁面附着最优通量结构周围的统计平均流场, 其中箭头代表(
$\{v'\},\{w'\} $ ). 透明等值面代表最优动量通量, 黄色等值面为雷诺切应力$\{u'v'\}+ $ = −2.1 (Osawa & Jiménez 2018)图 17 Reτ ≈ 1000的槽道湍流受到展向压力梯度(dP/dz = 60dP/dx)后不同时刻Q2−Q4对周围的统计平均流场 (Lozano-Durán et al. 2019)
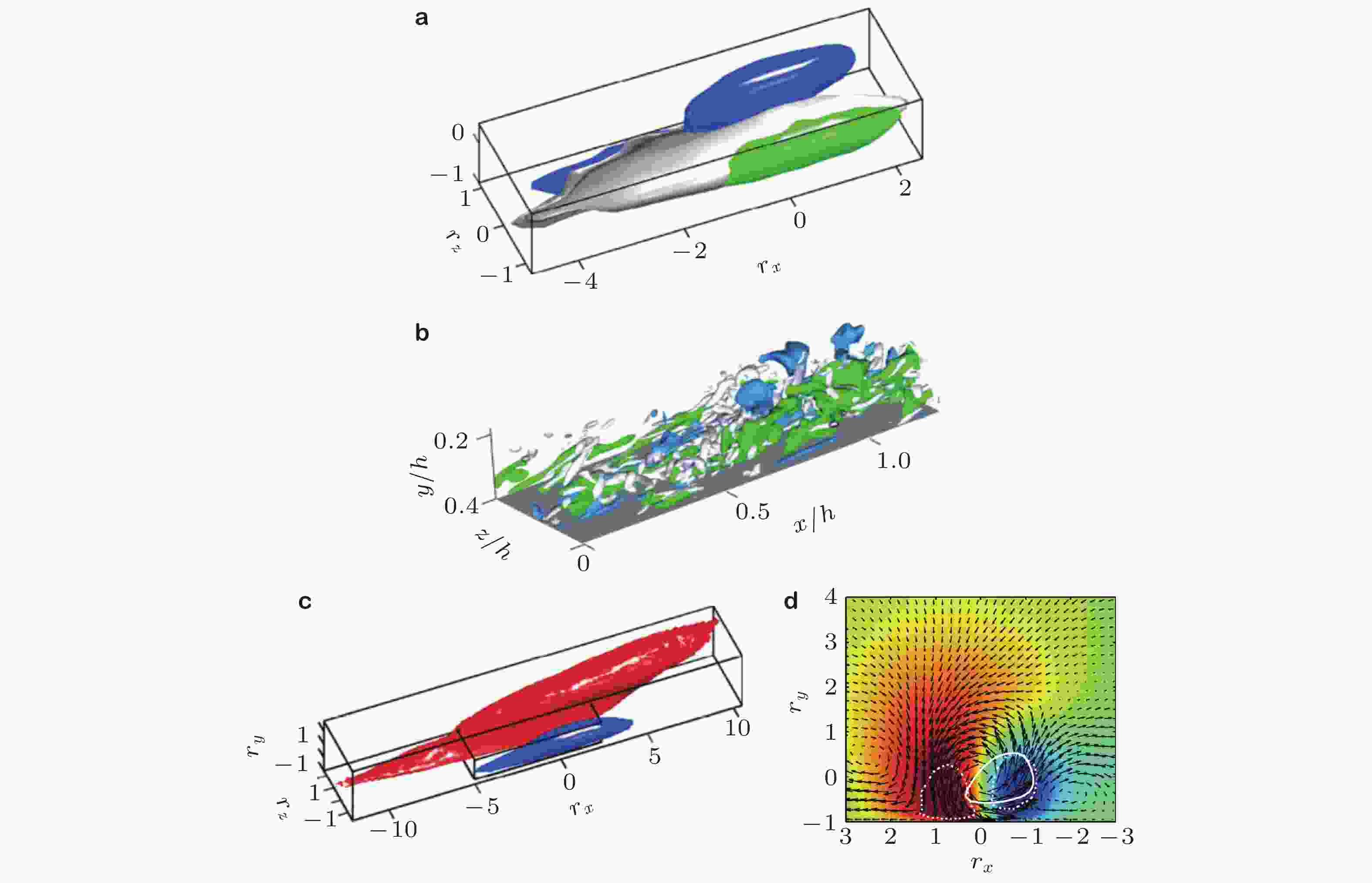
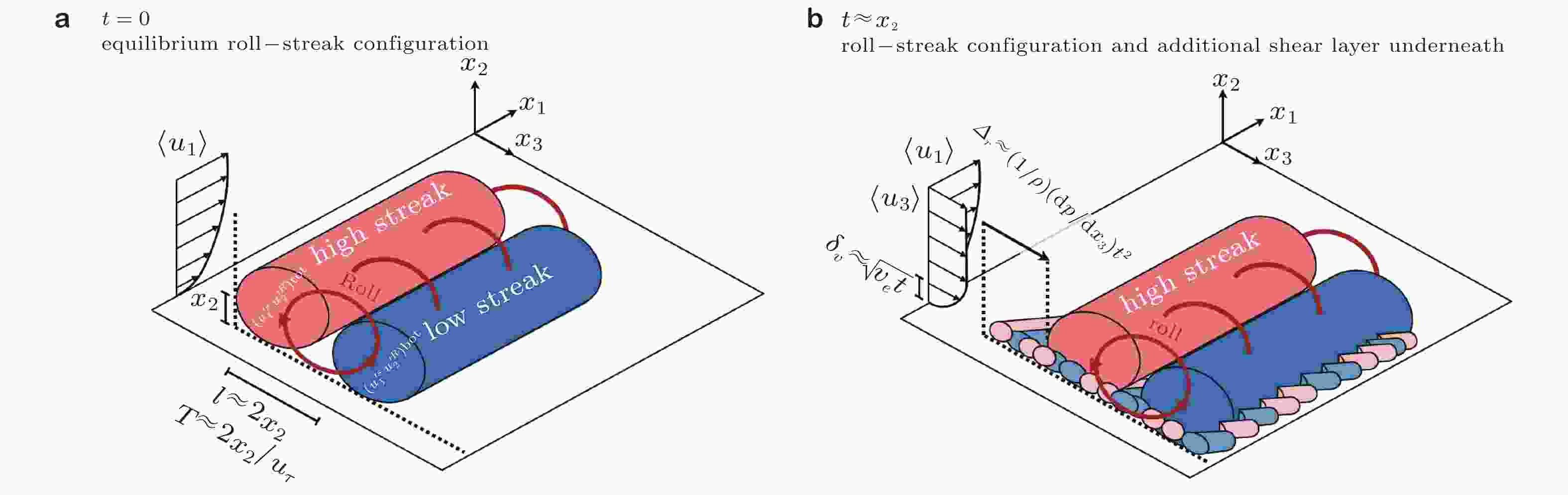
图 18 (a)二维平稳状态湍流边界层和(b)三维非平稳状态湍流边界层中的低速条带−高速条带−流向涡模型 (Lozano-Durán et al. 2019)
图 19 (a) δ+ ≈ 1200 ~ 1415的零压力梯度平板湍流边界层中的u结构(u'+ > 2). 图中省略了流向长度小于δ/2的结构. (b) δ+ ≈ 1800处的一个大尺度壁面附着u结构. 大小为(Δx, Δy, Δz) = (2.42, 0.89, 0.90)δ (Sillero 2014)
图 20 δ+ ≈ 1000的零压力梯度平板湍流边界层中壁面附着的(a)流向、(b)展向和(c)法向速度结构. 红色和蓝色分别代表正和负脉动ui' = ±1.5ui,rms. 颜色的明暗代表离壁面的距离 (Hwang & Sung 2018)
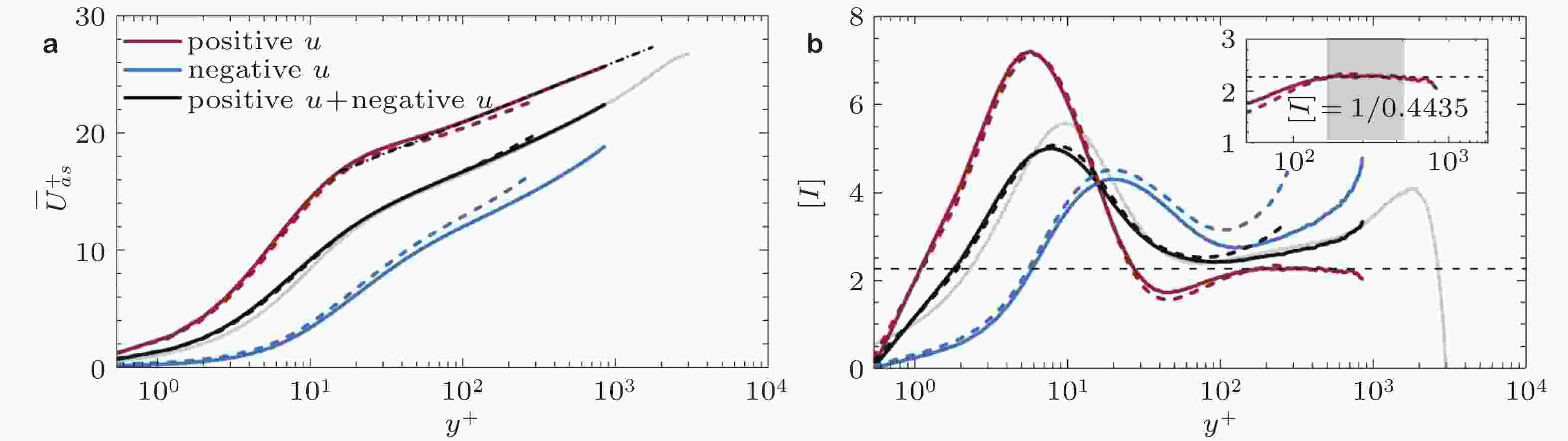
图 21 (a)全流场、高速和低速条带中的平均流向速度剖面, (b)为图(a)中的对数律指示因子 (Hwang & Sung 2019)
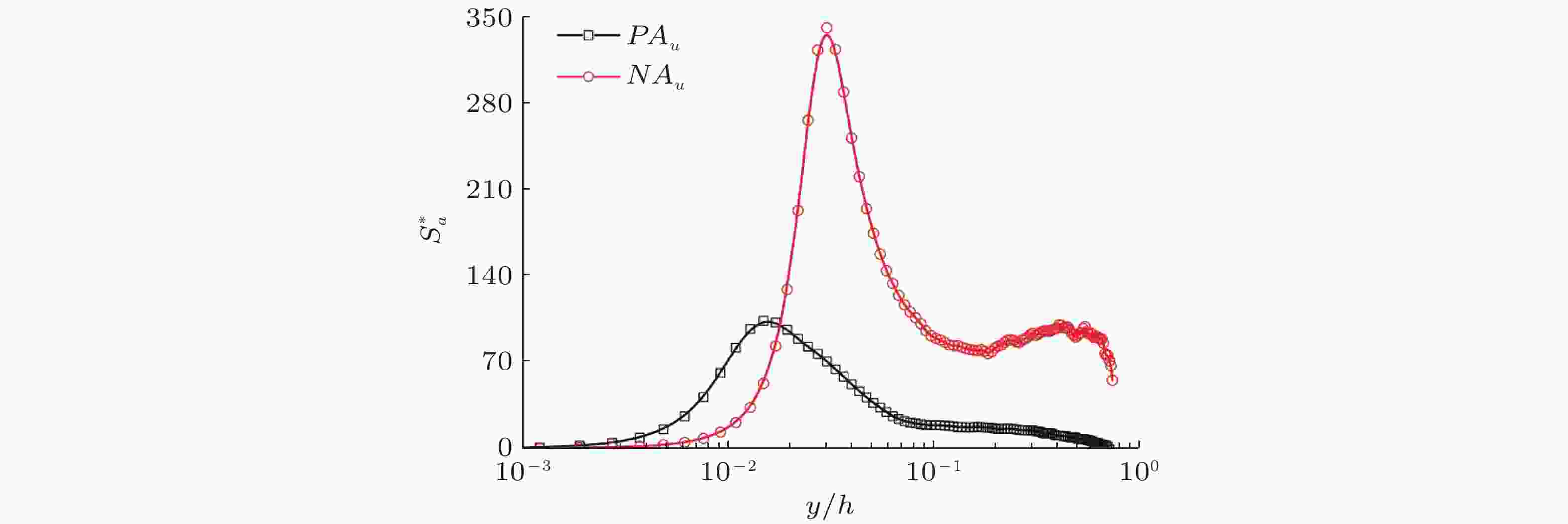
图 22 高(PAu)、低(NAu)速流向速度条带中的剪切常数在法向的变化 (Cheng et al. 2020a)
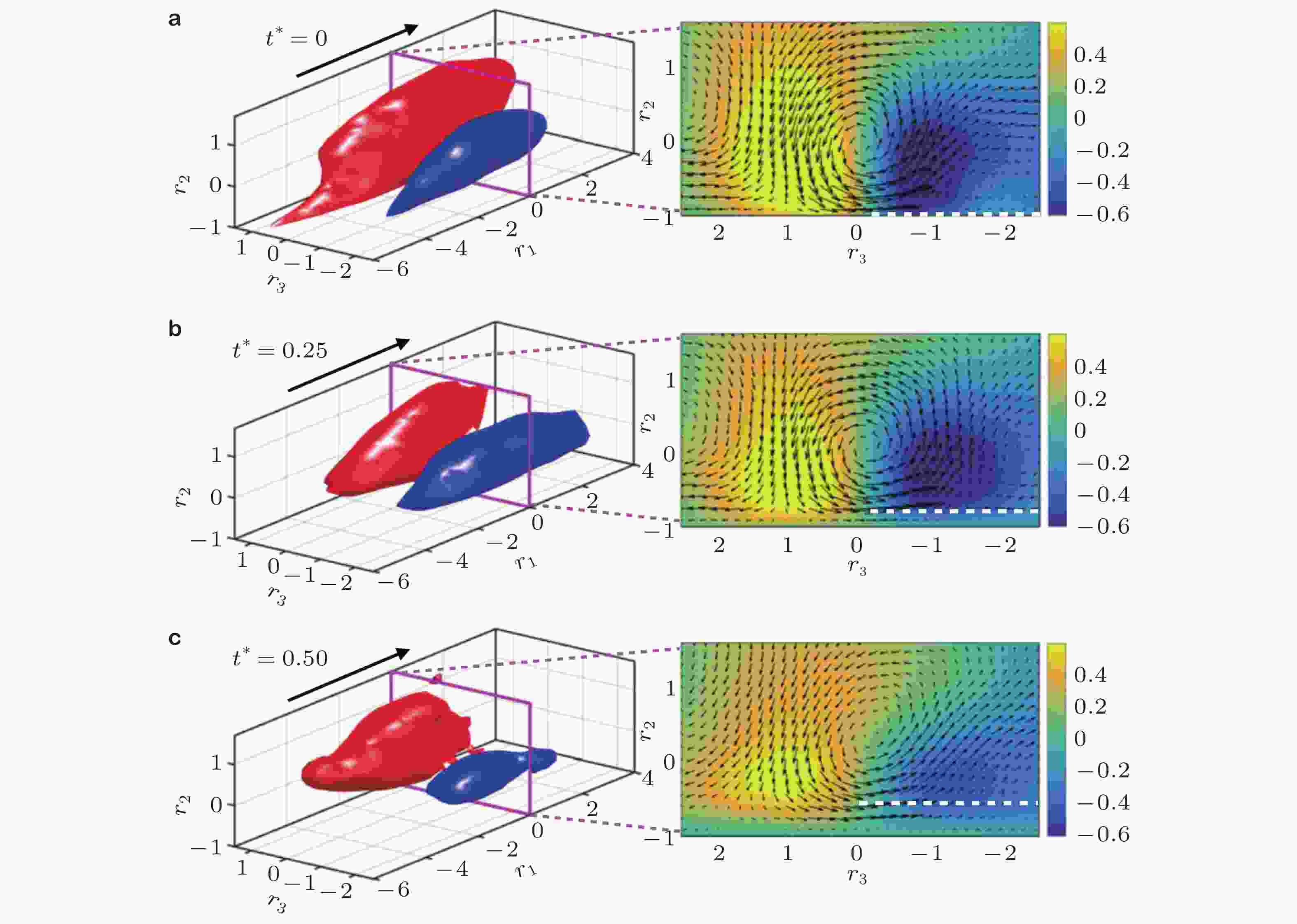
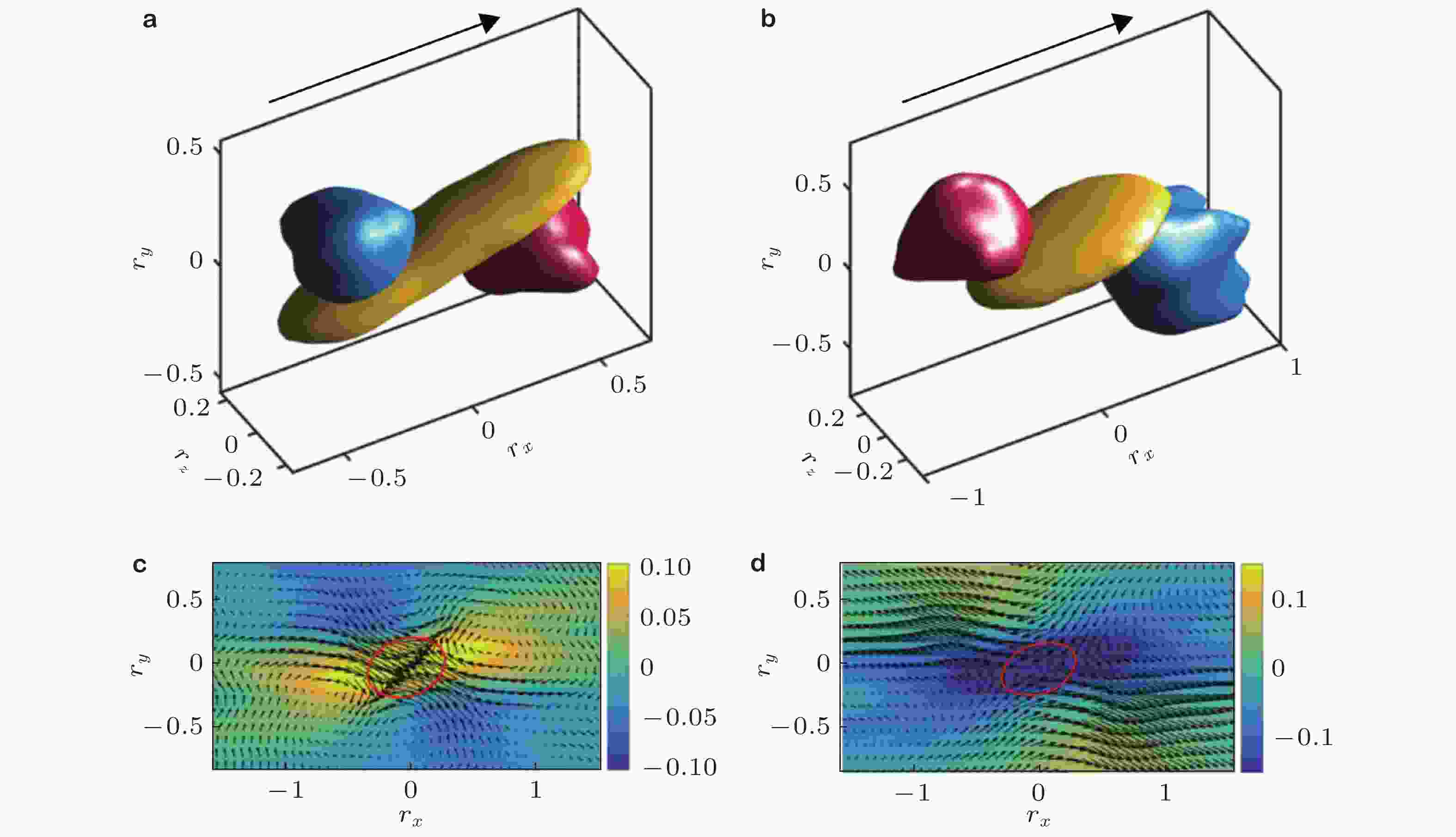
图 23 (a, c)正向和(b, d)逆向级串周围的统计平均速度场, 其中红、蓝和黄分别代表上抛、下扫和剪切层. (c, d)中云图表示剪切
$\partial \{\tilde u'\}/\partial y$ , 箭头代表($\{\tilde u'\}$ ,$\{\tilde v'\}$ ), 红色实线为属于级串事件的概率密度函数等值线 (Dong et al. 2020)图 24 条件平均获得的三维(a)正级串和(b)逆级串周围平均涡量的拟涡能(黄色和蓝色). 红色代表级串事件, 箭头表示平均涡量的方向 (Dong et al. 2020)
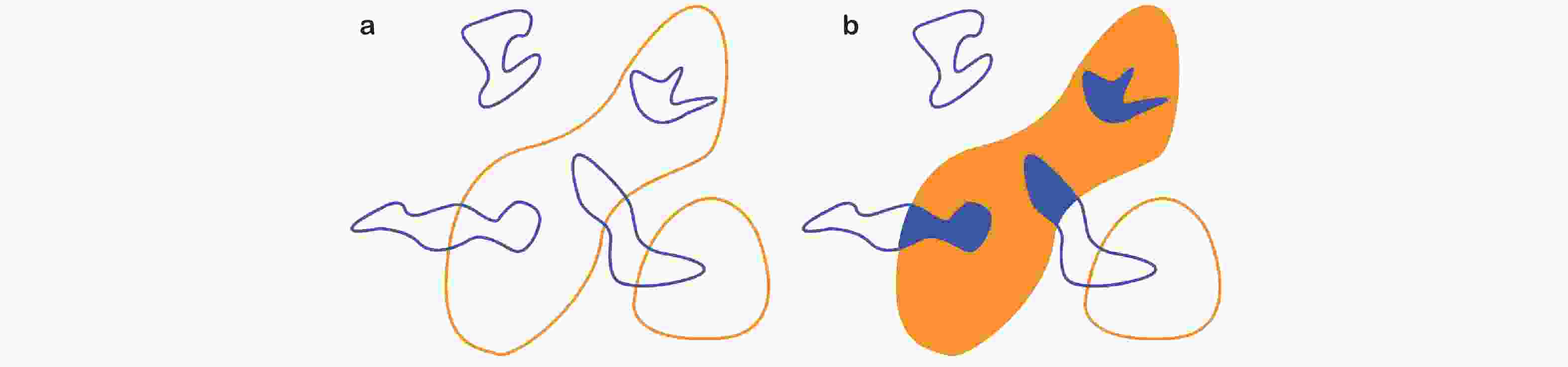
图 25 不同滤波尺度所得结构的空间重叠示意图 (Cardesa et al. 2017)
图 26 采用不同尺度滤波之后的湍动能谱 (Cardesa et al. 2017)
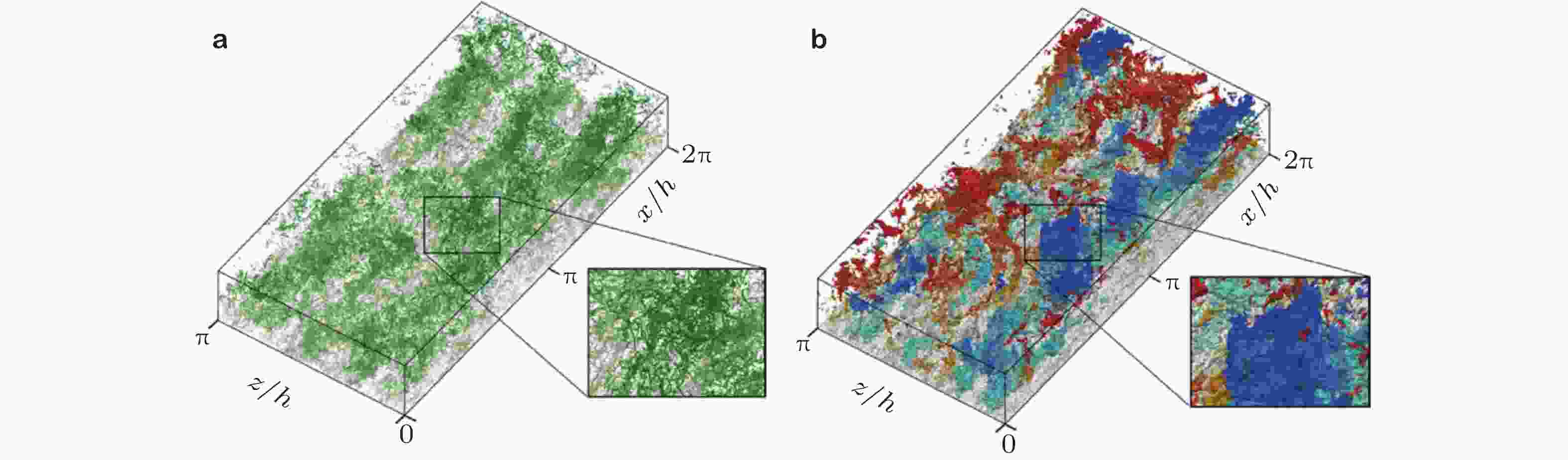
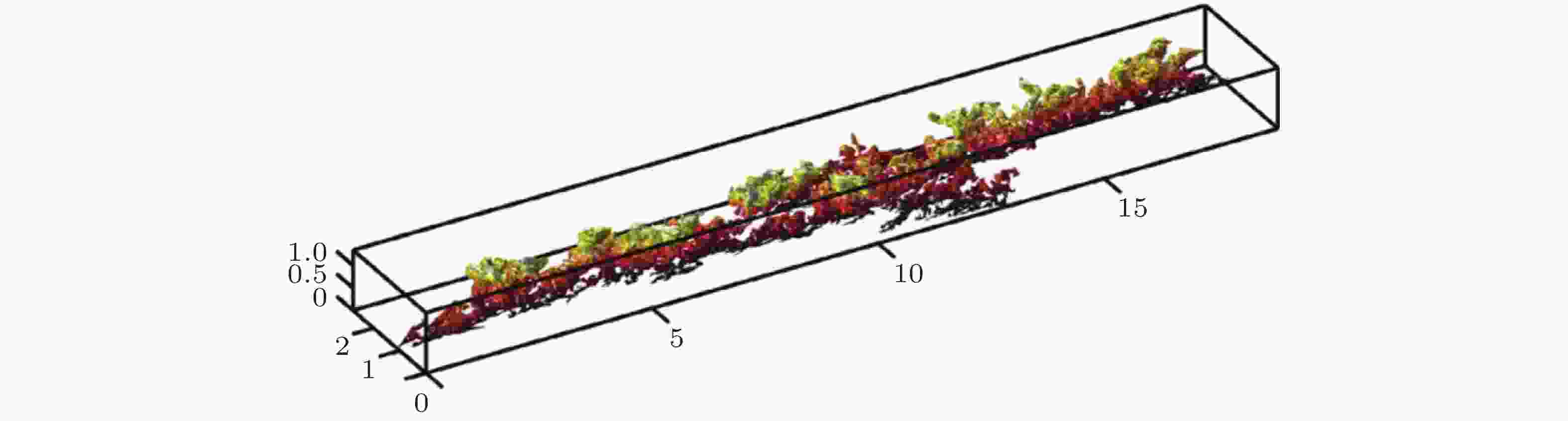
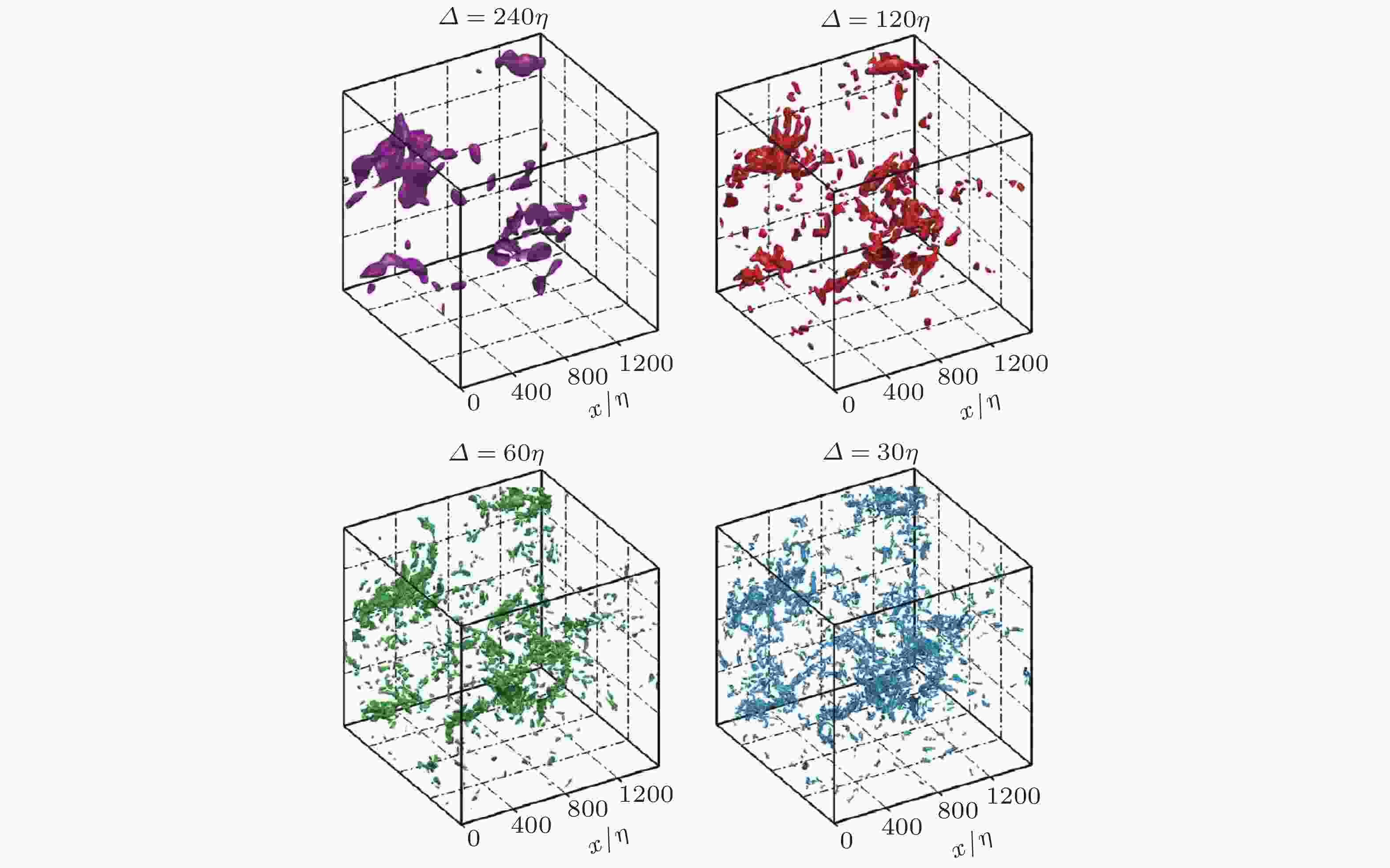
图 27 不同滤波尺度滤波之后提取的三维含能结构 (Cardesa et al. 2017)
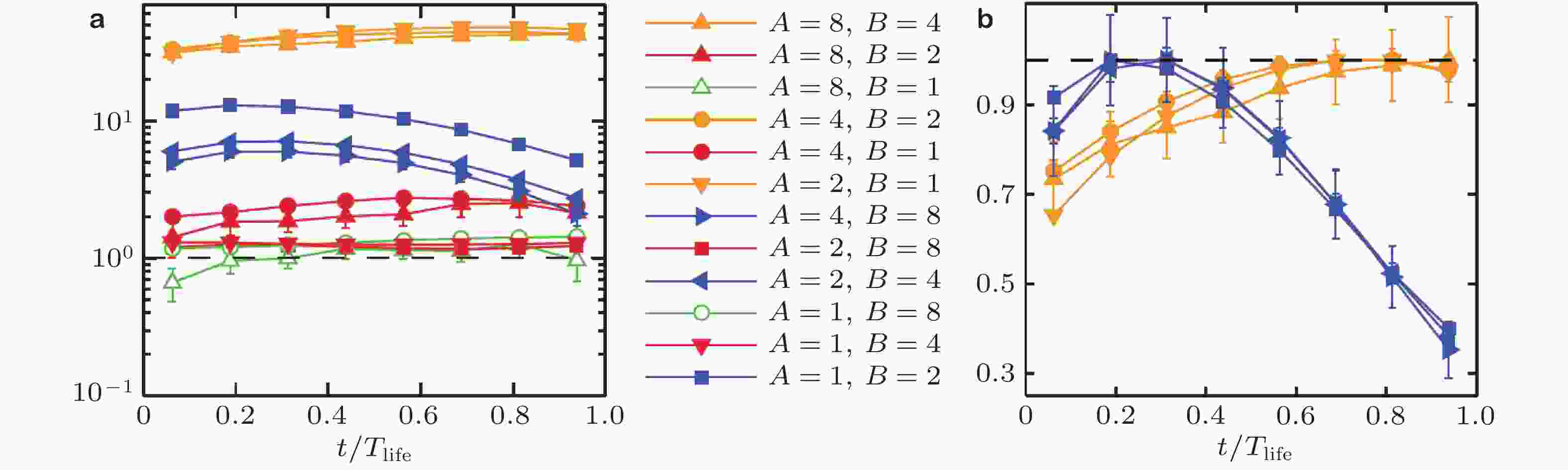
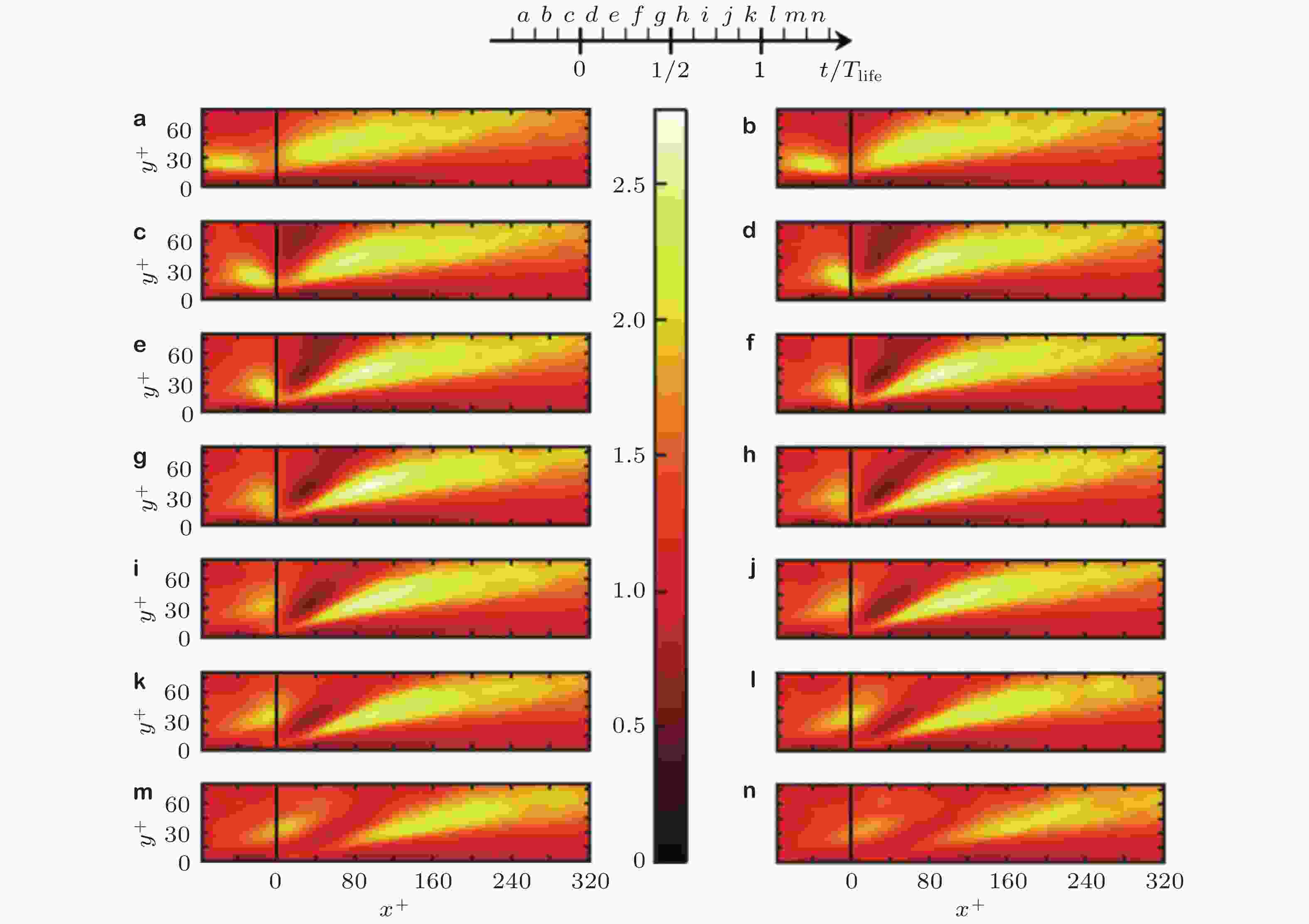
图 28 (a)生命周期的不同阶段不同滤波尺度间含能结构的体积重叠, (b)用整个生命周期中体积重叠最大值归一化了的体积重叠 (Cardesa et al. 2017)
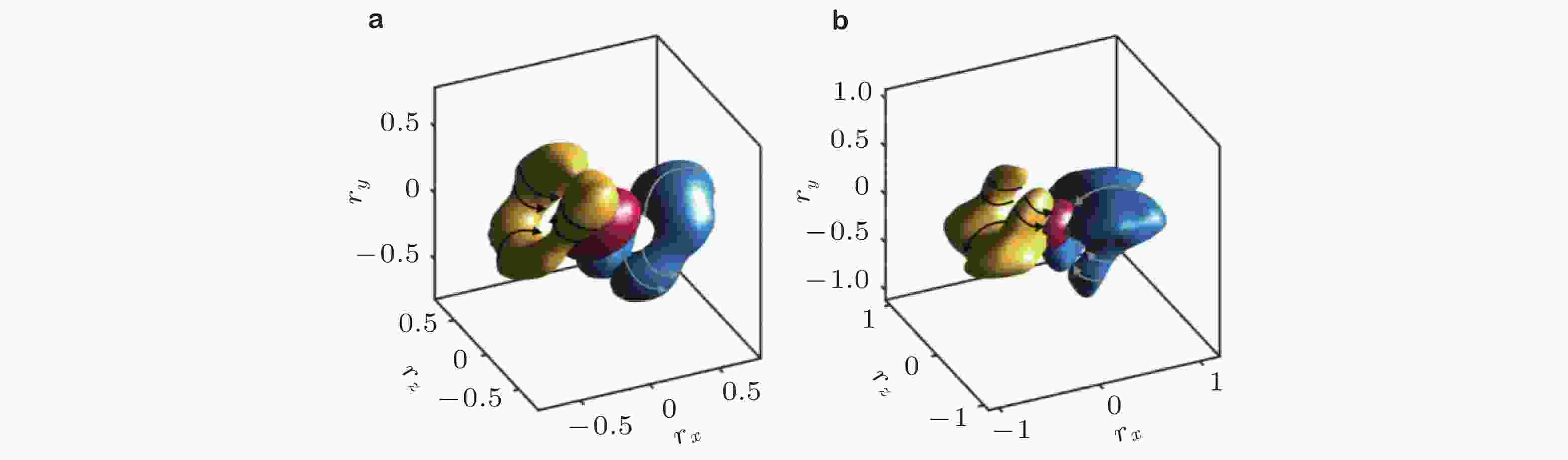
图 29 回流结构1/8生命周期时的统计平均流场. 红色, 蓝色和绿色等值面分别表示
$\{\omega_z\} $ = 2$\left\langle {{\omega _z}} \right\rangle $ ,$\{\omega_y\} $ = 0.5$\{\omega_y\}_{\rm{max}}$ 和$\{\omega_y\}$ = −0.5$\{\omega_y\}_{\rm{max}} $ . 黑色区域为回流结构的外接长方体 (Cardesa et al. 2019)图 30 回流结构中心xy截面上整个生命周期内的平均展向涡量 (Cardesa et al. 2019)
表 1 采用聚类连通法(基于种子填充算法)在槽道湍流中提取三维低速条带的耗时
阈值 0.1 0.5 1.0 1.5 2.0 网格量 4.0542×107 2.7366×107 1.4686×107 6.544×106 2.408×106 耗时/s 2.089 1.434 0.777 0.416 0.232 表 2 采用聚类连通法进行湍流拟序结构研究的代表性工作
代表作 主要贡献 Moisy & Jiménez (2004) 首次研究了三维拟序结构的性质, 并确定了阈值的选取方法 Lozano-Durán 等 (2012) 首次揭示了三维上抛、下扫和涡簇的空间构成 Hwang & Sung (2019) 首次发现高速条带中的平均速度剖面更符合对数律 Cheng 等 (2020a) 首次发现高速条带符合附着涡模型, 并揭示了高低速条带不对称的原因 Lozano-Durán & Jiménez (2014a) 首次研究了三维拟序结构的时空演化过程 Cardesa 等 (2017) 首次揭示了能量在空间−时间−尺度间的五维级串 -
[1] 黄真理. 2000. 湍流的分形特征. 力学进展, 30: 581-596 (Huang Z. 2000. Fractal nature in turbulence. Advances in Mechanics, 30: 581-596). [2] 李存标, 佘振苏. 2001. 湍流级串的动力学过程. 钱学森技术科学思想与力学论文集. [3] 许春晓. 2015. 壁湍流相干结构和减阻控制机理. 力学进展, 45: 201504 (Xu C X. 2015. Coherent structures and drag-reduction mechanism in wall turbulence. Advances in Mechanics, 45: 201504). [4] 郑晓静, 王国华. 2020. 高雷诺数壁湍流的研究进展及挑战. 力学进展, 50: 202001 (Zheng X J, Wang G H. 2020. Progresses and challenges of high Reynolds number wall-bounded turbulence. Advances in Mechanics, 50: 202001). [5] Adrian R J. 2007. Hairpin vortex organization in wall turbulence. Phys. Fluids, 19: 041301. doi: 10.1063/1.2717527 [6] Adrian R J, Meinhart C D, Tomkins C D. 2000. Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech., 422: 1-53. doi: 10.1017/S0022112000001580 [7] Adrian R J, Moin P. 1988. Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech., 190: 531-559. doi: 10.1017/S0022112088001442 [8] Atzori M, Vinuesa R, Lozano-Durán A, Schlatter P. 2019. Coherent structures in turbulent boundary layers over an airfoil. J. Phys. Conference Series, 1522: 012020. [9] del Álamo J C, Jiménez J, Zandonade P, Moser R D. 2004. Scaling of the energy spectra of turbulent channels. J. Fluid Mech., 500: 135-144. doi: 10.1017/S002211200300733X [10] del Álamo J C, Jiménez J, Zandonade P, Moser R D. 2006. Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech., 561: 329-358. doi: 10.1017/S0022112006000814 [11] Bernard P S, Thomas J M, Handler R A. 1993. Vortex dynamics and the production of Reynolds stress. J. Fluid Mech., 253: 385-419. doi: 10.1017/S0022112093001843 [12] van den Berg B, Elsenaar A, Lindhout A, Wesseling P. 1975. Measurements in an incompressible three-dimensional turbulent boundary layer, under infinite swept-wing conditions, and comparison with theory. J. Fluid Mech., 70: 127-148. doi: 10.1017/S0022112075001930 [13] Bradshaw P, Pontikos N S. 1985. Measurements in the turbulent boundary layer on an ‘infinite’ swept wing. J. Fluid Mech., 159: 105-130. doi: 10.1017/S0022112085003123 [14] Cardesa J I, Monty J P, Soria J, Chong M S. 2019. The structure and dynamics of backflow in turbulent channels. J. Fluid Mech., 880: R3. doi: 10.1017/jfm.2019.774 [15] Cardesa J I, Vela-Martin A, Jiménez J. 2017. The turbulent cascade in five dimensions. Science, 357: 782-784. doi: 10.1126/science.aan7933 [16] Christensen K T, Adrian R J. 2001. Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech., 431: 433-443. doi: 10.1017/S0022112001003512 [17] Chandra D, Baidya R, Monty J P, Marusic I. 2017. Two-dimensional energy spectra in high-Reynolds-number turbulent boundary layers. J. Fluid Mech., 826: R1. doi: 10.1017/jfm.2017.359 [18] Cheng C, Li W, Lozano-Durán A, Liu H. 2020a. Uncovering Townsend’s wall-attached eddies in low-Reynolds-number wall turbulence. J. Fluid Mech., 889: A29. doi: 10.1017/jfm.2020.100 [19] Cheng C, Li W, Lozano-Durán A, Liu H. 2020b. On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows. J. Fluid Mech., 903: A29. doi: 10.1017/jfm.2020.639 [20] Chen J, Dong S, Chen X, Yuan X, Xu G. 2021. Stationary crossflow breakdown in a high-speed swept-wing boundary layer. Phys. Fluids, 33: 024108. doi: 10.1063/5.0039901 [21] Coleman G N, Kim J, Spalart P R. 2000. A numerical study of strained three-dimensional wall-bounded turbulence. J. Fluid Mech., 416: 75-116. doi: 10.1017/S0022112000008806 [22] Dong S. 2016. Coherent structures in statistically-stationary homogeneous shear turbulence. [PhD Thesis]. Madrid: School of Aeronauticos, U. Politecnica de Madrid. [23] Dong S, Lozano-Durán A, Sekimoto A, Jiménez J. 2017. Coherent structures in statistically stationary homogeneous shear turbulence. J. Fluid Mech., 816: 167-208. doi: 10.1017/jfm.2017.78 [24] Dong S, Huang Y, Yuan X, Lozano-Durán A. 2020. The coherent structure of the kinetic energy transfer in shear turbulence. J. Fluid Mech., 892: A22. doi: 10.1017/jfm.2020.195 [25] Degani A T, Smith F T, Walker J D A. 2013. The structure of a three dimensional turbulent boundary layer. J. Fluid Mech., 250: 43-68. [26] Deng S C, Pan C, Wang J J, He G S. 2018. On the spatial organization of hairpin packets in a turbulent boundary layer at low-to-moderate Reynolds number. J. Fluid Mech., 844: 635-668. doi: 10.1017/jfm.2018.160 [27] Encinar M P, Jiménez J. 2020. Momentum transfer by linearised eddies in turbulent channel flows. J. Fluid Mech., 895: A23. doi: 10.1017/jfm.2020.302 [28] Flores O, Jiménez J, del Álamo J C. 2007. Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech., 591: 145-154. doi: 10.1017/S0022112007008506 [29] Flores O, Jimenez J. 2010. Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids, 22: 071704. doi: 10.1063/1.3464157 [30] Ganapathisubramani B. 2008. Statistical structure of momentum sources and sinks in the outer region of a turbulent boundary layer. J. Fluid Mech., 606: 225-237. doi: 10.1017/S0022112008001675 [31] Gilles J. 2013. Empirical wavelet transform. IEEE Trans. Signal Process, 61: 3999-4010. doi: 10.1109/TSP.2013.2265222 [32] Haidari A H, Smith C R. 1994. The generation and regeneration of single hairpin vortices. J. Fluid Mech., 277: 135-162. doi: 10.1017/S0022112094002715 [33] Hamilton J M, Kim J, Waleffe F. 1995. Regeneration mechanisms of near wall turbulence structures. J. Fluid Mech., 287: 317-348. doi: 10.1017/S0022112095000978 [34] Hernan M A, Jiménez J. 1982. Computer analysis of a high-speed film of the plane turbulent mixing layer. J. Fluid Mech., 119: 323-345. doi: 10.1017/S0022112082001372 [35] Hong J, Katz J, Meneveau C, Schultz M P. 2012. Coherent structures and associated subgrid-scale energy transfer in a rough-wall turbulent channel flow. J. Fluid Mech., 712: 92-128. doi: 10.1017/jfm.2012.403 [36] Huang N E, Shen Z, Long S R, Wu M C, Shih H H, Zheng Q, Yen N C, Tung C C, Liu H H. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A, 454: 903-995. doi: 10.1098/rspa.1998.0193 [37] Hultmark M, Vallikivi M, Bailey S C C, Smits A J. 2012. Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett., 108: 094501. doi: 10.1103/PhysRevLett.108.094501 [38] Hwang J, Sung H J. 2018. Wall-attached structures of velocity fluctuations in a turbulent boundary layer. J. Fluid Mech., 856: 958-983. doi: 10.1017/jfm.2018.727 [39] Hwang J, Sung H J. 2019. Wall-attached clusters for the logarithmic velocity law in turbulent pipe flow. Phys. Fluids, 31: 055109. doi: 10.1063/1.5096433 [40] Jeong J, Hussain F, Shoppa W, Kim J. 1997. Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech., 332: 185-214. doi: 10.1017/S0022112096003965 [41] Jiménez J, Wray A A. 1998. On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech., 373: 255-285. [42] Jiménez J. 2012. Cascades in wall-bounded turbulence. Ann. Rev. Fluid Mech., 44: 27-45. doi: 10.1146/annurev-fluid-120710-101039 [43] Jimenez J. 2013a. Near-wall turbulence. Phys. Fluids, 25: 101302. doi: 10.1063/1.4824988 [44] Jiménez J. 2013b. How linear is wall-bounded turbulence? Phys. Fluids, 25: 110814. [45] Jiménez J. 2015. Direct detection of linearized bursts in turbulence. Phys. Fluids, 27: 065102. doi: 10.1063/1.4921748 [46] Jiménez J. 2016. Optimal fluxes and Reynolds stresses. J. Fluid Mech., 809: 585-600. doi: 10.1017/jfm.2016.692 [47] Jiménez J. 2018a. Coherent structures in wall-bounded turbulence. J. Fluid Mech., 842: 1-100. doi: 10.1017/jfm.2018.154 [48] Jiménez J. 2018b. Machine-assisted turbulence theory. J. Fluid Mech., 854: R1. doi: 10.1017/jfm.2018.660 [49] Jiménez J. 2020. Dipoles and streams in two-dimensional turbulence. J. Fluid Mech., 904: A39. doi: 10.1017/jfm.2020.769 [50] Jiménez J, del Álamo J C, Flores O. 2004. The large scale dynamics of near-wall turbulence. J. Fluid Mech., 505: 179-199. doi: 10.1017/S0022112004008389 [51] Jiménez J, Cogollos M, Bernal L P. 1985. A perspective view of the plane mixing layer. J. Fluid Mech., 152: 125-143. doi: 10.1017/S002211208500060X [52] Jiménez J, Kawahara G, Simens M, Nagata M, Shiba M. 2005. Characterization of near-wall turbulence in terms of equilibrium and ‘bursting’ solutions. Phys. Fluids, 17: 015105. doi: 10.1063/1.1825451 [53] Jiménez J, Moin P. 1991. The minimal flow unit in near-wall turbulence. J. Fluid Mech., 225: 213-240. doi: 10.1017/S0022112091002033 [54] Jiménez J, Navalon J L. 1982. Some experiments in image vectorization. IBM J. Res. Develop., 26: 724-734. doi: 10.1147/rd.266.0724 [55] Jiménez J, Wray A A, Saffman P G, Rogallo R R. 1993. The structure of intense vorticity in isotropic turbulence. J. Fluid Mech., 255: 65-90. doi: 10.1017/S0022112093002393 [56] Jovanović M R, Schimid P J, Nichols J W. 2014. Sparsity-promoting dynamic mode decomposition. Phys. Fluids, 26: 024103. doi: 10.1063/1.4863670 [57] Kim J, Moin P. 1986. The structure of the vorticity field in turbulent channel flow. Part 2. Study of ensemble-averaged fields. J. Fluid Mech., 162: 339-363. doi: 10.1017/S0022112086002070 [58] Kim J, Moin P. 1987. The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech., 176: 33-66. doi: 10.1017/S0022112087000569 [59] Kim J. 1985. Evolution of a vortical structure associated with the bursting event in a channel flow. Turbulent Shear Flows, 5: 221-232. [60] Kline S J, Reynolds W C, Schraub F A, Runstadler P W. 1967. The structure of turbulent boundary layers. J. Fluid Mech., 30: 741-773. doi: 10.1017/S0022112067001740 [61] Kolmogrov A N. 1941. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR, 30: 301-305. [62] Lee J H, Sung H J. 2013. Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids, 25: 045103. doi: 10.1063/1.4802048 [63] Lee M, Moser R D. 2015. Direct numerical simulation of turbulent channel flow up to Re τ ≈ 5200. J. Fluid Mech., 774: 395-415. doi: 10.1017/jfm.2015.268 [64] Li W, Fan Y, Modesti D, Cheng C. 2019. Decomposition of the mean skin-friction drag in compressible turbulent channel flows. J. Fluid Mech., 875: 101-123. doi: 10.1017/jfm.2019.499 [65] Lozano-Durán A, Flores O, Jiménez J. 2012. The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech., 694: 100-130. doi: 10.1017/jfm.2011.524 [66] Lozano-Durán A, Jiménez J. 2014a. Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascade. J. Fluid Mech., 759: 432-471. doi: 10.1017/jfm.2014.575 [67] Lozano-Durán A, Bae H J, Encinar M P. 2020. Causality of energy-containing eddies in wall turbulence. J. Fluid Mech., 882: A2. [68] Lozano-Durán A, Borrell G. 2016. An efficient algorithm to compute the genus of discrete surfaces and applications to turbulent flows. ACM Trans. Math. Softw., 42: 34. [69] Lozano-Durán A, Jiménez J. 2014b. Effect of the computational domain on direct simulations of turbulent channels up to Re τ=4200. Phys. Fluids, 26: 011702. doi: 10.1063/1.4862918 [70] Lozano-Durán A. 2015. Time-resolved evolution of coherent structures in turbulent channels. [PhD Thesis]. Madrid: School of Aeronauticos, U. Politecnica de Madrid. [71] Lozano-Durán A, Giometto M G, Park G I, Moin P. 2019. Non-equilibrium three-dimensional boundary layers at moderate Reynolds numbers. J. Fluid Mech., 883: A20. [72] Lumley J L. 1967. The structure of inhomogeneous turbulent flows//Proceedings of the International Colloquium on the Fine Scale Structure of the Atmosphere and Its Influence on Radio Wave Propagation, Doklady Akademii Nauk SSSR, Moscow. [73] Lu S S, Willmarth W W. 1973. Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech., 60: 481-511. doi: 10.1017/S0022112073000315 [74] Marusic I, Monty J P, Hultmark M, Smits A J. 2013. On the logarithmic region in wall turbulence. J. Fluid Mech., 716: R3. doi: 10.1017/jfm.2012.511 [75] McKeon B J, Sharma A S. 2010. A critical-layer framework for turbulent pipe flow. J. Fluid Mech., 658: 336-382. [76] Mehrez A, Philip J, Yamamoto Y, Tsuji Y. 2019. Pressure and spanwise velocity fluctuations in turbulent channel flow: Logarithmic behacior of moment and coherent structures. Phys. Rev. Fluids, 4: 044601. [77] Meneveau C, Marusic I. 2013. Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech., 719: R11. [78] Mizuno Y, Jiménez J. 2013. Wall turbulence without walls. J. Fluid Mech., 723: 429-455. doi: 10.1017/jfm.2013.137 [79] Moin P. 1987. Analysis of turbulence data generated by numerical simulations. AIAA Paper, 87-0194. [80] Moisy F, Jiménez J. 2004. Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech., 513: 111-133. doi: 10.1017/S0022112004009802 [81] Needham M, Hodler A E. 2019. Graph Algorithms. O'Reilly Media, Inc. [82] Noack B R, Stankiewicz W, Morzyński M, Schmid P J. 2016. Recursive dynamic mode decomposition of transient and post-transient wake flows. J. Fluid Mech., 809: 843-872. doi: 10.1017/jfm.2016.678 [83] Obukhov A M. 1941. On the distribution of energy in the spectrum of turbulent flow. Izv. Akad. Nauk USSR, Ser. Geogr. Geofiz, 5: 453-466. [84] Örlü R, Fiorini T, Segalini A, Bellani G, Talamelli A, Alfredsson P H. 2017. Reynolds stress scaling in pipe flow turbulence-First results from CICLoPE. Philos. Trans. R. Soc. A, 375: 20160187. doi: 10.1098/rsta.2016.0187 [85] Osawa K, Jiménez J. 2018. Intense structures of different momentum fluxes in turbulent channels. Phys. Rev. Fluids, 3: 084603. doi: 10.1103/PhysRevFluids.3.084603 [86] Perry A E, Chong M S. 1982. On the mechanism of wall turbulence. J. Fluid Mech., 119: 173-217. doi: 10.1017/S0022112082001311 [87] Piomelli U, Cabot W H, Moin P, Lee S. 1991. Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids, 3: 1766-1771. [88] Piomelli U, Yu Y, Adrian R J. 1996. Subgrid-scale energy transfer and near-wall turbulence structure. Phys. Fluids, 8: 215-224. doi: 10.1063/1.868829 [89] Porté-Agel F, Pahlow M, Meneveau C, Parlange M B. 2001. Atmospheric stability effect on subgrid-scale physics for large-eddy simulation. Adv. Water Resour, 24: 1085-1102. doi: 10.1016/S0309-1708(01)00039-2 [90] Porté-Agel F, Parlange M B, Meneveau C, Eichinger W E. 2002. A priori field study of the subgrid-scale heat fluxes and dissipation in the atmospheric surface layer. J. Atmos. Sci., 58: 2673-2698. [91] Perry A E, Abell C J. 1977. Asymptotic similarity of turbulence structures in smooth- and rough-walled pipes. J. Fluid Mech., 79: 785-799. doi: 10.1017/S0022112077000457 [92] Pirozzoli S, Bernadini M, Grasso F. 2008. Coherent structures in a supersonic boundary layer. J. Fluid Mech., 613: 205-231. doi: 10.1017/S0022112008003005 [93] Pumir A. 1994. A numerical study of pressure fluctuations in three-dimensional incompressible, homogeneous, isotropic turbulence. Phys. Fluids, 6: 2071-2083. doi: 10.1063/1.868213 [94] Pumir A. 1996. Turbulence in homogeneous shear flows. Phys. Fluids, 8: 3112-3127. doi: 10.1063/1.869100 [95] Richardson L F. 1920. The supply of energy from and to atmospheric eddies. Proc. R. Soc. Lond. A, 97: 354-373. doi: 10.1098/rspa.1920.0039 [96] Robinson S K, Kline S J, Spalart P R. 1989. A review of quasi-coherent structures in a numerically simulated turbulent boundary layer. NASA Technical Memorandum 102191. [97] Robinson S K. 1991. Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech., 23: 601-639. doi: 10.1146/annurev.fl.23.010191.003125 [98] Rowley C W. 2005. Model reduction for fluids, using balanced proper orthogonal decomposition. Int. J. Bifurcation Chaos, 15: 997-1013. doi: 10.1142/S0218127405012429 [99] Ren J, Mao X, Fu S. 2021. Imaged-based flow decomposition using empirical wavelet transform. J. Fluid Mech., 906: A22. [100] Renard N, Deck S. 2016. A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer. J. Fluid Mech., 790: 339-367. doi: 10.1017/jfm.2016.12 [101] Schmid P J. 2010. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech., 656: 5-28. doi: 10.1017/S0022112010001217 [102] Schoppa W, Hussain F. 2002. Coherent structure generation in near-wall turbulence. J. Fluid Mech., 453: 57-108. doi: 10.1017/S002211200100667X [103] Sekimoto A, Dong S, Jiménez J. 2016. Direct numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. Phys. Fluids, 28: 035101. doi: 10.1063/1.4942496 [104] Sekimoto A, Jiménez J. 2017. Vertically localised equilibrium solutions in large-eddy simulations of homogeneous shear flow. J. Fluid Mech., 827: 225-249. doi: 10.1017/jfm.2017.450 [105] Sillero J, Jiménez J, Moser R D. 2013. One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to δ+≈2000. Phys. Fluids, 25: 105102. doi: 10.1063/1.4823831 [106] Sillero J. 2014. High Reynolds numbers turbulent boundary layers. [PhD Thesis]. Madrid: School of Aeronauticos, U. Politecnica de Madrid. [107] Sillero J, Jiménez J, Moser R D. 2014. Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to δ+ ≈ 2000. Phys. Fluids, 26: 105109. doi: 10.1063/1.4899259 [108] Singer B A, Joslin R D. 1994. Metamorphosis of a hairpin vortex into a young turbulent spot. Phys. Fluids, 6: 3724-3736. doi: 10.1063/1.868363 [109] Stanislas M, Perret L, Foucaut J M. 2008. Vortical structures in the turbulent boundary layer: a possible route to a universal representation. J. Fluid Mech., 602: 327-382. doi: 10.1017/S0022112008000803 [110] Stauffer D, Aharony A. 1994. Introduction to Percolation Theory. Abingdon: Taylor and Francis. [111] Suponitsky V, Avital E, Gaster M. 2005. On three-dimensionality and control of incompressible cavity flow. Phys. Fluids, 17: 104103. doi: 10.1063/1.2084230 [112] Tanahashi M, Iwase S, Miyauchi T. 2001. Appearance and alignment of strain rate of coherent fine scale eddies in turbulent mixing layer. J. Turbul., 2: 1-17. doi: 10.1088/1468-5248/2/1/001 [113] Towne A, Schmidt O T, Colonius T. 2018. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech., 847: 821-867. doi: 10.1017/jfm.2018.283 [114] Townsend A A. 1976. The Structure of Turbulent Shear Flow, 2nd edn. Cambridge: Cambridge University Press. [115] Tuerke F, Jiménez J. 2013. Simulations of turbulent channels with prescribed velocity profiles. J. Fluid Mech., 723: 587-603. doi: 10.1017/jfm.2013.143 [116] Wallace J M. 2012. Highlights from 50 years of turbulent boundary layer research. J. Turbul., 13: 1-70. doi: 10.1080/14685248.2011.633522 [117] Wallace J M. 2016. Quadrant analysis in turbulence research: History and evolution. Annu. Rev. Fluid Mech., 48: 131-158. doi: 10.1146/annurev-fluid-122414-034550 [118] Wallace J M, Brodkey R S, Eckelmann H. 1972. The wall region in turbulent shear flow. J. Fluid Mech., 54: 39-48. doi: 10.1017/S0022112072000515 [119] Wang W, Pan C, Wang J. 2021. Energy transfer structures associated with large-scale motions in a turbulent boundary layer. J. Fluid Mech., 906: A21. doi: 10.1017/jfm.2020.785 [120] Willmarth W W, Lu S S. 1972. Structure of the Reynolds stress near the wall. J. Fluid Mech., 55: 65-92. doi: 10.1017/S002211207200165X [121] Vela-Martin A, Encinar M P, Garcia-Gutierrez A, Jiménez J. 2019. A second-order consistent, low-storage method for time-resolved channel flow simulations up to Reτ = 5300, Technical Note, ETSIAE /MF-0219. [122] Xiong S, Yang Y. 2019. Identifying the tangle of vortex tubes in homogeneous isotropic turbulence. J. Fluid Mech., 874: 952-978. doi: 10.1017/jfm.2019.487 [123] Yang Q, Willis A P, Hwang Y. 2019. Exact coherent states of attached eddies in channel flow. J. Fluid Mech., 862: 1029-1059. doi: 10.1017/jfm.2018.1017 [124] Yang X, Baidya R, Lv Y, Marusic I. 2018. Hierarchical random additive model for the spanwise and wall-normal velocities in wall-bounded flows at high Reynolds numbers. Phys. Rev. Fluids, 3: 124606. doi: 10.1103/PhysRevFluids.3.124606 [125] Yeung P K, Zhai X M, Sreenivasan K R. 2015. Extreme events in computational turbulence. PNAS, 112: 12633-12638. doi: 10.1073/pnas.1517368112 [126] Yoon M, Hwang J, Yang J, Sung H J. 2020. Wall-attached structures of streamwise velocity fluctuations in an adverse-pressure-gradient turbulent boundary layer. J. Fluid Mech., 885: A12. doi: 10.1017/jfm.2019.950 [127] Zhao Y, Yang Y, Chen S. 2016. Evolution of material surfaces in the temporal transition in channel flow. J. Fluid Mech., 793: 840-876. doi: 10.1017/jfm.2016.152 [128] Zheng W, Yang Y, Chen S. 2016. Evolutionary geometry of Lagrangian structures in a transitional boundary layer. Phys. Fluids, 28: 035110. doi: 10.1063/1.4944047 [129] Zhou J, Adrian R J, Balachandar S, Kendall T M. 1999. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech., 387: 353-396. doi: 10.1017/S002211209900467X [130] Zheng W, Ruan S, Yang Y, Chen S. 2019. Image-based modelling of the skin-friction coefficient in compressible boundary layer transition. J. Fluid Mech., 875: 1175-1203. -





 下载:
下载: