板壳结构中的非线性兰姆波

刘瑶璐; 胡宁; 邓明晰; 赵友选; 李卫彬

doi:10.6052/1000-0992-16-032

板壳结构中的非线性兰姆波

doi: 10.6052/1000-0992-16-032

刘瑶璐¹,
胡宁^{1, 2,†,},
邓明晰^{1, 3,*,},
赵友选¹,
李卫彬^{1, 4}

1.
重庆大学航空航天学院, 重庆400044
2.
重庆大学机械传动国家重点实验室, 重庆400044
3.
中国人民解放军后勤工程学院, 重庆401331
4.
厦门大学航空航天学院, 厦门361005

详细信息

作者简介:
胡宁, 教授, 51 岁, 1991 年在重庆大学获得固体力学博士学位, 先后在南京航空航天大学、日本东北大学、清华大学、Johns Hopkins 大学、日本千叶大学、湖南大学等单位工作, 2013 年回国时任日本千叶大学人工系统科学专攻(含机械、电子、医疗器械3 个系) 的专攻长、机械系主任、教授.现任重庆大学航空航天学院院长、澳洲QUT 兼职教授、南京航空航天大学客座教授、中国复合材料学会理事、日本复合材料学会评议员、重庆航空学会常务副理事长、国际智能结构委员会(ICAST) 委员、世界华人计算力学协会常务理事等职. 主要研究领域有: 固体力学; 金属与复合材料及其结构的力电热等性能评价、设计、反问题等; 结构与功能型工业与纳米复合材料制备与加工; 基于Lamb 超声波的结构和材料无损检测和实时监控技术等.目前担任Scientifc Reports (Nature 集团) 等9 份国际杂志(其中6 份SCI 杂志) 和2 份中、日杂志的副主编、牵头客座主编、编委等职. 出版了英文书籍2 部; 申报和获批日本、中国专利近10 项; 发表中、日、英期刊论文230 篇, 其中SCI 论文150 篇、被引用3200 次、H-index=30、多篇ESI 高被引论文作者、入选爱思唯尔中国学者高被引榜单(材料力学, 2014, 2015). 曾在40 多个国际、国内会议上做特邀、专题和大会报告等; 曾获得过国家基金委杰出青年基金(B 类,2007)、重庆市百人计划(短期项目, 2007)、四川省百人计划(短期项目, 2007)、国家千人计划特聘专家(创新型,A 类, 2013) 等荣誉.在中国和日本, 作为项目负责人和副主研获得的包括中国国家自然科学基金(主研: 杰青B类、重点项目1 项与面上项目2 项)、中国863 项目、中国科技部国际合作项目、日本国家科学基金、即日本文部省JSPS(日本学术振兴会) 科研补助费(S 级, A, B, C 级)、JST(日本科学技术振兴机构)、美国空军亚太地区研发机构、JAXA(日本宇宙航空研究开发机构)、东芝(株)、新日铁化学(株)、铃木汽车公司(株) 等单位在内的各项科研经费超过500 万美元.E-mail: ninghu@cqu.edu.cn

邓明晰, 教授, 51 岁, 先后于四川大学、南京大学和同济大学获得理学学士、硕士和博士学位. 现任中国声学学会常务理事、重庆市声学学会副理事长、教育部近代声学重点实验室(南京大学) 学术委员. 长期从事超声学和非线性声学的理论、实验及应用研究, 先后负责7 项国家自然科学基金项目和1 项教育部新世纪优秀人才支持计划项目, 在科学出版社出版学术专著《固体板中的非线性兰姆波》, 发表学术论文180 余篇, 其中被SCI收录60 余篇、被EI 收录90 余篇. 在超声导波非线性研究方面取得一系列开创性成果, 发表的相关论文荣获中国声学学会会刊——《声学学报》年度最佳优秀论文奖, 以及第五届中国科协期刊优秀学术论文奖. 作为项目负责人, 获得国家教育部自然科学奖二等奖1 项(2013)、重庆市自然科学奖二等奖1 项(2013)、重庆市科技进步奖三等奖2 项(2000,2000); 作为项目主研人员, 获得国家科技进步奖二等奖1 项(2004)、上海市自然科学奖一等奖1 项(2015)、军队科技进步奖一等奖1 项(2000).E-mail: dengmx65@yahoo.com

中图分类号: O347
计量
- 文章访问数: 3583
- HTML全文浏览量: 852
- PDF下载量: 1372
- 被引次数: 0
出版历程
- 收稿日期: 2016-10-17
- 网络出版日期: 2017-01-20
- 刊出日期: 2017-02-24

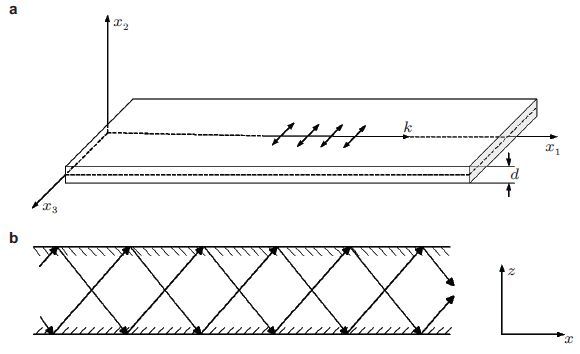
Nonlinear Lamb waves in plate/shell structures

LIU Yaolu¹,
HU Ning^{1, 2,†
,},
DENG Mingxi^{1, 3,*
,},
ZHAO Youxuan¹,
LI Weibin^{1, 4}

1.
College of Aerospace Engineering, Chongqing University, Chongqing 400044, China
2.
The State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, China
3.
Logistics Engineering University of PLA, Chongqing 401331, China
4.
School of Aerospace Engineering, Xiamen University, Xiamen 361005, China

摘要

摘要: 鉴于常规超声检测技术对分布式材料细微损伤和接触类结构损伤的检测效果不佳, 近年来非线性超声技术逐渐引起广泛关注. 超声波在板壳结构中通常以兰姆波的形式进行传播, 然而由于兰姆波的频散及多模特性, 使得非线性兰姆波的理论和实验研究进展缓慢. 本文从经典非线性理论出发,总结了源于材料固有非线性诱发的非线性兰姆波的理论和实验两个方面的研究进展, 并综述了兰姆波的二次谐波发生效应在材料损伤评价方面的若干应用; 从接触声非线性理论出发, 讨论了目前由于接触类结构损伤诱发的非线性兰姆波的研究现状. 最后展望了非线性兰姆波的未来研究重点及发展趋势.
- 非线性兰姆波 /
- 经典非线性理论 /
- 接触声非线性理论 /
- 材料性能评估 /
- 微裂纹检测
Abstract: In view of the fact that conventional ultrasonic detection technology is not effective for the detection of distributed fne damage and contact-type structural damage in materials, nonlinear ultrasound technology has been attracting more and more attention in recent years. Ultrasonic waves propagate in the form of Lamb wave modes in the structure of plates and shells. However, due to the dispersion and multimode characteristics of Lamb waves, the progress of theoretical and experimental research on nonlinear Lamb waves is slow. Based on the classical nonlinear theory, this paper summarizes the theoretical and experimental research progress of nonlinear Lamb waves induced by the inherent nonlinear-ity of material, and summarizes the application of the second harmonics of Lamb waves in damage evaluation of material. The current status of the research on nonlinear Lamb waves induced by contact-type structural damage is discussed based on contact acoustic nonlin-earity. At the end, this paper envisions the future research topics and trends in nonlinear Lamb waves.
- nonlinear lamb waves /
- classical nonlinear theory /
- contact acoustic nonlinearity /
- material performance evaluation /
- microcrack detection

HTML全文

图 1 水平剪切波的传播,其中传播方向为x₁,质点位移方向为x₃

下载: 全尺寸图片幻灯片

图 2 铝板中的SH模态的相速度频散曲线(c_T=3 100 m/s)其中实线代表对称模态虚线代表反对称模态

下载: 全尺寸图片幻灯片

图 3 对称型兰姆波(S模式)和反对称型兰姆波(A模式)

下载: 全尺寸图片幻灯片

图 4 兰姆波在铝板中传播的频散曲线.(a)相速度,(b)群速度

下载: 全尺寸图片幻灯片

图 5 在厚度为h的YZ-LiNbO₃压电薄板中伴随基频导波模式传播所发生的二倍频导波模式在薄板表面的振幅随传播距离的关系曲线.(a)离面位移,(b)面内位移(Deng & Xiang 2015)

下载: 全尺寸图片幻灯片

图 6 基波为S₀波(0.5 MHz)时二次谐波幅值和传播距离之间的关系(Chillara & Lissenden 2016)

下载: 全尺寸图片幻灯片

图 7 在铝板的相速度频散曲线中显示基波和二次谐波之间相速度的关系(Chillara & Lissenden 2016)

下载: 全尺寸图片幻灯片

图 8 基波为S₁波(3.6 MHz)时二次谐波幅值和传播距离之间的关系(Chillara & Lissenden 2016)

下载: 全尺寸图片幻灯片

图 9 三种应力状态下兰姆波的群速度随板内应力变化的相对改变(Pau & Scalea 2015)

下载: 全尺寸图片幻灯片

图 10 三种应力状态下二次谐波位移分量的变化曲线(Pau & Scalea 2015)

下载: 全尺寸图片幻灯片

图 11 非线性超声实验测量系统

下载: 全尺寸图片幻灯片

图 12 基频与二倍频兰姆波的频散曲线(P点: c^(ω) =c^(2ω))(Deng et al. 2005)

下载: 全尺寸图片幻灯片

图 13 频率为5.099 MHz时二次谐波幅值与基频兰姆波振幅平方比值与传播距离的关系曲线(Deng et al. 2005)

下载: 全尺寸图片幻灯片

图 14 铝板(6061-T6型号)中三组模式对的归一化非线性系数c_β₂ A₂ /A₁₂ ω ₂ 与传播距离的关系(Liu et al. 2012)

下载: 全尺寸图片幻灯片

图 15 S₁-S₂模式对、S₂-S₄模式对的非线性系数与传播距离的关系(Matlack et al. 2011)

下载: 全尺寸图片幻灯片

图 16 一定传播距离处相对非线性系数β' = A₂A₁₂与激励电压的关系(Bermes et al. 2008)

下载: 全尺寸图片幻灯片

图 17 在不同型号铝板中S1-S2模式对的相对非线性系数β' = A₂A₁₂与传播距离的关系(Bermes et al. 2008)

下载: 全尺寸图片幻灯片

图 18 超声兰姆波的归一化应力波因子与循环次数的关系(邓明晰 & 裴俊峰,2008).(a)基波,试件#A,(b)二次谐波试件#A,(c)基波试件#B,(d)二次谐波,试件#B

下载: 全尺寸图片幻灯片

图 19 频率为2.45 MHz时兰姆波声非线性系数与热退化时间的关系(Xiang et al. 2011)

下载: 全尺寸图片幻灯片

图 20 比较兰姆波的群速度、衰减系数和相对声非线性系数对热疲劳加载周期数的敏感度(Li et al. 2012)

下载: 全尺寸图片幻灯片

图 21 兰姆波的非线性与塑性变形的关系(Pruell et al. 2007)

下载: 全尺寸图片幻灯片

图 22 实验方案示意图(Rauter & Lammering 2015)

下载: 全尺寸图片幻灯片

图 23 实验结果:(a)群速度与冲击能量的关系(b)相对超声非线性系数与冲击能量的关系(Rauter & Lammering 2015)

下载: 全尺寸图片幻灯片

图 24 超声波传播通过呼吸裂纹示意图(Shen & Giurgiutiu 2012)

下载: 全尺寸图片幻灯片

图 25 S₁-S₂模式对的非线性系数与传播路径到裂纹的距离的关系(Hong et al. 2014)

下载: 全尺寸图片幻灯片

图 26 (a)铆钉圆孔边疲劳初期裂纹的检测方案示意图(单位mm,疲劳微裂纹被放大示意),(b)检测结果图(Hong et al. 2014)

下载: 全尺寸图片幻灯片

表 1 三种粘接情形的非线性兰姆波实验结果(邓明晰2015)

参考文献(77)

[1]	邓明晰, Price D C, Scott D A. 2005. 兰姆波非线性效应的实验观察. 声学学报, 30: 37-46 http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200501007.htm Deng M X, Price D C, Scott D A. 2005. Experimental observations of nonlinear effects of Lamb waves. Acta Acustica, 30: 37-46. http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200501007.htm
[2]	邓明晰, 裴俊峰. 2008. 无损评价固体板材疲劳损伤的非线性超声兰姆波方法. 声学学报, 33: 360-369 (Deng M X, Pei J F. 2008. Nondestructive evaluation of fatigue damage in solid plates using nonlinear ultrasonic Lamb wave method. Acta Acustica, 33: 360-369). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200804013.htm
[3]	邓明晰, 项延训, 裴俊峰, 刘良兵. 2012. 基于群速度失配的超声兰姆波二次谐波的时域测量方法. 声学学报, 37: 621-628 (Deng M X, Xiang Y X, Pei J F, Liu L B. 2012. Time-domain measurement technique of second harmonic of ultrasonic Lamb waves using mismatch of group velocities. Acta Acustica, 37: 621-628). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA201206010.htm
[4]	邓明晰. 1996. 兰姆波的非线性研究. 声学学报, 21: 429-436 (Deng M X. 1996. Research on nonlinearity of Lamb waves. Acta Acustica, 21: 429-436). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA6S1.006.htm
[5]	邓明晰. 1997. 兰姆波的非线性研究(II). 声学学报, 22: 182-187 (Deng M X. 1997. Research on nonlinearity of Lamb waves (II). Acta Acustica, 22: 182-187).
[6]	邓明晰. 2005. 分层结构中兰姆波二次谐波发生的模式展开分析. 声学学报, 30: 132-142 (Deng M X. 2005. Modal expansion analyses of second-harmonic generation of the Lamb waves in layered structures. Acta Acustica, 30: 132-142). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200502007.htm
[7]	邓明晰. 2005. 一种定征复合板材粘接层性质的非线性超声兰姆波方法. 声学学报, 30: 542-551 (Deng M X. 2005. Characterization of adhesive joints of composite solid layers using a nonlinear Lamb wave approach. Acta Acustica, 30: 542-551). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200506010.htm
[8]	邓明晰. 2006. 兰姆波非线性效应的实验观察(II). 声学学报, 31: 1-7 (Deng M X. 2006. Experimental observations of nonlinear effects of Lamb waves (II). Acta Acustica, 31: 1-7). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200601001.htm
[9]	税国双, 汪越胜, 曲建民. 2005. 材料力学性能退化的超声无损检测与评价. 力学进展, 35: 52-65. (Shui G S, Wang Y S, Qu J M. 2005. Advances in nondestructive test and evaluation of material degradation using nonlinear ultrasound. Advances in Mechanics, 35: 52-65). http://lxjz.cstam.org.cn/CN/abstract/abstract132738.shtml
[10]	Aleshin V, Van Den Abeele KEA. 2007. Micro contact-based theory for acoustics in micro damage materials. J. Mech. Phys. Solids, 55: 366-390. doi: 10.1016/j.jmps.2006.07.002
[11]	Auld B A. 1973. Acoustic Fields and Waves in Solids. New York: John Wiley.
[12]	Baltazar A, Rokhlin S I, Pecorari C. 2002. On the relationship between ultrasonic and micromechanical properties of contacting rough surfaces. J. Mech. Phys. Solids, 50: 1397-1416. doi: 10.1016/S0022-5096(01)00119-3
[13]	Belyaeva I Y, Zaitsev V Y, Ostrovsky L A. 1993. Nonlinear acousto-elastic properties of granular media. Acoust. Phys., 39: 11-15.
[14]	Bermes C, Kim J Y, Qu J M, Jacobs L J. 2008. Nonlinear Lamb waves for the detection of material nonlinearity. Mech. Syst. Signal PR., 22: 638-646. doi: 10.1016/j.ymssp.2007.09.006
[15]	Cantrell J H, Yost W T. 2001. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue, 23: 487-490. doi: 10.1016/S0142-1123(01)00162-1
[16]	Cantrell J H. 2003. Fundamentals and Application of Nonlinear Ultrasonic Nondestructive Evaluation. Florida: CRC Press LLC.
[17]	Chillara V K, Lissenden C J. 2014. Nonlinear guided waves in plates: a numerical perspective. Ultrasonics, 54: 1553-1558. doi: 10.1016/j.ultras.2014.04.009
[18]	Chillara V K, Lissenden C J. 2016. Review of nonlinear ultrasonic guided wave nondestructive evaluaton: theory, numerics, and experiments. Opt. Eng., 55: 011002.
[19]	Demer L J, Fentnor L H. 1969. Lamb wave techniques in nondestructive testing. International Journal of Nondestructive Testing, 1: 251-283.
[20]	Deng M X, Pei J F. 2007. Assessment of accumulated fatigue damage in solid plates using nonlinear Lamb wave approach. Appl. Phys. Lett., 90: Art. No. 121902.
[21]	Deng M X, Xiang Y X, Liu L B. 2011. Time-domain analysis and experimental examination of cumulative second-harmonic generation by primary Lamb wave propagation. J. Appl. Phys., 109: 113525. doi: 10.1063/1.3592672
[22]	Deng M X, Xiang Y X. 2015. Analysis of second-harmonic generation by primary ultrasonic guided wave propagation in a piezoelectric plate. Ultrasonics, 61: 121-125. doi: 10.1016/j.ultras.2015.04.005
[23]	Deng M X,Wng P, Lv X F. 2005. Experimental observation of cumulative secondharmonic generation of Lamb-wave propagation in an elastic plate. J. Phys. D -Appl. Phys., 38: 344-353 doi: 10.1088/0022-3727/38/2/020
[24]	Deng M X. 1999. Cumulative second-harmonic generation of Lamb mode propagation in a solid plate. J. Appl. Phys., 85: 3051-3058. doi: 10.1063/1.369642
[25]	Deng M X. 2003. Analysis of second-harmonic generation of Lamb modes using a modal analysis approach. J. Appl. Phys., 94: 4153-4159.
[26]	Deng M X, Yang J. 2007. Characterization of elastic anisotropy of a solid plate using nonlinear Lamb wave approach. J. Sound Vib., 308: 201-211. doi: 10.1016/j.jsv.2007.07.029
[27]	Diamanti K, Soutis C, Hodgkinson J M. 2007. Piezoelectric transducer arrangement for the inspection of large composite structures. Composites Part A, 38: 1121-1130. doi: 10.1016/j.compositesa.2006.06.011
[28]	Donskoy D. 2006. Assessment of initial material damage and remaining life prediction with nonlinear acoustics. J. Acoust. Soc. Am., 119: 3293.
[29]	Friswell M I, Penny J E T. 2002. Crack modeling for structural health monitoring. Struct. Health. Monit., 1: 139-148. doi: 10.1177/1475921702001002002
[30]	Giurgiutiu V. 2003. Lamb wave generation with piezoelectric wafer active sensors for structural health monitoring// Smart Structures and Materials 2003: Smart structures and Integrated systems, 111-122.
[31]	Giurgiutiu V. 2005. Tuned Lamb wave excitation and detection with piezoelectric wafer active sensors for structural health monitoring. J Intell. Mater. Syst. Struct.,16: 291-305. doi: 10.1177/1045389X05050106
[32]	Gusev V E, Lauriks W, Thoen J. 1998. New evolution equations for the nonlinear surface acoustic waves on an elastic solid of general anisotropy. J. Acoust. Soc. Am., 103: 3203-3215. doi: 10.1121/1.423036
[33]	Guyer R A, Johnson P A. 1999. Nonlinear mesoscopic elasticity: evidence for a new class of materials. Phys. Today, 52: 30-36.
[34]	Hong M, Su Z, Lu Ye, Cheng L. 2014. Temporal information of linear and nonlinear Lamb waves for fatigue damage localization: analysis and synthesis//7th European workshop on Structural Health Monitoring, July 8-11, 2014, La Cite, Nantes, France.
[35]	Hong M, Su Z, Wang Q, Cheng L, Qing X. 2014. Modeling nonlinearities of ultrasonic waves for fatigue damage characterization: theory, simulation, and experimental validation. Ultrasonics, 54: 770-778. doi: 10.1016/j.ultras.2013.09.023
[36]	Kumon R E, Hamilton M F. 2002. Directional dependence of nonlinear surface acoustic waves in the (001) plane of cubic crystals. J. Acoust. Soc. Am., 115: 2060-2069.
[37]	Lamb H. 1917. On the waves in an elastic plate. Proceedings of the Royal Society A, 293-312.
[38]	Li W, Cho Y, Achenbach J D. 2012. Detection of thermal fatigue in composites by second harmonic Lamb waves. Smart Mater. Struct., 21: 085019. doi: 10.1088/0964-1726/21/8/085019
[39]	Lima W J de, Hamilton M F. 2003. Finite-amplitude waves in isotropic elastic plates. J. Sound Vib., 265: 819-839. doi: 10.1016/S0022-460X(02)01260-9
[40]	Liu Y L, Hu N, Xu H, Yuan W F, Yan C, Li Y, Goda R, Alamusi, Qiu J H, Ning H M, Wu L K. 2014. Damage evaluation based on a wave energy flow map using multiple PZT sensors. Sensors, 14: 1902-1917. doi: 10.3390/s140201902
[41]	Liu Y, Kim J Y, Jacobs L J, Qu J M, Li Z. 2012. Experimental investigation of symmetry properties of second harmonic Lamb waves. J. Appl. Phys., 111: 053511. doi: 10.1063/1.3691225
[42]	Lu X, Lu M, Zhou L M, Su Z, Cheng L, Ye L, Meng G. 2011. Evaluation of welding damage in welded tubular steel structures using guided waves and a probability-based imaging approach. Smart Mater. Struct., 20: 015018. doi: 10.1088/0964-1726/20/1/015018
[43]	Luo W, Rose J L. 2007. Phased array focusing with guided waves in a viscoelastic coated hollow cylinder. J. Acoust. Soc. Am., 121: 1945-1955. doi: 10.1121/1.2711145
[44]	Matlack K H, Kim J Y, Jacobs L J, Qu J M. 2011. Experimental characterization of efficient second harmonic generation of Lamb wave modes in a nonlinear elastic isotropic plate. J. Appl. Phys., 109: 014905. doi: 10.1063/1.3527959
[45]	Miao H, Huan Q, Li F. 2016. Excitation and reception of pure shear horizontal waves by using face-shear d24 mode piezoelectric wafers. Smart Mater. Struct., 25: 11LT01. doi: 10.1088/0964-1726/25/11/11LT01
[46]	Muller M F, Kim J Y, Qu J, Jacobs L J. 2010. Characteristics of second harmonic generation of Lamb waves in nonlinear elastic plates. J. Acoust. Soc. Am., 174: 2141-2152.
[47]	Ostrocsky L A, Johnson P A. 2001. Dynamic nonlinear elasticity in geomaterials. Riv. Nuovo Cimento, 24: 1-46.
[48]	Ostrocsky L A, Johnson P A. 2001. Dynamic nonlinear elasticity in geomaterials. Riv. Nuovo Cimento, 24: 1-46.
[49]	Pau A, Scalea F L di. 2015. Nonlinear guided wave propagation in prestressed plates. J. Acoust. Soc. Am., 137: 1529-1540. doi: 10.1121/1.4908237
[50]	Pecorari C. 2003. Nonlinear interaction of plane ultrasonic waves with an interface between rough surfaces in contact. J. Acoust. Soc. Am., 113: 3065-3072. doi: 10.1121/1.1570437
[51]	Pruell C, Kim J-Y, Qu J, Jacobs L J. 2007. Evaluation of plasticity driven material damage using Lamb waves. Appl. Phys. Lett., 91: 231911. doi: 10.1063/1.2811954
[52]	Purekar A S, Pines D J. 2010. Damage detection in thin composite laminates using piezoelectric phased sensor arrays and guided Lamb wave interrogation. J. Intel. Mat. Syst. Str., 21: 955-1010. doi: 10.1177/1045389X10374163
[53]	Qian Z W. 1995. Second order harmonics of surface-waves in isotropic solids. J. Sound Vib., 187: 369-379. doi: 10.1006/jsvi.1995.0530
[54]	Qiu L, Yuan S F, Zhang X Y, Wang Y. 2011. A time reversal focusing based impact imaging method and its evaluation on complex composite structures. Smart Mater. Struct., 20: 105014. doi: 10.1088/0964-1726/20/10/105014
[55]	Qiu, L., Liu, M.L., Qing, X.L., Yuan, S.F. 2013. A quantitative multidamage monitoring method for large-scale complex composite. Struct. Health. Monit., 12: 183-196. doi: 10.1177/1475921713479643
[56]	Rauter N, Lammering R. 2015. Impact damage detection in composite structures considering Nonlinear Lamb wave propagation. Mech. Adv. Mater. Struc., 22: 44-51. doi: 10.1080/15376494.2014.907950
[57]	Shen Y, Giurgiutiu V. 2012. Simulation of interaction between Lamb waves and cracks for structural health monitoring with piezoelectric wafer active sensors//ASME 2012 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Stone Moutain, Georgia, USA.
[58]	Shui G S, Kim J Y, Qu J M, Jacobs L J. 2008. Nonlinear Lamb waves for the detection of material nonlinearity. Mech. Syst Signal Pr., 22: 638-646. doi: 10.1016/j.ymssp.2007.09.006
[59]	Sicard R, Goyette J, Zellouf D E. 2002. A SAFT algorithm for lamb wave imaging of isotropic plate-like structures. Ultrasonics, 39: 487-494. doi: 10.1016/S0041-624X(01)00087-7
[60]	Solodov I Y, Krohn N, Busse G. 2002. CAN: an example of nonclassical acoustic nonlinearity in solids. Ultrasonics, 40: 621-625. doi: 10.1016/S0041-624X(02)00186-5
[61]	Solodov I Y. 1998. Ultrasonic of nonlinear contacts: propagation, reflection and NDE application. Ultrasonics, 36: 383-390. doi: 10.1016/S0041-624X(97)00041-3
[62]	Sonti V R, Kim S J, Jones J D. 1995. Equivalent forces and wavenumber spectra of shaped piezoelectric actuators. J. Sound Vib., 187: 111-131. doi: 10.1006/jsvi.1995.0505
[63]	Srivastava A, Scalea F L di. 2009. On the existence of antisymmetric or symmetric Lamb waves at nonlinear higher harmonics. J. Sound Vib., 323: 932-943. doi: 10.1016/j.jsv.2009.01.027
[64]	Su Z, Ye L. 2005. Lamb wave propagation-based damage identification for quasi-isotropic cf/ep composite laminates using aritificial neural algorithm: part i-methodology and database development. J. Intel. Mat. Syst. Str., 16: 97-111. doi: 10.1177/1045389X05047599
[65]	Su Z, Ye L. 2009. Identification of damage using Lamb waves: from fundamentals to applications. Springer, 2009.
[66]	Van Den Abeele K, De Visscher J. 2000. Damage assessment in reinforced concrete using spectral and temporal nonlinear vibration techniques. Cement Concrete Res., 30: 1453-1464. doi: 10.1016/S0008-8846(00)00329-X
[67]	Van Den Abeele KEA., Sutin A, Carmeliet J, Johnson P A. 2001. Micro-damage diagnostics using nonlinear elastic wave spectroscopy (NEWS). NDT & E Int., 34: 239-248.
[68]	Viktorov I A. 1965. Ultrasonic Lamb wave (Review). Ultrasonics, 11: 1.
[69]	Vishnuvardhan J, Krishnamurthy C V, Balasubramaniam K, 2007. Genetic algorithm based reconstruction of the elastic moduli of orthotropic plates using an ultrasonic guided wave single-transmitter-multiple-receiver SHM array. Smart Mater. Struct., 16: 1639-1650.
[70]	Wan X, Zhang Q, Xu G, Tse P W. 2014. Numerical simulation of nonlinear Lamb waves used in a thin plate for detecting buried micro-cracks. Sensors, 14: 8528-8546. doi: 10.3390/s140508528
[71]	Wang D, Ye L, Su Z, Lu Y, Li F, Meng G. 2010. Probabilistic damage identification based on correlation analysis using guided wave signals in aluminum plates. Struct. Health. Monit., 9: 133-144. doi: 10.1177/1475921709352145
[72]	Worden K, Tomlinson G R. 2001. Nonlinearity in structural dynamics: Detection, Identification and Modelling. Bristol: IOP Publishing Ltd.
[73]	Worlton D C. 1961. Experimental confirmation of Lamb waves at Megacycle Frequencies. J. Appl. Phys., 32: 967-971. doi: 10.1063/1.1736196
[74]	Wright W, Hutchins D, Jansen D, Schindel D. 1997. Air-coupled lamb wave tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 44: 53-59. doi: 10.1109/58.585190
[75]	Xiang Y, Deng M, Xuan F-Z, Liu C-J. 2011. Experimental study of thermal degradation in ferritic Cr-Ni alloy steel plates using nonlinear Lamb waves. NDT & E Int., 44: 768-774.
[76]	Zabolotskaya E A. 1992. Nonlinear propagation of plane and circular Rayleigh waves in isotropic solids. J. Acoust. Soc. Am., 91: 2569-2575. doi: 10.1121/1.402993
[77]	Zhu W J, Deng M X, Xiang Y X, Xuan F Z, Liu C J. 2016. Second harmonic generation of Lamb wave in numerical perspective. Chin. Phys. Lett., 33: 104301. doi: 10.1088/0256-307X/33/10/104301