数智力学−驾驭数智时代的力学

杨卫

doi:10.6052/1000-0992-24-042

数智力学−驾驭数智时代的力学

doi: 10.6052/1000-0992-24-042 cstr: 32046.14.1000-0992-24-042

杨卫^,

浙江大学交叉力学中心, 杭州 310027

基金项目: 著者对国家自然科学基金咨询委员会对该基础研究专题的支持表示感谢. 南京航空航天大学郭万林教授建议了“数智力学”的题目. 韩杰才、高华健、胡海岩、何国威、郭万林、段慧玲、冷劲松提供了咨询意见. 郭旭、罗喜胜、彭志科、杨越、曲绍兴、卢同庆、田强、张维声、张助华、孟松鹤、贾铮、马寅佶等提供了协助性意见. 赵沛、常若菲协助了文稿形成及绘图.

详细信息

作者简介:
杨卫, 中国科学院院士, 发展中国家科学院院士, 美国工程院外籍院士, 固体力学专家, 浙江大学教授、博士生导师. 现任中国学位与研究生教育学会会长, 曾任国家自然科学基金委员会主任、浙江大学校长. 　　研究方向包括宏微观破坏力学、结构完整性评价、材料的增强与增韧、微小型航天器研制等, 提出X-Mechanics (交叉力学)的概念

通讯作者:
yangw@zju.edu.cn

中图分类号: O3
计量
- 文章访问数: 2762
- HTML全文浏览量: 100
- PDF下载量: 935
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-28
- 录用日期: 2024-12-02
- 网络出版日期: 2024-12-03
- 刊出日期: 2024-12-26

Digintel mechanics—Governing the digintel era

YANG Wei^,

Center for X-Mechanics, Zhejiang University, Hangzhou 310027, China

More Information

Corresponding author: yangw@zju.edu.cn

摘要

摘要: 数智力学意指可驾驭数智时代的力学. 本文将数智力学定义为: 探讨物理空间、信息空间、认知空间的自身与相互之间的作用机理, 并表达为因果性或关联性的规律. 文中列出了数智力学所面临的8个科学问题, 并给出在X-4范式四面体中探讨数智力学的7条方法论路径. 文中展述了当前可推动数智力学研究的5个研究方向, 分别为: 数智力学框架、智柔体力学、数智融合计算、交叉尺度力学、具身智能力学.
- 数智力学 /
- X-4 范式 /
- 智柔体 /
- 数智融合
Abstract: Digintel mechanics refers to the mechanics studies that would govern the scientific rules for the digintel era, with digintel abbreviates the combination of digital and intelligence. Digintel mechanics is defined herein as the exploration for the mechanisms concerning the interactions, both within and between, physical space, cyber space and cognition space, and as the revelation of causation or/and correlation laws. Eight basic scientific issues concerning digintel mechanics are listed. Attention is then focused on 7 routes of methodologies confined in the X-4 tetrahedron. Five research thrusts suitable for the preliminary development of digintel mechanics are enumerated, they are digintel mechanics formalism, mechanics of intelligent flexors, convergent digintel computation, cross-scale mechanics, and mechanics for embodied intelligence.
- digintel mechanics /
- X-4 paradigm /
- intelligent flexors /
- digintel convergence

HTML全文

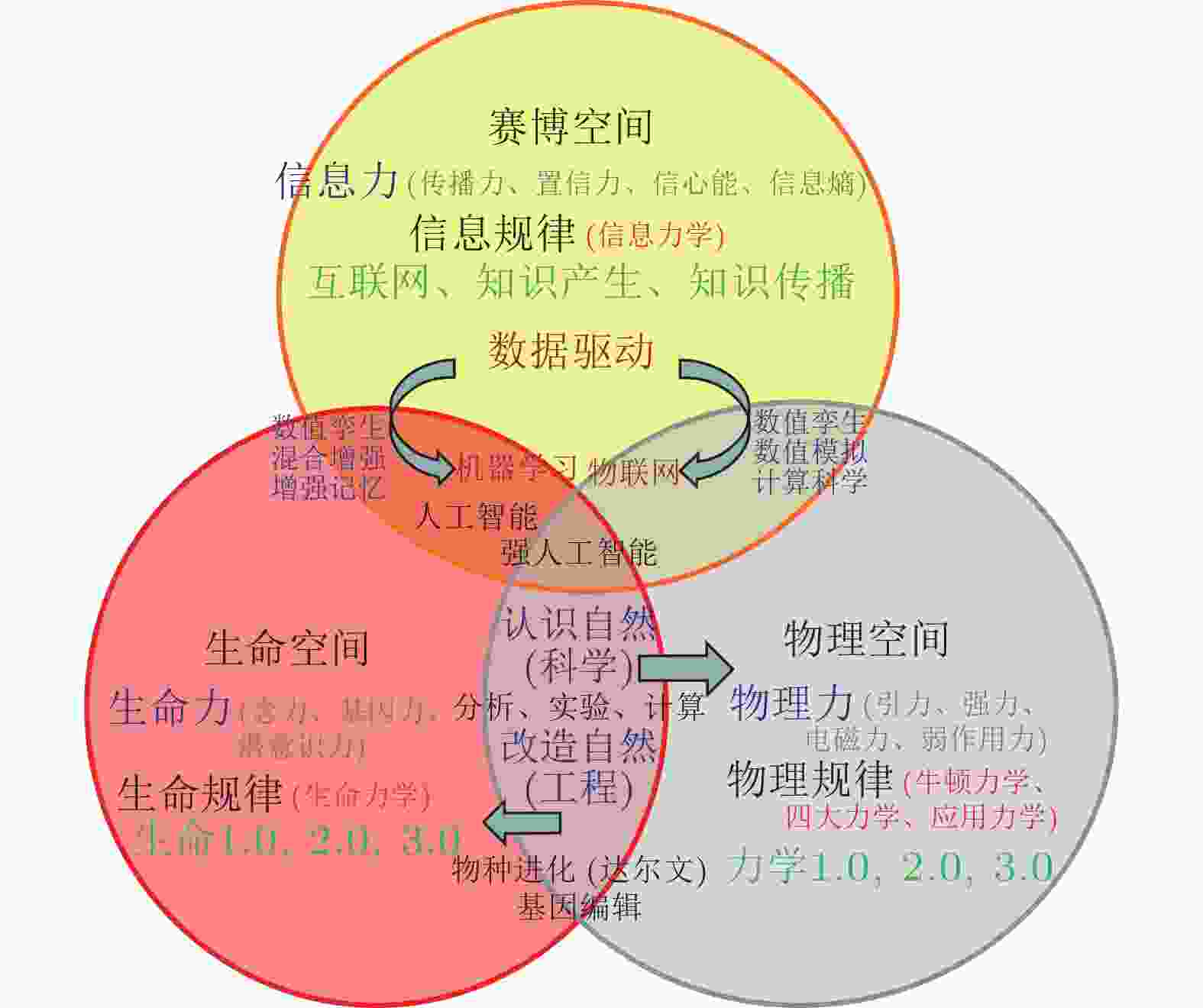
图 1 物理空间、信息空间与生命空间 (杨卫 2024)

下载: 全尺寸图片幻灯片

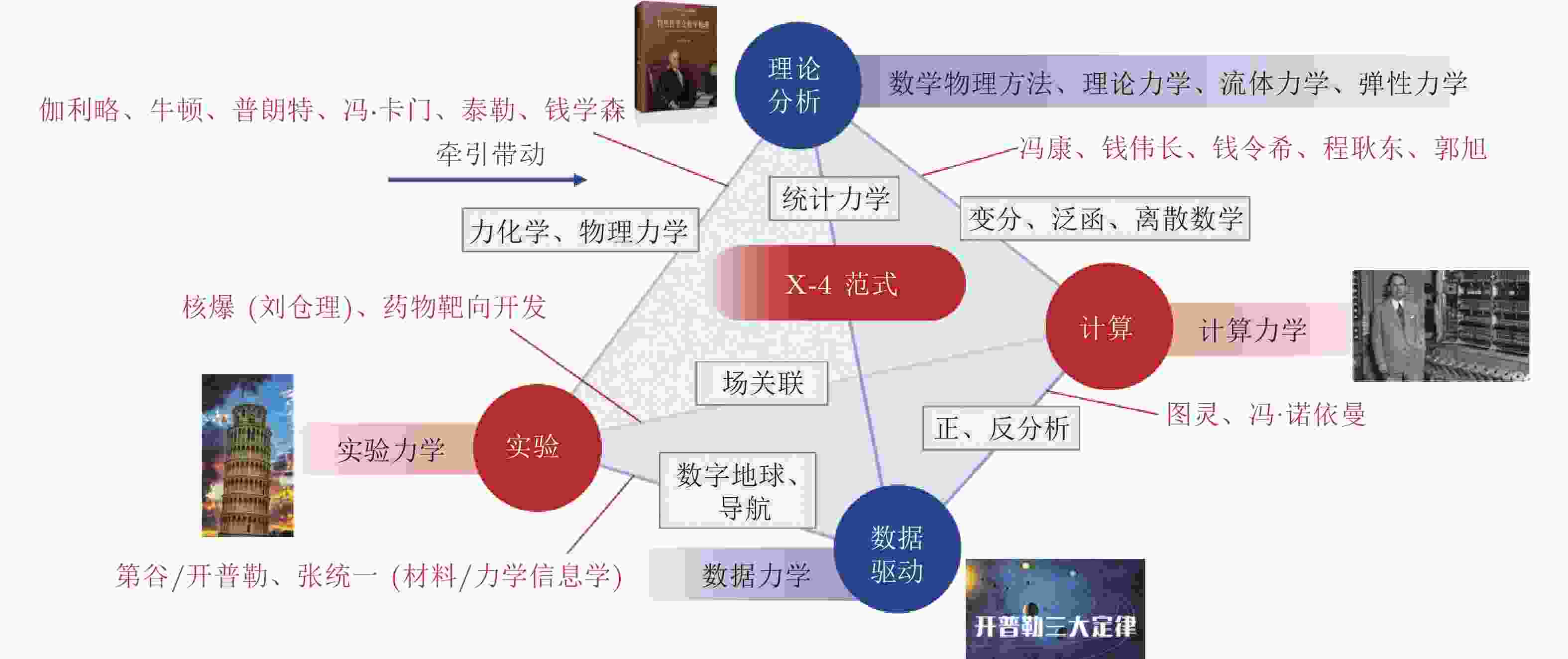
图 2 X-4范式(杨卫和赵沛 2024a)

下载: 全尺寸图片幻灯片

参考文献(18)

[1]	牛顿. 2018. 自然哲学之数学原理 (王克迪译). 北京: 北京大学出版社 (原著出版于1687年). 原著出版于1687年
[2]	托马斯·库恩. 2012. 科学革命的结构(伊安·哈金导读, 金吾伦和胡新和译). 北京: 北京大学出版社 (原著出版于1962年). 原著出版于1962年
[3]	王鹏, 孙升, 张庆, 张统一. 2019. 力学信息学简介. 自然杂志, 40(5): 313-322. doi: 10.3969/j.issn.0253-9608.2019.05.001
[4]	杨卫. 2024. 力学基本问题. 北京: 科学出版社.
[5]	杨卫, 赵沛. 2024a. 范式融合导向的数智时代力学专业核心课程. 力学与实践, doi: 10.6052/1000-0879-24-452.
[6]	杨卫, 赵沛. 2024b. 基础学科领域本科教育教学改革试点工作—力学“101计划”. 力学与实践, doi: 10.6052/1000-0879-24-451.
[7]	Gao H, Ji B, Jager I L, et al. 2003. Materials become insensitive to flaws at nanoscale: Lessons from nature. Proceedings of the National Academy of Sciences, 100(10): 5597-5600. doi: 10.1073/pnas.0631609100
[8]	He G, Jin G, Yang Y. 2017. Space-time correlations and dynamic coupling in turbulent flows. Annual Review of Fluid Mechanics, 49: 51-70. doi: 10.1146/annurev-fluid-010816-060309
[9]	Huang M C, Liu C, Guo Y L, et al. 2024. A mechanics-based data-free problem independent machine learning (PIML) model for large-scale structural analysis and design optimization. Journal of the Mechanics and Physics of Solids, 193: 105893. doi: 10.1016/j.jmps.2024.105893
[10]	Jin Y B, Liu X W, Shao Y C, et al. 2022. High-speed quadrupedal locomotion by imitation-relaxation reinforcement learning. Nature Machine Intelligence, 4(12): 1198-1208. doi: 10.1038/s42256-022-00576-3
[11]	Karapiperis K, Stainier L, Ortiz M, et al. 2021. Data-driven multiscale modeling in mechanics. Journal of the Mechanics and Physics of Solids, 147: 104239. doi: 10.1016/j.jmps.2020.104239
[12]	Kepler J. 1622. Summary of copernican astronomy. Austria: Johann Planck.
[13]	Kepler J. 1997. The harmony of the world (Aiton E J, Duncan A M, Field J V Trans). Pennsylvania: American Philosophical Society. (Original work published 1619).
[14]	Meng Z Y, Zhong J R, Xu S B, et al. 2024. Simulating unsteady flows on a superconducting quantum processor. Communications Physics, 7(1): 349. doi: 10.1038/s42005-024-01845-w
[15]	Raissi M, Perdikaris P, Karniadakis G E. 2019. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378: 686-707. doi: 10.1016/j.jcp.2018.10.045
[16]	Raissi M, Yazdani A, Karniadakis G E. 2020. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science, 367(6481): 1026-1030. doi: 10.1126/science.aaw4741
[17]	Shen W, Yao J, Yang Y. 2024. Designing turbulence with entangled vortices. Proceedings of the National Academy of Sciences, 121 (35): e2405351121.
[18]	Zhao Q, Zhu Q, Zhang Z, Yin B, Gao H, Zhou H. 2024. A machine learning–based framework for mapping hydrogen at the atomic scale. Proceedings of the National Academy of Sciences, 121 (39): e2410968121.