-
摘要: 螺旋度与湍流的拓扑结构以及动力学演化过程密切相关. 本文首先详细阐述了螺旋度与流动结构之间具体的关联关系. 随后, 本文重点探讨了螺旋度在湍流输运中的作用, 以及与其他物理效应之间的耦合关系. 由于螺旋度对流动结构的表征作用以及对湍流动力学演化的重要影响, 本文随后简要介绍了螺旋度在湍流建模中的应用. 最后, 本文对当前的研究进展进行了总结, 指出了螺旋度与湍流相关研究的未来主要发展方向.Abstract: Helicity is closely related to the topology of flow. This paper first explains the specific connection between helicity and flow structures. Subsequently, this paper focuses on elaborating the role of helicity in turbulence, as well as its coupling with other physical effects. Based on the crucial influence of helicity on flow structures and turbulent dynamics, this paper then briefly introduces the current applications of helicity in turbulence theory and simulation modeling. Finally, this paper summarizes the current research progress, outlining the overall advancement of helicity and the main directions for future studies.
-
Key words:
- helicity /
- turbulent theory /
- turbulent simulation /
- helical dynamics /
- helical wave decomposition
-
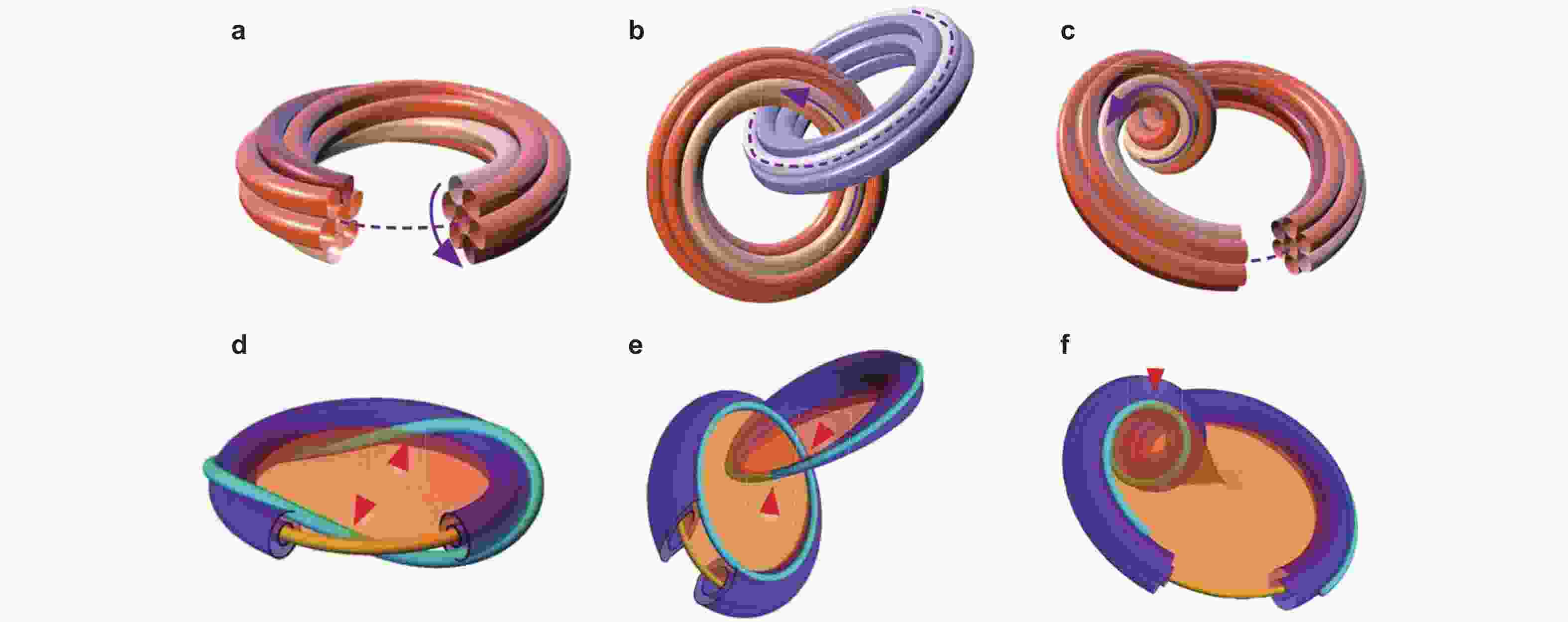
图 2 三种基本涡线构型. (a)和(d) 扭转, (b)和(e) 链接, (c)和(f) 缠绕(Scheeler et al. 2017)
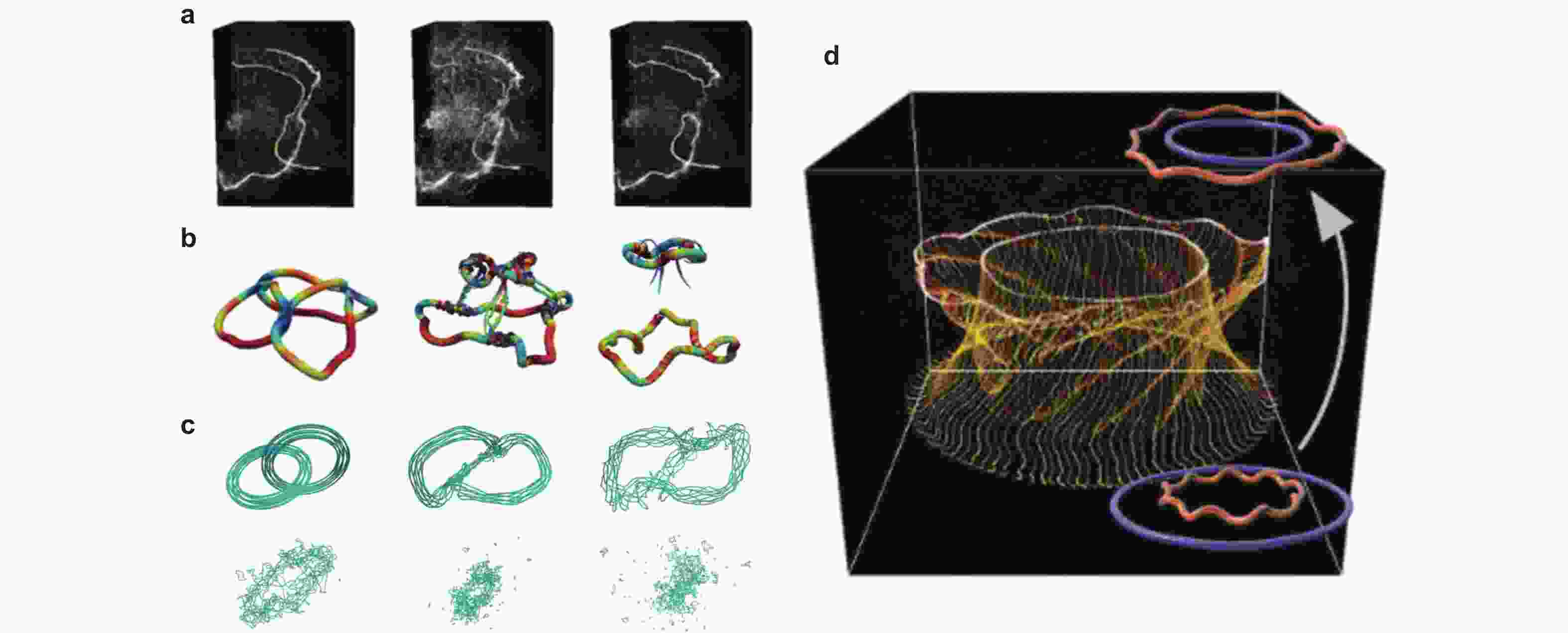
图 3 三种螺旋度之间的转换. (a)一对涡环之间的链接螺旋度在涡重联后转换为单个涡环的缠绕, 经过局部放大(Scheeler et al. 2014); (b) “三叶形结”的涡重联, 链接转化为缠绕(Alexakis & Biferale 2018, Yao et al. 2021); (c) Hopf link 的涡重联, 链接转化为缠绕(Kivotides & Leonard 2021); (d) 涡的追击过程中缠绕通过涡拉伸转换为扭转(Scheeler et al. 2017)
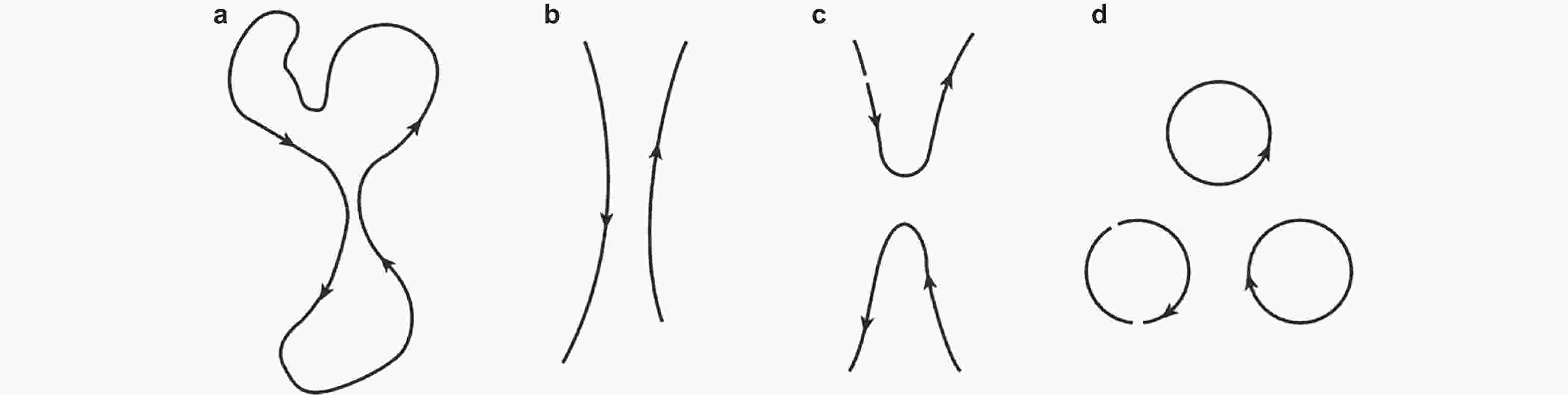
图 4 Feynman (1955)所预测的涡环 (a)能够发生重联 (b)→(c), 形成若干较小的涡环 (d)
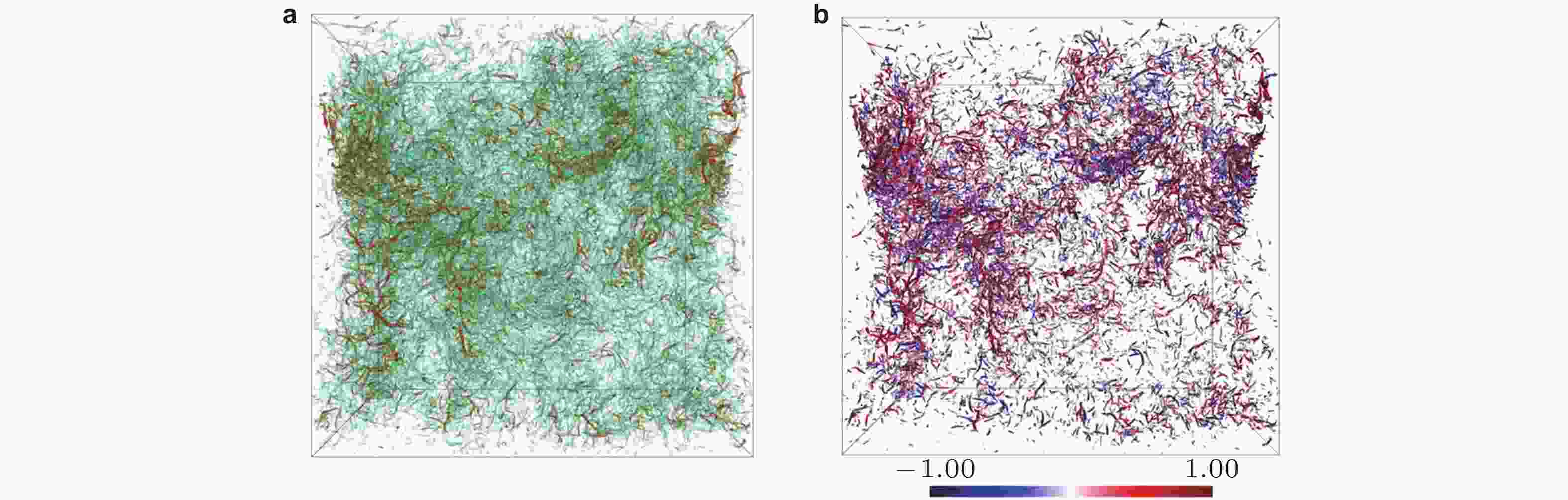
图 5 螺旋湍流中的 (a) 涡结构与 (b) 相对螺旋度分布(Kitamura 2021)
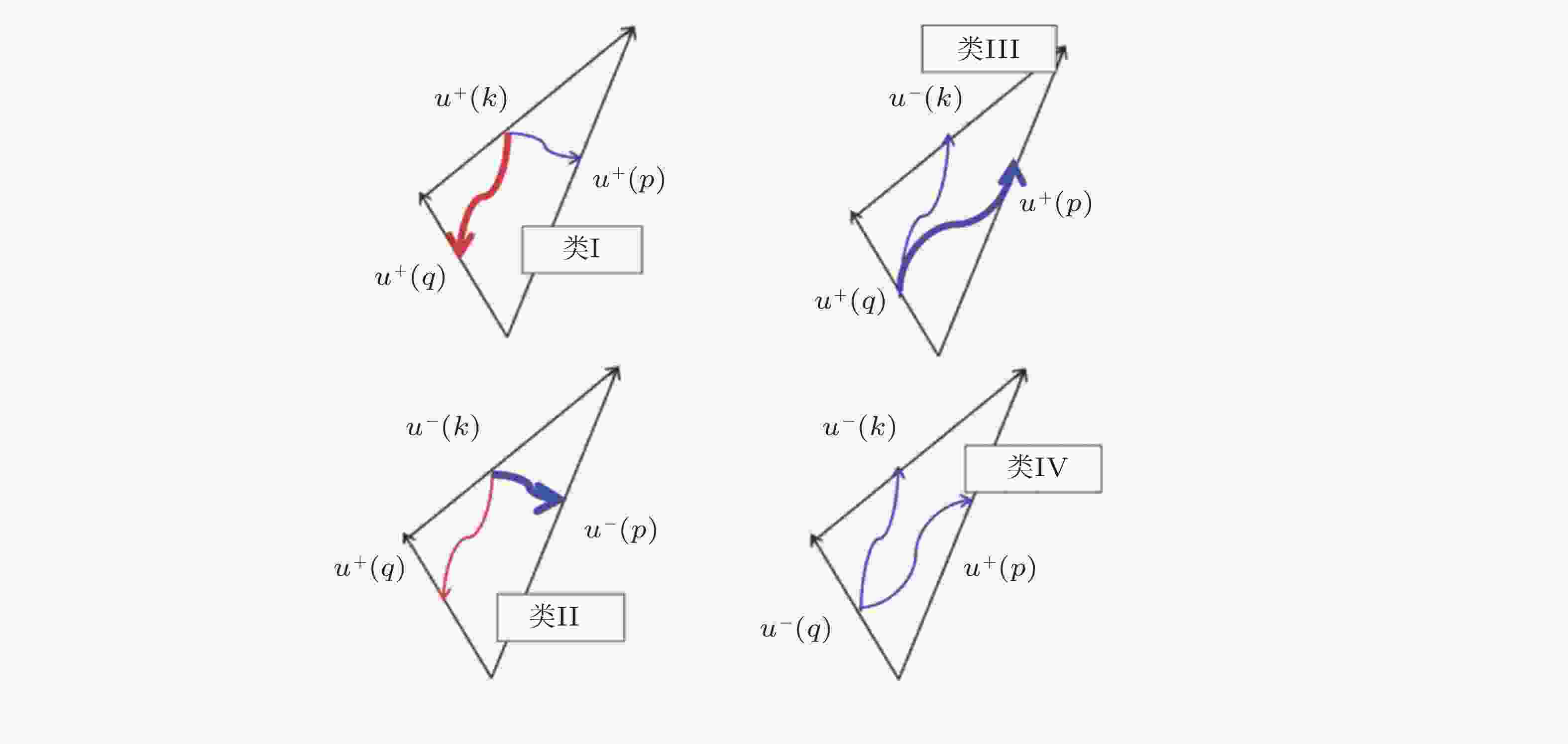
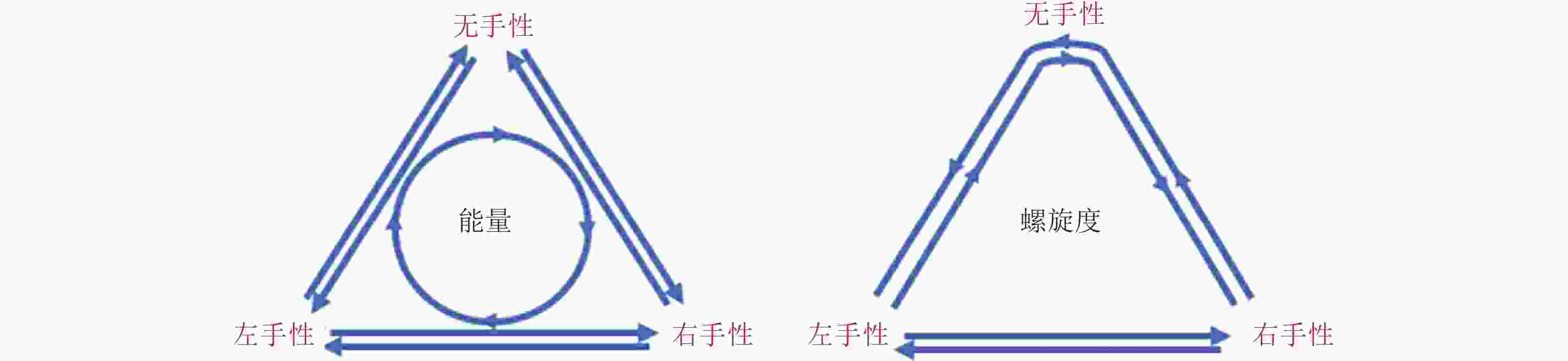
图 6 三波交互的四种分类(Waleffe 1992, Alexakis & Biferale 2018); 箭头代表了能量输运的方向, 线条粗细代表了能量通量的大小; 蓝色代表正向级串, 红色代表反向级串
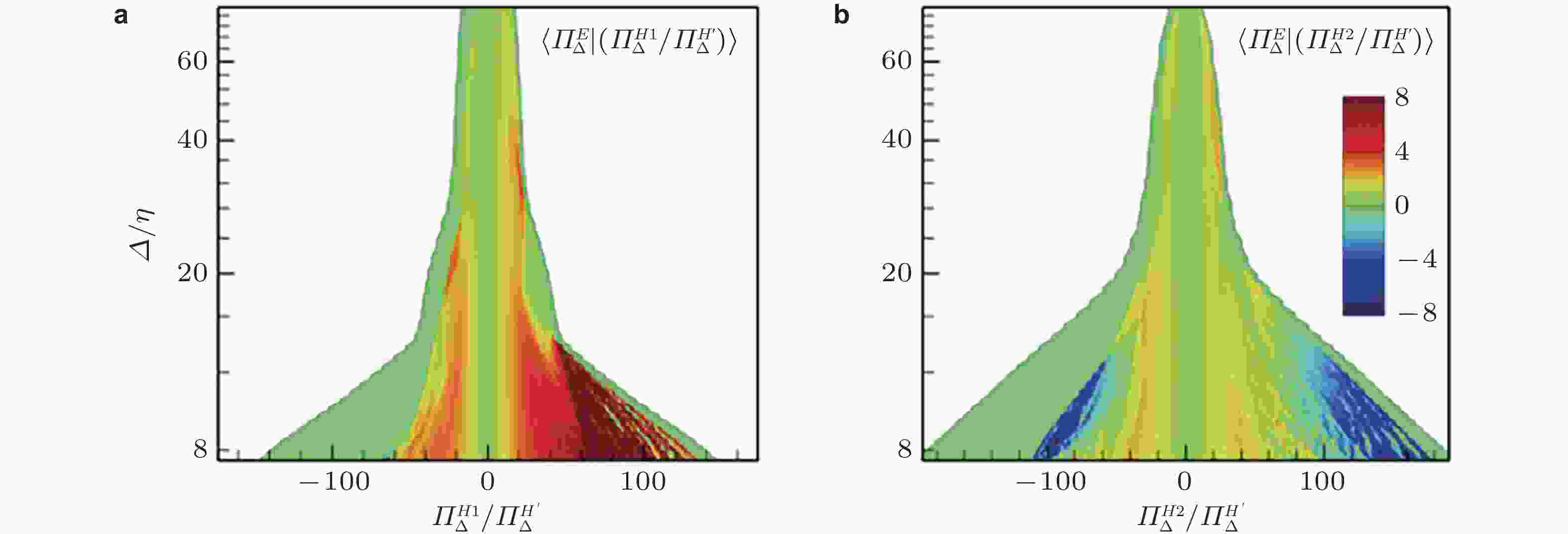
图 8 螺旋度级串的双通道对能量级串的影响(Yan et al. 2020c). (a)
$ \varPi _\Delta ^{H1} $ , (b)$ \varPi _\Delta ^{H2} $ 图 9 带有螺旋度的典型旋转湍流. (a) 螺旋旋转湍流(Hu et al. 2022), (b) 旋转壁湍流(Hu et al. 2024), (c) 旋转射流(Luginsland et al. 2016)
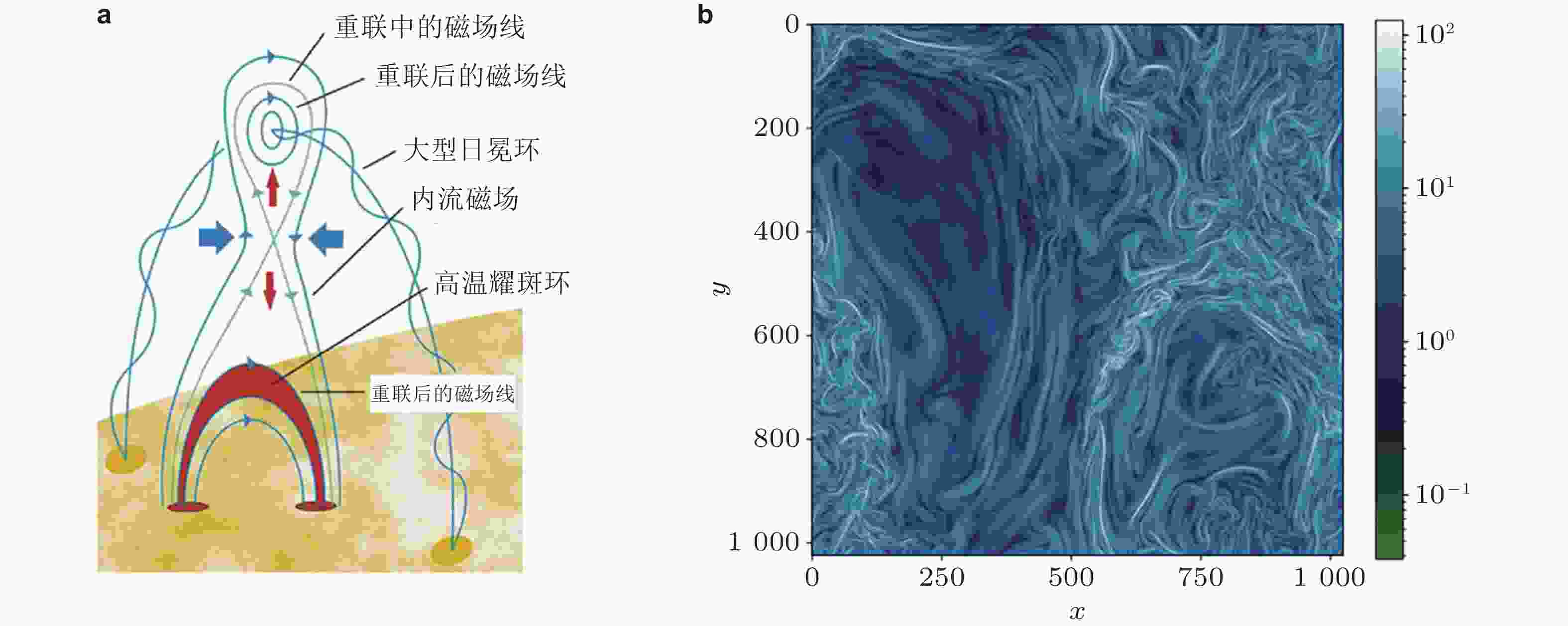
图 10 MHD 流动. (a) 日冕中的磁重联过程(Shibata & Magara 2011), (b) 霍尔 MHD 湍流中的电流密度(Ferrand 2021)
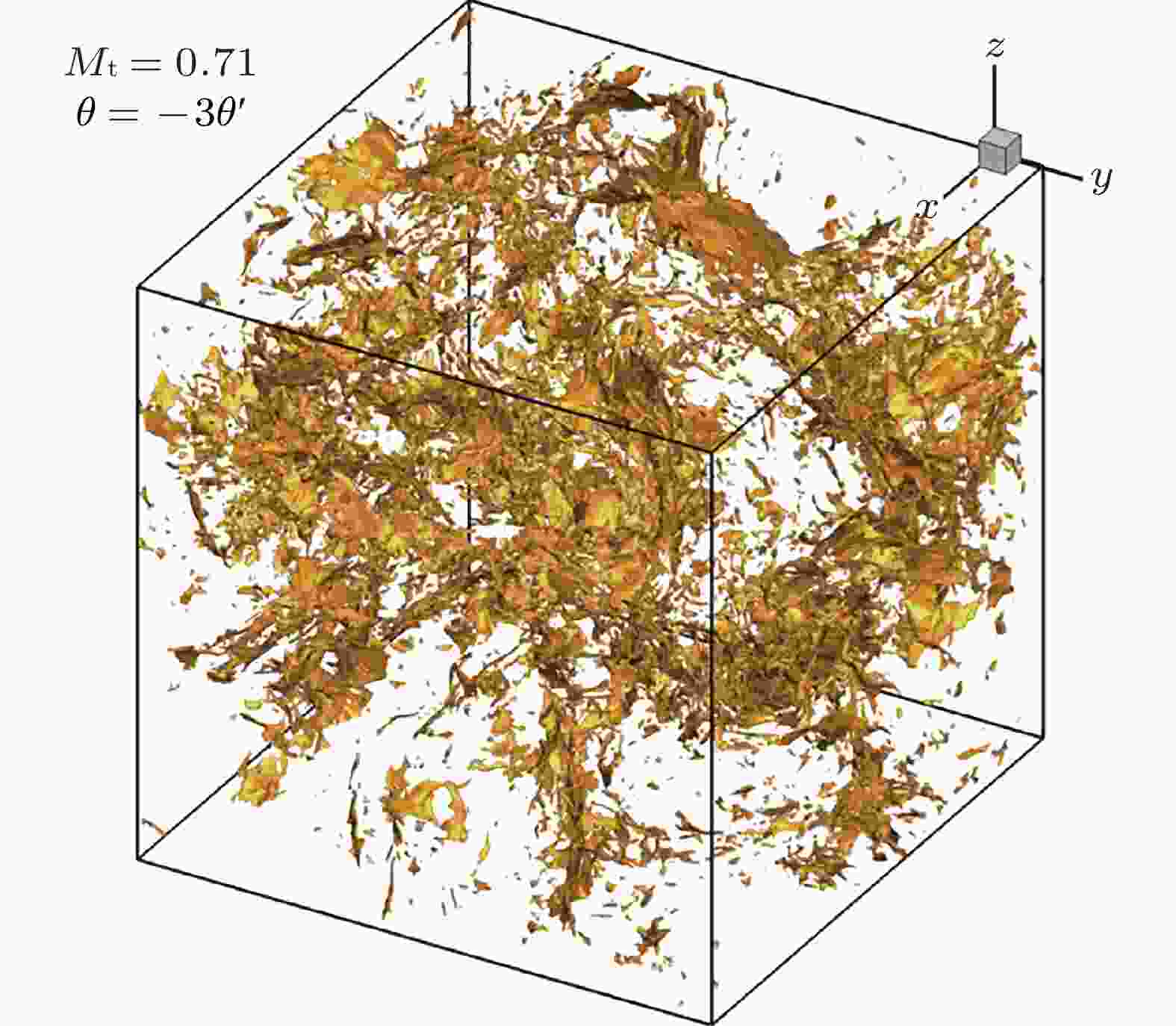
图 11 可压缩螺旋湍流中的速度散度(Yan et al. 2019)
图 12 可压缩螺旋湍流中动能与螺旋度的输运(Yan et al. 2020b)
图 13 压气机流动中不同模型和实验结果等总压图对比(Sun 2023)
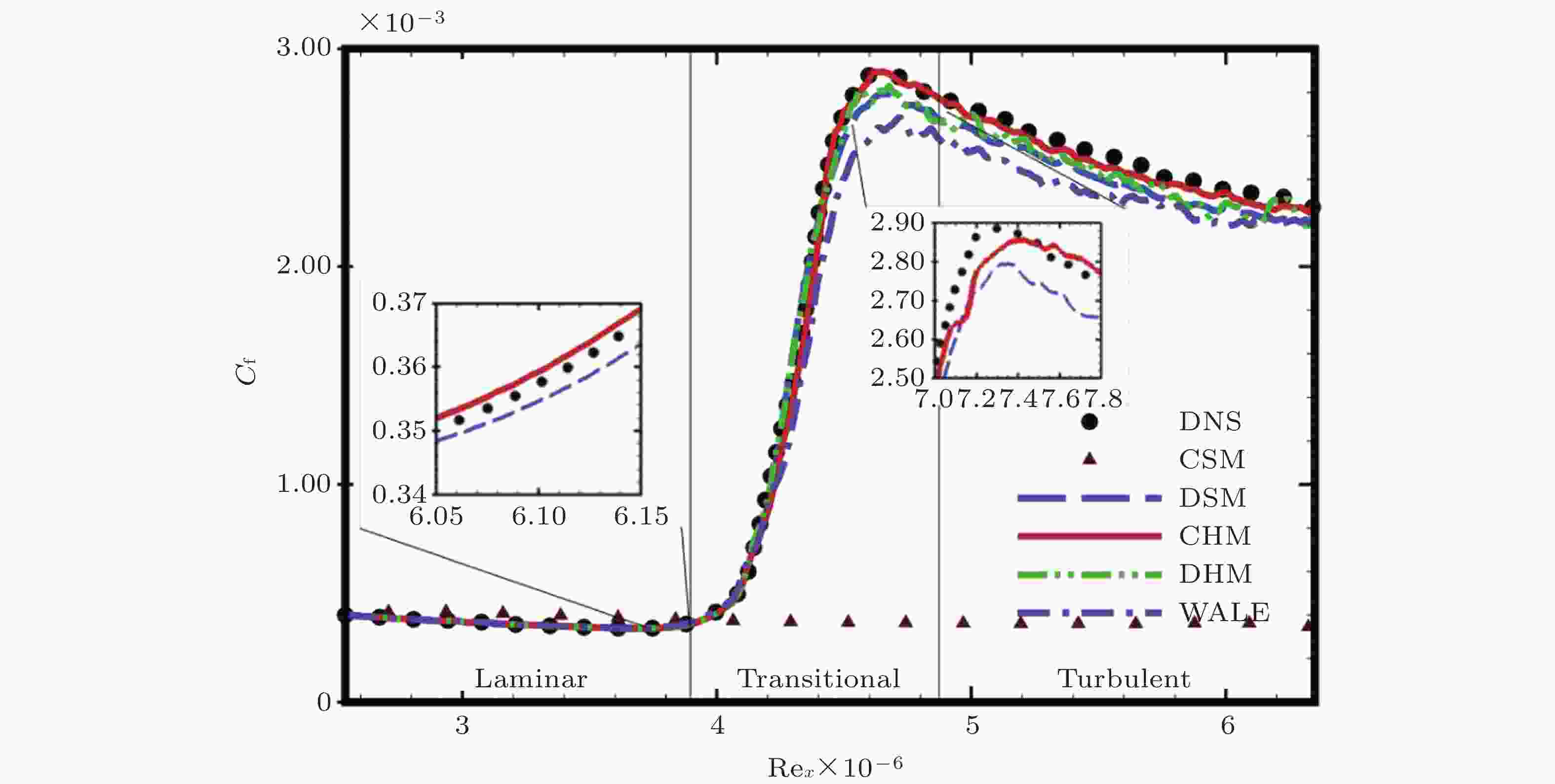
图 14 边界层转捩中模型效果比较(Zhou et al. 2019b). DNS为直接数值模拟结果, CSM与DSM分别是常系数与动态Smagorinsky模型, CHM与DHM分别是常系数与动态螺旋度模型, WALE是壁面自适应局部涡粘模型
-
[1] 杜一鸣, 王猛, 庞超, 等. 2023. 基于螺旋度的边界层横流转捩模型及其应用. 气动研究与试验, 1: 70-89. [2] 李耀东, 刘健文, 高守亭 . 2005. 螺旋度在对流天气预报中的应用研究进展. 气象科技, 33: 7-11 [3] 孙鹏. 2009. 湍流壳模型的非线性动力学. [博士论文]. 中国工程物理研究院. [4] 唐嘉蕙. 2019. 一次龙卷的高分辨数值模拟和螺旋度诊断分析. [硕士论文]. 南京信息工程大学. [5] 王革, 陈亮, 郜冶, 等. 2008. 旋转对固体火箭发动机燃烧室燃气流动的影响. 空气动力学学报, 26: 208-211. doi: 10.3969/j.issn.0258-1825.2008.02.013 [6] 姚冉. 2021. 基于非线性涡黏假设的γ-Re_θ转捩模型和γ转捩模型研究. [硕士论文]. 北京理工大学. [7] 张兆顺, 崔桂香, 许春晓. 2005. 湍流理论与模拟. 北京: 清华大学出版社有限公司. [8] 郑峰. 2005. 螺旋度及其在天气诊断分析中应用研究的进展. 贵州气象, 29: 2-5 [9] Agullo O, Müller W-C, Knaepen B, et al. 2001. Large eddy simulation of decaying magnetohydrodynamic turbulence with dynamic subgrid-modeling. Physics of Plasmas, 8: 3502-3505. doi: 10.1063/1.1372337 [10] Alexakis A. 2017. Helically decomposed turbulence. Journal of Fluid Mechanics, 812: 752-770. doi: 10.1017/jfm.2016.831 [11] Alexakis A, Biferale L. 2018. Cascades and transitions in turbulent flows. Physics Reports, 767-769: 1-101. doi: 10.1016/j.physrep.2018.08.001 [12] Aluie H. 2011. Compressible turbulence: The cascade and its locality. Physical Review Letters, 106: 174502. doi: 10.1103/PhysRevLett.106.174502 [13] André J C, Lesieur M. 1977. Influence of helicity on the evolution of isotropic turbulence at high Reynolds number. Journal of Fluid Mechanics, 81: 187-207. doi: 10.1017/S0022112077001979 [14] Andreopoulos Y. 2008. Vorticity and velocity alignment in compressible flows: An experimental study of helicity density in turbulence and vortices. Russian Journal of Electrochemistry, 44: 390-396. doi: 10.1134/S1023193508040046 [15] Baroud C N, Plapp B B, She Z S, et al. 2002. Anomalous self-similarity in a turbulent rapidly rotating fluid. Phys Rev Lett, 88: 114501. doi: 10.1103/PhysRevLett.88.114501 [16] Benavides S J, Alexakis A. 2017. Critical transitions in thin layer turbulence. Journal of Fluid Mechanics, 822: 364-385. doi: 10.1017/jfm.2017.293 [17] Benzi R, Biferale L, Kerr R M, et al. 1996. Helical shell models for three-dimensional turbulence. Physical Review E, 53: 3541-3550. doi: 10.1103/PhysRevE.53.3541 [18] Berger M A. 1999. Introduction to magnetic helicity. Plasma Physics and Controlled Fusion, 41: B167. doi: 10.1088/0741-3335/41/12B/312 [19] Bhattacharjee A. 2004. Impulsive magnetic reconnection in the Earth’s magnetotail and the Solar corona. Annual Review of Astronomy and Astrophysics, 42: 365-384. doi: 10.1146/annurev.astro.42.053102.134039 [20] Biferale L, Kerr R M. 1995. Role of inviscid invariants in shell models of turbulence. Physical Review E, 52: 6113-6122. doi: 10.1103/PhysRevE.52.6113 [21] Biferale L, Lambert A, Lima R, et al. 1995. Transition to chaos in a shell model of turbulence. Physica D: Nonlinear Phenomena, 80: 105-119. doi: 10.1016/0167-2789(95)90065-9 [22] Biferale L, Musacchio S, Toschi F. 2012. Inverse energy cascade in three-dimensional isotropic turbulence. Physical Review Letters, 108: 164501. doi: 10.1103/PhysRevLett.108.164501 [23] Biferale L, Musacchio S, Toschi F. 2013. Split energy–helicity cascades in three-dimensional homogeneous and isotropic turbulence. Journal of Fluid Mechanics, 730: 309-327. doi: 10.1017/jfm.2013.349 [24] Billant P, Chomaz J-M, Huerre P. 1998. Experimental study of vortex breakdown in swirling jets. Journal of Fluid Mechanics, 376: 183-219. doi: 10.1017/S0022112098002870 [25] Birkhoff G. 1954. Fourier synthesis of homogeneous turbulence. Communications on Pure and Applied Mathematics, 7: 19-44. doi: 10.1002/cpa.3160070104 [26] Boffetta G, Ecke R E. 2012. Two-dimensional turbulence. Annual Review of Fluid Mechanics, 44: 427-451. doi: 10.1146/annurev-fluid-120710-101240 [27] Boileau M, Staffelbach G, Cuenot B, et al. 2008. LES of an ignition sequence in a gas turbine engine. Combustion and Flame, 154: 2-22. doi: 10.1016/j.combustflame.2008.02.006 [28] Briard A, Biferale L, Gomez T. 2017. Closure theory for the split energy-helicity cascades in homogeneous isotropic homochiral turbulence. Physical Review Fluids, 2: 102602. doi: 10.1103/PhysRevFluids.2.102602 [29] Briard A, Gomez T. 2017. Dynamics of helicity in homogeneous skew-isotropic turbulence. Journal of Fluid Mechanics, 821: 539-581. doi: 10.1017/jfm.2017.260 [30] Brissaud A, Frisch U, Leorat J, et al. 1973. Helicity cascades in fully developed isotropic turbulence. Physics of Fluids, 16: 1366-1367. doi: 10.1063/1.1694520 [31] Burgess D W, Foster M. 1990. Test of helicity as a forecast parameter. Preprints, 16th Conf. on Severe Local Storms, Kananaskis Park, AB, Canada, 1990. [32] Buzzicotti M, Aluie H, Biferale L, et al. 2018. Energy transfer in turbulence under rotation. Physical Review Fluids, 3: 034802. doi: 10.1103/PhysRevFluids.3.034802 [33] Cassak P A, Shay M A, Drake J F. 2005. Catastrophe model for fast magnetic reconnection onset. Physical Review Letters, 95: 235002. doi: 10.1103/PhysRevLett.95.235002 [34] Celani A, Musacchio S, Vincenzi D. 2010. Turbulence in more than two and less than three dimensions. Physical Review Letters, 104: 184506. doi: 10.1103/PhysRevLett.104.184506 [35] Chen Q, Chen S, Eyink G L. 2003a. The joint cascade of energy and helicity in three-dimensional turbulence. Physics of Fluids, 15: 361-374. doi: 10.1063/1.1533070 [36] Chen Q, Chen S, Eyink G L, et al. 2003b. Intermittency in the joint cascade of energy and helicity. Phys. Rev. Lett., 90: 214503. doi: 10.1103/PhysRevLett.90.214503 [37] Chen Q, Chen S, Eyink G L, et al. 2005. Resonant interactions in rotating homogeneous three-dimensional turbulence. Journal of Fluid Mechanics, 542: 139-164. doi: 10.1017/S0022112005006324 [38] Chernyshov A A, Karelsky K V, Petrosyan A S. 2007. Development of large eddy simulation for modeling of decaying compressible magnetohydrodynamic turbulence. Physics of Fluids, 19: 055106. doi: 10.1063/1.2728936 [39] Chigier N A, Chervinsky A. 1967. Aerodynamic study of turbulent burning free jets with swirl. Symposium (International) on Combustion, 11: 489-499. doi: 10.1016/S0082-0784(67)80173-5 [40] Chkhetiani O G. 1996. On the third moments in helical turbulence. Journal of Experimental and Theoretical Physics Letters, 63: 808-812. doi: 10.1134/1.567095 [41] Cho J Y K. 2008. Atmospheric dynamics of tidally synchronized extrasolar planets. Philosophical Transactions of the Royal Society A-mathematical Physical and Engineering Sciences, 366: 4477-4488. doi: 10.1098/rsta.2008.0177 [42] Chollet J-P, Lesieur M. 1981. Parameterization of small scales of three-dimensional isotropic turbulence utilizing spectral closures. Journal of Atmospheric Sciences, 38: 2747-2757. doi: 10.1175/1520-0469(1981)038<2747:POSSOT>2.0.CO;2 [43] Crow S C. 1970. Stability theory for a pair of trailing vortices. AIAA Journal, 8: 2172-2179. doi: 10.2514/3.6083 [44] Deusebio E, Lindborg E. 2014. Helicity in the Ekman boundary layer. Journal of Fluid Mechanics, 755: 654-671. doi: 10.1017/jfm.2014.307 [45] Di Leoni P C, Mininni P D, Brachet M. 2016. Helicity, topology, and Kelvin waves in reconnecting quantum knots. Physical Review A, 94: 043605. doi: 10.1103/PhysRevA.94.043605 [46] Domaradzki J, Rogallo R. 1988. Energy transfer in isotropic turbulence at low Reynolds numbers. Stanford Univ., Studying Turbulence Using Numerical Simulation Databases, 2. Proceedings of the 1988 Summer Program, 89: 169-177. [47] Domaradzki J A, Carati D. 2007. A comparison of spectral sharp and smooth filters in the analysis of nonlinear interactions and energy transfer in turbulence. Physics of Fluids, 19: 085111. doi: 10.1063/1.2760281 [48] Dorelli J C, Glocer A, Collinson G, et al. 2015. The role of the Hall effect in the global structure and dynamics of planetary magnetospheres: Ganymede as a case study. Journal of Geophysical Research: Space Physics, 120: 5377-5392. doi: 10.1002/2014JA020951 [49] Ebrahimi F. 2020. An alfvenic reconnecting plasmoid thruster. Journal of Plasma Physics, 86: 905860614. doi: 10.1017/S0022377820001476 [50] Ebrahimi F, Raman R, Hooper E B, et al. 2014. Physics of forced magnetic reconnection in coaxial helicity injection experiments in national spherical torus experiment. Physics of Plasmas, 21: 056109. doi: 10.1063/1.4875337 [51] Ecke R E. 2017. From 2D to 3D in fluid turbulence: Unexpected critical transitions. Journal of Fluid Mechanics, 828: 1-4. doi: 10.1017/jfm.2017.507 [52] Eyink G L. 2005. Locality of turbulent cascades. Physica D: Nonlinear Phenomena, 207: 91-116. doi: 10.1016/j.physd.2005.05.018 [53] Eyink G L. 2006. Multi-scale gradient expansion of the turbulent stress tensor. Journal of Fluid Mechanics, 549: 159-190. doi: 10.1017/S0022112005007895 [54] Eyink G L, Drivas T D. 2018. Cascades and dissipative anomalies in relativistic fluid turbulence. Physical Review X, 8: 011023. [55] Ferrand R. 2021. Multi-scale compressible turbulence in astrophysical plasmas viewed through theoretical, numerical and observational methods. Earth and Planetary Astrophysics. Université Paris-Saclay. [56] Ferrand R, Sahraoui F, Galtier S, et al. 2022. An in-depth numerical study of exact laws for compressible Hall magnetohydrodynamic turbulence. The Astrophysical Journal, 927: 205. doi: 10.3847/1538-4357/ac517a [57] Feynman R P. 1955. Chapter II application of quantum mechanics to liquid helium//Progress in low temperature physics. Elsevier: 17-53. [58] Galanti B, Tsinober A. 2006. Physical space properties of helicity in quasi-homogeneous forced turbulence. Physics Letters A, 352: 141-149. doi: 10.1016/j.physleta.2005.11.066 [59] Gallaire F, Chomaz J-M. 2003. Mode selection in swirling jet experiments: A linear stability analysis. Journal of Fluid Mechanics, 494: 223-253. doi: 10.1017/S0022112003006104 [60] Galtier S. 2003. Weak inertial-wave turbulence theory. Physical Review E, 68: 015301. doi: 10.1103/PhysRevE.68.015301 [61] Galtier S. 2014. Weak turbulence theory for rotating magnetohydrodynamics and planetary flows. Journal of Fluid Mechanics, 757: 114-154. doi: 10.1017/jfm.2014.490 [62] Galtier S. 2016. Introduction to modern magnetohydrodynamics. Cambridge University Press. [63] Gledzer E B. 1973. System of hydrodynamic type admitting two quadratic integrals of motion. Soviet Physics Doklady, 18: 216. [64] Gomez T, Politano H, Pouquet A. 2000. Exact relationship for third-order structure functions in helical flows. Physical Review E, 61: 5321-5325. doi: 10.1103/PhysRevE.61.5321 [65] Gorce J-B, Falcon E. 2022. Statistical equilibrium of large scales in three-dimensional hydrodynamic turbulence. Physical Review Letters, 129: 054501. doi: 10.1103/PhysRevLett.129.054501 [66] Grabe C, Shengyang N, Krumbein A. 2018. Transport modeling for the prediction of crossflow transition. AIAA Journal, 56: 3167-3178. doi: 10.2514/1.J056200 [67] Hao G, Zuccher S, Ricca R, et al. 2020. Topological fluid mechanics and its new developments. SCIENTIA SINICA Physica, Mechanica & Astronomica, 50 : 054701. [68] Hellinger P, Papini E, Verdini A, et al. 2021. Spectral transfer and Kármán–Howarth–Monin equations for compressible Hall magnetohydrodynamics. The Astrophysical Journal, 917: 101. doi: 10.3847/1538-4357/ac088f [69] Herbert C. 2014. Restricted partition functions and inverse energy cascades in parity symmetry breaking flows. Physical Review E, 89: 013010. doi: 10.1103/PhysRevE.89.013010 [70] Hiejima T. 2015a. A factor involved in efficient breakdown of supersonic streamwise vortices. Physics of Fluids, 27: 034103. doi: 10.1063/1.4914100 [71] Hiejima T. 2015b. Stability of compressible streamwise vortices. Physics of Fluids, 27: 074107. doi: 10.1063/1.4927484 [72] Hiejima T. 2020. Helicity effects on inviscid instability in batchelor vortices. Journal of Fluid Mechanics, 897: A37. doi: 10.1017/jfm.2020.388 [73] Houghton J T. 2002. The physics of atmospheres. Cambridge University Press. [74] Hu R, Li X, Yu C. 2022. Transfers of energy and helicity in helical rotating turbulence. Journal of Fluid Mechanics, 946: A19. doi: 10.1017/jfm.2022.580 [75] Hu R, Li X, Yu C. 2024. Effects of streamwise rotation on helicity and vortex in channel turbulence. Journal of Fluid Mechanics, 980: A50. doi: 10.1017/jfm.2024.37 [76] Huerre P, Monkewitz P A. 1990. Local and global instabilities in spatially developing flows. Annual Review of Fluid Mechanics, 22: 473-537. doi: 10.1146/annurev.fl.22.010190.002353 [77] Inagaki K. 2018. Modeling the effect of helicity on the transport of the Reynolds stress in rotating inhomogeneous turbulence. The University of Tokyo. [78] Irvine W T. 2018. Moreau’s hydrodynamic helicity and the life of vortex knots and links. Comptes Rendus. Mécanique, 346: 170-174. [79] Jadhav K, Chandy A J. 2021. Large eddy simulations of high-magnetic Reynolds number magnetohydrodynamic turbulence for non-helical and helical initial conditions: A study of two sub-grid scale models. Physics of Fluids, 33: 085131. doi: 10.1063/5.0060925 [80] Kadanoff L P, Lohse D, Wang J C, et al. 1994. Scaling and dissipation in the GOY shell model. Physics of Fluids, 7: 617-629. [81] Käpylä M J, Gent F A, Väisälä M S, et al. 2018. The supernova-regulated ISM-III. Generation of vorticity, helicity, and mean flows. Astronomy & Astrophysics, 611: A15. [82] Kessar M, Plunian F, Stepanov R, et al. 2015. Non-Kolmogorov cascade of helicity-driven turbulence. Physical Review E, 92: 031004. doi: 10.1103/PhysRevE.92.031004 [83] Kida S, Takaoka M. 1988. Reconnection of vortex tubes. Fluid Dynamics Research, 3: 257-261. doi: 10.1016/0169-5983(88)90075-5 [84] Kitamura T. 2021. Constant-energetics control-based forcing methods in isotropic helical turbulence. Physical Review Fluids, 6: 044608. doi: 10.1103/PhysRevFluids.6.044608 [85] Kivotides D, Leonard A. 2021. Helicity spectra and topological dynamics of vortex links at high Reynolds numbers. Journal of Fluid Mechanics, 911: A25. doi: 10.1017/jfm.2020.1003 [86] Kleckner D, Kauffman L H, Irvine W T. 2016. How superfluid vortex knots untie. Nature Physics, 12: 650-655. doi: 10.1038/nphys3679 [87] Kolmogorov A N. 1941. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Numbers. In Dokl. Akad. Nauk SSSR, 30: 301-305. [88] Koprov B M, Koprov V M, Kurgansky M V, et al. 2015. Helicity and potential vorticity in surface turbulence. Izvestiya, Atmospheric and Oceanic Physics, 51: 565-575. doi: 10.1134/S0001433815060092 [89] Koprov B M, Koprov V M, Ponomarev V M, et al. 2005. Experimental studies of turbulent helicity and its spectrum in the atmospheric boundary layer//Doklady Physics. Nauka/Interperiodica, 50: 419-422. [90] Kraichnan R H. 1967. Inertial ranges in two-dimensional turbulence. The Physics of fluids, 10: 1417-1423. doi: 10.1063/1.1762301 [91] Kraichnan R H. 1971. Inertial-range transfer in two-and three-dimensional turbulence. Journal of Fluid Mechanics, 47: 525-535. doi: 10.1017/S0022112071001216 [92] Kraichnan R H. 1973. Helical turbulence and absolute equilibrium. Journal of Fluid Mechanics, 59: 745-752. doi: 10.1017/S0022112073001837 [93] Kraichnan R H. 1974. On Kolmogorov’s inertial-range theories. Journal of Fluid Mechanics, 62: 305-330. doi: 10.1017/S002211207400070X [94] Kurien S, Taylor M A, Matsumoto T. 2004. Isotropic third-order statistics in turbulence with helicity: The 2/15-law. Journal of Fluid Mechanics, 515: 87-97. doi: 10.1017/S0022112004000424 [95] L’vov V S, Podivilov E, Pomyalov A, et al. 1998. Improved shell model of turbulence. Physical Review E, 58: 1811-1822. doi: 10.1103/PhysRevE.58.1811 [96] Laing C E, Ricca R L, Sumners D W L. 2015. Conservation of writhe helicity under anti-parallel reconnection. Scientific Reports, 5: 9224. doi: 10.1038/srep09224 [97] Langtry R. 2015. Extending the gamma-rethetat correlation based transition model for crossflow effects (Invited). [98] Lessinnes T, Plunian F, Carati D. 2009. Helical shell models for MHD. Theoretical and Computational Fluid Dynamics, 23: 439-450. [99] Levshin A, Chkhetiani O G. 2014. Decay of helicity in homogeneous turbulence. JETP letters, 98: 598-602. doi: 10.1134/S0021364013230070 [100] Li W, Liu Y. 2019. Evaluation of Spalart-Allmaras model with various modifications for predicting corner separation in a compressor cascade. [101] Li W, Liu Y. 2022. Numerical investigation of corner separation flow using Spalart-Allmaras model with various modifications. Aerospace Science and Technology, 127: 107682. doi: 10.1016/j.ast.2022.107682 [102] Li Y, Meneveau C, Chen S, et al. 2006. Subgrid-scale modeling of helicity and energy dissipation in helical turbulence. Physical Review E, 74: 026310. doi: 10.1103/PhysRevE.74.026310 [103] Liang H, Maxworthy T. 2005. An experimental investigation of swirling jets. Journal of Fluid Mechanics, 525: 115-159. doi: 10.1017/S0022112004002629 [104] Lilly D K. 1983. Stratified turbulence and the mesoscale variability of the atmosphere. Journal of the Atmospheric Sciences, 40: 749-761. doi: 10.1175/1520-0469(1983)040<0749:STATMV>2.0.CO;2 [105] Lilly D K. 1986. The structure, energetics and propagation of rotating convective storms. Part II: Helicity and storm stabilization. Journal of Atmospheric Sciences, 43: 126-140. doi: 10.1175/1520-0469(1986)043<0126:TSEAPO>2.0.CO;2 [106] Linkmann M. 2018. Effects of helicity on dissipation in homogeneous box turbulence. Journal of Fluid Mechanics, 856: 79-102. doi: 10.1017/jfm.2018.709 [107] Liu S, Meneveau C, Katz J. 1994. On the properties of similarity subgrid-scale models as deduced from measurements in a turbulent jet. Journal of Fluid Mechanics, 275: 83-119. doi: 10.1017/S0022112094002296 [108] Liu W, Qi H, Shi H, et al. 2023. Helical model based on artificial neural network for large eddy simulation of compressible wall-bounded turbulent flows. Physics of Fluids, 35: 045120. doi: 10.1063/5.0137607 [109] Liu Y, Lu L, Fang L, et al. 2011. Modification of Spalart-Allmaras model with consideration of turbulence energy backscatter using velocity helicity. Physics Letters A, 375: 2377-2381. doi: 10.1016/j.physleta.2011.05.023 [110] Liu Y, Tang Y, Scillitoe A D, et al. 2020. Modification of shear stress transport turbulence model using helicity for predicting corner separation flow in a linear compressor cascade. Journal of Turbomachinery, 142: 021004. doi: 10.1115/1.4045658 [111] Lucca-Negro O, O’doherty T. 2001. Vortex breakdown: A review. Progress in Energy and Combustion Science, 27: 431-481. doi: 10.1016/S0360-1285(00)00022-8 [112] Luginsland T, Gallaire F, Kleiser L. 2016. Impact of rotating and fixed nozzles on vortex breakdown in compressible swirling jet flows. European Journal of Mechanics-B/Fluids, 57: 214-230. doi: 10.1016/j.euromechflu.2016.01.006 [113] Marchand P, Tomida K, Commerçon B, et al. 2019. Impact of the Hall effect in star formation, improving the angular momentum conservation. Astronomy & Astrophysics, 631: A66. [114] Marino R, Sorriso-Valvo L. 2023. Scaling laws for the energy transfer in space plasma turbulence. Physics Reports, 1006: 1-144. doi: 10.1016/j.physrep.2022.12.001 [115] Marino R, Sorriso-Valvo L, D’amicis R, et al. 2012. On the occurrence of the third-order scaling in high latitude solar wind. The Astrophysical Journal, 750: 41. doi: 10.1088/0004-637X/750/1/41 [116] Melander M V, Hussain F. 1993. Polarized vorticity dynamics on a vortex column. Physics of Fluids A: Fluid Dynamics, 5: 1992-2003. doi: 10.1063/1.858826 [117] Melander M V, Hussain F. 1994. Core dynamics on a vortex column. Fluid Dynamics Research, 13: 1-37. doi: 10.1016/0169-5983(94)90061-2 [118] Meyrand R, Galtier S. 2012. Spontaneous chiral symmetry breaking of hall magnetohydrodynamic turbulence. Physical Review Letters, 109: 194501. doi: 10.1103/PhysRevLett.109.194501 [119] Milanese L M, Loureiro N F, Boldyrev S. 2021. Dynamic phase alignment in Navier-Stokes turbulence. Physical Review Letters, 127: 274501. doi: 10.1103/PhysRevLett.127.274501 [120] Mininni P D, Alexakis A, Pouquet A. 2009. Scale interactions and scaling laws in rotating flows at moderate Rossby numbers and large Reynolds numbers. Physics of Fluids, 21: 015108. doi: 10.1063/1.3064122 [121] Mininni P D, Pouquet A. 2009. Helicity cascades in rotating turbulence. Physical Review E, 79: 026304. doi: 10.1103/PhysRevE.79.026304 [122] Mininni P D, Rosenberg D, Pouquet A. 2012. Isotropization at small scales of rotating helically driven turbulence. Journal of Fluid Mechanics, 699: 263-279. doi: 10.1017/jfm.2012.99 [123] Moffatt H K. 1969. The degree of knottedness of tangled vortex lines. Journal of Fluid Mechanics, 35: 117-129. doi: 10.1017/S0022112069000991 [124] Moffatt H K. 2014. Helicity and singular structures in fluid dynamics. Proceedings of the National Academy of Sciences of the United States of America, 111: 3663-3670. [125] Moiseev S S, Chkhetiani O. 1996. Helical scaling in turbulence. Journal of Experimental and Theoretical Physics, 83: 192-198. [126] Montagud-Camps V, Hellinger P, Verdini A, et al. 2022. Quantification of the cross-helicity turbulent cascade in compressible MHD simulations. The Astrophysical Journal, 938: 90. doi: 10.3847/1538-4357/ac9281 [127] Moreau J J. 1961. Constantes d’un îlot tourbillonnaire en fluide parfait barotrope. Comptes rendus hebdomadaires des séances de l'Académie des sciences, 252: 2810-2812. [128] Morinishi Y, Nakabayashi K, Ren S. 2001. Effects of helicity and system rotation on decaying homogeneous turbulence. JSME International Journal Series B Fluids and Thermal Engineering, 44: 410-418. doi: 10.1299/jsmeb.44.410 [129] Moyal J E. 1952. The spectra of turbulence in a compressible fluid; eddy turbulence and random noise//Mathematical Proceedings of the Cambridge Philosophical Society. Cambridge University Press, 48: 329-344. [130] Müller-Schindewolffs C, Herbst F. 2014. Modelling of crossflow-induced transition based on local variables. [131] Müller S B, Kleiser L. 2008. Large-eddy simulation of vortex breakdown in compressible swirling jet flow. Computers & Fluids, 37: 844-856. [132] Müller W-C, Carati D. 2002. Dynamic gradient-diffusion subgrid models for incompressible magnetohydrodynamic turbulence. Physics of Plasmas, 9: 824-834. doi: 10.1063/1.1448498 [133] Müller W-C, Malapaka S K, Busse A. 2012. Inverse cascade of magnetic helicity in magnetohydrodynamic turbulence. Physical Review E, 85: 015302. doi: 10.1103/PhysRevE.85.015302 [134] Musacchio S, Boffetta G. 2017. Split energy cascade in turbulent thin fluid layers. Physics of Fluids, 29. [135] Norman C, Heyvaerts J. 1985. Anomalous magnetic field diffusion during star formation. Astronomy and Astrophysics, 147: 247-256. [136] Oberlack M. 2002. On the decay exponent of isotropic turbulence//PAMM: Proceedings in applied mathematics and mechanics. Wiley Online Library, 1: 294-297. [137] Panickacheril John J, Donzis D A, Sreenivasan K R. 2022. Laws of turbulence decay from direct numerical simulations. Philosophical Transactions of the Royal Society A, 380: 20210089. doi: 10.1098/rsta.2021.0089 [138] Paoletti M S, Lathrop D P. 2011. Quantum turbulence. Annual Review of Condensed Matter Physics, 2: 213-234. doi: 10.1146/annurev-conmatphys-062910-140533 [139] Pariat E, Wyper P, Linan L. 2023. Comparison of magnetic energy and helicity in coronal jet simulations. Astronomy & Astrophysics, 669: A33. [140] Pela A, Marconcini M, Arnone A, et al. 2023. On the feasibility of helicity-based corrections of turbulence models for improving RANS predictions of centrifugal compressor stages//turbo expo: Power for land, sea, and air. American Society of Mechanical Engineers, 87110: V13DT35A026. [141] Plunian F, Teimurazov A, Stepanov R, et al. 2020. Inverse cascade of energy in helical turbulence. Journal of Fluid Mechanics, 895: A13. doi: 10.1017/jfm.2020.307 [142] Polifke W. 1991. Statistics of helicity fluctuations in homogeneous turbulence. Physics of Fluids A: Fluid Dynamics, 3: 115-129. doi: 10.1063/1.857871 [143] Politano H, Gomez T, Pouquet A. 2003. von Kármán-Howarth relationship for helical magnetohydrodynamic flows. Physical Review E, 68 : 026315. [144] Politano H, Pouquet A. 1998. von Karman-Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Physical Review E, 57: R21-R24. doi: 10.1103/PhysRevE.57.R21 [145] Pope S B. 2001. Turbulent flows. Measurement Science and Technology, 12: 2020-2021. [146] Pouquet A, Marino R. 2013. Geophysical turbulence and the duality of the energy flow across scales. Physical Review Letters, 111: 1-5. [147] Qi H, Li X, Yu C. 2021. Subgrid-scale helicity equation model for large-eddy simulation of turbulent flows. Physics of Fluids, 33: 035128. doi: 10.1063/5.0038165 [148] Rathmann N M, Ditlevsen P D. 2016. Role of helicity in triad interactions in three-dimensional turbulence investigated by a new shell model. Physical Review E, 94: 033115. doi: 10.1103/PhysRevE.94.033115 [149] Richner N J, Bodner G M, Bongard M W, et al. 2022. Magnetic turbulence and current drive during local helicity injection. Physical Review Letters, 128: 105001. doi: 10.1103/PhysRevLett.128.105001 [150] Saffman P. 1967. The large-scale structure of homogeneous turbulence. Journal of Fluid Mechanics, 27: 581-593. doi: 10.1017/S0022112067000552 [151] Sagaut P. 2005. Large eddy simulation for incompressible flows: An introduction. Springer Science & Business Media. [152] Sahoo G, Biferale L. 2015. Disentangling the triadic interactions in Navier-Stokes equations. The European Physical Journal E, 38: 114. doi: 10.1140/epje/i2015-15114-4 [153] Sahoo G, Bonaccorso F, Biferale L. 2015. Role of helicity for large- and small-scale turbulent fluctuations. Physical Review E, 92: 051002. doi: 10.1103/PhysRevE.92.051002 [154] Sahoo G, De Pietro M, Biferale L. 2017. Helicity statistics in homogeneous and isotropic turbulence and turbulence models. Physical Review Fluids, 2: 024601. doi: 10.1103/PhysRevFluids.2.024601 [155] Scheeler M W, Kleckner D, Proment D, et al. 2014. Helicity conservation by flow across scales in reconnecting vortex links and knots. Proceedings of the National Academy of Sciences, 111: 15350-15355. doi: 10.1073/pnas.1407232111 [156] Scheeler M W, Van Rees W M, Kedia H, et al. 2017. Complete measurement of helicity and its dynamics in vortex tubes. Science, 357: 487-491. doi: 10.1126/science.aam6897 [157] Sharma M K, Verma M K, Chakraborty S. 2019. Anisotropic energy transfers in rapidly rotating turbulence. Physics of Fluids, 31: 085117. doi: 10.1063/1.5109856 [158] Shibata K, Magara T. 2011. Solar flares: Magnetohydrodynamic processes. Living Reviews in Solar Physics, 8: 6. [159] Siggia E D. 1985. Collapse and amplification of a vortex filament. The Physics of fluids, 28: 794-805. doi: 10.1063/1.865047 [160] Smagorinsky J. 1963. General circulation experiments with the primitive equations: I. The basic experiment. Monthly Weather Review, 91: 99-164. doi: 10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 [161] Smith C W, Stawarz J E, Vasquez B J, et al. 2009. Turbulent cascade at 1 AU in high cross-helicity flows. Physical Review Letters, 103: 201101. doi: 10.1103/PhysRevLett.103.201101 [162] Sommeria J. 1986. Experimental study of the two-dimensional inverse energy cascade in a square box. Journal of Fluid Mechanics, 170: 139-168. doi: 10.1017/S0022112086000836 [163] Sommeria J, Moreau R. 1982. Why, how, and when, MHD turbulence becomes two-dimensional. Journal of Fluid Mechanics, 118: 507-518. doi: 10.1017/S0022112082001177 [164] Stalp S R, Skrbek L, Donnelly R J. 1999. Decay of grid turbulence in a finite channel. Physical Review Letters, 82: 4831. doi: 10.1103/PhysRevLett.82.4831 [165] Suman S, Girimaji S S. 2010. Velocity gradient invariants and local flow-field topology in compressible turbulence. Journal of Turbulence, 11: N2. doi: 10.1080/14685241003604751 [166] Suman S, Girimaji S S. 2012. Velocity-gradient dynamics in compressible turbulence: Influence of Mach number and dilatation rate. Journal of Turbulence, 13: N8. doi: 10.1080/14685248.2011.649850 [167] Suman S, Girimaji S S. 2013. Velocity gradient dynamics in compressible turbulence: Characterization of pressure-Hessian tensor. Physics of Fluids, 25. [168] Sun W. 2022. Assessment of rans and sbes methods for the prediction of corner separation in axial flow compressors. [169] Sun W. 2023. Assessment of advanced RANS turbulence models for prediction of complex flows in compressors. Chinese Journal of Aeronautics, 36: 162-177. doi: 10.1016/j.cja.2023.06.007 [170] Tabeling P. 2002. Two-dimensional turbulence: A physicist approach. Physics Reports-review Section of Physics Letters-Phys Rep-rev Sect Phys Lett, 362: 1-62. [171] Teimurazov A S, Stepanov R A, Verma M K, et al. 2018. Direct numerical simulation of homogeneous isotropic helical turbulence with the TARANG code. Journal of Applied Mechanics and Technical Physics, 59: 1279-1287. doi: 10.1134/S0021894418070131 [172] Teitelbaum T, Mininni P D. 2009. Effect of helicity and rotation on the free decay of turbulent flows. Physical Review Letters, 103: 1-4. [173] Theobald M L, Fox P A, Sofia S. 1994. A subgrid-scale resistivity for magnetohydrodynamics. Physics of Plasmas, 1: 3016-3032. doi: 10.1063/1.870542 [174] Vallefuoco D, Naso A, Godeferd F S. 2018. Small-scale anisotropy induced by spectral forcing and by rotation in non-helical and helical turbulence. Journal of Turbulence, 19: 107-140. doi: 10.1080/14685248.2017.1400667 [175] Waleffe F. 1992. The nature of triad interactions in homogeneous turbulence. Physics of Fluids, 4: 350-363. doi: 10.1063/1.858309 [176] Waleffe F. 1993. Inertial transfers in the helical decomposition. Physics of Fluids A: Fluid Dynamics, 5: 677-685. doi: 10.1063/1.858651 [177] Wan M, Servidio S, Oughton S, et al. 2009. The third-order law for increments in magnetohydrodynamic turbulence with constant shear. Physics of Plasmas, 16: 090703. doi: 10.1063/1.3240333 [178] Wang J, Gotoh T, Watanabe T. 2017. Spectra and statistics in compressible isotropic turbulence. Physical Review Fluids, 2: 013403. doi: 10.1103/PhysRevFluids.2.013403 [179] Wang J, Shi Y, Wang L-P, et al. 2012. Scaling and statistics in three-dimensional compressible turbulence. Physical Review Letters, 108: 214505. doi: 10.1103/PhysRevLett.108.214505 [180] Wang J, Wang L P, Xiao Z, et al. 2010. A hybrid numerical simulation of isotropic compressible turbulence. Journal of Computational Physics, 229: 5257-5279. doi: 10.1016/j.jcp.2010.03.042 [181] Wu J-Z, Ma H-Y, Zhou M-D. 2015. Vortical flows. Springer. [182] Xiong S, Yang Y. 2019. Construction of knotted vortex tubes with the writhe-dependent helicity. Physics of Fluids, 31: 047101. doi: 10.1063/1.5088015 [183] Yamada M, Ohkitani K. 1988. The inertial subrange and non-positive Lyapunov exponents in fully-developed turbulence. Progress of Theoretical Physics, 79: 1265-1268. doi: 10.1143/PTP.79.1265 [184] Yan Z, Li X, Wang J, et al. 2019. Effect of pressure on joint cascade of kinetic energy and helicity in compressible helical turbulence. Physical Review E, 99: 033114. doi: 10.1103/PhysRevE.99.033114 [185] Yan Z, Li X, Yu C. 2020a. Scale locality of helicity cascade in physical space. Physics of Fluids, 32: 061705. doi: 10.1063/5.0013009 [186] Yan Z, Li X, Yu C, et al. 2020b. Cross-chirality transfer of kinetic energy and helicity in compressible helical turbulence. Physical Review Fluids, 5: 084604. doi: 10.1103/PhysRevFluids.5.084604 [187] Yang X, Domaradzki J A. 2004. Large eddy simulations of decaying rotating turbulence. Physics of Fluids, 16: 4088-4104. doi: 10.1063/1.1790452 [188] Yan Z, Li X, Yu C, Wang J, Shen S. 2022c. Dual channels of helicity cascade in turbulent flows. Journal of Fluid Mechanics, 894: R2 [189] Yang Y, Ostilla-Mónico R, Wu J, et al. 2015. Inertial waves and mean velocity profiles in a rotating pipe and a circular annulus with axial flow. Physical Review E-Statistical, Nonlinear, and Soft Matter Physics, 91: 1-7. [190] Yang Y, Zhu J-Z. 2022. Turbulence compressibility reduction with helicity. Physics of Fluids, 34: 045113. doi: 10.1063/5.0089333 [191] Yang Y T, Su W D, Wu J Z. 2010. Helical-wave decomposition and applications to channel turbulence with streamwise rotation. Journal of Fluid Mechanics, 662: 91-122. doi: 10.1017/S0022112010003071 [192] Yang Y T, Wu J Z. 2012. Channel turbulence with spanwise rotation studied using helical wave decomposition. Journal of Fluid Mechanics, 692: 137-152. doi: 10.1017/jfm.2011.500 [193] Yao D, Xue H, Yin J, et al. 2018. Investigation into the formation, structure, and evolution of an EF4 tornado in east china using a high-resolution numerical simulation. Journal of Meteorological Research, 32: 157-171. doi: 10.1007/s13351-018-7083-0 [194] Yao J, Hussain F. 2021. Polarized vortex reconnection. Journal of Fluid Mechanics, 922: A19. doi: 10.1017/jfm.2021.517 [195] Yao J, Hussain F. 2022. Vortex reconnection and turbulence cascade. Annual Review of Fluid Mechanics, 54: 317-347. doi: 10.1146/annurev-fluid-030121-125143 [196] Yao J, Yang Y, Hussain F. 2021. Dynamics of a trefoil knotted vortex. Journal of Fluid Mechanics, 923: A19. doi: 10.1017/jfm.2021.580 [197] Yeung P K, Zhou Y. 1998. Numerical study of rotating turbulence with external forcing. Physics of Fluids, 10: 2895-2909. doi: 10.1063/1.869810 [198] Yokoi N, Brandenburg A. 2016. Large-scale flow generation by inhomogeneous helicity. Physical Review E, 93: 033125. doi: 10.1103/PhysRevE.93.033125 [199] Yokoi N, Yoshizawa A. 1993. Statistical analysis of the effects of helicity in inhomogeneous turbulence. Physics of Fluids A: Fluid Dynamics, 5: 464-477. doi: 10.1063/1.858869 [200] Yu C, Hong R, Xiao Z, et al. 2013. Subgrid-scale eddy viscosity model for helical turbulence. Physics of Fluids, 25: 095101. doi: 10.1063/1.4819765 [201] Yu C, Hu R, Yan Z, et al. 2022. Helicity distributions and transfer in turbulent channel flows with streamwise rotation. Journal of Fluid Mechanics, 940: A18. doi: 10.1017/jfm.2022.250 [202] Yu C, Xiao Z. 2013. Refined subgrid-scale model for large-eddy simulation of helical turbulence. Physical Review E, 87: 013006. doi: 10.1103/PhysRevE.87.013006 [203] Yu C, Xiao Z, Shi Y, et al. 2014. Joint-constraint model for large-eddy simulation of helical turbulence. Physical Review E, 89: 043021. doi: 10.1103/PhysRevE.89.043021 [204] Yu Z, Defoe J. 2024. Validation of helicity-corrected Spalart-Allmaras model for corner separation prediction in incompressible flow with OpenFOAM. Journal of the Global Power and Propulsion Society, 8: 73-83. doi: 10.33737/jgpps/186057 [205] Yu Z, Raza H, Defoe J. 2023. Assessment of fan stall point identification ability of steady RANS computations with the helicity-corrected Spalart-Allmaras turbulence model//Turbo Expo: Power for land, sea, and air. American Society of Mechanical Engineers, 87103 [206] Zhao X, Scalo C. 2021. Helicity dynamics in reconnection events of topologically complex vortex flows. Journal of Fluid Mechanics, 920: A30. doi: 10.1017/jfm.2021.455 [207] Zhou H, Li X, Qi H, et al. 2019a. Subgrid-scale model for large-eddy simulation of transition and turbulence in compressible flows. Physics of Fluids, 31. [208] Zhou H, Li X, Qi H, et al. 2019b. Subgrid-scale model for large-eddy simulation of transition and turbulence in compressible flows. Physics of Fluids, 31: 125118. doi: 10.1063/1.5128061 [209] Zhou Y. 1995. A phenomenological treatment of rotating turbulence. Physics of Fluids, 7: 2092-2094. doi: 10.1063/1.868457 [210] Zhu J-Z. 2021. Compressible helical turbulence: Fastened-structure geometry and statistics. Physics of Plasmas, 28: 032302. doi: 10.1063/5.0031108 [211] Zuccher S, Ricca R L. 2015. Helicity conservation under quantum reconnection of vortex rings. Physical Review E, 92: 061001. doi: 10.1103/PhysRevE.92.061001 [212] Zuccher S, Ricca R L. 2017. Relaxation of twist helicity in the cascade process of linked quantum vortices. Physical Review E, 95: 053109. doi: 10.1103/PhysRevE.95.053109 [213] Zuccher S, Ricca R L. 2018. Twist effects in quantum vortices and phase defects. Fluid Dynamics Research, 50: 011414. doi: 10.1088/1873-7005/aa8164 [214] Zweibel E G, Yamada M. 2009. Magnetic reconnection in astrophysical and laboratory plasmas. Annual Review of Astronomy and Astrophysics, 47: 291-332. doi: 10.1146/annurev-astro-082708-101726 -




 下载:
下载: