近场动力学在断裂力学领域的研究进展

张恒; 张雄; 乔丕忠

doi:10.6052/1000-0992-22-023

近场动力学在断裂力学领域的研究进展

doi: 10.6052/1000-0992-22-023

张恒¹,
张雄^1, ,,
乔丕忠^2, ,

1.
清华大学航天航空学院, 北京 100084
2.
上海交通大学海洋工程国家重点实验室和船舶海洋与建筑工程学院, 上海 200240

基金项目: 国家自然科学基金 (12172192, 11972224, 12102226)、中国博士后科学基金 (2021M691798) 资助项目.

详细信息

作者简介:
张雄, 清华大学航天航空学院长聘教授, 主要从事强冲击载荷作用下材料与结构力学行为数值分析方法的研究. 2004年入选教育部首批新世纪优秀人才支持计划, 获北京市高等学校教学名师奖、教育部自然科学奖二等奖和一等奖、北京市教育创新标兵、钱令希计算力学成就奖、ICACM Computational Mechanics Award和Fellows Award等奖励. 兼任北京振动工程学会副理事长、《International Journal of Mechanics and Materials in Design》副主编和多本国内外期刊编委. 已出版专著4部、教材3部, 发表期刊论文150余篇, 自2015年连续入选爱思唯尔中国高被引学者榜单, 1篇论文入选2012年度中国百篇最具影响国内学术论文. 出版了国内首部《无网格法》专著、国际首部《物质点法》专著及其英文版, 研发了三维显式并行物质点法数值仿真软件MPM3D, 已成功应用于多个实际工程问题中

乔丕忠, 上海交通大学“致远”讲席教授, 国家特聘专家, 教育部长江学者特聘教授; 美国土木工程协会会士 (ASCE Fellow) 和工程力学院会士 (EMI Fellow). 主要从事先进结构材料与力学的研究, 尤其致力于复合、智能和高性能材料在航空航天和土木水利工程中的发展和应用. 首次提出双层梁剪切和界面变形理论 (被波音公司命名为“乔方法”), 拓展了断裂力学的适用空间; 创建了离散板理论及结构局部稳定显式解, 已被航空业成功用于结构分析; 创新地提出了以剪切变形角为变量参数的板壳结构后屈曲分析方法, 为复材结构非线性大变形分析提供了理论基础; 研究了智能材料用于结构健康监测的关键性基础问题并发展了损伤识别的新理论与方法; 提出了几种破坏模型, 提升了复合材料对传统结构加固和修复的理论研究水平; 给出了态基近场动力学临界伸长准则与断裂释放能表达式, 推动了计算断裂力学的发展; 建立了近场动力学临界歪斜 (critical skew) 准则, 为II型断裂和剪切变形提供了分析手段. 现任《Journal of Engineering Mechanics》《 Journal of Aerospace Engineering》和《Structural Health Monitoring-An International Journal》三个国际期刊副主编和《力学季刊》副主编

通讯作者:
qiao@sjtu.edu.cn

xzhang@tsinghua.edu.cn

中图分类号: O34
计量
- 文章访问数: 3151
- HTML全文浏览量: 685
- PDF下载量: 758
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-02
- 录用日期: 2022-07-11
- 网络出版日期: 2022-07-12
- 刊出日期: 2022-12-29

Advances of peridynamics in fracture mechanics

ZHANG Heng¹,
ZHANG Xiong^{1
, ,},
QIAO Pizhong^{2
, ,}

1.
School of Aerospace, Tsinghua University, Beijing 100084, China
2.
State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

More Information

Corresponding author: qiao@sjtu.edu.cn; xzhang@tsinghua.edu.cn

摘要

摘要: 近场动力学采用非局部积分计算节点内力, 利用统一数学框架描述空间连续与非连续, 避免了非连续区局部空间导数引起的应力奇异, 数值上具有无网格属性, 可自然模拟材料结构的断裂问题. 本文概述了近场动力学的弹性本构力模型, 系统介绍了近场动力学临界伸长率、临界能量密度以及材料强度相关的键失效准则. 详细介绍了近场动力学在断裂力学领域的研究进展, 包括断裂参数能量释放率与应力强度因子的求解、J积分、混合型裂纹、弹塑性断裂、黏聚力模型、动态断裂、材料界面断裂以及疲劳裂纹扩展等. 最后讨论了断裂问题近场动力学研究的发展方向.
- 近场动力学 /
- 断裂力学 /
- 裂纹扩展 /
- 键失效
Abstract: In peridynamics, nonlocal integrals are proposed to calculate the node internal forces, and a unified mathematical framework is utilized to describe spatial continuity and discontinuity, which thus avoid the stress singularity caused by the local spatial derivative in the discontinuous region. Numerical peridynamic models have meshfree property, which is naturally capable of analyzing the fracture problems. In this paper, the elastic peridynamic model is briefly introduced, and the critical stretch, critical energy density, and strength-based peridynamic bond failure criteria are successively presented. Then, the research advances of peridynamics in the field of fracture mechanics are systematically introduced, including the computations of energy release rate and stress intensity factor, J integral, mixed-mode crack fracture, elastoplastic fracture, cohesive zone model, dynamic fracture, hybrid material interface fracture, and fatigue crack growth. Finally, the prospects for further research of peridynamics in fracture mechanics is provided.
- peridynamics /
- fracture mechanics /
- crack growth /
- bond failure.

HTML全文

图 1 常规态近场动力学模型.

下载: 全尺寸图片幻灯片

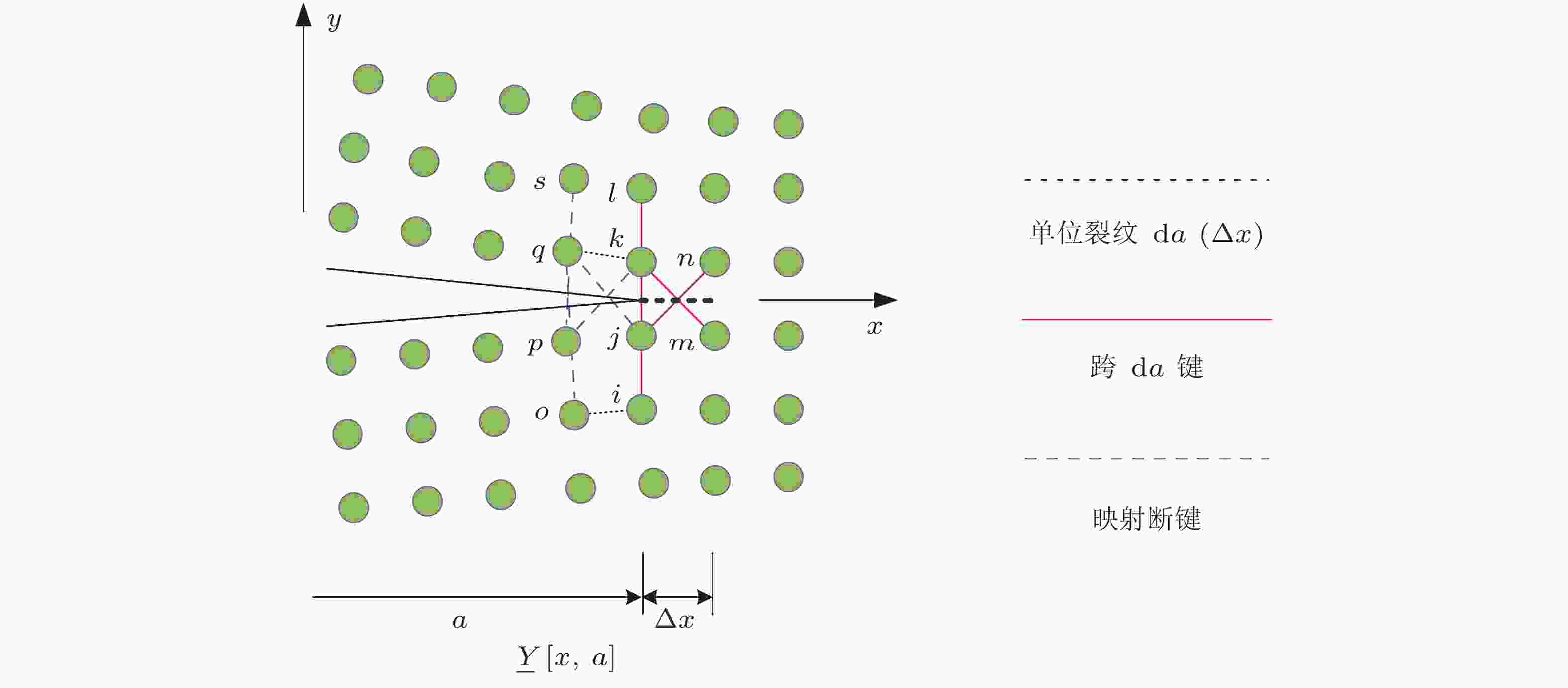
图 2 近场动力学虚拟裂纹闭合技术 (Zhang H & Qiao 2020c).

下载: 全尺寸图片幻灯片

图 3 近场动力学J积分 (Hu W K et al. 2012a).

下载: 全尺寸图片幻灯片

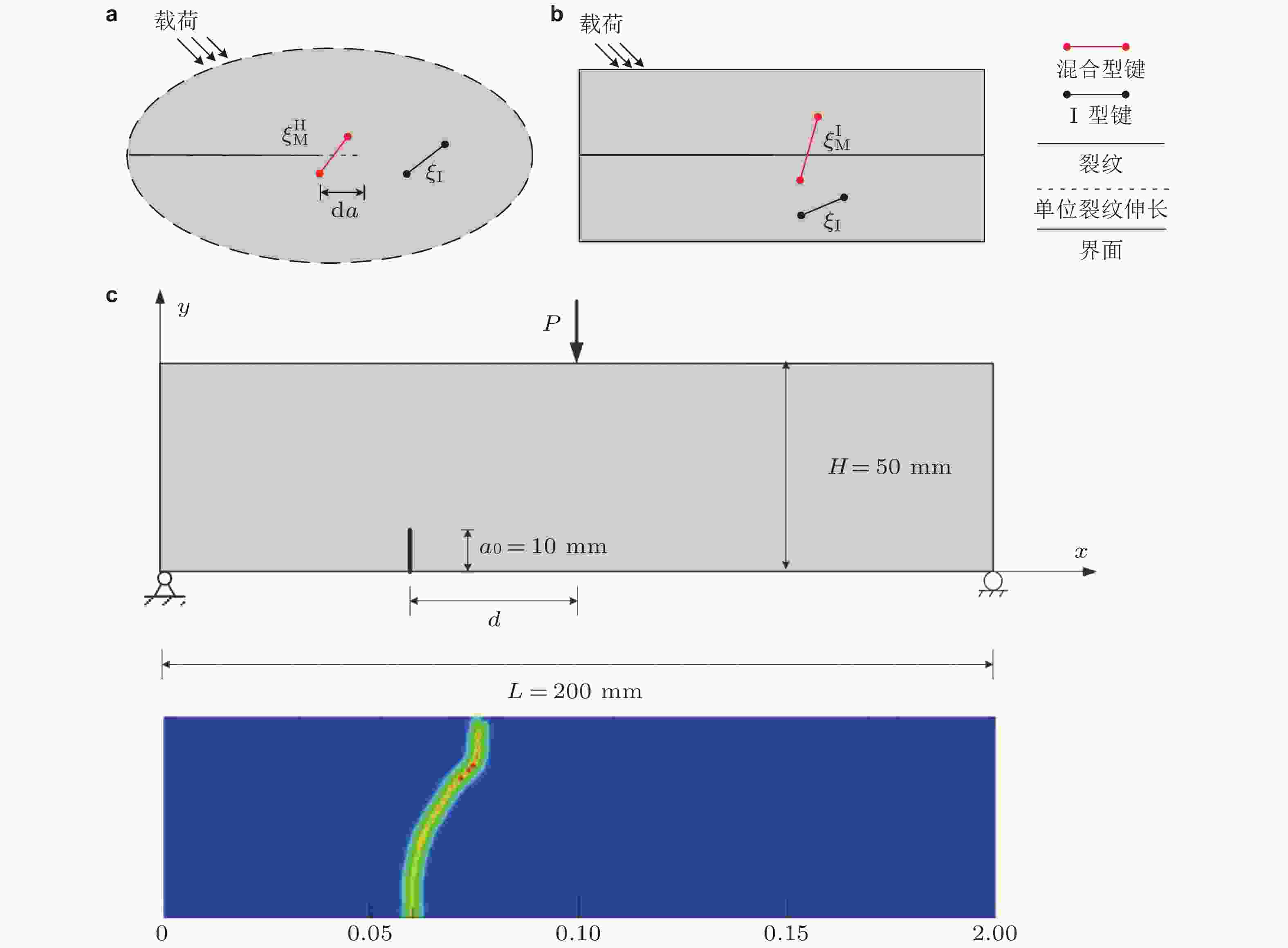
图 4 混合型裂纹的近场动力学模型 (Zhang H et al. 2021). (a) 各向同性材料, (b) 材料界面, (c) 应用展示.

下载: 全尺寸图片幻灯片

图 5 位移载荷下弹塑性材料断裂中的等效应力分布 (Madenci & Oterkus 2016). (a) u = 0.0025 m, (b) u = 0.003 m; (c) u = 0.0035 m, (d) u = 0.004 m.

下载: 全尺寸图片幻灯片

图 6 传统断裂力学和近场动力学粘聚力模型. (a) 传统断裂力学粘聚力模型, (b) 近场动力学粘聚力模型 (Yang et al. 2018).

下载: 全尺寸图片幻灯片

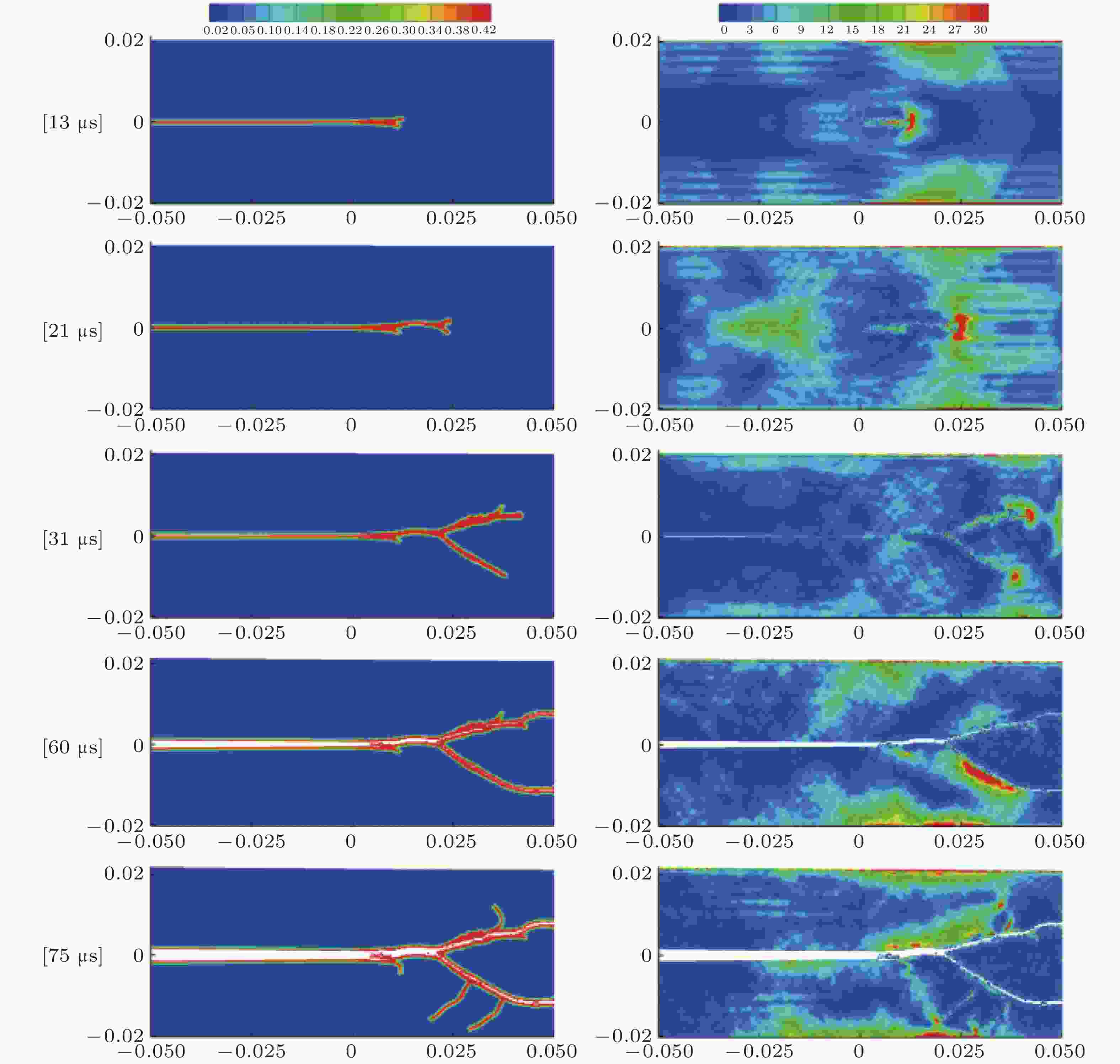
图 7 应力载荷σ = 23 MPa下不同时刻裂纹动态扩展和分叉以及应变能密度分布 (Ha & Bobaru 2011).

下载: 全尺寸图片幻灯片

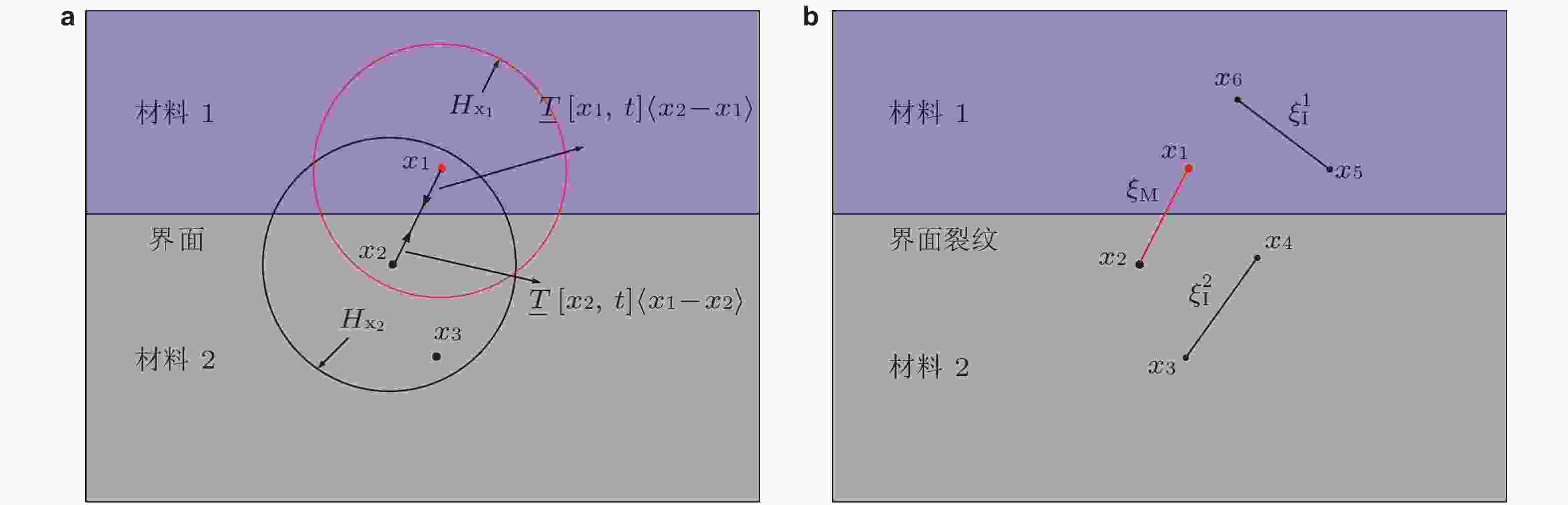
图 8 双弹性材料界面的近场动力学模型 (Zhang H et al. 2022). (a) 材料界面非局部力传递, (b) 近场动力学跨界面键与母材内部键.

下载: 全尺寸图片幻灯片

图 9 近场动力学疲劳模型 (Silling & Askari 2014). (a) 裂纹尖端近场动力学键, (b) 近场动力学疲劳模型参数校正.

下载: 全尺寸图片幻灯片

表 1 不同维度下常规态近场动力学弹性本构力模型


问题维度	力密度函数 t	体积膨胀量 θ	弹性参数 κ	弹性参数 α
三维	$ 3\dfrac{{\underline {\omega x} }}{q}\kappa \theta + \alpha \underline {\omega e} $	$ 3\dfrac{{\underline {\omega x} \cdot \underline e }}{q} $	$ \dfrac{E}{{3\left( {1 - 2v} \right)}} - \dfrac{{5\mu }}{3} $	$ \dfrac{{15\mu }}{q} $
平面应力	$ 2\dfrac{{\underline {\omega x} }}{q}\kappa \theta + \alpha \underline {\omega e} $	$ 2\dfrac{{\underline {\omega x} \cdot \underline e }}{q} $	$ \dfrac{E}{{2\left( {1 - v} \right)}} - 2\mu $	$ \dfrac{{8\mu }}{q} $
平面应变	$ 2\dfrac{{\underline {\omega x} }}{q}\kappa \theta + \alpha \underline {\omega e} $	$ 2\dfrac{{\underline {\omega x} \cdot \underline e }}{q} $	$ \dfrac{E}{{2\left( {1 + v} \right)\left( {1 - 2v} \right)}} - 2\mu $	$ \dfrac{{8\mu }}{q} $
一维	$ \alpha \underline {\omega e} $	$ \dfrac{{\underline {\omega x} \cdot \underline e }}{q} $	0	$\dfrac{E}{q}$

下载: 导出CSV

参考文献(109)

黄丹, 章青, 乔丕忠, 沈峰. 2010. 近场动力学方法及其应用. 力学进展, 40: 448-459 (Huang D, Zhang Q, Qiao P Z, Shen F. 2010. A review on peridynamics (PD) method and its application. Advances in Mechanics, 40: 448-459). doi: 10.6052/1000-0992-2010-4-J2010-002

乔丕忠, 张勇, 张恒, 张律文. 2017. 近场动力学研究进展. 力学季刊, 38: 1-13 (Qiao P Z, Zhang Y, Zhang H, Zhang L W. 2017. A review on advances in peridynamics. Chinese Quarterly of Mechanics, 38: 1-13).

顾鑫, 章青, Erdogan M. 2019. 多物理场耦合作用分析的近场动力学理论与方法. 力学进展, 49: 576-598 (Gu X, Zhang Q, Madenci E. 2019. Review of peridynamics for multi-physics coupling modeling. Advances in Mechanics, 49: 576-598).

Agwai A, Guven I. 2011. Predicting crack propagation with peridynamics : a comparative study. International Journal of Fracture, 171: 65-78. doi: 10.1007/s10704-011-9628-4

Alali B, Gunzburger M. 2015. Peridynamics and Material Interfaces. Journal of Elasticity, 120: 225-248.

Anh H, Hanlin N, Satoyuki W, et al. 2022. An in-depth investigation of bimaterial interface modeling using ordinary state-based peridynamics. Journal of Peridynamics and Nonlocal Modeling, 4: 112-138. doi: 10.1007/s42102-021-00058-x

Asgari M, Kouchakzadeh M A. 2019. An equivalent von Mises stress and corresponding equivalent plastic strain for elastic–plastic ordinary peridynamics. Meccanica, 54: 1001-1014. doi: 10.1007/s11012-019-00975-8

Bang D J, Ince A, Oterkus E, Oterkus S. 2021. Crack growth modeling and simulation of a peridynamic fatigue model based on numerical and analytical solution approaches. Theoretical and Applied Fracture Mechanics, 114: 103026. doi: 10.1016/j.tafmec.2021.103026

Behera D, Roy P, Madenci E. 2021. Peridynamic modeling of bonded-lap joints with viscoelastic adhesives in the presence of finite deformation. Computer Methods in Applied Mechanics and Engineering, 374: 113584. doi: 10.1016/j.cma.2020.113584

Caimmi F, Haddadi E, Choupani N, et al. 2016. Modelling mixed-mode fracture in poly(methylmethacrylate) using peridynamics. Procedia Structural Integrity, 2: 166-173. doi: 10.1016/j.prostr.2016.06.022

Cheng Z Q, Zhang G F, Wang Y N, Bobaru F. 2015. A peridynamic model for dynamic fracture in functionally graded materials. Composite Structures, 133: 529-546. doi: 10.1016/j.compstruct.2015.07.047

Chu B F, Liu Q W, Liu L S, et al. 2020. A rate-dependent peridynamic model for the dynamic behavior of ceramic materials. CMES - Computer Modeling in Engineering and Sciences, 124: 151-178. doi: 10.32604/cmes.2020.010115

Dai M J, Tanaka S, Oterkus S, Oterkus E. 2021. Mixed-mode stress intensity factors evaluation of flat shells under in-plane loading employing ordinary state-based peridynamics. Theoretical and Applied Fracture Mechanics, 112: 102841. doi: 10.1016/j.tafmec.2020.102841

Diehl P, Prudhomme S, Lévesque M. 2019. A review of benchmark experiments for the validation of peridynamics models. Journal of Peridynamics and Nonlocal Modeling, 1: 14-35. doi: 10.1007/s42102-018-0004-x

Dipasquale D, Zaccariotto M, Galvanetto U. 2014. Crack propagation with adaptive grid refinement in 2D peridynamics. International Journal of Fracture, 190: 1-22. doi: 10.1007/s10704-014-9970-4

Dipasquale D, Sarego G, Zaccariotto M, Galvanetto U. 2017. A discussion on failure criteria for ordinary state-based peridynamics. Engineering Fracture Mechanics, 186: 378-398. doi: 10.1016/j.engfracmech.2017.10.011

Foster J T, Silling S A, Chen W N. 2011. An energy based failure criterion for use with peridynamic states. International Journal for Multiscale Computational Engineering, 9: 675-687. doi: 10.1615/IntJMultCompEng.2011002407

Gerstle W, Sau N, Silling S A. 2005. Peridynamic modeling of plain and reinforced concrete structures//18th International Conference on Structural Mechanics in Reactor Technology (SMiRT 18), Beijing.

Ghajari M, Iannucci L, Curtis P. 2014. A peridynamic material model for the analysis of dynamic crack propagation in orthotropic media. Computer Methods in Applied Mechanics and Engineering, 276: 431-452. doi: 10.1016/j.cma.2014.04.002

Gui Y J, Yu Y, Hu Y L, et al. 2021. A peridynamic cohesive zone model for composite laminates. Journal of Peridynamics and Nonlocal Modeling, 3: 383-409. doi: 10.1007/s42102-021-00052-3

Ha Y D, Bobaru F. 2010. Studies of dynamic crack propagation and crack branching with peridynamics. International Journal of Fracture, 162: 229-244. doi: 10.1007/s10704-010-9442-4

Ha Y D, Bobaru F. 2011. Characteristics of dynamic brittle fracture captured with peridynamics. Engineering Fracture Mechanics, 78: 1156-1168. doi: 10.1016/j.engfracmech.2010.11.020

Han F, Lubineau G, Azdoud Y, Yan A. 2016. Adaptive coupling between damage mechanics and peridynamics: A route for objective simulation of material degradation up to complete failure. Journal of the Mechanics and Physics of Solids, 94: 453-472. doi: 10.1016/j.jmps.2016.05.017

Hattori G, Trevelyan J, Coombs W M. 2018. A non-ordinary state-based peridynamics framework for anisotropic materials. Computer Methods in Applied Mechanics and Engineering, 339: 416-442. doi: 10.1016/j.cma.2018.05.007

Hong K, Oterkus S, Oterkus E. 2021. Peridynamic analysis of fatigue crack growth in fillet welded joints. Ocean Engineering, 235: 109348.

Hu W K, Ha Y D, Bobaru F, Silling S A. 2012a. The formulation and computation of the nonlocal J-integral in bond-based peridynamics. International Journal of Fracture, 176: 195-206. doi: 10.1007/s10704-012-9745-8

Hu W K, Ha Y D, Bobaru F. 2012b. Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites. Computer Methods in Applied Mechanics and Engineering, 217–220: 247–261.

Hu Y L, De Carvalho N V, Madenci E. 2015. Peridynamic modeling of delamination growth in composite laminates. Composite Structures, 132: 610-620. doi: 10.1016/j.compstruct.2015.05.079

Hu Y L, Madenci E. 2017. Peridynamics for fatigue life and residual strength prediction of composite laminates. Composite Structures, 160: 169-184. doi: 10.1016/j.compstruct.2016.10.010

Imachi M, Tanaka S, Bui T Q, et al. 2019. A computational approach based on ordinary state-based peridynamics with new transition bond for dynamic fracture analysis. Engineering Fracture Mechanics, 206: 359-374. doi: 10.1016/j.engfracmech.2018.11.054

Imachi M, Tanaka S, Quoc T, Bui T Q. 2018. Mixed-mode dynamic stress intensity factors evaluation using ordinary state-based peridynamics. Theoretical and Applied Fracture Mechanics, 93: 97-104. doi: 10.1016/j.tafmec.2017.07.008

Imachi M, Tanaka S, Ozdemir M, et al. 2020. Dynamic crack arrest analysis by ordinary state-based peridynamics. International Journal of Fracture, 221: 155-169.

Isiet M, Mišković I, Mišković S. 2021. Review of peridynamic modelling of material failure and damage due to impact. International Journal of Impact Engineering, 147: 103740. doi: 10.1016/j.ijimpeng.2020.103740

Javili A, McBride A T, Mergheim J, Steinmann P. 2021. Towards elasto-plastic continuum-kinematics-inspired peridynamics. Computer Methods in Applied Mechanics and Engineering, 380: 113809. doi: 10.1016/j.cma.2021.113809

Jung J, Seok J. 2016. Fatigue crack growth analysis in layered heterogeneous material systems using peridynamic approach. Composite Structures, 152: 403-407. doi: 10.1016/j.compstruct.2016.05.077

Jung J, Seok J. 2017. Mixed-mode fatigue crack growth analysis using peridynamic approach. International Journal of Fatigue, 103: 591-603. doi: 10.1016/j.ijfatigue.2017.06.008

Kilic B. 2008. Peridynamic theory for progressive failure prediction in homogeneous and heterogeneous materials. [PhD Thesis]. Tucson: The University of Arizona.

Le Q V, Chan W K, Schwartz J. 2014. A two-dimensional ordinary, state-based peridynamic model for linearly elastic solids. International Journal for Numerical Methods in Engineering, 98: 547-561. doi: 10.1002/nme.4642

Li H X, Hao Z M, Li P, et al. 2022. A low cycle fatigue cracking simulation method of non-ordinary state-based peridynamics. International Journal of Fatigue, 156: 106638. doi: 10.1016/j.ijfatigue.2021.106638

Liu B C, Wang K, Bao R, Sui F. 2020. The effects of α/β phase interfaces on fatigue crack deflections in additively manufactured titanium alloy: A peridynamic study. International Journal of Fatigue, 137: 105622. doi: 10.1016/j.ijfatigue.2020.105622

Liu Y X, Liu L S, Mei H, et al. 2022. A modified rate-dependent peridynamic model with rotation effect for dynamic mechanical behavior of ceramic materials. Computer Methods in Applied Mechanics and Engineering, 388: 114246. doi: 10.1016/j.cma.2021.114246

Liu Z M, Bie Y H, Cui Z Q, Cui X Y. 2020. Ordinary state-based peridynamics for nonlinear hardening plastic materials’ deformation and its fracture process. Engineering Fracture Mechanics, 223: 106782. doi: 10.1016/j.engfracmech.2019.106782

Ma X C, Wang L, Xu J H, et al. 2022. A two-dimensional ordinary state-based peridynamic model for surface fatigue crack propagation in railheads. Engineering Fracture Mechanics, 265: 108362. doi: 10.1016/j.engfracmech.2022.108362

Macek R W, Silling S A. 2007. Peridynamics via finite element analysis. Finite Elements in Analysis and Design, 43: 1169-1178. doi: 10.1016/j.finel.2007.08.012

Madenci E. 2017. Peridynamic integrals for strain invariants of homogeneous deformation. Zeitschrift fur Angewandte Mathematik und Mechanik, 97: 1236-1251. doi: 10.1002/zamm.201600242

Madenci E, Barut A, Phan N. 2021. Bond-based peridynamics with stretch and rotation kinematics for opening and shearing modes of fracture. Journal of Peridynamics and Nonlocal Modeling, 3: 211-254. doi: 10.1007/s42102-020-00049-4

Madenci E, Colavito K, Phan N. 2016. Peridynamics for unguided crack growth prediction under mixed-mode loading. Engineering Fracture Mechanics, 167: 34-44. doi: 10.1016/j.engfracmech.2016.04.009

Madenci E, Oterkus E. 2015. Peridynamic Theory and Its Applications. New York: Springer.

Madenci E, Oterkus S. 2016. Ordinary state-based peridynamics for plastic deformation according to von Mises yield criteria with isotropic hardening. Journal of the Mechanics and Physics of Solids, 86: 192-219. doi: 10.1016/j.jmps.2015.09.016

Madenci E, Roy P, Behera D. 2022. Advances in Peridynamics. Springer Nature.

Mitchell J A. 2011. A nonlocal, ordinary, state-based plasticity model for peridynamics. SAND2011-3166, Sandia National Laboratories, Albuquerque.

Mousavi F, Jafarzadeh S, Bobaru F. 2021. An ordinary state-based peridynamic elastoplastic 2D model consistent with J2 plasticity. International Journal of Solids and Structures, 229: 111146. doi: 10.1016/j.ijsolstr.2021.111146

Nguyen C T, Oterkus S, Oterkus E. 2021. An energy-based peridynamic model for fatigue cracking. Engineering Fracture Mechanics, 241: 107373. doi: 10.1016/j.engfracmech.2020.107373

Ni T, Zhu Q Z, Zhao L Y, Li P F. 2018. Peridynamic simulation of fracture in quasi brittle solids using irregular finite element mesh. Engineering Fracture Mechanics, 188: 320-343. doi: 10.1016/j.engfracmech.2017.08.028

Oterkus E, Guven I, Madenci E. 2010. Fatigue failure model with peridynamic theory//12th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, Las Vegas.

Oterkus E, Madenci E. 2012. Peridynamic analysis of fiber-reinforced composite materials. Journal of Mechanics of Materials and Structures, 7: 45-84. doi: 10.2140/jomms.2012.7.45

Oterkus S, Madenci E. 2015. Peridynamics for antiplane shear and torsional deformations. Journal of Mechanics of Materials and Structures, 10: 167-193. doi: 10.2140/jomms.2015.10.167

Ozdemir M, Akb C, Mi D, et al. 2020. Dynamic fracture analysis of functionally graded materials using ordinary state-based peridynamics. Composite Structures, 244: 112296. doi: 10.1016/j.compstruct.2020.112296

Panchadhara R, Gordon P A. 2016. Application of peridynamic stress intensity factors to dynamic fracture initiation and propagation. International Journal of Fracture, 201: 81-96. doi: 10.1007/s10704-016-0124-8

Qin M Q, Yang D S, Chen W Z, Yang S Q. 2021. Hydraulic fracturing model of a layered rock mass based on peridynamics. Engineering Fracture Mechanics, 258: 108088. doi: 10.1016/j.engfracmech.2021.108088

Rahaman M M, Roy P, Roy D, et al. 2017. A peridynamic model for plasticity: Micro-inertia based flow rule, entropy equivalence and localization residuals. Computer Methods in Applied Mechanics and Engineering, 327: 369-391. doi: 10.1016/j.cma.2017.07.034

Ren H L, Zhuang X Y, Rabczuk T. 2016. A new peridynamic formulation with shear deformation for elastic solid. Journal of Micromechanics and Molecular Physics, 1: 1-24.

Rossi C N, Invaldi M A, Barrios D R, Iturrioz I. 2019. An alternative bilinear peridynamic model to simulate the damage process in quasi-brittle materials. Engineering Fracture Mechanics, 216: 106494. doi: 10.1016/j.engfracmech.2019.106494

Seleson P, Gunzburger M, Parks M L. 2013. Interface problems in nonlocal diffusion and sharp transitions between local and nonlocal domains. Computer Methods in Applied Mechanics and Engineering, 266: 185-204. doi: 10.1016/j.cma.2013.05.018

Shojaei A, Mossaiby F, Zaccariotto M, Galvanetto U. 2018. An adaptive multi-grid peridynamic method for dynamic fracture analysis. International Journal of Mechanical Sciences, 144: 600-617. doi: 10.1016/j.ijmecsci.2018.06.020

Silling S A. 2000. Reformulation of elasticity theory for discontinuities and long-range forces. Journal of the Mechanics and Physics of Solids, 48: 175-209. doi: 10.1016/S0022-5096(99)00029-0

Silling S A. 2003. Dynamic fracture modeling with a meshfree peridynamic code//Bathe KJ (ed) Computational fluid and solid mechanics 2003, Amsterdam, 641–644.

Silling S A, Askari A. 2014. Peridynamic model for fatigue cracks. SAND2014-18590, Sandia National Laboratories, Albuquerque.

Silling S A, Askari E. 2005. A meshfree method based on the peridynamic model of solid mechanics. Computers and Structures, 83: 1526-1535. doi: 10.1016/j.compstruc.2004.11.026

Silling S A, Epton M, Weckner O, et al. 2007. Peridynamic states and constitutive modeling. Journal of Elasticity, 88: 151-184. doi: 10.1007/s10659-007-9125-1

Silling S A, Lehoucq R B. 2010. Peridynamic theory of solid mechanics. Advances in Applied Mechanics, 44: 73-168.

Stenström C, Eriksson K. 2019. The J-contour integral in peridynamics via displacements. International Journal of Fracture, 216: 173-183. doi: 10.1007/s10704-019-00351-3

Stenström C, Eriksson K. 2021. The J-area integral applied in peridynamics. International Journal of Fracture, 228: 127-142. doi: 10.1007/s10704-020-00505-8

Stewart R J, Jeon B. 2019. Decoupling strength and grid resolution in peridynamic theory. Journal of Peridynamics and Nonlocal Modeling, 1: 97-106. doi: 10.1007/s42102-019-00008-8

Sun C Y, Huang Z X. 2016. Peridynamic simulation to impacting damage in composite laminate. Composite Structures, 138: 335-341. doi: 10.1016/j.compstruct.2015.12.001

Tong Y, Shen W Q, Shao J F. 2020a. An adaptive coupling method of state-based peridynamics theory and finite element method for modeling progressive failure process in cohesive materials. Computer Methods in Applied Mechanics and Engineering, 370: 113248. doi: 10.1016/j.cma.2020.113248

Tong Y, Shen W Q, Shao J F, Chen J L. 2020b. A new bond model in peridynamics theory for progressive failure in cohesive brittle materials. Engineering Fracture Mechanics, 223: 106767. doi: 10.1016/j.engfracmech.2019.106767

Wang F, Liu L, Liu Q, et al. 2014. Studies of bimaterial interface fracture with peridynamics//11th World Congress on Computational Mechanics (WCCM), Barcelona.

Wang Y W, Han F, Lubineau G. 2021. Strength-induced peridynamic modeling and simulation of fractures in brittle materials. Computer Methods in Applied Mechanics and Engineering, 374: 113558. doi: 10.1016/j.cma.2020.113558

Wang Y T, Zhou X P, Wang Y, Shou Y D. 2018. A 3-D conjugated bond-pair-based peridynamic formulation for initiation and propagation of cracks in brittle solids. International Journal of Solids and Structures, 134: 89-115. doi: 10.1016/j.ijsolstr.2017.10.022

Wang Y T, Zhou X P, Xu X. 2016. Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics. Engineering Fracture Mechanics, 163: 248-273. doi: 10.1016/j.engfracmech.2016.06.013

Wu L W, Huang D. 2022. Peridynamic modeling and simulations on concrete dynamic failure and penetration subjected to impact loadings. Engineering Fracture Mechanics, 259: 108135. doi: 10.1016/j.engfracmech.2021.108135

Wu L W, Huang D, Bobaru F. 2021. A reformulated rate-dependent visco-elastic model for dynamic deformation and fracture of PMMA with peridynamics. International Journal of Impact Engineering, 149: 103791. doi: 10.1016/j.ijimpeng.2020.103791

Wu L W, Huang D, Xu Y P, Wang L. 2020. A rate-dependent dynamic damage model in peridynamics for concrete under impact loading. International Journal of Damage Mechanics, 29: 1035-1058. doi: 10.1177/1056789519901162

Wu P, Yang F, Chen Z G, Bobaru F. 2021. Stochastically homogenized peridynamic model for dynamic fracture analysis of concrete. Engineering Fracture Mechanics, 253: 107863. doi: 10.1016/j.engfracmech.2021.107863

Yang D, Dong W, Liu X F, et al. 2018. Investigation on mode-I crack propagation in concrete using bond-based peridynamics with a new damage model. Engineering Fracture Mechanics, 199: 567-581. doi: 10.1016/j.engfracmech.2018.06.019

Yang D, He X Q, Liu X F, et al. 2020. A peridynamics-based cohesive zone model (PD-CZM) for predicting cohesive crack propagation. International Journal of Mechanical Sciences, 184: 105830. doi: 10.1016/j.ijmecsci.2020.105830

Yang D, He X Q, Zhu J Q, Bie Z W. 2021. A novel damage model in the peridynamics-based cohesive zone method (PD-CZM) for mixed mode fracture with its implicit implementation. Computer Methods in Applied Mechanics and Engineering, 377: 113721. doi: 10.1016/j.cma.2021.113721

Yu H T, Chen X Z, Sun Y Q. 2020. A generalized bond-based peridynamic model for quasi-brittle materials enriched with bond tension–rotation–shear coupling effects. Computer Methods in Applied Mechanics and Engineering, 372: 113405. doi: 10.1016/j.cma.2020.113405

Yu H C, Li S F. 2020. On energy release rates in Peridynamics. Journal of the Mechanics and Physics of Solids, 142: 104024. doi: 10.1016/j.jmps.2020.104024

Zeng Z X, Zhang H, Zhang X, et al. 2022. An adaptive peridynamics material point method for dynamic fracture. Computer Methods in Applied Mechanics and Engineering, 393: 114786. doi: 10.1016/j.cma.2022.114786

Zhan J M, Yao X H, Han F, Zhang X Q. 2021. A rate-dependent peridynamic model for predicting the dynamic response of particle reinforced metal matrix composites. Composite Structures, 263: 113673. doi: 10.1016/j.compstruct.2021.113673

Zhang G F, Le Q, Loghin A, et al. 2016. Validation of a peridynamic model for fatigue cracking. Engineering Fracture Mechanics, 162: 76-94. doi: 10.1016/j.engfracmech.2016.05.008

Zhang H, Qiao P Z. 2018a. A state-based peridynamic model for quantitative fracture analysis. International Journal of Fracture, 211: 217-235. doi: 10.1007/s10704-018-0285-8

Zhang H, Qiao P Z. 2018b. A coupled peridynamic strength and fracture criterion for open-hole failure analysis of plates under tensile load. Engineering Fracture Mechanics, 204: 103-118. doi: 10.1016/j.engfracmech.2018.09.037

Zhang H, Qiao P Z. 2018c. An extended state-based peridynamic model for damage growth prediction of bimaterial structures under thermomechanical loading. Engineering Fracture Mechanics, 189: 81-97. doi: 10.1016/j.engfracmech.2017.09.023

Zhang H, Qiao P Z. 2020a. A two-dimensional ordinary state-based peridynamic model for elastic and fracture analysis. Engineering Fracture Mechanics, 232: 107040. doi: 10.1016/j.engfracmech.2020.107040

Zhang H, Qiao P Z. 2020b. On the computation of energy release rates by a peridynamic virtual crack extension method. Computer Methods in Applied Mechanics and Engineering, 363: 112883. doi: 10.1016/j.cma.2020.112883

Zhang H, Qiao P Z. 2020c. Virtual crack closure technique in peridynamic theory. Computer Methods in Applied Mechanics and Engineering, 372: 113318. doi: 10.1016/j.cma.2020.113318

Zhang H, Zhang X, Liu Y, Qiao P Z. 2022. Peridynamic modeling of elastic bimaterial interface fracture. Computer Methods in Applied Mechanics and Engineering, 390: 114458. doi: 10.1016/j.cma.2021.114458

Zhang H, Zhang X, Qiao P Z. 2021. A new peridynamic mixed-mode bond failure model for interface delamination and homogeneous materials fracture analysis. Computer Methods in Applied Mechanics and Engineering, 379: 113728. doi: 10.1016/j.cma.2021.113728

Zhang Y, Qiao P Z. 2019a. A new bond failure criterion for ordinary state-based peridynamic mode II fracture analysis. International Journal of Fracture, 215: 105-128. doi: 10.1007/s10704-018-00341-x

Zhang Y, Qiao P Z. 2019b. Peridynamic simulation of two-dimensional axisymmetric pull-out tests. International Journal of Solids and Structures, 168: 41-57. doi: 10.1016/j.ijsolstr.2019.03.014

Zhou X P, Shou Y D, Berto F. 2018. Analysis of the plastic zone near the crack tips under the uniaxial tension using ordinary state-based peridynamics. Fatigue and Fracture of Engineering Materials and Structures, 41: 1159-1170. doi: 10.1111/ffe.12760

Zhou X P, Wang Y T. 2016. Numerical simulation of crack propagation and coalescence in pre-cracked rock-like Brazilian disks using the non-ordinary state-based peridynamics. International Journal of Rock Mechanics and Mining Sciences, 89: 235-249. doi: 10.1016/j.ijrmms.2016.09.010

Zhou X P, Wang Y T, Qian Q H. 2016. Numerical simulation of crack curving and branching in brittle materials under dynamic loads using the extended non-ordinary state-based peridynamics. European Journal of Mechanics, A/Solids, 60: 277-299.

Zhou X P, Zhang T, Qian Q H. 2021. A two-dimensional ordinary state-based peridynamic model for plastic deformation based on Drucker-Prager criteria with non-associated flow rule. International Journal of Rock Mechanics and Mining Sciences, 146: 104857. doi: 10.1016/j.ijrmms.2021.104857

Zhu N, Kochan C, Oterkus E, Oterkus S. 2021. Fatigue analysis of polycrystalline materials using Peridynamic Theory with a novel crack tip detection algorithm. Ocean Engineering, 222: 108572. doi: 10.1016/j.oceaneng.2021.108572

Zhu N, Oterkus E. 2020. Calculation of stress intensity factor using displacement extrapolation method in peridynamic framework. Journal of Mechanics, 36: 235-243. doi: 10.1017/jmech.2019.62

施引文献

资源附件(0)

访问统计