引用本文
张家忠, 刘雁, 孙旭, 陈嘉辉, 王乐. 2018. 柔性结构气弹效应在流动控制中的应用及进展. 力学进展, 48: 201806
Zhang J Z, Liu Y, Sun X, Chen J H, Wang L. 2018. Applications and developments of aeroelasticity of flexible structure in flow controls. Advanced in Mechanics 48: 201806  
Doi:10.6052/1000-0992-16-034
Permissions
Copyright©2018, 中国力学学会
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
柔性结构气弹效应在流动控制中的应用及进展
张家忠1†, 刘雁2, 孙旭3, 陈嘉辉1, 王乐1
1西安交通大学能源与动力工程学院, 西安 710049
2西北工业大学机电学院, 西安 710072
3中国石油大学(北京)机械与储运工程学院, 北京 102249

作者简介：张家忠, 教授, 博导. 研究方向: 在基础研究方面,一直致力于力学(流体力学、固体及流--固耦合)方面的动力系统的运动稳定性、分岔、混沌理论、动力学数值方法的研究;在应用研究方面,主要围绕国家能源动力装备、飞行器、大气及海洋动力学等领域开展了相应的基础和应用研究工作. 承担973计划、863计划、国家科技支撑计划、创新探索等项目. 担任International scientific committee and organizing committee for Nonlinear Science and Complexity, Committee for Chaos, Complexity and Transport, Committee for Analysis and Control~of Chaotic Systems, Committee for Chaotic Modeling and Simulation, Committee member for Topical Problems of Nonlinear Wave Physics等组织委员. 担任中国机械工程学会 流体工程分会第六届委员会委员等职务. 担任 Journal of Applied Nonlinear Dynamics、 《推进技术》《风机技术》等杂志编委, 担任 Journal of Vibration Testing and System Dynamics亚洲区主编.


收稿日期: 2017-05-03; 录用日期: 2017-05-03; 在线出版日期: 2017-05-30 †E-mail: jzzhang@mail.xjtu.edu.cn
基金项目: 国家973计划项目(2012CB026002)、国家自然科学基金(51305355)资助.
摘要

柔性结构与空气动力耦合形成的系统呈现出丰富的非定常、非线性流动和结构动力学行为,对其气动弹性效应合理地控制和利用,能够大幅度提高飞机机翼、风力机叶片等结构的气动性能,并使其具有气动自适应能力.本文总结了近年来与气弹效应应用相关的研究进展及存在的问题,具体介绍了薄膜翼型的流动控制特性、柔性壁面减阻技术以及Sinha扰流装置的发展过程、主要成果以及未来发展趋势,着重对相关试验、流固耦合数值分析、Lagrangian拟序结构动力学等理论分析方法进行总结,展示了气弹效应在流动控制方面的巨大潜力和深远的学术意义,以便更多的研究人员开展该领域的研究工作.

关键词: 气弹效应, 流动控制, 薄膜翼型, 柔性壁面, 拉格朗日拟序结构
中图分类号: O368 文献标志码: A
Applications and developments of aeroelasticity of flexible structure in flow controls
ZHANG Jiazhong1†, LIU Yan2, SUN Xu3, CHEN Jiahui1, WANG Le1
1School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
2School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, China
3School of Mechanical and Transportation Engineering,University of Petroleum-Beijing, Beijing 1002249, China
Abstract

There exists a very rich variety of distinctive properties which are relevant to unsteady, nonlinear flows and structural dynamics, as the flexible structures and fluids are coupled dynamically. If the aeroelastic effects are controlled and utilized properly, the aerodynamic performances and self-adaptability of aircraft wings and wind turbine blades could be improved significantly. In this paper, the progress and major challenges in aeroelasticity and its applications in flow control are reviewed, and three main directions, including the aerodynamic characteristics of the membrane wing, the drag reduction technique using flexible wall and the Sinha disturbers, are discussed in detail. In particular, the relevant studies including the experimental techniques, the numerical methods for fluid-structure interactions and theoretical methods such as nonlinear dynamics, Lagrangian coherent structure are summarized, and the great potential of the aeroelasticity in flow control and its academic values are emphasized, in order to pave the way for the researchers who are engaged in this field.

Key words: aeroelasticity, flow control, membrane wing, flexible wall, Lagrangian coherent structure
1 引 言

在传统空气动力学研究中, 飞机的颤振和抖振、建筑结构的风致振动、风力机及压气机叶片的颤振等气弹效应均被视为安全隐患, 须通过一些措施将其消除或控制在合理的范围内, 以防止发生结构破坏, 酿成事故. 相比之下, 自然界中的情况则不同, 如鸟类、昆虫、蝙蝠、鱼类、海洋哺乳动物等都具有柔性/弹性外形, 在飞行或游动过程中鱼鳍、翅膀、皮肤等身体结构随来流进行适当的变形和振动, 使它们获得非凡的飞行或游动性能(童秉纲和陆夕云 2004).这些生物的飞行或游动模式都是经过亿万年环境适应和自然选择进化而来的, 展示了弹性结构在流动控制方面的积极作用.

受自然界的启发, 越来越多的学者开始了气弹效应主动应用的相关研究.一方面, 通过试验观测、理论建模、数值模拟等手段, 分析弹性翅膀、柔性表皮分别在鸟类飞行和鱼类游动时的变形和振动过程, 及其对推进效率、升力、阻力、机动性等气动特性的影响规律, 获得对这些自然界中的气弹现象更深的认识; 另一方面, 研究人员也对开发全新气弹气动结构或利用气弹效应控制工程流动进行了探索, 期望使人造飞行器、风力机、流体机械等工程机械具有更加优良的气动性能.

在过去几十年里, 人们在柔性扑翼和薄膜翼型、柔性壁面减阻特性、局部弹性扰流装置、主动气动弹性机翼等方面做了大量的研究工作, 并取得了可喜的成果. 本文将从气弹效应利用的角度, 对几个主要研究方向的进展情况进行概述, 并对存在的问题和未来的发展趋势加以分析.

2 薄膜翼型的流动控制特性

随着微型飞行器(MAV)的发展, 人类对扑翼飞行方式的研究不断深入, 在机理分析和设计制造方面都取得了进展. 在早期的研究中, 人们主要利用有限自由度的二维/三维刚体模型, 对不同扑翼运动方式所对应的气动特性进行分析, 发现了扑翼利用非定常效应实现高升力的机制(Weis-Fogh 1973, Ellington et al. 1996, Dickinson et al. 1999, Sun & Tang 2002), 合理地解释了鸟类、昆虫、蝙蝠等生物扑翼飞行的原理, 为扑翼式MAV的研制奠定了基础. 近年来, 扑翼气弹效应的附加影响也受到了越来越多的关注(张兴伟等 2012, Thiria& Godoy-Diana 2010, Percin et al. 2011, Nakata & Liu 2012, Kang et al. 2011, Eldredge et al. 2010, Du & Sun 2010). 研究发现, 柔性扑翼可以进一步起到增升、减阻、增大推力、提高飞行效率的效果. 然而, 由于扑翼式飞行过程的复杂性, 对柔性翼在拍打过程中的变形和振动、结构与周围流体的耦合过程、以及它们与扑翼瞬时气动特性之间的关系等细节问题的分析显得非常困难.

为了更加深入、透彻地分析柔性翼型的气动特性, 很多学者对更加简单的固定薄膜翼型绕流问题进行了研究, 主要表现在试验研究和数值分析方面.

试验研究方面, Galvao等(2006)对一小展弦比薄膜翼型进行了风洞试验.发现薄膜在压差作用下将向上拱起, 并且在失速之前变形幅度随攻角增大而不断增大. 与刚性模型相比, 弹性薄膜的升力大幅增大, 失速攻角也延迟出现. Song和Breuer (2007)进一步考察了薄膜尺寸和预应力对Galvao模型的影响. 事实上, Galvao等(2006)和Song和Breuer (2007)的主要工作是研究薄膜变形的影响.之后, Rojratsirikul等(2009, 2010, 2011)借助高速摄像机、粒子图像测速法(PIV)等显示技术对弹性薄膜在大攻角下自激振动的非定常运动过程进行了更加详细的分析, 观测到了不同条件下薄膜自激振动的模态形式, 发现:(1)流动分离、薄膜自激振动开始之后, 薄膜时均变形随攻角增大不再发生显著变化; (2)攻角较小时薄膜振动可以使剪切层更加靠近壁面, 大攻角时振动可以使分离流再附, 如图1所示.两种情况均缩小了分离区, 减小了阻力.

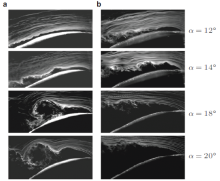图1 部分攻角下薄膜翼型的绕流流场(Rojratsirikul et al. 2009). (a)弹性薄膜, (b)刚性模型

数值分析方面, 20世纪90年代Smith和Shyy (1995, 1996)提出了一种薄膜振动模型, 并通过与N-S方程、雷诺时均(RANS)方程和SST k - \(\omega\)湍流模型相结合, 先后求解了低速 (Re = 4\(\times\) 103)和高速(Re =1.3\(\times\) 106)气流的薄膜绕流问题, 重点分析了流体黏性对薄膜振动和变形的影响. 之后, 一些学者在Smith和Shyy (1995, 1996)研究的基础上, 采用更高精度的算法对该问题进行了分析.Persson(2007)提出了一种高精度间断有限元的求解方法.Gordnier等(2009)针对低速和高速流动情况分别采用了六阶精度有限差分法和大涡模拟方法(LES).Molki和Breuer(2010)采用了将薄膜振动模型与Fluent流场计算软件相结合的求解方式.其中, Gordnierder等(2009)在研究中对不同情况下薄膜变形、振动以及对应的气动特性进行了深入研究, 得到了与Rojratsirikul等(2009)的实验结果相一致的结论. 目前, 低雷诺数(层流)下薄膜自激振动的数值模拟方法已经相对成熟.对于高雷诺数问题, 流动情况非常复杂, RANS方程和湍流模型相结合的计算方式不能准确地描述该非定常问题, 而LES和直接数值模拟(DNS)将成为主要的求解手段.

3 柔性壁面减阻技术

柔性壁面的减阻特性最早是由Kramer (1960)发现的. 1946年, Kramer在穿越大西洋时曾细致地观察过大洋中的海豚.海豚的非凡游动能力给了他很大的启发, 于是在后来的实验中(Kramer (1960)), 他仿照海豚表皮, 在刚性壁面上附以橡胶表层, 用来测试柔性壁面对流动的影响.

Kramer结构(如图2所示)由底部的刚性结构, 中间的橡胶支架和上层的弹性表面组成. 其中, 在支架缝隙填充有不同黏性系数的流体以提供阻尼.通过拖曳试验测量具有该弹性表面的模型, 发现当Re = 1.5\(\times \)106时, 相对于同样条件下的刚性模型, 阻力降低了59%.Kramer对这一现象的机理进行了初步的猜想, 他认为柔性表面与流体发生了相互作用, 从而使得流动变得稳定, 推迟了从层流到湍流的转捩.

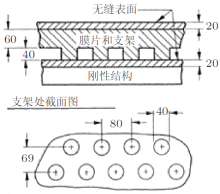图2 Kramer柔性壁面结构示意图(Kramer 1960)

Kramer试验的成功引起了极大的关注, 很多学者在20世纪60年代和70年代都进行了重复性试验. Puryear (1962)对6种柔性壁面模型的减阻效果进行了检验. 通过对比标准模型, 发现6组模型都没能实现减阻效果. Nisewanger (1964)采用Kramer柔性结构对某水下航行器模型进行了处理, 并在湖中进行了气球拖曳试验, 结果显示柔性壁面使阻力增大了6%.在同一时期, Ritter和Messum (1964)以及Ritter和Porteous (1964)也做过类似试验, 也没有发现柔性壁面减阻效果. 这些结果公开发表之后, 人们对Kramer的实验结果产生了质疑, 认为Kramer试验的减阻效果可能是由于附加柔性表皮改变了模型形状、或是试验时充在表层内部的润滑油发生了泄漏导致的. 在之后的20年里, 学术界在该问题上的争执一直都没有停止. 直到1985年, Carpenter和Garrad (1985, 1986)对Kramer (1960)所做的工作重新进行了理论分析, 证实了柔性壁面的减阻性能, 并合理解释了之前多次重复性试验失败的原因, 即由于柔性壁面材料的影响, 结构出现了流致不稳定性. 在Carpenter和Garrad理论分析结果的指导下, Gaster (1995)、Lee等(1995)再次进行了相关试验. 实验结果与Carpenter等(1985)的理论分析非常吻合, Kramer柔性壁面结构的减阻特性最终得到确认.

理论研究方面, Benjamin (1960)和Landahl (1962)等最先从边界层稳定性的角度对Kramer柔性结构的减阻机理进行了探讨. Benjamin (1960)通过将柔性壁面与原有的刚性壁面边界层稳定性问题进行对比, 建立了柔性边界流动稳定性理论. 并将柔性壁面边界层中的不稳定模式划分为三种形式: 第一种是与刚性壁面边界层相似的不稳定波; 第二种是共振效应; 第三种是Kelvin-Helmholtz不稳定性. 通过对三种不稳定形式的分析, Benjamin (1960)首次对Kramer (1960)的实验进行了解释, 指出由于柔性壁面的存在, T-S不稳定性受到破坏, 使T-S波转换为表面波; 又因为柔性壁面的阻力可以有效抑制表面波的发展, 因此柔性壁面具有稳定流场的作用. Landahl (1962)在Benjamin工作的基础上做了进一步分析, 具体讨论了阻尼对边界层稳定性的影响. 但是, 限于当时的计算条件, 他们分析结果主要由估算得到, 不具有足够的说服力. 1985年, Carpenter和Garrad (1985, 1986)在Benjamin (1960)和Landahl (1962)的工作基础上, 利用当时更加先进的计算技术, 给出了精确的数值计算结果. 在他们的研究中, 一方面采用由边界层方程得到的小扰动方程(Orr-Sommerfeld方程)描述流体部分, 另一方面采用梁方程作为柔性表面的控制方程. 通过计算刚性平板的Blasius流动与弹簧支撑膜结构流动, 并对比前人计算结果和实验数据, 发现结果吻合很好(如图3所示), 证实了其模型和算法的准确性. 同时, 他们的分析结果表明, Kramer型表面在理论上具有延迟转捩的能力, 但是当一些不利的条件存在时, 诸如逆压梯度或来流的湍流度较高时, 柔性表面的性能会受到较大影响. 另外, Kramer模型表面只在一定雷诺数范围内存在稳定区域, 不同柔性结构参数所对应的有效雷诺数是不同的. 如果试验雷诺数没有在其有效范围之内, 则不会起到延迟转捩的效果. 该发现很好地解释了之前重复性试验失败的原因.

图3 流动稳定性理论分析验证算例(Carpenter & Garrad 1985). (a) 刚性平板的Blasius流动稳定性分析, (b)弹簧支撑膜结构的流动稳定性分析

之后, 研究者们利用Carpernter和Garrad (1985, 1986)的线性稳定性分析方法对更多的柔性表面模型进行了分析. 在这些研究中, 柔性表面结构被分为基于表面的和基于体积的两类, 如图4, 所示. 其中, 基于表面的模型(图4(a))将柔性结构简化为一维模型, 分析和计算都比较简单, 可以在一定程度上反映弹性表面的影响. Carpenter和Garrad (1985, 1986)在对Kramer型表面进行讨论时, 采用的就是该种模型. 另外, Domaradzki和Metcalfe (1987), Davies和Carpenter (1997), Musleh和Frendi (2011)等也采用了该模型. 基于体积的模型(图4(b)和图4(c))由各向同性或各向异性的单层或多层表层构成, 该类模型比基于表面的模型更加接近实际情况. Duncan等(1985)、Yeo (1988, 1990)在研究中使用了该类模型. 此外, Carpenter (1993)还对一种复合柔性壁面模型进行过研究, 针对平板绕流, 同样达到了延迟转捩的效果.

图4 不同结构的柔性壁面模型(Lucey & Carpenter 2006). (a)一维模型, (b)单层柔性壁面, (c) 双层柔性壁面

近年来, 随着计算机性能的提高和计算流体力学的飞速发展, 很多学者开始通过耦合求解N-S方程和弹性壁面振动方程对该问题进行研究. Wang等(2005)通过直接数值模拟(DNS)求解不可压缩三维扰动N-S方程、有限差分法求解薄膜振动方程, 研究了线性和非线性波在刚性壁面和柔性壁面边界层中的发展过程, 并分析了柔性壁面对T-S波二次不稳定性的影响. Lucey和Carpenter (2006)通过将N-S方程和柔性壁面振动方程直接耦合对该问题进行了分析. 在他们的工作中, 流场求解采用边界元方法, 结构计算采用有限元方法, 在流固界面上交换压力、位移和速度等信息. 计算结果再次印证了柔性壁面的减阻特性. 目前, 柔性壁面减阻的数值分析仍处于起步阶段.

在工程应用方面, 柔性壁面在水下航行器减阻方面的潜力已得到初步证实. 研究表明(Gad-el-Hak 2002, Carpenter et al. 2001), 对于水翼(对应雷诺数1\(\times\)107)和鱼雷(对应雷诺数5\(\times\)107), 如果改用柔性壁面, 其层流区域可分别扩展23%和5%, 减阻效果达到83%和19%. 但是, 柔性壁面减阻技术对环境影响非常敏感, 工程流动中的杂质、高湍流度、壁面加工粗糙度、环境噪声等因素都会破坏减阻效果. 因此, 目前该技术还停留在理论分析和试验研究阶段.

4 Sinha扰流装置

以上研究结果表明, 柔性/弹性结构通过自适应变形、自激振动可以实现增升、减阻、延迟流动分离、推迟层流边界层转捩等效果. 进一步, 对气弹效应进行合理利用, 能够提高人造飞行器、风力机、透平压缩机等工程机械的气动性能, 该内容已经成为当前空气动力学领域中一个新的发展方向. 早在20世纪80年代, 美国就提出了"主动气动弹性机翼(AAW)"的设计理念, 并在型号飞机上作了系列的设计研究(陈桂彬等 2004). 与此同时, 关于整体弹性化引起的结构振动和控制问题, 不少研究者(Munday & Jacob 2002; Greenblatt & Wygnanski 2000; Mani et al. 2008; Jahanmiri 2011; Osborn et al. 2004; Pal & Sinha 1998; Sinha et al. 1999a, 1999b, 2001, 2004, 2007, 2008, 2010; Mangla & Sinha 2004; Sinha & Ravande 2006a, 2006b; Sinha & Hyvärinen 2008, 2009; Wang et al. 2012; 康伟和张家忠 2011; Kang et al. 2012, 2015; Li & Zhang 2015; Sun et al. 2012)对局部弹性结构在流场控制中的应用进行了探索. 本节将重点介绍Sinha等的研究工作.

20世纪90年代, 受到柔顺壁减阻技术和声激励等主动流场控制技术的启发, Pal等(1998)和Sinha等(1999a, 1999b, 2001)设计了一种利用弹性壁面控制非定常分离的装置AFW. 如图5所示, 该装置主要由外表面弹性薄膜、绝缘底板、金属条状支撑结构、交流/直流电源及控制器组成. 其中, 弹性薄膜外表面进行镀铝处理. 电源两极分别与薄膜表面金属层、内部金属条状支撑结构相连. 利用直流电源可以控制薄膜和支撑结构的距离, 也可以测量流动导致的薄膜振动. 而利用交流电源可以使薄膜产生周期性强迫振动, 进行主动控制. AFW的弹性薄膜和底板都具有较好的弹性, 可以粘附在叶片、机翼等结构表面上. 试验研究表明, 在1.2\(\times\)105\(\sim\) 1.5\(\times\)105的雷诺数范围内, AFW装置有效地推迟了圆柱表面的流动分离, 缩小了尾涡区, 实现了12% \(\sim \) 20%的减阻效果. 对于NACA0012翼型, 该装置可以使大攻角下的分离流再附.

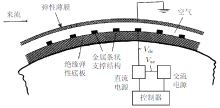图5 Sinha主动扰流装置示意图(Sinha 1999b)

对于图5所示的AFW模型, 当外部流体压力较高时, 条状支撑结构和弹性薄膜之间的空气间隙变得很小, 将影响到薄膜振动的幅度. 为了解决该问题, Sinha和Zou (2000)以及Mangla 和 Sinha(2004)提出了一种改进的AFW模型, 如图6所示. 在改进模型中, 采用了高低相间排列的条状支撑结构. 其中, 较高的条状结构主要起支撑的作用, 较低的条状结构与表面弹性薄膜间始终存在一定的距离, 主要用于薄膜自激振动的监测和主动控制. 通过风洞和飞行试验, Sinha和Zou(2000)研究了该装置对NACA0012翼型和NLF-0414F机翼的控制效果. 其中NACA0012翼型升力系数增大了4%, NLF-0414机翼阻力降低了2%. Mangla和Sinha (2004)通过风洞试验考察了该装置对动态失速的影响. 实验采用NACA0012翼型, 对应雷诺数为6\(\times\)105, 扭转振动缩减频率范围0.05 \(\sim \)0.15. 试验结果表明, 当安装位置位于翼型前缘、激振频率的无量纲参数Strouhal数为1时, AFW装置可以将动态失速攻角向后推迟2° 左右.

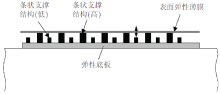图6 Sinha主动扰流装置(改进)示意图(Mangla & Sinha 2004)

图5和图6所示AFW装置采用的是主动控制方式, 需要从外界输入能量使弹性薄膜产生强迫振动. 能否利用流场自身能量, 通过薄膜自激振动实现流场的自动调节? Sinha在这方面做了大量的工作. 2004年, Sinha在AIAA年会上展示了他发明的被动扰流装置FCSD (Sinha 2004). 如图7所示, FCSD与AFW装置具有类似的主体结构, 只是去掉了外部电源, 并增大了相邻支撑之间的间距(为了促进薄膜自激振动). 与AFW相比, FCSD装置没有能耗、结构简单、并具有自适应特性. 从2004年至今, Sinha等通过大量的试验, 考察了该装置对于不同流场形态的控制效果. 从表1, 可以看出, FCSD对于机翼等流线型结构和卡车等钝体结构的流场都具有很好的控制效果. 基于该技术, Sinha申请了多项专利(2008---2010), 并成立了Sinhatech公司. 目前, Sinhatech生产的FCSD装置已经进入美国市场, 用于长途货运卡车的减阻控制. 在未来的几十年里, FCSD有望用于客机、战斗机、风力机、透平机械等更多工程领域.

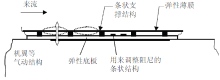图7 Sinha被动扰流装置示意图(Sinha 2004)

表1 Sinha-FCSD 装置测试试验和主要结果

Sinha等设计的AFW和FCSD装置, 都是利用弹性薄膜的局部振动实现流场控制的. 运行过程中外层弹性薄膜的振动幅度和速度虽然只有微米和毫米每秒量级, 却具有非常明显的流场调节效果. 对于AFW和FCSD装置的作用机理, Sinha结合试验结果进行了初步分析. 首先, Sinha在试验过程中发现两种扰动装置的位置非常关键. 如图8所示, 原流场沿流向存在从顺压梯度(dp/dx < 0)到逆压梯度(dp/dx > 0)的变化. 为了解释该现象, Sinha利用层流边界层方程研究了壁面非定常小扰动在边界层中的传播过程. 发现在dp/dx = 0处边界层对外加扰动的感受性最强, 此处壁面扰动可以穿过边界层对主流产生显著影响. 该发现对于其他流动控制技术也有一定的参考价值. 其次, 对于FCSD装置, 试验结果表明弹性壁面的扰动使机翼表面形成了紧贴壁面的分离层(图9). 该分离层具有层流边界层的特性, 壁面流体的速度梯度较低, 对应壁面摩擦阻力也很低. 但是, 与层流不同, 分离层内动量交换非常明显, 可以有效地抑制流动分离. 关于该分离层的形成机制, Sinha给出了如下解释: 当湍流边界层中的大尺度涡结构与FCSD表面薄膜结构接触时, 弹性薄膜将在大涡作用下变形和振动, 并把大涡破碎成一系列的小涡, 然后小涡在黏性作用下不断耗散, 把最初大涡的机械能转化为热能. 在此过程中, 大涡的耗散速度加快了, FCSD起到了与大涡破碎器(LEBU)类似的效果. 因此, FCSD形成的分离层同时具有层流、湍流边界层的部分特性. 该解释具有合理性, 但还没有经过实验或理论的证实. 为了获得更多的流动细节, Wang等(2012)在Sinha的指导下对FCSD的绕流流场进行了数值模拟. 他们利用RANS方程和k -\( \omega \)湍流模型, 通过缩小FCSD周围的流场的湍流混合长度研究了其对平板和S809翼型气动特性的影响. 由于没有考虑FCSD的振动, 因此结果还不能很好地反映真实情况.

图8 Sinha扰流装置与边界层的相互作用示意图(Sinha & Ravande 2006)

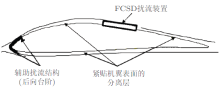图9 FCSD装置控制原理示意图(Sinha 2009)

这些效果明显的实验结果为该技术的研究提供了希望和基础, 然而由于所研究问题是一个多学科交叉问题, 涉及到空气动力学、固体力学以及结构动力学, 目前对其机理的理解尚不明确. 近年来, 张家忠课题组在该技术的理论分析和应用方面作了大量的工作. 他们提出了一种简化的具有局部弹性壁面的翼型模型(康伟和张家忠 2011, Kang et al, 2012), 并开发了流--固耦合求解程序(Li & Zhang 2015; Kang et al. 2014; Guanhua et al. 2013, 2014; 孙旭等 2010, 2011; Sun et al. 2012)对其气动特性进行了初步分析, 在低雷诺数下获得了显著的增升和减阻效果. 同时, 他们从非线性动力学角度, 对翼型静态失速的动力学特性进行了新的诠释(张家忠和李凯伦 2011), 并研发了Lagrangian拟序结构(Lagrangian Coherent Structures)方法, 在此基础上研究了局部弹性壁面对翼型非定常分离等流场细节的影响规律及动力学特性(雷鹏飞等 2008, 2012; Lei et al. 2014, 2015). 目前, 更加深入的研究仍在进行之中.

5 对相关数值、理论分析方法的一些思考

薄膜翼型、柔顺壁面和Sinha扰流装置的研究成果展示了弹性结构在增升、减阻、降噪等方面的巨大潜力. 为了理解气弹效应作用的机理并更好地对其加以控制和利用, 对相关数值分析方法、理论分析方法的研究显得非常关键.

数值分析方面, 由高速气流与弹性结构两种连续介质耦合而成的动力系统表现出比静载荷作用下单 一介质更加丰富、复杂的非定常、非线性动力学现象, 其数值模拟和分析方法还存在很多问题. 首先, 虽然目前连续体和结构的有限元解法、低速非定常流动问题的数值解法已经比较成熟, 但流--固耦合算法方面的研究还相对较少. 流--固耦合算法并不只是结构求解模块、流场求解模块的简单叠加, 还要考虑耦合精度、收敛性、稳定性、附加质量效应等众多因素. 近年来, 同时求解流场和结构控制方程的全耦合解法(Hü bner et al. 2004, Jog & Pal 2011)、交替求解流场和结构并在每个时间步上进行迭代的紧耦合解法(Kü ttler & Wall 2008, Degroote et al. 2010)已经成为该领域的研究热点, 也是未来非线性气弹问题求解方法的发展趋势. 其次, 对于低速层流非定常流动问题, 当前解法已经可以获得较为精确的结果, 与试验数据吻合得很好. 但是, 当高速流场存在转捩或湍流状态时, 数值结果与试验之间往往存在明显的偏差. 通常会通过修正转捩或湍流模型来缩小该偏差, 使计算结果对于工程流动问题有一定的参考价值. 然而, 对于非定常效应较强的气弹问题, 该近似方法不再适用, 所得到的结果并不能反映真实的非定常流动过程. 对于高速非定常流动问题, LES和DNS方法将成为主要分析手段. 最后, 从动力学的角度看, 流--固耦合系统是强非线性且关于时间二阶耗散的无穷维动力系统, 采用目前的数值方法, 如有限元方法、有限差分法、有限体积法等, 对系统进行离散逼近, 将产生大量的自由度. 大多数学者对该类动力学方程的求解主要采用直接数值积分方法确定其稳定解(很少完全跟踪出非稳定的解分枝), 并模拟系统的长时间行为, 这将对现有计算机的容量和速度提出更高要求. 另外, 非线性动力系统的一个主要特点就是对某些初边值的极端敏感性, 微小的初边值扰动(如: 大规模矩阵运算的数值误差积累等), 经过一段时间后将导致系统解的形态发生拓扑性改变, 进而增大定量分析非线性动力学行为的难度. 因此, 高维或无穷维非线性动力系统的降维(即减少离散后系统的自由度)就很自然地成为该领域中的一项急需解决的问题, 也是当前非线性学科的研究前沿. 近几年来, 初步研究显示流--固耦合系统的长期行为仅由少数或有限模态主导. 部分学者在进行另一类连续介质的试验时, 也观察到系统的复杂时空斑图是由``少数奇怪模态''组成的. 为此, 通过引入一种光滑的有限维流形, 即近似惯性流形, 在其上分析系统的整体性质, 可以大幅降低系统的自由度. 根据该思路, 张家忠等采用多级有限元方法, 成功构造出了该近似惯性流形, 并应用到了翼型绕流(Zhang & Ren 2011)、浅拱屈曲(Zhang et al. 2007, 张家忠等 2008)、壁板颤振等问题(梅冠华和张家忠 2011, 李凯伦等 2011, Zhang et al. 2011, 康伟等 2011)的数值分析之中, 为进一步分析气动弹性问题的分岔和稳定性问题提供了基础.

理论分析方面, 目前对气弹问题所包含的非线性现象的数学描述还很少. 在已有数值解法的基础上, 从非线性动力学角度进行更加深入的分析, 可以加深对各种流动、结构振动以及流--固耦合现象的理解. 以翼型失速问题为例, 静态失速所表现的突跳行为, 即滞后、多值性等现象, 可以确定是典型的由非线性动力系统鞍--结分岔描述的跳跃现象(Liu et al. 2012). 考虑到鞍--结分岔对外界的小扰动(可视为缺陷)很敏感, 适当的小扰动可以消除或延迟鞍--结分岔的发生, 在翼型局部施加自激振动这一非定常扰动可以延迟失速也就不难理解了. 另外, 分岔理论是描述系统拓扑结构发生变化的学科, 具有普适性. 已有研究发现, 利用分岔等理论, 可以解释绕流、空化等流动问题的复杂非线性现象的机理(Kang et al. 2012, Ren et al. 2012). 事实上, 与单一的流动或结构问题相比, 气弹问题具有更加丰富的非线性特性. 对于气弹问题, 高速气动力不是单一的周期运动, 与结构耦合将诱发出多种流动模态之间的激烈竞争, 并产生多周期解分枝同步、阵发性分岔、流动边界层拟序结构(斑图动力学)的改变、无穷维系统中复杂斑图的不稳定性等现象. 而这些问题的数学描述和解释, 是研究机翼等气动结构增升减阻等机理的关键和前提. 如果采用经典的线性化方法近似地、简化地分析系统, 这些非线性行为将被``过滤''掉, 有可能出现规律性失真(Zhang et al. 2005). 因此, 从非线性动力学观点出发, 用分岔和奇异性理论研究流动中的复杂现象, 从深层揭示系统气动弹性效应的内在机理是一重要的研究方向.

另外, 大多数流动采用基于Euler观点的描述和分析方法. 然而Euler描述方法存在局限性, 对于流动中的物质及能量输运特征等动力学行为缺乏有效的描述. 而Lagrangian描述是对动力系统的动力学描述方法, 能够采用非线性动力学相关理论对其进行分析. 基于此, 提出了Lagrangian拟序结构(Lagrangian Coherent Structure, 简称LCS)的概念, 可以用来分析非定常流动中的物质输运和混合作用. 张家忠课题组发展了LCS方法, 并成功应用于机翼、叶片绕流的动力学分析中, 解释了一些奇异现象(雷鹏飞等 2008, 2012; Lei et al. 2014).

6 总结与展望

经过几十年的努力, 人们对于气弹效应在流动控制方面的潜力有了更多的了解, 在应用方面也取得了成功. 然而, 该方面的研究仍处于起步阶段, 在很多方面都有待完善. 首先, 为了从自然界获得更多的灵感, 需要观测和分析昆虫/鸟类飞行、鱼类游动时的气弹现象, 这对试验设备和方法提出了严峻的挑战. 高分辨率、高精度的非定常流场显示和测试技术将成为未来试验研究的主要发展方向. 其次, 气弹问题是一个多学科交叉领域, 通常具有非定常、非线性、高自由度的特性, 给数值分析过程带来了一定的困难. 近年来, 针对低速层流流动, 发展了大量非线性气弹问题的流--固耦合数值解法, 以及高维或无穷维非线性动力系统的数值降维方法. 然而, 对于高雷诺数情形, 能够综合考虑转捩、湍流等复杂流动形态的流--固耦合算法尚不成熟. 另外, 传统气弹分析的理论基础是建立在颤振控制上的, 气弹效应主动利用的理论研究几乎空白.

总之, 该问题的研究不仅可以揭示出气弹效应实现流动控制的机理, 为开发透平机械、飞行器增升减阻技术提供新的途径, 而且将促进非线性科学向无穷维动力系统的发展和应用(如: 复杂的涡时--空斑图动力学、波--涡共振), 因此是一个多学科交叉(非线性偏微分发展方程、非线性动力学、流--固耦合等)、具有重要学术意义和应用价值的方向.

参考文献
[1] 陈桂彬, 邹丛青, 杨超. 2004. 气动弹性设计基础. 北京: 北京航空航天大学出版社
(Chen G B, Zou C Q, Yang C. 2004. Design Fundamentals of Aeroelasticity. Beijing: Beihang University Press). [本文引用:1]
[2] 康伟, 张家忠. 2011. 翼型局部弹性自激振动的增升减阻效应研究. 西安交通大学学报, 45: 94-101
(Kang W, Zhang J Z. 2011. Numerical analysis of lift enhancement and drag reduction by self-induced vibration of localized elastic airfoil. Journal of Xi'an Jiaotong University, 45: 94-101). [本文引用:1]
[3] 康伟, 张家忠, 李凯伦. 2011. 利用本征正交分解的非线性Galerkin 降维方法. 西安交通大学学报, 45: 58-62
(Kang W, Zhang J Z, Li K L. 2011. Nonlinear Galerkin method for dimension reduction using proper orthogonal decomposition. Journal of Xi'an Jiaotong University, 45: 58-62). [本文引用:1]
[4] 李凯伦, 张家忠, 周振堂. 2011. 传热时间迟滞影响的薄板热气动弹性耦合振荡模型. 航空动力学报, 26: 1-8
(Li K L, Zhang J Z, Zhou Z T. 2011. Aerothermoelastic coupling dynamic model of panel flutter with time delay of heat transfer. Journal of Aerospace Power, 26: 1-8). [本文引用:1]
[5] 雷鹏飞, 张家忠, 孙旭, 康伟, 苏哲. 2008. 机翼绕流边界层分离的分岔特性研究//第八届全国动力学与控制学术会议, 哈尔滨
(Lei P F, Zhang J Z, Sun X, Kang W, Su Z. 2008. Bifurcation in the separation flow near the wall of wing//The 8th National Conference on Dynamics & Control, Harbin). [本文引用:2]
[6] 雷鹏飞, 张家忠, 陈嘉辉. 2012. 局部弹性翼型非定常分离的动力学特性. 力学学报, 44: 13-22
(Lei P F, Zhang J Z, Chen J H. 2012. Unsteady separation of flow around airfoil with local elastic structure. Chinese Journal of Theoretical and Applied Mechanics, 44: 13-22 ). [本文引用:2]
[7] 梅冠华, 张家忠. 2011. 时滞惯性流形在三维壁板颤振数值分析中的应用. 西安交通大学学报, 45: 40-45
(Mei G H, Zhang J Z. 2011. Numerical analysis of 3-D panel flutter by inertial manifolds with delay. Journal of Xi'an Jiaotong University, 45: 40-45). [本文引用:1]
[8] 孙旭, 张家忠, 周志宏, 徐忠. 2010. 不可压黏性流动的CBS有限元解法. 计算力学学报, 27: 862-867
(Sun X, Zhang J Z. Zhou Z H, Xu Z. 2010. On the application of the CBS finite element method to the incompressible flow. Chinese Journal of Computational Mechanics, 27: 862-867). [本文引用:1]
[9] 孙旭, 张家忠. 2011. 具有运动边界不可压缩黏性流动的CBS有限元解法. 西安交通大学学报, 45: 97-104
(Sun X, Zhang J Z. 2011. A characteristic based Split-FEM scheme for incompressible viscous flow with moving boundaries. Journal of Xi'an Jiaotong University, 45: 97-104). [本文引用:1]
[10] 童秉纲, 陆夕云. 2004. 关于飞行和游动的生物力学研究. 力学进展, 34: 1-8
(Tong B G, Lu X Y. 2004. A review on biomechanics of animal flight and swimming. Advances in Mechanics, 34: 1-8). [本文引用:1]
[11] 张兴伟, 周超英, 谢鹏. 2012. 扑翼柔性变形对悬停气动特性影响的数值研究. 哈尔滨工业大学学报, 44: 115-119
(Zhang X W, Zhou C Y, Xie P. 2012. Numerical study on the effect of flapping wing deformation on aerodynamic performance in hovering flight. Journal of Harbin Institute of Technology, 44: 115-119). [本文引用:1]
[12] 张家忠, 陈丽莺, 梅冠华, 周志宏, 苏哲. 2008. 基于时滞惯性流形的浅拱动力屈曲研究//第八届全国动力学与控制学术会议, 哈尔滨
(Zhang J Z, Chen L Y, Mei G H, Zhou Z H, Su Z. 2008. Dynamic bucking analysis of shallow parabolic arch based on the method of inertial manifolds with time delay//The 8th National Conference on Dynamics & Control, Harbin). [本文引用:1]
[13] 张家忠, 李凯伦, 陈丽莺. 2011. 翼型失速的非线性动力学特性及其控制. 航空学报, 32: 2163-2173
(Zhang J Z, Li K L, Chen L Y. 2011. Nonlinear dynamics of static stall of airfoil and its control. Acta Aeronautica ET Astronautica Sinica, 32: 2163-2173). [本文引用:1]
[14] Al Musleh A, Frendi A. 2011. On the effects of a flexible structure on boundary layer stability and transition. Journal of Fluids Engineering, 133: 071103. [本文引用:1]
[15] Benjamin T B. 1960. Effects of a flexible boundary on hydrodynamic stability. Journal of Fluid Mechanics, 9: 513-532. [本文引用:1]
[16] Carpenter P W, Garrad A D. 1985. Hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 1: Tollmien-Schlichting instabilities. Journal of Fluid Mechanics, 155: 465-510. [本文引用:4]
[17] Carpenter P W, Garrad A D. 1986. Hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 2: Flow-induced surface instabilities. Journal of Fluid Mechanics, 170: 199-232. [本文引用:3]
[18] Carpenter P W. 1993. Optimization of multiple-panel compliant walls for delay of laminar-turbulent transition. AIAA Journal, 31: 1187-1188. [本文引用:1]
[19] Carpenter P W, Lucey A D, Davies C. 2001. Progress on the use of compliant walls for laminar-flow control. Journal of aircraft, 38: 504-512. [本文引用:1]
[20] Davies C, Carpenter P W. 1997. Instabilities in a plane channel flow between compliant walls. Journal of Fluid Mechanics, 352: 205-243. [本文引用:1]
[21] Davies C, Carpenter P W. 1997. Numerical simulation of the evolution of Tollmien-Schlichting waves over finite compliant panels. Journal of Fluid Mechanics, 335: 361-392. [本文引用:1]
[22] Degroote J, Haelterman R, Annerel S, Bruggeman P, Vierendeels J. 2010. Performance of partitioned procedures in fluid-structure interaction. Computers & Structures, 88: 446-457. [本文引用:1]
[23] Dickinson M H, Lehmann F O, Sane S P. 1999. Wing rotation and the aerodynamic basis of insect flight. Science, 284: 1954-1960. [本文引用:1]
[24] Domaradzki J A, Metcalfe R W. 1987. Stabilization of laminar boundary layers by compliant membranes. Physics of Fluids, 30: 695-705. [本文引用:1]
[25] Du G, Sun M. 2010. Effects of wing deformation on aerodynamic forces in hovering hoverflies. Journal of Experimental Biology, 213: 2273-2283. [本文引用:1]
[26] Duncan J, Waxman A, Tulin M. 1985. The dynamics of waves at the interface between a viscoelastic coating and a fluid flow. Journal of Fluid Mechanics, 158: 177-197. [本文引用:1]
[27] Ellington C P, Van Den Berg C, Willmott A P, Thomas A L R. 1996. Leading-edge vortices in insect flight. Nature, 384: 626-30. [本文引用:5]
[28] Eldredge J D, Toomey J, Medina A. 2010. On the roles of chord-wise flexibility in a flapping wing with hovering kinematics. Journal of Fluid Mechanics, 659: 94-115. [本文引用:1]
[29] Galvao R, Israeli E, Song A, Tian X D, Bishop K, Swartz S, Breuer K. 2006. The aerodynamics of compliant membrane wings modeled on mammalian flight mechanics. AIAA Paper, 2006-2866. [本文引用:1]
[30] Gad-el-Hak M. 2002. Compliant coatings for drag reduction. Progress in Aerospace Sciences, 38: 77-99. [本文引用:2]
[31] Gordnier R E. 2009. High fidelity computational simulation of a membrane wing airfoil. Journal of Fluids and Structures, 25: 897-917. [本文引用:1]
[32] Gordnier R E, Attar P J. 2009. Implicit les simulations of a low Reynolds number flexible Membrane Wing Airfoil. AIAA Paper, 2009-579. [本文引用:1]
[33] Greenblatt D, Wygnanski I J. 2000. The control of flow separation by periodic excitation. Progress in Aerospace Sciences, 36: 487-545. [本文引用:1]
[34] Mei G H, Zhang J Z, Sun X. 2014. Analysis of supersonic and transonic panel flutter using a fluid-structure coupling algorithm. ASME Journal of Vibration and Acoustics, 136: 031013-031013-11. [本文引用:1]
[35] Mei G H, Zhang J Z, Wang Z P. 2013. Numerical analysis of panel flutter on inertial manifolds with delay. ASME Journal of Computational and Nonlinear Dynamics, 8: 1-11. [本文引用:1]
[36] Hübner B, Walhorn E, Dinkler D. 2004. A monolithic approach to fluid--structure interaction using space--time finite elements. Computer Methods in Applied Mechanics and Engineering, 193: 2087-2104. [本文引用:1]
[37] Jahanmiri M. 2011. Aircraft drag reduction: An overview. Chalmers University of Technology, Research Report, 02. [本文引用:1]
[38] Jog C, Pal R. 2011. A monolithic strategy for fluid--structure interaction problems. International Journal for Numerical Methods in Engineering, 85: 429-460. [本文引用:2]
[39] Kang C, Aono H, Cesnik C, Shyy W. 2011. Effects of flexibility on the aerodynamic performance of flapping wings. Journal of Fluid Mechanics, 689: 32-74. [本文引用:1]
[40] Kang W, Zhang J Z, Feng P H. 2012. Aerodynamic analysis of a localized flexible airfoil at low Reynolds numbers. Communications in Computational Physics, 11: 1300-1310. [本文引用:2]
[41] Kang W, Zhang J Z, Lei P F, Min Xu. 2015. Effects of local oscillation of airfoil surface on lift enhancement at low Reynolds number. Journal of Fluid and Structure, 57: 49-65. [本文引用:3]
[42] Kang W, Zhang J Z, Lei P F, Min X. 2014. Computation of unsteady viscous flow around a locally flexible airfoil at low Reynolds number. Journal of Fluid and Structure, 46: 42-58. [本文引用:1]
[43] Kramer M O. 1960. Boundary layer stabilization by distributed damping. Journal of the American Society for Naval Engineers, 72: 25-34. [本文引用:2]
[44] Küttler U, Wall W A. 2008. Fixed-point fluid-- structure interaction solvers with dynamic relaxation. Computational Mechanics, 43: 61-72. [本文引用:1]
[45] Land ahl M T. 1962. On the stability of a laminar incompressible boundary layer over a flexible surface. Journal of Fluid Mechanics, 13: 609-362. [本文引用:1]
[46] Lei P F, Zhang J Z, Kang W, Ren S, Wang L. 2014. Unsteady flow separation and high performance of airfoil with local flexible structure at low Reynolds number. Communications in Computational Physics, 16: 699-717. [本文引用:2]
[47] Lei P F, Zhang J Z, Li K L, Wei D. 2015. Study on the transports in transient flow over impulsively started circular cylinder using Lagrangian coherent structures. Communications in Nonlinear Science and Numerical Simulation, 22: 953-963. [本文引用:1]
[48] Li K L, Zhang J Z, Ren J H, Yan Y. 2015. Investigation of aerothermoelastic behaviors of functionally graded panels in supersonic flows. Journal of Thermal Stresses, 38: 882-903. [本文引用:1]
[49] Liu Y, Li K L, Wang H, Liu L. 2012. Numerical bifurcation analysis of static stall of airfoil and dynamic stall under unsteady perturbation. Communications in Nonlinear Science and Numerical Simulation, 17: 3427-3434. [本文引用:1]
[50] Lucey A, Carpenter P. 1995. Boundary layer instability over compliant walls: Comparison between theory and experiment. Physics of Fluids, 7: 2355-2363. [本文引用:1]
[51] Lee T, Fisher M, Schwarz W. 1995. Investigation of the effects of a compliant surface on boundary-layer stability. Journal of Fluid Mechanics, 288: 37-58. [本文引用:1]
[52] Lucey A D, Carpenter P M, Werle J. 2006. Numerical simulation of the interaction of a uniform mean flow and a compliant boundary//1st International Conference on Computational Methods, 189-193. [本文引用:2]
[53] Mani R, Lagoudas D C, Rediniotis O K. 2008. Active skin for turbulent drag reduction. Smart Materials and Structures, 17: 035004. [本文引用:1]
[54] Mangla N L, Sinha S K. 2004. Controlling dynamic stall with an active flexible wall. AIAA Paper, 2004-2325. [本文引用:1]
[55] Molki M, Breuer K. 2010. Oscillatory motions of a prestrained compliant membrane caused by fluid-membrane interaction. Journal of Fluids and Structures, 26: 339-358. [本文引用:1]
[56] Munday D, Jacob J, Hauser T, Huang G. 2002 . Experimental and numerical investigation of aerodynamic flow control using oscillating adaptive surfaces. AIAA Paper, 2002-2837. [本文引用:1]
[57] Munday D, Jacob J. 2002. Active control of separation on a wing with oscillating camber. Journal of aircraft, 39: 187-189. [本文引用:4]
[58] Nakata T, Liu H. 2012. A fluid-structure interaction model of insect flight with flexible wings. Journal of Computational Physics, 233: 1822-1847. [本文引用:1]
[59] Nisewanger C. 1964. Flow noise and drag measurements of vehicle with compliant coating. US Naval Ordnance Test Station Report No. 8518, NOTS No. TP-3510China Lake, California. [本文引用:1]
[60] Osborn R, Kota S, Hetrick J A, Geister D E, Tilmann C P, Joo J Y. 2004. Active flow control using high-frequency compliant structures. Journal of Aircraft, 41: 603-609. [本文引用:3]
[61] Pal D, Sinha S K. 1998. Controlling unsteady separation on a cylinder with a driven flexible wall. AIAA Journal, 36: 1023-1028. [本文引用:2]
[62] Percin M, Hu Y, Van Oudheusden B, Remes B, Scarano F. 2011. Wing flexibility effects in clap-and -fling. International Journal of Micro Air Vehicles, 3: 217-228. [本文引用:1]
[63] Persson P O, Peraire J, Bonet J. 2007. A high order discontinuous Galerkin method for fluid-structure interaction. AIAA Paper, 2007-4327. [本文引用:1]
[64] Puryear F. 1962. Boundary layer control: Drag reduction by use of compliant coatings. David Taylor Model Basin Report No. 1668, Bethesda, MD. [本文引用:1]
[65] Rojratsirikul P, Wang Z, Gursul I. 2009. Unsteady fluid--structure interactions of membrane airfoils at low Reynolds numbers. Experiments in Fluids, 46: 859-872. [本文引用:1]
[66] Rojratsirikul P, Wang Z, Gursul I. 2010. Effect of pre-strain and excess length on unsteady fluid-structure interactions of membrane airfoils. Journal of Fluids and Structures, 26: 359-376. [本文引用:1]
[67] Rojratsirikul P, Genc M, Wang Z, Gursul. 2011. Flow-induced vibrations of low aspect ratio rectangular membrane wings. Journal of Fluids and Structures, 27: 1296-1309. [本文引用:1]
[68] Ritter H, Messum L T. 1964. Water tunnel measurements of turbulent skin friction on six different compliant surfaces of 1 Ft length. British Admiralty Research Laboratory Report No. ARL/N4/GHY/9/7, London, Great Britain. [本文引用:1]
[69] Ritter H, Porteous J S. 1964. Water tunnel measurements of skin friction on a compliant coating. British Admiralty Research Laboratory Report No. ARL/N3/G/HY/9/7, London, Great Britain. [本文引用:1]
[70] Ren S, Zhang J Z, Li K L. 2012. Mechanisms for oscillations in volume of single spherical bubble due to sound excitation in water. Chinese Physics Letters, 29: 020504-1-020504-3. [本文引用:1]
[71] Sinha S K. 1999. Active flexible walls for efficient aerodynamic flow separation control. AIAA Paper, 99-3132. [本文引用:3]
[72] Sinha S K. 1999. System for efficient control of flow separation using a driven flexible wall. U. S. Patents 5 961 080. [本文引用:2]
[73] Sinha S K. 2001. Flow separation control with microflexural wall vibrations. Journal of Aircraft, 38: 496-503. [本文引用:3]
[74] Sinha S K, Zou J. 2000. On controlling flows with micro-vibratory wall motion. AIAA Paper, 2000-4413. [本文引用:2]
[75] Sinha S K. 2004. Aircraft drag reduction with flexible composite surface boundary layer control. AIAA Paper, 2004-2121. [本文引用:3]
[76] Sinha S K, Ravand e S V. 2006. Sailplane performance improvement using a flexible composite surface deturbulator. AIAA Paper, 2006-447. [本文引用:2]
[77] Sinha S K, Ravand e S V. 2006. Drag reduction of natural laminar flow airfoils with a flexible surface deturbulator. AIAA Paper, 2006-3030. [本文引用:1]
[78] Sinha S K. 2007. Optimizing Wing lift to drag ratio enhancement with flexible-wall turbulence control. AIAA Paper, 2007-4425. [本文引用:1]
[79] Sinha S K, Hyvärinen J. 2008. Flexible-wall turbulence control for drag reduction on streamlined and bluff bodies. AIAA Paper, 2008-4207. [本文引用:1]
[80] Sinha S K, Hendrix J. 2009. Obtaining extremely high lift to drag ratios with flexible-wall turbulence control. AIAA Paper, 2009-896. [本文引用:1]
[81] Sinha S K, Sinha S. 2009. Method of reducing drag and increasing lift due to flow of a fluid over solid objects. U. S. Patents 2009/0294596. [本文引用:1]
[82] Sinha S K. 2008. System and method for using a flexible composite surface for pressure-drop free heat transfer enhancement and flow drag reduction. U. S. Patents 7 422 051. [本文引用:1]
[83] Sinha S K. 2010. Deturbulator fuel economy Enhancement for trucks. U. S. Patents 2010/0194144. [本文引用:1]
[84] Smith R, Shyy W. 1995. Computation of unsteady laminar flow over a flexible two-dimensional membrane wing. Physics of Fluids, 7: 2175-2184. [本文引用:1]
[85] Smith R, Shyy W. 1996. Computation of aerodynamic coefficients for a flexible membrane airfoil in turbulent flow: A comparison with classical theory. Physics of Fluids, 8: 3346-3353. [本文引用:1]
[86] Song A, Breuer K. 2007. Dynamics of a compliant membrane as related to mammalian flight. AIAA Paper, 2007-665. [本文引用:2]
[87] Sun M, Tang J. 2002. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion. Journal of Experimental Biology, 205: 55-70. [本文引用:1]
[88] Sun X, Zhang J Z, Ren X L. 2012. Characteristic-Based Split (CBS) finite element method for incompressible viscous flow with moving boundaries. Engineering Applications of Computational Fluid Mechanics, 6: 461-474. [本文引用:2]
[89] Tong B G, Lu X Y. 2004. A review on biomechanics of animal fight and swimming. Advances in Mechanics, 34: 1-8. [本文引用:1]
[90] Thiria B, Godoy-Diana R. 2010. How wing compliance drives the efficiency of self-propelled flapping flyers. Physical Review E, 82: 015303. [本文引用:1]
[91] Visbal M R, Gordnier R E, Galbraith M C. 2009. High-fidelity simulations of moving and flexible airfoils at low Reynolds numbers. Experiments in Fluids, 46: 903-922. [本文引用:1]
[92] Weis-Fogh T. 1973. Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. Journal of Experimental Biology, 59: 169-230. [本文引用:1]
[93] Wang Z, Yeo K, Khoo B. 2005. Spatial direct numerical simulation of transitional boundary layer over compliant surfaces. Computers and Fluids, 34: 1062-1095. [本文引用:1]
[94] Wang X, Walters K, Coley L, Barton M, Sinha S. 2012. Modeling turbulence control effect of the Sinha flexible composite surface deturbulator. AIAA Paper, 2012-3204. [本文引用:1]
[95] Wang Y T, Zhang J Z. 2011. An improved ALE and CBS-based finite element algorithm for analyzing flows around forced oscillating bodies. Finite Elements in Analysis and Design, 47: 1058-10659. [本文引用:1]
[96] Yeo K. 1988. The stability of boundary-layer flow over single- and multi-layer viscoelastic walls. Journal of Fluid Mechanics, 196: 259-408. [本文引用:1]
[97] Yeo K. 1990. The hydrodynamic stability of boundary-layer flow over a class of anisotropic compliant walls. Journal of Fluid Mechanics, 220: 125-160. [本文引用:1]
[98] Zhang J Z, Ren S, Mei G H. 2011. Model reduction on inertial manifolds for~N-S equations approached by multilevel finite element method. Communications in Nonlinear Science and Numerical Simulation, 16: 195-205. [本文引用:1]
[99] Zhang J Z, Liu Y, Lei P F, Sun X. 2007. Dynamic snap-through buckling analysis of shallow arches under impact load based on approximate inertial manifolds. Dynamics of Continuous, Discrete and Impulsive Systems, Series B, 14: 287-291. [本文引用:1]
[100] Zhang J Z, Liu Y, Feng P H. 2011. Approximate inertial manifolds of burgers equation approached by nonlinear Galerkin's procedure and its application. Communications in Nonlinear Science and Numerical Simulation, 16: 4666-4670. [本文引用:1]
[101] Zhang J Z, Liu Y, Cheng D M. 2005. Error estimate for the influence of model reduction of nonlinear dissipative autonomous dynamical system on the long-term behaviors. Journal of Applied Mathematics and Mechanics(English Edition), 26: 938-943. [本文引用:1]