研究领域为材料力学性能, 断裂力学与结构力学. 主要学术成果有: 提出了合金材料超高周疲劳裂纹萌生存在内禀特征区的新观点, 揭示了裂纹萌生特征区形成机理并提出了描述模型, 提出了裂纹表面和内部萌生竞争模型; 提出了材料中疲劳短裂纹"群体损伤"和"群体演化"的学术概念, 揭示了微结构影响短裂纹群体损伤演化的机制; 表明了亚微米/纳米材料中微结构影响塑性变形的规律; 获得了孔边裂纹断裂力学解答并用于孔边疲劳裂纹扩展模型; 揭示了材料微结构影响断裂和应力腐蚀开裂的机制, 提出了计及微结构作用的应力腐蚀开裂模型; 提出了水中悬浮隧道动力响应过程的 "协同浮重比"和"松弛--张紧区域图"新概念.相关成果用于成功解决悬索大桥国产高强度钢丝的高强韧性问题和高铁车轴的损伤容限与安全寿命评估问题.
发表论文290余篇; 获授权专利13项.获1996年度中科院自然科学一等奖(第二获奖人); 获2013年度国家自然科学二等奖(第三获奖人).曾获1995年度国家杰出青年科学基金.
近年, 关于超高周疲劳的研究成果促进了该领域的新进展.2016年在第21届欧洲断裂学术大会作首场大会邀请报告, 2017年在第7届国际超高周疲劳学术大会作首场大会邀请报告, 并受邀在2018年的第12届国际疲劳学术大会作大会邀请报告.
1 引 言
在循环载荷作用下, 合金材料发生裂纹萌生、扩展直至断裂的周次在107 以上的过程被称为超高周疲劳(Sakai 2009 , 洪友士等2009 ). 合金材料超高周疲劳(very-high-cycle fatigue, VHCF) 行为是对传统疲劳理念的挑战, 因为传统疲劳知识认为, 合金材料存在疲劳极限, 即对应107 载荷周次的疲劳强度被确定为疲劳极限 (ASTME468-90, 2004), 循环应力低于疲劳极限不发生疲劳损伤和破坏.
合金材料在载荷循环107 周次以上仍可发生疲劳损伤破坏的报道最早可追溯到20世纪60年代.Kikukawa等 (1965) 采用超声频率加载, 断裂周次超过108 , 研究了频率对低碳钢疲劳强度的影响, 但他们未对107 周次后的疲劳过程和特征进行专门研究.
20世纪80年代, 超高周疲劳现象开始得到专门研究. 最早的报道是Naito等(1983 , 1984 ) 关于渗碳钢的研究和Atrens等 (1983) 关于钛合金的研究.
人类对金属疲劳的研究起始于19世纪中叶 (W\"{o}hler 1867 ), 疲劳早已成为力学与材料科学相交融的分支学科之一. 超高周疲劳研究的萌发, 给这一古老的分支学科注入了崭新的内涵. 超高周疲劳即是对传统疲劳理念的挑战, 也是对传统疲劳领域的拓展, 使疲劳研究领域包含低周疲劳、高周疲劳和超高周疲劳三个部分.
从20世纪80年代至今, 超高周疲劳研究逐渐得到越来越广泛的重视.这是因为, 一方面, 在越来越多的工程应用中, 包括飞行器、高铁、汽车、桥梁、船舶等, 其结构和部件需要具有107 乃至1010 周次的 (安全) 疲劳寿命; 实际上, 若载荷频率为1 Hz, 服役3年2个月就达到108 载荷周次.另一方面, 超高周疲劳的裂纹萌生和初始扩展机理与传统高周疲劳、低周疲劳范畴的情形不同, 新的疲劳机理有待揭示.
1998年, 国际超高周疲劳学术会议应运而生, 而后每3年1届, 至今已举办7届. 超高周疲劳研究在日本和西欧得到特别重视, 这也许与所在地域先进制造业发达的需求有关.在2016年6月举行的第21届欧洲断裂学术大会上, 有4个大会报告关于超高周疲劳, 占12个大会报告的三分之一; 此外, 还有一个超高周疲劳专题研讨会.
值得回味的是, 在疲劳研究的起始, 关注的问题是火车车轴的疲劳断裂(W\"{o}hler 1867 ); 一个半世纪后, 当年时速10 km的蒸汽机车已经发展到如今时速300 km以上的高铁, 其车轴全寿命周期的载荷周次为109 量级, 超高周疲劳仍被认为是高铁车轴的第一个难点和不可确定的问题 (Zerbst et al. 2013 ).
超高周疲劳的关键科学问题可提练为4个方面: (1)超高周阶段的疲劳强度变化趋势, 即S-N曲线特征; (2)超高周疲劳裂纹萌生和初始扩展机理, 包括裂纹萌生方式的变化及其竞争机制; (3)表征超高周疲劳裂纹萌生和初始扩展的特征参量; (4)描述超高周疲劳机理和疲劳性能的模型.
关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型.
2 超高周疲劳研究的起源
关于超高周疲劳的研究可以从采用超声频率 (如20 kHz)进行疲劳加载说起. 采用如此高的加载频率是为了提高疲劳实验效率以研究合金材料更高加载周次的疲劳性能和更低裂纹扩展速率的疲劳行为. Manson (1956) 最早采用超声频率进行疲劳实验. 20世纪50 \(\sim\) 60年代, 仅有为数不多的报道, 其中Kikukawa等 (1965) 发展了超声轴向振动加载设备, 频率范围13 \(\sim \) 100 kHz, 最大加载周次达109 , 研究了加载频率对低碳钢疲劳性能的影响, 表明较高的加载频率导致较高的疲劳极限.这是采用超声频率进行超高周疲劳研究的雏形, 然而他们并未就加载频率对疲劳性能影响的机理进行研究, 也未点明"超高周疲劳"特征.
Willertz (1980) 的文章综述了20世纪50 \(\sim\) 70年代采用超声频率进行疲劳实验研究的情况. 随后, 1981年在美国召开了第一届"直至超声频率的疲劳和腐蚀疲劳"学术会议, 并以"超声疲劳"为题出版了论文集 (Wells et al. 1982 ).在该文集所收集的40篇论文里, 约有1/4论文的实验结果涉及疲劳断裂周次在107 以上直至1010 , 但这些研究并未关注107 周次之后疲劳性能和机理的变化. 注意到Tien (1982) 在该会上的Keynote综述报告的结论里提到"超高周疲劳数据(very high cycle fatigue data)".
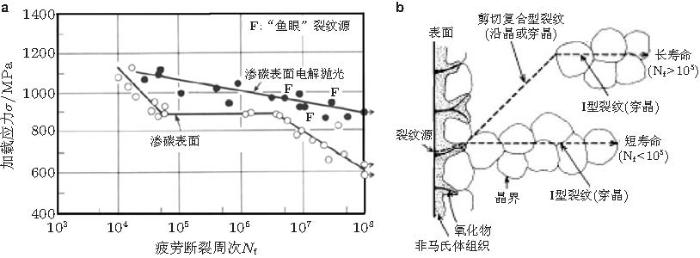
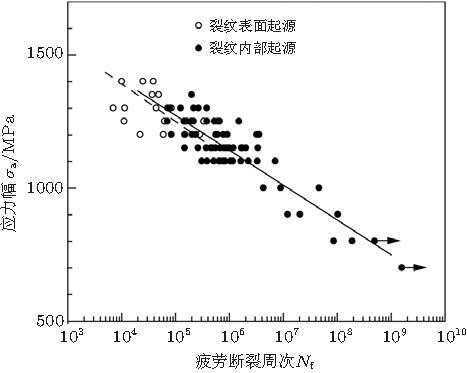
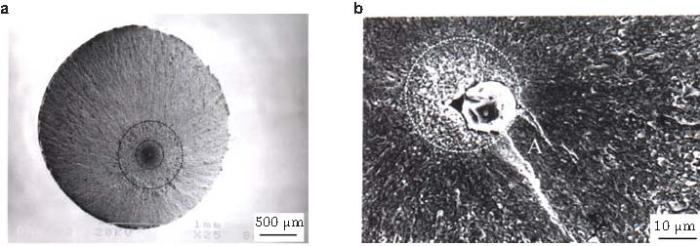
20世纪80年代, Naito等(1983 , 1984 )采用旋转弯曲加载技术 (50 Hz)研究了表面渗碳强化钢的疲劳特性. 所得到的S-N曲线有两个拐点, 一个位于105 周次附近, 另一个位于5\(\times \)106 周次附近; 直至108 周次, 疲劳强度随载荷周次下降, 不存在疲劳极限 (图1 (a)). 他们用电解抛光去除渗碳强化钢50 \(\mu\)m的微结构不均匀表层, 如此试样的疲劳强度得到明显提升且S-N曲线为无拐点的单一线性趋势(图1 (a)). 他们注意到在5\(\times\) 106 周次之后, 部分试样断口呈现"鱼眼 (fish-eye)"特征 (图2 ).这是最早关于高强钢超高周疲劳强度特性与断口特征的报道.
图 1 SCM415钢旋转弯曲实验结果 (Naito et al. 1984 ). (a)S-N曲线, 表面渗碳状态呈现"阶梯状", (b) 裂纹萌生和初始扩展解释示意图
图 2 裂纹亚表面萌生的鱼眼特征 (Naito et al. 1984 )
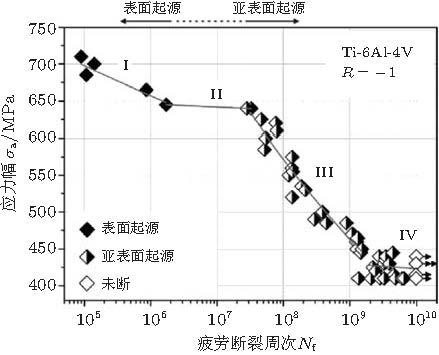
同一时期, Atrens等 (1983) 分别采用60 Hz, 150 Hz和20 kHz研究了Ti-6Al-4V合金的疲劳特性, 显示S-N曲线在\(10^{6}\sim 10 ^{7}\)周次趋于平缓, 107 周次之后疲劳强度又明显下降; 在\(10^{9}\sim 10 ^{10}\)周次, S-N曲线再趋于平缓, 对应的疲劳极限值较低 (图3 ).该文还研究了马氏体不锈钢\(10^{5}\sim 10 ^{10}\)周次的疲劳特性.他们指出, 对于钛合金在107 周次之后, 对于马氏体不锈钢在108 周次之后, 疲劳损伤机制不同, 疲劳裂纹萌生由试样表面转为试样内部, 但文章并未点明所观察到的"鱼眼"特征.
图 3 Ti-6Al-4V合金的S-N曲线, 低于107 周次, 裂纹表面萌生; 高于107 周次, 裂纹亚表面萌生 (Atrens et al. 1983 )
此外, Asami和Sugiyama (1985) 也采用旋转弯曲加载技术研究了若干表面强化钢的疲劳性能, 同样表明表面渗碳强化钢的S-N曲线有两个拐点 (图4 ), 所得到断口观察结果及其解释与Naito等 (1984) 相似.
图 4 表面渗碳强化SCM 420钢的S-N曲线 (Asami & Sugiyama 1985 )
Naito等(1983 , 1984 ) 和Atrens等 (1983) 的文章是关于高强钢和钛合金超高周疲劳研究的最先报道, 他们指出在"长寿命"阶段, 疲劳性能、特征、机理均发生了变化, 尽管在他们的文章里并无"超高周"的名词, 而表达为"长寿命".
随后, Stanzl等 (1986) 采用超声频率 (20 kHz) 研究了一种低碳钢在随机载荷下的疲劳特性, 疲劳断裂周次从3 \(\times\) 106 至3 \(\times \) 109 , 他们称此为"超高周疲劳范围 (very high cycle fatigue range)". 尽管他们并未关注超高周疲劳范围的特有行为, 但这是在研究论文里最早出现的"超高周疲劳 (very high cycle fatigue)"的表述.
Naito等(1983 , 1984 )、Atrens等 (1983) 、Asami和Sugiyama (1985) 和Stanzl等 (1986) 的研究报道, 标志了与传统低周疲劳和高周疲劳内涵不同的超高周疲劳研究的起源.
3 超高周疲劳的主要特征
超高周疲劳之所以成为疲劳研究的新领域, 不仅是因为其疲劳断裂周次大于107 且疲劳强度逐渐降低, 而且是因为其S-N曲线趋势发生了变化并呈现了独特的疲劳裂纹萌生和初始扩展特征.
换言之, 在超高周疲劳阶段, 疲劳裂纹萌生与初始扩展的方式与机理不同于传统的低周、高周疲劳的情形, 由此导致了超高周疲劳特异的力学特性.
3.1 高强钢超高周疲劳的S-N曲线及其裂纹萌生特征
作为最早报道的结果之一, 图1 (a)显示了表面渗碳强化钢的S-N曲线在 5\(\times 10^6\)周次发生二次拐折, 疲劳强度继续下降, 传统疲劳极限不复存在 (Naito et al. 1984 )的现象.长寿命的疲劳裂纹表面萌生后形成尺度约90 \(\mu \)m的光滑断面区(图5 (a)), 该断面区与拉应力方向夹角约45\(^\circ\); 这不同于短寿命的情形: 裂纹表面沿晶萌生后以I型裂纹方式发生初始扩展(图5 (b)). 图1 (b) 是对这一结果的解释.该S-N曲线及其裂纹萌生观察结果是重要的, 但其解释值得质疑: 图5 (a) 显示的裂纹萌生区光滑断面不完全与拉应力呈倾斜夹角, 此断面很可能是裂纹萌生过程形成的区域, 即裂纹亚表面萌生而不是表面萌生的特征.
图 5 裂纹萌生特征. (a) 长寿命试样\(\sigma _{\rm a} =690 {\rm MPa}\), \(N_{\rm f} = 4.65\times 10^7\), (b) 短寿命试样, \(\sigma _{\rm a} =930 {\rm MPa}\), \(N_{\rm f} = 5.81\times 10^4\) (Naito et al. 1984 )
对于图1 (a)中表面抛光去除了不均匀微结构层后的S-N曲线在107 周次后虽未出现拐点而保持原有下降趋势, 但却观察到裂纹亚表面起源的"鱼眼"特征 (图2 ).这是关于超高周疲劳裂纹内部起源呈现"鱼眼"特征的最早报道的观察图像.
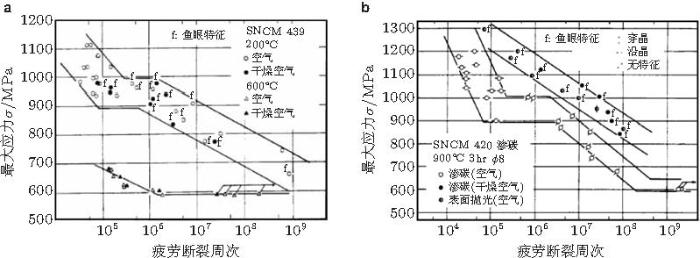
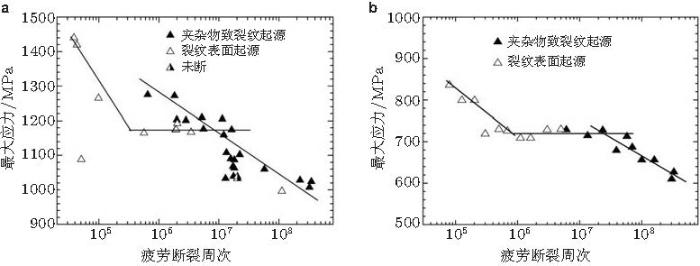
Asami和Emura (1990) 报道了若干高强钢在实验室环境和干燥空气中的超高周疲劳特性. 图6 (a) 是SNCM439 (0.4%C-Ni-Cr-Mo) 钢经淬火并低温(200\(^\circ\)C) 和高温 (600\(^\circ\)C) 回火的S-N曲线, 显示低温回火态的S-N曲线是具有两个拐点的双线形; 在第2个拐点后, 即106 \(\sim \) 109 周次区间主要为亚表面裂纹萌生的鱼眼特征.
图6 (b) 是SNCM420 (0.2%C-Ni-Cr-Mo)钢经表面渗碳强化的S-N曲线, 显示表面处理态的S-N曲线为双线形; 去除不均匀表层后, 裂纹主要为亚表面萌生, 具有"鱼眼"特征.
图 6 (a) 2组SNCM 439钢的S-N数据, (b) 3组SNCM 420钢的S-N数据(Asami & Emura 1990 )
Nishijima和Kanazawa (1999) 归纳分析了早期关于以表面硬化钢为代表的高强钢S-N曲线的结果 (图7 ). 他们认为, 表面起源和内部起源两种疲劳裂纹萌生模式导致了两套S-N曲线; 裂纹内部起源对应的载荷条件低于表面起源的载荷条件, 只有表面起源受到抑制, 才可能发生裂纹内部起源.
图 7 双重S-N曲线示意图 (Nishijima & Kanazawa 1999 )
Sakai等 (2000) 联络了6个实验室的研究者, 采用相同类型的旋转弯曲设备(52 Hz) 和相同类型的SUJ2钢 (1% C, 1.5% Cr) 试样, 所获得的大量数据表明"双重S-N曲线"特征 (图8 ).在106 周次之前, 裂纹于表面萌生, 即传统的疲劳行为; 在106 \(\sim \) 109 周次, 裂纹于内部萌生, 裂纹源区呈现"鱼眼"特征 (图9 (a)).起源处的高倍图像显示尺度为几十微米的亮区 (图9 (b)), 并称其为FGA (fine granular area). Sakai 2009 还给出了SUJ2钢轴向循环加载 (50 Hz) 的S-N数据, 其特征为单一线性下降趋势, "双重S-N曲线"特征不明显 (图10 ).在105 \(\sim \) 109 周次, 裂纹于内部萌生 (图11 (a)), 同样观察到起源处有尺度为几十微米的FGA特征 (图11 (b)).裂纹萌生位置在截面上随机分布, 这与轴向加载应力分布特征相对应.对于旋转弯曲加载具有的"双重S-N曲线"的一种解释是, 试样截面受力从表面到中心线性减小, 裂纹萌生和初始扩展点的应力小于名义应力; 而对于轴向加载, 试样整个截面受力一致. 换言之, 旋转弯曲加载和轴向加载分别对应的控制体积不同.控制体积是试样中发生裂纹起源的潜在区域, 通常取不小于 90%最大应力的截面所对应的试样体积为控制体积 (Murakami et al. 2002 , Furuya 2011 , Lei et al. 2014 , Sun et al. 2016 ).
图 8 SUJ2钢旋转弯曲加载的超高周疲劳双重S-N曲线 (Sakai et al. 2000 )
图 9 (a) 裂纹亚表面起源的鱼眼特征 \((\sigma _{\rm a} =1300 {\rm MPa}\), \(N_{\rm f} = 2.66\times 10^6)\), (b)高倍图像显示鱼眼中部环绕裂纹源夹杂物的FGA (Sakai et al. 2000 )
图 10 SUJ2钢轴向循环加载的超高周疲劳S-N曲线 (Sakai 2009 )
图 11 (a) 裂纹萌生于内部的鱼眼特征 \((\sigma _{\rm a} =900 {\rm MPa}\), \(N_{\rm f} = 1.94\times 10^8)\), (b) 高倍图像显示鱼眼中部环绕夹杂物的FGA (Sakai et al. 2002 )
笔者 (Hong et al. 2012 ) 对GCr15 (1% C, 1.5% Cr) 和40Cr(0.4% C, 1% Cr) 的旋转弯曲实验 (52 Hz)显示了疲劳性能具有"双重S-N曲线"特征 (图12 ). 图13 显示了裂纹亚表面起源所呈现的鱼眼特征 (图13 (b))和FGA特征 (图13 (c)). 光学显微镜图像 (图13 (b))显示鱼眼区域内的FGA为灰度大的深色特征, 因而也被称为暗区 (optical dark area, ODA) (Murakami et al. 2000 ); 而扫描电子显微镜(SEM)图像(图13 (c)) 显示的FGA是灰度相对小的亮区, 因而也被称为颗粒状亮面区 (granular bright facet, GBF) (Shiozawa etal. 2001 ), 这是由于扫描电镜对粗糙断面成像的缘故.
图 12 旋转弯曲加载的双重S-N曲线. (a) GCr15钢, (b) 40Cr钢 (Hong et al. 2012 )
图 13 GCr15钢超高周疲劳裂纹起源于亚表面 \((\sigma _{\max} =1024 {\rm MPa}\), \(N_{\rm f} = 3.5\times 10^8)\).(a)断口全貌光镜图像, (b) 鱼眼光镜图像, (c) FGA SEM图像(Hong et al. 2012 )
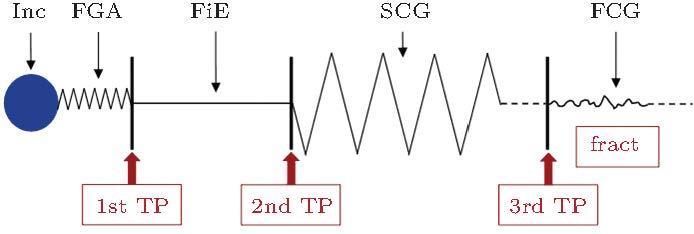
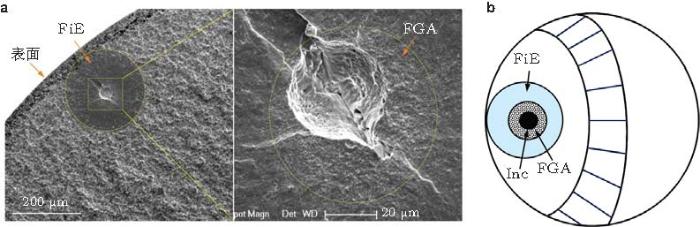
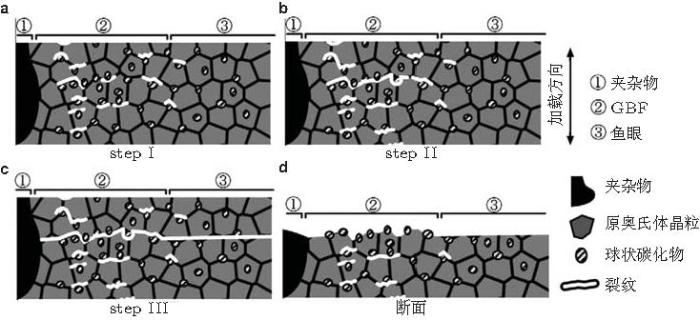
本文用图14 示意表达高强钢超高周疲劳裂纹萌生于夹杂物直至断裂的过程.裂纹萌生于试样内的夹杂物, 裂纹萌生和初始扩展呈现鱼眼 (FiE) 特征, FiE包含裂纹萌生区FGA. FGA断面相对粗糙; FGA外的FiE区断面相对平整; FiE区之外为裂纹稳态扩展区, 裂纹面粗糙度较大.
图 14 高强钢超高周疲劳裂纹内部萌生至断裂全过程示意图. Inc: 夹杂物, FGA: 细颗粒区, FiE: 鱼眼, SCG: 稳态裂纹扩展, FCG: 快速裂纹扩展, TP: 转捩点, Fract: 断裂 (完整的FiE包含Inc和FGA, 图中FiE指FGA之外的部分)
关于裂纹面粗糙度, Shiozawa等 (2006a , 2006b ) 对旋弯加载 (52.5 Hz)断裂周次\(N_{\rm f} = 6.3\times 10^8\)的SUJ2试样, 采用扫描电镜3D分析, 测量了FGA, FGA外FiE区和FiE外SCG断面的粗糙度(表1 ), 表明FGA的平均粗糙度\(R_{\rm a}\)值是FiE区的2.2倍, SCG区的平均粗糙度\(R_{\rm a}\)值是FiE区的3.5倍. 钱桂安 (2009)对旋弯加载 (52.5 Hz) 断裂周次\(N_{\rm f} = 1.34\times 10^7\)的40Cr试样, 采用原子力显微镜测量获得3个区域的断面粗糙度(表1 ), 表明FGA的平均粗糙度\(R_{\rm a}\)值是FiE区的3.4倍, SCG区的平均粗糙度\(R_{\rm a}\)值是FiE区的4.9倍.
3.2 钛合金超高周疲劳的S-N曲线及其裂纹萌生特征
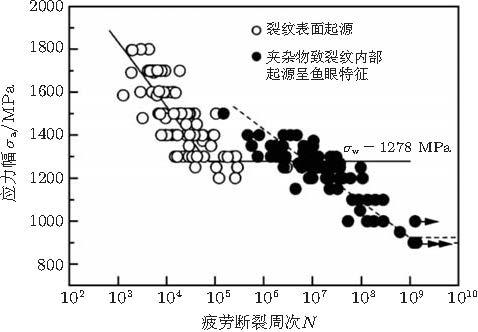
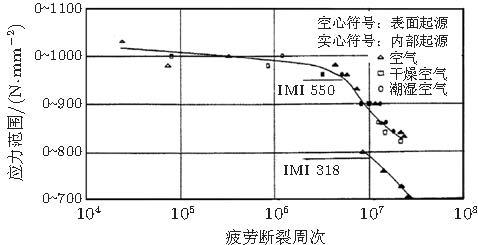
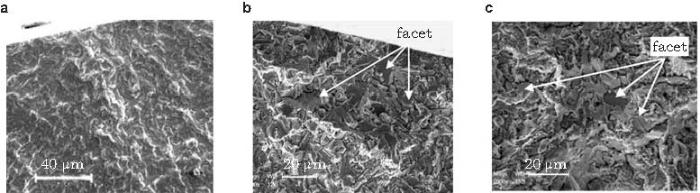
关于钛合金, Neal和Blenkinsop (1976) 给出了IMI 550(Ti-4Al-4Mo-2Sn-0.55Si) 和IMI 318 (Ti-6Al-4V) 轴向循环加载(应力比\(R=0\), 频率150 Hz) 的S-N曲线 (图15 ), 表明在\(3\times 10 ^{6}\sim 2.5\times 10^{7}\)周次范围疲劳裂纹主要从内部萌生, 裂纹起源特征为\(\alpha\)相解理导致的 "facet (小解理面)". 此结果是关于钛合金\(\alpha \)相"facet" 为特征裂纹萌生的最早报道. 但断裂周次仅略高于107 , 即初步涉及到超高周疲劳阶段.
图 15 IMI 550 (Ti-4Al-4Mo-2Sn-0.55Si) 和IMI 318 (Ti-6Al-4V)轴向循环加载的S-N结果 (Neal & Blenkinsop 1976 )
图3 是较完整的关于钛合金超高周疲劳特性的早期结果, 显示了Ti-6Al-4V的S-N曲线 (Atrens et al. 1983 ), 在107 周次的拐折点前后, 裂纹萌生机理发生了变化: 疲劳寿命\(N_{\rm f}\)低于 107 周次, 裂纹萌生于试样表面; \(N_{\rm f}\)高于107 周次, 裂纹萌生于亚表面即试样内部.
钛合金 (如Ti-6Al-4V) 的微结构包含hcp晶体结构的\(\alpha\)相和bcc晶体结构的\(\beta \)相; 这2种相的比例和形状决定了钛合金的微结构特征.钛合金基本不含夹杂物和孔洞缺陷. \(\alpha \)相的脆性特征明显, 超高周疲劳裂纹往往以\(\alpha \)相解理并呈现 facet 特征的方式起源.Zuo等(2008) 的结果表明, 在Ti-6Al-4V中, 对于双态组织形态, 超高周疲劳裂纹可萌生于\(\alpha _{\rm p}\)晶粒 (下标p表示初生)或\(\alpha _{\rm p}\)晶界, 对于网篮组织形态, 裂纹萌生于\(\alpha\)-\(\beta \)相界. Szczepanski等(2008) 的结果表明, 在Ti-6Al-2Sn-4Zr-6Mo合金中, 超高周疲劳裂纹萌生局域为\(\alpha _{\rm p}\)晶粒断裂而成的小解理面 (facet), 形成facet的\(\alpha _{\rm p}\)晶粒尺度对应于其平均值; 裂纹萌生局域的facet取向为高剪应力导向, 即与拉应力轴近似成45\(^\circ\).
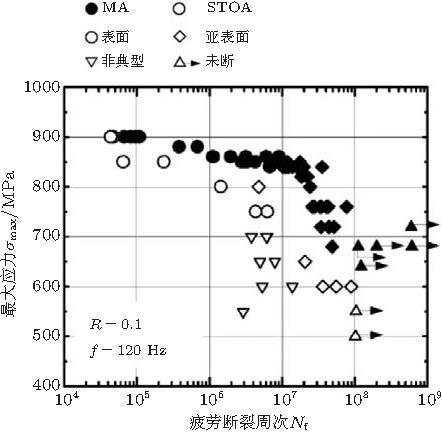
图16 是采用常规频率 (120 Hz) 对钛合金 (Ti-6Al-4V)轴向疲劳加载 \((R= 0.1)\) 的超高周疲劳特性典型结果 (Oguma & Nakamura 2010 ), 给出了退火态 (MA) 和固溶--时效态 (STOA)的超高周疲劳特性. 表明S-N曲线在107 周次发生显著拐折, 对应的疲劳裂纹起源由表面转为内部, 裂纹源区为\(\alpha\)相晶粒萌发的"小解理面"构成.
图 16 Ti-6Al-4V 轴向疲劳加载 (120 Hz) 的S-N特性 (Oguma & Nakamura 2010 )
图17 是采用超声频率 (20 kHz) 对Ti-6Al-4V轴向振动加载 \((R =-1)\) 的超高周疲劳特性典型结果 (Heinz et al. 2013 ), 表明S-N曲线在\(2\times 10^{7}\)周次发生显著拐折, SEM观察显示超高周疲劳裂纹萌生于试样内部 (图18 (a)), 并呈现"鱼眼"特征 (图18 (b)中的②), 裂纹源区有类似于FGA的粗糙区 (图18 (b)中的①), 粗糙区的高倍图像 (图18 (c)) 显示断面起伏特征.
图 17 Ti-6Al-4V超声振动加载 (20 kHz) 的S-N特性 (Heinz et al. 2013 )
图 18 Ti-6Al-4V超声轴向振动加载SEM断面图像 \((\sigma _{\rm a}= 1024 {\rm MPa}\), \(N_{\rm f} = 3.2\times 10^9)\).(a)全貌,(b) 裂纹萌生区, (c) 粗糙区①形貌 (Heinz et al. 2013 )
Furuya和Takeuchi (2014) 报道了Ti-6Al-4V在120 Hz和20 kHz轴向循环加载的超高周疲劳行为. 图19 是2组试样的S-N数据, 图中2组试样的化学成分以及屈服强度和拉伸强度基本一致, 但微结构形态不同. A组\(\alpha \)相晶粒为等轴状, 平均 (等效)直径约7 \(\mu \)m; B组\(\alpha \)相晶粒沿轧制方向拉长, 平均 (等效)直径约20 \(\mu \)m. 对于A组, 3 \(\times\) 105 周次后裂纹基本内部起源; 对于B组, 3 \(\times\) 106 周次后裂纹基本内部起源.加载频率对2组试样的疲劳强度基本无影响; 而疲劳强度随应力比增大而明显降低. 他们 (Takeuchi et al. 2008 , Furuya & Takeuchi 2014 ) 观察表明, 对于A组选取的试样 (20 kHz, \(R = -1)\), 裂纹内部萌生区有明显"鱼眼"特征 (图20 (a), \(N_{\rm f}= 2.10\times 10^{8})\), "鱼眼"中部包含表面起伏较大的粗糙区; 当裂纹源即粗糙区位于试样表面附近, "鱼眼"特征不明显(图20 (b), \(N_{\rm f}= 6.97\times 10^{7})\).对于B组选取的试样 (20 kHz, \(R = 0\), \(N_{\rm f} = 5.10\times 10^{8})\), 内部萌生的裂纹由facet组成 (图21 ). Furuya和Takeuchi(2014) 认为, 裂纹内部萌生局域\(\alpha \)相形成的小解理面群, 其单个小解理面尺度与\(\alpha \)晶粒相当.
图 19 2组Ti-6Al-4V在120 Hz和20 kHz 轴向循环加载 \((R = -1\), 0, 0.3)的S-N数据 (Furuya & Takeuchi 2014 )
图 20 A组试样裂纹内部萌生特征. (a) 裂纹萌生区鱼眼特征(20 kHz, \(R = -1\), \(N_{\rm f} = 2.10\times 10^8)\); (b)裂纹源靠近试样表面, 鱼眼特征不明显 (120 Hz, \(R = -1\), \(N_{\rm f}= 6.97\times 10^7)\)(Takeuchi et al. 2008 )
图 21 B组试样裂纹内部萌生特征 (20 kHz, \(R = 0\), \(N_{\rm f} =5.10\times 10^8)\). (a) 低倍图像显示萌生区全貌, (b)高倍图像显示萌生区facet特征 (Furuya & Takeuchi 2014 )
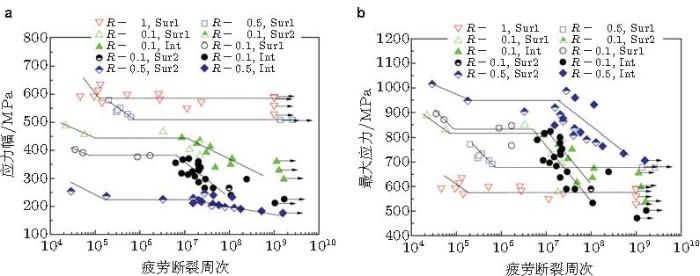
近期, 笔者采用超声轴向加载 (20 kHz)获得了不同应力比条件下Ti-6Al-4V的超高周疲劳特性 (Liu et al. 2015 ), 对于应力比R=-0.1, 0.1, 0.5情形, S-N曲线在107 周次附近发生二次拐折, 裂纹主要萌生于内部; 而\(R =-1\), \(-0.5\)的S-N曲线不发生拐折, 裂纹均于表面萌生 (图22 ).观察到3种裂纹萌生模式: 表面滑移、表面解理和内部解理 (图23 ).
图 22 Ti-6Al-4V在 \(R = -1\), \(-0.5\), \(-0.1\), 0.1, 0.5的S-N特性(Sur1: 表面滑移起源, Sur2: 表面解理起源, Int: 内部解理起源). (a)应力幅表达, (b) 最大应力表达(Liu et al. 2015 )
图 23 (a) 表面滑移起源: \(R = -1\), \(\sigma _{\rm a} ={550} {\rm MPa}\), \(N_{\rm f} = 1.13\times 10^7\); (b)表面解理起源: \(R = 0.5\), \(\sigma _{\rm a} = {202} {\rm MPa}\), \(N_{\rm f} = {4.03}\times 10^7\); (c) 内部解理起源: \(R = 0.1\), \(\sigma _{\rm a} = {339} {\rm MPa}\), \(N_{\rm f} = {2.26}\times10^7\)(Liu et al. 2015 )
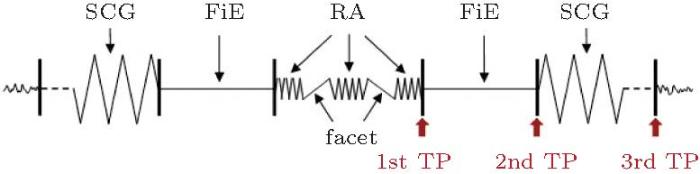
钛合金 (如Ti-6Al-4V) 超高周疲劳裂纹往往以\(\alpha\)相解理并呈现facet 特征的方式起源.裂纹萌生区由若干facet以及它们的汇合而构成, 形成相对粗糙的断面, 被称为rough area (RA). RA之后是FiE区, 然后进入裂纹稳态扩展. 图24 是钛合金超高周疲劳裂纹内部萌生及其发展的示意图. Liu 等(2016) 对超声轴向加载 (20 kHz) 断裂周次\(N_{\rm f} = {2.02}\times10^7\)的Ti-6Al-4V试样, 采用原子力显微镜测量表明, facet起伏很小, 最大值为14 nm, 连接facet的局域粗糙度很大, 最大值达2217 nm, 而FiE区的最大起伏为209 nm, 即RA区的粗糙度比FiE区大1个量级.
图 24 钛合金超高周疲劳裂纹内部萌生至断裂全过程示意图, RA: 粗糙区, Facet: 小刻面, FiE: 鱼眼, SCG: 稳态裂纹扩展, TP: 转捩点(完整的FiE包含facet和RA, 图中FiE指RA之外的部分)
3.3 裂纹不同萌生模式的竞争
合金材料超高周疲劳最主要的特征之一是裂纹从材料 (试样) 内部萌生. 这样, 裂纹内部起源与通常的裂纹表面起源存在竞争关系. 此外, 即使裂纹内部萌生, 也有不同类型裂纹源的情形 (如夹杂物或基体), 也存在竞争关系.超高周疲劳裂纹萌生方式的竞争关系是研究的一个关注点和重要科学问题.
Yu等 (2011) 对6组贝氏体/马氏体高强钢的研究表明超高周疲劳裂纹萌生于试样内部, 裂纹源可以是非金属夹杂物, 也可以是基体, 两种起源模式相互竞争.这一竞争与材料加工所经历的金属物理和金属化学过程有关; 金属物理方法使微结构均匀化、细化和强韧化, 而金属化学方法控制了非金属夹杂物的尺度和分布.只有同时优化金属物理方法和金属化学方法才能改善材料的超高周疲劳性能.
他们认为, 裂纹是否萌生于基体 (而不萌生于夹杂物) 与夹杂物尺度无关.只要微结构的细化程度和均匀性不佳, 裂纹将萌生于基体且具有较低的疲劳抗力; 反之, 裂纹将萌生于夹杂物且具有较高的疲劳抗力.
合金材料的超高周疲劳裂纹以内部起源为主, 但对于不同的材料, 裂纹萌发点和裂纹初始扩展特征可能存在差异.为了说明疲劳裂纹表面起源向内部起源的转移和竞争, 笔者 (Hong et al. 2009 , 2012 , Qian et al. 2011 ) 引入了一个新的参数\(D^\ast \)
\[D^\ast = N_{\rm i} / N_{\rm s} \ \ (1)\] 其中, \(N_{\rm i}\)是裂纹在内部萌生所需的周次, \(N_{\rm s}\)是裂纹在表面萌生所需的周次. 当\(N_{\rm s}<N_{\rm i} \), 即\(D^\ast >1\), 裂纹在表面萌生; 反之, 当\(N_{\rm s}>N_{\rm i} \), 即\(D^\ast<1\), 裂纹在内部萌生. 实际上, \(D^\ast\)是2个广义时间参量之比, 可称其为Deborah数. 模拟结果 (图25 )表明, 较小的载荷下, 较大的夹杂物尺度、较小的晶粒尺度和较大的位错阻力(即材料具有较高的强度), 这些因素均增加疲劳裂纹在内部萌生的可能性.这一预测与实验结果趋势一致.
图 25 \(D^*\)随\(\varphi = 0.5 \Delta \sigma /k\)和\(\psi =r/l\)的变化, 其中\(k\)是位错阻力, \(r\)是夹杂物半径, \(l\)是晶粒半径. (a)夹杂物与基体弱结合, (b) 夹杂物与基体强结合 (Hong et al. 2012 )
近期, Zhang等 (2016) 采用超声频率 (20 kHz)研究了马氏体时效硬化不锈钢(FV520B-I) 的超高周疲劳行为, 表明107 周次后裂纹于内部起源. 他们采用文献 (Hong et al. 2009 , 2012 ) 提出的\(D^*\)模型分析了裂纹表面萌生和内部萌生的竞争机理; 鉴于GBF (FGA) 的发展速率很低、寿命很长, 因此认为GBF (FGA)消耗的周次\(N_{\rm G}\)可以作为裂纹内部萌生寿命\(N_{\rm i}\)来分析萌生竞争机理.
笔者近期的研究结果 (Liu et al. 2015 ) 表明, 钛合金的高周和超高周疲劳裂纹萌生存在3种类型, 即表面滑移裂纹萌生、表面解理裂纹萌生和内部解理裂纹萌生 (图23 ). 3种断口类型包含两种裂纹萌生机制, 即滑移和解理.在分析3种断口类型的竞争关系时, 首先要分析滑移机制和解理机制的竞争, 然后再分析解理机制中表面解理和内部解理之间的竞争.
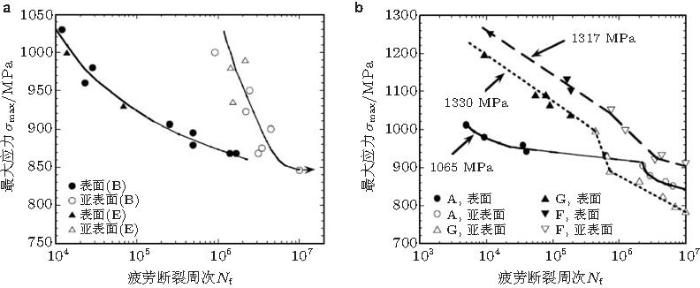
Jha和Ravi Chandran (2003) 、Ravi Chandran (2005) 和Ravi Chandran和Jha (2005) 报道了初生\(\alpha\)相比例对Ti-10V-2Fe-3Al疲劳行为的影响, 表明初生\(\alpha\)相体积比例较低时 (10%), 具有同样微结构形态的试样在所有应力水平下发生疲劳裂纹表面萌生和内部萌生的概率基本一样(图26 (a)). 初生\(\alpha \)相体积比例较高时 (45%), 高应力状态裂纹趋于表面萌生, 低应力状态趋于内部萌生 (图26 (b)).
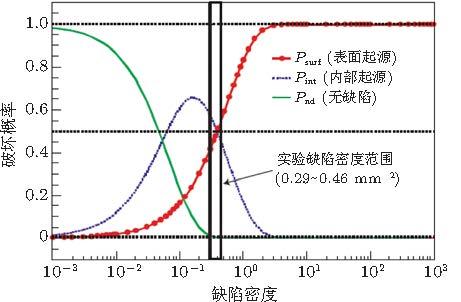
针对这一结果, 并将钛合金初生\(\alpha \)相晶粒团簇看作缺陷, Ravi Chandran 等 (Ravi Chandran 2005 , Ravi Chandran & Jha 2005 )提出了基于Poisson缺陷模型分析得到的3种疲劳破坏类型的发生概率, 以此解释不同初生\(\alpha \)相体积比例下, 钛合金疲劳裂纹表面萌生和内部萌生的竞争行为 (图27 ). 图中表明, 当 \(\lambda = 15\) mm\(^{ - 2}\), \(P_{\rm int}\)达到极值 (0.66); 该处对应\(P_{\rm surf }= 0.23\), \(P_{\rm nd }= 0.11\), 即23%的试样将从亚表面发生裂纹萌生. 当 \(\lambda = 15\) mm-2 , \(P_{\rm nd }= 0\), 意味着所有试样将由\(\alpha\)相晶粒团簇缺陷萌生裂纹导致断裂, 包括: 裂纹萌生于表面缺陷和萌生于内部缺陷. 这一预测与实验结果相符合; 即 \(\lambda = 0.29 \sim 0.46 \) mm\(^{ - 2}\)时, \(P_{\rm nd }=0\), \(P_{\rm int}\)和\(P_{\rm surf}\)数值相近, \(\alpha\)相晶粒团簇缺陷导致裂纹萌生于表面或萌生于内部.
图 26 Ti-10V-2Fe-3Al裂纹表面起源和内部起源对应的S-N曲线 (Jha& Ravi Chandran 2003 ). (a) \(\alpha _{\rm p}\)比例10%, B: 条状\(\alpha _{\rm p}\), E: 粒状\(\alpha _{\rm p}\); (b) \(\alpha _{\rm p}\)比例45%, A: 条状\(\alpha _{\rm p}\), F和G: 粒状\(\alpha _{\rm p}\)
图 27 计算结果显示裂纹表面起源和内部起源概率随缺陷密度的变化(Ravi Chandran 2005 , Ravi Chandran & Jha 2005 )
笔者 (Liu et al. 2015 )在研究应力比对钛合金高周和超高周疲劳3种裂纹萌生类型竞争关系时, 同样基于Poisson缺陷模型, 计算了3种裂纹萌生类型的发生概率, 其中, 表面解理裂纹萌生的发生概率为\[P_{\rm surf} = P_{\rm surf} (n \geq 1) = 1 - {\rm e}^{ -N_{\rm surf} } \ \ (2)\]内部解理裂纹萌生的发生概率为\[P_{\rm int} = P_{\rm surf} (n = 0)P_{\rm int} (n \geq 1) = (1- {\rm e}^{ - N_{\rm int} }){\rm e}^{ - N_{\rm surf} } \ \ (3)\]表面滑移裂纹萌生的发生概率为\[ P_{\rm sli} = P_{\rm surf} (n = 0)P_{\rm int} (n = 0)= {\rm e}^{ - (N_{\rm int} + N_{\rm surf} )} \ \ (4)\]图28 (a) 显示了式 (2)\(\sim \)(4)得到的裂纹萌生类型发生概率与最大应力的关系: 随着最大应力增加, 表面滑移裂纹萌生 (surface-without-facets) 减少, 表面解理裂纹萌生(surface-with-facets) 增加, 内部解理裂纹萌生(interior-with-facets) 先增加后减少. 图28 (b)是裂纹萌生类型随应力比变化的实验结果. 对于所涉及的情况, 应力比变化趋势与最大应力变化趋势相对应 (图22 (b)). 图28 (a) 与图28 (b)对比, 可见随着应力比增大, 即随着最大应力增大, 3种疲劳裂纹萌生类型随加载过程变化的模型计算结果与实验结果的趋势一致.
图 28 (a)3种疲劳裂纹萌生类型的发生概率与最大应力关系的计算结果, (b)疲劳裂纹萌生类型所占比例随应力比变化的实验结果 (Liu et al. 2015 )
4 超高周疲劳裂纹萌生特征区和特征参量
4.1 裂纹萌生特征区
高强合金超高周疲劳裂纹萌生的主要特点是起源于材料 (试样) 内部, 这是超高周疲劳不同于低周疲劳和高周疲劳的基本特征.内部萌生的裂纹在断面上呈现"鱼眼" 特征 (图2 , 图9 , 图11 , 图13 , 图18 , 图2 0); 在其范围内, 往往可见一表面相对粗糙的小区域. 对于高强钢, 该区域被称为光学暗区(ODA), 或GBF或FGA, 本文将其称为FGA; 对于钛合金, 该区域被称为粗糙区(RA). 笔者的研究指出, FGA和FiE是高强钢超高周疲劳裂纹萌生的特征区, FGA和FiE所对应的参量是高强钢超高周疲劳裂纹萌生特征参量 (Hong et al. 2014 ).
图29 (a) 是高强钢超高周疲劳裂纹内部萌生特征区的典型图像(Hong et al. 2014 ); 图29 (b) 是示意图: 裂纹起源于内部夹杂物 (Inc), 形成萌生区FGA, 而后发展形成FiE, 直至断裂. 其中, \(2a_{\rm Inc } = 35.3 \mu \)m, \(2a_{\rm FGA } =66.3 \mu \)m, \(2a_{\rm FiE } =235 \mu \)m.
图 29 (a) 高强钢超高周疲劳裂纹内部萌生特征区的典型图像, Cr钢(1% C, 1% Cr) 旋弯加载, \(N_{\rm f} = 1.79\times 10^7\) (Hong et al. 2014 ); (b) 超高周疲劳裂纹内部萌生特征区及发展至断裂示意图, FiE: 鱼眼, Inc: 夹杂物如图14 所示, 裂纹从FGA经过第1转捩点发展到FiE, 再从FiE经过第2转捩点进入稳态裂纹扩展阶段. FGA对应的疲劳寿命\(N_{\rm i}\), FiE对应的疲劳寿命\(N_{1}\), 稳态裂纹扩展对应的疲劳寿命\(N_{2}\).这里将特别关注第1转捩点之前FGA的特征和对应的参量.
需要说明, 在超高周疲劳领域, 应力强度因子\(K\)通常被作为描述裂纹萌生和扩展的表征量. 对此, Murakami等 (1989) 的分析结果给出了表面或内部缺陷萌生裂纹的应力强度因子最大值\(K_{\rm Imax} \)表达式. 对于表面缺陷\[ K_{\rm {Imax}} = 0.65\sigma _0 \left( {\pi \sqrt{area_{\rm s} } } \right) ^{1 / 2} \ \ (5)\] 式中, \(\sigma _0\)是最大拉伸应力, \(area_{\rm s}\)是表面缺陷在垂直于拉应力平面的投影面积. 对于内部缺陷\[K_{\rm {Imax}} = 0.5\sigma _0 \left( {\pi \sqrt{area_{\rm i} } } \right) ^{1 / 2} \ \ (6)\] 式中, \(area_{\rm i} \)是内部缺陷在垂直于拉应力平面的投影面积.
4.2 特征区FGA和FiE的特征参量
FGA 和FiE是超高周疲劳裂纹萌生的特征区, 其尺度及其关联的物理量是裂纹萌生特征区的特征参量.
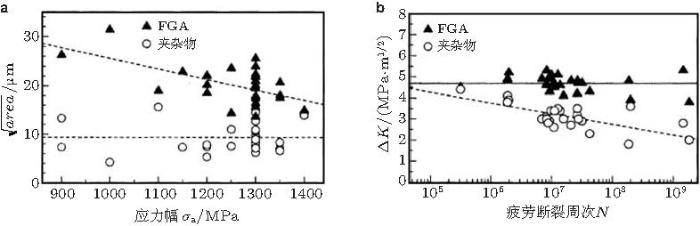
Sakai等 (2001) 给出了SUJ2钢 (旋弯加载) FGA尺度\(\sqrt {area}\)随加载应力增大而减小的趋势 (图30 (a)), 其尺度范围从15 \(\mu \)m至32 \(\mu \)m; 而导致裂纹起源的夹杂物尺度不随加载应力变化 (图30 (a)).对于FiE, 其尺度范围相对较大, 从50 \(\mu \)m至300 \(\mu \)m(Sakai et al. 2001 ).
重要的是, 疲劳断裂周次从105 到10 9 , FGA对应的应力强度因子幅值 \(\Delta K\)不随疲劳断裂周次变化且基本保持恒定, 其平均值为4.74 MPa\( \cdot \)m\(^{1 / 2}\); 而导致裂纹起源的夹杂物对应的应力强度因子幅值\(\Delta K\)随断裂周次增大而降低(图30 (b)).
Shiozawa和Lu (2002) 也对SUJ2钢得到了类似的结果, 表明疲劳断裂周次在\(10^{5}\sim 10 ^{9}\)范围, FGA尺度为12 \(\mu\)m至40 \(\mu \)m, 其对应的 \(\Delta K\)值不随断裂周次变化, 为4 \(\sim \) 6 MPa\( \cdot \)m\(^{1 / 2}\).
图 30 (a) FGA和裂纹源夹杂物尺度与加载应力幅的关系, (b)FGA和裂纹源夹杂物的应力强度因子幅值与疲劳寿命的关系 (Sakai et al. 2001 )
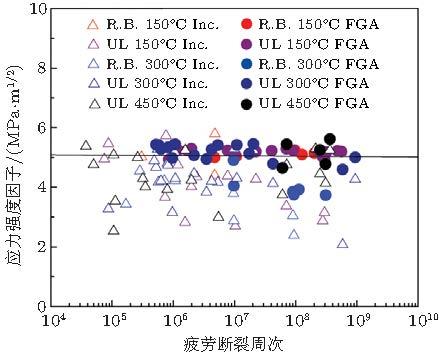
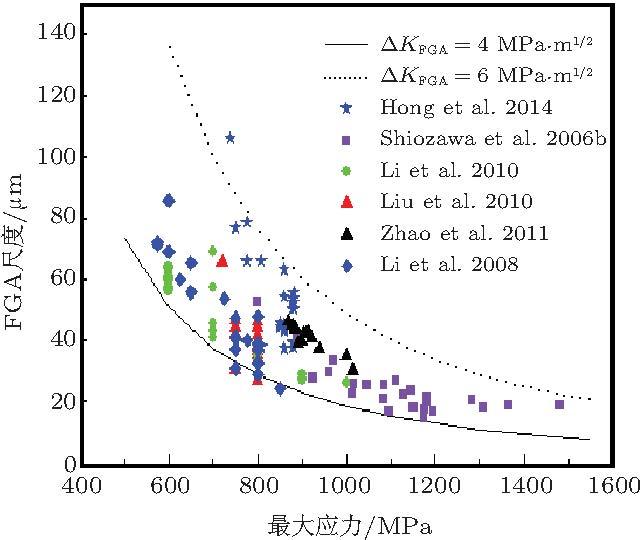
笔者 (Zhao et al. 2011 , 2012 ) 对GCr15钢 (与SUJ2相似)的若干强度状态分别进行旋转弯曲和超声轴向振动加载, 得到FGA对应的\(\Delta K\)值范围同样在4 \(\sim \) 6 MPa\( \cdot \)m\(^{1 / 2}\) (图31 ). 进一步地, 图32 (Hong et al. 2014 )汇集了我们和诸多其他研究者关于高强钢超高周疲劳FGA的结果, 表明绝大多数FGA尺度在15 \(\mu \)m至100 \(\mu \)m之间, 该尺度随加载应力减小而增大, 即循环应力越小, FGA发展的尺度越大, 对应的疲劳寿命越长. FGA裂纹尺度与加载应力可由应力强度因子关联, 即式 (6). 这样, 在图32 中标出了\(\Delta K_{\rm FGA} = 4 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)和\(6 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)的等值线, 显示绝大多数数据都被包络在这两条等值线范围内. 这一结果表明, \(\Delta K_{\rm FGA} \)是超高周疲劳裂纹萌生的一个稳定特征参量.从而我们明确提出FGA是超高周疲劳裂纹萌生的基本特征区 (Hong et al. 2014 ), 对应的\(\Delta K_{\rm FGA} \)即为裂纹萌生阈值\(\Delta K_{{\rm th}} \). 对于超高周疲劳过程, 这一特征区具有本征存在性.
图 31 FGA和夹杂物对应的应力强度因子幅值与疲劳寿命的关系 (Zhao et al. 2011 )
图 32 FGA尺度随加载最大应力的变化, 下界实线对应\(4 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 上界虚线对应{\fangsong \(6 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\) (Hong et al. 2014 )
FGA裂纹属短裂纹范畴, 其扩展受材料微结构尺度制约.因此笔者分析了FGA裂尖塑性区与材料微结构尺度的关系 (Zhao et al. 2011 , 2012 ). 对于平面应变I型裂纹, 裂尖塑性区尺度\(r_{\rm p}\)的表达式为 (Hertzberg et al. 2012 )\[r_{\rm p} = \dfrac{\left({1 - 2\nu } \right) ^2}{\pi }\left( {\dfrac{\Delta K}{\sigma_{\rm y} }} \right)^2 \approx \dfrac{1}{6\pi }\left({\dfrac{\Delta K}{\sigma _{\rm y} }} \right)^2 \ \ (7)\] 式中, \(\nu \)是泊松比, \(\sigma _{\rm y}\)是屈服强度. 另一方面, 材料微结构特征尺度\(l_{\rm m}\)与材料基本力学性能有如下关系 (Nix& Gao 1998 )\[l_{\rm m} = b\left( {\mu / \sigma _{\rm y} }\right) ^2 \ \ (8)\] 式中, b为材料柏氏矢量模, \(\mu\)为材料剪切模量. 假定当FGA裂尖塑性区尺寸与材料微结构特征尺度相等, FGA裂纹终止发展. 这样\( \Delta K_{\rm FGA} = \mu \sqrt {\pi b} =4.342\mu \sqrt { b} \ \ (9)\)\( 式 (9) 表明, 超高周疲劳裂纹萌生特征区FGA对应的特征参量\(\Delta K_{\rm FGA}\)可简单表达为材料剪切模量和柏氏矢量的函数.
对于钢, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 5.54} {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与文献实验结果 (如Sakai et al. 2002 , Ochi et al. 2002 , Shiozawa et al. 2006b , Yang et al. 2008 , Zhao et al. 2011 , Lei et al. 2012 ) 得到的\(4\sim 6 {\rm MPa} \cdot{\rm m}^{{\rm 1 / 2}}\)相符合.
对于铝合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\(1.911 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与诸多实验结果 (如Paris et al. 1999 , Papakyriacou et al. 2002, Holper et al. 2004 , Borrego et al. 2004 , Huang & Moan 2007 ) 得到的\(1.5\sim 2.8 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\)相符合.
对于钛合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 3.385} {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\), 与诸多实验结果 (如Ritchie et al. 1999 , Petit & Sarrazin-Baudoux 2006 , Huang & Moan 2007 ) 得到的\(3.4\sim 4.0 {\rm MPa} \cdot {\rm m}^{{\rm 1 /2}}\)相符合.
对于镁合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 1.179} {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\), 这与Papakyriacou 等 (2002) 的多组结果\(1.3\sim 1.5 {\rm MPa} \cdot {\rm m}^{{\rm 1 /2}}\)相符合.
4.3 裂纹萌生区FGA消耗的寿命和裂纹扩展速率
FGA是裂纹萌生区, FGA对应的疲劳寿命即是裂纹萌生寿命.关于高强钢超高周疲劳裂纹萌生阶段消耗的疲劳寿命已有若干结果, 如Wang等 (1999) 对2组中碳高强钢 (20 kHz轴向加载) 的估算结果显示, 对应断裂周次为3.8 \(\times \) 10\(^{7}\sim \) 5 \(\times\) 108 , 裂纹萌生寿命占总寿命的96.2% \(\sim \) 99.9%.Murakami等 (2000b) 对SCM435钢 (30 \(\sim \) 100 Hz轴向加载)的估算结果显示, 对应断裂周次5 \(\times \) 108 , 裂纹萌生寿命占总寿命的99.8%. Tanaka和Akiniwa (2002) 对SUJ2钢(52.5 Hz旋弯加载) 的估算结果给出, 对应断裂周次10\(^{7}\sim\) 5 \(\times \) 1010 , 裂纹萌生寿命占总寿命的95% \(\sim\) 99%.
关于高强钢超高周疲劳裂纹萌生阶段的裂纹扩展速率也已有若干结果, 如Murakami等 (1999) 对SCM435钢 (30 \(\sim \) 100 Hz轴向加载)的估算表明, 对于1 \(\sim \) 4 mm的大尺度FiE, 断裂周次108 , FiE对应的裂纹扩展速率10\(^{-11}\sim \) 10-12 m/cyc.他们注意到这一速率明显小于材料晶格尺度, 认为裂纹不是每个载荷周次都发生扩展. Tanaka等 (2002) 对SUJ2钢的估算表明, 对于断裂周次107 以上的超高周疲劳, 裂纹萌生阶段的速率 小于10-12 m/cyc.对于这一远小于材料柏氏矢量的速率, 他们认为裂纹萌生过程是沿其周边不均匀生长, 且裂纹生长不是通常的位错运动机制.
近期笔者进一步分析了FGA寿命和裂纹扩展速率 (Hong et al. 2014 ).对于VHCF裂纹萌生特征区FGA (等效直径\(2a_{\rm FGA})\), 可以估算其所消耗的疲劳寿命和裂纹扩展速率. FGA是裂纹萌生区, \(\Delta K_{\rm FGA} \)对应\(\Delta K_{{\rm th}} \), \(2a_{\rm FGA}\)之后裂纹发生稳态扩展. 假定Paris公式 (式(10))适用于描述\(2a_{\rm FGA}\)之后裂纹扩展速率\({\rm d}a /{\rm d}N\)与\(\Delta K\)的关系, 即 \( \dfrac{{\rm d}a}{{\rm d}N} = A\Delta K^m \ \ (10) \)式中, A和m是材料参数. 对式 (10) 积分可得\(a_{\rm FGA}\)到\(a_{\rm FiE}\)的疲劳寿命\(N_{1}\)和从\(a_{\rm FiE}\)到最后断裂的裂纹长度\(a_{\rm c}\)的疲劳寿命\(N_{2}\) (见图14 ). 这样, FGA消耗的寿命即裂纹萌生寿命\(N_{\rm i}\)为\(\( N_{\rm i} = N_{\rm f} - N_1 - N_2 \ \ (11)\)
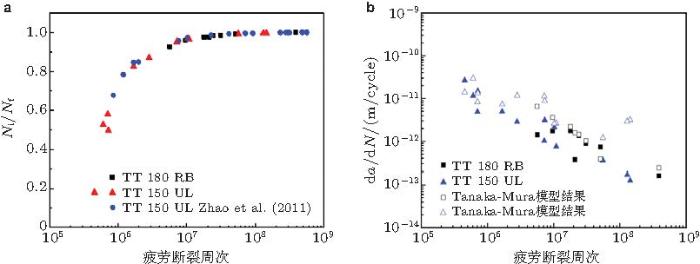
图33 是对一种GCr15钢的计算结果. 图33 (a)表明当疲劳寿命在10\(^{6}\sim \) 107 之间, FGA消耗的疲劳周次即裂纹萌生寿命占总寿命的70% \(\sim \) 95%; 当疲劳寿命在107 以上, FGA消耗的疲劳周次即裂纹萌生寿命占总寿命的95%以上; 当疲劳寿命在5 \(\times \) 107 以上, FGA消耗的疲劳周次即裂纹萌生寿命占总寿命对于99%. 图33 (b)表明, FGA裂纹的发展速率随疲劳断裂周次急剧下降, 当疲劳寿命在10\(^{6}\sim \) 107 之间, 速率为10\(^{-11}\sim\) 10-12 m/cyc, 当疲劳寿命在107 \(\sim \) 4\(\times\) 108 之间, 速率为10\(^{-12}\sim \) 10-13 m/cyc.笔者发展了Tanaka-Mura模型, 模拟得到的FGA裂纹扩展速率与实验估算结果的趋势一致 (图33 (b)).
图 33 (a) FGA裂纹萌生寿命与疲劳总寿命的关系, (b)FGA裂纹扩展速率与疲劳寿命的关系. 实心点为实验估算结果, 空心点为模型预测结果(Hong et al. 2014 )
近期, 笔者对Ti-6Al-4V多组实验数据 (应力比R=-1, -0.1, 0.1, 0.5)的推算结果表明, 在疲劳寿命10\(^{7}\sim \) 109 周次范围, 裂纹萌生寿命占总寿命的96.1% \(\sim \) 99.9%, 对应的裂纹扩展速率10\(^{-11}\sim \) 10-13 m/cyc (Su et al. 2017 ).
4.4 裂纹萌生区裂纹扩展速率的实验测量
近年, 有若干实验研究采用专门方法尝试测量裂纹萌生阶段的扩展速率.
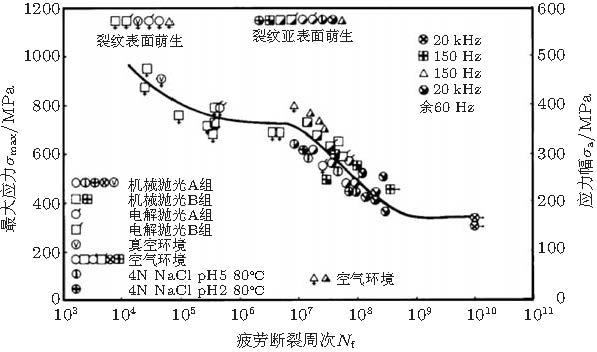
Stanzl-Tschegg和Schonbauer (2010) 对12%Cr (AISI 410)高强钢厚度2 mm的薄壁试样制备尖锐缺口, 采用超声轴向加载 (19 kHz, \(R = 0.05\)和0.5), 在真空环境测得裂纹萌生速率为5\(\times \)10-13 m/cyc. 对于空气环境, \(R = 0.05\), 测得裂纹萌生速率为2\(\times\)10-11 m/cyc; 对于R = 0.5, 测得裂纹萌生速率为6\(\times\)10-12 m/cyc. 他们通过裂纹萌生过程的断面微观特征比对, 推断FGA速率为10-12 m/cyc; FGA外的FiE区域裂纹扩展速率为10-11 m/cyc; 在FiE外的区域, 裂纹扩展速率为10-9 m/cyc.
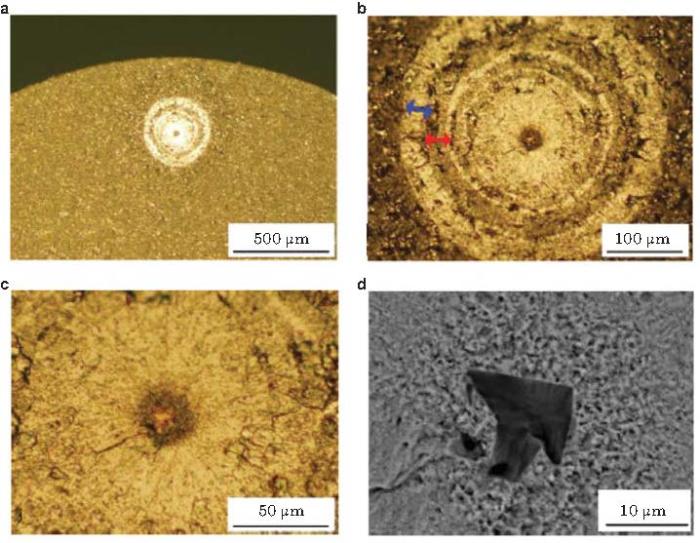
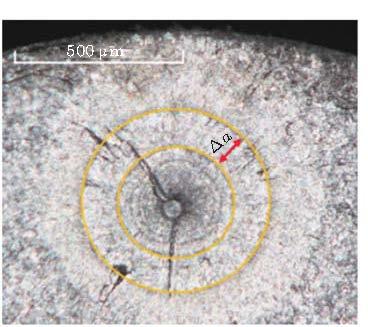
Ishida等 (2012) 和Ogawa等 (2014) 对SUJ2高强钢超声轴向加载(20 kHz, R = -1), 采用两级载荷往复阶梯加载 \((\Delta \sigma_{\rm H}= 1200\) MPa, \(n_{\rm H}= 1\times 10 ^{3}\), \(\Delta \sigma_{\rm L}= 850\) MPa, nL = 1\(\times\) 10 4 , \(N_{\rm f}=2.87\times \)10 8 ), 使断面呈现与阶梯载荷相对应的环状裂纹扩展特征(图34 ), 基于环状裂纹特征测得FGA外FiE区域的裂纹扩展速率, 再推得FGA的裂纹扩展速率. 他们所得到的结果为: FGA区域裂纹扩展速率10\(^{-13}\sim \) 10-14 m/cyc; 在FGA外的FiE区域, 裂纹扩展速率107 \(\sim \) 10-9 m/cyc.
图 34 (a) 光镜图像显示裂纹萌生区的"鱼眼"特征; (b)"鱼眼"区放大图像, 显示"海滩"斑图, 箭头表示阶梯加载的裂纹扩展增量, (c) 裂纹源区放大图像, 显示裂纹萌生区的ODA (FGA), (d) SEM图像显示裂纹源夹杂物及其周围的FGA特征(Ogawa et al. 2014 )
Sander等 (2014 , 2016 )对34CrNiMo6高强钢, 采用超声轴向加载 (21 kHz), 通过周期性变幅加载, 使得裂纹萌生区呈现裂纹扩展环状特征(图35 ), 从而测得在FGA之外的FiE区的裂纹扩展速率为3 \(\times\) 10\(^{-11}\sim \) 2 \(\times \) 10-12 m/cyc.
图 35 由变幅加载导致的裂纹萌生区环状扩展特征即鱼眼区域内裂纹扩展分界线(Sander et al. 2016 )
Ishida等 (2012) 和Ogawa等 (2014) 采用往复两级阶梯加载方法和Sander等 (2014, 2016) 采用周期性变幅加载方法, 导致萌生区的裂纹呈现环状扩展特征, 使得有可能直接观测到萌生阶段裂纹扩展特征并测量裂纹扩展速率.但他们观察到的环状裂纹特征及其测量均是在FGA外的FiE区域. 至今, 还未有关于FGA区域裂纹扩展速率的有效观察和测量的结果.
5 裂纹萌生区的形成机理与模型
超高周疲劳的裂纹往往萌生于材料 (试样) 内部. 对于高强钢, 裂纹萌生区呈现FiE和FGA特征. 尽管FiE尺度仅为100 \(\mu \)m量级, FGA尺度仅为10 \(\mu \)m量级; 作为超高周疲劳裂纹萌生特征区, FGA消耗了疲劳总寿命的95%以上 (Tanaka & Akiniwa 2002 , Hong et al. 2014 ). 因此, 揭示裂纹萌生区FGA的形成机理对于理解超高周疲劳的特有行为和寿命预测格外重要.
5.1 若干已有模型
在近10余年里, 有若干研究者提出了解释超高周疲劳裂纹萌生区的形成机理及其模型, 简述如下.
(1) "氢助裂纹萌生" 机理与模型
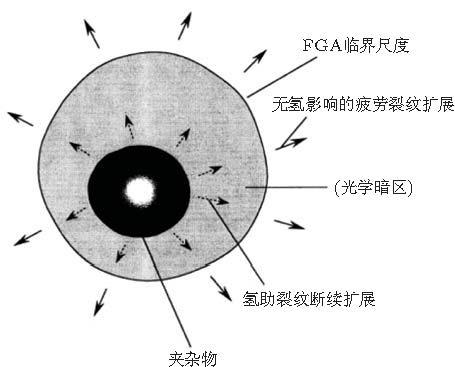
Murakami等 (2000a, 2000b)采用光学显微镜观察到高强钢超高周疲劳裂纹起源处有一灰度明显大的小局域, 称为光学暗区 (ODA, 即FGA).SEM和原子力显微镜观察显示FGA具有粗糙表面. 他们依据Takai 等 (1995 , 1996 ) 实验检测到在非金属夹杂物与基体的界面有氢富集的结果, 并依据他们对高强钢超高周疲劳实验结果, 推测FGA是由非金属夹杂物所捕获的氢与疲劳应力共同作用所致. 他们认为, 夹杂物周围局部富集的氢促进FGA形成.夹杂物捕获氢导致裂纹不连续生长且裂纹扩展速率相当低, 从而形成粗糙裂纹面. 当FGA达到临界尺度, 裂纹生长不再受氢的影响而稳定扩展. 图36 是该模型的示意图.
图 36 氢助裂纹环绕夹杂物萌生示意图 (Murakami et al. 2000a , 2000b )
(2) "球状碳化物弥散分离"机理与模型
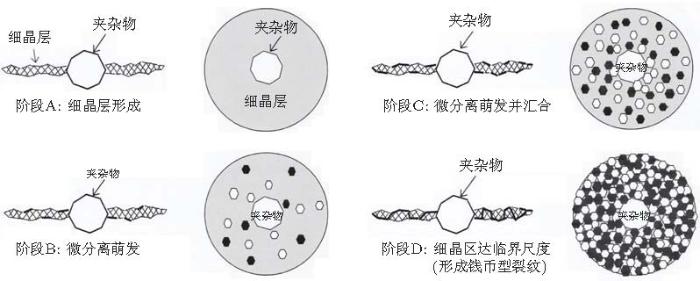
Shiozawa等 (2001 , 2002 , 2006a , 2006b )采用SEM和扫描探针显微镜观察表明, GBF (即FGA) 具有相对粗糙的表面, 其对应的应力强度因子幅值\(\Delta K\)与裂纹扩展门槛值\(\Delta K_{\rm th}\)基本一致.他们检测到FGA区域的微小隆起和凹陷的尺寸分布与细小碳化物的尺寸分布对应, 并通过电子探针显微分析表明FGA为富碳区; 另一方面, 采用断面形貌分析法模拟显示, 在非金属夹杂物周围发生弥散球状碳化物与基体分离而形成的微裂纹萌生、扩展和汇合; 当FGA达到临界尺度, 裂纹扩展不再依赖于球状碳化物与基体分离. 图37 是"球状碳化物弥散分离"模型描述超高周疲劳裂纹源区FGA形成机理的示意图(Shiozawa et al. 2006a , 2006b ).
图 37 夹杂物周围"球状碳化物弥散分离"形成GBF即FGA (Shiozawa et al. 2006a , 2006b )
(3) "细晶层形成与分离"机理与模型
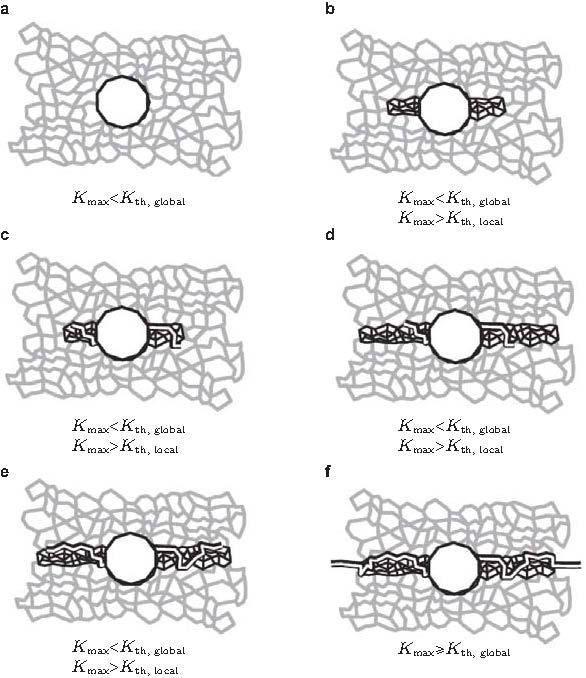
Sakai (2009) 认为, 由于长周次载荷循环, 在夹杂物周围裂纹萌生潜在局域由塑性变形导致的微结构多边形化, 使得在夹杂物周边 (裂纹萌生之前) 形成细晶层 (图38 stage A); 而后细晶层与基体分离形成裂纹面粗糙的萌生区, 即FGA (图38 stage B, stage C). 当FGA在夹杂物周边发展成钱币形的裂纹, FGA达到临界尺度, 裂纹进入Paris裂纹扩展区 (图38 stage D).
图 38 夹杂物周围发生"细晶层形成与分离"而形成裂纹萌生区示意图 (Sakai 2009 )
这一模型的关键点是: 细晶层在裂纹萌生之前形成且裂纹沿细晶层与基体分离, 即裂纹不是在细晶层内生长. Sakai与合作者 (Oguma et al. 2003 , Sakai et al. 2015 ) 对高强钢超高周疲劳裂纹萌生的精细观察表明同一试样断面一边有细晶层, 另一边仍是原始状态的粗晶, 以此来支持所提出的模型.
类似地, Grad等 (2012) 在高强钢观察到尺度约70 nm的细晶, 并提出"裂尖局部晶粒细化"模型, 如图39 所描述.这一模型与Sakai (2009) 模型的思路相似. 此类模型认为, 细晶层形成于裂纹萌生之前, 并且在已萌生的裂纹前沿不断形成细晶层.
图 39 夹杂物周围"细晶层形成与分离"示意图 (Grad et al. 2012 ). (a) 初始状态, (b) 局域晶粒细化, (c) 裂纹萌生, (d)
裂尖局域继续晶粒细化, (e)裂纹继续在细晶层发展, (f) FGA达到临界尺度
(4)"涡动塑性流动导致纳米微结构薄层形成"机理与模型
以上3个模型主要针对高强钢超高周疲劳裂纹萌生区的特点, 而Shanyavskiy (2013) 所提出的模型不仅针对高强钢, 而且也涉及其他高强合金. 他认为, 由于涡动塑性流动而形成纳米晶薄层且纳米晶粒在每一压缩/拉伸循环中转动(图40 (a) 和图40 (b)), 晶界强度消失使得晶粒颗粒化(即萌发裂纹), 从而形成FGA区域的粗糙断面 (图40 (c) 和图40 (d)). 这是一个有想象力的模型, 但其相关物理过程有待于验证.此模型亦认为, 在裂纹萌生之前, 在夹杂物周围形成了细晶层, 这一点与Sakai (2009) 模型相似.
图 40 夹杂物周围"涡动塑性流动导致形成纳米微结构薄层"示意图(Shanyavskiy 2013 ).(a) 载荷上升, (b) 载荷下降, (c)和(d) 裂纹面相互接触
(5) "萌生区裂纹面冷焊"机理与模型
Oguma和Nakamura (2013) 在研究钛合金超高周疲劳裂纹萌生时注意到裂纹萌生区的FGA特征往往是在真空环境下形成的, 并联系到高强钢和高强铝合金的类似情况, 从而提出了"萌生区裂纹面冷焊"机理 (图41 ), 即萌生的裂纹面在真空中往复接触发生"冷焊"过程, 导致萌生区晶粒细化. 这也是具有想象力的模型, 但其关键点, 即裂纹面发生"冷焊"过程并无实验依据.
图 41 基于"冷焊"的细晶区形成模型 (Oguma & Nakamura 2013 )
5.2 已有模型不能解释的反例
一种 (描述超高周疲劳裂纹萌生区形成的)机理及其模型的合理性和有效性, 在于能够解释不同情形下的实验结果.前节所介绍的机理及其模型, 只能对个别结果给予解释.在面对不同加载条件或不同断裂周次的多样结果时, 这些机理和模型遇到了困难.这里将这些机理和模型不能解释的实验结果权且称为"反例".
反例1 在Murakami等 (1999) 提出"氢助裂纹萌生"机理的同时, 他们对SCM435高强钢, 轴向循环 (30 \(\sim \) 100 Hz, \(R = -1)\)的实验结果给出了ODA即FGA尺度随疲劳断裂周次而增大的趋势, 特别是观察到对于断裂周次较低的试样, 疲劳裂纹于试样内部的夹杂物萌生, 断面呈现"鱼眼"特征, 但在裂纹源夹杂物周围并无ODA即FGA特征 (图42 ).
前节所述的模型不能解释如此实验结果.
图 42 SCM435高强钢, 轴向循环 (30 \(\sim \) 100 Hz, \(R =-1)\), 应力\(\sigma = 682 \) MPa, \(N_{\rm f} = 5.40\times 10^5\), 夹杂物尺度\(\sqrt {area} = 47.8 \mu{\rm m}\). (a) 光学显微镜图像, (b)SEM图像 (Murakami et al. 1999 )
反例2 在Shiozawa 等 (2006a , 2006b )提出"球状碳化物分离"机理的同时, 在他们对SUJ2高强钢经旋弯加载的断面图像里, 对于疲劳断裂周次较高的情况, 内部夹杂物起源的裂纹萌生区呈现"鱼眼"包含FGA的特征 (图43 (a)); 而对于疲劳断裂周次较低的情况, 内部夹杂物起源的裂纹萌生区仍有"鱼眼"但无FGA特征 (图43 (b)).前节所述的模型不能解释此实验结果.
图 43 (a) SUJ2钢旋弯加载\(\sigma _{\rm a }= 950\) MPa, \(N_{\rm f}= 6.3\times 10^{8}\) 的裂纹萌生区断面的鱼眼包含FGA特征; (b)经表面喷丸处理的SUJ2钢旋弯加载\(\sigma _{\rm a}= 1600\) MPa, \(N_{\rm f}= 3.7\times 10 ^{5}\) 的裂纹萌生区断面的鱼眼但无FGA特征, 图中AB是测量表面起伏的标志线, 结果列于表1 (Shiozawa et al. 2006b )
反例3 Kovacs等 (2013) 对12%Cr 马氏体钢(X10CrNiMoV12-2-2) 采用不同应力比 \((R= -1\), 0.1, 0.5, 0.7)进行超声频率轴向加载. 对于R=-1, 观察到裂纹起源于内部夹杂物的萌生区呈现鱼眼和FGA特征 (图44 (a)). 而对于正应力比加载的试样, 超高周疲劳裂纹仍萌生于内部夹杂物, 但裂纹萌生区呈现鱼眼特征但无FGA, 图44 (b) 是\(R= 0.5\)的图像. 他们采用FIB (focused ion beam)方法截取裂纹萌生区局域小样品, 采用SEM观察到, 对于R=-1, 裂纹面有厚度约3 \(\mu \)m的纳米晶层; 而对于R=0.1, 裂纹面无纳米晶层, 为原有的马氏体组织形态. R=-1 和 R=0.1, 0.5的裂纹萌生区具有截然不同的特征, 这不能被前节所述模型所解释.
图 44 12%Cr 马氏体钢, 超声轴向加载 (20 kHz)裂纹萌生区特征. (a) R=-1, \(\sigma _{\rm a}= 550\) MPa, \(N_{\rm f}= 4.66\times 10^{7}\); (b) \(R = 0.5\), \(\sigma _{\rm a}=250\) MPa, \(N_{\rm f}=4.87\times 10^{7}\) (Kovacs et al. 2013 )
反例4 Sander等 (2014) 采用超声轴向加载 (21 kHz)对34CrNiMo6高强钢进行应力比R=-1和\(R= 0\)加载, 给出了不同尺度和形状的夹杂物 (作为裂纹源) 导致不同断裂周次的结果, 观察到所有断面均有"鱼眼"特征但无FGA. 图45 是\(\sigma _{\rm a }= 430\) MPa, \(R = 0\), 断裂周次从\(N = 6.61\times 10 ^{5}\)到\( N = 2.57\times 10 ^{8}\)的4种情形的裂纹萌生区均无FGA特征.前节所述的模型不能解释此实验结果.
图 45 34CrNiMo6高强钢经超声轴向加载 (21 kHz, \(\sigma _{\rm a}= 430\) MPa, \(R = 0)\) 的裂纹萌生区特征 (Sander et al. 2014 ). (a)\(N_{\rm f}= 6.61\times 10^{5}\), (b) \(N_{\rm f}= 1.21\times10^{6}\), (c) \(N_{\rm f}= 2.24\times 10^{6}\),(d) \(N_{\rm f}=2.57\times 10^{8}\)
以上的反例可以归纳为3种情况: (1) 对于同一材料, 同一加载方式, 包括轴向循环和旋弯加载, 断裂周次长的试样内部夹杂物起源的裂纹萌生区为"鱼眼"包含FGA特征, 而断裂周次短的试样 (105 周次量级), 内部夹杂物起源的裂纹萌生区有"鱼眼"但无FGA特征 (反例1和反例2); (2) 对于同一材料, 同一加载方式, 加载应力比\(R < 0\)时, 内部夹杂物起源的裂纹萌生区为"鱼眼"包含FGA特征, 而应力比\(R >0\)时, 内部夹杂物起源的裂纹萌生区为"鱼眼"但无FGA特征 (反例3); (3)对于中碳合金钢, 断裂周次在10\(^{5}\sim 10^{8}\)范围, 从内部夹杂物起源的裂纹萌生区有"鱼眼"但无FGA特征 (反例4).前节叙述的模型不能解释这些实验结果. 因此, 需要发展新的模型来理解超高周疲劳裂纹萌生区的形成机理.
5.3 FGA剖面精细微结构
超高周疲劳裂纹萌生区剖面微结构特征与5.4节将要叙述的"大数往复挤压"机理与模型密切相关.因此, 在叙述提出的 "大数往复挤压 (numerous cyclic pressing)"机理与模型之前, 先介绍超高周疲劳裂纹萌生区剖面微结构观察的若干结果.这类实验研究是采用FIB方法, 在裂纹萌生区精确截取剖面小样品, 由透射电子显微镜(TEM)等方法进行精细观察.
Sakai和Oguma等 (Oguma et al. 2003, Sakai 2009 ) 对SUJ2 高强钢, 加载条件为旋弯加载 (52.5 Hz), \(\sigma _{\rm a }= 1100\) MPa, \(N_{\rm f} = 5.46\times 10 ^{7}\), 采用TEM 配合选区电子衍射 (SAD), SAD的直径为250 nm, 在FGA表面附近观察到厚度400 nm的细晶层, 晶粒尺度40 nm (图46 中C所在局域), 而远离FGA表面, 为粗晶组织(图46 中D所在局域). 在这些观察的基础上, 他们提出了"细晶层形成与分离"机理与模型 (Sakai 2009 ).
图 46 SUJ2高强钢旋弯加载 (52.5 Hz), \(\sigma _{\rm a }=1100\) MPa, \(N_{\rm f} = 5.46\times 10 ^{7}\), 裂纹起源区FGA局域剖面TEM图像, 在FGA表层附近 (C点)的SAD为纳米晶特征, 远离FGA表层 (D点)的SAD为粗晶特征 (Oguma et al. 2003 )
近期, Sakai等 (2015) 进一步给出了SUJ2高强钢 (旋弯加载)超高周疲劳裂纹起源区FGA的剖面特征.他们对同一试样断面的两侧观察表明, 一侧有细晶 (图47 (b)), 另一侧无细晶 (图47 (a)). 通过这一结果, 支持他们所提出的裂纹沿夹杂物周围形成的细晶层与基体分离而扩展的"细晶层形成与分离"模型.
图 47 (a) SUJ2高强钢 (旋弯加载), 同一试样断面FGA两侧剖面的SEM图像, 其中一侧的FGA表层为纳米晶; (b)另一侧的FGA表层为粗晶 (Sakai et al. 2015 )
Grad 等 (2012) 对100Cr6 (与SUJ2相似) 高强钢, 采用超声轴向加载(20 kHz), 通过TEM和SAD (直径650 nm)观察到超高周疲劳裂纹萌生区FGA剖面为细晶组织, 平均晶粒尺度70 nm; 而远离FGA的表面为粗晶组织 (图48 ). 基于这一观察结果, 他们认为夹杂物周围晶粒细化, 裂纹沿细晶层与基体之间分离而扩展, 并提出了与Sakai模型相似的FGA形成机理.
图 48 100Cr6高强钢, 超声轴向加载 (20 kHz), \(N_{\rm f} = 8.96\times 10 ^{8}\), 夹杂物周围FGA剖面的TEM图像, FGA表层附近的SAD显示纳米晶特征, 远离FGA表层的SAD显示粗晶特征 (Grad et al. 2012 )
Kovacs等 (2013) 对12%Cr 马氏体钢 (X10CrNiMoV12-2-2)采用不同加载应力比进行超声频率 (20 kHz) 轴向加载. 对于R= -1, 观察到FGA剖面有3 \(\mu \)m厚的细晶层 (图49 (a) 和图49 (b)), 而对于R= 0.5, 无细晶层, 为原始的马氏体组织 (图49 (c)和图49 (d)).
图 49 12%Cr 马氏体钢, 超声轴向加载, FGA剖面图像. (a), (b)\(\sigma_{\rm a}= 550\) MPa, R=-1, \(N_{\rm f} = 6.15\times 10^{7}\); (c), (d) \(\sigma_{\rm a}= 370\) MPa, R=0.1, \(N_{\rm f} = 1.24\times 10 ^{8}\) (Kovacs et al. 2013 )
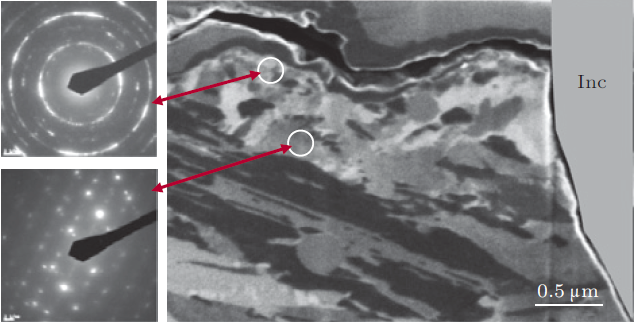
关于钛合金, 近期笔者采用超声轴向加载 (20 kHz)对Ti-6Al-4V超高周疲劳裂纹萌生区剖面进行了观测 (Liu et al. 2016b ).图50 (a) 是包含2处裂纹萌生区的典型断面 \((R = 0.1\), \(\sigma_{\rm a} = 367\) MPa, \(N_{\rm f} = 9.14\times 10 ^6)\) 的SEM图像.利用截面离子抛光方法沿虚线PQ切出该区域的剖面, 然后用EBSD(电子背散射衍射) 方法对该剖面进行观测. 结果显示, 裂纹萌生处A和B以及非裂纹萌生处的微结构 (包括初生\(\alpha \)相比例, 晶粒尺寸和晶体学取向) 基本无差别 (图50 (b)).因此认为对于钛合金, 内部裂纹起源可以发生在材料中的随机位置.
图 50 (a) Ti-6Al-4V \((R = 0.1\), \(\sigma _{\rm a }= 367\) MPa, \(N_{\rm f}= 9.14\times 10 ^{6})\) 断面包含裂纹萌生处A, B的SEM图像; (b) 虚线PQ对应的断口剖面的晶体取向图像 (Liu et al. 2016b )
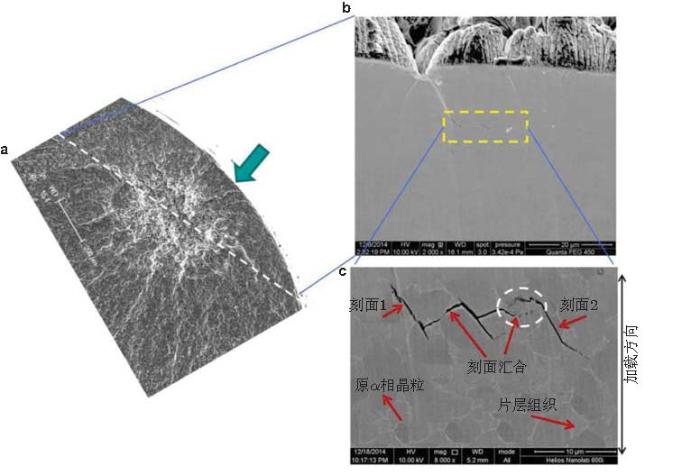
笔者 (Liu et al. 2016b )在截面离子抛光方法制备的Ti-6Al-4V裂纹萌生区的剖面试样上, 观察到在距断面20 \(\mu \)m位置的早期裂纹损伤 (图51 ).图51 (c) 显示facet 1和facet 2由初生\(\alpha\)相晶粒解理而成. 在两个facet之间, 裂纹沿晶界汇合而连接; 在虚线圆圈区域可见两处facet裂纹还未完全汇合. 这一观测结果表明, 钛合金裂纹萌生和初始扩展的方式是先由初生\(\alpha\)相晶粒独立解理形成facet裂纹, 再各自沿晶界扩展而汇合.进而提出了钛合金解理裂纹萌生的机制 (图52 ): (1)材料初始状态中存在可发生解理的初生\(\alpha \)相晶粒 (图52 (a)); (2) 一些初生\(\alpha \)晶粒发生解理, 形成facet裂纹 (图52 (b)); (3) facet裂纹发生汇合 (图52 (c)); (4) 汇合的裂纹进一步发展, 形成主裂纹 (图52 (d)), 最后导致试样破坏.
图 51 Ti-6Al-4V超声轴向加载 \((R = 0.5\), \(\sigma _{\rm a }=205 \) MPa, \(N_{\rm f} = 5.80\times 10 ^{7})\) 裂纹萌生区SEM图像.(a) 断面裂纹萌生区, (b) 萌生区剖面, (c) 对(b)放大观察显示已连接和未连接的裂纹 (Liu et al. 2016b )
图 52 小解理面损伤导致裂纹萌生示意图. (a) 初始微结构, (b)原\(\alpha\)相晶粒解理, (c) 小解理面汇合, (d) 形成主裂纹 (Liu et al. 2016b )
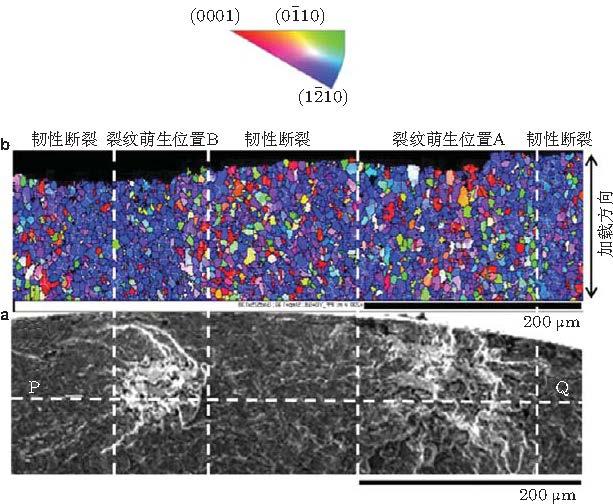
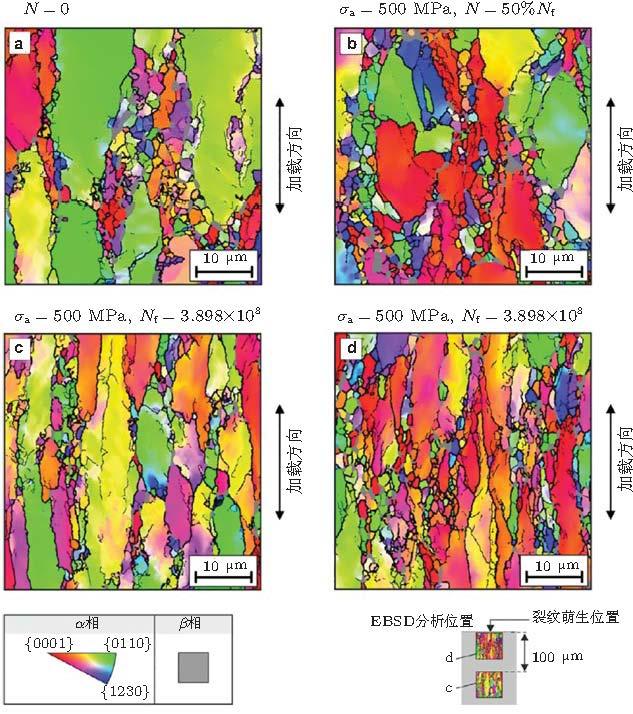
近期, Heinz 和Eifler (2016) 对Ti-6Al-4V合金, 以超声轴向加载(频率20 kHz, \(R = -1)\), SEM对裂纹源区剖面样品观测到FGA沿深度方向的微裂纹损伤特征.微裂纹萌生于大颗粒的初始\(\alpha \)相, 并受阻于\(\beta \)相 (图53 ). 微裂纹团簇是FGA的起源点, 微裂纹汇合形成与拉应力垂直的主裂纹. 他们还采用EBSD检测裂纹萌生位置的晶粒特征 (图54 ). 对于初始态, 晶粒尺度很不均匀 (图54 (a)), 尺度1 \(\mu \)m至60 \(\mu \)m, 粗晶为hcp的\(\alpha \)相, 细晶为bcc的\(\beta \)相.当加载至总寿命的50%, 局部塑性变形导致\(\alpha \)相晶粒细化 (图54 (b)). 断裂时, 累积塑性变形导致FGA裂纹面附近晶粒明显细化 (图54 (c)和图54 (d)), 且紧靠FGA裂纹面局域的晶粒细化更明显(图54 (d)). 测量结果为\(N = 0\), 平均晶粒面积\(A = 8.8 \mu\)m2 ; \(N = 50% N_{\rm f}\), \(A = 5.8 \mu \)m2 ; \(N = N_{\rm f}\), \(A= 3.8 \mu \)m2 .
图 53 Ti-6Al-4V超声轴向加载 (20 kHz, R=-1, \(\sigma _{\rm a }= 460\) MPa, \(N_{\rm f}= 1.2\times 10 ^{9})\), 裂纹萌生区中心位置剖面的SEM图像, (b) 是(a) 的局部放大图 (Heinz & Eifler 2016 )
图 54 Ti-6Al-4V超声轴向加载 (20 kHz, R=-1, \(\sigma _{\rm a }= 500\) MPa, \(N_{\rm f}= 3.9\times 10 ^{8})\)裂纹萌生区剖面的EBSD图像. (a) 初始状态, (b) \(N= 50% N_{\rm f}\), (c) \(N=N_{\rm f}\), (d) \(N=N_{\rm f}\) (Heinz et al. 2016 )
5.4 "大数往复挤压"机理与模型
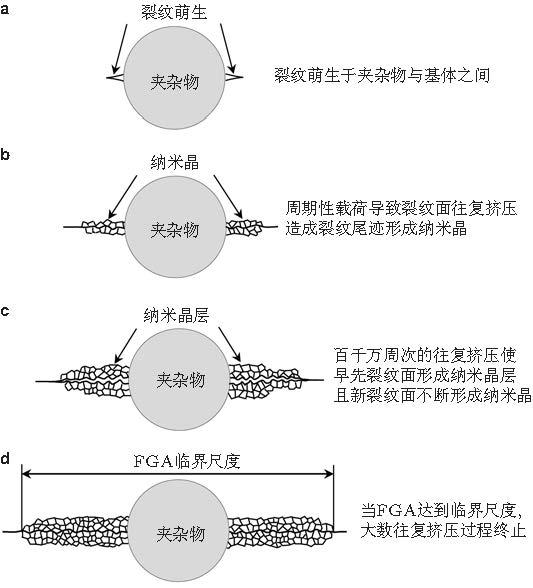
笔者针对典型的GCr15高强钢超高周疲劳裂纹萌生特征, 对旋弯加载的超高周疲劳裂纹萌生区制备FIB试样, 采用TEM观测并配有电子选区衍射 (SAD直径\(200 \sim 250\) nm) 检测, 直接观测到FGA是一层独特的细晶层, 而FGA之外的FiE区域为粗晶组织.对FGA细晶层的精细测量给出平均晶粒尺度48 nm, 厚度500 \(\sim \) 800 nm (图55 ). 随后, 对同一试样断面两侧相对应的局域观察到FGA均具有纳米晶特征 (图56 ). 从而, 提出了"大数往复挤压模型 (numerous cyclic pressing, NCP)": 萌生裂纹面之间经百万、千万周次的往复挤压, 造成裂纹尾迹的晶粒细化从而形成FGA, 此过程与裂纹闭合效应和残余应力释放相联系 (Hong et al. 2016 ).
图 55 GCr15, 旋弯加载, \(\sigma _{\max } = 775\) MPa, \(N_{\rm f} = 2.40\times 10 ^{7}\). (a) SEM图像显示裂纹源夹杂物及其周边的FGA(虚线范围), 长方形框为FIB取样位置; (b)TEM图像显示FGA截面有厚度500 \(\sim \) 800 nm的细晶层; (c)FGA细晶层的SAD图, 断续衍射环表明200 nm衍射区内有若干纳米晶; (d)距FGA表面2.5 \(\mu \)m处的SAD图, 衍射斑表明衍射区内为单晶; (e)FGA细晶层的高倍TEM图像; (f) FGA细晶层的SAD图, 基本连续的衍射环表明纳米晶及其\(\alpha \)-Fe晶面指数标定 (Hong et al. 2016 )
图 56 GCr15, 旋弯加载, \(\sigma _{\max }= 850\) MPa, \(N_{\rm f}= 9.64\times 10^{6}\). (a)和(d) 同一试样断面两侧的SEM图像, 虚线范围为FGA, 长方形框为FIB取样位置; (b) FGA截面的TEM图像, SAD断续衍射环表明200 nm衍射区内有若干纳米晶; (c)FGA之外FiE区的TEM图像, SAD衍射斑表明衍射区为单晶; (e)另一侧FGA截面的TEM图像, SAD图表明衍射区为纳米晶特征 (Hong et al.2016)
图57 说明了FGA形成的过程与机理 (Hong et al. 2016 ).在裂纹源夹杂物周边局域的塑性变形累积导致裂纹萌生 (图57 (a)).萌生裂纹面受到循环载荷导致的往复挤压, 这一过程与裂纹闭合作用和残余应力释放相联系; 由于局部剧烈塑性变形, 萌生裂纹表层的微结构发生碎化使得原有的粗晶细化为纳米晶 (图57 (b)). 经过百万、千万周次的循环载荷, 两侧裂纹面形成一层纳米晶层并具有粗糙裂纹面特征 (图57 (c)).当达到裂纹萌生与稳定扩展的转捩点, NCP过程终止, FGA达到其临界尺度(图57 (d)). 进而分析了这一尺度. 根据式 (6), 可以写出\(a_{\rm FGA} = {Y}'\left( {\dfrac{\Delta K_{\rm FGA} }{\sigma_{\max} }} \right)^2 \ \ (12)\)式中, \(a_{\rm FGA} \)是FGA尺度, \(\Delta K_{\rm FGA}\)是FGA对应的应力强度因子幅值. 联系到式 (9)有\( a_{\rm FGA} = Yb \left( {\dfrac{\mu }{\sigma _{\max} }}\right)^2 \ \ (13)\)式中, \(\mu \) 是材料剪切模量, b是材料柏氏矢量模, \(\sigma _{\max}\)是循环加载的最大应力, \(Y = 6\pi {Y}' = 24\). 式 (13) 表明, 对于给定的材料, FGA尺度与循环载荷最大应力的平方成反比. 实际上, 式(13) 表达了存在形成FGA条件情况的FGA临界尺度.
图 57 大数往复挤压 (NCP) 模型示意图 (Hong et al. 2016 )
NCP模型表明形成FGA纳晶层需要2个基本条件: (1)萌生的裂纹面之间存在压应力以导致裂纹面之间的接触挤压作用; (2)足够的载荷循环周次以使得裂纹面之间有充分多次数的接触挤压.
由此, NCP模型有2个推论: (1)形成FGA纳米晶层的倾向与加载应力比成反比; 即负应力比具有高倾向, 正应力比具有低倾向; 因为正应力比情况弱化了裂纹面接触挤压的可能性.(2) 即使是负应力比的情形, 若载荷周次相对低, 形成FGA纳米晶层的倾向也相对低; 因为相对低的载荷周次使得裂纹面接触挤压的次数不够充分.
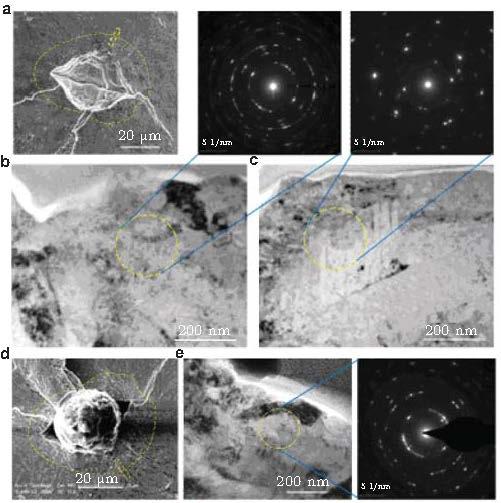
随后, 笔者 (Hong et al. 2016 ) 继续针对GCr15高强钢, 采用超声轴向不同应力比加载 (R = -1, -0.5, 0.1, 0.3), 观察到R=-1情形超高周疲劳的FGA仍为纳米晶层; 对于R=-1但周次较少的情况, SAD为稍拉长的衍射斑 (图58 (a)), 表明晶粒略有细化或具有织构特征. 对于R=-0.5, 超高周疲劳裂纹萌生虽有一定的FGA特征, 但FGA剖面的SAD为拉长的衍射斑(图58 (b)), 表明晶粒有一定细化, 但不像R=-1明显细化的特征.对于R=0.1和0.3, 裂纹萌生区未见粗糙的FGA特征, 对裂纹萌生区剖面试样的SAD检测结果为单晶衍射斑 (图58 (c)和图58 (d)), 表明正应力比状态的超高周疲劳裂纹萌生区不出现纳米晶层.这一结果证实了前述的NCP模型的2个推论, 即证实了所提出的"大数往复挤压模型 (NCP)".
图 58 (a) R=-1, \(\sigma _{\rm a}= 1029\) MPa, \(N_{\rm f}=1.28\times 10^{5}\), 裂纹萌生区表层的TEM图像, SAD图显示稍拉长的衍射斑; (b) \(R = -0.5\), \(\sigma _{\rm a}=633\) MPa, \(N_{\rm f}= 4.81\times 10 ^{8}\), 裂纹萌生区表层的TEM图像, SAD图显示明显拉长的衍射斑; (c) \(R = 0.1\), \(\sigma _{\rm a}= 534\) MPa, \(N_{\rm f} = 1.84\times 10 ^{7}\), 裂纹萌生区表层的TEM图像, SAD图显示单晶衍射斑; (d) \(R = 0.3\), \(\sigma _{\rm a}= 422\) MPa, \(N_{\rm f}= 9.76\times 10 ^{7}\), 裂纹萌生区表层的TEM图像, SAD图显示单晶衍射斑 (Hong et al. 2016 )
近期, 笔者 (Jiang et al. 2016 ) 对一种中碳结构钢 (0.42%C)超高周疲劳研究结果表明, 由夹杂物起源而形成的FGA表层确实为纳米晶层; 而由晶界作为裂纹源, 萌生区仍有粗糙面特征, 但无纳米晶特征 (图59 ). 对于由表面缺陷发生裂纹起源的情形, 裂纹萌生区无纳米晶特征(图60 ).
图 59 R=-1, \(\sigma _{\max}= 850\) MPa, \(N_{\rm f}=5.3\times 10^{6}\), 晶界引发的裂纹内部起源形成FiE情形.(a) 裂纹萌生区表层的TEM图像, (b) \(\sim \) (d)紧邻裂纹面的SAD结果, (e) 远离裂纹面的SAD结果 (Jiang et al. 2016 )
图 60 \(\sigma _{\max}= 500\) MPa, \(N_{\rm f}= 1.8\times 10^{8}\), 缺口引发的裂纹表面起源情形. (a) 裂纹萌生区表层的TEM图像, (b)和(c)紧邻裂纹面的SAD结果, (e) 离开裂纹面的SAD结果 (Jiang et al. 2016 )
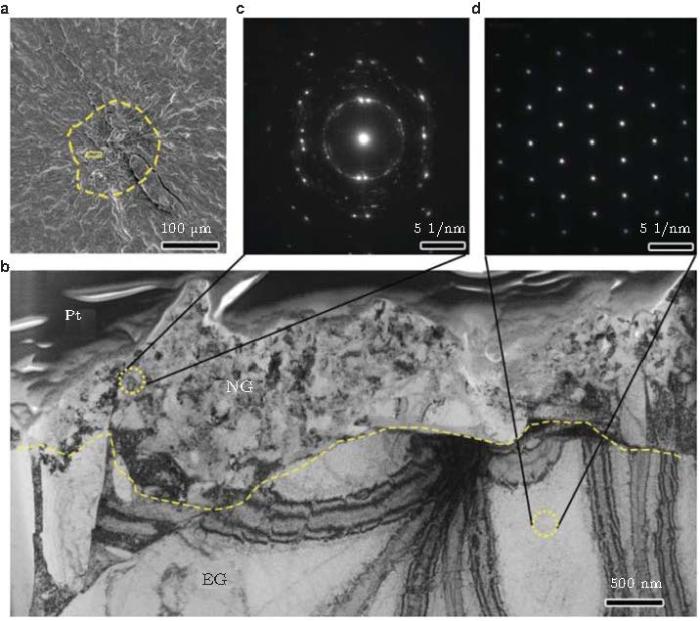
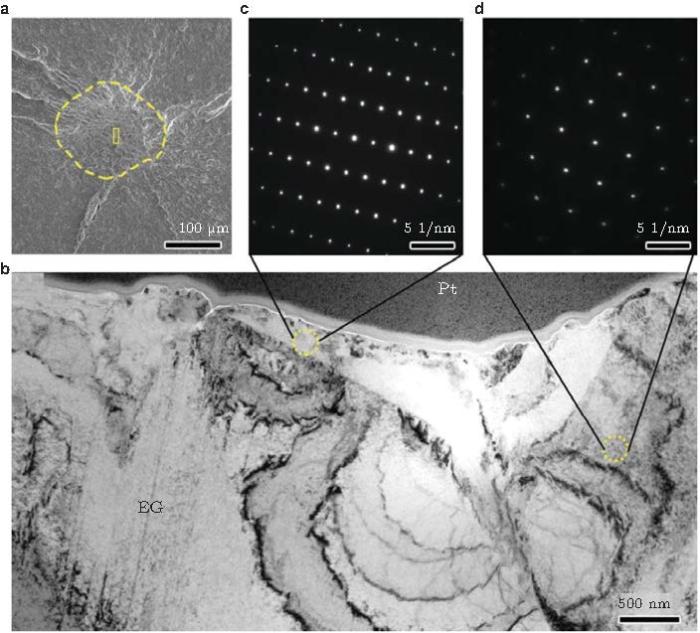
对于钛合金 (Ti-6Al-4V), 笔者的最新结果 (Su et al. 2017 ) 表明, 对于R=-1 (超声轴向加载, 20 kHz), 超高周疲劳裂纹内部萌生呈现RA(粗糙区) 特征, RA区为纳米晶层, 厚度800 \(\sim \) 1500 nm, 平均晶粒尺度105 nm (图61 ). 而对于\(R = 0.5\), 超高周疲劳裂纹内部萌生仍呈现RA特征, 但RA截面无纳米晶特征 (图62 ). 这一研究结果表明, NCP模型适用于解释钛合金超高周疲劳裂纹萌生特征区的形成机理.
图 61 Ti-6Al-4V, R=-1, \(\sigma _{\rm a}= 550\) MPa, \(N_{\rm f}= 4.52\times \)107 . (a) 裂纹内部萌生区的SEM 图像, 虚线范围显示RA, 长方形框为FIB 取样位置; (b) TEM图像显示裂纹萌生区截面特征, NG表示纳晶层, EG表示粗晶基体层; (c)紧邻RA表面的SAD 图, 显示纳米晶特征; (d) 距裂纹面2 \(\mu\)m处的SAD 图, 显示单晶特征 (Su et al. 2017 )
图 62 Ti-6Al-4V, R = 0.5, \(\sigma _{\rm a}= 240\) MPa, \(N_{\rm f}= 4.30\times \)10 7 . (a) 裂纹内部萌生区的低倍SEM 图像, 虚线范围显示RA, 长方形框为FIB 取样位置; (b) TEM图像显示裂纹萌生区截面特征, EG表示粗晶基体层; (c)紧邻RA裂纹面的SAD 图, 显示单晶特征; (d) 距裂纹面1.2 \(\mu\)m处的SAD图, 显示单晶特征 (Su et al. 2017 )
6 超高周疲劳性能预测模型
6.1 超高周疲劳寿命/疲劳强度预测模型
近20年来, 陆续有研究报道了针对高强钢超高周疲劳寿命或疲劳强度的预测模型, 如Murakami等 (Murakami & Usuki 1989 , Murakami et al. 1999 ), Harlow等 (2006) , Zhao 等 (2009) , Sun等 (2012 , 2013 ), Stepanskiy(2012) , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响.
Wang 等 (1999) 对Murakami模型进行了改进, 引入了疲劳寿命的影响, 给出了预测低合金高强钢疲劳寿命的模型 \[ \sigma _w = \dfrac{\beta (Hv + 120)}{\left({\sqrt {area_{{\rm In}} } } \right)^{1 / 6}}\left( {\dfrac{1 -R}{2}} \right)^\alpha \ \ (15)\]对于4种中碳低合金高强度钢, \(\beta = 3.09 - 0.12\log N_{\rm f} \((内部夹杂或缺陷) 或\)\beta = 2.79 - 0.108\log N_{\rm f} \((表面夹杂或缺陷), \)area_{{\rm In}}\(为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\). 式 (15)和式 (14) 对疲劳强度的预测结果与实验结果比较表明, 引入疲劳寿命影响的式 (15) 给出了较好的预测结果 (Wang et al. 1999 ).
Chapetti 等 (2003) 对SUJ2, SCM435和SNCM439钢的实验数据整理归纳出式(16), 用于描述FGA尺寸、夹杂物尺寸和疲劳寿命之间的关系 \[\dfrac{\sqrt {area_{\rm FGA} } }{ \sqrt {area_{\rm Inc} }} =0.25N_{\rm f}^{0.125} \ \ (16)\]
进而给出如下关联疲劳寿命、夹杂物尺寸和门槛应力\(\sigma _{{\rm th}}\)的关系 \[ \Delta \sigma _{{\rm th}} N_{\rm f}^{\frac{1}{48}} =4.473\dfrac{Hv + 120}{R_i^{1 / 6} } \ \ (17)\]式中\(\Delta \sigma _{{\rm th}} \)单位为MPa, \(R_i = \sqrt {area_{\rm Inc} / \pi } \)单位为\(\mu {\rm m}\), Hv单位为kgf/mm2 .记\(\Delta \sigma _{{\rm th}} = 2\sigma _a \), 式(17) 可写成 \[\sigma _a = 2.460\dfrac{Hv + 120}{\left( {\sqrt{area_{\rm Inc} } } \right)^{1 / 6}}N_{\rm f}^{ - \frac{1}{48}}\ \ (18)\]
Akiniwa 等 (2006) 假定Paris关系对FGA内的裂纹扩展行为仍然成立, 导出了疲劳强度和载荷周次之间的关系 \[ \sigma _a = \dfrac{2}{\sqrt \pi }\left({\dfrac{2}{C_{\rm A} (m_{\rm A} - 2)}} \right)^{\frac{1}{m_{\rm A}}}\left( {\sqrt {area_{\rm Inc} } } \right)^{\frac{1}{m_{\rm A} }- \frac{1}{2}}N_{\rm f}^{ - \frac{1}{m_{\rm A} }} \ \ (19)\]式中, 下角标 "Inc" 表示夹杂物, \(C_{\rm A}\(和\)m_{\rm A}\)是材料参数.
Mayer 等 (2009) 认为, 疲劳寿命、夹杂物尺寸和应力幅之间可以近似地用如下关系描述 \[ \left[ {\sigma _a \left( {\sqrt {area_{\rm Inc} } }\right)^{1 / 6}} \right]^nN_{\rm f} = C \ \ (20)\]即 \[ \sigma _a = C^{\frac{1}{n}}\dfrac{1}{\left( {\sqrt{area_{\rm Inc} } } \right)^{1 / 6}}N_{\rm f}^{ - \frac{1}{n}}\ \ (21)\]\(式中, \(\sigma _a \(单位为MPa, \)area_{\rm Inc} \)单位为\(\mu {\rm m}^2\).
Liu 等 (2010) 基于106 和109 周次的疲劳强度预测结果, 采用Basquin公式的形式对S-N曲线进行预测 \[ \sigma _a = \sigma '_{\rm f} (2N_{\rm f} )^b\ \ (22)\]式中, \(\sigma'_{\rm f} = 1.12(Hv + 120)^{9 / 8} / (\sqrt{area_{\rm Inc} } )^{1 / 8}\(, \)b = 3^{ - 1}\lg [1.35(Hv + 120)^{ -1 / 16}(\sqrt {area_{\rm Inc} } )^{ - 1 / 48}]\), \(\sigma _a\)单位为MPa, \(\sqrt {area_{\rm Inc} } \)单位为\(\mu {\rm m}\), H v单位为kgf/mm2 . 式 (22) 可表示成 \[ \sigma _a = 1.12\dfrac{2^b(Hv + 120)^{9 /8}}{\left( {\sqrt {area_{\rm Inc} } } \right)^{1 / 8}}N_{\rm f}^b\ \ (23)\]
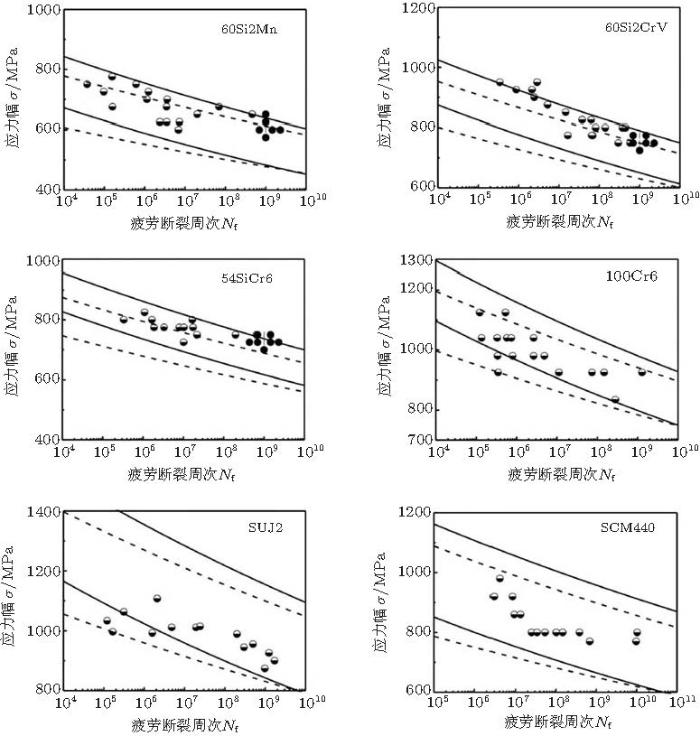
图63 给出了式 (22) 和式 (17)对疲劳强度预测结果与实验结果的比较.
图 63 式 (22) (实线) 和式 (17) (虚线)对疲劳强度预测结果与实验结果的比较 (Liu et al. 2010 )
Sun等 (2013) 在对大量实验数据研究的基础上, 给出了如下包含应力比影响的超高周疲劳强度预测模型 \[ \sigma _a = CN_{\rm f}^l a_0^m \left( {\dfrac{1 - R}{2}}\right)^\alpha \ \ (24)\]式中, \(a_0 = \sqrt {area_{\rm Inc} } \)是夹杂物尺寸, C, l, m和 \(\alpha \)是材料参数.
实际上, 式 (14)、式(15)、式(17)、式(19)、式(20) 和式(22)可以看作是式 (24) 的特殊形式.这些模型表达夹杂物尺度对疲劳强度影响的形式一样, 即以夹杂物尺度的幂函数形式出现.
Marines-Garcia 等 (2007, 2008)采用如下公式来估算FiE消耗的疲劳寿命. 对于门槛拐角之下 \[\dfrac{{\rm d}a}{{\rm d}N} = b\left( {\dfrac{\Delta K_{{\rm eff}}}{E\sqrt b }} \right)^\alpha , \qquad \alpha > 3\ \ (25)\]对于门槛拐角之上, 小裂纹与长裂纹的转折点之间 \[\dfrac{{\rm d}a}{{\rm d}N} = b\left( {\dfrac{\Delta K_{{\rm eff}}}{E\sqrt b }} \right)^3\ \ (26)\]门槛拐角处满足\[\dfrac{{\rm d}a}{{\rm d}N} = b \mbox{且} \dfrac{\Delta K_{{\rm eff}} }{E\sqrt b } = 1 \ \ (27)\]式中, b是Burgers矢量模, E是弹性模量.
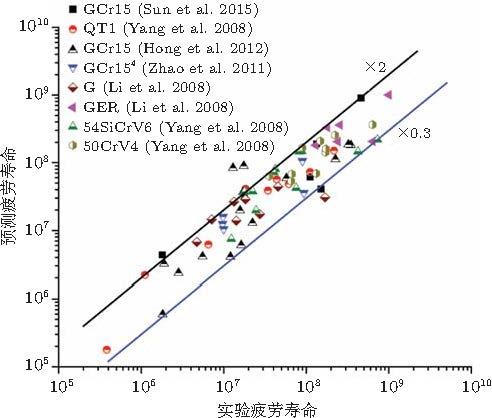
Sun 等 (2015) 假定FGA内每一周次的等效裂纹增长长度与裂纹尖端的塑性区尺寸有关, 给出了如下具有FiE和FGA断裂模式的高强钢疲劳寿命模型 \[ N_{\rm f} = \dfrac{1}{\alpha }\left( {\dfrac{\sigma _a}{\sigma _{\rm Y} }} \right)^{ - l}\ln \dfrac{a_{\rm FGA} }{a_{\rm 0} } \ \ (27)\]式中, \(a_0 = \sqrt {area_{\rm Inc} } \]是夹杂物尺寸, \(\alpha\)和l是材料参数. 该模型考虑了材料的宏观力学量 (屈服强度)对疲劳寿命的影响.图64 给出了模型预测的疲劳寿命与实验测得的疲劳寿命的比较.
图 64 式 (27) 预测的疲劳寿命与实验测得的疲劳寿命的比较 (Sun et al. 2015 )
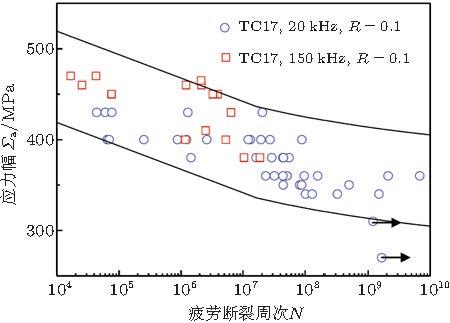
Huang等 (2014, 2015)研究了TC4和TC17钛合金超高周疲劳过程的热耗散行为, 并将S-N曲线描述成Basquin公式形式, 从而给出了一种预测钛合金不同失效概率下疲劳寿命的方法. 图65 和图66 分别给出了TC4和TC17在不同失效概率下的S-N曲线预测结果.
图 65 20%和80%失效概率下TC4 S-N曲线预测结果 (Huang et al.2014)
图 66 10%和90%失效概率下TC17 S-N曲线预测结果 (Huang et al.2015)
Wang等 (2002) 采用Tanaka-Mura位错模型 (Tanaka et al. 1982 )和Paris公式, 给出了预测超高周疲劳寿命模型 \[ N_{\rm f} = \dfrac{9GW_{\rm s} \Delta \sigma _{\rm R}}{\left(\Delta \sigma - \Delta \sigma _{\rm D}^{\rm R}\right)^2a_{\rm o} } + \dfrac{a_{\rm o}^{{\rm (1} - n / 2)}}{C\Delta \sigma ^n\beta _1^n \pi ^{n / 2}(0.5n - 1)} \ \ (28)\]式中, \(N_{\rm f}\)是疲劳寿命, \(\sigma _{\rm D}^{\rm R}\)是应力比为R时的疲劳极限, \(W_{\rm s}\)是断裂能, \(a_{\rm o} \)是初始夹杂物尺寸, G是基体材料剪切模量, C, n是与材料常数, \(\beta _{\rm 1} \)是几何常数.
Hong等 (2014) 将位错不可逆因子引入到Tanaka-Mura位错模型 (Tanaka et al. 1982 ) 中, 提出了描述超高周疲劳形核阶段寿命模型 \[ N_{\rm i} = A\left( {\dfrac{\Delta \sigma - \Delta \sigma _{\rm R} }{\Delta \sigma }} \right)^\alpha\dfrac{1}{(\Delta \sigma - \Delta \sigma _{\rm R} )^2a_{\rm Inc} }\ \ (29)\]式中, \(N_{\rm i}\)是疲劳形核阶段寿命, \(\Delta \sigma _{\rm R}\)是应力比为R时的疲劳极限, \(a_{\rm Inc} = \sqrt {area_{\rm Inc}} / 2\), \(area_{\rm Inc} \)为缺陷在最大主应力垂直方向上的投影面积(单位: \(\mu \(m\)^{2})\), A和\(\alpha \)是材料参数.
Mughrabi (1999 , 2002 , 2009 )假设Manson-Coffin关系在超高周疲劳中仍然成立, 并假定当局部不可逆累积塑性应变达到某一临界值时材料发生破坏, 从而提出了描述超高周疲劳寿命的关系式 \[ N_{\rm f}^{c + 1} \cdot p(\Delta \varepsilon _{{\rm pl}} ) = \dfrac{\varepsilon _{{\rm pl,cum,f}}^{{\rm irr}}}{4\varepsilon '_{\rm f} \cdot 2^c} = {\rm const} \ \ (30)\]式中, \(\varepsilon '_{\rm f} \)为疲劳韧性系数, c为疲劳韧性指数, \(\Delta \varepsilon _{{\rm pl}} \)为塑性应变幅值, \(N_{\rm f}\)为疲劳周次, \(p(\Delta \varepsilon _{\rm pl} )\)为不可逆循环滑移, 定义为 \[] p = \dfrac{\mbox{irreversible plastic shear strain}}{\mbox{cumulative total plastic shear strain}} \ \ (31)\]当滑移完全可逆时p=0, 滑移完全不可逆时p = 1, 部分可逆时, 0 < p < 1, p取决于塑性应变幅值的大小. 其中的临界值\(\varepsilon_{{\rm pl,cum,f}}^{{\rm irr}} \)和临界表面粗糙度相关, 并取决于(局部) 滑移面之间均方根位移的临界值.
该公式的进一步应用还需要对\(p\)与\(\Delta \varepsilon _{{\rm pl}}\)之间的关系进行仔细研究, 并确定破坏时不可逆累积塑性应变的临界值.在延性金属中, 疲劳损伤以驻留滑移带 (PSB) 的形式出现, PSB的平均宽度\(\bar {w}\)可用下式表述 (Mughrabi 2009 ) \[ \bar {w} \approx \sqrt {6bhpN\gamma _{{\rm pl},{\rm PSB}} }\ \ (32)\]其中, b为Burgers矢量模,h为滑移区厚度, N为疲劳循环加载周次, \(\gamma _{{\rm pl},{\rm PSB}} \)为PSB区域中的剪切塑性变形.利用AFM或FIB可以测量出\(\bar {w}\)和h, 从而可以计算出不可逆滑移分量p.
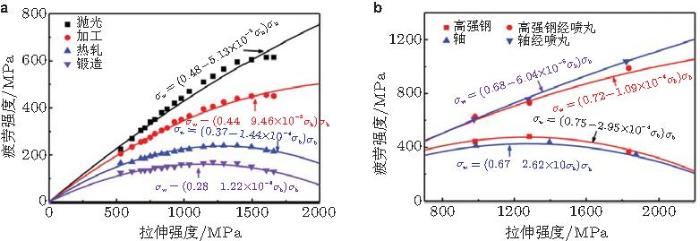
Pang等 (2014) 分析了多种合金材料疲劳强度与硬度、拉伸强度(屈服强度)、韧性之间的关系, 表明疲劳强度\(\sigma _{\rm w}\)与拉伸强度\(\sigma _{\rm b}\)之间的关系可以描述为 \[ \sigma _{\rm w}= \sigma _{\rm b} (C - P\sigma _{\rm b} ) \ \ (33)\]式中, C和P是材料参数.他们给出了经不同技术处理的零部件和高强钢拉伸强度与疲劳强度之间关系的模型结果与实验结果的比较(图67 ).
图 67 (a)具有不同表面状态的手动变速杆的拉伸强度与疲劳强度的关系, (b)经和未经喷丸处理的一种高强钢和一种轴的拉伸强度与疲劳强度的关系(Pang et al. 2014 )
6.2 应力比对疲劳寿命或疲劳强度的影响
研究表明, 传统的Goodman关系不能很好地描述应力比对合金材料超高周疲劳强度的影响(Takeuchi et al. 2010 , Sakai et al. 2006 ). Sun等 (2014) 分析了不同加载应力比条件下若干合金材料的近门槛区裂纹扩展速率(特别是远低于10-10 m/cyc的裂纹扩展速率) 的特征, 推导了应力比 (或平均应力) 对高周和超高周疲劳强度的影响关系, 即 \[ \sigma _{a,R} = \sigma _{ - 1} \left( {\dfrac{1 -R}{2}} \right)^\alpha = \sigma _{ - 1} \left( {1 - \dfrac{\sigma_{{\rm avg},R} }{\sigma _{{\rm max},R} }} \right)^\alpha \ \ (34)\]或 \[ \sigma _{a,R} = \left\{ \begin{array}{ll} \sigma _{ - 1} \dfrac{(1 - R)^\alpha }{2} = 2^{\alpha - 1}\sigma _{ - 1}\left( {1 - \dfrac{\sigma _{{\rm avg},R} }{\sigma _{{\rm max},R}}} \right)^\alpha, & \mbox{for} R \geq 0 \ [2mm] \sigma _{ - 1} \dfrac{1 - R}{2} = \sigma _{ - 1} \left( {1 - \dfrac{\sigma_{{\rm avg},R} }{\sigma _{{\rm max},R} }} \right),& \mbox{for} R < 0\\ \end{array} \right.\ \ (35)\]
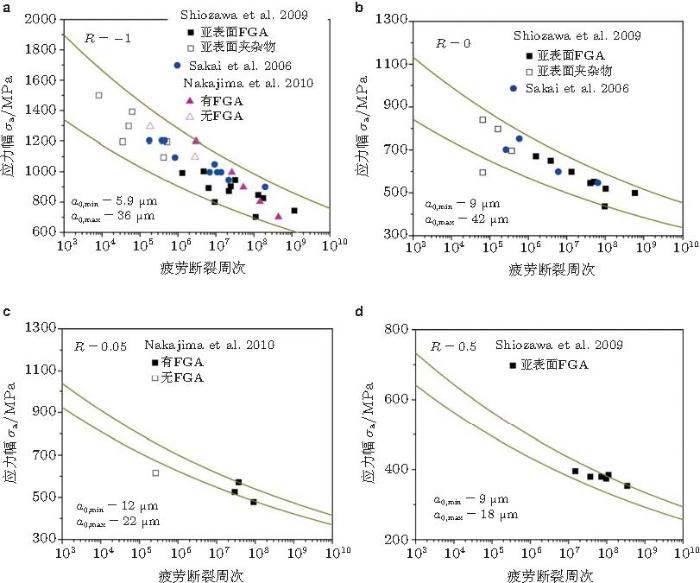
在上述若干关于超高周疲劳强度预测模型中已引入了应力比对疲劳强度的影响, 如式 (14)、式(15) 和 式(24).这些模型中有关应力比对疲劳强度的影响形式与式 (34) 相一致.图68 给出了采用式 (24)给出的不同应力比和夹杂物尺度条件下预测的疲劳n强度与实验结果的比较 (Sun et al. 2013 ). 式 (24)中的参数C和l通过文献 (Shiozawa et al. 2009 ) 中R = -1情况的裂纹源夹杂物周围具有FGA的实验数据点拟合得到, m = -0.192. \(\alpha \)= 0.627, 该值是通过R = -1和R = 0下\(N_{\rm f} = 4\times \)106 周次附近具有几乎相同夹杂物尺寸的试样的疲劳强度计算得到 (Sun et al. 2012 ). 从图68 看出, 此模型较好地反映了应力比和夹杂物尺度对超高周疲劳强度的影响, 采用最小和最大夹杂物尺度的预测结果可以看作是疲劳强度的上限和下限.
图 68 式 (24) 得到的4组预测结果与相应实验结果比较 (Sun et al. 2013 )
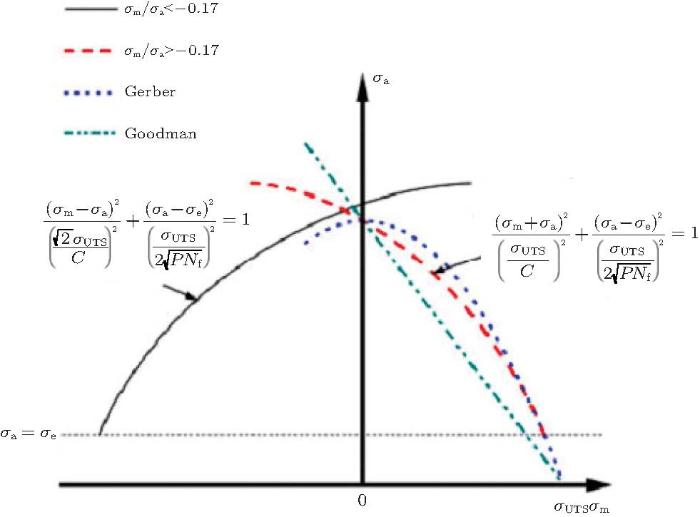
此外, Zhao 等 (2014) 基于Tanaka-Mura位错累积疲劳损伤模型, 通过引入弹性能释放项, 给出了一个考虑能量平衡的疲劳微观模型. 图69 显示了模型给出的拉压疲劳等寿命图并与Goodman, Gerber关系的对比. 由于存在II型裂纹开裂的弹性能释放, 在较高的压缩平均应力作用下, 疲劳裂纹可以形核.平均应力与应力幅的比值存在一个临界值\(-0.17\), 当该比值小于临界值时, 随平均压应力的增大, 疲劳形核寿命下降.
图 69 能量平衡模型给出的等寿命图与Goodman关系和Gerber关系比较(Zhao et al. 2014 )
综上, 关于超高周疲劳寿命或强度的预测模型, 基本上是建立在对实验数据的分析和拟合的基础上, 并未以材料及其损伤的微观物理和力学机制作为建模的出发点.这些模型虽然在一定程度上反映了材料的微结构 (如夹杂物)对疲劳寿命或疲劳强度的影响, 而且可以较好地对实验结果进行预测, 但这些模型的普适性和可靠性值得质疑. 因此, 期待发展基于材料微观物理与力学机制的描述超高周疲劳强度和寿命的模型.另外, 关于钛合金、铝合金等的超高周疲劳寿命或强度预测模型很少, 期待发展这方面的研究工作.
7 结语
7.1 合金材料超高周疲劳的特征、机理与模型
以时间轴为角度, 客观审视了材料疲劳研究的进程, 表明关于合金材料超高周疲劳的研究起源于20世纪80年代.
以高强钢和钛合金为例, 翔实归纳了合金材料超高周疲劳S-N曲线趋势变化规律和以内部起源为主导的裂纹萌生特征.
鲜明表述了合金材料超高周疲劳裂纹萌生特征区和特征参量的学术观点; 尺度仅为几十微米量级的特征区的疲劳寿命占据了总寿命的95%以上, 其扩展速率仅为每周次皮米量级或更小.
裂纹萌生特征区的特征参量 \(\Delta K_{\rm FGA}\)即为裂纹萌生阈值\(\Delta K_{\rm th}\); 对于给定材料, \(\Delta K_{\rm FGA}\)是伯格斯矢量和剪切模量的函数.
全面分析了现行的关于超高周疲劳裂纹内部萌生的模型, 通过多个反例指出了现行模型的缺陷; 进而阐述了笔者提出的关于超高周疲劳裂纹内部萌生的 "大数往复挤压(NCP)" 机理与模型, 并通过多方面的实验结果证实了NCP模型.
简明评述了关于超高周疲劳寿命和疲劳强度的预测模型; 这类模型在一定程度上反映了材料缺陷尺度、基本力学性能以及载荷条件对超高周疲劳寿命或疲劳强度的影响规律, 但基本上是以实验数据为基础的唯象模型.
7.2 未专门评述的合金材料超高周疲劳行为
诚然, 合金材料超高周疲劳的研究进展十分丰富, 不可毕其所有内容于一文, 例如, 下列这些内容本文未专门评述: (1) 高强钢超高周疲劳裂纹内部萌生主要由夹杂物起源, 但在某些情况, 裂纹也可以由非夹杂物起源, 如晶界等; 此外, 夹杂物的类型和尺度对裂纹萌生有影响. 本文在第5.2节和第5.4节中略有提到此方面的问题, 但未专门评述. 这方面的内容可参阅洪友士等(2009) 、Li等 (2012) 、Zimmermann (2012) 、Sander等 (2014) 文献.
(2) 采用超声频率 (如20 kHz)加载使得109 以至1010 加载周次成为不难的事情; 如此高的加载频率对合金材料超高周疲劳行为的影响是一个倍受关注的问题.本文在每个部分里都涉及到超声频率加载的结果, 但未对频率的影响专门评述. 这方面的内容可参阅洪友士等(2009) 、Zhao等 (2012)、Mayer (2016)文献.
(3) 加载环境对合金材料超高周疲劳行为的影响; 一方面这种影响涉及到环境影响的特有机理, 另一方面工程构件总是处在某种环境介质中. 本文在第4.4节和第5.1节提到真空环境, 但基本未涉及到腐蚀环境.弱腐蚀介质甚至中性水对超高周疲劳性能影响十分显著.这方面的内容可参阅: 洪友士等 (2009) , Qian等 (2015) , Mayer (2016) .
7.3 合金材料超高周疲劳研究领域值得进一步深入研究的问题
超高周疲劳裂纹萌生和初始扩展的演化过程: 采用不断发展的先进实验设备和技术, 设计独特的测试方法, 探测超高周疲劳裂纹萌生和初始扩展过程, 特别是几十微米范围的FGA裂纹萌生特征区的演化和形成过程; 一旦裂纹萌生特征区FGA的形成过程被直接揭示, 将意味着超高周疲劳研究的新突破.
基于物理机理的力学模型: 从物理机理出发, 包括微结构受力演化的微观机理, 缺陷形成和生长的微观机理等, 建立定量描述超高周疲劳的损伤行为和预测疲劳性能的力学模型, 从而建立超高周疲劳领域物理和力学的理论框架.
加载频率和加载环境对超高周疲劳特性的影响规律: 加载频率和加载环境对超高周疲劳特性的影响已有一些研究报道, 但似仍处于数据累积阶段, 相关因素对超高周疲劳行为的影响似还未说透; 另一方面, 加载频率和加载环境对超高周疲劳特性的影响程度及其规律往往是工程实际中需要回答的问题.
致谢:国家自然科学基金(11572325)、中国科学院战略性先导科技专项(B类)(XDB22040503, XDB22020201) 资助项目.
The authors have declared that no competing interests exist.
作者已声明无竞争性利益关系。The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
洪友士 , 赵爱国 , 钱桂安 . 2009 . 合金材料超高周疲劳行为的基本特征和影响因素
. 金属学报 , 45 : 769 -780
[本文引用: 5]
(Hong Y S Zhao A G Qian G A 2009 . Essential characteristics and influential factors for very-high-cycle fatigue behavior of metallic materials
. Acta Metallurgica Sinica, 45: 769-780).
[本文引用: 5]
[2]
钱桂安 . 2009 . 不同介质环境中低合金钢的高周和超高周疲劳实验研究. [博士论文]
. 北京: 中国科学院力学研究所
(Qian G A 2009 . Experimental investigation on high cycle and very-high-cycle fatigue behavior of low alloy steel under different environmental media
. [PhD Thesis]. Beijing: Institute of Mechanics, Chinese Academy of Sciences).
[3]
ASTM E468-90 2004 . Annual book of ASTM standards 2006
, Section 3 , 03.01: 556 -561 .
[4]
Akiniwa Y Miyamoto N Tsuru H Tanaka K 2006 . Notch effect on fatigue strength reduction of bearing steel in the very high cycle regime
. International Journal of Fatigue , 28 : 1555 -1565 .
[本文引用: 1]
[5]
Asami K Sugiyama Y 1985 . Fatigue~strength~of~various~surface~hardened~steels. Journal of the Japan Society for Heat~
Treatment , 25 : 147 -150 .
[本文引用: 3]
[6]
Asami K Emura H 1990 . Fatigue strength characteristics of high-strength steel. JSME International Journal Series I-Solid Mechanics Strength of
Materials , 33 : 367 -374 .
[本文引用: 2]
[7]
Atrens A Hoffelner W Duerig T W Allison J E 1983 . Subsurface crack initiation in high cycle fatigue in Ti6Al4V and in a typical martensitic stainless steel
. Scripta Metallurgica , 17 : 601 -606 .
[本文引用: 6]
[8]
Bathias C Paris P C 2005 . Gigacycle Fatigue in Mechanical Practice.
New York:Marcel Dekker.
[本文引用: 1]
[9]
Borrego L P Costa J M Silva S Ferreira J M 2004 . Microstructure dependent fatigue crack growth in aged hardened aluminium alloys
. International Journal of Fatigue , 26 : 1321 -1331 .
[本文引用: 1]
[10]
Chapetti M D Tagawa T Miyata T 2003 . Ultra-long cycle fatigue of high-strength carbon steels part II: Estimation of fatigue limit for failure from internal inclusions
. Materials Science & Engineering A , 356 : 236 -244 .
[本文引用: 1]
[11]
Furuya Y 2011 . Notable size effects on very high cycle fatigue properties of high-strength steel
. Materials Science & Engineering A , 528 : 5234 -5240 .
[本文引用: 1]
[12]
Furuya Y Takeuchi E 2014 . Gigacycle fatigue properties of Ti-6Al-4V alloy under tensile mean stress
. Materials Science & Engineering A , 598 : 135 -140 .
[本文引用: 5]
[13]
Grad P Reuscher B Brodyanski A Kopnarski M Kerscher E 2012 . Mechanism of fatigue crack initiation and propagation in the very high cycle fatigue regime of high-strength steels
. Scripta Materialia , 67 : 838 -641 .
[本文引用: 4]
[14]
Harlow D G Wei R P Sakai T Oguma N 2006 . Crack growth based probability modeling of S-N response for high strength steel
. International Journal of Fatigue , 28 : 1479 -85 .
[本文引用: 1]
[15]
Heinz S Balle F Wagner G Eifler D 2013 . Analysis of fatigue properties and failure mechanisms of Ti6Al4V in the very high cycle fatigue regime using ultrasonic technology and 3D laser scanning vibrometry
. Ultrasonics , 53 : 1433 -1440 .
[本文引用: 3]
[16]
Heinz S Eifler D 2016 . Crack initiation mechanisms of Ti6A14V in the very high cycle fatigue regime
. International Journal of Fatigue , 93 : 301 -308 .
[本文引用: 3]
[17]
Hertzberg R W Vinci R P Hertzberg J L 2012 . Deformation and Fracture Mechanics of Engineering Materials. 5th ed. New York:
Wiley.
[本文引用: 1]
[18]
Holper B Mayer H Vasudevan A K Stanzl-Tschegg S E 2004 . Near threshold fatigue crack growth at positive load ratio in aluminium alloys at low and ultrasonic frequency: influences of strain rate, slip behaviour and air humidity
. International Journal of Fatigue , 26 : 27 -38 .
[本文引用: 1]
[19]
Hong Y Qian G Zhou C 2009 . Experiment and simulation of very-high-cycle fatigue behavior for low alloy steels//Proceedings of the 12th International Conference on Fracture, July 12-17, 2009, Ottawa, Canada, ICF12 CD-ROM
, T26 .003 .
[本文引用: 2]
[20]
Hong Y Zhao A Qian G Zhou C 2012 . Fatigue strength and crack initiation mechanism of very-high-cycle fatigue for low alloy steels
. Metallurgical and Materials Transactions A , 43 : 2753 -2762 .
[本文引用: 6]
[21]
Hong Y Lei Z Sun C Zhao A 2014 . Propensities of crack interior initiation and early growth for very-high-cycle fatigue of high strength steels
. International Journal of Fatigue , 58 : 144 -151 .
[本文引用: 9]
[22]
Hong Y Liu X Lei Z Sun C 2016 . The formation mechanism of characteristic region at crack initiation for very-high-cycle fatigue of high-strength steels
. International Journal of Fatigue , 89 : 108 -118 .
[本文引用: 6]
[23]
Huang X Moan T 2007 . Improved modeling of the effect of R-ratio on crack growth rate
. International Journal of Fatigue , 29 : 591 -602 .
[本文引用: 2]
[24]
Huang Z Y Wang C Wagner D Bathias C 2014 . A very high cycle fatigue thermal dissipation investigation for titanium alloy TC4
. Materials Science & Engineering A , 600 : 153 -158
[25]
Huang Z Y Liu H Q Wang C Wang Q Y 2015 . Fatigue life dispersion and thermal dissipation investigations for titanium alloy TC17 in very high cycle regime
. Fatigue & Fracture of Engineering Materials & Structures , 38 : 1285 -1293 .
[26]
Ishida W Yamamoto T Kaneda S Ogawa T 2012 . Fatigue strength and internal crack growth behavior of high strength steel under variable amplitude stressing in very high cycle regime
. Transaction of Japan Society of Mechanical Engineers A , 78 : 23 -33 .
[本文引用: 2]
[27]
Jha S K Ravi Chandran K S 2003 . An unusual fatigue phenomenon: duality of the S-N fatigue curve in the \(\beta \)-titanium alloy Ti-10V-2Fe-3Al
. Scripta Materialia , 48 : 1207 -1212 .
[本文引用: 2]
[28]
Jiang Q Sun C Liu X Hong Y 2016. Very-high-cycle fatigue behavior of a structural steel with and without induced surface defects
. International Journal of Fatigue , 2016 , 93 : 352 -362 .
[本文引用: 3]
[29]
Kikukawa M Ohji K Ogura K 1965 . Push-pull fatigue strength of mild steel at very high frequencies of stress up to 100 kc/s. Journal of Basic Engineering,
Transactions of the ASME , 87 : 857 -864 .
[本文引用: 2]
[30]
Kovacs S Beck T Singheiser L 2013 . Influence of mean stresses on fatigue life and damage of a turbine blade steel in the VHCF-regime
. International Journal of Fatigue , 49 : 90 -99 .
[本文引用: 4]
[31]
Lei Z Hong Y Xie J Sun C Zhao A 2012 . Effects of inclusion size and location on very-high-cycle fatigue behavior for high strength steels
. Materials Science & Engineering A , 558 : 234 -241 .
[本文引用: 1]
[32]
Lei Z Xie J Sun C Hong Y 2014 . Effect of loading condition on very-high-cycle fatigue behavior and dominant variable analysis. Science China-Physics Mechanics &
Astronomy , 57 : 74 -82 .
[本文引用: 1]
[33]
Li S X 2012 . Effects of inclusions on very high cycle fatigue properties of high strength steels
. International Materials Reviews , 57 : 92 -114 .
[本文引用: 2]
[34]
Li W Sakai T Li Q Lu L T Wang P 2010 . Reliability evaluation on very high cycle fatigue property of GCr15 bearing steel
. International Journal of Fatigue , 32 : 1096 -1107 .
[35]
Li Y D Yang Z G Li S X Liu Y B Chen S M 2008 . Correlations between very high cycle fatigue properties and inclusions of GCr15 bearing steel
. Acta Metallurgica Sinica , 44 : 968 -972 .
[36]
Liu X Sun C Hong Y 2015 . Effects of stress ratio on high-cycle and very-high-cycle fatigue behavior of a Ti-6Al-4V alloy
. Materials Science & Engineering A , 622 : 228 -235 .
[本文引用: 6]
[37]
Liu X Sun C Zhou Y Hong Y 2016 a. Effects of microstructure and stress ratio on high-cycle and very-high-cycle fatigue of Ti-6Al-4V alloy
. Acta Metallurgica Sinica , 52 : 923 -930 .
[本文引用: 1]
[38]
Liu X Sun C Hong Y 2016 b. Faceted crack initiation characteristics for high-cycle and very-high-cycle fatigue of a titanium alloy under different stress ratios
. International Journal of Fatigue ,92 : 434 -441 .
[本文引用: 5]
[39]
Liu Y B Li Y D Li S X Yang Z G Chen S M Hui W J Weng Y Q 2010 . Prediction of the S-N curves of high-strength steels in the very high cycle fatigue regime
. International Journal of Fatigue , 32 : 1351 -1357 .
[本文引用: 2]
[40]
Marines-Garcia I Paris P C Tada H Bathias C 2007 . Fatigue crack growth from small to long cracks in very-high-cycle fatigue with surface and internal "fish-eye" failures for ferrite-perlitic low carbon steel SAE 8620
. Materials Science & Engineering A, 468- 470 : 120 -128 .
[41]
Marines-Garcia I Paris P C Tada H Bathias C Lados D 2008 . Fatigue crack growth from small to large cracks on very high cycle fatigue with fish-eye failures
. Engineering Fracture Mechanics , 75 : 1657 -1665 .
[42]
Mason W P 1956 . Internal friction and fatigue in metals at large strain amplitudes
. Journal of the Acoustical Society of America , 28 : 1207 -1218 .
[本文引用: 1]
[43]
Mayer H 1999 . Fatigue crack growth and threshold measurements at very high frequencies
. International Materials Reviews , 44 : 1 -36 .
[本文引用: 1]
[44]
Mayer H Haydn W Schuller R Issler S Furtner B Bacher-H\"{o}chst M 2009 . Very high cycle fatigue properties of bainitic high carbon-chromium steel
. International Journal of Fatigue , 31 : 242 -249 .
[本文引用: 1]
[45]
Mayer H 2016 . Recent developments in ultrasonic fatigue
. Fatigue & Fracture of Engineering Materials & Structures , 39 : 3 -29 .
[本文引用: 2]
[46]
Mughrabi H 1999 . On the life-controlling microstructural fatigue mechanisms in ductile metals and alloys in the gigacycle regime
. Fatigue & Fracture of Engineering Materials & Structures , 22 : 633 -641 .
[本文引用: 1]
[47]
Mughrabi H 2002 . On "multi-stage" fatigue life diagrams and the relevant life-controlling mechanisms in ultrahigh-cycle fatigue
. Fatigue & Fracture of Engineering Materials & Structures , 25 : 755 -764 .
[本文引用: 1]
[48]
Mughrabi H 2009 . Cyclic slip irreversibilities and the evolution of fatigue damage
. Metallurgical and Materials Transactions A , 40A : 1257 -1279 .
[本文引用: 2]
[49]
Mughrabi H 2010 . Fatigue, an everlasting materials problem-still en vogue
. Procedia Engineering , 2 : 3 -26 .
[本文引用: 1]
[50]
Murakami Y Kodama S Konuma S 1988 . Quantitative evaluation of effects of nonmetallic inclusions on fatigue strength of high strength steel
. Transactions of the Japan Society of Mechanical Engineers , 54A : 688 -695 .
[51]
Murakami Y Kodama S Konuma S 1989 . Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. I: Basic fatigue mechanism and evaluation of correlation between the fatigue fracture stress and the size and location of non-metallic inclusions
. International Journal of Fatigue , 11 : 291 -298 .
[本文引用: 2]
[52]
Murakami Y Usuki H 1989 . Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. II: Fatigue limit evaluation based on statistics for extreme values of inclusion size
. International Journal of Fatigue , 11 : 299 -307 .
[53]
Murakami Y Nomoto T Ueda T 1999 . Factors influencing the mechanism of superlong fatigue failure in steels
. Fatigue & Fracture of Engineering Materials & Structures , 22 : 581 -590 .
[本文引用: 5]
[54]
Murakami Y Nomoto T Ueda T Murakami Y 2000 a. On the mechanism of fatigue failure in the superlong life regime \((N > 10^{7}\) cycles), Part I: influence of hydrogen trapped by inclusions
. Fatigue & Fracture of Engineering Materials & Structures , 23 : 893 -902 .
[本文引用: 3]
[55]
Murakami Yu Nomoto T Ueda T Murakami Ya 2000 b. On the mechanism of fatigue failure in the superlong life regime \((N > 10 ^{7}\) cycles), Part II: a fractographic investigation
. Fatigue & Fracture of Engineering Materials & Structures , 23 : 903 -910 .
[本文引用: 1]
[56]
Murakami Y 2002 . Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions.
London:Elservier.
[57]
Murakami Y Yokoyama N N Nagata J 2002 b. Mechanism of fatigue failure in ultralong life regime
. Fatigue & Fracture of Engineering Materials & Structures , 25 : 735 -746 .
[本文引用: 2]
[58]
Naito T Ueda H Kikuchi M 1983 . Observation of fatigue fracture surface of carburized steel. Journal of the Society of Materials Science,
Japan , 32 : 1162 -1166 .
[本文引用: 4]
[59]
Naito T Ueda H Kikuchi M 1984 . Fatigue behavior of carburized steel with internal oxides and nonmartensitic microstructure near the surface
. Metallurgical Transactions A , 15A : 1431 -1436 .
[本文引用: 9]
[60]
Nakajima M Tokaji K Itoga H Shimizu T 2010 . Effect of loading condition on very high cycle fatigue behavior in a high strength steel
. International Journal of Fatigue , 32 : 475 -480 .
[61]
Neal D F Blenkinsop P A 1976 . Internal fatigue origins in \(\alpha -\beta \) titanium alloys
. Acta Metallurgica , 24 : 59 -63 .
[本文引用: 2]
[62]
Nishijima S Kanazawa K 1999 . Stepwise S-N curve and fish-eye failure in gigacycle fatigue
. Fatigue & Fracture of Engineering Materials & Structures , 22 : 601 -607 .
[本文引用: 2]
[63]
Nix W D Gao H J 1998 . Indentation size effects in crystalline materials: A law for strain gradient plasticity
. Journal of the Mechanics and Physics of Solids , 46 : 411 -425 .
[本文引用: 1]
[64]
Ochi Y Matsumura T Masaki K Yoshida S 2002 . High-cycle rotating bending fatigue property in very long-life regime of high-strength steels
. Fatigue & Fracture of Engineering Materials & Structures , 25 : 823 -830 .
[本文引用: 1]
[65]
Ogawa T Stanzl-Tschegg S Schonbauer B 2014 . A fracture mechanics approach to interior fatigue crack growth in the very high cycle regime
. Engineering Fracture Mechanics , 115 : 241 -254 .
[本文引用: 3]
[66]
Oguma N Harada H Sakai T 2003 . Mechanism of long life fatigue fracture induced by interior inclusion for bearing steel in rotating bending.
Journal of the Society of Materials Science,Japan , 52 : 1292 -1297 .
[本文引用: 2]
[67]
Oguma H Nakamura T 2010 . The effect of microstructure on very high cycle fatigue properties in Ti-6Al-4V
. Scripta Materialia , 63 : 32 -34 .
[本文引用: 2]
[68]
Oguma H Nakamura T 2013 . Fatigue crack propagation properties of Ti-6Al-4V in vacuum environments
. International Journal of Fatigue , 50 : 89 -93 .
[本文引用: 3]
[69]
Pang J C Li S X Wang Z G Zhang Z F 2014 . Relations between fatigue strength and other mechanical properties of metallic materials
. Fatigue & Fracture of Engineering Materials & Structures , 37 : 958 -976 .
[本文引用: 2]
[70]
Papakyriacou M Mayer H Fuchs U Stanzl-Tschegg S E Wei R P 2002 . Influence of atmospheric moisture on slow fatigue crack growth at ultrasonic frequency in aluminium and magnesium alloys
. Fatigue & Fracture of Engineering Materials & Structures , 25 : 795 -804 .
[本文引用: 2]
[71]
Paris P C Tada H Donald J K 1999 . Service load fatigue damage-a historical perspective
. International Journal of Fatigue , 21 : S35 -S46 .
[本文引用: 1]
[72]
Petit J Sarrazin-Baudoux C 2006 . An overview on the influence of the atmosphere environment on ultra-high-cycle fatigue and ultra-slow fatigue crack propagation
. International Journal of Fatigue , 28 : 1471 -1478 .
[本文引用: 1]
[73]
Qian G Zhou C Hong Y 2011 . Experimental and theoretical investigation of environmental media on very-high-cycle fatigue behavior for a structural steel
. Acta Materialia , 59 : 1321 -1327 .
[本文引用: 1]
[74]
Qian G Zhou C Hong Y 2015 . A model to predict S-N curves for surface and subsurface crack initiations in different environmental media
. International {\it Journal of Fatigue} , 71 : 35 -44 .
[本文引用: 1]
[75]
Ravi Chandran K S 2005 . Duality of fatigue failures of materials caused by Poisson defect statistics of competing failure modes
. Nature Materials , 4 : 303 -308 .
[本文引用: 3]
[76]
Ravi Chandran K S Jha S K 2005 . Duality of the S-N fatigue curve caused by competing failure modes in a titanium alloy and the role of Poisson defect statistics
. Acta Materialia , 53 : 1867 -1881 .
[本文引用: 3]
[77]
Ritchie R O Davidson D L Boyce B L Campbell J P Roder O 1999 . High-cycle fatigue of Ti-6Al-4V
. Fatigue & Fracture of Engineering Materials & Structures , 22 : 621 -631 .
[本文引用: 1]
[78]
Sakai T. Takeda M Shiozawa K Ochi Y Nakajima M Nakamura T Oguma N 2000 . Experimental reconfirmation of characteristic S-N property for high carbon chromium bearing steel in wide life region in rotating bending. Journal of the Society of Materials Science,
Japan , 49 : 779 -785 .
[本文引用: 2]
[79]
Sakai T Takeda M Tanaka N Kanemitsu M Oguma N Shiozawa K 2001 . S-N property and fractography of high carbon chromium bearing steel over ultra wide life region under rotating bending
. Transactions of the Japan Society of Mechanical Engineers , 67A : 1805 -1812 .
[本文引用: 3]
[80]
Sakai T Sato Y Oguma N 2002 . Characteristic S-N properties of high-carbon-chromium-bearing steel under axial loading in long-life fatigue
. Fatigue & Fracture of Engineering Materials & Structures , 25 : 765 -773 .
[本文引用: 2]
[81]
Sakai T Sato Y Nagano Y Takeda M Oguma N 2006 . Effect of stress ratio on long life fatigue behavior of high carbon chromium bearing steel under axial loading
. International Journal of Fatigue , 28 : 1547 -1554 .
[本文引用: 1]
[82]
Sakai T 2009 . Review and prospects for current studies on very high cycle fatigue of metallic materials for machine structural use
. Journal of Solid Mechanics and Materials Engineering , 3 : 425 -39 .
[本文引用: 9]
[83]
Sakai T Oguma N Morikawa A 2015 . Microscopic and nanoscopic observations of metallurgical structures around inclusions at interior crack initiation site for a bearing steel in very high-cycle fatigue
. Fatigue & Fracture of Engineering Materials & Structures , 38 : 1305 -1314 .
[本文引用: 4]
[84]
Sander M M\"{u}ller T Lebahn J 2014 . Influence of mean stress and variable amplitude loading on the fatigue behaviour of a high-strength steel in VHCF regime
. International Journal of Fatigue , 62 : 10 -20 .
[本文引用: 4]
[85]
Sander M M\"{u}ller T St\"{a}cker C 2016 . Very high cycle fatigue behavior under constant and variable amplitude loading
. Procedia Structural Integrity , 2 : 34 -41 .
[本文引用: 2]
[86]
Shanyavskiy A A 2013 . Mechanisms and modeling of subsurface fatigue cracking in metals
. Engineering Fracture Mechanics , 110 : 350 -363 .
[本文引用: 2]
[87]
Shiozawa K Lu L Ishihara S 2001 . S-N curve characteristics and subsurface crack initiation behaviour in ultra-long life fatigue of a high carbon-chromium bearing steel
. Fatigue & Fracture of Engineering Materials & Structures , 24 : 781 -790 .
[本文引用: 2]
[88]
Shiozawa K Lu L 2002 . Very high-cycle fatigue behaviour of shot-peened high-carbon-chromium bearing steel
. Fatigue & Fracture of Engineering Materials & Structures , 25 : 813 -822 .
[本文引用: 2]
[89]
Shiozawa K Morii Y Nishino S 2006 a. Subsurface crack initiation and propagation mechanism under the super-long fatigue regime for high speed tool steel (JIS SKH51) by fracture surface topographic analysis
. JSME International Journal Series A-Solid Mechanics and Material Engineering , 49 : 1 -10 .
[本文引用: 5]
[90]
Shiozawa K Morii Y Nishino S Lu L 2006 b. Subsurface crack initiation and propagation mechanism in high strength steel in a very high cycle fatigue regime
. International Journal of Fatigue , 28 : 1521 -1532 .
[本文引用: 7]
[91]
Shiozawa K Hasegawa T Kashiwagi Y Lu L 2009 . Very high cycle fatigue properties of bearing steel under axial loading condition
. International Journal of Fatigue , 31 : 880 -888 .
[本文引用: 1]
[92]
Stanzl S E Tschegg E K Mayer H 1986 . Lifetime measurements for random loading in the very high cycle fatigue range
. International Journal of Fatigue , 8 : 195 -200 .
[本文引用: 2]
[93]
Stanzl-Tschegg S Schonbauer B 2010 . Near-threshold crack propagation and internal cracks in steel
. Procedia Engineering , 2 : 1547 -1555 .
[本文引用: 1]
[94]
Stanzl-Tschegg S 2014 . Very high cycle fatigue measuring techniques
. International Journal of Fatigue , 60 : 2 -17 .
[本文引用: 1]
[95]
Stepanskiy L G 2012 . Cumulative model of very high cycle fatigue
. Fatigue & Fracture of Engineering Materials & Structures , 35 : 513 -522 .
[本文引用: 1]
[96]
Su H Liu X Sun C Hong Y 2017 . Nanograin layer formation at crack initiation region for very-high-cycle fatigue of a Ti-6Al-4V alloy
. Fatigue & Fracture of Engineering Materials & Structures , 40 : 979 -993 .
[本文引用: 4]
[97]
Sun C Xie J Zhao A Hong Y 2012 . A cumulative damage model for fatigue life estimation of high-strength steels in high-cycle and very-high-cycle fatigue regimes
. Fatigue & Fracture of Engineering Materials & Structures , 35 : 638 -647 .
[本文引用: 2]
[98]
Sun C Lei Z Xie J Hong Y 2013 . Effects of inclusion size and stress ratio on fatigue strength for high-strength steels with fish-eye mode failure
. International Journal of Fatigue , 48 : 19 -27 .
[本文引用: 4]
[99]
Sun C Lei Z Hong Y 2014 . Effects of stress ratio on crack growth rate and fatigue strength for high cycle and very-high-cycle fatigue of metallic materials
. Mechanics of Materials , 69 : 227 -236 .
[本文引用: 1]
[100]
Sun C Liu X Hong Y 2015 . A two-parameter model to predict fatigue life of high-strength steels in a very high cycle fatigue regime
. Acta Mechanica Sinica , 31 : 383 -391 .
[本文引用: 2]
[101]
Sun C Zhang X Liu X Hong Y 2016 . Effects of specimen size on fatigue life of metallic materials in high-cycle and very-high-cycle fatigue regimes
. Fatigue & Fracture of Engineering Materials & Structures , 39 : 770 -779 .
[本文引用: 1]
[102]
Szczepanski C J Jha S K Larsen J M Jones J W 2008 . Microstructural influences on very high cycle fatigue crack initiation in Ti-6246
. Metallurgical and Materials Transactions A , 39 : 2841 -2851 .
[本文引用: 1]
[103]
Takai K Seki J Seki J Honma Y 1995 . Observation of trapping sites of hydrogen and deuterium in high-strength steels by using secondary ion mass spectrometry.
Materials Transactions,JIM , 36 : 1134 -1139 .
[本文引用: 1]
[104]
Takai K Honma Y Izutsu K Nagumo M 1996 . Identification of trapping sites in high-strength steels by secondary ion mass spectrometry for thermally desorbed hydrogen
. The Journal of the Japan Institute of Metals , 60 : 1155 -1162 .
[本文引用: 1]
[105]
Takeuchi E Furuya Y Nagashima N Matsuoka S 2008 . The effect of frequency on the giga-cycle fatigue properties of a Ti-6Al-4V alloy
. Fatigue & Fracture of Engineering Materials & Structures , 31 : 599 -605 .
[本文引用: 2]
[106]
Takeuchi E Furuya Y Nagashima N Matsuoka S 2010 . Effect of stressratio on giga-cycle fatigue properties for Ti-6Al-4V Alloy
. Tetsu-to-Hagan\'{e} , 96 : 36 -41 .
[本文引用: 1]
[107]
Tanaka K Mura T 1982 . A theory of fatigue crack initiation at inclusions
. Metallurgical Transactions A , 13A : 117 -123 .
[本文引用: 2]
[108]
Tanaka K Akiniwa Y 2002 . Fatigue crack propagation behaviour derived from S-N data in very high cycle regime
. Fatigue & Fracture of Engineering Materials & Structures , 25 : 775 -784 .
[本文引用: 3]
[109]
Tien J K 1982 . The state of ultrasonic fatigue (keynote address). Ultrasonic Fatigue//Proceedings of the First International Conference on Fatigue and Corrosion Fatigue up to Ultrasonic Frequencies, The Metallurgical Society of AIME,
New York: 1 -14 .
[本文引用: 1]
[110]
Wang Q Y Berard J Y Rathery S Bathias C 1999 . High-cycle fatigue crack initiation and propagation gehaviour of high-strength spring steel wires
. Fatigue & Fracture of Engineering Materials & Structures , 22 : 673 -677 .
[本文引用: 2]
[111]
Wang Q Y Bathias C Kawagoishi N Chen Q 2002 . Effect of inclusion on subsurface crack initiation and gigacycle fatigue strength
. International Journal of Fatigue , 24 : 1269 -1274 .
[本文引用: 1]
[112]
Willertz L E 1980 . Ultrasonic fatigue
. International Metals Reviews , 25 : 65 -78 .
[本文引用: 1]
[113]
Wells J M Buck O Roth L D Tien J K 1982 . Ultrasonic fatigue//Proceedings of the First International Conference on Fatigue and Corrosion Fatigue up to Ultrasonic Frequencies, The Metallurgical Society of AIME
. New York.
[本文引用: 1]
[114]
W\"{o}hler A 1867 . W\"{o}hler's experiments on the strength of metals
. Engineering , 4 : 160 -161 .
[本文引用: 2]
[115]
Yang Z G Li S X Liu Y B Li Y D Li G Y Hui W J Weng Y Q 2008 . Estimation of the size of GBF area on fracture surface for high strength steels in very high cycle fatigue regime
. International Journal of Fatigue , 30 : 1016 -1023 .
[本文引用: 1]
[116]
Yu Y Gu J L Shou F L Xu L Bai B Z Liu Y B 2011 . Competition mechanism between microstructure type and inclusion level in determining VHCF behavior of bainite/martensite dual phase steels
. International Journal of Fatigue , 33 : 500 -506 .
[本文引用: 1]
[117]
Zerbst U Beretta S Koehler G Lawton A Vormwald M Beier H Th Klinger C Cerny I Rudlin J Heckel T Klingbeil D 2013 . Safe life and damage tolerance aspects of railway axles---A review
. Engineering Fracture Mechanics , 98 : 214 -271 .
[本文引用: 1]
[118]
Zhang M Wang W Wang P Liu Y Li J 2016 . The fatigue behavior and mechanism of FV520B-I with large surface roughness in a very high cycle regime
. Engineering Failure Analysis , 66 : 432 -444 .
[119]
Zhao A Xie J Sun C Lei Z Hong Y 2011 . Prediction of threshold value for FGA formation
. Materials Science & Engineering A , 528 : 6872 -6877 .
[本文引用: 4]
[120]
Zhao A Xie J Sun C Lei Z Hong Y 2012 . Effects of strength level and loading frequency on very-high-cycle fatigue behavior for a bearing steel
. International Journal of Fatigue , 38 : 46 -56 .
[本文引用: 2]
[121]
Zhao S Xie J Zhao A Wu X 2014 . An energy-equilibrium model for complex stress effect on fatigue crack initiation. Science China Physics,
Mechanics & Astronomy , 57 : 916 -926 .
[本文引用: 2]
[122]
Zhao Y X Yang B Feng M F Wang H 2009 . Probabilistic fatigue S-N curves including the super-long life regime of a railway axle steel
. International Journal of Fatigue , 31 : 1550 -1558 .
[本文引用: 1]
[123]
Zimmermann M 2012 . Diversity of damage evolution during cyclic loading at very high numbers of cycles
. International Materials Reviews , 57 : 73 -91 .
[本文引用: 2]
[124]
Zuo J H Wang Z G Han E H 2008 . Effect of microstructure on ultra-high cycle fatigue behavior of Ti-6Al-4V
. Materials Science & Engineering A , 473 : 147 -152 .
[本文引用: 1]
合金材料超高周疲劳行为的基本特征和影响因素
5
2009
... 在循环载荷作用下, 合金材料发生裂纹萌生、扩展直至断裂的周次在107 以上的过程被称为超高周疲劳(Sakai 2009 , 洪友士等2009 ). 合金材料超高周疲劳(very-high-cycle fatigue, VHCF) 行为是对传统疲劳理念的挑战, 因为传统疲劳知识认为, 合金材料存在疲劳极限, 即对应107 载荷周次的疲劳强度被确定为疲劳极限 (ASTME468-90, 2004), 循环应力低于疲劳极限不发生疲劳损伤和破坏. ...
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
... 诚然, 合金材料超高周疲劳的研究进展十分丰富, 不可毕其所有内容于一文, 例如, 下列这些内容本文未专门评述: (1) 高强钢超高周疲劳裂纹内部萌生主要由夹杂物起源, 但在某些情况, 裂纹也可以由非夹杂物起源, 如晶界等; 此外, 夹杂物的类型和尺度对裂纹萌生有影响. 本文在第5.2节和第5.4节中略有提到此方面的问题, 但未专门评述. 这方面的内容可参阅洪友士等(2009) 、Li等 (2012) 、Zimmermann (2012) 、Sander等 (2014) 文献. ...
... (2) 采用超声频率 (如20 kHz)加载使得109 以至1010 加载周次成为不难的事情; 如此高的加载频率对合金材料超高周疲劳行为的影响是一个倍受关注的问题.本文在每个部分里都涉及到超声频率加载的结果, 但未对频率的影响专门评述. 这方面的内容可参阅洪友士等(2009) 、Zhao等 (2012)、Mayer (2016)文献. ...
... (3) 加载环境对合金材料超高周疲劳行为的影响; 一方面这种影响涉及到环境影响的特有机理, 另一方面工程构件总是处在某种环境介质中. 本文在第4.4节和第5.1节提到真空环境, 但基本未涉及到腐蚀环境.弱腐蚀介质甚至中性水对超高周疲劳性能影响十分显著.这方面的内容可参阅: 洪友士等 (2009) , Qian等 (2015) , Mayer (2016) . ...
合金材料超高周疲劳行为的基本特征和影响因素
5
2009
... 在循环载荷作用下, 合金材料发生裂纹萌生、扩展直至断裂的周次在107 以上的过程被称为超高周疲劳(Sakai 2009 , 洪友士等2009 ). 合金材料超高周疲劳(very-high-cycle fatigue, VHCF) 行为是对传统疲劳理念的挑战, 因为传统疲劳知识认为, 合金材料存在疲劳极限, 即对应107 载荷周次的疲劳强度被确定为疲劳极限 (ASTME468-90, 2004), 循环应力低于疲劳极限不发生疲劳损伤和破坏. ...
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
... 诚然, 合金材料超高周疲劳的研究进展十分丰富, 不可毕其所有内容于一文, 例如, 下列这些内容本文未专门评述: (1) 高强钢超高周疲劳裂纹内部萌生主要由夹杂物起源, 但在某些情况, 裂纹也可以由非夹杂物起源, 如晶界等; 此外, 夹杂物的类型和尺度对裂纹萌生有影响. 本文在第5.2节和第5.4节中略有提到此方面的问题, 但未专门评述. 这方面的内容可参阅洪友士等(2009) 、Li等 (2012) 、Zimmermann (2012) 、Sander等 (2014) 文献. ...
... (2) 采用超声频率 (如20 kHz)加载使得109 以至1010 加载周次成为不难的事情; 如此高的加载频率对合金材料超高周疲劳行为的影响是一个倍受关注的问题.本文在每个部分里都涉及到超声频率加载的结果, 但未对频率的影响专门评述. 这方面的内容可参阅洪友士等(2009) 、Zhao等 (2012)、Mayer (2016)文献. ...
... (3) 加载环境对合金材料超高周疲劳行为的影响; 一方面这种影响涉及到环境影响的特有机理, 另一方面工程构件总是处在某种环境介质中. 本文在第4.4节和第5.1节提到真空环境, 但基本未涉及到腐蚀环境.弱腐蚀介质甚至中性水对超高周疲劳性能影响十分显著.这方面的内容可参阅: 洪友士等 (2009) , Qian等 (2015) , Mayer (2016) . ...
不同介质环境中低合金钢的高周和超高周疲劳实验研究. [博士论文]
0
2009
不同介质环境中低合金钢的高周和超高周疲劳实验研究. [博士论文]
0
2009
Annual book of ASTM standards 2006
0
2004
Notch effect on fatigue strength reduction of bearing steel in the very high cycle regime
1
2006
... Akiniwa 等 (2006) 假定Paris关系对FGA内的裂纹扩展行为仍然成立, 导出了疲劳强度和载荷周次之间的关系 \[ \sigma _a = \dfrac{2}{\sqrt \pi }\left({\dfrac{2}{C_{\rm A} (m_{\rm A} - 2)}} \right)^{\frac{1}{m_{\rm A}}}\left( {\sqrt {area_{\rm Inc} } } \right)^{\frac{1}{m_{\rm A} }- \frac{1}{2}}N_{\rm f}^{ - \frac{1}{m_{\rm A} }} \ \ (19)\]式中, 下角标 "Inc" 表示夹杂物, \(C_{\rm A}\(和\)m_{\rm A}\)是材料参数. ...
Fatigue~strength~of~various~surface~hardened~steels. Journal of the Japan Society for Heat~
3
1985
... 此外, Asami和Sugiyama (1985) 也采用旋转弯曲加载技术研究了若干表面强化钢的疲劳性能, 同样表明表面渗碳强化钢的S-N曲线有两个拐点 (图4 ), 所得到断口观察结果及其解释与Naito等 (1984) 相似. ...
... 表面渗碳强化SCM 420钢的S-N曲线 (Asami & Sugiyama 1985 ) ...
... Naito等(1983 , 1984 )、Atrens等 (1983) 、Asami和Sugiyama (1985) 和Stanzl等 (1986) 的研究报道, 标志了与传统低周疲劳和高周疲劳内涵不同的超高周疲劳研究的起源. ...
Fatigue strength characteristics of high-strength steel. JSME International Journal Series I-Solid Mechanics Strength of
2
1990
... Asami和Emura (1990) 报道了若干高强钢在实验室环境和干燥空气中的超高周疲劳特性. 图6 (a) 是SNCM439 (0.4%C-Ni-Cr-Mo) 钢经淬火并低温(200\(^\circ\)C) 和高温 (600\(^\circ\)C) 回火的S-N曲线, 显示低温回火态的S-N曲线是具有两个拐点的双线形; 在第2个拐点后, 即106 \(\sim \) 109 周次区间主要为亚表面裂纹萌生的鱼眼特征. ...
... (a) 2组SNCM 439钢的S-N数据, (b) 3组SNCM 420钢的S-N数据(Asami & Emura 1990 ) ...
Subsurface crack initiation in high cycle fatigue in Ti6Al4V and in a typical martensitic stainless steel
6
1983
... 20世纪80年代, 超高周疲劳现象开始得到专门研究. 最早的报道是Naito等(1983 , 1984 ) 关于渗碳钢的研究和Atrens等 (1983) 关于钛合金的研究. ...
... 同一时期, Atrens等 (1983) 分别采用60 Hz, 150 Hz和20 kHz研究了Ti-6Al-4V合金的疲劳特性, 显示S-N曲线在\(10^{6}\sim 10 ^{7}\)周次趋于平缓, 107 周次之后疲劳强度又明显下降; 在\(10^{9}\sim 10 ^{10}\)周次, S-N曲线再趋于平缓, 对应的疲劳极限值较低 (图3 ).该文还研究了马氏体不锈钢\(10^{5}\sim 10 ^{10}\)周次的疲劳特性.他们指出, 对于钛合金在107 周次之后, 对于马氏体不锈钢在108 周次之后, 疲劳损伤机制不同, 疲劳裂纹萌生由试样表面转为试样内部, 但文章并未点明所观察到的"鱼眼"特征. ...
... Ti-6Al-4V合金的S-N曲线, 低于107 周次, 裂纹表面萌生; 高于107 周次, 裂纹亚表面萌生 (Atrens et al. 1983 ) ...
... Naito等(1983 , 1984 ) 和Atrens等 (1983) 的文章是关于高强钢和钛合金超高周疲劳研究的最先报道, 他们指出在"长寿命"阶段, 疲劳性能、特征、机理均发生了变化, 尽管在他们的文章里并无"超高周"的名词, 而表达为"长寿命". ...
... Naito等(1983 , 1984 )、Atrens等 (1983) 、Asami和Sugiyama (1985) 和Stanzl等 (1986) 的研究报道, 标志了与传统低周疲劳和高周疲劳内涵不同的超高周疲劳研究的起源. ...
... 图3 是较完整的关于钛合金超高周疲劳特性的早期结果, 显示了Ti-6Al-4V的S-N曲线 (Atrens et al. 1983 ), 在107 周次的拐折点前后, 裂纹萌生机理发生了变化: 疲劳寿命\(N_{\rm f}\)低于 107 周次, 裂纹萌生于试样表面; \(N_{\rm f}\)高于107 周次, 裂纹萌生于亚表面即试样内部. ...
Gigacycle Fatigue in Mechanical Practice.
1
2005
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
Microstructure dependent fatigue crack growth in aged hardened aluminium alloys
1
2004
... 对于铝合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\(1.911 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与诸多实验结果 (如Paris et al. 1999 , Papakyriacou et al. 2002, Holper et al. 2004 , Borrego et al. 2004 , Huang & Moan 2007 ) 得到的\(1.5\sim 2.8 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\)相符合. ...
Ultra-long cycle fatigue of high-strength carbon steels part II: Estimation of fatigue limit for failure from internal inclusions
1
2003
... Chapetti 等 (2003) 对SUJ2, SCM435和SNCM439钢的实验数据整理归纳出式(16), 用于描述FGA尺寸、夹杂物尺寸和疲劳寿命之间的关系 \[\dfrac{\sqrt {area_{\rm FGA} } }{ \sqrt {area_{\rm Inc} }} =0.25N_{\rm f}^{0.125} \ \ (16)\] ...
Notable size effects on very high cycle fatigue properties of high-strength steel
1
2011
... Sakai等 (2000) 联络了6个实验室的研究者, 采用相同类型的旋转弯曲设备(52 Hz) 和相同类型的SUJ2钢 (1% C, 1.5% Cr) 试样, 所获得的大量数据表明"双重S-N曲线"特征 (图8 ).在106 周次之前, 裂纹于表面萌生, 即传统的疲劳行为; 在106 \(\sim \) 109 周次, 裂纹于内部萌生, 裂纹源区呈现"鱼眼"特征 (图9 (a)).起源处的高倍图像显示尺度为几十微米的亮区 (图9 (b)), 并称其为FGA (fine granular area). Sakai 2009 还给出了SUJ2钢轴向循环加载 (50 Hz) 的S-N数据, 其特征为单一线性下降趋势, "双重S-N曲线"特征不明显 (图10 ).在105 \(\sim \) 109 周次, 裂纹于内部萌生 (图11 (a)), 同样观察到起源处有尺度为几十微米的FGA特征 (图11 (b)).裂纹萌生位置在截面上随机分布, 这与轴向加载应力分布特征相对应.对于旋转弯曲加载具有的"双重S-N曲线"的一种解释是, 试样截面受力从表面到中心线性减小, 裂纹萌生和初始扩展点的应力小于名义应力; 而对于轴向加载, 试样整个截面受力一致. 换言之, 旋转弯曲加载和轴向加载分别对应的控制体积不同.控制体积是试样中发生裂纹起源的潜在区域, 通常取不小于 90%最大应力的截面所对应的试样体积为控制体积 (Murakami et al. 2002 , Furuya 2011 , Lei et al. 2014 , Sun et al. 2016 ). ...
Gigacycle fatigue properties of Ti-6Al-4V alloy under tensile mean stress
5
2014
... Furuya和Takeuchi (2014) 报道了Ti-6Al-4V在120 Hz和20 kHz轴向循环加载的超高周疲劳行为. 图19 是2组试样的S-N数据, 图中2组试样的化学成分以及屈服强度和拉伸强度基本一致, 但微结构形态不同. A组\(\alpha \)相晶粒为等轴状, 平均 (等效)直径约7 \(\mu \)m; B组\(\alpha \)相晶粒沿轧制方向拉长, 平均 (等效)直径约20 \(\mu \)m. 对于A组, 3 \(\times\) 105 周次后裂纹基本内部起源; 对于B组, 3 \(\times\) 106 周次后裂纹基本内部起源.加载频率对2组试样的疲劳强度基本无影响; 而疲劳强度随应力比增大而明显降低. 他们 (Takeuchi et al. 2008 , Furuya & Takeuchi 2014 ) 观察表明, 对于A组选取的试样 (20 kHz, \(R = -1)\), 裂纹内部萌生区有明显"鱼眼"特征 (图20 (a), \(N_{\rm f}= 2.10\times 10^{8})\), "鱼眼"中部包含表面起伏较大的粗糙区; 当裂纹源即粗糙区位于试样表面附近, "鱼眼"特征不明显(图20 (b), \(N_{\rm f}= 6.97\times 10^{7})\).对于B组选取的试样 (20 kHz, \(R = 0\), \(N_{\rm f} = 5.10\times 10^{8})\), 内部萌生的裂纹由facet组成 (图21 ). Furuya和Takeuchi(2014) 认为, 裂纹内部萌生局域\(\alpha \)相形成的小解理面群, 其单个小解理面尺度与\(\alpha \)晶粒相当. ...
... , Furuya & Takeuchi 2014 ) 观察表明, 对于A组选取的试样 (20 kHz, \(R = -1)\), 裂纹内部萌生区有明显"鱼眼"特征 (图20 (a), \(N_{\rm f}= 2.10\times 10^{8})\), "鱼眼"中部包含表面起伏较大的粗糙区; 当裂纹源即粗糙区位于试样表面附近, "鱼眼"特征不明显(图20 (b), \(N_{\rm f}= 6.97\times 10^{7})\).对于B组选取的试样 (20 kHz, \(R = 0\), \(N_{\rm f} = 5.10\times 10^{8})\), 内部萌生的裂纹由facet组成 (图21 ). Furuya和Takeuchi(2014) 认为, 裂纹内部萌生局域\(\alpha \)相形成的小解理面群, 其单个小解理面尺度与\(\alpha \)晶粒相当. ...
... ). Furuya和Takeuchi(2014) 认为, 裂纹内部萌生局域\(\alpha \)相形成的小解理面群, 其单个小解理面尺度与\(\alpha \)晶粒相当. ...
... 2组Ti-6Al-4V在120 Hz和20 kHz 轴向循环加载 \((R = -1\), 0, 0.3)的S-N数据 (Furuya & Takeuchi 2014 ) ...
... B组试样裂纹内部萌生特征 (20 kHz, \(R = 0\), \(N_{\rm f} =5.10\times 10^8)\). (a) 低倍图像显示萌生区全貌, (b)高倍图像显示萌生区facet特征 (Furuya & Takeuchi 2014 ) ...
Mechanism of fatigue crack initiation and propagation in the very high cycle fatigue regime of high-strength steels
4
2012
... 类似地, Grad等 (2012) 在高强钢观察到尺度约70 nm的细晶, 并提出"裂尖局部晶粒细化"模型, 如图39 所描述.这一模型与Sakai (2009) 模型的思路相似. 此类模型认为, 细晶层形成于裂纹萌生之前, 并且在已萌生的裂纹前沿不断形成细晶层. ...
... 夹杂物周围"细晶层形成与分离"示意图 (Grad et al. 2012 ). (a) 初始状态, (b) 局域晶粒细化, (c) 裂纹萌生, (d) ...
... Grad 等 (2012) 对100Cr6 (与SUJ2相似) 高强钢, 采用超声轴向加载(20 kHz), 通过TEM和SAD (直径650 nm)观察到超高周疲劳裂纹萌生区FGA剖面为细晶组织, 平均晶粒尺度70 nm; 而远离FGA的表面为粗晶组织 (图48 ). 基于这一观察结果, 他们认为夹杂物周围晶粒细化, 裂纹沿细晶层与基体之间分离而扩展, 并提出了与Sakai模型相似的FGA形成机理. ...
... 100Cr6高强钢, 超声轴向加载 (20 kHz), \(N_{\rm f} = 8.96\times 10 ^{8}\), 夹杂物周围FGA剖面的TEM图像, FGA表层附近的SAD显示纳米晶特征, 远离FGA表层的SAD显示粗晶特征 (Grad et al. 2012 ) ...
Crack growth based probability modeling of S-N response for high strength steel
1
2006
... 近20年来, 陆续有研究报道了针对高强钢超高周疲劳寿命或疲劳强度的预测模型, 如Murakami等 (Murakami & Usuki 1989 , Murakami et al. 1999 ), Harlow等 (2006) , Zhao 等 (2009) , Sun等 (2012 , 2013 ), Stepanskiy(2012) , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响. ...
Analysis of fatigue properties and failure mechanisms of Ti6Al4V in the very high cycle fatigue regime using ultrasonic technology and 3D laser scanning vibrometry
3
2013
... 图17 是采用超声频率 (20 kHz) 对Ti-6Al-4V轴向振动加载 \((R =-1)\) 的超高周疲劳特性典型结果 (Heinz et al. 2013 ), 表明S-N曲线在\(2\times 10^{7}\)周次发生显著拐折, SEM观察显示超高周疲劳裂纹萌生于试样内部 (图18 (a)), 并呈现"鱼眼"特征 (图18 (b)中的②), 裂纹源区有类似于FGA的粗糙区 (图18 (b)中的①), 粗糙区的高倍图像 (图18 (c)) 显示断面起伏特征. ...
... Ti-6Al-4V超声振动加载 (20 kHz) 的S-N特性 (Heinz et al. 2013 ) ...
... Ti-6Al-4V超声轴向振动加载SEM断面图像 \((\sigma _{\rm a}= 1024 {\rm MPa}\), \(N_{\rm f} = 3.2\times 10^9)\).(a)全貌,(b) 裂纹萌生区, (c) 粗糙区①形貌 (Heinz et al. 2013 ) ...
Crack initiation mechanisms of Ti6A14V in the very high cycle fatigue regime
3
2016
... 近期, Heinz 和Eifler (2016) 对Ti-6Al-4V合金, 以超声轴向加载(频率20 kHz, \(R = -1)\), SEM对裂纹源区剖面样品观测到FGA沿深度方向的微裂纹损伤特征.微裂纹萌生于大颗粒的初始\(\alpha \)相, 并受阻于\(\beta \)相 (图53 ). 微裂纹团簇是FGA的起源点, 微裂纹汇合形成与拉应力垂直的主裂纹. 他们还采用EBSD检测裂纹萌生位置的晶粒特征 (图54 ). 对于初始态, 晶粒尺度很不均匀 (图54 (a)), 尺度1 \(\mu \)m至60 \(\mu \)m, 粗晶为hcp的\(\alpha \)相, 细晶为bcc的\(\beta \)相.当加载至总寿命的50%, 局部塑性变形导致\(\alpha \)相晶粒细化 (图54 (b)). 断裂时, 累积塑性变形导致FGA裂纹面附近晶粒明显细化 (图54 (c)和图54 (d)), 且紧靠FGA裂纹面局域的晶粒细化更明显(图54 (d)). 测量结果为\(N = 0\), 平均晶粒面积\(A = 8.8 \mu\)m2 ; \(N = 50% N_{\rm f}\), \(A = 5.8 \mu \)m2 ; \(N = N_{\rm f}\), \(A= 3.8 \mu \)m2 . ...
... Ti-6Al-4V超声轴向加载 (20 kHz, R=-1, \(\sigma _{\rm a }= 460\) MPa, \(N_{\rm f}= 1.2\times 10 ^{9})\), 裂纹萌生区中心位置剖面的SEM图像, (b) 是(a) 的局部放大图 (Heinz & Eifler 2016 ) ...
... Ti-6Al-4V超声轴向加载 (20 kHz, R=-1, \(\sigma _{\rm a }= 500\) MPa, \(N_{\rm f}= 3.9\times 10 ^{8})\)裂纹萌生区剖面的EBSD图像. (a) 初始状态, (b) \(N= 50% N_{\rm f}\), (c) \(N=N_{\rm f}\), (d) \(N=N_{\rm f}\) (Heinz et al. 2016 ) ...
Deformation and Fracture Mechanics of Engineering Materials. 5th ed. New York:
1
2012
... FGA裂纹属短裂纹范畴, 其扩展受材料微结构尺度制约.因此笔者分析了FGA裂尖塑性区与材料微结构尺度的关系 (Zhao et al. 2011 , 2012 ). 对于平面应变I型裂纹, 裂尖塑性区尺度\(r_{\rm p}\)的表达式为 (Hertzberg et al. 2012 )\[r_{\rm p} = \dfrac{\left({1 - 2\nu } \right) ^2}{\pi }\left( {\dfrac{\Delta K}{\sigma_{\rm y} }} \right)^2 \approx \dfrac{1}{6\pi }\left({\dfrac{\Delta K}{\sigma _{\rm y} }} \right)^2 \ \ (7)\] 式中, \(\nu \)是泊松比, \(\sigma _{\rm y}\)是屈服强度. 另一方面, 材料微结构特征尺度\(l_{\rm m}\)与材料基本力学性能有如下关系 (Nix& Gao 1998 )\[l_{\rm m} = b\left( {\mu / \sigma _{\rm y} }\right) ^2 \ \ (8)\] 式中, b为材料柏氏矢量模, \(\mu\)为材料剪切模量. 假定当FGA裂尖塑性区尺寸与材料微结构特征尺度相等, FGA裂纹终止发展. 这样\( \Delta K_{\rm FGA} = \mu \sqrt {\pi b} =4.342\mu \sqrt { b} \ \ (9)\)\( 式 (9) 表明, 超高周疲劳裂纹萌生特征区FGA对应的特征参量\(\Delta K_{\rm FGA}\)可简单表达为材料剪切模量和柏氏矢量的函数. ...
Near threshold fatigue crack growth at positive load ratio in aluminium alloys at low and ultrasonic frequency: influences of strain rate, slip behaviour and air humidity
1
2004
... 对于铝合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\(1.911 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与诸多实验结果 (如Paris et al. 1999 , Papakyriacou et al. 2002, Holper et al. 2004 , Borrego et al. 2004 , Huang & Moan 2007 ) 得到的\(1.5\sim 2.8 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\)相符合. ...
Experiment and simulation of very-high-cycle fatigue behavior for low alloy steels//Proceedings of the 12th International Conference on Fracture, July 12-17, 2009, Ottawa, Canada, ICF12 CD-ROM
2
2009
... 合金材料的超高周疲劳裂纹以内部起源为主, 但对于不同的材料, 裂纹萌发点和裂纹初始扩展特征可能存在差异.为了说明疲劳裂纹表面起源向内部起源的转移和竞争, 笔者 (Hong et al. 2009 , 2012 , Qian et al. 2011 ) 引入了一个新的参数\(D^\ast \) ...
... 近期, Zhang等 (2016) 采用超声频率 (20 kHz)研究了马氏体时效硬化不锈钢(FV520B-I) 的超高周疲劳行为, 表明107 周次后裂纹于内部起源. 他们采用文献 (Hong et al. 2009 , 2012 ) 提出的\(D^*\)模型分析了裂纹表面萌生和内部萌生的竞争机理; 鉴于GBF (FGA) 的发展速率很低、寿命很长, 因此认为GBF (FGA)消耗的周次\(N_{\rm G}\)可以作为裂纹内部萌生寿命\(N_{\rm i}\)来分析萌生竞争机理. ...
Fatigue strength and crack initiation mechanism of very-high-cycle fatigue for low alloy steels
6
2012
... 笔者 (Hong et al. 2012 ) 对GCr15 (1% C, 1.5% Cr) 和40Cr(0.4% C, 1% Cr) 的旋转弯曲实验 (52 Hz)显示了疲劳性能具有"双重S-N曲线"特征 (图12 ). 图13 显示了裂纹亚表面起源所呈现的鱼眼特征 (图13 (b))和FGA特征 (图13 (c)). 光学显微镜图像 (图13 (b))显示鱼眼区域内的FGA为灰度大的深色特征, 因而也被称为暗区 (optical dark area, ODA) (Murakami et al. 2000 ); 而扫描电子显微镜(SEM)图像(图13 (c)) 显示的FGA是灰度相对小的亮区, 因而也被称为颗粒状亮面区 (granular bright facet, GBF) (Shiozawa etal. 2001 ), 这是由于扫描电镜对粗糙断面成像的缘故. ...
... 旋转弯曲加载的双重S-N曲线. (a) GCr15钢, (b) 40Cr钢 (Hong et al. 2012 ) ...
... GCr15钢超高周疲劳裂纹起源于亚表面 \((\sigma _{\max} =1024 {\rm MPa}\), \(N_{\rm f} = 3.5\times 10^8)\).(a)断口全貌光镜图像, (b) 鱼眼光镜图像, (c) FGA SEM图像(Hong et al. 2012 ) ...
... 合金材料的超高周疲劳裂纹以内部起源为主, 但对于不同的材料, 裂纹萌发点和裂纹初始扩展特征可能存在差异.为了说明疲劳裂纹表面起源向内部起源的转移和竞争, 笔者 (Hong et al. 2009 , 2012 , Qian et al. 2011 ) 引入了一个新的参数\(D^\ast \) ...
... \(D^*\)随\(\varphi = 0.5 \Delta \sigma /k\)和\(\psi =r/l\)的变化, 其中\(k\)是位错阻力, \(r\)是夹杂物半径, \(l\)是晶粒半径. (a)夹杂物与基体弱结合, (b) 夹杂物与基体强结合 (Hong et al. 2012 ) ...
... 近期, Zhang等 (2016) 采用超声频率 (20 kHz)研究了马氏体时效硬化不锈钢(FV520B-I) 的超高周疲劳行为, 表明107 周次后裂纹于内部起源. 他们采用文献 (Hong et al. 2009 , 2012 ) 提出的\(D^*\)模型分析了裂纹表面萌生和内部萌生的竞争机理; 鉴于GBF (FGA) 的发展速率很低、寿命很长, 因此认为GBF (FGA)消耗的周次\(N_{\rm G}\)可以作为裂纹内部萌生寿命\(N_{\rm i}\)来分析萌生竞争机理. ...
Propensities of crack interior initiation and early growth for very-high-cycle fatigue of high strength steels
9
2014
... 高强合金超高周疲劳裂纹萌生的主要特点是起源于材料 (试样) 内部, 这是超高周疲劳不同于低周疲劳和高周疲劳的基本特征.内部萌生的裂纹在断面上呈现"鱼眼" 特征 (图2 , 图9 , 图11 , 图13 , 图18 , 图2 0); 在其范围内, 往往可见一表面相对粗糙的小区域. 对于高强钢, 该区域被称为光学暗区(ODA), 或GBF或FGA, 本文将其称为FGA; 对于钛合金, 该区域被称为粗糙区(RA). 笔者的研究指出, FGA和FiE是高强钢超高周疲劳裂纹萌生的特征区, FGA和FiE所对应的参量是高强钢超高周疲劳裂纹萌生特征参量 (Hong et al. 2014 ). ...
... 图29 (a) 是高强钢超高周疲劳裂纹内部萌生特征区的典型图像(Hong et al. 2014 ); 图29 (b) 是示意图: 裂纹起源于内部夹杂物 (Inc), 形成萌生区FGA, 而后发展形成FiE, 直至断裂. 其中, \(2a_{\rm Inc } = 35.3 \mu \)m, \(2a_{\rm FGA } =66.3 \mu \)m, \(2a_{\rm FiE } =235 \mu \)m. ...
... (a) 高强钢超高周疲劳裂纹内部萌生特征区的典型图像, Cr钢(1% C, 1% Cr) 旋弯加载, \(N_{\rm f} = 1.79\times 10^7\) (Hong et al. 2014 ); (b) 超高周疲劳裂纹内部萌生特征区及发展至断裂示意图, FiE: 鱼眼, Inc: 夹杂物 ...
... 笔者 (Zhao et al. 2011 , 2012 ) 对GCr15钢 (与SUJ2相似)的若干强度状态分别进行旋转弯曲和超声轴向振动加载, 得到FGA对应的\(\Delta K\)值范围同样在4 \(\sim \) 6 MPa\( \cdot \)m\(^{1 / 2}\) (图31 ). 进一步地, 图32 (Hong et al. 2014 )汇集了我们和诸多其他研究者关于高强钢超高周疲劳FGA的结果, 表明绝大多数FGA尺度在15 \(\mu \)m至100 \(\mu \)m之间, 该尺度随加载应力减小而增大, 即循环应力越小, FGA发展的尺度越大, 对应的疲劳寿命越长. FGA裂纹尺度与加载应力可由应力强度因子关联, 即式 (6). 这样, 在图32 中标出了\(\Delta K_{\rm FGA} = 4 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)和\(6 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)的等值线, 显示绝大多数数据都被包络在这两条等值线范围内. 这一结果表明, \(\Delta K_{\rm FGA} \)是超高周疲劳裂纹萌生的一个稳定特征参量.从而我们明确提出FGA是超高周疲劳裂纹萌生的基本特征区 (Hong et al. 2014 ), 对应的\(\Delta K_{\rm FGA} \)即为裂纹萌生阈值\(\Delta K_{{\rm th}} \). 对于超高周疲劳过程, 这一特征区具有本征存在性. ...
... 中标出了\(\Delta K_{\rm FGA} = 4 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)和\(6 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)的等值线, 显示绝大多数数据都被包络在这两条等值线范围内. 这一结果表明, \(\Delta K_{\rm FGA} \)是超高周疲劳裂纹萌生的一个稳定特征参量.从而我们明确提出FGA是超高周疲劳裂纹萌生的基本特征区 (Hong et al. 2014 ), 对应的\(\Delta K_{\rm FGA} \)即为裂纹萌生阈值\(\Delta K_{{\rm th}} \). 对于超高周疲劳过程, 这一特征区具有本征存在性. ...
... FGA尺度随加载最大应力的变化, 下界实线对应\(4 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 上界虚线对应{\fangsong \(6 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\) (Hong et al. 2014 ) ...
... 近期笔者进一步分析了FGA寿命和裂纹扩展速率 (Hong et al. 2014 ).对于VHCF裂纹萌生特征区FGA (等效直径\(2a_{\rm FGA})\), 可以估算其所消耗的疲劳寿命和裂纹扩展速率. FGA是裂纹萌生区, \(\Delta K_{\rm FGA} \)对应\(\Delta K_{{\rm th}} \), \(2a_{\rm FGA}\)之后裂纹发生稳态扩展. 假定Paris公式 (式(10))适用于描述\(2a_{\rm FGA}\)之后裂纹扩展速率\({\rm d}a /{\rm d}N\)与\(\Delta K\)的关系, 即 \( \dfrac{{\rm d}a}{{\rm d}N} = A\Delta K^m \ \ (10) \)式中, A和m是材料参数. 对式 (10) 积分可得\(a_{\rm FGA}\)到\(a_{\rm FiE}\)的疲劳寿命\(N_{1}\)和从\(a_{\rm FiE}\)到最后断裂的裂纹长度\(a_{\rm c}\)的疲劳寿命\(N_{2}\) (见图14 ). 这样, FGA消耗的寿命即裂纹萌生寿命\(N_{\rm i}\)为\(\( N_{\rm i} = N_{\rm f} - N_1 - N_2 \ \ (11)\) ...
... (a) FGA裂纹萌生寿命与疲劳总寿命的关系, (b)FGA裂纹扩展速率与疲劳寿命的关系. 实心点为实验估算结果, 空心点为模型预测结果(Hong et al. 2014 ) ...
... 超高周疲劳的裂纹往往萌生于材料 (试样) 内部. 对于高强钢, 裂纹萌生区呈现FiE和FGA特征. 尽管FiE尺度仅为100 \(\mu \)m量级, FGA尺度仅为10 \(\mu \)m量级; 作为超高周疲劳裂纹萌生特征区, FGA消耗了疲劳总寿命的95%以上 (Tanaka & Akiniwa 2002 , Hong et al. 2014 ). 因此, 揭示裂纹萌生区FGA的形成机理对于理解超高周疲劳的特有行为和寿命预测格外重要. ...
The formation mechanism of characteristic region at crack initiation for very-high-cycle fatigue of high-strength steels
6
2016
... 笔者针对典型的GCr15高强钢超高周疲劳裂纹萌生特征, 对旋弯加载的超高周疲劳裂纹萌生区制备FIB试样, 采用TEM观测并配有电子选区衍射 (SAD直径\(200 \sim 250\) nm) 检测, 直接观测到FGA是一层独特的细晶层, 而FGA之外的FiE区域为粗晶组织.对FGA细晶层的精细测量给出平均晶粒尺度48 nm, 厚度500 \(\sim \) 800 nm (图55 ). 随后, 对同一试样断面两侧相对应的局域观察到FGA均具有纳米晶特征 (图56 ). 从而, 提出了"大数往复挤压模型 (numerous cyclic pressing, NCP)": 萌生裂纹面之间经百万、千万周次的往复挤压, 造成裂纹尾迹的晶粒细化从而形成FGA, 此过程与裂纹闭合效应和残余应力释放相联系 (Hong et al. 2016 ). ...
... GCr15, 旋弯加载, \(\sigma _{\max } = 775\) MPa, \(N_{\rm f} = 2.40\times 10 ^{7}\). (a) SEM图像显示裂纹源夹杂物及其周边的FGA(虚线范围), 长方形框为FIB取样位置; (b)TEM图像显示FGA截面有厚度500 \(\sim \) 800 nm的细晶层; (c)FGA细晶层的SAD图, 断续衍射环表明200 nm衍射区内有若干纳米晶; (d)距FGA表面2.5 \(\mu \)m处的SAD图, 衍射斑表明衍射区内为单晶; (e)FGA细晶层的高倍TEM图像; (f) FGA细晶层的SAD图, 基本连续的衍射环表明纳米晶及其\(\alpha \)-Fe晶面指数标定 (Hong et al. 2016 ) ...
... 图57 说明了FGA形成的过程与机理 (Hong et al. 2016 ).在裂纹源夹杂物周边局域的塑性变形累积导致裂纹萌生 (图57 (a)).萌生裂纹面受到循环载荷导致的往复挤压, 这一过程与裂纹闭合作用和残余应力释放相联系; 由于局部剧烈塑性变形, 萌生裂纹表层的微结构发生碎化使得原有的粗晶细化为纳米晶 (图57 (b)). 经过百万、千万周次的循环载荷, 两侧裂纹面形成一层纳米晶层并具有粗糙裂纹面特征 (图57 (c)).当达到裂纹萌生与稳定扩展的转捩点, NCP过程终止, FGA达到其临界尺度(图57 (d)). 进而分析了这一尺度. 根据式 (6), 可以写出\(a_{\rm FGA} = {Y}'\left( {\dfrac{\Delta K_{\rm FGA} }{\sigma_{\max} }} \right)^2 \ \ (12)\)式中, \(a_{\rm FGA} \)是FGA尺度, \(\Delta K_{\rm FGA}\)是FGA对应的应力强度因子幅值. 联系到式 (9)有\( a_{\rm FGA} = Yb \left( {\dfrac{\mu }{\sigma _{\max} }}\right)^2 \ \ (13)\)式中, \(\mu \) 是材料剪切模量, b是材料柏氏矢量模, \(\sigma _{\max}\)是循环加载的最大应力, \(Y = 6\pi {Y}' = 24\). 式 (13) 表明, 对于给定的材料, FGA尺度与循环载荷最大应力的平方成反比. 实际上, 式(13) 表达了存在形成FGA条件情况的FGA临界尺度. ...
... 大数往复挤压 (NCP) 模型示意图 (Hong et al. 2016 ) ...
... 随后, 笔者 (Hong et al. 2016 ) 继续针对GCr15高强钢, 采用超声轴向不同应力比加载 (R = -1, -0.5, 0.1, 0.3), 观察到R=-1情形超高周疲劳的FGA仍为纳米晶层; 对于R=-1但周次较少的情况, SAD为稍拉长的衍射斑 (图58 (a)), 表明晶粒略有细化或具有织构特征. 对于R=-0.5, 超高周疲劳裂纹萌生虽有一定的FGA特征, 但FGA剖面的SAD为拉长的衍射斑(图58 (b)), 表明晶粒有一定细化, 但不像R=-1明显细化的特征.对于R=0.1和0.3, 裂纹萌生区未见粗糙的FGA特征, 对裂纹萌生区剖面试样的SAD检测结果为单晶衍射斑 (图58 (c)和图58 (d)), 表明正应力比状态的超高周疲劳裂纹萌生区不出现纳米晶层.这一结果证实了前述的NCP模型的2个推论, 即证实了所提出的"大数往复挤压模型 (NCP)". ...
... (a) R=-1, \(\sigma _{\rm a}= 1029\) MPa, \(N_{\rm f}=1.28\times 10^{5}\), 裂纹萌生区表层的TEM图像, SAD图显示稍拉长的衍射斑; (b) \(R = -0.5\), \(\sigma _{\rm a}=633\) MPa, \(N_{\rm f}= 4.81\times 10 ^{8}\), 裂纹萌生区表层的TEM图像, SAD图显示明显拉长的衍射斑; (c) \(R = 0.1\), \(\sigma _{\rm a}= 534\) MPa, \(N_{\rm f} = 1.84\times 10 ^{7}\), 裂纹萌生区表层的TEM图像, SAD图显示单晶衍射斑; (d) \(R = 0.3\), \(\sigma _{\rm a}= 422\) MPa, \(N_{\rm f}= 9.76\times 10 ^{7}\), 裂纹萌生区表层的TEM图像, SAD图显示单晶衍射斑 (Hong et al. 2016 ) ...
Improved modeling of the effect of R-ratio on crack growth rate
2
2007
... 对于铝合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\(1.911 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与诸多实验结果 (如Paris et al. 1999 , Papakyriacou et al. 2002, Holper et al. 2004 , Borrego et al. 2004 , Huang & Moan 2007 ) 得到的\(1.5\sim 2.8 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\)相符合. ...
... 对于钛合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 3.385} {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\), 与诸多实验结果 (如Ritchie et al. 1999 , Petit & Sarrazin-Baudoux 2006 , Huang & Moan 2007 ) 得到的\(3.4\sim 4.0 {\rm MPa} \cdot {\rm m}^{{\rm 1 /2}}\)相符合. ...
A very high cycle fatigue thermal dissipation investigation for titanium alloy TC4
0
2014
Fatigue life dispersion and thermal dissipation investigations for titanium alloy TC17 in very high cycle regime
0
2015
Fatigue strength and internal crack growth behavior of high strength steel under variable amplitude stressing in very high cycle regime
2
2012
... Ishida等 (2012) 和Ogawa等 (2014) 对SUJ2高强钢超声轴向加载(20 kHz, R = -1), 采用两级载荷往复阶梯加载 \((\Delta \sigma_{\rm H}= 1200\) MPa, \(n_{\rm H}= 1\times 10 ^{3}\), \(\Delta \sigma_{\rm L}= 850\) MPa, nL = 1\(\times\) 10 4 , \(N_{\rm f}=2.87\times \)10 8 ), 使断面呈现与阶梯载荷相对应的环状裂纹扩展特征(图34 ), 基于环状裂纹特征测得FGA外FiE区域的裂纹扩展速率, 再推得FGA的裂纹扩展速率. 他们所得到的结果为: FGA区域裂纹扩展速率10\(^{-13}\sim \) 10-14 m/cyc; 在FGA外的FiE区域, 裂纹扩展速率107 \(\sim \) 10-9 m/cyc. ...
... Ishida等 (2012) 和Ogawa等 (2014) 采用往复两级阶梯加载方法和Sander等 (2014, 2016) 采用周期性变幅加载方法, 导致萌生区的裂纹呈现环状扩展特征, 使得有可能直接观测到萌生阶段裂纹扩展特征并测量裂纹扩展速率.但他们观察到的环状裂纹特征及其测量均是在FGA外的FiE区域. 至今, 还未有关于FGA区域裂纹扩展速率的有效观察和测量的结果. ...
An unusual fatigue phenomenon: duality of the S-N fatigue curve in the \(\beta \)-titanium alloy Ti-10V-2Fe-3Al
2
2003
... Jha和Ravi Chandran (2003) 、Ravi Chandran (2005) 和Ravi Chandran和Jha (2005) 报道了初生\(\alpha\)相比例对Ti-10V-2Fe-3Al疲劳行为的影响, 表明初生\(\alpha\)相体积比例较低时 (10%), 具有同样微结构形态的试样在所有应力水平下发生疲劳裂纹表面萌生和内部萌生的概率基本一样(图26 (a)). 初生\(\alpha \)相体积比例较高时 (45%), 高应力状态裂纹趋于表面萌生, 低应力状态趋于内部萌生 (图26 (b)). ...
... Ti-10V-2Fe-3Al裂纹表面起源和内部起源对应的S-N曲线 (Jha& Ravi Chandran 2003 ). (a) \(\alpha _{\rm p}\)比例10%, B: 条状\(\alpha _{\rm p}\), E: 粒状\(\alpha _{\rm p}\); (b) \(\alpha _{\rm p}\)比例45%, A: 条状\(\alpha _{\rm p}\), F和G: 粒状\(\alpha _{\rm p}\) ...
2016. Very-high-cycle fatigue behavior of a structural steel with and without induced surface defects
3
2016
... 近期, 笔者 (Jiang et al. 2016 ) 对一种中碳结构钢 (0.42%C)超高周疲劳研究结果表明, 由夹杂物起源而形成的FGA表层确实为纳米晶层; 而由晶界作为裂纹源, 萌生区仍有粗糙面特征, 但无纳米晶特征 (图59 ). 对于由表面缺陷发生裂纹起源的情形, 裂纹萌生区无纳米晶特征(图60 ). ...
... R=-1, \(\sigma _{\max}= 850\) MPa, \(N_{\rm f}=5.3\times 10^{6}\), 晶界引发的裂纹内部起源形成FiE情形.(a) 裂纹萌生区表层的TEM图像, (b) \(\sim \) (d)紧邻裂纹面的SAD结果, (e) 远离裂纹面的SAD结果 (Jiang et al. 2016 ) ...
... \(\sigma _{\max}= 500\) MPa, \(N_{\rm f}= 1.8\times 10^{8}\), 缺口引发的裂纹表面起源情形. (a) 裂纹萌生区表层的TEM图像, (b)和(c)紧邻裂纹面的SAD结果, (e) 离开裂纹面的SAD结果 (Jiang et al. 2016 ) ...
Push-pull fatigue strength of mild steel at very high frequencies of stress up to 100 kc/s. Journal of Basic Engineering,
2
1965
... 合金材料在载荷循环107 周次以上仍可发生疲劳损伤破坏的报道最早可追溯到20世纪60年代.Kikukawa等 (1965) 采用超声频率加载, 断裂周次超过108 , 研究了频率对低碳钢疲劳强度的影响, 但他们未对107 周次后的疲劳过程和特征进行专门研究. ...
... 关于超高周疲劳的研究可以从采用超声频率 (如20 kHz)进行疲劳加载说起. 采用如此高的加载频率是为了提高疲劳实验效率以研究合金材料更高加载周次的疲劳性能和更低裂纹扩展速率的疲劳行为. Manson (1956) 最早采用超声频率进行疲劳实验. 20世纪50 \(\sim\) 60年代, 仅有为数不多的报道, 其中Kikukawa等 (1965) 发展了超声轴向振动加载设备, 频率范围13 \(\sim \) 100 kHz, 最大加载周次达109 , 研究了加载频率对低碳钢疲劳性能的影响, 表明较高的加载频率导致较高的疲劳极限.这是采用超声频率进行超高周疲劳研究的雏形, 然而他们并未就加载频率对疲劳性能影响的机理进行研究, 也未点明"超高周疲劳"特征. ...
Influence of mean stresses on fatigue life and damage of a turbine blade steel in the VHCF-regime
4
2013
... 反例3 Kovacs等 (2013) 对12%Cr 马氏体钢(X10CrNiMoV12-2-2) 采用不同应力比 \((R= -1\), 0.1, 0.5, 0.7)进行超声频率轴向加载. 对于R=-1, 观察到裂纹起源于内部夹杂物的萌生区呈现鱼眼和FGA特征 (图44 (a)). 而对于正应力比加载的试样, 超高周疲劳裂纹仍萌生于内部夹杂物, 但裂纹萌生区呈现鱼眼特征但无FGA, 图44 (b) 是\(R= 0.5\)的图像. 他们采用FIB (focused ion beam)方法截取裂纹萌生区局域小样品, 采用SEM观察到, 对于R=-1, 裂纹面有厚度约3 \(\mu \)m的纳米晶层; 而对于R=0.1, 裂纹面无纳米晶层, 为原有的马氏体组织形态. R=-1 和 R=0.1, 0.5的裂纹萌生区具有截然不同的特征, 这不能被前节所述模型所解释. ...
... 12%Cr 马氏体钢, 超声轴向加载 (20 kHz)裂纹萌生区特征. (a) R=-1, \(\sigma _{\rm a}= 550\) MPa, \(N_{\rm f}= 4.66\times 10^{7}\); (b) \(R = 0.5\), \(\sigma _{\rm a}=250\) MPa, \(N_{\rm f}=4.87\times 10^{7}\) (Kovacs et al. 2013 ) ...
... Kovacs等 (2013) 对12%Cr 马氏体钢 (X10CrNiMoV12-2-2)采用不同加载应力比进行超声频率 (20 kHz) 轴向加载. 对于R= -1, 观察到FGA剖面有3 \(\mu \)m厚的细晶层 (图49 (a) 和图49 (b)), 而对于R= 0.5, 无细晶层, 为原始的马氏体组织 (图49 (c)和图49 (d)). ...
... 12%Cr 马氏体钢, 超声轴向加载, FGA剖面图像. (a), (b)\(\sigma_{\rm a}= 550\) MPa, R=-1, \(N_{\rm f} = 6.15\times 10^{7}\); (c), (d) \(\sigma_{\rm a}= 370\) MPa, R=0.1, \(N_{\rm f} = 1.24\times 10 ^{8}\) (Kovacs et al. 2013 ) ...
Effects of inclusion size and location on very-high-cycle fatigue behavior for high strength steels
1
2012
... 对于钢, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 5.54} {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与文献实验结果 (如Sakai et al. 2002 , Ochi et al. 2002 , Shiozawa et al. 2006b , Yang et al. 2008 , Zhao et al. 2011 , Lei et al. 2012 ) 得到的\(4\sim 6 {\rm MPa} \cdot{\rm m}^{{\rm 1 / 2}}\)相符合. ...
Effect of loading condition on very-high-cycle fatigue behavior and dominant variable analysis. Science China-Physics Mechanics &
1
2014
... Sakai等 (2000) 联络了6个实验室的研究者, 采用相同类型的旋转弯曲设备(52 Hz) 和相同类型的SUJ2钢 (1% C, 1.5% Cr) 试样, 所获得的大量数据表明"双重S-N曲线"特征 (图8 ).在106 周次之前, 裂纹于表面萌生, 即传统的疲劳行为; 在106 \(\sim \) 109 周次, 裂纹于内部萌生, 裂纹源区呈现"鱼眼"特征 (图9 (a)).起源处的高倍图像显示尺度为几十微米的亮区 (图9 (b)), 并称其为FGA (fine granular area). Sakai 2009 还给出了SUJ2钢轴向循环加载 (50 Hz) 的S-N数据, 其特征为单一线性下降趋势, "双重S-N曲线"特征不明显 (图10 ).在105 \(\sim \) 109 周次, 裂纹于内部萌生 (图11 (a)), 同样观察到起源处有尺度为几十微米的FGA特征 (图11 (b)).裂纹萌生位置在截面上随机分布, 这与轴向加载应力分布特征相对应.对于旋转弯曲加载具有的"双重S-N曲线"的一种解释是, 试样截面受力从表面到中心线性减小, 裂纹萌生和初始扩展点的应力小于名义应力; 而对于轴向加载, 试样整个截面受力一致. 换言之, 旋转弯曲加载和轴向加载分别对应的控制体积不同.控制体积是试样中发生裂纹起源的潜在区域, 通常取不小于 90%最大应力的截面所对应的试样体积为控制体积 (Murakami et al. 2002 , Furuya 2011 , Lei et al. 2014 , Sun et al. 2016 ). ...
Effects of inclusions on very high cycle fatigue properties of high strength steels
2
2012
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
... 诚然, 合金材料超高周疲劳的研究进展十分丰富, 不可毕其所有内容于一文, 例如, 下列这些内容本文未专门评述: (1) 高强钢超高周疲劳裂纹内部萌生主要由夹杂物起源, 但在某些情况, 裂纹也可以由非夹杂物起源, 如晶界等; 此外, 夹杂物的类型和尺度对裂纹萌生有影响. 本文在第5.2节和第5.4节中略有提到此方面的问题, 但未专门评述. 这方面的内容可参阅洪友士等(2009) 、Li等 (2012) 、Zimmermann (2012) 、Sander等 (2014) 文献. ...
Reliability evaluation on very high cycle fatigue property of GCr15 bearing steel
0
2010
Correlations between very high cycle fatigue properties and inclusions of GCr15 bearing steel
0
2008
Effects of stress ratio on high-cycle and very-high-cycle fatigue behavior of a Ti-6Al-4V alloy
6
2015
... 近期, 笔者采用超声轴向加载 (20 kHz)获得了不同应力比条件下Ti-6Al-4V的超高周疲劳特性 (Liu et al. 2015 ), 对于应力比R=-0.1, 0.1, 0.5情形, S-N曲线在107 周次附近发生二次拐折, 裂纹主要萌生于内部; 而\(R =-1\), \(-0.5\)的S-N曲线不发生拐折, 裂纹均于表面萌生 (图22 ).观察到3种裂纹萌生模式: 表面滑移、表面解理和内部解理 (图23 ). ...
... Ti-6Al-4V在 \(R = -1\), \(-0.5\), \(-0.1\), 0.1, 0.5的S-N特性(Sur1: 表面滑移起源, Sur2: 表面解理起源, Int: 内部解理起源). (a)应力幅表达, (b) 最大应力表达(Liu et al. 2015 ) ...
... (a) 表面滑移起源: \(R = -1\), \(\sigma _{\rm a} ={550} {\rm MPa}\), \(N_{\rm f} = 1.13\times 10^7\); (b)表面解理起源: \(R = 0.5\), \(\sigma _{\rm a} = {202} {\rm MPa}\), \(N_{\rm f} = {4.03}\times 10^7\); (c) 内部解理起源: \(R = 0.1\), \(\sigma _{\rm a} = {339} {\rm MPa}\), \(N_{\rm f} = {2.26}\times10^7\)(Liu et al. 2015 ) ...
... 笔者近期的研究结果 (Liu et al. 2015 ) 表明, 钛合金的高周和超高周疲劳裂纹萌生存在3种类型, 即表面滑移裂纹萌生、表面解理裂纹萌生和内部解理裂纹萌生 (图23 ). 3种断口类型包含两种裂纹萌生机制, 即滑移和解理.在分析3种断口类型的竞争关系时, 首先要分析滑移机制和解理机制的竞争, 然后再分析解理机制中表面解理和内部解理之间的竞争. ...
... 笔者 (Liu et al. 2015 )在研究应力比对钛合金高周和超高周疲劳3种裂纹萌生类型竞争关系时, 同样基于Poisson缺陷模型, 计算了3种裂纹萌生类型的发生概率, 其中, 表面解理裂纹萌生的发生概率为\[P_{\rm surf} = P_{\rm surf} (n \geq 1) = 1 - {\rm e}^{ -N_{\rm surf} } \ \ (2)\]内部解理裂纹萌生的发生概率为\[P_{\rm int} = P_{\rm surf} (n = 0)P_{\rm int} (n \geq 1) = (1- {\rm e}^{ - N_{\rm int} }){\rm e}^{ - N_{\rm surf} } \ \ (3)\]表面滑移裂纹萌生的发生概率为\[ P_{\rm sli} = P_{\rm surf} (n = 0)P_{\rm int} (n = 0)= {\rm e}^{ - (N_{\rm int} + N_{\rm surf} )} \ \ (4)\]图28 (a) 显示了式 (2)\(\sim \)(4)得到的裂纹萌生类型发生概率与最大应力的关系: 随着最大应力增加, 表面滑移裂纹萌生 (surface-without-facets) 减少, 表面解理裂纹萌生(surface-with-facets) 增加, 内部解理裂纹萌生(interior-with-facets) 先增加后减少. 图28 (b)是裂纹萌生类型随应力比变化的实验结果. 对于所涉及的情况, 应力比变化趋势与最大应力变化趋势相对应 (图22 (b)). 图28 (a) 与图28 (b)对比, 可见随着应力比增大, 即随着最大应力增大, 3种疲劳裂纹萌生类型随加载过程变化的模型计算结果与实验结果的趋势一致. ...
... (a)3种疲劳裂纹萌生类型的发生概率与最大应力关系的计算结果, (b)疲劳裂纹萌生类型所占比例随应力比变化的实验结果 (Liu et al. 2015 ) ...
a. Effects of microstructure and stress ratio on high-cycle and very-high-cycle fatigue of Ti-6Al-4V alloy
1
2016
... 钛合金 (如Ti-6Al-4V) 超高周疲劳裂纹往往以\(\alpha\)相解理并呈现facet 特征的方式起源.裂纹萌生区由若干facet以及它们的汇合而构成, 形成相对粗糙的断面, 被称为rough area (RA). RA之后是FiE区, 然后进入裂纹稳态扩展. 图24 是钛合金超高周疲劳裂纹内部萌生及其发展的示意图. Liu 等(2016) 对超声轴向加载 (20 kHz) 断裂周次\(N_{\rm f} = {2.02}\times10^7\)的Ti-6Al-4V试样, 采用原子力显微镜测量表明, facet起伏很小, 最大值为14 nm, 连接facet的局域粗糙度很大, 最大值达2217 nm, 而FiE区的最大起伏为209 nm, 即RA区的粗糙度比FiE区大1个量级. ...
b. Faceted crack initiation characteristics for high-cycle and very-high-cycle fatigue of a titanium alloy under different stress ratios
5
2016
... 关于钛合金, 近期笔者采用超声轴向加载 (20 kHz)对Ti-6Al-4V超高周疲劳裂纹萌生区剖面进行了观测 (Liu et al. 2016b ).图50 (a) 是包含2处裂纹萌生区的典型断面 \((R = 0.1\), \(\sigma_{\rm a} = 367\) MPa, \(N_{\rm f} = 9.14\times 10 ^6)\) 的SEM图像.利用截面离子抛光方法沿虚线PQ切出该区域的剖面, 然后用EBSD(电子背散射衍射) 方法对该剖面进行观测. 结果显示, 裂纹萌生处A和B以及非裂纹萌生处的微结构 (包括初生\(\alpha \)相比例, 晶粒尺寸和晶体学取向) 基本无差别 (图50 (b)).因此认为对于钛合金, 内部裂纹起源可以发生在材料中的随机位置. ...
... (a) Ti-6Al-4V \((R = 0.1\), \(\sigma _{\rm a }= 367\) MPa, \(N_{\rm f}= 9.14\times 10 ^{6})\) 断面包含裂纹萌生处A, B的SEM图像; (b) 虚线PQ对应的断口剖面的晶体取向图像 (Liu et al. 2016b ) ...
... 笔者 (Liu et al. 2016b )在截面离子抛光方法制备的Ti-6Al-4V裂纹萌生区的剖面试样上, 观察到在距断面20 \(\mu \)m位置的早期裂纹损伤 (图51 ).图51 (c) 显示facet 1和facet 2由初生\(\alpha\)相晶粒解理而成. 在两个facet之间, 裂纹沿晶界汇合而连接; 在虚线圆圈区域可见两处facet裂纹还未完全汇合. 这一观测结果表明, 钛合金裂纹萌生和初始扩展的方式是先由初生\(\alpha\)相晶粒独立解理形成facet裂纹, 再各自沿晶界扩展而汇合.进而提出了钛合金解理裂纹萌生的机制 (图52 ): (1)材料初始状态中存在可发生解理的初生\(\alpha \)相晶粒 (图52 (a)); (2) 一些初生\(\alpha \)晶粒发生解理, 形成facet裂纹 (图52 (b)); (3) facet裂纹发生汇合 (图52 (c)); (4) 汇合的裂纹进一步发展, 形成主裂纹 (图52 (d)), 最后导致试样破坏. ...
... Ti-6Al-4V超声轴向加载 \((R = 0.5\), \(\sigma _{\rm a }=205 \) MPa, \(N_{\rm f} = 5.80\times 10 ^{7})\) 裂纹萌生区SEM图像.(a) 断面裂纹萌生区, (b) 萌生区剖面, (c) 对(b)放大观察显示已连接和未连接的裂纹 (Liu et al. 2016b ) ...
... 小解理面损伤导致裂纹萌生示意图. (a) 初始微结构, (b)原\(\alpha\)相晶粒解理, (c) 小解理面汇合, (d) 形成主裂纹 (Liu et al. 2016b ) ...
Prediction of the S-N curves of high-strength steels in the very high cycle fatigue regime
2
2010
... Liu 等 (2010) 基于106 和109 周次的疲劳强度预测结果, 采用Basquin公式的形式对S-N曲线进行预测 \[ \sigma _a = \sigma '_{\rm f} (2N_{\rm f} )^b\ \ (22)\]式中, \(\sigma'_{\rm f} = 1.12(Hv + 120)^{9 / 8} / (\sqrt{area_{\rm Inc} } )^{1 / 8}\(, \)b = 3^{ - 1}\lg [1.35(Hv + 120)^{ -1 / 16}(\sqrt {area_{\rm Inc} } )^{ - 1 / 48}]\), \(\sigma _a\)单位为MPa, \(\sqrt {area_{\rm Inc} } \)单位为\(\mu {\rm m}\), H v单位为kgf/mm2 . 式 (22) 可表示成 \[ \sigma _a = 1.12\dfrac{2^b(Hv + 120)^{9 /8}}{\left( {\sqrt {area_{\rm Inc} } } \right)^{1 / 8}}N_{\rm f}^b\ \ (23)\] ...
... 式 (22) (实线) 和式 (17) (虚线)对疲劳强度预测结果与实验结果的比较 (Liu et al. 2010 ) ...
Fatigue crack growth from small to long cracks in very-high-cycle fatigue with surface and internal "fish-eye" failures for ferrite-perlitic low carbon steel SAE 8620
0
2007
Fatigue crack growth from small to large cracks on very high cycle fatigue with fish-eye failures
0
2008
Internal friction and fatigue in metals at large strain amplitudes
1
1956
... 关于超高周疲劳的研究可以从采用超声频率 (如20 kHz)进行疲劳加载说起. 采用如此高的加载频率是为了提高疲劳实验效率以研究合金材料更高加载周次的疲劳性能和更低裂纹扩展速率的疲劳行为. Manson (1956) 最早采用超声频率进行疲劳实验. 20世纪50 \(\sim\) 60年代, 仅有为数不多的报道, 其中Kikukawa等 (1965) 发展了超声轴向振动加载设备, 频率范围13 \(\sim \) 100 kHz, 最大加载周次达109 , 研究了加载频率对低碳钢疲劳性能的影响, 表明较高的加载频率导致较高的疲劳极限.这是采用超声频率进行超高周疲劳研究的雏形, 然而他们并未就加载频率对疲劳性能影响的机理进行研究, 也未点明"超高周疲劳"特征. ...
Fatigue crack growth and threshold measurements at very high frequencies
1
1999
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
Very high cycle fatigue properties of bainitic high carbon-chromium steel
1
2009
... Mayer 等 (2009) 认为, 疲劳寿命、夹杂物尺寸和应力幅之间可以近似地用如下关系描述 \[ \left[ {\sigma _a \left( {\sqrt {area_{\rm Inc} } }\right)^{1 / 6}} \right]^nN_{\rm f} = C \ \ (20)\]即 \[ \sigma _a = C^{\frac{1}{n}}\dfrac{1}{\left( {\sqrt{area_{\rm Inc} } } \right)^{1 / 6}}N_{\rm f}^{ - \frac{1}{n}}\ \ (21)\]\(式中, \(\sigma _a \(单位为MPa, \)area_{\rm Inc} \)单位为\(\mu {\rm m}^2\). ...
Recent developments in ultrasonic fatigue
2
2016
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
... (3) 加载环境对合金材料超高周疲劳行为的影响; 一方面这种影响涉及到环境影响的特有机理, 另一方面工程构件总是处在某种环境介质中. 本文在第4.4节和第5.1节提到真空环境, 但基本未涉及到腐蚀环境.弱腐蚀介质甚至中性水对超高周疲劳性能影响十分显著.这方面的内容可参阅: 洪友士等 (2009) , Qian等 (2015) , Mayer (2016) . ...
On the life-controlling microstructural fatigue mechanisms in ductile metals and alloys in the gigacycle regime
1
1999
... Mughrabi (1999 , 2002 , 2009 )假设Manson-Coffin关系在超高周疲劳中仍然成立, 并假定当局部不可逆累积塑性应变达到某一临界值时材料发生破坏, 从而提出了描述超高周疲劳寿命的关系式 \[ N_{\rm f}^{c + 1} \cdot p(\Delta \varepsilon _{{\rm pl}} ) = \dfrac{\varepsilon _{{\rm pl,cum,f}}^{{\rm irr}}}{4\varepsilon '_{\rm f} \cdot 2^c} = {\rm const} \ \ (30)\]式中, \(\varepsilon '_{\rm f} \)为疲劳韧性系数, c为疲劳韧性指数, \(\Delta \varepsilon _{{\rm pl}} \)为塑性应变幅值, \(N_{\rm f}\)为疲劳周次, \(p(\Delta \varepsilon _{\rm pl} )\)为不可逆循环滑移, 定义为 \[] p = \dfrac{\mbox{irreversible plastic shear strain}}{\mbox{cumulative total plastic shear strain}} \ \ (31)\]当滑移完全可逆时p=0, 滑移完全不可逆时p = 1, 部分可逆时, 0 < p < 1, p取决于塑性应变幅值的大小. 其中的临界值\(\varepsilon_{{\rm pl,cum,f}}^{{\rm irr}} \)和临界表面粗糙度相关, 并取决于(局部) 滑移面之间均方根位移的临界值. ...
On "multi-stage" fatigue life diagrams and the relevant life-controlling mechanisms in ultrahigh-cycle fatigue
1
2002
... Mughrabi (1999 , 2002 , 2009 )假设Manson-Coffin关系在超高周疲劳中仍然成立, 并假定当局部不可逆累积塑性应变达到某一临界值时材料发生破坏, 从而提出了描述超高周疲劳寿命的关系式 \[ N_{\rm f}^{c + 1} \cdot p(\Delta \varepsilon _{{\rm pl}} ) = \dfrac{\varepsilon _{{\rm pl,cum,f}}^{{\rm irr}}}{4\varepsilon '_{\rm f} \cdot 2^c} = {\rm const} \ \ (30)\]式中, \(\varepsilon '_{\rm f} \)为疲劳韧性系数, c为疲劳韧性指数, \(\Delta \varepsilon _{{\rm pl}} \)为塑性应变幅值, \(N_{\rm f}\)为疲劳周次, \(p(\Delta \varepsilon _{\rm pl} )\)为不可逆循环滑移, 定义为 \[] p = \dfrac{\mbox{irreversible plastic shear strain}}{\mbox{cumulative total plastic shear strain}} \ \ (31)\]当滑移完全可逆时p=0, 滑移完全不可逆时p = 1, 部分可逆时, 0 < p < 1, p取决于塑性应变幅值的大小. 其中的临界值\(\varepsilon_{{\rm pl,cum,f}}^{{\rm irr}} \)和临界表面粗糙度相关, 并取决于(局部) 滑移面之间均方根位移的临界值. ...
Cyclic slip irreversibilities and the evolution of fatigue damage
2
2009
... Mughrabi (1999 , 2002 , 2009 )假设Manson-Coffin关系在超高周疲劳中仍然成立, 并假定当局部不可逆累积塑性应变达到某一临界值时材料发生破坏, 从而提出了描述超高周疲劳寿命的关系式 \[ N_{\rm f}^{c + 1} \cdot p(\Delta \varepsilon _{{\rm pl}} ) = \dfrac{\varepsilon _{{\rm pl,cum,f}}^{{\rm irr}}}{4\varepsilon '_{\rm f} \cdot 2^c} = {\rm const} \ \ (30)\]式中, \(\varepsilon '_{\rm f} \)为疲劳韧性系数, c为疲劳韧性指数, \(\Delta \varepsilon _{{\rm pl}} \)为塑性应变幅值, \(N_{\rm f}\)为疲劳周次, \(p(\Delta \varepsilon _{\rm pl} )\)为不可逆循环滑移, 定义为 \[] p = \dfrac{\mbox{irreversible plastic shear strain}}{\mbox{cumulative total plastic shear strain}} \ \ (31)\]当滑移完全可逆时p=0, 滑移完全不可逆时p = 1, 部分可逆时, 0 < p < 1, p取决于塑性应变幅值的大小. 其中的临界值\(\varepsilon_{{\rm pl,cum,f}}^{{\rm irr}} \)和临界表面粗糙度相关, 并取决于(局部) 滑移面之间均方根位移的临界值. ...
... 该公式的进一步应用还需要对\(p\)与\(\Delta \varepsilon _{{\rm pl}}\)之间的关系进行仔细研究, 并确定破坏时不可逆累积塑性应变的临界值.在延性金属中, 疲劳损伤以驻留滑移带 (PSB) 的形式出现, PSB的平均宽度\(\bar {w}\)可用下式表述 (Mughrabi 2009 ) \[ \bar {w} \approx \sqrt {6bhpN\gamma _{{\rm pl},{\rm PSB}} }\ \ (32)\]其中, b为Burgers矢量模,h为滑移区厚度, N为疲劳循环加载周次, \(\gamma _{{\rm pl},{\rm PSB}} \)为PSB区域中的剪切塑性变形.利用AFM或FIB可以测量出\(\bar {w}\)和h, 从而可以计算出不可逆滑移分量p. ...
Fatigue, an everlasting materials problem-still en vogue
1
2010
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
Quantitative evaluation of effects of nonmetallic inclusions on fatigue strength of high strength steel
0
1988
Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. I: Basic fatigue mechanism and evaluation of correlation between the fatigue fracture stress and the size and location of non-metallic inclusions
2
1989
... 需要说明, 在超高周疲劳领域, 应力强度因子\(K\)通常被作为描述裂纹萌生和扩展的表征量. 对此, Murakami等 (1989) 的分析结果给出了表面或内部缺陷萌生裂纹的应力强度因子最大值\(K_{\rm Imax} \)表达式. 对于表面缺陷\[ K_{\rm {Imax}} = 0.65\sigma _0 \left( {\pi \sqrt{area_{\rm s} } } \right) ^{1 / 2} \ \ (5)\] 式中, \(\sigma _0\)是最大拉伸应力, \(area_{\rm s}\)是表面缺陷在垂直于拉应力平面的投影面积. 对于内部缺陷\[K_{\rm {Imax}} = 0.5\sigma _0 \left( {\pi \sqrt{area_{\rm i} } } \right) ^{1 / 2} \ \ (6)\] 式中, \(area_{\rm i} \)是内部缺陷在垂直于拉应力平面的投影面积. ...
... 近20年来, 陆续有研究报道了针对高强钢超高周疲劳寿命或疲劳强度的预测模型, 如Murakami等 (Murakami & Usuki 1989 , Murakami et al. 1999 ), Harlow等 (2006) , Zhao 等 (2009) , Sun等 (2012 , 2013 ), Stepanskiy(2012) , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响. ...
Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. II: Fatigue limit evaluation based on statistics for extreme values of inclusion size
0
1989
Factors influencing the mechanism of superlong fatigue failure in steels
5
1999
... 关于高强钢超高周疲劳裂纹萌生阶段的裂纹扩展速率也已有若干结果, 如Murakami等 (1999) 对SCM435钢 (30 \(\sim \) 100 Hz轴向加载)的估算表明, 对于1 \(\sim \) 4 mm的大尺度FiE, 断裂周次108 , FiE对应的裂纹扩展速率10\(^{-11}\sim \) 10-12 m/cyc.他们注意到这一速率明显小于材料晶格尺度, 认为裂纹不是每个载荷周次都发生扩展. Tanaka等 (2002) 对SUJ2钢的估算表明, 对于断裂周次107 以上的超高周疲劳, 裂纹萌生阶段的速率 小于10-12 m/cyc.对于这一远小于材料柏氏矢量的速率, 他们认为裂纹萌生过程是沿其周边不均匀生长, 且裂纹生长不是通常的位错运动机制. ...
... 反例1 在Murakami等 (1999) 提出"氢助裂纹萌生"机理的同时, 他们对SCM435高强钢, 轴向循环 (30 \(\sim \) 100 Hz, \(R = -1)\)的实验结果给出了ODA即FGA尺度随疲劳断裂周次而增大的趋势, 特别是观察到对于断裂周次较低的试样, 疲劳裂纹于试样内部的夹杂物萌生, 断面呈现"鱼眼"特征, 但在裂纹源夹杂物周围并无ODA即FGA特征 (图42 ). ...
... SCM435高强钢, 轴向循环 (30 \(\sim \) 100 Hz, \(R =-1)\), 应力\(\sigma = 682 \) MPa, \(N_{\rm f} = 5.40\times 10^5\), 夹杂物尺度\(\sqrt {area} = 47.8 \mu{\rm m}\). (a) 光学显微镜图像, (b)SEM图像 (Murakami et al. 1999 ) ...
... 近20年来, 陆续有研究报道了针对高强钢超高周疲劳寿命或疲劳强度的预测模型, 如Murakami等 (Murakami & Usuki 1989 , Murakami et al. 1999 ), Harlow等 (2006) , Zhao 等 (2009) , Sun等 (2012 , 2013 ), Stepanskiy(2012) , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响. ...
... , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响. ...
a. On the mechanism of fatigue failure in the superlong life regime \((N > 10^{7}\) cycles), Part I: influence of hydrogen trapped by inclusions
3
2000
... 笔者 (Hong et al. 2012 ) 对GCr15 (1% C, 1.5% Cr) 和40Cr(0.4% C, 1% Cr) 的旋转弯曲实验 (52 Hz)显示了疲劳性能具有"双重S-N曲线"特征 (图12 ). 图13 显示了裂纹亚表面起源所呈现的鱼眼特征 (图13 (b))和FGA特征 (图13 (c)). 光学显微镜图像 (图13 (b))显示鱼眼区域内的FGA为灰度大的深色特征, 因而也被称为暗区 (optical dark area, ODA) (Murakami et al. 2000 ); 而扫描电子显微镜(SEM)图像(图13 (c)) 显示的FGA是灰度相对小的亮区, 因而也被称为颗粒状亮面区 (granular bright facet, GBF) (Shiozawa etal. 2001 ), 这是由于扫描电镜对粗糙断面成像的缘故. ...
... FGA是裂纹萌生区, FGA对应的疲劳寿命即是裂纹萌生寿命.关于高强钢超高周疲劳裂纹萌生阶段消耗的疲劳寿命已有若干结果, 如Wang等 (1999) 对2组中碳高强钢 (20 kHz轴向加载) 的估算结果显示, 对应断裂周次为3.8 \(\times \) 10\(^{7}\sim \) 5 \(\times\) 108 , 裂纹萌生寿命占总寿命的96.2% \(\sim \) 99.9%.Murakami等 (2000b) 对SCM435钢 (30 \(\sim \) 100 Hz轴向加载)的估算结果显示, 对应断裂周次5 \(\times \) 108 , 裂纹萌生寿命占总寿命的99.8%. Tanaka和Akiniwa (2002) 对SUJ2钢(52.5 Hz旋弯加载) 的估算结果给出, 对应断裂周次10\(^{7}\sim\) 5 \(\times \) 1010 , 裂纹萌生寿命占总寿命的95% \(\sim\) 99%. ...
... 氢助裂纹环绕夹杂物萌生示意图 (Murakami et al. 2000a , 2000b ) ...
b. On the mechanism of fatigue failure in the superlong life regime \((N > 10 ^{7}\) cycles), Part II: a fractographic investigation
1
2000
... 氢助裂纹环绕夹杂物萌生示意图 (Murakami et al. 2000a , 2000b ) ...
Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions.
0
2002
b. Mechanism of fatigue failure in ultralong life regime
2
2002
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
... Sakai等 (2000) 联络了6个实验室的研究者, 采用相同类型的旋转弯曲设备(52 Hz) 和相同类型的SUJ2钢 (1% C, 1.5% Cr) 试样, 所获得的大量数据表明"双重S-N曲线"特征 (图8 ).在106 周次之前, 裂纹于表面萌生, 即传统的疲劳行为; 在106 \(\sim \) 109 周次, 裂纹于内部萌生, 裂纹源区呈现"鱼眼"特征 (图9 (a)).起源处的高倍图像显示尺度为几十微米的亮区 (图9 (b)), 并称其为FGA (fine granular area). Sakai 2009 还给出了SUJ2钢轴向循环加载 (50 Hz) 的S-N数据, 其特征为单一线性下降趋势, "双重S-N曲线"特征不明显 (图10 ).在105 \(\sim \) 109 周次, 裂纹于内部萌生 (图11 (a)), 同样观察到起源处有尺度为几十微米的FGA特征 (图11 (b)).裂纹萌生位置在截面上随机分布, 这与轴向加载应力分布特征相对应.对于旋转弯曲加载具有的"双重S-N曲线"的一种解释是, 试样截面受力从表面到中心线性减小, 裂纹萌生和初始扩展点的应力小于名义应力; 而对于轴向加载, 试样整个截面受力一致. 换言之, 旋转弯曲加载和轴向加载分别对应的控制体积不同.控制体积是试样中发生裂纹起源的潜在区域, 通常取不小于 90%最大应力的截面所对应的试样体积为控制体积 (Murakami et al. 2002 , Furuya 2011 , Lei et al. 2014 , Sun et al. 2016 ). ...
Observation of fatigue fracture surface of carburized steel. Journal of the Society of Materials Science,
4
1983
... 20世纪80年代, 超高周疲劳现象开始得到专门研究. 最早的报道是Naito等(1983 , 1984 ) 关于渗碳钢的研究和Atrens等 (1983) 关于钛合金的研究. ...
... 20世纪80年代, Naito等(1983 , 1984 )采用旋转弯曲加载技术 (50 Hz)研究了表面渗碳强化钢的疲劳特性. 所得到的S-N曲线有两个拐点, 一个位于105 周次附近, 另一个位于5\(\times \)106 周次附近; 直至108 周次, 疲劳强度随载荷周次下降, 不存在疲劳极限 (图1 (a)). 他们用电解抛光去除渗碳强化钢50 \(\mu\)m的微结构不均匀表层, 如此试样的疲劳强度得到明显提升且S-N曲线为无拐点的单一线性趋势(图1 (a)). 他们注意到在5\(\times\) 106 周次之后, 部分试样断口呈现"鱼眼 (fish-eye)"特征 (图2 ).这是最早关于高强钢超高周疲劳强度特性与断口特征的报道. ...
... Naito等(1983 , 1984 ) 和Atrens等 (1983) 的文章是关于高强钢和钛合金超高周疲劳研究的最先报道, 他们指出在"长寿命"阶段, 疲劳性能、特征、机理均发生了变化, 尽管在他们的文章里并无"超高周"的名词, 而表达为"长寿命". ...
... Naito等(1983 , 1984 )、Atrens等 (1983) 、Asami和Sugiyama (1985) 和Stanzl等 (1986) 的研究报道, 标志了与传统低周疲劳和高周疲劳内涵不同的超高周疲劳研究的起源. ...
Fatigue behavior of carburized steel with internal oxides and nonmartensitic microstructure near the surface
9
1984
... 20世纪80年代, 超高周疲劳现象开始得到专门研究. 最早的报道是Naito等(1983 , 1984 ) 关于渗碳钢的研究和Atrens等 (1983) 关于钛合金的研究. ...
... 20世纪80年代, Naito等(1983 , 1984 )采用旋转弯曲加载技术 (50 Hz)研究了表面渗碳强化钢的疲劳特性. 所得到的S-N曲线有两个拐点, 一个位于105 周次附近, 另一个位于5\(\times \)106 周次附近; 直至108 周次, 疲劳强度随载荷周次下降, 不存在疲劳极限 (图1 (a)). 他们用电解抛光去除渗碳强化钢50 \(\mu\)m的微结构不均匀表层, 如此试样的疲劳强度得到明显提升且S-N曲线为无拐点的单一线性趋势(图1 (a)). 他们注意到在5\(\times\) 106 周次之后, 部分试样断口呈现"鱼眼 (fish-eye)"特征 (图2 ).这是最早关于高强钢超高周疲劳强度特性与断口特征的报道. ...
... SCM415钢旋转弯曲实验结果 (Naito et al. 1984 ). (a)S-N曲线, 表面渗碳状态呈现"阶梯状", (b) 裂纹萌生和初始扩展解释示意图 ...
... 裂纹亚表面萌生的鱼眼特征 (Naito et al. 1984 ) ...
... 此外, Asami和Sugiyama (1985) 也采用旋转弯曲加载技术研究了若干表面强化钢的疲劳性能, 同样表明表面渗碳强化钢的S-N曲线有两个拐点 (图4 ), 所得到断口观察结果及其解释与Naito等 (1984) 相似. ...
... Naito等(1983 , 1984 ) 和Atrens等 (1983) 的文章是关于高强钢和钛合金超高周疲劳研究的最先报道, 他们指出在"长寿命"阶段, 疲劳性能、特征、机理均发生了变化, 尽管在他们的文章里并无"超高周"的名词, 而表达为"长寿命". ...
... Naito等(1983 , 1984 )、Atrens等 (1983) 、Asami和Sugiyama (1985) 和Stanzl等 (1986) 的研究报道, 标志了与传统低周疲劳和高周疲劳内涵不同的超高周疲劳研究的起源. ...
... 作为最早报道的结果之一, 图1 (a)显示了表面渗碳强化钢的S-N曲线在 5\(\times 10^6\)周次发生二次拐折, 疲劳强度继续下降, 传统疲劳极限不复存在 (Naito et al. 1984 )的现象.长寿命的疲劳裂纹表面萌生后形成尺度约90 \(\mu \)m的光滑断面区(图5 (a)), 该断面区与拉应力方向夹角约45\(^\circ\); 这不同于短寿命的情形: 裂纹表面沿晶萌生后以I型裂纹方式发生初始扩展(图5 (b)). 图1 (b) 是对这一结果的解释.该S-N曲线及其裂纹萌生观察结果是重要的, 但其解释值得质疑: 图5 (a) 显示的裂纹萌生区光滑断面不完全与拉应力呈倾斜夹角, 此断面很可能是裂纹萌生过程形成的区域, 即裂纹亚表面萌生而不是表面萌生的特征. ...
... 裂纹萌生特征. (a) 长寿命试样\(\sigma _{\rm a} =690 {\rm MPa}\), \(N_{\rm f} = 4.65\times 10^7\), (b) 短寿命试样, \(\sigma _{\rm a} =930 {\rm MPa}\), \(N_{\rm f} = 5.81\times 10^4\) (Naito et al. 1984 ) ...
Effect of loading condition on very high cycle fatigue behavior in a high strength steel
0
2010
Internal fatigue origins in \(\alpha -\beta \) titanium alloys
2
1976
... 关于钛合金, Neal和Blenkinsop (1976) 给出了IMI 550(Ti-4Al-4Mo-2Sn-0.55Si) 和IMI 318 (Ti-6Al-4V) 轴向循环加载(应力比\(R=0\), 频率150 Hz) 的S-N曲线 (图15 ), 表明在\(3\times 10 ^{6}\sim 2.5\times 10^{7}\)周次范围疲劳裂纹主要从内部萌生, 裂纹起源特征为\(\alpha\)相解理导致的 "facet (小解理面)". 此结果是关于钛合金\(\alpha \)相"facet" 为特征裂纹萌生的最早报道. 但断裂周次仅略高于107 , 即初步涉及到超高周疲劳阶段. ...
... IMI 550 (Ti-4Al-4Mo-2Sn-0.55Si) 和IMI 318 (Ti-6Al-4V)轴向循环加载的S-N结果 (Neal & Blenkinsop 1976 ) ...
Stepwise S-N curve and fish-eye failure in gigacycle fatigue
2
1999
... Nishijima和Kanazawa (1999) 归纳分析了早期关于以表面硬化钢为代表的高强钢S-N曲线的结果 (图7 ). 他们认为, 表面起源和内部起源两种疲劳裂纹萌生模式导致了两套S-N曲线; 裂纹内部起源对应的载荷条件低于表面起源的载荷条件, 只有表面起源受到抑制, 才可能发生裂纹内部起源. ...
... 双重S-N曲线示意图 (Nishijima & Kanazawa 1999 ) ...
Indentation size effects in crystalline materials: A law for strain gradient plasticity
1
1998
... FGA裂纹属短裂纹范畴, 其扩展受材料微结构尺度制约.因此笔者分析了FGA裂尖塑性区与材料微结构尺度的关系 (Zhao et al. 2011 , 2012 ). 对于平面应变I型裂纹, 裂尖塑性区尺度\(r_{\rm p}\)的表达式为 (Hertzberg et al. 2012 )\[r_{\rm p} = \dfrac{\left({1 - 2\nu } \right) ^2}{\pi }\left( {\dfrac{\Delta K}{\sigma_{\rm y} }} \right)^2 \approx \dfrac{1}{6\pi }\left({\dfrac{\Delta K}{\sigma _{\rm y} }} \right)^2 \ \ (7)\] 式中, \(\nu \)是泊松比, \(\sigma _{\rm y}\)是屈服强度. 另一方面, 材料微结构特征尺度\(l_{\rm m}\)与材料基本力学性能有如下关系 (Nix& Gao 1998 )\[l_{\rm m} = b\left( {\mu / \sigma _{\rm y} }\right) ^2 \ \ (8)\] 式中, b为材料柏氏矢量模, \(\mu\)为材料剪切模量. 假定当FGA裂尖塑性区尺寸与材料微结构特征尺度相等, FGA裂纹终止发展. 这样\( \Delta K_{\rm FGA} = \mu \sqrt {\pi b} =4.342\mu \sqrt { b} \ \ (9)\)\( 式 (9) 表明, 超高周疲劳裂纹萌生特征区FGA对应的特征参量\(\Delta K_{\rm FGA}\)可简单表达为材料剪切模量和柏氏矢量的函数. ...
High-cycle rotating bending fatigue property in very long-life regime of high-strength steels
1
2002
... 对于钢, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 5.54} {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与文献实验结果 (如Sakai et al. 2002 , Ochi et al. 2002 , Shiozawa et al. 2006b , Yang et al. 2008 , Zhao et al. 2011 , Lei et al. 2012 ) 得到的\(4\sim 6 {\rm MPa} \cdot{\rm m}^{{\rm 1 / 2}}\)相符合. ...
A fracture mechanics approach to interior fatigue crack growth in the very high cycle regime
3
2014
... Ishida等 (2012) 和Ogawa等 (2014) 对SUJ2高强钢超声轴向加载(20 kHz, R = -1), 采用两级载荷往复阶梯加载 \((\Delta \sigma_{\rm H}= 1200\) MPa, \(n_{\rm H}= 1\times 10 ^{3}\), \(\Delta \sigma_{\rm L}= 850\) MPa, nL = 1\(\times\) 10 4 , \(N_{\rm f}=2.87\times \)10 8 ), 使断面呈现与阶梯载荷相对应的环状裂纹扩展特征(图34 ), 基于环状裂纹特征测得FGA外FiE区域的裂纹扩展速率, 再推得FGA的裂纹扩展速率. 他们所得到的结果为: FGA区域裂纹扩展速率10\(^{-13}\sim \) 10-14 m/cyc; 在FGA外的FiE区域, 裂纹扩展速率107 \(\sim \) 10-9 m/cyc. ...
... (a) 光镜图像显示裂纹萌生区的"鱼眼"特征; (b)"鱼眼"区放大图像, 显示"海滩"斑图, 箭头表示阶梯加载的裂纹扩展增量, (c) 裂纹源区放大图像, 显示裂纹萌生区的ODA (FGA), (d) SEM图像显示裂纹源夹杂物及其周围的FGA特征(Ogawa et al. 2014 ) ...
... Ishida等 (2012) 和Ogawa等 (2014) 采用往复两级阶梯加载方法和Sander等 (2014, 2016) 采用周期性变幅加载方法, 导致萌生区的裂纹呈现环状扩展特征, 使得有可能直接观测到萌生阶段裂纹扩展特征并测量裂纹扩展速率.但他们观察到的环状裂纹特征及其测量均是在FGA外的FiE区域. 至今, 还未有关于FGA区域裂纹扩展速率的有效观察和测量的结果. ...
Mechanism of long life fatigue fracture induced by interior inclusion for bearing steel in rotating bending.
2
2003
... 这一模型的关键点是: 细晶层在裂纹萌生之前形成且裂纹沿细晶层与基体分离, 即裂纹不是在细晶层内生长. Sakai与合作者 (Oguma et al. 2003 , Sakai et al. 2015 ) 对高强钢超高周疲劳裂纹萌生的精细观察表明同一试样断面一边有细晶层, 另一边仍是原始状态的粗晶, 以此来支持所提出的模型. ...
... SUJ2高强钢旋弯加载 (52.5 Hz), \(\sigma _{\rm a }=1100\) MPa, \(N_{\rm f} = 5.46\times 10 ^{7}\), 裂纹起源区FGA局域剖面TEM图像, 在FGA表层附近 (C点)的SAD为纳米晶特征, 远离FGA表层 (D点)的SAD为粗晶特征 (Oguma et al. 2003 ) ...
The effect of microstructure on very high cycle fatigue properties in Ti-6Al-4V
2
2010
... 图16 是采用常规频率 (120 Hz) 对钛合金 (Ti-6Al-4V)轴向疲劳加载 \((R= 0.1)\) 的超高周疲劳特性典型结果 (Oguma & Nakamura 2010 ), 给出了退火态 (MA) 和固溶--时效态 (STOA)的超高周疲劳特性. 表明S-N曲线在107 周次发生显著拐折, 对应的疲劳裂纹起源由表面转为内部, 裂纹源区为\(\alpha\)相晶粒萌发的"小解理面"构成. ...
... Ti-6Al-4V 轴向疲劳加载 (120 Hz) 的S-N特性 (Oguma & Nakamura 2010 ) ...
Fatigue crack propagation properties of Ti-6Al-4V in vacuum environments
3
2013
... Oguma和Nakamura (2013) 在研究钛合金超高周疲劳裂纹萌生时注意到裂纹萌生区的FGA特征往往是在真空环境下形成的, 并联系到高强钢和高强铝合金的类似情况, 从而提出了"萌生区裂纹面冷焊"机理 (图41 ), 即萌生的裂纹面在真空中往复接触发生"冷焊"过程, 导致萌生区晶粒细化. 这也是具有想象力的模型, 但其关键点, 即裂纹面发生"冷焊"过程并无实验依据. ...
... 基于"冷焊"的细晶区形成模型 (Oguma & Nakamura 2013 ) ...
... Sakai和Oguma等 (Oguma et al. 2003, Sakai 2009 ) 对SUJ2 高强钢, 加载条件为旋弯加载 (52.5 Hz), \(\sigma _{\rm a }= 1100\) MPa, \(N_{\rm f} = 5.46\times 10 ^{7}\), 采用TEM 配合选区电子衍射 (SAD), SAD的直径为250 nm, 在FGA表面附近观察到厚度400 nm的细晶层, 晶粒尺度40 nm (图46 中C所在局域), 而远离FGA表面, 为粗晶组织(图46 中D所在局域). 在这些观察的基础上, 他们提出了"细晶层形成与分离"机理与模型 (Sakai 2009 ). ...
Relations between fatigue strength and other mechanical properties of metallic materials
2
2014
... Pang等 (2014) 分析了多种合金材料疲劳强度与硬度、拉伸强度(屈服强度)、韧性之间的关系, 表明疲劳强度\(\sigma _{\rm w}\)与拉伸强度\(\sigma _{\rm b}\)之间的关系可以描述为 \[ \sigma _{\rm w}= \sigma _{\rm b} (C - P\sigma _{\rm b} ) \ \ (33)\]式中, C和P是材料参数.他们给出了经不同技术处理的零部件和高强钢拉伸强度与疲劳强度之间关系的模型结果与实验结果的比较(图67 ). ...
... (a)具有不同表面状态的手动变速杆的拉伸强度与疲劳强度的关系, (b)经和未经喷丸处理的一种高强钢和一种轴的拉伸强度与疲劳强度的关系(Pang et al. 2014 ) ...
Influence of atmospheric moisture on slow fatigue crack growth at ultrasonic frequency in aluminium and magnesium alloys
2
2002
... 对于铝合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\(1.911 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与诸多实验结果 (如Paris et al. 1999 , Papakyriacou et al. 2002, Holper et al. 2004 , Borrego et al. 2004 , Huang & Moan 2007 ) 得到的\(1.5\sim 2.8 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\)相符合. ...
... 对于镁合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 1.179} {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\), 这与Papakyriacou 等 (2002) 的多组结果\(1.3\sim 1.5 {\rm MPa} \cdot {\rm m}^{{\rm 1 /2}}\)相符合. ...
Service load fatigue damage-a historical perspective
1
1999
... 对于铝合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\(1.911 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与诸多实验结果 (如Paris et al. 1999 , Papakyriacou et al. 2002, Holper et al. 2004 , Borrego et al. 2004 , Huang & Moan 2007 ) 得到的\(1.5\sim 2.8 {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\)相符合. ...
An overview on the influence of the atmosphere environment on ultra-high-cycle fatigue and ultra-slow fatigue crack propagation
1
2006
... 对于钛合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 3.385} {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\), 与诸多实验结果 (如Ritchie et al. 1999 , Petit & Sarrazin-Baudoux 2006 , Huang & Moan 2007 ) 得到的\(3.4\sim 4.0 {\rm MPa} \cdot {\rm m}^{{\rm 1 /2}}\)相符合. ...
Experimental and theoretical investigation of environmental media on very-high-cycle fatigue behavior for a structural steel
1
2011
... 合金材料的超高周疲劳裂纹以内部起源为主, 但对于不同的材料, 裂纹萌发点和裂纹初始扩展特征可能存在差异.为了说明疲劳裂纹表面起源向内部起源的转移和竞争, 笔者 (Hong et al. 2009 , 2012 , Qian et al. 2011 ) 引入了一个新的参数\(D^\ast \) ...
A model to predict S-N curves for surface and subsurface crack initiations in different environmental media
1
2015
... (3) 加载环境对合金材料超高周疲劳行为的影响; 一方面这种影响涉及到环境影响的特有机理, 另一方面工程构件总是处在某种环境介质中. 本文在第4.4节和第5.1节提到真空环境, 但基本未涉及到腐蚀环境.弱腐蚀介质甚至中性水对超高周疲劳性能影响十分显著.这方面的内容可参阅: 洪友士等 (2009) , Qian等 (2015) , Mayer (2016) . ...
Duality of fatigue failures of materials caused by Poisson defect statistics of competing failure modes
3
2005
... Jha和Ravi Chandran (2003) 、Ravi Chandran (2005) 和Ravi Chandran和Jha (2005) 报道了初生\(\alpha\)相比例对Ti-10V-2Fe-3Al疲劳行为的影响, 表明初生\(\alpha\)相体积比例较低时 (10%), 具有同样微结构形态的试样在所有应力水平下发生疲劳裂纹表面萌生和内部萌生的概率基本一样(图26 (a)). 初生\(\alpha \)相体积比例较高时 (45%), 高应力状态裂纹趋于表面萌生, 低应力状态趋于内部萌生 (图26 (b)). ...
... 针对这一结果, 并将钛合金初生\(\alpha \)相晶粒团簇看作缺陷, Ravi Chandran 等 (Ravi Chandran 2005 , Ravi Chandran & Jha 2005 )提出了基于Poisson缺陷模型分析得到的3种疲劳破坏类型的发生概率, 以此解释不同初生\(\alpha \)相体积比例下, 钛合金疲劳裂纹表面萌生和内部萌生的竞争行为 (图27 ). 图中表明, 当 \(\lambda = 15\) mm\(^{ - 2}\), \(P_{\rm int}\)达到极值 (0.66); 该处对应\(P_{\rm surf }= 0.23\), \(P_{\rm nd }= 0.11\), 即23%的试样将从亚表面发生裂纹萌生. 当 \(\lambda = 15\) mm-2 , \(P_{\rm nd }= 0\), 意味着所有试样将由\(\alpha\)相晶粒团簇缺陷萌生裂纹导致断裂, 包括: 裂纹萌生于表面缺陷和萌生于内部缺陷. 这一预测与实验结果相符合; 即 \(\lambda = 0.29 \sim 0.46 \) mm\(^{ - 2}\)时, \(P_{\rm nd }=0\), \(P_{\rm int}\)和\(P_{\rm surf}\)数值相近, \(\alpha\)相晶粒团簇缺陷导致裂纹萌生于表面或萌生于内部. ...
... 计算结果显示裂纹表面起源和内部起源概率随缺陷密度的变化(Ravi Chandran 2005 , Ravi Chandran & Jha 2005 ) ...
Duality of the S-N fatigue curve caused by competing failure modes in a titanium alloy and the role of Poisson defect statistics
3
2005
... Jha和Ravi Chandran (2003) 、Ravi Chandran (2005) 和Ravi Chandran和Jha (2005) 报道了初生\(\alpha\)相比例对Ti-10V-2Fe-3Al疲劳行为的影响, 表明初生\(\alpha\)相体积比例较低时 (10%), 具有同样微结构形态的试样在所有应力水平下发生疲劳裂纹表面萌生和内部萌生的概率基本一样(图26 (a)). 初生\(\alpha \)相体积比例较高时 (45%), 高应力状态裂纹趋于表面萌生, 低应力状态趋于内部萌生 (图26 (b)). ...
... 针对这一结果, 并将钛合金初生\(\alpha \)相晶粒团簇看作缺陷, Ravi Chandran 等 (Ravi Chandran 2005 , Ravi Chandran & Jha 2005 )提出了基于Poisson缺陷模型分析得到的3种疲劳破坏类型的发生概率, 以此解释不同初生\(\alpha \)相体积比例下, 钛合金疲劳裂纹表面萌生和内部萌生的竞争行为 (图27 ). 图中表明, 当 \(\lambda = 15\) mm\(^{ - 2}\), \(P_{\rm int}\)达到极值 (0.66); 该处对应\(P_{\rm surf }= 0.23\), \(P_{\rm nd }= 0.11\), 即23%的试样将从亚表面发生裂纹萌生. 当 \(\lambda = 15\) mm-2 , \(P_{\rm nd }= 0\), 意味着所有试样将由\(\alpha\)相晶粒团簇缺陷萌生裂纹导致断裂, 包括: 裂纹萌生于表面缺陷和萌生于内部缺陷. 这一预测与实验结果相符合; 即 \(\lambda = 0.29 \sim 0.46 \) mm\(^{ - 2}\)时, \(P_{\rm nd }=0\), \(P_{\rm int}\)和\(P_{\rm surf}\)数值相近, \(\alpha\)相晶粒团簇缺陷导致裂纹萌生于表面或萌生于内部. ...
... 计算结果显示裂纹表面起源和内部起源概率随缺陷密度的变化(Ravi Chandran 2005 , Ravi Chandran & Jha 2005 ) ...
High-cycle fatigue of Ti-6Al-4V
1
1999
... 对于钛合金, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 3.385} {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\), 与诸多实验结果 (如Ritchie et al. 1999 , Petit & Sarrazin-Baudoux 2006 , Huang & Moan 2007 ) 得到的\(3.4\sim 4.0 {\rm MPa} \cdot {\rm m}^{{\rm 1 /2}}\)相符合. ...
Experimental reconfirmation of characteristic S-N property for high carbon chromium bearing steel in wide life region in rotating bending. Journal of the Society of Materials Science,
2
2000
... SUJ2钢旋转弯曲加载的超高周疲劳双重S-N曲线 (Sakai et al. 2000 ) ...
... (a) 裂纹亚表面起源的鱼眼特征 \((\sigma _{\rm a} =1300 {\rm MPa}\), \(N_{\rm f} = 2.66\times 10^6)\), (b)高倍图像显示鱼眼中部环绕裂纹源夹杂物的FGA (Sakai et al. 2000 ) ...
S-N property and fractography of high carbon chromium bearing steel over ultra wide life region under rotating bending
3
2001
... Sakai等 (2001) 给出了SUJ2钢 (旋弯加载) FGA尺度\(\sqrt {area}\)随加载应力增大而减小的趋势 (图30 (a)), 其尺度范围从15 \(\mu \)m至32 \(\mu \)m; 而导致裂纹起源的夹杂物尺度不随加载应力变化 (图30 (a)).对于FiE, 其尺度范围相对较大, 从50 \(\mu \)m至300 \(\mu \)m(Sakai et al. 2001 ). ...
... (a)).对于FiE, 其尺度范围相对较大, 从50 \(\mu \)m至300 \(\mu \)m(Sakai et al. 2001 ). ...
... (a) FGA和裂纹源夹杂物尺度与加载应力幅的关系, (b)FGA和裂纹源夹杂物的应力强度因子幅值与疲劳寿命的关系 (Sakai et al. 2001 ) ...
Characteristic S-N properties of high-carbon-chromium-bearing steel under axial loading in long-life fatigue
2
2002
... (a) 裂纹萌生于内部的鱼眼特征 \((\sigma _{\rm a} =900 {\rm MPa}\), \(N_{\rm f} = 1.94\times 10^8)\), (b) 高倍图像显示鱼眼中部环绕夹杂物的FGA (Sakai et al. 2002 ) ...
... 对于钢, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 5.54} {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与文献实验结果 (如Sakai et al. 2002 , Ochi et al. 2002 , Shiozawa et al. 2006b , Yang et al. 2008 , Zhao et al. 2011 , Lei et al. 2012 ) 得到的\(4\sim 6 {\rm MPa} \cdot{\rm m}^{{\rm 1 / 2}}\)相符合. ...
Effect of stress ratio on long life fatigue behavior of high carbon chromium bearing steel under axial loading
1
2006
... 研究表明, 传统的Goodman关系不能很好地描述应力比对合金材料超高周疲劳强度的影响(Takeuchi et al. 2010 , Sakai et al. 2006 ). Sun等 (2014) 分析了不同加载应力比条件下若干合金材料的近门槛区裂纹扩展速率(特别是远低于10-10 m/cyc的裂纹扩展速率) 的特征, 推导了应力比 (或平均应力) 对高周和超高周疲劳强度的影响关系, 即 \[ \sigma _{a,R} = \sigma _{ - 1} \left( {\dfrac{1 -R}{2}} \right)^\alpha = \sigma _{ - 1} \left( {1 - \dfrac{\sigma_{{\rm avg},R} }{\sigma _{{\rm max},R} }} \right)^\alpha \ \ (34)\]或 \[ \sigma _{a,R} = \left\{ \begin{array}{ll} \sigma _{ - 1} \dfrac{(1 - R)^\alpha }{2} = 2^{\alpha - 1}\sigma _{ - 1}\left( {1 - \dfrac{\sigma _{{\rm avg},R} }{\sigma _{{\rm max},R}}} \right)^\alpha, & \mbox{for} R \geq 0 \ [2mm] \sigma _{ - 1} \dfrac{1 - R}{2} = \sigma _{ - 1} \left( {1 - \dfrac{\sigma_{{\rm avg},R} }{\sigma _{{\rm max},R} }} \right),& \mbox{for} R < 0\\ \end{array} \right.\ \ (35)\] ...
Review and prospects for current studies on very high cycle fatigue of metallic materials for machine structural use
9
2009
... 在循环载荷作用下, 合金材料发生裂纹萌生、扩展直至断裂的周次在107 以上的过程被称为超高周疲劳(Sakai 2009 , 洪友士等2009 ). 合金材料超高周疲劳(very-high-cycle fatigue, VHCF) 行为是对传统疲劳理念的挑战, 因为传统疲劳知识认为, 合金材料存在疲劳极限, 即对应107 载荷周次的疲劳强度被确定为疲劳极限 (ASTME468-90, 2004), 循环应力低于疲劳极限不发生疲劳损伤和破坏. ...
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
... Sakai等 (2000) 联络了6个实验室的研究者, 采用相同类型的旋转弯曲设备(52 Hz) 和相同类型的SUJ2钢 (1% C, 1.5% Cr) 试样, 所获得的大量数据表明"双重S-N曲线"特征 (图8 ).在106 周次之前, 裂纹于表面萌生, 即传统的疲劳行为; 在106 \(\sim \) 109 周次, 裂纹于内部萌生, 裂纹源区呈现"鱼眼"特征 (图9 (a)).起源处的高倍图像显示尺度为几十微米的亮区 (图9 (b)), 并称其为FGA (fine granular area). Sakai 2009 还给出了SUJ2钢轴向循环加载 (50 Hz) 的S-N数据, 其特征为单一线性下降趋势, "双重S-N曲线"特征不明显 (图10 ).在105 \(\sim \) 109 周次, 裂纹于内部萌生 (图11 (a)), 同样观察到起源处有尺度为几十微米的FGA特征 (图11 (b)).裂纹萌生位置在截面上随机分布, 这与轴向加载应力分布特征相对应.对于旋转弯曲加载具有的"双重S-N曲线"的一种解释是, 试样截面受力从表面到中心线性减小, 裂纹萌生和初始扩展点的应力小于名义应力; 而对于轴向加载, 试样整个截面受力一致. 换言之, 旋转弯曲加载和轴向加载分别对应的控制体积不同.控制体积是试样中发生裂纹起源的潜在区域, 通常取不小于 90%最大应力的截面所对应的试样体积为控制体积 (Murakami et al. 2002 , Furuya 2011 , Lei et al. 2014 , Sun et al. 2016 ). ...
... SUJ2钢轴向循环加载的超高周疲劳S-N曲线 (Sakai 2009 ) ...
... Sakai (2009) 认为, 由于长周次载荷循环, 在夹杂物周围裂纹萌生潜在局域由塑性变形导致的微结构多边形化, 使得在夹杂物周边 (裂纹萌生之前) 形成细晶层 (图38 stage A); 而后细晶层与基体分离形成裂纹面粗糙的萌生区, 即FGA (图38 stage B, stage C). 当FGA在夹杂物周边发展成钱币形的裂纹, FGA达到临界尺度, 裂纹进入Paris裂纹扩展区 (图38 stage D). ...
... 夹杂物周围发生"细晶层形成与分离"而形成裂纹萌生区示意图 (Sakai 2009 ) ...
... 以上3个模型主要针对高强钢超高周疲劳裂纹萌生区的特点, 而Shanyavskiy (2013) 所提出的模型不仅针对高强钢, 而且也涉及其他高强合金. 他认为, 由于涡动塑性流动而形成纳米晶薄层且纳米晶粒在每一压缩/拉伸循环中转动(图40 (a) 和图40 (b)), 晶界强度消失使得晶粒颗粒化(即萌发裂纹), 从而形成FGA区域的粗糙断面 (图40 (c) 和图40 (d)). 这是一个有想象力的模型, 但其相关物理过程有待于验证.此模型亦认为, 在裂纹萌生之前, 在夹杂物周围形成了细晶层, 这一点与Sakai (2009) 模型相似. ...
... Sakai和Oguma等 (Oguma et al. 2003, Sakai 2009 ) 对SUJ2 高强钢, 加载条件为旋弯加载 (52.5 Hz), \(\sigma _{\rm a }= 1100\) MPa, \(N_{\rm f} = 5.46\times 10 ^{7}\), 采用TEM 配合选区电子衍射 (SAD), SAD的直径为250 nm, 在FGA表面附近观察到厚度400 nm的细晶层, 晶粒尺度40 nm (图46 中C所在局域), 而远离FGA表面, 为粗晶组织(图46 中D所在局域). 在这些观察的基础上, 他们提出了"细晶层形成与分离"机理与模型 (Sakai 2009 ). ...
... 中D所在局域). 在这些观察的基础上, 他们提出了"细晶层形成与分离"机理与模型 (Sakai 2009 ). ...
Microscopic and nanoscopic observations of metallurgical structures around inclusions at interior crack initiation site for a bearing steel in very high-cycle fatigue
4
2015
... 这一模型的关键点是: 细晶层在裂纹萌生之前形成且裂纹沿细晶层与基体分离, 即裂纹不是在细晶层内生长. Sakai与合作者 (Oguma et al. 2003 , Sakai et al. 2015 ) 对高强钢超高周疲劳裂纹萌生的精细观察表明同一试样断面一边有细晶层, 另一边仍是原始状态的粗晶, 以此来支持所提出的模型. ...
... 类似地, Grad等 (2012) 在高强钢观察到尺度约70 nm的细晶, 并提出"裂尖局部晶粒细化"模型, 如图39 所描述.这一模型与Sakai (2009) 模型的思路相似. 此类模型认为, 细晶层形成于裂纹萌生之前, 并且在已萌生的裂纹前沿不断形成细晶层. ...
... 近期, Sakai等 (2015) 进一步给出了SUJ2高强钢 (旋弯加载)超高周疲劳裂纹起源区FGA的剖面特征.他们对同一试样断面的两侧观察表明, 一侧有细晶 (图47 (b)), 另一侧无细晶 (图47 (a)). 通过这一结果, 支持他们所提出的裂纹沿夹杂物周围形成的细晶层与基体分离而扩展的"细晶层形成与分离"模型. ...
... (a) SUJ2高强钢 (旋弯加载), 同一试样断面FGA两侧剖面的SEM图像, 其中一侧的FGA表层为纳米晶; (b)另一侧的FGA表层为粗晶 (Sakai et al. 2015 ) ...
Influence of mean stress and variable amplitude loading on the fatigue behaviour of a high-strength steel in VHCF regime
4
2014
... Sander等 (2014 , 2016 )对34CrNiMo6高强钢, 采用超声轴向加载 (21 kHz), 通过周期性变幅加载, 使得裂纹萌生区呈现裂纹扩展环状特征(图35 ), 从而测得在FGA之外的FiE区的裂纹扩展速率为3 \(\times\) 10\(^{-11}\sim \) 2 \(\times \) 10-12 m/cyc. ...
... 反例4 Sander等 (2014) 采用超声轴向加载 (21 kHz)对34CrNiMo6高强钢进行应力比R=-1和\(R= 0\)加载, 给出了不同尺度和形状的夹杂物 (作为裂纹源) 导致不同断裂周次的结果, 观察到所有断面均有"鱼眼"特征但无FGA. 图45 是\(\sigma _{\rm a }= 430\) MPa, \(R = 0\), 断裂周次从\(N = 6.61\times 10 ^{5}\)到\( N = 2.57\times 10 ^{8}\)的4种情形的裂纹萌生区均无FGA特征.前节所述的模型不能解释此实验结果. ...
... 34CrNiMo6高强钢经超声轴向加载 (21 kHz, \(\sigma _{\rm a}= 430\) MPa, \(R = 0)\) 的裂纹萌生区特征 (Sander et al. 2014 ). (a)\(N_{\rm f}= 6.61\times 10^{5}\), (b) \(N_{\rm f}= 1.21\times10^{6}\), (c) \(N_{\rm f}= 2.24\times 10^{6}\),(d) \(N_{\rm f}=2.57\times 10^{8}\) ...
... 诚然, 合金材料超高周疲劳的研究进展十分丰富, 不可毕其所有内容于一文, 例如, 下列这些内容本文未专门评述: (1) 高强钢超高周疲劳裂纹内部萌生主要由夹杂物起源, 但在某些情况, 裂纹也可以由非夹杂物起源, 如晶界等; 此外, 夹杂物的类型和尺度对裂纹萌生有影响. 本文在第5.2节和第5.4节中略有提到此方面的问题, 但未专门评述. 这方面的内容可参阅洪友士等(2009) 、Li等 (2012) 、Zimmermann (2012) 、Sander等 (2014) 文献. ...
Very high cycle fatigue behavior under constant and variable amplitude loading
2
2016
... Sander等 (2014 , 2016 )对34CrNiMo6高强钢, 采用超声轴向加载 (21 kHz), 通过周期性变幅加载, 使得裂纹萌生区呈现裂纹扩展环状特征(图35 ), 从而测得在FGA之外的FiE区的裂纹扩展速率为3 \(\times\) 10\(^{-11}\sim \) 2 \(\times \) 10-12 m/cyc. ...
... 由变幅加载导致的裂纹萌生区环状扩展特征即鱼眼区域内裂纹扩展分界线(Sander et al. 2016 ) ...
Mechanisms and modeling of subsurface fatigue cracking in metals
2
2013
... 以上3个模型主要针对高强钢超高周疲劳裂纹萌生区的特点, 而Shanyavskiy (2013) 所提出的模型不仅针对高强钢, 而且也涉及其他高强合金. 他认为, 由于涡动塑性流动而形成纳米晶薄层且纳米晶粒在每一压缩/拉伸循环中转动(图40 (a) 和图40 (b)), 晶界强度消失使得晶粒颗粒化(即萌发裂纹), 从而形成FGA区域的粗糙断面 (图40 (c) 和图40 (d)). 这是一个有想象力的模型, 但其相关物理过程有待于验证.此模型亦认为, 在裂纹萌生之前, 在夹杂物周围形成了细晶层, 这一点与Sakai (2009) 模型相似. ...
... 夹杂物周围"涡动塑性流动导致形成纳米微结构薄层"示意图(Shanyavskiy 2013 ).(a) 载荷上升, (b) 载荷下降, (c)和(d) 裂纹面相互接触 ...
S-N curve characteristics and subsurface crack initiation behaviour in ultra-long life fatigue of a high carbon-chromium bearing steel
2
2001
... 笔者 (Hong et al. 2012 ) 对GCr15 (1% C, 1.5% Cr) 和40Cr(0.4% C, 1% Cr) 的旋转弯曲实验 (52 Hz)显示了疲劳性能具有"双重S-N曲线"特征 (图12 ). 图13 显示了裂纹亚表面起源所呈现的鱼眼特征 (图13 (b))和FGA特征 (图13 (c)). 光学显微镜图像 (图13 (b))显示鱼眼区域内的FGA为灰度大的深色特征, 因而也被称为暗区 (optical dark area, ODA) (Murakami et al. 2000 ); 而扫描电子显微镜(SEM)图像(图13 (c)) 显示的FGA是灰度相对小的亮区, 因而也被称为颗粒状亮面区 (granular bright facet, GBF) (Shiozawa etal. 2001 ), 这是由于扫描电镜对粗糙断面成像的缘故. ...
... Shiozawa等 (2001 , 2002 , 2006a , 2006b )采用SEM和扫描探针显微镜观察表明, GBF (即FGA) 具有相对粗糙的表面, 其对应的应力强度因子幅值\(\Delta K\)与裂纹扩展门槛值\(\Delta K_{\rm th}\)基本一致.他们检测到FGA区域的微小隆起和凹陷的尺寸分布与细小碳化物的尺寸分布对应, 并通过电子探针显微分析表明FGA为富碳区; 另一方面, 采用断面形貌分析法模拟显示, 在非金属夹杂物周围发生弥散球状碳化物与基体分离而形成的微裂纹萌生、扩展和汇合; 当FGA达到临界尺度, 裂纹扩展不再依赖于球状碳化物与基体分离. 图37 是"球状碳化物弥散分离"模型描述超高周疲劳裂纹源区FGA形成机理的示意图(Shiozawa et al. 2006a , 2006b ). ...
Very high-cycle fatigue behaviour of shot-peened high-carbon-chromium bearing steel
2
2002
... Shiozawa和Lu (2002) 也对SUJ2钢得到了类似的结果, 表明疲劳断裂周次在\(10^{5}\sim 10 ^{9}\)范围, FGA尺度为12 \(\mu\)m至40 \(\mu \)m, 其对应的 \(\Delta K\)值不随断裂周次变化, 为4 \(\sim \) 6 MPa\( \cdot \)m\(^{1 / 2}\). ...
... Shiozawa等 (2001 , 2002 , 2006a , 2006b )采用SEM和扫描探针显微镜观察表明, GBF (即FGA) 具有相对粗糙的表面, 其对应的应力强度因子幅值\(\Delta K\)与裂纹扩展门槛值\(\Delta K_{\rm th}\)基本一致.他们检测到FGA区域的微小隆起和凹陷的尺寸分布与细小碳化物的尺寸分布对应, 并通过电子探针显微分析表明FGA为富碳区; 另一方面, 采用断面形貌分析法模拟显示, 在非金属夹杂物周围发生弥散球状碳化物与基体分离而形成的微裂纹萌生、扩展和汇合; 当FGA达到临界尺度, 裂纹扩展不再依赖于球状碳化物与基体分离. 图37 是"球状碳化物弥散分离"模型描述超高周疲劳裂纹源区FGA形成机理的示意图(Shiozawa et al. 2006a , 2006b ). ...
Subsurface crack initiation and propagation mechanism under the super-long fatigue regime for high speed tool steel (JIS SKH51) by fracture surface topographic analysis
5
2006
... 关于裂纹面粗糙度, Shiozawa等 (2006a , 2006b ) 对旋弯加载 (52.5 Hz)断裂周次\(N_{\rm f} = 6.3\times 10^8\)的SUJ2试样, 采用扫描电镜3D分析, 测量了FGA, FGA外FiE区和FiE外SCG断面的粗糙度(表1 ), 表明FGA的平均粗糙度\(R_{\rm a}\)值是FiE区的2.2倍, SCG区的平均粗糙度\(R_{\rm a}\)值是FiE区的3.5倍. 钱桂安 (2009)对旋弯加载 (52.5 Hz) 断裂周次\(N_{\rm f} = 1.34\times 10^7\)的40Cr试样, 采用原子力显微镜测量获得3个区域的断面粗糙度(表1 ), 表明FGA的平均粗糙度\(R_{\rm a}\)值是FiE区的3.4倍, SCG区的平均粗糙度\(R_{\rm a}\)值是FiE区的4.9倍. ...
... Shiozawa等 (2001 , 2002 , 2006a , 2006b )采用SEM和扫描探针显微镜观察表明, GBF (即FGA) 具有相对粗糙的表面, 其对应的应力强度因子幅值\(\Delta K\)与裂纹扩展门槛值\(\Delta K_{\rm th}\)基本一致.他们检测到FGA区域的微小隆起和凹陷的尺寸分布与细小碳化物的尺寸分布对应, 并通过电子探针显微分析表明FGA为富碳区; 另一方面, 采用断面形貌分析法模拟显示, 在非金属夹杂物周围发生弥散球状碳化物与基体分离而形成的微裂纹萌生、扩展和汇合; 当FGA达到临界尺度, 裂纹扩展不再依赖于球状碳化物与基体分离. 图37 是"球状碳化物弥散分离"模型描述超高周疲劳裂纹源区FGA形成机理的示意图(Shiozawa et al. 2006a , 2006b ). ...
... 是"球状碳化物弥散分离"模型描述超高周疲劳裂纹源区FGA形成机理的示意图(Shiozawa et al. 2006a , 2006b ). ...
... 夹杂物周围"球状碳化物弥散分离"形成GBF即FGA (Shiozawa et al. 2006a , 2006b ) ...
... 反例2 在Shiozawa 等 (2006a , 2006b )提出"球状碳化物分离"机理的同时, 在他们对SUJ2高强钢经旋弯加载的断面图像里, 对于疲劳断裂周次较高的情况, 内部夹杂物起源的裂纹萌生区呈现"鱼眼"包含FGA的特征 (图43 (a)); 而对于疲劳断裂周次较低的情况, 内部夹杂物起源的裂纹萌生区仍有"鱼眼"但无FGA特征 (图43 (b)).前节所述的模型不能解释此实验结果. ...
b. Subsurface crack initiation and propagation mechanism in high strength steel in a very high cycle fatigue regime
7
2006
... 关于裂纹面粗糙度, Shiozawa等 (2006a , 2006b ) 对旋弯加载 (52.5 Hz)断裂周次\(N_{\rm f} = 6.3\times 10^8\)的SUJ2试样, 采用扫描电镜3D分析, 测量了FGA, FGA外FiE区和FiE外SCG断面的粗糙度(表1 ), 表明FGA的平均粗糙度\(R_{\rm a}\)值是FiE区的2.2倍, SCG区的平均粗糙度\(R_{\rm a}\)值是FiE区的3.5倍. 钱桂安 (2009)对旋弯加载 (52.5 Hz) 断裂周次\(N_{\rm f} = 1.34\times 10^7\)的40Cr试样, 采用原子力显微镜测量获得3个区域的断面粗糙度(表1 ), 表明FGA的平均粗糙度\(R_{\rm a}\)值是FiE区的3.4倍, SCG区的平均粗糙度\(R_{\rm a}\)值是FiE区的4.9倍. ...
... 对于钢, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 5.54} {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与文献实验结果 (如Sakai et al. 2002 , Ochi et al. 2002 , Shiozawa et al. 2006b , Yang et al. 2008 , Zhao et al. 2011 , Lei et al. 2012 ) 得到的\(4\sim 6 {\rm MPa} \cdot{\rm m}^{{\rm 1 / 2}}\)相符合. ...
... Shiozawa等 (2001 , 2002 , 2006a , 2006b )采用SEM和扫描探针显微镜观察表明, GBF (即FGA) 具有相对粗糙的表面, 其对应的应力强度因子幅值\(\Delta K\)与裂纹扩展门槛值\(\Delta K_{\rm th}\)基本一致.他们检测到FGA区域的微小隆起和凹陷的尺寸分布与细小碳化物的尺寸分布对应, 并通过电子探针显微分析表明FGA为富碳区; 另一方面, 采用断面形貌分析法模拟显示, 在非金属夹杂物周围发生弥散球状碳化物与基体分离而形成的微裂纹萌生、扩展和汇合; 当FGA达到临界尺度, 裂纹扩展不再依赖于球状碳化物与基体分离. 图37 是"球状碳化物弥散分离"模型描述超高周疲劳裂纹源区FGA形成机理的示意图(Shiozawa et al. 2006a , 2006b ). ...
... , 2006b ). ...
... 夹杂物周围"球状碳化物弥散分离"形成GBF即FGA (Shiozawa et al. 2006a , 2006b ) ...
... 反例2 在Shiozawa 等 (2006a , 2006b )提出"球状碳化物分离"机理的同时, 在他们对SUJ2高强钢经旋弯加载的断面图像里, 对于疲劳断裂周次较高的情况, 内部夹杂物起源的裂纹萌生区呈现"鱼眼"包含FGA的特征 (图43 (a)); 而对于疲劳断裂周次较低的情况, 内部夹杂物起源的裂纹萌生区仍有"鱼眼"但无FGA特征 (图43 (b)).前节所述的模型不能解释此实验结果. ...
... (a) SUJ2钢旋弯加载\(\sigma _{\rm a }= 950\) MPa, \(N_{\rm f}= 6.3\times 10^{8}\) 的裂纹萌生区断面的鱼眼包含FGA特征; (b)经表面喷丸处理的SUJ2钢旋弯加载\(\sigma _{\rm a}= 1600\) MPa, \(N_{\rm f}= 3.7\times 10 ^{5}\) 的裂纹萌生区断面的鱼眼但无FGA特征, 图中AB是测量表面起伏的标志线, 结果列于表1 (Shiozawa et al. 2006b ) ...
Very high cycle fatigue properties of bearing steel under axial loading condition
1
2009
... 在上述若干关于超高周疲劳强度预测模型中已引入了应力比对疲劳强度的影响, 如式 (14)、式(15) 和 式(24).这些模型中有关应力比对疲劳强度的影响形式与式 (34) 相一致.图68 给出了采用式 (24)给出的不同应力比和夹杂物尺度条件下预测的疲劳n强度与实验结果的比较 (Sun et al. 2013 ). 式 (24)中的参数C和l通过文献 (Shiozawa et al. 2009 ) 中R = -1情况的裂纹源夹杂物周围具有FGA的实验数据点拟合得到, m = -0.192. \(\alpha \)= 0.627, 该值是通过R = -1和R = 0下\(N_{\rm f} = 4\times \)106 周次附近具有几乎相同夹杂物尺寸的试样的疲劳强度计算得到 (Sun et al. 2012 ). 从图68 看出, 此模型较好地反映了应力比和夹杂物尺度对超高周疲劳强度的影响, 采用最小和最大夹杂物尺度的预测结果可以看作是疲劳强度的上限和下限. ...
Lifetime measurements for random loading in the very high cycle fatigue range
2
1986
... 随后, Stanzl等 (1986) 采用超声频率 (20 kHz) 研究了一种低碳钢在随机载荷下的疲劳特性, 疲劳断裂周次从3 \(\times\) 106 至3 \(\times \) 109 , 他们称此为"超高周疲劳范围 (very high cycle fatigue range)". 尽管他们并未关注超高周疲劳范围的特有行为, 但这是在研究论文里最早出现的"超高周疲劳 (very high cycle fatigue)"的表述. ...
... Naito等(1983 , 1984 )、Atrens等 (1983) 、Asami和Sugiyama (1985) 和Stanzl等 (1986) 的研究报道, 标志了与传统低周疲劳和高周疲劳内涵不同的超高周疲劳研究的起源. ...
Near-threshold crack propagation and internal cracks in steel
1
2010
... Stanzl-Tschegg和Schonbauer (2010) 对12%Cr (AISI 410)高强钢厚度2 mm的薄壁试样制备尖锐缺口, 采用超声轴向加载 (19 kHz, \(R = 0.05\)和0.5), 在真空环境测得裂纹萌生速率为5\(\times \)10-13 m/cyc. 对于空气环境, \(R = 0.05\), 测得裂纹萌生速率为2\(\times\)10-11 m/cyc; 对于R = 0.5, 测得裂纹萌生速率为6\(\times\)10-12 m/cyc. 他们通过裂纹萌生过程的断面微观特征比对, 推断FGA速率为10-12 m/cyc; FGA外的FiE区域裂纹扩展速率为10-11 m/cyc; 在FiE外的区域, 裂纹扩展速率为10-9 m/cyc. ...
Very high cycle fatigue measuring techniques
1
2014
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
Cumulative model of very high cycle fatigue
1
2012
... 近20年来, 陆续有研究报道了针对高强钢超高周疲劳寿命或疲劳强度的预测模型, 如Murakami等 (Murakami & Usuki 1989 , Murakami et al. 1999 ), Harlow等 (2006) , Zhao 等 (2009) , Sun等 (2012 , 2013 ), Stepanskiy(2012) , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响. ...
Nanograin layer formation at crack initiation region for very-high-cycle fatigue of a Ti-6Al-4V alloy
4
2017
... 近期, 笔者对Ti-6Al-4V多组实验数据 (应力比R=-1, -0.1, 0.1, 0.5)的推算结果表明, 在疲劳寿命10\(^{7}\sim \) 109 周次范围, 裂纹萌生寿命占总寿命的96.1% \(\sim \) 99.9%, 对应的裂纹扩展速率10\(^{-11}\sim \) 10-13 m/cyc (Su et al. 2017 ). ...
... 对于钛合金 (Ti-6Al-4V), 笔者的最新结果 (Su et al. 2017 ) 表明, 对于R=-1 (超声轴向加载, 20 kHz), 超高周疲劳裂纹内部萌生呈现RA(粗糙区) 特征, RA区为纳米晶层, 厚度800 \(\sim \) 1500 nm, 平均晶粒尺度105 nm (图61 ). 而对于\(R = 0.5\), 超高周疲劳裂纹内部萌生仍呈现RA特征, 但RA截面无纳米晶特征 (图62 ). 这一研究结果表明, NCP模型适用于解释钛合金超高周疲劳裂纹萌生特征区的形成机理. ...
... Ti-6Al-4V, R=-1, \(\sigma _{\rm a}= 550\) MPa, \(N_{\rm f}= 4.52\times \)107 . (a) 裂纹内部萌生区的SEM 图像, 虚线范围显示RA, 长方形框为FIB 取样位置; (b) TEM图像显示裂纹萌生区截面特征, NG表示纳晶层, EG表示粗晶基体层; (c)紧邻RA表面的SAD 图, 显示纳米晶特征; (d) 距裂纹面2 \(\mu\)m处的SAD 图, 显示单晶特征 (Su et al. 2017 ) ...
... Ti-6Al-4V, R = 0.5, \(\sigma _{\rm a}= 240\) MPa, \(N_{\rm f}= 4.30\times \)10 7 . (a) 裂纹内部萌生区的低倍SEM 图像, 虚线范围显示RA, 长方形框为FIB 取样位置; (b) TEM图像显示裂纹萌生区截面特征, EG表示粗晶基体层; (c)紧邻RA裂纹面的SAD 图, 显示单晶特征; (d) 距裂纹面1.2 \(\mu\)m处的SAD图, 显示单晶特征 (Su et al. 2017 ) ...
A cumulative damage model for fatigue life estimation of high-strength steels in high-cycle and very-high-cycle fatigue regimes
2
2012
... 近20年来, 陆续有研究报道了针对高强钢超高周疲劳寿命或疲劳强度的预测模型, 如Murakami等 (Murakami & Usuki 1989 , Murakami et al. 1999 ), Harlow等 (2006) , Zhao 等 (2009) , Sun等 (2012 , 2013 ), Stepanskiy(2012) , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响. ...
... 在上述若干关于超高周疲劳强度预测模型中已引入了应力比对疲劳强度的影响, 如式 (14)、式(15) 和 式(24).这些模型中有关应力比对疲劳强度的影响形式与式 (34) 相一致.图68 给出了采用式 (24)给出的不同应力比和夹杂物尺度条件下预测的疲劳n强度与实验结果的比较 (Sun et al. 2013 ). 式 (24)中的参数C和l通过文献 (Shiozawa et al. 2009 ) 中R = -1情况的裂纹源夹杂物周围具有FGA的实验数据点拟合得到, m = -0.192. \(\alpha \)= 0.627, 该值是通过R = -1和R = 0下\(N_{\rm f} = 4\times \)106 周次附近具有几乎相同夹杂物尺寸的试样的疲劳强度计算得到 (Sun et al. 2012 ). 从图68 看出, 此模型较好地反映了应力比和夹杂物尺度对超高周疲劳强度的影响, 采用最小和最大夹杂物尺度的预测结果可以看作是疲劳强度的上限和下限. ...
Effects of inclusion size and stress ratio on fatigue strength for high-strength steels with fish-eye mode failure
4
2013
... 近20年来, 陆续有研究报道了针对高强钢超高周疲劳寿命或疲劳强度的预测模型, 如Murakami等 (Murakami & Usuki 1989 , Murakami et al. 1999 ), Harlow等 (2006) , Zhao 等 (2009) , Sun等 (2012 , 2013 ), Stepanskiy(2012) , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响. ...
... Sun等 (2013) 在对大量实验数据研究的基础上, 给出了如下包含应力比影响的超高周疲劳强度预测模型 \[ \sigma _a = CN_{\rm f}^l a_0^m \left( {\dfrac{1 - R}{2}}\right)^\alpha \ \ (24)\]式中, \(a_0 = \sqrt {area_{\rm Inc} } \)是夹杂物尺寸, C, l, m和 \(\alpha \)是材料参数. ...
... 在上述若干关于超高周疲劳强度预测模型中已引入了应力比对疲劳强度的影响, 如式 (14)、式(15) 和 式(24).这些模型中有关应力比对疲劳强度的影响形式与式 (34) 相一致.图68 给出了采用式 (24)给出的不同应力比和夹杂物尺度条件下预测的疲劳n强度与实验结果的比较 (Sun et al. 2013 ). 式 (24)中的参数C和l通过文献 (Shiozawa et al. 2009 ) 中R = -1情况的裂纹源夹杂物周围具有FGA的实验数据点拟合得到, m = -0.192. \(\alpha \)= 0.627, 该值是通过R = -1和R = 0下\(N_{\rm f} = 4\times \)106 周次附近具有几乎相同夹杂物尺寸的试样的疲劳强度计算得到 (Sun et al. 2012 ). 从图68 看出, 此模型较好地反映了应力比和夹杂物尺度对超高周疲劳强度的影响, 采用最小和最大夹杂物尺度的预测结果可以看作是疲劳强度的上限和下限. ...
... 式 (24) 得到的4组预测结果与相应实验结果比较 (Sun et al. 2013 ) ...
Effects of stress ratio on crack growth rate and fatigue strength for high cycle and very-high-cycle fatigue of metallic materials
1
2014
... 研究表明, 传统的Goodman关系不能很好地描述应力比对合金材料超高周疲劳强度的影响(Takeuchi et al. 2010 , Sakai et al. 2006 ). Sun等 (2014) 分析了不同加载应力比条件下若干合金材料的近门槛区裂纹扩展速率(特别是远低于10-10 m/cyc的裂纹扩展速率) 的特征, 推导了应力比 (或平均应力) 对高周和超高周疲劳强度的影响关系, 即 \[ \sigma _{a,R} = \sigma _{ - 1} \left( {\dfrac{1 -R}{2}} \right)^\alpha = \sigma _{ - 1} \left( {1 - \dfrac{\sigma_{{\rm avg},R} }{\sigma _{{\rm max},R} }} \right)^\alpha \ \ (34)\]或 \[ \sigma _{a,R} = \left\{ \begin{array}{ll} \sigma _{ - 1} \dfrac{(1 - R)^\alpha }{2} = 2^{\alpha - 1}\sigma _{ - 1}\left( {1 - \dfrac{\sigma _{{\rm avg},R} }{\sigma _{{\rm max},R}}} \right)^\alpha, & \mbox{for} R \geq 0 \ [2mm] \sigma _{ - 1} \dfrac{1 - R}{2} = \sigma _{ - 1} \left( {1 - \dfrac{\sigma_{{\rm avg},R} }{\sigma _{{\rm max},R} }} \right),& \mbox{for} R < 0\\ \end{array} \right.\ \ (35)\] ...
A two-parameter model to predict fatigue life of high-strength steels in a very high cycle fatigue regime
2
2015
... Sun 等 (2015) 假定FGA内每一周次的等效裂纹增长长度与裂纹尖端的塑性区尺寸有关, 给出了如下具有FiE和FGA断裂模式的高强钢疲劳寿命模型 \[ N_{\rm f} = \dfrac{1}{\alpha }\left( {\dfrac{\sigma _a}{\sigma _{\rm Y} }} \right)^{ - l}\ln \dfrac{a_{\rm FGA} }{a_{\rm 0} } \ \ (27)\]式中, \(a_0 = \sqrt {area_{\rm Inc} } \]是夹杂物尺寸, \(\alpha\)和l是材料参数. 该模型考虑了材料的宏观力学量 (屈服强度)对疲劳寿命的影响.图64 给出了模型预测的疲劳寿命与实验测得的疲劳寿命的比较. ...
... 式 (27) 预测的疲劳寿命与实验测得的疲劳寿命的比较 (Sun et al. 2015 ) ...
Effects of specimen size on fatigue life of metallic materials in high-cycle and very-high-cycle fatigue regimes
1
2016
... Sakai等 (2000) 联络了6个实验室的研究者, 采用相同类型的旋转弯曲设备(52 Hz) 和相同类型的SUJ2钢 (1% C, 1.5% Cr) 试样, 所获得的大量数据表明"双重S-N曲线"特征 (图8 ).在106 周次之前, 裂纹于表面萌生, 即传统的疲劳行为; 在106 \(\sim \) 109 周次, 裂纹于内部萌生, 裂纹源区呈现"鱼眼"特征 (图9 (a)).起源处的高倍图像显示尺度为几十微米的亮区 (图9 (b)), 并称其为FGA (fine granular area). Sakai 2009 还给出了SUJ2钢轴向循环加载 (50 Hz) 的S-N数据, 其特征为单一线性下降趋势, "双重S-N曲线"特征不明显 (图10 ).在105 \(\sim \) 109 周次, 裂纹于内部萌生 (图11 (a)), 同样观察到起源处有尺度为几十微米的FGA特征 (图11 (b)).裂纹萌生位置在截面上随机分布, 这与轴向加载应力分布特征相对应.对于旋转弯曲加载具有的"双重S-N曲线"的一种解释是, 试样截面受力从表面到中心线性减小, 裂纹萌生和初始扩展点的应力小于名义应力; 而对于轴向加载, 试样整个截面受力一致. 换言之, 旋转弯曲加载和轴向加载分别对应的控制体积不同.控制体积是试样中发生裂纹起源的潜在区域, 通常取不小于 90%最大应力的截面所对应的试样体积为控制体积 (Murakami et al. 2002 , Furuya 2011 , Lei et al. 2014 , Sun et al. 2016 ). ...
Microstructural influences on very high cycle fatigue crack initiation in Ti-6246
1
2008
... 钛合金 (如Ti-6Al-4V) 的微结构包含hcp晶体结构的\(\alpha\)相和bcc晶体结构的\(\beta \)相; 这2种相的比例和形状决定了钛合金的微结构特征.钛合金基本不含夹杂物和孔洞缺陷. \(\alpha \)相的脆性特征明显, 超高周疲劳裂纹往往以\(\alpha \)相解理并呈现 facet 特征的方式起源.Zuo等(2008) 的结果表明, 在Ti-6Al-4V中, 对于双态组织形态, 超高周疲劳裂纹可萌生于\(\alpha _{\rm p}\)晶粒 (下标p表示初生)或\(\alpha _{\rm p}\)晶界, 对于网篮组织形态, 裂纹萌生于\(\alpha\)-\(\beta \)相界. Szczepanski等(2008) 的结果表明, 在Ti-6Al-2Sn-4Zr-6Mo合金中, 超高周疲劳裂纹萌生局域为\(\alpha _{\rm p}\)晶粒断裂而成的小解理面 (facet), 形成facet的\(\alpha _{\rm p}\)晶粒尺度对应于其平均值; 裂纹萌生局域的facet取向为高剪应力导向, 即与拉应力轴近似成45\(^\circ\). ...
Observation of trapping sites of hydrogen and deuterium in high-strength steels by using secondary ion mass spectrometry.
1
1995
... Murakami等 (2000a, 2000b)采用光学显微镜观察到高强钢超高周疲劳裂纹起源处有一灰度明显大的小局域, 称为光学暗区 (ODA, 即FGA).SEM和原子力显微镜观察显示FGA具有粗糙表面. 他们依据Takai 等 (1995 , 1996 ) 实验检测到在非金属夹杂物与基体的界面有氢富集的结果, 并依据他们对高强钢超高周疲劳实验结果, 推测FGA是由非金属夹杂物所捕获的氢与疲劳应力共同作用所致. 他们认为, 夹杂物周围局部富集的氢促进FGA形成.夹杂物捕获氢导致裂纹不连续生长且裂纹扩展速率相当低, 从而形成粗糙裂纹面. 当FGA达到临界尺度, 裂纹生长不再受氢的影响而稳定扩展. 图36 是该模型的示意图. ...
Identification of trapping sites in high-strength steels by secondary ion mass spectrometry for thermally desorbed hydrogen
1
1996
... Murakami等 (2000a, 2000b)采用光学显微镜观察到高强钢超高周疲劳裂纹起源处有一灰度明显大的小局域, 称为光学暗区 (ODA, 即FGA).SEM和原子力显微镜观察显示FGA具有粗糙表面. 他们依据Takai 等 (1995 , 1996 ) 实验检测到在非金属夹杂物与基体的界面有氢富集的结果, 并依据他们对高强钢超高周疲劳实验结果, 推测FGA是由非金属夹杂物所捕获的氢与疲劳应力共同作用所致. 他们认为, 夹杂物周围局部富集的氢促进FGA形成.夹杂物捕获氢导致裂纹不连续生长且裂纹扩展速率相当低, 从而形成粗糙裂纹面. 当FGA达到临界尺度, 裂纹生长不再受氢的影响而稳定扩展. 图36 是该模型的示意图. ...
The effect of frequency on the giga-cycle fatigue properties of a Ti-6Al-4V alloy
2
2008
... Furuya和Takeuchi (2014) 报道了Ti-6Al-4V在120 Hz和20 kHz轴向循环加载的超高周疲劳行为. 图19 是2组试样的S-N数据, 图中2组试样的化学成分以及屈服强度和拉伸强度基本一致, 但微结构形态不同. A组\(\alpha \)相晶粒为等轴状, 平均 (等效)直径约7 \(\mu \)m; B组\(\alpha \)相晶粒沿轧制方向拉长, 平均 (等效)直径约20 \(\mu \)m. 对于A组, 3 \(\times\) 105 周次后裂纹基本内部起源; 对于B组, 3 \(\times\) 106 周次后裂纹基本内部起源.加载频率对2组试样的疲劳强度基本无影响; 而疲劳强度随应力比增大而明显降低. 他们 (Takeuchi et al. 2008 , Furuya & Takeuchi 2014 ) 观察表明, 对于A组选取的试样 (20 kHz, \(R = -1)\), 裂纹内部萌生区有明显"鱼眼"特征 (图20 (a), \(N_{\rm f}= 2.10\times 10^{8})\), "鱼眼"中部包含表面起伏较大的粗糙区; 当裂纹源即粗糙区位于试样表面附近, "鱼眼"特征不明显(图20 (b), \(N_{\rm f}= 6.97\times 10^{7})\).对于B组选取的试样 (20 kHz, \(R = 0\), \(N_{\rm f} = 5.10\times 10^{8})\), 内部萌生的裂纹由facet组成 (图21 ). Furuya和Takeuchi(2014) 认为, 裂纹内部萌生局域\(\alpha \)相形成的小解理面群, 其单个小解理面尺度与\(\alpha \)晶粒相当. ...
... A组试样裂纹内部萌生特征. (a) 裂纹萌生区鱼眼特征(20 kHz, \(R = -1\), \(N_{\rm f} = 2.10\times 10^8)\); (b)裂纹源靠近试样表面, 鱼眼特征不明显 (120 Hz, \(R = -1\), \(N_{\rm f}= 6.97\times 10^7)\)(Takeuchi et al. 2008 ) ...
Effect of stressratio on giga-cycle fatigue properties for Ti-6Al-4V Alloy
1
2010
... 研究表明, 传统的Goodman关系不能很好地描述应力比对合金材料超高周疲劳强度的影响(Takeuchi et al. 2010 , Sakai et al. 2006 ). Sun等 (2014) 分析了不同加载应力比条件下若干合金材料的近门槛区裂纹扩展速率(特别是远低于10-10 m/cyc的裂纹扩展速率) 的特征, 推导了应力比 (或平均应力) 对高周和超高周疲劳强度的影响关系, 即 \[ \sigma _{a,R} = \sigma _{ - 1} \left( {\dfrac{1 -R}{2}} \right)^\alpha = \sigma _{ - 1} \left( {1 - \dfrac{\sigma_{{\rm avg},R} }{\sigma _{{\rm max},R} }} \right)^\alpha \ \ (34)\]或 \[ \sigma _{a,R} = \left\{ \begin{array}{ll} \sigma _{ - 1} \dfrac{(1 - R)^\alpha }{2} = 2^{\alpha - 1}\sigma _{ - 1}\left( {1 - \dfrac{\sigma _{{\rm avg},R} }{\sigma _{{\rm max},R}}} \right)^\alpha, & \mbox{for} R \geq 0 \ [2mm] \sigma _{ - 1} \dfrac{1 - R}{2} = \sigma _{ - 1} \left( {1 - \dfrac{\sigma_{{\rm avg},R} }{\sigma _{{\rm max},R} }} \right),& \mbox{for} R < 0\\ \end{array} \right.\ \ (35)\] ...
A theory of fatigue crack initiation at inclusions
2
1982
... Wang等 (2002) 采用Tanaka-Mura位错模型 (Tanaka et al. 1982 )和Paris公式, 给出了预测超高周疲劳寿命模型 \[ N_{\rm f} = \dfrac{9GW_{\rm s} \Delta \sigma _{\rm R}}{\left(\Delta \sigma - \Delta \sigma _{\rm D}^{\rm R}\right)^2a_{\rm o} } + \dfrac{a_{\rm o}^{{\rm (1} - n / 2)}}{C\Delta \sigma ^n\beta _1^n \pi ^{n / 2}(0.5n - 1)} \ \ (28)\]式中, \(N_{\rm f}\)是疲劳寿命, \(\sigma _{\rm D}^{\rm R}\)是应力比为R时的疲劳极限, \(W_{\rm s}\)是断裂能, \(a_{\rm o} \)是初始夹杂物尺寸, G是基体材料剪切模量, C, n是与材料常数, \(\beta _{\rm 1} \)是几何常数. ...
... Hong等 (2014) 将位错不可逆因子引入到Tanaka-Mura位错模型 (Tanaka et al. 1982 ) 中, 提出了描述超高周疲劳形核阶段寿命模型 \[ N_{\rm i} = A\left( {\dfrac{\Delta \sigma - \Delta \sigma _{\rm R} }{\Delta \sigma }} \right)^\alpha\dfrac{1}{(\Delta \sigma - \Delta \sigma _{\rm R} )^2a_{\rm Inc} }\ \ (29)\]式中, \(N_{\rm i}\)是疲劳形核阶段寿命, \(\Delta \sigma _{\rm R}\)是应力比为R时的疲劳极限, \(a_{\rm Inc} = \sqrt {area_{\rm Inc}} / 2\), \(area_{\rm Inc} \)为缺陷在最大主应力垂直方向上的投影面积(单位: \(\mu \(m\)^{2})\), A和\(\alpha \)是材料参数. ...
Fatigue crack propagation behaviour derived from S-N data in very high cycle regime
3
2002
... FGA是裂纹萌生区, FGA对应的疲劳寿命即是裂纹萌生寿命.关于高强钢超高周疲劳裂纹萌生阶段消耗的疲劳寿命已有若干结果, 如Wang等 (1999) 对2组中碳高强钢 (20 kHz轴向加载) 的估算结果显示, 对应断裂周次为3.8 \(\times \) 10\(^{7}\sim \) 5 \(\times\) 108 , 裂纹萌生寿命占总寿命的96.2% \(\sim \) 99.9%.Murakami等 (2000b) 对SCM435钢 (30 \(\sim \) 100 Hz轴向加载)的估算结果显示, 对应断裂周次5 \(\times \) 108 , 裂纹萌生寿命占总寿命的99.8%. Tanaka和Akiniwa (2002) 对SUJ2钢(52.5 Hz旋弯加载) 的估算结果给出, 对应断裂周次10\(^{7}\sim\) 5 \(\times \) 1010 , 裂纹萌生寿命占总寿命的95% \(\sim\) 99%. ...
... 关于高强钢超高周疲劳裂纹萌生阶段的裂纹扩展速率也已有若干结果, 如Murakami等 (1999) 对SCM435钢 (30 \(\sim \) 100 Hz轴向加载)的估算表明, 对于1 \(\sim \) 4 mm的大尺度FiE, 断裂周次108 , FiE对应的裂纹扩展速率10\(^{-11}\sim \) 10-12 m/cyc.他们注意到这一速率明显小于材料晶格尺度, 认为裂纹不是每个载荷周次都发生扩展. Tanaka等 (2002) 对SUJ2钢的估算表明, 对于断裂周次107 以上的超高周疲劳, 裂纹萌生阶段的速率 小于10-12 m/cyc.对于这一远小于材料柏氏矢量的速率, 他们认为裂纹萌生过程是沿其周边不均匀生长, 且裂纹生长不是通常的位错运动机制. ...
... 超高周疲劳的裂纹往往萌生于材料 (试样) 内部. 对于高强钢, 裂纹萌生区呈现FiE和FGA特征. 尽管FiE尺度仅为100 \(\mu \)m量级, FGA尺度仅为10 \(\mu \)m量级; 作为超高周疲劳裂纹萌生特征区, FGA消耗了疲劳总寿命的95%以上 (Tanaka & Akiniwa 2002 , Hong et al. 2014 ). 因此, 揭示裂纹萌生区FGA的形成机理对于理解超高周疲劳的特有行为和寿命预测格外重要. ...
The state of ultrasonic fatigue (keynote address). Ultrasonic Fatigue//Proceedings of the First International Conference on Fatigue and Corrosion Fatigue up to Ultrasonic Frequencies, The Metallurgical Society of AIME,
1
1982
... Willertz (1980) 的文章综述了20世纪50 \(\sim\) 70年代采用超声频率进行疲劳实验研究的情况. 随后, 1981年在美国召开了第一届"直至超声频率的疲劳和腐蚀疲劳"学术会议, 并以"超声疲劳"为题出版了论文集 (Wells et al. 1982 ).在该文集所收集的40篇论文里, 约有1/4论文的实验结果涉及疲劳断裂周次在107 以上直至1010 , 但这些研究并未关注107 周次之后疲劳性能和机理的变化. 注意到Tien (1982) 在该会上的Keynote综述报告的结论里提到"超高周疲劳数据(very high cycle fatigue data)". ...
High-cycle fatigue crack initiation and propagation gehaviour of high-strength spring steel wires
2
1999
... FGA是裂纹萌生区, FGA对应的疲劳寿命即是裂纹萌生寿命.关于高强钢超高周疲劳裂纹萌生阶段消耗的疲劳寿命已有若干结果, 如Wang等 (1999) 对2组中碳高强钢 (20 kHz轴向加载) 的估算结果显示, 对应断裂周次为3.8 \(\times \) 10\(^{7}\sim \) 5 \(\times\) 108 , 裂纹萌生寿命占总寿命的96.2% \(\sim \) 99.9%.Murakami等 (2000b) 对SCM435钢 (30 \(\sim \) 100 Hz轴向加载)的估算结果显示, 对应断裂周次5 \(\times \) 108 , 裂纹萌生寿命占总寿命的99.8%. Tanaka和Akiniwa (2002) 对SUJ2钢(52.5 Hz旋弯加载) 的估算结果给出, 对应断裂周次10\(^{7}\sim\) 5 \(\times \) 1010 , 裂纹萌生寿命占总寿命的95% \(\sim\) 99%. ...
... Wang 等 (1999) 对Murakami模型进行了改进, 引入了疲劳寿命的影响, 给出了预测低合金高强钢疲劳寿命的模型 \[ \sigma _w = \dfrac{\beta (Hv + 120)}{\left({\sqrt {area_{{\rm In}} } } \right)^{1 / 6}}\left( {\dfrac{1 -R}{2}} \right)^\alpha \ \ (15)\]对于4种中碳低合金高强度钢, \(\beta = 3.09 - 0.12\log N_{\rm f} \((内部夹杂或缺陷) 或\)\beta = 2.79 - 0.108\log N_{\rm f} \((表面夹杂或缺陷), \)area_{{\rm In}}\(为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\). 式 (15)和式 (14) 对疲劳强度的预测结果与实验结果比较表明, 引入疲劳寿命影响的式 (15) 给出了较好的预测结果 (Wang et al. 1999 ). ...
Effect of inclusion on subsurface crack initiation and gigacycle fatigue strength
1
2002
... Wang 等 (1999) 对Murakami模型进行了改进, 引入了疲劳寿命的影响, 给出了预测低合金高强钢疲劳寿命的模型 \[ \sigma _w = \dfrac{\beta (Hv + 120)}{\left({\sqrt {area_{{\rm In}} } } \right)^{1 / 6}}\left( {\dfrac{1 -R}{2}} \right)^\alpha \ \ (15)\]对于4种中碳低合金高强度钢, \(\beta = 3.09 - 0.12\log N_{\rm f} \((内部夹杂或缺陷) 或\)\beta = 2.79 - 0.108\log N_{\rm f} \((表面夹杂或缺陷), \)area_{{\rm In}}\(为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\). 式 (15)和式 (14) 对疲劳强度的预测结果与实验结果比较表明, 引入疲劳寿命影响的式 (15) 给出了较好的预测结果 (Wang et al. 1999 ). ...
Ultrasonic fatigue
1
1980
... Willertz (1980) 的文章综述了20世纪50 \(\sim\) 70年代采用超声频率进行疲劳实验研究的情况. 随后, 1981年在美国召开了第一届"直至超声频率的疲劳和腐蚀疲劳"学术会议, 并以"超声疲劳"为题出版了论文集 (Wells et al. 1982 ).在该文集所收集的40篇论文里, 约有1/4论文的实验结果涉及疲劳断裂周次在107 以上直至1010 , 但这些研究并未关注107 周次之后疲劳性能和机理的变化. 注意到Tien (1982) 在该会上的Keynote综述报告的结论里提到"超高周疲劳数据(very high cycle fatigue data)". ...
Ultrasonic fatigue//Proceedings of the First International Conference on Fatigue and Corrosion Fatigue up to Ultrasonic Frequencies, The Metallurgical Society of AIME
1
1982
... Willertz (1980) 的文章综述了20世纪50 \(\sim\) 70年代采用超声频率进行疲劳实验研究的情况. 随后, 1981年在美国召开了第一届"直至超声频率的疲劳和腐蚀疲劳"学术会议, 并以"超声疲劳"为题出版了论文集 (Wells et al. 1982 ).在该文集所收集的40篇论文里, 约有1/4论文的实验结果涉及疲劳断裂周次在107 以上直至1010 , 但这些研究并未关注107 周次之后疲劳性能和机理的变化. 注意到Tien (1982) 在该会上的Keynote综述报告的结论里提到"超高周疲劳数据(very high cycle fatigue data)". ...
W\"{o}hler's experiments on the strength of metals
2
1867
... 人类对金属疲劳的研究起始于19世纪中叶 (W\"{o}hler 1867 ), 疲劳早已成为力学与材料科学相交融的分支学科之一. 超高周疲劳研究的萌发, 给这一古老的分支学科注入了崭新的内涵. 超高周疲劳即是对传统疲劳理念的挑战, 也是对传统疲劳领域的拓展, 使疲劳研究领域包含低周疲劳、高周疲劳和超高周疲劳三个部分. ...
... 值得回味的是, 在疲劳研究的起始, 关注的问题是火车车轴的疲劳断裂(W\"{o}hler 1867 ); 一个半世纪后, 当年时速10 km的蒸汽机车已经发展到如今时速300 km以上的高铁, 其车轴全寿命周期的载荷周次为109 量级, 超高周疲劳仍被认为是高铁车轴的第一个难点和不可确定的问题 (Zerbst et al. 2013 ). ...
Estimation of the size of GBF area on fracture surface for high strength steels in very high cycle fatigue regime
1
2008
... 对于钢, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 5.54} {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与文献实验结果 (如Sakai et al. 2002 , Ochi et al. 2002 , Shiozawa et al. 2006b , Yang et al. 2008 , Zhao et al. 2011 , Lei et al. 2012 ) 得到的\(4\sim 6 {\rm MPa} \cdot{\rm m}^{{\rm 1 / 2}}\)相符合. ...
Competition mechanism between microstructure type and inclusion level in determining VHCF behavior of bainite/martensite dual phase steels
1
2011
... Yu等 (2011) 对6组贝氏体/马氏体高强钢的研究表明超高周疲劳裂纹萌生于试样内部, 裂纹源可以是非金属夹杂物, 也可以是基体, 两种起源模式相互竞争.这一竞争与材料加工所经历的金属物理和金属化学过程有关; 金属物理方法使微结构均匀化、细化和强韧化, 而金属化学方法控制了非金属夹杂物的尺度和分布.只有同时优化金属物理方法和金属化学方法才能改善材料的超高周疲劳性能. ...
Safe life and damage tolerance aspects of railway axles---A review
1
2013
... 值得回味的是, 在疲劳研究的起始, 关注的问题是火车车轴的疲劳断裂(W\"{o}hler 1867 ); 一个半世纪后, 当年时速10 km的蒸汽机车已经发展到如今时速300 km以上的高铁, 其车轴全寿命周期的载荷周次为109 量级, 超高周疲劳仍被认为是高铁车轴的第一个难点和不可确定的问题 (Zerbst et al. 2013 ). ...
The fatigue behavior and mechanism of FV520B-I with large surface roughness in a very high cycle regime
0
2016
Prediction of threshold value for FGA formation
4
2011
... 笔者 (Zhao et al. 2011 , 2012 ) 对GCr15钢 (与SUJ2相似)的若干强度状态分别进行旋转弯曲和超声轴向振动加载, 得到FGA对应的\(\Delta K\)值范围同样在4 \(\sim \) 6 MPa\( \cdot \)m\(^{1 / 2}\) (图31 ). 进一步地, 图32 (Hong et al. 2014 )汇集了我们和诸多其他研究者关于高强钢超高周疲劳FGA的结果, 表明绝大多数FGA尺度在15 \(\mu \)m至100 \(\mu \)m之间, 该尺度随加载应力减小而增大, 即循环应力越小, FGA发展的尺度越大, 对应的疲劳寿命越长. FGA裂纹尺度与加载应力可由应力强度因子关联, 即式 (6). 这样, 在图32 中标出了\(\Delta K_{\rm FGA} = 4 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)和\(6 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)的等值线, 显示绝大多数数据都被包络在这两条等值线范围内. 这一结果表明, \(\Delta K_{\rm FGA} \)是超高周疲劳裂纹萌生的一个稳定特征参量.从而我们明确提出FGA是超高周疲劳裂纹萌生的基本特征区 (Hong et al. 2014 ), 对应的\(\Delta K_{\rm FGA} \)即为裂纹萌生阈值\(\Delta K_{{\rm th}} \). 对于超高周疲劳过程, 这一特征区具有本征存在性. ...
... FGA和夹杂物对应的应力强度因子幅值与疲劳寿命的关系 (Zhao et al. 2011 ) ...
... FGA裂纹属短裂纹范畴, 其扩展受材料微结构尺度制约.因此笔者分析了FGA裂尖塑性区与材料微结构尺度的关系 (Zhao et al. 2011 , 2012 ). 对于平面应变I型裂纹, 裂尖塑性区尺度\(r_{\rm p}\)的表达式为 (Hertzberg et al. 2012 )\[r_{\rm p} = \dfrac{\left({1 - 2\nu } \right) ^2}{\pi }\left( {\dfrac{\Delta K}{\sigma_{\rm y} }} \right)^2 \approx \dfrac{1}{6\pi }\left({\dfrac{\Delta K}{\sigma _{\rm y} }} \right)^2 \ \ (7)\] 式中, \(\nu \)是泊松比, \(\sigma _{\rm y}\)是屈服强度. 另一方面, 材料微结构特征尺度\(l_{\rm m}\)与材料基本力学性能有如下关系 (Nix& Gao 1998 )\[l_{\rm m} = b\left( {\mu / \sigma _{\rm y} }\right) ^2 \ \ (8)\] 式中, b为材料柏氏矢量模, \(\mu\)为材料剪切模量. 假定当FGA裂尖塑性区尺寸与材料微结构特征尺度相等, FGA裂纹终止发展. 这样\( \Delta K_{\rm FGA} = \mu \sqrt {\pi b} =4.342\mu \sqrt { b} \ \ (9)\)\( 式 (9) 表明, 超高周疲劳裂纹萌生特征区FGA对应的特征参量\(\Delta K_{\rm FGA}\)可简单表达为材料剪切模量和柏氏矢量的函数. ...
... 对于钢, 由式 (9) 算得\(\Delta K_{\rm FGA} \)为\({\rm 5.54} {\rm MPa}\cdot {\rm m}^{{\rm 1 / 2}}\), 这与文献实验结果 (如Sakai et al. 2002 , Ochi et al. 2002 , Shiozawa et al. 2006b , Yang et al. 2008 , Zhao et al. 2011 , Lei et al. 2012 ) 得到的\(4\sim 6 {\rm MPa} \cdot{\rm m}^{{\rm 1 / 2}}\)相符合. ...
Effects of strength level and loading frequency on very-high-cycle fatigue behavior for a bearing steel
2
2012
... 笔者 (Zhao et al. 2011 , 2012 ) 对GCr15钢 (与SUJ2相似)的若干强度状态分别进行旋转弯曲和超声轴向振动加载, 得到FGA对应的\(\Delta K\)值范围同样在4 \(\sim \) 6 MPa\( \cdot \)m\(^{1 / 2}\) (图31 ). 进一步地, 图32 (Hong et al. 2014 )汇集了我们和诸多其他研究者关于高强钢超高周疲劳FGA的结果, 表明绝大多数FGA尺度在15 \(\mu \)m至100 \(\mu \)m之间, 该尺度随加载应力减小而增大, 即循环应力越小, FGA发展的尺度越大, 对应的疲劳寿命越长. FGA裂纹尺度与加载应力可由应力强度因子关联, 即式 (6). 这样, 在图32 中标出了\(\Delta K_{\rm FGA} = 4 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)和\(6 {\rm MPa} \cdot {\rm m}^{{\rm 1 / 2}}\)的等值线, 显示绝大多数数据都被包络在这两条等值线范围内. 这一结果表明, \(\Delta K_{\rm FGA} \)是超高周疲劳裂纹萌生的一个稳定特征参量.从而我们明确提出FGA是超高周疲劳裂纹萌生的基本特征区 (Hong et al. 2014 ), 对应的\(\Delta K_{\rm FGA} \)即为裂纹萌生阈值\(\Delta K_{{\rm th}} \). 对于超高周疲劳过程, 这一特征区具有本征存在性. ...
... FGA裂纹属短裂纹范畴, 其扩展受材料微结构尺度制约.因此笔者分析了FGA裂尖塑性区与材料微结构尺度的关系 (Zhao et al. 2011 , 2012 ). 对于平面应变I型裂纹, 裂尖塑性区尺度\(r_{\rm p}\)的表达式为 (Hertzberg et al. 2012 )\[r_{\rm p} = \dfrac{\left({1 - 2\nu } \right) ^2}{\pi }\left( {\dfrac{\Delta K}{\sigma_{\rm y} }} \right)^2 \approx \dfrac{1}{6\pi }\left({\dfrac{\Delta K}{\sigma _{\rm y} }} \right)^2 \ \ (7)\] 式中, \(\nu \)是泊松比, \(\sigma _{\rm y}\)是屈服强度. 另一方面, 材料微结构特征尺度\(l_{\rm m}\)与材料基本力学性能有如下关系 (Nix& Gao 1998 )\[l_{\rm m} = b\left( {\mu / \sigma _{\rm y} }\right) ^2 \ \ (8)\] 式中, b为材料柏氏矢量模, \(\mu\)为材料剪切模量. 假定当FGA裂尖塑性区尺寸与材料微结构特征尺度相等, FGA裂纹终止发展. 这样\( \Delta K_{\rm FGA} = \mu \sqrt {\pi b} =4.342\mu \sqrt { b} \ \ (9)\)\( 式 (9) 表明, 超高周疲劳裂纹萌生特征区FGA对应的特征参量\(\Delta K_{\rm FGA}\)可简单表达为材料剪切模量和柏氏矢量的函数. ...
An energy-equilibrium model for complex stress effect on fatigue crack initiation. Science China Physics,
2
2014
... 此外, Zhao 等 (2014) 基于Tanaka-Mura位错累积疲劳损伤模型, 通过引入弹性能释放项, 给出了一个考虑能量平衡的疲劳微观模型. 图69 显示了模型给出的拉压疲劳等寿命图并与Goodman, Gerber关系的对比. 由于存在II型裂纹开裂的弹性能释放, 在较高的压缩平均应力作用下, 疲劳裂纹可以形核.平均应力与应力幅的比值存在一个临界值\(-0.17\), 当该比值小于临界值时, 随平均压应力的增大, 疲劳形核寿命下降. ...
... 能量平衡模型给出的等寿命图与Goodman关系和Gerber关系比较(Zhao et al. 2014 ) ...
Probabilistic fatigue S-N curves including the super-long life regime of a railway axle steel
1
2009
... 近20年来, 陆续有研究报道了针对高强钢超高周疲劳寿命或疲劳强度的预测模型, 如Murakami等 (Murakami & Usuki 1989 , Murakami et al. 1999 ), Harlow等 (2006) , Zhao 等 (2009) , Sun等 (2012 , 2013 ), Stepanskiy(2012) , 其中, Murakami等 (1999) 的模型较有影响.该模型认为材料内部的缺陷 (如夹杂、孔洞等) 均可看成小裂纹, 从而导出反映材料缺陷尺度影响的疲劳强度预测公式 \[ \sigma _w = \dfrac{C({ H}v + 120)}{\left( {\sqrt {area} } \right)^{1 /6}}\left( {\dfrac{1 - R}{2}} \right)^\alpha \ \ (14)\]式中, Hv为材料的硬度 (kgf\(\cdot \(mm\)^{ - 2})\), area为缺陷在最大主应力垂直方向上的投影面积 \(\mu \(m\)^{2})\), \(\sigma _w \)为疲劳极限 (MPa), 系数C = 1.43 (对应表面夹杂或缺陷)或C = 1.56 (对应内部夹杂或缺陷), R为应力比, \(\alpha = 0.226 + Hv\times 10^{ - 4}\). 需指出, 式 (14)最初是针对107 周次的疲劳性能, 并没有引入疲劳寿命的影响. ...
Diversity of damage evolution during cyclic loading at very high numbers of cycles
2
2012
... 关于超高周疲劳研究已有2本专著 (Murakami 2002 , Bathias & Paris 2005 ) 和若干综述文章, 如: Sakai 2009 , 洪友士等2009 , Mughrabi (2010) , Li (2012) , Zimmermann (2012) , Stanzl-Tschegg(2014) , Mayer (1999 , 2016 ).本文将侧重就以上所列的4个关键科学问题对超高周疲劳的研究进展进行综合评述, 并主要以高强钢和钛合金为例 (具有典型的超高周疲劳特征, 相关内容丰富), 阐述合金材料超高周疲劳行为的特征、机理与模型. ...
... 诚然, 合金材料超高周疲劳的研究进展十分丰富, 不可毕其所有内容于一文, 例如, 下列这些内容本文未专门评述: (1) 高强钢超高周疲劳裂纹内部萌生主要由夹杂物起源, 但在某些情况, 裂纹也可以由非夹杂物起源, 如晶界等; 此外, 夹杂物的类型和尺度对裂纹萌生有影响. 本文在第5.2节和第5.4节中略有提到此方面的问题, 但未专门评述. 这方面的内容可参阅洪友士等(2009) 、Li等 (2012) 、Zimmermann (2012) 、Sander等 (2014) 文献. ...
Effect of microstructure on ultra-high cycle fatigue behavior of Ti-6Al-4V
1
2008
... 钛合金 (如Ti-6Al-4V) 的微结构包含hcp晶体结构的\(\alpha\)相和bcc晶体结构的\(\beta \)相; 这2种相的比例和形状决定了钛合金的微结构特征.钛合金基本不含夹杂物和孔洞缺陷. \(\alpha \)相的脆性特征明显, 超高周疲劳裂纹往往以\(\alpha \)相解理并呈现 facet 特征的方式起源.Zuo等(2008) 的结果表明, 在Ti-6Al-4V中, 对于双态组织形态, 超高周疲劳裂纹可萌生于\(\alpha _{\rm p}\)晶粒 (下标p表示初生)或\(\alpha _{\rm p}\)晶界, 对于网篮组织形态, 裂纹萌生于\(\alpha\)-\(\beta \)相界. Szczepanski等(2008) 的结果表明, 在Ti-6Al-2Sn-4Zr-6Mo合金中, 超高周疲劳裂纹萌生局域为\(\alpha _{\rm p}\)晶粒断裂而成的小解理面 (facet), 形成facet的\(\alpha _{\rm p}\)晶粒尺度对应于其平均值; 裂纹萌生局域的facet取向为高剪应力导向, 即与拉应力轴近似成45\(^\circ\). ...