1 引言
颗粒材料是复杂的颗粒无序堆积的系统, 在自然界、工程建设和工业生产中广泛存在, 比如碎屑流灾害、堆石坝、流化床以及球床反应堆等, 可呈现剪切带、临界自组织、弛豫、类固体--类流体转变和流变等丰富力学现象.颗粒物质是多体相互作用体系. 宏观上, 它各向同性、均匀, 但是, 介观上又存在颗粒尺度的结构不均匀和动力学不均匀性, 因此从基本理论到实验手段上表征与建立颗粒结构与性能的相关性都极其困难.结构表征是理解和认识颗粒材料重要力学问题的基础和依据, 基于统计力学, 从颗粒结构和动力学开始建立颗粒材料体系的宏观连续介质力学理论框架是必然途径. 但是现有测试分析手段所描述的颗粒系统的组织结构过于简单化, 还不能建立颗粒尺度上的无序性和其力学和物理性能的对应关系, 缺乏对颗粒组织结构的真正认识. 所以, 颗粒系统中颗粒结构和动力学研究是制约颗粒物质基础研究和材料发展的瓶颈, 长期以来, 颗粒材料的基础研究进展缓慢, 面临很多的困难和挑战.
颗粒材料基础研究的发展和实验技术的进步紧密相关.测量颗粒平移和转动等运动学量, 测量结构量的空间分布及其演变, 引入新的概念、理论方法、新思路, 比如短程序、局域对称性等新概念, 新的结构描述方法和结构模型等, 定性和定量分析它们对宏观力学现象的影响, 始终是颗粒材料重要研究内容. 另外, 研究者多年来建立了描述颗粒材料弹性、塑性和黏性的大量模型和理论, 现代大型计算机也为颗粒结构的模拟提供了强有力的手段, 实验测量结果将验证其合理性和有效性, 为颗粒材料基础研究提供科学依据. 由于颗粒较大 (约\(100 \mu {\rm m}\sim 10\) {cm})且往往不透明,常用的光学和声学等测量方法的原理简单, 需要结合颗粒特点做改进和校验, 才能进行三维颗粒体系的有效测量, 目前针对颗粒的测量手段和分析能力依然非常有限.比如,光学技术(数字图像和透视技术)、核磁共振技术(MRI)和\(\mu \)-CT技术很难对颗粒三维运动进行高时间、高空间分辨率的测量; 光弹技术是测量片状颗粒位置及接触力的直观手段, 但是无法清晰显示三维颗粒体系的位置和接触力.内耗技术、动态力学分析仪(DMA)和声学谱等技术所测得的能量耗散和模量等都是宏观量, 这些物理量及其变化反映了内部发生的微观事件, 需要建立两者之间的联系.
近十年来, 笔者开展了颗粒结构和动力学性质的测量研究, 不断有表征颗粒尺度的结构和性能及其相关性的独特的实验技术被发展出来, 见表1 , 这些方法可以分为两类, (1)数字图像测速法、散斑能见度光谱法和X射线- CT等非侵入式测量技术在颗粒运动方面的应用, 这些工作在第2, 3和4节中介绍; (2)体积响应谱、力学谱(有效质量和内耗等)和声速测量技术等直接或间接测量颗粒接触力和颗粒结构技术, 这些工作在第5节中介绍. 在本文中, 笔者综述了这些实验手段的基本原理及其局限性, 取得的主要成果, 以及国际最新进展和困难, 最后建议开展多种技术联合测量, 从多方面和多角度认识颗粒体系复杂力学性质, 才能更好地、系统地研究颗粒结构与动力学特征等基础问题.
2 数字图像测速法
简易的图像分析方法是利用相机记录实验过程中不同时刻表层颗粒的图像, 识别颗粒并确定位置, 进而计算速度等信息.改进的基于数字图像的颗粒流速测量法主要有: 粒子图像测速(particle image velocimetry, PIV)、粒子跟踪测速(particle tracking velocimetry, PTV)以及空间滤波测速法(spatial filtering velocimetry, SFV), 其中, PIV或PTV技术在颗粒流实验测量中的应用较为广泛.
2.1 粒子图像测速技术(PIV)和粒子跟踪测速技术(PTV)
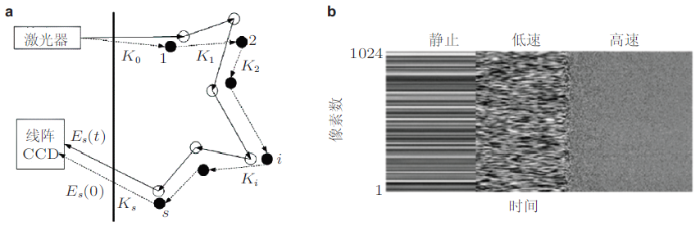
图1 所示为PIV技术原理图, 双脉冲激光经过柱面镜形成片光源, 照射在散布于颗粒流中的稀疏示踪粒子(近似一个点), 与脉冲激光同步的高速相机对粒子拍摄得到连续的双脉冲成像图, 再对双脉冲成像图中颗粒位移的相关性进行计算, 得到流场的分布(Adrian 2005 , Lueptow et al. 2000 ). 设粒子像点的光强度分布为\(I\left( \bar{x} \right)\), 它的自相关为 \[R\left( S \right) = \int {I\left(\bar {x} \right)I\left( {\bar {x} + \pmb s } \right)}{\rm d}x \ \ (1)\] 式中, \(\pmb s \)为二维位移矢量. \(\pmb s = 0\)代表每个像点自相关, 得到峰值\(R_{P}\). \(\pmb s\)等于诊断点内平均位移量, 出现第二个强的峰值\(R_{D}^{ + }\), 称为正位移峰值, 其物理意义为第一次光脉冲形成的粒子像和第二次光脉冲形成的粒子像重叠.同样会出现相同的峰值\(R_{D}^{ - }\), 称负位移峰值, 即第二次光脉冲形成的粒子像和第一次光脉冲形成的粒子像重合.假设原点峰值\(R_{P}\)的位置和正位移峰值\(R_{D}^{ +}\)的位置之间的位移矢量为\(\pmb S _D^ + \), 得到粒子像点的速度为\[\pmb V = \dfrac{\pmb S _D^ + }{M\Delta t} \ \ (2)\] 其中, \(M\)为系统放大倍数, \(\Delta t\)为曝光时间间隔.
PIV技术测量三维空间体内完整速度场是近年来的研究热点.研究曾尝试采用离焦成像、多视角成像和全息成像等方法通过对示踪粒子进行三维空间定位, 实现粒子追踪测速. 受粒子浓度的限制, 空间分辨率并不理想, 直到层析PIV概念的提出, 才使得三维PIV测量技术真正进入了实用阶段(Gao et al. 2013 ), 该技术通过三维互相关分析来得到具有较高空间分辨率的速度场, 实现了在较高粒子浓度下的测量. 三维PIV的核心技术包括粒子重构和速度场再现技术, 前者采用了医学领域光学层析技术中基于投影方法的代数重构技术, 后者采用三维互相关分析算法(Gao et al. 2011 , Percin et al. 2011 , Tang et al. 2012 ).
爱丁堡大学Rix等首次用PIV技术测量了鼓泡流化床中颗粒随气泡飞出时的速度场分布(Rix et al.1996 ), 但他们只是沿用了传统PIV的测量系统和算法(采用片激光光源和互相关算法), 没有针对密集颗粒体系的特点进行改进, 无法测量流化床中密集颗粒体系的速度分布.密集颗粒体系的一个特点是颗粒间隙小且互相遮挡, 激光无法在颗粒体系间传播, 因此测量密集颗粒体系的PIV系统一般不再采用片激光作为光源, 而是将激光束扩束或者采用多个直流卤素灯作为光源直接照射在待测颗粒流表面(Bokkers et al.2004 , Hagemeier et al. 2015 ).密集颗粒体系的另一个特点是速度场分布的梯度范围非常大, 如鼓泡流化床中气泡附近颗粒的速度梯度变化极大, 而在其他区域颗粒的位移几乎为零, 导致传统互相关算法的准确性大幅下降. 针对这一问题, 清华大学姚强课题组提出了一种改进PIV算法, 在梯度变化率不同的区域, 使用不同的互相关窗口(interrogation window, IW)和帧速率, 从而有效提高了系统的准确性(Liu et al. 2008 , Lim et al. 2007 , Hagemeier et al. 2015 ).
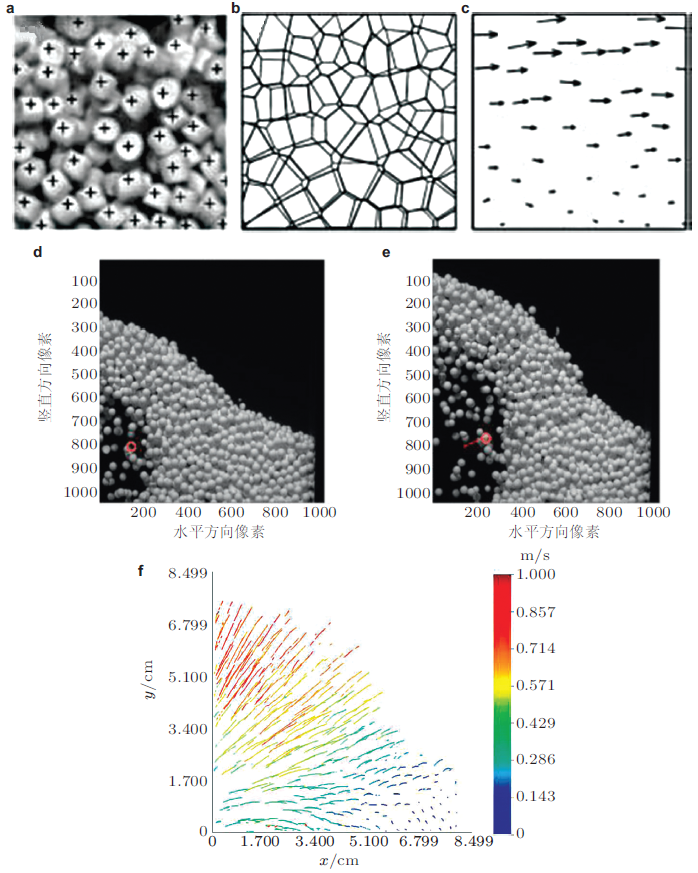
由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布.
图2 基于沃罗诺伊图的PTV测量结果(Hagemeier et al. 2015 ).(a)将颗粒中心以\(+\)表示其位置\(r_i \); (b)粗线表示以图(a)中颗粒位置为基础构成维诺网络, 细线表示下一帧中颗粒位置形成的沃罗诺伊图; (c)以沃罗诺伊图为基础匹配颗粒点, 得到了两帧之间的颗粒位移; (d)0.001 s 时刻颗粒位置; (e) 0.019 s 时刻颗粒位置; (f)通过连续20帧图像计算得到的轨迹分布
另外一种拓展的PTV法是通过测量一定曝光时间下的粒子光学轨迹长度, 进而计算出颗粒的运动速度(Orpe & Khakar 2007 ). 如图3 所示, 通过调节相机的增益和曝光时间得到颗粒的运动轨迹图, 然后对原始条纹(图3 (b))做二值化变换, 再用公式(3)对二值化图像(图3 (c))中的每个条纹进行拟合, 得到条纹灰度的分布函数\[I_{\rm th} = \left\{ {\begin{array}{l} C{\rm e}^{ - \bar {y}^2 / 4w^2,} \\ C{\rm e}^{[ - \bar {y}^2 - (\bar {x} - l)^2] / 4w^2,} \end{array}} \right.\begin{array}{l} \left| \bar {x} \right| \leq l \ \left| \bar {x} \right| > l \end{array} \ \ (4)\] 其中, \(\bar {x} = (X - X_C )\cos \theta + (Y - Y_C)\sin \theta \), \(\bar {y} = (Y - Y_C )\cos \theta + (X - X_C )\sin\theta \). \(\theta \) 为条纹与水平方向夹角, \(C\)为条纹的最大灰度值, \(X_{C}\)和\(Y_{C}\) 为条纹中心坐标. 计算得到速度\[v = {2L(l,w)} /{\Delta t} \ \ (5)\] 其中, \(L(l,w) = a_1 l + a_2w\) 通过对条纹长度\((2l)\)和宽度\((2w)\)线性拟合得到.拓展PTV法的优点是不需要高速相机和脉冲激光, 因此成本低、实时性强、操作简便, 但其精度和处理复杂流动的能力尚未得到认可, 目前还不是主流技术.
图3 拓展PTV法测量原理图(Orpe & Khakar 2007 ). (a)2 mm不锈钢球在准二维滚内连续流动图例(转速: 3 r\( \cdot \)min\(^{ -1})\), (b)颗粒轨迹条纹(streak), (c)颗粒轨迹条纹二值化图像, (d)用公式(4)对图(b)条纹进行拟合后的结果
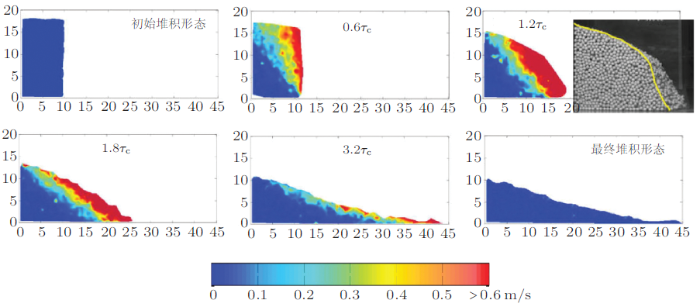
运动中的颗粒材料可能存在多种流态及其相互间复杂的转换过程, 例如, 土体边坡失稳、山体滑坡和泥石流的发生, 就是颗粒介质由固态转化为流态的复杂流变现象. 从理论上而言, 颗粒介质弹性失稳机理、不可恢复应变量化是研究颗粒材料固态和流态及固--流态转变的关键.在颗粒堆积体坍塌过程中, 体系依次经历了从静态堆积、失稳流动再到堆积的力学阶段, 是典型的颗粒介质固态与液态相互转换的过程.清华大学孙其诚课题组开展了25 167个陶颗粒堆积体坍塌过程的实验研究, 采用PTV技术测量了颗粒堆坍塌过程中的形态、速率大小分布等, 如图4 所示. 与此同时, 在颗粒堆底部铺设Tekscan薄膜压感器, 它是由美国Tekscan公司生产的一款接触式测量压力分布装置, 可以动态测量颗粒堆底部压力分布, 最大测量频率为200 Hz (Liu et al. 2011 ). Xu 等(2016)测量并确定了颗粒平均速率与体系体积分析、平均速率与底部压力的关系.
图4 颗粒堆塌落过程中的速率分布. 流动特征时间\(\tau _{\rm c}= \sqrt {{h_0 }/g} \), 其中\(h_{0}\)是颗粒堆初始高度, \(g\)是重力加速度; 速率大小用颜色表示.颗粒堆初始高度、厚度和长度分别为\(180 {\rm mm}\times 200 {\rm mm}\times 100 {\rm mm}\). 插图是时间\(1.2\tau_{\rm c} \) 时拍摄的颗粒堆(Xu et al. 2016 , 费明龙 等 2016 )
PIV和PTV技术的时空分辨率主要由高速相机决定, 其最大的优势在于不仅能追踪到单个颗粒的运动, 而且可以获得全场颗粒速度和加速度, 是目前应用最广泛的一种速度场测量方法.在测量密集颗粒体系时, 其局限性主要是图像中的待测颗粒必须能被有效识别, 才能进行后续计算, 因此适合测量颗粒流表面或二维颗粒流的速度场, 且不能测量小颗粒或不规则颗粒等图像无法有效识别的颗粒体系.
2.2 空间滤波测速技术(SFV)
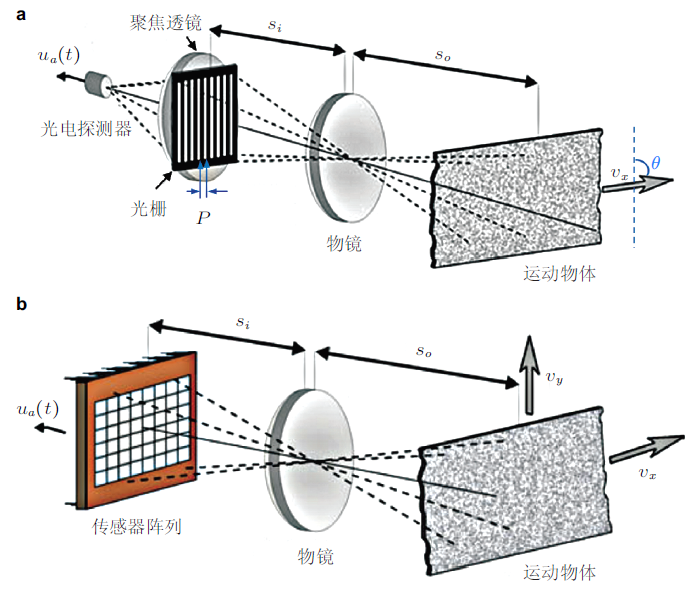
对于数字图像技术无法有效识别的小颗粒或不规则颗粒流, 可采用SFV技术测量其速度场(Aizu & Asakura 1987 ). 如图5 (a)所示, 采用对空间频率具有一定选择作用的栅格式空间滤波器, 被测运动物的像经过透镜成像在空间滤波器上, 经空间滤波器调制后再由聚焦透镜会聚到光电探测器上, 光电探测器输出周期性变化的正弦信号, 信号的中心频率\(f\)与物体的运动速度\(v\)满足如下关系\[v = \dfrac{pf}{M\sin \theta } \ \ (6)\] 其中, \(p\)为空间狭缝的空间周期, \(M\)为光学系统放大倍数, \(\theta\)为平行光栅中轴与运动物体速度的夹角.
图5 SFV系统原理图. (a)栅格式SFV系统, (b)传感器阵列SFV系统
实现空间滤波的方法有多种, 较早的空间滤波器是由如图5 (a)所示平行狭缝组成的光栅, 这种结构存在加工精度要求大, 空间周期不能调整, 且只能测量垂直于狭缝方向的运动速率等问题. 为了解决这一问题, 人们提出了利用传感器阵列实现空间滤波功能的光电探测器(如图5 (b)).Itakura 等 (1981) 利用一个液晶元件阵列构建了一种新型的空间滤波器, 并实现了二维速度分量的测量. 此后Kitagawa 等(1991)利用光纤阵列构建了一种空间滤波器, 有效简化了系统并提高了测量精度.但传感器或光纤阵列也存在分辨率较低, 安装调试困难, 传感器性能一致性差等问题.近年来, 随着光电技术及工业制造技术的发展, 传统的光栅和光电探测器阵列结构逐渐被线阵或面阵CCD/CMOS相机所取代. 如, Bergeler 和 Krambeer (2004) 对面阵CMOS相机像素在两个正交方向进行分组, 模拟空间滤波器件的功能, 实现了二维速度分量的测量, 并通过实验测量了毛细管中血流速度分布情况. 这种系统不仅结构简单, 性能稳定, 且可以通过软件调整空间周期, 提高空间滤波器用于速度测量的选择性, 测量精度高.另外, 还有采用静电传感阵列的空间滤波测量法(Xu et al. 2009 , Li et al. 2014 ), 该方法能够获得敏感区域内颗粒运动平均速度信息, 在一定程度上实现了对颗粒体系局部平均速度的测量.
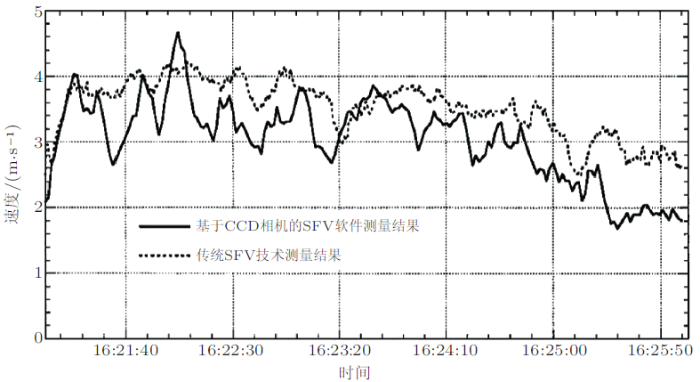
目前, SFV技术主要用于两相流的测量, 比如Petrak(2002) 采用基于光纤传感阵列的SFV技术测量了两相流中颗粒的大小和速度, Fiedler等(1997) 用基于CCD的空间滤波器测量了循环流化床中局部颗粒速度分布, Hosokawa等(2013) 采用SFV技术测量了鼓泡流化床中泡状流的泡沫速度, 并通过与PTV测量结果的比较, 发现在一定程度上SFV技术优于PTV技术.在密集颗粒流测量方面, Uddin等首次将SFV技术应用于泥石流表面速度的测量(Uddin et al.1998 ), 并对比了传统SFV技术和基于CCD相机的软件SFV的测量结果(如图6 所示), 发现两者结果基本一致, 而基于CCD相机的SFV技术结构更简单, 成本更低.
图6 传统的硬件SFV技术和基于CCD相机的软件SFV技术测得的泥石流表面速度比较(Uddin et al.1998)
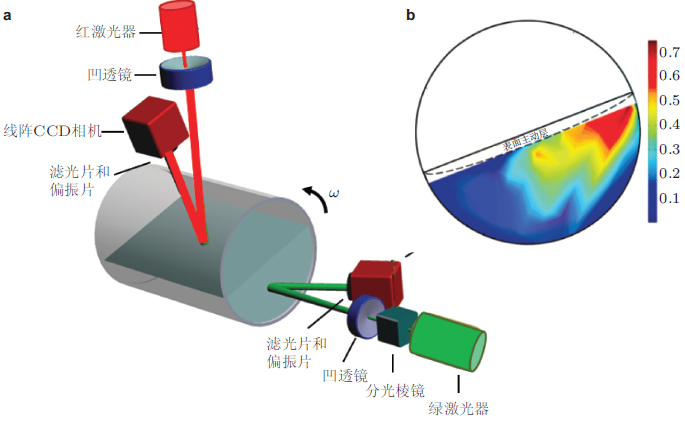
上海理工大学杨晖课题组针对密集颗粒流的特点, 提出了多种频谱校正和提取算法, 改进了基于线阵CCD空间滤波的颗粒运动速度测量系统(Gong et al. 2017 ), 并采用图7 (a)所示的滚筒实验装置进行了测试. 实验发现, 由于密集颗粒体系中颗粒的无序运动, 导致输出信号中掺杂有多种频率的干扰信号, 图7 (b)和图7 (c)所示分别为电机传送带(用于SFV标定)和滚筒内颗粒流表面的空间滤波信号频谱图, 可以明显看到, 电机传送带的空间滤波信号频谱具有非常确定的峰值, 而颗粒流信号的频谱图的噪声干扰非常严重, 为了准确得到信号峰值, 他们提出了采用平均重心法进行频谱校正, 进而提取中心频率的方法.并通过测量滚筒内不规则玻璃砂和小直径玻璃珠表层沿径向颗粒流速度分布进行了验证.从图7 (d)显示的玻璃珠和玻璃砂的速度分布曲线可以看到, 玻璃珠的速度分布呈现中间高两头低的对称分布, 这与理论分析以及大颗粒用PIV测量的先加速后减少结果一致(GDR MiDi 2003 ).而对于玻璃砂, 一方面在相同的滚筒转速下, 其速度值始终大于玻璃珠的速度值, 这一结果与玻璃砂的休止角较大, 因此动能较大的结果一致(Dub\'{e} et al. 2013 , Yang et al. 2017 ); 另一方面, 玻璃砂的速度分布呈现两次加速减速的过程, 这一结果与玻璃砂崩塌过程中速度变化类似, 原因是由于不规则颗粒在滚落过程中会在斜面中间形成一次小的堆积, 然后产生二次滚落(Yang et al. 2017 ).
图7 SFV测量滚筒内玻璃珠和玻璃砂的流动速度(Gong et al. 2017 ). (a)滚筒实验系统示意图, 滚筒直径15 cm, 转速为5.2 RPM; (b)电机传送带和 (c)滚筒内颗粒流表面的空间滤波信号频谱; (d)滚筒内玻璃砂\((\nabla )\)和玻璃珠\((\bigcirc )\) (颗粒粒度:1 \(\sim\) 1.5 mm)沿径向\((x\)方向)速度分布
综上所述, SFV技术的优势是无需识别颗粒, 对测量对象几乎没有要求(只要能反光, 且有一定的对比度变化), 结构简单, 光学及机械性能的稳定性好, 因此适用范围广.其不足之处就是, 相对于其他测速法(PIV和激光多普勒等), 由于颗粒的无序运动对空间滤波信号频谱影响较大, 导致其测量分辨率较低、精度较差, 因此, 不适用于高精度测量. 此外, 目前商业化的SFV仪器只能测量一维的速度分布(即与线阵CCD平行方向的速度分布), 采用高速面阵相机测量二维颗粒流速度场分布是SFV技术下一步研究的主要方向.
3 散斑能见度光谱法测量颗粒温度
颗粒介质的一个典型特征是能够对其外部扰动产生强烈的非仿射响应.当对晶体材料施加变形时, 它趋向于仿射地遵循宏观应变.而对颗粒材料施加变形时, 由于缺乏局部反转对称性, 每个颗粒除了产生一个仿射应变之外, 还产生一个附加的非仿射位移.并且, 颗粒的非仿射重排倾向于局部化, 但是对于导致这一过程的结构缺陷非常难以识别. Manning 和 Liu(2011) 提出了利用模式分析手段识别颗粒系统结构缺陷的方法, 即定义动力学矩阵频谱内前 \( N_m^\ast \)个最低频模式中的前\( N_p^\ast\) 个极化矢量最大的颗粒为软点(其中参数\(N_m^\ast \) 和\(N_p^\ast \)具有非常明确的物理意义, 对应于软点的能量尺度和长度尺度), 由这些软点组成的区域为软区(soft spots), 该工作为基于介观软区动力学行为的静态颗粒材料的宏观塑性理论铺平了道路.在实验测量方面, 由于颗粒无序运动的持续时间极短(微秒级), 位移极小(微米级), 需要足够高的时间和空间分辨率的技术来测定颗粒非仿射响应速度.
1905年, 爱因斯坦认为颗粒无序运动与微观粒子热运动有相似性; 直至1978年, Ogawa首次提出了颗粒温度 (granular temperature, \(T_{g})\)概念表征颗粒运动速度的无序程度, \(T_g \equiv\dfrac{1}{3}\left\langle {\left( {\delta v} \right)^2}\right\rangle \), 其中\(\delta v = v - \left\langle v \right\rangle\) 是颗粒脉动速度, \(\left\langle { \cdots} \right\rangle \)表示系综平均. 40多年以来, 以颗粒温度为核心概念, 建立了适用于稀疏颗粒流的颗粒动理学理论 (granular kinetics), 得到了稀疏颗粒流的黏滞系数和能量耗散等的解析表达, 但是颗粒温度的实验精细测量还缺乏. 散斑能见度光谱法(speckle visibility spectroscopy, SVS)测量颗粒温度是通过计算一定曝光时间内单幅散斑图像的对比度得到散斑的变化快慢, 进而得到颗粒流的速度脉动信息 (Dixon & Durian 2002 , Bandyopadhyay et al. 2005 ). 由于散斑图像是基于散射光场干涉的原理, 因此其空间分辨率可达到0.1 \(\mu \)m. 另一方面, 由于其采用线阵CCD相机测量散斑对比度变化, 因此其时间分辨率可达到1 \(\mu \)s.
SVS技术是在扩散波光谱(diffusing wave spectroscopy, DWS)技术上发展起来的(Pine et al. 1988 ), 其原理如图8 (a)所示, 激光经过凹透镜扩束后照射在密集的颗粒样品表面, 一部分光子在颗粒间多次散射后从入射反方向离开, 在CCD相机感光面上形成散斑. 当散射区域内颗粒发生运动时, 光子的光程就会发生变化, 从而引起散斑图像产生变化, 称为"动态散斑"或"时变散斑", 并且散斑的变化速率与颗粒的脉动速度有关. 图8 (b)显示了不同脉动速度下线阵CCD相机检测的颗粒流散斑图像随时间变化, 可以看到在一定曝光时间下, 散斑图像的对比度随颗粒脉动速度的增大而降低. 根据统计光学理论, 散斑图像的对比度\[V_2 (T) = \left( {\dfrac{\sigma _T }{\left\langle I \right\rangle_T }} \right)^2 = \dfrac{\left\langle {I^2} \right\rangle _T}{\left\langle I \right\rangle _T^2 } - 1 \ \ (7)\] 其中, \(I\)为散射光强, \(T\)为曝光时间, \(\left\langle I \right\rangle _T \)和\(\sigma _T ^2\) 分别为光强的均值和方差.结合高斯光束的Siegert公式, 由式(7)可以得到\[V_2 (T) = \beta \int_0^T {2(1 - t/T)} [g_1 (t)]^2{{\rm d}t}/T \ \ (8)\] 其中, \(\beta \) 为光学系统的相干因子, \(g_1 (t)\)为散射光场的自相关函数. 根据DWS理论, 后向散射光强的时间自相关函数\[g_1 (t) \approx \exp \left[ { - \gamma _0 k_0 \sqrt {\left\langle{\Delta r^2(t)} \right\rangle } } \right] = \exp \left[ { - 4\pi \sqrt {\left\langle {\left( {\delta v} \right)^2} \right\rangle }t / \lambda } \right] = \exp \left[ { - \varGamma t} \right] \ \ (9)\] 其中,\(\gamma _0 \)是一个与颗粒大小以及光学系统偏振态有关的常数. \(k_0 = {2\pi n}/\lambda \) 为散射矢量, \(n\)为空气折射率, \(\lambda \)为激光波长, \(\left\langle {\Delta r^2(t)} \right\rangle \)为颗粒系在两次测量间隔内的均方位移, 且与颗粒速度脉动具有\(\left\langle {\Delta r^2(t)} \right\rangle =\left( {\delta vt} \right)^2\)关系, \(\varGamma = {4\pi \delta v}/\lambda \) 称为自相关函数\(g_1 (t)\) 的衰减频率.
图8 SVS测量系统原理图. (a) SVS系统中光子相干散射示意图, (b)不同脉动速度下线阵CCD相机检测的颗粒流散斑图像随时间变化
由式(7) \(\sim \) 式(9)得到散斑图像的对比度与颗粒脉动速度的关系\[V_2 (t) = \beta \dfrac{\exp \left( { - 2\varGamma T} \right) - 1 +2\varGamma T}{2\left( {\varGamma T} \right)^2} \ \ (10)\]理论上, 相干因子\(\beta \)可以通过先测量静态散斑的对比度计算出来, 在实际应用中由于\(\beta \)的测量重复性不佳, 因此一般通过公式(11)将1倍和2倍曝光时间下的对比度值相除, 从而消去\(\beta \), 再求解出\(\varGamma \), 最后计算得到颗粒温度\(T_g\equiv \dfrac{1}{3}\left\langle {\left( {\delta v} \right)^2}\right\rangle \).\[\dfrac{V_2 \left( {2T} \right)}{V_2 \left( T \right)} =\dfrac{\exp \left( { - 4\varGamma T} \right) - 1 + 4\varGamma T}{4\left[ {\exp \left( { - 2\varGamma T} \right) - 1 + 2\varGamma T} \right]} \ \ (11)\]
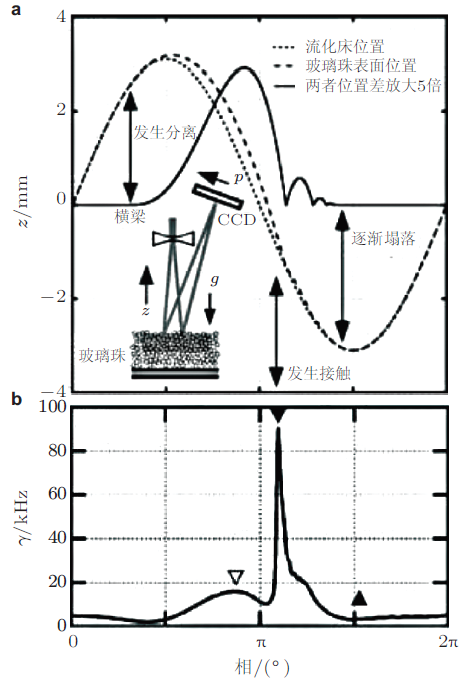
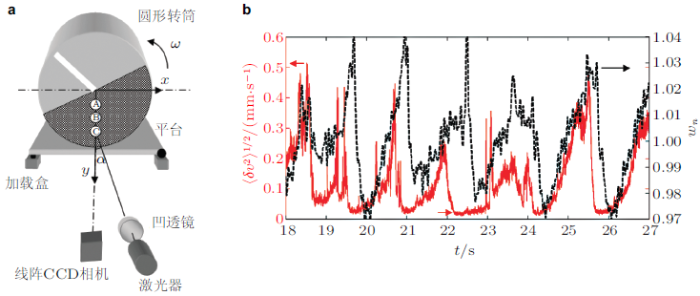
SVS法最早由美国宾夕法尼亚大学Durian团队提出用于测量振动流化床表层颗粒的运动(Dixon & Durian 2002 ), 如图9 所示在第一个1/4个周期, 玻璃珠随流化床一起以加速度\(1.25\sin \phi \cdot g\)上升, 玻璃珠间紧密挤压在一起, 颗粒温度几乎为0\(^{\circ}\)C; 在第二个1/4个周期, 流化床开始下降, 而玻璃珠由于惯性继续上升一段距离后开始下降, 在此过程中玻璃珠速度加快, 颗粒温度升高, 并在接近1/2周期时, 达到峰值(图9 (b)中空心三角处); 在第三个1/4个周期, 随着玻璃珠掉落到流化床上并互相碰撞, 颗粒温度形成一个尖峰; 此后随着玻璃珠再次堆积在流化床上, 颗粒温度逐渐下降, 并在最后一个1/4个周期趋于0. 此后, Durian团队进一步对该技术进行了完善, 将其用于泡沫(foam)和胶体(colloidal suspension)等研究(Gittings & Durian 2008 , Le et al. 2012 , Ianni et al. 2006 ).
图9 正弦垂直震荡流化床中玻璃珠的颗粒温度(Dixon & Durian 2002 ). (a)正弦震荡周期内流化床和玻璃珠层面的位置, 以及两者差的5倍, 最大加速度是1.25\(g\), 震荡周期10 Hz; (b)正弦震荡周期内颗粒温度变化曲线, 其中\(\gamma = {4\pi \delta v}/ \lambda \)
图10所示为Katsuragi 等(2010) 利用SVS技术和PTV技术测量准二维沙堆崩塌过程中颗粒速度\(v_x\)和颗粒脉动速度\(\delta v\)随深度变化, 从图10 (b)可以看到, 当深度大于0.6 cm, 颗粒脉动速度小于颗粒速度, 而当深度小于0.6 cm, 颗粒速度已经趋于0, 而颗粒脉动速度随深度衰减变慢, 颗粒间的挤压成为主导. 图10 (c)进一步显示\(\delta v\) 与\(\sqrt{v_x } \)在准二维沙堆的上半部分有较好的相关性.
图10 准二维沙堆崩塌过程中颗粒温度测量结果(Katsuragi et al. 2010 ). (a)准二维沙堆崩塌实验装置示意图, (b)崩塌过程中颗粒速度\(v_{x}\)和颗粒脉动速度\(\delta v\)随深度变化, (c)颗粒速度\(v_{x }\)与 颗粒脉动速度\(\delta v\)的关系
上海理工大学杨晖课题组较早将SVS技术应用于颗粒流研究(Yang et al. 2015 ), 图11 (a)所示为SVS技术测得滚筒内玻璃珠在崩塌模式下颗粒温度变化, 从图11 (b)的颗粒温度随时间变化可以看到, 玻璃珠的崩塌呈现明显的周期性, 进一步统计分析也证明了这种崩塌具有正态分布. 此外, 图11 (c)显示崩塌面的底部区域\((\bigcirc\!\!\!\!\!{\footnotesize\rm B}\)处)的颗粒温度高于顶部区域\((\bigcirc {\footnotesize\rm A}\)处)的结果也与速度分布结果一致.
图11 SVS技术测量转筒中颗粒流在崩塌模式下表层不同位置颗粒温度随时间变化及其统计结果(Yang et al.2015). (a)实验系统结构图, (b)颗粒物质崩塌模式下颗粒温度随时间变化曲线, (c)崩塌过程中\(\bigcirc {\footnotesize\rm A}\)和\(\bigcirc {\footnotesize\rm B}\)区域的颗粒温度峰值\(\delta v_{\rm p} ^2\) 的统计分布
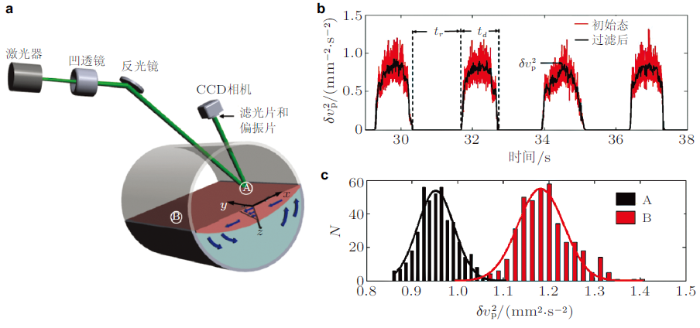
近期杨晖课题组提出了一种双SVS同步测量系统(图12 (a)) (Li et al. 2016 ), 对滚筒内颗粒流发生崩塌时, 表面主动层(active layer)和内部被动层(passive layer)的颗粒运动进行了测量, 首次通过实验测量了被动层的颗粒物质脉动速度分布(图12 (b)).
图12 转筒中颗粒流的双SVS同步测量系统(Li et al. 2016 ). (a)SVS测量转筒中颗粒流表层(主动层)和内部(被动层)的脉动速度, (b)颗粒流被动层颗粒脉动速度的空间分布
SVS技术还可以和其他技术结合, 从不同角度对颗粒物质的动力学特性进行同步测量研究. 图13 (a)所示为SVS技术与动态称重技术(测量颗粒物质崩塌过程中重力矩的变化)同步测量滚筒内不同黏性粉体的实验装置图(Yang et al.2016), 从图13 (b)可以看到, 颗粒脉动速度(红色实线)与黑色虚线下降段所示谷底颗粒材料重力矩高度吻合, 此时颗粒相对静止.
图13 SVS法与动态称重法同步测量滚筒内颗粒崩塌过程中的动力学特性(Yang et al. 2016 ). (a) 实验和测量装置, (b)颗粒脉动速度(红色实线)和重力矩(黑色虚线)随时间变化曲线
综上所述, SVS技术的优势在于其较高的时间分辨率(由线阵CCD相机的线速率决定, 最快可以到1 \(\mu \)s)和空间分辨率(1/4激光波长, 约0.1 \(\mu \)m), 并且与数字图像测速法不同的是, 散斑图像是光子在颗粒物质间多次散射后干涉的结果, 因此, SVS技术测量的是一定深度内(5到10层)的颗粒温度. 此外, 由于颗粒脉动速度和颗粒速度正相关, 因此SVS法还可以用于研究颗粒流态的瞬态、极小变化. 目前, 颗粒材料SVS法仍处于研发阶段, 其面临的难题在于如何对测量结果的准确性进行标定.一种比较可行的方案是, 对实验颗粒系统进行离散元模拟, 然后用图像测速法验证颗粒流表面的速度场仿真结果, 在此基础上计算颗粒体系的颗粒温度分布作为标准.
4 透视测速法
数字图像技术和激光散斑技术都只能测量颗粒流表面(数字图像技术)或一定深度内(SVS)的颗粒速度, 如果需要准确测量颗粒体系内部的颗粒运动速度, 就要采用可以透视的测量技术, 目前常用的方法有: 正电子发射颗粒跟踪(positron emission particle tracking, PEPT)、磁共振测速(magnetic resonance velocimetry, MRV)、以及同步X射线成像技术(synchrotron raditation Xray imaging technique, SR).
4.1 正电子发射颗粒跟踪技术(PEPT)
PEPT是利用正电子成像(positron emission tomography, PET)技术, 通过追踪具有放射性标识的颗粒位置, 进而计算出颗粒流速度的技术.如图14 所示其原理是利用同位素衰变时产生的正电子来实现显像的正电子发射型计算机断层扫描术, 具体为采用两个相对的探测器对正电子湮灭辐射产生的位于一条直线上、方向相反的两个光子产生的\(\gamma\)射线进行监测, 从而确定闪烁点位置.该系统包括一个正电子相机、跟踪剂位置和速度的定位算法以及跟踪标记技术.PEPT的示踪剂为发射正电子的放射性同位素, 其半衰期时间\( \left( {t_{1/ 2} } \right)\)应该保证实验完成,又要在使用后能够安全废弃, 通常使用的放射性同位素有: \( { }^{66}{\rm Ga}\left( {t_{1/2} =9.45\mbox{h}} \right)\), \({ }^{68}{\rm Ga}\left( {t_{1/2} =68 {\rm min}} \right)\), \({ }^{18}{\rm F}\left( {t_{1/2} =109 {\rm min}} \right)\), \({ }^{61}{\rm Cu}\left( {t_{1/2} =2.7 {\rm h}} \right)\)和\( { }^{64}{\rm Cu}\left( {t_{1/2} =204 {\rm min}} \right)\).
图14 PEPT测量原理图(Parker et al. 2002 ).(a)一对大矩形探测器组成的"正电子相机", (b) \(\gamma\)射线轨迹重构, (c)正电子发射原始位置
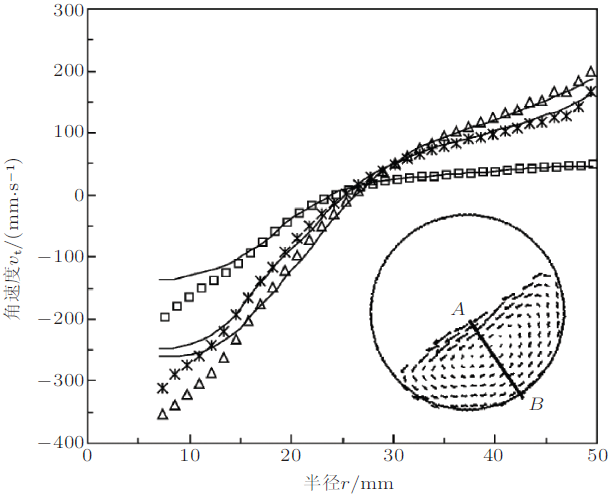
PEPT技术最早由英国伯明翰大学的Parker课题组提出(Hawkesworth & Parker. 1991 , Parker et al. 1993 ), 其追踪单个颗粒的空间分辨率可以达到0.5 mm, 时间分辨率主要由正电子相机决定(一般几十毫秒), 最大可以测量10 m/s的颗粒速度, 最多可以追踪3个示踪颗粒.由于其可追踪的示踪颗粒数量较少, 实际应用中比较适合测量具有周期边界的循环实验装置, 如滚筒、鼓泡气体流化床、振动流化床等. 与其他非侵入式测量技术相比, PEPT技术能够测出更加详细的固/液运动信息, 并且能够测量液体、有机聚合物、金属和矿物颗粒等众多材料.其不足之处在于, PEPT能跟踪颗粒数较少, 不适合复杂颗粒流速度场分布的测量. 此外, PEPT给出的是关于时间的平均速度场信息, 而不是颗粒瞬时速度场信息, 因此只适用于测量稳定流. 图15 所示为Parker 等(1997)用PEPT技术对准二维滚筒内(直径100 mm, 厚度16 mm, 颗粒直径3 mm)颗粒流速度的DEM计算结果进行了验证, 发现不同转速下, DEM计算的颗粒流表层速度总是大于PEPT的测量值, 造成这一结果主要是由于两方面原因, 一是DEM仿真时不考虑滚筒壁的作用, 二是DEM计算的速度是表层颗粒的平均速度, 而PEPT测得的是单个示踪颗粒的碰撞速度.
图15 不同转速下, 滚筒内沿径向( AB方向)的速度场分布.(符号为DEM计算值: \(\Box \) 20 r/mm, \(\triangle\) 42 r/mm, \(*\)65 r/mm; 实线为PEPT测量值) (Parker et al. 1997 )
Parker & Fan用PEPT技术测量了鼓泡流化床中的颗粒速度场分布(Parker & Fan 2008 ), 如图16 (a)所示, 并根据速度场分布将流化床分为底部、中部和顶部三个区域. 图16 (b)显示在流化床底部区域, 颗粒物质随着气泡在流化床边缘呈环状向上运动, 随后在流化床中间落下.这与图16 (a)中顶部区域颗粒流的运动方向正好相反. 在中间区域, 图16 (c)显示上升的气泡被从顶部边缘落下的颗粒挤到中间, 导致颗粒流速度场在流化床中间形成了一个小峰. 根据PEPT测量结果, 可以进一步计算出流化床中气泡的速度随高度变化, 如图16 (d)所示.
图16 鼓泡流化床中颗粒速度场的PEPT测量结果(Parker & Fan 2008 ). (a) 示踪颗粒在垂直平面内的速度矢量图, (b)流化床底部(高度10 \(\sim\)30 mm)颗粒速度\(y\)方向分布图,(c)流化床中部(高度120 \(\sim \)130 mm)颗粒速度\(y\)方向分布图, (d)根据PEPT测量值计算的气泡在流化床中上升速度
4.2 磁共振测速技术(MRV)
MRV是利用核磁共振(nuclear magnetic resonance, NMR)和磁共振成像(magnetic resonance imaging, MRI)原理来测量空间体内的三维速度场的一种技术(Haacke et al. 1999 , Sederman et al. 2007 ), 其工作介质通常为含氢原子的颗粒物质, 在外加磁场作用下, 原子核自旋系统逐步被磁化, 原子核以莫拉频率进动.在外部相同频率动射频脉冲激励下, 原子核产生磁共振现象, 而共振后恢复平衡状态的原子核会将吸收的射频脉冲能量释放出来, 探测器将这种磁共振信号转换成电信号再进行处理(如图17 所示).由于原子核自旋的共振频率与外部所加磁场相关, 因此外部磁场通常存在较弱的剃度渐变, 依此来实现空间定位, 起到追踪测量颗粒运动的目的.选用的颗粒物质要么本身含有质子\((^{1}\)H)比如芥菜籽、罂粟籽等; 要么是特殊制作包含质子的颗粒, 如胶囊中填充了液体维生素E(C\(_{29}\)H\(_{50}\)O\(_{2})\)等.
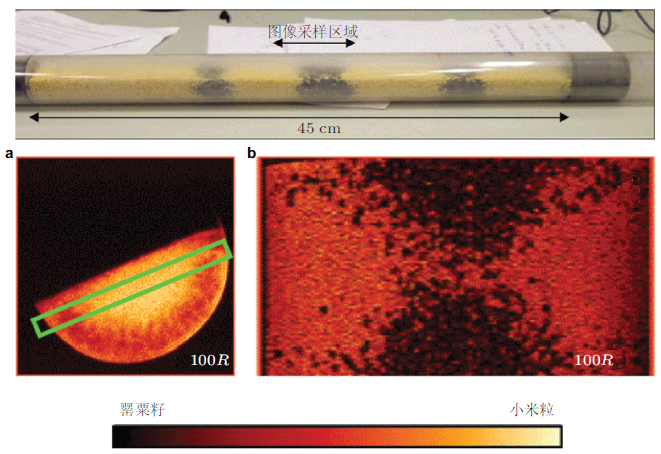
目前, 国际上从事颗粒流MRV研究的主要是英国剑桥大学和日本大阪大学, 比如: Sederman 等(2007) 利用该技术研究了罂粟籽和小米混合颗粒(如图18 )在滚筒内分选状态, 发现经过100转以后, 在径向, 粒度较小的罂粟籽颗粒集中在滚筒中间, 而粒度较大的小米颗粒分布在筒壁附近(如图18 (a)). 在轴向, 粒度较小的罂粟籽颗粒分布呈两头多、中间少的哑铃状(如图18 (b)), 再经过1 000转以后, 罂粟籽颗粒又偏向滚筒的一端.
图18 MRI测量小米和罂粟籽混合颗粒在滚筒内分选状态.罂粟籽和小米按体积比\(1:3\)的比例加入滚筒内, 黑色是罂粟籽(密度: 1 000 kg/m\(^{3}\), 粒度: 1.1 mm), 黄色是小米(密度: 1 150 kg/m\(^{3}\), 粒度: 2.3 mm) (Sederman et al. 2007 ). (a) 100转后径向分选, (b) 100转后轴向分选
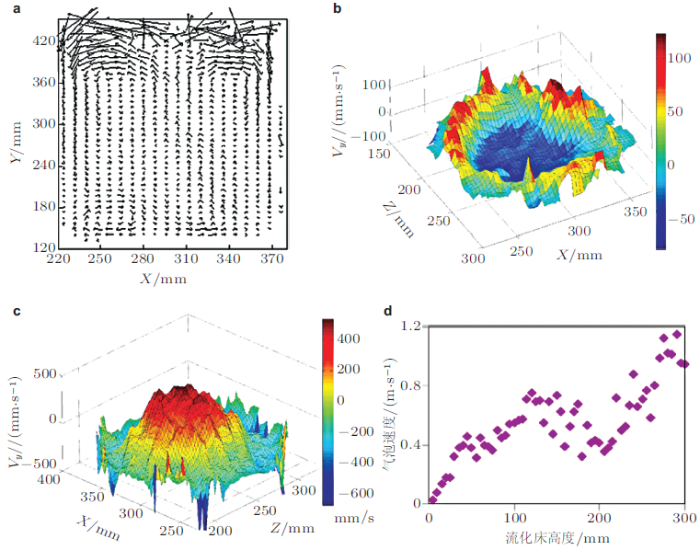
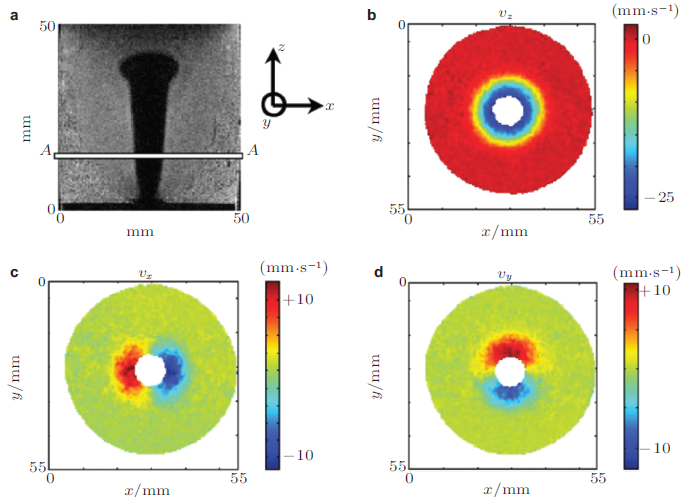
图19所示, Müller 等(2008) 用MRV测量了鼓泡流化床中的速度场, 其中图19 (b) \(\sim\) 图19 (d)分别给出了流化床中\(A\)位置截面上的\(z\), \(x\)和\(y\)方向颗粒速度分布, 可以看到, 只有在气泡周围的一小部分颗粒发生运动, 其余大部分区域的颗粒处于静止状态. 图20 显示测量的准二维鼓泡流化床的颗粒温度.
图19 MRV测量鼓泡流化床中颗粒流速度分布(Müller et al. 2008 ). (a)气泡喷射图像, \(A\)位置处 (b) \(z\) 方向, (c) \(x\)方向和 (d)\(y\)方向的速度场分布
图20 准二维鼓泡流化床的颗粒温度(Müller et al. 2008 ).(a)准二维鼓泡流化床, 流化速度为0.6 m/s, (b) DEM计算的颗粒温度, (c) MRV测量的颗粒温度MRV的空间分辨率较高(几十微米), 测量速度最高可达10 m/s的量级, 可以在几十到几百毫秒内完成普通二维图像的扫描, 但是对于高分辨率的三维测量需要花费数小时完成, 因此测量得到的速度场并不是瞬时速度场, 而是一种平均速度测量技术, 因此, MRV主要用于稳态颗粒流的测量.
4.3 同步辐射X射线成像技术(SR)
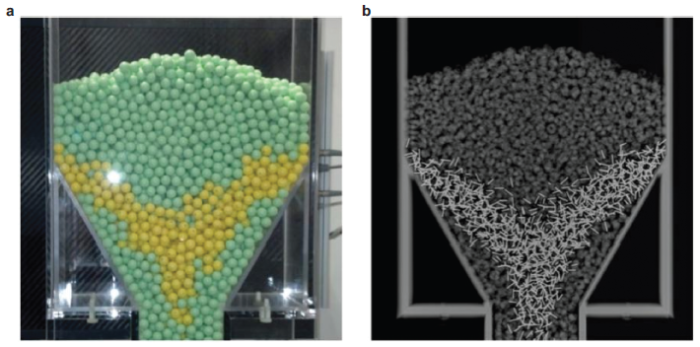
普通的X射线- CT可以研究颗粒运动和滚动信息(Beetstra et al. 2007 , Felice 1994 ), 实验时颗粒包裹着一根穿过球心的金属丝, 在X射线- CT图像中可以利用这根金属丝的形态得到塑料球的运动信息, 如图21 所示. 由于成像时间比较长, 实验装置内部设置挡板, 测量时挡住颗粒, 使其不发生运动, 然后X射线- CT成像; 成像完毕后, 抽开挡板, 颗粒流动, 然后再挡住颗粒, X射线- CT成像, 那么通过相邻两次成像就可以分析颗粒运动细节.不停的间断操作使得整个实验中颗粒运动是不连续的, 可能对整个流动产生扰动, 流动因此而发生改变.
图21 美国UC Berkeley开展的准二维楔形料仓中颗粒流X射线- CT测量(Laufer 2013 ). (a)包含金属针的黄色颗粒和没有包含金属针的白色颗粒; (b)CT测量得到的内部金属针形态, 由此可以确定颗粒旋转情况
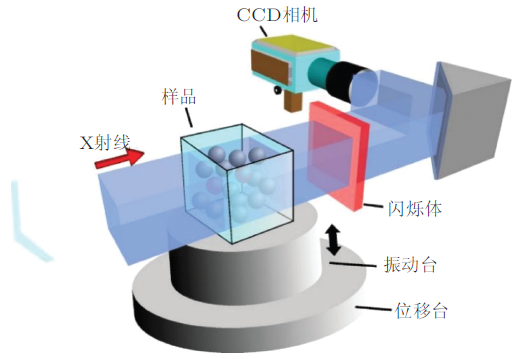
由于普通X射线光源亮度低, 穿透力差等原因使得成像的空间和时间分辨均较低, 且成像速度难以达到想要的结果, 所以具有高能量、高亮度、强穿透性等特点的同步辐射技术的出现能有效解决以上不足之处.同步辐射是电子在做高速曲线运动时沿轨道切线方向产生的电磁辐射, 具有其他辐射源难以比拟的优异特点, 比如光谱连续平滑、微米级脉冲、光强高、穿透性强、准直性好等.当前SR技术可以获得微米级的空间分辨率和微秒级的时间分辨率(Wang et al. 2008 ). 作为一种具有穿透性的非侵入测量手段, SR技术主要利用吸收衬度和相位衬度成像, 其中吸收衬度成像是X射线成像技术的主要手段.其主要原理是X射线在通过材料时会被吸收, 满足Beer-Lambert定律\[I = I_0 {\rm e}^{ - \mu L} \ \ (12)\] 其中, \(I_{0}\)和\(I\)分别为入射前和透射后的X射线强度, \(\mu\)为材料的线性衰减系数, \(L\)为X射线在材料中穿透的距离.由于不同材料对X射线的吸收系数不同, 因此沿X射线传播方向样品对X射线的吸收不同, 从而产生衬度.X射线成像对于颗粒流体研究的优势在于其具有穿透性, 可以得到光学不透明的颗粒体系内部的运动信息.这样排除了很多情况下颗粒微观动力学研究受到维度及边界效应影响的限制.在X射线实验中为了区分单独的颗粒, 可以使用与背景颗粒不同材质的颗粒作为示踪颗粒, 也可以在颗粒表面涂抹对X射线有强吸收的重金属元素涂层来增加吸收衬度.图22 显示了同步辐射研究颗粒运动的实验装置图.在容器中的颗粒受到震动台的连续震动形成密集颗粒气体, 对穿透的X射线吸收产生衬度.穿透的X射线打在荧光靶上产生可见光衬度像.这个衬度像可以通过一个45\(^{\circ}\)反射的镜子与CCD相机光学耦合成像.
自从1947年首次在美国通用电气公司的70 MeV电子同步加速器上观察到同步辐射现象以来, 同步辐射光源经历了三代的发展, 其中具有高能第三代同步辐射光源主要有美国的APS、欧洲的ESRF和日本的Spring-8, 美国和德国的第四代光源还在设计阶段.我国自20世纪90年代后期以来有北京、合肥两个同步辐射装置建成并投入运行, 分属第一、二代装置, 上海于2010年建成了目前国内先进的第三代同步辐射光源------"上海光源(SSRF)", 近年来已经在物理学、生命科学、材料科学等领域得到了广泛的应用.SR技术具备较高的空间分辨率\((\mu \)m)和时间分辨率\((\mu \)s), 可以利用动态X射线成像技术追踪视场内颗粒的轨迹(垂直光路平面内)和半径信息, 对于三维系统的CT扫描目前最快可达到亚秒量级.其不足在于同步辐射属于大科学装置, 建造费用昂贵, 专业化程度高, 实验机时较为稀缺. 同时SR技术是一种穿透技术, 不能得到颗粒沿X射线传播方向的位置信息. 要得到颗粒体系空间三维结构, 必须要利用CT技术, 但是对应的时间分辨率一般不能满足颗粒流体的动态结构演化研究.另外同步辐射X射线视场较小, 水平方向和垂直方向分别仅为几十毫米和几毫米, 对样品尺寸的限制非常大.
对颗粒体系的研究因受限于实验技术无法穿透一般不透明的颗粒材料而一直发展缓慢, 作为高速X射线成像技术的发展者, 上海交通大学王宇杰研究组用上海光源X射线成像及生物医学应用光束线站和美国阿贡国家实验室的先进光源32ID线站的高速SR技术, 对三维颗粒堆积体系的微观结构及动力学进行了实空间的成像, 并将其应用于研究非平衡态的颗粒体系.王宇杰等利用SR技术研究了三维棒状颗粒体系的性质和颗粒气体的运动(Zhang et al.2014 , Wang 2016 ) (如图23 所示), 同时还利用SR技术研究了单一分散颗粒硬球体系在有无液体时的微观结构, 同时将其与非晶玻璃化转变相关联(Xia et al. 2015 , Li et al. 2014 ); 研究发现颗粒体系中的玻璃化转变可能是非常类似于晶体结晶过程的一种特殊结构相变.其对应的玻璃结构序是一种局部紧密堆积的四面体结构, 这些四面体结构可以生长形成具有分形结构的团簇, 同时其形状及大小的增长符合位形熵驱动的成核模型, 这些都非常类似于快速降温的晶体生长模型.
图23 直径为0.5 cm, 长度为2 cm的ABS棒在20\(g\)振动加速度下的密集颗粒气体在某一瞬间的运动图像.少量示踪棒状颗粒表面涂有对X射线强吸收的氧化钕, 可以清晰地追踪其运动. X射线的拍摄速度是2 000帧/秒 (Zhang et al. 2014 , Wang 2016 )
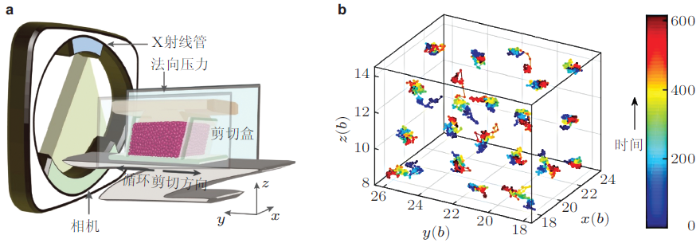
近期, 上海交通大学对椭球状颗粒施加准静态剪切应变循环加载(Kou et al. 2017 ), 等效于热扰动, 然后运用CT技术获取每个颗粒的位置与取向, 得到每一个颗粒在空间的三维轨迹, 从而确定位移与旋转随时间的变化规律(如图24 所示). 研究发现, 颗粒平移以及旋转位移平方的均值, 都与时间呈指数关系, 但幂指数与所施加的剪切应变有关, 且不存在普通流体在玻璃化转变时所出现的平台区, 即不存在所谓的笼效应(颗粒被临近颗粒暂时约束而失去流动性).进一步分析发现, 颗粒位移分布函数是非高斯的, 满足所谓的Gumbel关系, 与普通流体不同, 即在小位移下与高斯分布相似, 但大位移下有一个长尾, 如图24 (b)所示.研究人员认为这显示颗粒体系中存在两种弛豫机制的竞争, 即小尺度下由颗粒粗糙度所引起的扩散, 和大尺度下非可逆的弛豫. 此外, 其概率分布形状与应变、时间、以及位移方向无关, 显示其普适性.这个小尺度下由颗粒粗糙度所引起的微扩散过程, 是这一工作最关键的一个新的洞见.
图24 CT技术测量椭球状颗粒受到热扰动后, 位移与旋转随时间的变化规律(Kou et al. 2017 ). (a) CT实验装置示意图.剪切盒中包含椭球形颗粒, 在上表面沿\(z\)方向施加压力, 在下表面沿\(y\)方向施加循环加载剪切应变; (b) 剪切应变幅赋值为0.26, 615次循环加载条件下, 剪切盒中间20个颗粒的三维轨迹, 由此得到平移与旋转位移平方均值与时间及剪切应变关系
5 介尺度结构的测量
颗粒介质是多体相互作用体系, 其具有宏观均匀的结构特征, 介观上存在若干颗粒大小的介尺度结构.结构表征是理解和认识颗粒介质物理问题的基础和依据, 是当前制约颗粒介质力学和应用发展的瓶颈.随着研究的深入和结构分析实验手段的不断改进, 人们发现颗粒体系的结构存在非均匀性, 而结构不均匀是理解其动力学不均匀、力学性质转变等问题的基础.在颗粒介质的不同区域, 结构差别很大, 几乎每个颗粒周围的颗粒组成、体积分数、配位数和应力等都与其他区域的不同, 这种局域结构差异影响、甚至决定了颗粒介质的性质. 比如, 在颗粒介质中出现一种局域的本征态, 即某一位置颗粒的振动的振幅会随着距离快速衰减为零, 即颗粒的振动态只存在于体系局域的范围内, 这对颗粒介质的准静态性质有重要影响.
对于发生失稳流动的颗粒体系, 其黏性系数与剪切速率及力链长度的规律研究是动力学研究的重点课题.目前较为成功的是局域流变模型(local rheology), 比如法国科学家提出的\(\mu (I)\)流变, 在刻画准静态颗粒流方面存在问题. 此时颗粒之间密切接触, 使得速度脉动和力链网络都存在大尺度的空间关联, 应力紊动产生的弹性波在颗粒之间的传播长度由快速流态下的颗粒粒径尺度转变到力链长度尺度, 因而颗粒介质内部流动区域产生的扰动, 沿力链传递到远处区域, 颗粒介质表现出明显的非局域流变(non-local rheology)特性, 从而影响了动量输运.这一特殊的流变现象可以通过在局域模型中叠加考虑包含非局域特征长度影响的"二级流变"(secondary rheology)来实现, 引入特征长度构建的非局域流变模型, 或通过对各流层中的颗粒紊动进行积分处理引入颗粒之间的长程作用.尽管一些模型对准静态颗粒流的刻画上取得了成功, 可能抓住了问题的关键, 但对"二级流变"的机理探讨还存在很多争议, 需要从介尺度结构层面予以澄清.现有分析手段所描述的颗粒系统结构过于简单化, 还不能建立结构和其宏观力学性能的对应关系, 在基本理论和实验手段上的研究都非常困难.下面介绍光弹技术、声速测量技术、体积响应谱、力学谱(有效质量和内耗等)和声速测量技术等在直接或间接测量颗粒介尺度结构方面的进展.
5.1 二维力链结构的光弹技术(photoelastic technique)
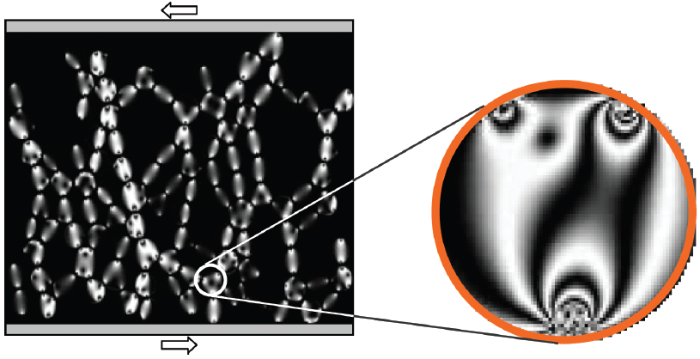
颗粒体系的基本特征是其内部本征的空间不均匀性, 径向分布函数\(g(r)\)可以给出重要的几何结构信息. 比如, 颗粒径向分布函数\(g(r)\) 在\(r >10\left\langle d \right\rangle \) 时变成直线(其中, \(r\)是颗粒质心到参考点的距离, \(\left\langle d \right\rangle\)是颗粒的平均直径), 而在\(r < 10\left\langle d \right\rangle \)时存在多个峰, 且随着 \(r\)增大, 峰值逐渐减弱. 从力空间看, 颗粒介质可以看作由相对硬的强力链和易于发生非仿射位移的弱力链这两类基本结构协调组成, 先进的物理学结构分析手段必然在结构辨识与演化规律分析方面发挥强大作用.光弹技术是应用光学原理研究弹性力学问题的一种实验应力分析方法, 是观测二维力链结构最为直接的手段.将具有双折射效应的透明塑料(如环氧树脂塑料或聚碳酸脂塑料)制成的结构模型置于偏振光场中, 当给模型施加载荷时, 即可看到模型上产生的干涉条纹图, 测量干涉条纹, 就能确定结构模型在受载情况下的应力分布. 在颗粒接触力检测时, 常用的制作颗粒的材料是聚碳酸酯, 它的光学灵敏度和透明度都较高, 时间–边缘效应小, 室温下蠕变小等优势. 颗粒接触处越亮, 则表示接触应力就越大, 这样就可以清晰地显示撞击床面瞬间接触力大小及其空间分布情况. 图25 (a)可清晰地看到颗粒间连成的强力链分布, 亮度越高, 应力越大, 图25 (b) 图是单颗粒上的应力光强分布情况, 可以细致反映颗粒内部应力的分布情况. 力链形态多种多样, 每种形态均具有独特性质, 如何高精度计算每个接触点上的力是难点.
图25 光弹实验显示了受压颗粒体系中的颗粒中的应力分布, 由此反推出颗粒接触点上的力
近10年来, 上海交通大学张洁研究组开展了力链结构表征及其演化规律分析的详细工作(Wang & Zhang 2015 ), 清华大学孙其诚研究组开展了二维颗粒光弹实验, 实现了基于应力条纹快速计算数千颗粒上所有接触点的法向力和切向力, 研究发现: 颗粒接触力的概率密度函数\(p(f)\)表征, 其中\(f\)为归一化力, 发现: \(f = 1\)处, \(p(f)\)达到极大值; 提出了准直性、应力阈值等标准, 定义了力链, 确定了力链长度概率密度分布, 发现力链约为8个颗粒长.近期, 美国Duke大学 Behringer 课题组结合光弹技术, 采用高速相机拍摄了颗粒受冲击过程中的力链变化, 测量了力的传播速度(Clark et al. 2015 ).
在力链结构刻画方面, Wyart 等 (2005) 认为: 设颗粒接触数\(Z\)与等静态接触数\(Z_{\rm iso} \) 之差为 \( \Delta Z = \left( {Z -Z_{\rm iso} } \right)\),则力链特征长度\(l^\ast \sim 1/{\Delta Z} \).近年来, 关于颗粒材料介观长度尺度及其随系统参数演化规律的数值研究已经取得了很大的进展.特别是, 一些研究者试图从动力学响应的角度研究颗粒体系中的特征长度.例如: Ellenbroek 等 (2006, 2009)研究了处于堵塞(jammed)固体样品中心的单个颗粒直径膨胀带来的力响应涨落, 发现当接近堵塞(jamming)点时的力响应涨落空间范围\(L^\ast \)发散, 暗示低于长度尺度\(L^\ast\)响应被涨落控制(变形场可以被视为一个扭曲软模式), 而在大于\(L^\ast\)的尺度, 系统的响应过渡到弹性. Karimi 和 Maloney(2011) 研究发现颗粒体系应力各向异性的特征长度随体积分数\(\varphi\)从上述趋近临界体积分数\(\varphi _{\rm c} \)时增大.Vitelli(2010)研究了无摩擦软球堵塞(jammed)体系剪切声波的长波衰减, 发现特征长度\(L^\ast \sim \left( {\varphi - \varphi _{\rm c} }\right)^{{ - 1} / 2}\).关于动力学关联长度随体积分数演化规律的研究方面, Flenner 等(2010) 实验发现在堵塞点附近, 水平振动单层颗粒床的动力学关联长度\(L^\ast \sim \left( {\varphi -\varphi _{\rm c} } \right)^{1/ 2}\).
5.2 声速测量技术
颗粒介质中颗粒的各种运动(包括振动、扩散、流变、弛豫等)可能导致颗粒间接触性质的变化, 反映在宏观性质上如弹性模量等的变化, 这就是弹性模量与颗粒介质结构、特性和性能存在关联性的物理原因.弹性模量的变化可以敏感地反映颗粒介质结构的变化.由于颗粒介质结构表征的困难, 弹性模量可以作为一个重要参数来研究和描述结构.
颗粒物质的一个基本特征是其能够对外部机械扰动产生线性和非线性响应, 亦即颗粒材料内部的强力链和易于发生非仿射位移的弱力链对外部声学激励分别产生本征不同的力学响应.一方面, 强力链骨架能够对外部扰动产生与均匀固体类似的线性响应, 这使得线性声学测量成为研究颗粒体系内部强力链骨架结构和力学性质的基本手段(孙其诚等2017), 其测量时间(频率范围是2 MHz \(\sim\) 5 MHz)短于颗粒本征弛豫时间(频率范围是0.1 Hz \(\sim\) 0.1 kHz), 测得的弹性模量即为力链瞬态模量. 目前, 研究已经取得了一些共识, 通过测量颗粒体系中横波和纵波的声速可以获得强力链骨架的剪切和压缩模量.但是仍然存在许多分歧. 例如: 有效介质理论预言在低压强下赫兹接触的球形颗粒体系中声速随压强满足幂律标度: \(V\sim p^{1 / 6}\), 而实验发现声速随压强的变化呈分段幂律标度, 即在高压下符合1/6幂律关系, 低压下符合1/4幂律关系. 另一方面, 颗粒介质中的弱力链则对外部扰动表现出与均匀固体不同的强烈非线性响应, 使得非线性效应成为研究弱力链及其动力学响应的重要工具.
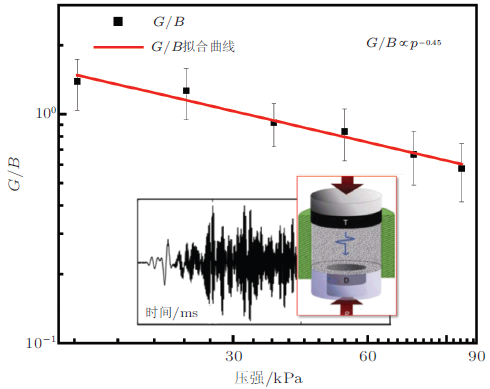
北京科技大学张国华课题组采用飞行时间法测了玻璃珠样品的横波声速\(V_{\rm s} \)和纵波声速\( V_{\rm p} \) 随压强的变化 (张攀等2016), 发现\(V_{\rm p} \)和\(V_{\rm s} \)随压强变化均呈现幂律标度, 即\(V_{\rm s} \sim p^{0.28}\), \(V_{\rm p} \sim p^{0.38}\), 不同压强下\({V_{\rm p} } /{V_{\rm s} } \approx 1.6\), 近似是常数. 根据经典弹性理论, 各向同性弹性体体积模量\(B\)和剪切模量\(G\), 与纵波波速\(V_{\rm p}\)和横波波速\(V_{\rm s} \)的关系为 \(B = \rho \left( {V_{\rm p} ^2 -\dfrac{4}{3}V_{\rm s} ^2} \right)\), \(G = \rho V_{\rm s} ^2\), 其中, \(\rho \)是弹性介质的质量密度,进一步得到\[\dfrac{G}{B} = \left( {\dfrac{V_{\rm p} ^2}{V_{\rm s} ^2} -\dfrac{4}{3}} \right)^{ - 1} \ \ (13)\]
图26 显示了玻璃珠样品的\(G /B\) 随\(P\)的变化规律, 发现实验给出的\( G /B = 0.58\sim 1.39\),且颗粒体系 \(G /B\)随\(P\)的增大而减小, 满足幂律关系: \(G /B\sim P^{ - 0.45}\), 如图26 中红色直线拟合所表示.根据(Tighe 2011 , Basu et al. 2014 , Goodrich et al. 2014 )的结果, 对于堵塞颗粒体系的\(G/B\sim\left( {\varphi - \varphi _{\rm c} } \right)^{1/ 2}\sim p^{1/3}\)(其中\(\varphi _{\rm c} \)是颗粒体系堵塞点的体积分数). 显然, 实验发现的\(G /B\)随\(P\)的变化规律与Hertz 接触理论不相符, 暗示连续弹性介质理论在低压强下可能不再成立.导致上述差异的因素可能有以下两个: (1) 理论模型要求颗粒是光滑的, 但是实际颗粒的表面是粗糙的, 这会使实际结果同Hertz接触理论预言存在一定偏差; (2)纵波对于应力场的各向异性更加敏感, 而横波对于结构各向异性更加敏感(Khidas & Jia 2010 ).
图26 颗粒体系的\(G /B\)随压强\(P\)的变化. 实线为拟合曲线, 插图是单轴压缩示意图和测量得到的纵波信号(张攀 等 2016 )
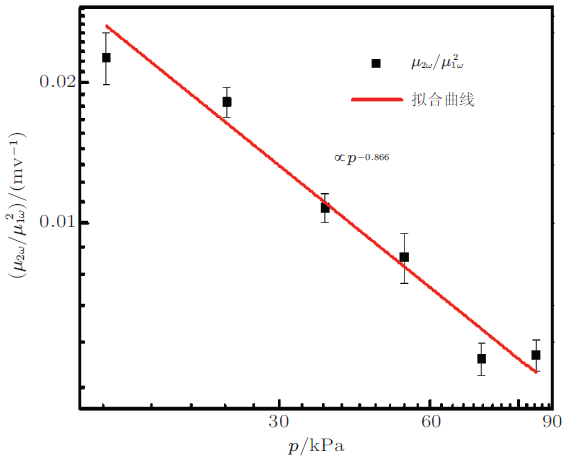
由于颗粒介质结构非均匀性的影响, 颗粒介质中声波除了一阶声波外, 还出现二阶甚至三阶的谐波. 非线性现象是研究弱力链规律的有效手段.目前, 各向异性介质非线性声学研究主要以纯模为主, 开展新的理论和实验具有非常迫切的需要.非线性效应对于弱力链的出现非常敏感. 一方面, 弱力链分数主要受材料应变的影响; 但是另一方面, 这些接触在线性弹性力学中很难被阐明. 因此, 颗粒介质重排的早期阶段引起的弱应变波很难通过线性声学传播来评估.相比之下, 高次谐波的产生表现出了对结构更高的敏感性.非线性声学研究固体结构受到越来越多的关注. 固体材料受力之后, 胡克定律几乎完美地描述了材料中的应力与应变(单位变形量)之间成线性关系, 而非线性声学就是处理应力应变的偏差.这个结果打破了弹性波的叠加效应, 使得非线性引起的波频谱分量水平增加可以作为这样"弱特征"的敏感指标, 可以用于颗粒材料弱力链网络的检测. 颗粒介质声学非线性可用系数\(\beta\)表征, 与二倍频振幅\(\mu _{2\omega } \)与基频振幅\(\mu _{1\omega }\)平方的比值有关(Brunet et al. 2008 )\[\left| {\dfrac{\mu _{2\omega } }{\mu _{1\omega } ^2}} \right| =\dfrac{\beta \omega ^2}{8\alpha V^2} \ \ (14)\] 其中, \(\mu_{2\omega } \)代表接收二倍频振幅, \(\mu _{1\omega }\) 代表接收基频振幅, \(V\)代表声速, \(\omega \)代表频率.\(\beta \)越大,波形畸变越严重. 利用傅立叶变换法分析了玻璃珠样品的 \({\mu _{2\omega } }/ {\mu _{1\omega } ^2}\) 随压强\(P\) 的变化曲线, 如图27 所示. \({\mu _{2\omega } }/{\mu _{1\omega } ^2}\)随压强的增大而幂率减小: \({\mu _{2\omega } }/ {\mu _{1\omega } ^2}\propto P^{ - 0.866}\), 如红色直线所示. 根据Hertz 接触理论, \({\mu_{2\omega } } /{\mu _{1\omega } ^2} \propto P^{ - 1 / 2}\), 实验得到的\({\mu _{2\omega } }/{\mu _{1\omega } ^2}\)随压强的幂指数\(( - 0.866)\)与理论预言的幂指数\(( - 1/2)\)存在差异.造成上述差异的原因可能是在低压强范围内颗粒物质的声速\(V_{\rm p} \), \(V_{\rm s} \) 及\(\beta \)随压强\(P\)的幂律标度指数都偏离Hertz接触理论的预言.
图27 二倍频振幅与基频振幅平方的比值\({\mu _{2\omega } }/ {\mu_{1\omega } ^2}\) 随压强\(P\)的变化关系图, 实线为拟合曲线(张攀 等 2016 )
5.3 体积谱技术
颗粒的表面摩擦和非弹性接触等因素使得颗粒体系能够快速耗散掉外部脉冲激励所产生的能量, 从而长时间停留在某一亚稳态. 另一方面, 连续的振动、摇晃等外部激励却可以推动颗粒体系动力学的演化, 例如, 用固定频率的大幅度垂直脉冲连续振动颗粒样品可以使系统快速达到一个稳定状态.达到稳态的颗粒材料的密度仅仅是脉冲振动幅度的单值函数, 而不依赖于制备的历史.为了进一步解释在外部激励脉冲作用下疏松颗粒材料的密度弛豫, Coniglio 等 (2004) 提出了基于能量的、用于描述颗粒物质稳态的统计力学方法.基于Edwards (1998)的统计力学框架, 给出了用位形温度\(T_{\rm conf}\)和颗粒数密度\(N_{\rm s} \)两个控制参量描述颗粒系统的平均场相图.在Coniglio的\(T_{\rm conf} - N_{\rm s} \) 相图中, 融化线和玻璃转变线把相图分成3个区域: 在熔化线之上(即在低\(N_{\rm s}\)、高\(T_{\rm conf} \)区)为具有水平平移不变性的类流体相; 在玻璃转变线之下(即在高\(N_{\rm s} \)、低\(T_{\rm conf} \)区)为玻璃相; 在熔化线和冻结线之间为超冷液体相. Coniglio的\(T_{\rm conf} - N_{\rm s} \)相图说明可以通过改变激励脉冲幅度来迫使颗粒系统经历从玻璃态到超冷液体以及从超冷液体到类流体的转变过程.
密度响应谱是探测颗粒体系内部弛豫动力学和研究颗粒材料热动力学理论的有效方法.Nowak 等(1998) 研究了垂直脉冲激励下圆柱形容器中单分散玻璃球体系的密度随时间的演化, 发现当用大于某个临界值\(\varGamma ^\ast\)的垂直脉冲振动足够长时间之后,系统密度最终达到一个仅依赖振幅的稳定值.Villarruel 等(2000) 进一步研究了垂直脉冲激励下的非均匀、圆柱形颗粒材料的状态随时间和空间的演变, 发现垂直脉冲振动驱动颗粒体系从无序、低聚集率状态到密实的、有序的、向列型状态演变.Ludewig 等 (2008) 研究了离散的垂直脉冲振动参数对系统密度的影响, 提出用一个全新的无量纲参数\(\varXi \)(垂直振动实验中注入颗粒体系的能量)作为描述颗粒压缩动力学(compaction dynamics)的特征量. Dijksman 和 van Hecke(2009) 则发现处于可逆分支的颗粒系统密度不仅与振动脉冲的强度有关, 还与单个脉冲的周期\(T\)有关, \(\varGamma {T}\)才是颗粒离散脉冲振动的控制参数. Zou(2010) 利用体积响应谱技术研究了垂直脉冲振动下颗粒体系的压缩动力学, 发现颗粒体系的体积响应因子表现出与自旋玻璃系统中动力学位形比热类似的行为, 暗示颗粒压缩过程中表现出的玻璃状动力学行为来源于颗粒的集体重排.
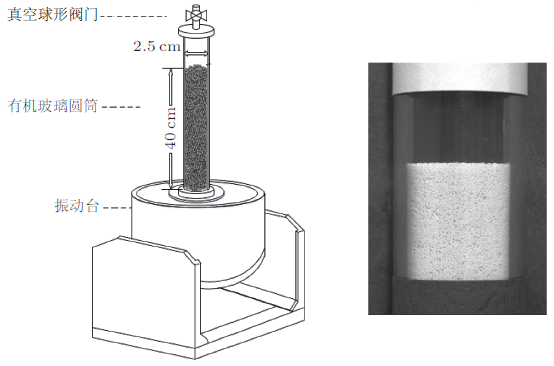
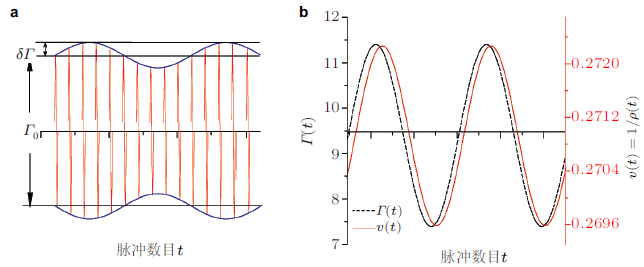
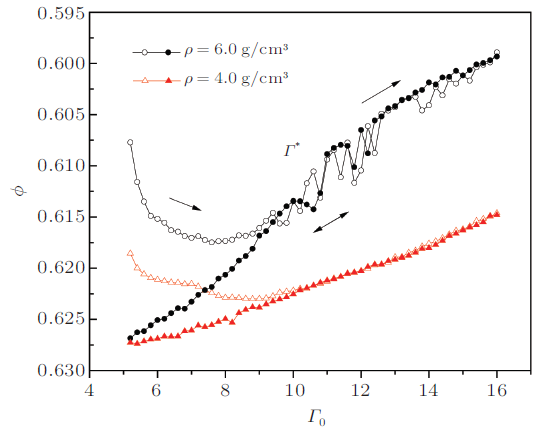
北京科技大学张国华研究组测量了垂直脉冲激励下球形氧化锆颗粒体系的动力学体积响应谱, 分析了氧化锆颗粒密度对颗粒体系体积响应谱的影响(马文波等2015), 如图28 所示. 实验使用球形氧化锆颗粒, 颗粒粒径\(d = 0.5 \sim0.6\) mm. 氧化锆颗粒的硬度比玻璃珠大, 表面也更加光滑, 可减少在压缩过程中的磨损.为了减小振动过程中由于颗粒与圆筒内壁摩擦而出现的静电, 在放入颗粒样品之前在圆筒内壁需涂抹一层防静电剂并烘干.样品池是内径23 mm, 高度500 mm的细长有机玻璃圆筒, 初始的颗粒填充高度约为400 mm. 为了减小空气对实验结果的影响, 实验前对样品池抽真空.选取细长圆筒可抑制振动过程中颗粒的大规模对流现象.为了限制在垂直振动过程有机玻璃筒的横向运动, 样品池被嵌套在一个圆筒形支架内. 实验中, 每个脉冲是单个周期的正弦振动(频率为30 Hz), 脉冲幅度\(\varGamma _0\)定义为脉冲的峰--峰加速度与重力加速度的比值,脉冲之间的间隔为5s.为了测量系统的动力学体积响应, 需要在振动的颗粒体系中引入微扰.如图29 所示, 将脉冲振幅\(\varGamma _0 \) 作为最重要的控制参数, 充当扰动场,并将其均值附近用正弦信号调制脉冲的振幅, \(\varGamma (t)\)为正弦调制过后的实时脉冲振幅为\[\varGamma (t) = \varGamma _0 + \delta \varGamma \sin (2\pi ft) \ \ (15)\] 其中, \(\varGamma _0 \)为脉冲振幅的平均值, 是最重要的控制参数, 而\(\delta \varGamma \) 为调制幅度, 充当微扰, \(f\)是调制频率, \(t\)是以脉冲振动数目为计量单位的时间.作为正弦调制脉冲振幅的响应, 颗粒体系的比容 \(v = 1/\rho\)可写成与式(15)类似的形式 \[ v(t) = v_0 + \delta v\sin (2\pi ft -\phi ) \ \ (16)\] 其中, \(\delta v\)是响应幅度, \(v_0\)是比容的平均值. \( \phi\) 为激发信号\( \varGamma (t)\)与体积响应信号\(v(t)\) 之间的相移, 由于系统中存在耗散, \(\phi \neq 0\).
图28 实验装置示意图(右图为顶部颗粒表面图)(马文波 等 2015 )
图29 (a)振动幅度\(\varGamma \)调制图示, (b)已调制振动幅度\(\varGamma(t)\) (虚线)与比容\(v(t)\) (实线)随脉冲数目\(t\)的变化(马文波 等 2015 )
为了研究垂直激励脉冲幅度\(\varGamma _0 \)对颗粒体系体积分数的影响, 测量了加速度增大和减小过程中密度为6.0 g/cm\(^3\)的氧化锆颗粒体系的体积分数\(\varphi (\varGamma _0)\)曲线,分别如图30 中的空心圆和实心圆曲线所示.实验过程中, 垂直脉冲幅度\(\varGamma _0 \)以步长\( \delta \varGamma = 0.2\), 从 5.2缓慢增大到16 (如空心圆曲线所示), 然后以相同的步长从16缓慢降低至5.2 (如实心圆曲线所示).在每一个脉冲幅度\(\varGamma _0 \)处, 系统经历100个垂直脉冲振动后再记录体积分数的值. 可以看出, 颗粒体系的体积分数\(\varphi (\varGamma _0 )\)依赖制备历史.当垂直脉冲幅度\(\varGamma _0 \) 小于某个特征幅度\(\varGamma ^\ast \)(约为11)时, 从最疏松状态增大\(\varGamma _0\)和从高密度状态减小\(\varGamma _0 \)过程中的\(\varphi (\varGamma _0)\)曲线不重合\((\varphi (\varGamma _0 )\)曲线不可逆), \(\varGamma _0\)增大过程的\(\varphi (\varGamma _0 )\)曲线高于\(\varGamma _0\)减小过程的\(\varphi (\varGamma _0 )\)曲线.从最疏松状态制备样品的\(\varphi (\varGamma _0 )\)曲线的不可逆性说明, 疏松的静态颗粒体系可以处于一种密度非常低的亚稳态, 当外部扰动时, 系统会获得额外的能量并弛豫到一个新的亚稳态.
另一方面, 当\(\varGamma _0 > \varGamma ^\ast \)时, \(\varGamma _0\)增大和减小过程的\(\varphi (\varGamma _0 )\)曲线重合\((\varphi(\varGamma _0 )\)曲线可逆), 说明在实验时间范围内系统达到稳态.进一步的实验表明, 一旦系统进入稳态, 系统的\(\varphi (\varGamma _0)\)曲线将变成可逆的, 即减小和增大\(\varGamma _0 \)过程中稳态体系的\(\varphi (\varGamma _0 )\)曲线重合(图中未显示).对于已经达到稳态的系统, 脉冲振动只能把颗粒体系从一个稳定的微观态激发到另一个的具有相同体积分数的微观态.此时, 系统的体积分数不再依赖历史, 而是脉冲振动幅度的单值函数.由于外部激励脉冲在颗粒系统中扮演了类似热系统中热激发的角色, 有可能通过控制脉冲幅度迫使系统经历Coniglio预言的从类玻璃态到类流体态的转变过程.
为了进一步研究氧化锆颗粒密度对颗粒体系体积分数的影响, 还测量了加速度增大和减小过程中密度为 4.0 g/cm\(^3\) 体系的\(\varphi(\varGamma _0 )\) 随\(\varGamma _0 \) 变化曲线, 分别空心三角和实心三角曲线所示. 可以看出, 相对于密度为6.0 g/cm\(^3\) 体系的\(\varphi (\varGamma _0 )\) 曲线, 密度为4.0 g/cm\(^3\) 体系的\(\varphi (\varGamma _0 )\) 曲线整体下移, 加速度增大和减小过程中\(\varphi (\varGamma _0 )\)曲线的可逆和不可逆分支的分界点处的加速度幅值\(\varGamma ^\ast \)有微小的变化, \(\varGamma ^\ast = 10.5\).
图30 垂直振动激励条件下颗粒体系体积分数\(\varphi\)随振动幅度\(\varGamma _0 \)的变化(马文波 等 2015 )
5.4 垂直振动激励下颗粒材料有效质量和耗散功率
目前, 颗粒物质的声学阻尼特性已经得到了广泛的应用, 但是关于颗粒材料中耗散机制的微观起源仍然不清楚, 需要进一步的研究.力学谱技术是研究材料中能量损耗规律的有效手段. 与其他谱学技术相比, 内耗测量采用的应力/应变振幅很小, 对被测物体没有任何破坏作用, 所以它是一种无损力学诊断方法, 并且对于微区成分和结构状态敏感, 可反映材料在各种复杂外界环境(如压力、高温、强核辐射等)下的力学性能等.因此, 内耗技术可以提供一些其他实验手段无法得到的信息, 在固体物理领域, 内耗与力学谱技术应用广泛(张进修 和 熊小敏 2013 , 吴学邦 等 2016 ). 随着内耗测量技术的不断发展, 近年来其应用领域已拓展到颗粒物质Jamming转变等, 一些工作表明, 内耗技术能够有效地探测和研究颗粒物质的结构转变与动力学弛豫行为.比如, 颗粒的种类、粒径大小、表面粗糙度以及外界压强等决定了力链网络结构的共振频率, 内耗技术还可用来探知颗粒体系力链在外场压强下的共振频率, 揭示密集颗粒物质的能量耗散性质.中国科学院固体物理所采用改进的低频内耗仪研究不同颗粒体系(如砂粒、铁粉和铝粉等)在外加剪切应力作用下的能量耗散性质, 比如发现了其内耗---频率谱中均分别出现 3个明显的能量耗散峰.随着外加压强(0 \(\sim \) 400 Pa)的增大, 各体系3个耗散峰均向高频端移动. 初步认为, 该耗散峰来源于颗粒体系中不同长度力链的共振耗散. 随着频率的降低, 内耗峰依次对应于双颗粒链、三颗粒链和四颗粒链的共振耗散(Wang et al. 2007 ). 动态力学分析仪(DMA) 是一种材料能耗测试仪, 与内耗仪一样可用于材料耗散性能测试.但目前DMA在测量颗粒材料的能量耗散性质方面的报道不多.
动态有效质量谱技术是研究垂直振动激励下颗粒材料声学耗散性质的重要手段(Hsu et al.2009 , Valenza et al. 2010 ). 彭政等(2013)研究了垂直激发下铜和玻璃珠系统的能量耗散, 发现体系在几十赫兹处出现共振, 且特定频率下的耗散功率随振动强度的变化呈现幂率规律. Valenza 等(2009)研究了湿度对钨颗粒体系有效质量的影响, 发现湿度越大, 颗粒物质的耗散越显著. 在钨颗粒涂上不同黏度的硅油, 研究了硅油黏度对有效质量的影响, 发现体系的耗散与黏度变化正相关.此外, Valenza 和 Johnson(2012)使用激光振动计观察到垂直振动过程中颗粒床侧壁与附近颗粒的相对位移近似为零, 表明有效质量测量是基于线性小振幅. 总之, 动态有效质量谱具有颗粒材料声学模式、弹性和时效的耗散特征, 正日益成为进一步理解颗粒体系耗散机理的主流技术之一.
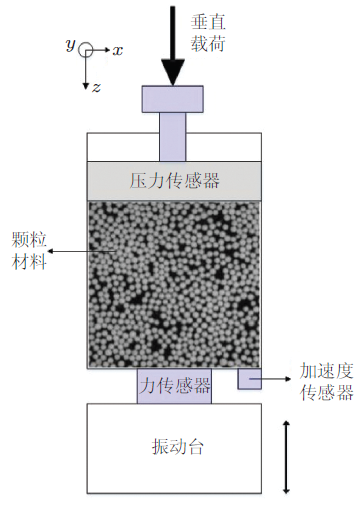
目前, 对颗粒材料自由表面颗粒体系的有效质量的研究已经取得了一些进展, 但是关于外部压强对颗粒体系有效质量和功率耗散影响的报导还不多见.北京科技大学张国华研究组研究了垂直振动激发下钨颗粒的动态有效质量\(\tilde{M}(\omega )\)和耗散功率\(p(\omega )\)随频率\(\omega \)的依赖关系, 进一步研究了有效质量实数部分的共振频率\(f_g\)和颗粒系统品质因子倒数\(1/ Q\)随表面压强\(P\)的变化规律(余田 等2015). 实验装置如图31 所示,样品池为一个圆柱形的铝杯, 铝杯质量261.1 g, 内径56 mm, 高82 mm.样品池中填充粒径约为100 \(\mu \)m, 总质量为791.7 g的钨颗粒.钨颗粒的上表面放置一活塞, 活塞的上表面连接一个压力传感器,穿过铝杯顶盖的螺杆顶在压力传感器上, 通过旋转螺杆可以给颗粒上表面施加压强\(P\).在铝杯的底座边缘刚性连接加速度传感器, 用于测量铝杯底部的加速度\(a(t)\).在铝杯和振动台之间刚性连接动态力传感器, 用以实时测量振动台对铝杯的作用力\(F(t)\).功率放大器通过固定在振动台面的加速度传感器的反馈信号, 控制振动台以恒定的加速度振动, 可产生频率 \(f = 10\sim2 000\) {Hz}的正弦信号.在振动台上放置另一加速度传感器, 其输出信号作为杯子底部动态力的传感器和加速度传感器的参考信号, 高速数采卡以500 kHz采样频率对加速度信号\(a(t)\), 力信号\(F(t)\), 颗粒上表面的压力信号\(P\)进行采集.
通过振动台对样品池和颗粒施加余弦力信号\(F(t) = F_0 \cos (wt + \phi_F )\), 由固定于样品池底部的加速度传感器测得样品池加速度\(a(t) = a_0\cos (wt + \phi _a )\), 其中\(F_0 \)和\(a_0\)分别是周期性驱动力和样品池加速度的振幅, \(\phi _F \)和\(\phi _a\)分别是周期性驱动力和样品池加速度的初相.颗粒体系有效质量定义为\(\tilde {M}(\omega ) = \dfrac{\tilde{F}(\omega )}{\tilde {a}(\omega )} - M_{\rm c} \), 其中\(M_{\rm c}\)为空杯质量, \(\tilde {M}(\omega ) = M_1 (\omega ) + {\rm i}M_2(\omega )\)为复数, \(M_1 (\omega ) = \dfrac{F_0 }{a_0 }\cos \left({\phi _F - \phi _a } \right) - M_{\rm c} \)描述了材料的惯性和弹性响应, \(M_{\rm c} (\omega ) = \dfrac{F_0}{a_0 }\sin \left( {\phi _F - \phi _a } \right)\)与颗粒材料的衰减有关.稳定状态下颗粒体系的平均能量耗散功率应该等于振动台和样品池的平均传递功率, 在一个周期\(T\)内平均功率损耗为\[p = \dfrac{1}{T}\int_0^T {F(t)\left( {\int_0^t {a({t}'){\rm d}{t}'} } \right)} {\rm d}t = \dfrac{1}{2\omega }F_0 a_0 \sin(\phi _a - \phi _F ) \ \ (17)\]
图31 垂直振动激发下钨颗粒实验装置示意图(余田 等 2015 )
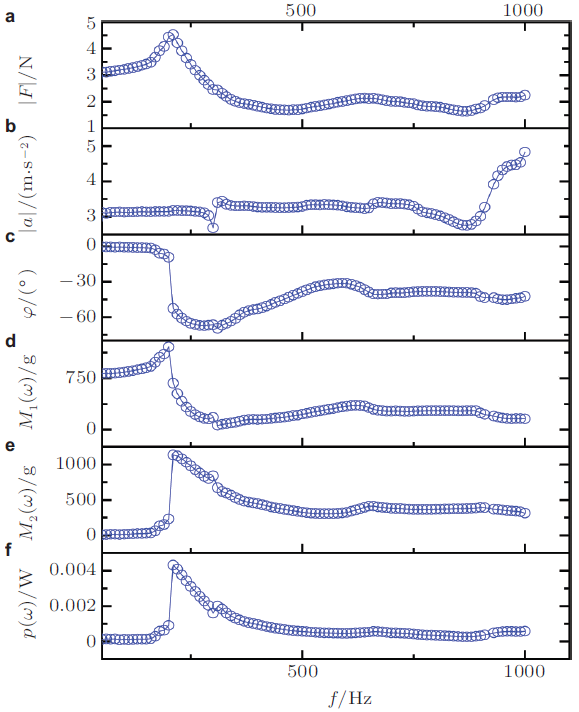
图32 (a) \(\sim\) 图32 (f)分别显示了样品池所受的驱动力振幅、加速度振幅、力和加速度的位相差、有效质量的实数部分\(M_1(\omega )\)、虚数部分\(M_2 (\omega )\)和耗散功率\(p(\omega )\)随驱动频率\(\omega \) 的依赖关系. 可以看出, 在低频极限中, \(M_1(\omega \to 0) \to 790g\), 接近系统的静态质量, \(M_2 (\omega \to 0)\to 0\). 在50 \(\sim \) 800 Hz频率范围内, 样品池的加速度幅与振动台的驱动幅度接近, 在3 m/s\(^{2}\)附近波动.\(\left| F \right|\), \(M_1 (\omega )\), \(M_2 (\omega )\) 和\(p(\omega)\) 在200 Hz左右出现较大的共振峰, 这可能是因为在200 Hz左右, 颗粒系统的结构产生了剧烈的调整, 接近于系统的共振状态(此频率处, 颗粒振动的幅度增大, 振动产生的噪音也较尖锐), 力振幅会出现一个峰值, 系统耗散也相应较大.颗粒的共振可能是力的振幅、有效质量及耗散功率峰值频率较一致的原因.在远离共振峰的频率区间\((f < 100\) {Hz} 低频区域和\(500 {\rm Hz} <f < 1 000 {\rm Hz}\) 高频区域), 耗散功率\(p(\omega )\) 都非常小.
图32 垂直振动激发下钨颗粒样品池所受的(a)力振幅\(\left| F\right|\), (b)加速度的振幅\(\left| a \right|\), (c)力和加速度的位相差\(\phi \), (d)有效质量的实数部分\(M_1 (\omega)\), (e)虚数部分 \(M_2 (\omega )\)和\((f)\)耗散功率\(p(\omega )\)随驱动频率\(\omega \) 的依赖关系(余田等 2015 )
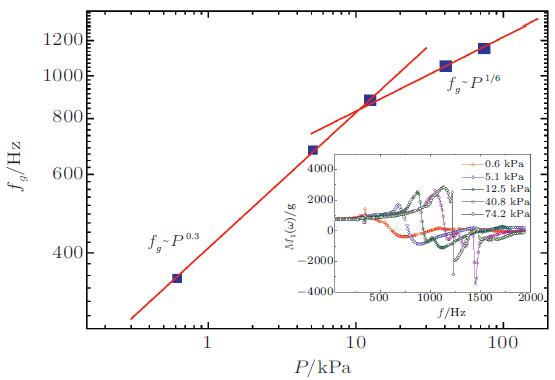
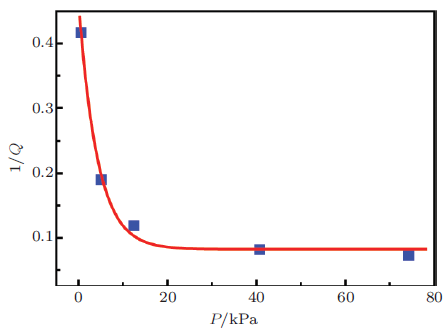
由图33 可知, 上表面压强对颗粒系统有效质量谱的影响很大.随着颗粒体系上表面压强的增大, \(M_1 (\omega )\) 和\(M_2 (\omega )\)的共振频率\(\omega _g \) 向高频处移动, 且共振处的峰值\(M_1 (\omega _g)\) 和\(M_2 (\omega _g )\) 也相应增大. 由内插图可得到\(M_1 (\omega )\)的主共振频率\(f_g \) 随压强的变化曲线, 发现共振频率\(f_g \)随外加压强\(P\) 的变化满足分段幂律的规律, 幂指数由\(P\) 的低值\((0.6 <P < 12 {\rm kPa})\)时的0.3, 减小为\(P\)的高值\((P > 12 {\rm kPa})\)时的\(1/ 6\). 在连续流体模型中, 颗粒介质被看做是一个有损耗的流体. 当颗粒体系产生共振时, \(f_g\propto \dfrac{1}{L}\sqrt {\dfrac{k}{\rho }} \), 其中\(\rho \)是颗粒的密度, \(k\) 为颗粒的体积模量, \(L\)为颗粒的填充深度, 容易得出共振频率\(f_g \) 与压强\(P\)的分段幂律关系: 即低压强处\(f_g\propto P^{1 / 4}\), 高压强处\(f_g \propto P^{1 / 3}\).
图33 双对数坐标系下\(M_1 (\omega )\) 的共振频率\(f_g\)随压强\(P\)的变化. 插图是为不同压强下有效质量的实数部分\(M_1 (\omega)\) 随\(f\)的变化, 由此确定共振频率\(f_g \)(余田 等 2015 )
\(Q\)值为共振频率与半峰高度的频宽的比值, 图34 显示了颗粒系统品质因子倒数\(1 /Q\)随压强\(P\)的变化曲线, \(1/Q\)随\(P\)增大满足指数衰减规律, 即\[\dfrac{1}{Q} = 0.4\exp \left( { - \dfrac{P}{4.25}} \right) + 0.08 \ \ (18)\]这可能是由于表面压强较小时, 体系较为疏松, 颗粒内部结构更容易发生调整, 耗散效率较高. 增大颗粒上表面的压强, 实际上不仅增加了颗粒之间紧密和更均匀接触的数量, 而且减少了切线应力接触和潜在的滑动接触的数量, 因此\(1/ Q\)随压强的增大而减小. 当压强足够高时, 颗粒体系被压缩至接近固体的状态, \(1/ Q\) 几乎不随压强变化.
图34 垂直振动激发下钨颗粒系统品质因子\(Q\)的倒数\(1/Q\)随压强\(P\)的变化, 满足指数衰减关系(余田等2015)
6 结论与展望
颗粒材料由大量粗颗粒密集堆积形成, 具有复杂和丰富的力学现象.由于颗粒材料在自然界、工程建设和工业生产中广泛存在, 在设计和调控其力学性质方面的需求巨大.发展颗粒材料宏观本构模型或本构理论, 实现对各种不同运动状态的统一描述, 是颗粒材料基础研究的前沿科学问题.
由于颗粒介质是多体相互作用体系, 其结构特征是宏观均匀, 又具有若干颗粒大小的介尺度结构.结构表征是理解和认识颗粒介质物理问题的基础和依据, 是当前制约颗粒介质力学和应用发展的瓶颈.随着研究的深入和结构分析实验手段的不断改进, 发现颗粒体系的结构存在非均匀性, 结构不均匀是认识动力学不均匀、力学性质转变等问题的基础.在颗粒介质的不同区域, 差别很大, 几乎每个颗粒周围的颗粒组成、体积分数、配位数和应力等与其他区域不同, 这种局域差异影响、甚至决定了颗粒介质的性质.这些就注定了表征与建立颗粒结构与性能的相关性从基本理论到实验手段上都极其困难.结构表征是理解和认识其颗粒材料重要力学问题的基础和依据, 基于统计力学, 从颗粒结构和动力学开始建立颗粒材料体系的宏观连续介质力学理论框架是必然途径.但是现有测试分析手段所描述的颗粒系统的组织结构过于简单化, 还不能建立颗粒尺度上的无序性和其力学和物理性能的对应关系, 缺乏对颗粒组织结构的真正认识. 所以, 颗粒系统中颗粒结构和动力学研究的困难是制约颗粒物质基础研究和材料发展的瓶颈, 这需要实验技术的进步. 测量颗粒平移和转动等运动学量, 测量结构量的空间分布及其演变, 引入新的概念、理论方法、新思路, 比如短程序、局域对称性等新概念, 新的结构描述方法和结构模型等, 定性和定量分析它们对宏观力学现象的影响, 始终是颗粒材料重要的研究内容. 另外, 人们多年来建立了描述颗粒材料弹性、塑性和黏性的大量模型和理论, 现代大型计算机也为颗粒结构的模拟提供了强有力的手段, 实验测量结果将验证其合理性和有效性, 为颗粒材料基础研究提供了科学依据.
结合笔者近十年来开展的颗粒结构和动力学性质的测量研究, 发展了表征颗粒尺度的结构和性能及其相关性的独特的实验技术.本文综述了这些实验手段的基本原理及其局限性, 以及取得的主要成果和国际最新进展和困难. 结合笔者的经验和教训, 认为今后开展多种技术联合测量, 从多方面和多角度认识颗粒体系复杂力学性质, 才能更好的、系统地研究颗粒结构与动力学特征等基础问题, 具体如下.
(1)描述颗粒材料弹性、塑性和黏性的大量模型和理论需要实验测量结果评判其合理性和有效性, 必须加强发展测量颗粒结构和动力学的独特的实验技术, 为颗粒材料宏观性能研究提供科学依据. 比如, SVS技术、PEPT和SR技术等测得的是颗粒运动信息, 这些物理量与宏观塑性和黏性等基本性质相关; 内耗技术、DMA和声学谱等技术所测得的能量耗散和模量等都是宏观量, 这些物理量及其变化反映了颗粒材料内部发生的微观事件.比较可行的方法是, 针对颗粒材料结构特征, 对现有测量技术进行改造, 会遇到许多实际问题, 需要逐步予以完善使其适用.把这些测量技术在应用于颗粒体系时, 注意发现的新规律以及遇到的问题, 力图研发原创性的测量手段, 解决工程实践特定需求.由于颗粒体系内在过程复杂和多样, 建议开展多种技术联合测量, 多方面和多角度认识颗粒体系力学现象.
(2)实验测量到的是颗粒运动学量和结构量, 要建立其与宏观力学量的联系, 亦即需要发展颗粒材料的粗粒化方法.粗粒化方法确定微观(或介观的)的物理量与某一恰当的、较大尺度上刻画体系的物理量之间的联系(包括本构关系), 并建立其演化方程, 定性和定量分析它们对宏观力学现象的影响, 从介观结构层次全面解释颗粒体系力学性质.颗粒介质的粗粒化方法出现的较晚, Goldhirsh曾开展了理论推导, 由颗粒接触力得到应力\(\sigma _{ij}^\varepsilon\), 以及由动量密度\(p_i\)得到应变\(\varepsilon _{ij} \) 等等概念上还有不清晰的方面, 比如\(\sigma _{ij}^\varepsilon \) 非对称性和偶应力量化, \(\varepsilon_{ij} \)定义中如何考虑颗粒自转等, 这些基本问题是颗粒介质所独有的.
(3)在透视测速领域, 目前的技术还不具有通用性, 这是由于一方面这些技术都需要极其专业而且昂贵的设备, 普通实验室很难实现; 另一方面, 这些技术都对人体健康有一定伤害, 如: PEPT, SR和CT等都具有辐射伤害, MRV虽然没有辐射但是长期在其强静磁场附近也会对人体产生影响. 因此, 开发一种安全、经济、具有普遍适用性的透视测速方法是当前迫切需要解决的问题.一种比较具有发展前景的技术就是采用无线传感技术的球形大颗粒运动测试技术, 该技术将各类传感器(如: 九轴运动传感器、温度传感器、应力传感器等)和2.4 G无线收发芯片, 通过单片机控制组成嵌入式系统构成测试节点, 植入颗粒内部(其中应变片贴在颗粒表面). 在颗粒运动过程中, 每个测试节点实时将测得的颗粒加速度和角速度、温度、以及应力等信息通过无线网络(局域网)发送到用户端, 用户端通过多线程智能采集技术, 高超采集各个节点的信息并计算出颗粒的速度、位移、角速度、应力等, 进而分析颗粒体系内部的速度流线、混流、停留时间、颗粒滑动和滚动等关键问题.但目前该技术的系统信噪比较差, 分辨率较低(空间分辨率: 1 cm以上, 时间分辨率: 0.1 s); 此外, 由于应力测量电路较复杂, 受体积的限制, 单个颗粒上应变片的数量有限(6个左右), 导致局部应力信息丢失. 因此, 选择精度更高、集成度更好的传感器, 以及开发适用性更强的信号处理算法(如卡尔曼滤波、深度学习等)是接下来重点研究方向.另一种安全的测试技术是目前最新的太赫兹(THz)技术, 太赫兹辐射是0.1 \(\sim\) 10 THz的电磁辐射(介于无线电波中的毫米波和光波中的远红外线之间), 优点安全无辐射、具有较强的穿透性, 不足之处是成像精度低(空间分辨率: 5 cm以上), 扫描速度慢(由待测区域决定, 一般需要几分钟), 价格高, 目前国际上还没有采用该技术测量颗粒流相关报道.
(4)声学手段已经成为研究颗粒材料力学性质的重要手段.人们已经能够利用探测颗粒材料横纵波声速、剪切与体积模量比值\(G/K\)、声衰减系数等, 进而研究颗粒材料的塑性转变和声学衰减机制; 此外, 人们正在尝试利用非线性声学手段研究颗粒材料的非线性系数、弱力及缺陷分布等, 进而探测颗粒材料内部与散射相关的结构. 但是, 受到声源功率等的限制, 能够直接进行颗粒材料声学测量(特别是非线性声学测量)的商业化仪器还不多见, 还需要研发新的声学测量手段以满足工程实践的需求.
The authors have declared that no competing interests exist.
作者已声明无竞争性利益关系。The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
费明龙 , 徐小蓉 , 孙其诚 , 周公旦 , 金峰 . 2016 . 颗粒介质固---流态转变的理论分析及实验研究
. 力学学报 , 48 : 48 -55
[本文引用: 1]
(Fei M L Xu X R Sun Q C Zhou G D Jin F. 2016 . Studies on the transition between solid- and fluid-like states of granular materials.
Chinese Journal of Theoretical and Applied Mechanics , 48 : 48 -55 ).
[本文引用: 1]
[2]
马文波 , 赵雪丹 , 张国华 , 孙其诚 , 侯志坚 ,董军军 . 颗粒密度对氧化锆颗粒系统的动力学体积响应的影响 . 2015 . 科学技术与工程
, 15 : 5 -11
[本文引用: 3]
(Ma W B Zhao X D Zhang G H Sun Q C Hou Z J The effect of the particle density on the spectrum of dynamical responses on packing volume of the granular system composed of spherical zirconium oxide
.2015 . Science Technology and Engineering,15 : 5 -11 ).
[本文引用: 3]
[3]
彭政 , 蒋亦民 , 刘锐 , 厚美瑛 . 垂直振动激发下颗粒物质的能量耗散 . 2013 . 物理学报
, 62 : 24502
(Peng Z Jiang Y M Liu R Hou M Y. 2013 . Energy dissipation of a granular system under vertical vibration.
Acta Physica Sinica , 62 : 24502 ).
[4]
孙其诚 , 王光谦 . 2009. 颗粒介质力学导论. 北京 : 科学出版社
(Sun Q C Wang G Q. An Introduction to the Mechanics of Granular Materials. Beijing : Science Press ).
[5]
吴学邦 , 刘长松 , 朱震刚 . 内耗技术在软物质研究中的一些应用
. 2016 . 物理 , 45 : 720 -728
[本文引用: 1]
(Wu X B Liu C S Zhu Z G. 2016 . Applications of internal friction technology in the study of soft matter.
Physics , 45 : 720 -728 ).
[本文引用: 1]
[6]
余田 , 张国华 , 孙其诚 , 赵雪丹 , 马文波 . 2015 . 垂直振动激励下颗粒材料有效质量和耗散功率的研究
. 物理学报 , 64 : 044501
[本文引用: 3]
(Yu T Zhang G Sun Q Zhao X Ma W . Dynamic effective mass and power dissipation of the granular material under vertical vibration.2015 .
Acta Phys.Sin. ,64 : 044501 ).
[本文引用: 3]
[7]
张进修 , 熊小敏 . 内耗频谱仪的应用及内耗频率峰机理的探讨
. 2003 . 金属学报 , 39 : 1127 -1132
[本文引用: 1]
(Zhang J X Xiong X M. 2003 . Applications of apparatus of internal friction frequency spectroscopy and interstation of mechanism of frequency internal friction peak.
Acta Metallurgica Sinica ,39 : 1127 -1132 ).
[本文引用: 1]
[8]
张攀 , 赵雪丹 , 张国华 , 张祺 , 孙其诚 , 侯志坚 ,董军军 . 垂直载荷下颗粒物质的声波探测和非线性响应
. 2016 . 物理学报 , 65 : 024501
[本文引用: 2]
( Zhang P Zhao X D Zhang G H Zhang Q Sun Q C Hou Z J Dong J J. 2016 . Acoustic detection and nonlinear response of granular materials under vertical vibrations.
Acta Phys. Sin., 65: 024501).
[本文引用: 2]
[9]
Adrian R. 2005 . Twenty years of particle image velocimetry.
Experiments in Fluids , 39 : 159 -169
[本文引用: 1]
[10]
Aizu Y Asakura T. 1987 . Principles and development of spatial filtering velocimetry.
Applied Physics B , 43 : 209 -224 .
[本文引用: 1]
[11]
Bandyopadhyay R Gittings A S Suh S S Dixon P K Durian D J. 2005 . Speckle-visibility spectroscopy: A tool to study time-varying dynamics.
Review of Scientific Instruments , 76 : 093110 .
[本文引用: 1]
[12]
Basu A Xu Y Still T Arratia P E Zhang Z Nordstrom K N Rieser J M Gollub J P Durian D J Yodh A G. 2014 . Rheology of soft colloids across the onset of rigidity: Scaling behavior, thermal, and non-thermal responses.
Soft Matter , 10 : 3027 -3035 .
[本文引用: 1]
[13]
Beetstra R Hoef M A V D , Kuipers J A M. 2007 . Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres.
Aiche Journal , 53 : 489 -501 .
[本文引用: 1]
[14]
Bendicks C Tarlet D Roloff C Bord\'{a}s R Wunderlich B Michaelis B Th\'{e}venin D. 2011 . Improved 3-D particle tracking velocimetry with colored particles. 2011.
Journal of Signal & Information Processing , 2 : 59 -71 .
[本文引用: 1]
[15]
Bergeler S Krambeer H. 2004 . Novel optical spatial filtering methods based on two-dimensional photodetector arrays.
Measurement Science and Technology , 15 : 1309 -1315 .
[本文引用: 1]
[16]
Bokkers G A Annaland M V S Kuipers J A M. 2004 . Mixing and segregation in a bidisperse gas--solid fluidised bed: a numerical and experimental study.
Powder Technology , 140 : 176 -186 .
[本文引用: 1]
[17]
Brunet T Jia X Johnson P A. 2008 . Transitional nonlinear elastic behaviour in dense granular media.
Geophysical Research Letters , 35 : L19308 .
[18]
Capart H Young D L Zech Y. 2002 . Vorono\"{\i} imaging methods for the measurement of granular flows.
Experiments in Fluids , 32 : 121 -135 .
[本文引用: 1]
[19]
Cao Y Zhang X Kou B Li X T Xiao X H Fezzaa K Wang Y J. 2014 . A dynamic synchrotron X射线 imaging study of effective temperature in a vibrated granular medium
. Soft Matter , 10 : 5398 -5404 .
[20]
Chung Y C Hsiau S S Liao H H Ooi J. 2010 . An improved PTV technique to evaluate the velocity field of non-spherical particles.
Powder Technology , 202 : 151 -161 .
[本文引用: 1]
[21]
Clark A H Petersen A J Kondic L Behringer R P. 2015 . Nonlinear force propagation during granular impact.
Physical Review Letters , 114 : 144502 .
[22]
Coniglio A de Candia A Fierro A Nicodemi M Pica Ciamarra M Tarzia M. 2004 . On Edwards' theory of powders.
Physica A , 339 : 1 -6 .
[23]
Dixon P K Durian D J. 2002 . Speckle visibility spectroscopy and variable granular fluidization.
Physical Review Letters , 90 : 184302 .
[本文引用: 1]
[24]
Dijksman J A van Hecke M. 2009 . The role of tap duration for the steady-state density of vibrated granular media.
EPL( Europhysics Letters ), 88 : 44001 .
[本文引用: 1]
[25]
Druckrey A M Alshibli K A. 3D Behavior of sand particles using X-ray synchrotron micro-tomography. 2014 . Geotechnical Special Publication
, 234 : 2814 -2821 .
[本文引用: 1]
[26]
Dub\'{e} O Alizadeh E Chaouki J Bertrand F. 2013 . Dynamics of non-spherical particles in a rotating drum.
\emph{Chemical Engineering Science} , 101 : 486 -502 .
[本文引用: 1]
[27]
Edwards S. 1998 . The equations of stress in a granular material.
Physica A , 249 : 226 -231 .
[28]
Ellenbroek W Somfai E van Hecke M van Saarloos W. 2006 . Critical scaling in linear response of frictionless granular packings near jamming.
Physical Review Letters , 97 : 258001 .
[29]
Ellenbroek W van Hecke M van Saarloos W. 2009 . Jammed frictionless disks: Connecting local and global response.2009.
Physical Review E , 80 : 061307 .
[本文引用: 1]
[30]
Felice R D. 1994 . The voidage function for fluid-particle interaction systems.
International Journal of Multiphase Flow , 20 : 153 -159 .
[本文引用: 2]
[31]
Flenner E Szamel G. Dynamic heterogeneity in a glass forming fluid: Susceptibility , structure factor correlation length. 2010 . Physical Review Letters
, 105 : 217801 .
[本文引用: 2]
[32]
Fiedler O Werther J Labahn N Christofori K. 1997 . Measurement of local particle velocities and velocity distributions in gas-solid flows by means of the spatial filter method.
Powder Technology , 94 : 51 -57 .
[33]
Gao Q Wang H P Shen G X. 2013 . Review on development of volumetric particle image velocimetry.
Science Bulletin , 58 : 4541 -4556 .
[34]
Gao Q Ortizdue\~{n}as C Longmire E K. 2011 . Analysis of vortex populations in turbulent wall-bounded flows.
Journal of Fluid Mechanics , 678 : 87 -123 .
[本文引用: 1]
[35]
GDR Midi. On dense granular flows. 2003 . European Physical Journal E
, 14 : 341 -365 .
[本文引用: 1]
[36]
Gittings A S Durian D J. Statistics of bubble rearrangement dynamics in a coarsening foam. 2008 . Physical Review E
, 78 : 066313 .
[本文引用: 1]
[37]
Gong J M Yang H Lin S H Li R Zivkovic V. 2018 . Spatial filtering velocimetry for surface velocity measurement of granular flow.
Powder Technology , 324 : 76 -84 .
[本文引用: 2]
[38]
Goodrich C P Liu A J Nagel S R. 2014 . Solids between the mechanical extremes of order and disorder.
Nature Physics , 10 : 578 -581 .
[本文引用: 1]
[39]
Haacke E M Brown R W Thompson M R Venkatesan R. 1999 . Magnetic Resonance Imaging: Physical Principles and Sequence Design. New York: JohnWiley and
Sons.
[本文引用: 2]
[40]
Hagemeier T B\"{o}rner M Bück A Tsotsas E. 2015 . A comparative study on optical techniques for the estimation of granular flow velocities.
Chemical Engineering Science , 131 : 63 -75 .
[本文引用: 3]
[41]
Hagemeier T B\"{o}rner M Bück A Tsotsas E. 2015 . Estimation of particle dynamics in 2-D fluidized beds using particle tracking velocimetry.
Particuology , 22 : 39 -51 .
[本文引用: 2]
[42]
Hawkesworth M R Parker D J. 1991 . Nonmedical applications of a positron camera.
Nuclear Instruments and Methods in Physics Research , 310 : 423 -434 .
[本文引用: 1]
[43]
Hsiau S S Jang H W. 1998 . Measurements of velocity fluctuations of granular materials in a shear cell.
Experimental Thermal & Fluid Science , 17 : 202 -209 .
[本文引用: 1]
[44]
Hosokawa S Matsumoto T Tomiyama A. 2013 . Measurement of bubble velocity using spatial filter velocimetry.
Experiments in Fluids , 54 : 1 -12 .
[45]
Hsu C J Johnson D L Ingale R A Valenza J J Gland N Makse H A. 2009 . Dynamic effective mass of granular media.
Physical Review Letters , 102 : 058001 .
[本文引用: 1]
[46]
Ianni F Lasne D Sarcia R H\'{e}braud P. 2006 . Relaxation of jammed colloidal suspensions after shear cessation.
Physical Review E , 74 : 011401 .
[本文引用: 1]
[47]
Itakura Y Sugimura A Tsutsumi S. 1981 . Amplitude-modulated reticle constructed by a liquid crystal cell array.
Applied Optics , 20 : 2819 -2826 .
[本文引用: 1]
[48]
Jesuthasan N Baliga B R Savage S B. 2006 . Use of particle tracking velocimetry for measurements of granular flows: Review and application particle tracking velocimetry for granular flow measurements.
Powder & Particle , 24 : 15 -26 .
[本文引用: 2]
[49]
Katsuragi H Abate A R Durian D J. 2010 . Jamming and growth of dynamical heterogeneities versus depth for granular heap flow.
Soft Matter , 6 : 3023 -3029 .
[本文引用: 1]
[50]
Khidas Y Jia X. 2010 . Anisotropic nonlinear elasticity in a spherical-bead pack: Influence of the fabric anisotropy.
Physical Review E , 81 : 021303 .
[51]
Kitagawa Y Hayashi A Minami S. 1991 . Particle velocity measurements using an optical fiber array spatial filter.
Transactions of the Society of Instrument and Control Engineers , 27 : 1041 -1043 .
[52]
Kou B Cao Y Li J Xia C Li Z Dong H Zhang A Zhang J Kob W Wang Y. 2017 . Granular materials flow like complex fluids.
Nature , 551 : 360 -363 .
[本文引用: 1]
[53]
Laufer M B. 2013 . Granular dynamics in pebble bed reactor cores. [PhD Thesis].
UC Berkeley
[54]
Le M M Cohenaddad S H\"{o}hler R. 2012 . Bubble rearrangement duration in foams near the jamming point.
Physical Review Letters , 108 : 188301 .
[本文引用: 1]
[55]
Li J Cao Y Xia C Kou B Xiao X H Fezzaa K Wang Y J. 2014 . Similarity of wet granular packing to gels.
Nature Communications , 5 : 5014 .
[56]
Liebling T M Tsukahara M. 2009 . Jamming in granular media.
EPFL.
[57]
Liu R Yin X Li H Shao Q York P He Y Xiao T Zhang J. 2013 . Visualization and quantitative profiling of mixing and segregation of granules using synchrotron radiation X射线 microtomography and three dimensional reconstruction
. International Journal of Pharmaceutics , 445 : 125 -133 .
[本文引用: 1]
[58]
Li R Yang H Zheng G Zhang B F Fei M L Sun Q C. 2016 . Double speckle visibility spectroscopy for the dynamics of a passive layer in a rotating drum.
Powder Technology , 295 : 167 -174 .
[本文引用: 1]
[59]
Liu J Sun Q Jin F. 2011 . The influence of flow rate on the decrease in pressure beneath a conical pile.
Powder Technology , 212 : 296 -298 .
[60]
Li J Xu C Wang S. 2014 . Spatial filtering characteristics of electrostatic sensor matrix for local velocity measurement of pneumatically conveyed particles.
Measurement , 53 : 194 -205 .
[本文引用: 4]
[61]
Lim E W C Wong Y S Wang C H. 2007 . Particle image velocimetry experiment and discrete-element simulation of voidage wave instability in a vibrated liquid-fluidized bed.
Industrial & Engineering Chemistry Research , 46 : 1375 -1389 .
[本文引用: 2]
[62]
Liu G Q Li S Q Zhao X L Yao Q. 2008 . Experimental studies of particle flow dynamics in a two-dimensional spouted bed.
Chemical Engineering Science , 63 : 1131 -1141 .
[本文引用: 1]
[63]
Lueptow R M Akonur A Shinbrot T. 2000 . PIV for granular flows.
Experiments in Fluids , 28 : 183 -186 .
[本文引用: 1]
[64]
Ludewig F Dorbolo S Gilet T Vandewalle N. 2008 . Energetic approach for the characterization of taps in granular compaction.
EPL ( Europhysics Letters ), 84 : 44001 .
[本文引用: 1]
[65]
Manning M Liu A. 2011 . Vibrational modes identify soft spots in a sheared disordered packing.
Physical Review Letters , 107 : 108302 .
[本文引用: 1]
[66]
Müller C R Holland D J Sederman A J Mantle M D Gladden L F Davidson J F. 2008 . Magnetic resonance imaging of fluidized beds.
Theoretical Foundations of Chemical Engineering , 42 : 469 -478 .
[本文引用: 2]
[67]
Müller C R Holland D J Sederman A J Mantle M D Gladden L F Davidson J F. 2008 . Granular temperature: Comparison of magnetic resonance measurements with discrete element model simulations.
Powder Technology , 184 : 241 -253 .
[本文引用: 3]
[68]
Natarajan V V R Hunt M L Taylor E D. 1995 . Local measurements of velocity fluctuations and diffusion coefficients for a granular material flow.
Journal of Fluid Mechanics , 304 : 1 -25 .
[本文引用: 1]
[69]
Nowak E R Knight J B Ben-Naim E Jaeger H M Nagel S R. 1998 . Density fluctuations in vibrated granular materials.
Physical Review E , 57 : 1971 -1982 .
[本文引用: 1]
[70]
Orpe A V Khakhar D V. 2007 . Rheology of surface granular flows.
Journal of Fluid Mechanics , 571 : 1 -32 .
[本文引用: 3]
[71]
Percin M Hu Y Oudheusden B W V Remes B Scarano F. 2011 . Wing flexibility effects in clap-and-fling.
Delft University of Technology , 3 : 217 -227 .
[本文引用: 1]
[72]
Petrak D. 2002 . Simultaneous measurement of particle size and particle velocity by the spatial filtering technique.
Particle & Particle Systems Characterization , 19 : 391 -400 .
[73]
Pine D J Weitz D A Chaikin P M Herbolzheimer E. 1988 . Diffusing wave spectroscopy.
Physical Review Letters , 60 : 1134 -1137 .
[74]
Karimi K Maloney C E. 2011 . Local anisotropy in globally isotropic granular packings.
Physical Review Letters , 107 : 268001 .
[本文引用: 2]
[75]
Parker D J Broadbent C J Fowles P Hawkesworth M R McNeil P. 1993 . Positron emission particle tracking: A technique for studying flow within engineering equipment.
Nuclear Instruments and Methods in Physics Research , 326 : 592 -607 .
[本文引用: 1]
[76]
Parker D J Forster R N Fowles P Takhar P S. 2002 . Positron emission particle tracking using the new Birmingham positron camera.
Nuclear Instruments and Methods in Physics Research Section A , 477 : 540 -546 .
[本文引用: 1]
[77]
Parker D J Dijkstra A E Martin T W Seville J P K. 1997 . Positron emission particle tracking studies of spherical particle motion in rotating drums.
Chemical Engineering Science , 52 : 2011 -2022 .
[78]
Parker D Fan X F. 2008 . Positron emission particle tracking---Application and labelling techniques.
Particuology , 6 : 16 -23 .
[79]
Qian M Liu J Yan M S Shen Z H Lu J Ni X W Li Q Xuan Y M. 2006 . Investigation on utilizing laser speckle velocimetry to measure the velocities of nanoparticles in nanofluids.
Optics Express , 14 : 7559 -7566 .
[80]
Rix S J L Glass D H Greated C A. 1996 . Preliminary studies of elutriation from gas-fluidised beds using particle image velocimetry.
Chemical Engineering Science , 51 : 3479 -3489 .
[本文引用: 1]
[81]
Sinha S K. 1988 . Improving the accuracy and resolution of particle image or laser speckle velocimetry.
Experiments in Fluids , 6 : 67 -68 .
[本文引用: 1]
[82]
Sederman A J Gladden L F Mantle M D. 2007 . Application of magnetic resonance imaging techniques to particulate systems.
Advanced Powder Technology , 18 : 23 -38 .
[本文引用: 1]
[83]
Shirsath S S Padding J T Clercx H J H Kuipers J A M. 2015 . Cross-validation of 3D particle tracking velocimetry for the study of granular flows down rotating chutes.
Chemical Engineering Science , 134 : 312 -323 .
[本文引用: 1]
[84]
Tang Z Q Jiang N Schroder A. 2012 . Tomographic PIV investigation of coherent structures in a turbulent boundary layer flow.
Acta Mechanica Sinica , 28 : 572 -582 .
[本文引用: 2]
[85]
Tighe B. 2011 . Relaxations and rheology near jamming.
Physical Review Letters , 107 : 158303 .
[本文引用: 2]
[86]
Uddin M S Inaba H Itakura Y Kasahara M. 1998 . Estimation of the surface velocity of debris flow with computer-based spatial filtering.
Applied Optics , 37 : 6234 -6239 .
[本文引用: 3]
[87]
Valenza J J Hsu C J Johnson D L. Effect of granular media on the vibrational response of a resonant structure: Theory and experiment. 2010 . The Journal of the Acoustical Society of America
, 128 : 2768 -2781 .
[本文引用: 1]
[88]
Valenza J Hsu C J Ingale R et al. 2009 .Dynamic effective mass of granular media and the attenuation of structure-borne sound.
Physical Review E , 80 : 051304 .
[89]
Valenza J Johnson D L. 2012 . Normal-mode spectrum of finite-sized granular systems: The effects of fluid viscosity at the grain contacts.
Physical Review E , 85 : 041302 .
[90]
Vitelli V. 2010 . Attenuation of shear sound waves in jammed solids.
Soft Matter , 6 : 3007 -3012 .
[本文引用: 2]
[91]
Villarruel F X Lauderdale B E Mueth D M Jaeger H M. 2000 . Compaction of rods: Relaxation and ordering in vibrated, anisotropic granular material.
Physical Review E , 61 : 6914 -6921 .
[本文引用: 1]
[92]
Wang W J Kong X Z Zhu Z G. 2007 . Friction and relative energy dissipation in sheared granular materials.
Physical Review E , 75 : 041302 .
[93]
Wang Y. 2016 . Granular packing as model glass formers.
Chinese Physics B , 1 : 1 -9 .
[本文引用: 2]
[94]
Wang Y Liu X Im K S Lee W-K Wang J Fezzaa K Hung DLS Winkelman J R. 2008 . Ultrafast X射线 study of dense-liquid-jet flow dynamics using structure-tracking velocimetry
. Nature Physics , 4 : 305 -309 .
[95]
Wang Z Zhang J. 2015 . Fluctuations of particle motion in granular avalanches - from the microscopic to the macroscopic scales.
Soft Matter , 11 : 5408 .
[96]
Wyart M Silbert L E Nagel S R Witten T A. 2005 . Effects of compression on the vibrational modes of marginally jammed solids.
Physical Review E , 72 : 051306 .
[97]
Xia C Li J Cao Y Kou B Xiao X Fezzaa K Xiao T Wang Y. 2015 . The structural origin of the hard-sphere glass transition in granular packing.
Nature Communications , 6 : 1 -9 .
[本文引用: 1]
[98]
Xu C Tang G Zhou B Wang S M. 2009 . The spatial filtering method for solid particle velocity measurement based on an electrostatic sensor.
Measurement Science and Technology , 20 : 045404 .
[本文引用: 1]
[99]
Xu X Sun Q Jin F Chen Y P. 2016 . Measurements of velocity and pressure of a collapsing granular pile.
Powder Technology , 303 : 147 -155 .
[本文引用: 2]
[100]
Yang H Jiang G L Sawe H Y Davies C Biggs M J Zivkovic V. 2016 . Granular dynamics of cohesive powders in a rotating drum as revealed by speckle visibility spectroscopy and synchronous measurement of forces due to avalanching.
Chemical Engineering Science , 149 : 1 -9 .
[本文引用: 1]
[101]
Yang H Zhang B F Li R Zheng G Zivkovic V. 2017 . Particle dynamics in avalanche flow of irregular sand particles in the slumping regime of a rotating drum.
Powder Technology , 311 : 439 -448 .
[102]
Yang H Li R Kong P Sun Q C Biggs M J Zivkovic V. 2015 . Avalanche dynamics of granular materials under the slumping regime in a rotating drum as revealed by speckle visibility spectroscopy.
Physical Review E , 91 : 042206 .
[本文引用: 1]
[103]
Zhang W Wang Y Sang J L. 2008 . Simultaneous PIV and PTV measurements of wind and sand particle velocities.
Experiments in Fluids , 45 : 241 -256 .
[本文引用: 2]
[104]
Zhang X D Xia C J Xiao X H Wang Y J. 2014 . Fast synchrotron X-ray tomography study of the packing structures of rods with different aspect ratios.
Chinese Physics B , 23 : 373 -376 .
[本文引用: 3]
[105]
Zou L N. 2010 . Spectral responses in granular compaction.
Physical Review E , 81 : 031302 .
颗粒介质固---流态转变的理论分析及实验研究
1
2016
... 颗粒堆塌落过程中的速率分布. 流动特征时间\(\tau _{\rm c}= \sqrt {{h_0 }/g} \), 其中\(h_{0}\)是颗粒堆初始高度, \(g\)是重力加速度; 速率大小用颜色表示.颗粒堆初始高度、厚度和长度分别为\(180 {\rm mm}\times 200 {\rm mm}\times 100 {\rm mm}\). 插图是时间\(1.2\tau_{\rm c} \) 时拍摄的颗粒堆(Xu et al. 2016 , 费明龙 等 2016 ) ...
颗粒介质固---流态转变的理论分析及实验研究
1
2016
... 颗粒堆塌落过程中的速率分布. 流动特征时间\(\tau _{\rm c}= \sqrt {{h_0 }/g} \), 其中\(h_{0}\)是颗粒堆初始高度, \(g\)是重力加速度; 速率大小用颜色表示.颗粒堆初始高度、厚度和长度分别为\(180 {\rm mm}\times 200 {\rm mm}\times 100 {\rm mm}\). 插图是时间\(1.2\tau_{\rm c} \) 时拍摄的颗粒堆(Xu et al. 2016 , 费明龙 等 2016 ) ...
科学技术与工程
3
2015
... 实验装置示意图(右图为顶部颗粒表面图)(马文波 等 2015 ) ...
... (a)振动幅度\(\varGamma \)调制图示, (b)已调制振动幅度\(\varGamma(t)\) (虚线)与比容\(v(t)\) (实线)随脉冲数目\(t\)的变化(马文波 等 2015 ) ...
... 垂直振动激励条件下颗粒体系体积分数\(\varphi\)随振动幅度\(\varGamma _0 \)的变化(马文波 等 2015 ) ...
科学技术与工程
3
2015
... 实验装置示意图(右图为顶部颗粒表面图)(马文波 等 2015 ) ...
... (a)振动幅度\(\varGamma \)调制图示, (b)已调制振动幅度\(\varGamma(t)\) (虚线)与比容\(v(t)\) (实线)随脉冲数目\(t\)的变化(马文波 等 2015 ) ...
... 垂直振动激励条件下颗粒体系体积分数\(\varphi\)随振动幅度\(\varGamma _0 \)的变化(马文波 等 2015 ) ...
内耗技术在软物质研究中的一些应用
1
2016
... 目前, 颗粒物质的声学阻尼特性已经得到了广泛的应用, 但是关于颗粒材料中耗散机制的微观起源仍然不清楚, 需要进一步的研究.力学谱技术是研究材料中能量损耗规律的有效手段. 与其他谱学技术相比, 内耗测量采用的应力/应变振幅很小, 对被测物体没有任何破坏作用, 所以它是一种无损力学诊断方法, 并且对于微区成分和结构状态敏感, 可反映材料在各种复杂外界环境(如压力、高温、强核辐射等)下的力学性能等.因此, 内耗技术可以提供一些其他实验手段无法得到的信息, 在固体物理领域, 内耗与力学谱技术应用广泛(张进修 和 熊小敏 2013 , 吴学邦 等 2016 ). 随着内耗测量技术的不断发展, 近年来其应用领域已拓展到颗粒物质Jamming转变等, 一些工作表明, 内耗技术能够有效地探测和研究颗粒物质的结构转变与动力学弛豫行为.比如, 颗粒的种类、粒径大小、表面粗糙度以及外界压强等决定了力链网络结构的共振频率, 内耗技术还可用来探知颗粒体系力链在外场压强下的共振频率, 揭示密集颗粒物质的能量耗散性质.中国科学院固体物理所采用改进的低频内耗仪研究不同颗粒体系(如砂粒、铁粉和铝粉等)在外加剪切应力作用下的能量耗散性质, 比如发现了其内耗---频率谱中均分别出现 3个明显的能量耗散峰.随着外加压强(0 \(\sim \) 400 Pa)的增大, 各体系3个耗散峰均向高频端移动. 初步认为, 该耗散峰来源于颗粒体系中不同长度力链的共振耗散. 随着频率的降低, 内耗峰依次对应于双颗粒链、三颗粒链和四颗粒链的共振耗散(Wang et al. 2007 ). 动态力学分析仪(DMA) 是一种材料能耗测试仪, 与内耗仪一样可用于材料耗散性能测试.但目前DMA在测量颗粒材料的能量耗散性质方面的报道不多. ...
内耗技术在软物质研究中的一些应用
1
2016
... 目前, 颗粒物质的声学阻尼特性已经得到了广泛的应用, 但是关于颗粒材料中耗散机制的微观起源仍然不清楚, 需要进一步的研究.力学谱技术是研究材料中能量损耗规律的有效手段. 与其他谱学技术相比, 内耗测量采用的应力/应变振幅很小, 对被测物体没有任何破坏作用, 所以它是一种无损力学诊断方法, 并且对于微区成分和结构状态敏感, 可反映材料在各种复杂外界环境(如压力、高温、强核辐射等)下的力学性能等.因此, 内耗技术可以提供一些其他实验手段无法得到的信息, 在固体物理领域, 内耗与力学谱技术应用广泛(张进修 和 熊小敏 2013 , 吴学邦 等 2016 ). 随着内耗测量技术的不断发展, 近年来其应用领域已拓展到颗粒物质Jamming转变等, 一些工作表明, 内耗技术能够有效地探测和研究颗粒物质的结构转变与动力学弛豫行为.比如, 颗粒的种类、粒径大小、表面粗糙度以及外界压强等决定了力链网络结构的共振频率, 内耗技术还可用来探知颗粒体系力链在外场压强下的共振频率, 揭示密集颗粒物质的能量耗散性质.中国科学院固体物理所采用改进的低频内耗仪研究不同颗粒体系(如砂粒、铁粉和铝粉等)在外加剪切应力作用下的能量耗散性质, 比如发现了其内耗---频率谱中均分别出现 3个明显的能量耗散峰.随着外加压强(0 \(\sim \) 400 Pa)的增大, 各体系3个耗散峰均向高频端移动. 初步认为, 该耗散峰来源于颗粒体系中不同长度力链的共振耗散. 随着频率的降低, 内耗峰依次对应于双颗粒链、三颗粒链和四颗粒链的共振耗散(Wang et al. 2007 ). 动态力学分析仪(DMA) 是一种材料能耗测试仪, 与内耗仪一样可用于材料耗散性能测试.但目前DMA在测量颗粒材料的能量耗散性质方面的报道不多. ...
垂直振动激励下颗粒材料有效质量和耗散功率的研究
3
2015
... 垂直振动激发下钨颗粒实验装置示意图(余田 等 2015 ) ...
... 垂直振动激发下钨颗粒样品池所受的(a)力振幅\(\left| F\right|\), (b)加速度的振幅\(\left| a \right|\), (c)力和加速度的位相差\(\phi \), (d)有效质量的实数部分\(M_1 (\omega)\), (e)虚数部分 \(M_2 (\omega )\)和\((f)\)耗散功率\(p(\omega )\)随驱动频率\(\omega \) 的依赖关系(余田等 2015 ) ...
... 双对数坐标系下\(M_1 (\omega )\) 的共振频率\(f_g\)随压强\(P\)的变化. 插图是为不同压强下有效质量的实数部分\(M_1 (\omega)\) 随\(f\)的变化, 由此确定共振频率\(f_g \)(余田 等 2015 ) ...
垂直振动激励下颗粒材料有效质量和耗散功率的研究
3
2015
... 垂直振动激发下钨颗粒实验装置示意图(余田 等 2015 ) ...
... 垂直振动激发下钨颗粒样品池所受的(a)力振幅\(\left| F\right|\), (b)加速度的振幅\(\left| a \right|\), (c)力和加速度的位相差\(\phi \), (d)有效质量的实数部分\(M_1 (\omega)\), (e)虚数部分 \(M_2 (\omega )\)和\((f)\)耗散功率\(p(\omega )\)随驱动频率\(\omega \) 的依赖关系(余田等 2015 ) ...
... 双对数坐标系下\(M_1 (\omega )\) 的共振频率\(f_g\)随压强\(P\)的变化. 插图是为不同压强下有效质量的实数部分\(M_1 (\omega)\) 随\(f\)的变化, 由此确定共振频率\(f_g \)(余田 等 2015 ) ...
内耗频谱仪的应用及内耗频率峰机理的探讨
1
2003
... 目前, 颗粒物质的声学阻尼特性已经得到了广泛的应用, 但是关于颗粒材料中耗散机制的微观起源仍然不清楚, 需要进一步的研究.力学谱技术是研究材料中能量损耗规律的有效手段. 与其他谱学技术相比, 内耗测量采用的应力/应变振幅很小, 对被测物体没有任何破坏作用, 所以它是一种无损力学诊断方法, 并且对于微区成分和结构状态敏感, 可反映材料在各种复杂外界环境(如压力、高温、强核辐射等)下的力学性能等.因此, 内耗技术可以提供一些其他实验手段无法得到的信息, 在固体物理领域, 内耗与力学谱技术应用广泛(张进修 和 熊小敏 2013 , 吴学邦 等 2016 ). 随着内耗测量技术的不断发展, 近年来其应用领域已拓展到颗粒物质Jamming转变等, 一些工作表明, 内耗技术能够有效地探测和研究颗粒物质的结构转变与动力学弛豫行为.比如, 颗粒的种类、粒径大小、表面粗糙度以及外界压强等决定了力链网络结构的共振频率, 内耗技术还可用来探知颗粒体系力链在外场压强下的共振频率, 揭示密集颗粒物质的能量耗散性质.中国科学院固体物理所采用改进的低频内耗仪研究不同颗粒体系(如砂粒、铁粉和铝粉等)在外加剪切应力作用下的能量耗散性质, 比如发现了其内耗---频率谱中均分别出现 3个明显的能量耗散峰.随着外加压强(0 \(\sim \) 400 Pa)的增大, 各体系3个耗散峰均向高频端移动. 初步认为, 该耗散峰来源于颗粒体系中不同长度力链的共振耗散. 随着频率的降低, 内耗峰依次对应于双颗粒链、三颗粒链和四颗粒链的共振耗散(Wang et al. 2007 ). 动态力学分析仪(DMA) 是一种材料能耗测试仪, 与内耗仪一样可用于材料耗散性能测试.但目前DMA在测量颗粒材料的能量耗散性质方面的报道不多. ...
内耗频谱仪的应用及内耗频率峰机理的探讨
1
2003
... 目前, 颗粒物质的声学阻尼特性已经得到了广泛的应用, 但是关于颗粒材料中耗散机制的微观起源仍然不清楚, 需要进一步的研究.力学谱技术是研究材料中能量损耗规律的有效手段. 与其他谱学技术相比, 内耗测量采用的应力/应变振幅很小, 对被测物体没有任何破坏作用, 所以它是一种无损力学诊断方法, 并且对于微区成分和结构状态敏感, 可反映材料在各种复杂外界环境(如压力、高温、强核辐射等)下的力学性能等.因此, 内耗技术可以提供一些其他实验手段无法得到的信息, 在固体物理领域, 内耗与力学谱技术应用广泛(张进修 和 熊小敏 2013 , 吴学邦 等 2016 ). 随着内耗测量技术的不断发展, 近年来其应用领域已拓展到颗粒物质Jamming转变等, 一些工作表明, 内耗技术能够有效地探测和研究颗粒物质的结构转变与动力学弛豫行为.比如, 颗粒的种类、粒径大小、表面粗糙度以及外界压强等决定了力链网络结构的共振频率, 内耗技术还可用来探知颗粒体系力链在外场压强下的共振频率, 揭示密集颗粒物质的能量耗散性质.中国科学院固体物理所采用改进的低频内耗仪研究不同颗粒体系(如砂粒、铁粉和铝粉等)在外加剪切应力作用下的能量耗散性质, 比如发现了其内耗---频率谱中均分别出现 3个明显的能量耗散峰.随着外加压强(0 \(\sim \) 400 Pa)的增大, 各体系3个耗散峰均向高频端移动. 初步认为, 该耗散峰来源于颗粒体系中不同长度力链的共振耗散. 随着频率的降低, 内耗峰依次对应于双颗粒链、三颗粒链和四颗粒链的共振耗散(Wang et al. 2007 ). 动态力学分析仪(DMA) 是一种材料能耗测试仪, 与内耗仪一样可用于材料耗散性能测试.但目前DMA在测量颗粒材料的能量耗散性质方面的报道不多. ...
垂直载荷下颗粒物质的声波探测和非线性响应
2
2016
... 颗粒体系的\(G /B\)随压强\(P\)的变化. 实线为拟合曲线, 插图是单轴压缩示意图和测量得到的纵波信号(张攀 等 2016 ) ...
... 二倍频振幅与基频振幅平方的比值\({\mu _{2\omega } }/ {\mu_{1\omega } ^2}\) 随压强\(P\)的变化关系图, 实线为拟合曲线(张攀 等 2016 ) ...
垂直载荷下颗粒物质的声波探测和非线性响应
2
2016
... 颗粒体系的\(G /B\)随压强\(P\)的变化. 实线为拟合曲线, 插图是单轴压缩示意图和测量得到的纵波信号(张攀 等 2016 ) ...
... 二倍频振幅与基频振幅平方的比值\({\mu _{2\omega } }/ {\mu_{1\omega } ^2}\) 随压强\(P\)的变化关系图, 实线为拟合曲线(张攀 等 2016 ) ...
Twenty years of particle image velocimetry.
1
2005
... 图1 所示为PIV技术原理图, 双脉冲激光经过柱面镜形成片光源, 照射在散布于颗粒流中的稀疏示踪粒子(近似一个点), 与脉冲激光同步的高速相机对粒子拍摄得到连续的双脉冲成像图, 再对双脉冲成像图中颗粒位移的相关性进行计算, 得到流场的分布(Adrian 2005 , Lueptow et al. 2000 ). 设粒子像点的光强度分布为\(I\left( \bar{x} \right)\), 它的自相关为 \[R\left( S \right) = \int {I\left(\bar {x} \right)I\left( {\bar {x} + \pmb s } \right)}{\rm d}x \ \ (1)\] 式中, \(\pmb s \)为二维位移矢量. \(\pmb s = 0\)代表每个像点自相关, 得到峰值\(R_{P}\). \(\pmb s\)等于诊断点内平均位移量, 出现第二个强的峰值\(R_{D}^{ + }\), 称为正位移峰值, 其物理意义为第一次光脉冲形成的粒子像和第二次光脉冲形成的粒子像重叠.同样会出现相同的峰值\(R_{D}^{ - }\), 称负位移峰值, 即第二次光脉冲形成的粒子像和第一次光脉冲形成的粒子像重合.假设原点峰值\(R_{P}\)的位置和正位移峰值\(R_{D}^{ +}\)的位置之间的位移矢量为\(\pmb S _D^ + \), 得到粒子像点的速度为\[\pmb V = \dfrac{\pmb S _D^ + }{M\Delta t} \ \ (2)\] 其中, \(M\)为系统放大倍数, \(\Delta t\)为曝光时间间隔. ...
Principles and development of spatial filtering velocimetry.
1
1987
... 对于数字图像技术无法有效识别的小颗粒或不规则颗粒流, 可采用SFV技术测量其速度场(Aizu & Asakura 1987 ). 如图5 (a)所示, 采用对空间频率具有一定选择作用的栅格式空间滤波器, 被测运动物的像经过透镜成像在空间滤波器上, 经空间滤波器调制后再由聚焦透镜会聚到光电探测器上, 光电探测器输出周期性变化的正弦信号, 信号的中心频率\(f\)与物体的运动速度\(v\)满足如下关系\[v = \dfrac{pf}{M\sin \theta } \ \ (6)\] 其中, \(p\)为空间狭缝的空间周期, \(M\)为光学系统放大倍数, \(\theta\)为平行光栅中轴与运动物体速度的夹角. ...
Speckle-visibility spectroscopy: A tool to study time-varying dynamics.
1
2005
... 1905年, 爱因斯坦认为颗粒无序运动与微观粒子热运动有相似性; 直至1978年, Ogawa首次提出了颗粒温度 (granular temperature, \(T_{g})\)概念表征颗粒运动速度的无序程度, \(T_g \equiv\dfrac{1}{3}\left\langle {\left( {\delta v} \right)^2}\right\rangle \), 其中\(\delta v = v - \left\langle v \right\rangle\) 是颗粒脉动速度, \(\left\langle { \cdots} \right\rangle \)表示系综平均. 40多年以来, 以颗粒温度为核心概念, 建立了适用于稀疏颗粒流的颗粒动理学理论 (granular kinetics), 得到了稀疏颗粒流的黏滞系数和能量耗散等的解析表达, 但是颗粒温度的实验精细测量还缺乏. 散斑能见度光谱法(speckle visibility spectroscopy, SVS)测量颗粒温度是通过计算一定曝光时间内单幅散斑图像的对比度得到散斑的变化快慢, 进而得到颗粒流的速度脉动信息 (Dixon & Durian 2002 , Bandyopadhyay et al. 2005 ). 由于散斑图像是基于散射光场干涉的原理, 因此其空间分辨率可达到0.1 \(\mu \)m. 另一方面, 由于其采用线阵CCD相机测量散斑对比度变化, 因此其时间分辨率可达到1 \(\mu \)s. ...
Rheology of soft colloids across the onset of rigidity: Scaling behavior, thermal, and non-thermal responses.
1
2014
... 图26 显示了玻璃珠样品的\(G /B\) 随\(P\)的变化规律, 发现实验给出的\( G /B = 0.58\sim 1.39\),且颗粒体系 \(G /B\)随\(P\)的增大而减小, 满足幂律关系: \(G /B\sim P^{ - 0.45}\), 如图26 中红色直线拟合所表示.根据(Tighe 2011 , Basu et al. 2014 , Goodrich et al. 2014 )的结果, 对于堵塞颗粒体系的\(G/B\sim\left( {\varphi - \varphi _{\rm c} } \right)^{1/ 2}\sim p^{1/3}\)(其中\(\varphi _{\rm c} \)是颗粒体系堵塞点的体积分数). 显然, 实验发现的\(G /B\)随\(P\)的变化规律与Hertz 接触理论不相符, 暗示连续弹性介质理论在低压强下可能不再成立.导致上述差异的因素可能有以下两个: (1) 理论模型要求颗粒是光滑的, 但是实际颗粒的表面是粗糙的, 这会使实际结果同Hertz接触理论预言存在一定偏差; (2)纵波对于应力场的各向异性更加敏感, 而横波对于结构各向异性更加敏感(Khidas & Jia 2010 ). ...
Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres.
1
2007
... 普通的X射线- CT可以研究颗粒运动和滚动信息(Beetstra et al. 2007 , Felice 1994 ), 实验时颗粒包裹着一根穿过球心的金属丝, 在X射线- CT图像中可以利用这根金属丝的形态得到塑料球的运动信息, 如图21 所示. 由于成像时间比较长, 实验装置内部设置挡板, 测量时挡住颗粒, 使其不发生运动, 然后X射线- CT成像; 成像完毕后, 抽开挡板, 颗粒流动, 然后再挡住颗粒, X射线- CT成像, 那么通过相邻两次成像就可以分析颗粒运动细节.不停的间断操作使得整个实验中颗粒运动是不连续的, 可能对整个流动产生扰动, 流动因此而发生改变. ...
Improved 3-D particle tracking velocimetry with colored particles. 2011.
1
2011
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
Novel optical spatial filtering methods based on two-dimensional photodetector arrays.
1
2004
... 实现空间滤波的方法有多种, 较早的空间滤波器是由如图5 (a)所示平行狭缝组成的光栅, 这种结构存在加工精度要求大, 空间周期不能调整, 且只能测量垂直于狭缝方向的运动速率等问题. 为了解决这一问题, 人们提出了利用传感器阵列实现空间滤波功能的光电探测器(如图5 (b)).Itakura 等 (1981) 利用一个液晶元件阵列构建了一种新型的空间滤波器, 并实现了二维速度分量的测量. 此后Kitagawa 等(1991)利用光纤阵列构建了一种空间滤波器, 有效简化了系统并提高了测量精度.但传感器或光纤阵列也存在分辨率较低, 安装调试困难, 传感器性能一致性差等问题.近年来, 随着光电技术及工业制造技术的发展, 传统的光栅和光电探测器阵列结构逐渐被线阵或面阵CCD/CMOS相机所取代. 如, Bergeler 和 Krambeer (2004) 对面阵CMOS相机像素在两个正交方向进行分组, 模拟空间滤波器件的功能, 实现了二维速度分量的测量, 并通过实验测量了毛细管中血流速度分布情况. 这种系统不仅结构简单, 性能稳定, 且可以通过软件调整空间周期, 提高空间滤波器用于速度测量的选择性, 测量精度高.另外, 还有采用静电传感阵列的空间滤波测量法(Xu et al. 2009 , Li et al. 2014 ), 该方法能够获得敏感区域内颗粒运动平均速度信息, 在一定程度上实现了对颗粒体系局部平均速度的测量. ...
Mixing and segregation in a bidisperse gas--solid fluidised bed: a numerical and experimental study.
1
2004
... 爱丁堡大学Rix等首次用PIV技术测量了鼓泡流化床中颗粒随气泡飞出时的速度场分布(Rix et al.1996 ), 但他们只是沿用了传统PIV的测量系统和算法(采用片激光光源和互相关算法), 没有针对密集颗粒体系的特点进行改进, 无法测量流化床中密集颗粒体系的速度分布.密集颗粒体系的一个特点是颗粒间隙小且互相遮挡, 激光无法在颗粒体系间传播, 因此测量密集颗粒体系的PIV系统一般不再采用片激光作为光源, 而是将激光束扩束或者采用多个直流卤素灯作为光源直接照射在待测颗粒流表面(Bokkers et al.2004 , Hagemeier et al. 2015 ).密集颗粒体系的另一个特点是速度场分布的梯度范围非常大, 如鼓泡流化床中气泡附近颗粒的速度梯度变化极大, 而在其他区域颗粒的位移几乎为零, 导致传统互相关算法的准确性大幅下降. 针对这一问题, 清华大学姚强课题组提出了一种改进PIV算法, 在梯度变化率不同的区域, 使用不同的互相关窗口(interrogation window, IW)和帧速率, 从而有效提高了系统的准确性(Liu et al. 2008 , Lim et al. 2007 , Hagemeier et al. 2015 ). ...
Transitional nonlinear elastic behaviour in dense granular media.
0
2008
Vorono\"{\i} imaging methods for the measurement of granular flows.
1
2002
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
A dynamic synchrotron X射线 imaging study of effective temperature in a vibrated granular medium
0
2014
An improved PTV technique to evaluate the velocity field of non-spherical particles.
1
2010
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
Nonlinear force propagation during granular impact.
0
2015
On Edwards' theory of powders.
0
2004
Speckle visibility spectroscopy and variable granular fluidization.
1
2002
... 1905年, 爱因斯坦认为颗粒无序运动与微观粒子热运动有相似性; 直至1978年, Ogawa首次提出了颗粒温度 (granular temperature, \(T_{g})\)概念表征颗粒运动速度的无序程度, \(T_g \equiv\dfrac{1}{3}\left\langle {\left( {\delta v} \right)^2}\right\rangle \), 其中\(\delta v = v - \left\langle v \right\rangle\) 是颗粒脉动速度, \(\left\langle { \cdots} \right\rangle \)表示系综平均. 40多年以来, 以颗粒温度为核心概念, 建立了适用于稀疏颗粒流的颗粒动理学理论 (granular kinetics), 得到了稀疏颗粒流的黏滞系数和能量耗散等的解析表达, 但是颗粒温度的实验精细测量还缺乏. 散斑能见度光谱法(speckle visibility spectroscopy, SVS)测量颗粒温度是通过计算一定曝光时间内单幅散斑图像的对比度得到散斑的变化快慢, 进而得到颗粒流的速度脉动信息 (Dixon & Durian 2002 , Bandyopadhyay et al. 2005 ). 由于散斑图像是基于散射光场干涉的原理, 因此其空间分辨率可达到0.1 \(\mu \)m. 另一方面, 由于其采用线阵CCD相机测量散斑对比度变化, 因此其时间分辨率可达到1 \(\mu \)s. ...
The role of tap duration for the steady-state density of vibrated granular media.
1
2009
... 密度响应谱是探测颗粒体系内部弛豫动力学和研究颗粒材料热动力学理论的有效方法.Nowak 等(1998) 研究了垂直脉冲激励下圆柱形容器中单分散玻璃球体系的密度随时间的演化, 发现当用大于某个临界值\(\varGamma ^\ast\)的垂直脉冲振动足够长时间之后,系统密度最终达到一个仅依赖振幅的稳定值.Villarruel 等(2000) 进一步研究了垂直脉冲激励下的非均匀、圆柱形颗粒材料的状态随时间和空间的演变, 发现垂直脉冲振动驱动颗粒体系从无序、低聚集率状态到密实的、有序的、向列型状态演变.Ludewig 等 (2008) 研究了离散的垂直脉冲振动参数对系统密度的影响, 提出用一个全新的无量纲参数\(\varXi \)(垂直振动实验中注入颗粒体系的能量)作为描述颗粒压缩动力学(compaction dynamics)的特征量. Dijksman 和 van Hecke(2009) 则发现处于可逆分支的颗粒系统密度不仅与振动脉冲的强度有关, 还与单个脉冲的周期\(T\)有关, \(\varGamma {T}\)才是颗粒离散脉冲振动的控制参数. Zou(2010) 利用体积响应谱技术研究了垂直脉冲振动下颗粒体系的压缩动力学, 发现颗粒体系的体积响应因子表现出与自旋玻璃系统中动力学位形比热类似的行为, 暗示颗粒压缩过程中表现出的玻璃状动力学行为来源于颗粒的集体重排. ...
Geotechnical Special Publication
1
2014
... 由于颗粒介质结构非均匀性的影响, 颗粒介质中声波除了一阶声波外, 还出现二阶甚至三阶的谐波. 非线性现象是研究弱力链规律的有效手段.目前, 各向异性介质非线性声学研究主要以纯模为主, 开展新的理论和实验具有非常迫切的需要.非线性效应对于弱力链的出现非常敏感. 一方面, 弱力链分数主要受材料应变的影响; 但是另一方面, 这些接触在线性弹性力学中很难被阐明. 因此, 颗粒介质重排的早期阶段引起的弱应变波很难通过线性声学传播来评估.相比之下, 高次谐波的产生表现出了对结构更高的敏感性.非线性声学研究固体结构受到越来越多的关注. 固体材料受力之后, 胡克定律几乎完美地描述了材料中的应力与应变(单位变形量)之间成线性关系, 而非线性声学就是处理应力应变的偏差.这个结果打破了弹性波的叠加效应, 使得非线性引起的波频谱分量水平增加可以作为这样"弱特征"的敏感指标, 可以用于颗粒材料弱力链网络的检测. 颗粒介质声学非线性可用系数\(\beta\)表征, 与二倍频振幅\(\mu _{2\omega } \)与基频振幅\(\mu _{1\omega }\)平方的比值有关(Brunet et al. 2008 )\[\left| {\dfrac{\mu _{2\omega } }{\mu _{1\omega } ^2}} \right| =\dfrac{\beta \omega ^2}{8\alpha V^2} \ \ (14)\] 其中, \(\mu_{2\omega } \)代表接收二倍频振幅, \(\mu _{1\omega }\) 代表接收基频振幅, \(V\)代表声速, \(\omega \)代表频率.\(\beta \)越大,波形畸变越严重. 利用傅立叶变换法分析了玻璃珠样品的 \({\mu _{2\omega } }/ {\mu _{1\omega } ^2}\) 随压强\(P\) 的变化曲线, 如图27 所示. \({\mu _{2\omega } }/{\mu _{1\omega } ^2}\)随压强的增大而幂率减小: \({\mu _{2\omega } }/ {\mu _{1\omega } ^2}\propto P^{ - 0.866}\), 如红色直线所示. 根据Hertz 接触理论, \({\mu_{2\omega } } /{\mu _{1\omega } ^2} \propto P^{ - 1 / 2}\), 实验得到的\({\mu _{2\omega } }/{\mu _{1\omega } ^2}\)随压强的幂指数\(( - 0.866)\)与理论预言的幂指数\(( - 1/2)\)存在差异.造成上述差异的原因可能是在低压强范围内颗粒物质的声速\(V_{\rm p} \), \(V_{\rm s} \) 及\(\beta \)随压强\(P\)的幂律标度指数都偏离Hertz接触理论的预言. ...
Dynamics of non-spherical particles in a rotating drum.
1
2013
... 上海理工大学杨晖课题组针对密集颗粒流的特点, 提出了多种频谱校正和提取算法, 改进了基于线阵CCD空间滤波的颗粒运动速度测量系统(Gong et al. 2017 ), 并采用图7 (a)所示的滚筒实验装置进行了测试. 实验发现, 由于密集颗粒体系中颗粒的无序运动, 导致输出信号中掺杂有多种频率的干扰信号, 图7 (b)和图7 (c)所示分别为电机传送带(用于SFV标定)和滚筒内颗粒流表面的空间滤波信号频谱图, 可以明显看到, 电机传送带的空间滤波信号频谱具有非常确定的峰值, 而颗粒流信号的频谱图的噪声干扰非常严重, 为了准确得到信号峰值, 他们提出了采用平均重心法进行频谱校正, 进而提取中心频率的方法.并通过测量滚筒内不规则玻璃砂和小直径玻璃珠表层沿径向颗粒流速度分布进行了验证.从图7 (d)显示的玻璃珠和玻璃砂的速度分布曲线可以看到, 玻璃珠的速度分布呈现中间高两头低的对称分布, 这与理论分析以及大颗粒用PIV测量的先加速后减少结果一致(GDR MiDi 2003 ).而对于玻璃砂, 一方面在相同的滚筒转速下, 其速度值始终大于玻璃珠的速度值, 这一结果与玻璃砂的休止角较大, 因此动能较大的结果一致(Dub\'{e} et al. 2013 , Yang et al. 2017 ); 另一方面, 玻璃砂的速度分布呈现两次加速减速的过程, 这一结果与玻璃砂崩塌过程中速度变化类似, 原因是由于不规则颗粒在滚落过程中会在斜面中间形成一次小的堆积, 然后产生二次滚落(Yang et al. 2017 ). ...
The equations of stress in a granular material.
0
1998
Critical scaling in linear response of frictionless granular packings near jamming.
0
2006
Jammed frictionless disks: Connecting local and global response.2009.
1
2009
... 近10年来, 上海交通大学张洁研究组开展了力链结构表征及其演化规律分析的详细工作(Wang & Zhang 2015 ), 清华大学孙其诚研究组开展了二维颗粒光弹实验, 实现了基于应力条纹快速计算数千颗粒上所有接触点的法向力和切向力, 研究发现: 颗粒接触力的概率密度函数\(p(f)\)表征, 其中\(f\)为归一化力, 发现: \(f = 1\)处, \(p(f)\)达到极大值; 提出了准直性、应力阈值等标准, 定义了力链, 确定了力链长度概率密度分布, 发现力链约为8个颗粒长.近期, 美国Duke大学 Behringer 课题组结合光弹技术, 采用高速相机拍摄了颗粒受冲击过程中的力链变化, 测量了力的传播速度(Clark et al. 2015 ). ...
The voidage function for fluid-particle interaction systems.
2
1994
... 普通的X射线- CT可以研究颗粒运动和滚动信息(Beetstra et al. 2007 , Felice 1994 ), 实验时颗粒包裹着一根穿过球心的金属丝, 在X射线- CT图像中可以利用这根金属丝的形态得到塑料球的运动信息, 如图21 所示. 由于成像时间比较长, 实验装置内部设置挡板, 测量时挡住颗粒, 使其不发生运动, 然后X射线- CT成像; 成像完毕后, 抽开挡板, 颗粒流动, 然后再挡住颗粒, X射线- CT成像, 那么通过相邻两次成像就可以分析颗粒运动细节.不停的间断操作使得整个实验中颗粒运动是不连续的, 可能对整个流动产生扰动, 流动因此而发生改变. ...
... 颗粒的表面摩擦和非弹性接触等因素使得颗粒体系能够快速耗散掉外部脉冲激励所产生的能量, 从而长时间停留在某一亚稳态. 另一方面, 连续的振动、摇晃等外部激励却可以推动颗粒体系动力学的演化, 例如, 用固定频率的大幅度垂直脉冲连续振动颗粒样品可以使系统快速达到一个稳定状态.达到稳态的颗粒材料的密度仅仅是脉冲振动幅度的单值函数, 而不依赖于制备的历史.为了进一步解释在外部激励脉冲作用下疏松颗粒材料的密度弛豫, Coniglio 等 (2004) 提出了基于能量的、用于描述颗粒物质稳态的统计力学方法.基于Edwards (1998)的统计力学框架, 给出了用位形温度\(T_{\rm conf}\)和颗粒数密度\(N_{\rm s} \)两个控制参量描述颗粒系统的平均场相图.在Coniglio的\(T_{\rm conf} - N_{\rm s} \) 相图中, 融化线和玻璃转变线把相图分成3个区域: 在熔化线之上(即在低\(N_{\rm s}\)、高\(T_{\rm conf} \)区)为具有水平平移不变性的类流体相; 在玻璃转变线之下(即在高\(N_{\rm s} \)、低\(T_{\rm conf} \)区)为玻璃相; 在熔化线和冻结线之间为超冷液体相. Coniglio的\(T_{\rm conf} - N_{\rm s} \)相图说明可以通过改变激励脉冲幅度来迫使颗粒系统经历从玻璃态到超冷液体以及从超冷液体到类流体的转变过程. ...
Physical Review Letters
2
2010
... SVS法最早由美国宾夕法尼亚大学Durian团队提出用于测量振动流化床表层颗粒的运动(Dixon & Durian 2002 ), 如图9 所示在第一个1/4个周期, 玻璃珠随流化床一起以加速度\(1.25\sin \phi \cdot g\)上升, 玻璃珠间紧密挤压在一起, 颗粒温度几乎为0\(^{\circ}\)C; 在第二个1/4个周期, 流化床开始下降, 而玻璃珠由于惯性继续上升一段距离后开始下降, 在此过程中玻璃珠速度加快, 颗粒温度升高, 并在接近1/2周期时, 达到峰值(图9 (b)中空心三角处); 在第三个1/4个周期, 随着玻璃珠掉落到流化床上并互相碰撞, 颗粒温度形成一个尖峰; 此后随着玻璃珠再次堆积在流化床上, 颗粒温度逐渐下降, 并在最后一个1/4个周期趋于0. 此后, Durian团队进一步对该技术进行了完善, 将其用于泡沫(foam)和胶体(colloidal suspension)等研究(Gittings & Durian 2008 , Le et al. 2012 , Ianni et al. 2006 ). ...
... 正弦垂直震荡流化床中玻璃珠的颗粒温度(Dixon & Durian 2002 ). (a)正弦震荡周期内流化床和玻璃珠层面的位置, 以及两者差的5倍, 最大加速度是1.25\(g\), 震荡周期10 Hz; (b)正弦震荡周期内颗粒温度变化曲线, 其中\(\gamma = {4\pi \delta v}/ \lambda \) ...
Measurement of local particle velocities and velocity distributions in gas-solid flows by means of the spatial filter method.
0
1997
Review on development of volumetric particle image velocimetry.
0
2013
Analysis of vortex populations in turbulent wall-bounded flows.
1
2011
... PIV技术测量三维空间体内完整速度场是近年来的研究热点.研究曾尝试采用离焦成像、多视角成像和全息成像等方法通过对示踪粒子进行三维空间定位, 实现粒子追踪测速. 受粒子浓度的限制, 空间分辨率并不理想, 直到层析PIV概念的提出, 才使得三维PIV测量技术真正进入了实用阶段(Gao et al. 2013 ), 该技术通过三维互相关分析来得到具有较高空间分辨率的速度场, 实现了在较高粒子浓度下的测量. 三维PIV的核心技术包括粒子重构和速度场再现技术, 前者采用了医学领域光学层析技术中基于投影方法的代数重构技术, 后者采用三维互相关分析算法(Gao et al. 2011 , Percin et al. 2011 , Tang et al. 2012 ). ...
European Physical Journal E
1
2003
... 上海理工大学杨晖课题组针对密集颗粒流的特点, 提出了多种频谱校正和提取算法, 改进了基于线阵CCD空间滤波的颗粒运动速度测量系统(Gong et al. 2017 ), 并采用图7 (a)所示的滚筒实验装置进行了测试. 实验发现, 由于密集颗粒体系中颗粒的无序运动, 导致输出信号中掺杂有多种频率的干扰信号, 图7 (b)和图7 (c)所示分别为电机传送带(用于SFV标定)和滚筒内颗粒流表面的空间滤波信号频谱图, 可以明显看到, 电机传送带的空间滤波信号频谱具有非常确定的峰值, 而颗粒流信号的频谱图的噪声干扰非常严重, 为了准确得到信号峰值, 他们提出了采用平均重心法进行频谱校正, 进而提取中心频率的方法.并通过测量滚筒内不规则玻璃砂和小直径玻璃珠表层沿径向颗粒流速度分布进行了验证.从图7 (d)显示的玻璃珠和玻璃砂的速度分布曲线可以看到, 玻璃珠的速度分布呈现中间高两头低的对称分布, 这与理论分析以及大颗粒用PIV测量的先加速后减少结果一致(GDR MiDi 2003 ).而对于玻璃砂, 一方面在相同的滚筒转速下, 其速度值始终大于玻璃珠的速度值, 这一结果与玻璃砂的休止角较大, 因此动能较大的结果一致(Dub\'{e} et al. 2013 , Yang et al. 2017 ); 另一方面, 玻璃砂的速度分布呈现两次加速减速的过程, 这一结果与玻璃砂崩塌过程中速度变化类似, 原因是由于不规则颗粒在滚落过程中会在斜面中间形成一次小的堆积, 然后产生二次滚落(Yang et al. 2017 ). ...
Physical Review E
1
2008
... SVS法最早由美国宾夕法尼亚大学Durian团队提出用于测量振动流化床表层颗粒的运动(Dixon & Durian 2002 ), 如图9 所示在第一个1/4个周期, 玻璃珠随流化床一起以加速度\(1.25\sin \phi \cdot g\)上升, 玻璃珠间紧密挤压在一起, 颗粒温度几乎为0\(^{\circ}\)C; 在第二个1/4个周期, 流化床开始下降, 而玻璃珠由于惯性继续上升一段距离后开始下降, 在此过程中玻璃珠速度加快, 颗粒温度升高, 并在接近1/2周期时, 达到峰值(图9 (b)中空心三角处); 在第三个1/4个周期, 随着玻璃珠掉落到流化床上并互相碰撞, 颗粒温度形成一个尖峰; 此后随着玻璃珠再次堆积在流化床上, 颗粒温度逐渐下降, 并在最后一个1/4个周期趋于0. 此后, Durian团队进一步对该技术进行了完善, 将其用于泡沫(foam)和胶体(colloidal suspension)等研究(Gittings & Durian 2008 , Le et al. 2012 , Ianni et al. 2006 ). ...
Spatial filtering velocimetry for surface velocity measurement of granular flow.
2
2018
... 上海理工大学杨晖课题组针对密集颗粒流的特点, 提出了多种频谱校正和提取算法, 改进了基于线阵CCD空间滤波的颗粒运动速度测量系统(Gong et al. 2017 ), 并采用图7 (a)所示的滚筒实验装置进行了测试. 实验发现, 由于密集颗粒体系中颗粒的无序运动, 导致输出信号中掺杂有多种频率的干扰信号, 图7 (b)和图7 (c)所示分别为电机传送带(用于SFV标定)和滚筒内颗粒流表面的空间滤波信号频谱图, 可以明显看到, 电机传送带的空间滤波信号频谱具有非常确定的峰值, 而颗粒流信号的频谱图的噪声干扰非常严重, 为了准确得到信号峰值, 他们提出了采用平均重心法进行频谱校正, 进而提取中心频率的方法.并通过测量滚筒内不规则玻璃砂和小直径玻璃珠表层沿径向颗粒流速度分布进行了验证.从图7 (d)显示的玻璃珠和玻璃砂的速度分布曲线可以看到, 玻璃珠的速度分布呈现中间高两头低的对称分布, 这与理论分析以及大颗粒用PIV测量的先加速后减少结果一致(GDR MiDi 2003 ).而对于玻璃砂, 一方面在相同的滚筒转速下, 其速度值始终大于玻璃珠的速度值, 这一结果与玻璃砂的休止角较大, 因此动能较大的结果一致(Dub\'{e} et al. 2013 , Yang et al. 2017 ); 另一方面, 玻璃砂的速度分布呈现两次加速减速的过程, 这一结果与玻璃砂崩塌过程中速度变化类似, 原因是由于不规则颗粒在滚落过程中会在斜面中间形成一次小的堆积, 然后产生二次滚落(Yang et al. 2017 ). ...
... SFV测量滚筒内玻璃珠和玻璃砂的流动速度(Gong et al. 2017 ). (a)滚筒实验系统示意图, 滚筒直径15 cm, 转速为5.2 RPM; (b)电机传送带和 (c)滚筒内颗粒流表面的空间滤波信号频谱; (d)滚筒内玻璃砂\((\nabla )\)和玻璃珠\((\bigcirc )\) (颗粒粒度:1 \(\sim\) 1.5 mm)沿径向\((x\)方向)速度分布 ...
Solids between the mechanical extremes of order and disorder.
1
2014
... 图26 显示了玻璃珠样品的\(G /B\) 随\(P\)的变化规律, 发现实验给出的\( G /B = 0.58\sim 1.39\),且颗粒体系 \(G /B\)随\(P\)的增大而减小, 满足幂律关系: \(G /B\sim P^{ - 0.45}\), 如图26 中红色直线拟合所表示.根据(Tighe 2011 , Basu et al. 2014 , Goodrich et al. 2014 )的结果, 对于堵塞颗粒体系的\(G/B\sim\left( {\varphi - \varphi _{\rm c} } \right)^{1/ 2}\sim p^{1/3}\)(其中\(\varphi _{\rm c} \)是颗粒体系堵塞点的体积分数). 显然, 实验发现的\(G /B\)随\(P\)的变化规律与Hertz 接触理论不相符, 暗示连续弹性介质理论在低压强下可能不再成立.导致上述差异的因素可能有以下两个: (1) 理论模型要求颗粒是光滑的, 但是实际颗粒的表面是粗糙的, 这会使实际结果同Hertz接触理论预言存在一定偏差; (2)纵波对于应力场的各向异性更加敏感, 而横波对于结构各向异性更加敏感(Khidas & Jia 2010 ). ...
Magnetic Resonance Imaging: Physical Principles and Sequence Design. New York: JohnWiley and
2
1999
... MRV是利用核磁共振(nuclear magnetic resonance, NMR)和磁共振成像(magnetic resonance imaging, MRI)原理来测量空间体内的三维速度场的一种技术(Haacke et al. 1999 , Sederman et al. 2007 ), 其工作介质通常为含氢原子的颗粒物质, 在外加磁场作用下, 原子核自旋系统逐步被磁化, 原子核以莫拉频率进动.在外部相同频率动射频脉冲激励下, 原子核产生磁共振现象, 而共振后恢复平衡状态的原子核会将吸收的射频脉冲能量释放出来, 探测器将这种磁共振信号转换成电信号再进行处理(如图17 所示).由于原子核自旋的共振频率与外部所加磁场相关, 因此外部磁场通常存在较弱的剃度渐变, 依此来实现空间定位, 起到追踪测量颗粒运动的目的.选用的颗粒物质要么本身含有质子\((^{1}\)H)比如芥菜籽、罂粟籽等; 要么是特殊制作包含质子的颗粒, 如胶囊中填充了液体维生素E(C\(_{29}\)H\(_{50}\)O\(_{2})\)等. ...
... 在力链结构刻画方面, Wyart 等 (2005) 认为: 设颗粒接触数\(Z\)与等静态接触数\(Z_{\rm iso} \) 之差为 \( \Delta Z = \left( {Z -Z_{\rm iso} } \right)\),则力链特征长度\(l^\ast \sim 1/{\Delta Z} \).近年来, 关于颗粒材料介观长度尺度及其随系统参数演化规律的数值研究已经取得了很大的进展.特别是, 一些研究者试图从动力学响应的角度研究颗粒体系中的特征长度.例如: Ellenbroek 等 (2006, 2009)研究了处于堵塞(jammed)固体样品中心的单个颗粒直径膨胀带来的力响应涨落, 发现当接近堵塞(jamming)点时的力响应涨落空间范围\(L^\ast \)发散, 暗示低于长度尺度\(L^\ast\)响应被涨落控制(变形场可以被视为一个扭曲软模式), 而在大于\(L^\ast\)的尺度, 系统的响应过渡到弹性. Karimi 和 Maloney(2011) 研究发现颗粒体系应力各向异性的特征长度随体积分数\(\varphi\)从上述趋近临界体积分数\(\varphi _{\rm c} \)时增大.Vitelli(2010)研究了无摩擦软球堵塞(jammed)体系剪切声波的长波衰减, 发现特征长度\(L^\ast \sim \left( {\varphi - \varphi _{\rm c} }\right)^{{ - 1} / 2}\).关于动力学关联长度随体积分数演化规律的研究方面, Flenner 等(2010) 实验发现在堵塞点附近, 水平振动单层颗粒床的动力学关联长度\(L^\ast \sim \left( {\varphi -\varphi _{\rm c} } \right)^{1/ 2}\). ...
A comparative study on optical techniques for the estimation of granular flow velocities.
3
2015
... 爱丁堡大学Rix等首次用PIV技术测量了鼓泡流化床中颗粒随气泡飞出时的速度场分布(Rix et al.1996 ), 但他们只是沿用了传统PIV的测量系统和算法(采用片激光光源和互相关算法), 没有针对密集颗粒体系的特点进行改进, 无法测量流化床中密集颗粒体系的速度分布.密集颗粒体系的一个特点是颗粒间隙小且互相遮挡, 激光无法在颗粒体系间传播, 因此测量密集颗粒体系的PIV系统一般不再采用片激光作为光源, 而是将激光束扩束或者采用多个直流卤素灯作为光源直接照射在待测颗粒流表面(Bokkers et al.2004 , Hagemeier et al. 2015 ).密集颗粒体系的另一个特点是速度场分布的梯度范围非常大, 如鼓泡流化床中气泡附近颗粒的速度梯度变化极大, 而在其他区域颗粒的位移几乎为零, 导致传统互相关算法的准确性大幅下降. 针对这一问题, 清华大学姚强课题组提出了一种改进PIV算法, 在梯度变化率不同的区域, 使用不同的互相关窗口(interrogation window, IW)和帧速率, 从而有效提高了系统的准确性(Liu et al. 2008 , Lim et al. 2007 , Hagemeier et al. 2015 ). ...
... , Hagemeier et al. 2015 ). ...
... 目前, SFV技术主要用于两相流的测量, 比如Petrak(2002) 采用基于光纤传感阵列的SFV技术测量了两相流中颗粒的大小和速度, Fiedler等(1997) 用基于CCD的空间滤波器测量了循环流化床中局部颗粒速度分布, Hosokawa等(2013) 采用SFV技术测量了鼓泡流化床中泡状流的泡沫速度, 并通过与PTV测量结果的比较, 发现在一定程度上SFV技术优于PTV技术.在密集颗粒流测量方面, Uddin等首次将SFV技术应用于泥石流表面速度的测量(Uddin et al.1998 ), 并对比了传统SFV技术和基于CCD相机的软件SFV的测量结果(如图6 所示), 发现两者结果基本一致, 而基于CCD相机的SFV技术结构更简单, 成本更低. ...
Estimation of particle dynamics in 2-D fluidized beds using particle tracking velocimetry.
2
2015
... PIV技术测量三维空间体内完整速度场是近年来的研究热点.研究曾尝试采用离焦成像、多视角成像和全息成像等方法通过对示踪粒子进行三维空间定位, 实现粒子追踪测速. 受粒子浓度的限制, 空间分辨率并不理想, 直到层析PIV概念的提出, 才使得三维PIV测量技术真正进入了实用阶段(Gao et al. 2013 ), 该技术通过三维互相关分析来得到具有较高空间分辨率的速度场, 实现了在较高粒子浓度下的测量. 三维PIV的核心技术包括粒子重构和速度场再现技术, 前者采用了医学领域光学层析技术中基于投影方法的代数重构技术, 后者采用三维互相关分析算法(Gao et al. 2011 , Percin et al. 2011 , Tang et al. 2012 ). ...
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
Nonmedical applications of a positron camera.
1
1991
... PEPT技术最早由英国伯明翰大学的Parker课题组提出(Hawkesworth & Parker. 1991 , Parker et al. 1993 ), 其追踪单个颗粒的空间分辨率可以达到0.5 mm, 时间分辨率主要由正电子相机决定(一般几十毫秒), 最大可以测量10 m/s的颗粒速度, 最多可以追踪3个示踪颗粒.由于其可追踪的示踪颗粒数量较少, 实际应用中比较适合测量具有周期边界的循环实验装置, 如滚筒、鼓泡气体流化床、振动流化床等. 与其他非侵入式测量技术相比, PEPT技术能够测出更加详细的固/液运动信息, 并且能够测量液体、有机聚合物、金属和矿物颗粒等众多材料.其不足之处在于, PEPT能跟踪颗粒数较少, 不适合复杂颗粒流速度场分布的测量. 此外, PEPT给出的是关于时间的平均速度场信息, 而不是颗粒瞬时速度场信息, 因此只适用于测量稳定流. 图15 所示为Parker 等(1997)用PEPT技术对准二维滚筒内(直径100 mm, 厚度16 mm, 颗粒直径3 mm)颗粒流速度的DEM计算结果进行了验证, 发现不同转速下, DEM计算的颗粒流表层速度总是大于PEPT的测量值, 造成这一结果主要是由于两方面原因, 一是DEM仿真时不考虑滚筒壁的作用, 二是DEM计算的速度是表层颗粒的平均速度, 而PEPT测得的是单个示踪颗粒的碰撞速度. ...
Measurements of velocity fluctuations of granular materials in a shear cell.
1
1998
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
Measurement of bubble velocity using spatial filter velocimetry.
0
2013
Dynamic effective mass of granular media.
1
2009
... 动态有效质量谱技术是研究垂直振动激励下颗粒材料声学耗散性质的重要手段(Hsu et al.2009 , Valenza et al. 2010 ). 彭政等(2013)研究了垂直激发下铜和玻璃珠系统的能量耗散, 发现体系在几十赫兹处出现共振, 且特定频率下的耗散功率随振动强度的变化呈现幂率规律. Valenza 等(2009)研究了湿度对钨颗粒体系有效质量的影响, 发现湿度越大, 颗粒物质的耗散越显著. 在钨颗粒涂上不同黏度的硅油, 研究了硅油黏度对有效质量的影响, 发现体系的耗散与黏度变化正相关.此外, Valenza 和 Johnson(2012)使用激光振动计观察到垂直振动过程中颗粒床侧壁与附近颗粒的相对位移近似为零, 表明有效质量测量是基于线性小振幅. 总之, 动态有效质量谱具有颗粒材料声学模式、弹性和时效的耗散特征, 正日益成为进一步理解颗粒体系耗散机理的主流技术之一. ...
Relaxation of jammed colloidal suspensions after shear cessation.
1
2006
... SVS法最早由美国宾夕法尼亚大学Durian团队提出用于测量振动流化床表层颗粒的运动(Dixon & Durian 2002 ), 如图9 所示在第一个1/4个周期, 玻璃珠随流化床一起以加速度\(1.25\sin \phi \cdot g\)上升, 玻璃珠间紧密挤压在一起, 颗粒温度几乎为0\(^{\circ}\)C; 在第二个1/4个周期, 流化床开始下降, 而玻璃珠由于惯性继续上升一段距离后开始下降, 在此过程中玻璃珠速度加快, 颗粒温度升高, 并在接近1/2周期时, 达到峰值(图9 (b)中空心三角处); 在第三个1/4个周期, 随着玻璃珠掉落到流化床上并互相碰撞, 颗粒温度形成一个尖峰; 此后随着玻璃珠再次堆积在流化床上, 颗粒温度逐渐下降, 并在最后一个1/4个周期趋于0. 此后, Durian团队进一步对该技术进行了完善, 将其用于泡沫(foam)和胶体(colloidal suspension)等研究(Gittings & Durian 2008 , Le et al. 2012 , Ianni et al. 2006 ). ...
Amplitude-modulated reticle constructed by a liquid crystal cell array.
1
1981
... 实现空间滤波的方法有多种, 较早的空间滤波器是由如图5 (a)所示平行狭缝组成的光栅, 这种结构存在加工精度要求大, 空间周期不能调整, 且只能测量垂直于狭缝方向的运动速率等问题. 为了解决这一问题, 人们提出了利用传感器阵列实现空间滤波功能的光电探测器(如图5 (b)).Itakura 等 (1981) 利用一个液晶元件阵列构建了一种新型的空间滤波器, 并实现了二维速度分量的测量. 此后Kitagawa 等(1991)利用光纤阵列构建了一种空间滤波器, 有效简化了系统并提高了测量精度.但传感器或光纤阵列也存在分辨率较低, 安装调试困难, 传感器性能一致性差等问题.近年来, 随着光电技术及工业制造技术的发展, 传统的光栅和光电探测器阵列结构逐渐被线阵或面阵CCD/CMOS相机所取代. 如, Bergeler 和 Krambeer (2004) 对面阵CMOS相机像素在两个正交方向进行分组, 模拟空间滤波器件的功能, 实现了二维速度分量的测量, 并通过实验测量了毛细管中血流速度分布情况. 这种系统不仅结构简单, 性能稳定, 且可以通过软件调整空间周期, 提高空间滤波器用于速度测量的选择性, 测量精度高.另外, 还有采用静电传感阵列的空间滤波测量法(Xu et al. 2009 , Li et al. 2014 ), 该方法能够获得敏感区域内颗粒运动平均速度信息, 在一定程度上实现了对颗粒体系局部平均速度的测量. ...
Use of particle tracking velocimetry for measurements of granular flows: Review and application particle tracking velocimetry for granular flow measurements.
2
2006
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
... 基于沃罗诺伊图的PTV测量结果(Hagemeier et al. 2015 ).(a)将颗粒中心以\(+\)表示其位置\(r_i \); (b)粗线表示以图(a)中颗粒位置为基础构成维诺网络, 细线表示下一帧中颗粒位置形成的沃罗诺伊图; (c)以沃罗诺伊图为基础匹配颗粒点, 得到了两帧之间的颗粒位移; (d)0.001 s 时刻颗粒位置; (e) 0.019 s 时刻颗粒位置; (f)通过连续20帧图像计算得到的轨迹分布 ...
Jamming and growth of dynamical heterogeneities versus depth for granular heap flow.
1
2010
... 图10所示为Katsuragi 等(2010) 利用SVS技术和PTV技术测量准二维沙堆崩塌过程中颗粒速度\(v_x\)和颗粒脉动速度\(\delta v\)随深度变化, 从图10 (b)可以看到, 当深度大于0.6 cm, 颗粒脉动速度小于颗粒速度, 而当深度小于0.6 cm, 颗粒速度已经趋于0, 而颗粒脉动速度随深度衰减变慢, 颗粒间的挤压成为主导. 图10 (c)进一步显示\(\delta v\) 与\(\sqrt{v_x } \)在准二维沙堆的上半部分有较好的相关性. ...
Anisotropic nonlinear elasticity in a spherical-bead pack: Influence of the fabric anisotropy.
0
2010
Particle velocity measurements using an optical fiber array spatial filter.
0
1991
Granular materials flow like complex fluids.
1
2017
... 目前, SFV技术主要用于两相流的测量, 比如Petrak(2002) 采用基于光纤传感阵列的SFV技术测量了两相流中颗粒的大小和速度, Fiedler等(1997) 用基于CCD的空间滤波器测量了循环流化床中局部颗粒速度分布, Hosokawa等(2013) 采用SFV技术测量了鼓泡流化床中泡状流的泡沫速度, 并通过与PTV测量结果的比较, 发现在一定程度上SFV技术优于PTV技术.在密集颗粒流测量方面, Uddin等首次将SFV技术应用于泥石流表面速度的测量(Uddin et al.1998 ), 并对比了传统SFV技术和基于CCD相机的软件SFV的测量结果(如图6 所示), 发现两者结果基本一致, 而基于CCD相机的SFV技术结构更简单, 成本更低. ...
Granular dynamics in pebble bed reactor cores. [PhD Thesis].
0
2013
Bubble rearrangement duration in foams near the jamming point.
1
2012
... SVS法最早由美国宾夕法尼亚大学Durian团队提出用于测量振动流化床表层颗粒的运动(Dixon & Durian 2002 ), 如图9 所示在第一个1/4个周期, 玻璃珠随流化床一起以加速度\(1.25\sin \phi \cdot g\)上升, 玻璃珠间紧密挤压在一起, 颗粒温度几乎为0\(^{\circ}\)C; 在第二个1/4个周期, 流化床开始下降, 而玻璃珠由于惯性继续上升一段距离后开始下降, 在此过程中玻璃珠速度加快, 颗粒温度升高, 并在接近1/2周期时, 达到峰值(图9 (b)中空心三角处); 在第三个1/4个周期, 随着玻璃珠掉落到流化床上并互相碰撞, 颗粒温度形成一个尖峰; 此后随着玻璃珠再次堆积在流化床上, 颗粒温度逐渐下降, 并在最后一个1/4个周期趋于0. 此后, Durian团队进一步对该技术进行了完善, 将其用于泡沫(foam)和胶体(colloidal suspension)等研究(Gittings & Durian 2008 , Le et al. 2012 , Ianni et al. 2006 ). ...
Similarity of wet granular packing to gels.
0
2014
Jamming in granular media.
0
2009
Visualization and quantitative profiling of mixing and segregation of granules using synchrotron radiation X射线 microtomography and three dimensional reconstruction
1
2013
... 准二维沙堆崩塌过程中颗粒温度测量结果(Katsuragi et al. 2010 ). (a)准二维沙堆崩塌实验装置示意图, (b)崩塌过程中颗粒速度\(v_{x}\)和颗粒脉动速度\(\delta v\)随深度变化, (c)颗粒速度\(v_{x }\)与 颗粒脉动速度\(\delta v\)的关系 ...
Double speckle visibility spectroscopy for the dynamics of a passive layer in a rotating drum.
1
2016
... 图26 显示了玻璃珠样品的\(G /B\) 随\(P\)的变化规律, 发现实验给出的\( G /B = 0.58\sim 1.39\),且颗粒体系 \(G /B\)随\(P\)的增大而减小, 满足幂律关系: \(G /B\sim P^{ - 0.45}\), 如图26 中红色直线拟合所表示.根据(Tighe 2011 , Basu et al. 2014 , Goodrich et al. 2014 )的结果, 对于堵塞颗粒体系的\(G/B\sim\left( {\varphi - \varphi _{\rm c} } \right)^{1/ 2}\sim p^{1/3}\)(其中\(\varphi _{\rm c} \)是颗粒体系堵塞点的体积分数). 显然, 实验发现的\(G /B\)随\(P\)的变化规律与Hertz 接触理论不相符, 暗示连续弹性介质理论在低压强下可能不再成立.导致上述差异的因素可能有以下两个: (1) 理论模型要求颗粒是光滑的, 但是实际颗粒的表面是粗糙的, 这会使实际结果同Hertz接触理论预言存在一定偏差; (2)纵波对于应力场的各向异性更加敏感, 而横波对于结构各向异性更加敏感(Khidas & Jia 2010 ). ...
The influence of flow rate on the decrease in pressure beneath a conical pile.
0
2011
Spatial filtering characteristics of electrostatic sensor matrix for local velocity measurement of pneumatically conveyed particles.
4
2014
... 实现空间滤波的方法有多种, 较早的空间滤波器是由如图5 (a)所示平行狭缝组成的光栅, 这种结构存在加工精度要求大, 空间周期不能调整, 且只能测量垂直于狭缝方向的运动速率等问题. 为了解决这一问题, 人们提出了利用传感器阵列实现空间滤波功能的光电探测器(如图5 (b)).Itakura 等 (1981) 利用一个液晶元件阵列构建了一种新型的空间滤波器, 并实现了二维速度分量的测量. 此后Kitagawa 等(1991)利用光纤阵列构建了一种空间滤波器, 有效简化了系统并提高了测量精度.但传感器或光纤阵列也存在分辨率较低, 安装调试困难, 传感器性能一致性差等问题.近年来, 随着光电技术及工业制造技术的发展, 传统的光栅和光电探测器阵列结构逐渐被线阵或面阵CCD/CMOS相机所取代. 如, Bergeler 和 Krambeer (2004) 对面阵CMOS相机像素在两个正交方向进行分组, 模拟空间滤波器件的功能, 实现了二维速度分量的测量, 并通过实验测量了毛细管中血流速度分布情况. 这种系统不仅结构简单, 性能稳定, 且可以通过软件调整空间周期, 提高空间滤波器用于速度测量的选择性, 测量精度高.另外, 还有采用静电传感阵列的空间滤波测量法(Xu et al. 2009 , Li et al. 2014 ), 该方法能够获得敏感区域内颗粒运动平均速度信息, 在一定程度上实现了对颗粒体系局部平均速度的测量. ...
... 对颗粒体系的研究因受限于实验技术无法穿透一般不透明的颗粒材料而一直发展缓慢, 作为高速X射线成像技术的发展者, 上海交通大学王宇杰研究组用上海光源X射线成像及生物医学应用光束线站和美国阿贡国家实验室的先进光源32ID线站的高速SR技术, 对三维颗粒堆积体系的微观结构及动力学进行了实空间的成像, 并将其应用于研究非平衡态的颗粒体系.王宇杰等利用SR技术研究了三维棒状颗粒体系的性质和颗粒气体的运动(Zhang et al.2014 , Wang 2016 ) (如图23 所示), 同时还利用SR技术研究了单一分散颗粒硬球体系在有无液体时的微观结构, 同时将其与非晶玻璃化转变相关联(Xia et al. 2015 , Li et al. 2014 ); 研究发现颗粒体系中的玻璃化转变可能是非常类似于晶体结晶过程的一种特殊结构相变.其对应的玻璃结构序是一种局部紧密堆积的四面体结构, 这些四面体结构可以生长形成具有分形结构的团簇, 同时其形状及大小的增长符合位形熵驱动的成核模型, 这些都非常类似于快速降温的晶体生长模型. ...
... 近期, 上海交通大学对椭球状颗粒施加准静态剪切应变循环加载(Kou et al. 2017 ), 等效于热扰动, 然后运用CT技术获取每个颗粒的位置与取向, 得到每一个颗粒在空间的三维轨迹, 从而确定位移与旋转随时间的变化规律(如图24 所示). 研究发现, 颗粒平移以及旋转位移平方的均值, 都与时间呈指数关系, 但幂指数与所施加的剪切应变有关, 且不存在普通流体在玻璃化转变时所出现的平台区, 即不存在所谓的笼效应(颗粒被临近颗粒暂时约束而失去流动性).进一步分析发现, 颗粒位移分布函数是非高斯的, 满足所谓的Gumbel关系, 与普通流体不同, 即在小位移下与高斯分布相似, 但大位移下有一个长尾, 如图24 (b)所示.研究人员认为这显示颗粒体系中存在两种弛豫机制的竞争, 即小尺度下由颗粒粗糙度所引起的扩散, 和大尺度下非可逆的弛豫. 此外, 其概率分布形状与应变、时间、以及位移方向无关, 显示其普适性.这个小尺度下由颗粒粗糙度所引起的微扩散过程, 是这一工作最关键的一个新的洞见. ...
... CT技术测量椭球状颗粒受到热扰动后, 位移与旋转随时间的变化规律(Kou et al. 2017 ). (a) CT实验装置示意图.剪切盒中包含椭球形颗粒, 在上表面沿\(z\)方向施加压力, 在下表面沿\(y\)方向施加循环加载剪切应变; (b) 剪切应变幅赋值为0.26, 615次循环加载条件下, 剪切盒中间20个颗粒的三维轨迹, 由此得到平移与旋转位移平方均值与时间及剪切应变关系 ...
Particle image velocimetry experiment and discrete-element simulation of voidage wave instability in a vibrated liquid-fluidized bed.
2
2007
... 爱丁堡大学Rix等首次用PIV技术测量了鼓泡流化床中颗粒随气泡飞出时的速度场分布(Rix et al.1996 ), 但他们只是沿用了传统PIV的测量系统和算法(采用片激光光源和互相关算法), 没有针对密集颗粒体系的特点进行改进, 无法测量流化床中密集颗粒体系的速度分布.密集颗粒体系的一个特点是颗粒间隙小且互相遮挡, 激光无法在颗粒体系间传播, 因此测量密集颗粒体系的PIV系统一般不再采用片激光作为光源, 而是将激光束扩束或者采用多个直流卤素灯作为光源直接照射在待测颗粒流表面(Bokkers et al.2004 , Hagemeier et al. 2015 ).密集颗粒体系的另一个特点是速度场分布的梯度范围非常大, 如鼓泡流化床中气泡附近颗粒的速度梯度变化极大, 而在其他区域颗粒的位移几乎为零, 导致传统互相关算法的准确性大幅下降. 针对这一问题, 清华大学姚强课题组提出了一种改进PIV算法, 在梯度变化率不同的区域, 使用不同的互相关窗口(interrogation window, IW)和帧速率, 从而有效提高了系统的准确性(Liu et al. 2008 , Lim et al. 2007 , Hagemeier et al. 2015 ). ...
... 美国UC Berkeley开展的准二维楔形料仓中颗粒流X射线- CT测量(Laufer 2013 ). (a)包含金属针的黄色颗粒和没有包含金属针的白色颗粒; (b)CT测量得到的内部金属针形态, 由此可以确定颗粒旋转情况 ...
Experimental studies of particle flow dynamics in a two-dimensional spouted bed.
1
2008
... 爱丁堡大学Rix等首次用PIV技术测量了鼓泡流化床中颗粒随气泡飞出时的速度场分布(Rix et al.1996 ), 但他们只是沿用了传统PIV的测量系统和算法(采用片激光光源和互相关算法), 没有针对密集颗粒体系的特点进行改进, 无法测量流化床中密集颗粒体系的速度分布.密集颗粒体系的一个特点是颗粒间隙小且互相遮挡, 激光无法在颗粒体系间传播, 因此测量密集颗粒体系的PIV系统一般不再采用片激光作为光源, 而是将激光束扩束或者采用多个直流卤素灯作为光源直接照射在待测颗粒流表面(Bokkers et al.2004 , Hagemeier et al. 2015 ).密集颗粒体系的另一个特点是速度场分布的梯度范围非常大, 如鼓泡流化床中气泡附近颗粒的速度梯度变化极大, 而在其他区域颗粒的位移几乎为零, 导致传统互相关算法的准确性大幅下降. 针对这一问题, 清华大学姚强课题组提出了一种改进PIV算法, 在梯度变化率不同的区域, 使用不同的互相关窗口(interrogation window, IW)和帧速率, 从而有效提高了系统的准确性(Liu et al. 2008 , Lim et al. 2007 , Hagemeier et al. 2015 ). ...
PIV for granular flows.
1
2000
... 图1 所示为PIV技术原理图, 双脉冲激光经过柱面镜形成片光源, 照射在散布于颗粒流中的稀疏示踪粒子(近似一个点), 与脉冲激光同步的高速相机对粒子拍摄得到连续的双脉冲成像图, 再对双脉冲成像图中颗粒位移的相关性进行计算, 得到流场的分布(Adrian 2005 , Lueptow et al. 2000 ). 设粒子像点的光强度分布为\(I\left( \bar{x} \right)\), 它的自相关为 \[R\left( S \right) = \int {I\left(\bar {x} \right)I\left( {\bar {x} + \pmb s } \right)}{\rm d}x \ \ (1)\] 式中, \(\pmb s \)为二维位移矢量. \(\pmb s = 0\)代表每个像点自相关, 得到峰值\(R_{P}\). \(\pmb s\)等于诊断点内平均位移量, 出现第二个强的峰值\(R_{D}^{ + }\), 称为正位移峰值, 其物理意义为第一次光脉冲形成的粒子像和第二次光脉冲形成的粒子像重叠.同样会出现相同的峰值\(R_{D}^{ - }\), 称负位移峰值, 即第二次光脉冲形成的粒子像和第一次光脉冲形成的粒子像重合.假设原点峰值\(R_{P}\)的位置和正位移峰值\(R_{D}^{ +}\)的位置之间的位移矢量为\(\pmb S _D^ + \), 得到粒子像点的速度为\[\pmb V = \dfrac{\pmb S _D^ + }{M\Delta t} \ \ (2)\] 其中, \(M\)为系统放大倍数, \(\Delta t\)为曝光时间间隔. ...
Energetic approach for the characterization of taps in granular compaction.
1
2008
... 密度响应谱是探测颗粒体系内部弛豫动力学和研究颗粒材料热动力学理论的有效方法.Nowak 等(1998) 研究了垂直脉冲激励下圆柱形容器中单分散玻璃球体系的密度随时间的演化, 发现当用大于某个临界值\(\varGamma ^\ast\)的垂直脉冲振动足够长时间之后,系统密度最终达到一个仅依赖振幅的稳定值.Villarruel 等(2000) 进一步研究了垂直脉冲激励下的非均匀、圆柱形颗粒材料的状态随时间和空间的演变, 发现垂直脉冲振动驱动颗粒体系从无序、低聚集率状态到密实的、有序的、向列型状态演变.Ludewig 等 (2008) 研究了离散的垂直脉冲振动参数对系统密度的影响, 提出用一个全新的无量纲参数\(\varXi \)(垂直振动实验中注入颗粒体系的能量)作为描述颗粒压缩动力学(compaction dynamics)的特征量. Dijksman 和 van Hecke(2009) 则发现处于可逆分支的颗粒系统密度不仅与振动脉冲的强度有关, 还与单个脉冲的周期\(T\)有关, \(\varGamma {T}\)才是颗粒离散脉冲振动的控制参数. Zou(2010) 利用体积响应谱技术研究了垂直脉冲振动下颗粒体系的压缩动力学, 发现颗粒体系的体积响应因子表现出与自旋玻璃系统中动力学位形比热类似的行为, 暗示颗粒压缩过程中表现出的玻璃状动力学行为来源于颗粒的集体重排. ...
Vibrational modes identify soft spots in a sheared disordered packing.
1
2011
... 在力链结构刻画方面, Wyart 等 (2005) 认为: 设颗粒接触数\(Z\)与等静态接触数\(Z_{\rm iso} \) 之差为 \( \Delta Z = \left( {Z -Z_{\rm iso} } \right)\),则力链特征长度\(l^\ast \sim 1/{\Delta Z} \).近年来, 关于颗粒材料介观长度尺度及其随系统参数演化规律的数值研究已经取得了很大的进展.特别是, 一些研究者试图从动力学响应的角度研究颗粒体系中的特征长度.例如: Ellenbroek 等 (2006, 2009)研究了处于堵塞(jammed)固体样品中心的单个颗粒直径膨胀带来的力响应涨落, 发现当接近堵塞(jamming)点时的力响应涨落空间范围\(L^\ast \)发散, 暗示低于长度尺度\(L^\ast\)响应被涨落控制(变形场可以被视为一个扭曲软模式), 而在大于\(L^\ast\)的尺度, 系统的响应过渡到弹性. Karimi 和 Maloney(2011) 研究发现颗粒体系应力各向异性的特征长度随体积分数\(\varphi\)从上述趋近临界体积分数\(\varphi _{\rm c} \)时增大.Vitelli(2010)研究了无摩擦软球堵塞(jammed)体系剪切声波的长波衰减, 发现特征长度\(L^\ast \sim \left( {\varphi - \varphi _{\rm c} }\right)^{{ - 1} / 2}\).关于动力学关联长度随体积分数演化规律的研究方面, Flenner 等(2010) 实验发现在堵塞点附近, 水平振动单层颗粒床的动力学关联长度\(L^\ast \sim \left( {\varphi -\varphi _{\rm c} } \right)^{1/ 2}\). ...
Magnetic resonance imaging of fluidized beds.
2
2008
... 近期杨晖课题组提出了一种双SVS同步测量系统(图12 (a)) (Li et al. 2016 ), 对滚筒内颗粒流发生崩塌时, 表面主动层(active layer)和内部被动层(passive layer)的颗粒运动进行了测量, 首次通过实验测量了被动层的颗粒物质脉动速度分布(图12 (b)). ...
... 转筒中颗粒流的双SVS同步测量系统(Li et al. 2016 ). (a)SVS测量转筒中颗粒流表层(主动层)和内部(被动层)的脉动速度, (b)颗粒流被动层颗粒脉动速度的空间分布 ...
Granular temperature: Comparison of magnetic resonance measurements with discrete element model simulations.
3
2008
... 运动中的颗粒材料可能存在多种流态及其相互间复杂的转换过程, 例如, 土体边坡失稳、山体滑坡和泥石流的发生, 就是颗粒介质由固态转化为流态的复杂流变现象. 从理论上而言, 颗粒介质弹性失稳机理、不可恢复应变量化是研究颗粒材料固态和流态及固--流态转变的关键.在颗粒堆积体坍塌过程中, 体系依次经历了从静态堆积、失稳流动再到堆积的力学阶段, 是典型的颗粒介质固态与液态相互转换的过程.清华大学孙其诚课题组开展了25 167个陶颗粒堆积体坍塌过程的实验研究, 采用PTV技术测量了颗粒堆坍塌过程中的形态、速率大小分布等, 如图4 所示. 与此同时, 在颗粒堆底部铺设Tekscan薄膜压感器, 它是由美国Tekscan公司生产的一款接触式测量压力分布装置, 可以动态测量颗粒堆底部压力分布, 最大测量频率为200 Hz (Liu et al. 2011 ). Xu 等(2016)测量并确定了颗粒平均速率与体系体积分析、平均速率与底部压力的关系. ...
... 颗粒介质的一个典型特征是能够对其外部扰动产生强烈的非仿射响应.当对晶体材料施加变形时, 它趋向于仿射地遵循宏观应变.而对颗粒材料施加变形时, 由于缺乏局部反转对称性, 每个颗粒除了产生一个仿射应变之外, 还产生一个附加的非仿射位移.并且, 颗粒的非仿射重排倾向于局部化, 但是对于导致这一过程的结构缺陷非常难以识别. Manning 和 Liu(2011) 提出了利用模式分析手段识别颗粒系统结构缺陷的方法, 即定义动力学矩阵频谱内前 \( N_m^\ast \)个最低频模式中的前\( N_p^\ast\) 个极化矢量最大的颗粒为软点(其中参数\(N_m^\ast \) 和\(N_p^\ast \)具有非常明确的物理意义, 对应于软点的能量尺度和长度尺度), 由这些软点组成的区域为软区(soft spots), 该工作为基于介观软区动力学行为的静态颗粒材料的宏观塑性理论铺平了道路.在实验测量方面, 由于颗粒无序运动的持续时间极短(微秒级), 位移极小(微米级), 需要足够高的时间和空间分辨率的技术来测定颗粒非仿射响应速度. ...
... 图19所示, Müller 等(2008) 用MRV测量了鼓泡流化床中的速度场, 其中图19 (b) \(\sim\) 图19 (d)分别给出了流化床中\(A\)位置截面上的\(z\), \(x\)和\(y\)方向颗粒速度分布, 可以看到, 只有在气泡周围的一小部分颗粒发生运动, 其余大部分区域的颗粒处于静止状态. 图20 显示测量的准二维鼓泡流化床的颗粒温度. ...
Local measurements of velocity fluctuations and diffusion coefficients for a granular material flow.
1
1995
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
Density fluctuations in vibrated granular materials.
1
1998
... 密度响应谱是探测颗粒体系内部弛豫动力学和研究颗粒材料热动力学理论的有效方法.Nowak 等(1998) 研究了垂直脉冲激励下圆柱形容器中单分散玻璃球体系的密度随时间的演化, 发现当用大于某个临界值\(\varGamma ^\ast\)的垂直脉冲振动足够长时间之后,系统密度最终达到一个仅依赖振幅的稳定值.Villarruel 等(2000) 进一步研究了垂直脉冲激励下的非均匀、圆柱形颗粒材料的状态随时间和空间的演变, 发现垂直脉冲振动驱动颗粒体系从无序、低聚集率状态到密实的、有序的、向列型状态演变.Ludewig 等 (2008) 研究了离散的垂直脉冲振动参数对系统密度的影响, 提出用一个全新的无量纲参数\(\varXi \)(垂直振动实验中注入颗粒体系的能量)作为描述颗粒压缩动力学(compaction dynamics)的特征量. Dijksman 和 van Hecke(2009) 则发现处于可逆分支的颗粒系统密度不仅与振动脉冲的强度有关, 还与单个脉冲的周期\(T\)有关, \(\varGamma {T}\)才是颗粒离散脉冲振动的控制参数. Zou(2010) 利用体积响应谱技术研究了垂直脉冲振动下颗粒体系的压缩动力学, 发现颗粒体系的体积响应因子表现出与自旋玻璃系统中动力学位形比热类似的行为, 暗示颗粒压缩过程中表现出的玻璃状动力学行为来源于颗粒的集体重排. ...
Rheology of surface granular flows.
3
2007
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
... 另外一种拓展的PTV法是通过测量一定曝光时间下的粒子光学轨迹长度, 进而计算出颗粒的运动速度(Orpe & Khakar 2007 ). 如图3 所示, 通过调节相机的增益和曝光时间得到颗粒的运动轨迹图, 然后对原始条纹(图3 (b))做二值化变换, 再用公式(3)对二值化图像(图3 (c))中的每个条纹进行拟合, 得到条纹灰度的分布函数\[I_{\rm th} = \left\{ {\begin{array}{l} C{\rm e}^{ - \bar {y}^2 / 4w^2,} \\ C{\rm e}^{[ - \bar {y}^2 - (\bar {x} - l)^2] / 4w^2,} \end{array}} \right.\begin{array}{l} \left| \bar {x} \right| \leq l \ \left| \bar {x} \right| > l \end{array} \ \ (4)\] 其中, \(\bar {x} = (X - X_C )\cos \theta + (Y - Y_C)\sin \theta \), \(\bar {y} = (Y - Y_C )\cos \theta + (X - X_C )\sin\theta \). \(\theta \) 为条纹与水平方向夹角, \(C\)为条纹的最大灰度值, \(X_{C}\)和\(Y_{C}\) 为条纹中心坐标. 计算得到速度\[v = {2L(l,w)} /{\Delta t} \ \ (5)\] 其中, \(L(l,w) = a_1 l + a_2w\) 通过对条纹长度\((2l)\)和宽度\((2w)\)线性拟合得到.拓展PTV法的优点是不需要高速相机和脉冲激光, 因此成本低、实时性强、操作简便, 但其精度和处理复杂流动的能力尚未得到认可, 目前还不是主流技术. ...
... 拓展PTV法测量原理图(Orpe & Khakar 2007 ). (a)2 mm不锈钢球在准二维滚内连续流动图例(转速: 3 r\( \cdot \)min\(^{ -1})\), (b)颗粒轨迹条纹(streak), (c)颗粒轨迹条纹二值化图像, (d)用公式(4)对图(b)条纹进行拟合后的结果 ...
Wing flexibility effects in clap-and-fling.
1
2011
... PIV技术测量三维空间体内完整速度场是近年来的研究热点.研究曾尝试采用离焦成像、多视角成像和全息成像等方法通过对示踪粒子进行三维空间定位, 实现粒子追踪测速. 受粒子浓度的限制, 空间分辨率并不理想, 直到层析PIV概念的提出, 才使得三维PIV测量技术真正进入了实用阶段(Gao et al. 2013 ), 该技术通过三维互相关分析来得到具有较高空间分辨率的速度场, 实现了在较高粒子浓度下的测量. 三维PIV的核心技术包括粒子重构和速度场再现技术, 前者采用了医学领域光学层析技术中基于投影方法的代数重构技术, 后者采用三维互相关分析算法(Gao et al. 2011 , Percin et al. 2011 , Tang et al. 2012 ). ...
Simultaneous measurement of particle size and particle velocity by the spatial filtering technique.
0
2002
Diffusing wave spectroscopy.
0
1988
Local anisotropy in globally isotropic granular packings.
2
2011
... MRV测量鼓泡流化床中颗粒流速度分布(Müller et al. 2008 ). (a)气泡喷射图像, \(A\)位置处 (b) \(z\) 方向, (c) \(x\)方向和 (d)\(y\)方向的速度场分布 ...
... 准二维鼓泡流化床的颗粒温度(Müller et al. 2008 ).(a)准二维鼓泡流化床, 流化速度为0.6 m/s, (b) DEM计算的颗粒温度, (c) MRV测量的颗粒温度 ...
Positron emission particle tracking: A technique for studying flow within engineering equipment.
1
1993
... PEPT技术最早由英国伯明翰大学的Parker课题组提出(Hawkesworth & Parker. 1991 , Parker et al. 1993 ), 其追踪单个颗粒的空间分辨率可以达到0.5 mm, 时间分辨率主要由正电子相机决定(一般几十毫秒), 最大可以测量10 m/s的颗粒速度, 最多可以追踪3个示踪颗粒.由于其可追踪的示踪颗粒数量较少, 实际应用中比较适合测量具有周期边界的循环实验装置, 如滚筒、鼓泡气体流化床、振动流化床等. 与其他非侵入式测量技术相比, PEPT技术能够测出更加详细的固/液运动信息, 并且能够测量液体、有机聚合物、金属和矿物颗粒等众多材料.其不足之处在于, PEPT能跟踪颗粒数较少, 不适合复杂颗粒流速度场分布的测量. 此外, PEPT给出的是关于时间的平均速度场信息, 而不是颗粒瞬时速度场信息, 因此只适用于测量稳定流. 图15 所示为Parker 等(1997)用PEPT技术对准二维滚筒内(直径100 mm, 厚度16 mm, 颗粒直径3 mm)颗粒流速度的DEM计算结果进行了验证, 发现不同转速下, DEM计算的颗粒流表层速度总是大于PEPT的测量值, 造成这一结果主要是由于两方面原因, 一是DEM仿真时不考虑滚筒壁的作用, 二是DEM计算的速度是表层颗粒的平均速度, 而PEPT测得的是单个示踪颗粒的碰撞速度. ...
Positron emission particle tracking using the new Birmingham positron camera.
1
2002
... 目前, SFV技术主要用于两相流的测量, 比如Petrak(2002) 采用基于光纤传感阵列的SFV技术测量了两相流中颗粒的大小和速度, Fiedler等(1997) 用基于CCD的空间滤波器测量了循环流化床中局部颗粒速度分布, Hosokawa等(2013) 采用SFV技术测量了鼓泡流化床中泡状流的泡沫速度, 并通过与PTV测量结果的比较, 发现在一定程度上SFV技术优于PTV技术.在密集颗粒流测量方面, Uddin等首次将SFV技术应用于泥石流表面速度的测量(Uddin et al.1998 ), 并对比了传统SFV技术和基于CCD相机的软件SFV的测量结果(如图6 所示), 发现两者结果基本一致, 而基于CCD相机的SFV技术结构更简单, 成本更低. ...
Positron emission particle tracking studies of spherical particle motion in rotating drums.
0
1997
Positron emission particle tracking---Application and labelling techniques.
0
2008
Investigation on utilizing laser speckle velocimetry to measure the velocities of nanoparticles in nanofluids.
0
2006
Preliminary studies of elutriation from gas-fluidised beds using particle image velocimetry.
1
1996
... 爱丁堡大学Rix等首次用PIV技术测量了鼓泡流化床中颗粒随气泡飞出时的速度场分布(Rix et al.1996 ), 但他们只是沿用了传统PIV的测量系统和算法(采用片激光光源和互相关算法), 没有针对密集颗粒体系的特点进行改进, 无法测量流化床中密集颗粒体系的速度分布.密集颗粒体系的一个特点是颗粒间隙小且互相遮挡, 激光无法在颗粒体系间传播, 因此测量密集颗粒体系的PIV系统一般不再采用片激光作为光源, 而是将激光束扩束或者采用多个直流卤素灯作为光源直接照射在待测颗粒流表面(Bokkers et al.2004 , Hagemeier et al. 2015 ).密集颗粒体系的另一个特点是速度场分布的梯度范围非常大, 如鼓泡流化床中气泡附近颗粒的速度梯度变化极大, 而在其他区域颗粒的位移几乎为零, 导致传统互相关算法的准确性大幅下降. 针对这一问题, 清华大学姚强课题组提出了一种改进PIV算法, 在梯度变化率不同的区域, 使用不同的互相关窗口(interrogation window, IW)和帧速率, 从而有效提高了系统的准确性(Liu et al. 2008 , Lim et al. 2007 , Hagemeier et al. 2015 ). ...
Improving the accuracy and resolution of particle image or laser speckle velocimetry.
1
1988
... SVS技术是在扩散波光谱(diffusing wave spectroscopy, DWS)技术上发展起来的(Pine et al. 1988 ), 其原理如图8 (a)所示, 激光经过凹透镜扩束后照射在密集的颗粒样品表面, 一部分光子在颗粒间多次散射后从入射反方向离开, 在CCD相机感光面上形成散斑. 当散射区域内颗粒发生运动时, 光子的光程就会发生变化, 从而引起散斑图像产生变化, 称为"动态散斑"或"时变散斑", 并且散斑的变化速率与颗粒的脉动速度有关. 图8 (b)显示了不同脉动速度下线阵CCD相机检测的颗粒流散斑图像随时间变化, 可以看到在一定曝光时间下, 散斑图像的对比度随颗粒脉动速度的增大而降低. 根据统计光学理论, 散斑图像的对比度\[V_2 (T) = \left( {\dfrac{\sigma _T }{\left\langle I \right\rangle_T }} \right)^2 = \dfrac{\left\langle {I^2} \right\rangle _T}{\left\langle I \right\rangle _T^2 } - 1 \ \ (7)\] 其中, \(I\)为散射光强, \(T\)为曝光时间, \(\left\langle I \right\rangle _T \)和\(\sigma _T ^2\) 分别为光强的均值和方差.结合高斯光束的Siegert公式, 由式(7)可以得到\[V_2 (T) = \beta \int_0^T {2(1 - t/T)} [g_1 (t)]^2{{\rm d}t}/T \ \ (8)\] 其中, \(\beta \) 为光学系统的相干因子, \(g_1 (t)\)为散射光场的自相关函数. 根据DWS理论, 后向散射光强的时间自相关函数\[g_1 (t) \approx \exp \left[ { - \gamma _0 k_0 \sqrt {\left\langle{\Delta r^2(t)} \right\rangle } } \right] = \exp \left[ { - 4\pi \sqrt {\left\langle {\left( {\delta v} \right)^2} \right\rangle }t / \lambda } \right] = \exp \left[ { - \varGamma t} \right] \ \ (9)\] 其中,\(\gamma _0 \)是一个与颗粒大小以及光学系统偏振态有关的常数. \(k_0 = {2\pi n}/\lambda \) 为散射矢量, \(n\)为空气折射率, \(\lambda \)为激光波长, \(\left\langle {\Delta r^2(t)} \right\rangle \)为颗粒系在两次测量间隔内的均方位移, 且与颗粒速度脉动具有\(\left\langle {\Delta r^2(t)} \right\rangle =\left( {\delta vt} \right)^2\)关系, \(\varGamma = {4\pi \delta v}/\lambda \) 称为自相关函数\(g_1 (t)\) 的衰减频率. ...
Application of magnetic resonance imaging techniques to particulate systems.
1
2007
... MRV是利用核磁共振(nuclear magnetic resonance, NMR)和磁共振成像(magnetic resonance imaging, MRI)原理来测量空间体内的三维速度场的一种技术(Haacke et al. 1999 , Sederman et al. 2007 ), 其工作介质通常为含氢原子的颗粒物质, 在外加磁场作用下, 原子核自旋系统逐步被磁化, 原子核以莫拉频率进动.在外部相同频率动射频脉冲激励下, 原子核产生磁共振现象, 而共振后恢复平衡状态的原子核会将吸收的射频脉冲能量释放出来, 探测器将这种磁共振信号转换成电信号再进行处理(如图17 所示).由于原子核自旋的共振频率与外部所加磁场相关, 因此外部磁场通常存在较弱的剃度渐变, 依此来实现空间定位, 起到追踪测量颗粒运动的目的.选用的颗粒物质要么本身含有质子\((^{1}\)H)比如芥菜籽、罂粟籽等; 要么是特殊制作包含质子的颗粒, 如胶囊中填充了液体维生素E(C\(_{29}\)H\(_{50}\)O\(_{2})\)等. ...
Cross-validation of 3D particle tracking velocimetry for the study of granular flows down rotating chutes.
1
2015
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
Tomographic PIV investigation of coherent structures in a turbulent boundary layer flow.
2
2012
... PIV技术测量三维空间体内完整速度场是近年来的研究热点.研究曾尝试采用离焦成像、多视角成像和全息成像等方法通过对示踪粒子进行三维空间定位, 实现粒子追踪测速. 受粒子浓度的限制, 空间分辨率并不理想, 直到层析PIV概念的提出, 才使得三维PIV测量技术真正进入了实用阶段(Gao et al. 2013 ), 该技术通过三维互相关分析来得到具有较高空间分辨率的速度场, 实现了在较高粒子浓度下的测量. 三维PIV的核心技术包括粒子重构和速度场再现技术, 前者采用了医学领域光学层析技术中基于投影方法的代数重构技术, 后者采用三维互相关分析算法(Gao et al. 2011 , Percin et al. 2011 , Tang et al. 2012 ). ...
... PEPT测量原理图(Parker et al. 2002 ).(a)一对大矩形探测器组成的"正电子相机", (b) \(\gamma\)射线轨迹重构, (c)正电子发射原始位置 ...
Relaxations and rheology near jamming.
2
2011
... 不同转速下, 滚筒内沿径向( AB方向)的速度场分布.(符号为DEM计算值: \(\Box \) 20 r/mm, \(\triangle\) 42 r/mm, \(*\)65 r/mm; 实线为PEPT测量值) (Parker et al. 1997 ) ...
... 图26 显示了玻璃珠样品的\(G /B\) 随\(P\)的变化规律, 发现实验给出的\( G /B = 0.58\sim 1.39\),且颗粒体系 \(G /B\)随\(P\)的增大而减小, 满足幂律关系: \(G /B\sim P^{ - 0.45}\), 如图26 中红色直线拟合所表示.根据(Tighe 2011 , Basu et al. 2014 , Goodrich et al. 2014 )的结果, 对于堵塞颗粒体系的\(G/B\sim\left( {\varphi - \varphi _{\rm c} } \right)^{1/ 2}\sim p^{1/3}\)(其中\(\varphi _{\rm c} \)是颗粒体系堵塞点的体积分数). 显然, 实验发现的\(G /B\)随\(P\)的变化规律与Hertz 接触理论不相符, 暗示连续弹性介质理论在低压强下可能不再成立.导致上述差异的因素可能有以下两个: (1) 理论模型要求颗粒是光滑的, 但是实际颗粒的表面是粗糙的, 这会使实际结果同Hertz接触理论预言存在一定偏差; (2)纵波对于应力场的各向异性更加敏感, 而横波对于结构各向异性更加敏感(Khidas & Jia 2010 ). ...
Estimation of the surface velocity of debris flow with computer-based spatial filtering.
3
1998
... 目前, SFV技术主要用于两相流的测量, 比如Petrak(2002) 采用基于光纤传感阵列的SFV技术测量了两相流中颗粒的大小和速度, Fiedler等(1997) 用基于CCD的空间滤波器测量了循环流化床中局部颗粒速度分布, Hosokawa等(2013) 采用SFV技术测量了鼓泡流化床中泡状流的泡沫速度, 并通过与PTV测量结果的比较, 发现在一定程度上SFV技术优于PTV技术.在密集颗粒流测量方面, Uddin等首次将SFV技术应用于泥石流表面速度的测量(Uddin et al.1998 ), 并对比了传统SFV技术和基于CCD相机的软件SFV的测量结果(如图6 所示), 发现两者结果基本一致, 而基于CCD相机的SFV技术结构更简单, 成本更低. ...
... Parker & Fan用PEPT技术测量了鼓泡流化床中的颗粒速度场分布(Parker & Fan 2008 ), 如图16 (a)所示, 并根据速度场分布将流化床分为底部、中部和顶部三个区域. 图16 (b)显示在流化床底部区域, 颗粒物质随着气泡在流化床边缘呈环状向上运动, 随后在流化床中间落下.这与图16 (a)中顶部区域颗粒流的运动方向正好相反. 在中间区域, 图16 (c)显示上升的气泡被从顶部边缘落下的颗粒挤到中间, 导致颗粒流速度场在流化床中间形成了一个小峰. 根据PEPT测量结果, 可以进一步计算出流化床中气泡的速度随高度变化, 如图16 (d)所示. ...
... 鼓泡流化床中颗粒速度场的PEPT测量结果(Parker & Fan 2008 ). (a) 示踪颗粒在垂直平面内的速度矢量图, (b)流化床底部(高度10 \(\sim\)30 mm)颗粒速度\(y\)方向分布图,(c)流化床中部(高度120 \(\sim \)130 mm)颗粒速度\(y\)方向分布图, (d)根据PEPT测量值计算的气泡在流化床中上升速度 ...
The Journal of the Acoustical Society of America
1
2010
... 动态有效质量谱技术是研究垂直振动激励下颗粒材料声学耗散性质的重要手段(Hsu et al.2009 , Valenza et al. 2010 ). 彭政等(2013)研究了垂直激发下铜和玻璃珠系统的能量耗散, 发现体系在几十赫兹处出现共振, 且特定频率下的耗散功率随振动强度的变化呈现幂率规律. Valenza 等(2009)研究了湿度对钨颗粒体系有效质量的影响, 发现湿度越大, 颗粒物质的耗散越显著. 在钨颗粒涂上不同黏度的硅油, 研究了硅油黏度对有效质量的影响, 发现体系的耗散与黏度变化正相关.此外, Valenza 和 Johnson(2012)使用激光振动计观察到垂直振动过程中颗粒床侧壁与附近颗粒的相对位移近似为零, 表明有效质量测量是基于线性小振幅. 总之, 动态有效质量谱具有颗粒材料声学模式、弹性和时效的耗散特征, 正日益成为进一步理解颗粒体系耗散机理的主流技术之一. ...
Dynamic effective mass of granular media and the attenuation of structure-borne sound.
0
2009
Normal-mode spectrum of finite-sized granular systems: The effects of fluid viscosity at the grain contacts.
0
2012
Attenuation of shear sound waves in jammed solids.
2
2010
... 目前, 国际上从事颗粒流MRV研究的主要是英国剑桥大学和日本大阪大学, 比如: Sederman 等(2007) 利用该技术研究了罂粟籽和小米混合颗粒(如图18 )在滚筒内分选状态, 发现经过100转以后, 在径向, 粒度较小的罂粟籽颗粒集中在滚筒中间, 而粒度较大的小米颗粒分布在筒壁附近(如图18 (a)). 在轴向, 粒度较小的罂粟籽颗粒分布呈两头多、中间少的哑铃状(如图18 (b)), 再经过1 000转以后, 罂粟籽颗粒又偏向滚筒的一端. ...
... MRI测量小米和罂粟籽混合颗粒在滚筒内分选状态.罂粟籽和小米按体积比\(1:3\)的比例加入滚筒内, 黑色是罂粟籽(密度: 1 000 kg/m\(^{3}\), 粒度: 1.1 mm), 黄色是小米(密度: 1 150 kg/m\(^{3}\), 粒度: 2.3 mm) (Sederman et al. 2007 ). (a) 100转后径向分选, (b) 100转后轴向分选 ...
Compaction of rods: Relaxation and ordering in vibrated, anisotropic granular material.
1
2000
... 密度响应谱是探测颗粒体系内部弛豫动力学和研究颗粒材料热动力学理论的有效方法.Nowak 等(1998) 研究了垂直脉冲激励下圆柱形容器中单分散玻璃球体系的密度随时间的演化, 发现当用大于某个临界值\(\varGamma ^\ast\)的垂直脉冲振动足够长时间之后,系统密度最终达到一个仅依赖振幅的稳定值.Villarruel 等(2000) 进一步研究了垂直脉冲激励下的非均匀、圆柱形颗粒材料的状态随时间和空间的演变, 发现垂直脉冲振动驱动颗粒体系从无序、低聚集率状态到密实的、有序的、向列型状态演变.Ludewig 等 (2008) 研究了离散的垂直脉冲振动参数对系统密度的影响, 提出用一个全新的无量纲参数\(\varXi \)(垂直振动实验中注入颗粒体系的能量)作为描述颗粒压缩动力学(compaction dynamics)的特征量. Dijksman 和 van Hecke(2009) 则发现处于可逆分支的颗粒系统密度不仅与振动脉冲的强度有关, 还与单个脉冲的周期\(T\)有关, \(\varGamma {T}\)才是颗粒离散脉冲振动的控制参数. Zou(2010) 利用体积响应谱技术研究了垂直脉冲振动下颗粒体系的压缩动力学, 发现颗粒体系的体积响应因子表现出与自旋玻璃系统中动力学位形比热类似的行为, 暗示颗粒压缩过程中表现出的玻璃状动力学行为来源于颗粒的集体重排. ...
Friction and relative energy dissipation in sheared granular materials.
0
2007
Granular packing as model glass formers.
2
2016
... 对颗粒体系的研究因受限于实验技术无法穿透一般不透明的颗粒材料而一直发展缓慢, 作为高速X射线成像技术的发展者, 上海交通大学王宇杰研究组用上海光源X射线成像及生物医学应用光束线站和美国阿贡国家实验室的先进光源32ID线站的高速SR技术, 对三维颗粒堆积体系的微观结构及动力学进行了实空间的成像, 并将其应用于研究非平衡态的颗粒体系.王宇杰等利用SR技术研究了三维棒状颗粒体系的性质和颗粒气体的运动(Zhang et al.2014 , Wang 2016 ) (如图23 所示), 同时还利用SR技术研究了单一分散颗粒硬球体系在有无液体时的微观结构, 同时将其与非晶玻璃化转变相关联(Xia et al. 2015 , Li et al. 2014 ); 研究发现颗粒体系中的玻璃化转变可能是非常类似于晶体结晶过程的一种特殊结构相变.其对应的玻璃结构序是一种局部紧密堆积的四面体结构, 这些四面体结构可以生长形成具有分形结构的团簇, 同时其形状及大小的增长符合位形熵驱动的成核模型, 这些都非常类似于快速降温的晶体生长模型. ...
... 直径为0.5 cm, 长度为2 cm的ABS棒在20\(g\)振动加速度下的密集颗粒气体在某一瞬间的运动图像.少量示踪棒状颗粒表面涂有对X射线强吸收的氧化钕, 可以清晰地追踪其运动. X射线的拍摄速度是2 000帧/秒 (Zhang et al. 2014 , Wang 2016 ) ...
Ultrafast X射线 study of dense-liquid-jet flow dynamics using structure-tracking velocimetry
0
2008
Fluctuations of particle motion in granular avalanches - from the microscopic to the macroscopic scales.
0
2015
Effects of compression on the vibrational modes of marginally jammed solids.
0
2005
The structural origin of the hard-sphere glass transition in granular packing.
1
2015
... 对颗粒体系的研究因受限于实验技术无法穿透一般不透明的颗粒材料而一直发展缓慢, 作为高速X射线成像技术的发展者, 上海交通大学王宇杰研究组用上海光源X射线成像及生物医学应用光束线站和美国阿贡国家实验室的先进光源32ID线站的高速SR技术, 对三维颗粒堆积体系的微观结构及动力学进行了实空间的成像, 并将其应用于研究非平衡态的颗粒体系.王宇杰等利用SR技术研究了三维棒状颗粒体系的性质和颗粒气体的运动(Zhang et al.2014 , Wang 2016 ) (如图23 所示), 同时还利用SR技术研究了单一分散颗粒硬球体系在有无液体时的微观结构, 同时将其与非晶玻璃化转变相关联(Xia et al. 2015 , Li et al. 2014 ); 研究发现颗粒体系中的玻璃化转变可能是非常类似于晶体结晶过程的一种特殊结构相变.其对应的玻璃结构序是一种局部紧密堆积的四面体结构, 这些四面体结构可以生长形成具有分形结构的团簇, 同时其形状及大小的增长符合位形熵驱动的成核模型, 这些都非常类似于快速降温的晶体生长模型. ...
The spatial filtering method for solid particle velocity measurement based on an electrostatic sensor.
1
2009
... 实现空间滤波的方法有多种, 较早的空间滤波器是由如图5 (a)所示平行狭缝组成的光栅, 这种结构存在加工精度要求大, 空间周期不能调整, 且只能测量垂直于狭缝方向的运动速率等问题. 为了解决这一问题, 人们提出了利用传感器阵列实现空间滤波功能的光电探测器(如图5 (b)).Itakura 等 (1981) 利用一个液晶元件阵列构建了一种新型的空间滤波器, 并实现了二维速度分量的测量. 此后Kitagawa 等(1991)利用光纤阵列构建了一种空间滤波器, 有效简化了系统并提高了测量精度.但传感器或光纤阵列也存在分辨率较低, 安装调试困难, 传感器性能一致性差等问题.近年来, 随着光电技术及工业制造技术的发展, 传统的光栅和光电探测器阵列结构逐渐被线阵或面阵CCD/CMOS相机所取代. 如, Bergeler 和 Krambeer (2004) 对面阵CMOS相机像素在两个正交方向进行分组, 模拟空间滤波器件的功能, 实现了二维速度分量的测量, 并通过实验测量了毛细管中血流速度分布情况. 这种系统不仅结构简单, 性能稳定, 且可以通过软件调整空间周期, 提高空间滤波器用于速度测量的选择性, 测量精度高.另外, 还有采用静电传感阵列的空间滤波测量法(Xu et al. 2009 , Li et al. 2014 ), 该方法能够获得敏感区域内颗粒运动平均速度信息, 在一定程度上实现了对颗粒体系局部平均速度的测量. ...
Measurements of velocity and pressure of a collapsing granular pile.
2
2016
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
... 颗粒堆塌落过程中的速率分布. 流动特征时间\(\tau _{\rm c}= \sqrt {{h_0 }/g} \), 其中\(h_{0}\)是颗粒堆初始高度, \(g\)是重力加速度; 速率大小用颜色表示.颗粒堆初始高度、厚度和长度分别为\(180 {\rm mm}\times 200 {\rm mm}\times 100 {\rm mm}\). 插图是时间\(1.2\tau_{\rm c} \) 时拍摄的颗粒堆(Xu et al. 2016 , 费明龙 等 2016 ) ...
Granular dynamics of cohesive powders in a rotating drum as revealed by speckle visibility spectroscopy and synchronous measurement of forces due to avalanching.
1
2016
... 目前, 颗粒物质的声学阻尼特性已经得到了广泛的应用, 但是关于颗粒材料中耗散机制的微观起源仍然不清楚, 需要进一步的研究.力学谱技术是研究材料中能量损耗规律的有效手段. 与其他谱学技术相比, 内耗测量采用的应力/应变振幅很小, 对被测物体没有任何破坏作用, 所以它是一种无损力学诊断方法, 并且对于微区成分和结构状态敏感, 可反映材料在各种复杂外界环境(如压力、高温、强核辐射等)下的力学性能等.因此, 内耗技术可以提供一些其他实验手段无法得到的信息, 在固体物理领域, 内耗与力学谱技术应用广泛(张进修 和 熊小敏 2013 , 吴学邦 等 2016 ). 随着内耗测量技术的不断发展, 近年来其应用领域已拓展到颗粒物质Jamming转变等, 一些工作表明, 内耗技术能够有效地探测和研究颗粒物质的结构转变与动力学弛豫行为.比如, 颗粒的种类、粒径大小、表面粗糙度以及外界压强等决定了力链网络结构的共振频率, 内耗技术还可用来探知颗粒体系力链在外场压强下的共振频率, 揭示密集颗粒物质的能量耗散性质.中国科学院固体物理所采用改进的低频内耗仪研究不同颗粒体系(如砂粒、铁粉和铝粉等)在外加剪切应力作用下的能量耗散性质, 比如发现了其内耗---频率谱中均分别出现 3个明显的能量耗散峰.随着外加压强(0 \(\sim \) 400 Pa)的增大, 各体系3个耗散峰均向高频端移动. 初步认为, 该耗散峰来源于颗粒体系中不同长度力链的共振耗散. 随着频率的降低, 内耗峰依次对应于双颗粒链、三颗粒链和四颗粒链的共振耗散(Wang et al. 2007 ). 动态力学分析仪(DMA) 是一种材料能耗测试仪, 与内耗仪一样可用于材料耗散性能测试.但目前DMA在测量颗粒材料的能量耗散性质方面的报道不多. ...
Particle dynamics in avalanche flow of irregular sand particles in the slumping regime of a rotating drum.
0
2017
Avalanche dynamics of granular materials under the slumping regime in a rotating drum as revealed by speckle visibility spectroscopy.
1
2015
... 由于普通X射线光源亮度低, 穿透力差等原因使得成像的空间和时间分辨均较低, 且成像速度难以达到想要的结果, 所以具有高能量、高亮度、强穿透性等特点的同步辐射技术的出现能有效解决以上不足之处.同步辐射是电子在做高速曲线运动时沿轨道切线方向产生的电磁辐射, 具有其他辐射源难以比拟的优异特点, 比如光谱连续平滑、微米级脉冲、光强高、穿透性强、准直性好等.当前SR技术可以获得微米级的空间分辨率和微秒级的时间分辨率(Wang et al. 2008 ). 作为一种具有穿透性的非侵入测量手段, SR技术主要利用吸收衬度和相位衬度成像, 其中吸收衬度成像是X射线成像技术的主要手段.其主要原理是X射线在通过材料时会被吸收, 满足Beer-Lambert定律\[I = I_0 {\rm e}^{ - \mu L} \ \ (12)\] 其中, \(I_{0}\)和\(I\)分别为入射前和透射后的X射线强度, \(\mu\)为材料的线性衰减系数, \(L\)为X射线在材料中穿透的距离.由于不同材料对X射线的吸收系数不同, 因此沿X射线传播方向样品对X射线的吸收不同, 从而产生衬度.X射线成像对于颗粒流体研究的优势在于其具有穿透性, 可以得到光学不透明的颗粒体系内部的运动信息.这样排除了很多情况下颗粒微观动力学研究受到维度及边界效应影响的限制.在X射线实验中为了区分单独的颗粒, 可以使用与背景颗粒不同材质的颗粒作为示踪颗粒, 也可以在颗粒表面涂抹对X射线有强吸收的重金属元素涂层来增加吸收衬度.图22 显示了同步辐射研究颗粒运动的实验装置图.在容器中的颗粒受到震动台的连续震动形成密集颗粒气体, 对穿透的X射线吸收产生衬度.穿透的X射线打在荧光靶上产生可见光衬度像.这个衬度像可以通过一个45\(^{\circ}\)反射的镜子与CCD相机光学耦合成像. ...
Simultaneous PIV and PTV measurements of wind and sand particle velocities.
2
2008
... 由于PIV技术的本质是一种欧拉方法(对窗口内所有粒子位移的统计平均), 无法解决速度场梯度过大的问题, 目前对密集颗粒体系速度场进行测量时, PTV技术已成为主流(Orpe & Khakar 2007 , Zhang et al. 2008 , Chung et al. 2010 , Shirsath et al. 2015 , Xu et al. 2016 ).传统PTV测量法的基本原理与PIV类似, 也是对连续两幅图像的相关性进行计算, 两者的主要区别是PTV技术是跟随某个流体质点一起运动, 了解该质点的速度随时间的变化情况, 然后综合流场中的所有流体质点得到整个流场的流动情况, 属于拉格朗日方法, 在一定程度上可以解决速度场梯度较大的问题.PTV技术的主要难点在于粒子的跟踪算法, 简单的解决办法是在待测颗粒物质中加入不同颜色或者荧光的颗粒(Natarajan et al.1995 , Hsiau & Jang 1998 , Bendicks et al. 2011 ), 但这种方法可操作性较差, 如果示踪颗粒太少则不能完整表征流速场, 如果示踪颗粒太多则颗粒容易混叠影响测量结果.更有效的解决办法是基于沃罗诺伊图(Voronoi diagram)的PTV测量(Capart et al. 2002 , Jesuthasan et al. 2006 , Hagemeier et al. 2015 ). 该方法通过确定图像中可识别的颗粒位置, 由连接两邻点直线的垂直平分线构成连续多边形, 完成划分区域并标记颗粒, 匹配连续多帧中的同一颗粒进而确定其位置变化(轨迹). 对于\(T_{i - 1} \)到\(T_{i + 2} \) 时刻连续的多帧图像, 可识别的颗粒记为\(P_{i - 1}, \cdots, P_{i + 2} \), 相应的轨迹距离表示为\[{\rm dis} t_T \left( {P_i ,P_{i + 1} } \right) = \min \left({\left| {r_i^ - - r_i } \right|,\left| {r_{i + 1}^ + - r_{i + 1} }\right|} \right) \ \ (3)\] 其中, \(r_i^ - = 2r_{i + 1} - r_{i +2} \), \(r_{i + 1}^ + = 2r - r_{i - 1} \), \(r_{i + 1}^ + = 2r - r_{i- 1} \); \(r_{i - 1}, \cdots, r_{i + 2} \)为\(P_{i - 1}, \cdots, P_{i + 2} \)在各帧图像中的颗粒位置. 图2 为连续20帧图像用PTV算法测得的颗粒速度分布. ...
... 近10年来, 上海交通大学张洁研究组开展了力链结构表征及其演化规律分析的详细工作(Wang & Zhang 2015 ), 清华大学孙其诚研究组开展了二维颗粒光弹实验, 实现了基于应力条纹快速计算数千颗粒上所有接触点的法向力和切向力, 研究发现: 颗粒接触力的概率密度函数\(p(f)\)表征, 其中\(f\)为归一化力, 发现: \(f = 1\)处, \(p(f)\)达到极大值; 提出了准直性、应力阈值等标准, 定义了力链, 确定了力链长度概率密度分布, 发现力链约为8个颗粒长.近期, 美国Duke大学 Behringer 课题组结合光弹技术, 采用高速相机拍摄了颗粒受冲击过程中的力链变化, 测量了力的传播速度(Clark et al. 2015 ). ...
Fast synchrotron X-ray tomography study of the packing structures of rods with different aspect ratios.
3
2014
... 对颗粒体系的研究因受限于实验技术无法穿透一般不透明的颗粒材料而一直发展缓慢, 作为高速X射线成像技术的发展者, 上海交通大学王宇杰研究组用上海光源X射线成像及生物医学应用光束线站和美国阿贡国家实验室的先进光源32ID线站的高速SR技术, 对三维颗粒堆积体系的微观结构及动力学进行了实空间的成像, 并将其应用于研究非平衡态的颗粒体系.王宇杰等利用SR技术研究了三维棒状颗粒体系的性质和颗粒气体的运动(Zhang et al.2014 , Wang 2016 ) (如图23 所示), 同时还利用SR技术研究了单一分散颗粒硬球体系在有无液体时的微观结构, 同时将其与非晶玻璃化转变相关联(Xia et al. 2015 , Li et al. 2014 ); 研究发现颗粒体系中的玻璃化转变可能是非常类似于晶体结晶过程的一种特殊结构相变.其对应的玻璃结构序是一种局部紧密堆积的四面体结构, 这些四面体结构可以生长形成具有分形结构的团簇, 同时其形状及大小的增长符合位形熵驱动的成核模型, 这些都非常类似于快速降温的晶体生长模型. ...
... 直径为0.5 cm, 长度为2 cm的ABS棒在20\(g\)振动加速度下的密集颗粒气体在某一瞬间的运动图像.少量示踪棒状颗粒表面涂有对X射线强吸收的氧化钕, 可以清晰地追踪其运动. X射线的拍摄速度是2 000帧/秒 (Zhang et al. 2014 , Wang 2016 ) ...
... 在力链结构刻画方面, Wyart 等 (2005) 认为: 设颗粒接触数\(Z\)与等静态接触数\(Z_{\rm iso} \) 之差为 \( \Delta Z = \left( {Z -Z_{\rm iso} } \right)\),则力链特征长度\(l^\ast \sim 1/{\Delta Z} \).近年来, 关于颗粒材料介观长度尺度及其随系统参数演化规律的数值研究已经取得了很大的进展.特别是, 一些研究者试图从动力学响应的角度研究颗粒体系中的特征长度.例如: Ellenbroek 等 (2006, 2009)研究了处于堵塞(jammed)固体样品中心的单个颗粒直径膨胀带来的力响应涨落, 发现当接近堵塞(jamming)点时的力响应涨落空间范围\(L^\ast \)发散, 暗示低于长度尺度\(L^\ast\)响应被涨落控制(变形场可以被视为一个扭曲软模式), 而在大于\(L^\ast\)的尺度, 系统的响应过渡到弹性. Karimi 和 Maloney(2011) 研究发现颗粒体系应力各向异性的特征长度随体积分数\(\varphi\)从上述趋近临界体积分数\(\varphi _{\rm c} \)时增大.Vitelli(2010)研究了无摩擦软球堵塞(jammed)体系剪切声波的长波衰减, 发现特征长度\(L^\ast \sim \left( {\varphi - \varphi _{\rm c} }\right)^{{ - 1} / 2}\).关于动力学关联长度随体积分数演化规律的研究方面, Flenner 等(2010) 实验发现在堵塞点附近, 水平振动单层颗粒床的动力学关联长度\(L^\ast \sim \left( {\varphi -\varphi _{\rm c} } \right)^{1/ 2}\). ...
Spectral responses in granular compaction.
0
2010