1 引言
作为一种典型的智能材料, 形状记忆合金 (shape memory alloys, SMAs)因其特有的超弹性和形状记忆效应已经在很多领域得到了广泛的应用(Van Humbeeck 1999 , Duerig et al. 1999 , Morgan 2004 ).在实际的服役过程中, 形状记忆合金构件和器件通常会承受循环载荷的作用(包括温度循环、磁力循环和机械循环载荷以及它们之间的耦合), 循环变形和疲劳失效行为是这些构件或器件疲劳寿命预测和可靠性评价中的关键问题, 已得到了国内外研究者的广泛关注. 众所周知, 形状记忆合金的超弹性和形状记忆效应来自于该类材料特殊的、由温度场或应力(应变)场以及磁场的变化诱发的马氏体相变及其逆相变所致.因此, 可以按照形状记忆合金的相变诱发方式将其分为两大类:由温度或应力(应变)场诱发的热致形状记忆合金, 如近等原子比的NiTi形状记忆合金和高温NiTiX形状记忆合金; 由温度、应力和磁场单独或共同诱发的磁致形状记忆合金, 如NiMnGa铁磁形状记忆合金.在这两类形状记忆合金的反复相变过程中都涉及到相变潜热的释放和吸收, 因而必然涉及到热--力和磁--热--力耦合的问题, 特别是在加载速率相对较大的情形下. 由此可见, 有必要深入探讨形状记忆合金的热--力和磁--热--力耦合循环变形和疲劳失效行为并进行理论描述.
自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述.
因此, 本文将对热致和磁致形状记忆合金的热--力和磁--力耦合循环变形和疲劳失效行为的宏微观实验和理论研究的现状进行综述.第2和第3部分首先分析了热致形状记忆合金(包括NiTi形状记忆合金和NiTiX高温形状记忆合金)热--力耦合循环变形和疲劳失效行为的研究成果; 在第4和第5部分分别分析了磁致形状记忆合金(以NiMnGa为典型代表)的磁--力耦合循环变形和疲劳失效行为的研究成果; 最后, 第6部分对全文进行简要总结并对后续进一步研究工作进行了展望, 以便能促进形状记忆合金材料和相关智能器件的开发与应用.
2 热致形状记忆合金的热--力耦合循环变形行为
热致形状记忆合金是最先问世的形状记忆合金, 并且是目前研究最为集中的智能材料之一.在这类形状记忆合金中应用最为广泛的是近等原子比的NiTi形状记忆合金和NiTiX高温形状记忆合金, 同时其他的热致形状记忆合金(诸如Cu基和Fe基形状记忆合金等)的热--力耦合循环变形行为与前述两种合金的非常相似(赵连城等 2002 ), 因此本节仅对NiTi和NiTiX形状记忆合金的相关研究成果进行总结, 对这两类合金的基本力学行为及其相变机理等不做阐述, 相关内容可参见文献(Lagoudas 2008 , 赵连城等 2002 ).
2.1 NiTi形状记忆合金的循环变形行为
近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ).
2.1.1 实验研究
由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变.
2.1.1.1 超弹性NiTi形状记忆合金的率相关循环变形行为
(1) 宏观变形行为
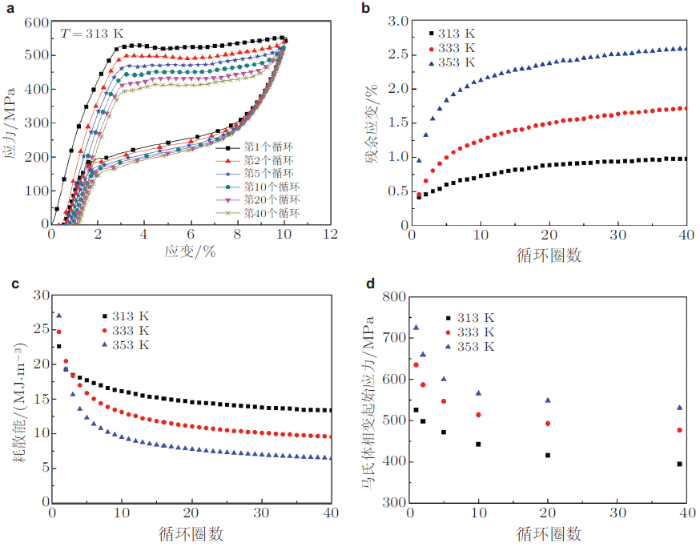
已有研究表明, 超弹性NiTi形状记忆合金的相变应力明显依赖于实验环境温度, 由Clausius-Clapeyron关系式可知实验温度每升高1K, 该合金的马氏体相变开始应力将升高8 MPa左右 (Lagoudas 2008 , 赵连城等 2002 ).NiTi形状记忆合金的热--力耦合行为与相变潜热的释放和吸收以及由此而引起的温度变化密切相关, Yu等(2014a)专门讨论了超弹性NiTi形状记忆合金在应变控制循环变形过程中出现的超弹性劣化效应的温度相关性, 结果如图1 所示. 由图1 (b) \(\sim \) 图1 (d)可见: 随实验环境温度的升高, 残余应变的累积效果随循环次数的增大越显著, 耗散能密度和马氏体相变开始应力减小就越明显, 即循环变形对NiTi形状记忆合金的超弹性劣化作用就越显著, 相变棘轮行为发展就更为迅速.
图1 超弹性劣化效应的温度依赖性 (Yu et al. 2014a ). (a)应力--应变曲线, (b) 残余应变\(\varepsilon ^{\rm r}\)演变曲线, (c)耗散能\(W\)演变曲线, (d)马氏体相变开始应力\(\sigma _{\rm MA}^{\rm s}\)演变曲线
众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\).
图2 超弹性NiTi形状记忆合金微管的率相关应力--应变曲线 (Kan et al.2016). (a) 第1周, (b) 第5周, (c) 第20周, (d) 第50周
图3 超弹性NiTi形状记忆合金微管在3.3 \(\times \) 10\(^{ -4}\) s\(^{-1}\)加载速率下的表面温度场及其在循环变形过程中的变化情况(Kan et al.2016).(a) 应变--应变曲线上的特定观察点, (b)特定点上的温度分布情况
图4 超弹性NiTi形状记忆合金微管在3.3 \(\times \) 10\(^{ -2}\) s\(^{-1}\)加载速率下的表面温度场及其在循环变形过程中的变化情况(Kan et al.2016).(a) 应变--应变曲线上的特定观察点, (b)特定点上的温度分布情况
图5 超弹性NiTi形状记忆合金微管在不同加载速率下的平均温度随相对时间(当前时间/循环一周所花时间)的变化曲线(Kan et al.2016 ). (a) 3.3 \(\times \) 10\(^{ - 4}\) s\(^{-1}\),(b) 3.3 \(\times \) 10\(^{ - 2}\) s\(^{-1}\)
由图2 得到的应力--应变关系曲线可见: (1)加载速率的变化显著影响超弹性NiTi形状记忆合金微管的循环应力--应变响应, 拉伸部分体现出的相变硬化程度在高加载速率下变得更加显著, 如图2 (a)所示. (2) 残余应变的累积同样依赖于加载速率, 在高加载速率下演变更为迅速, \(3.3\times 10^{ - 2}\) s\(^{ -1}\)下的饱和残余应变值明显高于其他加载速率下的结果, 如图2 (b) \(\sim\) 图2 (d)所示. (3)随着加载速率的增大, 每一次循环中的耗散能密度下降也更为迅速, 并且饱和的耗散能密度值也变得更小. 这说明, 超弹性的循环劣化和耗散能密度减小在高加载速率的循环过程中变得更加显著, 进而更易导致超弹性NiTi形状记忆合金的功能性疲劳失效. 此外, 超弹性NiTi形状记忆合金循环劣化和耗散能密度还随着加载应力水平的提高(Kang et al. 2009 )和温升的提高 (Yu et al. 2014a )变得更加显著.
由图3 \(\sim\) 图5 可见, NiTi合金微管的表面温度在循环变形过程中会发生明显变化, 变化的最大值随加载速率的增加而增大. 然而, 整个工作段的平均温度即使在加载速率为\(3.3\times 10^{ - 2}\) s\(^{ -1 }\)(在最大应变为9%时, 相当于加载频率为0.15 Hz)的工况下却会随着循环次数的增大而逐渐下降, 如图5 (b)所示. 这与Yin等(2014) 在加载频率高于1 Hz的单轴拉伸--卸载循环加载下观察到的、平均温度随循环次数增大而不断升高的现象不同(如图6 所示). 由于Kan 等(2016) 采用的最高加载速率比Yin 等(2014) 的要低, 因而只能观察到平均温度随循环次数增大而逐渐下降的现象.当加载速率较小时, 微管与外界的热交换在循环过程中会随着循环次数的增大而逐渐充分, 虽然在循环变形过程中有温度的波动, 但平均温度将随循环次数的增大而逐渐下降, 最后趋近于环境温度, 或是没有明显的升高 (见图5 (a)); 当加载速率较大时 (如Yin等(2014) 讨论的1 Hz), 微管与外界的热交换不能充分进行, 材料内部在循环变形过程中将产生热量的集中, 并随循环次数的增大而变得更加显著, 因此, 平均温度将随循环次数增大而逐渐上升, 如图6 (a)所示.
图6 超弹性NiTi形状记忆合金微管在高加载速率下的平均温度随循环次数的变化曲线(Yin et al.2014 ). (a) 温度变化, (b) 应力--应变响应
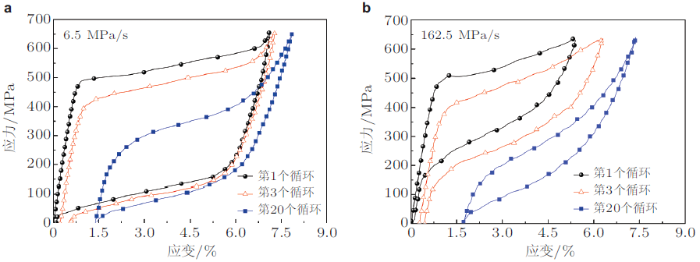
尽管如此, Kan等(2016) 完成的相关实验还是揭示了超弹性NiTi形状记忆合金明显的热--力耦合效应以及由此而引起的率相关循环变形特性, 并且表明在相应的本构模型构建中应该合理考虑这种与内部热生成和外部热交换密切相关的热--力耦合循环变形行为.同时, Xie等(2016a) 还通过不同加载速率下的应力控制循环拉伸--卸载实验, 揭示了不同应力率下超弹性NiTi形状记忆合金板材的单轴相变棘轮行为演化特征, 如图7 所示. 图7 表明: NiTi合金板材的单轴相变棘轮行为也体现出明显的应力率相关性, 拉伸部分的相变硬化程度也随应力率(即加载应力随时间的变化率)的增大而增大, 并且高应力率下的相变棘轮行为更为显著. 另外, 由图7 还可以看出, 在高应力率情形下, 每一次循环中的耗散能密度(即应力--应变滞回环的面积)明显小于低应力率下的结果. 这也说明, 在应力控制的循环变形过程中, 超弹性劣化和耗散能下降也随应力率的增大而变得更加迅速.这些率相关性也是依赖于循环变形过程中体现出的、明显的热--力耦合效应.值得注意的是, 尽管目前已有一些文献讨论了超弹性NiTi形状记忆合金的率相关相变棘轮行为, 但与应变控制下的率相关循环变形行为相比, 已有的研究还不系统, 特别是NiTi形状记忆合金多轴循环变形行为的率相关性方面还需要在未来的研究中进行更为深入和系统的实验观察.
图7 超弹性NiTi形状记忆合金板材在不同应力率下的单轴相变棘轮行为(Xie et al. 2016a ). (a) 6.5 MPa/s, (b) 162.5 MPa/s
(2) 相变图案及其演化
尽管NiTi形状记忆合金中的热弹性马氏体相变是一种快速的切变式固态相变过程, 但是, 在多晶NiTi形状记忆合金材料中, 因晶粒晶体学位向的不同和晶界对相变过程的阻碍作用, 使得马氏体相变过程是一种局部切变形核而逐渐扩展长大的过程, 特别是在超细晶的多晶NiTi形状记忆合金中.对于这一种局部的、非均匀马氏体相变过程, Shaw & Kyriakides(1995 , 1997 )对细晶多晶NiTi形状记忆合金条带通过全场像和应力--应变的同时测量进行了早期的观察, 揭示了在外加载荷作用下非均匀马氏体相变的产生以及宏观可观察的相变图案(transformation domain)形成和扩展. 近年来, Zhang 等(2010) , Sun 等(2002) , He 和 Sun(2010a) 及 Feng 和 Sun(2006) 利用CCD相机和高速摄像仪进一步观察了细晶超弹性NiTi形状记忆合金在应变控制的单轴拉伸--卸载过程中相变图案的形成和演化以及这一过程的加载速率依赖性, 进而揭示了单轴拉伸和卸载过程中马氏体相变过程的局部性. Zhang等(2010)得到的细晶超弹性NiTi形状记忆合金薄材典型的实验结果如图8 和图9 所示.
图8 NiTi形状记忆合金在3.3 \(\times \) 10\(^{ -4}\) s\(^{-1}\)下的(a)拉伸--卸载曲线和(b)相变图案演化 (Zhang et al. 2010 )
图9 NiTi形状记忆合金在3.3 \(\times \) 10\(^{ -2}\) s\(^{-1}\)下的(a)拉伸--卸载曲线和(b)相变图案演化 (Zhang et al. 2010 )
由图8 和图9 可见:(1) 当应变率较低(如3.3 \(\times\) 10\(^{-4}\) s\(^{-1}\))时, 在拉伸过程中, 宏观可见的马氏体图案首先出现在试样工作段的上端部, 并且伴随着响应应力从\(a\)点到\(c\)点的下降过程, 如图8 (a)所示.在后续的加载过程中, 马氏体图案朝试样中部扩展. 当载荷施加到\(e\)点时, 在试样下端部萌生并扩展形成了一条新的马氏体图案, 且也对应于响应应力值的下降. 在此之后, 随着外加载荷的增大, 这两条马氏体图案继续向试样中部扩展, 最后在\(m\)点处二者合并为一, 马氏体相变完成. 在卸载过程中, 当外加载荷卸载到一定程度时(例如到达\(p\)点时), 将会发生马氏体向奥氏体的逆相变, 表现为加载过程中形成的马氏体图案从试样工作段两端开始的逐步收缩.在\(t\)点时, 马氏体图案因逆相变进行完毕而完全消失. (2)当应变率较高(如3.3 \(\times \) 10\(^{-2}\) s\(^{-1}\))时, 如图9 所示, 马氏体图案的形成和扩展规律明显不同于应变率较低时的情形.在拉伸过程中的相变开始点\(a\), 在高应变率下是在试样的工作段同时形成多个马氏体图案, 其数目远大于低应变率下观察到的2条. 在后续的加载过程中, 形成的马氏体图案进一步扩展并相互汇聚, 直至加载过程结束.在卸载过程中, 与加载过程中观察到的马氏体图案的萌生和扩展规律相似, 多条奥氏体图案萌生和扩展, 然后在逆相变结束时完全汇聚, 如图9 (b)所示.
结合实际变形过程中的温度变化的测量, Zhang等(2010) 进一步对相变图案形成和演化及其率相关性的物理本质进行了解释, 强调了这一物理过程中的材料局部失稳特性和热--力耦合特性. 然而, 上述研究仅针对应变控制的拉伸--卸载过程, 没有涉及多次循环、不同加载水平以及在应力控制加载条件下相变图案的形成和演化, 还需要进一步观察和讨论. 为此, Xie等(2016a) 采用非接触数字图像相关(DIC)和红外热成像(IR)方法直接观测了超弹性NiTi形状记忆合金板材在应力控制拉伸--卸载循环过程的相变图案和温度场分布及其演化, 讨论了不同峰值应力(即650, 750和800 MPa)作用下NiTi合金板材相变图案的循环演化特征及其形成机理, 典型的实验结果如图10 和图11 所示. 结果表明: (1)超弹性NiTi形状记忆合金在拉伸--卸载循环初期表现出变形局部化的特征, 马氏体条带逐渐形成、长大和扩展以及卸载过程中的奥氏体条带的形成、长大或扩展, 如图10 (a)和图11 (a)所示. (2)然而, 循环稳定后相变图案的演化则依赖于外加的应力峰值大小.应力峰值较小(如650 MPa)时, 循环稳定后无明显的相变图案形成, 表现出较为均匀化的变形特征; 但当应力峰值较高(如750和800 MPa)时, 循环稳定时仍会出现明显的相变图案, 产生马氏体条带的残留现象. Xie等(2016a) 进一步通过测得的应变场和温度场的变化, 认为宏观马氏体条带的残留是由高峰值应力循环后富集的位错对马氏体的钉扎作用造成的, 马氏体条带的残留也与该NiTi合金在高峰值应力下显著的相变棘轮行为是相对应的.
图10 NiTi形状记忆合金在峰值应力为650 MPa的循环拉伸--卸载过程中的相变图案演化(Xie et al.2016a). (a) 第1周, (b) 第20周. 图中\(a\)为正相变开始点, \(b\)为加载中点, \linebreak\(c\)为峰值应力点, \(d\)为逆相变开始点, \(e\)为卸载中点, \(f\)为零应力点
图11 NiTi形状记忆合金在峰值应力为800 MPa的循环拉伸--卸载过程中的相变图案演化(Xie et al.2016a ). (a) 第1周, (b) 第20周. 图中\(a\)为正相变开始点, \(b\)为加载中点, \(c\)为峰值应力点, \(d\)为逆相变开始点, \(e\)为卸载中点; \(f\)为零应力点
Xie等(2016b) 进一步分别讨论了在应变控制和应力控制拉伸--卸载循环变形过程中相变图案的形成和演化对加载速率的依赖性.研究表明: (1)相变条带的数目随加载速率的增大而单调增大; (2)在加载速率较低时, 随循环次数的增大, 变形逐渐由明显的局部化特征过渡到均匀变形, 残余马氏体条带不明显; (3)在加载速率较大时, 在循环稳定时将会有明显的残余马氏体条带产生, 这是因为加载速率较快时, 相变棘轮行为更为显著, 增加的位错密度将对马氏体逆相变产生显著的抑制作用的缘故; (4)在应力控制的循环拉伸--卸载加载的稳定变形阶段, 观察到的应变和温度场要比应变控制下的更为均匀.材料内部的相变热生成和与外界的热交换之间的相互竞争是相变图案率相关性的根本原因, 而在稳定的循环变形阶段这两种因素的竞争达到一个动态的平衡.
综上所述, 通过超细晶的多晶NiTi形状记忆合金热--力耦合变形过程中相变图案的形成和演化过程的观察, 可以直观地揭示多晶NiTi合金材料相变及由此而引起的变形过程的局部化特性, 能够为进一步了解该合金热--力耦合循环变形的微观机理提供一定的信息, 应该是一个值得深入而系统研究的问题. 然而, 上述研究仅仅提供了超弹性NiTi形状记忆合金(初始相为奥氏体)在单轴循环拉伸--卸载加载过程中观察到的信息, 对于多轴循环加载下超弹性NiTi合金以及形状记忆效应NiTi合金(初始相为孪生的马氏体相)的相变图案观察还未能涉及.
2.1.1.2 形状记忆效应NiTi合金的率相关热--力耦合循环变形行为
初始相为孪生马氏体的NiTi形状记忆合金在热--力耦合的加载过程中会体现出特有的形状记忆效应, 包括有单程、双程和全程记忆效应 (Lagoudas 2008 ).在具有形状记忆效应的NiTi合金中, 其记忆效应是通过温度诱导的马氏体逆相变(即解孪马氏体向奥氏体的转变)来实现的, 而解孪(或重取向)马氏体则是通过施加位移或力载荷由孪生马氏体转变而得, 因此, 这是一个显著的热--力耦合过程, 需要同时考虑机械载荷和温度以及两者之间的耦合作用的影响.
由于初始相为孪生马氏体的NiTi形状记忆合金在单纯的机械载荷作用下是通过马氏体的解孪和重取向来产生材料的宏观变形的, 不涉及任何相变过程的发生, 因此, 在机械载荷完全卸载以后, 由马氏体的解孪和重取向发生的变形绝大部分不能恢复, 产生类似于塑性应变的残余变形.这一部分残余应变只有在后续的升温过程中才能因解孪(重取向)马氏体转变为奥氏体而逐渐消失, 为此, 人们认为在不涉及温度变化的纯机械载荷作用下, 形状记忆NiTi合金的循环变形行为与普通金属类似, 进而没有对其进行较为系统的研究. 然而, Kang等(2009) 对初始相为孪生马氏体的NiTi形状记忆合金的室温单轴应力控制循环变形实验研究却表明, 由于该合金的非弹性变形机制是马氏体的解孪和重取向, 是一种外加载荷作用下马氏体孪生关系和晶体学位向的改变, 并不是普通金属室温循环变形过程中涉及的位错的滑移或孪晶的形成, 因此, 其应力控制的单轴循环变形行为与普通金属材料有明显的不同.
对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示.
图12 形状记忆NiTi合金在恒定轴向应力的温度循环下的实验结果(Bo & Lagoudas 1999 ). (a) 温度--应变曲线(恒定应力为35 MPa, 前20周), (b) 不同恒定应力下的塑性应变演变曲线
由图12 可见: (1)在恒定轴向应力的温度循环变形过程中, 在反复的马氏体--奥氏体相变过程的同时, 由于恒定轴向应力的作用, 在升温和降温的过程中均产生一定的应变, 并且一个温度循环内得到的温度--应变滞回环随循环次数的增大逐渐在轴向方向发生平移, 形成塑性变形的累积, 但累积的速率会逐渐降低, 经过一定的循环次数后逐渐趋于稳定, 如图12 (a)所示.(2)累积的塑性变形与施加的轴向应力水平有关, 在所给定的应力范围内轴向应力越大、塑性应变越大并且累积速率越大.(3)马氏体相变的开始温度随循环次数的增大而逐渐降低, 表明循环过程中由于塑性变形的产生使得热弹性马氏体相变的驱动力有所增大, 马氏体相变的困难程度提高.
由上述综述情况来看, 目前对于具有形状记忆效应的NiTi合金热--力耦合循环变形行为的实验研究还不是非常全面, 对于发生在循环变形过程中的形状记忆退化现象研究还不深入, 集中讨论的热--力耦合循环加载工况也仅限于恒定应力下的温度循环加载, 未能涉及机械载荷和温度载荷同时为交变载荷的热--力耦合加载工况或是针对单程记忆效应的应力(或应变)--升温--降温--应力 (或应变)循环加载条件. 更为突出的是, 目前的研究还没有涉及到温度循环的速度, 也就是温度加载频率的变化对形状记忆效应的热--力耦合特性的影响还未能涉及.可见, 目前已有研究中涉及到的加载工况还未能合理考虑NiTi形状记忆合金器件的实际服役条件, 还需要开展更为符合实际服役条件的热--力耦合循环变形行为的实验研究.
2.1.2 微观实验观察
尽管文献 (康国政等2015)对NiTi形状记忆合金循环变形过程中的微观结构研究现状进行了一定的综述(具体细节可参见原文献), 但未能对近年来取得的NiTi形状记忆合金循环变形过程中的微观结构演变特征研究成果进行合理的评述, 因此, 本小节在这方面做一个简要的概述.
Pelton 等(2011, 2012)采用透射电子显微镜(TEM)对NiTi形状记忆合金在温度循环过程中的微观结构演变进行了观察, 结果发现位错密度会随着温度循环次数的增大而逐渐增大, 如图13 所示, 并且累积的位错会影响材料的温度和力学响应.
图13 NiTi形状记忆合金经历10个循环次数和100个循环次数温度导致的位错分布图(Pelton et al.2012)
最近, Zotov等(2017) 通过原位X射线衍射仪(XRD)测量了超弹性NiTi形状记忆合金相变过程中马氏体体积分数随循环次数的演变图像, 如图14 所示. 可以看出, 马氏体分布随着循环次数的增大趋于均匀化, 位移控制下的平均马氏体体积分数高于载荷控制下的平均马氏体体积分数, 这表明载荷控制比位移控制产生了更多的累积残余应变.试样标距段的统计平均马氏体分数值随着循环次数的增大而下降, 即马氏体相变过程被逐渐抑制. Zotov 等(2017)进一步基于XRD测量结果, 确定了平均位错密度的演变曲线, 如图15 所示, 为相变过程中位错密度的循环变化提供了定量数据.
图14 循环变形过程马氏体体积分数随循环次数的演化 (Zotov et al. 2017 ).(a) \(\sim\) (f) 载荷控制, (g) 位移控制
图15 奥氏体相中平均保留位错密度随循环次数的演变曲线 (Zotov et al.2017)
Tadayyon等(2017) 通过TEM观察研究了初始相为马氏体的NiTi形状记忆合金在拉伸载荷作用下的变形行为和相关的微结构演变, 如图16 所示. 结果表明: 初始拉伸阶段首先发生孪晶马氏体的弹性变形, 然后发生马氏体解孪并进一步产生位错, 而位错的移动则会促进解孪和孪生变形; 随着变形的增大, 位错之间的相互约束增强, 最后发生剪切带和堆垛层错的滑移. Tadayyon等(2017) 指出位错运动和孪生变形可以细化晶粒, 导致合金强度提高以及延展性增强, 而堆垛层错进一步使得材料发生加工硬化. 这些研究结果表明, NiTi形状记忆合金发生马氏体重定向时也会产生大量的位错缺陷, 且位错缺陷甚至会演变成堆垛层错, 进一步影响该合金的性能.
图16 初始相为马氏体相的NiTi形状记忆合金在拉伸变形过程中微结构的演化图(Tadayyon et al. 2017 )
综上所述, 已有研究在NiTi形状记忆合金热--力耦合循环变形过程中微结构的形成和演变的微观观察以及宏观变形行为微观机理的总结方面还存在很多不足, 相关研究还不系统、不深入, 需要开展大力的研究, 特别是可以借用扫描电子显微镜(SEM)原位(高温)疲劳试验与TEM观察相结合的技术优势, 获得更多的形状记忆合金试样表面或亚表面微结构的演变行为、损伤机制的实验数据以及微结构在相变演变过程中的形貌变化机制及影响因素等(王习术 2010 ).
2.1.3 微/纳尺度的数值模拟
Cisse等(2016) 在对形状记忆合金的本构模型和模拟技术的综述过程中对相关的分子动力学模拟和相场分析进行了简要评述, 但并没有涉及到一些具体细节和重要结果, 并且对形状记忆合金在微纳米尺度下的热--力耦合循环变形行为数值模拟讨论较少.
因此, 本小节将对NiTi形状记忆合金的相场模拟和分子动力学计算方面的研究现状进行必要的补充介绍, 给出一些典型的以及最新的研究成果, 并且着重突出在该合金热--力耦合微观循环变形过程数值模拟方面的最新进展.
2.1.3.1 相场模拟
2.1.1.1节中讨论了相变图案及其演化结果, NiTi形状记忆合金的相变过程是一个局部形核、逐渐长大的变化过程, 而采用一般的本构模型是无法模拟形状记忆合金这种局部相变行为的演化.但相场模拟可以通过系统总能量最小化得到材料微结构演变, 在得到了材料系统的自由能泛函之后, 根据相场动力学方程进行序参量的求解.相场分析方法由于具有处理复杂的几何和拓扑变化的灵活性特点, 已广泛应用于模拟相变过程中微观结构的演变.不同序参量满足的动力学方程不同, 根据序参数的保守和非保守性, 描述材料微结构演变的相场动力学方程有两种简单的近似形式:
(1) Cahn-Hilliard模型 (Cahn & Hilliard 1958 , 1959 ), 这种模型的相由保守的场变量唯一决定; (2) Allen-Cahn模型 (Cahn {\rm&} Allen 1977 , Allen & Cahn 1979 ), 这种模型的相无法由浓度、温度和压强等唯一决定, 而需要引入一个或多个额外的非保守场变量即序参量来决定局部相. 目前, 大部分的相场模拟是基于Allen-Cahn模型及其改进模型开展的.Allen-Cahn模型的动力学方程通常也称之为时间相关Ginzburg-Landau(TDGL)方程, 求解该动力学方程的数值解法有很多, 最常见的是基于统一空间网格和精确时间步长的简单二阶有限差分法 (Fan & Chen 1997 ). 从已有研究中可归纳出相场模拟的4个步骤: (1)为研究材料系统确定合适的序参数; (2)将局部能量密度表示为所选序参数的函数, 并得出材料系统的自由能泛函, 这些函数必须正确描述系统的对称性和热力学性质; (3)由自由能泛函得到相场动力学方程, 并将从实验数据或基础计算中得到的唯象系数带入动力学方程; (4)确定正确的初始和边界条件并选择适当的方法求解动力学方程.
近些年来, 在已有的研究中所采用的相场模型主要差异在于选择的序参量不同. 表1 总结了近年来采用不同序参量的相场模型开展的单晶和多晶形状记忆合金相变过程的模拟情况.
为了进一步考虑NiTi形状记忆合金相变和塑性的交互作用, Levitas等(2003) 采用相状态作为序参量, 从理论上研究了马氏体相变和孪生过程, 并引入位错密度作为序参量考虑位错对相变过程的影响. Malik等(2012) 采用弹塑性相场模型, 基于有限元法研究了塑性自适应对马氏体相变的影响, 结果显示, 塑性自适应会粗化马氏体微观结构. 之后, Malik等(2013) 采用弹塑性相场模型研究了多晶材料晶粒边界和孪晶边界对马氏体相变的影响, 结果发现, 晶粒边界会阻断马氏体的扩展而孪晶边界则不会. Kundin等(2011) 采用类似的方法, 在只考虑单晶奥氏体塑性变形的情况下, 模拟了蝶形马氏体相变的微结构演变, 结果表明奥氏体和马氏体边界处位错密度最大. 之后, Kundin等(2015) 进一步研究了马氏体锋面与奥氏体引发的塑性变形之间的交互作用, 包括位错穿过界面由马氏体承受和位错被马氏体锋面湮灭两种情况.
Paranjape 等(2016) 基于相场理论的有限元模拟方法, 采用晶体塑性理论模拟形状记忆合金单晶温度诱发马氏体相变和塑性滑移之间的交互作用, 如图17 所示. 模拟结果表明: (1)奥氏体和马氏体界面的局部变形不协调诱发的高应力容易导致奥氏体发生塑性滑移; (2)马氏体和马氏体界面附近材料点的等效塑性应变较大; (3)冷却阶段塑性滑移量的增加比升温阶段要慢; (4)塑性滑移较小区域促进马氏体相变;(5)塑性滑移较大区域处马氏体相变受阻.
图17 无应力热循环过程中马氏体和塑性的交互作用 (Paranjape et al. 2016 ). (a) 第一个循环中的马氏体分布, (b)第一个循环中的塑性滑移分布, (c)第二个循环中的马氏体分布, (d)第二个循环中的塑性滑移分布, (e)第一个循环冷却过程中的马氏体分布, (f)第一个循环冷却过程中的塑性滑移分布, (g)第一个循环加热过程中的马氏体分布, (h) 第一个循环加热过程中的塑性滑移分布
Levitas 和 Javanakht (2012) 引入位错序参量, 采用有限元法研究了奥氏体相和奥氏体--马氏体界面处位错的形核和扩展过程.之后, Levitas 和 Javanakht (2013) 同时引入相变序参量和位错序参量, 采用有限元方法研究了纳米尺度平面应变大变形情况下马氏体(单个变体)相变、位错对奥氏体--马氏体界面扩展的影响、温度诱发马氏体相变时马氏体片的演化和应力诱发马氏体相变时微结构的演化.同时, Levitas 和 Javanbakht(2015) 还详细介绍了纳米尺度大变形情况下马氏体(多个变体)相变、孪生和位错之间交互作用理论的推导和依据. 然后, Javanbakht和 Levitas (2015) 采用有限元方法对该模型进行了数值实现, 进而研究了纳米尺度应力诱发双晶马氏体相变与位错之间的交互作用, 发现位错引起的应力集中可以促进马氏体形核, 而位错引起的应力释放又会阻碍马氏体相变. 此外, 他们还研究了温度诱发马氏体相变时马氏体片在双晶之间的扩展与位错之间的交互作用.
因此, 相场分析方法为微观组织演变的模拟提供了有效的手段, 无论对枝晶生长的模拟, 还是对多晶演变过程的模拟, 相场分析方法都表现出明显的优越性. 随着相场方法的提出及不断完善, 其应用也越来越广泛. 然而, 相场模型计算结果对输入参数十分敏感, 通常这些参数都是经验参数或很难测量, 相场模型发展的新趋势是与其他模拟方法结合, 实现对微结构演变的定量模拟. 目前, 相场模拟尚有以下工作有待进一步开展: (1)优化数值求解方法, 提高计算效率. 相场模型变量多, 控制方程多, 求解非常复杂, 因此计算效率问题尤其突出.(2)相场模拟虽然在理论上解决了微观结构的演化问题, 但其微观实验的验证还有待进一步开展.(3)已有的相场模拟均针对单调加载情形, 鲜有涉及到循环加载过程下的微结构演变模拟.
2.1.3.2 分子动力学模拟
近二十年来, 随着人们对NiTi形状记忆合金的了解和认识的深入, 越来越多的学者更加关注该合金在纳米尺度下的变形机制, 已经在NiTi形状记忆合金的热--力耦合变形行为的分子动力学(MD)模拟方面取得了众多成果, Kastner (2012) 和Cisse等(2016) 对形状记忆合金相变过程及相关变形行为的分子动力学模拟方面的研究现状进行了较为系统的介绍, 特别是针对NiTi原子间相互作用势、NiTi形状记忆合金的超弹性和形状记忆效应原子模拟方面的研究.因此, 关于NiTi形状记忆合金分子动力学模拟的基本过程以及不同原子间势函数的特征和选择原则等方面的内容请参见文献Kastner(2012) 和Cisse 等(2016) , 本小节仅针对已有的热--力耦合循环变形行为的分子动力学模拟结果做一个必要的补充.
所谓的NiTi形状记忆合金超弹性效应的分子动力学模拟实际上就是在原子模型的初始结构为奥氏体结构时, 采用合适的原子间相互作用势, 通过施加一定的机械载荷并考虑卸载过程, 在原子尺度下讨论形状记忆合金的马氏体相变及其逆相变过程以及由此而引起的超弹性变形行为.例如: Zhong等(2012) 采用EAM原子间作用势研究了NiTi形状记忆合金纳米柱超弹性效应的载荷和温度效应, 计算结果表明, 在高温(奥氏体结束温度之上50K范围)和低载荷(压缩应变为6.6%)的加载和卸载过程中纳米柱仍然呈现明显的超弹性效应, 如图18 所示; 然而由于孪晶界的位错钉扎导致形变孪晶的不可逆性, 在高应变情况下纳米柱丧失超弹性能力.
图18 NiTi合金纳米柱在400 K的压缩变形 (Zhong et al. 2012 ).(a)加载(蓝色)和卸载(红色)的应力应变曲线, (b)纳米柱的横截面视图, (c) BCO晶胞的示意图, (d) B2和BCO晶胞的平面投影视图, (e)纳米柱在压缩过程的快照, 左边描述了孪生剪切带的形成, 右边描述了孪生剪切带的生长, (f)卸载到零应变时的纳米柱快照, 左边描述了残余孪生剪切带, 右边是B2相的横截面视图
Ko等(2017) 则采用考虑第二近邻的MEAM势在奥氏体相变结束温度以上模拟了不同晶粒尺寸(应变率为5 \(\times\) 10\(^{8}\) s\(^{ - 1})\)和不同应变率 (晶粒尺寸为8nm)下NiTi形状记忆合金的超弹性行为, 分子动力学模拟结果表明: (1)加/卸载过程中的相变应力随着晶粒尺寸的减小而增加, 如图19 所示; (2)在没有内部缺陷的模型中再现了实验中观察到的温度和应力诱导马氏体相变, 证实了内部缺陷贡献机制不是马氏体相变的主要诱发机制.基于分子动力学模拟结果, Ko等(2017) 提出了相变诱发的应变贡献机制并成功地解释了马氏体相变和逆相变中的非对称形核和生长行为, 如图20 所示(图中原子的颜色根据CNA模式进行标记, 在每幅截图中蓝色的原子对应B2奥氏体相, 红色的原子对应B19'马氏体相, 灰色的原子对应晶界和域边界).(3)超弹性NiTi形状记忆合金在拉伸过程的应力--应变响应强烈依赖于加载速率, 加载速率越大, 相变硬化程度越高, 进而相同应变值下对应的应力值越高; 同时, 相变开始应力也随加载速率的增大而升高, 如图21 所示.
图19 不同平均晶粒尺寸下NiTi纳米晶体的超弹性应力应变曲线 (Ko et al.2017)
图20 超弹性加卸载过程中NiTi纳米晶体的原子排列 (Ko et al. 2017 )
图21 400 K下平均晶粒尺寸为8 nm的NiTi晶体拉伸--卸载时的应力--应变曲线 (Ko et al. 2017 )
Mirzaeifar 等(2014) 采用Zhong等(2012)修正的NiTi形状记忆合金原子间相互作用势(EAM势)对温度和应力驱动下NiTi形状记忆合金纳米柱的相变过程进行了分子动力学模拟, 结果发现: (1)减小NiTi合金纳米柱的表面能可以使B2相奥氏体转变成B19相马氏体, 模型在弛豫后处于B19相(B19相中构成变体2的原子以红色表示), 如图22 所示.(2)在轴向加载过程中变体2(V2)重定向成变体1(V1):当应变加载到0.02时, 变体2(V2)中三个区域沿着大约\(\pm 45^\circ\)的方向转变成变体1(V1); 随后, 更多的变体2(V2)转变成变体1(V1); 在应变加载到0.1时, 变体2(V2)几乎全部转变成变体1(V1), 如图22 (b)所示. (3)NiTi形状记忆合金纳米柱在三个不同温度下马氏体重定向过程的应力--应变曲线中明显可以看出重取向应力随着温度的升高而升高, 如图23 所示.
图22 NiTi纳米柱在275 K下的马氏体重定向过程 (Mirzaeifar et al. 2014 ). (a) [110]\(_{\rm B2}\)方向的两个不同的B19变体和B2相, (b)单轴拉伸过程中纳米柱的重定向, 变体1和2分别采用蓝色和红色表示, (c)纳米柱多个变体界面的放大视图, Ni和Ti原子分别采用蓝色和红色表示
图23 不同温度下NiTi纳米柱在单轴拉伸卸载过程中的马氏体重定向应力--应变曲线(Mirzaeifar et al. 2014 )
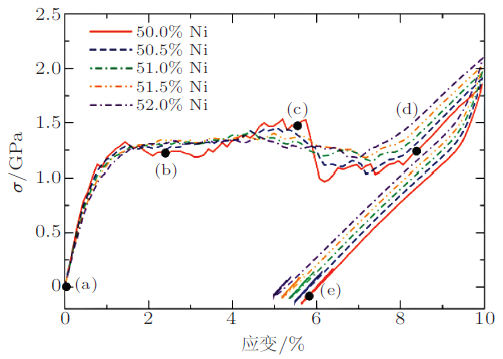
Mutter 和 Nielaba(2013) 采用EAM势对包含不同方向变体的马氏体相NiTi形状记忆合金纳米柱的拉伸--卸载和升温过程进行了原子模拟, 研究了纳米尺度下NiTi形状记忆合金的形状记忆效应, 在1K下具有5种不同Ni原子含量的NiTi形状记忆合金纳米柱的应力--应变曲线如图24 所示, 结果表明NiTi形状记忆合金纳米柱在拉伸过程中多取向变体构型转变成单个变体构型, 卸载后NiTi合金纳米柱存在残余应变, 升温后并没有发现奥氏体产生.
图24 NiTi纳米柱在不同Ni原子含量下的应力--应变曲线(Mutter & Nielaba 2013 )
Wang 等(2017) 采用EAM势, 通过分子动力学模拟研究了循环压缩--卸载过程中NiTi形状记忆合金纳米柱的超弹性行为, 发现位错和孪生对原子模型的物理结构和力学响应的改变、累积不可逆应变和超弹性行为的衰减有着重要影响.图25 给出了NiTi形状记忆合金纳米柱在400 K下峰值应变为7.46%时的单轴循环压缩--卸载模拟结果, 可见在循环变形过程中会产生明显的残余变形以及超弹性劣化现象, 循环7周以后即达到稳定状态, 超弹性滞回环消失.
图25 NiTi形状记忆合金纳米柱单轴循环压缩--卸载过程的模拟结果(Wang et al. 2017 ). (a)应力--应变曲线, (b) CNA与应变曲线, (c)第5周循环中应变压缩到7.36%时的模型, \(Z\)方向距离表面5 {\AA}的原子不可见, (d)纳米柱的位错演化过程, (e)位错滑移平面示意图, 滑移面由红色虚线构成
分子动力学对模拟纳米尺度下NiTi形状记忆合金的相变行为是一个强大和可行的方法.在NiTi合金势能研究方面, 目前已提出10多种NiTi合金势函数. 但是, 由于NiTi合金在超弹性及形状记忆相变过程中涉及到多种晶体结构及理论预测和实验测量的弹性模量的差异性, 并没有一种势函数可以描述所有与NiTi合金相关的物理现象.在超弹性NiTi形状记忆合金研究方面, 目前的研究工作主要集中在应变加载下应变率、环境温度和中间相对变形过程的影响, 缺少一些工艺参数, 如初始相态、加载路径、应力水平等在纳米尺度下对超弹性NiTi形状记忆合金变形行为影响方面的研究.在NiTi合金形状记忆效应方面, 目前的工作主要集中在单纯温度循环加载过程的分子动力学研究, 对热--力耦合循环加载条件下NiTi形状记忆合金的形状记忆退化效应的分子动力学模拟尚不完善, 还需进一步研究.
2.1.4 热--力耦合本构理论
基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ).
为了考虑NiTi形状记忆合金变形过程中体现出的强烈热--力耦合作用, 通过考虑材料非弹性变形过程中的内部热效应(包括相变潜热和非弹性耗散生热)和热边界条件, Müller 和 Bruhns (2006) , Auricchio 等(2008) , Christ 和 Reese(2009) 和Mirzaeifar 等(2011) 建立了NiTi形状记忆合金热--力耦合本构模型.这些本构模型能够合理描述NiTi形状记忆合金的率相关变形特性, 但由于未引入与循环变形相关的内变量, 无法对NiTi形状记忆合金循环变形过程中体现出的率相关超弹性和形状记忆效应劣化现象进行合理的描述.
为了描述NiTi形状记忆合金的率相关循环变形特性, Morin 等(2011) 通过在Z-M本构模型 (Zaki & Moumni 2007 )中引入考虑热--力耦合超弹性退化效应的演化方程, 将Z-M模型拓展到了非等温情形, 拓展后的本构模型能很好地对超弹性NiTi形状记忆合金的相变棘轮行为及其率相关特性进行理论描述.然而, 该模型将残余应变的累积演变假定成指数函数形式, 因而无法描述Kan等(2016)在超弹性NiTi形状记忆合金率相关循环变形实验中观察到的新现象, 即残余应变对加载率的依赖性. 为此, Yu 等(2014a)将超弹性NiTi形状记忆合金率相关的超弹性劣化效应归结为相变--位错交互作用和热--力耦合效应, 建立了基于物理机制的宏观唯象本构模型, 合理预测了该合金在不同加载速率下的超弹性劣化行为和温度场演化特性.下面对该模型的主要部分进行简要介绍.
Yu 等 (2014a) 在小变形框架下, 将材料点总的应变张量\(\pmb \varepsilon\)分解为四个部分, 即弹性应变张量\(\pmb \varepsilon ^{\rm e}\)、热膨胀应变张量\(\pmb \varepsilon ^{\rm T}\)、相变应变张量\(\pmb\varepsilon ^{\rm tr}\)和相变诱发塑性应变张量\(\pmb \varepsilon^{\rm p}\), 即\[\pmb \varepsilon = \pmb \varepsilon ^{\rm e} +\pmb \varepsilon ^{\rm T} + \pmb \varepsilon ^{\rm tr} + \pmb\varepsilon ^{\rm p}\ \ (1)\]热膨胀应变和温度的关系为\[\pmb \varepsilon ^{\rm T} = \pmb \alpha(T - T_{\rm r} )\ \ (2)\]其中, \(\pmb \alpha\), \(T\), \(T_{\rm r}\)分别是二阶热膨胀张量、当前温度和参考温度.
根据Lagoudas (2008) 的工作, 相变应变率张量\(\dot{\pmb\varepsilon}^{\rm tr}\)与马氏体体积分数率\(\dot {\xi}\)的关系可取为\[\dot {\pmb\varepsilon}^{\rm tr} = g^{\rm tr}\pmb N _{\rm tr} \dot {\xi } , \qquad \pmb N _{\rm tr} = \left\{{\begin{array}{ll} \sqrt {\dfrac{3}{2}} \dfrac{\pmb \sigma ^{\rm dev} + \pmb B }{\left\| {\pmb \sigma ^{\rm dev} + \pmb B } \right\|},& \dot {\xi } > 0 \\ \dfrac{\pmb \varepsilon _{\rm recent}^{\rm tr} }{g^{\rm tr}\xi _{\rm recent} },& \dot {\xi } < 0 \\ \end{array}} \right.\ \ (3)\]其中, \(\pmb N _{\rm tr} \)是马氏体相变的方向张量, \(g ^{\rm tr}\)是马氏体完全相变产生的相变应变大小, \(\pmb \sigma ^{\rm dev}\)是偏应力张量. \(\pmb B \)是相变内应力, 用来刻画位错造成的局部内应力对马氏体相变形核的帮助作用, 即描述马氏体相变应力随着循环过程而逐渐降低的现象. \(\xi _{\rm recent} \)和\(\pmb \varepsilon _{\rm recent}^{\rm tr}\)分别是逆向变开始点的马氏体体积分数和相变应变张量.
考虑位错对马氏体相变的正向和逆向钉扎, 即针对宏观实验观测到的最大相变应变逐渐减小和残余马氏体累积的现象, 将马氏体体积分数的取值范围定为\[\xi < 1 - \xi _{\rm d} , \qquad \xi > \xi _{\rm r}\ \ (4)\]其中, \(\xi _{\rm d}\)是由于正向钉扎效应导致的未完全转换成马氏体的残余奥氏体体积分数, \(\xi _{\rm r}\)是由于逆向钉扎效应导致的未完全转换成奥氏体的残余马氏体体积分数.需要指出的是\(\xi _{\rm d} \)和\(\xi _{\rm r} \)并不是常数, 而是随着循环变形的进行而演化.
采用黏性形式的马氏体体积分数演化方程\[\left\{\!\! \begin{array}{ll} \dot {\xi } = \left( {\dfrac{\pi _{\rm tr} }{Y}} \right)^{m_{\rm tr} },& \pi_{\rm tr} > 0 \\ \dot {\xi } = - \left( {\dfrac{ - \pi _{\rm tr} }{Y}} \right)^{m_{\rm tr} },& \pi _{\rm tr} < 0\\ \dot {\xi } = 0,& \mbox{其他条件} \\ \end{array} \right.\ \ (5)\]其中, \(m_{\rm tr} \)是材料参数, 用来控制黏性大小. 当\(m_{\rm tr} \to \infty \)时, 黏性效应消失, 即退化为无黏性情形. \(\pi _{\rm tr}\)为热力学相变驱动力, \(Y\)是一个控制应力--应变曲线相变滞回环宽度的变量.
与相变应变张量类似, 塑性应变率张量\(\dot {\pmb\varepsilon}^{\rm p}\)可以写成如下形式\[\dot {\pmb\varepsilon}^{\rm p} = \pmb N _{\rm p} \dot{\gamma },\qquad \pmb N _{\rm p} = \sqrt {\dfrac{3}{2}}\dfrac{\pmb \sigma ^{\rm dev}}{\left\| {\pmb \sigma ^{\rm dev}}\right\|}\ \ (6)\]其中, \(\dot {\gamma }\)是非负的塑性滑移量\((\dot {\gamma } \geq 0)\), \(\pmb N _{\rm p} \)是塑性应变率的方向.
相变过程中奥氏体--马氏体界面处的高局部应力会诱发奥氏体内位错滑移的启动, 这和普通金属材料中位错滑移完全由外加应力诱发有所不同. 为此, Yu等(2014a) 提出了如下描述相变诱发塑性的演化方程\[\left\{\!\! \begin{array}{ll} \dot {\gamma } = (1 - \xi )\gamma _0 \left( \dfrac{\pmb \sigma :\pmb N _{\rm p} }{\mu } \right)^2 \exp \left( \dfrac{ - \Delta G_{\rm slip} }{k_{\rm b} T}\left( 1 - \left( \dfrac{\pi _{\rm p}}{\tau _0 } \right)^{p} \right)^q \right)\left| \dot {\xi }\right|, &\qquad \pi _{\rm p} > 0\\ \dot {\gamma } = 0, &\qquad \pi _{\rm p} \leq 0 \end{array}\right. \ \ (7)\]其中, \(\gamma _0 \)是参考滑移率; \(p\)和\(q\)是两个材料参数, 需要满足如下限制条件\(0 < p \leq 1\)和\(1 < q \leq 2\); \(\mu\)是剪切模量; \(\Delta G_{\rm slip} \)为无应力条件下的位错激活能, \(k_{\rm b} \)是玻尔兹曼常数; \(\tau _0 \)是在\(T=0\) K时的晶格阻力.
位错密度的演变为 (Mecking & Kocks 1981 )\[\dot {\rho } = \left( {k_1 \sqrt \rho - k_2 \rho } \right)\dot{\gamma }\ \ (8)\]其中, \(k_1 \)和\(k_2 \)是两个材料参数.
在循环变形过程中, 位错滑移的各向同性抗力\(\tau _{\rm c}\)随着位错密度的增大而增大, 根据Franciosi (1985) 可以写成\[\tau _{\rm c} = \dfrac{1}{2}\mu b\sqrt \rho \ \ (9)\]其中, \(b\)是材料的Burgers矢量大小.
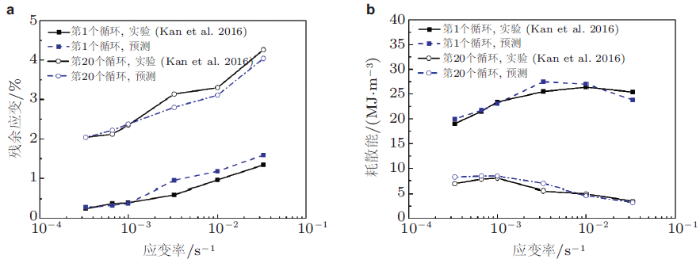
进一步在马氏体体积分数、内应力和各向同性变形抗力中引入与位错密度相关的演变方程, 即可考虑相变--位错的交互作用. 在引入应力平衡方程和变形几何方程后, 结合本构方程和热动平衡方程, 采用有限差分法求解描述NiTi形状记忆合金率相关循环变形特性的封闭方程组即可得到应力、应变和温度随循环次数的演化规律.图26 给出了超弹性NiTi形状记忆合金在应变率为 3.3 \(\times\) 10\(^{ - 3}\) s\(^{-1}\)时热--力耦合循环变形特性的模拟结果.需要指出的是, 模拟过程中试样的整体应力、应变和温度都是通过对有限差分节点上相应物理量的代数平均得到.从图26 可以看出, 模拟结果和实验结果吻合得很好, 所提出的模型能够定量地描述超弹性劣化特性和循环变形过程中试样整体温度的振荡以及相应的演化特征.另外, 图27 给出了第1周和第20周中残余应变、耗散能和应变率之间关系曲线的模拟结果.可以看出, 所提出的热--力耦合本构模型能够合理地描述和预测NiTi形状记忆合金的率相关循环变形特性.
图26 应变率为3.3 \(\times \) 10\(^{ -3}\) s\(^{-1}\)时的实验和模拟的结果 (Yu et al. 2014a ). (a)第1周和第5周的应力--应变曲线, (b) 第10周和第50周的应力--应变曲线, (c) 残余应变随循环次数演变曲线, (d)平均温度随循环次数演变曲线
图27 实验和模拟的超弹性退化 (Yu et al. 2014a ). (a)第1周和第20周的残余应变随应变率变化曲线, (b)第1周和第20周的耗散能随应变率变化曲线
为了描述NiTi形状记忆合金在热--力耦合循环变形过程中体现出的形状记忆效应劣化现象, Auricchio 等(2008) , Zaki 和 Moumni (2007) 和Hartl等(2010) 通过引入必要的非弹性变形机制, 建立了相应的本构模型; 但是, 这些本构模型没有很好地考虑在热--力耦合循环载荷作用下冷却阶段发生的附加非弹性变形, 也不能对形状记忆效应退化现象的加载水平依赖性进行合理的描述. 最近, Yu 等 (2016) 在Popov 和 Lagoudas (2007) 提出的本构模型基础上, 针对NiTi形状记忆合金循环加载条件下出现的形状记忆效应退化现象, 发展了一个宏观多机制本构模型. 该模型根据实验观测结果, 考虑了NiTi形状记忆合金热--力循环过程中的四种变形机制, 即马氏体相变、相变诱发塑性、马氏体重取向和重取向诱发塑性, 并且重点突出了马氏体相变和重取向与位错的交互作用.根据宏观实验结果, Yu 等 (2016) 认为: 随循环次数的增大, 相变和重定向模量增大, 马氏体相变开始温度升高, 重定向开始应力下降; 某些区域位错诱发的局部应力的投影为正, 该内应力将促进马氏体相变和重定向, 其结果是循环过程中马氏体相变开始温度升高; 同时, 位错诱发的应力梯度会阻碍孪晶和解孪相的形核, 导致相变和重定向模量增大. 下面对Yu 等(2016) 发展的本构模型进行简要介绍.
为了考虑NiTi形状记忆合金的形状记忆效应, Popov 和 Lagoudas(2007) 将形状记忆过程的微结构状态分为三相, 即奥氏体、孪晶马氏体和解孪马氏体, 相应的体积分数记作: \(\xi _{\rm A} \), \(\xi _{\rm M}^{\rm t} \)和 \(\xi _{\rm M}^{\rm d} \).为了描述每两相之间的转变, 引入内变量\(\lambda _1 \), \(\lambda _2\)和\(\lambda _3\) \[\left\{{\begin{array}{l} \lambda _1 :\xi _{\rm A} \leftrightarrow \xi _{\rm M}^{\rm t} \\ \lambda _2 :\xi _{\rm A} \leftrightarrow \xi _{\rm M}^{\rm d} \\ \lambda _3 :\xi _{\rm M}^{\rm t} \to \xi _{\rm M}^{\rm d} ,\qquad \dot {\lambda }_3 \geq 0 \\ \end{array}} \right.\ \ (10)\]这里\(\lambda _1 \), \(\lambda _2 \)和\(\lambda _3\)分别代表奥氏体--孪晶马氏体、奥氏体--解孪马氏体、孪晶马氏体--解孪马氏体的相变程度, 它们与三相体积分数相关\[\xi _{\rm A} = \xi _{\rm A}^0 - \lambda _1 - \lambda _2 \ \ (11)\]\[\xi _{\rm M}^{\rm t} = \xi _{\rm M}^{{\rm t}0} + \lambda _1 - \lambda _3 \ \ (12)\]\[\xi _{\rm M}^{\rm d} = \xi _{\rm M}^{{\rm d}0} + \lambda _2 + \lambda _3 \ \ (13)\]这里\(\xi _{\rm A}^0 \), \(\xi _{\rm M}^{{\rm t}0} \) 和\(\xi _{\rm M}^{{\rm d}0} \)是\(\xi _{\rm A} \), \(\xi _{\rm M}^{\rm t} \)和 \(\xi_{\rm M}^{\rm d} \)的初始值.
在此基础上, Yu 等 (2016) 首先基于小变形假设, 将总应变张量\(\pmb\varepsilon \)分解为五部分, 即弹性应变 \(\pmb \varepsilon ^{\rm e}\), 相变应变\(\pmb \varepsilon ^{\rm tr}\), 重定向应变\(\pmb \varepsilon^{\rm reo}\), 相变诱发塑性应变 \(\pmb \varepsilon ^{\rm tp}\)和重定向诱发塑性应变\(\pmb \varepsilon ^{\rm rp}\)\[\pmb \varepsilon = \pmb \varepsilon ^{\rm e} + \pmb \varepsilon^{\rm tr} + \pmb \varepsilon ^{\rm reo} + \pmb \varepsilon ^{\rm tp} + \pmb \varepsilon ^{\rm rp}\ \ (14)\]相变应变率张量可表示为\[\dot {\pmb\varepsilon}^{\rm tr} = g\pmb N _{\rm tr} \dot{\lambda }_2 \ \ (15)\]\[\pmb N _{\rm tr} = \left\{ {\begin{array}{ll} \sqrt {\dfrac{3}{2}} \dfrac{\pmb \sigma _{\rm dev} + \pmb B _{\rm tr}}{\left\| {\pmb \sigma _{\rm dev} + \pmb B _{\rm tr} }\right\|},&\qquad \dot {\lambda }_2 > 0 \\ \sqrt {\dfrac{3}{2}} \dfrac{\pmb \varepsilon ^{\rm tr} + \pmb \varepsilon ^{\rm reo}} {\left\| {\pmb \varepsilon ^{\rm tr} + \pmb \varepsilon ^{\rm reo}} \right\|},&\qquad\dot {\lambda }_2 < 0 \\ \end{array}} \right.\ \ (16)\]其中, \(g\)为向前相变全部完成时相变应变值, \(\pmb N _{\rm tr} \)为马氏体相变方向张量, \(\pmb \sigma _{\rm dev} \)为应力张量\(\pmb\sigma \)的偏量. 为了描述马氏体相变开始温度随循环次数增大而升高, 引入一个内应力张量\(\pmb B _{\rm tr} \), 其为相变应变率张量的共轭变量.
重定向应变率张量可表示为\[\dot {\pmb\varepsilon}^{\rm reo} = g\pmb N _{\rm reo} \dot {\lambda }_3\ \ (17)\] \[\pmb N _{\rm reo} = \sqrt {\dfrac{3}{2}} \dfrac{\pmb \sigma _{\rm dev} +\pmb B _{\rm reo} }{\left\| {\pmb \sigma _{\rm dev} + \pmb B _{\rm reo} } \right\|}\ \ (18)\]其中, \(\pmb N _{\rm reo} \)为马氏体重定向的方向张量.为描述马氏体相变开始应力随循环次数的下降过程, 也引入一个内应力张量\(\pmb B _{\rm reo} \), 其为重定向应变率张量\(\dot {\pmb\varepsilon} ^{\rm reo}\)的共轭变量.
相变诱发塑性应变率\(\dot {\pmb\varepsilon}^{\rm tp}\)和重定向诱发塑性应变率\(\dot {\pmb\varepsilon}^{\rm rp}\)张量表示如下\[\dot {\pmb\varepsilon}^{\rm tp} = \pmb N _{\rm tr} \dot {\gamma}_{\rm tp}\ \ (19)\]\[\dot {\pmb\varepsilon}^{\rm rp} = \pmb N _{\rm reo} \dot {\gamma }_{\rm rp}\ \ (20)\]其中, \(\dot {\gamma }_{\rm tp} \)和 \(\dot {\gamma }_{\rm rp}\)分别是相变诱发塑性和重定向诱发塑性的滑移率, 假定其方向分别与相变方向和重定向方向相同.
考虑马氏体相变对位错滑移的影响, 相变诱发塑性演变方程如下\[\n \left\{\!\! \begin{array}{ll} \dot {\gamma }_{\rm tp} = \xi _{\rm A} \gamma _0 \left( {\dfrac{\pmb \sigma :\pmb N _{\rm tr} }{\mu }} \right)^2 \exp \left\{ {\dfrac{ - \Delta G_{\rm slip} }{k_{\rm b} T}\left[ {1 - \left( {\dfrac{\pi _{\rm tp} }{\tau _0 }} \right)^{p}} \right]^q} \right\}\left( {\left|{\dot {\lambda }_1 } \right| + \left| {\dot {\lambda }_2 }\right|} \right),& \pi _{\rm tp} > 0 \\ \dot {\gamma }_{\rm tp} = 0,& \pi _{\rm tp} \leq 0 \\ \end{array} \right.\ \ (21)\]其中, \(\left| {\dot {\lambda }_1 } \right| + \left| {\dot {\lambda}_2 } \right|\)反映马氏体相变诱发的塑性变形, 当\(\left| {\dot{\lambda }_1 } \right| + \left| {\dot {\lambda }_2 } \right|=0\)时, 塑性变形不能发生; \(\xi _{\rm A} \)反映与相变诱发塑性相关的位错滑移, 且仅发生在奥氏体相中; \(\pi _{\rm tp}\)为相变诱发塑性的热力学驱动力.
相似地, 重定向诱发塑性的演变方程可写为\[\n \left\{\!\! \begin{array}{ll} \dot {\gamma }_{\rm rp} = \left( {1 - \xi _{\rm A} } \right)\gamma _0 \left({\dfrac{\pmb \sigma :\pmb N _{\rm reo} }{\mu }} \right)^2\exp\left\{ {\dfrac{ - \Delta G_{\rm slip} }{k_{\rm b} T}\left[ {1 -\left( {\dfrac{\pi _{\rm rp} }{\tau _0 }} \right)^{p}} \right]^q}\right\}\left| {\dot {\lambda }_3 } \right|,& \pi _{\rm rp} >0\\ \dot {\gamma }_{\rm rp} = 0,& \pi _{\rm rp} \leq 0 \\ \end{array} \right.\ \ (22)\]其中, \(\left| {\dot {\lambda }_3 }\right|\)反映马氏体重定向诱发的塑性应变, 当\(\left| {\dot {\lambda}_3 } \right|\)=0时, 塑性变形不能发生; \(\left( {1 - \xi _{\rm A} }\right)\)反映与重定向诱发相关的位错滑移, 且仅能发生在马氏体相中; \(\pi _{\rm rp} \)为重定向诱发塑性的热力学驱动力.
图28 给出了峰值应力为500 MPa、不同循环次数下的NiTi形状记忆合金形状记忆效应退化的实验和模拟结果, 而图29 给出了实验和模拟得到的残余应变、塑性应变和峰值应变随循环次数的演变曲线.对比图28 和图29 中的实验和模拟结果可知, Yu 等(2016) 发展的模型能够合理地预测NiTi形状记忆合金热--力循环变形过程中不同次数下的应力--应变--温度曲线以及残余应变、塑性应变和峰值应变的演变曲线, 能够对在热--力耦合循环变形过程中体现出的形状记忆效应退化现象进行合理的描述.
图28 峰值应力为500 MPa时形状记忆退化效应的实验和模拟结果(Yu et al. 2016 ). (a) 第1周和第10周应力--应变曲线, (b) 第1周和第10周温度--应变曲线
图29 形状记忆循环过程中残余应变、塑性应变和峰值应变的实验和模拟结果(Yu et al. 2016 ). (a) 残余应变, (b) 塑性应变, (c) 峰值应变
2.2 高温NiTiX形状记忆合金的循环变形行为
尽管近等原子比NiTi形状记忆合金已经得到了广泛应用, 但是其使用温度较低, 不能超过373 K. 然而, 在一些工程领域会面临373 K以上的高温环境, 因此, 为了满足高温智能材料的需要, 在NiTi形状记忆合金的基础上通过引入第三种元素, 开发了三元的NiTiX高温形状记忆合金. 三元NiTiX合金中的X可以分别是Pd, Pt, Hf和Zr, 其使用温度可以提高至523 \(\sim \) 773 K, 其中NiTi(Pd, Pt)合金是用第三相置换NiTi合金中的Ni原子, 而NiTi (Zr, Hf)合金则用第三相置换Ti原子. 对于高温形状记忆合金, Ma等(2010) 对工程中使用的高温形状记忆合金按相变温度范围分为三类, 即373 \(\sim \) 673 K为第一类, 673 \(\sim \) 973 K为第二类, 973 K以上为第三类; 同时对不同类别的高温形状记忆合金的一些基本变形行为特征的研究现状进行了综述, 对2010年以前取得的相关研究成果进行了很好的总结. 因此, 本小节将主要对近年来三元NiTiX高温形状记忆合金(即第一类高温形状记忆合金)的循环变形行为研究现状和研究成果进行评述, 其他合金体系和类别的高温形状记忆合金的研究进展参见Ma 等(2010) 的综述论文以及近年来发表的相关文献.
2.2.1 实验研究
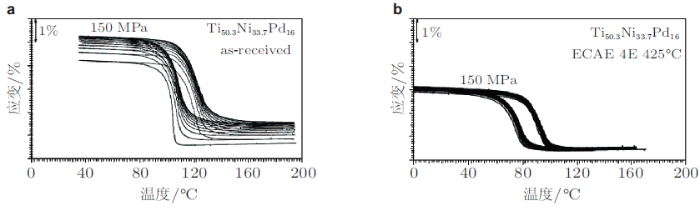
与二元NiTi形状记忆合金相比, 高温形状记忆合金的循环变形实验研究相对较少, 并且大部分集中在温度循环加载方式, 即讨论其形状记忆效应在恒定应力和温度循环加载过程中的演化规律.已有的实验表明, 高温形状记忆合金的温度循环变形特性与原子组分、加工方式和外加应力等密切相关.例如, Bigelow等(2007) 首先对Ni\(_{19.4}\)Ti\(_{50.6}\)Pd\(_{30}\)合金在外加恒定应力为200 MPa的情况下进行温度循环实验, 发现温度循环30周后材料达到稳定的温度--变形响应状态, 并且相变温度上升了16\(^{\circ}\)C; 但是, 他们的结果还显示该合金在无外加应力的温度循环情况下, 相变温度会降低5 \(\sim \) 10\(^{\circ}\)C. 后来, Bigelow等(2010) 通过对不同合金含量的NiTiPd高温形状记忆合金在外加恒定应力下的温度循环加载实验研究, 揭示了该合金的温度循环稳定性随Pd元素含量的增加逐渐下降, 并且不可恢复应变也随之增大的变化规律. Kockar 等(2006, 2010)通过对不同加工状态下的Ni\(_{33.7}\)Ti\(_{50.3}\)Pd\(_{16}\)高温形状记忆合金的热--力耦合循环变形实验, 揭示了温度循环中在外加应力方向上的塑性变形累积现象, 如图30 所示. 由图30 可见, 经过等通道转角挤压的高温形状记忆合金在循环过程中的塑性应变明显减小, 相变应变远大于未经加工的初始材料; 同时, 将转角挤压的Ni\(_{33.7}\)Ti\(_{50.3}\)Pd\(_{16}\)高温形状记忆合金材料继续在425\(^{\circ}\)C退火15min, 可以得到更加稳定的温度循环响应结果, 循环10周后的累积塑性应变在外加拉伸应力为100 MPa时仅有0.05%, 并且在200 MPa时也不超过0.2%. 另外, Saghaian等(2016) 对富Ni的NiTiHf高温形状记忆合金的温度循环变形实验研究表明, 温度循环时的外加应力越大, 相变温度越高, 热滞回环越大, 不可恢复应变也随之增大.
图30 供货态与挤压态NiTiPd高温形状记忆合金的循环温度--应变响应 (Kockar et al.2010 ). (a) 供货态, (b) 挤压态
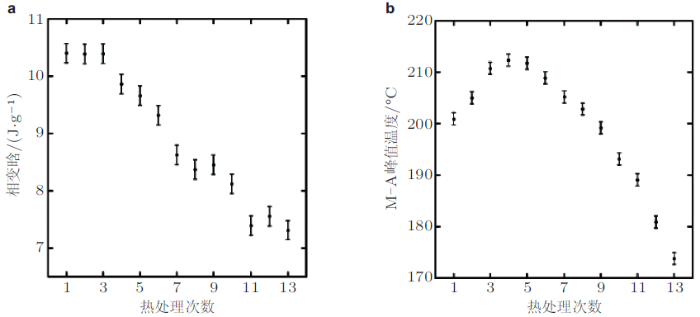
已有的研究还表明, 在高温热处理条件下, 材料内部的微观结构(如沉淀相等)会极大程度地影响其温度循环变形特性(如初始相变温度等), 而上述微观结构的粒子尺寸与含量还会在温度循环过程中逐渐演化, 进一步影响材料的循环变形行为. McCluskey等(2011) 对于NiTiZr薄片材料进行了加热至900\(^{\circ}\)C后退火的高温循环实验, 发现马氏体向奥氏体转化的相变焓在循环初期(3次数内)保持稳定, 而后线性下降. 与此同时, 相变峰值温度也在达到最高值后随循环圈数增大呈抛物线型降低, 见图31 . McCluskey等(2011) 认为产生上述现象的原因为沉淀相造成材料中的应力松弛, 降低了整体的应变能, 在循环初期使马氏体向奥氏体转化的相变温度升高; 而在高温循环的过程中, 由于沉淀相的含量逐渐增大, 改变了基体的组分, 导致相变温度和相变焓均迅速降低. 同时, McCluskey等(2011) 还对经历了3次及13次高温循环加载的NiTiZr薄片分别进行了100次的低温(50 \(\sim\) 250\(^{\circ}\)C)循环实验研究, 结果表明: 经过13次高温循环的材料在循环初期相变温度迅速降低, 但在随后的循环过程中, 其平均下降速率与经历了3次高温循环的情况并无较大差别; 在Zr原子含量增大的情况下, 相变温度也随之升高, 同时温度循环的稳定性也较高; 而对于经过13次高温循环的材料, 其不同Zr原子含量材料的低温循环初始/结束温度较经历了3次高温循环的情况更加接近, 见图32 .
图31 Ni\(_{44.7}\)Ti\(_{35.7}\)Zr\(_{19.6}\)高温形状记忆合金经历高温循环后的物理量变化(McCluskey et al. 2011 ). (a) 相变焓, (b) 相变温度
图32 Ni\(_{44.7}\)Ti\(_{35.7}\)Zr\(_{19.6}\)高温形状记忆合金在低温循环时的相变温度变化(McCluskey et al. 2011 ). (a) 3次高温循环后, (b) 13次高温循环后
同样, 对于高温形状记忆合金的超弹性循环变形实验研究目前进行得也不充分, 实验研究多集中在不同温度下的多级循环加载情形, 并且循环次数较小(通常小于10周). Tian 和 Wu(2002)研究了当环境温度刚刚达到奥氏体相变结束温度和在该温度之上20及70\(^{\circ}\)C的情况下NiTiPd高温形状记忆合金可恢复应变的变化情况, 并且对不同加载条件下应力--应变滞回环的宽度进行了比较, 结果表明: 与二元NiTi形状记忆合金的情况类似, 环境温度越高, 加载应力越大, 循环累积的塑性应变则越大. Wu 和Tian(2003)对NiTiPd合金进行了不同温度及应力下的多级循环加载实验研究, 发现施加应力越高, 达到循环稳定所需的循环次数则越小; 并且认为对于B19马氏体变体的NiTiPd合金, 织构是影响其超弹性的重要因素. Karaca等(2013)则研究了具有不同时效时间的挤压态NiTiHf合金在不同温度多级循环加载条件下的超弹性性能变化, 结果如图33 所示. 实验表明: 经过3 h \(\times\) 550\(^{\circ}\)C时效处理的NiTiHf合金在高温下具有非常好的超弹性行为, 在220\(^{\circ}\)C及240\(^{\circ}\)C的环境温度下, 完全恢复的压缩应变可以达到4%; 然而, 当时效温度提高至650\(^{\circ}\)C时, 超弹性行为则发生了明显劣化, 可恢复变形量明显下降.这是由于过时效引起沉淀相的粗化所导致的(Sasaki et al. 2013 ).事实上, 沉淀相的尺寸及含量会极大影响高温形状记忆合金的超弹性和形状记忆特性.例如, Kockar 等(2010)对于NiTiHf合金得研究表明: 在Ni原子质量分数为50.3% \(\sim\) 52.0%的范围内时, 随着Ni原子含量的增加, 沉淀相的尺寸(大于100 nm)及体积分数均增大, 材料的可恢复应变逐渐降低; 然而, 当Ni原子质量分数较低时, 沉淀尺寸较小(5 \(\sim \) 15 nm), 沉淀相易于被马氏体变体所吸收而不影响马氏体相变的过程, 可以获得较高的可恢复应变值.
图33 NiTiHf高温形状记忆合金在不同温度下的压缩方向超弹性实验结果 (Karaca et al.2013). (a) 挤压态, (b) 550\(^{\circ}\)C \(\times \) 3 h, (c)650\(^{\circ}\)C \(\times\) 3 h
2.2.2 微观实验研究
尽管对NiTiX高温形状记忆合金的微观结构特征已有较多的微观实验观察, 但绝大多数集中在材料改性的范畴, 对热--力耦合循环加载下该类合金的微观结构观察少有报道, 需在今后进一步开展系统的研究. 例如, Karaca等(2013) 对不同温度下的挤压态NiTiHf高温形状记忆合金的沉淀相进行了观察, 证明了550\(^{\circ}\)C \(\times \) 3 h后, 材料中即有纳米级沉淀出现, 并且时效温度提高到650\(^{\circ}\)C后, 相同时效时间下的沉淀尺寸增大; Satamarta等(2013) 对NiTiHf及NiTiZr材料的微观实验观察中证明炉内冷却的方法可以比高温时效更易使材料内部产生更大的沉淀粒子; Yang 等(2013) 在实验观察的基础上进一步提出, 对于NiTiHf高温形状记忆合金, 这些沉淀粒子并非普通的Ni\(_{4}\) (Ti, Hf)\(_{3}\)相, 而是一种具有不同原子结构的新相, 即H相.
Kockar 等(2006 , 2010 )对供货态和挤压态NiTiPd和NiTiHf高温形状记忆合金的马氏体形貌分别进行了对比, 发现经过等通道转角挤压的高温形状记忆合金中马氏体尺寸比供货态有大幅度的减小, 进而材料的力学性能则有大幅度的提高. Meng 等(2002) 对NiTiHf高温形状记忆合金在单次加载下的应力诱发马氏体形貌进行了观察, 发现: 在548 K下施加8%的应变时, 形成的马氏体具有方向性, 且边界较为清晰; 而应变增大到16%的时候, 马氏体的边界则变得模糊不清; 同时, 当实验温度升高到573 K时, 施加8%的应变即出现马氏体边界不清的情况, 与较低温度时的剧烈变形情况相似, 见图34 .
图34 NiTiHf高温形状记忆合金在不同应变及温度下的应力诱发马氏体形貌 (Meng et al.2002 ). (a) 8%, 548 K; (b) 16%, 548 K; (c) 8%, 573 K; (d) 16%, 573 K
Kumar & Lagoudas(2010) 利用TEM对蠕变以及温度循环后的NiTiPd高温形状记忆合金的马氏体形貌分别进行了观察, 实验表明: 供货态材料中的马氏体以\{1 \ 1 \ 1\}取向的第一类孪晶构成, 见图35 (a); 而蠕变加载下的马氏体则主要由\{0 \ 1 \ 1\}取向的复合孪晶和\{1 \ 1 \ 1\}取向的第一类孪晶同时组成, 并且复合孪晶在材料的微结构中占主导地位(图35 (b)), 这些复合孪晶常出现在材料中的沉淀及缺陷周围; 同时, 蠕变加载中的位错攀移会导致位错在材料中出现随机分布的形式, 在取向不占优的滑移平面, 这些位错也会引起应力集中, 导致材料中复合孪晶的形成; 在温度循环中形成的马氏体尺寸比蠕变情况下更大, 且边界更为清晰, 其中\{1 \ 1 \ 1\}取向的孪晶在温度循环加载时占主导地位; 将试样加热到更高的温度, 材料中的马氏体恢复为奥氏体的比率也会相应增大, 见图36 .
图35 NiTiPd高温形状记忆合金蠕变加载前后的马氏体形貌对比(Kumar & Lagoudas 2010 ). (a) 供货态材料, 由\{1 \ 1 \ 1\}第一类孪晶组成; (b) 200 MPa蠕变加载后, 其中区域1为\{0 \ 1 \ 1\}复合孪晶, 区域2为\{1 \ 1 \ 1\}第一类孪晶
图36 经过温度循环后的NiTiPd高温形状记忆合金加热至不同温度后的马氏体形貌对比(Kumar & Lagoudas 2010 ). (a) 加热至523\({^\circ}\)C, 其中区域3, 4, 5为残余马氏体, 区域6, 7恢复为奥氏体; (b)加热至640\({^\circ}\)C, 其中区域8为残余马氏体, 区域9恢复为奥氏体
2.2.3 本构理论
目前, 专门针对NiTiX高温形状记忆合金热--力耦合变形行为的本构模型研究较少, 已有研究均是在二元NiTi形状记忆合金对应的本构模型基础上进行拓展, 并且均为宏观唯象的本构模型, 主要针对高温形状记忆合金在恒定应力作用下温度循环加载过程中的热--力耦合变形行为进行本构描述.对于三元NiTiX高温形状记忆合金的超弹性行为, 因其与二元NiTi形状记忆合金的区别主要体现在相变温度上, 也就是说其使用的环境温度与二元NiTi形状记忆合金不同, 其应力诱发的相变机制以及由此而产生的超弹性变形行为与二元NiTi形状记忆合金基本相同, 因此, 可以采用已有的、能够合理描述NiTi形状记忆合金超弹性行为的本构模型直接描述NiTiX高温形状记忆合金的超弹性行为及其在循环变形过程中的劣化现象和对环境温度的依赖性(如图33 (b)所示).针对NiTiX高温形状记忆合金在恒定应力作用下的温度循环加载过程中的热--力耦合变形行为, Lagoudas 等(2009a) 及其合作者(Hartl et al. 2010, Chemisky et al. 2014 )在其本构模型构建方面开展了一系列较为重要的探索性工作.Lagoudas 等(2009a)首先根据对高温形状记忆合金的蠕变现象(位错攀移)的观察, 通过将总应变分为弹性应变\(\varepsilon ^{\rm e}\)、热应变\(\varepsilon ^{\rm T}\)、相变应变\(\varepsilon ^{\rm t}\)、相变诱发塑性应变\(\varepsilon ^{\rm tp}\)和黏塑性(蠕变)应变\(\varepsilon ^{\rm vp}\)五个部分, 进而将蠕变机制引入NiTiX高温形状记忆合金的宏观唯象本构模型中, 提出了适用于NiTiX高温形状记忆合金热--力耦合变形行为的一维本构模型, 模型中假设相变与蠕变过程是独立进行的, 不考虑其交互作用; Hartl等(2010)将上述本构模型推广到了三维的情况, 并同时考虑了相变及黏塑性变形间的交互作用; 针对上述两种本构模型均不能合理描述多次循环加载下NiTiX高温形状记忆合金的热--力耦合响应的问题, Chemisky等(2014)通过合理考虑三种非弹性变形机制(即相变、相变诱发塑性及黏塑性变形)对高温形状记忆合金热--力学耦合行为的共同作用, 建立了可描述高温形状记忆合金在温度循环加载下热--力耦合循环变形行为的本构模型.该模型沿用了Lagoudas 等(2009a)的处理方式, 仍然将相变和蠕变变形看作是两个独立的过程, 并假设蠕变变形仅在奥氏体相中发生, 一旦材料发生马氏体相变, 则蠕变机制停止, 直到材料逆相变全部恢复为奥氏体后蠕变才继续进行.另外, 该模型同时考虑了残余马氏体在循环变形中的作用, 较为合理地反映了高温形状记忆合金的残余应变随温度循环的演化情况.下面对该模型(Chemisky et al. 2014 )进行简要的介绍.
首先, 将总应变看成是五部分之和, 即\[\pmb\varepsilon=\pmb\varepsilon ^{\rm e} + \pmb\varepsilon ^{\rm T} +\pmb \varepsilon ^{\rm t} +\pmb \varepsilon ^{\rm tp} +\pmb\varepsilon ^{\rm vp} \ \ (23)\] 其中, \(\pmb \varepsilon^{\rm e}\)为弹性应变, \(\pmb \varepsilon ^{\rm T}\)为热膨胀应变, \(\pmb \varepsilon ^{ \rm t }\)为相变应变, \(\pmb \varepsilon ^{ \rm tp} \)为相变诱发塑性应变, \(\pmb \varepsilon ^{\rm vp}\)为表示蠕变引发的黏塑性应变.令相变应变、相变诱发塑性应变和黏塑性应变的演化方程分别如下\[ \dot{\pmb \varepsilon}^{\rm t}=\pmb\varLambda^{\rm t}\dot{\xi},\qquad \dot{\pmb \varepsilon}^{\rm tp}=\pmb\varLambda^{\rm tp}\dot{\xi},\qquad \dot{\pmb\varepsilon}^{\rm vp}=\pmb\varLambda^{\rm vp}\dot{p} \ \ (24)\]其中 \(\pmb\varLambda^{\rm t}\)、 \(\pmb\varLambda^{\rm tp}\)、\(\pmb\varLambda^{\rm vp}\)分别为相变、相变诱发塑性和黏塑性方向张量.
(1)相变变形
将 \(\pmb\varLambda^{\rm t}\)分为正相变 \(\pmb\varLambda^{\rm t}_{\rm fwd}\)和逆相变\(\pmb\varLambda^{\rm t}_{\rm rev}\)两部分, 其定义沿用Lagoudas 等(2009a) 中的形式, 记为\[\pmb\varLambda^{\rm t}_{\rm fwd}=\dfrac{3}{2}H^{\rm cur}\dfrac{\pmb\sigma'}{\bar{\sigma}},\qquad \dot{\xi}>0 \ \ {\rm (25a)}\]
\[\pmb\varLambda^{\rm t}_{\rm rev}=\dfrac{\pmb\varepsilon^{t-r}}{\xi^{r}},\qquad \dot{\xi}<0 \ \ {\rm (25b)}\]其中, \(\pmb\sigma'\)为偏应力张量, \(\bar{\sigma}\)为von-Mises等效应力, \(H^{\rm cur}\)为最大相变应变, \(\pmb\varepsilon^{t-r}\)为逆相变开始时的相变应变张量, \(\xi^{\rm r}\)为逆相变时的马氏体体积分数. 对于正相变过程, 相变面\(\varPhi_{\rm fwd}^{\rm t}\)定义为\[ \varPhi_{\rm fwd}^{\rm t}=\pi_{\rm fwd}^{\rm t}-Y_{\rm fwd}^{\rm t}\ \ (26)\] 其中, \(\pi_{\rm fwd}^{\rm t}\)为正相变时的热力学驱动力, \(Y_{\rm fwd}^{\rm t}\)为临界能.\(Y_{\rm fwd}^{\rm t}\)可以写为(Hartl et al. 2010 )\[ Y_{\rm fwd}^{\rm t}(\pmb\sigma)=Y_0^{\rm t}+D\pmb\sigma:\left(\pmb\varLambda_{\rm fwd}^{\rm t}+\pmb\varLambda_{\rm fwd}^{\rm tp}\right) \ \ (27)\] 其中, \(D\)为描述热力学驱动力对应力依赖程度的参数, \(Y_0^{\rm t}\)为常数.
同样地, 逆相变方程\(\varPhi_{\rm rev}^{\rm t}\)可定义为\[\varPhi_{\rm rev}^{\rm t}=-\pi_{\rm rev}^{\rm t}-Y_{\rm rev}^{\rm t}\ \ (28)\] 逆相变的临界能可写为\[ Y_{\rm rev}^{\rm t}(\pmb\sigma)=Y_0^{\rm t}+D\pmb\sigma:\left(\pmb\varLambda_{\rm rev}^{\rm t} +\pmb\varLambda_{\rm rev}^{\rm tp}\right) \ \ (29)\]
(2)相变诱发塑性变形
相变诱发塑性变形的方向张量可假设为与马氏体体积分数有关, 则由Lagoudas 和 Entchev (2004) 中的形式, 可得\[ \dot{\pmb \varepsilon}^{\rm tp}=\pmb\varLambda^{\rm tp}\dot{\xi}\ \ (30)\]\[\pmb\varLambda^{\rm tp}_{\rm fwd}=\dfrac{3}{2}\dfrac{\pmb\sigma'}{\bar{\sigma}}w_1\left(C_0^{\rm tp}+C_1^{\rm tp}e^{-\zeta^{\rm d}/C_2^{\rm tp}}\right)\dfrac{H^{\rm cur}}{H^{\rm sat}},\qquad \dot{\xi}>0\ \ (31)\]\[ \pmb\varLambda^{\rm tp}_{\rm rev}=\dfrac{\pmb\varepsilon^{t-r}}{\bar{\varepsilon}^{t-r}}(1-w_1)\left(C_0^{\rm tp}+C_1^{\rm tp}e^{-\zeta^{\rm d}/C_2^{\rm tp}}\right)\dfrac{H^{\rm cur}}{H^{\rm sat}},\qquad \dot{\xi}<0\ \ (32)\] 其中, \(C_0^{\rm tp}\)和\(C_1^{\rm tp}\)为与应力相关的函数, \(C_2^{\rm tp}\)为常数. \(C_1^{\rm tp}\)和\(C_2^{\rm tp}\)描述了相变诱发塑性应变在第一个循环时的指数演化; 而\(C_0^{\rm tp}\)描述了相变诱发塑性应变在随后的循环过程中的线性演化.\(\zeta^{\rm d}\)为累积解孪马氏体体积分数.
(3)黏塑性变形
黏塑性应变率张量\(\dot{\pmb \varepsilon}^{\rm vp}\)和等效累积黏塑性应变率\(\dot{p}\)可写为(Lemaitre & Chaboche 1994 )\[ \dot{\pmb \varepsilon}^{\rm vp}=\pmb\varLambda^{\rm vp}\dot{p},\qquad \pmb\varLambda^{\rm vp}=\dfrac{3}{2}\dfrac{\pmb\sigma'}{\bar{\sigma}} \ \ (33)\]\[p'=\left\langle {\dfrac{\bar {\sigma } - f^{\rm vp} -Y^{\rm vp}}{K_{\rm a} }} \right\rangle ^{N_{\rm a} } \ \ (34)\]其中, \(Y^{\rm vp}=Y^{\rm vp}(T)\)为温度相关的蠕变启动临界应力, \(K_{\rm a}=K_{\rm a}(T)\)是拖应力, \(N_{\rm a}=N_{\rm a}(T)\)为应力指数, 均与温度相关, \(f^{\rm vp}=Q_1p+Q_2(1-e^{-Q_3p})\)且\(Q_{1}\), \(Q_{2}\)和\(Q_{3}\)是温度相关的材料参数.
该模型可对NiTiPb高温形状记忆合金不同恒定应力下的温度循环加载过程中的热--力耦合循环变形行为做出较为准确的理论模拟(仅限于循环开始的2 \(\sim\) 3周), 如图37 所示.
图37 NiTiPd高温形状记忆合金在不同压缩载荷下的温度循环加载时热--力耦合循环变形行为的实验和模拟结果(Chemisky et al. 2014 ). (a) 400 MPa, (b) 500 MPa
3 温度诱发形状记忆合金的热--力耦合疲劳失效行为
3.1 NiTi形状记忆合金的疲劳失效行为
随着对NiTi形状记忆合金循环变形行为研究的开展和深入, 正如Eggeler等(2004)和Mahtabi 等(2015)综述的那样, NiTi形状记忆合金的疲劳问题已经得到了较为广泛的研究. Eggeler等(2004)进一步将NiTi形状记忆合金的疲劳失效行为分为两类, 即:结构疲劳失效, 代表NiTi形状记忆合金在一定循环载荷寿命下的物理失效或断裂; 功能疲劳失效则代表因超弹性和形状记忆效应等功能的劣化而发生的功能性丧失.例如, Wagner等(2004)就将超弹性NiTi形状记忆合金在循环变形过程中产生的累积残余应变的某一个临界值作为其功能失效的一种判据; 而Predki 等(2006), Dunand-Ch\^{a}tellet 和 Moumni (2012) 以及Song等(2015)则将每次循环中的耗散能密度下降到某一个临界值作为超弹性NiTi形状记忆合金的功能失效判据.由第2部分讨论的NiTi形状记忆合金的循环变形行为可知, 在NiTi形状记忆合金的循环变形过程中, 经过一定的循环次数后均会达到一个相对稳定的循环变形状态, 累积残余应变或降低的耗散能密度都会无限接近于一个稳定值, 并且在功能失效发生时没有材料的断裂发生, 因此, NiTi形状记忆合金的功能失效行为在设定了失效判据(也就是残余应变或耗散能密度等的临界值)以后, 完全可以和前节综述的NiTi形状记忆合金的循环变形行为一起来讨论.为此, 本节将主要讨论NiTi形状记忆合金的结构疲劳失效行为, 对于其功能失效行为的研究现状可参见Eggeler 等(2004)和Mahtabi等(2015)综述论文. 针对NiTi形状记忆合金的结构疲劳失效行为, Kang 和Song(2015) 已经着重对不同试样形式下的宏观疲劳失效行为的实验研究现状进行了较为详细的评述, 讨论了NiTi形状记忆合金单轴和多轴以及热--力耦合疲劳失效行为的研究进展.为了保证本文内容的完整性, 本小节结合一些最新的研究进展, 对该合金的结构疲劳失效行为的失效机制微观观察和疲劳失效模型(特别是基于损伤的疲劳失效模型)的研究现状进行补充评述.本节未涉及到的相关研究进展可参见文献(Kang & Song 2015 ).同样, 由于Cu-基和Fe-基形状记忆合金的循环变形和疲劳失效行为与NiTi形状记忆合金的类似, 本节也就仅针对NiTi形状记忆合金的疲劳失效行为来进行评述.
3.1.1 失效机理的微观实验研究
正如Kang 和 Song (2015) 综述的那样, 通过对疲劳断口的SEM观察发现, 超弹性NiTi合金(初始相为奥氏体)的断口形貌和形状记忆NiTi合金(初始相为马氏体)基本相同, 均可见明显的疲劳条纹、二次裂纹和河流状解理图案以及一些大而浅的韧窝.在NiTi形状记忆合金疲劳断口的SEM观察结果基础上, 进一步总结得出:NiTi形状记忆合金的疲劳断裂可分为两阶段, 即疲劳裂纹萌生阶段和扩展阶段; 在疲劳断裂过程中, 同时会出现由疲劳载荷引起的稳态的裂纹长大和由大而浅的韧窝代表的塑性过载断裂.另外, 从整个疲劳失效过程中的应力--应变响应曲线可以看到, 在循环稳定后(从200周开始直至疲劳断裂发生), 滞回环形状和大小基本上不会发生可观察的变化, 疲劳断裂突然毫无宏观征兆地发生. 这说明, NiTi形状记忆合金在疲劳失效过程中的裂纹萌生和扩展机制与普通金属有明显不同.Charkaluk 等(2000 , 2002 ), Skelton 等(1991 , 1998 )以及Dunand-Chatellet 和 Moumni (2012) 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为.
最近, Song等(2016) 对超弹性NiTi形状记忆合金微管单轴和非比例多轴疲劳断口形貌进行了SEM观察, 讨论了单轴和多轴疲劳失效过程中不同的微观结构形貌, 总结了该合金的多轴疲劳失效机制. 研究结果表明: (1)由于该合金微管的壁厚仅为150 \(\mu \)m, 远小于Robertson等(2012) 总结出的宏观裂纹的最小物理尺寸(1 mm), 同时, 在疲劳断面上裂纹扩展区和终断区交替出现, 因此, 其疲劳失效主要由微裂纹的萌生与扩展控制, 不涉及宏观裂纹的扩展阶段.(2)在单轴疲劳失效过程中, 微裂纹萌生于微管试样的内外表面和内部的空洞和夹杂处, 并随循环次数增大而逐渐扩展, 形成疲劳条纹, 同时形成大量的二次裂纹, 最终导致微管的疲劳破坏. (3)在多轴疲劳失效过程中, 除了能够观察到与单轴疲劳失效过程类似的疲劳条纹和二次裂纹外, 还可以观察到V型犁沟、穿透型疲劳台阶、斜断裂、划伤和表面多裂纹源这样一些独有的微观结构伤损模式, 如图38 所示.
(4)超弹性NiTi形状记忆合金微管的多轴疲劳失效过程中在裂纹萌生阶段出现的较高程度的损伤以及特有的多方向、多平面微裂纹扩展模式使得其疲劳寿命远低于相同加载水平下的单轴疲劳寿命.
图38 NiTi形状记忆合金多轴疲劳断口形貌 (Song et al. 2016 ).(a) V型犁沟, (b) 疲劳台阶, (c) 斜断裂, (d) 划伤, (e) 表面多裂纹源
对于NiTi形状记忆合金的原位测试目前也在一定程度上展开了研究, 如DiCocco 等(2014) , Frotscher 等(2008) , Niendorf 等(2011) 和\v{S}ittner等(2007).采用的测试手段包括SEM、XRD、选区电子衍射(EBSD)、中子衍射(neutron diffraction)等, 其中SEM和XRD最为常见. 研究者采用上述测试方法, 对NiTi形状记忆合金的应力诱发马氏体相变以及裂纹扩展等过程进行了实时观测.Di Cocco等(2014) 用原位SEM和XRD观测了2个循环周次中裂纹萌生及扩展的过程.研究表明, 应力诱发马氏体相变在裂尖处发生, 导致NiTi形状记忆合金的裂纹扩展与普通金属具有较大区别.实验中并未观察到裂尖钝化的情况, 但逆相变过程中会观察到完全的裂纹闭合, 见图39 .灰色箭头指示主裂纹的扩展, 白色箭头指示二次裂纹的扩展. 图39 清晰地描述了随应变增大, 裂纹尖端张开位移不断增大的过程.
图39 不同变形程度的预制裂纹扩展SEM原位观察 (Di Cocco et al. 2014 ).(a) 10%, (b) 11%, (c) 12%, (d) 拉伸断裂
Frotscher等(2008) 利用原位SEM观测了NiTi形状记忆合金菱形结构的疲劳断裂过程.研究表明, 表面划痕以及缺陷等应力集中处易于出现裂纹萌生, 但实验中也发现一些表面缺陷处在循环过程中并不会造成裂纹萌生. 图40 描述了在结构循环至第34周, 应变为24%时微裂纹的扩展情况.此时当应变仅增加0.06%时, 对比图40 (a)与图40 (b), 可见表面微裂纹尺寸明显增大. 继续施加应力时, 则材料迅速破坏.这也说明了裂纹萌生阶段占疲劳寿命的比例较大, 宏观裂纹一旦出现, 材料则在短时间内即发生破坏.
图40 宏观裂纹的演变 (Frotscher et al. 2008 ). (a)结构应变24%时; (b) 结构应变24.06%时, 可观察到裂纹尺寸明显增大; (c) 继续加载, 结构破坏
除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为.
3.1.2 半经验型疲劳失效模型
如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内.
Zhang 等(2016) 在室温下对NiTi合金丝进行了不同应变频率下的疲劳实验, 基于实验结果, 将非弹性耗散能分为两部分: 一部分通过热传导和热对流释放到环境中, 另一部分则储存于材料内部促进应力诱发马氏体相变的晶体缺陷.随加载速率的变化, 这两部分非弹性耗散能的比例发生变化, 由于释放到环境中的非弹性耗散能不会引起裂纹的萌生和扩展, 因此只考虑非弹性耗散能中储存于材料内部的部分达到一定临界值时, 裂纹开始萌生和扩展. 当加载速率越高, 材料内部储存的能量越大, 从而引起更低的寿命. Zhang等(2016)在此基础上发展了如下基于耗散能的疲劳准则\[ W_{\rm sat} = \gamma \dot {\varepsilon }^{ - \eta}N_{\rm f}^\beta \ \ (36)\]其中, \(\dot {\varepsilon }\)为应变率, \(\gamma \), \(\eta \)和\(\beta\)为材料参数, 可通过实验数据的拟合得到.该模型能够较合理的预测NiTi合金丝在不同应变率下的疲劳失效寿命.
Zhang 等(2017) 为了进一步考虑加载模式和载荷比对NiTi合金丝疲劳寿命的影响, 提出了基于应变能的疲劳寿命预测模型\[ e_0 = \alpha N_{\rm f}^\beta\ \ (37)\]其中, \(e_{0}\)为应变能, \(\alpha \)和\(\beta \)为材料参数.该模型能够较为合理的预测应变控制不同应变幅值和应力控制不同应力幅值下的疲劳失效寿命.
然而, 半经验型疲劳失效模型直接来自于宏观实验结果的数据拟合, 没有涉及疲劳断裂的物理本质, 也没有考虑疲劳裂纹萌生寿命和裂纹扩展寿命在整个疲劳寿命中的贡献, 因而, 预测误差偏大. 为了提高疲劳失效模型的合理性和准确性, 需要对NiTi形状记忆合金疲劳失效的微观机理进行分析, 了解疲劳失效过程中损伤机制以及损伤演化规律, 建立基于损伤演化的疲劳寿命预测模型.
3.1.3 基于损伤演变的寿命预测模型
由于NiTi形状记忆合金的疲劳失效行为较为复杂, 涉及热弹性马氏体相变及其相关的复杂微观结构变化, 因此, 目前对其疲劳损伤机理的研究还不多, 其复杂的损伤演化过程还需要进行深入而系统的实验观察, 合理而准确的损伤演变方程还需要进一步探讨. 最近, Song等(2015) 和宋迪(2015)在超弹性NiTi形状记忆合金应力控制的单轴和多轴疲劳实验研究的基础上, 引入一个基于耗散能密度的损伤变量, 揭示了定义的损伤变量在疲劳失效过程中的演变特征, 建立了相应的损伤演变方程, 进而在基于损伤演变的NiTi形状记忆合金疲劳失效寿命预测模型构建方面进行了很有意义的尝试.
Song等(2015) 首先在超弹性NiTi形状记忆合金单轴应力控制疲劳实验的基础上, 将损伤变量\(D\)定义为一定循环次数\(N\)下的累积耗散能密度与材料疲劳失效时\((N_{\rm f})\)总的累积耗散能密度之比, 即\[ D = \dfrac{\sum\limits_{i = 1}^N {W_i }}{\sum\limits_{i = 1}^{N_{\rm f} } {W_i } } \ \ (38)\]其中, \(W_{i}\)为一个循环次数内的耗散能密度.该损伤变量的定义考虑了稳定循环达到之前的循环变形行为对总的疲劳损伤的影响.
同时, 结合已有的实验结果, Song 等(2015) 将超弹性NiTi形状记忆合金的单轴疲劳损伤进一步看成是如下三部分之和, 即
(1)由位错滑移引起的微裂纹萌生造成的损伤\(D_{\rm ini}\)\[D_{\rm ini} = g_1 \cdot \int_0^{N_{\rm sat} } {W_N } {\rm d}N,\qquad N \leq N_{\rm sat} \ \ (39)\]
(2)微裂纹稳态扩展造成的损伤\(D_{\rm pro}\)\[D_{\rm pro} = g_2 \cdot \left( {N - N_{\rm sat} - 1} \right),\qquad N >N_{\rm sat} \ \ (40)\]
(3)由循环马氏体相变和相变诱发塑性造成的损伤\(D_{\rm trans}\)\[ D_{\rm trans} = g_3 \cdot \left[ {\int_0^{N_{\rm sat} }{W_N {\rm d}N + (N - N_{\rm sat} - 1)} \cdot W_{\rm sat} } \right]\ \ (41)\]其中\[ g_1 = b_1 \cdot \left( {\dfrac{\sigma _{\rm peak} - \sigma_{\rm AM}^{\rm s} }{\sigma _{\rm MA}^{\rm s} }} \right)^{n_1 }\ \ (42)\]\[ g_2 = a_1 \cdot \dfrac{\sigma _{\rm peak} ^2 + \left[{\sigma _{\rm valley} \cdot H(\sigma _{\rm valley} )}\right]^2}{W_{\rm sat} } \ \ (43)\]\[ g_3 = b_2 \cdot \left\{ {\left[ {\dfrac{F_1 (\sigma_{\rm peak} ) + F_2 (\sigma _{\rm peak} ,\sigma _{\rm valley})}{\sigma _{\rm AM}^{\rm f} - \sigma _{\rm AM}^{\rm s} + \sigma_{\rm MA}^{\rm s} - \sigma _{\rm MA}^{\rm f} }} \right]^{n_2 } +\left[ {\dfrac{F_1 (\sigma _{\rm peak} ) + F_2 (\sigma _{\rm peak},\sigma _{\rm valley} )}{\sigma _{\rm AM}^{\rm f} - \sigma _{\rm AM}^{\rm s} + \sigma _{\rm MA}^{\rm s} - \sigma _{\rm MA}^{\rm f}}} \right]^{\frac{1}{n_2 }}} \right\} \ \ (44)\]\[ F_1 = (\sigma _{\rm peak} - \sigma _{\rm AM}^{\rm s} ) \cdot H(\sigma _{\rm peak} - \sigma _{\rm AM}^{\rm s} ) + (\sigma _{\rm AM}^{\rm f} - \sigma _{\rm peak} ) \cdot H(\sigma _{\rm peak} -\sigma _{\rm AM}^{\rm f} ) \ \ (45)\]\[ F_2 = [(\sigma _{\rm MA}^{\rm s} - \sigma _{\rm valley} ) \cdot H(\sigma _{\rm MA}^{\rm f} - \sigma _{\rm valley} ) +\]\[ (\sigma_{\rm valley} - \sigma _{\rm MA}^{\rm f} ) \cdot H(\sigma _{\rm MA}^{\rm s} - \sigma _{\rm valley} )] \cdot H(\sigma _{\rm peak} -\sigma _{\rm AM}^{\rm s} ) \ \ (46)\]其中, \(H\)是Heaviside函数, \(\sigma _{\rm AM}^{\rm s} \)和\(\sigma_{\rm AM}^{\rm f} \)是马氏体相变开始和结束应力, \(\sigma _{\rm MA}^{\rm s} \)和\(\sigma _{\rm MA}^{\rm f} \)是逆相变开始和结束应力, \(a_{1}\), \(b_{1}\), \(b_{2}\), \(n_{1}\)和\(n_{2}\)是材料参数, \(\sigma_{\rm peak}\)和 \(\sigma _{\rm valley}\)为施加的峰值应力和谷值应力, \(W_{N}\)和\(W_{\rm sat}\)为当前和循环稳定时的耗散能密度.函数\(F_{1}\)和\(F_{2}\)反映了马氏体相变和逆相变在每一个加载工况下的进行程度, 如果马氏体相变和逆相变都是完全进行的, 则式(44)中指数\(n_{2}\)和\(1/n_{2}\)都等于1.
令总的损伤变量\(D=D_{\rm ini}+D_{\rm pro}+D_{\rm trans}=1\)时材料发生破坏, 则可得到了如下的寿命预测模型\[ N_{\rm f} = N_{\rm sat} + 1 + \dfrac{1 - \left( {g_1 + g_3\int_0^{N_{\rm sat} } {W_N {\rm d}N} } \right)}{g_2 + W_{\rm sat}\cdot g_3 } \ \ (47)\]
利用该模型, Song等(2015) 对超弹性NiTi形状记忆合金的单轴应力控制疲劳失效寿命进行了预测, 预测结果和实验结果的比较见图41 (a)所示. 由图可见, 所有的点都位于1.5倍误差带以内, 这说明基于损伤演化的寿命预测模型预测效果良好.
图41 NiTi形状记忆合金单轴和多轴疲劳寿命比较图. (a) 单轴(Song et al. 2015 ), (b) 多轴 (宋迪 2015)
后来, 宋迪(2015) 在此基础上进一步拓展建立了基于损伤演化的NiTi形状记忆合金非比例多轴疲劳寿命预测模型.为了反映多轴加载路径下出现的马氏体重取向以及重取向诱发塑性对疲劳失效寿命的影响, 在前述三种损伤机制上, 引入了一项新的马氏体重取向损伤\(D_{\rm reo}\), 并定义为\[ D_{\rm reo} = g_4 \cdot N\ \ (48)\]\[g_4 = c \cdot \lambda \ \ (49)\]其中, \(c\)为材料常数, \(\lambda\)为考虑不同形状的多轴加载路径对NiTi形状记忆合金疲劳失效寿命影响的加载路径因子, 但其定义不同于Song等(2017) 在半经验型多轴疲劳寿命预测模型(即式(35))中引入的定义, 具体可见文献(宋迪2015). 最后, 在失效判据\(D=D_{\rm ini}+D_{\rm pro}+D_{\rm trans}+D_{\rm reo}=1\)的基础上, 得到了如下的寿命预测模型\[ N_{\rm f} = \dfrac{1 - (g_1 + g_3 ) \cdot \int_0^{N_{\rm sat} } {W_N{\rm d}N + (g_2 + W_{\rm sat} \cdot g_3 ) \cdot (1 +N_{\rm sat} )} }{g_2 + W_{\rm sat} \cdot g_3 + g_4 } \ \ (50)\]
利用该模型, 宋迪(2015) 对超弹性NiTi形状记忆合金的非比例多轴应力控制疲劳失效寿命进行了预测, 预测结果与实验结果的比较见图41 (b)所示. 由图可见, 所有的点都位于2倍分散带内, 并且大部分点位于1.5倍误差带以内, 这说明基于损伤演化的非比例多轴疲劳寿命预测模型预测效果良好.
由于NiTi形状记忆合金疲劳失效过程的复杂性, 目前已经开展的一些寿命预测的尝试工作都还未能获得满意的结果, 预测误差仍然偏大, 因此, 在今后的一段时期内还需要对该合金疲劳损伤的微观机理和演化模型进行更为深入和系统的研究.
3.2 高温NiTiX形状记忆合金的疲劳失效行为
Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究.
König等(2011) 则观察了利用磁控溅射制备的NiTiHf多层纳米薄片材料中存在的三元Laves相沉淀, 深入讨论了该沉淀相对薄膜材料温度循环变形行为的影响. König等(2011) 指出, 三元Laves相的出现可以增加材料的可恢复应力, 提高其功能性疲劳(温度循环)特性, 并认为该沉淀相是造成多层纳米薄片材料与沉积制备的单层薄片材料和块体材料循环变形行为不同的原因.König等(2011) 对不同Hf原子含量的NiTiHf高温形状记忆合金薄膜材料分别进行了温度循环实验, 结果表明: 在温度循环的初始时期, Laves相的出现可增大材料的可恢复应力; 但随着循环的进行, 第二相粒子数目逐渐增加, 则会导致可恢复应力逐渐降低. 同时, König 等(2011) 根据实验结果, 将每一个温度循环次数下的应力幅值\(\sigma (T)\)随循环次数线性变化的斜率定义为功能性疲劳因子\(c_{\rm f}\), 并且探讨了\(c_{\rm f}\)与Hf原子含量的关系. 结果表明, Laves相的存在会抵消由Hf含量增大而增大的滞回环宽度, 使材料的功能性疲劳因子\(c_{\rm f}\)在Hf含量达到17%后迅速下降, 见图42 .
图42 功能性疲劳因子\(c_{\rm f}\)及其随Hf含量的变化 (König et al.2011). (a) \(c_{\rm f}\)的定义, (b) 随Hf原子含量的变化
4 磁致形状记忆合金的磁--力耦合循环变形行为
虽然NiTi形状记忆合金具有超弹性、形状记忆特性、良好的生物相容性和耐磨性等优点, 但其在温度驱动条件下热传导时间较长, 响应频率低, 无法满足高频响应器件的要求. 然而, 铁磁形状记忆合金除了具备传统NiTi形状记忆合金的优良特性之外, 还具有在磁场驱动条件下响应频率高这一优点. 因此, 近年来, 铁磁形状记忆合金得到了越来越多的关注, 具有广阔的应用前景.自从Ullakko等(1996) 首次报道了NiMnGa合金单晶在中等磁场强度下(小于1T)能够产生0.2%的磁致伸缩应变后, 铁磁形状记忆合金就以其优越的热--力--磁学特性引起了固体力学界和材料科学界学者的广泛关注和研究, 取得了丰硕的研究成果.关于磁致形状记忆合金一些基本变形特征的阐述可参见Kiefer 和 Lagoudas (2005) 的工作, 本节仅针对其磁--力耦合循环变形行为的研究现状进行评述.
4.1 实验研究
4.1.1 磁--力耦合变形机理分析
磁致形状记忆合金的变形机制较为为复杂, 除了具有与NiTi形状记忆合金所共有的马氏体相变、马氏体重定向机制外, 还包含了磁畴旋转以及畴壁运动这两种与磁性相关的变形机制.针对铁磁形状记忆合金的磁--力耦合变形机制, 根据变形的诱发条件不同, 可以总结为以下四类.
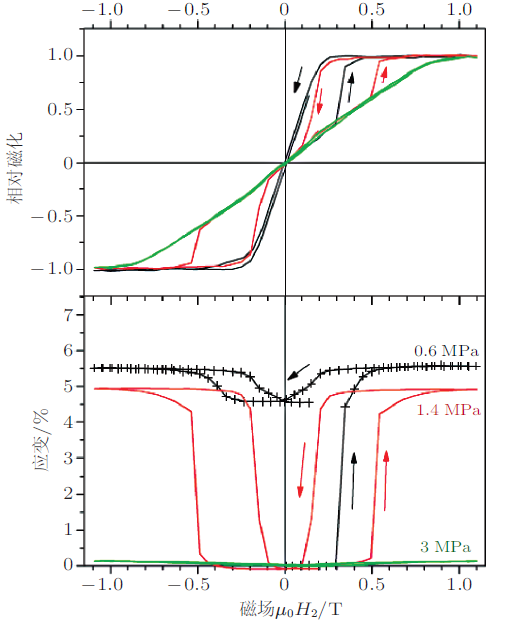
(1)磁场诱发马氏体重定向:Tickle和 James (1999) , Tickle 等(1999) , Heczko (2005) , Straka 和 Heczko (2003) 以及Karaca等(2006) 研究了环境温度在马氏体完成温度\((M_{\rm f})\)以下时铁磁形状记忆合金单晶在轴向恒定压应力、横向交变磁场作用下磁场诱发马氏体重定向特性.此时, 材料的初始相为马氏体, 图43 给出了该加载工况下典型的磁场--相对磁化曲线及磁场--应变曲线.以压应力为1.4 MPa的工况为例, 由图可见: 在变形的初始阶段(即磁场低于0.5 T), 由于磁场低于马氏体重定向临界磁场, 无非弹性应变出现, 并且磁化量随着磁场的增大而线性增大, 该阶段的磁化机制主要为磁化矢量的旋转; 当磁场高于0.5 T时, 马氏体重定向发生, 伴随着很大的非弹性应变出现, 同时磁化率出现跳跃并远高于低磁场(小于0.5 T)时的磁化率, 在该阶段马氏体重定向和磁化矢量旋转这两种磁化机制同时发生; 当磁场达到0.8 T时, 马氏体重定向完成, 磁化饱和出现, 并在后续磁场加载过程中, 非弹性应变和磁化量不再变化; 在卸载过程中, 当磁场达到0.25 T时, 逆向重定向发生, 非弹性应变和磁化量剧烈变化; 当磁场完全卸载后, 马氏体重定向完成, 非弹性应变及磁化量完全归零.另外, 对比图43 中不同应力水平下的磁--力响应可以看出:磁致伸缩应变的大小随着轴向压应力的增大而逐渐减小, 并且轴向压应力对磁场诱发马氏体重定向有抑制作用, 即临界磁场强度随着轴向压应力的增加而逐渐升高; 在压应力较小时(0.6 MPa), 磁场诱发出的重定向应变无法完全恢复; 在压应力较大时(3 MPa), 试样在发生马氏体重定向之前已经通过磁化矢量旋转机制完成了磁化, 无法诱发马氏体重定向机制. 这说明, 铁磁形状记忆合金存在着一个"闭锁应力", 在应力低于"闭锁应力"时, 磁场能够诱发马氏体重定向; 在应力高于"闭锁应力"时, 磁场无法诱发马氏体重定向. 铁磁形状记忆合金的"闭锁应力"一般较低, 大约在3 MPa左右. Karaca等(2006) 进一步提出了发生马氏体重定向的两个必要条件, 即高的磁晶各向异性能和低的孪生界面运动能, 并通过增大测试温度与居里温度之差以及减小测试温度和马氏体相变温度之差分别提高和降低磁晶各向异性能和孪生界面运动能, 进而获得了较高的应力闭锁值(5.7 MPa).
图43 NiMnGa形状记忆合金单晶磁场诱发马氏体重定向特性 (Heczko 2005 ):磁场--相对磁化曲线及磁场--应变曲线
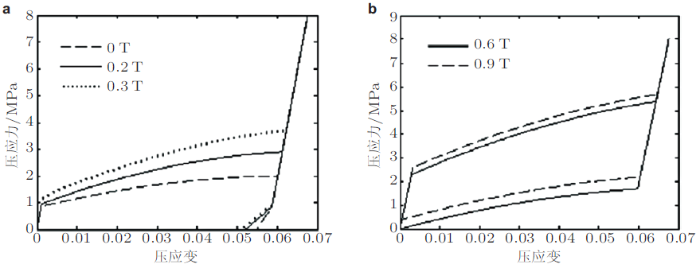
(2)应力诱发马氏体重定向. Heczko (2005) , Karaca 等(2006) , Chen等(2014) 和Heidi 等(2016) 研究了环境温度在马氏体完成温度\(M_{\rm f}\)以下时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体重定向特性.图44 给出了在该加载工况下典型的应力应变曲线. 由图可见: 在无磁场作用下时, 加载诱发出的非弹性应变在应力完全卸载后不能恢复, 这是由于马氏体逆向重定向开始应力大于零; 而在磁场作用下, 马氏体重定向平台随着磁场的增大的逐渐升高, 这表明横向磁场对轴向应力诱发马氏体重定向有抑制作用; 当磁场达到8 kG时, 重定向应变在应力卸载后能够完全恢复, 材料展示出超弹性效应. 需要说明的是, 铁磁形状记忆合金在\(M_{\rm f}\)以下的超弹性机制是正向和逆向马氏体重定向, 这与NiTi形状记忆合金在奥氏体完成温度\(A_{\rm f}\)以上由正向和逆向马氏体相变所导致的超弹性有本质区别.
图44 NiMnGa形状记忆合金单晶应力诱发马氏体重定向特性的不同横向恒定磁场下的应力--应变曲线(Karaca et al.2006)
(3)应力诱发马氏体相变. Chernenko 等(2005) , Segu\'{\i} 等(2005) , Kim 等(2006) 和Karaca 等(2007) 研究了环境温度在奥氏体完成温度A\(_{\rm f}\)以上时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体相变特性.和NiTi形状记忆合金类似, 铁磁形状记忆环境在应力作用下展示出良好的超弹性特性, 如图45 所示. 同时, 可以看出横向磁场对马氏体相变具有抑制作用, 即向前相变和逆相变平台均随着横向磁场的增加而升高, 并且相变特性对温度有很强的依赖性. 需要说明的是, 为了便于比较, 图43 中每个温度下的应变初始值均为零, 坐标轴的刻度间隔为1%.
图45 NiMnGa形状记忆合金单晶应力诱发马氏体相变的不同温度和不同磁场下的应力--应变曲线(Karaca et al.2007)
(4)磁场诱发马氏体相变. 与马氏体重定向相比, 单纯的磁场诱发马氏体相变十分困难, 需要的临界磁场通常高于5T(Kakeshita et al. 2000 , Haldar et al. 2014 ), 这极大地限制了铁磁形状记忆合金的应用范围.为了能使铁磁形状记忆合金在较低磁场下仍然能够诱发马氏体相变机制, Karaman 等(2006)和Karaca 等(2007)提出了一种行之有效的方法, 即应力辅助磁场诱发马氏体相变:首先施加应力, 使试样发生马氏体相变, 然后卸载至无磁场下逆相变开始应力和1.6 T磁场下逆相变开始应力之间, 如图46 所示. 此时, 保持应力不变, 施加磁场, 即可在较小的磁场强度下(0.8 T)诱发马氏体相变机制, 同时可以观察到较大的相变应变, 如图44 所示. 需要指出的是, 磁场诱发马氏体相变是一种很重要的机制, 这是由于在同样磁场强度下, 磁场诱发马氏体相变的输出功率远高于磁场诱发马氏体重定向, 这对铁磁形状记忆合金磁驱动器的设计提供了新的理论基础.
图46 NiMnGa形状记忆合金单晶磁场诱发马氏体相变的磁场--应变曲线(Karaca et al.2007)
4.1.2 磁--力耦合循环变形行为
在铁磁形状记忆合金循环载荷下的功能性劣化方面, Karaca等(2006) 通过对NiMnGa单晶施加循环磁载荷, 发现随着循环过程的进行, 残余应变会逐渐累积, 如图47 所示, 这与NiTi形状记忆合金在温度诱发循环相变过程中残余应变累积的现象类似.Aaltio 等(2010) 研究了NiMnGa单晶在单纯机械载荷作用下的循环变形特性, 结果表明: 与NiTi形状记忆合金类似, NiMnGa在循环变形过程中出现了明显的功能性劣化, 即重定向开始应力和重定向模量均随着循环次数的增大而升高, 如图48 所示. Aaltio 等(2010) 指出, 上述的功能性劣化现象来源于两个方面:一是在循环机械载荷作用下, 晶体缺陷会逐渐形核并累积; 二是缺陷的存在阻碍了马氏体孪生界面运动, 从而造成重定向开始应力和重定向模量逐渐升高.
图47 NiMnGa形状记忆合金单晶在循环磁场作用下的磁场--应变曲线(Karaca et al. 2006 )
图48 NiMnGa形状记忆合金单晶在循环应力作用下的应力--应变曲线(Aaltio et al. 2010 )
上述研究主要集中在铁磁形状记忆合金单晶方面. Murray 等(1998) , Jeong等(2003) 研究了铁磁形状记忆合金多晶的磁--力耦合特性, 发现相对于单晶材料, 多晶能产生的磁致伸缩应变很小. Marioni(2002) 进一步指出, 针对多晶铁磁形状记忆合金, 可以通过定向凝固法调控择优取向的初始织构来获取较大的磁致伸缩应变.近年来, 众多学者研究了铁磁形状记忆合金定向凝固多晶在不同方向上的磁场诱发马氏体重定向特性(Pötschke et al.2010 , Yu et al. 2014b ), 应力诱发马氏体重定向特性(Chulist et al. 2010 , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性.
综上所述, 虽然铁磁形状记忆合金在实验研究方面已取得了长足的发展, 但大多数实验研究仅仅关注了材料在磁--力加卸载下的马氏体重定向及相变特性.虽然Karaca 等(2006) 和Aaltio等(2010) 研究了材料在循环载荷作用下的循环变形特性, 但载荷模式仅仅是单一磁或机械载荷, 尚缺少在热--力--磁多场环境下对材料循环变形特性的宏观实验观察.因此, 随着铁磁形状记忆合金日益广泛的应用, 对材料在热--力--磁多场环境下循环变形特性的实验研究工作亟待开展.
4.2 磁--力耦合本构理论
基于铁磁形状记忆合金磁--力耦合变形行为的实验研究成果, 目前已经建立了一些相应的磁--力耦合本构模型, 根据所采用的方法不同可以大致分为4类: (1)基于微磁学约束理论模型.James 和Wuttig (1998) , DeSimone 和 James(2002) 基于微观磁学通过引入Zeeman能、静磁能和弹性能得到了系统的自由能函数, 假定磁化矢量在磁化过程中始终与易轴平行(即磁晶各向异性能无穷大而导致磁畴无法发生旋转), 采用能量最小化原理预测了铁磁形状记忆合金微结构的变形、宏观磁致应变以及磁化响应, 并预测在铁磁形状记忆合金中马氏体以层状结构形式存在. 然而, 由于该类模型的复杂性, 较难应用到具体的工程问题中. (2)能量模型.Murray等(2001)基于能量分析法来预测铁磁形状记忆合金发生马氏体重定向的条件, 提出了一个考虑双马氏体变体的二维能量模型, 将两个变体内磁能之差作为孪生变体界面运动的驱动力. Müllner等(2002)进一步考虑了机械能的存在对马氏体重定向的影响. He等(2011) 建立了一个适用于复杂多轴力--磁场条件下, 并考虑了磁滞效应的一般性能量模型.
(3)基于不可逆热力学的宏观唯象模型.该类模型通过引入内变量并结合外变量来表征材料的热力学状态, 通过建立的Helmholtz或Gibbs自由能, 采用热力学第二定律推导出各种非弹性变形机制生成的耗散, 进而定义与内变量共轭的热力学驱动力, 最后基于热力学约束和实验观察, 提出内变量演化方程, 得到描述材料本构关系的封闭微分方程组.这类模型由于概念较为简单, 便于工程应用, 目前得到了较为广泛的关注.(4)基于Eshelby夹杂理论的细观力学模型.该类模型将初始相为马氏体相的铁磁形状记忆合金中的一个变体看作基体, 另外一个变体看作夹杂, 通过引入Eshelby张量度量材料内部应力--应变场的非均匀性, 并采用Mori-Tanaka方法得到材料的宏观性能.这类模型物理概念清晰、能够反映铁磁形状记忆合金的细观非均匀性以及微结构的交互作用, 进而具有良好的发展前景.
4.2.1 宏观唯象本构理论
如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景.
Mousavi 和 Arghavani (2017) 考虑了三种与磁致应变相关的变形机制, 即马氏体重定向、畴壁运动和磁畴旋转, 因此, 在本构方程中引入了三个马氏体变体体积分数(即 \(\xi _{1}\), \(\xi _{2}\)和 \(\xi _{3})\), 第\(i\)个马氏体变体中的两种磁畴体积分数(即\(\alpha _{i}\)和\(1-\alpha _{i})\)和第\(i\)个马氏体变体中两种磁畴中磁化矢量方向\((\pmb m_{ +i} , \pmb m_{ - i})\)作为内变量来描述材料所处的热力学状态, 系统的自由能\(g\)写成\[ g=g^{\rm mec} + g^{\rm mag} + g^{\rm T} +g^{\rm int} + g^{\rm con} \ \ (51)\] 其中, \(g^{\rm mec}\), \(g^{\rm mag}\), \(g^{\rm T}\), \(g^{\rm int}\)和\(g^{\rm con}\)分别是力学能、磁能、温度相关内能、硬化能以及约束能.它们的具体形式为\[g^{\rm mec}=-\dfrac{1}{2\rho}\pmb\sigma:\pmb S:\pmb\sigma-\dfrac{1}{\rho}\pmb\sigma:\pmb \varepsilon^{\rm r} \ \ (52)\]\[g^{\rm mag}=-\dfrac{\mu_0}{\rho}\pmb M\cdot\pmb H+\sum_{i=1}^3\xi_i\alpha_iK_I\left[1-(\pmb e_i\cdot\pmb m_{+i})^2\right]+ \sum_{i=1}^3\xi_i(1-\alpha_i)K_I\left[1-(\pmb e_i\cdot\pmb m_{-i})^2\right] \ \ (53)\]\[g^{\rm T}=C_p\left[T-T_0-T\ln\left(\dfrac{T}{T_0}\right)\right]\ \ (54)\]\[g^{\rm int}=\dfrac{1}{\rho n}k_1\left(\xi_1^n +\xi_2^n +\xi_3^n \right) \ \ (55)\]\[g^{\rm con}=\dfrac{1}{\rho } [\lambda_\xi \left(\xi_1 +\xi_2 +\xi_3-1\right)+I^{\xi_1}(\xi_1)+I^{\xi_2}(\xi_2)+I^{\xi_3}(\xi_3)+I^{\alpha_1}(\alpha_1)+I^{\alpha_2}(\alpha_2)+\]\[I^{\alpha_3}(\alpha_3)+\lambda_{+1}(\|\pmb m_{+1}\|-1)+\lambda_{-1}(\|\pmb m_{-1}\|-1)+\lambda_{+2}(\|\pmb m_{+2}\|-1)+\]\[\lambda_{-2}(\|\pmb m_{-2}\|-1) + \lambda_{+3}(\|\pmb m_{+3}\|-1)+\lambda_{-3}(\|\pmb m_{-3}\|-1) \ \ (56)\] 其中, \(\rho \)是材料密度, \(\pmb\sigma \)是应力张量, \(\pmb S\)是柔度张量, \(\pmb \varepsilon ^{r}\)是重定向应变张量, \(\mu_{0}\)是真空磁导率, \(\pmb M\)是磁化矢量, \(\pmb H\)是磁场强度; \(\pmb e_{i}\)是坐标基础矢量; \(C_{p}\)是比热容, \(T_{0}\)是平衡温度; \(K_{I}\), \(n\), \(k_{1}\)是材料参数; \(\lambda_{\xi }\), \(\lambda_{ + 1}\), \(\lambda_{ - 1}\), \(\lambda_{ + 2}\), \(\lambda_{ - 2}\), \(\lambda_{ + 3}\)和 \(\lambda _{ -3}\)是拉格朗日乘子; \(I^{\xi i} ( \xi _{i})\)和\(I^{\alpha i} (\alpha_{i})\)是约束函数.
根据实验观察, Mousavi 和 Arghavani(2017) 给出了马氏体变体中磁畴体积分数和外加磁场之间的关系\[\alpha_i=\left\{\begin{array}{ll}\dfrac{1}{2}+\dfrac{H_i}{2H_{\rm sat}}, |H_i| < H_{\rm sat} \\ \dfrac{1}{2}+ \dfrac{1}{2}{\rm sign}H_i, |H_i|\geq H_{\rm sat}\\ \end{array}\right. (57)\], \(H_{i}\)是外加磁场矢量的第\(i\)个方向分量, \(H_{\rm sat}\)是饱和磁场强度. 根据热力学关系, 可推导出磁化矢量旋转方程为\[\alpha_i=\left\{\begin{array}{l}\left(\pmb I-\pmb m_{ + i}\bigotimes\pmb m_{ + i}\right)\cdot\left[\mu_0M^{\rm sat}\pmb H+2\rho K_I\left(\pmb e_i\bigotimes\pmb e_i\right)\cdot\pmb m_{ + i}\right]=0\\ \left(\pmb I-\pmb m_{ - i}\bigotimes\pmb m_{ - i}\right)\cdot \left[\mu_0M^{\rm sat}\pmb H+2\rho K_I\left(\pmb e_i\bigotimes \pmb e_i\right)\cdot\pmb m_{ - i}\right]=0 \\ \end{array}\right.\ \ (58)\] 其中, \(\pmb I\)是二阶单位张量.通过求解公式(58)即可得到\(\pmb m_{ + i}\)和\(\pmb m_{ - i}\).
Mousavi 和 Arghavani(2017) 进一步根据热力学关系推导出与每个马氏体变体对应的热力学驱动力, 即\[\pi ^{\xi_i}=-\rho\dfrac{\partial g}{\partial \xi_i}=-\varepsilon^{r,\max}\sigma_{ii}+\mu_0 M^{\rm sat}\left\{\left[\alpha_i\pmb m_{ + i}+(1-\alpha_i)\pmb m_{-i}\right]\cdot\pmb H\right\}-\]\[\rho K_I \alpha_i\left\{1-\left(\pmb e_i\cdot\pmb m_{ + i}\right)^2\right\}- \rho K_I(1-\alpha_i)\left\{1-\left(\pmb e_i\cdot\pmb m_{-i}\right)^2\right\}-k_1\xi_i^{n-1}-\lambda_\xi-\dfrac{\partial I^{\xi_i}( \xi_i)}{\partial \xi_i} \ \ (59)\] 同时, 将马氏体重定向的驱动力定义为最大的马氏体变体驱动力和最小的马氏体变体驱动力之差, 并认为当驱动力之差达到一个定值之后, 马氏体重定向发生, 即\[F=\pi ^{\xi p}-\pi ^{\xi R}=Y \ \ (60)\] 其中, \(\pi ^{\xi p}\)和 \(\pi ^{\xi R}\)分别是最大的和最小的马氏体变体热力学驱动力.
Mousavi 和 Arghavani (2017)对提出的本构模型进行了数值实现, 并通过将模拟结果和实验结果的对比验证了模型的正确性. 图49 和图50 分别给出了Mousavi 和Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型(LaMaster et al. 2014 )在应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和应力诱发重定向实验结果 (Chen et al. 2014 )与对应的模拟结果的比较情况. 由图可以看出, 三个模型都能够较好地捕捉到实验现象, 但是, Mousavi 和 Arghavani模型(Mousavi & Arghavani 2017 )与实验数据吻合得更好.
图49 应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比 (Mousavi & Arghavani 2017 )
图50 应力诱发重定向实验结果(Chen et al. 2014 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al.2014)以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比(Mousavi & Arghavani 2017 )
4.2.2 基于Eshelby夹杂理论的细观力学本构理论
基于Eshelby夹杂理论的细观力学本构模型能反映铁磁形状记忆合金磁--力耦合变形行为的细观非均匀性, 具有良好的发展前景, 目前已经得到了研究者的广泛重视. 例如:Zhu 和Dui (2007) 建立了基于Eshelby夹杂理论的铁磁形状记忆合金细观力学模型, 并通过该模型进一步研究了应力状态(拉伸、压缩)对磁场诱发马氏体重定向的影响(Zhu & Dui 2008 )以及磁矢量旋转对马氏体重定向的影响 (Zhu & Dui 2010 ); Wang 和 Li(2010) 通过考虑夹杂的各向异性拓展了细观力学模型.由于细观力学模型充分考虑了微结构之间的非均匀性与交互作用, 因此能够很好地描述铁磁形状记忆合金的重定向特性.需要指出的是现有的铁磁形状记忆合金细观力学模型均为二维模型.下面将简要的介绍 Zhu和 Dui (2007) 建立的细观力学本构模型.
Zhu 和 Dui (2007) 将第一个马氏体变体视为基体, 第二个马氏体视为夹杂, 并将宏观整体应变\(\bar{\pmb\varepsilon}\)分解为弹性应变\(\bar{\pmb\varepsilon }^{\rm e}\)和非弹性应变\(\bar{\pmb\varepsilon }^{\rm in}\), 即 \[\bar{\pmb\varepsilon } = \bar{\pmb\varepsilon }^{\rm e} +\bar{\pmb\varepsilon }^{\rm in} \ \ (61)\]其中, \(\bar{\pmb\varepsilon }^{\rm e}\)和\(\bar{\pmb\varepsilon }^{\rm in}\)分别可以表示为 \[ \bar{\pmb\varepsilon }^{\rm e} = \overline{\pmb M}\bar {\pmb \sigma } \ \ {\rm (62a)}\] \[ \bar{\pmb\varepsilon }^{\rm in} = \xi \left( {1 - \xi} \right)\left\{ {\pmb L_0 + \left( {\pmb L_1 - \pmb L_0 }\right)\left[ {\pmb S - \xi \left( {\pmb S - \pmb I} \right)}\right]} \right\}^{ - 1}\left( {\pmb L_0 - \pmb L_1 }\right)\left( {\pmb S - \pmb I} \right)\left( {\pmb \varepsilon^{\rm r} - \pmb \varepsilon ^{\rm ph}} \right)+\] \[ \pmb \varepsilon^{\rm ph} + \xi \pmb \varepsilon ^{\rm r} \ \ {\rm (62b)}\]其中, \(\xi \)是第二个马氏体变体的体积分数, \(\pmb L_0 \)和\(\pmb L_1\)分别是基体和夹杂的弹性柔度张量, \(\pmb S\)是Eshelby张量, \(\pmb I\)是四阶单位张量, \(\pmb \varepsilon ^{\rm r}\)和\(\pmb \varepsilon^{\rm ph}\)分别是重定向和相变应变张量, \( \bar {\pmb\sigma }\)是宏观整体应力. \(\overline{\pmb M}\)是宏观整体有效弹性柔度张量 \[ \overline{\pmb M} = \left\{ {\pmb I + \xi \left\{ {\pmb L_0 + \left( {\pmb L_1 - \pmb L_0 } \right)\left[{\pmb S - \xi \left( {\pmb S - \pmb I} \right)} \right]}\right\}^{ - 1}\left( {\pmb L_0 - \pmb L_1 } \right)} \right\}\pmb M_0 \ \ (63)\]Zhu 和 Dui (2007) 将两个马氏体变体的Gibbs自由能之差分成三项, 即 \[ \Delta G = \Delta G_{\rm me} + \Delta G_{\rm ze} + \Delta G_{\rm an} \ \ (64)\]其中, \(\Delta G_{\rm me} \), \(\Delta G_{\rm ze} \)和\(\Delta G_{\rm an} \)分别是机械能、Zeeman能和磁晶各向异性能, 即 \[ \Delta G_{\rm me} = - \dfrac{1}{2}\xi \left( {1 - \xi }\right)\pmb L_0 \left( {\pmb S - \pmb I} \right)\pmb \varepsilon^{\rm r}\pmb \varepsilon ^{\rm r} \ \ {\rm (65a)}\] \[ \Delta G_{\rm ze} = \left( {1 - \xi } \right)\mu _0 M^{\rm sat}H\left\{ \left[{\alpha \cos \beta _3 - \left( {1 - \alpha } \right)\cos \beta _1} \right]\cos \theta +\right.\] \[ \left. \left[ {\alpha \sin \beta _3 - \left( {1 -\alpha } \right)\sin \beta _1 } \right]\sin \theta \right\} + \xi \mu _0 M^{\rm sat}H\left\{ \left[ { - \alpha \sin \beta _4 +\left( {1 - \alpha } \right)\sin \beta _2 } \right]\cos \theta+\right.\] \[\left.\left[ {\alpha \cos \beta _4 - \left( {1 - \alpha } \right)\cos\beta _2 } \right]\sin \theta \right\}\ \ {\rm (65b)}\] \[ \Delta G_{\rm an} = \left( {1 - \xi } \right)\left[{\alpha K_u \sin ^2\beta _3 + \left( {1 - \alpha } \right)K_u \sin^2\beta _1 } \right] +\] \[ \xi \left[ {\alpha K_u \sin ^2\beta _4 +\left( {1 - \alpha } \right)K_u \sin ^2\beta _2 } \right]\ \ {\rm (65c)}\] 式中, \(\beta_1\)和\(\beta_2\)为第一个马氏体变体中两种磁畴磁化矢量与磁化易轴的夹角, \(\beta_3\)和\(\beta_4\)为第二个马氏体变体中两种磁畴磁化矢量与磁化易轴的夹角, \(K_u\)为磁晶各向异性能, \(\alpha \)和\(1-\alpha\)为马氏体变体中两种磁畴的体积分数.
Zhu 和 Dui (2007) 将两个马氏体变体的Gibbs自由能之差对体积分数\(\xi\)的导数作为马氏体重定向的驱动力, 即 \[ f_{\rm drv} = - \dfrac{\partial \Delta G}{\partial \xi }= - \dfrac{\partial \Delta G_{\rm me} }{\partial \xi } -\dfrac{\partial \Delta G_{\rm ze} }{\partial \xi } -\dfrac{\partial \Delta G_{\rm an} }{\partial \xi } \ \ (66)\]进一步考虑了两种马氏体重定向的能垒, 即界面能和界面摩擦耗散能 \[ \Delta G_{\rm s} = {2\xi \gamma _{\rm s} } /t \ \ {\rm (67a)}\] \[\Delta G_{\rm d} = D\left( {e^{b\xi } - 1} \right)\ \ {\rm (67b)}\]其中, \(\gamma _{\rm s} \)是马氏体--马氏体界面能密度, \(t\)是界面厚度, \(D\)和\(b\)是材料参数. 同时, 将两种能垒之和对体积分数\(\xi\)的导数作为马氏体重定向的阻力 \[ f_{\rm res} = \dfrac{\partial \Delta G_{\rm s} }{\partial \xi }+ \dfrac{\partial \Delta G_{\rm d} }{\partial \xi } \ \ (68)\]同时, 提出如下马氏体重定向演化准则 \[f_{\rm drv} = f_{\rm res} \ \ (69)\]
为了简化起见, Zhu 和 Dui(2007) 忽略了磁畴壁运动和磁化矢量旋转这两种机制. 因此, 在已知外加应力和磁场的情况下就可以完全计算出体积分数\(\xi \).
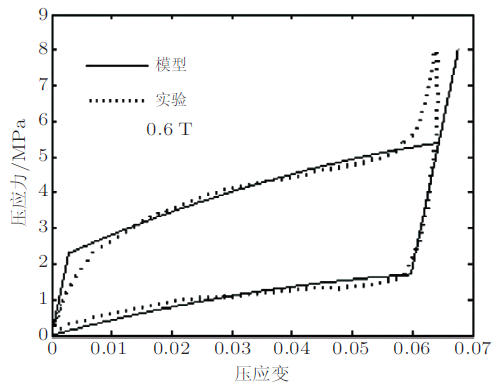
图51 给出了Zhu-Dui模型对恒定磁场(0.6 T)下应力诱发重定向实验结果的模拟.由图可以看出, Zhu-Dui模型能够很好地描述磁场作用下马氏体重定向特性.图52 给出了Zhu-Dui模型对不同恒定磁场下应力诱发重定向实验结果的预测, 可以看出:Zhu-Dui模型能够预测出随着横向磁场强度增大, 重定向及逆向重定向平台逐渐上升这一现象, 这与实验观察是吻合的.
图51 Zhu-Dui模型对恒定磁场(0.6 T)下应力诱发重定向实验结果的模拟(Zhu & Dui 2007 )
图52 Zhu-Dui模型对不同恒定磁场下应力诱发重定向实验结果的预测(Zhu & Dui 2007 )
需要指出的是, 虽然铁磁形状记忆合金在理论模型研究方面已取得了较大的突破, 所建立起的本构模型能够较为合理地预测材料的磁--力耦合变形特性, 但绝大多数本构模型主要关注铁磁形状记忆合金在磁--力载荷下的马氏体重定向特性, 而对马氏体相变机制研究较少, 尚缺少一个能够全面考虑铁磁形状记忆合金不同变形机制, 即马氏体相变、马氏体重定向、磁畴壁运动及磁化矢量旋转的磁--力耦合本构模型.同时, 由于缺乏对铁磁形状记忆合金热--力--磁多场环境下循环变形特性的实验观察, 已有的本构模型并未引入与材料功能性劣化相关的非弹性变形机制, 因而无法描述和预测材料的循环变形特性. 同时, 已有的本构模型中也未能考虑与相变潜热的吸收和释放相关的热--磁--力耦合问题, 并且目前也缺乏磁致形状记忆合金热--磁--力耦合变形(特别是循环变形)的实验数据.这表明, 铁磁形状记忆合金热--力--磁耦合循环变形行为及其本构模型理论建立这一个关键科学问题还需要进行深入而系统的研究.
5 磁致形状记忆合金的磁--力耦合疲劳失效行为
与传统的NiTi形状记忆合金相比, 对铁磁形状记忆合金疲劳失效行为的报道要少很多, 已有的研究主要可以分为磁场诱发和机械载荷诱发疲劳失效两个方面.
(1)磁场诱发疲劳失效. Chmielus等(2008) 通过对NiMnGa单晶施加循环旋转磁场(磁场强度保持恒定, 方向改变)观察了磁致应变在循环变形过程中的演化, 如图53 所示.
图53 NiMnGa铁磁形状记忆合金单晶在旋转磁场下磁致应变随循环次数的演化(Chmielus et al. 2008 )
由图53 可见, 磁致应变的演化可以分为三个阶段, 即稳定区A、稳定增长区B和下降区C; 同时, 在不同区间的交接区附近, 最大磁致应变的改变非常迅速. Chmielus等(2008) 进一步解释了三个区域特性所对应的微观机制:在施加磁场之前, 材料未经有效训练, 初始态为孪生马氏体态, 单个马氏体厚度很小, 仅为10 nm到1 \(\mu \)m之间, 马氏体各个变体以高密度的交错形式存在, 变体--变体界面的运动阻力很高, 在0.97T磁场作用下, 仅仅观察到了0.2%的磁致重定向应变, 如图53 中区域A所示; 随着循环变形的进行, 由于晶体缺陷的逐渐累积, 择优取向马氏体逐渐相互吞噬, 形成大的马氏体区域, 马氏体各个变体逐渐以低密度的交错形式存在, 变体--变体界面的运动阻力显著降低, 磁致应变随着循环变形的进行而逐渐增大, 如图53 中区域B所示; 由于马氏体变体之间的本征应变不同, 在变体--变体界面处存在着应变突跳, 造成应力集中, 随着循环变形的进一步进行, 缺陷和微裂纹逐渐在变体--变体界面处累积, 导致材料性能劣化, 当循环次数达到5 \(\times \) 10\(^{5}\)之后, 磁致应变随着循环次数的增大而逐渐降低, 如图53 中区域C所示.需要指出的是, NiMnGa铁磁形状记忆合金单晶具有很好的抗疲劳特性, 在经历10\(^{8}\)次循环磁场载荷后, 试样出现了宏观裂纹, 但并未发生断裂.
Guldbakke 等(2010) 也研究了NiMnGaFe单晶在相同加载模式下的疲劳特性, 结果表明, NiMnGaFe单晶的磁致应变演化特性和NiMnGa单晶非常类似, 也分为上述三个阶段, 但其抗疲劳特性较差, 试样在经历2 \(\times\) 10\(^{6}\)次循环磁场载荷后出现断裂.Lawrence 等(2016) 则观察了NiMnGa单晶在磁场诱发疲劳后的试样微观形貌, 发现三种典型的裂纹形式同时存在, 即: I型裂纹沿\(<100>\)方向扩展, II型裂纹沿\(<100>\)方向扩展, III型裂纹沿小角度晶界扩展, 如图54 所示(图中所示的1, 2和3分别代表I型、II型和III型裂纹).
需要指出的是, 虽然Lawrence等(2016) 采用Bridgman-Stockbarger方法生长单晶, 但制备出的试样仍然存在小角度晶界. Lawrence等(2016) 进一步研究了表面划痕以及表面粗糙度对试样疲劳寿命的影响.结果表明, 表面的划痕和较高的粗糙度会造成试样表面应力集中, 同时马氏体孪晶与表面缺陷的相互作用导致孪生位错的逐渐累积, 造成局部内应力, 导致裂纹萌生, 从而大大降低材料的疲劳寿命. Lawrence等(2016) 指出, 若想获得较好的疲劳寿命, 要同时避免单晶生长过程中出现的小角度晶界和表面划痕以及保证材料具有较低的表面粗糙度.
图54 磁场诱发疲劳后的试样微观形貌 (Lawrence et al. 2016 )
(2)机械载荷诱发疲劳失效. Aaltio等(2010) 研究了机械循环载荷作用下NiMnGa单晶的疲劳特性, 所得的典型循环应力--应变曲线如图48 所示. 由图可见, 与普通NiTi形状记忆合金类似, NiMnGa单晶在循环变形中也会出现明显的功能性劣化, 即重定向开始应力和重定向模量均随着循环次数的增大而升高. Aaltio等(2010) 指出, 上述的功能性劣化现象来源于两个方面: 一是在机械循环载荷作用下, 马氏体孪晶结构逐渐从大孪晶转变为细孪晶, 导致新孪晶形成后自由运动空间变小, 从而增大了新孪晶的运动阻力, 如图55 所示; 二是在循环变形过程中, 晶体缺陷(如位错、空洞)逐渐累积, 这些缺陷的存在增大了材料内部的应力场梯度, 从而阻碍了马氏体孪生界面运动, 从而造成重定向模量逐渐升高. 同时, Aaltio 等(2010) 的研究还表明: 材料的疲劳寿命随着应变幅值的增大而显著降低; 由于马氏体重定向机制是二级相变, 相变前后不涉及到潜热的释放, 因此材料对加载频率的依赖性很低; 虽然在循环变形过程中应力--应变曲线发生明显改变, 然而马氏体相变温度和居里温度保持不变; 材料中加工时预先存在的一些裂纹易于成为继发的裂纹源, 然而, 裂纹的扩展方向并不平行于预先存在的裂纹方向, 而是沿着马氏体孪晶的(101)晶面扩展, 因此, 在宏观上可以观察到裂纹与外加应力方向呈45\(^\circ\)角, 如图56 所示.
图55 NiMnGa形状记忆合金单晶在循环过程中的马氏体孪晶结构.左侧为循环7 \(\times \) 10\(^{5}\)次后的试样表面; 右侧为循环7.1 \(\times \) 10\(^{7}\)次后的试样表面 (Aaltio et al. 2010 )
图56 NiMnGa形状记忆合金单晶表面裂纹形貌(预先存在裂纹和新裂纹) (Aaltio et al.2010 )
6 总结与展望
通过对热致和磁致形状记忆合金热--力和磁--力耦合循环变形和疲劳失效行为研究现状的评述, 本文得到了如下结论.
(1)热致NiTi形状记忆合金.目前对NiTi形状记忆合金热--力耦合循环变形行为和疲劳失效的研究最为广泛, 已经在循环载荷作用下的超弹性和形状记忆退化效应(功能疲劳)和相关疲劳失效行为研究方面取得了较为丰硕的成果, 积累了很多宝贵的实验数据, 并已建立了一系列的热--力耦合本构模型和疲劳失效模型. 然而, 由于NiTi形状记忆合金循环变形行为的强烈热--力耦合特性和相变过程的局部失稳特性等, 目前对热--力耦合循环变形的微观机理以及损伤演化规律还未得到清楚的认识, 因而, 建立的理论模型预测精度还不够, 还有较大的改进空间.
尽管目前已经将分子动力学和相场分析等微细观数值分析手段用来对NiTi形状记忆合金变形机理进行研究, 但相关研究对热--力耦合循环载荷作用下的变形机理还少有涉及. 另外, 目前针对超弹性NiTi合金的热--力耦合循环变形和疲劳失效行为的研究较多, 针对形状记忆效应NiTi合金的研究相对较少, 仅见恒定应力下的温度循环实验和理论研究成果.对于应力和载荷同时为交变载荷的热--力耦合加载工况以及针对单程记忆效应的应力(或应变)--升温--降温--应力(或应变)循环加载条件下的形状记忆NiTi合金的热--力耦合循环变形和疲劳失效行为的实验和理论研究还少见文献报道.
(2)热致高温NiTiX形状记忆合金. 与NiTi形状记忆合金相比, 高温NiTiX形状记忆合金的热--力耦合循环变形和疲劳失效行为的研究要少很多, 目前已有的研究主要集中在恒定应力的温度循环方面, 并且局限于宏观循环变形实验和本构模型研究方面, 对于变形的微观机理和热--力耦合疲劳失效方面涉及甚少, 还需进行系统而深入的研究. 另外, 即使是在宏观唯象的本构模型研究方面, 已有的模型大都是基于NiTi形状记忆合金的本构模型拓展而来, 专门针对NiTiX高温形状记忆合金热--力耦合循环变形行为的本构模型研究较少.
(3)磁致形状记忆合金.
已有工作理清了磁致形状记忆合金磁--力耦合变形机制, 即除了具有与NiTi形状记忆合金所共有的马氏体相变、马氏体重定向机制外, 还包含了磁畴旋转以及畴壁运动这两种与磁性相关的变形机制, 然而, 尚缺少在热--力--磁多场环境下磁致形状记忆合金循环变形特性的宏微观实验观察; 同时, 已有研究主要集中在磁场诱发和机械载荷诱发疲劳失效两个方面, 尚缺乏磁--力耦合疲劳失效行为研究; 尽管目前已建立了基于不可逆热力学的宏观唯象模型和基于Eshelby夹杂理论的细观力学模型等, 但所建立的本构模型大都关注铁磁形状记忆合金在磁--力载荷下的马氏体重定向特性, 而对马氏体相变机制研究较少, 尚缺少一个能够全面考虑铁磁形状记忆合金不同变形机制的磁--力耦合本构模型; 已有本构模型并未引入与功能性劣化相关的非弹性变形机制, 无法描述和预测该合金的热--磁--力耦合循环变形特性; 目前针对磁致形状记忆合金疲劳失效行为的研究仅限于机械循环载荷和磁场循环载荷单独作用下的情形, 对该合金实际服役过程中涉及的热--磁--力耦合疲劳失效行为的研究尚未涉及, 有待于进一步深入开展.
基于对已有工作的总结, 对今后的工作作如下展望:
(1)开展热致和磁致形状记忆合金的热--力和磁--热--力耦合循环变形和疲劳失效行为的宏微观实验, 积累丰富的第一手实验数据.
(2)结合宏微观实验观察, 利用分子动力学和相场分析以及有限元分析等多尺度数值模拟方法, 探究热致和磁致形状记忆合金循环变形和失效行为的微观机理, 揭示形状记忆合金复杂的微观结构与宏观力学行为的关系, 优化材料设计.
(3)基于揭示的微观机理, 建立热致和磁致形状记忆合金的热--力和磁--热--力耦合循环本构模型和疲劳失效模型.
(4)基于建立的理论模型, 开展热致和磁致形状记忆合金器件的多场耦合分析, 对其服役寿命和可靠性进行评价.
The authors have declared that no competing interests exist.
作者已声明无竞争性利益关系。
参考文献
文献选项
[1]
康国政 , 于超 , 阚前华 . 2015 . NiTi 形状记忆合金热--力耦合循环变形行为宏微观实验和理论研究进展
. 固体力学学报 , 36 : 461 -480
[本文引用: 4]
(Kang G Z Yu C Kan Q H. 2015 . Progress in thermo-mechanical cyclic deformation of NiTi shape memory alloy: Macroscopic/Microscopic experiments and theory.
Chinese Jounral of Solid Mechanics ,36 : 461 -480 ).
[本文引用: 4]
[2]
康国政 . 2011 . 超弹性镍钛形状记忆合金循环变形行为的研究进展
. 西南交通大学学报 , 46 : 355 -364
[本文引用: 4]
(Kang G Z. 2011 . Research progress in cyclic deformation of super-elastic NiTi shape memory alloy.
Journal of Southwest Jiaotong University ,46 : 355 -364 ).
[本文引用: 4]
[3]
宋迪 . 2015 . 超弹性 NiTi 形状记忆合金微管的疲劳行为及损伤演化模型研究. [博士论文]
. 成都: 西南交通大学
(Song D. 2015 . Study on the fatigue behavior and damage evolution model of super-elastic NiTi shape memory alloy microtubes.
[PhD Thesis]. Chengdu: Southwest Jiaotong University ).
[4]
王习术 . 2010. 材料力学行为试验与分析 (第2版). 北京 : 清华大学出版社 , 77 -91
[本文引用: 1]
(Wang X S. 2010. Test and Analysis on Mechanical Behavior of Materials (Second Edition ). Beijing : Tsinghua University Press, 77-91) .
[本文引用: 1]
[5]
赵连城 , 蔡伟 , 郑玉峰 . 2002.合金的形状记忆合金效应与超弹性.第一版. 北京 :国防工业出版社
[本文引用: 6]
(Zhao L C Cai W Zheng Y F. 2002. Shape Memory Effect and Superelasticity of Alloys. (First Edition) . Beijing : National Defence Industry Press) .
[本文引用: 6]
[6]
左舜贵 , 金学军 , 金明江 . 2014 . 高温形状记忆合金的研究进展
. 机械工程材料 , 38 : 1 -5
[本文引用: 9]
(Zuo S G Jin X J Jin M J. 2014 . Research progress in high temperature shape memory alloys.
Materials for Mechanical Engineering ,38 : 1 -5 ).
[本文引用: 9]
[7]
周廷 , 阚前华 , 康国政 , 邱博 . 2017 . 超弹性镍钛形状记忆合金单轴相变棘轮行为的宏观唯象本构模型
. 力学学报 , 49 : 588 -596
[本文引用: 1]
(Zhou T Kan Q H Kang G Z Qiu B. 2017 . A macroscopic phenomenological constitutive model for the uniaxial transformation ratcheting of super-elastic NiTi shape memory alloy.
Chinese Journal of Theoretical and Applied Mechanics ,49 : 588 -596 ).
[本文引用: 1]
[8]
Aaltio I Soroka A Ge Y Söderberg O Hannula S P. 2010 . High-cycle fatigue of 10M Ni-Mn-Ga magnetic shape memory alloy in reversed mechanical loading.
Smart Mater. Struct. , 19 : 075014 .
[本文引用: 5]
[9]
Ahadi A Sun Q. 2013 . Stress hysteresis and temperature dependence of phase transition stress in nanostructured NiTi---Effects of grain size.
Appl. Phys. Lett. , 103 : 021902 .
[本文引用: 1]
[10]
Ahadi A Sun Q. 2014 . Effects of grain size on the rate-dependent thermomechanical responses of nanostructured superelastic NiTi.
Acta Mater. , 76 : 186 -197 .
[本文引用: 1]
[11]
Allen S M Cahn J W. 1979 . A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening.
Acta Metall. , 27 : 1085 -1095 .
[本文引用: 1]
[12]
Auricchio F Bessoud A-L Reali A Stefanelli U. 2015 . A phenomenological model for the magneto-mechanical response of single-crystal magnetic shape memory alloys. Eur. J. Mech. A
-Solid , 52 : 1 -11 .
[本文引用: 1]
[13]
Auricchio F Fugazza D Desroches R. 2008 . Rate-dependent thermomechanical modelling of superelastic shape-memory alloys for seismic applications. J
. Intell. Mater. Syst. Struct. , 19 : 47 -61 .
[14]
Benafan O Noebe R D Ii S A P Brown D W Vogel S Vaidyanathan R. 2014 . Thermomechanical cycling of a NiTi shape memory alloy-macroscopic response and microstructural evolution. Int. J
. Plast. , 56 : 99 -118 .
[本文引用: 1]
[15]
Bigelow G S Padula Ii S A Garg A Noebe R D. 2007 . Correlation between mechanical behavior and actuator-type performance of Ni-Ti-Pd high-temperature shape memory alloys.
International Symposium on: Smart Structures & Materials & Nondestructure Evaluation & Health Monitorying, 6526: 6526B-6526B-12.
[本文引用: 4]
[16]
Bigelow G S Padula S A Garg A Gaydosh D Noebe R D. 2010 . Characterization of ternary nitipd high-temperature shape-memory alloys under load-biased thermal cycling. Metall. Mater. Trans.
A , 41 : 3065 -3079 .
[17]
Bo Z Lagoudas D C. 1999 . Thermomechanical modeling of polycrystalline SMAs under cyclic loading, Part III: Evolution of plastic strains and two-way shape memory effect. Int. J
. Eng. Sci. , 37 : 1175 -1203 .
[本文引用: 1]
[18]
Cahn J W Allen S M. 1977 . Microscopic theory for domain wall motion and its experimental verification in fe-al alloy domain growth kinetics.
J. Phy. Colloques, 38: C7-51-C7-54.
[本文引用: 1]
[19]
Cahn J W Hilliard J E. 1958 . Free energy of a nonuniform system. I. Interfacial free energy. J
. Chem. Phys. , 28 : 258 -267 .
[20]
Cahn J W Hilliard J E. 1959 . Free energy of a nonuniform system. iii. nucleation in a two---component incompressible fluid. J
. Chem. Phys. , 31 : 688 -699 .
[本文引用: 2]
[21]
Charkaluk E Bignonnet A Constantinescu A Dang Van K. 2002 . Fatigue design of structures under thermomechanical loadings.
Fatigue Fract. Eng. Mater. Struct. , 25 : 1199 -1206 .
[本文引用: 1]
[22]
Charkaluk E Constantinescu A. 2000 . An energetic approach in thermomechanical fatigue for silicon molybdenum cast iron.
Mater. High Temp. , 17 : 373 -380 .
[本文引用: 2]
[23]
Chemisky Y Chatzigeorgiou G Kumar P Lagoudas D C. 2014 . A constitutive model for cyclic actuation of high-temperature shape memory alloys.
Mech. Mater. , 68 : 120 -136 .
[本文引用: 1]
[24]
Chen X Moumni Z He Y Zhang W. 2014 . A three-dimensional model of magneto-mechanical behaviors of martensite reorientation in ferromagnetic shape memory alloys. J. Mech. Phys.
Solids , 64 : 249 -286 .
[本文引用: 1]
[25]
Chernenko V A Pons J Cesari E Ishikawa K. 2005 . Stress-temperature phase diagram of a ferromagnetic Ni-Mn-Ga shape memory alloy.
Acta Mater. , 53 : 5071 -5077 .
[26]
Chmielus M Chernenko V A Knowlton W B Kostorz G Müllner P. 2008 . Training, constraints, and high-cycle magneto-mechanical properties of Ni-Mn-Ga magnetic shape-memory alloys. Eur. Phys. J
. Spec. Top. , 158 : 79 -85 .
[本文引用: 1]
[27]
Christ D Reese S. 2009 . A finite element model for shape memory alloys considering thermomechanical couplings at large strains. Int. J
. Solids. Struct. , 46 : 3694 -3709 .
[本文引用: 2]
[28]
Chulist R Skrotzki W Oertel C G Böhm A Pötschke M. 2010 . Change in microstructure during training of a Ni50Mn29Ga21 bicrystal.
Scripta Mater. , 63 : 548 -551 .
[本文引用: 1]
[29]
Cisse C Zaki W Ben Zineb T. 2016 . A review of constitutive models and modeling techniques for shape memory alloys. Int. J
. Plast. , 76 : 244 -284 .
[本文引用: 6]
[30]
Creton N Hirsinger L. 2005 . Rearrangement surfaces under magnetic field and/or stress in Ni-Mn-Ga.
J. Magn. Magn. Mater., 290- 291 : 832 -835 .
[本文引用: 4]
[31]
Delville R Malard B Pilch J Sittner P Schryvers D. 2010 . Microstructure changes during non-conventional heat treatment of thin Ni-Ti wires by pulsed electric current studied by transmission electron microscopy.
Acta Mater. , 58 : 4503 -4515 .
[本文引用: 7]
[32]
Delville R Malard B Pilch J Sittner P Schryvers D. 2011 . Transmission electron microscopy investigation of dislocation slip during superelastic cycling of Ni-Ti wires. Int. J
. Plast. , 27 : 282 -297 .
[本文引用: 2]
[33]
DeSimone A James R D. 2002 . A constrained theory of magnetoelasticity. J. Mech. Phys.
Solids , 50 : 283 -320 .
[本文引用: 4]
[34]
Dhote R P Gomez H Melnik R N V Zu J. 2015 . 3D coupled thermo-mechanical phase-field modeling of shape memory alloy dynamics via isogeometric analysis.
Comput. Struct. , 154 : 48 -58 .
[35]
Di Cocco V Iacoviello F Maletta C Natali S. 2014 . Cyclic microstructural transitions and fracture micromechanisms in a near equiatomic NiTi alloy. Int. J.
Fatigue , 58 : 136 -143 .
[本文引用: 3]
[36]
Duerig T Pelton A Stöckel D. 1999 . An overview of nitinol medical applications.
Mater. Sci. Eng. A, 273- 275 : 149 -160 .
[本文引用: 2]
[37]
Dunand-Ch\^{a}tellet C Moumni Z. 2012 . Experimental analysis of the fatigue of shape memory alloys through power-law statistics. Int. J.
Fatigue , 36 : 163 -170 .
[本文引用: 1]
[38]
Eggeler G Hornbogen E Yawny A Heckmann A Wagner M. 2004 . Structural and functional fatigue of NiTi shape memory alloys. Mater. Sci. Eng.
A , 378 : 24 -33 .
[39]
Falk F. 1983 a. Ginzburg-Landau theory of static domain walls in shape-memory alloys. Z. Phys.
B , 51 : 177 -185 .
[40]
Falk F. 1983 b. One-dimensional model of shape memory alloys. Arch.
Mech , 35 : 63 -84 .
[41]
Fan D Chen L Q. 1997 . Computer simulation of grain growth using a continuum field model.
Acta Mater. , 45 : 611 -622 .
[42]
Feng P Sun Q P. 2006 . Experimental investigation on macroscopic domain formation and evolution in polycrystalline NiTi microtubing under mechanical force. J. Mech. Phys.
Solids , 54 : 1568 -1603 .
[本文引用: 1]
[43]
Franciosi P. 1985 . The concepts of latent hardening and strain hardening in metallic single crystals.
Acta Metall. , 33 : 1601 -1612 .
[本文引用: 1]
[44]
Frotscher M Neuking K Böckmann R Wolff KD Eggeler G. 2008 . In situ scanning electron microscopic study of structural fatigue of struts, the characteristic elementary building units of medical stents.
Mater. Sci. Eng. A, 481- 482 : 160 -165 .
[45]
Gauthier J Y Lexcellent C Hubert A Abadie J Chaillet N. 2006 . Modeling rearrangement process of martensite platelets in a magnetic shape memory alloy Ni\(_{2}\)MnGa single crystal under magnetic field and (or) stress action. J
. Intell. Mater. Syst. Struct. , 18 : 289 -299 .
[本文引用: 2]
[46]
Grabe C Bruhns O T. 2008 . On the viscous and strain rate dependent behavior of polycrystalline NiTi. Int. J
. Solids. Struct. , 45 : 1876 -1895 .
[本文引用: 1]
[47]
Grandi D Maraldi M Molari L. 2012 . A macroscale phase-field model for shape memory alloys with non-isothermal effects: Influence of strain rate and environmental conditions on the mechanical response.
Acta Mater. , 60 : 179 -191 .
[48]
Guldbakke J M Chmielus M Rolfs K Schneider R Müllner P Raatz A. 2010 . Magnetic, mechanical and fatigue properties of a Ni\(_{45.4}\)Mn\(_{29.1}\)Ga\(_{21.6}\)Fe\(_{3.9}\) single crystal
. Scripta Mater. , 62 : 875 -878 .
[本文引用: 1]
[49]
Guo X H Shi S-Q Ma X Q. 2005 . Elastoplastic phase field model for microstructure evolution.
Appl. Phys. Lett. , 87 : 221910 .
[50]
Haldar K Lagoudas D C Karaman I. 2014 . Magnetic field-induced martensitic phase transformation in magnetic shape memory alloys: Modeling and experiments. J. Mech. Phys.
Solids , 69 : 33 -66 .
[本文引用: 1]
[51]
Hamilton R F Sehitoglu H Chumlyakov Y Maier H J. 2004 . Stress dependence of the hysteresis in single crystal NiTi alloys.
Acta Mater. , 52 : 3383 -3402 .
[本文引用: 3]
[52]
Hartl D J Chatzigeorgiou G Lagoudas D C. 2010 . Three-dimensional modeling and numerical analysis of rate-dependent irrecoverable deformation in shape memory alloys. Int. J
. Plast. , 26 : 1485 -1507 .
[本文引用: 2]
[53]
He Y J Chen X Moumni Z. 2011 . Two-dimensional analysis to improve the output stress in ferromagnetic shape memory alloys. J
. Appl. Phys. , 110 : 063905 .
[54]
He Y J Sun Q P. 2010 a. Rate-dependent domain spacing in a stretched NiTi strip. Int. J
. Solids. Struct. , 47 : 2775 -2783 .
[本文引用: 2]
[55]
He Y J Sun Q P. 2010 b. Frequency-dependent temperature evolution in NiTi shape memory alloy under cyclic loading
. Smart Mater. Struct. , 19 : 115014 .
[本文引用: 2]
[56]
Hebda D A White S R. 1998 . Effect of training conditions and extended thermal cycling on nitinol two-way shape memory behavior.
Smart Mater. Struct. , 4 : 298 .
[本文引用: 1]
[57]
Heczko O. 2005 . Magnetic shape memory effect and magnetization reversal.
J. Magn. Magn. Mater., 290- 291 : 787 -794 .
[58]
Heidi P F Constantin C Eberle J L Jason L D. 2016 . Experimental characterization and modeling of a three-variant magnetic shape memory alloy.
Smart Mater. Struct. , 25 : 104004 .
[本文引用: 2]
[59]
Hirsinger L Lexcellent C. 2003 . Modelling detwinning of martensite platelets under magnetic and (or) stress actions on Ni-Mn-Ga alloys.
J. Magn. Magn. Mater., 254- 255 : 275 -277 .
[本文引用: 2]
[60]
James R D Wuttig M. 1998 . Magnetostriction of martensite. Philos. Mag.
A , 77 : 1273 -1299 .
[本文引用: 3]
[61]
Javanbakht M Levitas V I. 2015 . Interaction between phase transformations and dislocations at the nanoscale. Part 2: Phase field simulation examples. J. Mech. Phys.
Solids , 82 : 164 -185 .
[62]
Jeong S Inoue K Inoue S Koterazawa K Taya M Inoue K. 2003 . Effect of magnetic field on martensite transformation in a polycrystalline Ni\(_{2}\)MnGa. Mater. Sci. Eng.
A , 359 : 253 -260 .
[本文引用: 1]
[63]
Kakeshita T Takeuchi T Fukuda T Tsujiguchi M Saburi T Oshima R Muto S. 2000 . Giant magnetostriction in an ordered Fe\(_{3}\)Pt single crystal exhibiting a martensitic transformation.
Appl. Phys. Lett. , 77 : 1502 -1504 .
[本文引用: 1]
[64]
Kan Q H Kang G Z Yan W Y Dong Y W Yu C. 2011 . An energy-based fatigue failure model for super-elastic NiTi alloys under pure mechanical cyclic loading.
SPIE Conference Series , 8409 .
[本文引用: 6]
[65]
Kan Q H Yu C Kang G Z Li J Yan W Y. 2016 . Experimental observations on rate-dependent cyclic deformation of super-elastic NiTi shape memory alloy.
Mech. Mater. , 97 : 48 -58 .
[本文引用: 4]
[66]
Kang G Z Song D. 2015 . Review on structural fatigue of NiTi shape memory alloys: Pure mechanical and thermo-mechanical ones.
Theor. Appl. Mech. Lett. , 5 : 245 -254 .
[本文引用: 5]
[67]
Kang G Z. 2013 . Advances in transformation ratcheting and ratcheting-fatigue interaction of NiTi shape memory alloy. Acta. Mech.
Solida Sin , 26 : 221 -236 .
[本文引用: 4]
[68]
Kang G Z Kan Q H Qian L Liu Y. 2009 . Ratchetting deformation of super-elastic and shape-memory NiTi alloys.
Mech. Mater. , 41 : 139 -153 .
[本文引用: 1]
[69]
Karaca H E Acar E Ded G S Basaran B Tobe H Noebe R D Bigelow G Chumlyakov Y I. 2013 . Shape memory behavior of high strength NiTiHfPd polycrystalline alloys.
Acta Mater. , 61 : 5036 -5049 .
[70]
Karaca H E Karaman I Basaran B Chumlyakov Y I Maier H J. 2006 . Magnetic field and stress induced martensite reorientation in NiMnGa ferromagnetic shape memory alloy single crystals.
Acta Mater. , 54 : 233 -245 .
[本文引用: 1]
[71]
Karaca H E Karaman I Basaran B Lagoudas D C Chumlyakov Y I Maier H J. 2007 . On the stress-assisted magnetic-field-induced phase transformation in Ni\(_{2}\)MnGa ferromagnetic shape memory alloys.
Acta Mater. , 55 : 4253 -4269 .
[本文引用: 1]
[72]
Karaman I Karaca H E Basaran B Lagoudas D C Chumlyakov Y I Maier H J. 2006 . Stress-assisted reversible magnetic field-induced phase transformation in Ni2MnGa magnetic shape memory alloys.
Scripta Mater. , 55 : 403 -406 .
[本文引用: 1]
[73]
Kastner O. 2012 . First Principles Modelling of Shape Memory Alloys. Berlin Heidelberg:
Springer.
[本文引用: 2]
[74]
Ke C B Cao S Zhang X P. 2015 . Phase field modeling of Ni-concentration distribution behavior around Ni\(_{4}\)Ti\(_{3}\) precipitates in NiTi alloys.
Comp. Mater. Sci. , 105 : 55 -65 .
[75]
Kiefer B Lagoudas D C. 2005 . Magnetic field-induced martensitic variant reorientation in magnetic shape memory alloys.
Philos. Mag. , 85 : 4289 -4329 .
[本文引用: 4]
[76]
Kim J H Inaba F Fukuda T Kakeshita T. 2006 . Effect of magnetic field on martensitic transformation temperature in Ni-Mn-Ga ferromagnetic shape memory alloys.
Acta Mater. , 54 : 493 -499 .
[本文引用: 1]
[77]
Ko W S Maisel S B Grabowski B Jeon J B Neugebauer J. 2017 . Atomic scale processes of phase transformations in nanocrystalline NiTi shape-memory alloys.
Acta Mater. , 123 : 90 -101 .
[本文引用: 5]
[78]
Kockar B Atli K C Ma J Haouaoui M Karaman I Nagasako M Kainuma R. 2010 . Role of severe plastic deformation on the cyclic reversibility of a Ti\(_{50.3}\)Ni\(_{33.7}\)Pd\(_{16}\) high temperature shape memory alloy
. Acta Mater. , 58 : 6411 -6420 .
[本文引用: 4]
[79]
Kockar B Karaman I Kim J I Chumlyakov Y. 2006 . A method to enhance cyclic reversibility of NiTiHf high temperature shape memory alloys.
Scripta Mater. , 54 : 2203 -2208 .
[本文引用: 2]
[80]
König D Zarnetta R Savan A Brunken H Ludwig A. 2011 . Phase transformation, structural and functional fatigue properties of Ti-Ni-Hf shape memory thin films.
Acta Mater. , 59 : 3267 -3275 .
[本文引用: 5]
[81]
Kumar P K Lagoudas D C. 2010 . Experimental and microstructural characterization of simultaneous creep, plasticity and phase transformation in high-temperature shape memory alloy.
Acta Mater. , 58 : 1618 -1628 .
[本文引用: 1]
[82]
Kundin J Pogorelov E Emmerich H. 2015 . Numerical investigation of the interaction between the martensitic transformation front and the plastic strain in austenite. J. Mech. Phys.
Solids , 76 : 65 -83 .
[83]
Kundin J Raabe D Emmerich H. 2011 . A phase-field model for incoherent martensitic transformations including plastic accommodation processes in the austenite. J. Mech. Phys.
Solids , 59 : 2082 -2102 .
[本文引用: 1]
[84]
Lagoudas D C. 2008 . Shape Memory Alloys: Modeling and Engineering Applications.
Springer.
[本文引用: 11]
[85]
Lagoudas D C Chatzigeorgiou G Kumar P K. 2009 a. Modeling and experimental study of simultaneous creep and transformation in polycrystalline high-temperature shape memory Alloys. J
. Intell. Mater. Syst. Struct. , 20 : 2257 -2267 .
[本文引用: 2]
[86]
Lagoudas D C Entchev P B. 2004 . Modeling of transformation-induced plasticity and its effect on the behavior of porous shape memory alloys. Part I: constitutive model for fully dense
SMAs. Mech. Mater. , 36 : 865 -892 .
[本文引用: 1]
[87]
Lagoudas D C Miller D A Rong L Kumar P K. 2009 b. Thermomechanical fatigue of shape memory alloys
. Smart Mater. Struct. , 18 : 085021 .
[本文引用: 1]
[88]
LaMaster D H Feigenbaum H P Ciocanel C Nelson I D. 2014 . A full 3D thermodynamic-based model for magnetic shape memory alloys. J
. Intell. Mater. Syst. Struct. , 26 : 663 -679 .
[本文引用: 2]
[89]
Lawrence T Lindquist P Ullakko K Müllner P. 2016 . Fatigue life and fracture mechanics of unconstrained Ni-Mn-Ga single crystals in a rotating magnetic field. Mater. Sci. Eng.
A , 654 : 221 -227 .
[本文引用: 2]
[90]
Lemaitre J Chaboche J L. 1994. Mechanics of solid materials. Cambridge University Press. .
[本文引用: 2]
[91]
Levitas V I Javanbakht M. 2012 . Advanced phase-field approach to dislocation evolution. Phys. Rev. B, 86:
140101(R ).
[本文引用: 2]
[92]
Levitas V I Javanbakht M. 2013 . Phase field approach to interaction of phase transformation and dislocation evolution.
Appl. Phys. Lett. , 102 : 251904 .
[本文引用: 1]
[93]
Levitas V I Javanbakht M. 2015 . Interaction between phase transformations and dislocations at the nanoscale. Part 1. General phase field approach. J. Mech. Phys.
Solids , 82 : 287 -319 .
[94]
Levitas V I Preston D L Lee D W. 2003 . Three-dimensional Landau theory for multivariant stress-induced martensitic phase transformations. III. Alternative potentials, critical nuclei, kink solutions, and dislocation theory. Phys. Rev.
B , 68 .
[95]
Lim T J Mcdowell D L. 1999 . Mechanical behavior of an Ni-Ti shape memory alloy under axial-torsional proportional and nonproportional loading. J
. Eng. Mater. Technol. , 121 : 9 -18 .
[本文引用: 5]
[96]
Liu Y McCormick P G. 1990 . Factors influencing the development of two-way shape memory in NiTi.
Acta Mater. , 38 : 1321 -1326 .
[本文引用: 5]
[97]
Liu Y Xie Z Van Humbeeck J Delaey L. 1998 . Asymmetry of stress-strain curves under tension and compression for NiTi shape memory alloys.
Acta Mater. , 46 : 4325 -4338 .
[98]
Ma J Karaman I Noebe R D. 2010 . High temperature shape memory alloys.
Int. Mater. Rev. , 55 : 257 -315 .
[本文引用: 1]
[99]
Mahtabi M J Shamsaei N Mitchell M R. 2015 . Fatigue of nitinol: The state-of-the-art and ongoing challenges. J
. Mech. Behav. Biomed. , 50 : 228 -254 .
[100]
Maletta C Sgambitterra E Furgiuele F Casati R Tuissi A. 2012 . Fatigue of pseudoelastic NiTi within the stress-induced transformation regime: A modified Coffin-Manson approach.
Smart Mater. Struct. , 21 : 112001 .
[本文引用: 2]
[101]
Maletta C Sgambitterra E Furgiuele F Casati R Tuissi A. 2014 . Fatigue properties of a pseudoelastic NiTi alloy: Strain ratcheting and hysteresis under cyclic tensile loading. Int. J.
Fatigue , 66 : 78 -85 .
[本文引用: 2]
[102]
Malik A Amberg G Borgenstam A {\AA}gren J. 2013 . Phase-field modelling of martensitic transformation: the effects of grain and twin boundaries.
Modell. Simul. Mater. Sci. Eng. , 21 : 085003 .
[103]
Malik A Yeddu H K Amberg G Borgenstam A {\AA}gren J. 2012 . Three dimensional elasto-plastic phase field simulation of martensitic transformation in polycrystal. Mater. Sci. Eng.
A , 556 : 221 -232 .
[104]
Marioni M A O'Handley R C Allen S M. 2002 . Analytical model for field-induced strain in ferromagnetic shape-memory alloy polycrystals. J
. Appl. Phys. , 91 : 7807 -7809 .
[本文引用: 2]
[105]
Mccluskey P J Zhao C Kfir O Vlassak J J. 2011 . Precipitation and thermal fatigue in Ni-Ti-Zr shape memory alloy thin films by combinatorial nanocalorimetry.
Acta Mater. , 59 : 5116 -5124 .
[本文引用: 7]
[106]
Mecking H Kocks U F. 1981 . Kinetics of flow and strain-hardening.
Acta Metall. , 29 : 1865 -1875 .
[107]
Meng X L Cai W Zheng Y F Tong Y X Zhao L C Zhou L M. 2002 . Stress-induced martensitic transformation behavior of a Ti-Ni-Hf high temperature shape memory alloy.
Mater. Lett. , 55 : 111 -115 .
[本文引用: 2]
[108]
Meng X L Zheng Y F Wang Z Zhao L C. 2000 . Shape memory properties of the Ti\(_{36}\)Ni\(_{49}\)Hf\(_{15}\) high temperature shape memory alloy.
Mater. Lett. , 45 : 128 -132 .
[本文引用: 1]
[109]
Miller D A Lagoudas D C. 2000 . Thermomechanical characterization of NiTiCu and NiTi SMA actuators: Influence of plastic strains.
Smart Mater. Struct. , 9 : 640 .
[本文引用: 2]
[110]
Mirzaeifar R Desroches R Yavari A. 2011 . Analysis of the rate-dependent coupled thermo-mechanical response of shape memory alloy bars and wires in tension.
Continuum Mech. Thermodyn. , 23 : 363 -385 .
[本文引用: 2]
[111]
Mirzaeifar R Gall K Zhu T Yavari A DesRoches R. 2014 . Structural transformations in NiTi shape memory alloy nanowires. J
. Appl. Phys. , 115 : 194307 .
[112]
Miyazaki S Imai T Igo Y Otsuka K. 1986 . Effect of cyclic deformation on the pseudoelasticity characteristics of Ti-Ni alloys. Metall. Mater. Trans.
A , 17 : 115 -120 .
[本文引用: 1]
[113]
Miyazaki S Oshiba M Nadai T. 1981 . Precaution on use of hydrochloride salts in pharmaceutical formulation. J
. Pharm. Sci. , 70 : 594 .
[本文引用: 2]
[114]
Mohd Jani J Leary M Subic A Gibson M A. 2014 . A review of shape memory alloy research, applications and opportunities.
Materials & Design ( 1980-2015 ), 56 : 1078 -1113 .
[本文引用: 2]
[115]
Morgan N B. 2004 . Medical shape memory alloy applications---the market and its products. Mater. Sci. Eng.
A , 378 : 16 -23 .
[本文引用: 1]
[116]
Morin C Moumni Z Zaki W. 2011 . Thermomechanical coupling in shape memory alloys under cyclic loadings: Experimental analysis and constitutive modeling. Int. J
. Plast. , 27 : 1959 -1980 .
[本文引用: 2]
[117]
Moumni Z Herpen A V Riberty P. 2005 . Fatigue analysis of shape memory alloys: Energy approach.
Smart Mater. Struct. , 14 : S287 .
[118]
Mousavi M R Arghavani J. 2017 . A three-dimensional constitutive model for magnetic shape memory alloys under magneto-mechanical loadings.
Smart Mater. Struct. , 26 : 015014 .
[本文引用: 7]
[119]
Müller C Bruhns O T. 2006 . A thermodynamic finite-strain model for pseudoelastic shape memory alloys. Int. J
. Plast. , 22 : 1658 -1682 .
[本文引用: 1]
[120]
Müllner P Chernenko V Wollgarten M Kostorz G. 2002 . Large cyclic deformation of a Ni-Mn-Ga shape memory alloy induced by magnetic fields. J
. Appl. Phys. , 92 : 6708 -6713 .
[121]
Murray S Farinelli M Kantner C Huang J Allen S O'Handley R. 1998 . Field-induced strain under load in Ni-Mn-Ga magnetic shape memory materials. J
. Appl. Phys. , 83 : 7297 -7299 .
[本文引用: 1]
[122]
Murray S O'Handley R Allen S. 2001 . Model for discontinuous actuation of ferromagnetic shape memory alloy under stress. J
. Appl. Phys. , 89 : 1295 -1301 .
[123]
Mutter D Nielaba P. 2013 . Simulation of the shape memory effect in a NiTi nano model system. J
. Alloys Compd. , 577 : S83 -S87 .
[本文引用: 1]
[124]
Niendorf T Lackmann J Gorny B Maier HJ. 2011 . In situ characterization of martensite variant formation in nickel-titanium shape memory alloy under biaxial loading.
Scripta Mater. , 65 , 915 -918 .
[本文引用: 1]
[125]
Norfleet D M Sarosi P M Manchiraju S Wagner M F X Uchic M D Anderson P M Mills M J. 2009 . Transformation-induced plasticity during pseudoelastic deformation in Ni-Ti microcrystals.
Acta Mater. , 57 : 3549 -3561 .
[本文引用: 6]
[126]
Paranjape H M Manchiraju S Anderson P M. 2016 . A phase field - Finite element approach to model the interaction between phase transformations and plasticity in shape memory alloys. Int. J
. Plast. , 80 : 1 -18 .
[127]
Pelton A R Huang G H Moine P Sinclair R. 2012 . Effects of thermal cycling on microstructure and properties in Nitinol. Mater. Sci. Eng.
A , 532 : 130 -138 .
[本文引用: 1]
[128]
Pelton A R. 2011 . Nitinol Fatigue: A Review of Microstructures and Mechanisms. J
. Mater. Eng. Perform. , 20 : 613 -617 .
[本文引用: 1]
[129]
Popov P Lagoudas D C. 2007 . A 3-D constitutive model for shape memory alloys incorporating pseudoelasticity and detwinning of self-accommodated martensite. Int. J
. Plast. , 23 : 1679 -1720 .
[本文引用: 2]
[130]
Pötschke M Weiss S Gaitzsch U Cong D Hürrich C Roth S Schultz L. 2010 . Magnetically resettable 0.16% free strain in polycrystalline Ni-Mn-Ga plates
. Scripta Mater. , 63 : 383 -386 .
[本文引用: 3]
[131]
Predki W Klönne M Knopik A. 2006 . Cyclic torsional loading of pseudoelastic NiTi shape memory alloys: Damping and fatigue failure. Mater. Sci. Eng.
A , 417 : 182 -189 .
[本文引用: 1]
[132]
Rao A Srinivasa A R Reddy J N. 2015 . Design of Shape Memory Alloy (SMA) Actuators.
Springer , 3 .
[本文引用: 2]
[133]
Robertson S Pelton A Ritchie R. 2012 . Mechanical fatigue and fracture of Nitinol.
Int. Mater. Rev. , 57 : 1 -37 .
[本文引用: 3]
[134]
Runciman A Xu D Pelton A R Ritchie R O. 2011 . An equivalent strain/Coffin-Manson approach to multiaxial fatigue and life prediction in superelastic Nitinol medical devices.
Biomaterials , 32 : 4987 -4993 .
[本文引用: 1]
[135]
Saghaian S M Karaca H E Tobe H Pons J Santamarta R Chumlyakov Y I Noebe R D. 2016 . Effects of Ni content on the shape memory properties and microstructure of Ni-rich NiTi-20Hf alloys.
Smart Mater. Struct. , 25 : 095029 .
[本文引用: 1]
[136]
Saleeb A F Kumar A Ii S A P Dhakal B. 2013 . The cyclic and evolutionary response to approach the attraction loops under stress controlled isothermal conditions for a multi-mechanism based multi-axial SMA model.
Mech. Mater. , 63 : 21 -47 .
[137]
Santamarta R Arr\'{o}yave R Pons J Evirgen A Karaman I Karaca H E Noebe R D. 2013 . TEM study of structural and microstructural characteristics of a precipitate phase in Ni-rich Ni-Ti-Hf and Ni-Ti-Zr shape memory alloys.
Acta Mater. , 61 : 6191 -6206 .
[本文引用: 1]
[138]
Sasaki T T Hornbuckle B C Noebe R D Bigelow G S Weaver M L Thompson G B. 2013 . Effect of aging on microstructure and shape memory properties of a Ni-48Ti-25Pd (At. Pct) alloy. Metall. Mater. Trans.
A , 44 : 1388 -1400 .
[139]
Saxena A Wu Y Lookman T Shenoy S Bishop A. 1997 . Hierarchical pattern formation in elastic materials. Phy.
A , 239 : 18 -34 .
[140]
Segu\'{\i} C Chernenko V A Pons J Cesari E Khovailo V Takagi T. 2005 . Low temperature-induced intermartensitic phase transformations in Ni-Mn-Ga single crystal.
Acta Mater. , 53 : 111 -120 .
[本文引用: 1]
[141]
Shaw J A Kyriakides S. 1995 . Thermomechanical aspects of NiTi. J. Mech. Phys.
Solids , 43 : 1243 -1281 .
[本文引用: 2]
[142]
Shaw J A Kyriakides S. 1997 . Initiation and propagation of localized deformation in elasto-plastic strips under uniaxial tension. Int. J
. Plast. , 13 : 837 -871 .
[本文引用: 2]
[143]
Shchyglo O Salman U Finel A. 2012 . Martensitic phase transformations in Ni-Ti-based shape memory alloys: The Landau theory.
Acta Mater. , 60 : 6784 -6792 .
[本文引用: 1]
[144]
\v{S}ittner P Nov\'{a}k V Landa M Luk\'{a}\v{s} P. 2007 . Deformation processes in functional materials studied by in situ neutron diffraction and ultrasonic techniques. Mater. Sci. Eng.
A , 462 , 12 -22 .
[本文引用: 1]
[145]
Skelton R P Vilhelmsen T Webster G A. 1998 . Energy criteria and cumulative damage during fatigue crack growth. Int. J.
Fatigue , 20 : 641 -649 .
[本文引用: 2]
[146]
Skelton R. 1991 . Energy criterion for high temperature low cycle fatigue failure.
Mater. Sci. Technol. , 7 : 427 -440 .
[本文引用: 1]
[147]
Song D Kang G Z Kan Q H Yu C Zhang C. 2015 . Damage-based life prediction model for uniaxial low-cycle stress fatigue of super-elastic NiTi shape memory alloy microtubes.
Smart Mater. Struct. , 24 : 085007 .
[148]
Song D Kang G Z Kan Q H Yu C Zhang C. 2016 . Multiaxial low-cycle fatigue failure mechanism of super-elastic NiTi shape memory alloy micro-tubes. Mater. Sci. Eng.
A , 665 : 17 -25 .
[149]
Song D Kang G Z Kan Q H Yu C Zhang C. 2017 . Effects of peak stress and stress amplitude on multiaxial transformation ratchetting and fatigue life of superelastic NiTi SMA micro-tubes: Experiments and life-prediction model. Int. J.
Fatigue , 96 : 252 -260 .
[本文引用: 1]
[150]
Song G Ma N Li H N. 2006 . Applications of shape memory alloys in civil structures.
Eng. Struct. , 28 : 1266 -1274 .
[本文引用: 1]
[151]
Straka L Heczko O. 2003 . Superelastic response of Ni-Mn-Ga martensite in magnetic fields and a simple model.
IEEE Trans. Magn. , 39 : 3402 -3404 .
[本文引用: 1]
[152]
Sun L Huang W M Ding Z Zhao Y Wang C C Purnawali H Tang C. 2012 a. Stimulus-responsive shape memory materials: A review
. Mater. Des. , 33 : 577 -640 .
[153]
Sun Q P Li Z Q. 2002 . Phase transformation in superelastic NiTi polycrystalline micro-tubes under tension and torsion--from localization to homogeneous deformation. Int. J
. Solids. Struct. , 39 : 3797 -3809 .
[本文引用: 1]
[154]
Sun Q P Zhao H Zhou R Saletti D Yin H. 2012 b. Recent advances in spatiotemporal evolution of thermomechanical fields during the solid-solid phase transition. C. R.
Mecanique , 340 : 349 -358 .
[本文引用: 1]
[155]
Tadayyon G Guo Y Mazinani M Zebarjad S M Tiernan P Tofail S A M Biggs M J P. 2017 . Effect of different stages of deformation on the microstructure evolution of Ti-rich NiTi shape memory alloy.
Mater. Charact. , 125 : 51 -66 .
[本文引用: 2]
[156]
Tian Q Wu J. 2002 . Tensile behavior of Ti\(_{50.6}\)Pd\(_{30}\)Ni1\(_{9.4}\) alloy under different tensile conditions. Mater. Sci. Eng.
A , 325 : 249 -254 .
[本文引用: 1]
[157]
Tickle R James R D Shield T Wuttig M Kokorin V V. 1999 . Ferromagnetic shape memory in the NiMnGa system.
IEEE Trans. Magn. , 35 : 4301 -4310 .
[158]
Tickle R James R D. 1999 . Magnetic and magnetomechanical properties of Ni\(_{2}\)MnGa. J
. Magn. Magn. Mater. , 195 : 627 -638 .
[159]
Tobushi H Nakahara T Shimeno Y Hashimoto T. 2000 . Low-cycle fatigue of TiNi shape memory alloy and formulation of fatigue life. T.
Asme , 122 : 186 -191 .
[160]
Ullakko K Huang J K Kantner C Ohandley R C Kokorin V V. 1996 . Large magnetic-field-induced strains in Ni2MnGa single crystals.
Appl. Phys. Lett. , 69 : 1966 -1968 .
[本文引用: 2]
[161]
Van Humbeeck J. 1999 . Non-medical applications of shape memory alloys.
Mater. Sci. Eng. A, 273- 275 : 134 -148 .
[本文引用: 1]
[162]
Wagner M Sawaguchi T Kausträter G Höffken D Eggeler G. 2004 . Structural fatigue of pseudoelastic NiTi shape memory wires. Mater. Sci. Eng.
A , 378 : 105 -109 .
[本文引用: 3]
[163]
Wang B Kang G Z Kan Q H Zhou K Yu C. 2017 . Molecular dynamics simulations to the pseudo-elasticity of NiTi shape memory alloy nano-pillar subjected to cyclic compression.
Comp. Mater. Sci. , 131 : 132 -138 .
[164]
Wang X Li F. 2010 . A kinetics model for martensite variants rearrangement in ferromagnetic shape memory alloys. J
. Appl. Phys. , 108 : 113921 .
[本文引用: 3]
[165]
Wang Y Khachaturyan A. 1997 . Three-dimensional field model and computer modeling of martensitic transformations.
Acta Mater. , 45 : 759 -773 .
[166]
Wu J Tian Q. 2003 . The superelasticity of TiPdNi high temperature shape memory alloy.
Intermetallics , 11 : 773 -778 .
[本文引用: 1]
[167]
Xie X Kan Q H Kang G Z Li J Qiu B Yu C. 2016 a. Observation on the transformation domains of super-elastic NiTi shape memory alloy and their evolutions during cyclic loading
. Smart Mater. Struct. , 25 : 045003 .
[本文引用: 5]
[168]
Xie X Kan Q H Kang G Z Lu F C Chen K J. 2016 b. Observation on rate-dependent cyclic transformation domain of super-elastic NiTi shape memory alloy. Mater. Sci. Eng.
A , 671 : 32 -47 .
[本文引用: 1]
[169]
Xie Z Liu Y Van Humbeeck J. 1998 . Microstructure of NiTi shape memory alloy due to tension-compression cyclic deformation.
Acta Mater. , 46 : 1989 -2000 .
[本文引用: 1]
[170]
Yang F Coughlin D R Phillips P J Yang L Devaraj A Kovarik L Noebe R D Mills M J. 2013 . Structure analysis of a precipitate phase in an Ni-rich high-temperature NiTiHf shape memory alloy.
Acta Mater. , 61 : 3335 -3346 .
[本文引用: 2]
[171]
Yin H He Y Sun Q. 2014 . Effect of deformation frequency on temperature and stress oscillations in cyclic phase transition of NiTi shape memory alloy. J. Mech. Phys.
Solids , 67 : 100 -128 .
[本文引用: 4]
[172]
Yin H Yan Y Huo Y Sun Q. 2013 . Rate dependent damping of single crystal CuAlNi shape memory alloy.
Mater. Lett. , 109 : 287 -290 .
[173]
Yu C Kang G Z Kan Q H. 2014 a. A physical mechanism based constitutive model for temperature-dependent transformation ratchetting of NiTi shape memory alloy: One-dimensional model
. Mech. Mater. , 78 : 1 -10 .
[本文引用: 6]
[174]
Yu C Kang G Z Kan Q H. 2016 . A macroscopic multi-mechanism based constitutive model for the thermo-mechanical cyclic degeneration of shape memory effect of NiTi shape memory alloy.
Acta Mech. Sinica , 1 -16 .
[本文引用: 1]
[175]
Yu S Y Wei J J Kang S S Chen J L Wu G H. 2014 b. Large temperature and magnetic field induced strain in polycrystalline Ni\(_{50}\)Mn\(_{36}\)In\(_{14}\)-xSbx alloys. J
. Alloys Compd. , 586 : 328 -332 .
[本文引用: 1]
[176]
Zaki W Moumni Z. 2007 . A three-dimensional model of the thermomechanical behavior of shape memory alloys. J. Mech. Phys.
Solids , 55 : 2455 -2490 .
[本文引用: 1]
[177]
Zhang X Feng P He Y Yu T Sun Q. 2010 . Experimental study on rate dependence of macroscopic domain and stress hysteresis in NiTi shape memory alloy strips. Int. J
. Mech. Sci. , 52 : 1660 -1670 .
[本文引用: 1]
[178]
Zhang Y You Y Moumni Z Anlas G Zhu J Zhang W. 2017 . Experimental and theoretical investigation of the frequency effect on low cycle fatigue of shape memory alloys. Int. J. Plast., 90: 1-30. Zhang Y, Zhu J, Moumni Z, Herpen A V, Zhang W. 2016. Energy-based fatigue model for shape memory alloys including thermomechanical coupling
. Smart Mater. Struct. , 25 : 035042 .
[本文引用: 2]
[179]
Zhong Y Gall K Zhu T. 2012 . Atomistic characterization of pseudoelasticity and shape memory in NiTi nanopillars.
Acta Mater. , 60 : 6301 -6311 .
[本文引用: 1]
[180]
Zhong Y Zhu T. 2014 . Phase-field modeling of martensitic microstructure in NiTi shape memory alloys.
Acta Mater. , 75 : 337 -347 .
[181]
Zhu Y Chen T Teng Y Liu B Xue L. 2016 . Experimental study of directionally solidified ferromagnetic shape memory alloy under multi-field coupling. J
. Magn. Magn. Mater. , 417 : 249 -257 .
[本文引用: 7]
[182]
Zhu Y Dui G. 2007 . Micromechanical modeling of the stress-induced superelastic strain in magnetic shape memory alloy.
Mech. Mater. , 39 : 1025 -1034 .
[本文引用: 6]
[183]
Zhu Y Dui G. 2008 . Model for field-induced reorientation strain in magnetic shape memory alloy with tensile and compressive loads. J
. Alloys Compd. , 459 : 55 -60 .
[本文引用: 1]
[184]
Zhu Y Dui G. 2010 . Influence of magnetization rotation on martensite reorientation in magnetic shape memory alloy.
Acta Mech. Solida Sin. , 23 : 13 -19 .
[本文引用: 4]
[185]
Zotov N Pfund M Polatidis E Mark A F Mittemeijer E J. 2017 . Change of transformation mechanism during pseudoelastic cycling of NiTi shape memory alloys. Mater. Sci. Eng.
A , 682 : 178 -191 .
[本文引用: 1]
NiTi 形状记忆合金热--力耦合循环变形行为宏微观实验和理论研究进展
4
2015
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
... 由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变. ...
... 基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ). ...
NiTi 形状记忆合金热--力耦合循环变形行为宏微观实验和理论研究进展
4
2015
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
... 由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变. ...
... 基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ). ...
超弹性镍钛形状记忆合金循环变形行为的研究进展
4
2011
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
... 由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变. ...
... 基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ). ...
超弹性镍钛形状记忆合金循环变形行为的研究进展
4
2011
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
... 由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变. ...
... 基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ). ...
超弹性 NiTi 形状记忆合金微管的疲劳行为及损伤演化模型研究. [博士论文]
0
2015
超弹性 NiTi 形状记忆合金微管的疲劳行为及损伤演化模型研究. [博士论文]
0
2015
1
... 综上所述, 已有研究在NiTi形状记忆合金热--力耦合循环变形过程中微结构的形成和演变的微观观察以及宏观变形行为微观机理的总结方面还存在很多不足, 相关研究还不系统、不深入, 需要开展大力的研究, 特别是可以借用扫描电子显微镜(SEM)原位(高温)疲劳试验与TEM观察相结合的技术优势, 获得更多的形状记忆合金试样表面或亚表面微结构的演变行为、损伤机制的实验数据以及微结构在相变演变过程中的形貌变化机制及影响因素等(王习术 2010 ). ...
1
... 综上所述, 已有研究在NiTi形状记忆合金热--力耦合循环变形过程中微结构的形成和演变的微观观察以及宏观变形行为微观机理的总结方面还存在很多不足, 相关研究还不系统、不深入, 需要开展大力的研究, 特别是可以借用扫描电子显微镜(SEM)原位(高温)疲劳试验与TEM观察相结合的技术优势, 获得更多的形状记忆合金试样表面或亚表面微结构的演变行为、损伤机制的实验数据以及微结构在相变演变过程中的形貌变化机制及影响因素等(王习术 2010 ). ...
6
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 热致形状记忆合金是最先问世的形状记忆合金, 并且是目前研究最为集中的智能材料之一.在这类形状记忆合金中应用最为广泛的是近等原子比的NiTi形状记忆合金和NiTiX高温形状记忆合金, 同时其他的热致形状记忆合金(诸如Cu基和Fe基形状记忆合金等)的热--力耦合循环变形行为与前述两种合金的非常相似(赵连城等 2002 ), 因此本节仅对NiTi和NiTiX形状记忆合金的相关研究成果进行总结, 对这两类合金的基本力学行为及其相变机理等不做阐述, 相关内容可参见文献(Lagoudas 2008 , 赵连城等 2002 ). ...
... , 赵连城等 2002 ). ...
... 已有研究表明, 超弹性NiTi形状记忆合金的相变应力明显依赖于实验环境温度, 由Clausius-Clapeyron关系式可知实验温度每升高1K, 该合金的马氏体相变开始应力将升高8 MPa左右 (Lagoudas 2008 , 赵连城等 2002 ).NiTi形状记忆合金的热--力耦合行为与相变潜热的释放和吸收以及由此而引起的温度变化密切相关, Yu等(2014a)专门讨论了超弹性NiTi形状记忆合金在应变控制循环变形过程中出现的超弹性劣化效应的温度相关性, 结果如图1 所示. 由图1 (b) \(\sim \) 图1 (d)可见: 随实验环境温度的升高, 残余应变的累积效果随循环次数的增大越显著, 耗散能密度和马氏体相变开始应力减小就越明显, 即循环变形对NiTi形状记忆合金的超弹性劣化作用就越显著, 相变棘轮行为发展就更为迅速. ...
... 后来, 宋迪(2015) 在此基础上进一步拓展建立了基于损伤演化的NiTi形状记忆合金非比例多轴疲劳寿命预测模型.为了反映多轴加载路径下出现的马氏体重取向以及重取向诱发塑性对疲劳失效寿命的影响, 在前述三种损伤机制上, 引入了一项新的马氏体重取向损伤\(D_{\rm reo}\), 并定义为\[ D_{\rm reo} = g_4 \cdot N\ \ (48)\]\[g_4 = c \cdot \lambda \ \ (49)\]其中, \(c\)为材料常数, \(\lambda\)为考虑不同形状的多轴加载路径对NiTi形状记忆合金疲劳失效寿命影响的加载路径因子, 但其定义不同于Song等(2017) 在半经验型多轴疲劳寿命预测模型(即式(35))中引入的定义, 具体可见文献(宋迪2015). 最后, 在失效判据\(D=D_{\rm ini}+D_{\rm pro}+D_{\rm trans}+D_{\rm reo}=1\)的基础上, 得到了如下的寿命预测模型\[ N_{\rm f} = \dfrac{1 - (g_1 + g_3 ) \cdot \int_0^{N_{\rm sat} } {W_N{\rm d}N + (g_2 + W_{\rm sat} \cdot g_3 ) \cdot (1 +N_{\rm sat} )} }{g_2 + W_{\rm sat} \cdot g_3 + g_4 } \ \ (50)\] ...
... 利用该模型, 宋迪(2015) 对超弹性NiTi形状记忆合金的非比例多轴应力控制疲劳失效寿命进行了预测, 预测结果与实验结果的比较见图41 (b)所示. 由图可见, 所有的点都位于2倍分散带内, 并且大部分点位于1.5倍误差带以内, 这说明基于损伤演化的非比例多轴疲劳寿命预测模型预测效果良好. ...
6
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 热致形状记忆合金是最先问世的形状记忆合金, 并且是目前研究最为集中的智能材料之一.在这类形状记忆合金中应用最为广泛的是近等原子比的NiTi形状记忆合金和NiTiX高温形状记忆合金, 同时其他的热致形状记忆合金(诸如Cu基和Fe基形状记忆合金等)的热--力耦合循环变形行为与前述两种合金的非常相似(赵连城等 2002 ), 因此本节仅对NiTi和NiTiX形状记忆合金的相关研究成果进行总结, 对这两类合金的基本力学行为及其相变机理等不做阐述, 相关内容可参见文献(Lagoudas 2008 , 赵连城等 2002 ). ...
... , 赵连城等 2002 ). ...
... 已有研究表明, 超弹性NiTi形状记忆合金的相变应力明显依赖于实验环境温度, 由Clausius-Clapeyron关系式可知实验温度每升高1K, 该合金的马氏体相变开始应力将升高8 MPa左右 (Lagoudas 2008 , 赵连城等 2002 ).NiTi形状记忆合金的热--力耦合行为与相变潜热的释放和吸收以及由此而引起的温度变化密切相关, Yu等(2014a)专门讨论了超弹性NiTi形状记忆合金在应变控制循环变形过程中出现的超弹性劣化效应的温度相关性, 结果如图1 所示. 由图1 (b) \(\sim \) 图1 (d)可见: 随实验环境温度的升高, 残余应变的累积效果随循环次数的增大越显著, 耗散能密度和马氏体相变开始应力减小就越明显, 即循环变形对NiTi形状记忆合金的超弹性劣化作用就越显著, 相变棘轮行为发展就更为迅速. ...
... 后来, 宋迪(2015) 在此基础上进一步拓展建立了基于损伤演化的NiTi形状记忆合金非比例多轴疲劳寿命预测模型.为了反映多轴加载路径下出现的马氏体重取向以及重取向诱发塑性对疲劳失效寿命的影响, 在前述三种损伤机制上, 引入了一项新的马氏体重取向损伤\(D_{\rm reo}\), 并定义为\[ D_{\rm reo} = g_4 \cdot N\ \ (48)\]\[g_4 = c \cdot \lambda \ \ (49)\]其中, \(c\)为材料常数, \(\lambda\)为考虑不同形状的多轴加载路径对NiTi形状记忆合金疲劳失效寿命影响的加载路径因子, 但其定义不同于Song等(2017) 在半经验型多轴疲劳寿命预测模型(即式(35))中引入的定义, 具体可见文献(宋迪2015). 最后, 在失效判据\(D=D_{\rm ini}+D_{\rm pro}+D_{\rm trans}+D_{\rm reo}=1\)的基础上, 得到了如下的寿命预测模型\[ N_{\rm f} = \dfrac{1 - (g_1 + g_3 ) \cdot \int_0^{N_{\rm sat} } {W_N{\rm d}N + (g_2 + W_{\rm sat} \cdot g_3 ) \cdot (1 +N_{\rm sat} )} }{g_2 + W_{\rm sat} \cdot g_3 + g_4 } \ \ (50)\] ...
... 利用该模型, 宋迪(2015) 对超弹性NiTi形状记忆合金的非比例多轴应力控制疲劳失效寿命进行了预测, 预测结果与实验结果的比较见图41 (b)所示. 由图可见, 所有的点都位于2倍分散带内, 并且大部分点位于1.5倍误差带以内, 这说明基于损伤演化的非比例多轴疲劳寿命预测模型预测效果良好. ...
高温形状记忆合金的研究进展
9
2014
... 正如Kang 和 Song (2015) 综述的那样, 通过对疲劳断口的SEM观察发现, 超弹性NiTi合金(初始相为奥氏体)的断口形貌和形状记忆NiTi合金(初始相为马氏体)基本相同, 均可见明显的疲劳条纹、二次裂纹和河流状解理图案以及一些大而浅的韧窝.在NiTi形状记忆合金疲劳断口的SEM观察结果基础上, 进一步总结得出:NiTi形状记忆合金的疲劳断裂可分为两阶段, 即疲劳裂纹萌生阶段和扩展阶段; 在疲劳断裂过程中, 同时会出现由疲劳载荷引起的稳态的裂纹长大和由大而浅的韧窝代表的塑性过载断裂.另外, 从整个疲劳失效过程中的应力--应变响应曲线可以看到, 在循环稳定后(从200周开始直至疲劳断裂发生), 滞回环形状和大小基本上不会发生可观察的变化, 疲劳断裂突然毫无宏观征兆地发生. 这说明, NiTi形状记忆合金在疲劳失效过程中的裂纹萌生和扩展机制与普通金属有明显不同.Charkaluk 等(2000 , 2002 ), Skelton 等(1991 , 1998 )以及Dunand-Chatellet 和 Moumni (2012) 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
... 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
... 由于NiTi形状记忆合金的疲劳失效行为较为复杂, 涉及热弹性马氏体相变及其相关的复杂微观结构变化, 因此, 目前对其疲劳损伤机理的研究还不多, 其复杂的损伤演化过程还需要进行深入而系统的实验观察, 合理而准确的损伤演变方程还需要进一步探讨. 最近, Song等(2015) 和宋迪(2015)在超弹性NiTi形状记忆合金应力控制的单轴和多轴疲劳实验研究的基础上, 引入一个基于耗散能密度的损伤变量, 揭示了定义的损伤变量在疲劳失效过程中的演变特征, 建立了相应的损伤演变方程, 进而在基于损伤演变的NiTi形状记忆合金疲劳失效寿命预测模型构建方面进行了很有意义的尝试. ...
... Song等(2015) 首先在超弹性NiTi形状记忆合金单轴应力控制疲劳实验的基础上, 将损伤变量\(D\)定义为一定循环次数\(N\)下的累积耗散能密度与材料疲劳失效时\((N_{\rm f})\)总的累积耗散能密度之比, 即\[ D = \dfrac{\sum\limits_{i = 1}^N {W_i }}{\sum\limits_{i = 1}^{N_{\rm f} } {W_i } } \ \ (38)\]其中, \(W_{i}\)为一个循环次数内的耗散能密度.该损伤变量的定义考虑了稳定循环达到之前的循环变形行为对总的疲劳损伤的影响. ...
... 同时, 结合已有的实验结果, Song 等(2015) 将超弹性NiTi形状记忆合金的单轴疲劳损伤进一步看成是如下三部分之和, 即 ...
... 利用该模型, Song等(2015) 对超弹性NiTi形状记忆合金的单轴应力控制疲劳失效寿命进行了预测, 预测结果和实验结果的比较见图41 (a)所示. 由图可见, 所有的点都位于1.5倍误差带以内, 这说明基于损伤演化的寿命预测模型预测效果良好. ...
... NiTi形状记忆合金单轴和多轴疲劳寿命比较图. (a) 单轴(Song et al. 2015 ), (b) 多轴 (宋迪 2015) ...
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
高温形状记忆合金的研究进展
9
2014
... 正如Kang 和 Song (2015) 综述的那样, 通过对疲劳断口的SEM观察发现, 超弹性NiTi合金(初始相为奥氏体)的断口形貌和形状记忆NiTi合金(初始相为马氏体)基本相同, 均可见明显的疲劳条纹、二次裂纹和河流状解理图案以及一些大而浅的韧窝.在NiTi形状记忆合金疲劳断口的SEM观察结果基础上, 进一步总结得出:NiTi形状记忆合金的疲劳断裂可分为两阶段, 即疲劳裂纹萌生阶段和扩展阶段; 在疲劳断裂过程中, 同时会出现由疲劳载荷引起的稳态的裂纹长大和由大而浅的韧窝代表的塑性过载断裂.另外, 从整个疲劳失效过程中的应力--应变响应曲线可以看到, 在循环稳定后(从200周开始直至疲劳断裂发生), 滞回环形状和大小基本上不会发生可观察的变化, 疲劳断裂突然毫无宏观征兆地发生. 这说明, NiTi形状记忆合金在疲劳失效过程中的裂纹萌生和扩展机制与普通金属有明显不同.Charkaluk 等(2000 , 2002 ), Skelton 等(1991 , 1998 )以及Dunand-Chatellet 和 Moumni (2012) 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
... 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
... 由于NiTi形状记忆合金的疲劳失效行为较为复杂, 涉及热弹性马氏体相变及其相关的复杂微观结构变化, 因此, 目前对其疲劳损伤机理的研究还不多, 其复杂的损伤演化过程还需要进行深入而系统的实验观察, 合理而准确的损伤演变方程还需要进一步探讨. 最近, Song等(2015) 和宋迪(2015)在超弹性NiTi形状记忆合金应力控制的单轴和多轴疲劳实验研究的基础上, 引入一个基于耗散能密度的损伤变量, 揭示了定义的损伤变量在疲劳失效过程中的演变特征, 建立了相应的损伤演变方程, 进而在基于损伤演变的NiTi形状记忆合金疲劳失效寿命预测模型构建方面进行了很有意义的尝试. ...
... Song等(2015) 首先在超弹性NiTi形状记忆合金单轴应力控制疲劳实验的基础上, 将损伤变量\(D\)定义为一定循环次数\(N\)下的累积耗散能密度与材料疲劳失效时\((N_{\rm f})\)总的累积耗散能密度之比, 即\[ D = \dfrac{\sum\limits_{i = 1}^N {W_i }}{\sum\limits_{i = 1}^{N_{\rm f} } {W_i } } \ \ (38)\]其中, \(W_{i}\)为一个循环次数内的耗散能密度.该损伤变量的定义考虑了稳定循环达到之前的循环变形行为对总的疲劳损伤的影响. ...
... 同时, 结合已有的实验结果, Song 等(2015) 将超弹性NiTi形状记忆合金的单轴疲劳损伤进一步看成是如下三部分之和, 即 ...
... 利用该模型, Song等(2015) 对超弹性NiTi形状记忆合金的单轴应力控制疲劳失效寿命进行了预测, 预测结果和实验结果的比较见图41 (a)所示. 由图可见, 所有的点都位于1.5倍误差带以内, 这说明基于损伤演化的寿命预测模型预测效果良好. ...
... NiTi形状记忆合金单轴和多轴疲劳寿命比较图. (a) 单轴(Song et al. 2015 ), (b) 多轴 (宋迪 2015) ...
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
超弹性镍钛形状记忆合金单轴相变棘轮行为的宏观唯象本构模型
1
2017
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
超弹性镍钛形状记忆合金单轴相变棘轮行为的宏观唯象本构模型
1
2017
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
High-cycle fatigue of 10M Ni-Mn-Ga magnetic shape memory alloy in reversed mechanical loading.
5
2010
... 在铁磁形状记忆合金循环载荷下的功能性劣化方面, Karaca等(2006) 通过对NiMnGa单晶施加循环磁载荷, 发现随着循环过程的进行, 残余应变会逐渐累积, 如图47 所示, 这与NiTi形状记忆合金在温度诱发循环相变过程中残余应变累积的现象类似.Aaltio 等(2010) 研究了NiMnGa单晶在单纯机械载荷作用下的循环变形特性, 结果表明: 与NiTi形状记忆合金类似, NiMnGa在循环变形过程中出现了明显的功能性劣化, 即重定向开始应力和重定向模量均随着循环次数的增大而升高, 如图48 所示. Aaltio 等(2010) 指出, 上述的功能性劣化现象来源于两个方面:一是在循环机械载荷作用下, 晶体缺陷会逐渐形核并累积; 二是缺陷的存在阻碍了马氏体孪生界面运动, 从而造成重定向开始应力和重定向模量逐渐升高. ...
... 所示. Aaltio 等(2010) 指出, 上述的功能性劣化现象来源于两个方面:一是在循环机械载荷作用下, 晶体缺陷会逐渐形核并累积; 二是缺陷的存在阻碍了马氏体孪生界面运动, 从而造成重定向开始应力和重定向模量逐渐升高. ...
... 综上所述, 虽然铁磁形状记忆合金在实验研究方面已取得了长足的发展, 但大多数实验研究仅仅关注了材料在磁--力加卸载下的马氏体重定向及相变特性.虽然Karaca 等(2006) 和Aaltio等(2010) 研究了材料在循环载荷作用下的循环变形特性, 但载荷模式仅仅是单一磁或机械载荷, 尚缺少在热--力--磁多场环境下对材料循环变形特性的宏观实验观察.因此, 随着铁磁形状记忆合金日益广泛的应用, 对材料在热--力--磁多场环境下循环变形特性的实验研究工作亟待开展. ...
... (2)机械载荷诱发疲劳失效. Aaltio等(2010) 研究了机械循环载荷作用下NiMnGa单晶的疲劳特性, 所得的典型循环应力--应变曲线如图48 所示. 由图可见, 与普通NiTi形状记忆合金类似, NiMnGa单晶在循环变形中也会出现明显的功能性劣化, 即重定向开始应力和重定向模量均随着循环次数的增大而升高. Aaltio等(2010) 指出, 上述的功能性劣化现象来源于两个方面: 一是在机械循环载荷作用下, 马氏体孪晶结构逐渐从大孪晶转变为细孪晶, 导致新孪晶形成后自由运动空间变小, 从而增大了新孪晶的运动阻力, 如图55 所示; 二是在循环变形过程中, 晶体缺陷(如位错、空洞)逐渐累积, 这些缺陷的存在增大了材料内部的应力场梯度, 从而阻碍了马氏体孪生界面运动, 从而造成重定向模量逐渐升高. 同时, Aaltio 等(2010) 的研究还表明: 材料的疲劳寿命随着应变幅值的增大而显著降低; 由于马氏体重定向机制是二级相变, 相变前后不涉及到潜热的释放, 因此材料对加载频率的依赖性很低; 虽然在循环变形过程中应力--应变曲线发生明显改变, 然而马氏体相变温度和居里温度保持不变; 材料中加工时预先存在的一些裂纹易于成为继发的裂纹源, 然而, 裂纹的扩展方向并不平行于预先存在的裂纹方向, 而是沿着马氏体孪晶的(101)晶面扩展, 因此, 在宏观上可以观察到裂纹与外加应力方向呈45\(^\circ\)角, 如图56 所示. ...
... NiMnGa形状记忆合金单晶表面裂纹形貌(预先存在裂纹和新裂纹) (Aaltio et al.2010 ) ...
Stress hysteresis and temperature dependence of phase transition stress in nanostructured NiTi---Effects of grain size.
1
2013
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
Effects of grain size on the rate-dependent thermomechanical responses of nanostructured superelastic NiTi.
1
2014
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening.
1
1979
... (1) Cahn-Hilliard模型 (Cahn & Hilliard 1958 , 1959 ), 这种模型的相由保守的场变量唯一决定; (2) Allen-Cahn模型 (Cahn {\rm&} Allen 1977 , Allen & Cahn 1979 ), 这种模型的相无法由浓度、温度和压强等唯一决定, 而需要引入一个或多个额外的非保守场变量即序参量来决定局部相. 目前, 大部分的相场模拟是基于Allen-Cahn模型及其改进模型开展的.Allen-Cahn模型的动力学方程通常也称之为时间相关Ginzburg-Landau(TDGL)方程, 求解该动力学方程的数值解法有很多, 最常见的是基于统一空间网格和精确时间步长的简单二阶有限差分法 (Fan & Chen 1997 ). 从已有研究中可归纳出相场模拟的4个步骤: (1)为研究材料系统确定合适的序参数; (2)将局部能量密度表示为所选序参数的函数, 并得出材料系统的自由能泛函, 这些函数必须正确描述系统的对称性和热力学性质; (3)由自由能泛函得到相场动力学方程, 并将从实验数据或基础计算中得到的唯象系数带入动力学方程; (4)确定正确的初始和边界条件并选择适当的方法求解动力学方程. ...
A phenomenological model for the magneto-mechanical response of single-crystal magnetic shape memory alloys. Eur. J. Mech. A
1
2015
... 如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景. ...
Rate-dependent thermomechanical modelling of superelastic shape-memory alloys for seismic applications. J
0
2008
Thermomechanical cycling of a NiTi shape memory alloy-macroscopic response and microstructural evolution. Int. J
1
2014
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
Correlation between mechanical behavior and actuator-type performance of Ni-Ti-Pd high-temperature shape memory alloys.
4
2007
... NiMnGa形状记忆合金单晶在循环应力作用下的应力--应变曲线(Aaltio et al. 2010 ) ...
... (2)机械载荷诱发疲劳失效. Aaltio等(2010) 研究了机械循环载荷作用下NiMnGa单晶的疲劳特性, 所得的典型循环应力--应变曲线如图48 所示. 由图可见, 与普通NiTi形状记忆合金类似, NiMnGa单晶在循环变形中也会出现明显的功能性劣化, 即重定向开始应力和重定向模量均随着循环次数的增大而升高. Aaltio等(2010) 指出, 上述的功能性劣化现象来源于两个方面: 一是在机械循环载荷作用下, 马氏体孪晶结构逐渐从大孪晶转变为细孪晶, 导致新孪晶形成后自由运动空间变小, 从而增大了新孪晶的运动阻力, 如图55 所示; 二是在循环变形过程中, 晶体缺陷(如位错、空洞)逐渐累积, 这些缺陷的存在增大了材料内部的应力场梯度, 从而阻碍了马氏体孪生界面运动, 从而造成重定向模量逐渐升高. 同时, Aaltio 等(2010) 的研究还表明: 材料的疲劳寿命随着应变幅值的增大而显著降低; 由于马氏体重定向机制是二级相变, 相变前后不涉及到潜热的释放, 因此材料对加载频率的依赖性很低; 虽然在循环变形过程中应力--应变曲线发生明显改变, 然而马氏体相变温度和居里温度保持不变; 材料中加工时预先存在的一些裂纹易于成为继发的裂纹源, 然而, 裂纹的扩展方向并不平行于预先存在的裂纹方向, 而是沿着马氏体孪晶的(101)晶面扩展, 因此, 在宏观上可以观察到裂纹与外加应力方向呈45\(^\circ\)角, 如图56 所示. ...
... 所示. 由图可见, 与普通NiTi形状记忆合金类似, NiMnGa单晶在循环变形中也会出现明显的功能性劣化, 即重定向开始应力和重定向模量均随着循环次数的增大而升高. Aaltio等(2010) 指出, 上述的功能性劣化现象来源于两个方面: 一是在机械循环载荷作用下, 马氏体孪晶结构逐渐从大孪晶转变为细孪晶, 导致新孪晶形成后自由运动空间变小, 从而增大了新孪晶的运动阻力, 如图55 所示; 二是在循环变形过程中, 晶体缺陷(如位错、空洞)逐渐累积, 这些缺陷的存在增大了材料内部的应力场梯度, 从而阻碍了马氏体孪生界面运动, 从而造成重定向模量逐渐升高. 同时, Aaltio 等(2010) 的研究还表明: 材料的疲劳寿命随着应变幅值的增大而显著降低; 由于马氏体重定向机制是二级相变, 相变前后不涉及到潜热的释放, 因此材料对加载频率的依赖性很低; 虽然在循环变形过程中应力--应变曲线发生明显改变, 然而马氏体相变温度和居里温度保持不变; 材料中加工时预先存在的一些裂纹易于成为继发的裂纹源, 然而, 裂纹的扩展方向并不平行于预先存在的裂纹方向, 而是沿着马氏体孪晶的(101)晶面扩展, 因此, 在宏观上可以观察到裂纹与外加应力方向呈45\(^\circ\)角, 如图56 所示. ...
... NiMnGa形状记忆合金单晶在循环过程中的马氏体孪晶结构.左侧为循环7 \(\times \) 10\(^{5}\)次后的试样表面; 右侧为循环7.1 \(\times \) 10\(^{7}\)次后的试样表面 (Aaltio et al. 2010 ) ...
Characterization of ternary nitipd high-temperature shape-memory alloys under load-biased thermal cycling. Metall. Mater. Trans.
0
2010
Thermomechanical modeling of polycrystalline SMAs under cyclic loading, Part III: Evolution of plastic strains and two-way shape memory effect. Int. J
1
1999
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
Microscopic theory for domain wall motion and its experimental verification in fe-al alloy domain growth kinetics.
1
1977
... (1) Cahn-Hilliard模型 (Cahn & Hilliard 1958 , 1959 ), 这种模型的相由保守的场变量唯一决定; (2) Allen-Cahn模型 (Cahn {\rm&} Allen 1977 , Allen & Cahn 1979 ), 这种模型的相无法由浓度、温度和压强等唯一决定, 而需要引入一个或多个额外的非保守场变量即序参量来决定局部相. 目前, 大部分的相场模拟是基于Allen-Cahn模型及其改进模型开展的.Allen-Cahn模型的动力学方程通常也称之为时间相关Ginzburg-Landau(TDGL)方程, 求解该动力学方程的数值解法有很多, 最常见的是基于统一空间网格和精确时间步长的简单二阶有限差分法 (Fan & Chen 1997 ). 从已有研究中可归纳出相场模拟的4个步骤: (1)为研究材料系统确定合适的序参数; (2)将局部能量密度表示为所选序参数的函数, 并得出材料系统的自由能泛函, 这些函数必须正确描述系统的对称性和热力学性质; (3)由自由能泛函得到相场动力学方程, 并将从实验数据或基础计算中得到的唯象系数带入动力学方程; (4)确定正确的初始和边界条件并选择适当的方法求解动力学方程. ...
Free energy of a nonuniform system. I. Interfacial free energy. J
0
1958
Free energy of a nonuniform system. iii. nucleation in a two---component incompressible fluid. J
2
1959
... 为了考虑NiTi形状记忆合金变形过程中体现出的强烈热--力耦合作用, 通过考虑材料非弹性变形过程中的内部热效应(包括相变潜热和非弹性耗散生热)和热边界条件, Müller 和 Bruhns (2006) , Auricchio 等(2008) , Christ 和 Reese(2009) 和Mirzaeifar 等(2011) 建立了NiTi形状记忆合金热--力耦合本构模型.这些本构模型能够合理描述NiTi形状记忆合金的率相关变形特性, 但由于未引入与循环变形相关的内变量, 无法对NiTi形状记忆合金循环变形过程中体现出的率相关超弹性和形状记忆效应劣化现象进行合理的描述. ...
... 为了描述NiTi形状记忆合金在热--力耦合循环变形过程中体现出的形状记忆效应劣化现象, Auricchio 等(2008) , Zaki 和 Moumni (2007) 和Hartl等(2010) 通过引入必要的非弹性变形机制, 建立了相应的本构模型; 但是, 这些本构模型没有很好地考虑在热--力耦合循环载荷作用下冷却阶段发生的附加非弹性变形, 也不能对形状记忆效应退化现象的加载水平依赖性进行合理的描述. 最近, Yu 等 (2016) 在Popov 和 Lagoudas (2007) 提出的本构模型基础上, 针对NiTi形状记忆合金循环加载条件下出现的形状记忆效应退化现象, 发展了一个宏观多机制本构模型. 该模型根据实验观测结果, 考虑了NiTi形状记忆合金热--力循环过程中的四种变形机制, 即马氏体相变、相变诱发塑性、马氏体重取向和重取向诱发塑性, 并且重点突出了马氏体相变和重取向与位错的交互作用.根据宏观实验结果, Yu 等 (2016) 认为: 随循环次数的增大, 相变和重定向模量增大, 马氏体相变开始温度升高, 重定向开始应力下降; 某些区域位错诱发的局部应力的投影为正, 该内应力将促进马氏体相变和重定向, 其结果是循环过程中马氏体相变开始温度升高; 同时, 位错诱发的应力梯度会阻碍孪晶和解孪相的形核, 导致相变和重定向模量增大. 下面对Yu 等(2016) 发展的本构模型进行简要介绍. ...
Fatigue design of structures under thermomechanical loadings.
1
2002
... 正如Kang 和 Song (2015) 综述的那样, 通过对疲劳断口的SEM观察发现, 超弹性NiTi合金(初始相为奥氏体)的断口形貌和形状记忆NiTi合金(初始相为马氏体)基本相同, 均可见明显的疲劳条纹、二次裂纹和河流状解理图案以及一些大而浅的韧窝.在NiTi形状记忆合金疲劳断口的SEM观察结果基础上, 进一步总结得出:NiTi形状记忆合金的疲劳断裂可分为两阶段, 即疲劳裂纹萌生阶段和扩展阶段; 在疲劳断裂过程中, 同时会出现由疲劳载荷引起的稳态的裂纹长大和由大而浅的韧窝代表的塑性过载断裂.另外, 从整个疲劳失效过程中的应力--应变响应曲线可以看到, 在循环稳定后(从200周开始直至疲劳断裂发生), 滞回环形状和大小基本上不会发生可观察的变化, 疲劳断裂突然毫无宏观征兆地发生. 这说明, NiTi形状记忆合金在疲劳失效过程中的裂纹萌生和扩展机制与普通金属有明显不同.Charkaluk 等(2000 , 2002 ), Skelton 等(1991 , 1998 )以及Dunand-Chatellet 和 Moumni (2012) 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
An energetic approach in thermomechanical fatigue for silicon molybdenum cast iron.
2
2000
... 与二元NiTi形状记忆合金相比, 高温形状记忆合金的循环变形实验研究相对较少, 并且大部分集中在温度循环加载方式, 即讨论其形状记忆效应在恒定应力和温度循环加载过程中的演化规律.已有的实验表明, 高温形状记忆合金的温度循环变形特性与原子组分、加工方式和外加应力等密切相关.例如, Bigelow等(2007) 首先对Ni\(_{19.4}\)Ti\(_{50.6}\)Pd\(_{30}\)合金在外加恒定应力为200 MPa的情况下进行温度循环实验, 发现温度循环30周后材料达到稳定的温度--变形响应状态, 并且相变温度上升了16\(^{\circ}\)C; 但是, 他们的结果还显示该合金在无外加应力的温度循环情况下, 相变温度会降低5 \(\sim \) 10\(^{\circ}\)C. 后来, Bigelow等(2010) 通过对不同合金含量的NiTiPd高温形状记忆合金在外加恒定应力下的温度循环加载实验研究, 揭示了该合金的温度循环稳定性随Pd元素含量的增加逐渐下降, 并且不可恢复应变也随之增大的变化规律. Kockar 等(2006, 2010)通过对不同加工状态下的Ni\(_{33.7}\)Ti\(_{50.3}\)Pd\(_{16}\)高温形状记忆合金的热--力耦合循环变形实验, 揭示了温度循环中在外加应力方向上的塑性变形累积现象, 如图30 所示. 由图30 可见, 经过等通道转角挤压的高温形状记忆合金在循环过程中的塑性应变明显减小, 相变应变远大于未经加工的初始材料; 同时, 将转角挤压的Ni\(_{33.7}\)Ti\(_{50.3}\)Pd\(_{16}\)高温形状记忆合金材料继续在425\(^{\circ}\)C退火15min, 可以得到更加稳定的温度循环响应结果, 循环10周后的累积塑性应变在外加拉伸应力为100 MPa时仅有0.05%, 并且在200 MPa时也不超过0.2%. 另外, Saghaian等(2016) 对富Ni的NiTiHf高温形状记忆合金的温度循环变形实验研究表明, 温度循环时的外加应力越大, 相变温度越高, 热滞回环越大, 不可恢复应变也随之增大. ...
... 正如Kang 和 Song (2015) 综述的那样, 通过对疲劳断口的SEM观察发现, 超弹性NiTi合金(初始相为奥氏体)的断口形貌和形状记忆NiTi合金(初始相为马氏体)基本相同, 均可见明显的疲劳条纹、二次裂纹和河流状解理图案以及一些大而浅的韧窝.在NiTi形状记忆合金疲劳断口的SEM观察结果基础上, 进一步总结得出:NiTi形状记忆合金的疲劳断裂可分为两阶段, 即疲劳裂纹萌生阶段和扩展阶段; 在疲劳断裂过程中, 同时会出现由疲劳载荷引起的稳态的裂纹长大和由大而浅的韧窝代表的塑性过载断裂.另外, 从整个疲劳失效过程中的应力--应变响应曲线可以看到, 在循环稳定后(从200周开始直至疲劳断裂发生), 滞回环形状和大小基本上不会发生可观察的变化, 疲劳断裂突然毫无宏观征兆地发生. 这说明, NiTi形状记忆合金在疲劳失效过程中的裂纹萌生和扩展机制与普通金属有明显不同.Charkaluk 等(2000 , 2002 ), Skelton 等(1991 , 1998 )以及Dunand-Chatellet 和 Moumni (2012) 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
A constitutive model for cyclic actuation of high-temperature shape memory alloys.
1
2014
... 与二元NiTi形状记忆合金相比, 高温形状记忆合金的循环变形实验研究相对较少, 并且大部分集中在温度循环加载方式, 即讨论其形状记忆效应在恒定应力和温度循环加载过程中的演化规律.已有的实验表明, 高温形状记忆合金的温度循环变形特性与原子组分、加工方式和外加应力等密切相关.例如, Bigelow等(2007) 首先对Ni\(_{19.4}\)Ti\(_{50.6}\)Pd\(_{30}\)合金在外加恒定应力为200 MPa的情况下进行温度循环实验, 发现温度循环30周后材料达到稳定的温度--变形响应状态, 并且相变温度上升了16\(^{\circ}\)C; 但是, 他们的结果还显示该合金在无外加应力的温度循环情况下, 相变温度会降低5 \(\sim \) 10\(^{\circ}\)C. 后来, Bigelow等(2010) 通过对不同合金含量的NiTiPd高温形状记忆合金在外加恒定应力下的温度循环加载实验研究, 揭示了该合金的温度循环稳定性随Pd元素含量的增加逐渐下降, 并且不可恢复应变也随之增大的变化规律. Kockar 等(2006, 2010)通过对不同加工状态下的Ni\(_{33.7}\)Ti\(_{50.3}\)Pd\(_{16}\)高温形状记忆合金的热--力耦合循环变形实验, 揭示了温度循环中在外加应力方向上的塑性变形累积现象, 如图30 所示. 由图30 可见, 经过等通道转角挤压的高温形状记忆合金在循环过程中的塑性应变明显减小, 相变应变远大于未经加工的初始材料; 同时, 将转角挤压的Ni\(_{33.7}\)Ti\(_{50.3}\)Pd\(_{16}\)高温形状记忆合金材料继续在425\(^{\circ}\)C退火15min, 可以得到更加稳定的温度循环响应结果, 循环10周后的累积塑性应变在外加拉伸应力为100 MPa时仅有0.05%, 并且在200 MPa时也不超过0.2%. 另外, Saghaian等(2016) 对富Ni的NiTiHf高温形状记忆合金的温度循环变形实验研究表明, 温度循环时的外加应力越大, 相变温度越高, 热滞回环越大, 不可恢复应变也随之增大. ...
A three-dimensional model of magneto-mechanical behaviors of martensite reorientation in ferromagnetic shape memory alloys. J. Mech. Phys.
1
2014
... 形状记忆NiTi合金在恒定轴向应力的温度循环下的实验结果(Bo & Lagoudas 1999 ). (a) 温度--应变曲线(恒定应力为35 MPa, 前20周), (b) 不同恒定应力下的塑性应变演变曲线 ...
Stress-temperature phase diagram of a ferromagnetic Ni-Mn-Ga shape memory alloy.
0
2005
Training, constraints, and high-cycle magneto-mechanical properties of Ni-Mn-Ga magnetic shape-memory alloys. Eur. Phys. J
1
2008
... (1) Cahn-Hilliard模型 (Cahn & Hilliard 1958 , 1959 ), 这种模型的相由保守的场变量唯一决定; (2) Allen-Cahn模型 (Cahn {\rm&} Allen 1977 , Allen & Cahn 1979 ), 这种模型的相无法由浓度、温度和压强等唯一决定, 而需要引入一个或多个额外的非保守场变量即序参量来决定局部相. 目前, 大部分的相场模拟是基于Allen-Cahn模型及其改进模型开展的.Allen-Cahn模型的动力学方程通常也称之为时间相关Ginzburg-Landau(TDGL)方程, 求解该动力学方程的数值解法有很多, 最常见的是基于统一空间网格和精确时间步长的简单二阶有限差分法 (Fan & Chen 1997 ). 从已有研究中可归纳出相场模拟的4个步骤: (1)为研究材料系统确定合适的序参数; (2)将局部能量密度表示为所选序参数的函数, 并得出材料系统的自由能泛函, 这些函数必须正确描述系统的对称性和热力学性质; (3)由自由能泛函得到相场动力学方程, 并将从实验数据或基础计算中得到的唯象系数带入动力学方程; (4)确定正确的初始和边界条件并选择适当的方法求解动力学方程. ...
A finite element model for shape memory alloys considering thermomechanical couplings at large strains. Int. J
2
2009
... (1) Cahn-Hilliard模型 (Cahn & Hilliard 1958 , 1959 ), 这种模型的相由保守的场变量唯一决定; (2) Allen-Cahn模型 (Cahn {\rm&} Allen 1977 , Allen & Cahn 1979 ), 这种模型的相无法由浓度、温度和压强等唯一决定, 而需要引入一个或多个额外的非保守场变量即序参量来决定局部相. 目前, 大部分的相场模拟是基于Allen-Cahn模型及其改进模型开展的.Allen-Cahn模型的动力学方程通常也称之为时间相关Ginzburg-Landau(TDGL)方程, 求解该动力学方程的数值解法有很多, 最常见的是基于统一空间网格和精确时间步长的简单二阶有限差分法 (Fan & Chen 1997 ). 从已有研究中可归纳出相场模拟的4个步骤: (1)为研究材料系统确定合适的序参数; (2)将局部能量密度表示为所选序参数的函数, 并得出材料系统的自由能泛函, 这些函数必须正确描述系统的对称性和热力学性质; (3)由自由能泛函得到相场动力学方程, 并将从实验数据或基础计算中得到的唯象系数带入动力学方程; (4)确定正确的初始和边界条件并选择适当的方法求解动力学方程. ...
... 为了考虑NiTi形状记忆合金变形过程中体现出的强烈热--力耦合作用, 通过考虑材料非弹性变形过程中的内部热效应(包括相变潜热和非弹性耗散生热)和热边界条件, Müller 和 Bruhns (2006) , Auricchio 等(2008) , Christ 和 Reese(2009) 和Mirzaeifar 等(2011) 建立了NiTi形状记忆合金热--力耦合本构模型.这些本构模型能够合理描述NiTi形状记忆合金的率相关变形特性, 但由于未引入与循环变形相关的内变量, 无法对NiTi形状记忆合金循环变形过程中体现出的率相关超弹性和形状记忆效应劣化现象进行合理的描述. ...
Change in microstructure during training of a Ni50Mn29Ga21 bicrystal.
1
2010
... 上述研究主要集中在铁磁形状记忆合金单晶方面. Murray 等(1998) , Jeong等(2003) 研究了铁磁形状记忆合金多晶的磁--力耦合特性, 发现相对于单晶材料, 多晶能产生的磁致伸缩应变很小. Marioni(2002) 进一步指出, 针对多晶铁磁形状记忆合金, 可以通过定向凝固法调控择优取向的初始织构来获取较大的磁致伸缩应变.近年来, 众多学者研究了铁磁形状记忆合金定向凝固多晶在不同方向上的磁场诱发马氏体重定向特性(Pötschke et al.2010 , Yu et al. 2014b ), 应力诱发马氏体重定向特性(Chulist et al. 2010 , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性. ...
A review of constitutive models and modeling techniques for shape memory alloys. Int. J
6
2016
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
... 由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变. ...
... 近二十年来, 随着人们对NiTi形状记忆合金的了解和认识的深入, 越来越多的学者更加关注该合金在纳米尺度下的变形机制, 已经在NiTi形状记忆合金的热--力耦合变形行为的分子动力学(MD)模拟方面取得了众多成果, Kastner (2012) 和Cisse等(2016) 对形状记忆合金相变过程及相关变形行为的分子动力学模拟方面的研究现状进行了较为系统的介绍, 特别是针对NiTi原子间相互作用势、NiTi形状记忆合金的超弹性和形状记忆效应原子模拟方面的研究.因此, 关于NiTi形状记忆合金分子动力学模拟的基本过程以及不同原子间势函数的特征和选择原则等方面的内容请参见文献Kastner(2012) 和Cisse 等(2016) , 本小节仅针对已有的热--力耦合循环变形行为的分子动力学模拟结果做一个必要的补充. ...
... 和Cisse 等(2016) , 本小节仅针对已有的热--力耦合循环变形行为的分子动力学模拟结果做一个必要的补充. ...
... 基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ). ...
Rearrangement surfaces under magnetic field and/or stress in Ni-Mn-Ga.
4
2005
... 目前, 专门针对NiTiX高温形状记忆合金热--力耦合变形行为的本构模型研究较少, 已有研究均是在二元NiTi形状记忆合金对应的本构模型基础上进行拓展, 并且均为宏观唯象的本构模型, 主要针对高温形状记忆合金在恒定应力作用下温度循环加载过程中的热--力耦合变形行为进行本构描述.对于三元NiTiX高温形状记忆合金的超弹性行为, 因其与二元NiTi形状记忆合金的区别主要体现在相变温度上, 也就是说其使用的环境温度与二元NiTi形状记忆合金不同, 其应力诱发的相变机制以及由此而产生的超弹性变形行为与二元NiTi形状记忆合金基本相同, 因此, 可以采用已有的、能够合理描述NiTi形状记忆合金超弹性行为的本构模型直接描述NiTiX高温形状记忆合金的超弹性行为及其在循环变形过程中的劣化现象和对环境温度的依赖性(如图33 (b)所示).针对NiTiX高温形状记忆合金在恒定应力作用下的温度循环加载过程中的热--力耦合变形行为, Lagoudas 等(2009a) 及其合作者(Hartl et al. 2010, Chemisky et al. 2014 )在其本构模型构建方面开展了一系列较为重要的探索性工作.Lagoudas 等(2009a)首先根据对高温形状记忆合金的蠕变现象(位错攀移)的观察, 通过将总应变分为弹性应变\(\varepsilon ^{\rm e}\)、热应变\(\varepsilon ^{\rm T}\)、相变应变\(\varepsilon ^{\rm t}\)、相变诱发塑性应变\(\varepsilon ^{\rm tp}\)和黏塑性(蠕变)应变\(\varepsilon ^{\rm vp}\)五个部分, 进而将蠕变机制引入NiTiX高温形状记忆合金的宏观唯象本构模型中, 提出了适用于NiTiX高温形状记忆合金热--力耦合变形行为的一维本构模型, 模型中假设相变与蠕变过程是独立进行的, 不考虑其交互作用; Hartl等(2010)将上述本构模型推广到了三维的情况, 并同时考虑了相变及黏塑性变形间的交互作用; 针对上述两种本构模型均不能合理描述多次循环加载下NiTiX高温形状记忆合金的热--力耦合响应的问题, Chemisky等(2014)通过合理考虑三种非弹性变形机制(即相变、相变诱发塑性及黏塑性变形)对高温形状记忆合金热--力学耦合行为的共同作用, 建立了可描述高温形状记忆合金在温度循环加载下热--力耦合循环变形行为的本构模型.该模型沿用了Lagoudas 等(2009a)的处理方式, 仍然将相变和蠕变变形看作是两个独立的过程, 并假设蠕变变形仅在奥氏体相中发生, 一旦材料发生马氏体相变, 则蠕变机制停止, 直到材料逆相变全部恢复为奥氏体后蠕变才继续进行.另外, 该模型同时考虑了残余马氏体在循环变形中的作用, 较为合理地反映了高温形状记忆合金的残余应变随温度循环的演化情况.下面对该模型(Chemisky et al. 2014 )进行简要的介绍. ...
... )在其本构模型构建方面开展了一系列较为重要的探索性工作.Lagoudas 等(2009a)首先根据对高温形状记忆合金的蠕变现象(位错攀移)的观察, 通过将总应变分为弹性应变\(\varepsilon ^{\rm e}\)、热应变\(\varepsilon ^{\rm T}\)、相变应变\(\varepsilon ^{\rm t}\)、相变诱发塑性应变\(\varepsilon ^{\rm tp}\)和黏塑性(蠕变)应变\(\varepsilon ^{\rm vp}\)五个部分, 进而将蠕变机制引入NiTiX高温形状记忆合金的宏观唯象本构模型中, 提出了适用于NiTiX高温形状记忆合金热--力耦合变形行为的一维本构模型, 模型中假设相变与蠕变过程是独立进行的, 不考虑其交互作用; Hartl等(2010)将上述本构模型推广到了三维的情况, 并同时考虑了相变及黏塑性变形间的交互作用; 针对上述两种本构模型均不能合理描述多次循环加载下NiTiX高温形状记忆合金的热--力耦合响应的问题, Chemisky等(2014)通过合理考虑三种非弹性变形机制(即相变、相变诱发塑性及黏塑性变形)对高温形状记忆合金热--力学耦合行为的共同作用, 建立了可描述高温形状记忆合金在温度循环加载下热--力耦合循环变形行为的本构模型.该模型沿用了Lagoudas 等(2009a)的处理方式, 仍然将相变和蠕变变形看作是两个独立的过程, 并假设蠕变变形仅在奥氏体相中发生, 一旦材料发生马氏体相变, 则蠕变机制停止, 直到材料逆相变全部恢复为奥氏体后蠕变才继续进行.另外, 该模型同时考虑了残余马氏体在循环变形中的作用, 较为合理地反映了高温形状记忆合金的残余应变随温度循环的演化情况.下面对该模型(Chemisky et al. 2014 )进行简要的介绍. ...
... NiTiPd高温形状记忆合金在不同压缩载荷下的温度循环加载时热--力耦合循环变形行为的实验和模拟结果(Chemisky et al. 2014 ). (a) 400 MPa, (b) 500 MPa ...
... 如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景. ...
Microstructure changes during non-conventional heat treatment of thin Ni-Ti wires by pulsed electric current studied by transmission electron microscopy.
7
2010
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
... (2)应力诱发马氏体重定向. Heczko (2005) , Karaca 等(2006) , Chen等(2014) 和Heidi 等(2016) 研究了环境温度在马氏体完成温度\(M_{\rm f}\)以下时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体重定向特性.图44 给出了在该加载工况下典型的应力应变曲线. 由图可见: 在无磁场作用下时, 加载诱发出的非弹性应变在应力完全卸载后不能恢复, 这是由于马氏体逆向重定向开始应力大于零; 而在磁场作用下, 马氏体重定向平台随着磁场的增大的逐渐升高, 这表明横向磁场对轴向应力诱发马氏体重定向有抑制作用; 当磁场达到8 kG时, 重定向应变在应力卸载后能够完全恢复, 材料展示出超弹性效应. 需要说明的是, 铁磁形状记忆合金在\(M_{\rm f}\)以下的超弹性机制是正向和逆向马氏体重定向, 这与NiTi形状记忆合金在奥氏体完成温度\(A_{\rm f}\)以上由正向和逆向马氏体相变所导致的超弹性有本质区别. ...
... 如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景. ...
... Mousavi 和 Arghavani (2017)对提出的本构模型进行了数值实现, 并通过将模拟结果和实验结果的对比验证了模型的正确性. 图49 和图50 分别给出了Mousavi 和Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型(LaMaster et al. 2014 )在应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和应力诱发重定向实验结果 (Chen et al. 2014 )与对应的模拟结果的比较情况. 由图可以看出, 三个模型都能够较好地捕捉到实验现象, 但是, Mousavi 和 Arghavani模型(Mousavi & Arghavani 2017 )与实验数据吻合得更好. ...
... )和应力诱发重定向实验结果 (Chen et al. 2014 )与对应的模拟结果的比较情况. 由图可以看出, 三个模型都能够较好地捕捉到实验现象, 但是, Mousavi 和 Arghavani模型(Mousavi & Arghavani 2017 )与实验数据吻合得更好. ...
... 应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比 (Mousavi & Arghavani 2017 ) ...
... 应力诱发重定向实验结果(Chen et al. 2014 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al.2014)以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比(Mousavi & Arghavani 2017 ) ...
Transmission electron microscopy investigation of dislocation slip during superelastic cycling of Ni-Ti wires. Int. J
2
2011
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
... (3)应力诱发马氏体相变. Chernenko 等(2005) , Segu\'{\i} 等(2005) , Kim 等(2006) 和Karaca 等(2007) 研究了环境温度在奥氏体完成温度A\(_{\rm f}\)以上时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体相变特性.和NiTi形状记忆合金类似, 铁磁形状记忆环境在应力作用下展示出良好的超弹性特性, 如图45 所示. 同时, 可以看出横向磁场对马氏体相变具有抑制作用, 即向前相变和逆相变平台均随着横向磁场的增加而升高, 并且相变特性对温度有很强的依赖性. 需要说明的是, 为了便于比较, 图43 中每个温度下的应变初始值均为零, 坐标轴的刻度间隔为1%. ...
A constrained theory of magnetoelasticity. J. Mech. Phys.
4
2002
... 基于铁磁形状记忆合金磁--力耦合变形行为的实验研究成果, 目前已经建立了一些相应的磁--力耦合本构模型, 根据所采用的方法不同可以大致分为4类: (1)基于微磁学约束理论模型.James 和Wuttig (1998) , DeSimone 和 James(2002) 基于微观磁学通过引入Zeeman能、静磁能和弹性能得到了系统的自由能函数, 假定磁化矢量在磁化过程中始终与易轴平行(即磁晶各向异性能无穷大而导致磁畴无法发生旋转), 采用能量最小化原理预测了铁磁形状记忆合金微结构的变形、宏观磁致应变以及磁化响应, 并预测在铁磁形状记忆合金中马氏体以层状结构形式存在. 然而, 由于该类模型的复杂性, 较难应用到具体的工程问题中. (2)能量模型.Murray等(2001)基于能量分析法来预测铁磁形状记忆合金发生马氏体重定向的条件, 提出了一个考虑双马氏体变体的二维能量模型, 将两个变体内磁能之差作为孪生变体界面运动的驱动力. Müllner等(2002)进一步考虑了机械能的存在对马氏体重定向的影响. He等(2011) 建立了一个适用于复杂多轴力--磁场条件下, 并考虑了磁滞效应的一般性能量模型. ...
... (1)磁场诱发疲劳失效. Chmielus等(2008) 通过对NiMnGa单晶施加循环旋转磁场(磁场强度保持恒定, 方向改变)观察了磁致应变在循环变形过程中的演化, 如图53 所示. ...
... NiMnGa铁磁形状记忆合金单晶在旋转磁场下磁致应变随循环次数的演化(Chmielus et al. 2008 ) ...
... 由图53 可见, 磁致应变的演化可以分为三个阶段, 即稳定区A、稳定增长区B和下降区C; 同时, 在不同区间的交接区附近, 最大磁致应变的改变非常迅速. Chmielus等(2008) 进一步解释了三个区域特性所对应的微观机制:在施加磁场之前, 材料未经有效训练, 初始态为孪生马氏体态, 单个马氏体厚度很小, 仅为10 nm到1 \(\mu \)m之间, 马氏体各个变体以高密度的交错形式存在, 变体--变体界面的运动阻力很高, 在0.97T磁场作用下, 仅仅观察到了0.2%的磁致重定向应变, 如图53 中区域A所示; 随着循环变形的进行, 由于晶体缺陷的逐渐累积, 择优取向马氏体逐渐相互吞噬, 形成大的马氏体区域, 马氏体各个变体逐渐以低密度的交错形式存在, 变体--变体界面的运动阻力显著降低, 磁致应变随着循环变形的进行而逐渐增大, 如图53 中区域B所示; 由于马氏体变体之间的本征应变不同, 在变体--变体界面处存在着应变突跳, 造成应力集中, 随着循环变形的进一步进行, 缺陷和微裂纹逐渐在变体--变体界面处累积, 导致材料性能劣化, 当循环次数达到5 \(\times \) 10\(^{5}\)之后, 磁致应变随着循环次数的增大而逐渐降低, 如图53 中区域C所示.需要指出的是, NiMnGa铁磁形状记忆合金单晶具有很好的抗疲劳特性, 在经历10\(^{8}\)次循环磁场载荷后, 试样出现了宏观裂纹, 但并未发生断裂. ...
3D coupled thermo-mechanical phase-field modeling of shape memory alloy dynamics via isogeometric analysis.
0
2015
Cyclic microstructural transitions and fracture micromechanisms in a near equiatomic NiTi alloy. Int. J.
3
2014
... 对于NiTi形状记忆合金的原位测试目前也在一定程度上展开了研究, 如DiCocco 等(2014) , Frotscher 等(2008) , Niendorf 等(2011) 和\v{S}ittner等(2007).采用的测试手段包括SEM、XRD、选区电子衍射(EBSD)、中子衍射(neutron diffraction)等, 其中SEM和XRD最为常见. 研究者采用上述测试方法, 对NiTi形状记忆合金的应力诱发马氏体相变以及裂纹扩展等过程进行了实时观测.Di Cocco等(2014) 用原位SEM和XRD观测了2个循环周次中裂纹萌生及扩展的过程.研究表明, 应力诱发马氏体相变在裂尖处发生, 导致NiTi形状记忆合金的裂纹扩展与普通金属具有较大区别.实验中并未观察到裂尖钝化的情况, 但逆相变过程中会观察到完全的裂纹闭合, 见图39 .灰色箭头指示主裂纹的扩展, 白色箭头指示二次裂纹的扩展. 图39 清晰地描述了随应变增大, 裂纹尖端张开位移不断增大的过程. ...
... 和\v{S}ittner等(2007).采用的测试手段包括SEM、XRD、选区电子衍射(EBSD)、中子衍射(neutron diffraction)等, 其中SEM和XRD最为常见. 研究者采用上述测试方法, 对NiTi形状记忆合金的应力诱发马氏体相变以及裂纹扩展等过程进行了实时观测.Di Cocco等(2014) 用原位SEM和XRD观测了2个循环周次中裂纹萌生及扩展的过程.研究表明, 应力诱发马氏体相变在裂尖处发生, 导致NiTi形状记忆合金的裂纹扩展与普通金属具有较大区别.实验中并未观察到裂尖钝化的情况, 但逆相变过程中会观察到完全的裂纹闭合, 见图39 .灰色箭头指示主裂纹的扩展, 白色箭头指示二次裂纹的扩展. 图39 清晰地描述了随应变增大, 裂纹尖端张开位移不断增大的过程. ...
... 不同变形程度的预制裂纹扩展SEM原位观察 (Di Cocco et al. 2014 ).(a) 10%, (b) 11%, (c) 12%, (d) 拉伸断裂 ...
An overview of nitinol medical applications.
2
1999
... 作为一种典型的智能材料, 形状记忆合金 (shape memory alloys, SMAs)因其特有的超弹性和形状记忆效应已经在很多领域得到了广泛的应用(Van Humbeeck 1999 , Duerig et al. 1999 , Morgan 2004 ).在实际的服役过程中, 形状记忆合金构件和器件通常会承受循环载荷的作用(包括温度循环、磁力循环和机械循环载荷以及它们之间的耦合), 循环变形和疲劳失效行为是这些构件或器件疲劳寿命预测和可靠性评价中的关键问题, 已得到了国内外研究者的广泛关注. 众所周知, 形状记忆合金的超弹性和形状记忆效应来自于该类材料特殊的、由温度场或应力(应变)场以及磁场的变化诱发的马氏体相变及其逆相变所致.因此, 可以按照形状记忆合金的相变诱发方式将其分为两大类:由温度或应力(应变)场诱发的热致形状记忆合金, 如近等原子比的NiTi形状记忆合金和高温NiTiX形状记忆合金; 由温度、应力和磁场单独或共同诱发的磁致形状记忆合金, 如NiMnGa铁磁形状记忆合金.在这两类形状记忆合金的反复相变过程中都涉及到相变潜热的释放和吸收, 因而必然涉及到热--力和磁--热--力耦合的问题, 特别是在加载速率相对较大的情形下. 由此可见, 有必要深入探讨形状记忆合金的热--力和磁--热--力耦合循环变形和疲劳失效行为并进行理论描述. ...
... Cisse等(2016) 在对形状记忆合金的本构模型和模拟技术的综述过程中对相关的分子动力学模拟和相场分析进行了简要评述, 但并没有涉及到一些具体细节和重要结果, 并且对形状记忆合金在微纳米尺度下的热--力耦合循环变形行为数值模拟讨论较少. ...
Experimental analysis of the fatigue of shape memory alloys through power-law statistics. Int. J.
1
2012
... 正如Kang 和 Song (2015) 综述的那样, 通过对疲劳断口的SEM观察发现, 超弹性NiTi合金(初始相为奥氏体)的断口形貌和形状记忆NiTi合金(初始相为马氏体)基本相同, 均可见明显的疲劳条纹、二次裂纹和河流状解理图案以及一些大而浅的韧窝.在NiTi形状记忆合金疲劳断口的SEM观察结果基础上, 进一步总结得出:NiTi形状记忆合金的疲劳断裂可分为两阶段, 即疲劳裂纹萌生阶段和扩展阶段; 在疲劳断裂过程中, 同时会出现由疲劳载荷引起的稳态的裂纹长大和由大而浅的韧窝代表的塑性过载断裂.另外, 从整个疲劳失效过程中的应力--应变响应曲线可以看到, 在循环稳定后(从200周开始直至疲劳断裂发生), 滞回环形状和大小基本上不会发生可观察的变化, 疲劳断裂突然毫无宏观征兆地发生. 这说明, NiTi形状记忆合金在疲劳失效过程中的裂纹萌生和扩展机制与普通金属有明显不同.Charkaluk 等(2000 , 2002 ), Skelton 等(1991 , 1998 )以及Dunand-Chatellet 和 Moumni (2012) 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
Structural and functional fatigue of NiTi shape memory alloys. Mater. Sci. Eng.
0
2004
a. Ginzburg-Landau theory of static domain walls in shape-memory alloys. Z. Phys.
0
1983
b. One-dimensional model of shape memory alloys. Arch.
0
1983
Computer simulation of grain growth using a continuum field model.
0
1997
Experimental investigation on macroscopic domain formation and evolution in polycrystalline NiTi microtubing under mechanical force. J. Mech. Phys.
1
2006
... 尽管NiTi形状记忆合金中的热弹性马氏体相变是一种快速的切变式固态相变过程, 但是, 在多晶NiTi形状记忆合金材料中, 因晶粒晶体学位向的不同和晶界对相变过程的阻碍作用, 使得马氏体相变过程是一种局部切变形核而逐渐扩展长大的过程, 特别是在超细晶的多晶NiTi形状记忆合金中.对于这一种局部的、非均匀马氏体相变过程, Shaw & Kyriakides(1995 , 1997 )对细晶多晶NiTi形状记忆合金条带通过全场像和应力--应变的同时测量进行了早期的观察, 揭示了在外加载荷作用下非均匀马氏体相变的产生以及宏观可观察的相变图案(transformation domain)形成和扩展. 近年来, Zhang 等(2010) , Sun 等(2002) , He 和 Sun(2010a) 及 Feng 和 Sun(2006) 利用CCD相机和高速摄像仪进一步观察了细晶超弹性NiTi形状记忆合金在应变控制的单轴拉伸--卸载过程中相变图案的形成和演化以及这一过程的加载速率依赖性, 进而揭示了单轴拉伸和卸载过程中马氏体相变过程的局部性. Zhang等(2010)得到的细晶超弹性NiTi形状记忆合金薄材典型的实验结果如图8 和图9 所示. ...
The concepts of latent hardening and strain hardening in metallic single crystals.
1
1985
... 在循环变形过程中, 位错滑移的各向同性抗力\(\tau _{\rm c}\)随着位错密度的增大而增大, 根据Franciosi (1985) 可以写成\[\tau _{\rm c} = \dfrac{1}{2}\mu b\sqrt \rho \ \ (9)\]其中, \(b\)是材料的Burgers矢量大小. ...
In situ scanning electron microscopic study of structural fatigue of struts, the characteristic elementary building units of medical stents.
0
2008
Modeling rearrangement process of martensite platelets in a magnetic shape memory alloy Ni\(_{2}\)MnGa single crystal under magnetic field and (or) stress action. J
2
2006
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
On the viscous and strain rate dependent behavior of polycrystalline NiTi. Int. J
1
2008
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
A macroscale phase-field model for shape memory alloys with non-isothermal effects: Influence of strain rate and environmental conditions on the mechanical response.
0
2012
Magnetic, mechanical and fatigue properties of a Ni\(_{45.4}\)Mn\(_{29.1}\)Ga\(_{21.6}\)Fe\(_{3.9}\) single crystal
1
2010
... (1) Cahn-Hilliard模型 (Cahn & Hilliard 1958 , 1959 ), 这种模型的相由保守的场变量唯一决定; (2) Allen-Cahn模型 (Cahn {\rm&} Allen 1977 , Allen & Cahn 1979 ), 这种模型的相无法由浓度、温度和压强等唯一决定, 而需要引入一个或多个额外的非保守场变量即序参量来决定局部相. 目前, 大部分的相场模拟是基于Allen-Cahn模型及其改进模型开展的.Allen-Cahn模型的动力学方程通常也称之为时间相关Ginzburg-Landau(TDGL)方程, 求解该动力学方程的数值解法有很多, 最常见的是基于统一空间网格和精确时间步长的简单二阶有限差分法 (Fan & Chen 1997 ). 从已有研究中可归纳出相场模拟的4个步骤: (1)为研究材料系统确定合适的序参数; (2)将局部能量密度表示为所选序参数的函数, 并得出材料系统的自由能泛函, 这些函数必须正确描述系统的对称性和热力学性质; (3)由自由能泛函得到相场动力学方程, 并将从实验数据或基础计算中得到的唯象系数带入动力学方程; (4)确定正确的初始和边界条件并选择适当的方法求解动力学方程. ...
Elastoplastic phase field model for microstructure evolution.
0
2005
Magnetic field-induced martensitic phase transformation in magnetic shape memory alloys: Modeling and experiments. J. Mech. Phys.
1
2014
... (4)磁场诱发马氏体相变. 与马氏体重定向相比, 单纯的磁场诱发马氏体相变十分困难, 需要的临界磁场通常高于5T(Kakeshita et al. 2000 , Haldar et al. 2014 ), 这极大地限制了铁磁形状记忆合金的应用范围.为了能使铁磁形状记忆合金在较低磁场下仍然能够诱发马氏体相变机制, Karaman 等(2006)和Karaca 等(2007)提出了一种行之有效的方法, 即应力辅助磁场诱发马氏体相变:首先施加应力, 使试样发生马氏体相变, 然后卸载至无磁场下逆相变开始应力和1.6 T磁场下逆相变开始应力之间, 如图46 所示. 此时, 保持应力不变, 施加磁场, 即可在较小的磁场强度下(0.8 T)诱发马氏体相变机制, 同时可以观察到较大的相变应变, 如图44 所示. 需要指出的是, 磁场诱发马氏体相变是一种很重要的机制, 这是由于在同样磁场强度下, 磁场诱发马氏体相变的输出功率远高于磁场诱发马氏体重定向, 这对铁磁形状记忆合金磁驱动器的设计提供了新的理论基础. ...
Stress dependence of the hysteresis in single crystal NiTi alloys.
3
2004
... 对于NiTi形状记忆合金的原位测试目前也在一定程度上展开了研究, 如DiCocco 等(2014) , Frotscher 等(2008) , Niendorf 等(2011) 和\v{S}ittner等(2007).采用的测试手段包括SEM、XRD、选区电子衍射(EBSD)、中子衍射(neutron diffraction)等, 其中SEM和XRD最为常见. 研究者采用上述测试方法, 对NiTi形状记忆合金的应力诱发马氏体相变以及裂纹扩展等过程进行了实时观测.Di Cocco等(2014) 用原位SEM和XRD观测了2个循环周次中裂纹萌生及扩展的过程.研究表明, 应力诱发马氏体相变在裂尖处发生, 导致NiTi形状记忆合金的裂纹扩展与普通金属具有较大区别.实验中并未观察到裂尖钝化的情况, 但逆相变过程中会观察到完全的裂纹闭合, 见图39 .灰色箭头指示主裂纹的扩展, 白色箭头指示二次裂纹的扩展. 图39 清晰地描述了随应变增大, 裂纹尖端张开位移不断增大的过程. ...
... Frotscher等(2008) 利用原位SEM观测了NiTi形状记忆合金菱形结构的疲劳断裂过程.研究表明, 表面划痕以及缺陷等应力集中处易于出现裂纹萌生, 但实验中也发现一些表面缺陷处在循环过程中并不会造成裂纹萌生. 图40 描述了在结构循环至第34周, 应变为24%时微裂纹的扩展情况.此时当应变仅增加0.06%时, 对比图40 (a)与图40 (b), 可见表面微裂纹尺寸明显增大. 继续施加应力时, 则材料迅速破坏.这也说明了裂纹萌生阶段占疲劳寿命的比例较大, 宏观裂纹一旦出现, 材料则在短时间内即发生破坏. ...
... 宏观裂纹的演变 (Frotscher et al. 2008 ). (a)结构应变24%时; (b) 结构应变24.06%时, 可观察到裂纹尺寸明显增大; (c) 继续加载, 结构破坏 ...
Three-dimensional modeling and numerical analysis of rate-dependent irrecoverable deformation in shape memory alloys. Int. J
2
2010
... 为了描述NiTi形状记忆合金在热--力耦合循环变形过程中体现出的形状记忆效应劣化现象, Auricchio 等(2008) , Zaki 和 Moumni (2007) 和Hartl等(2010) 通过引入必要的非弹性变形机制, 建立了相应的本构模型; 但是, 这些本构模型没有很好地考虑在热--力耦合循环载荷作用下冷却阶段发生的附加非弹性变形, 也不能对形状记忆效应退化现象的加载水平依赖性进行合理的描述. 最近, Yu 等 (2016) 在Popov 和 Lagoudas (2007) 提出的本构模型基础上, 针对NiTi形状记忆合金循环加载条件下出现的形状记忆效应退化现象, 发展了一个宏观多机制本构模型. 该模型根据实验观测结果, 考虑了NiTi形状记忆合金热--力循环过程中的四种变形机制, 即马氏体相变、相变诱发塑性、马氏体重取向和重取向诱发塑性, 并且重点突出了马氏体相变和重取向与位错的交互作用.根据宏观实验结果, Yu 等 (2016) 认为: 随循环次数的增大, 相变和重定向模量增大, 马氏体相变开始温度升高, 重定向开始应力下降; 某些区域位错诱发的局部应力的投影为正, 该内应力将促进马氏体相变和重定向, 其结果是循环过程中马氏体相变开始温度升高; 同时, 位错诱发的应力梯度会阻碍孪晶和解孪相的形核, 导致相变和重定向模量增大. 下面对Yu 等(2016) 发展的本构模型进行简要介绍. ...
... 目前, 专门针对NiTiX高温形状记忆合金热--力耦合变形行为的本构模型研究较少, 已有研究均是在二元NiTi形状记忆合金对应的本构模型基础上进行拓展, 并且均为宏观唯象的本构模型, 主要针对高温形状记忆合金在恒定应力作用下温度循环加载过程中的热--力耦合变形行为进行本构描述.对于三元NiTiX高温形状记忆合金的超弹性行为, 因其与二元NiTi形状记忆合金的区别主要体现在相变温度上, 也就是说其使用的环境温度与二元NiTi形状记忆合金不同, 其应力诱发的相变机制以及由此而产生的超弹性变形行为与二元NiTi形状记忆合金基本相同, 因此, 可以采用已有的、能够合理描述NiTi形状记忆合金超弹性行为的本构模型直接描述NiTiX高温形状记忆合金的超弹性行为及其在循环变形过程中的劣化现象和对环境温度的依赖性(如图33 (b)所示).针对NiTiX高温形状记忆合金在恒定应力作用下的温度循环加载过程中的热--力耦合变形行为, Lagoudas 等(2009a) 及其合作者(Hartl et al. 2010, Chemisky et al. 2014 )在其本构模型构建方面开展了一系列较为重要的探索性工作.Lagoudas 等(2009a)首先根据对高温形状记忆合金的蠕变现象(位错攀移)的观察, 通过将总应变分为弹性应变\(\varepsilon ^{\rm e}\)、热应变\(\varepsilon ^{\rm T}\)、相变应变\(\varepsilon ^{\rm t}\)、相变诱发塑性应变\(\varepsilon ^{\rm tp}\)和黏塑性(蠕变)应变\(\varepsilon ^{\rm vp}\)五个部分, 进而将蠕变机制引入NiTiX高温形状记忆合金的宏观唯象本构模型中, 提出了适用于NiTiX高温形状记忆合金热--力耦合变形行为的一维本构模型, 模型中假设相变与蠕变过程是独立进行的, 不考虑其交互作用; Hartl等(2010)将上述本构模型推广到了三维的情况, 并同时考虑了相变及黏塑性变形间的交互作用; 针对上述两种本构模型均不能合理描述多次循环加载下NiTiX高温形状记忆合金的热--力耦合响应的问题, Chemisky等(2014)通过合理考虑三种非弹性变形机制(即相变、相变诱发塑性及黏塑性变形)对高温形状记忆合金热--力学耦合行为的共同作用, 建立了可描述高温形状记忆合金在温度循环加载下热--力耦合循环变形行为的本构模型.该模型沿用了Lagoudas 等(2009a)的处理方式, 仍然将相变和蠕变变形看作是两个独立的过程, 并假设蠕变变形仅在奥氏体相中发生, 一旦材料发生马氏体相变, 则蠕变机制停止, 直到材料逆相变全部恢复为奥氏体后蠕变才继续进行.另外, 该模型同时考虑了残余马氏体在循环变形中的作用, 较为合理地反映了高温形状记忆合金的残余应变随温度循环的演化情况.下面对该模型(Chemisky et al. 2014 )进行简要的介绍. ...
Two-dimensional analysis to improve the output stress in ferromagnetic shape memory alloys. J
0
2011
a. Rate-dependent domain spacing in a stretched NiTi strip. Int. J
2
2010
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
... 尽管NiTi形状记忆合金中的热弹性马氏体相变是一种快速的切变式固态相变过程, 但是, 在多晶NiTi形状记忆合金材料中, 因晶粒晶体学位向的不同和晶界对相变过程的阻碍作用, 使得马氏体相变过程是一种局部切变形核而逐渐扩展长大的过程, 特别是在超细晶的多晶NiTi形状记忆合金中.对于这一种局部的、非均匀马氏体相变过程, Shaw & Kyriakides(1995 , 1997 )对细晶多晶NiTi形状记忆合金条带通过全场像和应力--应变的同时测量进行了早期的观察, 揭示了在外加载荷作用下非均匀马氏体相变的产生以及宏观可观察的相变图案(transformation domain)形成和扩展. 近年来, Zhang 等(2010) , Sun 等(2002) , He 和 Sun(2010a) 及 Feng 和 Sun(2006) 利用CCD相机和高速摄像仪进一步观察了细晶超弹性NiTi形状记忆合金在应变控制的单轴拉伸--卸载过程中相变图案的形成和演化以及这一过程的加载速率依赖性, 进而揭示了单轴拉伸和卸载过程中马氏体相变过程的局部性. Zhang等(2010)得到的细晶超弹性NiTi形状记忆合金薄材典型的实验结果如图8 和图9 所示. ...
b. Frequency-dependent temperature evolution in NiTi shape memory alloy under cyclic loading
2
2010
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
... Guldbakke 等(2010) 也研究了NiMnGaFe单晶在相同加载模式下的疲劳特性, 结果表明, NiMnGaFe单晶的磁致应变演化特性和NiMnGa单晶非常类似, 也分为上述三个阶段, 但其抗疲劳特性较差, 试样在经历2 \(\times\) 10\(^{6}\)次循环磁场载荷后出现断裂.Lawrence 等(2016) 则观察了NiMnGa单晶在磁场诱发疲劳后的试样微观形貌, 发现三种典型的裂纹形式同时存在, 即: I型裂纹沿\(<100>\)方向扩展, II型裂纹沿\(<100>\)方向扩展, III型裂纹沿小角度晶界扩展, 如图54 所示(图中所示的1, 2和3分别代表I型、II型和III型裂纹). ...
Effect of training conditions and extended thermal cycling on nitinol two-way shape memory behavior.
1
1998
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
Magnetic shape memory effect and magnetization reversal.
0
2005
Experimental characterization and modeling of a three-variant magnetic shape memory alloy.
2
2016
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
... (2)应力诱发马氏体重定向. Heczko (2005) , Karaca 等(2006) , Chen等(2014) 和Heidi 等(2016) 研究了环境温度在马氏体完成温度\(M_{\rm f}\)以下时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体重定向特性.图44 给出了在该加载工况下典型的应力应变曲线. 由图可见: 在无磁场作用下时, 加载诱发出的非弹性应变在应力完全卸载后不能恢复, 这是由于马氏体逆向重定向开始应力大于零; 而在磁场作用下, 马氏体重定向平台随着磁场的增大的逐渐升高, 这表明横向磁场对轴向应力诱发马氏体重定向有抑制作用; 当磁场达到8 kG时, 重定向应变在应力卸载后能够完全恢复, 材料展示出超弹性效应. 需要说明的是, 铁磁形状记忆合金在\(M_{\rm f}\)以下的超弹性机制是正向和逆向马氏体重定向, 这与NiTi形状记忆合金在奥氏体完成温度\(A_{\rm f}\)以上由正向和逆向马氏体相变所导致的超弹性有本质区别. ...
Modelling detwinning of martensite platelets under magnetic and (or) stress actions on Ni-Mn-Ga alloys.
2
2003
... \[\pmb\varLambda^{\rm t}_{\rm rev}=\dfrac{\pmb\varepsilon^{t-r}}{\xi^{r}},\qquad \dot{\xi}<0 \ \ {\rm (25b)}\]其中, \(\pmb\sigma'\)为偏应力张量, \(\bar{\sigma}\)为von-Mises等效应力, \(H^{\rm cur}\)为最大相变应变, \(\pmb\varepsilon^{t-r}\)为逆相变开始时的相变应变张量, \(\xi^{\rm r}\)为逆相变时的马氏体体积分数. 对于正相变过程, 相变面\(\varPhi_{\rm fwd}^{\rm t}\)定义为\[ \varPhi_{\rm fwd}^{\rm t}=\pi_{\rm fwd}^{\rm t}-Y_{\rm fwd}^{\rm t}\ \ (26)\] 其中, \(\pi_{\rm fwd}^{\rm t}\)为正相变时的热力学驱动力, \(Y_{\rm fwd}^{\rm t}\)为临界能.\(Y_{\rm fwd}^{\rm t}\)可以写为(Hartl et al. 2010 )\[ Y_{\rm fwd}^{\rm t}(\pmb\sigma)=Y_0^{\rm t}+D\pmb\sigma:\left(\pmb\varLambda_{\rm fwd}^{\rm t}+\pmb\varLambda_{\rm fwd}^{\rm tp}\right) \ \ (27)\] 其中, \(D\)为描述热力学驱动力对应力依赖程度的参数, \(Y_0^{\rm t}\)为常数. ...
... 如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景. ...
Magnetostriction of martensite. Philos. Mag.
3
1998
... (1)磁场诱发马氏体重定向:Tickle和 James (1999) , Tickle 等(1999) , Heczko (2005) , Straka 和 Heczko (2003) 以及Karaca等(2006) 研究了环境温度在马氏体完成温度\((M_{\rm f})\)以下时铁磁形状记忆合金单晶在轴向恒定压应力、横向交变磁场作用下磁场诱发马氏体重定向特性.此时, 材料的初始相为马氏体, 图43 给出了该加载工况下典型的磁场--相对磁化曲线及磁场--应变曲线.以压应力为1.4 MPa的工况为例, 由图可见: 在变形的初始阶段(即磁场低于0.5 T), 由于磁场低于马氏体重定向临界磁场, 无非弹性应变出现, 并且磁化量随着磁场的增大而线性增大, 该阶段的磁化机制主要为磁化矢量的旋转; 当磁场高于0.5 T时, 马氏体重定向发生, 伴随着很大的非弹性应变出现, 同时磁化率出现跳跃并远高于低磁场(小于0.5 T)时的磁化率, 在该阶段马氏体重定向和磁化矢量旋转这两种磁化机制同时发生; 当磁场达到0.8 T时, 马氏体重定向完成, 磁化饱和出现, 并在后续磁场加载过程中, 非弹性应变和磁化量不再变化; 在卸载过程中, 当磁场达到0.25 T时, 逆向重定向发生, 非弹性应变和磁化量剧烈变化; 当磁场完全卸载后, 马氏体重定向完成, 非弹性应变及磁化量完全归零.另外, 对比图43 中不同应力水平下的磁--力响应可以看出:磁致伸缩应变的大小随着轴向压应力的增大而逐渐减小, 并且轴向压应力对磁场诱发马氏体重定向有抑制作用, 即临界磁场强度随着轴向压应力的增加而逐渐升高; 在压应力较小时(0.6 MPa), 磁场诱发出的重定向应变无法完全恢复; 在压应力较大时(3 MPa), 试样在发生马氏体重定向之前已经通过磁化矢量旋转机制完成了磁化, 无法诱发马氏体重定向机制. 这说明, 铁磁形状记忆合金存在着一个"闭锁应力", 在应力低于"闭锁应力"时, 磁场能够诱发马氏体重定向; 在应力高于"闭锁应力"时, 磁场无法诱发马氏体重定向. 铁磁形状记忆合金的"闭锁应力"一般较低, 大约在3 MPa左右. Karaca等(2006) 进一步提出了发生马氏体重定向的两个必要条件, 即高的磁晶各向异性能和低的孪生界面运动能, 并通过增大测试温度与居里温度之差以及减小测试温度和马氏体相变温度之差分别提高和降低磁晶各向异性能和孪生界面运动能, 进而获得了较高的应力闭锁值(5.7 MPa). ...
... 基于铁磁形状记忆合金磁--力耦合变形行为的实验研究成果, 目前已经建立了一些相应的磁--力耦合本构模型, 根据所采用的方法不同可以大致分为4类: (1)基于微磁学约束理论模型.James 和Wuttig (1998) , DeSimone 和 James(2002) 基于微观磁学通过引入Zeeman能、静磁能和弹性能得到了系统的自由能函数, 假定磁化矢量在磁化过程中始终与易轴平行(即磁晶各向异性能无穷大而导致磁畴无法发生旋转), 采用能量最小化原理预测了铁磁形状记忆合金微结构的变形、宏观磁致应变以及磁化响应, 并预测在铁磁形状记忆合金中马氏体以层状结构形式存在. 然而, 由于该类模型的复杂性, 较难应用到具体的工程问题中. (2)能量模型.Murray等(2001)基于能量分析法来预测铁磁形状记忆合金发生马氏体重定向的条件, 提出了一个考虑双马氏体变体的二维能量模型, 将两个变体内磁能之差作为孪生变体界面运动的驱动力. Müllner等(2002)进一步考虑了机械能的存在对马氏体重定向的影响. He等(2011) 建立了一个适用于复杂多轴力--磁场条件下, 并考虑了磁滞效应的一般性能量模型. ...
... 基于微观磁学通过引入Zeeman能、静磁能和弹性能得到了系统的自由能函数, 假定磁化矢量在磁化过程中始终与易轴平行(即磁晶各向异性能无穷大而导致磁畴无法发生旋转), 采用能量最小化原理预测了铁磁形状记忆合金微结构的变形、宏观磁致应变以及磁化响应, 并预测在铁磁形状记忆合金中马氏体以层状结构形式存在. 然而, 由于该类模型的复杂性, 较难应用到具体的工程问题中. (2)能量模型.Murray等(2001)基于能量分析法来预测铁磁形状记忆合金发生马氏体重定向的条件, 提出了一个考虑双马氏体变体的二维能量模型, 将两个变体内磁能之差作为孪生变体界面运动的驱动力. Müllner等(2002)进一步考虑了机械能的存在对马氏体重定向的影响. He等(2011) 建立了一个适用于复杂多轴力--磁场条件下, 并考虑了磁滞效应的一般性能量模型. ...
Interaction between phase transformations and dislocations at the nanoscale. Part 2: Phase field simulation examples. J. Mech. Phys.
0
2015
Effect of magnetic field on martensite transformation in a polycrystalline Ni\(_{2}\)MnGa. Mater. Sci. Eng.
1
2003
... 上述研究主要集中在铁磁形状记忆合金单晶方面. Murray 等(1998) , Jeong等(2003) 研究了铁磁形状记忆合金多晶的磁--力耦合特性, 发现相对于单晶材料, 多晶能产生的磁致伸缩应变很小. Marioni(2002) 进一步指出, 针对多晶铁磁形状记忆合金, 可以通过定向凝固法调控择优取向的初始织构来获取较大的磁致伸缩应变.近年来, 众多学者研究了铁磁形状记忆合金定向凝固多晶在不同方向上的磁场诱发马氏体重定向特性(Pötschke et al.2010 , Yu et al. 2014b ), 应力诱发马氏体重定向特性(Chulist et al. 2010 , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性. ...
Giant magnetostriction in an ordered Fe\(_{3}\)Pt single crystal exhibiting a martensitic transformation.
1
2000
... (4)磁场诱发马氏体相变. 与马氏体重定向相比, 单纯的磁场诱发马氏体相变十分困难, 需要的临界磁场通常高于5T(Kakeshita et al. 2000 , Haldar et al. 2014 ), 这极大地限制了铁磁形状记忆合金的应用范围.为了能使铁磁形状记忆合金在较低磁场下仍然能够诱发马氏体相变机制, Karaman 等(2006)和Karaca 等(2007)提出了一种行之有效的方法, 即应力辅助磁场诱发马氏体相变:首先施加应力, 使试样发生马氏体相变, 然后卸载至无磁场下逆相变开始应力和1.6 T磁场下逆相变开始应力之间, 如图46 所示. 此时, 保持应力不变, 施加磁场, 即可在较小的磁场强度下(0.8 T)诱发马氏体相变机制, 同时可以观察到较大的相变应变, 如图44 所示. 需要指出的是, 磁场诱发马氏体相变是一种很重要的机制, 这是由于在同样磁场强度下, 磁场诱发马氏体相变的输出功率远高于磁场诱发马氏体重定向, 这对铁磁形状记忆合金磁驱动器的设计提供了新的理论基础. ...
An energy-based fatigue failure model for super-elastic NiTi alloys under pure mechanical cyclic loading.
6
2011
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
... (1)磁场诱发马氏体重定向:Tickle和 James (1999) , Tickle 等(1999) , Heczko (2005) , Straka 和 Heczko (2003) 以及Karaca等(2006) 研究了环境温度在马氏体完成温度\((M_{\rm f})\)以下时铁磁形状记忆合金单晶在轴向恒定压应力、横向交变磁场作用下磁场诱发马氏体重定向特性.此时, 材料的初始相为马氏体, 图43 给出了该加载工况下典型的磁场--相对磁化曲线及磁场--应变曲线.以压应力为1.4 MPa的工况为例, 由图可见: 在变形的初始阶段(即磁场低于0.5 T), 由于磁场低于马氏体重定向临界磁场, 无非弹性应变出现, 并且磁化量随着磁场的增大而线性增大, 该阶段的磁化机制主要为磁化矢量的旋转; 当磁场高于0.5 T时, 马氏体重定向发生, 伴随着很大的非弹性应变出现, 同时磁化率出现跳跃并远高于低磁场(小于0.5 T)时的磁化率, 在该阶段马氏体重定向和磁化矢量旋转这两种磁化机制同时发生; 当磁场达到0.8 T时, 马氏体重定向完成, 磁化饱和出现, 并在后续磁场加载过程中, 非弹性应变和磁化量不再变化; 在卸载过程中, 当磁场达到0.25 T时, 逆向重定向发生, 非弹性应变和磁化量剧烈变化; 当磁场完全卸载后, 马氏体重定向完成, 非弹性应变及磁化量完全归零.另外, 对比图43 中不同应力水平下的磁--力响应可以看出:磁致伸缩应变的大小随着轴向压应力的增大而逐渐减小, 并且轴向压应力对磁场诱发马氏体重定向有抑制作用, 即临界磁场强度随着轴向压应力的增加而逐渐升高; 在压应力较小时(0.6 MPa), 磁场诱发出的重定向应变无法完全恢复; 在压应力较大时(3 MPa), 试样在发生马氏体重定向之前已经通过磁化矢量旋转机制完成了磁化, 无法诱发马氏体重定向机制. 这说明, 铁磁形状记忆合金存在着一个"闭锁应力", 在应力低于"闭锁应力"时, 磁场能够诱发马氏体重定向; 在应力高于"闭锁应力"时, 磁场无法诱发马氏体重定向. 铁磁形状记忆合金的"闭锁应力"一般较低, 大约在3 MPa左右. Karaca等(2006) 进一步提出了发生马氏体重定向的两个必要条件, 即高的磁晶各向异性能和低的孪生界面运动能, 并通过增大测试温度与居里温度之差以及减小测试温度和马氏体相变温度之差分别提高和降低磁晶各向异性能和孪生界面运动能, 进而获得了较高的应力闭锁值(5.7 MPa). ...
... NiMnGa形状记忆合金单晶磁场诱发马氏体重定向特性 (Heczko 2005 ):磁场--相对磁化曲线及磁场--应变曲线 ...
... (2)应力诱发马氏体重定向. Heczko (2005) , Karaca 等(2006) , Chen等(2014) 和Heidi 等(2016) 研究了环境温度在马氏体完成温度\(M_{\rm f}\)以下时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体重定向特性.图44 给出了在该加载工况下典型的应力应变曲线. 由图可见: 在无磁场作用下时, 加载诱发出的非弹性应变在应力完全卸载后不能恢复, 这是由于马氏体逆向重定向开始应力大于零; 而在磁场作用下, 马氏体重定向平台随着磁场的增大的逐渐升高, 这表明横向磁场对轴向应力诱发马氏体重定向有抑制作用; 当磁场达到8 kG时, 重定向应变在应力卸载后能够完全恢复, 材料展示出超弹性效应. 需要说明的是, 铁磁形状记忆合金在\(M_{\rm f}\)以下的超弹性机制是正向和逆向马氏体重定向, 这与NiTi形状记忆合金在奥氏体完成温度\(A_{\rm f}\)以上由正向和逆向马氏体相变所导致的超弹性有本质区别. ...
... Mousavi 和 Arghavani (2017)对提出的本构模型进行了数值实现, 并通过将模拟结果和实验结果的对比验证了模型的正确性. 图49 和图50 分别给出了Mousavi 和Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型(LaMaster et al. 2014 )在应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和应力诱发重定向实验结果 (Chen et al. 2014 )与对应的模拟结果的比较情况. 由图可以看出, 三个模型都能够较好地捕捉到实验现象, 但是, Mousavi 和 Arghavani模型(Mousavi & Arghavani 2017 )与实验数据吻合得更好. ...
... 应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比 (Mousavi & Arghavani 2017 ) ...
Experimental observations on rate-dependent cyclic deformation of super-elastic NiTi shape memory alloy.
4
2016
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
... 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
... 超弹性NiTi形状记忆合金微管在不同加载速率下的平均温度随相对时间(当前时间/循环一周所花时间)的变化曲线(Kan et al.2016 ). (a) 3.3 \(\times \) 10\(^{ - 4}\) s\(^{-1}\),(b) 3.3 \(\times \) 10\(^{ - 2}\) s\(^{-1}\) ...
... 由图3 \(\sim\) 图5 可见, NiTi合金微管的表面温度在循环变形过程中会发生明显变化, 变化的最大值随加载速率的增加而增大. 然而, 整个工作段的平均温度即使在加载速率为\(3.3\times 10^{ - 2}\) s\(^{ -1 }\)(在最大应变为9%时, 相当于加载频率为0.15 Hz)的工况下却会随着循环次数的增大而逐渐下降, 如图5 (b)所示. 这与Yin等(2014) 在加载频率高于1 Hz的单轴拉伸--卸载循环加载下观察到的、平均温度随循环次数增大而不断升高的现象不同(如图6 所示). 由于Kan 等(2016) 采用的最高加载速率比Yin 等(2014) 的要低, 因而只能观察到平均温度随循环次数增大而逐渐下降的现象.当加载速率较小时, 微管与外界的热交换在循环过程中会随着循环次数的增大而逐渐充分, 虽然在循环变形过程中有温度的波动, 但平均温度将随循环次数的增大而逐渐下降, 最后趋近于环境温度, 或是没有明显的升高 (见图5 (a)); 当加载速率较大时 (如Yin等(2014) 讨论的1 Hz), 微管与外界的热交换不能充分进行, 材料内部在循环变形过程中将产生热量的集中, 并随循环次数的增大而变得更加显著, 因此, 平均温度将随循环次数增大而逐渐上升, 如图6 (a)所示. ...
Review on structural fatigue of NiTi shape memory alloys: Pure mechanical and thermo-mechanical ones.
5
2015
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
... 由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变. ...
... 基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ). ...
... 随着对NiTi形状记忆合金循环变形行为研究的开展和深入, 正如Eggeler等(2004)和Mahtabi 等(2015)综述的那样, NiTi形状记忆合金的疲劳问题已经得到了较为广泛的研究. Eggeler等(2004)进一步将NiTi形状记忆合金的疲劳失效行为分为两类, 即:结构疲劳失效, 代表NiTi形状记忆合金在一定循环载荷寿命下的物理失效或断裂; 功能疲劳失效则代表因超弹性和形状记忆效应等功能的劣化而发生的功能性丧失.例如, Wagner等(2004)就将超弹性NiTi形状记忆合金在循环变形过程中产生的累积残余应变的某一个临界值作为其功能失效的一种判据; 而Predki 等(2006), Dunand-Ch\^{a}tellet 和 Moumni (2012) 以及Song等(2015)则将每次循环中的耗散能密度下降到某一个临界值作为超弹性NiTi形状记忆合金的功能失效判据.由第2部分讨论的NiTi形状记忆合金的循环变形行为可知, 在NiTi形状记忆合金的循环变形过程中, 经过一定的循环次数后均会达到一个相对稳定的循环变形状态, 累积残余应变或降低的耗散能密度都会无限接近于一个稳定值, 并且在功能失效发生时没有材料的断裂发生, 因此, NiTi形状记忆合金的功能失效行为在设定了失效判据(也就是残余应变或耗散能密度等的临界值)以后, 完全可以和前节综述的NiTi形状记忆合金的循环变形行为一起来讨论.为此, 本节将主要讨论NiTi形状记忆合金的结构疲劳失效行为, 对于其功能失效行为的研究现状可参见Eggeler 等(2004)和Mahtabi等(2015)综述论文. 针对NiTi形状记忆合金的结构疲劳失效行为, Kang 和Song(2015) 已经着重对不同试样形式下的宏观疲劳失效行为的实验研究现状进行了较为详细的评述, 讨论了NiTi形状记忆合金单轴和多轴以及热--力耦合疲劳失效行为的研究进展.为了保证本文内容的完整性, 本小节结合一些最新的研究进展, 对该合金的结构疲劳失效行为的失效机制微观观察和疲劳失效模型(特别是基于损伤的疲劳失效模型)的研究现状进行补充评述.本节未涉及到的相关研究进展可参见文献(Kang & Song 2015 ).同样, 由于Cu-基和Fe-基形状记忆合金的循环变形和疲劳失效行为与NiTi形状记忆合金的类似, 本节也就仅针对NiTi形状记忆合金的疲劳失效行为来进行评述. ...
Advances in transformation ratcheting and ratcheting-fatigue interaction of NiTi shape memory alloy. Acta. Mech.
4
2013
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
... 由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变. ...
... 基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ). ...
Ratchetting deformation of super-elastic and shape-memory NiTi alloys.
1
2009
... Levitas 和 Javanakht (2012) 引入位错序参量, 采用有限元法研究了奥氏体相和奥氏体--马氏体界面处位错的形核和扩展过程.之后, Levitas 和 Javanakht (2013) 同时引入相变序参量和位错序参量, 采用有限元方法研究了纳米尺度平面应变大变形情况下马氏体(单个变体)相变、位错对奥氏体--马氏体界面扩展的影响、温度诱发马氏体相变时马氏体片的演化和应力诱发马氏体相变时微结构的演化.同时, Levitas 和 Javanbakht(2015) 还详细介绍了纳米尺度大变形情况下马氏体(多个变体)相变、孪生和位错之间交互作用理论的推导和依据. 然后, Javanbakht和 Levitas (2015) 采用有限元方法对该模型进行了数值实现, 进而研究了纳米尺度应力诱发双晶马氏体相变与位错之间的交互作用, 发现位错引起的应力集中可以促进马氏体形核, 而位错引起的应力释放又会阻碍马氏体相变. 此外, 他们还研究了温度诱发马氏体相变时马氏体片在双晶之间的扩展与位错之间的交互作用. ...
Shape memory behavior of high strength NiTiHfPd polycrystalline alloys.
0
2013
Magnetic field and stress induced martensite reorientation in NiMnGa ferromagnetic shape memory alloy single crystals.
1
2006
... 综上所述, 虽然铁磁形状记忆合金在实验研究方面已取得了长足的发展, 但大多数实验研究仅仅关注了材料在磁--力加卸载下的马氏体重定向及相变特性.虽然Karaca 等(2006) 和Aaltio等(2010) 研究了材料在循环载荷作用下的循环变形特性, 但载荷模式仅仅是单一磁或机械载荷, 尚缺少在热--力--磁多场环境下对材料循环变形特性的宏观实验观察.因此, 随着铁磁形状记忆合金日益广泛的应用, 对材料在热--力--磁多场环境下循环变形特性的实验研究工作亟待开展. ...
On the stress-assisted magnetic-field-induced phase transformation in Ni\(_{2}\)MnGa ferromagnetic shape memory alloys.
1
2007
... (3)应力诱发马氏体相变. Chernenko 等(2005) , Segu\'{\i} 等(2005) , Kim 等(2006) 和Karaca 等(2007) 研究了环境温度在奥氏体完成温度A\(_{\rm f}\)以上时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体相变特性.和NiTi形状记忆合金类似, 铁磁形状记忆环境在应力作用下展示出良好的超弹性特性, 如图45 所示. 同时, 可以看出横向磁场对马氏体相变具有抑制作用, 即向前相变和逆相变平台均随着横向磁场的增加而升高, 并且相变特性对温度有很强的依赖性. 需要说明的是, 为了便于比较, 图43 中每个温度下的应变初始值均为零, 坐标轴的刻度间隔为1%. ...
Stress-assisted reversible magnetic field-induced phase transformation in Ni2MnGa magnetic shape memory alloys.
1
2006
... 尽管如此, Kan等(2016) 完成的相关实验还是揭示了超弹性NiTi形状记忆合金明显的热--力耦合效应以及由此而引起的率相关循环变形特性, 并且表明在相应的本构模型构建中应该合理考虑这种与内部热生成和外部热交换密切相关的热--力耦合循环变形行为.同时, Xie等(2016a) 还通过不同加载速率下的应力控制循环拉伸--卸载实验, 揭示了不同应力率下超弹性NiTi形状记忆合金板材的单轴相变棘轮行为演化特征, 如图7 所示. 图7 表明: NiTi合金板材的单轴相变棘轮行为也体现出明显的应力率相关性, 拉伸部分的相变硬化程度也随应力率(即加载应力随时间的变化率)的增大而增大, 并且高应力率下的相变棘轮行为更为显著. 另外, 由图7 还可以看出, 在高应力率情形下, 每一次循环中的耗散能密度(即应力--应变滞回环的面积)明显小于低应力率下的结果. 这也说明, 在应力控制的循环变形过程中, 超弹性劣化和耗散能下降也随应力率的增大而变得更加迅速.这些率相关性也是依赖于循环变形过程中体现出的、明显的热--力耦合效应.值得注意的是, 尽管目前已有一些文献讨论了超弹性NiTi形状记忆合金的率相关相变棘轮行为, 但与应变控制下的率相关循环变形行为相比, 已有的研究还不系统, 特别是NiTi形状记忆合金多轴循环变形行为的率相关性方面还需要在未来的研究中进行更为深入和系统的实验观察. ...
First Principles Modelling of Shape Memory Alloys. Berlin Heidelberg:
2
2012
... 近二十年来, 随着人们对NiTi形状记忆合金的了解和认识的深入, 越来越多的学者更加关注该合金在纳米尺度下的变形机制, 已经在NiTi形状记忆合金的热--力耦合变形行为的分子动力学(MD)模拟方面取得了众多成果, Kastner (2012) 和Cisse等(2016) 对形状记忆合金相变过程及相关变形行为的分子动力学模拟方面的研究现状进行了较为系统的介绍, 特别是针对NiTi原子间相互作用势、NiTi形状记忆合金的超弹性和形状记忆效应原子模拟方面的研究.因此, 关于NiTi形状记忆合金分子动力学模拟的基本过程以及不同原子间势函数的特征和选择原则等方面的内容请参见文献Kastner(2012) 和Cisse 等(2016) , 本小节仅针对已有的热--力耦合循环变形行为的分子动力学模拟结果做一个必要的补充. ...
... 随着对NiTi形状记忆合金循环变形行为研究的开展和深入, 正如Eggeler等(2004)和Mahtabi 等(2015)综述的那样, NiTi形状记忆合金的疲劳问题已经得到了较为广泛的研究. Eggeler等(2004)进一步将NiTi形状记忆合金的疲劳失效行为分为两类, 即:结构疲劳失效, 代表NiTi形状记忆合金在一定循环载荷寿命下的物理失效或断裂; 功能疲劳失效则代表因超弹性和形状记忆效应等功能的劣化而发生的功能性丧失.例如, Wagner等(2004)就将超弹性NiTi形状记忆合金在循环变形过程中产生的累积残余应变的某一个临界值作为其功能失效的一种判据; 而Predki 等(2006), Dunand-Ch\^{a}tellet 和 Moumni (2012) 以及Song等(2015)则将每次循环中的耗散能密度下降到某一个临界值作为超弹性NiTi形状记忆合金的功能失效判据.由第2部分讨论的NiTi形状记忆合金的循环变形行为可知, 在NiTi形状记忆合金的循环变形过程中, 经过一定的循环次数后均会达到一个相对稳定的循环变形状态, 累积残余应变或降低的耗散能密度都会无限接近于一个稳定值, 并且在功能失效发生时没有材料的断裂发生, 因此, NiTi形状记忆合金的功能失效行为在设定了失效判据(也就是残余应变或耗散能密度等的临界值)以后, 完全可以和前节综述的NiTi形状记忆合金的循环变形行为一起来讨论.为此, 本节将主要讨论NiTi形状记忆合金的结构疲劳失效行为, 对于其功能失效行为的研究现状可参见Eggeler 等(2004)和Mahtabi等(2015)综述论文. 针对NiTi形状记忆合金的结构疲劳失效行为, Kang 和Song(2015) 已经着重对不同试样形式下的宏观疲劳失效行为的实验研究现状进行了较为详细的评述, 讨论了NiTi形状记忆合金单轴和多轴以及热--力耦合疲劳失效行为的研究进展.为了保证本文内容的完整性, 本小节结合一些最新的研究进展, 对该合金的结构疲劳失效行为的失效机制微观观察和疲劳失效模型(特别是基于损伤的疲劳失效模型)的研究现状进行补充评述.本节未涉及到的相关研究进展可参见文献(Kang & Song 2015 ).同样, 由于Cu-基和Fe-基形状记忆合金的循环变形和疲劳失效行为与NiTi形状记忆合金的类似, 本节也就仅针对NiTi形状记忆合金的疲劳失效行为来进行评述. ...
Phase field modeling of Ni-concentration distribution behavior around Ni\(_{4}\)Ti\(_{3}\) precipitates in NiTi alloys.
0
2015
Magnetic field-induced martensitic variant reorientation in magnetic shape memory alloys.
4
2005
... 由图2 得到的应力--应变关系曲线可见: (1)加载速率的变化显著影响超弹性NiTi形状记忆合金微管的循环应力--应变响应, 拉伸部分体现出的相变硬化程度在高加载速率下变得更加显著, 如图2 (a)所示. (2) 残余应变的累积同样依赖于加载速率, 在高加载速率下演变更为迅速, \(3.3\times 10^{ - 2}\) s\(^{ -1}\)下的饱和残余应变值明显高于其他加载速率下的结果, 如图2 (b) \(\sim\) 图2 (d)所示. (3)随着加载速率的增大, 每一次循环中的耗散能密度下降也更为迅速, 并且饱和的耗散能密度值也变得更小. 这说明, 超弹性的循环劣化和耗散能密度减小在高加载速率的循环过程中变得更加显著, 进而更易导致超弹性NiTi形状记忆合金的功能性疲劳失效. 此外, 超弹性NiTi形状记忆合金循环劣化和耗散能密度还随着加载应力水平的提高(Kang et al. 2009 )和温升的提高 (Yu et al. 2014a )变得更加显著. ...
... 由于初始相为孪生马氏体的NiTi形状记忆合金在单纯的机械载荷作用下是通过马氏体的解孪和重取向来产生材料的宏观变形的, 不涉及任何相变过程的发生, 因此, 在机械载荷完全卸载以后, 由马氏体的解孪和重取向发生的变形绝大部分不能恢复, 产生类似于塑性应变的残余变形.这一部分残余应变只有在后续的升温过程中才能因解孪(重取向)马氏体转变为奥氏体而逐渐消失, 为此, 人们认为在不涉及温度变化的纯机械载荷作用下, 形状记忆NiTi合金的循环变形行为与普通金属类似, 进而没有对其进行较为系统的研究. 然而, Kang等(2009) 对初始相为孪生马氏体的NiTi形状记忆合金的室温单轴应力控制循环变形实验研究却表明, 由于该合金的非弹性变形机制是马氏体的解孪和重取向, 是一种外加载荷作用下马氏体孪生关系和晶体学位向的改变, 并不是普通金属室温循环变形过程中涉及的位错的滑移或孪晶的形成, 因此, 其应力控制的单轴循环变形行为与普通金属材料有明显的不同. ...
... 虽然NiTi形状记忆合金具有超弹性、形状记忆特性、良好的生物相容性和耐磨性等优点, 但其在温度驱动条件下热传导时间较长, 响应频率低, 无法满足高频响应器件的要求. 然而, 铁磁形状记忆合金除了具备传统NiTi形状记忆合金的优良特性之外, 还具有在磁场驱动条件下响应频率高这一优点. 因此, 近年来, 铁磁形状记忆合金得到了越来越多的关注, 具有广阔的应用前景.自从Ullakko等(1996) 首次报道了NiMnGa合金单晶在中等磁场强度下(小于1T)能够产生0.2%的磁致伸缩应变后, 铁磁形状记忆合金就以其优越的热--力--磁学特性引起了固体力学界和材料科学界学者的广泛关注和研究, 取得了丰硕的研究成果.关于磁致形状记忆合金一些基本变形特征的阐述可参见Kiefer 和 Lagoudas (2005) 的工作, 本节仅针对其磁--力耦合循环变形行为的研究现状进行评述. ...
... 如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景. ...
Effect of magnetic field on martensitic transformation temperature in Ni-Mn-Ga ferromagnetic shape memory alloys.
1
2006
... 尽管对NiTiX高温形状记忆合金的微观结构特征已有较多的微观实验观察, 但绝大多数集中在材料改性的范畴, 对热--力耦合循环加载下该类合金的微观结构观察少有报道, 需在今后进一步开展系统的研究. 例如, Karaca等(2013) 对不同温度下的挤压态NiTiHf高温形状记忆合金的沉淀相进行了观察, 证明了550\(^{\circ}\)C \(\times \) 3 h后, 材料中即有纳米级沉淀出现, 并且时效温度提高到650\(^{\circ}\)C后, 相同时效时间下的沉淀尺寸增大; Satamarta等(2013) 对NiTiHf及NiTiZr材料的微观实验观察中证明炉内冷却的方法可以比高温时效更易使材料内部产生更大的沉淀粒子; Yang 等(2013) 在实验观察的基础上进一步提出, 对于NiTiHf高温形状记忆合金, 这些沉淀粒子并非普通的Ni\(_{4}\) (Ti, Hf)\(_{3}\)相, 而是一种具有不同原子结构的新相, 即H相. ...
Atomic scale processes of phase transformations in nanocrystalline NiTi shape-memory alloys.
5
2017
... (1)磁场诱发马氏体重定向:Tickle和 James (1999) , Tickle 等(1999) , Heczko (2005) , Straka 和 Heczko (2003) 以及Karaca等(2006) 研究了环境温度在马氏体完成温度\((M_{\rm f})\)以下时铁磁形状记忆合金单晶在轴向恒定压应力、横向交变磁场作用下磁场诱发马氏体重定向特性.此时, 材料的初始相为马氏体, 图43 给出了该加载工况下典型的磁场--相对磁化曲线及磁场--应变曲线.以压应力为1.4 MPa的工况为例, 由图可见: 在变形的初始阶段(即磁场低于0.5 T), 由于磁场低于马氏体重定向临界磁场, 无非弹性应变出现, 并且磁化量随着磁场的增大而线性增大, 该阶段的磁化机制主要为磁化矢量的旋转; 当磁场高于0.5 T时, 马氏体重定向发生, 伴随着很大的非弹性应变出现, 同时磁化率出现跳跃并远高于低磁场(小于0.5 T)时的磁化率, 在该阶段马氏体重定向和磁化矢量旋转这两种磁化机制同时发生; 当磁场达到0.8 T时, 马氏体重定向完成, 磁化饱和出现, 并在后续磁场加载过程中, 非弹性应变和磁化量不再变化; 在卸载过程中, 当磁场达到0.25 T时, 逆向重定向发生, 非弹性应变和磁化量剧烈变化; 当磁场完全卸载后, 马氏体重定向完成, 非弹性应变及磁化量完全归零.另外, 对比图43 中不同应力水平下的磁--力响应可以看出:磁致伸缩应变的大小随着轴向压应力的增大而逐渐减小, 并且轴向压应力对磁场诱发马氏体重定向有抑制作用, 即临界磁场强度随着轴向压应力的增加而逐渐升高; 在压应力较小时(0.6 MPa), 磁场诱发出的重定向应变无法完全恢复; 在压应力较大时(3 MPa), 试样在发生马氏体重定向之前已经通过磁化矢量旋转机制完成了磁化, 无法诱发马氏体重定向机制. 这说明, 铁磁形状记忆合金存在着一个"闭锁应力", 在应力低于"闭锁应力"时, 磁场能够诱发马氏体重定向; 在应力高于"闭锁应力"时, 磁场无法诱发马氏体重定向. 铁磁形状记忆合金的"闭锁应力"一般较低, 大约在3 MPa左右. Karaca等(2006) 进一步提出了发生马氏体重定向的两个必要条件, 即高的磁晶各向异性能和低的孪生界面运动能, 并通过增大测试温度与居里温度之差以及减小测试温度和马氏体相变温度之差分别提高和降低磁晶各向异性能和孪生界面运动能, 进而获得了较高的应力闭锁值(5.7 MPa). ...
... 中不同应力水平下的磁--力响应可以看出:磁致伸缩应变的大小随着轴向压应力的增大而逐渐减小, 并且轴向压应力对磁场诱发马氏体重定向有抑制作用, 即临界磁场强度随着轴向压应力的增加而逐渐升高; 在压应力较小时(0.6 MPa), 磁场诱发出的重定向应变无法完全恢复; 在压应力较大时(3 MPa), 试样在发生马氏体重定向之前已经通过磁化矢量旋转机制完成了磁化, 无法诱发马氏体重定向机制. 这说明, 铁磁形状记忆合金存在着一个"闭锁应力", 在应力低于"闭锁应力"时, 磁场能够诱发马氏体重定向; 在应力高于"闭锁应力"时, 磁场无法诱发马氏体重定向. 铁磁形状记忆合金的"闭锁应力"一般较低, 大约在3 MPa左右. Karaca等(2006) 进一步提出了发生马氏体重定向的两个必要条件, 即高的磁晶各向异性能和低的孪生界面运动能, 并通过增大测试温度与居里温度之差以及减小测试温度和马氏体相变温度之差分别提高和降低磁晶各向异性能和孪生界面运动能, 进而获得了较高的应力闭锁值(5.7 MPa). ...
... (2)应力诱发马氏体重定向. Heczko (2005) , Karaca 等(2006) , Chen等(2014) 和Heidi 等(2016) 研究了环境温度在马氏体完成温度\(M_{\rm f}\)以下时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体重定向特性.图44 给出了在该加载工况下典型的应力应变曲线. 由图可见: 在无磁场作用下时, 加载诱发出的非弹性应变在应力完全卸载后不能恢复, 这是由于马氏体逆向重定向开始应力大于零; 而在磁场作用下, 马氏体重定向平台随着磁场的增大的逐渐升高, 这表明横向磁场对轴向应力诱发马氏体重定向有抑制作用; 当磁场达到8 kG时, 重定向应变在应力卸载后能够完全恢复, 材料展示出超弹性效应. 需要说明的是, 铁磁形状记忆合金在\(M_{\rm f}\)以下的超弹性机制是正向和逆向马氏体重定向, 这与NiTi形状记忆合金在奥氏体完成温度\(A_{\rm f}\)以上由正向和逆向马氏体相变所导致的超弹性有本质区别. ...
... 在铁磁形状记忆合金循环载荷下的功能性劣化方面, Karaca等(2006) 通过对NiMnGa单晶施加循环磁载荷, 发现随着循环过程的进行, 残余应变会逐渐累积, 如图47 所示, 这与NiTi形状记忆合金在温度诱发循环相变过程中残余应变累积的现象类似.Aaltio 等(2010) 研究了NiMnGa单晶在单纯机械载荷作用下的循环变形特性, 结果表明: 与NiTi形状记忆合金类似, NiMnGa在循环变形过程中出现了明显的功能性劣化, 即重定向开始应力和重定向模量均随着循环次数的增大而升高, 如图48 所示. Aaltio 等(2010) 指出, 上述的功能性劣化现象来源于两个方面:一是在循环机械载荷作用下, 晶体缺陷会逐渐形核并累积; 二是缺陷的存在阻碍了马氏体孪生界面运动, 从而造成重定向开始应力和重定向模量逐渐升高. ...
... NiMnGa形状记忆合金单晶在循环磁场作用下的磁场--应变曲线(Karaca et al. 2006 ) ...
Role of severe plastic deformation on the cyclic reversibility of a Ti\(_{50.3}\)Ni\(_{33.7}\)Pd\(_{16}\) high temperature shape memory alloy
4
2010
... 供货态与挤压态NiTiPd高温形状记忆合金的循环温度--应变响应 (Kockar et al.2010 ). (a) 供货态, (b) 挤压态 ...
... Kockar 等(2006 , 2010 )对供货态和挤压态NiTiPd和NiTiHf高温形状记忆合金的马氏体形貌分别进行了对比, 发现经过等通道转角挤压的高温形状记忆合金中马氏体尺寸比供货态有大幅度的减小, 进而材料的力学性能则有大幅度的提高. Meng 等(2002) 对NiTiHf高温形状记忆合金在单次加载下的应力诱发马氏体形貌进行了观察, 发现: 在548 K下施加8%的应变时, 形成的马氏体具有方向性, 且边界较为清晰; 而应变增大到16%的时候, 马氏体的边界则变得模糊不清; 同时, 当实验温度升高到573 K时, 施加8%的应变即出现马氏体边界不清的情况, 与较低温度时的剧烈变形情况相似, 见图34 . ...
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
... ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
A method to enhance cyclic reversibility of NiTiHf high temperature shape memory alloys.
2
2006
... Kockar 等(2006 , 2010 )对供货态和挤压态NiTiPd和NiTiHf高温形状记忆合金的马氏体形貌分别进行了对比, 发现经过等通道转角挤压的高温形状记忆合金中马氏体尺寸比供货态有大幅度的减小, 进而材料的力学性能则有大幅度的提高. Meng 等(2002) 对NiTiHf高温形状记忆合金在单次加载下的应力诱发马氏体形貌进行了观察, 发现: 在548 K下施加8%的应变时, 形成的马氏体具有方向性, 且边界较为清晰; 而应变增大到16%的时候, 马氏体的边界则变得模糊不清; 同时, 当实验温度升高到573 K时, 施加8%的应变即出现马氏体边界不清的情况, 与较低温度时的剧烈变形情况相似, 见图34 . ...
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
Phase transformation, structural and functional fatigue properties of Ti-Ni-Hf shape memory thin films.
5
2011
... 近二十年来, 随着人们对NiTi形状记忆合金的了解和认识的深入, 越来越多的学者更加关注该合金在纳米尺度下的变形机制, 已经在NiTi形状记忆合金的热--力耦合变形行为的分子动力学(MD)模拟方面取得了众多成果, Kastner (2012) 和Cisse等(2016) 对形状记忆合金相变过程及相关变形行为的分子动力学模拟方面的研究现状进行了较为系统的介绍, 特别是针对NiTi原子间相互作用势、NiTi形状记忆合金的超弹性和形状记忆效应原子模拟方面的研究.因此, 关于NiTi形状记忆合金分子动力学模拟的基本过程以及不同原子间势函数的特征和选择原则等方面的内容请参见文献Kastner(2012) 和Cisse 等(2016) , 本小节仅针对已有的热--力耦合循环变形行为的分子动力学模拟结果做一个必要的补充. ...
... König等(2011) 则观察了利用磁控溅射制备的NiTiHf多层纳米薄片材料中存在的三元Laves相沉淀, 深入讨论了该沉淀相对薄膜材料温度循环变形行为的影响. König等(2011) 指出, 三元Laves相的出现可以增加材料的可恢复应力, 提高其功能性疲劳(温度循环)特性, 并认为该沉淀相是造成多层纳米薄片材料与沉积制备的单层薄片材料和块体材料循环变形行为不同的原因.König等(2011) 对不同Hf原子含量的NiTiHf高温形状记忆合金薄膜材料分别进行了温度循环实验, 结果表明: 在温度循环的初始时期, Laves相的出现可增大材料的可恢复应力; 但随着循环的进行, 第二相粒子数目逐渐增加, 则会导致可恢复应力逐渐降低. 同时, König 等(2011) 根据实验结果, 将每一个温度循环次数下的应力幅值\(\sigma (T)\)随循环次数线性变化的斜率定义为功能性疲劳因子\(c_{\rm f}\), 并且探讨了\(c_{\rm f}\)与Hf原子含量的关系. 结果表明, Laves相的存在会抵消由Hf含量增大而增大的滞回环宽度, 使材料的功能性疲劳因子\(c_{\rm f}\)在Hf含量达到17%后迅速下降, 见图42 . ...
... 则观察了利用磁控溅射制备的NiTiHf多层纳米薄片材料中存在的三元Laves相沉淀, 深入讨论了该沉淀相对薄膜材料温度循环变形行为的影响. König等(2011) 指出, 三元Laves相的出现可以增加材料的可恢复应力, 提高其功能性疲劳(温度循环)特性, 并认为该沉淀相是造成多层纳米薄片材料与沉积制备的单层薄片材料和块体材料循环变形行为不同的原因.König等(2011) 对不同Hf原子含量的NiTiHf高温形状记忆合金薄膜材料分别进行了温度循环实验, 结果表明: 在温度循环的初始时期, Laves相的出现可增大材料的可恢复应力; 但随着循环的进行, 第二相粒子数目逐渐增加, 则会导致可恢复应力逐渐降低. 同时, König 等(2011) 根据实验结果, 将每一个温度循环次数下的应力幅值\(\sigma (T)\)随循环次数线性变化的斜率定义为功能性疲劳因子\(c_{\rm f}\), 并且探讨了\(c_{\rm f}\)与Hf原子含量的关系. 结果表明, Laves相的存在会抵消由Hf含量增大而增大的滞回环宽度, 使材料的功能性疲劳因子\(c_{\rm f}\)在Hf含量达到17%后迅速下降, 见图42 . ...
... 指出, 三元Laves相的出现可以增加材料的可恢复应力, 提高其功能性疲劳(温度循环)特性, 并认为该沉淀相是造成多层纳米薄片材料与沉积制备的单层薄片材料和块体材料循环变形行为不同的原因.König等(2011) 对不同Hf原子含量的NiTiHf高温形状记忆合金薄膜材料分别进行了温度循环实验, 结果表明: 在温度循环的初始时期, Laves相的出现可增大材料的可恢复应力; 但随着循环的进行, 第二相粒子数目逐渐增加, 则会导致可恢复应力逐渐降低. 同时, König 等(2011) 根据实验结果, 将每一个温度循环次数下的应力幅值\(\sigma (T)\)随循环次数线性变化的斜率定义为功能性疲劳因子\(c_{\rm f}\), 并且探讨了\(c_{\rm f}\)与Hf原子含量的关系. 结果表明, Laves相的存在会抵消由Hf含量增大而增大的滞回环宽度, 使材料的功能性疲劳因子\(c_{\rm f}\)在Hf含量达到17%后迅速下降, 见图42 . ...
... 对不同Hf原子含量的NiTiHf高温形状记忆合金薄膜材料分别进行了温度循环实验, 结果表明: 在温度循环的初始时期, Laves相的出现可增大材料的可恢复应力; 但随着循环的进行, 第二相粒子数目逐渐增加, 则会导致可恢复应力逐渐降低. 同时, König 等(2011) 根据实验结果, 将每一个温度循环次数下的应力幅值\(\sigma (T)\)随循环次数线性变化的斜率定义为功能性疲劳因子\(c_{\rm f}\), 并且探讨了\(c_{\rm f}\)与Hf原子含量的关系. 结果表明, Laves相的存在会抵消由Hf含量增大而增大的滞回环宽度, 使材料的功能性疲劳因子\(c_{\rm f}\)在Hf含量达到17%后迅速下降, 见图42 . ...
Experimental and microstructural characterization of simultaneous creep, plasticity and phase transformation in high-temperature shape memory alloy.
1
2010
... Kumar & Lagoudas(2010) 利用TEM对蠕变以及温度循环后的NiTiPd高温形状记忆合金的马氏体形貌分别进行了观察, 实验表明: 供货态材料中的马氏体以\{1 \ 1 \ 1\}取向的第一类孪晶构成, 见图35 (a); 而蠕变加载下的马氏体则主要由\{0 \ 1 \ 1\}取向的复合孪晶和\{1 \ 1 \ 1\}取向的第一类孪晶同时组成, 并且复合孪晶在材料的微结构中占主导地位(图35 (b)), 这些复合孪晶常出现在材料中的沉淀及缺陷周围; 同时, 蠕变加载中的位错攀移会导致位错在材料中出现随机分布的形式, 在取向不占优的滑移平面, 这些位错也会引起应力集中, 导致材料中复合孪晶的形成; 在温度循环中形成的马氏体尺寸比蠕变情况下更大, 且边界更为清晰, 其中\{1 \ 1 \ 1\}取向的孪晶在温度循环加载时占主导地位; 将试样加热到更高的温度, 材料中的马氏体恢复为奥氏体的比率也会相应增大, 见图36 . ...
Numerical investigation of the interaction between the martensitic transformation front and the plastic strain in austenite. J. Mech. Phys.
0
2015
A phase-field model for incoherent martensitic transformations including plastic accommodation processes in the austenite. J. Mech. Phys.
1
2011
... (3)应力诱发马氏体相变. Chernenko 等(2005) , Segu\'{\i} 等(2005) , Kim 等(2006) 和Karaca 等(2007) 研究了环境温度在奥氏体完成温度A\(_{\rm f}\)以上时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体相变特性.和NiTi形状记忆合金类似, 铁磁形状记忆环境在应力作用下展示出良好的超弹性特性, 如图45 所示. 同时, 可以看出横向磁场对马氏体相变具有抑制作用, 即向前相变和逆相变平台均随着横向磁场的增加而升高, 并且相变特性对温度有很强的依赖性. 需要说明的是, 为了便于比较, 图43 中每个温度下的应变初始值均为零, 坐标轴的刻度间隔为1%. ...
Shape Memory Alloys: Modeling and Engineering Applications.
11
2008
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 热致形状记忆合金是最先问世的形状记忆合金, 并且是目前研究最为集中的智能材料之一.在这类形状记忆合金中应用最为广泛的是近等原子比的NiTi形状记忆合金和NiTiX高温形状记忆合金, 同时其他的热致形状记忆合金(诸如Cu基和Fe基形状记忆合金等)的热--力耦合循环变形行为与前述两种合金的非常相似(赵连城等 2002 ), 因此本节仅对NiTi和NiTiX形状记忆合金的相关研究成果进行总结, 对这两类合金的基本力学行为及其相变机理等不做阐述, 相关内容可参见文献(Lagoudas 2008 , 赵连城等 2002 ). ...
... 近等原子比NiTi形状记忆合金是研究最为系统、应用最为广泛的热致形状记忆合金材料之一.因此, 本节首先对近等原子比NiTi形状记忆合金热--力循环变形行为的宏微观实验观察、数值模拟和本构模型的研究现状进行较为全面的综述.需要指出的是, 本节讨论的NiTi形状记忆合金的热弹性马氏体相变温度通常低于373 K, 无法在高于373 K的温度环境下使用.针对使用温度高于393 K的高温形状记忆合金(如三元系的NiTiX高温形状记忆合金)的相关变形行为将在2.2节中进行讨论.本小节将着重对NiTi形状记忆合金循环变形行为的强烈热--力耦合效应及其理论模型研究的最新进展进行评述, 其他的研究现状综述可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 , 周廷等 2017 ). ...
... 由于NiTi形状记忆合金在不同的加载条件下将分别呈现出超弹性效应和形状记忆效应, 而这两大效应都与施加的热--力耦合循环载荷有密切的联系, 因此将分超弹性和形状记忆NiTi形状记忆合金来进行总结. 但是, 如前所述, 本小节仅着重介绍在不同加载速率或加载频率下体现出的率相关热--力耦合循环变形行为, 其他的相关实验研究成果可参见文献 (Lagoudas 2008 , 康国政 2011 , Kang2013 , 康国政等 2015 , Kang & Song 2015 , Cisse et al. 2016 )中的相关综述内容. 需要指出的是, 下面讨论应力--应变曲线时, 应变由引伸计测得, 而在相变局部化观测过程中, 由DIC测得应变场, 然后对试样工作段应变进行平均得到名义应变. ...
... 已有研究表明, 超弹性NiTi形状记忆合金的相变应力明显依赖于实验环境温度, 由Clausius-Clapeyron关系式可知实验温度每升高1K, 该合金的马氏体相变开始应力将升高8 MPa左右 (Lagoudas 2008 , 赵连城等 2002 ).NiTi形状记忆合金的热--力耦合行为与相变潜热的释放和吸收以及由此而引起的温度变化密切相关, Yu等(2014a)专门讨论了超弹性NiTi形状记忆合金在应变控制循环变形过程中出现的超弹性劣化效应的温度相关性, 结果如图1 所示. 由图1 (b) \(\sim \) 图1 (d)可见: 随实验环境温度的升高, 残余应变的累积效果随循环次数的增大越显著, 耗散能密度和马氏体相变开始应力减小就越明显, 即循环变形对NiTi形状记忆合金的超弹性劣化作用就越显著, 相变棘轮行为发展就更为迅速. ...
... Ko等(2017) 则采用考虑第二近邻的MEAM势在奥氏体相变结束温度以上模拟了不同晶粒尺寸(应变率为5 \(\times\) 10\(^{8}\) s\(^{ - 1})\)和不同应变率 (晶粒尺寸为8nm)下NiTi形状记忆合金的超弹性行为, 分子动力学模拟结果表明: (1)加/卸载过程中的相变应力随着晶粒尺寸的减小而增加, 如图19 所示; (2)在没有内部缺陷的模型中再现了实验中观察到的温度和应力诱导马氏体相变, 证实了内部缺陷贡献机制不是马氏体相变的主要诱发机制.基于分子动力学模拟结果, Ko等(2017) 提出了相变诱发的应变贡献机制并成功地解释了马氏体相变和逆相变中的非对称形核和生长行为, 如图20 所示(图中原子的颜色根据CNA模式进行标记, 在每幅截图中蓝色的原子对应B2奥氏体相, 红色的原子对应B19'马氏体相, 灰色的原子对应晶界和域边界).(3)超弹性NiTi形状记忆合金在拉伸过程的应力--应变响应强烈依赖于加载速率, 加载速率越大, 相变硬化程度越高, 进而相同应变值下对应的应力值越高; 同时, 相变开始应力也随加载速率的增大而升高, 如图21 所示. ...
... 所示; (2)在没有内部缺陷的模型中再现了实验中观察到的温度和应力诱导马氏体相变, 证实了内部缺陷贡献机制不是马氏体相变的主要诱发机制.基于分子动力学模拟结果, Ko等(2017) 提出了相变诱发的应变贡献机制并成功地解释了马氏体相变和逆相变中的非对称形核和生长行为, 如图20 所示(图中原子的颜色根据CNA模式进行标记, 在每幅截图中蓝色的原子对应B2奥氏体相, 红色的原子对应B19'马氏体相, 灰色的原子对应晶界和域边界).(3)超弹性NiTi形状记忆合金在拉伸过程的应力--应变响应强烈依赖于加载速率, 加载速率越大, 相变硬化程度越高, 进而相同应变值下对应的应力值越高; 同时, 相变开始应力也随加载速率的增大而升高, 如图21 所示. ...
... 超弹性加卸载过程中NiTi纳米晶体的原子排列 (Ko et al. 2017 ) ...
... 400 K下平均晶粒尺寸为8 nm的NiTi晶体拉伸--卸载时的应力--应变曲线 (Ko et al. 2017 ) ...
... 基于已有的热--力耦合循环变形实验研究, 近年来众多学者建立了一系列的本构模型来描述NiTi形状记忆合金的热--力耦合循环变形行为.Lagoudas (2008), 康国政 (2011), Kang (2013), 康国政等(2015), Kang和 Song (2015)和Cisse等(2016)对NiTi形状记忆合金的本构模型研究现状也分别进行了一定的综述, 并着重对描述NiTi形状记忆合金的超弹性行为及其循环劣化的本构模型进行了评述, 将它们归纳为宏观本构模型、晶体塑性模型和基于Eshelby夹杂理论的细观本构模型三大类.但是, 他们对NiTi形状记忆合金热--力耦合循环变形行为及其本构描述突出得还不够, 因此, 本小节将着重对NiTi形状记忆合金的热--力耦本构模型研究的最新进展进行评述, 其他方面的研究现状可参见文献 (Lagoudas 2008 , 康国政2011 , Kang 2013 , 康国政等2015 , Kang & Song 2015 , Cisse et al. 2016 ). ...
... 根据Lagoudas (2008) 的工作, 相变应变率张量\(\dot{\pmb\varepsilon}^{\rm tr}\)与马氏体体积分数率\(\dot {\xi}\)的关系可取为\[\dot {\pmb\varepsilon}^{\rm tr} = g^{\rm tr}\pmb N _{\rm tr} \dot {\xi } , \qquad \pmb N _{\rm tr} = \left\{{\begin{array}{ll} \sqrt {\dfrac{3}{2}} \dfrac{\pmb \sigma ^{\rm dev} + \pmb B }{\left\| {\pmb \sigma ^{\rm dev} + \pmb B } \right\|},& \dot {\xi } > 0 \\ \dfrac{\pmb \varepsilon _{\rm recent}^{\rm tr} }{g^{\rm tr}\xi _{\rm recent} },& \dot {\xi } < 0 \\ \end{array}} \right.\ \ (3)\]其中, \(\pmb N _{\rm tr} \)是马氏体相变的方向张量, \(g ^{\rm tr}\)是马氏体完全相变产生的相变应变大小, \(\pmb \sigma ^{\rm dev}\)是偏应力张量. \(\pmb B \)是相变内应力, 用来刻画位错造成的局部内应力对马氏体相变形核的帮助作用, 即描述马氏体相变应力随着循环过程而逐渐降低的现象. \(\xi _{\rm recent} \)和\(\pmb \varepsilon _{\rm recent}^{\rm tr}\)分别是逆向变开始点的马氏体体积分数和相变应变张量. ...
a. Modeling and experimental study of simultaneous creep and transformation in polycrystalline high-temperature shape memory Alloys. J
2
2009
... 目前, 专门针对NiTiX高温形状记忆合金热--力耦合变形行为的本构模型研究较少, 已有研究均是在二元NiTi形状记忆合金对应的本构模型基础上进行拓展, 并且均为宏观唯象的本构模型, 主要针对高温形状记忆合金在恒定应力作用下温度循环加载过程中的热--力耦合变形行为进行本构描述.对于三元NiTiX高温形状记忆合金的超弹性行为, 因其与二元NiTi形状记忆合金的区别主要体现在相变温度上, 也就是说其使用的环境温度与二元NiTi形状记忆合金不同, 其应力诱发的相变机制以及由此而产生的超弹性变形行为与二元NiTi形状记忆合金基本相同, 因此, 可以采用已有的、能够合理描述NiTi形状记忆合金超弹性行为的本构模型直接描述NiTiX高温形状记忆合金的超弹性行为及其在循环变形过程中的劣化现象和对环境温度的依赖性(如图33 (b)所示).针对NiTiX高温形状记忆合金在恒定应力作用下的温度循环加载过程中的热--力耦合变形行为, Lagoudas 等(2009a) 及其合作者(Hartl et al. 2010, Chemisky et al. 2014 )在其本构模型构建方面开展了一系列较为重要的探索性工作.Lagoudas 等(2009a)首先根据对高温形状记忆合金的蠕变现象(位错攀移)的观察, 通过将总应变分为弹性应变\(\varepsilon ^{\rm e}\)、热应变\(\varepsilon ^{\rm T}\)、相变应变\(\varepsilon ^{\rm t}\)、相变诱发塑性应变\(\varepsilon ^{\rm tp}\)和黏塑性(蠕变)应变\(\varepsilon ^{\rm vp}\)五个部分, 进而将蠕变机制引入NiTiX高温形状记忆合金的宏观唯象本构模型中, 提出了适用于NiTiX高温形状记忆合金热--力耦合变形行为的一维本构模型, 模型中假设相变与蠕变过程是独立进行的, 不考虑其交互作用; Hartl等(2010)将上述本构模型推广到了三维的情况, 并同时考虑了相变及黏塑性变形间的交互作用; 针对上述两种本构模型均不能合理描述多次循环加载下NiTiX高温形状记忆合金的热--力耦合响应的问题, Chemisky等(2014)通过合理考虑三种非弹性变形机制(即相变、相变诱发塑性及黏塑性变形)对高温形状记忆合金热--力学耦合行为的共同作用, 建立了可描述高温形状记忆合金在温度循环加载下热--力耦合循环变形行为的本构模型.该模型沿用了Lagoudas 等(2009a)的处理方式, 仍然将相变和蠕变变形看作是两个独立的过程, 并假设蠕变变形仅在奥氏体相中发生, 一旦材料发生马氏体相变, 则蠕变机制停止, 直到材料逆相变全部恢复为奥氏体后蠕变才继续进行.另外, 该模型同时考虑了残余马氏体在循环变形中的作用, 较为合理地反映了高温形状记忆合金的残余应变随温度循环的演化情况.下面对该模型(Chemisky et al. 2014 )进行简要的介绍. ...
... 将 \(\pmb\varLambda^{\rm t}\)分为正相变 \(\pmb\varLambda^{\rm t}_{\rm fwd}\)和逆相变\(\pmb\varLambda^{\rm t}_{\rm rev}\)两部分, 其定义沿用Lagoudas 等(2009a) 中的形式, 记为\[\pmb\varLambda^{\rm t}_{\rm fwd}=\dfrac{3}{2}H^{\rm cur}\dfrac{\pmb\sigma'}{\bar{\sigma}},\qquad \dot{\xi}>0 \ \ {\rm (25a)}\] ...
Modeling of transformation-induced plasticity and its effect on the behavior of porous shape memory alloys. Part I: constitutive model for fully dense
1
2004
... 相变诱发塑性变形的方向张量可假设为与马氏体体积分数有关, 则由Lagoudas 和 Entchev (2004) 中的形式, 可得\[ \dot{\pmb \varepsilon}^{\rm tp}=\pmb\varLambda^{\rm tp}\dot{\xi}\ \ (30)\]\[\pmb\varLambda^{\rm tp}_{\rm fwd}=\dfrac{3}{2}\dfrac{\pmb\sigma'}{\bar{\sigma}}w_1\left(C_0^{\rm tp}+C_1^{\rm tp}e^{-\zeta^{\rm d}/C_2^{\rm tp}}\right)\dfrac{H^{\rm cur}}{H^{\rm sat}},\qquad \dot{\xi}>0\ \ (31)\]\[ \pmb\varLambda^{\rm tp}_{\rm rev}=\dfrac{\pmb\varepsilon^{t-r}}{\bar{\varepsilon}^{t-r}}(1-w_1)\left(C_0^{\rm tp}+C_1^{\rm tp}e^{-\zeta^{\rm d}/C_2^{\rm tp}}\right)\dfrac{H^{\rm cur}}{H^{\rm sat}},\qquad \dot{\xi}<0\ \ (32)\] 其中, \(C_0^{\rm tp}\)和\(C_1^{\rm tp}\)为与应力相关的函数, \(C_2^{\rm tp}\)为常数. \(C_1^{\rm tp}\)和\(C_2^{\rm tp}\)描述了相变诱发塑性应变在第一个循环时的指数演化; 而\(C_0^{\rm tp}\)描述了相变诱发塑性应变在随后的循环过程中的线性演化.\(\zeta^{\rm d}\)为累积解孪马氏体体积分数. ...
b. Thermomechanical fatigue of shape memory alloys
1
2009
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
A full 3D thermodynamic-based model for magnetic shape memory alloys. J
2
2014
... NiTiPd高温形状记忆合金蠕变加载前后的马氏体形貌对比(Kumar & Lagoudas 2010 ). (a) 供货态材料, 由\{1 \ 1 \ 1\}第一类孪晶组成; (b) 200 MPa蠕变加载后, 其中区域1为\{0 \ 1 \ 1\}复合孪晶, 区域2为\{1 \ 1 \ 1\}第一类孪晶 ...
... 经过温度循环后的NiTiPd高温形状记忆合金加热至不同温度后的马氏体形貌对比(Kumar & Lagoudas 2010 ). (a) 加热至523\({^\circ}\)C, 其中区域3, 4, 5为残余马氏体, 区域6, 7恢复为奥氏体; (b)加热至640\({^\circ}\)C, 其中区域8为残余马氏体, 区域9恢复为奥氏体 ...
Fatigue life and fracture mechanics of unconstrained Ni-Mn-Ga single crystals in a rotating magnetic field. Mater. Sci. Eng.
2
2016
... 为了进一步考虑NiTi形状记忆合金相变和塑性的交互作用, Levitas等(2003) 采用相状态作为序参量, 从理论上研究了马氏体相变和孪生过程, 并引入位错密度作为序参量考虑位错对相变过程的影响. Malik等(2012) 采用弹塑性相场模型, 基于有限元法研究了塑性自适应对马氏体相变的影响, 结果显示, 塑性自适应会粗化马氏体微观结构. 之后, Malik等(2013) 采用弹塑性相场模型研究了多晶材料晶粒边界和孪晶边界对马氏体相变的影响, 结果发现, 晶粒边界会阻断马氏体的扩展而孪晶边界则不会. Kundin等(2011) 采用类似的方法, 在只考虑单晶奥氏体塑性变形的情况下, 模拟了蝶形马氏体相变的微结构演变, 结果表明奥氏体和马氏体边界处位错密度最大. 之后, Kundin等(2015) 进一步研究了马氏体锋面与奥氏体引发的塑性变形之间的交互作用, 包括位错穿过界面由马氏体承受和位错被马氏体锋面湮灭两种情况. ...
... Guldbakke 等(2010) 也研究了NiMnGaFe单晶在相同加载模式下的疲劳特性, 结果表明, NiMnGaFe单晶的磁致应变演化特性和NiMnGa单晶非常类似, 也分为上述三个阶段, 但其抗疲劳特性较差, 试样在经历2 \(\times\) 10\(^{6}\)次循环磁场载荷后出现断裂.Lawrence 等(2016) 则观察了NiMnGa单晶在磁场诱发疲劳后的试样微观形貌, 发现三种典型的裂纹形式同时存在, 即: I型裂纹沿\(<100>\)方向扩展, II型裂纹沿\(<100>\)方向扩展, III型裂纹沿小角度晶界扩展, 如图54 所示(图中所示的1, 2和3分别代表I型、II型和III型裂纹). ...
2
... 为了进一步考虑NiTi形状记忆合金相变和塑性的交互作用, Levitas等(2003) 采用相状态作为序参量, 从理论上研究了马氏体相变和孪生过程, 并引入位错密度作为序参量考虑位错对相变过程的影响. Malik等(2012) 采用弹塑性相场模型, 基于有限元法研究了塑性自适应对马氏体相变的影响, 结果显示, 塑性自适应会粗化马氏体微观结构. 之后, Malik等(2013) 采用弹塑性相场模型研究了多晶材料晶粒边界和孪晶边界对马氏体相变的影响, 结果发现, 晶粒边界会阻断马氏体的扩展而孪晶边界则不会. Kundin等(2011) 采用类似的方法, 在只考虑单晶奥氏体塑性变形的情况下, 模拟了蝶形马氏体相变的微结构演变, 结果表明奥氏体和马氏体边界处位错密度最大. 之后, Kundin等(2015) 进一步研究了马氏体锋面与奥氏体引发的塑性变形之间的交互作用, 包括位错穿过界面由马氏体承受和位错被马氏体锋面湮灭两种情况. ...
... 黏塑性应变率张量\(\dot{\pmb \varepsilon}^{\rm vp}\)和等效累积黏塑性应变率\(\dot{p}\)可写为(Lemaitre & Chaboche 1994 )\[ \dot{\pmb \varepsilon}^{\rm vp}=\pmb\varLambda^{\rm vp}\dot{p},\qquad \pmb\varLambda^{\rm vp}=\dfrac{3}{2}\dfrac{\pmb\sigma'}{\bar{\sigma}} \ \ (33)\]\[p'=\left\langle {\dfrac{\bar {\sigma } - f^{\rm vp} -Y^{\rm vp}}{K_{\rm a} }} \right\rangle ^{N_{\rm a} } \ \ (34)\]其中, \(Y^{\rm vp}=Y^{\rm vp}(T)\)为温度相关的蠕变启动临界应力, \(K_{\rm a}=K_{\rm a}(T)\)是拖应力, \(N_{\rm a}=N_{\rm a}(T)\)为应力指数, 均与温度相关, \(f^{\rm vp}=Q_1p+Q_2(1-e^{-Q_3p})\)且\(Q_{1}\), \(Q_{2}\)和\(Q_{3}\)是温度相关的材料参数. ...
Advanced phase-field approach to dislocation evolution. Phys. Rev. B, 86:
2
2012
... 初始相为孪生马氏体的NiTi形状记忆合金在热--力耦合的加载过程中会体现出特有的形状记忆效应, 包括有单程、双程和全程记忆效应 (Lagoudas 2008 ).在具有形状记忆效应的NiTi合金中, 其记忆效应是通过温度诱导的马氏体逆相变(即解孪马氏体向奥氏体的转变)来实现的, 而解孪(或重取向)马氏体则是通过施加位移或力载荷由孪生马氏体转变而得, 因此, 这是一个显著的热--力耦合过程, 需要同时考虑机械载荷和温度以及两者之间的耦合作用的影响. ...
... Levitas 和 Javanakht (2012) 引入位错序参量, 采用有限元法研究了奥氏体相和奥氏体--马氏体界面处位错的形核和扩展过程.之后, Levitas 和 Javanakht (2013) 同时引入相变序参量和位错序参量, 采用有限元方法研究了纳米尺度平面应变大变形情况下马氏体(单个变体)相变、位错对奥氏体--马氏体界面扩展的影响、温度诱发马氏体相变时马氏体片的演化和应力诱发马氏体相变时微结构的演化.同时, Levitas 和 Javanbakht(2015) 还详细介绍了纳米尺度大变形情况下马氏体(多个变体)相变、孪生和位错之间交互作用理论的推导和依据. 然后, Javanbakht和 Levitas (2015) 采用有限元方法对该模型进行了数值实现, 进而研究了纳米尺度应力诱发双晶马氏体相变与位错之间的交互作用, 发现位错引起的应力集中可以促进马氏体形核, 而位错引起的应力释放又会阻碍马氏体相变. 此外, 他们还研究了温度诱发马氏体相变时马氏体片在双晶之间的扩展与位错之间的交互作用. ...
Phase field approach to interaction of phase transformation and dislocation evolution.
1
2013
... Levitas 和 Javanakht (2012) 引入位错序参量, 采用有限元法研究了奥氏体相和奥氏体--马氏体界面处位错的形核和扩展过程.之后, Levitas 和 Javanakht (2013) 同时引入相变序参量和位错序参量, 采用有限元方法研究了纳米尺度平面应变大变形情况下马氏体(单个变体)相变、位错对奥氏体--马氏体界面扩展的影响、温度诱发马氏体相变时马氏体片的演化和应力诱发马氏体相变时微结构的演化.同时, Levitas 和 Javanbakht(2015) 还详细介绍了纳米尺度大变形情况下马氏体(多个变体)相变、孪生和位错之间交互作用理论的推导和依据. 然后, Javanbakht和 Levitas (2015) 采用有限元方法对该模型进行了数值实现, 进而研究了纳米尺度应力诱发双晶马氏体相变与位错之间的交互作用, 发现位错引起的应力集中可以促进马氏体形核, 而位错引起的应力释放又会阻碍马氏体相变. 此外, 他们还研究了温度诱发马氏体相变时马氏体片在双晶之间的扩展与位错之间的交互作用. ...
Interaction between phase transformations and dislocations at the nanoscale. Part 1. General phase field approach. J. Mech. Phys.
0
2015
Three-dimensional Landau theory for multivariant stress-induced martensitic phase transformations. III. Alternative potentials, critical nuclei, kink solutions, and dislocation theory. Phys. Rev.
0
2003
Mechanical behavior of an Ni-Ti shape memory alloy under axial-torsional proportional and nonproportional loading. J
5
1999
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
... 如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景. ...
... Mousavi 和 Arghavani (2017)对提出的本构模型进行了数值实现, 并通过将模拟结果和实验结果的对比验证了模型的正确性. 图49 和图50 分别给出了Mousavi 和Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型(LaMaster et al. 2014 )在应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和应力诱发重定向实验结果 (Chen et al. 2014 )与对应的模拟结果的比较情况. 由图可以看出, 三个模型都能够较好地捕捉到实验现象, 但是, Mousavi 和 Arghavani模型(Mousavi & Arghavani 2017 )与实验数据吻合得更好. ...
... 应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比 (Mousavi & Arghavani 2017 ) ...
... 应力诱发重定向实验结果(Chen et al. 2014 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al.2014)以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比(Mousavi & Arghavani 2017 ) ...
Factors influencing the development of two-way shape memory in NiTi.
5
1990
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
... 需要指出的是, 虽然Lawrence等(2016) 采用Bridgman-Stockbarger方法生长单晶, 但制备出的试样仍然存在小角度晶界. Lawrence等(2016) 进一步研究了表面划痕以及表面粗糙度对试样疲劳寿命的影响.结果表明, 表面的划痕和较高的粗糙度会造成试样表面应力集中, 同时马氏体孪晶与表面缺陷的相互作用导致孪生位错的逐渐累积, 造成局部内应力, 导致裂纹萌生, 从而大大降低材料的疲劳寿命. Lawrence等(2016) 指出, 若想获得较好的疲劳寿命, 要同时避免单晶生长过程中出现的小角度晶界和表面划痕以及保证材料具有较低的表面粗糙度. ...
... 采用Bridgman-Stockbarger方法生长单晶, 但制备出的试样仍然存在小角度晶界. Lawrence等(2016) 进一步研究了表面划痕以及表面粗糙度对试样疲劳寿命的影响.结果表明, 表面的划痕和较高的粗糙度会造成试样表面应力集中, 同时马氏体孪晶与表面缺陷的相互作用导致孪生位错的逐渐累积, 造成局部内应力, 导致裂纹萌生, 从而大大降低材料的疲劳寿命. Lawrence等(2016) 指出, 若想获得较好的疲劳寿命, 要同时避免单晶生长过程中出现的小角度晶界和表面划痕以及保证材料具有较低的表面粗糙度. ...
... 进一步研究了表面划痕以及表面粗糙度对试样疲劳寿命的影响.结果表明, 表面的划痕和较高的粗糙度会造成试样表面应力集中, 同时马氏体孪晶与表面缺陷的相互作用导致孪生位错的逐渐累积, 造成局部内应力, 导致裂纹萌生, 从而大大降低材料的疲劳寿命. Lawrence等(2016) 指出, 若想获得较好的疲劳寿命, 要同时避免单晶生长过程中出现的小角度晶界和表面划痕以及保证材料具有较低的表面粗糙度. ...
... 磁场诱发疲劳后的试样微观形貌 (Lawrence et al. 2016 ) ...
Asymmetry of stress-strain curves under tension and compression for NiTi shape memory alloys.
0
1998
High temperature shape memory alloys.
1
2010
... 尽管近等原子比NiTi形状记忆合金已经得到了广泛应用, 但是其使用温度较低, 不能超过373 K. 然而, 在一些工程领域会面临373 K以上的高温环境, 因此, 为了满足高温智能材料的需要, 在NiTi形状记忆合金的基础上通过引入第三种元素, 开发了三元的NiTiX高温形状记忆合金. 三元NiTiX合金中的X可以分别是Pd, Pt, Hf和Zr, 其使用温度可以提高至523 \(\sim \) 773 K, 其中NiTi(Pd, Pt)合金是用第三相置换NiTi合金中的Ni原子, 而NiTi (Zr, Hf)合金则用第三相置换Ti原子. 对于高温形状记忆合金, Ma等(2010) 对工程中使用的高温形状记忆合金按相变温度范围分为三类, 即373 \(\sim \) 673 K为第一类, 673 \(\sim \) 973 K为第二类, 973 K以上为第三类; 同时对不同类别的高温形状记忆合金的一些基本变形行为特征的研究现状进行了综述, 对2010年以前取得的相关研究成果进行了很好的总结. 因此, 本小节将主要对近年来三元NiTiX高温形状记忆合金(即第一类高温形状记忆合金)的循环变形行为研究现状和研究成果进行评述, 其他合金体系和类别的高温形状记忆合金的研究进展参见Ma 等(2010) 的综述论文以及近年来发表的相关文献. ...
Fatigue of nitinol: The state-of-the-art and ongoing challenges. J
0
2015
Fatigue of pseudoelastic NiTi within the stress-induced transformation regime: A modified Coffin-Manson approach.
2
2012
... Levitas 和 Javanakht (2012) 引入位错序参量, 采用有限元法研究了奥氏体相和奥氏体--马氏体界面处位错的形核和扩展过程.之后, Levitas 和 Javanakht (2013) 同时引入相变序参量和位错序参量, 采用有限元方法研究了纳米尺度平面应变大变形情况下马氏体(单个变体)相变、位错对奥氏体--马氏体界面扩展的影响、温度诱发马氏体相变时马氏体片的演化和应力诱发马氏体相变时微结构的演化.同时, Levitas 和 Javanbakht(2015) 还详细介绍了纳米尺度大变形情况下马氏体(多个变体)相变、孪生和位错之间交互作用理论的推导和依据. 然后, Javanbakht和 Levitas (2015) 采用有限元方法对该模型进行了数值实现, 进而研究了纳米尺度应力诱发双晶马氏体相变与位错之间的交互作用, 发现位错引起的应力集中可以促进马氏体形核, 而位错引起的应力释放又会阻碍马氏体相变. 此外, 他们还研究了温度诱发马氏体相变时马氏体片在双晶之间的扩展与位错之间的交互作用. ...
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
Fatigue properties of a pseudoelastic NiTi alloy: Strain ratcheting and hysteresis under cyclic tensile loading. Int. J.
2
2014
... 为了进一步考虑NiTi形状记忆合金相变和塑性的交互作用, Levitas等(2003) 采用相状态作为序参量, 从理论上研究了马氏体相变和孪生过程, 并引入位错密度作为序参量考虑位错对相变过程的影响. Malik等(2012) 采用弹塑性相场模型, 基于有限元法研究了塑性自适应对马氏体相变的影响, 结果显示, 塑性自适应会粗化马氏体微观结构. 之后, Malik等(2013) 采用弹塑性相场模型研究了多晶材料晶粒边界和孪晶边界对马氏体相变的影响, 结果发现, 晶粒边界会阻断马氏体的扩展而孪晶边界则不会. Kundin等(2011) 采用类似的方法, 在只考虑单晶奥氏体塑性变形的情况下, 模拟了蝶形马氏体相变的微结构演变, 结果表明奥氏体和马氏体边界处位错密度最大. 之后, Kundin等(2015) 进一步研究了马氏体锋面与奥氏体引发的塑性变形之间的交互作用, 包括位错穿过界面由马氏体承受和位错被马氏体锋面湮灭两种情况. ...
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
Phase-field modelling of martensitic transformation: the effects of grain and twin boundaries.
0
2013
Three dimensional elasto-plastic phase field simulation of martensitic transformation in polycrystal. Mater. Sci. Eng.
0
2012
Analytical model for field-induced strain in ferromagnetic shape-memory alloy polycrystals. J
2
2002
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
... 上述研究主要集中在铁磁形状记忆合金单晶方面. Murray 等(1998) , Jeong等(2003) 研究了铁磁形状记忆合金多晶的磁--力耦合特性, 发现相对于单晶材料, 多晶能产生的磁致伸缩应变很小. Marioni(2002) 进一步指出, 针对多晶铁磁形状记忆合金, 可以通过定向凝固法调控择优取向的初始织构来获取较大的磁致伸缩应变.近年来, 众多学者研究了铁磁形状记忆合金定向凝固多晶在不同方向上的磁场诱发马氏体重定向特性(Pötschke et al.2010 , Yu et al. 2014b ), 应力诱发马氏体重定向特性(Chulist et al. 2010 , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性. ...
Precipitation and thermal fatigue in Ni-Ti-Zr shape memory alloy thin films by combinatorial nanocalorimetry.
7
2011
... 尽管近等原子比NiTi形状记忆合金已经得到了广泛应用, 但是其使用温度较低, 不能超过373 K. 然而, 在一些工程领域会面临373 K以上的高温环境, 因此, 为了满足高温智能材料的需要, 在NiTi形状记忆合金的基础上通过引入第三种元素, 开发了三元的NiTiX高温形状记忆合金. 三元NiTiX合金中的X可以分别是Pd, Pt, Hf和Zr, 其使用温度可以提高至523 \(\sim \) 773 K, 其中NiTi(Pd, Pt)合金是用第三相置换NiTi合金中的Ni原子, 而NiTi (Zr, Hf)合金则用第三相置换Ti原子. 对于高温形状记忆合金, Ma等(2010) 对工程中使用的高温形状记忆合金按相变温度范围分为三类, 即373 \(\sim \) 673 K为第一类, 673 \(\sim \) 973 K为第二类, 973 K以上为第三类; 同时对不同类别的高温形状记忆合金的一些基本变形行为特征的研究现状进行了综述, 对2010年以前取得的相关研究成果进行了很好的总结. 因此, 本小节将主要对近年来三元NiTiX高温形状记忆合金(即第一类高温形状记忆合金)的循环变形行为研究现状和研究成果进行评述, 其他合金体系和类别的高温形状记忆合金的研究进展参见Ma 等(2010) 的综述论文以及近年来发表的相关文献. ...
... 已有的研究还表明, 在高温热处理条件下, 材料内部的微观结构(如沉淀相等)会极大程度地影响其温度循环变形特性(如初始相变温度等), 而上述微观结构的粒子尺寸与含量还会在温度循环过程中逐渐演化, 进一步影响材料的循环变形行为. McCluskey等(2011) 对于NiTiZr薄片材料进行了加热至900\(^{\circ}\)C后退火的高温循环实验, 发现马氏体向奥氏体转化的相变焓在循环初期(3次数内)保持稳定, 而后线性下降. 与此同时, 相变峰值温度也在达到最高值后随循环圈数增大呈抛物线型降低, 见图31 . McCluskey等(2011) 认为产生上述现象的原因为沉淀相造成材料中的应力松弛, 降低了整体的应变能, 在循环初期使马氏体向奥氏体转化的相变温度升高; 而在高温循环的过程中, 由于沉淀相的含量逐渐增大, 改变了基体的组分, 导致相变温度和相变焓均迅速降低. 同时, McCluskey等(2011) 还对经历了3次及13次高温循环加载的NiTiZr薄片分别进行了100次的低温(50 \(\sim\) 250\(^{\circ}\)C)循环实验研究, 结果表明: 经过13次高温循环的材料在循环初期相变温度迅速降低, 但在随后的循环过程中, 其平均下降速率与经历了3次高温循环的情况并无较大差别; 在Zr原子含量增大的情况下, 相变温度也随之升高, 同时温度循环的稳定性也较高; 而对于经过13次高温循环的材料, 其不同Zr原子含量材料的低温循环初始/结束温度较经历了3次高温循环的情况更加接近, 见图32 . ...
... . McCluskey等(2011) 认为产生上述现象的原因为沉淀相造成材料中的应力松弛, 降低了整体的应变能, 在循环初期使马氏体向奥氏体转化的相变温度升高; 而在高温循环的过程中, 由于沉淀相的含量逐渐增大, 改变了基体的组分, 导致相变温度和相变焓均迅速降低. 同时, McCluskey等(2011) 还对经历了3次及13次高温循环加载的NiTiZr薄片分别进行了100次的低温(50 \(\sim\) 250\(^{\circ}\)C)循环实验研究, 结果表明: 经过13次高温循环的材料在循环初期相变温度迅速降低, 但在随后的循环过程中, 其平均下降速率与经历了3次高温循环的情况并无较大差别; 在Zr原子含量增大的情况下, 相变温度也随之升高, 同时温度循环的稳定性也较高; 而对于经过13次高温循环的材料, 其不同Zr原子含量材料的低温循环初始/结束温度较经历了3次高温循环的情况更加接近, 见图32 . ...
... 认为产生上述现象的原因为沉淀相造成材料中的应力松弛, 降低了整体的应变能, 在循环初期使马氏体向奥氏体转化的相变温度升高; 而在高温循环的过程中, 由于沉淀相的含量逐渐增大, 改变了基体的组分, 导致相变温度和相变焓均迅速降低. 同时, McCluskey等(2011) 还对经历了3次及13次高温循环加载的NiTiZr薄片分别进行了100次的低温(50 \(\sim\) 250\(^{\circ}\)C)循环实验研究, 结果表明: 经过13次高温循环的材料在循环初期相变温度迅速降低, 但在随后的循环过程中, 其平均下降速率与经历了3次高温循环的情况并无较大差别; 在Zr原子含量增大的情况下, 相变温度也随之升高, 同时温度循环的稳定性也较高; 而对于经过13次高温循环的材料, 其不同Zr原子含量材料的低温循环初始/结束温度较经历了3次高温循环的情况更加接近, 见图32 . ...
... Ni\(_{44.7}\)Ti\(_{35.7}\)Zr\(_{19.6}\)高温形状记忆合金经历高温循环后的物理量变化(McCluskey et al. 2011 ). (a) 相变焓, (b) 相变温度 ...
... Ni\(_{44.7}\)Ti\(_{35.7}\)Zr\(_{19.6}\)高温形状记忆合金在低温循环时的相变温度变化(McCluskey et al. 2011 ). (a) 3次高温循环后, (b) 13次高温循环后 ...
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
Kinetics of flow and strain-hardening.
0
1981
Stress-induced martensitic transformation behavior of a Ti-Ni-Hf high temperature shape memory alloy.
2
2002
... NiTiHf高温形状记忆合金在不同应变及温度下的应力诱发马氏体形貌 (Meng et al.2002 ). (a) 8%, 548 K; (b) 16%, 548 K; (c) 8%, 573 K; (d) 16%, 573 K ...
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
Shape memory properties of the Ti\(_{36}\)Ni\(_{49}\)Hf\(_{15}\) high temperature shape memory alloy.
1
2000
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
Thermomechanical characterization of NiTiCu and NiTi SMA actuators: Influence of plastic strains.
2
2000
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
... 为了进一步考虑NiTi形状记忆合金相变和塑性的交互作用, Levitas等(2003) 采用相状态作为序参量, 从理论上研究了马氏体相变和孪生过程, 并引入位错密度作为序参量考虑位错对相变过程的影响. Malik等(2012) 采用弹塑性相场模型, 基于有限元法研究了塑性自适应对马氏体相变的影响, 结果显示, 塑性自适应会粗化马氏体微观结构. 之后, Malik等(2013) 采用弹塑性相场模型研究了多晶材料晶粒边界和孪晶边界对马氏体相变的影响, 结果发现, 晶粒边界会阻断马氏体的扩展而孪晶边界则不会. Kundin等(2011) 采用类似的方法, 在只考虑单晶奥氏体塑性变形的情况下, 模拟了蝶形马氏体相变的微结构演变, 结果表明奥氏体和马氏体边界处位错密度最大. 之后, Kundin等(2015) 进一步研究了马氏体锋面与奥氏体引发的塑性变形之间的交互作用, 包括位错穿过界面由马氏体承受和位错被马氏体锋面湮灭两种情况. ...
Analysis of the rate-dependent coupled thermo-mechanical response of shape memory alloy bars and wires in tension.
2
2011
... 为了进一步考虑NiTi形状记忆合金相变和塑性的交互作用, Levitas等(2003) 采用相状态作为序参量, 从理论上研究了马氏体相变和孪生过程, 并引入位错密度作为序参量考虑位错对相变过程的影响. Malik等(2012) 采用弹塑性相场模型, 基于有限元法研究了塑性自适应对马氏体相变的影响, 结果显示, 塑性自适应会粗化马氏体微观结构. 之后, Malik等(2013) 采用弹塑性相场模型研究了多晶材料晶粒边界和孪晶边界对马氏体相变的影响, 结果发现, 晶粒边界会阻断马氏体的扩展而孪晶边界则不会. Kundin等(2011) 采用类似的方法, 在只考虑单晶奥氏体塑性变形的情况下, 模拟了蝶形马氏体相变的微结构演变, 结果表明奥氏体和马氏体边界处位错密度最大. 之后, Kundin等(2015) 进一步研究了马氏体锋面与奥氏体引发的塑性变形之间的交互作用, 包括位错穿过界面由马氏体承受和位错被马氏体锋面湮灭两种情况. ...
... 为了考虑NiTi形状记忆合金变形过程中体现出的强烈热--力耦合作用, 通过考虑材料非弹性变形过程中的内部热效应(包括相变潜热和非弹性耗散生热)和热边界条件, Müller 和 Bruhns (2006) , Auricchio 等(2008) , Christ 和 Reese(2009) 和Mirzaeifar 等(2011) 建立了NiTi形状记忆合金热--力耦合本构模型.这些本构模型能够合理描述NiTi形状记忆合金的率相关变形特性, 但由于未引入与循环变形相关的内变量, 无法对NiTi形状记忆合金循环变形过程中体现出的率相关超弹性和形状记忆效应劣化现象进行合理的描述. ...
Structural transformations in NiTi shape memory alloy nanowires. J
0
2014
Effect of cyclic deformation on the pseudoelasticity characteristics of Ti-Ni alloys. Metall. Mater. Trans.
1
1986
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
Precaution on use of hydrochloride salts in pharmaceutical formulation. J
2
1981
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
... 位错密度的演变为 (Mecking & Kocks 1981 )\[\dot {\rho } = \left( {k_1 \sqrt \rho - k_2 \rho } \right)\dot{\gamma }\ \ (8)\]其中, \(k_1 \)和\(k_2 \)是两个材料参数. ...
A review of shape memory alloy research, applications and opportunities.
2
2014
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... Kockar 等(2006 , 2010 )对供货态和挤压态NiTiPd和NiTiHf高温形状记忆合金的马氏体形貌分别进行了对比, 发现经过等通道转角挤压的高温形状记忆合金中马氏体尺寸比供货态有大幅度的减小, 进而材料的力学性能则有大幅度的提高. Meng 等(2002) 对NiTiHf高温形状记忆合金在单次加载下的应力诱发马氏体形貌进行了观察, 发现: 在548 K下施加8%的应变时, 形成的马氏体具有方向性, 且边界较为清晰; 而应变增大到16%的时候, 马氏体的边界则变得模糊不清; 同时, 当实验温度升高到573 K时, 施加8%的应变即出现马氏体边界不清的情况, 与较低温度时的剧烈变形情况相似, 见图34 . ...
Medical shape memory alloy applications---the market and its products. Mater. Sci. Eng.
1
2004
... 作为一种典型的智能材料, 形状记忆合金 (shape memory alloys, SMAs)因其特有的超弹性和形状记忆效应已经在很多领域得到了广泛的应用(Van Humbeeck 1999 , Duerig et al. 1999 , Morgan 2004 ).在实际的服役过程中, 形状记忆合金构件和器件通常会承受循环载荷的作用(包括温度循环、磁力循环和机械循环载荷以及它们之间的耦合), 循环变形和疲劳失效行为是这些构件或器件疲劳寿命预测和可靠性评价中的关键问题, 已得到了国内外研究者的广泛关注. 众所周知, 形状记忆合金的超弹性和形状记忆效应来自于该类材料特殊的、由温度场或应力(应变)场以及磁场的变化诱发的马氏体相变及其逆相变所致.因此, 可以按照形状记忆合金的相变诱发方式将其分为两大类:由温度或应力(应变)场诱发的热致形状记忆合金, 如近等原子比的NiTi形状记忆合金和高温NiTiX形状记忆合金; 由温度、应力和磁场单独或共同诱发的磁致形状记忆合金, 如NiMnGa铁磁形状记忆合金.在这两类形状记忆合金的反复相变过程中都涉及到相变潜热的释放和吸收, 因而必然涉及到热--力和磁--热--力耦合的问题, 特别是在加载速率相对较大的情形下. 由此可见, 有必要深入探讨形状记忆合金的热--力和磁--热--力耦合循环变形和疲劳失效行为并进行理论描述. ...
Thermomechanical coupling in shape memory alloys under cyclic loadings: Experimental analysis and constitutive modeling. Int. J
2
2011
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
... 为了描述NiTi形状记忆合金的率相关循环变形特性, Morin 等(2011) 通过在Z-M本构模型 (Zaki & Moumni 2007 )中引入考虑热--力耦合超弹性退化效应的演化方程, 将Z-M模型拓展到了非等温情形, 拓展后的本构模型能很好地对超弹性NiTi形状记忆合金的相变棘轮行为及其率相关特性进行理论描述.然而, 该模型将残余应变的累积演变假定成指数函数形式, 因而无法描述Kan等(2016)在超弹性NiTi形状记忆合金率相关循环变形实验中观察到的新现象, 即残余应变对加载率的依赖性. 为此, Yu 等(2014a)将超弹性NiTi形状记忆合金率相关的超弹性劣化效应归结为相变--位错交互作用和热--力耦合效应, 建立了基于物理机制的宏观唯象本构模型, 合理预测了该合金在不同加载速率下的超弹性劣化行为和温度场演化特性.下面对该模型的主要部分进行简要介绍. ...
Fatigue analysis of shape memory alloys: Energy approach.
0
2005
A three-dimensional constitutive model for magnetic shape memory alloys under magneto-mechanical loadings.
7
2017
... Mirzaeifar 等(2014) 采用Zhong等(2012)修正的NiTi形状记忆合金原子间相互作用势(EAM势)对温度和应力驱动下NiTi形状记忆合金纳米柱的相变过程进行了分子动力学模拟, 结果发现: (1)减小NiTi合金纳米柱的表面能可以使B2相奥氏体转变成B19相马氏体, 模型在弛豫后处于B19相(B19相中构成变体2的原子以红色表示), 如图22 所示.(2)在轴向加载过程中变体2(V2)重定向成变体1(V1):当应变加载到0.02时, 变体2(V2)中三个区域沿着大约\(\pm 45^\circ\)的方向转变成变体1(V1); 随后, 更多的变体2(V2)转变成变体1(V1); 在应变加载到0.1时, 变体2(V2)几乎全部转变成变体1(V1), 如图22 (b)所示. (3)NiTi形状记忆合金纳米柱在三个不同温度下马氏体重定向过程的应力--应变曲线中明显可以看出重取向应力随着温度的升高而升高, 如图23 所示. ...
... NiTi纳米柱在275 K下的马氏体重定向过程 (Mirzaeifar et al. 2014 ). (a) [110]\(_{\rm B2}\)方向的两个不同的B19变体和B2相, (b)单轴拉伸过程中纳米柱的重定向, 变体1和2分别采用蓝色和红色表示, (c)纳米柱多个变体界面的放大视图, Ni和Ti原子分别采用蓝色和红色表示 ...
... 不同温度下NiTi纳米柱在单轴拉伸卸载过程中的马氏体重定向应力--应变曲线(Mirzaeifar et al. 2014 ) ...
... 如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景. ...
... Mousavi 和 Arghavani (2017) 考虑了三种与磁致应变相关的变形机制, 即马氏体重定向、畴壁运动和磁畴旋转, 因此, 在本构方程中引入了三个马氏体变体体积分数(即 \(\xi _{1}\), \(\xi _{2}\)和 \(\xi _{3})\), 第\(i\)个马氏体变体中的两种磁畴体积分数(即\(\alpha _{i}\)和\(1-\alpha _{i})\)和第\(i\)个马氏体变体中两种磁畴中磁化矢量方向\((\pmb m_{ +i} , \pmb m_{ - i})\)作为内变量来描述材料所处的热力学状态, 系统的自由能\(g\)写成\[ g=g^{\rm mec} + g^{\rm mag} + g^{\rm T} +g^{\rm int} + g^{\rm con} \ \ (51)\] 其中, \(g^{\rm mec}\), \(g^{\rm mag}\), \(g^{\rm T}\), \(g^{\rm int}\)和\(g^{\rm con}\)分别是力学能、磁能、温度相关内能、硬化能以及约束能.它们的具体形式为\[g^{\rm mec}=-\dfrac{1}{2\rho}\pmb\sigma:\pmb S:\pmb\sigma-\dfrac{1}{\rho}\pmb\sigma:\pmb \varepsilon^{\rm r} \ \ (52)\]\[g^{\rm mag}=-\dfrac{\mu_0}{\rho}\pmb M\cdot\pmb H+\sum_{i=1}^3\xi_i\alpha_iK_I\left[1-(\pmb e_i\cdot\pmb m_{+i})^2\right]+ \sum_{i=1}^3\xi_i(1-\alpha_i)K_I\left[1-(\pmb e_i\cdot\pmb m_{-i})^2\right] \ \ (53)\]\[g^{\rm T}=C_p\left[T-T_0-T\ln\left(\dfrac{T}{T_0}\right)\right]\ \ (54)\]\[g^{\rm int}=\dfrac{1}{\rho n}k_1\left(\xi_1^n +\xi_2^n +\xi_3^n \right) \ \ (55)\]\[g^{\rm con}=\dfrac{1}{\rho } [\lambda_\xi \left(\xi_1 +\xi_2 +\xi_3-1\right)+I^{\xi_1}(\xi_1)+I^{\xi_2}(\xi_2)+I^{\xi_3}(\xi_3)+I^{\alpha_1}(\alpha_1)+I^{\alpha_2}(\alpha_2)+\]\[I^{\alpha_3}(\alpha_3)+\lambda_{+1}(\|\pmb m_{+1}\|-1)+\lambda_{-1}(\|\pmb m_{-1}\|-1)+\lambda_{+2}(\|\pmb m_{+2}\|-1)+\]\[\lambda_{-2}(\|\pmb m_{-2}\|-1) + \lambda_{+3}(\|\pmb m_{+3}\|-1)+\lambda_{-3}(\|\pmb m_{-3}\|-1) \ \ (56)\] 其中, \(\rho \)是材料密度, \(\pmb\sigma \)是应力张量, \(\pmb S\)是柔度张量, \(\pmb \varepsilon ^{r}\)是重定向应变张量, \(\mu_{0}\)是真空磁导率, \(\pmb M\)是磁化矢量, \(\pmb H\)是磁场强度; \(\pmb e_{i}\)是坐标基础矢量; \(C_{p}\)是比热容, \(T_{0}\)是平衡温度; \(K_{I}\), \(n\), \(k_{1}\)是材料参数; \(\lambda_{\xi }\), \(\lambda_{ + 1}\), \(\lambda_{ - 1}\), \(\lambda_{ + 2}\), \(\lambda_{ - 2}\), \(\lambda_{ + 3}\)和 \(\lambda _{ -3}\)是拉格朗日乘子; \(I^{\xi i} ( \xi _{i})\)和\(I^{\alpha i} (\alpha_{i})\)是约束函数. ...
... 根据实验观察, Mousavi 和 Arghavani(2017) 给出了马氏体变体中磁畴体积分数和外加磁场之间的关系\[\alpha_i=\left\{\begin{array}{ll}\dfrac{1}{2}+\dfrac{H_i}{2H_{\rm sat}}, |H_i| < H_{\rm sat} \\ \dfrac{1}{2}+ \dfrac{1}{2}{\rm sign}H_i, |H_i|\geq H_{\rm sat}\\ \end{array}\right. (57)\], \(H_{i}\)是外加磁场矢量的第\(i\)个方向分量, \(H_{\rm sat}\)是饱和磁场强度. 根据热力学关系, 可推导出磁化矢量旋转方程为\[\alpha_i=\left\{\begin{array}{l}\left(\pmb I-\pmb m_{ + i}\bigotimes\pmb m_{ + i}\right)\cdot\left[\mu_0M^{\rm sat}\pmb H+2\rho K_I\left(\pmb e_i\bigotimes\pmb e_i\right)\cdot\pmb m_{ + i}\right]=0\\ \left(\pmb I-\pmb m_{ - i}\bigotimes\pmb m_{ - i}\right)\cdot \left[\mu_0M^{\rm sat}\pmb H+2\rho K_I\left(\pmb e_i\bigotimes \pmb e_i\right)\cdot\pmb m_{ - i}\right]=0 \\ \end{array}\right.\ \ (58)\] 其中, \(\pmb I\)是二阶单位张量.通过求解公式(58)即可得到\(\pmb m_{ + i}\)和\(\pmb m_{ - i}\). ...
... Mousavi 和 Arghavani(2017) 进一步根据热力学关系推导出与每个马氏体变体对应的热力学驱动力, 即\[\pi ^{\xi_i}=-\rho\dfrac{\partial g}{\partial \xi_i}=-\varepsilon^{r,\max}\sigma_{ii}+\mu_0 M^{\rm sat}\left\{\left[\alpha_i\pmb m_{ + i}+(1-\alpha_i)\pmb m_{-i}\right]\cdot\pmb H\right\}-\]\[\rho K_I \alpha_i\left\{1-\left(\pmb e_i\cdot\pmb m_{ + i}\right)^2\right\}- \rho K_I(1-\alpha_i)\left\{1-\left(\pmb e_i\cdot\pmb m_{-i}\right)^2\right\}-k_1\xi_i^{n-1}-\lambda_\xi-\dfrac{\partial I^{\xi_i}( \xi_i)}{\partial \xi_i} \ \ (59)\] 同时, 将马氏体重定向的驱动力定义为最大的马氏体变体驱动力和最小的马氏体变体驱动力之差, 并认为当驱动力之差达到一个定值之后, 马氏体重定向发生, 即\[F=\pi ^{\xi p}-\pi ^{\xi R}=Y \ \ (60)\] 其中, \(\pi ^{\xi p}\)和 \(\pi ^{\xi R}\)分别是最大的和最小的马氏体变体热力学驱动力. ...
A thermodynamic finite-strain model for pseudoelastic shape memory alloys. Int. J
1
2006
... 为了考虑NiTi形状记忆合金变形过程中体现出的强烈热--力耦合作用, 通过考虑材料非弹性变形过程中的内部热效应(包括相变潜热和非弹性耗散生热)和热边界条件, Müller 和 Bruhns (2006) , Auricchio 等(2008) , Christ 和 Reese(2009) 和Mirzaeifar 等(2011) 建立了NiTi形状记忆合金热--力耦合本构模型.这些本构模型能够合理描述NiTi形状记忆合金的率相关变形特性, 但由于未引入与循环变形相关的内变量, 无法对NiTi形状记忆合金循环变形过程中体现出的率相关超弹性和形状记忆效应劣化现象进行合理的描述. ...
Large cyclic deformation of a Ni-Mn-Ga shape memory alloy induced by magnetic fields. J
0
2002
Field-induced strain under load in Ni-Mn-Ga magnetic shape memory materials. J
1
1998
... 上述研究主要集中在铁磁形状记忆合金单晶方面. Murray 等(1998) , Jeong等(2003) 研究了铁磁形状记忆合金多晶的磁--力耦合特性, 发现相对于单晶材料, 多晶能产生的磁致伸缩应变很小. Marioni(2002) 进一步指出, 针对多晶铁磁形状记忆合金, 可以通过定向凝固法调控择优取向的初始织构来获取较大的磁致伸缩应变.近年来, 众多学者研究了铁磁形状记忆合金定向凝固多晶在不同方向上的磁场诱发马氏体重定向特性(Pötschke et al.2010 , Yu et al. 2014b ), 应力诱发马氏体重定向特性(Chulist et al. 2010 , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性. ...
Model for discontinuous actuation of ferromagnetic shape memory alloy under stress. J
0
2001
Simulation of the shape memory effect in a NiTi nano model system. J
1
2013
... Mutter 和 Nielaba(2013) 采用EAM势对包含不同方向变体的马氏体相NiTi形状记忆合金纳米柱的拉伸--卸载和升温过程进行了原子模拟, 研究了纳米尺度下NiTi形状记忆合金的形状记忆效应, 在1K下具有5种不同Ni原子含量的NiTi形状记忆合金纳米柱的应力--应变曲线如图24 所示, 结果表明NiTi形状记忆合金纳米柱在拉伸过程中多取向变体构型转变成单个变体构型, 卸载后NiTi合金纳米柱存在残余应变, 升温后并没有发现奥氏体产生. ...
In situ characterization of martensite variant formation in nickel-titanium shape memory alloy under biaxial loading.
1
2011
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
Transformation-induced plasticity during pseudoelastic deformation in Ni-Ti microcrystals.
6
2009
... Mousavi 和 Arghavani (2017)对提出的本构模型进行了数值实现, 并通过将模拟结果和实验结果的对比验证了模型的正确性. 图49 和图50 分别给出了Mousavi 和Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型(LaMaster et al. 2014 )在应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和应力诱发重定向实验结果 (Chen et al. 2014 )与对应的模拟结果的比较情况. 由图可以看出, 三个模型都能够较好地捕捉到实验现象, 但是, Mousavi 和 Arghavani模型(Mousavi & Arghavani 2017 )与实验数据吻合得更好. ...
... )与对应的模拟结果的比较情况. 由图可以看出, 三个模型都能够较好地捕捉到实验现象, 但是, Mousavi 和 Arghavani模型(Mousavi & Arghavani 2017 )与实验数据吻合得更好. ...
... 应力保持下\((-1.4\) MPa)磁场诱发重定向导致的磁致应变实验结果(Heczko 2005 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al. 2014 )以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比 (Mousavi & Arghavani 2017 ) ...
... )的模拟结果对比 (Mousavi & Arghavani 2017 ) ...
... 应力诱发重定向实验结果(Chen et al. 2014 )和Mousavi & Arghavani模型(Mousavi & Arghavani 2017 )、Chen模型 (Chen et al.2014)以及LaMaster模型 (LaMaster et al. 2014 )的模拟结果对比(Mousavi & Arghavani 2017 ) ...
... )的模拟结果对比(Mousavi & Arghavani 2017 ) ...
A phase field - Finite element approach to model the interaction between phase transformations and plasticity in shape memory alloys. Int. J
0
2016
Effects of thermal cycling on microstructure and properties in Nitinol. Mater. Sci. Eng.
1
2012
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
Nitinol Fatigue: A Review of Microstructures and Mechanisms. J
1
2011
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
A 3-D constitutive model for shape memory alloys incorporating pseudoelasticity and detwinning of self-accommodated martensite. Int. J
2
2007
... 为了描述NiTi形状记忆合金在热--力耦合循环变形过程中体现出的形状记忆效应劣化现象, Auricchio 等(2008) , Zaki 和 Moumni (2007) 和Hartl等(2010) 通过引入必要的非弹性变形机制, 建立了相应的本构模型; 但是, 这些本构模型没有很好地考虑在热--力耦合循环载荷作用下冷却阶段发生的附加非弹性变形, 也不能对形状记忆效应退化现象的加载水平依赖性进行合理的描述. 最近, Yu 等 (2016) 在Popov 和 Lagoudas (2007) 提出的本构模型基础上, 针对NiTi形状记忆合金循环加载条件下出现的形状记忆效应退化现象, 发展了一个宏观多机制本构模型. 该模型根据实验观测结果, 考虑了NiTi形状记忆合金热--力循环过程中的四种变形机制, 即马氏体相变、相变诱发塑性、马氏体重取向和重取向诱发塑性, 并且重点突出了马氏体相变和重取向与位错的交互作用.根据宏观实验结果, Yu 等 (2016) 认为: 随循环次数的增大, 相变和重定向模量增大, 马氏体相变开始温度升高, 重定向开始应力下降; 某些区域位错诱发的局部应力的投影为正, 该内应力将促进马氏体相变和重定向, 其结果是循环过程中马氏体相变开始温度升高; 同时, 位错诱发的应力梯度会阻碍孪晶和解孪相的形核, 导致相变和重定向模量增大. 下面对Yu 等(2016) 发展的本构模型进行简要介绍. ...
... 为了考虑NiTi形状记忆合金的形状记忆效应, Popov 和 Lagoudas(2007) 将形状记忆过程的微结构状态分为三相, 即奥氏体、孪晶马氏体和解孪马氏体, 相应的体积分数记作: \(\xi _{\rm A} \), \(\xi _{\rm M}^{\rm t} \)和 \(\xi _{\rm M}^{\rm d} \).为了描述每两相之间的转变, 引入内变量\(\lambda _1 \), \(\lambda _2\)和\(\lambda _3\) \[\left\{{\begin{array}{l} \lambda _1 :\xi _{\rm A} \leftrightarrow \xi _{\rm M}^{\rm t} \\ \lambda _2 :\xi _{\rm A} \leftrightarrow \xi _{\rm M}^{\rm d} \\ \lambda _3 :\xi _{\rm M}^{\rm t} \to \xi _{\rm M}^{\rm d} ,\qquad \dot {\lambda }_3 \geq 0 \\ \end{array}} \right.\ \ (10)\]这里\(\lambda _1 \), \(\lambda _2 \)和\(\lambda _3\)分别代表奥氏体--孪晶马氏体、奥氏体--解孪马氏体、孪晶马氏体--解孪马氏体的相变程度, 它们与三相体积分数相关\[\xi _{\rm A} = \xi _{\rm A}^0 - \lambda _1 - \lambda _2 \ \ (11)\]\[\xi _{\rm M}^{\rm t} = \xi _{\rm M}^{{\rm t}0} + \lambda _1 - \lambda _3 \ \ (12)\]\[\xi _{\rm M}^{\rm d} = \xi _{\rm M}^{{\rm d}0} + \lambda _2 + \lambda _3 \ \ (13)\]这里\(\xi _{\rm A}^0 \), \(\xi _{\rm M}^{{\rm t}0} \) 和\(\xi _{\rm M}^{{\rm d}0} \)是\(\xi _{\rm A} \), \(\xi _{\rm M}^{\rm t} \)和 \(\xi_{\rm M}^{\rm d} \)的初始值. ...
Magnetically resettable 0.16% free strain in polycrystalline Ni-Mn-Ga plates
3
2010
... NiTi纳米柱在不同Ni原子含量下的应力--应变曲线(Mutter & Nielaba 2013 ) ...
... 上述研究主要集中在铁磁形状记忆合金单晶方面. Murray 等(1998) , Jeong等(2003) 研究了铁磁形状记忆合金多晶的磁--力耦合特性, 发现相对于单晶材料, 多晶能产生的磁致伸缩应变很小. Marioni(2002) 进一步指出, 针对多晶铁磁形状记忆合金, 可以通过定向凝固法调控择优取向的初始织构来获取较大的磁致伸缩应变.近年来, 众多学者研究了铁磁形状记忆合金定向凝固多晶在不同方向上的磁场诱发马氏体重定向特性(Pötschke et al.2010 , Yu et al. 2014b ), 应力诱发马氏体重定向特性(Chulist et al. 2010 , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性. ...
... , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性. ...
Cyclic torsional loading of pseudoelastic NiTi shape memory alloys: Damping and fatigue failure. Mater. Sci. Eng.
1
2006
... 对于NiTi形状记忆合金的原位测试目前也在一定程度上展开了研究, 如DiCocco 等(2014) , Frotscher 等(2008) , Niendorf 等(2011) 和\v{S}ittner等(2007).采用的测试手段包括SEM、XRD、选区电子衍射(EBSD)、中子衍射(neutron diffraction)等, 其中SEM和XRD最为常见. 研究者采用上述测试方法, 对NiTi形状记忆合金的应力诱发马氏体相变以及裂纹扩展等过程进行了实时观测.Di Cocco等(2014) 用原位SEM和XRD观测了2个循环周次中裂纹萌生及扩展的过程.研究表明, 应力诱发马氏体相变在裂尖处发生, 导致NiTi形状记忆合金的裂纹扩展与普通金属具有较大区别.实验中并未观察到裂尖钝化的情况, 但逆相变过程中会观察到完全的裂纹闭合, 见图39 .灰色箭头指示主裂纹的扩展, 白色箭头指示二次裂纹的扩展. 图39 清晰地描述了随应变增大, 裂纹尖端张开位移不断增大的过程. ...
Design of Shape Memory Alloy (SMA) Actuators.
2
2015
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
Mechanical fatigue and fracture of Nitinol.
3
2012
... Paranjape 等(2016) 基于相场理论的有限元模拟方法, 采用晶体塑性理论模拟形状记忆合金单晶温度诱发马氏体相变和塑性滑移之间的交互作用, 如图17 所示. 模拟结果表明: (1)奥氏体和马氏体界面的局部变形不协调诱发的高应力容易导致奥氏体发生塑性滑移; (2)马氏体和马氏体界面附近材料点的等效塑性应变较大; (3)冷却阶段塑性滑移量的增加比升温阶段要慢; (4)塑性滑移较小区域促进马氏体相变;(5)塑性滑移较大区域处马氏体相变受阻. ...
... 无应力热循环过程中马氏体和塑性的交互作用 (Paranjape et al. 2016 ). (a) 第一个循环中的马氏体分布, (b)第一个循环中的塑性滑移分布, (c)第二个循环中的马氏体分布, (d)第二个循环中的塑性滑移分布, (e)第一个循环冷却过程中的马氏体分布, (f)第一个循环冷却过程中的塑性滑移分布, (g)第一个循环加热过程中的马氏体分布, (h) 第一个循环加热过程中的塑性滑移分布 ...
... 最近, Song等(2016) 对超弹性NiTi形状记忆合金微管单轴和非比例多轴疲劳断口形貌进行了SEM观察, 讨论了单轴和多轴疲劳失效过程中不同的微观结构形貌, 总结了该合金的多轴疲劳失效机制. 研究结果表明: (1)由于该合金微管的壁厚仅为150 \(\mu \)m, 远小于Robertson等(2012) 总结出的宏观裂纹的最小物理尺寸(1 mm), 同时, 在疲劳断面上裂纹扩展区和终断区交替出现, 因此, 其疲劳失效主要由微裂纹的萌生与扩展控制, 不涉及宏观裂纹的扩展阶段.(2)在单轴疲劳失效过程中, 微裂纹萌生于微管试样的内外表面和内部的空洞和夹杂处, 并随循环次数增大而逐渐扩展, 形成疲劳条纹, 同时形成大量的二次裂纹, 最终导致微管的疲劳破坏. (3)在多轴疲劳失效过程中, 除了能够观察到与单轴疲劳失效过程类似的疲劳条纹和二次裂纹外, 还可以观察到V型犁沟、穿透型疲劳台阶、斜断裂、划伤和表面多裂纹源这样一些独有的微观结构伤损模式, 如图38 所示. ...
An equivalent strain/Coffin-Manson approach to multiaxial fatigue and life prediction in superelastic Nitinol medical devices.
1
2011
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
Effects of Ni content on the shape memory properties and microstructure of Ni-rich NiTi-20Hf alloys.
1
2016
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
The cyclic and evolutionary response to approach the attraction loops under stress controlled isothermal conditions for a multi-mechanism based multi-axial SMA model.
0
2013
TEM study of structural and microstructural characteristics of a precipitate phase in Ni-rich Ni-Ti-Hf and Ni-Ti-Zr shape memory alloys.
1
2013
... 尽管对NiTiX高温形状记忆合金的微观结构特征已有较多的微观实验观察, 但绝大多数集中在材料改性的范畴, 对热--力耦合循环加载下该类合金的微观结构观察少有报道, 需在今后进一步开展系统的研究. 例如, Karaca等(2013) 对不同温度下的挤压态NiTiHf高温形状记忆合金的沉淀相进行了观察, 证明了550\(^{\circ}\)C \(\times \) 3 h后, 材料中即有纳米级沉淀出现, 并且时效温度提高到650\(^{\circ}\)C后, 相同时效时间下的沉淀尺寸增大; Satamarta等(2013) 对NiTiHf及NiTiZr材料的微观实验观察中证明炉内冷却的方法可以比高温时效更易使材料内部产生更大的沉淀粒子; Yang 等(2013) 在实验观察的基础上进一步提出, 对于NiTiHf高温形状记忆合金, 这些沉淀粒子并非普通的Ni\(_{4}\) (Ti, Hf)\(_{3}\)相, 而是一种具有不同原子结构的新相, 即H相. ...
Effect of aging on microstructure and shape memory properties of a Ni-48Ti-25Pd (At. Pct) alloy. Metall. Mater. Trans.
0
2013
Hierarchical pattern formation in elastic materials. Phy.
0
1997
Low temperature-induced intermartensitic phase transformations in Ni-Mn-Ga single crystal.
1
2005
... (3)应力诱发马氏体相变. Chernenko 等(2005) , Segu\'{\i} 等(2005) , Kim 等(2006) 和Karaca 等(2007) 研究了环境温度在奥氏体完成温度A\(_{\rm f}\)以上时铁磁形状记忆合金单晶在横向恒定磁场、轴向交变压应力作用下应力诱发马氏体相变特性.和NiTi形状记忆合金类似, 铁磁形状记忆环境在应力作用下展示出良好的超弹性特性, 如图45 所示. 同时, 可以看出横向磁场对马氏体相变具有抑制作用, 即向前相变和逆相变平台均随着横向磁场的增加而升高, 并且相变特性对温度有很强的依赖性. 需要说明的是, 为了便于比较, 图43 中每个温度下的应变初始值均为零, 坐标轴的刻度间隔为1%. ...
Thermomechanical aspects of NiTi. J. Mech. Phys.
2
1995
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
... 尽管NiTi形状记忆合金中的热弹性马氏体相变是一种快速的切变式固态相变过程, 但是, 在多晶NiTi形状记忆合金材料中, 因晶粒晶体学位向的不同和晶界对相变过程的阻碍作用, 使得马氏体相变过程是一种局部切变形核而逐渐扩展长大的过程, 特别是在超细晶的多晶NiTi形状记忆合金中.对于这一种局部的、非均匀马氏体相变过程, Shaw & Kyriakides(1995 , 1997 )对细晶多晶NiTi形状记忆合金条带通过全场像和应力--应变的同时测量进行了早期的观察, 揭示了在外加载荷作用下非均匀马氏体相变的产生以及宏观可观察的相变图案(transformation domain)形成和扩展. 近年来, Zhang 等(2010) , Sun 等(2002) , He 和 Sun(2010a) 及 Feng 和 Sun(2006) 利用CCD相机和高速摄像仪进一步观察了细晶超弹性NiTi形状记忆合金在应变控制的单轴拉伸--卸载过程中相变图案的形成和演化以及这一过程的加载速率依赖性, 进而揭示了单轴拉伸和卸载过程中马氏体相变过程的局部性. Zhang等(2010)得到的细晶超弹性NiTi形状记忆合金薄材典型的实验结果如图8 和图9 所示. ...
Initiation and propagation of localized deformation in elasto-plastic strips under uniaxial tension. Int. J
2
1997
... 尽管NiTi形状记忆合金中的热弹性马氏体相变是一种快速的切变式固态相变过程, 但是, 在多晶NiTi形状记忆合金材料中, 因晶粒晶体学位向的不同和晶界对相变过程的阻碍作用, 使得马氏体相变过程是一种局部切变形核而逐渐扩展长大的过程, 特别是在超细晶的多晶NiTi形状记忆合金中.对于这一种局部的、非均匀马氏体相变过程, Shaw & Kyriakides(1995 , 1997 )对细晶多晶NiTi形状记忆合金条带通过全场像和应力--应变的同时测量进行了早期的观察, 揭示了在外加载荷作用下非均匀马氏体相变的产生以及宏观可观察的相变图案(transformation domain)形成和扩展. 近年来, Zhang 等(2010) , Sun 等(2002) , He 和 Sun(2010a) 及 Feng 和 Sun(2006) 利用CCD相机和高速摄像仪进一步观察了细晶超弹性NiTi形状记忆合金在应变控制的单轴拉伸--卸载过程中相变图案的形成和演化以及这一过程的加载速率依赖性, 进而揭示了单轴拉伸和卸载过程中马氏体相变过程的局部性. Zhang等(2010)得到的细晶超弹性NiTi形状记忆合金薄材典型的实验结果如图8 和图9 所示. ...
... 与二元NiTi形状记忆合金相比, 高温形状记忆合金的循环变形实验研究相对较少, 并且大部分集中在温度循环加载方式, 即讨论其形状记忆效应在恒定应力和温度循环加载过程中的演化规律.已有的实验表明, 高温形状记忆合金的温度循环变形特性与原子组分、加工方式和外加应力等密切相关.例如, Bigelow等(2007) 首先对Ni\(_{19.4}\)Ti\(_{50.6}\)Pd\(_{30}\)合金在外加恒定应力为200 MPa的情况下进行温度循环实验, 发现温度循环30周后材料达到稳定的温度--变形响应状态, 并且相变温度上升了16\(^{\circ}\)C; 但是, 他们的结果还显示该合金在无外加应力的温度循环情况下, 相变温度会降低5 \(\sim \) 10\(^{\circ}\)C. 后来, Bigelow等(2010) 通过对不同合金含量的NiTiPd高温形状记忆合金在外加恒定应力下的温度循环加载实验研究, 揭示了该合金的温度循环稳定性随Pd元素含量的增加逐渐下降, 并且不可恢复应变也随之增大的变化规律. Kockar 等(2006, 2010)通过对不同加工状态下的Ni\(_{33.7}\)Ti\(_{50.3}\)Pd\(_{16}\)高温形状记忆合金的热--力耦合循环变形实验, 揭示了温度循环中在外加应力方向上的塑性变形累积现象, 如图30 所示. 由图30 可见, 经过等通道转角挤压的高温形状记忆合金在循环过程中的塑性应变明显减小, 相变应变远大于未经加工的初始材料; 同时, 将转角挤压的Ni\(_{33.7}\)Ti\(_{50.3}\)Pd\(_{16}\)高温形状记忆合金材料继续在425\(^{\circ}\)C退火15min, 可以得到更加稳定的温度循环响应结果, 循环10周后的累积塑性应变在外加拉伸应力为100 MPa时仅有0.05%, 并且在200 MPa时也不超过0.2%. 另外, Saghaian等(2016) 对富Ni的NiTiHf高温形状记忆合金的温度循环变形实验研究表明, 温度循环时的外加应力越大, 相变温度越高, 热滞回环越大, 不可恢复应变也随之增大. ...
Martensitic phase transformations in Ni-Ti-based shape memory alloys: The Landau theory.
1
2012
... 对于具有形状记忆效应的NiTi合金, 学者们更多关心的是其作为温度诱导的主动控制器件时涉及到的热--力耦合循环变形行为的研究, 也就是探讨该合金在恒定应力作用下温度循环变化时的热--力耦合响应. Miyazaki等(1981 , 1986 ), Liu 和 McCormick (1990) , Lim和McDowell (1999) , Hebda和White(1998) , Bo和Lagoudas (1999) , Miller和Lagoudas (2000) , Saleeb等(2013) 和Benafan 等(2014) 对此进行了相关的实验研究, 在施加不同恒定轴向应力的温度循环加载过程中得到的典型实验结果如图12 所示. ...
Deformation processes in functional materials studied by in situ neutron diffraction and ultrasonic techniques. Mater. Sci. Eng.
1
2007
... Ma 等(2010)指出, 由于NiTiX高温形状记忆合金随着第三相元素的加入, 虽然相变温度得到了大幅提高, 但是其延展性则会发生剧烈的下降. 同时, 许多研究 (Kockar et al. 2006 , 2010 ; Meng et al. 2000 , 2002 ; 左舜贵等 2014 )也都揭示了高温形状记忆合金的脆性断裂性质. Ma等(2010)和Kockar 等(2010)进一步指出, 在温度循环加载中, 高温形状记忆合金的脆性更为明显, 在200 MPa的恒定拉伸应力下经历几次温度循环即可导致材料发生断裂.Kockar等(2010)认为高温形状记忆合金疲劳性能差的原因是由于加工时引入了过量的碳化物所导致的.若排除加工因素的影响, 事实上, 高温形状记忆合金由于其本身的材料成分及较高的工作温度, 其疲劳性质也会受到较大的影响, 主要涉及以下几个方面: (1)高温形状记忆合金的位错滑移临界应力(CSS)较低, 会使相变和塑性变形同时发生, 在微观上也可观察到大量的位错聚集以及破碎的马氏体形貌等剧烈变形的特征(Meng et al.2002), 这严重劣化了材料的抗疲劳性能; (2)高温形状记忆合金在较高的服役温度下, 蠕变也是导致附加变形的重要因素, 并且循环加载时蠕变的作用比静载下更为显著(Ma et al. 2010 ), 进一步影响材料的疲劳行为; (3) 在高温服役环境下, 材料中的沉淀相会随着时间的推移而逐渐粗化, 同样会对材料的疲劳行为产生一定的影响(Santamarta et al. 2013 ).目前, 一些学者通过在NiTiX高温合金中添加第四相成分或采用转角挤压和高温时效的加工方式来提高该材料的位错滑移临界应力, 使相变在位错滑移前即可发生, 较大程度地提高了材料的超弹性及形状记忆特性(Kockar et al. 2010 , Saghaian et al. 2016 ). 可以推断, 上述经过改性的高温形状记忆合金的疲劳行为也应得到一定程度的改善; 然而, 对此目前尚未见文献报道, 有待于进一步深入研究. ...
Energy criteria and cumulative damage during fatigue crack growth. Int. J.
2
1998
... 同样, 对于高温形状记忆合金的超弹性循环变形实验研究目前进行得也不充分, 实验研究多集中在不同温度下的多级循环加载情形, 并且循环次数较小(通常小于10周). Tian 和 Wu(2002)研究了当环境温度刚刚达到奥氏体相变结束温度和在该温度之上20及70\(^{\circ}\)C的情况下NiTiPd高温形状记忆合金可恢复应变的变化情况, 并且对不同加载条件下应力--应变滞回环的宽度进行了比较, 结果表明: 与二元NiTi形状记忆合金的情况类似, 环境温度越高, 加载应力越大, 循环累积的塑性应变则越大. Wu 和Tian(2003)对NiTiPd合金进行了不同温度及应力下的多级循环加载实验研究, 发现施加应力越高, 达到循环稳定所需的循环次数则越小; 并且认为对于B19马氏体变体的NiTiPd合金, 织构是影响其超弹性的重要因素. Karaca等(2013)则研究了具有不同时效时间的挤压态NiTiHf合金在不同温度多级循环加载条件下的超弹性性能变化, 结果如图33 所示. 实验表明: 经过3 h \(\times\) 550\(^{\circ}\)C时效处理的NiTiHf合金在高温下具有非常好的超弹性行为, 在220\(^{\circ}\)C及240\(^{\circ}\)C的环境温度下, 完全恢复的压缩应变可以达到4%; 然而, 当时效温度提高至650\(^{\circ}\)C时, 超弹性行为则发生了明显劣化, 可恢复变形量明显下降.这是由于过时效引起沉淀相的粗化所导致的(Sasaki et al. 2013 ).事实上, 沉淀相的尺寸及含量会极大影响高温形状记忆合金的超弹性和形状记忆特性.例如, Kockar 等(2010)对于NiTiHf合金得研究表明: 在Ni原子质量分数为50.3% \(\sim\) 52.0%的范围内时, 随着Ni原子含量的增加, 沉淀相的尺寸(大于100 nm)及体积分数均增大, 材料的可恢复应变逐渐降低; 然而, 当Ni原子质量分数较低时, 沉淀尺寸较小(5 \(\sim \) 15 nm), 沉淀相易于被马氏体变体所吸收而不影响马氏体相变的过程, 可以获得较高的可恢复应变值. ...
... 正如Kang 和 Song (2015) 综述的那样, 通过对疲劳断口的SEM观察发现, 超弹性NiTi合金(初始相为奥氏体)的断口形貌和形状记忆NiTi合金(初始相为马氏体)基本相同, 均可见明显的疲劳条纹、二次裂纹和河流状解理图案以及一些大而浅的韧窝.在NiTi形状记忆合金疲劳断口的SEM观察结果基础上, 进一步总结得出:NiTi形状记忆合金的疲劳断裂可分为两阶段, 即疲劳裂纹萌生阶段和扩展阶段; 在疲劳断裂过程中, 同时会出现由疲劳载荷引起的稳态的裂纹长大和由大而浅的韧窝代表的塑性过载断裂.另外, 从整个疲劳失效过程中的应力--应变响应曲线可以看到, 在循环稳定后(从200周开始直至疲劳断裂发生), 滞回环形状和大小基本上不会发生可观察的变化, 疲劳断裂突然毫无宏观征兆地发生. 这说明, NiTi形状记忆合金在疲劳失效过程中的裂纹萌生和扩展机制与普通金属有明显不同.Charkaluk 等(2000 , 2002 ), Skelton 等(1991 , 1998 )以及Dunand-Chatellet 和 Moumni (2012) 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
Energy criterion for high temperature low cycle fatigue failure.
1
1991
... 正如Kang 和 Song (2015) 综述的那样, 通过对疲劳断口的SEM观察发现, 超弹性NiTi合金(初始相为奥氏体)的断口形貌和形状记忆NiTi合金(初始相为马氏体)基本相同, 均可见明显的疲劳条纹、二次裂纹和河流状解理图案以及一些大而浅的韧窝.在NiTi形状记忆合金疲劳断口的SEM观察结果基础上, 进一步总结得出:NiTi形状记忆合金的疲劳断裂可分为两阶段, 即疲劳裂纹萌生阶段和扩展阶段; 在疲劳断裂过程中, 同时会出现由疲劳载荷引起的稳态的裂纹长大和由大而浅的韧窝代表的塑性过载断裂.另外, 从整个疲劳失效过程中的应力--应变响应曲线可以看到, 在循环稳定后(从200周开始直至疲劳断裂发生), 滞回环形状和大小基本上不会发生可观察的变化, 疲劳断裂突然毫无宏观征兆地发生. 这说明, NiTi形状记忆合金在疲劳失效过程中的裂纹萌生和扩展机制与普通金属有明显不同.Charkaluk 等(2000 , 2002 ), Skelton 等(1991 , 1998 )以及Dunand-Chatellet 和 Moumni (2012) 进一步指出:对于NiTi形状记忆合金, 与大多数金属材料类似, 达到稳定的应力--应变响应的时刻可以被看成是位错控制的微裂纹萌生阶段向微裂纹扩展阶段的转变点.根据这一观点, 可以非常直接地从NiTi形状记忆合金在疲劳失效过程中宏观应力--应变响应曲线的变化情况来得到上述转变对应的循环次数.尽管如此, 由于微裂纹扩展阶段向宏观裂纹扩展阶段的过渡点不能直接从应力--应变曲线等宏观响应中确定, 因此, NiTi形状记忆合金总的疲劳寿命并不能直接根据宏观应力--应变响应来分成裂纹萌生寿命和扩展寿命两部分.这使得NiTi形状记忆合金的疲劳失效寿命的理论预测非常困难. 另一方面, 根据Kang 和 Song (2015) 的综述可知, 裂纹尖端的应力诱发马氏体相变将会大幅度降低NiTi形状记忆合金中裂纹尖端的应力集中程度, 进而延缓裂纹的扩展, 使得NiTi形状记忆合金成为所有合金中裂纹扩展速率最小的材料.这也说明裂纹扩展寿命是NiTi形状记忆合金的疲劳寿命中的重要组成部分, 同时也使得该合金的疲劳寿命显著依赖于试样的几何尺寸.使用几何尺寸相对较大的试样得到的NiTi形状记忆合金的疲劳寿命不能直接用于评价合金几何尺寸相对较小时(例如NiTi形状记忆合金微管等)的疲劳失效行为. ...
Damage-based life prediction model for uniaxial low-cycle stress fatigue of super-elastic NiTi shape memory alloy microtubes.
0
2015
Multiaxial low-cycle fatigue failure mechanism of super-elastic NiTi shape memory alloy micro-tubes. Mater. Sci. Eng.
0
2016
Effects of peak stress and stress amplitude on multiaxial transformation ratchetting and fatigue life of superelastic NiTi SMA micro-tubes: Experiments and life-prediction model. Int. J.
1
2017
... 后来, 宋迪(2015) 在此基础上进一步拓展建立了基于损伤演化的NiTi形状记忆合金非比例多轴疲劳寿命预测模型.为了反映多轴加载路径下出现的马氏体重取向以及重取向诱发塑性对疲劳失效寿命的影响, 在前述三种损伤机制上, 引入了一项新的马氏体重取向损伤\(D_{\rm reo}\), 并定义为\[ D_{\rm reo} = g_4 \cdot N\ \ (48)\]\[g_4 = c \cdot \lambda \ \ (49)\]其中, \(c\)为材料常数, \(\lambda\)为考虑不同形状的多轴加载路径对NiTi形状记忆合金疲劳失效寿命影响的加载路径因子, 但其定义不同于Song等(2017) 在半经验型多轴疲劳寿命预测模型(即式(35))中引入的定义, 具体可见文献(宋迪2015). 最后, 在失效判据\(D=D_{\rm ini}+D_{\rm pro}+D_{\rm trans}+D_{\rm reo}=1\)的基础上, 得到了如下的寿命预测模型\[ N_{\rm f} = \dfrac{1 - (g_1 + g_3 ) \cdot \int_0^{N_{\rm sat} } {W_N{\rm d}N + (g_2 + W_{\rm sat} \cdot g_3 ) \cdot (1 +N_{\rm sat} )} }{g_2 + W_{\rm sat} \cdot g_3 + g_4 } \ \ (50)\] ...
Applications of shape memory alloys in civil structures.
1
2006
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
Superelastic response of Ni-Mn-Ga martensite in magnetic fields and a simple model.
1
2003
... (1)磁场诱发马氏体重定向:Tickle和 James (1999) , Tickle 等(1999) , Heczko (2005) , Straka 和 Heczko (2003) 以及Karaca等(2006) 研究了环境温度在马氏体完成温度\((M_{\rm f})\)以下时铁磁形状记忆合金单晶在轴向恒定压应力、横向交变磁场作用下磁场诱发马氏体重定向特性.此时, 材料的初始相为马氏体, 图43 给出了该加载工况下典型的磁场--相对磁化曲线及磁场--应变曲线.以压应力为1.4 MPa的工况为例, 由图可见: 在变形的初始阶段(即磁场低于0.5 T), 由于磁场低于马氏体重定向临界磁场, 无非弹性应变出现, 并且磁化量随着磁场的增大而线性增大, 该阶段的磁化机制主要为磁化矢量的旋转; 当磁场高于0.5 T时, 马氏体重定向发生, 伴随着很大的非弹性应变出现, 同时磁化率出现跳跃并远高于低磁场(小于0.5 T)时的磁化率, 在该阶段马氏体重定向和磁化矢量旋转这两种磁化机制同时发生; 当磁场达到0.8 T时, 马氏体重定向完成, 磁化饱和出现, 并在后续磁场加载过程中, 非弹性应变和磁化量不再变化; 在卸载过程中, 当磁场达到0.25 T时, 逆向重定向发生, 非弹性应变和磁化量剧烈变化; 当磁场完全卸载后, 马氏体重定向完成, 非弹性应变及磁化量完全归零.另外, 对比图43 中不同应力水平下的磁--力响应可以看出:磁致伸缩应变的大小随着轴向压应力的增大而逐渐减小, 并且轴向压应力对磁场诱发马氏体重定向有抑制作用, 即临界磁场强度随着轴向压应力的增加而逐渐升高; 在压应力较小时(0.6 MPa), 磁场诱发出的重定向应变无法完全恢复; 在压应力较大时(3 MPa), 试样在发生马氏体重定向之前已经通过磁化矢量旋转机制完成了磁化, 无法诱发马氏体重定向机制. 这说明, 铁磁形状记忆合金存在着一个"闭锁应力", 在应力低于"闭锁应力"时, 磁场能够诱发马氏体重定向; 在应力高于"闭锁应力"时, 磁场无法诱发马氏体重定向. 铁磁形状记忆合金的"闭锁应力"一般较低, 大约在3 MPa左右. Karaca等(2006) 进一步提出了发生马氏体重定向的两个必要条件, 即高的磁晶各向异性能和低的孪生界面运动能, 并通过增大测试温度与居里温度之差以及减小测试温度和马氏体相变温度之差分别提高和降低磁晶各向异性能和孪生界面运动能, 进而获得了较高的应力闭锁值(5.7 MPa). ...
a. Stimulus-responsive shape memory materials: A review
0
2012
Phase transformation in superelastic NiTi polycrystalline micro-tubes under tension and torsion--from localization to homogeneous deformation. Int. J
1
2002
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
b. Recent advances in spatiotemporal evolution of thermomechanical fields during the solid-solid phase transition. C. R.
1
2012
... 自形状记忆合金问世以来, 正如一些综述性论文 (Sun et al. 2012a , Mohd Jani et al. 2014 , Song et al. 2006 , Eggeler et al. 2004 )和专著(Rao et al. 2015 , Lagoudas 2008 )中评述的那样, 目前已经开展了许多关于形状记忆合金变形和疲劳失效行为(包括结构疲劳和功能疲劳(Eggeler et al. 2004 ))的实验和理论研究, 然而, 上述这些综述论文和专著中对热致形状记忆合金的热--力耦合循环变形行为、超弹性和形状记忆效应循环劣化行为及相关疲劳失效行为的研究现状评述还不够全面, 特别是针对近年来取得的相关研究成果. 2010年以来, 康国政等 (康国政2011 , Kang 2013 , 康国政等 2015 , Kang & Song 2015 )和Cisse 等(2016) 进一步对热致形状记忆合金的热--力耦合循环变形和疲劳失效行为研究的最新进展进行了评述, 弥补了已有综述文献的不足, 但是, 他们的评述主要集中在NiTi形状记忆合金的相关研究成果方面, 几乎没有涉及高温形状记忆合金和磁致形状记忆合金的热--力和热--磁--力耦合循环变形和相关疲劳失效行为.另一方面, 已有的综述文献主要集中在宏观层次的形状记忆合金循环变形行为实验研究和理论模型构建方面, 对于细微观层次上的实验观察以及基于分子动力学和相场理论的数值模拟等方面的研究成果少有涉及, 仅见Cisse 等(2016) 对NiTi形状记忆合金力学行为的分子动力学和相场分析(即基于Ginzburge-Landau理论的微观力学分析)进行了简要的评述. ...
Effect of different stages of deformation on the microstructure evolution of Ti-rich NiTi shape memory alloy.
2
2017
... 最近, Song等(2016) 对超弹性NiTi形状记忆合金微管单轴和非比例多轴疲劳断口形貌进行了SEM观察, 讨论了单轴和多轴疲劳失效过程中不同的微观结构形貌, 总结了该合金的多轴疲劳失效机制. 研究结果表明: (1)由于该合金微管的壁厚仅为150 \(\mu \)m, 远小于Robertson等(2012) 总结出的宏观裂纹的最小物理尺寸(1 mm), 同时, 在疲劳断面上裂纹扩展区和终断区交替出现, 因此, 其疲劳失效主要由微裂纹的萌生与扩展控制, 不涉及宏观裂纹的扩展阶段.(2)在单轴疲劳失效过程中, 微裂纹萌生于微管试样的内外表面和内部的空洞和夹杂处, 并随循环次数增大而逐渐扩展, 形成疲劳条纹, 同时形成大量的二次裂纹, 最终导致微管的疲劳破坏. (3)在多轴疲劳失效过程中, 除了能够观察到与单轴疲劳失效过程类似的疲劳条纹和二次裂纹外, 还可以观察到V型犁沟、穿透型疲劳台阶、斜断裂、划伤和表面多裂纹源这样一些独有的微观结构伤损模式, 如图38 所示. ...
... NiTi形状记忆合金多轴疲劳断口形貌 (Song et al. 2016 ).(a) V型犁沟, (b) 疲劳台阶, (c) 斜断裂, (d) 划伤, (e) 表面多裂纹源 ...
Tensile behavior of Ti\(_{50.6}\)Pd\(_{30}\)Ni1\(_{9.4}\) alloy under different tensile conditions. Mater. Sci. Eng.
1
2002
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
Ferromagnetic shape memory in the NiMnGa system.
0
1999
Magnetic and magnetomechanical properties of Ni\(_{2}\)MnGa. J
0
1999
Low-cycle fatigue of TiNi shape memory alloy and formulation of fatigue life. T.
0
2000
Large magnetic-field-induced strains in Ni2MnGa single crystals.
2
1996
... 尽管NiTi形状记忆合金中的热弹性马氏体相变是一种快速的切变式固态相变过程, 但是, 在多晶NiTi形状记忆合金材料中, 因晶粒晶体学位向的不同和晶界对相变过程的阻碍作用, 使得马氏体相变过程是一种局部切变形核而逐渐扩展长大的过程, 特别是在超细晶的多晶NiTi形状记忆合金中.对于这一种局部的、非均匀马氏体相变过程, Shaw & Kyriakides(1995 , 1997 )对细晶多晶NiTi形状记忆合金条带通过全场像和应力--应变的同时测量进行了早期的观察, 揭示了在外加载荷作用下非均匀马氏体相变的产生以及宏观可观察的相变图案(transformation domain)形成和扩展. 近年来, Zhang 等(2010) , Sun 等(2002) , He 和 Sun(2010a) 及 Feng 和 Sun(2006) 利用CCD相机和高速摄像仪进一步观察了细晶超弹性NiTi形状记忆合金在应变控制的单轴拉伸--卸载过程中相变图案的形成和演化以及这一过程的加载速率依赖性, 进而揭示了单轴拉伸和卸载过程中马氏体相变过程的局部性. Zhang等(2010)得到的细晶超弹性NiTi形状记忆合金薄材典型的实验结果如图8 和图9 所示. ...
... 虽然NiTi形状记忆合金具有超弹性、形状记忆特性、良好的生物相容性和耐磨性等优点, 但其在温度驱动条件下热传导时间较长, 响应频率低, 无法满足高频响应器件的要求. 然而, 铁磁形状记忆合金除了具备传统NiTi形状记忆合金的优良特性之外, 还具有在磁场驱动条件下响应频率高这一优点. 因此, 近年来, 铁磁形状记忆合金得到了越来越多的关注, 具有广阔的应用前景.自从Ullakko等(1996) 首次报道了NiMnGa合金单晶在中等磁场强度下(小于1T)能够产生0.2%的磁致伸缩应变后, 铁磁形状记忆合金就以其优越的热--力--磁学特性引起了固体力学界和材料科学界学者的广泛关注和研究, 取得了丰硕的研究成果.关于磁致形状记忆合金一些基本变形特征的阐述可参见Kiefer 和 Lagoudas (2005) 的工作, 本节仅针对其磁--力耦合循环变形行为的研究现状进行评述. ...
Non-medical applications of shape memory alloys.
1
1999
... 作为一种典型的智能材料, 形状记忆合金 (shape memory alloys, SMAs)因其特有的超弹性和形状记忆效应已经在很多领域得到了广泛的应用(Van Humbeeck 1999 , Duerig et al. 1999 , Morgan 2004 ).在实际的服役过程中, 形状记忆合金构件和器件通常会承受循环载荷的作用(包括温度循环、磁力循环和机械循环载荷以及它们之间的耦合), 循环变形和疲劳失效行为是这些构件或器件疲劳寿命预测和可靠性评价中的关键问题, 已得到了国内外研究者的广泛关注. 众所周知, 形状记忆合金的超弹性和形状记忆效应来自于该类材料特殊的、由温度场或应力(应变)场以及磁场的变化诱发的马氏体相变及其逆相变所致.因此, 可以按照形状记忆合金的相变诱发方式将其分为两大类:由温度或应力(应变)场诱发的热致形状记忆合金, 如近等原子比的NiTi形状记忆合金和高温NiTiX形状记忆合金; 由温度、应力和磁场单独或共同诱发的磁致形状记忆合金, 如NiMnGa铁磁形状记忆合金.在这两类形状记忆合金的反复相变过程中都涉及到相变潜热的释放和吸收, 因而必然涉及到热--力和磁--热--力耦合的问题, 特别是在加载速率相对较大的情形下. 由此可见, 有必要深入探讨形状记忆合金的热--力和磁--热--力耦合循环变形和疲劳失效行为并进行理论描述. ...
Structural fatigue of pseudoelastic NiTi shape memory wires. Mater. Sci. Eng.
3
2004
... Tadayyon等(2017) 通过TEM观察研究了初始相为马氏体的NiTi形状记忆合金在拉伸载荷作用下的变形行为和相关的微结构演变, 如图16 所示. 结果表明: 初始拉伸阶段首先发生孪晶马氏体的弹性变形, 然后发生马氏体解孪并进一步产生位错, 而位错的移动则会促进解孪和孪生变形; 随着变形的增大, 位错之间的相互约束增强, 最后发生剪切带和堆垛层错的滑移. Tadayyon等(2017) 指出位错运动和孪生变形可以细化晶粒, 导致合金强度提高以及延展性增强, 而堆垛层错进一步使得材料发生加工硬化. 这些研究结果表明, NiTi形状记忆合金发生马氏体重定向时也会产生大量的位错缺陷, 且位错缺陷甚至会演变成堆垛层错, 进一步影响该合金的性能. ...
... 所示. 结果表明: 初始拉伸阶段首先发生孪晶马氏体的弹性变形, 然后发生马氏体解孪并进一步产生位错, 而位错的移动则会促进解孪和孪生变形; 随着变形的增大, 位错之间的相互约束增强, 最后发生剪切带和堆垛层错的滑移. Tadayyon等(2017) 指出位错运动和孪生变形可以细化晶粒, 导致合金强度提高以及延展性增强, 而堆垛层错进一步使得材料发生加工硬化. 这些研究结果表明, NiTi形状记忆合金发生马氏体重定向时也会产生大量的位错缺陷, 且位错缺陷甚至会演变成堆垛层错, 进一步影响该合金的性能. ...
... 初始相为马氏体相的NiTi形状记忆合金在拉伸变形过程中微结构的演化图(Tadayyon et al. 2017 ) ...
Molecular dynamics simulations to the pseudo-elasticity of NiTi shape memory alloy nano-pillar subjected to cyclic compression.
0
2017
A kinetics model for martensite variants rearrangement in ferromagnetic shape memory alloys. J
3
2010
... (1)磁场诱发马氏体重定向:Tickle和 James (1999) , Tickle 等(1999) , Heczko (2005) , Straka 和 Heczko (2003) 以及Karaca等(2006) 研究了环境温度在马氏体完成温度\((M_{\rm f})\)以下时铁磁形状记忆合金单晶在轴向恒定压应力、横向交变磁场作用下磁场诱发马氏体重定向特性.此时, 材料的初始相为马氏体, 图43 给出了该加载工况下典型的磁场--相对磁化曲线及磁场--应变曲线.以压应力为1.4 MPa的工况为例, 由图可见: 在变形的初始阶段(即磁场低于0.5 T), 由于磁场低于马氏体重定向临界磁场, 无非弹性应变出现, 并且磁化量随着磁场的增大而线性增大, 该阶段的磁化机制主要为磁化矢量的旋转; 当磁场高于0.5 T时, 马氏体重定向发生, 伴随着很大的非弹性应变出现, 同时磁化率出现跳跃并远高于低磁场(小于0.5 T)时的磁化率, 在该阶段马氏体重定向和磁化矢量旋转这两种磁化机制同时发生; 当磁场达到0.8 T时, 马氏体重定向完成, 磁化饱和出现, 并在后续磁场加载过程中, 非弹性应变和磁化量不再变化; 在卸载过程中, 当磁场达到0.25 T时, 逆向重定向发生, 非弹性应变和磁化量剧烈变化; 当磁场完全卸载后, 马氏体重定向完成, 非弹性应变及磁化量完全归零.另外, 对比图43 中不同应力水平下的磁--力响应可以看出:磁致伸缩应变的大小随着轴向压应力的增大而逐渐减小, 并且轴向压应力对磁场诱发马氏体重定向有抑制作用, 即临界磁场强度随着轴向压应力的增加而逐渐升高; 在压应力较小时(0.6 MPa), 磁场诱发出的重定向应变无法完全恢复; 在压应力较大时(3 MPa), 试样在发生马氏体重定向之前已经通过磁化矢量旋转机制完成了磁化, 无法诱发马氏体重定向机制. 这说明, 铁磁形状记忆合金存在着一个"闭锁应力", 在应力低于"闭锁应力"时, 磁场能够诱发马氏体重定向; 在应力高于"闭锁应力"时, 磁场无法诱发马氏体重定向. 铁磁形状记忆合金的"闭锁应力"一般较低, 大约在3 MPa左右. Karaca等(2006) 进一步提出了发生马氏体重定向的两个必要条件, 即高的磁晶各向异性能和低的孪生界面运动能, 并通过增大测试温度与居里温度之差以及减小测试温度和马氏体相变温度之差分别提高和降低磁晶各向异性能和孪生界面运动能, 进而获得了较高的应力闭锁值(5.7 MPa). ...
... 如前所述, 铁磁形状记忆合金磁--力耦合变形行为的宏观唯象本构模型因其概念简单、便于工程应用等优点已经得到了较为广泛的关注.例如:Hirsinger 和 Lexcellent(2003) 通过假定磁晶各向异性能无穷大和磁化矢量不发生旋转, 首先提出了一个描述NiMnGa铁磁形状记忆合金磁--力耦合变形行为的一维宏观唯象本构模型; 然后, Creton 和 Hirsinger (2005) 以及Gauthier等(2006)对该模型做了进一步的拓展, 给出了磁化矢量旋转量与外加磁场之间的关系; Kiefer 和 Lagoudas(2005) 通过同时考虑马氏体孪生界面运动、磁畴的旋转和畴壁运动三种机制建立了一个较为全面的双马氏体变体二维唯象本构模型, 对铁磁形状记忆合金的力--磁学特性以及微结构演变进行了合理的描述; Wang 和 Li (2010) 通过引入二阶张量型马氏体重定向驱动力, 建立了一个新的铁磁形状记忆合金本构模型, 很好的描述了马氏体在外加应力和磁场作用下的马氏体重定向特性; Chen等(2014) , LaMaster 等(2014) 和Auricchio等(2015) 基于真实的晶体学位向关系, 引入三个马氏体变体, 从而建立了三维的单晶唯象本构模型, 对铁磁形状记忆合金在复杂加载条件下的马氏体相变和重定向给出了合理的描述和预测.最近, Mousavi 和 Arghavani(2017) 建立了一个既能更全面描述铁磁形状记忆合金力--磁耦合变形行为, 又易于进行数值实现的三维宏观唯象本构模型.该模型具有较好的应用前景. ...
... 基于Eshelby夹杂理论的细观力学本构模型能反映铁磁形状记忆合金磁--力耦合变形行为的细观非均匀性, 具有良好的发展前景, 目前已经得到了研究者的广泛重视. 例如:Zhu 和Dui (2007) 建立了基于Eshelby夹杂理论的铁磁形状记忆合金细观力学模型, 并通过该模型进一步研究了应力状态(拉伸、压缩)对磁场诱发马氏体重定向的影响(Zhu & Dui 2008 )以及磁矢量旋转对马氏体重定向的影响 (Zhu & Dui 2010 ); Wang 和 Li(2010) 通过考虑夹杂的各向异性拓展了细观力学模型.由于细观力学模型充分考虑了微结构之间的非均匀性与交互作用, 因此能够很好地描述铁磁形状记忆合金的重定向特性.需要指出的是现有的铁磁形状记忆合金细观力学模型均为二维模型.下面将简要的介绍 Zhu和 Dui (2007) 建立的细观力学本构模型. ...
Three-dimensional field model and computer modeling of martensitic transformations.
0
1997
The superelasticity of TiPdNi high temperature shape memory alloy.
1
2003
... 如Kang 和 Song (2015) 指出, 在单轴疲劳失效实验研究的基础上已经建立了一些疲劳失效模型, 对NiTi形状记忆合金的疲劳失效寿命进行了预测.但这些已有的疲劳失效模型中, 绝大部分都是基于宏观实验结果的半经验型模型. 例如, Tobushi等(2000) 基于NiTi形状记忆合金丝在水和油中的低周旋转弯曲疲劳实验数据, 直接采用与Manson-Coffin公式类似的方程对实验数据进行了校核, 提出了一个半经验型的寿命预测模型; 为了引入NiTi形状记忆合金特有的马氏体相变过程对疲劳寿命的影响, Maletta 等(2012 , 2014 )通过考虑不同的变形机制, 对Manson-Coffin公式进行了修正, 提出了一个新的疲劳寿命预测模型; 类似的还包括Lagoudas 等(2009b) 和Runciman 等(2011) 的工作.值得注意的是, 这些模型都是基于应变幅值的寿命预测模型, 不能很好地反映NiTi形状记忆合金在循环变形过程中的能量耗散及其演化情况, 预测效果不理想. 近年来, Moumni 等(2005) 和Kan等(2011) 以NiTi形状记忆合金饱和的耗散能密度(即一个加载循环中的响应的应力--应变滞回环面积)作为基本变量, 建立了半经验型的、基于能量的疲劳寿命预测模型, 对NiTi形状记忆合金的单周疲劳寿命进行了合理的预测. Song等(2017) 通过不同峰值应力下超弹性NiTi形状记忆合金微管的单轴和非比例多轴疲劳实验, 讨论了峰值应力和相变程度对单轴和多轴疲劳寿命的影响, 并在此基础上通过引入初始耗散能密度\(W_{\rm first}\)和稳定耗散能密度\(W_{\rm sat}\)以及加载路径参数 \(\lambda\)分别来反映峰值应力水平和相变程度以及非比例多轴加载路径对疲劳寿命的影响, 提出了基于能量的超弹性NiTi形状记忆合金多轴疲劳失效寿命预测模型, 即\[ N_{\rm f} = \dfrac{\alpha \ln (W_{\rm sat} / \beta )}{\ln W_{\rm first} }\cdot \dfrac{1}{\lambda } \ \ (35)\]其中, \(\alpha \)和\(\beta \)为材料参数, 可以通过实验数据的拟合而得.加载路径参数 \(\lambda \)定义为多轴加载路径的周长和其外接圆周长之比.预测结果和实验结果的对比表明, 所有的点都位于2倍分散带以内, 并且有85%的点位于1.5倍分散带以内. ...
a. Observation on the transformation domains of super-elastic NiTi shape memory alloy and their evolutions during cyclic loading
5
2016
... 尽管如此, Kan等(2016) 完成的相关实验还是揭示了超弹性NiTi形状记忆合金明显的热--力耦合效应以及由此而引起的率相关循环变形特性, 并且表明在相应的本构模型构建中应该合理考虑这种与内部热生成和外部热交换密切相关的热--力耦合循环变形行为.同时, Xie等(2016a) 还通过不同加载速率下的应力控制循环拉伸--卸载实验, 揭示了不同应力率下超弹性NiTi形状记忆合金板材的单轴相变棘轮行为演化特征, 如图7 所示. 图7 表明: NiTi合金板材的单轴相变棘轮行为也体现出明显的应力率相关性, 拉伸部分的相变硬化程度也随应力率(即加载应力随时间的变化率)的增大而增大, 并且高应力率下的相变棘轮行为更为显著. 另外, 由图7 还可以看出, 在高应力率情形下, 每一次循环中的耗散能密度(即应力--应变滞回环的面积)明显小于低应力率下的结果. 这也说明, 在应力控制的循环变形过程中, 超弹性劣化和耗散能下降也随应力率的增大而变得更加迅速.这些率相关性也是依赖于循环变形过程中体现出的、明显的热--力耦合效应.值得注意的是, 尽管目前已有一些文献讨论了超弹性NiTi形状记忆合金的率相关相变棘轮行为, 但与应变控制下的率相关循环变形行为相比, 已有的研究还不系统, 特别是NiTi形状记忆合金多轴循环变形行为的率相关性方面还需要在未来的研究中进行更为深入和系统的实验观察. ...
... 超弹性NiTi形状记忆合金板材在不同应力率下的单轴相变棘轮行为(Xie et al. 2016a ). (a) 6.5 MPa/s, (b) 162.5 MPa/s ...
... 结合实际变形过程中的温度变化的测量, Zhang等(2010) 进一步对相变图案形成和演化及其率相关性的物理本质进行了解释, 强调了这一物理过程中的材料局部失稳特性和热--力耦合特性. 然而, 上述研究仅针对应变控制的拉伸--卸载过程, 没有涉及多次循环、不同加载水平以及在应力控制加载条件下相变图案的形成和演化, 还需要进一步观察和讨论. 为此, Xie等(2016a) 采用非接触数字图像相关(DIC)和红外热成像(IR)方法直接观测了超弹性NiTi形状记忆合金板材在应力控制拉伸--卸载循环过程的相变图案和温度场分布及其演化, 讨论了不同峰值应力(即650, 750和800 MPa)作用下NiTi合金板材相变图案的循环演化特征及其形成机理, 典型的实验结果如图10 和图11 所示. 结果表明: (1)超弹性NiTi形状记忆合金在拉伸--卸载循环初期表现出变形局部化的特征, 马氏体条带逐渐形成、长大和扩展以及卸载过程中的奥氏体条带的形成、长大或扩展, 如图10 (a)和图11 (a)所示. (2)然而, 循环稳定后相变图案的演化则依赖于外加的应力峰值大小.应力峰值较小(如650 MPa)时, 循环稳定后无明显的相变图案形成, 表现出较为均匀化的变形特征; 但当应力峰值较高(如750和800 MPa)时, 循环稳定时仍会出现明显的相变图案, 产生马氏体条带的残留现象. Xie等(2016a) 进一步通过测得的应变场和温度场的变化, 认为宏观马氏体条带的残留是由高峰值应力循环后富集的位错对马氏体的钉扎作用造成的, 马氏体条带的残留也与该NiTi合金在高峰值应力下显著的相变棘轮行为是相对应的. ...
... (a)所示. (2)然而, 循环稳定后相变图案的演化则依赖于外加的应力峰值大小.应力峰值较小(如650 MPa)时, 循环稳定后无明显的相变图案形成, 表现出较为均匀化的变形特征; 但当应力峰值较高(如750和800 MPa)时, 循环稳定时仍会出现明显的相变图案, 产生马氏体条带的残留现象. Xie等(2016a) 进一步通过测得的应变场和温度场的变化, 认为宏观马氏体条带的残留是由高峰值应力循环后富集的位错对马氏体的钉扎作用造成的, 马氏体条带的残留也与该NiTi合金在高峰值应力下显著的相变棘轮行为是相对应的. ...
... NiTi形状记忆合金在峰值应力为800 MPa的循环拉伸--卸载过程中的相变图案演化(Xie et al.2016a ). (a) 第1周, (b) 第20周. 图中\(a\)为正相变开始点, \(b\)为加载中点, \(c\)为峰值应力点, \(d\)为逆相变开始点, \(e\)为卸载中点; \(f\)为零应力点 ...
b. Observation on rate-dependent cyclic transformation domain of super-elastic NiTi shape memory alloy. Mater. Sci. Eng.
1
2016
... Xie等(2016b) 进一步分别讨论了在应变控制和应力控制拉伸--卸载循环变形过程中相变图案的形成和演化对加载速率的依赖性.研究表明: (1)相变条带的数目随加载速率的增大而单调增大; (2)在加载速率较低时, 随循环次数的增大, 变形逐渐由明显的局部化特征过渡到均匀变形, 残余马氏体条带不明显; (3)在加载速率较大时, 在循环稳定时将会有明显的残余马氏体条带产生, 这是因为加载速率较快时, 相变棘轮行为更为显著, 增加的位错密度将对马氏体逆相变产生显著的抑制作用的缘故; (4)在应力控制的循环拉伸--卸载加载的稳定变形阶段, 观察到的应变和温度场要比应变控制下的更为均匀.材料内部的相变热生成和与外界的热交换之间的相互竞争是相变图案率相关性的根本原因, 而在稳定的循环变形阶段这两种因素的竞争达到一个动态的平衡. ...
Microstructure of NiTi shape memory alloy due to tension-compression cyclic deformation.
1
1998
... 除了上述对疲劳断口的SEM形貌观察以外, 人们还对NiTi形状记忆合金在疲劳失效过程中的微观缺陷, 例如位错等的形成和长大过程进行了TEM观察, 以期讨论疲劳微裂纹的萌生机制. Hamilton 等(2004) , Norfleet等(2009) , Pelton 等(2011 , 2012 ), Delville 等(2010 , 2011 ), Liu等(1998) 和Xie 等(1998) 的研究表明, 在循环变形过程中, 位错主要在奥氏体和诱发马氏体的界面和具有不同晶体学位向的马氏体变体间的界面附近以及夹杂和沉淀相的周围形成和聚集; Ahadi和 Sun (2013 , 2014 )的观察进一步表明, 位错的形成和聚集只能发生在具有大尺度晶粒(大于300 \(\mu\)m)的NiTi形状记忆合金中, 在具有小尺度晶粒的NiTi形状记忆合金中观察不到大范围的位错聚集.这是因为晶界对位错运动的阻碍作用将随晶粒尺度的减小而增加的缘故.需要指出的是, 已经获得的这些微观缺陷的形成和演化信息仍然偏少, 还不足以清楚地说明NiTi形状记忆合金在整个以及在不同加载方式下的疲劳失效过程中微观缺陷的形成和演化特征, 在今后的研究中还需要进一步加强, 特别是针对NiTi形状记忆合金的热--力耦合疲劳失效行为. ...
Structure analysis of a precipitate phase in an Ni-rich high-temperature NiTiHf shape memory alloy.
2
2013
... Wang 等(2017) 采用EAM势, 通过分子动力学模拟研究了循环压缩--卸载过程中NiTi形状记忆合金纳米柱的超弹性行为, 发现位错和孪生对原子模型的物理结构和力学响应的改变、累积不可逆应变和超弹性行为的衰减有着重要影响.图25 给出了NiTi形状记忆合金纳米柱在400 K下峰值应变为7.46%时的单轴循环压缩--卸载模拟结果, 可见在循环变形过程中会产生明显的残余变形以及超弹性劣化现象, 循环7周以后即达到稳定状态, 超弹性滞回环消失. ...
... NiTi形状记忆合金纳米柱单轴循环压缩--卸载过程的模拟结果(Wang et al. 2017 ). (a)应力--应变曲线, (b) CNA与应变曲线, (c)第5周循环中应变压缩到7.36%时的模型, \(Z\)方向距离表面5 {\AA}的原子不可见, (d)纳米柱的位错演化过程, (e)位错滑移平面示意图, 滑移面由红色虚线构成 ...
Effect of deformation frequency on temperature and stress oscillations in cyclic phase transition of NiTi shape memory alloy. J. Mech. Phys.
4
2014
... 由图3 \(\sim\) 图5 可见, NiTi合金微管的表面温度在循环变形过程中会发生明显变化, 变化的最大值随加载速率的增加而增大. 然而, 整个工作段的平均温度即使在加载速率为\(3.3\times 10^{ - 2}\) s\(^{ -1 }\)(在最大应变为9%时, 相当于加载频率为0.15 Hz)的工况下却会随着循环次数的增大而逐渐下降, 如图5 (b)所示. 这与Yin等(2014) 在加载频率高于1 Hz的单轴拉伸--卸载循环加载下观察到的、平均温度随循环次数增大而不断升高的现象不同(如图6 所示). 由于Kan 等(2016) 采用的最高加载速率比Yin 等(2014) 的要低, 因而只能观察到平均温度随循环次数增大而逐渐下降的现象.当加载速率较小时, 微管与外界的热交换在循环过程中会随着循环次数的增大而逐渐充分, 虽然在循环变形过程中有温度的波动, 但平均温度将随循环次数的增大而逐渐下降, 最后趋近于环境温度, 或是没有明显的升高 (见图5 (a)); 当加载速率较大时 (如Yin等(2014) 讨论的1 Hz), 微管与外界的热交换不能充分进行, 材料内部在循环变形过程中将产生热量的集中, 并随循环次数的增大而变得更加显著, 因此, 平均温度将随循环次数增大而逐渐上升, 如图6 (a)所示. ...
... 采用的最高加载速率比Yin 等(2014) 的要低, 因而只能观察到平均温度随循环次数增大而逐渐下降的现象.当加载速率较小时, 微管与外界的热交换在循环过程中会随着循环次数的增大而逐渐充分, 虽然在循环变形过程中有温度的波动, 但平均温度将随循环次数的增大而逐渐下降, 最后趋近于环境温度, 或是没有明显的升高 (见图5 (a)); 当加载速率较大时 (如Yin等(2014) 讨论的1 Hz), 微管与外界的热交换不能充分进行, 材料内部在循环变形过程中将产生热量的集中, 并随循环次数的增大而变得更加显著, 因此, 平均温度将随循环次数增大而逐渐上升, 如图6 (a)所示. ...
... (a)); 当加载速率较大时 (如Yin等(2014) 讨论的1 Hz), 微管与外界的热交换不能充分进行, 材料内部在循环变形过程中将产生热量的集中, 并随循环次数的增大而变得更加显著, 因此, 平均温度将随循环次数增大而逐渐上升, 如图6 (a)所示. ...
... 超弹性NiTi形状记忆合金微管在高加载速率下的平均温度随循环次数的变化曲线(Yin et al.2014 ). (a) 温度变化, (b) 应力--应变响应 ...
Rate dependent damping of single crystal CuAlNi shape memory alloy.
0
2013
a. A physical mechanism based constitutive model for temperature-dependent transformation ratchetting of NiTi shape memory alloy: One-dimensional model
6
2014
... 超弹性劣化效应的温度依赖性 (Yu et al. 2014a ). (a)应力--应变曲线, (b) 残余应变\(\varepsilon ^{\rm r}\)演变曲线, (c)耗散能\(W\)演变曲线, (d)马氏体相变开始应力\(\sigma _{\rm MA}^{\rm s}\)演变曲线 ...
... 由图2 得到的应力--应变关系曲线可见: (1)加载速率的变化显著影响超弹性NiTi形状记忆合金微管的循环应力--应变响应, 拉伸部分体现出的相变硬化程度在高加载速率下变得更加显著, 如图2 (a)所示. (2) 残余应变的累积同样依赖于加载速率, 在高加载速率下演变更为迅速, \(3.3\times 10^{ - 2}\) s\(^{ -1}\)下的饱和残余应变值明显高于其他加载速率下的结果, 如图2 (b) \(\sim\) 图2 (d)所示. (3)随着加载速率的增大, 每一次循环中的耗散能密度下降也更为迅速, 并且饱和的耗散能密度值也变得更小. 这说明, 超弹性的循环劣化和耗散能密度减小在高加载速率的循环过程中变得更加显著, 进而更易导致超弹性NiTi形状记忆合金的功能性疲劳失效. 此外, 超弹性NiTi形状记忆合金循环劣化和耗散能密度还随着加载应力水平的提高(Kang et al. 2009 )和温升的提高 (Yu et al. 2014a )变得更加显著. ...
... Yu 等 (2014a) 在小变形框架下, 将材料点总的应变张量\(\pmb \varepsilon\)分解为四个部分, 即弹性应变张量\(\pmb \varepsilon ^{\rm e}\)、热膨胀应变张量\(\pmb \varepsilon ^{\rm T}\)、相变应变张量\(\pmb\varepsilon ^{\rm tr}\)和相变诱发塑性应变张量\(\pmb \varepsilon^{\rm p}\), 即\[\pmb \varepsilon = \pmb \varepsilon ^{\rm e} +\pmb \varepsilon ^{\rm T} + \pmb \varepsilon ^{\rm tr} + \pmb\varepsilon ^{\rm p}\ \ (1)\]热膨胀应变和温度的关系为\[\pmb \varepsilon ^{\rm T} = \pmb \alpha(T - T_{\rm r} )\ \ (2)\]其中, \(\pmb \alpha\), \(T\), \(T_{\rm r}\)分别是二阶热膨胀张量、当前温度和参考温度. ...
... 相变过程中奥氏体--马氏体界面处的高局部应力会诱发奥氏体内位错滑移的启动, 这和普通金属材料中位错滑移完全由外加应力诱发有所不同. 为此, Yu等(2014a) 提出了如下描述相变诱发塑性的演化方程\[\left\{\!\! \begin{array}{ll} \dot {\gamma } = (1 - \xi )\gamma _0 \left( \dfrac{\pmb \sigma :\pmb N _{\rm p} }{\mu } \right)^2 \exp \left( \dfrac{ - \Delta G_{\rm slip} }{k_{\rm b} T}\left( 1 - \left( \dfrac{\pi _{\rm p}}{\tau _0 } \right)^{p} \right)^q \right)\left| \dot {\xi }\right|, &\qquad \pi _{\rm p} > 0\\ \dot {\gamma } = 0, &\qquad \pi _{\rm p} \leq 0 \end{array}\right. \ \ (7)\]其中, \(\gamma _0 \)是参考滑移率; \(p\)和\(q\)是两个材料参数, 需要满足如下限制条件\(0 < p \leq 1\)和\(1 < q \leq 2\); \(\mu\)是剪切模量; \(\Delta G_{\rm slip} \)为无应力条件下的位错激活能, \(k_{\rm b} \)是玻尔兹曼常数; \(\tau _0 \)是在\(T=0\) K时的晶格阻力. ...
... 应变率为3.3 \(\times \) 10\(^{ -3}\) s\(^{-1}\)时的实验和模拟的结果 (Yu et al. 2014a ). (a)第1周和第5周的应力--应变曲线, (b) 第10周和第50周的应力--应变曲线, (c) 残余应变随循环次数演变曲线, (d)平均温度随循环次数演变曲线 ...
... 实验和模拟的超弹性退化 (Yu et al. 2014a ). (a)第1周和第20周的残余应变随应变率变化曲线, (b)第1周和第20周的耗散能随应变率变化曲线 ...
A macroscopic multi-mechanism based constitutive model for the thermo-mechanical cyclic degeneration of shape memory effect of NiTi shape memory alloy.
1
2016
... 为了描述NiTi形状记忆合金在热--力耦合循环变形过程中体现出的形状记忆效应劣化现象, Auricchio 等(2008) , Zaki 和 Moumni (2007) 和Hartl等(2010) 通过引入必要的非弹性变形机制, 建立了相应的本构模型; 但是, 这些本构模型没有很好地考虑在热--力耦合循环载荷作用下冷却阶段发生的附加非弹性变形, 也不能对形状记忆效应退化现象的加载水平依赖性进行合理的描述. 最近, Yu 等 (2016) 在Popov 和 Lagoudas (2007) 提出的本构模型基础上, 针对NiTi形状记忆合金循环加载条件下出现的形状记忆效应退化现象, 发展了一个宏观多机制本构模型. 该模型根据实验观测结果, 考虑了NiTi形状记忆合金热--力循环过程中的四种变形机制, 即马氏体相变、相变诱发塑性、马氏体重取向和重取向诱发塑性, 并且重点突出了马氏体相变和重取向与位错的交互作用.根据宏观实验结果, Yu 等 (2016) 认为: 随循环次数的增大, 相变和重定向模量增大, 马氏体相变开始温度升高, 重定向开始应力下降; 某些区域位错诱发的局部应力的投影为正, 该内应力将促进马氏体相变和重定向, 其结果是循环过程中马氏体相变开始温度升高; 同时, 位错诱发的应力梯度会阻碍孪晶和解孪相的形核, 导致相变和重定向模量增大. 下面对Yu 等(2016) 发展的本构模型进行简要介绍. ...
b. Large temperature and magnetic field induced strain in polycrystalline Ni\(_{50}\)Mn\(_{36}\)In\(_{14}\)-xSbx alloys. J
1
2014
... 上述研究主要集中在铁磁形状记忆合金单晶方面. Murray 等(1998) , Jeong等(2003) 研究了铁磁形状记忆合金多晶的磁--力耦合特性, 发现相对于单晶材料, 多晶能产生的磁致伸缩应变很小. Marioni(2002) 进一步指出, 针对多晶铁磁形状记忆合金, 可以通过定向凝固法调控择优取向的初始织构来获取较大的磁致伸缩应变.近年来, 众多学者研究了铁磁形状记忆合金定向凝固多晶在不同方向上的磁场诱发马氏体重定向特性(Pötschke et al.2010 , Yu et al. 2014b ), 应力诱发马氏体重定向特性(Chulist et al. 2010 , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性. ...
A three-dimensional model of the thermomechanical behavior of shape memory alloys. J. Mech. Phys.
1
2007
... 为了描述NiTi形状记忆合金在热--力耦合循环变形过程中体现出的形状记忆效应劣化现象, Auricchio 等(2008) , Zaki 和 Moumni (2007) 和Hartl等(2010) 通过引入必要的非弹性变形机制, 建立了相应的本构模型; 但是, 这些本构模型没有很好地考虑在热--力耦合循环载荷作用下冷却阶段发生的附加非弹性变形, 也不能对形状记忆效应退化现象的加载水平依赖性进行合理的描述. 最近, Yu 等 (2016) 在Popov 和 Lagoudas (2007) 提出的本构模型基础上, 针对NiTi形状记忆合金循环加载条件下出现的形状记忆效应退化现象, 发展了一个宏观多机制本构模型. 该模型根据实验观测结果, 考虑了NiTi形状记忆合金热--力循环过程中的四种变形机制, 即马氏体相变、相变诱发塑性、马氏体重取向和重取向诱发塑性, 并且重点突出了马氏体相变和重取向与位错的交互作用.根据宏观实验结果, Yu 等 (2016) 认为: 随循环次数的增大, 相变和重定向模量增大, 马氏体相变开始温度升高, 重定向开始应力下降; 某些区域位错诱发的局部应力的投影为正, 该内应力将促进马氏体相变和重定向, 其结果是循环过程中马氏体相变开始温度升高; 同时, 位错诱发的应力梯度会阻碍孪晶和解孪相的形核, 导致相变和重定向模量增大. 下面对Yu 等(2016) 发展的本构模型进行简要介绍. ...
Experimental study on rate dependence of macroscopic domain and stress hysteresis in NiTi shape memory alloy strips. Int. J
1
2010
... 尽管对NiTiX高温形状记忆合金的微观结构特征已有较多的微观实验观察, 但绝大多数集中在材料改性的范畴, 对热--力耦合循环加载下该类合金的微观结构观察少有报道, 需在今后进一步开展系统的研究. 例如, Karaca等(2013) 对不同温度下的挤压态NiTiHf高温形状记忆合金的沉淀相进行了观察, 证明了550\(^{\circ}\)C \(\times \) 3 h后, 材料中即有纳米级沉淀出现, 并且时效温度提高到650\(^{\circ}\)C后, 相同时效时间下的沉淀尺寸增大; Satamarta等(2013) 对NiTiHf及NiTiZr材料的微观实验观察中证明炉内冷却的方法可以比高温时效更易使材料内部产生更大的沉淀粒子; Yang 等(2013) 在实验观察的基础上进一步提出, 对于NiTiHf高温形状记忆合金, 这些沉淀粒子并非普通的Ni\(_{4}\) (Ti, Hf)\(_{3}\)相, 而是一种具有不同原子结构的新相, 即H相. ...
Experimental and theoretical investigation of the frequency effect on low cycle fatigue of shape memory alloys. Int. J. Plast., 90: 1-30. Zhang Y, Zhu J, Moumni Z, Herpen A V, Zhang W. 2016. Energy-based fatigue model for shape memory alloys including thermomechanical coupling
2
2017
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
... Zhang 等(2016) 在室温下对NiTi合金丝进行了不同应变频率下的疲劳实验, 基于实验结果, 将非弹性耗散能分为两部分: 一部分通过热传导和热对流释放到环境中, 另一部分则储存于材料内部促进应力诱发马氏体相变的晶体缺陷.随加载速率的变化, 这两部分非弹性耗散能的比例发生变化, 由于释放到环境中的非弹性耗散能不会引起裂纹的萌生和扩展, 因此只考虑非弹性耗散能中储存于材料内部的部分达到一定临界值时, 裂纹开始萌生和扩展. 当加载速率越高, 材料内部储存的能量越大, 从而引起更低的寿命. Zhang等(2016)在此基础上发展了如下基于耗散能的疲劳准则\[ W_{\rm sat} = \gamma \dot {\varepsilon }^{ - \eta}N_{\rm f}^\beta \ \ (36)\]其中, \(\dot {\varepsilon }\)为应变率, \(\gamma \), \(\eta \)和\(\beta\)为材料参数, 可通过实验数据的拟合得到.该模型能够较合理的预测NiTi合金丝在不同应变率下的疲劳失效寿命. ...
Atomistic characterization of pseudoelasticity and shape memory in NiTi nanopillars.
1
2012
... 众所周知, 超弹性NiTi形状记忆合金在循环变形过程中会经历反复的热弹性马氏体相变及其逆相变过程, 并且在循环相变过程中还存在相变潜热的释放和吸收过程. 也就是说, 在该合金的循环变形过程中必然涉及到合金与环境介质之间的热交换, 这是一个显著的热--力耦合问题; 同时, 这种热交换进行的程度取决于发生循环相变的时间和频率, 也就是取决于外加载荷的加载速率和加载频率, 体现出显著的率相关性.正如Shaw 和 Kyriakides (1995) , Grabe和Bruhns (2008) , Yin等 (2013) , He和Sun (2010a) 以及Sun和He (2012b) 指出, 超弹性NiTi形状记忆合金的率相关特性主要源自其内部热效应和与外部热交换之间的竞争, 而不是材料的黏性. 因此, 讨论加载速率或加载频率对超弹性NiTi形状记忆合金循环变形行为的影响对于揭示其热--力耦合物理本质是非常有意义的.为此, 近年来, Morin 等(1959) , He 和 Sun (2010b) , Yin 等(2014) 和Kan等(2016) 在应变控制的单轴循环加载条件下对超弹性NiTi形状记忆合金的率相关循环变形行为及相关的热--力耦合响应进行了较为系统的实验研究.图2 \(\sim\) 图5 分别给出了Kan 等(2016) 在最大应变为9%和采用6种不同应变率 (即3.3 \(\times \) 10\(^{ -4}\), 6.6 \(\times \) 10\(^{ - 4}\), 1 \(\times \) 10\(^{ - 3}\), 3.3 \(\times \) 10\(^{ - 3}\), 1 \(\times \) 10\(^{ - 2}\)和\(3.3\times 10^{ - 2}\) s\(^{ -1})\)的单轴循环拉伸--卸载实验中得到的超弹性NiTi形状记忆合金微管的循环变形和试样表面温度变化的实验结果.其中, 温度场分布通过FLIR A655sc型高分辨率红外热像仪进行测量, 测量精度为0.5\({^\circ}\). ...
Phase-field modeling of martensitic microstructure in NiTi shape memory alloys.
0
2014
Experimental study of directionally solidified ferromagnetic shape memory alloy under multi-field coupling. J
7
2016
... 为了描述NiTi形状记忆合金在热--力耦合循环变形过程中体现出的形状记忆效应劣化现象, Auricchio 等(2008) , Zaki 和 Moumni (2007) 和Hartl等(2010) 通过引入必要的非弹性变形机制, 建立了相应的本构模型; 但是, 这些本构模型没有很好地考虑在热--力耦合循环载荷作用下冷却阶段发生的附加非弹性变形, 也不能对形状记忆效应退化现象的加载水平依赖性进行合理的描述. 最近, Yu 等 (2016) 在Popov 和 Lagoudas (2007) 提出的本构模型基础上, 针对NiTi形状记忆合金循环加载条件下出现的形状记忆效应退化现象, 发展了一个宏观多机制本构模型. 该模型根据实验观测结果, 考虑了NiTi形状记忆合金热--力循环过程中的四种变形机制, 即马氏体相变、相变诱发塑性、马氏体重取向和重取向诱发塑性, 并且重点突出了马氏体相变和重取向与位错的交互作用.根据宏观实验结果, Yu 等 (2016) 认为: 随循环次数的增大, 相变和重定向模量增大, 马氏体相变开始温度升高, 重定向开始应力下降; 某些区域位错诱发的局部应力的投影为正, 该内应力将促进马氏体相变和重定向, 其结果是循环过程中马氏体相变开始温度升高; 同时, 位错诱发的应力梯度会阻碍孪晶和解孪相的形核, 导致相变和重定向模量增大. 下面对Yu 等(2016) 发展的本构模型进行简要介绍. ...
... 提出的本构模型基础上, 针对NiTi形状记忆合金循环加载条件下出现的形状记忆效应退化现象, 发展了一个宏观多机制本构模型. 该模型根据实验观测结果, 考虑了NiTi形状记忆合金热--力循环过程中的四种变形机制, 即马氏体相变、相变诱发塑性、马氏体重取向和重取向诱发塑性, 并且重点突出了马氏体相变和重取向与位错的交互作用.根据宏观实验结果, Yu 等 (2016) 认为: 随循环次数的增大, 相变和重定向模量增大, 马氏体相变开始温度升高, 重定向开始应力下降; 某些区域位错诱发的局部应力的投影为正, 该内应力将促进马氏体相变和重定向, 其结果是循环过程中马氏体相变开始温度升高; 同时, 位错诱发的应力梯度会阻碍孪晶和解孪相的形核, 导致相变和重定向模量增大. 下面对Yu 等(2016) 发展的本构模型进行简要介绍. ...
... 在此基础上, Yu 等 (2016) 首先基于小变形假设, 将总应变张量\(\pmb\varepsilon \)分解为五部分, 即弹性应变 \(\pmb \varepsilon ^{\rm e}\), 相变应变\(\pmb \varepsilon ^{\rm tr}\), 重定向应变\(\pmb \varepsilon^{\rm reo}\), 相变诱发塑性应变 \(\pmb \varepsilon ^{\rm tp}\)和重定向诱发塑性应变\(\pmb \varepsilon ^{\rm rp}\)\[\pmb \varepsilon = \pmb \varepsilon ^{\rm e} + \pmb \varepsilon^{\rm tr} + \pmb \varepsilon ^{\rm reo} + \pmb \varepsilon ^{\rm tp} + \pmb \varepsilon ^{\rm rp}\ \ (14)\]相变应变率张量可表示为\[\dot {\pmb\varepsilon}^{\rm tr} = g\pmb N _{\rm tr} \dot{\lambda }_2 \ \ (15)\]\[\pmb N _{\rm tr} = \left\{ {\begin{array}{ll} \sqrt {\dfrac{3}{2}} \dfrac{\pmb \sigma _{\rm dev} + \pmb B _{\rm tr}}{\left\| {\pmb \sigma _{\rm dev} + \pmb B _{\rm tr} }\right\|},&\qquad \dot {\lambda }_2 > 0 \\ \sqrt {\dfrac{3}{2}} \dfrac{\pmb \varepsilon ^{\rm tr} + \pmb \varepsilon ^{\rm reo}} {\left\| {\pmb \varepsilon ^{\rm tr} + \pmb \varepsilon ^{\rm reo}} \right\|},&\qquad\dot {\lambda }_2 < 0 \\ \end{array}} \right.\ \ (16)\]其中, \(g\)为向前相变全部完成时相变应变值, \(\pmb N _{\rm tr} \)为马氏体相变方向张量, \(\pmb \sigma _{\rm dev} \)为应力张量\(\pmb\sigma \)的偏量. 为了描述马氏体相变开始温度随循环次数增大而升高, 引入一个内应力张量\(\pmb B _{\rm tr} \), 其为相变应变率张量的共轭变量. ...
... 图28 给出了峰值应力为500 MPa、不同循环次数下的NiTi形状记忆合金形状记忆效应退化的实验和模拟结果, 而图29 给出了实验和模拟得到的残余应变、塑性应变和峰值应变随循环次数的演变曲线.对比图28 和图29 中的实验和模拟结果可知, Yu 等(2016) 发展的模型能够合理地预测NiTi形状记忆合金热--力循环变形过程中不同次数下的应力--应变--温度曲线以及残余应变、塑性应变和峰值应变的演变曲线, 能够对在热--力耦合循环变形过程中体现出的形状记忆效应退化现象进行合理的描述. ...
... 峰值应力为500 MPa时形状记忆退化效应的实验和模拟结果(Yu et al. 2016 ). (a) 第1周和第10周应力--应变曲线, (b) 第1周和第10周温度--应变曲线 ...
... 形状记忆循环过程中残余应变、塑性应变和峰值应变的实验和模拟结果(Yu et al. 2016 ). (a) 残余应变, (b) 塑性应变, (c) 峰值应变 ...
... 上述研究主要集中在铁磁形状记忆合金单晶方面. Murray 等(1998) , Jeong等(2003) 研究了铁磁形状记忆合金多晶的磁--力耦合特性, 发现相对于单晶材料, 多晶能产生的磁致伸缩应变很小. Marioni(2002) 进一步指出, 针对多晶铁磁形状记忆合金, 可以通过定向凝固法调控择优取向的初始织构来获取较大的磁致伸缩应变.近年来, 众多学者研究了铁磁形状记忆合金定向凝固多晶在不同方向上的磁场诱发马氏体重定向特性(Pötschke et al.2010 , Yu et al. 2014b ), 应力诱发马氏体重定向特性(Chulist et al. 2010 , Pötschke et al. 2010 ). 最近Zhu等(2016) 更为系统地研究了在热--磁耦合作用下, 铁磁形状记忆合金定向凝固多晶不同方向上的磁场诱发马氏体重定向以及温度诱发马氏体相变特性.结果表明, 由于定向凝固造成的强烈初始织构, 铁磁形状记忆合金多晶展示出强烈的热--磁--力各向异性特性. ...
Micromechanical modeling of the stress-induced superelastic strain in magnetic shape memory alloy.
6
2007
... 基于Eshelby夹杂理论的细观力学本构模型能反映铁磁形状记忆合金磁--力耦合变形行为的细观非均匀性, 具有良好的发展前景, 目前已经得到了研究者的广泛重视. 例如:Zhu 和Dui (2007) 建立了基于Eshelby夹杂理论的铁磁形状记忆合金细观力学模型, 并通过该模型进一步研究了应力状态(拉伸、压缩)对磁场诱发马氏体重定向的影响(Zhu & Dui 2008 )以及磁矢量旋转对马氏体重定向的影响 (Zhu & Dui 2010 ); Wang 和 Li(2010) 通过考虑夹杂的各向异性拓展了细观力学模型.由于细观力学模型充分考虑了微结构之间的非均匀性与交互作用, 因此能够很好地描述铁磁形状记忆合金的重定向特性.需要指出的是现有的铁磁形状记忆合金细观力学模型均为二维模型.下面将简要的介绍 Zhu和 Dui (2007) 建立的细观力学本构模型. ...
... 通过考虑夹杂的各向异性拓展了细观力学模型.由于细观力学模型充分考虑了微结构之间的非均匀性与交互作用, 因此能够很好地描述铁磁形状记忆合金的重定向特性.需要指出的是现有的铁磁形状记忆合金细观力学模型均为二维模型.下面将简要的介绍 Zhu和 Dui (2007) 建立的细观力学本构模型. ...
... Zhu 和 Dui (2007) 将第一个马氏体变体视为基体, 第二个马氏体视为夹杂, 并将宏观整体应变\(\bar{\pmb\varepsilon}\)分解为弹性应变\(\bar{\pmb\varepsilon }^{\rm e}\)和非弹性应变\(\bar{\pmb\varepsilon }^{\rm in}\), 即 \[\bar{\pmb\varepsilon } = \bar{\pmb\varepsilon }^{\rm e} +\bar{\pmb\varepsilon }^{\rm in} \ \ (61)\]其中, \(\bar{\pmb\varepsilon }^{\rm e}\)和\(\bar{\pmb\varepsilon }^{\rm in}\)分别可以表示为 \[ \bar{\pmb\varepsilon }^{\rm e} = \overline{\pmb M}\bar {\pmb \sigma } \ \ {\rm (62a)}\] \[ \bar{\pmb\varepsilon }^{\rm in} = \xi \left( {1 - \xi} \right)\left\{ {\pmb L_0 + \left( {\pmb L_1 - \pmb L_0 }\right)\left[ {\pmb S - \xi \left( {\pmb S - \pmb I} \right)}\right]} \right\}^{ - 1}\left( {\pmb L_0 - \pmb L_1 }\right)\left( {\pmb S - \pmb I} \right)\left( {\pmb \varepsilon^{\rm r} - \pmb \varepsilon ^{\rm ph}} \right)+\] \[ \pmb \varepsilon^{\rm ph} + \xi \pmb \varepsilon ^{\rm r} \ \ {\rm (62b)}\]其中, \(\xi \)是第二个马氏体变体的体积分数, \(\pmb L_0 \)和\(\pmb L_1\)分别是基体和夹杂的弹性柔度张量, \(\pmb S\)是Eshelby张量, \(\pmb I\)是四阶单位张量, \(\pmb \varepsilon ^{\rm r}\)和\(\pmb \varepsilon^{\rm ph}\)分别是重定向和相变应变张量, \( \bar {\pmb\sigma }\)是宏观整体应力. \(\overline{\pmb M}\)是宏观整体有效弹性柔度张量 \[ \overline{\pmb M} = \left\{ {\pmb I + \xi \left\{ {\pmb L_0 + \left( {\pmb L_1 - \pmb L_0 } \right)\left[{\pmb S - \xi \left( {\pmb S - \pmb I} \right)} \right]}\right\}^{ - 1}\left( {\pmb L_0 - \pmb L_1 } \right)} \right\}\pmb M_0 \ \ (63)\]Zhu 和 Dui (2007) 将两个马氏体变体的Gibbs自由能之差分成三项, 即 \[ \Delta G = \Delta G_{\rm me} + \Delta G_{\rm ze} + \Delta G_{\rm an} \ \ (64)\]其中, \(\Delta G_{\rm me} \), \(\Delta G_{\rm ze} \)和\(\Delta G_{\rm an} \)分别是机械能、Zeeman能和磁晶各向异性能, 即 \[ \Delta G_{\rm me} = - \dfrac{1}{2}\xi \left( {1 - \xi }\right)\pmb L_0 \left( {\pmb S - \pmb I} \right)\pmb \varepsilon^{\rm r}\pmb \varepsilon ^{\rm r} \ \ {\rm (65a)}\] \[ \Delta G_{\rm ze} = \left( {1 - \xi } \right)\mu _0 M^{\rm sat}H\left\{ \left[{\alpha \cos \beta _3 - \left( {1 - \alpha } \right)\cos \beta _1} \right]\cos \theta +\right.\] \[ \left. \left[ {\alpha \sin \beta _3 - \left( {1 -\alpha } \right)\sin \beta _1 } \right]\sin \theta \right\} + \xi \mu _0 M^{\rm sat}H\left\{ \left[ { - \alpha \sin \beta _4 +\left( {1 - \alpha } \right)\sin \beta _2 } \right]\cos \theta+\right.\] \[\left.\left[ {\alpha \cos \beta _4 - \left( {1 - \alpha } \right)\cos\beta _2 } \right]\sin \theta \right\}\ \ {\rm (65b)}\] \[ \Delta G_{\rm an} = \left( {1 - \xi } \right)\left[{\alpha K_u \sin ^2\beta _3 + \left( {1 - \alpha } \right)K_u \sin^2\beta _1 } \right] +\] \[ \xi \left[ {\alpha K_u \sin ^2\beta _4 +\left( {1 - \alpha } \right)K_u \sin ^2\beta _2 } \right]\ \ {\rm (65c)}\] 式中, \(\beta_1\)和\(\beta_2\)为第一个马氏体变体中两种磁畴磁化矢量与磁化易轴的夹角, \(\beta_3\)和\(\beta_4\)为第二个马氏体变体中两种磁畴磁化矢量与磁化易轴的夹角, \(K_u\)为磁晶各向异性能, \(\alpha \)和\(1-\alpha\)为马氏体变体中两种磁畴的体积分数. ...
... 将第一个马氏体变体视为基体, 第二个马氏体视为夹杂, 并将宏观整体应变\(\bar{\pmb\varepsilon}\)分解为弹性应变\(\bar{\pmb\varepsilon }^{\rm e}\)和非弹性应变\(\bar{\pmb\varepsilon }^{\rm in}\), 即 \[\bar{\pmb\varepsilon } = \bar{\pmb\varepsilon }^{\rm e} +\bar{\pmb\varepsilon }^{\rm in} \ \ (61)\]其中, \(\bar{\pmb\varepsilon }^{\rm e}\)和\(\bar{\pmb\varepsilon }^{\rm in}\)分别可以表示为 \[ \bar{\pmb\varepsilon }^{\rm e} = \overline{\pmb M}\bar {\pmb \sigma } \ \ {\rm (62a)}\] \[ \bar{\pmb\varepsilon }^{\rm in} = \xi \left( {1 - \xi} \right)\left\{ {\pmb L_0 + \left( {\pmb L_1 - \pmb L_0 }\right)\left[ {\pmb S - \xi \left( {\pmb S - \pmb I} \right)}\right]} \right\}^{ - 1}\left( {\pmb L_0 - \pmb L_1 }\right)\left( {\pmb S - \pmb I} \right)\left( {\pmb \varepsilon^{\rm r} - \pmb \varepsilon ^{\rm ph}} \right)+\] \[ \pmb \varepsilon^{\rm ph} + \xi \pmb \varepsilon ^{\rm r} \ \ {\rm (62b)}\]其中, \(\xi \)是第二个马氏体变体的体积分数, \(\pmb L_0 \)和\(\pmb L_1\)分别是基体和夹杂的弹性柔度张量, \(\pmb S\)是Eshelby张量, \(\pmb I\)是四阶单位张量, \(\pmb \varepsilon ^{\rm r}\)和\(\pmb \varepsilon^{\rm ph}\)分别是重定向和相变应变张量, \( \bar {\pmb\sigma }\)是宏观整体应力. \(\overline{\pmb M}\)是宏观整体有效弹性柔度张量 \[ \overline{\pmb M} = \left\{ {\pmb I + \xi \left\{ {\pmb L_0 + \left( {\pmb L_1 - \pmb L_0 } \right)\left[{\pmb S - \xi \left( {\pmb S - \pmb I} \right)} \right]}\right\}^{ - 1}\left( {\pmb L_0 - \pmb L_1 } \right)} \right\}\pmb M_0 \ \ (63)\]Zhu 和 Dui (2007) 将两个马氏体变体的Gibbs自由能之差分成三项, 即 \[ \Delta G = \Delta G_{\rm me} + \Delta G_{\rm ze} + \Delta G_{\rm an} \ \ (64)\]其中, \(\Delta G_{\rm me} \), \(\Delta G_{\rm ze} \)和\(\Delta G_{\rm an} \)分别是机械能、Zeeman能和磁晶各向异性能, 即 \[ \Delta G_{\rm me} = - \dfrac{1}{2}\xi \left( {1 - \xi }\right)\pmb L_0 \left( {\pmb S - \pmb I} \right)\pmb \varepsilon^{\rm r}\pmb \varepsilon ^{\rm r} \ \ {\rm (65a)}\] \[ \Delta G_{\rm ze} = \left( {1 - \xi } \right)\mu _0 M^{\rm sat}H\left\{ \left[{\alpha \cos \beta _3 - \left( {1 - \alpha } \right)\cos \beta _1} \right]\cos \theta +\right.\] \[ \left. \left[ {\alpha \sin \beta _3 - \left( {1 -\alpha } \right)\sin \beta _1 } \right]\sin \theta \right\} + \xi \mu _0 M^{\rm sat}H\left\{ \left[ { - \alpha \sin \beta _4 +\left( {1 - \alpha } \right)\sin \beta _2 } \right]\cos \theta+\right.\] \[\left.\left[ {\alpha \cos \beta _4 - \left( {1 - \alpha } \right)\cos\beta _2 } \right]\sin \theta \right\}\ \ {\rm (65b)}\] \[ \Delta G_{\rm an} = \left( {1 - \xi } \right)\left[{\alpha K_u \sin ^2\beta _3 + \left( {1 - \alpha } \right)K_u \sin^2\beta _1 } \right] +\] \[ \xi \left[ {\alpha K_u \sin ^2\beta _4 +\left( {1 - \alpha } \right)K_u \sin ^2\beta _2 } \right]\ \ {\rm (65c)}\] 式中, \(\beta_1\)和\(\beta_2\)为第一个马氏体变体中两种磁畴磁化矢量与磁化易轴的夹角, \(\beta_3\)和\(\beta_4\)为第二个马氏体变体中两种磁畴磁化矢量与磁化易轴的夹角, \(K_u\)为磁晶各向异性能, \(\alpha \)和\(1-\alpha\)为马氏体变体中两种磁畴的体积分数. ...
... Zhu 和 Dui (2007) 将两个马氏体变体的Gibbs自由能之差对体积分数\(\xi\)的导数作为马氏体重定向的驱动力, 即 \[ f_{\rm drv} = - \dfrac{\partial \Delta G}{\partial \xi }= - \dfrac{\partial \Delta G_{\rm me} }{\partial \xi } -\dfrac{\partial \Delta G_{\rm ze} }{\partial \xi } -\dfrac{\partial \Delta G_{\rm an} }{\partial \xi } \ \ (66)\]进一步考虑了两种马氏体重定向的能垒, 即界面能和界面摩擦耗散能 \[ \Delta G_{\rm s} = {2\xi \gamma _{\rm s} } /t \ \ {\rm (67a)}\] \[\Delta G_{\rm d} = D\left( {e^{b\xi } - 1} \right)\ \ {\rm (67b)}\]其中, \(\gamma _{\rm s} \)是马氏体--马氏体界面能密度, \(t\)是界面厚度, \(D\)和\(b\)是材料参数. 同时, 将两种能垒之和对体积分数\(\xi\)的导数作为马氏体重定向的阻力 \[ f_{\rm res} = \dfrac{\partial \Delta G_{\rm s} }{\partial \xi }+ \dfrac{\partial \Delta G_{\rm d} }{\partial \xi } \ \ (68)\]同时, 提出如下马氏体重定向演化准则 \[f_{\rm drv} = f_{\rm res} \ \ (69)\] ...
... 为了简化起见, Zhu 和 Dui(2007) 忽略了磁畴壁运动和磁化矢量旋转这两种机制. 因此, 在已知外加应力和磁场的情况下就可以完全计算出体积分数\(\xi \). ...
Model for field-induced reorientation strain in magnetic shape memory alloy with tensile and compressive loads. J
1
2008
... 为了描述NiTi形状记忆合金的率相关循环变形特性, Morin 等(2011) 通过在Z-M本构模型 (Zaki & Moumni 2007 )中引入考虑热--力耦合超弹性退化效应的演化方程, 将Z-M模型拓展到了非等温情形, 拓展后的本构模型能很好地对超弹性NiTi形状记忆合金的相变棘轮行为及其率相关特性进行理论描述.然而, 该模型将残余应变的累积演变假定成指数函数形式, 因而无法描述Kan等(2016)在超弹性NiTi形状记忆合金率相关循环变形实验中观察到的新现象, 即残余应变对加载率的依赖性. 为此, Yu 等(2014a)将超弹性NiTi形状记忆合金率相关的超弹性劣化效应归结为相变--位错交互作用和热--力耦合效应, 建立了基于物理机制的宏观唯象本构模型, 合理预测了该合金在不同加载速率下的超弹性劣化行为和温度场演化特性.下面对该模型的主要部分进行简要介绍. ...
Influence of magnetization rotation on martensite reorientation in magnetic shape memory alloy.
4
2010
... 尽管NiTi形状记忆合金中的热弹性马氏体相变是一种快速的切变式固态相变过程, 但是, 在多晶NiTi形状记忆合金材料中, 因晶粒晶体学位向的不同和晶界对相变过程的阻碍作用, 使得马氏体相变过程是一种局部切变形核而逐渐扩展长大的过程, 特别是在超细晶的多晶NiTi形状记忆合金中.对于这一种局部的、非均匀马氏体相变过程, Shaw & Kyriakides(1995 , 1997 )对细晶多晶NiTi形状记忆合金条带通过全场像和应力--应变的同时测量进行了早期的观察, 揭示了在外加载荷作用下非均匀马氏体相变的产生以及宏观可观察的相变图案(transformation domain)形成和扩展. 近年来, Zhang 等(2010) , Sun 等(2002) , He 和 Sun(2010a) 及 Feng 和 Sun(2006) 利用CCD相机和高速摄像仪进一步观察了细晶超弹性NiTi形状记忆合金在应变控制的单轴拉伸--卸载过程中相变图案的形成和演化以及这一过程的加载速率依赖性, 进而揭示了单轴拉伸和卸载过程中马氏体相变过程的局部性. Zhang等(2010)得到的细晶超弹性NiTi形状记忆合金薄材典型的实验结果如图8 和图9 所示. ...
... NiTi形状记忆合金在3.3 \(\times \) 10\(^{ -4}\) s\(^{-1}\)下的(a)拉伸--卸载曲线和(b)相变图案演化 (Zhang et al. 2010 ) ...
... NiTi形状记忆合金在3.3 \(\times \) 10\(^{ -2}\) s\(^{-1}\)下的(a)拉伸--卸载曲线和(b)相变图案演化 (Zhang et al. 2010 ) ...
... 结合实际变形过程中的温度变化的测量, Zhang等(2010) 进一步对相变图案形成和演化及其率相关性的物理本质进行了解释, 强调了这一物理过程中的材料局部失稳特性和热--力耦合特性. 然而, 上述研究仅针对应变控制的拉伸--卸载过程, 没有涉及多次循环、不同加载水平以及在应力控制加载条件下相变图案的形成和演化, 还需要进一步观察和讨论. 为此, Xie等(2016a) 采用非接触数字图像相关(DIC)和红外热成像(IR)方法直接观测了超弹性NiTi形状记忆合金板材在应力控制拉伸--卸载循环过程的相变图案和温度场分布及其演化, 讨论了不同峰值应力(即650, 750和800 MPa)作用下NiTi合金板材相变图案的循环演化特征及其形成机理, 典型的实验结果如图10 和图11 所示. 结果表明: (1)超弹性NiTi形状记忆合金在拉伸--卸载循环初期表现出变形局部化的特征, 马氏体条带逐渐形成、长大和扩展以及卸载过程中的奥氏体条带的形成、长大或扩展, 如图10 (a)和图11 (a)所示. (2)然而, 循环稳定后相变图案的演化则依赖于外加的应力峰值大小.应力峰值较小(如650 MPa)时, 循环稳定后无明显的相变图案形成, 表现出较为均匀化的变形特征; 但当应力峰值较高(如750和800 MPa)时, 循环稳定时仍会出现明显的相变图案, 产生马氏体条带的残留现象. Xie等(2016a) 进一步通过测得的应变场和温度场的变化, 认为宏观马氏体条带的残留是由高峰值应力循环后富集的位错对马氏体的钉扎作用造成的, 马氏体条带的残留也与该NiTi合金在高峰值应力下显著的相变棘轮行为是相对应的. ...
Change of transformation mechanism during pseudoelastic cycling of NiTi shape memory alloys. Mater. Sci. Eng.
1
2017
... Zhang 等(2017) 为了进一步考虑加载模式和载荷比对NiTi合金丝疲劳寿命的影响, 提出了基于应变能的疲劳寿命预测模型\[ e_0 = \alpha N_{\rm f}^\beta\ \ (37)\]其中, \(e_{0}\)为应变能, \(\alpha \)和\(\beta \)为材料参数.该模型能够较为合理的预测应变控制不同应变幅值和应力控制不同应力幅值下的疲劳失效寿命. ...