-
摘要: 在20世纪80年代由徐皆苏教授创建的胞映射方法一直受非线性科学界同仁的欢迎.近几年胞映射方法有了许多新的应用和算法.本文介绍了一些控制应用和算法的文献.另外,还介绍和讨论胞映射方法应用与多目标优化问题的研究和方法,多目标优化控制设计和非线性代数方程找零解.文中指出胞映射方法在并行计算的帮助下,现在可以解决中等高维空间中的各类问题,新的应用还会不断出现.
-
关键词:
- 胞映射方法 /
- 全局分析 /
- 最优控制 /
- 多目标优化 /
- 非线性代数方程的零解
Abstract: The cell mapping methods created by Hsu in 1980s have been popular choices for the researchers in nonlinear science communities. There have been new applications and new algorithm developments of the cell mapping methods. This paper presents a discussion of the literature of some control applications and recent algorithm developments of the cell mapping methods. In particular, we present studies of multi-objective optimization problems with the cell mapping methods, multi-objective optimal control designs, and zeros finding of nonlinear algebraic equations. The problems solved with the cell mapping methods are now in moderately high dimensional space with the help of parallel computing.-
Key words:
- cell mapping methods /
- global analysis /
- optimal control /
- multi-objective optimization /
- finding zeros
-
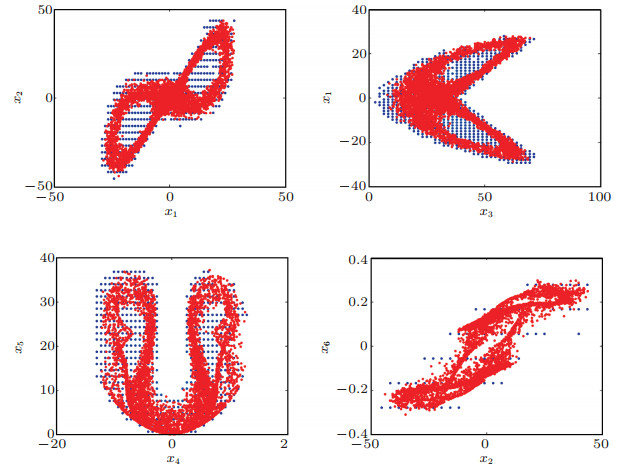
Figure 2. The 5-dimensional Pareto front of the objective functions, projected on to 2-dimensional sub-spaces of the objective space. The color code indicates the level of Mp, x1, IAEx2, max |x2|, and tp, x1 in subplots from upper left in counterclockwise order. The conflicting nature among these objectives can be observed clearly. For example, the overshoot and peak time are conflicting for tracking control, which can be seen in the upper left plot of x1
-
[1] Azhmyakov V. 2008. An approach to controlled mechanical systems based on the multiobjective optimization technique. Journal of Industrial and Management Optimization, 4:697-712. doi: 10.3934/jimo [2] Bhaya A, Kaszkurewicz E. 2004. Newton algorithms via control Liapunov functions for polynomial zero finding//Proceedings of the 43rd IEEE Conference on Decision and Control (CDC), Piscataway, NJ, USA, 2:1629-34. [3] Blesken M, Ruckert U, Steenken D, Witting K, Dellnitz M. 2009. Multiobjective optimization for transistor sizing of CMOS logic standard cells using set-oriented numerical techniques//Proceedings of NORCHIP, Piscataway, New Jersey, 1-4. [4] Borre M, Flashner H. 2011. Periodic solutions and their regions of attraction for flexible structures under relay feedback control with nonlinear control law//Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference and the 23rd Biennial Conference on Mechanical Vibration and Noise, Washington, DC. 1:609-618. [5] Borre M, Flashner H. 2012a. Computation of periodic solutions and their regions of attraction for flexible structures under nonlinear feedback control. Journal of Vibration and Control, 18:745-756. doi: 10.1177/1077546311411754 [6] Borre M, Flashner H. 2012b. Periodic solutions for flexible structures under relay feedback control with time delay//Proceedings of the ASME 5th Annual Dynamic Systems and Control Division Conference and JSME 11th Motion and Vibration Conference, Fort Lauderdale, Florida, 2:607-616. [7] Bosman P A N. 2012. On gradients and hybrid evolutionary algorithms for real-valued multi-objective optimization. IEEE Transaction on Evolutionary Computation, 16:51-69. doi: 10.1109/TEVC.2010.2051445 [8] Bursal F H, Hsu C S. 1989. Application of a cell-mapping method to optimal control problems. International Journal of Control, 49:1505-1522. doi: 10.1080/00207178908559722 [9] Bursal F H, Tongue B H. 1992. A new method of nonlinear system identification using interpolated cell mapping//Proceedings of American Control Conference, 3160-3164. [10] Carniel R. 1994. Quasi cell mapping approach to the global dynamical analysis of Newton's root-finding algorithm. Applied Numerical Mathematics, 15:133-152. doi: 10.1016/0168-9274(94)00016-6 [11] Chandrupatla T R. 1997. New hybrid quadratic/bisection algorithm for finding the zero of a nonlinear function without using derivatives. Advances in Engineering Software, 28:145-149. doi: 10.1016/S0965-9978(96)00051-8 [12] Chen Y Y, Tsao T C. 1988. A new approach for the global analysis of fuzzy dynamical systems//Proceedings of the 27th IEEE Conference on Decision and Control, 2:1415-1420. [13] Chen Y Y, Tsao T C. 1989. A description of the dynamic behavior of fuzzy systems. IEEE Transactions on Systems, Man, and Cybernetics, 19:745-755. doi: 10.1109/21.35338 [14] Chiha I, Liouane N, Borne P. 2012. Tuning PID controller using multiobjective ant colony optimization.Applied Computational Intelligence and Soft Computing, 536326 http://www.academia.edu/8345209/Tuning_PID_Controller_Using_Multiobjective_Ant_Colony_Optimization [15] Chung K L. 1967. Markov Chains with Stationary Transition Probabilities. Springer-Verlag, New York. [16] Cominos P, Munro N. 2002. PID controllers:Recent tuning methods and design to specification. IEEE Proceedings-Control Theory and Applications, 149:46-53. doi: 10.1049/ip-cta:20020103 [17] Crespo L G, Sun J Q. 2000a. Optimal control of target tracking via simple cell mapping. AIAA Journal of Guidance and Control, 24:1029-1031. [18] Crespo L G, Sun J Q. 2000b. Solution of fixed final state optimal control problems via simple cell mapping.Nonlinear Dynamics, 23:391-403. doi: 10.1023/A:1008375230648 [19] Crespo L G, Sun J Q. 2003a. Fixed final time optimal control via simple cell mapping. Nonlinear Dynamics, 31:119-131. doi: 10.1023/A:1022041418604 [20] Crespo L G, Sun J Q. 2003b. Stochastic optimal control of nonlinear dynamic systems via Bellman's principle and cell mapping. Automatica, 39:2109-2114. doi: 10.1016/S0005-1098(03)00238-3 [21] Custodio A L, Madeira J F A, Vaz A I F, Vicente L N. 2011. Direct multisearch for multiobjective optimization. SIAM Journal on Optimization, 21:1109-1140. doi: 10.1137/10079731X [22] Dellnitz M, Hohmann A. 1997. A subdivision algorithm for the computation of unstable manifolds and global attractors. Numerische Mathematik, 75:293-317. doi: 10.1007/s002110050240 [23] Dellnitz M, Junge O. 1998. An adaptive subdivision technique for the approximation of attractors and invariant measures. Computing and Visualization in Science, 1:63-68. doi: 10.1007/s007910050006 [24] Dellnitz M, Junge O. 2002. Set oriented numerical methods for dynamical systems. Handbook of Dynamical Systems, 2:221-264. doi: 10.1016/S1874-575X(02)80026-1 [25] Dellnitz M, Schütze O, Hestermeyer T. 2005. Covering Pareto sets by multilevel subdivision techniques.Journal of Optimization Theory and Applications, 124:113-155. doi: 10.1007/s10957-004-6468-7 [26] Dellnitz M, Schütze O, Zheng Q. 2002a. Locating all the zeros of an analytic function in one complex variable. Journal of Computational and Applied Mathematics, 138:325-333. doi: 10.1016/S0377-0427(01)00371-5 [27] Dellnitz M, Schutze O, Sertl S. 2002b. Finding zeros by multilevel subdivision techniques. IMA Journal of Numerical Analysis, 22:167-185. doi: 10.1093/imanum/22.2.167 [28] Ding Q, Cooper J E, Leung A Y T. 2005. Application of an improved cell mapping method to bilinear stiffness aeroelastic systems. Journal of Fluids and Structures, 20:35-49. doi: 10.1016/j.jfluidstructs.2004.09.003 [29] Eason R P, Dick A J. 2014. A parallelized multi-degrees-of-freedom cell mapping method. Nonlinear Dynamics, 77:467-479. doi: 10.1007/s11071-014-1310-8 [30] Fei J, Isik C. 1990. The analysis of fuzzy knowledge-based systems using cell-to-cell mapping//Proceedings of the 5th IEEE International Symposium on Intelligent Control, 1:633-637. [31] Feng J, Xu W. 2011. Chaotic boundary crisis in the Duffing Van der Pol vibro-imapct oscillator//Proceedings of International Conference on Multimedia Technology, 2431-2434. [32] Fernández J, Schüütze O, Hernández C, Sun J Q, Xiong F R. 2016. Parallel simple cell mapping for multiobjective optimization. Engineering Optimization, 48:1845-1868 (doi:10.1080/0305215X. 2016.1145215). [33] Flashner H, Burns T F. 1990. Spacecraft momentum unloading:the cell mapping approach. Journal of Guidance, Control and Dynamics, 13:89-98. doi: 10.2514/3.20521 [34] Fliege J, Svaiter B F. 2000. Steepest descent methods for multicriteria optimization, Mathematical Methods of Operations Research, 51:479-494. doi: 10.1007/s001860000043 [35] Gambier A, Badreddin E. 2007. Multi-objective optimal control:An overview//Proceedings of 16th IEEE International Conference on Control Applications. Part of IEEE Multi-conference on Systems and Control, Piscataway, NJ, USA, 170-175. [36] Ge Z M, Lee S C. 1997. A modified interpolated cell mapping method. Journal of Sound and Vibration, 199:189-206. doi: 10.1006/jsvi.1996.0619 [37] Grune L, Junge H. 2005. A set oriented approach to optimal feedback stabilization. Systems & Control Letters, 54:169-180. https://www.researchgate.net/publication/222555590_A_set_oriented_approach_to_optimal_feedback_stabilization [38] Han Q, Xu W, Sun J Q. 2016. Stochastic response and bifurcation of periodically driven nonlinear oscillators by the generalized cell mapping method. Physica A:Statistical Mechanics and Its Applications, 458:115-125. doi: 10.1016/j.physa.2016.04.006 [39] Hernández C, Naranjani Y, Sardahi Y, Liang W, Schütze O, Sun J Q. 2013a. Simple cell mapping method for multiobjective optimal PID control design. International Journal of Dynamics and Control, 1:231. doi: 10.1007/s40435-013-0021-1 [40] Hernández C, Sun J Q, Schütze O. 2013b. Computing the set of approximate solutions of a multi-objective optimization problem by means of cell mapping techniques//Proceedings of EVOLVE 2013-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computing, Leiden, The Netherland. [41] Hernández C, Schütze O, Emmerich M, Xiong F R, Sun J Q. 2014. Barrier tree for continuous landscapes by means of generalized cell mapping//Proceedings of EVOLVE 2014-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computing, Beijing, China. [42] Hillermeier C. 2001. Nonlinear Multiobjective Optimization:A Generalized Homotopy Approach, Birkhauser, Berlin, Germany. [43] Hong L, Jiang J, Sun J Q. 2015a. Fuzzy responses and bifurcations of a forced duffing oscillator with a triple-well potential. International Journal of Bifurcation and Chaos, 25:1550005. doi: 10.1142/S0218127415500054 [44] Hong L, Jiang J, Sun J Q. 2015b. Response analysis of fuzzy nonlinear dynamical systems. Nonlinear Dynamics, 78:1221-1232. https://www.researchgate.net/publication/271677975_Response_analysis_of_fuzzy_nonlinear_dynamical_systems [45] Hong L, Sun J Q. 2006a. Bifurcations of a forced Duffing oscillator in the presence of fuzzy noise by the generalized cell mapping method. International Journal of Bifurcation and Chaos, 16:3043-3051. doi: 10.1142/S0218127406016641 [46] Hong L, Sun J Q. 2006b. Bifurcations of fuzzy nonlinear dynamical systems. Communications in Nonlinear Science and Numerical Simulation, 11:1-12. doi: 10.1016/j.cnsns.2004.11.001 [47] Hong L, Sun J Q. 2006c. Codimension two bifurcations of nonlinear systems driven by fuzzy noise. Physica D:Nonlinear Phenomena, 213:181-189. doi: 10.1016/j.physd.2005.11.005 [48] Hong L, Sun J Q. 2006d. Global bifurcations of complex nonlinear dynamical systems with cell mapping methods//Sun J Q, Luo A C J. eds. Bifurcation and Chaos in Complex Systems, Elsevier Science, Ltd., Oxford, U.K., 1:191-298. [49] Hsu C S. 1982. A probabilistic theory of nonlinear dynamical systems based on the cell state space concept.Journal of Applied Mechanics, 49:895-902. doi: 10.1115/1.3162633 [50] Hsu C S. 1985. A discrete method of optimal control based upon the cell state space concept. Journal of Optimization Theory and Applications, 46:547-569. doi: 10.1007/BF00939159 [51] Hsu C S. 1995. Global analysis of dynamical systems using posets and digraphs. International Journal of Bifurcation and Chaos, 5:1085-1118. doi: 10.1142/S021812749500079X [52] Jahn J. 2006. Multiobjective search algorithm with subdivision technique. Computational Optimization and Applications, 35:161-175. doi: 10.1007/s10589-006-6450-4 [53] Jiang J, Guo X. 2011. Study of evolution of global structure into chaotic itinerancy by point mapping under cell reference method//Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference and the 23rd Biennial Conference on Mechanical Vibration and Noise, Washington, DC. 1:625-629. [54] Junge O, Osinga H M. 2004. A set oriented approach to global optimal control. ESAIM Control, Optimisation and Calculus of Variations, 10:259-270. doi: 10.1051/cocv:2004006 [55] Kerschke P, Preuss M, Hernández C, Schütze O, Sun J Q, Grimme C, Rudolph G, Bischl B, Trautmann H. 2014. Cell mapping techniques for exploratory landscape analysis//Proceedings of EVOLVE 2014-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computing, Beijing, China. [56] Khoie M, Salahshoor K, Nouri E, Sedigh A K. 2012. PID controller tuning using multi-objective optimization based on fused genetic-immune algorithm and immune feedback mechanism//Lecture Notes in Computer Science-Advanced Intelligent Computing Theories and Applications, Vol. 6839 of Advanced Intelligent Computing Theories and Applications. With Aspects of Artificial Intelligence. 7th International Conference, ICIC 2011. Revised Selected Papers, Springer Verlag, Berlin, Germany, 267-276. [57] Kim J, Lee S. 2009. Fast neighbor cells finding method for multiple octree representation//Proceedings of IEEE International Symposium on Computational Intelligence in Robotics and Automation, 540-545. [58] Kumar C A, Nair N K. 2011. Multi-objective PI controller design with an application to speed control of permanent magnet DC motor drives//Proceedings of International Conference on Signal Processing, Communication, Computing and Networking Technologies, Piscataway, New Jersey, 424-429. [59] Lee W K, Ghang M R. 1994. Domains of attraction of a forced beam by interpolated mapping. Journal of Applied Mechanics, 61:144-151. doi: 10.1115/1.2901389 [60] Lee W K, Hsu C S. 1994. A global analysis of an harmonically excited spring-pendulum system with internal resonance. Journal of Sound and Vibration, 171:335-359. doi: 10.1006/jsvi.1994.1125 [61] Leu M C, Kim T Q. 1998. Cell mapping based fuzzy control of car parking//Proceedings of IEEE International Conference on Robotics and Automation, 3:2494-2499. [62] Li L, Wang F Y. 2002. Vehicle trajectory generation for optimal driving guidance//Proceedings of the IEEE 5th International Conference on Intelligent Transportation Systems, 231-235. [63] Li L, Wang F Y. 2003a. An integrated design framework for driver/passenger-oriented trajectory planning//Proceedings of IEEE Intelligent Transportation Systems, 2:1764-1769. [64] Li L, Wang F Y. 2003b. Trajectory generation for driving guidance of front wheel steering vehicles//Proceedings of IEEE Intelligent Vehicles Symposium, 231-236. [65] Lin J H, Isik C. 1997. Fuzzy modeling and control based on maximum entropy self-organizing nets and cell state mapping//Proceedings of Annual Meeting of the North American Fuzzy Information Processing Society, 45-50. [66] Liu L M, Tian Y T, Sui Z, Huang X l. 2009. Finite-time robust trajectory tracking control for the underactuated biped robot based on Poincare-like-alter-cell-to-cell mapping method//Proceedings of the 4th International Conference on Autonomous Robots and Agents, 686-691. [67] Liu L, Tian Y. 2009. Numerical method to estimate the initial state of the stable gaits for the underactuated biped robot with knees//Proceedings of International Conference on Information and Automation, 60-65. [68] Liu N, Li J, Wang T. 2007. The effects of parameter variation on the basins of attraction of passive walking models//Proceedings of International Conference on Mechatronics and Automation, 1908-1913. [69] Liu Z J. 1990. An algorithm for finding all isolated zeros of polynomial systems//Proceedings of the International Symposium on Symbolic and Algebraic Computation, New York, USA. [70] Madsen K. 1973. A root-finding algorithm based on Newton's method. BIT Numerical Mathematics, 13:71-75. doi: 10.1007/BF01933524 [71] Moon J S, Spong M W. 2010. Bifurcations and chaos in passive walking of a compass-gait biped with asymmetries//Proceedings of IEEE International Conference on Robotics and Automation, 1721-1726. [72] Naranjani Y, Hernández C, Xiong F R, Schütze O, Sun J Q. 2013. A hybrid algorithm for the simple cell mapping method in multi-objective optimization//Proceedings of EVOLVE-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computing, Leiden, The Netherland. [73] Naranjani Y, Hernández C, Xiong F R, Schütze O, Sun J Q. 2016. A hybrid method of evolutionary algorithm and simple cell mapping for multi-objective optimization problems. International Journal of Dynamics and Control, 1-13. doi: 10.1007/s40435-016-0250-1. [74] Naranjani Y, Sardahi Y, Sun J Q. 2014. A genetic algorithm and cell mapping hybrid method for multiobjective optimization problems//Proceedings of the 11th International Conference on Electrical Engineering, Computing Science and Automatic Control, Carmen, Mexico, 1-5. [75] Naranjani Y, Sun J Q. 2015. A multi-objective path planning algorithm for mobile robots based on cellular automata//Proceedings of ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Boston, Massachusetts. [76] Neumann N, Sattel T, Wallaschek J. 2007. On set-oriented numerical methods for global analysis of nonsmooth mechanical systems. Journal of Vibration and Control, 13:1393-1405. doi: 10.1177/1077546307077500 [77] Panda S. 2011. Multi-objective PID controller tuning for a FACTS-based damping stabilizer using nondominated sorting genetic algorithm-Ⅱ. International Journal of Electrical Power & Energy Systems, 33:1296-1308. [78] Pareto V. 1971. Manual of Political Economy. The MacMillan Press, London, (original edition in French in 1927). [79] Rega G, Lenci S. 2015. A global dynamics perspective for system safety from macro-to nanomechanics:Analysis, control, and design engineering. Applied Mechanics Reviews, 67:050802. doi: 10.1115/1.4031705 [80] Rizk C G, Smith S M. 1997. Automatic design of nonlinear controllers with optimal global performance using best estimate directed search and continued propagation cell mapping//Proceedings of IEEE International Conference on Systems, Man, and Cybernetics-Computational Cybernetics and Simulation, 4:3861-3866. [81] Schütze O, Witting K, Ober-Blöbaum S, Dellnitz M. 2013. Setoriented methods for the numerical treatment of multiobjective optimization problems//EVOLVE-A Bridge between Probability, Set Oriented Numerics and Evolutionary Computation, Springer, 447:187-219. [82] Schütze O, Vasile M, Junge O, Dellnitz M, Izzo D. 2009. Designing optimal low thrust gravity assist trajectories using space pruning and a multi-objective approach. Engineering Optimization, 41:155-181. doi: 10.1080/03052150802391734 [83] Silva V V R E, Khatib W, Fleming P J. 2006. Nonlinear control system design using variable complexity modelling and multiobjective optimization. Sba:Controle & Automação Sociedade Brasileira de Automatica, 17:24-31. [84] Smith S M, Comer D J. 1990. Self-tuning of a fuzzy logic controller using a cell state space algorithm//Proceedings of IEEE International Conference on Systems, Man and Cybernetics, 445-450. [85] Smith S M, Comer D J. 1991. Automated calibration of a fuzzy logic controller using a cell state space algorithm. IEEE Control Systems, 11:18-28. https://www.researchgate.net/publication/3206175_Automated_Calibration_of_a_Fuzzy_Logic_Controller_Using_a_Cell_State_Space_Algorithm [86] Solihin M I, Tack L F, Kean M L. 2011. Tuning of PID controller using particle swarm optimization (PSO). International Journal on Advanced Science, Engineering and Information Technology, 1:458-461. doi: 10.18517/ijaseit.1.4.93 [87] Sun H, Yu J, Zhang S. 2015. Bifurcation analysis of the asymmetric rolling missiles//Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 230:1273-1283. [88] Sun J Q, Luo A C J. 2012. Global Analysis of Nonlinear Dynamics. Springer, New York. [89] Sun J Q, Song B. 2012. Analysis and control of deterministic and stochastic dynamical systems with time delay//Luo A C J, Sun J Q. eds. Complex Systems, Vol. 0 of Nonlinear Physical Science, Springer Berlin Heidelberg, 119-203. [90] Sun J Q. 2013. Control of nonlinear dynamic systems with the cell mapping method//Schütze O, Coello C A, Tantar A A, Tantar E, Bouvry P, DelMoral P, Legrand P. eds. EVOLVE-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation Ii, Vol. 175 of Advances in Intelligent Systems and Computing, Springer-Verlag Berlin, Berlin, 3-18. [91] Tai H M, Hu H T, Shenoi S. 1995. Auto-tuning of fuzzy controllers using cell mapping//Proceedings of International IEEE/IAS Conference on Industrial Automation and Control:Emerging Technologies, 492-499. [92] Tai H M, Papa M, Shenoi S. 1996. On global analysis and design of fuzzy control systems//Proceedings of the 22nd International Conference on Industrial Electronics, Control, and Instrumentation, 1:372-377. [93] Tongue B H, Gu K, 1988a. A higher order method of interpolated cell mapping. Journal of Sound and Vibration, 125:169-179. doi: 10.1016/0022-460X(88)90424-5 [94] Tongue B H, Gu K. 1988b. A theoretical basis for interpolated cell mapping. SIAM Journal on Applied Mathematics, 48:1206-1214. doi: 10.1137/0148072 [95] Tongue B H, Gu K. 1988c. Interpolated cell mapping of dynamical systems. Journal of Applied Mechanics, 55:461-466. doi: 10.1115/1.3173700 [96] Tongue B H. 1987. On obtaining global nonlinear system characteristics through interpolated cell mapping. Physica D:Nonlinear Phenomena, 28:401-408. doi: 10.1016/0167-2789(87)90028-5 [97] Ungarala S. 2012. Fixed interval smoothing of nonlinear/non-Gaussian dynamic systems in cell space//Proceedings of the 8th IFAC Symposium on Advanced Control of Chemical Processes, Singapore. 45:298-303. [98] Vroemen B, De Jager B. 1997. Multiobjective control:An overview//Proceedings of Proceedings of the 36th IEEE Conference on Decision and Control, New York, NY, USA, 1:440-445. [99] Wang F Y, Lever P J A. 1994. A cell mapping method for general optimum trajectory planning of multiple robotic arms. Robotics and Autonomous Systems, 12:15-27. doi: 10.1016/0921-8890(94)90044-2 [100] Wang L, Wang B, Guo Y. 2007. Analyzing quantization effect of digital control system by cell mapping method//Proceedings of Chinese Control Conference, 97-99. [101] Wang Q G, Lee T H, Fung H W, Bi Q, Zhang Y. 1999. PID tuning for improved performance. IEEE Transactions on Control Systems Technology, 7:457-465. doi: 10.1109/87.772161 [102] Wang Y, Zheng H, Guan Z, Gao F. 2011. Application of cell mapping method in global analysis of fault gear system//Proceedings of International Conference on Network Computing and Information Security (NCIS), Los Alamitos, CA, USA, 2:352-354. [103] Wang Y, Zheng H, Li H, Guan Z. 2012. Cell mapping global dynamic analysis of gear wear fault. Journal of Vibration, Measurement and Diagnosis, 32:135-137. http://en.cnki.com.cn/Article_en/CJFDTotal-ZDCS201201029.htm [104] White M, Tongue B. 1995. Application of interpolated cell mapping to an analysis of the Lorenz equations.Journal of Sound and Vibration, 188:209-226. doi: 10.1006/jsvi.1995.0587 [105] Xiong F R, Qin Z C, Schütze O, Ding Q, Sun J Q. 2014a. Finding zeros of nonlinear functions using the hybrid cell mapping method//Proceedings of EVOLVE-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computing, Beijing, China. [106] Xiong F R, Qin Z C, Xue Y, Schütze O, Ding Q, Sun J Q, 2014b. Multi-objective optimal design of feedback controls for dynamical systems with hybrid simple cell mapping algorithm. Communications in Nonlinear Science and Numerical Simulation, 19:1465-1473. doi: 10.1016/j.cnsns.2013.09.032 [107] Xiong F R, Qin Z C, Ding Q, Hernández C, Fernandez J, Schütze O, Sun J Q. 2015. Parallel cell mapping method for global analysis of high-dimensional nonlinear dynamical systems. Journal of Applied Mechanics, 82:111010. doi: 10.1115/1.4031149 [108] Xiong F R, Schütze O, Ding Q, Sun J Q. 2016. Finding zeros ofnonlinear functions using the hybrid parallel cell mapping method. Communications in Nonlinear Science and Numerical Simulation, 34:23-37. doi: 10.1016/j.cnsns.2015.10.008 [109] Xu W, Sun C, Sun J Q, He Q. 2013. Development and study on cell mapping methods. Advances in Mechanics, 43:91-100. http://lxjz.cstam.org.cn/CN/abstract/abstract143925.shtml [110] Xue Y, Xiong F R, Qin Z C, Li X, Sun J Q. 2014. An algorithm for robot path planning with obstacle avoidance using cell mapping//Proceedings of EVOLVE 2014-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computing, Beijing, China. [111] Yen J Y, Tarng S W. 1996. A fuzzy cell-mapping feedback control algorithm for the satellite attitude maneuvering control//Proc-eedings of the Asian Fuzzy Systems Symposium-Soft Computing in Intelligent Systems and Information Processing, 567-572. [112] Yen J Y. 1992. Computer disk file track accessing controller design based upon cell to cell mapping//Proceedings of the American Control Conference, 216-220. [113] Zang X, Bai J, Zhu Y, Zhao J. 2013. The global stability analysis of passive biped robot based on gradual point mapping-cell mapping method//Proceedings of the 2nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation, 800-804. [114] Zhao H, Tsu T. 2003. Research on multiobjective optimization control for nonlinear unknown systems//Proceedings of 12th International Fuzzy Systems Conference, Piscataway, NJ, USA, 1:402-407. [115] Zhao J, Wu X, Zang X, Zhu Y, Zhu L. 2011. The analysis on period doubling gait and chaotic gait of the compass-gait biped model//2011 IEEE International Conference on Proceedings of Robotics and Automation (ICRA), 2015-2020. [116] Zhong X, Fan W, Lin J, Zhao Z. 2010. A novel multi-objective compass search//Proceedings of the 1st IEEE International Conference on Progress in Informatics and Computing, Shanghai, China, 1:24-29. [117] Zhu W H, Leu M C. 1990. Planning optimal robot trajectories by cell mapping//Proceedings of IEEE International Conference on Robotics and Automation, 3:1730-1735. -





 下载:
下载: